专题04 三角函数的图象和性质-2017年高考数学文母题题源系列新课标1专版 含解析 精品
高三数学三角函数的图象与性质试题答案及解析

高三数学三角函数的图象与性质试题答案及解析1.函数的最小正周期为.【答案】π【解析】因为,所以函数f(x)=cos2x-sin2x的最小正周期为【考点】三角函数的周期2.已知函数,下面结论错误的是()A.函数的最小正周期为2B.函数在区间[0,]上是增函数C.函数的图象关于直线=0对称D.函数是奇函数【答案】D.【解析】A:最小正周期,∴A正确;B:当时,,∴B正确;C:∵,∴C正确;D:∵,∴是偶函数,∴D错误.【考点】三角函数的图象和性质.3.已知函数f(x)=4sinxcos(x-)-1(1)求函数f(x)的最小正周期; (2)当x∈[-π,]时,求函数f(x)的取值范围.【答案】(1)π;(2)[-2,1]【解析】(1)先化简函数表达式,利用T=求周期;(2)根据已知条件,先确定出整体变量(2x-)的范围,然后根据正弦函数的性质求出f(x)的取值范围.试题解析:(1)∵函数f(x)=4sinxcos(x-)-1=4sinx(cosxcos+sinxsin)-1=2sinxcosx+2sin2x-1=sin2x-cos2x=2sin(2x-),∴T=,∴函数f(x)的最小正周期π;(2)∵x∈[-,],∴2x∈[-,],∴2x-∈[-π,],∴f(x)∈[-2,1].【考点】两角和与差的三角函数,正弦型函数的性质,最小正周期,值域4.函数的最小正周期是()A.B.C.D.【答案】B【解析】由周期公式,又,所以函数的周期,故选B.【考点】三角函数的最小正周期.5.设函数f(x)=3sin(x+),若存在这样的实数x1,x2,对任意的x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为________.【答案】2【解析】f(x)=3sin(x+)的最小正周期T=2π×=4,f(x1),f(x2)应分别为函数f(x)的最小值和最大值,故|x1-x2|的最小值为=2.6.已知函数(1)求的值;(2)当时,求函数的值域.【答案】(1)2 ;(2).【解析】本题主要考查倍角公式、两角和的正弦公式、诱导公式、三角函数值域等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用倍角公式和两角和的正弦公式化简表达式,使之化简成的形式,将代入解析式,用诱导公式化简得到数值;第二问,利用第一问化简的表达式,将代入,先得到角的范围,再利用数形结合得到函数的值域.(1) .2分4分6分(2), 8分, 10分,即的值域是 12分【考点】倍角公式、两角和的正弦公式、诱导公式、三角函数值域.7.江西高考设f(x)=sin 3x+cos 3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.【答案】[2,+∞)【解析】由于f(x)=sin 3x+cos 3x=2sin,则|f(x)|=2≤2,要使|f(x)|≤a恒成立,则a≥2.8.已知函数的部分图象如图所示,则( ) A.B.C.D.【答案】D【解析】由题意得:,又,,所以.【考点】三角函数图像与性质9.已知函数的图象由的图象向右平移个单位得到,这两个函数的部分图象如图所示,则的值为( )A.B.C.D.【答案】A【解析】函数的图象在轴右侧的第一个对称轴为,所以,关于对称的直线为,由图象可知,通过向右平移之后,横坐标为的点平移到,所以,故应选A.10.已知函数f(x)=(2cos2x-1)sin2x+cos4x(1)求f(x)的最小正周期及最大值。
超实用高考数学重难点专题复习:专题四 三角函数 第一讲 三角函数的图像及性质

,又因为 f ( x) 2 tan 3x 1
6
18
的图象是由 f ( x) 2 tan 3 x 的图象向上平移1个单
6
位得到的,所以对称中心可以为 ,1 .故选D.
18
考点3:三角函数 y A sin( x ) 的图像及性质
6
12
6
且为单调递减时候零点,∴
5π π
π 2kπ, k Z
12 6
24k
12
, k Z ,由图象知 T 2π 2 5π ,∴
,又∵
(
n
)
12
5
5
0 ,∴ 2
∴ 2
π
∴ f ( x) 2 sin 2 x ,∵函数 f x 的图象可由 y A sin x
[解析] 由 1 tan( x ) 0 ,得
4
2
4
4
4
解得 k
x k , k Z ,故所求函数的定义域为
4
2
k
,
k
,k Z
4
2
,故选C.
考点2:三角函数的性质
1.三角函数的单调性、奇偶性、对称性和周期性
[典型例题]
π
1.函数 y 2sin 2 x 是( )
应用
2.根据图象求解析式或参数
(三)核心知识整合
考点1:三角函数的定义域、值域、最值
1.三角函数的图像
三角函数的图像与性质-2017年高考数学(文)备考学易黄金易错点无答案

专题06 三角函数的图像与性质2017年高考数学(文)备考学易黄金易错点1.为了得到函数y=sin错误!的图象,只需把函数y =sin2x的图象上所有的点( )A.向左平行移动π3个单位长度B.向右平行移动错误!个单位长度C.向左平行移动错误!个单位长度D.向右平行移动π6个单位长度2.若将函数y=2sin2x的图象向左平移错误!个单位长度,则平移后图象的对称轴为()A.x=错误!-错误!(k∈Z) B.x=错误!+错误!(k∈Z)3.已知函数f(x)=sin(ωx+φ)错误!,x=-错误!为f (x)的零点,x=错误!为y=f(x)图象的对称轴,且f(x)在错误!上单调,则ω的最大值为()A.11B.9C.7D.54.已知函数f(x)=sin错误!(x∈R,ω>0)图象的相邻两条对称轴之间的距离为π2。
为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象( )A.向左平移错误!个单位长度B.向右平移错误!个单位长度C.向左平移错误!个单位长度D.向右平移π5个单位长度5.如图,函数f(x)=A sin(ωx+φ)(其中A>0,ω>0,|φ|≤错误!)与坐标轴的三个交点P、Q、R满足P(2,0),∠PQR =错误!,M为QR的中点,PM=2错误!,则A的值为()A.错误!错误!B.错误!错误!C.8 D.166.义在区间0,3π]上的函数y=sin2x的图象与y=cos x 的图象的交点个数是________.7.已知函数f(x)=2a sinωx·cosωx+23cos2ωx-错误!(a>0,ω>0)的最大值为2,x1,x2是集合M={x∈R|f (x)=0}中的任意两个元素,且|x1-x2|的最小值为6。
(1)求函数f(x)的解析式及其图象的对称轴方程;(2)将函数y =f (x )的图象向右平移2个单位后得到函数y =g (x )的图象,当x ∈(-1,2]时,求函数h (x )=f (x )·g (x )的值域.易错起源1、 三角函数的概念、诱导公式及同角关系式例1、(1)点P 从(1,0)出发,沿单位圆x 2+y 2=1逆时针方向运动2π3弧长到达Q 点,则Q 点的坐标为( )A . (-错误!,错误!)B .(-错误!,-错误!)C .(-错误!,-错误!)D .(-错误!,错误!)(2)已知sin α+2cos α=0,则2sin αcos α-cos 2α的值是________.【变式探究】(1)已知点P 错误!落在角θ的终边上,且θ∈0,2π),则θ的值为( )A.π4B 。
03三角函数的图象与性质-2017年高考数学(理)母题题源系列(新课标1专版)含解析

母题三三角函数的图象与性质【母题原题1】【2017新课标1,理9】已知曲线C1:y=cos x,C2:y=sin (2x+2π),则下面结论正确的是3A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,个单位长度,得到曲线C2再把得到的曲线向右平移π6B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,个单位长度,得到曲线C2再把得到的曲线向左平移π12倍,纵坐标不变,C.把C1上各点的横坐标缩短到原来的12再把得到的曲线向右平移π个单位长度,得到曲线C26倍,纵坐标不变,D.把C1上各点的横坐标缩短到原来的12再把得到的曲线向左平移π个单位长度,得到曲线C212【答案】D【考点】三角函数图像变换.【名师点睛】对于三角函数图像变换问题,首先要将不同名函数转换成同名函数,利用诱导公式,需要重点记住sin cos(),cos sin()22ππαααα=-=+;另外,在进行图像变换时,提倡先平移后伸缩,而先伸缩后平移在考试中经常出现,无论哪种变换,记住每一个变换总是对变量x 而言.【母题原题2】【2016新课标1,理12】已知函数ππ()sin()(0),24f x x+x ,ωϕωϕ=>≤=-为()f x 的 零点,π4x =为()y f x =图像的对称轴,且()f x 在π5π()1836,单调,则ω的最大值为(A)11 (B)9 (C )7 (D )5【答案】B【考点】三角函数的性质【名师点睛】本题将三角函数的单调性与对称性结合在一起进行考查,题目新颖,是一道考查能力的好题.注意本题求解中用到的两个结论:①()()()sin 0,0f x A x A ωϕω=+≠≠的单调区间长度是最小正周期的一半;②若()()()sin 0,0f x A x A ωϕω=+≠≠的图像关于直线0x x = 对称,则()0f x A = 或()0f x A =-。
【母题原题3】【2015新课标1,理8】函数()f x =cos()x ωϕ+的部分图像如图所示,则()f x 的单调递减区间为( )(A )13(,),44k k k Z ππ-+∈ (B)13(2,2),44k k k Z ππ-+∈ (C )13(,),44k k k Z -+∈ (D)13(2,2),44k k k Z -+∈【答案】D【解析】由五点作图知,1+4253+42πωϕπωϕ⎧=⎪⎪⎨⎪=⎪⎩,解得=ωπ,=4πϕ,所以()cos()4f x x ππ=+,令22,4k x k k Z πππππ<+<+∈,解得124k -<x <324k +,k Z ∈,故单调减区间为(124k -,324k +),k Z ∈,故选D. 【考点】三角函数图像与性质【名师点睛】本题考查函数cos()y A x ωϕ=+的图像与性质,先利用五点作图法列出关于ωϕ,方程,求出ωϕ,,或利用利用图像先求出周期,用周期公式求出ω,利用特殊点求出ϕ,再利用复合函数单调性求其单调递减区间,是中档题,正确求ωϕ,使解题的关键.【命题意图】 高考主要考查函数y =Asin (ωx+φ)的图象变换,考查函数y =Asin (ωx+φ)解析式中参数φ的求法.【命题规律】 三角函数的图象与性质是高考考查的重点和热点内容,主要从以下两个方面进行考查:1。
(完整版)高中数学必修一三角函数图像性质总结(精华版)
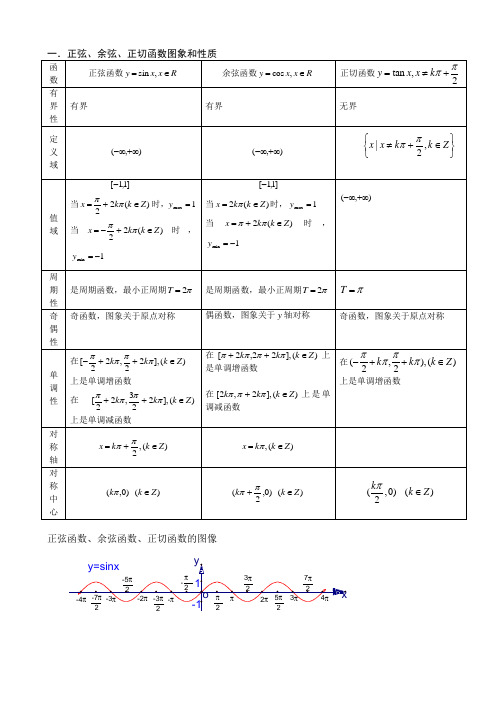
正弦函数、余弦函数、正切函数的图像1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy xy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx(一)三角函数的性质 1、定义域与值域2、奇偶性(1)基本函数的奇偶性 奇函数:y =sinx ,y =tanx ; 偶函数:y =cosx. (2)型三角函数的奇偶性(ⅰ)g (x )= (x ∈R )g (x )为偶函数由此得 ; 同理, 为奇函数.(ⅱ)为偶函数; 为奇函数.3、周期性(1)基本公式(ⅰ)基本三角函数的周期 y =sinx ,y =cosx 的周期为 ; y =tanx ,y =cotx的周期为 . (ⅱ)型三角函数的周期的周期为 ;的周期为 .(2)认知(ⅰ)型函数的周期的周期为;的周期为 .(ⅱ)的周期的周期为;的周期为 .均同它们不加绝对值时的周期相同,即对y=的解析式施加绝对值后,该函数的周期不变.注意这一点与(ⅰ)的区别.(ⅱ)若函数为型两位函数之和,则探求周期适于“最小公倍数法”.(ⅲ)探求其它“杂”三角函数的周期,基本策略是试验――猜想――证明.(3)特殊情形研究(ⅰ)y=tanx-cotx的最小正周期为;(ⅱ)的最小正周期为;(ⅲ)y=sin4x+cos4x的最小正周期为 .由此领悟“最小公倍数法”的适用类型,以防施错对象.4、单调性(1)基本三角函数的单调区间(族)依从三角函数图象识证“三部曲”:①选周期:在原点附近选取那个包含全部锐角,单调区间完整,并且最好关于原点对称的一个周期;②写特解:在所选周期内写出函数的增区间(或减区间);③获通解:在②中所得特解区间两端加上有关函数的最小正周期的整数倍,即得这一函数的增区间族(或减区间族)循着上述三部曲,便可得出课本中规范的三角函数的单调区间族.揭示:上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域.(2)y=型三角函数的单调区间此类三角函数单调区间的寻求“三部曲”为 ①换元、分解:令u =,将所给函数分解为内、外两层:y =f (u ),u =;②套用公式:根据对复合函数单调性的认知,确定出f (u )的单调性,而后利用(1)中公式写出关于u 的不等式; ③还原、结论:将u = 代入②中u 的不等式,解出x 的取值范围,并用集合或区间形成结论.()ϕω+=x A y sin (A 、ω>0)定义域 R R R 值域 ]1,1[+- ]1,1[+-R R []A A ,-周期性 π2 π2ππωπ2 奇偶性 奇函数偶函数 奇函数 奇函数当,0≠ϕ非奇非偶 当,0=ϕ奇函数单调性]22,22[ππππk k ++-上为增函数;]223,22[ππππk k ++上为减函数(Z k ∈)()]2,12[ππk k -;上为增函数()]12,2[ππ+k k上为减函数(Z k ∈)⎪⎭⎫⎝⎛++-ππππk k 2,2上为增函数(Z k ∈)()()ππ1,+k k 上为减函数(Z k ∈)⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--+--)(212),(22A k A k ωϕππωϕππ上为增函数;⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--+-+)(232),(22A k A k ωϕππωϕππ上为减函数(Z k ∈)注意:①x y sin -=与x y sin =的单调性正好相反;x y cos -=与x y cos =的单调性也同样相反.一般地,若)(x f y =在],[b a 上递增(减),则)(x f y -=在],[b a 上递减(增). ②x y sin =与xy cos =的周期是π.③)sin(ϕω+=x y 或)cos(ϕω+=x y (0≠ω)的周期ωπ2=T .2tanxy =的周期为2π(πωπ2=⇒=T T ,如图,翻折无效).④)sin(ϕω+=x y 的对称轴方程是2ππ+=k x (Z k ∈),对称中心(0,πk );)cos(ϕω+=x y 的对称轴方程是πk x =(Z k ∈),对称中心(0,21ππ+k );)tan(ϕω+=x y 的对称中心(0,2πk ). ⎭⎬⎫⎩⎨⎧∈+≠∈Z k k x R x x ,21|ππ且{}Z k k x R x x ∈≠∈,|π且xy cot =x y tan =x y cos =xy sin =▲Oyxx x y x y 2cos )2cos(2cos -=--=−−−→−=原点对称⑤当αtan ·,1tan =β)(2Z k k ∈+=+ππβα;αtan ·,1tan -=β)(2Z k k ∈+=-ππβα.⑥x y cos =与⎪⎭⎫ ⎝⎛++=ππk x y 22sin 是同一函数,而)(ϕω+=x y 是偶函数,则)cos()21sin()(x k x x y ωππωϕω±=++=+=.⑦函数x y tan =在R 上为增函数.(×) [只能在某个单调区间单调递增. 若在整个定义域,x y tan =为增函数,同样也是错误的].⑧定义域关于原点对称是)(x f 具有奇偶性的必要不充分条件.(奇偶性的两个条件:一是定义域关于原点对称(奇偶都要),二是满足奇偶性条件,偶函数:)()(x f x f =-,奇函数:)()(x f x f -=-)奇偶性的单调性:奇同偶反. 例如:x y tan =是奇函数,)31tan(π+=x y 是非奇非偶.(定义域不关于原点对称)奇函数特有性质:若x ∈0的定义域,则)(x f 一定有0)0(=f .(x ∉0的定义域,则无此性质)⑨x y sin =不是周期函数;x y sin =为周期函数(π=T );xy cos =是周期函数(如图);x y cos =为周期函数(π=T );212cos +=x y 的周期为π(如图),并非所有周期函数都有最小正周期,例如:R k k x f x f y ∈+===),(5)(.⑩abb a b a y =+++=+=ϕϕαβαcos )sin(sin cos 22有y b a ≥+22.二、形如sin()y A x ωϕ=+的函数:1、几个物理量:A ―振幅;1f T=―频率(周期的倒数);x ωϕ+―相位;ϕ―初相;2、函数sin()y A x ωϕ=+表达式的确定:A 由最值确定;ω由周期确定;ϕ由图象上的特殊点确定,如()sin()(0,0f x A x A ωϕω=+>>,||)2πϕ<=_____(答:15()2sin()23f x x π=+);3.函数B x A y ++=)sin(ϕω),(其中00>>ωA最大值是B A +,最小值是A B -,周期是ωπ2=T ,最小正周期||2ωπ=T 频率是πω2=f ,相位是ϕω+x ,初相是ϕ;其图象的对称轴是直线)(2Z k k x ∈+=+ππϕω,凡y=cos |x|图象y=|cos2x +1/2|图象是该图象与直线B y =的交点都是该图象的对称中心。
2017高考数学(理)(新课标版)考前冲刺复习:第2部分专题2第1讲三角函数的图象与性质含答案

课时作业1.(2016·广州市五校联考)下列函数中,周期为π的奇函数是( ) A .y =sin x cos x B .y =sin 2x C .y =tan 2xD .y =sin 2x +cos 2xA [解析] y =sin 2x 为偶函数;y =tan 2x 的周期为π2;y =sin 2x +cos 2x 为非奇非偶函数,故B 、C 、D 都不正确,选A.2.已知角α的终边与单位圆x 2+y 2=1交于P ⎝ ⎛⎭⎪⎫12,y 0,则sin ⎝ ⎛⎭⎪⎫π2+2α=( )A .-12B .1 C.12D .-32A [解析] 由题意知当x =12时,y 0=-32或y 0=32,即sin α=-32或sin α=32,又因为sin ⎝ ⎛⎭⎪⎫π2+2α=cos 2α=1-2sin 2α,所以sin ⎝ ⎛⎭⎪⎫π2+2α=1-2×34=-12.3.(2016·福建省毕业班质量检测)若sin ⎝ ⎛⎭⎪⎫π2+α=-35,且α∈⎝ ⎛⎭⎪⎫π2,π,则sin(π-2α)=( )A.2425 B.1225 C .-1225D .-2425D [解析] 由sin ⎝ ⎛⎭⎪⎫π2+α=cos α=-35,且α∈⎝ ⎛⎭⎪⎫π2,π,得sin α=45,所以sin(π-2α)=sin 2α=2sin α·cos α=-2425,选项D 正确.4.(2016·沈阳市教学质量监测(一))某函数部分图象如图所示,它的函数解析式可能是( )A .y =sin ⎝ ⎛⎭⎪⎫-56x +3π5B .y =sin ⎝ ⎛⎭⎪⎫65x -2π5C .y =sin ⎝ ⎛⎭⎪⎫65x +3π5 D .y =-cos ⎝ ⎛⎭⎪⎫56x +3π5C [解析] 不妨令该函数解析式为y =A sin(ωx +φ)(ω>0),由图知A =1,T 4=3π4-π3=5π12,于是2πω=5π3,即ω=65,π3是函数的图象递减时经过的零点,于是65×π3+φ=2k π+π,k ∈Z ,所以φ可以是3π5,选C.5.已知ω>0,函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π4在⎝ ⎛⎭⎪⎫π2,π上单调递减,则ω的取值范围是( )A.⎣⎢⎡⎦⎥⎤12,54B.⎣⎢⎡⎦⎥⎤12,34 C.⎝ ⎛⎦⎥⎤0,12 D .(0,2]A [解析] 由π2<x <π得π2ω+π4<ωx +π4<πω+π4,由题意知⎝ ⎛⎭⎪⎫π2ω+π4,πω+π4⊆⎣⎢⎡⎦⎥⎤π2,3π2,所以⎩⎪⎨⎪⎧π2ω+π4≥π2,πω+π4≤3π2,所以12≤ω≤54.6.(2016·山西考前质量检测)若函数f (x )=sin(2x +φ)⎝ ⎛⎭⎪⎫||φ<π2的图象关于直线x =π12对称,且当x 1,x 2∈⎝ ⎛⎭⎪⎫-π6,π3,x 1≠x 2时,f (x 1)=f (x 2),则f (x 1+x 2)=( )A.12B.22C.32D .1C [解析] 由题意得,2×π12+φ=π2+k π,k ∈Z ,所以φ=π3+k π,k ∈Z ,因为|φ|<π2,所以k =0,φ=π3,又x 1,x 2∈⎝ ⎛⎭⎪⎫-π6,π3,所以2x 1+π3,2x 2+π3∈(0,π),所以2x 1+π3+2x 2+π32=π2,解得x 1+x 2=π6,所以f (x 1+x 2)=sin ⎝⎛⎭⎪⎫2×π6+π3=32.7.已知-π2<α<0,sin α+cos α=15,则sin α-cos α=________.[解析] sin α+cos α=15,平方可得sin 2α+2sin α·cos α+cos 2α=125,即2sin α·cos α=-2425,因为(sin α-cos α)2=1-2sin α·cos α=4925,又-π2<α<0,所以sin α<0,cos α>0,所以sin α-cos α<0,所以sin α-cos α=-75.[答案] -758.已知函数y =cos x 与y =sin(2x +φ)(0≤φ<π),它们的图象有一个横坐标为π3的交点,则φ的值是________.[解析] 由题意,得sin ⎝ ⎛⎭⎪⎫2×π3+φ=cos π3,因为0≤φ<π,所以φ=π6.[答案] π69.已知f (x )=sin 2x -3cos 2x ,若对任意实数x ∈⎝⎛⎦⎥⎤0,π4,都有|f (x )|<m ,则实数m 的取值范围是________.[解析] 因为f (x )=sin 2x -3cos 2x =2sin ⎝ ⎛⎭⎪⎫2x -π3,x ∈⎝ ⎛⎦⎥⎤0,π4,所以⎝⎛⎭⎪⎫2x -π3∈⎝ ⎛⎦⎥⎤-π3,π6,所以2sin ⎝⎛⎭⎪⎫2x -π3∈(-3,1], 所以|f (x )|=⎪⎪⎪⎪⎪⎪2sin ⎝ ⎛⎭⎪⎫2x -π3<3,所以m ≥ 3.[答案] [3,+∞)10.已知f (x )=sin(ωx +φ)⎝⎛⎭⎪⎫ω>0,|φ|<π2满足f (x )=-f (x +π),f (0)=12,则g (x )=2cos(ωx +φ)在区间⎣⎢⎡⎦⎥⎤0,π2上的最大值为________.[解析] 由f (x )=-f (x +π)可得f (x +2π)=f (x ),即函数f (x )的周期为2π,所以ω=2π2π=1.由f (0)=12得sin φ=12,又|φ|<π2,所以φ=π6,因为g (x )=2cos ⎝ ⎛⎭⎪⎫x +π6,且0≤x ≤π2,所以π6≤x +π6≤2π3,所以-12≤cos ⎝ ⎛⎭⎪⎫x +π6≤32,因此g (x )max = 3.[答案] 311.已知a =(sin 2x ,2cos 2x -1),b =(sin θ,cos θ)(0<θ<π),函数f (x )=a ·b的图象经过点⎝ ⎛⎭⎪⎫π6,1.(1)求θ及f (x )的最小正周期;(2)当x ∈⎣⎢⎡⎦⎥⎤-π6,π4时,求f (x )的最大值和最小值. [解] (1)因为f (x )=a ·b =sin 2x sin θ+cos 2x cos θ=cos(2x -θ), 所以f (x )的最小正周期为T =π.因为y =f (x )的图象经过点⎝ ⎛⎭⎪⎫π6,1, 所以cos ⎝ ⎛⎭⎪⎫π3-θ=1.因为0<θ<π,所以θ=π3.(2)由(1)得f (x )=cos ⎝ ⎛⎭⎪⎫2x -π3. 因为-π6≤x ≤π4,所以-2π3≤2x -π3≤π6.故当2x -π3=0,即x =π6时,f (x )取得最大值1;当2x -π3=-2π3,即x =-π6时,f (x )取得最小值-12.12.设函数f (x )=2cos 2x +sin 2x +a (a ∈R ). (1)求函数f (x )的最小正周期和单调递增区间;(2)当x ∈⎣⎢⎡⎦⎥⎤0,π6时,f (x )的最大值为2,求a 的值,并求出y =f (x )(x ∈R )的对称轴方程.[解] (1)f (x )=2cos 2x +sin 2x +a =1+cos 2x +sin 2x +a =2sin ⎝ ⎛⎭⎪⎫2x +π4+1+a ,则f (x )的最小正周期T =2π2=π,且当2k π-π2≤2x +π4≤2k π+π2(k ∈Z )时f (x )单调递增,即k π-38π≤x ≤k π+π8(k ∈Z ). 所以⎣⎢⎡⎦⎥⎤k π-3π8,k π+π8(k ∈Z )为f (x )的单调递增区间. (2)当x ∈⎣⎢⎡⎦⎥⎤0,π6时,π4≤2x +π4≤7π12, 当2x +π4=π2,即x =π8时,sin ⎝ ⎛⎭⎪⎫2x +π4=1.所以f (x )max =2+1+a =2⇒a =1- 2. 由2x +π4=k π+π2得x =k π2+π8(k ∈Z ),故y =f (x )的对称轴方程为x =k π2+π8,k ∈Z .13.(2016·湖北省七市(州)协作体联考)已知函数f (x )=2sin x +6cos x (x ∈R ). (1)若α∈[0,π]且f (α)=2,求α;(2)先将y =f (x )的图象上所有点的横坐标缩短到原来的12(纵坐标不变),再将得到的图象上所有点向右平行移动θ(θ>0)个单位长度,得到的图象关于直线x =3π4对称,求θ的最小值.[解] (1)f (x )=2sin x +6cos x=22⎝ ⎛⎭⎪⎫12sin x +32cos x =22sin ⎝ ⎛⎭⎪⎫x +π3.由f (α)=2,得sin ⎝⎛⎭⎪⎫α+π3=22,即α+π3=2k π+π4或α+π3=2k π+3π4,k ∈Z .于是α=2k π-π12或α=2k π+5π12,k ∈Z .又α∈[0,π],故α=5π12.(2)将y =f (x )图象上所有点的横坐标缩短到原来的12(纵坐标不变),得到y =22sin ⎝ ⎛⎭⎪⎫2x +π3的图象,再将y =22sin ⎝ ⎛⎭⎪⎫2x +π3图象上所有点的横坐标向右平行移动θ个单位长度,得到y =22sin ⎝⎛⎭⎪⎫2x -2θ+π3的图象.由于y =sin x 的图象关于直线x =k π+π2(k ∈Z )对称,令2x -2θ+π3=k π+π2,解得x =k π2+θ+π12,k ∈Z .由于y =22sin ⎝ ⎛⎭⎪⎫2x -2θ+π3的图象关于直线x =3π4对称,令k π2+θ+π12=3π4,解得θ=-k π2+2π3,k ∈Z . 由θ>0可知,当k =1时,θ取得最小值π6.14.已知定义在区间⎣⎢⎡⎦⎥⎤-π,3π2上的函数y =f (x )的图象关于直线x =π4对称,当x ≥π4时,f (x )=-sin x . (1)作出y =f (x )的图象;(2)求y =f (x )的解析式;(3)若关于x 的方程f (x )=a 有解,将方程中的a 取一确定的值所得的所有解的和记为M a ,求M a 的所有可能的值及相应的a 的取值范围.[解] (1)y =f (x )的图象如图所示.(2)任取x ∈⎣⎢⎡⎦⎥⎤-π,π4, 则π2-x ∈⎣⎢⎡⎦⎥⎤π4,3π2, 因为函数y =f (x )的图象关于直线x =π4对称,则f (x )=f ⎝ ⎛⎭⎪⎫π2-x ,又当x ≥π4时,f (x )=-sin x , 则f (x )=f ⎝ ⎛⎭⎪⎫π2-x =-sin ⎝ ⎛⎭⎪⎫π2-x=-cos x ,即f (x )=⎩⎪⎨⎪⎧-cos x ,x ∈⎣⎢⎡⎭⎪⎫-π,π4,-sin x ,x ∈⎣⎢⎡⎦⎥⎤π4,3π2.(3)当a =-1时,f (x )=a 的两根为0,π2,则M a =π2;当a ∈⎝ ⎛⎭⎪⎫-1,-22时,f (x )=a 的四根满足x 1<x 2<π4<x 3<x 4,由对称性得x 1+x 2=0,x 3+x 4=π,则M a =π;当a =-22时,f (x )=a 的三根满足x 1<x 2=π4<x 3,由对称性得x 3+x 1=π2,则M a =3π4;当a ∈⎝ ⎛⎦⎥⎤-22,1时,f (x )=a 的两根为x 1,x 2,由对称性得M a =π2.综上,当a ∈⎝ ⎛⎭⎪⎫-1,-22时,M a =π; 当a =-22时,M a =3π4; 当a ∈⎝⎛⎦⎥⎤-22,1∪{-1}时,M a =π2.。
三角函数的图像及其性质

三角函数的图像及其性质1、三角函数的图像及性质sin y xsin y A x k图像值域周期对称轴2x k2x k对称中心(零点)令x k 代入求y令x k 代入,求出x 和y 单调增区间2,222x k k2,222x k k单调减区间32,222x k k32,222x k kcos y xcos y A x k图像值域周期对称轴x kx k 对称中心(零点)2x k代入,求y 2x k求出x 和y 单调增区间 2,2x k k 2,2x k k 单调减区间2,2x k k2,2x k k tan y x图像定义域值域周期单调性与对称性性质【考点分类】考点一:图像变换:1.把函数y =sin x 的图象向右平移个单位得到y =g (x )的图象,再把y =g (x )图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),所得到图象的解析式为()A.B.C.D.2.将函数f (x )=sin x 图象上所有点的横坐标变为原来的(ω>0),纵坐标不变,得到函数g (x )的图象,若g (x )的最小正周期为6π,则ω=()A.B.6C.D.33.将函数y =2sin2x 图象上的所有点向右平移个单位,然后把图象上所有点的横坐标缩短为原来的倍,(纵坐标不变)得到y =f (x )的图象,则f (x )等于()A.2sin(x ﹣)B.2sin(x ﹣)C.2sin(4x ﹣)D.2sin(4x ﹣)4.已知曲线C 1:y =cos x ,C 2:y =sin(2x +),则下面结论正确的是()A.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再向右平移个单位长度,得到曲线C 2B.把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再向左平移个单位长度,得到曲线C 2C.把C 1上各点的横坐标缩短到原来的,纵坐标不变,再向右平移个单位长度,得到曲线C 2D.把C 1上各点的横坐标缩短到原来的,纵坐标不变,再向左平移个单位长度,得到曲线C 25.把函数y =cos(3x +4)的图象适当变动就可以得到y =sin(-3x )的图象,这种变动可以是()A 向右平移4 B 向左平移4 C 向右平移12 D 向左平移126..函数32sin( x y 的图象是由2sin xy 的图象沿x 轴()得到的。
三角函数的图象与性质-2017年高考数学(理)母题题源系列(新课标2专版)含解析

【母题原题1】【2017新课标卷II ,理14】函数23()sin 34f x x x =-([0,])2x π∈的最大值是 ____________. 【答案】1 【解析】化简得()22311cos 3cos 344f x x x x x =-+-=-+=23(cos 12x --+,由 [0,]2x π∈可得cos [0,1]x ∈,当3cos x =时,函数()f x 取得最大值1.【考点】 三角变换、复合型二次函数的最值【名师点睛】本题经三角函数式的化简将三角函数的问题转化为二次函数的问题,二次函数、二次方程与二次不等式统称“三个二次”,它们常结合在一起,有关二次函数的问题,数形结合、密切联系图象是探求解题思路的有效方法.一般从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面进行分析.【母题原题2】【2016新课标卷II,理7】若将函数y =2sin 2x 的图像向左平移12π个单位长度,则平移后图像的对称轴为(A )x =26k ππ-(k ∈Z ) (B )x =26k ππ+(k ∈Z )(C )x =212k ππ-(k ∈Z ) (D)x =212k ππ+(k ∈Z )【答案】B【考点】三角函数图像的变换与对称性【名师点睛】平移变换和伸缩变换都是针对x 而言,即x 本身加或减多少值,而不是依赖于ωx 加或减多少值.【命题意图】 三角函数的图象与性质,高考重点考查三角函数的性质、图象及平移变换、运算能力、等价转化及数学结合思想.【命题规律】 高考对该部分内容考查一般以选择填空题形式出现,难度中等或中等以下,热点是三角函数的值域、最值、单调性、对称性及三角函数解析式的确定,且常常与三角变换结合在一起考查.【答题模板】解答本类题目,以2017年试题为例,一般考虑如下三步:第一步:把所给函数化为最简 化简的思路一般是化分式为整式,化高次为低次,且是项数尽可能的少,配方与辅助角公式是常用的2种方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题四 三角函数的图象和性质【母题来源一】【2017全国卷1文数8】 【母题原题】函数sin21cos xy x=-的部分图像大致为A .B .C .D .【答案】C【考点】函数图像【名师点睛】函数图象问题首先关注定义域,从图象的对称性,分析函数的奇偶性,根据函数的奇偶性排除部分选择项,从图象的最高点、最低点,分析函数的最值、极值,利用特值检验,较难的需要研究单调性、极值等,从图象的走向趋势,分析函数的单调性、周期性等.【母题来源二】【2016全国卷1文数6】【母题原题】将函数y =2sin (2x +π6)的图象向右平移14个周期后,所得图象对应的函数为 (A )y =2sin(2x +π4) (B )y =2sin(2x +π3) (C )y =2sin(2x –π4) (D )y =2sin(2x –π3)【答案】D 【解析】试题分析:函数2sin(2)6y x π=+的周期为π,将函数2sin(2)6y x π=+的图像向右平移14个周期即4π个单位,所得图像对应的函数为2sin[2())]2sin(2)463y x x πππ=-+=-,故选D. 【考点】三角函数图像的平移【名师点睛】函数图像的平移问题易错点有两个,一是平移方向,注意“左加右减”;二是平移多少个单位是对x 而言的,不要忘记乘以系数. 【母题来源三】【2015全国卷1文数8】【母题原题】函数()cos()f x x ωϕ=+的部分图像如图所示,则()f x 的单调递减区间为( )(A )13(,),44k k k Z ππ-+∈ (B )13(2,2),44k k k Z ππ-+∈ (C )13(,),44k k k Z -+∈ (D )13(2,2),44k k k Z -+∈【答案】D【考点定位】三角函数图像与性质【名师点睛】本题考查函数cos()y A x ωϕ=+的图象与性质,先利用五点作图法列出关于ωϕ,方程,求出ωϕ,,或利用利用图象先求出周期,用周期公式求出ω,利用特殊点求出ϕ,再利用复合函数单调性求其单调递减区间,是中档题,正确求ωϕ,使解题的关键.【命题意图】考查函数()y Asin x ωϕ=+的图象变换、解析式中参数,ωϕ的求法,考查三角函数的奇偶性、周期性、单调性.考查函数式化简变形能力及数形结合思想.【命题规律】三角函数的图象与性质是三角函数的重要内容,高考中比较重视考查三角函数图象变换及三角函数的周期性、最值、奇偶性、单调性、对称性等,同时往往注重考查三角函数和差倍半公式的应用.从历年高考题目看,以选择题、填空题为主,少有解答题. 【答题模板】(1)先平移后伸缩 (2)先伸缩后平移【方法总结】1.一个区别——两种图像变换的区别由y =sin x 的图像变换到y =Asin(ωx +φ)的图像,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是|φ|个单位长度;而先周期变换(伸缩变换)再相位变换,平移的量是|φ|ω(ω>0)个单位长度。
原因在于相位变换和周期变换都是针对x 而言,即x 本身加减多少值,而不是依赖于ωx 加减多少值。
2. 三种方法——由函数图像求解析式的方法(1)如果从图像可确定振幅和周期,则可直接确定函数表达式y =Asin(ωx +φ)中的参数A 和ω,再选取 “第一零点”(即五点作图法中的第一个点)的数据代入“ωx +φ=0”(要注意正确判断哪一点是“第一零点”)求得φ。
(2)通过若干特殊点代入函数式,可以求得相关待定系数A ,ω,φ,依据是五点法。
(3)运用逆向思维的方法,根据图像变换可以确定相关的参数。
3.确定y =Asin(ωx +φ)+b(A>0,ω>0)的步骤和方法 (1)求A ,b ,确定函数的最大值M 和最小值m ,则A =M -m 2,b =M +m2(2)求ω,确定函数的周期T ,则可得ω=2πT(3)求φ,常用的方法有:①代入法:把图像上的一个已知点代入(此时A ,ω,b 已知)或代入图像与直线y =b 的交点求解(此时要注意交点在上升区间上还是在下降区间上)。
②五点法:确定φ值时,往往以寻找“五点法”中的某一个点为突破口。
具体如下:“第一点”(即图像上升时与x 轴的交点)时ωx +φ=0;“第二点”(即图像的“峰点”)时ωx +φ=π2;“第三点”(即图像下降时与x 轴的交点)时ωx +φ=π;“第四点”(即图像的“谷点”)时ωx +φ=3π2;“第五点”时ωx +φ=2π。
4.解答有关平移伸缩变换的题目时,向左(或右)平移m 个位时,用x+m(或x-m)代替x,向下(或上)平移n 个单位时,用y+n(或y-n)代替y,横(或纵)坐标伸长或缩短到原来的k 倍,用k x 代替x(或ky代替y),即可获得解决.5.解答三角函数性质(单调性、周期性、最值等)问题时,通常是利用三角函数的有关公式,将三角函数化为“只含”一个函数名称且角度唯一,最高次数为一次(一角一函)的形式,再依正(余)弦型函数依次对所求问题作出解答.1.【2017广东佛山二模】为了得到函数2cos 26y x π⎛⎫=- ⎪⎝⎭的图象,只需将函数2sin2y x =图象上所有的点( )A. 向左平移12π个单位长度B. 向右平移12π个单位长度 C. 向左平移6π个单位长度 D. 向右平移6π个单位长度【答案】C【解析】2sin22cos 22cos 2266y x x x πππ⎡⎤⎛⎫⎛⎫==-=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以向左平移6π个单位长度,选C.2.【2017湖南娄底二模】已知函数()()sin f x x ωϕ=+(0ω>, 0ϕπ<<)的最小正周期是π,将函数()f x 的图象向左平移6π个单位长度后所得的函数图象过点()0,1P ,则函数()()sin f x x ωϕ=+( )A. 有一个对称中心,012π⎛⎫⎪⎝⎭B. 有一条对称轴6x π=C. 在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递减D. 在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递增 【答案】B3.【2017重庆二诊】已知函数()2sin (0,0)y x ωϕωϕπ=+><<的部分图象如图所示,则ϕ=( )A.6π B. 4π C. 3π D. 2π 【答案】B【解析】由图象得,25221212πππωω⎡⎤⎛⎫=⨯--⇒= ⎪⎢⎥⎝⎭⎣⎦,则函数的解析式为()2sin 2y x ϕ=+,将点212π⎛⎫⎪⎝⎭,代入得, 2sin 2212πϕ⎛⎫⨯+= ⎪⎝⎭,又0ϕπ<<,所以623πππϕϕ+=⇒=,故选C.4.【2017四川资阳4月模拟】已知函数()sin 6f x x πω⎛⎫=+ ⎪⎝⎭(其中0ω>)图象的一条对称轴方程为12x π=,则ω的最小值为A. 2B. 4C. 10D. 16 【答案】B【解析】解:由三角函数的性质可知,当12x π=时:(),12462x k k k Z ππωπω+=+∴=+∈ ,取0k = 可得ω 的最小值为4ω= . 本题选择B 选项.5.【2017福建漳州5月质检】为了得到函数cos2y x =的图象,只要把函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象上所有的点( )A. 向右平行移动512π个单位长度B. 向左平行移动512π个单位长度C. 向右平行移动56π个单位长度D. 向左平行移动56π个单位长度【答案】B6.【2017河北唐山三模】函数()cos 6f x x πω⎛⎫=+⎪⎝⎭(0ω>)的最小正周期为π,则()f x 满足( ) A. 在0,3π⎛⎫⎪⎝⎭上单调递增 B. 图象关于直线6x π=对称C. 3f π⎛⎫=⎪⎝⎭当512x π=时有最小值1- 【答案】D【解析】由函数()cos 6f x x πω⎛⎫=+⎪⎝⎭(0ω>)的最小正周期为π得2ω=,则()cos 26f x x π⎛⎫=+ ⎪⎝⎭,当0,3x π⎛⎫∈ ⎪⎝⎭时, 52,666x πππ⎛⎫+∈ ⎪⎝⎭,显然此时()f x 不单调递增,A 错误; 当6x π=时, cos 062f ππ⎛⎫==⎪⎝⎭,B 错误;5cos 36f ππ⎛⎫== ⎪⎝⎭C 错误;故选择D.7.【2017河北武邑四模】已知函数()cos2f x x x =-的图象在区间0,3a ⎡⎤⎢⎥⎣⎦和42,3a π⎡⎤⎢⎥⎣⎦上均单调递增,则正数的取值范围是( ) A. 5,612ππ⎡⎤⎢⎥⎣⎦ B. 5,12ππ⎡⎤⎢⎥⎣⎦ C. ,4ππ⎡⎤⎢⎥⎣⎦ D. 2,43ππ⎡⎤⎢⎥⎣⎦【答案】B8.【2017安徽马鞍山三模】已知函数()cos 2sin26f x x x π⎛⎫=-+ ⎪⎝⎭,则()f x 的一个单调递减区间是( ) A. ,36ππ⎡⎤-⎢⎥⎣⎦ B. 2,33ππ⎡⎤-⎢⎥⎣⎦ C. 5,66ππ⎡⎤-⎢⎥⎣⎦ D. 2,63ππ⎡⎤⎢⎥⎣⎦【答案】D【解析】()3sin2226f x x x x π⎛⎫=+=+ ⎪⎝⎭ , ()3222262k x k k Z πππππ+≤+≤+∈,解得()263k x k k Z ππππ+≤≤+∈ ,当0k =时, 263x ππ≤≤ ,故选D.9.【2017福建4月质检】已知函数()sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭在,123ππ⎛⎫ ⎪⎝⎭上有最大值,但没有最小值,则ω的取值范围是__________. 【答案】3,34⎛⎫⎪⎝⎭【解析】函数()sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭在,123ππ⎛⎫ ⎪⎝⎭上有最大值,但没有最小值,所以33(,3)12423424ππππππωωω+<<+≤⇒∈.10.【2017北京丰台5月综合测试】已知函数()2πsin 2f x xsin x x ⎛⎫=- ⎪⎝⎭. (Ⅰ)求()f x 的最小正周期; (Ⅱ)求()f x 的单调递增区间. 【答案】(1)最小正周期为(2)5ππ[π,π]()1212k k k Z -++∈(Ⅱ)由πππ2π22π()232k x k k Z -+≤+≤+∈求得5ππππ()1212k x k k Z -+≤≤+∈, 所以()f x 的单调递增区间为5ππ[π,π]()1212k k k Z -++∈。
