基于GM(1,1)模型的煤矿百万吨死亡率的预测研究
基于灰色GM(1,1)模型的煤炭需求量预测

基于灰色GM(1,1)模型的煤炭需求量预测张珏赟;姚轲;徐旭东;南莹浩【摘要】以2010~2016年我国的煤炭需求消费总量作为数据基础,应用灰色系统理论,建立了GM(1,1)模型,预测出了2017~2019三年我国的煤炭需求量并分析了预测结果,表明该模型经检验有较高的精确度,其预测结果可信度高,为保障我国能源安全、制定能源发展战略提供科学依据.【期刊名称】《华北科技学院学报》【年(卷),期】2016(013)006【总页数】3页(P106-108)【关键词】GM(1,1)模型;煤炭需求量;预测【作者】张珏赟;姚轲;徐旭东;南莹浩【作者单位】华北科技学院研究生院,北京东燕郊 101601;华北科技学院研究生院,北京东燕郊 101601;华北科技学院研究生院,北京东燕郊 101601;华北科技学院研究生院,北京东燕郊 101601【正文语种】中文【中图分类】F426.21自改革开放30多年来,随着中国经济高速增长所引起的能源消费需求急剧扩大,受国内能源后备资源相对不足及以煤为主的能源消费结构所带来的环境影响压力加大,能源供需矛盾日益突出,并已成为制约未来中国经济实现可持续发展的关键因素[1]。
煤炭是我国的主导能源,但据预测,如果按现在的开采速度,我国的煤炭的供给年限保守估计在60年左右。
我国以煤为主的能源消费结构是由资源条件决定的,我国是一个富煤、缺油、少气的国家,以煤炭为主的能源格局是难以在短期内彻底改变的,在能源结构的调整的过程中,不可盲目地用大量的石油或天然气等我国相对短缺的能源来替代煤炭。
能源消费结构预测是制定能源发展战略和能源规划的重要组成部分,通过能源消费结构预测,可以制定最优的能源发展战略、安排能源建设以及优化配置等。
灰色系统理论[2-5]中的GM(1,1)模型因其所需要的信息少、运算方便而广泛应用于各种预测领域。
本文结合我国能源消费的历史数据,用GM(1,1)模型来预测2017~2019年我国的煤炭需求量,为制定能源发展战略提供科学依据。
关于我国煤矿百万吨死亡率的灰色预测探讨

矿 业 安 全 与 环 保
第 3 卷第4 3 期
一
曰 =
05x ( + D2] . l 1 :() [D ) 05x () D 3] . l 2 + () [D 05x ( 一1 + D /] .El n ) (, D 1 )
‘() ‘( )T 。 3 … 。 n I ’ ’
供依据。在 G M(n k 模 型中, ,) n代表 阶数 , k代表 变 量个 数 。 12 G 11 模型 【 . M(,) 1
G 11 模 型是 目前应 用最 为广 泛 的灰 色 预测 M( ,) 系统模 型 。
1 灰 色预 测
1 1 灰 色预 测概述 .
设 ‘ 为非负序列 , 为 ∞ 的一阶累加生成 。 ‘ ’ 序列( —A O序列) ‘ I G : ‘ [ 。 1,‘( ) ‘( )…,‘ ( ) ‘() 。 2 , 。 3 , 。 n ]
亡人数 一直 徘徊 在 六 七 千 人 , 不仅 给 职工 家 属 带 这
的信 息, 立 一个 从 过去 引伸 到 未来 的 G g y 建 M(r e
m d1 型 , oe) 模 以发 现 和掌 握 系 统 的发展 规 律 , 系统 对
的未来状态作出科学的定量 预测 , 并为规划决策提
来了极大痛苦 , 也给 国家造成 巨大 的经济损失。因 此, 对事故进行科学 的分析及 预测 , 可以避免计划的 盲目 , 性 对安全管理起到辅助作用。
摘 要: 通过对 G ( ,) M 11灰色预测模型的分析 , 对我国近几年来煤矿百万吨死亡率进行统计预测, 并通过对灰色模型预测结果与一元线性回归模型预测结果 的对比, 说明该模型基本正确, 预测精度是基 本可靠的。由此可对事故进行科学的分析及预测 , 以最大限度地减少事故的发生, 降低损失。
基于GM(1

di1 .9 9ji n 10 2 9 .0 2 0 .0 o:0 36 /. s.0 5— 7 8 2 1 .3 0 1 s
基 于 G 1 1 模 型 的 山 西煤 矿 百 万 吨 M( , ) 死 亡 率 的预 测 研 究 张金 山 , 王 浩 , 侯
d cin mo e .T ec a n n S a x r vn e i e e t e r n l o o s mo ai t t t sp e i t h rd ci n a c r c s it d 1 h o mie i h n i o ic n r c n a so emi in t n r t sai i r d c ,te p e it c u a y i o l P y l t y l sc o v i a e .T er s l h w t a h r d cin mo e ft e sr cu e i c re t o o n aey p o u t n p o i e r cs h oy l a d td h e ut s o h tt e p e it d l tu t r s or c rc a mi e s f t rd ci r v d sp e ie t e r s o o h f l o b ss a i.
对煤 矿的安全 生产 提供 了精确 的理论依据 。 关键词 : M( ,) G 1 1 模型 ; 灰色 系统 ; 百万吨死亡率
中 图 分 类 号 :9 8 0 X 2 .3 文献标识码 : A 文章 编 号 :0 5 2 9 (0 2 0 — 0 1 0 10 — 7 8 2 1 )3 00 . 2
炭主产 地之 一 , 炭 产量 约 占全 国三 分 之 一 。 由于 加 法 、 煤 自适应 性 累加法 等逐 步使 根本 没有 规 律 的 、 杂 煤 层赋存 条件 非 常 复 杂 , 质构 造对 煤 层 的破 坏 非 乱 无章 的一组 原 始 数 据 白化 , 而构 造 相 应 于 微 分 地 从 常严重 , 大部 分煤 层 的开采普 遍存 在 着生 产效 率 低 、 方程解的模型并作 出预报, 一般仅要求较少 的原始 安 全状 况差 等 问题 。煤 矿 的安全生 产 又是 一个 庞 大 数 据就 可 以构 造 模 型 _ 。G 1 1 是 在 灰 色 系 统 1 M( , ) J 复杂 的系统 , 受到 地方 经济 、 自然 条件 、 国家政 策 、 采 预测理 论 中经 常用 到 的单 变量 数 列 预 测 模 型 , 个 这
GM(1,1)灰色预测模型在矿井瓦斯涌出量预测中的应用

GM(1,1)灰色预测模型在矿井瓦斯涌出量预测中的应用杨武艳;郁钟铭【摘要】瓦斯是造成煤矿生产过程中事故频发的重要因素.以预测矿井瓦斯涌出量为研究目的,运用灰色系统理论,通过对矿井瓦斯涌出资料进行分析、研究建立GM(1,1)瓦斯涌出量灰色预测模型对瓦斯涌出量变化趋势进行预测,并与现场实际瓦斯涌出量比较,结果表明该模型精度较高,能够很好用于矿井瓦斯涌出量的预测,为井下安全生产和瓦斯监测提供依据,从而避免瓦斯事故的发生.%Gas is an important factor which causes frequent accidents in coal production. By taking mine gas emission prediction as the research purposes and using grey system theory, this paper analyzes mine gas emission data, and establishes GM ( 1,1 ) grey forecasting model to forecast the change trend of the gas emission. By comparing with the actual gas emission quantity, results show that the model can better predict mine gas emission, and provide basis for downhole safety production and gas monitor. In this way gas accidents can be avoided.【期刊名称】《矿业工程研究》【年(卷),期】2012(027)004【总页数】4页(P46-49)【关键词】瓦斯涌出量;灰色理论;GM(1;1)模型;灰色预测【作者】杨武艳;郁钟铭【作者单位】贵州大学矿业学院,贵州贵阳550025;六盘水师范学院,贵州六盘水553000【正文语种】中文【中图分类】TD712.5瓦斯涌出量的大小是造成煤矿生产中发生事故频发的主要影响因素之一,瓦斯涌出量过大会引起煤与瓦斯突出,造成不必要的人员伤亡和经济损失;在通风效果不好的情况下,瓦斯涌出量过大会造成作业人员窒息甚至死亡;如遇火源,还有可能会引发瓦斯爆炸,酿成重大瓦斯事故[1].因此,在进行煤层开采的过程中,必须事先对瓦斯涌出情况进行预测,以避免事故的发生.通常情况下影响瓦斯涌出的主要有开采方法、煤层厚度、瓦斯含量、地质构造等多种因素,但在现有的生产条件下,很难把这些因素考虑的全面而准确,即瓦斯涌出量的大小是已知和未知因素综合作用的结果,所以瓦斯涌出实际上是一个灰色系统.因此,可以利用灰色系统理论来进行煤层瓦斯涌出量的预测[2].1 灰色系统及其模型的建立1.1 灰色系统的特点灰色系统理论是20世纪80年代,由中国华中理工大学邓聚龙教授首先提出并创立的一门新兴学科,它是基于数学理论的系统工程学科,它是一种研究少数据、贫信息不确定性问题的新方法.灰色系统理论以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对“部分”已知信息的生成、开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控.灰色系统理论的主要优点是通过一系列数据生成方法,如直接累加法、移动平均法、加权累加法、自性累加法等,将本没有规律的、杂乱无章的或规律性不强的一组原始数据序列变得具有明显的规律性[3].灰色系统预测模型是一种将矿井瓦斯涌出量看作是在一定区间内变化的灰色量,将矿井瓦斯涌出量变化的过程看成是在一定幅间区、一定时区间变化的随机过程.这种方法具有数据样本少,不需要典型的分布规律的特点,当煤矿新建、改建、扩建时,没有长时期的瓦斯涌出量历史数据资料,且所收集数据少、数据波动不大的情况下,可以使用灰色预测模型.采用灰色理论的预测模型,对矿井今后一段时间内瓦斯涌出量的大小及发展趋势进行预测,为矿井瓦斯涌出量时间动态数列的预测提供了一种新的途径[4].1.2 GM(1,1)模型的建立1)确定任一子数据序列 X(0)=[X(0)(1),X(0)(2),…,X(0)(n)].n为灰色数据总长度,对子数据序列作一次累加生成(1-AGO)则生成的序列为2)建立GM(1,1)的微分方程称式(1)为一阶单变量灰微分方程模型,记为GM(1,1);式中的a,b为待定参数的元素,可以用最小二乘法求解,即3)求常数向量Yn及构造累加矩阵B4)数学模型的求解利用初始条件对白化方程进行求解,可得微分方程(1)的解,即根据式(5)求得x(1)(k+1)为所求数据序列预测值的累加生成值,故需要将其还原为变化后的数据序列,对)求导数,得出还原模型从理论上说,式(5)和式(6)可以对所建立的GM(1,1)模型进行求解,对所规定的数据序列的发展趋势作出具体的预测[5].5)GM(1,1)模型的精度检验上述模型只是数据序列的初始模型,此类模型的预测在一定程度上还不能反映该序列的客观变化规律,需对其做进一步的精度检验.在此处采用残差序列法来进行修正[6].假设残差序列为,即q(0)(k)=x(0)(k)-(k)=(q(0)(1),q(0)(2),…,q(0)(n)),对此序列 q(0)(k)同样采用上述方法建立GM(1,1)模型,其时间响应函数为将式(7)代入式(6)中,则得式中2 应用灰色GM(1,1)模型进行某矿采掘工作面的瓦斯涌出量预测矿井瓦斯涌出量的大小受多种因素的影响,各因素之间的关系错综复杂,表现为既非确定的也非随即的,而是一种模糊的系统状态[7].因此,利用灰色系统理论,可对采掘工作面的近期瓦斯涌出量作出合理的预测,这无疑对矿井的瓦斯管理有重要的指导意义.以某矿为例进行采掘工作面瓦斯涌出量的预测.利用灰色系统理论,对该矿2011年05~11月份采煤工作面的瓦斯涌出资料进行分析、研究建立矿井瓦斯涌出量灰色预测模型,并利用文中的灰色模型对该矿12月份的瓦斯涌出量进行预测[8].2011年5~11月采煤工作面瓦斯涌出量分别为 17.50,19.18,20.80,22.93,26.81,29.31,29.93 m3/t.1)对原始数据做一次累加处理(1-AGO)2)构造数据矩阵B和数据列Yn3)计算参数向量则 a=-0.094 6,b=16.778 2.4)所以,该矿的瓦斯涌出GM(1,1)模型为其时间响应函数为该方程的解为某煤矿瓦斯涌出量的灰色预测模型.5)对模型进行检验(表1)利用式x(0)(k)=x(1)(k)-x∧(1)(k+1)进行还原检验,见表2.表1 计算值与实际累加值Tab.1 Calculated values and actual accumulative values序号计算值实际累加值k=1x∧(1)(2)=36.84x(1)(2)=36.68k=2x∧(1)(3)=50.09x(1)(3)=57.48 k=3x∧(1)(4)=81.46x(1)(4)=80.41k=4x∧(1)(5)=107.14x(1)(5)=107.22 k=5x∧(1)(6)=135.37x(1)(6)=163.54k=6x∧(1)(7)=166.46x(1)(7)=166.46表2 还原检验Tab.2 Reduction test序号计算值原始值残差相对误差/%k=1 19.34 19.18 -0.16 0.83 k=2 21.26 20.80 -0.46 2.20 k=3 23.38 22.93 -0.45 1.96 k=4 25.71 26.81 1.10 4.10 k=5 28.27 29.31 1.04 3.55 k=6 31.08 29.93 -1.15 3.846)预测该矿12月份的瓦斯涌出量,根据下列模型可计算出当k=6时当k=7时根据得:这表示该矿12月份的瓦斯涌出量为34.18 m3/t.3 结论1)应用灰色系统理论建立的GM(1,1)预测模型,适合矿井瓦斯涌出量的灰色预测,实际瓦斯涌出量与预测瓦斯涌出量的误差很小,为实际瓦斯监测提供可靠的依据. 2)在运用灰色理论建立瓦斯涌出量预测GM(1,1)模型时,要不断根据实测的新数据,建立新的GM(1,1)模型,提高预测精度.3)利用灰色系统理论进行瓦斯涌出量预测,具有所需样本少、运算量小、收集资料比较容易,对瓦斯涌出量的预测结果准确可靠,能够反映矿井瓦斯涌出量的发展趋势.参考文献:【相关文献】[1]张淑玲,崔洪庆,刘国兴,等.灰色关联理论在矿井瓦斯涌出灾害预测中的应用[J].煤炭技术,2008,27(3):67-69.CHEN Shuling,CUI Hongqing,LIU Guoxing,et al.The application of the grey relation theory in the hazard prediction of mine gas emission[J].Coal Technology,2008,27(3):67-69.[2]孙强,张振文.基于灰色理论的矿井瓦斯涌出量预测模型研究[J].煤炭技术,2009,28(9):94-96.SUN Qiang,ZHANG Zhenwen.Based on the grey theory of mine gas emission prediction model research[J].Coal Technology,2009,28(9):94-96.[3]王文才,李刚,张世明,等.基于灰色理论的矿井瓦斯涌出量预测研究[J].煤矿开采,2011,16(3):56-58.WANG Wencai,LI Gang,ZHANG Shiming,et al.Based on the grey theory of mine gas emission prediction research[J].Coal Mining,2011,16(3):56-58.[4]肖鹏,李树刚,宋莹,等.瓦斯涌出量的灰色建模及其预测[J].采矿与安全工程学报,2009,26(3):318-321.XIAO Peng,LI Shugang,SONG Ying,et al.Gas emission amount of grey modeling and its prediction[J].Mining and Safety Engineering Journal,2009,26(3):318-321.[5]张瑞林,刘晓,郑立军.基于灰色动态建模的瓦斯涌出量预测方法研究[J].中国矿业,2006,15(12):110-112.ZHANG Ruilin,LIU Xiao,ZHENG Lijun.Based on the grey dynamic modeling method to forecast the gas emission[J].China Mining,2006,15(12):110-112. [6]吕光华.矿业灰色系统[M].北京.煤炭工业出版社.1993.LV Guanghua.Mining grey system[M].Beijing:Coal Industry Press,1993.[7]伍爱友,田云丽,宋译,等.灰色系统理论在矿井瓦斯涌出量预测中的应用[J].煤炭学报,2005,30(5):589-592.WU Aiyou,TIAN Yunli,SONG Yi,et al.The application of the grey system theory in the mine gas emission prediction[J].Journal of China Coal Society,2005,30(5):589-592.[8]徐君.基于GM(1,1)模型的矿井瓦斯涌出量预测研究[J].矿业研究与开发,2005,25(3):87-88.XU Jun.Based on the GM(1,1)model of the mine gas emission prediction research[J].Mining Research and Development,2005,25(3):87-88.。
对煤炭业年死亡人数和百万吨死亡率的模拟预测研究
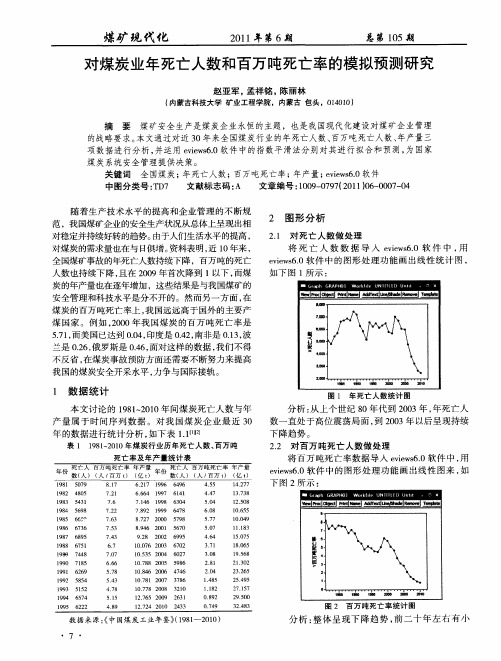
死 亡 率 及 年 产 量 统 计 表
… 、
图 1 年 死 亡 人 数 统 计 图
分 析 : 上 个 世纪 8 代 到 20 从 0年 03年 , 死亡 人 年 数 一 直处 于高 位震 荡 局 面 , 20 到 0 3年 以后 呈 现 持续 下 降趋 势 。 22 对 百 万 吨死 亡 人数 做 处理 . 将 百万 吨死 亡 率数 据 导 入 eiw60软 件 中 , v s. e 用 ei s. 件 中 的 图形 处 理 功 能 画 出线 性 图 来 , v w60软 e 如
下 图 2所示 :
…
死 亡人 百万 吨死亡率 年产 量 死亡人 百 万吨死亡 率 年 产量 数( ) ( / 人 人 百万 t ( t … 数( ) ( / ) 亿 ) 人 人 百万 t ( t ) 亿 )
图 2 百 万 吨 死 亡 率统 计 图
数 据来 源 : 中国煤 炭工业年鉴》 1 8— 2 1 《 (9 1 0 0)
2 图形 分 析
21 对 死 亡 人数 做 处 理 .
将 死 亡 人 数 数 据 导 入 ei s. 件 中 , v w6 e 0软 用 ei s. 件 中 的 图形 处 理 功 能 画 出线 性 统 计 图 , ve 60软 w
如下图 1 所示 :
l 数据统计
本 文 讨论 的 18 00年 间煤炭 死 亡 人数 与 年 9 12 1 产 量 属 于 时 间 序 列 数 据 。对 我 国 煤 炭 企 业 最 近 3 0 年 的数 据进 行 统计 分 析 , 势 , 二十年左 右有小 前
7 ・
煤矿 现 代化
21 年第6 01 期
应用灰色系统理论进行煤矿百万吨死亡率预测

应用灰色系统理论进行煤矿百万吨死亡率预测摘要:本文从煤矿百万吨死亡率的统计结果来评估煤矿产业的安全性能,在此基础上,通过灰色预测系统理论来建立GM(1,1)煤矿百万吨死亡率预测模型,使用Matlab 编程实现灰色预测算法,大大减少了计算量和出错几率,提高预测质量。
并深入分析该模型的基本原理,以及合成运用。
对2003年―2013年的煤矿百万吨死亡率进行实例与预测研究,以此论证,以灰色系统为理论建立的煤矿百万吨死亡率预测模型的有效性。
关键词:GM(1,1)模型;灰色预测;煤矿;百万吨死亡率;Matlab引言中国是一个煤炭生产大国,也是煤炭消费大国。
当前,在一次性能源的消费中,煤炭的消费约占70%,从当今的中国能源消费状况[2]看,在今后很长的时间内,煤炭将继续充当非常重要的角色,是我国的经济和社会的发展过程中的助推器。
在我国,绝大多数煤矿的开采都是地下作业,由于煤矿安全生产受多方面因素的影响和制约,事故频发、伤亡惨重、经济损失巨大的状况尚未得到根本好转,每年煤矿安全生产事故死亡人数一直位于各行业之首,安全生产形势十分严峻。
这不但严重制约了煤炭工业的持续发展,而且造成了企业及国家财产和人民生命的巨大损失。
但由于煤矿系统的复杂性和关联性,预测技术还不尽成熟,甚至由于在数据运算的误差或模型适用性等原因,出现预测精度较低甚至偏离其原有的发展方向。
仍需在原有基础上探究新方法,解决许多限制。
因此,对我国煤矿百万吨死亡率进行统计分析,并对其发展规律进行了预测具有重要的意义。
一来可以为国家制定有关煤矿安全生产的政策提供理论依据,对生产过程中的安全性指标提供参考的标准;二来有利于对全国的各个地区的煤矿安全系统有一个全面整体的认知,从而通过采取相应的方法和措施,提高我国煤矿安全生产的安全指数,促进煤矿安全生产的持续发展。
一. 煤矿百万吨死亡率预测模型的建立1.1 模型建立的理论基础-灰色系统理论传统的系统理论大多研究那些信息比较充分的系统,对一些信息比较贫乏的系统,利用黑箱方法也取得了较为成功的经验。
优化GM_1_1_预测模型对煤炭产量的预测研究(精)

优化GM_1_1_预测模型对煤炭产量的预测研究表 1。
记残差为εk= xk( 1)-^x( 1)k,残差序列εk与原始序列x( 0)的方差分别为 s1和 s2,则后验差比值为:c = s1/ s2. ( 9)误差概率P 为:P = P{ | e( 0)( k) - e | < 0. 6745s2} . ( 10)表 1 精度检验参照表精度等级好( 一级)合格( 二级)勉强( 三级)不合格( 四级)后验差比值 c ≤0. 35 0. 35 ~0. 50 0.50 ~0.65 >0. 65P 值≥0. 95 0. 8 ~0. 95 0. 7 ~ 0. 8 < 0. 72 优化 GM( 1,1) 模型的原理与求解过程前面背景值的求法实际上就是数值积分中的梯形公式,而梯形公式的误差较大,精度低,为此提出了基于连分式理论[5]的有理插值与广义梯形公式来重构背景值。
2. 1 连分式插值原理设{ an} ,{ bn} 为 2 个实数数列,称形如式( 11)的分式为连分式,记作b0= k∞1( an/ bn) 。
b0+a1b1+a2b2+a3b3+a4b4+ …. ( 11)对于给定的插值点( xi,yi) ,yi= f( xi) ,i = 0,1…,其中 x0,x1,…xm + n互异。
函数 f( x) 在 xi,yi处的反商差:φ( xi,xj) =xj- xiyj- yi.( i ≠ j) ( 12)函数 f( x) 在 xi,yi处的 k 阶反商差:φ( x0,x1,…,xk -1,xk) =xk- xk -1φ( x0,x1,…,xk -2,xk) -φ( x0,x1,…,xk -2,xk -1), ( 13)Rn( x) = φ( x0) +x -x0φ( x0,x1) +x - x1φ( x0,x1,…,xn -1) +x - xn -1φ( x0,x1,…,xn -1,xn), ( 14)式中,φ = φ( x0,x1,…,xn) ≠0,∞,k =0,1,…,n,为 f( x) 在 x0,x1,…,xk处的反商差,则有Rn( x) = f( xi) ,i = 0,1,…,n . ( 15)即函数 Rn( x) 为函数 f( xi) 在点 x0,x1,…,xk处的有理插值函数。
改进欧拉法的GM(1,1)模型及其在非煤矿山事故预测中的应用

ma k e t h e s t a t i s t i c a l j u d g e m e n t t o t h e t r e n d o f n o n — c o a l mi n e a c c i d e n t s , a n d a c c u r a t e l y p r e d i c t s o me r e c e n t d a t a ,
Ab s t r a c t : B a s e d o n t h e n u me i r c a l a l g o i r t h m t o s o ] v e t h e d i f f e r e n t i a l e q u a t i o n s o f t h e G M( 1 , 1 )m o d e l , a G M( 1 ,
文章编号 : 1 6 7 3—1 9 3 X( 2 0 1 3 ) 一0 8— 0 1 8 8— 0 5
改进 欧拉 法 的 G M( 1 , 1 ) 模 型及 其在 非煤 矿 山 事 故 预 测 中的应 用
李 明洋 , 姜福川 , 陈思帆
( 昆明理工 大学 国土资源工 程学院 , 云南 昆明 6 5 0 0 9 3 ) 摘 要: 通过对 G M( 1 , 1 ) 模 型中的微分方程 使用 数值 算法求解 , 提 出一种改进欧 拉算法 G M( 1 , 1 )
第 9卷 第 8期 2 0 1 3年 8月
中 国 安 全 生 产 科 学 技 术
J o u r n a l o f S a f e t y S c i e n c e a n d T e c h n o l o g y
Vo 1 . 9 No . 8 Au g .2 01 3
基于GM(1,1)模型的沉降预测及应用

·72·文章编号:2095-6835(2023)15-0072-04基于GM(1,1)模型的沉降预测及应用陶舜禹(华北理工大学,河北唐山063200)摘要:地表沉降的防治已经成为近年来人们研究的重点问题。
沉降灾害严重地破坏了人们的生活环境,限制了城市的发展速度。
选用GM (1,1)模型对某市沉降区域内的6个特征点进行预测。
结果表明,GM (1,1)模型可以作为基于时间序列的预测模型在沉降的预防治理中应用。
关键词:沉降预测模型;地表沉降;GM (1,1);模型精度中图分类号:TD327文献标志码:ADOI :10.15913/ki.kjycx.2023.15.021地表沉降是造成自然灾害的原因之一,严重地威胁到的人们的生活和生命财产安全,制约了城市发展。
当沉降速率到达一定程度时,城市的地下建设也会受到严重的威胁和破坏[1]。
沉降的防治工作已成为城市建设的重点研究问题。
灰色系统中被应用最广泛的模型就是GM (1,1)模型,GM (1,1)模型通过对原始数据的累加,并采用累加后的数据进行模型计算,对计算得出的模型值进行累减计算后得到预测值[2-3]。
本文采用GM (1,1)模型针对南湖地区地表沉降观测数据进行预测,并结合采用均方根误差(Root Mean Square Rrror ,RMSE )、平均绝对百分比误差(Mean Absolute Percent Error ,MAPE )2个指标对模型精度进行评估[4]。
1GM(1,1)模型生成设原始数据列为:X (0)={x (0)(1),x (0)(2),…,x (0)(n )}将原始数据累加后得到的数据列为:X (1)={x (1)(1),x (1)(2),…,x (1)(n )}其中:n k i x k x ki ,,,),()()( 211(0)1==∑=灰色GM (1,1)模型的白化微分方程为:b aX tX =+)1()1(d d 通过对方程离散化处理得到灰色GM (1,1)模型为:X (0)(k )+aZ (1)(k )=b(1)其中,Z (1)为X (1)的紧邻均值数据列,即:[])()()(k x k x k Z )0()0()1(121+-=通过最小二乘法求解出的灰参数a 、b ,即:[]YB B B b a a ˆΤ1-ΤΤ)(==其中:Y =[x (0)(2)x (0)(3)…x (0)(n )]T(2)⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---=11312111)()()()()()(n Z Z Z B 将参数a 、b 代入式(1)中得到模型的时间响应函数为:a b e a b x k x ˆak +⎥⎦⎤⎢⎣⎡-=+-)()()()(1111将式(2)的计算结果递减得到模型的预测值为:)()()()()()(k x ˆk x ˆk x ˆ11011-+=+2算例分析以水准数据的测量结果作为模型输入数据,选取了唐山南湖地区测量范围内的沉降不稳定区域的监测点BM66,主要分布在天鹅湖动物园区域内和薰衣草庄园—爱尚庄园,属于基本稳定区域的监测点BM60、BM61、BM63、BM68,以及稳定区域内的监测点BM57。
改进GM(1,1)预测模型对我国煤炭消费需求的预测分析

改进GM(1,1)预测模型对我国煤炭消费需求的预测分析周晓明;罗文柯;李润球【期刊名称】《矿业工程研究》【年(卷),期】2010(025)002【摘要】为了预测未来煤炭消费需求状况,利用1998-2008年度我国煤炭消费需求的历史数据直接作为传统GM(1,1)及其残差模型的原始序列,通过生成处理后所得模型分别为勉强合格(三级)和合格(二级)等级,而通过对原始数据取自然对数为基础,并进行二阶弱化处理后所得的改进GM(1,1)模型及其残差GM(1,1)模型,经过点对点的残差检验发现,改进GM(1,1)模型及其残差GM(1,1)模型均提升至好的预测模型(一级)等级,其预测精度较高.用其预测未来3年的煤炭消费需求总量继续呈增长趋势,说明煤炭在未来短期内的主导地位没有改变.因此,国家和各级政府应加大对煤炭行业的资金投入与政策支持的力度,以保障我国经济持续稳定发展.【总页数】4页(P65-68)【作者】周晓明;罗文柯;李润球【作者单位】湖南省白山坪矿业公司,湖南,耒阳,421828;煤矿安全开采技术湖南省重点实验室,湖南,湘潭,411201;湖南科技大学能源与安全工程学院,湖南,湘潭,411201;煤矿安全开采技术湖南省重点实验室,湖南,湘潭,411201;湖南科技大学能源与安全工程学院,湖南,湘潭,411201【正文语种】中文【中图分类】X936;TD173【相关文献】1.“十二五”期间我国中药产业发展趋势预测分析--基于灰色GM(1,1)预测模型 [J], 肖瑜;刘永军2.我国农村用电量预测分析——基于最小二乘法的改进GM(1,1)模型 [J], 姚飞;王波;顾继发3.我国居民消费价格指数的预测分析--基于残差修正的改进GM(1,1)模型 [J], 卜宾宾;蒋艳;吴天魁4.我国居民消费价格指数的预测分析——基于残差修正的改进GM(1,1)模型 [J], 卜宾宾;蒋艳;吴天魁;5.我国农村用电量预测分析——基于最小二乘法的改进GM(1,1)模型 [J], 姚飞;王波;顾继发因版权原因,仅展示原文概要,查看原文内容请购买。
基于GM(1,1)模型的矿山开采沉陷预测

基于GM(1,1)模型的矿山开采沉陷预测李新新;沈震【摘要】矿山开采沉陷的因素具有复杂性,但可以利用预测理论加以预测.在分析矿山开采沉陷系统灰色因素的基础之上,提出了将开采沉陷下沉量作为矿山开采沉陷系统的特征量处理,运用灰色理论对开采沉陷下沉量进行预测.灰色理论运用预测对象自身的时间序列,而与预测对象相关联的其他因素没有参与运算和建模,因此运用起来比较简单使用,不用考虑其他复杂的要素.灰色理论在矿山开采沉陷预测中发挥了重要的作用.【期刊名称】《北京测绘》【年(卷),期】2015(000)006【总页数】3页(P62-64)【关键词】矿山开采沉陷;灰色理论;预测【作者】李新新;沈震【作者单位】安徽理工大学,安徽淮南232000;安徽理工大学,安徽淮南232000【正文语种】中文【中图分类】P2581 引言随着我国煤炭开采规模的不断扩大,开采强度的不断提高,由于采矿而引起的地面沉陷对地面建筑物、铁路以及公路等的损坏不断加大,这既破坏了当地的环境,也给人民的生活和安全造成重大的威胁。
因此对矿山开采的沉陷进行预测,不仅对建筑物和生态环境的保护有重大意义,而且可以指导矿山的开采。
所以,基于以上的背景,笔者以某工作面为例,通过此工作面上观测点的沉降数据,运用灰色预测模型对矿山开采沉陷进行预测。
2 灰色预测原理灰色系统就是指既含有已知信息又含有未知的或非确知信息的系统,灰色系统理论主要研究系统模型不明确、行为信息不完全、运行机制不清楚这类系统的建模、预测、决策和控制等问题,它就是利用灰色动态GM模型(Grey Model)对系统的行为特征量或者模型指标发展变化到未来一定时刻现的数值进行预测,它只是运用预测对象自身的时间序列,而与预测对象相关联的其他因素没有参与运算和建模[1]。
如果把矿山开采的沉陷作为一个系统来看,这个系统中存在着一些确定因素即白色信息,也存在着一些不确定因素即灰色信息,如地质因素、水文因素。
基于GM(1,1)模型的恶性肿瘤死亡率的预测

基于GM(1,1)模型的恶性肿瘤死亡率的预测马尉瑶【摘要】目的:了解辽阳市辽阳县恶性肿瘤死亡情况,介绍GM(1,1)模型预测辽阳市辽阳县恶性肿瘤死亡率。
方法收集辽阳市辽阳县2008-2015年恶性肿瘤死亡数据,并应用GM(1,1)模型对其进行动态预测。
结果 GM(1,1)预测模型为x^(1)k+1=(x1(0)-μ/α)e-αk+μ/α=6315.220.023Ik-6177.06,预测精度优,预测2016年和2017年辽阳市辽阳县恶性肿瘤死亡率分别为173.50/10万和177.55/10万。
结论 GM(1,1)模型能够用于恶性肿瘤死亡率预测。
%Objective To comprehend the mortality of malignant tumors in Liaoyang County and to predict it with GM(1,1) model. Methods The data of the mortality of malignant tumors in Liaoyang County from 2008 to 2015 were col-lected and predicted with GM(1,1) model. Results It showed the GM (1,1) prediction model was x^(1)k+1=(x1(0)-μ/α)e-αk+μ/α=6 315.220.023Ik-6 177.06, and the model was advanced by the precision-test. The predictive values of the mortality of ma-lignant tumors were 173.50/100 000 and 177.55/100 000 respectively during 2016 and 2017. Conclusion The GM(1,1) model can be applied to predict the mortality of malignant tumors.【期刊名称】《海南医学》【年(卷),期】2017(028)001【总页数】2页(P155-156)【关键词】恶性肿瘤;GM(1,1);模型;预测;死亡率【作者】马尉瑶【作者单位】辽阳市疾病预防控制中心,辽宁辽阳 111000【正文语种】中文【中图分类】R730.720世纪70~90年代我国恶性肿瘤死亡率呈上升趋势,死亡率上升了29.42%,年龄调整死亡率上升了11.56%[1]。
优化GM(1,1)预测模型对煤炭产量的预测研究

济社 会有 重 要 的意义 。
k =1 2 … , ,,
造方 法 是 影 响其 精 度 和 适 应 性 的 关 键 因素 j 。为 了提高灰 色 预测 的 精度 , 用基 于 连 分式 理 论 的有 采
‘ n ( )
z ( k+1 = ( )
厶
( )+ k
( k+1 ), )
() 5
理插值构造背景值 , 建立了 G ( ,) M 1 1 煤炭产量预测
— i一 十0 [
C
+ 0 ( ) = / [ 1 /
,
,
,
( 1 )
式 中 , 、/为待 辨识参 数 , O / L , 序列 ¨ 为对原 始数 列 的 ’
一
已广 泛地 应用 于 国 民经济 的各 个领 域 。特别 是 在显 著不 确定 性 和缺 乏数 据信 息 的领域 得 到 了成 功 的应 用 。灰色 预测 理论 是灰 色 系统 的重要 组 成 部分 ,利
地方 经济 的发展 密切 相关 。 灰色 系 统理论 在 经过 了 2 0多年 的发 展后 , 现
‘ ‘ : { 。( ) ‘ ( ) … , 。( } 。 ‘ 1 , 。 2 , ‘ ) . ’ 生成一 阶累加 生成模 块 ¨ ( ) ’k : ( )= { ¨, ( ) … , ’n }. k ‘ 2 , ( ) ’ ¨ ( ) 以建立 下述 微分 白化 方程 : ’k 可
() 9
基于GM(1,1)的灰色系统理论对煤矿顶板死亡人数预测

基于GM(1,1)的灰色系统理论对煤矿顶板死亡人数预测管洪;刘超;姜佩文【摘要】从2004年起国家强制要求高瓦斯矿井对煤层瓦斯进行先抽后采,低瓦斯矿井也安装了瓦斯监测监控系统后,由瓦斯爆炸、矿井突水、火灾引起的特大型人员死亡事故大大降低,因此由顶板引起的人员死亡事故就进入公众的视野成为公众关注的焦点。
以2003—2010年我国煤矿顶板造成的人员死亡数据为初始数据,建立GM(1,1)模型对2011年及未来两年我国由煤矿顶板引起的人员亡人数进行预测。
【期刊名称】《甘肃科技》【年(卷),期】2015(000)007【总页数】3页(P8-10)【关键词】灰色系统理论;矿难死亡人数;预测GM(1,1)【作者】管洪;刘超;姜佩文【作者单位】黔西南州安全生产监督管理局,贵州黔西南 562400;贵州建设职业技术学院,贵州贵阳 551400;贵州建设职业技术学院,贵州贵阳 551400【正文语种】中文【中图分类】N941.5中国煤炭资源丰富,我国目前已探明的能源储量显示煤炭占94%,这也就决定了我国仍会将煤炭作为第一能源。
因而由煤炭开采引起的人员伤亡事故就成为了公众关注的焦点。
从2004年起国家强制要求高瓦斯矿井对煤层瓦斯进行先抽后采,低瓦斯矿井也安装了瓦斯监测监控系统后,由瓦斯爆炸、矿井突水、火灾等引起的特大型人员死亡事故大大降低,因此由顶板引起的人员死亡事故就进入公众的视野成为公众关注的焦点。
以2003-2010年我国煤矿顶板造成的人员死亡数据为为初始数据,通过建立GM(1,1)模型对2011年及未来两年我国由煤矿顶板引起的人员亡人数进行预测。
1 GM(1,1)模型的基本原理与分析过程灰色理论认为一切随机量都是在一定范围内、一定时间段上变化的灰色量及灰色过程。
数据处理不去寻找其统计规律和概率分布,而是对原始数据作一定处理后,使其成为有规律的时间序列数据,在此基础上建立数学模型。
灰色系统理论的实质是将无规律的原始数据进行累加生成,得到规律性较强的生成数列再重新建模;由生成模型得到的数据通过累加生成的逆运算——累减生成得到还原模型,由还原模型作为预测模型。
煤矿安全事故预测报告

(0)
(0) (k ) (k ) (0) (k )
0.0000 -0.0515 0.0644 -0.0134 0.1110 0.0202 -0.0778 -0.0837 -0.1492 -0.0954
(0)
0.5
1.0000 0.3952 0.3676 0.7906 0.3334 0.7914 0.5747 0.6121 0.5397 0.6861
对其进行一次累加生成,得其1-AGO序列为:
X(1) ={5.07 , 9.706 , 13.876 , 16.957 , 19.768 , 21.809 , 23.294 , 24.476,25.368,26.1 17}
北京科技大学
5/21
建立GM(1,1)模型
X(1)的紧邻均值生成序列: Z(1)={7.3880 , 11.7910 , 15.4165 , 18.3625 , 20.7885 , 22.5500 , 23.8850,24.9220,25.7425} 以最小二乘法估计参数a和b
起始年 2010 2009 2008 合计 起始状态 E1 E1 E1 表4 灰色马尔可夫预测表 E1 转移步数 1 3/4 2 2/4 3 1/4 3/2 E2 0 0 0 0 E3 0 0 0 0
根据上表的状态转移概率可知,2011年处于E1状态的可能性最大,则 2011年预测值为0.657*(0.85+0.95)/2=0.591
北京科技大学
3/21
预测步骤与计算过程
累加生成—邻近生成
建立GM(1,1)模型
计算参数,得出模型公式
模型的精度检验
预测结果
北京科技大学
4/21
建立GM(1,1)模型
基于GMM模型的煤矿顶板事故致死人数预测

基于GMM模型的煤矿顶板事故致死人数预测李闯;袁梅;王玉丽;许石青;杨萌萌【摘要】为了解决目前常用预测模型对随机波动性较大数据预测精度偏低的问题,文章在灰色预测GM(1,1)的基础上引入马尔可夫状态转移矩阵,建立了灰色马尔可夫预测模型(GMM),并将该法运用到煤矿顶板致死人数的预测中.经计算GMM模型的预测平均相对误差为1.181%,最大相对误差3.426%,与GM(1,1)法相比,后者精度分别提高了21倍和13倍.【期刊名称】《工业安全与环保》【年(卷),期】2017(043)008【总页数】4页(P9-12)【关键词】灰色系统;马尔可夫预测;转移概率;顶板事故【作者】李闯;袁梅;王玉丽;许石青;杨萌萌【作者单位】贵州大学矿业学院贵阳 550025;贵州大学矿业学院贵阳 550025;贵州省非金属矿产资源综合利用重点实验室贵阳 550025;贵州省优势矿产资源高效利用工程实验室贵阳 550025;复杂地质矿山开采安全技术工程中心贵阳 550025;贵州大学矿业学院贵阳 550025;贵州大学矿业学院贵阳 550025;贵州省非金属矿产资源综合利用重点实验室贵阳 550025;贵州省优势矿产资源高效利用工程实验室贵阳 550025;复杂地质矿山开采安全技术工程中心贵阳 550025;贵州大学矿业学院贵阳 550025【正文语种】中文近年来在我国调整产业机构、转变经济发展方式的大背景下,煤矿行业发生着巨大的变革。
由原来只注重产量的高能耗、高污染、高死亡率的发展模式逐步向高安全、低能耗、低排放的绿色发展的模式转变。
得益于此煤矿行业的煤矿事故起数和事故造成的死亡人数呈现连年递减的良好态势。
但是目前我国的煤矿百万吨产量死亡率较西方发达国家仍有较大差距,瓦斯事故、顶板事故、水灾和火灾等事故仍是制约煤矿安全生产的重要因素。
为了更好地掌握煤矿安全事故的发生规律,了解煤矿的安全状况及其安全事故发生发展趋势,制定合理的煤矿生产安全事故预防措施,进行合理、有效的事故预测具有十分重要的意义。
GM1,1)模型在我国亿元GDP死亡率预测中的应用

GM(1,1)模型在我国亿元GDP死亡率预测中的应用周焕明黄浪(中钢集团武汉安全环保研究院)摘要:文章在统计2001~2012年全国安全状况参数(事故起数、死亡人数、亿元GDP死亡率、十万人死亡率)的基础上,通过相关性分析,选取亿元GDP死亡率作为所研究的安全状况参数,应用灰色系统预测理论,引入光滑性检验方法,建立亿元GDP死亡率的GM(1,1)动态预测模型,结果显示预测模型具有良好的拟合度,可以用于预测,因此也对2013、2014、2015年的相关安全状况参数(亿元GDP死亡率)进行了预测。
关键词:灰色系统预测;GM(1,1);光滑性检验;亿元GDP死亡率随着全国经济的发展,国民生活水平的提高,人们越来越关注安全与健康。
近几年来,我国安全状况虽然有所好转,但是形式依然不容乐观,和西方发达国家差距明显,且重大、特大事故时有发生。
因此,为了为相关机构的安全决策提供参考依据,对安全事故状态参数,比如事故起数、死亡人数、亿元GDP死亡率、十万人死亡率进行分析预测显得尤为重要。
如果把全国的安全事故作为一个系统,则该系统中有的信息是已知的、确定的,有的信息是未知的、不确定的,具有明显的灰色特征,可以利用灰色系统理论对全国安全状况参数进行预测分析[1],本文采用相关系数法先确定亿元GDP死亡率作为所研究的全国安全状况参数,然后用GM(1,1)动态预测模型,对亿元GDP死亡率进行建模和预测。
1 灰色系统预测模型GM(1,1)1.1灰色系统预测模型的基本原理灰色系统预测是通过鉴别系统因素之间发展趋势的相异程度,把已有的原始数据序列比作随时间变化的不确定量或不确定过程,进行关联度分析,并对观测到的反映预测对象特征的一系列数值进行生成处理,建立相应的微分方程模型,来预测事物未来发展趋势的状况[2]。
GM(1,1)是在灰色系统预测理论中经常用到的单变量数列预测模型,这个模型应用原始非负数据数列,经过累加运算生成另一个数据序列,通过生成数列的矩阵变换,使用最小二乘法,构造白化微分方程,解此方程得到模型计算值,再与原始数据进行比较,得到残差,进行模型精度检验,符合相关标准则可以适用于建模预测。
基于GM(1,1)-Markov 模型的火灾事故预测

科技与创新┃Science and Technology&Innovation ·96·2022年第14期文章编号:2095-6835(2022)14-0096-03基于GM(1,1)-Markov模型的火灾事故预测童乐1,赵玲1,2(1.江西理工大学资源与环境工程学院,江西赣州341000;2.江西省矿业工程重点实验室,江西赣州341000)摘要:根据火灾事故的灰色特征及随机性等特点,建立了GM(1,1)-Markov火灾事故预测模型。
应用该模型对火灾死亡人数进行预测,结果表明所建立的GM(1,1)-Markov火灾事故预测模型能较好地反映死亡人数的变化趋势及波动性特点,预测结果的相对误差的绝对平均值为1.9%,其精度高于GM(1,1)模型。
预测结果可以作为制定安全目标的依据,为消防安全管理与决策提供科学的指导。
关键词:火灾事故;GM(1,1)-Markov模型;状态转移概率;相对误差中图分类号:X928.7文献标志码:A DOI:10.15913/ki.kjycx.2022.14.031中国火灾事故具有发生频率高、时空跨度大、造成的人员伤亡及经济损失大等特点,严重影响着经济发展及社会稳定。
近年来虽然火灾事故数据整体呈下降趋势,但安全形势依然严峻,2020年中国发生火灾25.2万起,死亡1183人,直接财产损失达40.09亿元。
对火灾事故进行科学准确的预测与分析可以避免计划的盲目性,为消防安全管理提供重要依据。
本文建立了GM(1,1)-Markov火灾预测模型,并对火灾死亡人数进行了预测。
预测结果可以为消防安全投入、确定安全目标等提供科学依据,促进安全管理水平的提高。
1火灾事故预测方法事故预测方法主要有滑动平均法、指数滑动平均法、回归分析法、灰色预测法、马尔柯夫链预测法等。
以GM(1,1)模型为代表的灰色预测模型得到了广泛的应用,该模型的优势在于通过一系列数据生成方法将无规律或规律不强的一组原始数据序列变得具有明显的规律性,解决了数学界一直认为不能解决的微积分方程建模问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
G i n 5 0 5 hn ) uy g 50 2 ,C ia a
Abta t ya i G 11)moe s stu o h et—a e lo o s i mie y src: d n m c M(, A d li e p f t d a rt p rmiin tn n ns b r e h e l
u i g t e g a y t m h o y r y p e it n f r t e d ah r t e l o o s i n s h s sn h r y s se t e r ,a g a r d c i h e t - a e p r mi in tn n mi e a o o l b e c mp ee i r c n y a sa d h e a c r c o p e it n s a i r l b e T e e u t e n o lt d n e e t e r ,n t c u a y f r d ci i b s o c ei l . h r s l a i d c t s t a h d l i c re t a d h s c r i l r c ia au ,t e r s l f p e it n i n i ae h t t e mo e s o r c n a e t ny p a t l v e h e u t o r d ci s a c l s o s i n i c a d r l l ,t r v d n a c r t h o y f r s ft n g me t i n s ce t i n ei e o p o i e a c u a e t e r o a ey ma a e n n mi e . f b a
贵阳 5 0 2) 5 0 5
摘 要: 应用灰 色系统理论 , 建立 了煤矿百 万吨死亡率的 G 11 M(, 动态预测模型 , ) 对我 国近几年 的煤矿百万 吨死亡 率进行灰色预测 , 预测精度基本可靠。 结果表 明: 该模型的建立是正确 的, 并具有一定的实用价值 , 使预测结果科学 可靠 , 为煤矿的安全管理提供 了准确 的理论依据。 关键词:M(, 模型 ;灰色预测 ;百万 吨死亡率 G 11) 中图分类号:D 6 T 7 文献标识码: A 文章编号: 0 — 7 5 2 1 0 ~ 0 10 1 8 8 2 (0 0) 0 8 — 3 0 4
Ke o d : M(, m d l ry pe i i ; et—a e lo o s y w r sG 11) o e; e rdc o d a rt p rmiin tn g tn h e l
0 前 言
居第二。由于煤矿事故多 , 死亡人数多 , 造成了我国
1 灰色预测模 型 G 1 的建立 M(, 1)
S u y o P e i t g De t t e i i n To s td f r d c i a h Ra e P r M l o n n l
i ie a e n GM n M n s B sd o
( , 1 )M o e 1 dl
JANG h n v I C u — u U He g y I C e — u,L h n h i ,S n — u
( .C l g f Miig G i o n es y 1 ol e o n , uz u U i ri ,G i n 5 0 3 C ia .F c l f L n eo re E g e r g e n h v t uy g 5 0 0 hn ;2 a ut o a d R suc n i ei . a y n n
他 国家 。 目前 , 国加 强 了对煤 炭行 业 的科 技 投入 我
ห้องสมุดไป่ตู้
设 卿 为非负序列 ,
:
和安全资金投入 , 开展 了各种安全技术培训和安全 宣传活动 , 加强了安全意识 的教育 , 使我国的百万 吨死亡率保持了连续 的下降, 由于煤矿开采 的复 但 杂性 、 特殊性 , 国煤矿的安全事故还未得到根本 全 性的好转 , 致使煤矿事故给员工和国家带来 了巨大 的损失。因此 , 对煤矿事故进行科学的分析和预测 , G 1 的动态预测模型对我国未来 的百万 吨死 M(, 1)
我 国煤炭 行业 的安全 事故 仅次 于 交通 事故 , 位 11 GM (, 模 型 . 1 1)
G 1 模型是 目前应用最广泛 的灰色 系统 M(, 1) 煤矿的百万吨死亡率一直居高不下 , 与世界其他主 预测模 型 。符 号 G 1 的含 义是 :(ry 色 , M(, 1) Gge) 灰 M 要产煤 国家相 比, 我国的百万吨死亡率远远高于其 (oe模型,11分别表示 1 m d1 ) ( ,) 阶方程、 个变量 。 1
第 2 卷第 4 9 期 2 1 年4 0 0 期
煤
炭
技
术
Co lT c n lg a e h oo y
V0.9No0 1 . .4 2 Ap l 01 i 2 r, 0
基于 G 1 模型 的煤矿 百万吨死亡率 的预测研究 M(, 1)
江成玉 ,李春辉 ,苏恒瑜。
(.贵州大学 矿业学院, 阳 5 0 0 ;2 1 贵 50 3 .昆明理工大学 国土资源工程学 院,昆明 6 0 9 ;3 50 3 .贵州省煤矿设计研究院 ,
K n n i e i f S in e a d T c n l g ,Ku mi g 6 0 9 C ia .Guz o a n sg n t u e u mig Un v r t o ce c n e h o o y s y n n 5 0 3 h n ;3 ih u Co l Mi e De i n I si t , t
