6.2平面直角坐标系练习纸
专题训练八--平面直角坐标系(共20张)

数学八年级上浙教版6.2平面直角坐标系同步练习7

6.2 平面直角坐标系同步练习一、选择题1、如图是在方格纸上画出的小旗图案,假设用(0,0)表示A点,(0,4)表示B点,那么C点的位置可表示为( )A、(0,3)B、(2,3)C、(3,2)D、(3,0)BCA图12.点A〔a,b〕在第四象限,那么点B〔b,a〕在〔〕 A.第一象限 B.第二象限 C.第三象限3.点P〔x,y〕在第四象限,且│x│=3,│y│=5,那么点P的坐标是〔〕A.〔-3,5〕 B.〔5,-3〕 C.〔3,-5〕 D.〔-5,3〕4、一个正方形在平面直角坐标系中三个点的坐标为〔-2,-3〕、〔-2,-1〕、〔2,1〕,那么第四个顶点的坐标为 ( )A、〔2,2〕B、〔3,2〕C、〔2,-3〕D、〔2,3〕5、点P〔m+3,m+1〕在x轴上,那么P点坐标为〔〕A.〔0,-2〕 B.〔2,0〕 C.〔4,0〕 D.〔0,-4〕6、点P到x轴距离为3,到y轴的距离为2,那么P点坐标一定为〔〕A、(3,2)B、(2,3)C、(-3,-2)D、以上答案都不对7.点P〔m,1〕在第二象限内,那么点Q〔-m,0〕在〔〕A.x轴正半轴上 B.x轴负半轴上C.y轴正半轴上 D.y轴负半轴上8.过两点A〔3,4〕,B〔-2,4〕作直线AB,那么直线AB( )A、经过原点B、平行于y轴C、平行于x轴D、以上说法都不对9、平行于x轴的直线上的任意两点的坐标之间的关系是( )A、横坐标相等B、纵坐标相等C、横坐标的绝对值相等D、纵坐标的绝对值相等二、填空题〔每题6分,共30分,〕10.点P 在第二象限,它的横坐标与纵坐标的和为1,点P 的坐标是________〔写出符合条件的一个点即可〕. 11.坐标平面内一点A(1,-2)x 轴上任意一点的纵坐标是_______,y 轴上任意一点的纵坐标是_______. 12.点A 〔2,0〕,B 〔-3,0〕,C 〔0,2〕,那么△ABC 的面积=_______. 13、点M 〔-3,2〕到x 轴的距离是_____,到y 轴的距离是______. 14、如图2,根据坐标平面内点的位置,写出以下各点的坐标: A( ),B( ),C( )。
新人教数学 7年级下:同步测控优化训练(6.2坐标方法的简单应用)

精品资料七年级数学复习专用Word精排版,可随意编辑6.2 坐标方法的简单应用5分钟训练(预习类训练,可用于课前)1.如果点A既在x轴的上方,又在y轴的左边,且距离x轴、y轴分别为5、4个单位,那么A 点的坐标为( )A.(5,-4)B.(4,-5)C.(-5,4)D.(-4,5)解析:点A在x轴的上方,则纵坐标大于零;在y轴的左边横坐标小于零.答案:C2.小华若将直角坐标系中的一只猫的图案向左平移了3个单位长度,而猫的形状、大小都不变,则图案上各点的坐标的变化情况为( )A.横坐标加3,纵坐标不变B.纵坐标加3,横坐标不变C.横坐标减小3,纵坐标不变D.纵坐标减小3,横坐标不变解析:若将直角坐标系中的一个图案左、右平移,而图案的形状、大小都不变,只需将原图案的横坐标加或减去一个值,纵坐标不变.答案:C3.若将直角坐标系中的一只鱼的图案向下平移了3个单位长度,而鱼的形状、大小都不变,则图案上各点的坐标的变化情况为( )A.横坐标加3,纵坐标不变B.纵坐标加3,横坐标不变C.横坐标减小3,纵坐标不变D.纵坐标减小3,横坐标不变解析:若将直角坐标系中的一个图案上、下平移,而图案的形状、大小都不变,只需将原图案的纵坐标加或减去一个值,横坐标不变.答案:D4.在平面内,将一个图形沿_____________移动_____________,这样的图形移动称为平移.平移前后两个图形的_____________和_____________不变.答案:某个方向一定的距离形状大小10分钟训练(强化类训练,可用于课中)1.(2010浙江温州模拟,5)点A(1,2)向右平移2个单位得到对应点A′,则点A′的坐标是( )A.(1,4)B.(1,0)C.(-1,2)D.(3,2)解析:向左右平移各点的纵坐标不变,横坐标增加.答案:D2.图6-2-1是画在方格纸上的某行政区简图,(1)地点B,E,H,R的坐标是________________.(2)点(2,4),(5,3),(7,7)所代表的地点分别为点_______________.图6-2-1 图6-2-2解析:根据坐标的定义及画法解题.各点分别向x轴(y轴)作垂线,垂足对应的数字即为横(纵)坐标.答案:(1)B(4,8),E(11,4),H(10,4),R(6,1)(2)M,I,C3.小华、小明、小强、小彬、小亮是很要好的伙伴,正北、正东分别在y轴、x轴的正方向,他们家的位置如图6-2-2所示.比例尺为1∶10 000(1个单位长度,代表10 000 cm). (1)从小华家向____________走____________米到小彬家,再向____________走____________米可到小明家;(2)从小刚家向北走____________米再向____________走____________米到小华家.解析:本题的解题关键是首先要理解坐标的意义及比例尺的计算,如小华与小彬家的距离为5×10 000=50 000(cm)=500(m).答案:(1)东500 北300(2) 200 西4004.(2010湖北十堰模拟,15(1))如图6-2-3,在平面直角坐标系中,请按下列要求分别作出△ABC 变换后的图形(图中每个小正方形的边长为1个单位):向右平移8个单位.图6-2-3解:向右平移8个单位,横坐标加8,各点的纵坐标不变.其图象如下图所示,5.在上一个题目中若△ABC内有一个点M(a,b),平移后其坐标变成什么?解:△ABC向右平移8个单位,点M(a,b)也跟着平移,平移后其坐标变成(a+8,b).6.在直角坐标系中描出下列各点(-1,-2),(0,0),(2,4),并顺次连结各点观察其形状特点,点(1,2)是否在它们的连线上?解:如图所示,是一条直线;点(1,2)在这条直线上.30分钟训练(巩固类训练,可用于课后)1.如果长方形的三个顶点的坐标分别为(-3,2),(3,2),(3,-2),则这个长方形的面积为( )A.32B.24C.6D.8解析:如图所示,长方形的长为6,宽为4,所以面积为24.答案:B2.(1)小明在直角坐标系中画出了一个长方形,他想把这个长方形向右平移3个单位长度,再向上平移2个单位长度,所得图形与原图形相比_______________;(2)若他将此长方形的横坐标都不变,纵坐标变为原来的21,则所得的长方形与原长方形相比_____________.解析:(1)在变化过程中,横坐标分别加3,纵坐标加2即可;(2)若将此长方形的横坐标都不变,纵坐标变为原来的21,则所得的长方形与原长方形相比,图案横向未发生改变,纵向被压缩为原来的一半;答案:(1)横坐标分别加3,纵坐标加2(2)横向未发生改变,纵向压缩为原来的一半3.将一梯形的各顶点的横坐标变为原来的2倍,纵坐标变为原来的21,则所得图形的面积与原来图形的面积_____________.解析:将一梯形的各顶点的横坐标变为原来的2倍,所得的梯形与原梯形相比,图案纵向未发生改变,纵坐标没变,整个图形横向拉长为原来2倍,则面积是原梯形面积的2倍;再将该梯形的各顶点的纵坐标变为原来的21,图案纵向未发生改变,纵向被压缩为原来的一半,即面积又缩小为新梯形的21.综上所述,所得图形的面积与原来图形的面积相等. 答案:相等4.在平面直角坐标系中,(1)将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连结起来形成一个图案.(2)若横坐标保持不变,纵坐标分别加3呢?解:(1)下图虚线即为所求;(2)横坐标保持不变,纵坐标分别加3,相当于把原图案向上平移了3个单位,所以其形状、大小都不发生改变.5.(2010海南模拟,21(2))△ABC 在平面直角坐标系中的位置如图6-2-4所示.将△ABC 向右平移6个单位,作出平移后的△A 2B 2C 2,并写出△A 2B 2C 2各顶点的坐标.图6-2-4分析:△ABC 向右平移6个单位,各点的纵坐标不变,横坐标加6.解:(1)如图所示,(2)△ABC 中点的坐标分别是A (0,4)、B (-2,2)、C (-1,1);所以A 2(6,4),B 2(4,2),C 2(5,1).6.小明头顶上方A 处5 000米的高空有一架飞机飞过,飞机的速度为300米/秒,若飞行方向不变,飞行10秒后来到B 处,用1∶100 000的比例尺,你能否用直角坐标系来表示飞机前后A 、B 的坐标,通过测量试求出小明与B 点的大概距离.解:以小明为原点竖直方向为纵轴,飞行方向为横轴建立如图所示的直角坐标系,则A (0,5),B (3,5).经过测量图中OB 约为5.8 cm ,所以根据公式:比例尺=实际距离图上距离,可求得小明与B 点的大概距离为5.8×100 000=5 800(米).7.(1)在直角坐标系中描出下列各点A (2,1),B (-2,1),C (3,2),D (-3,2);(2)连结AB 、CD 观察它们与y 轴的关系,(3)猜想(a,1)(-a,1)两点的连线是否遵循上述规律.解:(1)描点如图所示;(2)y 轴是AB 、CD 的垂直平分线;(3)已知点的坐标规律是A 与B ,C 与D 的横坐标互为相反数纵坐标相同;点(a,1),(-a,1)具备上述规律,所以y 轴是(a,1)、(-a,1)两点的连线的垂直平分线.8.图6-2-5是游乐城的平面示意图,借助刻度尺、量角器,解决如下问题:图6-2-5(1)建立适当的平面直角坐标系,写出各景点的坐标.(2)用量角器量出海底世界位于入口处的什么方向,在同一方向上还有什么景点?(3)用刻度尺量出球幕电影到入口处的图上距离,并求出它们的实际距离.解:(1)答案不唯一.若以“海底世界”为原点,则入口处(4,-1);童趣花园(4,2);梦幻艺馆(1,3);球幕电影(2,-4);(2)海底世界位于入口处北偏西约76°,在同一方向上还有太空秋千;(3)球幕电影到入口处图上距离约为1.8 cm,实际距离为1.8÷100001=270(米). 9.如图6-2-6所示,在直角坐标系下,图(1)中的图案“A”经过变换分别变成图(2)至图(6)中的相应图案(虚线对应于原图案),试写出图(2)至图(6)中各顶点的坐标,探索每次变换前后图案发生了什么变化,对应点的坐标之间有什么关系.(1) (2) (3)(4) (5) (6)图6-2-6解:由题图可知.由图(1)到图(2)是横坐标变为原来的2倍,纵坐标没变,整个图形横向拉长为原来2倍.由图(1)到图(3)是横坐标都加3,纵坐标不变,整个图形整体向右移动3个单位. 由图(1)到图(4)是横坐标不变,纵坐标都乘以-1,两个图形的大小和形状相同.由图(1)到图(5)是横坐标不变,纵坐标变为原来的2倍,图形被纵向拉长为原来的2倍.由图(1)到图(6)是横坐标、纵坐标都变为原来的2倍,形状不变,大小放大为原来的4倍.。
浙教版八年级上册作业题电子稿 第6章 图形与坐标
2
A组
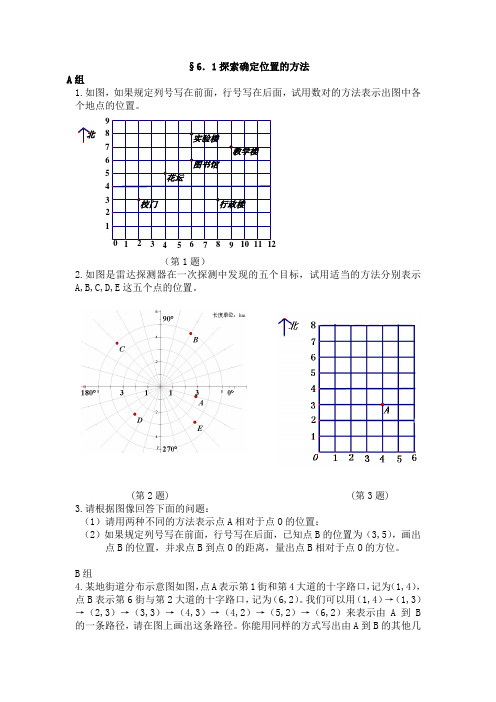
1.如图,在直角坐标系中,点A的坐标是(1.5,2)。把点A,已知直线l分别作下列变换,请作出变换后的像(只要求作出图形):
(1)把点A向下平移4个单位;
(2)把点A向左平移2.5个单位;
(3)把直线l向左平移4个单位。
2.(1)把点P(-2,7)向左平移2个单位,得点;
(2)把点P(-2,7)向下平移7个单位,得点;
(第4题)
§6.2平面直角坐标系
A组
1.在如图所示的平面直角坐标系中画出点M(-1,0),N(2,2),P(1.5,-1.5),
Q(4,-4)。
(第1题)
2.指出图中点A,B,C,D,E,F,G分别在哪一个象限内,并写出各点的坐标。
(第2题)
3.根据图中各点的位置填写下表:
点
坐标
所在象限或坐标轴
A
B
9.点A的坐标是(1.5,2)。点A向右平移2个单位后的坐标是____________,点A向下平移3.5个单位后的坐标是___________。
10.如图,直线l上的点的什么坐标不变?若把直线l上任意一点的坐标记为(-2,y),则把它向右平移5个单位所得到像的坐标应怎样表示?请在直角坐标系中做出这个像。
11.△ABC的三个顶点A,B,C的坐标分别为A(0,-4),B(-4.5,3),C(4.5,5)。
(1)在直角坐标系中画出△ABC;
(2)以y轴为对称轴,将△ABC作轴对称变换,作出变换后所得的像,并求出像的各个顶点的坐标。
12.已知线段AB的两个端点A,B的坐标分别为(-2,3),(1,3)。
(1)在直是传说中的一张藏宝岛图,藏宝人生前通过建立直角坐标系(以南北方向为纵轴,东西方向为横轴)画出这幅藏宝图。现在我们知道图上两块大石头的坐标为A(1,2),B(8,9),而藏宝地的坐标为(5,7),试设法在地图上找到宝藏,并表示出来。
6.2平面直角坐标系(2)

镇政府
镇中心小学 0
0
农技站 X
y
5 4 3 2 1 -4 -3 -2 -1
, ) ·(4,4) , ) · (3,2)
O
-1 -2 -3
·
1
2
3
4
5
X
·
(3,-2) , )
-4 在一次“寻宝”游戏中, 在一次“寻宝”游戏中,寻宝人已经找到了坐标为 (3,2)和(3,-2)的两个标志点,并且知道藏宝 , ) , )的两个标志点, 地点的坐标为( , ),除此之外不知道其他信息, ),除此之外不知道其他信息 地点的坐标为(4,4),除此之外不知道其他信息, 如何确定直角坐标系找到“宝藏” 请跟同伴交流。 如何确定直角坐标系找到“宝藏”?请跟同伴交流。
5 4
第二象限
3 2 1
第一象限
6
5
4
3
2
1
O 1 2 3 4 5
1
2
3
4
5
6
7
x
第三象限
第四象限
(二)点在平面内的坐标:
y
Q.
(- 4,4)
5 4 3 2 1
.
1 2 3
(3,2) M
4 5 6 7 x
6
5
4
3
2
1 O 1 2 3
(-3,-4) N
.
4 5
. P (4,- 4)
一般,先在x轴上得到横坐标 再在y轴上得到纵坐标 先 横坐标,再 纵坐标。 横坐标 纵坐标
2
(一) 平面直角坐标系的概念: 一 平面直角坐标系的概念:
画成水平的轴叫x轴或横轴,取向右的方向为正方向; 轴 横轴, 横轴 画成铅垂的轴叫y轴或纵轴 轴 纵轴,取向上的方向为正方向。 纵轴
数学八年级上浙教版6.2平面直角坐标系同步检测2

6.2 平面直角坐标系同步检测一、选择题〔本大题共8小题,每题4分,共32分,在每题所给出的四个选项中,只有一项为哪一项符合题目要求的〕1.点P〔m,1〕在第二象限内,那么点Q〔-m,0〕在〔〕A.x轴正半轴上 B.x轴负半轴上 C.y轴正半轴上 D.y轴负半轴上2.点A〔a,b〕在第四象限,那么点B〔b,a〕在〔〕A.第一象限 B.第二象限 C.第三象限 D.第四象限3.点P〔1,-2〕关于y轴的对称点的坐标是〔〕A.〔-1,-2〕 B.〔1,2〕 C.〔-1,2〕 D.〔-2,1〕4.点P〔x,y〕在第四象限,且│x│=3,│y│=5,那么点P的坐标是〔〕A.〔-3,5〕 B.〔5,-3〕 C.〔3,-5〕 D.〔-5,3〕5.点P〔m+3,m+1〕在x轴上,那么P点坐标为〔〕A.〔0,-2〕 B.〔2,0〕 C.〔4,0〕 D.〔0,-4〕6.三角形ABC三个顶点的坐标分别是A〔-4,-1〕,B〔1,1〕,C〔-1,4〕,将三角形ABC向右平移2个单位长度,再向上平移3个单位长度,那么平移后三个顶点的坐标是〔〕A.〔2,2〕,〔3,4〕,〔1,7〕 B.〔-2,2〕,〔4,3〕,〔1,7〕C.〔-2,2〕,〔3,4〕,〔1,7〕 D.〔2,-2〕,〔3,3〕,〔1,7〕7.假设点M在第一、三象限的角平分线上,且点M到x轴的距离为2,那么点M的坐标是〔〕A.〔2,2〕 B.〔-2,-2〕 C.〔2,2〕或〔-2,-2〕 D.〔2,-2〕或〔-2,2〕8.假设a>0,b<-2,那么点〔a,b+2〕应在〔〕A.第一象限 B.第二象限 C.第三象限 D.第四象限二、填空题〔本大题共6小题,每题4分,共24分,把答案填在题中横线上〕9.点P在第二象限,它的横坐标与纵坐标的和为1,点P的坐标是________〔写出符合条件的一个点即可〕.10.小刚家位于某住宅楼12层B座,可记为B12;按这种方法小红家住8层A•座应记为____________.11.点M〔-6,5〕到x轴的距离是_____,到y轴的距离是______.12.点A〔1-a,5〕,B〔3,b〕关于y轴对称,那么a+b=_______.13.如图,中国象棋中的“象〞,在图中的坐标为〔1,0〕,•假设“象〞再走一步,试写出下一步它可能走到的位置的坐标________.14.过点A〔-2,5〕作x轴的垂线L,那么直线L上的点的坐标特点是_________.三、解答题〔本大题共6小题,共44分.解容许写出文字说明,•证明过程或演算步骤〕15.〔8分〕〔1〕写出图中点A、B、C、D、E、F的坐标.〔2〕如图是一台雷达探测相关目标得到的结果,假设记图中目标A的位置为〔•2,90°〕,那么其余各目标的位置分别是多少?16.〔6分〕将以下图方格中的图案作以下变换,请画出相应的图案:〔1〕沿y•轴正向平移4个单位;〔2〕关于y轴轴对称.17.〔7分〕以下图中标明了小英家附近的一些地方.以小英家为坐标原点,建立如下图的坐标系.〔1〕写出汽车站和消防站的坐标;〔2〕某星期日早晨,小英同学从家里出发,沿〔3,2〕,〔3,-1〕,〔0,-1〕,〔-1,-2〕,〔•-3,-1〕的路线转了一下,又回到家里,写出路上她经过的地方.18.〔9分〕用围棋棋子可以在棋盘中摆出许多有趣的图案.如图6-6,•在棋盘上建立平面直角坐标系,以直线y=x 为对称轴,我们可以摆出一个轴对称图案〔其中A 与A ′是对称点〕,你看它像不像一只美丽的鱼.〔1〕请你在图6-7中,也用10枚以上..的棋子摆出一个以直线...y=x ...为对称轴....的轴对称图案,并在所作的图形中找出两组对称点,分别标为B 、B ′、C 、C ′〔•注意棋子要摆在格点上〕.〔2〕在给定的平面直角坐标系中,你标出的B 、B•′、•C•、•C•′的坐标分别是:B______,B ′______,C_______,C ′_______;根据以上对称点坐标的规律,写出点P 〔a ,b 〕关于对称轴y=x 的对称点P ′的坐标是________.〔1〕 〔2〕 19.〔7分〕“假设点P 、Q 的坐标是〔x 1,y 1〕、〔x 2,y 2〕,那么线段PQ 中点的坐标为〔122x x +122y y +,〕.〞点A 、B 、C 的坐标分别为〔-5,0〕、〔3,0〕、〔1,4〕,利用上述结论求线段AC 、BC 的中点D 、E 的坐标,并判断DE 与AB 的位置关系.20.〔7分〕如图,三角形AOB中,A、B两点的坐标分别为〔-4,-6〕,〔-6,-3〕,求三角形AOB的面积〔提示:三角形AOB的面积可以看作一个梯形的面积减去一些小三角形的面积〕.答案:1.A 点拨:因为点P〔m,1〕在第二象限,所以m<0,所以-m>0,于是点Q〔-m,0〕在x轴正半轴上,应选A.2.B 点拨:因为点A〔a,b〕在第四象限,所以a>0,b<0,于是点B〔b,a〕在第二象限,应选B.3.A 点拨:点〔a,b〕关于y轴对称的点为〔-a,b〕.4.C 点拨:因为点P〔x,y〕在第四象限,所以x>0,y<0.又│x│=3,│y│=5,•所以x=3,y=-5.所以点P的坐标为〔3,-5〕,应选C.5.B 点拨:因为点P〔m+3,m+1〕在x轴上,所以m+1=0,解得m=-1,所以m+3=2.•应选B.6.C7.C 点拨:在第一、三象限角平分线上的点的横坐标与纵坐标相等.8.D 9.〔-2,3〕 10.A0811.5;6 点拨:注意坐标与距离的关系.12.913.〔3,2〕,〔3,-2〕,〔-1,2〕,〔-1,-2〕点拨:象走“田〞字.14.直线L上所有点的横坐标都是-215.解:〔1〕A〔-2,-2〕,B〔-5,4〕,C〔5,-4〕,D〔0,-3〕,E〔2,5〕,F〔-3,0〕.〔2〕B〔5,•30°〕,C〔4,240°〕,D〔3,300°〕,E〔6,120°〕.16.解:如答图所示.〔16题〕〔18题〕17.解:〔1〕汽车站〔1,1〕,消防站〔2,-2〕.〔2〕小英路上经过的地方:游乐场,公园,姥姥家,宠物店,邮局.18.解:〔1〕如答图所示.〔2〕〔3,10〕;〔10,3〕;〔7,10〕;〔10,7〕;〔b,a〕19.解:由“中点公式〞得D〔-2,2〕,E〔2,2〕,DE∥AB.20.解:做辅助线如图.S△AOB=S梯形BCDO-〔S△ABC+S△OAD〕=12×〔3+6〕×6-〔12×2×3+12×4×6〕=27-〔3+12〕=12.。
平面直角坐标系练习完美A4版打印

竹西公园 荷花池图1图2第六章整章复习一、耐心填一填,一锤定音! 1.电影票上“4排5号”,记作(4,5),则“5排4号”记作______. 2.点(2-,3)向右平移2个单位后的坐标是______. 3.所有纵坐标为零的点都在______轴上.4.已知点P 在第二象限,且到x 轴的距离是2,到y 轴的距离是3,则点P 的坐标为______. 5.如果0a <,0b >,则点()A a b ,在第______象限.点()Q a b b a -++,在第______象限.6.在矩形ABCD 中,(4)A -1,,(01)B ,,(03)C ,,则D 点的坐标为______. 7.如图1是具有2 000多年历史的古城扬州市区内的几个旅游景点分布示意图.(图中每个小正方形的边长均为1个单位长度)(1)请以国家AAAA 级(最高级)旅游景点瘦西湖为坐标原点,以水平向右为x 轴的正方向,以竖直向上为y 轴的正方向.用坐标表示下列景点的位置:荷花池______、平山堂______、汪氏小苑______; (2)如果建立适当的直角坐标系(不以瘦西湖为坐标原点),例如:以______为原点,以水平向右为x 轴的正方向,以竖直向上为y 轴的正方向.用坐标表示下列景点的位置:平山堂______、竹西公园______.8.如图2,如果点A 的位置为(1-,0),那么点B ,C ,D ,E 的位置分别为______、______、______、______.9.在如图3所示的直角坐标系中,A 点的坐标是______,B 点的坐标是______,C 点的坐标是______,点A ,B ,C 都在______上.10.在同一平面直角坐标系中,过x 轴上坐标是(-4,0)的点作x 轴的垂线,过y 轴上坐标是(0,-2)的点作y 轴的垂线,两垂线相交于点P ,则点P 的坐标是______. 11.已知线段MN 平行于y 轴,且M (3,-5),N (x ,2),那么x =______. 12.已知点M (A ,B ),且AB <0,则点M 在第______象限. 13.观察图象,与图4中的鱼相比,图5中的鱼__________. 14.三角形ABC 中,A (-4,-2),B (-1,-3),C (-2,-1),将三角形ABC 先向右平移4个单位长度,再向上平移3个单位长度,则对应点A ′,B ′,C ′的坐标分别为______,______,______. 7.如图6所示,从2街4巷到4街2巷,走最短的路线共有______种走法.图4 图3 图58.在一座共8层的商业大厦中,每层的摊位布局基本相同,如图7所示.小明的父亲在6楼,其位置可以表示为(6,2,3).若小明的母亲在5楼,则小明的母亲的摊位的位置可以表示为______. 二、心选一选,慧眼识金!1.下表是沈阳市地图简图的一部分,图中“故宫”、“鼓楼”所在的区域分别是( ).A.D 7,E 6 B.D 6,E 7 C.E 7,D 6 D.E 6,D 72.如图8,横坐标是正数,纵坐标是负数的点是( ). A.A B.B C.C D.3.在平面直角坐标系中,点(2-,4)所在的象限 是( ).A.第一象限 B.第二象限C.第三象限 D.第四象限 4.已知点A (3-,2),B (3,2),则A ,B 两点相距( ). A.3个单位长度 B.4个单位长度 C.5个单位长度 D.6个单位长度 5.点P (m ,1)在第二象限内,则点Q (m -,0)在( ). A.x 轴正半轴上 B.x 轴负半轴上 C.y 轴正半轴上 D.y 轴负半轴上 6.平面直角坐标系中,一个三角形的三个顶点的坐标,横坐标保持不变,纵坐标增加3个单位,则所得的图形与原图形相比( ).A.形状不变,大小扩大了3倍 B.形状不变,向右平移了3个单位 C.形状不变,向上平移了3个单位 D.三角形被纵向拉伸为原来的3倍7.利用平面直角坐标系绘制区域内一些地点分布情况平面图的过程如下:①根据具体问题确定适当的单位长度;②建立平面直角坐标系;③在坐标平面内画出各点.其中顺序正确的是( ). A.①②③ B.②①③ C.③①② D.①③② 8.下列说法错误的是( ).A.平行于x 轴的直线上的所有点的纵坐标相同B.平行于y 轴的直线上的所有点的横坐标相同 C.若点P (a ,b )在x 轴上,则0a = D.(3-,4)与(4,3-)表示两个不同的点 9.点P (M +3,M +1)在平面直角坐标系的x 轴上,则P 点的坐标为( ). A.(0,-2) B.(2,0) C.(0,2) D.(0,-4)10.新华电影院是具有三层楼座位的大型电影院,且每层楼只有一个电影厅.小强买了一张该电影院的门票,若他想知道他在哪个位置,需从电影票上找到相关数据的个数是( ). A.1 B.2 C.3 D.4 11.小明家的坐标为(1,2),小丽家的坐标为(-2,-1),则小明家在小丽家的( ).图8图7A.东南方向 B.东北方向 C.西南方向 D.西北方向12.若点P 在第四象限,且点P 到x 轴,y 轴的距离分别为4,3,则点P 的坐标为( ). A.(4,-3) B.(-4,3) C.(-3,4) D.(3,-4)13.课间操时,小华,小军,小刚的位置如图9所示,小华对小刚说,就你,我,小军我们三人的位置而言,如果我的位置用(0,0)来表示,小军的位置用(2,1)表示,那么你的位置可表示成( ). A.(5,4) B.(4,5) C.(3,4) D.(4,3)14.如图10,四边形ABCD 是矩形,原点D 是矩形的中心,AD 边平行于x 轴,则下列叙述正确的个数是( ).①A ,D 两点纵坐标相同,横坐标相反 ②A ,B 两点横坐标相同,纵坐标相反 ③A ,C 两点横纵坐标都相反A.1 B.2 C.3 D.015.正方形网格中的每个小正方形边长都为1,每个小方格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.如图11中,B ,C 两点的位置分别记为( )(2,0),(4,0),若格点三角形ABC 不是锐角三角形且面积为4,则满足条件的A 点的位置记法不对的是( ). A.(0,4) B.(1,4)C.(2,4) D.(3,4) 16.在平面直角坐标系中,已知A (2,-2),在y 轴的负半轴上 确定点P ,使三角形AOP 为等腰三角形,则符合条件的点P 共有( ).A.2个 B.3个 C.4个 D.5个三、用心做一做,马到成功!1.用有序数对表示物体位置时,(3-,2)与(2,3-) 表示的位置相同吗?请结合图形说明.2.你用过计算机中的画图软件吗?当你的鼠标在空白的工作区域移动时,状态栏上就会显示两个变化的数字,这实际上就是鼠标的“坐标”,你还能举出一些身边关于坐标的例子吗?3.如果点A 的坐标为(23a --,22b +),那么点A 在第几象限?说说你的理由.图9 图10图114.已知A (a ,21-),B (13-,b ),且A ,B 两点所在直线平行于x 轴.求a ,b 的值.5.在直角坐标系中描出下列各组点,并将各组内的点用线段依次连结起来. (1)(1,0)、(6,0)、(6,1)、(5,0)、(6,-1)、(6,0);(2)(2,0)、(5,3)、(4,0); (3)(2,0)、(5,-3)、(4,0).观察所得到的图形像什么?如果要将此图形向上平移到x 轴上方, 那么至少要向上平移几个单位长度.6.如图12,在平面直角坐标系中,已知点A (2-,0),B (2,0). (1)画出等腰三角形ABC (画一个即可);(2)写出(1)中画出的三角形ABC 的顶点C 的坐标. 7.图13为一辆公交车的行驶路线,“Ο”表示该公交车的中途停车点,现在请你帮助小明完成对该公交车行驶路线的描述:起点站→(1,1)→…→终点站.图13t128.如图14,点A 用(3,1)表示,点B 用(8,5)表示.若(3,1)→(5,1)→(5,4)→(8,4)→(8,5)表示由A 到B 的一种走法,并规定A 到B 只能向上或向右走,用上述表示法再写出两种走法, 并判断这几种走法的路程是否相等.9.如图15,三角形ABC 中任意一点00()P x y ,,经平移后对应点为100(35)P x y +-,,将三角形ABC 作同样平移得到三角形111A B C ,求1A ,1B ,1C 的坐标,并在图中画出111A B C 的位置.10.观察图16中图形由(1)→(2)→(3)→(4)的变化过程,写出每一步图形是如何变化的,图形中各顶点的坐标是如何变化的.图14图15图165.正方形ABCD的邻边分别与x轴,y轴平行,A点坐标为(2,4),且正方形面积为25(平方单位),则顶点A的对角的顶点坐标可能是多少?6.如图17,矩形ABCD的宽AB=4,长BC=6,按下列要求分别建立直角坐标系:(1)使D点坐标为(6,4);(2)使D点坐标为(0,4);(3)使B点坐标为(-3,-2);(4)使B点坐标为(-3,-4).图17。
6.2.1 用坐标表示地理位置 同步作业(含答案)

6.2.1 用坐标表示地理位置◆典型例题【例1】古城黄州以其名胜古迹吸引了不少游客.从地图上看,较有名的六外景点在黄州城内的分布是∶东坡赤壁在市政府以西2km再往南3km处,黄冈中学在市政府以东1 km 处,宝塔公园在市政府以东3km处,鄂黄长江桥在市政府以东7 km再往北8 km处,遗爱湖在市政府以东4km再往北4km处,博物馆在市政府以北2 km再往西1 km处.请画图表示出这六个景点的位置,并用坐标表示出来.【解析】各景点的位置是相对某一地点(市政府)而言的,因此市政府可作为参照点.以市政府为坐标原点,在东西方向上画出x轴,在南北方向上画y轴建立平面直角坐标系.然后,标出各景点的位置,写出各点的坐标.【答案】如图6-20所示.图6-20其坐标分别为∶A(-2,-3),B(1,0),C(3,0),D(7,8),E(4,4),F(-1,2).【例2】如图6-21,请建立适当的平面直角坐标系,写出各景点或设方向的坐标.[解析) 首先选择一个合适的景点作为原点,再建立坐标系.图6-21【解析】首先选择一个合适的时景点作为原点,再建坐标系.【答案】以学校为原点、水平向右方向和坚直向上方向为x轴正方向和y轴正方向建立平面直角坐标系,则学校A(0,0),体训基地B(5,0),网球场C(8,0),炮台D(2,3.5),京山E(-2,4),海洋大学(-7,0),百花苑G(-1,-2).【例3】在雷达探测区域,可以建立平面直角坐标系表示位置.在某次行动中,当我两架飞机在A(-1,2)与B(3,2)位置时,可疑飞机在(-1,-3)位置,你能找到这个直角坐标系的横、纵坐标的位置吗?把它们表示出来并确定可疑飞机的位置,说说你的做法.【解析】A、B两点纵坐标相同说明AB平行于x轴,线段AB长为4个单位,则y 轴把它分成1∶3两部分,由于纵标是2,原点在y轴下方2个单位处(如图6-22所示).图6-22【答案】如图6-22所示,先把AB四等分,然后过靠近A点的分点M作AB的垂线即为y轴,以AM为单位长度沿y轴向下2个单位即为O点,过点O作x轴垂直于y轴,然后描出敌机位置(如图6-22中的N点).◆课前热身1.用坐标表示地理位置时,所建立的坐标系不同,表示同一点的坐标__________.(填“相同”或“不同”)2.如图6-23,五间亭的位置是__________,飞虹桥的位置是__________,下棋亭的位置是__________,碑亭的位置是__________.图6-23 图6-24◆课上作业3.方格纸上有A、B两点,以B为原点,建立平面直角坐标系(如图6-24),则A点坐标为(5,3),若以A点为坐标原点建立直角坐标系,则B点坐标为__________.4.张老师住在学校正东200m处,从张老师家出发向北走150m就到李老师家,若选取李老师家为原点,分别以正东、正北方向为x、y轴正方向建立平面直角坐标系,则学校的坐标是_________.5.图6-25是我市市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度)请以某景区为原点,画出平面直角坐标系,并用坐标表示下列景点的位置∶光岳楼__________,金凤广场__________,动物园__________.图6-25 图6-266.某人出火车站向南走300m到平价超市,再从平价超市向西走100m到汽车站,若将平价超市的坐标记为(0,-300),则汽车站的纵坐标为__________.◆课下作业一、填空题7.从学校向东走600 m,再向南走500m到达小伟家;从学校向南走500m,再向西走300m 到小亮家,则小亮家在小伟家的__________.8.某军事行动中,对军队部署的方位,采用代码的方式来表示.例如,北偏东30°方向45 km 的位置与钟面相结合,以钟面圆心为基准,时针指向北偏东30°的时刻是1∶00,那么这个地点就用代码010045表示。
第六章平面直角坐标系单元测试题与答案

2010-2011学年度下期七年级6.2《 平面直角坐标系的应用》检测题班级姓名得分一.填空题(每小题3分,共30分):1. 在平面直角坐标系中,把点P (-1,-2)向上平移4个单位长 度所得点的坐标是.2. 将点A (4,3)向平移个单位长度后,其坐标的 变化是( 6, 3 ) .3. 已知点A(-4,-6),将点A 先向右平移4个单位长度,再向上平移6 个单位长度,得到A ′,则A ′的坐标为________.4.如果将点A (-3,-2)向右移2个单位长度再向上平移3个单位长度单位得到点B ,,那么点B ,在第象限,点B 的坐标是.5.已知正方形的一个顶点A (-4,2),把此正方形向上平移2个单位长度,再向左平移3个单位长度时,此时点A 的坐标是.6.点(-2,3)先向右平移2个单位,再向下平移3个单位,此时的位置是.7.△ABC 的三个顶点A (1,2),B (-1,-2),C (-2,3)将其平移到点A ′(-1,-2)处,使A 与A ′重合,则B ′、C ′两点坐标分别为, .8.如图所示,如果点A 的位置为(-1,0),那么点B 的位置为___,点C 的位置,点D 和点E 的位置分别为、.9.正方形各个点的纵坐标都减去3,相应的新图形就是把原图形向平移个单位长度.10.如图,将边长为1的正方形OAPB 沿x 轴正方向边连续 翻转2006次,点P 依次落在点1232006,,P P P P的位置,则2006P 的横坐标2006x =____________二.选择题(每小题3分,共21分):11,把点P 1(2,一3)向右平移3个单位长度再向下平移2个单位长度到达点P 2处,则P 2的坐标是( )A.(5,-1)B.(-1,-5)C.(5,-5)D.(-1,-1) 12.如图,将三角形向右平移2个单位长度,再向(3)第8题 第10题图x8题图上平移3个单位长度,则平移后三个的坐标是( ) A.(2,2)(3,4)(1,7) B.(一2,2)(4,3)(1,7) C.(一2,2)(3,4)(1,7) D.(2,一2)(3,3)(1,7)13.在直角坐标系中,A (1,2)点的横坐标乘 -1,纵坐标不变,得到A ′点,则A 与A ′的关系 是( )A.关于x 轴对称B.关于y 轴对C.关于原点对称D.将A 点向x 轴负方向平移一个单位14.以如图所示的方格纸中,每个小正方形的边长为1,如果以MN 所在的直线为Y 轴,以小正方形的边长为单位长度建立平面直角坐标系,使A 点与B 点关于原点对称,则这时C 点的坐标可能是( ) A 、(1,3);B 、(2,-1);C 、2,1);D 、(3,1)15.小虫在小方格上沿着小方格的边爬行,它的起始位置是A (2,2)先爬到B (2,4),再爬到C (5,4),最后爬到D(5,6),则小虫共爬了( ) A 、7个单位长度 B 、5个单位长度 C 、4个单位长度 D 、3个单位长度 16.线段MN 是由线段EF 经过平移得到的若点E(-1,3)的对应点M (2,5),则点F (-3,-2)的对应点N 的坐标是( )A (-1,0)B (-6,0)C (0,-4)D (0,0)17.已知△ABC 平移后得到△A ′B ′C ′,且A ′(-2,3)、B ′(-4,-1)、C ′(m,n )、 C (m+5,n+3),则A 、B 两点的坐标为( ) A. (3,6)、(1,2) B. (-7,0)、(-9,-4) C.(1,8)、(-1,4) D.(-7,-2)、(0,-9)三.解答题(本大题69分): 17(8分).如图,将△ABC 向右平移2下平移3个单位长度,得到对应的△A 1B 1C 1, 并写出点A 1,B 1,C 1,的坐标。
第七章平面直角坐标系练习题

第七章 平面直角坐标系课时作业1 有序实数对总分:100分 时间:40分钟 成绩评定 一、选择题(每小题5分,共30分) 1.[A]如图在正方形网格中,若)1,1(A ,)0,2(B ,则C 点的坐标为( )A .)2,3(--B .)2,3(-C .)3,2(--D .)3,2(-2.[A]根据下列表述,能确定位置的是 ( )A .红星电影院第2排B .北京市四环路C .北偏东30°D .东经118°,北纬40°3.[A]电影院里的座位按“×排×号”编排,小明的座位简记为(12,6),小菲的位置简记为(12,12),则小明与小菲坐的位置为 ( )A .同一排B .前后同一条直线上C .中间隔着六个人D .前后隔六排4.[A]下列关于有序数对的说法正确的是 ( )A .(3,2)与(2,3)表示的位置相同B .(,)a b 与(,)b a 表示的位置一定不相同C .(3,2)-与(2,3)-是表示不同位置的两个有序数对D .(4,4)与(4,4)表示两个不同的位置5.[B]王东坐在教室的第3列第2行,用(3,2)表示,李军坐在王东正后方的第一个位置上,李军的位置是 ( )A .(4,3)B .(3,4)C .(1,3)D .(3,3)6.[C]如图,已知校门的位置是(1,1),图中单位长度表示100m ,那么下列对于 实验楼的位置的叙述:①实验楼的位置是(3,2);②实验楼的位置是(3,3);③实验楼的位置在校门的东北方向300m 处,其中正确的个数为( )A .0B .1C .2D .3二、填空题(每小题5分,共20分)7.[A]如果用)8,7(表示七年级八班,那么八年级六班可表示成 ;8.[B]如图,O 对应的有序数对为)3,1(有一个英文单词的字母顺序对应如图中的有序数对分别为)2,1(,)1,5(,)2,5(,)2,5(,)3,1(,请你把这个英文单词写出来为 ;第8题图 第9题图 第10题图9.[B]如图,每个小正方格都是边长为1个单位长度的正方形,如果用()0,0表示A 点的位置,用()4,3表示B 点的位置,那么C 点的位置可表示为 ;10.[C]将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形。
八年级数学上册 6.2平面直角坐标系同步练习 浙教版

6.2平面直角坐标系[同步练习]复习巩固1.如图3,将△AOB绕点O逆时针旋转90°,得到△A′OB′,若点A的坐标为(a,b),则点A′的坐标为 .2.△ABC在直角坐标系中的位置如图4所示,若△A ′B′C′与△ABC关于y轴对称,则点A的对应点A ′的坐标为 ,3.如图5,在直角坐标系中,右边的图案是由左边的图案经过平移得到的,左图案中左右眼的坐标分别是(-4,2),(-2,2),右图案中左眼的坐标是(3,4),则右图中右眼的坐标是 .4.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2005的值为 .5.若点A(-2,n)在x轴上,则点B(n-1,n+1)在().(A) 第一象限 (B) 第二象限 (C) 第三象限 (D)第四象限6.若点M(a+2,3-2a)在y轴上,则点M的坐标是().(A) (-2,7) (B) (0,3) (C) (0,7) D. (7,0)7.如图6,若平行四边形的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是().(A) (3,7) (B) (5,3) (C) (7,3) (D) (8,2)8.直角梯形ABCD在直角坐标系中的位置如图7,若AD=5,A点坐标为(-2,7),则D点坐标为().(A) (2,2) (B) (2,12) (C) (3,7) (D) (7,7)9.如图8,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).(1)把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形并写出点B1的坐标;(2)把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C的图形并写出点B2的坐标.10.中国象棋棋盘中蕴含着平面直角坐标系,如图9是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走. 例如:图中“马”所在的位置可以直接走到点A、B处.(1)如果“帅”位于点(0,0),“相”位于点(4,2),则“马”所在的点的坐标为,点C的坐标为,点D的坐标为 .(2)若“马”的位置在C点,为了到达D点,请按“马”走的规则,在图中画出一种你认为合理的行走路线,并用坐标表示.11.如图10,是某学校的平面示意图,在10×10的正方形网格中(每个小方格都是边长为1的正方形),若分别用(3,1)、(3,5)表示图中图书馆和教学楼的位置,那么实验楼的位置应表示为 .图3图4图5图6 图7图8图9图10y探索拓展12.在平面直角坐标系中,有四个定点A(-3,0),B(1,-1),C (0,3),D(-1,3)及一动点P ,则PA+PB+PC+PD 的最小值是 . 13.一个长方形在平面直角坐标系中三个顶点的坐标分别为(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标为( ).(A) (2,2) (B) (3,2) (C) (3,3) (D) (2,3)14.已知坐标平面内平行四边形三个顶点的坐标分别是(0,0),(4,0),(2,3),求另一个顶点的坐标.复习巩固1.(-b,a) 2. ( 4,2) 3. (5,6) 4. –15. B6. C7. C8. C9.点B 1、B 2坐标分别为(-9,-1),(5,5)10. (1) (-3,0)、(1,3)、(3,1);11.(-3,4)12. 明显地当P 是四边形对角线交点时,PA+PB+PC+PD 为最小数:13. B 14. 有三种情形,坐标分别为(6,3),(-2,3),(2,3)A BC D x。
2023年新高考数学一轮复习6-2 平面向量的基本定理及坐标表示(真题测试)含详解

专题6.2 平面向量的基本定理及坐标表示(真题测试)一、单选题1.(2019·全国·高考真题(文))已知向量()()2332a b ==,,,,则|–|a b =( ) AB .2C .D .502.(2019·全国·高考真题(理))已知AB =(2,3),AC =(3,t ),BC =1,则AB BC ⋅=( ) A .-3 B .-2 C .2D .33.(2020·山东·高考真题)已知点()4,3A ,()4,2B -,点P 在函数243y x x =--图象的对称轴上,若PA PB ⊥,则点P 的坐标是( ) A .()2,6-或()2,1 B .()2,6--或()2,1- C .()2,6或()2,1-D .()2,6-或()2,1--4.(2022·全国·高三专题练习)正方形ABCD 的边长为2,以AB 为直径的圆M ,若点P 为圆M 上一动点,则·PC PD 的取值范围为( )A .[]04,B .[]08,C .[]18-,D .[]14-, 5.(2022·广东·大埔县虎山中学高三阶段练习)已知ABC 是边长为a 的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是( ) A .22a -B .238a -C .243a -D .2a -6.(2022·上海奉贤·二模)已知平面向量a ,m ,n ,满足4a =,221010m a m n a n ⎧-⋅+=⎪⎨-⋅+=⎪⎩,则当m 与n 的夹角最大时,m n -的值为( ) A .4B .2CD .17.(2017·全国·高考真题(理))已知ABC 是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC +的最小值是( ) A .2-B .32-C .43-D .1-8.(2016·四川·高考真题(文))已知正三角形ABC 的边长为,平面ABC 内的动点P ,M 满足||1AP =,PM MC =,则2||BM 的最大值是( )A .B .C .D .二、多选题9.(2022·广东广州·三模)已知向量()3,1a =-,()1,2b =-,则下列结论中正确的是( ) A .5a b ⋅= B .5a b -=C .,4a b π=D .a b ∥10.(2022·湖北·模拟预测)正方形ABCD 的边长为2,E 是BC 中点,如图,点P 是以AB 为直径的半圆上任意点,AP λ=AD AE μ+,则( )A .λ最大值为12B .μ最大值为1C .AP AD ⋅最大值是2 D .AP AE ⋅211.(2022·湖北·荆州中学模拟预测)已知向量()3,1a =,()()cos ,sin 0b θθθπ=≤≤,则下列命题正确的是( )A .若a b ⊥,则tan θ=B .存在θ,使得a b a b +=-C .与a 共线的单位向量只有一个为12)D .向量a 与b 夹角的余弦值范围是[ 12.(2022·湖南·长郡中学模拟预测)已知向量(1,sin ),(cos ,2)a b θθ==,则下列命题正确的是( )A .存在θ,使得 //a bB .当tan θ=时,a 与b 垂直C .对任意θ,都有||||a b ≠D .当3a b ⋅=-时,tan θ=三、填空题13.(2020·全国高考真题(理))设,a b 为单位向量,且||1a b +=,则||a b -=______________. 14.(2018·全国·高考真题(理))已知向量()=1,2a ,()=2,2b -,()=1,c λ.若()2+ca b ,则λ=________.15.(2021·全国·高考真题(理))已知向量()()1,3,3,4a b ==,若()a b b λ-⊥,则λ=__________. 16.(2022·浙江·高考真题)设点P 在单位圆的内接正八边形128A A A 的边12A A 上,则222182PA PA PA +++的取值范围是_______. 四、解答题17.(2022·全国·高三专题练习)已知平行四边形ABCD 的三个顶点A 、B 、C 的坐标分别是(2,1)-、(1,3)-、(3,4). 若OB OA OD λμ=+,求λμ+的值18.(2022·全国·高三专题练习)已知平行四边形ABCD 的三个顶点A 、B 、C 的坐标分别是(-2,1)、(-1,3)、(3,4). O 为坐标原点,若动点S 满足向量2DS =,求OS 的最大值19.(2023·全国·高三专题练习)已知平行四边形ABCD 中,2EC DE =,2FC BF =,2FG GE =.(1)用AB ,AD 表示AG ;(2)若6AB =,32AD =45BAD ∠=︒,如图建立直角坐标系,求GB 和DF 的坐标. 20.(2023·全国·高三专题练习)已知向量a →=(1,2),b →=(-3,k ). (1)若a →∥b →,求b →的值;(2)若a →⊥(a →+2b →),求实数k 的值;(3)若a →与b →的夹角是钝角,求实数k 的取值范围.21.(2022·全国·高三专题练习)已知平行四边形ABCD 的三个顶点A 、B 、C 的坐标分别是(-2,1)、(-1,3)、(3,4). 若Q 是线段BC 上的动点,求·AQ DQ 的最值22.(2017·江苏·高考真题)已知向量()([]330a cosx sinx b x π==-∈,,,,,.(1)若a b,求x的值;(2)记()f x a b=⋅,求函数y=f(x)的最大值和最小值及对应的x的值.专题6.2 平面向量的基本定理及坐标表示(真题测试)一、单选题1.(2019·全国·高考真题(文))已知向量()()2332a b ==,,,,则|–|a b =( ) AB .2C .D .50【答案】A 【解析】 【分析】本题先计算a b -,再根据模的概念求出||a b -. 【详解】由已知,(2,3)(3,2)(1,1)a b -=-=-,所以2||(1)a b -=-= 故选A2.(2019·全国·高考真题(理))已知AB =(2,3),AC =(3,t ),BC =1,则AB BC ⋅=( ) A .-3 B .-2 C .2 D .3【答案】C 【解析】 【分析】根据向量三角形法则求出t ,再求出向量的数量积. 【详解】由(1,3)BC AC AB t =-=-,211BC =,得3t =,则(1,0)BC =,(2,3)(1,0)21302AB BC ==⨯+⨯=.故选C .3.(2020·山东·高考真题)已知点()4,3A ,()4,2B -,点P 在函数243y x x =--图象的对称轴上,若PA PB ⊥,则点P 的坐标是( ) A .()2,6-或()2,1B .()2,6--或()2,1-C .()2,6或()2,1-D .()2,6-或()2,1--【答案】C 【解析】 【分析】由二次函数对称轴设出P 点坐标,再由向量垂直的坐标表示计算可得. 【详解】由题意函数243y x x =--图象的对称轴是2x =,设(2,)P y ,因为PA PB ⊥,所以(2,3)(6,2)12(3)(2)0PA PB y y y y ⋅=-⋅--=-+--=,解得6y =或1y =-,所以(2,6)P 或(2,1)P -, 故选:C .4.(2022·全国·高三专题练习)正方形ABCD 的边长为2,以AB 为直径的圆M ,若点P 为圆M 上一动点,则·PC PD 的取值范围为( )A .[]04,B .[]08,C .[]18-,D .[]14-, 【答案】B 【解析】 【分析】以AB 为x 轴,线段AB 的中垂线为y 轴建立平面直角坐标系,写出,C D 坐标,设(cos ,sin )P θθ,用数量积的坐标表示计算数量积后由正弦函数性质得范围. 【详解】以AB 为x 轴,线段AB 的中垂线为y 轴建立平面直角坐标系,如图,则(1,2)C ,(1,2)D -, 圆方程为221x y +=,P 在圆上,设(cos ,sin )P θθ, (1cos ,2sin )PC θθ=--,(1cos ,2sin )PD θθ=---,2(1cos )(1cos )(2sin )PC PD θθθ⋅=---+-22cos 144sin sin θθθ=-+-+44sin θ=-,sin [1,1]θ∈-,所以[0,8]PC PD ⋅∈.故选:B .5.(2022·广东·大埔县虎山中学高三阶段练习)已知ABC 是边长为a 的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是( ) A .22a - B .238a -C .243a -D .2a -【答案】B 【解析】 【分析】建立平面直角坐标系,用坐标表示出PA 、PB 和PC ,计算()PA PB PC ⋅+的最小值即可. 【详解】解:以BC 中点为坐标原点,建立如图所示的坐标系,则30,2A a ⎛⎫ ⎪ ⎪⎝⎭,1,02B a ⎛⎫- ⎪⎝⎭,1,02C a ⎛⎫ ⎪⎝⎭,设(,)P x y ,则PA x y ⎛⎫=-- ⎪ ⎪⎝⎭,1,2PB a x y ⎛⎫=--- ⎪⎝⎭,1,2PC a x y ⎛⎫=-- ⎪⎝⎭,所以()2,2PB x y PC --+=,所以()22(2)(2)22PA PB PC x x y y x y ⎫⋅+=-⋅-+-⋅-=+⎪⎪⎝⎭2223228x y a ⎛⎫=+- ⎪ ⎪⎝⎭;所以当0x =,y =时,()PA PB PC ⋅+取得最小值是238a -.故选:B .6.(2022·上海奉贤·二模)已知平面向量a ,m ,n ,满足4a =,221010m a m n a n ⎧-⋅+=⎪⎨-⋅+=⎪⎩,则当m 与n 的夹角最大时,m n -的值为( ) A .4 B .2 CD .1【答案】C 【解析】 【分析】以O 为原点建立平面坐标系,设(4,0)a =,(,)m x y =,根据向量的数量积的运算公式,分别求得向量,m n 的终点所表示的轨迹方程,进而根据圆的性质,即可求解. 【详解】设,,a m n 的起点均为O ,以O 为原点建立平面坐标系,如图所示, 不妨设(4,0)a =,(,)m x y =,则222m x y =+,4a m x ⋅=, 由210m a m -⋅+=可得22410x y x +-+=,即22(2)3x y -+=, ∴m 的终点M 在以(2,0) 同理n 的终点N 在以(2,0)显然当OM ,ON 为圆的两条切线时,MON ∠最大,即m 与n 的夹角最大.设圆心为A ,则AM =1OM =,则sin MOA ∠= ∴60MOA ∠=︒,设MN 与x 轴交于点B ,由对称性可知MN x ⊥轴,且2MN MB =,∴22sin 21MN MB OM MOA ==⋅∠=⨯= 即当m 与n 的夹角最大时,3m n -= 故选:C7.(2017·全国·高考真题(理))已知ABC 是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC +的最小值是( ) A .2- B .32-C .43-D .1-【答案】B 【解析】 【分析】根据条件建立坐标系,求出点的坐标,利用坐标法结合向量数量积的公式进行计算即可. 【详解】建立如图所示的坐标系,以BC 中点为坐标原点,则A ,(1,0)B -,(1,0)C ,设(,)P x y ,则()PA x y =-,(1,)PB x y =---,(1,)PC x y =--,则22223()222[(]4PA PB PC x y x y +=-+=+-∴当0x =,y =332()42⨯-=-,故选:B .8.(2016·四川·高考真题(文))已知正三角形ABC 的边长为,平面ABC 内的动点P ,M 满足||1AP =,PM MC =,则2||BM 的最大值是( )A .B .C .D .【答案】B 【解析】 【详解】试题分析:如图可得120,2ADC ADB BDC DA DB DC ∠=∠=∠=︒===.以D 为原点,直线DA 为x 轴建立平面直角坐标系,则()((2,0,1,,.A B C --设(),,P x y 由已知1AP =,得()2221x y -+=,又131,,,,222x y x PM MC M BM ⎛⎫⎛-++=∴∴= ⎪ ⎪ ⎝⎭⎝⎭()()222133||4x y BM +++∴=,它表示圆()2221x y -+=上的点(),x y 与点()1,33--的距离的平方的14,()()2222max149333144BM⎛⎫∴=++= ⎪⎝⎭,故选B. 【考点】向量的夹角,解析几何中与圆有关的最值问题【名师点睛】本题考查平面向量的夹角与向量的模,由于结论是要求向量模的平方的最大值,因此我们要把它用一个参数表示出来,解题时首先对条件进行化简变形,本题中得出120ADC ADB BDC ∠=∠=∠=︒,且2DA DB DC ===,因此我们采用解析法,即建立直角坐标系,写出点,,,A B C D 的坐标,同时动点P 的轨迹是圆,则()(22214x y BM +++=,因此可用圆的性质得出最值.因此本题又考查了数形结合的数学思想. 二、多选题9.(2022·广东广州·三模)已知向量()3,1a =-,()1,2b =-,则下列结论中正确的是( ) A .5a b ⋅= B .5a b -=C .,4a b π=D .a b ∥【答案】ABC 【解析】 【分析】按照向量数量积的坐标运算、模的坐标运算、夹角公式及平行的坐标公式依次判断即可. 【详解】31(1)(2)5a b ⋅=⨯+-⨯-=,A 正确;2(2,1),21a b a b -=-=+B 正确;22223(1)10,1(2)5a b =+-==+-=,则52cos ,,,2452a b a b a b a bπ⋅====,C 正确; ()()3211⨯-≠-⨯,D 错误.故选:ABC.10.(2022·湖北·模拟预测)正方形ABCD 的边长为2,E 是BC 中点,如图,点P 是以AB 为直径的半圆上任意点,AP λ=AD AE μ+,则( )A .λ最大值为12 B .μ最大值为1C .AP AD ⋅最大值是2 D .AP AE ⋅2【答案】BCD 【解析】 【分析】以AB 中点O 为原点建立平面直角坐标系,利用坐标表示向量,根据三角函数的性质可判断各选项. 【详解】以AB 中点O 为原点建立平面直角坐标系,()1,0A -,()1,2D -,()1,1E ,设BOP α∠=,则()cos ,sin P αα,()cos 1,sin AP αα=+,()0,2AD =,由AP AD AE λμ=+,得2cos 1μα=+且2sin λμα+=,[]0,απ∈()()112sin cos 144λαααθ=--=--A 错; 0α=时max 1μ=,故B 正确;2sin 2AP AD α⋅=≤,故C 正确;()sin 2cos 222AP AE αααφ⋅=++=++,故D 正确. 故选:BCD.11.(2022·湖北·荆州中学模拟预测)已知向量()3,1a =,()()cos ,sin 0b θθθπ=≤≤,则下列命题正确的是( )A .若a b ⊥,则tan θ=B .存在θ,使得a b a b +=-C .与a 共线的单位向量只有一个为12)D .向量a 与b 夹角的余弦值范围是[ 【答案】AB 【解析】 【分析】根据向量垂直的坐标表示判断A 、B ,根据单位向量的定义判断C ,根据向量夹角的坐标表示及正弦函数的性质判断D ; 【详解】解:对于A 选项:若a b ⊥,则0a b ⋅=, ∴sin 0θθ+=,∴tan θ=A 正确;对于B :若a b a b +=-,则22a b a b +=-,即222222a a b b a a b b +⋅+=-⋅+,所以0a b ⋅=,即a b ⊥,由A 可知,tan θ=0θπ≤≤,所以23πθ=,故B 正确;对于C 选项:与a 共线的单位向量为aa ±,故为12⎫⎪⎪⎝⎭或12⎛⎫- ⎪ ⎪⎝⎭,故C 选项错误;对于D 选项:设向量a 与b 夹角为α,则cos sin 3πθα⎛⎫+ ⎪⎝=⎭,因为0θπ≤≤,所以4333πππθ≤+≤,所以sin 13πθ⎛⎫≤+≤ ⎪⎝⎭,故cos 1α≤≤,故D 错误;故选:AB .12.(2022·湖南·长郡中学模拟预测)已知向量(1,sin ),(cos ,2)a b θθ==,则下列命题正确的是( )A .存在θ,使得 //a bB .当tan θ=时,a 与b 垂直C .对任意θ,都有||||a b ≠D .当3a b ⋅=-时,tan θ=【答案】BD 【解析】 【分析】A 选项,利用向量平行及三角函数恒等变换得到方程,sin 21θ=,故A 错误;B 选项,利用垂直得到方程,求出正切值;C 选项,计算出两向量的模长,得到ππ,2k k Z θ=+∈,C 错误;利用向量的数量积列出cos a b θθ⋅==2tan 20θ-θ+=,求出正切值.【详解】对于选项A :若 //a b sin cos =θθ,即sin 21θ=, 所以不存在这样的θ,故A 错误;对于选项B :若a b ⊥,则cos 0θθ=,即cos θ=θ,得tan 2θ=,故B 正确; 对于选项C :22||1sin ,||2cos a b θθ=+=+,当||||a b =时,cos21θ=-, 此时ππ,2k k Z θ=+∈,故C 错误;对于选项D :cos a b θθ⋅==两边同时平方得2222cos 2sin sin 3cos 3sin θθθθθθ++⋅=+,化简得222cos sin cos 0θ+θ-θθ=,等式两边同除以2cos θ得2tan 20θ-θ+=,即2(tan 0θ-=,所以tan θ=D 正确.故选:BD. 三、填空题13.(2020·全国高考真题(理))设,a b 为单位向量,且||1a b +=,则||a b -=______________.【解析】因为,a b 为单位向量,所以1a b == 所以()2222221a b a b a a b b a b +=+=+⋅+=+⋅=解得:21a b ⋅=- 所以()22223a b a b a a b b -=-=-⋅+=14.(2018·全国·高考真题(理))已知向量()=1,2a ,()=2,2b -,()=1,c λ.若()2+c a b ,则λ=________.【答案】12 【解析】 【分析】由两向量共线的坐标关系计算即可. 【详解】由题可得()24,2a b +=()//2,c a b +()1,c λ=4λ20∴-=,即1λ2=故答案为1215.(2021·全国·高考真题(理))已知向量()()1,3,3,4a b ==,若()a b b λ-⊥,则λ=__________.【答案】35【解析】 【分析】根据平面向量数量积的坐标表示以及向量的线性运算列出方程,即可解出. 【详解】因为()()()1,33,413,34a b λλλλ-=-=--,所以由()a b b λ-⊥可得,()()3134340λλ-+-=,解得35λ=. 故答案为:35.16.(2022·浙江·高考真题)设点P 在单位圆的内接正八边形128A A A 的边12A A 上,则222182PA PA PA +++的取值范围是_______.【答案】[12+ 【解析】 【分析】根据正八边形的结构特征,分别以圆心为原点,37A A 所在直线为x 轴,51A A 所在直线为y 轴建立平面直角坐标系,即可求出各顶点的坐标,设(,)P x y ,再根据平面向量模的坐标计算公式即可得到()2222212888PA PA PA x y +++=++,然后利用cos 22.5||1OP ≤≤即可解出.【详解】以圆心为原点,37A A 所在直线为x 轴,51A A 所在直线为y 轴建立平面直角坐标系,如图所示:则1345726222222(0,1),,,(1,0),,,(0,1),,,(1,0)222222A A A A A A A ⎛⎫⎛⎫⎛⎫----- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,822,22A ⎛⎫- ⎪ ⎪⎝⎭,设(,)P x y ,于是()2222212888PA PA PA x y +++=++,因为cos 22.5||1OP ≤≤,所以221cos 4512x y +≤+≤,故222128PA PA PA +++的取值范围是[12+.故答案为:[12+. 四、解答题17.(2022·全国·高三专题练习)已知平行四边形ABCD 的三个顶点A 、B 、C 的坐标分别是(2,1)-、(1,3)-、(3,4). 若OB OA OD λμ=+,求λμ+的值【答案】136【解析】【分析】设出D ,利用向量的坐标公式求出四边对应的向量,据对边平行得到向量相等,利用向量相等的充要条件列出方程组求出D 的坐标,从而求出OB 、OA 、OD 的坐标,再根据平面向量线性运算的坐标表示得到方程组,解得即可. 【详解】解:设(,)D x y ,(2,1)A -,(1,3)B -,(3,4)C ,则(1,2)AB =,(3,4)DC x y =--,又AB DC =,3142x y -=⎧∴⎨-=⎩,解得22x y =⎧⎨=⎩,即()2,2D , 所以()1,3OB =-,()2,1OA =-,()2,2OD =,因为OB OA OD λμ=+,所以()()()1,32,12,2λμ-=-+,所以22123λμλμ-+=-⎧⎨+=⎩,解得4356λμ⎧=⎪⎪⎨⎪=⎪⎩,所以136λμ+= 18.(2022·全国·高三专题练习)已知平行四边形ABCD 的三个顶点A 、B 、C 的坐标分别是(-2,1)、(-1,3)、(3,4). O 为坐标原点,若动点S 满足向量2DS =,求OS 的最大值【答案】2 【解析】 【分析】先利用AB DC =求出D 点坐标,再结合2DS =求出S 的轨迹是圆,最后利用O 到圆心的距离加半径求出最大值即可. 【详解】设(,)D a b ,()(1,2),3,4AB DC a b ==--,由AB DC =得3142a b -=⎧⎨-=⎩,解得22a b =⎧⎨=⎩,故(2,2)D ,设(,)S x y ,(2,2)DS x y =--,则由2DS =得()()22224x y -+-=,即S 的轨迹是以()2,2为圆心,2为半径的圆,故OS 的最大值为O22=.19.(2023·全国·高三专题练习)已知平行四边形ABCD 中,2EC DE =,2FC BF =,2FG GE =.(1)用AB ,AD 表示AG ;(2)若6AB =,32AD =45BAD ∠=︒,如图建立直角坐标系,求GB 和DF 的坐标. 【答案】(1)5799=+AD AG AB (2)17,33GB ⎛⎫=- ⎪⎝⎭,()4,2DF =-【解析】 【分析】(1)根据向量的加法及数乘运算求解;(2)建立平面直角坐标系,利用坐标运算求解即可. (1)13AE AD AB =+,13AF AD AB =+,又2FG GE =,所以2()AG AF AE AG -=- 所以21573399AG AE AF AB AD =+=+(2)过点D 作AB 的垂线交AB 于点D ,如图,于是在Rt ADD '△中,由45BAD ∠=︒可知,3AD '=根据题意得各点坐标:()0,0A ,()6,0B ,()9,3C ,()3,3D ,()5,3E ,()7,1F ,5757(60)(3,3)9999AG AB AD =+=+=,177,33⎛⎫ ⎪⎝⎭所以177,33G ⎛⎫ ⎪⎝⎭所以()6,0AB =,177,33AG =⎛⎫⎪⎝⎭,()4,2DF =-,17,33GB AB AG ⎛⎫=-=- ⎪⎝⎭20.(2023·全国·高三专题练习)已知向量a →=(1,2),b →=(-3,k ).(1)若a →∥b →,求b →的值;(2)若a →⊥(a →+2b →),求实数k 的值;(3)若a →与b →的夹角是钝角,求实数k 的取值范围.【答案】(2)k =14;(3)k <32且k ≠-6.【解析】 【分析】(1)解方程1×k -2×(3)-=0即得解; (2)解方程1×(5)-+2×(22)k +=0即得解; (3)解不等式1×(3)-+2×k <0且k ≠-6,即得解. (1)解:因为向量a →=(1,2),b →=(-3,k ),且a →∥b →, 所以1×k -2×(3)-=0,解得k =-6,所以b →(2)解:因为a →+2b →=(5,22)k -+,且a →⊥(2)a b →→+,所以1×(5)-+2×(22)k +=0,解得k =14.(3)解:因为a →与b →的夹角是钝角,则a b →→⋅<0且a →与b →不共线.即1×(3)-+2×k <0且k ≠-6,所以k <32且k ≠-6.21.(2022·全国·高三专题练习)已知平行四边形ABCD 的三个顶点A 、B 、C 的坐标分别是(-2,1)、(-1,3)、(3,4). 若Q 是线段BC 上的动点,求·AQ DQ 的最值 【答案】最小值614- ,最大值57. 【解析】 【分析】根据平行四边形,求出D 点的坐标,分别求出AQ DQ 的解析式, 根据解析式求出最值,再综合考虑即可. 【详解】依题意作上图,点D 的位置有3个,分别为12,,D D D ,下面分别求出这3个位置的坐标:设(),D x y ,则有()()1,23,4AB DC x y ===-- ,解得()2,2,2,2x y D ==∴ ;()(),1,23,4AB CD x y ==-- ,解得()14,6,4,6x y D === ; ()(),4,12,1BC DA x y ==--- ,解得()26,0,6,0x y D =-=- ;∵点Q 在BC 上,设(),,Q m n BQ BC λ= ,则有()()1,34,1m n λ+-= , 41,3m n λλ=-=+ ([]0,1λ∈) ,()41,2AQ λλ=++ ,()43,1DQ λλ=-+ ,()145,3DQ λλ=-- , ()245,3D Q λλ=++ ,21751AQ DQ λλ=-- ,当534λ=时,取最小值=9368- ,最大值=11;21171711AQ DQ λλ=-- ,当12λ= 时,取最小值=614-,最大值=-11; 22172911AQ D Q λλ=++,当0λ= 时,取最小值=11,最大值=57;所以在以A ,B ,C 为顶点的平行四边形中,AQ DQ 的最小值为614-,最大值为57;综上,最小值为614-,最大值为57. 22.(2017·江苏·高考真题)已知向量()([]330a cosx sinx b x π==-∈,,,,,. (1)若a b ,求x 的值;(2)记()f x a b =⋅,求函数y =f (x )的最大值和最小值及对应的x 的值.【答案】(1)5π6x =(2)0x =时,()f x 取到最大值3; 5π6x =时,()f x 取到最小值- 【解析】 【分析】(1)根据a b ,利用向量平行的充要条件建立等式,即可求x 的值.(2)根据()f x a b =⋅求解求函数y =f (x )解析式,化简,结合三角函数的性质即可求解最大值和最小值及对应的x 的值. 【详解】解:(1)∵向量()([]330a cosx sinx b x π==-∈,,,,,. 由a b ,可得:3sinx =,即tanx = ∵x ∈[0,π] ∴56x π=.(2)由()233f x a b cosx x π⎛⎫=⋅==+ ⎪⎝⎭∵x ∈[0,π],∴225333x πππ⎡⎤+∈⎢⎥⎣⎦,∴当2233x ππ+=时,即x =0时f (x )max =3;当2332x ππ+=,即56x π=时()min f x =-。
七年级第六章平面直角坐标系单元测试题(含答案)-(K12教育文档)

七年级第六章平面直角坐标系单元测试题(含答案)-(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级第六章平面直角坐标系单元测试题(含答案)-(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级第六章平面直角坐标系单元测试题(含答案)-(word版可编辑修改)的全部内容。
第六章平面直角坐标系单元测试题(时间:45分钟 满分:100分)姓名________一、选择题(每小题3分,共18分)1.课间操时,小华、小军、小刚的位置如图,小华对小网说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )A .(5,4)B .(4,5)C .(3,4)D .(4,3)小华小军小刚(第1题图) (第2题图) (第7题图) 2.如图,下列说法正确的是( )A .A 与D 的横坐标相同。
B .C 与D 的横坐标相同。
C .B 与C 的纵坐标相同。
D .B 与D 的纵坐标相同。
3.若x 轴上的点P 到y 轴的距离为3,则点P 的坐标为( ) A .(3,0) B .(3,0)或(–3,0)C .(0,3)D .(0,3)或(0,–3)4.如果点P(5,y)在第四象限,则y 的取值范围是( ) A .y <0 B .y >0 C .y ≤0 D .y ≥05.线段CD 是由线段AB 平移得到的,点A (–1,4)的对应点为C (4,7),则点B (—4,–1)的对应点D 的坐标为( )A .(2,9)B .(5,3)C .(1,2)D .(– 9,– 4)6.一个长方形在平面直角坐标系中三个顶点的坐标为(–1,–1)、(–1,2)、(3,–1),则第四个顶点的坐标为( )A.(2,2) B.(3,2) C.(3,3) D.(2,3)二、填空题(每小题3分,共12分)7.如图是小刚画的一张脸,他对妹妹说“如果我用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成 .8.点A在x轴上,位于原点的右侧,距离坐标原点5个单位长度,则此点的坐标为;点B在y轴上,位于原点的下方,距离坐标原点5个单位长度,则此点的坐标为;点C在y轴左侧,在x轴下方,距离每个坐标轴都是5个单位长度,则此点的坐标为。
数学八年级上浙教版6.2平面直角坐标系同步练习1

6.2 平面直角坐标系 同步练习1、在坐标平面内,〔1〕x 轴上点的纵坐标有什么特点? 〔2〕y 轴上点的横坐标有什么特点?〔3〕第一、三象限角平分线上点的坐标有什么特点? 〔4〕第二、四象限角平分线上点的坐标有什么特点?2、平面直角坐标系的建立是在平面内取______两条数轴;取______为正方向;两条数轴的______一样;所有横标为O 的点在______上; 所有纵标为O 的点在______上;所有横、纵坐标相等的点在______上;所有横、纵坐标互为相反数的点在______上;P(x ,y)为第一象限内的点,那么x______,y______; P(x ,y)为第二象限内的点,那么x______,y______;P(x ,y)为第三象限内的点,那么x_______,y______; P(x ,y)为第四象限内的点,那么x______,y______.3、P 〔x ,y 〕是平面直角坐标系内的点,写出它的坐标满足的条件。
〔1〕在x 轴上 ; 〔2〕在第四象限 ;〔3〕在二、四象限的角的平分线上 ;4、在平面直角坐标系中,P 〔-3,4〕关于轴的对称点Q 的坐标是 ,关于轴的对称点R 的坐标是 ,点Q 和点R 关于 对称。
5、函数x x y -+-=321的自变量x 的取值范围是 。
6、点P 在第二象限,且到x 轴的距离是2,到y 轴的距离是3,那么点P 的坐标为_____________。
7、假设点M 〔1-x ,x+2〕在第二象限内,那么x 的取值范围为 。
8、点P 〔2a-8,2-a 〕是第三象限的整点那么P 点的坐标是 。
9、点(a ,-2)与点B(31,b)关于y 轴对称,那么a= ,b= 。
10、点Q 〔2m 2+4,m 2+m+6〕在第一象限的角平分线上,那么m = 。
11、点A(3,0),B(-1,0)两点,分别以A 、B 两点为圆心的两圆相交于点M(a-1,-2)、N(1,2b-2a),那么a= ,b= 。
八年级数学上册6.2平面直角坐标系同步练习2

6.2 平面直角坐标系 同步练习1、画一个直角坐标系;并在坐标系中描出下列各点:A (–2;0)B (3;–2)C (0;4)D (–1;–2)E (0;–2)求出下列线段的长:AC__________ ;AD=` ___________ ;CE=___________ ;BD=____________ 。
2、x 轴上的点的特点是________________________;y 轴上的点的特点是________________; 分别说出各象限点的特点是____________________________________________________。
3、坐标系中到两轴距离相等的点的坐标的特点是__________________________________;这些点在直线_____________________上。
4、说出下列点所在的位置:A (m 2+1;|m|)B (2-a ;0)5、若点(212,323-+-m m )在第三象限;则m 的取值范围是_____________。
6、在第一象限到x 轴距离为4;到y 轴距离为7的点的坐标是______________;在第四象限到x 轴距离为5;到y 轴距离为2的点的坐标是________________;在第二象限到x 轴距离为a ;到y 轴距离为b 的点的坐标是________________。
7、在x 轴上到原点距离为3的点的坐标为________________;到(–2;0)距离为5个单位的点的坐标是_____________;到)0,38(-距离4.5个单位的点的坐标为_______________。
8、点(1;0)(4;0)的中点的坐标为__________;点(–2;0)(7;0)的中点坐标为________。
9、点(–1;0)(5;0)关于直线________对称;点(4;0)(–2;0)关于直线______对称。
数学八年级上浙教版6.2平面直角坐标系同步练习3

6.2 平面直角坐标系 同步练习一、填空:1、点A 的坐标是〔-2,3〕,那么它在第 象限。
2、点P 〔4,-6〕x 轴的距离是 ,到y 轴的距离是_____;M(-5,4〕到x 轴的距离是_____,到y 轴的距离是_____。
3、当x= 时,点M 〔2x-4,6〕在y 轴上。
4、当x= 时,A 〔4,x+2〕与B(-3,6-3x)的连线平行于x 轴。
假设P 〔a, 3-b 〕,Q(5, 2)关于x 轴对称,那么a=___,b=___5、点P 在第二象限,且到x 轴的距离是2,到y 轴的距离是3,那么P 点坐标为___________6、直角坐标系中,点A 〔2,1〕向左平移4个单位长度,再向下平移2个单位长度后的坐标为 。
7、点P 〔x,y 〕满足()02y 2x 2=++- ,那么点P 的坐标在第 象限。
8、△ABC 的三个顶点的坐标为A(-5,2)、B(1,2)、C(3,-1),那么△ABC 的面积为 。
9.假设点A 〔a-1,a 〕在第二象限,那么点B 〔a,1-a 〕在第 象限。
10.假设点M 〔a,b 〕在第四象限,那么点M 〔b -a,a -b 〕在第 象限. 假设点 A(a ,b 〕在第三象限,那么点 C 〔-a+1,3b -5〕在第_____________象限.11.点P(3,-4〕关于y 轴的对称点坐标为_______,它关于x 轴的对称点坐标为_______.它关于原点的对称点坐标为_______.二、选择题:1、点A 〔0,-2〕在 〔 〕A 、x 轴上B 、y 轴上C 、第三象限D 、第四象限2、在直角坐标系中,点A 〔3,1〕和点B 〔3,3〕,那么线段AB 的中点坐标是〔 〕A 、〔2,3〕B 、〔3,2〕C 、〔6,2〕D 、〔6,4〕3、点A 〔-3,-4〕到原点的距离为〔 〕A 、3B 、4C 、5D 、74、点A(2x-4,x+2)在y 轴上,那么x 的值等于〔 〕A 、2B 、-2C 、2或-2D 、非上述答案点5、 P 〔m ,1〕在第二象限内,那么点Q 〔-m ,0〕在〔 〕A .x 轴正半轴上B .x 轴负半轴上C .y 轴正半轴上D .y 轴负半轴上6、假设a >0,b <-2,那么点〔a ,b+2〕应在〔 〕A .第一象限B .第二象限C .第三象限D 第四象限7、在平面直角坐标系中,A 、B 、C 三点的坐标分别为〔0,0〕,〔0,-5〕,〔-2,-2〕,以这三点为平行四边形的三个顶点,那么第四个顶点不可能在〔 〕A.第一象限B.第二象限C.第三象限D.第四象限三、解答题:1、在直角坐标系中描出以下各组的点,并将各组的点用线段依次连接起来:⑴(0,0),(2,1),(4,0),(2,-1),(0,0); ⑵(0,0),(1,2),(0,4),(-1,2),(0,0);⑶(0,0),(-2,1),(-4,0),(-2,-1),(0,0) ⑷(0,0),(-1,-2),(0,-4),(1,-2),(0,0)观察所得的图形,其形状如同。
数学八年级上浙教版6.2平面直角坐标系同步练习6

6.2 平面直角坐标系 同步练习〔1〕点A 在y 轴右侧,距y 轴6个单位长度,距轴8个单位长度,那么A 点的坐标是 ,A点离开原点的距离是 。
〔2〕点〔-3,2〕,〔,1+a 〕在函数1-=kx y 的图像上,那么______,==a k 〔3〕正比例函数的图像经过点〔-3,5〕,那么函数的关系式是 。
〔4〕函数25+-=x y 与x 轴的交点是 ,与y 轴的交点是 。
与两坐标轴围成的三角形面积是 。
〔5〕函数25+-=x y 与x 轴的交点是 ,与y 轴的交点是 。
6〕y 与4x-1成正比例,且当x=3时,y=6,写出y 与x 的函数关系式 。
〔7〕写出以下函数关系式①速度60千米的匀速运动中,路程S 与时间t 的关系②等腰三角形顶角y 与底角x 之间的关系③汽车油箱中原有油100升,汽车每行驶50千米耗油9升,油箱剩余油量y 〔升〕与汽车行驶路程x 〔千米〕之间的关系④矩形周长30,那么面积y 与一条边长x 之间的关系在上述各式中, 是一次函数, 是正比例函数〔只填序号〕〔8〕正比例函数的图像一定经过点 。
〔9〕假设点〔3,〕在一次函数13+=x y 的图像上,那么=a 。
〔10〕一次函数1-=kx y 的图像经过点〔-3,0〕,那么k= 。
〔11〕某地的 月租费24元,通话费每分钟0.15元,那么每月话费y 〔元〕与通话时间x 〔分钟〕之间的关系式是 ,某居民某月的 费是38.7元,那么通话时间是 分钟,假设通话时间62分钟,那么 费为 元。
〔12〕y 与2x+1成正比例,且当x=3时,y=6,写出y 与x 的函数关系式 。
〔13〕个人出幅员书获得的稿费的纳税计算方法是:稿费不高于800元的不纳税;稿费高于800元又不高于4000元的应缴纳超过800元的那一局部稿费的14%的税;稿费高于4000元的应缴纳全部稿费的11%的税。
假设某人获得一笔稿费后,缴纳个人所得税420元,那么稿费 元,假设缴税为280元,稿费为 元。
