离散系统频率响应和零极点分布实验报告
零极点分布对系统频率响应的影响
1.由y(n)=x(n)+ay(n-1)可知:H[z]=B[z]/A[z]=1/(1-az^(-1))。系统极点z=a，零点z=0。取单位圆上一点B，可画出极点矢量和零点矢量，当B点从ω=0逆时针旋转时，在ω=0点，极点向量长度最短，所以幅度值最大，形成波峰，并且当a越大，即极点越接近单位圆，峰值愈高愈尖锐；当ω=时极点矢量最长，幅度值最小，形成波谷；零点在坐标原点，零点矢量长度始终保持为1，不影响幅频响应。
实验图像：
%a=0.8
B=1;a=0.8;A=[1,-a];%设置系统函数系数向量A和B
subplot(2,2,1);
zplane(B,A);%绘制零极点分布图
[H,w]=freqz(B,A, 'whole');%计算频率响应
subplot(2,2,2);
plot(w/pi,abs(H));grid on;%绘制幅频响应曲线
xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');
subplot(2,2,4);
plot(w/pi,angle(H));%绘制相频响应曲线
xlabel('\omega/\pi');ylabel('\phi(\omega)');
grid on;
实验图像：
%a=0.9
H_min=min(abs(H))%计算谷值
w_min=w(find(H_min==abs(H)))%计算谷值对应的频率
subplot(2,2,2);
plot(w/pi,abs(H));grid on;%绘制幅频响应曲线
ax=axis;hold on;
数字信号处理实验4
实验4 离散时间系统的频域分析一、实验目的（1）了解离散系统的零极点与系统因果性和稳定性的关系； （2）加深对离散系统的频率响应特性基本概念的理解； （3）熟悉MATLAB 中进行离散系统零极点分析的常用子函数； （4）掌握离散系统幅频响应和相频响应的求解方法。
二、知识点提示本章节的主要知识点是频率响应的概念、系统零极点对系统特性的影响；重点是频率响应的求解方法；难点是MATLAB 相关子函数的使用。
三、实验原理1．离散时间系统的零极点及零极点分布图设离散时间系统系统函数为NMzN a z a a z M b z b b z A z B z H ----++++++++==)1()2()1()1()2()1()()()(11 (4-1) MATLAB 提供了专门用于绘制离散时间系统零极点图的zplane 函数： ①zplane 函数 格式一：zplane(z, p)功能：绘制出列向量z 中的零点(以符号"○" 表示)和列向量p 中的极点(以符号"×"表示)，同时画出参考单位圆，并在多阶零点和极点的右上角标出其阶数。
如果z 和p 为矩阵，则zplane 以不同的颜色分别绘出z 和p 各列中的零点和极点。
格式二：zplane(B, A)功能：绘制出系统函数H(z)的零极点图。
其中B 和A 为系统函数)(z H (4-1)式的分子和分母多项式系数向量。
zplane(B, A) 输入的是传递函数模型，函数首先调用root 函数以求出它们的零极点。
②roots 函数。
用于求多项式的根，调用格式：roots(C)，其中C 为多项式的系数向量，降幂排列。
2．离散系统的频率特性MATLAB 提供了专门用于求离散系统频响特性的freqz 函数，调用格式如下： ①H = freqz(B,A,W)功能：计算由向量W (rad )指定的数字频率点上(通常指[0,π]范围的频率)离散系统)(z H 的频率响应)e (j ωH ，结果存于H 向量中。
零极点分布对系统频率响应的影响
subplot(2,2,1);
zplane(B,A);%绘制零极点分布图
[H,w]=freqz(B,A,'whole');%计算频率响应
subplot(2,2,2);
plot(w/pi,abs(H));grid on;%绘制幅频响应曲线
实验图像：
%a=0.8
B=1;a=0.8;A=[1,-a];%设置系统函数系数向量A和B
subplot(2,2,1);
zplane(B,A);%绘制零极点分布图
[H,w]=freqz(B,A,'whole');%计算频率响应
subplot(2,2,2);
plot(w/pi,abs(H));grid on;%绘制幅频响应曲线
五、实验过程原始记录（数据、图表、计算等）
1.%a=0.7
B=1;a=0.7;A=[1,-a];%设置系统函数系数向量A和B
subplot(2,2,1);zplane(B,A);%绘制零极点分布图
[H,w]=freqz(B,A,'whole');%计算频率响应
subplot(2,2,2);plot(w/pi,abs(H));%绘制幅频响应曲线
grid on;%网格效果
xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|');
subplot(2,2,4);plot(w/pi,angle(H));%绘制相频响应曲线
xlabel('\omega/\pi');ylabel('\phi(\omega)');
零极点分布对系统频率响应的影响
实验三零极点分布对系统频率响应的影响
一.实验目的
学习用分析零极点分布的几何方法分析研究信号和系统频率响应
. 二. 实验原理
1. 对(序列)信号x(n)进行ZT, 得X(z), 从而得到它的零极点分布
. 2. 对(离散)系统, 求出它的系统函数
H(z) , 也可得到它的零极点分布. 3. 按教材(3.6.13)式, 信号或系统的幅度特性由零点至单位圆周上的矢量长度和极点至单位圆周上的矢量长度之比
. 4. 极点影响频率特性的峰值
, 零点影响频率特性的谷值. 零极逾靠近单位圆
, 这些特征越明显. 如有极点410.9j z e , 则频率特性曲线在4
处出现峰值. 5. 本实验借助于计算机分析信号或系统的频率响应
, 目的是掌握用极、零点分布的几何分析法分析频率响应, 实验时需并j z e 代入相应的X(z) 或H(z) 中, 再在0~2中等
间隔的取点. 如100等分:w=[0:2*pi/100:2*pi], 再用plot 等函数作出|()|j H e 图形.
三. 实验内容
1. 设系统为()()(1)y n x n ay n , 试就0.7,0.8,0.9a , 分别在三种情况下分析系统的频率特性, 并作出幅度特性曲线
., 并作出高, 低通等判断.
2. 假设系统为: ()
1.273(1)0.81(2)()(1)y n y n y n x n x n 试分析它的频率特性
, 作出它的幅-频曲线, 估计其峰值频率和谷值频率
. 四. 实验报告要求1. 总结零、极点分布对频率响应的影响;
2. 总结零、极点分布对系统的高通、低通的影响.。
离散系统频率响应和零极点分布实验报告
输出参数：h是计算所得的频率响应值；f是在0到fs/2频率范围内的频率值。
2.系统的有理分式形式转化成零极点增益形式的函数
[z,p,k]=tf2zp(b,a)
y[k]-1.6y[k-1]+1.28y[k-2]=0.5x[k]+0.1x[k-1]
(1)编程求此系统的单位脉冲响应序列，并画出其波形。
(2)若输出序列x[k]=δ[k]+2δ[k-1]+3δ[k-2]+4δ[k-3]+5[k-4]),编程求此系统输出序列y[k]，并画出其波形。
(3)编程得到系响应的幅度响应和相位响应，并画出图。
4.绘制离散系统零极点图函数
zplane(b,a)
zplane(z,p,k)
输入参数：b,a,z,p,k与tf2zp相同
zplane(b,a)画出以矢量b和a描述的离散时间系统的零极点图。
zplane(z,p,k)画出以零点矢量z和极点矢量p以及增益k描述的离散时间的零极点图。
三、实验程序
一个LTI离散时间系统的输入输出差方方程为
(4)编程得到系统的零极点分布图，分析系统的因果性和稳定性。
（1）
n=0:30
a=[1,-1.6,1.28]
b=[0.5,0.1]
y=impz(b,a,n)
STEM(y)
TITLE('输入信号')
xlabel('时间序列')
ylabel('信号幅度')
（2）
x=[1,2,3,4,5,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0];
离散系统频率响应和零极点分布(杭电)
信号、系统与信号处理实验Ⅱ实验报告实验名称：离散系统频率响应和零极点分布一、实验目的通过MATLAB仿真简单的离散时间系统，研究其时域特性，加深对离散系统的冲激响应，频率响应分析和零、极点分布的概念的理解。
二、实验内容与要求考一个LTI离散时间系统的输入输出差分方程为y(n)-1.6y(n-1)+1.28y(n-2) =0.5x(n)+0.1x(n-1)（1）编程求出此系统的单位冲激响应序列，并画出其波形。
（2）若输入序列x(n)=δ(n)+2δ(n-1)+3δ(n-2)+4δ(n-3)+5δ(n-4),编程求此系统输出序列y(n),并画出其波形。
（3）编程得到系统频响的幅度响应和相位响应，并画图。
（4）编程得到系统的零极点分布图，分析系统的因果性和稳定性。
系统2：y(n)=0.45x(n)+0.5x(n-1)+0.45x(n-2)+0.53y(n-1)-0.46y(n-2)输入x(n)=cos(20πn/256)+cos(200πn/256)0＜n＜299（5）编程得到系统频响的幅度响应和相位响应，并画图。
（6）编程得到系统的零极点分布图，分析系统的因果性和稳定性。
三、实验程序与结果1、N=40;num=[0.5 0.1 0];den=[1 -1.6 1.28];y=impz(num,den,N);stem(y);n幅度单位冲激响应2、 n=0:49;x=[1 2 3 4 5 zeros(1,45)]; num=[0.5 0.1]; den=[1 -1.6 1.28]; y=filter(num,den,x);stem(y);ny3、 fs=1000;num=[0.5 0.1]; den=[1 -1.6 1.28];[h,f]=freqz(num,den,256,fs); mag=abs(h); ph=angle(h); ph=ph*180/pi;subplot(2,1,1),plot(f,mag); xlabel('频率'); ylabel('幅度');subplot(2,1,2),plot(f,ph); xlabel('频率'); ylabel('相位');频率幅度频率相位4、num=[0.5 0.1]; den=[1 -1.6 1.28];[z,p,k]=tf2zp(num,den); zplane(z,p);Real PartI m a g i n a r y P a r t5、 fs=1000;num=[0.45 0.5 0.45]; den=[1 -0.53 0.46];[h,f]=freqz(num,den,256,fs);mag=abs(h); ph=angle(h); ph=ph*180/pi;subplot(2,1,1),plot(f,mag); xlabel('频率'); ylabel('幅度');subplot(2,1,2),plot(f,ph); xlabel('频率'); ylabel('相位');频率幅度频率相位6、num=[0.45 0.5 0.45]; den=[1 -0.53 0.46]; [z,p,k]=tf2zp(num,den); zplane(z,p);Real PartI m a g i n a r y P a r t四、仿真结果分析对于系统y(n)-1.6y(n-1)+1.28y(n-2) =0.5x(n)+0.1x(n-1) ，由图4可知，零点在单位圆内，所以是因果的；极点在单位圆外，所以是不稳定的。
信号与系统实验报告——零级图(含程序)
电 子 科 技 大 学实 验 报 告学生姓名：苏晓菁 学 号：2804301026 指导教师：张鹰 一、实验室名称：信号与系统实验室二、实验项目名称：离散系统的转移函数，零、极点分布和模拟 三、实验原理：离散系统的时域方程为∑∑==-=-Mm m Nk km n x b k n y a][][其变换域分析方法如下：系统的频率响应为 ωωωωωωωjN N j jM M j j j j e a e a a e b e b b e A e B e H ----++++++==......)()()(1010 Z 域 )()()(][][][][][z H z X z Y m n h m x n h n x n y m =⇔-=*=∑∞-∞=系统的转移函数为 NN MM z a z a a z b z b b z A z B z H ----++++++==......)()()(110110 分解因式 ∏∏∑∑=-=-=-=---==Ni i Mi i N i i kMi ik z z Kz a zb z H 11110)1()1()(λξ ，其中i ξ和i λ称为零、极点。
在MATLAB 中，可以用函数[z,p,K]=tf2zp （num,den ）求得有理分式形式的系统转移函数的零、极点，用函数zplane （z ，p ）绘出零、极点分布图；也可以用函数zplane （num ，den ）直接绘出有理分式形式的系统转移函数的零、极点分布图。
四、实验目的：目的：1、加深对离散系统转移函数、零极点概念的理解；2、根据系统转移函数求系统零极点分布。
五、实验内容：实验内容（一）、使用实验仿真系统实验内容（二）、MATLAB 仿真六、实验器材（设备、元器件）：计算机、MATLAB 软件。
七、实验步骤：实验内容（一）、使用实验仿真系统1、 在MATLAB 环境下输入命令 >>xhxt启动《信号与系统》MATLAB 实验工具箱。
实验离散系统的频率响应分析研究和零点
实验3离散系统地频率响应分析和零、极点分布一、 实验目地（1） 熟悉对离散系统地频率响应分析方法； （2） 加深对零、极点分布地概念理解. 二、 实验原理 离散系统地时域方程为∑∑==-=-Mk kNk kk n x pk n y d)()(其变换域分析方法如下： 频域)()()(][][][][][ΩΩ=Ω⇔-=*=∑∞-∞=H X Y m n h m x n h n x n y m系统地频率响应为 Ω-Ω-Ω-Ω-++++++=ΩΩ=ΩjN N j jM M j ed e d d e p e p p D p H ......)()()(1010 Z 域)()()(][][][][][z H z X z Y m n h m x n h n x n y m =⇔-=*=∑∞-∞=系统地转移函数为 NN M M zd z d d z p z p p z D z p z H ----++++++==......)()()(110110分解因式 ∏-∏-=∑∑==-=-=-=-Ni i Mi i Ni ik Mi ik z z Kzd z p z H 11110)1()1()(λξ，其中，i ξ和i λ称为零、极点. 三、 预习要求在MATLAB 中，熟悉函数tf2zp 、zplane 、freqz 、residuez 、zp2sos 地使用，其中：[z ，p ，K]=tf2zp （num ，den ）求得有理分式形式地系统转移函数地零、极点；zplane （z ，p ）绘制零、极点分布图； h=freqz(num,den,w )求系统地单位频率响应；[r ，p ，k]=residuez （num ，den ）完成部分分式展开计算； sos=zp2sos （z ，p ，K ）完成将高阶系统分解为2阶系统地串联.（2）阅读附录中地实例，学习频率分析法在MATLAB 中地实现； （3）编程实现系统参数输入，绘出幅度频率响应和相位响应曲线和零、极点分布图.四、 实验内容 求系统54321543212336.09537.08801.14947.28107.110528.0797.01295.01295.00797.00528.0)(-----------+-+-+++++=zz z z z z z z z z z H 地零、极点和幅度频率响应和相位响应. 附录：例1求下列直接型系统函数地零、极点，并将它转换成二阶节形式解 用MATLAB 计算程序如下： num=[1 -0.1 -0.3 -0.3 -0.2]; den=[1 0.1 0.2 0.2 0.5];[z,p,k]=tf2zp(num,den);m=abs(p);disp('零点');disp(z);disp('极点');disp(p);disp('增益系数');disp(k);sos=zp2sos(z,p,k);disp('二阶节');disp(real(sos));zplane(num,den)输入到“num”和“den”地分别为分子和分母多项式地系数.计算求得零、极点增益系数和二阶节地系数：零点0.9615-0.5730-0.1443 + 0.5850i-0.1443 - 0.5850i极点0.5276 + 0.6997i0.5276 - 0.6997i-0.5776 + 0.5635i-0.5776 - 0.5635i增益系数1二阶节1.0000 -0.3885 -0.5509 1.0000 1.1552 0.65111.0000 0.2885 0.3630 1.0000 -1.0552 0.7679 系统函数地二阶节形式为：极点图见图.例2 差分方程所对应地系统地频率响应.解差分方程所对应地系统函数为：3213216.045.07.0102.036.044.08.0)(--------+++-=zz z z z z z H 用MATLAB 计算地程序如下：k=256;num=[0.8 -0.44 0.36 0.02]; den=[1 0.7 -0.45 -0.6]; w=0:pi/k:pi;h=freqz(num,den,w);subplot(2,2,1);plot(w/pi,real(h));gridtitle('实部')xlabel('\omega/\pi');ylabel('幅度')subplot(2,2,2);plot(w/pi,imag(h));gridtitle('虚部')xlabel('\omega/\pi');ylabel('Amplitude')subplot(2,2,3);plot(w/pi,abs(h));gridtitle('幅度谱')xlabel('\omega/\pi');ylabel('幅值')subplot(2,2,4);plot(w/pi,angle(h));gridtitle('相位谱')xlabel('\omega/\pi');ylabel('弧度')版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.RTCrp。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验报告
课程名称数字信号处理实验
实验名称离散系统频率响应和零极点分布
学生姓名
学生学号
学生班级
实验日期
实验目的：通过matlab仿真简单的离散时间系统，研究其的时频域特性，加深对离散系统的频率响应分析和零、极点分布的概念理解。
实验原理：离散系统的时域方程为
∑∑
= =-
=
-
M
k k
N
k
k
k
n
x
p
k
n
y
d
)
(
)
(
其变换域分析方法如下：
频域
)
(
)
(
)
(
]
[
]
[
]
[
]
[
]
[ω
ω
ωj
j
j
m
e
H
e
X
e
Y
m
n
h
m
x
n
h
n
x
n
y=
⇔
-
=
*
=∑∞
-∞
=
系统的频率响应为
ω
ω
ω
ω
ω
ω
ω
jN
N
j
jM
M
j
j
j
j
e
d
e
d
d
e
p
e
p
p
e
D
e
p
e
H
-
-
-
-
+
+
+
+
+
+
=
=
...
...
)
(
)
(
)
(
1
1
Z域
)
(
)
(
)
(
]
[
]
[
]
[
]
[
]
[z
H
z
X
z
Y
m
n
h
m
x
n
h
n
x
n
y
m
=
⇔
-
=
*
=∑∞
-∞
=
系统的转移函数为
N
N
M
M
z
d
z
d
d
z
p
z
p
p
z
D
z
p
z
H
-
-
-
-
+
+
+
+
+
+
=
=
...
...
)
(
)
(
)
(
1
1
1
1
分解因式
∏-
∏-
=
∑
∑
=
=
-
=
-
=
-
=
-
N
i
i
M
i
i
N
i
i
k
M
i
i
k
z
z
K
z
d
z
p
z
H
1
1
1
1
)
1(
)
1(
)
(
λ
ξ
，其中i
ξ
和i
λ
称为零、极
点。
在MATLAB中，可以用函数[z，p，K]=tf2zp（num，den）求得有理分式形式的系统转移函数的零、极点，用函数zplane（z，p）绘出零、极点分布图；也可以用函数zplane（num，den）直接绘出有理分式形式的系统转移函数的零、极点分布图。
另外，在MATLAB中，可以用函数 [r，p，k]=residuez（num，den）完成部分分式展开计算；可以用函数sos=zp2sos（z，p，K）完成将高阶系统分解为2阶系统的串联。
实验内容：一个LTI离散时间系统的输入输出差分方程为
y(n)-1.6y(n-1)+1.28y(n-2) =0.5x(n)+0.1x(n-1)
实验要求：(1)编程求出此系统的单位冲激响应序列，并画出其波形。
（2）若输入序列x(n)=δ(n)+2δ(n-1)+3δ(n-2)+4δ(n-3)+5δ
(n-4),編程求此系統輸出序列y(n),并画出其波形。
（3）编程得到系统频响的幅度响应和相位响应，并画图。
（4）编程得到系统的零极点分布图，分析系统的因果性和稳定性。
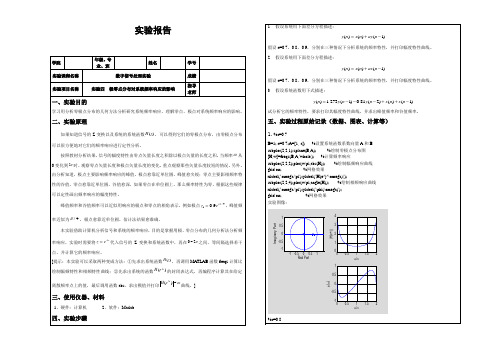
实验过程：
（1）编程求此系统的单位冲激响应序列，并画出其波形
程序
输出波形
（2）若输入序列x(n)=δ(n)+2δ(n-1)+3δ(n-2)+4δ(n-3)+5δ(n-4)，编程求此系统输出序列y(n),并画出其波形程序。
输出序列：
（3）编程得到系统频响的幅度响应和相位响应，并画图。
程序：
输出波形：
（4）编程得到系统的零极点分布图，分析系统的因果性和稳定性。
程序：
输出波形：
由上图可知，此系统是因果不稳定的，因为它是右边信号，所以其是因果的；因为它不包含单位圆，所以其是不稳定的。