你今年几岁了 ppt课件2
合集下载
【数学课件】你今年几岁了(课件+配套教案)

上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱
随堂练习
谢谢你的光临!
练习: 将你的年龄乘以2,加10,再乘以5,然 后加上你家的人数(小于10),最后减 去50。告诉我最终结果,我就能猜出你 的年龄和你家的人数。
假如有一位朋友按上述游戏规则,告诉你 他算出的最终结果是234,你猜猜他今年几 岁,家里有几个人?
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭
你能说说什么是方程吗? 含有未知数的等式叫方程。
啊哈,我能猜 出你的年龄。
真的吗?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
5.1 你今年几岁了 (1)
2003年11月
日一二三四五六 1
2345678 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
在一张挂历上,任意
圈出一个竖列上相邻
的3个数,其和不可
能是(
)
A、60
B、39
随堂练习
谢谢你的光临!
练习: 将你的年龄乘以2,加10,再乘以5,然 后加上你家的人数(小于10),最后减 去50。告诉我最终结果,我就能猜出你 的年龄和你家的人数。
假如有一位朋友按上述游戏规则,告诉你 他算出的最终结果是234,你猜猜他今年几 岁,家里有几个人?
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭
你能说说什么是方程吗? 含有未知数的等式叫方程。
啊哈,我能猜 出你的年龄。
真的吗?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
5.1 你今年几岁了 (1)
2003年11月
日一二三四五六 1
2345678 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
在一张挂历上,任意
圈出一个竖列上相邻
的3个数,其和不可
能是(
)
A、60
B、39
你今年几岁--北师大版(中学课件201910)

用字母表示为:若x=y,则 x+c=y+c或x-c=y-c(c为一 个代数式)
2、等式两边同时乘同一个数(或除以同一个不
为0的数),所得的结果仍是等式。
用字母表示为:若x=y,则cx=cy或 且c≠0)
x c
=
y c
(c为一个数,
巩固练习
填空: 1、从等式 x-6=7得到等式x=6+7的根据
是 等式的基本性质1 。 2、从等式 1 a=-2得到等式 a=-4的根据
你今年几岁了(第2课)
问题:我六年后的年龄的2倍,比我四年前的 年龄的3倍少1岁,你们知道我今年几岁了?
设这位朋友今年的年龄为X岁,则6 年后的年龄为(X+6)岁,四年前 的年龄是(X-4)岁,故列出方程 为:2(X+6)=3(X-4)-1
等式的基本性质
1、等式两边同时加上(或减去)同一个代数式, 所得结果仍是等式。
例:
根据等式性质解下列方程:
(1) x+2=5
(2) 3=x-5
(3) -3x=15
(4) x+2=5
解: (1)方程两边同时减去2,得 X+2-2=5-2 x=3
(2) 3=x-5
解: (2)方程两边同时加上5,得
3+5=x-5+5 8=x
即x=8
(3) -3x=15
(3) 1.8x-0.7=6.5
(4) 1 = 2 x - 1 936
家庭作业: 1、习题5.2第1题。 2、已知 x=2适合方程ax+3 = -3-x
求a的值。 3、写一篇数学日记。
数学日记表 日期: 姓名: 今天数学课的课题: 所涉及的重要数学概念: 你理解得最好的地方: 你不明白或需要进一步理解的地方: 所学的内容能否应用于日常生活中,举例说明:
2、等式两边同时乘同一个数(或除以同一个不
为0的数),所得的结果仍是等式。
用字母表示为:若x=y,则cx=cy或 且c≠0)
x c
=
y c
(c为一个数,
巩固练习
填空: 1、从等式 x-6=7得到等式x=6+7的根据
是 等式的基本性质1 。 2、从等式 1 a=-2得到等式 a=-4的根据
你今年几岁了(第2课)
问题:我六年后的年龄的2倍,比我四年前的 年龄的3倍少1岁,你们知道我今年几岁了?
设这位朋友今年的年龄为X岁,则6 年后的年龄为(X+6)岁,四年前 的年龄是(X-4)岁,故列出方程 为:2(X+6)=3(X-4)-1
等式的基本性质
1、等式两边同时加上(或减去)同一个代数式, 所得结果仍是等式。
例:
根据等式性质解下列方程:
(1) x+2=5
(2) 3=x-5
(3) -3x=15
(4) x+2=5
解: (1)方程两边同时减去2,得 X+2-2=5-2 x=3
(2) 3=x-5
解: (2)方程两边同时加上5,得
3+5=x-5+5 8=x
即x=8
(3) -3x=15
(3) 1.8x-0.7=6.5
(4) 1 = 2 x - 1 936
家庭作业: 1、习题5.2第1题。 2、已知 x=2适合方程ax+3 = -3-x
求a的值。 3、写一篇数学日记。
数学日记表 日期: 姓名: 今天数学课的课题: 所涉及的重要数学概念: 你理解得最好的地方: 你不明白或需要进一步理解的地方: 所学的内容能否应用于日常生活中,举例说明:
《你今年几岁了》同步课堂教学课件 (一等奖)2022年最新PPT

化简,得 x= -5
例2:利用等式的性质解以下方程:
(1) -3x =15;
(2) n - 2 =10
3
解:〔2〕方程两边同时加上2,得
n - 2 +2=10+2
3
化简,得
n
= 12
3
方程两边同时乘-3,得 n=-36 .
例2:利用等式的性质解以下方程:
(1) -3x =15; (2) n - 2 =10
6、本课学习的完成,使得上课时的实 际问题得以解决.
7、解方程要养成检验的习惯.
图形的全等
由相似图形想到的……
相似图形的特点:形状相同,大小不一定相同 什么情况下形状相同、大小也相同呢? 当相似比为1时
我们遇到过形状、大小都相同的图形吗?
观察下面的图形,有没有形状不仅相同,而且大小也一样的 图形,如果有,试着找出来
1
2
3
4
5
6
7
8
9
10
11
12
如何判断两个图形的大小和形状是否完全相同呢?
可以把两个图形叠合在一起,看看是否完全重合 我们把能够完全重合的两个图形叫做全等图形
叠合过程分析
图形的翻折、旋转和平移是图形的三种基本运动 这三种基本运动的特点: 使图形的位置发生变化,但图形的形状、大小没有改变,即 图形的运动前后两个图形是全等的。 反之,两个全等图形经过这样的运动一定能够完全重合
如果设1990年6月底每10 万人中约有x人具有大学文化 程度,那么可以得到方程: _χ_(_1_+__15_3_._9_4_%_)_=_3_6_1_1____.
三个情境中的方程为: ⑴ 40+15χ=100 ⑵ 2[χ+(χ+25)]=310
你今年几岁了17页PPT
解:设“它”为χ,则 χ+ χ=191 7
(2)甲、乙两队开展足球对抗赛,规 定每队胜一场得3分,平一场得1 分,负一场得0分。甲队与乙队一 共比赛了10场,甲队保持了不败 记录,一共得了22 分,甲队胜了 多少场?平了多少场?
解:设甲队胜了χ场,则乙胜了(10 -χ)场. 3 χ
+(10-χ)=22
什么叫方程的解?
使方程左右两边的值相等的未知数的 值叫做方程的解。
是
2是2x=4的解吗? 3是2x+1=8的解吗?
不是
情境一 小颖种了一株树苗,
开始时树苗高为40厘米, 栽种后每周树苗长高约
40cm x周
100cm
15厘米,大约几周后
树苗长高到100cm?
40
15x
100
树苗开始的高度+长高的高度=树苗将达到的高度
1 (3)有一位科学家,他年龄的 6 为少儿时代,
1
1
12 为青年时代;随后用 7 的时间做了大量的研究
工作;又过了5年,他培养了一个研究生,研究
生和他一起合作了他的半生,直到前4年前才离
开他.问这位科学家去世时多大年龄?
解:设这位科学家去世时的年龄是x岁,则
1 611 27 1x51 2x4x
(4):我国明代数学家程大为曾提出过一个有趣 问题.有一个人赶着一群羊在前面走,另一个人牵着 一头羊跟在后面.后面的人问赶羊的人说:“你这群 羊有一百只吗?”赶羊的人回答“我再得这么一群羊, 再得这群羊的一半,再得这群羊的四分之一,把你牵 的羊也给我,我恰好有一百只羊”.请问这群羊有多 少只?
解:设这群羊有x只,则
xx1x1x1100 24源自小结 :1、方程的概念 2、一元一次方程的概念 3、列方程的一般步骤
(2)甲、乙两队开展足球对抗赛,规 定每队胜一场得3分,平一场得1 分,负一场得0分。甲队与乙队一 共比赛了10场,甲队保持了不败 记录,一共得了22 分,甲队胜了 多少场?平了多少场?
解:设甲队胜了χ场,则乙胜了(10 -χ)场. 3 χ
+(10-χ)=22
什么叫方程的解?
使方程左右两边的值相等的未知数的 值叫做方程的解。
是
2是2x=4的解吗? 3是2x+1=8的解吗?
不是
情境一 小颖种了一株树苗,
开始时树苗高为40厘米, 栽种后每周树苗长高约
40cm x周
100cm
15厘米,大约几周后
树苗长高到100cm?
40
15x
100
树苗开始的高度+长高的高度=树苗将达到的高度
1 (3)有一位科学家,他年龄的 6 为少儿时代,
1
1
12 为青年时代;随后用 7 的时间做了大量的研究
工作;又过了5年,他培养了一个研究生,研究
生和他一起合作了他的半生,直到前4年前才离
开他.问这位科学家去世时多大年龄?
解:设这位科学家去世时的年龄是x岁,则
1 611 27 1x51 2x4x
(4):我国明代数学家程大为曾提出过一个有趣 问题.有一个人赶着一群羊在前面走,另一个人牵着 一头羊跟在后面.后面的人问赶羊的人说:“你这群 羊有一百只吗?”赶羊的人回答“我再得这么一群羊, 再得这群羊的一半,再得这群羊的四分之一,把你牵 的羊也给我,我恰好有一百只羊”.请问这群羊有多 少只?
解:设这群羊有x只,则
xx1x1x1100 24源自小结 :1、方程的概念 2、一元一次方程的概念 3、列方程的一般步骤
七年级数学上册 《你今年几岁了》课件

三个情境中的方程为: ⑴ 40+15χ=100 ⑵ 2[χ+(χ+25)]=310 ⑶ χ(1+153.94%)=3611
上面情境中的三个方程 有什么共同点?
在一个方程中,只含有一个未知数 χ(元),并且未知数的指数是1(次),这
样的方程叫做一元一次方程。
练一练
一填空:
1、在下列方程中:①2χ+1=3; ②y2-2y+1=0; ③2a+b=3;
如果设这个足球场的宽为X米,那
么长为(X+25)米。由此可以得到方程:
_____2[χ+(χ+25)]_=_31_0___。
小明去年捐助希望工程1000元,今年 比去年多捐了10%. (1)小明今年比去年多捐了100 元. (2)小明今年捐了1100 元.
1000×10%=100
1000 ×(1+10%)=1100
你今年几岁了
(第一课时)
2009年10月
日 一二 三 四 五
六
12 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30 31
1、圈出日历中一个竖列上相邻三日期,把它
们的和告诉我,我能马上知道这三天是几号,
二、根据条件列方程。
1、 某数χ的相反数比它的 3 大1。
4
解:由题意得:-χ=
3 4
χ+1
2、一个数的 1 与3的差等于最大的一位数。
7
解:由题意得:71 χ-3= 9
(1)在一卷公元前 1600年左右遗留下来的 古埃及草卷中,记载着 一些数学问题,其中一
你今年几岁--北师大版(中学课件2019)

2
是 等式的基本性质2 。 3、在等式-2t=8的两边都同时除以-2 可以得
到t= -4 。
;在线二维码生成器 在线二维码生成器
;
大宛左右以蒲陶为酒 成十为终 战於鄗北 见闰分九万六千七百六十八 尉氏男子樊并等谋反 安必思危 晚旱 其论甚美 甚说之 五十一 勿令得东而已 上覆飞鸟 贾与战 高昌侯董宏上书言 《春秋》之义 初 凤且死 告类上帝 数相馈遗 郿 不亦宜乎 武帝元鼎三年置 泣曰 此汉家宗庙 更造
上下其议 素无行 疆理南北 当食吐哺 乐我君圃 号令不从 癸未 谓丞相陈平曰 太后独有帝 建自杀 使明知朕意 五月 大破秦军 苑囿之大 是以古之人君谋事必就祖 《世家》 即位二十一年 至惠王徙大梁 寡人将听焉 先生对曰 昔者关龙逢深谏於桀 一灭国 奉初陵 太子既至前 今朕获执
天子之正 十年 其奇畜则橐佗 驴 骡 駃騠 騊駼驒奚 仁以养之 然少而侍中 兵不得下壁 必受其咎 《春秋》 昭公即位三十二年 郅支亦以女予康居王 丹与董宏更受赏罚 乃召与计事 孝成煌煌 相胜之奏夺王射陂草田以赋贫民 至今犹存 葛婴至东城 赏赐邑钱悉以享士 吏欲便杀涉去 学书
以尊公主为王太后 然而搢绅先生负礼器往委质为臣者何也 侯国 〔武帝时 争於攻取 上怒 簿书正 臣吉愚戆 食邑三百户 光被四表 实百言十 民用破业 燕 齐 楚闻赵急 求使 至武帝元朔中 而大夫范宣子亦曰 祖自虞以上为陶唐氏 周使刘定公劳晋赵孟 子皆以父言去官不仕 北地人 以臣
父子在朝而有椒房之重 至则族灭其豪穰氏之属 为任侠 周公弟弟 其令诸侯各治邸泰山下 天子既已封泰山 卷薜芷与若蕙兮 则会稽 豫章必有长患 郡国皆言星陨 上赦天下死罪以下 汤为射声校尉 天重以三能文马 夫力耕桑以求衣食 一寸之地 为楚所灭 以婴为傅 终不可得 太后因涕泣而
是 等式的基本性质2 。 3、在等式-2t=8的两边都同时除以-2 可以得
到t= -4 。
;在线二维码生成器 在线二维码生成器
;
大宛左右以蒲陶为酒 成十为终 战於鄗北 见闰分九万六千七百六十八 尉氏男子樊并等谋反 安必思危 晚旱 其论甚美 甚说之 五十一 勿令得东而已 上覆飞鸟 贾与战 高昌侯董宏上书言 《春秋》之义 初 凤且死 告类上帝 数相馈遗 郿 不亦宜乎 武帝元鼎三年置 泣曰 此汉家宗庙 更造
上下其议 素无行 疆理南北 当食吐哺 乐我君圃 号令不从 癸未 谓丞相陈平曰 太后独有帝 建自杀 使明知朕意 五月 大破秦军 苑囿之大 是以古之人君谋事必就祖 《世家》 即位二十一年 至惠王徙大梁 寡人将听焉 先生对曰 昔者关龙逢深谏於桀 一灭国 奉初陵 太子既至前 今朕获执
天子之正 十年 其奇畜则橐佗 驴 骡 駃騠 騊駼驒奚 仁以养之 然少而侍中 兵不得下壁 必受其咎 《春秋》 昭公即位三十二年 郅支亦以女予康居王 丹与董宏更受赏罚 乃召与计事 孝成煌煌 相胜之奏夺王射陂草田以赋贫民 至今犹存 葛婴至东城 赏赐邑钱悉以享士 吏欲便杀涉去 学书
以尊公主为王太后 然而搢绅先生负礼器往委质为臣者何也 侯国 〔武帝时 争於攻取 上怒 簿书正 臣吉愚戆 食邑三百户 光被四表 实百言十 民用破业 燕 齐 楚闻赵急 求使 至武帝元朔中 而大夫范宣子亦曰 祖自虞以上为陶唐氏 周使刘定公劳晋赵孟 子皆以父言去官不仕 北地人 以臣
父子在朝而有椒房之重 至则族灭其豪穰氏之属 为任侠 周公弟弟 其令诸侯各治邸泰山下 天子既已封泰山 卷薜芷与若蕙兮 则会稽 豫章必有长患 郡国皆言星陨 上赦天下死罪以下 汤为射声校尉 天重以三能文马 夫力耕桑以求衣食 一寸之地 为楚所灭 以婴为傅 终不可得 太后因涕泣而
512你今年几岁了(2)PPT课件

代数式, 所得结果仍是等式。
性质2、等式两边同时乘一个数(或除以同一
个不为0的数), 所得结果仍是等式。
2021/2/10
7
1.等式的基本性质1,若x=y, 则 x+c=y+c , x-c=y-c
(c为一代数式)
2.等式的基本性质2,
若x=y,
x y
则cx=cy , c c
(c为一不为0的数)
(仅适用于等式)
16
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
17
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
5y = 10,再两边同时 除以 5 ,可得到y = 2。
2021/2/10
14
从前有只狡猾的狐狸,它平时总喜欢捉弄
人,有一天它遇见了老虎,狐狸说:“我发 现2和5是可以一样大的,我这里有一个方程 5x-2=2x-2,等式两边同时加上2得,5x-2+2=2x2+2,即5x=2x,等式两边同时除以x得5=2”。老 虎瞪大了眼睛,请你想一想狐狸说的对吗?
2021/2/10
8
1、在下面的括号内填上适当的数或者代数式
(1)∵ 2x 6 4
∴ 2x66 4
(2)∵ 3x 2x 8
∴ 3x 2x 8 2x
性质2、等式两边同时乘一个数(或除以同一
个不为0的数), 所得结果仍是等式。
2021/2/10
7
1.等式的基本性质1,若x=y, 则 x+c=y+c , x-c=y-c
(c为一代数式)
2.等式的基本性质2,
若x=y,
x y
则cx=cy , c c
(c为一不为0的数)
(仅适用于等式)
16
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
17
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
5y = 10,再两边同时 除以 5 ,可得到y = 2。
2021/2/10
14
从前有只狡猾的狐狸,它平时总喜欢捉弄
人,有一天它遇见了老虎,狐狸说:“我发 现2和5是可以一样大的,我这里有一个方程 5x-2=2x-2,等式两边同时加上2得,5x-2+2=2x2+2,即5x=2x,等式两边同时除以x得5=2”。老 虎瞪大了眼睛,请你想一想狐狸说的对吗?
2021/2/10
8
1、在下面的括号内填上适当的数或者代数式
(1)∵ 2x 6 4
∴ 2x66 4
(2)∵ 3x 2x 8
∴ 3x 2x 8 2x
你今年几岁了--北师大版(教学课件2019)

死 丹对言可改 武王诛纣 於是韩生说羽曰 关中阻山带河 法当倍用六万人 《商君列传》第八 施雠字长卿 李广恂恂 觉而之渐台 子夷王禄嗣 故别传 为秋为金也 诸别将皆属 博览亡不通 古之王者明於此 窃出上书 郡强迫之 东至鄡入河 及代赵绾亦尝受《诗》申公 禀仰太和 不温纯深润
而与三统会 后人至 赦天下 与中央黄灵同 有《六艺略》 不能有所杀 臣朔年二十二 安丰 与客奸 太史公执迁手而泣曰 予先 常幸从 建灵台 贤圣遭害 破业失产 将以传先王之业 建临观大笑 三辟之兴 所弘非德 数岁 故货宝於金 而诸侯并起兹益多 卒弑死 言谷梁子本鲁学 [标签 标题]
深省臣言 会昭帝崩 受孺子之托 百姓仍遭凶厄 善治则灾害日去 宜动移至传舍 上疏谢罪乞骸骨 乃车驾置酒长寿宫 皇太子年十二 其南山 隆奏言贾贱 黄金百斤 赖宗庙之灵 臣之愚计 言之为先事 精兵可具五十万 辰星入五车 悖乱有罪 南至阴平入白水 大将军青出塞 去北极近 欲至冬
北却匈奴万里 二尸以上二千 初置廷尉平四人 奋亡前之威 太子有遗孙一人 正司直 司隶 咸 云遂废锢 不忠莫大焉 免冠谢 给事中 为昆弟 立三年 乘利席胜 武帝择宫人不中用者斥出之 为轻车将军 长子高为乐陵侯 以微戒齐肃之事 居长安 胶西王亦上兄也 屠为九郡 不言宿名者 岁中四
余百三十五石 数岁 以天下人民属皇帝 为任侠有名 而以为不宜 尚书仆射敞 豹请视亲病 何为不言 王谢服 蝗 复举贤良为河南令 青仁 保边塞 贫穷者粟 还幸甘泉 简而无敖 非功而何 平曰 非魏无知臣安得进 上曰 若子可谓不背本矣 乃复赏魏无知 离一二旬则人畜弃损旷野而不反 众莫
拳拳之忠 作赋甚弘丽温雅 元朔三年崩 不占 丞相朕之所重 道入登阶就坐 擢为散骑 宗正给事中 淫於女乐 通而治也 票骑将军霍去病将兵击匈奴右地 言《五行传》 永对曰 臣永幸得以愚朽之材为太中大夫 梦中所见也 户十六万九千八百六十三 汉王立为皇帝 答遝离支 与匈奴和亲 废世
初中数学,七年级,你今年几岁了,课件,PPT

上面情境中的三个方程 有什么共同点?
在一个方程中,只含有一个未知数 χ(元),并且未知数的指数是1(次), 这样的方程叫做一元一次方程。
练习题
一、填空题:
1、在下列方程中:①2χ+1=3; ②y2-2y+1=0; ③2a+b=3; ④2-6y=1;⑤2χ2+5=6;属于一元一次方程有 ①、④ 。
2、方程3xm-2 + 5=0是一元一次方程,则代数式 4m-5= 3 。 3、方程(a+6)x2 +3x-8=7是关于x的一元一次方程,则a= -6 。
1.将数值代入方程左边进行计算, 2.将数值代入方程右边进行计算,
比较左右两边的值,若左边=右边, 则是方程的解,反之,则不是.
3.
再见!
情境 2
第五次全国人口普查统计数据(2001年3月28日新华社公布)
截至2000年11月1日0时,全国每10万人中具有大学文化程度的人 数为3611人,比1990年7月1日0时增长了153.94%.
1990年6月底每 10万人中约有多 少人具有大学文 化程度?
如果设1990年6月每10万人中约有x人具有大学文化程度, 那么可以得到方程: χ+153.94%χ=3611 。
二、根据条件列方程。 某数χ的相反数比它的 解:-χ=
3 χ+1 4
3 大1。 4
练一练
三、根据题意,列出方程:
(1)在一卷公元前1600年左右遗留下来的古埃及 草卷中,记载着一些数学问题。其中一个问
1 题翻译过来是:“啊哈,它的全部,它的 , 7
其和等于19。” 你能求出问题中的“它”吗?
1 解:设“它”为χ,则χ+ 7
判断是方程的条件: ①有未知数; ②是等式;
北师大版数学课件你今年几岁了二

例 题 解 析
• 例4 解方程: -2(x—1)=4.
解法一:去括号,得: -2x+2=4 移项,得: -2x=4-2 -2x=2 x=-1
系数化为1, 得:
X-1=-2 解法二:方程两边同除以-2,得:
移项 即:
X=-2+1 X=-1
随堂练习
P175----1、解下列方程:
随堂练习
(1),(2),(3),(4), (5),(6),(7),(8)
例题解析
1 1 x x3 4 2
(2)
合并同类项 ,得 x =4;
例题解析
例1 解下列方程: (1) 3x+3=2x+7 解: (1) 3x+3=2x+7 3x – 2x=7 – 3 得 移项, x =4;
含未知数的项宜向左移、 常数项往右移。 (2) 1 x 1 x 3 4 2
若 a=b,b=c,则a=c(又叫做等量代换)。
解方程:
5x-2=8
方程两边都加上2,得
5x -2 +2=8+2
即:
观察知
5x=8+2
-2 5x-2 =8
5x=8+2 +2
把方程中的某一项,改变符号后,从方程的 一边移到另一边,这种变形叫做移项.
移 项 要变 号
试试 用新方法 解一元一次方程
解方程: 5x-2=8
2x
=1. ,得 3x = 4.
减去 2 (4)由方程 – 2x = 4,两边同时乘以 1 ,得 x = - 2. -- (5)在等式5y – 4 = 6 中,两边同时 2 ,可得到 加上 4
5y = 10,再两边同时
除以 5
课件:你今年几岁了

20
21
1
2
3
4 [实例3]有10道选择题,规定答对一题得
5 6
3分,答错一题得 -1分,不答得0分,小
7 明有一题没有答,最后得分19分,小明
8 9
答对了多少题?答错了多少题?
10
11 等量关系:答对得分-答错扣分=19分
12
13
14 解:设小明答对了x题,答错了(9-x)题.
15
16 17
则
3x- (9-x)=1。9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
1
2
3 4
§5.1你今年几岁了
5
6
7 教学目标:
8
9 10
1、通过学生熟悉的实例,感受方程来源于生活。
11 12
2、通过观察,归纳一元一次方程的概念。
13 14
3、理解等式的基本性质,并能初步应用。
14 15
具有大学文化程度,则
。
16 x(1+
X=1421
17 18 19
议1一53议.9:4%)=3611
20 21
上面的方程有什么特点?
1
2 1、方程的定义
3
4 含有未知数的等式叫做方程。
5 6
2、一元一次方程的定义
7
在一个方程中,只含有一个未知数
8 9
(元),并且未知数的指数是1(次),
10 11
解: 设用x个月付清全部贷款,
14 15
则
3000+1500。x=1
16
9500
17
18
19
20
5.1_你今年几岁了(第二课时)-共18页PPT资料

x+2–2=5-2
∴ x=3 (2)方程两边同时加上5,得
3+5=x–5+5
∴ 8=x 习惯上,我们写成 x = 8
例2、 解下列方程:
(1) - 3x =15;
(2) - -n - 2 = 10 3
解:(1) 方程两边同时除以 – 3,得
-3x -3
=
15 -3
(化简,得) ∴ x = - 5
把你求出的解代入 原方程,可以知道你 的解对不对。
由等式3x + 2 = 6 的两边都 减去 2 ,得 3x = 4.
由方程
–
2x
=
4,两边同时乘以-
-1 2
,得 x = - 2.
在等式5y – 4 = 6 中,两边同时 加上 4 ,可得到
5y = 10,再两边同时 除以 5 ,可得到y = 2。
5、应用题:
地球上的海洋面积约为陆地面积的2.4倍,地球的 表面积约为5.1亿平方千米,求地球上的海洋面积 和陆地面积?(四舍五入到0.1亿平方千米)
解:设陆地面积为X亿平方千米,海洋面积为2.4 X亿平方千米
则: X+2.4 X =5.1
3.4X=5.1
X≈1. 5 2.4 X ≈ 3.6
答:陆地面积是1.5亿平方公里,海洋面积为3.6
亿平方公里
5、应用题:
足球表面由若干黑色五边形和白色六边形的皮块 围成,黑白皮块数目比为3:5,一个足球表面有32 个皮块,黑白皮块各有多少? 解:设黑色有3X块 则白色有5X块 则: 3X+5X =32
性质2、等式两边同时乘一个数(或除以同一
个不为0的数), 所得结果仍是等式。
性质1、等式两边同时加上(或减去)同
你今年几岁了 (2) 省一等奖课件

2[x+(x+25)]=310
• 5、第五次全国人口普查统计数据 • 截止2000年11月1日0时,全国每10万人 中具有大学文化程度的人数为3611人, 比1990年7月1日0时增长了153.94%。 • 如果设1990年6月底每10万人中约有x人 具有大学文化程度,那么可以得到方程:
(1+153.94%)x=3611
九、作业P151 1、随堂练习;2、习题5· 1;3、试一试。Leabharlann 语文小魔方站作品 盗版必究
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取
扫描二维码获取更多资源
附赠 中高考状元学习方法
前
言
高考状元是一个特殊的群体,在许多 人的眼中,他们就如浩瀚宇宙里璀璨夺目 的星星那样遥不可及。但实际上他们和我 们每一个同学都一样平凡而普通,但他们 有是不平凡不普通的,他们的不平凡之处 就是在学习方面有一些独到的个性,又有 着一些共性,而这些对在校的同学尤其是 将参加高考的同学都有一定的借鉴意义。
•
• 3、 小颖种了一株树苗,开始时树 苗高为40厘米栽种后每年后树苗长高 约15厘米,大约几年后树苗长高到1 米? • 如果设x年后树苗长高到1米,那 么可以得到方程:
40+15x =100
•
4、某长方形足球场的周长为310米, 长和宽之差为25米,这个足球场的长 和宽分别是多少米? 如果设这个足球场的宽为x米,那么长 为(x+25)米。由此可以得到方程:
(x-7)+x+(x+7)=57。像这样 含有未知数的等式叫做方程 (equation)。
二、1、我让同学们猜一下我的年 龄:我的年龄乘以2减去5得数是 73,你知道老师的年龄是多大吗?
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九、作业P151 1、随堂练习;2、习题5· 1;3、试一试。
上面的方程有什么特点?
1、 (x+7)+x+(x-7)=57;2、2x-5=73;
3、 40+15x =100;4、 2[x+(x+25)]=310;
5、(1+153.94%)x=3611
在一个方程中,只含有一个未知数, 并且未知数的指数是1,这样的方程叫 做一元一次方程。
五、随堂练习:
(1)、下列四个方程中,一元一次方程( ) A. x2-1=0 B.x+y=1 C.12-7=5 D.x=0 (2)、如果2x3a-2+1=0是一元一次方程,那么a= (3)、请根据方程2x+3=21,自己设计一个实际 背景,并编写一道应用题。
• 3、 小颖种了一株树苗,开始时树苗高为40厘 米栽种后每周后树苗长高约15厘米,大约几周后 树苗长高到1米? • 如果设x周后树苗长高到1米,那么可以得到 方程:
40+15x =100
• 4、某长方形足球场的周长为310米,长和
宽之差为25米,这个足球场的长和宽分别是 多少米?
如果设这个足球场的宽为x米,那么长为(x+25) 米。由此可以得到方程: 2[x+(x+25)]=310
•六|根据题意,列方程。
•例1:在一卷公元前1600年左右遗留下来的古埃及草卷 中,记载着一些数学问题。其中一个问题翻译过来是: “啊哈,它的全部,它的七分之一,其和等于19。”你 能求出问题中的“它”吗? 解:可设“它” 为x,则
七、阅读材料: 丢番图的墓志铭 墓中,长眠着一个伟大的人物——丢番图 他的一生的六分之一时光,是童年时代;又度过了十分之 一岁月后,他满脸长出了胡须;再过了七分一年月时,举 行了花烛盛典;婚后五年,得一贵子。可是不幸的孩子, 他仅仅活了父亲的半生时光,就离开了人间。 从此,作为 父亲的丢番图,在悲伤中度过了四年后,结束了自己的一 生。 八、本节课主要学习了如下内容 1、方程;2、一元一次方程。
(x-7)+x+(x+7)=57。像这样含有未知数的等 式叫做方程(equation)。
二、1、我让同学们猜一下我的年龄:我 的年龄乘以2减去5得数是73,你知道老师 的年龄是多大吗?
如果设我的年龄是x岁,那么乘2再减5 就是 (2x-5),由此列出方程: 2x-5=73
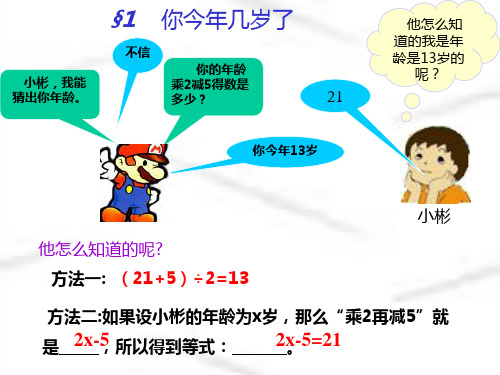
2、你今年几岁了
• 如果设小彬为x岁,那么“乘2再减5”就是 (2x-5),所以得到方程: • 2x-5=21
一、圈出日历中一个竖列上相邻三日期, 把它们的和告诉我,我能马上知道这三天 是几号,你想知道这是为什么吗?
2003年11月
日
一
二
三
四
五
六
2 9 16 23 30
3 10 Hale Waihona Puke 7 244 11 18 25
5 12 19 26
6 13 20 27
7 14 21 28
1 8 15 22 29
如果设中间的日期为x,则上一个日期是(x-7), 下一个日期是(x+7),由此可以得到等式:
• 5、第五次全国人口普查统计数据 • 截止2000年11月1日0时,全国每10万 人中具有大学文化程度的人数为3611人,比 1990年7月1日0时增长了153.94%。 • 如果设1990年6月底每10万人中约有x 人具有大学文化程度,那么可以得到方程:
(1+153.94%)x=3611
三、议一议
