初一上找规律专题(完整资料).doc
七年级上找规律

找规律知识点写出下面数列的第n项1.(1)1,4,7……(2)5,9,13……2.(1)1,2,4,8……-1,2,-4,8……(2)2,6,18,54……2,-6,18,-54……-1,4,-7,10……5,-9,13,-17……3.(1)0,1,4,9……(2)1,2,5,10……4. (1)3,8,15,24……(2)0,4,10,18……(3)1,5,13,25……5. (1)1130325,,,……(1)数与式排列找规律【例1】 观察一列单项式:1x ,3x 2,5x 2,7x ,9x 2,11x 2,…,则第2013个单项式是 .【例2】 一个叫巴尔末的中学教师成功地从光谱数据59,1216,2125,3236,…中得到巴尔末公式,从而打开了光谱奥秘的大门,请你按照这种规律,写出第n 个数据是___________【例3】 按照规律填上所缺的单项式并回答问题:(1)a 、22a -、33a 、44a -,________,__________; (2)试写出第2007个和第2008个单项式 (3) 试写出第n 个单项式(2)尾数问题【例4】 观察下列算式,用你所发现的规律得出20102的末位数字是( ) 21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…A .2B .4C .6D .8【例5】 观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187解答下列问题:3+32+33+34…+32013的末位数字是( )A .0B .1C .3D .7【例6】 已知123456789101112…997998999是由连续整数1至999排列组成的一个数,在该数中从左往右数第2013位上的数字为 .(3)数与式计算找规律 【例7】 已知123112113114,,,...,1232323438345415a a a =+==+==+=⨯⨯⨯⨯⨯⨯依据上述规律,则99a =【例8】 22222233445522334455338815152424已知:,,,,+=⨯+=⨯+=⨯+=⨯21010+b ba a=⨯符合前面的式子,则a b +=【例9】 观察下列计算:211211-=⨯3121321-=⨯4131431-=⨯5141541-=⨯ … 从计算结果中找规律,利用规律计算+⨯+⨯+⨯+⨯541431321211…=⨯+201020091.【例10】 已知下列等式: ① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102;由此规律知,第⑤个等式是 .(二)图形类找规律【例11】 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n 个图形需要黑色棋子的个数是________________.【例12】 用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第n 个“口”字需用棋子___________第2个“口” 第1个“口” 第3个“口”第n 个“口”………………?第1个图形 第2个图形第3个图形第4个图形【例13】用“O”摆出如图所示的图案,若按照同样的方式构造图案,则第10个图案需要____________个“O”.【例14】搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②,图③的方式串起来搭建,则串7顶这样的帐篷需要_______________根钢管.图1 图2 图3【例15】把一个正三角形分成四个全等的三角形,第一次挖去中间的一个小三角形,对剩下的三个小正三角形再重复以上做法……一直到第n次挖去后剩下的三角形有___________个.第一次第二次第三次第四次【例16】图1是棱长为a的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层的小正方体的个数为s.解答下列问题:图3图2图1⑴按照要求填表:⑵写出当10n=时,s=.【例17】图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是()A.25B.66C.91D.120(三)定义新运算【例18】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为图1 图2 图324,第二次输出的结果为12,…,则第2010次输出的结果为___________(A )6 (B )3 (C )200623 (D )10033231003⨯+【例19】 (2012•青浦区一模)定义某种新运算⊙:s=a ⊙b 的运算原理如图流程图所示,则5⊙4-3⊙4=___________课堂练习【题1】 已知一组数2,4,8,16,32,…,按此规律,则第n 个数是 .(第11题)【题2】 观察下列一组数:21,43,65,87,……,它们是按一定规律排列的.那么这一组数的第k 个数是 .【题3】 一组按规律排列的式子:a2,43a ,65a ,87a ,….则第n 个式子是 .【题4】 观察式子:),7151(21751),5131(21531),311(21311-=⨯-=⨯-=⨯……. 由此计算:+⨯+⨯+⨯751531311…=⨯+201120091_____________.【题5】 先找规律,再填数:111111*********1,,,,122342125633078456............111+_______.2011201220112012+-=+-=+-=+-=-=⨯则【题6】 用同样大小的黑色棋子按如图所示的规律摆放:(1)第5个图形有多少黑色棋子?(2)第几个图形有2013颗黑色棋子?请说明理由.【题7】 定义一种新运算:b a b a -=*21,那么4*(-1)= _______【题8】 现定义一种新运算:★,对于任意整数a 、b ,有a ★b=a+b-1,求4★[(6★8)★(3★5)]的值【题9】 用“”、“”定义新运算:对于任意实数a ,b ,都有a b=a 和ab=b ,例如32=3,32=2.则(20102009)(20072008)的值是.【题10】 定义新运算“⊗”,规定:a ⊗b =13a -4b ,则12⊗ (-1)= .A .15B .25C .55D .1225【题11】 观察下面三个特殊的等式()2103213121⨯⨯-⨯⨯=⨯ ()3214323132⨯⨯-⨯⨯=⨯()4325433143⨯⨯-⨯⨯=⨯将这三个等式的两边相加,可以得到1×2+2×3+3×4=2054331=⨯⨯⨯ 读完这段材料,请你思考后回答:⑴ =⨯++⨯+⨯1011003221⑵ ()()=++++⨯⨯+⨯⨯21432321n n n ⑶ ()()=++++⨯⨯+⨯⨯21432321n n n【题12】 定义一种新的运算a ﹠b=a b,如2﹠3=23=8,那么请试求(3﹠2)﹠2= _______ .课后作业1. 观察下面的单项式:a ,﹣2a 2,4a 3,﹣8a 4,…根据你发现的规律,第8个式子是_______. 2. 填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m 的值是 .3. 观察表一,寻找规律.表二、表三分别是从表一中截取的一部分,其中a +b 的值为_____________.4. 观察上面的图形,它们是按一定规律排列的,依照此规律,第7个图形共有_________个。
(完整)初一找规律练习题

精心整理初一数学找规律一、数字排列规律题1、下面数列后两位应该填上什么数字呢?23581217 ___2、请填出下面横线上的数字。
112358 ____ 213、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么?4、有一串数字36101521_ 第6个是什么数?|| 75、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,吊门心八H I,1那么第2005个数是().A. 1 B . 2 C. 3 D . 46、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1 , 0,那么这100个数中“0”的个数为_________ .7、一组按规律排列的数:1, 3, 7, 13, 21,……请你推断第9个数是.4 9 16 25 36&已知下列等式:① 13= 12;② 13+ 23= 32;③ 13+ 23+ 33= 62;④13+ 23+ 33+ 43= 102; .... 由此规律知,第⑤个等式是.9、观察下列各式;①、12+1 = 1X2;②、22+2=2X 3;③、32+3=3X4; ....... 请把你猜想到的规律用自然数n表示出来。
10、观察下面的几个算式:①、1+2+仁4;②、1+2+3+2+仁9③、1+2+3+4+3+2+1 = 16 ④、1+2+3+4+5+4+3+2+1=25 ……根据你所发现的规律,请你直接写出第n个式子11、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,精心整理那么第2005个数是()A. 1B. 2 C . 3 D. 412、把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行、……,中间用虚线围的一列,从上至下依次为1、5、13、25、……,则第10个数为________ 。
七年级数学找规律经典题型

七年级数学找规律经典题型一、数字规律1. 数列规律例1:观察数列1,3,5,7,9,…,求第n个数。
解析:首先观察这个数列,发现相邻两个数的差值都是2。
第1个数是1 = 2×1 1;第2个数是3 = 2×2 1;第3个数是5 = 2×3 1;第4个数是7 = 2×4 1;第5个数是9 = 2×5 1。
所以可以得出第n个数为2n 1。
例2:观察数列2,4,8,16,32,…,求第n个数。
解析:这个数列中,后一个数都是前一个数的2倍。
第1个数是2 = 2^1;第2个数是4 = 2^2;第3个数是8 = 2^3;第4个数是16 = 2^4;第5个数是32 = 2^5。
所以第n个数为2^n。
2. 数字循环规律例:有一组数按照1, 1,1, 1,…的规律排列,求第n个数。
解析:观察这组数字,发现数字是1和 1交替出现。
当n为奇数时,第n个数为1;当n为偶数时,第n个数为 1。
可以用(-1)^(n + 1)来表示,当n = 1时,(-1)^(1+1)=1;当n = 2时,(-1)^(2 + 1)= 1。
二、图形规律1. 图形数量规律例1:用火柴棒搭三角形,搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒,搭3个三角形需要7根火柴棒,…,求搭n个三角形需要多少根火柴棒。
解析:搭1个三角形需要3根火柴棒,即2×1+1;搭2个三角形时,第二个三角形和第一个三角形共用一条边,所以需要3 + 2 = 5根火柴棒,即2×2+1;搭3个三角形时,第三个三角形和前面的三角形共用两条边,所以需要3+2×2 = 7根火柴棒,即2×3 + 1。
所以搭n个三角形需要2n+1根火柴棒。
例2:观察下列图形的点数规律:第1个图形有1个点;第2个图形有1 + 3 = 4个点;第3个图形有1+3 + 5 = 9个点;第4个图形有1+3+5 + 7 = 16个点;求第n个图形的点数。
初一上找规律专题

初一数学找规律找规律:数列中每一个数,或者图形所关联的数,用它们的序列号(n)的式子表示1、一些基本数字数列(1)自然数列:1、2、3、4……n(2)奇数列:1、3、5、7……2n-1(3)偶数列:2、4、6、8……2n(4)平方数列:1、4、9、16……n²(5)2的乘方数列:2、4、8、16……2 n(6)符号性质数列:-1、1、-1、1……(-1) n 1、-1、1、-1……(-1) n+1 1、-1、1、-1……(-1) n-12、数字数列的变形(1)数列的平移:有些数列里,每个数并不直接与它们的序列号形成基本的数字数列关系;比如下面的数列,是2的乘方数列变形而成的1、2、4、8、16……2 n-1数列中的每个数往右平移了一位,n就变成了n-1(2)考虑符号性质的数列:有些数列本身就是基本数字数列,但必须考虑符号性质,如:1、-4、9、-16……(-1) n-1n²很明显,是自然数的平方数列和符号性质数列的综合(3)基本数字数列的拓展:有些数列只是改变了基本数字数列的某个部份,如:5、25、125、625……5 n这个数列,只是2的乘方数列的拓展;(4)综合数列:有些数列看起来很复杂,其实只是多个基本数列的综合,如:3/2、-5/4、7/8、-9/16……(-1) n-1 (2n+1)/2n上面的数列是三个基本数列及其变型数列的综合。
数列中的每一个数都可以看成三个部分组成:符号部份是符号性质数列;分子部分是奇数列的平移数列;分母部分是2的乘方数列练习:按以下的数排列:8,9,11,15,23,39……,则第11个数是1031 ,第n个数是2 n-1+73、特殊数列(1)等差数列:数列中的每一个数减去它前面的数的差相等的数列叫等差数列。
如:2、5、8、11……2+(n-1)d其中数列中的第一个数叫首项,记作a1;相等的差叫公差,记作d;第n项的数记作an,称为通项an=a1+(n-1)d练习:凸多边形的所有内角的角度之和称为多边形的内角和。
(完整word版)初一数学找规律题讲解【重点】
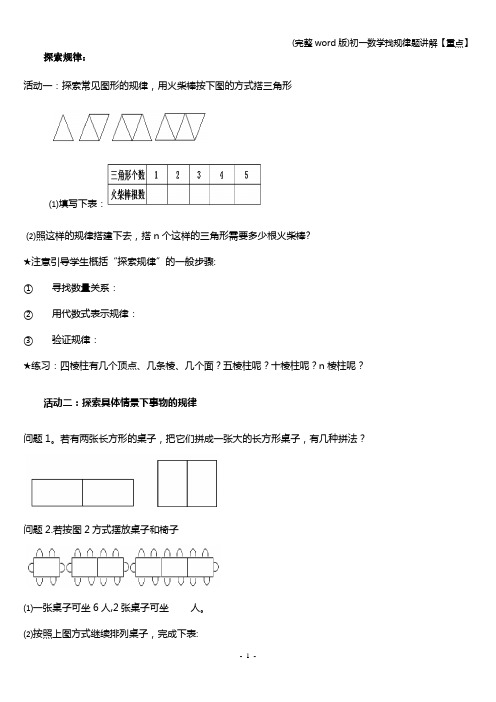
探索规律:活动一:探索常见图形的规律,用火柴棒按下图的方式搭三角形⑴填写下表:⑵照这样的规律搭建下去,搭n个这样的三角形需要多少根火柴棒?★注意引导学生概括“探索规律”的一般步骤:①寻找数量关系:②用代数式表示规律:③验证规律:★练习:四棱柱有几个顶点、几条棱、几个面?五棱柱呢?十棱柱呢?n棱柱呢?活动二:探索具体情景下事物的规律问题1。
若有两张长方形的桌子,把它们拼成一张大的长方形桌子,有几种拼法?问题2.若按图2方式摆放桌子和椅子⑴一张桌子可坐6人,2张桌子可坐人。
⑵按照上图方式继续排列桌子,完成下表:问题3。
如果按图3的方式将桌子拼在一起⑴2张桌子拼在一起可坐多少人?3张呢?n张呢?⑵教室有40张这样的桌子,按上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐人。
⑶在⑵中,改成每8张桌子拼成1张大桌子,则共可坐人。
活动三:探索图表的规律下面是2000年八月份的日历:⑴日历中的绿色方框中的9个数之和与该方框正中间的数有什么关系?⑵这个关系对其它这样的方框成立吗?你能用代数式表示这个关系吗?⑶这个关系对任何一个月的日历都成立吗?为什么?⑷你还能发现这样的方框中9个数之间的其他关系吗?用代数式表示。
⑸你还能提出那些问题?中考数学探索题训练—找规律1、我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。
在电子数字计算机中用的是二进制,只要两个数码:0和1。
如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数 .2、从1开始,将连续的奇数相加,和的情况有如下规律:1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52;…按此规律请你猜想从1开始,将前10个奇数(即当最后一个奇数是19时),它们的和是 。
七年级上期规律探索题集锦(完整资料).doc
此文档下载后即可编辑1.一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是( )A. 6 个B. 7个C. 8个D. 9 个2.如下表,从左到右在每一个小格中都填入一个整数,使任意三个相邻的格子所填的整数之和都相等,则第2017个格子中的整数是( )- 4 a b c 6 b - 2 ......3.四个电子宠物排座位,一开始,小鼠、小猴、小兔、小猫分别坐在1、2、3、4号座位上(如图所示),以后它们不停地变换位置,第一次上下两排交换,第二次是在第一次换位后,再左右两列交换位置,第三次上下两排交换,第四次再左右两列交换……这样一直下去,则第2005次交换位置后,小兔子坐在( )号位上。
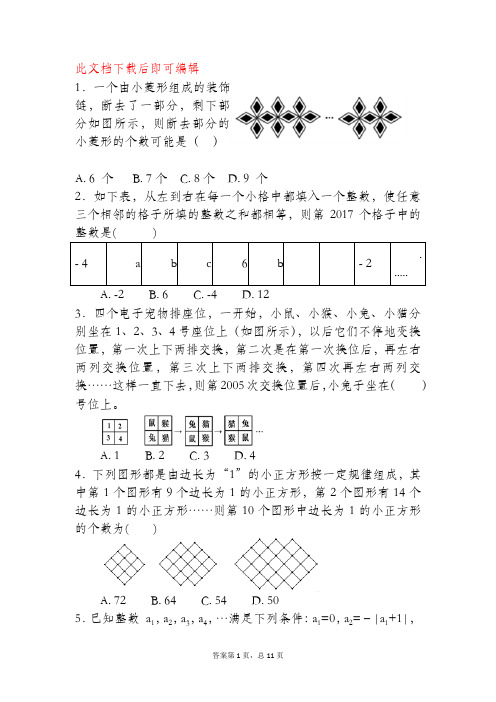
A. 1B. 2C. 3D. 44.下列图形都是由边长为“1”的小正方形按一定规律组成,其中第1个图形有9个边长为1的小正方形,第2个图形有14个边长为1的小正方形……则第10个图形中边长为1的小正方形的个数为( )A. 72B. 64C. 54D. 505.已知整数 a 1,a 2,a 3,a 4,…满足下列条件:a 1=0,a 2=﹣|a 1+1|,a 3=﹣|a 2+2|,a 4=﹣|a 3+3|,…,依此类推,则a 2017的值为( )A. ﹣1005B. ﹣1006C. ﹣1007D. ﹣10086.观察图中菱形四个顶点所标的数字规律,可知数2017应标在( )A. 第504个菱形的左边B. 第505个菱形的下边C. 第504个菱形的上边D. 第505个菱形的右边7.如图所示是一副“三角形图”,第一行有1个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第八行有____个三角形.8.在一次猜数字游戏中,小红写出如下一组数:1, 69415,,,57311…,小军猜想出的第六个数字是1813,也是正确的,根据此规律,第n 个数是_____.9.观察下列各式及其展开式:(a +b)2=a 2+2ab +b 2;(a +b)3=a 3+3a 2b +3ab 2+b 3;(a +b)4=a 4+4a 3b +6a 2b 2+4ab 3+b 4;(a +b)5=a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+b 5;…请你猜想(a +b)10的展开式第三项的系数是________.10.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,…,试猜想,32016的个位数字是__.11.一个自然数的立方,可以分裂成若干个连续奇数的和.例如: 32, 33和34分别可以如图所示的方式“分裂”成2个,3个和4个连续奇数的和.若36也按照此规律进行“分裂”。
(完整版)七年级找规律经典题汇总带答案

……一、数字排列规律题1、观察下列各算式: 1+3=4=22,1+3+5=9=23,1+3+5+7=16=24… 按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个( )二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称).三、数、式计算规律题 1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ;由此规律知,第⑤个等式是 . 2、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,… 根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ =+⨯=+b a aba b 则符合前面式子的规律,,若…21010 规律发现专题训练1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖 块。
七年级上册找规律数学题

七年级上册找规律数学题一、数字规律题。
1. 观察下列数:1,4,9,16,25,…,按此规律,第n个数是()- 解析:- 第1个数是1 = 1^2;- 第2个数是4=2^2;- 第3个数是9 = 3^2;- 第4个数是16=4^2;- 第5个数是25 = 5^2。
- 所以第n个数是n^2。
2. 有一组数:1, - 2,3,-4,5,-6,·s,按此规律,第n个数是()- 解析:- 当n为奇数时,数为正数,即第n个数为n;- 当n为偶数时,数为负数,即第n个数为-n。
- 所以第n个数是( - 1)^n + 1n。
3. 观察数列:2,5,8,11,·s,则第n个数是()- 解析:- 可以发现每一个数都比前一个数大3。
- 第1个数2 = 3×1 - 1;- 第2个数5=3×2 - 1;- 第3个数8 = 3×3-1;- 所以第n个数是3n - 1。
4. 数列1,(1)/(2),(1)/(3),(1)/(4),(1)/(5),·s,第n个数是()- 解析:- 很明显,第n个数是(1)/(n)。
5. 找规律:0,3,8,15,24,·s,第n个数是()- 解析:- 第1个数0 = 1^2-1;- 第2个数3=2^2-1;- 第3个数8 = 3^2-1;- 第4个数15=4^2-1;- 第5个数24 = 5^2-1;- 所以第n个数是n^2-1。
二、图形规律题。
6. 用火柴棒按下图的方式搭三角形:- 照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?- 解析:- 搭1个三角形需要3根火柴棒;- 搭2个三角形需要3 + 2=5根火柴棒;- 搭3个三角形需要3+2×2 = 7根火柴棒;- 搭n个三角形需要3 + 2(n - 1)=2n + 1根火柴棒。
7. 观察下列图形的构成规律,根据此规律,第n个图形中有多少个圆?- 第1个图形有1个圆;- 第2个图形有1 + 2 = 3个圆;- 第3个图形有1+2 + 3=6个圆;- 第4个图形有1+2+3 + 4 = 10个圆;- 解析:- 第n个图形中圆的个数为1 + 2+3+·s+n=(n(n + 1))/(2)。
初一上找规律专题

初一数学找规律找规律:数列中每一个数,或者图形所关联的数,用它们的序列号(n)的式子表示1、一些基本数字数列(1)自然数列:1、2、3、4……n(2)奇数列:1、3、5、7……2n-1(3)偶数列:2、4、6、8……2n(4)平方数列:1、4、9、16……n²(5)2的乘方数列:2、4、8、16……2 n(6)符号性质数列:-1、1、-1、1……(-1) n 1、-1、1、-1……(-1) n+1 1、-1、1、-1……(-1) n-12、数字数列的变形(1)数列的平移:有些数列里,每个数并不直接与它们的序列号形成基本的数字数列关系;比如下面的数列,是2的乘方数列变形而成的1、2、4、8、16……2 n-1数列中的每个数往右平移了一位,n就变成了n-1(2)考虑符号性质的数列:有些数列本身就是基本数字数列,但必须考虑符号性质,如:1、-4、9、-16……(-1) n-1n²很明显,是自然数的平方数列和符号性质数列的综合(3)基本数字数列的拓展:有些数列只是改变了基本数字数列的某个部份,如:5、25、125、625……5 n这个数列,只是2的乘方数列的拓展;(4)综合数列:有些数列看起来很复杂,其实只是多个基本数列的综合,如:3/2、-5/4、7/8、-9/16……(-1) n-1 (2n+1)/2n上面的数列是三个基本数列及其变型数列的综合。
数列中的每一个数都可以看成三个部分组成:符号部份是符号性质数列;分子部分是奇数列的平移数列;分母部分是2的乘方数列练习:按以下的数排列:8,9,11,15,23,39……,则第11个数是1031 ,第n个数是2 n-1+73、特殊数列(1)等差数列:数列中的每一个数减去它前面的数的差相等的数列叫等差数列。
如:2、5、8、11……2+(n-1)d其中数列中的第一个数叫首项,记作a1;相等的差叫公差,记作d;第n项的数记作an,称为通项an=a1+(n-1)d练习:凸多边形的所有内角的角度之和称为多边形的内角和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
此文档下载后即可编辑初一数学找规律找规律:数列中每一个数,或者图形所关联的数,用它们的序列号(n)的式子表示1、一些基本数字数列(1)自然数列:1、2、3、4……n(2)奇数列:1、3、5、7……2n-1(3)偶数列:2、4、6、8……2n(4)平方数列:1、4、9、16……n²(5)2的乘方数列:2、4、8、16……2 n(6)符号性质数列:-1、1、-1、1……(-1) n 1、-1、1、-1……(-1) n+1 1、-1、1、-1……(-1) n-12、数字数列的变形(1)数列的平移:有些数列里,每个数并不直接与它们的序列号形成基本的数字数列关系;比如下面的数列,是2的乘方数列变形而成的1、2、4、8、16……2 n-1数列中的每个数往右平移了一位,n就变成了n-1(2)考虑符号性质的数列:有些数列本身就是基本数字数列,但必须考虑符号性质,如:1、-4、9、-16……(-1) n-1n²很明显,是自然数的平方数列和符号性质数列的综合(3)基本数字数列的拓展:有些数列只是改变了基本数字数列的某个部份,如:5、25、125、625……5 n这个数列,只是2的乘方数列的拓展;(4)综合数列:有些数列看起来很复杂,其实只是多个基本数列的综合,如:3/2、-5/4、7/8、-9/16……(-1) n-1 (2n+1)/2n上面的数列是三个基本数列及其变型数列的综合。
数列中的每一个数都可以看成三个部分组成:符号部份是符号性质数列;分子部分是奇数列的平移数列;分母部分是2的乘方数列练习:按以下的数排列:8,9,11,15,23,39……,则第11个数是1031 ,第n个数是2 n-1+73、特殊数列(1)等差数列:数列中的每一个数减去它前面的数的差相等的数列叫等差数列。
如:2、5、8、11……2+(n-1)d其中数列中的第一个数叫首项,记作a1;相等的差叫公差,记作d;第n项的数记作an,称为通项an=a1+(n-1)d练习:凸多边形的所有内角的角度之和称为多边形的内角和。
已知三角形的内角和等于180º,四边形的内角和等于360º,五边形的内角和等于540º,六边形的内角和等于720º,则十边形的内角和等于1440º ,n边形的内角和等于(n-2)180º 。
(2)等比数列:数列中的每一个数除以它前面的数的商相等的数列叫等比数列。
如:2、10、50、250……2*q n-1其中数列中的第一个数叫首项,记作a1;相等的商叫公比,记作q;第n项的数记作an,称为通项an=a1* q n-14、自然数列中各数的和等于:n(n+1)/2下面的数列中各数的和等于:1、2、3、4、5……n-1练习:在足球双循环比赛中,每支球队要和其它球队踢两场比赛,如果有12支球队参加,一共要踢132 场比赛;如果有n支球队参加,一共要踢n(n-1) 场比赛。
5、在计算中找规律:裂项法:1 - 1/2=1/2;1/2 - 1/3=1/6;1/3 - 1/4=1/12……1/n -1/(n+1)=1/[n(n+1)]练习1/2+1/6+1/12+1/20+……+1/[n(n+1)]分组:2004+2003-2002-2001+2000+1999-1998-1997+……+4+3-2-1新运算:“⊙”表示一种新运算符。
已知1⊙2=3,2⊙3=9,3⊙4=18,4⊙4=22,按此规律计算16⊙4;(规律:从前面一个数字开始加起,到(第后面一个数)个数结束,如1⊙2=3=1+2,从1开始加,加到2,两个数)s=12n=4s=8n=3s=4n=26、几何图形变化规律题(1)观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球_____个.(2)下列是由同型号黑白两种颜色的正三角形瓷砖按一定规律铺设的图形, 仔细观察图形可知:图①有1块黑色的瓷砖,可表示为(11)112+⨯=;图②有3块黑色的瓷砖,可表示为(12)2122+⨯+=图③有6块黑色的瓷砖,可表示为(13)31232+⨯++=;实践与探索:请在图④的虚线框内画出第4个图形;(只须画出草图)第10个图形有 ______块黑色的瓷砖;(直接填写结果)第n 个图形有 ________块黑色的瓷砖.(用含n 的代数式表示)(2)小强用黑白两种颜色的正六边形地面砖按如图拼成了三个图案,他发现了规律,若继续这样拼出第4个,第5个,…,那么第n 个图案中白色地面砖有 ______块.(3)观察右面的图案,每条边上有n(n≥2)个方格,每个图案中方格的总数是S.请写出n=5时,S= ____;请写出n=18时,S=____;按上述规律,写出S与n的关系式S=_______(4)如图,按一定的规律用火柴棒搭图形:①②③按图示的规律填表:7、阅读理解(1)已知下列等式:①13=12;②13+23=32;③13+23+33=62;④13+23+33+43=102;由此规律知,第⑤个等式是..(2)观察下面的几个算式:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1=____.,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+=+⨯=+b a a ba b 则符合前面式子的规律,,若 (21010)8、数形结合观察下面一列数:-1,2,-3,4,-5,6,-7,...,将这列数排成下列形式按照上述规律排下去,那么第10行从左边第9个数是 .9、观察下面三行数:① 2,-4,8,-16,··· ② -1,2,-4,8··· ③ 3,-3,9,-15···(1)第①行数按什么规律排列?(2)第②③行数与第①行数分别有什么关系? (3)取每行数的第9个数,计算这三个数的和练习:1、观察下列各算式:1+3=4=2的平方,1+3+5=9=3的平方,1+3+5+7=16=4的平方…......16-1514-1312-1110-9-76-54-32-1第8题按此规律(1)试猜想:1+3+5+7+…+2005+2007的值?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢?2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么?5、有一串数字 3 6 10 15 21 ___ 第6个是什么数?6、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是( ). A .1B .2C .3D .47、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 _________个.8、我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非。
”如图,在一个边长为1的正方形纸版上,依次贴上面积为21,41,81,…,n21的矩形彩色纸片(n 为大于1的整数)。
请你用“数形结合”的思想,依数形变化的规律,计算n21814121++++Λ=________。
9、 观察下面一列有规律的数ΛΛ,486,355,244,153,82,31,根据这个规律可知第n 个数是______(n 是正整数)10、某校的一间阶梯教室,第1排的座位数为12,从第2排开始,每一排都比前一排增加a 个座位。
(1)请你在下表的空格里填写一个适当的代数式:(2)已知第15排座位数是第5排座位数的2倍,求a 的值,并计算第21排有多少座位?10、裂项法:计算)1(1431321211+++⨯+⨯+⨯n n Λ的值.11、观察右图并寻找规律,x 处填上的数字是A .-136B .-15011235...C .-158D .-16212、意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造如下正方形:再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、 …相应长方形的周长如下表所示:仔细观察图形,上表中的=x ____,=y _____.若按此规律继续作长方形,则序号为⑧的长方形周长是_____. 16、26、17811231511211321④③②①…。
