2020届湖北省四地七校联盟高三第七次调研考试数学(文)试题
2020届湖北省高三年级4月线上调研考试数学(文)试题

2020年湖北省高三(4月)线上调研考试文科数学试卷一、选择题:本大题共 12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}0542<--=x x x A ,集合{}0>=y y B ,则A ∩B=( )A .{}50<<x xB .{}05<<-x xC .),1(+∞-D .{}101≤<-x x2.已知),(33R b a i b iia ∈+=-,其中i 为虚数单位,则复数bi a z -=在复平面内对应的点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.已知2log ,2log ,25.051.0===z y x ,则( )A .y <x <zB .y <z <xC .z <x <yD .z <y <x 4.已知平面向量,均为单位向量,若向量,的夹角为3π,则n m 3+( ) A .37 B .25 C .37 D .55.若不等式m x x ≥-+4111,对)41,0(∈x 恒成立,则实数m 的最大值为( ) A .7 B .8 C .9 D .106.某城市在进行创建文明城市的活动中,为了解居民对“创建文明城”的满意程度,组织居民给活动打分(分数为整数,满分100分),从中随机抽取一个容量为120的样本,发现所给数据均在[40,100]内.现将这些分数分成以下6组并画出样本的频率分布直方图,但不小心污损了部分图形,如图所示.观察图形则下列说法中有错误..的是( ) A .第三组的频数为18人B .根据频率分布直方图估计众数为75分C .根据频率分布直方图估计样本的平均数为75分D .根据频率分布直方图估计样本的中位数为75分7.我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,常用函数的图像研究函数的性质,也常用函数的解析式来琢磨函数的图像特征.如函数]2,2[,1cos cos 22ππ-∈++-=x x x y 的图象大致为( )8.函数)2cos()22cos(3)(x x x f ++-=ππ的单调增区间为( )A .Z k k k ∈++-],3,6[ππππB .Z k k k ∈++-],6,3[ππππC .Z k k k ∈++-],12,125[ππππ D .Z k k k ∈++-],125,12[ππππ 9.已知F 是抛物线x y 42=的焦点,过焦点F 的直线l 交抛物线的准线于点P ,点A 在抛物线上,且3==AF AP ,则直线l 的斜率为( )A .1±B .2C .2±D .210.已知函数⎩⎨⎧>-≤+-=1,731,)(2x ax x ax x x f ,若存在R x x ∈21,,且21x x ≠,使得)()(21x f x f =成立,则实数a 的取值范围是( )A .(-∞,3)B .(-∞,3]C .(-2,2)D .(-2,2]11.平面四边形ABCD 中,3,,13,23150=⊥===∠CD AB BD AC BC AB ABC ,ο,则四边形ABCD的面积为( )A .232+B .13+C .37D .23712.已知双曲线)0,0(12222>>=-b a by a x C :的左右焦点分别为21,F F ,过1F 的直线与C 的两条渐近线分别交于A 、B 两点,若以21F F 为直径的圆过点B ,且A 为B F 1的中点,则C 的离心率为( )A .13+B .2C .3D .2 二、填空题:本大题共4小题,每小题5分,共20分.13.设曲线y=e x+1上点P 处的切线平行于直线01=--y x ,则点P 的坐标是 .14.已知θsin()5cos 24πθθθ+=,则tan θ = .15.已知A ,B ,C 是球O 球面上的三点,AC=BC=6,AB=OABC 的体积为24.则球O 的表面积为 .16.自湖北爆发新型冠状病毒肺炎疫情以来湖北某市医护人员和医疗、生活物资严重匮乏,全国各地纷纷驰援.某运输队接到从武汉送往该市物资的任务,该运输队有8辆载重为6t 的A 型卡车,6辆载重为10t 的B 型卡车,10名驾驶员,要求此运输队每天至少运送240t 物资.已知每辆卡车每天往返的次数为A 型卡车5次,B 型卡车4次,每辆卡车每天往返的成本A 型卡车1200元,B 型卡车1800元,则每天派出运输队所花的成本最低为 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答. (一)必考题:共 60分. 17.(本小题满分12分)已知函数)(log )(3b ax x f +=的图像经过点A (2,1)和B (5,2),)(*N n b an a n ∈+=.(1)求{}n a ;(2)设数列{}n a 的前n 项和为S n ,2(2)n b n n =++,求{}n b 的前n 项和T n .18.(本小题满分12分)2020年春节期间,新型冠状病毒(2019-nCoV )疫情牵动每一个中国人的心,危难时刻全国人民众志成城.共克时艰,为疫区助力.我国S 省Q 市共100家商家及个人为缓解湖北省抗疫消毒物资压力,募捐价值百万的物资对口输送湖北省H 市.(1)现对100家商家抽取5家,其中2家来自A 地,3家来自B 地,从选中的这5家中,选出3家进行调研.求选出3家中1家来自A 地,2家来自B 地的概率.(2)该市一商家考虑增加先进生产技术投入,该商家欲预测先进生产技术投入为49千元的月产增量.现用以往的先进技术投入i x (千元)与月产增量i y (千件)(i=1,2,3,…,8)的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线x b a y +=的附近,且:8.6,563,6.46===t y x ,281()289.9ii x x =-=∑,281() 1.6i i t t =-=∑,81()()1469i i i x x y y =--=∑,81()()108.8i i i t t y y =--=∑,其中,i t =8118i i t t ==∑,根据所给的统计量,求y 关于x 回归方程,并预测先进生产技术投入为49千元时的月产增量.附:对于一组数据),)(,(2211v u v u ,其回归直线u v βα+=的斜率和截距的最小二乘法估计分别为u v u uv v u uni ini i iβαβˆˆ)())((ˆ121-=---=∑∑==,19.(本小题满分12分)如图,在四棱锥S -ABCD 中,侧面SCD 为钝角三角形且垂直于底面ABCD ,CD =SD ,点M 是SA 的中点,AD// BC ,∠ABC =90°,AB =AD=12BC=a . (1)求证:平面MBD ⊥平面SCD ;(2)若∠SDC=120°,求三棱锥C —MBD 的体积20.(本小题满分12分)已知椭圆:22221x y a b+= (a >b >0)过点E (2,1),其左、右顶点分别为A ,B ,左、右焦点为F 1,F 2,其中F 1(2-,0).(1)求栖圆C 的方程:(2)设M (x 0,y 0)为椭圆C 上异于A ,B 两点的任意一点,MN ⊥AB 于点N ,直线042:00=-+y y x x l ,设过点A 与x 轴垂直的直线与直线l 交于点P ,证明:直线BP 经过线段MN 的中点.21.(本小题满分12分)已知函数x a x x f cos )(2+=(1)求函数f (x )的奇偶性.并证明当2≤a 时函数f (x )只有一个极值点; (2)当π=a 时,求f (x )的最小值;(二)选考题:共10分.请考生在22,23题中任选一题作答.如果多做,则按所做的第一题计分.作答时写清题号.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,曲线1C 的参数方程为⎩⎨⎧=+=θθsin 2cos 22y x (θ为参数),以原点为极点,x 轴非负半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为αρ22sin 314+=.(1)求曲线1C 的极坐标方程以及曲线2C 的直角坐标方程;(2)若直线kx y l =:与曲线1C 、曲线2C 在第一象限交于P 、Q ,且PQ OQ =,点M 的直角坐标为)0,1(,求PMQ ∆的面积.23.[选修4-5:不等式选讲](10分)已知实数a ,b 满足322=-+ab b a . (1)求b a -的取值范围; (2)若ab >0,求证:abb a 4431122≥++.。
湖北省武汉市2020届高三毕业生学习质量检测文科数学试题及参考答案

(2)由(1)知 an = 2n−1 ,由 an > n +100 得 an − n −100 > 0 ,即 2n−1 − n −100 > 0 设 bn = 2n−1 − n −100 (n ∈ N ∗ ) ,则需 bn > 0 , bn+1 − bn = (2n − n −1−100) − (2n−1 − n −100) = 2n−1 −1 , 显然 n = 1 时, bn+1 = bn , n ≥ 2 时, bn+1 > bn ,……8 分
即 b1 = b2 < b3 < b4 < L < bn < L , 而 b7 = −43 < 0 , b8 = 20 > 0 , 即 n ≤ 7 时 bn < 0 ;当 n > 8 时, bn > 0 , 故 n 的取值范围是: n ≥ 8 ……12 分
18.(1)取 DC 的中点 H , AB 的中点 M ,连接 QH 、 在正方体 ABCD − A1B1C1D1 中, Q 为 C1D1 的中点, 则 QH ⊥ CD ,则 QH ⊥ 面 ABCD , 所以 QH ⊥ AC ,…… 2 分 在正方形 ABCD 中, H 、 L 分别为 CD 、 BC 的中点, 所以 BD // HL ,而 AC ⊥ BD ,则 HL ⊥ AC ,……4 分 又 QH I HL = H ,所以 AC ⊥ 面 QHL ,所以 AC ⊥ QL .……6 分 连接 ML 、 MP ,显然 PQ // ML 且 PQ = ML ,故四边形 PQLM 为平行四边形, 则 SΔPQL = SΔPML ,
题号 1
2
3
4
5
6
7
2020年湖北省高三(5月)调研模拟考试文科数学试卷(答案)

2020 年湖北省高三(5 月)调研模拟考试
文科数学参考答案
一、选择题
题号 1
2
3
4
5
6
7
8
9 10 11 12
答案 C A C C B C B D D A A D
二、填空题
13. x y 2 0 14.
15. ᧳
粘贴在答题卡上 的指定位置 。
2.选择题 的作答 :每 小题选 出答 案后 ,用 2B铅 笔 把答 题 卡上 对应 题 目的答 案标 号涂
黑 。写在试题卷 、草稿纸和答题卡上 的非答题 区域均无效 。 3.非 选择题 的作答 :用 签字笔 直接答在答 题 卡上对应 的答 题 区域 内。写在试 题卷 、草
C· 一钅卜
手 D。
5.如 图 ,网 格纸上每个小格都是边长为 1 的正方形 ,粗线 画 出的是一个几何体 的三视 图 ,则 该几何体 的体积为
A.1
B.争
昔 C。
D.÷
6.若 △⒕BC三 边长分别为 3,5,7,则 △⒕BC的 面积为
⒏f
7.某 校 随机抽取 1CXl名 同学进行 “垃圾分类 ”的问卷测试 ,测 试结果发现这 100名 同学 的得
是符合题 目要求的。
1.设 全集 σ=N丰 ,集 合⒕={1,2,3,4,5},B={2,4,6,8},则 图中的阴影部分表示的集合为
A.{1,3,5}
B.{2,4}
C.{6,8}
D.{2,4,6,8}
2.已 知 i是 虚数单位,复 数 z满 足(i+1)z=i,则 z的 虚部是
÷ A·
:· ÷i
C.÷i
2020年湖北省部分高中调考 高三数学试卷文科
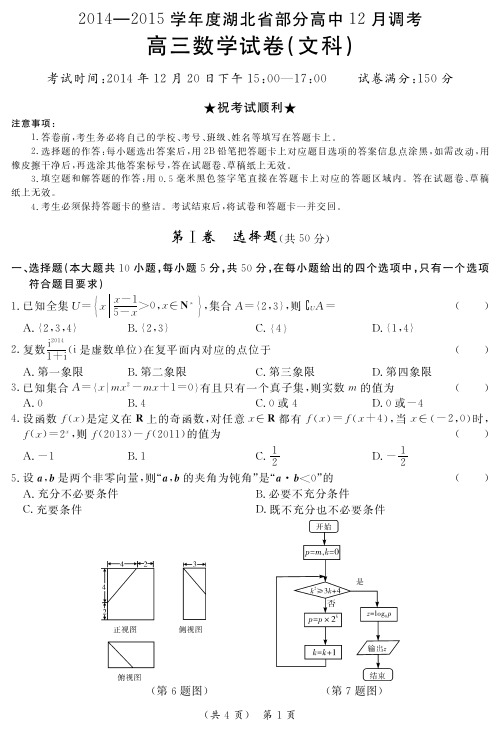
#$'%")分&已知数列 '&+ (的 前+ 项 和5+ *&+ 0+# +"!数 列 ''+ (满 足 )+ +'+0" * %+0"&&+0" + +&+!且'"*)# %&求&+!'+. %&设 6+ 为数列 ''+ (的前+ 项和!求 6+!并求满足 6+(&时+ 的最大值#
共 ! 页 ! 第!) 页
.''"!!(
#'复 数"/#0$"!/%/是 虚 数 单 位 &在 复 平 面 内 对 应 的 点 位 于
%! ! &
,'第 一 象 限
('第 二 象 限
-'第 三 象 限
.'第 四 象 限
)'已知集合 #*'"'$"#+$"0"*$(有且只有一个真子集!则实数 $ 的值为
%!;!
橡 皮 擦 干 净 后 !再 选 涂 其 他 答 案 标 号 !答 在 试 题 卷 "草 稿 纸 上 无 效 # )'填空题和解答题的作答$用$'%毫米黑色 签 字 笔 直 接 在 答 题 卡 上 对 应 的 答 题 区 域 内# 答 在 试 题 卷"草 稿
纸上无效# !'考 生 必 须 保 持 答 题 卡 的 整 洁 # 考 试 结 束 后 !将 试 卷 和 答 题 卡 一 并 交 回 #
湖南湖北四校2020届高三学情调研联考数学(文)试题及答案

湖南湖北四校2020届高三学情调研联考文科数学试题卷 考试时间:2020年4月24日本试卷共5页,满分150分,考试用时120分钟. 考生注意:1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.祝考试顺利一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}04P x R x =∈≤≤,{}3Q x R x =∈<,则P Q =U ( ) A.[]3,4B.(]3,4-C.(],4-∞D.()3,-+∞2.x ,y 互为共轭复数,且()2346x y xyi i +-=-则x y +=( ) A.2B.1C.22D.43.如图所示,三国时代数学家在《周脾算经》中利用弦图,给出了勾股定理的绝妙证明.图中包含四个全等的直角三角形及一个小正方形(阴影),设直角三角形有一个内角为30︒,若向弦图内随机抛掷200颗米粒(大小忽略不计,取3 1.732≈),则落在小正方形(阴影)内的米粒数大约为( )A.20B.27C.54D.644.如图,在ABC △中,点D 在线段BC 上,且3BD DC =,若AD AB AC λμ=+uuu v uu u v uuu v,则λμ=( )A.13B.12C.23D.25.已知定义在R 上的函数()21x mf x -=-(m 为实数)为偶函数,记()0.5log 3a f =,()2log 5b f =,()2c f m =+,则,,a b c 的大小关系为( )A.a b c <<B.c b a <<C.c a b <<D.a c b <<6.如图所示是某多面体的三视图,左上为正视图,右上为侧视图,左下为俯视图,且图中小方格单位长度为1,则该多面体的侧面最大面积为( )A.23B.6C.22D.27.已知双曲线()2222:10,0x y C a b a b -=>>的左,右焦点分别为()1,0F c -,()2,0F c ,又点23,2b N c a ⎛⎫- ⎪⎝⎭.若双曲线C 左支上的任意一点M 均满足24MF MN b +>,则双曲线C 的离心率的取值范围为( )A.1353⎛⎝B.)131,5,3⎛+∞ ⎝⎭UC.()513,+∞UD.5,138.为计算11111123499100S =-+-++-L ,设计了下面的程序框图,则在空白框中应填入( ) A.1i i =+B.2i i =+C.3i i =+D.4i i =+9.已知ABC △的内角,,A B C 所对的边分别为,,a b c ,且3cos cos 5a Bb Ac -=,则()tan A B -的最大值为( )B.32C.3410.已知函数()()22π2sin cos sin 024r f x x x ωωωω⎛⎫=⋅-->⎪⎝⎭在区间2π5π,36⎡⎤-⎢⎥⎣⎦上是增函数,且在区间[]0,π上恰好取得一次最大值1,则w 的取值范围是( )A.30,5⎛⎤ ⎥⎝⎦B.13,25⎡⎤⎢⎥⎣⎦C.13,24⎡⎤⎢⎥⎣⎦D.15,22⎡⎫⎪⎢⎣⎭11.过双曲线()222210x y a b a b-=>>右焦点F 的直线交两渐近线于A 、B 两点,若0OA AB ⋅=uu r uu u r ,O 为坐标原点,且OAB △内切圆半径为12a ,则该双曲线的离心率为( )112.已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC △是边长为2的正三角形,,E F 分别是,PA AB 的中点,90CEF ∠=︒,则球O 的体积为( )A.B.C.二、填空题:本题共4小题,每小题5分,共20分. 13.命题“()00,x ∃∈+∞,00ln 1x x =-”的否定是. 14.观察分析下表中的数据:猜想一般凸多面体中,,F V E 所满足的等式是.15.设函数()()1xf x ex =-,函数()g x mx =,若对于任意的[]12,2x ∈-,总存在[]21,2x ∈,使得()()12f x g x >,则实数m 的取值范围是.16.某小商品生产厂家计划每天生产A 型、B 型、C 型三种小商品共100个,生产一个型小商品需5分钟,生产一个B 型小商品需7分钟,生产一个C 型小商品需4分钟,已知总生产时间不超过10小时.若生产一个A 型小商品可获利润8元,生产一个B 型小商品可获利润9元,生产一个C 型小商品可获利润6元.该厂家合理分配生产任务使每天的利润最大,则最大日利润是元.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:60分.17.已知数列{}{},n n a b 满足:114a=,1n n a b +=,121n n n b b a +=-.(1)证明:11n b ⎧⎫⎨⎬-⎩⎭是等差数列,并求数列{}n b 的通项公式; (2)设1223341n n n S a a a a a a a a +=++++L ,求实数a 为何值时4n n aS b <恒成立.18.如图,ABCD 是边长为2的菱形,60DAB ∠=︒,EB ⊥平面ABCD ,FD ⊥平面ABCD ,24EB FD ==.(1)求证:EF AC ⊥; (2)求几何体EFABCD 的体积.19.在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由3个人依次出场解密,每人限定时间是1分钟内,否则派下一个人.3个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲100次的测试记录,绘制了如下的频率分布直方图.(1)若甲解密成功所需时间的中位数为47,求a 、b 的值,并求出甲在1分钟内解密成功的频率; (2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为()11911,2,31010n n n P P n --⎛⎫=+= ⎪⎝⎭,其中i P 表示第i 个出场选手解密成功的概率,并且1P 定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立. ①求该团队挑战成功的概率;②该团队以i P 从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人数X 的可能值及其概率.20.如图,设抛物线()21:40C y mx m =->的准线l 与x 轴交于椭圆22222:1(0)x y C a b a b+=>>的右焦点21,F F 为2C 的左焦点.椭圆的离心率为12e =,抛物线1C 与椭圆2C 交于x 轴上方一点P ,连接1PF 并延长其交1C 于点Q ,M 为1C 上一动点,且在,P Q 之间移动.(1)当32a b+取最小值时,求1C 和2C 的方程; (2)若12PF F △的边长恰好是三个连续的自然数,当MPQ △面积取最大值时,求面积最大值以及此时直线MP 的方程. 21.已知函数()ln xf x a x e=+,其中a 为常数.(1)若直线2y x e=是曲线()y f x =的一条切线,求实数a 的值; (2)当1a =-时,若函数()()ln xg x f x b x=-+在[)1,+∞上有两个零点.求实数b 的取值范围.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22.[选修4—4:坐标系与参数方程]在平面直角坐标系xOy 中,直线l 的参数方程为21x ty t=--⎧⎨=+⎩,(t 为参数),曲线1:C y =以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为π4ρα⎛⎫= ⎪⎝⎭-. (1)若直线l 与x ,y 轴的交点分别为,A B ,点P 在1C 上,求BA BP ⋅uu r uu r的取值范围;(2)若直线l 与2C 交于M N ,两点,点Q 的直角坐标为()2,1-,求QM QN -的值. 23.[选修4–5:不等式选讲]已知函数()223f x x x m =+++,R m ∈. (1)当2m =-时,求不等式()3f x ≤的解集; (2)若(),0x ∀∈-∞,都有()2f x x x≥+恒成立,求m 的取值范围.湖南湖北四校2020届高三学情调研联考文科数学试题卷参考答案及解析一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.B【解析】由题意得,[]0,4P =,()3,3Q =-,(]3,4P Q =-∴U ,故选B. 2.C 【解析】设x a bi =+,y a bi =-,代入得()()2222346a a bi i -+=-,所以()224a =,()2236a b +=,解得1a =,1b =,所以x y +=3.B 解析:设大正方体的边长为x ,12x x -,设落在小正方形内的米粒数大约为N ,则2212200x x N x ⎫-⎪⎝⎭=,解得:27N ≈. 4.A 【解析】()33134444AD AB BD AB BC AB AC AB AC AB =+=+=+-=+u u u r u u u r u u u r u u u u u r u u uu r u u u r u u u r u u u r r u u u r ,所以14λ=,34μ=,从而求得13λμ=.5.D 解析:Q 函数()f x 是偶函数,()()f x f x ∴=-在R 上恒成立,0m ∴=,∴当0x ≥时,易得()21x f x =-为增函数,()()0.52log 3log 3af f ∴==,,()2log5b f =,()2c f =,22log 32log 5<<Q,a c b ∴<<6.C 由三视图可知多面体是棱长为2的正方体中的三棱锥P ABC -, 故1AC =,2PA =,BC PC ==AB =PB =12112ABC PAC S S ∴==⨯⨯=△△,122PAB S =⨯⨯=△12PBC S =⨯=△,∴该多面体的侧面最大面积为.故选C.7.B 解析:双曲线C 左支上的任意一点M 均满足24MF MN b +>, 即()2min4MF MNb +>,又2 21232222b MF MN aMF MN a NF aa+≥++≥+=+2223244382ba b a b aba∴+>⇒+>34802b a ba b a⇒⋅+->⇒>或23ba<2221bea∴=+,5e>或131N<<8.B详解:由11111123499100S=-+-++-L得程序框图先对奇数项累加,偶数项累加,最后再相减.因此在空白框中应填入2i i=+,选B.9.C【解析】3cos cos5a Bb A c-=Q∴由正弦定理,得3sin cos sin cos sin5A B B A C-=,()()sin sinC A B C A Bπ=-+⇒=+Q,()3sin cos sin cos sin cos cos sin5A B B A A B A B∴-=+,整理,得sin cos4sin cosA B B A=,同除以cos cosA B,得tan4tanA B=,由此可得()2tan tan3tan3tan11tan tan14tan4tantanA B BA BA B B BB--===+++,AQ、B是三角形内角,且tan A与tan B同号,A∴、B都是锐角,即tan0A>,tan0B>,114tan4tan4tan tanB BB B+≥⋅=Q()33tan144tantanA BBB-=≤+,当且仅当14tantanBB=,即1tan2B=时,()tan A B-的最大值为34.10.B解析:2ππ2cos1cos1sin242xx xωωω⎛⎫⎛⎫-=+-=+⎪ ⎪⎝⎭⎝⎭Q,()()2sin1sin sin sinf x x x x xωωωω=+-=.令π2π2x kω=+可得π2π2kxωω=+,()f xQ在区间[]0,π上恰好取得一次最大值,π0π2ω∴≤≤解得12ω≥.令ππ2π2π22k x kω-+≤≤+,解得:π2ππ2π22k kxωωωω-+≤≤+,()f xQ在区间2π5π,36⎡⎤-⎢⎥⎣⎦上是增函数,2ππ325π365ωω⎧-≥-⎪⎪∴⎨⎪≤≤⎪⎩,解得35ω≤.综上,1325ω≤≤.故选:B.11.A解析:因为0a b>>,所以双曲线的渐近线如图所示,设内切圆圆心为M,则M在AOB∠平分线OF上,过点M分别作MN OA⊥于N,MT AB⊥于T,由FA OA⊥得四边形MTAN为正方形,由焦点到渐近线的距离为b得FA b=,又OF c=,所以OA a=,312NA MN a==-,所以332NO a=-,所以tan3MNbAOFa NO=∠==,得23213bea⎛⎫=+=⎪⎝⎭.故选A.12.D解析:方法一:本题也可用解三角形方法,达到求出棱长的目的.适合空间想象能力略差学生.设2PA PB PC x===,,E F分别为,PA AB中点,EF PB∴∥,且12EF PB x==,ABC△Q为边长为2的等边三角形,3CF∴=又90CEF∠=︒23CE x∴=-12AE PA x==AEC△中余弦定理()2243cos22x xEACx+--∠=⨯⨯,作PD AC⊥于D,PA PC=Q,DQ为AC中点,1cos2ADEACPA x∠==,2243142x xx x+-+∴=,2212x ∴+=,212x ∴=,2x =,PA PB PC ∴===2AB BC AC ===,,,PA PB PC∴两两垂直,2R ∴==2R ∴=,344338V R ππ∴==⨯=,故选D. 方法二:PA PB PC ==Q ,ABC △为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA 、AB 中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,CE AC C =I ,EF ∴⊥平面PAC ,PB ⊥平面PAC ,PAB ∴∠=90︒,PA PB PC ∴===,P ABC ∴-为正方体一部分,2R ==R =,34433V R ππ∴===,故选D. 二、填空题:本题共4小题,每小题5分,共20分. 13.()0,x ∀∈+∞,ln 1x x ≠- 14.2F V E +-=解析:凸多面体的面数为F .顶点数为V 和棱数为E ,①正方体:6F =,8V =,12E =,得86122F V E +-=+-=; ②三棱柱:5F =,6V =,9E =,得5692F V E +-=+-=; ③三棱锥:4F =,4V =,6E =,得4462F V E +-=+-=.根据以上几个例子,猜想:凸多面体的面数F .V 和棱数E 满足如下关系:2F V E +-= 再通过举四棱锥、六棱柱、…等等,发现上述公式都成立. 因此归纳出一般结论:2F V E +-= 故答案为:2F V E +-= 15.1,2⎛⎫-∞-⎪⎝⎭解析:()()1x f x e x =-Q ,()xf x xe '∴=,∴对于任意的[]2,2x ∈-,当[)2,0x ∈-时,()0f x '<,当(]0,2x ∈时,()0f x '>,即()f x 在[)2,0-上为减函数,在(]0,2上为增函数.0x ∴=为()f x 在[]2,2-上的极小值点,也是最小值点且最小值为[]2,2-,∴对于任意的[]12,2x ∈-,()1min 1f x =-,而总存在[]21,2x ∈,使得()()12f x g x >,()()12min min f x g x >.()g x mx =∵,∴①0m =时,()20g x =,不合题意,②0m >时,()[]22,2g x mx m m =∈,此时1m <-,不合题意,③0m <时,()[]222,g x mx m m =∈,()2min 2g x m ∴=,21m ∴<-,12m <-. 16.850【解析】依题意,每天生产的玩具A 型商品x 个、B 商品y 个、C 商品的个数等于:100x y --,所以每天的利润()89610023600T x y x y x y =++--=++.约束条件为:()*57410060010000,0,,x y x y x y x y x y N ++--≤⎧⎪--≥⎨⎪≥≥∈⎩,整理得*3200100,x y x y x y N ⎧+≤⎪+≤⎨⎪∈⎩.目标函数为23600T x y =++.如图所示,做出可行域.初始直线0:230l x y +=,平移初始直线经过点A 时,T 有最大值.由3200100x y x y +=⎧⎨+=⎩得5050x y =⎧⎨=⎩.最优解为()50,50A ,此时max 850T =(元).即最大日利润是850元.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.17.(1)()()()111122n n n n n n n n b b b a a b b b +===-+--Q ,11112n nb b +∴-=--,12111111n n n n b b b b +-∴==-+---.∴数列11n b ⎧⎫⎨⎬-⎩⎭是以4-为首项,1-为公差的等差数列. ∴14(1)31n n n b =---=---,∴12133n n b n n +=-=++. (2)113n n a b n =-=+Q . ()()()12231111114556344444n n n n S a a a a a a n n n n +∴=++⋅⋅⋅+=++⋅⋅⋅=-=⨯⨯++++ ()()()()21368244334n n a n a n an n aS b n n n n -+--+∴-=-=++++.由条件可知()()213680a n a n -+--<恒成立即可满足条件,设()()()21328f n a n a n =-+--,当1a =时,()380f n n =--<恒成立,当1a >时,由二次函数的性质知不可能成立.当1a <时,对称轴3231102121a a a -⎛⎫-⋅=--< ⎪--⎝⎭,()f n 在[)1,+∞为单调递减函数. ()()()113684150f a a a =-+--=-<,154a ∴<,∴时4n aSb <恒成立.综上知:1a <时,4n aS b <恒成立. 18.【解析】(1)连接DB ,DF ⊥平面ABCD ,EB ⊥平面ABCD ,EB FD ∴∥,E ∴,F ,D ,B 四点共面,AC EB ∴⊥,设DB AC O =I ,ABCD Q 为菱形,AC DB ∴⊥.DB EB B =I ,AC ∴⊥平面EFDB ,EF ⊂Q 平面EFDB ,AC EF ∴⊥.(2)EB FD ∥Q ,EB BD ⊥,EFDB ∴为直角梯形,在菱形ABCD 中,60DAB ∠︒=,2AB =,2BD =,3AO CO ==∴梯形EFDB 的面积()24262S +⨯==,AC ⊥Q 平面EFDB ,114333EFABCD C EFDB A EFDB V V V S AO S CO --∴==⨯+⨯=+. 19.解析:(1)甲解密成功所需时间的中位数为47,()0.0150.014550.03450.0447450.5b ∴⨯+⨯+⨯+⨯+⨯-=,解得0.026b =;0.0430.032550.010100.5a ∴⨯+⨯+⨯+⨯=,解得0.024a =;∴甲在1分钟内解密成功的频率是10.01100.9f =-⨯=(2)①由题意及(1)可知第一个出场选手解密成功的概率为10.9P =;第二个出场选手解密成功的概率为2910.910.911010P =⨯+⨯=, 第三个出场选手解密成功的概率为23910.920.9291010P ⎛⎫=+⨯= ⎪⎝⎭⨯, 所以该团队挑战成功的概率为0.90.10.910.10.090.9290.999361P =+⨯+⨯⨯=(或令“该团队挑战成功”的事件为A ,“挑战不成功”的事件为A ,()()()()10.910.9110.9290.10.090.0710.000639P A ⨯=---=⨯=,∴该团队挑战成功的概率为()()110.00016390.999361P A P A =-=-=②由①可知按i P 从小到大的顺序的概率分别1p ,2p ,3p ,根据题意知X 的取值为1,2,3;则()10.9P X ==,()()210.90.910.091P X ==-⨯=, ()()()310.910.910.10.090.009P X ==--=⨯=.20.(1)因为1,2c c m e a ===,则2,a m b ==,所以2a b +取最小值时1m =, 此时抛物线21:4C y x =-,此时22,3a b ==,所以椭圆2C 的方程为22143x y +=; (2)因为1,2c c m e a ===,则2,a m b ==,设椭圆的标准方程为2222143x y m m +=, ()()0011,,,P x y Q x y 由2222214334x y m m y mx ⎧+=⎪⎨⎪=-⎩得22316120x mx m --=,所以023x m =-或06x m =(舍去),代入抛物线方程得03y m =,即23m P ⎛- ⎝⎭, 于是153m PF =,21723m PF a PF =-=,12623m F F m ==,又12PF F △的边长恰好是三个连续的自然数,所以3m =.此时抛物线方程为212y x =-,()(13,0,F P --,则直线PQ的方程为)3y x =+.联立)2312y x y x⎧=+⎪⎨=-⎪⎩,得192x =-或12x =-(舍去),于是9,2Q ⎛-- ⎝.所以252PQ ==,设(()2,12t M t t ⎛⎫-∈- ⎪⎝⎭到直线PQ的距离为d,则2753022d t ⎛=⨯+- ⎝⎭,当t =max 752d ==,所以MPQ △的面积最大值为12522⨯=.此时:MP y =+.21.(1)函数()f x 的定义域为()0,+∞,()1a x ae f x e x ex+'=+=,曲线()y f x =在点()00,x y 处的切线方程为2y x e =.由题意得000012,2ln a e x e x x a x ee ⎧+=⎪⎪⎨⎪=+⎪⎩解得1a =,0x e =.所以a 的值为1. (2)当1a =-时,()ln xf x x e =-,则()11x e f x e x ex-'=-=,由()0f x '>,得x e >,由()0f x '<,得0x e <<,则()f x 有最小值为()0f e =,即()0f x ≥,所以()ln ln x x g x x b e x=--+,()0x >,由已知可得函数ln ln x x y x x e =+-的图象与直线y b =有两个交点, 设()()ln ln 0x x h x x x x e=+->,则()22211ln 1ln x ex e e x x h x x x e ex -+--'=+-=, 令()2ln x ex e e x x ϕ=+--,()222e ex e x x e x x x ϕ--'=--=, 由220ex e x --<,可知()0x ϕ'<,所以()x ϕ在()0,+∞上为减函数,由()0e ϕ=,得0x e <<时,()0x ϕ>,当x e >时,()0x ϕ<,即当0x e <<时,()0h x '>,当x e >时,()0h x '<,则函数()h x 在()0,e 上为增函数,在(),e +∞上为减函数,所以,函数()h x 在x e =处取得极大值()1h e e =, 又()11h e =-,()322331341h e e e e e=+-<-<-<-, 所以,当函数()g x 在[)1,+∞上有两个零点时,b 的取值范围是11b e e -≤<, 即11,b e e ⎡⎫∈-⎪⎢⎣⎭. 22.(1)由题意可知:直线l 的普通方程为10x y ++=,()1,0A ∴-,()0,1B -1C 的方程可化为()2210x y y +=≥,设点P 的坐标为()cos ,sin θθ,0θπ≤≤,cos sin 1114BA BP πθθθ⎛⎫⎡⎤∴⋅=-++=-+∈ ⎪⎣⎦⎝⎭uu r uu r(2)曲线2C 的直角坐标方程为:()()22228x y ++-=直线l的标准参数方程为212x m y m ⎧=-⎪⎪⎨⎪=+⎪⎩(m 为参数),代入2C得:270m -=设,M N 两点对应的参数分别为12,m m121270m m m m +=-<故12,m m异号12QM QN m m ∴-=+=23.答案:(1)当2m =-时,()()410322321023452x x f x x x x x x ⎧⎪+≥⎪⎪⎛⎫=++--<<⎨ ⎪⎝⎭⎪⎪⎛⎫--≤-⎪ ⎪⎝⎭⎩当4130x x +≤⎧⎨≥⎩解得102x ≤≤当30,132x -<<≤恒成立. 当45332x x --≤⎧⎪⎨≤-⎪⎩解得322x -≤≤-,此不等式的解集为12,2⎡⎤-⎢⎥⎣⎦. (2)()()43032233023432x m x f x x x m m x x m x ⎧⎪++≥⎪⎪⎛⎫=+++=+-<<⎨ ⎪⎝⎭⎪⎪⎛⎫--+≤-⎪ ⎪⎝⎭⎩, 当(),0x ∈-∞时,()33022233432m x f x x x m x m x ⎧⎛⎫+-<< ⎪⎪⎪⎝⎭=+++=⎨⎛⎫⎪--+≤- ⎪⎪⎝⎭⎩当302x -<<时,()3f x m =+,当()3,432x f x x m ≤-=--+单调递减, ()f x ∴的最小值为3m +设()()20g x x x x=+<当20,x x x ->-+≥-,当且仅当2x x -=-时,取等号2x x ∴+≤-即x =()g x取得最大值-.要使()2f x x x≥+恒成立,只需3m +≥-3m ≥-.。
2019-2020年高三第七次调研考试文数试题 含解析

2019-2020年高三第七次调研考试文数试题 含解析一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}{}23,log ,,M a N a b ==,若{}0M N =,则MN =( )A .{}0,1,2B .{}0,1,3C .{}0,2,3D .{}1,2,3【答案】B考点:集合的交集、并集运算.2.设:12,:21x p x q <<>,则p 是q 成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件【答案】A 【解析】 试题分析:21,0x x >∴>,所以p 是q 成立的充分不必要条件.考点:充分、必要条件的判断.【方法点睛】充分不必要条件、必要不充分条件、既不充分也不必要条件的判断的一般方法: ①充分不必要条件:如果p q ⇒,且p q ⇐/,则说p 是q 的充分不必要条件; ②必要不充分条件:如果p q ⇒/,且p q ⇐,则说p 是q 的必要不充分条件; ③既不充分也不必要条件:如果p q ⇒/,且p q ⇐/,则说p 是q 的既不充分也不必要条件. 3.已知角α的顶点在原点,始边与x 轴正半轴重合,终边过点()39,2a a -+,且cos 0,sin 0αα≤>,则a 的范围是( )A .()2,3-B .[)2,3-C .(]2,3-D .[]2,3-【答案】C考点:三角函数的定义.4.在各项均为正数的等比数列{}n a 中,2109a a =,则57a a +=( ) A .有最小值6B .有最大值6C .有最大值9D .有最小值3【答案】A 【解析】试题分析:因为在等比数列2213x y +=中,2109a a =,所以572109a a a a ==,所以由基本不等式可得,576a a +≥=,当且仅当573a a ==时等号成立,故应选A . 考点:1、等比数列;2、基本不等式的应用.5.一个几何体的三视图如图所示,则这个几何体的外接球的体积为( )A .3BC .2πD .3【答案】A考点:空间几何体的三视图.6.在ABC ∆中,若点D 满足2BD DC =,则AD =( ) A .1233AC AB + B .5233AB AC - C .2133AC AB - D .2133AC AB + 【答案】D 【解析】试题分析:根据题意画出图形如下所示:∵2BD DC =,∴ 2()AD AB AC AD -=-u u u r u u u r u u u r u u u r,∴32AD AB AC =+uuu r uu u r uu u r ,∴1233AD AB AC =+uuu r uu u r uuu r ,故选D .考点:平面向量的共线定理. 7.函数()()sin 0,06f x A x A πωω⎛⎫=+>> ⎪⎝⎭的图象与x 轴的交点的横坐标构成一个公差为2π的等差数列,要得到函数()cos g x A x ω=的图象,只需将()f x 的图象( ) A .向左平移6π B .向左平移3π C .向左平移23π D .向右平移23π【答案】A 【解析】试题分析:由题意知,函数)0,0)(6sin()(>>+=ωπωA x A x f 的周期为π,所以2ππω=,即2ω=.要得到函数x A x g ωcos )(=sin[2()]66x ππ=++的图像,只需将()f x 的图像向左平移6π个单位即可,故应选A . 考点:1、函数()sin()f x A x ωϕ=+的图像及其变换.8.若下框图所给的程序运行结果为35S =,那么判断框中应填入的关于k 的条件是( ) A .7k =B .6k ≤C .6k <D .6k >【答案】D考点:程序构图.9.已知函数()2211x x f x x ++=+,若()23f a =,则()f a -=( ) A .23B .23-C .43D .43-【答案】C 【解析】 试题分析:()2221111x x xf x x x ++==+++,()222111313a a f a a a ∴=+=∴=-++,所以()()22141111331aa f a a a -⎛⎫-=+=-=--= ⎪+⎝⎭-+,故选C. 考点:函数的奇偶性. 10.已知函数()213ln 22f x x x =-+在其定义域内的一个子区间()1,1a a -+内不是单调函数,则实数a 的取值范围是( ) A .13,22⎛⎫-⎪⎝⎭B .51,4⎡⎫⎪⎢⎣⎭C .31,2⎛⎫ ⎪⎝⎭D .31,2⎡⎫⎪⎢⎣⎭【答案】D 【解析】试题分析:因为函数()23ln 212+-=x x x f 在区间()1,1+-a a 上不单调,所以考点:函数的单调性与导数的关系.11.设,,a b c 为三角形ABC 三边长,1,a b c ≠<,若l o g l o g2l o gl o g c bc b c b c b a a aa +-+-+=,则三角形ABC 的形状为( ) A .锐角三角形 B .直角三角形C .钝角三角形D .无法确定【答案】B 【解析】试题分析:∵log log 2log log c b c b c b c b a a a a +-+-+=,∴112log log c b c b a a-++=,即()()l o g l o g 2a a c b c b -++=,∴()22log 2a c b -=,即222c b a -=,故三角形ABC 的形状为直角三角形,故选:B . 考点:三角形的形状判断.【思路点睛】本题考查的知识点是三角形形状判断,对数的运算性质,熟练掌握对数的换底公式是解决本题的关键,结合对数的运算性质,及换底公式的推论,可将已知化为:222c b a -=,再由勾股定理判断出三角形的形状.12.已知点P 为双曲线()222210,0x y a b a b -=>>右支上一点,12,F F 分别为双曲线的左右焦点,且212,b F F I a=为三角形12PF F 的内心,若1212IPF IPF IF F S S S λ∆∆∆=+成立,则λ的值为( )A .12+B .1C 1D 1【答案】D 【解析】试题分析:设12PF F V 的内切圆半径为r ,由双曲线的定义得1212||22PF PF aF F c -==,,1212|1122|||IPF IPF S PF r S PF r =⋅=⋅V V ,,12122IF F S c r cr =⋅⋅=V ,由题意得,121122||||PF r PF r cr λ⋅=⋅+,故122PF PF a cc λ-===,212||b F F a =Q ,2222b c a c a a-∴==2210a ac c ⎛⎫∴+-= ⎪⎝⎭,1a c ∴=故选:D .考点:1.双曲线的简单性质;2.圆锥曲线的定义、性质与方程.【思路点睛】本题考查双曲线的定义和简单性质,利用待定系数法求出参数的值,设12PF F V 的内切圆半径为r ,由1212||22PF PF a F F c -==,,用12PF F V 的边长和r 表示出等式中的三角形的面积,解此等式求出λ.第Ⅱ卷(非选择题,共90分)二、填空题(共4小题,每题5分,满分20分,将答案填在答题纸上) 13.若复数a iz i+=(其中i 为虚数单位)的实部与虚部相等,则实数a =______. 【答案】-1考点:复数概念.14.已知0m >,实数,x y 满足0,0,,x y x y m ≥⎧⎪≥⎨⎪+≤⎩若2z x y =+的最大值为2,则实数m =______.【答案】1 【解析】试题分析:由已知的约束条件可知,目标函数2z x y =+在点(0,)m 处取得最大值,即max 022z m =+=,所以1m =,故应填1. 考点:简单的线性规划.15.顶点在原点,经过圆22:20C x y x +-+=的圆心且准线与x 轴垂直的抛物线方程为______. 【答案】22yx =.考点:1.抛物线的标准方程;2.圆的标准方程.【思路点睛】本题主要考查抛物线的标准方程和圆的标准方程,重点考查抛物线的标准方程的求法,属中档题.其解题的一般思路为:首先设出抛物线的标准方程,然后利用已知条件知其图像过点(1,,代入即可求出抛物线中的参数,最后得出所求的抛物线的标准方程即可.16.设函数()f x 在()0,+∞内可导,且()1312xxf e x e =++,且()1f '=______. 【答案】27【解析】试题分析:令xt e=,则ln x t =,()3ln 12t f t t ∴=++,()213+='∴t t f ,()272131=+='∴f . 考点:求导数值.【思路点睛】本题考查了求导的运算以及换元法求外层函数的解析式,属于基本题型;由题设知,可先用换元法令xt e =,求出函数()f x 的解析式,再根据求导公式,求出函数()f x 它的导数,然后再将1x =代入,进而求出()1f '.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知函数()22sin 2,,442f x x x x πππ⎛⎫⎡⎤=+∈ ⎪⎢⎥⎝⎭⎣⎦.设x α=时()f x 取得最大值. (1)求()f x 的最大值及α的值;(2)在ABC ∆中,内角,,A B C 的对边分别为,,,12a b c A πα=-,且2sin sin sin B C A =,求b c -的值.【答案】(1)3;(2)0b c -=试题解析:解:(1)由题意,()1cos 221sin 2212sin 223f x x x x x x ππ⎡⎤⎛⎫⎛⎫=-+=+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.又,42x ππ⎡⎤∈⎢⎥⎣⎦,则22633x πππ≤-≤. 故当232x ππ-=,即512x πα==时,()max 3f x =. (2)由(1)知123A ππα=-=.由2sin sin sin B C A =,即2bc a =.又222222cos a b c bc A b c bc =+-=+-.则22b c bc bc +-=,即()20b c -=.故0b c -=.考点:1.三角恒等变换;2.正弦定理;3.余弦定理.18.根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:(1)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;(2)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.【答案】(1)35;(2)去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.(2)去年该居民区PM2.5年平均浓度为:12.50.1537.50.662.50.1587.50.142.5⨯+⨯+⨯+⨯=(微克/立方米).因为42.535>,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.考点:1古典概型概率;2平均数.19.在如图所示的多面体ABCDE 中,已知,,ABDE AB AD ACD ⊥∆是正三角形,22,AD DE AB BC F ===是CD 的中点.(1)求证://AF 平面BCE ;(2)求直线CE 与平面ABED 所成角的余弦值.【答案】(1)见解析;(2)4(3(2)因为ACD ∆是正三角形,所以2AC AD CD ===,在ABC ∆中,1,2,AB AC BC ==222AB AC BC +=,故AB AC ⊥,又,AB AD AC AD A ⊥=,所以AB ⊥平面ACD .取AD 的中点H ,连接,CH EH ,则AB CH ⊥,又AC CD =,所以CH AD ⊥,又AB AD A =,所以CH ⊥平面ABED ,所以CEH ∠是直线CE 与平面ABED 所成的角.在Rt CHE ∆中,CH EH CE ===cos CEH ∠=. 考点:1.线面平行、垂直的判定与性质;2.线面角的求法;3.多面体的体积.【方法点睛】本题主要考查线面平行、垂直的判定与性质,线面角的求法及多面体体积的求法,属中档题.判断线面平行的常用方法有:1.利用线面平行的定义;2.利用线面平行的判定定理;3.利用面面平行的性质(即若两个平面平行,一个平面内的任意一条直线平行于另一个平面).20.如图,已知圆()221:11C x y ++=,圆()()222:341C x y -+-=.(1)若过点1C 的直线l 被圆2C 截得的弦长为65,求直线l 的方程; (2)设动圆C 同时平分圆1C 、圆2C 的周长.①求证:动圆圆心C 在一条定直线上运动;②动圆C 是否过定点?若过,求出定点的坐标;若不过,请说明理由.【答案】(1)3430x y -+=或4340x y -+=;(2)①详见解析;②动圆C 过定点12⎛++ ⎝⎭和12⎛ ⎝⎭(2)①证明:设动圆圆心(),C x y ,由题可知12CC CC ==化简得30x y +-=,所以动圆圆心C 在定直线30x y +-=上运动.②动圆C 过定点设(),3C m m-,则动圆C=动圆C 的方程为()()()()22223113x m y m m m -+-+=+++-整理得()2262210x y y m x y +----+= 2262010x y y x y ⎧+--=⎨-+=⎩,解得12x y ⎧=+⎪⎪⎨⎪=⎪⎩12x y ⎧=⎪⎪⎨⎪=⎪⎩所以动圆C过定点12⎛+⎝⎭和12⎛- ⎝⎭. 考点:1.圆与圆的位置关系及其判定;2.直线与圆的位置关系.21.已知函数()ln 1f x ax x =+-,其中a 为常数.(1)当1,a e ⎛⎫∈-∞- ⎪⎝⎭时,若()f x 在区间()0,e 上的最大值为4-,求a 的值;(2)当1a e =-时,若函数()()ln 2x b g x f x x =--存在零件,求实数b 的取值范围. 【答案】(1)2a e =-;(2)22b e≥- 试题解析:解(1)由题意()1f x a x '=+,令()0f x '=解得1x a =- 因为1,a e ⎛⎫∈-∞ ⎪⎝⎭,所以10e a<-<,由()0f x '>解得10x a <<-,由()0f x '<解得1x e a-<< 从而()f x 的单调递增区间为10,a ⎛⎫- ⎪⎝⎭,减区间为1,e a ⎛⎫- ⎪⎝⎭所以,()max 1111ln 4f x f a a ⎛⎫⎛⎫=-=--+-=- ⎪ ⎪⎝⎭⎝⎭,解得2a e =-. (2)函数()()ln 2x b g x f x x =--存在零点,即方程()ln 2x b f x x =+有实数根, 由已知,函数()f x 的定义域为{}0x x >,当1a e =-时,()1ln x f x x e=--+,所以()11x e f x e x ex -'=-+=-, 当0x e <<时,()0f x '>;当x e >时,()0f x '<,所以()f x 的单调增区间为()0,e ,减区间为(),e +∞,所以()()max 1f x f e ==-,所以()1f x ≥.令()ln 2x b h x x =+,则()21ln x h x x -'=.当0x e <<时,()0h x '>;当x e >时,从而()()h x g x 在()0,e 上单调递增,在(),e +∞上单调递减,所以()()max 12b h x h e e ==+,要使方程()ln 2x b f x x =+有实数根, 只需()()max 112b h x h e e ==+≥即可,则22b e≥-. 考点:1.利用导数研究函数的单调性;2.利用导数求闭区间上函数的最值.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-1:几何证明选讲如图,AB 是圆O 的直径,,C D 是圆O 上两点,AC 与BD 相交于点,,E GC GD 是圆O 的切线,点F 在DG 的延长线上,且DG GF =.求证:(1),,,D E C F 四点共圆;(2)GE AB ⊥.【答案】(1)证明过程详见解析;(2)证明过程详见解析.(2)延长GE 交AB 于点H .因为GD GC GF ==,所以点G 是经过,,,D E C F 四点的圆的圆心,所以GE GC =,所以GCE GEC ∠=∠.又因为390,13GCE ∠+∠=︒∠=∠,所以190GEC ∠+∠=︒, 所以190AEH ∠+∠=︒,所以90EHA ∠=︒,即GE AB ⊥.考点:1.切线的性质;2.圆心角与圆周角的关系;3.四点共圆的判定.23.选修4-4:坐标系与参数方程已知直线l的参数方程为122x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),曲线C 的极坐标方程为2cos21ρθ=.(1)求曲线C 的普通方程;(2)求直线l 被曲线C 截得的弦长.【答案】(1)221x y -=;(2)考点:1.参数方程化成普通方程;2.简单曲线的极坐标方程.【方法点睛】1.极坐标方程化直角坐标方程,一般通过两边同时平方,两边同时乘以ρ等方式,构造或凑配2cos sin ρρθρθ,,,再利用互化公式转化.常见互化公式有()222cos sin tan 0y x y x y x x ρρθρθθ=+===≠,,,等. 2.参数方程化普通方程,关键是消参,常见消参方式有:代入法,两式相加、减,两式相乘除,方程两边同时平方等.3.若直线与曲线相交于()()1122A x y B x y ,,,,直线的斜率为k ,联立直线与曲线的方程,消去y ,再利用韦达定理将12x x +及12x x ⋅的值整体代入弦长公式AB =24.选修4-5:不等式选讲已知函数()2123f x x x =++-.(1)求不等式()6f x ≤的解集;(2)若关于x 的不等式()()22log 32f x a a -->恒成立,求实数a 的取值范围. 【答案】(1){}12x x -≤≤;(2)10a -<<或3 4.a <<【解析】试题分析:(1)首先分三种情况进行讨论:①32x >,②1322x -≤≤,③12x <-,并分别化去绝对值,得到相应的不等式组,最后运用一元二次不等式的解法即可得出所求的结果;(2)首先将已知的恒成立问题转化为22log (3)22123a a x x -+<++-,然后运用三角不等式即可得出2123x x ++-的最小值,考点:1、含绝对值不等式的解法;2、对数不等式.。
2020届湖北省武汉市四中高三数学测试卷(文)

数学试题(文科)考试时间:120分钟, 满分:150分第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的,将正确选项的字母填在答题卡相应的表格中.) 1.设2:x x f →是集合A 到集合B 的映射,若B={1,2},则B A I 为 ( )A .ΦB .{1}C .Φ或{2}D .Φ或{1} 2.如果9,,,,1--c b a 成等比数列,那么( )A .9,3==ac bB .9,3=-=ac bC .9,3-==ac bD .9,3-=-=ac b3.当,10时<<<b a 下列不等式中正确的是( )A .ba b a )1()1(->- B .bab a )1()1(+>+C .2)1()1(b ba a ->-D .bbb a )1()1(1->-4.已知等差数列{n a }的前n 项和为S n ,若,201OC a OA a OB +=且A 、B 、C 三点共线(该直线不过点O ),则S 20=( )A .10B .11C .20D .215.已知函数2)4()(),0(2)(=+>=b f a f x x f x若ba 11+则的最小值是 ( )A .6B .7C .8D .96.已知△ABC 的三个内角A 、B 、C 所对的三边分别为a 、b 、c ,若△ABC 的面积22)(b a c S --=,则2tanC等于 ( )A .21 B .41 C .81 D .47.已知A 、B 、C 、D 是同一球面上的四点,且每两点间距离都等于2,则球心到平面BCD 的距离是 ( ) A .36B .66 C .126 D .1868.过点M (3,0)的直线交⊙4)2(:22=+-y x C 于A 、B 两点,C 为圆心,则⋅ 的最小值是( )A .8B .6C .532 D .49.设双曲线)1,0(,1:222C y ax M 过点=-且斜率为1的直线,交双曲线的两渐近线于A 、B两点,若2CB AC =,则双曲线的离心率为( )A .10B .5C .310 D .25 10.设定义域为R 的函数)(),(x g x f 都有反函数,并且)22()1(1---x g x f 和函数的图像关于直线)1(,2008)2(,f g x y 则若对称==的值为( )A .1005B .2020C .1003D .以上结果均不对第Ⅱ卷(非选择题,共100分)二、填空题(本大题共5小题,每小题5分,共25分,将答案写在答题卡相应的横线上.) 11.△ABC 与△DBC 所在平面互相垂直,且AB=BC=BD ,∠ABC=∠DBC=60°,则二面角A —BD —C 的正切值是 . 12.设数列}{},{n n b a 是等差数列,T n 、S n 分别是数列}{},{n n b a 的前n 项和,且,12--n nS T n n 则=66b a .13.给出下列命题:①函数)6,2()3sin(πππ--=的区间x y 内单调递增; ②函数|sin 2|x y =的最小正周期为π; ③函数)3cos(π+=x y 的图形是关于直线6π=x 成轴对称的图形;④函数)3tan(π+=x y 的图形是关于点)0,6(π成中心对称的图形. 其中正确命题有 .14.设F 为抛物线的焦点x y 42=A 、B 、C 为该抛物线上三点,若032=++FC FB FA ,则||3||2||FC FB FA ++= .15.已知A (3,3),O 为原点,点||,002303),(OA OP OA y y x y x y x P ⎪⎪⎩⎪⎪⎨⎧≥≥+-≤-则的坐标满足的最大值是 ,此时点P 的坐标是 .三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程和演算步骤,将答案写在答题卡相应处.) 16.(本小题满分12分)已知集合}.,0)1(2|{},,0)13(2)33(|{22R x a x ax x B R x a x a x x A ∈<+--=∈<+++-=集合(1)求B ∉4时,求实数a 的取值范围; (2)求使A B ⊆的实数a 的取值范围。
2020年5月湖北省七市(州)教科研协作体高三联合考试文科数学参考答案

2020年5月湖北省七市(州)教科研协作体高三联合考试数学(文史类)参考答案一、选择题二、填空题13.4-14.1315.13x x⎧⎫>⎨⎬⎩⎭16. 22三、解答题(一)必考题17.解:(1)……………………………4分(2)由题可知,当车速在[]85,90时超速,此时车辆共有:201001.0200=⨯⨯(辆);……………………………8分这200辆汽车在该路段的平均速度为:721001.08506.07502.06501.055=⨯⨯+⨯+⨯+⨯)((公路/小时)……………12分18.解:(1)当2n≥时,11(*)2nnnaa n Na--=∈+15:DABDC610:CACAB1112:CB11112(1)n n a a -∴+=+……………………………4分所以数列是以2为公比,以为首项的等比数列,从而……………………………6分(2)由(1)121n n a =-,12(21)(21)nn n n b +∴=--1112121n n +=--- ……………8分 2231111111()()()212121212121n n n T +∴=-+-+⋅⋅⋅+-------11121n +=-- …………………12分 19.解:(1)证明:AD BC //Θ,ADMN AD ADMN BC 平面平面⊂⊄,,∴ADMN BC 平面//. ……………………………2分又BC ⊂平面PBC ,平面PBC I 平面ADMN MN = BC ∴∥MN ……………………………4分(2) 平面⊥PA ΘABCD ,BC ⊂平面ABCDBC PA ⊥∴,又A AB PA AB BC =⊥I ,,PAB BC 平面⊥∴………………………6分 AN ⊂Q 平面PAB ,BC AN ∴⊥,又BC ∥MN ,AN MN ∴⊥ Q 平面ADMN ⊥平面PBC 平面ADMN I 平面PBC MN = AN ∴⊥平面PBC AN PB ∴⊥ ………………………8分 AB PA =Θ,N ∴为PB 中点,又BC ∥MN ,∴21=PC PM 1122P BDM C BDM B CDM B PCD P BCD V V V V V -----∴==== ………………………10分 11n a ⎧⎫+⎨⎬⎩⎭1112a ⎛⎫+= ⎪⎝⎭12111221n n n n a a -+=⨯⇒=-11123213BCD P BCD M BCDP ABCD P ABCD ABCD S h V V V V S h ∆----∆⋅⋅∴=⋅,又13BCD ABCD S S ∆∆= 16M BCD P ABCD V V --∴= ………………………12分 20.解:(1)由题可知1c =,又221112a b +=,221a b =+ 2221112(1)a a ∴+=- 422520a a ∴-+= 22(2)(21)0a a ∴--=又21a > 22a ∴=,21b = ………………………4分(2)设11(,)A x y ,22(,)B x y ,AB 中点00(,)P x y ,直线AB 的方程为:(1)y k x =+ 由22(1)12y k x x y =+⎧⎪⎨+=⎪⎩可得2222(21)4220k x k x k +++-= 212221224212221k x x k k x x k ⎧-+=⎪⎪+∴⎨-⎪⋅=⎪+⎩………………………6分 122221k y y k ∴+=+ 2222(,)2121k k P k k -∴++ ………………………8分 HA HB =Q 1PH AB k k ∴⋅=- 22221121213kk k k k +∴⋅=--++ ………………………10分 21k ∴= 1k ∴=± :1AB l y x ∴=+或1y x =--,AB ∴==………………………12分21.解:(1)当1a e=时,1)(-=='x x e ae x f Θ1)1(='∴f ,又1)1(=f , ∴函数)(x f y =在))1(,1(f 处的切线方程为x y = ………………………4分(2)1a e≥Q ,1-≥∴x x e ae 令x e x m x -=-1)(,则1)(1-='-x e x m ,令1,0)(=='x x m 则 当)1,0(∈x 时,0)(<'x m ,)(x m 单调递减;当),1(+∞∈x 时,0)(>'x m ,)(x m 单调递增,∴0)1()(min ==m x m 故x e x ≥-1恒成立, ………………………6分 只需证1ln +≥xx x ,即证0ln 2≥--x x x ………………………8分 令x x x x n --=ln )(2,则xx x x x x x x x n )1)(12(12112)(2-+=--=--=' 令1,0)(=='x x n 则 当)1,0(∈x 时,0)(<'x n ,)(x n 单调递减;当),1(+∞∈x 时,0)(>'x n ,)(x n 单调递增 ∴min ()(1)0n x n ==,∴ 0)(≥x n 恒成立 ln 1x x x∴≥+ ………………………10分 1ln 1x x x ae e x x -∴≥≥≥+,()()f x g x ∴≥ ()()0f x g x ∴-≥恒成立. ………………………12分(此种解法仅供参考,其它解法斟情给分)(二)选考题22.【选修4—4:坐标系与参数方程】解:(1)(I)直线0y ++= 曲线C :2239()24x y ++= …………………5分 (2)方法一:联立直线与曲线C得:22139(2))224t --++= 化简得:21202t t +-=, ∴1212t t +=-l lO 到直线的距离d == ………………………8分1211||| |||| |=||2224APO BPO S S AP d BP d t t ∆∆-=⋅-⋅+=.………………10分 方法二:联立直线与曲线C得:22039(2)24y y ++=⎨-++=⎪⎩化简得:2302y y -=,∴12y y += ………………………8分121211||||||||||| |=||224APO BPO S S OP y OP y y y ∆∆-=⋅-⋅+=……………10分 21. 解:(1)由题可知,3,2()21,213,1x f x x x x -≤-⎧⎪=+-<<⎨⎪≥⎩, ……………2分当21x -<<时,212x +≥-312x ∴-≤<; 当1x ≥时,成立, ……………4分 故()2f x ≥-的解集为32x x ⎧⎫≥-⎨⎬⎩⎭. ……………5分 (2)由(1)可知,()f x 的最大值为3,23a b c ∴++= ……………6分 2229()()()24a b c ab ac bc c a c b c ++∴+++=++≤=. ……………10分l l。
2020年湖北省高考数学(文科)模拟试卷(7) 含详细答案解析

3??- ??- 6 ≤ 0 x, y 满足约束条件 { ??- ??+ 2 ≥ 0 ,若目标函数
??≥ 0,??≥ 0
z= ax+by( a> 1, b
2
3
> 1)的最大值为 12,则
+
的最小值为
.
??-1 ??-1
三.解答题(共 5 小题,满分 60 分,每小题 12 分)
17.( 12 分)已知函数 f( x)= x2+bx+c( b, c∈R),且 f ( x)< 0 的解集为 { x|﹣ 3< x< 1} ; 数列 { an} 的前 n 项和为 Sn,对任意 n∈N * ,满足 Sn= f( n) +3﹣ n.
2 >(
11 10
)
4
????对
n∈N* 恒成立,求实
数 x 的取值范围.
18.( 12 分)在改革开放 40 年成就展上有某地区某衣产品近几年的产扯统计如表:
年份
2014
2015
2016
2017
2018
2019
年份代码 x
1
2
3
4
5
6
第 3页(共 20页)
年产量(万吨)
6.6
6.7
7
7.1
7.2
( 1)求 a1 的值及数列 { an} 的通项公式;
( 2)已知数列 { bn} 的前
n 项和为
Tn,满足 ????=
2????-
1,n∈N* ,求数列 2
{ an?bn} 的前
n项
和 An;
( 3)已知数列
{c n} 满足 ????=
(
10 11
)
2020届全国名师联盟高三第七次联考数学(文)试题.pdf

( I )证明:平面 AEC 平面 BED ;
( II )若 BAD , AE EC 三棱锥 E ACD 的体 3
积为 6 ,求 BE 的长 . 3
2
18.(本小题共 12 分)已知正项数列 an 的前 n 项和满足 2Sn 2an an 1(n N )
-3-
( 1)求数列 an 的通项公式;
( 2)设 bn
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.若抛物线 y2 tx 的焦点是双曲线 x2 y2 1 的一个焦点,则正数 t 等( ) 22
A. 9
B. 2
C.8
D. 4
4.已知直线 ax y 2 0 与圆 C : ( x 1)2 ( y a) 2 4 相交于 A, B 两点, 且线段 AB 是圆
4、答题前,请先将自己的姓名、准考证号用
0.5 毫米黑色签字笔填写在试题卷和答题卡
上的相应位置, 并将准考证号条形码粘贴在答题卡上的指定位置。
用 2B 铅笔将答题卡上试卷
类型 A 后的方框涂黑。
5、选择题的作答:每个小题选出答案后,用
2B 铅笔把答题卡上对应题目的答案标号涂
黑。写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
1 , Tn 是数列 bn 的前 n 项的和,求证: Tn 2 .
an an 1
19.(本小题共 12 分)已知函数 f ( x)
3 sin xcos x
1 cos2x
1
.
2
4
4
( 1)求函数 f ( x) 的单调递减区间;
( 2)在 ABC 中,角 A, B ,C 的对边分别为 a,b,c ,且 a 8 5 , D 为边 AB 上一点, 5
2020届湖北省名师联盟高三入学调研考试数学(文)试题(PDF版)

x
的方程[
f
( x)]2
mf
(x)
n
0的
以下叙述中,正确的个数为( )
① m 1 , n 0 时,方程有三个不等的实根; 2
② m n 1时,方程必有一根为 0 ;
③ n 0 且 m n 1时,方程有三个不等实根.
A. 0 个
B.1个
C. 2 个
D.3 个
2 OR 2 9 OP OQ ,求点 Q 的轨迹的直角坐标方程.
-8-
23.(10 分)【选修 4-5:不等式选讲】 已知函数 f (x) x 3 x 1 , M 为不等式 f (x) 2 的解集. (1)求 M ; (2)证明:当 loga b M 时, 2a 2b 2ab1 2 .
-9-
2020 届高三入学调研考试卷
文 科 数 学答 案
一 、选择题 :本大题 共 12 小 题,每小 题 5 分 ,在每小 题给 出的四 个选 项中 ,只 有一项 是符合题目要求的.
1.【答案】C 2.【答案】B 3.【答案】B 4.【答案】C 5.【答案】A 6.【答案】D 7.【答案】C 8.【答案】D 9.【答案】B 10.【答案】B 11.【答案】A 12.【答案】D 二、填空题:本大题共 4 小题,每小题 5 分.
2n
1.
(2) bn
log2 (an
1)
n,
bn
1 bn1
1 n(n 1)
1 n
1, n 1
∴
Sn
1 1
1 2
1 2
1 3
[首发]湖南湖北四校2020届高三学情调研联考数学(文)试题含答案+详解
![[首发]湖南湖北四校2020届高三学情调研联考数学(文)试题含答案+详解](https://img.taocdn.com/s3/m/9497d2f727284b73f342504c.png)
,
5 2
11.过双曲线
x2 a2
y2 b2
1a
b
0
右焦点
F
的直线交两渐近线于
A、B
两点,若
uur OA
uuur AB
0
,O
为
坐标原点,且 △OAB 内切圆半径为 3 1 a ,则该双曲线的离心率为
2
A. 2 3
3
B. 3
C. 4 3
3
D. 3 1
12.已知三棱锥 P ABC 的四个顶点在球 O 的球面上, PA PB PC ,△ABC 是边长为 2 的正三
ta(n A
B)
tanA tanB 1 tanAtanB
3tanB 1 4tan2B
1
3
, A、B 是三角形内角,且
4tanB
tanB
tanA 与 tanB 同号, A、B 都是锐角,即 tanA>0,tanB>0,
1 4tanB 2 1 4tanB 4
tanB
tanB
ta(n A B)
9 、C【解析】 acosB bcosA 3 c ∴由正弦定理,得 5
sinAcosB sinBcosA 3 sinC, 5
C (A B) sinC si(n A B) ,,
∴ sinAcosB sinBcosA 3(sinAcosB cosAsinB), 5
整理,得 sinAcosB 4sinBcosA ,同除以 cosAcosB,得 tanA 4tanB ,由此可得
日利润是__________元.
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题, 每个试题考生都必须作答。第 22、23 题为选考题,考生根据要求作答。 (一)必考题:60 分。
湖北省2020届高三(5月)调研模拟考试数学(文科)试卷 含答案

19:(本小题满分 12 分)
如图,已知椭圆
C:x a
2 2
+
y2 b2
= 1(a
b
0) 的左、右焦点分别为 F1、F2 ,
F1F2
=2
5 ,Q 是 y 轴的正
半轴上一点, QF2 交椭圆于 P,且 PF1 ⊥ PF2 , PQF1 的内切圆⊙M 半径为 1.
(1)求椭圆 C 的标准方程;
(2)若 N 点为圆 M 上一点,求 NF1 NF2 的取值范围.
湖北省 2020 年高三(5 月)调研模拟考试
文科数学试卷
本试卷共 5 页,23 题(含选考题)。全卷满分 150 分。考试用时 120 分钟。
2020.5
★祝考试顺利★
注意事项:
1.答题前先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上 的指定位置。
2.选择题的作答:每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑。写在试题卷 草稿纸和答题卡上的非答题区域均无效。
一工厂工作的概率为
A. 1 6
B. 1 3
C. 1 2
2
D. 5 6
10.函数 y = x − 4x − x2 的值城为
A.[2 − 2 2,4]
B.[0,4]
C.[0,2 + 2 2]
D.[2 − 2 2,2 + 2 2]
11.已知函数 f (x) = sin(x − )( 0) 在[0, ]有且仅有 4 个零点,则 的取值范围为 3
(2)若 bn = (2n +1) an ,求数列bn的前 n 项和Tn 。
3
18.(本小题满分 12 分)
已知如图 1 直角△ABC 中,AC⊥BC,AC=6,BC= 6 3 ,点 D 为 AB 的中点,BC=3BF,将△ACD
2020年5月湖北省七市(州)教科研协作体高三联合考试文科数学试卷答案
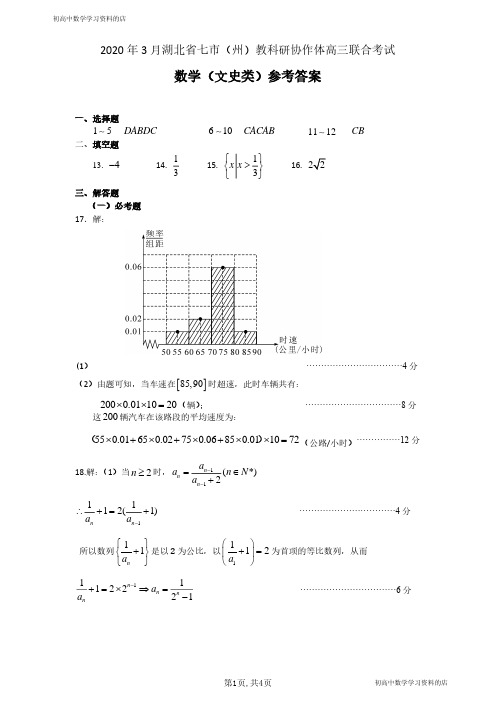
x
x
x
令 n(x) = 0,则x =1 当 x (0,1) 时 , n(x) 0 , n(x) 单 调 递 减 ; 当 x (1,+) 时 ,
n(x) 0 , n(x) 单 调 递 增 n(x)min = n(1) = 0 , n(x) 0 恒 成 立
x ln x +1 x
aex ex−1 x ln x +1, f (x) g(x) x
函数 y = f (x) 在 (1, f (1))处的切线方程为 y = x
………………………4 分
(2) a 1 ,aex ex−1 令 m(x) = ex−1 − x ,则 m(x) = ex−1 −1,令 m(x) = 0,则x =1 e
当 x (0,1) 时, m(x) 0 , m(x) 单调递减;当 x (1,+) 时, m(x) 0 , m(x) 单调递
………………………10 分
第3页,共4页
初高中数学学习资料的店
初高中数学学习资料的店
f (x) − g(x) 0 恒成立. ………………………12 分
(此种解法仅供参考,其它解法斟情给分)
(二)选考题
22.【选修 4—4:坐标系与参数方程】
解:(1)(I)直线 l : 3x + y + 2 3 = 0 曲线 C : (x + 3)2 + y2 = 9 …………………5 分
பைடு நூலகம்
2
4
(2)方法一:联立直线 l 与曲线 C 得: (−2 − 1 t + 3)2 + ( 3 t)2 = 9
PA ⊥ BC ,又 BC ⊥ AB, PA AB = A ,BC ⊥ 平面PAB ………………………6 分
2020届湖北省高三年级调研考试数学(文)试题及答案

2020届湖北省高三年级调研考试数学(文)试题及答案一、单选题1.已知集合{}1,2,3,4,5A =,{}|3B x x =-<-,则A B =()A .{}5B .{}1,2C .{}3,4,5D .{}4,5【答案】D【解析】首先求出集合B ,再根据交集的定义,即可得解. 【详解】解:因为{}|3B x x =-<-{}|3B x x ∴=>,{}1,2,3,4,5A ={}4,5A B ∴=.故选:D 【点睛】本题考查交集的运算,属于基础题. 2.复数5iz i =+上的虚部为( )A .526B .526iC .526-D .526i -【答案】A【解析】化简得到152626z i =+计算虚部得到答案. 【详解】()515262626i i z i -==+,所以5i z i =+的虚部为526. 故选:A 【点睛】本题考查了复数虚部的计算,属于简单题.3.已知,αβ是两个不同的平面,,m l 是两条不同的直线,且,,m l αβααβ⊥⊂⋂=,则“m l ⊥”是“m β⊥”的( )条件 A .充分不必要 B .必要不充分 C .充要D .既不充分也不必要【答案】C【解析】由面面垂直的性质定理、线面垂直的概念,结合充分、必要条件,判断出正确选项. 【详解】若m l ⊥,根据面面垂直的性质定理可知m β⊥;若m β⊥,则由l β⊂可得m l ⊥.所以“m l ⊥”是“m β⊥”的充要条件 故选:C. 【点睛】本小题主要考查面面垂直的性质定理,考查充分、必要条件的判断,属于基础题.4.某地有两个国家AAAA 级旅游景区——甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的月客流量(单位:百人),得到如图所示的茎叶图.关于2019年1月至6月这两个景区的月客流量,以下结论错误..的是( )A .甲景区月客流量的中位数为12950人B .乙景区月客流量的中位数为12450人C.甲景区月客流量的极差为3200人D.乙景区月客流量的极差为3100人【答案】D【解析】分别计算甲乙景区流量的中位数和极差得到答案.【详解】根据茎叶图的数据:甲景区月客流量的中位数为12950人,乙景区月客流量的中位数为12450人.甲景区月客流量的极差为3200人,乙景区月客流量的极差为3000人.故选:D【点睛】本题考查了茎叶图中位数和极差的计算,意在考查学生的应用能力.5.执行下边的程序框图,若输入的x的值为5,则输出的n的值为()A.2 B.3 C.4 D.5【答案】C【解析】根据程序框图依次计算得到答案. 【详解】执行程序框图:(),x n 依次为()5,0,()7,1,()9,2,()11,3,()13,4∵21313132+>∴输出的n 的值为4. 故选:C 【点睛】本题考查了程序框图的计算,意在考查学生对于程序框图的理解能力. 6.设函数ln(),0()()1,0x x f x g x x -<⎧=⎨+>⎩若()f x 是奇函数,则()2g e =( )A .-3B .-9C .-1D .1【答案】A【解析】首先根据函数()f x 是奇函数可得()()222f e f e =--=-,又()()221g e f e =-,据此即可求出结果.【详解】因为函数()f x 是奇函数,所以()()222ln 2f ef e e=--=-=-,又()()221g e f e =-,所以()23g e =-.故选:A. 【点睛】本题主要考查了函数的奇偶性,以及利用分段函数求函数值,属于基础题.7.已知等比数列{}n a 的前n 项和为n S ,且54S =,1010S =,则15S =( )A .16B .19C .20D .25【答案】B【解析】利用5S ,105S S -,1510S S -成等比数列求解 【详解】因为等比数列{}n a 的前n 项和为n S ,所以5S ,105S S -,1510S S -成等比数列,因为54S =,1010S =,所以1056S S -=,15109S S -=,故1510919S =+=. 故选:B 【点睛】本题考查等比数列前n 项性质,熟记性质是关键,是基础题8.将曲线sin 2y x =向左平移()0ϕϕ>个单位长度,得到曲线5cos 26y x π⎛⎫=+ ⎪⎝⎭,则tan ϕ=( )AB .C .3D .3-【答案】B【解析】变换得到sin 2cos 22x x π⎛⎫=- ⎪⎝⎭,根据平移得到()23k k πϕπ=+∈N ,计算得到答案. 【详解】sin 2cos 22x x π⎛⎫=- ⎪⎝⎭,所以52cos 2cos 2632x x πππ⎡⎤⎛⎫⎛⎫+=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 所以()23k k πϕπ=+∈N ,则tan ϕ=故选:B 【点睛】本题考查了三角函数的平移,变换sin 2cos 22x x π⎛⎫=- ⎪⎝⎭是解题的关键.9.已知抛物线24y x =的焦点为F ,M ,N 是该抛物线上的两点,且12MF NF +=,则线段MN 的中点到x 轴的距离是( )A .14B .18C .316D .516【答案】C【解析】先判断线段MN 的中点到其准线的距离是14,再计算到x 轴的距离. 【详解】12MF NF +=,所以线段MN 的中点到其准线的距离是14由题意可知18p =,则线段MN 的中点到x 轴的距离是134216p -=. 故选:C 【点睛】本题考查了抛物线上的点到准线的距离问题,意在考查学生的转化能力和计算能力. 10.已知函数()1cos 2cos xf x x+=+,()()20g x ax a =->.若1x R ∀∈,[]21,2x ∃∈,()()12f x g x =,则a 的取值范围是()A .21,3⎡⎤⎢⎥⎣⎦B .2,23⎡⎤⎢⎥⎣⎦C .4,23⎡⎤⎢⎥⎣⎦D .4,3⎡⎫+∞⎪⎢⎣⎭【答案】C【解析】根据条件求出()f x 的值域,与()g x 的值域,由1x R ∀∈,[]21,2x ∃∈,()()12f x g x =,可得两值域的包含关系,即可求得参数a 的取值范围. 【详解】 解:因为()2cos 1112cos 2cos x f x x x+-==-++,12cos 3x +,所以()f x 的值域为20,3⎡⎤⎢⎥⎣⎦. 因为0a >,所以()g x 在[]1,2上的值域为[]2,22a a --,依题意得[]20,2,223a a ⎡⎤⊆--⎢⎥⎣⎦,则 20,222,3a a -⎧⎪⎨-⎪⎩解得423a . 故选:C 【点睛】本题考查函数方程思想的综合应用,属于中档题. 11.唐朝著名的凤鸟花卉纹浮雕银杯如图1所示,它的盛酒部分可以近似地看作是半球与圆柱的组合体(如图2).当这种酒杯内壁表面积(假设内壁表面光滑,表面积为S 平方厘米,半球的半径为R 厘米)固定时,若要使得酒杯的容积不大于半球体积的2倍,则R 的取值范围为()A .⎛ ⎝B .⎫+∞⎪⎪⎭ C .D . 【答案】D【解析】根据题意,酒杯内壁表面积为圆柱与半球的表面积,列出S 的表达式,再求出体积V ,解不等式即可. 【详解】解:设圆柱的高度与半球的半径分别为h ,R ,则222S R Rh ππ=+,则22SRh R ππ=-, 所以酒杯的容积323233224()332323S S V R R h R R R R R R ππππππ=+=+-=-+, 又0h >,所以202SR π->,所以22523S R R ππ<2S R π<,故选:D . 【点睛】考查了组合体的体积和表面积计算,属于中档题.12.双曲线()222210,0x y a b a b -=>>的左、右焦点分别为1F ,2F ,渐近线分别为1l ,2l ,过点1F 且与1l 垂直的直线l 交1l 于点P ,交2l 于点Q ,若12PQ F P =,则双曲线的离心率为( ) AB C .2 D .3【答案】B【解析】设1l :b y x a =-,2l :by x a =,联立方程得到2,a ab P c c ⎛⎫- ⎪⎝⎭,再计算2PQ b =,OQ =4224430c a c a -+=,计算得到答案.【详解】记O 为坐标原点.由题意可得()1,0F c -,不妨设1l :by x a =-,2l :b y x a=则直线l :()a y x c b =+.联立()a y x c b b y x a ⎧=+⎪⎪⎨⎪=-⎪⎩,解得2a x cab y c ⎧=-⎪⎪⎨⎪=⎪⎩则2,a ab P c c ⎛⎫- ⎪⎝⎭故1PF b =,OP a =.因为12PQ F P =,所以12PQ PF =所以2PQ b =,OQ =22221cos QOF ∠=.因为2tan bQOF a ∠=,所以2cos aQOF c ∠=,22220ac=,整理得4224430c a c a -+=,则42430e e -+=解得e =故选:B 【点睛】本题考查了双曲线的离心率问题,综合性强,计算量大,意在考查学生的综合应用能力和计算能力.二、填空题13.若函数()e x f x mx =-在[2,0]-上为减函数,则m 的取值范围为___________.【答案】[)1,+∞【解析】将问题转化为导函数在[]2,0-上恒小于零,从而根据恒成立思想求解出m 的取值范围. 【详解】由题意可知()e 0x f x m '=-≤,即x m e ≥对[2,0]x ∈-恒成立, 所以()maxxm e≥,所以0e1m ≥=即[)1,m ∈+∞.故答案为:[)1,+∞. 【点睛】本题考查根据函数的单调性求解参数范围,难度一般.已知函数()f x 为指定区间的单调增(或减)函数,则()()()00f x f x ''≥≤在指定区间上恒成立.14.第28届金鸡百花电影节将在福建省厦门市举办,近日首批影展片单揭晓,《南方车站的聚会》《春江水暖》《第一次的离别》《春潮》《抵达之谜》五部优秀作品将在电影节进行展映.若从这五部作品中随机选择两部放在展映的前两位,则《春潮》与《抵达之谜》至少有一部被选中的概率为 _____. 【答案】710.【解析】首先根据题意,列举出从这五部作品中随机选择两部放在展映的前两位的所有情况,共10种情况,其中《春潮》与《抵达之谜》至少有一部被选中的有7种,根据古典概型概率计算公式即可求结果. 【详解】从这五部作品中随机选择两部放在展映的前两位的所有情况为(《南方车站的聚会》,《春江水暖》),(《南方车站的聚会》,《第一次的离别》),(《南方车站的聚会》,《春潮》),(《南方车站的聚会》,《抵达之谜》),(《春江水暖》,《第一次的离别》),(《春江水暖》,《春潮》),(《春江水暖》,《抵达之谜》),(《第一次的离别》,《春潮》),(《第一次的离别》,《抵达之谜》),(《春潮》,《抵达之谜》),共10种情况,其中《春潮》与《抵达之谜》至少有一部被选中的有7种,故所求概率为710.故答案为:710.【点睛】本题主要考查了古典概型概率的计算,属于基础题. 15.根据记载,最早发现勾股定理的人应是我国西周时期的数学家商高,商高曾经和周公讨论过“勾3股4弦5”的问题.现有ABC ∆满足“勾3股4弦5”,其中“股”4AB =,D 为“弦”BC 上一点(不含端点),且ABD ∆满足勾股定理,则()CB CA AD -⋅=______.【答案】14425【解析】先由等面积法求得AD ,利用向量几何意义求解即可. 【详解】由等面积法可得341255AD ⨯==,依题意可得,AD BC ⊥, 所以()214425CB CA AD AB AD AD -⋅=⋅==. 故答案为:14425【点睛】本题考查向量的数量积,重点考查向量数量积的几何意义,属于基础题.16.在数列{}n a 中,13a =,且()()12(1)22n n n a n a n +-=++- (1){}n a 的通项公式为________;(2)在1a ,2a ,3a , ,2019a 这2019项中,被10除余2的项数为________.【答案】222n a n n =-+ 403【解析】(1)等式两边同除()1n n +构造数列为等差数列即可求出通项公式;(2)利用通项公式及被10除余2 的数的特点即可求解 【详解】(1)因为()()12(1)22n n n a n a n +-=++-,所以122221n n n a a n a n n n+-+--==+ 2+,即12221n n a a n n +---=+,则2n a n -⎧⎫⎨⎬⎩⎭为等差数列且首项为1,差为2,所以212(1)n a n n -=+-21n =-,故222n a n n =-+(2)因为(21)2n n n a =-+,所以当n 能被10整除或n 为偶数且21n -能被5整除时,n a 被10除余2,所以8,10,18,20,,2010,2018n =,故被10除余2的项数为201014035+=. 故答案为:222n a n n =-+;403 【点睛】本题考查数列的通项,考查构造法,注意解题方法的积累,属于中档题.三、解答题17.某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.(1)求购买金额不少于45元的频率;(2)根据以上数据完成22⨯列联表,并判断是否有95%的把握认为购买金额是否少于60元与性别有关.附:参考公式和数据:()()()()()22n ad bcKa b c d a c b d-=++++,n a b c d =+++.附表:【答案】(1)12(或0.5);(2)列联表见解析,有95%的把握认为购买金额是否少于60元与性别有关.【解析】(1)根据统计表及古典概型的概率计算公式即可计算出不少于45元的频率;(2)完善列联表,计算出2K 跟参考数据比较得出结论. 【详解】解:(1)购买金额不少于45元的频率为1520101902++=. (2)22⨯列联表如下:()22901220401814405 3.84130605238247K ⨯⨯-⨯==>>⨯⨯⨯,因此有95%的把握认为购买金额是否少于60元与性别有关. 【点睛】本题考查独立性检验,以及古典概型的概率计算问题,属于基础题.18.设函数23()cos sin 2f x x x x =+-,a ,b ,c 分别为ABC∆内角A ,B ,C 的对边.已知()0f A =,2b =. (1)若a =B ;(2)若2a c =,求ABC ∆的面积.【答案】(1)6B π=. (2) 6【解析】(1)运用二倍角正余弦公式和辅助角公式,化简f (x ),并求得3A π=,再利用正弦定理求得1sin 2B =,可得结论;(2)由三角形的余弦定理得13c -+=结合面积公式,求得b ,c 的关系,即可得到所求三角形的周长. 【详解】(1)1cos23()2sin 212226x f x x x π-⎛⎫=+-=-- ⎪⎝⎭, 因为()0f A =,所以262A ππ-=,即3A π=.因为sin sin a b A B =,所以sin 1sin 2b A B a ==, 因为(0,)B π∈,所以6B π=或56π,又b a <,所以6B π=.(2)由余弦定理,可得222(2)222cos 3c c c π=+-⨯⨯,即23240c c +-=,解得c =(负根舍去),故ABC ∆的面积为11sin 2sin 223bc A π=⨯=【点睛】本题考查三角函数的恒等变换,正弦函数的图形和性质,考查解三角形的余弦定理和面积公式,考查化简整理的运算能力,属于中档题.19.如图,在正方体1111ABCD A B C D -中,F ,G 分别是棱1CC ,1AA 的中点,E ,M 分别为棱AB ,11A B 上一点,113B M MA =,且GM 平面1B EF .(1)证明:E 为AB 的中点. (2)若四棱锥1F B MGE -的体积为32,求正方体1111ABCD A B C D -的表面积.【答案】(1)见解析;(2)24【解析】(1)取11A B 的中点N ,连接AN ,可证GM AN ,再由线面平行得到1ANB E ,又1B NAE ,所以四边形1AEB N 为平行四边形,即可得证.(2)设棱长为a ,易知F 到平面11ABB A 的距离为a ,由1113F B MGE B MGE V h S -=⋅⋅求出a 的值,即可求出表面积.【详解】解:(1)证明:取11A B 的中点N ,连接AN因为113B M MA =,所以M 为1A N 的中点,又G 为1AA 的中点,所以GMAN .因为GM 平面1B EF ,GM ⊂平面11ABB A ,平面11ABB A 平面11B EF B E =.所以1GM B E ,即1AN B E .又1B NAE ,所以四边形1AEB N 为平行四边形,则1AE B N =,所以E 为AB 的中点.(2)设AB a ,则1A MG ∆,AGE ∆,1BEB ∆的面积分别为2a 16,28a ,24a ,易知F 到平面11ABB A 的距离为a ,所以11222321133331684162F B MGEB MGE a a a a V h S a a -⎛⎫==⋅⋅⨯---⨯== ⎪⎝⎭, 解得2a =,故所求正方体的表面积为2624a =. 【点睛】本题考查锥体的体积计算以及线面平行的性质,属于基础题.20.已知椭圆()2222:10x y a b a b Ω+=>>的焦距为2622(1)求Ω的方程;(2)若直线2y x =+与Ω相交于A 、B 两点,求以线段AB 为直径的圆的标准方程.【答案】(1)22182x y +=;(2)2282485525x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭. 【解析】(1)根据题意求出a 和b 的值,即可求出椭圆Ω的方程;(2)设点()11,A x y 、()22,B x y ,将直线AB 的方程与椭圆Ω的方程联立,列出韦达定理,求出线段AB 的中点和AB ,即可得出所求圆的标准方程. 【详解】(1)设椭圆Ω的焦距为()20c c >,则2c =,2b =所以c =b =2228a b c =+=,所以Ω的方程为22182x y +=;(2)设点()11,A x y 、()22,B x y ,联立222182y x x y =+⎧⎪⎨+=⎪⎩,消去y ,得251680x x ++=.由韦达定理得12165x x +=-,1285x x =, 所以12825x x +=-,线段AB 的中点坐标为82,55⎛⎫- ⎪⎝⎭.12AB x x =-===,所以,所求圆的标准方程为2282485525x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭. 【点睛】本题考查椭圆方程的求解,同时也考查了直线截圆所得弦长的计算以及圆的标准方程的求解,一般将直线方程与椭圆方程联立,利用韦达定理设而不求法来计算,考查运算求解能力,属于中等题. 21.已知函数()()33114ln 10f f x ax x x '=--的图象在点()()1,1f 处的切线方程为100++=x y b . (1)求a ,b 的值;(2)若()13f x m >对()0,x ∈+∞恒成立,求m 的取值范围. 【答案】(1)13a =,403=-b (2)2642ln 2<-m 【解析】(1)求导可得()()23114310f f x ax x''=--,由题,切线方程斜率为()1f k '=,解得13a =,代回函数求得()1013f =,即10103b =--,可求得403=-b ; (2)如果求()13f x m >对0x ∈+∞(,)恒成立,即求()min 13f x m >,利用导数判断单调性求得最小值即可求解不等式 【详解】解:(1)()()23114310f f x ax x''=--, 因为()f x 在()()1,1f 处的切线方程为100++=x y b ,即10y x b =--,此时切线斜率10k =-, 则()3(1)13141010f f a k ''=--==-,解得13a =,所以()()333101114ln 314ln 3103f x x x x x x x ⨯-=--=+-, 所以()31110113114ln13333f =⨯+⨯-=+=,则10103b =--,解得403=-b(2)由(1)知()31314ln 3f x x x x =+-,()32143143x x f x x x x+-'=+-=,设函数()()33140g x xx x =+->,则()2330g x x '=+>,所以()g x 在()0,∞+为增函数,因为()20g =,令()0g x <,得02x <<;令()0g x >,得2x >, 所以当02x <<时,()0f x '<;当2x >时,()0f x '>, 所以()()3min 126223214ln 214ln 233f x f ==⨯+⨯-=-, 从而12614ln 233<-m ,即2642ln 2<-m 【点睛】本题考查利用导数的几何意义求值,考查利用导数研究不等式恒成立问题,考查转化思想,考查运算能力22.在直角坐标系xOy 中,直线l的参数方程为212x t y ⎧=-⎪⎪⎨⎪=+⎪⎩(t为参数),曲线C 的参数方程为cos sin x m y a n αα=⎧⎨=+⎩(0m >,0n >,α为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,且曲线C 的极坐标方程为8sin ρθ=. (1)求a ,m ,n 的值;(2)已知点P 的直角坐标为()0,1,l 与曲线C 交于A ,B 两点,求PA PB +.【答案】(1)4a m n ===;(2.【解析】(1)根据极坐标方程得到()22416x y +-=,根据参数方程得到答案.(2)将参数方程代入圆方程得到270t --=,根据韦达定理得到120t t +=>,1270t t =-<,计算12PA PB t t +=-得到答案.【详解】 (1)由8sin ρθ=,得28sin ρρθ=,则228x y y +=,即()22416x y +-=.因为0m >,0n >,所以4a m n ===.(2)将1x y ⎧=⎪⎪⎨⎪=⎪⎩代入()22416x y +-=,得270t --=. 设A ,B 两点对应的参数分别为1t ,2t,则120t t +=>,1270t t =-<. 所以12t t P PB A =-==+.【点睛】 本题考查了极坐标方程和参数方程,利用直线的参数方程可以简化计算,是解题的关键. 23.已知函数()3124f x x x =+--.(1)求不等式()3f x >的解集;(2)若对任意x ∈R ,不等式()228f x x tt --≤-恒成立,求t 的取值范围,【答案】(1)4(,10),5⎛⎫-∞-+∞ ⎪⎝⎭;(2)(][),19,-∞-+∞.【解析】(1)利用分段讨论法去掉绝对值,求出不等式()3f x >的解集;(2)利用绝对值三角不等式求出()2f x x --的最大值,得出关于t 的不等式,求出解集即可.【详解】(1)当1x <-时,()3(1)(24)3f x x x =-++->,解得10x <-; 当12x -≤≤时,()3(1)(24)3f x x x =++->,解得45x >,则425x <≤; 当2x >时,()3(1)(24)3f x x x =+-->,解得4x >-,则2x >. 综上,不等式()3f x >的解集为4(,10),5⎛⎫-∞-+∞ ⎪⎝⎭; (2)()|2|3|1||24||2|f x x x x x --=+----3|1|3|2|x x =+-- |33||36|x x =+--|33(36)|9x x ≤+--=,若对任意x ∈R ,不等式2()|2|8f x x t t --≤-恒成立, 则289t t -≥,解得1t ≤-或9t ≥.因此,实数t 的取值范围是(][),19,-∞-+∞.【点睛】本题考查了含有绝对值的不等式解法与应用,同时考查了不等式恒成立问题,属于中档题.。
2020届湖北省四地七校联盟高三第七次联考数学(文)试题

2020届湖北省四地七校联盟高三第七次联考文科数学试题 ★祝考试顺利★ 注意事项:1、考试范围:高考范围。
2、试题卷启封下发后,如果试题卷有缺页、漏印、重印、损坏或者个别字句印刷模糊不清等情况,应当立马报告监考老师,否则一切后果自负。
3、答题卡启封下发后,如果发现答题卡上出现字迹模糊、行列歪斜或缺印等现象,应当马上报告监考老师,否则一切后果自负。
4、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
5、选择题的作答:每个小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
6、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
7、保持答题卡卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
8、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
第I 卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每个小题所给出的四个选项中,只 有一项是符合题目要求的,把正确选项的代号填在答题卡的指定位置.) 1.设集合1|02x A x x +⎧⎫=≥⎨⎬-⎩⎭,{}1,0,1,2B =-,则A B = A .{}1,0,1-B .{}0,1,2C .{}1,0,1,2-D .{}1,22.设复数z 满足i z 32-=,则=z A .3B .13C .2D .133.“1x <”是“ln(1)0x +<”的 A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.在ABC ∆中,1a =,30A =,60B =,则b 等于A B .12C D .25.若某空间几何体的三视图如图所示,则该几何体的体积是A .2B .1C .D .6.若椭圆2221x y a +=经过点1,3P ⎛⎫ ⎪ ⎪⎝⎭,则椭圆的离心率e =A .2B 1C .3D .37.设数列{}n a 满足32111232n n a a a a n +++=-,则n a = A .112n -B .312n -C .12nD .2n n 8.已知α满足972cos =α,则cos cos 44ππαα⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭A. 718B. 2518C. 718-D. 2518-9.如果123,,,P P P 是抛物线2:4C y x =上的点,它们的横坐标123,,,x x x ,F 是抛物线C的焦点,若12201820x x x +++=,则122018PF P F P F +++=A .2028B .2038C .4046D .405610.已知()f x 是定义在R 上的奇函数,且在(),-∞+∞上是减函数,()12f =-,则满足()232f x -<的实数x 的取值范围是A .()1,1-B .()2,0-C .()2,2-D .()0,211.一个圆锥SC 的高和底面直径相等,且这个圆锥SC 和圆柱OM 的底面半径及体积也都相等,则圆锥SC 和圆柱OM 的侧面积的比值为 A.2BCD12.已知函数(1)2y f x =+-是奇函数,21()1x g x x -=-,且()f x 与()g x 的图像的交点为11(,)x y ,22(,)x y ,,66(,)x y ,则126126x x x y y y +++++++=A .0B .6C .12D .18第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每小题5分,满分20分)13.双曲线2212516y x -=的渐近线方程为_____________14.设x ,y 满足约束条件⎪⎩⎪⎨⎧≤-+≥+-≥+0530101y x y x y ,则y x z +-=2的最小值为 .15.设,a b ∈R ,222a b +=,则221411a b +++的最小值为______. 16.若两曲线21y x =-与ln 1y a x =-存在公切线,则正实数a 的取值范围是 . 三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤,第17 ~ 21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.) 17.(12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c2cos Asin C-=. (1)求角A 的大小; (2)若cos(B +6π)=14,求cosC 的值.18.(12分)2019年10月28日至10月31日,中国共产党第十九届四中全会在北京召开。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020届湖北省四地七校联盟高三第七次调研考试高三 文科数学 ★祝考试顺利★ 注意事项:1、考试范围:高考范围。
2、试题卷启封下发后,如果试题卷有缺页、漏印、重印、损坏或者个别字句印刷模糊不清等情况,应当立马报告监考老师,否则一切后果自负。
3、答题卡启封下发后,如果发现答题卡上出现字迹模糊、行列歪斜或缺印等现象,应当马上报告监考老师,否则一切后果自负。
4、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
5、选择题的作答:每个小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
6、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
7、保持答题卡卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
8、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{1,2,6},{2,4},{1,2,3,4}A B C ===,则()AB C =( )A . {2}B .{1,2,4}C .{1,2,4,6}D .{1,2,3,4,6} 2.若a 为实数,且2+a i1+i =3+i ,则a =( )A .-4B .-3C .3D .4 3.下列函数中,定义域是R 且为增函数的是( )A .x e y -=B .x y =C .x y ln =D .3x y =4.已知命题p :,x ∃∈R 210x x -+≥;命题q :若22a b <,则a<b.下列命题为真命题的是( )A .p q ∧ B.p q ∧⌝ C.p q ⌝∧ D.p q ⌝∧⌝ 5.已知54)cos(=-απ,且α为第三象限角,则α2tan 的值等于()A. 34 B .-34 C .-247 D .2476.已知函数⎩⎨⎧=x x x f 3log )(2)0()0(≤>x x ,则)]41([f f 的值是( )A.9B.91-C. 91D .9-7.设x R ∈ ,向量(,1),(1,2),a x b ==-且a b ⊥ ,则||a b +=( )A.5B.10C.52D. 108.要得到函数⎪⎭⎫ ⎝⎛-=34sin πx y 的图象,只需将函数x y 4sin =的图象()A .向右平移π12个单位B .向左平移π12个单位 C .向左平移π3个单位D .向右平移π3个单位9.从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为( )A.B.C.D.10.我国古代数学名著《算法统宗》中有如下问题:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( ) A. 1盏 B.2盏 C .3盏 D .9盏 11.设曲线x x y sin cos 1+=在点)1,2(π处的切线与直线01=+-ay x 平行,则实数=a ( )A .1B -1C .2D .-2 12.已知函数()f x '是函数()f x 的导函数,1(1)f e=,对任意实数都有()()0f x f x '->,则不等式2()x f x e -<的解集为( ) A .(1,)+∞B .(,)e -∞C .(1,)eD .(,)e +∞二、填空题:本题共4小题,每小题5分,共20分。
13. 已知)(x f 是奇函数,且当0>x 时,12)(2-=x x f ,那么=-)1(f ________.14.已知向量a ,b 的夹角为2=1=,=________.15. 已知x ,y 满足约束条件0401x y x y y -≥⎧⎪+-≤⎨⎪≥⎩,则z= -2x+y 的最大值是________.16. 已知函数()y f x =的周期为2,当[1,1]x ∈-时2()f x x =,那么函数()y f x =的图象与函数|lg |y x =的图象的交点个数为________.三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17. (本题满分10分)记n S 为等差数列{}n a 的前n 项和,已知71-=a ,153-=S .(1)求{}n a 的通项公式; (2)求n S ,并求n S 的最小值.18. (本题满分12分)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos C (a cos B +b cos A )=c . ①求C ;②若c =7,△ABC 的面积为332,求△ABC 的周长.19.(本题满分12分)已知是各项均为正数的等比数列,且,.(1)求数列的通项公式;(2)为各项非零的等差数列,其前项和为.已知,求数列⎭⎬⎫⎩⎨⎧n n a b 的前项和n T .20. (本题满分12分)在平面直角坐标系xOy 中,已知向量⎪⎪⎭⎫ ⎝⎛-=22,22,()x x cos ,sin =,⎪⎭⎫ ⎝⎛∈2,0πx . (1)若⊥,求x tan 的值; (2)若与的夹角为π3,求x 的值.21. (本题满分12分)已知e 是自然对数的底数,实数a 是常数,函数1)(--=ax e x f x 的定义域为(0,+∞). (1)设e a =,求函数f (x )的图象在点()()1,1f 处的切线方程; (2)判断函数)(x f 的单调性.22. (本题满分12分)已知常数0≠a,x x a x f 2ln )(+=.(1)当a =-4时,求)(x f 的极值;(2)当)(x f 的最小值不小于a -时,求实数a 的取值范围.高三数学答案一、选择题(本大题共12小题,每小题5分,共60分)二、填空题(本大题共4小题,每小题5分,共20分)(文科)13.-1; 14.23; 15. -1; 16.10 (理科)13.3 14.23; 15. -1; 16.10 三、解答题(本大题共6小题,共70分) 17. (本题满分10分)解 (1)设{a n }的公差为d ,由题意得3a 1+3d =-15.由a 1=-7得d =2.所以{a n }的通项公式为a n =a 1+(n -1)d =2n -9(n ∈N *).………..5分(2)由(1)得S n =a 1+a n2·n =n 2-8n =(n -4)2-16.所以当n =4时,S n 取得最小值,最小值为-16. ………..5分 18.(本题满分12分)[解] ①由已知及正弦定理得2cos C (sin A cos B +sin B cos A )=sin C , 即2cos C sin(A +B )=sin C , 故2sin C cos C =sin C .可得cos C =12,所以C =π3. ..............................................6分②由已知得12ab sin C =332. 又C =π3,所以ab =6.由已知及余弦定理得a 2+b 2-2ab cos C =7, 故a 2+b 2=13,从而(a +b )2=25.所以△ABC 的周长为5+7. ……………………..12分 19. (本题满分12分)解:(1)设{a n }的公比为q , 由题意知a 1(1+q )=6,a 21q =a 1q 2. 又a n >0,解得a 1=2,q =2, 所以a n =2n . ………..5分 (2)由题意知,S 2n +1=(2n +1)(b 1+b 2n +1)2=(2n +1)b n +1, 又S 2n +1=b n b n +1,b n +1≠0, 所以b n =2n +1.令c n =b n a n ,则c n =2n +12n ,因此T n =c 1+c 2+…+c n =32+522+723+…+2n -12n -1+2n +12n , 又12T n =322+523+724+…+2n -12n +2n +12n +1, 两式相减得12T n =32+⎝ ⎛⎭⎪⎫12+122+…+12n -1-2n +12n +1 =32+1-⎝ ⎛⎭⎪⎫12n -1-2n +12n +1 =52-2n +52n +1,所以T n =5-2n +52n .………..12分 20. (本题满分12分)解 (1)因为m =⎝ ⎛⎭⎪⎫22,-22,n =(sin x ,cos x ),m ⊥n . 所以m ·n =0,即22sin x -22cos x =0, 所以sin x =cos x ,所以tan x =1.(2)因为|m |=|n |=1,所以m ·n =cos π3=12, 即22sin x -22cos x =12,所以sin ⎝ ⎛⎭⎪⎫x -π4=12,因为0<x <π2,所以-π4<x -π4<π4,所以x -π4=π6,即x =5π12. 21. (本题满分12分)解:(1)∵a =e ,∴ f (x )=e x-e x -1, ∴f ′(x )=e x-e ,f (1)=-1,f ′(1)=0.∴当a =e 时,函数f (x )的图象在点(1,f (1))处的切线方程为y =-1. (2)∵f (x )=e x -ax -1,∴f ′(x )=e x -a . 易知f ′(x )=e x -a 在(0,+∞)上单调递增.∴当a ≤1时,f ′(x )>0,故f (x )在(0,+∞)上单调递增; 当a >1时,由f ′(x )=e x-a =0,得x =ln a ,∴当0<x <ln a 时,f ′(x )<0,当x >ln a 时,f ′(x )>0, ∴f (x )在(0,ln a )上单调递减,在(ln a ,+∞)上单调递增. 综上,当a ≤1时,f (x )在(0,+∞)上单调递增;当a >1时,f (x )在(0,ln a )上单调递减,在(ln a ,+∞)上单调递增. 22.(本题满分12分)解:(1)由已知得f (x )的定义域为x ∈(0,+∞),f ′(x )=a x +2=a +2x x .当a =-4时,f ′(x )=2x -4x .∴当0<x <2时,f ′(x )<0,即f (x )单调递减; 当x >2时,f ′(x )>0,即f (x )单调递增.∴f (x )只有极小值,且在x =2时,f (x )取得极小值f (2)=4-4ln 2,无极大值.…….6分(2)∵f ′(x )=a +2xx ,∴当a >0,x ∈(0,+∞)时,f ′(x )>0,即f (x )在x ∈(0,+∞)上单调递增,没有最小值;当a <0时,由f ′(x )>0得,x >-a2,∴f (x )在⎝ ⎛⎭⎪⎫-a 2,+∞上单调递增; 由f ′(x )<0得,0<x <-a2,∴f (x )在⎝ ⎛⎭⎪⎫0,-a 2上单调递减.∴当a <0时,f (x )的最小值为f ⎝ ⎛⎭⎪⎫-a 2=a ln ⎝ ⎛⎭⎪⎫-a 2+2×⎝ ⎛⎭⎪⎫-a 2.根据题意得f ⎝ ⎛⎭⎪⎫-a 2=a ln ⎝ ⎛⎭⎪⎫-a 2+2×⎝ ⎛⎭⎪⎫-a 2≥-a ,即a [ln(-a )-ln 2]≥0.∵a <0,∴ln(-a )-ln 2≤0,解得-2≤a <0,∴实数a的取值范围是[-2, 0).……………………….12分。
