广州市海珠区2013届高三上学期综合测试(二)数学理试题_word版
【2013珠海二模】广东省珠海市2013届高三5月综合试题(二)数学理试题-推荐下载

A.1
B.0 C.-1 D. 9 2
第 1 页 共 14 页
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
必学必懂 广东省珠海市2013届高三上学期期末质检数学理试题

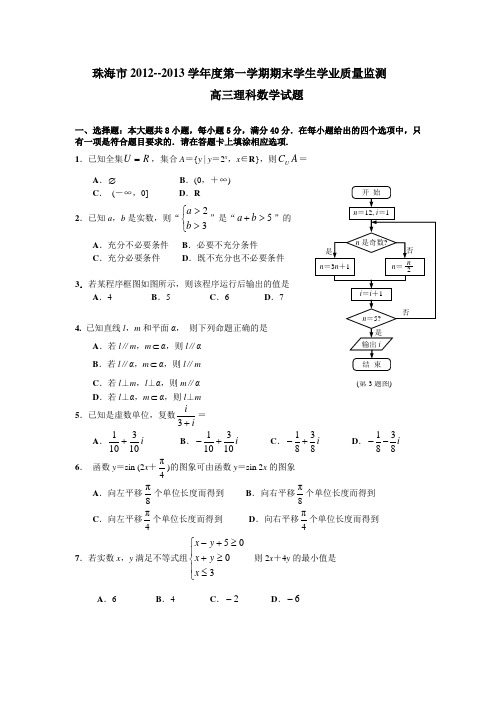
珠海市2012--2013学年度第一学期期末学生学业质量监测 高三理科数学试题一、 选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项. 1.已知全集,集合A ={y | y =2x ,x ∈R},则=A .B .(0,+∞)C . (-∞,0]D .R 2.已知a ,b 是实数,则“”是“”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.若某程序框图如图所示,则该程序运行后输出的值是 A .4 B .5 C .6 D .74. 已知直线l ,m 和平面α, 则下列命题正确的是A .若l ∥m ,m α,则l ∥αB .若l ∥α,mα,则l ∥mC .若l ⊥m ,l ⊥α,则m ∥αD .若l ⊥α,mα,则l ⊥m5.已知是虚数单位,复数=A .B .C .D .6. 函数y =sin (2x +)的图象可由函数y =sin 2x 的图象A .向左平移个单位长度而得到B .向右平移个单位长度而得到C .向左平移个单位长度而得到 D .向右平移个单位长度而得到7.若实数x ,y 满足不等式组 则2x +4y 的最小值是A .6B .4C .D .8. 对于直角坐标平面内的任意两点、,定义它们之间的一种“距离”:‖AB ‖=,给出下列三个命题:①若点C 在线段AB 上,则‖AC ‖+‖CB ‖=‖AB ‖;②在△ABC 中,若∠C =90°,则‖AC ‖+‖CB ‖=‖AB ‖; ③在△ABC 中,‖AC ‖+‖CB ‖>‖AB ‖. 其中真命题的个数为A. 0B. 1C. 2D.3(第3题图)二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.请将答案填在答题卡相应位置. (一)必做题(9-13题) 9.函数的导函数.10.在递增等比数列{a n }中,,则公比= .11.某学校三个社团的人员分布如下表(每名同学只参加一个社团):学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取人,结果合唱社被抽出人,则这三个社团人数共有_______________.12.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知C =,,若△ABC 的面积为,则= .13.如图,F 1,F 2是双曲线C :(a >0,b >0) 的左、右焦点,过F 1的直线与的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3 : 4 : 5,则双 曲线的离心率为 .(二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在直角坐标系x O y 中, 已知曲线:, (为参数)与曲线 :,(为参数)相交于两个点、,则线段的长为 . 15.(几何证明选讲选做题)如图,PAB 、PCD 为⊙O 的两条割线, 若PA=5,AB=7,CD=11,AC=2,则BD 等于 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)设向量a =,b =,θ为锐角.(1)若a ·b =136,求sin θ+cos θ的值;(2)若a ∥b ,求sin(2θ+π3)的值.17.(本小题满分12分)某中学校本课程共开设了A ,B ,C ,D 共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:武术社20xy OA BF 1F 2 (第13题图)3(1)求这3名学生选修课所有选法的总数;(2)求恰有2门选修课没有被这3名学生选择的概率; (3)求A 选修课被这3名学生选择的人数的数学期望.18.(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形 (1)求证:; (2)求证:; (3)设为中点,在边上找一点,使平面,并求的值.19.(本题满分14分)已知椭圆:,左、右两个焦点分别为、,上顶点,为正三角形且周长为6. (1)求椭圆的标准方程及离心率;(2)为坐标原点,是直线上的一个动点,求的最小值,并求出此时点的坐标.20.(本小题满分14分)已知函数,.(1)如果函数在上是单调减函数,求的取值范围;(2)是否存在实数,使得方程在区间内有且只有两个不相等的实数根?若存在,请求出的取值范围;若不存在,请说明理由. 21.(本题满分14分)已知正项数列的前项和为,且.(1)求的值及数列的通项公式;(2)求证:;(3)是否存在非零整数,使不等式对一切都成立?若存在,求出的值;若不存在,说明理由.8 主视图 侧视图俯视图4珠海市2012~2013学年第一学期普通高中学生学业质量监测高三理科数学试题参考答案及评分标准一、选择题:CABD AADB 二、填空题: 9、2sin cos x xx x - 10、2 11、150 12、7 13、13 14、 4 15、 6三、解答题: 16.(本小题满分12分)设向量a =)sin ,2(θ,b =)cos ,1(θ,θ为锐角. (1)若a ·b =136,求sin θ+cos θ的值;(2)若a ∥b ,求sin(2θ+π3)的值.17.(本小题满分12分)某中学校本课程共开设了A ,B ,C ,D 共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:(1)求这3名学生选修课所有选法的总数;(2)求恰有2门选修课没有被这3名学生选择的概率; (3)求A 选修课被这3名学生选择的人数的数学期望.18.(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形 (1)求证:N B C BC 11//平面; (2)求证:BN 11C B N ⊥平面; (3)设M 为AB 中点,在BC 边上找一点P ,使MP //平面1CNB ,并求PCBP的值.19.(本题满分14分)8 主视图侧视图俯视图45已知椭圆:,左、右两个焦点分别为1F 、2F ,上顶点),0(b A ,21F AF ∆为正三角形且周长为6. (1)求椭圆的标准方程及离心率;(2)O 为坐标原点,P 是直线A F 1上的一个动点,求||||2PO PF +的最小值,并求出此时点P 的坐标.20.(本小题满分14分)已知函数,.(1)如果函数在上是单调减函数,求的取值范围;(2)是否存在实数,使得方程在区间内有且只有两个不相等的实数根?若存在,请求出的取值范围;若不存在,请说明理由. 21.(本题满分14分)已知正项数列{}n a 的前n 项和为n S ,且(2)4n n n a a S += *()n ∈N . (1)求1a 的值及数列{}n a 的通项公式;(2)求证:33331231111532n a a a a ++++<*()n ∈N ; (3)是否存在非零整数λ,使不等式112111(1)(1)(1)cos 2n n a a a a πλ+--⋅⋅-<对一切*n ∈N 都成立?若存在,求出λ的值;若不存在,说明理由.三、解答题: 16.(本小题满分12分) 解:(1) 因为a ·b =2+sin θcos θ=136,所以sin θcos θ=16. ……………… 3分 所以 (sin θ+cos θ)2=1+2 sin θcos θ=43.又因为θ为锐角,所以sin θ+cos θ=233. ……………… 6分(2) 解法一 因为a ∥b ,所以tan θ=2. ……………… 8分 所以 sin2θ=2 sin θcos θ=2 sin θcos θ sin 2θ+cos 2θ= 2 tan θ tan 2θ+1=45, cos2θ=cos 2θ-sin 2θ=cos 2θ-sin 2θ sin 2θ+cos 2θ=1-tan 2θ tan 2θ+1=-35.……………… 10分所以sin(2θ+π3 )=12sin2θ+32cos2θ=12×45+32×(-35 )=4-3310. ……………… 12分 解法二 因为a ∥b ,所以tan θ=2. ……………… 8分 所以 sin θ=255,cos θ=55.因此 sin2θ=2 sin θcos θ=45, cos2θ=cos 2θ-sin 2θ=-35. ……………… 10分所以sin(2θ+π3 )=12sin2θ+32cos2θ=12×45+32×(-35 )=4-3310. ……………… 12分17、(本小题满分12分)解析:(Ⅰ)每个学生有四个不同选择,根据乘法法则,选法总数N=64444=⨯⨯ …… 3分 (Ⅱ) 恰有2门选修课这3名学生都没选择的概率为……………… 7分(Ⅲ) 设A 选修课被这3名学生选择的人数为ξ,则ξ=0,1,2,3P(ξ=0)=64274333= P(ξ=1)=6427433213=⋅C P(ξ=2)=64943313=⋅C P(ξ=3)= 6414333=C ……………… 9分的分布列是………… 10分………… 12分18.解:(1)证明: 该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴1,,BB BC BA 两两互相垂直。
广东省珠海市2013届高三上学期期末质检数学理试卷

珠海市2012--2013学年度第一学期期末学生学业质量监测高三理科数学试题一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项. 1.已知全集R U =,集合A ={y | y =2x ,x ∈R },则A C U =A .∅B .(0,+∞)C . (-∞,0]D .R 2.已知a ,b 是实数,则“⎩⎨⎧>>32b a ”是“5>+b a ”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.若某程序框图如图所示,则该程序运行后输出的值是 A .4 B .5 C .6 D .74. 已知直线l ,m 和平面α, 则下列命题正确的是A .若l ∥m ,m ⊂α,则l ∥αB .若l ∥α,m ⊂α,则l ∥mC .若l ⊥m ,l ⊥α,则m ∥αD .若l ⊥α,m ⊂α,则l ⊥m 5.已知是虚数单位,复数ii+3= A .i 103101+ B .i 103101+- C .i 8381+- D .i 8381--6. 函数y =sin (2x +π4)的图象可由函数y =sin 2x 的图象 A .向左平移π8个单位长度而得到 B .向右平移π8个单位长度而得到 C .向左平移π4个单位长度而得到 D .向右平移π4个单位长度而得到7.若实数x ,y 满足不等式组⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x 则2x +4y 的最小值是A .6B .4C .2-D .6-(第3题图)8. 对于直角坐标平面内的任意两点11(,)A x y 、22(,)B x y ,定义它们之间的一种“距离”: ‖AB ‖=1212x x y y -+-,给出下列三个命题:①若点C 在线段AB 上,则‖AC ‖+‖CB ‖=‖AB ‖;②在△ABC 中,若∠C =90°,则‖AC ‖+‖CB ‖=‖AB ‖; ③在△ABC 中,‖AC ‖+‖CB ‖>‖AB ‖. 其中真命题的个数为A. 0B. 1C. 2D.3二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.请将答案填在答题卡相应位置. (一)必做题(9-13题) 9.函数=y xxsin 的导函数='y . 10.在递增等比数列{a n }中,4,2342=-=a a a ,则公比q = .11.某学校三个社团的人员分布如下表(每名同学只参加一个社团):学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果合唱社被抽出12人,则这三个社团人数共有_______________. 12.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知C =3π,3=b ,若△ABC 的面积为233 ,则c = . 13.如图,F 1,F 2是双曲线C :22221x y a b-=(a >0,b >0) 的左、右焦点,过F 1的直线与C 的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3 : 4 : 5,则双 曲线的离心率为 .(二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在直角坐标系x O y 中, 已知曲线1C :⎩⎨⎧-=+=t y t x 212 , (为参数)与曲线2C :⎩⎨⎧==θθsin 3cos 3y x ,(θ为参数)相交于两个点A 、B ,则线段AB 的长为 .xy OA BF 1F 2(第13题图)(第15题图) 15.(几何证明选讲选做题)如图,PAB 、PCD 为⊙O 的两条割线,若PA=5,AB=7,CD=11,AC=2,则BD 等于 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)设向量a =)sin ,2(θ,b =)cos ,1(θ,θ为锐角. (1)若a ·b =136,求sin θ+cos θ的值;(2)若a ∥b ,求sin(2θ+π3)的值.17.(本小题满分12分)某中学校本课程共开设了A ,B ,C ,D 共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生: (1)求这3名学生选修课所有选法的总数;(2)求恰有2门选修课没有被这3名学生选择的概率; (3)求A 选修课被这3名学生选择的人数的数学期望.18.(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形(1)求证:N B C BC 11//平面; (2)求证:BN 11C B N ⊥平面; (3)设M 为AB 中点,在BC 边上找一点P ,使MP //平面1CNB ,并求PCBP的值.8主视图侧视图俯视图419.(本题满分14分)已知椭圆C :)0(12222>>=+b a by a x ,左、右两个焦点分别为1F 、2F ,上顶点),0(b A ,21F AF ∆为正三角形且周长为6.(1)求椭圆C 的标准方程及离心率;(2)O 为坐标原点,P 是直线A F 1上的一个动点,求||||2PO PF +的最小值,并求出此时点P 的坐标.20.(本小题满分14分)已知函数21()22f x ax x =+,()g x lnx =. (1)如果函数()y f x =在[1,)+∞上是单调减函数,求a 的取值范围;(2)是否存在实数0a >,使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根?若存在,请求出a 的取值范围;若不存在,请说明理由.21.(本题满分14分)已知正项数列{}n a 的前n 项和为n S ,且(2)4n n n a a S += *()n ∈N . (1)求1a 的值及数列{}n a 的通项公式;(2)求证:33331231111532n a a a a ++++<*()n ∈N ; (3)是否存在非零整数λ,使不等式112111(1)(1)(1)cos 2n n a a a a πλ+--⋅⋅-<对一切*n ∈N 都成立?若存在,求出λ的值;若不存在,说明理由.珠海市2012~2013学年第一学期普通高中学生学业质量监测高三理科数学试题参考答案及评分标准一、选择题:CABD AADB 二、填空题:(第15题图)9.函数=y xxsin 的导函数='y . 10.在递增等比数列{a n }中,4,2342=-=a a a ,则公比q = .11.某学校三个社团的人员分布如下表(每名同学只参加一个社团):学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果合唱社被抽出12人,则这三个社团人数共有_______________. 12.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知C =3π,3=b ,若△ABC 的面积为233 ,则c = .13.如图,F 1,F 2是双曲线C :22221x y a b-=(a >0,b >0) 的左、右焦点,过F 1的直线与C 的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3 : 4 : 5,则双 曲线的离心率为 .(二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在直角坐标系x O y 中, 已知曲线1C :⎩⎨⎧-=+=t y t x 212 , (为参数)与曲线2C :⎩⎨⎧==θθsin 3cos 3y x ,(θ为参数)相交于两个点A 、B ,则线段AB 的长为 . 15.(几何证明选讲选做题)如图,PAB 、PCD 为⊙O 的两条割线,若PA=5,AB=7,CD=11,AC=2,则BD 等于 .9、2sin cos x xx x - 10、2 11、150 12、713、13 14、 4 15、 6 三、解答题:12+12+14+14+14+14=80 16.(本小题满分12分)xy OA BF 1F 2(第13题图)设向量a =)sin ,2(θ,b =)cos ,1(θ,θ为锐角. (1)若a ·b =136,求sin θ+cos θ的值;(2)若a ∥b ,求sin(2θ+π3)的值.17.(本小题满分12分)某中学校本课程共开设了A ,B ,C ,D 共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生: (1)求这3名学生选修课所有选法的总数;(2)求恰有2门选修课没有被这3名学生选择的概率; (3)求A 选修课被这3名学生选择的人数的数学期望.18.(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形(1)求证:N B C BC 11//平面; (2)求证:BN 11C B N ⊥平面; (3)设M 为AB 中点,在BC 边上找一点P ,使MP //平面1CNB ,并求PCBP的值.19.(本题满分14分)已知椭圆C :)0(12222>>=+b a by a x ,左、右两个焦点分别为1F 、2F ,上顶点),0(b A ,21F AF ∆为正三角形且周长为6.(1)求椭圆C 的标准方程及离心率;(2)O 为坐标原点,P 是直线A F 1上的一个动点,求||||2PO PF +的最小值,并求出此时点P 的坐标.8 主视图 侧视图俯视图420.(本小题满分14分)已知函数21()22f x ax x =+,()g x lnx =. (1)如果函数()y f x =在[1,)+∞上是单调减函数,求a 的取值范围;(2)是否存在实数0a >,使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根?若存在,请求出a 的取值范围;若不存在,请说明理由.21.(本题满分14分)已知正项数列{}n a 的前n 项和为n S ,且(2)4n n n a a S += *()n ∈N . (1)求1a 的值及数列{}n a 的通项公式;(2)求证:33331231111532n a a a a ++++<*()n∈N ; (3)是否存在非零整数λ,使不等式112111(1)(1)(1)cos 2n n a a a a πλ+--⋅⋅-<对一切*n ∈N 都成立?若存在,求出λ的值;若不存在,说明理由.三、解答题: 16.(本小题满分12分) 解:(1) 因为a ·b =2+sin θcos θ=136,所以sin θcos θ=16. ……………… 3分 所以 (sin θ+cos θ)2=1+2 sin θcos θ=43.又因为θ为锐角,所以sin θ+cos θ=233. ……………… 6分(2) 解法一 因为a ∥b ,所以tan θ=2. ……………… 8分 所以 sin2θ=2 sin θcos θ= 2 sin θcos θ sin 2θ+cos 2θ= 2 tan θ tan 2θ+1=45,cos2θ=cos 2θ-sin 2θ=cos 2θ-sin 2θ sin 2θ+cos 2θ=1-tan 2θ tan 2θ+1=-35.……………… 10分 所以sin(2θ+π3 )=12sin2θ+32cos2θ=12×45+32×(-35 )=4-3310. ……………… 12分 解法二 因为a ∥b ,所以tan θ=2. ……………… 8分 所以 sin θ=255,cos θ=55.因此 sin2θ=2 sin θcos θ=45, cos2θ=cos 2θ-sin 2θ=-35. ……………… 10分所以sin(2θ+π3 )=12sin2θ+32cos2θ=12×45+32×(-35 )=4-3310. ……………… 12分17、(本小题满分12分)解析:(Ⅰ)每个学生有四个不同选择,根据乘法法则,选法总数N=64444=⨯⨯ …… 3分(Ⅱ) 恰有2门选修课这3名学生都没选择的概率为1694442332432223242=⨯⨯⨯⨯⨯==A C C P ……………… 7分(Ⅲ) 设A 选修课被这3名学生选择的人数为ξ,则ξ=0,1,2,3P(ξ=0)=64274333= P(ξ=1)=6427433213=⋅C P(ξ=2)=64943313=⋅C P(ξ=3)= 6414333=C ……………… 9分ξ的分布列是………… 10分43641364926427164270=⨯+⨯+⨯+⨯=ξE ………… 12分18.解:(1)证明: 该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴1,,BB BC BA 两两互相垂直。
广东省珠海市2013届高三上学期期末学业质量监测数学理试题
珠海市2012--2013学年度第一学期期末学生学业质量监测高三理科数学试题一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项. 1.已知全集R U =,集合A ={y | y =2x ,x ∈R },则A C U =A .∅B .(0,+∞)C . (-∞,0]D .R 2.已知a ,b 是实数,则“⎩⎨⎧>>32b a ”是“5>+b a ”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.若某程序框图如图所示,则该程序运行后输出的值是 A .4 B .5 C .6 D .74. 已知直线l ,m 和平面α, 则下列命题正确的是A .若l ∥m ,m ⊂α,则l ∥αB .若l ∥α,m ⊂α,则l ∥mC .若l ⊥m ,l ⊥α,则m ∥αD .若l ⊥α,m ⊂α,则l ⊥m 5.已知是虚数单位,复数ii+3= A .i 103101+ B .i 103101+- C .i 8381+- D .i 8381--6. 函数y =sin (2x +π4)的图象可由函数y =sin 2x 的图象 A .向左平移π8个单位长度而得到 B .向右平移π8个单位长度而得到 C .向左平移π4个单位长度而得到 D .向右平移π4个单位长度而得到7.若实数x ,y 满足不等式组⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x 则2x +4y 的最小值是A .6B .4C .2-D .6-n =12, i =1n =3n +1开 始 n 是奇数?输出i 结 束 是 否 n = n =5?是 否n 2i =i +1 (第3题图)8. 对于直角坐标平面内的任意两点11(,)A x y 、22(,)B x y ,定义它们之间的一种“距离”: ‖AB ‖=1212x x y y -+-,给出下列三个命题:①若点C 在线段AB 上,则‖AC ‖+‖CB ‖=‖AB ‖;②在△ABC 中,若∠C =90°,则‖AC ‖+‖CB ‖=‖AB ‖; ③在△ABC 中,‖AC ‖+‖CB ‖>‖AB ‖. 其中真命题的个数为A. 0B. 1C. 2D.3二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.请将答案填在答题卡相应位置. (一)必做题(9-13题) 9.函数=y xxsin 的导函数='y . 10.在递增等比数列{a n }中,4,2342=-=a a a ,则公比q = . 11.某学校三个社团的人员分布如下表(每名同学只参加一个社团):学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果合唱社被抽出12人,则这三个社团人数共有_______________. 12.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知C =3π,3=b ,若△ABC 的面积为233 ,则c = . 13.如图,F 1,F 2是双曲线C :22221x y a b-=(a >0,b >0) 的左、右焦点,过F 1的直线与C 的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3 : 4 : 5,则双 曲线的离心率为 .(二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在直角坐标系x O y 中, 已知曲线1C :⎩⎨⎧-=+=t y t x 212 , (为参数)与曲线2C :⎩⎨⎧==θθsin 3cos 3y x ,(θ为参数)相交于两个点A 、B ,则线段AB 的长为 .合唱社 粤曲社 武术社 高一 45 30 a高二 15 10 20xy OA BF 1F 2(第13题图)ODCB AP(第15题图)15.(几何证明选讲选做题)如图,PAB 、PCD 为⊙O 的两条割线,若PA=5,AB=7,CD=11,AC=2,则BD 等于 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)设向量a =)sin ,2(θ,b =)cos ,1(θ,θ为锐角. (1)若a ·b =136,求sin θ+cos θ的值;(2)若a ∥b ,求sin(2θ+π3)的值.17.(本小题满分12分)某中学校本课程共开设了A ,B ,C ,D 共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生: (1)求这3名学生选修课所有选法的总数;(2)求恰有2门选修课没有被这3名学生选择的概率; (3)求A 选修课被这3名学生选择的人数的数学期望.18.(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形(1)求证:N B C BC 11//平面; (2)求证:BN 11C B N ⊥平面; (3)设M 为AB 中点,在BC 边上找一点P ,使MP //平面1CNB ,并求PCBP的值.88 4主视图 侧视图俯视图44819.(本题满分14分)已知椭圆C :)0(12222>>=+b a by a x ,左、右两个焦点分别为1F 、2F ,上顶点),0(b A ,21F AF ∆为正三角形且周长为6.(1)求椭圆C 的标准方程及离心率;(2)O 为坐标原点,P 是直线A F 1上的一个动点,求||||2PO PF +的最小值,并求出此时点P 的坐标.20.(本小题满分14分)已知函数21()22f x ax x =+,()g x lnx =. (1)如果函数()y f x =在[1,)+∞上是单调减函数,求a 的取值范围;(2)是否存在实数0a >,使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根?若存在,请求出a 的取值范围;若不存在,请说明理由.21.(本题满分14分)已知正项数列{}n a 的前n 项和为n S ,且(2)4n n n a a S += *()n ∈N . (1)求1a 的值及数列{}n a 的通项公式;(2)求证:33331231111532n a a a a ++++<*()n ∈N ; (3)是否存在非零整数λ,使不等式1121111(1)(1)(1)cos 21n n n a a a a a πλ+--⋅⋅-<+ 对一切*n ∈N 都成立?若存在,求出λ的值;若不存在,说明理由.ODCBAP(第15题图)珠海市2012~2013学年第一学期普通高中学生学业质量监测高三理科数学试题参考答案及评分标准一、选择题:CABD AADB 二、填空题: 9.函数=y xxsin 的导函数='y . 10.在递增等比数列{a n }中,4,2342=-=a a a ,则公比q = . 11.某学校三个社团的人员分布如下表(每名同学只参加一个社团):学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果合唱社被抽出12人,则这三个社团人数共有_______________. 12.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知C =3π,3=b ,若△ABC 的面积为233 ,则c = .13.如图,F 1,F 2是双曲线C :22221x y a b-=(a >0,b >0) 的左、右焦点,过F 1的直线与C 的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3 : 4 : 5,则双 曲线的离心率为 .(二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在直角坐标系x O y 中, 已知曲线1C :⎩⎨⎧-=+=t y t x 212 , (为参数)与曲线2C :⎩⎨⎧==θθsin 3cos 3y x ,(θ为参数)相交于两个点A 、B ,则线段AB 的长为 .15.(几何证明选讲选做题)如图,PAB 、PCD 为⊙O 的两条割线,若PA=5,AB=7,CD=11,AC=2,则BD 等于 .合唱社 粤曲社 武术社 高一 45 30 a高二 15 10 20xy OA BF 1F 2(第13题图)9、2sin cos x xx x - 10、2 11、150 12、713、13 14、 4 15、 6 三、解答题:12+12+14+14+14+14=80 16.(本小题满分12分)设向量a =)sin ,2(θ,b =)cos ,1(θ,θ为锐角. (1)若a ·b =136,求sin θ+cos θ的值;(2)若a ∥b ,求sin(2θ+π3)的值.17.(本小题满分12分)某中学校本课程共开设了A ,B ,C ,D 共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生: (1)求这3名学生选修课所有选法的总数;(2)求恰有2门选修课没有被这3名学生选择的概率; (3)求A 选修课被这3名学生选择的人数的数学期望.18.(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形(1)求证:N B C BC 11//平面; (2)求证:BN 11C B N ⊥平面; (3)设M 为AB 中点,在BC 边上找一点P ,使MP //平面1CNB ,并求PCBP的值.19.(本题满分14分)88 4主视图 侧视图俯视图448已知椭圆C :)0(12222>>=+b a by a x ,左、右两个焦点分别为1F 、2F ,上顶点),0(b A ,21F AF ∆为正三角形且周长为6.(1)求椭圆C 的标准方程及离心率;(2)O 为坐标原点,P 是直线A F 1上的一个动点,求||||2PO PF +的最小值,并求出此时点P 的坐标.20.(本小题满分14分)已知函数21()22f x ax x =+,()g x lnx =. (1)如果函数()y f x =在[1,)+∞上是单调减函数,求a 的取值范围;(2)是否存在实数0a >,使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根?若存在,请求出a 的取值范围;若不存在,请说明理由.21.(本题满分14分)已知正项数列{}n a 的前n 项和为n S ,且(2)4n n n a a S += *()n ∈N . (1)求1a 的值及数列{}n a 的通项公式;(2)求证:33331231111532n a a a a ++++<*()n ∈N ; (3)是否存在非零整数λ,使不等式1121111(1)(1)(1)cos 21n n n a a a a a πλ+--⋅⋅-<+ 对一切*n ∈N 都成立?若存在,求出λ的值;若不存在,说明理由.三、解答题:16.(本小题满分12分)解:(1) 因为a ·b =2+sin θcos θ=136,所以sin θcos θ=16. ……………… 3分所以 (sin θ+cos θ)2=1+2 sin θcos θ=43.又因为θ为锐角,所以sin θ+cos θ=233. ……………… 6分(2) 解法一 因为a ∥b ,所以tan θ=2. ……………… 8分所以 sin2θ=2 sin θcos θ= 2 sin θcos θ sin 2θ+cos 2θ= 2 tan θ tan 2θ+1=45, cos2θ=cos 2θ-sin 2θ=cos 2θ-sin 2θ sin 2θ+cos 2θ=1-tan 2θ tan 2θ+1=-35.……………… 10分所以sin(2θ+π3 )=12sin2θ+32cos2θ=12×45+32×(-35 )=4-3310. ……………… 12分 解法二 因为a ∥b ,所以tan θ=2. ……………… 8分 所以 sin θ=255,cos θ=55.因此 sin2θ=2 sin θcos θ=45, cos2θ=cos 2θ-sin 2θ=-35. ……………… 10分所以sin(2θ+π3 )=12sin2θ+32cos2θ=12×45+32×(-35 )=4-3310. ……………… 12分17、(本小题满分12分)解析:(Ⅰ)每个学生有四个不同选择,根据乘法法则,选法总数N=64444=⨯⨯ …… 3分(Ⅱ) 恰有2门选修课这3名学生都没选择的概率为1694442332432223242=⨯⨯⨯⨯⨯==A C C P ……………… 7分(Ⅲ) 设A 选修课被这3名学生选择的人数为ξ,则ξ=0,1,2,3=64274333= P(ξ=1)=P(ξ=0)6427433213=⋅C P(ξ=2)=64943313=⋅C P(ξ=3)= 6414333=C ……………… 9分ξ的分布列是………… 10分43641364926427164270=⨯+⨯+⨯+⨯=ξE ………… 12分18.解:(1)证明: 该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴1,,BB BC BA 两两互相垂直。
广东省广州市2013年普通高中毕业班综合测试(二)理科数学考试试卷(word版)

试卷类型:A2013年广州市普通高中毕业班综合测试(二)数 学(理科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号.用黑色字迹的钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型 (A) 填涂在答题卡相应位置上.2.选择题每小题选出答案后.用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:如果事件A 、B 互斥,那么()()()P A B P A P B +=+. 如果事件A 、B 相互独立,那么()()()P A B P A P B = .如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率()(1)(0,1,2,,)k k n kn n P k C p p k n -=-= . 两数立方差公式:3322() ()a b a b a ab b -=-++.一、选择题:本大题共8小题.每小题5分,满分40分.在每小题给出的四个选项中.只有一项是符合题目要求的 l .已知i 为虚数单位,若复数(1)(1)a a -++i 为实数,则实数a 的值为A .-1B .0C . 1D .不确定2.已知全集U A B = 中有m 个元素,()()U UA A痧中有n 个元索,若A B 非空,则A B 的元素个数为A .mnB .m n +C .m n -D .n m -3.已知向量()sin ,cos a x x =,向量(b =,则a b +的最大值为A .1BC .3D .94.若m ,n 是互不相同的空间直线,α是平面,则下列命题中正确的是A .若//m n ,n α⊂,则//m αB .若//m n ,//n α,则//m αC .若//m n ,n α⊥,则m α⊥D .若m n ⊥,n α⊥,则m α⊥5.在如图1所示的算法流程图中,若()2x f x =,()3g x x =,则()2h 的值为(注:框图中的赋值符号“=”也可以写成“←”或“=”) A .9 B .8 C .6 D .46.已知点(),p x y 的坐标满足10,30,2x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩O 为坐标原点,则PO 的最小值为A.2B.2CD7.已知函数()sin f x x =,若12,[,]22x x ππ∈-且()()12f x f x <,则下列不等式中正确的是A .12x x >B .12x x <C .120x x +<D .2212x x < 8.一个人以6米/秒的匀速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始作变速直线行驶 (汽车与人的前进方向相同),汽车在时刻t 的速度为()v t t =米/秒.那么.此人A .可在7秒内追上汽车B .可在9秒内追上汽车C .不能追上汽车,但其间最近距离为14米D .不能追上汽车,但其间最近距离为7米二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分 (一) 必做题 (9~13题)9.若函数()cos() cos() (>0)2f x x x πωωω=-的最小正周期为π,则m 的值为 .10.已知椭圆C的离心率2e =,且它的焦点与双曲线2224x y -=的焦点重台,则椭圆C 的方程为 .11.甲、乙两工人在一天生产中出现废品数分别是两个随机变量ξ、η,其分布列分别为:若甲、乙两人的日产量相等,则甲、乙两人中技术较好的是. 12.图2是一个有n 层(2)n ≥的六边形点阵.它的中心是一个点,算作 第一层.第2层每边有2个点.第3层每边有3个点,…,第n 层 每边有n 个点,则这个点阵的点数共有 个.13.已知2nx ⎫⎪⎭的展开式中第5项的系数与第3项的系数比为56:3,则该展开式中2x 的系数为 . (二) 选做题 (14~15题.考生只能从中选做一题)14.(坐标系与参数方程选做题) 已知直线l 的参数方程为142x ty t =+⎧⎨=-⎩(参数t R ∈),圆C 的参数方程为2cos 22sin x y θθ=+⎧⎨=⎩ (参数[0,2]θπ∈),则直线l 被圆C 所截得的弦长为 .15.(几何证明选讲选做题) 如图3,半径为5的圆O 的两条弦AD 和BC 相交于点P ,OD BC ⊥,P 为AD 的中点,6BC =,则弦AD 的长度为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知tan 24πα⎛⎫+=⎪⎝⎭,1tan 2β=.(1) 求tan α值;(2) 求sin()2sin cos 2sin sin cos()αβαβαβαβ+-++的值.17.(本小题满分12分)如图4,在直角梯形ABCD 中,90ABC DAB ∠=∠=°.30CAB ∠=°,1BC =,AD CD =,把DAC ∆沿对角线AC 折起后如图5所示 (点D 记为点P ).点P 在平面ABC 上的正投影E 落在线段AB 上,连接PB . (1) 求直线PC 与平面PAB 所成的角的大小;(2) 求二面角P AC B --的大小的余弦值.18.(本小题满分14分)一射击运动员进行飞碟射击训练,每一次射击命中飞碟的概率p 与运动员离飞碟的距离s (米)成反比.每一个飞碟飞出后离运动员的距离s (米)与飞行时间t (秒)满足15(1) (04)s t t =+≤≤,每个飞碟允许该运动员射击两次 (若第一次射击命中,则不再进行第二次射击).该运动员在每一个飞碟飞出0.5秒时进行第一次射击.命中的概率为45,当第一次射击没有命中飞碟,则在第一次射击后0.5秒进行第二次射击,子弹的飞行时间忽略不计.(1) 在第一个飞碟的射击训练时,若该运动员第一次射击没有命中,求他第二次射击命中飞碟的概率;(2) 求第一个飞碟被该运动员命中的概率;(3) 若该运动员进行三个飞碟的射击训练 (每个飞碟是否被命中互不影响),求他至少命中两个飞碟的概率19.(本小题满分14分)已知抛物线C :22 (0)x py p => 的焦点为F ,A 、B 是抛物线C 上异于坐标原点O 的不同两点,抛物线C 在点A 、B 处的切线分别为1l 、2l ,且12l l ⊥,1l 与2l 相交于点D .(1) 求点D 的纵坐标;(2) 证明:A 、B 、F 三点共线;(3) 假设点D 的坐标为3,12⎛⎫- ⎪⎝⎭,问是否存在经过A 、B 两点且与1l 、2l 都相切的圆,若存在,求出该圆的方程;若不存在,请说明理由.20.(本小题满分14分)已知函数()32(,)f x x x ax b a b R =-++∈的一个极值点为1x =.方程20ax x b ++=的两个实根为α,()βαβ<,函数()f x 在区间[,]αβ上是单调的(1) 求a 的值和b 的取值范围;(2) 若1x ,2[,]x αβ∈证明:()()121f x f x -≤.21.(本小题满分14分)已知数列{}n a 和{}n b 满足11a b =,且对任意n N ∈*都有1n n a b +=,211n n n na ba a +=-. (1) 求数列{}n a 和{}nb 的通项公式; (2) 证明:31324122341123...1 (1) ...n n n na a aa a a a a n nb b b b b b b b ++++++<+<++++.。
2013珠海二模理科数学试题与参考答案

2013年5月珠海市高三综合测试(二)理科数学参考答案及评分标准本试卷共4页,21小题, 满分150分。
考试用时120分钟。
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|12},{|0},A x x B x x =-≤-<=-≥则A B 等于C A .{|02}x x ≤<B . {|21}x x -<≤-C .{|20}x x -<≤D . {|10}x x -<≤2.设i 为虚数单位,则复数43ii+的虚部为 ( )A A .-4 B .-4i C .4 D .4i3.已知非零向量a ,b 满足错误!未找到引用源。
,则函数()()()2f x ax bx R =+∈是 ( )AA.偶函数B. 奇函数C.既是奇函数又是偶函数D.非奇非偶函数4.设随机变量ξ服从正态分布),2(2σN ,若a c P =>)(ξ,则)4(c P ->ξ等于BA. B. C. D.5.已知变量x y、满足030330x y x y x y -≤⎧⎪+-≤⎨⎪+-≥⎩,则2z x y =-的值域是DA .[03],B .(03),C .3(3)2-, D .3[3]2-, 6.已知实数4,,9m 构成一个等比数列,则圆锥曲线 C ) A B C 7 7.如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体的体积是 ( A ) A 【答案】A8.已知)(x f 是R 上的偶函数,2)0(=f ,若)(x f 的图象向右平移一个单位后,则得到一个奇函数的图象,a 21-a a -1a 2那么)9()7()5()3()1(f f f f f ++++的值为( )BA .1B .0C .-1 D二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.某程序框图如图所示,该程序运行后输出的k 的值是 。
广东省海珠区12—13上学期高三数学(理科)综合测试(二)考试试卷

海珠区2012学年高三综合测试(二)数学(理科)本试卷共6页,21小题,满分150分.考试用时120分钟. 注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室 号、座位号填写在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息 点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷 上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指 定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案; 不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后,将答题卡一并交回. 参考公式:如果事件A 、B 互斥,那么)()()(B P A P B A P +=+若在每次试验中,事件A 发生的概率为P ,则在n 次独立重复试验中,事件W A 恰好发生k 次的概率为n k p p C k XP k n kk n ,,1,0,)1()( =-==-.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.i 是虚数单位,复数31i i+对应的点位于 A .第一象限B 第二象限C .第二象限D .第四象限2.若集合},1{2a A =,集合}9,6{=B ,则 “a = 3”是“}9{=⋂B A .的 A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.已知函数x x f -=1)(,若)2(),11(lg ),8.0(lg 21-===f c f b f a ,则 A .a c < a D .a < c <b4.如图1所示,则 A .6π,21-==ϕωB .3π,2-==ϕωC .3π,21==ϕωD .6π,2==ϕω 5.已知正二棱柱(侧棱与底面垂直,底面是正二角形)的高与底面边长均为1,其直观图 和正(主)视图如图2所示,则它的左(侧)视图的面积是 A .3B .1C .31 D .23 6.已知双曲线)0,0(12222>>=-b a by a x 的一个焦点与抛物线y 2 =12x 的焦点重合,且双曲线的离心率等 于3,则该双曲线的标准方程为A .16322=-y xB .1241222=-y x C .1182722=-y x D .1271822=-y x 7.已知各项不为O 的等差数列}{n a 满足:06π6π12272=+-a a a ,数列}{n b 是各项均为 正值的等比数列,且b 7=a 7,则)tan(104b b 等于 A .3B .3-C .3±D .338.用},max{b a 表示a ,b 两个数中的最大数,设)41}(,max{)(2≥=x x x x f ,那么山函数)(x f y =的图象、X 轴、直线41=x 和直线X = 2所围成的封闭图形的面积是 A .1235 B .2459 C .857D .1291二、填空题:本大题共 7 小题,考生作答 6 小题,每小题 5 分,满分 30 分.(一)必做题(9~13 题9.6)12(xx +的二项展丌式的常数项为_______.(用数字作答)11.已知实数X ,满足约束条件⎪⎩⎨≤+-≤512y x x y ,则目标函数Z = X-y 的最小值等于______.12.某程序框图如图4所示,该程序运行后输出的值依次为_____. 13.给出下列四个命题:①命题1sin ,R :≤∈∀x x p ,则1sin ,R :<∈∃x x p , ②当1≥a 时,不等式a x x <-+-|3||4|的解集为非空;③当X >1时,有2ln 1ln ≥+xx ④设有五个函数.x y x y x y x y x y 2,,,,2321=====-,其中既是偶函数又在),0(+∞上是增函数的有2个.其中真命题的序号是_____.(二)选做题(14、15 题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在极坐标系中,点A 的坐标为),4π,22(曲线c 的方程为θρsin 4=,则0A (O 为极点)所在直线被曲线C 所截弦的长度为____. 15.(几何证明选讲选做题D 如图5所示,过圆C 外一点尸做一条直线与圆C 交于A ,B 两 点,AB = 2AP ,PT 与圆c 相切于T 点.已知圆C 的半径为2,∠30=CAB °,则PT =_______.三、解答题:本大题共 6 小题,满分 80 分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知函数x x x x x f cos sin 2)6π2cos()6π2cos()(+-++= (1)求f (X )的最小正周期; (2)求函数)(x f 在区间]3π,3π[-上的最大值和最小值,并求此时X 的值.17.(本小题满分12分)现有3个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.约定:每个人将质地均匀的硬币抛掷2次决定自己去参加哪个游戏.2次抛出的硬币朝上的面均为正面的 人去参加甲游戏,2次抛出的硬币朝上的面为其它情形的去参加乙游戏.(1)求这3个人中恰有2人去参加甲游戏的概率;(2)求这3个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;18.用;分别表示这3个人中去参加甲、乙游戏的人数,记||Y X -=ξ,求随机变 量ξ的分布列和数学期望.(本小题满分14分)如图6,四棱锥P -ABCD 中,PA 丄底面ABCD ,M ,N 分别是PB ,PC 的中点, PA = AB ,在四边形ABCD 中,AB 丄AD ,AB 丄 BC .(1)求证:MN //平面PAD ,(2)求证:平面MN 丄平面PBC ;(3)若AD - AB = 1,5=PD ,∠ 45=CAD ,求二面角P -AB -N 的大小.19.(本小题满分14分)设椭圆)0(12:222>=+a y a x C 的左、右顶点分别为A 、B ,点尸在椭圆上且异于A 、B 两点,O 为坐标原点.(1)若直线AP 与BP 的斜率之积为21-,求椭圆的离心率; (2)对于由(1)得到的椭圆C ,过点P 的直线l 交X 轴于点Q (-1,0),交x 轴于点M , 若||2||=,求直线l 的斜率.20.(本小题满分14分)已知点)N )(,(,),,(),,(*222111∈n b a P b a P b a P n n n ?在函数x y 21log =的图象上.(1)若数列}{n b 是等差数列,求证数列}{n a 是等比数列;(2)若数列}{n a 的前《项和是nn S --=21,过点1,+n n P P 的直线与两坐标轴所围二角形面积为C n ,求最小的实数t 使*N ∈≤n t c n 对:恒成立;(3)若数列}{n b 为山(2)中{a 」得到的数列,在k b 与1+k b 之间插入)N (3*1∈-k k 个3, 得一新数列}{n d ,问是杏存在这样的正整数m ,使数列}{n d 的前m 项的和2008=m S ,如果存在,求出m 的值,如果不存在,请说明理由21.(本小题满分14分)已知函数)ln()(a x x x f +-=的最小值为0,其中a >0. (1)求a 的值;(2)若对任意的),0[+∞∈x ,有2)(kx x f ≤成立,求实数k 的最小值;(3)证明)N (2)12ln(122*1∑=∈<+--ni n n i海珠区2012学年高三综合测试(二)理科数学参考答案与评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分. 3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题. 9.16010.025.0,180 11.1- 12.34,55 13.③④14.2215.3(第10题第一空2分,第二空3分)三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查三角两角和的正余弦公式,三角特殊值的运算,函数()()()()()ϕωϕω+=+=x A x f x A x f c o s s i n 或的周期,最值等知识,考查化归、转化、换元的数学思想方法,以及运算求解能力)解:(1)()cos 2cos 22sin cos 66f x x x x x ππ⎛⎫⎛⎫=++-+ ⎪ ⎪⎝⎭⎝⎭6sin 2sin 6cos2cos ππx x -=+6sin2sin 6cos2cos ππx x +x x cos sin 2+ 2分x 2cos 232⨯=x 2sin + x 2cos 3=x 2sin + 3分⎪⎪⎭⎫ ⎝⎛+=x x 2sin 212cos 232 4分 ⎪⎭⎫⎝⎛+=x x 2sin 3cos 2cos 3sin 2ππ 5分⎪⎭⎫ ⎝⎛+=32sin 2πx …………6分∴()f x 的最小正周期为ππ==22T …7分 (2)由(1)知()x f ⎪⎭⎫⎝⎛+=32sin 2πx , 由33ππ≤≤-x ,得πππ≤+≤-323x , ……8分∴当232ππ=+x ,即12π=x 时, ()f x 取得最大值2; …………10分 当332ππ-=+x ,即3π-=x 时, ()f x 取得最小值3-.…………12分17.(本小题满分12分)(本小题主要考查互斥事件,古典概型,独立重复试验,数学期望等知识,考查随机思想以及数据处理能力、抽象思维能力、运算求解能力和应用意识)解:将质地均匀的两枚硬币抛掷两次朝上的面有等可能的四种结果:()正正,,()反正,,()正反,,()反反,, 1分所以3个人中,每个人去参加甲游戏的概率为41,去参加乙游戏的概率为43.…………2分 设“这3个人中恰有i 人去参加甲游戏”为事件()3,2,1,0=i A i则()iii i C A P -⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛=334341.…………3分 (1)这3个人中恰有2人去参加甲游戏的概率()6494341232232=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=-C A P .…………5分 (2)设“这3个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B ,则23A A B ⋃=,由于23A A 与互斥,故()()()23A P A P B P +==325649641434141223333=+=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛C C . 所以, 这3个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为325.………7分 (3)ξ的所有可能取值为3,1, 8分由于1A 与2A ,0A 与3A 互斥,故()()()=+==211A P A P P ξ+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2134341C 16964964274341223=+=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛C ,…………9分()()()=+==303A P A P P ξ+⎪⎭⎫ ⎝⎛30343C 167641642741333=+=⎪⎭⎫ ⎝⎛C .…………10分所以, ξ的分布列为……11分所以随机变量ξ的数学期望815163016731691==⨯+⨯=ξE .…………12分 18.(本小题满分14分)(本小题主要考查空间线面关系、空间向量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)解:(1)证明: N M ,分别是PC PB ,的中点MN ∴是PBC ∆的中位线,BC MN //∴, 又 AD AB ⊥,AB ⊥BC∴AD BC //,AD MN //∴, …………1分 ⊂AD 平面PAD , …………2分⊄MN 平面PAD , …………3分 //MN 平面PAD .…………4分PAB ,⊂AB 平面PAB ,⊥∴BC 平面PAB ,⊂AM 平面PAB BC AM ⊥∴.…………6分B BC PB =⋂,⊂PB 平面PBC ,⊂BC 平面PBC ⊥∴AM 平面PBC .…………7分又⊂AM 平面AMN ……8分∴平面AMN ⊥平面PBC .…………9分(3) ⊥PA 底面ABCD ,AD ⊂平面ABCD ,AD PA ⊥∴,又AB PA =222PD AD PA =+∴又AB PA =,,5=PD5222==+∴PD AD AB联立⎩⎨⎧=+=-5122AD AB AB AD ,解得⎩⎨⎧==21AD AB . 过点C 作AD CH ⊥于H ,在DHC Rt ∆中,1,450===∠AB CH CDH1=∴DH ,1==∴AH BC .…………10分方法一(向量法):以A 为坐标原点,分别以直线AP AB AD ,,为x 轴,y 轴,z 轴建立空间直角坐标系xyz O -,如图所示.…………11分则()()()0,1,1,0,1,0,0,0,0C B A ,()⎪⎭⎫⎝⎛21,21,21,1,0,0N P , ()0,0,1=BC ,⎪⎭⎫⎝⎛=21,21,21AN ,()0,1,0=AB .由(2)知()0,0,1=是平面PAB 的一个法向量; 设平面NAB 的法向量为()z y x ,,=,则⎪⎩⎪⎨⎧=⋅=⋅00AN n ,即⎪⎩⎪⎨⎧==++0212121y z y x ,得 ⎩⎨⎧=-=0y zx .取()1,0,1-=. …………12分()()22101001100011222222=-++⨯++-⨯+⨯+⨯==. …………13分结合图可知, 二面角N AB P --的大小为045.…………14分∴12BN=.同理易证12AN PC=.AN BN∴=.取AB的中点Q,连AQ,则AB NQ⊥.连MQ,易知//MQ PA,MQ AB∴⊥.MQ⊂平面PAB,NQ⊂平面NAB,MQN∴∠即是二面角NABP--的平面角.…………11分在Rt PBC∆中,PB PC==∴== BN∴=∴在Rt BQN∆中,NQ==1122MQ PA==,1122MN BC==, 12分∴在MQN∆中,222MQ MN NQ+=,又有MN MQ=,∴MQN∆是以NMQ∠为直角的等腰直角三角形,MQN ∴∠045=.…………13分∴二面角N AB P --的大小为045.…………14分19.(本小题14分)(本小题主要考查直线斜率、椭圆的方程、离心率、向量的运算等知识,考查数形结合、化归与转化、方程的思想方法,考查综合运用能力以及运算求解能力)解:(1)由已知()()0,,0,a B a A -,设()()a x y x P ±≠000,.…………1分 则直线AP 的斜率ax y k AP +=00,直线BP 的斜率ax y k AP -=00.由1220220=+y a x ,得()2202202a x a y -=.…………2分 ∴⨯AP k AP k a x y +=00()()2202222220200022a x a a x a a x y a x y -=---=-=-⨯ …3分 2122-=-∴a,得42=a , 4分 ∴214242=-=e .…………5分 ∴椭圆的离心率22=e .…………6分 (2)由题意知直线l 的斜率存在.…………7分设直线l 的斜率为k , 直线l 的方程为()1+=x k y ……8分 则有()k M ,0,设()()a x y x P ±≠000,,由于Q M P ,,= 根据题意,得()()0000,12,y x k y x +±=- …………9分解得⎩⎨⎧-=-=k y x 002或⎪⎪⎩⎪⎪⎨⎧=-=33200k y x …………11分又点P 在椭圆上,又由(1)知椭圆C 的方程为12422=+y x 所以()()124222=-+-k …………①或12343222=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-k …………② 由①解得02=k ,即0=k ,此时点P 与椭圆左端点A 重合, 0=∴k 舍去; 12分由②解得162=k ,即4±=k 13分∴直线直线l 的斜率4±=k .…………14分20.(本小题满分14分)(本小题主要考查等差、等比数列的定义、通项、求和、对数的运算、直线方程与不等式等知识,考查化归、转化、方程的数学思想方法,以及抽象概括能力、运算求解能力、创新能力和综合应用能力)解:(1)证明:数列{}n b 是等差数列,设公差为d ,则1n n b b d +-=对*n N ∈恒成立, 1分依题意12log n n b a =,1()2n bn a =, 2分所以1111()()22n n b b d n n a a +-+==是定值, 3分 从而数列{}n a 是等比数列.……………… 4分 (2)解:当1n =时,112a =,当2n ≥时,11()2nn n n a S S -=-=,1n =也适合此式,即数列{}n a 的通项公式是1()2nn a =.……………… 5分 由12log n n b a =,数列{}n b 的通项公式是n b n =, 6分 所以1(,)2n n P n ,111(,1)2n n P n +++. 过这两点的直线方程是:11211(1)22n n nx y n n n +--=+--, 可得与坐标轴的交点是12(,0)2n n n A ++和(0,2)n B n +.……………… 7分221(2)22n n n n n c OA OB ++=⨯⨯=,……………… 8分由于212(22n n n n n n n n n c c +++++++-+-=-=232102n n n ++-=>……………9分即数列{}n c 的各项依次单调递减,所以198t c ≥=.……………… 10分 (3)数列{}n d 中,k b (含k b 项)前的所有项的和是121(12)(333)k k -+++++++()13322k k k +-=+ …… 11分 估算知,当7k =时,其和是73328112020082-+=<, ………… 12分当8k =时,其和是83336331520082-+=>, 又因为200811208882963-==⨯,是3的倍数,故存在这样的m ,使得2008m S =, … 13分此时257(1333)296667m =++++++=.……………… 14分21.(本小题满分14分)(本小题主要考查导数的运算,利用导数研究函数的单调性、不等式等基础知识,考查函数思想,分类讨论思想,以及抽象概括能力、运算求解能力、创新能力和综合应用能力)解(Ⅰ)解:)(x f 的定义域为()+∞-,a 1分ax a x a x x f +-+=+-=111)('.……… 2分 由.0)('=x f 得a a x ->-=1当x 变化时,)(),('x f x f 的变化情况如下表:……………… 3分因此,)(x f 在a x -=1处取得最小值,故由题意,01)1(=-=-a a f 所以.1=a 5分(2)解:当0≤k 时,取1=x ,有().02ln 11>-=f 故0≤k 不合题意.… 6分当0>k 时,令()(),2kx x f x g -=即()().1ln 2kx x x x g -+-=()()[].121221'+---=-+=x k kx x kx x x x g 令()0'=x g , 得.1221,021->-==kkx x 7分 ①当21≥k 时,0221≤-k k.()0'<x g 在()+∞,0上恒成立,因此,()x g 在[)+∞,0上单调递减.从而对于任意的的[)+∞∈,0x ,总有()(),00=≤g x g 即()2kx x f ≤在()+∞,0上恒成立.故21≥k 符合题意.……………… 8分 ②当210<<k 时,,0221>-k k 对于()0,221,0'>⎪⎭⎫ ⎝⎛-∈x g k k x ,故()x g 在⎪⎭⎫ ⎝⎛-k k 221,0内单调递增.因此当⎪⎭⎫⎝⎛-∈k k x 221,00时,()(),000=>g x g 即()200kx x f ≤不成立.故210<<k 不合题意.……………… 9分 综上,k 的最小值为21.……………… 10分(3)证明:当1=n 时,不等式左边=<-=23ln 2右边.所以不等式成立.……………… 11分 当2≥n 时,∑∑==⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+--=⎪⎭⎫ ⎝⎛-n i ni i i i f 111221ln 122122 ()()[]∑∑==--+--=ni ni i i i 1112ln 12ln 122()12ln 1221+--=∑=n i n i … 12分 在(2)中取21=k ,得()()022≥≤x x x f ,从而 ()()()(),2,123221221222≥∈--<-≤⎪⎭⎫ ⎝⎛-*i N i i i i i f … 13分 所以有()()()()∑∑∑∑====--+-<⎪⎭⎫⎝⎛-+=⎪⎭⎫ ⎝⎛-=+--n i ni n i ni i i i f f i f n i 2211123223ln 2122212212ln 122212113ln 21213213ln 22<--+-=⎪⎭⎫ ⎝⎛---+-=∑=n i i ni 综上,()()*=∈<+--∑N n n i ni 212ln 1221 14分。
广东省珠海市2013届高三5月综合测试(二)数学理考试试题

广东省珠海市2013届高三5月综合测试(二)数学理考试试题2013年5月珠海市高三综合测试(二)理科数学本试卷共4页,21小题, 满分150分。
考试用时120分钟。
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|12},{|0},A x x B x x =-≤-<=-≥则A B 等于A .{|02}x x ≤<B . {|21}x x -<≤-C .{|20}x x -<≤D . {|10}x x -<≤2.设i 为虚数单位,则复数43ii+的虚部为 A .-4 B .-4i C .4 D .4i3.已知非零向量a ,b 满足a b ⊥,则函数()()()2f x ax bx R =+∈是A.偶函数B. 奇函数C.既是奇函数又是偶函数D.非奇非偶函数 4.设随机变量ξ服从正态分布),2(2σN ,若a c P =>)(ξ,则)4(c P ->ξ等于A.B. C. D.5.已知变量x y 、满足030330x y x y x y-≤⎧⎪+-≤⎨⎪+-≥⎩,则2z x y =-的值域是A .[03],B .(03),C .3(3)2-, D .3[3]2-,6.已知实数4,,9m 构成一个等比数列,则圆锥曲线A B C 7 7.如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长 为2的等腰直角三角形,则该几何体的体积是A 8.已知)(x f 是R 上的偶函数,2)0(=f ,若)(x f 的图象向右平移一个单位后,则得到一个奇函数的图象,那么)9()7()5()3()1(f f f f f ++++的值为A .1B .0C .-1D a 21-a a -1a 2第7题二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.某程序框图如图所示,该程序运行后输出的k 的值是 .10. 某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表。
广东省海珠区2013届高三上学期综合测试(二)数学理试题 word版

海珠区2012学年高三综合测试(二)数学(理科)本试卷共6页,21小题,满分150分。
考试用时120分钟。
注意事项:1答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3. 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁。
考试结束后,将答题卡一并交回。
参考公式:如果事件A、B互斥,那么若在每次试验中,事件A发生的概率为P,则在n次独立重复试验中,事件WA恰好发生k次的概率为.一、选择题:本大题共 8 小题,每小题 5 分,满分 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. i是虚数单位,复数对应的点位于A第一象限B第二象限 C.第二象限 D.第四象限2. 若集合.,集合,则“a = 3”是“.的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3. 已知函数,若,,则A. a < b < cB. c < a < bC. b < c < aD. a < c <b4. 已知函数的一部分图象如图1所示,则A. B.C. D.5. 已知正二棱柱(侧棱与底面垂直,底面是正二角形)的高与底面边长均为1,其直观图和正(主)视图如图2所示,则它的左(侧)视图的面积是A. B. 1 C. D.6. 已知双曲线的一个焦点与抛物线y2=12x的焦点重合,且双曲线的离心率等于,则该双曲线的标准方程为A. B. C. D.7. 已知各项不为O的等差数列满足:,数列是各项均为正值的等比数列,且b7=a7,则等于A. B. C. D.8. 用表示a,b两个数中的最大数,设,那么山函数的图象、X轴、直线和直线X = 2所围成的封闭图形的面积是A. B. C. D.二、填空题:本大题共 7 小题,考生作答 6 小题,每小题 5 分,满分 30 分.(一)必做题(9~13 题9. 的二项展丌式的常数项为_______.(用数字作答)10. 公路部门对通过某路段的300辆汽车的车速进行检测,将所得数据按[40,50), [50,60), [60,70), [70,80]分组,绘制成如图3所示的频率分布直方图.图示中a的值等于_____;这300辆汽车中车速低于的汽车有_____辆.11. 已知实数X,满足约束条件,则目标函数Z = X -y的最小值等于______.12. 某程序框图如图4所示,该程序运行后输出的值依次为_____.13. 给出下列四个命题:①命题,则,②当时,不等式的解集为非空;③当X>1时,有④设有五个函数.,其中既是偶函数又在上是增函数的有2个.其中真命题的序号是_____.(二)选做题(14、15 题,考生只能从中选做一题)14. (坐标系与参数方程选做题)在极坐标系中,点A的坐标为曲线c的方程为,则0A (O为极点)所在直线被曲线C所截弦的长度为____.15. (几何证明选讲选做题D如图5所示,过圆C外一点尸做一条直线与圆C交于A,B两点,AB = 2AP,PT与圆c相切于T点.已知圆C的半径为2,,则PT=_______.三、解答题:本大题共 6 小题,满分 80 分.解答须写出文字说明、证明过程和演算步骤.16. (本小题满分12分)已知函数(1) 求f(X)的最小正周期;(2) 求函数在区间上的最大值和最小值,并求此时X的值.17. (本小题满分12分)现有3个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.约定:每个人将质地均匀的硬币抛掷2次决定自己去参加哪个游戏.2次抛出的硬币朝上的面均为正面的人去参加甲游戏,2次抛出的硬币朝上的面为其它情形的去参加乙游戏.(1) 求这3个人中恰有2人去参加甲游戏的概率;(2) 求这3个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;18. 用;分别表示这3个人中去参加甲、乙游戏的人数,记,求随机变量的分布列和数学期望.(本小题满分14分)如图6,四棱锥P-ABCD中,PA丄底面ABCD,M,N分别是PB,PC的中点,PA = AB,在四边形ABCD中,AB丄 AD,AB丄 BC .(1)求证:MN//平面PAD,(2) 求证:平面MN丄平面PBC;(3)若AD- AB = 1,,,求二面角P-AB-N的大小.19. (本小题满分14分)设椭圆的左、右顶点分别为A、B,点尸在椭圆上且异于A、B两点,O 为坐标原点.(1) 若直线AP与BP的斜率之积为,求椭圆的离心率;(2) 对于由(1)得到的椭圆C,过点P的直线l交X轴于点Q(-1,0),交x轴于点M,若,求直线l的斜率.20. (本小题满分14分)已知点?在函数_的图象上.(1) 若数列是等差数列,求证数列是等比数列;(2) 若数列的前《项和是,过点的直线与两坐标轴所围二角形面积为C n,求最小的实数t使:恒成立;(3) 若数列为山(2)中{a」得到的数列,在与之间插入个3,得一新数列,问是杏存在这样的正整数m,使数列的前m项的和,如果存在,求出m的值,如果不存在,请说明理由21. (本小题满分14分)已知函数的最小值为0,其中a>0.(1)求a的值;(2)若对任意的,有成立,求实数k的最小值;(3)证明海珠区2012学年高三综合测试(二)理科数学参考答案与评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分。
(整理)海珠区届高三上学期综合测试二理综

海珠区2013届高三上学期综合测试(二)理科综合本试卷分第一部分(选择题)和第二部分(非选择题)两部分;第一部分 1-5 页,第二部分6-12 页,满分300 分。
考试时间150 分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的学校、班级、姓名、考场试室号、座位号填写在答题卡上;填写准考证号,并用2B 铅笔把对应号码的标号涂黑。
2.选择题每小题选出答案后,用 2B 铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束,将答题卡交回。
第一部分选择题(共118 分)一、单项选择题:本大题共16 小题,每小题4分,共64 分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4分,选错或不答的得0分。
1.下列有关猪的肝细胞和胰岛细胞的叙述中,正确的是A.各种细胞器的种类和数目相同B.与呼吸酶相关的基因能得到表达C.信使R NA 的种类和数目相同D.肝细胞中缺少胰岛素基因2.在下图所示的细胞类型转换过程中,有关叙述错.误.的是全能干细胞骨髓干细胞未成熟红细胞红细胞A.这一过程称做细胞分化B.这一过程伴随着细胞分裂C.这一过程细胞的全能性降低D.这一过程在生物体内是可逆转的3.右图表示某二倍体植物一对同源染色体上的部分基因。
下列叙述正确的是A.图示同源染色体上共存在4对等位基因B.花顶生是隐性性状,该植物不.能表现出此性状C.基因D (d)与E(e)的遗传不.遵循基因自由组合定律D.用秋水仙素处理萌发的种子,可得到三倍体幼苗长茎A短茎花顶生b b 花顶生红花D d 白花皱粒e E 圆粒A 4.我国棉花产量位居世界首位。
广东省海珠区2013届高三上学期综合测试(二)数学文(word版)

海珠区2012学年高三综合测试(二)数学(文科)本试卷共6页,21小题,满分150分。
考试用时120分钟。
注意事项1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3. 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁。
考试结束后,将答题卡一并交回。
参考公式:锥体体积公式,其中s为锥体的底面积,h为锥体的高.如果事件A、B互斥,那么.线性回归方程中系数计算公式其中表示样本平均值.一、选择题:本大题共 10 小题,每小题 5 分,满分 50 分.在每小题给出的四个选项中,只有一项是符合题目要求的1. i是虚数单位,复数对应的点位于A第一象限 B第二象限 c.第二象限 D.第四象限2. 若集合集合5 = {6,9},则“ a = 3,,是“”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3. 已知函数,若,则A. a < b < cB. c < a <bC. b < c < aD. a < c <b4. 已知实数x,y满足不约束条件,则目标函数Z=x-y 的最大值等于A. 7B. 4C. 3D. 55. 在中,若,则.的形状是A.为钝角的二角形 B.为直角的直角二角形C.锐角二角形D.为直角的直角二角形6. 已知函数的一部分图象如图1所示,则A. B.C. D.7. 已知正二棱柱(侧棱与底面垂直,底面是正二角形)的高与底面边长均为1,其直观图和正(主)视图如图2,则它的左(侧)视图的面积是A. B. 1C. D.8. 已知双曲线的一个焦点与抛物线的焦点S合,且双曲线的离心率等于,则该双曲线的标准方程为A. B. C. D.9. 已知各项不为O的等差数列满足:,数列.是各项均为正值的等比数列,且,则等于A. B.C. D.10. 给出下列四个命题:①命题,则;②当x>l时,有③函数.的零点个数有3个;④设有五个函数,其中既是偶函数又在上是增函数的有2个.其中真命题的个数是A l个 B.2个 C. 3个Z). 4个二、填空题:本大题共 5 小题,考生作答 4 小题,每小题 5 分,满分 20 分.(一)必做题(11~13 题)11. 公路部门对通过某路段的300辆汽车的车速进行检测,将所得数据按[40,50),[50,60),[60,70),[70,80]分组,绘制成如图3所示的频率分布直方图.图示中a的值等于_______;这300辆汽车中车速低于的汽车有_______辆.12. 某程序框图如图4所示,该程序运行后输出M, N的值依次为_______.713. 对大于或等于2的自然数m的n次幂有如下分解方式:根据上述分解规律,则的分解中最小的数为73,则m的值为_______.(二)选做题(14、15 题,考生只能从中选做一题14. (坐标系与参数方程选做题)在极坐标系中,点J的坐标为,曲线c的方程为,则04 (O为极点)所在直线被曲线C所截弦的长度为______.15. (几何证明选讲选做题)如图5所示,过圆c外一点P做一条直线与圆C交于A,B两点,AB-2AP,PT与圆C相切于T点.已知圆c的半径为2,,则PT=_____.三、解答题:本大题共 6 小题,满分 80 分.解答须写出文字说明、证明过程和演算步骤.16. (本小题满分12分)已知函数(1)求f(X)的最小正周期;(2)求函数f(X)在区间上的最大值和最小值,并求此时X的值.17. (本小题满分12分)一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了 5次试验,收集数据如下:(1) 在5次试验中任取2次,记加工时间分别为a,b求事件a,b均小于80分钟”的概率;(2) 请根据第二次,第二次,第四次试验的数据,求出y关于X的线性回归方程(3)根据(2)得到的线性回归方程预测加工70个零件所需要的时间.18. (本小题满分14分)如图6,在四棱锥P-ABC D中,PA丄平面AB CD,底面AB CD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB= 2,:(1) 求证:OM//平面PAB;(2) 平面PBD丄平面PA C;(3) 当四棱锥P-ABCD的体积等于.时,求PB的长.19. (本小题满分14分)设椭圆的左、右顶点分别为A、B,点P在椭圆上且异于A、B两点,O为坐标原点.(1) 若直线AP与BP的斜率之积为,求椭圆的离心率;(2)对于由(1)得到的椭圆C,过点p的直线l交X轴于点-1,0),交y轴于点M,若,求直线l 的斜率.20. (本小题满分14分)已知函数丨(1)若a= 1,求曲线_在点处的切线方程;(2) 若f(X)在的最小值为,求a的值;(3) 若在上恒成立,求a的取值范围.21. (本小题满分14分)已知点」都在函数的图象上.(1) 若数列是等差数列,求证数列是等比数列;(2) 若数列的前《项和是,过点的直线与两坐标轴所围二角 形面积为,求最小的实数t 使恒成立; (3) 若数列为山(2)中得到的数列,在与之间插入个3, 得一新数列,问是杏存在这样的正整数w ,使数列的前m 项的和,如果存在,求出m 的值,如果不存在,请说明理由海珠区2012学年高三综合测试(二)文科数学参考答案与评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查共10小题,每小题5分,满分50分.二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题. 11. 025.0,180 12. 34, 55 13. 9; 14. 22 15. 3 (第11题第一空2分,第二空3分)三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查三角两角和的正余弦公式,三角特殊值的运算,函数()()()()()ϕωϕω+=+=x A x f x A x f cos sin 或的周期,最值等知识,考查化归、转化、换元的数学思想方法,以及运算求解能力)解:(1)()cos 2cos 22sin cos 66f x x x x x ππ⎛⎫⎛⎫=++-+ ⎪ ⎪⎝⎭⎝⎭ 6sin2sin 6cos2cos ππx x -=+6sin2sin 6cos2cos ππx x +x x cos sin 2+…………2分x 2cos 232⨯=x 2sin + x 2cos 3=x 2sin + …………3分⎪⎪⎭⎫ ⎝⎛+=x x 2sin 212cos 232 …………4分 ⎪⎭⎫⎝⎛+=x x 2sin 3cos 2cos 3sin 2ππ …………5分⎪⎭⎫ ⎝⎛+=32sin 2πx …………6分∴()f x 的最小正周期为ππ==22T …………7分 (2)由(1)知()x f ⎪⎭⎫⎝⎛+=32sin 2πx , 由33ππ≤≤-x ,得πππ≤+≤-323x , …………8分∴当232ππ=+x ,即12π=x 时, ()f x 取得最大值2; …………10分 当332ππ-=+x ,即3π-=x 时, ()f x 取得最小值3-.…………12分17.( 本小题满分12分)(本小题主要考查考查互斥事件、古典概型、线性回归,样本估计总体等知识,考查或然与必然,样本估计总体的统计思想方法,以及数据观察能力、抽象思维能力和应用意识) 解:(1)b a ,构成的基本事件()b a ,有:()()()()()()()89,67,80,67,75,67,89,62,80,62,75,62,67.62,(),80,75()()89,80,89,75共有10个. …………2分其中“b a ,均小于80分钟”的有()()()75,67,75,62,67.62共3个. …………3分∴事件 “b a ,均小于80分钟”的概率为103. …………4分 (2)()3040302031=++=x , …………5分M OP D C BA ()1677580743y =++= …………6分 ()()()()()()()()()222304030303020748030407475303074673020-+-+--⨯-+-⨯-+-⨯-=∧b2013=. …………8分 …………9分∴y 关于x 的线性回归方程∧y 1354.520x =+ …………10分(3)由(2)知y 关于x 的线性回归方程为∧y 1354.520x =+, 当70=x 时,1005.54702013=+⨯=y . …………11分 ∴预测加工70个零件需要100分钟的时间. …………12分18.(本小题满分14分)(本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力) 解:(1) 在PBD ∆中,O 、M 分别是BD 、PD 的中点, OM ∴是PBD ∆的中位线,PB OM //∴, …………1分 ⊄OM 平面PBD ,⊂PB 平面PBD ,……3分 //OM ∴平面PAB . …………4分 (2) 底面ABCD 是菱形,AC BD ⊥∴, ………5分PA ⊥平面ABCD ,⊂BD 平面ABCDPA BD ⊥∴. …………6分 ⊂AC 平面PAC ,⊂PA 平面PAC ,⋂AC A PA =,…………7分⊥∴BD 平面PAC , …………8分⊂BD 平面PBD , …………9分∴平面PBD ⊥平面PAC . …………10分(3) 底面ABCD 是菱形,,60,20=∠=BAD AB∴菱形ABCD的面积为32232260sin 2120=⨯⨯=⨯⨯⨯⨯=AD AB S ABCD 菱形,…………11分 四棱锥ABCD P -的高为PA ,∴33231=⨯⨯PA ,得23=PA …………12分PA ⊥平面ABCD ,⊂AB 平面ABCD ,AB PA ⊥∴. …………13分在PAB Rt ∆中,252232222=+⎪⎭⎫ ⎝⎛=+=AB PA PB . …………14分19.(本小题14分)(本小题主要考查直线斜率、椭圆的方程、离心率、向量的运算等知识,考查数形结合、化归与转化、方程的思想方法,考查综合运用能力以及运算求解能力)解:(1) 由已知()()0,,0,a B a A -,设()()a x y x P ±≠000,. …………1分 则直线AP 的斜率ax y k AP +=00,直线BP 的斜率ax y k AP -=00.由1220220=+y ax ,得()2202202a x a y -=. …………2分∴⨯AP k APk a x y +=00()()2202222220200022ax a a x a a x y a x y -=---=-=-⨯ …………3分 2122-=-∴a,得42=a , …………4分 ∴214242=-=e . …………5分∴椭圆的离心率22=e . …………6分 (2) 由题意知直线l 的斜率存在. …………7分 设直线l 的斜率为k , 直线l 的方程为()1+=x k y …………8分 则有()k M ,0,设()()a x y x P ±≠000,,由于Q M P ,,= 根据题意,得()()0000,12,y x k y x +±=- …………9分解得⎩⎨⎧-=-=k y x 002或⎪⎪⎩⎪⎪⎨⎧=-=33200k y x …………11分又点P 在椭圆上,又由(1)知椭圆C 的方程为12422=+y x 所以()()124222=-+-k …………①或12343222=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-k …………② 由①解得02=k ,即0=k ,此时点P 与椭圆左端点A 重合, 0=∴k 舍去; …………12分由②解得162=k ,即4±=k …………13分∴直线直线l 的斜率4±=k . …………14分20. (本小题满分14分)(本小题主要考查导数、不等式、函数的单调性、最值等知识,考查化归与转化、分类与讨论的数学思想方法,以及数学探究能力、综合运用能力和运算求解能力) 解:(1)当1=a 时, (),1ln xx x f -= ()2'11xx x f +=. ……………… 1分 ()1.111ln 1-=-=f()2111112'=+=f∴曲线()x f y =在点()1,1-处的切线方程为()121-=+x y ,即32-=x y . ………3分(2) ()2'xa x x f+=. ……………… 4分①若1-≥a ,则0≥+a x ,即()0'≥x f在[]e ,1上恒成立,此时()x f 在[]e ,1上为增函数,……………… 5分()()231min =-==∴a f x f , 23-=∴a (舍去); ……………… 6分②若e a -≤,则0≤+a x ,即()0'≤x f在[]e ,1上恒成立,此时()x f 在[]e ,1上为减函数,……………… 7分()()231min =-==∴e a e f x f ,2e a -=∴(舍去); ……………… 8分 ③若1-<<-a e ,令()0'=x f得a x -=, 当e x a <<-时,()0'>x f,∴()x f 在()e a ,-上为增函数, 当a x -<<1时,()0'<x f ,∴()x f 在()a -,1上为减函数, ……………… 9分()()()231ln min =+-=-=∴a a f x f , e a -=∴.综上所述,e a -=. ……………… 10分(3)(),ln ,22x x a x x x f <-∴< 又.ln ,03x x x a x ->∴> ……………… 11分 令(),ln 3x x x x g -=则()(),3ln 12'x x x g x h -+==()x x x x x h 2'6161--=-=. ……… 12分 当()+∞∈,1x 时,()0'<x h ,()x h ∴在()+∞,1上是减函数.()()021<-=<∴h x h ,即()0'<x g ,()x g ∴在()+∞,1上也是减函数.()()11-=<∴g x g , ……………… 13分 ∴当1-≥a 时,()2x x f < 在()+∞,1上恒成立. ……………… 14分21.(本小题满分14分)(本小题主要考查等差、等比数列的定义、通项、求和、对数的运算、直线方程与不等式等知识,考查化归、转化、方程的数学思想方法,以及抽象概括能力、运算求解能力、创新能力和综合应用能力)解:(1)证明:数列{}n b 是等差数列,设公差为d ,则1n n b b d +-=对*n N ∈恒成立, ……………… 1分 依题意12log n n b a =,1()2n bn a =, ……………… 2分 所以1111()()22n n b b d n n a a +-+==是定值, ……………… 3分 从而数列{}n a 是等比数列. ……………… 4分(2)解:当1n =时,112a =,当2n ≥时,11()2n n n n a S S -=-=,1n =也适合此式, 即数列{}n a 的通项公式是1()2n n a =. ……………… 5分 由12log n n b a =, 数列{}n b 的通项公式是n b n =, ……………… 6分 所以1(,)2n n P n ,111(,1)2n n P n +++. 过这两点的直线方程是:11211(1)22n n nx y n n n +--=+--, 可得与坐标轴的交点是12(,0)2n n n A ++和(0,2)n B n +. ……………… 7分 221(2)22n n n n n c OA OB ++=⨯⨯=,……………… 8分 由于22221233(2)(3)2(2)(3)222n n n n n n n n n c c +++++++-+-=-=232102n n n ++-=>……………9分 即数列{}n c 的各项依次单调递减,所以198t c ≥=. ……………… 10分 (3)数列{}n d 中,k b (含k b 项)前的所有项的和是121(12)(333)k k -+++++++()13322k k k +-=+ ……… 11分 估算知,当7k =时,其和是73328112020082-+=<, ……………… 12分 当8k =时,其和是83336331520082-+=>, 又因为200811208882-==⨯,是3的倍数,故存在这样的m ,使得2008m S =, ……………… 13分 此时257(1333)296667m =++++++=. ……………… 14分。
广东省海珠区2013届高三上学期综合测试(二)理综(扫描版)

2 012学年高三综合测试(二)试题答案理科综合一、单项选择题:本大题包括16小题,每小题给出的四个选项中,只有一个选项最符合题目要求, 每题4分,共64分。
二、双项选择题:本大题包括9小题,每小题给出的四个选项中,只有两个选项符合题目要求, 全选对得6分,只选一个且正确得3分,错选、不选得0分,共54分。
三、非选择题:本大题包括11小题,共182分。
26.(16分,每空2分)(1)Si4+ 不同种类的载体的数量根细胞进行无氧呼吸,积累酒精所致(2)①光照强度和CO2浓度②a点的夜温过低导致植物夜间新陈代谢过弱,不利于物质合成、细胞分裂等生理活动的进行③不认同(1分),因为没有在其他日温和夜温条件下对番茄植株的生长速率进行实验(3)翻译愈伤组织27.(16分,每空2分)(1)次生(2)60偏大(3)逐级递减3%(4)生长、发育和繁殖热能(5)生物的种间关系28.(16分,除特别说明,每空2分)(1)胞吞(1分)构成细胞膜的重要成分(1分)(2)转录酶的合成来控制代谢过程(3)反馈(4)①常染色体显性遗传1/6 ②限制性核酸内切患29.(16分,除特别说明,每空2分)(1)UV-B辐射剂量0 对照(2)每个组设置多个平行实验组(或进行重复实验)(1分),并算出平均值(1分)(3)3(4)溶解度(5)中(1分)观察小球藻细胞染色体数目记录表:(3分)30.(共15分)(1)(3分)(2) ABCD (4分)(对一个给一分共4分)(3)(4分) (4)(4分)31.(16分)(1) 0.003mol/L·min (3分,单位错扣1分)(2)CD (4分,对一个给2分,全对4分,错一个扣2分,扣完为止,不出现负分) (3)(5分) CO(g) + H2O(g) CO2(g) + H2(g)c起始(mol·L -1)0.1 0.1 0 0c转化(mol·L -1)0.03 0.03 0.03 0.03c平衡(mol·L -1)0.07 0.07 0.03 0.03(4)该反应未达平衡状态(1分);由于该状态下生成物浓度幂之积与反成物浓度幂之积的比值不等于K(3分)。
导数与积分(2) Word版(含答案)

广东省2013届高三最新理科试题精选(37套含13大市区的二模)分类汇编17:导数与积分(2)一、选择题1 .(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))由曲线sin ,cos y x y x ==与直线0,2x x π==所围成的平面图形(图1中的阴影部分)的面积是( )A .1B .4πC .3D .2【答案】D2 .(广东省汕头市2013年普通高中高三教学质量测试试题(二)理科数学试卷)如图所示,图中曲线方程为21y x =-,用定积分表达围成封闭图形(阴影部分)的面积是【答案】C3 .(广东省茂名市2013届高三4月第二次高考模拟数学理试题(WORD 版))曲线f(x)=xlnx在点x=1处的切线方程为( )A .y=2x+2B .y=2x-2C .y=x-1C .y=x+1【答案】C4 .(广东省江门佛山两市2013届高三4月教学质量检测(佛山二模)数学理试题)将边长为2的等边三角形PAB 沿x 轴滚动,某时刻P 与坐标原点重合(如图),设顶点(,)P x y 的轨迹方程是()y f x =,关于函数()y f x =的有下列说法:①()f x 的值域为[0,2];②()f x 是周期函数;③( 1.9)()(2013)f f f π-<<;④69()2f x dx π=⎰.其中正确的说法个数为: ( )A .0B .C .2D .3【答案】C5 .(广东省广州市2013届高三4月综合测试(二)数学理试题(WORD 版))已知函数()yf x =的图象如图1所示,则其导函数()y f x '=的图象可能是【答案】A二、填空题6 .(广东省茂名市2013届高三第一次模拟考试数学(理)试题)计算________.【答案】2e ;7 .(广东省江门市2013年高考模拟考试(即一模)数学(理)试题 )在平面直角坐标系Oxy中,直线a y =(0>a )与抛物线2x y =所围成的封闭图形的面积为328,则=a _______. 【答案】28 .(广东省海珠区2013届高三上学期综合测试一数学(理)试题)不等式211x -<的解集为(),a b ,计算定积分)2b ax dx -=⎰_______.【答案】139.(广东省广州市2013届高三调研测试数学(理)试题)若直线2y x m =+是曲线ln y x x=图1A .B .C .D .O x P A 第8题图的切线,则实数m 的值为_________.【答案】e -分析:设切点为000(,ln )x x x ,由1(ln )ln ln 1y x x x x x x''==+=+ 得0ln 1k x =+, 故切线方程为0000ln (ln 1)()y x x x x x -=+-,整理得00(ln 1)y x x x =+-, 与2y x m =+比较得00ln 12x x m+=⎧⎨-=⎩,解得0e x =,故e m =-10.(广东省广州市2013届高三3月毕业班综合测试试题(一)数学(理)试题)10x cos ⎰d x =______________.【答案】1sin11.(广东省肇庆市2013届高三4月第二次模拟数学(理)试题)20(3sin )x x dx π+=⎰________________.【答案】2318π+解析:22220033(3sin )(cos )|128x x dx x x πππ+=-=+⎰.12.(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD 版))曲线y= x 3-x + 3在点(1,3)处的切线方程为_______【答案】21x y -+13.(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))若直线y kx =与曲线ln y x =相切,则k =__________________.【答案】1e14.(广东省潮州市2013届高三第二次模拟考试数学(理)试题)计算= ________.【答案】2e .三、解答题15.(广东省揭阳市2013届高三3月第一次高考模拟数学(理)试题(含解析))已知函数()ln f x x =,2()()g x f x ax bx =++,函数()g x 的图象在点(1,(1))g 处的切线平行于x 轴.(1)确定a 与b 的关系;(2)试讨论函数()g x 的单调性; (3)证明:对任意*n N ∈,都有()211ln 1ni i n i=-+>∑成立.【答案】解:(1)依题意得2()ln g x x axbx =++,则1'()2g x ax b x=++ 由函数()g x 的图象在点(1,(1))g 处的切线平行于x 轴得:'(1)120g a b =++= ∴21b a =--(2)由(1)得22(21)1'()ax a x g x x -++=(21)(1)ax x x--=∵函数()g x 的定义域为(0,)+∞∴当0a ≤时,210ax -<在(0,)+∞上恒成立, 由'()0g x >得01x <<,由'()0g x <得1x >, 即函数()g x 在(0,1)上单调递增,在(1,)+∞单调递减; 当0a >时,令'()0g x =得1x =或12x a=, 若112a <,即12a >时,由'()0g x >得1x >或102x a <<,由'()0g x <得112x a<<,即函数()g x 在1(0,)2a ,(1,)+∞上单调递增,在1(,1)2a单调递减;若112a >,即102a <<时,由'()0g x >得12x a>或01x <<,由'()0g x <得112x a<<, 即函数()g x 在(0,1),1(,)2a +∞上单调递增,在1(1,)2a单调递减;若112a =,即12a =时,在(0,)+∞上恒有'()0g x ≥, 即函数()g x 在(0,)+∞上单调递增,综上得:当0a ≤时,函数()g x 在(0,1)上单调递增,在(1,)+∞单调递减; 当102a <<时,函数()g x 在(0,1)单调递增,在1(1,)2a 单调递减;在1(,)2a+∞上单调递增;当12a =时,函数()g x 在(0,)+∞上单调递增, 当12a >时,函数()g x 在1(0,)2a 上单调递增,在1(,1)2a单调递减;在(1,)+∞上单调递增.(3)证法一:由(2)知当1a =时,函数2()ln 3g x x x x =+-在(1,)+∞单调递增,2ln 3(1)2x x x g ∴+-≥=-,即2ln 32(1)(2)x x x x x ≥-+-=---,令*11,x n N n =+∈,则2111ln(1)n n n+>-, 2222111111111111ln(1)ln(1)ln(1)...ln(1)...123112233n n n∴++++++++>-+-+-++-2222111111111111ln[(1)(1)(1)...(1)]...123112233n n n∴++++++>-+-+-++-即()211ln 1ni i n i=-+>∑ 【证法二:构造数列{}n a ,使其前n 项和ln(1)n T n =+, 则当2n ≥时,111ln()ln(1)n n n n a T T n n-+=-==+, 显然1ln 2a =也满足该式, 故只需证221111ln(1)n n n n n-+>=- 令1x n=,即证2ln(1)0x x x +-+>,记2()ln(1)h x x x x =+-+,0x > 则11(21)'()12120111x x h x x x x x x +=-+=-+=>+++,()h x 在(0,)+∞上单调递增,故()(0)0h x h >=,∴221111ln(1)n n n n n -+>=-成立,2222111111111111ln(1)ln(1)ln(1)...ln(1)...123112233n n n∴++++++++>-+-+-++-即()211ln 1ni i n i =-+>∑ 】 【证法三:令211()ln(1)i ni i n n i ϕ==-=+-∑,则2(1)()ln(2)ln(1)(1)n n n n n n ϕϕ+-=+--++2111ln(1)11(1)n n n =+-++++ 令11,1x n =++则(1,2]x ∈,*11,,1x n N n =-∈+ 记22()ln (1)(1)ln 32h x x x x x x x =--+-=+-+∵1(21)(1)()230x x h x x x x--'=+-=>∴函数()h x 在(1,2]单调递增, 又(1)0,(1,2],()0,h x h x =∴∈>当时即(1)()0n n ϕϕ+->, ∴数列()n ϕ单调递增,又(1)ln 20ϕ=>,∴()211ln 1ni i n i =-+>∑ 】 16.(广东省江门市2013年高考模拟考试(即一模)数学(理)试题 )已知x a a x a x x f ln )()12(21)(22+++-=(0>x ,a 是常数),若对曲线)(x f y =上任意一点) , (00y x P 处的切线)(x g y =,)()(x g x f ≥恒成立,求a 的取值范围.江门市2013年高考模拟考【答案】解:依题意,xaa a x x f +++-=2/)12()()(00x f y =,曲线)(x f y =在点) , (00y x P 处的切线为))((00/0x x x f y y -=- ,即))((00/0x x x f y y -+=,所以))(()(00/0x x x f y x g -+= 直接计算得)1)(ln ()12(21)(002200-++++--=x x x a a x a x x x x g , 直接计算得)()(x g x f ≥等价于0)1)(ln ()(2100220≥+-++-x xx x a a x x 记)1)(ln ()(21)(00220+-++-=x xx x a a x x x h ,则 )1)(()11)(()()(020020/xx aa x x x x a a x x x h +--=-++-=若02≤+a a ,则由0)(/=x h ,得0x x = ,且当00x x <<时,0)(/<x h ,当0x x >时,0)(/>x h ,所以)(x h 在0x x =处取得极小值,从而也是最小值,即0)()(0=≥x h x h ,从而)()(x g x f ≥恒成立 .若02>+a a ,取a a x +=20,则0)1)(()(020/≥+--=xx aa x x x h 且当01x x ≠时0)(/>x h ,)(x h 单调递增 ,所以当00x x <<时,0)()(0=<x h x h ,与)()(x g x f ≥恒成立矛盾,所以02≤+a a ,从而a 的取值范围为01≤≤-a17.(广东省海珠区2013届高三上学期综合测试一数学(理)试题)(本小题满分14分)已知函数()()2ln f x x a x x =+--在0x =处取得极值.(1)求实数a 的值;(2)若关于x 的方程()52f x x b =-+在区间[]0,2上恰有两个不同的实数根,求实数b 的取值范围;(3)证明:对任意的正整数n ,不等式()23412ln 149n n n+++++>+ 都成立. 【答案】(本小题主要考查导数、函数的单调性、不等式、最值、方程的根等知识,考查化归转化、分类讨论、数形结和的数学思想方法,以及抽象概括能力、运算求解能力、创新能力和综合应用能力) 解:(1)()'121,f x x x a=--+ 0x = 时,()f x 取得极值, ()'00,f ∴=故12010,0a-⨯-=+解得 1.a =经检验1a =符合题意 (2)由1a =知()()2ln 1,f x x x x =+--由()52f x x b =-+,得()23ln 10,2x x x b +-+-= 令()()23ln 1,2x x x x b ϕ=+-+-则()52f x x b =-+在区间[]0,2上恰有两个不同的实数根等价于()0x ϕ=在区间[]0,2上恰有两个不同的实数根()()()()'451132,1221x x x x x x ϕ-+-=-+=++当[]0,1x ∈时,()'0x ϕ>,于是()x ϕ在[)0,1上单调递增; 当(]1,2x ∈时,()'0x ϕ<,于是()x ϕ在(]1,2上单调递减依题意有()()()()()0031ln 111022ln 12430b b b ϕϕϕ=-≤⎧⎪⎪=+-+->⎨⎪⎪=+-+-≤⎩,解得,1ln 31ln 2.2b -≤<+(3) ()()2ln 1f x x x x =+--的定义域为{}1x x >-,由(1)知()()()'231x x f x x -+=+,令()'0fx =得,0x =或32x =-(舍去), ∴当10x -<<时, ()'0f x >,()f x 单调递增;当0x >时, ()'0fx <,()f x 单调递减.()0f ∴为()f x 在()1,-+∞上的最大值. ()()0f x f ∴≤,故()2ln 10x x x +--≤(当且仅当0x =时,等号成立)对任意正整数n ,取10x n=> 得,2111ln 1,n n n⎛⎫+<+⎪⎝⎭ 211ln n n n n++⎛⎫∴< ⎪⎝⎭.故()23413412ln 2ln ln ln ln 14923n n n n n++++++>++++=+ . 18.(广东省广州市2013届高三3月毕业班综合测试试题(一)数学(理)试题)已知二次函数()21fx x a x m =+++,关于x的不等式()()2211f x m x m <-+-的解集为()1m m ,+,其中m 为非零常数.设()()1f xg x x =-.(1)求a 的值;(2)k k (∈R )如何取值时,函数()x ϕ()g x =-()1k x ln -存在极值点,并求出极值点;(3)若1m =,且x 0>,求证:()()1122nn ng x g x n (⎡⎤+-+≥-∈⎣⎦N *). 【答案】(本小题主要考查二次函数、一元二次不等式、一元二次方程、函数应用、均值不等式等基础知识,考查数形结合、函数与方程、分类与整合、化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力、创新意识) (1)解:∵关于x 的不等式()()2211fx m x m <-+-的解集为()1m m ,+,即不等式()22120x a m x m m ++-++<的解集为()1m m ,+,∴()2212x a m x m m ++-++=()()1x mx m ---.∴()2212x a m x m m ++-++=()()2211x m x m m -+++.∴()1221a m m +-=-+. ∴2a =-(2)解法1:由(1)得()()1f xg x x =-()221111x x m m x x x -++==-+--.∴()()xg x ϕ=-()1k x ln -()11mx x =-+-()1k x ln --的定义域为()1,+∞.∴()1x ϕ'=-()211mkx x ---()()22211x k x k m x -++-+=- 方程()2210x k x k m -++-+=(*)的判别式()()222414Δk k m k m =+--+=+①当0m >时,0Δ>,方程(*)的两个实根为11x ,=<21x ,=>则()21x x ,∈时,()0x ϕ'<;()2x x ,∈+∞时,()0x ϕ'>. ∴函数()x ϕ在()21x ,上单调递减,在()2x ,+∞上单调递增. ∴函数()x ϕ有极小值点2x②当0m <时,由0Δ>,得k <-k >若k <-,则11x ,=<21x ,=<故x ∈()1,+∞时,()0x ϕ'>∴函数()x ϕ在()1,+∞上单调递增. ∴函数()x ϕ没有极值点若k >时,1212k x ,+-=>2212k x ,++=>则()11x x ,∈时,()0x ϕ'>;()12x x x ,∈时,()0x ϕ'<;()2x x ,∈+∞时,()0x ϕ'>.∴函数()x ϕ在()11x ,上单调递增,在()12x x ,上单调递减,在()2x ,+∞上单调递增. ∴函数()x ϕ有极小值点2x ,有极大值点1x综上所述, 当0m >时,k 取任意实数, 函数()x ϕ有极小值点2x ; 当0m <时,k >函数()x ϕ有极小值点2x ,有极大值点1x (其中122k x +-=, 222k x ++=解法2:由(1)得()()1f xg x x =-()221111x x m m x x x -++==-+--.∴()()xg x ϕ=-()1k x ln -()11mx x =-+-()1k x ln --的定义域为()1,+∞.∴()1x ϕ'=-()211mkx x ---()()22211x k x k m x -++-+=- 若函数()()x g x ϕ=-()1k x ln -存在极值点等价于函数()x ϕ'有两个不等的零点,且至少有一个零点在()1,+∞上 令()x ϕ'()()22211x k x k m x -++-+=-0=,得()221x k x k m -++-+0=, (*)则()()2224140Δkk m k m =+--+=+>,(**)方程(*)的两个实根为1x =2x =设()h x=()221x k x k m -++-+,①若1211x x ,<>,则()10h m =-<,得0m >,此时,k 取任意实数, (**)成立.则()21x x ,∈时,()0x ϕ'<;()2x x ,∈+∞时,()0x ϕ'>. ∴函数()x ϕ在()21x ,上单调递减,在()2x ,+∞上单调递增. ∴函数()x ϕ有极小值点2x②若1211x x ,>>,则()10212h m k ,.⎧=->⎪⎨+>⎪⎩得00m k ,.⎧<⎨>⎩又由(**)解得k >k <-故k >则()11x x ,∈时,()0x ϕ'>;()12x x x ,∈时,()0x ϕ'<;()2x x ,∈+∞时,()0x ϕ'>.∴函数()x ϕ在()11x ,上单调递增,在()12x x ,上单调递减,在()2x ,+∞上单调递增. ∴函数()x ϕ有极小值点2x ,有极大值点1x综上所述, 当0m >时,k 取任何实数, 函数()x ϕ有极小值点2x ; 当0m <时,k >函数()x ϕ有极小值点2x ,有极大值点1x (其中122k x +-=, 222k x ++=(2)证法1:∵1m =, ∴()g x=()111x x -+-.∴()()1111nnn n n g x g x x x x x ⎛⎫⎛⎫⎡⎤+-+=+-+ ⎪ ⎪⎣⎦⎝⎭⎝⎭ 112212111111n n n n n n n n n n n n n x C x C x C x C x x x x x x ----⎛⎫=+⋅+⋅++⋅+-+ ⎪⎝⎭ 122412n n n n n n n C x C x C x ----=+++令T 122412n n n nn n n C xC x C x ----=+++ , 则T 122412n nn n n n n n C xC x C x -----=+++122412n n n n n n n C x C x C x ----=+++ .∵x 0>, ∴2T ()()()122244122n n n n n n n n n n C xx C x x C x x -------=++++++≥121n nn n C C C -⋅+⋅++⋅ ()1212n n n n C C C -=+++()012102n n n n n n n n n n C C C C C C C -=+++++--()222n =-∴22n T ≥-,即()()1122nn n g x g x ⎡⎤+-+≥-⎣⎦证法2:下面用数学归纳法证明不等式11nn n x x x x ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭22n ≥-.① 当1n =时,左边110x x x x ⎛⎫⎛⎫=+-+= ⎪ ⎪⎝⎭⎝⎭,右边1220=-=,不等式成立;② 假设当n k =k (∈N *)时,不等式成立,即11kk k x x x x ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭22k≥-,则 11111k k k x x x x +++⎛⎫⎛⎫+-+ ⎪⎪⎝⎭⎝⎭11111111kk k k k k k x x x x x x x x x x x x ++⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥=++-++++-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦111kk k x x x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=++-++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦111k k x x --⎛⎫+ ⎪⎝⎭()22k ≥⋅-+122k +=-也就是说,当1n k =+时,不等式也成立.由①②可得,对∀n ∈N *,()()1122nn n g x g x ⎡⎤+-+≥-⎣⎦都成立19.(广东省潮州市2013届高三上学期期末教学质量检测数学(理)试题)二次函数()f x 满足(0)(1)0f f ==,且最小值是14-.(1)求()f x 的解析式; (2)设常数1(0,)2t ∈,求直线l :2y t t =-与()f x 的图象以及y 轴所围成封闭图形的面积是()S t ;(3)已知0m ≥,0n ≥,求证:211()()24m n m n +++≥【答案】解:(1)由二次函数()f x 满足(0)(1)0f f ==.设()(1)(0)f x ax x a =-≠,则221()()24af x ax ax a x =-=--又()f x 的最小值是14-,故144a -=-.解得1a =.∴2()f x x x =-;(2)依题意,由22x x t t -=-,得x t =,或1x t =-.(1t - t) 由定积分的几何意义知3232222002()[()()]()|3232ttx x t t S t x x t t dx t x tx =---=--+=-+⎰(3)∵()f x 的最小值为14-,故14m -,14n -∴12m n +-≥-,故12m n ++≥∵1()02m n +,102m n ++, ∴11()()22m n m n +++=∴211()()24m n m n +++≥20.(2013年广东省佛山市普通高中高三教学质量检测(一)数学(理)试题)设()x g x e =,()[(1)]()f x g x a g x =λ+-λ-λ,其中,a λ是常数,且01λ<<.(1)求函数()f x 的极值;(2)证明:对任意正数a ,存在正数x ,使不等式11x e a x--<成立; (3)设12,λλ∈+R ,且121λλ+=,证明:对任意正数21,a a 都有:12121122a a a a λλ≤λ+λ.【答案】解析:(1)∵()[(1)]()f x g x a g x λλλλ'''=+--,由()0f x '>得,[(1)]()g x a g x λλ''+->,∴(1)x a x λλ+->,即(1)()0x a λ--<,解得x a <, 故当x a <时,()0f x '>;当x a >时,()0f x '<; ∴当x a =时,()f x 取极大值,但()f x 没有极小值(2)∵111x x e e x x x----=, 又当0x >时,令()1xh x e x =--,则()10xh x e '=->, 故()(0)0h x h >=,因此原不等式化为1x e x a x--<,即(1)10x e a x -+-<, 令()(1)1x g x e a x =-+-,则()(1)xg x e a '=-+, 由()0g x '=得:1xe a =+,解得ln(1)x a =+,当0ln(1)x a <<+时,()0g x '<;当ln(1)x a >+时,()0g x '>. 故当ln(1)x a =+时,()g x 取最小值[ln(1)](1)ln(1)g a a a a +=-++,令()ln(1),01a s a a a a =-+>+,则2211()0(1)1(1)a s a a a a '=-=-<+++. 故()(0)0s a s <=,即[ln(1)](1)ln(1)0g a a a a +=-++<.因此,存在正数ln(1)x a =+,使原不等式成立(3)对任意正数12,a a ,存在实数12,x x 使11x a e =,22x a e =, 则121122112212xx x x a a e ee λλλλλλ+=⋅=,12112212x x a a e e λλλλ+=+,原不等式12121122a a a a λλλλ≤+11221212x x x x e e e λλλλ+⇔≤+,11221122()()()g x x g x g x λλλλ⇔+≤+由(1)()(1)()f x g a λ≤-恒成立,故[(1)]()(1)()g x a g x g a λλλλ+-≤+-, 取1212,,,1x x a x λλλλ===-=, 即得11221122()()()g x x g x g x λλλλ+≤+, 即11221212x x x x e e e λλλλ+≤+,故所证不等式成立21.(广东省肇庆市2013届高三4月第二次模拟数学(理)试题)已知函数321,(1)()(1),(1)x x ax bx x f x c e x -⎧-++<⎪=⎨-≥⎪⎩在32,0==x x 处存在极值. (1)求实数b a ,的值;(2)函数)(x f y =的图像上存在两点B A ,使得AOB ∆是以坐标原点O 为直角顶点的直角三角形,且斜边AB 的中点在y 轴上,求实数c 的取值范围; (3)当e c =时,讨论关于x 的方程()f x kx =()k R ∈的实根的个数.【答案】解(1)当1x <时,2()32f x x ax b '=-++.因为函数f(x)在20,3x x ==处存在极值,所以(0)0,2()0,3f f '=⎧⎪⎨'=⎪⎩解得1,0a b ==. (2) 由(1)得321,(1),()(1),(1),x x x x f x c e x -⎧-+<⎪=⎨-≥⎪⎩根据条件知A,B 的横坐标互为相反数,不妨设32(,),(,()),(0)A t t t B t f t t -+>.若1t <,则32()f t t t =-+,由AOB ∠是直角得,0OA OB ⋅= ,即23232()()0t t t t t -++-+=,即4210t t -+=.此时无解;若1t ≥,则1()(1)t f t c e -=-. 由于AB 的中点在y 轴上,且AOB ∠是直角,所以B 点不可能在x 轴上,即1t ≠. 由0OA OB ⋅= ,即2321()(1)t t t t c e --++⋅-=0,即()11(1)1t c t e -=+-..因为函数()1(1)1t y t e -=+-在1t >上的值域是(0,)+∞,所以实数c 的取值范围是(0,)+∞.(3)由方程()f x kx =,知32,(1),(1)x x x x kx e e x ⎧-+<⎪=⎨-≥⎪⎩,可知0一定是方程的根,所以仅就0x ≠时进行研究:方程等价于2,(10),,(1).x x x x x k e e x x ⎧-+<≠⎪=⎨-≥⎪⎩且构造函数2,(10),(),(1),x x x x x g x e e x x⎧-+<≠⎪=⎨-≥⎪⎩且对于10x x <≠且部分,函数2()g x x x =-+的图像是开口向下的抛物线的一部分, 当12x =时取得最大值14,其值域是1(,0)(0,]4-∞ ; 对于1x ≥部分,函数()x e e g x x -=,由2(1)()0x e x e g x x-+'=>,知函数()g x 在()1,+∞上单调递增.所以,①当14k >或0k ≤时,方程()f x kx =有两个实根; ②当14k =时,方程()f x kx =有三个实根; ③当104k <<时,方程()f x kx =有四个实根.22.(广东省湛江市2013届高三4月高考测试(二)数学理试题(WORD 版))已知a <2,(1) 求f(x)的单调区间; (2)若存在x 1∈[e,e2],使得对任意的x 2∈[—2,0],f (x 1)<g(x 2)恒成立,求实数a 的取值范围.【答案】23.(广东省深圳市2013届高三第二次调研考试数学理试题(2013深圳二模))定义(,)|||ln |x x y e y y x y ρ=---,其中,x R y R +∈∈.(1)设0a >,函数()(,)f x x a ρ=,试判断()f x 的定义域内零点的个数; (2)设0a b <<,函数()(,)(,)F x x a x b ρρ=-,求()F x 的最小值; (3)记(2)中最小值为(,)T a b ,若{}n a 是各项均为正数的单调递增数列,证明:1111(,)()ln 2nii n i T a aa a ++=<-∑.【答案】24.(广东省韶关市2013届高三4月第二次调研测试数学理试题)设函数32()()f x ax a b x bx c =-+++其中0,,a b c R ≥∈(1)若1()3f '=0,求()f x 的单调区间;(2)设M 表示'(0)f 与'(1)f 两个数中的最大值,求证:当0≤x ≤1时,|()f x '|≤M .【答案】设函数32()()f x ax a b x bx c =-+++其中0,,a b c R ≥∈(1)若1()3f '=0,求()f x 的单调区间(2)设M 表示'(0)f 与'(1)f 两个数中的最大值,求证:当0≤x ≤1时,|()f x '|≤M . 解:(1)由1()3f '=0,得a =b .当0a =时,则0b =,()f x c =不具备单调性 故f (x )= ax 3-2ax 2+ax +c .由()f x '=a (3x 2-4x +1)=0,得x 1=13,x 2=1列表:由表可得,函数f (x )的单调增区间是(-∞,13)及(1,+∞) .单调减区间是1[,1]3(2)当0a =时,()f x '=2bx b -+ 若0b = ()0f x '=,若0b >,或0b <,()f x '在[0,1]是单调函数,'(0)(1)f f '-=≤()f x '≤(0)f ',或'(1)f -=(0)f '≤()f x '≤(1)f '所以,()f x '≤M当0a >时,()f x '=3ax 2-2(a +b )x +b =3222()33a b a b aba x a a++---. ①当1,033a b a b a a++≥或≤时,则()f x '在[0,1]上是单调函数,所以(1)f '≤()f x '≤(0)f ',或(0)f '≤()f x '≤(1)f ',且(0)f '+(1)f '=a >0.所以M -()f x '<≤M②当013a ba +<<,即-a <b <2a ,则223a b ab a +--≤()f x '≤M . (i) 当-a <b ≤2a 时,则0<a +b ≤32a. 所以 (1)f '223a b ab a +--=22223a b ab a --=223()3a a b a -+≥214a >0.所以 M -()f x '<≤M (ii) 当2a <b <2a 时,则()(2)2a b b a --<0,即a 2+b 2-52ab <0. 所以223a b ab b a +--=2243ab a b a -->22523ab a b a-->0,即(0)f '>223a b ab a +-.所以 M -()f x '<≤M综上所述:当0≤x ≤1时,|()f x '|≤M25.(广东省汕头市2013年普通高中高三教学质量测试试题(二)理科数学试卷)已知函数2(),()ln f x x ax g x x =-=.(1)若()()f x g x ≥对于定义域内的任意x 恒成立,求实数a 的取值范围; (2)设()()()h x f x g x =+有两个极值点12,x x ,且11(0,)2x ∈,证明:123()()ln 24h x h x ->-; (3)设1()()()2ax r x f x g +=+对于任意的(1,2)a ∈,总存在01[,1]2x ∈,使不等式2()(1)r x k a >- 成立,求实数k 的取值范围.【答案】解析:(Ⅰ)由题意:)()(x g x f ≥⇔≥-ax x 2x ln ,)0(>x分离参数a 可得:)0(ln >-≤x xx x a设x x x x ln )(-=φ,则22/1ln )(x x x x -+=φ由于函数2x y =,x y ln =在区间),0(+∞上都是增函数,所以函数1ln 2-+=x x y 在区间),0(+∞上也是增函数,显然1=x 时,该函数值为0 所以当)1,0(∈x 时,0)(/<x ϕ,当),1(+∞∈x 时,0)(/>x ϕ所以函数)(x φ在)1,0(∈x 上是减函数,在),1(+∞∈x 上是增函数 所以1)1()(min ==φφx ,所以1)(min =≤x a φ即]1,(-∞∈a(Ⅱ)由题意知道:x ax x x h ln )(2+-=,且)0(,12)(2|>+-=x x ax x x h所以方程)0(0122>=+-x ax x 有两个不相等的实数根21,x x ,且)21,0(1∈x , 又因为,2121=x x 所以),1(2112+∞∈=x x ,且)2,1(,122=+=i x ax i i而)ln ()()(112121x ax x x h x h +-=-)ln (2222x ax x +--]ln )12([12121x x x ++-=]ln )12([22222x x x ++--212122lnx x x x +-=22222221ln )21(x x x x +-=2222222ln 41x x x --=,)1(2>x设)1(,2ln 41)(222≥--=x x x x x u ,则02)12()(322/≥-=x x x u所以2ln 43)1()(-=>u x u ,即2ln 43)()(21->-x h x h(Ⅲ))21()()(ax g x f x r ++=21ln2++-=ax ax x 所以12)(|++-=ax a a x x r 12222++-=ax x x a ax 1)22(22+--=ax a a x ax 因为(1,2)a ∈,所以21212212222=-≤-=-a a a a 所以当),21(+∞∈x 时,)(x r 是增函数,所以当01[,1]2x ∈时, 21ln1)1()(max 0++-==a a r x r ,(1,2)a ∈所以,要满足题意就需要满足下面的条件:)1(21ln12a k a a ->++-,令)1(21ln 1)(2a k a a a --++-=ϕ,(1,2)a ∈即对任意(1,2)a ∈,)1(21ln1)(2a k a a a --++-=ϕ0>恒成立 因为)122(11222111)(2/-++=+-+=+++-=k ka a aa a ka ka ka a a ϕ分类讨论如下:(1)若0=k ,则1)(/+-=a aa ϕ,所以)(a ϕ在)2,1(∈a 递减,此时0)1()(=<ϕϕa 不符合题意(2)若0<k ,则)121(12)(/+-+=k a a ka a ϕ,所以)(a ϕ在)2,1(∈a 递减,此时0)1()(=<ϕϕa 不符合题意.(3)若0>k ,则)121(12)(/+-+=k a a ka a ϕ,那么当1121>-k 时,假设t 为2与121-k中较小的一个数,即}121,2min{-=k t ,则)(a ϕ在区间})121,2min{,1(-k 上递减,此时0)1()(=<ϕϕa 不符合题意.综上可得⎪⎩⎪⎨⎧≤->11210k k 解得41≥k ,即实数k 的取值范围为),41[+∞26.(广东省茂名市2013届高三4月第二次高考模拟数学理试题(WORD 版))已知函数32(),()ln ,(0)f x x x bx g x a x a =-++=>.(1)若()f x 存在极值点,求实数b 的取值范围;(3)当b=0时,令(),1()(),1f x x F xg x x <⎧=⎨≥⎩.P(11,()x F x ),Q(22,()x F x )为曲线y=()F x 上的两动点,O 为坐标原点,请完成下面两个问题:①能否使得POQ 是以O 为直角顶点的直角三角形,且斜边中点在y 轴上?请说明理由. ②当1<12x x <时,若存在012(,)x x x ∈,使得曲线y=F(x)在x=x 0处的切线l ∥PQ, 求证:1202x x x +<【答案】27.(广东省揭阳市2013年高中毕业班第二次高考模拟考试理科数学试题)设函数2()(1)n n f x x x =-在1[,1]2上的最大值为n a (1,2,n = ).(1)求12,a a 的值;(2)求数列{}n a 的通项公式;(3)证明:对任意*n N ∈(2n ≥),都有21(2)n a n ≤+成立.【答案】解:(1)解法1:∵121'()(1)2(1)(1)[(1)2]n n n n f x nx x x x x x n x x --=---=---当1n =时,1'()(1)(13)f x x x =--当1[,1]2x ∈时,1'()0f x ≤,即函数1()f x 在1[,1]2上单调递减, ∴1111()28a f ==, 当2n =时,2'()f x 2(1)(12)x x x =--当1[,1]2x ∈时,2'()0f x ≤,即函数2()f x 在1[,1]2上单调递减, ∴2211()216a f ==【解法2:当1n =时,21()(1)f x x x =-,则21'()(1)2(1)(1)(13)f x x x x x x =---=-- 当1[,1]2x ∈时,1'()0f x ≤,即函数1()f x 在1[,1]2上单调递减,∴1111()28a f ==, 当2n =时,222()(1)f x x x =-,则222'()2(1)2(1)f x x x x x =---2(1)(12)x x x =--当1[,1]2x ∈时,2'()0f x ≤,即函数2()f x 在1[,1]2上单调递减,∴2211()216a f ==】 (2)令'()0n f x =得1x =或2n x n =+,∵当3n ≥时,1[,1]22n n ∈+且当1[,)22nx n ∈+时'()0n f x >,当(,1]2nx n ∈+时'()0n f x <, 故()n f x 在2nx n =+处取得最大值,即当3n ≥时,22()()()222n n n n n a f n n n ==+++24(2)nn n n +=+,------(*) 当2n =时(*)仍然成立,综上得21,184.2(2)n nn n a n n n +⎧=⎪⎪=⎨⎪≥⎪+⎩(3)当2n ≥时,要证2241(2)(2)n n n n n +≤++,只需证明2(1)4n n +≥∵01222(1)()()n nnn n n C C C nnn+=+++ 2(1)41212142n n n-≥++⋅≥++=∴对任意*n N ∈(2n ≥),都有21(2)n a n ≤+成立 28.(广东省惠州市2013届高三4月模拟考试数学理试题(WORD 版))已知函数2()1f x a bx x =++在3x =处的切线方程为58y x =-. (1)求函数()f x 的解析式;(2)若关于x 的方程()x f x k e =恰有两个不同的实根,求实数k 的值; (3)数列{}n a 满足12(2)a f =,1(),n n a f a n N *+=∈, 求12320131111S a a a a =+++⋅⋅⋅⋅+的整数部分.惠州市2013届高三第一次模拟考【答案】解: (1) f'(x)=2ax+b ,依题设,有`(3)5(3)7f f =⎧⎨=⎩,即659317a b a b +=⎧⎨++=⎩,解得11a b =⎧⎨=-⎩2()=1f x x x ∴-+(2)方程()=k x f x e ∴,即21k xx x e -+=,得2k (1)xx x e -=-+, 记2F(x)(1)xx x e -=-+,则22F'(x)=(21)(1)(32)(1)(2)x x x x x e x x e x x e x x e -------+=--+=---令F'(x)=0,得121,2x x ==当x 变化时,F'(x)、F(x)的变化情况如下表:∴当1x =时,F(x)取极小值1e ;当2x =时,F(x)取极大值23e作出直线y x =和函数2F(x)(1)xx x e -=-+的大致图象,可知当1k e =或23k e =时,它们有两个不同的交点,因此方程()x f x k e =恰有两个不同的实根,(3) 12(2)3a f ==,得1312a >>,又21()1n n n n a f a a a +==-+.22121(1)0n n n n n a a a a a +∴-=-+=->,11n n a a +∴>>由211n n n a a a +=-+,得11=(1)n n n a a a +--,111111(1)1n nnnnaa a a a+∴==----,即111111nnn aa a+=---122013122320132014111111111()()()111111S a aaa aaaaa∴=+++=-+-++-------12014201411111122a aa=-=-<---又1211242637211S a a>++==>即12S <<,故S 的整数部分为. l4分。
广东省珠海市2013届高三上学期期末质检数学理(附答案)

珠海市2012--2013学年度第一学期期末学生学业质量监测高三理科数学试题一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请在答题卡上填涂相应选项. 1.已知全集R U =,集合A ={y | y =2x,x ∈R},则A C U =A .∅B .(0,+∞)C . (-∞,0]D .R2.已知a ,b 是实数,则“⎩⎨⎧>>32b a ”是“5>+b a ”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.若某程序框图如图所示,则该程序运行后输出的值是 A .4 B .5 C .6 D .74. 已知直线l ,m 和平面α, 则下列命题正确的是A .若l ∥m ,m ⊂α,则l ∥αB .若l ∥α,m ⊂α,则l ∥mC .若l ⊥m ,l ⊥α,则m ∥αD .若l ⊥α,m ⊂α,则l ⊥m 5.已知是虚数单位,复数ii+3= A .i 103101+ B .i 103101+- C .i 8381+- D .i 8381--6. 函数y =sin (2x +π4)的图象可由函数y =sin 2x 的图象 A .向左平移π8个单位长度而得到 B .向右平移π8个单位长度而得到C .向左平移π4个单位长度而得到D .向右平移π4个单位长度而得到7.若实数x ,y 满足不等式组⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x 则2x +4y 的最小值是A .6B .4C .2-D .6-(第3题图)(第15题图)8. 对于直角坐标平面内的任意两点11(,)A x y 、22(,)B x y ,定义它们之间的一种“距离”: ‖AB ‖=1212x x y y -+-,给出下列三个命题:①若点C 在线段AB 上,则‖AC ‖+‖CB ‖=‖AB ‖;②在△ABC 中,若∠C=90°,则‖AC ‖+‖CB ‖=‖AB ‖; ③在△ABC 中,‖AC ‖+‖CB ‖>‖AB ‖. 其中真命题的个数为A. 0B. 1C. 2D.3二、填空题:本大题共7小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.请将答案填在答题卡相应位置. (一)必做题(9-13题) 9.函数=y xxsin 的导函数='y . 10.在递增等比数列{a n }中,4,2342=-=a a a ,则公比q = .11.某学校三个社团的人员分布如下表(每名同学只参加一个社团):学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果合唱社被抽出12人,则这三个社团人数共有_______________. 12.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知C =3π,3=b ,若△ABC 的面积为233 ,则c = . 13.如图,F 1,F 2是双曲线C :22221x y a b-=(a >0,b >0) 的左、右焦点,过F 1的直线与C 的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3 : 4 : 5,则双 曲线的离心率为 .(二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在直角坐标系xOy 中, 已知曲线1C :⎩⎨⎧-=+=t y t x 212 , (为参数)与曲线2C :⎩⎨⎧==θθsin 3cos 3y x ,(θ为参数)相交于两个点A 、B ,则线段AB 的长为 .xy OA BF 1F 2(第13题图)15.(几何证明选讲选做题)如图,PAB 、PCD 为⊙O 的两条割线, 若PA=5,AB=7,CD=11,AC=2,则BD 等于 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)设向量a =)sin ,2(θ,b =)cos ,1(θ,θ为锐角. (1)若a·b =136,求sin θ+cos θ的值;(2)若a ∥b ,求sin(2θ+π3)的值. 17.(本小题满分12分)某中学校本课程共开设了A ,B ,C ,D 共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:(1)求这3名学生选修课所有选法的总数;(2)求恰有2门选修课没有被这3名学生选择的概率; (3)求A 选修课被这3名学生选择的人数的数学期望.18.(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形(1)求证:N B C BC 11//平面; (2)求证:BN 11C B N ⊥平面; (3)设M 为AB 中点,在BC 边上找一点P ,使MP //平面1CNB ,并求PCBP的值.19.(本题满分14分)已知椭圆C :)0(12222>>=+b a by a x ,左、右两个焦点分别为1F 、2F ,上顶点),0(b A ,21F AF ∆为正三角形且周长为6.8 主视图侧视图俯视图4(1)求椭圆C 的标准方程及离心率;(2)O 为坐标原点,P 是直线A F 1上的一个动点,求||||2PO PF +的最小值,并求出此时点P 的坐标.20.(本小题满分14分)已知函数21()22f x ax x =+,()g x lnx =. (1)如果函数()y f x =在[1,)+∞上是单调减函数,求a 的取值范围;(2)是否存在实数0a >,使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根?若存在,请求出a 的取值范围;若不存在,请说明理由.21.(本题满分14分)已知正项数列{}n a 的前n 项和为n S ,且(2)4n n n a a S += *()n ∈N . (1)求1a 的值及数列{}n a 的通项公式;(2)求证:33331231111532n a a a a ++++<*()n ∈N ; (3)是否存在非零整数λ,使不等式112111(1)(1)(1)cos 2n n a a a a πλ+--⋅⋅-<对一切*n ∈N 都成立?若存在,求出λ的值;若不存在,说明理由.(第15题图)珠海市2012~2013学年第一学期普通高中学生学业质量监测高三理科数学试题参考答案及评分标准一、选择题:CABD AADB 二、填空题: 9.函数=y xxsin 的导函数='y . 10.在递增等比数列{a n }中,4,2342=-=a a a ,则公比q = .11.某学校三个社团的人员分布如下表(每名同学只参加一个社团):学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果合唱社被抽出12人,则这三个社团人数共有_______________. 12.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知C =3π,3=b ,若△ABC 的面积为233 ,则c = .13.如图,F 1,F 2是双曲线C :22221x y a b-=(a >0,b >0) 的左、右焦点,过F 1的直线与C 的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3 : 4 : 5,则双 曲线的离心率为 .(二)选做题(14-15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在直角坐标系xOy 中, 已知曲线1C :⎩⎨⎧-=+=t y t x 212 , (为参数)与曲线2C :⎩⎨⎧==θθsin 3cos 3y x ,(θ为参数)相交于两个点A 、B ,则线段AB 的长为 . 15.(几何证明选讲选做题)如图,PAB 、PCD 为⊙O 的两条割线, 若PA=5,AB=7,CD=11,AC=2,则BD 等于 .xy OA BF 1F 2(第13题图)9、2sin cos xxx x - 10、2 11、150 12、 7 13、13 14、 4 15、 6 三、解答题:12+12+14+14+14+14=80 16.(本小题满分12分)设向量a =)sin ,2(θ,b =)cos ,1(θ,θ为锐角. (1)若a·b =136,求sin θ+cos θ的值;(2)若a ∥b ,求sin(2θ+π3)的值. 17.(本小题满分12分)某中学校本课程共开设了A ,B ,C ,D 共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生:(1)求这3名学生选修课所有选法的总数;(2)求恰有2门选修课没有被这3名学生选择的概率; (3)求A 选修课被这3名学生选择的人数的数学期望.18.(本小题满分14分)已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形(1)求证:N B C BC 11//平面; (2)求证:BN 11C B N ⊥平面; (3)设M 为AB 中点,在BC 边上找一点P ,使MP //平面1CNB ,并求PCBP的值.19.(本题满分14分)已知椭圆C :)0(12222>>=+b a by a x ,左、右两个焦点分别为1F 、2F ,上顶点),0(b A,8 主视图 侧视图俯视图421F AF ∆为正三角形且周长为6.(1)求椭圆C 的标准方程及离心率;(2)O 为坐标原点,P 是直线A F 1上的一个动点,求||||2PO PF +的最小值,并求出此时点P 的坐标.20.(本小题满分14分)已知函数21()22f x ax x =+,()g x lnx =. (1)如果函数()y f x =在[1,)+∞上是单调减函数,求a 的取值范围;(2)是否存在实数0a >,使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根?若存在,请求出a 的取值范围;若不存在,请说明理由.21.(本题满分14分)已知正项数列{}n a 的前n 项和为n S ,且(2)4n n n a a S += *()n ∈N . (1)求1a 的值及数列{}n a 的通项公式;(2)求证:33331231111532n a a a a ++++<*()n∈N ; (3)是否存在非零整数λ,使不等式112111(1)(1)(1)cos 2n n a a a a πλ+--⋅⋅-<对一切*n ∈N 都成立?若存在,求出λ的值;若不存在,说明理由.三、解答题: 16.(本小题满分12分)解:(1) 因为a ·b =2+sin θcos θ=136,所以sin θcos θ=16. ……………… 3分所以 (sin θ+cos θ)2=1+2 sin θcos θ=43.又因为θ为锐角,所以sin θ+cos θ=233. ……………… 6分(2) 解法一 因为a ∥b ,所以tan θ=2. ……………… 8分 所以 sin2θ=2 sin θcos θ=2 sin θcos θ sin 2θ+cos 2θ= 2 tan θ tan 2θ+1=45, cos2θ=cos 2θ-sin 2θ=cos 2θ-sin 2θ sin 2θ+cos 2θ=1-tan 2θ tan 2θ+1=-35.……………… 10分所以sin(2θ+π3 )=12sin2θ+32cos2θ=12×45+32×(-35 )=4-3310. ……………… 12分 解法二 因为a ∥b ,所以tan θ=2. ……………… 8分 所以 sin θ=255,cos θ=55.因此 sin2θ=2 sin θcos θ=45, cos2θ=cos 2θ-sin 2θ=-35. (10)分所以sin(2θ+π3 )=12sin2θ+32cos2θ=12×45+32×(-35 )=4-3310. ……………… 12分17、(本小题满分12分)解析:(Ⅰ)每个学生有四个不同选择,根据乘法法则,选法总数N=64444=⨯⨯ …… 3分(Ⅱ) 恰有2门选修课这3名学生都没选择的概率为1694442332432223242=⨯⨯⨯⨯⨯==A C C P ……………… 7分(Ⅲ) 设A 选修课被这3名学生选择的人数为ξ,则ξ=0,1,2,30)=64274333= P(ξ=1)=P(ξ=433213⋅C P(ξ=2)=64943313=⋅C P(ξ=3)= 6414333=C ……………… 9分ξ的分布列是………… 10分43641364926427164270=⨯+⨯+⨯+⨯=ξE ………… 12分18.解:(1)证明: 该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴1,,BB BC BA 两两互相垂直。
海珠区2013届高三上学期综合测试(二)(理综)

海珠区2013届高三上学期综合测试(二)理科综合本试卷分第一部分(选择题)和第二部分(非选择题)两部分;第一部分1-5 页,第二部分6-12 页,满分300 分。
考试时间150 分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的学校、班级、姓名、考场试室号、座位号填写在答题卡上;填写准考证号,并用2B 铅笔把对应号码的标号涂黑。
2.选择题每小题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束,将答题卡交回。
第一部分选择题(共118 分)一、单项选择题:本大题共16 小题,每小题4分,共64 分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4分,选错或不答的得0分。
1.下列有关猪的肝细胞和胰岛细胞的叙述中,正确的是A.各种细胞器的种类和数目相同B.与呼吸酶相关的基因能得到表达C.信使R NA 的种类和数目相同D.肝细胞中缺少胰岛素基因2.在下图所示的细胞类型转换过程中,有关叙述错.误.的是全能干细胞骨髓干细胞未成熟红细胞红细胞A.这一过程称做细胞分化B.这一过程伴随着细胞分裂C.这一过程细胞的全能性降低D.这一过程在生物体内是可逆转的3.右图表示某二倍体植物一对同源染色体上的部分基因。
下列叙述正确的是A.图示同源染色体上共存在4对等位基因B.花顶生是隐性性状,该植物不.能表现出此性状C.基因D (d)与E(e)的遗传不.遵循基因自由组合定律D.用秋水仙素处理萌发的种子,可得到三倍体幼苗长茎A短茎花顶生b b 花顶生红花D d 白花皱粒e E 圆粒A 4.我国棉花产量位居世界首位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海珠区2012学年高三综合测试(二)数学(理科)本试卷共6页,21小题,满分150分。
考试用时120分钟。
注意事项:1答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3. 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁。
考试结束后,将答题卡一并交回。
参考公式:如果事件A、B互斥,那么若在每次试验中,事件A发生的概率为P,则在n次独立重复试验中,事件WA恰好发生k次的概率为.一、选择题:本大题共 8 小题,每小题 5 分,满分 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. i是虚数单位,复数对应的点位于A第一象限B第二象限 C.第二象限 D.第四象限2. 若集合.,集合,则“a = 3”是“.的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3. 已知函数,若,,则A. a < b < cB. c < a < bC. b < c < aD. a < c <b4. 已知函数的一部分图象如图1所示,则A. B.C. D.5. 已知正二棱柱(侧棱与底面垂直,底面是正二角形)的高与底面边长均为1,其直观图和正(主)视图如图2所示,则它的左(侧)视图的面积是A. B. 1 C. D.6. 已知双曲线的一个焦点与抛物线y2=12x 的焦点重合,且双曲线的离心率等于,则该双曲线的标准方程为A. B. C. D.7. 已知各项不为O的等差数列满足:,数列是各项均为正值的等比数列,且b7=a7,则等于A. B. C. D.8. 用表示a,b两个数中的最大数,设,那么山函数的图象、X轴、直线和直线X = 2所围成的封闭图形的面积是A. B. C. D.二、填空题:本大题共 7 小题,考生作答 6 小题,每小题 5 分,满分 30 分.(一)必做题(9~13 题9. 的二项展丌式的常数项为_______.(用数字作答)10. 公路部门对通过某路段的300辆汽车的车速进行检测,将所得数据按[40,50), [50,60), [60,70), [70,80]分组,绘制成如图3所示的频率分布直方图.图示中a的值等于_____;这300辆汽车中车速低于的汽车有_____辆.11. 已知实数X,满足约束条件,则目标函数Z = X -y的最小值等于______.12. 某程序框图如图4所示,该程序运行后输出的值依次为_____.13. 给出下列四个命题:①命题,则,②当时,不等式的解集为非空;③当X>1时,有④设有五个函数.,其中既是偶函数又在上是增函数的有2个.其中真命题的序号是_____.(二)选做题(14、15 题,考生只能从中选做一题)14. (坐标系与参数方程选做题)在极坐标系中,点A的坐标为曲线c的方程为15.线与圆C交于A,B两点,AB = 2AP,PT与圆c相切于T点.已知圆C的半径为2,,则PT=_______.三、解答题:本大题共 6 小题,满分 80 分.解答须写出文字说明、证明过程和演算步骤.16. (本小题满分12分)已知函数(1) 求f(X)的最小正周期;(2) 求函数在区间上的最大值和最小值,并求此时X的值.17. (本小题满分12分)现有3个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.约定:每个人将质地均匀的硬币抛掷2次决定自己去参加哪个游戏.2次抛出的硬币朝上的面均为正面的人去参加甲游戏,2次抛出的硬币朝上的面为其它情形的去参加乙游戏.(1) 求这3个人中恰有2人去参加甲游戏的概率;(2) 求这3个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;18. 用;分别表示这3个人中去参加甲、乙游戏的人数,记,求随机变量的分布列和数学期望.(本小题满分14分)如图6,四棱锥P-ABCD中,PA丄底面ABCD,M,N分别是PB,PC的中点,PA = AB,在四边形ABCD中,AB丄 AD,AB丄 BC .(1)求证:MN//平面PAD,(2) 求证:平面MN丄平面PBC;(3)若AD- AB = 1,,,求二面角P-AB-N的大小.19. (本小题满分14分)设椭圆的左、右顶点分别为A、B,点尸在椭圆上且异于A、B两点,O为坐标原点.(1) 若直线AP与BP的斜率之积为,求椭圆的离心率;(2) 对于由(1)得到的椭圆C,过点P的直线l交X轴于点Q(-1,0),交x轴于点M,若,求直线l的斜率.20. (本小题满分14分)已知点?在函数_的图象上.(1) 若数列是等差数列,求证数列是等比数列;(2) 若数列的前《项和是,过点的直线与两坐标轴所围二角形面积为C n,求最小的实数t使:恒成立;(3) 若数列为山(2)中{a」得到的数列,在与之间插入个3,得一新数列,问是杏存在这样的正整数m,使数列的前m项的和,如果存在,求出m的值,如果不存在,请说明理由21. (本小题满分14分)已知函数的最小值为0,其中a>0.(1)求a的值;(2)若对任意的,有成立,求实数k的最小值;(3)证明海珠区2012学年高三综合测试(二)理科数学参考答案与评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题考查基本知识和基本运算.共8小题,每小题5分,满分40分.14~15题是选做题,考生只能选做一题.9. 160 10. 025.0,180 11. 1- 12. 34,55 13. ③④ 14. 22 15. 3(第10题第一空2分,第二空3分)三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查三角两角和的正余弦公式,三角特殊值的运算,函数()()()()()ϕωϕω+=+=x A x f x A x f cos sin 或的周期,最值等知识,考查化归、转化、换元的数学思想方法,以及运算求解能力) 解:(1)()cos 2cos 22sin cos 66f x x x x x ππ⎛⎫⎛⎫=++-+ ⎪ ⎪⎝⎭⎝⎭ 6sin2sin 6cos2cos ππx x -=+6sin2sin 6cos2cos ππx x +x x cos sin 2+…………2分x 2cos 232⨯=x 2sin +x 2cos 3=x 2sin + …………3分⎪⎪⎭⎫ ⎝⎛+=x x 2sin 212cos 232 …………4分 ⎪⎭⎫ ⎝⎛+=x x 2sin 3cos 2cos 3sin 2ππ …………5分⎪⎭⎫ ⎝⎛+=32sin 2πx …………6分∴()fx 的最小正周期为ππ==22T…………7分(2)由(1)知()x f ⎪⎭⎫⎝⎛+=32sin 2πx , 由33ππ≤≤-x ,得πππ≤+≤-323x , ……8分∴当232ππ=+x ,即12π=x 时, ()f x 取得最大值2; …………10分 当332ππ-=+x ,即3π-=x 时, ()f x 取得最小值3-.…………12分17. (本小题满分12分)(本小题主要考查互斥事件,古典概型,独立重复试验,数学期望等知识,考查随机思想以及数据处理能力、抽象思维能力、运算求解能力和应用意识)解:将质地均匀的两枚硬币抛掷两次朝上的面有等可能的四种结果:()正正,,()反正,,()正反,,()反反,, …………1分所以3个人中,每个人去参加甲游戏的概率为41,去参加乙游戏的概率为43.…………2分设“这3个人中恰有i 人去参加甲游戏”为事件()3,2,1,0=i A i 则()iii i C A P -⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=334341. …………3分(1)这3个人中恰有2人去参加甲游戏的概率()6494341232232=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=-C A P .…………5分(2)设“这3个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B ,则23A A B ⋃=, 由于23A A 与互斥,故()()()23A P A P B P +==325649641434141223333=+=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛C C . 所以, 这3个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为325.………7分(3)ξ的所有可能取值为3,1, …………8分 由于1A 与2A ,0A 与3A 互斥,故()()()=+==211A P A P P ξ+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛2134341C 16964964274341223=+=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛C ,…………9分()()()=+==303A P A P P ξ+⎪⎭⎫ ⎝⎛30343C 167641642741333=+=⎪⎭⎫⎝⎛C . …………10分 所以, ξ的分布列为……11分所以随机变量ξ的数学期望815163016731691==⨯+⨯=ξE . …………12分18. (本小题满分14分)(本小题主要考查空间线面关系、空间向量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力) 解: (1)证明: N M ,分别是PB ,MN ∴是PBC ∆的中位线,BC MN //∴, 又 AD AB ⊥,∴AD BC //,AD MN //∴, ⊂AD 平面PAD , ⊄MN 平面PAD , …………//MN 平面PAD . …………(2) AB PA =,M 是PB 的中点PB AM ⊥∴…………5分⊥PA 底面ABCD , BC ⊂平面ABCD , PA BC ⊥∴又 BC ⊥AB ,A AB PA =⋂,⊂PA 平面PAB ,⊂AB 平面PAB ,⊥∴BC 平面PAB ,⊂AM 平面PABBC AM ⊥∴. …………6分 B BC PB =⋂,⊂PB 平面PBC ,⊂BC 平面PBC⊥∴AM 平面PBC . …………7分又⊂AM 平面AMN …………8分∴平面AMN ⊥平面PBC . …………9分(3) ⊥PA 底面ABCD ,AD ⊂平面ABCD , AD PA ⊥∴,又AB PA =222PD AD PA =+∴Q又AB PA =,,5=PD5222==+∴PDADAB联立⎩⎨⎧=+=-5122AD AB AB AD ,解得⎩⎨⎧==21AD AB . 过点C 作AD CH ⊥于H , 在DHC Rt ∆中,1,450===∠AB CH CDH1=∴DH ,1==∴AH BC . …………10分方法一(向量法):以A 为坐标原点,分别以直线AP AB AD ,,为x 轴,y 轴,z 轴建立空间直角坐标系xyz O -,如图所示. …………11分则()()()0,1,1,0,1,0,0,0,0C B A ,()⎪⎭⎫⎝⎛21,21,21,1,0,0N P , ()0,0,1=BC ,⎪⎭⎫⎝⎛=21,21,21AN ,()0,1,0=AB .由(2)知()0,0,1=BC 是平面PAB 的一个法向量; 设平面NAB 的法向量为()z y x n ,,=,则⎪⎩⎪⎨⎧=⋅=⋅00AB n AN n ,即⎪⎩⎪⎨⎧==++00212121y z y x ,得 ⎩⎨⎧=-=0y zx .取()1,0,1-=n . …………12分()()22101001100011cos 222222=-++⨯++-⨯+⨯+⨯==.…………13分结合图可知, 二面角N AB P --的大小为045. …………14分 方法二(几何法)由(2)知⊥BC 平面PAB ,⊂PB 平面PABB C P B ∴⊥,N 是直角三角形R t P B C ∆斜边上的中线,∴12B N PC =.同理易证12A N P C =.A NB N ∴=.取AB 的中点Q ,连AQ ,则AB NQ ⊥. 连MQ ,易知//M Q PA ,MQ AB ∴⊥.MQ ⊂平面PAB ,NQ ⊂平面NAB ,M QN ∴∠即是二面角N AB P --的平面角. …………11分在R t P B C ∆中,PB PC ==∴==2BN ∴=∴在Rt BQN ∆中,1N Q ===,1122M Q PA ==,1122M N B C ==, …………12分∴在MQN ∆中,222M Q M N N Q +=,又有MN MQ =, ∴MQN ∆是以NMQ ∠为直角的等腰直角三角形,M QN ∴∠045=. …………13分∴二面角N AB P --的大小为045. …………14分19.(本小题14分)(本小题主要考查直线斜率、椭圆的方程、离心率、向量的运算等知识,考查数形结合、化归与转化、方程的思想方法,考查综合运用能力以及运算求解能力)解:(1) 由已知()()0,,0,a B a A -,设()()a x y x P ±≠000,. …………1分 则直线AP 的斜率a x y k AP +=00,直线BP 的斜率ax y k AP -=00.由1220220=+y ax ,得()222202ax a y -=. …………2分∴⨯AP k AP k ax y +=00()()222220222020022ax aax a a x y ax y -=---=-=-⨯…………3分2122-=-∴a,得42=a , …………4分∴214242=-=e . …………5分∴椭圆的离心率22=e . …………6分(2) 由题意知直线l 的斜率存在. …………7分 设直线l 的斜率为k , 直线l 的方程为()1+=x k y …………8分 则有()k M ,0,设()()a x y x P ±≠000,,由于Q M P ,,= 根据题意,得()()0000,12,y x k y x +±=- …………9分 解得⎩⎨⎧-=-=k y x 002或⎪⎪⎩⎪⎪⎨⎧=-=33200k y x …………11分又点P 在椭圆上,又由(1)知椭圆C 的方程为12422=+yx所以()()124222=-+-k …………①或12343222=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛-k …………②由①解得02=k,即0=k ,此时点P 与椭圆左端点A 重合, 0=∴k 舍去; …………12分由②解得162=k,即4±=k …………13分∴直线直线l 的斜率4±=k . …………14分20. (本小题满分14分)(本小题主要考查等差、等比数列的定义、通项、求和、对数的运算、直线方程与不等式等知识,考查化归、转化、方程的数学思想方法,以及抽象概括能力、运算求解能力、创新能力和综合应用能力)解:(1)证明:数列{}n b 是等差数列,设公差为d ,则1n n b b d +-=对*n N ∈恒成立, ……………… 1分 依题意12log n n b a =,1()2nb n a =, ……………… 2分所以1111()()22n n b b dn na a +-+==是定值, ……………… 3分 从而数列{}n a 是等比数列. ……………… 4分 (2)解:当1n =时,112a =,当2n ≥时,11()2n n n n a S S -=-=,1n =也适合此式,即数列{}n a 的通项公式是1()2nn a =. ……………… 5分由12log n n b a =,数列{}n b 的通项公式是n b n =, ……………… 6分 所以1(,)2n nP n ,111(,1)2n n P n +++.过这两点的直线方程是:11211(1)22nn nx y n n n+--=+--,可得与坐标轴的交点是12(,0)2n n n A ++和(0,2)n B n +. ……………… 7分221(2)22n n n n n c OA OB ++=⨯⨯=,……………… 8分由于22221233(2)(3)2(2)(3)222n n n n n n n n n c c +++++++-+-=-=232102n n n ++-=>……………9分即数列{}n c 的各项依次单调递减,所以198t c ≥=. ……………… 10分(3)数列{}n d 中,k b (含k b 项)前的所有项的和是121(12)(333)k k -+++++++ ()13322kk k +-=+……………… 11分估算知,当7k =时,其和是73328112020082-+=<, ……………… 12分当8k =时,其和是83336331520082-+=>,又因为20081120888-==⨯,是3的倍数,故存在这样的m ,使得2008m S =, ……………… 13分此时257(1333)296667m =++++++= . ……………… 14分21. (本小题满分14分)(本小题主要考查导数的运算,利用导数研究函数的单调性、不等式等基础知识,考查函数思想,分类讨论思想,以及抽象概括能力、运算求解能力、创新能力和综合应用能力) 解(Ⅰ)解:)(x f 的定义域为()+∞-,a ……………… 1分ax a x ax x f +-+=+-=111)('. ……… 2分由.0)('=x f 得a a x ->-=1当x 变化时,)(),('x f x f 的变化情况如下表:……………… 3分因此,)(x f 在a x -=1处取得最小值,故由题意,01)1(=-=-a a f 所以.1=a ……………… 5分(2)解:当0≤k 时,取1=x ,有().02ln 11>-=f 故0≤k 不合题意. ……………… 6分当0>k 时,令()(),2kx x f x g -=即()().1ln 2kx x x x g -+-=()()[].121221'+---=-+=x k kx x kx x x x g 令()0'=x g ,得.1221,021->-==k k x x ……………… 7分①当21≥k 时,0221≤-kk . ()0'<x g 在()+∞,0上恒成立,因此,()x g 在[)+∞,0上单调递减.从而对于任意的的[)+∞∈,0x ,总有()(),00=≤g x g 即()2kx x f ≤在()+∞,0上恒成立. 故21≥k 符合题意. ……………… 8分②当210<<k 时,,0221>-kk 对于()0,221,0'>⎪⎭⎫ ⎝⎛-∈x g k k x ,故()x g 在⎪⎭⎫⎝⎛-k k 221,0内单调递增.因此当⎪⎭⎫ ⎝⎛-∈k k x 221,00时,()(),000=>g x g 即()200kx x f ≤不成立. 故210<<k 不合题意. ……………… 9分综上,k 的最小值为21. ……………… 10分(3)证明:当1=n 时,不等式左边=<-=23ln 2右边.所以不等式成立. ……………… 11分 当2≥n 时,∑∑==⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+--=⎪⎭⎫ ⎝⎛-ni ni i i i f 111221ln 122122 ()()[]∑∑==--+--=ni ni i i i 1112ln 12ln 122()12ln 1221+--=∑=n i ni ……………… 12分在(2)中取21=k ,得()()022≥≤x xx f ,从而()()()(),2,123221221222≥∈--<-≤⎪⎭⎫ ⎝⎛-*i N i i i i i f ……………… 13分 所以有()()()()∑∑∑∑====--+-<⎪⎭⎫⎝⎛-+=⎪⎭⎫ ⎝⎛-=+--ni ni ni ni i i i f f i f n i 2211123223ln 2122212212ln 122212113ln 21213213ln 22<--+-=⎪⎭⎫ ⎝⎛---+-=∑=n i i ni 综上, ()()*=∈<+--∑Nn n i ni 212ln 1221……… 14分。
