高中数学选修4-5课件(人教版)2.1比较法 (共46张PPT)
合集下载
人教版选修A4-5数学课件:2.1 比较法 (共21张PPT)

-9-
一 比较法
探究一 探究二 思维辨析
首页
X 新知导学 D答疑解惑
INZHIDAOXUE
AYIJIEHUO
D当堂检测
ANGTANGJIANCE
变式训练1 若a,b均为负数,求证a3+b3≤a2b+ab2. 证明:a3+b3-(a2b+ab2)=(a3-a2b)+(b3-ab2) =a2(a-b)-b2(a-b)=(a-b)2(a+b). 因为a,b均为负数,所以a+b<0,(a-b)2≥0, 所以(a-b)2(a+b)≤0. 故a3+b3≤a2b+ab2.
1 1 2 + 与 的大小. 2������ 2������ ������+������
因为 a<0,b<0, 所以 (a-b)2≥0,ab>0,(a+b)<0.
(������-������)2 所以 ≤0, 2������������(������+������) 1 1 2 故 + ≤ . 2������ 2������ ������+������
-8-
一 比较法
探究一 探究二 思维辨析
首页
X 新知导学 D答疑解惑
INZHIDAOXUE
AYIJIEHUO
D当堂检测
ANGTANGJIANCE
反思感悟作差比较法证明不等式的技巧 1.在作差比较法中,变形具有承上启下的作用,变形的目的在于判 断差的符号,而不用考虑差能否化简或值是多少. 2.变形所用的方法有配方、因式分解等,要具体情况具体分析. 3.因式分解是常用的变形手段,为了便于判断差式的符号,常将差 式变形为一个常数,或几个因式积的形式,当所得的差式是某字母 的二次三项式时,常用判别式法判断符号.
人教版高中数学选修4-5课件:2.1比较法

b
b
综上可知,对任意a>0,b>0,都有aabb≥ ab
ab 2 .
林老师网络编辑整理
21
【延伸探究】
1.典例中的条件不变,试证明:abba≤ ab
ab 2 .
【证明】因为abba>0, ab>0,
ab 2
所以
所以当aaabb=baa2bb 时 a,b显-2 a b然a-2有b (ba)b-2=a,1;
=aa-baa-cbb-cbb-acc-acc-b(=a )ab ( a )ac ( b )bc. bcc
林老师网络编辑整理
24
因为a>b>0,所以a >1,a-b>0,所以(a )ab >1.
b
b
同理
(
b
>1, )bc
>( a1)a.c
所以 c >1,所以c a2ab2bc2c>ab+cbc+aca+b.
26
【变式训练】已知a>2,求证:loga(a-1)<log(a+1)a.
【证明】因为a>2,则a-1>1,所以loga(a-1)>0,
log(a+1)a>0,
由于 loga a=l1o ga(a-1)·loga(a+1)
loga1a
<[ loga a 1 loga a 1 ]2 [loga a2 1 ]2.
第二讲 证明不等式的基本方法 一比较法
林老师网络编辑整理
1
【自主预习】 比较法的定义 比较法证明不等式可分为作差比较法和作商比较法两 种.
林老师网络编辑整理
2
(1)作差比较法:要证明a>b,只要证明_a_-_b_>_0_;要证明
人教数学选修4-5全册精品课件

不等式的综合应用 不等式的应用主要体现在两大方面:一是不 等式作为一种重要工具在研究解答数学学科 本身有关问题及其他学科有关问题方面的应 用;二是解决现实生活、生产及科学技术领 域中的实际问题.
不等式应用主要是:利用不等式求函数的定 义域、值域;利用不等式求函数最大值、最 小值;利用不等式讨论方程根及有关性质; 利用不等式解应用题.
1 则 f(x)= (1-t2), 2 1 2 ∴y=f(x)+ 1-2fx= (1-t )+t 2 1 1 1 ≤ t ≤ =- (t-1)2+1 . 2 2 3 1 1 ∵在 t∈ , 上函数 y 是增函数, 2 3 1 7 ∴当 t= 时,y 有最小值为 , 3 9 1 7 当 t= 时,y 有最大值为 . 2 8
例4
【思路点拨】 首先应根据函数单调性去掉 函数符号,转化为关于 sinx的不等式恒成立 问题. 【解】 ∵f(x)在(-∞,1]上是减函数,
∴k-sinx≤k2-sin2x≤1.
假设存在实数k符合题设.
∵k2-sin2x≤1即k2-1≤sin2x对一切x∈R恒 成立,且sin2x≥0, ∴k2-1≤0,-1≤k≤1.①
本讲优化总结
本 讲 优 化 总 结
知识体系网络
专题探究精讲
讲末综合检测
知识体系网络
专题探究精讲
柯西不等式证法一 构造二次函数(ai≠0,i=1,2,„,n) 2 2 2 f(x ) = (a 1 +a2 +„+an )x2 - 2(a1b1 + a2b2 + „ + 2 2 anbn)x+(b2 + b +„+ b 1 2 n). ∵ f(x)= (a1x-b1)2+ (a2x- b2)2+„+ (anx- bn)2≥0, 2 2 ∴ Δ = 4(a1b1 + a2b2 +„+ anbn)2 - 4(a 1 +a2 +„+ 2 2 2 2 an )· (b1 +b2 +„+bn )≤0. 2 2 2 ∴ (a1b1+ a2b2+„+ anbn)2≤(a2 + a +„+ a )( b 1 2 n 1+ 2 2 b2+„+bn).
最新人教版高三数学选修4-5(全套)精品课件

引言
最新人教版高三数学选修4-5(全 套)精品课件Biblioteka 第一讲 不等式和绝对值不等 式
最新人教版高三数学选修4-5(全 套)精品课件
一 不等式
最新人教版高三数学选修4-5(全 套)精品课件
1.不等式的基本性质
最新人教版高三数学选修4-5(全 套)精品课件
最新人教版高三数学选修4-5(全 套)精品课件目录
0002页 0092页 0130页 0209页 0266页 0326页 1168页 1201页 1230页 1301页 1399页
引言 一 不等式 2.基本不等式 二 绝对值不等式 2.绝对值不等式的解法 一 比较法 三 反证法与放缩法 一 二维形式柯西不等式 三 排序不等式 一 数学归纳法 学习总结报告
高中数学(人教版选修4-5)配套课件第二讲 2.1 比较法

第二讲
证明不等式的基本方法 2.1 比较法
栏 目 链 接
1.了解用作差比较法证明不等式.
2.了解用作商比较法证明不等式.
3.提高综合应用知识解决问题的能力.
栏 目 链 接
栏 目 链 接
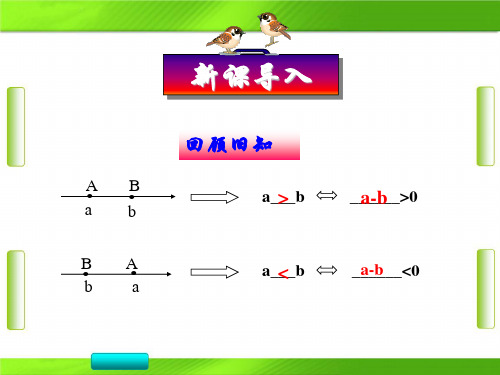
要比较两个实数的大小,只要考查它们的差的符号即
可,即利用不等式的性质:
> a>b⇔a-b________0 = a=b⇔a-b________0 < a<b⇔a-b________0 思考1 比较两个代数式值的大小: x2与x2-x+1.
栏 目 链 接
变 式 训 练
2. 已知 a≥1, 利用作商比较法求证: a+1- a< a- a-1.
左边 a+1- a a+ a-1 证明: = = <1, 右边 a- a-1 a+1+ a 又 a+1- a>0, a- a-1>0. ∴原不等式成立. 点评:根据左、右两边都含无理号的特点,也可以采取两边平方的方 法来比较,但是应先判断两边的符号,都大于 0 时,两边平方是等价 变形,否则要改变不等号.
栏 目 链 接
变 式 训 练 1.已知a,b∈R+,求证: (a+b)(an+bn)≤2(an+1+bn+1)(n∈N*). 证明:(a+b)(an+bn)-2(an+1+bn+1) =an+1+abn+anb+bn+1-2an+1-2bn+1 =an(b-a)+bn(a-b)=(a-b)(bn-an), 又∵a,b∈R+,n∈N*,
题型二
作商比较法证明不等式
+
a+b 例 3 已知 a,b∈R ,求证:a b ≥(ab) . 2
a b
aabb a-b b-a aa-b 证明: =a ·b = . b a+b 2 2 2 ab
2 aa-b 当 a=b 时, =1 ; b 2 aa-b a a -b 当 a>b 时, >1, >0,由指数函数的性质知 >1, b b 2 2 aa-b a a -b 当 a<b 时,0< <1, <0,由指数函数的性质知 >1. b b 2 2 a+b a b ∴a b ≥(ab) . 2
证明不等式的基本方法 2.1 比较法
栏 目 链 接
1.了解用作差比较法证明不等式.
2.了解用作商比较法证明不等式.
3.提高综合应用知识解决问题的能力.
栏 目 链 接
栏 目 链 接
要比较两个实数的大小,只要考查它们的差的符号即
可,即利用不等式的性质:
> a>b⇔a-b________0 = a=b⇔a-b________0 < a<b⇔a-b________0 思考1 比较两个代数式值的大小: x2与x2-x+1.
栏 目 链 接
变 式 训 练
2. 已知 a≥1, 利用作商比较法求证: a+1- a< a- a-1.
左边 a+1- a a+ a-1 证明: = = <1, 右边 a- a-1 a+1+ a 又 a+1- a>0, a- a-1>0. ∴原不等式成立. 点评:根据左、右两边都含无理号的特点,也可以采取两边平方的方 法来比较,但是应先判断两边的符号,都大于 0 时,两边平方是等价 变形,否则要改变不等号.
栏 目 链 接
变 式 训 练 1.已知a,b∈R+,求证: (a+b)(an+bn)≤2(an+1+bn+1)(n∈N*). 证明:(a+b)(an+bn)-2(an+1+bn+1) =an+1+abn+anb+bn+1-2an+1-2bn+1 =an(b-a)+bn(a-b)=(a-b)(bn-an), 又∵a,b∈R+,n∈N*,
题型二
作商比较法证明不等式
+
a+b 例 3 已知 a,b∈R ,求证:a b ≥(ab) . 2
a b
aabb a-b b-a aa-b 证明: =a ·b = . b a+b 2 2 2 ab
2 aa-b 当 a=b 时, =1 ; b 2 aa-b a a -b 当 a>b 时, >1, >0,由指数函数的性质知 >1, b b 2 2 aa-b a a -b 当 a<b 时,0< <1, <0,由指数函数的性质知 >1. b b 2 2 a+b a b ∴a b ≥(ab) . 2
高中数学人教A版选修4-5课件:2-1比较法

目标导航
知识梳理
重难聚焦
典例透析
1
2
3
【做一做1-1】 当a<b<0时,下列关系式中成立的是 (
)
A. ������2 < ������2 C. > 1
������ ������
B. lg ������2 < lg ������2 D.
2 ������ 1
2
>
2 ������ 1
2
解析:方法一:取特殊值a=-4,b=-1,则知选项A,C,D不正确,选项B 正确,故选B; 方法二:∵a<b<0,∴a2>b2. 而函数y=lg x(x>0)为增函数, ∴lg b2<lg a2,B项正确. 答案:B
答案:A
目标导航
知识梳理
重难聚焦
典例透析
1
2
3
3.作商比较法 ������ = ������⇔ ������ = 1, (1)作商比较法的证明依据:当 a,b>0 时, ������ > ������⇔ ������ > 1,. ������ < ������⇔ < 1
(2)基本步骤:①作商;②变形;③判断与“1”的大小;④下结论.
分析:因不等式的两边进行分子有理化相减后,可判断差的符号, 故可用作差比较法进行证明.
证明: ∵( ������ + 1 − ������) − ( ������ − ������-1) =
1 − ������+1+ ������
1 ������+ ������-1
������-1- ������ + 1 = < 0, ∴ ������ + 1 − ������ < ������ − ������-1. ( ������ + 1 + ������)( ������ + ������-1)
2.1 比较法 课件(人教A选修4-5)

解:设A地到B地距离为m千米.起步价内行驶的路程为a千米.
显然当m≤a时,选起步价为8元的出租车比较便宜.
当m>a时,设m=a+x(x>0),乘坐起步价为10元的出租车费用 为P(x)元.乘坐起步价为8元的出租车费用为Q(x)元,则P(x)=
10+1.2 x,
Q(x)=8+1.4x ∵P(x)-Q(x)=2-0.2x=0.2(10-x)
[例1]
设△ABC的三边长分别是a、b、c,求证:
4(ab+bc+ac)>(a+b+c)2. [思路点拨] 作差法证明,注意条件“在同一个三角形
中,任意两边之和大于第三边”的应用.
[证明] ∵a、b、c是△ABC的三边长.
∴a>0,b>0,c>0,且b+c-a>0,c+a-b>0,a+b-c>0. ∴4(ab+bc+ac)-(a+b+c)2 =2(ab+bc+ac)-(a2+b2+c2) =(b+c-a)a+(c+a-b)b+(a+b-c)c>0. ∴4(ab+bc+ac)>(a+b+c)2.
甲有一半时间以速度m行走,另一半以速度n行走;乙有
一半路程以速度m行走,另一半路程以速度n行走.如果
m≠n,问甲、乙二人谁先到达指定地点? [思路点拨] 先用m、n表示甲、乙两人走完全程所用
时间,再进行比较.
[解]
设从出发地点至指定地点的路程为 s,甲、乙二人走
完这段路程所用的时间分别为 t1,t2 ,依题意有: t1 t1 m+ n=s, 2 2 s s + =t . 2m 2n 2 sm+n 2s ∴t1= ,t = . 2mn m+n 2 sm+n 2s ∴t1-t2= - 2mn m+n s[4mn-m+n2] sm-n2 = =- . 2mnm+n 2mnm+n 其中 s,m,n 都是正数,且 m≠n, ∴t1-t2<0.即 t1<t2. 从而知甲比乙先到达指定地点.
人教版高中数学选修4-5 第一讲 一 不等式 (共46张PPT)教育课件
解得:1 5 x1 5
2
2
由上可知,当 x 1 5 或x1 5时,M大于N;
2
2
当
1 2
5
x1 2
5 时,M小于N。
–
凡 事 都 是 多 棱 镜 , 不 同 的 角 度 会 看到 不 同 的 结 果 。 若 能 把 一 些事 看 淡 了 , 就 会 有 个 好 心 境, 若 把 很 多 事 看开 了 , 就 会 有 个 好 心 情 。 让 聚 散 离 合 犹如 月 缺 月 圆 那 样 寻 常 ,
当且仅当a b时,等号成立。
探究
观察下图,如果AD=a,BD=b,OC是 斜边AB的中线,你能给出基本不等式的 几何意义吗?
C
A
O
DB
分析
在图中,CD⊥AB,AO=OB,于是OC= 1 AB= 1(a+b),
2
2
因为∠DCA+ ∠A=90o, ∠B+∠A=90o
所以∠DCA= ∠B.
于是Rt△DCA和Rt△DBC相似.
3
当且仅当a=b=c时,等号成立。
推广
对于n个正数a1,a2,…,an,它们的算术平 均数不小于它们的几何平均数,
即 当: 且a仅1 当+ aa12=n+a2.=..…+=aann时 ,n a等1a号2 .成..a立n 。
例4 已知x,y,z R+,求证(x+y+z)3≥27xyz
提示 本题涉及三个实数的和积, 可以考虑基本不等式的推广。
1 8
4
由上可知,y的最大值是
1
8
2.若M=(2x+3)(x-4),N=(x-7)(x+3)+8,讨论M 与N的大小关系。
2019年高中数学人教版选修4-5课件:第二讲2.1比较法

当 b>a>0 时,0<ab<1,且 a-b<0,故aababbab>1; 当 a=b 时,aababbab=1. 答案:B
4. 设 P=a2b2+5,Q=2ab-a2-4a,若 P>Q,则实 数 a,b 满足的条件为________.
解析:P-Q=a2b2+5-2ab+a2+4a=(ab-1)2+(a +2)2,因为 P>Q⇒P-Q>0.所以 ab≠1 或 a≠-2.
以 ω≥u.
答案:C
3.已知 a,b 都是正实数,则下列关系式成立的是 ()
A.aabb=abba B.aabb≥abba C.aabb<abba D.aabb≤abba 解析:因为 a,b∈R+,故 abba>0.
又aaabbbba=aba·bab=aba-b, 当 a>b>0 时,ab>1,且 a-b>0,故aaabbbba>1;
解:设截面的周长为 l,依题意知,截面是圆的水管 的截面面积为π·2lπ2,截面是正方形的水管的截面面积 为4l 2.
因为π·2lπ2-4l 2=l42π1 -14=(4-16ππ)l2.
(4-π)l2
由于 l>0,0<π<4,所以
归纳升华 1.应用不等式解决实际问题时,关键是如何把等量 关系、不等量关系转化为不等式的问题来解决,也即建立 数学模型是解应用题的关键. 2.在实际应用不等式问题时,常用比较法来判断数 的大小关系.若是选择题或填空题,则可用特殊值加以判 断.
[变式训练] 通过水管放水,当流速相同时,如果水 管截面(指横截面)的周长相等,试问:截面为圆的水管流 量大还是截面为正方形的水管流量大?
作差比较法的基本步骤是:作差、变形、判断符号.变 形是关键,目的在于能判断差的符号.为便于判断差式 的符号.通常将差式变形为常数或几个因式的积、商形 式或平方和形式.多项式不等式、分式不等式或对数不 等式常用作差比较法证明.作商比较法的基本步骤是: 作商、变形、判断商值与 1 的大小,适用于两边都是正值 的幂或积的形式的不等式.其中判断差值的正负及商值 与 1 的大小是用比较法证明不等式的难点.
