第6章 弯曲变形2
材料力学(理工科课件)第六章 弯曲变形)

§6-1 基本概念及工程实例 (Basic concepts and example problems)
一、工程实例(Example problem)
(Deflection of Beams)
但在另外一些情况下,有时却要求构件具有较大的弹性变 形,以满足特定的工作需要.
例如,车辆上的板弹簧,要求有足够大的变形,以缓解车辆受
M 0 w 0
x
O
M 0 w 0
M
(Deflection of Beams)
w (1 w )
2 3 2
M ( x) EI
2 w 与 1 相比十分微小而可以忽略不计,故上式可近似为
w"
M ( x) EI
(6.5)
此式称为 梁的挠曲线近似微分方程(differential equation of the deflection curve) 近似原因 : (1) 略去了剪力的影响; (2) 略去了 w2项; (3) tan w w( x )
x Cx D
4
(Deflection of Beams)
边界条件x=0 和 x=l时, w 0
梁的转角方程和挠曲线方程 A 分别为 q 2 3 3 (6lx 4 x l ) 24 EI qx 2 3 3 w (2lx x l ) 24 EI 最大转角和最大挠度分别为 在 x=0 和 x=l 处转角的绝对值相等且都是最大值,
A a l D B
b
(Deflection of Beams)
解: 梁的两个支反力为
FRA F FRB F b l a l
x
l x
F FRA
A 1 a D b 2
材料力学第六章 弯曲变形

4
2
C
B
)
=
A
( A)q C
l q
( B )q
(b)
B
( wC )q
l
θ B ( θ B )q ( θ B ) M e
+
Me
(c)
Mel ql 24 EI 6 EI
3
A
B
( B ) M e
( A ) MC ( wC ) M
e
e
l
例题3
AB梁的EI为已知,求梁中间C截面挠度.
F1l 2 F2 la 0.4 400 200 B ( ) 16 EI 3 EI 210 1880 16 3 +0.423 10-4 (rad)
F1l a F2a F2a l wC 5.19 106 m 16 EI 3 EI 3 EI wmax w (3)校核刚度: l l
x A
dx
F
x
C' dω
B
d tg dx
二、挠曲线的微分方程
1.纯弯曲时曲率与弯矩的关系
M EI
1
横力弯曲时, M 和 都是x的函数.略去剪力对梁的位移的影 响, 则
1 M ( x) ( x) EI
2.由数学得到平面曲线的曲率
F
1 | w | 3 2 2 ( x) (1 w )
q
A x B
w w F wq
+
w wF wq
例1 已知:EI, F,q .求C点挠度 F q
A
C a a
B
Fa 3 ( wC )F 6 EI
材料力学刘鸿文第六版最新课件第六章 弯曲变形

内容回顾
6.1:基本概念 挠度;转角;挠曲线;挠度和转角的关系;挠度 和转角的符号定义。
6.2:挠曲线的微分方程
d2w M dx2 EI
6.3:积分法求弯曲变形
w" M(x) EI
EIw M ( x )dx C1 (转角方程) EIw M ( x )dxdx C1 x C 2 (挠度方程)
确定积分常数C1和C2
确定积分常数C1和C2
(1)在简支梁中, 左右两铰支座处的
挠度 w A 和 wB 都等于0。
A
wA 0
(2)在悬臂梁中,固定端处的挠度 w A
和转角 A 都应等于0。
(3)在弯曲变形对称点,转角为0。
A
wA 0
A 0
B
wB 0
B
42
(4)若B支座改为弹簧支撑,则: (5)若B支座改为
又:
1M
EI
B
d2w M
ds
A
此式称为
dx2 EI
梁的挠曲线近似微分方15程
横力弯曲梁:
w" M(x) EI
近似原因 : (1) 略去了剪力的影响; (2) 略去了 w2项;
(3) tan w w ( x )
16
§6-3 用积分法求弯曲变形
一、微分方程的积分 w M ( x) EI
x a时,wC 左 wC 右
x L, w FBy
B
k
B kx
h F EA
A
C
a
bB
L
x 0, wA 0
x a时,C左 C右
x a时,wC左 wC右
x
L, wB
lBD
FByh EA
例题1 图示一抗弯刚度为 EI 的悬臂梁, 在自由端受一集中力 F
材料力学第6章弯曲变形

M1 EIw1
Fb x1 l
2 x1
" EIw2
Fb M2 x2 F ( x2 a ) l
2 x2 2
EIw1
Fb C1 l 2
x2 a Fb F C2 (i) EIw2 l 2 2
工学院
§6.2 挠曲线的微分方程
纯弯曲情况下,弯矩与曲率 间的关系(5.1):
M EI
1
--(a)
横力弯曲时,梁截面上有弯矩也有剪力,对于跨 度远大于截面高度的梁,剪力对弯曲变形的影响可以 省略,(a)式便可以作为横力弯曲变形的基本方程。其 中,M和1/ρ都是x的函数。
工学院
§6.2 挠曲线的微分方程
(o) (p)
CB段 (a x2 l )
Fb 2 3l 2 2 2 l b 3 x ( x a ) 2 2 6l b Fb 2 l 2 2 3 EIw2 l b x x ( x a ) 2 2 6l b 2 EIw2
车床主轴的变形过大会影响 齿轮的啮合和轴承的配合, 造成磨损不匀,产生噪音, 降低寿命以及影响加工精度。
工学院
§6.1 工程中的弯曲变形问题
吊车梁的变形过大,会 使梁上小车行走困难, 出现爬坡现象,还会引 起较严重的振动。
变形超过允许数值,即 使在弹性范围内,也被 认为是一种失效现象。
工学院
§6.1 工程中的弯曲变形问题
l
2
b
2
3
工学院
§6.3 用积分法求弯曲变形—实例3
7). 讨论
上面得到最大挠度表达式为: 3 1 Fb 2 2 wmax l b 9 3 EIl
材料力学习题册答案_第6章_弯曲变形

得 x=0.519l
所以
W
m
ax
=0.00652
ql 4 EI
3 用叠加法求如图 7 所示各梁截面 A 的挠度和转角。EI 为已知常数。
解 A 截面的挠度为 P 单独作用与 M 0 单独作用所产生的挠度之和。 查表得:
y AP
Pl 3 24 EI
y = M 0l 2 Pl 3
AM 0
8EI
度 y = Fl 3 。 C 32 EI
4. 如图 4 所示两梁的横截面大小形状均相同,跨度为 l , 则两梁的力 图 相同 ,两梁的变形 不同 。(填“相同”或“不同”)
5. 提高梁的刚度措施有 提高Wz 、 降低 M MAX 等。 四、计算题 1 用积分法求图 5 所示梁 A 截面的挠度和 B 截面的转角。
8EI
y y 则 y A
AP
= Pl 3
AM0 12 EI
同理,A 截面的转角为 P 单独作用与 M 0 单独作用所产生的转角之和。
查表得
AP
Pl 2 8EI
对于 AM0 可求得该转角满足方程 EI =-Plx+C 边界条件 x=0 0 可得 C=0
现 4 个积分常数,这些积分常数需要用梁的 边界 条件和 光滑连
续 条件来确定。
2. 用积分法求图 2 所示梁变形法时,边界条件为:YA 0,A 0,YD 0 ;
连续条件为:
YA
1
YA
2
,
B
1
B
2
,
YC3.
如图
3
所示的外伸梁,已知
B
截面转角
B
=
Fl 2 16 EI
,则 C 截面的挠
于零的截面处。
刘鸿文版材料力学第六章

F6bl
(l2
b2 ) x1
CB 段: a x2 l
y
F
A A
DC
FAy x1
x2
a
ym ax b
B B x
FBy
EI
Fb 2 2l
2
x2
F 2
(
x2
a)2
Fb (l2 6l
b2 )
EIy2
Fb 6l
x32
F 6
(
x2
a)3
F6lb (l2 b2 ) x2
目录
§6-3 用积分法求弯曲变形
目录
§6-5 简单超静定梁
例7 梁AB 和BC 在B 处铰接,A、C 两端固定,梁的抗弯刚度均为EI,F = 40kN, q = 20kN/m。画梁的剪力图和弯矩图。
解 从B 处拆开,使超静定结构变成两个悬臂 梁。
MA
FA FB
FB FB
yB2
yB1
FB
变形协调方程为: 物理关系
yB1 yB 2
4
EI
ql 4 48EI
ql 4 16 EI
11ql 4 ( ) 384 EI
3
ql 3
B i 1 Bi 24EI
ql 3 16EI
ql 3 3EI
11ql 3 ( ) 48EI
目录
§6-4 用叠加法求弯曲变形
例4 已知:悬臂梁受力如图示,q、l、
yC
EI均为已知。求C截面的挠度yC和转角C
§6-4 用叠加法求弯曲变形
讨论 叠加法求变形有什么优缺点?
目录
§6-5 简单超静定梁
1.基本概念: 超静定梁:支反力数目大于有效平衡方程数目的梁 多余约束:从维持平衡角度而言,多余的约束 超静定次数:多余约束或多余支反力的数目。 相当系统:用多余约束力代替多余约束的静定系统
弯曲变形——精选推荐

第六章弯曲变形判断弯曲变形1、“平面弯曲梁的挠曲线必定是一条与外力作用面重合或平行的平面曲线”2、“由于挠曲线的曲率与弯矩成正比,因此横截面的挠度与转角也与横截面的弯矩成正比”3、“只要满足线弹性条件,就可以应用挠曲线的近似微分方程”4、“两梁的抗弯刚度相同、弯矩方程相同,则两梁的挠曲线形状相同”5、“梁的挠曲线方程随弯矩方程的分段而分段,只要梁不具有中间铰,梁的挠曲线仍然是一条光滑、连续的曲线。
”6、“最大挠度处的截面转角一定为0”7、“最大弯矩处的挠度也一定是最大”8、“梁的最大挠度不一定是发生在梁的最大弯矩处。
”9、“只要材料服从虎克定律,则构件弯曲时其弯矩、转角、挠度都可以用叠加方法来求”10、“两根几何尺寸、支撑条件完全相同的静定梁,只要所受的载荷相同,则两梁所对应的截面的挠度和转角相同,而与梁的材料是否相同无关”11、“一铸铁简支梁在均布载荷的作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力和变形均相同”选择弯曲变形1、圆截面的悬臂梁在自由端受集中力的作用,当梁的直径减少一半而其他条件不变时,最大正应力是原来的倍;最大挠度是原来的倍。
若梁的长度增大一倍,其他条件不变,最大弯曲正应力是原来的倍,最大挠度是原来的倍。
A:2; B:16 C:8 D:4;2、y’’=M(x)/EI在条件下成立。
A:小变形; B:材料服从虎克定律;C:挠曲线在xoy面内; D:同时满足A、B、C;3、等直梁在弯曲变形时,挠曲线最大曲率发生在处。
A:挠度最大; B:转角最大 C:剪力最大; D:弯矩最大;4、在简支梁中,对于减少弯曲变形效果最明显。
A:减小集中力P; B:减小梁的跨度;C:采用优质钢; D:提高截面的惯性矩5、板条弯成1/4圆,设梁始终处于线弹性范围内:①σ=My/I Z,②y’’=M(x)/EI Z哪一个会得到正确的计算结果?A:①正确、②正确;B:①正确、②错误; C:①错误、②正确; D:①错误、②错误;6、应用叠加原理求横截面的挠度、转角时,需要满足的条件是。
工程力学c材料力学部分第六章 弯曲变形

A l/2
C l
B
解:此梁上的荷载可视为 正对称和反对称荷载的叠加, 正对称和反对称荷载的叠加, 如图所示。 如图所示。 正对称荷载作用下:
q/2
5(q / 2)l 4 5ql 4 wC1 = − =− 384 EI 768 EI
B
(q / 2)l 3 ql 3 θ A1 = −θ B1 = =− 24 EI 48EI
w P A a D
a
A C a H a B
EI
Pl 3 wB = − 3 EI
P
B
l
Pl 2 θB = − 2 EI
P A a 2a 2a C B
P/2
P/2 B
P/2
=
A
+
P/2
力分解为关于中截面的对称和反对称力( )之和的形式。 解:将P力分解为关于中截面的对称和反对称力(P/2)之和的形式。 力分解为关于中截面的对称和反对称力 显然,在反对称力( / )作用下, 显然,在反对称力(P/2)作用下,wc=0 对称力作用的简支梁, 对称力作用的简支梁,可以等效为悬臂梁受到两个力的作用 的问题。 的问题。
wA=0 θA=0
B
②、变形连续条件 变形连续条件: 连续条件
P A C θC左 wC左= wC右, =θ C右 B
的悬臂梁, 例1:图示一弯曲刚度为 的悬臂梁,在自由端受一集中力 作 :图示一弯曲刚度为EI的悬臂梁 在自由端受一集中力F 试求梁的挠曲线方程,并求最大挠度及最大转角。 用,试求梁的挠曲线方程,并求最大挠度及最大转角。 解:① 建立坐标系并写出弯矩方程 ①
在小变形情况下, 曲线弯曲平缓, 在小变形情况下,挠曲线弯曲平缓,
∴ w′ ≪ 1
2
弯曲变形求解方法

①建立刚度条件,解决刚度问题
②建立变形协调条件,解决超静定问题
③为振动计算奠定基础。
§6.2挠曲线的微分方程
一、概念
以简支梁为例,以变形前的轴线为x轴,垂直向上为y轴,xoy平面为梁的纵向对称面。
①挠曲线:
在对称弯曲情况下,变形后梁的轴线为xoy平面内的一条曲线,此曲线称为挠曲线。
②挠度:
一、梁的刚度条件
在工程中,梁除了要满足强度条件外,还要满足刚度条件。梁的刚度条件为
式中 ——最大挠跨比;
——许用挠跨比。许用挠跨比可从设计规范中查得,一般在 ~ 之间。
[例6-2]受力情况如图9-42a所示的简支梁,由型号为45a工字钢制成。材料的许用应力 MPa, ,材料的弹性模量为 GPa,试校核梁的强度和刚度。
梁的任一截面形心的竖直位移称为挠度。
③挠曲线的方程式:
w=f(x)
④转角:弯曲变形中,梁的横截面对其原来位置转过的角度θ,称为截面转角。根据平面假设,梁的横截面变形前,垂直于轴线,变形后垂直于挠曲线。故
⑤挠度w和转角θ是度量弯曲变形的两个基本量。
⑥挠度与转角符号规定:在图示坐标中,挠度向上为正,反时针的转角为正。
[解](1)作梁的弯矩图(图9-42b)。
由图可知: kN·m
(2)校核梁的强度。
查型号为45a工字钢知,惯性矩 cm4,抗弯截面系数 cm3。
梁内最大正应力
N/mm2=103.18MPa<
梁满足强度要求。
(3)校核梁的刚度
用叠加法计算梁跨中的挠度为
mm
=18.5mm
< =0.002
梁满足刚度要求。此梁安全。
二、提高梁刚度的措施
要提高梁的刚度,应从影响梁刚度的各个因素来考虑。梁的挠度和转角与作用在梁上的荷载、梁的跨度、支座条件及梁的抗弯刚度有关,因此,要降低挠度,提高刚度,可采用以下措施:
材料力学 第6章 梁的弯曲变形

(c)
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
在本章所取的坐标系中,
上凸的曲线w″为正值,下凸的为负值。
如图6-5所示。 按弯矩正负号的规定,正弯矩对应着负的w″, 负弯矩对应着正的w″,故(c)式
w
M (x)
(1
w2 )3 2
EI z
在小变形情况下, w dw 是一个很小的量, dx
则 w'2为高阶微量,可略去不计,故
挠曲线的近似微分方程
M x
w EI z
EIw''= −M (x)
(6-1b)
图6-5
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
6.4 积分法计算梁的变形
对于等直梁,可以直接积分,计算梁的挠度和转角。 将式(6-1b)积分一次,得到
EIw′ = EIθ = −∫ M (x) dx + C
maxFl 2 2EI来自A xyF
θmax B
x
wmax
l
图6-7 例题 6-1 图
wm a x
Fl 3 3EI
θ max为正值,表明梁变形后,截面B顺时针转动;
wmax为正值,表明点B位移向下。
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
例题6-2 一简支梁受均布荷载q作用,如图6-8所示。试求梁的转角方程和 挠度方程, 并确定最大挠度和A、B截面的转角。设梁的弯曲刚度为EI。
A x
y
F
θmax B
x
wmax
l
进行两次积分,得到
EIw EI Flx Flx2 C
(a)
2
EIw Flx2 Fx3 Cx D
材料力学简明教程(景荣春)课后答案第六章

( ) wA
= − q0l 4 30EI
↓
,θB
= q0l3 24EI
(顺)
讨论:请读者按右手坐标系求 wA ,θB 并与以上解答比较。
(c)
(c1)
解 图(c1)
( ) ∑ M B = 0 , FC
= − Me l
↓
CA 段
M
=
−
Me l
x1
⎜⎛ 0 ⎝
≤
x1
<
l 2
⎟⎞ ⎠
AB 段
M
=
−
Me l
l 2
≤
x2
≤
l ⎟⎞ ⎠
Ew1′′
=
3 8
qlx1
−
1 2
qx12
EIw1′
=
3 16
qlx12
−
1 6
qx13
+
C1
EIw1
=
1 16
qlx13
−
1 24
qx14
+
C1 x1
+
D1
EIw′2′
=
3 8
qlx2
−
ql 2
⎜⎛ ⎝
x2
−
l ⎟⎞ 4⎠
EIw′2
=
3 16
qlx22
−
ql 4
⎜⎛ ⎝
x2
24
EIw′(l) = 0 ,− q l 3 + 3Al 2 + 2Bl = 0
6
解式(a),(b)得
A = ql , B = − ql 2
12
24
即挠曲线方程为
EIw = − q x4 + ql x3 − ql 2 x2 24 12 24
第六章弯曲变形分析
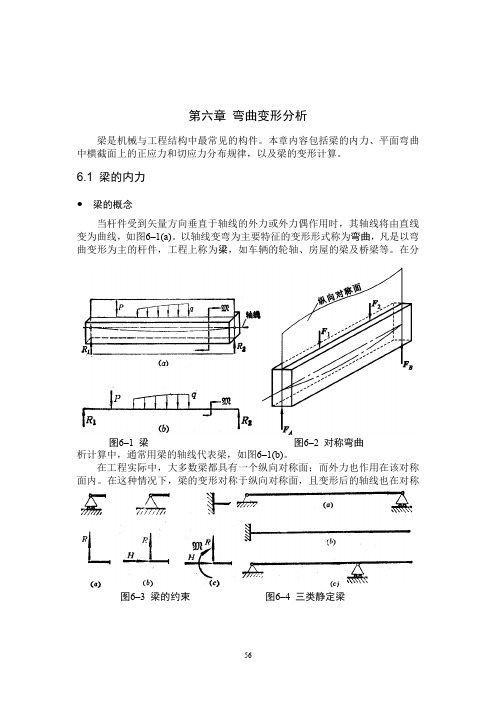
第六章 弯曲变形分析梁是机械与工程结构中最常见的构件。
本章内容包括梁的内力、平面弯曲中横截面上的正应力和切应力分布规律,以及梁的变形计算。
6.1 梁的内力● 梁的概念当杆件受到矢量方向垂直于轴线的外力或外力偶作用时,其轴线将由直线变为曲线,如图6–1(a)。
以轴线变弯为主要特征的变形形式称为弯曲,凡是以弯曲变形为主的杆件,工程上称为梁,如车辆的轮轴、房屋的梁及桥梁等。
在分析计算中,通常用梁的轴线代表梁,如图6–1(b)。
在工程实际中,大多数梁都具有一个纵向对称面;而外力也作用在该对称面内。
在这种情况下,梁的变形对称于纵向对称面,且变形后的轴线也在对称图6–1 梁 图6–2 对称弯曲图6–3 梁的约束 图6–4 三类静定梁面内,即所谓的对称弯曲,如图6–2。
它是弯曲问题中最基本、最常见的情况。
本章只讨论梁的对称弯曲。
图6–3表示了梁的三种常见约束形式及相应的约束力:可动铰支座(图6–3(a)),固定铰支座(图6–3(b))和(平面)固定端约束(图6–3(c))。
在以上三种约束方式下,有三种常见的梁形式,如图6–4所示。
图6–4(a)为简支梁,两端分别为固定铰支座和活动铰支座;图6–4(b)为悬臂梁,一端固定端约束,一端自由;图6–4(b)为外伸梁,它是具有一个或两个外伸部分的简支梁。
这三种梁都是静定梁。
作用在梁上的外载荷,常见的有集中力偶M (图6–5(a))、分布载荷q (图6–5(b))和集中力F (图6–5(c))。
在实际问题中,q 为常数的均布载荷较为常见。
● 梁的剪力与弯矩在4.2中已经介绍了求杆件内力的通用方法,即截面法。
具体到梁,其内力分量为剪力和弯矩,规定当剪力相对于横截面的转向为顺时针为正,使杆件发生上凹下凸的弯矩为正,如图4–5(b)和(c)。
例6–1:如图6–6所示悬臂梁,受均布载荷q ,在B 点处受矩为2qa M =的力偶作用,试绘梁的剪力图与弯矩图。
解:设固定端的约束力和约束力偶为C R 和C M ,则由平衡方程00=-=∑qa R F C y ,qa R C =05.102=--⋅=∑C C M qa qa a m ,221qa M C = 以杆件左端为坐标原点,以B 为分界面,将梁分为AB 和BC 两段。
精品课件-材料力学(张功学)-第6章

图6-4
6.1 引 言
解(1)求约束力。建立坐标系如图所示,求得约束力为
方向均竖直向上。
FAy
b l
F
,
FBy
a l
F
(2)写出弯矩方程。由于集中力加在两支座之间,弯矩方
程在AC、BC两段各不相同。
AC段:
M
1(
x)
b l
Fx
w(a )w(a ), (a ) (a )
(f)
利用式(e)和式(f),即可解得
D1 D2 0,
C1
C2
Fb(b 6l
2
l
2
)
于是,求得梁的转角方程和挠曲线方程分别为
6.1 引 言
AC段:
EI (x) Fb(3x2 b2 l 2 )
6l
EIw(x) Fbx[x3 (b2 l 2 )x] 6l
(a) (b) (c)
6.1 引 言
确定积分常数C和D的边界条件为:在固定端截面处,挠度 和转角均为零。即
w00, 00
将(b)、(c)两式代入,得
D0, C0
将所得积分常数代入(b)、(c)两式,得到梁的转角方程和挠
度方程分别为
(x)dw
1
Wx 2 (
Wlx )
dx EI 2
w(x) 1 (Wx 3 Wlx 2 ) EI 6 2
6.1 引 言 显然在自由端处转角与挠度最大,即当x=l时,得
m
ax
B
1 EI
(Wl 2
2
Wl
2
Wl 2 )
2EI
1 Wl 3 Wl 3 Wl 3
工程力学(第二版)章图文 (6)

(1) 一体重为700 N (2) 要求两名体重均为700 N的工人抬着1500 N的货物安全 走过,木板的宽度不变,重新设计木板厚度h。
第6章 弯 曲
解 (1) 计算弯矩的最大值Mmax。当工人行走到跳板中央
(2) 横截面上的弯矩在数值上等于该截面左侧(或右侧)所 有外力对该截面形心的力矩的代数和。
第6章 弯 曲
为了使所求得的剪力与弯矩符合前面的符号规定,按此 规律计算剪力时,截面左侧梁上外力向上取正值,向下取负 值,截面右侧梁上外力向下取正值,向上取负值;计算弯矩 时,截面左侧梁上外力对该截面形心的力矩顺时针转向取正 值,逆时针转向取负值,截面右侧外力对该截面形心的力矩 逆时针转向取正值,顺时针转向取负值。可以将这个规则归 纳为一个简单的口诀:左上右下,剪力为正;左顺右逆,弯 矩为正。
第6章 弯 曲 图 6.10
第6章 弯 曲 解 设截面m-m与B端之间的距离为x,取m-m截面的右段
为研究对象,画出受力图,如图6.10(b)所示。 根据平衡条件:
由Fs=qx可绘出剪力图,如图6.10(c)所示;由 描点可绘出弯矩图,如图6.10(d)
第6章 弯 曲
6.3 弯曲时的正应力与强度计算
m,材料的许用应力[σ]=150 MPa, 求此悬臂梁的许可载荷。
图 6.15
第6章 弯 曲 解 绘出悬臂梁的弯矩图,如图6.15(b)所示。 图中,Mmax=Fl=4000F 梁的横截面抗弯截面系数为
由梁的弯曲正应力强度条件得
因此, 悬臂梁的许可载荷为F=25 000 N。
第6章 弯 曲 【例6.5】 某建筑工地上, 用长l=3 m的矩形截面木板做
第06章弯曲变形题解
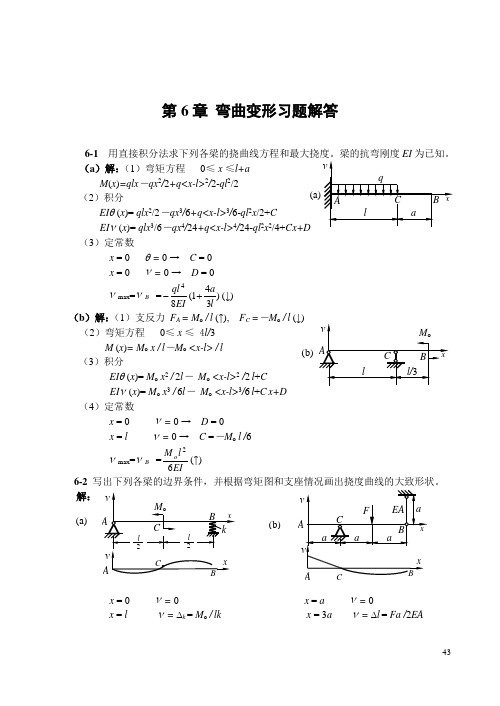
第6章 弯曲变形习题解答6-1 用直接积分法求下列各梁的挠曲线方程和最大挠度。
梁的抗弯刚度EI 为已知。
(a )解:(1)弯矩方程 0≤ x ≤l+aM (x )=qlx -qx 2/2+q<x-l>2/2-ql 2/2(2)积分 EI θ (x )= qlx 2/2-qx 3/6+q<x-l>3/6-ql 2x /2+CEI ν(x )= qlx 3/6-qx 4/24+q<x-l>4/24-ql 2x 2/4+Cx+D (3)定常数x = 0 θ = 0 → C = 0 x = 0 ν= 0 → D = 0νmax =ν B =)341(84laEI ql +-(↓)(b )解:(1)支反力 F A = M o / l (↑), F C =-M o / l (↓) (2)弯矩方程 0≤ x ≤ 4l/3M (x )= M o x / l -M o <x-l> / l (3)积分EI θ (x )= M o x 2 / 2l - M o <x-l>2 /2 l +CEI ν(x )= M o x 3 / 6l - M o <x-l>3/6 l +C x+D (4)定常数x = 0 ν= 0 → D = 0x = l ν= 0 → C =-M o l /6νmax =ν B =EIl M o 62(↑)6-2 写出下列各梁的边界条件,并根据弯矩图和支座情况画出挠度曲线的大致形状。
解:x = 0 ν= 0 x = a ν= 0x = l ν= ∆k = M o / lk x = 3a ν= ∆l = Fa /2EA(b) ν(b) (a)x = 0 θ = 0 x = 0 ν= 0 x = 0 ν=0 x = 3a ν= 0x = 0 ν= 0 x = 0 ν= 0 , θ = 0x =2a ν=0 x = 2a ν= 06-3 用叠加法求下列各梁C 截面的挠度和B 截面的转角。
弯曲变形

3)建立相当系统 (以多余约束反力代 替多余约束。) 4)变形协调条件
f B = f BP + f BY = 0
B
f B = 0(VB = 0)
5)物理关系 查表 : Pa 2 f BP = + ( 3L − a ) 6 EI Z 3 YB L f BY = − B 3EI Z
6)补充方程:
Pa 2 YB L3 ( 3L − a ) − =0 6 EI Z 3EI Z
PL2 → D1 = D2 = 0, C1 = C2 = 24
4)求θC和VC: θ
4)求θC和VC: θ
1 3 1 L 3 PL2 BC段:EI zV = − Px + P( x − ) + x 6 3 2 24 PL3 1 L 3 PL2 PL3 V |x = L = − + P( L − ) + ×L= − (↓) 6 3 2 24 12 EI Z
6)刚度校核:
令 = 0(即 = 0处) V' θ L →x= 3
f
max
M 0 2 M 0L − x + =0 2L 6
=
M 0 L2 9 3EI Z
< [ f ] 刚度满足要求。
例二、长度为L的梁AC,其EI为常数,在自由端承 受集中力P(如图),试求自由端C的挠度和转角。 解: 1)外力分析: RA = P(↓), R B = 2 P ( ↑ ) 2)内力分析及挠曲线 微分方程及其积分 AB段:0 ≤ x ≤ L / 2 ) (
M 0L C = 6
5)求θA,θB。
M 0L ( θ A = θ (0 ) = 6 EI Z M 0L θ B = θ (L ) = − ( 3EI Z
建筑力学—组合变形及答案讲解
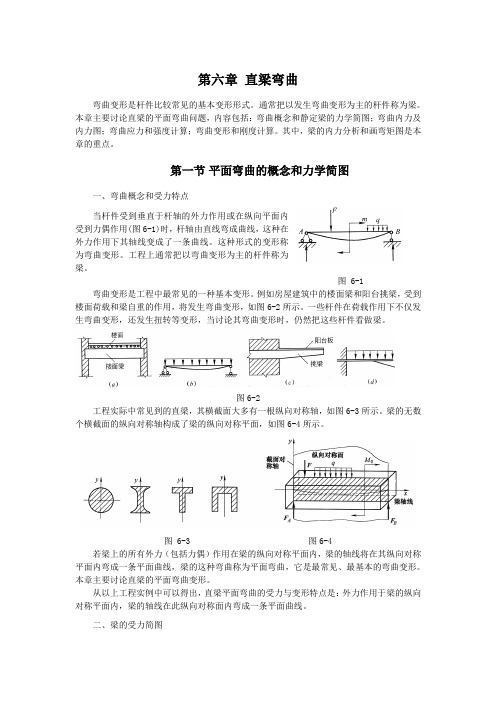
第六章直梁弯曲弯曲变形是杆件比较常见的基本变形形式。
通常把以发生弯曲变形为主的杆件称为梁。
本章主要讨论直梁的平面弯曲问题,内容包括:弯曲概念和静定梁的力学简图;弯曲内力及内力图;弯曲应力和强度计算;弯曲变形和刚度计算。
其中,梁的内力分析和画弯矩图是本章的重点。
第一节平面弯曲的概念和力学简图一、弯曲概念和受力特点当杆件受到垂直于杆轴的外力作用或在纵向平面内受到力偶作用(图6-1)时,杆轴由直线弯成曲线,这种在外力作用下其轴线变成了一条曲线。
这种形式的变形称为弯曲变形。
工程上通常把以弯曲变形为主的杆件称为梁。
图 6-1 弯曲变形是工程中最常见的一种基本变形。
例如房屋建筑中的楼面梁和阳台挑梁,受到楼面荷载和梁自重的作用,将发生弯曲变形,如图6-2所示。
一些杆件在荷载作用下不仅发生弯曲变形,还发生扭转等变形,当讨论其弯曲变形时,仍然把这些杆件看做梁。
图6-2工程实际中常见到的直梁,其横截面大多有一根纵向对称轴,如图6-3所示。
梁的无数个横截面的纵向对称轴构成了梁的纵向对称平面,如图6-4所示。
图 6-3 图6-4若梁上的所有外力(包括力偶)作用在梁的纵向对称平面内,梁的轴线将在其纵向对称平面内弯成一条平面曲线,梁的这种弯曲称为平面弯曲,它是最常见、最基本的弯曲变形。
本章主要讨论直梁的平面弯曲变形。
从以上工程实例中可以得出,直梁平面弯曲的受力与变形特点是:外力作用于梁的纵向对称平面内,梁的轴线在此纵向对称面内弯成一条平面曲线。
二、梁的受力简图为了便于分析和计算直梁平面弯曲时的强度和刚度,需建立梁的力学简图。
梁的力学简图(力学模型)包括梁的简化、荷载的简化和支座的简化。
1、梁的简化由前述平面弯曲的概念可知,载荷作用在梁的纵向对称平面内,梁的轴线弯成一条平面曲线。
因此,无论梁的外形尺寸如何复杂,用梁的轴线来代替梁可以使问题得到简化。
例如,图6-1a和图6-2a所示的火车轮轴和桥式起重机大梁,可分别用梁的轴线AB代替梁进行简化(图6-1b和图6-2b)。
材料力学(赵振伟)梁的弯曲变形2

3. 应用叠加原理的若干情况 1 ) 荷载的分解或重组
q m
q
L/2 L/2
L
F
q
q
m L/2 L/2
F
例
q0
EI
A 求图示自由端的挠度。
L2
L2
q0
L
w1
q0
w3
B
w2
L2
L2
w1
q0 L4 8EI
w2
q0 L 24
8EI
q0 L4 128EI
w3
B
L 2
q0 L 23
6EI
L 2
q0 L4 96EI
wA
w1
w2
w3
41q0 L4 384EI
2) 逐段刚化法
依据: 若结构可分为若干部分,且各部分在荷载作用下的 变形不是相互独立的,那么,结构中 A 点的位移是各个部 分在这一荷载作用下的变形在 A 点所引起的位移的叠加。
A EI a
变形刚体
F
F
Fa 2
B
C
a/2
wwww1122
B (F1, F2,, Fn ) B1(F1) B2 (F2 ) Bn(Fn )
yB (F1, F2,, Fn ) yB1(F1) yB2 (F2 ) yBn(Fn )
叠加法的特征: 1、梁在简单载荷作用下挠度、转角应为已知或有变形表可查; 2、叠加法适用于求梁个别截面的挠度或转角值。
分析和讨论
q
在下列不同的支承方 式中,哪一种刚度最高?
q
q
分析和讨论
q
梁由混凝土材料制成,如果横截面从左图改为右图,能 够改善强度吗?能够改善刚度吗?
梁的材料由普通钢改为优质钢,能够改善强度吗? 梁的材料由普通钢改为优质钢,能够改善刚度吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲变形
但在另外一些情况下,有时却要求构 件具有较大的弹性变形,以满足特定 的工作需要.
例如,车辆上的板弹簧,要求有足够大
的变形,以缓解车辆受到的冲击和振 动作用.
F 2
F 2
F
4/73
弯曲变形
二、基本概念(basic concepts)
1、挠度( Deflection ) 横截面形心 C (即轴线上的点)在垂直于 x 轴方向的线位移,称 为该截面的挠度,用w表示。
1
(0 x a )
Fb 2 2 2 ( 1 w1 l b 3x ) 6lEI Fbx 2 2 [ l b x 2] w1 6lEI
2
(a x l )
Fb l 1 2 2 2 2 [ ( x a ) x ( l b )] 2 w 2' 2lEI b 3 Fb l 3 3 2 2 [ ( ( x a ) w2 x l b ) x] 6lEI b
Fl 2 Fl 2 Fl 2 ( ) max | x l EI 2 EI 2 EI Fl 3 wmax w | x l ( ) 3 EI
18/73
弯曲变形
【例题2】 图示一抗弯刚度为 EI 的简支梁,在全梁上受集度为q
的均布荷载作用.试求此梁的挠曲线方程和转角方程,并确定其
挠曲线的微分方程
弯曲变形
M w EI 1 w2 3/2
w'
2
与 1 相比十分微小而可以忽略不计,故上式可近似为
M w" EI
此式称为 梁的挠曲线近似微分方程
12/73
弯曲变形
6–3 用积分法求弯曲变形
(Beam deflection by integration )
M 一、挠曲线近似微分方程 w EI tg w ' w '( x ) 1、积分一次得转角方程
x l/2
时, w 0
A
l
B
梁的转角方程和挠曲线方程分别为
RB
q (6lx 2 4 x 3 l 3 ) 24 EI
最大转角和最大挠度分别为
qx w (2lx 2 x 3 l 3 ) 24 EI
ql 3 A B 24 EI
21/73
在 x=0 和 x=l 处转角的绝对值相等且都是最大值, max
Pab( l a ) B 6lEI
28/73
弯曲变形
w' 0 处 先研究第一段梁,令 w1 0 得
简支梁的最大挠度应在
Fb 2 2 (l b 3 x 2) 0 1 w 1' 6lEI
l 2 b2 a (a 2b ) x1 3 3
当 a > b时, x1 < a 最大挠度确实在第一段梁中
M w EI
ql 3 q 4 EIw x x Cx D 12 24
20/73
弯曲变形
EIw
边界条件 或者
ql 2 q 3 x x C 4 6
EIw
ql 3 q 4 x x Cx D 12 24
q wmax B
x 0, l
时,
w0
A x RA
31/73
弯曲变形
1、载荷叠加(Superposition of loads) 多个载荷同时作用于结构而 引起的变形等于每个载荷单独作用于结构而引起的变形的代 数和.
( F1 , F2 , , Fn ) 1 ( F1 ) 2 ( F2 ) n ( Fn )
2 Fb Fbl 2 2 3 w | ( l b ) 0.0642 w max x x1 EI 9 3lEI
弯曲变形
梁中点 C 处的挠度为
Fb Fbl 2 2 wC (3l 4b ) 0.0625 48 EI EI
2
2 Fb Fbl 2 2 3 y | ( l b ) 0.0642 w max x x1 EI 9 3lEI
EIw Md x C1
2、再积分一次, 得挠度方程
EIw Mdxdx C1 x C 2
13/73
弯曲变形
二、积分常数的确定
1、边界条件(Boundary condition) 2、连续条件 (Continuum condition) 在简支梁中, 左右两铰支座处的 挠度 w A 和 w B 都等于0
弯曲变形
D点的连续条件
在x=a处
w2 w1 w1 w2
F
RA
A
1
D
2
RB
B
边界条件 在 x = 0 处, w1 0 在 x = l 处, w2 0
a
b
l
代入方程可解得:
D1 D 2 0
Fb 2 2 (l b ) C1 C 2 6l
26/73
弯曲变形
w
A
C
B
x w挠度
C'
B'
5/73
弯曲变形
2、转角 (slope)
横截面对其原来位置的角位移,称为该截面的转角, 用 表示。
w
A
C' C B
x
w挠度(
B
转角
6/73
弯曲变形
3、挠曲线 (Deflection curve) 挠曲线方程为 梁变形后的轴线称为挠曲线
w f ( x)
式中,x 为梁变形前轴线上任一点的横坐标,w 为该点的挠度。 w
C2 0
梁的转角方程和挠曲线方程分别为
Fx EIw Flx 2
2
Flx Fx EIw 2 6
17/73
弯曲变形
y A
F
B x
wmax
l
Fx 2 EIw Flx 2 2 3 Flx Fx EIw 2 6
max
max 和 wmax都发生在自由端截面处
(4)
16/73
弯曲变形
Fx 2 EIw Flx C1 (3) 2 2 3 EIw Flx Fx C 1x C 2 2 6 边界条件 x 0, w 0
x 0,
将边界条件代入(3)
w A
F
B x
(4)
x
l
w 0
(4)两式中,可得
C1 0
2 3
结论: 在简支梁中, 不论它受什么荷载作用, 只要挠曲线上无 拐点, 其最
大挠度值都可用梁跨中点处的挠度值来代替, 其精确度是能满足工程要求 的.
30/73
弯曲变形
6–4 用叠加法求弯曲变形
( Beam deflections by superposition )
一、叠加原理 (Superposition )
27/73
弯曲变形
将 x = 0 和 x = l 分别代入两个转角方程, 两支座处截面的转角
Pab( l b ) A 1 | x 0 6lEI Pab( l a ) B 2 | x l 6lEI
当 a > b 时, 右支座处截面的转角绝对值为最大
max
两段梁的弯矩方程分别为
F RA
A 1 a D b l 2
RB
B
x
b M 1 RA x F x l
(0 x a ) (a x l )
23/73
b M2 F x F ( x a) l
弯曲变形
两段梁的挠曲线方程 1 ( 0 x a) 挠曲线微分方程
b M 1 RA x F x l
w( F1 , F2 , , Fn ) w1 ( F1 ) w2 ( F2 ) wn ( Fn )
A B
wA 0
A
wB 0
B
在悬臂梁中,固定端处的挠度 w A 和转角 A 都应等于零.
wA 0
A 0
14/73
弯曲变形
【例题1】 图示一抗弯刚度为 EI 的悬臂梁, 在自由端受一 集中力 F 作用。试求梁的挠曲线方程和转角方程, 并确定 其最大挠度 wmax 和最大转角 max 。 F
max 和 wmax
q A l B
19/73
弯曲变形
q
解: 由对称性可知,梁的 两个支反力为
A x
B
ql RA RB 2
RA
l
RB
此梁的弯矩方程及挠曲线微分方程分别为
ql q 2 M ( x) x x 2 2 ql q 2 EIw x x 2 2
ql 2 q 3 EIw x x C 4 6
Chapter 6 Deflection of Beams
弯曲变形
目 录
6-1 基本概念及工程实例
6-2 挠曲线的微分方程
6-3 用积分法求弯曲变形
6-4 用叠加法求弯曲变形
6-5 静不定梁的解法
6-6 提高弯曲刚度的措施
弯曲变形
6–1 基本概念及工程实例
一. 工程实例
构件的变形不能超过允许值
3/73
挠度 向上为正,向下为负; 转角 自x 转至切线方向,逆时针转为正,顺时针转为负。 w
A C B x
挠曲线
C'
w挠度
转角
B
9/73
弯曲变形
6–2 挠曲线的微分方程
( Differential equation of the deflection curve)
一、挠曲线方程的建立
1、纯弯曲时曲率与弯矩的关系
(0 x a )
b EIw 1 M 1 F x l
