2018届一轮复习人教A版三角函数图象及运算 课件
合集下载
人教A版高考总复习一轮理科数学精品课件 第4章 三角函数、解三角形 解答题专项二 三角函数与解三角形

令
1
− 2 cos
2x-
3
sin
4
2
π
+6
π
2x+6
∈
π
2
π
3
2 +
1
-2(cos
+
2x-1)=
3
sin
2
2
1
2x-2cos
2π
)
3
1-cos (2-
2x+1=-
2
1
-2cos
3
sin
4
−
1
cos
2
1
2x+2
1
2x+2
1
2x-4cos
2x+1
+1.
3π
2π, 2
+ 2π ,k∈Z,则 x∈
解答题
专项二
三角函数与解三角形
考情分析:高考对三角函数与解三角形的考查有较强的规律性,三角解答题
与数列解答题交替考查.只考小题的试卷有三道题目,共15分;考解答题时
有一大一小两个题目,共17分.在三个小题中,分别考查三角函数的图象与
性质、三角变换、解三角形;在一个小题和一个大题中,小题要么考查三角
π
6
+1,
,
1
≥-2,
结合正弦函数的图象与性质可知
π
−2
1
+1=- sin
2
π
2x-6
∈
7π
5π
− 6 ,− 6
∪
π 5π
−6, 6
,
,
即所求实数 x 的取值集合为 ∣
π
−
2
2018学年高一数学人教A版必修四课件:第一章 三角函数1 章末高效整合 精品

2.明确三角函数的定义,牢记三角函数值的符号 (1)定义:角 α 的顶点放在坐标原点,始边与 x 轴非负半轴重合,角 α 的终边 与单位圆的交点为 P(x,y),则 y=sin α,x=cos α,xy=tan α(x≠0). 即①y 叫作 α 的正弦,记作 sin α; ②x 叫作 α 的余弦,记作 cos α; ③xy叫作 α 的正切,记作 tan α.
A.ω=2π,φ=π6 B.ω=π,φ=π6 C.ω=π,φ=π3 D.ω=2π,φ=π3
(2)经过怎样的变换由函数 y=sin 2x 的图象可得到 y=cos x+π4的图象? 解析: (1)由函数的图象可知 A=2,T=4×56-13=2,所以 ω=2Tπ=π,因 为函数的图象经过13,2,所以 2=2sinπ3+φ,得π3+φ=2kπ+π2,k∈Z,因为|φ| <π2,所以取 k=0,所以 φ=π6,所以 ω=π,φ=π6.
(2)利用诱导公式,可以把任意角的正弦、余弦函数值化为锐角三角函数值, 其一般步骤为:负化正(公式三或一)、大化小(公式一)、锐角求值(公式二或四).
化简求值中注意利用角与角之间隐含的互余或互补关系,从而简化解题过 程.
5.探究性质应用,对比周期公式 (1)函数 y=sin x 和 y=cos x 的周期是 2π,y=tan x 的周期是 π;函数 y= Asin(ωx+φ)和 y=Acos(ωx+φ)的周期是|2ωπ|,y=Atan(ωx+φ)的周期是|ωπ|. (2)函数 y=sin x 和 y=cos x 的有界性为-1≤sin x≤1,-1≤cos x≤1;函数 y= tan x 没有最值,其有界性可用来解决三角函数的最值问题. (3)利用函数的单调性比较同名三角函数值的大小时,注意利用诱导公式将角 转化到同一单调区间内.求形如 f(ωx+φ)(f 为 sin,cos,tan)的单调区间时,应 采用整体代换的思想将 ωx+φ 视为整体,求解时注意 x 的范围以及 ω,f 的符号 对单调性的影响.
高考数学一轮复习三角函数的图像与性质培优课件

π
3
5π
2kπ6
5π
π
, 2π +
6
6
,∴函数的递增区间为
π
0, 6
.
π
≤x≤2kπ+ (k∈Z).
6
(k∈Z).
考向2.由单调性求参数
典例突破
例 4.已知 ω>0,函数 f(x)=sin
是
.
π
+4
在
π
,π
2
上是减少的,则 ω 的取值范围
答案:
1 5
,
2 4
π
π
解析:由2 <x<π,ω>0,得 2
3π ∴0<a≤ π ,∴a 的最大值为π .
≤ 4 ,
4
4
> 0,
π 3π
−4, 4
,
(2)由题意可知,[a,2]⊆
π
π
− ,
π
2π + 4
, 2π +
5π
4
(k∈Z).
突破技巧1.三角函数定义域的求法
将求复杂函数的定义域问题转化为求解简单的三角函数不等式.
2.简单三角不等式的解法
(1)利用三角函数线求解.
(2)利用三角函数的图像求解.
1
y=tan -1的定义域为
.
(2)函数 y=lg(sin 2x)+ 9- 2 的定义域为
π
3
的递减区间是函数 y=sin 2 −
的递增区间.
由
π
2kπ-2
π
≤2x-3
π
≤2kπ+ 2 ,k∈Z,得
故所给函数的递减区间为 π −
人教A版高中数学必修一课件 《三角函数的图象与性质》三角函数(第二课时正、余弦函数的周期性与奇偶性)

15
三角函数奇偶性的判断 【例 2】 判断下列函数的奇偶性: (1)f(x)=sin-12x+π2; (2)f(x)=lg(1-sin x)-lg(1+sin x); (3)f(x)=1+s1i+n xs-in cxos2x.
16
[思路点拨]
17
[解] (1)显然x∈R,f(x)=cos12x,
A.-12
B.12
C.-
3 2
D.
3 2
24
[思路点拨] (1)先作出选项A,B中函数的图象,化简选项C、D中函 数的解析式,再判断奇偶性、周期性.
(2)先依据f(x+π)=f(x)化简f53π;再依据f(x)是偶函数和x∈0,π2,f(x) =sin x求值.
25
(1)D (2)D [(1)y=cos|2x|是偶函数,y=|sin 2x|是偶函数,y= sinπ2+2x=cos 2x是偶函数,y=cos32π-2x=-sin 2x是奇函数,根据公 式得其最小正周期T=π.
32
[提示] (1)×.因为对任意 x,sin23π+x与 sin x 并不一定相等. (2)×.不是所有的函数都有最小正周期,如函数 f(x)=5 是周期函数, 就不存在最小正周期. (3)×.函数 y= sin x的定义域为{x|2kπ≤x≤2kπ+π,k∈Z},不关于 原点对称,故非奇非偶. [答案] (1)× (2)× (3)×
23
【例3】 (1)下列函数中是奇函数,且最小正周期是π的函数是
() A.y=cos|2x|
B.y=|sin 2x|
C.y=sinπ2+2x
D.y=cos32π-2x
(2)定义在R上的函数f(x)既是偶函数,又是周期函数,若f(x)的最小正
周期为π,且当x∈0,π2时,f(x)=sin x,则f53π等于( )
三角函数奇偶性的判断 【例 2】 判断下列函数的奇偶性: (1)f(x)=sin-12x+π2; (2)f(x)=lg(1-sin x)-lg(1+sin x); (3)f(x)=1+s1i+n xs-in cxos2x.
16
[思路点拨]
17
[解] (1)显然x∈R,f(x)=cos12x,
A.-12
B.12
C.-
3 2
D.
3 2
24
[思路点拨] (1)先作出选项A,B中函数的图象,化简选项C、D中函 数的解析式,再判断奇偶性、周期性.
(2)先依据f(x+π)=f(x)化简f53π;再依据f(x)是偶函数和x∈0,π2,f(x) =sin x求值.
25
(1)D (2)D [(1)y=cos|2x|是偶函数,y=|sin 2x|是偶函数,y= sinπ2+2x=cos 2x是偶函数,y=cos32π-2x=-sin 2x是奇函数,根据公 式得其最小正周期T=π.
32
[提示] (1)×.因为对任意 x,sin23π+x与 sin x 并不一定相等. (2)×.不是所有的函数都有最小正周期,如函数 f(x)=5 是周期函数, 就不存在最小正周期. (3)×.函数 y= sin x的定义域为{x|2kπ≤x≤2kπ+π,k∈Z},不关于 原点对称,故非奇非偶. [答案] (1)× (2)× (3)×
23
【例3】 (1)下列函数中是奇函数,且最小正周期是π的函数是
() A.y=cos|2x|
B.y=|sin 2x|
C.y=sinπ2+2x
D.y=cos32π-2x
(2)定义在R上的函数f(x)既是偶函数,又是周期函数,若f(x)的最小正
周期为π,且当x∈0,π2时,f(x)=sin x,则f53π等于( )
高三数学一轮复习精品课件1:三角函数的图像与性质

(2)把函数 y=tanπ3-2x变为 y=-tan2x-π3. 由 kπ-π2<2x-π3<kπ+π2,k∈Z, 得 kπ-π6<2x<kπ+56π,k∈Z, 即k2π-1π2<x<k2π+51π2,k∈Z. 故函数 y=tanπ3-2x的单调减区间为 k2π-1π2,k2π+51π2(k∈Z).
________.
解析:当 x∈0,π2时,2x-π6∈-π6,56π,sin2x-π6∈
-12,1,
故 3sin2x-π6∈-32,3, 即此时函数 f(x)的值域是-32,3.
答案:-32,3
2.(2014·湛江调研)函数 y=lg(sin x)+
义域为________.
解析:要使函数有意义必须有
故 y=2cos2x+5sin x-4 的值域为[-9,1].
(2)∵x∈π6,76π,∴sin x∈-12,1. 又 y=3-sin x-2cos2x=3-sin x-2(1-sin2x)=
2sin
x-142+78.
∴当 sin x=14时,ymin=78,
当 sin x=-12或 sin x=1 时,ymax=2.
1.三角函数存在多个单调区间时易错用“∪”联结. 2.研究三角函数单调性、对称中心、奇偶性及对称轴 时易忽视“k∈Z”这一条件.
[试一试]
1.函数 y=tanπ4-x的定义域是________.
答案:xx≠kπ+34π
,k∈Z,x∈R
2.(2013·南京三模)函数 y=sin x-π4≤x≤34π的值域是
第四章 三角函数
4.3三角函数的图像与性质
君不见,黄河之水天上来,奔流到海不复回。 君不见,高堂明镜悲白发,朝如青丝暮成雪。 人生得意须尽欢,莫使金樽空对月。 天生我材必有用,千金散尽还复来。 烹羊宰牛且为乐,会须一饮三百杯。 岑夫子,丹丘生,将进酒,杯莫停。 与君歌一曲,请君为我倾耳听。 钟鼓馔玉不足贵,但愿长醉不复醒。 古来圣贤皆寂寞,惟有饮者留其名。 陈王昔时宴平乐,斗酒十千恣欢谑。 主人何为言少钱,径须沽取对君酌。 五花马,千金裘,呼儿将出换美酒,与尔同销万古愁
高考数学一轮复习第三章第五讲三角函数的图象与性质课件

由于 f(x)=tan 2x-π4的最小正周期为π2,故排除 D.故选 C.
答案:C
2.(考向 2)若函数 f(x)=sin ωx+4π(ω>0)在π2,π上单调递增, 则 ω 的取值范围是( )
A.12,54
B.12,34
C.0,
1 4
D.(0,2]
解析:∵函数 f(x)=sin ωx+π4(ω>0)在π2,π上单调递增, 则 ω·π2+π4≥-π2+2kπ,且 ω·π+π4≤π2+2kπ,k∈Z, 求得 4k-32≤ω≤2k+14,取 k=0,得-32≤ω≤14. ∵ω>0,∴可得 ω 的取值范围为0,41.故选 C. 答案:C
考点一 三角函数的定义域
1.(2023 年金牛区校级月考)函数 y=tan2x-π4的定义域为
()
A.xx≠kπ+π2,
k∈Z
B.xx≠k2π+ 83π,k∈Z
C.xx≠2kπ+π2,
k∈Z
D.xx≠2kπ+38π,
k∈Z
解析:由题意,得 2x-π4≠kπ+π2,k∈Z,解得 x≠k2π+83π,k∈Z, 故定义域为xx≠k2π+ 83π,k∈Z.故选 B.
正数;若 A<0,借助导公式 sin α=-sin (α±π)或 cos α=-cos (α±π)
将 A 化为正数. (2)根据 y=sin x 和 y=cos x 的单调区间列不等式求解.
[例 3]函数 f(x)=3sin 23π-2x的一个单调递减区间是(
)
A.71π2,1132π
B.1π2,71π2
2.正弦、余弦、正切函数的图象与性质(下表中 k∈Z)
函数
y=sin x
y=cos x
y=tan x
答案:C
2.(考向 2)若函数 f(x)=sin ωx+4π(ω>0)在π2,π上单调递增, 则 ω 的取值范围是( )
A.12,54
B.12,34
C.0,
1 4
D.(0,2]
解析:∵函数 f(x)=sin ωx+π4(ω>0)在π2,π上单调递增, 则 ω·π2+π4≥-π2+2kπ,且 ω·π+π4≤π2+2kπ,k∈Z, 求得 4k-32≤ω≤2k+14,取 k=0,得-32≤ω≤14. ∵ω>0,∴可得 ω 的取值范围为0,41.故选 C. 答案:C
考点一 三角函数的定义域
1.(2023 年金牛区校级月考)函数 y=tan2x-π4的定义域为
()
A.xx≠kπ+π2,
k∈Z
B.xx≠k2π+ 83π,k∈Z
C.xx≠2kπ+π2,
k∈Z
D.xx≠2kπ+38π,
k∈Z
解析:由题意,得 2x-π4≠kπ+π2,k∈Z,解得 x≠k2π+83π,k∈Z, 故定义域为xx≠k2π+ 83π,k∈Z.故选 B.
正数;若 A<0,借助导公式 sin α=-sin (α±π)或 cos α=-cos (α±π)
将 A 化为正数. (2)根据 y=sin x 和 y=cos x 的单调区间列不等式求解.
[例 3]函数 f(x)=3sin 23π-2x的一个单调递减区间是(
)
A.71π2,1132π
B.1π2,71π2
2.正弦、余弦、正切函数的图象与性质(下表中 k∈Z)
函数
y=sin x
y=cos x
y=tan x
高考数学一轮复习课件:三角函数的图像与性质

4.sinxcosx 与 sinx±cosx 同时存在型可换元转化. 5.y=acssiinnxx++db(或 y=acccoossxx++db)型,可用分离常数法或由 |sinx|≤1 来解决. 6.y=cacsoinsxx++bd型,可用斜率公式来解决.
求下列函数的值域: (文)(1)y=2s1in+x·scionsx2x,x∈[0,2π]; (2)y=sin2x+2sinx·cosx+3cos2x.
(2)求三角函数定义域时,通常归结为解三角不等式或不 等式组.
求下列各函数的定义域: (1)y=1-1cosx;(2)y= sinx+ 1-tanx. [分析]
[解析] (1)函数 y=1-1cosx有意义时,1-cosx≠0,即 cosx≠1,所以 x≠2kπ(k∈Z),所以函数的定义域为{x|x≠2kπ, x∈R,k∈Z}.
(2)第(2)小题解不等式组 2
,然后利用数轴求
tanx≥0
解.
[解析] (1)要使原函数有意义,必须有:
2sinx-1>0, 1-2cosx≥0,
即csionsxx>≤12,12.
由图知,原函数的定义域为:
[2kπ+3π,2kπ+56π)(k∈Z).
(2)要使函数有意义 2+log12 x≥0,
() A.[-2,2]
B.[- 3, 3]
C.[-1,1]
D.[-
23,
3 2]
[答案] B
[解析] 本题考查两角和的余弦公式、辅助角公式,三角 函数的值域.
由题意知,f(x)=sinx-cosxcosπ6+sinxsin6π=32sinx-
3 2 cosx
= 3( 23sinx-12cosx)= 3sin(x-6π),
一轮复习三角函数PPT课件

[自主解答] (1)∵在(0,π)内终边在直线 y= 3x 上的角 是π3,∴终边在直线 y= 3x 上的角的集合为
α|α=π3+kπ,k∈Z. (2)∵θ=67π+2kπ(k∈Z), ∴θ3=27π+2k3π(k∈Z). 依题意 0≤27π+2k3π<2π⇒-37≤k<178,k∈Z.
[备考方向要明了]
考什么 1.了解任意角的概念. 2.了解弧度制的概念,能进
行弧度与角度的互化. 3.理解任意角三角函数(正
弦、余弦、正切)的定 义.
1.三角函怎数么的定考义与三 角恒等变换等相结 合,考查三角函数
求 值问 题,如2008
年 高考T15等.
[归纳
1.角的有关概念
知识整合]
角的特点
三角函数线
有向线段 ____ 有向线段____ 有向线段____
MP
OM
AT
为正弦线
为余弦线
为正切线
[探究] 3.三角函数线的长度及方向各有什么 意义?
提示:三角函数线的长度表示三角函数值的绝 对值,方向表示三角函数值的正负.
[自测 牛刀小试] 1.(教材习题改编)下列与94π的终边相同的角 α 的集合为___.
解析:∵94π=94×180°=360°+45° ∴与94π 终边相同的角可表示为 k·360°+45°(k∈Z)
答案:{α|α=k·360°+ 45°(k∈Z)}
2.(教材习题改编)若角θ同时满足sin θ<0且tan θ<0, 则角θ的终边一定落在第________象限. 解析:由sin θ<0,可知θ的终边可能位于第三或第 四象限,也可能与y轴的非正半轴重合.由tan θ<0, 可知θ的终边可能位于第二象限或第四象限,可知θ的
2.弧度的概念与公式
人教版高中总复习一轮数学精品课件 第4章 三角函数与解三角形 4.1 任意角和弧度制、三角函数的概念
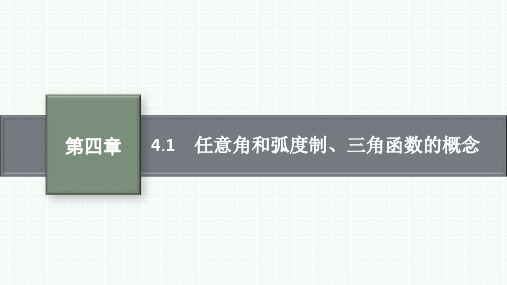
由三角函数的定义可得 cos
3
D.-5
A 在第二象限,又因为圆 O 为单位圆,
3
α=-5.
(2)已知角α的终边在直线3x+4y=0上,则5sin α+5cos α+4tan α= -2或-4 .
由题意,设点 P(-4a,3a)为角 α 终边上的任意一点,
r=|OP|=|5a|(a≠0)(O 为坐标原点).
在的象限即可.
3.确定角 kα, (k≥2,且 k∈N*)的终边的位置:先用终边相同角的形式表示出
角 α 的范围,再写出 kα 或 的范围,最后根据 k 的可能取值讨论确定角 kα 或
的终边所在位置.
对点训练 1
3π
4π
(1)给出下列四个命题:①- 4 是第二象限角;② 3 是第三象限角;③-400°是
象限,所以 是第二或第四象限角.
2
能力形成点2 利用三角函数定义求三角函数值
例 2 (1)如图,在平面直角坐标系 Oxy 中,角 α 的终边与单位圆交于点 A,
4
点 A 的纵坐标为5,则 cos α 的值为( D )
4
A.5
因为点
所以点
4
B.-5
3
C.5
4
A 的纵坐标为 ,且点
5
3
A 的横坐标为-5.
,
.
3
7 21 21
(3)已知角α为第三象限角,则2α的终边在 第一或第二象限或y轴的非负半轴
.
3π
由α是第三象限角,得 π+2kπ<α< 2 +2kπ(k∈Z),
则2π+4kπ<2α<3π+4kπ(k∈Z).
人教A版高中数学必修一课件 《三角恒等变换》三角函数PPT(第4课时二倍角的正弦、余弦、正切公式)

判断正误(正确的打“√”,错误的打“×”) (1)10α 是 5α 的倍角,5α 是52α的倍角.( √ ) (2)二倍角的正弦、余弦、正切公式的适用范围是任意角.( × ) (3)存在角 α,使得 sin 2α=2sin α 成立.( √ ) (4)对于任意角 α,总有 tan 2α=1-2tatannα2α.( × )
解:(1)1-tatnan3023°0°=121×-2ttaann23300°°
=12tan 60°= 23.
(2)原式=cossi1n01°0°-co3ss1in0°10°
=212cossin1100°°-co2s31si0n°10°
=4(sin
30°cos 10°-cos 30°sin 2sin 10°cos 10°
=ccooss 22αα=1.
(2)证明:法一:左边=csoinsπ4π4++αα-csionsπ4π4--αα=
sinπ4+αcosπ4-α-sinπ4-αcosπ4+α cosπ4+αcosπ4-α
=cosisnπ4π4++ααs-inπ4π4++αα
=12sinsinπ2+2α2α=2csions 22αα=2tan 2α=右边. 所以等式成立.
=cos
π6=
3 2.
答案:
3 2
4.已知 α∈π2,π,sin α= 55. (1)求 sin 2α,cos 2α 的值; (2)求 cos56π-2α的值.
解:(1)因为 α∈π2,π,sin α= 55,
所以 cos α=-
1-sin2α=-2
5
5 .
sin 2α=2sin αcos α=2× 55×-255=-45,
cos α
sin α
cos α sin α
数学一轮文科复习课件三角函数的图像和性质

精品课件,精彩无限!
21
• 第(2)问中平移图象使这个函数为偶函数 是本题考查的重心,试题设计的使解题方
向有选择的余地,一是借助于直观的函数 图象,根据偶函数图象关于y轴对称解决, 二是根据偶函数的定义通过g(x)=g(-x) 对任意x恒成立,在得到的恒等式中不含x 的部分必须为0,求出m值.试题设计步 步深入,是一道考查三角函数图象与性质 的优秀试题.
(2)先求出 ωx+φ 在[-2π,0]上的范围,然后根据单调性 求解.
精品课件,精彩无限!
16
变式迁移 1 用五点作图法画出函数 y= 3sin2x+cos2x的图象.
精品课件,精彩无限!
17
【例 2】 (1)已知函数 y=-sin2x+ 3sinx+54,求其取得 最大值和最小值时的 x,并说出最大值和最小值是什么;
精品课件,精彩无限!
12
4.函数 y=cos(x+π3),x∈(0,3π]的值域是________.
解析:∵0<x≤π3,∴π3<x+π3≤23π, 又 y=cosx 在[0,π]上是减函数, ∴cos23π≤cos(x+π3)<cos3π, 即-12≤y<12.
精品课件,精彩无限!
13
探 究 热 点
(2)若 x∈[-π3,π4],求函数 f(x)=co1s2x+2tanx+1 的最值及 相应的 x 值.
• 思路分析: • (1)式可以看做关于 sinx 的二次函数,故可以用配方法解决,需
要注意 sinx 的有界性; • (2)式切化弦后不好处理,结合式子特点,可把 1 换成 sin2x+
cos2x,统一为关于 tanx 的二次函数求最值,这里要注意 x 有范 围限制,可由其确定 tanx 的取值范围.
高三数学一轮复习课件第18讲三角函数的图像与性质

π
平移 个单位长度,则平移后图像的对称轴为 (
12
π π
A.x= 2 - 6 (k∈Z)
π π
C.x= 2 -12 (k∈Z)
π
π
B.x= 2 + 6 (k∈Z)
π
π
D.x= 2 +12 (k∈Z)
[答案]
B
)
[解析] 平移后的图像对应的解析式为
π
π
π
y=2sin 2 x+12 ,令 2 + 12 =kπ+ 2 (k∈
π
T= .
||
2.正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半周期,相邻的对称
1
中心与对称轴之间的距离是 周期.正切曲线相邻两对称中心之间的距离是半周期.
4
3.三角函数中奇函数一般可化为 y=Asin ωx 或 y=Atan ωx 的形式,偶函数一般可化为 y=Acos
ωx+b 的形式.
D.与 b 无关,但与 c 有关
)
[答案]
B
[解析] 若 b=0,则
f(x)=sin2x+c=
1-cos 2
2
1
1
2
2
+c=- cos 2x+ +c 的
最小正周期是 π;若 b≠0,则
f(x)=sin2x+bsin x+c 的最小正周期是 2π.
故选 B.
教学参考
3.[2017·天津卷] 设函数
A
5π
8
=2,f
11π
=0,∴
8
3π
- 8 =4 (2m+1),m∈N,解得 T=2 +1,m∈
平移 个单位长度,则平移后图像的对称轴为 (
12
π π
A.x= 2 - 6 (k∈Z)
π π
C.x= 2 -12 (k∈Z)
π
π
B.x= 2 + 6 (k∈Z)
π
π
D.x= 2 +12 (k∈Z)
[答案]
B
)
[解析] 平移后的图像对应的解析式为
π
π
π
y=2sin 2 x+12 ,令 2 + 12 =kπ+ 2 (k∈
π
T= .
||
2.正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半周期,相邻的对称
1
中心与对称轴之间的距离是 周期.正切曲线相邻两对称中心之间的距离是半周期.
4
3.三角函数中奇函数一般可化为 y=Asin ωx 或 y=Atan ωx 的形式,偶函数一般可化为 y=Acos
ωx+b 的形式.
D.与 b 无关,但与 c 有关
)
[答案]
B
[解析] 若 b=0,则
f(x)=sin2x+c=
1-cos 2
2
1
1
2
2
+c=- cos 2x+ +c 的
最小正周期是 π;若 b≠0,则
f(x)=sin2x+bsin x+c 的最小正周期是 2π.
故选 B.
教学参考
3.[2017·天津卷] 设函数
A
5π
8
=2,f
11π
=0,∴
8
3π
- 8 =4 (2m+1),m∈N,解得 T=2 +1,m∈
人教版高中总复习一轮数学精品课件 第4章 三角函数与解三角形 4.3 三角函数的图象与性质
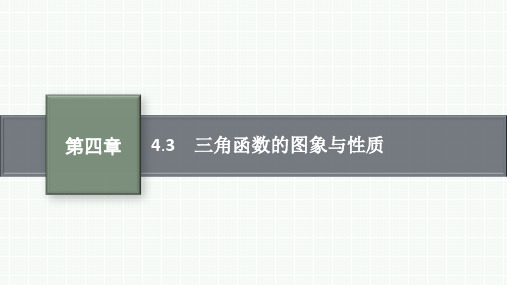
f(x)=√3sin ωx+cos
由函数 y=f(x)的图象与直线 y=2 的相邻两个交点的距离为 π,
知函数 y=f(x)的最小正周期 T=π,
又
令
得
2π
ω>0,所以 T= =π,解得 ω=2,即 f(x)=2sin
π
π
π
2kπ- ≤2x+ ≤2kπ+ (k∈Z),
2
6
2
π
π
kπ-3 ≤x≤kπ+6(k∈Z).
(2)f(x)为奇函数的充要条件是φ=kπ(k∈Z).
【知识巩固】
1.下列说法正确的画“√”,错误的画“×”.
(1)y=cos x是减函数.( × )
(2)若y=ksin x+1(k∈R),则y的最大值是k+1.( × )
(3)若非零实数T是函数f(x)的周期,则kT(k是非零整数)也是函数f(x)的周
3 7
的取值范围是 [2 , 4]
.
函数 y=cos x 的单调递增区间为[-π+2kπ,2kπ](k∈Z),
π π
+
≥
-π
+
2π,
5
1
2
4
则
(k∈Z),解得 4k-2 ≤ ≤2k-4(k∈Z),
π
π + ≤ 2π
又由
所以
4
5
1
4k-2-(2k-4)≤0(k∈Z),且
3 7
ω∈[2 , 4].
③当A>0(A<0)时,所列不等式的方向与y=sin x,y=cos x的单调区间对应的
不等式方向相同(反).
π
(2)对于函数 y=Atan(ωx+φ)(A,ω,φ 为常数),其周期 T=||,利用
高考数学一轮总复习 第3章 第4节 三角函数的图像与性

ω
ω
拓展延伸
1. 三角函数的周期 (1)若T是函数y=f(x)的周期,则必须是对于定义域内的每一个x值
都具有f(x+T)=f(x)(T≠0). (2)周期和最小正周期的区别:周期函数不一定有最小正周期(如y=
c(c为常数),任何非零实数都是它的周期,显然无最小正周期), 而三角函数的周期一般指最小正周期.
选 B.
3. 已知函数 f(x)=sinx-π2(x∈R),下面结论错误的是(
)
A. 函数 f(x)的最小正周期为 2π
B. 函数 f(x)在区间0,π2上是增函数
C. 函数 f(x)的图像关于直线 x=0 对称 D. 函数 f(x)是奇函数
解析: ∵y=sinx-π2=-cos x,∴T=2π,在0,π2上是增函数,图 像关于 y 轴对称,为偶函数.选 D
解析: (1)错误.正弦函数y=sin x在 2kπ-π2,2kπ+π2(k∈Z)内单调 递增,并不是在第一、四象限内递增.
(2)错误.如常数函数是周期函数但无最小正周期.
(3)正确.由cos(-x)=cos x可知余弦函数在定义域内是偶函数. π
(4)错误.由y=sin x的图像可知,当x=2kπ+ 2 ,k∈Z时 y=sin x取 得最大值.
最新考纲
基础梳理
第
自主测评
Байду номын сангаас
四
节
典例研析
特色栏目
备课优选
基础梳理
1. “五点法”作图原理
在确定正弦函数y=sinx在[0,2π]上的图像的形状时,起关键作用的五个 点是(0,0)、 π2,1 、(π, 0 )、32π,-1 、(2π,0). 在确定
余弦函数 y=cosx在[0,2π]上的图像的形状时,起关键作用的五个点是
新教材人教A版5.4三角函数的图像和性质课件(18张)

y
余弦函数的图象 叫做余弦曲线
正弦函数的图象 叫做正弦曲线
如何作出三角函数的图象
(3)如何利用周期性得到y=sinx,x∈R的图象
-
-
-
1
-1
正弦函数的图象 叫做正弦曲线
三角函数的图象
三角函数
正弦函数
余弦函数
图象
定义域
值域
R
R
[-1,1]
[-1,1]
五点作图法
【回顾】 作出y=sinx,x∈[0,2π]的图象
12等分x轴上区间[0,2π] 在x轴负半轴上取一点O1,以此为圆心作半径为1的圆 12等分圆周角,作出各角的正弦线 把角x的正弦线向右平移,使它的起点与x轴上表示数x的点重合 用光滑的曲线把这些平移后的正弦线的终点连结起来
-
-
-1
1
-
-
-1
-
-
如何作出三角函数的图象
(4)如何利用正弦曲线得到y=cosx,x∈R的图象
x
0
π
2π
y
0
0
0
1
-1
列表
描点连线
如何作出三角函数的图象
(1)列表描点法
用Excel软件绘制y=sinx,x∈[0,2π]的图象
如何作出三角函数的图象
(2)三角函数线法——几何法
O
P
M
y
.
x
如何作出三角函数的图象
(2)三角函数线法——几何法
问题2 如何借助前面的几何法作出 y=sinx,x∈[0,2π]的图象?
【方法总结】 在精确度要求不高时,先作出函数y=sinx和y=cosx的五个关键点,再用光滑的曲线将它们顺次连结起来,就得到函数的简图。这种作图法叫做“五点(画图)法”。
高考总复习一轮数学精品课件 第5章 三角函数、解三角形 第4节 三角恒等变换

2.cos2α-sin2α=(cos α+sin α)(cos α-sin α).
3.sin α±cos α= 2sin(α± ).
4
4.函数 y=asin ωx±bcos ωx 的最大值是 2 + 2 ,最小值是- 2 + 2 ,最小正
2
周期为 .
|ω|
自主诊断
题组一 思考辨析(判断下列结论是否正确,正确的画“ ”,错误的画“×”)
π 7π
π 7π
D,x∈(4 , 12)时,2x∈(2 , 6 ),f(x)不单调,故 D 错误.故选 C.
研考点
精准突破
考点一
三角函数式的化简
2 18°×(3 2 9°- 2 9°-1)
例 1(1)(2024·重庆模拟)式子
化简的结果为
6°+ 3 6°
1
A.
B.1
C. 3 或- 3
2
D. 3
解析 因为 tan α,tan β 是方程 x2+3 3x+4=0 的两根,
所以 tan α+tan β=-3 3,tan αtan β=4,所以
tan+tan
tan(α+β)=
1-tantan
= 3.
因为 tan α+tan β=-3 3,tan αtan β=4,
1. 1- =
2sin2 .(
× )
2.y=3sin x+4cos x 的最大值是 7.( × )
3.半角的正弦、余弦公式实质就是将倍角的余弦公式逆用得来的.(
θ
4.tan2
=
θ
1+ θ
=
1- θ
3.sin α±cos α= 2sin(α± ).
4
4.函数 y=asin ωx±bcos ωx 的最大值是 2 + 2 ,最小值是- 2 + 2 ,最小正
2
周期为 .
|ω|
自主诊断
题组一 思考辨析(判断下列结论是否正确,正确的画“ ”,错误的画“×”)
π 7π
π 7π
D,x∈(4 , 12)时,2x∈(2 , 6 ),f(x)不单调,故 D 错误.故选 C.
研考点
精准突破
考点一
三角函数式的化简
2 18°×(3 2 9°- 2 9°-1)
例 1(1)(2024·重庆模拟)式子
化简的结果为
6°+ 3 6°
1
A.
B.1
C. 3 或- 3
2
D. 3
解析 因为 tan α,tan β 是方程 x2+3 3x+4=0 的两根,
所以 tan α+tan β=-3 3,tan αtan β=4,所以
tan+tan
tan(α+β)=
1-tantan
= 3.
因为 tan α+tan β=-3 3,tan αtan β=4,
1. 1- =
2sin2 .(
× )
2.y=3sin x+4cos x 的最大值是 7.( × )
3.半角的正弦、余弦公式实质就是将倍角的余弦公式逆用得来的.(
θ
4.tan2
=
θ
1+ θ
=
1- θ
人教A版高中数学必修一课件《三角函数的图象与性质》三角函数(第一课时正弦函数、余弦函数的图象)

33
观察图象可知,在[0,2π]上,当π6<x≤π3或23π≤x<56π时,不等式12<sin
x≤ 23成立,
所以12<sin x≤ 23的解集为
xπ6+2kπ<x≤π3+2kπ
或
23π+2kπ≤x<56π+2kπ,k∈Z
.
34
1.用三角函数的图象解sin x>a(或cos x>a)的方法 (1)作出y=a,y=sin x(或y=cos x)的图象. (2)确定sin x=a(或cos x=a)的x值. (3)确定sin x>a(或cos x>a)的解集. 2.利用三角函数线解sin x>a(或cos x>a)的方法 (1)找出使sin x=a(或cos x=a)的两个x值的终边所在的位置. (2)根据变化趋势,确定不等式的解集.
6
思考:y=cos x(x∈R)的图象可由 y=sin x(x∈R)的图象平移得到的原 因是什么?
提示:因为 cos x=sinx+π2,所以 y=sin x(x∈R)的图象向左平移π2个 单位可得 y=cos x(x∈R)的图象.
7
A [五个关键点的横坐标依次
1.用五点法画 y=3sin x, x∈[0,2π]的图象时,下列哪个点不是
[0,2π]上简图的步骤
(1)列表:
x
0
π 2
π
3π 2
2π
sin x (或cos x)
0(或1)
-1 1(或0) 0(或-1)
(或0)
0(或1)
b
A+b
b
-A+b
b
y
(或A+b) (或b) (或-A+b) (或b) (或A+b)
23
(2)描点:在平面直角坐标系中描出五个点(0,y1),π2,y2,(π, y3),32π,y4,(2π,y5),这里的yi(i=1,2,3,4,5)值是通过函数解析式计算 得到的.
观察图象可知,在[0,2π]上,当π6<x≤π3或23π≤x<56π时,不等式12<sin
x≤ 23成立,
所以12<sin x≤ 23的解集为
xπ6+2kπ<x≤π3+2kπ
或
23π+2kπ≤x<56π+2kπ,k∈Z
.
34
1.用三角函数的图象解sin x>a(或cos x>a)的方法 (1)作出y=a,y=sin x(或y=cos x)的图象. (2)确定sin x=a(或cos x=a)的x值. (3)确定sin x>a(或cos x>a)的解集. 2.利用三角函数线解sin x>a(或cos x>a)的方法 (1)找出使sin x=a(或cos x=a)的两个x值的终边所在的位置. (2)根据变化趋势,确定不等式的解集.
6
思考:y=cos x(x∈R)的图象可由 y=sin x(x∈R)的图象平移得到的原 因是什么?
提示:因为 cos x=sinx+π2,所以 y=sin x(x∈R)的图象向左平移π2个 单位可得 y=cos x(x∈R)的图象.
7
A [五个关键点的横坐标依次
1.用五点法画 y=3sin x, x∈[0,2π]的图象时,下列哪个点不是
[0,2π]上简图的步骤
(1)列表:
x
0
π 2
π
3π 2
2π
sin x (或cos x)
0(或1)
-1 1(或0) 0(或-1)
(或0)
0(或1)
b
A+b
b
-A+b
b
y
(或A+b) (或b) (或-A+b) (或b) (或A+b)
23
(2)描点:在平面直角坐标系中描出五个点(0,y1),π2,y2,(π, y3),32π,y4,(2π,y5),这里的yi(i=1,2,3,4,5)值是通过函数解析式计算 得到的.
中学高三数学三角函数的图像与性质复习课件新人教A版

注:较复杂的三角函数要先化简,再利用公式求周期;有时
可用数形结合或定义法求周期
2P.9研3,1究下列f(x函)数= 中As周in期(为x2+的) 是性(质D的方) 法:类比研究y=sinx的性质,
A只 要.y需 特=s将别in注x2ω意x, +AφB和看.yω=成s的inx符2,x号但C.,y在=通c求o过sfx4(诱x)导=DA公.ys=i式cno(先s4x将x+ω)化的正单。调区间时,
解: ∵f(x)=sin(x+)(>0, 0≤≤) 是 R 上的偶函数,
∴f(0)=±1 ∴cos=0.
又∵0≤≤,
∴=
2
.
∴f(x)=cosx.
∵f(x) 的图象关于点 M 对称, ∴ f( 34) =0.
∴
3
4
=k+
2
(kZ).
∴=
4k+2 3
(kZ).
∵>0,
∴f(x)=cosx 在区间 [0,
纵向伸长3倍
y y=3sinx
y=sinx
- O 6
y=3sinx
横向缩短
1 2
y=3sin2x
y=3sin2x
左移π6
y=3sin(2x+π ) 3
y=3sin(2x+ ) )
3
x
返回目录
例3已知函数
y=
1 2
cos2x+
3 2
sinxcosx+1,
xR.
(1)求当
y
取得
最大值时自变量 x 的集合; (2)该函数可由y=sinx(xR) 的图象
∴∴2当(-x=8-)+8时=k,+y
