人教版九年级数学下册27.2.1相似三角形的判定同步练习(1)b.docx

合集下载

2017-2018 人教版九年级数学下册第27章相似 27.2 相似三角形 27.2.1相似三角形的判定同步练习含答案

人教版九年级数学下册第27章相似 27.2 相似三角形 27.2.1相似三角形的判定同步练习1．如图，DF ∥AC ，若AF BF ＝35，则△DBF 和△CBA 的相似比为( )A.53 B ．35 C ．32D ．582．如图，在平行四边形ABCD 中，EF ∥AB 交AD 于E ，交BD 于F ，DE ∶EA ＝3∶4，EF ＝3，则CD 的长为( )A ．4B ．7C ．3D ．123．如图，直线l 1∥l 2∥l 3，直线AC 分别交l 1、l 2、l 3于点A 、B 、C ；直线DF 分别交l 1、l 2、l 3于点D 、E 、F.AC 与DF 相交于点H ，且AH ＝2，HB ＝1，BC ＝5，则DEEF 的值为( ) A.12 B ．2 C ．25D ．354．如图，若DE∥BC，DE＝12，BC＝15，则△OED∽，相似比为，△ABC ∽△ADE，相似比为.5．如图，直线l1、l2、…、l6是一组等距离的平行线，过直线l1上的点A作两条射线，分别与直线l3、l6相交于点B、E、C、F，若BC＝2，则EF的长是.6．已知△ABC和△DEF，∠C＝∠E＝75°，AC＝4cm，BC＝5cm，DE＝6cm，要使△ABC ∽△DFE，则EF的长应为.7．如图所示，在△ABC中，D、E分别在边AC、AB上，且AD∶AB＝AE∶AC＝1∶3，BC ＝12，则DE＝.8．如图，在△ABC和△A′B′C′中，∠A＝60°，∠B＝40°，∠A′＝60°，当∠C′＝时，则△ABC∽△A′B′C′.9．如图，点D、E分别在AB、AC上，且∠ABC＝∠AED.若DE＝4，AE＝5，BC＝8，则AB的长为.10．如图，在△ABC 中，DE ∥BC ，M 为DE 中点，CM 的延长线交AB 于N ，若AD ∶AB ＝2∶3，求ND ∶BD.11．如图所示，l 1∥l 2∥l 3，且AB ＝2BC ，DF ＝5cm ，AG ＝4cm ，求GF 、AF 、EF 的长．12．已知线段OA ⊥OB ，C 为OB 的中点，D 为AO 上一点，连接AC 、BD 交于P 点． (1)如图①，当OA ＝OB 且D 为AO 中点时，求APPC 的值；(2)如图②，当OA ＝OB ，AD AO ＝14时，求APAC的值．答案： 1. D 2. B 3. D4. △OBC 45 545. 56.7.5cm 7. 48. 80°9. 1010. 解：∵DE∥BC ，∴△ADE∽△ABC.∴DE BC ＝AD AB ＝23.∵M 为DE 中点，∴DMBC ＝13.∵DM∥BC，∴△NDM∽△NBC.∴ND NB ＝DM BC ＝13，∴ND∶BD＝1∶2. 11. 解：∵l 1∥l 2∥l 3，∴AB BC ＝DE EF .又∵AB＝2BC ，∴DE EF ＝2，∴DF＝3EF.∴EF＝13DF ＝13×5＝53cm.∵l 1∥l 2∥l 3，∴AB BC ＝AG GF ，∴2＝AG GF ，∴GF＝42＝2cm ，∴AF＝AG ＋GF ＝4＋2＝6cm.故GF ＝2cm ，AF ＝6cm ，EF ＝53cm.12. 解：(1)过C 作CE∥OA 交BD 于E ，则△BCE∽△BOD，得CE ＝12OD ＝12AD.再由△ECP∽△DAP 得AP PC ＝ADCE＝2；(2)过C 作CE∥OA 交BD 于E ，设AD ＝x ，则AO ＝OB ＝4x ，则OD ＝3x.由△BCE∽△BOD 得CE ＝12OD ＝32x.再由△ECP∽△DAP 得AP PC ＝AD EC ＝23.则AP AC ＝25.。

人教版数学九年级下册数学：27.2.1 相似三角形的判定同步练习(附答案)

27．2.1 相似三角形的判定第1课时平行线分线段成比例1．如图所示，△ADE ∽△ACB ，∠AED ＝∠B ，那么下列比例式成立的是( ) A.AD AC ＝AE AB ＝DE BC B.AD AB ＝AE ACC.AD AE ＝AC AB ＝DE BC D.AD AB ＝AE EC ＝DE BC2．两个三角形相似，且相似比k ＝1，则这两个三角形．3．如图，在△ABC 中，DE ∥BC ，AD ＝6，DB ＝3，AE ＝4，则EC 的长为( )A ．1B ．2C ．3D ．44．如图，直线l 1∥l 2∥l 3，直线AC 交l 1，l 2，l 3于点A ，B ，C ，直线DF 交l 1，l 2，l 3于点D ，E ，F ，已知AB AC ＝13，则EFDE＝．5．如图，在▱ABCD 中，EF ∥AB 交AD 于点E ，交BD 于点F ，DE ∶EA ＝3∶4，EF ＝3，则CD 的长为( )A ．4B ．7C ．3D ．126．如图，点E ，F 分别在△ABC 的边AB ，AC 上，且EF ∥BC ，点M 在边BC 上，AM 与EF 交于点D ，则图中相似三角形共有( )A ．4对B ．3对C ．2对D ．1对7．在△ABC 中，AB ＝6，AC ＝9，点P 是直线AB 上一点，且AP ＝2，过点P 作BC 边的平行线，交直线AC 于点M ，则MC 的长为．8．如图，在△ABC中，点D在BC边上，连接AD，点G在线段AD上，GE∥BD，且交AB 于点E，GF∥AC，且交CD于点F，则下列结论一定正确的是()A.ABAE＝AGADB.DFCF＝DGADC.FGAC＝EGBDD.AEBE＝CFDF9．如图，AG∶GD＝4∶1，BD∶DC＝2∶3，则AE∶EC的值是()A．3∶2B．4∶3C．6∶5D．8∶510．如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点A，B，C都在横格线上，若线段AB＝4 cm，则线段BC＝cm.11．如图，在△ABC中，点D，E分别为AB，AC的中点，连接DE，线段BE，CD相交于点O，若OD＝2，则OC＝.12．如图，在▱ABCD中，对角线AC、BD相交于点O，在BA的延长线上取一点E，连接OE交AD于点F，若CD＝5，BC＝8，AE＝2，则AF＝．13．中国高铁近年来用震惊世界的速度不断发展，已成为当代中国一张耀眼的“国家名片”，修建高铁时常常要逢山开道、遇水搭桥，如图，某高铁在修建时需打通一直线隧道MN(M、N为山的两侧)，工程人员为了计算M、N两点之间的直线距离，选择作MN的平行线BC，并测得AM＝900米， AB＝30米，BC＝45米，求直线隧道MN的长．14．如图，延长正方形ABCD的一边CB至点E，ED与AB相交于点F，过点F作FG∥BE 交AE于点G，求证：GF＝FB.15．如图，AD∥EG∥BC，EG分别交AB，DB，AC于点E，F，G，已知AD＝6，BC＝10，AE＝3，AB＝5，求EG，FG的长．第2课时相似三角形的判定定理1，21．将一个三角形的各边长都缩小12后，得到的三角形与原三角形( )A ．一定相似B ．一定不相似C ．不一定相似D ．无法确定2．若△ABC 各边分别为AB ＝10 cm ，BC ＝8 cm ，AC ＝6 cm ，△DEF 的两边为DE ＝5 cm ，EF ＝4 cm ，则当DF ＝ cm 时，△ABC ∽△DEF. 3．试判断图中的两个三角形是否相似，并说明理由．4．网格图中每个方格都是边长为1的正方形．若A ，B ，C ，D ，E ，F 都是格点，试说明△ABC ∽△DEF.5．能判定△ABC ∽△A ′B ′C ′的条件是( )A.AB A ′B ′＝ACA ′C ′B.AB AC ＝A ′B ′A ′C ′且∠A ＝∠A ′ C.AB BC ＝A ′B ′A ′C ′且∠B ＝∠C ′ D.AB A ′B ′＝ACA ′C ′且∠B ＝∠B ′6．如图，已知△ABC，则下列4个三角形中，与△ABC相似的是()7．如图，AB与CD相交于点O，OA＝3，OB＝5，OD＝6，当OC＝时，△AOC∽△BOD.8．如图，点C，D在线段AB上，∠A＝∠B，AE＝3，AD＝2，BC＝3，BF＝4.5，DE＝5，求CF的长．9．在△ABC中，AB＝6，AC＝5，点D在边AB上，且AD＝2，点E在边AC上，当AE＝时，以A，D，E为顶点的三角形与△ABC相似．10．如图，在方格纸中，△ABC和△EPD的顶点均在格点上，要使△ABC∽△EPD，则点P所在的格点为()A．P 1B．P2C．P3D．P411．如图，在△ABC中，点P在AB上，下列四个条件：①AP∶AC＝AC∶AB；②AC2＝AP·AB；③AB·CP＝AP·CB.其中能满足△APC和△ACB相似的条件有()A．1个 B．2个C．3个D．0个12．如图，已知∠DAB＝∠CAE，请补充一个条件：，使△ABC∽△ADE.13．如图，AB∥DE，AC∥DF，BC∥EF，求证：△DEF∽△ABC.14．如图，在△ABC中，AB＝AC，D为CB延长线上一点，E为BC延长线上一点，且满足AB2＝DB·CE.求证：△ADB∽△EAC.15．如图，正方形ABCD中，P是BC上的点，且BP＝3PC，Q是CD的中点，求证：△ADQ ∽△QCP.16．如图，在钝角三角形ABC中，AB＝6 cm，AC＝12 cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1 cm/s，点E运动的速度为2 cm/s.如果两点同时运动，那么当以点A，D，E为顶点的三角形与△ABC相似时，运动的时间是．第3课时相似三角形的判定定理31．下列各组图形中有可能不相似的是()A．各有一个角是45°的两个等腰三角形B．各有一个角是60°的两个等腰三角形C．各有一个角是105°的两个等腰三角形D．两个等腰直角三角形2．已知△ABC中，∠A＝40°，∠B＝75°，下图各三角形中与△ABC相似的是.3．如图，锐角三角形ABC的边AB，AC上的高线EC，BF相交于点D，请写出图中的两对相似三角形．(用相似符号连接) 4．如图，点B，D，C，F在一条直线上，且AB∥EF，AC∥DE，求证：△ABC∽△EFD.5．如图，∠1＝∠2，∠C ＝∠D.求证：△ABC ∽△AED.6．在△ABC 和△A ′B ′C ′中，∠C ＝∠C ′＝90°，AC ＝12，AB ＝15，A ′C ′＝8，则当A ′B ′＝时，△ABC ∽△A ′B ′C ′.7．一个直角三角形的一条直角边长和斜边长分别为8 cm 和15 cm ，另一个直角三角形的一条直角边长和斜边长分别是6 cm 和454 cm ，这两个直角三角形 (填“是”或“不是”)相似三角形．8．一个直角三角形的两边长分别为3和6，另一个直角三角形的两边长分别为2和4，那么这两个直角三角形 (填“一定”“不一定”或“一定不”)相似．9．如图，在△ABC 中，点D ，E 分别在AB ，AC 边上，DE ∥BC ，且∠DCE ＝∠B.那么下列判断中，错误的是( )A ．△ADE ∽△ABCB ．△ADE ∽△ACDC ．△DEC ∽△CDBD ．△ADE ∽△DCB10．如图，在△ABC 中，点D 是边AB 上的一点，∠ADC ＝∠ACB ，AD ＝2，BD ＝6，则边AC 的长为( )A ．2B ．4C ．6D ．811．《九章算术》是我国古代数学名著，书中有下列问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为：“今有直角三角形，勾(短直角边)长为5步，股(长直角边)长为12步，问该直角三角形能容纳的正方形边长最大是多少步？”该问题的答案是步．12．如图，已知∠ACB＝∠ABD＝90°，AB＝6，AC＝2，求AD的长为多少时，图中两直角三角形相似？13．如图，在▱ABCD中，过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE＝∠D.求证：△ABF∽△BEC.14．如图，矩形ABCD中，AB＝20，BC＝10，点P为AB边上一动点，DP交AC于点Q.(1)求证：△APQ∽△CDQ；(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动，移动时间为t秒．当t为何值时，DP⊥AC?15．如图，在△ABC中，AD，BF分别是BC，AC边上的高，过点D作AB的垂线交AB于点E，交BF于点G，交AC的延长线于点H，求证：DE2＝EG·EH.参考答案：27．2.1 相似三角形的判定第1课时平行线分线段成比例1．A2．全等．3．B4． 2．5．B6．B7． 6或12．8．D9．D10．12.11．4.12．169．13．解：∵BC ∥MN ，∴△ABC ∽△AMN.∴AB AM ＝BC MN ，即30900＝45MN .∴MN ＝1 350.答：直线隧道MN 的长为1 350米．14．证明：∵GF ∥AD ，∴GF AD ＝EFED .又FB ∥DC ，∴FB DC ＝EFED .又AD ＝DC ，∴GF AD ＝FBAD .∴GF ＝FB.15．解：∵在△ABC 中，EG ∥BC ，∴△AEG ∽△ABC ，∴EG BC ＝AEAB .∵BC ＝10，AE ＝3，AB ＝5，∴EG 10＝35，∴EG ＝6. ∵在△BAD 中，EF ∥AD ，∴△BEF ∽△BAD ，∴EF AD ＝BE AB. ∵AD ＝6，AE ＝3，AB ＝5，∴EF 6＝5－35.∴EF ＝125. ∴FG ＝EG －EF ＝185.第2课时相似三角形的判定定理1，21．A2．3.3．解：相似．理由如下：在Rt △ABC 中，BC ＝AB 2－AC 2＝32－2.42＝1.8，在Rt △DEF 中，DF ＝DE 2－EF 2＝62－3.62＝4.8，∴AB DE ＝BC EF ＝AC DF ＝12. ∴△ABC ∽△DEF.4．证明：∵AC ＝2，BC ＝12＋32＝10，AB ＝4，DF ＝22＋22＝22，EF ＝22＋62＝210，ED ＝8，∴AC DF ＝BC EF ＝AB DE ＝12. ∴△ABC ∽△DEF.5．B6．C7． 1858．解：∵AE BF ＝34.5＝23，AD BC ＝23，∴AE BF ＝AD BC.又∵∠A ＝∠B ，∴△AED ∽△BFC.∴AD BC ＝DE CF .∴23＝5CF. ∴CF ＝152. 9． 125或53． 10．C11．B12． AD AB ＝AE AC 13．证明：∵AB ∥DE ，∴△ODE ∽△OAB.∴DE AB ＝OE OB. ∵BC ∥EF ，∴△OEF ∽△OBC.∴EF BC ＝OE OB ＝OF OC. ∵AC ∥DF ，∴△ODF ∽△OAC.∴DF AC ＝OF OC. ∴DE AB ＝EF BC ＝DF AC. ∴△DEF ∽△ABC.14．证明：∵AB ＝AC ，∴∠ABC ＝∠ACB.∴∠ABD ＝∠ACE.∵AB 2＝DB ·CE ，∴AB CE ＝DB AB . 又AB ＝AC ，∴AB CE ＝DB AC. ∴△ADB ∽△EAC.15．证明：设正方形的边长为4a ，则AD ＝CD ＝BC ＝4a.∵Q 是CD 的中点，BP ＝3PC ，∴DQ ＝CQ ＝2a ，PC ＝a.∴DQ PC ＝AD CQ ＝21. 又∵∠D ＝∠C ＝90°，∴△ADQ ∽△QCP.16．3__s 或4.8__s ．第3课时相似三角形的判定定理31．A2． △EFD ，△HGK .3．答案不唯一，如△BDE ∽△CDF ，△ABF ∽△ACE 等．4．证明：∵AB ∥EF ，AC ∥DE ，∴∠B ＝∠F ，∠ACB ＝∠EDF.∴△ABC ∽△EFD.5．证明：∵∠1＝∠2，∴∠1＋∠CAD ＝∠2＋∠CAD ，即∠BAC ＝∠EAD.又∵∠C ＝∠D ，∴△ABC ∽△AED.6．10.7．是．8．不一定．9．D10．B11．6017． 12．解：①若△ABC ∽△ADB ，则AB AD ＝AC AB.∴AD ＝3； ②若△ABC ∽△DAB ，则AB AD ＝BC AB.∴AD ＝3 2.综上所述，当AD ＝3或32时，两直角三角形相似．13．证明：∵四边形ABCD 是平行四边形， ∴AB ∥CD ，AD ∥BC ，AD ＝BC.∴∠D ＋∠C ＝180°，∠ABF ＝∠BEC.又∵∠AFB ＋∠AFE ＝180°，且∠AFE ＝∠D ， ∴∠C ＝∠AFB.又∵∠ABF ＝∠BEC ，∴△ABF ∽△BEC.14．解：(1)证明：∵四边形ABCD 是矩形， ∴AB ∥CD.∴△APQ ∽△CDQ.(2)当DP ⊥AC 时，∠QCD ＋∠QDC ＝90°.∵∠ADQ ＋∠QDC ＝90°，∴∠DCA ＝∠ADP. 又∵∠ADC ＝∠DAP ＝90°，∴△ADC ∽△PAD.∴AD PA ＝DC AD .∴10PA ＝2010，解得PA ＝5. ∴t ＝5.15．证明：∵AD ，BF 分别是BC ，AC 边上的高， ∴∠ADB ＝∠BED ＝90°.∴∠EBD ＋∠EDB ＝∠EDB ＋∠ADE.∴∠EBD ＝∠EDA.∴△AED ∽△DEB.∴AE DE ＝DE BE，即DE 2＝AE ·BE. 又∵∠HFG ＝90°，∠BGE ＝∠HGF ，∴∠EBG ＝∠H.∵∠BEG ＝∠HEA ＝90°，∴△BEG ∽△HEA.∴EG AE ＝BE EH，即EG ·EH ＝AE ·BE. ∴DE 2＝EG ·EH.。

人教版九年级数学下册27.2 相似三角形同步练习1 含答案

27.2.1相似三角形的判定（1）1、已知D 、E 分别是ΔABC 的边AB 、AC 上的点，请你添加一个条件，使ΔABC 与ΔAED 相似. (只需添加一个你认为适当的条件即可).2、如图，已知DE ∥BC ，EF ∥AB ，则下列比例式中错误的是（）A AC AE AB AD = B FB EA CF CE =C BD AD BC DE = D CBCF AB EF =3、如图，E 是平行四边形ABCD 的边BC 的延长线上的一点，连结AE 交CD 于F ，则图中共有相似三角形（） A 1对 B 2对 C 3对 D 4对4、如图，在大小为4×4的正方形网格中，是相似三角形的是（）① ② ③ ④A.①和②B.②和③C.①和③D.②和④.5、如图，在正方形网格上有6个斜三角形：①ΔABC ，②ΔBCD ，③ΔBDE ，④ΔBFG ，⑤ΔFGH ，⑥ΔEFK.其中②～⑥中，与三角形①相似的是（）(A)②③④ (B)③④⑤ (C)④⑤⑥ (D)②③⑥6、在方格纸中，每个小格的顶点叫做格点.以格点连线为边的三角形叫做格点三角形.如图，请你在4×4的方格纸中，画一个格点三角形A 1B 1C 1，使ΔA 1B 1C 1与格点三角形AB C 相似(相似比不为1).7、如图，ΔABC 与ΔADB 中，∠ABC=∠ADB=90°，AC=5cm ，AB=4cm ，如果图中的两个直角三角形相似，求AD 的长.8、一个钢筋三角架三边长分别为20cm ，50cm ，60cm ，现要再做一个与其相似的钢筋三角架，而只有长为30cm 和50cm 的两根钢筋，要求以其中的一根为一边，从另一根截下两段(允许有余料)作为另两边，写出所有不同的截法？答案1、D E ∥BC2、C3、C4、C5、B6、略7、AD=516cm 8、两种截法（1）新截三角形的三边分别是10cm,25cm,30c m （2）新截三角形的三边分别是12cm,30cm,36cm。

2021年人教版数学九下27.2.1《相似三角形的判定1》同步练习(含答案)

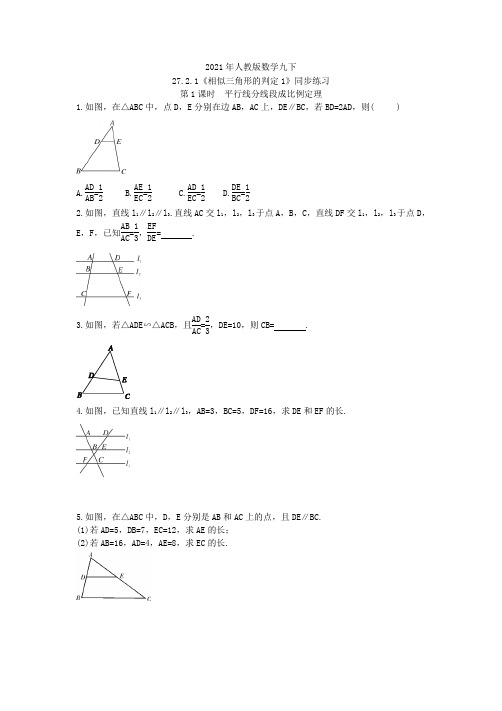
2021年人教版数学九下27.2.1《相似三角形的判定1》同步练习第1课时平行线分线段成比例定理1.如图，在△ABC 中，点D ，E 分别在边AB ，AC 上，DE ∥BC ，若BD=2AD ，则( )A.AD AB =12B.AE EC =12C.AD EC =12D.DE BC =122.如图，直线l 1∥l 2∥l3.直线AC 交l 1，l 2，l 3于点A ，B ，C ，直线DF 交l 1，l 2，l 3于点D ，E ，F ，已知AB AC =13，EF DE= .3.如图，若△ADE ∽△ACB ，且AD AC =23，DE=10，则CB= .4.如图，已知直线l 1∥l 2∥l 3，AB=3，BC=5，DF=16，求DE 和EF 的长.5.如图，在△ABC 中，D ，E 分别是AB 和AC 上的点，且DE ∥BC.(1)若AD=5，DB=7，EC=12，求AE 的长；(2)若AB=16，AD=4，AE=8，求EC 的长.6.如图，在△ABC 中，DE ∥BC ，∠ADE=∠EFC ，AD ∶DB=5∶3，FC=6，则DE 的长为( )A.6B.8C.10D.127.如图，在▱ABCD 中，AB=2，BC=3.以点C 为圆心，适当长为半径画弧，交BC 于点P ，交CD于点Q ，再分别以点P ，Q 为圆心，大于12PQ 的长为半径画弧，两弧相交于点N ，射线CN 交BA 的延长线于点E ，则AE 的长是( )A.0.5B.1C.1.2D.1.58.如图，已知AB ∥MN ，BC ∥NG ，求证：OA OM =OC OG.9.如图，在△ABC 中，DE ∥BC ，BF 平分∠ABC ，交DE 的延长线于点F.若AD=1，BD=2，BC=4，求EF.参考答案1.答案为：B2.答案为：23.答案为：154.答案为：DE=6，EF=105.答案为：(1)607(2)24 6.答案为：C7.答案为：B8.证明：∵AB ∥MN ，∴OA OM =OB ON. 又∵BC ∥NG ，∴OB ON =OC OG ，∴OA OM =OC OG. 9.答案为：23；。

人教版九年级数学下册第二十七章相似 27.2 相似三角形同步练习(含答案)

人教版九年级数学下册第二十七章相似27.2 相似三角形同步练习一、选择题1、能判定与相似的条件是（）A. B.，且C.且D.，且2、如图，下列条件中不能判定的是（）A. B.C. D.3、.如图，点D在△ABC的边AC上，要判断△ADB与△ABC相似，添加一个条件，不正确的是（）A.∠ABD=∠CB.∠ADB=∠ABCC.D.4、如图1，在三角形纸片ABC中，∠A=78°，AB=4，AC=6．将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形相似的有（）A．①②③ B．①②④ C．①③④ D．②③④5、如图，△ABC中，点D、E分别在AB、AC边上，则下列条件中，不一定能使△AED∽△ABC的是（）A．∠2=∠B B．∠1=∠C C．D．6、如图，△ABC中，BD是∠ABC的平分线，DE∥AB交BC于E，EC=6，BE=4，则AB长为（）A． 6 B． 8 C．D．7、如图，DE是△ABC的中位线，已知△ABC的面积为8，则△ADE的面积为（）．A． 2 B． 4 C． 6 D． 88、如图所示，在河的一岸边选定一个目标A，再在河的另一岸边选定B和C，使AB⊥BC，然后选定E，使EC⊥BC，用视线确定BC和AE相交于D，此时测得BD=120米，CD=60米，为了估计河的宽度AB，还需要测量的线段是（）A.CEB.DEC.CE或DED.无法确定9、已知：如图，∠ADE＝∠ACD＝∠ABC，图中相似三角形共有（）A.1对B.2对C.3对D.4对10、某班同学要测量学校升国旗的旗杆高度，在同一时刻，量得某同学的身高是1.5米，影长是1米，且旗杆的影长为8米，则旗杆的高度是（）A.12米 B．11米 C．10米 D．9米11、．如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S△COA=1：25，则的值为（）A． B． C． D．12、如图，在钝角三角形ABC中，AB＝6cm，AC＝12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是( )A. 4.5秒B.3秒C. 3秒或4.8秒D.4.5秒或4.8秒二、填空题13、如图，是的中位线，的面积为，则四边形的面积为．14、如图，已知零件的外径为25，现用一个交叉卡钳（两条尺长AC和BD相等，OC=OD）量零件的内孔直径AB．若OC∶OA=1∶2，量得CD＝10，则零件的厚度．15、如图，AC与BD交于点E，AB∥CD∥EF，AB=10，CD=15，则EF的长为16、已知△ABC∽△A′B′C′，且，△ABC的周长比△A′B′C′的周长少8cm，则△A′B′C′的周长为 cm 。

初中数学 27.2.1 相似三角形的判定同步练习

ABDCHG EFADEEABDC27.2.1 相似三角形的判定（一）A组1.如图27-2-1，E是平行四边形ABCD的边BC的延长线上的一点，连结AE交CD于F，则图中共有相似三角形（）A.1对B.2对C.3对D.4对图27-2-1 图27-2-22.如图27-2-2，在△ABC中，DE//BC，且AD：DB=2：1，那么DE：BC等于（）A.2：1B.1：2C.2：3D.3：23.如图27-2-3，在□ABCD中，F、H分别是BC、AD上任一点，EF平行AB，HG平行CD，则图中共有相似三角形的对数是（）A.2B.3C.4D.5图27-2-3 图27-2-44.如图27-2-4，在△ABC中，DE//BC，AD:CD=1:3，BE=6cm，则AE= cm．5.如图，在□ABCD中，E、F分别是AB、BC的中点，连接AC、EF.求证：△BEF∽△ACD.6.已知：如图，试用两种不同的方法在△ABC内部作一个三角形，使其与△ABC相似，且相似比为14.7.如图，物AB与其所成像A’B’平行，孔心O到蜡烛头A的距离是36cm，到蜡烛头的像A’的距离是12cm，你知道像长是物长的几分之几吗？你是怎样知道的？8.如图，AD与BC交于点O，且AB ∥ CD。

①已知BO：OC=1：3，CD=6cm，求AB的长。

②已知BO：BC=1：3，CD=6cm，求AB的长。

③已知BO：OC=1：3，AD=8cm，求OA的长。

C DA BOOABB’A’PC AGFB 组1.如图27-2-5，已知DE ∥BC ，EF ∥AB ，则下列比例式，错误．．的是（） A.AD AE =ABACB.CE EA =CFFBC.DE AD =BC BD D.EF CF=AB CB图27-2-5 图27-2-62.如图27-2-6，在△ABC 中，DG ∥A C ，EF ∥BC ，则图中与△PDE 相似三角形的个数是（） A.1B.2C.3D.43.如图，AB 是⊙O 的直径，C 、D 是圆上两点，且弧AC=弧BD ，射线AC 与射线BD 交于点E ，求证：△ECD∽△ABE.4.已知：如图，AB=AD ，AC=AE ，FG ∥DE.试说出与所有△ABC 相似的三角形，并说明理由.E OD C BADB CG FE5.如图，△ABC 中，AD ⊥BC ，D 是垂足，E 是BC 中点，FE ⊥BC 交AB 于F ，BD ＝6，DC ＝4，AB ＝8，求BF 长。

九年级数学下册 27.2.1 相似三角形的判定同步测试 (新版)新人教版 (优质)

相似三角形27．2.1 相似三角形的判定第1课时平行线分线段成比例定理 [见B 本P69]1．如图27－2－1，已知直线a ∥b ∥c ，直线m ，n 与a ，b ，c 分别交于点A ，C ，E ，B ，D ，F ，AC ＝4，CE ＝6，BD ＝3，则BF ＝( B )A ．7B ．7.5C ．8D ．8.5 【解析】 ∵a ∥b ∥c ，∴AC CE ＝BD DF ，∴46＝3DF，∴DF ＝4.5，∴BF ＝BD ＋DF ＝7.5.图27－2－1图27－2－22．如图27－2－2，若l 1∥l 2，那么以下比例式中正确的是( D ) A.MR NR ＝RP RQ B.MR NP ＝NRMQ C.MR MQ ＝RP NP D.MR RQ ＝NR RP3．如图27－2－3，已知BD ∥CE ，则下列等式不成立的是( A )图27－2－3A.AB BC ＝BD CEB.AB AC ＝BD CEC.AD AE ＝BD CE D.AB AC ＝AD AE4. 如图27－2－4，在△ABC 中，点D ，E 分别在边AB ，AC 上，DE ∥BC .已知AE ＝6，ADDB＝34，则EC 的长是( B )图27－2－4A ．4.5B ．8C ．10.5D ．14【解析】根据平行线分线段成比例定理，列出比例式求解即可得到答案． ∵DE ∥BC ，∴AD DB ＝AEEC，∵AE ＝6，∴34＝6EC，解得EC ＝8，则EC 的长是8.5．如图27－2－5所示，△ABC 中，DE ∥BC ，AD ＝5，BD ＝10，AE ＝3，则CE 的值为( B )图27－2－5A ．9B ．6C ．3D ．4 【解析】 ∵DE ∥BC ，∴AD BD ＝AE CE .∵AD ＝5，BD ＝10，AE ＝3，∴510＝3CE，∴CE ＝6，故选B.6．如图27－2－6，△ABC 中，点D 在线段BC 上，且△ABC ∽△DBA ，则下列结论一定正确的是( A )图27－2－6 A ．AB 2＝BC ·BD B ．AB 2＝AC ·BD C ．AB ·AD ＝BD ·BC D ．AB ·AD ＝AD ·CD【解析】由△ABC ∽△DBA 可得对应边成比例，即AB DB ＝BC BA，再根据比例的性质可知AB 2＝BC ·BD ，故选A.7．如图27－2－7，在梯形ABCD 中，AD ∥BC ，对角线AC ，BD 相交于点O ，若AD ＝1，BC ＝3，则AOCO的值为( B ) A.12 B.13 C.14 D.19图27－2－7图27－2－88．如图27－2－8，已知DE ∥AB ，DF ∥BC ，下列结论中不正确的是( D ) A.AD DC ＝AF DE B.CE CB ＝BF AB C.CD AD ＝CE DF D.AF BF ＝DF BC【解析】 A 正确，∵DE ∥AB ，DF ∥BC ， ∴四边形DEBF 是平行四边形，∴DE ＝BF .∵DF ∥BC ，∴AD DC ＝AF BF ，∴AD DC ＝AFDE；B 正确，∵DE ∥AB ，∴CE CB ＝CDCA ，又DF ∥BC ，∴CD CA ＝BF AB，∴CE CB ＝BFAB； C 正确，∵四边形DEBF 是平行四边形， ∴DF ＝BE . ∵DE ∥AB ，∴CD AD ＝CE BE ，∴CD AD ＝CEDF；D 不正确，∵DF ∥BC ，∴AF AB ＝ADAC ，又DE ∥AB ，∴AD AC ＝BE BC ，∴AF AB ＝BEBC，又BE ＝DF ，∴AF AB ＝DF BC.9．如图27－2－9，已知AC ∥DB ，OA ∶OB ＝3∶5，OA ＝9，CD ＝32，则OB ＝__15__，OD ＝__20__．【解析】 ∵OA OB ＝35，∴OB ＝53OA ＝53×9＝15.设OD ＝x ，则OC ＝32－x . ∵AC ∥DB ，∴OA OB ＝OC OD ，∴35＝32－xx，解得x ＝20.图27－2－9图27－2－1010．如图27－2－10，已知l 1∥l 2∥l 3，AM ＝3 cm ，BM ＝5 cm ，CM ＝4.5 cm ，EF ＝12 cm ，则DM ＝__7.5__cm ，EK ＝__4.5__cm ，FK ＝__7.5__cm. 【解析】 ∵l 1∥l 2∥l 3，∴AM BM ＝CM DM， ∴35＝4.5DM，∴DM ＝7.5 cm. ∵l 1∥l 2∥l 3，∴EK EF ＝AM AB ，∴EK 12＝38，∴EK ＝4.5 cm ，∴FK ＝EF －EK ＝12－4.5＝7.5(cm)．11. 如图27－2－11，已知在△ABC 中，点D ，E ，F 分别是边AB ，AC ，BC 上的点，DE ∥BC ，EF ∥AB ，且AD ∶DB ＝ 3∶5，那么CF ∶CB 等于( A )图27－2－11 A. 5∶8 B ．3∶8 C. 3∶5 D ．2∶5【解析】 ∵AD ∶DB ＝3∶5，∴BD ∶AB ＝5∶8， ∵DE ∥BC ，∴CE ∶AC ＝BD ∶AB ＝5∶8， ∵EF ∥AB ，∴CF ∶CB ＝CE ∶AC ＝5∶8.12．如图27－2－12，点F 是▱ABCD 的边CD 上一点，直线BF 交AD 的延长线于点E ，则下列结论错误的是( C ) A.ED EA ＝DF AB B.DE BC ＝EFFBC.BC DE ＝BF BE D.BF BE ＝BC AE图27－2－12图27－2－1313．如图27－2－13，已知FG ∥BC ，AE ∥GH ∥CD ，求证：AB BF ＝EDDH.【解析】观察图形，我们会发现AE ∥GH ∥CD ，具备了平行线分线段成比例定理的基本图形，可推得ED DH ＝ACCG；由FG ∥BC ，知它具备了定理推论中的“A ”型的基本图形，可推得AC CG ＝AB BF ，从而可证得ED DH ＝AB BF. 证明：∵AE ∥GH ∥CD ，∴ED DH ＝ACCG. ∵FG ∥BC ，∴AC CG ＝AB BF ，∴ED DH ＝ABBF.14．如图27－2－14，已知AB ∥MN ，BC ∥NG ，求证：OA OM ＝OCOG. 证明：∵AB ∥MN ，∴OA OM ＝OB ON，又∵BC ∥NG ，∴OB ON ＝OC OG ，∴OA OM ＝OCOG.图27－2－14图27－2－1515．如图27－2－15，▱ABCD 中，E 在CD 延长线上，BE 交AD 于F .若AB ＝3，BC ＝4，DF ＝1，求DE 的长．解：∵四边形ABCD 是平行四边形， ∴AB ＝DC ，AD ＝BC . ∵AB ∥DC ，AD ∥BC ， ∴AF DF ＝BF FE ＝CD DE ， ∴AB DE ＝AF DF，又∵AF ＝AD －DF ＝BC －DF ＝3， ∴3DE ＝31，∴DE ＝1.16．如图27－2－16，已知AD 是△ABC 的角平分线，CE ∥AD 交BA 的延长线于点E . 求证：AB AC ＝BD DC.图27－2－16证明：∵AD ∥CE ，∴∠BAD ＝∠E ，∠DAC ＝∠ACE . 又∵∠BAD ＝∠DAC ，∴∠E＝∠ACE，∴AE＝AC.又∵CE∥AD，∴ABAE＝BDDC，∴ABAC＝BDDC.第2课时相似三角形判定定理1、2 [见A 本P71]1．如图27－2－17，在△ABC 中，DE ∥BC ，若AD BD ＝12，DE ＝4 cm ，则BC 的长为( B )图27－2－17 A ．8 cm B ．12 cm C ．11 cm D ．10 cm 【解析】 ∵DE ∥BC ， ∴△ADE ∽△ABC ，∴AD AB ＝DE BC. ∵AD BD ＝12，∴AD AB ＝13，∴13＝4BC， ∴BC ＝12 cm ，选择B.2. 能说明△ABC ∽△A ′B ′C ′的条件是( D ) A.AB A ′B ′＝AC A ′C ′≠BCB ′C ′ B.AB AC ＝A ′B ′A ′C ′，∠A ＝∠C ′ C.AB A ′B ′＝BCA ′C ′，且∠B ＝∠A ′ D.AB A ′B ′＝BCB ′C ′，且∠B ＝∠B ′ 3．如图27－2－18，四边形ABCD 的对角线AC ，BD 相交于O ，且将这个四边形分成①，②，③，④四个三角形，若OA ∶OC ＝OB ∶OD ，则下列结论中一定正确的是( B )图27－2－18A ．①和②相似B ．①和③相似C ．①和④相似D ．②和④相似【解析】两个三角形两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似．4．如图27－2－19，在△ABC 中，点D ，E 分别是AB ，AC 的中点，则下列结论：①BC ＝2DE ；②△ADE ∽△ABC ；③AD AE ＝ABAC.其中正确的有( A ) A ．3个 B ．2个 C ．1个 D ．0个【解析】点D ，E 分别是AB ，AC 的中点，所以由中位线定理得DE ∥BC ，且DE ＝12BC ，①正确；因为DE ∥BC ，所以△ADE ∽△ABC ，②正确；由②得AD AE ＝AB AC，③正确．故选A.图27－2－19图27－2－205．如图27－2－20，在▱ABCD 中，E 是AD 上一点，连接CE 并延长交BA 的延长线于点F ，则下列结论中错误的是( B )A ．∠AEF ＝∠DECB ．FA ∶CD ＝AE ∶BC C ．FA ∶AB ＝FE ∶ECD ．AB ＝DC 【解析】 ∵DC ∥AB ，∴△DCE ∽△AFE ， ∴FA CD ＝AEDE，故结论B 错误． ∵AE ∥BC ，∴△FAE ∽△FBC ， ∴FA FB ＝FE FC ，即FB FA ＝FC FE ，∴FA ＋AB FA ＝FE ＋EC FE， ∴AB FA ＝ECFE，即FA ∶AB ＝FE ∶EC ，故结论C 正确．而A ，D 显然正确，∴应选B. 6．在△ABC 中，AB ＝9，AC ＝12，BC ＝18，D 为AC 上一点，DC ＝23AC ，在AB 上取一点E ，得到△ADE ，若△ADE 与△ABC 相似，则DE 长为__6或8__．【解析】 (1)当△AED ∽△ABC 时，此时图形为(a)，可得DE ＝6；(2)当△AED ∽△ACB 时，此时图形为(b)，可得DE ＝8.7．如图27－2－21，在△ABC 中，已知DE ∥BC ，AD ＝4，DB ＝8，DE ＝3.(1)求AD AB的值；(2)求BC .图27－2－21解：(1)∵AD ＝4，DB ＝8， ∴AB ＝AD ＋DB ＝4＋8＝12， ∴AD AB ＝412＝13. (2)∵DE ∥BC ，∴△ADE ∽△ABC ，∴DE BC ＝AD AB.∵DE ＝3，∴3BC ＝13，∴BC ＝9.8．网格图中每个方格都是边长为1的正方形．若A ，B ，C ，D ，E ，F 都是格点，试说明△ABC ∽△DEF .图27－2－22【解析】利用图形与勾股定理可以推知图中两个三角形的三条对应边成比例，由此可以证得△ABC ∽△DEF .解：∵AC ＝2，BC ＝12＋32＝10，AB ＝4，DF ＝22＋22＝22，EF ＝22＋62＝210，ED ＝8，∴AC DF ＝BC EF ＝AB DE ＝12， ∴△ABC ∽△DEF .9．如图27－2－23，D ，E ，F 分别是△ABC 的三边BC ，CA ，AB 的中点．图27－2－23(1)求证：△DEF ∽△ABC ；(2)图中还有哪几个三角形与△ABC 相似？解：(1)证明：∵D ，F 分别是△ABC 的边BC ，BA 的中点， ∴DF ＝12AC ，同理EF ＝12CB ，DE ＝12AB ，则DF AC ＝EF CB ＝ED AB， ∴△DEF ∽△ABC ；(2)∵E ，F 分别是△ABC 的三边CA ，AB 的中点， ∴EF ∥BC ， ∴△AFE ∽△ABC .同理，△FBD ∽△ABC ，△EDC ∽△ABC .∴图中与△ABC 相似的三角形还有△AFE ，△FBD ，△EDC .10．如图27－2－24，△ABC 是等边三角形，D ，E 在BC 边所在的直线上，且AB ·AC ＝BD ·CE . 求证：△ABD ∽△ECA .图27－2－24证明：∵△ABC 是等边三角形(已知)，∴∠ABC ＝∠ACB ＝60°(等边三角形的三个内角相等，都等于60°)，∴∠ABD ＝∠ACE (等角的补角相等)．又AB ·AC ＝BD ·CE (已知)，即AB EC ＝BDCA，∴△ABD ∽△ECA (两边对应成比例且夹角相等的两三角形相似)．11．如图27－2－25，已知正方形ABCD 中，F 为BC 上一点，且BF ＝3FC ，E 为DC 的中点．求证：△ADE ∽△ECF .图27－2－25证明：∵正方形ABCD 中，E 为CD 中点， ∴CE ＝ED ＝12CD ＝12AD .∵BF ＝3FC ，∴FC ＝14BC ＝14AD ＝12CE .∴CF CE ＝DE AD ＝12，即CF DE ＝CE AD. ∵∠C ＝∠D ＝90°， ∴△ADE ∽△ECF .12．如图27－2－26，∠DAB ＝∠CAE ，且AB ·AD ＝AE ·AC ，请在图中找出与∠ADE 相等的角，并说明理由．图27－2－26【解析】由AB ·AD ＝AE ·AC 得AB AE ＝ACAD，如果证得它们的夹角相等，就可得到三角形相似，于是就有与∠ADE 相等的角．解：∠C ＝∠ADE ，理由如下： ∵∠DAB ＝∠CAE ，∴∠DAB ＋∠BAE ＝∠CAE ＋∠BAE ， ∴∠DAE ＝∠BAC . ∵AB ·AD ＝AE ·AC ， ∴AB AE ＝ACAD，∴△ABC ∽△AED ， ∴∠ADE ＝∠C .13. 如图27－2－27，∠AOB＝90°，OA＝OB＝BC＝CD.请找出图中的相似三角形，并说明理由．图27－2－27解：△ABC∽△DBA.理由如下：设OA＝OB＝BC＝CD＝x，根据勾股定理，AB＝x2＋x2＝2x，AC＝x2＋（2x）2＝5x，AD＝x2＋（3x）2＝10x，∵BCAB＝x2x＝22，ABBD＝2x2x＝22，ACAD＝5x10x＝22，∴BCAB＝ABBD＝ACAD，∴△ABC∽△DBA.第3课时相似三角形判定定理3 [见B本P71]1．已知如图27－2－28(1)，(2)中各有两个三角形，其边长和角的度数已在图上标注，图(2)中AB，CD交于O点，对于各图中的两个三角形而言，下列说法正确的是( A )图27－2－28A．都相似 B．都不相似C．只有(1)相似 D．只有(2)相似【解析】两角对应相等，或者两组对应边的比相等，并且相应的夹角相等的两个三角形相似．2．△ABC和△DEF满足下列条件，其中使△ABC与△DEF不相似的是( C )A．∠A＝∠D＝45°38′，∠C＝26°22′，∠E＝108°B．AB＝1，AC＝1.5，BC＝2，DE＝12，EF＝8，DF＝16C．BC＝a，AC＝b，AB＝c，DE＝a，EF＝b，DF＝cD．AB＝AC，DE＝DF，∠A＝∠D＝40°3．如图27－2－29，在△ABC中，∠C＝90°，D是AC上一点，DE⊥AB于点E，若AC＝8，BC＝6，DE＝3，则AD的长为( C )图27－2－29A ．3B ．4C ．5D ．6【解析】在△ABC 中，∠C ＝90°，AC ＝8，BC ＝6，由勾股定理得AB ＝AC 2＋BC 2＝82＋62＝10.在△ADE 和△ABC 中，∵∠A ＝∠A ，∠AED ＝∠C ，∴△ADE ∽△ABC ，∴DE BC ＝AD AB ，即36＝AD10，∴AD ＝5.4．如图27－2－30所示，给出下列条件：①∠B ＝∠ACD ；②∠ADC ＝∠ACB ；③AC CD ＝ABBC；④AC 2＝AD ·AB .其中单独能够判定△ABC ∽△ACD 的个数为( C ) A ．1 B ．2 C ．3 D ．4【解析】图中△AB C 与△ACD 有一组公共角，根据相似三角形的判定方法，可再补充另一组对应角相等，①②符合条件；或补充夹公共角的两边对应成比例，④符合条件，所以补充①②④能判定△ABC ∽△ACD .图27－2－30图27－2－315．如图27－2－31，在△ABC 中，AB ＝5，AC ＝4，点D 在边AB 上，∠ACD ＝∠B ，则AD的长为__165__．6. [2013·安顺]如图27－2－32，在▱ABCD 中，点E 在DC 上，若DE ∶EC ＝1∶2，则BF ∶BE ＝__3∶5__．图27－2－32图27－2－337．如图27－2－33，∠1＝∠2，添加一个条件，使得△ADE ∽△ACB ：__∠D ＝∠C 或∠E ＝∠B 或AD AC ＝AEAB__．【解析】由∠1＝∠2可得∠DAE ＝∠CAB .只需还有一对角对应相等或夹边对应成比例即可使得△ADE ∽△ACB .8. [2013·六盘水]如图27－2－34，添加一个条件：__∠ADE ＝∠C 或∠AED ＝∠B 或ADAC＝AEAB__，使得△ADE ∽△ACB .(写出一个即可) 【解析】由题意得，∠A ＝∠A (公共角)，则可添加：∠ADE ＝∠C 或∠AED ＝∠B ，利用两角法可判定△ADE ∽△ACB ，添加AD AC ＝AE AB也可以．图27－2－34图27－2－359. 如图27－2－35，在△ABC中，AB＝AC，BD＝CD，CE⊥AB于E.求证：△ABD∽△CBE. 证明：在△ABC中，AB＝AC，BD＝CD，∴AD⊥BC，∵CE⊥AB，∴∠ADB＝∠CEB＝90°，又∵∠B＝∠B，∴△ABD∽△CBE.10．如图27－2－36，点P在平行四边形ABCD的CD边上，连接BP并延长与AD的延长线交于点Q.(1)求证：△DQP∽△CBP；(2)当△DQP≌△CBP，且AB＝8时，求DP的长．图27－2－36解：(1)∵四边形ABCD是平行四边形，∴AQ∥BC，∴∠Q＝∠PBC，∠PDQ＝∠C，∴△DQP∽△CBP；(2)∵△DQP≌△CBP，∴DP ＝CP ＝12CD .∵AB ＝CD ＝8，∴DP ＝4.图27－2－3711.如图27－2－37所示，在平行四边形ABCD 中，AC 与BD 相交于点O ，E 为OD 的中点，连接AE 并延长交DC 于点F ，则DF ∶FC ＝( D ) A ．1∶4 B ．1∶3 C ．2∶3 D ．1∶2【解析】在平行四边形ABCD 中，AB ∥DC ，则△DFE ∽△BAE ，∴DF AB ＝DE EB， ∵O 为对角线的交点，∴DO ＝BO ，又∵E 为OD 的中点，∴DE ＝14DB ，则DE ∶EB ＝1∶3，∴DF ∶AB ＝1∶3，∵DC ＝AB ，∴DF ∶DC ＝1∶3，∴DF ∶FC ＝1∶2.图27－2－3812．如图27－2－38，△ABC 中，AE 交BC 于点D ，∠C ＝∠E ，AD ＝4，BC ＝8，BD ∶DC ＝5∶3，则DE 的长等于( B ) A.203 B.154 C.163 D.174【解析】∵∠ADC ＝∠BDE ，∠C ＝∠E ，∴△ADC ∽△BDE ，∴AD BD ＝DC DE ，∵AD ＝4，BC ＝8，BD ∶DC ＝5∶3，∴BD ＝5，DC ＝3，∴DE ＝BD ·DC AD ＝154. 故选B.13．如图27－2－39，AC 是⊙O 的直径，弦BD 交AC 于点E .(1)求证：△ADE ∽△BCE ；(2)如果AD 2＝AE ·AC ，求证：CD ＝CB .图27－2－39第13题答图解：(1)证明：∵∠A 与∠B 是CD ︵所对的圆周角，∴∠A ＝∠B ，又∵∠AED ＝∠BEC ，∴△ADE ∽△BCE ；(2)证明：如图，∵AD 2＝AE ·AC ，∴AE AD ＝AD AC，又∵∠A ＝∠A ，∴△ADE ∽△ACD ，∴∠AED＝∠ADC，又∵AC是⊙O的直径，∴∠ADC＝90°，即∠AED＝90°，∴直径AC⊥BD，∴CD＝CB.14．已知AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点(不与点A，B，G重合)，直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.(1)如图(1)，当点E在直径AB上时，试证明：OE·OP＝r2；图27－2－40(2)当点E在AB(或BA)的延长线上时，以图(2)中点E的位置为例，请你画出符合题意的图形，标注上字母，(1)中的结论是否成立？请说明理由．解：(1)证明：如图(1)，连接FO并延长交⊙O于Q，连接DQ.∵FQ是⊙O的直径，∴∠FDQ＝90°，∴∠QFD＋∠Q＝90°.∵CD⊥AB，∴∠P＋∠C＝90°.∵∠Q＝∠C，∴∠QFD＝∠P.∵∠FOE＝∠POF，∴△FOE∽△POF，∴OEOF＝OFOP，∴OE·OP＝OF2＝r2.图(1)图(2)(2)(1)中的结论成立．理由：如图(2)，依题意画出图形，连接FO并延长交⊙O于M，连接CM. ∵FM是⊙O的直径，∴∠FCM＝90°，∴∠M＋∠CFM＝90°.∵CD⊥AB，∴∠E＋∠D＝90°.∵∠M＝∠D，∴∠CFM＝∠E.∵∠POF＝∠FOE，∴△POF∽△FOE，∴OPOF＝OFOE，∴OE·OP＝OF2＝r2.。

人教版九年级数学下册27.2.1相似三角形的判定基础训练(有答案)

人教版九年级数学下学期27.2.1相似三角形的判定基础训练一、单选题1．下列命题是假命题的是（）A．所有等边三角形一定相似B．所有等腰直角三角形一定相似C．有一个角为120︒的两个等腰三角形相似D．有一条边对应成比例的两个等腰三角形相似2．如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（）A．∠ABP=∠C B．∠APB=∠ABCC．AP ABAB AC=D．AB ACBP CB=3．如图，AD、BC相交于点O，由下列条件不能判定△AOB与△DOC相似的是（）A．AB∥CD B．A D∠=∠C．OA OBOD OC=D．OA ABOD CD=4．如图，△ACB≌△A′CB′，∠BCB′=30°，则∠ACA′的度数为（）A．20°B．30°C．35°D．40°5．如图，点D，E分别在△ABC的AB，AC边上，增加下列哪些条件，①∠AED=∠B，②AE DE AB BC=，③AD AEAC AB=，使△ADE与△ACB一定相似（）12A ．①②B ．②C ．①③D ．①②③6．如图，在△ABC 中，点D ，E ，F 分别是边AB ，AC ，BC 上的点，DE ∥BC ，EF ∥AB ，且AD ∶DB ＝3∶5，那么CF ∶CB 等于( )A ．5∶8B ．3∶8C ．3∶5D ．2∶57．如图，E 是▱ABCD 的边BC 的延长线上一点，连接AE 交CD 于F ，则图中共有相似三角形( )A ．4对B ．3对C ．2对D ．1对8．如图，在△ABC 中，∠B=80°，∠C=40°，直线l 平行于BC ．现将直线l 绕点A 逆时针旋转，所得直线分别交边AB 和AC 于点M 、N ，若△AMN 与△ABC 相似，则旋转角为（）A ．20°B ．40°C ．60°D ．80°9．如图，点A 在线段BD 上，在BD 的同侧作等腰Rt ABC ∆和等腰Rt ADE ∆，CD 与BE 、AE 分别交于点P 、M .对于下列结论：①BAE CAD ∆~∆；②MP MD MA ME ⋅=⋅；③22CB CP CM =⋅.其中正确的是（）3A ．①②③B ．①C ．①②D ．②③10．如图，D 是等边△ABC 边AB 上的一点，且AD ：DB ＝1：2，现将△ABC 折叠，使点C 与D 重合，折痕为EF ，点E 、F 分别在AC 和BC 上，则CE ：CF 的值为（）A ．45B ．35C ．56D ．67二、填空题11．如图：使△AOB ∽△COD ，则还需添加一个条件是：．（写一个即可）12．如图，E 为平行四边形ABCD 的对角线BD 上一点，AE 的延长线交边CD 于点F ．在不添加辅助线的情况下，请写出图中一对相似三角形:________________．13．如图，////,::2:3:4DE FG BC AD DF FB =，如果4EG =，那么AC =________．14．若线段AB ＝2，且点C 是AB 的黄金分割点且AC ＞BC ，则BC 等于_____．415．如图，在四边形ABCD 中，∠ABC ＝90°，AB ＝3，BC ＝4，CD ＝10，DA ＝，则BD 的长为_______．16．如图，已知,20,60AB BC AC BAD DAE AD DE AE︒︒==∠=∠=，则DAC ∠的度数为_________．17．如图，在矩形ABCD 中，6AB =，12AD =，点E 在边AD 上，8AE =，点F 在边DC 上，则当EF =________时，ABE △与DEF V 相似．18．如图，ABC ∆中，AB AC =，AD BC ⊥于D 点，DE AB ⊥于点E ，BF AC ⊥于点F ，3cm DE =，则BF =__________cm .19．如图，正方形ABCD 的边长为2，连接BD ，点P 是线段AD 延长线上的一个动点，45PBQ ∠=︒，点Q 是BQ 与线段CD 延长线的交点，当BD 平分PBQ ∠时，PD ______QD （填“>”“<”或“=”）：当BD 不平分PBQ ∠时，PD QD ⋅=__________.三、解答题20．在△ABC和△A′B′C′中，已知：AB＝6cm，BC＝8cm，AC＝10cm，A′B′＝18cm，B′C′＝24cm，A′C′＝30cm．试证明△ABC与△A′B′C′相似．21．如图，E是□ ABCD的边BA延长线上一点，连接EC，交AD于点F．求证：△EBC∽△CDF．22．在△ABC中，点D、E分别边AB、AC上的点，若AD＝2，DB＝7，AE＝3，EC＝3，求DE：BC的值．523．如图，已知AB∥EF∥CD，AD与BC相交于点O.（1）如果CE=3，EB=9，DF=2，求AD的长；（2）如果BO：OE：EC=2：4：3，AB=3，求CD的长．24．如图，在△ABC中，∠C＝90°，DE⊥AB于E，DF⊥BC于F．求证：△DEH∽△BCA．25．已知：如图，在△ABC中，点D、E分别在边AB、AC上，且∠ABE =∠ACD，BE、CD交于点G．（1）求证：△AED∽△ABC；（2）如果BE平分∠ABC，求证：DE=CE．6726．如图所示，⊙O 的半径为4，点A 是⊙O 上一点，直线l 过点A ；P 是⊙O 上的一个动点（不与点A 重合），过点P 作PB ⊥l 于点B ，交⊙O 于点E ，直径PD 延长线交直线l 于点F ，点A 是»DE的中点．（1）求证：直线l 是⊙O 的切线；（2）若PA=6，求PB 的长．27．已知，如图1，抛物线2l y ax bx c =++：过(1,0),(3,0),(0,3)A B C -三点，顶点为点D ，连接,,AC CD DB ，点P 为抛物线对称轴上一点，连接,PC PA ，直线'l y kx n =+：过点,B C 两点．（1）求抛物线l 及直线'l 的函数解析式；（2）求PC PA +的最小值；（3）求证：AOC ∆∽DCB ∆；（4）如图2，若点M 是在抛物线l 上且位于第一象限内的一动点，请直接写出MBC ∆面积的最大值及此时点M 的坐标．8参考答案1．D2．D3．D4．B5．C6．A7．B8．B9．A10．A11．∠A=∠C（答案不唯一）．12．△ABE∽△FDE13．1214．315．16．40°17．5或20318．619．= 820．略21．略22．1323．（1）8；（2）21224．略25．略26．（1）略；（2）PB=92．27．（1）2y x 2x 3=-++，3y x =-+；（2）（3）详见解析；（4）（4）278MBC S ∆=最大，此时315(,)24M ．。

人教版九年级数学下册【推荐】27.2.1 相似三角形的判定-同步练习(1)B(含答案)

相似三角形判定练习题1．如图1，（1）若OAOB=_____，则△OAC∽△OBD，∠A=________．（2）若∠B=________，则△OAC∽△OBD，________与________是对应边．（3）请你再写一个条件，_________，使△OAC∽△OBD．2．如图2，若∠BEF=∠CDF，则△_______∽△________，△______∽△_______．(1) (2) (3)3．如图3，已知A（3，0），B（0，6），且∠ACO=•∠BAO，•则点C•的坐标为________，•AC=_______．4．已知，如图4，△ABC中，DE∥BC，DF∥AC，则图中共有________对相似三角形．5．下列各组图形一定相似的是（）．A．有一个角相等的等腰三角形 B．有一个角相等的直角三角形C．有一个角是100°的等腰三角形 D．有一个角是对顶角的两个三角形6．如图5，AB=BC=CD=DE，∠B=90°，则∠1+∠2+∠3等于（）．A．45° B．60° C．75° D．90°(4) (5) (6)7．如图6，若∠ACD=∠B，则△_______∽△______，对应边的比例式为_____________，∠ADC=________．8．如图，在△ABC中，CD，AE是三角形的两条高，写出图中所有相似的三角形，简要说明理由．9．如图，D，E是AB边上的三等分点，F，G是AC边上的三等分点，•写出图中的相似三角形，并求出对应的相似比．10．如图，在直角坐标系中，已知点A （2，0），B （0，4），在坐标轴上找到点C （1，0）•和点D ，使△AOB 与△DOC 相似，求出D 点的坐标，并说明理由．11．已知：如图是一束光线射入室内的平面图，•上檐边缘射入的光线照在距窗户2.5m 处，已知窗户AB 高为2m ，B 点距地面高为1.2m ，求下檐光线的落地点N•与窗户的距离NC ．12．如图，等腰直角三角形ABC 中，顶点为C ，∠MCN=45°，试说明△BCM ∽△ANC ．13．在Y ABCD 中，M ，N 为对角线BD 的三等分点，连接AM 交BC 于E ，连接EN 并延长交AD于F ．（1）试说明△AMD ∽△EMB ；（2）求FNNE的值．14．在△ABC 中，M 是AB 上一点，若过M 的直线所截得的三角形与原三角形相似，•试说明满足条件的直线有几条，画出相应的图形加以说明．15．为了测量一大楼的高度，在地面上放一平面镜，镜子与楼的距离AE=27m，他与镜子的距离是2.1m时，刚好能从镜子中看到楼顶B，已知他的眼睛到地面的高度CD为1.6m，结果他很快计算出大楼的高度AB，你知道是什么吗？试加以说明．16．在△ABC和△A′B′C′中，∠A=∠A′=80°，∠B=30°，∠B′=20°．•试分别在△ABC 和△A′B′C′中画一条直线，使分得的两个三角形相似．在下图中分别画出符合条件的直线，并标注有关数据．17．如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC，DE∥BC，那么在下列三角形中，与△ABC相似的三角形是（）．A．△DBE B．△ADE C．△ABD D．△BDC18．如第17题图，已知等腰三角形ABC中，顶角∠A=36°，BD平分∠ABC，•则ADAC的值为（）．A．12B．5151.1.C D-+19．如图，△ABC和△DEF均为正三角形，D，E分别在AB，BC上，请找出一个与△DBE相似的三角形并证明．20．如图，四边形ABCD是平行四边形，点F在BA的延长线上，连接CF交AD•于点E．（1）求证：△CDE∽△FAE．（2）当E是AD的中点且BC=2CD时，求证：∠F=∠BCF．。

人教版-数学-九年级下册-27.2 相似三角形的判定同步练习

相似三角形的判定1．如果两个三角形的________，________，那么这两个三角形相似．若△ABC和△A′B′C′相似，可记为________．2．相似三角形________叫做相似比．如果△ABC∽△A′B′C′，且相似比为k，那么________________________ABA B===''．3．两条直线被一组平行线所截，所得的________；平行于三角形一边的直线截其他两边(或两边的延长线)，所得的________．4．平行于三角形一边的直线和其他两边相交，所构成的三角形与________．5．平行于三角形一边的直线与三角形两边的延长线相交，所构成的三角形与________．6．如图，如果AB∥CD∥EF，那么下列结论正确的是( )A．AD BCDF CE=B．BC DFCE AD=C．CD BCEF BE=D．CD ADEF AF=7．如图，F是□ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是( )A．ED DFEA AB=B．DE EF BC FB=C．BC BF DE BE=D．BF BC BE AE=8．(2015·淮安)如图，l1∥l2∥l3，直线A.b与l1、l2、l3分别相交于点A.B.C和点D.E.F，若23ABBC=，DE＝4，则EF的长是( )A．8 3B．20 3C．6D．109．(2014·沈阳)如图，在△ABC中，点D在边AB上，BD＝2AD，DE∥BC交AC于点E．若线段DE＝5，则线段BC的长为________．10．如图，l1∥l2∥l3，AC＝8，DF＝5，EF＝3，求AB的长．11．(2015·乐山)如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A.B.C和点D.E.F，已知32ABBC，则DEDF的值为( )A．32B．23C．25D．3512．如图，在△ABC中，DE∥BC，MN∥AB，则图中与△ABC相似的三角形有( )A．1个B．2个C．3个D．4个13．如图，在菱形ABCD中，EF⊥AC于点G，分别交AD及CB的延长线于点E.F，EF交AB于点H，AH︰FB＝1︰2，则AG︰GC的值为( )A．13B．15C．25D．1414．如图，l1∥l2∥l3，AE＝4cm，BE＝3cm，CD＝14cm，则CF＝________cm，DF＝________cm．15．如图，在□ABCD中，点E在AB上，CE.BD交于点F．若AE︰BE＝4︰3，且BF＝2，则DF＝________．16．如图，在△ABC中，DE∥BC，EF∥CD，求证：AF ADAD AB．17．如图，P是菱形ABCD的对角线AC上的一点，连接DP，并延长DP交边AB于点E，连接BP，并延长BP交边AD于点F，交CD的延长线于点G．(1)求证：△APB≌△APD；(2)已知DF︰FA＝1︰2，设线段PD的长为x，线段FP的长为y．①求y与x之间的函数解析式；②当x＝6时，求线段FG的长．参考答案1．三个角分别相等三条边成比例△ABC∽△A′B′C′2．对应边的比BCB C''ACA C'' k3．对应线段成比例对应线段成比例4．原三角形相似5．原三角形相似6．A7．C8．C9．1510．∵l1∥l2∥l3，∴AB DE BC EF =．∵DF ＝5，EF ＝3，∴DE ＝2．∴23DE EF =．∴23AB AB BC AC AB ==-．∴283AB AB =-．∴165AB =11．D12．C13．B14．8 615．14316．∵DE ∥BC ，∴△ADE ∽△ABC ．∴AD AE AB AC =．∵EF ∥CD ，∴△AEF ∽△ACD ．∴AF AE AD AC =．∴AF AD AD AB =17．(1)∵四边形ABCD ．是菱形，∴AB ＝AD ，AC 平分∠DAB ．∴∠DAP ＝∠BAP ．在△APB 和△APD 中，,,,AB AD BAP DAP AP AP =⎧⎪∠=∠⎨⎪=⎩，∴△APB ≌△APD(2)①∵四边形ABCD 是菱形，∴AD ∥BC ，AD ＝BC ．∴△AFP ∽△CBP ．∴AF FP BC BP =．∵DF︰FA ＝1︰2，∴AF ︰BC ＝AF ︰AD ＝AF ︰(DF ＋AF)＝2︰3．∴23FP BP =．由(1)知BP ＝PD ＝x ．又∵FP ＝y ，∴23y x =，即23y x =．∴y 与x 之间的函数解析式为23y x = ②当x ＝6时，2643y =⨯=．∴FB ＝FP ＋PB ＝10．∵DG ∥AB ，∴△DFG ∽△AFB ．∴12FG FD FB FA ==．∴11052FG =⨯=．∴线段FG 的长为5。

人教版九年级数学下册27.2.1相似三角形的判定同步练习及答案【新改】

27.2.1 相似三角形的判定（3）一、基础练习1．已知线段AC 、BD 交于O ，如图1，OC ：OB=1：2，OA=6cm ，•OD=•3cm ，•AB=•7cm ，则CD=____．OBACDBA C DGF BACE D M G F(1) (2) (3)2．如图2，△ABC 中，∠C=90°，四边形DEFG 是正方形，点G 、F 分别在AC 、BC 上，DE 在AB 上，则图中相似的三角形共有_______对，它们分别是____________．3．如图3，△ABC 中，DE ∥BC ，GF ∥AC ，则图中与△ABC 相似的三角形为_________．4．•如图4，•∠1=•∠2=•∠3，•则图中相似三角形共有______•对，•它们分别是_________．BAC 31ED 2BA CE DP(4) (5) (6) 5．如图5，有下列条件：①∠B=∠C ；②∠ADB=∠AEC ；③AD AE AC AB =；④AD AE AB AC =；⑤PE BPPD PC=，•其中一个条件就能使△BPE ∽△CPD 的条件有_______个，它们分别是_________．（填序号就可以）6．如图6，在△ABC 中，AB=24，AC=18，D 是AC 上一的点，AD=12，在AB 上取一点E ，使A 、D 、E 三点组成的三角形与△ABC 相似，则AE 的长为________． 7．如图7，在Rt △ABC 的直角边AC 上有一点P （P 不同于A 、C ），过P 作直线截△ABC ，使截得的三角形与△ABC 相似，满足条件的直线共有_______条，这些直线与△ABC•的边的位置关系分别是______________．B AC ED F(7) (8) (9)8．如图8，在YABCD 中，AB=10，AD=6，E 是AD 的中点，在AB 上取一点F ，使△CBF ∽△CDE ，则BF 的长为__________．9．如图9，弦AB 和CD 相交于⊙O 内一点P ，AP=4cm ，BP=3cm ，CP=5cm ，则DP=______cm ．10．如图，在正方形网格上，请你画两个三角形，使它们不全等且分别与图中的△ABC 相似，其相似比不为1，三角形的顶点都在正方形的顶点上，并注明相应的字母．BAC二、整合练习1．如图，已知△ABC 的高CD 、BE 相交于点F ，求证：CF ·FD=BF ·FE ．BAC E DF2．如图，D 是△ABC 的边BC 上的一点，且BD ABDC AC，BE ⊥AD 于E ，CF ⊥AD 于F ，求证：AB ·DF=AC ·DE ． BA CE DF3．如图，已知正方形ABCD 中，P 是BC 边上的点，BP=3PC ，Q 是CD 的中点．求证：（1）△ADQ ∽△QCP ；（2）AQ ⊥QP ；（3）AQ=2AQ ；（4）AQ 平分∠DAP ．BA CQD P答案:一、基础练习1．3．5cm 2．6 △ABC 与△GFC △ABC 与△AGD △ABC 与△FBE • •△AGD•与△GFC △AGD 与△FBE △GFC 与△FBE 3．△ADE △GBF △GDM4．4 △ADE 与△ABC △ACD 与△ABC △ACD 与△ADE △DEC 与△CDB 5．4 ①②④⑤6．16或9（△AED ∽△ABC 或△ADE ∽△ABC ）7．3 一条与AB 平行，一条与BC 平行，一条与BC 垂直 8．1．8 9．125（连结AC 、BD ，证明△APC ∽△DPB ） 10．如图B 2C 1A 2C 2B 1A 1B A C二、整合练习1．因为BE ⊥AC ，CD ⊥AB ，∠CEF=∠BDF=90°，∠CFE=∠BFD ，△CFE ∽△BFD （两角对应相等，两三角形相似），CF FEBF FD=，即CF ·FD=BF ·FE ． 2．因为BE ⊥AD ，CF ⊥AD ，可证△BDE ∽△CDF ，得BD DE DC DF =，又BD ABDC AC=，所以AB DE AC DF=，即AB ．DF=AC ．DE ． 3．（1）∠D=∠C=90°，AD DQQC PC==2．（2）证∠AQD+∠PQC=90° （3）由（1）得AQ ADPQ QC==2 （4）•证△ADQ ∽△AQP。

人教版数学九年级下册27.2《相似三角形的判定》同步练习1

相似三角形的判定1．以下各组三角形中，两个三角形能够相似的是〔〕A.△ABC 中，∠A ＝42 o ，∠B ＝118 o ，△A`B`C`中，∠A`＝118 o ，∠B`＝15 oB.△ABC 中，AB=8，AC=4, ∠A ＝105 o ，△A`B`C`中，A`B`＝16，B`C`＝8，∠A`＝100oC.△ABC 中，AB=18，BC ＝20，CA ＝35，△A`B`C`中，A`B`＝36，B`C`＝40，C`A`＝70D.△ABC 和△A`B`C`中，有````C B BC B A AB ，∠C ＝∠C` 2．△ABC 和△DEF 满足以下条件，其中使△ABC 和△DEF 不相似的是〔〕A ．∠A ＝∠D ＝45 o 38`，∠C ＝26 o 22`，∠E ＝108 oB ．AB ＝1，AC ＝1.5，BC ＝2，DE ＝12，EF ＝8，DF ＝16C ．BC ＝a ，AC ＝b ，AB ＝c ，DE ＝a ，EF ＝b ，DF ＝cD ．AB ＝AC ，DE ＝DF ，∠A ＝∠D ＝40 o3．如图，△ABC 中∠ACB ＝90o ，CD ⊥AB 于D 。

那么图中能够相似的三角形共有〔〕A ．1对B ．2对C ．3对D ．4对4．△ABC 中，D 是AB 上一固定点。

E 是AC 上的一个动点，假设使△ABC 和△ADE 相似，那么这样的点E 有〔〕A ．1个B ．2个C ．3个D ．很多5．以下说法①所有等腰三角形都相似；②有一个底角相等的两个等腰三角形相似；③有一个角相等的等腰三角形相似；④有一个角为60 o 的两个直角三角形相似，其中正确的说法是〔〕A ．②④B ．①③C ．①②④D ．②③④6．如图，假设点D 为△ABC 中AB 边上的一点，且∠ABC ＝∠ACD ，AD ＝3cm ，AB ＝4cm ，那么AC 的长为〔〕A ．12cmB ．32cmC ．3cmD ．2cm7．如图，BD 平分∠ABC ，且AB ＝4，BC ＝6，那么当BD ＝_________时， △ABC ∽△DBC 。

人教版九年级下册数学 27.2.1相似三角形的判定同步测试

27.2.1相似三角形的判定同步测试一．选择题1．下列条件中，不能判断△ABC与△DEF相似的是（）A．∠A＝∠D，∠B＝∠F B．且∠B＝∠DC．D．且∠A＝∠D2．如图，已知△ABC中，D是AB上一点，连结CD，不能判定△ACD∽△ABC的条件是（）A．∠ACD＝∠B B．∠ADC＝∠ACB C．D．AC2＝AD•AB 3．如图，在△ABC中，点D、E分别在边AB、AC上，下列条件中能判断△ABC∽△AED 的是（）①∠AED＝∠B；②∠ADE＝∠C；③＝；④＝．A．①②B．①②③C．①②④D．①②③④4．如图，点D、E分别在△ABC的边AB、BC上，下列条件中，不能判定DE∥AC的条件是（）A．B．C．D．5．已知△ABC中，D、E分别是边AB、AC上的点，下列各式中，不能判断DE∥BC的是（）A．＝B．＝C．＝D．＝6．已知△ABC如图所示．则下列4个三角形中．与△ABC相似的是（）A．B．C．D．7．如图，在4×4的正方形网格中，画2个相似三角形，在下列各图中，正确的画法有（）A．1个B．2个C．3个D．4个8．如图．在△ABC中，DE∥BC，∠B＝∠ACD，则图中相似三角形有（）A．2对B．3对C．4对D．5对9．如图，在正方形ABCD中，点E为边AD上的一个动点（与点A、D不重合），∠EBM＝45°，BE交对角线AC于点F，BM交对角线AC于点G，交边CD于点M，那么下列结论中，错误的是（）A．△AEF∽△CBF B．△CMG∽△BFG C．△ABG∽△CFB D．△ABF∽△CBG 10．如图，正方形ABCD中，点F是BC边上一点，连接AF，以AF为对角线作正方形AEFG，边FG与正方形ABCD的对角线AC相交于点H，连接DG．以下四个结论：①∠EAB＝∠GAD；②△AFC∽△AGD；③2AE2＝AH•AC；④DG⊥AC．其中正确的个数为（）A．1个B．2个C．3个D．4个二．填空题11．已知△ABC，P是边AB上的一点，连接CP，请你添加一个条件，使△ACP∽△ABC，这个条件可以是．（写出一个即可）12．在平面直角坐标系中有两点A（4，0），B（0，2），如果点C在x轴上（C与A不重合），当点C的坐标为时，使得△BOC∽△AOB．13．在Rt△ABC中，∠C＝90°，∠A＝30°，点P为AC中点，经过点P的直线截△ABC，使截得的三角形与△ABC相似，这样的直线共有条．14．如图，在△ABC中，AB＝6cm，AC＝8cm，D是AB上一点且AD＝2cm，点E在边AC 上，当AE＝cm时，使得△ADE与△ABC相似．15．如图，点P是边长为5的正方形ABCD内一点，且PB＝2，PB⊥BF，垂足为点B，请在射线BF上找一点M，使得以B，M，C为顶点的三角形与△ABP相似，则BM＝．三．解答题16．如图，在△ABC中，点D、E分别在AB、AC上，DE、BC的延长线相交于点F，且EF•DF＝CF•BF．求证：△CAB∽△DAE．17．如图，已知∠DAB＝∠ECB，∠ABD＝∠CBE．求证：△ABC∽△DBE．18．如图，在Rt△ABC中，∠B＝90°，AC＝10cm，BC＝6cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以2cm/s的速度沿AB向终点B移动；点Q以1cm/s 的速度沿BC向终点C移动，其中一点到终点，另一点也随之停止．连接PQ．设动点运动时间为x秒．（1）含x的代数式表示BQ、PB的长度；（2）x为何值时，△PBQ为等腰三角形？当△BPQ和△BAC相似时，求此时x的值．参考答案一．选择题1．解：A、∠A＝∠D，∠B＝∠F，可以得出△ABC∽△DFE，故此选项不合题意；B、＝且∠B＝∠D，不是两边成比例且夹角相等，故此选项符合题意；C、＝＝，可以得出△ABC∽△DEF，故此选项不合题意；D、＝且∠A＝∠D，可以得出△ABC∽△DEF，故此选项不合题意；故选：B．2．解：因△ACD和△ABC已有一公共角，要使△ACD∽△ABC，则需再有一角对应相等，如∠ACD＝∠B，∠ADC＝∠ACB，故A，B正确；或公共角的两边对应相等，如AD：AC＝AC：AB，即AC2＝AD•AB，故D正确，C错误．故选：C．3．解：∵∠A＝∠A，∴∠AED＝∠B或∠ADE＝∠C时，△ABC∽△AED．∵＝，∴＝∵∠A＝∠A，∴△ABC∽△AED，故①②③可以判断三角形相似，故选：B．4．解：A、∵，不能判定DE∥AC，选项符合题意；B、∵，∴DE∥AC，选项不符合题意；C、∵，∴，∴DE∥AC，选项不符合题意；D、∵，∴，∴DE∥AC，选项不符合题意；故选：A．5．解：如图，若使线段DE∥BC，则其对应边必成比例，即＝，＝，＝，故B选项答案错误；故选：B．6．解：∵由图可知，AB＝AC＝6，∠B＝75°，∴∠C＝75°，∠A＝30°，A、三角形各角的度数分别为75°，52.5°，52.5°，B、三角形各角的度数都是60°，C、三角形各角的度数分别为75°，30°，75°，D、三角形各角的度数分别为40°，70°，70°，∴只有C选项中三角形各角的度数与题干中三角形各角的度数相等，故选：C．7．解：第1个网格中两个三角形对应边的比例满足＝＝，所以这两个三角形相似；第2个网格中两个三角形对应边的比例＝＝，所以这两个三角形相似；第3个网格中两个三角形对应边的比例满足＝＝＝，所以这两个三角形相似；第4个网格中两个三角形对应边的比例＝＝，所以这两个三角形相似；故选：D．8．解：∵∠B＝∠ACD，∠A＝∠A，∴△ACD∽△ABC，∵DE∥BC，∴△ADE∽△ABC，∴△ACD∽△ADE，∵DE∥BC，∴∠EDC＝∠DCB，∵∠B＝∠DCE，∴△CDE∽△BCD，故共4对，故选：C．9．解：∵四边形ABCD是正方形，∴AB∥CD，AD∥BC，∠DCA＝∠ACB＝∠DAC＝∠CAB＝∠EBM＝45°，∴△AEF∽△CBF，故选项A不合题意；∵∠EBM＝∠DCA，∠MGC＝∠BGF，∴△CMG∽△BFG，故选项B不合题意；∴∠CMG＝∠CFB，∵CD∥AB，∴∠CMG＝∠ABG，∴∠CFB＝∠ABG，又∵∠CAB＝∠BCF＝45°，∴△BCF∽△GAB，故选项C不合题意；∵∠CAB＝∠ACB＝∠FBG＝45°，∴∠ABF+∠CBG＝45°，∴∠ABF≠∠CBG，∴△ABF与△CBG不相似，故选项D符合题意；故选：D．10．解：∵四边形ABCD，四边形AEFG都是正方形，∴∠EAG＝∠BAD＝90°，∠F AG＝∠AFG＝∠DAC＝∠ACB＝45°，AF＝AG，AC ＝AD，∴∠EAG﹣∠BAG＝∠BAD﹣∠BAG，∴∠EAB＝∠DAG，故①正确；∵AF＝AG，AC＝AD，∴＝，∵∠F AG＝∠CAD＝45°，∴∠F AC＝∠DAG，∴△F AC∽△DAG，故②正确，∴∠ADG＝∠ACB＝45°，延长DG交AC于N，∵∠CAD＝45°，∠ADG＝45°，∴∠AND＝90°，∴DG⊥AC，故④正确，∵∠F AC＝∠F AH，∠AFG＝∠ACF＝45°，∴△AFH∽△ACF，∴，∴AF2＝AH•AC，∴2AE2＝AH•AC，故③正确，故选：D．二．填空题11．解：∵∠A＝∠A，∴当∠ACP＝∠B，或∠APC＝∠ACB或＝时，△ACP∽△ABC，故答案为：∠ACP＝∠B，或∠APC＝∠ACB或＝．12．解：∵点A为（4，0），∴AO＝4；∵点B为（0，2），∴OB＝2．若△BOC∽△AOB．则：＝．即：＝，∴OC＝1．故点C为（﹣1，0）或者（1，0）．故答案为：（﹣1，0）或者（1，0）．13．解：过点P作PE∥AB交AB于点E，△CPE∽△CAB．过点P作PF∥BC交AB于点F，△APF∽△ACB．过点P作PG⊥AB交AB于点G，△PGA∽△BCA．故满足条件的直线有3条，故答案为：3．14．解：有两种情形：如图，当DE∥BC时，△ADE∽△ABC，∴＝，∴＝，∴AE＝（cm），当∠ADE′＝∠C时，∵∠A＝∠A，∴△ADE′∽△ACB，∴＝，∴＝，∴AE′＝1.5（cm），故答案为或1.5．15．解：∵四边形ABCD为正方形，∴∠ABC＝90°，BA＝BC，∵PB⊥BF，∴∠PBM＝90°，∵∠ABP+∠CBP＝90°，∠CBP+∠CBM＝90°，∴∠ABP＝∠CBM，∴当＝时，△BAP∽△BCM，即＝，解得BM＝2；当＝时，△BAP∽△BMC，即＝，解得BM＝，综上所述，当BM为2或时，以B，M，C为顶点的三角形与△ABP相似．故答案为2或．三．解答题16．证明：∵EF•DF＝CF•BF．∴，∵∠EFC＝∠BFD，∴△EFC∽△BFD，∴∠CEF＝∠B，∴∠B＝∠AED，∵∠CAB＝∠DAE，∴△CAB∽△DAE．17．证明：∵∠DAB＝∠ECB，∠ABD＝∠CBE，∴△ABD∽△CBE，∴＝，即，∵∠ABC＝∠ABD+∠DBC，∠DBE＝∠DBC+CBE，∵，∠ABC＝∠DBE，∴△ABC∽△DBE．18．解：（1）∵∠B＝90°，AC＝10cm，BC＝6cm，∴AB＝＝＝8（cm）．由运动可知：BQ＝x（cm），P A＝2x（cm），∴PB＝（8﹣2x）cm．（2）由题意，得8﹣2x＝x，∴x＝．∴当x＝时，△PBQ为等腰三角形．当BP：BA＝BQ：BC时，两三角形相似，此时（8﹣2x）：8＝x：6，解得x＝，当BP：BC＝BQ：AB时，两三角形相似，此时（8﹣2x）：6＝x：8，解得x＝，综上所述，满足条件的x的值为或．。

九年级数学下册第二十七章相似27.2相似三角形27.2.1相似三角形的判定同步练习新版新人教版

相似三角形的判断一、基础题目1．如图，△ ADE∽△ ACB，∠ AED＝∠ B，那么以下比率式成立的是()A.AD AE DE AD AEC.AD AC DE AE DE ＝＝ B.＝AC＝＝ D.＝AC AB BC AB AE AB BC EC BC2．如图，在△ ABC中，点 D， E 分别在边AB， AC上， DE∥ BC，若 BD＝2AD，则()A.AD1B.AE1C.AD1D.DE1＝2＝2＝2＝2 AB EC EC BC3．如图，已知直线a∥ b∥ c，直线 m交直线 a， b， c 于点 A， B， C，直线 n 交直线 a，b， c 于点 D， E，F，若AB1DE)＝，则＝(BC2EF112A. 3B.2C.3D． 1第 1题图第2题图第3题图4．假如△ ABC∽△ A′B′C′，△ ABC 与△ A′B′C′的相似比为2，那么△ A′B′C′与△ ABC 的相似比为．BC．5．如图， AB∥ CD∥ EF， AF 与 BE订交于点 G，且 AG＝ 2， GD＝ 1， DF＝ 5，那么的值等于CE6．如图，AB、CD订交于点 O，OC＝ 2，OD＝ 3，AC∥ BD.EF 是△ ODB的中位线，且 EF＝2，则 AC的长为．DE．7．如图，在△ ABC中， DE∥ BC，且 AD＝ 2， DB＝ 3，则＝BC第 5题图第6题图第7题图8．如图，EG∥BC，GF∥CD，AE＝3，EB＝2，AF＝ 6，求AD的值．二、训练题目9．如图，△ABC中，DE∥BC，EF∥AB，则图中相似三角形的对数是()A．1 对B． 2 对C． 3 对D． 4 对10. 如图，在 ?ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF∶FC等于() A．3∶2B．3∶1C．1∶1D．1∶211．如图 , 在ABC 中,DE∥BC,AD 3, BD2, 则ADE和ABC的相似比是；若DE6则BC，第9题图第10题图第11题图12．一个三角形的三边长分别为8 cm,6 cm,12 cm,另一个与它相似的三角形的最短边为 3 cm，则其余两边长为 ______________.13. 如图 , 在ABC 中, DE∥ BC, DE分别与AB,AC订交于 D、E ，若AD 4 ,DB 2,求DE :BC的值。

人教版数学九年级下册第二十七章相似 27.2.1 相似三角形的判定同步练习

人教版数学九年级下册第二十七章相似 27.2.1 相似三角形的判定同步练习一、单选题（共9题；共18分）1.如图，在 △ABC 中， ∠B =70° ， AB =4 ， BC =6 ，将 △ABC 沿图示中的虚线 DE 剪开，剪下的三角形与原三角形不．相似的是（）A. B. C. D.2.下列各组长度的线段（单位： cm ）中，成比例线段的是（）A. 1，2，3，4B. 1，2，3，5C. 2，3，4，5D. 2，3，4，6 3.已知四条线段a,b,c,d 是成比例线段，即 ab ＝ cd ，下列说法错误的是（） A. ad=bc B. a+cb+d ＝ ab C. a−b b＝c−b dD. a 2b2 ＝c 2d 24.下列判断中，错误的有（）A. 三边对应成比例的两个三角形相似B. 两边对应成比例，且有一个角相等的两个三角形相似C. 有一个锐角相等的两个直角三角形相似D. 有一个角是100°的两个等腰三角形相似 5.如图，在△ABC 中，DE ∥BC ，EF ∥AB ，AD ：BD=5：3，CF=6，则DE 的长为（）A. 6B. 8C. 10D. 12 6.下列条件中，不能判断△ABC 与△DEF 相似的是（） A. ∠A =∠D ， ∠B =∠F B. BCEF =ACDF 且∠B =∠D C. ABDE =BCEF =ACDF D. ABDE =ACDF 且∠A =∠D7.如图所示，在▱ABCD.BE 交AC ，CD 于G ，F ，交AD 的延长线于E ，则图中的相似三角形有（）A. 3对B. 4对C. 5对D. 6对8.如图，下列条件中不能判定△ACD∽△ABC的是（）A. ∠ADC＝∠ACBB. ABBC =ACCDC. ∠ACD＝∠BD. AC2＝AD•AB9.如图，AG：GD=4：1，BD：DC=2：3，则AE：EC 的值是（）A. 3：2B. 4：3C. 6：5D. 8：5二、填空题（共4题；共4分）10.如图，在△ABC中，D，E两点分别在AB，AC边上，DE∥B C．如果ADDB =32，AC＝10，那么EC＝________．11.如图，在△ABC中，∠C＝90°，BC＝16 cm，AC＝12 cm，点P从点B出发，沿BC以2 cm/s的速度向点C移动，点Q从点C出发，以1 cm/s的速度向点A移动，若点P、Q分别从点B、C同时出发，设运动时间为ts，当t＝________时，△CPQ与△CBA相似．12.ΔABC的边长分别为a,b,c,ΔA1B1C1的边长分别√a,√b,√c，则ΔABC与ΔA1B1C1________（选填“一定”“不一定” “一定不”）相似13.如图所示，在△ABC中，已知BD＝2DC，AM＝3MD，过M作直线交AB，AC于P，Q两点．则ABAP +2ACAQ＝________．三、解答题（共4题；共20分）14.如图，在△ABC中，BD平分∠ABC，交AC于点D，点E是AB上一点，连接DE，BD2=BC·BE.证明：△BCD∽△BDE.15.如图，直线a//b//c，直线m,n相交于点O，且分别与直线a,b,c相交于点A,B,C和点D,E,F，已知OA=3，OB=4，BC=6，EF=5，求DO的长度．16.已知：如图，ΔABC中，点D、E分别在边AB、AC上，且DE//BC,BE与CD交于点S,AS与BC交于点M．求证：点M是线段BC的中点．17.如图，把一块直角三角板的直角顶点P放在正方形ABCD的边BC上，并且使一条直角边经过点D，另一条直角边与AB交于点Q，请写出一对相似三角形，并加以证明（图中不添加字幕和线段）四、综合题（共1题；共7分）18.如图1，在正方形ABCD中，E是边BC上的点，将线段DE绕点E逆时针旋转90°得到EF，过点C作CG∥EF交BA（或其延长线）于点G，连接DF，FG.（1）FG与CE的数量关系是________，位置关系是________.（2）如图2，若点E是CB延长线上的点，其它条件不变.①（1）中的结论是否仍然成立？请作出判断，并给予证明；.②DE，DF分别交BG于点M，N，若BC＝2BE，求MNBC答案解析部分一、单选题1.【答案】C【解析】【解答】解：A.∵∠B=∠EDC, ∠C=∠C,∴△ABC∽△EDC;B.∵∠B=∠DEC, ∠C=∠C,∴△ABC∽△DEC;D.∵A、B、C、D在同一个圆上，∴∠A+∠DEC=180°,又∵∠DEB+∠DEC=180°,∴∠A=∠DEB, ∠B=∠B,∴△ABC∽△EBD;故剪下的三角形与原三角形不相似的是C.故答案为：C.【分析】根据相似三角形的判定定理逐项进行判断，即可求解.2.【答案】D【解析】【解答】解：A.1：2≠3：4，故四条线段不成比例，不合题意；B. 1：2≠3：5，故四条线段不成比例，不合题意；C.2：3≠4：5，故四条线段不成比例，不合题意；D. 2：3=4：6，故四条线段成比例，符合题意；故答案为：D．【分析】如果其中两条线段的乘积等于另外两条线段的乘积，则四条线段叫成比例线段．判定四条线段是否成比例，只要把四条线段按大小顺序排列好，判断前两条线段之比与后两条线段之比是否相等即可．3.【答案】C【解析】【解答】解：∵四条线段a，b，c，d是成比例线段，即ab ＝cd，∴A．利用内项之积等于外项之积，ad=bc，不符合题意，B．利用内项之积等于外项之积，a（b+d）=b（a+c），ab+ad=ab+bc，即ad=bc，不符合题意，C．∵a−bb = c−dd，∴a−bb＝c−bd，符合题意，D．∵ab ＝cd，∴a2b2＝c2d2，不符合题意．故答案为：C．【分析】根据比例的性质分别将原式变形，然后判断即可.4.【答案】B【解析】【解答】解：A、三边对应成比例的两个三角形相似，故A选项不合题意；B、两边对应成比例，且夹角相等的两个三角形相似，故B选项符合题意；C、有一个锐角相等的两个直角三角形相似，故C选项不合题意；D、有一个角是100°的两个等腰三角形，则它们的底角都是40°，所以有一个角是100°的两个等腰三角形相似，故D选项不合题意；故答案为：B．【分析】三边对应成比例、两边对应成比例且夹角相等、两角分别相等的两个三角形相似，据此逐一判断即可.5.【答案】C【解析】【解答】解：∵DE∥BC，EF∥AB∴四边形BFED是平行四边形∴DE=BF∵ DE∥BC AD：BD=5：3∴ADDB =AEEC=53∴CECA =38又EF∥AB∴CECA =CFCB=38又∵CF=6∴CB=16∴BF=BC−FC=10即DE=10故答案为：C【分析】根据DE∥BC，EF∥AB，判断出DE=BF，在根据DE∥BC，EF∥AB，便可以找到分的线段成比例。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初中数学试卷
鼎尚图文**整理制作
相似三角形判定练习题
1．如图1，（1）若OA
OB
=_____，则△OAC∽△OBD，∠A=________．
（2）若∠B=________，则△OAC∽△OBD，________与________是对应边．（3）请你再写一个条件，_________，使△OAC∽△OBD．
2．如图2，若∠BEF=∠CDF，则△_______∽△________，△______∽△_______．
(1) (2) (3)
3．如图3，已知A（3，0），B（0，6），且∠ACO=•∠BAO，•则点C•的坐标为________，•AC=_______．4．已知，如图4，△ABC中，DE∥BC，DF∥AC，则图中共有________对相似三角形．
5．下列各组图形一定相似的是（）．
A．有一个角相等的等腰三角形 B．有一个角相等的直角三角形
C．有一个角是100°的等腰三角形 D．有一个角是对顶角的两个三角形
6．如图5，AB=BC=CD=DE，∠B=90°，则∠1+∠2+∠3等于（）．
A．45° B．60° C．75° D．90°
(4) (5) (6)
7．如图6，若∠ACD=∠B，则△_______∽△______，对应边的比例式为_____________，∠ADC=________．8．如图，在△ABC中，CD，AE是三角形的两条高，写出图中所有相似的三角形，简要说明理由．
9．如图，D，E是AB边上的三等分点，F，G是AC边上的三等分点，•写出图中的相似三角形，并求出对应的相似比．
10．如图，在直角坐标系中，已知点A （2，0），B （0，4），在坐标轴上找到点C （1，0）•和点D ，使△AOB 与△DOC 相似，求出D 点的坐标，并说明理由．
11．已知：如图是一束光线射入室内的平面图，•上檐边缘射入的光线照在距窗户2.5m 处，已知窗户AB 高为2m ，B 点距地面高为1.2m ，求下檐光线的落地点N•与窗户的距离NC ．
12．如图，等腰直角三角形ABC 中，顶点为C ，∠MCN=45°，试说明△BCM ∽△ANC ．
13．在ABCD 中，M ，N 为对角线BD 的三等分点，连接AM 交BC 于E ，连接EN 并延长交AD 于F ．（1）试说明△AMD ∽△EMB ；（2）求FN NE
的值．
14．在△ABC 中，M 是AB 上一点，若过M 的直线所截得的三角形与原三角形相似，•试说明满足条件的直线有几条，画出相应的图形加以说明．
15．为了测量一大楼的高度，在地面上放一平面镜，镜子与楼的距离AE=27m ，他与镜子的距离是2.1m 时，
刚好能从镜子中看到楼顶B ，已知他的眼睛到地面的高度CD 为1.6m ，结果他很快计算出大楼的高度AB ，你知道是什么吗？试加以说明．
16．在△ABC 和△A ′B ′C ′中，∠A=∠A ′=80°，∠B=30°，∠B ′=20°．•试分别在△ABC 和△A ′B ′C ′中画一条直线，使分得的两个三角形相似．在下图中分别画出符合条件的直线，并标注有关数据．
17．如图，在△ABC 中，AB=AC ，∠A=36°，BD 平分∠ABC ，DE ∥BC ，那么在下列三角形中，与△ABC 相似的三角形是（）．
A ．△DBE
B ．△ADE
C ．△AB
D D ．△BDC
18．如第17题图，已知等腰三角形ABC 中，顶角∠A=36°，BD 平分∠ABC ，•则AD AC
的值为（）．
A ．12
B ．5151.1.22
C D -+ 19．如图，△ABC 和△DEF 均为正三角形，D ，E 分别在AB ，BC 上，请找出一个与△DBE 相似的三角形并证明．
20．如图，四边形ABCD 是平行四边形，点F 在BA 的延长线上，连接CF 交AD•于点E ．
（1）求证：△CDE ∽△FAE ．（2）当E 是AD 的中点且BC=2CD 时，求证：∠F=∠BCF ．。

人教版九年级数学下册27.2.1相似三角形的判定同步练习(1)b.docx

2017-2018 人教版九年级数学下册 第27章 相似 27.2 相似三角形 27.2.1相似三角形的判定 同步练习 含答案

人教版数学九年级下册数学：27.2.1 相似三角形的判定 同步练习(附答案)

人教版九年级数学下册27.2 相似三角形 同步练习1 含答案