专题16 圆的问题-备战2016中考-江苏省各地数学模拟试题分项汇编
苏科版九年级数学上册《圆有关的最值问题》专题(解析版)

圆有关的最值问题一、求解方法:1.根据“三角形三边关系”求解:-≤≤+a b c a b2.动中有静,抓住不变量求解.3.旋转必产生圆,很多情况在相切位置产生最值.4.四点共圆(补充).五个基本判断方法:(1)若四个点到一个定点的距离相等,则这四个点共圆.(2)若一个四边形的一组对角互补(和为180。
),则这个四边形的四个点共圆.(3)若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆.(4)若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆.(5)同斜边的直角三角形的顶点共圆,二、解题策略1.直观感觉,画出图形;2.特殊位置,比较结果;3.理性分析动点过程中所维系的不变条件,通过几何构建,寻找动量与定量(常量)之间的关系,建立等式,进行转化.三、中考展望与题型训练例一、圆外一点与圆的最近点、最远点1.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D是平面内的一个动点,且AD=2,M为BD的中点,在D点运动过程中,线段CM长度的取值范围是.例二、正弦定理2.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为.3.如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD 的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,PM=l,则l的最大值是.例三、不等式、配方法4.如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接P A、PB,设PC的长为x(2<x<4).当x为何值时,PD•CD的值最大?最大值是多少?5.如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为()A.4B.C.D.26.如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O是一动点且P在第一象限内,过P作⊙O切线与x轴相交于点A,与y轴相交于点B.则线段AB 的最小值是.例四、相切的应用(有公共点、最大或最小夹角)7.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D为AB边上一点,过点D作CD的垂线交直线BC于点E,则线段CE长度的最小值是____8.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一点O为圆心OA为半径作⊙O,若⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是.9.如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为()A.B.C.3D.2【题型训练】10.如图,在平面直角坐标系中,O为原点,点A的坐标为(﹣4,0),点B的坐标为(0,4),点C、D分别为OA、OB的中点,若正方形OCED绕点O顺时针旋转,得正方形OC′E′D′.记旋转角为a(0°<a<360°),连结AC′、BD′,设直线AC′与直线BD′相交于点F,则点F的纵坐标的最大值为.11.如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为()A.4B.C.D.12.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是()A.4.75B.4.8C.5D.413.如图,在等腰Rt△ABC中,∠A=90°,AC=AB=4,D是BC的中点,点E在AB边上运动(点E不与点A重合),过A、D、E三点作⊙O,⊙O交AC于另一点F,在此运动变化的过程中,线段EF长度的最小值为____14.如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是()A.2B.1C.D.15.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是()A.3B.C.D.416.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=4,⊙C的半径为1,点P在斜边AB上,PQ切⊙O于点Q,则切线长PQ长度的最小值为()A.B.2C.3D.417.如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,P A长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE 长度的最大值为.18.在坐标系中,点A的坐标为(3,0),点P是y轴右侧一点,且AP=2,点B是直线y =x+1上一动点,且PB⊥AP于点P,则tan∠ABP=m,则m的取值范围是.19.在平面直角坐标系中,M(6,8),P是以M为圆心,2为半径的⊙M上一动点,A(﹣2,0)、B(2,0),连接P A、PB,则P A2+PB2最大值是.20.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC =6,圆A和圆B相切于点D,且分别交线段AC,BC于点E,F.则阴影部分(在△ABC内,且在两圆外)面积的最大值是____.21.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为()A.2﹣2B.C.D.22.如图,平面直角坐标系中,分别以点M(2,3)、N(3,﹣5)为圆心,以1、2为半径作⊙M、⊙N,A、B分别是⊙M、⊙N上的动点,P为y轴上的动点,则P A+PB的最小值等于.23.如图,在平面直角坐标系中,已知点A(0,1),B(0,1+m),C(0,1﹣m)(m>0),点P在以D(﹣4,﹣2)为圆心,为半径的圆上运动,且始终满足∠BPC=90°,则m的取值范围是.24.如图,等边三角形ABC内接于⊙O,点D是弧ACB上的一个动点(不与点A、B重合).连接BD.过点A作AE⊥BD,垂足为E,连接CE.若⊙O的半径为2cm,则CE长的最小值为cm.25.在平面直角坐标系中,点A是直线y=x上动点,以点B(0,4)为圆心,半径为1的圆上有一点C,若直线AC与⊙B相切,切点为C,则线段AC的最小值为()A.B.C.3D.26.如图,矩形ABCD中,AB=2,BC=3,分别以A、D为圆心,1为半径画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是()A.2B.3C.4D.527.如图,在△ABC中,∠C=90°,AC=2,BC=1,点A,C分别在x轴、y轴上,当点A在x轴运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为.28.如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为cm.29.如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是.30.已知条件如图所示,点D是AC上动点,求弦EF长度的最小值.31.如图,在平行四边形ABCD中,AB=AD=2,∠A=60°,M是AD边的中点,若线段MA绕点M旋转得到线段MA′,如图,连接A′C,则A′C长度的最小值是.32.在平面直角坐标系中,以点A(10,8)为圆心的⊙A与y轴相切。
江苏中考数学历年真题分类 圆的性质及变换

江苏中考数学历年真题分类圆的性质及变换一、单选题1.(2021·常州)如图,BC是⊙O的直径,AB是⊙O的弦.若∠AOC=60°,则∠OAB的度数是()A.20°B.25°C.30°D.35°【答案】C【解析】【解答】解:∵∠AOC=60°,∴∠AOB=180°-60°=120°,∵OA=OB,∴∠OAB=∠OBA=(180°-120°)÷2=30°,故答案为:C.【分析】由圆周角定理可得∠AOB的度数,然后根据等腰三角形的性质以及三角形内角和定理求解即可.2.(2021·镇江)如图,∠BAC=36°,点O在边AB上,∠O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于()A.27°B.29°C.35°D.37°【答案】A【解析】【解答】解:连接OD,∵∠O与边AC相切于点D,∴∠ADO=90°,∵∠BAC=36°,∴∠AOD=90°﹣36°=54°,∴∠AFD=12∠AOD=12×54°=27,故答案为:A.【分析】连接OD,根据切线的性质得出∠ADO=90°,然后根据直角三角形的性质求出∠AOD,最后利用三角形的外角性质求∠AFD即可.3.(2021·镇江)设圆锥的底面圆半径为r,圆锥的母线长为l,满足2r+l=6,这样的圆锥的侧面积()A.有最大值94πB.有最小值94πC.有最大值92πD.有最小值92π【答案】C【解析】【解答】解:∵2r+l=6,∴l=6﹣2r,∴圆锥的侧面积S侧=πrl=πr(6﹣2r)=﹣2π(r2﹣3r)=﹣2π[(r﹣32)2﹣94]=﹣2π(r﹣32)2+ 92π,∴当r=32时,S侧有最大值92π.故答案为:C.【分析】先把l用含r的代数式表示,代入圆锥的侧面积公式,得出一个关于S侧和r的二次函数关系式,再利用二次函数的性质求圆锥侧面积的最值即可.4.如图,AB是⊙O的弦,点C在过点B的切线上,OC⊥OA,OC交AB于点P.若∠BPC=70°,则∠ABC的度数等于()A.75°B.70°C.65°D.60°【答案】B【解析】【解答】解:∵∠BPC=70°,∴∠APO=70°,∵OC⊥OA,∴∠AOP=90°,∴∠A=20°,又∵OA=OB,∴∠ABO=20°,又∵点C在过点B的切线上,∴∠OBC=90°,∴∠ABC=∠OBC−∠ABO=90°−20°=70°,故答案为:B.【分析】根据题意可求出∠APO、∠A的度数,进一步可得∠ABO度数,从而推出答案. 5.(2020·扬州)如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则sin∠ADC的值为()A.2√1313B.3√1313C.23D.32【答案】A【解析】【解答】∵∠ADC和∠ABC所对的弧长都是AC⌢,∴根据圆周角定理知,∠ABC=∠ADC,∴在Rt∠ACB中,AB= √AC2+BC2=√22+32=√13根据锐角三角函数的定义知,sin∠ABC=ACAB=2√13=2√1313,∴sin∠ADC= 2√1313,故答案为:A.【分析】首先根据圆周角定理可知,∠ABC=∠ADC,在Rt∠ACB中,根据锐角三角函数的定义求出∠ABC的正弦值.6.(2020·南京)如图,在平面直角坐标系中,点P在第一象限,∠P与x轴、y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D,若∠P的半径为5,点A的坐标是(0,8),则点D的坐标是()A.(9,2)B.(9,3)C.(10,2)D.(10,3)【答案】A【解析】【解答】设切点分别为G,E,连接PG,PE,PC,PD,并延长EP交BC与F,则PG=PE=PC=5,四边形OBFE是矩形.∵OA=8,∴CF=8-5=3,∴PF=4,∴OB=EF=5+4=9.∵PF过圆心,∴DF=CF=3,∴BD=8-3-3=2,∴D(9,2).故答案为:A.【分析】在Rt∠CPF中根据勾股定理求出PF的长,再根据垂径定理求出DF的长,进而求出OB,BD的长,从而求出点D的坐标.7.(2020·淮安)如图,点A,B,C在圆O上,∠ACB=54∘,则∠ABO的度数是()A.54∘B.27∘C.36∘D.108∘【答案】C【解析】【解答】解:∵在圆O中,∠ACB=54º,∴∠AOB=2∠ACB=108º,∵OA=OB,∴∠OAB=∠OBA= 180∘−108∘2=36º,故答案为:C.【分析】先由圆周角定理得到∠AOB,再利用等腰三角形的性质求解即可.8.(2020·常州)如图,AB是⊙O的弦,点C是优弧AB上的动点(C不与A、B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是()A.3B.4C.5D.6【答案】A【解析】【解答】解:∵CH⊥AB∴∠BHC=90°∵在Rt∠BHC中,点M是BC的中点∴MH= 12BC∵BC为⊙O的弦∴当BC为直径时,MH最大∵⊙O的半径是3∴MH最大为3.故答案为:A.【分析】根据直角三角形斜边上的中线等于斜边的一半可知MH= 12BC,当BC为直径时长度最大,即可求解.9.(2019·镇江)如图,四边形ABCD是半圆的内接四边形,AB是直径,DC⌢=CB⌢.若∠C= 110°,则∠ABC的度数等于()A.55°B.60°C.65°D.70°【答案】A【解析】【解答】解:连接AC,∵四边形ABCD是半圆的内接四边形,∴∠DAB=180°-∠C=70°,∵DC⌢=CB⌢,∴∠CAB= 12∠DAB=35°,∵AB是直径,∴∠ACB=90°,∴∠ABC=90°-∠CAB=55°。
江苏省2016届高三数学一轮复习优题精练:直线与圆-Word版含答案

江苏省2016年高考一轮复习突破训练直线与圆一、填空题1、(2015年江苏高考)在平面直角坐标系xoy 中,以点(1,0)为圆心且与直线210mx y m ---=()m R ∈相切的所有圆中,半径最大的圆的标准方程为____22(1)2x y -+=_____________。
2、(2014年江苏高考)在平面直角坐标系xOy 中,直线032x =-+y 被圆4)1(2x 22=++-y )(截得的弦长为 ▲ .3、(2015届南京、盐城市高三二模)在平面直角坐标系xoy 中,已知⊙C:5)1(22=-+y x ,A为⊙C与x 负半轴的交点,过A 作⊙ 。
4、(南通、扬州、连云港2015届高三第二次调研(淮安三模))在平面直角坐标系xOy 中,圆1C :22(1)(6)25x y ++-=,圆2C :222(17)(30)x y r -+-=.若圆2C 上存在一点P ,使得过点P 可作一条射线与圆1C 依次交于点A ,B ,满足2PA AB =, 则半径r 的取值范围是 ▲ .5、(苏锡常镇四市2015届高三教学情况调研(一))在平面直角坐标系xOy 中,已知圆C :22(3)2x y +-=,点A 是x 轴上的一个动点,AP ,AQ 分别切圆C 于P ,Q 两点,则线段PQ 长的取值范围为 . 6、(连云港、徐州、淮安、宿迁四市2015届高三第一次调研考试)已知a ,b 为正数,且直线60ax by +-=与直线()2350x b y +-+=互相平行,则23a b +的最小值为 ▲7、(南京市、盐城市2015届高三第一次模拟)在平面直角坐标系xOy 中,设直线2y x =-+与圆222(0)x y r r +=>交于,A B 两点,O 为坐标原点,若圆上一点C 满足5344OC OA OB =+,则r = ▲ .8、(苏州市2015届高三2月调研测试)已知圆22:(1)(1)4M x y -+-=,直线:60,l x y A+-=为直线l 上一点,若圆M 上存在两点,B C ,使得60BAC ∠=︒,则点A 的横坐标的取值范围是 9、(2015届江苏南通市直中学高三9月调研)已知圆22:24200C x y x y +---=,直线l 过点P (3,1),则当直线l 被圆C 截得的弦长最短时,直线l 的方程为 ▲10、(2015届江苏苏州高三9月调研)已知圆()()()22:10C x a y a a -+-=>与直线3y x =相交于,P Q 两点,则当CPQ ∆的面积最大时,此时实数a 的值为 ▲11、(南京市2014届高三第三次模拟)在平面直角坐标系xOy 中,圆C 的方程为(x -1)2+y 2=4,P 为圆C 上一点.若存在一个定圆M ,过P 作圆M 的两条切线P A ,PB ,切点分别为A ,B ,当P 在圆C 上运动时,使得∠APB 恒为60︒,则圆M 的方程为12、(2014江苏百校联考一)已知圆22:(2)1C x y -+=,点P 在直线:10l x y ++=上,若过点P 存在直线m 与圆C 交于A 、B 两点,且点A 为PB 的中点,则点P 横坐标0x 的取值范围是 . 13、(南京、盐城市2014届高三第二次模拟(淮安三模))在平面直角坐标系xOy 中,过点P (5,3)作直线l 与圆x 2+y 2=4相交于A ,B 两点,若OA ⊥OB ,则直线l 的斜率为 ▲ 14、(无锡市2015届高三上学期期末)已知点0,2A 位圆22:2200M x y ax ay a 外一点,圆M 上存在点T 使得45MAT ,则实数a 的取值范围是 .15、(宿迁市2015届高三11月摸底考试)已知光线通过点()3,4M -,被直线l :30x y -+=反射,反射光线通过点()2,6N , 则反射光线所在直线的方程是 ▲二、解答题1、(2013年江苏高考)本小题满分14分。
苏教版初三数学中考_圆_复习卷

AO B C (第2题) 苏教版初三数学“圆”中考复习一、选择题1. 当两圆无公共点时,这两圆的位置关系一定是 ··········· ( )A .外离B .内含C .同心圆D .外离或内含 答案:D .解析:本题为容易题,考查了圆与圆的位置关系.根据两圆的位置关系,当两圆外离或内含时,两圆没有公共点,因此本题选D .2. 如图,已知AB 为⊙O 的直径,点C 在⊙O 上,若∠B =50°,则∠A 等于 ······················· ()A .80°B .60°C .50°D .40° 答案:D .解析:本题为容易题,考查了直径所对圆周角的特征.直径所对的圆周角是直角,故∠A 与∠B 互余,因此本题选D .3. 如图,圆周角∠ACB 的度数为48°,则圆心角∠AOB 的度数为······················· ( ) A .48° B .24° C .96°D .90°答案:C .解析:本题为容易题,考查了圆周角与圆心角的关系.同弧所对的圆周角是圆心角的一半,因此本题选C .4. 如图,⊙O 的半径为5,弦AB 的长为8,M 是弦AB 上的动点,则线段OM 长的最小值 ··············· ( )A .2B .3C .4D .5答案:B .解析:本题为容易题,考查了垂径定理及其推论.当OM ⊥AB 时OM 最短,由垂径定理得AM =BM =4,根据勾股定理解得OM =3,因此本题选B .5. 两圆半径分别为2 cm 和6 cm ,若两圆相切,则圆心距为 ······ ( )A(第3题)O CBA BMO(第4题)A .4 cmB .8 cmC .10 cm 或2 cmD .8 cm 或4 cm答案:D .解析:本题为容易题,考查了圆与圆的位置关系.两圆相切分为外切与内切,当两圆外切时,圆心距d =R +r ,当两圆内切时,圆心距d =R -r ,因此本题选D .6. 如图,P 为正△ABC 外接圆上一点,则∠APB 为 ··· ( )A .150°B .135°C .115°D .120°答案:D .解析:本题为容易题,考查了圆周角与圆心角的关系.由圆内接四边形的性质得∠P +∠C =180°,因此本题选D .7. 一个扇形的圆心角是120°,它的面积为3π cm 2,那么这个扇形的半径是 ( )A 3B .3 cmC .6 cmD .9 cm答案:B .解析:本题为容易题,考查了计算扇形的面积.扇形面积公式为S =2360n r ,因此本题选B .8. 已知两圆的圆心距是3,两圆半径分别是一元二次方程x 2-3x +2=0的两个根,则这两个圆的位置关系是 ······················ ( )A .外离B .外切C .相交D .内切答案:B .解析:本题为容易题,考查了圆与圆的位置关系.方程的两个根为1和2,由d =R +r 得两圆外切,因此本题选B .9. 如图,四边形ABCD 为⊙O 的内接四边形,∠BOD =120°,则∠BCD的度数为 ····················( )A .120°B .90°C .60°D .30°答案:A .解析:本题为容易题,考查了圆周角与圆心角的关系.由题意得∠A =60°,又根据圆内接四边形的性质得∠A +∠C =180°,因此本题选A .BDC OA(第9题)AB C P(第6题)10.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( )A .30°B .30°或150°C .60°D .60°或120°答案:B .解析:本题为容易题,考查了圆周角与圆心角的关系.该弦与两半径围成一个正三角形,因此圆心角为60°,根据同弧所对的圆周角是圆心角的一半得30°,再根据圆内接四边形性质得优弧所对的圆周角为150°,因此本题选B .11.在Rt △ABC 中,∠C =90°,AB =10 cm ,AC =5 cm ,若以C 为圆心,4 cm 为直径的⊙C 与AB 的关系是 ·························· ( )A .相离B .相交C .相切D .不能确定答案:A .解析:本题为中档题,考查了直线与圆的位置关系.通过计算可得BC =3从而点C 到AB 5325322,因此本题选A .12.如图,梯形ABCD 内接于⊙O ,AB ∥CD ,AB 为直径,DO 平分∠ADC ,则∠DAO 的度数是 ················ ( )A .90°B .80°C .70°D .60°答案:D .解析:本题为中档题,考查了圆的有关概念和平行的性质.由条件可得△AOD 为正三角形,因此本题选D .13.过⊙O 内一点M 的最长弦长为10 cm ,最短弦长为8 cm ,那么OM 的长为 ( )A .3 cmB .6 cmC 41D .9 cm答案:A .解析:本题为中档题,考查了垂径定理及其推论.最长弦为直径,故半径为5 cm ,最短弦为垂直于直径的弦,由垂径定理构造直角三角形后由勾股定理得OM =3,因此本题选A .14.若圆锥的母线长为4 cm ,底面半径为3 cm ,则圆锥的侧面展开图的面积是 ( )A .6π cm 2B .12π cm 2C .18π cm 2D .24π cm 2答案:B .解析:本题为中档题,考查了计算圆锥的侧面积.圆锥的底面周长为6π,即为扇形的弧长,由扇形面积公式S =12lR ,因此本题选B .ABODC(第12题)15.如图,在△ABC 中,AB =2,AC =1,以AB 为直径的圆与AC 相切,与边BC 交于点D ,则AD 的长为 ··········· ( )A .255B .455C .235D .435答案:A .解析:本题为中档题,考查了切线与过切线的半径之间的关系和直径所对圆周角的性质.由切线的概念得△ABC 为Rt △,可得BC =5,又由直径所对圆周角是90°,用面积法可解出AD ,因此本题选A .16.两圆相交,圆心距为5 cm ,两圆半径分别为3 cm 和4 cm ,则公共弦长为 ( )A .2.4 cmB .4.8 cmC .1.8 cmD .3.6 cm答案:B .解析:本题为稍难题,考查了圆与圆的位置关系和解直角三角形.由条件可得,圆心和一个交点围成一个直角三角形,且斜边上的高为2.4 cm ,因此本题选B .17. 已知Rt △ABC 的两条直角边长为6和8,则它的内切圆与外接圆的圆心距为 ( )A .32B .332C .3D .5答案:D .解析:本题为稍难题,考查了切线长定理和三角形的内心、外心.外心是三条边垂直平分线的交点,在斜边中点。
2016中考《圆》综合试题及答案
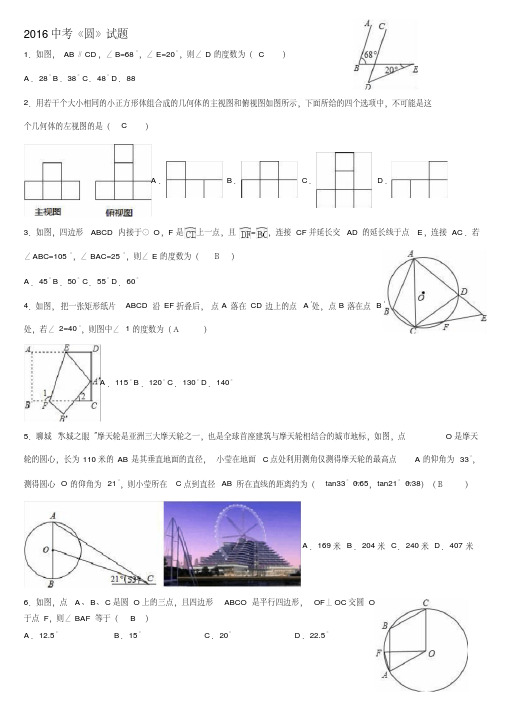
2016中考《圆》试题1.如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为(C)A.28° B.38° C.48° D.882.用若干个大小相同的小正方形体组合成的几何体的主视图和俯视图如图所示,下面所给的四个选项中,不可能是这个几何体的左视图的是(C)A.B.C.D.3.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为(B)A.45° B.50° C.55° D.60°4.如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为(A)A.115° B.120° C.130° D.140°5.聊城“水城之眼”摩天轮是亚洲三大摩天轮之一,也是全球首座建筑与摩天轮相结合的城市地标,如图,点O是摩天轮的圆心,长为110米的AB是其垂直地面的直径,小莹在地面C点处利用测角仪测得摩天轮的最高点A的仰角为33°,测得圆心O的仰角为21°,则小莹所在C点到直径AB所在直线的距离约为(tan33°≈0.65,tan21°≈0.38)(B)A.169米B.204米C.240米D.407米6.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于(B)A.12.5°B.15°C.20°D.22.5°7.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于(D)A.1:B.1:C.1:2 D.2:38.如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为.9.如图,○O的半径为1,AD,BC是⊙O的两条互相垂直的直径,点P从点O出发(P点与O点不重合),沿O→C→D的路线运动,设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是(B)A.B.C.D.10.如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为cm2.11.如图,已知圆锥的高为,高所在直线与母线的夹角为30°,圆锥的侧面积为2π.12.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标;(2)若△ABC和△A1B2C2关于原点O成中心对称图形,写出△A1B2C2的各顶点的坐标;(3)将△ABC绕着点O按顺时针方向旋转90°得到△A2B3C3,写出△A2B3C3的各顶点的坐标.解:(1)如图,△A1B1C1为所作,因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);13.如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.证明:∵AF∥CD,∴∠AFE=∠CDE,在△AFE和△CDE中,,∴△AEF≌△CED,∴AF=CD,∵AF∥CD,∴四边形ADCF是平行四边形,∵∠B=90°,∠ACB=30°,∴∠CAB=60°,∵AD平分∠CAB,∴∠DAC=∠DAB=30°=∠ACD,∴DA=DC,∴四边形ADCF是菱形.14.如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在的中点,连接AF并延长与CB的延长线相交于点G,连接OF.(1)求证:OF=BG;网](2)若AB=4,求DC的长.(1)证明:∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在的中点,∴=,∴∠AOF=∠BOF,∵∠ABC=∠ABG=90°,∴∠AOF=∠ABG,∴FO∥BG,∵AO=BO,∴FO是△ABG的中位线,∴FO=BG;(2)解:在△FOE和△CBE中,,∴△FOE≌△CBE(ASA),∴BC=FO=AB=2,∴AC==2,连接DB,∵AB为⊙O直径,∴∠ADB=90°,∴∠ADB=∠ABC,∵∠BCD=∠ACB,∴△BCD∽△ACB,∴=,∴=,解得:DC=.15.如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D连接BD.(1)求证:BD平分∠PBC;(2)若⊙O的半径为1,PD=3DE,求OE及AB的长.(1)证明:连接OB.∵PB是⊙O切线,∴OB⊥PB,∴∠PBO=90°,∴∠PBD+∠OBD=90°,∵OB=OD,∴∠OBD=∠ODB,∵OP⊥BC,∴∠BED=90°,∴∠DBE+∠BDE=90°,∴∠PBD=∠EBD,∴BD平分∠PBC.(2)解:作DK⊥PB于K,∵==,∵BD平分∠PBE,DE⊥BE,DK⊥PB,∴DK=DE,∴==,∵∠OBE+∠PBE=90°,∠PBE+∠P=90°,∴∠OBE=∠P,∵∠OEB=∠BEP=90°,∴△BEO∽△PEB,∴=,∴==,∵BO=1,∴OE=,∵OE⊥BC,∴BE=EC,∵AO=OC,∴AB=2OE=.。
江苏各地5年数学中考题(2016-2020)分类汇编专题16多边形与平行四边形逐题详解

五年(2016-2020)中考数学真题+1年模拟新题分项汇编(江苏专用)专题16多边形与平行四边形【真题42道模拟50道】一.选择题(共8小题)1.(2020•无锡)正十边形的每一个外角的度数为()A.36°B.30°C.144°D.150°2.(2020•扬州)如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为()A.100米B.80米C.60米D.40米3.(2020•淮安)六边形的内角和为()A.360°B.540°C.720°D.1080°4.(2018•南通)若一个凸多边形的内角和为720°,则这个多边形的边数为()A.4B.5C.6D.75.(2018•无锡)若一个多边形的每一个外角都是40°,则这个多边形是()A.七边形B.八边形C.九边形D.十边形6.(2017•苏州)如图,在正五边形ABCDE中,连接BE,则∠ABE的度数为()五年中考真题A.30°B.36°C.54°D.72°7.(2016•南通)若一个多边形的内角和与它的外角和相等,则这个多边形是()A.三角形B.四边形C.五边形D.六边形8.(2017•常州)如图,已知▱ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是()A.12B.13C.6√5D.8√3二.填空题(共19小题)9.(2020•扬州)如图,在▱ABCD中,∠B=60°,AB=10,BC=8,点E为边AB上的一个动点,连接ED并延长至点F,使得DF=14DE,以EC、EF为邻边构造▱EFGC,连接EG,则EG的最小值为.10.(2019•南通)如图,▱ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则PB+√32PD 的最小值等于.11.(2019•徐州)如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则∠OAD=.12.(2019•淮安)若一个多边形的内角和是540°,则该多边形的边数是.13.(2019•泰州)八边形的内角和为°.14.(2018•南京)如图,五边形ABCDE是正五边形.若l1∥l2,则∠1﹣∠2=°.15.(2018•徐州)五边形的内角和是°.16.(2018•宿迁)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是.17.(2017•徐州)正六边形的每个内角等于°.18.(2017•南京)如图,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=°.19.(2016•连云港)如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=.20.(2016•常州)一个多边形的每个外角都是60°,则这个多边形边数为.21.(2016•镇江)正五边形每个外角的度数是.22.(2018•常州)如图,在▱ABCD中,∠A=70°,DC=DB,则∠CDB=.23.(2018•泰州)如图,▱ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为.24.(2017•连云港)如图,在▱ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=56°,则∠B=°.25.(2017•扬州)在平行四边形ABCD中,∠B+∠D=200°,则∠A=.26.(2016•无锡)如图,已知▱OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为.27.(2018•无锡)如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC 为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD ∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是.三.解答题(共15小题)28.(2020•扬州)如图,▱ABCD的对角线AC、BD相交于点O,过点O作EF⊥AC,分别交AB、DC于点E、F,连接AF、CE.(1)若OE=32,求EF的长;(2)判断四边形AECF的形状,并说明理由.29.(2019•无锡)如图,在▱ABCD中,点E、F分别在边AD、BC上,且DE=BF,直线EF与BA、DC 的延长线分别交于点G,H.求证:(1)△DEH≌△BFG;(2)AG=CH.30.(2019•淮安)已知:如图,在▱ABCD中,点E、F分别是边AD、BC的中点.求证:BE=DF.31.(2019•扬州)如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.(1)求证:∠BEC=90°;(2)求cos∠DAE.32.(2018•淮安)已知:如图,▱ABCD的对角线AC、BD相交于点O,过点O的直线分别与AD、BC相交于点E、F.求证:AE=CF.33.(2018•无锡)如图,平行四边形ABCD中,E、F分别是边BC、AD的中点,求证:∠ABF=∠CDE.34.(2018•宿迁)如图,在▱ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H.求证:AG=CH.35.(2017•无锡)已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.36.(2017•南京)如图,在▱ABCD中,点E、F分别在AD、BC上,且AE=CF,EF、BD相交于点O,求证:OE=OF.37.(2017•淮安)已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.38.(2016•徐州)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证:(1)△ABE≌△CFE;(2)四边形ABFD是平行四边形.39.(2020•淮安)如图,在▱ABCD中,点E、F分别在BC、AD上,AC与EF相交于点O,且AO=CO.(1)求证:△AOF≌△COE;(2)连接AE、CF,则四边形AECF(填“是”或“不是”)平行四边形.40.(2017•无锡)如图,已知点E、F分别在边AB、BC上,ED∥BC,EF∥AC,BE=CF.求证:BD是△ABC的角平分线.41.(2017•镇江)如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.(1)求证:四边形BCED是平行四边形;(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.42.(2016•宿迁)如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.一.选择题(共12小题)1.(2020•滨海县二模)如图,正六边形ABCDEF的一个内角的度数是()A.60°B.120°C.135°D.150°2.(2020•广陵区二模)已知正多边形的一个内角是140°,则这个正多边形的边数是()A.九B.八C.七D.六3.(2020•海安市一模)如图,M是正五边形ABCDE的边CD延长线上一点.连接AD,则∠ADM的度数是()A.108°B.120°C.144°D.150°4.(2020•梁溪区模拟)如图,点E在四边形ABCD的CD边的延长线上,若∠ADE=120°,则∠A+∠B+∠C的度数为()A.240°B.260°C.300°D.320°5.已知一个多边形的外角和比它的内角和少540°,则该多边形的边数为()一年模拟新题A.7B.8C.9D.106.(2020•邗江区校级一模)平行四边形的一边长为6cm,则它的两条对角线长可以是()A.4cm,6cm B.5cm,6cm C.4cm,8cm D.2cm,12cm7.(2020•工业园区一模)如图,平行四边形ABCD的周长为36cm,对角线AC,BD相交于点O,AC=12cm.若点E是AB的中点,则△AOE的周长为()A.10cm B.15cm C.20cm D.30cm8.(2020•江苏模拟)如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为()A.1:2B.1:3C.1:4D.1:59.(2020•天宁区校级模拟)下列给出的条件中,不能判断四边形ABCD是平行四边形的是()A.AB∥CD,AD=BC B.∠A=∠C,∠B=∠DC.AB∥CD,AD∥BC D.AB=CD,AD=BC10.(2020•惠山区一模)六边形的外角和为()A.180°B.720°C.360°D.1080°11.(2020•海门市校级模拟)已知一个正多边形的一个内角为150度,则它的边数为()A.12B.8C.9D.712.(2020•海淀区校级模拟)一个多边形的每一个外角都是72°,这个多边形的内角和为()A.360°B.540°C.720°D.900°二.填空题(共19小题)13.(2020•邗江区一模)在平面直角坐标系中,▱OABC的三个顶点O(0,0)、A(3,0)、B(5,3),则其第四个顶点C的坐标是.14.(2020•灌南县一模)如图,在平行四边形ABCD中,AE⊥BC于点E,AF⊥CD于点F,若∠EAF=70°,则∠B的度数为.15.(2020•宜兴市一模)已知平面直角坐标系xoy中,O(0,0),A(﹣6,8),B(m,−43m﹣4),则平行四边形OABD的面积是.16.(2020•昆山市一模)如图,已知在△ABC中,AB=AC=13,BC=10,点M是AC边上任意一点,连接MB,以MB、MC为邻边作▱MCNB,连接MN,则MN的最小值为.17.(2020•新吴区一模)定理“对角线互相平分的四边形是平行四边形”的逆定理是.18.(2020•邗江区二模)若一个多边形的内角和比外角和大180°,则这个多边形的边数为.19.(2020•徐州模拟)若一个正多边形的外角与它的内角相等,则这个多边形为.20.(2020•南京一模)如图,将正六边形ABCDEF绕点D逆时针旋转27°得正六边形A′B′C′DE′F′,则∠1=°.21.(2020•宝应县一模)如图,1角硬币边缘镌刻的是正九边形,则这个正九边形每个内角的度数是°.22.(2020•兴化市模拟)任意多边形的外角和等于.23.(2020•江阴市模拟)正十边形的外角和为.24.(2020•泰兴市一模)如果一个正多边形的内角和等于720°,那么该正多边形的一个外角等于度.25.(2020•海门市校级模拟)若一个多边形的内角和为其外角和的6倍,则这个多边形的边数为.26.(2020•无锡一模)如果一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数为.27.(2020•姜堰区二模)一个多边形的每个外角都是45°,则这个多边形的边数为.28.(2020•滨湖区模拟)已知一个多边形的内角和是外角和的3倍,那么这个多边形是边形.29.(2020•如皋市校级模拟)已知一个多边形的内角和为540°,则这个多边形是边形.30.(2020•天桥区一模)一个多边形的内角和是1440°,那么这个多边形边数是.31.(2020•徐州模拟)已知多边形的每个内角都等于120°,则这个多边形是边形.三.解答题(共19小题)32.(2020•邗江区二模)如图,平行四边形ABCD中,点E、F分别在边BC、AD上,EA⊥AC,FC⊥AC.(1)求证:△ABE≌△CDF;(2)若∠B=30°,∠AEC=45°,求证:AB=AF.33.(2020•仪征市一模)如图,在▱ABCD中,DE⊥BC于点E,过点A作AF∥DE,交CB的延长线于点F,连接DF,交AB于点P.(1)若AD=4,tan C=3,BF=1,求DF的长;(2)若∠APD=2∠ADP,求证:DF=2AP.34.(2020•金湖县一模)如图,在平行四边形ABCD中,作∠BAD和∠BCD平分线分别交对角线BD于点E、F,求证:BF=DE.35.(2020•惠山区一模)如图,BD为▱ABCD的对角线,AE∥CF,点E、F在BD上.求证:BE=DF.36.(2020•滨海县一模)如图,B、C在直线EF上,AE∥FD,AE=FD,且BE=CF.(1)求证:△ABE≌△DCF;(2)求证:以A、B、D、C为顶点的四边形是平行四边形.37.(2020•徐州模拟)已知,如图,在▱ABCD中,E是AB的中点,连接CE并延长交DA的延长线于点F.(1)求证:△AEF≌△BEC;(2)若DE平分∠ADC,求证:DC=DF.38.(2020•江都区二模)如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:△ABE≌△FCE;(2)过点D作DG⊥AE于点G,H为DG的中点.判断CH与DG的位置关系,并说明理由.39.(2020•无锡模拟)在▱ABCD中,点E、F分别在AB、CD上,且AE=CF.求证:DE=BF.40.(2020•滨湖区模拟)如图所示,在▱ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.41.(2020•锡山区一模)如图,在▱ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.(1)求证:△AEB≌△CFD;(2)若四边形EBFD是菱形,求∠ABD的度数.42.(2020•玄武区模拟)如图在平行四边形ABCD中,点E、F分别在BC、AD上,且AF=CE,求证:△ABE≌△CDF.43.(2020•梁溪区模拟)如图,四边形ABCD是平行四边形,E、F分别是AD、BC的中点,EF与BD交于点G.求证:EF与BD互相平分.44.(2020•邗江区一模)如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF.(1)求证:四边形BEFD是平行四边形;(2)若∠AFB=90°,AB=4,求四边形BEFD的周长.45.(2020•盐城模拟)已知点E、F分别是▱ABCD的边BC、AD的中点.(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,求▱AECF的周长.46.(2020•海门市校级模拟)如图,点E是平行四边形ABCD边CD上的中点,AE、BC的延长线交于点F,连接DF.求证:四边形ACFD为平行四边形.47.(2020•徐州模拟)如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE ⊥AE,点F在AB上,且BF=DE.(1)求证:四边形BDEF是平行四边形;(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.48.(2020•江阴市二模)已知,如图,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE =CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.49.(2020•无锡二模)如图,在平行四边形ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:BE ∥DF.50.(2020•吴中区二模)已知:如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,求证:BE =DF.五年(2016-2020)中考数学真题+1年模拟新题分项汇编(江苏专用)专题16多边形与平行四边形【真题42道模拟50道】一.选择题(共8小题)1.(2020•无锡)正十边形的每一个外角的度数为()A.36°B.30°C.144°D.150°【分析】根据多边形的外角和为360°,再由正十边形的每一个外角都相等,进而求出每一个外角的度数.【解析】正十边形的每一个外角都相等,因此每一个外角为:360°÷10=36°,故选:A.2.(2020•扬州)如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为()A.100米B.80米C.60米D.40米【分析】根据题意,小明走过的路程是正多边形,先用360°除以45°求出边数,然后再乘以10米即可.【解析】∵小明每次都是沿直线前进10米后向左转45度,∴他走过的图形是正多边形,∴边数n=360°÷45°=8,∴他第一次回到出发点A时,一共走了8×10=80(m).故选:B.3.(2020•淮安)六边形的内角和为()A.360°B.540°C.720°D.1080°【分析】利用多边形的内角和=(n﹣2)•180°即可解决问题.【解析】根据多边形的内角和可得:(6﹣2)×180°=720°.故选:C.4.(2018•南通)若一个凸多边形的内角和为720°,则这个多边形的边数为()A.4B.5C.6D.7【分析】设这个多边形的边数为n,根据多边形的内角和定理得到(n﹣2)×180°=720°,然后解方程即可.【解析】设这个多边形的边数为n,则(n﹣2)×180°=720°,解得n=6,故这个多边形为六边形.故选:C.5.(2018•无锡)若一个多边形的每一个外角都是40°,则这个多边形是()A.七边形B.八边形C.九边形D.十边形【分析】根据任何多边形的外角和都是360度,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.【解析】360÷40=9,即这个多边形的边数是9,故选:C.6.(2017•苏州)如图,在正五边形ABCDE中,连接BE,则∠ABE的度数为()A.30°B.36°C.54°D.72°【分析】在等腰三角形△ABE中,求出∠A的度数即可解决问题.【解析】在正五边形ABCDE中,∠A=15×(5﹣2)×180=108°又知△ABE是等腰三角形,∴AB=AE,∴∠ABE=12(180°﹣108°)=36°.故选:B.7.(2016•南通)若一个多边形的内角和与它的外角和相等,则这个多边形是()A.三角形B.四边形C.五边形D.六边形【分析】根据多边形的内角和公式(n﹣2)•180°与多边形的外角和定理列式进行计算即可得解.【解析】设多边形的边数为n,根据题意得(n﹣2)•180°=360°,解得n=4.故这个多边形是四边形.故选:B.8.(2017•常州)如图,已知▱ABCD的四个内角的平分线分别相交于点E、F、G、H,连接AC.若EF=2,FG=GC=5,则AC的长是()A.12B.13C.6√5D.8√3【分析】如图,作AP⊥CH交CH的延长线与P.利用勾股定理即可解决问题;【解析】如图,作AP⊥CH交CH的延长线与P.∵四边形ABCD是平行四边形,▱ABCD的四个内角的平分线分别相交于点E、F、G、H,∴易证四边形EFGH是矩形,四边形AEHP是矩形,△ABE≌△CDG,可得P A=FG=5,AE=PH=CG=5,CP=CG+PH+GH=2+10=12,在Rt△APC中,AC=√PA2+PC2=√122+52=13.故选:B.二.填空题(共19小题)9.(2020•扬州)如图,在▱ABCD中,∠B=60°,AB=10,BC=8,点E为边AB上的一个动点,连接ED并延长至点F,使得DF=14DE,以EC、EF为邻边构造▱EFGC,连接EG,则EG的最小值为9√3.【分析】根据题意和平行四边形的性质,可以得到ED和EF的比值,再根据三角形相似和最短距离,即可得到EG的最小值,本题得以解决.【解析】作CH⊥AB于点H,∵在▱ABCD中,∠B=60°,BC=8,∴CH=4√3,∵四边形ECGF是平行四边形,∴EF∥CG,∴△EOD∽△GOC,∴EOGO =DOOC=EDGC,∵DF =14DE ,∴DE EF =45, ∴ED GC =45, ∴EO GO =45,∴当EO 取得最小值时,EG 即可取得最小值,当EO ⊥CD 时,EO 取得最小值,∴CH =EO ,∴EO =4√3,∴GO =5√3,∴EG 的最小值是9√3,故答案为:9√3.10.(2019•南通)如图,▱ABCD 中,∠DAB =60°,AB =6,BC =2,P 为边CD 上的一动点,则PB +√32PD 的最小值等于 3√3 .【分析】过点P 作PE ⊥AD ,交AD 的延长线于点E ,有锐角三角函数可得EP =√32PD ,即PB +√32PD =PB +PE ,则当点B ,点P ,点E 三点共线且BE ⊥AD 时,PB +PE 有最小值,即最小值为BE .【解析】如图,过点P 作PE ⊥AD ,交AD 的延长线于点E ,∵AB∥CD∴∠EDP=∠DAB=60°,∴sin∠EDP=EPDP=√32∴EP=√32PD∴PB+√32PD=PB+PE∴当点B,点P,点E三点共线且BE⊥AD时,PB+PE有最小值,即最小值为BE,∵sin∠A=BEAB=√32∴BE=3√3故答案为3√311.(2019•徐州)如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则∠OAD=30°.【分析】连接OB、OC,利用任意凸多边形的外角和均为360°,正多边形的每个外角相等即可求出多边形的边数,再根据多边形的内角和公式计算即可.【解析】连接OB、OC,多边形的每个外角相等,且其和为360°,据此可得多边形的边数为:360°40°=9,∴∠AOB=360°9=40°,∴∠AOD=40°×3=120°.∴∠OAD=180°−∠AOD2=30°.故答案为:30°12.(2019•淮安)若一个多边形的内角和是540°,则该多边形的边数是5.【分析】n边形的内角和公式为(n﹣2)•180°,由此列方程求n.【解析】设这个多边形的边数是n,则(n﹣2)•180°=540°,解得n=5,故答案为:5.13.(2019•泰州)八边形的内角和为1080°.【分析】根据多边形的内角和公式(n﹣2)•180°进行计算即可得解.【解析】(8﹣2)•180°=6×180°=1080°.故答案为:1080°.14.(2018•南京)如图,五边形ABCDE是正五边形.若l1∥l2,则∠1﹣∠2=72°.【分析】过B点作BF∥l1,根据正五边形的性质可得∠ABC的度数,再根据平行线的性质以及等量关系可得∠1﹣∠2的度数.【解析】过B点作BF∥l1,∵五边形ABCDE是正五边形,∴∠ABC=108°,∵BF∥l1,l1∥l2,∴BF∥l2,∴∠3=180°﹣∠1,∠4=∠2,∴180°﹣∠1+∠2=∠ABC=108°,∴∠1﹣∠2=72°.故答案为:72.15.(2018•徐州)五边形的内角和是540°.【分析】根据多边形的内角和是(n﹣2)•180°,代入计算即可.【解析】(5﹣2)•180°=540°,故答案为:540°.16.(2018•宿迁)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是八.【分析】任何多边形的外角和是360°,即这个多边形的内角和是3×360°.n边形的内角和是(n﹣2)•180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.【解析】设多边形的边数为n,根据题意,得(n﹣2)•180=3×360,解得n=8.则这个多边形的边数是八.17.(2017•徐州)正六边形的每个内角等于120°.【分析】根据多边形内角和公式即可求出答案.【解析】六边形的内角和为:(6﹣2)×180°=720°,∴正六边形的每个内角为:720°6=120°,故答案为:120°18.(2017•南京)如图,∠1是五边形ABCDE的一个外角,若∠1=65°,则∠A+∠B+∠C+∠D=425°.【分析】根据补角的定义得到∠AED=115°,根据五边形的内角和即可得到结论.【解析】∵∠1=65°,∴∠AED =115°,∴∠A +∠B +∠C +∠D =540°﹣∠AED =425°,故答案为:425.19.(2016•连云港)如图,正十二边形A 1A 2…A 12,连接A 3A 7,A 7A 10,则∠A 3A 7A 10= 75° .【分析】如图,作辅助线,首先证得A 3A 7A 10̂=512⊙O 的周长,进而求得∠A 3OA 10=512×360°=150°,运用圆周角定理问题即可解决.【解析】设该正十二边形的中心为O ,如图,连接A 10O 和A 3O ,由题意知,A 3A 7A 10̂=512⊙O 的周长, ∴∠A 3OA 10=512×360°=150°,∴∠A 3A 7A 10=75°,故答案为:75°.20.(2016•常州)一个多边形的每个外角都是60°,则这个多边形边数为 6 .【分析】利用外角和除以外角的度数即可得到边数.【解析】360÷60=6.故这个多边形边数为6.故答案为:6.21.(2016•镇江)正五边形每个外角的度数是 72° .【分析】利用正五边形的外角和等于360度,除以边数即可求出答案.【解析】360°÷5=72°.故答案为:72°.22.(2018•常州)如图,在▱ABCD中,∠A=70°,DC=DB,则∠CDB=40°.【分析】根据等腰三角形的性质,平行四边形的性质以及三角形内角和定理即可解决问题.【解析】∵四边形ABCD是平行四边形,∴∠A=∠C=70°,∵DC=DB,∴∠C=∠DBC=70°,∴∠CDB=180°﹣70°﹣70°=40°,故答案为40°.23.(2018•泰州)如图,▱ABCD中,AC、BD相交于点O,若AD=6,AC+BD=16,则△BOC的周长为14.【分析】根据平行四边形的性质,三角形周长的定义即可解决问题;【解析】∵四边形ABCD是平行四边形,∴AD=BC=6,OA=OC,OB=OD,∵AC+BD=16,∴OB+OC=8,∴△BOC的周长=BC+OB+OC=6+8=14,故答案为14.24.(2017•连云港)如图,在▱ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=56°,则∠B=56°.【分析】根据四边形的内角和等于360°求出∠C,再根据平行四边形的邻角互补列式计算即可得解.【解析】∵AE⊥BC,AF⊥CD,∴∠AEC=∠AFC=90°,在四边形AECF中,∠C=360°﹣∠EAF﹣∠AEC﹣∠AFC=360°﹣56°﹣90°﹣90°=124°,在▱ABCD中,∠B=180°﹣∠C=180°﹣124°=56°.故答案为:56.25.(2017•扬州)在平行四边形ABCD中,∠B+∠D=200°,则∠A=80°.【分析】利用平行四边形的对角相等、邻角互补可求得答案.【解析】∵四边形ABCD为平行四边形,∴∠B=∠D,∠A+∠B=180°,∵∠B+∠D=200°,∴∠B=∠D=100°,∴∠A=180°﹣∠B=180°﹣100°=80°,故答案为:80°.26.(2016•无锡)如图,已知▱OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为5.【分析】过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E.则OB=√OE2+BE2.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,从而可求.【解析】过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,如图:∵四边形OABC是平行四边形,∴∠OAB=∠BCO,OC∥AB,OA=BC,∵直线x=1与直线x=4均垂直于x轴,∴AM ∥CN ,∴四边形ANCM 是平行四边形,∴∠MAN =∠NCM ,∴∠OAF =∠BCD ,∵∠OF A =∠BDC =90°,∴∠FOA =∠DBC ,在△OAF 和△BCD 中,{∠FOA =∠DBCOA =BC ∠OAF =∠BCD,∴△OAF ≌△BCD .∴BD =OF =1,∴OE =4+1=5,∴OB =√OE 2+BE 2.由于OE 的长不变,所以当BE 最小时(即B 点在x 轴上),OB 取得最小值,最小值为OB =OE =5. 故答案为:5.27.(2018•无锡)如图,已知∠XOY =60°,点A 在边OX 上,OA =2.过点A 作AC ⊥OY 于点C ,以AC 为一边在∠XOY 内作等边三角形ABC ,点P 是△ABC 围成的区域(包括各边)内的一点,过点P 作PD ∥OY 交OX 于点D ,作PE ∥OX 交OY 于点E .设OD =a ,OE =b ,则a +2b 的取值范围是 2≤a +2b ≤5 .【分析】作辅助线,构建30度的直角三角形,先证明四边形EODP 是平行四边形,得EP =OD =a ,在Rt △HEP 中,∠EPH =30°,可得EH 的长,计算a +2b =2OH ,确认OH 最大和最小值的位置,可得结论.【解析】如图1,过P 作PH ⊥OY 交于点H ,∵PD ∥OY ,PE ∥OX ,∴四边形EODP 是平行四边形,∠HEP =∠XOY =60°,∴EP =OD =a ,Rt △HEP 中,∠EPH =30°,∴EH =12EP =12a ,∴a +2b =2(12a +b )=2(EH +EO )=2OH , 当P 在AC 边上时,H 与C 重合,此时OH 的最小值=OC =12OA =1,即a +2b 的最小值是2;当P 在点B 时,如图2,OC =1,AC =BC =√3,Rt △CHP 中,∠HCP =30°,∴PH =√32,CH =32,则OH 的最大值是:OC +CH =1+32=52,即(a +2b )的最大值是5,∴2≤a +2b ≤5.三.解答题(共15小题)28.(2020•扬州)如图,▱ABCD的对角线AC、BD相交于点O,过点O作EF⊥AC,分别交AB、DC于点E、F,连接AF、CE.(1)若OE=32,求EF的长;(2)判断四边形AECF的形状,并说明理由.【分析】(1)判定△AOE≌△COF(ASA),即可得OE=OF=32,进而得出EF的长;(2)先判定四边形AECF是平行四边形,再根据EF⊥AC,即可得到四边形AECF是菱形.【解析】(1)∵四边形ABCD是平行四边形,∴AB∥CD,AO=CO,∴∠FCO=∠EAO,又∵∠AOE=∠COF,∴△AOE≌△COF(ASA),∴OE=OF=3 2,∴EF=2OE=3;(2)四边形AECF是菱形,理由:∵△AOE≌△COF,∴AE=CF,又∵AE∥CF,∴四边形AECF是平行四边形,又∵EF⊥AC,∴四边形AECF是菱形.29.(2019•无锡)如图,在▱ABCD中,点E、F分别在边AD、BC上,且DE=BF,直线EF与BA、DC 的延长线分别交于点G,H.求证:(1)△DEH≌△BFG;(2)AG=CH.【分析】(1)依据四边形ABCD是平行四边形,即可得到∠D=∠B,∠H=∠G,DE=BF,进而得出△DEH≌△BFG;(2)依据△DEH≌△BFG,即可得到GB=HD,再根据AB=CD,即可得出AG=CH.【解析】(1)∵四边形ABCD是平行四边形,∴AB∥CD,∠B=∠D,AB=CD,∴∠G=∠H,∵∠D=∠B,∠H=∠G,DE=BF,∴△DEH≌△BFG(AAS);(2)∵△DEH≌△BFG,∴GB=HD,又∵AB=CD,∴GB﹣AB=HD﹣CD,∴AG=CH.30.(2019•淮安)已知:如图,在▱ABCD中,点E、F分别是边AD、BC的中点.求证:BE=DF.【分析】由四边形ABCD是平行四边形,可得AD∥BC,AD=BC,又由点E、F分别是▱ABCD边AD、BC的中点,可得DE=BF,继而证得四边形BFDE是平行四边形,即可证得结论.【解答】证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∵点E、F分别是▱ABCD边AD、BC的中点,∴DE=12AD,BF=12BC,∴DE=BF,∴四边形BFDE是平行四边形,∴BE=DF.31.(2019•扬州)如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.(1)求证:∠BEC=90°;(2)求cos∠DAE.【分析】(1)根据平行四边形的性质得出DC=AB,AD=CB,DC∥AB,推出∠DEA=∠EAB,再根据角平分线性质得出∠DAE=∠DEA,推出AD=DE=10,得出AB=CD=16,由勾股定理的逆定理即可得出结论;(2)由平行线得出∠ABE=∠BEC=90°,由勾股定理求出AE=√AB2+BE2=8√5,得出cos∠DAE=cos∠EAB,即可得出结果.【解答】(1)证明:∵四边形ABCD是平行四边形,∴DC=AB,AD=BC,DC∥AB,∴∠DEA=∠EAB,∵AE平分∠DAB,∴∠DAE=∠EAB,∴∠DAE=∠DEA∴AD=DE=10,∴BC=10,AB=CD=DE+CE=16,∵CE 2+BE 2=62+82=100=BC 2,∴△BCE 是直角三角形,∠BEC =90°;(2)解:∵AB ∥CD ,∴∠ABE =∠BEC =90°,∴AE =√AB 2+BE 2=√162+82=8√5,∴cos ∠DAE =cos ∠EAB =AB AE =168√5=2√55. 32.(2018•淮安)已知:如图,▱ABCD 的对角线AC 、BD 相交于点O ,过点O 的直线分别与AD 、BC 相交于点E 、F .求证:AE =CF .【分析】利用平行四边形的性质得出AO =CO ,AD ∥BC ,进而得出∠EAC =∠FCO ,再利用ASA 求出△AOE ≌△COF ,即可得出答案.【解答】证明:∵▱ABCD 的对角线AC ,BD 交于点O ,∴AO =CO ,AD ∥BC ,∴∠EAC =∠FCO ,在△AOE 和△COF 中{∠EAO =∠FCOAO =CO ∠AOE =∠COF,∴△AOE ≌△COF (ASA ),∴AE =CF .33.(2018•无锡)如图,平行四边形ABCD 中,E 、F 分别是边BC 、AD 的中点,求证:∠ABF =∠CDE .【分析】根据平行四边形的性质以及全等三角形的性质即可求出答案.【解析】在▱ABCD 中,AD =BC ,∠A =∠C ,∵E 、F 分别是边BC 、AD 的中点,∴AF =CE ,在△ABF 与△CDE 中,{AB =CD ∠A =∠C AF =CE∴△ABF ≌△CDE (SAS )∴∠ABF =∠CDE34.(2018•宿迁)如图,在▱ABCD 中,点E 、F 分别在边CB 、AD 的延长线上,且BE =DF ,EF 分别与AB 、CD 交于点G 、H .求证:AG =CH .【分析】利用平行四边形的性质得出AF =EC ,再利用全等三角形的判定与性质得出答案.【解答】证明:∵四边形ABCD 是平行四边形,∴AD =BC ,∠A =∠C ,AD ∥BC ,∴∠E =∠F ,∵BE =DF ,∴AF =EC ,在△AGF 和△CHE 中{∠A =∠CAF =EC ∠F =∠E,∴△AGF ≌△CHE (ASA ),∴AG =CH .35.(2017•无锡)已知,如图,平行四边形ABCD 中,E 是BC 边的中点,连DE 并延长交AB 的延长线于点F ,求证:AB =BF .【分析】根据线段中点的定义可得CE =BE ,根据平行四边形的对边平行且相等可得AB ∥CD ,AB =CD ,再根据两直线平行,内错角相等可得∠DCB =∠FBE ,然后利用“角边角”证明△CED 和△BEF 全等,根据全等三角形对应边相等可得CD =BF ,从而得证.【解答】证明:∵E 是BC 的中点,∴CE =BE ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,AB =CD ,∴∠DCB =∠FBE ,在△CED 和△BEF 中,{∠DCB =∠FBECE =BE ∠CED =∠BEF,∴△CED ≌△BEF (ASA ),∴CD =BF ,∴AB =BF .36.(2017•南京)如图,在▱ABCD 中,点E 、F 分别在AD 、BC 上,且AE =CF ,EF 、BD 相交于点O ,求证:OE =OF .【分析】方法1、连接BE 、DF ,由已知证出四边形BEDF 是平行四边形,即可得出结论.方法2、先判断出DE =BF ,进而判断出△DOE ≌△BOF 即可.【解答】证明:方法1,连接BE 、DF ,如图所示:∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∴DE ∥BF ,∵AE =CF ,∴DE =BF ,∴四边形BEDF 是平行四边形,∴OF =OE .方法2,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∴∠ODE =∠OBF ,又∵AE =CF ,∴DE =BF ,在△DOE 和△BOF 中,{∠DOE =∠BOF∠ODE =∠OBF DE =BF,∴△DOE ≌△BOF (AAS ),∴OE =OF .37.(2017•淮安)已知:如图,在平行四边形ABCD 中,AE ⊥BD ,CF ⊥BD ,垂足分别为E ,F .求证:△ADE ≌△CBF .【分析】证出∠ADE =∠CBF ,AD =CB ,由AAS 证△ADE ≌△CBF 即可.【解答】证明:∵四边形ABCD 是平行四边形,∴AD =CB ,AD ∥BC ,∴∠ADE =∠CBF ,∵AE ⊥BD ,CF ⊥BD ,∴∠AED =∠CFB =90°,在△ADE 和△CBF 中,{∠ADE =∠CBF∠AED =∠CFB AD =CB,∴△ADE ≌△CBF (AAS ).38.(2016•徐州)如图,在△ABC 中,∠ABC =90°,∠BAC =60°,△ACD 是等边三角形,E 是AC 的中点,连接BE 并延长,交DC 于点F ,求证:(1)△ABE ≌△CFE ;(2)四边形ABFD 是平行四边形.【分析】(1)根据等边三角形的性质得到∠DCA =60°等量代换得到∠DCA =∠BAC ,根据全等三角形的判定定理即可得到结论;(2)根据已知条件得到△ABE 是等边三角形,推出△CEF 是等边三角形,证得∠CFE =∠CDA ,求得BF ∥AD ,即可得到结论;【解答】证明:(1)∵△ACD 是等边三角形,∴∠DCA =60°,∵∠BAC =60°,∴∠DCA =∠BAC ,在△ABE 与△CFE 中,{∠DCA =∠BACAE =CE ∠BEA =∠FEC,∴△ABE ≌△CFE ;(2)∵E 是AC 的中点,∴BE =EA ,∵∠BAE =60°,∴△ABE 是等边三角形,∴△CEF 是等边三角形,∴∠CFE =60°,∵△ACD 是等边三角形,∴∠CDA =∠DCA =60°,∴∠CFE =∠CDA ,∴BF ∥AD ,∵∠DCA =∠BAC =60°,∴AB ∥DC ,∴四边形ABFD 是平行四边形.39.(2020•淮安)如图,在▱ABCD 中,点E 、F 分别在BC 、AD 上,AC 与EF 相交于点O ,且AO =CO .(1)求证:△AOF ≌△COE ;(2)连接AE 、CF ,则四边形AECF 是 (填“是”或“不是”)平行四边形.【分析】(1)由ASA 证明△AOF ≌△COE 即可;(2)由全等三角形的性质得出FO =EO ,再由AO =CO ,即可得出结论.【解答】(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠OAF =∠OCE ,在△AOF 和△COE 中,{∠OAF =∠OCEAO =CO ∠AOF =∠COE,∴△AOF ≌△COE (ASA )(2)解:四边形AECF 是平行四边形,理由如下:由(1)得:△AOF ≌△COE ,∴FO =EO ,又∵AO =CO ,∴四边形AECF 是平行四边形;故答案为:是.40.(2017•无锡)如图,已知点E 、F 分别在边AB 、BC 上,ED ∥BC ,EF ∥AC ,BE =CF .求证:BD 是△ABC 的角平分线.【分析】先证明四边形EFCD是平行四边形,得ED=CF,再证明△BED是等腰三角形,得∠EBD=∠EDB,再由平行线的性质得结果.【解答】证明:∵ED∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴ED=CF,∵BE=CF,∴BE=ED,∴∠EBD=∠EDB,∵ED∥BC,∴∠EDB=∠DBC,∴EBD=∠DBC,∴BD是△ABC的角平分线.41.(2017•镇江)如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.(1)求证:四边形BCED是平行四边形;(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.【分析】(1)由已知角相等,利用对顶角相等,等量代换得到同位角相等,进而得出DB与EC平行,再由内错角相等两直线平行得到DE与BC平行,即可得证;(2)由角平分线得到一对角相等,再由两直线平行内错角相等,等量代换得到一对角相等,再利用等角对等边得到CN=BC,再由平行四边形对边相等即可确定出所求.【解答】(1)证明:∵∠A=∠F,∴DE∥BC,∵∠1=∠2,且∠1=∠DMF,∴∠DMF=∠2,∴DB∥EC,则四边形BCED为平行四边形;。
2021年江苏各市(苏州扬州泰州盐城无锡等)中考数学真题分项汇编16 圆含详解

专题16圆一、圆的基本性质1.(2021·江苏无锡市)用半径为50,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径为________.2.(2021·江苏扬州市)如图是某圆柱体果罐,它的主视图是边长为10cm 的正方形,该果罐侧面积为_____2cm .3.(2021·江苏盐城市)一圆锥的底面半径为2,母线长为3,则这个圆锥的侧面积为_______.4.(2021·江苏宿迁市)已知圆锥的底面圆半径为4,侧面展开图扇形的圆心角为120°,则它的侧面展开图面积为_____________.二、圆锥与扇形5.(2021·江苏徐州市)如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3:1,则圆的面积约为正方形面积的( )A .27倍B .14倍C .9倍D .3倍6.(2021·江苏南京市)如图,AB 是O 的弦,C 是AB 的中点,OC 交AB 于点D .若8cm,2cm AB CD ==,则O 的半径为________cm .7.(2021·江苏常州市)如图,BC 是O 的直径,AB 是O 的弦.若60AOC ∠=︒,则OAB ∠的度数是( )A .20︒B .25︒C .30D .35︒8.(2021·江苏宿迁市)如图,在Rt△ABC 中,△ABC =90°,△A =32°,点B 、C 在O 上,边AB 、AC 分别交O 于D 、E 两点﹐点B 是CD 的中点,则△ABE =__________.9.(2021·江苏盐城市)如图,在△O 内接四边形ABCD 中,若100ABC ∠=︒,则ADC ∠=________︒.10.(2021·江苏连云港市)如图,OA 、OB 是O 的半径,点C 在O 上,30AOB ∠=︒,40OBC ∠=︒,则OAC ∠=______︒.11.(2021·江苏南京市)如图,,,,,FA GB HC ID JE 是五边形ABCDE 的外接圆的切线,则BAF CBG DCH EDI AEJ ∠+∠+∠+∠+∠=______︒.12.(2021·江苏徐州市)如图,AB 是O 的直径,点C D 、在O 上,若58ADC ∠=︒,则BAC ∠=_________°.13.(2021·江苏连云港市)如图,正方形ABCD 内接于O ,线段MN 在对角线BD 上运动,若O 的面积为2π,1MN =,则AMN 周长的最小值是( )A .3B .4C .5D .614.(2021·江苏常州市)如图,在Rt ABC 中,90,30,1ACB CBA AC ∠=︒∠=︒=,D 是AB 上一点(点D 与点A 不重合).若在Rt ABC 的直角边上存在4个不同的点分别和点A 、D 成为直角三角形的三个顶点,则AD 长的取值范围是________.15.(2021·江苏扬州市)在一次数学探究活动中,李老师设计了一份活动单:“追梦”学习小组通过操作、观察、讨论后汇报:点A 的位置不唯一,它在以BC 为弦的圆弧上(点B 、C 除外),…….小华同学画出了符合要求的一条圆弧(如图1).(1)小华同学提出了下列问题,请你帮助解决.△该弧所在圆的半径长为___________;△ABC 面积的最大值为_________;(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A ',请你利用图1证明30BA C '∠>︒;(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形ABCD 的边长2AB =,3BC =,点P 在直线CD 的左侧,且4tan 3DPC ∠=. △线段PB 长的最小值为_______;△若23PCD PAD S S =,则线段PD 长为________.三、圆的切线16.(2021·江苏泰州市)如图,平面直角坐标系xOy 中,点A 的坐标为(8,5),△A 与x 轴相切,点P 在y 轴正半轴上,PB 与△A 相切于点B .若△APB =30°,则点P 的坐标为 ___.17.(2021·江苏南京市)如图,已知P 是O 外一点.用两种不同的方法过点P 作O 的一条切线.要求: (1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.18.(2021·江苏南通市)如图,AB 为O 的直径,C 为O 上一点,弦AE 的延长线与过点C 的切线互相垂直,垂足为D ,35CAD ∠=︒,连接BC .(1)求B 的度数;(2)若2AB =,求EC 的长.19.(2021·江苏盐城市)如图,O 为线段PB 上一点,以O 为圆心OB 长为半径的△O 交PB 于点A ,点C 在△O 上,连接PC ,满足2PC PA PB =⋅.(1)求证:PC 是△O 的切线;(2)若3AB PA =,求AC BC的值. 20.(2021·江苏无锡市)如图,四边形ABCD 内接于O ,AC 是O 的直径,AC 与BD 交于点E ,PB 切O 于点B .(1)求证:PBA OBC ∠=∠;(2)若20PBA ,40ACD ∠=︒,求证:OAB CDE ∽.21.(2021·江苏宿迁市)如图,在Rt △AOB 中,△AOB =90°,以点O 为圆心,OA 为半径的圆交AB 于点C ,点D 在边OB 上,且CD= BD .(1)判断直线CD 与圆O 的位置关系,并说明理由;(2)已知24tan 7DOC ∠=,AB =40,求O 的半径.22.(2021·江苏苏州市)如图,四边形ABCD 内接于O ,12∠=∠,延长BC 到点E ,使得CE AB =,连接ED . (1)求证:BD ED =;(2)若4AB =,6BC =,60ABC ∠=︒,求tan DCB ∠的值.23.(2021·江苏扬州市)如图,四边形ABCD 中,//AD BC ,90BAD ∠=︒,CB CD =,连接BD ,以点B 为圆心,BA 长为半径作B ,交BD 于点E .(1)试判断CD 与B 的位置关系,并说明理由;(2)若AB =60BCD ∠=︒,求图中阴影部分的面积.24.(2021·江苏连云港市)如图,Rt ABC 中,90ABC ∠=︒,以点C 为圆心,CB 为半径作C ,D 为C 上一点,连接AD 、CD ,AB AD =,AC 平分BAD ∠.(1)求证:AD 是C 的切线;(2)延长AD 、BC 相交于点E ,若2EDC ABC S S =,求tan BAC ∠的值.25.(2021·江苏泰州市)如图,在△O中,AB为直径,P为AB上一点,P A=1,PB=m(m为常数,且m>0).过点P的弦CD△AB,Q为BC上一动点(与点B不重合),AH△QD,垂足为H.连接AD、BQ.(1)若m=3.△求证:△OAD=60°;△求BQDH的值;(2)用含m的代数式表示BQDH,请直接写出结果;(3)存在一个大小确定的△O,对于点Q的任意位置,都有BQ2﹣2DH2+PB2的值是一个定值,求此时△Q的度数.26.(2021·江苏苏州市)如图△,甲,乙都是高为6米的长方体容器,容器甲的底面ABCD是正方形,容器乙的底面EFGH是矩形.如图△,已知正方形ABCD与矩形EFGH满足如下条件:正方形ABCD外切于一个半径为5米的圆O,矩形EFGH内接于这个圆O,2EF EH=.(1)求容器甲,乙的容积分别为多少立方米?(2)现在我们分别向容器甲,乙同时持续注水(注水前两个容器是空的),一开始注水流量均为25立方米/小时,4小时后.把容器甲的注水流量增加a立方米/小时,同时保持容器乙的注水流量不变,继续注水2小时后,把容器甲的注水流量再一次增加50立方米/小时,同时容器乙的注水流量仍旧保持不变.直到两个容器的水位高度相同,停止注水.在整个注水过程中,当注水时间为t时,我们把容器甲的水位高度记为h甲,容器乙的水位高度记为h乙,设h h h-=乙甲,已知h(米)关于注水时间t(小时)的函数图像如图△所示,其中MN平行于横轴.根据图中所给信息,解决下列问题:△求a的值;△求图△中线段PN所在直线的解析式.专题16圆一、圆的基本性质1.(2021·江苏无锡市)用半径为50,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面半径为________.【答案】50 3【分析】先求出扇形的弧长,再根据圆的周长公式,即可求解.【详解】△扇形的弧长=120501001803ππ⨯=,△圆锥的底面半径=1003π÷2π=503.故答案是:503.【点睛】本题主要考查扇形的弧长公式,掌握圆锥的底面周长等于圆锥展开扇形的弧长,是解题的关键.2.(2021·江苏扬州市)如图是某圆柱体果罐,它的主视图是边长为10cm的正方形,该果罐侧面积为_____2cm.【答案】100π【分析】根据圆柱体的主视图为边长为10cm的正方形,得到圆柱的底面直径和高,从而计算侧面积.【详解】解:△果罐的主视图是边长为10cm的正方形,为圆柱体,△圆柱体的底面直径和高为10cm,△侧面积为1010π⨯=100π,故答案为:100π.【点睛】本题考查了几何体的三视图,解题的关键是根据三视图得到几何体的相关数据.3.(2021·江苏盐城市)一圆锥的底面半径为2,母线长为3,则这个圆锥的侧面积为_______.【答案】6π【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.【详解】解:该圆锥的侧面积=12×2π×2×3=6π.故答案为6π.【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.4.(2021·江苏宿迁市)已知圆锥的底面圆半径为4,侧面展开图扇形的圆心角为120°,则它的侧面展开图面积为_____________.【答案】48π【分析】首先根据底面圆的半径求得扇形的弧长,然后根据弧长公式求得扇形的半径,然后利用公式求得面积即可.【详解】解:△底面圆的半径为4,△底面周长为8π,△侧面展开扇形的弧长为8π,设扇形的半径为r,△圆锥的侧面展开图的圆心角是120°,△120180rπ=8π,解得:r=12,△侧面积为π×4×12=48π,故答案为:48π.【点睛】考查了圆锥的计算,解题的关键是了解圆锥的侧面展开扇形的弧长等于底面圆的周长,难度不大.二、圆锥与扇形5.(2021·江苏徐州市)如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3:1,则圆的面积约为正方形面积的()A .27倍B .14倍C .9倍D .3倍【答案】C【分析】 设OB =x ,则OA =3x ,BC =2x ,根据圆的面积公式和正方形的面积公式,求出面积,进而即可求解.【详解】解:由圆和正方形的对称性,可知:OA =OD ,OB =OC ,△圆的直径与正方形的对角线之比为3:1,△设OB =x ,则OA =3x ,BC =2x ,△圆的面积=π(3x )2=9πx 2,正方形的面积=()2122x =2x 2, △9πx 2÷2x 2=9142π≈,即:圆的面积约为正方形面积的14倍, 故选C .【点睛】本题主要考查圆和正方形的面积以及对称性,根据题意画出图形,用未知数表示各个图形的面积,是解题的关键.6.(2021·江苏南京市)如图,AB 是O 的弦,C 是AB 的中点,OC 交AB 于点D .若8cm,2cm AB CD ==,则O 的半径为________cm .【答案】5【分析】连接OA ,由垂径定理得AD =4cm ,设圆的半径为R ,根据勾股定理得到方程2224(2)R R =+-,求解即可【详解】解:连接OA ,△C 是AB 的中点,△OC AB ⊥ △14cm 2AD AB ==设O 的半径为R ,△2cm CD =△(2)cm OD OC CD R =-=-在Rt OAD ∆中,222OA AD OD =+,即2224(2)R R =+-,解得,5R =即O 的半径为5cm故答案为:5【点睛】本题考查的是垂径定理及勾股定理,根据垂径定理判断出OC 是AB 的垂直平分线是解答此题的关键.7.(2021·江苏常州市)如图,BC 是O 的直径,AB 是O 的弦.若60AOC ∠=︒,则OAB ∠的度数是()A .20︒B .25︒C .30D .35︒【答案】C【分析】先根据平角的定义求出△AOB ,再根据等腰三角形的性质求解,即可.【详解】解:△60AOC ∠=︒,△△AOB =180°-60°=120°,△OA =OB ,△OAB ∠=△OBA =(180°-120°)÷2=30°,故选C .【点睛】本题主要考查圆的基本性质以及等腰三角形的性质,掌握圆的半径相等,是解题的关键.8.(2021·江苏宿迁市)如图,在Rt△ABC 中,△ABC =90°,△A =32°,点B 、C 在O 上,边AB 、AC 分别交O 于D 、E 两点﹐点B 是CD 的中点,则△ABE =__________.【答案】13︒【分析】如图,连接,DC 先证明,BDC BCD ∠=∠再证明,ABE ACD ∠=∠利用三角形的外角可得:,BDC A ACD A ABE ∠=∠+∠=∠+∠再利用直角三角形中两锐角互余可得:()2902,BDC A ABE ∠=︒-∠+∠再解方程可得答案.【详解】解:如图,连接,DC B 是CD 的中点,,,BD BC BDC BCD ∴=∠=∠,DE DE =,ABE ACD ∴∠=∠,BDC A ACD A ABE ∴∠=∠+∠=∠+∠90,32,ABC A ∠=︒∠=︒()2902,BDC A ABE ∴∠=︒-∠+∠45453213.ABE A ∴∠=︒-∠=︒-︒=︒故答案为:13.︒【点睛】本题考查的是圆周角定理,三角形的外角的性质,直角三角形的两锐角互余,掌握圆周角定理的含义是解题的关键. 9.(2021·江苏盐城市)如图,在△O 内接四边形ABCD 中,若100ABC ∠=︒,则ADC ∠=________︒.【答案】80【分析】根据圆内接四边形的性质计算出18080ADC ABC ∠∠=︒-=︒即可.【详解】解:△ABCD 是△O 的内接四边形,△ABC =100°,△△ABC +△ADC =180°,△180********ADC ABC ∠∠=︒-=︒-︒=︒.故答案为80.【点睛】本题考查了圆内接四边形的性质、解题的关键是熟练掌握圆内接四边形的性质.10.(2021·江苏连云港市)如图,OA 、OB 是O 的半径,点C 在O 上,30AOB ∠=︒,40OBC ∠=︒,则OAC ∠=______︒.【答案】25【分析】连接OC ,根据等腰三角形的性质和三角形内角和定理得到△BOC =100°,求出△AOC ,根据等腰三角形的性质计算.【详解】解:连接OC,△OC=OB,△△OCB=△OBC=40°,△△BOC=180°-40°×2=100°,△△AOC=100°+30°=130°,△OC=OA,△△OAC=△OCA=25°,故答案为:25.【点睛】本题考查的是圆的基本性质、等腰三角形的性质,三角形内角和定理,掌握三角形内角和等于180°是解题的关键.FA GB HC ID JE是五边形ABCDE的外接圆的切线,则11.(2021·江苏南京市)如图,,,,,∠+∠+∠+∠+∠=______︒.BAF CBG DCH EDI AEJ【答案】180︒【分析】由切线的性质可知切线垂直于半径,所以要求的5个角的和等于5个直角减去五边形的内角和的一半.【详解】如图:过圆心连接五边形ABCDE的各顶点,∠+∠+∠+∠+∠则OAB OBC OCD ODE OEA=∠+∠+∠+∠+∠OBA OCB ODC OED OAE1=-⨯︒=︒(52)1802702∴BAF CBG DCH EDI AEJ∠+∠+∠+∠+∠=⨯︒-∠+∠+∠+∠+∠590()OAB OBC OCD ODE OEA=︒-︒450270180=︒.故答案为:180︒.【点睛】本题考查了圆的切线的性质,多边形的内角和公式2180()n -⨯︒(n 为多边形的边数),由半径相等可得“等边对等角”,正确的理解题意作出图形是解题的关键.12.(2021·江苏徐州市)如图,AB 是O 的直径,点C D 、在O 上,若58ADC ∠=︒,则BAC ∠=_________°.【答案】32【分析】由同弧所对的圆周角相等和直径所对的圆周角为90°然后根据三角形内角和即可求出BAC ∠的度数.【详解】△58ADC ∠=︒,△58ABC ADC ∠=∠=︒,又△AB 是直径,△90ACB ∠=︒,△905832BAC =︒-︒=︒∠.故答案为:32.【点睛】此题考查了同弧所对圆周角的性质和直径所对圆周角的性质,解题的关键是熟练掌握同弧所对圆周角的性质和直径所对圆周角的性质.13.(2021·江苏连云港市)如图,正方形ABCD 内接于O ,线段MN 在对角线BD 上运动,若O 的面积为2π,1MN =,则AMN 周长的最小值是( )A .3B .4C .5D .6【答案】B【分析】 利用将军饮马之造桥选址的数学方法进行计算.【详解】如图所示,(1)N 为BD 上一动点,A 点关于线段BD 的对称点为点C ,连接CN ,则=CN AN ,过A 点作CN 的平行线AG ,过C 点作BD 的平行线CG ,两平行线相交于点G ,AG 与BD 相交于点M .//,//,CN MG NM CG∴四边形CNMG 是平行四边形∴MG CN =∴MG AN =则=1AMN C AN AM NM MG AM ++=++(2)找一点'N , 连接'CN ,则'='CN AN ,过G 点作'CN 的平行线MG ,连接'AM 则''=''''''''''1AM N C AN AM N M AN AM CG AN AM NM AN AM ++=++=++=++.此时1''1AN AM AN AM ++<++∴''AMN AM N C C <∴(1)中AMN 周长取到最小值四边形CNMG 是平行四边形∴CNM NMA ∠=∠四边形ABCD 是正方形∴CO OA =,AC BD ⊥又CNM NMA ∠=∠,NOC MOA ∠=∠,CO OA =∴()CNO AOM AAS ≅∴ON OM =又AC BD∴AN AM =∴ANM 是等腰三角形22S r ππ==,则圆的半径r =1111222OM MN ==⨯= 2222219+24AM r OM ⎛⎫==+= ⎪⎝⎭ 32AM ∴= 3=2+1=42AMN C ∴⨯ 故选:B .【点睛】本题难度较大,需要具备一定的几何分析方法.关键是要找到AMN 周长取最小值时M N 、的位置.14.(2021·江苏常州市)如图,在Rt ABC 中,90,30,1ACB CBA AC ∠=︒∠=︒=,D 是AB 上一点(点D 与点A 不重合).若在Rt ABC 的直角边上存在4个不同的点分别和点A 、D 成为直角三角形的三个顶点,则AD 长的取值范围是________.【答案】43<AD <2 【分析】以AD 为直径,作O 与BC 相切于点M ,连接OM ,求出此时AD 的长;以AD 为直径,作O ,当点D 与点B 重合时,求出AD 的长,进入即可得到答案.【详解】解:以AD 为直径,作O 与BC 相切于点M ,连接OM ,则OM △BC ,此时,在Rt ABC 的直角边上存在3个不同的点分别和点A 、D 成为直角三角形,如图,△在Rt ABC 中,90,30,1ACB CBA AC ∠=︒∠=︒=,△AB =2,△OM △BC , △1sin 302OM OB ︒==, 设OM =x ,则AO =x , △122x x =-,解得:23x =, △AD =2×23=43, 以AD 为直径,作O ,当点D 与点B 重合时,如图,此时AD =AB =2,△在Rt ABC 的直角边上存在4个不同的点分别和点A 、D 成为直角三角形的三个顶点,则AD 长的取值范围是:43<AD <2. 故答案是:43<AD <2.【点睛】本题主要考查圆的综合问题,熟练掌握圆周角定理的推论,解直角三角形,画出图形,分类讨论,是解题的关键.15.(2021·江苏扬州市)在一次数学探究活动中,李老师设计了一份活动单:“追梦”学习小组通过操作、观察、讨论后汇报:点A 的位置不唯一,它在以BC 为弦的圆弧上(点B 、C 除外),…….小华同学画出了符合要求的一条圆弧(如图1).(1)小华同学提出了下列问题,请你帮助解决.△该弧所在圆的半径长为___________;△ABC 面积的最大值为_________;(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A ',请你利用图1证明30BA C '∠>︒;(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形ABCD 的边长2AB =,3BC =,点P 在直线CD 的左侧,且4tan 3DPC ∠=. △线段PB 长的最小值为_______;△若23PCD PAD S S =,则线段PD 长为________.【答案】(1)△2;2;(2)见解析;(3) 【分析】(1)△设O 为圆心,连接BO ,CO ,根据圆周角定理得到△BOC =60°,证明△OBC 是等边三角形,可得半径; △过点O 作BC 的垂线,垂足为E ,延长EO ,交圆于D ,以BC 为底,则当A 与D 重合时,△ABC 的面积最大,求出OE ,根据三角形面积公式计算即可;(2)延长BA ′,交圆于点D ,连接CD ,利用三角形外角的性质和圆周角定理证明即可;(3)△根据4tan 3DPC ∠=,连接PD ,设点Q 为PD 中点,以点Q 为圆心,12PD 为半径画圆,可得点P 在优弧CPD 上,连接BQ ,与圆Q 交于P ′,可得BP ′即为BP 的最小值,再计算出BQ 和圆Q 的半径,相减即可得到BP ′; △根据AD ,CD 和23PCD PAD S S =推出点P 在△ADC 的平分线上,从而找到点P 的位置,过点C 作CF △PD ,垂足为F ,解直角三角形即可求出DP .【详解】解:(1)△设O 为圆心,连接BO ,CO ,△△BAC =30°,△△BOC =60°,又OB =OC ,△△OBC 是等边三角形,△OB =OC =BC =2,即半径为2;△△△ABC 以BC 为底边,BC =2,△当点A 到BC 的距离最大时,△ABC 的面积最大,如图,过点O 作BC 的垂线,垂足为E ,延长EO ,交圆于D ,△BE =CE =1,DO =BO =2,△OE△DE 2,△△ABC 的最大面积为)1222⨯⨯2;(2)如图,延长BA ′,交圆于点D ,连接CD ,△点D 在圆上,△△BDC =△BAC ,△△BA ′C =△BDC +△A ′CD ,△△BA ′C >△BDC ,△△BA ′C >△BAC ,即△BA ′C >30°;(3)△如图,当点P在BC上,且PC=32时,△△PCD=90°,AB=CD=2,AD=BC=3,△tan△DPC=CDPC =43,为定值,连接PD,设点Q为PD中点,以点Q为圆心,12PD为半径画圆,△当点P在优弧CPD上时,tan△DPC=43,连接BQ,与圆Q交于P′,此时BP′即为BP的最小值,过点Q作QE△BE,垂足为E,△点Q是PD中点,△点E为PC中点,即QE=12CD=1,PE=CE=12PC=34,△BE=BC-CE=3-34=94,△BQ,△PD 52,△圆Q的半径为155 224⨯=,△BP′=BQ-P′Q BP△△AD=3,CD=2,23PCD PADS S=,则23 CDAD=,△△P AD中AD边上的高=△PCD中CD边上的高,即点P到AD的距离和点P到CD的距离相等,则点P到AD和CD的距离相等,即点P在△ADC的平分线上,如图,过点C作CF△PD,垂足为F,△PD平分△ADC,△△ADP=△CDP=45°,△△CDF为等腰直角三角形,又CD=2,△CF=DF△tan△DPC=CFPF=43,△PF△PD=DF+PF.【点睛】本题是圆的综合题,考查了圆周角定理,三角形的面积,等边三角形的判定和性质,最值问题,解直角三角形,三角形外角的性质,勾股定理,知识点较多,难度较大,解题时要根据已知条件找到点P的轨迹.三、圆的切线16.(2021·江苏泰州市)如图,平面直角坐标系xOy中,点A的坐标为(8,5),△A与x轴相切,点P在y轴正半轴上,PB与△A相切于点B.若△APB=30°,则点P的坐标为___.【答案】()0,11.【分析】连接AB,作AD△x轴,AC△y轴,根据题意和30°直角三角形的性质求出AP的长度,然后由圆和矩形的性质,根据勾股定理求出OC的长度,即可求出点P的坐标.【详解】如下图所示,连接AB ,作AD △x 轴,AC △y 轴,△PB 与△A 相切于点B△AB △PB ,△△APB =30°,AB △PB ,△P A =2AB =2510⨯=.△90,90,90O OCA ADO =︒=︒=︒∠∠∠,△四边形ACOD 是矩形,点A 的坐标为(8,5),所以AC =OD =8,CO =AD =5,在Rt PAC △中,6PC ==.如图,当点P 在C 点上方时,△5611OP OC CP =+=+=,△点P 的坐标为()0,11.【点睛】此题考查了勾股定理,30°角直角三角形的性质和矩形等的性质,解题的关键是根据题意作出辅助线.17.(2021·江苏南京市)如图,已知P 是O 外一点.用两种不同的方法过点P 作O 的一条切线.要求: (1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.【答案】答案见解析.【分析】方法一:作出OP 的垂直平分线,交OP 于点A ,再以点A 为圆心,P A 长为半径画弧,交O 于点Q ,连结PQ ,PQ 即为所求.方法二:作出以OP 为底边的等腰三角形BPO ,再作出△OBP 的角平分线交OP 于点A ,再以点A 为圆心,P A 长为半径画弧,交O 于点Q ,连结PQ ,PQ 即为所求.【详解】解:作法:连结PO ,分别以P 、O 为圆心,大于12PO 的长度为半径画弧,交于两点,连结两点交PO 于点A ;以点A 为圆心,P A 长为半径画弧,交O 于点Q ,连结PQ ,PQ 即为所求.作法:连结PO ,分别以P 、O 为圆心,以大于12PO 的长度为半径画弧交PO 上方于点B ,连结BP 、BO ;以点B 为圆心,任意长为半径画弧交BP 、BO 于C 、D 两点,分别以于C 、D 两点为圆心,大于12CD 的长度为半径画弧交于一点,连结该点与B 点,并将其反向延长交PQ 于点A ,以点A 为圆心,P A 长为半径画弧,交O 于点Q ,连结PQ ,PQ 即为所求.【点睛】本题考查了作图——复杂作图,涉及垂直平分线的作法,角平分线的作法,等腰三角形的作法,圆的作法等知识点.复杂作图是在五种基本作图的基础上进行作图.解题的关键是熟悉基本几何图形的性质,结合基本几何图形的性质把复杂作图拆解成基本作图,逐步操作.18.(2021·江苏南通市)如图,AB 为O 的直径,C 为O 上一点,弦AE 的延长线与过点C 的切线互相垂直,垂足为D ,35CAD ∠=︒,连接BC .(1)求B的度数;(2)若2AB=,求EC的长.【答案】(1)55°;(2)718π.【分析】(1)连接OC,如图,利用切线的性质得到OC△CD,则判断OC△AE,所以△DAC=△OCA,然后利用△OCA=△OAC 得到△OAB的度数,即可求解;(2)利用(1)的结论先求得△AEO=△EAO=70°,再平行线的性质求得△COE=70°,然后利用弧长公式求解即可.【详解】解:(1)连接OC,如图,△CD是△O的切线,△OC△CD,△AE△CD,△OC△AE,△△DAC=△OCA,△OA=OC,△CAD=35°,△△OAC=△OCA=△CAD=35°,△AB为△O的直径,△△ACB=90°,△△B=90°-△OAC=55°;(2)连接OE,OC,如图,由(1)得△EAO =△OAC +△CAD =70°,△OA =OE ,△△AEO =△EAO =70°,△OC △AE ,△△COE =△AEO =70°,△AB =2,则OC =OE =1,△EC 的长为70718018018n r πππ==. 【点睛】本题考查了切线的性质,圆周角定理,弧长公式等知识,解题的关键是学会添加常用辅助线.19.(2021·江苏盐城市)如图,O 为线段PB 上一点,以O 为圆心OB 长为半径的△O 交PB 于点A ,点C 在△O 上,连接PC ,满足2PC PA PB =⋅.(1)求证:PC 是△O 的切线;(2)若3AB PA =,求AC BC的值. 【答案】(1)见解析;(2)12【分析】(1) 连接OC ,把2PC PA PB =⋅转化为比例式,利用三角形相似证明90PCO ∠=︒即可;(2)利用勾股定理和相似三角形的性质求解即可.【详解】(1)证明:连接OC△2PC PA PB =⋅ △PC PB PA PC=, 又△△P =△P ,△PAC PCB ∽△PAC PCB =∠∠,PCA PBC ∠=∠△PCO PCB OCB ∠=∠-∠△PCO PAC OCB ∠=∠-∠又△OC OB =△OCB OBC ∠=∠△PCO PAC ABC ACB ∠=∠-∠=∠已知C 是O 上的点,AB 是直径,△90ACB ∠=︒,△90PCO ∠=︒△AC PO ⊥,△PC 是圆的切线;(2)设AP a =,则3AB a =, 1.5r a =△ 1.5OC a =在Rt △PCO 中△ 2.5OP a =, 1.5OC a =,△2PC a =已知PAC PCB ∽,AC PA BC PC= △12AC BC =. 【点睛】本题考查了切线的判定,三角形相似的判定和性质,勾股定理,熟练掌握切线的判定方法,灵活运用三角形相似的判定证明相似,运用勾股定理计算是解题的关键.20.(2021·江苏无锡市)如图,四边形ABCD 内接于O ,AC 是O 的直径,AC 与BD 交于点E ,PB 切O 于点B .(1)求证:PBA OBC ∠=∠;(2)若20PBA ,40ACD ∠=︒,求证:OAB CDE ∽.【答案】(1)见详解;(2)见详解【分析】(1)由圆周角定理的推论,可知△ABC =90°,由切线的性质可知△OBP =90°,进而即可得到结论;(2)先推出20OCB OBC ∠=∠=︒,从而得△AOB =40°,继而得△OAB =70°,再推出△CDE =70°,进而即可得到结论.【详解】证明:(1)△AC 是O 的直径,△△ABC =90°,△PB 切O 于点B ,△△OBP =90°,△90PBA ABO OBC ABO ∠+∠=∠+∠=︒,△PBA OBC ∠=∠;(2)△20PBA ,PBA OBC ∠=∠,△20OBC ∠=︒,△OB =OC ,△20OCB OBC ∠=∠=︒,△△AOB =20°+20°=40°,△OB =OA ,△△OAB =△OBA =(180°-40°)÷2=70°,△△ADB =12△AOB =20°,△AC 是O 的直径,△△ADC =90°,△△CDE =90°-20°=70°,△△CDE =△OAB ,△40ACD ∠=︒,△40ACD AOB ∠=∠=︒,△OAB CDE ∽.【点睛】本题主要考查圆的性质以及相似三角形的判定定理,掌握圆周角定理的推论,相似三角形的判定定理,切线的性质定理,是解题的关键.21.(2021·江苏宿迁市)如图,在Rt △AOB 中,△AOB =90°,以点O 为圆心,OA 为半径的圆交AB 于点C ,点D 在边OB 上,且CD= BD .(1)判断直线CD 与圆O 的位置关系,并说明理由;(2)已知24tan 7DOC ∠=,AB =40,求O 的半径.【答案】(1)直线CD 与圆O 相切,理由见解析;(2)【分析】(1)连接,OC 证明90,DCB OCA ∠+∠=︒可得90,OCD ∠=︒ 从而可得答案;(2)由24,tan ,7CD OC CD DOC OC ⊥∠== 设24,CD x = 则7,OC x = 再求解25,7,OD x OA x == 再表示49,OB OD BD x =+= 再利用222,AO BO AB += 列方程解方程,可得答案.【详解】解:(1)直线CD 与圆O 相切,理由如下:如图,连接,OC90,,AOB OA OC ∠=︒=90,,B OAC OAC OCA ∴∠+∠=︒∠=∠,CD BD =,B DCB ∴∠=∠90,DCB OCA ∴∠+∠=︒1809090,OCD ∴∠=︒-︒=︒,OC CD ∴⊥ OC 为O 的半径,CD ∴是O 的切线.(2)24,tan ,7CD OC CD DOC OC ⊥∠== 设24,CD x = 则7,OC x =25,7,OD x OA OC x ∴===,CD BD =24,BD x ∴=49,OB OD BD x ∴=+=40,90,AB AOB =∠=︒222,AO BO AB ∴+=()()22274940,x x ∴+= 232,49x ∴=12x x ∴==(负根舍去)O ∴的半径为:777OC x ==⨯= 【点睛】本题考查的是切线的判定与性质,勾股定理的应用,等腰三角形的性质,锐角三角函数的应用,一元二次方程的解法,熟练应用基础知识,把知识串联起来是解题的关键.22.(2021·江苏苏州市)如图,四边形ABCD 内接于O ,12∠=∠,延长BC 到点E ,使得CE AB =,连接ED . (1)求证:BD ED =;(2)若4AB =,6BC =,60ABC ∠=︒,求tan DCB ∠的值.【答案】(1)见解析;(2 【分析】(1)由圆内接四边形的性质可知180A BCD ∠+∠=︒,再由180DCE BCD ∠+∠=︒,即可得出A DCE ∠=∠.根据圆周角定理结合题意可知AD CD =,即得出AD CD =.由此易证()ABD CED SAS △≌△,即得出BD ED =. (2)过点D 作DM BE ⊥,垂足为M .根据题意可求出10BE =,结合(1)可知152BM EM BE ===,即可求出1CM =.根据题意又可求出230∠=︒,利用三角函数即可求出DM =最后再利用三角函数即可求出最后结果. 【详解】(1)证明:△四边形ABCD 是圆的内接四边形,△180A BCD ∠+∠=︒.△180DCE BCD ∠+∠=︒,△A DCE ∠=∠.△12∠=∠,△AD CD =,△AD CD =. 在ABD △和CED 中,AB CE A DCE AD CD =⎧⎪∠=∠⎨⎪=⎩△()ABD CED SAS △≌△,△BD ED =.(2)解:如图,过点D 作DM BE ⊥,垂足为M .△6BC =,4AB CE ==,△10BE BC CE =+=.由(1)知BD ED =. △152BM EM BE ===. △1CM BC BM =-=.△60ABC ∠=︒,12∠=∠,△230∠=︒.△tan 305DM BM =⋅︒==.△tan DM DCB CM ∠== 【点睛】 本题为圆的综合题.考查圆内接四边形的性质,圆周角定理,全等三角形的判定和性质,等腰三角形的判定和性质以及解直角三角形.利用数形结合的思想并正确作出辅助线是解答本题的关键.23.(2021·江苏扬州市)如图,四边形ABCD 中,//AD BC ,90BAD ∠=︒,CB CD =,连接BD ,以点B 为圆心,BA 长为半径作B ,交BD 于点E .(1)试判断CD 与B 的位置关系,并说明理由;(2)若AB =60BCD ∠=︒,求图中阴影部分的面积.【答案】(1)相切,理由见解析;(2)π【分析】(1)过点B 作BF △CD ,证明△ABD △△FBD ,得到BF =BA ,即可证明CD 与圆B 相切;(2)先证明△BCD 是等边三角形,根据三线合一得到△ABD =30°,求出AD ,再利用S △ABD -S 扇形ABE 求出阴影部分面积.【详解】解:(1)过点B 作BF △CD ,△AD △BC ,△△ADB =△CBD ,△CB =CD ,△△CBD =△CDB ,△△ADB =△CDB ,又BD =BD ,△BAD =△BFD =90°,△△ABD △△FBD (AAS ),△BF =BA ,则点F 在圆B 上,△CD 与圆B 相切;(2)△△BCD =60°,CB =CD ,△△BCD 是等边三角形,△△CBD =60°△BF △CD ,△△ABD =△DBF =△CBF =30°,△△ABF =60°,△AB =BF =△AD =DF =tan30AB ⋅︒=2,△阴影部分的面积=S △ABD -S 扇形ABE=(230122360π⨯⨯⨯-=π.【点睛】本题考查了切线的判定,全等三角形的判定和性质,等边三角形的判定和性质,扇形面积,三角函数的定义,题目的综合性较强,难度不小,解题的关键是正确做出辅助线.24.(2021·江苏连云港市)如图,Rt ABC 中,90ABC ∠=︒,以点C 为圆心,CB 为半径作C ,D 为C 上一点,连接AD 、CD ,AB AD =,AC 平分BAD ∠.(1)求证:AD 是C 的切线;(2)延长AD 、BC 相交于点E ,若2EDC ABC S S =,求tan BAC ∠的值.【答案】(1)见解析;(2【分析】 (1)利用SAS 证明≌∆∆BAC DAC ,可得90ADC ABC ∠=∠=︒,即可得证;(2)由已知条件可得EDC EBA ∆∆∽,可得出:=DC BA :=CB BA tan BAC ∠;【详解】(1)△AC 平分BAD ∠,△BAC DAC ∠=∠.△AB AD =,AC AC =,△≌∆∆BAC DAC .△90ADC ABC ∠=∠=︒.△CD AD ⊥,△AD 是C 的切线.(2)由(1)可知,90EDC ABC ∠=∠=︒,又E E ∠=∠,△EDC EBA ∆∆∽.△2∆∆=EDC ABC S S ,且≌∆∆BAC DAC ,△:1:2∆∆=EDC EBA S S ,△:=DC BA△DC CB =,△:=CB BA△90ABC ∠=︒△tan ∠=CB BAC BA 【点睛】此题考查了切线的判定与性质,正切的性质,以及相似三角形的性质判定,熟练掌握基础知识是解本题的关键. 25.(2021·江苏泰州市)如图,在△O 中,AB 为直径,P 为AB 上一点,P A =1,PB =m (m 为常数,且m >0).过点P 的弦CD △AB ,Q 为BC 上一动点(与点B 不重合),AH △QD ,垂足为H .连接AD 、BQ .(1)若m =3.△求证:△OAD =60°;△求BQ DH的值; (2)用含m 的代数式表示BQ DH ,请直接写出结果; (3)存在一个大小确定的△O ,对于点Q 的任意位置,都有BQ 2﹣2DH 2+PB 2的值是一个定值,求此时△Q 的度数.【答案】(1)△见解析;△2;(2(3)存在半径为1的圆,45°【分析】(1)△连接OD ,则易得CD 垂直平分线段OA ,从而OD =AD ,由OA =OD ,即可得△OAD 是等边三角形,从而可得结论;△连接AQ ,由圆周角定理得:△ABQ =△ADH ,从而其余弦值相等,因此可得BQ AB DH AD= ,由△可得AB 、AD 的值,从而可得结论;(2)连接AQ 、BD , 首先与(1)中的△相同,有BQ AB DH AD =,由△APD △△ADB ,可求得AD 的长,从而求得结果; (3)由(2)的结论可得:22(1)BQ m DH =+,从而BQ 2﹣2DH 2+PB 222(1)m DH m =-+当m =1时,即可得是一个定值,从而可求得△Q 的值.【详解】(1)△如图,连接OD ,则OA =OD△AB =P A +PB =1+3=4△OA =122AB = △OP =AP =1即点P 是线段OA 的中点△CD △AB△CD 垂直平分线段OA△OD =AD△OA =OD =AD。
江苏省中考数学真题《圆》专题汇编(解答)
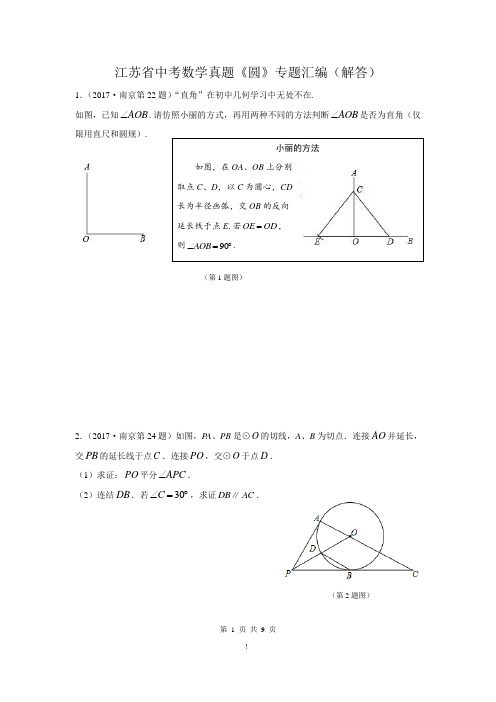
第 1 页 共 9 页 江苏省中考数学真题《圆》专题汇编(解答)1.(2017·南京第22题)“直角”在初中几何学习中无处不在.如图,已知AOB ∠.请仿照小丽的方式,再用两种不同的方法判断AOB ∠是否为直角(仅限用直尺和圆规).2.(2017·南京第24题)如图,P A 、PB 是⊙O 的切线,A 、B 为切点.连接AO 并延长,交PB 的延长线于点C .连接PO ,交⊙O 于点D .(1)求证:PO 平分APC ∠.(2)连结DB .若30C ∠=︒,求证DB ∥AC .(第1题图) (第2题图)3.(2017·无锡第24题)如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):(1)作△ABC的外心O;(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC 和AC上.(第3题图)4.(2017·无锡第27题)如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2,求点P的坐标.(第4题图)第 2 页共9 页第 3 页 共 9 页5.(2017·常州第28题)如图,已知一次函数443y x =-+的图像是直线l ,设直线l 分别与y 轴、x 轴交于点A B 、.(1)求线段AB 的长度;(2)设点M 在射线AB 上,将点M 绕点A 按逆时针方向旋转90°到点N ,以点N 为圆心,NA 的长为半径作N .①当N 与x 轴相切时,求点M 的坐标;②在①的条件下,设直线AN 与x 轴交于点C ,与N 的另一个交点为D ,连接MD 交x 轴于点E ,直线m 过点N 分别与y 轴、直线l 交于点P Q 、,当APQ ∆与CDE ∆相似时,求点P 的坐标.(第5题图)第 4 页 共 9 页6.(2017·苏州第27题)如图,已知△ABC 内接于⊙O ,AB 是直径,点D 在⊙O 上,OD ∥BC ,过点D 作DE ⊥AB ,垂足为E ,连接CD 交OE 边于点F .(1)求证:△DOE ∽△ABC ;(2)求证:∠ODF=∠BDE ;(3)连接OC ,设△DOE 的面积为S 1,四边形BCOD 的面积为S 2,若7221 S S ,求sinA 的值.7.(2017·南通第24题)如图,Rt △ABC 中,∠C=90°,BC=3,点O 在AB 上,OB=2,以OB 为半径的⊙O 与AC 相切于点D ,交BC 于点E ,求弦BE 的长.(第6题图)(第7题图)8.(2017·淮安第25题)如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.(1)试判断直线EF与⊙O的位置关系,并说明理由;(2)若OA=2,∠A=30°,求图中阴影部分的面积.(第8题图)9.(2017·盐城第24题)如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.(第9题图)第 5 页共9 页第 6 页 共 9 页10.(2017·盐城第25题)如图,在平面直角坐标系中,Rt △ABC 的斜边AB 在y 轴上,边AC 与x 轴交于点D ,AE 平分∠BAC 交边BC 于点E ,经过点A 、D 、E 的圆的圆心F 恰好在y 轴上,⊙F 与y 轴相交于另一点G .(1)求证:BC 是⊙F 的切线;(2)若点A 、D 的坐标分别为A (0,1 ),D (2,0),求⊙F 的半径;(3)试探究线段AG 、AD 、CD 三者之间满足的等量关系,并证明你的结论.11.(2017·扬州第25题)如图,已知平行四边形OABC 的三个顶点A 、B 、C 在以O 为圆心的半圆上,过点C 作CD ⊥AB ,分别交AB 、AO 的延长线于点D 、E ,AE 交半圆O 于点F ,连接CF .(1)判断直线DE 与半圆O 的位置关系,并说明理由;(2)①求证:CF=OC ;②若半圆O 的半径为12,求阴影部分的周长.(第10题图)(第11题图)12.(2017·扬州第28题)如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上,对角线EG、PF相交于点O.(1)若AP=1,则AE= ;(2)①求证:点O一定在△APE的外接圆上;②当点P从点A运动到点B时,点O也随之运动,求点O经过的路径长;(3)在点P从点A到点B的运动过程中,△APE的外接圆的圆心也随之运动,求该圆心到AB边的距离的最大值.(第12题图)第7 页共9 页第 8 页 共 9 页13.(2017·镇江第26题)如图1,Rt △ACB 中,∠C=90°,点D 在AC 上,∠CBD=∠A ,过A 、D 两点的圆的圆心O 在AB 上.(1)利用直尺和圆规在图1中画出⊙O (不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);(2)判断BD 所在直线与(1)中所作的⊙O 的位置关系,并证明你的结论;(3)设⊙O 交AB 于点E ,连接DE ,过点E 作EF ⊥BC ,F 为垂足.若点D 是线段AC 的黄金分割点(即AC AD AD DC ),如图2,试说明四边形DEFC 是正方形.(第13题图)第 9 页 共 9 页14.(2017·泰州第24题)如图,⊙O 的直径AB=12cm ,C 为AB 延长线上一点,CP 与⊙O 相切于点P ,过点B 作弦BD ∥CP ,连接PD .(1)求证:点P 为BD ⌒的中点;(2)若∠C=∠D ,求四边形BCPD 的面积.15.(2017·宿迁第22题)如图,AB 与⊙O 相切于点B ,BC 为⊙O 的弦,OC ⊥OA ,OA 与BC 相交于点P .(1)求证:AP=AB ;(2)若OB=4,AB=3,求线段BP 的长.(第14题图)(第15题图)。
16年江苏各市中考卷解析及试卷

16年江苏各市中考卷解析及试卷一、选择题(每题4分,共40分)1. 下列哪个城市的中考数学试卷难度最大?()A. 南京B. C. 苏州D. 徐州A. 《背影》B. 《济南的冬天》C. 《小石潭记》D. 《苏州园林》A. happinessB. challengeC. friendshipD. strangerA. 物体在不受力时,保持静止或匀速直线运动B. 物体在受力时,保持静止或匀速直线运动C. 物体在不受力时,一定保持静止D. 物体在受力时,一定保持匀速直线运动A. Zn + H2SO4 → ZnSO4 + H2↑B. 2H2 + O2 → 2H2OC. CaCO3 → CaO + CO2↑D. NaOH + HCl → NaCl + H2OA. 玄武门之变B. 陈桥兵变C. 靖康之变D.土木堡之变A. 苏州B. 无锡C. 常州D. 南京A. 细胞壁B. 细胞膜C. 叶绿体D. 中心体A. 计划经济B. 商品经济C. 社会主义市场经济D. 自然经济A. 50米跑B. 立定跳远C. 引体向上D. 跳绳二、填空题(每题4分,共40分)1. 2016年江苏省中考数学试卷中,二次函数y = ax^2 + bx + c (a≠0)的图像是一个_________。
2. 2016年江苏省中考语文试卷中,诗句“山重水复疑无路,柳暗花明又一村”出自宋代诗人_________的《游山西村》。
3. 2016年江苏省中考英语试卷中,现在进行时表示正在进行的动作或状态,其结构为:be动词(am/is/are)+_________。
4. 2016年江苏省中考物理试卷中,力的单位是_________。
5. 2016年江苏省中考化学试卷中,氢氧化钠的化学式为_________。
6. 2016年江苏省中考历史试卷中,秦始皇统一六国后,实行了_________制度。
7. 2016年江苏省中考地理试卷中,我国最大的淡水湖是_________。
专题16圆的问题-备战2016中考江苏省各地数学模拟分项汇编
2015年江苏省各地中考数学模拟优质试题分项版解析汇编专题16:圆的问题一、选择题1.【无锡市崇安区一模】如图,AB是半圆O的直径,点C是»AB的中点,点D是»AC的中点,连接AC、BD交于点E,则DEBE=()A、15B、316C、122-D、221-2.【江阴市青阳片一模】已知圆锥的侧面积是20πcm2,母线长为5cm,则圆锥的底面半径为()A、2cmB、3cmC、4cmD、6cm3.【盐城市滨海县一模】如图,正方形ABCD的四个顶点分别在⊙O上,点P在»CD上不同于点C的任意一点,则∠BPC的度数是()A、45°B、60°C、75°D、90°4.【扬州市江都市一模】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=22,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为()A、2 B23 D、35.【南京市建邺区二模】如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是()A 、42°B 、48°C 、52°D 、58°6.【苏州市一模】如图,⊙O 上A 、B 、C 三点,若∠B=50,∠A=20°,则∠AOB 等于( ) A 、30° B 、50° C 、70°D 、60°7.【徐州市二模】如图,AB 为半圆的直径,且AB=4,半圆绕点B 顺时针旋转45°,点A 旋转到A ′的位置,则图中阴影部分的面积为( )A 、πB 、2πC 、2D 、4π8.【宿迁市泗阳县一模】若一个圆锥的主视图是一个腰长为6,底角为α的等腰三角形,且cosα=13,则其圆锥的全面积是()A . 9πB . 16πC . 27πD . 36π9.【江阴市要塞片二模】如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O 的圆心O 在格点上,则∠AED 的正切值等于( )A 、55 B 、55 C 、2 D 、12»BD的度数是()10.【南京市高淳区二模】如图,四边形ABCD内接于⊙O,∠A=100°,则劣弧A、80°B、100°C、130°D、160°二、填空题1.【昆山市二模】如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为 cm.2.【昆山市二模】如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=3,CE=1.则弧BD的长是.3.【泰兴市二模】如图,△ABC内接于⊙O,半径为5,BC=6,CD⊥AB于D点,则tan∠ACD的值为.4.【泰兴市二模】如图,P为△ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=120°.若3PAB 的面积为.5.【泰兴市二模】如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,PM=l,则l的最大值是6.【南京市鼓楼区二模】已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为 cm.7.【无锡市崇安区一模】已知扇形的圆心角为120°,半径为6,则扇形的弧长是.8.【南京市建邺区一模】如图,四边形ABCD是⊙O的内接四边形,若⊙O的半径为3cm,∠A=110°,则劣»BD的长为 cm.弧9.【南京市建邺区一模】如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE= cm.10.【江阴市青阳片一模】如图,正方形ABCD的边长等于3,点E是AB延长线上一点,且AE=5,以AE为直径的半圆交BC于点F,则BF= .11.【盐城市滨海县一模】若一个圆锥的主视图是一个腰长为6cm,底边长为2cm的等腰三角形,则这个圆锥的侧面积为 cm2.12.【盐城市滨海县一模】如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为.13.【高邮市二模】半径为6cm,圆心角为120°的扇形的面积为.14.【高邮市二模】如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点逆时针旋转,使点D落在⊙O上.若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为cm.15.【扬州市宝应县一模】如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为.(结果保留π)16.【扬州市江都市一模】如图,圆锥体的高h=23,底面半径r=2cm,则圆锥体的侧面积为cm2.17.【南京市高淳区一模】用一个半径为6cm的半圆围成一个圆锥的侧面,则这个圆锥底面圆的半径为 cm.18.【南京市高淳区一模】如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=80°,则∠A= °.19.【南京市鼓楼区一模】已知Rt△ABC,∠C=90°,AB=13,AC=12,以AC所在直线为轴,将此三角形旋转1周,所得圆锥的侧面积是.20.【南京市鼓楼区一模】如图,⊙O的直径为10,弦AB长为8,点P在AB上运动,则OP的最小值是.21.【南京市建邺区二模】如图,在⊙O中,AO∥CD,∠1=30°,弧AB的长为3300π千米,则⊙O的半径用科学记数法表示为千米.22.【南京市建邺区二模】如图,在半径为2的⊙O中,两个顶点重合的内接正四边形与正六边形,则阴影部分的面积为.23.【苏州市一模】在Rt△ABC中,斜边AB=4,∠B=60°,将△ABC绕点B旋转60°,顶点C运动的路线长是(结果保留π).24.【苏州市一模】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为.25.【徐州市一模】如图,弦AB与⊙O相交于A、B两点,已知⊙O的直径为10,若圆心O到AB的距离为3,那么弦AB长为26.【徐州市一模】如果圆锥的底面半径为2cm,母线长为6cm,那么这个圆锥的侧面积为 cm2.(结果保留π)27.【徐州市一模】一个正多边形的边长为2cm,它的一个外角是60°,则这个正多边形的面积是 cm2.28.【徐州市二模】】如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA= .29.【徐州市二模】圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为 cm2.30.【徐州市二模】在⊙O中,AB是⊙O的直径,AB=8cm,»»»AC CD BD==,M是AB上一动点,CM+DM的最小值是 cm.31.【仪征市一模】将一个圆心角为120°,半径为6cm的扇形围成一个圆锥的侧面,则所得圆锥的高为 cm.32.【仪征市一模】小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A处的三角板读数为12cm,点B处的量角器的读数为74°和106°,由此可知三角板的较短直角边的长度为 cm.(参考数据:tan37°=0.75)33.【常州市武进区一模】若扇形的半径为3cm,扇形的面积为2πcm2,则该扇形的圆心角为°,弧长为 cm.34.【江阴市要塞片二模】将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为.35.【盐城市大丰市一模】如图,圆锥的母线长为2,底面圆的周长为3,则该圆锥的侧面积为.36.【盐城市大丰市一模】如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6、3,则图中阴影部分的面积是.37.【盐城市大丰市一模】如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.38.【南京市高淳区二模】如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,-1),则△ABC外接圆的圆心坐标为.39.【南京市高淳区二模】如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧MN 的长度为.40.【泰州市姜堰区一模】已知圆锥的母线为10,底面圆的直径为12,则此圆锥的侧面积是.41.【铜山县】圆锥底面圆的半径为3m,其侧面展开图是半圆,则圆锥母线长为m.42.【铜山县】如图,△ABC是⊙O的内接三角形,∠C=50°,则∠OAB= °.43.【苏州市吴江区一模】如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径为5,则图中阴影部分的面积是 .44.【南京市浦口区一模】如图,正六边形ABCDEF的边长为2,则对角线AC= .45.【南京市浦口区一模】某体育馆的圆弧形屋顶如图所示,最高点C到弦AB的距离是20m,圆弧形屋顶的跨度AB是80m,则该圆弧所在圆的半径为m.三、解答题1.【昆山市二模】如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.(1)求证:BC平分∠PBD;(2)求证:BC2=AB•BD;(3)若PA=6,PC=62,求BD的长.2.【泰兴市二模】如图线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.(1)请你用尺规在所给的网格中画出线段AC及点B经过的路径;(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(-2,-1),则点C 的坐标为;(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为;(4)若有一张与(3)中所说的区域形状相同的纸片,将它围成一个几何体的侧面,则该几何体底面圆的半径长为3.【泰兴市二模】如图,在△ABC中,AB=AC,点D在边AB上,以点A为圆心,线段AD的长为半径的⊙A 与边AC相交于点E,AF⊥DE,垂足为点F,AF的延长线与边BC相交于点G,联结GE.已知DE=10,cos∠BAG=1213,12ADDB.求:(1)⊙A的半径AD的长;(2)∠EGC的余切值.4.【南京市鼓楼区二模】如图,OA、OB是⊙O的半径且OA⊥OB,作OA的垂直平分线交⊙O于点C、D,连接CB、AB.求证:∠ABC=2∠CBO.5.【南京市建邺区】在正方形ABCD中,AD=2,l是过AD中点P的一条直线.O是l上一点,以O为圆心的圆经过点A、D,直线l与⊙O交于点E、F(E、F不与A、D重合,E在F的上面).(1)如图,若点F在BC上,求证:BC与⊙O相切.并求出此时⊙O的半径.(2)若⊙O半径为23,请直接写出∠AED的度数.6.【盐城市滨海县一模】如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.(1)判断BC、MD的位置关系,并说明理由;(2)若AE=16,BE=4,求线段CD的长;(3)若MD恰好经过圆心O,求∠D的度数.7.【高邮市二模】(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,2.①求∠ABC的度数;②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;(2)如图2,已知▱ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.8.【扬州市宝应县一模】如图,点C是半圆O的半径OB上的动点,作PC⊥AB于C.点D是半圆上位于PC 左侧的点,连接BD交线段PC于E,且PD=PE.(1)求证:PD是⊙O的切线;(2)若⊙O的半径为43,PC=83,设OC=x,PD2=y.①求y关于x的函数关系式;②当x=3时,求tanB的值.9.【扬州市江都市一模】如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA,PB,切点分别为点A,B.(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;(2)填空:①当DP=cm时,四边形AOBD是菱形;②当DP=cm时,四边形AOBP是正方形.10.【南京市高淳区一模】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C 作CE⊥DB,垂足为E,直线AB与CE相交于F点.(1)求证:CF为⊙O的切线;(2)若⊙O的半径为52cm,弦BD的长为3cm,求CF的长.11.【南京市鼓楼区一模】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,(1)求证:CD是⊙O的切线.(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.12.【南京市建邺区二模】如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA 交于点E、与OB交于点F,连接CE、CF.(1)AB与⊙O相切吗,为什么?(2)若∠AOB=∠ECF,试判断四边形OECF的形状,并说明理由.13.【苏州市一模】如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD ⊥AE的延长线于D点,直线CD与射线AB交于P点.(1)求证:DC为⊙O切线;(2)若DC=1,5O半径长;②求EB的长.14.【宿迁市泗阳县一模】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.(1)试判断:直线BF与⊙O的位置关系,并说明理由;(2)若AB=6,BF=8,求tan∠CBF.15【盐城市大丰市一模】如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.(1)求证:AC平分∠DAB;(2)若点E为»AB的中点,AD=325,AC=8,求AB和CE的长.16.【南京市高淳区二模】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.(1)求证:直线BC是⊙O的切线;(2)若OA=3,AB=2,求BP的长.17.【泰州市姜堰区一模】如图,已知△ABD为⊙O的内接正三角形,AB=27,E、F分别为边AD、AB上的»BD于点C,连接CD.动点,且AE=BF,DF与BE相交于G点,过B点作BC∥DF交(1)求∠BCD的度数;(2)求证:四边形BCDG为平行四边形;(3)连接CG,当CG与△BCD的一边垂直时,求CG的长度.18.【铜山县】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O 于点E.(1)求证:AC平分∠DAB;(2)若∠B=60°,CD=23,求AE的长.19.【苏州市吴江区一模】如图所示,D是以AB为直径的半圆O上的一点,C是弧AD的中点,点M在AB上,AD与CM交于点N,CN=AN.(1)求证:CM⊥AB;(2)若AC=23,BD=2,求半圆的直径.20.【南京市浦口区一模】如图,四边形ABCD是⊙O的内接四边形,AC为直径,»»BD AD,DE⊥BC,垂足为E.(1)求证:CD平分∠ACE;(2)判断直线ED与⊙O的位置关系,并说明理由;(3)若CE=1,AC=4,求阴影部分的面积.。
专题 16 圆(第01期)-决胜2016年中考全国名校试题数学分项汇编(江苏特刊)(解析版)

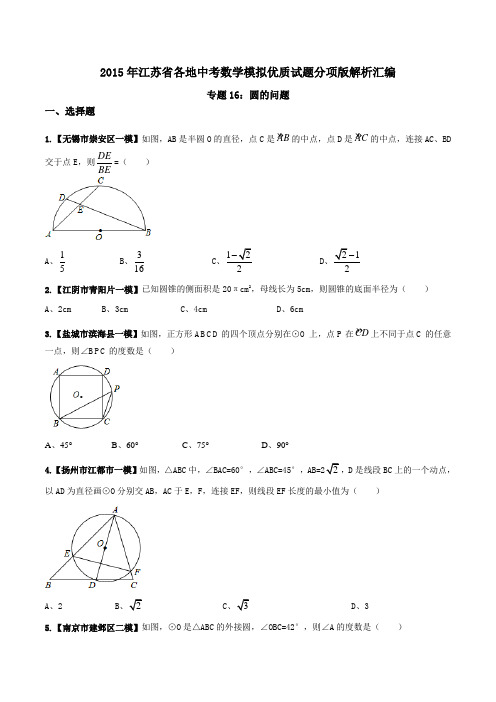
2015年江苏省各地中考数学模拟优质试题分项版解析汇编专题16:圆的问题一、选择题1.【无锡市惠山区】如图,在平面直角坐标系中,过格点A、B、C作圆弧,点B与下列格点的连线中,能够与该圆弧相切的是 ( )A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1)【答案】C【解析】考点:垂径定理,平面直角坐标系2.【无锡市惠山区】如图,在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )A.1 B. 5 C.13 D.5【答案】B考点:图形的变换2.【南京市秦淮区】如图,⊙O 的半径为1,A 为⊙O 上一点,过点A 的直线l 交⊙O 于点B ,将直线l 绕点A 旋转180°,当AB 的长度由1变为3时,l 在圆内扫过的面积为( )A .πB .π3C .π3 或 π2+ 3D .π6 或 π2+ 3 2【答案】D【解析】试题分析:由题意知∠OAB=60°,如图,直线l 在旋转过程中,AB 由1,根据垂径定理可知,根据cos ∠OAB 1,可求得∠OAB 1=30°,因此这时l 旋转角∠BAB 1=60°-30°=30°,因此可求扫过的面积为△OAB 的面积+扇形OBB 1的面积-△OAB 1=6π;当直线l 旋转至AB 2时,根据垂径定理及三角函数,同样可求∠BAB 2=60°+30°=90°,这时扫过的面积为△AOB 的面积+△AOB 2的面积+扇形B 1OB 2的面积=2π+. 故选D考点:垂径定理,三角形的面积,扇形的面积,勾股定理3.【江阴市华士片】圆锥的底面半径为3,高为4,则圆锥侧面展开图的面积为……( )A .π5B .π10C .π15D .π20【答案】C【解析】考点:圆锥的侧面积4.【江阴市华士片】如图,已知扇形的圆心角为2α(定值),半径为R (定值),分别在图一、二中作扇形的内接矩形,若按图一作出的矩形面积的最大值为21tan 2R α,则按图二作出的矩形面积的最大值为……………( )A .2tan R α B .2tan 2R α C .21tan 22R α D .21tan 2R α【答案】B【解析】考点:圆,解直角三角形5.【连云港市海州区】如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )A. 1π B. 1.5π C.2π D.3π【答案】C【解析】考点:弧长公式6. 【无锡市锡山区】一个圆锥形的圣诞帽底面半径为12cm ,母线长为13cm ,则圣诞帽的表面积为( )A .312π2cmB .156π2cmC .78π2cmD .60π2cm【答案】B【解析】试题分析:圆锥的底面周长是:12×13π=156π,则圣诞帽的表面积是:12×12π×13=156π. 故选:B考点:圆锥的计算7.【南京市溧水区】如图,在平面直角坐标系中,⊙M 与y 轴相切于原点O ,平行 于x 轴的直线交⊙M 于P ,Q 两点,点P 在点Q 的右方,若点P 的坐标是(-1,2),则点Q 的坐标是( )A .(-4,2)B .(-4.5,2)C .(-5,2)D .(-5.5,2)【答案】A【解析】试题分析:∵⊙M 与y 轴相切于原点O ,平行于x 轴的直线交⊙M 于P ,Q 两点,点P 在点Q 的右方,点P 的坐标是(-1,2),∴点Q 的纵坐标是2设PQ=2x ,作MA ⊥PQ ,利用垂径定理可知QA=PA=x ,连接MP ,则MP=MO=x+1,在Rt △AMP 中,MA 2+AP 2=MP 2,∴22+x 2=(x+1)2∴x=1.5∴PQ=3,Q 的横坐标=-(1+3)=-4,∴Q (-4,2)故选:A考点:垂径定理8.【无锡市南长区】如图,矩形ABCD 为⊙O 的内接四边形,AB=2,BC=3,点E 为BC 上一点,且BE=1,延长 AE 交⊙O 于点F ,则线段AF 的长为 ( )A .75 5B .5C .5+1D .325【答案】A【解析】考点:1.矩形的性质;2.勾股定理;3. 相交弦定理.9.【连云港市东海县】如图,点A 、B 、C 都在⊙O 上,⊙O 的半径为2,∠ACB =30°,则弧AB 的长是A. π2B. πC. π32D. π31【答案】C【解析】试题分析:因为∠ACB =30°,所以∠AOB =60°,又⊙O 的半径为2,所以弧AB 的长=60221803ππ⨯=,故选:C.考点:1.圆周角定理;2.弧长计算.10.【南京市江宁区】如图,⊙P 经过点A (0,3)、O (0,0)、B (1,0),点C 在第一象限的上,则∠BCO 的度数为( )A.15°B.30°C.45°D.60°【答案】B【解析】考点:圆的基本性质.11.【无锡市滨湖区】已知圆锥的侧面积为10πcm 2,侧面展开图的圆心角为36°,则该圆锥的母线长为( )A .100cmB .10cmC 【答案】B【解析】试题分析:根据扇形的面积计算公式可得:S=223610360360n r r p p p ==,解得:r=10cm ,即圆锥的母线长为10cm.考点:扇形的面积计算.12.【无锡市北塘区】在一个圆中,给出下列命题,其中正确的是( )A .若圆心到两条直线的距离都等于圆的半径,则这两条直线不可能垂直.B .若圆心到两条直线的距离都小于圆的半径,则这两条直线与圆一定有四个公共点.C .若两条弦所在直线平行,则这两条弦之间的距离一定小于圆的直径.D .若两条弦所在直线不平行,则这两条弦一定在圆内有公共点.【答案】C【解析】试题分析:根据圆的基本性质可得两弦所在的直线平行,则两弦之间的距离一定小于圆的直径. 考点:圆的基本性质.13.【苏州市高新区】如图,有一锐角为30°的直角三角板ABC 的斜边AB 与量角器的直径重合,点D 对应54°,则∠BCD 的度数为( )A .27°B .54°C .63°D .36°【答案】C .【解析】考点:圆心角、弧、弦的关系.14.【南京市六合区】半径为1,圆心角为60°的扇形的面积是( ) A.3p B.16 C.6p D.13【答案】C【解析】试题分析:根据扇形的面积计算公式可得:S=2360n r p =6013606p p ´=. 考点:扇形的面积计算.15.【南京市六合区】如图,在平面直角坐标系中,x 轴上一点A 从点(-3,0)出发沿x 轴向右平移,当以A为圆心,半径为1的圆与函数y =33x 的图像相切时,点A 的坐标变为( ) A.(-2,0) B.(,0)或,0) C.(,0) D.(-2,0)或(2,0)【答案】D考点:直线与圆的位置关系.16.【南京市玄武区】如图,半径为1的⊙O 与正五边形ABCDE 相切于点A 、C ,则劣弧 ⌒AC的长度为( ). A .35π B .45π C .34π D .23π【答案】B.【解析】E(第6题) (第6题)试题分析:根据正五边形的有关计算可知,∠D=∠E=108°,由切线的性质可知,∠OAE=∠OCD=90°,根据多边形的内角和公式可知,五边形OAEDCA 的内角和为540°,所以∠AOC 的度数为144°,根据弧长计算公式可得劣弧 ⌒AC 的长度为1441180π⨯=45π. 故选:B.考点:多边形内角和的计算;弧长公式.17.【无锡市新区】已知⊙O 的半径为5,直线l 上有一点P 满足PO=5,则直线l 与⊙O 的位置关系是( )A .相切B .相离C .相离或相切D .相切或相交【答案】D【解析】试题分析:当OP 与l 垂直时,直线l 与圆相切;当OP 与l 不垂直的时候,直线l 与圆相交.考点:直线与圆的位置关系.18.【无锡市新区】如图,AB 是半圆O 直径,半径OC ⊥AB ,连接AC ,∠CAB 的平分线AD 分别交OC 于点E ,交BC ︵于点D ,连接CD 、OD ,以下三个结论:①AC ∥OD ;②AC =2CD ;③线段CD 是CE 与CO 的比例中项,其中所有正确结论的序号是( )A .①②B .①③C .②③D .①②③【答案】B【解析】考点:圆的基本性质、三角形性质.二、填空题1.【南京市秦淮区】如图,⊙O是△ABD的外接圆,AB=AD,点C在⊙O上,若∠C=76°,则∠ABD=°.A(第13题)【答案】38°【解析】考点:圆内接四边形2.【江阴市华士片】如图,⊙O是△ABC的外接圆,已知∠B=60°,则∠CAO的度数是.【答案】30°【解析】试题分析:连接OA,由圆周角定理,易求得∠COA=2∠B=120°,在等腰△OAC中,已知顶角∠COA的度数,即可求出底角∠CAO=30°.考点:圆周角定理,三角形的内角和定理3.【连云港市海州区】如图,在O ⊙中,40ACB =∠°,则AOB =∠ 度.【答案】80【解析】试题分析:根据圆周角定理同弧做对的圆周角等于它所对的圆心角的一半,可直接求得∠AOB=2∠ACB=80°. 考点:圆周角定理4.【连云港市海州区】如图,一块直角边分别为6cm 和8cm 的三角木板,绕6cm 的边旋转一周,则斜边扫过的面积是 2cm (结果用含π的式子表示).【答案】80π【解析】考点:圆锥的侧面积5.【无锡市锡山区】如图,已知A 、B 两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是.【答案】11 3【解析】考点:切线的性质6.【南京市溧水区】圆锥的底面直径是6,母线长为5,则圆锥侧面展开图的圆心角是度.【答案】216【解析】试题分析:设圆锥侧面展开图的圆心角为n°,所以••56180nππ=,解得n=216.故答案为:216考点:圆锥计算7.【南京市溧水区】如图,AB 为O ⊙的直径,CD 为O ⊙的弦,25ACD∠,则BAD ∠的度数为 °.【答案】65【解析】考点:圆周角定理8.【南京市溧水区】如图,正六边形ABCDEF 的边长为,点P 为六边形内任一点.则点P 到各边距离之和为 cm .【答案】18【解析】试题分析:过P 作AB 的垂线,交AB 、DE 分别为H 、K ,连接BD ,∵六边形ABCDEF 是正六边形,∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,∵BC=CD,∠BCD=∠ABC=∠CDE=120°,∴∠CBD=∠BDC=30°,∴BD∥HK,且BD=HK,∵CG⊥BD,∴BD=2BG=2×BC×cos∠CBD=2×,∴点P到各边距离之和为3BD=3×6=18.故答案为:18考点:正多边形9.【盐都区实验学校】如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于°.【答案】32.【解析】试题分析:∵AB是⊙O的直径,∴∠ADB=90°,∵∠ABD=58°,∴∠BAD=90°﹣∠ABD=32°,∴∠BCD=∠BAD=32°.故答案为:32.考点:圆周角定理.10.【无锡市南长区】一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积...是 .【答案】3π【解析】考点:圆锥的侧面展开图.11.【南京市江宁区】如图,⊙O是正五边形ABCDE的外接圆,则∠CAD= °.【答案】36°考点:正五边形的性质.12.【无锡市滨湖区】将量角器按如图所示的方式放置在三角形纸片上,使点C在半圆圆心上,点B在半圆上,边AB、AC分别交圆于点E、F,点B、E、F对应的读数分别为160°、70°、50°,则∠A的度数为.【答案】25°【解析】试题分析:根据图示可得:∠C=110°,∠B=45°,则∠A=180°-110°-45°=25°.考点:圆的基本性质.13.【泰州市】如图,点A、B在直线MN上,AB=8cm,⊙A、⊙B的半径均为1cm.⊙A以每秒1cm的速度自左向右运动;与此同时,⊙B的半径也随之增大,其半径r(cm)与时间t(秒)之间满足关系式r=1+t(t ≥0).则当点A出发后秒,两圆相切.【答案】3和4.【解析】试题分析:根据两圆相切时,两圆的半径与圆心距的关系,注意有4种情况.试题解析:分四种情况考虑:如图,考点:圆与圆的位置关系.14.【泰州市】小明要制作一个圆锥模型,其侧面是由一个半径为9cm,圆心角为240°的扇形纸板制成的,还需要一块圆形纸板做底面,那么这块圆形纸板的半径为cm.【答案】6.【解析】试题分析:24092180rππ⨯=,解得r=6.故答案为:6.考点:弧长的计算.15.【南京市六合区】如图,在正六边形ABCDEF中,连接AE,则tan∠1= .【解析】试题分析:根据正六边形的性质可得∠F=120°,AF=EF ,则∠1=∠AEF=30°,则tan ∠1=tan30°. 考点:正多边形的性质.16.【南京市玄武区】若圆锥的高为2,底面半径为1,则这个圆锥的侧面积为 . 【答案】5π.【解析】,底面圆的周长为2π,所以这个圆锥的侧面积为122π=. 故答案为:5π.考点:圆锥的有关计算.17.【南京市玄武区】如图为一个半径为4 m 的圆形广场,其中放有六个宽为1m 的长方形临时摊位,这些摊位均有两个顶点在广场边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为 m . 【答案】37-32. 【解析】(第16题)考点:勾股定理;正多边形的计算.18.【仪征市】将一个圆心角为120°,半径为6cm 的扇形围成一个圆锥的侧面,则所得圆锥的高为 cm .【答案】.考点:弧长,圆锥,解直角三角形.19.【扬州市邗江区】如图,在⊙O 中,弦AB ∥CD ,若∠ABC=40°,则∠BOD 的度数为 .【答案】80°【解析】试题分析:根据平行可得:∠BCD=∠ABC=40°,则∠BOD=2∠BCD=80°.考点:圆的基本性质、平行线的性质20.【无锡市新区】已知圆锥的底面半径为2cm ,母线长为5cm ,则圆锥的侧面积是 .【答案】10π2cm【解析】试题分析:S=rl p =10π2cm .考点:圆锥的侧面积计算.21.【无锡市新区】如图,扇形OMN 与正三角形ABC ,半径OM 与AB 重合,扇形弧MN 的长为AB 的长,已知AB=10,扇形沿着正三角形翻滚到首次与起始位置相同,则点O 经过的路径长.【答案】10+703p.考点:弧长的计算公式.三、解答题1.【南京市秦淮区】如图,AB 是⊙O 的直径,C 是AB⌒ 的中点,延长AC 至点D ,使AC =CD ,DB 的延长线交CE 的延长线于点F ,AF 交⊙O 于点M ,连接BM .(1)求证:DB 是⊙O 的切线;(2)若⊙O 的半径为2,E 是OB 的中点,求BM 的长.【答案】(2【解析】 试题分析:(1)连接OC ,根据C 是 AB 的中点,可知∠AOC=90°,由AC=CD 可知C 为AD 的中点,根据三角形的中位线可得证AB ⊥DF ,从而得证结论;(2)根据中位线的结论OC ∥DB ,可得△COE ≌△FBE ,进而得到BF =CO =2,再根据勾股定理可得AF=根据sin∠BAM =BF AF ,sin∠BAM =BM AB ,可相应的求出结论. (第26题) A试题解析:(1)证明:连接OC .∵C 是AB⌒ 的中点, ∴∠COA =12∠AOB =90°. ∵AC =CD ,AO =BO ,∴CO 是△ADB 的中位线.∴CO ∥DB .∴∠ABD =∠COA =90°.∴BD ⊥OB .又∵点B 在⊙O 上,∴DB 是⊙O 的切线.ABDF在Rt△ABM 中, sin∠BAM =BM AB=,∴BM考点:中位线的性质,切线的判定,解直角三角形2.【无锡市锡山区】已知:如图,点E 是正方形ABCD 中AD 边上的一动点,连结BE ,作∠BEG =∠BEA 交CD 于G ,再以B 为圆心作弧AC ,连结BG .(1)求证:EG 与AC ︵相切(2)求∠EBG 的度数;G BCA DE【答案】【解析】∵BA为 AC的半径,∴BF为 AC的半径,∴EG与 AC相切;(2)由(1)可得△ABE≌△FBE,∴∠1=∠ABE=12∠ABF,∵四边形ABCD是正方形,∴∠C=∠ABC=90°,∴CD是⊙O切线,由(1)可得EG与 AC相切,∴GF=GC,∵BF⊥EG,BC⊥CD,∴∠2=∠CBG=12∠FBC,∴∠EBG=∠1+∠2=12(∠ABF+∠FBC)=12∠ABC=45°考点:切线的判定3.【无锡市锡山区】图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.【答案】见解析【解析】考点:简单作图4.【南京市溧水区】如图,跷跷板AB 的一端B 碰到地面时,AB 与地面的夹角为18°,且OA =OB =3m .(1)求此时另一端A 离地面的距离(精确到0.1 m );(2)跷动AB ,使端点A 碰到地面,请画出点A 运动的路线(写出画法,并保留画图痕迹),并求出点A 运动路线的长.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)【答案】(1)另一端A 离地面的距离约为1.9 m(2)端点A 运动路线的长为35m 【解析】ABO(第22题) 18º∴AC =AB ·sin ∠ABC =6·sin18°≈6×0.31≈1.9.答:另一端A 离地面的距离约为1.9 m考点:弧长的计算5.【南京市溧水区】已知,Rt△ABC 中,∠C =90°,AC =4, BC =3.以AC 上一点O 为圆心的⊙O 与BC 相切于点C ,与AC 相交于点D .(1)如图1,若⊙O 与AB 相切于点E ,求⊙O 的半径;(2)如图2,若⊙O 与AB 相交,且在AB 边上截得的弦FGO 的半径. 【答案】(1)⊙O 的半径为23; (2)⊙O 的半径为74【解析】 试题分析:(1)由于AB 和圆相切,所以连接OE ,利用相似即可 .(2)作弦的弦心距,构造直角三角形,利用勾股定理求出未知量.B 图1图2试题解析:(1)连接OE ,因为⊙O 与AB 相切于点E ,所以OE ⊥AB设OE =x ,则CO =x ,AO =4-x由Rt △AOE ∽Rt △ABC ,得AB AO BC OE = ∴543x x -=,解得:x =23 ∴⊙O 的半径为23;图1E考点:1.切线性质2.三角形相似6.【盐都区实验学校】如图,已知AB 是⊙O 的直径,C 为⊙O 外一点,连结CO 并延长交⊙O 于点D 、E ,连结BD 并延长交AC 于点F ,连结AD ,∠DAF =∠B .(1)求证:CA 是⊙O 的切线;(2)若AB =6,CA =4,求CD 的长;(3)在(2)的条件下,求tan ∠CDF 的值.【答案】(1)证明见试题解析;(2)2;(3)21. 【解析】考点:1.切线的判定;2.勾股定理;3.相似三角形的判定与性质.7.【无锡市南长区】如图,以O 为圆心的 BD 度数为60 o ,∠BOE=45o,DA ⊥OB,EB ⊥OB . (1)求BE DA的值;(2)若OE 与 BD交于点M,OC 平分∠BOE,连接CM.说明:CM 为⊙O 的切线; (3)在(2)的条件下,若BC=1,求tan ∠BCO 的值.【答案】(1)BE DA ;(2)见解析;(3) tan ∠+1. 【解析】D MECB O A考点:1.切线的判定;2.解直角三角形;3.全等三角形的判定与性质.8.【连云港市东海县】如图,在⊙O 中,AB 为直径,AC 为弦,过点C 作CD ⊥AB 于点D ,将△ACD 沿AC 翻折,点D 落在点E 处,AE 交⊙O 于点F ,连接OC 、FC.(1)求证:CE 是⊙O 的切线.(2)若FC ∥AB ,求证:四边形 AOCF 是菱形.【答案】(1)见解析(2)见解析【解析】考点:1.图形折叠的性质;2.切线的判定;3.菱形的判定.9.【南京市江宁区】如图,△ABC 内接于⊙O ,AB 是⊙O 的直径,点D 在⊙O 上,且∠BAC =∠CAD ,过点C 作CE ⊥AD ,垂足为点E .(1)试判断CE 与⊙O 的位置关系,并说明理由;(2)若AB =5,AC =4,求CE .A B第23题图【答案】相切;125【解析】考点:圆的基本性质、三角形相似.10.【无锡市滨湖区】如图,在△ABC 中,AB=AC ,D 是BC 上的任意一点.(1)过A 、B 、D 三点作⊙O ,交线段AC 于点E (用直尺和圆规作图,保留作图痕迹,不写作法);(2)若 ⌒ DE = ⌒ DB,求证:AB 是⊙O 的直径; (3)在(2)的条件下,若AB=5,BC=6,求AE 的长BA【答案】略;AE=1.4【解析】(3)如图3,连结BE∵AB是⊙O的直径,∴BE⊥AC,由勾股定理可得,AB2—AE2=BC2—(AC—AE)2,即52—AE2=62—(5—AE)2,解得AE=1.4.故AE的长是1.4.考点:圆的基本性质.11.【泰州市】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.(1)求证:CF为⊙O的切线;(2)若⊙O的半径为52cm,弦BD的长为3 cm,求CF的长.【答案】(1)证明见解析;(2)CF=103.【解析】考点:切线的判定.12.【苏州市高新区】如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC 交于点E,F在DA的延长线上,且AF=AE.(1)试判断BF与⊙O的位置关系,并说明理由;(2)若BF=5,cos∠C=45,求⊙O的直径;(3)若cos∠F=35,则ACEABESSVV.(直接填写结果)【答案】(1)相切;(2)203;(3)725.【解析】考点:1.切线的判定;2.解直角三角形.13.【南京市六合区】已知,如图,在矩形ABCD中,AB=6cm,BC=8cm,动点E、F同时从B点出发,点E 沿射线BC方向以5cm/s运动,点F沿线段BD方向以4cm/s运动,当点F到达D时,运动停止,连接DE,设运动时间为t(s).(1)请判断△DEF的形状,并说明理由;(2)线段DE 的中点O 的运动路径长 cm ;(3)当t 为何值时,△DEF 的外接圆与矩形ABCD 的边相切?【答案】(1)、直角三角形;(2)、254;(3)、t=940或t=85【解析】(第26题)所以,当t =940或t =85时,△DEF 的外接圆⊙O 与矩形ABCD 的边相切.考点:动点问题、直线与圆的位置关系.14.【南京市玄武区】如图,四边形ABCD 是菱形,对角线BD 上有一点O ,以O 为圆心,OD 长为半径的圆记作⊙O.(1)当⊙O 经过点A 时,用尺规作出⊙O;此时,点C 在⊙O 上吗?为什么?(2)当⊙O 与AB 相切于点A 时,①求证:BC 与⊙O 相切;②若OB =1,⊙O 的面积= .【答案】(1)作图略;点C 在⊙O 上,理由详见解析;(2)①证明详见解析;②14π. 【解析】连接OC , C BAD (第23题) O G MDCE B A H考点:菱形的性质;全等三角形的判定和性质;切线的判定.15.【仪征市】如图,在□ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE∠CDE=∠BCE.(1)求证:AD=CE;(2)判断直线BC与⊙O的位置关系,并说明理由;(3)若BC=3,DE=6,求BE的长.【答案】(1)略;(2)相切.(3)32【解析】(3)∵□ABCD ∴AD =BC ,AB ∥CD ,由(1)AD =CE ∴BC =CEA B C DE∵AB ∥CD ,∴∠BEC =∠DCE .又∵∠BCE =∠CDE ,∴△BCE ∽△EDC .∴BC DE =BE CE, ∵BC =3 ∴CE=3.即 36=BE 3. 解得,BE =32. 考点:圆.16.【扬州市邗江区】如图,⊙O 是△ABC 的外接圆,AB 是直径,作OD ∥BC 与过点A 的切线交于点D ,连接DC 并延长交AB 的延长线于点E .(1)、求证:DE 是⊙O 的切线;(2)、若AE=6,CE=32,求线段CE 、BE 与劣弧BC 所围成的图形面积.(结果保留根号和π)【答案】略;23p -. 【解析】考点:切线的性质、勾股定理、扇形面积计算.。
江苏省中考数学第一部分考点研究复习第六章圆第28课时与圆有关的计算练习(含解析)

第六章圆第28课时与圆有关的计算基础过关1。
(2016遵义)如图,半圆的圆心为O,直径AB的长为12,C为半圆上一点,∠CAB=30°,错误!的长是()A。
12π B。
6π C。
5π D。
4π第1题图第2题图2。
(2016青岛)如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120˚,AB长为25 cm,贴纸部分的宽BD为15 cm,若纸扇两面贴纸,则贴纸的面积为( )A. 175π cm2 B。
350π cm2 C。
错误!π cm2 D. 150π cm23. (2016十堰)如图,从一张腰长为60 cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )A。
10 cm B。
15 cm C. 10错误! cm D. 20错误! cm第3题图 第4题图4. (2016贵港)如图,点A 在以BC 为直径的⊙O 内,且AB =AC ,以点A 为圆心,AC 长为半径作弧,得到扇形ABC ,剪下扇形ABC 围成一个圆锥(AB 和AC 重合),若∠BAC =120°,BC =2错误!,则这个圆锥底面圆的半径是( )A 。
错误!B 。
错误! C. 错误! D. 错误!5. (2016兰州)如图,用一个半径为 5 cm 的定滑轮带动重物上升,滑轮上一点P 旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )A. π cm B 。
2π cm C 。
3π cm D. 5π cm第5题图6。
(2016山西)如图,在▱ABCD 中,AB 为⊙O 的直径,⊙O 与DC 相切于点E ,与AD 相交于点F ,已知AB =12,∠C =60°,则FE ︵的长为( ) A.π3B 。
错误!C .πD .2π第6题图第7题图7。
(2016深圳)如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是错误!的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2错误!时,则阴影部分的面积为()A。
江苏中考数学--圆的填空、选择、证明和计算-中高难度

1、一个扇形的弧长为cm,面积为cm2,那么扇形的圆心角是。
2、一个圆锥的侧面积是底面积的2倍,那么这个圆锥的侧面展开图的圆心角是。
3、如图,在△ABC中,AB=AC,∠C=72°,圆O过A、B两点,且与BC切与点B,与AC交于点D,连结BD,假设BC=,那么AC= 。
4、如图,在Rt△ABC中,△ACB=90度.点P是半圆弧AC的中点,连接BP交AC于点D,,S 2之间的关系是。
116、以下结论正确的选项是()A.长度相等的两条弧是等弧B.半圆是弧C.相等的圆心角所对的弧相等D.弧是半圆17、以下语句中,正确的选项是()A.同一平面上的三点确定一个圆B.三角形的外心是三角形三边中垂线的交点C.三角形的内心到三角形三个顶点的距离相等D.菱形的四个顶点在同一圆上18、以下说法:①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④长度相等的两条弧是等弧;⑤完全重合的两条弧是等弧.正确的命题有()A.1个B.2个C.3个D.4个19、在以下命题中:①三点确定一个圆;②同弧或等弧所对圆周角相等;③所有直角三角形都相似;④所有菱形都相似;其中正确的命题个数是()A.0B.1C.2D.320、以下命题错误的选项是()A.经过三个点一定可以作圆B.三角形的外心到三角形各顶点的距离相等C.同圆或等圆中,相等的圆心角所对的弧相等D.经过切点且垂直于切线的直线必经过圆心21、以下命题:①相交两圆的公共弦垂直平分连心线;②不在同一条直线上的三点确定一个圆;③正多边形的中心是它的对称中心;④一条直线垂直于圆的半径,这条直线一定就是圆的切线.其中正确的命题有()A.1个B.2个C.3个D.4个22、如以下图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与M,N重合,当P点在上移动时,矩形PAOB的形状、大小随之变化,那么PA 2+PB 2的值()A.逐渐变大B.逐渐变小C.不变D.不能确定( 第22题) ( 第23题)23、如上图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A△B△C△D△A滑动到A止,同时点R从点B出发,沿图中所示方向按B△C△D△A△B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为()A.2B.4-πC.πD.π-124、如图,以点O为圆心的两个同心圆,半径分别为5和3,假设大圆的弦AB与小圆相交,那么弦长AB的取值范围是()A.8≤AB≤10B.AB≥8C.8<AB≤10D.8<AB<10( 第24题) ( 第25题) ( 第26题)25、高速公路的隧道和桥梁最多.如图是一个隧道的横截面,假设它的形状是以O为圆心的圆的一局部,路面AB=10米,净高CD=7米,那么此圆的半径OA=()A.5B.7C.D.26、如图,△O的半径为1,AB是△O的一条弦,且AB= ,那么弦AB所对圆周角的度数为()A.30°B.60°C.30°或150°D.60°或120°27、过△O内一点M的最长的弦长为6cm,最短的弦长为4cm.那么OM的长为()A.cmB.cmC.2cmD.3cm28、如图,点A、B、P在△O上,且△APB=50°.假设点M是△O上的动点,要使△ABM为等腰三角形,那么所有符合条件的点M有()A.1个B.2个C.3个D.4个( 第28题) ( 第29题) ( 第30题)29、如图,MN是半径为1的△O的直径,点A在△O上,△AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,那么PA+PB的最小值为()A. B. C.1 D.230、如图是武汉某座天桥的设计图,设计数据如下图,桥拱是圆弧形,那么桥拱的半径为()A.13mB.15mC.20mD.26m31、如图,四边形PAOB是扇形OMN的内接矩形,顶点P在上,且不与M,N重合,当P 点在上移动时,矩形PAOB的形状、大小随之变化,那么AB的长度()A.变大B.变小C.不变D.不能确定( 第31题) ( 第32题) ( 第33题)32、如图,是半圆,O为AB中点,C、D两点在上,且AD△OC,连接BC、BD.假设=62°,那么的度数为何?()A.56B.58C.60D.6233、如图,AB是半圆的直径,点D是的中点,△ABC=50°,那么△DAB等于()A.55°B.60°C.65°D.70°34、如图,BE是半径为6的圆D的圆周,C点是上的任意一点,△ABD是等边三角形,那么四边形ABCD的周长P的取值范围是()A.12<P≤18B.18<P≤24C.18<P≤18+6D.12<P≤12+635、一条弦分圆为1:5两局部,那么这条弦所对的圆周角的度数为()A.30°B.150°C.30°或150°D.不能确定36、如图,△C=15°,且,那么△E的度数为()A.30°B.35°C.40°D.45°( 第34题) ( 第36题) ( 第37题)37、:如图,ABCD是△O的内接正方形,AB=4,F是BC的中点,AF的延长线交△O于点E,那么AE的长是()A. B. C. D.38、如图,AB是△O的直径,C是△O外一点,CA、CB交△O分别于D、E点,且AB=1,那么cos△C=()A.DEB.BCC.DCD.CE39、如图,O为原点,点A的坐标为(3,0),点B的坐标为(0,4),△D过A、B、O三点,点C为上一点(不与O、A两点重合),那么cosC的值为()A. B. C. D.40、:如图,在△O的内接四边形ABCD中,AB是直径,△BCD=130°,过D点的切线PD与直线AB交于P点,那么△ADP的度数为()A.40°B.45°C.50°D.65°( 第38题) ( 第39题) ( 第40题)41、如图,Rt△ABC中,AB=AC=4,以AB为直径的圆交AC于D,那么阴影局部的面积为( )A.2πB.π+1C.π+2D.4+42、如图,半圆O的直径AB=7,两弦AC、BD相交于点E,弦CD= ,且BD=5,那么DE等于()A. B. C. D.43、如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,那么=()A. B. C.1- D.( 第41题) ( 第42题) ( 第43题)44、以下说法错误的选项是()A.圆内接四边形的对角互补B.圆内接四边形的邻角互补C.圆内接平行四边形是矩形D.圆内接梯形是等腰梯形45、平行四边形的四个顶点在同一圆上,那么该平行四边形一定是()A.正方形B.菱形C.矩形D.等腰梯形46、如图,AB、AC是△O的切线,B、C为切点,△A=50°,点P是圆上异于B、C,且在上的动点,那么△BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°47、如图,,PD为△O的直径,直线BC切△O于点C,BP的延长线与CD的延长线交于点A,△A=28°,△B=26°,那么△PDC等于()A.34°B.36°C.38°D.40°48、如图,点I为△ABC的内心,点O为△ABC的外心,∠O=140°,那么∠I为()A.140°B.125°C.130°D.110°( 第46题) ( 第47题) ( 第48题)49、如图,Rt△ABC中,△C=90°,AC= ,BC=1,假设以C为圆心,CB为半径的圆交AB于点P,那么AP=____________.50、如图,△O的半径为3,OA=6,AB切△O于B,弦BC△OA,连接AC,图中阴影局部的面积为____________.51、如图,AB是△O的直径,弦CD△AB,AC=2 ,BC=1,那么sin△ABD的值是____________.( 第49题) ( 第50题) ( 第51题)52、如图,AD=30,点B,C是AD上的三等分点,分别以AB,BC,CD为直径作圆,圆心分别为E,F,G,AP切△G于点P,交△F于M,N,那么弦MN的长是____________.53、如图,AB是半圆的直径,O是圆心,C是半圆上一点,E是弧AC的中点,OE交弦AC 于D.假设AC=8cm,DE=2cm,那么OD的长为____________cm.54、如图,AB是△O的直径,弦BC=2cm,F是弦BC的中点,△ABC=60°.假设动点E以2cm/s 的速度从A点出发沿着A→B方向运动,设运动时间为t(s),连接EF、CE,当t为____________秒时,CE+EF最小,其最小值是____________.( 第52题) ( 第53题) ( 第54题)55、如图,AB是△O的直径,AB=10cm,M是半圆AB的一个三等分点,N是半圆AB的一个六等分点,P是直径AB上一动点,连接MP、NP,那么MP+NP的最小值是____________cm.56、如图,在△ABC中,BC=4,以点A为圆心,2为半径的△A与BC相切于点D,交AB于E,交AC于F,点P是△A上的一点,且△EPF=40°,那么图中阴影局部的面积是__________.57、如图,AB是△O的一条弦,点C是△O上一动点,且△ACB=30°,点E、F分别是AC、BC 的中点,直线EF与△O交于G、H两点.假设△O的半径为7,那么GE+FH的最大值为____________.( 第55题) ( 第56题) ( 第57题)58、如图,AB是△O的直径,弦BC=2cm,F是弦BC的中点,△ABC=60°.假设动点E以2cm/s 的速度从A点出发沿着A△B△A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当t为____________s时,△BEF是直角三角形.59、如图,圆O的半径为4,△A=45°,假设一个圆锥的侧面展开图与扇形OBC能完全重合,那么该圆锥的底面圆的半径为____________.60、如图,AD、AC分别是直径和弦,△CAD=30°,B是AC上一点,BO△AD,垂足为O,BO=5cm,那么CD等于____________cm.( 第58题) ( 第59题) ( 第60题)61、在圆内接四边形ABCD中,△A:△B:△C=4:3:5,那么△D=__________.62、如果圆中一条弦长与半径相等,那么此弦所对的圆周角的度数为___________.63、如图:EB、EC是△O的两条切线,B、C是切点,A、D是△O上两点,如果△E=46°,△DCF=32°,那么△A的度数是__________.64、如图,半径为1cm都5个圆,圆心顺次连线得到五边形ABCDE,那么图中阴影局部面积之和为。
专题16 圆解答题(精选34道)-三年(2021-2023)中考数学真题分项汇编【山东】(原卷版)

三年(2021-2023)中考数学真题分项汇编【山东专用】专题16圆解答题(精选34道)一.解答题(共34小题)1.(2023•威海)如图,在平面直角坐标系中,点P在第一象限内,⊙P与x轴相切于点C,与y轴相交于点A(0,8),B(0,2).连接AC,BC.(1)求点P的坐标;(2)求cos∠ACB的值.2.(2023•日照)在探究“四点共圆的条件”的数学活动课上,小霞小组通过探究得出:在平面内,一组对角互补的四边形的四个顶点共圆.请应用此结论,解决以下问题:如图1,△ABC中,AB=AC,∠BAC=α(60°<α<180°).点D是BC边上的一动点(点D不与B,C 重合),将线段AD绕点A顺时针旋转α到线段AE,连接BE.(1)求证:A,E,B,D四点共圆;(2)如图2,当AD=CD时,⊙O是四边形AEBD的外接圆,求证:AC是⊙O的切线;(3)已知α=120°,BC=6,点M是边BC的中点,此时⊙P是四边形AEBD的外接圆,直接写出圆心P与点M距离的最小值.3.(2023•威海)已知:射线OP平分∠MON,A为OP上一点,⊙A交射线OM于点B,C,交射线ON于点D,E,连接AB,AC,AD.(1)如图1,若AD∥OM,试判断四边形OBAD的形状,并说明理由;(2)如图2,过点C作CF⊥OM,交OP于点F;过点D作DG⊥ON,交OP于点G.求证:AG=AF.4.(2023•东营)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC,垂足为E.(1)求证:DE是⊙O的切线;(2)若∠C=30°,CD=2,求的长.5.(2023•菏泽)如图,AB为⊙O的直径,C是圆上一点,D是的中点,弦DE⊥AB,垂足为点F.(1)求证:BC=DE;(2)P是上一点,AC=6,BF=2,求tan∠BPC;(3)在(2)的条件下,当CP是∠ACB的平分线时,求CP的长.6.(2023•济宁)如图,已知AB是⊙O的直径,CD=CB,BE切⊙O于点B,过点C作CF⊥OE交BE于点F,EF=2BF.(1)如图1,连接BD,求证:△ADB≌△OBE;(2)如图2,N是AD上一点,在AB上取一点M,使∠MCN=60°,连接MN.请问:三条线段MN,BM,DN有怎样的数量关系?并证明你的结论.7.(2023•聊城)如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AD交BC于点D,∠ADC的平分线DE交AC于点E.以AD上的点O为圆心,OD为半径作⊙O,恰好过点E.(1)求证:AC是⊙O的切线;(2)若CD=12,tan∠ABC=,求⊙O的半径.8.(2023•滨州)如图,点E是△ABC的内心,AE的延长线与边BC相交于点F,与△ABC的外接圆交于点D.(1)求证:S△ABF:S△ACF=AB:AC;(2)求证:AB:AC=BF:CF;(3)求证:AF2=AB•AC﹣BF•CF;(4)猜想:线段DF,DE,DA三者之间存在的等量关系.(直接写出,不需证明.)9.(2023•枣庄)如图,AB为⊙O的直径,点C是的中点,过点C做射线BD的垂线,垂足为E.(1)求证:CE是⊙O的切线;(2)若BE=3,AB=4,求BC的长;(3)在(2)的条件下,求阴影部分的面积(用含有π的式子表示).10.(2023•临沂)如图,⊙O是△ABC的外接圆,BD是⊙O的直径,AB=AC,AE∥BC,E为BD的延长线与AE的交点.(1)求证:AE是⊙O的切线;(2)若∠ABC=75°,BC=2,求的长.11.(2023•烟台)如图,在菱形ABCD中,对角线AC,BD相交于点E,⊙O经过A,D两点,交对角线AC于点F,连接OF交AD于点G,且AG=GD.(1)求证:AB是⊙O的切线;(2)已知⊙O的半径与菱形的边长之比为5:8,求tan∠ADB的值.12.(2022•菏泽)如图,在△ABC中,以AB为直径作⊙O交AC、BC于点D、E,且D是AC的中点,过点D作DG⊥BC于点G,交BA的延长线于点H.(1)求证:直线HG是⊙O的切线;(2)若HA=3,cos B=,求CG的长.13.(2022•聊城)如图,点O是△ABC的边AC上一点,以点O为圆心,OA为半径作⊙O,与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F,∠AOD=∠EOD.(1)连接AF,求证:AF是⊙O的切线;(2)若FC=10,AC=6,求FD的长.14.(2022•泰安)问题探究(1)在△ABC中,BD,CE分别是∠ABC与∠BCA的平分线.①若∠A=60°,AB=AC,如图1,试证明BC=CD+BE;②将①中的条件“AB=AC”去掉,其他条件不变,如图2,问①中的结论是否成立?并说明理由.迁移运用(2)若四边形ABCD是圆的内接四边形,且∠ACB=2∠ACD,∠CAD=2∠CAB,如图3,试探究线段AD,BC,AC之间的等量关系,并证明.15.(2022•日照)如图,在Rt△ABC中,∠C=90°,∠B=30°,点D为边AB的中点,点O在边BC上,以点O为圆心的圆过顶点C,与边AB交于点D.(1)求证:直线AB是⊙O的切线;(2)若AC=,求图中阴影部分的面积.16.(2022•临沂)如图,AB是⊙O的切线,B为切点,直线AO交⊙O于C,D两点,连接BC,BD.过圆心O作BC的平行线,分别交AB的延长线、⊙O及BD于点E,F,G.(1)求证:∠D=∠E;(2)若F是OE的中点,⊙O的半径为3,求阴影部分的面积.17.(2022•枣庄)如图,在半径为10cm的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,点E是BC的中点,OE=6cm.(1)求证:CD是⊙O的切线;(2)求AD的长.18.(2022•东营)如图,AB为⊙O的直径,点C为⊙O上一点,BD⊥CE于点D,BC平分∠ABD.(1)求证:直线CE是⊙O的切线;(2)若∠ABC=30°,⊙O的半径为2,求图中阴影部分的面积.19.(2022•德州)如图1,在等腰三角形ABC中,AB=AC,O为底边BC的中点,过点O作OD⊥AB,垂足为D,以点O为圆心,OD为半径作圆,交BC于点M,N.(1)AB与⊙O的位置关系为;(2)求证:AC是⊙O的切线;(结果保留小数点后一位.参考数据:sin24°≈0.41,(3)如图2,连接DM,DM=4,∠A=96°,求⊙O的直径.cos24°≈0.91,tan24°≈0.45)20.(2022•济南)已知:如图,AB为⊙O的直径,CD与⊙O相切于点C,交AB延长线于点D,连接AC,BC,∠D=30°,CE平分∠ACB交⊙O于点E,过点B作BF⊥CE,垂足为F.(1)求证:CA=CD;(2)若AB=12,求线段BF的长.21.(2022•潍坊)在数学实验课上,小莹将含30°角的直角三角尺分别以两个直角边为轴旋转一周,得到甲、乙两个圆锥,并用作图软件Geogebra画出如下示意图.小亮观察后说:“甲、乙圆锥的侧面都是由三角尺的斜边AB旋转得到,所以它们的侧面积相等.”你认同小亮的说法吗?请说明理由.22.(2022•威海)如图,四边形ABCD是⊙O的内接四边形,连接AC,BD,延长CD至点E.(1)若AB=AC,求证:∠ADB=∠ADE;(2)若BC=3,⊙O的半径为2,求sin∠BAC.23.(2022•淄博)已知△ABC是⊙O的内接三角形,∠BAC的平分线与⊙O相交于点D,连接DB.(1)如图①,设∠ABC的平分线与AD相交于点I,求证:BD=DI;(2)如图②,过点D作直线DE∥BC,求证:DE是⊙O的切线;(3)如图③,设弦BD,AC延长后交⊙O外一点F,过F作AD的平行线交BC的延长线于点G,过G 作⊙O的切线GH(切点为H),求证:FG=HG.24.(2021•菏泽)如图,在⊙O中,AB是直径,弦CD⊥AB,垂足为H,E为上一点,F为弦DC延长线上一点,连接FE并延长交直径AB的延长线于点G,连接AE交CD于点P,若FE=FP.(1)求证:FE是⊙O的切线;(2)若⊙O的半径为8,sin F=,求BG的长.25.(2021•威海)如图,AB是⊙O直径,弦CD⊥AB,垂足为点E.弦BF交CD于点G,点P在CD延长线上,且PF=PG.(1)求证:PF为⊙O切线;(2)若OB=10,BF=16,BE=8,求PF的长.26.(2021•枣庄)如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作⊙O的切线与AC的延长线交于点P.(1)求证:DP∥BC;(2)求证:△ABD∽△DCP;(3)当AB=5cm,AC=12cm时,求线段PC的长.27.(2021•泰安)如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD 的延长线相交于点E.(1)求证:CD=ED;(2)AD与OC,BC分别交于点F,H.①若CF=CH,如图2,求证:CF•AF=FO•AH;②若圆的半径为2,BD=1,如图3,求AC的值.28.(2021•德州)已知⊙O为△ACD的外接圆,AD=CD.(1)如图1,延长AD至点B,使BD=AD,连接CB.①求证:△ABC为直角三角形;②若⊙O的半径为4,AD=5,求BC的值;(2)如图2,若∠ADC=90°,E为⊙O上的一点,且点D,E位于AC两侧,作△ADE关于AD对称的图形△ADQ,连接QC,试猜想QA,QC,QD三者之间的数量关系并给予证明.29.(2021•济宁)如图,点C在以AB为直径的⊙O上,点D是BC的中点,连接OD并延长交⊙O于点E,作∠EBP=∠EBC,BP交OE的延长线于点P.(1)求证:PB是⊙O的切线;(2)若AC=2,PD=6,求⊙O的半径.30.(2021•济南)已知:如图,AB是⊙O的直径,C,D是⊙O上两点,过点C的切线交DA的延长线于点E,DE⊥CE,连接CD,BC.(1)求证:∠DAB=2∠ABC;(2)若tan∠ADC=,BC=4,求⊙O的半径.31.(2021•东营)如图,以等边三角形ABC的BC边为直径画圆,交AC于点D,DF⊥AB于点F,连接OF,且AF=1.(1)求证:DF是⊙O的切线;(2)求线段OF的长度.32.(2021•烟台)如图,已知Rt△ABC中,∠C=90°.(1)请按如下要求完成尺规作图(不写作法,保留作图痕迹).①作∠BAC的角平分线AD,交BC于点D;②作线段AD的垂直平分线EF与AB相交于点O;③以点O为圆心,以OD长为半径画圆,交边AB于点M.(2)在(1)的条件下,求证:BC是⊙O的切线;(3)若AM=4BM,AC=10,求⊙O的半径.33.(2021•临沂)如图,已知在⊙O中,==,OC与AD相交于点E.求证:(1)AD∥BC;(2)四边形BCDE为菱形.34.(2021•潍坊)如图,半圆形薄铁皮的直径AB=8,点O为圆心,C是半圆上一动点(不与A,B重合),连接AC并延长到点D,使AC=CD,过点D作AB的垂线DH交,CB,AB于点E,F,H,连接OC,记∠ABC=θ,θ随点C的移动而变化.(1)移动点C,当点H,O重合时,求sinθ的值;(2)当θ<45°时,求证:BH•AH=DH•FH;(3)当θ=45°时,将扇形OAC剪下并卷成一个圆锥的侧面,求该圆锥的底面半径和高.。
江苏初三圆练习题大题

江苏初三圆练习题大题(文章)江苏初三圆练习题大题近年来,江苏省初中教育在教学改革和素质教育方面取得了显著成绩。
为了进一步提高学生的学习兴趣和能力,促进他们的全面发展,江苏省教育部门特别设计了一套圆练习题大题,以检验学生对数学知识的掌握程度和解题能力。
本文将针对江苏初三圆练习题大题进行分析和解答,帮助学生们更好地应对考试。
第一大题:填选第一大题是填选题,要求学生根据给定的条件填写表格中的空白处。
这类题目主要考察学生的计算能力和逻辑思维能力。
在解答这类题目时,学生首先需要仔细阅读题目,理清思路,然后运用所学知识进行计算。
在填写答案时,学生要注意排版整齐,答案清晰可辨。
第二大题:证明与判断第二大题属于证明与判断类题目,要求学生根据已知条件证明或判断给定结论的真假。
这类题目要求学生具备较强的逻辑思维能力和推理能力。
在解答这类题目时,学生应先熟悉相关概念和定理,然后根据已知条件运用合适的推理方法进行证明或判断。
在书写答案时,学生要注重论证过程的严密性,语句通顺流畅,排版整齐美观。
第三大题:设计与计算第三大题要求学生根据给定条件进行问题的设计和计算。
这类题目既考察学生对数学知识的灵活应用能力,又要求学生具备一定的创新思维能力。
在解答这类题目时,学生应先理解问题的意义和目标,然后根据已给条件进行整体规划,合理设计解决方案。
在计算时,学生要注意运用正确的计算方法,计算过程清晰可见,结果准确无误。
第四大题:实例与推广第四大题要求学生在理论学习的基础上,通过实例进行问题探究与推广。
这类题目既考察学生对数学知识的理解和应用能力,也要求学生具备较强的分析和推理能力。
在解答这类题目时,学生应先选择合适的实例进行分析,并根据实例总结规律,然后运用所学知识进行推广。
在书写答案时,学生要注意实例的选择和分析,推广过程的逻辑性和连贯性。
综上所述,江苏初三圆练习题大题涵盖了填选、证明与判断、设计与计算以及实例与推广等各类题型。
解答这些题目需要学生具备扎实的数学基础,灵活运用数学知识的能力,以及良好的逻辑思维和推理能力。
江苏省中考数学真题《圆》专题汇编(解答题)
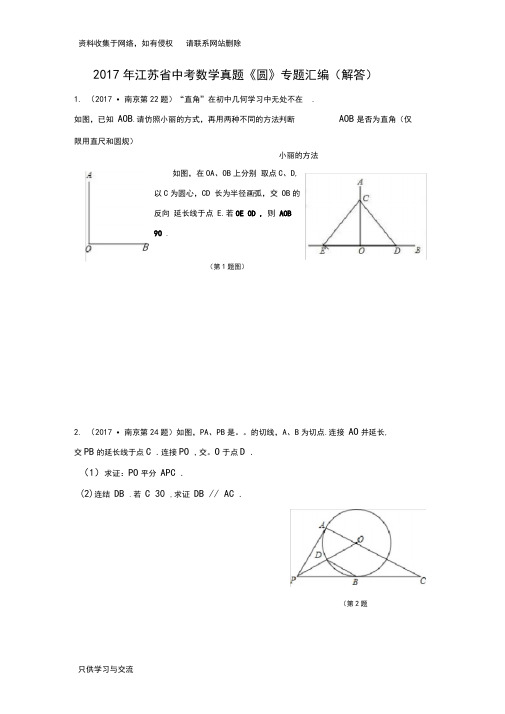
2017年江苏省中考数学真题《圆》专题汇编(解答)1.(2017 •南京第22题)“直角”在初中几何学习中无处不在.如图,已知AOB.请仿照小丽的方式,再用两种不同的方法判断AOB是否为直角(仅限用直尺和圆规)小丽的方法如图,在OA、OB上分别取点C、D,以C为圆心,CD 长为半径画弧,交OB的反向延长线于点E.若OE OD , 则AOB90 .B(第1题图)2.(2017 •南京第24题)如图,PA、PB是。
的切线,A、B为切点.连接AO并延长,交PB的延长线于点C .连接PO ,交。
O于点D .(1)求证:PO平分APC .(2)连结DB .若C 30 ,求证DB // AC .(第2题图)4. (2017 ・无锡第27题)如图,以原点 。
为圆心,3为半径的圆与 x 轴分别交于 A, B 两 点(点B 在点A 的右边),P 是半径OB 上一点,过 P 且垂直于AB 的直线与。
分别交于 C, D 两点(点 C 在点D 的上方),直线 AC, DB 交于点E.若AC: CE=1 : 2,求点P 的 坐标.3. (2017 ・无锡第24题)如图,已知等边△ ABC,要求作图(不要求写作法,但要保留作图痕迹):(1)作4ABC 的外心O;(2)设D 是AB 边上一点,在图中作出一个正六边形和AC 上.请用直尺(不带刻度)和圆规,按下列DEFGHI ,使点F,点H 分别在边 BC(第4题图)5. (2017 •常州第28题)如图,已知一次函数 y与y 轴、x 轴交于点A B.(1)求线段AB 的长度;(2)设点M 在射线AB 上,将点M 绕点A 按逆时针方向旋转 90°到点N ,以点N 为圆心, NA 的长为半径作e N .①当e N 与x 轴相切时,求点 M 的坐标;②在①的条件下,设直线 AN 与x 轴交于点C ,与e N 的另一个交点为 D ,连接MD 交x 轴于点E ,直线m 过点N 分别与y 轴、直线l 交于点P 、Q ,当 APQ 与 CDE 相似时, 求点P 的坐标.4-x 4的图像是直线l ,设直线l 分别 36. (2017 •苏州第27题)如图,已知△ ABC 内接于。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题16:圆的问题一、选择题1.如图,AB是半圆O的直径,点C是 AB的中点,点D是 AC的中点,连接A C、BD交于点E,则DEBE=()A、15B、316C、122-D、221-2.已知圆锥的侧面积是20πcm2,母线长为5cm,则圆锥的底面半径为()A、2cmB、3cmC、4cmD、6cm3.如图,正方形ABCD的四个顶点分别在⊙O上,点P在 CD上不同于点C的任意一点,则∠BPC的度数是()A、45°B、60°C、75°D、90°4.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=22,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为()A、2B、2C、3D、35如图,⊙O是△ABC的外接圆,∠OBC=42°,则∠A的度数是()A 、42°B 、48°C 、52°D 、58°6.如图,⊙O 上A 、B 、C 三点,若∠B =50,∠A =20°,则∠AOB 等于( )A 、30°B 、50°C 、70°D 、60°7.如图,AB 为半圆的直径,且AB =4,半圆绕点B 顺时针旋转45°,点A 旋转到A ′的位置,则图中阴影部分的面积为( )A 、πB 、2πC 、2D 、4π8.若一个圆锥的主视图是一个腰长为6,底角为α的等腰三角形,且cosα=13,则其圆锥的全面积是()A . 9πB . 16πC . 27πD . 36π 9.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O 的圆心O 在格点上,则∠AED 的正切值等于( )A 、55B 、255C 、2D 、1210.如图,四边形ABCD内接于⊙O,∠A=100°,则劣弧 BD的度数是()A、80°B、100°C、130°D、160°二、填空题1.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为cm.2.如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=3,CE=1.则弧BD的长是.3.如图,△ABC内接于⊙O,半径为5,BC=6,CD⊥AB于D点,则tan∠ACD的值为.4.如图,P为△ABC内一点,∠BAC=30°,∠ACB=90°,∠BPC=120°.若BP=3,则△PAB 的面积为.5.如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD 的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,PM=l,则l的最大值是6.已知等腰△ABC中,AB=AC=13cm,BC=10cm,则△ABC的内切圆半径为cm.7.已知扇形的圆心角为120°,半径为6,则扇形的弧长是.8.如图,四边形ABCD是⊙O的内接四边形,若⊙O的半径为3cm,∠A=110°,则劣弧 BD 的长为cm.9.如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE= cm.10.如图,正方形ABCD的边长等于3,点E是AB延长线上一点,且AE=5,以AE为直径的半圆交BC于点F,则BF= .11.若一个圆锥的主视图是一个腰长为6cm,底边长为2cm的等腰三角形,则这个圆锥的侧面积为cm2.12.如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为.13.半径为6cm,圆心角为120°的扇形的面积为.14.如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD 绕点逆时针旋转,使点D落在⊙O上.若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为cm.15.如图,小正方形的边长均为1,扇形OAB是某圆锥的侧面展开图,则这个圆锥的底面周长为.(结果保留π)16.如图,圆锥体的高h=23cm,底面半径r=2cm,则圆锥体的侧面积为cm2.17.用一个半径为6cm的半圆围成一个圆锥的侧面,则这个圆锥底面圆的半径为cm.18.如图,四边形ABCD内接于⊙O,A D、BC的延长线相交于点E,A B、DC的延长线相交于点F.若∠E+∠F=80°,则∠A= °.19.已知Rt△ABC,∠C=90°,AB=13,AC=12,以AC所在直线为轴,将此三角形旋转1周,所得圆锥的侧面积是.20.如图,⊙O的直径为10,弦AB长为8,点P在AB上运动,则OP的最小值是.21.如图,在⊙O中,AO∥CD,∠1=30°,弧AB的长为3300π千米,则⊙O的半径用科学记数法表示为千米.22.如图,在半径为2的⊙O中,两个顶点重合的内接正四边形与正六边形,则阴影部分的面积为.23.在Rt△ABC中,斜边AB=4,∠B=60°,将△ABC绕点B旋转60°,顶点C运动的路线长是(结果保留π).24.如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为.25.如图,弦AB与⊙O相交于A、B两点,已知⊙O的直径为10,若圆心O到AB的距离为3,那么弦AB长为26.如果圆锥的底面半径为2cm,母线长为6cm,那么这个圆锥的侧面积为cm2.(结果保留π)27.一个正多边形的边长为2cm,它的一个外角是60°,则这个正多边形的面积是cm2.28.如图,⊙O的半径为3,P是CB延长线上一点,PO=5,PA切⊙O于A点,则PA= .29.圆锥的底面半径为6cm,母线长为10cm,则圆锥的侧面积为cm2.30.在⊙O 中,AB 是⊙O 的直径,AB =8cm , AC CDBD ==,M 是AB 上一动点,CM +DM 的最小值是 cm .31.将一个圆心角为120°,半径为6cm 的扇形围成一个圆锥的侧面,则所得圆锥的高为 cm .32.小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A 处的三角板读数为12cm ,点B 处的量角器的读数为74°和106°,由此可知三角板的较短直角边的长度为 cm .(参考数据:tan 37°=0.75)33.若扇形的半径为3cm ,扇形的面积为2πcm 2,则该扇形的圆心角为 °,弧长为 cm .34.将量角器按如图所示的方式放置在三角形纸片上,使点C 在半圆圆心上,点B 在半圆上,边A B 、AC 分别交圆于点E 、F ,点B 、E 、F 对应的读数分别为160°、70°、50°,则∠A 的度数为 .35.如图,圆锥的母线长为2,底面圆的周长为3,则该圆锥的侧面积为 .36.如图,两同心圆的圆心为O ,大圆的弦AB 切小圆于P ,两圆的半径分别为6、3,则图中阴影部分的面积是.37.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC= 度.38.如图,在直角坐标系中,点A、B、C的坐标分别为(0,3)、(4,3)、(0,-1),则△ABC外接圆的圆心坐标为.39.如图,半径为1的⊙O与正五边形ABCDE的边A B、AE相切于点M、N,则劣弧MN的长度为.40.已知圆锥的母线为10,底面圆的直径为12,则此圆锥的侧面积是.41.圆锥底面圆的半径为3m,其侧面展开图是半圆,则圆锥母线长为m.42.如图,△ABC是⊙O的内接三角形,∠C=50°,则∠OAB= °.43.如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,且AC=OC,若⊙O的半径为5,则图中阴影部分的面积是.44.如图,正六边形ABCDEF的边长为2,则对角线AC=.45.某体育馆的圆弧形屋顶如图所示,最高点C到弦AB的距离是20m,圆弧形屋顶的跨度AB是80m,则该圆弧所在圆的半径为m.三、解答题1.如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接B C.(1)求证:BC平分∠PBD;(2)求证:BC2=AB•BD;(3)若PA=6,PC=62,求BD的长.2.如图线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段A C.(1)请你用尺规在所给的网格中画出线段AC及点B经过的路径;(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(-2,-1),则点C的坐标为;(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为;(4)若有一张与(3)中所说的区域形状相同的纸片,将它围成一个几何体的侧面,则该几何体底面圆的半径长为3.如图,在△ABC中,AB=AC,点D在边AB上,以点A为圆心,线段AD的长为半径的⊙A 与边AC相交于点E,AF⊥DE,垂足为点F,AF的延长线与边BC相交于点G,联结GE.已知DE=10,cos∠BAG=1213,12ADDB.求:(1)⊙A的半径AD的长;(2)∠EGC的余切值.4.如图,O A、OB是⊙O的半径且OA⊥OB,作OA的垂直平分线交⊙O于点C、D,连接C B、A B.求证:∠ABC=2∠CBO.5.在正方形ABCD中,AD=2,l是过AD中点P的一条直线.O是l上一点,以O为圆心的圆经过点A、D,直线l与⊙O交于点E、F(E、F不与A、D重合,E在F的上面).(1)如图,若点F在BC上,求证:BC与⊙O相切.并求出此时⊙O的半径.(2)若⊙O半径为233,请直接写出∠AED的度数.6.如图,已知AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,∠M=∠D.(1)判断B C、MD的位置关系,并说明理由;(2)若AE=16,BE=4,求线段CD的长;(3)若MD恰好经过圆心O,求∠D的度数.7.(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=42.①求∠ABC的度数;②已知AP是⊙O的切线,且AP=4,连接P C.判断直线PC与⊙O的位置关系,并说明理由;(2)如图2,已知▱ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O 于点E,连接DE.求证:DE=D C.8.如图,点C是半圆O的半径OB上的动点,作PC⊥AB于C.点D是半圆上位于PC左侧的点,连接BD交线段PC于E,且PD=PE.(1)求证:PD是⊙O的切线;(2)若⊙O的半径为43,PC=83,设OC=x,PD2=y.①求y关于x的函数关系式;②当x=3时,求tanB的值.9.如图,CD是⊙O的直径,且CD=2cm,点P为CD的延长线上一点,过点P作⊙O的切线PA,PB,切点分别为点A,B.(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;(2)填空:①当DP=cm时,四边形AOBD是菱形;②当DP=cm时,四边形AOBP是正方形.10.如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BA C.过点C 作CE⊥DB,垂足为E,直线AB与CE相交于F点.(1)求证:CF为⊙O的切线;(2)若⊙O的半径为52cm,弦BD的长为3cm,求CF的长.11.如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,(1)求证:CD是⊙O的切线.(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.12.如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C,且与OA交于点E、与OB交于点F,连接CE、CF.(1)AB与⊙O相切吗,为什么?(2)若∠AOB=∠ECF,试判断四边形OECF的形状,并说明理由.13.如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于C点,过C点作CD⊥AE的延长线于D点,直线CD与射线AB交于P点.(1)求证:DC为⊙O切线;(2)若DC=1,AC=5,①求⊙O半径长;②求EB的长.14.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交A C、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.(1)试判断:直线BF与⊙O的位置关系,并说明理由;(2)若AB=6,BF=8,求tan∠CBF.15如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.(1)求证:AC平分∠DAB;(2)若点E为 AB的中点,AD=325,AC=8,求AB和CE的长.16.如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C 在OP上,且BC=P C.(1)求证:直线BC是⊙O的切线;(2)若OA=3,AB=2,求BP的长.17.如图,已知△ABD为⊙O的内接正三角形,AB=27,E、F分别为边A D、AB上的动点,且AE=BF,DF与BE相交于G点,过B点作BC∥DF交 BD于点C,连接C D.(1)求∠BCD的度数;(2)求证:四边形BCDG为平行四边形;(3)连接CG,当CG与△BCD的一边垂直时,求CG的长度.18.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.(1)求证:AC 平分∠DAB ;(2)若∠B =60°,CD =23,求AE 的长.19.如图所示,D 是以AB 为直径的半圆O 上的一点,C 是弧AD 的中点,点M 在AB 上,AD 与CM 交于点N ,CN =AN .(1)求证:CM ⊥AB ;(2)若AC =23,BD =2,求半圆的直径.20.如图,四边形ABCD 是⊙O 的内接四边形,AC 为直径, BD AD ,DE ⊥BC ,垂足为E .(1)求证:CD 平分∠ACE ;(2)判断直线ED 与⊙O 的位置关系,并说明理由;(3)若CE =1,AC =4,求阴影部分的面积.。
