广东省东莞市2016届高三备考研讨会材料:《函数与数列(2)
广东省14市2016届高三上学期期末考试数学理试题分类汇编:数列

广东省14市2016届高三上学期期末考试数学理试题分类汇编数列一、选择题1、(清远市2016届高三上期末)已知数列{}n a 满足:111,(*)2nn n a a a n N a +==∈+,12(1)()1n n C a n λ=+-+,若{}n C 是单调递减数列,则实数λ的取值范围是( ) A 、λ13≥B 、λ13>C 、λ43≥D 、λ43> 2、(东莞市2016届高三上期末)已知各项为正的数列{}n a 的前n 项的乘积为n T ,点(2,15)n T n n -在函数12log y x =的图象上,则数列{}2log n a 的前10项和为(A )-140 (B )100 (C )124 (D )1563、(广州市2016届高三1月模拟考试)各项均为正数的等差数列{}n a 中,3694=a a ,则前12项和12S 的最小值为(A )78 (B )48 (C )60(D )724、(揭阳市2016届高三上期末)在等差数列{}n a 中,已知35710132,9a a a a a +=++=,则此数列的公差为 (A )13 (B )3 (C )12 (D )165、(清远市2016届高三上期末)已知数列{}n a 的前n 项和为22n S n n =-,则317a a +=( )A 、36B 、35C 、34D 、336、(汕尾市2016届高三上期末)已知是等差数列{}n a ,且28a a +=16,则数列{}n a 的前9 项和等于( )A.36B.72C.144D.2887、(湛江市2016年普通高考测试(一))设n S 为等差数列{}n a 的前n 项和,若11a =,公差d =2,2n n S S +-=36,则n =A 、5B 、6C 、7D 、88、(肇庆市2016届高三第二次统测(期末))设等差数列{}n a 的前n 项和为n S ,若11a =,315S =,则6S =(A )62 (B )66 (C )70 (D )74选择题答案:1、B2、C3、D4、A5、C6、B7、D8、 B 二、填空题 1、(惠州市2016届高三第三次调研考试)设数列{}n a 的前n 项和为n S ,且121a a ==,{}(2)n n nS n a ++为等差数列,则数列{}n a 的通项公式n a = .2、(揭阳市2016届高三上期末)设n S 是数列{}n a 的前n 项和,且1111,n n n a a S S ++=-=学科网,则数列{}n a 的通项公式n a = 3、(汕尾市2016届高三上期末)已知数列为等比数列,,若数列满足则的前n 项和n S = .填空题答案1、12n n- 2、1,(1)1.(2)(1)n n n n -=⎧⎪⎨≥⎪-⎩3、1n n +三、解答题1、(潮州市2016届高三上期末)已知正项等差数列{}n a 的前n 项和为n S ,且满足215313a a a +=,756S =。
高三数列讲座心得体会

时光荏苒,转眼间我们已迈入高三这个紧张而关键的阶段。
在这个阶段,数列作为高中数学的重要组成部分,对我们的数学学习提出了更高的要求。
近期,我有幸参加了一场关于数列的讲座,通过这次讲座,我对数列有了更深入的理解,以下是我的一些心得体会。
一、数列的概念与性质讲座伊始,讲师首先向我们介绍了数列的基本概念和性质。
数列是由一系列按一定顺序排列的数组成的,它可以是有限数列,也可以是无限数列。
数列的通项公式是描述数列中每一项的规律的关键。
通过学习数列的性质,我认识到数列的有序性、递增性、递减性等特点,这些特点在解决数列问题时具有重要作用。
二、数列的求和问题在讲座中,讲师详细讲解了数列的求和问题。
求和问题是数列学习中的核心问题,也是高中数学考试中的热点。
通过学习,我了解到数列求和的方法有很多,如分组求和、错位相减、裂项相消等。
这些方法在解决不同类型的数列求和问题时具有很好的效果。
例如,在解决等差数列求和问题时,我们可以运用分组求和的方法;而在解决等比数列求和问题时,则可以运用错位相减的方法。
通过这次讲座,我对数列求和问题有了更加全面的认识。
三、数列的应用讲座中,讲师还向我们展示了数列在现实生活中的应用。
例如,在经济学中,我们可以用数列来描述经济指数的变化;在物理学中,我们可以用数列来描述物体的运动轨迹。
这些应用使我认识到数列知识的重要性,也让我对数学学习产生了更浓厚的兴趣。
四、学习方法与技巧在讲座的最后,讲师分享了学习数列的方法与技巧。
以下是我在讲座中总结的一些学习心得:1. 注重基础知识:数列学习的基础是掌握数列的概念、性质和通项公式,只有对这些基础知识有扎实的掌握,才能在解决数列问题时游刃有余。
2. 善于归纳总结:在学习数列的过程中,我们要善于归纳总结各种类型数列的求和方法和解题技巧,以便在考试中能够迅速找到解题思路。
3. 勤于练习:数列知识的应用需要大量的练习,只有通过不断的练习,我们才能熟练掌握各种解题方法,提高解题速度。
广东省东莞市2016届高三备考研讨会材料:2016届高三备考建议

(5)东莞市高中数学青年教师培训
(6)东莞市高中数学骨干教师培训 (7)高三备考研讨(分区域)
后果:乏味、疲劳、缺乏兴趣 观点:要站在系统、整体的高度审视教材,做到层次分
明,结构清晰,让不同模块之间的知识汇成一个系统, 交织成一张网,复习课也可用好教材,上出新意。 知识结构;(3)研究习题,提炼思想方法;(4)因材施教, 促进分层教学.
建议:(1)梳理系统,构建知识网络;(2)知识重讲,完善
2016届高三数学备考建议
重基础 抓落实 促发展
2016届高三数学备考建议
(1)处理好教材与教辅的关系 (2)将知识化为能力,将能力转化为分数 (3)处理习题教学几个环节:选题、审题、解题、反思提炼 (4)关注学生:课堂听课状态、作业、考试策略、心态
处理好教材与教辅的关系
现象:复习就是重复、“炒冷饭”
试Байду номын сангаас争取科学,把握好梯度,控制好难度。
审题:要站在系统的高度引领学生解题,强化学生的
“联系”、“联想”的习惯和能力,适度的“模型
化”“模式化”。
解题:规范步骤,凸显通性通法,让解题方法来得更加
自然,讲推理,更要讲道理。
反思:找联系,找规律,找本源。
关注学生
听课状态:将教育的关怀指向每一位孩子。
作业情况:做好跟踪落实,做到有布置就有检查,有检
查就有反馈,加强个性化作业布置的研究。
考试策略:指导学生学习,指导学生答题,对于部分重
点关注的学生做到面批面改。
意志品质:通过复习、解题,锻炼学生的意志品质,多
鼓励,增强学生信心,关注学生的心态。
常规工作
(1)期市末统考范围 (2)东莞市高中数学竞赛 (3)东莞市青年教师优质课比赛 (4)微课优课资源建设及应用
高三函数专题训练

函数专题训练1. (安徽省示范高中2016届高三第二次联考数学、理、1)函数22()x x f x x-++=的定义域为( ) A-(-1,0) (0,2) B .(-1,0)(0,+∞) C .(一∞,-1)(2,+∞) D .(-1,2) 2.(广东省惠州市2016届高三调研、理、6)已知函数⎩⎨⎧≤>=0,20,log )(3x x x x f x ,则))91((f f =( ).(A )12 (B )14(C )16 (D )18 3.(广东省廉江一中2016届高三月考、理、10)函数⎪⎩⎪⎨⎧<-=>=010001)(x x x x f ,),1()(2-⋅=x f x x g 则函数)(x g 的递减区间是( )A .),0[+∞B .)1,0[C .)1,(-∞D .)1,1(-4. (安徽省示范高中2016届高三第二次联考数学、理、3)已知225535232(),(),log ,,,555a b c a b c ===则的大小关系是( ) A. a<c<b B. b<a<e C. c<a<b D. a<b<c5.(吉林省实验中学2016届高三上学期第一次模拟、理、3)下列函数中,既是偶函数又在(),0-∞上单调递增的函数是( )(A )2y x = (B )2x y = (C )21log y x= (D )sin y x =6.(广东省廉江一中2016届高三月考、理、6)函数)32(log 3++=x y a 的图象必经过定点P 的坐标为( )A .)3,1(-B .)4,1(-C .)1,0(D .)2,2(7.(广东省廉江一中2016届高三月考、理、7)已知函数,⎪⎩⎪⎨⎧<+≥=3)1(3)21()(x x f x x f x 则(l)f 的值是( )A .121B .81 C .24 D .12 8.(黑龙江省大庆铁人中学2016届高三第一阶段考试、理、5)定义在R 上的偶函数f(x),对任意12,[0,)x x ∈+∞ (12x x ≠),有2121()()0f x f x x x -<-,则( ) A .(3)(2)(1)f f f <-< B .(1)(2)(3)f f f <-<C .(2)(1)(3)f f f -<<D .(3)(1)(2)f f f <<-9.(辽宁省五校协作体2016届高三上学期期初考试数学、理、7)设函数()f x 是定义在R 上的奇函数,当0x >时,()23,x f x x =+-则()f x 的零点个数为( )A .1B .2C .3D .410.(安徽省合肥市第八中学2016届高三阶段考试、理、13)若2log (2)2a +=,则3a = .11.(安徽省合肥市第八中学2016届高三阶段考试、理、14)20(cos sin )x x dx π-=⎰ 。
2016年高考数学数列问题解法与技巧_答题技巧

2016年高考数学数列问题解法与技巧_答题技巧数列是高中数学的重要内容,又是学习高等数学的基础。
下面是查字典数学网整理的数列问题解法与技巧,请考生学习。
高考对本章的考查比较全面,等差数列,等比数列的考查每年都不会遗漏。
有关数列的试题经常是综合题,经常把数列知识和指数函数、对数函数和不等式的知识综合起来,试题也常把等差数列、等比数列,求极限和数学归纳法综合在一起。
探索性问题是高考的热点,常在数列解答题中出现。
本章中还蕴含着丰富的数学思想,在主观题中着重考查函数与方程、转化与化归、分类讨论等重要思想,以及配方法、换元法、待定系数法等基本数学方法。
近几年来,高考关于数列方面的命题主要有以下三个方面;(1)数列本身的有关知识,其中有等差数列与等比数列的概念、性质、通项公式及求和公式。
(2)数列与其它知识的结合,其中有数列与函数、方程、不等式、三角、几何的结合。
(3)数列的应用问题,其中主要是以增长率问题为主。
试题的难度有三个层次,小题大都以基础题为主,解答题大都以基础题和中档题为主,只有个别地方用数列与几何的综合与函数、不等式的综合作为最后一题难度较大。
1、在掌握等差数列、等比数列的定义、性质、通项公式、前n项和公式的基础上,系统掌握解等差数列与等比数列综合题的规律,深化数学思想方法在解题实践中的指导作用,灵活地运用数列知识和方法解决数学和实际生活中的有关问题。
2、在解决综合题和探索性问题实践中加深对基础知识、基本技能和基本数学思想方法的认识,沟通各类知识的联系,形成更完整的知识网络,提高分析问题和解决问题的能力。
进一步培养学生阅读理解和创新能力,综合运用数学思想方法分析问题与解决问题的能力。
3、培养学生善于分析题意,富于联想,以适应新的背景,新的设问方式,提高学生用函数的思想、方程的思想研究数列问题的自觉性、培养学生主动探索的精神和科学理性的思维方法.数列问题解法与技巧的内容就是这些,查字典数学网预祝考生可以取得优异的成绩。
2016届广东省高考数学二轮专题复习等差数列、等比数列01
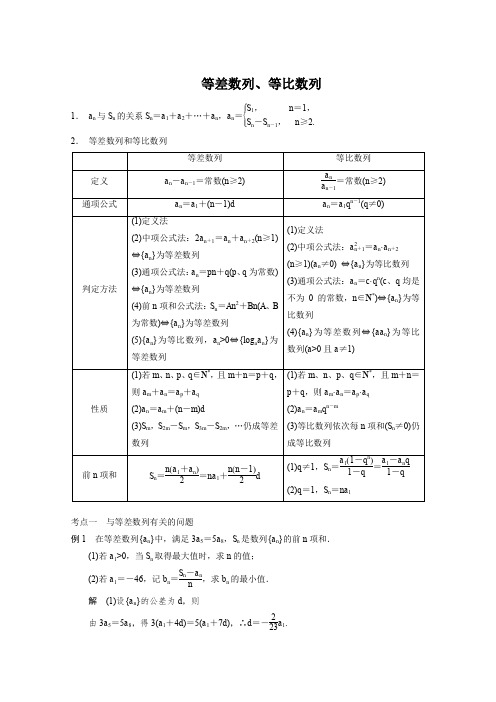
等差数列、等比数列1. a n 与S n 的关系S n =a 1+a 2+…+a n ,a n =⎩⎪⎨⎪⎧S 1, n =1,S n -S n -1, n ≥2.2. 等差数列和等比数列考点一 与等差数列有关的问题例1 在等差数列{a n }中,满足3a 5=5a 8,S n 是数列{a n }的前n 项和.(1)若a 1>0,当S n 取得最大值时,求n 的值; (2)若a 1=-46,记b n =S n -a nn ,求b n 的最小值.解 (1)设{a n }的公差为d ,则由3a 5=5a 8,得3(a 1+4d )=5(a 1+7d ),∴d =-223a 1.∴S n =na 1+n (n -1)2×⎝⎛⎭⎫-223a 1=-123a 1n 2+2423a 1n=-123a 1(n -12)2+14423a 1.∵a 1>0,∴当n =12时,S n 取得最大值. (2)由(1)及a 1=-46,得d =-223×(-46)=4,∴a n =-46+(n -1)×4=4n -50, S n =-46n +n (n -1)2×4=2n 2-48n .∴b n =S n -a n n =2n 2-52n +50n=2n +50n-52≥22n ×50n-52=-32,当且仅当2n =50n ,即n =5时,等号成立.故b n 的最小值为-32.(1)在等差数列问题中其最基本的量是首项和公差,只要根据已知条件求出这两个量,其他问题就可随之而解,这就是解决等差数列问题的基本方法,其中蕴含着方程思想的运用.(2)等差数列的性质①若m ,n ,p ,q ∈N *,且m +n =p +q ,则a m +a n =a p +a q ; ②S m ,S 2m -S m ,S 3m -S 2m ,…,仍成等差数列; ③a m -a n =(m -n )d ⇔d =a m -a nm -n(m ,n ∈N *);④a n b n =A 2n -1B 2n -1(A 2n -1,B 2n -1分别为{a n },{b n }的前2n -1项的和). (3)数列{a n }是等差数列的充要条件是其前n 项和公式S n =f (n )是n 的二次函数或一次函数且不含常数项,即S n =An 2+Bn (A 2+B 2≠0).(1)设S n 是公差为d (d ≠0)的无穷等差数列{a n }的前n 项和,则下列命题错误..的是________.(填序号)①若d <0,则数列{S n }有最大项; ②若数列{S n }有最大项,则d <0;③若数列{S n }是递增数列,则对任意n ∈N *,均有S n >0; ④若对任意n ∈N *,均有S n >0,则数列{S n }是递增数列.(2)设等差数列{a n }的前n 项和为S n ,S m -1=-2,S m =0,S m +1=3,则m =________. 答案 (1)③ (2)5【详细分析】(1)利用函数思想,通过讨论S n =d2n 2+⎝⎛⎭⎫a 1-d 2n 的单调性判断. 设{a n }的首项为a 1,则S n =na 1+12n (n -1)d =d2n 2+⎝⎛⎭⎫a 1-d 2n . 由二次函数性质知S n 有最大值时,则d <0,故①②正确;因为{S n }为递增数列,则d >0,不妨设a 1=-1,d =2,显然{S n }是递增数列,但S 1=-1<0,故③错误;对任意n ∈N *,S n 均大于0时,a 1>0,d >0,{S n }必是递增数列,④正确. (2)a m =2,a m +1=3,故d =1, 因为S m =0,故ma 1+m (m -1)2d =0,故a 1=-m -12,因为a m +a m +1=5, 故a m +a m +1=2a 1+(2m -1)d =-(m -1)+2m -1=5, 即m =5.考点二 与等比数列有关的问题例2 (1)已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=________.(2)设公比为q (q >0)的等比数列{a n }的前n 项和为S n .若S 2=3a 2+2,S 4=3a 4+2,则q =________.答案 (1)-7 (2)32【详细分析】(1)利用等比数列的性质求解.由⎩⎪⎨⎪⎧ a 4+a 7=2,a 5a 6=a 4a 7=-8解得⎩⎪⎨⎪⎧ a 4=-2,a 7=4或⎩⎪⎨⎪⎧a 4=4,a 7=-2. ∴⎩⎪⎨⎪⎧q 3=-2,a 1=1或⎩⎪⎨⎪⎧q 3=-12,a 1=-8,∴a 1+a 10=a 1(1+q 9)=-7.(2)利用等比数列的通项公式及前n 项和公式求解. S 4=S 2+a 3+a 4=3a 2+2+a 3+a 4=3a 4+2, 将a 3=a 2q ,a 4=a 2q 2代入得,3a 2+2+a 2q +a 2q 2=3a 2q 2+2,化简得2q 2-q -3=0, 解得q =32(q =-1不合题意,舍去).(1)证明数列是等比数列的两个方法:①利用定义:a n +1a n(n ∈N *)是常数,②利用等比中项a 2n =a n -1a n +1(n ≥2,n ∈N *).(2)等比数列中的五个量:a 1,a n ,q ,n ,S n 可以“知三求二”. (3){a n }为等比数列,其性质如下:①若m 、n 、r 、s ∈N *,且m +n =r +s ,则a m ·a n =a r ·a s ; ②a n =a m q n -m ;③S n ,S 2n -S n ,S 3n -S 2n 成等比数列(q ≠-1). (4)等比数列前n 项和公式 S n =⎩⎪⎨⎪⎧na 1(q =1),a 1(1-q n )1-q=a 1-a n q 1-q (q ≠1).①能“知三求二”;②注意讨论公比q 是否为1;③a 1≠0.已知S n 是等比数列{a n }的前n 项和,S 4,S 2,S 3成等差数列,且a 2+a 3+a 4=-18. (1)求数列{a n }的通项公式;(2)是否存在正整数n ,使得S n ≥2 013?若存在,求出符合条件的所有n 的集合;若不存在,说明理由.解 (1)设等比数列{a n }的公比为q ,则a 1≠0,q ≠0.由题意得⎩⎪⎨⎪⎧ S 2-S 4=S 3-S 2,a 2+a 3+a 4=-18.即⎩⎪⎨⎪⎧-a 1q 2-a 1q 3=a 1q 2,a 1q (1+q +q 2)=-18, 解得⎩⎪⎨⎪⎧a 1=3,q =-2.故数列{a n }的通项公式为a n =3×(-2)n -1.(2)由(1)有S n =3[1-(-2)n ]1-(-2)=1-(-2)n .假设存在n ,使得S n ≥2 013,则1-(-2)n ≥2 013,即(-2)n ≤-2 012. 当n 为偶数时,(-2)n >0.上式不成立; 当n 为奇数时,(-2)n =-2n ≤-2 012, 即2n ≥2 012,则n ≥11.综上,存在符合条件的正整数n ,且所有这样的n 的集合为{n |n =2k +1,k ∈N ,k ≥5}. 考点三 等差数列、等比数列的综合应用 例3 已知等差数列{a n }的公差为-1,且a 2+a 7+a 12=-6.(1)求数列{a n }的通项公式a n 与前n 项和S n ;(2)将数列{a n }的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{b n }的前3项,记{b n }的前n 项和为T n ,若存在m ∈N *,使对任意n ∈N *,总有S n <T m +λ恒成立,求实数λ的取值范围.解 (1)由a 2+a 7+a 12=-6得a 7=-2,∴a 1=4, ∴a n =5-n ,从而S n =n (9-n )2.(2)由题意知b 1=4,b 2=2,b 3=1, 设等比数列{b n }的公比为q , 则q =b 2b 1=12,∴T m =4[1-(12)m ]1-12=8[1-(12)m ],∵(12)m 随m 增加而递减, ∴{T m }为递增数列,得4≤T m <8. 又S n =n (9-n )2=-12(n 2-9n )=-12[(n -92)2-814],故(S n )max =S 4=S 5=10,若存在m ∈N *,使对任意n ∈N *总有S n <T m +λ, 则10<4+λ,得λ>6.等差(比)数列的综合问题的常见类型及解法(1)等差数列与等比数列交汇的问题,常用“基本量法”求解,但有时灵活地运用性质,可使运算简便.(2)等差数列、等比数列与函数、方程、不等式等的交汇问题,求解时用等差(比)数列的相关知识,将问题转化为相应的函数、方程、不等式等问题求解即可. 已知数列{a n }满足a 1=3,a n +1-3a n =3n (n ∈N *),数列{b n }满足b n =3-n a n .(1)求证:数列{b n }是等差数列;(2)设S n =a 13+a 24+a 35+…+a n n +2,求满足不等式1128<S n S 2n <14的所有正整数n 的值.(1)证明 由b n =3-n a n 得a n =3n b n ,则a n +1=3n +1b n +1.代入a n +1-3a n =3n 中,得3n +1b n +1-3n +1b n =3n ,即得b n +1-b n =13.所以数列{b n }是等差数列.(2)解 因为数列{b n }是首项为b 1=3-1a 1=1,公差为13的等差数列,则b n =1+13(n -1)=n +23,则a n =3n b n =(n +2)×3n -1,从而有a n n +2=3n -1, 故S n =a 13+a 24+a 35+…+a nn +2=1+3+32+…+3n -1=1-3n 1-3=3n -12,则S n S 2n =3n-132n -1=13n +1, 由1128<S n S 2n <14,得1128<13n +1<14, 即3<3n <127,得1<n ≤4.故满足不等式1128<S n S 2n <14的所有正整数n 的值为2,3,4.1. 在等差(比)数列中,a 1,d (q ),n ,a n ,S n 五个量中知道其中任意三个,就可以求出其他两个.解这类问题时,一般是转化为首项a 1和公差d (公比q )这两个基本量的有关运算. 2. 等差、等比数列的性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 3. 等差、等比数列的单调性(1)等差数列的单调性d >0⇔{a n }为递增数列,S n 有最小值. d <0⇔{a n }为递减数列,S n 有最大值. d =0⇔{a n }为常数列. (2)等比数列的单调性当⎩⎪⎨⎪⎧ a 1>0,q >1或⎩⎪⎨⎪⎧ a 1<0,0<q <1时,{a n }为递增数列,当⎩⎪⎨⎪⎧ a 1>0,0<q <1或⎩⎪⎨⎪⎧a 1<0,q >1时,{a n }为递减数列. 4. 常用结论(1)若{a n },{b n }均是等差数列,S n 是{a n }的前n 项和,则{ma n +kb n },{S nn }仍为等差数列,其中m ,k 为常数.(2)若{a n },{b n }均是等比数列,则{ca n }(c ≠0),{|a n |},{a n ·b n },{ma n b n }(m 为常数),{a 2n },{1a n}等也是等比数列. (3)公比不为1的等比数列,其相邻两项的差也依次成等比数列,且公比不变,即a 2-a 1,a 3-a 2,a 4-a 3,…成等比数列,且公比为a 3-a 2a 2-a 1=(a 2-a 1)qa 2-a 1=q .(4)等比数列(q ≠-1)中连续k 项的和成等比数列,即S k ,S 2k -S k ,S 3k -S 2k ,…成等比数列,其公差为q k .等差数列中连续k 项的和成等差数列,即S k ,S 2k -S k ,S 3k -S 2k ,…成等差数列,公差为k 2d . 5. 易错提醒(1)应用关系式a n =⎩⎪⎨⎪⎧S 1,n =1,S n -S n -1,n ≥2时,一定要注意分n =1,n ≥2两种情况,在求出结果后,看看这两种情况能否整合在一起.(2)三个数a ,b ,c 成等差数列的充要条件是b =a +c2,但三个数a ,b ,c 成等比数列的必要条件是b 2=ac .。
广东省东莞市六校2016届高三上学期联考数学理试题

东莞市2015—2016学年度第一学期六校联考考试高三数学(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数z 满足2)1()1(i z i ,其中i 为虚数单位,则在复平面上复数z 对应的点位于()A .第一象限B .第二象限C .第三象限D .第四象限2.已知集合2{|log 3}M x x ,{|21,}N x x n n N ,则M N () A .(0,8)B .{3,5,7}C .{0,1,3,5,7}D .{1,3,5,7}3.如右图所示的程序框图,若输出的41S ,则判断框内应填入的条件是()A .3?k B .4?k C .5?k D .6?k 4.下列函数中既是奇函数,又在区间1,1上是增函数的为()A .y xB .x x y e eC .sin y xD .3yx 5.设向量a,b 满足10b a ,6b a ,则b a =()A .1 B.2 C .3 D .5 6.已知))2,0[,0)(sin(x y的部分图象如图所示,则()A .23B .43C .2D .47.钝角三角形ABC 的面积是12,AB=1,BC=2,则AC=()A .1 B .2 C .5 D .58.函数y =ln 1|2x -3|的大致图象为()9.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于()A .40 cm 3B .30 cm 3C .20 cm 3D .10 cm310.已知斜率为2的直线l 双曲线2222:1(0,0)xy C ab a b 交,A B 两点,若点(2,1)P 是AB 的中点,则C 的离心率等于()A .22B .2 C .3D .2。
2016届广东省高考数学二轮专题复习三角函数的图象与性质02

(2)已知函数f (x )=4cos ωx ·sin ⎝⎛⎭⎫ωx +π4(ω>0)的最小正周期为π. ①求ω的值;②讨论f (x )在区间⎣⎡⎦⎤0,π2上的单调性. 解 ①f (x )=4cos ωx ·sin ⎝⎛⎭⎫ωx +π4 =22sin ωx ·cos ωx +22cos 2ωx =2(sin 2ωx +cos 2ωx )+ 2=2sin ⎝⎛⎭⎫2ωx +π4+ 2. 因为f (x )的最小正周期为π,且ω>0.从而有2π2ω=π,故ω=1. ②由①知,f (x )=2sin ⎝⎛⎭⎫2x +π4+ 2. 若0≤x ≤π2, 则π4≤2x +π4≤5π4. 当π4≤2x +π4≤π2, 即0≤x ≤π8时,f (x )单调递增; 当π2≤2x +π4≤5π4, 即π8≤x ≤π2时,f (x )单调递减. 综上可知,f (x )在区间⎣⎡⎦⎤0,π8上单调递增, 在区间⎣⎡⎦⎤π8,π2上单调递减.1. 求函数y =A sin(ωx +φ)(或y =A cos(ωx +φ),或y =A tan(ωx +φ))的单调区间(1)将ω化为正.(2)将ωx +φ看成一个整体,由三角函数的单调性求解.2. 已知函数y =A sin(ωx +φ)+B (A >0,ω>0)的图象求解析式(1)A =y max -y min 2,B =y max +y min 2. (2)由函数的周期T 求ω,ω=2πT.(3)利用与“五点法”中相对应的特殊点求φ.3. 函数y =A sin(ωx +φ)的对称轴一定经过图象的最高点或最低点.4. 求三角函数式最值的方法(1)将三角函数式化为y =A sin(ωx +φ)+B 的形式,进而结合三角函数的性质求解.(2)将三角函数式化为关于sin x ,cos x 的二次函数的形式,进而借助二次函数的性质求解.5. 特别提醒:进行三角函数的图象变换时,要注意无论进行什么样的变换都是变换变量本身.提高练习1. 假设若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”.给出下列函数:①f (x )=sin x -cos x ;②f (x )=2(sin x +cos x );③f (x )=2sin x +2;④f (x )=sin x .则其中属于“互为生成函数”的是________.(填序号)答案 ①②2. 已知函数f (x )=sin ωx ·cos ωx +3cos 2ωx -32(ω>0),直线x =x 1,x =x 2是y =f (x )图象的任意两条对称轴,且|x 1-x 2|的最小值为π4. (1)求f (x )的表达式;(2)将函数f (x )的图象向右平移π8个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数y =g (x )的图象,若关于x 的方程g (x )+k =0在区间[0,π2]上有且只有一个实数解,求实数k 的取值范围.解 (1)f (x )=12sin 2ωx +3×1+cos 2ωx 2-32=12sin 2ωx +32cos 2ωx =sin(2ωx +π3), 由题意知,最小正周期T =2×π4=π2, T =2π2ω=πω=π2,所以ω=2, ∴f (x )=sin ⎝⎛⎭⎫4x +π3. (2)将f (x )的图象向右平移π8个单位后, 得到y =sin(4x -π6)的图象,再将所得图象所有点的横坐标伸长到原来的2倍,纵坐标不变,得到y =sin(2x -π6)的图象. 所以g (x )=sin(2x -π6). 令2x -π6=t ,∵0≤x ≤π2,∴-π6≤t ≤5π6. g (x )+k =0在区间[0,π2]上有且只有一个实数解, 即函数g (t )=sin t 与y =-k 在区间[-π6,5π6]上有且只有一个交点. 如图,由正弦函数的图象可知-12≤-k <12或-k =1. ∴-12<k ≤12或k =-1.(推荐时间:60分钟)一、填空题1. 点P 从(1,0)出发,沿单位圆x 2+y 2=1逆时针方向运动2π3弧长到达Q 点,则Q 点的坐标为________.答案 ⎝⎛⎭⎫-12,32 【详细分析】记α=∠POQ ,由三角函数的定义可知,Q 点的坐标(x ,y )满足x =cos α=cos2π3=-12, y =sin α=sin 2π3=32. 2. 已知角θ的顶点为坐标原点,始边为x 轴的正半轴,若P (4,y )是角θ终边上一点,且sinθ=-255,则y =________. 答案 -8【详细分析】因为sin θ=y 42+y 2=-255,所以y <0,且y 2=64,所以y =-8.3. 已知α为第二象限角,sin α+cos α=33,则cos 2α等于________. 答案 -53【详细分析】因为sin α+cos α=33, 两边平方得1+2sin αcos α=13,所以sin 2α=-23. 由于sin α+cos α=2sin ⎝⎛⎭⎫α+π4=33>0, 且α为第二象限角,所以2k π+π2<α<2k π+3π4,k ∈Z , 所以4k π+π<2α<4k π+3π2,k ∈Z , 所以cos 2α=-1-sin 22α=-1-49=-53. 4. 将函数y =cos ⎝⎛⎭⎫x -π3的图象上各点横坐标伸长到原来的2倍(纵坐标不变),再向左平移π6个单位,所得函数的解析式为________.答案 y =cos ⎝⎛⎭⎫12x -π4【详细分析】y =cos ⎝⎛⎭⎫x -π3―――――――――→横坐标伸长到原来的2倍纵坐标不变5. 若函数y =A sin(ωx +φ)(A >0,ω>0,|φ|<π2)在一个周期内的图象如图所 示,M ,N 分别是这段图象的最高点与最低点,且OM →·ON →=0,则A ·ω等于________.答案 7π6 【详细分析】由题中图象知T 4=π3-π12, 所以T =π,所以ω=2.则M ⎝⎛⎭⎫π12,A ,N ⎝⎛⎭⎫7π12,-A 由OM →·ON →=0,得7π2122=A 2, 所以A =7π12,所以A ·ω=7π6.6. 已知函数f (x )=2sin(ωx +φ) (ω>0)的图象关于直线x =π3对称,且f ⎝⎛⎭⎫π12=0,则ω的最小值为________.答案 2【详细分析】由f ⎝⎛⎭⎫π12=0知⎝⎛⎭⎫π12,0是f (x )图象的一个对称中心,又x =π3是一条对称轴,所以应有⎩⎪⎨⎪⎧ω>02πω≤4⎝⎛⎭⎫π3-π12, 解得ω≥2,即ω的最小值为2.7. 已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是________. 答案 ⎣⎡⎦⎤12,54【详细分析】由π2<x <π, ω>0得ωπ2+π4<ωx +π4<ωπ+π4, 又y =sin x 在⎝⎛⎭⎫π2,3π2上递减, 所以⎩⎨⎧ ωπ2+π4≥π2ωπ+π4≤3π2,解得12≤ωπ≤54.。
广东省2016届高三数学二轮复习精选试题汇编:合情推理与演绎推理 Word版含答案

合情推理与演绎推理一、填空题1. 下面给出三个类比推理命题(其中Q 为有理数集,R 为实数集,C 为复数集); ①",,0,"a b R a b a b ∈-==若则类比推出",,a b C ∈若0";a b a b -==,则 ②",,,,,,"a b c d R a bi c di a c b d ∈+=+==若复数则类比推出",,,a b c d Q ∈,若,,";a c a c b d +=+==则③",,0,"a b R a b a b ∈->>若则类比推出",,0,";a b C a b a b ∈->>若则其中类比结论正确的序号是_____________(写出所有正确结论的序号)2. 已知21111()12f n n n n n=++++++,则()f n 中共有 项. 3. 设()()()()f x x a x b x c =---(,,a b c 是两两不等的常数),则///()()()a b cf a f b f c ++的值是 ______________.二、选择题4. “所有金属都能导电,铁是金属,所以铁能导电,”此推理类型属于A .演绎推理B .类比推理C .合情推理D .归纳推理5. 用三段论推理命题:“任何实数的平方大于0,因为a 是实数,所以2a >0”,你认为这个推理( )A .大前题错误B .小前题错误C .推理形式错误D .是正确的6. 已知扇形的弧长为l ,所在圆的半径为r ,类比三角形的面积公式:12S =⨯底⨯高,可得扇形的面积公式为( )A.212r B.212l C.12rl D.不可类比7. 下列给出的平面图形中,与空间的平行六面体作为类比对象较为合适的是( ) A.三角形 B.梯形 C.平行四边形 D.矩形8. 图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第七个叠放的图形中,小正方体木块总数就是( )A.25 B.66 C.91 D.120 9. 若,,x y R ∈则"1"xy ≤是22"1"x y +≤的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件10. 设115114113112log 1log 1log 1log 1+++=P ,则( ) A .10<<P B .21<<P C .32<<P D .43<<P11. 关于x 的方程229430x x a -----⋅-=有实根的充要条件是( )A .4a ≥-B .40a -≤<C .0a <D .30a -≤<12. 计算机中常用的十六进制是逢16进1的计数制,采用数字09和字母A F 共16个计例如,用十六进制表示,则( ) A .6E B .72 C .5F D .0B13. 设b a b a b a +=+∈则,62,,22R 的最小值是( )A .22-B .335-C .-3D .27-三、解答题 14. 已知)()1(12t n N n n a ∈+=记)1()1)(1()(21n a a a n f -⋯--=试通过计算)3(),2(),1(f f f 的值,推测出)(n f 的值。
【三维设计】(新课标)2016届高考数学5年真题备考题库 第二章 第8节 函数与方程 理(含解析)

第2章 函数、导数及其应用第8节 函数与方程1. (2014山东,5分)已知函数f(x)=|x -2|+1,g(x)=kx ,若方程f(x)=g(x)有两个不相等的实根,则实数k 的取值范围是( )A.⎝ ⎛⎭⎪⎫0,12 B.⎝ ⎛⎭⎪⎫12,1 C .(1,2)D .(2,+∞)解析:在同一坐标系中分别画出函数f(x),g(x)的图象如图所示,方程f(x)=g(x)有两个不相等的实根等价于两个函数的图象有两个不同的交点,结合图象可知,当直线y =kx 的斜率大于坐标原点与点(2,1)连线的斜率且小于直线y =x -1的斜率时符合题意,故12<k<1.答案:B2. (2014天津,5分)已知函数f (x )=|x 2+3x |,x ∈R .若方程f (x )-a |x -1|=0恰有4个互异的实数根,则实数a 的取值范围为________.解析:画出函数f (x )=|x 2+3x |的大致图象,如图,令g (x )=a |x-1|,则函数f (x )的图象与函数g (x )的图象有且仅有4个不同的交点,显然a >0.联立⎩⎪⎨⎪⎧y =-x 2-3x ,y =a 1-x消去y ,得x 2+(3-a )x +a =0,由Δ>0,解得a <1或a >9;联立⎩⎪⎨⎪⎧y =x 2+3x ,y =a 1-x消去y ,得x2+(3+a )x -a =0,由Δ>0,解得a >-1或a <-9.综上,实数a 的取值范围为(0,1)∪(9,+∞).3. (2014江苏,5分)已知f (x )是定义在R 上且周期为3的函数,当x ∈[0,3)时,f (x )=⎪⎪⎪⎪⎪⎪x 2-2x +12.若函数y =f (x )-a 在区间[-3,4]上有10个零点(互不相同),则实数a 的取值范围是________.解析:函数y =f (x )-a 在区间[-3,4]上有互不相同的10个零点,即函数y =f (x ),x∈[-3,4]与y =a 的图象有10个不同交点.作出函数y =f (x )在[-3,4]上的图象,f (-3)=f (-2)=f (-1)=f (0)=f (1)=f (2)=f (3)=f (4)=12,观察图象可得0<a <12.答案:⎝ ⎛⎭⎪⎫0,124. (2014新课标全国卷Ⅰ,5分)已知函数f (x )=ax 3-3x 2+1,若f (x )存在唯一的零点x 0,且x 0>0,则a 的取值范围为( )A .(2,+∞)B .(-∞,-2)C .(1,+∞)D .(-∞,-1)解析:当a =0时,f (x )=-3x 2+1有两个零点,不符合题意,故a ≠0.f ′(x )=3ax2-6x =3x (ax -2),令f ′(x )=0,得x =0或x =2a,由题意得a <0且f ⎝ ⎛⎭⎪⎫2a >0,解得a <-2,选B.答案:B5.(2013安徽,5分)已知函数f (x )=x 3+ax 2+bx +c 有两个极值点x 1,x 2.若f (x 1)=x 1<x 2,则关于x 的方程3(f (x ))2+2af (x )+b =0的不同实根个数为( )A .3B .4C .5D .6解析:本题主要考查函数与导数以及函数与方程的基础知识,意在考查考生的数形结合思想、推理论证能力以及创新意识.因为函数f (x )=x 3+ax 2+bx +c 有两个极值点x 1,x 2,可知关于导函数的方程f ′(x )=3x 2+2ax +b =0有两个不等的实根x 1,x 2.则方程3(f (x ))2+2af (x )+b =0有两个不等的实根,即f (x )=x 1或f (x )=x 2,原方程根的个数就是这两个方程f (x )=x 1和f (x )=x 2的不等实根的个数之和.由上述可知函数f (x )在区间(-∞,x 1),(x 2,+∞)上是单调递增的,在区间(x 1,x 2)上是单调递减的,又f (x 1)=x 1<x 2,如图所示,由数形结合可知,f (x )=x 1时,有两个不同实根,f (x )=x 2时有一个实根,所以不同实根的个数为3.答案:A6.(2013天津,5分)函数f (x )=2x|log 0.5x |-1的零点个数为( ) A .1 B .2 C .3D .4解析:本题考查函数零点,意在考查考生的数形结合能力.函数f(x)=2x|log0.5x|-1的零点个数即为函数y=|log0.5x|与y=12图象的交点个数.在同一直角坐标系中作出函数y=|log0.5x|与y=12x的图象,易知有2个交点.答案:B7.(2013湖南,5分)函数f(x)=2ln x的图象与函数g(x)=x2-4x+5的图象的交点个数为( )A.3 B.2C.1 D.0解析:本小题主要考查二次函数和对数函数的图象及性质,考查对数值的取值范围的探究及数形结合思想.由已知g(x)=(x-2)2+1,所以其顶点为(2,1),又f(2)=2ln 2∈(1,2),可知点(2,1)位于函数f(x)=2ln x图象的下方,故函数f(x)=2ln x的图象与函数g(x)=x2-4x+5的图象有2个交点.答案:B8.(2013重庆,5分)若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)·(x-c)+(x-c)(x-a)的两个零点分别位于区间( )A.(a,b) 和(b,c)内B.(-∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(-∞,a) 和(c,+∞)内解析:本题考查函数的零点,意在考查考生数形结合的能力.由已知易得f(a)>0,f(b)<0,f(c)>0,故函数f(x)的两个零点分别位于区间(a,b)和(b,c)内.答案:A9.(2013福建,5分)满足a,b∈{-1,0,1,2},且关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为( )A.14 B.13C.12 D.10解析:本题考查集合、方程的根、计数原理等基础知识,意在考查考生的综合能力.因为a,b∈{-1,0,1,2},可分为两类:①当a=0时,b可能为-1或1或0或2,即b有4种不同的选法;②当a≠0时,依题意得Δ=4-4ab≥0,所以ab≤1.当a=-1时,b有4种不同的选法,当a=1时,b可能为-1或0或1,即b有3种不同的选法,当a=2时,b 可能为-1或0,即b有2种不同的选法.根据分类加法计数原理,(a,b)的个数共有4+4+3+2=13.答案:B10.(2012辽宁,5分)设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x ∈[0,1]时,f (x )=x 3.又函数g (x )=|x cos(πx )|,则函数h (x )=g (x )-f (x )在[-12,32]上的零点个数为( )A .5B .6C .7D .8解析:由题意知函数f (x )是偶函数,且周期是2.作出g (x ),f (x )的函数图像,如图.由图可知函数y =g (x ),y =f (x )在[-12,32]图像有6个交点,故h (x )=g (x )-f (x )在[-12,32]上的零点有6个.答案:B11.(2012天津,5分)函数f (x )=2x +x 3-2在区间(0,1)内的零点个数是( ) A .0 B .1 C .2D .3解析:法一:函数f (x )=2x+x 3-2在区间(0,1)内的零点个数即为函数y =2x,y =2-x 3在区间(0,1)内的图像的交点个数,作出图像即可知两个函数图像在区间(0,1)内有1个交点,故原函数在区间(0,1)内的零点个数是1.法二:由题意知f (x )为单调增函数且f (0)=-1<0,f (1)=1>0, 所以在区间(0,1)内有且只有一个零点. 答案:B12.(2012湖北,5分)函数f (x )=x cos x 2在区间[0,4]上的零点个数为( ) A .4 B .5 C .6D .7解析:令x cos x 2=0,则x =0,或x 2=k π+π2,又x ∈[0,4],因此x k =k π+π2(k =0,1,2,3,4),共有6个零点.答案:C13.(2011新课标全国,5分)函数y =11-x 的图像与函数y =2sin πx (-2≤x ≤4)的图像所有交点的横坐标之和等于( )A .2B .4C .6D .8解析:如图,两个函数图像都关于点(1,0)成中心对称,两个图像在[-2,4]上共8个公共点,每两个对应交点横坐标之和为2,故所有交点的横坐标之和为8.答案:D。
2016届高考数学经典例题集锦:数列(含答案)

数列题目精选精编【典型例题】(一)研究等差等比数列的有关性质 1. 研究通项的性质例题1. 已知数列}{n a 满足1111,3(2)n n n a a a n --==+≥.(1)求32,a a ;(2)证明:312n n a -=. 解:(1)21231,314,3413a a a =∴=+==+=Q . (2)证明:由已知113--=-n n n a a ,故)()()(12211a a a a a a a n n n n n -++-+-=---Λ1213133312n n n a ---+=++++=L , 所以证得312n n a -=.例题2. 数列{}n a 的前n 项和记为11,1,21(1)n n n S a a S n +==+≥(Ⅰ)求{}n a 的通项公式;(Ⅱ)等差数列{}n b 的各项为正,其前n 项和为n T ,且315T =,又112233,,a b a b a b +++成等比数列,求n T .解:(Ⅰ)由121n n a S +=+可得121(2)n n a S n -=+≥,两式相减得:112,3(2)n n n n n a a a a a n ++-==≥,又21213a S =+=∴213a a = 故{}n a 是首项为1,公比为3的等比数列∴13n n a -=(Ⅱ)设{}n b 的公差为d ,由315T =得,可得12315b b b ++=,可得25b = 故可设135,5b d b d =-=+,又1231,3,9a a a ===,由题意可得2(51)(59)(53)d d -+++=+,解得122,10d d ==∵等差数列{}n b 的各项为正,∴0d > ∴2d =∴2(1)3222n n n T n n n -=+⨯=+例题3. 已知数列{}n a 的前三项与数列{}n b 的前三项对应相同,且212322...aa a +++128n n a n -+=对任意的*N n ∈都成立,数列{}n n b b -+1是等差数列.⑴求数列{}n a 与{}n b 的通项公式;⑵是否存在N k *∈,使得(0,1)k k b a -∈,请说明理由.点拨:(1)2112322...28n n a a a a n -++++=左边相当于是数列{}12n n a -前n 项和的形式,可以联想到已知n S 求na 的方法,当2n ≥时,1n n n S S a --=.(2)把k k a b -看作一个函数,利用函数的思想方法来研究k k a b -的取值情况.解:(1)已知212322a a a +++ (1)2n n a -+8n =(n ∈*N )① 2n ≥时,212322a a a +++ (2)128(1)n n a n --+=-(n ∈*N )②①-②得,128n n a -=,求得42n n a -=,在①中令1n =,可得得41182a -==,所以42nn a -=(n ∈N*). 由题意18b =,24b =,32b =,所以214b b -=-,322b b -=-, ∴数列}{1n n b b -+的公差为2)4(2=---, ∴1n nb b +-=2)1(4⨯-+-n 26n =-,121321()()()n n n b b b b b b b b -=+-+-++-L(4)(2)(28)n =-+-++-L 2714n n =-+(n ∈*N ).(2)k k b a -=2714k k -+-42k-,当4k ≥时,277()()24f k k =-+-42k-单调递增,且(4)1f =, 所以4k ≥时,2()714f k k k =-+-421k -≥, 又(1)(2)(3)0f f f ===,所以,不存在k ∈*N ,使得(0,1)k k b a -∈.例题4. 设各项均为正数的数列{a n }和{b n }满足:a n 、b n 、a n+1成等差数列,b n 、a n+1、b n+1成等比数列,且a 1 = 1, b 1 = 2 , a 2 = 3 ,求通项a n ,b n 解: 依题意得:2b n+1 = a n+1 + a n+2 ① a 2n+1 = b n b n+1 ②∵ a n 、b n 为正数, 由②得21211,+++++==n n n n n n b b a b b a , 代入①并同除以1+n b 得:212+++=n n n b b b , ∴}{n b 为等差数列∵ b 1 = 2 , a 2 = 3 ,29,22122==b b b a 则 ,∴ 2)1(),1(22)229)(1(22+=∴+=--+=n b n n b n n ,∴当n ≥2时,2)1(1+==-n n b b a n n n , 又a 1 = 1,当n = 1时成立, ∴2)1(+=n n a n2. 研究前n 项和的性质例题5. 已知等比数列}{n a 的前n 项和为2nn S a b =⋅+,且13a =. (1)求a 、b 的值及数列}{n a 的通项公式;(2)设n n nb a =,求数列}{n b 的前n 项和n T .解:(1)2≥n 时,a S S a n n n n ⋅=-=--112.而}{n a 为等比数列,得a a a =⋅=-1112, 又31=a ,得3=a ,从而123-⋅=n n a .又123,3a a b b =+=∴=-Q .(2)132n n n n n b a -==⋅, 21123(1)3222n n n T -=++++L231111231(2322222n n n n n T --=+++++L ) ,得2111111(1)232222n n n n T -=++++-L , 111(1)2412[](1)13232212n n n n n n n T +⋅-=-=---.例题6. 数列{}n a 是首项为1000,公比为110的等比数列,数列{b }n 满足121(lg lg lg )k k b a a a k =+++L*()N k ∈, (1)求数列{b }n 的前n 项和的最大值;(2)求数列{|b |}n 的前n 项和n S '. 解:(1)由题意:410nn a -=,∴lg 4n a n =-,∴数列{lg }n a 是首项为3,公差为1-的等差数列,∴12(1)lg lg lg 32k k k a a a k -+++=-L ,∴1(1)7[3]22n n n nb n n --=-=由100n n b b +≥⎧⎨≤⎩,得67n ≤≤,∴数列{b }n 的前n 项和的最大值为67212S S ==.(2)由(1)当7n ≤时,0n b ≥,当7n >时,0n b <,∴当7n ≤时,212731132()244n n n S b b b n n n -+'=+++==-+L当7n >时,12789n n S b b b b b b '=+++----L L 27121132()2144n S b b b n n =-+++=-+L∴22113(7)4411321(7)44n n n n S n n n ⎧-+≤⎪⎪'=⎨⎪-+>⎪⎩.例题7. 已知递增的等比数列{n a }满足23428a a a ++=,且32a +是2a ,4a 的等差中项. (1)求{n a }的通项公式n a ;(2)若12log n n nb a a =,12n n S b b b =+++L 求使1230n n S n ++⋅>成立的n 的最小值.解:(1)设等比数列的公比为q (q >1),由a 1q +a 1q 2+a 1q 3=28,a 1q +a 1q 3=2(a 1q 2+2),得:a 1=2,q =2或a 1=32,q =12(舍)∴a n =2·2(n -1)=2n(2) ∵12log 2nn n n b a a n ==-⋅,∴S n =-(1·2+2·22+3·23+…+n ·2n ) ∴2S n =-(1·22+2·23+…+n ·2n +1),∴S n =2+22+23+…+2n -n ·2n +1=-(n -1)·2n +1-2, 若S n +n ·2n +1>30成立,则2n +1>32,故n >4,∴n 的最小值为5.例题8. 已知数列}{n a 的前n 项和为S n ,且11,,n n S a +-成等差数列,*1,1N n a ∈=. 函数3()log f x x =.(I )求数列}{n a 的通项公式;(II )设数列{}n b 满足1(3)[()2]n n b n f a =++,记数列{}n b 的前n 项和为T n ,试比较52512312n n T +-与的大小. 解:(I )11,,n n S a +-Q 成等差数列,121n n S a +∴=-① 当2n ≥时,121n n S a -=-②. ①-②得:112()n n n n S S a a -+-=-,13+=∴n n a a ,13.n na a +∴=当n =1时,由①得112221S a a ∴==-, 又11,a =2213,3,a a a ∴=∴={}n a ∴是以1为首项3为公比的等比数列,13.n n a -∴=(II )∵()x log x f 3=,133()log log 31n n n f a a n -∴===-, 11111()(3)[()2](1)(3)213n n b n f a n n n n ===-++++++,1111111111111()224354657213n T n n n n ∴=-+-+-+-++-+-+++L11111()22323n n =+--++525,122(2)(3)n n n +=-++比较52512312n n T +-与的大小,只需比较2(2)(3)n n ++与312 的大小即可. 222(2)(3)3122(56156)2(5150)n n n n n n ++-=++-=+-又2(15)(10)n n =+-∵*,N n ∈∴当*19N n n ≤≤∈且时,5252(2)(3)312,;12312nn n n T +++<<-即当10n =时,5252(2)(3)312,;12312n n n n T +++==-即当*10N n n >∈且时,5252(2)(3)312,12312nn n n T +++>>-即.3. 研究生成数列的性质例题9. (I ) 已知数列{}n c ,其中nn n c 32+=,且数列{}n n pc c -+1为等比数列,求常数p ;(II ) 设{}n a 、{}n b 是公比不相等的两个等比数列,n n n b a c +=,证明数列{}n c 不是等比数列.解:(Ⅰ)因为{c n +1-pc n }是等比数列,故有 (c n +1-pc n )2=( c n +2-pc n+1)(c n -pc n -1), 将c n =2n +3n 代入上式,得 [2n +1+3n +1-p (2n +3n )]2=[2n +2+3n +2-p (2n +1+3n +1)]·[2n +3n -p (2n -1+3n -1)], 即[(2-p )2n +(3-p )3n ]2=[(2-p )2n+1+(3-p )3n+1][ (2-p )2n -1+(3-p )3n -1],整理得61(2-p )(3-p )·2n ·3n =0,解得p =2或p =3. (Ⅱ)设{a n }、{b n }的公比分别为p 、q ,p ≠q ,c n =a n +b n .为证{c n }不是等比数列只需证22c ≠c 1·c 3.事实上,22c =(a 1p +b 1q )2=21a p 2+21b q 2+2a 1b 1pq ,c 1·c 3=(a 1+b 1)(a 1p 2+b 1q 2)=21a p 2+21b q 2+a 1b 1(p 2+q 2).由于p ≠q ,p 2+q 2>2pq ,又a 1、b 1不为零,因此≠22c c 1·c 3,故{c n }不是等比数列.例题10. n 2( n ≥4)个正数排成n 行n 列:其中每一行的数成等差数列,每一列的数成等比数列,并且所有公比相等已知a 24=1,163,814342==a a 求S=a 11 + a 22 + a 33 + … + a nn解: 设数列{1k a }的公差为d , 数列{ik a }(i=1,2,3,…,n )的公比为q则1k a = a 11 + (k -1)d , a kk = [a 11 + (k -1)d]q k -1依题意得:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+==+==+=163)2(81)(1)3(31143311421124q d a a q d a a q d a a ,解得:a 11 = d = q = ±21 又n 2个数都是正数,∴a 11 = d = q = 21 , ∴a kk = kk2n n S 212132122132⨯++⨯+⨯+=Λ,1432212132122121+⨯++⨯+⨯+=n n S Λ,两式相减得:n n nS 22121--=-例题11. 已知函数3()log ()f x ax b =+的图象经过点)1,2(A 和)2,5(B ,记()*3,.f n n a n N =∈(1)求数列}{n a 的通项公式;(2)设n n n nn b b b T a b +++==Λ21,2,若)(Z m m T n ∈<,求m 的最小值;(3)求使不等式12)11()11)(11(21+≥+++n p a a a nΛ对一切*N n ∈均成立的最大实数p .解:(1)由题意得⎩⎨⎧=+=+2)5(log 1)2(log 33b a b a ,解得⎩⎨⎧-==12b a ,)12(log )(3-=∴x x f *)12(log ,1233N n n a n n ∈-==- (2)由(1)得n n n b 212-=, nn n n n T 2122322523211321-+-++++=∴-Λ ① 1132212232252232121+--+-+-+++=n n n n n n n T Λ ② ①-②得)21212121(2121n 22222222221T 211n 2n 2111n n 1n 321n --+-+++++=--+++++=ΛΛ1n 1n 1n 21n 2212321n 2+-+---=--.n n 2n n 23n 2321n 2213T +-=---=∴-, 设*,232)(N n n n f n ∈+=,则由1512132121)32(252232252)()1(1<+≤++=++=++=++n n n n n n f n f n n 得*,232)(Nn n n f n ∈+=随n 的增大而减小+∞→∴n 当时,3→n T 又)(Z m m T n ∈<恒成立,3min =∴m(3)由题意得*21)11()11)(11(121N n a a a n p n ∈++++≤对Λ恒成立记)11()11)(11(121)(21n a a a n n F ++++=Λ,则 ()()11n 21n 2)1n ()1n (4)1n (2)3n 2)(1n 2(2n 2)a 11()a 11)(a 11(1n 21)a 11)(a 11()a 11)(a 11(3n 21)n (F )1n (F 2n 211n n 21=++>+-++=+++=+++++++++=++ΛΛ)(),()1(,0)(n F n F n F n F 即>+∴>Θ是随n 的增大而增大)(n F 的最小值为332)1(=F ,332≤∴p ,即332max =p .(二)证明等差与等比数列 1. 转化为等差等比数列.例题12. 数列{}n a 中,2,841==a a 且满足n n n a a a -=++122,*N n ∈. ⑴求数列{}n a 的通项公式;⑵设||||||21n n a a a S +++=Λ,求n S ;⑶设n b =1(12)n n a -**12(),()N N n n n T b b b n ∈=+++∈L ,是否存在最大的整数m ,使得对任意*N n ∈,均有>n T 32m成立?若存在,求出m 的值;若不存在,请说明理由.解:(1)由题意,n n n n a a a a -=-+++112,}{n a ∴为等差数列,设公差为d , 由题意得2832d d =+⇒=-,82(1)102n a n n ∴=--=-. (2)若50210≤≥-n n 则,||||||,521n n a a a S n +++=≤Λ时21281029,2n na a a n n n +-=+++=⨯=-L6n ≥时,n n a a a a a a S ---+++=ΛΛ765212555()2940n n S S S S S n n =--=-=-+故⎪⎩⎪⎨⎧+--=40n 9n n n 9S 22n 56n n ≤≥ (3)11111()(12)2(1)21n n b n a n n n n ===--++Q ,∴n T 1111111111[(1)()()()()]22233411n n n n =-+-+-++-+--+L .2(1)n n =+若32n m T >对任意*N n ∈成立,即116n mn >+对任意*N n ∈成立,*()1N n n n ∈+Q的最小值是21,1,162m ∴<m ∴的最大整数值是7.即存在最大整数,7=m 使对任意*N n ∈,均有.32n m T >例题13. 已知等比数列{}n b 与数列{}n a 满足3,n an b n =∈N *. (1)判断{}n a 是何种数列,并给出证明; (2)若8131220,a a m b b b +=L 求.解:(1)设{}n b 的公比为q ,∵3n an b =,∴()q log 1n a a 3q 331n a 1n a n 1-+=⇒=⋅-。
高考模拟试题_广东省东莞市六校2016届高三上学期联考文科数学试卷_人教新课标

第Ⅱ卷
本卷包括必考题和选考题两部分。第 13--21 题为必考题,每个试题考生都必须作答。 第 22--24 题为选考题,考生根据要求作答. 二、填空题(本大概题共 4 小题,每小题 5 分,共 20 分)
x + y ≥ 1 13.(虎中)若变量 x,y 满足约束条件 y − x ≤ 1 ,则= z 2 x − y 的最小值为 x ≤1
[60, 65) , [65, 70 ) , [70, 75) , [75,80 ) , [80,85) , [85,90 )
后得到如图的频率分布直方图. (1)求这 40 辆小型车辆车速的众数和中位数的估计值. (2)若从车速在 [ 60, 70 ) 的车辆中任抽取 2 辆,求车速在 [ 65, 70 ) 的车辆恰有一辆的概率. 19.(厚中) (本小题满分 12 分)某公司生产的某产品每件成本为 40 元,经市场调查整理出 如下信息: ①该产品 90 天内日销量( m 件)与时间(第 x 天)满足一次函数关系,部分数据如
c sin A + 3a cos C = 0
⑴ 求 C 的值; ⑵ 若 cos A =
3 , c = 5 3 ,求 sin B 和 b 的值. 5
18. (济中) (本小题满分 12 分) 2014 年“双节”期间,高速公路车辆较多.某调查公司 在一服务区从七座以下小型汽车中按进服务区的先后每间隔 50 辆就抽取一辆的抽样方法抽取 40 名驾驶员进行询问调查, 将他们在某段高速公路的车速(km/t)分成六段:
.
14. (厚中)圆 O 是等边 ∆ABC 的内切圆,在 ∆ABC 内任取一点 P,则点 P 落在圆
2
O 内的概率是
广东省东莞市2016届高三上学期期末调研测试数学文试题 含解析

东莞市2016届高三上学期期末调研测试数学(文)试题一、选择题(共12小题,60分)(1)若复数z 满足(1)3z i i +=+,其中i 是虚数单位,则复数z 的其轭复数为(A )2+i (B)2-i (C)-2+i (D )-2-i(2)已知全集U =R ,集合A ={}2|l g (2)2x o x -<,UC B =(,1)[4,)-∞+∞,则A B=(A )(4,6] (B )[1,6) (C )(2,4] (D)(2,4)(3)已知命题:p m R ∃∈,使得函数32()(1)2f x x m x =+--是奇函数,命题q :向量1122(,),(,)a x y b x y ==,则“1122xy x y ="是“a b ”的充要条件,则下列命题为真命题的是(A )p q ∧ (B )()p q ⌝∧ (C )()p q ∧⌝ (D )()()p q ⌝∧⌝ (4)网上大型汽车销售店销售某品牌A 型汽车,在2015双十一期间,进行了降价促销,该型汽车的价格与月销售量之间有如下关系:已知A 型汽车的购买量y 与价格x 符合如下线性回归方程:80y bx =+,若A 型汽车价格降到19万元,预测月销售量大约是(A )39 (B)42 (C)45 (D)50 (5)已知圆22()4x m y -+=上存在两点关于直线20x y --=对称,若离心率为2的双曲线22221(0,0)x y a b a b-=>>的两条渐近线与圆相交,则它们的交点构成的图形的面积为 (A )1 (B)3(C)23 (D )4(6)已知一个几何体的三视图如图所示,图中小正方形的边长为1,则该几何体的体积为(A )103(B )4 (C )6 (D )10(7)已知点P(t ,3)为锐角ϕ终边上的一点,且cos 2t ϕ=,若函数()2sin()(0)f x x ωϕω=+>的图象与直线y=2相邻的两交点之间的距离为π,则函数()f x 的一条对称轴方程为(A )12x π= (B )6x π= (C )3x π= (D )2x π=(8)在△ABC 中,||||AB CA CB =+,||4,||3CA CB ==,2BP PA =,则CP AB 的值为 (A)233(B )72- (C )-233(D )-8(9)已知各项为正的数列{}na 的前n 项的乘积为nT ,点(2,15)nT nn -在函数12log y x =的图象上,则数列{}2log na 的前10项和为 (A )-140 (B )100 (C )124 (D )156(10)执行如右图所示的程序框图,输出的结果为1538,则判断框内可填入的条件为(A)n >6? (B)n >7? (C)n >8? (D )n >9? (11)设抛物线E :22(0)ypx p =>的焦点为F,点M 为抛物线E 上一点,|MF |的最小值为3,若点P 为抛物线E 上任意一点,A(4,1),则|PA |+|PF |的最小值为(A )4+32(B)7 (C )4+23(D )10(12) 如图,某时刻P 与坐标原点重合,将边长为2的等边三角形PAB 沿x 轴正方向滚动,设顶点P (x,y )的轨迹方程是y =f(x ),若对于任意的t ∈[1,2],函数()g x =32(4)[(4)]2f mxx f x +-++在区间(t ,3)上都不是单调函数,则m 的取值范围为(A) (-373,-5) (B) (-9,-5) (C ) (-373,-9) (D )(-∞,-373)第II 卷二、填空题(共20分)(13)如图,等腰直角三角形ABC ,|AB 2L ,三角形ABC绕直线L 旋转一周,得到的几何体的体积为(14)已知函数1,10()10lg(2),10x x f x x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪-+>⎩,若2(8)(2)f m f m -<,则实数m 的取值范围是(15)已知实数x ,y满足4230y x x y x y ≥⎧⎪+≤⎨⎪+-≥⎩,则12x z y ⎛⎫=- ⎪⎝⎭的取值范围为(16)已知各项为正的等比数列{}na 的前n 项和为nS ,430S =,过点P(2,logn n a )和Q (212,logn n a ++)(*n N ∈)的直线的斜率为1,设2122212log log log n nn na ba a ++=,则数列{}nb 的前n 项和为nT =三、解答题(17)(本小题满分12分)已知△ABC 中,角A ,B,C 所对的分别为,,a b c ,设3(,),(cos ,)2m a n C c ==,且m n b =。
广东省东莞市东莞中学2016届高三第一次月考数学(理)试题Word版含答案

绝密★启封并使用完毕前试题类型:A2015-2016第一学期教学质量自查高三理科数学一、选择题(本题共12题,每题5分,满分60分)1.已知集合{1,0,1}A =-,{|11}B x x =-≤<,则A B =( ) A. {0} B. {0,1} C. {1,0}- D. {1,0,1}-2、若复数=+=z i iiz 为虚数单位),则(1( ) A 、1-i B 、1+i C 、-1-i D 、i 3、计算:=-+)8sin 8)(cos 8sin 8(cos ππππ( )A 、22 B 、22- C 、23 D 、23- 4、运行如图的程序框图,则输出s 的结果是( ) A. 16 B.2524 C.34 D.11125、某校开设A 类选修课2门,B 类选修课3门,一位同学从中选3门。
若要求两类课程至少选一门,则不同选法共有( )种 A 、3 B 、6 C 、9 D 、186、在边长为1的正方形OABC 中任取一点P ,则点P 恰好落在正方形与曲线y =围成的区域内(阴影部分)的概率为( )A .12B .23C .34D .457、已知等比数列}{n a 中,首项,11=a 公比,cos 2θ=q 前100项和0100=S ,则=θ( )A 、)(3Z k k ∈±ππ B 、)(32Z k k ∈±ππ C 、)(322Z k k ∈±ππ D 、以上都不对8、在△ABC 中,若,2222c b a =+则C cos 的最小值是( )A 、21B 、22-C 、23D 、23-OCxy =AB9、设函数|,|)(a x x x f -=若函数)(x f 在),3[+∞上单调递增,则a 的取值范围是( )A 、]3,(--∞B 、]0,3[-C 、]3,0(D 、]3,(-∞10、给定区域D :⎪⎩⎪⎨⎧≥≤+≥+0444x y x y x ,令点集上取得在是D y x z y x Z y x y x T +=∈=),(,,|,{(000000}最大值或最小值的点,则T 中的点共确定( )条不同的直线A 、3B 、4C 、5D 、611、若点P 为共焦点的椭圆1C 和双曲线2C 的一个交点,1F 、2F 分别是它们的左右焦点。
东莞市高中数学高三备考交流材料

东莞市高中数学高三备考交流材料三角函数与平面向量 东莞高级中学 赵永红【三角函数部分】一、近三年广东省数学卷三角函数部分分析再看全国高考题可以发现:2004年,在15套试题中,除辽宁、上海两个省市没有命制三角函数解答试题外,其他的13道三角函数解答题,均处在解答题的第一个位置,涉及三角形的三角函数题有3题;三角函数知识内部综合的有11道,与学科外的知识(数列、向量)综合的有2道。
2005年,高考的16套试题中,出现三角函数解答试题的有12套,其中涉及三角形的三角函数求值7道,关联三角形的求值的4道,一求三角函数的最值或值域的有2道,与导数结合的有3道。
2006年,高考的18套试题中,出现三角函数解答试题的有18道(江苏没有,但上海有2道,其中一个为三角函数应用题),其中涉及三角形的有6道,求三角函数的最值的8道,和向量结合的4道。
由此可见:三角函数解答题是高考命题的一个常考的基础性题形,其命题的热点是章节内部的三角函数求值、图象的性质问题,命题的冷点是跨章节的学科综合问题。
二、课标解读:新课程标准(讨论搞): 1.三角函数(1)任意角的概念、弧度制 ① 了解任意角的概念.② 了解弧度制概念,能进行弧度与角度的互化. (2)三角函数① 理解任意角三角函数(正弦、余弦、正切)的定义. ② 能利用单位圆中的三角函数线推导出±π2α,π±α的正弦、余弦、正切的诱导公式,能画出sin ,cos ,tan y x y x y x ===的图像,了解三角函数的周期性.③ 理解正弦函数、余弦函数在区间[0,2π]的性质(如单调性、最大和最小值与x 轴交点等).理解正切函数在区间(2,2ππ-)的单调性. ④ 理解同角三角函数的基本关系式:,1cos sin 22=+x x.tan cos sin x xx= ⑤ 了解函数sin()y A x ωϕ=+的物理意义;能画出sin()y A x ωϕ=+的图像,了解参数,,A ωϕ对函数图像变化的影响.⑥ 了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一些简单实际问题 2.简单的三角恒等变换能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆). 解三角形(1)正弦定理和余弦定理掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.(2) 应用能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.新课标强调三角函数是描述周期现象的重要函数模型,重点是三角函数的图象性质(含三角形应用)和应用。
2016届广东省高考数学二轮专题复习推理与证明02

1. 将全体正奇数排成一个三角形数阵:按照以上排列的规律,第45行从左向右的第17个数为________. 答案 2 013【详细分析】观察数阵,记第n 行的第1个数为a n ,则有 a 2-a 1=2, a 3-a 2=4, a 4-a 3=6, a 5-a 4=8, ……a n -a n -1=2(n -1).将以上各等式两边分别相加,得a n -a 1=2+4+6+8+…+2(n -1)=n (n -1), 所以a n =n (n -1)+1,所以a 45=1 981.又从第3行起数阵每一行的数都构成一个公差为2的等差数列,则第45行从左向右的第17个数为1 981+16×2=2 013.2. 在计算“1×2+2×3+…+n (n +1)”时,某同学学到了如下一种方法:先改写第k 项,k (k +1)=13[k (k +1)(k +2)-(k -1)k (k +1)],由此得1×2=13(1×2×3-0×1×2),2×3=13(2×3×4-1×2×3),…n (n +1)=13[n (n +1)(n +2)-(n -1)n (n +1)].相加,得1×2+2×3+…+n (n +1)=13n (n +1)(n +2).类比上述方法,计算“1×2×3+2×3×4+…+n (n +1)(n +2)”的结果为________. 答案 14n (n +1)(n +2)(n +3)【详细分析】类比k (k +1)=13[k (k +1)(k +2)-(k -1)k (k +1)],可得到k (k +1)(k +2)=14[k (k +1)(k +2)(k +3)-(k -1)k (k +1)(k +2)],先逐项裂项,然后累加即得14n (n +1)(n +2)(n +3).(推荐时间:60分钟)一、填空题1. 下列关于五角星的图案构成一个数列,该数列的一个通项公式是________.答案 a n =n (n +1)2【详细分析】从图中观察五角星构成规律, n =1时,有1个; n =2时,有3个; n =3时,有6个; n =4时,有10个;…所以a n =1+2+3+4+…+n =n (n +1)2.2. 已知结论:在正三角形ABC 中,若D 是边BC 的中点,G 是三角形ABC 的重心,则AG GD=2.若把该结论推广到空间中,则有结论:在棱长都相等的四面体ABCD 中,若△BCD 的中心为M ,四面体内部一点O 到四面体各面的距离都相等,则AOOM 等于________.答案 3【详细分析】设四面体内部一点O 到四面体各面都相等的距离为d ,则题意知d =OM ,设各个面的面积为S ,则由等体积法得:4·13S ·OM =13S ·AM,4OM =AM =AO +OM ,从而AOOM =31=3. 3. 已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个数对是________. 答案 (5,7)【详细分析】依题意,就每组整数对的和相同的分为一组,不难得知每组整数对的和为n +1,且每组共有n 个整数时,这样的前n 组一共有n (n +1)2个整数时,注意到10(10+1)2<60<11(11+1)2,因此第60个整数对处于第11组(每对整数对的和为12的组)的第5个位置,结合题意可知每对整数对的和为12的组中的各数对依次为(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个整数对是(5,7).4. 已知正三角形内切圆的半径是其高的13,把这个结论推广到空间正四面体,类似的结论是________________________________________________________________________. 答案 正四面体的内切球的半径是其高的14【详细分析】原问题的解法为等面积法, 即S =12ah =3×12ar ⇒r =13h ,类比问题的解法应为等体积法, V =13Sh =4×13Sr ⇒r =14h ,即正四面体的内切球的半径是其高的14.5. 把非零自然数按一定的规则排成了如图所示的三角形数表(每行比上一行多一个数).设a ij (i 、j ∈N *)是位于这个三角形数表中从上往下数第i 行、从左往右数第j 个数,如a 42=8,若a ij =2 014,则i ,j 的值的和为________.答案 79【详细分析】观察偶数行的变化规律,2 014是数列:2,4,6,8,…的第1 007项,前31个偶数行的偶数的个数为(2+62)×312=32×31=992,所以2 014是偶数行的第32行第15个数,即三角形数表中的第64行第15个数,所以i =64,j =15,所以i +j =79. 6. 有一个奇数列1,3,5,7,9,…,现在进行如下分组:第一组含一个数{1},第二组含两个数{3,5},第三组含三个数{7,9,11},第四组含四个数{13,15,17,19},…,现观察猜想每组内各数之和为a n 与其组的编号数n 的关系为________. 答案 a n =n 3【详细分析】由题意知a 1=1=13,a 2=3+5=8=23,a 3=7+9+11=27=33,a 4=13+15+17+19=64=43,….因此可归纳出a n =n 3.7. 观察下列等式:(1+1)=2×1(2+1)(2+2)=22×1×3(3+1)(3+2)(3+3)=23×1×3×5 …照此规律,第n 个等式可为______________. 答案 (n +1)(n +2)…(n +n )=2n ×1×3×…×(2n -1)【详细分析】由已知的三个等式左边的变化规律,得第n 个等式左边为(n +1)(n +2)…(n+n ),由已知的三个等式右边的变化规律,得第n 个等式右边为2n 与n 个奇数之积,即2n ×1×3×…×(2n -1).8. 如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n 个数,且两端的数均为1n ,每个数是它下一行左右相邻两数的和,如11=12+12,12=13+16,13=14+112,…,则第10行第3个数(从左往右数)为________.答案1360【详细分析】由上面的规律可知第n 行的第一个数为1n ,第二个数为1n (n -1),所以第9行的第二个数为18×9,第10行的第一个数为110,第二个数为19×10=190,设第3个数为x ,即x +190=19×8⇒x =1360.9. 对大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”:23⎩⎨⎧35,33⎩⎪⎨⎪⎧7911,43⎩⎪⎨⎪⎧13151719,….仿此,若m 3的“分裂数”中有一个是59,则m 的值为________.答案 8【详细分析】由已知可观察出m 3可分裂为m 个连续奇数,最小的一个为(m -1)m +1.当m =8 时,最小的数为57,第二个便是59.∴m =8. 二、解答题10.已知a >0且a ≠1,f (x )=1a x+a. (1)求值:f (0)+f (1),f (-1)+f (2);(2)由(1)的结果归纳概括对所有实数x 都成立的一个等式,并加以证明; (3)若n ∈N *,求和:f (-(n -1))+f (-(n -2))+…+f (-1)+f (0)+f (1)+…+f (n ). 解 (1)f (0)+f (1)=11+a +1a +a =1a =aa, f (-1)+f (2)=1a -1+a +1a 2+a =1a =aa .(2)由(1)归纳得到对一切实数x ,有f (x )+f (1-x )=a a. 证明如下f (x )+f (1-x )=1a x +a +1a 1-x +a=1a x +a +a xa (a +a x ) =a +a x a (a +a x )=1a =a a. (3)设S =f (-(n -1))+f (-(n -2))+…+f (-1)+f (0)+f (1)+…+f (n ), 又S =f (n )+f (n -1)+…+f (2)+f (1)+f (0)+…+f (-(n -1)), 两式相加,得(由(2)的结论) 2S =2n ·a a ,∴S =n a a.11.等差数列{a n }的前n 项和为S n ,a 1=1+2,S 3=9+3 2.(1)求数列{a n }的通项a n 与前n 项和S n ;(2)设b n =S nn(n ∈N *),求证:数列{b n }中任意不同的三项都不可能成为等比数列.(1)解 由已知得⎩⎨⎧a 1=2+1,3a 1+3d =9+32,∴d =2,故a n =2n -1+2,S n =n (n +2). (2)证明 由(1)得b n =S nn=n + 2.假设数列{b n }中存在三项b p ,b q ,b r (p ,q ,r 互不相等)成等比数列,则b 2q =b p b r .即(q +2)2=(p +2)(r +2). ∴(q 2-pr )+(2q -p -r )2=0.∵p ,q ,r ∈N *,∴⎩⎪⎨⎪⎧q 2-pr =0,2q -p -r =0,∵(p +r 2)2=pr ,(p -r )2=0,∴p =r .与p ≠r 矛盾.所以数列{b n }中任意不同的三项都不可能成等比数列.12.设数列{a n }的前n 项和为S n ,并且满足2S n =a 2n +n ,a n >0(n ∈N *).(1)求a 1,a 2,a 3;(2)猜想{a n }的通项公式,并加以证明;(3)设x >0,y >0,且x +y =1,证明:a n x +1+a n y +1≤2(n +2). (1)解 分别令n =1,2,3,得⎩⎪⎨⎪⎧2a 1=a 21+1,2(a 1+a 2)=a 22+2,2(a 1+a 2+a 3)=a 23+3,∵a n >0,∴a 1=1,a 2=2,a 3=3. (2)解 猜想:a n =n , 由2S n =a 2n +n ,① 可知,当n ≥2时,2S n -1=a 2n -1+(n -1),②①-②,得2a n =a 2n -a 2n -1+1,即a 2n =2a n +a 2n -1-1. (ⅰ)当n =2时,a 22=2a 2+12-1,∵a 2>0,∴a 2=2;(ⅱ)假设当n =k (k ≥2)时,a k =k . 那么当n =k +1时,⇒[a k +1-(k +1)][a k +1+(k -1)]=0, ∵a k +1>0,k ≥2,∴a k +1+(k -1)>0, ∴a k +1=k +1.这就是说,当n =k +1时也成立, ∴a n =n (n ≥2).显然n =1时,也适合. 故对于n ∈N *,均有a n =n .(3)证明 要证a n x +1+a n y +1≤2(n +2). 即证nx +1+ny +1≤2(n +2),只要证nx +1+2(nx +1)(ny +1)+ny +1≤2(n +2), 即n (x +y )+2+2n 2xy +n (x +y )+1≤2(n +2), 将x +y =1代入,得2n 2xy +n +1≤n +2, 即要证4(n 2xy +n +1)≤(n +2)2,即4xy ≤1. ∵x >0,y >0,且x +y =1,∴xy ≤x +y 2=12,即xy ≤14,故4xy ≤1成立,所以原不等式成立.。
2016届高考数学总复习课件:第5章-第2节 等差数列及其前n项和

战 沙 场
切
点
脉 搏
[(2n+1+3)-3]=1,
兵
核
心 突 破
∴数列{bn}是首项为a1+2 3=-32+3=0,公差为 1 的等差 课
时
数列.
提 升
练
菜单
第十六页,编辑于星期五:二十一点 四分。
高三总复习·数学(理)
提
考向二 等差数列的基本运算
素
养
满
分
研
[典例剖析]
指
动
导
向
考 纲
【例 2】 (2014·浙江高考)已知等差数列{an}的公差 d>
高三总复习·数学(理)
提
素
养
满
分
研
指
动
导
向
考
纲
考
演
向
实
第二节 等差数列及其前 n 项和
战 沙
场
切
点
脉
兵
搏
核
心
突
破
课
时
提
升
练
菜单
第一页,编辑于星期五:二十一点 四分。
高三总复习·数学(理)
提
素
养
满
分
研
指
动
导
向
考
纲 考
考纲要求 1.理解等差数列的概念.2.掌握等差数列的通项 演
向
实
公式.3.了解等差数列与一次函数的关系.4.等差数列的基本量
养
满
分
研
指
动
导
向 考
1.等差数列运算问题的通性通法
纲
考 向
(1)等差数列运算问题的一般求法是设出首项 a1 和公差
