高中数学原创试题(8)
高中数学测试题及答案doc原创

高中数学测试题及答案doc原创一、选择题(每题4分,共40分)1. 下列哪个选项不是实数集的子集?A. 有理数集B. 整数集C. 无理数集D. 复数集答案:D2. 若函数f(x)=2x+1,则f(-1)的值为:A. -1B. 1C. 3D. -3答案:A3. 一个圆的半径为5,那么它的面积是:A. 25πB. 50πC. 100πD. 25答案:B4. 等差数列{an}的首项a1=3,公差d=2,那么a5的值为:A. 13B. 11C. 9D. 7答案:A5. 已知集合A={1,2,3},B={2,3,4},则A∩B的值为:A. {1}B. {2,3}C. {3,4}D. {1,2,3,4}答案:B6. 函数y=x^2-4x+3的顶点坐标是:A. (2,-1)B. (2,1)C. (-2,1)D. (-2,-1)答案:A7. 一个等腰三角形的两边长分别为3和4,那么它的周长是:A. 10B. 11C. 12D. 13答案:C8. 已知数列{an}满足a1=1,an+1=2an+1,那么a3的值为:A. 7B. 5C. 3D. 1答案:A9. 函数y=1/x的图像关于:A. 原点对称B. y轴对称C. x轴对称D. 直线y=x对称答案:A10. 一个正方体的体积为27,那么它的表面积是:A. 54B. 108C. 216D. 486答案:A二、填空题(每题4分,共20分)1. 若sinα=3/5,且α为锐角,则cosα=______。
答案:4/52. 一个数列的前三项为1,2,4,从第四项开始,每一项是前三项的和,那么这个数列的第五项是______。
答案:73. 已知函数f(x)=x^3-3x+1,求f'(x)=______。
答案:3x^2-34. 一个圆的直径为10,那么它的周长是______。
答案:π*105. 一个等比数列的首项为2,公比为3,那么它的第五项是______。
答案:486三、解答题(每题10分,共40分)1. 已知函数f(x)=x^2-6x+8,求函数的顶点坐标和对称轴。
高中数学立体几何测试题(10套)

∴ BD ∥平面 PMN ,
位置关系为
平行
。
∴ O 到平面 PMN 的距离即为 BD 到平面 PMN 的距离。
11 、a,b 为异面直线,且 a,b 所成角为 40 °,直线 c 与 a,b 均异面,且所成角均为
∵ BD ⊥ AC , MN ∥ BD
∵ PA⊥面 ABCD
θ,若这样的 c 共有四条,则 θ的范围为 (70 °, 90° ) 。
D
C
A
B
D1 A1
C1 B1
17 、 已知异面直线 a, b 的公垂线段 AB 的中点为 O,平面 满足 a∥ , b∥ , 且 O , M 、 N 是 a, b 上的任意两点, MN ∩ = P,求证: P 是 MN 的中
点
A aM
O
P
BN b
.
立几面测试 001
参考答 案
一、 1- 8 ACDDBDBA
2、已知 m, n 为异面直线, m∥平面 , n∥平面 , ∩ =l ,则 l( ) ( A)与 m, n 都相交 ( B)与 m,n 中至少一条相交 ( C)与 m, n 都不相交 ( D )与 m, n 中一条相交
3、已知 a, b 是两条相交直线, a∥ ,则 b 与 的位置关系是 ( )
A 、 b∥
PAM
∵ AB=2 , BM=1 , CM=1
∴ AM= 5 ,
P
A H
O
.
B
F M
B
D N C
立几面测试 003
一、选择题
1.异面直线是指
(A) 在空间内不能相交的两条直线
(B) 分别位于两个不同平面的两条直线
(C) 某一个平面内的一条直线和这个平面外的一条直线
高中数学试卷原创题

一、选择题(每题5分,共60分)1. 已知函数f(x)=2x²-3x+1,则f(-1)的值为()A. -4B. -2C. 2D. 42. 若log₂(x-1)+log₂(x+1)=3,则x的值为()A. 2B. 3C. 4D. 53. 已知等差数列{an}的前n项和为Sn,若S₂=5,S₄=14,则a₁₀的值为()A. 11B. 12C. 13D. 144. 在△ABC中,若sinA=3/5,cosB=1/2,则sinC的值为()A. 1/10B. 1/5C. 3/10D. 2/55. 已知集合A={x|0<x<1},B={x|-1<x<0},则A∪B=()A. {x|-1<x<0}B. {x|0<x<1}C. {x|-1<x<1}D. {x|x<-1或x>1}6. 若(1+i)²=a+bi,则a+b的值为()A. 0B. 1C. 2D. 37. 已知函数f(x)=x³-2x²-5x+6,则方程f(x)=0的三个根之和为()A. -2B. -1C. 1D. 28. 若(cosθ+isinθ)⁴=a+bi,则a的值为()A. -1B. 0C. 1D. 29. 在平面直角坐标系中,点P(-1,2)关于直线y=x的对称点坐标为()A. (1,-2)B. (2,-1)C. (-2,1)D. (-1,2)10. 已知双曲线C: x²/a²-y²/b²=1(a>0,b>0)的左、右顶点分别为F₁(-c,0),F₂(c,0),若|F₁F₂|=8,则双曲线C的方程为()A. x²/16-y²/12=1B. x²/12-y²/16=1C. x²/16+y²/12=1D. x²/12+y²/16=111. 设f(x)是定义在R上的奇函数,且f(1)=2,则f(-3)的值为()A. -6B. -2C. 2D. 612. 已知椭圆C: x²/a²+y²/b²=1(a>b>0)的焦点为F₁,F₂,若|F₁F₂|=6,且C的右顶点坐标为(5,0),则椭圆C的方程为()A. x²/25+y²/16=1B. x²/16+y²/25=1C. x²/25+y²/9=1D. x²/9+y²/25=1二、填空题(每题5分,共20分)1. 已知log₂8=3,则log₄32=________。
人教版高中数学必修4综合测试试题含答案(原创,难度适中)

人教版高中数学必修4综合测试试题含答案(原创,难度适中)高中数学必修4综合测试满分:150分时间:120分钟注意事项:客观题请在答题卡上用2B铅笔填涂,主观题请用黑色水笔书写在答题卡上。
一、选择题:(共12小题,每小题5分,共60分。
)1.sin300°的值为A。
-31 B。
3 C。
22 D。
1/22.角α的终边过点P(4,-3),则cosα的值为A。
4 B。
-3 C。
2/5 D。
-4/53.cos25°cos35°-sin25°sin35°的值等于A。
3/11 B。
3/4 C。
2/11 D。
-2/114.对于非零向量AB,BC,AC,下列等式中一定不成立的是A。
AB+BC=AC B。
AB-AC=BCC。
AB-BC=BC D。
AB+BC=AC5.下列区间中,使函数y=sinx为增函数的是A。
[0,π] B。
[π,2π] C。
[-π/2,π/2] D。
[-π,0]6.已知tan(α-π/3)=1/√3,则tanα的值为A。
4/3 B。
-3/5 C。
-5/3 D。
-3/47.将函数y=sinx图象上所有的点向左平移π/3个单位长度,再将图象上所有的点的横坐标伸长到原来的2倍(纵坐标不变),则所得图象的函数解析式为A。
y=sin(2x+π/3) B。
y=sin(2x+2π/3)C。
y=sin(2x-π/3) D。
y=sin(2x-2π/3)8.在函数y=sinx、y=sin(2x+π/2)、y=cos(2x+π)中,最小正周期为π的函数的个数为()A。
1个 B。
2个 C。
3个 D。
4个9.下列命题中,正确的是A。
|a|=|b|→a=b B。
|a|>|b|→a>bC。
|a|=0→a=0 D。
a=b→a∥b10.函数y=Asin(ωx+φ)在一个周期内的图象如右图所示,此函数的解析式为y=2sin(2x-π/3)11.方程sin(πx)=x的解的个数是()A。
第7绝对值函数

Y.P.M 数学竞赛讲座 1绝对值函数在这里绝对值函数f(x)特指函数f(x)=a 1|x-x 1|+a 2|x-x 2|+…+a n |x-x n |.1.图像变换[例1]:(1989年全国高中数学联赛试题)设函数f 0(x)=|x|,f 1(x)=|f 0(x)-1|,f 2(x)=|f 1(x)-2|,则函数y=f 2(x)的图像与x 轴所围成图形中的封闭部分的面积是_________.[解析]:[评注]:①函数y=f(|x|)是偶函数,图像关于y 轴对称,在y 轴右侧的图像与y=f(x)的图像重合;②函数y=|f(x)|是非负函数,y=f(x)在x 轴上方的图像与y=|f(x)|的图像重合,y=f(x)在x 轴下方的图像与y=|f(x)|的图像关于轴对称.[类题]:1.(2006年湖北高考试题)关于x 的方程(x 2-1)2-|x 2-1|+k=0,给出下列四个命题:①存在实数k,使得方程恰有2个不同的实根; ②存在实数k,使得方程恰有4个不同的实根; ③存在实数k,使得方程恰有5个不同的实根; ④存在实数k,使得方程恰有8个不同的实根.其中假命题的个数是( )(A)0 (B)1 (C)2 (D)32.(2005年上海高考试题)设定义域为R 的函数f(x)=⎩⎨⎧=≠-1,01||,1|lg |x x x ,则关于x 的方程f 2(x)+bf(x)+c=0有7个不同实数解的充要条件是( )(A)b<0,且c>0 (B)b<0,且c=0 (C)b>0,且c<0 (D)b ≥0,且c=03.(1986年全国高中数学联赛试题)已知f(x)=|1-2x|,x ∈[0,1].那么方程f(f(f(x)))=21x 的解的个数是 . 2.几何意义[例2]:(2005年全国高中数学联赛北京初赛试题)2005个实数x 1,x 2,…,x 2005满足|x 1-x 2|+|x 2-x 3|+…+|x 2004-x 2005|+|x 2005 -x 1|=1,则|x 1|+|x 2|+…+|x 2005|的最小值等于 .[解析]:[评注]:数轴上的点P 、A 对应的实数分别是x 、a,则|PA|=|x-a|.这就是绝对值的几何意义.利用该几何意义可得|x-a|+ |x-b|≥|a-b|;|x-a|-|x-b|≤|a-b|.[类题]:1.(2011年全国高中数学联赛四川初赛试题)己知实数x 满足|2x+1|+|2x-5|=6,则x 的取值范围是 .2.(2009年重庆高考试题)不等式|x+3|-|x-1|≤a 2-3a 对任意实数x 恒成立,则实数a 的取值范围为( )(A)(-∞,-1]∪[4,+∞) (B)(-∞,-2]∪[5,+∞) (C)[1,2] (D)(-∞,1]∪[2,+∞)3.(2007年全国高中数学联赛天津初赛试题)在平面直角坐标系中定义两点P(x 1,y 1),Q(x 2,y 2)之间的交通距离为d(P,Q)=|x 1-x 2|+|y 1-y 2|.若C(x,y)到点A(1,3),B(6,9)的交通距离相等,其中实数x,y 满足0≤x ≤10,0≤y ≤10,则所有满足条件的点C 的轨迹的长之和为________. 3.三角不等[例3]:(2009年全国高中数学联赛安徽初赛试题)当实数a ∈ 时,不存在实数x,使得|x+a+1|+|x+a 2-2|<3.[解析]:[评注]:绝对值三角不等式:||a|-|b||≤|a ±b|≤|a|+|b|,|a-c|≤|a-b|+|b-c|.[类题]:1.(2009年辽宁高考试题)设函数f(x)=|x-1|+|x-a|.如果∀x ∈R,f(x)≥2,则a 的取值范围是 .2.(2004年第十五届希望杯全国数学邀请赛(高一)试题)对于任意实数x,若不等式|x-3|+|x-4|>a(a>0)恒成立,则实数a 应满足( )(A)0<a<1 (B)0<a ≤1 (C)a>1 (D)a ≥13.(2004年第十五届希望杯全国数学邀请赛(高一)试题)已知不等式|x-a|+|x-b|<1(其中a,b 是常数)的解集是空集,则2 Y.P.M 数学竞赛讲座 |a-b|的取值范围是( )(A)(-1,1) (B)(0,1) (C)[1,+∞) (D)(1,+∞)4.零点方法[例4]:(2002年全国高中数学联赛北京初赛试题)已知f(x+1)=|x-1|-|x+1|,且f(f(x))=f(2002)+1,则x= .[解析]:[评注]:零点法,即令函数f(x)中每个绝对值内的式子等于零,分别求出x 的值,并把求出的值表示在数轴上,然后按这些点把数轴分成的部分,由左至右分类去绝对值.[类题]:1.(1993年第四届希望杯全国数学邀请赛(高一)试题)函数f(x)=|2x-1|-|x-1|的最小值为_______.2.(2009年全国高中数学联赛四川初赛试题)若实数x 满足log 2x=1+cos θ,其中θ∈[-2π,0],则函数f(x)=|x-1|+2|x-3|的最大值等于 .3.(2007年第十八届“希望杯”全国数学邀请赛(高一)试题)函数y=2143--+x x +3168--+x x 的最小值为 ,此时x = . 5.二阶函数[例5]:(2007年全国高中数学联赛福建初赛试题)设函数f(x)=|1-2x|-3|x+1|,如果方程f(x)=a 恰有两个不同的实数根u,v,满足2≤|u-v|≤10,则实数a 的取值范围是 .[解析]:[评注]:二阶函数f(x)=a|x-x 1|+b|x-x 2|(x 1<x 2)有如下性质:①当a+b>0时,f(x)有最小值=min{f(x 1),f(x 2)},当a+b<0时,f(x)有最大值=max{f(x 1),f(x 2)},当a+b=0时,f(x)有最小值=min{f(x 1),f(x 2)},也有最大值=max{f(x 1),f(x 2)};②当且仅当a=b 时,f(x)的图像是轴对称图形,且对称轴为x=221x x +;③当且仅当a+b=0时,f(x)的图像是中心对称图形,且对称中心为(221x x +,f(221x x +)). [类题]:1.(2007年全国高中数学联赛试题)设实数a 使得不等式|2x-a|+|3x-2a|≥a 2对任意实数x 恒成立,则满足条件的a 所组成的集合是 .2.(2008年山东高考试题)设函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a 的值为( )(A)3 (B)2 (C)1 (D)-13.(2010年湖南高考试题)用min{a,b}表示a,b 两数中的最小值.若函数f(x)=min{|x|,|x+t|}的图像关于直线x=-21对称,则t 的值为( )(A)-2 (B)2 (C)-1 (D)1 6.最值问题[例6]:(2011年北大等十三校联考(北约)自主招生试题)函数f(x)=|x-1|+|2x-1|+…+|2011x-1|的最小值为_______.[解析]:[评注]:关于函数f(x)=a 1|x-x 1|+a 2|x-x 2|+…+a n |x-x n |有如下结论:①函数f(x)的极值在零点x 1,x 2,…,x n 处取得;②当a 1+a 2+…+a n >0时,f(x)有最小值;当a 1+a 2+…+a n <0时,f(x)有最大值;当a 1+a 2+…+a n =0时,f(x)有最小值,也有最大值;③当|a i |为正整数时,零点x i 计|a i |次,把这些零点由小到大的排列.当|a 1|+|a 2|+…+|a n |为奇数时,所有零点的中间数是其极值点;当|a 1|+|a 2|+…+|a n |为偶数时,所有零点的中间两数(包括这两个数)之间的任意一个数都是其极值点.[类题]:1.(2008年全国高中数学联赛四川初赛试题)函数f(x)=|x-1|+|x-3|+|x-5|+|x-7|的最小值为_______.2.⑴(2007年第十八届希望杯全国数学邀请赛(高二)试题)函数f(x)=∑=--101|)1 2(| nnx的最小值是( )(A)40 (B)50 (C)60 (D)80⑵(2006年全国Ⅱ高考试题)函数f(x)=∑=-191| |nnx的最小值为( )(A)190 (B)171 (C)90 (D)453.(2009年上海高考试题)某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点(-2,2),(3,1),(3,4),(-2,3),(4,5),(6,6)为报刊零售点.请确定一个格点(除零售点外)__________为发行站.使6个零售点沿街道到发行站之间路程的和最短.7.图象性质[例7]:(2007年全国高中数学联赛江苏初赛试题)(2008年全国高中数学联赛贵州初赛试题)已知f(x)=|x+1|+|x+2|+ …+|x+2007|+|x−1|+|x−2|+…+|x−2007|(x∈R),且f(a2−3a+2)=f(a−1),则a的值有( )(A)2个 (B)3个 (C)4个 (D)无数个[解析]:[评注]:关于函数f(x)=a1|x-x1|+a2|x-x2|+…+a n|x-x n|的图像有如下结论:①函数f(x)图像的两端是两条射线,这两条射线所在直线的斜率及在y轴上的截距分别互为相反数;②函数f(x)图像的是轴对称图形的充要条件是:所有零点关于其中位数对称,且关于中位数对称的两零点所对应的系数相等,其对称轴为x=中位数;③函数f(x)图像的是中心对称图形的充要条件是所有零点关于其中位数对称,关于中位数对称的两零点所对应的系数互为相反数,且所有系数和为零,其对称中心为(x0,f(x0)),其中x0为零点的中位数.奇数阶绝对值函数不是中心对称图形.[类题]:1.(2012北约自主招生试题)求x的范围,使得|x+2|+|x|+|x-1|是增函数.2.(原创题)若函数f(x)=|x+1|+2|x+a|+(b-1)|x+3|的图像为轴对称图形,则a+b= .3.(原创题)函数f(x)=|x-1|+|x-2|+…+|x-1006|-|x-1007|-|x-1008|-…-|x-2012|图像的对称中心为 .8.综合函数[例8]:(2009年全国高中数学联赛福建初赛试题)若对于任意的实数x,函数f(x)=x2-2x-|x-1-a|-|x-2|+4的值都是非负实数,则实数a的最小值为 .[解析]:[评注]:[类题]:1.(2005年全国Ⅱ高考试题)设函数f(x)=2|x+1|-|x-1|,则使f(x)≥22的x的取值范围为 .2.(2011年辽宁高考试题)已知函数f(x)=|x-2|-|x-5|.则不等式f(x)≥x2-8x+15的解集为 .3.(2008年广东高考试题)己知a∈R,若关于x的方程x2+x+|a-41|+|a|=0有实根,则a的取值范围是.绝对值函数在这里绝对值函数f(x)特指函数f(x)=a 1|x-x 1|+a 2|x-x 2|+…+a n |x-x n |.1.图像变换[例1]:(1989年全国高中数学联赛试题)设函数f 0(x)=|x|,f 1(x)=|f 0(x)-1|,f 2(x)=|f 1(x)-2|,则函数y=f 2(x)的图像与x 轴所围成图形中的封闭部分的面积是_________. y y y[解析]:f 0(x)=|x|,f 1(x)=|f 0(x)-1|, 1 2 f 2(x)=|f 1(x)-2|的图像如图: O -1 O 1 x 1其面积为8-1=7. -3 O 3 x [评注]:①函数y=f(|x|)是偶函数,图像关于y 轴对称,在y 轴右侧的图像与y=f(x)的图像重合;②函数y=|f(x)|是非负函数,y=f(x)在x 轴上方的图像与y=|f(x)|的图像重合,y=f(x)在x 轴下方的图像与y=|f(x)|的图像关于轴对称.[类题]:1.(2006年湖北高考试题)关于x 的方程(x 2-1)2-|x 2-1|+k=0,给出下列四个命题:①存在实数k,使得方程恰有2个不同的实根; ②存在实数k,使得方程恰有4个不同的实根; ③存在实数k,使得方程恰有5个不同的实根; ④存在实数k,使得方程恰有8个不同的实根.其中假命题的个数是( )(A)0 (B)1 (C)2 (D)3解:令f(x)=|x 2-1|,设方程(x 2-1)2-|x 2-1|+k=0的两根分别为y 1、y 2,则y 1+y 2=1,y 1y 2=k,k ≤41,且f(x)=y 1,f(x)=y 2,①由图知,方程恰有2个实根⇔y 1>1,y 2<0,如y 1=2,y 2=-1,k=-2满足条件,所以①正确;②由图知,方程恰有4个实根⇔y 1=y 2=21,k=41所以②正确;③由图知,方程恰有5个实根⇔y 1=1,y 2=0,k=0所以③正确;④由图知,方程恰有8个实根⇔y 1≠y 2,且y 1、y 2∈(0,1),如y 1=31,y 2=32,k=92满足条件,所以④正确.综上,正确命题的个数为4,假命题的个数为0,故选(A).2.(2005年上海高考试题)设定义域为R 的函数f(x)=⎩⎨⎧=≠-1,01||,1|lg |x x x ,则关于x 的方程f 2(x)+bf(x)+c=0有7个不同实数解的充要条件是( )(A)b<0,且c>0 (B)b<0,且c=0 (C)b>0,且c<0 (D)b ≥0,且c=03.(1986年全国高中数学联赛试题)已知f(x)=|1-2x|,x ∈[0,1].那么方程f(f(f(x)))=21x 的解的个数是 . 解:f(x)=|1-2x|=|2x-1|的图像如图: y y yf(f(x))=|2|2x-1|-1|的图像如图: 1(求该函数的零点41,43); O 21 x O 41 43 x O 81 41 43 87 x f(f(f(x)))=|2|2|2x-1|-1|-1|(求该函数的零点81,41,43,87),共有8个解. 由y=f(x)到y=|2f(x)-1|的变换:纵坐标伸长2倍,得值域[0,2];再向下平移1个单位,最后作绝对值变换.2.几何意义[例2]:(2005年全国高中数学联赛北京初赛试题)2005个实数x 1,x 2,…,x 2005满足|x 1-x 2|+|x 2-x 3|+…+|x 2004-x 2005|+|x 2005 -x 1|=1,则|x 1|+|x 2|+…+|x 2005|的最小值等于 .[解析]:在数轴上取点P i :x i ,则|x 1|+|x 2|+…+|x 2005|=|OP 1|+|OP 2|+…+|OP 2005|,|x 1-x 2|+|x 2-x 3|+…+|x 2004-x 2005|+|x 2005-x 1| =1⇔|P 1P 3|+|P 2P 3|+…+|P 2004P 2005|+|P 1P 2005|=1⇒2|P 1P 2005|≥1,为使|OP 1|+|OP 2|+…+|OP 2005|最小,取P 1,P 2…,P 2004为O,P 2004, 0.5⇒|x 1|+|x 2|+…+|x 2005|的最小值等于0.5.2 Y.P.M 数学竞赛讲座[评注]:数轴上的点P 、A 对应的实数分别是x 、a,则|PA|=|x-a|.这就是绝对值的几何意义.利用该几何意义可得|x-a|+ |x-b|≥|a-b|;|x-a|-|x-b|≤|a-b|.[类题]:1.(2011年全国高中数学联赛四川初赛试题)己知实数x 满足|2x+1|+|2x-5|=6,则x 的取值范围是 .2.(2009年重庆高考试题)不等式|x+3|-|x-1|≤a 2-3a 对任意实数x 恒成立,则实数a 的取值范围为( )(A)(-∞,-1]∪[4,+∞) (B)(-∞,-2]∪[5,+∞) (C)[1,2] (D)(-∞,1]∪[2,+∞)3.(2007年全国高中数学联赛天津初赛试题)在平面直角坐标系中定义两点P(x 1,y 1),Q(x 2,y 2)之间的交通距离为d(P,Q)=|x 1-x 2|+|y 1-y 2|.若C(x,y)到点A(1,3),B(6,9)的交通距离相等,其中实数x,y 满足0≤x ≤10,0≤y ≤10,则所有满足条件的点C 的轨迹的长之和为________.解:由条件得|x-1|+|y-3|=|x-6|+|y-9|.①当x ≤1,y ≤3时,无解;②当x ≤1,3≤y ≤9时,y=8.5,线段长为1;③当x ≤1,y ≥9时,无解;④当1≤x ≤6,y ≤3时,无解;⑤当1≤x ≤6,3≤y ≤9时,x+y=9.5,线段长为52;⑥当1≤x ≤6,y ≥9时,无解;⑦当x ≥6,y ≤3时,无解;⑧当x ≥6,3≤y ≤9时,y=3.5,线段长为4;⑨当x ≥6,y ≥9时,无解.综上所述,点C 的轨迹构成的线段的长之和为1+52+4=5(1+2). 3.三角不等[例3]:(2009年全国高中数学联赛安徽初赛试题)当实数a ∈ 时,不存在实数x,使得|x+a+1|+|x+a 2-2|<3.[解析]:不存在实数x,使得|x+a+1|+|x+a 2-2|<3⇔∀x ∈R,|x+a+1|+|x+a 2-2|≥3⇔|(a 2-2)-(a+1)|≥3⇔a 2-a ≤0,或a 2-a-6≥0⇔a ∈(-∞,-2]∪[0,1]∪[3,+∞). [评注]:绝对值三角不等式:||a|-|b||≤|a ±b|≤|a|+|b|,|a-c|≤|a-b|+|b-c|.[类题]:1.(2009年辽宁高考试题)设函数f(x)=|x-1|+|x-a|.如果∀x ∈R,f(x)≥2, 则a 的取值范围是 .2.(2004年第十五届希望杯全国数学邀请赛(高一)试题)对于任意实数x,若不等式|x-3|+|x-4|>a(a>0)恒成立,则实数a 应满足( )(A)0<a<1 (B)0<a ≤1 (C)a>1 (D)a ≥13.(2004年第十五届希望杯全国数学邀请赛(高一)试题)已知不等式|x-a|+|x-b|<1(其中a,b 是常数)的解集是空集,则|a-b|的取值范围是( )(A)(-1,1) (B)(0,1) (C)[1,+∞) (D)(1,+∞)4.零点方法[例4]:(2002年全国高中数学联赛北京初赛试题)已知f(x+1)=|x-1|-|x+1|,且f(f(x))=f(2002)+1,则x= .[解析]:f(x+1)=|x-1|-|x+1|⇒f(x)=|x-2|-|x|⇒f(x)=⎪⎩⎪⎨⎧>-≤≤-<)2(2)20(22)0(2x x x x ,f(2002)=-2⇒f(2002)+1=-1,①当x<0时,f(x)=2⇒f(f(x))=f(2)=-2;②当x>2时,f(x)=-2⇒f(f(x))=f(-2)=2;③当0≤x ≤2时,f(x)=2-2x ⇒f(f(x))= f(2-2x)=2|x|-2|x-1|=2x-2|x-1|=-1⇒2x+1=2|x-1|⇒x=41. [评注]:零点法,即令函数f(x)中每个绝对值内的式子等于零,分别求出x 的值,并把求出的值表示在数轴上,然后按这些点把数轴分成的部分,由左至右分类去绝对值.[类题]:1.(1993年第四届希望杯全国数学邀请赛(高一)试题)函数f(x)=|2x-1|-|x-1|的最小值为_______.2.(2009年全国高中数学联赛四川初赛试题)若实数x 满足log 2x=1+cos θ,其中θ∈[-2π,0],则函数f(x)=|x-1|+2|x-3|的最大值等于 .3.(2007年第十八届“希望杯”全国数学邀请赛(高一)试题)函数y=2143--+x x +3168--+x x 的最小值为 ,Y.P.M 数学竞赛讲座 3 此时x = .5.二阶函数[例5]:(2007年全国高中数学联赛福建初赛试题)设函数f(x)=|1-2x|-3|x+1|,如果方程f(x)=a 恰有两个不同的实数根u,v,满足2≤|u-v|≤10,则实数a 的取值范围是 .[解析]:因为函数f(x)=⎪⎪⎪⎩⎪⎪⎪⎨⎧>+-≤≤----<+)21)(4()211(25)1(4x x x x x x 的图像如图: 当a>3时,f(x)=a 无解;当a=3时,f(x)=a 只有一个解;当-29≤a<3时,直线y=a 与y=x+4和y=-5x-2有两个交点,故此时f(x)=a 有两个不同的解u=a-4,v=-51(a+2),2≤|u-v|≤10⇔-316≤a ≤34;当a<-29时,直线y=a 与y=x+4和y=-x-4有两个交点,故此时f(x)=a 有两个不同的解u=a-4,v=-(a+4),2≤|u-v|≤10⇔-5≤a ≤-1,得实数a 的取值范围是[-5,34]. [评注]:二阶函数f(x)=a|x-x 1|+b|x-x 2|(x 1<x 2)有如下性质:①当a+b>0时,f(x)有最小值=min{f(x 1),f(x 2)},当a+b<0时,f(x)有最大值=max{f(x 1),f(x 2)},当a+b=0时,f(x)有最小值=min{f(x 1),f(x 2)},也有最大值=max{f(x 1),f(x 2)};②当且仅当a=b 时,f(x)的图像是轴对称图形,且对称轴为x=221x x +;③当且仅当a+b=0时,f(x)的图像是中心对称图形,且对称中心为(221x x +,f(221x x +)). [类题]:1.(2007年全国高中数学联赛试题)设实数a 使得不等式|2x-a|+|3x-2a|≥a 2对任意实数x 恒成立,则满足条件的a 所组成的集合是 .解:令x=at,则原不等式为|a||2t-1|+|a||3t-2|≥a 2⇔|a|≤|2t-1|+|3t-2|⇔|a|≤31.2.(2008年山东高考试题)设函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a 的值为( )(A)3 (B)2 (C)1 (D)-13.(2010年湖南高考试题)用min{a,b}表示a,b 两数中的最小值.若函数f(x)=min{|x|,|x+t|}的图像关于直线x=-21对称,则t 的值为( )(A)-2 (B)2 (C)-1 (D)1 6.最值问题[例6]:(2011年北大等十三校联考(北约)自主招生试题)函数f(x)=|x-1|+|2x-1|+…+|2011x-1|的最小值为_______.[解析]:f(x)=|x-1|+2|x-21|+…+2011|x-20111|,所有零点由小到大:20111(2011个),20101(2010个),…,21(2个), 1(1个),共有1+2+…+2011=1006×2011个,所以在503×2011个与503×2011+1个零点之间取得最小值,令1+2+…+n<503×2011⇒n 的最小值=1421⇒第503×2011个与503×2011+1个零点均为14221⇒f(x)的最小值为f(14221)= 711592043. [评注]:关于函数f(x)=a 1|x-x 1|+a 2|x-x 2|+…+a n |x-x n |有如下结论:①函数f(x)的极值在零点x 1,x 2,…,x n 处取得;②当a 1+a 2+…+a n >0时,f(x)有最小值;当a 1+a 2+…+a n <0时,f(x)有最大值;当a 1+a 2+…+a n =0时,f(x)有最小值,也有最大值;③4 Y.P.M 数学竞赛讲座 当|a i |为正整数时,零点x i 计|a i |次,把这些零点由小到大的排列.当|a 1|+|a 2|+…+|a n |为奇数时,所有零点的中间数是其极值点;当|a 1|+|a 2|+…+|a n |为偶数时,所有零点的中间两数(包括这两个数)之间的任意一个数都是其极值点.[类题]:1.(2008年全国高中数学联赛四川初赛试题)函数f(x)=|x-1|+|x-3|+|x-5|+|x-7|的最小值为_______.2.⑴(2007年第十八届希望杯全国数学邀请赛(高二)试题)函数f(x)=∑=--101|)12(|n n x 的最小值是( )(A)40 (B)50 (C)60 (D)80 ⑵(2006年全国Ⅱ高考试题)函数f(x)=∑=-191||n n x 的最小值为( ) (A)190 (B)171 (C)90 (D)453.(2009年上海高考试题)某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点(-2,2),(3,1),(3,4),(-2,3),(4,5),(6,6)为报刊零售点.请确定一个格点(除零售点外)__________为发行站.使6个零售点沿街道到发行站之间路程的和最短.7.图象性质[例7]:(2007年全国高中数学联赛江苏初赛试题)(2008年全国高中数学联赛贵州初赛试题)已知f(x)=|x+1|+|x+2|+ …+|x+2007|+|x −1|+|x −2|+…+|x −2007|(x ∈R ),且f(a 2−3a+2)=f(a −1),则a 的值有( )(A)2个 (B)3个 (C)4个 (D)无数个 [解析]:由题设知f(x)为偶函数,则考虑在−1≤x ≤1时,恒有f(x)=2×(1+2+3+…+ 2007)=2008×2007.所以当−1≤a 2−3a+2≤1,且−1≤a −1≤1时,恒有f(a 2−3a+2)=f(a −1).故选(D).[评注]:关于函数f(x)=a 1|x-x 1|+a 2|x-x 2|+…+a n |x-x n |的图像有如下结论:①函数f(x)图像的两端是两条射线,这两条射线所在直线的斜率及在y 轴上的截距分别互为相反数;②函数f(x)图像的是轴对称图形的充要条件是:所有零点关于其中位数对称,且关于中位数对称的两零点所对应的系数相等,其对称轴为x=中位数;③函数f(x)图像的是中心对称图形的充要条件是所有零点关于其中位数对称,关于中位数对称的两零点所对应的系数互为相反数,且所有系数和为零,其对称中心为(x 0,f(x 0)),其中x 0为零点的中位数.奇数阶绝对值函数不是中心对称图形.[类题]:1.(2012北约自主招生试题)求x 的范围,使得|x+2|+|x|+|x-1|是增函数.2.(原创题)若函数f(x)=|x+1|+2|x+a|+(b-1)|x+3|的图像为轴对称图形,则a+b= .3.(原创题)函数f(x)=|x-1|+|x-2|+…+|x-1006|-|x-1007|-|x-1008|-…-|x-2012|图像的对称中心为 .8.综合函数[例8]:(2009年全国高中数学联赛福建初赛试题)若对于任意的实数x,函数f(x)=x 2-2x-|x-1-a|-|x-2|+4的值都是非负实数,则实数a 的最小值为 .[解析]:由条件知⎩⎨⎧≥+-=≥++-=02||)1(02|1|)0(a f a f ,解得-2≤a ≤1.当a=-2时,f(x)= x 2-2x-|x+1|-|x-2|+4,对于任意的实数x,f(x)的值都是非负实数,因此a=-2符合要求.所以,实数a 的最小值为-2.[评注]:[类题]:1.(2005年全国Ⅱ高考试题)设函数f(x)=2|x+1|-|x-1|,则使f(x)≥22的x 的取值范围为 .2.(2011年辽宁高考试题)已知函数f(x)=|x-2|-|x-5|.则不等式f(x)≥x 2-8x+15的解集为 .3.(2008年广东高考试题)己知a ∈R,若关于x 的方程x 2+x+|a-41|+|a|=0有实根,则a 的取值范围是 .。
第8无理函数

无理函数的值域问题求无理函数的值域问题是初等数学的难点,因该类问题内涵丰富,灵活多变,涉及多个知识点,技巧性、综合性较强,解法灵活多样,因此成为数学竞赛的热点.本文通过对各种解法进行对比研究,试图寻找解决各种类型问题的最佳方法.1.单调性质法[例1]:(2010年全国高中数学联赛试题)函数f(x)=5-x -x 324-的值域是 .[解析]:[评注]:一个函数我们直接或作一些变形就能判断函数的单调性,用单调求值域是一种比较快捷的方法.无理函数f (x)=b ax ++d cx +(a 与c 同号)型,或f (x)=b ax +-d cx +(a 与c 异号)型,或f (x)=b ax +-d cx +(a 与c 相等)型等,可判断函数单调性,均可用此法.用单调性质法求无理函数的值域时,必须注意到函数隐含的正负性特征和定义域.[类题]:1.(2011年全国高中数学联赛湖南初赛试题)函数y=1+x -x 525-的值域是 .2.(1995年第六届“希望杯”全国数学邀请赛(高一)试题)函数y=2+x -2-x ( ) (A)是非单调函数,没有反函数 (B)有反函数,且反函数是增函数 (C)有反函数,且反函数是减函数 (D)有反函数,且反函数是非单调函数3.(原创题)求函数y=27+x +x -13-x 的最大值和最小值.4.(原创题)求函数y=27+x +x -14-x -13的最大值和最小值.2.平方分析法[例2]:(2005年全国高中数学联赛试题)使关于x 的不等式3-x +x -6≥k 有解的实数k 的最大值是 .[解析]:[评注]:求无理函数值域的难点是解析式中含有的根式,而平方法是去掉根式的根本方法.无理函数f (x)=b ax ++ax d -(a>0,b>0,d>0)型,或f (x)=ax+b ±q px x a ++22型等,可使用平方法分析求解.用平方法求无理函数的值域时,必须注意到平方前函数中隐含的非负性特征和定义域.[类题]:1.(1994年全国高中数学联赛上海初赛试题)函数y=x -1994+1993-x 的值域是_____.2.(2003年第十四届“希望杯”全国数学邀请赛(高二)试题)函数y=232+-x x +232x x -+的最大值是 ,最小值是 .3.(2005年全国高中数学联赛吉林初赛试题)若x 2+y 2=169,则函数f(x,y)=3381024+-x y +3381024++x y 的最大值是 .4.(2001年全国高中数学联赛试题)函数y=x+232+-x x 的值域为 .3.代数换元法[例3]:(2006年江苏高考试题)设a 为实数,设函数f(x)=a21x -+x +1+x -1的最大值为g(a).(Ⅰ)设t=x +1+x -1,求t 的取值范围,并把f(x)表示为t 的函数m(t); (Ⅱ)求g(a); (Ⅲ)试求满足g(a)=g(a1)的所有实数a. [解析]:[评注]:此法适用于函数f(x)=ax+b+md cx +,一般令t=d cx +,将原函数转化为t 的二次函数,当然也适用于函数f(x)=ax 2+b+m d cx +2、f(x)=ax 2+bx+k+m d cx +、f(x)=qpx cbx ax +++等.用代数换元法求无理函数的值域时,必须注意到换元后的新变元的取值范围.[类题]:1.(1997年第八届“希望杯”全国数学邀请赛(高一))函数y=x-x -1的值域为 . 2,(2011年全国高中数学联赛山西初赛试题)函数y=2x-5+x 311-的最大值是 . 3.(原创题)函数f(x)=x 2+21x -的值域为 .4.(2011年全国高中数学联赛试题)函数f(x)=112-+x x 的值域为 . 4.三角换元法(Ⅰ)[例4]:(2010年全国高中数学联赛安徽初赛试题)函数f(x)=2x-24x x -的值域是_________.[解析]:[评注]:若|x|≤R,则可作代换x=Rcos α,且α∈[0,π].此法适用于无理函数f(x)中的无理式是22)(a x R --的形式.用三角换元法求无理函数的值域时,必须给定换元中角α的取值范围.如作代换x=Rsin α,则α∈[-2π,2π],使得换元恰取值好为原函数的定义域.[类题]:1.(2010年全国高中数学联赛江西初赛试题)函数f(x)=212+-x x 的值域是 . 2.(典型题)函数y=x 21x -+x 2的值域是 .3.(1986年全国高中数学联赛上海初赛试题)已知函数y=)56)(96(22-+-+-x x x x ,那么它的值域是__________.4.⑴(2011年全国高中数学联赛内蒙古初赛试题)函数f(x)=9102-+-x x +184502-+-x x 的最大值为 . ⑵(2004年第十五届“希望杯”全国数学邀请赛(高一))已知函数f(x)=232-+-x x +652-+-x x ,则函数f(x)的最大值与最小值之差是________.5.三角换元法(Ⅱ)[例5]:(2006年全国高中数学联赛江西初赛试题)函数f(x)=3-x +x 312-的值域为 .[解析]:[评注]:若x ∈[a,b],则可作代换x=(b-a)sin 2α+a,且α∈[0,2π],或x=2a b -cos α+2b a +,且α∈[0,π].此法适用于无理函数f(x)中的无理式的定义域为[a,b]的函数.如无理函数f (x)=b ax ++d cx +(a 与c 异号)型,或f (x)=ax 2+bx+c+ m t qx px ++2(a<0,q 2-4pr>0)型.用三角换元法求无理函数的值域时,必须给定换元中角α的取值范围.使得换元恰取值好为原函数的定义域.[类题]:1.(2008年重庆高考试题)(2009年全国高中数学联赛河南初赛试题)已知函数y=x -1+3+x 的最大值为M,最小值为m,则Mm的值为 .2.(2010年全国高中数学联赛湖南初赛试题)设函数f(x)=x -4+2+x 的最大值为M,最小值为m,则M 与m 的乘积为 .3.(2006年全国高中数学联赛福建初赛试题)函数y=43+x +x 34-的最大值与最小值之和为 .4.(典型题)函数y=x+2+23102-+-x x 的值域是________.6.三角换元法(Ⅲ)[例6]:(2011年全国高中数学联赛试题)函数f(x)=112-+x x 的值域为 . [解析]:[评注]:若无理函数f(x)中的无理式是c b x a ++2)((a>0,c>0)的形式,可作代换x+b=actan α,且α∈(-2π,2π),则c b x a ++2)(=αcos c.用三角换元法求无理函数的值域时,必须给定换元中角α的取值范围.使得换元恰取值好为原函数的定义域.[类题]:1.(原创题)函数f(x)=212+-x x 的值域为 .2.(200年全国高考试题改编题)若函数f(x)=12+x -ax(a>0)在[0,+∞)上单调递减,则实数a 的取值范围是 .3.(原创题)函数f(x)=5422+-x x -x 的值域为 .4.(2002年全国高中数学联赛上海初赛试题)已知函数f(x)=x21(1-x+2221x x +-),x ∈[2,4],则该函数的值域是_____. 7.距离分析法[例7]:(2008年全国高中数学联赛江西初赛试题)设x ∈R,则函数f(x)=12+x +16)12(2+-x 的最小值为 .[解析]:[评注]:对于有些无理函数的值域问题,巧妙地应用平面上两点间的距离公式,可以起到化难为易,化繁为简的作用,同时借助几何直观,使问题得到顺利解答.[类题]:1.(2006年全国高中数学联赛四川初赛试题)函数f(x)=222++x x +222+-x x 的最小值是 . ⑵(2011年台湾高校(对澳门地区)试题)设f(x)=522+-x x +1342+-x x ,则f(x)的最小值为 . ⑶(2011年第二十二届“希望杯”全国数学邀请赛(高一)试题)522+-x x +2582+-x x 的最小值为______. ⑷(2010年第二十一届“希望杯”全国数学邀请赛(高二))函数f(x)=50102+-x x +252+x 的值域是 .2.(2011年全国高中数学联赛安徽初赛试题)设a 是正数,若f(x)=22106a ax x +-+2252a ax x ++(x ∈R)的最小值为10, 则a= .3.⑴(2004年第十五届“希望杯”全国数学邀请赛(高二))函数y=222++x x -332+-x x 达到最大值时,x 的值是 .⑵(2007年第十八届“希望杯”全国数学邀请赛(高二))当x ∈R 时,函数y=1022++x x -102+-x x ( ) (A)没有最大值和最小值 (B)有最大值,没有最小值 (C)没有最大值,有最小值 (D)有最大值和最小值 4.⑴(1992年全国高中数学联赛试题)函数f(x)=136324+--x x x -124+-x x 的最大值是 .⑵(2011年全国高中数学联赛河南初赛试题)函数f(x)=106324+-+x x x -52324++-x x x 的最大值是 .8.曲线分析法[例8]:(2001年全国高中数学联赛试题)函数y=x+232+-x x 的值域为 .[解析]:[评注]:利用函数解析式的几何意义,把求函数值域的问题转化为距离或截距的范围问题.数形结合是解决求值域和最值问题的重要方法,运用图形的直观性,通过数形结合使抽象问题直观化,复杂问题简单化,综合问题浅显化,充分训练发散思维.[类题]:1.(2005年第十六届“希望杯”全国数学邀请赛(高二)试题)函数y=2-x +x -5的最大值是 ,最小值是 .2.(2011年全国高中数学联赛四川初赛试题)函数f(x)=5-x +x 324-的最大值是 .3.(典型题)函数y=4x+223x x -+的值域为 .4.(数学奥林匹克高中训练题(73))函数y=212x x -+-2215x x --的值域为 .9.向量分析法[例9]:(2009年全国高中数学联赛试题)求函数y=27+x +x -13+x 的最大和最小值. [解析]:[评注]:根据向量的数量积的定义ab =|a ||b |cos<a,b>⇒(ab )2=|a |2|b |2cos 2<a,b>⇒(ab )2≤|a |2|b |2,等号当且仅当a ∥b 时成立.如求函数f(x)=m x a -+n b x -的最值,可令a =(m,n),b =(x a -,b x -),由(x a -)2+(b x -)2=a-b,f 2(x) =(ab )2=|a |2|b |2cos 2<a,b>⇒<a,b>∈[0,θ],tan θ=n/m,或cot θ=n/m ⇒cos<a,b>∈[t,1],其中t=min{22nm n +,22nm m +}⇒f 2(x)∈[(m 2+n 2)t,(m 2+n 2)(a-b)].[类题]:1.(2011年全国高中数学联赛四川初赛试题)函数f(x)=5-x +x 324-的最大值为 .2.(2003年全国高中数学联赛试题)设23≤x ≤5,证明不等式21+x +32-x +x 315-<219. 10.不等式法[例10]:(2003年全国高中数学联赛试题)设23≤x ≤5,证明不等式21+x +32-x +x 315-<219.[解析]: [类题]:1.(数学奥林匹克高中训练题(147))设0≤x ≤8则函数f(x)=1)8)(8(2+-+x x x x 的值域为 .2.(《中等数学》2006年笫6期.数学奥林匹克高中训练题(1))设x ∈R +,则函数y=211x++2xx+1的最大值为 . 3.(数学奥林匹克高中训练题(126))函数f(x)=x(x +1+x -1)的值域为 . 4.(2009年全国高中数学联赛试题)求函数y=27+x +x -13+x 的最大和最小值.无理函数的值域问题求无理函数的值域问题是初等数学的难点,因该类问题内涵丰富,灵活多变,涉及多个知识点,技巧性、综合性较强,解法灵活多样,因此成为数学竞赛的热点.本文通过对各种解法进行对比研究,试图寻找解决各种类型问题的最佳方法.Ⅰ.解法分析1.单调性质法[例1]:(2010年全国高中数学联赛试题)函数f(x)=5-x -x 324-的值域是 .[解析]:函数f(x)的定义域为[5,8],且函数y=5-x 在定义域[5,8]内单调递减,y=x 324-在定义域[5,8]内单调递增⇒f(x)在定义域[5,8]内单调递增⇒f(x)的值域是[f(5),f(8)]=[-3,3].[评注]:一个函数我们直接或作一些变形就能判断函数的单调性,用单调求值域是一种比较快捷的方法.无理函数f (x)=b ax ++d cx +(a 与c 同号)型,或f (x)=b ax +-d cx +(a 与c 异号)型,或f (x)=b ax +-d cx +(a 与c 相等)型等,可判断函数单调性,均可用此法.用单调性质法求无理函数的值域时,必须注意到函数隐含的正负性特征和定义域.[类题]:1.(2011年全国高中数学联赛湖南初赛试题)函数y=1+x -x 525-的值域是 .2.(1995年第六届“希望杯”全国数学邀请赛(高一)试题)函数y=2+x -2-x ( ) (A)是非单调函数,没有反函数 (B)有反函数,且反函数是增函数 (C)有反函数,且反函数是减函数 (D)有反函数,且反函数是非单调函数 解:y=2+x -2-x =224-++x x 在[-2,2]上单调递减⇒有反函数,且反函数是减函数.3.(原创题)求函数y=27+x +x -13-x 的最大值和最小值. 解:函数的定义域为[0,13],y=27+x -x =xx ++2727在[0,13]上单调递减⇒函数y=27+x +x -13-x 在[0,13]上单调递减⇒x=13时,y min =210-13,x=0时,y max =33+13. 4.(原创题)求函数y=27+x +x -14-x -13的最大值和最小值. 解:函数的定义域为[-27,,13],y=x -14-x -13=xx -+-14131在[-27,13]上单调递增⇒y=27+x +x -14-x -13在[-27,13]上单调递增⇒2.平方分析法[例2]:(2005年全国高中数学联赛试题)使关于x 的不等式3-x +x -6≥k 有解的实数k 的最大值是 .[解析]:令y=3-x +x -6,3≤x ≤6,则y 2=3+2)6)(3(x x --(或用二次函数)≤3+[(x-3)+(6-x)]=6,实数k 的最大值是6.[评注]:求无理函数值域的难点是解析式中含有的根式,而平方法是去掉根式的根本方法.无理函数f (x)=b ax ++ax d -(a>0,b>0,d>0)型,或f (x)=ax+b ±q px x a ++22型等,可使用平方法分析求解.用平方法求无理函数的值域时,必须注意到平方前函数中隐含的非负性特征和定义域.[类题]:1.(1994年全国高中数学联赛上海初赛试题)函数y=x -1994+1993-x 的值域是_____.2.(2003年第十四届“希望杯”全国数学邀请赛(高二)试题)函数y=232+-x x +232x x -+的最大值是 ,最小值是 .解:令x 2-3x=t,y=2+t +t -2.3.(2005年全国高中数学联赛吉林初赛试题)若x 2+y 2=169,则函数f(x,y)=3381024+-x y +3381024++x y 的最大值是 .解:f 2(x,y)=48y+676+222)10()33824(x y -+=48y+676+22222210169338338242)1024(⨯-+⨯⨯++y y ,y=13,x=0时,f(x)max=1026.4.(2001年全国高中数学联赛试题)函数y=x+232+-x x 的值域为 .解:y=x+232+-x x ⇒y-x=232+-x x ≥0⇒(y-x)2=x 2-3x+2⇒(2y-3)x=y 2-2⇒y ≠23,x=3222--y y ⇒y ≥3222--y y ⇒1≤y <23,或y ≥2. 3.代数换元法[例3]:(2006年江苏高考试题)设a 为实数,设函数f(x)=a21x -+x +1+x -1的最大值为g(a).(Ⅰ)设t=x +1+x -1,求t 的取值范围,并把f(x)表示为t 的函数m(t); (Ⅱ)求g(a); (Ⅲ)试求满足g(a)=g(a1)的所有实数a. [解析]:(Ⅰ)t 2=2+221x -∈[2,4]⇒t ∈[2,2],f(x)=m(t)=21at 2-a+t; (Ⅱ)①当a=0时,m(t)=t ⇒g(a)=m(2)=2;②当a>0时,函数m(t)过定点(2,2),对称轴t=-a1⇒g(a)=m(2)=a+2;③当a<0时,函数m(t)过定点(2,2),对称轴t=-a1. 综上[评注]:此法适用于函数f(x)=ax+b+md cx +,一般令t=d cx +,将原函数转化为t 的二次函数,当然也适用于函数f(x)=ax 2+b+m d cx +2、f(x)=ax 2+bx+k+m d cx +、f(x)=qpx cbx ax +++等.用代数换元法求无理函数的值域时,必须注意到换元后的新变元的取值范围.[类题]:1.(1997年第八届“希望杯”全国数学邀请赛(高一))函数y=x-x -1的值域为 . 解:令x -1=t,则t ≥0,且x=1-t 2,则y=1-t 2-t ≤1.2,(2011年全国高中数学联赛山西初赛试题)函数y=2x-5+x 311-的最大值是 . 解:令x 311-=t,则t ≥0,且x=31(11-t 2),则3y=-2t 2+3t+7≤865⇒y 的最大值是2465. 3.(原创题)函数f(x)=x 2+21x -的值域为 .解:令21x -=t,则t ∈[0,1],且x 2=1-t 2,y=1-t 2+t.4.(2011年全国高中数学联赛试题)函数f(x)=112-+x x 的值域为 . 解:令x-1=t,则f(x)=tt 1)1(2++.当t>0时,f(x)=2221t t ++>1;当t<0时,f(x)=-2221t t ++=-21)211(22++t ≤-22. 4.三角换元法(Ⅰ)[例4]:(2010年全国高中数学联赛安徽初赛试题)函数f(x)=2x-24x x -的值域是_________.[解析]:f(x)=2x-24x x -=2x-2)2(4--x ,设x-2=2cos α,α∈[0,π],则y=4cos α-2sin α+4=25cos(α+φ)+4,其中cos φ=52,φ为锐角,所以当α=0时,y max =8,当α+φ=π时,y min =4-25.[评注]:若|x|≤R,则可作代换x=Rcos α,且α∈[0,π].此法适用于无理函数f(x)中的无理式是22)(a x R --的形式.用三角换元法求无理函数的值域时,必须给定换元中角α的取值范围.如作代换x=Rsin α,则α∈[-2π,2π],使得换元恰取值好为原函数的定义域.[类题]:1.(2010年全国高中数学联赛江西初赛试题)函数f(x)=212+-x x 的值域是 . 解:设x=cos α,且α∈[0,π].则y=2cos sin +αα,作P(cos α,sin α),A(-2,0),k AP =2cos sin +αα∈[0,33].2.(典型题)函数y=x 21x -+x 2的值域是 .解:设x=sin α(|α|≤2π),则y=sin αcos α+sin 2α=21+22sin(2α-4π),故所求函数值域为[21-22,21+22]. 3.(1986年全国高中数学联赛上海初赛试题)已知函数y=)56)(96(22-+-+-x x x x ,那么它的值域是__________. 解:f(x)的定义域为[1,5],令x-3=2cos α,α∈[0,π],y=])3(4[)3(22---x x =αα22cos sin 16=2|sin2α|∈[0,2]. 4.⑴(2011年全国高中数学联赛内蒙古初赛试题)函数f(x)=9102-+-x x +184502-+-x x 的最大值为 . 解:f(x)=22)5(4--x -22)25(21--x ,令x-5=4cos α,x-25=21cos β,α,β∈[0,π],4cos α-21cos β=20,f(x)=4sin α+21sin β,f 2(x)+202=(4sin α+21sin β)2+(4cos α-21cos β)2=16+441-168cos(α+β)⇒f 2(x)=57-168cos(α+β)⇒cos(α+β)=-1时,f(x)max =16857+=15.⑵(2004年第十五届“希望杯”全国数学邀请赛(高一))已知函数f(x)=232-+-x x +652-+-x x ,则函数f(x)的最大值与最小值之差是________. 解:f(x)=2)23(41--x +2)25(41--x ,令x-23=21cos α,x-25=21cos β,α,β∈[0,π],cos α-cos β=2⇒f(x)=21(sinα+sin β)⇒4+4f 2(x)=2-2cos(α+β)≤4⇒f(x)=0.5.三角换元法(Ⅱ)[例5]:(2006年全国高中数学联赛江西初赛试题)函数f(x)=3-x +x 312-的值域为 .[解析]:f(x)的定义域为[3,4],令x=(4-3)sin 2θ,θ∈[0,2π],则f(x)=sin θ+3cos θ=2sin(θ+3π),3π≤θ+3π≤65π⇒21≤sin(θ+3π)≤1⇒f(x)=3-x +x 312-的值域为[1,2].[评注]:若x ∈[a,b],则可作代换x=(b-a)sin 2α+a,且α∈[0,2π],或x=2a b -cos α+2b a +,且α∈[0,π].此法适用于无理函数f(x)中的无理式的定义域为[a,b]的函数.如无理函数f (x)=b ax ++d cx +(a 与c 异号)型,或f (x)=ax 2+bx+c+ m t qx px ++2(a<0,q 2-4pr>0)型.用三角换元法求无理函数的值域时,必须给定换元中角α的取值范围.使得换元恰取值好为原函数的定义域.[类题]:1.(2008年重庆高考试题)(2009年全国高中数学联赛河南初赛试题)已知函数y=x -1+3+x 的最大值为M,最小值为m,则Mm的值为 . 2.(2010年全国高中数学联赛湖南初赛试题)设函数f(x)=x -4+2+x 的最大值为M,最小值为m,则M 与m 的乘积为 .3.(2006年全国高中数学联赛福建初赛试题)函数y=43+x +x 34-的最大值与最小值之和为 .4.(典型题)函数y=x+2+23102-+-x x 的值域是________.解:由-x 2+10x-23≥0⇒5-2≤x ≤5+2,令x=2cos α+5,α∈[0,π],则y=2cos α+7+2sin α=2sin(α+4π)+7,由 α∈[0,π]⇒α+4π∈[4π,45π]⇒sin(α+4π)∈[-22,1]⇒y ∈[7-2,9]. 6.三角换元法(Ⅲ)[例6]:(2011年全国高中数学联赛试题)函数f(x)=112-+x x 的值域为 . [解析]:令x=tan α,α∈(-2π,2π),α≠4π,f(x)=ααcos sin 1-=)4sin(21πα-,α-4π∈(-43π,4π)⇒sin(α-4π)∈[-1,0)∪(0,22)⇒f(x)∈(-∞,-22]∪(1,+∞).[评注]:若无理函数f(x)中的无理式是c b x a ++2)((a>0,c>0)的形式,可作代换x+b=actan α,且α∈(-2π,2π),则c b x a ++2)(=αcos c.用三角换元法求无理函数的值域时,必须给定换元中角α的取值范围.使得换元恰取值好为原函数的定义域.[类题]:1.(原创题)函数f(x)=212+-x x 的值域为 .解:令x=2tan α,α∈(-2π,2π),则f(x)=22(sin α-cos α)=sin(α-4π)∈[-1,22). 2.(200年全国高考试题改编题)若函数f(x)=12+x -ax(a>0)在[0,+∞)上单调递减,则实数a 的取值范围是 .解:令x=tan α,α∈(-2π,2π),则f(x)=αcos 1-atan α=ααcos sin 1a -=a ααcos sin 1-a ,取单位圆上的点P(cos α,sin α),A(0,a 1),-k PA =ααcos sin 1-a ,f(x)递减⇔k PA 递增⇔a 1≤1⇔a ≥1. 3.(原创题)函数f(x)=5422+-x x -x 的值域为 . 解:f(x)=3)1(22+-x -12+x ,令x-1=26tan α,α∈(-2π,2π),则f(x)=αcos 3-26tan α-1=26ααcos sin 2--1,取单位圆上的点P(cos α,sin α),A(0,2),-k PA =ααcos sin 2-,k PA ≤-1⇒-k PA ≥1⇒f(x)≥26-1.4.(2002年全国高中数学联赛上海初赛试题)已知函数f(x)=x21(1-x+2221x x +-),x ∈[2,4],则该函数的值域是_____. 解:f(x)=x 21(1-x+2221x x +-)=21(x1-1+2212+-xx)=21[x 1-1+1)11(2+-x ],令1-x 1=tan α∈[21,43],则y=f(x)=21(-tan α+αcos 1)=21ααcos sin 1-,取单位圆上的点P(cos α,sin α),A(0,1),-k PA =ααcos sin 1-,k OA 递增,ααcos sin 1-递减,当tan α=21时,sin α=55,cos α=552⇒f(x)max =415-;当tan α=43时,sin α=53,cos α=54⇒f(x)min =41.7.距离分析法[例7]:(2008年全国高中数学联赛江西初赛试题)设x ∈R,则函数f(x)=12+x +16)12(2+-x 的最小值为 .[解析]:[评注]:对于有些无理函数的值域问题,巧妙地应用平面上两点间的距离公式,可以起到化难为易,化繁为简的作用,同时借助几何直观,使问题得到顺利解答.[类题]:1.(2006年全国高中数学联赛四川初赛试题)函数f(x)=222++x x +222+-x x 的最小值是 . ⑵(2011年台湾高校(对澳门地区)试题)设f(x)=522+-x x +1342+-x x ,则f(x)的最小值为 . ⑶(2011年第二十二届“希望杯”全国数学邀请赛(高一)试题)522+-x x +2582+-x x 的最小值为______. ⑷(2010年第二十一届“希望杯”全国数学邀请赛(高二))函数f(x)=50102+-x x +252+x 的值域是 .2.(2011年全国高中数学联赛安徽初赛试题)设a 是正数,若f(x)=22106a ax x +-+2252a ax x ++(x ∈R)的最小值为10,则a= .3.⑴(2004年第十五届“希望杯”全国数学邀请赛(高二))函数y=222++x x -332+-x x 达到最大值时,x 的值是 . ⑵(2007年第十八届“希望杯”全国数学邀请赛(高二))当x ∈R 时,函数y=1022++x x -102+-x x ( ) (A)没有最大值和最小值 (B)有最大值,没有最小值 (C)没有最大值,有最小值 (D)有最大值和最小值4.⑴(1992年全国高中数学联赛试题)函数f(x)=136324+--x x x -124+-x x 的最大值是 .⑵(2011年全国高中数学联赛河南初赛试题)函数f(x)=106324+-+x x x -52324++-x x x 的最大值是 .8.曲线分析法[例8]:(2001年全国高中数学联赛试题)函数y=x+232+-x x 的值域为 .[解析]:取点P(x-23,232+-x x ),则点P 在x 2-y 2=41(y ≥0)上,u=x+y+23,直线x+y=u-23在x 轴上的截矩u-23满足-21≤u-23<0,u-23≥21⇔u ∈[1,23)∪[2,+∞). [评注]:利用函数解析式的几何意义,把求函数值域的问题转化为距离或截距的范围问题.数形结合是解决求值域和最值问题的重要方法,运用图形的直观性,通过数形结合使抽象问题直观化,复杂问题简单化,综合问题浅显化,充分训练发散思维.[类题]:1.(2005年第十六届“希望杯”全国数学邀请赛(高二)试题)函数y=2-x +x -5的最大值是 ,最小值是 . 解:取点P(2-x ,x -5),点P 在四分之一圆弧C:x 2+y 2=3(x ≥0,y ≥0)上,u=x+y,直线x+y=u 在x 轴上的截矩u 满足:3≤u ≤6.2.(2011年全国高中数学联赛四川初赛试题)函数f(x)=5-x +x 324-的最大值是 .解:取点P(5-x ,x -8),点P 在四分之一圆弧C:x 2+y 2=3(x ≥0,y ≥0)上,u=x+3y,直线x+y=u 在x 轴上的截矩u 满足:3≤u ≤23.3.(典型题)函数y=4x+223x x -+的值域为 .解:取点P(x,223x x -+),点P 在半圆圆弧C:(x-1)2+y 2=4(0≤y ≤2)上,u=4x+y,直线4x+y=u 在x 轴上的截矩u 满足:-1≤41u ≤217+1⇒-4≤u ≤4+217. 4.(数学奥林匹克高中训练题(73))函数y=212x x -+-2215x x --的值域为 . 解:f(x)的定义域为[-3,3],设y 1=212x x -+(y 1≥0),y 2=2215x x --(y 2≥0),则(x-21)2+y 12=(27)2,(x+1)2+y 22=42, 作此两圆,如图: B y 设直线x=t 与半圆C 1,C 2分别相交于A,B 两点,则有向线段BA 的数量, A即为x=t 时的函数值. C 2 C 1 显然,当x=-3时,y 取得最小值-23;当x=3时,y 取得最大值6. -5 -3 x=t O 3 4 x9.向量分析法[例9]:(2009年全国高中数学联赛试题)求函数y=27+x +x -13+x 的最大和最小值.[解析]:设a =(31,21,1),b =()13(3x -,x 2,27+x ),则|a |=666,|b |=66,ab =27+x +x -13+x ,其中0≤x ≤13,由(ab )2≤|a |2|b |2得y ≤66666=11,当且仅当a ∥b ,即x=9时,等号成立;又因()13(3x -)2+(x 2)2+(27+x )2=66⇒当且仅当b =(39,0,33),即x=0时,cos<a ,b >≥113313+⇒27+x +x -13+x =ab =|a ||b |cos<a ,b >≥13+33.[评注]:根据向量的数量积的定义ab =|a ||b |cos<a,b>⇒(ab )2=|a |2|b |2cos 2<a,b>⇒(ab )2≤|a |2|b |2,等号当且仅当a ∥b 时成立.如求函数f(x)=m x a -+n b x -的最值,可令a =(m,n),b =(x a -,b x -),由(x a -)2+(b x -)2=a-b,f 2(x) =(ab )2=|a |2|b |2cos 2<a,b>⇒<a,b>∈[0,θ],tan θ=n/m,或cot θ=n/m ⇒cos<a,b>∈[t,1],其中t=min{22nm n +,22nm m +}⇒f 2(x)∈[(m 2+n 2)t,(m 2+n 2)(a-b)].[类题]:Y.P.M 数学竞赛讲座 71.(2005年全国高中数学联赛试题)使关于x 的不等式3-x +x -6≥k 有解的实数k 的最大值是 .2.(2011年全国高中数学联赛四川初赛试题)函数f(x)=5-x +x 324-的最大值为 .3.(2003年全国高中数学联赛试题)设23≤x ≤5,证明不等式21+x +32-x +x 315-<219. 解:设a =(2,1,1),b =(1+x ,32-x ,x 315-),则|a |=6,|b |=13,ab =21+x +32-x +x 315-=|a ||b | cos<a ,b >=613cos<a ,b >.当b =(25,0,221),即x=23时,cos<a ,b >取得最大值⇒21+x +32-x +x 315-最大值=225+221<219. 10.不等式法[例10]:(2003年全国高中数学联赛试题)设23≤x ≤5,证明不等式21+x +32-x +x 315-<219.[解析]:由(x 1+x 2+…+x n )2=x 12+x 22+…+x n 2+2x 1x 2+2x 1x 3+…+2x n-1x n ≤x 12+x 22+…+x n 2+(n-1)(x 12+x 22+…+x n 2)=n(x 12+x 22+…+x n 2)⇒x 1+x 2+…+x n ≤n22221n x x x +⋅⋅⋅++,当且仅当x 1=x 2=…=x n 时取等号.21+x +32-x +x 315-=1+x +1+x +32-x +x 315-≤214+x ≤219,而等号不能成立.柯西不等式:(a 1x 1+a 2x 2+…+a n x n )2≤(a 12+a 22+…+a n 2)(x 12+x 22+…+x n 2),当且仅当a 1:x 1=a 2:x 2=…=a n :x n 时等号成立; (21+x +32-x +x 315-)2=(m1m mx 44++n1n nx 32-+k1kx k 315-)2≤(m 1+n 1+k1)[(4mx+4m)+(2nx-3n)+ (15k-3kx)],令4m+2n=3k,y 5≤(m 1+n 1+k1)(4m-3n+15k),取[评注]: [类题]:1.(数学奥林匹克高中训练题(147))设0≤x ≤8则函数f(x)=1)8)(8(2+-+x x x x 的值域为 .解:f(x)=1)8)(8(2+-+x x x x =1)8)(8(22+-+x x x x ≤)1(2)8()8(22+-++x x x x =4,当且仅当x=2时等号成立,值域为[0,4].2.(《中等数学》2006年笫6期.数学奥林匹克高中训练题(1))设x ∈R +,则函数y=211x++2xx+1的最大值为 . 解:设t=x1(t>0),y=21t t ++t+12≤2)1(2t t ++t+12=t t +12+t +12=2-t +12+t +12=2-2(t+11-22)2+22≤ 2+22=223,当且仅当t+11=22,即t=1时等号成立. 3.(数学奥林匹克高中训练题(126))函数f(x)=x(x +1+x -1)的值域为 .解:函数f(x)的定义域为[-1,1],且为奇函数,设21x -=t,0≤t ≤1,f 2(x)=x 2(2+221x -)=2(1-t 2)(1+t)=(1+t)(1+t)(2-2t)≤[3)22()1()1(t t t -++++]3=2764,当且仅当1+t=2-2t,t=31时等号成立⇒f max (x)=938⇒值域为[-938,938]. 4.(2009年全国高中数学联赛试题)求函数y=27+x +x -13+x 的最大和最小值.解:函数的定义域为[0,13],y=27+x +x -13+x =27+x +)13(213x x -+≥27+13=33+13,当且仅当x=0时等号成立;又由柯西不等式:(a 1x 1+a 2x 2+…+a n x n )2≤(a 12+a 22+…+a n 2)(x 12+x 22+…+x n 2),当且仅当a 1:x 1=a 2:x 2=…=a n :x n 时等号成立;y 2= (27+x +x -13+x )2=(m1m mx 27++n1nx n -13+k1kx )2≤(m 1+n 1+k1)[(mx+27m)+(13n-nx)+kx],令m+k=n,且m1:m mx 27+=n 1:nx n -13=k 1:kx ⇒m 2x+27m 2=13n 2-n 2x=k 2x ⇒x=22222713m n m n +-=22213k n n +∈[0,13],取m=1⇒k=2,n=3,则y 5≤(m 1+n 1+k1)(27m+13n)=112.x=9时等号成立;Ⅱ.类型分析1.函数f(x)=ax+b+m dcx +2.函数f(x)=3.函数f(x)=nbax ++mdcx +4.函数f(x)=ax+b+m t qx px ++25.函数f(x)=6.函数f(x)=7.函数f(x)=8.函数f(x)=9.函数f(x)= 10.函数f(x)=3.函数f(x)=n b ax ++m d cx ++k q px +4.f(x)=ax+b+m t qx px ++25.f(x)=ax 2+bx+c+m t qx px ++26.f(x)=n c bx ax ++2+m t qx px ++27.f(x)=qpx cbx ax +++4.(原创题)函数f(x)=5422+-x x -12+x 的值域为 . 解:设y 1=5422+-x x ,y 2=12+x ⇒。
高考数学原创试题的命题方向及典型题分析

高考数学原创试题的命题方向及典型题分析从2004年开始,全国高考11个省市独立命题。
高考数学形成了“百花齐放”的局面,各地数学试卷中出现了不少新颖的高质量原创试题. 从某种角度看, 原创试题的新颖性对考生是一种难度,可真正考查出考生的学习潜能和个性品质状况;而对命题者来说,更是命题成功与否的一个重要标志。
笔者在文[1]中已探讨了原创试题命题的七个方向,下面结合国内外课程标准,再提出原创试题的六个命题方向。
一、考查数学交流评价的试题在我国2003年制订的《普通高中数学课程标准》(下面简称《标准》)中,数学交流已作为一项教学目标被明确提出.使用交流去培养学生的数学理解力是数学交流的目标,但在我国高考数学中“数学交流”的试题现在基本上还没有涉及.以后会编制出不同种类的“数学交流”试题,让学生通过书面表述、图表、数学模式、数学图象、数学规律等方式进行数学交流,最终达到熟练掌握数学语言进行交流的目的.典型题1 (韩国高考数学题改编)下面是学生甲和学生乙争论集合的部分内容:甲:我们能够想象到的集合之全体的集合叫做S,那么(a)S将S自身作为元素所有,是吧?乙:那不成体统,哪有那样的事?甲:好,那么(b)不把自己本身作为元素的集合之全体的集合又怎么样呢?以数学方式表达上述争论中带有底线的(a),(b),哪一项最好?(A)S ∈S ,{A|A ∉A ,A 是集合};(B) S ∈S ,{A|A ⊄A ,A 是集合};(C) S ∈S ,{A|A ∉A ,A 是集合};(D) S ⊂S ,{A|A ⊂A ,A 是集合}.评注:此题通过两个学生的数学交流来表明他们对集合与集合、集合与元素之间关系的理解,同时让应试者参与讨论,并把一些观点与数学表达符号化.二、考查凸显数学文化的试题数学文化是多姿多彩的,它是人类文化宝库中的奇葩.《标准》中指出:数学是人类文化的重要组成部分。
数学是人类社会进步的产物,也是推动社会发展的动力。
高中数学公式测试题-三角、函数、数列部分[原创]-人教版
![高中数学公式测试题-三角、函数、数列部分[原创]-人教版](https://img.taocdn.com/s3/m/8e77b07da26925c52cc5bfcc.png)
高中数学公式测试题 一.三角函数1、 以角α的顶点为坐标原点,始边为x 轴正半轴建立直角坐标系,在角α的终边上任取一个异于原点的点),(y x P ,点P 到原点的距离记为r ,则sin α=ry ,cos α=rx ,tg α=xy ,sec α=xr ,2、 符号规律:2、同角三角函数的关系中,平方关系是:1cos sin 22=+αα,αα22sec 1=+tg ,αα22csc 1=+ctg ;倒数关系是:1=⋅ααctg tg ,1csc sin =⋅αα,1sec cos =⋅αα; 相除关系是:αααcos sin =tg ,αααsin cos =ctg 。
3、诱导公式可用十个字概括为:奇变偶不变,符号看象限。
如:=-)23sin(απαcos -,)215(απ-ctg =αtg ,=-)3(απtg αtg -。
4、 函数B x A y ++=)s in(ϕω),(其中00>>ωA 的最大值是B A +,最小值是A B -,周期是ωπ2=T ,频率是πω2=f ,相位是ϕω+x ,初相是ϕ;其图象的对称轴是直线)(2Z k k x ∈+=+ππϕω,凡是该图象与直线B y =的交点都是该图象的对称中心。
5、 三角函数的单调区间:x y s i n =的递增区间是⎥⎦⎤⎢⎣⎡+-2222ππππk k ,)(Z k ∈,递减区间是⎥⎦⎤⎢⎣⎡++23222ππππk k ,)(Z k ∈;x y cos =的递增区间是[]πππk k 22,-)(Z k ∈,递减区间是[]πππ+k k 22,)(Z k ∈,tgx y =的递增区间是⎪⎭⎫⎝⎛+-22ππππk k ,)(Z k ∈,ctgx y =的递减区间是()πππ+k k ,)(Z k ∈。
6、=±)sin(βαβαβαsin cos cos sin ±=±)c o s (βαβαβαs i n s i n c o s c o s =±)(βαtg βαβαtg tg tg tg ⋅± 17、二倍角公式是:sin2α=ααcos sin 2⋅cos2α=αα22sin cos -=1cos 22-α=α2sin 21- tg2α=αα212tg tg -。
高中数学原创新题思考题(含答案)

高中数学原创新题思考题(新高三)1.若向量x 、y 满足|x|=|y|=1,xy=21,向量z 满足|z-8x|+|z-5y|=7,则x ·z+y ·z 的最大值为.2.在平面直角坐标系xoy 中,设圆A :x 2+y 2+10x-6y+30=0,斜率为-3的直线l 1上有一点M ,直线l 2过点M 且与圆A 恒有公共点.⑴若l 1⊥l 2,点M 与点A 重合,求l 2的方程;⑵若l 2的斜率存在时可为任意实数,求点M 横坐标的取值范围;⑶设l 2与圆A 的一个公共点为T ,若|MT|2+|MA|2≤20,求l 1纵截距的取值范围.3.已知函数f(x)=a x -ax 2,a ∈R 且a>1.⑴若f(x)在区间(0,+∞)上有且仅有一个零点,求a ;⑵设f(x)的两个极值点为x 1、x 2(极值点是函数取极值时对应自变量的值),证明:f(2x x 21 )<e-aln a 21.|x|=|y|=1,xy=21,设x 、y 的夹角为A ,则cosA=21根据向量的几何意义作图:在△ABC 中,由余弦定理得BC 2=AB 2+AC 2-2AB ·ACcosA=64+25-40=49所以BC=7据|z-8x|+|z-5y|=7可作出z 向量,即z 的尾端恰在线段BC 上所以xz+yz=z(x+y),即z 与定向量x+y 的数量积z(x+y)=|x+y|·|k|,k 表示|z|在|x+y|上的投影据图形运动,xz+yz 的最大值在z 运动到C 时取得所以有xz+yz ≤8×1+8×1×21=12故xz+yz 的最大值为12.2.⑴圆A :x 2+y 2+10x-6y+30=0即(x+5)2+(y-3)2=4点M 与点A 重合,即M(-5,3)l 1⊥l 2,l 1的斜率为-3,则l 2的斜率为31-所以l 2的方程为y-3=31-(x+5),即x+3y-4=0(或y=31-x+34)⑵因为l 2的斜率存在时可为任意实数,l 2过点M 且与圆A 恒有公共点,据平面知识考察以下两种情况:当点M 在圆A 外时,过M 总存在直线与圆A 无公共点即此时l 2的斜率不为任意实数x A BC y 85x A BCy 85z当点M 在圆A 上或圆A 内时,明显l 2始终与圆A 有公共点即此时l 2的斜率为任意实数所以点M 在圆A 上或圆A 内所以点M 的横坐标∈[-5-2,-5+2],即取值范围为[-7,-3]⑶已知|MT|2+|MA|2≤20解法一:连结AT 并取AT 中点为K ,有|AT|=2|MK|2=|)MA +MT (21|=)MT MA 2|MA |+|MT (|4122⋅+在△MAT 中由余弦定理得2|MT|·|MA|cos ∠AMT=|MT|2+|MA|2-4所以|MK|2=-4)|MA |+2|MT |(24122≤4)-20(241⨯=9,即|MK|≤3据圆的定义,点M 始终在以K 为圆心,3为半径的圆内或圆上;解法二:设M(x ,y),T(m ,n)所以|MT|2+|MA|2≤20即(x-m)2+(y-n)2+(x+5)2+(y-3)2≤20整理得得x 2+y 2+(5-m)x-(n+3)y+21(m 2+n 2)+7≤0即(x-2m 5-+)2+(y-2n 3+)2≤9,而AT 中点K 的坐标恰为(2m 5-+,2n 3+)所以点M 始终在以K 为圆心,3为半径的圆内或圆上;由T 在圆A 上运动,|AK|=1得点M 也始终在以A 为圆心,4为半径的圆内或圆上且可知M 可为该圆内或圆上的所有点设l 1纵截距为b ,则其方程为3x+y-b=0l 1与以A 为圆心,4为半径的圆有公共点即满足条件得l 1到圆心的距离=2213|b -31--5)(3|+⨯⨯≤4,解得-410-18≤b ≤410-18所以l 1纵截距的取值范围为[-410-18,410-18].3.⑴f(x)在区间(0,+∞)上有且仅有一个零点解法一:转化为方程a x =ax 2仅有一解由a>1,x>0,在a x =ax 2两边取自然对数,得xlna=lna+2lnx 令g(x)=xlna-2lnx-lna ,即g(x)有且仅有一个零点g '(x)=x 2-xlna ,令g '(x)<0、g '(x)>0解出单调区间得g(x)在(0,lna 2)减,(lna 2,+∞)增所以g(lna 2)=0,而g(1)=0,得lna 2=1,a=e 2下证g(lna 2)<0时,g(x)有两个零点先考察函数h(a)=a ln a 2,h '(a)=aln 2-lna 3令h '(a)<0,h '(a)>0解出单调区间,得h(a)在(1,e 2)减,(e 2,+∞)增所以h(a)≥h(e 2)=4e 2,据此可知有2a >lna ①lna 2<1时,只要证g(x)在(0,lna 2)有一个零点因为2a>2a >lna ,即a 1<lna2又g(a 1)=lna a lna >0,故g(x)在(a 1,lna 2)必有一个零点②lna 2>1时,只要证g(x)在(lna 2,+∞)有一个零点x>1时,2x >lnx ,即g(x)>xlna-4x -lna得g((lna 4+1)2)>(lna 4+1)2lna-4(lna4+1)-lna>0故g(x)在(lna 2,(lna 4+1)2)必有一个零点综上a=e 2解法二:考察原函数,f '(x)=a x lna-2ax=F(x),F '(x)=a x ln 2a-2a 由解法一中a ln a 2≥4e 2,得a ln 2a 2>1,因此令F '(x)<0、F '(x)>0可得F(x)在(0,log a (a ln 2a 2))减,(log a (a ln 2a 2),+∞)增同理得F(21)=a (lna-a )<0,又F(0)=lna>0所以F(x)在(0,21)上有一个零点,记为x 1又存在x>log a (a ln 2a 2),F(x)>0所以F(x)在(log a (a ln 2a 2),+∞)上有一个零点,记为x 2可得f(x)在(0,x 1)增,(x 1,x 2)减,(x 2,+∞)增由f(1)=0,有以下讨论F(1)>0时,存在x<1,f(x)<0,又f(0)=1>0得f(x)在(0,1)有零点,舍去F(1)<0时,存在x>1,f(x)<0,又存在x>x 2,f(x)>0得f(x)在(1,+∞)有零点,舍去所以F(1)=0,即alna-2a=0,a=e 2补证存在x>log a (a ln 2a 2),F(x)>0;存在x>x 2,f(x)>0只要证对于任意的x 2>a ln 6a 4,x>a ln 3a 3,F(x)>0,f(x)>0考察函数H(x)=3x x a ,H '(x)=4x x 3-xlna a )(得H(x)≥H(lna 3)>3a ln 3,故a x >3a ln 3x 3所以F(x)>3a ln 4x 3-2ax ,f(x)>3a ln 3x 3-ax 2由此可知得证综上a=e 2(解法二对下一问有帮助作用,但须较强能力)⑵注意到lna 1a =e ,所以f(2x x 21+)<e-a ln a 2即f(2x x 21+)<lna 1a -a 2)lna 1(故证f(2x x 21+)<e-a ln a 2,即证f(2x x 21+)<f(lna 1)f '(lna 1)=elna-2lna a =lna(a ln a -2e 2)<lna(2)2e (-2e )<0所以x=lna 1在f(x)的减区间上又由⑴解法二可知,x=2x x 21+也在f(x)的减区间上所以证明2x x 21+>lna 1即可x 1、x 2满足a x 1lna-2ax 1=0,a x 2lna-2ax 2=0将这两个式子相除,得21x -x 21a x x =,两边取自然对数,得ln 21x x =(x 1-x 2)lna 不妨设x 1<x 2,故证2x x 21+>lna 1即证ln 21x x <2121x x x -x 2+设t=21x x ,证lnt-1t )1-2(t +<0,其中t<1即可设G(t)=lnt-1t )1-2(t +,G '(t)=221)t(t 1)-(t +>0,所以G(t)在(0,1)单调增所以G(t)<G(1)=0,得证因此证明得f(2x x 21+)<e-aln a 2。
安徽省A10联盟2024届高三上学期11月段考数学试题及答案

A10联盟2024届高三上学期11月段考数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.请在答题卷上作答.第Ⅰ卷选择题(共60分)一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.2023i 25i-的虚部为()A.529-B.529C.229-D.2292.已知集合2,3k M x x k +⎧⎫==∈⎨⎬⎩⎭Z ,2,3N x x k k ⎧⎫==+∈⎨⎬⎩⎭Z ,则()A.M N M= B.M N M= C.M N =∅ D.M N=3.函数()3e e x xx f x -=-的部分图象大致为()A. B.C. D.4.在ABC △中,点M 是线段BC 上靠近B 的三等分点,点N 是线段AC 的中点,则AM =()A.23BN AC-+ B.2433BN AC-+ C.53BN AC-+D.2233BN AC-+ 5.在平面直角坐标系xOy 中,设角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,若角α的终边过点()4,3P -,则()3sin 2cos 22παπα⎛⎫++-= ⎪⎝⎭()A.1425-B.1425C.1725-D.17256.已知m ,n ,l 为三条不同的直线,α,β为两个不同的平面,则下列命题错误的是()A.若m n ∥,n α∥,m α⊄,则m α∥ B.若m n ⊥,m l ⊥,n α∥,l α∥,则m α⊥C.若m β∥,m α⊂,n αβ= ,则m n ∥ D.若αβ∥,m α⊥,n β⊥,则m n ∥7.已知定义在R 上的函数()F x 满足:()10F =,当1,32x ⎛⎫∈ ⎪⎝⎭时,()0F x '<.若()()f x xF x =,则下列说法错误的是()A.()10f '< B.()20f <C.()1,3x ∀∈,()0f x '< D.1,12x ⎛⎫∀∈⎪⎝⎭,()0f x >且()0f x '>8.已知正三棱锥S ABC -底面边长为1,侧棱长为2,过棱SA 的中点D 作与该棱垂直的截面分别交SB ,SC 于点E ,F ,则截面DEF 的面积为() A.1149B.21149 C.31149D.117二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.若函数()f x 的图象关于点()2,3中心对称,则()f x 的解析式可以是()A.()sin 3f x x π=+B.()372x f x x -=-C.()32619f x x x =-+ D.())lg 3f x x =+10.已知单位向量a ,b的夹角为θ,则()A.1cos 22a bθ=+ B.1sin 22a bθ=- C.若21a b += ,则56πθ=D.若21a b += ,则23πθ=11.已知a ,b ,c ,()0,d ∈+∞,且46a b +=,22c d +=,则()A.22542c d +≥B.22226485a b c d +++≥C.1153a b +≥+≤12.已知函数()()221f x x x λ=--+在11,22⎡⎤-⎢⎥⎣⎦上无极值点,则实数λ的值可能是()A.1- B.1 C.2D.4第Ⅱ卷非选择题(共90分)三、填空题(本题共4小题,每小题5分,共20分.)13.已知函数()ln f x x x =+,过原点作曲线()y f x =的切线l ,则切线l 的斜率为______.14.已知向量a ,b 满足2a b ⋅=- ,4a =,b 在a 方向上的投影向量为c ,则c = ______a .(用数字作答)15.,体积为3cm ,则经过该圆锥的两条母线的截面面积的最大值为______2cm .16.当异物卡在气管内迫使人咳嗽时,膈肌向上推动,导致肺部压力增加,与此同时,气管收缩,导致排出物移动更快,并增加异物的压力.已知咳嗽的数学模型()42121log log 1232v r r r r ⎛⎫=+≤≤ ⎪+⎝⎭,其中v (厘米/秒)表示通过人的气管的气流速度,r (厘米)表示气管半径,则咳嗽的气流最大速度约为______厘米/秒.(结果精确到0.1,参考数据:2log 3 1.585≈)四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分)已知幂函数()()22255m mf x m m x-=-+在()0,+∞上单调递减,函数()2xg x k =-.(1)求m 的值;(2)记集合()[]{},1,2A y y f x x ==∈,集合()[]{},1,1B y y g x x ==∈-,若A B A = ,求实数k 的取值范围.18.(本小题满分12分)已知M ,N 分别为函数()()()cos 0,0,0f x A x A ωϕωϕπ=+>><<图象上相邻的最高点和最低点,MN =,将函数()f x 的图象向左平移6π个单位长度后得到函数()g x 的图象,()g x 为奇函数.(1)求函数()f x 的解析式;(2)当3,04x π⎡⎤∈-⎢⎥⎣⎦时,关于x 的方程()0f x m -=有两个不同的实数解,求实数m 的取值范围.19.(本小题满分12分)如图,在直五棱柱ABCDE A B C D E '''''-中,22AB AE DE AA '====,BC CD ==,2BAE BCD π∠=∠=,F 为AE 的中点.(1)求证:B C E F ''⊥;(2)求平面B E F ''与平面CE F '夹角的余弦值.20.(本小题满分12分)如图,平面四边形ABCD 的对角线分别为AC ,BD ,其中AB =,BC CD ⊥,23BCD ABC ∠=∠.(1)若2BC =,ACD △的面积为3142,求BCD △的面积;(2)若13ADC BCD ∠=∠,2AD AB =,求cos ACD ∠的值.21.(本小题满分12分)已知()f x 是定义在R 上的奇函数,且当0x <时,()12xf x =-.(1)求函数()f x 的解析式;(2)若()2212n f n λλ--≤⋅对任意*n ∈N 恒成立,求实数λ的取值范围.22.(本小题满分12分)已知()()2e e213xxf x a a x -=-++-.(1)讨论函数()f x 的单调性;(2)若函数()f x 有两个零点,求a 的取值范围.·A10联盟2024届高三上学期11月段考数学参考答案一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)题号12345678答案CBADABDB1.C 由题意得,()()()2023i 25i i 52i 25i 25i 25i 2929-+==---+,故所求虚部为229-,故选C.2.B 由题意得,32,3k N x x k +⎧⎫==∈⎨⎬⎩⎭Z ,故N M Ü,则M N M = ,故选B.3.A 由题意得,()f x 的定义域为{}0x x ≠,且()()()33e e e ex xx x x x f x f x ----===--,所以()f x 为偶函数,排除CD ;又()1110e ef -=<-,排除B.故选A.4.D 作出图形如图,则12BN BA AN AB AC =+=-+,所以()1133AM AB BC AB AC AB =+=+- 21212223333333AB AC AB AC AC BN AC =+=-+=-+,故选D.5.A 由题意得,3sin 5α=-,则()3sin 2cos 2cos 2cos 22cos 22παπαααα⎛⎫++-=--=- ⎪⎝⎭()22314212sin 212525α⎡⎤⎛⎫=--=-⨯-⨯-=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.故选A.6.B B 中,若n l ∥,则未必有m α⊥,则B 的说法不一定正确.故选B.7.D由题意得,()()()f x F x xF x ''=+,∴()()()111f F F ''=+,∴()()110f F ''=<,故A 的说法正确;()()222f F =,∵1,32x ⎛⎫∈⎪⎝⎭时,()0F x '<,∴()F x 在1,32⎛⎫⎪⎝⎭上单调递减,又()10F =,∴()20F <,∴()20f <,故B 的说法正确;∵()()()f x F x xF x ''=+,()1,3x ∀∈,()0F x <,()0F x '<,∴()1,3x ∀∈,()0f x '<,故C 的说法正确;∵()F x 在1,32⎛⎫ ⎪⎝⎭上单调递减,又()10F =,∴1,12x ⎛⎫∀∈ ⎪⎝⎭,()0F x >,∴()()0f x xF x =>,∵1,12x ⎛⎫∀∈ ⎪⎝⎭,()0F x '<,∴()()()f x F x xF x ''=+的正负性无法判断,故D 的说法错误.故选D.8.B 由题易知,DE SA ⊥,DF SA ⊥,在SAB △中,由余弦定理得,4417cos 88ASB +-∠==,∴15tan 7ASB ∠=,157DE =,187cos 78SD SE ASB ===∠,同理,87SF SE ==,∴EF BC ∥,∴SE EF SB BC =,∴8721EF =,∴47EF =.过D 作DH EF ⊥于点H,则117DH ==,∴11411211227749DEF S EF DH =⨯⨯=⨯=△,故选B.二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)题号9101112答案ABCABDBDBD9.ABC对A ,sin y x π=关于()2,0中心对称,故()sin 3f x x π=+关于点()2,3中心对称,故A 正确;对B ,()371322x f x x x -==---,故()372x f x x -=-关于点()2,3中心对称,故B 正确:对C ,因为()()46f x f x +-=,所以()32619f x x x =-+关于点()2,3中心对称,故C 正确;对D ,易得()03f =,())4lg43f =+,不满足()()046f f +=,故D 错误.故选ABC.10.ABD由题意得,[]0,θπ∈,∴sin02θ≥,cos 02θ≥.∵()222211211cos a ba b a b θ+=++⋅=++⨯⨯⨯222cos 4cos 2θθ=+=,∴1cos 22a b θ=+ ,故A 正确;∵()2222a ba b a b -=+-⋅211211cos 22cos 4sin 2θθθ=+-⨯⨯⨯=-=,∴1sin 22a b θ=- ,故B正确;若21a b += ,则222221a b a b a b ++⋅=+⋅= ,∴12a b ⋅=- ,∴1cos 2θ=-,∴23πθ=,故C错误,D 正确.故选ABD.11.BD()2222422c d c d ++≥=,故A 错误;()()22222222886422a b c d a a d d +++=+-+-+()22464642415555a d ⎛⎫=-+-+≥ ⎪⎝⎭,故B 正确;()11111144566b a a b a b a b a b ⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭13562⎛≥+≥ ⎝,当且仅当2b a =时等号成立,故C 错误;()()42a b c d ++48242442ac bc ad bd ac bd ac bd=+++≥+=+(222==+≤,故D 正确.故选BD.12.BD方法一:设()()221h x x x λ=--+,要使()f x 在无极值点,即()f x 在11,22⎡⎤-⎢⎥⎣⎦上单调,只需要2122102h λ-⎧≥⎪⎪⎨⎛⎫⎪≥ ⎪⎪⎝⎭⎩或2122102h λ-⎧≥⎪⎪⎨⎛⎫⎪-≤ ⎪⎪⎝⎭⎩或2122102h λ-⎧≤-⎪⎪⎨⎛⎫⎪-≥ ⎪⎪⎝⎭⎩或2122102h λ-⎧≤-⎪⎪⎨⎛⎫⎪≤ ⎪⎪⎝⎭⎩,解得932λ≤≤或112λ-≤≤,所以实数λ的取值范围19,13,22⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦.故选BD.方法二:用区间没有零点也可解答.三、填空题(本题共4小题,每小题5分,共20分.)13.11e+由题意得,()11f x x '=+,设切点为()000,ln P x x x +,则切线方程为()000011ln y x x x x x ⎛⎫=+-++ ⎪⎝⎭,因为切线过原点,所以()00000101ln ln 1x x x x x ⎛⎫=+-++=-⎪⎝⎭,解得0e x =,所以()()01e 1ef x f ''==+.14.18-由投影向量定义知,b 在a 方向上的投影向量221168a ba abc a aa a⋅⋅-=⋅=⋅==-.15.4设该圆锥的底面半径和母线长分别为r ,l ,则213r π=,解得r =,∴)cm l ==.设SA ,SB 为圆锥的两条母线,当AB为底面直径时,221cos 2ASB +-∠==-,∴当2ASB π∠=时,经过该圆锥的两条母线的截面面积最大,为142⨯=.16.1.3由题意得,()42222212121212log log log log log log 2232323v r r r r r=+===++++()()22211log log 1log 31 1.585 1.322≤==+≈⨯+≈=,即23r =时取等号,即咳嗽的气流最大速度约为1.3厘米/秒.四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分)(1)由题意得,2551m m -+=,解得1m =或4m =,……2分当1m =时,()11f x xx-==,满足题意;……3分当4m =时,()8f x x =,此时()f x 在()0,+∞上单调递增,不满足题意.……4分综上,1m =.……5分(2)由(1)知,()1f x x =,则1,12A ⎡⎤=⎢⎥⎣⎦.……6分∵()2xg x k =-,∴1,22B k k ⎡⎤=--⎢⎥⎣⎦.……7分∵A B A = ,∴A B ⊆,∴112221k k ⎧-≤⎪⎨⎪-≥⎩,……9分解得01k ≤≤,即实数k 的取值范围为[]0,1.……10分18.(本小题满分12分)(1)由题意得,MN ==,……1分则2ω=,1A =,∴()()cos 2f x x ϕ=+,……2分∴()cos 2cos 263g x x x ππϕϕ⎡⎤⎛⎫⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,……3分∵()g x 为奇函数,∴()32k k ππϕπ+=+∈Z ,∴()6k k πϕπ=+∈Z ,……4分∵0ϕπ<<,∴6πϕ=,∴()cos 26f x x π⎛⎫=+ ⎪⎝⎭.……5分(2)∵304x π-≤≤,∴42366x πππ-≤+≤,作出函数()f x 在3,04x π⎡⎤∈-⎢⎥⎣⎦上的图象和直线y m =,……8分由图知,当131,22m ⎫⎛⎤∈--⎪⎢ ⎥⎪⎝⎦⎣⎭ 时,函数()f x 在3,04x π⎡⎤∈-⎢⎥⎣⎦上的图象和直线y m =有两个不同的交点,即关于x 的方程()0f x m -=有两个不同的实数解,……9分综上,实数m 的取值范围是131,22⎫⎛⎤--⎪ ⎥⎪⎝⎦⎣⎭ .……12分19.(本小题满分12分)(1)证明:连接BD ,A F ',FC,∵BC CD ==,2BCD π∠=,∴2BD =,∵2AB AE DE ===,2BAE π∠=,∴四边形ABDE 是正方形,∵F 为AE 的中点,∴CF AE ⊥.……1分由题意得,EE '⊥平面ABCDE ,∴EE CF '⊥,……2分∵AE EE E '= ,∴CF ⊥平面AEE A '',∴CF E F '⊥.……3分∵A B AB CF ''∥∥,∴A ',B ',C ,F 四点共面.……4分∵A F E F ''==,2A E ''=,∴222A F E F A E ''''+=,∴A F E F ''⊥,……5分∵CF A F F '= ,∴E F '⊥平面A B CF '',∴B C E F ''⊥.……6分(2)如图,分别以EA ,ED ,EE '为x ,y ,z 轴,建立空间直角坐标系,则()0,0,0E ,()1,0,0F ,()0,0,1E ',()2,2,1B ',()1,3,0C ,∴()2,2,0E B ''= ,()1,0,1E F '=- ,()0,3,0FC =.……7分设平面B E F ''的法向量为()111,,m x y z = ,由0m E B m E F ⎧''⋅=⎪⎨'⋅=⎪⎩可得11112200x y x z +=⎧⎨-=⎩,令11x =,得11y =-,11z =,∴()1,1,1m =-.……9分设平面CE F '的法向量为()222,,n x y z = ,由0n E F n FC ⎧'⋅=⎪⎨⋅=⎪⎩可得222030x z y -=⎧⎨=⎩,令21x =,得20y =,21z =,∴()1,0,1n =,……11分∴111011cos ,3m n m n m n⨯+-⨯+⨯⋅==,∴平面B EF ''与平面CE F '夹角的余弦值为3.……12分20.(本小题满分12分)(1)由题意得,2BCD π∠=,34ABC π∠=,在ABC △中,由余弦定理得,AC =……2分由余弦定理得,cos ACB ∠==3分∵2ACB ACD π∠+∠=,∴cos sin ACB ACD ∠=∠=,……4分∴11314sin 222ACD S AC CD ACD CD =⋅⋅⋅∠=⋅⋅△,故CD =5分∴11222BCD S BC CD =⋅⋅==△……6分(2)在ABC △中,由正弦定理得,sin sin AB AC ACB ABC =∠∠,∴1sin AC ACB =∠.……8分在ACD △中,由正弦定理得,sin sin AD AC ACD ADC =∠∠,∴2sin AC ACD =∠.……10分∵2ACB ACD π∠+∠=,∴cos sin ACD ACB ∠=∠,∴1cos sin ACD ACD=∠∠,∴sin 0ACD ACD ∠=∠>,……11分又22sin cos 1ACD ACD ∠+∠=,解得3cos 3ACD ∠=.……12分21.(本小题满分12分)(1)∵()f x 是定义在R 上的奇函数,∴()00f =.……1分当0x >时,0x -<,则()()122x x f x f x --=-=-=-,即()2x f x =.……3分综上,()1,020,02,0x x x f x x x ⎧-<⎪⎪==⎨⎪>⎪⎩.……4分(2)由(1)得,22122n n λλ--≤⋅对任意*n ∈N 恒成立.……5分①当0λ=时,20-≤成立,所以0λ=符合题意;……6分②当0λ>时,由22212n n λλ--≤恒成立,得22min212n n λλ⎛⎫--≤ ⎪⎝⎭.易知当1n =时,2102n n -=;当2n ≥时,2102n n ->,故2min102n n ⎛⎫-= ⎪⎝⎭.由220λλ-≤和0λ>,得0λ<≤;……8分③当0λ<时,由22212n n λλ--≥恒成立,得22min212n n λλ⎛⎫--≥ ⎪⎝⎭.由()2221111122222n n n n n n n +++---++-=,得当1n =,2时,()22111122n n n n ++-->;当3n ≥时,()22111122n n n n ++--<,且2223213122--<,∴223max 131122n n ⎛⎫--== ⎪⎝⎭.由221λλ-≥和0λ<,得10λ-≤<;……11分综上所述,实数λ的取值范围为⎡-⎣.……12分22.(本小题满分12分)(1)()()()()22e e 21e 2e 21e e e 2e 1x x x x x x x x f x a a a a a ---'⎡⎤=+++=+++=++⎣⎦.……1分当0a ≥时,()0f x '>,则()f x 在(),-∞+∞上单调递增;……2分当0a <时,令e 0xa +=,可得()ln x a =-,……3分当()(),ln x a ∈-∞-时,()0f x '<,()f x 在()(),ln a -∞-上单调递减;当()()ln ,x a ∈-+∞时,()0f x '>,()f x 在()()ln ,a -+∞上单调递增.……4分(2)由(1)得,要使函数()f x 有两个零点,则0a <,且()()()()()min ln 21ln 220f x f a a a a =-=+---<.……5分令()()()()21ln 220g x x x x x =+---<,则()()12ln g x x x'=-+,令()()()()12ln 0h x g x x x x '==-+<,则()()221110x h x x x x x -'=-=<,∴()h x 即()g x '在(),0-∞上单调递减.……6分∵()110g '-=-<,()1122ln 2ln 4022g '-=-=->,∴()02,1x ∃∈--,使得()()00012ln 0g x x x '=-+=,即()001ln 2x x -=-,......7分且()g x 在()0,x -∞上单调递增,在()0,0x 上单调递减,故只需()()0max 0g x g x =<,......8分即()()()000021ln 2200x x x x +---<<,则()()000012122002x x x x ⎛⎫+⨯---<< ⎪⎝⎭,即()200046100x x x ++<<, (10)分解得03344x --+<<,……11分故当3535,44a ⎛---+∈ ⎝⎭时,函数()f x 有两个零点.……12分以上各解答题如有不同解法并且正确,请按相应步骤给分.。
高中数学试题及答案doc原创

高中数学试题及答案doc原创一、选择题(每题5分,共20分)1. 下列函数中,为奇函数的是:A. y = x^2B. y = |x|C. y = x^3D. y = sin(x)答案:C2. 已知函数f(x) = 2x + 3,求f(-1)的值:A. -1B. 1C. 5D. -5答案:A3. 一个圆的半径为5,其面积是:A. 25πB. 50πC. 100πD. 25答案:B4. 直线y = 2x + 1与直线y = -x + 4相交于:A. (1, 3)B. (-1, 3)C. (1, -1)D. (-1, -1)答案:A二、填空题(每题5分,共20分)1. 等差数列的前n项和公式为:________答案:S_n = n/2 * (a_1 + a_n)2. 函数y = x^2 - 4x + 3的顶点坐标为:________答案:(2, -1)3. 一个三角形的内角和为:________答案:180°4. 圆的周长公式为:________答案:C = 2πr三、解答题(每题10分,共60分)1. 已知等比数列{a_n}的前三项依次为2, 6, 18,求该数列的通项公式。
答案:a_n = 2 * 3^(n-1)2. 求函数f(x) = x^2 - 6x + 8在区间[1, 4]上的最大值和最小值。
答案:最小值f(3) = -1,最大值f(1) = 33. 已知三角形ABC中,角A、B、C的对边分别为a、b、c,且满足a^2 + c^2 - b^2 = ac,求角B的大小。
答案:B = π/34. 已知函数f(x) = x^3 - 3x^2 + 4,求导数f'(x)。
答案:f'(x) = 3x^2 - 6x5. 一个圆的直径为10,求该圆的面积。
答案:A = 25π6. 已知直线l:y = 3x + 2与抛物线y^2 = 4x相交于点A和B,求A、B两点的坐标。
答案:A(1, 3),B(3, 9)四、证明题(每题10分,共20分)1. 证明:若一个三角形的两边长分别为3和4,且第三边长为整数,则该三角形的周长不可能为9。
高中数学竞赛holder不等式

高中数学竞赛holder不等式
(原创版)
目录
1.高中数学竞赛 holder 不等式的概念和背景
2.holder 不等式的基本原理
3.holder 不等式在数学竞赛中的应用
4.如何运用 holder 不等式解决竞赛题目
5.结论
正文
【1】高中数学竞赛 holder 不等式的概念和背景
在高中数学竞赛中,holder 不等式是一个非常重要的工具,它可以
帮助学生解决许多复杂的数学问题。
holder 不等式的全称是 Holder 不
等式,是由数学家 Holder 提出的。
【2】holder 不等式的基本原理
holder 不等式的基本原理是:对于任意的实数 a 和 b,都有|a+b|≤|a|+|b|。
这个不等式在数学中有着广泛的应用,可以帮助我们解决许
多复杂的数学问题。
【3】holder 不等式在数学竞赛中的应用
在高中数学竞赛中,holder 不等式常常被用来解决一些复杂的数学
问题。
例如,它可以用来解决一些涉及到绝对值的不等式问题,也可以用来解决一些涉及到概率的问题。
【4】如何运用 holder 不等式解决竞赛题目
在使用 holder 不等式解决竞赛题目时,学生需要先理解题目的要求,然后找到题目中可以使用 holder 不等式的地方,最后运用 holder 不等
式解决题目。
【5】结论
总的来说,holder 不等式是高中数学竞赛中一个非常重要的工具,它可以帮助学生解决许多复杂的数学问题。
2008年江苏高考数学原创压轴题

2008年江苏高考数学原创压轴题2010年将是不平静的一年,除了奥运会的举办等国际国内的大事以外,就数牵动千百万家庭的高考了,特别是江苏的高考,是进入新课程后的第一次高考,全新的课程标准、全新的教学方法、全新的高考模式、全新的录取形式,所以必然出现全新的高考命题模式.通过认真学习《高中数学课程标准》、《江苏省课程标准教学要求》等纲领性文件,反复研读了2005、2006、2007,2008.,2009五年高考江苏卷的试卷评析报告,下面给出几个原创题,供高三师生参考,权当抛砖引玉.1.如果复数()()21m i mi ++是实数,则实数m=____________________.解: ()()21m i mi ++展开后,“原始项”共四项,但是我们并 不关心实部项,虚部项为:21m mi i ⋅+⋅,只需310m +=即可,所以1m =-.【命题意图】考查复数的运算和相关基本概念的理解.过去复数在《选修Ⅱ》中,《选修Ⅰ》没有复数,所以,近几年江苏一直不讲复数,因此,复数成了新内容.2.设[]x 表示不大于x 的最大整数,集合{}2|2[]3A x x x =-=,1|288x B x ⎧⎫=<<⎨⎬⎩⎭,则A B = _________________.解:不等式1288x <<的解为33x -<<,所以(3,3)B =-. 若x A B ∈ ,则22[]333x x x ⎧-=⎨-<<⎩,所以[]x 只可能取值3,2,1,0,1,2---.若[]2x ≤-,则232[]0x x =+<,没有实数解;若[]1x =-,则21x =,解得1x =-; 若[]0x =,则23x =,没有符合条件的解;若[]1x =,则25x =,没有符合条件的解;若[]2x =,则27x =,有一个符合条件的解x =因此,{A B =- .【命题意图】此题是一元二次方程根分布问题,涉及指数不等式的解法,函数与方程思想,分类讨论思想等.数学的精华在于数学思想方法,思考问题的支撑点也是数学思想方法,只有理解了数学思想方法,才算真正学明白了数学.3.如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D .测得00153030BCD BDC CD ∠=∠==,,米,并在点C 测得塔顶A 的仰角为060,则塔高AB=_____ .解:由原解答得()tan sin 30tan 60sin 30sin()sin 1530s AB θβαβ⋅===++【命题意图】在2007年的课改区高考试题中,十分重视弘扬和发展学生的数学应用意识.新课标卷更注意数学应用意识和实践能力的考查,试题设计更加注意贴近生活实践.4.若关于,x y 的方程组22110ax by x y +=⎧⎨+=⎩有解,且所有的解都是整数,则有序数对(),a b 的数目为 .解:因为2210x y +=的整数解为:()()()()()()()()1,3,3,1,1,3,3,1,1,3,3,1,1,3,3,1--------,所以这八个点两两所连的不过原点的直线有24条,过这八个点的切线有8条,每条直线确定了唯一的有序数对(),a b ,所以有序数对(),a b 的数目为32.【命题意图】本题主要考察直线与圆的概念,以及组合的知识,既要数形结合,又要分类考虑,要结合圆上点的对称性来考虑过点的直线的特征.是较难问题.5.若数列{a n }的通项公式a n =21(1)n +,记12()2(1)(1)(1)n f n a a a =--⋅⋅⋅-,试通过计算(1)f ,(2)f ,(3)f 的值,推测出()f n = .解:∵ ()()1213(1)2121211f a ⎡⎤=-=⨯-=⎢⎥+⎢⎥⎣⎦,122314(2)2(1)(1)1233f a a ⎛⎫=⨯--=-= ⎪⎝⎭,()3415(3)(2)113164f f a ⎛⎫=-=-= ⎪⎝⎭,∴归纳猜想得2(1)n f n n +=+. 【命题意图】考查考生对归纳猜想和递推的理解和运用.此题涉及属探索性问题,考生可根据特殊情形归纳概括一般性结论.6.已知三个正数,,a b c 满足a b c <<. (1)若,,a b c 是从129,,101010⎧⎫⋅⋅⋅⎨⎬⎩⎭中任取的三个数,求,,a b c 能构成三角形三边长的概率; (2)若,,a b c 是从(0,1)中任取的三个数,求,,a b c 能构成三角形三边长的概率.分析:在(1)中,,a b c 的取值是有限可数的,可用列举法解决;(2)中,,a b c 的取值是无穷的,得用几何概型的方法求解.解:(1)若,,a b c 能构成三角形,则4,10a b c c +>≥. ①若410c =时,32,1010b a ==.共1种;②若510c =时.432,,101010b a ==.共2种; 同理610c =时,有3+1=4种;710c =时,有4+2=6种;810c =时,有5+3+1=9种;910c =时,有6+4+2=12种.于是共有1+2+4+6+9+12=34种. 下面求从129,,101010⎧⎫⋅⋅⋅⎨⎬⎩⎭中任取的三个数,,a b c (a b c <<)的种数: ①若110a =,210b =,则39,,1010c =⋅⋅⋅,有7种;349,,,101010b c ==⋅⋅⋅,有6种;410b =,59,,1010c =⋅⋅⋅,有5种;……; 89,1010b c ==,有1种.故共有7+6+5+4+3+2+1=28种.同理,210a =时,有6+5+4+3+2+1=21种;310a =时,有5+4+3+2+1=15种;410a =时,有4+3+2+1=10种;510a =时,有3+2+1=6种;610a =时,有2+1=3种;710a =时,有1种.这时共有28+21+15+10+6+3+1=84种. ∴,,a b c 能构成三角形的概率为34174824=. (2)a b c 、、能构成三角形的充要条件是0101a b c a b c c <<<<⎧⎪+>⎨⎪<<⎩.在坐标系aOb 内画出满足以上条件的区域(如右图阴影部分),由几何概型的计算方法可知,只求阴影部分的面积与图中正方形的面积比即可.又12S =阴影,于是所要求的概率为112.12P == 【命题意图】统计、概率对于现代社会(经济发达)越来越显得重要,也是学生由确定性数学向不确定性(随机性)数学的一个转变,有着基本的重要性,考查是必然的.7.请认真阅读下列程序框图:已知程序框图(1)i i x f x =-中的函数关系式为42()1x f x x -=+,程序框图中的D 为函数()f x 的定义域,把此程序框图中所输出的数i x组成一个数列{}n x .(理科考生请完成下列各题) (1) 若输入04965x =,请写出数列{}n x 的所有项; (2) 若输出的无穷数列{}n x 是一个常数列,试求输入的初始值0x 的值;(3) 若输入一个正数0x 时,产生的无穷数列{}n x 满足:*n N ∀∈,都有1n n x x +<,试求正数0x 的取值范围.(文科考生请完成下列各题)(1) 若输入04965x =,请写出输出的所有数i x ; (2) 若输出的所有数i x 都相等,试求输入的初始值0x 的值. 解:(1)当04965x =时,12349111111165191955x f x f x f ⎛⎫⎛⎫⎛⎫======- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,, 所以输出的数列为1111195-,,…………………(3分) (2)数列{}n x 是一个常数列,则有120n x x x x ==⋅⋅⋅== 即000042()1x x f x x -==-,解得:0012x x ==或 所以输入的初始值0x 为1或2时输出的为常数列. (3)由题意知 142()1n n n n n x x f x x x +-==>+,因00x >,0n x ∴>,有:421n n n x x x ->+得42(1)n n n x x x ->+即2320n n x x -+<,即(2)(1)0n n x x --<要使*n N ∀∈,都有1n n a a +>,须00(2)(1)0x x --<,解得:012x <<, 所以当正数0x 在(1,2)内取值时,所输出的数列{}n x 对任意正整数n 满足1n n x x +< (文科)解:(1)当04965x =时,12349111111165191955x f x f x f ⎛⎫⎛⎫⎛⎫======- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,所以输出的数为1111195-,,,要使输出的数i x 都相等,即11()i i i x f x x --==(2)此时有 100()x f x x ==,即00421x x -+=0x ,解得01x =或02x =,所以输入初始值01x =或02x =时,输出的数i x 均相等.【命题意图】算法思想可以贯穿于整个中学数学内容之中,有很丰富的层次递进的素材,而在算法的具体实现上又可以和信息技术相联系,因此,算法与函数,数列等知识的融合,有利于培养学生理性精神和实践能力,是实施探究性学习的良好素材.8.已知二次函数2(),f x ax bx c =++直线21:8l y t t =-+(其中t 为常数);2:2=x l .若直线12,l l 与函数()f x 的图象以及1l ,y 轴与函数()f x 的图象所围成的封闭图形如阴影所示. (Ⅰ)求a 、b 、c 的值(Ⅱ)求阴影面积S 关于t 的函数()S t 的解析式;(Ⅲ)若,ln 6)(m x x g +=问是否存在实数m ,使得()y f x =的图象与()y g x =的图象有且只有两个不同的交点?若存在,求出m 的值;若不存在,说明理由.解:(I )由图形知:2201880804164c a a b c b c ac b a⎧⎪==-⎧⎪⎪⎪⋅+⋅+==⎨⎨⎪⎪=-⎩⎪=⎪⎩,解之得:,∴函数()f x 的解析式为x x x f 8)(2+-= (Ⅱ)由⎪⎩⎪⎨⎧+-=+-=xx y t t y 8822得2128(8)0,,8,x x t t x t x t ---=∴==-∵0≤t ≤2,∴直线l 1与()f x 的图象的交点坐标为()8,2t t t +-由定积分的几何意义知:⎰⎰+--+-++--+-=102222]8()8[()]8()8[()(tdx t t x x dx x x t t t S12223222088(8)()()(8)32032tx x x x t t x t t x ⎡⎤⎡⎤=-+--++-+--+⋅⎢⎥⎢⎥⎣⎦⎣⎦34016103423+-+-=t t t(Ⅲ)令.ln 68)()()(2m x x x x f x g x ++-=-=ϕ因为x >0,要使函数()f x 与函数()g x 有且仅有2个不同的交点,则函数m x x x x ++-=ln 68)(2ϕ的图象与x 轴的正半轴有且只有两个不同的交点262862(1)(3)()28(0)x x x x x x x x x xϕ-+--'∴=-+==>当x ∈(0,1)时,()0,()x x ϕϕ'>是增函数; 当x ∈(1,3)时,()0,()x x ϕϕ'<是减函数 当x ∈(3,+∞)时,()0,()x x ϕϕ'>是增函数 当x=1或x=3时,()0x ϕ'=∴;7)1()(-=m x ϕϕ极大值为153ln 6)3()(-+=m x ϕϕ极小值为 又因为当x →0时,-∞→)(x ϕ 当+∞→+∞→)(x x ϕ时,所以要使0)(=x ϕ有且仅有两个不同的正根,必须且只须(1)0(3)0(3)0(1)0ϕϕϕϕ==⎧⎧⎨⎨'<>⎩⎩,或即706ln 31506ln 315070m m m m -=+-=⎧⎧⎨⎨+-<->⎩⎩,或,∴m=7或.3ln 615-=m∴当m=7或.3ln 615-=m 时,函数()f x 与函数()g x 的图象有且只有两个不同交点.【命题意图】对江苏来说,与以往不同的是,增加了正弦、余弦、指数、对数的导数,还有积的导数,商的导数.对理科另外还有求形如)(b ax f +的复合函数导数以及定积分.高校教师熟悉微积分,历来是命题的热点(江苏2003年21题就很难),加上新增加许多函数的导数,2008年大题考导数,定积分的可能性极大.。
高中数学考试试卷原创题(难度较大)

标题姓名: 校区:一、选择题(每题5分,共60分)1.已知集合{}122=+∈=y x Z x A ,集合{}12-==x y x B ,则B A ⋂的元素个数为( ) A.0 B.1 C.2 D.3 2.向量、,若)2,1(=,满足与+同方向的单位向量为)13133,13132(=b ( ) A.5 B.25 C.5 D.35 3.已知复数1z 、2z 满足21=z ,221=-z z ,i z z -=+3221,则=21z z ( ) A.i i -2528或 B.i i +-2528或C.i i 5157-或D.i i 5751+-或4.如图所示程序框图,若输出的结果为25=S ,则 输入的t =( )A.5B.9C.10D.155.抛物线y x 42=上两动点A 、B ,若8=AB 。
设()00,y x P 是线段AB 的中点,则=0y ( )A.4B.8C.41D.16156.若P 点是双曲线C :12222=-by a x (0,0>>b a )上任意一点;在P 点处作C 的切线l 与两坐标轴交于A 、B 两点。
已知△OAB 的面积为2a ,则双曲线C 的离心率为( ) A.5 B.3 C.2 D.257.从231、232、233···240这十个数字中随机抽取一个数字,则该数字的个位数字与十位数字之和是奇数的概率为( ) A.107 B.53 C.21 D.528.已知实数x 、y 满足⎪⎩⎪⎨⎧≥≤≤+-0001y x y x ,则223y x z +=的最小值为( )A.1B.43C.22D.09.已知三棱锥A -BCD 的所有棱长都为2,点P 是平面BCD 内的一个动点,AP=3,若M 、N 、Q 分别为AB 、AC 、AD 的中点,则三棱锥P -MNQ 的外接球表面积为( ) A.π3 B.π4 C.π5 D.π610.已知α是第二象限角,且1cos sin 5=+αα,则=+ααcos sin 18( ) A.5 B.6 C.7 D.8 11.已知几何体的三视图如图所示,正视图和侧视图是边长 为3的正方体,则该几何体的体积为( ) A.23B.3C.233 D.23 12.函数x x x f )3()(2+=的图像大致为( ) A.B.C. D.二、填空题(每题5分,共20分)13.()55)1(2+⋅+x x 的展开式中x 项的系数是 .14.已知ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,且满足c A b B a 53cos cos =-,则BAtan tan 的值为 .15.已知实数a 、b 满足1=+b a .则()()1122++++b b a a 的最小值是 .16.已知函数)1ln(2ln )(+-=x ax x f .若)(x f 在定义域内有且仅有一个零点,则a 的取值范围是 .三、解答题(每题12分,共60分)17.已知正项数列{}n a 的前n 项和为n S ,满足n S a a n n 442121++=+,且73a S =.(1)求n a 得通项公式;(2)求数列{}n n S ⋅2的前n 项和n T .18.如图所示的三棱锥P -BCA 中,PA=AB=1,PC=BC=3(1)求证:PB ⊥AC ; (2)若PB=26,AB ⊥BC.求二面角A -PC -B 的余弦值。
专题08 等比数列-高中数学必备考试技能之二级结论提高速度原创精品(2021版)(解析版)

S2 , S4 S2 , S6 S4 为等比数列,又 S2 k , S4 S2 2k , S6 S4 4k , S6 7 k ,
Hale Waihona Puke a96 a99 9S .
a96 a99 9S 36 .
8.已知等比数列 an 的各项均为正数,若 log 3 a1 log 3 a2 log 3 a12 12 ,则 a6 a7 =( )
A.1
B.3
C.6
D.9
【答案】D
【解析】由 log 3 a1 log 3 a2
也成等比数列,进而突破难点.
针对训练*举一反三
1.在各项均为正数的等比数列中 an , a3 2 2 , a5 2 1 ,则 a1a5 2a2 a6 a3 a7 (
A.1
B.9
C. 5 2 7
)
D. 3 2 9
【答案】B
【详解】因为 an 为各项为正的等比数列, a3 2 2 , a5 2 1 ,
高考数学必备考试技能之“二级结论*提高速度”原创精品【2021 版】
结论八:等比数列
已知等比数列{an},公比为 q,前 n 项和为 Sn.
n-m
m
n
*
(1)an=am·q ,an+m=anq =amq (m,n∈N ).
*
(2)若 m+n=p+q,则 am·an=ap·aq(m,n,p,q∈N );反之,不一定成立.
例
【答案】 64
解
析
【详解】等比数列 {an } 的前 n 项和为 S n ,则 S4 , S8 S4 , S12 S8 , S16 S12 也成等比数列,
漫谈高中数学原创试题的命制

决定将“ C 一÷” 改为“ C 一一1 ” , 此时, 解答过程需要
‘ 士
合 近年 来参 加南 通市 高三模 拟 考试 和海 安县 期 中、 期
末调研考 试 的命 题 经历 , 举 例 探 讨 原 创 题 的 命 制
过程。
对 首项 进行分 类讨 论 , 且 对第 ( 2 ) 问没 有 影 响 , 故 笔者 考 虑在 题 干 中直 接 给 出 c 的 值 ; 第( 2 ) 问 证 明“ A= = = 0 ” , “ O ” 对学 生解 题有 暗示作 用 , 故 考虑 改为 求值题 。
列 ?并说 明理 由 ;
命制 的一道 数列 题 , 命 题 方 法 主要 为 特 殊 与 一 般 、 抽
象概 括 ( 统一 形式 ) 、 逆 向思 维 。
( 2 ) 若数列 { a ) 是等 比数 列 , 求t 的值 。
审核 : 审核 时 , 主要 研 究 了等 比数 列 { ) 的存 在
1
列符 合题 设。通过探 究 , 公比q : = = n +1 , k 一 一÷
u 1
( 口 >O ) , 从而 最 <O 。同时 , 就第 ( 2 ) 问求 解 方 法 的 多
命 制一 道数 列综 合题 。
初稿 : 由等 差 数 列 口 一2 n 一 1的 前 项 和 S 一
满足 S :Aa : +B a +C 的形式 ) 。在 等 比数 列 ( 公 比 g ≠1 ) 中, s 一一 1 qj a + L பைடு நூலகம் 故也满足 s 一A口 : + B a +C ( 其 中 A—O ) 的形式 , 即 一 =A a +( B一1 )・
口 +c ( ≥2 ) 。若取 A一÷, B一音 , C一÷, 可求得
高中数学原创题命制的应用探析

高中高中数学原创题命制的应用探析?江苏省连云港市城头高级中学 穆加超命题作为一项系统性较强的技术型工作,具有一定的难度和挑战性.新时期教育背景下,为有效提升教育领域命题的质量,命题者有必要更新方法和技术,积累命题经验,并能够通过改编和原创两种方式,实现对试题的科学命制.现阶段,高质量的原创题在教育领域大受欢迎,应试教育制度下,高中数学教师为有效提高学生的应试能力和数学学科核心素养,不仅开始主动贯彻新课程改革的要求,还开始投入到数学题的命制工作中.在此过程中,教师要基于课堂实际,以适用性为原则,尊重学生间的差异性,在具体的教学实践中,对数学题进行命制和原创,以期实现对学生课堂所学知识的巩固作用,开发学生创新能力和思维意识,推动学生的全面发展,使其在应试教育背景下实现“素质”和“应试”的协调发展.高中数学教师基于课程标准相关要求、运用一定的命题原理和命题技术、在数学教学实践中进行原创题的命制,能够有效测试和提升学生的创新能力和实践意识.纵观应试教育背景下长期以来数学题的状况和形式,可以发现数学题型较为单一、与生活实际相背离,而新时期教师命制的原创题,则具有一定的新颖度、深度和广度,能够满足学生多样性和探索性的需求特点,进而实现对学生数学知识迁移、融合和运用能力的考查.此外,进行高中数学原创题的命制,还有助于更好地实现高考的人才选拔功能.作为高中阶段重要的选拔性考试,高考能够为高等院校选拔人才,在教育体系中占据着关键的位置,发挥着重要的作用.基于高中数学原创题命制背景新颖、形式多样的特点,能够实现对学生数学知识和技能掌握情况的判定,实现对学生思想方法和学习潜能的考查,减小高考中学生之间的分数差距,实现优秀人才的选拔.在本篇文章中,笔者基于自身为某高中高三学生一次模拟考试的命题经历,对命题方式展开详细的阐述.一、命题过程中要重视知识的内在联系作为一门复杂性和逻辑性极强的学科,数学科目十分重视知识的内在联系和衔接,因此,在进行原创题命制时,命题者要利用知识间的联系,将知识有机统一.下题为一道与高中数学必修5中数列知识相关的原创试题,在进行本题命制时,主要应用了抽象概括方法和逆向思维方式,同时,命题者还将考试实际和学生的接受情况纳入到考量范围中,基于学生接受能力的特点,构建了一道集等差、等比数列相关公式为一体的数列综合题,体现了一定的基础性和典型性特点.在初步设计阶段,命题者做出如下设计:犪狀=2狀-1为等差数列,基于前狀项和公式犛狀=狀2,得出犛狀=犪狀+12()2,还可以将该式进行展开,使其满足犛狀=犃犪2狀+犅犪狀+犆的形式.在公比不为1的等比数列犛狀=-狇1-狇犪狀+犪11-狇中,其也符合犛狀=犃犪2狀+犅犪狀+犆的形式,只是犃=0,也就是犛狀-1=犃犪2狀+(犅-1)犪狀+犆(狀≥2),在犃和犆分别等于14、犅等于12的情况下,得到犪狀=2狀-1,在{犪狀}是等比数列的情况下,能够证明出犃=0.基于以上设计,命题者进一步构建出初步命题内容为:数列{犪狀}的各项均为正数,狀为整数且狀≥2,犛狀-1=犃犪2狀+(犅-1)犪狀+犆.求:(1)犃=犆=14,犅=12时,该数列的通项公式;(2)该数列为等比数列情况下,证明犃=0.在完成初步命题后,教师还要科学地对构建的原创题内容进行调整,以完善命题的不足之处,在本题的命制中,第(1)问要求求出通项公式,过于直白简单,为了提升难度和区分度,命题者将犆的值改为“-1”,同时,在初步命题的第(2)问中,命题者给出的证明犃=0条件,在一定程度上会起到一定的提示和暗示作用,因此,要将此部分更换为求值题.最终,命题者构建了内容如下的原创试题:数列{犪狀}为各项均为正数的无穷数列,犛狀为前狀项和,在狀≥2的01命题考试命题研究 2021年4月Copyright©博看网 . All Rights Reserved.高中情况下,犛狀-1=狋犪2狀-犽犪狀-1,(犽,狋均为犚).求:(1)已知犽=12,狋=14,请猜想该数列能否为等差数列,并说明原因;(2)该数列为等比数列时,求犽值.二、命题过程中要重视原创空间的寻找和创设为保证命制的高中数学原创题具有一定的创新性元素和新颖性特点,命题者在进行原创题命制工作时,要重视寻找和创设原创空间.下题为笔者依据高中阶段数学必修1基本初等函数教学知识所设计的一道函数题,旨在考查学生的函数与方程的分类思想和整合能力.命题者通过细致梳理可以发现关于狔=狓犪和狔=log犪狓二者之间关系的考查相对来说较少,因此,命题者在对其中一个函数做特殊化处理、降低难度的基础上,构建了相应的原创题,以期实现对学生知识体系的良好考查.在初步设计阶段,命题者做出如下设计:研究狔=狓犪与狔=ln狓的交点个数.在0<犪<1e的情况下,存在两个交点,代数证明难度较高.构建题目如下:犳(狓)=狓犪,犵(狓)=e狓,犺(狓)=ln狓.求:(1)犪=1时,犺(狓)<犳(狓)<犵(狓);(2)犪=e时,求犳(狓)=犵(狓)正实根;(3)犪∈犚时,求犳(狓)=犺(狓)的实根个数.第(3)问过难且方法重复,因而删去,第(2)问已有研究,也删去,在对第(1)问进行调整的基础上,构建出最终的原创题:犳(狓)=狓犪,犵(狓)=ln狓.求:(1)犪=1时,证明狓>0时,犳(狓)>=犵(狓)+1;(2)犪∈犚的情况下,求犳(狓)=犵(狓)的实根个数.三、命题过程中要重视实验操作在高中阶段的数学教学中,通过实验操作,能够使学生对数学知识进行直观感知,发现有趣的数学现象和规律,提出有价值的新问题.命题者以A4纸为媒介,通过构建实验操作,提取有价值元素,命制了下方的高中数学原创题,旨在考查高中生函数的应用和数学阅读建模能力.在进行本题设计时,命题者首先将A4纸(制造过水装置的材料)分别折叠成截面三角形、等腰梯形、弓形的立体图形,并要求折痕与A4纸两边平行,尝试怎样折叠能实现过水量的最大化.基于图1可知,不同图形过水量证明方式存在明显的难度差异,并不适合将其作为考题.因而,命题者为图1了将本部分的命题贴近实际,帮助考生获取分数,最终构建了生活性较强的、简洁明了的考试试题,具体如下:某校园想要构建多边形花坛,要求花坛一边需靠着长度为30米以上的围墙,现有两种方案可供选择.如图2,花坛形状为直角三角形犃犈犅,犃犈+犈犅=30m.如图3,花坛为形状为等腰梯形犃犈犉犅,犃犈=犈犉=犅犉=10m.图2 图3请分别对两种形状花坛的面积进行求解,并选择最优方案.当然,除以上三种方法外,高中数学原创题的命制方法还有很多,本文不一一进行赘述.总之,在进行高中阶段数学原创题的命制工作时,教师发挥着极其关键和重要的作用.教师不仅要具备精湛的命题技术,还要具备雄厚的教学经验,要密切关注学生的学习情况,与学生密切配合,善于抓住教学实践中的灵感,发现新问题,最终实现高中数学原创题命制质量的有效提升.参考文献:[1]杨元餠,耿晓华.对一道试题的命制预设与测试反馈差异的思考[J].数学通报,2018(10).[2]庄志红.命制一道初中数学试题的艰难取舍[J].数学通报,2016(7).[3]马明.巧借数学史知识精心命制数列原创题[J].数学通讯,2018(12).[4]庄佩玉.课本题,巧设计,出新意———一道期中原创题的命制过程及感悟[J].中学数学(上),2018(6).犠112021年4月 命题研究命题考试Copyright©博看网 . All Rights Reserved.。
高中数学原创选编题
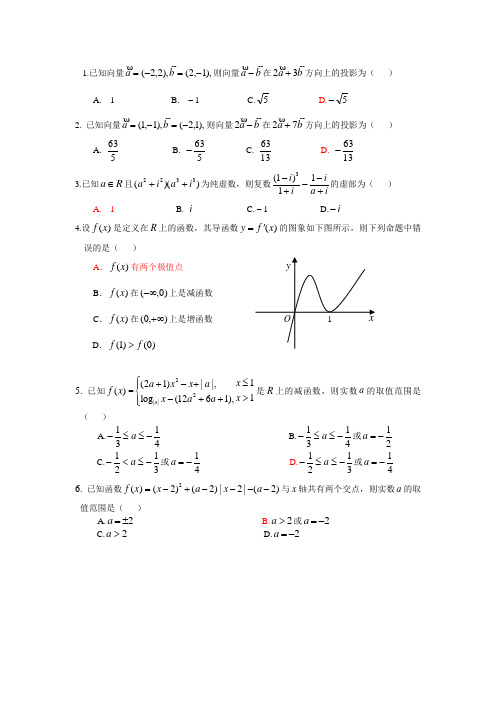
1.已知向量),1,2(),2,2(-=-=b a则向量b a -在b a 32+方向上的投影为( )A. 1B. – 1C.5D.5-2. 已知向量),1,2(),1,1(-=-=b a则向量b a -2在b a 72+方向上的投影为( )A.563 B. 563- C. 1363 D. 1363-3.已知R a ∈且))((3322i a i a ++为纯虚数,则复数ia ii i +--+-11)1(3的虚部为( ) A. 1 B. i C. – 1 D.i -4.设)(x f 是定义在R 上的函数,其导函数)(x f y '=的图象如下图所示,则下列命题中错误的是( )A .)(x f 有两个极值点B .)(x f 在)0,(-∞上是减函数C .)(x f 在),0(+∞上是增函数D .(1)(0)f f >5. 已知)(x f =22||1(21)||,1log (1261),a x a x x a x x a a ⎧≤+-+⎪⎨>-++⎪⎩是R 上的减函数,则实数a 的取值范围是( )A.4131-≤≤-a B.4131-≤≤-a 或21-=a C.3121-≤<-a 或41-=a D.3121-≤≤-a 或41-=a6. 已知函数2()(2)(2)|2|(2)f x x a x a =-+----与x 轴共有两个交点,则实数a 的取值范围是( )A.2a =±B.2a >或2a =-C.2a >D.2a =-不等式2ln(1)023x x x ++-≥的解集是{|101}x x x -<>或≤.不等式2ln(1)02x x x ++-≥的解集是{|101}x x x -<>或≤. 不等式2ln(2)023x x x ++-≥的解集是3{|11}2x x x -<->或≤. 不等式2ln(2)0||6x x x +--≤的解集是{|13}x x -<≤. 不等式2ln(1)02||3x x x +--≤的解集是{|03}x x <≤.不等式22||30ln(1)x x x --+≥的解集是{|103}x x x -<<或≥.不等式2ln(2)ln 203||2x x x +--+≥的解集是{|21012}x x x x -<<-<>或或≤.不等式23||20ln(2)ln 2x x x -++-≥的解集是{|21012}x x x x --<或或≤≤≤≥.不等式2ln(2)ln 203||2x x x +--+≤的解集是{|012}x x x <<<-1或≤.不等式22132x x x ->++的解集是{|21}x x -<<-.已知α为第四象限的角,cos ()2πα+=35,则cot (2)4πα-=1731-.向量及正余弦定理例题A1.设斜△ABC 的面积为S ,则S=A .1(AB AC)sin A 2⋅ B .1(AB AC)tan A 2⋅C .1|AB AC |sin A 2⋅D .1|AB AC |tan A 2⋅2.已知平面上O 、A 、B 三点不共线,设OA=a ,OB b =,则△OAB 的面积等于A BC D 3.已知||3a = ,||8b = ,,120a b <>=︒ ,求||a b +.(7)4.已知0a b c ++= ,且||3a = ,||5b = ,||7c = ,求,a b <>. (60°)5.已知(3,1)b =- ,(2,1)c =,a 与c 共线,求a b + 的模的最小值.习题A1.设△ABC 的面积为S ,若AB AC 1⋅=,tan A=2,则S=A .15 B C .1 D .2 2.若△ABC 的面积为S=1,且tan B=2,则AB BC ⋅=A .-1B .1C .-2D .23.已知△ABC 中,AB (3,4)= ,AC (5,12)=,则△ABC 的面积是 .(8) 4.若△ABC 的面积为S=1,且AB BC 1⋅=.(1)求tan B ;(-2) (2)求AC的模的最小值.(2)5.已知△ABC 的面积为S ,设CA a = ,CB b =.(1)求证:S =(2)若12(,)a a a = ,12(,)b b b = ,试用1a 、2a 、1b 、2b 表示S .(12211||2S a b a b =-)(3)若(1,2)a = ,(3,4)b = ,求S 及tan C .(1,2/11,提示:1()tan C 2S a b =⋅ )例题B1.叙述并证明正弦定理和余弦定理.2.证明:sin(A B)sin(A B)(sin A sin B)(sin A sin B).+-=+-3.在△ABC 中,角A 、B 、C 的对边分别为a b c 、、,求证:22A 2B.a b bc -=⇔= 4.已知△ABC 的三边长是连续整数,且最大角是最小角的2倍,求三边长.5. 已知a 、b 是两个非零向量,当()a tb t R +∈的模取最小值时,求t 的值,并证明此时.b a tb ⊥+习题B1.在△ABC 中,角A 、B 、C 的对边分别为a b c 、、,且22.a b bc -=(1)求证:A 2B =; (2)若ABC 12S ∆=,AB BC 3⋅=-,求cos C.2.在△ABC 中,角A 、B 、C 的对边a b c 、、成等差数列,且C 2A =. 求sin A :sin B:sin C的值.3.在△ABC 中,已知cot A cot B cot C 、、成等差数列,求证:222a b c 、、也成等差数列. 4.已知33(cos ,sin )22x x a = ,(cos ,sin )22x x b =- ,且3[,]22x ππ∈. (1)分别求出使得a b ⊥ 和a ∥b成立时的x 值;(2)求||a b +的取值范围;(3)求函数()||f x a b a b =⋅-+的值域,并求出()f x 取最小值时的x 值; (4)若函数()2||f x a b a b λ=⋅-+ 的最小值是32-,求λ的值.5.在△ABC 中,角A 、B 、C 的对边a b c 、、的倒数成等差数列.(1)求角B 的范围; (2)求2sin 2Bsin B cos By +=+的取值范围.。
高中原创试题出处及答案

高中原创试题出处及答案试题一:数学-几何题题目:在一个直角三角形ABC中,∠C为直角,已知AB=5,AC=3,求BC的长度。
解题思路:根据勾股定理,直角三角形的斜边的平方等于两直角边的平方和。
即AB² = AC² + BC²。
答案:首先计算AC² = 3² = 9,然后将AB² - AC² = 5² - 9 = 25 - 9 = 16,得到BC² = 16。
因此,BC = √16 = 4。
试题二:物理-力学题题目:一个质量为2千克的物体,从静止开始自由下落,忽略空气阻力,求物体在下落2秒时的速度。
解题思路:根据自由落体运动的公式,v = gt,其中v是速度,g是重力加速度(取9.8 m/s²),t是时间。
答案:将已知数值代入公式,v = 9.8 m/s² × 2 s = 19.6 m/s。
物体在下落2秒时的速度为19.6米每秒。
试题三:化学-物质的量题题目:在标准状况下,1摩尔的氧气(O₂)的体积是多少?解题思路:根据摩尔体积的定义,在标准状况下(0℃,1大气压),1摩尔任何气体的体积都是22.4升。
答案:1摩尔氧气(O₂)的体积是22.4升。
试题四:生物-遗传题题目:如果一个生物体的基因型为AaBb,其中A和B是两对独立遗传的基因,求其后代出现aaBB的概率。
解题思路:根据孟德尔的分离定律和独立分配定律,Aa与Aa的后代出现aa的概率是1/4,Bb与Bb的后代出现BB的概率也是1/4。
答案:后代出现aaBB的概率是1/4 × 1/4 = 1/16。
试题五:历史-年代题题目:请列举中国历史上的“文景之治”时期,并简述其主要特点。
解题思路:文景之治是中国西汉时期的一个历史时期,由汉文帝和汉景帝统治。
答案:文景之治时期指的是公元前180年至公元前141年,主要特点是政治清明、经济繁荣、社会稳定,是中国封建社会早期的一个黄金时期。
高中数学倒序相加例题

高中数学倒序相加例题
(原创版)
目录
1.倒序相加的概念
2.倒序相加的解题步骤
3.倒序相加的例题解析
4.倒序相加的技巧和注意事项
正文
【1.倒序相加的概念】
倒序相加法是高中数学中一种常用的解题方法,主要用于解决数列求和的问题。
倒序相加法的核心思想是将数列的求和问题转化为求解两个部分数列的乘积,从而简化问题。
【2.倒序相加的解题步骤】
倒序相加法的解题步骤如下:
Step 1:确定数列的求和问题,明确求和的上下限。
Step 2:将原数列倒序排列,即从下标 n-1 开始,到下标 0 结束。
Step 3:计算新数列的和,即原数列求和的下限与上限的和。
Step 4:计算原数列的和,即新数列的和乘以原数列的下标。
【3.倒序相加的例题解析】
例题:求数列 1, 2, 3,..., n 的和。
解:根据倒序相加法,首先将数列倒序排列,得到 n, n-1, n-2,..., 1。
然后计算新数列的和,即 n+(n-1)+(n-2)+...+1。
最后,计算原数列
的和,即新数列的和乘以原数列的下标,即 (n+(n-1)+(n-2)+...+1)×n/2。
【4.倒序相加的技巧和注意事项】
技巧:在运用倒序相加法时,可以先通过观察原数列的规律,尝试找到一个等差或等比数列,从而简化问题。
注意事项:
1.在进行倒序排列时,需要注意不要改变原数列的顺序,以免影响求和结果。
2.在计算新数列的和时,需要将原数列求和的上下限考虑在内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年数学原创试题(8)
1.(本题满分12分)设函数],0[,2
sin 2)6sin()(2ππ∈++
=x x x x f (Ⅰ)求)(x f 的值域;
(Ⅱ)记A ∆BC 的内角A 、B 、C 的对边长分别为a c b B f c b a 求若,3,1,1)(,,,===的值。
【解析】(I )x x x x x x f cos 1cos 2
1sin 232sin 2)6sin()(2-++=++=π
1)6
sin(1cos 21sin 23+-=+-=πx x x ………………3分
]65,6[6],,0[ππππ-∈-∴∈x x ]2,21[)(∈∴x f ………………6分
(II )由6,0)6sin(,1)(ππ==-=B B B f 故得 ………………7分
解法一:由余弦定理,cos 2222B a c a b -+= 得21,0222
或解得==+-a a a ………………12分 解法二:由正弦定理
323,23sin ,sin sin ππ或得===C C C c B b 当2,2,322=+===c b a A C 从而ππ ………………9分
当1,6,6,32=====b a B A C 从而又时πππ ………………11分 故a 的值为1或2 ………………12分
2.(本题满分12分)国庆前夕,我国具有自主知识产权的“人甲型H1N1流感病毒核酸检测
试剂盒”(简称试剂盒)在上海进行批量生产,这种“试剂盒”不仅成本低操作简单,而且可以准确诊断出“甲流感”病情,为甲型H1N1流感疫情的防控再添一道安全屏障、某医院在得到“试剂盒”的第一时间,特别选择了知道诊断结论的5位发热病人(其中“甲流感”患者只占少数),对病情做了一次验证性检测、已知如果任意抽检2人,恰有1位是“甲流感”患者的概率为
52。
(1)求出这5位发热病人中“甲流感”患者的人数; (2)若用“试剂盒”逐个检测这5位发热病人,直到能确定“甲流感”患者为止,设ξ
表示检测次数,求ξ的分布列及数学期望E ξ。
【解析】(1)设有x 人患“甲流感”,则由题意有5225151=⋅-C C C x x , ……………3分 解得 x =1或x =4(舍)、
∴ 这5位发热病人中有1人患“甲流感”、…………………………………5分
(2)ξ=1,2,3,4,则511)1(15===A P ξ,5
1
)2(251
4===A A P ξ, 51)3(352
4===A A P ξ,5
2
)4(454
434=+==A A A P ξ、
∴ ξ的分布列为
……………………………………………………………………………………10分 ∴8.252
451
351
251
1=⨯+⨯+⨯+⨯=ξE 、 ……………………………………12分。
