【数学】广西钦州市大寺中学2012-2013学年高二下学期期中(文)
广西钦州市大寺中学高二数学下学期期中试题 文 新人教A版

满分150分,考试时间为120分钟一、选择题:(本大题共12个小题,每小题5分,共60分)。
1、设集合A={4,5,7,9},B={3,4,7,8,9},则集合A ∪B 中的元素共有 ( )A.3个B.4个C.5个D.6个2、角α终边过点(-1,2),则cos α等于 ( )A.5B.5C.- 5D.- 53、椭圆22143x y +=的离心率为( )C.74D.21 4、在261()xx -的展开式中,2x 的系数是 ( ) A.20 B.15 C.-20 D.-155、在10张奖券中,有4张有奖,从中任抽2张,能中奖的概率为 ( ) A.12 B.13 C.23 D.456、函数( )A.(-4,-1)B.(-4,1)C.(-1,1)D.(-1,1]7、已知ab ≠0,a,b ∈R ,则下列式子总能成立的是 ( ) A.2b a a b +≥ B.2b a a b +≥- C.2b a a b +≤- D.2b a a b+≥ 8、在一个口袋中装有5个白球和3个黑球,这些球除颜色外完全相同,从中摸出3个球,至少摸到2个黑球的概率等于 ( ) A.27 B.38 C.37 D.9289、某校开设10门课供学生选修,其中A 、B 、C 这3门由于上课时间相同,至多选1门.学校规定,每位同学选修3门,则每位同学不同的选修方案种数是( )A.120B.98C.63D.5610、在空间四边形ABCD 中,已知AB=3,CD=4,BD=2,则异面直线AC 与BD 所成角的大小是 ( )A.30°B.45°C.60°D.90°11、等差数列{n a }的前n 项和为33,6,4,n S S a ==且,则公差d 等于 ( )A.1B.53C.2D.312、已知52345012345(1)x a a x a x a x a x a x -=+++++,那么024135()()a a a a a a ++++的值等于 ( )A 、—256B 、256C 、—512D 、512二、填空题:把答案填在题中横线上(本大题共4个小题,每题5分,共20分)。
广西钦州市大寺中学2012-2013学年高二下学期期中考试英语试题 Word版含答案.pdf

大寺中学2012-2013学年高二下学期期中考试英语试题 第一部分听力(共两节,满分30分) 第一节(共5小题:每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小脱.从题中所给的A. B.C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
What does the woman mean? She is going to have lunch with the man. She’d like to have lunch with Bill. She is going to make many phone call What can we learn from the conversation? The man went to New Zealand during Christmas. The man was at home during Christmas. The man’s parents live in New Zealand. What are the two speakers talking about?A. The woman’s shoes.B. The woman’s husband.C. The woman’s shoes store. What are the two speakers going to do?A. Check the weather.B. Go swimming.C. Take a walk. Where is Jocelyn going?A. To England.B. To American.C. To France. 第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话。
每段对话后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
广西钦州市高二下学期数学期中考试试卷

广西钦州市高二下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)(2018·龙泉驿模拟) 设集合,,则集合为()A .B .C .D .2. (2分)已知函数,给定区间E,对任意,当x1<x2时,总有f(x1)>f(x2)则下列区间可作为E的是()A . (-3,-1)B . (-1,0)C . (1,2)D . (3,6)3. (2分) (2019高一上·黄梅月考) 已知是第二象限角,为其终边上一点且,则的值()A . 5B .C .D .4. (2分) (2018高一上·兰州月考) 设,,,则a,b,c的大小关系是()A . a<b<cB . c<b<aC . c<a<bD . b<c<a5. (2分)已知,则f'(0)等于()A . 2B . 0C . -2D . -46. (2分) (2017高三上·珠海期末) 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)图象如图所示,则下列关于函数 f (x)的说法中正确的是()A . 对称轴方程是x= +kπ(k∈Z)B . 对称中心坐标是(+kπ,0)(k∈Z)C . 在区间(﹣,)上单调递增D . 在区间(﹣π,﹣)上单调递减7. (2分)若向量满足,与的夹角为600 ,则的值为()A .B .C .D . 28. (2分) (2018高一上·舒兰期中) 奇函数在[2,4]上是减函数且最小值是2,则在区间[-4,-2]上()A . 增函数且最大值为-2B . 增函数且最小值为-2C . 减函数且最大值为-2D . 减函数且最小值为-29. (2分) (2019高三上·榕城月考) 函数的大致图象是A .B .C .D .10. (2分)下列函数中在其定义域内即是增函数又是奇函数的是()A . y=x3+xB . y=-log2xC . y=3xD .二、双空题 (共4题;共4分)11. (1分) (2019高三上·建平期中) 若复数,满足,(是虚数单位),则 ________12. (1分) (2020高一下·昌吉期中) 在中,如果,则 ________.13. (1分)若函数f(x)=x2+ln(x+a)与g(x)=x2+ex﹣(x<0)的图象上存在关于y轴对称的点,则实数a的取值范围是________14. (1分) (2018高一下·安庆期末) 若一元二次不等式对一切实数都成立,则的取值范围为________.三、填空题 (共3题;共3分)15. (1分) (2019高一下·上海月考) 方程的解集为________.16. (1分) (2019高二下·吉林期中) 函数的最大值为________.17. (1分) (2019高三上·成都月考) 若非零向量,满足,,,则 ________.四、解答题 (共5题;共60分)18. (10分)(2017·南京模拟) 已知角α的终边上有一点p(1,2),(Ⅰ)求tan()的值;(Ⅱ)求sin(2 )的值.19. (10分) (2020高一下·怀仁期中) 在锐角三角形中,a,b,c分别为角A,B,C的对边,且(Ⅰ)求A的大小;(Ⅱ)若,求的周长L的最大值.20. (10分)(2017·南阳模拟) 某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理.现需决策此蛋糕店每天应该制作几个生日蛋糕,为此搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图3所示的柱状图,以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.(1)求当天的利润y(单位:元)关于当天需求量n(单位:个,n∈N)的函数解析式;(2)求当天的利润不低于750元的概率.21. (15分) (2020高二下·衢州期末) 已知函数(1)若,求函数的零点;(2)若不存在相异实数、,使得成立.求实数a的取值范围;(3)若对任意实数a,总存在实数、,使得成立,求实数k的最大值.22. (15分)(2020·肇庆模拟) 设函数,e为自然对数的底数.(1)若在上单调递增,求的取值范围;(2)证明:若,则.参考答案一、单选题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:二、双空题 (共4题;共4分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:三、填空题 (共3题;共3分)答案:15-1、考点:解析:答案:16-1、考点:解析:答案:17-1、考点:解析:四、解答题 (共5题;共60分)答案:18-1、考点:解析:答案:19-1、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、答案:21-2、答案:21-3、考点:解析:答案:22-1、答案:22-2、考点:解析:。
广西钦州市大寺中学高二下学期期中考试语文试题 Word版无答案.pdf

大寺中学2012-2013学年高二下学期期中考试语文试题 注意事项:本卷共150分,试卷共8页,考试时间150分钟。
第I卷(选择题,共30分) 一、选择题(12 分,每小题3分) 1、下列词语中,加点字的读音全都正确的一组是( ) 澄(chéng)莹 蛮横(hèng) 发怔(zhèng) 缱绻(qiǎn quǎn) 谷囤(tún) 打烊(yáng) 不啻(chì) 赍(jī)发 笑靥(yè) 央浼(méi) 玄(xuán)色 掎(jǐ)角之势 蹩(biě)进 拗(ǎo)断 纨绔(kuà) 插科打诨(hùn) 2、下列各句中加点的成语使用恰当的一句是:A.这个展览会规模宏大,其展品可以说是包罗万象,美不胜收。
B.他把相敬如宾当作与朋友交往的一条起码原则,但在生活中他却常常得不到别人的尊敬,他为之很苦恼。
C.王军和李刚是男篮的主力队员,他们既是同乡又是同学,两小无猜,在场上配合得非常好。
D.他们俩人在拜把兄弟时曾经海誓山盟,永不背叛,可到了商战的关键时刻,竟成了仇敌。
二、阅读下面的文章,完成5—7题。
(9 分,每小题3 分) 低碳经济是一种以低能耗、低排放、低污染为基础的经济发展模式。
它具有以下特征: 首先是经济性。
它包含两层含义:一是低碳经济应按照市场经济的原则和机制来发展,二是低碳经济的发展不应导致人们的生活条件和福利水平明显下降。
也就是说,既反对奢侈或能源浪费型的消费,又必须使人民生活水平不断提高。
更通俗地说,发展低碳经济不能也不是让人类回到农耕社会。
其次是技术性。
也就是通过技术进步,在提高能源效率的同时,也降低二氧化碳等温室气体的排放强度。
前者要求在消耗同样能源的条件下人们享受到的能源服务(如照明、家用电器消耗等)不降低;后者要求在排放同等温室气体情况下人们的生活条件和福利水平不降低,这两个“不降低”需要通过能效技术和温室气体减排技术的研发和产业化来实现。
广西钦州市大寺中学2012-2013学年高二第一次月考语文试题

高二中高二上学期第一次月考语文试卷 一、语言基础知识题(18分,每小题3分) 1.下列字词当中,读音有误的一项是( )A、央浼(m?i) 埋怨(mán) 干涸(hé)讥诮(qiào)B、辖制(xiá) 流憩(qì)潦水(lǎo)联袂(mèi)C、拮据(jié) 庇佑(pì)酩酊(dīng)仓廒(áo)D、一稔(rěn) 簪笏(hù)洗马(xiǎn)决起(xuè)3、下列加点的成语运用无误的一项是( ) A、翠翠生活在湘西的“边城”,是个下里巴人。
B、操场上锣鼓喧天,人声鼎沸,可是同学们却安然无恙地坐在教室里,看书的看书,做习题的做习题,谁也没有关注教室外的事情。
C、如果只为了一个小小的成就便踌躇满志,不但得不到别人的赞美,反而会遭人们嗤之以鼻。
D、在已经气息奄奄的暮年,他坐在公园的石凳上沉思往事,突然发现自己所崇拜的偶像不过是个华而不实、自私自利的小人。
4、下列各句中,没有语病的一句是( )w A、我们要以增强打赢信息化条件下局部战争能力为核心,提高解放军不断应对多种安全威胁、完成多样化军事任务的能力。
B、中国现代企业的灵魂在于“中国制造”,怎样才能摆脱故步自封,重振华夏雄风?事实证明,具有自主创新能力决定了它们的生死存亡。
C、英国伦敦高等法院日前裁决,《达·芬奇密码》的作者丹·布郎被控抄袭另一畅销书著作权的罪名不成立。
D、虽然农产品价格的上涨可使农民收入有所增加,但这并不很大的收益却会由于其他商品价格的上涨而被抵销,结果其实际总收入还有可能下降。
5、依次填入下而横线处的句子,与上下文衔接最恰当的一组是( ) 我独坐在书斋中,忘记了尘世间一切不愉快的事情,怡然自得。
世界之广,宇宙之大,此时却仿佛只有我和我的书友存在。
? , , , 。
①阳光照在玉兰花的肥大的绿叶子上 ②连平常我喜欢听的鸟鸣声“光棍好过”,也听而不问了 ③窗外粼粼碧水,丝丝垂柳 ④这都是我平常最喜爱的东西,现在也都视而不见了 A.③①④② B.①②③④ C.①③④② D.③④①② 6.下列各项中对作品的情节叙述和分析错误的一项是( ) A.赤壁之战前夕,曹操对明月,奠长江,横槊赋诗,高唱“对酒当歌,人生几何”,让我们看到一位慷慨壮志、壮志凌云的历史英雄。
广西钦州市高二下学期数学期中联考试卷

广西钦州市高二下学期数学期中联考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)(2019·山西模拟) 抛物线的焦点坐标为()A .B .C .D .2. (2分)当为任意实数时,直线恒过定点,则以为圆心,半径为的圆是()A .B .C .D .3. (2分)函数y=sinx﹣cosx,则f'(π)的值是()A . ﹣1B . 0C . 1D . π4. (2分) (2019高一下·涟水月考) 已知,是两个不同的平面,,为两条不重合的直线,则下列命题中正确的为()A . 若,,,则B . 若,,,则C . 若,,,则D . 若,,,则5. (2分) (2017高一下·扶余期末) 一个长方体被一个平面截去一部分后所剩几何体的三视图如图所示(单位:cm),则该几何体的体积为()A . 120 cm3B . 100 cm3C . 80 cm3D . 60 cm36. (2分) (2019高二下·温州期中) 已知函数f(x)=x3+px2+qx与x轴切于x0 点,且极小值为-4,则p+q=()A . 12B . 13C . 15D . 167. (2分)否定“自然数m,n,k中恰有一个奇数”时正确的反设为()A . m,n,k都是奇数B . m,n,k都是偶数C . m,n,k中至少有两个偶数D . m,n,k都是偶数或至少有两个奇数8. (2分) (2019高二上·恩施期中) 边长为6的两个等边,所在的平面互相垂直,则四面体的外接球的体积为().A .B .C .D .9. (2分) (2017高二上·莆田期末) 已知椭圆若其长轴在y轴上,焦距为4,则m等于()A . 4B . 5C . 7D . 810. (2分)在正方体中,异面直线与所成的角为()A .B .C .D .二、双空题 (共4题;共4分)11. (1分) (2019高二下·钦州期末) 若,则 ________12. (1分) (2020高二下·上海期末) 双曲线的虚轴长是实轴长的2倍,则 ________13. (1分) (2020高二下·金华月考) 已知,那么单调递增区间________;单调递减区间________.14. (1分) (2018高二上·太原期中) 已知直线.若,则实数m=________.三、填空题 (共3题;共3分)15. (1分) (2016高二下·武汉期中) 若函数f(x)=(1﹣x2)(x2+ax+b)的图象关于直线x=﹣2对称,则f(x)的最大值为________.16. (1分) (2019高一上·河南月考) 函数的最大值为________.17. (1分) (2019高二下·绍兴期中) 已知函数在上为增函数,则的取值范围为 ________四、解答题 (共5题;共50分)18. (10分) (2019高二下·湖州期末) 已知,为抛物线上的相异两点,且.(1)若直线过,求的值;(2)若直线的垂直平分线交x轴与点P,求面积的最大值.19. (10分) (2017高三上·安庆期末) 已知O为坐标原点,P(x,y)为函数y=1+lnx图象上一点,记直线OP的斜率k=f(x).(Ⅰ)若函数f(x)在区间(m,m+ )(m>0)上存在极值,求实数m的取值范围;(Ⅱ)当x≥1时,不等式f(x)≥ 恒成立,求实数t的取值范围.20. (10分)(2020·吉林模拟) 如图,已知三棱柱中,与是全等的等边三角形.(1)求证:;(2)若,求二面角的余弦值.21. (10分) (2018高三上·鄂州期中) 已知函数.求的单调区间;Ⅱ 证明:其中e是自然对数的底数,.22. (10分)(2018·山东模拟) 已知点,分别是椭圆的长轴端点、短轴端点,为坐标原点,若, .(1)求椭圆的标准方程;(2)如果斜率为的直线交椭圆于不同的两点 (都不同于点 ),线段的中点为,设线段的垂线的斜率为,试探求与之间的数量关系.参考答案一、单选题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:二、双空题 (共4题;共4分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:三、填空题 (共3题;共3分)答案:15-1、考点:解析:答案:16-1、考点:解析:答案:17-1、考点:解析:四、解答题 (共5题;共50分)答案:18-1、答案:18-2、考点:解析:答案:19-1、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、考点:解析:答案:22-1、答案:22-2、考点:解析:。
广西钦州市数学高二下期中经典练习(培优练)

一、选择题1.(0分)[ID :13609]已知向量a ,b 满足2a =,||1b =,且2b a +=,则向量a 与b 的夹角的余弦值为( )A .2B C D 2.(0分)[ID :13605]O 是平面上的一定点,,,A B C 是平面上不共线的三点,动点P 满足+OP OA λ= ()·cos ?cos AB AC AB B AC C+,(0,)λ∈∞,则动点P 的轨迹一定经过ABC ∆的( ) A .重心B .垂心C .外心D .内心3.(0分)[ID :13604]将函数y =2sin(2x +π6)的图象向右平移14个周期后,所得图象对应的函数为( )A .y =2sin(2x +π4) B .y =2sin(2x +π3) C .y =2sin(2x −π4) D .y =2sin(2x −π3)4.(0分)[ID :13600]函数()()sin 02f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭,的最小正周期是π,若其图象向左平移3π个单位后得到的函数为偶函数,则函数()f x 的图象( ) A .关于点012π⎛⎫⎪⎝⎭,对称 B .关于直线12x π=对称 C .关于点06π⎛⎫⎪⎝⎭,对称 D .关于直线6x π=对称5.(0分)[ID :13580]在ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,三边a ,b ,c 成等差数列,且6B π=,则()2cos cos A C -的值为( )A .1BC .2D .06.(0分)[ID :13554]设函数()2sin()f x x ωϕ=+,x ∈R ,其中0>ω,||ϕπ<.若5()28f π=,()08f 11π=,且()f x 的最小正周期大于2π,则 A .23ω=,12πϕ= B .23ω=,12ϕ11π=- C .13ω=,24ϕ11π=- D .13ω=,724πϕ=7.(0分)[ID :13553]函数()()()sin 102f x x πωϕωϕ=++><,的部分图像如图所示,将()f x 的图像向右平移4π个单位长度后得函数()g x 的图像,则()g x =()A .2sin 23x π⎛⎫+ ⎪⎝⎭B .sin 23x π⎛⎫- ⎪⎝⎭C .sin 213x π⎛⎫++ ⎪⎝⎭D .sin 213x π⎛⎫-+ ⎪⎝⎭8.(0分)[ID :13619]在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a bcosC <,则ABC 为( )A .钝角三角形B .直角三角形C .锐角三角形D .等边三角形9.(0分)[ID :13614]已知函数()()2cos 23042x f x x πωωω⎛⎫=-->⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减,则ω的最大值为( ). A .1B .65C .43D .3210.(0分)[ID :13613]已知在ABC 中,::3:2:4sinA sinB sinC =,那么cosC 的值为( )A .14-B .14C .23-D .2311.(0分)[ID :13590]在ABC 中,点D 是线段BC 上任意一点,M 是线段AD 的中点,若存在实数λ和μ,使得BM AB AC λμ=+,则λμ+= A .2 B .2- C .12 D .12-12.(0分)[ID :13588]在ABC ∆中,角,,A B C 的对边分别是,,a b c , 2cos 22A b c c+=,则ABC ∆的形状为 A .直角三角形 B .等腰三角形或直角三角形 C .等腰直角三角形D .正三角形13.(0分)[ID :13564]已知函数()sin()(0),24f x x+x ππωϕωϕ=>≤=-,为()f x 的零点,4x π=为()y f x =图象的对称轴,且()f x 在π5π()1836,单调,则ω的最大值为 A .11 B .9 C .7D .514.(0分)[ID :13542]以下命题①||||a b -||a b =+是,a b 共线的充要条件;②若{,,}a b c 是空间的一组基底,则{,,}a b b c c a +++是空间的另一组基底; ③|()|||||||a b c a b c ⋅=⋅⋅. 其中正确的命题有( ) A .0个B .1个C .2个D .3个15.(0分)[ID :13541]已知a ,b 均为非零向量,()2a b a -⊥,()2b a b -⊥,则a ,b 的夹角为( )A .3π B .2π C .23πD .56π 二、填空题16.(0分)[ID :13726]函数()sin 52sin x f x x+=-的最大值为__________.17.(0分)[ID :13722]已知函数f(x)=−4cos(ωx+φ)e |x |(ω>0,0<φ<π)的部分图像如图所示,则ωφ=__________.18.(0分)[ID :13692]已知tan 24x π⎛⎫+= ⎪⎝⎭,则tan tan 2xx=____________________. 19.(0分)[ID :13681]在ABC ∆中,M 是BC 的中点,120A ∠=︒,12AB AC ⋅=-,则线段AM 长的最小值为___________20.(0分)[ID :13678]菱形ABCD 的边长为2,60A ∠=︒,M 为DC 的中点,若N 为菱形内任意一点(含边界),则AM AN ⋅的最大值为____________.21.(0分)[ID :13666]设a b ,为单位向量,若向量c 满足()c a b a b -+=-,则c 的最大值是____________.22.(0分)[ID :13662]函数f (x )3 x +cos x 的最大值是___________. 23.(0分)[ID :13653]已知3cos 63πα⎛⎫-=⎪⎝⎭,则25sin cos 66παπα⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭的值为__________ .24.(0分)[ID :13650]在△ABC 中,3AB =,2AC =,60A =︒,AG mAB AC =+,则AG 的最小值为________25.(0分)[ID :13640]已知12(1,1),(2,3)P P =-=,若P 在12PP 的长线上,且1222PP P P =,则点P 的坐标为______.三、解答题26.(0分)[ID :13818]已知向量,a b 的夹角为60︒,且1a =,2b =,设3m a b =-,2n ta b =+.(1)试用t 来表示m n ⋅的值;(2)若m 与n 的夹角为钝角,试求实数t 的取值范围. 27.(0分)[ID :13770]已知函数()22cos cos 213f x x x π⎛⎫=-+- ⎪⎝⎭. (1)求函数()f x 的最小正周期和对称轴方程; (2)讨论函数()f x 在44ππ⎡⎤-⎢⎥⎣⎦,上的单调性. 28.(0分)[ID :13750]在平面上,给定非零向量b ,对任意向量a ,定义122()||a b a a b b ⋅=-⋅. (1)若(1,2)a =,(1,1)b =-,求1a ;(2)设(1,2)b =,证明:若位置向量a 的终点在直线3450x y ++=上,则位置向量1a 的终点轨迹是一条直线,并求此直线的方程.29.(0分)[ID :13803]已知点()0,2A ,()4,6B ,12OM t OA t AB =+,其中1t ,2t 为实数:(1)若点M 在第二或第三象限,且12t =,求2t 的取值范围; (2)求证:当11t =时,不论2t 为何值,A ,B ,M 三点共线;(3)若21t a =,OM AB ⊥,且三角形ABM 的面积为12,求a 和2t 的值.30.(0分)[ID :13802]设函数()cos 22sin sin .344f x x x x πππ⎛⎫⎛⎫⎛⎫=-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()1求()f x 的单调递减区间及其图象的对称轴方程;()2若()f x 在区间,12a π⎡⎤-⎢⎥⎣⎦上的值域为⎡⎤⎢⎥⎣⎦,求实数a 的取值范围.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1.D2.B3.D4.A5.A6.A7.D8.A9.C10.A11.D12.A13.B14.B15.A二、填空题16.6【解析】【分析】利用分离常数法分离常数然后结合不等式的性质求得最大值【详解】∵所以所以∴时故答案为:6【点睛】本题考查求函数的最值考查正弦函数的性质解题方法是利用分离常数法分离常数然后结合不等式的17.2【解析】f(0)=0⇒cosφ=0∵0<φ<π∴φ=π2f(1)=0⇒cos(ω+π2)=0⇒sinω=0⇒ω=kπ(k∈Z)∵0 <2πω<2∴ω=π所以ωφ=218.【解析】试题分析:考点:两角和的正切公式与正切的二倍角公式19.【解析】【分析】由平方得:再由可得进而利用基本不等式可得最小值【详解】由平方得:又所以所以当且仅当时取最小值故答案为:【点睛】本题主要考查了中线的向量表示及数量积的运算考查了利用基本不等式求最小值属20.9【解析】【分析】【详解】由数量积的几何意义知当在上的投影最大时最大从图可以看出当N点在点C处在上的投影最大所以的最大值为:21.【解析】试题分析:因为向量满足所以当所以+≤=当且仅当=即时等号成立所以的最大值考点:1平面向量模的运算性质;2平面向量的运算22.【解析】由23.【解析】分析:由同角三角函数关系得诱导公式得进而得解详解:由得所以故答案为:点睛:本题主要考查了同角三角函数的关系和诱导公式属于基础题24.【解析】【分析】先计算得到根据二次函数得到最小值【详解】则当时有最小值即的最小值为故答案为:【点睛】本题考查了向量模的计算意在考查学生的计算能力25.【解析】【分析】首先利用线段的比值求出λ进一步利用分点坐标公式即可求出结果【详解】由题意因为点P在的延长线上且所以可得又由设可得所以点的坐标为故答案为:【点睛】本题主要考查了定比分点的坐标公式的应用三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题 1.D 解析:D 【解析】 【分析】根据平方运算可求得12a b ⋅=,利用cos ,a b a b a b ⋅<>=求得结果. 【详解】由题意可知:2222324b a b a b a a b +=+⋅+=+⋅=,解得:12a b ⋅=1cos ,422a b a b a b⋅∴<>===本题正确选项:D 【点睛】本题考查向量夹角的求解问题,关键是能够通过平方运算求得向量的数量积.2.B解析:B 【解析】 【分析】解出AP ,计算AP BC ⋅并化简可得出结论. 【详解】AP OP OA =-=λ(AB AC AB cosBAC cosC+⋅⋅),∴()...0AB BC AC BC AP BC BC BC AB cosB AC cosC λλ⎛⎫⎪=+=-+= ⎪⋅⋅⎝⎭, ∴AP BC ⊥,即点P 在BC 边的高上,即点P 的轨迹经过△ABC 的垂心. 故选B . 【点睛】本题考查了平面向量的数量积运算在几何中的应用,根据条件中的角计算AP BC ⋅是关3.D解析:D 【解析】 【分析】 【详解】函数y =2sin(2x +π6)的周期为π,将函数y =2sin(2x +π6)的图象向右平移14个周期即π4个单位,所得图象对应的函数为y =2sin[2(x −π4)+π6)]=2sin(2x −π3), 故选D.4.A解析:A 【解析】 【分析】根据函数()f x 的最小正周期是π,求得2w =,即()()sin 2f x x ϕ=+,再根据三角函数的图象变换求得2()sin(2)3g x x πϕ=++,利用三角函数的对称性,求得6πϕ=-,得到函数()sin 26f x x π⎛⎫=- ⎪⎝⎭,再利用三角函数的性质,即可求解.【详解】由题意,函数()()sin f x x ωϕ=+的最小正周期是π,即2wππ=,解得2w =, 所以()()sin 2f x x ϕ=+, 将函数()f x 的向左平移3π个单位后得到函数2()sin[2()]sin(2)33g x x x ππϕϕ=++=++ 因为()g x 为偶函数,所以2(0)sin()13g πϕ=+=±,即2,32k k Z ππϕπ+=+∈, 解得,6k k Z πϕπ=-+∈,因为2πϕ<,所以6πϕ=-,所以()sin 26f x x π⎛⎫=- ⎪⎝⎭,令2,6x k k Z ππ-=∈,解得,122k x k Z ππ=+∈, 令0k =,则12x π=,所以函数()f x 关于012π⎛⎫⎪⎝⎭,对称,故选A. 【点睛】本题主要考查了三角函数的图象变换,以及三角函数的图象与性质的应用,其中解答中熟练应用三角函数的图象变换求得函数的解析式,再利用三角函数的图象与性质求解是解答的关键,着重考查了推理与运算能力,属于基础题.解析:A 【解析】 【分析】三边a ,b ,c 成等差数列,可得2b a c =+,利用正弦定理可得:2sin sin sin B A C =+,即sin sin 1A C +=,设cos cos A C m -=,平方相加即可得出. 【详解】解:三边a ,b ,c 成等差数列, 2b a c ∴=+,利用正弦定理可得:2sin sin sin B A C =+,sin sin 2sin16A C π∴+==,设cos cos A C m -=,则平方相加可得:222cos()1A C m -+=+,22cos 11m B ∴=+=.故选:A . 【点睛】本题考查了等差数列的通项公式性质、正弦定理、同角三角函数基本关系式、和差公式,考查了推理能力与计算能力,属于中档题.6.A解析:A 【解析】由题意125282118k k ωππϕπωπϕπ⎧+=+⎪⎪⎨⎪+=⎪⎩,其中12,k k Z ∈,所以2142(2)33k k ω=--,又22T ππω=>,所以01ω<<,所以23ω=,11212k ϕππ=+,由ϕπ<得12πϕ=,故选A .【考点】求三角函数的解析式【名师点睛】有关sin()y A x ωϕ=+问题,一种为提供函数图象求解析式或某参数的范围,一般先根据图象的最高点或最低点确定A ,再根据周期或12周期或14周期求出ω,最后再利用最高点或最低点坐标满足解析式,求出满足条件的ϕ值,另一种时根据题目用文字形容的函数图象特点,如对称轴或曲线经过的点的坐标,根据题意自己画出图象,再寻求待定的参变量,题型很活,求ω或ϕ的值或最值或范围等.7.D解析:D 【解析】 【分析】由图像可知,代入点,26π⎛⎫⎪⎝⎭和30,2⎛⎫⎪⎝⎭则可计算出()f x 表达式,再根据平移知识点左加右减即可得出()g x 表达式. 【详解】由函数()sin()10,||2f x x πωϕωϕ⎛⎫=++>< ⎪⎝⎭的部分图象知31sin 2ϕ+=,即1sin 2ϕ=. 因为||2ϕπ<,所以6π=ϕ.所以()sin 16f x x πω⎛⎫=++ ⎪⎝⎭.因为点,26π⎛⎫⎪⎝⎭在()f x 的图象上.所以sin 166ππω⎛⎫+= ⎪⎝⎭.所以2(Z)662k k πππωπ+=+∈.因为0>ω,结合图象可知2ω=,所以()sin 216f x x π⎛⎫=++ ⎪⎝⎭.将()f x 的图象向右平移4π个单位长度后得到函数()g x 的图象.则()sin 21sin 21463g x x x πππ⎡⎤⎛⎫⎛⎫=-++=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.【点睛】根据三角函数图像求表示时一般代入特殊点,如最值点和图像与坐标轴的交点进行运算.函数平移左加右减,注意平移的时候是x 整体变化,如果有系数记得加括号.8.A解析:A 【解析】 【分析】利用正弦定理,将a bcosC <,转化为sin sin A BcosC <,再利用两角和与差的三角函数得到cos sin 0B C <判断. 【详解】 因为a bcosC <, 所以sin sin A BcosC <, 所以()sin sin B C BcosC +<,所以sin cos cos sin sin B C B C BcosC +<, 所以cos sin 0B C <,所以,2B ππ⎛⎫∈⎪⎝⎭, 所以ABC 为钝角三角形. 故选:A 【点睛】本题主要考查正弦定理和两角和与差的三角函数的应用,还考查了运算求解的能力,属于中档题.9.C解析:C 【解析】 【分析】首先化简函数()2cos 3f x x πω⎛⎫=+ ⎪⎝⎭,需满足22T π≥,根据函数在区间0,2π⎡⎤⎢⎥⎣⎦单调递减,所以求3x πω+的范围,且是[]0,π的子集,最后求ω的范围.【详解】()cos 1cos 2f x x x πωω⎫⎛⎫=+- ⎪⎪⎝⎭⎭cos x x ωω=2cos 3x πω⎛⎫=+- ⎪⎝⎭()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减,22T π∴≥ ,即2ππω≥ 02ω∴<≤ ,当[0,]2x π∈时,[,]3323x ππωπωπ+∈+,∴ [,][0,]323πωπππ+⊆∴ 23ωπππ+≤, 403ω∴<≤, 综上可知403ω<≤.故选C 【点睛】本题考查三角函数的恒等变形,以及根据区间的单调性求参数的取值范围,属于中档题型,利用三角函数的奇偶性,周期性,对称性求解参数的值或范围是一个重点题型,首先将三角函数写成形如()sin y A x b ωϕ=++,或()cos y A x b ωϕ=++,()tan y A x b ωϕ=++的形式,然后利用三角函数的性质,借助公式,区间范围关系等将参数表示出来,得到函数参数的等式或不等式,求解.10.A解析:A 【解析】 【分析】 【详解】::sin :sin :sin 3:2:4a b c A B C == ,不妨设3,2,4a k b k c k ===,,则()()()2223241cos 2324k k k C k k+-==-⨯⨯ ,选A.11.D解析:D 【解析】 【分析】由题意结合中点的性质和平面向量基本定理首先表示出向量BD ,BM ,然后结合平面向量的运算法则即可求得最终结果. 【详解】如图所示,因为点D 在线段BC 上,所以存在t R ∈,使得()BD tBC t AC AB ==-, 因为M 是线段AD 的中点,所以:()()()111112222BM BA BD AB t AC t AB t AB t AC =+=-+-=-++, 又BM AB AC λμ=+,所以()112t λ=-+,12t μ=, 所以12λμ+=-. 本题选择D 选项.【点睛】(1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算.(2)用向量基本定理解决问题的一般思路是:先选择一组基底,并运用该基底将条件和结论表示成向量的形式,再通过向量的运算来解决.12.A解析:A 【解析】 【分析】先根据二倍角公式化简,再根据正弦定理化角,最后根据角的关系判断选择. 【详解】 因为2cos22A b c c+=,所以1cosA 22b cc ++=,() ccosA b,sinCcosA sinB sin A C ,sinAcosC 0===+=,因此cosC 0C 2π==,,选A.【点睛】本题考查二倍角公式以及正弦定理,考查基本分析转化能力,属基础题.13.B解析:B 【解析】 【分析】根据已知可得ω为正奇数,且ω≤12,结合x 4π=-为f (x )的零点,x 4π=为y =f (x )图象的对称轴,求出满足条件的解析式,并结合f (x )在(18π,536π)上单调,可得ω的最大值. 【详解】 ∵x 4π=-为f (x )的零点,x 4π=为y =f (x )图象的对称轴,∴2142n T π+⋅=,即21242n ππω+⋅=,(n ∈N ) 即ω=2n +1,(n ∈N ) 即ω为正奇数,∵f (x )在(18π,536π)上单调,则53618122T πππ-=≤, 即T 26ππω=≥,解得:ω≤12,当ω=11时,114π-+φ=k π,k ∈Z , ∵|φ|2π≤, ∴φ4π=-,此时f (x )在(18π,536π)不单调,不满足题意; 当ω=9时,94π-+φ=k π,k ∈Z , ∵|φ|2π≤,∴φ4π=,此时f (x )在(18π,536π)单调,满足题意;故ω的最大值为9, 故选B . 【点睛】本题将三角函数的单调性与对称性结合在一起进行考查,题目新颖,是一道考查能力的好题.注意本题求解中用到的两个结论:①()()()sin 0,0f x A x A ωϕω=+≠≠的单调区间长度是最小正周期的一半;②若()()()sin 0,0f x A x A ωϕω=+≠≠的图像关于直线0x x =对称,则()0f x A =或()0f x A =-.14.B解析:B 【解析】 【分析】①||||||a b a b -=+共线,反之不成立,即可判断出结论; ②利用基底的定义即可判断出真假;③|()||||||||cos ,|a b c a b c a b =<>,即可判断出真假. 【详解】①||||||a b a b a -=+⇒,b 共线,反之不成立,||||||a b a b -=+是a ,b 共线的充分不必要条件,因此不正确;②若{a ,b ,}c 是空间的一组基底,假设,,a b b c c a +++共面, 则存在唯一一组实数,x y ,使=()()a b x b c y c a ++++成立, 即()a b xb x y c ya +=+++,所以1,1,0x y x y ==+=,显然无解, 假设不成立,即,,a b b c c a +++不共面,则{a b +,b c +,}c a +是空间的另一组基底,正确; ③|()|||||||cos ,a b c a b c a b =<>,而cos ,a b <>不一定等于1, 因此不正确.其中正确的命题有一个. 故选:B . 【点睛】本题考查了向量共线、共面定理、数量积运算性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.15.A解析:A 【解析】由题意得,因为()()2,2a b a b a b -⊥-⊥所以()()22220,220a b a a a b b a b b a b -⋅=-⋅=-⋅=-⋅=, 即22222,2a a a b b ba b ==⋅==⋅,所以向量a 和b 的夹角为1cos ,2a b a b a b⋅〈〉==⋅,又,[0,]a b π〈〉∈,所以,3a b π〈〉=,故选A.考点:向量的夹角公式及向量的数量积的运算.二、填空题16.6【解析】【分析】利用分离常数法分离常数然后结合不等式的性质求得最大值【详解】∵所以所以∴时故答案为:6【点睛】本题考查求函数的最值考查正弦函数的性质解题方法是利用分离常数法分离常数然后结合不等式的 解析:6 【解析】 【分析】利用分离常数法分离常数,然后结合不等式的性质求得最大值. 【详解】()sin 52sin x f x x +=-712sin x=-+-,∵1sin 1x -≤≤,所以12sin 3x ≤-≤,77732sin x ≤≤-,所以4()63f x -≤≤, ∴sin 1x =时,max ()6f x =.故答案为:6. 【点睛】本题考查求函数的最值,考查正弦函数的性质.解题方法是利用分离常数法分离常数,然后结合不等式的性质求解.17.2【解析】f(0)=0⇒cosφ=0∵0<φ<π∴φ=π2f(1)=0⇒cos(ω+π2)=0⇒sinω=0⇒ω=k π(k∈Z)∵0<2πω<2∴ω=π所以ωφ=2 解析:2【解析】f(0)=0⇒cosφ=0∵0<φ<π∴φ=π2f(1)=0⇒cos(ω+π2)=0⇒sinω=0⇒ω=kπ(k ∈Z)∵0<2πω<2∴ω=π所以ωφ=218.【解析】试题分析:考点:两角和的正切公式与正切的二倍角公式 解析:49【解析】 试题分析:12tan 1133tan 22tan tan 2141tan 3419x x x x x π⨯+⎛⎫+=∴=∴=∴== ⎪-⎝⎭-1tan 433tan 294x x ∴== 考点:两角和的正切公式与正切的二倍角公式19.【解析】【分析】由平方得:再由可得进而利用基本不等式可得最小值【详解】由平方得:又所以所以当且仅当时取最小值故答案为:【点睛】本题主要考查了中线的向量表示及数量积的运算考查了利用基本不等式求最小值属解析:12【解析】 【分析】由1()2AM AB AC =+平方得:2221(1)4AM AB AC =+-,再由AB AC ⋅可得||||1AB AC ⋅=,进而利用基本不等式可得最小值.【详解】 由1()2AM AB AC =+平方得:2222211(2)(1)44AB A AM AB AC AB AC C =++=+-⋅.又11||||cos120||||22AB AC AB AC AB AC ⋅=⋅=-⋅=-,所以||||1AB AC ⋅=. 所以222221111(2)(1)(2||||1)4444AB AC AM AB AC AB AC AB AC ⋅=++=+-≥⋅-=. 当且仅当||||1AB AC ==时,AM 取最小值12.故答案为:12. 【点睛】本题主要考查了中线的向量表示及数量积的运算,考查了利用基本不等式求最小值,属于中档题.20.9【解析】【分析】【详解】由数量积的几何意义知当在上的投影最大时最大从图可以看出当N 点在点C 处在上的投影最大所以的最大值为:解析:9 【解析】 【分析】 【详解】由数量积的几何意义知,当AN 在AM 上的投影最大时,AM AN 最大. 从图可以看出,当N 点在点C 处,AN 在AM 上的投影最大,所以AM AN 的最大值为:1·()?()92AM AC AD AB AB AD =++=. 21.【解析】试题分析:因为向量满足所以当所以+≤=当且仅当=即时等号成立所以的最大值考点:1平面向量模的运算性质;2平面向量的运算解析:【解析】试题分析:因为向量c 满足()c a b a b -+=-,所以()a b c a b c a b -=-+≥-+,当所以c a b ≤++a b -≤22||)a b a b ++-=222(22)22a b +=,当且仅当a b +=a b -,即a b ⊥时等号成立,所以c 的最大值考点:1、平面向量模的运算性质;2、平面向量的运算.22.【解析】由 解析:2【解析】由max ()cos 2sin()()26f x x x x f x π=+=+⇒=.23.【解析】分析:由同角三角函数关系得诱导公式得进而得解详解:由得所以故答案为:点睛:本题主要考查了同角三角函数的关系和诱导公式属于基础题【解析】分析:由同角三角函数关系得222sin 11666cos cos πππααα⎛⎫⎛⎫⎛⎫-=--=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,诱导公式得5cos cos π cos 666πππααα⎡⎤⎛⎫⎛⎫⎛⎫+=--=--⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,进而得解.详解:由cos 6πα⎛⎫-=⎪⎝⎭,得22212sin 11166633cos cos πππααα⎛⎫⎛⎫⎛⎫-=--=--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.5cos cos π cos 666πππααα⎡⎤⎛⎫⎛⎫⎛⎫+=--=--= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.所以25sin cos 66παπα⎛⎫⎛⎫--+=⎪ ⎪⎝⎭⎝⎭点睛:本题主要考查了同角三角函数的关系和诱导公式,属于基础题.24.【解析】【分析】先计算得到根据二次函数得到最小值【详解】则当时有最小值即的最小值为故答案为:【点睛】本题考查了向量模的计算意在考查学生的计算能力【解析】 【分析】先计算得到2219()33AG m +=+,根据二次函数得到最小值. 【详解】AG mAB AC =+则222222219649()33AG m AB AC mAB A m m C m ⋅=++=++=++当13m =-时,2AG 有最小值3,即||AG【点睛】本题考查了向量模的计算,意在考查学生的计算能力.25.【解析】【分析】首先利用线段的比值求出λ进一步利用分点坐标公式即可求出结果【详解】由题意因为点P 在的延长线上且所以可得又由设可得所以点的坐标为故答案为:【点睛】本题主要考查了定比分点的坐标公式的应用解析:7,42⎛⎫⎪⎝⎭【解析】 【分析】首先利用线段的比值求出λ,进一步利用分点坐标公式,即可求出结果. 【详解】由题意,因为点P 在12PP 的延长线上,且122||2||PP P P =, 所以213PP PP =-,可得3λ=-, 又由121123P P =-=(,)、(,), 设P x y (,),可得121(3)271132x x x λλ+-+-⨯===+-,121(3)34113y y y λλ++-⨯===+- 所以点P 的坐标为7,42⎛⎫ ⎪⎝⎭. 故答案为:7,42⎛⎫ ⎪⎝⎭【点睛】本题主要考查了定比分点的坐标公式的应用,以及向量的共线条件的应用,着重考查了学生的运算能力和转化能力,属于基础题型..三、解答题 26.(1)22m n t ⋅=-;(2){|1t t <且6}t ≠-. 【解析】 【分析】(1)由数量积的运算律计算.(2)由0m n ⋅<解得t 的范围,排除,m n 反向的t 值. 【详解】(1)由已知12cos601a b ⋅=⨯⨯︒=,m n ⋅22(3)(2)3(6)23(6)822a b ta b ta t a b b t t t =-⋅+=+-⋅-=+--=-.(2)m 与n 的夹角为钝角,则220m n t ⋅=-<,1t <,设m kn =,即2(3)ta b k a b +=-,则32t k k =⎧⎨=-⎩,解得26k t =-⎧⎨=-⎩,此时m 与n 方向相反.所以t 的取值范围是{|1t t <且6}t ≠-. 【点睛】本题考查向量的数量积运算,掌握平面向量数量积运算律是解题关键.0m n ⋅<时,m 与n 的夹角为钝角或平角,即向量方向相反时,数量积也小于0.注意检验排除. 27.(1)最小正周期π,对称轴方程为62k x ππ=+,k Z ∈;(2)()f x 在区间46ππ⎡⎤-⎢⎥⎣⎦,上单调递增;在区间64ππ⎡⎤⎢⎥⎣⎦,上单调递减.【解析】分析:(1)利用二倍角公式、两角和的余弦公式化简函数表达式,再利用周期公式和整体思想进行求解;(2)利用整体思想和三角函数的单调性进行求解. 详解:(1)()22cos cos 213f x x x π⎛⎫=-+- ⎪⎝⎭1cos2cos2sin 226x x x x π⎛⎫=-=+ ⎪⎝⎭,因为2ω=,所以最小正周期2T ππω==,令2=62x k πππ++,所以对称轴方程为62k x ππ=+,k Z ∈. (2)令222262k x k πππππ-+≤+≤+,得36k x k ππππ-+≤≤+,k Z ∈,设44A ππ⎡⎤=-⎢⎥⎣⎦,,36B x k x k k Z ππππ⎧⎫-+≤≤+∈⎨⎬⎩⎭,,易知46A B ππ⎡⎤⋂=-⎢⎥⎣⎦,, 所以,当44x ππ⎡⎤∈-⎢⎥⎣⎦,时,()f x 在区间46ππ⎡⎤-⎢⎥⎣⎦,上单调递增;在区间64ππ⎡⎤⎢⎥⎣⎦,上单调递减.【名师点睛】本题考查二倍角公式、两角和公式、辅助角公式、三角函数的图象和性质等知识,意在考查学生的转化能力和基本计算能力.28.(1)(2,1)a =;(2)724250x y +-=. 【解析】 【分析】(1)由题意,计算a b ⋅和2b 的值,即可求解1a ;(2)用参数设出向量a ,求得1a ,再消去参数即可证明1a 的终点的轨迹是一条直线,并写出直线方程。
广西钦州市高二下学期期中数学试卷

广西钦州市高二下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分) (2019高三上·天津期末) 设全集,,,则()A .B .C .D .2. (2分) cos 的值为()A .B . ﹣C . ﹣D .3. (2分)下列四个命题中正确的是()A . 公比q>1的等比数列的各项都大于1B . 公比q<0的等比数列是递减数列C . 常数列是公比为1的等比数列D . {lg2n}是等差数列而不是等比数列4. (2分) (2017高一下·新乡期中) 已知向量 =(cos5°,sin5°),,则=()A . 1B .C .D .5. (2分)设是两条不同的直线,是两个不同的平面,给出下列条件,能得到的是()A .B .C .D .6. (2分)(2018·普陀模拟) 已知,,若,则对此不等式描叙正确的是()A . 若,则至少存在一个以为边长的等边三角形B . 若,则对任意满足不等式的都存在以为边长的三角形C . 若,则对任意满足不等式的都存在以为边长的三角形D . 若,则对满足不等式的不存在以为边长的直角三角形7. (2分)(2017·海淀模拟) 圆x2+y2﹣2y=0与曲线y=|x|﹣1的公共点个数为()A . 4B . 3C . 2D . 08. (2分)函数的部分图象如图所示,则的解析式为()A .B .C .D .9. (2分) (2016高一上·上杭期中) 已知f(x)= ,若函数f(x)是R上的增函数,则a的取值范围是()A . (1,3)B . (1,2)C . [2,3)D . (1,2]10. (2分)如图,已知正方体ABCD﹣A1B1C1D1棱长为4,点H在棱A1A上,且HA1=1.点E,F分别为棱B1C1 ,C1C的中点,P是侧面BCC1B1内一动点,且满足PE⊥PF.则当点P运动时,|HP|2的最小值是()A . 7﹣B . 27﹣6C . 51﹣14D . 14﹣2二、填空题 (共7题;共7分)11. (1分) (2017高二下·济南期末) 已知双曲线的离心率是,则n=________.12. (1分) (2016高一下·黄陵开学考) 对定义域分别为D1 , D2的函数y=f(x),y=g(x),规定:函数h(x)= ,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是________.13. (1分) (2016高三上·吉林期中) 已知数列{an}与{bn}满足an=2bn+3(n∈N*),若{bn}的前n项和为Sn= (3n﹣1)且λan>bn+36(n﹣3)+3λ对一切n∈N*恒成立,则实数λ的取值范围是________.14. (1分) (2016·德州模拟) 已知x,y满足,且z=2x﹣y的最大值是最小值的﹣2倍,则a的值是________.15. (1分)(2016·天津模拟) 一个几何体的三视图(单位:m)如图所示,则此几何体的表面积为________ m216. (1分)已知点A(﹣,),在抛物线C:y2=2px(p>0)的准线上,点M,N在抛物线C上,且位于x 轴的两侧,O是坐标原点,若=3,则点A到动直线MN的最大距离为________17. (1分) (2016高一下·盐城期末) 在平面直角坐标系xOy中,已知圆C:(x﹣3)2+(y﹣4)2=5,A、B 是圆C上的两个动点,AB=2,则的取值范围为________.三、解答题 (共5题;共55分)18. (10分) (2018高一下·长春期末) 在斜中,内角所对的边分别为 ,已知.(1)证明: ;(2)若的面积为边上的中点, ,求 .19. (10分) (2019高一上·汪清月考) 如图所示,在正方体中,分别是的中点.(1)求证:平面平面;(2)求证:平面平面 .20. (15分) (2016高一上·昆明期中) 已知函数f(x)=x2﹣4|x|+3,x∈R.(1)判断函数的奇偶性并将函数写成分段函数的形式;(2)画出函数的图象,根据图象写出它的单调区间;(3)若函数f(x)的图象与y=a的图象有四个不同交点,则实数a的取值范围.21. (10分) (2016高一下·岳池期末) 已知数列{an}的前n项和为Sn ,点(n,)在直线y= x+上.(1)求数列{an}的通项公式;(2)设bn= ,求数列{bn}的前n项和为Tn,并求使不等式Tn>对一切n∈N*都成立的最大正整数k的值.22. (10分)(2018·栖霞模拟) 已知椭圆的焦距为,且过点 .(1)求椭圆的方程;(2)若不经过点的直线与椭圆交于,两点,且直线与直线的斜率之和为,证明:直线的斜率为定值.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共7题;共7分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、三、解答题 (共5题;共55分) 18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、。
广西省钦州市大寺中学数学文科模拟考试卷二

广西省钦州市大寺中学2007届数学文科模拟考试卷二一.选择题(每小题5分,共60分)1.设集合M=},,2|{},0|{2R x x x N R x x x x ∈<=∈<-和集合则 A .N ⊂MB .M ∩N=MC .M ∪N=MD .M ∪N=R2.若平面向量()==︒-=b a b 则,且的夹角是与向量,53|b |1802,1A .(-3,6)B .(3,-6)C .(6,-3)D .(-6,3)3.已知)15(cos ,2cos )(sin f x x f 则=的值是A .21B .-21 C .23 D .23- 4.已知等差数列{a n }满足:30,8531==+S a a ,若等比数列{b n }满足,,4311a b a b ==则 5b 为A .16B .32C .64D .275.x x y 52sin 52cos3+=的图象相邻两对称轴之间的距离为A .52πB .45πC .25π D .π56.抛物线y = x 2+ bx + c 在点(1,2)处的切线与其平行直线bx + y + c = 0间的距离是A .42 B .22 C .223 D .27.函数|3||4|12-++-=x x x y 是A .奇函数B .偶函数C .非奇非偶函数D .既是奇函数又是偶函数 8.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是323π,那么这个三棱柱的体积是A . 9.设a 、b ∈R +,且a + b = 4,则有A .211≥ab B .111≥+b a C .2≥abD .41122≥+ba 10.某餐厅内抽取100人,其中有30人在15岁以下,35人在16至25岁之间,25人在26至45岁之间,10人在46岁以上,则数0.35是16至25岁人员占总体分布的 A.概率 B .频率 C.累积频率 D.频数11.已知22,05302-+⎩⎨⎧≥+-≤-y x y x y x 则的最大值是A .2B .-2C .1D .-112.某段街道旁边规划树立10块广告牌,广告底色选用红、绿两种颜色,则相邻两块广告底色不同为绿色的配色方案的种数为A .72B .78C .144D .156二.填空题(每小题4分,共16分)13.将一个容量为m 的样本分成3组,已知第一组的频数为8,第二、三组的频率为0.15和0.45,则m = . 14.若t an θ=2,则2si n 2θ-32si n 2θ=___________ 15.在)1()1(26x x x ++-的展开式中,3x 的系数是 (用数字作答). 16.对于不同的直线m , n 和不同的平面βα,,给出下列命题:①m n m α⊥⎫⇒⎬⊥⎭ n ∥α ② m n αα⊥⎫⇒⎬⊥⎭n ∥m③ //m n αβαβ⊂⎫⎪⊂⇒⎬⎪⎭m 与n 异面 ④ n m n m βααββ⊥⎫⎪=⇒⊥⎬⎪⊥⎭其中正确..的命题序号是 . 三.解答题(第17、18、19、20、21题每题12分,第22题14分,共74分) 17.已知实数等比数列{}n a 前n 项和为n S ,314S =,6126S =。
广西钦州市大寺中学2012-2013学年高二历史下学期期中试题新人教版

大寺中学2012-2013学年高二下学期期中考试历史试题一、选择题(2*25=50分)1、俄国二月革命是一场资产阶级民主革命,但其结果却超出了资产阶级民主革命的范围,具体表现为A、摧毁了沙皇专制统治B、结束了两个政权并存的局面C、无产阶级掌管国家事务D、资产阶级拥有强大武装2、苏联实行新经济政策和美国推行罗斯福新政的相似之处是①面临极为困难的经济形势②国家颁布法令强制干预经济③最主要内容是调整和复兴工业④通过发展商品生产来恢复农业()A.①②B.①③C.②③D.①④3、斯大林时期的经济体制最本质的特点是()A.用行政命令来管理经济 B.权力高度集中,缺少群众监督C.限制商品货币关系 D. 否定价值规律与市场机制的作用4、丘吉尔说:英国的政策并不考虑全力称霸欧洲和国家空间是哪一个国家……它唯一关心的是,谁是最强大的或具有支配力的暴君。
因此,我人不要怕别人说我们亲法反德。
如果情况有变,我们同样可以亲德反法。
”这一说反映出英国奉行的外交原则是A、民族处决B、势力均衡C、绥靖主义D、严守中立5、有人称苏俄新经济政策是“布尔什维克转向资本主义”,罗斯福新政是“社会主义计划”,这一看法的缺陷是①没有从政策实施的根本目的上看问题②没有看到政策在一定限度内调整③只看现象不看本质④没有从发展的、辩证的角度看问题A、①②③④B、①②③C、②③D、②③④6、在巴黎和会上,美国总统威尔逊提出:“不论平时和战时,在领海以外,海洋上的航行有绝对自由……”。
其真实目的是() A.维护公海航行自由B.限制德国潜艇的发展C.打破英国的海上优势D.维护美国的海上霸权7、凡尔赛——华盛顿体系中,最能够突出反映美国争夺海外市场力量增强的是()A.《凡尔赛合约》B.《五国海军条约》C.《国际联盟盟约》D.《九国公约》8、1929年-1933年经济危机爆发后,银行纷纷倒闭,罗斯福上台没几天,就下令全国银行休业4天进行整顿,淘汰丧失支付能力的小银行,扶持实力雄厚的大银行……通过工业复兴法……规定生产规模、价格水平、工资标准和工作日时数等。
广西钦州市大寺中学2012届高三第四次月考数学(文科)试题

钦州市大寺中学2 0 1 2届高三毕业班数学月考试题[文4]命题:李川华 审核:高三数学备课组 考试时间:2011—12—15班别: 姓名: 座号: 一.选择题(每小题5分,共60分) 1.sin15cos165的值为A .41B .14- C .21 D .12- 2.抛物线24y x =的焦点坐标为A.(1,0)B.1(0,)16C.(0,1) D 。
1(,0)83.已知数列{}na 是各项均为正数的等比数列,=++==54331,21,3a a a S a 则前三项和A .2B .33C .84D .1894.已知向量(1,2)a =,向量(,2)b x =-,且()a a b ⊥-,则实数x 等于A .9B .4C .0D .4-5.函数y =的定义域为A .(4,1)--B .(4,1)-C .(1,1)-D .(1,1]-6.(52x +的展开式中3x 的系数是A .18B .14C .10D .67.设 l 、m 、n 为不同的直线,α、β为不同的平面,则正确的命题是 A .若 α⊥β,l ⊥α,则 l ∥β B . 若 α⊥β,l α⊂,则 l ⊥βC . 若 l ⊥m ,m ⊥n ,则 l ∥nD . 若m ⊥α,n ∥β且α∥β,则 m ⊥n8.已知点A (3,1)和B (-4,6)在直线023=+-a y x 的两侧,则的a 取值范围是A .a <-7或 a >24B .a <-24或 a >7C .-7<a <24D .-24<a <79.已知函数()χ2=x f 的反函数()x f 1-满足()4)(11=+--b fa f ,则ba 11+的最小值为A .21B .31C .41D .110.双曲线)0,0(12222>>=-b a by a x 中,F 为右焦点,A 为左顶点,点BF AB b B ⊥且),0(,则此双曲线的离心率为A .2B .3C .213+ D .215+ 11.某班选派6人参加两项公益活动,每项活动最多安排4人,则不同的安排方法有A.50种 B 。
广西钦州市大寺中学2012-2013学年高二下学期期中考试生物试题及答案试题

大寺中学2012-2013学年高二下学期期中考试生物试题一、单项选择题(每题2分,共50分)1、一对夫妇第一胎是一个女孩,如果允许他们生第二胎,则他们生一个男孩的可能是()A.100%B.50%C.0%D.25%2、小明长得非常像他父亲,这可能是由于( )A.从父亲得到了较多的染色体B.从父亲得到的显性基因较多C.与父亲的性别相同D.长期主动地模仿和学习父亲3、设某一多肽链中有100个肽键,那么,作为合成该多肽链的模板mRNA和用来转录该mRNA的DNA分子,至少分别含有碱基的个数是( )A.1000个和2000个B.3000个和6000个C.3003个和6006个D.2997个和5994个4、有一种鸟类的生活习性是白天休息,夜晚觅食。
到秋季,此种鸟换冬羽越冬,影响这两种习性的关键生态因素依次是()A.阳光、阳光B.阳光、温度C.温度、水分D.水分、温度5.、玉米体细胞内有10对染色体,则其精子、卵细胞、子房壁细胞中各有多少染色体? ( )A.10,10,10B.10,10,20C.10,20,30D.20,20,206、我国科学家已成功破译了水稻基因组的全部信息。
下列叙述错误的是()A、水稻基因实质上是水稻DNA分子上起遗传作用的一些片段B、水稻抗病、抗倒伏、高产优质等一系列可遗传的性状均由基因决定C、水稻DNA分子是一种大分子化学物质,它们就是水稻的遗传物质D、将来水稻体内的DNA不再可能发生任何变7、孟德尔在对一对相对性状进行研究的过程中,发现了基因的分离定律。
下列有关基因分离定律的几组比例,能说明基因分离定律实质的是( )A.F2的表现型比为3∶1B.F1产生配子的比为1∶1C.F2基因型的比为1∶2∶1D.测交后代的比为1∶18、下列关于遗传物质、基因、性状关系的叙述中,不正确的是()A.遗传物质、基因的载体是染色体B.基因是遗传物质中决定性状的最小单位C.生物所有的性状都是由一对基因控制的D.基因对生物性状起决定作用9、下列关于变异的叙述,不正确的是 ( )A.生物的变异都是可以遗传的B.引起变异的原因是多种多样的C.变异在自然界是普遍存在的D.没有变异就没有新品种的产生10、决定生物进化方向的是()A. 突变和重组B. 生存斗争C. 自然选择D. 隔离11、下列说法正确的是()A. 一片森林中的全部蛇是一个种群B. 在自然条件下,种群的基因频率可以保持永久稳定C. 当生物体的体细胞出现基因突变时,这个生物体就成为了新物种的个体了D. 生殖隔离一旦形成,新的物种也就产生了12、基因型为AaBb和aaBb的个体杂交(两对基因独立遗传),F1的表现型比例是( ):3:3:1 B.1:1:1:1 C.3:1 D.3:1:3:113、2008年“神舟七号”成功发射,山东省宁阳县伏山镇选送的“伏春一号黄瓜”和“伏乐长茄”两个品种共10克种子,也搭载飞船遨游太空。
广西钦州市高二下学期数学期中考试试卷
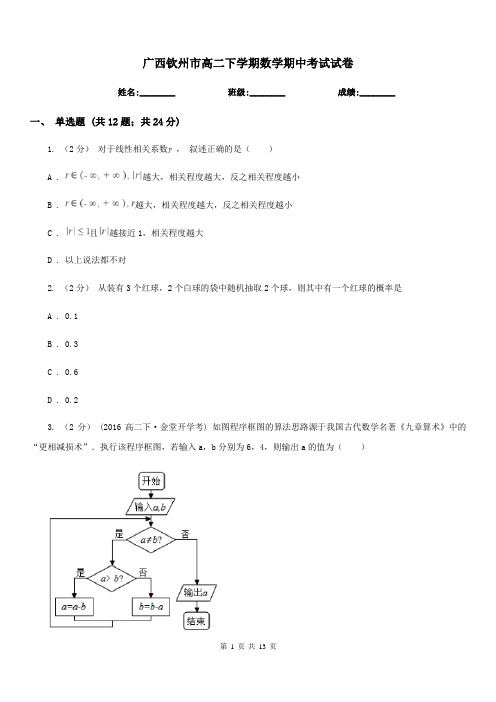
广西钦州市高二下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)对于线性相关系数,叙述正确的是()A . 越大,相关程度越大,反之相关程度越小B . 越大,相关程度越大,反之相关程度越小C . 且越接近1,相关程度越大D . 以上说法都不对2. (2分)从装有3个红球,2个白球的袋中随机抽取2个球,则其中有一个红球的概率是A . 0.1B . 0.3C . 0.6D . 0.23. (2分) (2016高二下·金堂开学考) 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b分别为6,4,则输出a的值为()B . 2C . 4D . 64. (2分)某考察团对全国10大城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)进行统计调查,y与x具有相关关系,回归方程为=0.66x+1.562.若某城市居民人均消费水平为7.675千元,估计该城市人均消费额占人均工资收入的百分比约为()A . 83%B . 72%C . 67%D . 66%5. (2分)(2019.全国Ⅰ卷文) 某学校为了解1000名新生的身体素质,将这些学生编号为1,2, (1000)从这些新生中用系统抽样方法等距抽取100名学生进行体质测验,若46号学生被抽到,则下面4名学生中被抽到的是()A . 8号学生B . 200号学生C . 616号学生D . 815号学生6. (2分)设a∈Z,且0≤a≤13,若512012+a能被13整除,则a=()A . 0B . 1C . 117. (2分)中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他活动的民间艺术,在中国,剪纸具有广泛的群众基础,交融于各族人民的社会生活,是各种民俗活动的重要组成部分.在如图所示的古代正八边形窗花矢量图片中,,则向正八边形窗花矢量图片中任投一点,落在正方形中的概率为()A .B .C .D .8. (2分) (2017高二下·中山期末) 在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布N(﹣1,1)的密度曲线)的点的个数的估计值为()附:若X~N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.A . 1 193B . 1 359C . 2 718D . 3 4139. (2分) (2016高二下·卢龙期末) 抛掷红、蓝两枚骰子,事件A=“红色骰子出现点数3”,事件B=“蓝色骰子出现偶数点”,则P(B|A)=()A .B .C .D .10. (2分)两人进行乒乓球比赛,先赢三局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有()A . 10种B . 15种C . 20种D . 30种11. (2分) (2016高二下·威海期末) 通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女合计爱好402060不爱好203050合计6050110根据上述数据能得出的结论是()(参考公式与数据:X2= .当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关;当X2<3.841时认为事件A与B无关.)A . 有99%的把握认为“爱好该项运动与性别有关”B . 有99%的把握认为“爱好该项运动与性别无关”C . 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D . 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”.12. (2分)(2017·深圳模拟) 一个三位数,个位、十位、百位上的数字依次为x、y、z,当且仅当y>x,y >z时,称这样的数为“凸数”(如243),现从集合{1,2,3,4}中取出三个不相同的数组成一个三位数,则这个三位数是“凸数”的概率为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2016高一下·无锡期末) 某人一周5次乘车上班的时间(单位:分钟)分别为10,11,9,x,11,已知这组数据的平均数为10,那么这组数据的方差为________.14. (1分)全国篮球职业联赛的某个赛季在H队与F队之间角逐.采取七局四胜制(无平局),即若有一队胜4场,则该队获胜并且比赛结束.设比赛双方获胜是等可能的.根据已往资料显示,每场比赛的组织者可获门票收入100万元.组织者在此赛季中,两队决出胜负后,门票收入不低于500万元的概率是________.15. (1分) (2019高三上·上海月考) 我国古代典籍《周易》用“卦”描述万物的变化,每一“重卦”由从下到上排列的6个爻组成,爻分为“阳爻”和“阴爻”,如图就是重卦,在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是________.16. (1分) (2018高二下·重庆期中) 袋中有6个黄色、4个白色的乒乓球,做不放回抽样,每次任取1个球,取2次,则事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率为________三、解答题 (共6题;共70分)17. (15分) (2018高二上·长安期末) 某旅游爱好者计划从3个亚洲国家和3个欧洲国家中选择2个国家去旅游.(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括但不包括的概率.18. (10分) (2016高一下·滑县期末) 如图,已知AB是半圆O的直径,O是半圆圆心,AB=8,M、N、P是将半圆圆周四等分的三个分点.(1)从A、B、M、N、P这5个点中任取3个点,求这3个点组成等腰三角形的概率;(2)在半圆内任取一点S,求△SOB的面积大于4 的概率.19. (10分) (2016高二下·长治期中) 随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:年份20102011201220132014时间代号t12345储蓄存款y(千亿元)567810(1)求y关于t的回归方程.(2)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.附:回归方程中.20. (10分)(2020·化州模拟) 改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:交(0,1000](1000,2000]大于2000付金额(元)支付方式仅使用A18人9人3人仅使用B10人14人1人(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.21. (10分)(2017·湖北模拟) 随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.22. (15分)(2012·湖南理) 已知数列{an}的各项均为正数,记A(n)=a1+a2+…+an , B(n)=a2+a3+…+an+1 ,C(n)=a3+a4+…+an+2 , n=1,2,….(1)若a1=1,a2=5,且对任意n∈N*,三个数A(n),B(n),C(n)组成等差数列,求数列{an}的通项公式.(2)证明:数列{an}是公比为q的等比数列的充分必要条件是:对任意n∈N*,三个数A(n),B(n),C(n)组成公比为q的等比数列.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共70分)17-1、18-1、18-2、19-1、19-2、20-1、21-1、21-2、22-1、22-2、。
广西钦州市数学高二下学期文数期中考试试卷

广西钦州市数学高二下学期文数期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)若是纯虚数,则的值为().A .B .C . 7D . 或2. (2分) (2017高二下·广州期中) 对两个变量Y与X进行回归分析,分别选择不同的模型,它们的相关系数r如下,其中拟合效果最好的模型是()A . 模型Ⅰ的相关系数r为0.96B . 模型Ⅱ的相关系数r为0.81C . 模型Ⅲ的相关系数r为0.53D . 模型Ⅳ的相关系数r为0.353. (2分)(2017·汕头模拟) 某厂家为了解销售轿车台数与广告宣传费之间的关系,得到如表统计数据表:根据数据表可得回归直线方程,其中,,据此模型预测广告费用为9万元时,销售轿车台数为()广告费用x(万元)23456销售轿车y(台数)3461012A . 17B . 18C . 19D . 204. (2分)已知,观察下列式子:,,,类比有,则a是()A .B . nC . n+1D . n-15. (2分) (2016高二下·珠海期中) 用反证法证明数学命题时首先应该做出与命题结论相矛盾的假设.否定“自然数a,b,c中恰有一个偶数”时正确的反设为()A . 自然数a,b,c都是奇数B . 自然数a,b,c都是偶数C . 自然数a,b,c中至少有两个偶数D . 自然数 a,b,c中至少有两个偶数或都是奇数6. (2分)设p:x>1, q:,则p是q的()A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件7. (2分)设是定义在R上的可导函数,且满足,对于任意的正数,下面不等式恒成立的是()A .B .C .D .8. (2分)(2018·淮南模拟) 在中,角的对边分别为,且,,则角等于()A .B . 或C .D .9. (2分) (2019高二上·会宁期中) 若,则的最小值为()A .B .C .D .10. (2分)若曲线C1:y2=2px(p>0)的焦点F恰好是曲线的右焦点,且C1与C2交点的连线过点F,则曲线C2的离心率为()A .B .C .D .11. (2分) (2018高三上·寿光期末) “干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。
广西钦州市大寺中学高一数学下学期期中试题新人教A版

大寺中学2012-2013学年高一下学期期中考试数学试题一、单项选择题:本大题共12小题,每小题5分,共60分.1. 某校在检查学生作业时,抽出每班学号尾数为4的学生作业进行检查,这里主要运用的抽样方法是( )A.分层抽样B.抽签抽样C.随机抽样D.系统抽样 2.从甲、乙、丙三人中任选2人作代表,则甲被选中的概率为( )A.12B.13C.23D . 1 3.为了在运行下面的程序之后输出的y 值为16,则输入x 的值应该是 ( ). INPUT xIF x<0 THENy=(x+1)(x+1) ELSEy=(x-1)(x-1)END IFPRINT y ENDA.3或-3 B . -5 C.5或-3 D.-5或54.废品率x%与每吨生铁成本y(元)之间的回归直线方程为yˆ=234+3x,表明:( ) A .废品率每增加1%,生铁成本增加3x 元 B .废品率每增加1%,生铁成本每吨增加3元 C .废品率每增加1%,生铁成本增加234元 D .废品率不变,生铁成本为234元5. 有一个容量为200的样本,其频率分布直方如图 所示.根据样本的频率分布直方图估计,样本数 据落在区间[10,12)内的频数为 ( ). A .18 B .36 C .54 D .726. 某射手一次射击中,击中10环、9环、8环的概 率分别是0.24,0.28,0.19,则这射手在一次射击中 不够9环的概率是( )A.0.48B.0.52C.0.71D.0.297. 在一个试验模型中,设A 表示一个随机事件,__A 表示A 的对立事件.以下给出了3 个结论: ①__()()P A P A =; ②__()1P A A +=; ③ 若()1P A =,则__()0P A =.其中错误的结论共有( )A .3个B . 2个C . 1个 D.0个 8 .执行如图所示的程序框图,输出的S 值为A .2B .4C .8D .169. 从装有两个白球和两个黄球的口袋中任取2个球,以下给 出了三组事件:① 至少有1个白球与至少有1个黄球; ②至少有1个黄球与都是黄球; ③恰有1个白球与恰有 1个黄球.其中互斥而不对立的事件共有( )组 A. 0 B. 1 C. 2 D. 310.在5件产品中,有3件一等品,2件二等品. 从中任取2件. 那么以710为概率的事件是 ( )A .都不是一等品B .至少有一件二等品C .恰有一件一等品D .至少有一件一等品 11.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有 点数1,2,3,4,5,6),骰子朝上的面的点数分别为X ,Y , 则log 2X Y =1的概率为( ).A .错误!未找到引用源。
广西钦州市高二下学期期中考试数学试题(解析版)

一、单选题1.数列满足,,则( ) {}n a 14a =1421n n a a n +=++4a =A .2 B .C .D .832-83-【答案】A【分析】运用代入法进行求解即可, 【详解】因为, 14a =所以, 23414244284212,,281142213313a a a a =+=+==+==+=+++故选:A2.在5道题中有3道数学题和2道物理题,如果不放回地依次抽取2道题,则在第一次抽到数学题条件下,第二次抽到数学题的概率是( ) A .B .C .D .310123513【答案】B【分析】法一:分析出第一次抽到数学题条件下,剩余试题的特征,从而求出概率;法二:设出事件,利用条件概率公式进行求解.【详解】法一:因为第一次抽到数学题条件下,还剩下4道试题,有2道数学题和2道物理题,因此第二次抽到数学题的概率是;12法二:设第二次抽到数学题为事件,第一次抽到数学题为事件,A B 则,,()2325C 3C 10P AB ==()1315C 3C 5P B ==则.()()()3110325P AB P A B P B ===故选:B3.已知,则( )14,3X B ⎛⎫⎪⎝⎭:(1)P X ==A . B . C .D .8813281427827【答案】B【分析】根据二项分布的知识求得正确答案.【详解】因为,所以. 14,3X B ⎛⎫ ⎪⎝⎭:3141232(1)C 3381P X ⎛⎫==⨯⨯= ⎪⎝⎭故选:B4.根据变量与的对应关系(如表),求得关于的线性回归方程为,则表中x y y x 6.517.5y x =+的值为( )m x 24 5 6 8y 30 40 m 50 70A .60B .55C .50D .45【答案】A【分析】先求得样本点中心,再根据回归直线过样本点中心即可求解. 【详解】由表中数据,计算,()12456855x =⨯++++=,()1304050703855m y m =⨯++++=+因为回归直线方程过样本中心, ˆ 6.517.5y x =+,解得, 38 6.6517.55m∴+=⨯+60m =故选:A5.{an }是首项为1,公差为3的等差数列,如果an =2 023,则序号n 等于( ) A .674 B .675C .676D .677【答案】B【分析】先求出等差数列的通项公式,再把代入求解即可.2023n a =【详解】因为数列是首项为1,公差为3的等差数列,所以. {}n a ()13132n a n n =+-=-当时,即,解得. 2023n a =322023n -=675n =故选:B6.已知数列对任意满足,且,则等于( ) {}n a *n ∈N 11n n a a a ++=11a =5a A . B .C .D .2345【答案】D【分析】由数列递推公式依次计算,,,,即可得答案. 2a 3a 4a 5a 【详解】由题意可得,,,2112a a a =+=321213a a a =+=+=,. 431314a a a =+=+=541415a a a =+=+=故选:D7.等比数列的前n 项和为,若,,则( ) {}n a n S 1010S =2030S =40S =A .60 B .70 C .80 D .150【答案】D【分析】根据等比数列前项和的片段和性质,结合题意,进行具体计算即可. n 【详解】因为是等比数列,{}n a 所以成等比数列, 10201030204030,,,S S S S S S S ---又因为,,, 1010S =2030S =201020S S -=则,, 302040S S -=403080S S -=所以,. 3070S =40150S =故选:D.8.已知数列为等差数列,若,,且数列的前项和有最大值,那么{}n a 2830a a +<670a a ⋅<{}n a n 取得最小正值时为( )n S n A .11 B .12 C .7 D .6【答案】A【分析】根据已知条件,判断出,的符号,再根据等差数列前项和的计算公式,即可67,a a 67a a +n 求得.【详解】因为等差数列的前项和有最大值,故可得, n 0d <因为,故可得,即, 2830a a +<10224+<a d 10112+<d a 所以,可得,7012-<a d 7102<<a d 又因为,670a a ⋅<故可得,所以数列的前6项和有最大值, 60a >{}n a 且, 6712110+=+<a a a d 又因为,, ()122711612602=⨯=++<a S a a a ()611111111102+>=⨯=⨯S a a a 故取得最小正值时n 等于.n S 11故选:A.二、多选题9.下列选项中能满足数列1,0,1,0,1,0,…的通项公式的有( )A .B . 11(1)2n n a ++=-πsin2n n a =C .D .()21πcos 2n n a -=10n n a n ⎧=⎨⎩,是奇数,是偶数【答案】ACD【分析】根据给定的通项公式求出前几项判断是否符合已知数列各项. 【详解】对A :当为奇数时,,当为偶数时,,符合数列1,0,1,n 1112n a +==n 1102n a -==0,1,0,…的通项公式; 对B :当为奇数时,或,当为偶数时,,不符合数列1,0,1,n πsin 12n n a ==1-n 1102n a -==0,1,0,…的通项公式;对C :当为奇数时,,当为偶数时,,符合数列1,0,1,0,1,0,…的通项公n 1n a =n 0n a =式;对D :当为奇数时,,当为偶数时,,符合数列1,0,1,0,1,0,…的通项公n 1n a =n 0n a =式; 故选:ACD10.下列命题中,正确的命题( )A .回归直线恒过样本点的中心,且至少过一个样本点 ˆˆˆybx a =+(,)x y B .将一组数据的每个数据都加一个相同的常数后,方差不变C .用相关系数来刻画回归效果,越接近,说明模型的拟合效果越好||r ||r 0D .若随机变量,且,则()23,N ξσ~()60.84P ξ<=()360.34P ξ<<=【答案】BD【分析】利用回归直线的性质判断A ;利用波动性判断B ;利用相关系数的意义判断C ;利用正态分布的对称性计算判断D 作答.【详解】对于A ,回归直线恒过样本点的中心,不一定过样本点,A 错误; ˆˆˆybx a =+(,)x y 对于B ,将一组数据的每个数据都加一个相同的常数后,数据的波动性不变,方差不变,B 正确;对于C ,用相关系数来刻画回归效果,越接近,说明模型的拟合效果越好,C 错误;r r 1对于D ,随机变量,则, D 正确.()23,N ξσ~()()3660.50.840.50.34P P ξξ<<=<-=-=故选:BD11.随机投掷一枚质地均匀的正方体骰子两次,记录朝上一面的点数.设事件“第一次为奇A =数”,“第二次为奇数”,“两次点数之和为奇数”,则( ) B =C =A . B .与互斥()()()P A P B P C ==A B ⋂C C .与相互独立 D .A C ()()()()P ABC P A PB PC =【答案】ABC【分析】设事件“第一次为奇数”,则,“第二次为奇数”, 则,A =()3162P A ==B =()3162P B ==“两次点数之和为奇数”,则,根据概率的概念及互斥事件与相互独立事C =()1111122222P C =⨯+⨯=件概率的概念求解判断即可.【详解】随机投掷一枚质地均匀的正方体骰子两次,记录朝上一面的点数. 设事件“第一次为奇数”,则, A =()3162P A ==“第二次为奇数”, 则, B =()3162P B ==“两次点数之和为奇数”,则,则,C =()1111122222P C =⨯+⨯=∴,A 正确;()()()P A P B P C ==为两次点数之和为偶数,与两次点数之和为奇数不可能同时发生,A B ⋂则与互斥,B 正确;A B ⋂C ,故A 与相互独立,C 正确;()()()1122P AC P A P C =⨯=C 事件A,B,C 不可能同时发生,则,故D 错误; ()0P ABC =故选:ABC.12.已知数列满足,前n 项的和为,关于,叙述正确的是( ) {}n a 3211n a n =-n S n a n S A .有最小值 B .有最小值 n a n S C .有最大值 D .有最大值n a n S 【答案】ABC【分析】利用函数性质研究数列的性质,结合,的单调性逐项分析判断.n a n S【详解】对于函数可知:在上单调递减, ()3112112f x x x ⎛⎫=≠ ⎪-⎝⎭()f x 1111,,,22⎛⎫⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭且当时,;当时,. 112x <()0f x <112x >()0f x >故对于数列可知: 3211n a n =-当,则;*15,n n ≤≤∈N 12345133a a a a a -=>>>>=-当,则数列为递减数列,且; *6,n n ≥∈N {}n a 603n a a <≤=故数列有最大值,有最小值,A 、C 正确; {}n a 63a =53a =-又∵当,;当,; *15,n n ≤≤∈N 0n a <*6,n n ≥∈N 0n a >故当,则; *15,n n ≤≤∈N 12345S S S S S >>>>当,则; *6,n n ≥∈N 51n n S S S +<<故有最小值,B 正确,D 错误; n S 5S 故选:ABC.三、填空题13.若随机变量,则_______.(附:若随机变量,则()~63,100X N ()73P X <=()2~,X N μσ,)()0.6827P X μσμσ-<<+=()220.9545P X μσμσ-<<+=【答案】0.84135【分析】根据正态分布的对称性,结合原则求解即可3σ【详解】因为,所以. ()~63,100X N ()()0.68277363100.50.841352P X P X <=<+=+=故答案为:0.8413514.从一批含有13件正品、2件次品的产品中,不放回地任取3件,设取得的次品数为,则X ________.(1)P X <=【答案】2235【分析】由题可得服从超几何分布,进而即得.X 【详解】由题意知服从超几何分布,则,X 30313152C C 22(0)C 35P X ===所以. 22(1)(0)35P X P X <===故答案为:. 223515.在等比数列中,若、是方程的两根,则的值是______. {}n a 3a 11a 2530x x ++=7a 【答案】【分析】分析出,利用韦达定理结合等比中项的性质可求得的值. 70a <7a 【详解】对于方程,, 2530x x ++=25430∆=-⨯>设等比数列的公比为,则,即、同号, {}n a q 1130a a >3a 11a 由韦达定理可得,则、均为负数,,, 31131135a a a a =⎧⎨+=-⎩3a 11a 4730a q a => 70a ∴<由等比中项的性质可得,273113a a a ==7a ∴=故答案为:.16.随机变量X 的分布列如表所示,若,则_________. ()13E X =(32)D X -=X -1 0 1 P 16a b【答案】5【分析】利用离散型随机变量的分布列、数学期望的性质,列出方程组,求出,,由此能求出a b 方差,再根据方差的性质计算可得.【详解】依题意可得,解得,1161110163a b a b ⎧++=⎪⎪⎨⎪-⨯+⨯+⨯=⎪⎩1312a b ⎧=⎪⎪⎨⎪=⎪⎩所以,()22211111151013633329D X ⎛⎫⎛⎫⎛⎫=--⨯+-⨯+-⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以.()()25323959D X D X -==⨯=故答案为:5.四、解答题17.已知等差数列中,{}n a 3262,8a a a =+=(1)求的通项公式;{}n a (2)求数列的前n 项和,并求的最小值 {}n a n S n S 【答案】(1)24n a n =-(2),23n S n n =-2-【分析】(1)设等差数列的公差为,根据题意列出关于的等式,联立可得{}n a d 1,a d 12,2a d =-=,即可求解;(2)利用等差的求和公式得到,然后判断的正负,即可求得的最小值 n S n a n S 【详解】(1)设等差数列的公差为,{}n a d 因为,所以,解得, 3262,8a a a =+=1122268a d a d +=⎧⎨+=⎩122a d =-⎧⎨=⎩所以; ()1124n a a n d n =+-=-(2),()21132n n n S na d n n -=+=-数列首项为负的,公差大于零,是递增数列, {}n a 令即,解得,因为,所以, 0n a <240n -<2n <*N n ∈1n =令即,解得, 0n a =240n -=2n =令即,解得,0n a >240n ->2n >所以第1项是负数,第2项是0,从第3项起变成正数, 所以当或2时,取得最小值,1n =n S 122S S ==-18.某箱子中原来装有除颜色外完全相同的6个小球,其中4个红球,2个白球.从箱子中每次随机取出1个球,如果取出的是红球,则不放回;如果取出的是白球,则放回,每一次操作,称为一次取球.(1)求取球两次后,箱子中小球的个数为5的概率;(2)记取球两次后,箱子中小球的个数为,求的分布列和数学期望. X X 【答案】(1)2245(2)分布列见解析, 21245【分析】(1)记“取球两次后,箱子中小球的个数为5”为事件,然后列出事件包含的事件,根A A 据概率公式进行求解即可;(2)依题意可得到的所有可能取值为4,求出对应的概率,列出分布列并求出期望即可 X 56,,【详解】(1)记“取球两次后,箱子中小球的个数为5”为事件,A 事件包含:“第一次取球为红色,第二次取球为白色”和“第一次取球为白色,第二次取球为红A 色”,则,()422422656645P A =⨯+⨯=取球两次后,箱子中小球的个数为5的概率为; 2245(2)依题意得的所有可能取值为4,X 56,,则, ()()()432222214,5,665545669P X P X P X ==⨯=====⨯=的分布列为 X ∴X 4 5 6P 25224519的数学期望 X ∴()2221212456545945E X =⨯+⨯+⨯=19.赤霉素在幼芽、幼根、未成熟的种子中合成,其作用是促进细胞的生长,使得植株变高,每粒种子的赤霉素含量(单位:ng/g )直接影响该粒种子后天的生长质量.现通过生物仪器采集了赤霉x 素含量分别为10,20,30,40,50的种子各20粒,并跟踪每粒种子后天生长的情况,收集种子后天生长的优质数量(单位:粒),得到的数据如下表:y 赤霉素含量 x 10 20 30 40 50 后天生长的优质数量y 237810(1)求关于的线性回归方程;y x (2)利用(1)中的回归方程,估计1000粒赤霉素含量为60ng/g 的种子后天生长的优质数量.附:回归直线的斜率和截距的最小二乘估计公式分别为,.()()()121nii i nii xx y ybxx==--=-∑∑ a y bx =-$$【答案】(1) 0.210.3y x =-(2)615【分析】(1)求出、、、,代入公式计算可得答案;x y ()()51i i i x x y y =--∑()521i i x x=-∑(2)将代入可得答案. 60x = 0.210.3y x =-【详解】(1),,1020304050305x ++++==23781065y ++++==,,()()51210i i i x xy y =--=∑()5211000i i x x=-=∑则,, 2100.211000b== 0.3ay bx =-=- 故关于的线性回归方程为; y x 0.210.3y x =-(2)将,代入,得到,60x = 0.210.3y x =- 12.3y =则估计1000粒赤霉素含量为60ng/g 的种子后天生长的优质数量为. 12.3100061520⨯=20.某校用随机抽样的方法调查学生参加校外补习情况,得到的数据如下表: 分数等级人数不及格 [)0,60及格 [)60,75良好 [)75,90优秀[]90,100学生人数 8 52 29 11 参加校外补习人数51573(1)从中任取一名学生,记“该生参加了校外补习”,“该生成绩为优秀”.求及A =B =()P B ()P B A ;(2)能否在犯错误的概率不超过0.1的前提下认为学生成绩优秀或良好与校外补习有关?附:,其中.()()()()()22n ad bc K a b c d a c b d -=++++n a b c d =+++()20P K k ≥0.10 0.05 0.01 0.005 0.0010k 2.706 3.841 6.635 7.879 10.828【答案】(1),;()0.11P B =()0.1P B A =(2)不能在犯错误的概率不超过为0.1的前提下认为学生成绩优秀或良好与校外补习有关.【分析】(1)根据给定的数表,利用古典概率及条件概率公式计算作答.(2)根据数表完善列联表,计算的观测值并比对作答.22⨯2K 【详解】(1)由给定的数表得:,,, ()110.118522911P B ==+++()30310010P A ==()3100P AB =所以. ()()()311000.131010P AB P B A P A ====(2)由已知得列联表:22⨯参加校外 不参加校外 合计 成绩优秀或良好10 30 40 成绩不为优秀且良好20 40 60 合计30 70 100 的观测值为, 2K 22100(10402030)500.794 2.7063070406063K ⨯⨯-⨯==≈<⨯⨯⨯所以不能在犯错误的概率不超过为0.1的前提下认为学生成绩优秀或良好与校外补习有关.21.已知正项数列的前项和为,且,.{}n a n n S 12a <2632n n n S a a =++(1)求数列的通项公式;{}n a (2)若,求数列的前项和. 13n n n b a a +=⋅{}n b n n T 【答案】(1);32n a n =-(2). 331=+n n T n【分析】(1)由已知,结合的关系可得、,根据等差数列的定义即可写出,n n a S 11a =13n n a a --=通项公式.(2)由(1)得,应用裂项相消法求前项和. 113231n b n n =--+n n T 【详解】(1)当时,且,所以.1n =2111632a a a =++12a <11a =当时,, 2n ≥2111623n n n S a a ---+=+所以,()221116633n n n n n n n S S a a a a a ----==-+-所以,又,()()()1113n n n n n n a a a a a a ---+=+-10n n a a ->+所以,即是首项为1,公差为3的等差数列,故.13n n a a --={}n a 32n a n =-(2)因为, ()()31132313231n b n n n n ==--+-+所以. 11111131144732313131n n T n n n n ⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪-+++⎝⎭⎝⎭⎝⎭22.某企业年初在一个项目上投资2000万元,据市场调查,每年获得的利润为投资的50%,为了企业长远发展,每年年底需要从利润中取出500万元进行科研、技术改造,其余继续投入该项目.设经过年后,该项目的资金为万元. ()*n n N ∈n a (1)求和的值;1a 2a (2)求证:数列为等比数列;{}1000-n a (3)若该项目的资金达到翻一番,至少经过几年?(,)log 30.5≈log 20.3≈【答案】(1),12500a =23250a =(2)证明见解析(3)年3【分析】(1)根据题意直接计算可得;(2)依题意可得递推公式,然后构造可证;(3)根据(2)先求通项,然后根据题意列不等式求解可得.【详解】(1)由题意知,()12000150%5002500a =+-=,()22500150%5003250a =+-=(2)证明:由题意知.()()1150%5002n n a a n -=+-≥即,所以. 135002n n a a -=-()()131000100022n n a a n --=-≥由110001500-=a 所以数列的首项为,{}1000n a -110001500a -=所以是首项为,公比为的等比数列. {}1000n a -150032(3)由(2)知数列的首项为,公比为. {}1000n a -110001500a -=32所以,所以. 1310001500·2n n a -⎛⎫-= ⎪⎝⎭131********n n a -⎛⎫=⋅+ ⎪⎝⎭当,得.4000n a ≥1322n -⎛⎫≥ ⎪⎝⎭两边取常用对数得,所以,所以, ()31lg lg22n -≥lg20.331lg3lg20.50.32n -≥≈=-- 2.5n ≥因为,所以. *n ∈N 3n ≥即至少经过年,该项目的资金达到翻一番. 3。
广西壮族自治区钦州市市大寺中学高二生物期末试卷含解析

广西壮族自治区钦州市市大寺中学高二生物期末试卷含解析一、选择题(本题共40小题,每小题1.5分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 下列不属于基因工程在植物中的应用的是A. 增强植物的抗逆性B. 改良植物的品质C. 获得多倍体植物D. 利用植物细胞生产动物蛋白参考答案:C通过基因工程,可以增强植物的抗逆性、改良植物的品质,或者利用植物细胞生产动物蛋白;获得多倍体植物可用秋水仙素处理植物的芽尖分身组织。
2. 甲.乙.丙三组小鼠不同的免疫器官被破坏,其中甲组仅有体液免疫功能,乙组和丙组丧失了特异性免疫功能。
现给三组小鼠分别输入造血干细胞,发现仅有乙组恢复了细胞免疫功能,出现这些现象的原因是A.甲组骨髓被破坏,乙组胸腺被破坏,丙组骨髓和胸腺均被破坏B.甲组胸腺被破坏,乙组骨髓被破坏,丙组骨髓和胸腺均被破坏C.乙组骨髓被破坏,丙组胸腺被破坏,甲组骨髓和胸腺均被破坏D.丙组骨髓被破坏,甲组胸腺被破坏,乙组骨髓和胸腺均被破坏参考答案:B3. 精子的变形过程中()演变为精子的尾A.高尔基体B.细胞核C.内质网D.中心体参考答案:D4. 下列关于生态系统信息传递特征的描述,正确的是 ( )A.生态系统的物理信息都来源于环境 B.植物都通过化学物质传递信息C.信息沿食物链从低营养级向高营养级传递 D.信息可以调节生物种间关系参考答案:D5. 右图表示某生态系统的食物网,关于此食物网的叙述,正确的是()A.绿色植物接受的太阳能是流经此生态系统的总能量B.向此生态系统大量引入外来物种,使其组成成分增多,食物网变得复杂,抵抗力稳定性增强C.如果土壤受到污染,鹰体内的污染物积累浓度可能最高D. 狼依据野兔留下的气味进行捕食,野兔依据狼的气味或行为特征躲避猎捕,说明生物体的生命活动必须依靠信息的传递参考答案:C6. 演替过程中灌木逐渐取代了草本植物,其中主要原因是A.灌木繁殖能力较强B.草本植物寿命较短C.草本植物较为低等D.灌木较为高大,能获得更高的阳光参考答案:D7. 以下属于种群范畴的是A.一座山上所有的马尾松 B.一块草地上所有的昆虫C.一个池塘内所有的鱼类 D.一个公园内所有的树木参考答案:A8. 顶端优势的现象表示植物生长素在植物体内的运输方式是()A.自由扩散B.协助扩散 C.主动运输 D.渗透作用参考答案:C9. 下列关于基因工程的叙述中正确的是( )A、基因工程经常以抗菌素抗性基因为目的基因B、细菌质粒是基因工程常用的运载体C、通常用一种限制酶处理目的基因的DNA,用另一种限制酶处理运载体DNAD、为育成抗除草剂的作物新品种,导入抗除草剂基因时只有以受精卵为受体参考答案:B10. 下列四组生物中,都属于原核生物的一组是A.T2噬菌体 HIV SARS病毒 B.毛霉根瘤菌硝化细菌C.乳酸菌酵母菌醋酸菌 D.大肠杆菌 Taq细菌蓝藻参考答案:D11. 实验一:用不带特殊病原体的小鼠进行如下特异性免疫实验,过程如图1,结果如图2,(1)实验中,对B组小鼠的处理是作为A组小鼠的________处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大寺中学2012-2013学年高二下学期期中考试(文)试题
一、选择题:(本大题共12个小题,每小题5分,共60分)。
1、设集合A={4,5,7,9},B={3,4,7,8,9},则集合A ∪B 中的元素共有 ( ) A.3个 B.4个 C.5个 D.6个 2、角α终边过点(-1,2),则cos α等于 ( )
3、椭圆22
143
x y +=的离心率为 ( )
74 D.2
1 4、在261
()x
x -的展开式中,
2x 的系数是 ( ) A.20 B.15 C.-20 D.-15
5、在10张奖券中,有4张有奖,从中任抽2张,能中奖的概率为 ( )
A.12
B.13
C.23
D.4
5
6、函数
的定义域为( )
A.(-4,-1)
B.(-4,1)
C.(-1,1)
D.(-1,1] 7、已知ab ≠0,a,b ∈R ,则下列式子总能成立的是 ( )
A .2b a
a b
+≥ B.
2b a a b +≥- C.2b a
a b
+≤- D.
2b a
a b
+≥ 8、在一个口袋中装有5个白球和3个黑球,这些球除颜色外完全相同,从中摸
出3个球,至少摸到2个黑球的概率等于( )
A.27
B.38
C.37
D.9
28
9、某校开设10门课供学生选修,其中A 、B 、C 这3门由于上课时间相同,至多选1门.学校规定,每位同学选修3门,则每位同学不同的选修方案种数是( ) A.120 B.98 C.63 D.56
10、在空间四边形ABCD 中,已知AB=3,CD=4,BD=2,则异面直线AC 与BD 所成角的大小是( ) A.30°
B.45°
C.60°
D.90°
11、等差数列{n a }的前n 项和为33,6,4,n S S a ==且,则公差d 等于
( ) A.1
B.5
3
C.2
D.3
12、已知52345012345(1)x a a x a x a x a x a x -=+++++,那么024135()()a a a a a a ++++的值等于( ) A 、—256
B 、256
C 、—512
D 、512
二、填空题:把答案填在题中横线上(本大题共4个小题,每题5分,共20分)。
13、在东经100°,北纬分别是30°和75°的地球表面上有A 、B 两地,设
地球半径为R ,则A 、B 两地的球面距离是________ 14、()()3
4
121x x +-展开式中2x 的系数为___________。
15、电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有_______种不同的播放方式(用数值表示).
16、在等比数列{}n a 中,32a =,732a =,则5a = 三、解答题:(17题10分,18-------22题每题12分,共70分). 17、有5个同学排队照相,求:
(1)甲、乙2个同学必须相邻的排法有多少种? (2)甲、乙、丙3个同学互不相邻的排法有多少种?
18、在△ABC 中,角,,A B C 所对的边分别为,,a b c ,已知2a =,3c =,1cos 4
B =
. (1)求b 的值; (2)求sin C 的值.
19、A、B、C、D、E五名实习老师被随机地分到甲、乙、丙、丁四个不同的学校实习,每个学校至少有一名实习老师.
(1)求A、B两人同时到甲学校实习的概率;
(2)求A、B两人不在同一个学校实习的概率;
20、某商场举行抽奖活动,从装有编号为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(1)求中三等奖的概率;
(2)求中奖的概率.
21、如图,长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接B1C,过B
作B1C的垂线交CC1于E,交B1C于F,
(1)求证:A1C⊥平面EBD;
(2)求点A到平面A1B1C的距离:
(3)求直线DE与平面A1B1C所成角的正弦值.
22、如图,四边形ABCD是边长为1的正方形,MD ABCD
⊥平面,
⊥平面,NB ABCD
且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值
(2)在线段AN上找点S,使得ES⊥平面AMN,并求线段AS的长;
高二数学(文科)参考答案
1、D
2、C
3、D
4、C
5、C
6、B
7、D
8、A
9、B 10、D 11、C 12、A
13、 14、 15、 48 16、 8
17、
解:(1)这是典型的相邻问题,采用捆绑法.先排甲、乙,有种方法,再与其他3名同学
排列,共有=48种不同排法.
(2)这是不相邻问题,采用插空法,先排其余的2名同学,有种排法,出现3个空,
将甲、乙、丙插空,所以共有·=12种排法.
18、
解:由余弦定理得:,
得,.
(2)由余弦定理,得
∵是的内角,∴.
19、
解析:(1)记A、B两人同时到甲学校实习为事件E A,那么
即A、B两人同时到甲学校实习的概率是.
(2)记A、B两人不同在一学校实习为事件E,那么
所以,A、B两人不同在一学校实习的概率是
20、
解:两个小球号码相加之和等于3中三等奖,两个小球号码相加之和不小于3中奖,设“中三等奖”的事件为A,“中奖”的事件为B,从四个小球中任选两个共有
(0,1),(0,2),(0,3),(1,2),(1,3),(2,3)六种不同的取法.
(1)两个小球号码相加之和等于3的取法有2种:(0,3),(1,2),故P(A)=.
(2)中奖的概率为P(B)=.
21、
解:如图建立空间直角坐标系A-xyz.
(1)A(0,0,0,),A1(0,0,2),E(1,1,)B(1,0,0),D(0,1,0),C(1,1,0),
.
,
即A1C⊥BE,A1C⊥DE.
∵BE∩DE=E所以A1C⊥平面EBD.
(2)设平面A1B1C的一个法向量为m=(x,y,z),
则,,令z=1,得m=(0,2,1).
=(0,0,2),
所以,所求的距离为.
(3)由(2)知,m=(0,2,1).,
设与m所成角为,则.22、解析:(1)在如图,以D为坐标原点,建立空间直角坐标
依题意,得。
,
所以异面直线与所成角的余弦值为.
………………………(6分)
(2)设是线段上的点,使得平面.
, 则
又.
由平面,得即
故,此时.
经检验,当时,平面.
故线段上存在点,使得平面,此时。
