材料力学作业6(弯曲应力)
材料力学——弯曲应力

公式推导
线应变的变化规律 与纤维到中性层的距离成正比。
从横截面上看: 点离开中性轴越远,该点的线应变越大。
2、物理关系
当σ<σP时 虎克定律
E
E
y
y
弯曲正应力的分布规律 a、与点到中性轴的距离成正比; 沿截面高度 线性分布; b、沿截面宽度 均匀分布; c、正弯矩作用下, 上压下拉; d、危险点的位置, 离开中性轴最远处.
M max ymax IZ
x
67.5 103 90 103 5.832 105
104.17MPa
6、已知E=200GPa,C 截面的曲率半径ρ q=60KN/m A FAY B 1m C 3m FBY
M C 60kN m
I z 5.832 105 m 4
M EI
4 103 88 103 46.1MPa 6 7.64 10
9KN
4KN
C截面应力计算
A FA
M 1m
C 1m
B
1m FB
C截面应力分布 应用公式
t ,max
My Iz
2.5KNm
2.5 103 88 103 28.8MPa 6 7.64 10
Fb Fa
C截面: max M C Fb3 62.5 160 32 46.4MPa d W 3
zC
2
0.13
32
(5)结论 轮轴满足强度条件
一简支梁受力如图所示。已知 [ ] 12MPa ,空心圆截面 的内外径之比 一倍,比值不变,则载荷 q 可增加到多大? q=0.5KN/m A B
反映了截面的几何形状、尺寸对强度的影响
最大弯曲正应力计算公式
材料力学作业6(弯曲应力)

第六章 弯曲应力一、是非题1 梁在纯弯曲时,横截面上各点只有正应力。
( )2 对于等截面梁,弯矩绝对值最大的截面,就是危险截面。
( )3 抗弯截面系数是反映梁横截面抵抗弯曲变形的一个几何量,它的大小与梁的材料有关。
( )4 钢梁和木梁的截面形状和尺寸相同,在受同样大的弯矩时,木梁的应力一定大于钢梁的应力。
( )5 对于矩形截面梁,无论平放还是立放,其抗弯强度相同。
( ) 二、选择或填空1 材料弯曲变形后( )长度不变。
A .外层B .中性层C .内层 2 梁弯曲时横截面上的最大正应力在( )。
A.中性轴上B.对称轴上C.离中性轴最远处的边缘上3 若矩形截面梁的高度h 和宽度b 分别增大一倍,其抗弯截面系数将增大 ( )。
A.2倍 B.4倍 C.8倍 D.16倍4一圆截面悬臂梁,受力弯曲变形时,若其它条件不变,而直径增加一倍,则其最大正应力是原来的________倍。
A :81B :8C :2D :21 5 图示悬臂梁,在外力偶矩M 的作用下,N-N 截面应力分布图正确的是( )A B C D 6 图示横截面上的应力分布图,其中属于直梁弯曲的是图( ),属于圆轴扭转的是图( )。
7 等强度梁各横截面上 数值近似相等。
A .最大正应力B .弯矩C .面积D .抗弯截面系数8 图示,用T 形截面形状的铸铁材料作悬臂梁,从提高梁的弯曲强度考虑,图( )的方案是合理的。
A B三计算题1 图示悬臂梁,梁长L =1m ,集中载荷F =10k N ,梁截面为工字形,已知其Z W =102 cm3 试求出该悬臂梁上最大正应力。
2 长度mm 250=l 、截面宽度mm 25=b 、高度mm 8.0=h 的薄钢尺,由于两端外力偶矩的作用而弯成中心角为 60的圆弧。
已知钢的弹性模量GPa 210=E ,试求钢尺横截面上的最大正应力。
3 图示矩形截面简支梁。
试求1-1截面上a 、b 两点的正应力。
8kN4图示木梁受移动载荷kN 40=F 作用。
弯曲应力-材料力学

弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
另外,根据不同的弯曲形式和受力情 况,还可以采用其他计算公式来求解 弯曲应力,如均布载荷下的简支梁、 集中载荷下的悬臂梁等。
弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
弯曲应力可能导致材料发生弯曲变形,影响结构的稳定性和精度。
弯曲应力对材料刚度的影响
弯曲应力对材料的刚度有影响,材料的刚度随着弯曲应力的增大而 减小。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
弯曲应力
材料的韧性和强度都会影响其弯曲应力的大小和分布。韧性好的材料能够更好地分散和 吸收弯曲应力,而高强度的材料则能够承受更大的弯曲应力而不发生断裂。
材料韧性、强度与弯曲应力的关系
韧性
是指材料在受到外力作用时吸收能量的能力。韧性好的材料能够吸收更多的能量,从而 减少因弯曲应力而产生的脆性断裂。
强度
剪切应力的分布
剪切应力在材料截面的边缘最大,向中性轴方向 逐渐减小。
3
剪切应力和弯曲应力的关系
剪切应力和弯曲应力共同作用,影响梁的承载能 力和稳定性,在设计时需要考虑两者的相互作用。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
材料力学06弯曲应力_3切应力_机

5
三、圆形截面梁
最大弯曲切应力发生于中性轴上各点处, 计算公式为
max
4FS 3A
式中,A 为圆形截面的面积
四、薄壁圆环形截面梁
薄壁圆环:壁厚 t 远小于平均半径 R
最大弯曲切应力发生于中性轴上各点
max
处,计算公式为
max
2
FS A
式中,A 为薄壁圆环形截面的面积
FS
max
z
x
14
FS max 9.75kN
M 26kN m max
2)校核弯曲正应力强度
由型钢表中查得 No. 18 工字钢截面的几何参数:d = 6.5 mm,Wz = 185 mm3 ,Iz : Sz = 15.4 cm
max
M max Wz
26 185
103 106
140.6 MPa < 170 MPa
y
FS R
max
z
t
y
6
五、弯曲切应力强度条件
其中
max ≤
max
3 FS max 2A
4 FS max 3A
2 FS max A
FS max
d
(Iz
:
S z max
)
矩形截面 圆形截面 薄壁圆环形截面 工字形截面
7
[例1] 图示矩形截面简支梁受均布载荷作用,试求梁的最大弯曲正 应力和最大弯曲切应力,并比较其大小。
b
FS
max h
z
缘各点处,弯曲切应力为
材料力学弯曲应力课件

材料力学弯曲应力课件曲在工程中的应用。
这是一个厂房,这是一个大梁,这个吊车可以在这个大梁上运动。
对于这样一个问题,我们可以把它简化成一个简支梁,这个吊车的移动呢可以处理成一个移动荷载。
那么对于这个移动荷载而言,它所导致的应力如何计算行车移动时,它的应力如何变化这就是本章的内容之一。
我们再看看这个图片,这是我们拍摄的汽车的下部分,大家注意一些这个部分,这是就是汽车的板簧,它的模型就是这个样子,可以看成好几个钢板的组合,那么,为什么要设计成这个样子呢它有什么优点呢这也是本章要解决的问题。
这是一个运动员,撑杆跳,对吧。
大家常常见到,利用这个杆的助力,人可以跳的更高。
我们可以处理成这样一个模型。
她在跳高的过程中,杆就发生了弯曲。
那么,这个时候,跳杆横截面上的应力和杆曲率半径有什么关系这个杆在什么情况下才满足强度要求大家看看这个场面,对于这个场面,我们截面几何性质那章提到过,都是薄壁杆件,那么薄壁杆件有弯曲正应力和弯曲切应力,专门有一小节来讲解它的弯曲切应力,看看这些切应力有什么特点如何避免薄壁杆件的强度失效这也是本章的问题这个大家都熟悉,著名的比萨斜塔。
对于这个结构,初步计算,我们可以简化成这样一个均质圆筒,那么它有哪些变形效应它的危险截面、危险点在哪儿如何计算其应力这也是本章可以解决的问题。
因此,本章所涉及的问题是比较广的。
基本内容那么本章到底需要同学们掌握哪些内容呢1、熟练张博横截面上弯曲正应力和弯曲切应力的分布规律,并能正确熟练的进行梁的强度分析。
2、熟悉提高梁强度的主要措施。
、正确理解薄壁杆件横截面上弯曲切应力的分布规律,了解弯曲中心的概念。
4、熟悉掌握梁在组合变形中的应力的计算方法。
第一、第四条是很重要的。
这是以后大家经常需要处理的问题。
基本概念平面弯曲首先我们来看弯曲正应力。
在这章具体内容介绍之前呢,我们先介绍一些概念。
关于梁弯曲的基本概念。
梁的平面弯曲。
什么是梁的平面弯曲呢这是一个悬臂梁,截面是矩形截面,那么这个横截面就有一个中心对称轴,整个梁就存在一个对称面,如果我们的所有的外荷载都作用在这个平面之内,比如外荷载是这样的,那么发生变形后,梁的轴线仍然在这个平面内,像这样的弯曲,我们就叫做平面弯曲。
材料力学--弯曲正应力及其强度条件
C
E
15 106 200 109
7.5 105
q 40 kN / m
A
C
1.5 m
1.5 m
B 300 200
例21:图示木梁,已知下边缘纵向总伸
长为 10 mm,E=10GPa,求载荷P的大小。
P
300
A
C
B 200
2m
2m
解: AC
l/2
(x) dx
0
l/2 (x) d x l/2 M ( x) d x
1m
例20:简支梁受均布荷载,在其C截面
的下边缘贴一应变片,已知材料的 E=200GPa,试问该应变片所测得的应变 值应为多大?
q 40 kN / m
A
C
1.5 m
1.5 m
B 300 200
解:C截面的弯矩
ql2 MC 8 45kN m
C截面下边缘的应力 C
MC Wz
15MPa
应变值
P
y1
y2
Cz
解:
max
M max y1 Iz
[ ]
(1)
max
M max y2 Iz
[ ]
(2)
(1) 得: y1 [ ]
(2)
y2 [ ]
例16:图示外伸梁,受均布载荷作用,
材料的许用应力[σ]=160 MPa,校核 该梁的强度。
10 kN / m
2m
4m
200 100
10 kN / m
变形几何关系 从三方面考虑: 物理关系
静力学关系
1、变形几何关系
m
mn
m
aa
bb
mn
m
m
观察到以下变形现象: (1)aa、bb弯成弧线,aa缩短,bb伸长 (2)mm、nn变形后仍保持为直线,且仍与变为
材料力学习题及答案4-6

第四章弯曲应力判断图弯矩的值等于梁截面一侧所有外力的代数和。
()负弯矩说明该截面弯矩值很小,在设计时可以忽略不计。
()简支梁上向下的集中力对任意横截面均产生负弯矩。
()横截面两侧所有外力对该截面形心力矩的代数和就是该截面的弯矩值。
()梁的任一横截面上的弯矩在数值上等于该截面任一侧所有外力对该截面形心的力矩代数和。
()在计算指定截面的剪力时,左段梁向下的荷载产生负剪力。
()在计算指定截面的剪力时,右段梁向下的荷载产生正剪力。
()梁纯弯曲时中性轴一定通过截面的形心。
()简支梁上受一集中力偶作用,当集中力偶在不改变转向的条件下,在梁上任意移动时,弯矩图发生变化,剪力图不发生变化。
()图示梁弯矩图的B点是二次抛物线的顶点。
()图示梁段上集中力偶作用点两侧的弯矩直线一定平行。
()(M图)下列三种斜梁A截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁B截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁C截面的弯矩均相同。
()l/2l/2l/2l/2l/2l/2梁弯曲时的内力有剪力和弯矩,剪力的方向总是和横截面相切,而弯矩的作用面总是垂直于横截面。
()一端(或两端)向支座外伸出的简支梁叫做外伸梁。
()##√悬臂梁的一端固定,另一端为自由端。
()##√弯矩的作用面与梁的横截面垂直,它们的大小及正负由截面一侧的外力确定。
()##√弯曲时剪力对细长梁的强度影响很小,所以在一般工程计算中可忽略。
()##√图示,外伸梁BC段受力F作用而发生弯曲变形,AB段无外力而不产生弯曲变形()##×由于弯矩是垂直于横截面的内力的合力偶矩,所以弯矩必然在横截面上形成正应力。
()##√抗弯截面系数是反映梁横截面抵抗弯曲变形的一个几何量,它的大小与梁的材料有关。
()##×无论梁的截面形状如何,只要截面面积相等,则抗弯截面系数就相等。
()##×梁弯曲变形时,弯矩最大的截面一定是危险截面。
6.材料力学——弯曲应力

y2 20
120
20
RA A
F1=9kN
RB
F2=4kN
解
RA = 2.5kN RB = 10.5kN 最大正弯矩在截面 C 上
C 1m 1m
B 1m
D
MC = 2.5kN ⋅ m
最大负弯矩在 截面 B 上
2.5kN 80 y1
M( x) ⋅ y σ= Iz
M( x) — 横截面上的弯矩
18
强度条件: 二. 强度条件:
σmax
Mmax ⋅ ymax = ≤ [σ ] Iz
σmax
拉压强度相等材料: 拉压强度相等材料: 拉压强度不等材料: 拉压强度不等材料: 强度计算: 强度计算: a. 强度校核 强度校核: b. 截面设计 截面设计:
σ = Eε
=E
ρ
y
对称轴
o
z
y
正应力与它到中性层的距离成正比, 正应力与它到中性层的距离成正比, 中性层上的正应力为零 上式只能用于定性分析, 上式只能用于定性分析, 而不能用于定量计算: 而不能用于定量计算: 的位置未确定, (1)由于中性轴 z 的位置未确定, ) 无法标定; 故 y 无法标定;
中性轴 中性层
y
z
对称轴
ρ
M
中性层
y
图6-4
m ∆θ n z o a′ 中性轴 a′ o′ o′ b′ y b关系
o
o
y 轴 — 截面的对称轴 Z 轴 — 截面的中性轴 —距中性层为 b′b′ 距中性层为 y 处的纤维变形后的长度
y
dϕ 的线应变: 纤维 bb 的线应变: γ p = ρ dx M (ρ + y)dθ − ρ ⋅ dθ = y ε= ρ ⋅ dθ ρ
材料力学-6-弯曲刚度

• 引言 • 弯曲刚度的基本原理 • 弯曲刚度的实验验证 • 弯曲刚度在工程中的应用 • 弯曲刚度的优化设计 • 结论与展望
01
引言
主题简介
01
弯曲刚度是材料力学中一个重要 的概念,主要研究材料在受到弯 曲力作用时的行为和性能。
02
弯曲刚度涉及到材料抵抗弯曲变 形的能力,对于工程结构的稳定 性、承载能力和使用寿命具有重 要意义。
车辆行驶安全
弯曲刚度影响桥梁的平顺性,从而 影响车辆行驶的安全性和舒适性。 弯曲刚度不足可能导致桥面不平整, 增加车辆颠簸和振动。
建筑度对其抗震性 能具有重要影响。在地震作用下, 具有较高弯曲刚度的建筑能够更 好地抵抗地震引起的振动,减少
破坏。
风载响应
弯曲刚度也决定了建筑结构对风 载的响应。弯曲刚度较大的建筑 能够更好地承受风力作用,减少
机械零件
在机械零件的设计中,弯曲刚度是评估零件性能的重要指标。例如,在汽车和 航空器的设计中,需要确保关键部件的弯曲刚度满足要求,以保证车辆和飞机 的安全性和稳定性。
03
弯曲刚度的实验验证
实验设备与材料
01
02
03
试样
选择具有代表性的材料试 样,如金属、塑料等。
实验设备
包括万能材料试验机、测 力计、测量工具等。
轻质材料
选择轻质材料,如铝合金、碳纤维复合材料等,以减小结构重量, 提高弯曲刚度。
高强度材料
选用高强度材料,如高强度钢、钛合金等,以提高结构承载能力, 降低弯曲变形。
材料属性优化
通过合金化、热处理等方法优化材料的力学性能,如提高弹性模量、 抗拉强度等,从而提高弯曲刚度。
结构设计优化
合理布局
(整理)材料力学试题库题解题6_弯曲应力

弯曲应力1.圆形截面简支梁A,B套成,A,B层间不计摩擦,材料的弹性模量E B=2E A求在外力偶矩M e作用下,A,B中最大正应力的比值^max有4个答案:Bmin1(A)-;61 (C)1;81(D)丄10答: B2.矩形截面纯弯梁,材料的抗拉弹性模量E t大于材料的抗压弹性模量E c,则正应力在截面上的分布图有以下4种答案:(A) (B) (C) (D) 答: C3.将厚度为2 mm的钢板尺与一曲面密实接触,已知测得钢尺点A处的应变为—,则该曲面在点A1000处的曲率半径为_________ m m。
答:999 mmP4.边长为a的正方形截面梁,按图示两种不同形式放置,在相同弯矩作用下,两者最大正应力之比匕丛= ___________(%x)bO(b)答:1/ , 25. 一工字截面梁,截面尺寸如图,h二b, b =10t。
试证明,此梁上,下翼缘承担的弯矩约为截面上总弯矩的88%证: — My M12MA y(ybdy) =1 820 罟3Iz4 l z=690tM1 Mt4 1勺8207 6904”88%I yh/2—- 丄h/2zt其中:积分限Bt? , A弓为翼缘弯矩6. 直径d =20 mm 的圆截面钢梁受力如图,已知弹性模量E = 200 GPa , a =200 mm ,欲将其中段AB 弯成 f m 的圆弧,试求所需载荷,并计算最大7. 钢筋横截面积为A ,密度为「,放在刚性平面上,一端加力F ,提起钢筋离 开地面长度-。
试问F 应多大?3解:截面C 曲率为零2Fl gA(l /3) 3 28. 矩形截面钢条长l ,总重为F ,放在刚性水平面上,在钢条A 端作用|向上的拉力时,试求钢条内最大正应力。
解:在截面C 处,有―罟丸弯曲正应力。
解:1 = M 而 M 二 Fa P EI Fmax64 =0.785 10 岀 m 4, 「旦 Pa = 0.654 kN21 Fad 21 3 3 0.654 1 03 0.2 20 10 2 0.785 10 出 = 167 MPa即M C =F Is3 l AC F (I AC )2 l 2 2l AC AC 段可视为受均布载荷q 作用的简支梁 max max 2q(U c ) /8 _ Fl bt 2/6 3bt 2iF/3 C9.图示组合梁由正方形的铝管和正方形钢杆套成,在两端用刚性平板牢固联接。
第六周 材料力学A_(弯曲变形的基本概念和分类, 正应力公式)

M ( x)
从梁中切出小分离体: x方向平衡: FN 2 FN 1 FS 0 M
y
M+dM
FN 2 dA
A1
A1
M dM ydA Iz
A1
dx FS
z b
y
假设: 横截面上各点切应力方向平行 于剪力的方向 横截面上切应力沿z方向均布
M dM 其中 S Sz z Iz M 同理 FN1 Sz
M=Fl/4
max
(5.7)
C
max
31
M=Fl/4
C
如T形、槽形截面等
32
2.弯曲切应力强度条件 梁弯曲时,横截面上切应力的危险点: 剪力最大截面的中性轴上(此处正应力恰好为零), ——纯剪切应力状态 F
A F/2 (FS) F/2 F/2 C B
3.梁的弯曲强度计算 (1)一般的细长非薄壁梁(跨高比 l/h 较大),可只 校核正应力强度条件(此时切应力强度条件多自动 满足)。 F h
h 1 h b h2 矩形截面: Sz ( y) b ( y) ( y ( y)) ( y2 ) 2 2 2 2 4
max
max
min
H
M
( y )
FS h 2 ( y2 ) 2I z 4
FS h2 3 F 3 S 3 bh 4 2 A 2 2 12
z
M
y
ymax2 z ymax1
max
Wz1
M
应分别计算 max max
Iz ymax1
由梁所受外力(已知载荷) 图,求得各截面上的弯矩)
材料力学第六章弯曲应力1
d c
M
b
d
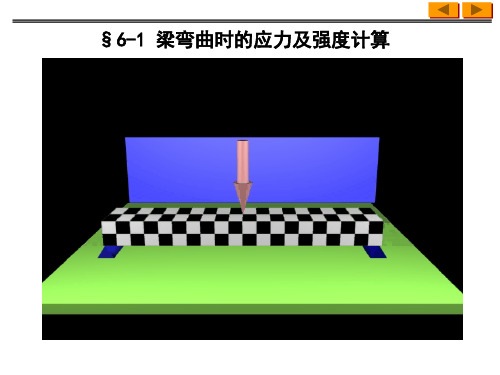
(1)弯曲平面假设:梁变形前原为平面的横截面变形后仍为平 面,且仍垂直于变形后的轴线,只是各横截面绕其上的某轴转 动了一个角度。
(2)纵向纤维假设:梁是由许多纵向纤维组成的,且各纵向纤维 之间无挤压。
凹入一侧纤维缩短 突出一侧纤维伸长
根据变形的连续性可知, 梁弯曲时从其凹入一侧的 纵向线缩短区到其凸出一 侧的纵向线伸长区,中间 必有一层纵向无长度改变 的过渡层--------称为中
q
y1 y2
y
z
b
解:1)画弯矩图
| M |max 0.5ql2 3 kNm
№10槽钢
2)查型钢表:
M
y1
y2
y
b 4.8cm, I z 25.6cm4 , y1 1.52cm y2 4.8 1.52 3.28cm
3)求应力:
M 3000 1.52 178 MPa t max y1 6 25 .6 10 Iz
中间层与横截面的交线 --中性轴
性层 。 梁的弯曲变形实际上是各截面绕各自的中性轴转 动了一个角度,等高度的一层纤维的变形完全相同。
4、线应变的变化规律:
A1 B1 AB AB
a
c
( y )d d d
A1 B1 OO1 OO1
y
y
...... (1)
Mycmax cmax Iz
几种简单截面的抗弯截面系数 b ⑴ 矩形截面
h
z
bh3 Iz 12 b3h Iy 12
⑵ 圆形截面
y d
Iz bh2 Wz h/2 6 Iy b2h Wy b/2 6
材料力学习题第六章应力状态分析答案详解

第6章 应力状态分析一、选择题1、对于图示各点应力状态,属于单向应力状态的是(A )。
(A )a 点;(B )b 点;(C )c 点;(D )d 点 。
2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==; (B)AC AC /2,/2ττσ==; (C)AC AC /2,/2ττσ==;(D)AC AC /2,/2ττσ=-=。
4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。
关于它们的正确性,现有四种答案,正确答案是( D )。
(A )点1、2的应力状态是正确的;(B )点2、3的应力状态是正确的; (C )点3、4的应力状态是正确的;(D )点1、5的应力状态是正确的。
5、对于图示三种应力状态(a )、(b )、(c )之间的关系,有下列四种答案,正确答案是( D )。
(A )三种应力状态均相同;(B )三种应力状态均不同; (C )(b )和(c )相同; (D )(a )和(c )相同;6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。
解答:max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围,有下列四种答案,正确答案是( C )。
(A )脆性材料;(B )塑性材料;(C )材料为各向同性,且处于线弹性范围内;(D )任何材料; 8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适用于( C )。
(A )任何材料在任何变形阶级; (B )各向同性材料在任何变形阶级; (C )各向同性材料应力在比例极限范围内;(D )任何材料在弹性变形范围内。
材料力学第六章

解 1)将梁上的载荷分解
wC wC1 wC2 wC3
B B1 B2 B3
2)查表得3种情形下C截面的 挠度和B截面的转角。
wC1
5ql 4 384EI
wC 2
ql 4 48EI
ql 4 wC3 16EI
B1
ql 3 24EI
B1
ql 3 16EI
B3
ql 3 3EI
wC1
wC2 wC3
3)进行变形比较,列出变形协调
条件
wB 0
4)叠加法
wB (wB )F (wB )FBy 0
MA A
MFAAy A
FAy A
A
MA A FA y
MA A AA
MA A A
F
B
C
2a (a) B
aF C
2a
Ba C
((ba))
B B (b)
F C
C
(c)
FBy F
B
FF C
BB
(c)
FBy
CC
B12 a
Fa 2l 3EI
w1 wB11 wB12
w2
B2a
Fl 2a 16 EI
w w1 w2
用叠加法求跨度中点挠度
解: wc wc1 wc2
由于 wc wc2
=
故
wc
1 2
wc1
1 5q0l 4 5q0l 4 2 384EI 768EI
-
解: wc wc1 wc2
当 d w 0 时,w为极值
dx
EI1
Fb 2l
x2 1
Fb 6l
(l 2
b2 )
E I 2
Fb 2l
x22
材料力学弯曲应力

(4)强度校核 B截面:
Fb Fa
max
MB WB
Fa
d13
62.5
267 0.163
32
32
41.5106 Pa 41.5MPa
C截面:
max
MC WC
Fb
d
3 2
62.5160 32
0.133
46.4106 Pa
46.4MPa
t,max t c,max c
14
常见截面的 IZ 和 WZ
空心矩形截面
IZ y2dA
A
WZ
IZ y max
圆截面
IZ
d 4
64
d 3
WZ 32
空心圆截面 矩形截面
IZ
D4
64
(1
4)
WZ
D3
32
(1
4)
bh3 IZ 12
5
§5.1 纯弯曲
凹入一侧纤维缩短 突出一侧纤维伸长 中间一层纤维长 度不变
--中性层
中间层与横截面 的交线
--中性轴
6
§5.2 纯弯曲时的正应力
一、变形几何关系
7
§5.2 纯弯曲时的正应力 y
二、物理关系:
当
时
p
z
E
E y
x 可确定横截面上的应力分布
y
问题:中性层( y 的起点)在哪里? 1 怎样算?
C
l = 3m
FS 90kN
B
x
180
实验6 弯曲性能测定 (2)

实验六 弯曲性能测定一、 目的要求1. 明确弯曲试验为何可作为复合材料的筛选试验缘故。
2. 了解方法要点,测试塑料及玻璃钢弯曲强度。
二、 原理复合材料的弯曲试验中试样的受力状态比较复杂,有拉力、压力、剪力、挤压力等,因而对成型工艺配方、试验条件等因素的敏感性较大。
用弯曲试验作为筛选试验是简单易行的,也是比较适宜的。
玻璃纤维增强塑料弯曲性能试验方法(GB1449-83)适用于测定玻璃纤维织物塑料板材和短切玻璃纤维增强塑料的弯曲性能,包括弯曲强度、弯曲弹性模量、规定挠度下的弯曲应力、弯曲载荷-挠度曲线。
GB1042-79适用于塑料弯曲性能测定。
1.弯曲强度。
弯曲试验一般采用三点加载简支梁,即将试样放在两支点上,在两支点间的试样上施加集中载荷,使试样变形直至破坏时的强度为弯曲强度223bhPlf =σ 式中f σ——弯曲强度(或挠度为1.5倍试样厚度时的弯曲应力),Mpa ; P ——破坏载荷(或最大载荷,或挠度为1.5倍试样厚度时的载荷),N ;l ——跨距,cm ;b 、h ——试样宽度、厚度,cm 。
2.弯曲弹性模量。
它是指在比例极限内应力与应变比值fbh Pl E f ∆⋅∆⋅=334 式中 f E ——弯曲弹性模量,Mpa ;P ∆——载荷-挠度曲线上初始直线段的载荷增量,N ; f ∆——与载荷增量P ∆对应的跨距中点处的挠度增量,cm 。
3.某些试验由于特殊要求,可测定表观弯曲强度,即超过规定挠度时(如超过跨距的10%)载荷达到最大值时的弯曲应力。
在此大挠度试验时,弯曲应力最好用下面的修正公式:]){41[2322l f bh Pl f+=σ式中 f ——试样跨距中点处的挠度,cm 。
三、 方法要点(一) 试样试样型式和尺寸见图55-1,表55-1、表55-2、表55-3。
(二) 试验条件与步骤弯曲试验装置示意图55-2。
加载上压头圆柱面半径R 为5±0.1mm ,支座圆角半径r 为2±0.2mm (当h ﹥3mm 时)和0.5±0.2mm (当h ≤3mm 时),若试样出现明显支座压痕,r应改为2mm 。
材料力学教案 第6章 弯曲应力

第6章弯曲应力教学目的:在本章的学习中要求熟练掌握梁纯弯曲时横截面上正应力计算公式的推导过程,理解推导过程中所作的假设。
掌握中性层、中性轴等基本概念和含义。
弯曲正应力和剪应力强度条件的建立和相应的计算。
理解横力弯曲正应力计算仍用纯弯曲公式的条件和近似程度。
从弯曲强度条件出发,掌握提高弯曲强度的若干措施。
教学重点:纯弯曲梁横截面上正应力公式的分析推导;横力弯曲横截面上正应力的计算,最大拉应力和最大压应力的计算;弯曲的强度计算;弯曲横截面上的剪应力。
教学难点:弯曲正应力、剪应力推导过程和结果以及弯曲中心的概念。
教具:多媒体。
教学方法:采用启发式教学,通过提问,引导学生思考,让学生回答问题。
教学内容:梁纯弯曲和横力弯曲时横截面上的正应力;梁横力弯曲时横截面上的切应力;提高弯曲强度的若干措施。
教学学时:6学时。
教学提纲:6.1 梁的纯弯曲1、几个基本概念(1)平面弯曲和弯曲中心变形后梁轴线的位移方向沿着加载方向的弯曲情况,称为平面弯曲。
怎样加载才能产生平面弯曲?若梁的横截面有对称平面时,载荷必须作用在对称平面内,才能发生平面弯曲。
若梁的横截面没有对称平面时,载荷的作用线必须通过截面的弯曲中心。
什么叫弯曲中心?当载荷的作用线通过横截面上某一点特定点时,杆件只产生弯曲而无扭转。
这样的特定点称为弯曲中心。
关于弯曲中心位置的确定及工程上常见图形的弯曲中心位置。
①具有两个对称轴或反对称的截面,如工字形、圆形、圆环形、空心矩形截面等,弯曲中心与形心(两对称轴的交点)重合,如图(a),(b),(c)所示。
②具有一个对称轴的截面,如槽形和T形截面,弯曲中心必在对称轴上,如图(d)、(e)所示。
③如果截面是由中线相交于一点的几个狭长矩形所组成,如L形或T形截面,则此交点就是弯曲中心,如图(e)、(f)所示。
④不对称实心截面的弯曲中心靠近形心。
这种截面在荷载作用线通过形心时也将引起扭转,但由于这种截面的抗扭刚度很大,弯曲中心与形心又非常靠近,故通常不考虑它的扭转影响。
弯曲应力

第六章 弯曲应力1 基本概念及知识要点1.1 基本概念纯弯曲、横力弯曲、弯曲正应力、惯性矩、抗弯截面系数、弯曲刚度、弯曲切应力(剪应力)。
应熟练理解和掌握这些基本概念。
1.2 平面弯曲工程实际中的梁,大多数是具有一个纵向对称面的等截面直梁。
外载荷作用在梁的纵向对称面内,并垂直于梁的轴线,梁弯曲时轴线将在对称平面内弯曲成平面曲线,这种弯曲叫平面弯曲。
当梁横截面上既有弯矩又有剪力时,梁的弯曲是横力弯曲(或剪切弯曲);梁横截面上只有弯矩而没有剪力时,梁的弯曲是纯弯曲。
1.3 弯曲正应力梁在纯弯曲时的正应力是综合运用变形几何关系、物理关系和静力平衡关系推导出来的,推导弯曲正应力公式的方法,与推导轴向拉压正应力公式和扭转切应力公式的方法相同。
弯曲正应力公式zI My=σ 式中M 为所研究截面的弯矩;z I 分为截面图形对中性轴的惯性矩;y 为所求应力点到中性轴的距离。
计算时,M 和y 均用代数值代入,由此得到所求点的应力符号,同样也可根据梁的变形情况来确定。
梁弯曲正应力公式适用材料处于线弹性范围内的纯弯曲梁,可推广到横力弯曲以及小曲率杆的弯曲中。
1.4 弯曲切应力弯曲切应力公式的推导不是按照变形几何关系、物理关系、平衡关系三方面进行的,而是根据分析对弯曲切应力的分布规律作出假定——平行于剪力F s 且沿截面厚度均匀分布,然后利用平衡关系直接导出矩形截面切应力公式*zzF S bI τ=s 式中,F s 为截面上的剪力;z I 为整个截面对中性轴的惯性矩;b 为所求切应力处横截面的宽度;*z S 为截面上距中性轴为y 的横线任一侧部分面积对中性轴的静矩。
1.5 弯曲强度条件1 正应力强度条件弯曲正应力是影响梁强度的主要因素,对梁(等截面梁)的强度计算主要是满足正应力强度条件][maxmax σσ≤=zW M 式中m axy I W zz =称为横截面的抗弯截面系数。
对于塑性材料,其抗拉和抗压能力相等,通常将梁设计为与中性轴对称的形状,强度条件为][maxmax σσ≤=zW M 对于脆性材料,其抗压能力远超过抗拉能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 8
B.8
C.2
D.
1 2
) , 属于圆轴扭转的是图 ( ) 。
5 、 图示横截面上的应力分布图, 其中属于直梁弯曲的是图 (
A B C 6、图示矩形截面悬臂梁,在外力 F 的作用下,画出 A-A 截面弯曲正应力和弯曲切应力分布 图。
7、等强度梁各横截面上( )数值近似相等。 A.最大正应力 B.弯矩 C.面积 D.抗弯截面系数 8、图示,用 T 形截面形状的铸铁材料作悬臂梁,从提高梁的弯曲强度考虑,图( 案是合理的。
4、图示 T 形截面铸铁梁承受载荷作用。已知铸铁的许用拉应力 [ t ] 40 MPa ,许用压应力
[ c ] 160 MPa 。试按正应力强度条件校核梁的强度。
第六章 弯曲应力
班级(
)学号(
)姓名(
)
5、图示梁,受力如图, (1)绘制梁的剪力图和弯矩图,标出最大剪力、弯矩的位置和值。 (2) 如果梁为矩形截面钢梁,矩形高 h = 80mm,宽 b = 60mm,a = 1m,q = 5kN/m,[σ] =160 MPa, 校核梁的强度。 (10 分)
2qa2 A a
q B 2a C a
2qa D
6、图示简支梁,有四块尺寸相同的木板胶接而成。已知载荷 F4=4kN,梁跨度 l=400mm,截
面 宽 度 b=50mm , 高 度 h=80mm , 木 板 的 许 用 应 力 [ ] 7 MPa , 胶 缝 的 许 用 切 应 力
[ ] 5 MPa ,试校核梁的强度。
第六章 弯曲应力
班级(
)学号(
)姓名(
)
第六章
弯曲应力
一、选择或填空 1、材料弯曲变形后( )长度不变。 A.外层 B.中性层 C.内层 2、梁弯曲时横截面上的最大正应力在( ) 。 A.中性轴上 B.对称轴上 C.离中性轴最远处的边缘上 3、若矩形截面梁的高度 h 和宽度 b 分别增大一倍,其抗弯截面系数将增大 ( ) 。 A.2 倍 B.4 倍 C.8 倍 D.16 倍 4、一圆截面悬臂梁,受力弯曲变形时,若其它条件不变,而直径增加一倍,则其最大正应力 是原来的( )倍。 A.
2、图示矩形截面简支梁。试求 1-1 截面上 a、b 两点的正应力。
8kN A 1000 1200 1000
1 1
10 B 150
.
75 b.
.
a
.
40
第六章 弯曲应力
班级(
)学号(
Hale Waihona Puke )姓名()3、图示简支梁,由 No18 工字钢制成,弹性模量 E = 200GPa,a = 1m。在均布载荷作用下, 测得横截面 C 底边的纵向正应变 = 3.0×10-4,试计算梁内的最大弯曲正应力。
)的方
A
B
9 、矩形截面梁(如图) ,若采用两种方式放置,则两种情况下的最大应力比 σ max,a / σ max,b 为 。
第六章 弯曲应力
班级(
)学号(
)姓名(
)
二、计算题
1、直径为 d 弹性模量为 E 的金属丝,绕在直径为 D 的轮缘上,试求金属丝内的最大弯曲正应变、 最大弯曲正应力和弯矩。
