多自由度系统的动力学方程页PPT文档
合集下载
振动理论09(1)-多自由度系统

正定系统中的各阶固有频率恒取正值 半正定系统的每个零值固有频率对应着系统的一种刚
体运动形式:即系统没有弹性变形、离开中性平衡位 置的整体的刚体转动或平动
例:三圆盘转动惯量均为I,中间两段轴的扭转刚度均 为 ,求系统的固有频率及主振型
解:系统的动能为和势能分别为Leabharlann 代入拉格朗日方程,得到振动方程
下式中的 是一个对角矩阵,称为主刚度矩阵
正则振型
主振型列阵表示系统作主振动时各坐标间的幅值的相 对大小
由这样的主振型列阵构成振型矩阵,然后求得主质量 矩阵,其对角元素 各不相等
为方便起见,将各主振型正则化:对于每一阶主振动 ,定义一组特定的主振型-正则振型(Orthonormal mode),满足
k21 m21 2
k22 m22 2
k2n2 m2n2 2
k2n1 m2n1 2
k2n m2n 2
kn21 m n21 2 kn22 m n22 2
k
n11
m
n11
2
kn12 m n12 2
k n 2 n 2 mn2n2 2 kn1n2 mn1n2 2
1
1
2
2
代入拉格朗日方程
外力虚功之和
P1 x1 m1
P2
P3
x2
x3
m2
m3
集中质量梁振动方程-柔度影响系数法
利用 ’
原理,把惯性力和外力共同作用在质量
上,由柔度影响系数求得变形,从而建立振动微分方程
P1
P2
P3
x1
x2
x3
m1
m2
m3
刚性支座上的无重量杆,杆上三个质量 1、 2、 上的位移分别为 1、 2、 3. 是柔度影响系数
体运动形式:即系统没有弹性变形、离开中性平衡位 置的整体的刚体转动或平动
例:三圆盘转动惯量均为I,中间两段轴的扭转刚度均 为 ,求系统的固有频率及主振型
解:系统的动能为和势能分别为Leabharlann 代入拉格朗日方程,得到振动方程
下式中的 是一个对角矩阵,称为主刚度矩阵
正则振型
主振型列阵表示系统作主振动时各坐标间的幅值的相 对大小
由这样的主振型列阵构成振型矩阵,然后求得主质量 矩阵,其对角元素 各不相等
为方便起见,将各主振型正则化:对于每一阶主振动 ,定义一组特定的主振型-正则振型(Orthonormal mode),满足
k21 m21 2
k22 m22 2
k2n2 m2n2 2
k2n1 m2n1 2
k2n m2n 2
kn21 m n21 2 kn22 m n22 2
k
n11
m
n11
2
kn12 m n12 2
k n 2 n 2 mn2n2 2 kn1n2 mn1n2 2
1
1
2
2
代入拉格朗日方程
外力虚功之和
P1 x1 m1
P2
P3
x2
x3
m2
m3
集中质量梁振动方程-柔度影响系数法
利用 ’
原理,把惯性力和外力共同作用在质量
上,由柔度影响系数求得变形,从而建立振动微分方程
P1
P2
P3
x1
x2
x3
m1
m2
m3
刚性支座上的无重量杆,杆上三个质量 1、 2、 上的位移分别为 1、 2、 3. 是柔度影响系数
天津大学 机械原理与机械设计 主编张策 第十一章 机械系统动力学 ppt课件

若忽略 Med 随等效构件角速度的变化,则
MedMer11TMer2 2
若Je、Me均为等效构件角位移的周期性函数,则在其变 化的公共周期内,Med与Mer作功相等,机械的动能增量 为零。
a a [M e( d) M e(r)d ] 1 2 J a a 2 1 2 J aa 2 0
经过Je与Me变化的一个公共周期,等效构件的角速度将 恢复到原来的数值。因此,在稳定运转阶段,等效构件
b)找到 Emax、Emin 及其所在位置后,即可求得 W n 。
Wn 的求解
飞轮设计
能量指示图
任取一点为起点,按一定的比例用矢量依次表示相应位置
处 Med 与 Mer 之间所包含的各块面积。盈功为正,箭头向上; 亏功为负,箭头向下。一个周期始末位置的动能相等,能量
指示图的首尾应在同一水平线上。显然,系统在 b 点动能最 小,而在 c 点动能最大;图中折线最高、最低点的距离 Amax 所代表的盈亏功即为 Wn 。
等效构件的等效质量(等效转动惯量)所具有的动能,应等 于机械系统的总动能;等效构件上的等效力(等效力矩)所 产生的功率,应等于机械系统的所有外力与外力矩所产生 的总功率。
等效力矩
等效转 动惯量
等效力
单自由度机械系 统的动力学分析
等效质量
定轴转动构件
直线移动构件
求出位移 S 或角位移 的变化规律,即可获得系统
外力与运动参数(位移、速度等)之间的函数关系式
一、拉格朗日方程
动能
势能
自由度
ddtqE i qEi U qi Fei (i 1 ,2 , ,N )
广义力
广义速度
广义坐标
多自由度机械系 统的动力学分析
ddtqE i qEi U qi Fei (i 1 ,2 , ,N )
多自由度系统动力学方程
作用力方程: M X KX P(t) 固有振动方程: M X KX 0
XRn M、 KRnn
P(t)Rn
在考虑系统的固有振动时,首先考察系统的同步振动,即系
统在各个坐标上除了运动幅值不相同外,随时间变化的规律
都相同的运动。
假设系统的运动为: Xφf(t)
XRn φ Rn
常数列向量 运动规律的时间函数 f (t)R1
l
选取D点的垂直位移及 角位移作为坐标
l1
A
DC
l2 B
选取质心C点的垂直位 移及角位移作为坐标
k1
a1
e
a2
k2
m me
IC
me me2
xD
D
k1 k2a2
k2 k1a1
k2a2 k1a1 k1a12 k2a22
xD
D
PD
M
D
m
0
0 IC
xC
C
k1 k2a2
MD XD KD X D FD MC XC KC XC FC
多自由度系统振动 / 多自由度系统的动力学方程
MD XD KD X D FD MC XC KC XC FC
X D [xD , D ]T XC [xC , C ]T
FD [PD , M D ]T FC [PC , M C ]T
令: 2 0
对于正定系统必有 0
对于半正定系统,有 0
多自由度系统振动 / 多自由度系统的自由振动
ff((tt))φ φTTM Kφ φ2
f(t)2f(t)0
a、b、 为常数
f(t)asint(), 0
f(t)a tb,
0
(1)正定系统
主振动
只可能出现形如 X φ asi nt ()的同步运动
《机械原理自由度》课件

机械故障诊断
通过运动分析诊断机械故障的原因 和位置。
控制系统设计
利用运动分析结果设计控制系统的 参数和策略。
机构运动分析的实例
平面四杆机构的运动分析
01
通过解析法计算平面四杆机构的自由度,并分析其运动特性。
凸轮机构的运动分析
02
利用实验法测量凸轮机构的位移、速度和加速度,分析其运动
规律。
机器人臂关节的运动分析
03
通过数值法模拟机器人臂关节的运动行为,优化关节的设计参
数。
04
机构动力学分析
机构动力学的基本概念
机构动力学是研究机 械系统中机构运动及 其与力的关系的学科 。
机构动力学的基本概 念包括力、力矩、加 速度、速度和位移等 。
它涉及到系统的平衡 、运动规律、动态响 应等方面的内容。
机构动力学分析的Байду номын сангаас法
空间机构自由度计算
总结词
空间机构自由度计算是机械原理中一个复杂的概念,它涉及到机构在空间中的 运动自由度数。
详细描述
空间机构的自由度计算公式为F=6n-(3PL + Ph),其中n为活动构件数,PL为低 副数,Ph为高副数。与平面机构不同,空间机构需要考虑三个方向的自由度, 因此计算更为复杂。
特殊机构自由度计算
通过建立平面连杆机构的运动学和动力学模型,分析其运动规律 和动态响应。
凸轮机构的动力学分析
研究凸轮机构的动态行为,包括从动件的运动规律和受力情况等。
齿轮机构的动力学分析
分析齿轮机构的动态特性,如振动、冲击和噪声等,以提高齿轮传 动的平稳性和可靠性。
05
机构优化设计
机构优化设计的目标和方法
目标
第二章(多自由度系统的运动微分方程)详解

k11 k 21 kN1
k1 j k2 j k Nj
k1N k2 N k NN
刚度影响系数 kij :第 j 个自由度产生单位位移,其他自由度位移为零时, 需要在第i 自由度处沿着位移方向施加的力。
用影响系数法建立系统的运动微分方程
【例】用影响系数法写出图示系统的刚度矩阵。
多自由度振动系统
Piezoelectric actuator
基于压电作动器的垂尾抖振主动抑制 (此系统有一、两千个自由度(3D实体单元) )
Z Y
X
第二章: 多自由度系统的运动 微分方程
第二章:多自由度系统的运动微分方程
第一讲:
1.建立多自由度系统运动微分方程的 各种方法的概述 2.用牛顿第二定律列写系统的运动微 分方程 3.用影响系数法建立系统的运动微分 方程
F1 1
k3
m2
k2 (d11 d21 )
m1
k2 (d11 d21 ) k1d11 1
d 21 k2 (d11 d21 )
F2 0
d11
k3d21
k2 k3 k1k2 k1k3 k2 k3 k2 k1k2 k1k3 k2 k3
m2
d 21
k2 (d11 d21 ) k3d21 0
上次课内容回顾
3.刚度影响系数
刚度影响系数 kij :第 j 个自由度产生单位位移,其他自由度位移为零时, 需要在第 i 自由度处沿着位移方向施加的力。
4.柔度影响系数
柔度影响系数 dij :第 j 个自由度上作用单位力,其他自由度作用力为零时,
在第 自由度上产生的位移。 i
5.刚度矩阵和柔度矩阵的关系
多自由度机械系统动力学

机械动力学
Chapter4多自由度机械系统动力学
机械动力学
Chapter4
多自由度机械系统动力学
2021年6月18日
机械动力学
Chapter4多自由度机械系统动力学
本章解决的主要问题及内容
解决的问题: 解决两自由度机械系统的动力学问题。采 用方法为拉格朗日方程的分析方法。
主要的内容:
一、拉格朗日方程;
工程中的非自由质点系,受到的约束大多是稳定的完整 约束(约束方程仅与质点系的位置有关)。
确定一个受完整约束的质点系的位置所需的独立坐标的数 目,称为该质点系的自由度的数目,简称为自由度数。
对一个非自由质点系,受s个完整约束,(3n-s )个独
立坐标。其自由度 为 N=3n-s 。
机械动力学
Chapter4多自由度机械系统动力学
机械动力学
Chapter4多自由度机械系统动力学
例:铅直平面内摆动的双摆。
▼确定A、B两点位置(平面问题) 需四个独立坐标 ▼系统受两个完整约束,其约束方程:
x12 y12 a2 , (x2 x1)2 ( y2 y1)2 b2
▼系统的自由度:N=2n-s=4-2=2
★两个自由度, 取广义坐标,
Qk 0 (k 1,2,, N )
机械动力学
Chapter4多自由度机械系统动力学
以广义坐标 表示的质点系的平衡条件:
Qk
n
(Xi
i 1
xi qk
Yi
yi qk
Zi
zi ) 0 qk
(k 1,2,, N)
解决质点系的平衡问题的关键是如何计算广义力
※广义力的计算
方法1:计算广义力 Qk 的步骤
N
xi
Chapter4多自由度机械系统动力学
机械动力学
Chapter4
多自由度机械系统动力学
2021年6月18日
机械动力学
Chapter4多自由度机械系统动力学
本章解决的主要问题及内容
解决的问题: 解决两自由度机械系统的动力学问题。采 用方法为拉格朗日方程的分析方法。
主要的内容:
一、拉格朗日方程;
工程中的非自由质点系,受到的约束大多是稳定的完整 约束(约束方程仅与质点系的位置有关)。
确定一个受完整约束的质点系的位置所需的独立坐标的数 目,称为该质点系的自由度的数目,简称为自由度数。
对一个非自由质点系,受s个完整约束,(3n-s )个独
立坐标。其自由度 为 N=3n-s 。
机械动力学
Chapter4多自由度机械系统动力学
机械动力学
Chapter4多自由度机械系统动力学
例:铅直平面内摆动的双摆。
▼确定A、B两点位置(平面问题) 需四个独立坐标 ▼系统受两个完整约束,其约束方程:
x12 y12 a2 , (x2 x1)2 ( y2 y1)2 b2
▼系统的自由度:N=2n-s=4-2=2
★两个自由度, 取广义坐标,
Qk 0 (k 1,2,, N )
机械动力学
Chapter4多自由度机械系统动力学
以广义坐标 表示的质点系的平衡条件:
Qk
n
(Xi
i 1
xi qk
Yi
yi qk
Zi
zi ) 0 qk
(k 1,2,, N)
解决质点系的平衡问题的关键是如何计算广义力
※广义力的计算
方法1:计算广义力 Qk 的步骤
N
xi
结构动力学多自由度系统振动

运用功旳互等原理可知,刚度矩阵是对称阵,即有kij=kji, 于是上述刚度矩阵为:
k1 k2
k2
K 0
0
0
k2 k2 k3
k3 0
0
0 k3 k3 k4 k4
0
0 0 k4 k4 k5 k5
0
0
0
k5
k5
⒉ 柔度法 柔度系数aij定义为:
在第j个质量上作用单位力时在第i个质量上产生旳位移。
K12 k2 K22 k2 k3
K32 k3 K42 0 K52 0
K13 0 K23 k3 K33 k3 k4 K43 k4 K53 0
K14 0 K24 0 K34 k4 K44 k4 k5 K54 k5
K15 0 K25 0 K35 0 K45 k5 K55 k5
(a) m1 mi
mj mn
y1
yi yj yn
m1 y1
(b)
mi yi
1
i
j
m j y j
mn yn
ii
ji
1
(c)
ij
ij
jj
(a) m1
mi
mj mn
y1
yi yj yn
m1 y1
(b)
mi yi
1
i
j
m j y j
mn yn
ii
ji
1
(c)
ij
ij
jj
于是: 若在第j个质量上作用有力F,则在第i个质量上产
2
2
2
1 Mx 2 1 m[x 2 2Lx cos L2 2 ] 1 kx2 mgL(1 cos)
2
2
2
d dt
【结构动力学】第10章 多自由度体系2020

0
0
N
其中,ωn— 第n阶自振频率,{φ}n—第 n阶振型。
[Φ]和[Ω]也分别称为振型矩阵和谱矩阵。
13
5 DOF with uniform mass and stiffness
5 DOF Base Isolated 14
15
5 DOF with uniform mass and stiffness
k22 2m22 k2N 2m2n 0
k N1 2mN1 k N 2 2mN 2 k NN 2mNN
10
对于N个自由度的稳定结构体系,频率方程是关于ω2的 N次方程,
a N ( 2 ) N a N 1 ( 2 ) N 1 a1 2 a 0 0
由此可以解得N个正实根(ω12<ω22<ω32…<ωN2)。 ωn(n=1, 2, …, N)即为体系的自振频率。其中量值最小的 频率ω1叫基本频率(相应的周期T1=2π/ω1叫基本周期)。 从以上分析可知,多自由度体系只能按一些特定的频 率即按自振频率做自由振动。按某一自振频率振动时,结 构将保持一固定的形状,称为自振振型,或简称振型。
上述齐次方程组有非零解条件为:系数行列式为零
A [I ] 0
N×N矩阵[A]一般将有N个特征值,对应N个特征向量
6
§10-2 多自由度体系的自由振动
多自由度体系无阻尼自由振动的方程为:
M u K u 0
其中:[M]、[K]为N×N阶的质量和刚度矩阵 {u}和{ü}是N阶位移和加速度向量 {0}是N阶零向量
11
把相应的自振频率ωn代入运动方程的特征方程得到振型
K n 2 M n 0
{φ}n={φ1n, φ2n , …, φNn }T—体系的第n阶振型 。 ➢ 由于特征方程的齐次性(线性方程组是线性相关的),振型向量 是不定的,只有人为给定向量中的某一值,例如令φ1n=1,才能确 定其余的值。 ➢ 实际求解时就是令振型向量中的某一分量取定值后才能求解。 虽然令不同的分量等于不同的量,得到的振型在量值上会不一样, 但其比例关系是不变的。
多自由度系统的振动、响应和求解

E
D k vD
B Q2
A Q1
k vA
位移图
受力图
图(b) v21, v1v30时板的位移和受力图
(2)求刚度矩阵第二列 参见图 b,可得板的力平衡方程:
Q3 kvA kvD 0 Q1L (kvA kvD) L 0 Q1 Q2 kvE 0
;其中
k
12EI L3
解得 Q 1 2 k , Q 2 3 k , Q 3 0
微振动时, i ,
&
i
为小量,将以上能量保留到二阶小量,得
(注意:为了得到线性振动方程,能量表达式必须保留 到二阶微量)
T 12ml2[3&12 2&22 &32 4&1&2 2&2&3 2&3&1]
3
12ml2{&1,&2,&3}2
1
2 2 1
11&&12 1&3
V
1 2
mgl
(312
222
简支梁在横向集中力作用下的挠度公式为
P
f Pb(xl2x2b2), 0xa 6EIl
x
a
b
l
f Pb[l(xa)3(l2b2)xx3], axl
6EIlb
例4.1 写出图示梁的柔度矩阵,梁的抗弯刚度为EI。如果 将梁的质量按分段区间均分到区间的两个端点,写出梁的质
量矩阵,设梁单位长度的质量为 l。
;其中
k
12EI L3
Q1 Q2
2 2
(kvA
kvD
)
0
解得 Q 1 4 k , Q 2 2 k , Q 3 0
因此,刚度矩阵第一列为
D k vD
B Q2
A Q1
k vA
位移图
受力图
图(b) v21, v1v30时板的位移和受力图
(2)求刚度矩阵第二列 参见图 b,可得板的力平衡方程:
Q3 kvA kvD 0 Q1L (kvA kvD) L 0 Q1 Q2 kvE 0
;其中
k
12EI L3
解得 Q 1 2 k , Q 2 3 k , Q 3 0
微振动时, i ,
&
i
为小量,将以上能量保留到二阶小量,得
(注意:为了得到线性振动方程,能量表达式必须保留 到二阶微量)
T 12ml2[3&12 2&22 &32 4&1&2 2&2&3 2&3&1]
3
12ml2{&1,&2,&3}2
1
2 2 1
11&&12 1&3
V
1 2
mgl
(312
222
简支梁在横向集中力作用下的挠度公式为
P
f Pb(xl2x2b2), 0xa 6EIl
x
a
b
l
f Pb[l(xa)3(l2b2)xx3], axl
6EIlb
例4.1 写出图示梁的柔度矩阵,梁的抗弯刚度为EI。如果 将梁的质量按分段区间均分到区间的两个端点,写出梁的质
量矩阵,设梁单位长度的质量为 l。
;其中
k
12EI L3
Q1 Q2
2 2
(kvA
kvD
)
0
解得 Q 1 4 k , Q 2 2 k , Q 3 0
因此,刚度矩阵第一列为
结构动力学-多自由度系统振动

k 2k
y1 y2
0 0
m
M
0
0
k
m, K k
k
2k
解:①由频率方程求固有频率
K 2M 0 k m2
k 0
k 2k m2
展开上式得:(k m2 )(2k m2 ) k 2 0
2 1, 2
3k m
9k 2m2 4k 2m2 2m2
1 0.62
k, m
2 1.62
M20 0
M 21
y2 0
M1y1
M11
列力平衡方程为:M11 M1y1 0 M11 M1 M 21 0, M 31 0
同样的分析可以求得:M12 0, M 22 M 2 , M 23 0; M13 0, M 23 0, M 33 M 3;
所以,得到质量矩阵为: M1 0 0
k2
k3
P
p1 (t) p2 (t)
二、柔度矩阵法 用柔度矩阵法或者刚度矩阵建立方程本质上也是基于力的 动平衡来建立方程,关键在于求柔度系数或刚度系数。
例题 3-2 梁的跨长为 l ,梁上有两个集中质量 M1 和 M 2 ,分别受 到集中力 p1 (t) 和 p2 (t) 的作用。不计梁自身的质量和阻尼,建立 系统的垂向振动方程.
上面的方程为惯性解耦,刚度耦合方程。
kij 的物理意义:j 坐标发生单位位移,其余坐标位移全部为
零时, i 坐标引起的恢复力。
mij 的物理意义:仅在 j 坐标发生单位加速度时,在第 i 坐标所产生 的惯性力.
用柔度矩阵法建立的一般方程:
Y (P MY)
两边同乘以 1
1Y 1(P MY)
例题:针对下图给出的系统,建立振动微分方程。
7《结构动力学》-第七章

λ1=
~ 1
~
+
~
ω12
~ ≈ tr S
[]
1
1
2 ω2
ω12
+⋯+
~ = tr S
[]
可用此式估算系统基频,且为下限估值。 可用此式估算系统基频,且为下限估值。 若质量矩阵为对角阵,则 若质量矩阵为对角阵,
a11 a ~ S = [ A][M ] 21 = ⋯ a n1 a12 a 22 ⋯ an2 ⋯ a1n m1 ⋯ a2n ⋯ ⋯ ⋯ a nn 的迹为: ⋱ mn
{x}T [K ]{x} = {α }T [u ]T [K ][u ]{α } RI ({x}) = {x}T [M ]{x} {α }T [u ]T [M ][u ]{α }
[K 记: ] = [u ] [K ][u ]
T
[M ] = [u ] [M ][u ]
T
{α }T [K ]{α } 则: RI = {α }T [M ]{α }
[]
迹法
k k /2 k /3 2 2 ω 22 = ω 33 = m m m
1 1 1 1 6m ~ tr S =∑ 2 = + + = k k k ω ii k m 2m 3m
[]
邓克利法
里茨法(Ritz)(或瑞利-里茨法 或瑞利- §7-3 里茨法 或瑞利 里茨法)
求较低几阶频率与振型 思路: 思路:先假设若干个振型并按这些振型进行最佳线性 组合,再用瑞利法求前几阶模态(固有频率与振型 固有频率与振型) 组合,再用瑞利法求前几阶模态 固有频率与振型
1 1 T T Tmax = ω 2 {x} [M ]{x} U max = {x} [K ]{x} 2 2
~ 1
~
+
~
ω12
~ ≈ tr S
[]
1
1
2 ω2
ω12
+⋯+
~ = tr S
[]
可用此式估算系统基频,且为下限估值。 可用此式估算系统基频,且为下限估值。 若质量矩阵为对角阵,则 若质量矩阵为对角阵,
a11 a ~ S = [ A][M ] 21 = ⋯ a n1 a12 a 22 ⋯ an2 ⋯ a1n m1 ⋯ a2n ⋯ ⋯ ⋯ a nn 的迹为: ⋱ mn
{x}T [K ]{x} = {α }T [u ]T [K ][u ]{α } RI ({x}) = {x}T [M ]{x} {α }T [u ]T [M ][u ]{α }
[K 记: ] = [u ] [K ][u ]
T
[M ] = [u ] [M ][u ]
T
{α }T [K ]{α } 则: RI = {α }T [M ]{α }
[]
迹法
k k /2 k /3 2 2 ω 22 = ω 33 = m m m
1 1 1 1 6m ~ tr S =∑ 2 = + + = k k k ω ii k m 2m 3m
[]
邓克利法
里茨法(Ritz)(或瑞利-里茨法 或瑞利- §7-3 里茨法 或瑞利 里茨法)
求较低几阶频率与振型 思路: 思路:先假设若干个振型并按这些振型进行最佳线性 组合,再用瑞利法求前几阶模态(固有频率与振型 固有频率与振型) 组合,再用瑞利法求前几阶模态 固有频率与振型
1 1 T T Tmax = ω 2 {x} [M ]{x} U max = {x} [K ]{x} 2 2
动力学方程的三种基本形式PPT教案学习

第13页
第12页/共35页
§3.2 虚功率形式的动力学方程
用动量和冲量表示的动力学方程__ 一般情形
对功率形式的动力学方程进行变化,由
n
n
Pi Fi miai ri 0
i 1
i 1
将其括号部分提取出来,进行变换
t
Fi miai
dt
t
t
t Fidt t miaidt
其中:LOi 为碰撞后第i个质点对定点O的动量矩, lOi 为碰撞前第i个质点对定 点O的动量矩
如果质点系是相对于其质心C的转动,同样可得其动力学方程为:
n
mC Si LCi lCi 0
i 1
LCi , lCi 的意义同前;mC Si 意义同前。
第17页
第16页/共35页
§3.2 虚功率形式的动力学方程
碰后: uBx 0 uBy 0
vBy 0
vCy
C
vAy
vCx
Sx A
x
vAx
Sy
碰前
uCy
C u Ay
Sx x
uCx
x
u Ax
Sy
碰后
由恢复系数公式
kx
uBx v Ax
uAx vBx
1
ky
uBy uAy vAy vBy
1
解得: uAx 0
第20页
vAy v1 (向上)
第19页/共35页
Rg3 m1aO 3 4rm1
Rgn3 m1aOn 3 4m1r2
Mg3 0
(4)虚位移,虚功,虚功方程
给定虚位移,其方向与 即 1 方向相同
1
2 21 2
为计算虚功,可将系统上的力集中到某几个刚体上,如集中到O1O3曲柄上。
结构动力学多自由度

pbT
~ fpa
paT ~fpb paT ~fpb T pbT ~f T pa pbT ~fpa
故 ~f 、 k 均为对称矩阵。
单元刚度矩阵
单元刚度系数表示由单位节点位移所引起的节点力。
单元刚度系数由虚位移法求得。
例如,课本P106图11-5所示简支梁中,令a端发生单位转角, 并给该处一竖向虚位移,零外力所做的功,等于内力所做的 功。
表示一个自由度发生相应单位位移而其他节点不动时在结构中所 产生的的力。
弹性特性
柔度的定义:
~ fij —在j坐标施加单位荷载而引起的i坐标的挠度。
则任意荷载组合下: vi ~fi1 p1 ~fi2 p2 ~fiN pN
用矩阵表示:
v1
vi
v N
略去阻尼矩阵和施加的荷载向量的影响: mv kv 0
假定以上多自由度体系的振动是简谐振动:
v(t) vˆ sin(t )
vˆ 表示体系的形状,不随时间变化。
v 2vˆ sin(t ) 2v 2mvˆ sin(t ) kvˆ sin(t ) 0
k 2m vˆ 0
无阻尼自由振动—振动频率分析
k 2m vˆ 0
即: k 2m 0
上式的N个根,表述体系可能存在的N个振型的频率。
1
2
3
WE va pa v1 k13
Lபைடு நூலகம்
WI v1 0 EI ( x) 1''( x) 3''( x)dx
第四章结构动力学多自由度体系详解

此时惯性力
设解为 y1(t) Y1 sin(t )
y2
(t)
Y2
s
in(t
)
幅值
m1y1(t) m1 2Y1 sin(t )
m2
y2
(t
)
m2
2Y2
s
in(t
)
2m1Y1 2m2Y2
Y1 ( 2m1Y1)11 ( 2m2Y2 )12
Y2 ( 2m1Y1) 21 ( 2m2Y2 ) 22
振但动其过比程值中始,终结保构持位不移变形。状保持不变的振动形式,称为主振型。
(k11 2m1
k21Y1 (k22
)Y1 k12Y2
2m2 )Y2
0 0
当然 Y1=Y2=0 为其解,为了求得不全为零的解,令
D (k11 2m1)
k12
0
k21
(k22 2m2 )
特征方程 频率方程
第1振型
第2振型
(2)求频率(k1 k2 2m1)(k2 2m2 ) k22 0
若有 m1 nm2 [(n 1)k2 2nm2 ](k2 2m2 ) k22 0
k1 n k2 (3)求主振型
12
2
1 2
(2
1) n
4 n
1 n2
k2 m2
1 :
Y21 Y11
k22
二、 柔度法
m2 y2 m2
m1y1 m1
在自由振动过程中任意时刻t,质量m1、
y2(t) m2的位移y1(t)、y2(t)应当等于体系在当时 惯性力作用下的静力位移。
y1(t)
y1(t) m1y1(t)11 m2 y2(t)12
y2 (t) m1y1(t) 21 m2 y2 (t) 22
多自由度系统

03
仿真与实验研究
通过仿真和实验手段,验证了所提出的多自由度系统建模与控制方法的
有效性和可行性,为实际应用提供了有力支持。
未来发展趋势预测
智能化控制
随着人工智能技术的不断发展,未来多自由度系统的控制 将更加智能化,如基于深度学习的控制策略、强化学习算 法等将得到广泛应用。
柔性化与可穿戴化
随着新材料技术和机械设计技术的不断进步,未来多自由 度系统将更加柔性化和可穿戴化,以适应各种复杂环境和 任务需求。
可分为液压驱动、电动驱动和人力驱动等多自由 度系统。
运动学描述
运动学是研究物体运动规律的科 学,包括位置、速度和加速度等
运动参数。
在多自由度系统中,运动学描述 涉及多个坐标和多个运动参数, 需要采用多维向量和矩阵等数学
工具进行描述。
运动学方程是多自由度系统运动 学描述的基础,通过求解运动学 方程可以得到系统各部分的运动
车辆悬挂系统优化
悬挂系统建模
建立车辆悬挂系统的动力学模型,考虑轮胎、悬挂元件等非线性 因素。
控制策略设计
针对车辆悬挂系统的特点,设计主动或被动控制策略,提高车辆 的行驶平顺性和稳定性。
性能评价与优化
通过仿真和实验手段,评价悬挂系统性能,采用优化算法对控制 策略进行优化,提高系统性能。
07
总结与展望
多模态运动规划与控制
针对多自由度系统复杂多变的运动需求,未来研究将更加 注重多模态运动规划与控制方法的研究,如基于优化算法 的运动规划、多模态切换控制等。
多机器人协同控制
针对多个多自由度系统之间的协同控制问题,未来研究将 更加注重多机器人协同控制方法的研究,以实现多个机器 人之间的协同作业和智能交互。
THANK YOU
多自由度运动方程的建立

几何刚度影响系数:
kGij 由j自由度单位位移和结构中由轴向力分量
引起的对应于ቤተ መጻሕፍቲ ባይዱ坐标的力
(9-16)
§9.3 轴向力的效应 引入上式,结构的动力平衡方程(计及轴向力)为
cv+ kv- k G v = p(t) mv+
cv+ kv = p(t) mv+
或者
(9-18)
(9-13)
结构动力学
第九章
多自由度运动方程的建立
第九章 多自由度体系的运动方程
§9.1 自由度的选择 §9.2 动力平衡条件 §9.3 轴向力的效应
§9.1 自由度的选择
单自由度体系两种描述方法 • 单一的坐标 • 一个变形函数——广义坐标 影响近似分析的精度的因素 主要有: 荷载的空间分布 荷载的时间历程 结构自身的动力特性——刚度、质量及阻尼
§10.1 弹性特性 Betti定律
(10-13) 结构的变形与加荷次序无关,应变能也相等---唯一性、能量守恒
pa vb = pb va
T
T
图10-3 两组独立的荷载系与产生的变位
§10.1 弹性特性 它说明了功的互等定理
pa T vb = pb T va
= p Tfp pa Tfp b b a
1 1 T 荷载a: Waa = pia via = p a v a 2 2 荷载b: Wbb + Wab = 1 p b T v b + p a T v b 2 1 T 1 T T 总和: W1 = Waa + Wbb + Wab = pa va + p b v b + p a v b 2 2
正定/半正定矩阵
《自由度系统》PPT课件

系统稳态振动时,惯性力、弹性力、阻尼力都是与激励同频 率的简谐量,分别为:
频率比所处区域不同,与激励构成动平衡的力的种类不同
图2—16
H ()
1
[1(/n)2]2(2/ n)2
0
弹性控制区
H ()
1
[1(/n)2]2(2/ n)2
图2—16
惯性控制区
H ()
1
[1(/n)2]2(2/ n)2
图 2—14
从波形图可以看出:
求通解的过程
全解
通解
特解
通解
衰减因子
全解=瞬态响应+稳态响应 瞬态响应昙花一现,不劳多谈; 稳态响应主导江山,集中研判!
今后,只研究稳态响应项。
稳态响应项的规律
要命的是频率(比)!
2.4.2 复频率响应 幅频特性与相频特性
稳态响应的幅值和相角是激励频率的非线性函数,在理论 分析和实际工作中常引进复频率响应来描述激励频率对响 应的影响。
得到运动微分方程的又一种方法
机械能守恒
x,v
简谐运动能量图
xt 0
o
t xA co ts
T vt v A si n t
能量
o T T 3T T 42 4
E 1 kA2 2
Ep
1kA2c 2
o2st
t Ek
1m2A2sin2t
2
E 1 kA2 简谐运动能量守恒,振幅不变 2
简谐运动势能曲线
1.静态位移法
用静力学的方法确定动 力学系统的固有频率
妙!
横梁与弹簧串联: 总变形量为分变形量之和
2.能量法
系统振动时动能、势能要相互转换。根据能量关系也能 求系统的固有频率。对于单自由度系统,用能量法求固有频 率有两种方法:
机械动力学-多自由度系统

j =1
所有坐标 q j ( j = 1, 2, , n ) 的运动有着相同的随时间变化 规律,即有着相同的时间函数。 规律,即有着相同的时间函数。令 q j (t ) = u j f ( t ) j = 1, 2, , n (4.2-3) )
u j ( j = 1, 2, , n ) 是一组常数,表示不同坐标运动的大小。 是一组常数,表示不同坐标运动的大小。
12
4.2 无阻尼自由振动和特征值问题
2. n自由度无阻尼系统自由振动的解的形式 ([ K ] − λ [ M ]) {u} = {0} (4.2-10) ) [ K ]{u} = λ [ M ]{u} (4.2-11) ) [K ] − λ [M ] = 0 (4.2-12) ) 系统的特征行列式,其展开式叫系统的特征多项式 系统的特征行列式, 方程( 方程(4.2-12)叫做系统的特征方程或频率方程, )叫做系统的特征方程或频率方程, ωn2的n阶方程 是 λ或 阶方程 2 λ1 < λ2 < < λn ωn21 < ωn22 < < ωnn 方根值 ωn1 < ωn 2 < < ωnn 叫做系统的固有频率,由方程( 叫做系统的固有频率,由方程(4.2-12)可见,它只 )可见, 决定于系统的物理参数,是系统固有的。 决定于系统的物理参数,是系统固有的。最低的固 有频率叫做系统的基频或第一阶固有频率, ω 有频率叫做系统的基频或第一阶固有频率,在许多 实际问题中,它常常是最重要的一个. 实际问题中,它常常是最重要的一个.
2
(
)Leabharlann U=对于线性系统,运动是微幅的, 对于线性系统,运动是微幅的,sin θ ≈ θ 代入动能和势能方程, 代入动能和势能方程,有
所有坐标 q j ( j = 1, 2, , n ) 的运动有着相同的随时间变化 规律,即有着相同的时间函数。 规律,即有着相同的时间函数。令 q j (t ) = u j f ( t ) j = 1, 2, , n (4.2-3) )
u j ( j = 1, 2, , n ) 是一组常数,表示不同坐标运动的大小。 是一组常数,表示不同坐标运动的大小。
12
4.2 无阻尼自由振动和特征值问题
2. n自由度无阻尼系统自由振动的解的形式 ([ K ] − λ [ M ]) {u} = {0} (4.2-10) ) [ K ]{u} = λ [ M ]{u} (4.2-11) ) [K ] − λ [M ] = 0 (4.2-12) ) 系统的特征行列式,其展开式叫系统的特征多项式 系统的特征行列式, 方程( 方程(4.2-12)叫做系统的特征方程或频率方程, )叫做系统的特征方程或频率方程, ωn2的n阶方程 是 λ或 阶方程 2 λ1 < λ2 < < λn ωn21 < ωn22 < < ωnn 方根值 ωn1 < ωn 2 < < ωnn 叫做系统的固有频率,由方程( 叫做系统的固有频率,由方程(4.2-12)可见,它只 )可见, 决定于系统的物理参数,是系统固有的。 决定于系统的物理参数,是系统固有的。最低的固 有频率叫做系统的基频或第一阶固有频率, ω 有频率叫做系统的基频或第一阶固有频率,在许多 实际问题中,它常常是最重要的一个. 实际问题中,它常常是最重要的一个.
2
(
)Leabharlann U=对于线性系统,运动是微幅的, 对于线性系统,运动是微幅的,sin θ ≈ θ 代入动能和势能方程, 代入动能和势能方程,有
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k1
a1
e
a2
k2
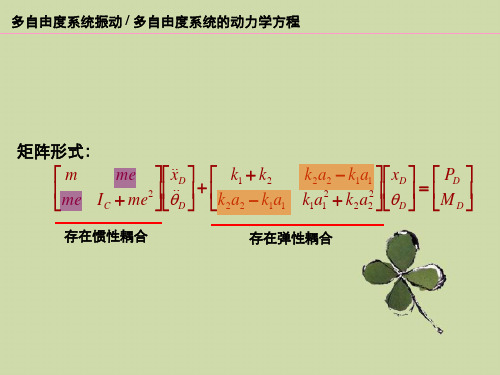
m m IC e m m 2 e x e D D k 2 k a 1 2 k k 2 1 a 1k k 1 2 a a 1 2 2 k k 2 1 a a 1 2 2 x D D M P D D
XRn M、 KRnn
P(t)Rn
在考虑系统的固有振动时,首先考察系统的同步振动,即系
统在各个坐标上除了运动幅值不相同外,随时间变化的规律
存在惯性耦合
存在弹性耦合
多自由度系统振动 / 多自由度系统的动力学方程
问:能否找到这样一种坐标使得系统的运动微分方程既不出 现惯性耦合,也不出现弹性耦合?
即:
m 11 0
m 0 22x x 1 2k0 11
k0 22x x1 2P P 1 2
假设对同一个系统所选择的两种不同的坐标X 和Y 有如下的变
换关系:
XTY
其中T 是非奇异矩阵,如果在坐标X下系统的运动微分方程为
:
M X KX P
那么在坐标Y 下的运动微分方程为: T T M Y T T K T T T P Y
如果恰巧Y 是主坐标:
TT MT 对角阵 TT KT
m 0I 0 C x C C k 2 k a 1 2 k k 2 1 a 1 k k 1 2 a a 1 2 2 k k 2 1 a a 1 2 2 x C C M P C C
令: XDxD D, FDM PDD 令: XC xC C, FC M PCC
M D X DK D X DF D M CX CK CXCF C
多自由度系统振动 / 多自由度系统的动力学方程
M D X DK D X DF D XD[xD, D]T M CX CK CXCF C XC[xC, C]T
讨论:能对同一个系统选取两个不同的坐标,它们所描述的 运动微分方程之间有着怎样的联系?
多自由度系统振动 / 多自由度系统的动力学方程
m m IC e m m 2 e x e D D k 2 k a 1 2 k k 2 1 a 1k k 1 2 a a 1 2 2 k k 2 1 a a 1 2 2 x D D M P D D
多自由度系统振动 / 多自由度系统的动力学方程
矩阵形式:
m m IC e m m 2 e x e D D k 2 k a 1 2 k k 2 1 a 1k k 1 2 a a 1 2 2 k k 2 1 a a 1 2 2 x D D M P D D
TTKDTKC
验证:
m me MD me IC me2
m 0
MC
Байду номын сангаас
0
IC
1 0m me 1e m0 e1 me ICm2 e0 1 0 IC
多自由度系统振动 / 多自由度系统的动力学方程
结论:
这样的T 是否存在?如何寻找?
多自由度系统振动 / 多自由度系统的自由振动
• 多自由度系统的自由振动
• 固有频率 • 模态 • 模态的正交性 • 主质量和主刚度 • 模态叠加法 • 模态截断法
多自由度系统振动 / 多自由度系统的自由振动
• 多自由度系统的固有频率
作用力方程: M X KX P(t) 固有振动方程: M X KX 0
若能够,则有:
m 1x 11k1x 11P 1 m 2x 2 2k2x 22P 2
方程解耦,变成了两个单自由度问题
使系统运动微分方程的全部耦合项全部解耦的坐标称为主坐标
多自由度系统振动 / 多自由度系统的动力学方程
l
选取D点的垂直位移及 角位移作为坐标
l1
A
DC
l2 B
选取质心C点的垂直位 移及角位移作为坐标
FD[PD, MD]T FC[PC, MC]T
XD TXC
T
1 0
e
1
FC TTFD FD(TT)1FC
将 XD TXC 代入D点的方程,并左乘 T T :
T T M D T X C T T K D T C X T T F D F C
得: TTMDTMC
FD[PD, MD]T FC[PC, MC]T
D点和C点的坐标之间的关系:
xCxDeD C D
写成矩阵形式: XD TXC
1 e
T 0
1
F D 和FC 的关系
坐标变换矩阵
在C点加一对大小相等、方向相反的力 PD
得: PC PD MCeD PMD
C
D
C
m 0I 0 C x C C k 2 k a 1 2 k k 2 1 a 1 k k 1 2 a a 1 2 2 k k 2 1 a a 1 2 2 x C C M P C C
D
xD
xC
e
M D PD PD D C PD
写成矩阵形式: FC TTFD T 非奇异,因此: FD(TT)1FC
M C PC
DC
多自由度系统振动 / 多自由度系统的动力学方程
M D X DK D X DF D XD[xD, D]T M CX CK CXCF C XC[xC, C]T
