12-2 毕奥-萨伐尔定律-磁感强度计算 (2014)
毕奥萨伐尔定律

1820年,法国物理学家比奥特(Biot)和萨瓦特(Savart)通过实验,测量了一条长直电流线附近的小磁针的力定律,并发表了一篇论文,题为“传递给运动中的金属的电的磁化力”。
后来被称为比奥-萨瓦特定律。
后来,在数学家拉普拉斯(Laplace)的帮助下,该定律以数学公式表示。
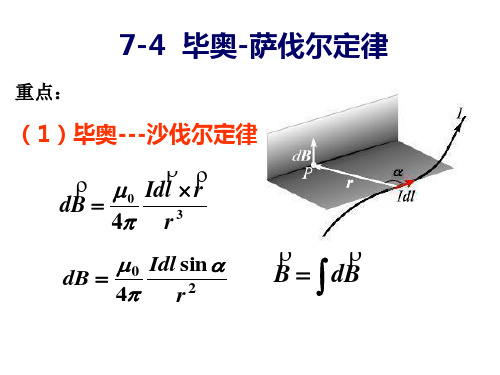
毕奥-萨伐尔定律:载流导线上的电流元Idl在真空中某点P的磁感度dB的大小与电流元Idl的大小成正比,与电流元Idl和从电流元到P点的位矢r之间的夹角θ的正弦成正比,与位矢r的大小的平方成反比。
dB的方向垂直于Idl和r所确定的平面,当右手弯曲,四指从方向沿小于π角转向r时,伸直的大拇指所指的方向为dB的方向,即dB、Idl、r三个矢量的方向符合右手螺旋法则。
叠加原理:
与点电荷的场强公式相似,毕奥——萨伐尔定律是求电流周围磁感强度的基本公式.磁感强度B也遵从叠加原理.因此,任一形状的载流导线在空间某一点P的磁感强度B,等于各电流元在该点所产生的磁感应强度dB的矢量和。
特点:
从课程论和物理学课自身特点的角度来分析毕奥-萨伐尔定律,它体现的学科特点有以下几点:(1)是稳恒电流磁场的关键知识点;(2)具有高度的抽象性;(3)使用数学工具的复杂性;(4)掌握“方法”比掌握“内容”更重要;(5)在探索知识的过程中体现“把握本质联
系,揭示事物发展内在规律性”的唯物辩证法观点。
磁感应强度毕奥—萨伐尔定律

R2dx R2x2 3/2
R2x2R2cs2c
B0nI2
2 1
R3cs2cd R3cs3cd
0nI2sind
2 1
讨论
B0 2nIco2sco1s
(1)P点位于管内轴线中点 1π2
co1sco2s
cos2
l/2
l/22 R2
B0ncIo 2s0 2 nIl2/4 lR 21/2
若 l R
dl
dB v40 nSdlrq3vvrv
运动电荷的磁场
实用条件 vc
BvddN Bv4d 0N qvv r3n rvd Sl
q+
r +
v
B
q
r
v
B
例: 半径 为 R的带电薄圆盘的电荷面密度
为 , 并以角速度 绕通过盘心垂直于盘面的轴转
动 ,求圆盘中心的磁感强度.
解法一 圆电流的磁场
oR
r
处的磁感强度
vv B dB
0Idlvrv 4 r3
v dB
0
4
Idlvrv r3
毕奥—萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
1
8
2
+
7
Idl + 3
R
6
+4
5
1、5 点 :dB0
3、7点
:dB
0Idl
4π R2
2、4、6、8 点 :
dB0Idl sin450
4πR2
二、 毕奥---萨伐尔定律应用举例
R
o
p*
dx
x
x
+++++++++++++ +
12-2 毕奥-萨伐尔定律

一 磁场
1 磁铁的磁场 N、S极同时存在; 同名磁极相斥,异名磁极相吸.
N S N S
磁 铁
磁场
磁
铁
第12章 恒定磁场
1
12-2 毕奥-萨伐尔定律
2 电流的磁场
奥斯特实验 电 流
3 磁现象的本质 运动电荷 磁场
磁 铁
磁场
第12章 恒定磁场
运动电荷
2
二. 磁感应强度(magnetic induction) B
Idl
R
0 IR 2 π R B dl 3 0 4πr
r
x
o
*p
dB
x
B
0 IR
2
2 2 3
( 2 x R )2
第12章 恒定磁场
13
12-2 毕奥-萨伐尔定律
讨 (1)若线圈有 N 匝 B 3 2 2 论 ( 2 x R )2
N 0 IR2Rr Nhomakorabeax
o
0 I x0 B ( 2) 2R B *p x
——描述磁场大小和方向的物理量
12-2 毕奥-萨伐尔定律
(1) 定义: B 的方向: 小磁针N极指向; B 的大小:
实验结果: a. F v 、B 组成的平面; b. F 大小正比于v 、q0 、sin q0 沿磁场方向运动, F=0 q0 垂直磁场方向运动, F = Fmax
实验: 正试验电荷q0以速率v 在场中 定义磁感强度的大小: 沿不同方向运动受力: Fmax B q0 v B q0 v 单位: 特斯拉(T)
I
第12章 恒定磁场
14
12-2 毕奥-萨伐尔定律
毕奥-萨伐尔定律

将实验结果与毕奥-萨伐尔定律的理论值进行对比,评估定律的准确性。
结果分析
分析实验误差来源,如设备精度、环境干扰等,提高实验的可靠性和准确性。
05
毕奥-萨伐尔定律的扩展与 推广
对三维空间的推广
总结词
毕奥-萨伐尔定律最初是在二维空间中 推导出来的,但通过引入矢量运算, 该定律可以扩展到三维空间中。
Idl
电流元,表示电流的一 部分。
r
观察点到电流元的径矢 ,表示观察点与电流元
之间的距离。
03
毕奥-萨伐尔定律的应用场 景
电场与磁场的关系
磁场是由电流产生的,而电场是由电 荷产生的。毕奥-萨伐尔定律描述了 电流和磁偶极子产生的磁场,以及变 化的电场产生的磁场。
毕奥-萨伐尔定律揭示了电场和磁场之 间的相互关系,表明它们是电磁场的 两个方面,而不是独立存在的。
THANKS
对微观尺度的适用性问题
毕奥-萨伐尔定律在描述微观尺度的电磁场时,其精确度受 到限制。在量子尺度下,电磁场的涨落和量子效应可能导 致定律的不适用。
未来研究需要进一步探索毕奥-萨伐尔定律在微观尺度下 的适用性和修正,以更好地描述量子电磁场的行为。
对超导态物质的适用性问题
毕奥-萨伐尔定律在描述超导态物质的 电磁场时,可能存在局限性。超导态 物质的电磁行为与常规物质有所不同, 需要更复杂的理论模型来描述。
电流与磁场的相互作用
根据毕奥-萨伐尔定律,电流产生磁场,而磁场对电流有作用 力。这种作用力被称为洛伦兹力,它描述了电流在磁场中所 受到的力。
毕奥-萨伐尔定律是电动机和发电机等电气设备工作的基础, 它解释了电流如何在磁场中受到作用力,从而产生旋转或线 性运动。
磁力线的描绘
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
毕奥萨伐尔定律公式详细解说

毕奥萨伐尔定律公式详细解说毕奥萨伐尔定律是电磁学中的基本定律之一,描述了通过一个导体回路所产生的磁场与通过该回路的电流的关系。
该定律由法国物理学家安德烈-玛丽·安普尔·毕奥萨伐尔于1820年发现并提出。
毕奥萨伐尔定律的数学表达式为:B = μ0 * I / (2 * π * r),其中B 表示磁场的强度,μ0为真空中的磁导率,I表示电流的强度,r表示距离导体回路的距离。
这个公式是通过实验观测得到的,可以用来计算任意一个导体回路所产生的磁场强度。
根据毕奥萨伐尔定律,当电流通过一个导体回路时,会在该回路周围产生一个环绕回路的磁场。
这个磁场的强度与电流的强度成正比,与距离导体回路的距离成反比。
磁场的方向则由右手定则来确定,即握住导线,大拇指指向电流方向,其他四指的弯曲方向就是磁场的方向。
毕奥萨伐尔定律的应用非常广泛。
在电磁学中,我们可以利用这个定律来计算各种不同形状和电流分布的导体回路所产生的磁场。
例如,在电磁铁中,通电线圈产生的磁场可以吸引铁磁物体;在电动机中,导线中的电流通过电磁场与磁场相互作用,产生力矩使电动机运转;在变压器中,通过调整线圈的匝数比可以改变磁场的强度,从而实现电能的传输和转换等。
除了应用于电磁学领域外,毕奥萨伐尔定律还有很多其他应用。
在电路中,我们可以利用这个定律来计算线圈的自感和互感。
自感是指通过一个线圈产生的磁场对该线圈自身电流的影响,而互感则是指线圈之间由于磁场耦合而产生的电流相互影响。
了解自感和互感的大小对于电路的设计和工作原理的理解非常重要。
毕奥萨伐尔定律还可以用于解释许多其他现象。
例如,当一个导体在磁场中运动时,会受到一个由毕奥萨伐尔定律描述的洛伦兹力的作用。
这个力可以使导体受到推动或制动,也可以用于实现电能与机械能的相互转换。
毕奥萨伐尔定律是电磁学中的重要定律,描述了电流通过一个导体回路所产生的磁场与磁场的强度、电流的关系。
它不仅在电磁学领域有广泛的应用,还可以用于解释和理解其他相关现象。
电磁学 毕奥-萨伐尔定律

I 2 dl
e
er
38
L2单位长度受到的力的大小是
f dF12 0 I1I 2
dz
2r0
(2.2-19)
令I1 = I2 = I , 当 r0 = 1米,并且测得f = 2×10 –7牛顿/ 米时,两导线中的电流强度I 就定义为“1安培”.
0
2r0
I2
f
2
1m 2 10 7 1A2
N
/
m
25
A
若两电流元关于平面A镜像对
称,证明:它们在A上的合磁 场B必垂直于A(除非B=0)
Idl r
Idl '
r'
z
dB dB'
0I 4
dl
r
r
3
0I 4
dl'r' r'3
0I 4r 3
(dl r dl 'r ')
dl
(lx
,
l
Hale Waihona Puke y,lz)
dl ' (lx ,ly ,lz )
11
2.安培定律(Amperes’ Law)
真空中,两个稳恒的电流回路L1和L2 ,
电d流F1元2 I1dIl21d对l2I2dlk2的I1作d用lr1122力e为12
在MKSA单位制中,比例常数
k 0 4
(2.2-2)
(2.2-1)
e12 I1dl1 r12
L1
I2dl2 L2
12
其中,0称为真空磁导率,它与真空介电常数e0
36
电磁相互作用宇称守恒
dB( x)
0 4
Idl e r
r2
毕奥萨伐尔定律

磁力发电机
磁力发电机是一种利用磁场产生电能的装置。根据毕奥萨 伐尔定律,当导体在磁场中运动时,会在导体中产生感应 电流。磁力发电机通过转子产生的旋转磁场与定子绕组相 对运动,使定子绕组中产生感应电流,实现发电的目的。
磁力发电机广泛应用于风力发电、水力发电、汽车发动机 等领域,为可再生能源的开发和节能减排做出了重要贡献 。
06
毕奥萨伐尔定律的未来研 究与展望
磁场产生的原因与机制
磁场产生的原因
毕奥-萨伐尔定律指出,运动电荷或电流会产生磁场,这是磁场产生的根本原因。
磁场产生的机制
磁场的产生与电荷或电流的运动有关,当电荷或电流运动时,会激发周围的磁场 ,磁场的大小和方向与电荷或电流的运动状态有关。
磁场对物质的作用与影响
核磁共振成像等磁现象在医疗领域具有广泛的应用前景,同时磁 约束核聚变等前沿技术也在积极探索中。
磁现象在太阳能领域的应用
太阳能电池板在吸收太阳能时,利用磁性原理可以提高太阳能利 用率。
感谢您的观看
THANKS
磁场强度的方向与单位
磁场强度的方向
在右手螺旋定则中,拇指指向电流的方向 ,四指环绕的方向就是磁场的方向。
VS
磁场强度的单位
安培/米(A/m),国际单位制中,磁场强度 的单位是安培/米。
03
毕奥萨伐尔定律的实验验 证
实验设计思路
确定实验目标
验证毕奥萨伐尔定律在特定情况下 的适用性,即通过实验手段测量物 理量以验证理论的准确性。
总结词
描述电磁场基本规律的方程组。
详细描述
麦克斯韦方程组是描述电磁场基本规律的方程组,其 中包括了电场、磁场和电荷密度等物理量的关系。毕 奥萨伐尔定律是麦克斯韦方程组的一个推论,它描述 了磁场与电流之间的关系。此外,麦克斯韦方程组还 预言了电磁波的存在,即光、无线电波等。
电磁学2毕奥-萨伐尔定律

β lr
β dB
a
P
§4-3 毕奥
萨伐尔定律的应用
1. 载流直导线的磁场
dB 的方向: I dl × r 的方向
dB
的大小:
dB
=
μo
4π
I
dl sina
r2
几何关系:
I dl
sin a =sin ( 900 +β ) dl a
= cosβ l = a tgβ
β lr
dl = a sec 2β dβ r = a secβ
I dl
r
IR
θ x
y dB θ P x
By= Bz=0
Idl r z
dB
B = dB x = dB
sinθ
=
μ
4π
o
I r
2
sinθ
dl
=
μo
4π
I r
2
sinθ
dl
sinθ
=
R r
I dl
r
r = (x 2 +R2 )1 2 I R
θ x
y dB θ x
z
B=
μo
4π
I r
2
sinθ
dl
=
×(
r r
)
B
=
μ
4π
o
I dl × r3
r
用矢量形式表示的毕奥 萨伐尔定律
dB =
μ o I dl × r
4π r 3
=
μo
4π
I dl r2
×(
r r
)
B
=
μ
4π
o
I dl × r3
高中物理(磁场)理解拓展辅导讲义与典型例题答案解析

1.磁感应强度B 磁感应强度可以采用如下三种定义方式: (1) B 的方向垂直于正电荷所受最大磁力的方向与电荷运动方向组成的平面,并满足右旋关系,即B v q F ⨯=.当v 垂直于B 时,电荷所受磁力最大(m F ),B 的大小等于单位试探电荷以单位速率运动时所受的最大磁力,即qv F B m /=,如图12-1所示.(2)B 的方向垂直于电流元所受最大磁力的方向与电流元方向组成的平面,并满足右旋关系,即B l Id F d ⨯=.当l d 垂直于B 时,电流元的受磁力最大,B 的大小等于单位电流元所受的最大磁力,即Idl F B m /=,如图12-2所示.(3)B 的方向垂直于线圈所受最大力矩的方向与磁矩方向所组成的平面,并满足右旋关系,即B m M ⨯=,当m 垂直于B 时,线圈所受力矩最大(m M ),B 的大小等于单位磁矩所受的最大力矩,即m M B m /=,如图12-3所示.理解与拓展:⑴ 磁感应强度B 是反映磁场(对运动电荷或电流有作用力)性质的基本量,它的重要性相当于电场中的E .它是一个矢量,一般是空间和时间的函数,磁场中某一点的B ,只依赖于磁场本身在该点的特性.⑵ 上述三种B 的定义都是等效的,方向都与小磁针N 极受力方向相同,大小也是一样的,因为有I d l qv =,l d F M m m '=,l Idld IS m '==,所以m M I d l F qv F B m m m ///===.相应的三个定义式B v q F m ⨯=,B l Id F m ⨯=和B m M m ⨯=也是可以互相推导的.2.磁场中的高斯定理 在磁场中通过任意封闭曲面的磁通量恒为零,即 0=∙=Φ⎰S d B SmF m Bv(a )q 图12-1F mB Id l(b ) 图12-2M Bm(c ) 图12-3理解与拓展:⑴ 同静电场中引入电场线一样,磁场中可以引入磁感应线(B 线),并规定它在某点的切线方向表示该处B 的方向,垂直穿过某点附近单位面积磁感应线的条数为B 的大小.⑵ 高斯定理反映了磁场的无源性.即磁感应线是连续的,在任何地方都不可断,磁场是无源场.假若B 线在某点中断,就一定能作出包围该点但B 通量不为零的闭合面.这是高斯定理所不允许的,场线中断的地方是场源,B 线不中断,说明磁场是无源场,它的本质是认为没有磁荷.⑶ 高斯定理的适用范围:它是由毕奥-萨伐尔定律导出的,它的适用条件也应当是稳恒电流的磁场,进一步的研究指出,高斯定理可以推广到任意非稳恒电流激发的磁场,但这时毕奥-萨伐尔定律不再成立.⑷ 通过某一有限面S 的磁通量可表示为 ⎰⎰=∙=ΦSSm dS B S d B θcos3.毕奥-萨伐尔定律如图12-4所示,电流元l Id 在距它为r的场点P 处产生的磁感应强度B d 为304r rl Id B d⨯=πμ毕奥-萨伐尔定律仅对线电流元的空间适用,即电流通过的横截面的线度远小于其到待求场点的距离,所以不存在0→r 时∞→B d 的困惑。
毕奥-萨伐尔定律

x
l 2
17
B
I0 I0
从以上分析可以看出长直载流螺线管的磁场 分布情况:在螺线管中心区域为均匀磁场,在 管端口处,磁场等于中心处的一半,在螺线管 外部距管轴中心约七个管半径处,磁场就几乎 等于零了。
18
例4. 在半径R=2cm的无限长的半圆形金属薄片中, 有电流I=6A自下而上的通过,如图求 圆柱轴线上任一点的磁感应强度。
位矢量,指向与电流的方向满足右螺旋关系。
多匝平面线圈电流I 应以线圈的总匝数与每匝
线圈的电流的乘积代替。
0 m m 0 圆电流 B n 3 3 2π x 2x
10
三 磁矩
m ISen
2
I
例2 中圆电流磁感强度 公式也可写成
S
en
m
B
0 IR
2x
3
0 IR 2
0 IR 2
a
4π a
25
例7 在玻尔的氢原子模型中,电子绕原子核运动相 当于一个圆电流,具有相应的磁矩(称为轨道磁 矩)。求轨道磁矩 与轨道角动量之间的关系。 解: 设电子的轨道半径为r,每秒转速为ν。 电流:
I e 2 磁矩: IS e πr
圆电流面积: S π r 2
4π d
R
o ( 3) I R
B0
0 I
4R
R2
*o
B0
o
0 I
8R
B0
0 I
4 R2
0 I
4 R1
0 I
4π R1
13
例3 载流直螺线管的磁场 如图所示,有一长为 l , 半径为R的载流密绕直螺 线管,螺线管的总匝数为N,通有电流 I. 设把螺线管 放在真空中,求管内轴线上一点处的磁感强度.
2.2 磁感应强度 毕奥一萨伐尔定律

实验结果:示零——不动,单位磁极受到的作用力矩相等。
结果分析: F1 H0 B1, F2 H0 B2 F1 B1 , F2 B2 单位磁极, H0=1,所以
1 2
F1r10 Br 1 10 1 F2 r20 B2 r20 B r 1 得到: 1 20 , 即 : B B2 r10 r0
两电流元——安培定律:
ˆ I I d l (d l r ) dF12 k 1 2 2 2 1 12 r 12 ˆ ˆ I d l (I d l r ) I dl r 0 2 2 21 1 12 I 2 d l2 0 1 1 12 ) ( 4 r 12 4 r 212 I 2 d l2 dB 0 I1d l1 r12 ˆ dB 4 r 212
电磁学电子教案
使用教材:
赵凯华、陈熙谋: 新概念物理学—电磁学
主讲:周贵德
沧州师范学院物电系
2012年2月修订
1
§2 磁感应强度 毕奥-萨伐尔定律
2.1 磁感应强度适量B
库仑定律: F 1 q1q2 ˆ r 2 4π 0 r
磁的库仑定律:
F
1 qm1qm 2 ˆ r 4πμ0 r 2
B
0
2
(cos 1 cos 2 )
B 0
B
0
2
16
几种载流导线的磁感应线
长直导线(电流元)
17
小结:
原则上,B-S定理加上叠加原理可以求任何载流导线在空 间某点的B 实际上,只在电流分布具有一定对称性,能够判断其磁场 方向,并可简化为标量积分时,才易于求解; 为完成积分,需要利用几何关系,统一积分变量; 一些重要的结果应牢记备用; 如果对称性有所削弱,求解将困难得多 如圆线圈非轴线上一点的磁场,就需要借助特殊函数 才能求解 又如在螺距不可忽略时,螺线管的电流既有环向分量 又有轴向分量,若除去密绕条件,就更为复杂。
12.2毕奥-萨伐尔定律

D C
x
C
1
0 Id sin dB 2 4r C
D
B
D
C
0 Id sin dB 2 4 r C
D
z
D 2
物理学教程 (第二版)
以 为变量如图: a a r sin sin
Id
I
actg actg
a d d sin 2
B dB
0 nI
2
R
x1
2
x2
R 2dx
2
x
2 3/ 2
x Rct g
dx R csc2 d
R2 x2 R2 csc2
B
B
0 nI
2
2
1
R 3csc2 d R 3 csc3
0 nI
2
cos 2 cos 1
B
0 pm 2 2 32 2(x R )
物理学教程 (第二版)
(1) I (2 )
R B x 0 0 I O B0 2R
I
( 4)
0 I BA 4π d
d *A
R1
R2
R
O
B0
0 I
4R
( 5) I
( 3) I R
O
* O
B0
0 I
8R
B0
0 I
0 ve B 4R 2
r
R
物理学教程 (第二版)
毕奥 — 萨伐尔定律
0 Idl r dB 3 4π r
dB 0 1、 5 点 :
3、7点 :dB
磁感应强度 毕奥-萨伐尔定律

µ0
r
2
B=
µ0 I
4 π r0
∫θ
θ2
1
sin θ d θ
v B 的方向沿 x 轴的负方向. 轴的负方向
无限长载流长直导线的磁场 无限长载流长直导线的磁场. 载流长直导线的磁场
z
D
θ2
v B
B=
(cosθ1 − cosθ 2) 4π r0
B=
µ0 I
I
o
x
C
θ1 → 0 θ2 →π
µ0I
2 π r0
r µ0 B= 4π
∫
L1
r ˆ ( I 1 d l1 × r12 )
2 r12
r r r dF2 = I 2 dl 2 × B
——磁感应强度矢量
讨论: 讨论:
r r r 为矢量式, (1) dF2 = I 2 dl2 × B 为矢量式,其标量式为 )
dF2 = I 2 dl2 B sin θ
θ
u r u r 是 I 2 dl2与 B 的夹角
d N = nS d l v v v v d B µ0 qv × r B= = d N 4π r 3
−q
v r
θ
v v
v B
例4 半径 为 R 的带电薄圆盘的电荷面密度 为 σ , 并以角速度 ω 绕通过盘心垂直于盘面的轴转 圆盘中心的磁感强度. 中心的磁感强度 动 ,求圆盘中心的磁感强度
σ R o
B
1 µ 0 nI 2
O
四 运动电荷的磁场
v v v µ0 Idl × r 毕— 萨定律 dB = 3 4π r v
v j
S
v v Id l = j S d l = nS d lq v v v v µ 0 nSdlqv × r dB = 3 4π r
12.1磁场 磁感强度§12.2毕奥-萨伐尔定律

第十二章恒定磁场§12.1 磁场磁感强度《大学物理》校级精品课程教学团队稳恒磁场: 磁感应强度不随时间变化的磁场.人类最早发现磁现象是从天然磁石(F吸引铁制物体的现象开始的.我国是发现天然磁铁最早的国家.公元前250年前韩非子“有度”篇中有“司南”的记基本磁现象1、磁铁的磁性2、电流的磁效应1820年,丹麦物理学家奥斯特发现电流的磁效应.同年,安培发现载流线框、螺线管或载流导线的行为像一块磁铁。
3.电流、磁铁的本源一致:安培分子环流假说:物体中的每一个分子都存在回路电流,称为分子电流,如果这些分子电流做定向排列,在宏观上会显现磁性。
地磁场Ø地球是一个大磁铁,目前它的N极位于地理南极一磁场运动电荷磁场vF=v+2.带电粒子在磁场中他方向运动时v v于与特定直线所组vv qFB max=-1-1-1-1 1T1N C m s1N A m =×××=××+B第十二章恒定磁场§12.2 毕奥-萨伐尔定律《大学物理》校级精品课程教学团队一、毕奥-萨伐尔定律:电流元的磁场(类比点电荷的静电场)r1.电流元矢量Idl0B d =m r 毕奥---萨伐尔定律的矢量式:二、毕奥---萨伐尔定律的应用1. 直电流的磁场(P已知:真空中I012(cos cos )4IB am q q p =-u 无限长载流直导线的磁场讨论aI B p m 20=半无限长载流直导线有限端的磁场aI B p m 40=04πI B am =’o=P B 0'=P B u 无限长载流直导线的磁场aI B p m 20=o2. 圆电流的磁场ê建立坐标系oxy ê任取电流元lId r2322202)x R (IR B +=m 方向:右手螺旋法则大小:B(1)圆心处:RI B 20m ==x RI R I B p q m p q m 42200=×=讨论nm IS e =u u r uu r nm NIS e =u u r uu r 讨论ne uu r载流圆弧,圆心处的设在半径为R的载流圆弧上通以电流为例1:一无限长载流直导线被弯成如图所示的形状,试计算O解:点O 的磁感强度是图中的4根载流导线在该点产生的磁感强度的矢量和,即12B B B =+v v v例2:求图中圆心O点的I3. 载流直螺线管内轴线上的磁场长直螺线管长为x变量代换:Q=x R bcot0(cos nI B m b =讨论nIB 0m =nIB 021m =练习:四条皆垂直于纸面的载流细长直导线,每条中的电流强度皆为I ,这四条导线被纸面截得的断面,如图所示。
第八讲 磁感应强度 毕奥萨伐尔定律

r
a
I
建立坐标系
θ
Idl
z
分析对称性、写出分量式 由对称性: B y Bz 0
19
B0
B dBx dB cos
21
国防科大
B dBx dB cos
0 I cosdl 4 r 2 I a I 0 2 cos dl 0 2 2a 4r r 4 r
0 Idl ( I ' dl 'r ) dF 4 r3 r x x ' , 4 10 N A I ' dl '( Idl r ') dF ' 0 4 r '3 r ' r
7 0
提出寻找电流、电流之间的相互作用的定量规律问题。
dB p
I ' dl 'r B dB 4 r
0 3
r
Biot-savert定律
dl '
I ' dl '
r
实验表明磁场满足叠加原理:
dl '
I'
dB p
点电荷的场强+场强叠加原理
1 dq E dE r 4 r
cos
a r
r ( x 2 a 2 )1 2
dB
例3. 在Bohr氢原子模型中,电子在圆轨道上绕核转动,试 证明电子的轨道磁矩 与轨道角动量 L 之间有关系:
x P
x
θ
dB
e L 2m
L
e为电子电荷,m为电子质量。 解:
Ia 2 0 Ia 2 0 3 2( x 2 a 2 )3 2 2r
磁感应强度毕奥-萨伐定律

Idl
L
0 B 4
Idl r 0 r2
毕奥-萨伐尔 定律应用
有限长载流 I 直导线
2
Idl
l
o
I
a
r0
r
P
0 Idl r 0 dB 4 r2 0 Idl r 0 B 2 4 r L
1
有限长 载流 I 直导线
B
2
0 4
Idl sin 2 r L
0 In
(cos 1 cos 2 )
1. 无限长 1 0 2 B 0 In 0i 所有磁力线全部被拘束在内部 2. 半无限长 1 0 2 B
B
0 nI
0 nI
2
2
O
0 In
2
0i
2
X
无限大载流平面 的B 讨论
Z
B 0i
I
2r
3
a
r
X
R sin
2
x l cot R
x
a
dl
b
Rd 1 R 3 sin 2 2( ) sin 2 In 0 In 0 B sin d (cos 1 cos 2 ) 1 2 2 B
0 InR 2
载流螺线管的讨论
2 讨论: B
12 C 8 . 85 10 两个常数: 0
N m
2
7 N 4 10 , 0 A2
Thanks
cos x r
Y
dB
0
dy
r
X
0 idy B By cos a 2 r a i dy x B 0 a 2 r r
我的电磁学讲义10:磁感应强度毕奥-萨伐尔定律

我的电磁学讲义10:磁感应强度毕奥-萨伐尔定律磁感应强度为了描述电场的分布,我们引⼊电场强度⽮量\vec{E},同样,为了描述磁场的分布,我们也需要引⼊⼀个新的⽮量,这个⽮量就是磁感应强度\vec{B}。
两个电流元的磁相互作⽤⼒满⾜安培定律\begin{equation*} \mathrm d\vec{F}_{12}=k\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrm d\vec{l}_1\times \hat{r_{12}})}{r_{12}^2}=\frac{\mu_0}{4\pi}\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrm d\vec{l}_1\times \hat{r_{12}})}{r_{12}^2} \end{equation*}在国际单位制中,\frac{\mu_0}{4\pi}=10^{-7}\mathrm {N/A^2}。
元电流之间的安培⼒的表达式分成两项:\begin{equation*} \mathrm d\vec{F}_{12}=I_2\mathrm d\vec{l}_2\times \mathrm d\vec{B} \end{equation*}\begin{equation*} \mathrm d\vec{B}=\frac{\mu_0}{4\pi}\frac{I_1\mathrm d\vec{l}_1\times \hat{r_{12}}}{r_{12}^2} \end{equation*}把电流元I_2 \mathrm d\vec{l} \_2看做试探电流元,则\mathrm d \vec{B}则为电流元I_1\mathrm d\vec{l} \_1的磁场在电流元I_2\mathrmd\vec{l} \_2所在位置处的磁感应强度。
整个回路1对电流元I_2\mathrm d\vec{l}_2的作⽤⼒为\begin{equation*} \begin{split} \mathrm d\vec{F}_{2}=&\frac{\mu_0}{4\pi}\oint_{L_1}\frac{I_2\mathrm d\vec{l}_2\times (I_1\mathrmd\vec{l}_1\times \hat{r_{12}})}{r_{12}^2}=\frac{\mu_0}{4\pi}I_2d\vec{l}_2\times\mathrm \oint_{L_1}\frac{ I_1\mathrm d\vec{l}_1\times\hat{r_{12}}}{r_{12}^2} \\ =&I_2d\vec{l}_2\times \vec{B} \end{split} \end{equation*}上式中\begin{equation*} \vec{B}=\frac{\mu_0}{4\pi}\oint_{L_1}\frac{I_1\mathrm d\vec{l}_1\times \hat{r_{12}}}{r_{12}^2} \end{equation*}即为闭合回路L_1的磁场在电流元I_2\mathrm d\vec{l}_2所在位置处的磁感应强度。
高中物理磁场中的毕奥-萨伐尔定律

高中物理磁场中的毕奥-萨伐尔定律高中物理磁场中的毕奥萨伐尔定律在高中物理的学习中,磁场是一个十分重要的概念,而毕奥萨伐尔定律则是描述磁场产生的基本规律之一。
理解并掌握毕奥萨伐尔定律,对于我们深入认识磁场的本质和特性具有至关重要的意义。
那么,什么是毕奥萨伐尔定律呢?简单来说,毕奥萨伐尔定律是用来计算电流元在空间中产生的磁场的大小和方向的。
我们先来看一下这个定律的数学表达式。
毕奥萨伐尔定律表述为:电流元 Idl 在空间某点 P 处产生的磁感应强度 dB 的大小与电流元的大小 Idl、电流元到 P 点的距离 r 的平方成反比,与电流元 Idl 和矢径 r 之间的夹角的正弦成正比,其方向垂直于 Idl 和 r 所组成的平面,并且遵循右手螺旋定则。
为了更直观地理解这个定律,我们来举一个简单的例子。
假设有一根直导线,通有电流 I。
我们想要知道这根导线在周围空间某一点产生的磁场强度。
我们可以把这根导线分割成无数个小段,每一小段都可以看作是一个电流元。
对于每一个电流元,我们都可以根据毕奥萨伐尔定律计算出它在该点产生的磁场强度。
然后,把所有电流元在该点产生的磁场强度进行矢量叠加,就可以得到这根导线在该点产生的总的磁场强度。
在实际计算中,我们常常会用到一些常见的几何关系和三角函数来简化计算。
比如说,如果电流元与矢径的夹角为 90 度,那么sinθ = 1,计算就会相对简单一些。
毕奥萨伐尔定律的应用非常广泛。
比如说,在计算环形电流在中心轴线上产生的磁场时,我们就可以利用这个定律。
对于一个环形电流,我们同样可以把它分成无数个小段电流元。
通过毕奥萨伐尔定律计算每个电流元在中心轴线上一点产生的磁场强度,然后进行矢量叠加,就可以得到环形电流在中心轴线上产生的磁场强度的表达式。
再比如,在分析螺线管内部的磁场时,也离不开毕奥萨伐尔定律。
螺线管是由很多圈环形电流组成的。
通过对每一圈环形电流应用毕奥萨伐尔定律,并考虑它们的叠加效果,我们可以得出螺线管内部磁场的分布规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dB
dB
P *
r
Idl
I
0 I dl r B dB 4π r 3
r
二、毕奥——萨伐尔定律 讨 论:
电流元在a、b、c、d四点产生的磁场大小及方向。
dB 0
c
0 Idl sin dB 2 b 4π R
两平行载流导线间有相互作用力
载流线圈受磁力矩作用而转动
I1
I2
F
I1
I2
N
I
F
S
I
一、磁力和磁场
磁感应强度
2.磁现象的电本质 (2)安培(A.M.Ampere法国科学家)实验 (1820年及以后)
电子束
S +
N
带电粒子在磁场中运动
一、磁力和磁场
磁感应强度
2.磁现象的电本质 (2)安培(A.M.Ampere法国科学家)实验 (1820年及以后)
2.磁现象的电本质 (1)奥斯特(H.C.Oersted丹麦物理学家)实 验(1819年春 ) ——小磁针在通电导线周围受磁
力作用发生偏转
I
揭示了电现象与磁现象的联系,宣告电磁学作为 一个统一学科诞生; 说明了磁力是横向力,突破了非接触物体之间只 存在有心力的观念。
一、磁力和磁场
磁感应强度
2.磁现象的电本质 (2)安培(A.M.Ampere法国科学家)实验 (1820年及以后)
a
R
0 Idl dB 4 π R2
d
Idl
0 Idl dB 4 π R2
二、毕奥——萨伐尔定律
3. 毕—萨定律的应用 0 I (cos 1 cos 2 ) 例1. 载流长直导线的磁场 B
4 π r0
z
D
2
dz
I
z
1
r
r0
0 I 无限长载流长直导线 B 2πr 0 I 半无限长载流长直导线 B 4πr 在导线及其延长线上 B 0
分量,最后由 B Bx i By j Bz k 确定。 (充分利用对称性)
3. 对于有些载流导体产生的磁场,可在上述典型计算 的基础上进一步求解。
二、毕奥——萨伐尔定律
3. 毕—萨定律的应用 例4. 载流直螺线管轴线上的磁场
R
o1 * p
2
x
dx
x
++ ++++ ++ +++ ++ +
分析:BO B1 B2 B3 B4
由右手螺旋法则可判断:方向均垂直向里。
1
R1
O R2
4 2 BO B1 B2 B3 B4 3 0 q1v 0 R1 R1 0 B1 B3 2 2 4 R1 4 4 R1 0 dqv 0 R dr r 0 R1 B2 B4 dB ln 2 2 4 r 4 R r 4 R2
B
0R
2
R o r
dr
将一根均匀带电(电荷线密度为 )的导线弯成 如图的形状,当导线绕 O点以角速度 转动时,求 O点的磁感应强度。
课堂测试
R1
O R2
课堂测试
将一根均匀带电(电荷线密度为 )的导线弯成 如图的形状,当导线绕 O点以角速度 转动时,求 O点的磁感应强度。
核磁共振成像
NMR(Nuclear Magnetic Resonance) Imaging
二、毕奥——萨伐尔定律
1. 磁场叠加原理
电荷元 电流元 点电荷系(带电体) 电流(载流体)
E dE
B dB
Idl
2. Biot—Savart Law 电流元在空间产生的磁场 0 Idl r dB 3 4π r 7 -2 ( 0 4 π10 N A )
克罗地亚男孩伊凡具有超能力, 他的身体能吸附金属物体。
3. 磁感应强度 B
一、磁力和磁场
Z
Fmax
磁感应强度 洛伦兹力:F qv B
q0 O
+
v F 0
B
X
Y
Fmax
q
+
方向:即运动电荷受力为零时的方1 2
0 R1 BO ( ln ) 2 R2
今日作业
7-10、 7-11、 7-12、 7-13、
带电粒子在磁场中运动 极光
一、磁力和磁场
2.磁现象的电本质
磁感应强度
(3)结论
一切磁现象都起源于运动电荷的相互作用; 物体具有磁性是由于其分子内形成分子电流; 磁相互作用通过磁场进行—— 磁场力。 运动电荷 传导电流 永久磁铁 磁场 运动电荷 传导电流 永久磁铁
2014年5月2日,西南交通大学超导技术研究所、 牵引动力国家重点实验室,建成国内首例载人高温超 导磁悬浮环形实验线。此前仅德国有先例。
er m 2
2
e m L 2me
m
解题布骤
(B-S定律和磁场叠加原理) 1. 在载流导体上取电流元 Idl,由 B-S定律,确定 电流元在给定点的磁感应强度 dB ; B dB求 B ; 2. 若各电流元的 方向相同,则直接用 d B 若各电流元的 dB 方向不同,则应选取适当的坐标系, 确定 dB 在各个方向的分量,由代数积分分别计算 的 B
ao
b
x
*P
0 I a b B ln 2πb a
二、毕奥——萨伐尔定律
3. 毕—萨定律的应用 例3. 圆形载流线圈轴线上的磁场
Id l
R
r
x
I
dB dB dB
中心磁场
0 I BO 2R
O
P
Idl
dB
X
2 2 3
磁偶极矩
I S
B
0 IR
2
( 2 x R )2
i
en
m
电流与磁感强度方向满足右手螺旋关系
m ISen
二、毕奥——萨伐尔定律
3. 毕—萨定律的应用
其它组合
R
I
×O
I
R1
R2
* o
0 I 0 I BO 2 2 R 4R
氢原子的轨道磁矩
0 I 0 I 0 I BO 4 R2 4 R1 4 π R1 L
N s N 单位:特斯拉 1T 1 1 Cm Am
v
B
自然界中一些磁场的值(T)
中子星 超导电磁铁 大型电磁铁 地球赤道附件 地球两极附件 108 5~40 1~2 3×10-5 6×10-5
人体磁场
10-12
AMS 计划
•1998.6.3, 2008 •丁肇中, •“发现者号”航天飞机, •α-磁谱仪 •(AMS, Alpha-Magnetic Spectrometer), •寻找太空中的反物质, 暗物质和磁荷, •中心磁场1.37 T。
0 nI B (cos 2 cos 1 ) 2
1 0 nI 2
B O
0 nI
电流与磁感强度成 右手螺旋关系
无限长螺线管轴线 x
B 0 nI
二、毕奥——萨伐尔定律
3. 毕—萨定律的应用 例5. 运动电荷的磁场
I
S
0 nSdlqv r dB 4π r3 dN nS dl
x
o
dB * P y
电流与磁感强度的方向满足:
右手螺旋关系
I I
X
C
B
二、毕奥——萨伐尔定律
3. 毕—萨定律的应用
P
BP 0
P
0 I BP r0
P P
0 I BP 4r0
BP
20 I r0
二、毕奥——萨伐尔定律
3. 毕—萨定律的应用 例2. 载流平板的磁场
I
x
dx
dB
d B 0 qv r B 3 d N 4π r
dl
+
r
P
适用条件 v c
q
v r ×B
q
r
v
B
二、毕奥——萨伐尔定律
3. 毕—萨定律的应用
例6. 半径为R的带电薄圆盘的电荷面密度为 , 并以角速度 绕通过盘心垂直于盘面的轴转动, 求圆盘中心的磁感强度.
内容概要
一、磁场、磁力、磁感应强度
二、毕奥——萨伐尔定律
三、应用毕—萨定律和磁场叠加原理 求载流导线(线圈)的磁场分布
一、磁力和磁场
1.磁现象
磁感应强度
磁铁能吸引铁、钴、镍等金属材料; 磁铁上磁力作用特别强的区域称为磁极 (N极与S极) ; 同号磁极相斥,异号磁极相吸;
S
N
S
N
一、磁力和磁场
磁感应强度
