第2章例题
第二章负债例题

第二章负债例题【例1】甲公司为增值税一般纳税人,适用的增值税税率为17%。
2010年12月甲公司董事会决定将本公司生产的500件产品作为福利发放给公司人员,其中生产工人400人,总部管理人员100人。
该批产品单件成本为1.2万元,市场销售价格为每件2万元(不含增值税),不考虑其他相关税费。
【例2】B公司2010年7月有关职工薪酬业务如下:(1)为生产工人100人提供免费住宿,月计提折旧合计为3万元。
(2)为总部部门经理级别以上职工每人提供一辆汽车免费使用,该公司总部共有部门经理以上职工10名,假定每辆汽车每月计提折旧0.2万元;【例3】企业缴纳的下列税金,应通过“应交税费”科目核算的有()。
(多选)A.印花税B.耕地占用税C.房产税D.土地增值税【例4】不通过“应交税费”科目核算?【例5】某企业为增值税一般纳税人,2010年实际已交纳税金情况如下:房产税850万元,消费税150万元,城市维护建设税70万元,车船税0.5万元,耕地占用税1.5万元,所得税120万元。
上述各项税金应记入“应交税费”科目的金额是()万元。
(单选)A.1 190B.1 190.5C.1 191.5D.1 192【例6】(单选)甲公司因意外火灾(管理不善导致)毁损一批存货,其中原材料的成本为100万元,增值税额l7万元;库存商品的实际成本800万元,经确认损失外购材料的增值税34万元。
该企业的有关会计分录不正确的是()。
A.借记“待处理财产损溢”科目951万元B.贷记“原材料”科目l00万元C.贷记“库存商品”科目800万元D.贷记“应交税费——应交增值税(进项税额转出)科目17万元【例7】【思考问题】如果为自然灾害造成的损失,如何处理?【例8】(多选)下列各项,增值税一般纳税企业需要转出进项税额的有()。
A.自制产成品用于职工福利B.自制产成品用于对外投资C.外购的生产用原材料发生非正常损失D.外购的生产用原材料改用于自建厂房【例9】(单选)2010年乙公司发出原材料一批,成本为100万元,其购入时支付的增值税为17万元。
第二章空气、物质的构成 知识点及典型例题总结
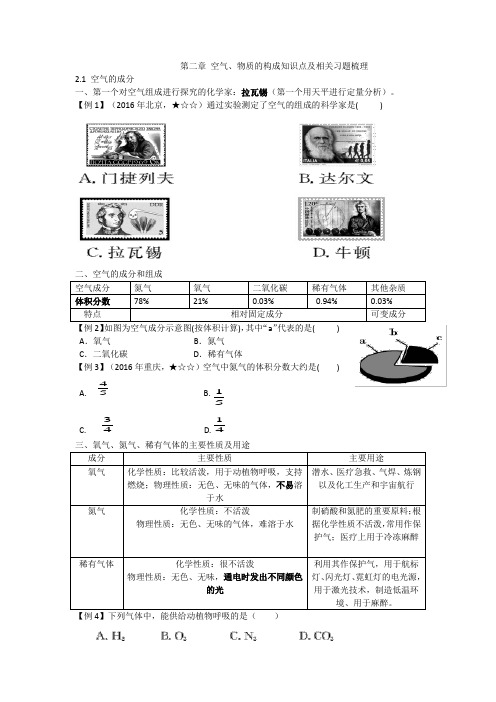
第二章空气、物质的构成知识点及相关习题梳理2.1 空气的成分一、第一个对空气组成进行探究的化学家:拉瓦锡(第一个用天平进行定量分析)。
【例1】(2016年北京,★☆☆)通过实验测定了空气的组成的科学家是( )空气成分氮气氧气二氧化碳稀有气体其他杂质体积分数78%21% 0.03% 0.94% 0.03%特点相对固定成分可变成分A.氧气B.氮气C.二氧化碳D.稀有气体【例3】(2016年重庆,★☆☆)空气中氮气的体积分数大约是( )A. 54B.51C. 43D.41成分主要性质主要用途氧气化学性质:比较活泼,用于动植物呼吸,支持燃烧;物理性质:无色、无味的气体,不易溶于水潜水、医疗急救、气焊、炼钢以及化工生产和宇宙航行氮气化学性质:不活泼物理性质:无色、无味的气体,难溶于水制硝酸和氮肥的重要原料;根据化学性质不活泼,常用作保护气;医疗上用于冷冻麻醉稀有气体化学性质:很不活泼物理性质:无色、无味,通电时发出不同颜色的光利用其作保护气,用于航标灯、闪光灯、霓虹灯的电光源,用于激光技术,制造低温环境、用于麻醉。
【例4】下列气体中,能供给动植物呼吸的是()【例5】空气中的下列气体,属于稀有气体的是( ) A .He B.N 2 C .O 2 D.CO 2 【例6】下列关于空气的说法正确的是( ) A .空气由空气分子构成 B.N 2、O 2等均匀混合C.N 2、O 2不再保持各自的化学性质D.N 2、O 2的体积比约为5∶1 四、空气的污染及防治1、空气的污染源:工业污染、生活污染、交通污染、农业污染2、对空气造成污染的主要是有害气体(二氧化硫、一氧化碳、二氧化氮、烟尘)3、空气污染的危害:损害人体健康,影响作物生长,破坏生态平衡,导致全球气候变暖、臭氧层破坏和酸雨等。
4、保护空气措施:加强大气质量监测,改善环境状况,使用清洁能源,积极植树、造林、种草等。
5、城市空气质量日报、预报空气质量日报的主要内容包括“空气污染指数”“首要污染物”“空气质量级别”“空气质量状况”等,根据我国空气污染的特点和污染防治重点,目前计入空气污染指数的项目暂定为:二氧化硫、一氧化碳、二氧化氮、可吸入颗粒物和臭氧等。
例题2

∆λ =
λ
m1
= 0.75 × 10−4 µm
第2章 光的干涉 例 2-5 观察迈克尔逊干涉仪,我们看到一个由同心明、暗 环所包围的圆形中心暗斑。该干涉仪的一个臂比另一个臂长2 cm,且λ=0.5µm。试求中心暗斑的级数,以及第6个暗环的级数。 解: 对于由虚平板产生的等倾干涉条纹, 最小值满足如 下干涉条件:
∆ = 2h n − n sin θ1 +
2 2 0 2
λ
2
m=1,2,…
在观察到膜最亮时,应满足干涉加强的条件
∆ = 2h n − n sin θ1 +
2 2 0 2
λ
2
= mλ
第2章 光的干涉 由此可得膜厚h为
1 m − λ 2 h= 2 2 n 2 − n0 sin 2 θ1
TM = 1 − A 0.1 = 1− = 63% 1− R 1 − 0.7314
由上面的讨论可以看出,提高光的透过率与压缩∆λ1/2 是相 互制约的, 需要根据实际要求折衷考虑。
θ1 N
1 = n0
nλ N d
第2章 光的干涉 因而第N个暗环半径的表示式为
rN = f tan θ1N ≈ fθ1N
第一个暗环的半径为
f = n0
nλ N d
f r1 = n0
nλ = 0.95cm d
为能看到干涉环,最大允许谱线宽度∆λ应满足
m1 (λ + ∆λ ) = ( m1 + 1)λ
第2章 光的干涉 例 2-3 用λ=0.5µm的绿光照射肥皂膜,若沿着与肥皂膜平面 成30°角的方向观察,看到膜最亮。假设此时的干涉级次最低, 并已知肥皂水的折射率为1.33,求此膜的厚度。当垂直观察时, 应改用多大波长的光照射才能看到膜最亮? 解: 已知由平行平板两表面反射的两支光的光程差表示式 为
第2章 资产 教材上的例题 自己写会计分录 答案在教材上

【例2-2】甲企业为增值税一般纳税人,向银行申请办理银行汇票用以购买原材料,将款项250000元交存银行转作银行汇票存款,根据银行盖章退回的申请书存根联,企业编制如下分录:甲企业购入原材料一批,取得的增值税专用发票上的原材料价款为200000元,增值税税额为34000元,已用银行汇票办理结算,多余款项16000元退回开户银行,企业已收到开户银行转来的银行汇票第四联(多余款收账通知)。
企业编制如下会计分录:【例2-3】甲企业为增值税一般纳税人,为取得银行本票,向银行填交“银行本票申请书”,并将10000元银行存款转作银行本票存款。
企业取得银行本票后,应根据银行盖章退回的银行本票申请书存根联填制银行付款凭证,企业编制如下会计分录:甲企业用银行本票购买办公用品10000元。
根据发票账单等有关凭证,编制会计分录:【例2-4】甲企业于2017年8月24日向银行申请信用卡,向银行交存50000元。
2017年9月10日,该公司用信用卡向新华书店支付购书款3000元,增值税专用发票上注明的增值税税额为390元。
甲企业编制如下分录:【例2-5】甲公司向银行申请开具信用证2000000元,用于支付境外采购材料价款,公司已向银行缴纳保证金,并收到银行盖章退回的进账单第一联。
甲公司编制如下会计分录:甲公司收到银行转来的境外销货单位信用证结算凭证以及所附发票账单、海关进口增值税专用缴款书等有关凭证,材料价款1500000元,增值税税额为255000元。
甲公司编制如下会计分录:甲公司收到银行收款通知,对该境外销货单位开出的信用证余款245000元已经转回银行账户。
甲公司编制如下会计分录:【例2-6】甲公司派采购员到异地采购原材料,2×12年8月10日委托开户银行汇款100000元到采购地设立采购专户,根据收到的银行汇款凭证回单联。
甲公司应编制如下会计分录:2×12年8月20日,采购员交来从采购专户付款购入材料的有关凭证,增值税专用发票上的原材料价款为80000元,增值税税额为13600元,甲公司应编制如下会计分录:2×12年8月30日,收到开户银行的收款通知,该采购专户中的结余款项已经转回,根据收账通知,甲公司编制如下会计分录:【例2-7】甲公司为一般纳税人,2017年9月1日向乙公司(为增值税一般纳税人)销售一批产品,价款为1500000元,尚未收到,已办妥托收手续,适用的增值税税率为17%。
第2章 例题习题
6. 结构的动弯矩幅值图:
返回目录 14
结构的动弯矩幅值图:
11
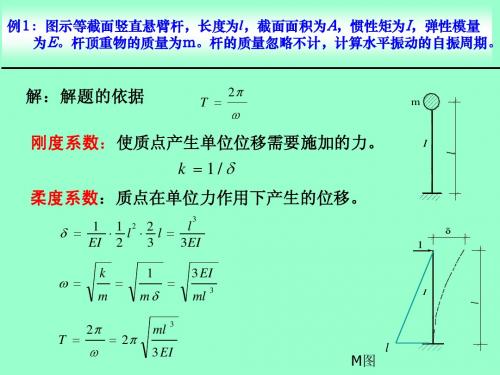
例7. 试求图示体系的自振频率及质量m的最大动力位移, 设θ=0.
5ω ,弹簧刚度k=0.05EI/l 3, 各杆EI相同。(天津大学1996年)
m B Fsin t θ A l C l/ 2 l/ 2 D F=1 l l/ 2 l/ 2 F= 1 l
MP
1P
1/2
M1
解:解题的依据
T
2
m I
l
刚度系数:使质点产生单位位移需要施加的力。
k 1/
柔度系数:质点在单位力作用下产生的位移。
1 1l 2l l
2
3
EI 2
3
3EI
1
k 1 3EI m m m l3
I
m l3 T 2图示结构的重量集中为柱顶,W=20KN,试计算结构 的自振周期。EI1=3.528107Nm2. I=∞
l
0.5 l
0.5 l
6
一、判断题
5. 在动力计算中,以下两图所示结构的动力自由
度相同(各杆均为无重弹性杆)。
m1 m2 m1
( ╳ )
m3
m4
m2
7
二、选择填空
1. 体系的跨度、约束、质点位置不变,下列哪种况自 振频率最小: ( D ) A.质量小,刚度小 B.质量大,刚度大 C.质量小,刚度大 D.质量大,刚度小 2. 已知一单自由度 体系的阻尼比为=1.2,则该体系自 由振动时的位移方程曲线的形状可能为。 ( D )
体系自由振动的频率: 3 1 1 1 l l 2 l 2 l k EI 2 2 4 3 4 48EI 动力系数: 5.93
第2章 2.1二元一次方程(主要知识点概述例题解析同步练习)

好题、较难题拓展训练打开思维,突破自我一、选择题1.甲、乙两人练习赛跑,若甲先跑半小时,则乙出发后40分钟可追上甲,设甲、乙每小时分别跑x千米、y千米,则可列方程()A.0.5x=40y B.C.(0.5+40)x=40y D.2.(2016•齐齐哈尔)足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队共进行了6场比赛,得了12分,该队获胜的场数可能是()A.1或2 B.2或3 C.3或4 D.4或53.(2016春•威远县校级期中)方程(m﹣2016)x|m|﹣2015+(n+4)y|n|﹣3=2018是关于x、y的二元一次方程,则()A.m=±2016;n=±4 B.m=2016,n=4 C.m=﹣2016,n=﹣4 D.m=﹣2016,n=4二、填空题4.(2016春•启东市校级期中)已知方程2x+y﹣4=0,当x与y互为相反数时,则x=.5.(2014春•吴中区期末)把二元一次方程﹣=1化为y=kx+b的形式,得.6.(2015春•宿迁校级期末)写出一个二元一次方程,使其满足x 的系数是大于2的自然数,y 的系数是小于﹣3的整数,且x=2,y=3是它的一个解. .三、解答题7.已知关于x 、y 二元一次方程3x +5y=10的两个解为,,若m ﹣s=3.(1)求的值;(2)若将二元一次方程“3x +5y=10”,改为二元一次方程“3x +by=10”,其他条件不变,求的值;(3)若将二元一次方程“3x +5y=10”,改为二元一次方程“3x +by=10”,“m ﹣s=3”改为“m ﹣s=k”,其他条件不变,求的值;(4)在(3)中,若将二元一次方程“3x +by=10”,改为二元一次方程“ax +by=c”其他条件不变,求的值.8.(2016春•重庆校级月考)进制也就是进位制,是人们利用符号进行计数的科学方法.对于任何一种进制X 进制,就表示某一位置上的数运算时逢X 进一位,如十进制数123=1×102+2×101+3×100,记作123(10); 七进制123=1×72+2×71+3×70,记作123(7).各进制之间可进行转化,如:将七进制转化为十进制:123(7)=1×72+2×7+3×70=66,即123(7)=66(10),将十进制转化为七进制:(因为72<66<73,所以做除法从72开始)66÷72=1…17,17÷71=2…3,即66(10)=123(7) (1)根据以上信息,若将八进制转化为十进制:15(8)=1×81+5×80=13,即15(8)=(10);若将十进制转化为九进制:98÷92=1…17,17÷91=1…8,即98(10)=(9)(2)若将一个十进制两位数转换成九进制和八进制数后,得到一个九进制两位数和一个八进制两位数,首位分别2,3,个位分别为x ,y . ①若x=7,则y= .②请求出满足上述条件的所有十进制两位数.9.(2015春•亭湖区期末)【方法阅读】一般地,二元一次方程的解有无数个,但是有些二元一次方程的正整数解却只有有限个,如二元一次方程2x+3y=15的正整数解只有和两个.那么,我们如何寻找二元一次方程的正整数解呢?不妨以方程2x+3y=15为例,首先过程方程各项的特征,发现2x和15分别是偶数和奇数,可以确定3y必然是奇数,即y是奇数,再运用特值法代入尝试,即将y=1,3,5,…等奇数代入原方程一次求出相应的x的值,从而获得2x+3y=15的正整数解.同学们还可以尝试运用列表法来探索二元一次方程的正整数解.【理解运用】(1)盒子里有若干个大小相同的红球和白球,规定从中摸出一个红球的3分,摸到一个白球的4分,假设小华摸到x个红球和y个白球,共得34分,请你列出关于x、y的方程,并写出这个方程符合实际意义的所有的解.【灵活运用】(2)已知△ABC的三边m,n,p都是正整数,m,n,p,且△ABC的周长为15,则符合条件的三角形共有个.10.(2015春•衡阳县期中)观察图,解答后面的问题.梯形个数1 2 3 4 5 6…周长5 8 11 14…(1)把表中的空格填上适当的数据:123456…梯形个数周长5811141720…(2)写出周长L和梯形个数n之间的二元一次方程;(3)求n=2015时L的值;(4)求L=6053时n的值.11.(2014春•宝应县期末)某电视台在黄金时段的2分钟广告时间内,计划插播长度为15秒和30秒的两种广告.15秒广告每播1次收费0.8万元,30秒广告每播1次收费1.5万元.若要求每种广告播放不少于2次.问:(1)两种广告的播放次数有几种安排方式?(2)电视台选择哪种方式播放收益较大?12.若整系数方程ax+by=c(ab≠0)有整数解,则(a,b)|c,反之,若(a,b)|c,则整系数方程ax+by=c(ab≠0)有整数解.其中(a,b)表示a,b的最大公约数,(a,b)|c表示(a,b)能整除c.根据这种方法判定下列二元一次方程有无整数解.(1)3x+4y=33;(2)2x+6y=15.参考答案:一、选择题1.解:设甲、乙每小时分别跑x千米、y千米,则可列方程:∵40÷60=,∴(0.5+)x=y.故选:D.2.解:设该队胜x场,平y场,则负(6﹣x﹣y)场,根据题意,得:3x+y=12,即:x=,∵x、y均为非负整数,且x+y≤6,∴当y=0时,x=4;当y=3时,x=3;即该队获胜的场数可能是3场或4场,故选:C.3.解:∵(m﹣2016)x|m|﹣2015+(n+4)y|n|﹣3=2018是关于x、y的二元一次方程,∴m﹣2016≠0,n+4≠0,|m|﹣2015=1,|n|﹣3=1.解得:m=﹣2016,n=4.故选:D.二、填空题4.解:∵x与y互为相反数,∴y=﹣x,∴2x﹣x﹣4=0,解得x=4.故答案为:4.5.解:把二元一次方程﹣=1化为y=kx+b的形式,得y=﹣x+.故答案为:y=﹣x+.6.解:答案不唯一,如3x﹣4y=﹣6.三、解答题7.解:(1)∵关于x、y二元一次方程3x+5y=10的两个解为,,∴3m+5n=10①,3s+5t=10②,①﹣②得,3m+5n﹣3s﹣5t=0,解得3(m﹣s)+5(n﹣t)=0,∴=﹣;(2)∵与是二元一次方程3x+by=10的解,m﹣s=3,∴3m+bn=10①,3s+bt=10②,①﹣②得,3m+bn﹣3s﹣bt=0,解得3(m﹣s)+b(n﹣t)=0,∴=﹣;(3)同(1)可得,=﹣;(4)同(1)可得,=﹣.8.解:(1)∵15(8)=1×81+5×80=13,∴15(8)=13(10);∵98÷92=1…17,17÷91=1…8,∴98(10)=118(9).故答案为:13;118.(2)①2x=2×9+x=25,(9)25÷81=3…1,∴y=1.故答案为:1.②由题意得:九进制两位数和八进制两位数分别是2x和3y,则2×9+x=3×8+y,∴x=6+y,∵x≤8,∴x=6、7、8.则九进制数分别是26、27、28.∴十进制两位数分别是24、25、26.9.解:(1)依题意得:3x+4y=34,有三个正整数解为,,;(2)设m≥n≥p,则由m+n+p=15,得m≥5.用试值法或者枚举法可得:,,,,,,.所以符合条件的三角形共有7个.故答案是:7.10.解:(1)由图中可以看出图形的周长=上下底的和+两腰长,梯形个数为1时,周长为3+2=5;梯形个数为2时,周长为2×3+2=8;梯形个数为3时,周长为3×3+2=11;…L=3n+2.当n=5时,L=3×5+2=17.当n=6时,L=3×6+2=20.故答案是:17;20.(2)由(1)知,周长L和梯形个数n之间的二元一次方程是:L=3n+2.(3)当n=2015时,L=3×2015+2=6047;(4)当L=6053时,3n+2=6043,解得n=2017.11.解:设15秒的广告播x次,30秒的广告播y次.则15x+30y=120,∵每种广告播放不少于2次,∴x=2,y=3,或x=4,y=2当x=2,y=3时,收益为:2×0.6+3×1=4.2万元;当x=4,y=2时,收益为4×0.6+1×2=4.4万元∴电视台在播放时收益最大的播放方式是:15秒的广告播放4次,30秒的广告播放2次.(2)当x=4,y=2时,0.8×4+1.5×2=6.2(万元)当x=2,y=3时,0.8×2+1.5×3=6.1(万元)所以,选择播放15秒的广告4次,播放30秒的广告2次,收益最大.12.解:(1)3,4的最大公约数是1,1能整除33,所以3x+4y=33有整数解;(2)2,6的最大公约数是2,2不能整除15,所以2x+6y=15无整数解.。
第二章例题总结

市场证券组合的报酬率为13%,国库券的利息率为5%。
要求:(1)计算市场风险报酬率;(2)当β值为1.5时,必要报酬率应为多少?(3)如果一个投资计划的β值为0.8,期望报酬率为11%,是否应当进行投资?(4)如果某种股票的必要报酬率为12.2%,其β值应为多少?(10分)1.市场风险报酬率=市场证券组合的报酬率-国库券的利息率=13%-5%=8%.2.必要报酬率=无风险利率+β*(预期报酬率-无风险利率)=8%+1.5*(13%-8%)=15.5%3投资计划必要报酬率=无风险利率+β*(预期报酬率-无风险利率)=8%+0.8*(11%-8%)=10.4%投资计划必要报酬率10.4%<期望报酬率为11%,所以不应当进行投资;4.12.2%=8%+β*(12.2%-8%)β=1第二章例题总结例一、将1000元钱存入银行,年利息率为7%,按复利计算,5年后终值应为多少?解答:FV5=P V·(1+i)5=1000*(1+7%)5=1403元或FV5=PV·FVIF5,%,7=1000*1.403=1043元例二、若计划在3年以后得到2000元,年利息率为8%,复利计息,则现在应存金额为多少?解答:PV=FVn ·PVIF3%,8=2000*0.794=1588元例三、某人在5年中每年年底存入银行1000元,年存款利率8%,复利计息,则第5年年末年金终值为多少元钱?解答:FV A5=A·FVIFA5,%,8=1000*5.867=5867元例四、某人准备在今后5年中每年年末从银行取1000元,如果利息率为10%,则现在应存入多少元钱?解答:PVA5=A·PVIFA5%,10=1000*3.791=3791元例五、某人每年年初存入银行1000元,银行年存款利率为8%,则第10年年末约本利和应为多少?解答:XFVA10=1000·FVIFA10%,8·(1+8%)=1000*14.487*1.08=15646元或XFVA10=1000*(FAIFA11%,8-1)=1000*(16.645-1)=15645元例六、某企业租用一套设备,在10年中每年年初要支付租金5000元,年利息率为8%,则这些租金的现值为多少?解答:XPVA10=5000·PVIFA10%,8·(1+8%)=5000*6.71*1.08=36234元或XPVA10=5000·(PVIFA9%,8+1)=5000*(6.247+1)=36235元例七、某企业向银行借入一笔款项,银行贷款的年利息率为8%,银行规定前10年不需要还本付息,但第11-12年每年年末偿还本息1000元,则这笔款项的现值是多少?解答:V0=1000·PVIFA10%,8·PVIF10%,8=1000*6.710*0.463=3107元或V0=1000·(PVIFA20%,8- PVIFA10%,8)=1000*(9.818-6.710)=3108元例八、一项每年年底的收入为800元的永续年金投资,利息率为8%,则其现值为多少?解答:V0=800*%81=10000元例九、某人每年年末都将节省下来的工资存入银行,其存款额如下表所示,贴现率为5%,求这笔不等额存款的现值。
第2章例题

6 1
0.047
x
n
0.047 6
0.019
若按正态分布计算,取 0.01 ,相应 的置信概率 p 1 0.99 ,由附录表1查得 t=2.60,则算术平均值的极限误差为:
lim x t x 2.60 0.019 0.049
因测量次数较少,应按t分布计算算术平均值的极限误差。 03 已知 v n 1 5 ,取 0.01,则由附录表3查得 ta 4., 则有:
求各测量结果的权。 解:由式(2-42)得
p1 : p2 : p3 1
2 x1
:
1
2 x2
:
1
2 x 3
1 1 1 : : 16 : 1 : 4 2 2 2 (0.05) (0.20) (0.10)
因此各组的权可取为
p1 16, p 2 1, p3 4
求例2-10 加权算术平均值
p1 3, p2 2, p3 5
选 x0 999.94mm,则有
3 0.0025 2 0.0016 5 0.0019 x 999.94mm mm 999.9420mm 3 25
例2-12 求例2-11的加权算术平均值的标准差。 x 解:由加权算术平均值 x 999.9420mm,可得各组 测量结果的残余误差:
pi
i
p
i 1
m
4 0.10 0.04mm 16 1 4
i
2 p v i xi
求例2-10 加权算术平均值标准差
x 1 2000.45mm, x1 0.05mm
x 2 2000.15mm, x 2 0.20mm p2 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
<1,1>~<2,2>~<3,3>~<4,4>.
<1,4>~<1,4>.
<4,1>~<4,1>.
差为±3.
集合与图论
1.12
哈尔滨工业大学软件学院பைடு நூலகம்
李东 副教授
R的等价划分有:{<1,2>,<2,3>,<3,4>}。
等价划分的 并集等于 AXA.
S ○ R ={< {Φ} ,{Φ}>}.
集合与图论
1.26
哈尔滨工业大学软件学院
李东 副教授
domR= {Φ,{{Φ}},{Φ}}. ran S= { Φ }. R-1= {<{{Φ}},{Φ}>,<{Φ},{{Φ}}>, <{Φ},Φ>}.
集合与图论
1.27
哈尔滨工业大学软件学院
李东 副教授
例12 已知R的关系图如下, 求r(R),s(R )和t(R )的关系图。
解:因为A =P({Φ}) ={Φ,{Φ}}. 所以,P(A)= {Φ,{Φ}, {{Φ}},{Φ,{Φ}}}. 则: P(A)X{Φ}={< Φ, Φ>, < {Φ} , Φ>, < {{Φ}} , Φ>, < {Φ,{Φ}}, Φ>}.
集合与图论
1.25
哈尔滨工业大学软件学院
李东 副教授
例题分析
集合与图论 1.10 哈尔滨工业大学软件学院 李东 副教授
例题分析(7)
例5 A={1,2,3,4},R为AXA上的等价关系
u, v , x, y A A, u, v R x, y u y x v
求出由R引起的A的划分。
解: u , v R
集合与图论 1.8 哈尔滨工业大学软件学院 李东 副教授
答:只有(4)中的R是A上的等价关系
(1)中的R不是自反的,因为x-x=0≠2。另 外,R也不是对称的,不是传递的。 (2)中的R不是传递的,因为1R3, 3R2 成 立,但1R2不成立. (3)中的R不是自反的,因为2R2不成立. (5)中的R不是传递的,例如X={a,b}. P(X)={Φ,{a},{b},{a,b}},则有{a}R{a,b}, {a,b}R{b},但没有{a}R{b}。
集合与图论 1.23 哈尔滨工业大学软件学院 李东 副教授
(4)由于要将弧度映射到实数.所 以,首先想到三角函数:
将π/2映射到 –1,将3π/2映射到1 ,正好是:f(x)=-sinx .
集合与图论
1.24
哈尔滨工业大学软件学院
李东 副教授
例题分析(6)
二.计算题:
例9 已知A=P({Φ}),求P(A)X{Φ}?
集合与图论
1.21
哈尔滨工业大学软件学院
李东 副教授
1 / 2, x 0, 1 / 4, x 1, (2) f ( x) n 2 n 1 / 2 , x 1 / 2 , n 1 , 2 , 3 ,... x, otherwise.
集合与图论
1.22
所以f(L)= {<2x+1,-1>|x∈R}=RX{-1}. (7)能构成函数,但既不是单射也不是满射.因 为f(<1,1>)=f(<2,2>)=0,2不属于ranf。 f(NX{0})= {n2-02|n∈N}= {n2|n∈N}.
集合与图论 1.19 哈尔滨工业大学软件学院 李东 副教授
例题分析(10)
例题分析(1)
一.概念题:
例1 判断下列命题是否为真:
(1)设A,B,C为任意集合,若AXB=AXC,则 B=C. (2)设A,B,C为任意集合,则A-(BXC)=(A-B) X(A-C). (3)若<2x+y,6>=<5,x+y>,则x=-1,y=7.
(4)若R1,R2在A上是反对称的,则R1∪R2 在A上也是反对称的.
x, y u y x v u v x y.
即两个有序对等价的充要条件是第1个元素 减第2个元素所得的差相等。
集合与图论 1.11 哈尔滨工业大学软件学院 李东 副教授
则AXA上等价的有序对有: 差为±1. <1,2>~<2,3>~<3,4>.
<2,1>~<3,2>~<4,3>.
集合与图论 1.2 哈尔滨工业大学软件学院 李东 副教授
例题分析(3)
(3)为真.
(4)为假. (5)为真. 例如A上的恒等关系既是等价关系 ,也是偏序关系. (6)不是恒真命题. 只能说:若f:A→B为单射,则f-1:ranf→A也为单 射.这里ranf B.
集合与图论
1.3
哈尔滨工业大学软件学院
李东 副教授
( x) 2 , (x R ). x 1 6.A=B=RXR,f(<x,y>)=<x+y,x-y>,令 L={<x,y>|x,y∈R∧y=x+1},计算f(L).
5.A=B=R+, f
x
7.A=NXN,B=N,f(<x,y>)=|x2-y2|,计算f(NX{0}). 答: (1)能构成函数,但既不是单射也不是满射. (2)不能构成函数,因为<1,7>∈f且<1,9>∈f.
集合与图论
1.5
哈尔滨工业大学软件学院
李东 副教授
例题分析(5)
例3 已知A={1,2,3},R为A上的关系,且
1 0 0 MR 1 1 0 . 1 0 0
写出R的关系表达式,画出R的关系图, 并说明R的性质。
集合与图论
1.6
哈尔滨工业大学软件学院
李东 副教授
解:R={<1,1>, <2,1>, <2,2>, <3,1>}。
例8对于给定的集合A、B,构造 双射函数f:A→B. 1.A=[0,1], B=[0.25, 0.5]。 2.A=[0,1], B=(0, 1)。 3.A=Z,B=N.
3 4.A=[
, ],B=[-1, 2 2
1].
集合与图论
1.20
哈尔滨工业大学软件学院
李东 副教授
答: 构造双射函数最简单的就是直 线方程.所以,(1)的解就是<0,0.25> 到<1,0.5>的直线方程: f(x)=(x+1)/4。 对于象(2)这样值域和定义域的开闭情 况不一样的问题,通常的做法是:在区间 内选择一个无穷序列,将端点对应到序列 的前部,其余的向后错位对应。
例10 已知R={<{Φ},{{Φ}}>, <{{Φ}},{Φ}>, <Φ,{Φ}>},S= {<{Φ},Φ>}. 求R2,R ○ S,S ○ R ,domR,ranS和R-1? 解: R2=R ○ R ={<{Φ},{Φ}>, <{{Φ}},{{Φ}}> ,<Φ,{{Φ}}>}.
R ○ S= {<{{Φ}},Φ>,< Φ,Φ>}.
集合与图论 1.9 哈尔滨工业大学软件学院 李东 副教授
(4)中的R是自反的,因为:
x A, xRx x x C.
R是对称的,因为:
x, y A, xRy yRx. x y y x.
R是传递的,因为:
x, y, z A, xRy, yRz xRz. x z x y y z ( x y ) ( y z ).
哈尔滨工业大学软件学院
李东 副教授
(3)由于要将整数集Z以双射的形 式映射到自然数集.所以,特构造如 下映射方法: Z: 0 1 -1 2 -2 3 -3……
N: 0 1 2 3 4 5 6…… 则这种映射对应的函数为:
f : Z N. 2 x, x 0. f ( x) 2 x 1, x 0
李东 副教授
例题分析(4)
例2 已知A={1,2,3,4},
列出以下关系中的元素?
(1)x, y A, xRy 3 | ( x y). (2)x, y A, xRy x | y x y. (3)x, y A, xRy | x || y | . (4)x, y A, xRy x y y x. (5)x, y A, xRy x y Z .
{<2,1>,<3,2>,<4,3>}。 {<3,1>,<4,2>}。 {<1,3>,<2,4>}。
{<1,1>,<2,2>,<3,3>,<4,4>}。
{<1,4>}。 {<4,1>}。
集合与图论
1.13
哈尔滨工业大学软件学院
李东 副教授
例题分析(8)
例6 已知X为集合,A=P(X)-{Φ}-{X},且 A≠Φ,问: 1.偏序集<A, R >是否存在最大元?
集合与图论 1.4 哈尔滨工业大学软件学院 李东 副教授
解: (1)R={<1,4>, <4,1>} ∪IA (2)R={<1,2>, <1,3>, <1,4>, <2,4>} (3)R={<1,2>, <1,3>, <1,4>, <2,3>, <2,4> ,<3,4>}. (4)R=EA-IA. (5)R=Φ.
