湖北省长阳县第一高级中学高二数学上学期期中试题理
湖北高二高中数学期中考试带答案解析

湖北高二高中数学期中考试班级:___________ 姓名:___________ 分数:___________一、选择题1.已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a+b互相垂直,则k的值是A.1B.-1C.D.2.曲线在点A(2,10)处的切线的斜率是A.4B.5C.6D.73.等于A.-2ln2B.2ln2C.-ln2D.ln24.已知点A(1,-2,0)和向量a=(-3,4,12),若向量a,且,则B点的坐标为A.(-5,6,24)B.(-5,6,24)或(7,-10,-24)C.(-5,16,-24)D.(-5,16,-24)或(7,-16,24)5.直线y=x与抛物线y=x(x+2)所围成的封闭图形的面积等于A.B.C.D.6.若向量a=(1,0),b=(2,0,0)且a与b的夹角为,则等于A.1B.C.-或D.-1或17.为正方形,平面,,则与所成角的度数为A.30°B.45°C.60°D.90°8.已知则当时,n的最小值是A.9B.10C.11D.129.在正方体中,E是棱的中点,则BE与平面所成角的正弦值为A.B.C.D.10.已知二次函数的导数为,,对于任意实数,有,则的最小值为A .B .C .D .二、填空题1.已知向量,若,则______;2.已知,对任意实数x ,不等式恒成立,则m 的取值范围是 。
3.从1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…,推广到第个等式为 _________________________.4.一桥拱的形状为抛物线,已知该抛物线拱的宽为8米,抛物线拱的面积为160平方米,则抛物线拱的高等于5.若函数的单调增区间为(0,+∞),则实数的取值范围是________.三、解答题1.(本题满分10分) 设函数为奇函数,其图象在点处的切线与直线垂直,导函数的最小值为.试求,,的值。
湖北省长阳县第一高级中学2014-2015学年高二上学期期中考试数学(理)试题

湖北省长阳县第一高级中学2014-2015学年高二上学期期中考试数学(理)试题考试时间:120分钟 试卷总分:150分第Ⅰ卷 选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 某研究性学习课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( ) A .6B . 8C .10D .122.已知α是第二象限角,且3sin()5πα+=-,则tan 2α的值为( ) A .54 B .723- C .724-D .3-3.如右图所示,程序框图(算法流程图)的输出结果是 ( ) A .16B .2524 C .34 D .11124.由表可得回归直线方程a x yˆ56.0ˆ+=,据此模型预报身高为cm 172的男生的体重大约为( )A .70.09 kgB .70.12 kgC .70.55 kgD .71.05 kg 5.若直线l :y =kx -3与直线x +y -3=0的交点位于第二象限,则直线l 的倾斜角的取值范围是( )A . 3(,]24ππB . 3[,)24ππC . 3(,)34ππD . 3(,)24ππ6.在△ABC 中,AB →2+AB →·BC →<0,则△ABC 为A .锐角三角形B .直角三角形C .钝角三角形D .锐角或钝角三角形7.已知函数x x x f ωωco s sin )(+=,如果存在实数1x ,使得对任意的实数x ,都有)2014()()(11+≤≤x f x f x f 成立,则ω的最小正值为( )1350A.2014πB.20141 C. 40281 D. 4028π 8.如图,四棱锥S-ABCD 的底面为正方形,SD ⊥底面ABCD , 则下列结论中不正确...的是( ) A .AC ⊥SBB .AB ∥平面SCDC .AB 与SC 所成的角等于DC 与SA 所成的角D .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 9.在区间[]3,3-上任取一个数a ,则圆221:450C x y x ++-=与圆()222:1C x a y -+=有公共点的概率为( )A .23 B .13C .16D .5610.已知ABC Rt ∆的斜边AB 的长为4,设P 是以C 为圆心1为半径的圆上的任意一点,则⋅的取值范围是( ) A. ]25,23[-B. ]25,25[- C. ]5,3[- D. ]321,321[+-第Ⅱ卷 非选择题部分(共100分)二、填空题:本大题共5小题,每小题5分,把答案填在相应题号后的横线上。
湖北省长阳县第一高级中学2014-2015学年高二上学期期中考试数学(文)试题

考试时间:120分钟 试卷总分:150分第Ⅰ卷 选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某研究型学习课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( ) A .6 B .8 C .10 D .12 2.已知α是第二象限角,且3sin()5πα+=-,则tan 2α的值为 ( ) A .45 B .237- C .247-D .257- 3.如右图所示,程序框图(算法流程图)的输出结果是( )A .16B .2524 C .34 D .11124.由上表可得回归直线方程ˆˆ0.56yx a =+,据此模型预报身高为172cm 的男生的体重大约为( )A .70.09kgB .70.12kgC .70.55kgD .71.05kg5.若直线l :y =kx -3与直线x +y -3=0的交点位于第二象限,则直线l 的倾斜角的取值范围是( ) A . 3(,]24ππB . 3[,)24ππC . 3(,)34ππD . 3(,)24ππ6.在△ABC 中,AB →2+AB →·BC →<0,则△ABC 为( )A .锐角三角形B .直角三角形C .钝角三角形D .锐角或钝角三角形 7.要得到函数sin cos y x x =-的图象,只需将函数sin cos y x x =+的图象 A .向右平移2π个单位长度 B .向左平移2π个单位长度C .向右平移π个单位长度D .向左平移π个单位长度8.如图,四棱锥S ABCD -的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确...的是( ) A .AC SB ⊥ B .AB ∥平面SCDC .AB 与SC 所成的角等于DC 与SA 所成的角D .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角9.已知函数x x x f ωωcos sin )(+=,如果存在实数1x ,使得对任意的实数x ,都有)2014()()(11+≤≤x f x f x f 成立,则ω的最小正值为( )A. 20141B. 2014πC. 40281D. 4028π10.已知ABC Rt ∆的斜边AB 的长为4,设P 是以C 为圆心1为半径的圆上的任意一点,则PB PA ⋅的取值范围是( ) A. ]25,23[-B. ]25,25[- C. ]5,3[- D. ]321,321[+- 第Ⅱ卷 非选择题部分(共100分)二、填空题:本大题共7小题,每小题5分,把答案填在相应题号后的横线上。
湖北省长阳县第一高级中学高二数学上学期第一次月考试题理(无答案)

长阳一中2016—2017学年度第一学期第一次月考高二数学试卷(理科)考试时间:120分钟 试卷总分:150分一、选择题(60分)1;条件:q 直线2y kx =+与圆221x y +=相切,则p ¬是q ¬的( )A .充分必要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件2. 下列四个结论:①ABC ∆中,P:A >B,Q:sinA >sinB,P 是Q 的充分不必要条件 ②在频率分布直方图中,中位数左边和右边的直方图的面积相等; ③“命题p q ∨为真”是“命题p q ∧为真”的充分不必要条件; ④命题“,ln 0x R x x +∀∈->”的否定是“000,ln 0x R x x +∃∈-≤”.其中正确结论的个数是 ( ) A .1个B .2个C .3个D .4个3.若直线(a+2)x+(1-a)y=3与直线(a-1)x+(2a+3)y+2=0互相垂直,则a 等于 ( )A .1B .-1C .±1D .-24.已知甲、乙两组数据如图茎叶图所示,若它们的中位数相同,平均数也相同,则图中的,m n 的)A B C D .1 5.已知x ∈(0,π],关于x 的方程2sin ⎝⎛⎭⎪⎫x +π3=a 有两个不同的实数解,则实数a 的取值范围为( )A .[-3,2]B .[3,2]C .(3,2]D .(3,2)6.把)8(2016化成二进制为( )A.)2(010********B.)2(010********C.)2(11000001110D.)2(010********7. 在区间[]1,1-上随机取一个数x ,0 )A B C . D 8. 称na 1+a 2+…+a n为n 个正数a 1+a 2+…+a n 的“均倒数”已知数列{a n }的各项均为正,且其前n项的“均倒数”为12n -1则数列{a n }的通项公式为( ). A .2n -1 B .4n -3C .4n -1D .4n -59.程序框图如下:如果上述程序运行的结果S 的值比2016小,若使输出的S 最大,那么判断框中应填入 A .10k ≤ ? B .10k ≥ ? C .9k ≤ ? D .9k ≥? 10.从甲袋中摸出1个红球的概率是31,从乙袋中摸出1个红球的概率是21,从两个袋子中个摸出一个球,则32等于() A .2个球都不是红球的概率 B.2个球都是红球的概率 C .2个球恰好有1个是红球的概率 D.至少有一个是红球的概率11.如图,四面体ABCD 中,,二面角A BD C --的平面角的大小为60,,E F 分别是,BC AD 的中点,则异面直线EF 与AC 所成的角的余弦值是( )A B C D 12.一个三位自然数abc 的百位,十位,个位上的数字依次为,,a b c ,当且仅当a b >且c b >时称为“凹数”.若}7,6,5,4{,,∈c b a ,且,,a b c 互不相同,任取一个三位数abc ,则它为“凹数”的概率是( )A B C D二.填空题(20分)13.某产品的广告费用x 与销售额y 的统计数据如表:根据表格已得回归方程为ˆ9.49.1yx =+,表中有一数据模糊不清,请推算该数据的值为____________.14.采用系统抽样方法从960人中抽取32人做问卷调查。
2020-2021学年湖北省宜昌市长阳一中高二(上)期中数学试卷

2020-2021学年湖北省宜昌市长阳一中高二(上)期中数学试卷一、选择题(每小题5分,共12小题60分)1.(5分)已知经过两点(5,m)和(2,8)的直线的斜率大于1,则m的取值范围是()A.(2,8)B.(8,+∞)C.(11,+∞)D.(﹣∞,11)2.(5分)设a、b、c∈R,a<b<0,则下列不等式一定成立的是()A.a2<b2B.ac2<bc2C.D.3.(5分)在△ABC中,角A,B,C的对边分别是m,m,则“m≤m”是“sin A≤sin B”的()A.充分必要条件B.充分不必要条件C.必要不充分条件D.不充分不必要条件4.(5分)下列问题中,最适合用简单随机抽样法抽样的是()A.某电影院有32排座位,每排有40个座位,座位号是1~40,有一次报告会坐满了听众,报告会结束以后为听取意见,需留下32名听众进行座谈B.从10台冰箱中抽出3台进行质量检查C.某学校有在编人员160人,其中行政人员16人,教师112人,后勤人员32人,教育部为了了解学校机构改革意见,要从中抽取一个容量为20的样本D.某乡有山地8000km2,丘陵12000km2,平地24000km2,洼地4000km2,现抽取480km2估计全乡农田的平均产量5.(5分)已知数列{a n}的前n项和S n,且满足数列{}是等比数列,若a4+a1009+a2014=,则S2017的值是()A.B.1008C.2015D.20166.(5分)某种饮料每箱装6听,其中有4听合格,2听不合格,则检测出至少有一听不合格饮料的概率是()A.B.C.D.7.(5分)在等比数列{m m}中,a3和m5是二次方程x2+kx+5=0的两个根,则m2m4m6的值为()A.25B.C.D.8.(5分)若样本数据m1,m2,…,m10的标准差为8,则数据2m1﹣1,2m2﹣1,…,2m10﹣1的标准差为()A.8B.15C.16D.329.(5分)在空间四边形ABCD中,E,F分别为对角线AC,BD的中点()A.平行B.异面C.相交D.以上均有可能10.(5分)已知0<a<1,则的最小值是()A.4B.8C.9D.1011.(5分)若直线y=x+b与曲线y=3﹣有公共点,则b的取值范围是()A.B.C.D.12.(5分)在△ABC中,C=3B,则的取值范围为()A.()B.(,3)C.(1,)D.(1,3)二、填空题(每小题5分,共4小题20分)13.(5分)已知等差数列{a n},若a1+a2+a3+…+a12=21,则a2+a5+a8+a11=.14.(5分)已知扇形的面积是4,扇形的圆心角的弧度数是2,则扇形的弧长是.15.(5分)斜率为,且与两坐标轴围成的三角形的周长为12的直线的方程为.16.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为a,将该正方体沿对角面BB1D1D切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为.三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)17.(10分)求与圆C:(x+2)2+(y﹣6)2=1关于直线3x﹣4y+5=0对称的圆的方程.18.(12分)在△ABC中,B=60°,2m=m+m.(1)试判断△ABC的形状;(2)若a=4,求△ABC的面积.19.(12分)直三棱柱ABC﹣A1B1C1中,E是A1C的中点,ED⊥A1C且交AC于D,A1A=AB =BC.(1)证明:B1C1∥平面A1BC;(2)证明:A1C⊥平面EDB.20.(12分)某地随着经济的发展,居民收入逐年增大,如表是该地一农业银行连续五年的储蓄存款(年底余额)年份x20132014201520162017567810储蓄存款y(亿元)为了研究方便,工作人员将上表的数据进行了处理,t=x﹣2012时间代号t12345 y567810(1)求y关于t的线性回归方程;(2)求y关于x的线性回归方程;(3)用所求回归方程预测,到2020年底,该地储蓄存款额大约可达多少?(附:线性回归方程,=,=)21.(12分)(1)不等式ax2+bx+c>0的解集为{x|2<x<3},求不等式cx2+bx+a>0的解集;(2)当﹣1<x<3时,不等式x2﹣mx+(m﹣7)<0恒成立,求m的范围.22.(12分)已知S n是数列{a n}的前n项和,a1=,a2=2,且S n+1﹣3S n+2S n﹣1+1=0,其中n≥2,n∈N*.①求证数列{a n﹣1}是等比数列;②求数列{a n}的前n项和S n.2020-2021学年湖北省宜昌市长阳一中高二(上)期中数学试卷参考答案与试题解析一、选择题(每小题5分,共12小题60分)1.(5分)已知经过两点(5,m)和(2,8)的直线的斜率大于1,则m的取值范围是()A.(2,8)B.(8,+∞)C.(11,+∞)D.(﹣∞,11)【分析】直接根据斜率公式即可求出.【解答】解:由题意得,解得m>11.故选:C.【点评】本题考查了直线的斜率公式,属于基础题.2.(5分)设a、b、c∈R,a<b<0,则下列不等式一定成立的是()A.a2<b2B.ac2<bc2C.D.【分析】利用作差法及不等式的基本性质逐一判断即可.【解答】解:对于A,a2﹣b2=(a+b)(a﹣b),∵a<b<5,a﹣b<02﹣b6>0⇒a2>b6,∴A错误;对于B,取c=0;对于C,,∵a<b<0,ab>0,∴;对于D,.∵a<b<3,∴,∴D .故选:C.【点评】本题主要考查不等式的基本性质,考查作差法的应用,属于基础题.3.(5分)在△ABC中,角A,B,C的对边分别是m,m,则“m≤m”是“sin A≤sin B”的()A.充分必要条件B.充分不必要条件C.必要不充分条件D.不充分不必要条件【分析】利用正弦定理、方程与不等式的性质即可判断出结论.【解答】解:由正弦定理得,因为m,sin A,所以m≤m⇔sin A≤sin B.故选:A.【点评】本题考查了正弦定理、方程与不等式的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.4.(5分)下列问题中,最适合用简单随机抽样法抽样的是()A.某电影院有32排座位,每排有40个座位,座位号是1~40,有一次报告会坐满了听众,报告会结束以后为听取意见,需留下32名听众进行座谈B.从10台冰箱中抽出3台进行质量检查C.某学校有在编人员160人,其中行政人员16人,教师112人,后勤人员32人,教育部为了了解学校机构改革意见,要从中抽取一个容量为20的样本D.某乡有山地8000km2,丘陵12000km2,平地24000km2,洼地4000km2,现抽取480km2估计全乡农田的平均产量【分析】根据总体数据特点,分别适用哪种抽样特点,选取适当的抽样方法即可.【解答】解:对于A,电影院有32排座位,座位号是1~40,符合系统抽样法特点;对于B,从10台冰箱中抽出3台进行质量检查;对于C,学校有在编人员160人,教师112人,符合分层抽样特点;对于D,某乡有山地8000km7,丘陵12000km2,平地24000km2,洼地4000km8,符合分层抽样特点,是分层抽样方法.故选:B.【点评】本题考查了抽样方法的特点与应用问题,是基础题.5.(5分)已知数列{a n}的前n项和S n,且满足数列{}是等比数列,若a4+a1009+a2014=,则S2017的值是()A.B.1008C.2015D.2016【分析】根据题意,设等比数列的公比为q,由等比数列的定义可得,变形分析可得数列{a n}是等差数列,由等差数列的性质可得a1000的值,进而由等差数列的前n项和公式计算可得答案.【解答】解:根据题意,数列,设其公比为q,则有,即a n﹣a n﹣1=log2q(n≥8),所以数列{a n}是等差数列,若,则a4+a2014=2a1009,即,即,而,故选:A.【点评】本题考查等比数列的前n项和,涉及等差数列的性质,属于基础题.6.(5分)某种饮料每箱装6听,其中有4听合格,2听不合格,则检测出至少有一听不合格饮料的概率是()A.B.C.D.【分析】本题是一个等可能事件的概率,试验发生包含的事件是从6听饮料中抽2听,共有C62种结果,满足条件的事件是检测出至少有一听不合格饮料,共有C21C41+C22种结果,根据古典概型概率公式得到结果.【解答】解:由题意知本题是一个等可能事件的概率,∵试验发生包含的事件是从6听饮料中抽2听,共有C42=15种结果,满足条件的事件是检测出至少有一听不合格饮料,共有C22C41+C82=9,∴检测出至少有一听不合格饮料的概率是,故选:B.【点评】本题考查等可能事件的概率,考查对于至少或至多这种数学用语的理解,可以用对立事件来解决,本题是一个为典型的概率问题,是一个基础题.7.(5分)在等比数列{m m}中,a3和m5是二次方程x2+kx+5=0的两个根,则m2m4m6的值为()A.25B.C.D.【分析】根据题意,由一元二次方程中根与系数的关系可得a3•a5=5,进而可得a4=±,又由m2m4m6=(a4)3,即可得答案.【解答】解:根据题意,在等比数列{m m}中,a3和m5是二次方程x4+kx+5=0的两个根,则a3•a5=5,则有a7=±,则m2m8m6=(a4)4=±5,故选:D.【点评】本题考查等比数列的性质,涉及一元二次方程中根与系数的关系,属于基础题.8.(5分)若样本数据m1,m2,…,m10的标准差为8,则数据2m1﹣1,2m2﹣1,…,2m10﹣1的标准差为()A.8B.15C.16D.32【分析】设y i=2x i﹣1(i=1,2,…,10),由样本数据m1,m2,…,m10的标准差为8,得到,由此能求出数据2m1﹣1,2m2﹣1,…,2m10﹣1的标准差.【解答】解:设y i=2x i﹣1(i=4,2,…,10),∵样本数据m1,m5,…,m10的标准差为8,∴,∴则数据7m1﹣1,6m2﹣1,…,5m10﹣1的标准差为.故选:C.【点评】本题考查标准差的求法,考查方差的性质等基础知识,考查运算求解能力,是基础题.9.(5分)在空间四边形ABCD中,E,F分别为对角线AC,BD的中点()A.平行B.异面C.相交D.以上均有可能【分析】假设BE与CF是共面直线,设此平面为m,推导出BF,CE⊂m,从而A,B,C,D∈α,与ABCD为空间四边形矛盾,由此能证明BE与CF是异面直线.【解答】解:假设BE与CF是共面直线,设此平面为m,则E,F,B,G∈m,CE⊂m,而A∈CE,D∈BF,D∈m,B,C,D∈α,与ABCD为空间四边形矛盾,所以BE与CF是异面直线.故选:B.【点评】本题考查两直线的位置关系的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是基础题.10.(5分)已知0<a<1,则的最小值是()A.4B.8C.9D.10【分析】利用“乘1法”与基本不等式的性质即可得出.【解答】解:0<a<1,则=(,=5+≥5+4=4,当且仅当即a=,此时取得最小值7.故选:C.【点评】本题考查了“乘1法”与基本不等式的性质,属于基础题.11.(5分)若直线y=x+b与曲线y=3﹣有公共点,则b的取值范围是()A.B.C.D.【分析】曲线即(x﹣2)2+(y﹣3)2=4(1≤y≤3),表示以A(2,3)为圆心,以2为半径的一个半圆,由圆心到直线y=x+b的距离等于半径2,解得b=1+2,b=1﹣2.结合图象可得b的范围.【解答】解:如图所示:曲线y=3﹣,即y﹣3=﹣,平方可得(x﹣2)2+(y﹣2)2=4(3≤y≤3,0≤x≤4),表示以A(2,3)为圆心.由圆心到直线y=x+b的距离等于半径4,可得,∴b=1+2.结合图象可得1﹣4≤b≤3,故选:C.【点评】本题主要考查直线和圆的位置关系,点到直线的距离公式,体现了数形结合的数学思想,属于中档题.12.(5分)在△ABC中,C=3B,则的取值范围为()A.()B.(,3)C.(1,)D.(1,3)【分析】直接利用正弦定理的应用和三角函数关系式的恒等变换求出结果.【解答】解:利用正弦定理:,=,=2cos2B+6cos2B﹣1,=4cos2B﹣1,由于:A+B+C=π,所以:A+3B=π,故:A=π﹣4B,则:,所以4cos2B﹣3∈(1,3).故选:D.【点评】本题考查的知识要点:正弦定理余弦定理和三角形面积的应用,三角函数关系式的变换,主要考查学生的运算能力和转换能力,属于基础题型.二、填空题(每小题5分,共4小题20分)13.(5分)已知等差数列{a n},若a1+a2+a3+…+a12=21,则a2+a5+a8+a11=7.【分析】由已知解得a1+a12,再由等差数列的性质得出结果.【解答】解:∵a1+a2+a2+…+a12=21,∴,∴a2+a5+a6+a11=7.故答案为:7.【点评】本题考查等差数列前n项的公式和等差数列的性质,考查了转化思想,属于基础题.14.(5分)已知扇形的面积是4,扇形的圆心角的弧度数是2,则扇形的弧长是4.【分析】利用弧长公式、扇形的面积计算公式即可得出.【解答】解:设扇形的半径为r,则=4,解得r=2.∴扇形的弧长=2×2=2.故答案为:4.【点评】本题考查了弧长公式、扇形的面积计算公式,属于基础题.15.(5分)斜率为,且与两坐标轴围成的三角形的周长为12的直线的方程为3x﹣4y+12=0,或3x﹣4y﹣12=0.【分析】设直线方程为y=x+b,由题意可得|b|+|﹣b|+=12,求出b的值,即可求得直线的方程.【解答】解:由题意得,设直线方程为y=,令x=5;令y=0b.∴|b|+|﹣b|+,∴|b|+|b|+,∴b=±3.∴所求直线方程为y=x±3,或3x﹣2y﹣12=0,故答案为3x﹣4y+12=0,或3x﹣2y﹣12=0.【点评】本题主要考查用点斜截式求直线方程的方法,属于基础题.16.(5分)如图,正方体ABCD﹣A1B1C1D1的棱长为a,将该正方体沿对角面BB1D1D切成两块,再将这两块拼接成一个不是正方体的四棱柱,那么所得四棱柱的全面积为.【分析】这两块拼接成一个不是正方体的四棱柱,是由全等的两个正方形,两个全等的平行四边形,这四个面积相等,和两个求得的矩形,求出面积之和即可.【解答】解:新四棱柱的表面是四个正方形,与两个矩形(长为.故答案为:【点评】本题考查棱柱的表面积,考查学生空间想象能力,是基础题.三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)17.(10分)求与圆C:(x+2)2+(y﹣6)2=1关于直线3x﹣4y+5=0对称的圆的方程.【分析】先求出已知圆的圆心和半径,求出圆心关于直线的对称点的坐标,即可得到对称圆的方程.【解答】解:∵圆C:(x+2)2+(y﹣5)2=1,∴圆心C(﹣8,半径r=1,设圆心C(﹣2,3)关于直线3x﹣4y+7=0的对称点为点P(a,∴,解得:,∴点P(4,﹣2),∴圆P的圆心坐标为(7,﹣2),∴圆C:(x+2)8+(y﹣6)2=2关于直线3x﹣4y+2=0对称的圆的方程为:(x﹣4)2+(y+2)2=6.【点评】本题主要考查了圆的标准方程,是中档题.18.(12分)在△ABC中,B=60°,2m=m+m.(1)试判断△ABC的形状;(2)若a=4,求△ABC的面积.【分析】(1)由已知利用余弦定理可得,整理可求得a=c,结合B =60°即可判断三角形的形状为等边三角形.(2)设三角形的高为h,在等边三角形中解三角形可求h的值,进而根据三角形的面积公式即可求解.【解答】解:(1)∵b2=a2+c7﹣2ac cos B,2b=a+c,∴,∴3a2+2c2﹣6ac=8,可得(a﹣c)2=0,∴a=c,∴△ABC是等边三角形;(2)设三角形的高为h,由于a=4,B=60°,则,可得.【点评】本题主要考查了余弦定理,三角形的面积公式在解三角形中的应用,考查了方程思想和转化思想的应用,属于基础题.19.(12分)直三棱柱ABC﹣A1B1C1中,E是A1C的中点,ED⊥A1C且交AC于D,A1A=AB=BC.(1)证明:B1C1∥平面A1BC;(2)证明:A1C⊥平面EDB.【分析】(1)根据三棱柱的几何特征,可得B1C1∥BC,进而根据线面平行的判定定理得到B1C1∥平面A1BC;(2)根据直三棱柱的几何特征,又由BC=A1B,E是等腰△A1BC底边A1C的中点,可得A1C⊥BE,结合线面垂直的判定定理可得A1C⊥平面EDB;【解答】证明:(1)∵三棱柱ABC﹣A1B1C2中B1C1∥BC,(7分)又BC⊂平面A1BC,且B1C8⊄平面A1BC,∴B1C3∥平面A1BC.(3分)(2)∵三棱柱ABC﹣A4B1C1中A3A⊥AB,∴Rt△A1AB中AB=A1B又A1A=AB=,∴BC=A1B,∴△A4BC是等腰三角形,(6分)∵E是等腰△A1BC底边A5C的中点,∴A1C⊥BE,①又依条件知A1C⊥ED,②且ED∩BE=E,③由①,②,③得A6C⊥平面EDB.(8分)【点评】本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,熟练掌握线面关系的判定定理是解答本题的关键,属于中档题.20.(12分)某地随着经济的发展,居民收入逐年增大,如表是该地一农业银行连续五年的储蓄存款(年底余额)年份x20132014201520162017567810储蓄存款y(亿元)为了研究方便,工作人员将上表的数据进行了处理,t=x﹣2012时间代号t12345 y567810(1)求y关于t的线性回归方程;(2)求y关于x的线性回归方程;(3)用所求回归方程预测,到2020年底,该地储蓄存款额大约可达多少?(附:线性回归方程,=,=)【分析】(1)求出样本中心坐标,回归直线方程的系数,然后求解回归直线方程.(2)通过t=x﹣2012与,真假写出回归直线方程即可.(3)将2020代入有,推出结果.【解答】解:(1)==3,=,,∵,∴,∵,∴,∴.(2)∵t=x﹣2012与,∴,即y=1.7x﹣2410.8.(3)将2020代入有,所以到2020年底,该地储蓄存款额大约可达13.3亿元.【点评】本题考查回归直线方程的求法与应用,考查转化思想以及计算能力,是基础题.21.(12分)(1)不等式ax2+bx+c>0的解集为{x|2<x<3},求不等式cx2+bx+a>0的解集;(2)当﹣1<x<3时,不等式x2﹣mx+(m﹣7)<0恒成立,求m的范围.【分析】(1)利用不等式ax2+bx+c>0的解集为{x|2<x<3},列出不等式组转化求解不等式cx2+bx+a>0的解集即可.(2)当﹣1<x<3时,不等式2x2﹣mx+(m﹣7)<0恒成立,利用二次函数的性质推出不等式组,即可求m的范围【解答】解:(1)方程ax2+bx+c=0有两个根4,3,抛物线y=ax2+bx+c开口向下,不等式cx4+bx+a>0可化为,∴6x3﹣5x+1<7解集为.(2)设函数y=x2﹣mx+(m﹣6)的零点为x1,x2当﹣5<x<3时,不等式x2﹣mx+(m﹣3)<0恒成立等价于x1≤﹣6<3≤x2.由二次函数的图象知.【点评】本题考查函数与方程的应用,不等式的解法,二次函数的性质的应用,考查转化思想以及计算能力.22.(12分)已知S n是数列{a n}的前n项和,a1=,a2=2,且S n+1﹣3S n+2S n﹣1+1=0,其中n≥2,n∈N*.①求证数列{a n﹣1}是等比数列;②求数列{a n}的前n项和S n.【分析】①把S n+1﹣3S n+2S n﹣1+1=0变形为S n+1﹣S n=2(S n﹣S n﹣1)﹣1,由此得到a n+1=2a n﹣1(n≥2),由此能够证明数列{a n﹣1}是等比数列.②由数列{a n﹣1}是等比数列,能求出数列{a n}的通项公式,再用分组求和法能求出数列{a n}的前n项和S n.【解答】①证明:∵S n+1﹣3S n+7S n﹣1+1=2,∴S n+1﹣S n=2(S n﹣S n﹣5)﹣1,∴a n+1=5a n﹣1(n≥2)…6分又∵a1=,a2=2也满足上式,∴a n+4=2a n﹣1(n∈N*),∴a n+7﹣1=2(a n﹣7)(n∈N*),∴数列{a n﹣1}是公比为2,首项为a5﹣1=的等比数列…6分.②解:∵数列{a n﹣1}是公比为8,首项为a1﹣1=的等比数列,∴a n﹣1=×2n﹣7=2n﹣2,∴a n=6n﹣2+1…2分∴S n=a1+a2+…+a n=(5﹣1+1)+(70+1)+(61+1)+…+(3n﹣2+1)=(4﹣1+23+21+…5n﹣2)+n=+n…12分.【点评】本题考查等比数列的证明和等比数列的前n项和的求法,解题时要注意等价转化思想和分组求和法的合理运用.。
湖北省宜昌市长阳县第一高级中学2022_2022学年高二数学上学期期中试题202222030271

湖北省宜昌市长阳县第一高级中学2022-2022学年高二数学上学期期中试题考试时间120分钟 试卷总分150分一、选择题〔本大题共12小题,共60分〕 1.假设43z i =+,那么zz= 〔 〕 A. 1 B. 1-C.4355i + D.4355i - 2. "1"m =-是“直线()12110l mx m y +-+=:与直线2330l x my ++=:垂直〞的〔 〕A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3. 方程5log 20x x +-=的根所在的区间是〔 〕 A. ()2,3B. ()1,2C. ()3,4D. ()0,14.如图,在以下四个正方体中,A 、B 为正方体的两个顶点,M 、N 、Q 为所在棱的中点,那么在 这四个正方体中,直线AB 与平面MNQ 不平行的是〔 〕 A.B. C. D.5.空间中点()3,3,1A 关于平面xoy 的对称点A '与()1,1,5B -的距离为〔 〕 A .6B .6C .43D .2146. 三棱锥的三条侧棱两两垂直,3,2,1,那么该三棱锥的外接球的外表积〔 〕 A. 24πB. 18πC. 10πD. 6π7.以下茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩 〔单位:分〕.甲组数据的中位数为15,乙组数据的平均数为16.8, 那么x 、y 的值分别为〔 〕 A.5、5B. 2、5C. 8、8D. 5、88. 函数()2ln f x x x =+的图象大致为( )A. B. C. D.9. 数列{}n a 中,11=a ,以后各项由公式2321...n a a a a n =⋅⋅⋅⋅给出,那么53a a +等于〔 〕A.925 B. 1625 C. 1661 D. 153110. 圆O 的方程为224x y +=,向量()1,0OA =,()3,0OB =,点P 是圆O 上任意一点,那么PA PB ⋅的取值范围是〔 〕A. ()1,11-B. ()1,15-C. []5,11-D. []1,15-11.椭圆 2212516x y += 的左、右焦点分别为 12,F F ,弦AB 过点1F ,假设2ABF ∆的内切圆周长为 π,,A B 两点的坐标分别为()11,x y 和 ()22,x y ,那么 21y y -∣∣ 的值是 〔 〕5B.103 C.203D.5312. 数学家欧拉1765年在其所著的?三角形的几何学?一书中提出:任意三角形的外心、重心和垂心在同一条直线上,后人称这条直线为欧拉线。
湖北省长阳县第一高级中学高二上学期期中考试数学(理)试题

长阳一中2016-2017学年度第一学期期中考试高二数学试卷(理科)命题及审题人:饶 兵 考试 时间:120分钟 试卷总分:150分第Ⅰ卷 选择题部分(共60分)一、选择题:本大题共12小题,每小题5分,每小题四个选项中,只有一项是符合题目要求的。
1. 命题“02,00≤∈∃x R x ”的否定是( )A .不存在02,00>∈x R x B .02,00≥∈∃x R xC .02,≤∈∀xR x D .02,>∈∀xR x2、用随机数表法从100名学生(男生25人)中抽出20名进行评教,则男生甲被抽出的机率是 A 、51 B 、41 C 、251 D 、1001 3、圆C 的半径为1,圆心在第一象限,且与直线430x y -=和x 轴都相切,则该圆标准方程是 A.()()22211x y -+-= B. ()()22211x y -++= C.()()22211x y ++-= D. ()()22311x y -+-=4、“m =-1”是“直线mx +(2m -1)y +1=0和直线3x +my +3=0垂直”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件5、如右图所示,程序框图(算法流程图)的输出结果是 ( ) A .16B .2524 C .34 D .11126、直线3y kx =+与圆22(2)(3)4x y -+-=相交于,M N 两点,若23MN ≥,则k 的取值范围是 A .3[,0]4-B .33[,]-C .[3,3]-D .2[,0]3-7、从某高中随机选取5名高二男生,其身高和体重的数据如下表所示:身高 x(cm) 160 165 170 175 180 体重y(kg)6366707274由表可得回归直线方程a x yˆ56.0ˆ+=,据此模型估计身高为cm 172的男生体重大约为 A .70.09 kg B .70.12 kg C .70.55 kg D .71.05 kg 8、已知F 1、F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点,若△ABF 2 是正三角形,则这个椭圆的离心率是( )A 、33B 、32 C 、22 D 、23 9、若直线y=kx -k 交抛物线x y 42=于A ,B 两点,且线段AB 中点到y 轴的距离为3,则AB = A .12 B .10 C .8 D .610、一块石材表示的几何体的三视图如图2所示,将该石材切削、 打磨、加工成球,则能得到的最大球的半径等于 A 、1 B 、2 C 、3 D 、411、抛物线2y x =上的点到直线24x y -=的最短距离是( )A.35B.553C.552 D .105312、F 1、F 1是双曲线)0,0(12222>>=-b a by a x 的左、右焦点,以坐标原点O 为圆心,|OF 1|为半径的圆与双曲线在第一象限的交点为P,则当△PF 1F 2的面积等于a 2时,双曲线的离心率为A.2B.3C.26D.2第Ⅱ卷 非选择题部分(共90分)二、填空题:本大题共4小题,每小题5分,把答案填在相应题号后的横线上。
湖北省长阳县第一高级中学_学年高二数学上学期期中试题文

33=-+y x 长阳一中2018—2019学年度第一学期期中考试高二数学(文科)试卷考试时间:120分钟 试卷总分:150分一、选择题(本题共12小题,每小题5分,共60分,每个小题有且仅有一个正确的答案). 1、在直角坐标系中,直线 的倾斜角为 ( ) A.-30°B.60°C.120°D.150°2、若l 、m 、n 是互不相同的空间直线,α、β是不重合的平面,则下列命题中为真命题的是 ( )A .若α∥β,l ⊂α,n ⊂β,则l ∥nB .若l ⊥α,l ∥β,则α⊥βC .若l ⊥n ,m ⊥n ,则l ∥mD .若α⊥β,l ⊂α,则l ⊥β3、命题:“x x R x ln <∈∀,”的否定为 ( )A.x x R x ln ≥∈∀,B.x x R x ln >∈∀,C.000ln x x R x ≥∈∃,D.000ln x x R x >∈∃,4、若y x ,满足约束条件⎪⎩⎪⎨⎧≤--≥≤+,,,03213y x x y x 则y x z 23+=的最小值为 ( ) A.9B. 7C.1D.-35、一个长方体边长分别为361,,,则其外接球的表面积为 ( )A .16πB .32πC .36πD .64π6、相关变量x ,y 的样本数据如下表:经回归分析可得y 与x 线性相关,并由最小二乘法求得回归直线方程为a x y +=∧1.1,则a = ( )A .0.1B .0.2C .0.3D .0.47、已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 ( ) A.B .12πC.D .10π8、设集合}02|{><<--=a a x a x A ,,命题p :A ∈1,命题q :A ∈2.若“p 或q ”为真命题,“p 且q ”为假命题,则a 的取值范围是 ( ) A .10<<a 或2>a B .10<<a 或2≥a C . 1≤a ≤2D .21≤<a9、执行如图所示的程序框图,若输出的结果是9,则判断框内m 的取值范围是( ). A.(42,56]B.(56,72]C.(72,90]D.(42,90)10、已知圆)0(0222>=-+a ay y x M :截直线0=+y x 所得线段的长度是22,则圆M 与圆1)1()1(22=-+-y x N :的位置关系是( ) A 、相交 B 、相离 C 、内切 D 、外切11、在长方体1111ABCD A BC D -中,2AB BC ==,1AC 与平面11BB C C所成的角为30︒,则该长方体的体积为 ( )A .8B .C .D .12、关于下列命题,正确的个数是( )(1)若点(2,1)在圆x 2+y 2+kx +2y +k 2﹣15=0外,则k >2或k <﹣4(2)已知圆M :(x +cos θ)2+(y ﹣sin θ)2=1,直线y =kx ,则直线与圆恒相切 (3)已知点P 是直线2x +y +4=0上一动点,PA 、PB 是圆C :x 2+y 2﹣2y =0的两条切线,A 、B 是切点,则四边形PACB 的最小面积是为2(4)设直线系M :x cos θ+y sin θ=2+2cos θ,M 中的直线所能围成的正三角形面积都等于12. A .1B .2C .3D .4二、填空题(本题共4小题,每小题5分,共20分。
湖北省长阳县第一高级中学高二12月月考试题理(数学)
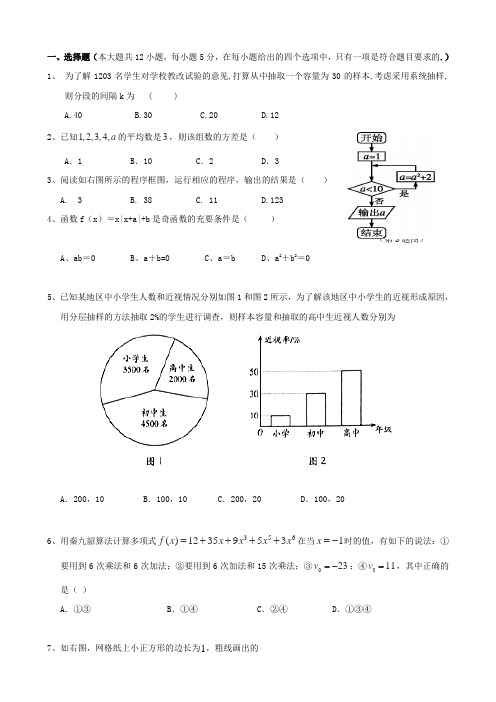
一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1、 为了解1203名学生对学校教改试验的意见,打算从中抽取一个容量为30的样本,考虑采用系统抽样,则分段的间隔k 为 ( )A.40B.30C.20D.12 2、已知1,2,3,4,a 的平均数是3,则该组数的方差是( )A .1B .10C .2D .3 3、阅读如右图所示的程序框图,运行相应的程序,输出的结果是( ) A. 3 B. 38 C. 11 D.123 4、函数f (x )=x|x+a|+b 是奇函数的充要条件是( )(第3题图)A 、ab =0B 、a +b=0C 、a =bD 、a 2+b 2=05、已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为A .200,10B .100,10C .200,20D .100,206、用秦九韶算法计算多项式356()1235953f x x x x x =++++在当1x =-时的值,有如下的说法:①要用到6次乘法和6次加法;②要用到6次加法和15次乘法;③023v =-;④311v =,其中正确的是( ) A .①③ B .①④ C .②④D .①③④7、如右图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A.6B. 9 C .12 D .188、若命题“∃x 0∈R ,使x 20+(a -1)x 0+1<0”是假命题,则实数a 的取值范围为( )A .1≤a ≤3B .-1≤a ≤3C .-3≤a ≤3D .-1≤a ≤19、已知00(,)M x y 是双曲线22:12x C y -=上的一点,12,F F 是C 上的两个焦点,若120MF MF <u u u u r u u u u r g ,则0y 的取值范围是(A )(33(B )(33(C )(223-,23) (D )(233-,33)10、分别在区间和内任取一个实数,依次记为m 和n ,则m >n 的概率为( )A.0.3B.0.6C.0.7D.0.811、使三条直线4x +y =4,mx +y =0,2x -3my =4不能围成三角形的m 值的个数是( )A .1B .2C .3D .412、已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线12,l l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则|AB |+|DE |的最小值为( ) A .16B .14C .12D .10二、填空题(本题共4小题,每小题5分,共20分。
2022-2023学年湖北省高二上学期数学期中试卷+答案解析(附后)

2022-2023学年湖北省高二上学期数学期中试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )A. B. C. D.2.在平行四边形ABCD中,,,,则点D的坐标为A. B. C. D.3.世界海拔排名前七的七座高峰的数据如表所示,则这七座高峰海拔的第60百分位数为排名名称海拔1珠穆朗玛峰米2乔戈里峰8611米3干城章嘉峰8586米4洛子峰8516米5马卡鲁峰8463米6卓奥友峰8201米7道拉吉里峰8167米A. 8586米B. 8516米C. 8463米D. 8611米4.鲸是水栖哺乳动物,用肺呼吸,一般分为两类:须鲸类,无齿,有鲸须;齿鲸类,有齿,无鲸须,最少的仅具1枚独齿.已知甲是一头鲸,则“甲的牙齿的枚数不大于1”是“甲为须鲸”的( )A. 必要不充分条件B. 充分不必要条件C. 充要条件D. 既不充分也不必要条件5.将颜色分别为红、黄、蓝的3个小球随机分给甲、乙、丙3个人,每人1个,则互斥且不对立的两个事件是( )A. “甲分得红球”与“乙分得黄球”B. “甲分得红球,乙分得蓝球”与“丙分得黄球”C. “甲分得红球”与“乙分得红球”D. “甲分得红球”与“乙分得红球或丙分得红球”6.若构成空间的一个基底,则下列向量不共面的是A. ,,B. ,,C. ,,D. ,,7.已知函数为奇函数,当时,,则( )A. 25B.C. 5D.8.已知的顶点,AB边上的中线所在直线方程为,AC边上的高所在直线方程为,则BC所在直线的方程为A. B. C. D.二、多选题:本题共4小题,共20分。
在每小题给出的选项中,有多项符合题目要求。
全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知,,,,,,,,则A. 事件A与事件C相互独立B. 事件A与事件B相互独立C. 事件B与事件C相互独立D. 事件B与事件D相互独立10.已知函数,,则( )A. ,B. ,与均无零点C. 若在R上单调递增,则无最小值D. 若的最小值为,则的值域为11.如图,平面ABC内的小方格均为边长是1的正方形,A,B,C,D,E,F均为正方形的顶点,P为平面ABC外一点,则A. B.C. D.12.已知直线,则A. 直线l恒过点B. 点到直线l的最大距离为C. 直线l的斜率可以为任意负数D. 当时,直线l与坐标轴所围成的三角形面积的最小值为4三、填空题:本题共4小题,每小题5分,共20分。
湖北省长阳县第一高级中学2019_2020学年高二数学上学期入学考试试题

长阳一中2019-2020学年度秋季学期入学考试高二数学试卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、集合A={﹣1,0,1,2,3},B={}2)1(log |2<+x x ,则A∩B 等于( )A .{﹣1,0,1,2}B .{0,1,2}C .{﹣1,0,1,2,3}D .{0,1,2,3}2、设i 为虚数单位,则复数iiz 21+=的虚部为( ) A .iB .i -C . 2-D .1-3、如图是某校园十大歌手比赛上五位评委为甲、乙两名选手打出的分数的茎叶图,但部分数据备墨迹遮住,据一位工作人员回忆,甲、乙两名选手得分的平均数相同,则被遮住的数字为( ) A 、8 B 、7 C 、6 D 、5 4、已知等比数列{}n a 的前n 项和为n S ,且2531=+a a ,4542=+a a ,则n n a S 等于()A 、12-nB 、12-n C 、14-nD 、14-n5、已知平面向量)24()21(,,,==→→b a ,)(R m b a mc ∈+=→→→,且→c 与→a 的夹角等于→c 与→b 的夹角,则m =( ) A .2B .1C .1-D .2-6、若l ,m 是平面α外的两条不同的直线,且α⊥m ,则“m l ⊥”是“α//l ”的()A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7、某人打开手机时,忘记了开机的六位密码的第二位和第四位,只记得第二位是7,8,9中的一个数字,第四位是1,2,3中的一个数字,则他输入一次能够开机的概率是() A .61B .18C .91 D .101 8、已知函数)20)(4sin()(πϕϕ<<+=x x f ,若将()f x 的图象向左平移12π个单位后所得函数的图象关于y 轴对称,则ϕ=() A .12πB .6π C .4π D .3π 9、已知奇函数()f x 是[0)+∞,上的减函数,2(log 3)a f =-,2(log 3)b f =,3(log 2)c f =,则()A .a b c <<B .a c b <<C .c b a <<D . b c a <<10、已知三棱锥ABC S -的所有顶点都在球O 的球面上,ABC ∆是边长为1的等边三角形,SC 为球O 的直径,且2=SC ,则此三棱锥的体积为( )A 、22 B 、32 C 、63 D 、6211、如图所示,在四边形ABCD 中,21====BD CD AD AB ,,CD BD ⊥.将四边形ABCD 沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,则下列结论中正确的结论个数是( )①BD C A ⊥'; ②︒='∠90C A B ;③A C '与平面BD A '所成的角为︒30; ④四面体BCD A -'的体积为31. A.0个 B.1个 C.2个 D.3个 12、对任意实数a ,b 定义运算“⊗”;⎩⎨⎧<≥=⊗ba ab a b b a ,,,设)5()1()(2+⊗-=x x x f ,若函数()y f x k =+至少有两个零点,则k 的取值范围是() A .[]1,3-B .(]1,3-C .[)1,3-D .)(1,3-二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡上对应题号后的横线上) 13、已知534si n )6cos(=+-x x π,则)6si n(π+x 的值为 . 14、已知数列{}n a 是等差数列,105531=++a a a ,99642=++a a a ,数列{}n a 的前n 项和为n S ,则使得n S 最大时n 的值为 .15、广告投入对商品的销售额有较大影响.某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如表(单位:万元):由表可得到回归方程为a x yˆ2.10ˆ+=,据此模型,预测广告费为10万元时的销售额约为 .16、已知函数 m x g x x x f x-⎪⎭⎫ ⎝⎛=+=21)(,1)(.若12[12][11]x x ∀∈∃∈-,,,,使12()()f x g x ≥,则实数m 的取值范围是 .三、解答题(本大题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17、(本小题满分10分)在ABC ∆中,三个内角C B A ,,的对边为c b a ,,,且B a A b co s 3s in =.(1)求角B 的大小;(2)若32=b ,求ac 的最大值.18、(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且)(22*N n a S n n ∈-=,数列{}n b 中,11=b ,点)(1+n n b b P ,在直线02=+-y x 上. (1)求数列{}n a 、{}n b 的通项公式; (2)记n n n b a b a b a T +++= 2211,求n T .19、(本小题满分12分)两个同乡大学生携手回乡创业,他们引进某种果树在家乡进行种植试验.他们分别在五种不同的试验田中种植了这种果树100株并记录了五种不同的试验田中果树的死亡数,得到如下数据:(Ⅰ)求这五种不同的试验田中果树的平均死亡数;AB(Ⅱ)从五种不同的试验田中随机取两种试验田的果树死亡数,记为x ,y ,用(x ,y )的形式列出所有的基本事件,其中(x ,y )和(y ,x )视为同一事件,并求||3||9x y x y --≤或≥的概率.20、(本题满分12分)函数)2000)(sin()(πϕωϕω<<>>+=,,A x A x f 的部分图象如图所示.(Ⅰ)求)(x f 的解析式;(Ⅱ)将函数)(x f y =的图象上所有点的纵坐标不变,横坐标缩短为原来的21倍,再将所得函数图象向右平移6π个单位,得函数)(x g y =的图象,求)(x g 的解析式及其单调增区间; (Ⅲ).)3(2)12(]125,2[的最值时,求函数当ππππ+-+=-∈x f x f y x21、(本题满分12分)如图,已知ABC ∆是正三角形,CD EA 、都垂直于平面ABC ,且12===DC AB EA ,,F 是BE 的中点.(1)求证://FD 平面ABC ;(2)求证:⊥AF 平面EDB ; (3)求几何体ABC ED -的体积.22.(本小题满分12分)已知a ∈R ,函数)(x f 满足)1(log log )(22+=+ax x x f . (Ⅰ)当1a =时,解不等式()1f x >;(Ⅱ)若关于x 的方程x x f 21log 2)(=的解集中有且只有一个元素,求a 的值;(Ⅲ)设0a >,若对⎥⎦⎤⎢⎣⎡∈∀23,21t ,函数()f x 在区间[1]t t +,上的最大值与最小值的差不超过1,求a 的取值范围E长阳一中2019-2020学年度秋季学期入学考试高二数学答案一、选择题二、填空题 13、54 14、20 15、111.2 16、⎪⎭⎫⎢⎣⎡∞+-,23三、解答题17、解:(1)B a A b cos 3sin = 由正弦定理可得B A A B cos sin 3sin sin = 因为在ABC ∆中,0si n ≠A B B cos 3si n =∴ 即3tan =Bπ<<B 0 3π=∴B(2)323==b B ,π,由余弦定理B ac c a b cos 2222-+=,得1222=-+ac c aac c a 222≥+ 12≤∴ac ,当且仅当32==c a 时,ac 取得最大值为1218、19、解:(Ⅰ)由题意,这5种试验田果树的的平均死亡数为:2332242917255++++=……………………………………………………2分(Ⅱ)(x ,y )的取值情况有:(23,32),(23,24),(23,29),(23,17),(32,24),(32,29),(32,17),(24,29),(24,17),(29,17)…………………4分基本事件总数n =10………………………………………………………………5分 设满足||9x y -≥的事件为A ,则事件A 包含的基本事件为:(23,32),(32,17),(29,17),共有m =3个, ∴3()10P A =…………8分 设满足||3x y -≤的事件为B ,则事件B 包含的基本事件为:(23,24),(32,29),共有2m '=个, ∴2()10P B =……………………10分 ∴||3||9x y x y --≤或≥的概率321()()10102P P A P B =+=+=…………12分 20、解析: (Ⅰ)由图得:34T =116π-π3=96π=32π,∴T =2π,∴ω=2πT=1.又f (116π)=0,得:A sin(116π+φ)=0,∴116π+φ=2k π,φ=2k π-116π,∵0<φ<π2,∴当k =1时,φ=π6.又由f (0)=2,得:A sin φ=2,A =4,∴f (x )=4sin(x+π6). (4分) (Ⅱ)将f (x )=4 sin(x +π6)的图象上所有点的横坐标缩短为原来的12倍,纵坐标不变得到y =4sin(2x +π6),再将图象向右平移π6个单位得到g (x )=4sin[2(x -π6)+π6]=4sin(2x -π6),由2k π-π2≤2x -π6≤2k π+π2(k ∈Z )得:k π-π6≤x ≤k π+π3(k ∈Z ),∴g (x )的单调增区间为[k π-π6,k π+π3](k ∈Z ). (8分)(Ⅲ)y =f (x +π12)-2f (x +π3)=4sin[(x +π12)+π6]-2×4sin[(x +π3)+π6]=4sin(x +π4)-42sin(x +π2) =4(sin x ·cos π4+cos x ·sin π4)-42cos x=22sin x +22cos x -42cos x =22sin x -22cos x =4sin(x -π4).∵x ∈[-π2,512π],x -π4∈[-34π,π6],∴sin(x -π4)∈[-1,12],∴函数的最小值为-4,最大值为2. (12分)22.解:(Ⅰ)由题意可得201log (1)110x x x >⎧⎪⎪+>⎨⎪+>⎪⎩,得112x +>,解得{|01}x x <<…………2分(Ⅱ)方程有且仅有一解,等价于210ax x +-=有且仅有一解,且0,10x ax >+>………………4分当0a =时,1x =符合题意;当0a ≠时,11404a a ∆=+==-,此时2=x 满足题意综上,0a =或14a =-…………………………………………………………6分 (Ⅲ)当120x x <<时,1211a a x x +>+,221211log ()log ()a a x x +>+所以()f x 在(0)+∞,上单调递减函数()f x 在区间[1]t t +,上的最大值与最小值分别为()f t ,(1)f t +,2211()(1)log ()log ()11f t f t a a t t -+=+-+≤+即2(1)10at a t ++-≥对任意⎥⎦⎤⎢⎣⎡∈23,21t 恒成立……………………………8分 因为0a >,所以函数2(1)1y at a t =++-在区间⎥⎦⎤⎢⎣⎡23,21上单调递增,所以12t =时,y 有最小值3142a -, 由31042a -≥,得23a ≥故a 的取值范围为2[)3+∞,………………………………………………12分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长阳一中2016-2017学年度第一学期期中考试高二数学试卷(理科)考试 时间:120分钟 试卷总分:150分第Ⅰ卷 选择题部分(共60分)一、选择题:本大题共12小题,每小题5分,每小题四个选项中,只有一项是符合题目要求的。
1. 命题“02,00≤∈∃xR x ”的否定是( )A .不存在02,00>∈x R x B .02,00≥∈∃x R xC .02,≤∈∀x R xD .02,>∈∀x R x2、用随机数表法从100名学生(男生25人)中抽出20名进行评教,则男生甲被抽出的机率是 A 、51 B 、41 C 、251 D 、1001 3、圆C 的半径为1,圆心在第一象限,且与直线430x y -=和x 轴都相切,则该圆标准方程是 A.()()22211x y -+-= B. ()()22211x y -++=C.()()22211x y ++-= D. ()()22311x y -+-=4、“m =-1”是“直线mx +(2m -1)y +1=0和直线3x +my +3=0垂直”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件5、如右图所示,程序框图(算法流程图)的输出结果是 ( ) A .16B .2524 C .34 D .11126、直线3y kx =+与圆22(2)(3)4x y -+-=相交于,M N 两点,若MN ≥k 的 取值范围是A .3[,0]4-B .[C .[D .2[,0]3-7、从某高中随机选取5名高二男生,其身高和体重的数据如下表所示:175由表可得回归直线方程a x yˆ56.0ˆ+=,据此模型估计身高为cm 172的男生体重大约为 A .70.09 kg B .70.12 kg C .70.55 kg D .71.05 kg 8、已知F 1、F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点,若△ABF 2 是正三角形,则这个椭圆的离心率是( )A 、33B 、32 C 、22 D 、23 9、若直线y=kx -k 交抛物线x y 42=于A ,B 两点,且线段AB 中点到y 轴的距离为3,则AB =A .12B .10C .8D .610、一块石材表示的几何体的三视图如图2所示,将该石材切削、 打磨、加工成球,则能得到的最大球的半径等于 A 、1 B 、2 C 、3 D 、411、抛物线2y x =上的点到直线24x y -=的最短距离是( )A.35B.553 C.552 D.105312、F 1、F 1是双曲线)0,0(12222>>=-b a by a x 的左、右焦点,以坐标原点O 为圆心,|OF 1|为半径的圆与双曲线在第一象限的交点为P,则当△PF 1F 2的面积等于a 2时,双曲线的离心率为A.2B.3C.26D.2第Ⅱ卷 非选择题部分(共90分)二、填空题:本大题共4小题,每小题5分,把答案填在相应题号后的横线上。
13.将二进制数110 101(2)化成十进制数,结果为________14、如图所示,正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角,则异面直线AD 与BF 所成角的余弦值是_______.15、甲、乙两人约定在10:00---12:00会面商谈事情,约定先到者应等另一个人30分钟,即可离去,求两人能会面的概率 (用最简分数表示).16、关于x,y 的方程组{202xx y m y x --==-+有两组不同解,则实数m 的取值范围是三、解答题:本大题共6小题,解答应写出文字说明、证明过程或演算步骤。
17、(10分)命题p :关于x 的不等式0422>++ax x ,对一切x ∈R 恒成立,命题q :指数函 数xa x f )23()(-=是增函数,为假为真,若q p q p ∧∨,求实数a 的取值范围.18.(12分)某高校2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185)得到的频率分布直方图如图所示.(1)求第3、4、5组的频率并估计这次考试成绩的中位数(精确到小数点后一位数字);(2)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求:第4组至少有一名学生被甲考官面试的概率?19.(12分)在正方体1111ABCD A BC D -中,设E 是棱1CC 的中点。
(1) 求证:BD AE ⊥; (2) 求证://AC 平面1B DE ; (3)求锐二面角E-BD-C 的余弦值20、(12分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(x 吨)与相应的生产能耗y (吨)标准煤的几组对照数据:(1)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程a bx y+=ˆ; (2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(1)求出的线性回归方 程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?(参考:用最小二乘法求线性回归方程系数公式 1221ˆni ii nii x y nx yb xnx ==-⋅=-∑∑,ˆa y bx =-)21、(12分)已知圆O :222x y +=,直线:2l y kx =-.(1)若直线l 与圆O 交于不同的两点A 、B ,当AOB ∠为锐角时,求k 的取值范围. (2)若12k =,P 是直线l 上的动点,过P 作圆O 的两条切线PC 、PD ,切点为C 、D ,探 究:直线CD 是否过定点。
22、(12分)已知椭圆1C :22221x y a b+=(0a b >>)经过点()1,e ,其中e 是椭圆1C 的离心率,以原点O 为圆心,以椭圆1C 的长轴长为直径的圆2C 与直线20x y -+=相切. (Ⅰ)求椭圆1C 和圆2C 的方程;(Ⅱ)过椭圆1C 的右焦点F 的直线1l 与椭圆1C 交于点A ,B ,过F 且与直线1l 垂直的直线2l 与圆2C 交于点C ,D ,以A ,B ,C ,D 为顶点的四边形的面积记为S ,求S 的取值范围数学试卷(理科)参考答案一、选择题:二、填空题:13、 53 14、 4215、 95 16、 )12,0[三、解答题17、∵p ∨q 为真,p ∧q 为假,∴p 为真,q 为假,或p 为假,q 为真. ①当p 为真,q 为假时,,解得1<a <.②当p 为假,q 为真时,,解得a ≤﹣2综上,实数a 的取值范围是{a|a ≤﹣2或1<a <}. ………………… 10分18(1)由题设可知,第3组的频率为0.06×5=0.3;第4组的频率为0.04×5=0.2 第5组的频率为0.02×5=0.1.估计这次考试成绩的众数为171.7 ………………… 4分 (2)第3,4,5组分别抽取出3人,2人和1人. ………………… 7分 (3)设第3组的3位同学为A 1,A 2,A 3,第4组的两位同学为B 1,B 2,第5组的1位同学为C 1,则从六位同学中抽两位同学有:(A 1,A 2),(A 1,A 3),(A 1,B 1),(A 1,B 2),(A 1,C 1),(A 2,A 3),(A 2,B 1)(A 2,B 2),(A 2,C 1),(A 3,B 1),(A 3,B 2),(A 3,C 1),(B 1,B 2),(B 1,C 1),(B 2,C 1)共15种可能.其中第4组的2位同学为B 1,B 2,至少有一位同学入选的有(A 1,B 1),(A 1,B 2),(A 2,B 1)(A 2,B 2),(A 3,B 1),(A 3,B 2),(B 1,B 2),(B 1,C 1),(B 2,C 1)共9种可能所以第4组至少有一名学生被甲考官面试的概率为……………12分19、(1))证明连接BD ,AE . 因四边形ABCD 为正方形,故BD AC ⊥, 因EC ⊥底面ABCD ,BD ⊂面ABCD ,故EC BD ⊥,又ECAC C =,故BD ⊥平面AEC ,AE ⊂平面AEC ,故BD AE ⊥. ----------- 4分 ⑵. 连接1AC ,设 11AC B D G =,连接GE ,则G 为1AC 中点,而E 为1C C 的中点,故GE 为三角形1ACC 的中位线,//AC GE ,GE ⊂平面1B DE ,AC ⊄平面1B DE ,故//AC 平面1B DE . ----------- 8分⑶二面角E-BD-C 的余弦值为36 ------- 12分20、(1)4166.5i ii X Y ==∑ 4222221345686ii X==+++=∑ 4.5X = 3.5Y =266.54 4.5 3.566.563ˆ0.7864 4.58681b -⨯⨯-===-⨯- ; ˆˆ 3.50.7 4.50.35a Y bX =-=-⨯= 所求的回归方程为 0.70.35y x =+ (2) 100x =时, 35.70=y (吨)预测生产100吨甲产品的生产能耗比技改前降低9070.3519.65-=(吨)21、(1)(2)22、解:(Ⅰ)由已知得222222211c a a b a a b c ⎧+=⎪⎪=⎪=+⎪⎩,解得1a b ⎧=⎪⎨=⎪⎩所以椭圆1C 的方程为2212x y +=,圆2C 的方程为222x y +=.---------- 5分 (Ⅱ)若直线AB 的斜率不存在,由12l l ⊥,得22b aAB ==CD =,此时122S ==. 若直线AB 的斜率为0,由12l l ⊥,得AB =,CD 2==,此时122S ==. 若直线AB 的斜率存在且不为0,设1l 的方程为()1y k x =-.设()11,x y A ,()22,x y B ,()22121x y y k x ⎧+=⎪⎨⎪=-⎩,消y 得()2222124220k x k x k +-+-=,所以2122412k x x k +=+,21222212k x x k -=+,()()42221641222880k k k k ∆=-+-=+>.12x AB ==-== 又2l 的方程为()11y x k=--,即10x ky +-=,得CD ==11CD 22S =AB ⨯==. 因为2k >,S =2k 是单调递减函数,(S =.综上得,S 的取值范围是2,⎡⎣.---------- 12分。
