应用统计学 第4章数据的概括性度量新
统计学第4章学习指导
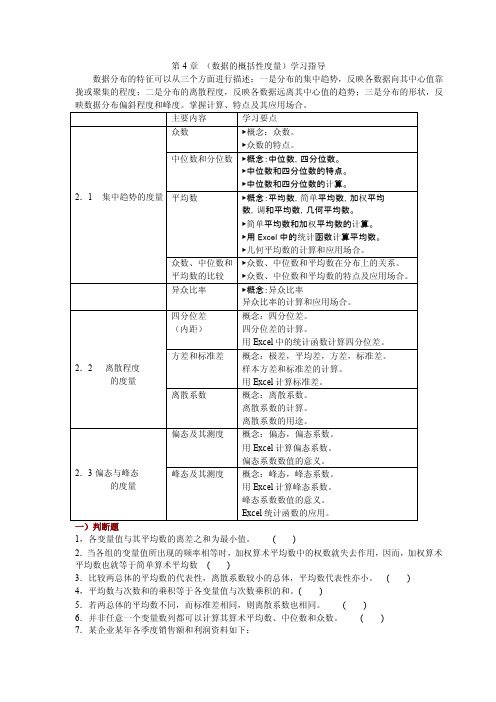
第4章(数据的概括性度量)学习指导数据分布的特征可以从三个方面进行描述:一是分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度;二是分布的离散程度,反映各数据远离其中心值的趋势;三是分布的形状,反映数据分布偏斜程度和峰度。
掌握计算、特点及其应用场合。
主要内容学习要点2.1 集中趋势的度量众数▶概念:众数。
▶众数的特点。
中位数和分位数▶概念:中位数,四分位数。
▶中位数和四分位数的特点。
▶中位数和四分位数的计算。
平均数▶概念:平均数,简单平均数,加权平均数,调和平均数,几何平均数。
▶简单平均数和加权平均数的计算。
▶用Excel中的统计函数计算平均数。
▶几何平均数的计算和应用场合。
众数、中位数和平均数的比较▶众数、中位数和平均数在分布上的关系。
▶众数、中位数和平均数的特点及应用场合。
异众比率▶概念:异众比率异众比率的计算和应用场合。
2.2离散程度的度量四分位差(内距)概念:四分位差。
四分位差的计算。
用Excel中的统计函数计算四分位差。
方差和标准差概念:极差,平均差,方差,标准差。
样本方差和标准差的计算。
用Excel计算标准差。
离散系数概念:离散系数。
离散系数的计算。
离散系数的用途。
2.3偏态与峰态的度量偏态及其测度概念:偏态,偏态系数。
用Excel计算偏态系数。
偏态系数数值的意义。
峰态及其测度概念:峰态,峰态系数。
用Excel计算峰态系数。
峰态系数数值的意义。
Excel统计函数的应用。
一)判断题1,各变量值与其平均数的离差之和为最小值。
( )2.当各组的变量值所出现的频率相等时,加权算术平均数中的权数就失去作用,因而,加权算术平均数也就等于简单算术平均数( )3.比较两总体的平均数的代表性,离散系数较小的总体,平均数代表性亦小。
( )4,平均数与次数和的乘积等于各变量值与次数乘积的和。
( )5.若两总体的平均数不同,而标准差相同,则离散系数也相同。
( )6.并非任意一个变量数列都可以计算其算术平均数、中位数和众数。
统计学第四章统计数据的概括性度量

4-3
经济、管理类 基础课程
统计学
一、统计数据的概括性度量方法—统计指标
1、概念:统计指标是反映现象总体综合数量特征的基本概念及其具体 数值的总称 2、特点:同质事物的可量性和量的综合性 3、作用: (1)是记录社会经济现象发展变化情况的工具,也是反映社会经济现 象数量规律的手段 (2)是进行社会经济管理和科学研究的基本依据 4、种类: (1)按作用和表现形式的不同分为:总量指标、相对指标、平均指标、 离散指标和形状指标 (2)按其所反映的内容和数量性质不同分为:数量指标和质量指标 (3)按其反映现象的时间状况不同分为:静态指标和动态指标 (4)按其计算范围不同分为:总体指标和样本指标 (5)按其计量单位不同可分为:实物指标、价值指标和劳动量指标
经济、管理类 基础课程
统计学
第四章 统计数据的概括性度量
4-1
经济、管理类 基础课程
统计学
第一节 第二节 第三节 第四节
第四章 统计数据的概括性度量
统计数据的概括性度量理论 集中趋势的度量 离散程度的度量 偏态与峰态的度量
4-2
经济、管理类 基础课程
统计学
第一节 统计数据的概括性度量理论
一、统计数据的概括性度量方法——统计指标 二、总量指标 三、相对指标 四、数据分布的特征及度量 (集中趋势、离中趋势、分布形状的测度)
4-8
经济、管理类 基础课程
统计学
三、相对指标
5、种类与计算方法
(3)比例相对数:是总体内部分与部分的数据对比,反映事物各组成部分 之间的数量联系程度,常用系数或倍数,以及n:1或n:100或1:m:n 的连比等形式表示 公式为: 比例相对指标=(总体中某一部分数值÷总体中另一部分数值)×100% 注意:分子分母指标可以互换、对比数值可以大于1或小于1,这一特点与 结构相对数不同。该指标有助于认识客观现象是否按比例协调发展 (4)比较相对数:是同类现象在不同国家、地区、部门、单位之间的数值 对比,用以表现同类现象在不同空间条件下的数量对比关系。常用百 分数、系数、倍数等表示。 公式为: 比较相对指标=某条件下的某类指标数值÷另一条件下同类指标数值 注意:分子分母可以互换,根据研究需要决定
第4章统计数据的概括性度量(新)

N
简写为:
x N
通常用于未分组数值型数据算术均值计算 且研究总量取决于各变量值的和。
简单算术均值
(例题分析)
【例】某班级40名同学统学的考试成绩 :
该班40名同学统计学的平均成绩为:
x 6 4 7 0 7 8 7 5 3 0 8 9 7 7 .2 3 (分)
总规模数据的计算要求
1.现象要具有同类性 2.要有明确、科学的涵义和科学的统计方法 3.要有统一的计量单位
第二节 相对水平的度量
一、相对数据的概述 二、相对水平的度量
一、相对数据的概述
1.相对数是由两个相互联系的变量值相除而得出的比 率,它反映了研究对象内部各部分之间或现象之间的 相互关系。
2.其数值表现形式有无名数和有名数两种,其中绝大 多数的相对数数值都采用无名数表现,常用的无 名数是系数、倍数和百分数。
3. 其计算公式为:
动态相对数=
报告期数值 基期数值
或
动态相对数=
报告期数值-基期数值 基期数值
如某年某国的经济增长率,某企业某月产品销售量
的发展速度,具体在第5章介绍。
17
强度相对数
1.是指两个性质不同但有联系的总体变量值的比率
2.强度相对数主要用来反映事物的密度、强度和普遍程度。
3. 强度相对数可用名数表示,也可用无名数表示。
13
二、相对水平的度量
常用的相对数:结构相对数,比较相对数, 动态相对数,强度相对数,计划完成程度相 对数。
结构相对数
1. 是指总体中某部分数值与全部数值的比率,可用 来反映研究现象内部的构成状况。 2. 常表现为比重,以百分数或系数表示。 3. 其计算公式为:
第四章 数据的概括性度量

第四章数据的概括性度量第四章 数据的概括性度量一.填空题 1. 是一组数据中出现次数最多的变量值。
2.一组数据排序后处于中间位置上的变量值称 。
3.不受极端值影响的集中趋势度量指标有 . 和 。
4.一组数据的最大值与最小值之差称 。
5. 是一组数据的标准差与其相应的平均数之比。
6.Excel 中计算中位数时选用的函数为 。
7. 某工厂13名工人某日生产零件数分别为(单位:件)10.11.13.11.14.11.12.11.15.16.12.11.13 ,则中位数为 ;众数为 。
8.某百货公司连续几天的销售额如下:257.276.297.252.238.310.240.236.265,则其下四分位数是 。
9.若一组数据的e oX M M 〈〈,则其属于_______________分布(左偏.右偏)。
10.如果一组数据服从标准正态分布,则峰态系数为___________。
11.假定一个总体由5个数据组成:3.7.8.9.13,该总体的方差为。
13.某班共有25名学生,期末统计学课程的考试分数分别为:68.73.66.76.86.74.61.89.65.90.69.67.76.62.81.63.68.81.70.73.60.87.75.64.56,该班考试分数的下四分位数和上四分位数分别是和。
14.在某行业中随机抽取10家企业,第一季度的利润额(单位:万元)分别为72.63.1.54.7.54.3.29.26.9.25.23.9.23.20,该组数据的极差为。
二.单项选择题1.对于对称分布的数据,众数.中位数和平均数的关系是:()。
A.众数>中位数>平均数B.众数=中位数=平均数C.平均数>中位数>众数D.中位数>众数>平均数2.可以计算平均数的数据类型有:()。
A.分类型数据B.顺序型数据C.数据型数据D.所有数据类型3.数值型数据的离散程度测度方法中,受极端变量值影响最大的是()。
A.极差B.方差C.均方差D.平均差4.当偏态系数为正数时,说明数据的分布是()。
(04)数据概括度量

调和平均数的应用
【例】某企业某日工人的日产量资料如下:
日产量(件) 各组工人日总产量(件)
X
10 11 12 13 14
m
700 1100 4560 1950 1400 9710
合计
计算该企业该日全部工人的平均日产量。
调和平均数的应用
解:
XH m 1 Xm 9710 700 1400 10 14
求解比值的平均数的方法
mi 比值 X i fi
X
m f
Xf f
m 1 X m
己知 m、f, 己知 X、f , 采用基本平 采用加权算术 均数公式 平均数公式
己知 X、m , 采用加权调和 平均数公式
求解比值的平均数的方法
【例A】某季度某工业公司18个工业企业 产值计划完成情况如下:
STAT
第四章 数据的概括性度量
统计学家与数学家
一名统计学家遇到一位数学家,统计学家 调侃数学家说道:“你们不是说若X=Y且Y =Z,则X=Z吗!那么想必你若是喜欢一个 女孩,那么那个女孩喜欢的男孩你也会喜欢 喽!?” 数学家想也没事吧!因为它们平均的温度 不过是五十度而已!”
计划完成程度 组中值 (﹪) (﹪) 85 90以下 95 90~100 105 100~110 115 110以上 — 合计 企业数 计划产值 (个) (万元) 2 800 3 2500 10 17200 3 4400 18 24900
计算该公司该季度的平均计划完成程度。
计划完成 实际产值m 求解比值的平均数的方法 X 分析:
1 1 1 1 4 ⒉再求算术平均数: 2 4 6 8
⒊再求倒数:
1 1 1 1 4 2 4 6 8
第四章 数据的概括性度量

第四章 数据的概括性度量
4.2.3 数值型数据:方差和标准差 1、极差 一组数据的最大值与最小值之差称为极差,也称全距,用R表示。 R=Max-Min 极差是描述数据离散程度的最简单的测度值,计算简单,易于理解,但容易受极 端值的影响。由于极差只是利用了一组数据两端的信息,不能反映出中间数据的 分散情况,因而不能准确表述出数据的分散程度。 2、平均差 也称平均绝对离差,是各变量值与其平均数离差绝对值的平均数,用Md表示。 Md=(∑ ∣Xi-X ∣)/n
第四章 数据的概括性度量
MEDIAN函数用于计算给定数值的中值,即一组数值中居于中间的数值,其语法是 MEDIAN(number1,number2,…)。其中,参数number1,number2…为数组或对单元格 的引用,参数的个数介于1—255之间。 2、四分位数 四分位数、十分位数和百分位数分别是用3个点、9个点和99个点将数据4等分、10 等分和100等分后各分位点上的值。 四分位数也称为四分位点,是一组数据排序后处于25%和75%位置上的值。四分位 数通过3个点将全部数据等分为4部分,其中每部分包含25%的数据。中间的四分位 数就是中位数。
变异指标:一组数值之间的差异程度称为标志变动度。测定标志变动度大小的指 标叫做标致变异指标。
第四章 数据的概括性度量
变异指标的作用:
① 反映总体各单位变量值分布的均衡性。一般来说,标致变异指标数值越大,总 体各单位变量值分布的离散趋势越高,均衡性越低;反之,变量值分布的离散 趋势越低,均衡性就越高。
数据的概括性度量
第四章 数据的概括性度量
利用图表展示数据,可以对数据分布的形状和特征有一个大致的了解。但要全面 把握数据分布的特征,还需要找到反映数据分布特征的各个代表值。 数据分布特征可以从三个方面进行测度和描述: •分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度。 •分布的离散程度,反映各数据远离其中心值的趋势。 •分布的形状,反映数据分布的偏态和峰态。
统计学第4章数据的概括性度量

https://
REPORTING
• 引言 • 集中趋势的度量 • 离散程度的度量 • 偏态与峰态的度量 • 数据分布形态的图形表示 • Excel在概括性度量中的应用
目录
PART 01
引言
REPORTING
WENKU DESIGN
概括性度量的定义
方差和标准差能够全面反映数据的离散程度,且计算相对简单。其中标
准差具有与原始数据相同的量纲,更便于比较不同数据集之间的离散程
度。
PART 04
偏态与峰态的度量
REPORTING
WENKU DESIGN
偏态及其度量
偏态定义
偏态是指数据分布的不对称性。 在统计学中,偏态通常通过计算 偏态系数来衡量。
特点
算术平均数对极端值敏感,当数 据集中存在极端异常值时,算术
平均数可能会受到较大影响。
中位数
定义
计算公式
中位数是一组数据按照大小顺序排列后, 位于中间位置的数值,用于反映数据集中 趋势的一个统计指标。
中位数 = 第(n+1)/2项数据(n为数据个数 )适用Fra bibliotek围特点
适用于数值型数据,且数据分布呈偏态或 存在极端异常值的情况。
偏态与峰态度量
包括偏态系数和峰态系数 等,用于描述数据分布的 形态特点。
PART 02
集中趋势的度量
REPORTING
WENKU DESIGN
算术平均数
定义
算术平均数是一组数据的总和 除以数据的个数,用于反映数 据集中趋势的一个统计指标。
计算公式
算术平均数 = 数据总和 / 数据 个数
适用范围
适用于数值型数据,且数据之 间没有极端异常值的情况。
贾俊平《统计学》(第5版)章节题库-第4章 数据的概括性度量【圣才出品】

第4章 数据的概括性度量一、单项选择题1.一组数据中出现频数最多的变量值称为( )。
A.众数B.中位数C.四分位数D.平均数【答案】A【解析】众数是一组数据中出现次数最多的变量值。
众数主要用于测度分类数据的集中趋势。
一般情况下,只有在数据量较大的情况下,众数才有意义。
2.下列关于众数的叙述,不正确的是( )。
A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不受极端值的影响【答案】C【解析】众数是一组数据中出现次数最多的变量值。
众数主要用于测度分类数据的集中趋势,当然也适用于作为顺序数据以及数值型数据集中趋势的测度值。
一般情况下,只有在数据量较大的情况下,众数才有意义。
一组数据可能存在多个众数,由于众数是一个位置代表值,因此它不受数据中极端值的影响。
3.一组数据排序后处于中间位置上的变量值称为( )。
A.众数B.中位数C.四分位数D.平均数【答案】B【解析】中位数是一组数据排序后处于中间位置上的变量值。
中位数将全部数据等分成两部分,每部分包含50%的数据,一部分数据比中位数大,另一部分则比中位数小。
4.一组数据排序后处于25%和75%位置上的值称为( )。
A.众数B.中位数C.四分位数D.平均数【答案】C【解析】四分位数也称四分位点,它是一组数据排序后处于25%和75%位置上的值。
四分位数是通过3个点将全部数据等分为4部分,其中每部分包含25%的数据。
5.非众数组的频数占总频数的比例称为( )。
A.异众比率B.离散系数C.平均差D.标准差【答案】A【解析】异众比率是指非众数组的频数占总频数的比例。
主要用于衡量众数对一组数据的代表程度。
6.四分位差是( )。
A.上四分位数减下四分位数的结果B.下四分位数减上四分位数的结果C.下四分位数加上四分位数D.四分位数与上四分位数的中间值【答案】A【解析】四分位差也称内距或四分间距,它是上四分位数与下四分位数之差。
四分位差反映了中间50%数据的离散程度,其数值越小,说明中间的数据越集中;其数值越大,说明中间的数据越分散。
统计学第四章统计数据的概括性度量

经济、管理类 基础课程
众数
(众数的不唯一性P87)
10 5 9 12 6 8
统计学
无众数 原始数据:
一个众数 原始数据:
4 6
5
9
8
5
5
多于一个众数 原始数据: 25 28 28 36 42 42
4 - 17
经济、管理类 基础课程
分类数据的众数
(算例)
统计学
【例 4.1】根据第三章表 3-1 中的 数据,计算众数
4-3
经济、管理类 基础课程
统计学
一、统计数据的概括性度量方法—统计指标
1、概念:统计指标是反映现象总体综合数量特征的基本概念及其具体 数值的总称 2、特点:同质事物的可量性和量的综合性 3、作用: (1)是记录社会经济现象发展变化情况的工具,也是反映社会经济现 象数量规律的手段 (2)是进行社会经济管理和科学研究的基本依据 4、种类: (1)按作用和表现形式的不同分为:总量指标、相对指标、平均指标、 离散指标和形状指标 (2)按其所反映的内容和数量性质不同分为:数量指标和质量指标 (3)按其反映现象的时间状况不同分为:静态指标和动态指标 (4)按其计算范围不同分为:总体指标和样本指标 (5)按其计量单位不同可分为:实物指标、价值指标和劳动量指标
统计学
1. 一组数据向其中心值靠拢的倾向和程度 2. 测度集中趋势就是寻找数据一般水平的代表值或中心值 3. 不同类型的数据用不同的集中趋势测度值
4. 低层次数据的集中趋势测度值适用于高层次的测量数据, 反过来,高层次数据的集中趋势测度值并不适用于低层次 的测量数据 5. 选用哪一个测度值来反映数据的集中趋势,要根据所掌握 的数据的类型来确定
统计学
6第四章、数据的概括性度量(一)

调侃统计学家
如果你的腳已經踩在爐子上, 而頭卻在冰箱裡,統計學家會告訴 你,平均而言,你相當舒服。
数据特征测度分类
数据的特征和测度
集中趋势
众数 中位数 均值
离散程度
分布的形状
异众比率 四分位差 方差和标准差 离散系数
偏态 峰度
集中趋势
指总体中各单位的次数分布从两边向 中间集中的趋势,用平均指标来反映。
广告类型
人数(人) 比例 频率(%)
商品广告 服务广告 金融广告 房地产广告 招生招聘广告 其他广告
合计
112
0.560
56.0
51
0.255
25.5
9
0.045
4.5
16
0.080
8.0
10
0.050
5.0
2
0.010
1.0
200
1
100
解:这里的变量为“广告类 型”,这是个分类变量,不 同类型的广告就是分类数据 我们看到,在所调查的200 人当中,关注商品广告的人 数 最 多 , 为 112 人 , 占 总 被 调查人数的56%,因此众数 为“商品广告”这一类别, 即
第四章 数据的概括性度量
第一节 集中趋势的测度 第二节 离散程度的测度 第三节 偏态与峰度的测度
统计学家与数学家
一名统计学家遇到一位数学家,统计学家 调侃数学家说道:“你们不是说若X=Y且Y =Z,则X=Z吗!那么想必你若是喜欢一个 女孩,那么那个女孩喜欢的男孩你也会喜欢 喽!?”
数学家想也没事吧!因为它们平均的温度不 过是五十度而已!”
50%
50%
Me 3. 不受极端值的影响
4. 主要用于顺序数据,也可用数值型数据,但不能用于分 类数据
应用统计课件:第 4 章 数据的概括性度量

第 4 章数据的概括性度量集中趋势(central tendency)分类数据:众数众数(mode)1.一组数据中出现次数最多的变量值2.适合于数据量较多时使用3.不受极端值的影响4.一组数据可能没有众数或有几个众数5.主要用于分类数据,也可用于顺序数据和数值型数据众数(不惟一性)无众数原始数据: 10 5 9 12 6 8分类数据的众数(例题分析)顺序数据的众数(例题分析)顺序数据:中位数和分位数中位数(median)1.排序后处于中间位置上的值中位数(位置和数值的确定)顺序数据的中位数(例题分析)数值型数据的中位数(9个数据的算例)【例】9个家庭的人均月收入数据原始数据: 1500 750 780 1080 850 960 2000 1250 1630排序: 750 780 850 960 1080 1250 1500 1630 2000位置: 1 2 3 4 5 6 7 8 9数值型数据的中位数(10个数据的算例)【例】:10个家庭的人均月收入数据排序: 660750 780 850 960 10801250 1500 1630 2000位置: 1 2 3 4 5 67 8 9 10 四分位数(quartile)1.排序后处于25%和75%位置上的值顺序数据的四分位数(例题分析)数值型数据的四分位数(9个数据的算例)【例】:9个家庭的人均月收入数据(4种方法计算)原始数据: 1500 750 780 1080 850 960 2000 1250 1630排序: 750 780 850960 1080 1250 1500 1630 2000位置: 1 2 3 4 5 67 8 9数值型数据:平均数平均数(mean)1.也称为均值2.集中趋势的最常用测度值3.一组数据的均衡点所在3.体现了数据的必然性特征4.易受极端值的影响5.有简单平均数和加权平均数之分6.根据总体数据计算的,称为平均数,记为μ;根据样本数据计算的,称为样本平均数,记为⎺x简单平均数(Simple mean)加权平均数(Weighted mean)几何平均数(geometric mean)1.n 个变量值乘积的n 次方根2.适用于对比率数据的平均3.主要用于计算平均增长率4.计算公式为几何平均数(例题分析)【例】一位投资者购持有一种股票,在2000、2001、2002和2003年收益率分别为4.5%、2.1%、25.5%、1.9%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四分位差为
Qd = QU - QL =3–2 =1
数值型数据:方差和标准差
极差
(range)
1. 2. 3. 4. 一组数据的最大值与最小值之差 离散程度的最简单测度值 易受极端值影响 未考虑数据的分布
5. 计算公式为
R = max(xi) - min(xi)
Me=一般
数值型数据的中位数
(9个数据的算例)
【例】
原始数据: 1630 排 序: 2000 位 置:
9个家庭的人均月收入数据
1500 750 780 1080 850 960 2000 1250 750 780 850 960 1080 1250 1500 1630
n 1 9 1 位置 5 2 2 中位数 1080
数值型数据:平均数
平均数
(mean)
1. 2. 3. 3. 4. 5. 6. 也称为均值 集中趋势的最常用测度值 x 一组数据的均衡点所在 体现了数据的必然性特征 易受极端值的影响 有简单平均数和加权平均数之分 根据总体数据计算的,称为平均数,记为;根据 样本数据计算的,称为样本平均数,记为x
(central tendency)
1. 一组数据向其中心值靠拢的倾向和程度 2. 测度集中趋势就是寻找数据水平的代表值或中心值 3. 不同类型的数据用不同的集中趋势测度值
4. 低层次数据的测度值适用于高层次的测量数据,但高 层次数据的测度值并不适用于低层次的测量数据
分类数据:众数
众数
(mode)
非常不满意 不满意 一般 满意 非常满意
合计
24 108 93 45 30
300
8 36 31 15 10
100.0
Mo=不满意
顺序数据:中位数和分位数
中位数 (median)
1. 排序后处于中间位置上的值
50%
Me
50%
2. 不受极端值的影响 3. 主要用于顺序数据,也可用数值型数据,但不能 用于分类数据 4. 各变量值与中位数的离差绝对值之和最小,即
甲城市 回答类别 非常不满意 不满意 一般 满意 非常满意 合计
户数 (户)
24 108 93 45 30 300
累计频数
24 132 225 270 300 —
满意”这一组别中; QU在 “一般”这一组别中 四分位数为 QL = 不满意 QU = 一般
数值型数据的四分位数
(9个数据的算例)
1. 一组数据中出现次数最多的变量值
2. 适合于数据量较多时使用 3. 不受极端值的影响 4. 一组数据可能没有众数或有几个众数 5. 主要用于分类数据,也可用于顺序数据和 数值型数据
众数
(不惟一性)
无众数 原始数据: 一个众数 原始数据:
10 6 5 5 9 9 12 8 5 6 5 8
多于一个众数 原始数据: 25 28 28 36 42 42
平均差
(mean deviation)
1. 各变量值与其平均数离差绝对值的平均数 2. 能全面反映一组数据的离散程度 3. 数学性质较差,实际中应用较少
4. 计算公式为
未分组数据
Md
x
i 1
n
i
x
n
组距分组数据 M d
M
i 1
k
i
x fi
n
平均差
(例题分析)
某电脑公司销售量数据平均差计算表 xx 按销售量分组 组中值(Mi) 频数(fi)
50 15 50 15 1 50 0.7 70%
顺序数据:四分位差
四分位差
(quartile deviation)
1. 对顺序数据离散程度的测度 2. 也称为内距或四分间距 3. 上四分位数与下四分位数之差
Qd = QU – Q L
4. 反映了中间50%数据的离散程度
5. 不受极端值的影响
x
M
i 1
k
i
fi
合计
—
120
22200
n 22200 185 120
几何平均数
(geometric mean)
1. n 个变量值乘积的 n 次方根 2. 适用于对比率数据的平均 3. 主要用于计算平均增长率 4. 计算公式为
Gm n x1 x2 xn n
5. 可看作是平均数的一种变形
x
i 1
n
i
n
1 lg Gm (lg x1 lg x 2 lg x n ) n
lg x
i 1
i
n
几何平均数
(例题分析)
【 例 】 一 位 投 资 者 购 持 有 一 种 股 票 , 在 2000 、 2001、2002和2003年收益率分别为4.5%、2.1%、 25.5%、1.9%。计算该投资者在这四年内的平均收益 率 几何平均:
G 4 104.5% 102.1% 125.5% 101.9% 1 8.0787% 算术平均: G 4.5% 2.1% 25.5% 1.9% 4 8.5%
众数、中位数和平均数的比较
众数、中位数和平均数的关系
均值 中位数 众数
均值 = 中位数 = 众数
数值确定
n为偶数
顺序数据的中位数
(例题分析)
甲城市家庭对住房状况评价的频数分布 回答类别 非常不满意 不满意 一般 满意 非常满意 合计 甲城市 户数 (户) 24 108 93 45 30 300 累计频数 24 132 225 270 300 —
解:中位数的位置为
(300+1)/2=150.5 从累计频数看, 中位数在“一般”这 一组别中 中位数为
解:
vr
果汁 矿泉水 绿茶 其他 碳酸饮料
合计
6 10 11 8 15
50
0.12 0.20 0.22 0.16 0.30
1
在所调查的50人当中,购 买其他品牌饮料的人数占 70%,异众比率比较大。因 此,用“碳酸饮料”代表消 100 费者购买饮料品牌的状况, 其代表性不是很好
12 20 22 16 30
分类数据的众数
(例题分析)
)
解:这里的变量为“饮 料品牌”,这是个分类 变量,不同类型的饮料 就是变量值 所 调 查 的 50 人 中 , 购买碳酸饮料的人数最 多,为15人,占总被调 查人数的30%,因此众 数为“可口可乐”这一 品牌,即
按销售量分组 140~150 150~160 160~170 170~180 180~190 190~200 200~210 210~220 220~230 230~240 组中值(Mi) 145 155 165 175 185 195 205 215 225 235 频数(fi) 4 9 16 27 20 17 10 8 4 5 Mi fi 580 1395 2640 4725 3700 3315 2050 1720 900 1175
3. 平均数
4.2 离散程度的度量
4.2.1 4.2.2 4.2.3 4.2.4 分类数据:异众比率 顺序数据:四分位差 数值型数据:方差和标准差 相对离散程度:离散系数
离中趋势
1. 数据分布的另一个重要特征
2. 反映各变量值远离其中心值的程度(离散程度) 3. 从另一个侧面说明了集中趋势测度值的代表程度 4. 不同类型的数据有不同的离散程度测度值
简单平均数
(Simple mean)
设一组数据为:x1 ,x2 ,… ,xn (总体数据xN)
样本平均数
x1 x 2 x n x n
x
i 1
n
i
n
总体平均数
x1 x 2 x N i 1 N N
x
N
i
加权平均数
(Weighted mean)
设各组的组中值为:M1 ,M2 ,… ,Mk 相应的频数为: f1 , f2 ,… ,fk 样本加权平均
1
2
3
4
5
6
7
8
9
数值型数据的中位数
(10个数据的算例)
【例】:10个家庭的人均月收入数据
排 序: 2000 位 置: 660 750 780 850 960 1080 1250 1500 1630
1 2
3
4
5
6
7
8
9
10
n 1 10 1 位置 5.5 2 2
960 1080 中位数 1020 2
【例】:9个家庭的人均月收入数据(4种方法计 算)
原始数据: 排 序: 位 置: 1500 750 780 1080 850 960 2000 1250 1630 750 780 850 960 1080 1250 1500 1630 2000
1
2
3
4
5
6
7
8
9
3 9 QU 位置 6.75 4 QL 780 (850 780) 0.25 QU 1250 (1500 1250) 0.75 1437.5 797.5 9 QL 位置 2.25 4
分类数据:异众比率
异众比率
(variation ratio)
1. 对分类数据离散程度的测度
2. 非众数组的频数占总频数的比例 3. 计算公式为
vr
f f f
i i
m
fm 1 fi
4. 用于衡量众数的代表性
异众比率
(例题分析)
不同品牌饮料的频数分布 饮料品牌 频数 比例 百分 比(%)
