大学物理:第 16 章 变化的电磁场
大学物理第16章麦克斯韦方程组和电磁辐射

位移电流 全电流安培环路定理
稳恒磁场中,安培环路定理 H dl I j ds
l s
S1
L
-
S2
+ + + +
(以 L 为边做任意曲面 S ) H dl j ds I
L S1
I
H dl j ds 0
第16章 麦克斯韦方程组和电 磁辐射
本章主要内容
§16.1 Maxwell电磁场方程组
§16.2 电磁波和电磁辐射 §16.4 电磁波的性质 §16.5 电磁波的能量 §16.6 电磁波的动量 光压
第16章 麦克斯韦方程组和电磁辐射
电现象/磁现象
电场/磁场(稳恒态)
我国:周朝(BC8世)/战国(BC4-3世) 西方:BC6世/ AD15世末
B
2
计算得
r dQ H 2 2 π R dt
Q
0 r dQ
2 π R dt
2
代入数据计算得
Q
I d 1.1 A
B 1.1110 T
5
Ic
R
P *r
Ic
例2. 一平行板电容器的两极板都是圆形板,面积为S,其上 的电荷随时间变化,变化率为 q q sint
m
求: 1)电容器中位移电流密度的大小。
麦克斯韦18311879英国物理学家1865年麦克斯韦在总结前人工作的基础上提出完整的电磁场理论他的主要贡献是提出了有旋电场和位移电流两个假设从而预言了电磁波的存在并计算出电磁波的速度即光1888年赫兹的实验证实了他的预言麦克斯韦理论奠定了经典电动力学的基础为无线电技术和现代电子通讯技术发展开辟了广阔前景
大学物理电磁学公式总结汇总

大学物理电磁学公式总结汇总普通物理学教程大学物理电磁学公式总结,下面给大家整理了关于大学物理电磁学公式总结,方便大家学习大学物理电磁学公式总结1定律和定理1. 矢量叠加原理:任意一矢量可看成其独立的分量的和。
即:=∑ (把式中换成、、、、、就分别成了位置、速度、加速度、力、电场强度和磁感应强度的叠加原理)。
2. 牛顿定律:=m (或= );牛顿第三定律:′= ;万有引力定律:3. 动量定理:→动量守恒:条件4. 角动量定理:→角动量守恒:条件5. 动能原理:(比较势能定义式:)6. 功能原理:A外+A非保内=ΔE→机械能守恒:ΔE=0条件A 外+A非保内=07. 理想气体状态方程:或P=nkT(n=N/V,k=R/N0)8. 能量均分原理:在平衡态下,物质分子的每个自由度都具有相同的平均动能,其大小都为kT/2。
克劳修斯表述:不可能把热量从低温物体传到高温物体而不产生其它影响。
开尔文表述:不可能从单一热源吸取热量,使之完全变为有用的功而不产生其它影响。
实质:在孤立系统内部发生的过程,总是由热力学概率小的宏观状态向热力学概率大的状态进行。
亦即在孤立系统内部所发生的过程总是沿着无序性增大的方向进行。
9. 热力学第一定律:ΔE=Q+A10.热力学第二定律:孤立系统:ΔS0(熵增加原理)11. 库仑定律:(k=1/4πε0)12. 高斯定理:(静电场是有源场)→无穷大平板:E=σ/2ε013. 环路定理:(静电场无旋,因此是保守场)θ2Ir P o Rθ1I14. 毕奥—沙伐尔定律:直长载流导线:无限长载流导线:载流圆圈:,圆弧:电磁学1. 定义:= /q0 单位:N/C =V/mB=Fmax/qv;方向,小磁针指向(S→N);单位:特斯拉(T)=104高斯(G)① 和:=q( + × )洛仑兹公式②电势:电势差:电动势:( )③电通量:磁通量:磁通链:ΦB=NφB单位:韦伯(Wb)Θ ⊕-q +qS④电偶极矩:=q 磁矩:=I =IS⑤电容:C=q/U 单位:法拉(F)乘自感:L=Ψ/I 单位:亨利(H)乘互感:M=Ψ21/I1=Ψ12/I2 单位:亨利(H)⑥电流:I = ; 乘位移电流:ID =ε0 单位:安培(A)⑦乘能流密度:2. 实验定律① 库仑定律:②毕奥—沙伐尔定律:③安培定律:d =I ×④电磁感应定律:ε感= –动生电动势:感生电动势:( i为感生电场)乘⑤欧姆定律:U=IR( =ρ )其中ρ为电导率3. 乘定理(麦克斯韦方程组)电场的高斯定理:( 静是有源场)( 感是无源场)磁场的高斯定理:( 稳是无源场)( 感是无源场)电场的环路定理:(静电场无旋)(感生电场有旋;变化的磁场产生感生电场)安培环路定理:(稳恒磁场有旋)(变化的电场产生感生磁场)4. 常用公式①无限长载流导线:螺线管:B=nμ0I② 带电粒子在匀强磁场中:半径周期磁矩在匀强磁场中:受力F=0;受力矩③电容器储能:Wc= CU2 乘电场能量密度:ωe= ε0E2 电磁场能量密度:ω= ε0E2+ B2乘电感储能:WL= LI2 乘磁场能量密度:ωB= B2 电磁场能流密度:S=ωV④ 乘电磁波:C= =3.0×108m/s 在介质中V=C/n,频率f=ν=波动学大学物理电磁学公式总结2概念(2113定义和相关公式)1. 位置矢量:,其5261在直角坐标系中:; 角位置:4102θ16532. 速度:平均速度:速率:( )角速度:角速度与速度的关系:V=rω3. 加速度:或平均加速度:角加速度:在自然坐标系中其中(=rβ),(=r2 ω)4. 力:=m (或= ) 力矩:(大小:M=rFcosθ方向:右手螺旋法则)5. 动量:,角动量:(大小:L=rmvcosθ方向:右手螺旋法则)6. 冲量:(= Δt);功:(气体对外做功:A=∫PdV)mg(重力) → mgh-kx(弹性力) → kx2/2F= (万有引力) → =Ep(静电力) →7. 动能:mV2/28. 势能:A保= –ΔEp不同相互作用力势能形式不同且零点选择不同其形式不同,在默认势能零点的情况下:机械能:E=EK+EP9. 热量:其中:摩尔热容量C与过程有关,等容热容量Cv 与等压热容量Cp之间的关系为:Cp= Cv+R10. 压强:11. 分子平均平动能:;理想气体内能:12. 麦克斯韦速率分布函数:(意义:在V附近单位速度间隔内的分子数所占比率)13. 平均速率:方均根速率:;最可几速率:14. 熵:S=KlnΩ(Ω为热力学几率,即:一种宏观态包含的微观态数)15. 电场强度:= /q0 (对点电荷:)16. 电势:(对点电荷);电势能:Wa=qUa(A= –ΔW)17. 电容:C=Q/U ;电容器储能:W=CU2/2;电场能量密度ωe=ε0E2/218. 磁感应强度:大小,B=Fmax/qv(T);方向,小磁针指向(S→N)。
大学物理变化的电磁场习题思考题

习题88-1.如图所示,金属圆环半径为R ,位于磁感应强度为B的均匀磁场中,圆环平面与磁场方向垂直。
当圆环以恒定速度v在环所在平面内运动时,求环中的感应电动势及环上位于与运动方向垂直的直径两端a 、b 间的电势差。
解:(1)由法拉第电磁感应定律i d dtεΦ=-,考虑到圆环内的磁通量不变,所以,环中的感应电动势0i ε=; (2)利用:()aab bv B dl ε=⨯⋅⎰,有:22ab Bv R Bv R ε=⋅=。
【注:相同电动势的两个电源并联,并联后等效电源电动势不变】8-2.如图所示,长直导线中通有电流A I 0.5=,在与其相距cm 5.0=d 处放有一矩形线圈,共1000匝,设线圈长cm 0.4=l ,宽cm 0.2=a 。
不计线圈自感,若线圈以速度cm/s 0.3=v 沿垂直于长导线的方向向右 运动,线圈中的感生电动势多大?解法一:利用法拉第电磁感应定律解决。
首先用0lB dl I μ⋅=∑⎰ 求出电场分布,易得:02I B rμπ=, 则矩形线圈内的磁通量为:00ln22x axI I l x al dr r xμμππ++Φ=⋅=⎰, 由i d Nd t εΦ=-,有:011()2i N I l d xx a x dtμεπ=--⋅+ ∴当x d =时,有:041.92102()i N I l a v V d a μεπ-==⨯+。
解法二:利用动生电动势公式解决。
由0lB dl I μ⋅=∑⎰ 求出电场分布,易得:02I B rμπ=, 考虑线圈框架的两个平行长直导线部分产生动生电动势, 近端部分:11NB l v ε=, 远端部分:22NB lv ε=, 则:12εεε=-=00411() 1.921022()N I N I al v l v V d d a d d a μμππ--==⨯++。
8-3.如图所示,长直导线中通有电流强度为I 的电流,长为l 的金属棒ab 与长直导线共面且垂直于导线放置,其a 端离导线为d ,并以速度v平行于长直导线作匀速运动,求金属棒中的感应电动势ε并比较U a 、U b 的电势大小。
大学物理电磁学

大学物理电磁学是物理学的一个重要分支,主要研究电磁现象的规律和本质。
电磁学在科学技术、工业生产和日常生活中都有着广泛的应用。
本文将从电磁学的基本概念、基本定律和电磁波的传播等方面对大学物理电磁学进行介绍。
一、基本概念1.电荷:电荷是物质的一种属性,分为正电荷和负电荷。
电荷间的相互作用规律是:同种电荷相互排斥,异种电荷相互吸引。
2.电场:电场是电荷及变化磁场周围空间里存在的一种特殊物质,它对放入其中的电荷有作用力。
电场的强度用电场强度E表示,单位是牛/库仑。
3.磁场:磁场是磁体周围空间里存在的一种特殊物质,它对放入其中的磁体有作用力。
磁场的强度用磁感应强度B表示,单位是特斯拉。
4.电磁波:电磁波是由同相振荡且互相垂直的电场与磁场在空间中以波的形式移动,其传播方向垂直于电场与磁场构成的平面,有效的传递能量。
电磁波在真空传播速度与光速一样,速度为30万千米/秒。
二、基本定律1.库仑定律:库仑定律是描述电荷之间相互作用的定律,其内容为:真空中两点电荷间的作用力与它们的电荷量的乘积成正比,与它们的距离的平方成反比,作用力在它们的连线上。
2.安培定律:安培定律是描述电流和电流激发磁场的定律,其内容为:电流I1通过一条无限长直导线时,在距离导线r处产生的磁场强度H1与I1成正比,与r成反比,即H1与I1r成反比。
磁场方向垂直于电流方向和通过点的平面。
3.法拉第电磁感应定律:法拉第电磁感应定律是描述磁场变化引起电场变化的定律,其内容为:穿过电路的磁通量发生变化时,产生感应电动势。
感应电动势的大小与磁通量变化率成正比,与电路的匝数成正比。
4.麦克斯韦方程组:麦克斯韦方程组是描述电磁场分布和电磁波传播的四个偏微分方程,包括库仑定律、法拉第电磁感应定律、安培定律和位移电流定律。
三、电磁波的传播1.电磁波的发射:电磁波的产生通常是通过振荡电路实现的。
当振荡电路中的电场和磁场相互垂直且同相振荡时,电磁波便会产生并向外传播。
大学物理电磁学部分总结

电磁学部分总结 静电场部分第一部分:静电场的基本性质和规律电场是物质的一种存在形态,它同实物一样也具有能量、动量、质量等属性。
静电场的物质特性的外在表现是:(1)电场对位于其中的任何带电体都有电场力的作用(2)带电体在电场中运动,电场力要作功——电场具有能量1、描述静电场性质的基本物理量是场强和电势,掌握定义及二者间的关系。
电场强度 电势2、反映静电场基本性质的两条定理是高斯定理和环路定理要掌握各个定理的内容,所揭示的静电场的性质,明确定理中各个物理量的含义及影响各个量的因素。
重点是高斯定理的理解和应用。
3、应用(1)、电场强度的计算a)、由点电荷场强公式 及场强叠加原理 计算场强q FE =⎰∞⋅==aa ar d E q W U 0∑⎰⎰=⋅=ΦiSe qS d E 01ε ⎰=⋅0r d E L 02041r rq E πε=iiE E ∑=一、离散分布的点电荷系的场强二、连续分布带电体的场强其中,重点掌握电荷呈线分布的带电体问题b)、由静电场中的高斯 定理计算场源分布具有高度对称性的带电体的场强分布一般诸如球对称分布、轴对称分布和面对称分布,步骤及例题详见课堂笔记。
还有可能结合电势的计算一起进行。
c)、由场强和电势梯度之间的关系来计算场强(适用于电势容易计算或电势分布已知的情形),掌握作业及课堂练习的类型即可。
(2)、电通量的计算2041i ii i i i r r q E E πε∑=∑=⎰⎰π==0204d r rq E d E εUgradU E -∇=-=)(k zU j y U i x U ∂∂+∂∂+∂∂-=a)、均匀电场中S 与电场强度方向垂直b)、均匀电场,S 法线方向与电场强度方向成q 角c)、由高斯定理求某些电通量(3)、电势的计算a)、场强积分法(定义法)——根据已知的场强分布,按定义计算b)、电势叠加法——已知电荷分布,由点电荷电势公式,利用电势叠加原理计算第二部分:静电场中的导体和电介质 一、导体的静电平衡状态和条件导体内部和表面都没有电荷作宏观定向运动的状态称为静电平衡状态。
大学物理变化的电磁场总复习内容深入超赞

dt
3.计算互感系数: (1)给任一回路通电流;
(2)计算穿过另一回路的磁通量;
(3)代入定义式或定义方程
例3:长直导线与矩形线圈共面,线圈中通有电
流I(t),计算长直导线中的互感电动势。
问题:长直导线是 解:设长直导线通有电流 I1
回路吗?
矩形线圈内的磁通量
I 1 I(t)
ds l
m S
BdS
=0
Lddtmddt(L)I
LdI dt
I
dL dt
当线圈形状、匝数、介质等不变时,L是常量.
εL
LdI dt
L L
dI dt
自感电动势与电流的变化率成正比
3.自感系数计算 考虑方法同计算电容。
(1)令回路通电流;
B
(2)计算穿过回路的磁通量;
(3)代入定义式或定义方程。
I
例1.计算长直螺线管(N,l,R)的自感系数:
da d
0 I1ldx 2 x
0Ill 2
nda d
o x d a
M m 0l lnd a
I1
M
2 d
dI 0llndadI
dt 2 d dt
三、磁场的能量
L
考虑自感线圈中电流的建立过程:
L
L di dt
K1
在移动dq=idt的过程中,电源反抗
自感电动势做功 dALdqLidt Lidi
在i从0到I过程中,做功
•单位:伏V
正
第十一章 变化的电磁场
§1 电磁感应 §2自感与互感 §3 Maxwell’s 方程组
本章重点:感应电动势、自感、互感 的计算
本章难点:涡旋电场,位移电流,场概念的理解
大学物理Ⅱ11变化的磁场和变化的电场(自感互感)

解: 1.假想原线圈C1 中通有电流 i1 ,
则螺线管内均匀磁场的磁感强度和磁通
量分别为
B
0
N 1i1 l
,
m
BS
0
N 1i1 l
S
所有磁感线都通过副线圈C2,即通过副线圈的磁通量也是Φm,
故副线圈的磁链为
N 2 m
0
N1 N 2i1 l
S
按互感系数的定义式,对N2匝线圈来说,当穿过每匝回路的磁
通量相同时,应有M i1 =N2Φm ,由此得两线圈的互感系数为
L
Wm
1 2
LI 2
1 2
n
2V
(
B
n
)
2
1 2
B2
V
wmV
磁场能量密度
wm矢量12式B
H
磁场能量
wm
B2
2
1 2
H 2
1 2
BH
与电场能量密度
Wm V wmdV
Байду номын сангаас
we
1
D
E
V
B22
2
dV
比较
磁场能量
Wm
V wmdV
V
B2
2
dV
磁场所储存的总能量:
Wm
wmdV
V
V
H B dV 2
小时,小线圈中的感应电动势为多大?
解: (1)设大线圈中通有电流为I1,由题设可知,S2<<S1=πR2,
故可视I1在面积S2上各点激发的磁场相同,其值为
B
N1
O I1
2 R1
通过 S2 的磁链为 互感系数为 M
21 N 2 21
大学物理习题答案16

第十六章 电磁场P177.16.1 一条铜棒长为L = 0.5m ,水平放置,可绕距离A 端为L /5处和棒垂直的轴OO'在水平面内旋转,每秒转动一周.铜棒置于竖直向上的匀强磁场中,如图所示,磁感应强度B = 1.0×10-4T .求铜棒两端A 、B 的电势差,何端电势高.[解答]设想一个半径为R 的金属棒绕一端做匀速圆周运动,角速度为ω,经过时间d t 后转过的角度为d θ = ωd t ,扫过的面积为d S = R 2d θ/2,切割的磁通量为d Φ = B d S = BR 2d θ/2,动生电动势的大小为ε = d Φ/d t = ωBR 2/2.根据右手螺旋法则,圆周上端点的电势高.AO 和BO 段的动生电动势大小分别为22()2550AO B LBL ωωε==, 22416()2550BOB LBL ωωε==. 由于BO > AO ,所以B 端的电势比A 端更高,A 和B 端的电势差为2310BO AOBL ωεεε=-=242332π 1.010(0.5)1010BL ω-⨯⨯⨯=== 4.71×10-4(V). [讨论]如果棒上两点到O 的距离分别为L 和l ,则两点间的电势差为222()(2)222B L l Bl B L Ll ωωωε++=-=.16.2 一长直载流导线电流强度为I ,铜棒AB 长为L ,A 端与直导线的距离为x A ,AB 与直导线的夹角为θ,以水平速度v 向右运动.求AB 棒的动生电动势为多少,何端电势高?[解答]在棒上长为l 处取一线元d l ,在垂直于速度方向上的长度为 d l ⊥ = d l cos θ;线元到直线之间的距离为r = x A + l sin θ,直线电流在线元处产生的磁感应强度为图16.1图16.2002π2π(sin )A IIB rx l μμθ==+.由于B ,v 和d l ⊥相互垂直,线元上动生电动势的大小为0cos d d d 2π(sin )A Iv lBv l x l μθεθ⊥==+,棒的动生电动势为00cos d 2πsin LAIv lx l μθεθ=+⎰00cos d(sin )2πsin sin LA A Iv x l x l μθθθθ+=+⎰ 0sin cot ln2πA AIvx L x μθθ+=,A 端的电势高.[讨论](1)当θ→π/2时,cot θ = cos θ/sin θ→0,所以ε→0,就是说:当棒不切割磁力线时,棒中不产生电动势.(2)当θ→0时,由于sin sin sin lnln(1)A A A Ax L L L x x x θθθ+=+→,所以02πAIvLx με→,这就是棒垂直割磁力线时所产生电动势.16.3 如图所示,平行导轨上放置一金属杆AB ,质量为m ,长为L .在导轨上的一端接有电阻R .匀强磁场B 垂直导轨平面向里.当AB 杆以初速度v 0向运动时,求:(1)AB 杆能够移动的距离;(2)在移动过程中电阻R 上放出的焦耳热为多少? [分析]当杆运动时会产生动生电动势,在电路中形成电流;这时杆又变成通电导体,所受的安培力与速度方向相反,所以杆将做减速运动.随着杆的速度变小,动生电动势也会变小,因而电流也会变小,所受的安培力也会变小,所以杆做加速度不断减小的减速运动,最后缓慢地停下来.[解答](1)方法一:速度法.设杆运动时间t 时的速度为v ,则动生电动势为ε = BLv ,电流为I = ε/R ,所受的安培力为F = -ILB = -εLB/R = -(BL )2v/R ,负号表示力的方向与速度方向相反.取速度的方向为正,根据牛顿第二定律F = ma 得速度的微分方程为BA图16.32()d d BL v v m R t-=,即: 2d ()d v B L t v m R=-积分得方程的通解为21()ln BL v t C mR=-+.根据初始条件,当t = 0时,v = v 0,可得常量C 1 = ln v 0.方程的特解为20()exp[]BL v v t mR=-.由于v = d x /d t ,可得位移的微分方程20()d exp[]d BL x v t t mR=-,方程的通解为20()exp[]d BL x v t t mR =-⎰2022()exp[]()mRv BL t C BL mR-=-+, 当t = 0时,x = 0,所以常量为022()mRv C BL =. 方程的特解为202(){1exp[]}()mRv BL x t BL mR=--. 当时间t 趋于无穷大时,杆运动的距离为2()mRv x BL =. 方法二:冲量定理.根据安培力的公式可得F = -(BL )2v/R ,负号表示安培力与速度的方向相反.因此2()d d BL x F t R-=,根据冲量定理得d 0tF t mv=-⎰,即:杆所受的冲量等于杆的动量的变化量.积分后可得02()mv Rx BL =. (2)方法一:焦耳定律.杆在移动过程中产生的焦耳热元为222()d d d d BLv Q I R t t t R R ε===220()2()exp[]d BLv BL t t R mR=-整个运动过程中产生的焦耳热为2200()2()exp[]d BLv BL Q t t R mR ∞=-⎰222002()exp[]22mv mv BL t mR ∞-=-=, 即:焦耳热是杆的动能转化而来的.方法二:动能定理.由于I = ε/R ,其中ε = BLv = BL d x /d t ,而安培力为F = -ILB ,负号表示安培力的方向与杆运动的方向相反.因此焦耳热元为d Q = I 2R d t = I εd t = IBL d x = -F d x .负号表示安培力做负功.根据动能定理,磁场的安培力对杆所做的功等于杆的动能的增量,因此安培力在杆的整个运动过程中所做的功为201d (0)2W F x mv =-=--⎰, 所以产生的焦耳热为212Q W mv ==. [小结]在求杆的运动距离时,用冲量定理可避免解微分方程.在求焦耳热时用动能定理可避免积分运算.16.4 如图所示,质量为m 、长度为L 的金属棒AB 从静止开始沿倾斜的绝缘框架滑下.磁感应强度B 的方向竖直向上(忽略棒AB 与框架之间的摩擦),求棒AB 的动生电动势.若棒AB 沿光滑的金属框架滑下,设金属棒与金属框组成的回路的电阻R 为常量,棒AB 的动生电动势又为多少?[解答](1)棒的加速度为a = g sin θ,经过时间t ,棒的速度为v = at = (g sin θ)t ,而切割磁力线的速度为v ⊥ = v cos θ,所以棒的动生电动势为ε = BLv ⊥ = BLg (sin θcos θ)t = BLg (sin2θ)t /2.(2)设棒运动时间t 时的速度为v ,则动生电动势为图16.4ε = BLv cos θ,电流为I = ε/R ,所受的安培力的大小为F = ILB = εLB/R = (BL )2v cos θ/R ,其方向水平向右.安培力沿着斜面向上的分量为F' = F cos θ,其方向与速度的方向相反.取速度的方向为正,根据牛顿第二定律ΣF = ma 得速度的微分方程为2(cos )d sin d BL v vmg m R tθθ-=,即 2d d sin (cos )mRt v mgR BL vθθ=-, 方程可化为222d[sin (cos )]d (cos )sin (cos )mR mgR BL v t BL mgR BL vθθθθθ--=-. 积分得方程的通解为22ln[sin (cos )](cos )mR t mgR BL v C BL θθθ-=-+.根据初始条件,当t = 0时,v = 0,可得常量2ln(sin )(cos )mRC mgR BL θθ=, 方程的特解为22[sin (cos )]ln (cos )sin mR mgR BL v t BL mgR θθθθ--=, 棒的速度为22sin (cos ){1exp[]}(cos )mgR BL v t BL mRθθθ=--, 动生电动势为cos BLv εθ=2(cos )tan {1exp[]}mgR BL t BL mRθθ=--. [讨论]当时间t 趋于无穷大时,最终速度为2sin (cos )mgR v BL θθ=,最终电动势为tan mgRBL εθ=, 最终电流为tan mgI BLθ=. 另外,棒最终做匀速运动,重力做功的功率等于感生电流做功的功率,重力做功的功率为P = mg sin θv ,感生电流做功的功率为222(cos )BLv P I R R Rεθ===, 两式联立也可得2sin (cos )mgR v BL θθ=,由此可以求出最终电动势和电流.[注意]只有当物体做匀速运动时,重力所做的功才等于电流所做的功,否则,重力还有一部分功转换成物体的动能.16.5 电磁涡流制动器是一个电导率为ζ,厚度为t 的圆盘,此盘绕通过其中心的垂直轴旋转,且有一覆盖小面积为a 2的均匀磁场B 垂直于圆盘,小面积离轴r (r >>a ).当圆盘角速度为ω时,试证此圆盘受到一阻碍其转动的磁力矩,其大小近似地表达为M ≈B 2a 2r 2ωζt .[解答]电导率是电阻率的倒数ζ = 1/ρ.不妨将圆盘与磁场相对的部分当成长、宽和高分别为a 、a 和t 的小导体,其横截面积为S = at ,电流将从横截面中流过,长度为a ,因此其电阻为1l R S tρσ==. 宽为a 的边扫过磁场中,速度大小为v = r ω,产生的感生电动势为ε = Bav = Bar ω,圆盘其他部分的电阻远小于小导体的电阻,因此通过小导体的电流强度为I ≈ε/R = Bar ωζt ,所受的安培力为F = IaB ≈B 2a 2r ωζt ,其方向与速度方向相反.产生的磁力矩为M = Fr ≈B 2a 2r 2ωζt .其方向与角速度的方向相反.16.6 如图,有一弯成θ角的金属架COD 放在磁场中,磁感应强度B 的方向垂直于金图16.5t属架COD 所在平面,一导体杆MN 垂直于OD 边,并在金属架上以恒定速度v 向右滑动,v 与MN 垂直,设t = 0时,x = 0,求下列两情形,框架内的感应电动势εi .(1)磁场分布均匀,且B 不随时间改变; (2)非均匀的交变磁场B = Kx cos ωt . [解答](1)经过时间t ,导体杆运动的距离为X = vt ,杆的有效长度为l = X tan θ = v (tan θ)t , 动生电动势为εi = Blv = Bv 2(tan θ)t . (2)导体杆在t 时刻运动到X 处,在三角形中取一个面积元 d S = y d x , 由于y = x tan θ,所以d S = x tan θd x ,通过该面元的磁通量为d Φ = B d S = K cos ωt tan θx 2d x ,通过三角形的磁通量为20tan cos d XK t x x Φθω=⎰31tan cos 3K tX θω=331tan cos 3Kv t t θω=,感应电动势为d d i t Φε=-323tan (3cos sin )3kv t t t t θωωω=--,即: 32tan (sin 3cos )3i kv t t t t θεωωω=-.[注意]公式B = Kx cos ωt 中的x 是场点到O 点的距离,不一定是杆运动的距离,为了区别两个距离,杆的距离用X 表示.16.7 如图所示的回路,磁感应强度B 垂直于回路平面向里,磁通量按下述规律变化Φ = 3t 2 + 2t + 1,式中Φ的单位为毫韦伯,t 的单位为秒.求:(1)在t = 2s 时回路中的感生电动势为多少? (2)电阻上的电流方向如何?[解答](1)将磁通量的单位化为韦伯得 Φ = (3t 2 + 2t + 1)/103,感生电动势大小为ε = |d Φ/d t | = 2(3t + 1)/103.t = 2s 时的感生电动势为1.4×10-2(V).(2)由于原磁场在增加,根据楞次定律,感应电流所产生的磁场的方向与原磁场的方向相反,所以在线圈中感生电流的方向是逆时针的,从电阻的左边流向右边.O图16.6图16.716.8 如图所示的两个同轴圆形导体线圈,小线圈在大线圈上面.两线圈的距离为x ,设x 远大于圆半径R .大线圈中通有电流I 时,若半径为r 的小线圈中的磁场可看作是均匀的,且以速率v = d x /d t 运动.求x = NR 时,小线圈中的感应电动势为多少?感应电流的方向如何?[解答]环电流在轴线上产生的磁感应强度为20223/22()IR B x R μ=+, 当x >>R 时,磁感应强度为2032IRB xμ≈.小线圈的面积为S = πr 2,通过的磁通量为2203π2IR r BS x μΦ=≈, 当小线圈运动时,感应电动势为22043πd d 2IR r vt xμΦε=-≈, 当x = NR 时,感应电动势为20423π2Ir vN Rμε≈. 感应电流的磁场与原磁场的方向相同,感应电流的方向与原电流的环绕方向相同.16.9 如图所示,匀强磁场B 与矩形导线回路的法线n 成θ = 60°角,B = kt (k 为大于零的常数).长为L 的导体杆AB 以匀速v 向右平动,求回路中t 时刻的感应电动势的大小和方向(设t = 0时,x = 0).[解答]经过时间t ,导体杆运动的距离为 x = vt , 扫过的面积为 S = Lx = Lvt ,通过此面积的磁通量为Φ = B ·S = BS cos θ = Lvkt 2/2. 感应电动势的大小为ε = d Φ/d t = Lvkt .由于回路中磁通量在增加,而感应电流的磁通量阻碍原磁通量增加,其磁场与原磁场的方向相反,所以感应电动势的方向是顺时针的.16.10 长为b ,宽为a 的矩形线圈ABCD 与无限长直截流导线共面,且线圈的长边平行于长直导线,线圈以速度v 向右平动,t 时刻基AD 边距离长直导线为x ;且长直导线中的电流按I = I 0cos ωt 规律随时间变化,如图所示.求回路中的电动势ε.[解答]电流I 在r 处产生的磁感应强度为图16.8图16.902πIB rμ=,穿过面积元d S = b d r 的磁通量为0d d d 2πIbB S r rμΦ==,穿过矩形线圈ABCD 的磁通量为001d ln()2π2πx axIbIb x a r r xμμΦ++==⎰, 回路中的电动势为d d t Φε=-0d 11d [ln()()]2πd d b x a I x I x t x a x tμ+=-+-+ 00cos [ln()sin ]2π()I bx a av tt x x x a μωωω+=++. 显然,第一项是由于磁场变化产生的感生电动势,第二项是由于线圈运动产生的动生电动势. *16.11 如图,一个矩形的金属线框,边长分别为a和b (b 足够长).金属线框的质量为m ,自感系数为L ,忽略电阻.线框的长边与x 轴平行,它以速度v 0沿x 轴的方向从磁场外进入磁感应强度为B 0的均匀磁场中,B 0的方向垂直矩形线框平面.求矩形线框在磁场中速度与时间的关系式v = v (t )和沿x 轴方向移动的距离与时间的关系式x = x (t ).[解答]由于b 边很长,所以线框只有右边在做切割磁力线的运动.当线框速度为v 时,产生的动生电动势为ε = B 0av .当线框中的电流为i 时,产生的自感电动势的大小为d d L i Ltε=. 根据欧姆定律得ε + εL = iR ,由于不计电阻,所以有0d 0d iB av Lt+=. ① 右边所受的力为F = iaB 0,根据牛顿第二定律得0d d v iaB mt=, 微分得图16.10图16.11202d d d d i vaB m t t=, ②联立①和②式得微分方程2202()d 0d aB v v t mL+=, 这是简谐振动的微分方程,其通解为v A B =+.当t = 0时,v = v 0,所以A = v 0.加速度a t = d v /dt )A B =-+,当t = 0时,a t = 0,所以B = 0.速度方程为0v v =. 由于v = d x /d t ,所以0d d x v t v t ==⎰⎰00v C =+. 当t = 0时,x = 0,所以C = 0,所以位移方程为0x v =.16.12 如图所示的圆面积内,匀强磁场B 的方向垂直于圆面积向里,圆半径R = 12cm ,d B /d t = 10-2T·s -1.求图中a 、b 、c 三点的涡旋电场为多少(b 为圆心)?设ab = 10cm ,bc = 15cm . [解答](1)当点在磁场之中时,以b 为圆心,以r 为半径作一圆形环中,其周长为C = 2πr ,面积为S = πr 2.取环路的逆时针方向为正,根据右手螺旋法则,面积的法向方向垂直纸面向外。
大学物理中的电磁波电磁场的传播与性质

大学物理中的电磁波电磁场的传播与性质电磁波是大学物理中的重要概念,它在电磁场中传播,并具有多种性质。
本文将从电磁波的定义、传播特性、电磁波谱和应用等方面进行探讨。
一、电磁波的定义电磁波是由变化的电场和磁场相互耦合产生的一种波动现象,具有电磁振荡和传播性质。
它的本质是通过电磁场的相互作用而传播能量和动量。
二、电磁波的传播特性1. 电磁波的速度:电磁波在真空中的传播速度为光速,即299792458米/秒(约为3.0×10^8 m/s),在其他介质中传播速度会发生变化。
2. 电磁波的周期和频率:电磁波的周期是指波的一个完整振动所经历的时间,单位为秒;频率是指单位时间内波的振动次数,单位为赫兹(Hz)。
3. 电磁波的波长和波数:电磁波的波长是指波的一个完整周期所对应的长度,通常用λ表示,单位为米;波数是指在单位长度内波的振动次数,通常用k表示,单位为1/米。
4. 电磁波的能量和强度:电磁波传播时会携带能量,能量与波的振幅和频率有关;强度是指单位面积内电磁波的能量流密度,与波的振幅和传播方向有关。
三、电磁波谱电磁波谱是指电磁波按照频率或波长划分的不同区域。
根据频率的不同,电磁波谱可以分为无线电波、微波、红外线、可见光、紫外线、X射线和γ射线等不同的频段。
不同频段的电磁波在应用上具有不同的特性和用途。
四、电磁波的应用1. 通信:无线电波和微波被广泛应用于通信领域,包括无线电广播、电视信号传输、移动通信等。
2. 显微镜和光学:可见光是光学仪器如显微镜的重要光源,通过光学设备的应用可以观察和研究物体的微观结构。
3. 医学诊断和治疗:X射线和γ射线在医学影像和肿瘤治疗中起到重要作用,可以帮助医生诊断和治疗疾病。
4. 遥感和雷达:微波和红外线被用于遥感技术和雷达系统,可以监测和探测地球表面的变化和异常情况。
5. 光电子学和半导体器件:光电子学和半导体器件利用电磁波与物质相互作用的特性,开发了各种光学传感器和光电子器件。
大学物理16-5

E E0 cos t x u 0
S E0 H 0 cos 2 t x u 0
一个周期内的时平均辐射强度
S E0 H 0 2
因 c 1 0 0以 0 E0 0 H 0及,得
S 0cE 2
2 0
E H
电磁波的性质
平面简谐电磁波的传播
y
u
E
z
H
x
电磁波的一般性质: (1)电磁波的电场和磁场都垂直于波的传播方向,电 磁波是横波。
电磁波的性质
(2)沿给定方向传播的电磁波,E 和H 分别在各自平 面内振动,这种特性称为偏振。 (3)E 和H 作周期性的变化,而且相位相同,同地 同时达到最大,同地同时减到最小。
电磁波的性质
积分得
E0 x x H cos t 0 H 0 cos t 0 u u u
E0 H0 E0 ——H的振幅 u
E0 H 0
H 和E 有相同的频率,且两者同相位,二者满足瞬 时关系:
S 0cH 02 2
(4)任一时刻、空间任一点,E 和H 在量值上满足
E H (5)电磁波的传播速度 u 1
通常 和 与电磁波的频率有关,在介质中不同 频率的电磁波具有不同的传播速度,此即电磁波在介 质中的色散现象。
3.电磁波的能量
电磁波所携带的电磁能量,称为辐射能。单位时间 内通过垂直于传播方向的单位面积的辐射能,称为能流 密度或辐射强度。 电场和磁场的能量体密度分别为
we E 2 , wm H 2
2 2
电磁场的总能量体密度:
w we wm (E H ) 2
大学物理下变化的电磁场

3、讨论:
•若有N匝线圈,它们彼此串联,总电动势等于各匝线圈所产生 的电动势之和。令每匝的磁通量为 1、 2 、 3
d1 d 2 dt dt
磁通链数:
1 2 3
d (1 2 3 ) d dt dt
故本题的结果为: r=2cm时
r dB 0.02 Ek =- 0.2 2 10 3V m 1 2 dt 2
R dB 0.05 Ek =- 0.2 5 10 3V m 1 2 dt 2
R 2 dB 0.052 Ek 0.2 2.5 10 3V m 1 2r dt 2 0.1
演示
11-2 动生电动势
引起磁通量变化的原因有两种: 1.磁场不变,回路全部或局部在稳恒磁场中运动——动生电动势 2.回路不动,磁场随时间变化——感生电动势 当上述两种情况同时存在时,则同时存在动生电动势与感生电 动势。 a
d
1、从运动导线切割磁场线导出 动生电动势公式
d d Blx d x i Bl Blv dt dt dt
d B i B dS dS S t dt S
不论空间是否存在导 体,变化的磁场总是 在周围空间激发电场
•感生电场的电场线是无头无尾的闭合曲线,所以又叫涡旋电场。
B dl 0 j dS
L S•感生电场和磁感应强Fra bibliotek的变化连在一起。
(b) 0, increase
n
n
i
direction
i
direction
(c) 0, decrease
(d ) 0, decrease
同济大学物理变化的电磁场活 答案

大作业解答变化的电磁场P.1一、选择题1.一导体圆线圈在均匀磁场中运动, 能使其中产生感应电流的一种情况是(A) 线圈绕自身直径轴转动, 轴与磁场方向平行.(B) 线圈绕自身直径轴转动, 轴与磁场方向垂直.(C) 线圈平面垂直于磁场并沿垂直磁场方向平移.(D) 线圈平面平行于磁场并沿垂直磁场方向平移.2.如图, 长度为l 的直导线ab 在均匀磁场中以速度移动, 直导线ab 中的电动势为(A) Bl v . (B) Bl v sin a . (C) Bl v cos a . (D) 0.B v Bva bα⎰⋅⨯ba lB d )(vP.23.如图所示, 直角三角形金属框架abc 放在均匀磁场中, 磁场平行于ab 边, bc 的长度为l . 当金属框架绕ab 边以匀角速度ω转动时, abc 回路中的感应电动势εi 和a 、c 两点间的电势差U a –U c 为B 2i 21,0)A (l B U U c a ωε=-=2i 21,0)B (l B U U c a ωε-=-=22i 21,)C (l B U U l B c a ωωε=-=22i 21,)D (l B U U l B c a ωωε-=-=Bl b acωP.34. 对于单匝线圈取自感系数的定义式为L =Φm /I . 当线圈的几何形状、大小及周围磁介质分布不变, 且无铁磁性物质时, 若线圈中的电流强度变小, 则线圈的自感系数L(A) 不变.(B) 变小.(C) 变大, 与电流成反比关系.(D) 变大, 但与电流不成反比关系.P.4VB LI W μ22m 2121==nI B μ=222πr l n V n L μμ==5.有两个长直密绕螺线管, 长度及线圈匝数均相同, 半径分别为r1和r 2, 管内充满均匀介质, 其磁导率分别为μ1和μ2. 设r 1:r 2=1:2, μ1:μ2=2:1, 当将两只螺线管串联在电路中通电稳定后, 其自感系数之比L1:L 2与磁能之比W m1:W m2分别为:(A)L1:L 2 = 1:1, W m1:W m2 = 1:1(B)L 1:L 2= 1:2, W m1:W m2= 1:1(C)L 1:L2 = 1:2, W m1:W m2 = 1:2(D)L 1:L 2 = 2:1, W m1:W m2= 2:1解: 已知自感系数与长直密绕螺线管内部磁场分别为磁场能量为P.5St B Sd ⋅∂∂=⎰ε6.在圆柱形空间内有一磁感应强度为的均匀磁场,如图所示. 的大小以速率变化. 有一长度为l 0的金属棒先后放在磁场的两个不同位置ab 和a 'b ',那么,金属棒在这两个位置时棒内的感应电动势的大小关系为(A)(B)(C)(D)Oa 'bb 'a ⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯B Bt B d d 0≠=''b a ab εεabb a εε>''abb a εε<''0==''ab b a εεB 解:P.67:电磁波的电场强度、磁场强度和传播速度的关系是(A) 三者互相垂直, 而和位相相差(B) 三者互相垂直, 而、、构成右旋系统(C) 三者中和是同方向的, 但都与垂直(D) 三者中和可以是任意方向的, 但都必须与垂直E H u u E E E E H H u u H H 2π/P.7St D S j I I l H S S d Ld d d 0⋅∂∂+⋅=+=⋅⎰⎰⎰8.如图所示, 平板电容器(忽略边缘效应)充电时, 沿环路L 1、L 2磁场强度的环流中, 必有:(A) (B) (C) (D) H⎰⎰⋅>⋅21d d L L l H l H ⎰⎰⋅=⋅21d d L L l H l H ⎰⎰⋅<⋅21d d L L l H l H 0d 1=⋅⎰L l H L 2L 1解:P.8二、填空题1.一根直导线在磁感应强度为的均匀磁场中以速度切割磁力线运动, 导线中对应于非静电力的场强(称作非静电场场强) ⎽⎽⎽⎽⎽⎽⎽⎽.B v =k E解:lE l B L Ld d )(i ⋅=⋅⨯=⎰⎰感v εB ⨯v 2.载有恒定电流I 的长直导线旁有一半圆环导线MN, 半圆环半径为b , 环面与直导线垂直, 且半圆环两端点连线的延长线与直导线相交, 如图所示.当半圆环以速度沿平行于直导线的方向平移时, 半圆环上的感应电动势的大小是⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.v abM O N 的方向I v 解:⎰⋅⨯==L l B d )(MN MN v εεba b a I -+⋅=ln π20v μP.9I o rωa 3.如图所示, 一半径为r 的很小的金属圆环, 在初始时刻与一半径为a (a >>r )的大金属圆环共面且同心. 在大圆环中通以恒定的电流I , 方向如图. 如果小圆环以角速度ω绕其任一方向的直径转动, 并设小圆环的电阻为R , 则任一时刻t 通过小圆环的磁通量Φm =⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽; 小圆环中的感应电流i = ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.解:t r a It BS Φωμωcos π2cos 20m =≈tr aR I t ΦR R i ωωμεsin π2d d 120===P.10 4.如图, 通有电流I0的长直导线旁, 有一与其共面、且相距为d 的U 形导轨, 在导轨上有电阻为R 的金属棒AB,其长度为a , 以速度向右沿导轨平动, 不计一切摩擦, 则AB 棒上的感应电动势为; AB 棒所受安培力的大小为, 方向为⎽⎽⎽⎽⎽⎽⎽⎽.v r r I l B a d d d 2πd )(00i v v ⎰⎰+=⋅⨯=με d ad I +ln 2π00vμ⎰⨯=B l I F d ⎰++⋅=ad d r r I d a d I R F d π2ln 2π0000μμv 向左Ad R aBR vIR d a d I v 200ln 2π⎥⎦⎤⎢⎣⎡+μP.115.自感系数L =0.3H 的长直螺线管中通以I =8A 的电流时, 螺线管存储的磁场能量W m =⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.解:221LI L =J6.983.0212=⨯⨯=6.将条形磁铁插入与冲击电流计串联的金属环中时,有q =2.0⨯10-5C 的电荷通过电流计. 若连接电流计的电路总电阻R =25Ω, 则穿过环的磁通量的变化∆Φm =⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.解:m 1ΦR q ∆-=RqΦ=∆m Wb 105.04-⨯P.127.由半径为r 的两块圆板组成的平行板电容器,在放电时两板间的电场强度的大小为,式中E 0、RC t E E -=e 0R 、C 均为常数. 则两板间的位移电流的大小为⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽; 其方向与场强方向⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.解:S t Dt ΦI d d d d d D ==St Ed d 0ε=RCtr RC E --=e π200ε流向与电场方向相反P.13试判断下列结论是包含于或者等效于哪一个麦克斯韦方程式的,将你确定的方程式用代号填在相应结论后的空白处::(1) 变化的磁场一定伴随有电场: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽;(2) 磁感应线是无头无尾的: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽;(3) 电荷总伴随有电场: ⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.231⎰∑==⋅s n i q S D 0i d ⎰-=⋅L t Φl E d d d m⎰=⋅sS B 0d ⎰∑+=⋅=L ni tΦI l H d d d D0i 8.反映电磁场基本性质和规律的积分形式的麦克斯韦方程组为:(1)(2)(4)(3)P.14三、计算题解:rr I l B t l a t a d 2πsin d )(0cos cos i μθεθθ⎰⎰+++-=⋅⨯=v v v v θθθμcos cosln sin 2π0t a t l a I v v v +++-=A 端电势髙a a +lO r 1. 如图所示, 一长直导线中通有电流I ,有一垂直于导线、长度为l 的金属棒AB 在包含导线的平面内, 以恒定的速度沿与棒成θ角的方向移动. 开始时, 棒的A 端到导线的距离为a , 求任意时刻金属棒中的动生电动势, 并指出棒哪端的电势高.v I a lA BvθP.15直于磁场方向,如图所示.回路的CD 段为滑动导线,以匀速远离A 端运动,且始终保持回路为等边三角形.设滑动导线CD 到A 端的垂直距离为x ,且初始x =0.试求回路ACDA 中的感应电动势ε和时间t 的关系.(其中为常矢量)的均匀磁场中,回路平面垂t B B 0=0Bv 2.将等边三角形平面回路ACDA 放在磁感应强度为⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯v A C DB x 解:⎰⎰=⋅=S S S t B S B Φd d 0mtS B S t B S 00d ==⎰320203330tan t B tx B v =︒=220m3d d t B t Φv -=-=εP.16220200013330tan d d d )d(d t B x B S B S t t B S t B v =︒===⋅∂∂-=⎰⎰⎰ ε220233230tan 2)(tB x B CD B v v v =︒⋅=⋅⨯= ε22022022021333233t B t B t B v v v =+=+=∴εεε⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯v A C D B x 另解:P.173.无限长直导线通以电流.有一与之共面的矩形线圈,其长边与长直导线平行.已知长边为L ,两长边距离长直导分别为a 、b ,位置如图所示.求:(1) 矩形线圈内的感应电动势的大小和感应电动势的方向; (2) 导线与线圈的互感系数.)4exp(0t I I -= b L Ia解: 建立坐标系Oxx L x I x BL S B Φd π2d d d 0m μ==⋅= O x abILx L x I Φb a ln π2d π200m μμ⎰==tIa bLt Φd d ln π2d d 0m i ⋅-=-=μεP.18tI t I I I 404t -0e 4d d e --== t i a b LI 400e ln π2-=∴με方向:顺时针 bLIaabLI abLI I ΦM ln π2ln π200m μμ===tIa bLt I M t Φi d d ln π2d d d d 0m ⋅-=-=-=μεP.19r L l 1R 2R I I 4.由半径为R 1和R 2的的两个薄圆筒形导体组成一同轴电缆,中间填充磁导率为μ的均匀磁介质.电缆内层导体通电流I ,外层导体作为电流返回路径,如图所示.求长度为l 的一段电缆内的磁场储存的能量.解:选图示的安培环路,由介质中的环路定理⎰∑=⋅L I l H d 得:)(π221R r R r IH <<=r IH B π2μμ==磁能密度:222m π821r I BH w μ==体积元:rrl V d π2d =磁场能量:122m m ln π4d 21R R l I V w W R R μ==⎰。
大学物理-16 麦克斯韦方程组

➢ 非稳恒电路中,在传导电流中断处必发生电荷分布的变化
I dq / dt 极板上电荷的时间变化率等于传导电流
➢ 极板上电荷的变化必引起电场的变化 (以平行板电容器为例)
电位移通量
ΦD DS ΦD t
Dσ
σ t σ t
I (t)
Dt
I (t)
ΦD t tS qt
S
I
dq 移电流(电场变化等效为一种电流)
⑶ 产生焦耳热 无焦耳热
⑷ 存在于导体 存在于真空、导体、电介质
l Ei
dl
S
B t
dS
L H d dl
D
dS
S t
(Hd为Id产生的涡旋磁场)
B
D
t
t
Ei 左旋
右旋 H d
对称美
二、电磁场 麦克斯韦电磁场方程的积分形式
法拉第电磁感应定律说明:变化的磁场激发电场,
麦克斯韦用数学形式,系统而完美地概括了电磁场 的基本规律,奠定了宏观电磁场理论的基础;预言了 电磁波的存在;并指出光波也是电磁波,从而将电磁 现象和光现象联系起来。
讨论 麦克斯韦方程组:
B
D dS q ①
E dl dS
S B dS 0 ③
L
H dl
(
S
j
t D
)
dS
判S 断下列结论包含于或等效L 于哪一S个方程 t式
② ④
(A)电荷总伴随有电场;
( ①)
(B) 静电场是保守场;
( ②)
(C) 磁感线是无头无尾的;
( ③)
(D) 变化的磁场一定伴随有电场; ( ② )
(E) 感生电场是有旋场;
( ②)
(F) 变化的电场总伴随有磁场; ( ④ )
《大学物理》下学期期中复习知识点总结
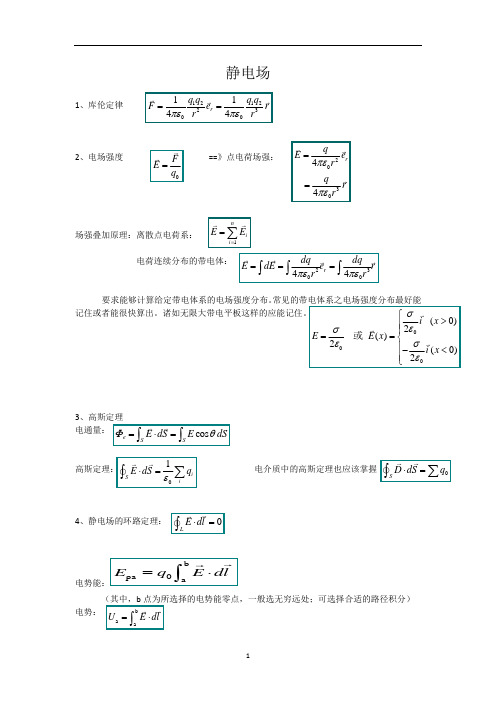
静电场1、库伦定律2、电场强度 ==》点电荷场强:场强叠加原理:离散点电荷系:电荷连续分布的带电体:要求能够计算给定带电体系的电场强度分布。
常见的带电体系之电场强度分布最好能记住或者能很快算出。
诸如无限大带电平板这样的应能记住。
3、高斯定理电通量:高斯定理: 电介质中的高斯定理也应该掌握4、静电场的环路定理:电势能:(其中,b 点为所选择的电势能零点,一般选无穷远处;可选择合适的路径积分)电势:bpa 0aE q E dl=⋅⎰121223001144rq q q q F e r r r πεπε==0F E q =1nii E E ==∑20304 4r q E e r q rrπεπε==230044rdq dq E dE e r r r πεπε===⎰⎰⎰(0)2 ()2(0)2i x E E x i x σεσσεε⎧>⎪⎪==⎨⎪-<⎪⎩或cos e S SE dS E dSΦθ=⋅=⎰⎰01iS i E dS q ε⋅=∑⎰SD dS q ⋅=∑⎰LE dl ⋅=⎰b a a U E dl=⋅⎰电势和电势能的关系:电场力做功:5、电势的计算:若取无穷远处为电势零点,方法一:从点电荷电势出发,利用电势叠加原理(空间某点的电势等于带电体系各部分产生之电势的叠加。
给定带电体如何分割可具体情况具体分析) 点电荷电势: 点电荷系:电荷连续分布的带电体:方法二:直接从电场强度分布出发 (反过来亦可由电势得到电场: )静电场中的导体和电介质1、导体的静电平衡电荷:净电荷分布只能分布在导体表面,一般电荷密度和导体表面曲率成正比 电场:导体内部电场为零,外表面附近电场垂直于导体表面电势:整个导体是等势体,导体表面是等势面若导体接地,则该导体与地等电势(一般视为零电势,至于此时该导体表面是否电荷为零,则要根据电势为零来分析)。
2、电容器:电容: 要能计算给定电容器的电容,常见电容器电容表达式最好记住E qU =00( )bab a b aW q U U q E dl=-=⋅⎰0()4qU U r rπε==04i i iiiq U U r πε==∑∑04dqU dU rπε==⎰⎰aU E dl∞=⋅⎰( )U U UE U i j k x y z∂∂∂=-∇=-++∂∂∂0n0n E e σε=ABQ C U =电容器的串并联3、电介质电极化强度:高斯定理:对线性各向同性介质,4、静电场的能量点电荷系:i U 为除第i q 点电荷以外的其它点电荷所产生的电场在i q 处的电势。
大学物理习题答案-第16章-电磁场

第16章 电磁场 参考答案一、选择题1(A),2(A),3(C),4(C),5(D),6(D),7(C),8(B),9(B),10(B) 二、填空题(1). )2/cos(/d d π+==t A NbB t x NbB ωωε 或t NBbA ωωεsin =. (2). πBnR 2, O . (3). 相同(或221R B ω), 沿曲线由中心向外.(4). 小于, 有关. (5). 0 (6). )8/(2220a I πμ. (7). 9.6 J.(8). ⎰⎰⋅∂∂S S D t ϖϖd 或 t D /d d Φ , ⎰⎰⋅∂∂-SS B t ϖϖd 或 t m /d d Φ-. (9). t E R d /d 02επ, 与E ϖ方向相同(或由正极板垂直指向负极板).(10).t B r d /d 21.三 计算题1. 如图所示,有一半径为r =10 cm 的多匝圆形线圈,匝数N =100,置于均匀磁场B ϖ中(B = 0.5 T ).圆形线圈可绕通过圆心的轴O 1O 2转动,转速 n =600 rev/min .求圆线圈自图示的初始位置转过π21时,(1) 线圈中的瞬时电流值(线圈的电阻R 为 100 Ω,不计自感);(2) 圆心处的磁感强度.(μ0 =4π×10-7 H/m)解:(1) 设线圈转至任意位置时圆线圈的法向与磁场之间的夹角为θ,则通过该圆线圈平面的磁通量为θΦcos 2r B π=, nt t π==2ωθ∴ nt r B ππ=2cos 2Φ在任意时刻线圈中的感应电动势为nt n r NB tNπππ=Φ-=2sin 2d d 2 nt n BNr ππ=2sin 222 t ΤI nt R n NBr R i m π=ππ==22sin 2sin 22 当线圈转过π /2时,t =T /4,则 987.0/22=π==2R NBn r I i m A(2) 由圆线圈中电流I m 在圆心处激发的磁场为==')2/(0r NI B m μ 6.20×10-4 T方向在图面内向下,故此时圆心处的实际磁感强度的大小500.0)(2/1220≈'+=B B B T 方向与磁场B ρ的方向基本相同.ϖ2. 如图所示,真空中一长直导线通有电流I (t ) =I 0e -λt (式中I 0、λ为常量,t 为时间),有一带滑动边的矩形导线框与长直导线平行共面,二者相距a .矩形线框的滑动边与长直导线垂直,它的长度为b ,并且以匀速v ϖ(方向平行长直导线)滑动.若忽略线框中的自感电动势,并设开始时滑动边与对边重合,试求任意时刻t 在矩形线框内的感应电动势 i 并讨论 i 方向.解:线框内既有感生又有动生电动势.设顺时针绕向为 i 的正方向.由 i = -d Φ /dt 出发,先求任意时刻t 的Φ (t )⎰⋅=S B t ρϖd )(Φy t x yt I ba ad )(2)(0⎰+π=μaba t x t I +π=ln )()(20μ 再求Φ (t )对t 的导数:)d d d d )((ln 2d )(d 0txI x t I b ba t t ++π=μΦ ab a t I t+-π=-ln )1(e 200λμλv )(t x v =∴ i ab a t I tt +-π=-=-ln )1(e 2d d 00λμΦλvi 方向:λ t <1时,逆时针;λ t >1时,顺时针.3. 如图所示,一根长为L 的金属细杆ab 绕竖直轴O 1O 2以角速度ω在水平面内旋转.O 1O 2在离细杆a 端L /5处.若已知地磁场在竖直方向的分量为B ϖ.求ab 两端间的电势差b a U U -.解:Ob 间的动生电动势:⎰⎰=⋅⨯=5/405/401d d )L L l Bl l B ωϖϖϖv ( 225016)54(21BL L B ωω== b 点电势高于O 点. Oa 间的动生电动势:⎰⎰⋅=⨯=5/05/02d d )L L l Bl l B ωϖϖϖv ( 22501)51(21BL L B ωω== a 点电势高于O 点. ∴ 22125016501BL BL U U b a ωω-=-=- 221035015BL BL ωω-=-=I (t )v ϖI (t ) x (t )b4. 有一很长的长方的U 形导轨,与水平面成θ角,裸导线ab 可在导轨上无摩擦地下滑,导轨位于磁感强度B ϖ竖直向上的均匀磁场中,如图所示.设导线ab 的质量为m ,电阻为R ,长度为l ,导轨的电阻略去不计,abcd 形成电路,t =0时,v =0. 试求:导线ab 下滑的速度v 与时间t 的函数关系.解:ab 导线在磁场中运动产生的感应电动势 θcos v Bl i = abcd 回路中流过的电流 θcos RBl R I ii v ==ab 载流导线在磁场中受到的安培力沿导轨方向上的分力为: θθθcos cos cos Bl RBl Bl I F i v ==由牛顿第二定律: t mBl R Bl mg d d cos cos sin vv =-θθθ mR l B g t θθ222cos sin d d v v-=令 θsin g A =,)/(cos 222mR l B c θ= 则 )/(d d v v c A t -=利用t = 0,v = 0 有⎰⎰⎰---=-=vv v v v v 000)d(1d c A c A c c A d t t Ac A ct v--=ln1 ∴ )e 1(cos sin )e 1(222ct ctl B mgR c A ---=-=θθv5. 一根长为l ,质量为m ,电阻为R 的导线ab 沿两平行的导电轨道无摩擦下滑,如图所示.轨道平面的倾角为θ,导线ab 与轨道组成矩形闭合导电回路abdc .整个系统处在竖直向上的均匀磁场B ϖ中,忽略轨道电阻.求ab 导线下滑所达到的稳定速度.解∶动生电动势θcos Bl i v = RBl RI iθcos v ==导线受到的安培力 lB I f m =ab 导线下滑达到稳定速度时重力和磁力在导轨方向的分力相平衡 θθcos sin m f mg =θθθcos cos sin lB RBl mg v =∴ θθ222cos sin l B mgR =vdϖ6. 已知,一根长的同轴电缆由半径为R 1的空心圆柱导体壳和另一半径为R 2的外圆柱导体壳组成,两导体壳间为真空.忽略电缆自身电阻,设电缆中通有电流i ,导体间电势差为U ,求(1) 两导体壳之间的电场强度E ϖ和磁感强度B ϖ. (2) 电缆单位长度的自感L 和电容C .解:(1) 根据安培环路定理i l B 0d μ⎰=⋅ϖϖ和长直条件及轴对称性可知,在R 2 >r > R 1 (r 为轴线到场点的半径)区域有 )2/(0r I B π=μB ϖ方向与内导体壳电流方向成右手螺旋关系.根据高斯定理:⎰⋅=0/d εQ S E ϖϖ和长直条件及轴对称性可知,在R 2 >r > R 1区域有r E 02/ελπ=E ϖ方向沿半径指向电势降落方向,式中λ为电缆内导体壳上单位长度上的电荷.由两导体间电势差U ,可求得 )/ln(2120R R U ελπ=, ∴ )/ln(12R R r UE =(2) 在电缆的两个导体壳之间单位长度的磁通量为 1200ln 2d 221R R ir riR R π=π=⎰μμΦ 单位长度电缆的自感系数为12ln2R R iL π==μΦ由电容定义又知单位长度电缆的电容应为 )/ln(2120R R UC ελπ==7. 两线圈顺接,如图(a),1、4间的总自感为1.0 H .在它们的形状和位置都不变的情况下,如图(b)那样反接后1、3之间的总自感为0.4 H .求两线圈之间的互感系数.解:设顺接的总自感为L S ,反接的总自感为L F . ∵ M L L L S 221++= M L L L F 221-+=∴ 4/)(F S L L M -== 0.15 H8. 如图所示,真空中一矩形线圈宽和长分别为2a 和b ,通有电流I 2,可绕其中心对称轴OO '转动.与轴平行且相距为d +a 处有一固定不动的长直电流I 1,开始时矩形线圈与长直电流在同一平面内,求:(1) 在图示位置时,I 1产生的磁场通过线圈平面的磁通量;(2) 线圈与直线电流间的互感系数. (3) 保持I 1、I 2不变,使线圈绕轴OO '转过90°外力要做多少功? 解:(1) 按题意是指图示位置时的Φ.123(a)顺接(b) 反接Ibdad bI bdx xI ad d2ln2210210+π=π=⎰+μμΦ (2) dad bI M 2ln201+π==μΦ(3)dad bI I I A 2ln22102+π==∆μΦ9. 一根电缆由半径为R 1和R 2的两个薄圆筒形导体组成,在两圆筒中间填充磁导率为μ 的均匀磁介质.电缆内层导体通电流I ,外层导体作为电流返回路径,如图所示.求长度为l 的一段电缆内的磁场储存的能量.解: ⎰∑⋅=i I l H ϖϖd , I rH =π2 (R 1< r < R 2)r I H π=2, r I H B π==2μμ2222)2(22r I B w m π==μμμ l r r w V w W m m m ⋅π==d 2d d r rl r Id 2)2(222ππ=μ∴ ⎰⎰π==2121d 4d 2R R R R m m rrl I W W μ122ln4R R lI π=μ四 研讨题1. 我们考虑这样一个例子: 设一个半径为R 的导体圆盘绕通过其中心的垂直轴在磁场中作角速度为ω的匀速转动,并假设磁场B 均匀且与轴线平行,如图所示。
大学物理11-22章例题习题答案

第十一章 静电场 例题答案:11-1 (B ) 11-2(B ) 11-3(B )11-4. ()30220824Rqdd R R qd εεπ≈-ππ;从O 点指向缺口中心点 11-5. 0/ελd ;()2204d R d-πελ ;沿矢径OP 11-6(D) 11-7.02εσ 向右 ; 023εσ向右 11-8 (1)o 2r 4r k E ε=,r <R ; (2) 204r r4R k E ε=,r >R 。
[解](1)作与球体同心、而半径r <R 的球面S 1。
球体内电荷密度ρ随r 变化,因此,球面S 1内包含的电荷()dr r r 4Q ro 21⎰ρπ=。
根据高斯定理和已知的电荷体密度ρ(r ),可求得球体内任意点的场强。
即()⎰⎰ρπε=⋅=Φr 02s o r dr r r 41s d E 1 ,得:o2r 4r k E ε=,r <R 。
(2)作与球体同心、半径r >R 的球面S 2,因R 外电荷为零,故S 2内的电荷Q 2=Q 1,根据高斯定理得:Φ=()⎰⎰ρπε=⋅R 02s 0r dr r r 41s d E 2 =4πr 2E r =⎰πεR30dr kr 41,∴204r r 4R kE ε=,r >R 。
11-9(D) 11-10(C) 11-11.d 0L⋅=⎰ E l 单位正电荷在静电场中沿任意闭合路径绕行一周,电场力作功等于零有势(或保守力)11-12. 45 V —15 V 11-13. -2000V 11-14. (B) 11-15.20R 4Q πε,0,R4Q 0πε,20r 4Qπε。
11-16()()a b b c R R R R /ln /ln 21=λλ [解]:设B 上带正电荷,内表面上电荷线密度为λ1,外表面上电荷线密度为λ2,而A 、C 上相应地感应等量负电荷,如图所示.则A 、B 间场强分布为E 1=λ1 / 2πε0r ,方向由B 指向AB 、C 间场强分布为 E 2=λ2 / 2πε0r ,方向由B 指向CB 、A 间电势差11100ln 22E r d d a a bbR R b BA R R aR r r R λλεε=⋅=-=ππ⎰⎰U B 、C 间电势差 22200ln 22E r d d c c bbR R c BC R R bR r U r R λλεε=⋅=-=ππ⎰⎰因U BA =U BC ,得到 ()()a b b c R R R R /ln /ln 21=λλ 练习详解:11-1. (1)E 0=0;(2)E 0=0;(3)0E=k2a q 4i ;(4)0E = k 2aq 2i[解](1)如图(a )所示,各点电荷在点o 处产生的场强两两对应相消,所以,点o 处场强E 0=0(2)取图中(b )所示坐标。
电磁学(第二版)___习题解答

电磁学(第二版)___习题解答本文档旨在概述《大学物理通用教程_电磁学(第二版)___题解答》的内容和目的。
章节结构本教程共包含以下章节:第一章:电磁学基础概念第二章:库仑定律和电场第三章:电场的高斯定理第四章:静电场的电势第五章:电场中的运动带电粒子第六章:稳恒电流第七章:磁场的基本特性第八章:安培定律和磁场的高斯定理第九章:磁场的矢量势与法拉第电磁感应定律第十章:电磁感应中的动生电动势第十一章:电磁感应中的感生电流第十二章:电磁场的能量与动量第十三章:交变电路理论第十四章:交变电磁场中的能流与坡印廷矢量第十五章:电磁波概论第十六章:辐射和天线每一章节都提供了对应题的解答,帮助读者更好地理解和应用所学的电磁学知识。
该题解答本是《大学物理通用教程_电磁学(第二版)___》的附属部分,旨在补充教材内容,提供题的详细解答,便于读者巩固所学知识。
本文档总结了《大学物理通用教程_电磁学(第二版)___题解答》中的题解答内容特点和方法。
本解答提供了《大学物理通用教程_电磁学(第二版)___题解答》中的题解答方式和思路的例子。
问题:如何计算两个点电荷间的电势差?答案:根据库仑定律可以计算出两个点电荷间的力,将该力乘以电荷间的距离即可得到电势差。
问题:如何确定一个圆环上的电场强度大小与方向?答案:根据环上各点的电荷之间的静电力作用,可以确定该点的电场强度大小和方向。
可以施用库仑定律以及数学公式来计算。
问题:如何计算一个球体内的电势分布?答案:根据球内各点的电荷密度以及球内各处的距离关系,利用电场的定义公式,可以计算出球体内各点的电势。
以上是一些《大学物理通用教程_电磁学(第二版)___题解答》的题目解答示例,希望对你的研究有所帮助。
本文档是《大学物理通用教程_电磁学(第二版)___题解答》的一部分,旨在为读者提供对电磁研究题的解答。
以下是总结本文档的重要性和帮助的几点观点:方便研究:本文档提供了电磁研究题的解答,可以帮助读者更好地理解和掌握这门学科。
习题讨论《电磁感应、位移电流、磁场能量》

R
2 r 2 fB
R
sin( 2 ft 0 )
2 r 2 fB
R
10
5. 长直导线与矩形单匝线圈共面放置,导线与线圈的长边平 行,矩形线圈的边长分别为a、b,它到直导线的距离为c (如图),当矩形线圈中通有电流I = I0sint时,求直导线中 的感应电动势。 参考:习题16.17
2
0 I (t ) 1 1 0 I0 l2 t e B1 B 2 ( ) 2 a ( l 2 a ) 2 a l 2 a
l1
v
a
l2
动生 v l1 ( B1 B 2 )
0 I0
l1l 2 v
2 a ( l 2 a )
e
t
0 I0
解:如果在直导线中通以稳恒电流I,在距离为 r处产生的磁感应强度为B =0I/2r.在矩形 线圈中取一面积元dS=bdr,通过线圈的磁通 量为
ac
a
I
b
BdS
S
c
0 Ib d r
2 r
0 Ib
2
ln
ac c
c
M12=M21=M
M
dI dt
互感系数为
M
I
t 0 2 ft 0
(t ) 0 1 2 B r cos( 2 ft 0 )
2
B
r
G
根据法拉第电磁感应定律,有 因此回路中的感应电流为
I (t )
d dt
r fB sin( 2 ft 0 )
2 2
则感应电流的最大值为
大学物理易考知识点电磁场的基本规律

大学物理易考知识点电磁场的基本规律大学物理易考知识点:电磁场的基本规律电磁场是电荷和电流所产生的物理现象,在电磁学中起着至关重要的作用。
了解电磁场的基本规律不仅可以帮助我们解决实际问题,还可以为日常生活中的电器使用提供指导。
本文将介绍电磁场的基本规律,包括库仑定律、电场的叠加原理、高斯定律、法拉第电磁感应定律以及安培环路定理等。
一、库仑定律库仑定律是描述电荷之间相互作用的规律。
根据库仑定律,两个电荷之间的相互作用力与它们的电荷量成正比,与它们之间的距离的平方成反比。
具体表达式为:\[F = k\frac{{|q_1q_2|}}{{r^2}}\]其中,\[F\]代表电荷之间的相互作用力,\[q_1\]和\[q_2\]分别代表两个电荷的电荷量,\[r\]代表两个电荷之间的距离,\[k\]为比例常数。
二、电场的叠加原理电场是由电荷产生的一种物理场。
电场可以用来描述在电荷存在的情况下,其他电荷所受到的力的情况。
如果有多个电荷同时存在,它们所产生的电场的叠加效应可以通过电场的叠加原理来描述。
根据电场的叠加原理,电场叠加后的总电场强度等于各个电场强度的矢量和。
这一原理可以用公式表示为:\[E = E_1 + E_2 + E_3 + ... + E_n\]其中,\[E_1\],\[E_2\],\[E_3\]等分别代表各个电荷所产生的电场强度,\[E\]代表叠加后的总电场强度。
三、高斯定律高斯定律是描述电场的分布与电荷之间的关系的定律。
根据高斯定律,电场通过一个闭合曲面的通量与该闭合曲面内的电荷量成正比,与电荷分布无关。
具体表达式为:\[Φ = \frac{Q}{{ε_0}}\]其中,\[Φ\]代表电场通过闭合曲面的通量,\[Q\]代表闭合曲面内的电荷量,\[ε_0\]为真空中的介电常数。
四、法拉第电磁感应定律法拉第电磁感应定律描述了磁场的变化所产生的感应电动势。
根据法拉第电磁感应定律,感应电动势的大小与磁场变化率成正比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d m d t 2. 非合闭合回路 B c (1) E dl l i S t dS c Ei Ei dl
a
b
a
d m abc cda ( 2) dt
d
abc cda
C
G G22
D
END
§16.4 自感和互感
一、 自感
自感电动势
I
i mi
d dt
I
B I m B dS I
S
LI
L——称为回路的自感。
自感由回路的形状、大小及周围介质决定
d dI dL L L I dt dt dt
第 16 章 变化的电磁场
第 16 章 变化的电磁场
§16.1 电磁感应定律 §16.2 动生电动势 §16.3 感生电动势 感应电场 §16.4 自感和互感 §16.5 电容和电感电路中的暂态电流 §16.6 磁场能量 §16.7 位移电流 §16.8 麦克斯韦电磁场方程组
§16.1 电磁感应定律
若L不变
dI L L dt
自感电动势阻碍电流的变化
——电磁惯性
自感之单位
H 1H 1Wb/A
LI L
计算自感系数的方法:
I
dI L L L L dI dt dt
二、 互感
互感应
I1 21 21 I 2 12 12
一段导线: Ei dl 闭合回路: l Ei dl a d m l Ei dl dt d m d B B dS dS S t dt dt S B 变化磁场产生电场! Ei dl dS l S t
L 以角速度 绕o点转动,
。
I
a
o
dl
A
vB dl
l
2πa l cos
0 I
dl
0I a a L cos d ln L 2π cos cos a
法拉第圆盘发电机
R
0
v B dl
一、楞次定则
楞次定则:感应电动势 产生的感应电流的方向 总是使感应电流的磁场 通过回路的磁通量阻碍 原磁通量的变化。
二、法拉第定律
法拉第通量法则:回路上感应电动势的大 小与通过回路的磁通量的变化率成正比。
d m dt
任意曲面的磁通量。
SI: (V), m ( Wb)
m:通过回路的磁通量—即通过以回路为边线的
u
外力做正功输入机械能,安培力做负功吸收它,同 时感应电动势在回路中做正功又以电能形式输出这个 份额的能量。
三、动生电动势的计算
1. 对于导线回路
(1) (2)
l
d m dt
b
v B dl
一般情况: mi N m——磁通链 i 1 d 设线圈电阻为R I R R dt 在t1到t2时间内流过的电量:
q
END
t2
t1
1 Idt R
2
1
1 d 2 1 R
§16.2 动生电动势
一、洛伦兹力产生动生电动势
设稳恒磁场 B ,导线运动! b dl v 载流子受力 F qv B 如 q>0 B a F Ek v B q b b Ek dl (v B) dl 如 0, // dl
B
lBdl
0
R
R
1 2 R B 2 1 2 并联 R B 2 思考: Δ 0, 0, ? m
dl
R
能否用法拉第定律求解?
t
时间内导体棒
a
扫过(切割)磁感应线数
Δ m
d m 1 2 BR 2 dt
方向:
1 2 BΔS BR 2
a a
对于导线回路
v B dl
l
d m v B dl l d t 证明:如图 Δ t 时间内 dl 扫过面积 dS dl v Δ t
左、右底面和侧面构成闭合曲面 S!
试证明:在稳恒磁场中,动生电动势
d
Eiz dz 0 Eiz 0 a
B l Ei dl Ei 2πr S t dS B 2 πr r R Ei 2 πr t
O r l R
r B m (B 2 ) Ei πr 2 t m B 2 ) r R Ei 2πr πR ( B 2 πR t
趋肤效应
B I Ei t
热功率
P
2
减小涡电流的方法: 使用硅钢片材料
趋肤效应(对于高频电流)
I
I2
I1
j r
有效截面 S 电阻 改善方法: (1)表面镀银以减小电阻 (2)分束法,增加导线表面积
o
(3)挖空中心,节省材料
四、感生电动势的计算
1. 导体为闭合回路
设均匀磁场
B
以恒定外力向右拉杆
f1
v f 2 v I IBl F qv u B qv B qu B f1 f 2 f1 u q(v B) u q B u v q u B v f 2 v
END
vB sin Rd Ek v B Eka Ekc vB
b d
向左
v B dl vBRsin d 2vBR
0
§16.3 感生电动势
一、 感生电动势
感应电场
I
d m I 变化时 Ii dt R
S2 S1
l
d m dt
B
m 0
B
Φm 0 0
Φm 0 0
m 0
约定:先规定回路正方向,从而得到磁通量,再求 感应电动势。若为正,则与规定的回路方向相同。 若为负,则其方向与假设方向相反。
若回路线圈有N匝,则由于串联关系
d m d ( N m ) d N dt dt dt
l S l
非闭合回路:
b
a
(v B) dl
d m dt
dt 时间内扫过 面积的磁通量
电磁阻尼:
v
F
v
F
二、动生电动势过程中的能量转化
r Ei B0 2
R
B
r
Ei
dl
B
[例16-6] 问: AB , 解:
如图均匀变化磁场B,导体AB=2R,CD=2R
i1 , CD , i2
B A
是否为零?
G1
AB
Ei dl 0
i1 0
CD 0
i2 0
A B R
静电场为有源场!
感应电场为无源场!
感应电场与磁场涡旋性质相似!
B dl 0 I 0 j dS
l S
B Ei
B
B l Ei dl S t dS B j t
B t
Ei
I
三、 感应涡电流
v dl
dl
l t l
t t ??
l S
B dS 0
S
B dS B dl v Δ t B dS 0
l
( ) ( ) ( ) v B dl Δ t B dS B dS
若既有动生电动势,又有感生电动势
或:
b
a
b v B dl Ei dl
a
l
B v B dl dS S t
[例16-3]
计算具有轴对称变化磁场产生的感应电场。
Eir
解:
Eiz S2
产生感生电动势的 非静电力是什么?
Ii l
G
1.
F q(E v B) v 0, B 0 f m 0
B(t )
2.
F
q
产生感生电动势的非静电力一定不是洛仑兹力。
麦克斯韦提出感应电场概念:当空间中的磁场 发生变化时,就在周围空间激起感应电场 , 在导体中产生感生电动势,并形成感应电流。
v
2. 对于一段导线
(1) v B d l ab a d m (2) ab dt
b
v a
[例16-1] 如图杆 OA 且与直电流共面, 求 解:
0 I B 2πa l cos d v B dl
Ei
R B Ei 2r t
2
o R
r
