2020年中考数学一轮复习课件:提分微课(01)关于中点的联想
2020年中考最全复习资料专题22 关于中点的联想
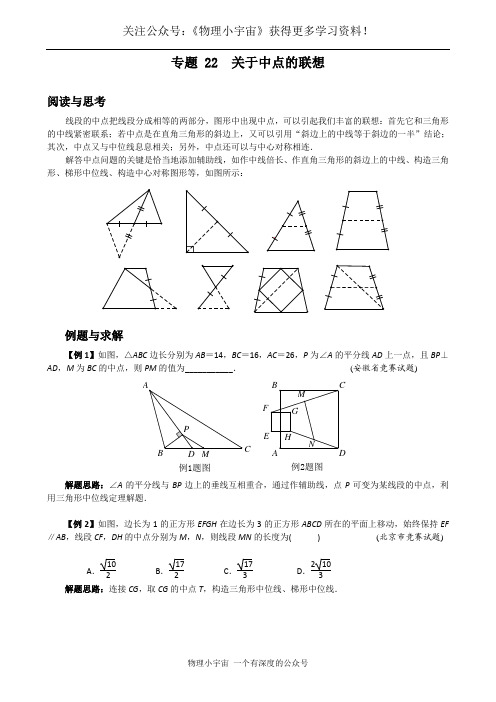
专题 22 关于中点的联想阅读与思考线段的中点把线段分成相等的两部分,图形中出现中点,可以引起我们丰富的联想:首先它和三角形的中线紧密联系;若中点是在直角三角形的斜边上,又可以引用“斜边上的中线等于斜边的一半”结论;其次,中点又与中位线息息相关;另外,中点还可以与中心对称相连.解答中点问题的关键是恰当地添加辅助线,如作中线倍长、作直角三角形的斜边上的中线、构造三角形、梯形中位线、构造中心对称图形等,如图所示:例题与求解【例1】如图,△ABC边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,则PM的值为___________.(安徽省竞赛试题)例2题图例1题图F解题思路:∠A的平分线与BP边上的垂线互相重合,通过作辅助线,点P可变为某线段的中点,利用三角形中位线定理解题.【例2】如图,边长为1的正方形EFGH在边长为3的正方形ABCD所在的平面上移动,始终保持EF ∥AB,线段CF,DH的中点分别为M,N,则线段MN的长度为( ) (北京市竞赛试题)A.102B.172C.173D.2103解题思路:连接CG,取CG的中点T,构造三角形中位线、梯形中位线.【例3】如图,在△ABC 中,AB =AC ,延长AB 到D ,使BD =AB ,E 为AB 中点,连接CE ,CD ,求证:CD =2EC . (宁波市竞赛试题)解题思路:图形中有两个中点E ,B ,联想到与中点相关的丰富知识,将线段倍分关系的证明转化为线段相等关系的证明,关键是恰当添加辅助线.【例4】如图1,P 是线段AB 上一点,在AB 的同侧作△APC 和△BPD ,使∠APC =∠BPD ,PC =PA ,PD =PB ,连接CD ,点E ,F ,G ,H 分别是AC ,AB ,BD ,CD 的中点,顺次连接E ,F ,G ,H .(1) 猜想四边形EFGH 的形状,直接回答,不必说明理由;(2) 当点P 在线段AB 的上方时,如图2,在△APB 的外部作△APC 和△BPD ,其他条件不变,(1)中的结论还成立吗?说明理由;(3) 如果(2)中,∠APC =∠BPD =90°,其他条件不变,先补全图3,再判断四边形EFGH 的形状,并说明理由. (营口市中考试题)BAPAFP BG D H CE HGF E PABC D图① 图② 图③解题思路:结论随着条件的改变也许发生变化,但解决问题的方法是一致的,即通过连线,为三角形中位线定理的应用创造条件.例3图CA D【例5】如图,以△ABC 的AB ,AC 边为斜边向形外作直角三角形ABD 和ACE ,且使∠ABD =∠ACE ,M 是BC 的中点,求证:DM =EM . (“祖冲之杯”邀请赛试题)解题思路:显然△DBM 不全等于△ECM ,必须通过作辅助线,构造全等三角形证明DM =EM .【例6】如图,已知△ABC 中,∠ACB =90°,AB 边上的高CH 与△ABC 的两条内角平分线AM ,BN 分别交于P ,Q 两点,PM ,QN 的中点分别为E ,F ,求证:EF ∥AB . (全国初中数学联赛题)解题思路:从图形的形成过程,逐步探索相应结论.将原问题分解为多个小问题.○能 ○力 ○训 ○练 A 级1.如图,若E ,F ,G ,H 分别是四边形ABCD 各边的中点,则四边形EFGH 是____________.(1)如果把条件中的四边形ABCD 依次改为矩形、菱形、正方形或等腰梯形,其他条件不变,那么所得的四边形EFGH 分别为_______________________;(2)如果把结论中的平行四边形EFGH 依次改为矩形、菱形、正方形,那么原四边形ABCD 应具备的条件是_______________________. (湖北省黄冈市中考试题)2.如图,已知AG ⊥BD ,AF ⊥CE ,BD ,CE 分别是∠ABC 和∠ACB 的角平分线,若BF =2,ED =3,GC 例5图EDM ABC例6图CB D第1题图第2题图C3.如图,在△ABC 中,AB =AC ,AD ⊥BC 于点D ,E 是AC 的中点,若BC =16,DE =5,则AD =______________. (南京市中考试题)4.如图,在△ABC 中,AB =AC ,M ,N 分别是AB ,AC 的中点,D ,E 为BC 上的点,连接DN ,EM ,若AB =13cm ,BC =10cm ,DE =5cm ,则图中阴影部分的面积为________________.(北京市中考试题)5.A ′,B ′,C ′,D ′顺次为四边形ABCD 的各边的中点,下面条件中使四边形A ′B ′C ′D ′为正方形的条件是( )A .四边形ABCD 是矩形B .四边形ABCD 是菱形C .四边形ABCD 是等腰梯形 D .四边形ABCD 中,AC ⊥BD 且AC =BD6.若等腰梯形的两条对角线互相垂直,中位线长为8cm ,则该等腰梯形的面积为( ) A .16cm 2 B .32cm 2 C .64cm 2 D .112cm 27.如图,梯形ABCD 中,AD ∥BC ,E ,F 分别是BD ,AC 的中点,若AD =6cm ,BC =18cm ,则EF 的长为( )A .8cmB .7cmC .6cmD .5cm8.如图,在梯形ABCD 中,AD ∥EF ∥GH ∥BC ,AE =EG =GB ,AD =18,BC =32,则EF +GH =( ) A .40 B .48 C .50 D .56 (泰州市中考试题)B第8题图 第9题图9.如图,在△ABC 中,∠B =2∠C ,AD ⊥BC 于点D ,M 是BC 的中点,求证:DM =12AB .第4题图第3题图A第7题图10. 如图,在△ABC 中,BD =CE ,BE ,CD 的中点分别是M ,N ,直线MN 分别交AB ,AC 于点P ,Q ,求证:AP =AQ .11.在图1至图3中,点B 是线段AC 的中点,点D 是线段CE 的中点.四边形BCGF 和CDHN 都是正方形.AE 的中点是M .(1)如图1,点E 在AC 的延长线上,点N 与点G 重合时,点M 与点C 重合,求证:FM = MH ,FM ⊥MH ; (2)将图1中的CE 绕点C 顺时针旋转一个锐角,得到图2,求证:△FMH 是等腰直角三角形; (3)将图2中的CE 缩短到图3的情况,△FMH 还是等腰直角三角形吗?(不必说明理由) (2009年河北省中考试题)12.在六边形ABCDEF 中,AB ∥DE ,BC ∥EF ,CD ∥FA ,AB +DE =BC +EF ,A 1,B 1,D 1,E 1分别是边AB ,BC ,DE ,EF 的中点,A 1D 1=B 1E 1.求证:∠CDE =∠AFE .第12题图F E第10题图图1AHC (M )DEBFG (N )G图2AHC DEBFNMAHCDE图3BFG MNB 级1.如图,正方形ABCD 两条对角线相交于点E ,∠CAD 的平分线AF 交DE 于点G ,交DC 于点F ,若GE =24,则FC =_________________.2.如图,四边形ABCD 的对角线AC ,BD 相交于点F ,M ,N 分别是AB ,CD 的中点,MN 分别交BD ,AC 于点P ,Q ,且∠FPQ =∠FQP ,BD =10,则AC =_________. (重庆市竞赛试题)3.如图,在△ABC 中,∠BAC =120°,以AB ,AC 为边分别向形外作正三角形ABD 和正三角形ACE ,M 为AD 的中点,N 为AE 的中点,P 为BC 的中点,则∠MPN =_________. (北京市竞赛试题)4.如图,已知A 为DE 的中点,设△DBC ,△ABC ,△EBC 的面积分别为S 1,S 2,S 3,则S 1,S 2,S 3之间的关系是( )A .S 2=32(S 1+S 3)B .S 2=12(S 3―S 1)C .S 2=12(S 1+S 3)D .S 2=32(S 3―S 1) 5.如图,在图形ABCD 中,AB ∥DC ,M 为DC 的中点,N 为AB 的中点,则 ( ) A .MN >12(AD +BC ) B .MN <12(AD +BC )C .MN =12(AD +BC ) D .无法确定MN 与12(AD +BC )的关系6.如图,凸四边形ABCD 的面积是a ,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,那么图中的阴影部分的面积为( )A .18aB .16aC .14aD .12a(江苏省竞赛试题)7.如图,在△ABC 中,D 为AB 的中点,分别延长CA ,CB 到点E ,F ,使DE =DF ,过E ,F 分别作CA ,CB 的垂线,相交于点P .求证:∠PAE =∠PBF . (全国初中数学联赛试题)第5题图DC M 第2题图CF第1题图F第3题图 第4题图D第6题图ABE第7题图EPF8.如图,锐角△ABC 中,作高BD 和CE ,过顶点B ,C 分别作DE 的垂线BF 和CG ,求证:EF =DG .(全俄奥林匹克数学竞赛试题)9. 如图,在△ABC 中,AD 是BC 边上的中线,点M 在AB 边上,点N 在AC 边上,并且∠MDN =90°,如果BM 2+CN 2=DM 2+DN 2.求证:AD 2=14(AB 2+AC 2). (北京市竞赛试题)10.已知:△ABD 和△ACE 都是直角三角形,且∠ABD =∠ACE =90°.如图1,连接DE ,设M 为DE 的中点.(1)求证:MB =MC ;(2)设∠BAD =∠CAE ,固定△ABD ,让Rt △ACE 绕顶点A 在平面内旋转到图2的位置,试问:MB =MC 是否还成立?请说明理由. (江苏省竞赛试题)图2图1第9题图 ABC D第8题图BG11.已知△OAB ,△OCD 都是等腰直角三角形,∠AOB =∠COD =90°.(1) 如图1,点C 在OA 边上,点D 在OB 边上,连接AD ,BC ,M 为线段AD 的中点,求证:OM ⊥BC . (2) 如图2,在图1的基础上,将△OCD 绕点O 逆时针旋转α(α为锐角),M 为线段AD 的中点.①求证:OM =12BC ;②OM ⊥BC 是否还成立?若成立,请证明;若不成立,请说明理由.图1图2BBODC12.如图1,在△ABC 中,点P 为BC 边的中点,直线a 绕顶点A 旋转,若点B ,P 在直线a 的异侧,BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接PM ,PN .(1)延长MP 交CN 于点E (如图2). ①求证:△BPM ≌△CPE ; ②求证:PM =PN .(2)若直线a 绕点A 旋转到如图3的位置时,点B ,P 在直线a 的同侧,其他条件不变,此时PM =PN 还成立吗?若成立,请证明;若不成立,请说明理由.(3) )若直线a 绕点A 旋转到与BC 边平行的位置时,其他条件不变.请直接判断四边形MBCN 的形状及此时PM =PN 是否成立.不必说明理由. (沈阳市中考试题)图3图2图1BB。
中点联想

中点联想线段的中点是几何图形中一个特殊的点,它关联着三角形中线、直角三角形斜边中线、中心对称图形、三角形中位线、梯形中位线等丰富的知识,恰当地利用中点,处理中点是解与中点有关问题的关键,由中点想到什么?常见的联想路径是:1.中线倍长;2.作直角三角形斜边中线;3.构造中位线;4.构造中心对称全等三角形等.基本图形:解读:(一)遇到中点时常见的五种思路:1.遇到等腰三角形底边的中点时考虑:三线合一2.遇到直角三角形斜边的中点时考虑:斜边的中线等于斜边的一半。
3.遇到三角形一边上的中线时考虑:倍长中线4.遇到平行线所截线段的中点时考虑:类倍长中线5.多个中点考虑(或构造):中位线(二)例题:1.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于()A. B. C. D.2.如图, 在△ABC中,BE,CF分别为边AC,AB的高,D为BC的中点,M为EF的中点。
求证:D M⊥EF3.如图,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF,求证:AC=BF.(三)练习1.已知,如图,在等腰△ABC中,AB=AC,D是BC的中点,过A 的直线MN//BC,在直线MN上点A的两侧分别取点E,F且AE=AF。
求证:DE=DF2.如图,在等腰三角形ABC中,AB=AC,D是BC的中点,过A作AE⊥DE,AF⊥DF,且AE=AF,求证:∠EDB=FDC.3.如图, 在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
如果点M,N分别在线段AB,AC上移动,在移动中保证AN=AM,请判断△OMN 的形状,并证明你的结论。
4.如图,△ABC中,BC=18,若BD⊥AC于D,CE⊥AB于E,F、G分别为BC、DE的中点,若ED=10,求FG的长.5. 如图,在△ABC中,AB≠AC,D、E在BC上,点E为DC的中点,过D作DF∥BA交AE于点F,DF=AC.求证:AE平分∠BAC.6. 如图,AD是△ABC的中线,E、F分别是AB、AC的中点,求证:AD与EF互相平分.7.如图,已知在矩形ABCD中,E为CB延长线上一点,CE=AC,F是AE 的中点.(1)求证BF⊥DF(用两种方法正明)(2)若AB=8,AD=6,求DF的长.8.如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE ⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是(把所有正确结论的序号都填在横线上)(1)∠DCF= ∠BCD,(2)EF=CF;(3)S ΔBEC =2S ΔCEF ;(4)∠DFE=3∠AEF ∙∙(四)中考重现1.如图,已知:在矩形ABCD中,O为AC的中点,直线l经过点B,且直线l绕着点B旋转,AM⊥l于点M,CN⊥l于点N,连接OM,ON(1)当直线l经过点D时,如图1,则OM、ON的数量关系为;(2)当直线l与线段CD交于点F时,如图2(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由;(3)当直线l与线段DC的延长线交于点P时,请在图3中做出符合条件的图形,并判断(1)中的结论是否仍然成立?不必说明理由.2.如图1,在正方形ABCD和正方形CGEF(CG>BC)中,点B,C,G在同一直线上,点M是AE的中点.(1)探究线段MD,MF的位置及数量关系,并证明.(2)若将图1中的正方形CGEF绕点C顺时针旋转,使D,C,G 三点在一条直线上,如图2,其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.(3)将图1中的正方形CGEF绕点C顺时针旋转,使正方形CGEF 的对角线CE恰好与正方形ABCD的边BC在同一条直线上,如图3,其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.3.我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)4..如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;(2)现将图①中的△CDE绕着点C顺时针旋转,得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;(3)若图②中的等腰直角三角形变成直角三角形,使BC=AC,CD=CE,如图③,写出PM与PN的数量关系,并加以证明.5.已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.。
提分微课(01) 中点问题

在 Rt△EFC 中,EC=2,∠C=60°,∴EF= 3.
∵G 为 EF 的中点,∴EG= 23. 在 Rt△DEG 中,DE=2,EG= 23, 由勾股定理得,DG= ������������2 + ������������2= 219.故答案为 219.
7. [2017·天津]如图W1-7,正方形ABCD和
点,P 为 AC 边上的动点,OQ⊥OP 交 BC 于点 Q,M 为 PQ 的中点,当点 P 从点 A 运动
到点 C 时,点 M 所经过的路线长为 ( )
A. 42π
B. 22π
C.1
D.2
图W1-10
[答案] C
[解析]连接 OM,CM,OC. ∵OQ⊥OP,且 M 是 PQ 的中点,∴OM=12PQ. ∵△ABC 是等腰直角三角形,∴∠ACB=90°,∴CM=12PQ,∴OM=CM, ∴△OCM 是等腰三角形,∴M 在 OC 的垂直平分线上.
6. [2018·天津]如图W1-6,在边长为4的等边三角形ABC中,D,E分别为AB,BC的
中点,EF⊥AC于点F,G为EF的中点,连接DG,则DG的长为
.
图W1-6
[答案]
19 2
[解析]连接 DE,∵D,E 分别为 AB,BC 的中点,∴DE∥AC,2DE=AC=4,EC=2,
∵EF⊥AC,∴DE⊥EF.∴△DEG 为直角三角形,
类型二 多个中点 构造 中位线
4.[2018·苏州]如图 W1-4,在△ABC 中,延长 [答案]B
BC
至
D,使得
CD=12BC,过
AC
的中点
E
作
[解析]取 BC 的中点 ∵E 是 AC 的中点,
G,连接
方法专题中点的联想PPT课件

联想之三
3、三角形中遇到两边的中点,常联想“三角形 的中位线定理”
如图,在△ABC中,D、E分别是AB、AC的中点, DE=4,则BC= .
第4页/共13页
联想之三
例:如图E为平行四边形ABCD中DC边的延长线 上一点,且CE=DC,连结AE,分别交BC、BD于 点F、G,连接AC交BD于O,连结OF. 求证: AB= 2 OF
•
•
5
N
6
第2页/共13页
联想之二
2、直角三角形中遇到斜边上的中点,常联想 “斜边上的中线,等于斜边的一半”
例:如图,点D为△ABC的BC边上一个动点(不与B、 C重合),连接AD,过点D分别作DE⊥AC于点E, DF⊥AB于点F,点M是AD的中点,连接ME,MF,在点 D的移动过程中,∠EMF的大小是否发生改变,请说 明理由。
如图点d为abc的bc边上一个动点不与bc重合连接ad过点d分别作deac于点edfab于点f点m是ad的中点连接memf在点d的移动过程中emf的大小是否发生改变请说明理由
方法专题
开县德阳初级中学数学 冯元辉
第1页/共13页
联想之一
1、等腰三角形中遇到底边上的中点,常 联想“三线合一”的性质;
如图1所示,在△ABC中,AB=AC=5,BC=6,点M为BC中点, MN⊥AC于点N
提示:证明△ABF≌ △ECF,
得BF=CF,再证OF是B
△ABC的中位线.
A O
G
F
D C
E
第5页/共13页
联想之四
4、遇到两平行线所截得的线段的中点时,常联想“八字型”全等三角形
如图, ∥ ,C是线段AB的中点,那么过点C的任何 直线都可以和AB构造“8字型”全等。
中考数学复习《中点联想解析》

中考数学复习中点联想训练本文基于教学实践和反思提出了在初中数学教学中对“中点”的一些认识。
并对中点问题进行了详细分类,对每种类型进行了举例、分析,特别是对各类中点问题的基本思路做了探讨和研究,并且针对学生在解题上存在的问题,提出了中点问题教学的几点建议:(1)在中点问题教学中,要积极培养学生的观察能力,提高学生的图形结合能力。
(2)在中点问题教学中,要培养学生的分析能力与概括能力,并帮助学生实现各部分知识之间的联系与转换,从而提高学生的综合分析问题和概括问题的能力。
(3)在中点问题教学中,要给学生有专题性的训练,从而提高学生解中点问题的能力。
1.与中点有关的定理(1)直角三角形斜边上的中线等于斜边的一半.(2)等腰三角形“三线合一”的性质.(3)三角形的中位线定理.(4)垂径定理及其推论.2.与中点有关的辅助线(1)构造三角形的中位线,如连结三角形两边的中点;取一边的中点,然后与另一边的中点相连结;过三角形一边的中点作另一边的平行线等等.(2)延长角平分线的垂线,构造等腰三角形的“三线合一”.(3)把三角形的中线延长一倍,构造平行四边形.一、中点在普通三角形中的应用【例题】(2017广西河池)三角形的下列线段中能将三角形的面积分成相等两部分的是()A.中线B.角平分线C.高D.中位线【考点】K3:三角形的面积;K2:三角形的角平分线、中线和高.【分析】根据等底等高的三角形的面积相等解答.【解答】解:∵三角形的中线把三角形分成两个等底同高的三角形,∴三角形的中线将三角形的面积分成相等两部分.故选A.【同步训练】(2017齐齐哈尔)如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.(1)求证:DE=DF,DE⊥DF;(2)连接EF,若AC=10,求EF的长.【考点】KD:全等三角形的判定与性质;KQ:勾股定理.【分析】(1)证明△BDG≌△ADC,根据全等三角形的性质、直角三角形的性质证明;(2)根据直角三角形的性质分别求出DE、DF,根据勾股定理计算即可.【解答】(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°,在△BDG和△ADC中,,∴△BDG≌△ADC,∴BG=AC,∠BGD=∠C,∵∠ADB=∠ADC=90°,E,F分别是BG,AC的中点,∴DE=BG=EG,DF=AC=AF,∴DE=DF,∠EDG=∠EGD,∠FDA=∠FAD,∴∠EDG+∠FDA=90°,∴DE⊥DF;(2)解:∵AC=10,∴DE=DF=5,由勾股定理得,EF==5.二、中点在等腰三角形中的应用【例题】(2016·广西桂林·3分)如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= .【考点】相似三角形的判定与性质;全等三角形的判定与性质;等腰直角三角形.【分析】在BD上截取BE=CH,连接CO,OE,根据相似三角形的性质得到,求得CH=,根据等腰直角三角形的性质得到AO=OB=OC,∠A=∠ACO=∠BCO=∠ABC=45°,等量代换得到∠OCH=∠ABD,根据全等三角形的性质得到OE=OH,∠BOE=∠HOC推出△HOE是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.【解答】解:在BD上截取BE=CH,连接CO,OE,∵∠ACB=90°CH⊥BD,∵AC=BC=3,CD=1,∴BD=,∴△CDH∽△BDC,∴,∴CH=,∵△ACB是等腰直角三角形,点O是AB中点,∴AO=OB=OC,∠A=∠ACO=∠BCO=∠ABC=45°,∴∠OCH+∠DCH=45°,∠ABD+∠DBC=45°,∵∠DCH=∠CBD,∴∠OCH=∠ABD,在△CHO与△BEO中,,∴△CHO≌△BEO,∴OE=OH,∠BOE=∠HOC,∵OC⊥BO,∴∠EOH=90°,即△HOE是等腰直角三角形,∵EH=BD﹣DH﹣CH=﹣﹣=,∴OH=EH×=,故答案为:.【同步训练】(2016·湖北随州·10分)爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.【特例探究】(1)如图1,当tan∠PAB=1,c=4时,a= 4,b= 4;如图2,当∠PAB=30°,c=2时,a= ,b= ;【归纳证明】(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.【拓展证明】(3)如图4,▱ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3,AB=3,求AF的长.【考点】四边形综合题.【分析】(1)①首先证明△APB,△PEF都是等腰直角三角形,求出PA、PB、PE、PF,再利用勾股定理即可解决问题.②连接EF,在RT△PAB,RT△PEF中,利用30°性质求出PA、PB、PE、PF,再利用勾股定理即可解决问题.(2)结论a2+b2=5c2.设MP=x,NP=y,则AP=2x,BP=2y,利用勾股定理分别求出a2、b2、c2即可解决问题.(3)取AB中点H,连接FH并且延长交DA的延长线于P点,首先证明△ABF是中垂三角形,利用(2)中结论列出方程即可解决问题.【解答】(1)解:如图1中,∵CE=AE,CF=BF,∴EF∥AB,EF=AB=2,∵tan∠PAB=1,∴∠PAB=∠PBA=∠PEF=∠PFE=45°,∴PF=PE=2,PB=PA=4,∴AE=BF==2.∴b=AC=2AE=4,a=BC=4.故答案为4,4.如图2中,连接EF,,∵CE=AE,CF=BF,∴EF∥AB,EF=AB=1,∵∠PAB=30°,∴PB=1,PA=,在RT△EFP中,∵∠EFP=∠PAB=30°,∴PE=,PF=,∴AE==,BF==,∴a=BC=2BF=,b=AC=2AE=,故答案分别为,.(2)结论a2+b2=5c2.证明:如图3中,连接EF.∵AF、BE是中线,∴EF∥AB,EF=AB,∴△FPE∽△APB,∴==,设FP=x,EP=y,则AP=2x,BP=2y,∴a2=BC2=4BF2=4(FP2+BP2)=4x2+16y2,b2=AC2=4AE2=4(PE2+AP2)=4y2+16x2,c2=AB2=AP2+BP2=4x2+4y2,∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2.(3)解:如图4中,在△AGE和△FGB中,,∴△AGE≌△FGB,∴BG=FG,取AB中点H,连接FH并且延长交DA的延长线于P点,同理可证△APH≌△BFH,∴AP=BF,PE=CF=2BF,即PE∥CF,PE=CF,∴四边形CEPF是平行四边形,∴FP∥CE,∵BE⊥CE,∴FP⊥BE,即FH⊥BG,∴△ABF是中垂三角形,由(2)可知AB2+AF2=5BF2,∵AB=3,BF=AD=,∴9+AF2=5×()2,∴AF=4.三、中点在直角三角形中的应用【例题】(2017毕节)如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD 上一点,且CF=CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为()A.6 B.4 C.7 D.12【考点】KX:三角形中位线定理;KP:直角三角形斜边上的中线.【分析】先根据直角三角形的性质求出CD的长,再由三角形中位线定理即可得出结论.【解答】解:∵Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,∴CD=AB=4.5.∵CF=CD,∴DF=CD=×4.5=3.∵BE∥DC,∴DF是△ABE的中位线,∴BE=2DF=6.故选A.【同步训练】(2017•黄石)如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=,则∠CDE+∠ACD=()A.60°B.75°C.90°D.105°【考点】KS:勾股定理的逆定理;KP:直角三角形斜边上的中线.【分析】根据直角三角形的性质得到BC=2CE=,根据勾股定理的逆定理得到∠ACB=90°,根据三角函数的定义得到∠A=60°,求得∠ACD=∠B=30°,得到∠DCE=60°,于是得到结论.【解答】解:∵CD⊥AB,E为BC边的中点,∴BC=2CE=,∵AB=2,AC=1,∴AC2+BC2=12+()2=4=22=AB2,∴∠ACB=90°,∵tan∠A==,∴∠A=60°,∴∠ACD=∠B=30°,∴∠DCE=60°,∵DE=CE,∴∠CDE=60°,∴∠CDE+∠ACD=90°,故选C.【点评】本题考查了勾股定理的逆定理,直角三角形的性质,三角函数的定义,熟练掌握勾股定理的逆定理是解题的关键.四、中位线在三角形的应用【例题】(2017毕节)如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD 上一点,且CF=CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为()A.6 B.4 C.7 D.12【考点】KX:三角形中位线定理;KP:直角三角形斜边上的中线.【分析】先根据直角三角形的性质求出CD的长,再由三角形中位线定理即可得出结论.【解答】解:∵Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,∴CD=AB=4.5.∵CF=CD,∴DF=CD=×4.5=3.∵BE∥DC,∴DF是△ABE的中位线,∴BE=2DF=6.故选A.【同步训练】(2017湖北宜昌)如图,要测定被池塘隔开的A,B两点的距离.可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED.现测得AC=30m,BC=40m,DE=24m,则AB=()A.50m B.48m C.45m D.35m【考点】KX:三角形中位线定理.【分析】根据中位线定理可得:AB=2DE=48m.【解答】解:∵D是AC的中点,E是BC的中点,∴DE是△ABC的中位线,∴DE=AB,∵DE=24m,∴AB=2DE=48m,故选B.五、中点在圆的性质中的应用【例题】(2017广西百色)已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若=,如图1,.(1)判断△ABC的形状,并证明你的结论;(2)设AE与DF相交于点M,如图2,AF=2FC=4,求AM的长.【考点】MI:三角形的内切圆与内心.【分析】(1)易证∠EOF+∠C=180°,∠DOE+∠B=180°和∠EOF=∠DOE,即可解题;(2)连接OB、OC、OD、OF,易证AD=AF,BD=CF可得DF∥BC,再根据AE长度即可解题.【解答】解:(1)△ABC为等腰三角形,∵△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,∴∠CFE=∠CEF=∠BDO=∠BEO=90°,∵四边形内角和为360°,∴∠EOF+∠C=180°,∠DOE+∠B=180°,∵=,∴∠EOF=∠DOE,∴∠B=∠C,AB=AC,∴△ABC为等腰三角形;(2)连接OB、OC、OD、OF,如图,∵等腰三角形ABC中,AE⊥BC,∴E是BC中点,BE=CE,∵在Rt△AOF和Rt△AOD中,,∴Rt△AOF≌Rt△AOD,∴AF=AD,同理Rt△COF≌Rt△COE,CF=CE=2,Rt△BOD≌Rt△BOE,BD=BE,∴AD=AF,BD=CF,∴DF∥BC,∴=,∵AE==4,∴AM=4×=.【同步训练】(2017呼和浩特)如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧的中点,AC与BD交于点E.(1)求证:DC2=CE•AC;(2)若AE=2,EC=1,求证:△AOD是正三角形;(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,求△ACH的面积.【考点】MR:圆的综合题.【分析】(1)由圆周角定理得出∠DAC=∠CDB,证明△ACD∽△DCE,得出对应边成比例,即可得出结论;(2)求出DC=,连接OC、OD,如图所示:证出BC=DC=,由圆周角定理得出∠ACB=90°,由勾股定理得出AB==2,得出OB=OC=OD=DC=BC=,证出△OCD、△OBC是正三角形,得出∠COD=∠BOC=∠OBC=60°,求出∠AOD=60°,即可得出结论;(3)由切线的性质得出OC⊥CH,求出∠H=30°,证出∠H=∠BAC,得出AC=CH=3,求出AH和高,由三角形面积公式即可得出答案.【解答】(1)证明:∵C是劣弧的中点,∴∠DAC=∠CDB,∵∠ACD=∠DCE,∴△ACD∽△DCE,∴=,∴DC2=CE•AC;(2)证明:∵AE=2,EC=1,∴AC=3,∴DC2=CE•AC=1×3=3,∴DC=,连接OC、OD,如图所示:∵C是劣弧的中点,∴OC平分∠DOB,BC=DC=,∵AB是⊙O的直径,∴∠ACB=90°,∴AB==2,∴OB=OC=OD=DC=BC=,∴△OCD、△OBC是正三角形,∴∠COD=∠BOC=∠OBC=60°,∴∠AOD=180°﹣2×60°=60°,∵OA=OD,∴△AOD是正三角形;(3)解:∵CH是⊙O的切线,∴OC⊥CH,∵∠COH=60°,∴∠H=30°,∵∠BAC=90°﹣60°=30°,∴∠H=∠BAC,∴AC=CH=3,∵AH=3,AH上的高为BC•sin60°=,∴△ACH的面积=×3×=.六、中点在四边形中的性质应用【例题】(2017•温州)四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2EF,则正方形ABCD的面积为()A.12S B.10S C.9S D.8S【考点】KR:勾股定理的证明.【分析】设AM=2a.BM=b.则正方形ABCD的面积=4a2+b2,由题意可知EF=(2a﹣b)﹣2(a﹣b)=2a﹣b﹣2a+2b=b,由此即可解决问题.【解答】解:设AM=2a.BM=b.则正方形ABCD的面积=4a2+b2由题意可知EF=(2a﹣b)﹣2(a﹣b)=2a﹣b﹣2a+2b=b,∵AM=2EF,∴2a=2b,∴a=b,∵正方形EFGH的面积为S,∴b2=S,∴正方形ABCD的面积=4a2+b2=9b2=9S,故选C.【点评】本题考查正方形的性质、勾股定理、线段的垂直平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考选择题中的压轴题.【同步训练】(2016·山东省德州市·4分)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH 的形状.(不必证明)【考点】平行四边形的判定与性质.【分析】(1)如图1中,连接BD,根据三角形中位线定理只要证明EH∥FG,EH=FG即可.(2)四边形EFGH是菱形.先证明△APC≌△BPD,得到AC=BD,再证明EF=FG即可.(3)四边形EFGH是正方形,只要证明∠EHG=90°,利用△APC≌△BPD,得∠ACP=∠BDP,即可证明∠COD=∠CPD=90°,再根据平行线的性质即可证明.【解答】(1)证明:如图1中,连接BD.∵点E,H分别为边AB,DA的中点,∴EH∥BD,EH=BD,∵点F,G分别为边BC,CD的中点,∴FG∥BD,FG=BD,∴EH∥FG,EH=GF,∴中点四边形EFGH是平行四边形.(2)四边形EFGH是菱形.证明:如图2中,连接AC,BD.∵∠APB=∠CPD,∴∠APB+∠APD=∠CPD+∠APD即∠APC=∠BPD,在△APC和△BPD中,,∴△APC≌△BPD,∴AC=BD∵点E,F,G分别为边AB,BC,CD的中点,∴EF=AC,FG=BD,∵四边形EFGH是平行四边形,∴四边形EFGH是菱形.(3)四边形EFGH是正方形.证明:如图2中,设AC与BD交于点O.AC与PD交于点M,AC与EH交于点N.∵△APC≌△BPD,∴∠ACP=∠BDP,∵∠DMO=∠CMP,∴∠COD=∠CPD=90°,∵EH∥BD,AC∥HG,∴∠EHG=∠ENO=∠BOC=∠DOC=90°,∵四边形EFGH是菱形,∴四边形EFGH是正方形.【点评】本题考查平行四边形的判定和性质、全等三角形的判定和性质、菱形的判定和性质、正方形的判定和性质等知识,解题的关键是灵活应用三角形中位线定理,学会添加常用辅助线,属于中考常考题型.七、中点在其它图形中的综合应用【达标训练】1.(2016·陕西·3分)如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有()A.2对 B.3对 C.4对 D.5对【考点】正方形的性质;全等三角形的判定.【分析】可以判断△ABD≌△BCD,△MDO≌△M′BO,△NOD≌△N′OB,△MON≌△M′ON′由此即可对称结论.【解答】解:∵四边形ABCD是正方形,∴AB=CD=CB=AD,∠A=∠C=∠ABC=∠ADC=90°,AD∥BC,在△ABD和△BCD中,,∴△ABD≌△BCD,∵AD∥BC,∴∠MDO=∠M′BO,在△MOD和△M′OB中,,∴△MDO≌△M′BO,同理可证△NOD≌△N′OB,∴△MON≌△M′ON′,∴全等三角形一共有4对.故选C .2. (2016·山东省东营市·3分)如图,在矩形ABCD 中,E 是AD 边的中点,BE ⊥AC ,垂足为点F ,连接DF ,分析下列四个结论:①△AEF ∽△CAB ;②CF =2AF ;③DF =DC ;④tan ∠CAD =2.其中正确的结论有( ) A.4个 B .3个 C .2个 D .1个第10题图F E DB CA【知识点】特殊平行四边形——矩形的性质、相似三角形——相似三角形的判定与性质、锐角三角函数——锐角三角函数值的求法【答案】B.【解析】∵矩形ABCD 中,∴AD ∥BC .∴△AEF ∽△CAB ….......................①正确; ∵△AEF ∽△CAB ,∴AF CF =AE BC =12,∴CF =2AF ……………………………②正确; 过点D 作DH ⊥AC 于点H .易证△ABF ≌△CDH (AAS ).∴AF =CH .∵EF ∥DH ,∴AF FH =AE ED=1.∴AF =FH .∴FH =CH . ∴DH 垂直平分CF .∴DF =DC . ……………………………………………③正确;第10题答案图G H F E D A C B设EF =1,则BF =2.∵△ABF ∽△EAF .∴AF EF =BF AF.∴AF =EF •BF =1×2= 2. ∴tan ∠ABF =AF BF =22.∵∠CAD =∠ABF ,∴tan ∠CAD =tan ∠ABF =22.…………④错误. 故选择B.【点拨】本题考查了矩形的性质、相似三角形的判定和性质,图形面积的计算,锐角三角函数值的求法,正确的作出辅助线是解本题的关键.3. (2016·湖北荆门·3分)如图,已知点A (1,2)是反比例函数y=图象上的一点,连接AO 并延长交双曲线的另一分支于点B ,点P 是x 轴上一动点;若△PAB 是等腰三角形,则点P 的坐标是 (﹣3,0)或(5,0)或(3,0)或(﹣5,0) .【考点】反比例函数图象上点的坐标特征;等腰三角形的性质.【分析】由对称性可知O 为AB 的中点,则当△PAB 为等腰三角形时只能有PA=AB 或PB=AB ,设P 点坐标为(x ,0),可分别表示出PA 和PB ,从而可得到关与x 的方程,可求得x ,可求得P 点坐标.【解答】解:∵反比例函数y=图象关于原点对称,∴A 、B 两点关于O 对称,∴O为AB的中点,且B(﹣1,﹣2),∴当△PAB为等腰三角形时有PA=AB或PB=AB,设P点坐标为(x,0),∵A(1,2),B(﹣1,﹣2),∴AB==2,PA=,PB=,当PA=AB时,则有=2,解得x=﹣3或5,此时P点坐标为(﹣3,0)或(5,0);当PB=AB时,则有=2,解得x=3或﹣5,此时P点坐标为(3,0)或(﹣5,0);综上可知P点的坐标为(﹣3,0)或(5,0)或(3,0)或(﹣5,0),故答案为:(﹣3,0)或(5,0)或(3,0)或(﹣5,0).4. (2017广西)如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是()A.45°B.60°C.75°D.85°【考点】M5:圆周角定理;M4:圆心角、弧、弦的关系.【分析】根据圆周角定理求得∠AOB的度数,则∠AOB的度数一定不小于∠AMB的度数,据此即可判断.【解答】解:∵B是的中点,∴∠AOB=2∠BDC=80°,又∵M是OD上一点,∴∠AMB≤∠AOB=80°.则不符合条件的只有85°.故选D.5.(2017江苏徐州)△ABC中,点D,E分别是AB,AC的中点,DE=7,则BC= 14 .【考点】KX:三角形中位线定理.【分析】根据三角形中位线定理三角形的中位线平行于第三边,并且等于第三边的一半可知,BC=2DE,进而由DE的值求得BC.【解答】解:∵D,E分别是△ABC的边AC和AC的中点,∴DE是△ABC的中位线,∵DE=7,∴BC=2DE=14.故答案是:14.6.(2017.江苏宿迁)如图,在△ABC中,∠ACB=90°,点D,E,F分别是AB,BC,CA的中点,若CD=2,则线段EF的长是 2 .【考点】KX:三角形中位线定理;KP:直角三角形斜边上的中线.【分析】首先利用直角三角形斜边上的中线等于斜边的一半求得AB的长,然后根据三角形的中位线定理求解.【解答】解:∵Rt△ABC中,∠ACB=90°,D是AB的中点,即CD是直角三角形斜边上的中线,∴AB=2CD=2×2=4,又∵E、F分别是BC、CA的中点,即EF是△ABC的中位线,∴EF=AB=×2=2,故答案为:2.7.(2017宁夏)在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=DM.当AM⊥BM时,则BC的长为8 .【分析】根据直角三角形的性质求出DM,根据题意求出DE,根据三角形中位线定理计算即可.【解答】解:∵AM⊥BM,点D是AB的中点,∴DM=AC=3,∵ME=DM,∴ME=1,∴DE=DM+ME=4,∵D是AB的中点,DE∥BC,∴BC=2DE=8,故答案为:8.【点评】本题考查的是三角形的中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.8.(2017哈尔滨)已知:AB是⊙O的弦,点C是的中点,连接OB、OC,OC交AB于点D.(1)如图1,求证:AD=BD;(2)如图2,过点B作⊙O的切线交OC的延长线于点M,点P是上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;(3)如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO=,求的值.【考点】MR:圆的综合题.【分析】(1)如图1,连接OA,利用垂径定理和圆周角定理可得结论;(2)如图2,延长BO交⊙O于点T,连接PT,由圆周角定理可得∠BPT=90°,易得∠APT=∠APB﹣∠BPT=∠APB﹣90°,利用切线的性质定理和垂径定理可得∠ABO=∠OMB,等量代换可得∠ABO=∠APT,易得结论;(3)如图3,连接MA,利用垂直平分线的性质可得MA=MB,易得∠MAB=∠MBA,作∠PMG=∠AMB,在射线MG上截取MN=MP,连接PN,BN,易得△APM≌△BNM,由全等三角形的性质可得AP=BN,∠MAP=∠MBN,延长PD至点K,使DK=DP,连接AK、BK,易得四边形APBK是平行四边形,由平行四边形的性质和平行线的性质可得∠PAB=∠ABK,∠APB+∠PBK=180°,由(2)得∠APB ﹣(90°﹣∠MBA)=90°,易得∠NBP=∠KBP,可得△PBN≌△PBK,PN=2PH,利用三角函数的定义可得sin∠PMH=,sin∠ABO=,设DP=3a,则PM=5a,可得结果.【解答】(1)证明:如图1,连接OA,∵C是的中点,∴,∴∠AOC=∠BOC,∵OA=OB,∴OD⊥AB,AD=BD;(2)证明:如图2,延长BO交⊙O于点T,连接PT∵BT是⊙O的直径∴∠BPT=90°,∴∠APT=∠APB﹣∠BPT=∠APB﹣90°,∵BM是⊙O的切线,又∠OBA+∠MBA=90°,∴∠ABO=∠OMB又∠ABO=∠APT∴∠APB﹣90°=∠OMB,∴∠APB﹣∠OMB=90°;(3)解:如图3,连接MA,∵MO垂直平分AB,∴MA=MB,∴∠MAB=∠MBA,作∠PMG=∠AMB,在射线MG上截取MN=MP,连接PN,BN,则∠AMP=∠BMN,∴△APM≌△BNM,∴AP=BN,∠MAP=∠MBN,延长PD至点K,使DK=DP,连接AK、BK,∴四边形APBK是平行四边形;AP∥BK,∴∠PAB=∠ABK,∠APB+∠PBK=180°,由(2)得∠APB﹣(90°﹣∠MBA)=90°,∴∠APB+∠MBA=180°∴∠PBK=∠MBA,∴∠MBP=∠ABK=∠PAB,∴∠MAP=∠PBA=∠MBN,∴∠NBP=∠KBP,∴△PBN≌△PBK,∴PN=PK=2PD,过点M作MH⊥PN于点H,∴PN=2PH,∴PH=DP,∠PMH=∠ABO,∵sin∠PMH=,sin∠ABO=,∴,∴,设DP=3a,则PM=5a,∴MQ=6DP=18a,∴.9.(2017黑龙江佳木斯)如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为4或4或4 .【考点】KQ:勾股定理;KH:等腰三角形的性质.【分析】分三种情况讨论:①当M在AB下方且∠AMB=90°时,②当M在AB上方且∠AMB=90°时,③当∠ABM=90°时,分别根据含30°直角三角形的性质、直角三角形斜边的中线的性质或勾股定理,进行计算求解即可.【解答】解:如图1,当∠AMB=90°时,∵O是AB的中点,AB=8,∴OM=OB=4,又∵∠AOC=∠BOM=60°,∴△BOM是等边三角形,∴BM=BO=4,∴Rt△ABM中,AM==4;如图2,当∠AMB=90°时,∵O是AB的中点,AB=8,∴OM=OA=4,又∵∠AOC=60°,∴△AOM是等边三角形,∴AM=AO=4;如图3,当∠ABM=90°时,∵∠BOM=∠AOC=60°,∴∠BMO=30°,∴MO=2BO=2×4=8,∴Rt△BOM中,BM==4,∴Rt△ABM中,AM==4,综上所述,当△ABM为直角三角形时,AM的长为4或4或4.故答案为:4或4或4.10.(2017•营口)如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是()A.∠ECD=112.5°B.DE平分∠FDC C.∠DEC=30° D.AB=CD【考点】KX:三角形中位线定理;KH:等腰三角形的性质.【分析】由AB=AC,∠C AB=45°,根据等边对等角及三角形内角和定理求出∠B=∠ACB=67.5°.由Rt△ADC中,∠CAD=45°,∠ADC=90°,根据三角形内角和定理求出∠ACD=45°,根据等角对等边得出AD=DC,那么∠ECD=∠ACB+∠ACD=112.5°,从而判断A正确;根据三角形的中位线定理得到FE=AB,FE∥AB,根据平行线的性质得出∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.根据直角三角形的性质以及等腰三角形的性质得到FD=AC,DF⊥AC,∠FDC=45°,等量代换得到FE=FD,再求出∠FDE=∠FED=22.5°,进而判断B正确;由∠FEC=∠B=67.5°,∠FED=22.5°,求出∠DEC=∠FEC﹣∠FED=45°,从而判断C错误;在等腰Rt△ADC中利用勾股定理求出AC=CD,又AB=AC,等量代换得到AB=CD,从而判断D正确.【解答】解:∵AB=AC,∠CAB=45°,∴∠B=∠ACB=67.5°.∵Rt△ADC中,∠CAD=45°,∠ADC=90°,∴∠ACD=45°,AD=DC,∴∠ECD=∠ACB+∠ACD=112.5°,故A正确,不符合题意;∵E、F分别是BC、AC的中点,∴FE=AB,FE∥AB,∴∠EFC=∠BAC=45°,∠FEC=∠B=67.5°.∵F是AC的中点,∠ADC=90°,AD=DC,∴FD=AC,DF⊥AC,∠FDC=45°,∵AB=AC,∴FE=FD,∴∠FDE=∠FED=(180°﹣∠EFD)=(180°﹣135°)=22.5°,∴∠FDE=∠FDC,∴DE平分∠FDC,故B正确,不符合题意;∵∠FEC=∠B=67.5°,∠FED=22.5°,∴∠DEC=∠FEC﹣∠FED=45°,故C错误,符合题意;∵Rt△ADC中,∠ADC=90°,AD=DC,∴AC=CD,∵AB=AC,∴AB=CD,故D正确,不符合题意.故选C.【点评】本题考查的是三角形中位线定理,等腰三角形的判定与性质,直角三角形的性质,平行线的性质,勾股定理等知识.掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.。
2020中考专题12——方法技巧之中点联想

2020中考专题12——方法技巧之中点联想班级姓名.【方法解读】1.与中点有关的定理:(1)直角三角形斜边上的中线等于斜边的一半.(2)等腰三角形“三线合一”的性质.(3)三角形的中位线定理.(4)垂径定理及其推论.2.与中点有关的辅助线:(1)构造三角形的中位线,如连结三角形两边的中点;取一边的中点,然后与另一边的中点相连结;过三角形一边的中点作另一边的平行线等.(2)延长角平分线的垂线,构造等腰三角形,利用等腰三角形的“三线合一”.(3)把三角形的中线延长一倍,构造平行四边形.【例题分析】例1.在正方形ABCD中,点P是射线CB上一个动点,连接PA,PD,点M、N分别为BC、AP 的中点,连接MN交PD于点Q.(1)如图1,当点P与点B重合时,QPM∆的形状是;(2)当点P在线段CB的延长线上时,如图2.①依题意补全图2;②判断QPM∆的形状并加以证明;(3)点P'于点P关于直线AB对称,且点P'在线段BC上,连接AP',若点Q恰好在直线AP'上,正方形ABCD的边长为2,请写出求此时BP长的思路(可以不写出计算结果).例2.在ABCD中,点B关于AD的对称点为B',连接AB',CB',CB'交AD于F点.(1)如图1,90ABC∠=︒,求证:F为CB'的中点;(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB'的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:过点B'作//B G CD'交AD于G点,只需证三角形全等;想法2:连接BB'交AD于H点,只需证H为BB'的中点;想法3:连接BB',BF,只需证90B BC∠'=︒.⋯请你参考上面的想法,证明F为CB'的中点.(一种方法即可)(3)如图3,当135ABC∠=︒时,AB',CD的延长线相交于点E,求CEAF的值.例3.在ABC ∆中,AB BC =,BD AC ⊥于点D .(1)如图1,当90ABC ∠=︒时,若CE 平分ACB ∠,交AB 于点E ,交BD 于点F .①求证:BEF ∆是等腰三角形;②求证:1()2BD BC BF =+;(2)点E 在AB 边上,连接CE .若1()2BD BC BE =+,在图2中补全图形,判断ACE ∠与ABC∠之间的数量关系,写出你的结论,并写出求解ACE ∠与ABC ∠关系的思路.【巩固训练】1.[2018·南充]如图1,在Rt △ABC 中,∠ACB=90°,∠A=30°,D ,E ,F 分别为AB ,AC ,AD 的中点,若BC=2,则EF 的长度为()A .21B .1C .23D .3图1图22.[2017·株洲]如图F6-2,点E ,F ,G ,H 分别为四边形ABCD 四条边AB ,BC ,CD ,DA 的中点,则下列关于四边形EFGH 的说法正确的是()A .一定不是平行四边形B .一定不会是中心对称图形C .可能是轴对称图形D .当AC=BD 时,它为矩形3.如图3,在正方形ABCD 和正方形CEFG 中,点D 在CG 上,BC=1,CE=3,H 是AF 的中点,那么CH 的长是()A .2.5B .5C .223D .2图3图4图54.[2019·海南]如图4,在Rt △ABC 中,∠C=90°,AB=5,BC=4,点P 是边AC 上一动点,过点P 作PQ ∥AB 交BC 于点Q ,D 为线段PQ 的中点,当BD 平分∠ABC 时,AP 的长度为()A .138B .1315C .1325D .13325.[2018·眉山]如图5,在▱ABCD 中,CD=2AD ,BE ⊥AD 于点E ,F 为DC 的中点,连结EF ,BF ,下列结论:①∠ABC=2∠ABF ;②EF=BF ;③S 四边形DEBC =2S △EFB ;④∠CFE=3∠DEF.其中正确的结论有()A .1个B .2个C .3个D .4个6.[2018·苏州]如图6,在△ABC 中,延长BC 至点D ,使得CD=21BC.过AC 的中点E 作EF ∥CD (点F 位于点E 右侧),且EF=2CD.连结DF ,若AB=8,则DF 的长为.图6图7图87.[2018·天津]如图7,在边长为4的等边三角形ABC 中,D ,E 分别为AB ,BC 的中点,EF ⊥AC 于点F ,G 为EF 的中点,连结DG ,则DG 的长为.8.[2018·哈尔滨]如图8,在平行四边形ABCD 中,对角线AC ,BD 相交于点O ,AB=OB ,点E ,F 分别是OA ,OD 的中点,连结EF ,∠CEF=45°,EM ⊥BC 于点M ,EM 交BD 于点N ,FN=10,则线段BC 的长为.9.[2019·泰安改编]如图9,矩形ABCD 中,AB=4,AD=2,E 为AB 的中点,F 为EC 上一动点,P 为DF 中点,连结PB ,则PB 的最小值是.图9图1010.[2019·桂林]如图10,在矩形ABCD 中,AB=3,AD=3,点P 是边AD 上的一个动点,连结BP ,作点A 关于直线BP 的对称点A 1,连结A 1C ,设A 1C 的中点为Q ,当点P 从点A 出发,沿边AD 运动到点D 时停止运动,点Q 的运动路径长为.11.[2019·广元]如图11,已知:在△ABC 中,∠BAC=90°,延长BA 到点D ,使AD=21AB ,点E ,F 分别是边BC ,AC 的中点.求证:DF=BE.图1112.[2019·泰安]如图12,四边形ABCD 是正方形,△EFC 是等腰直角三角形,点E 在AB 上,且∠CEF=90°,FG ⊥AD ,垂足为点G.(1)试判断AG 与FG 是否相等?并给出证明.(2)若点H 为CF 的中点,GH 与DH 垂直吗?若垂直,给出证明;若不垂直,说明理由.图1213.[2018·淄博](1)操作发现:如图F6-13①,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连结GM,GN,小明发现:线段GM与GN的数量关系是;位置关系是.(2)类比思考:如图②,小明在此基础上进行了深入思考,把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其他条件不变,小明发现的上述的结论还成立吗?请说明理由.(3)深入探究:如图③,小明在(2)的基础上,又作了进一步的探究,向△ABC的内侧分别作等腰直角三角形ABD,ACE,其他条件不变,试判断△GMN的形状,并给予证明.图13【参考答案】例1.解:(1)如图1,连接AC , 四边形ABCD 为正方形,AC BD ∴⊥,45DBC ∠=︒,点M 、N 分别为BC 、AP 的中点,//MN AC ∴,90BQM BOC ∴∠=∠=︒,45QMB ∴∠=︒,QPM ∴∆是等腰直角三角形,故答案为:等腰直角三角形.(2)①如图2,②QPM ∆的形状是等腰三角形,如图3,延长BC 至E ,使CE BP =,连接AE ,PB CE = ,PB BC CE BC ∴+=+,即CP BE =, 四边形ABCD 是正方形,AB DC ∴=,90ABC DCB ∠=∠=︒,在DCP ∆和ABE ∆中,DC AB DCP ABE CP BE =⎧⎪∠=∠⎨⎪=⎩DCP ABE ∴∆≅∆,DPC E ∴∠=∠,M 为BC 的中点,MB MC ∴=,MB BP MC CE ∴+=+,即MP ME =,M ∴为PE 的中点,N 为AP 的中点,//MN AE ∴,NMP E ∴∠=∠,DPC NMP ∴∠=∠,QM QP ∴=,QPM ∴∆是等腰三角形.(3)求解思路如下:a ,由题意画出图形,并延长BC 至E ,使CE BP =,连接AE ,如图4.b ,由(2)可得//QM AE ,可证P Q P MQA ME ''=.c ,由//PP AD ',可证△P PQ ADQ '∆∽,从而P Q P PQA AD''=.d ,可得P M P PME AD''=.e ,由点P '与点P 关于直线AB 对称,得到BP BP CE '==,设BP BP CE x '===,由2AD BC ==,可分别表示P M ',ME ,P P ',可求BP 的长.例2.(1)证明:四边形ABCD 为平行四边形,90ABC ∠=︒,ABCD ∴ 为矩形,AB CD =,90D BAD ∴∠=∠=︒,B ,B '关于AD 对称,90B AD BAD ∴∠'=∠=︒,AB AB =',B AD D ∴∠'=∠,AFB CFD ∠'=∠,在AFB ∆'与CFD ∆中,B AD D AFB CFD AB CD ∠'=∠⎧⎪∠'=∠⎨⎪'=⎩,()AFB CFD AAS ∴∆'≅∆,FB FC ∴'=,F ∴是CB '的中点;(2)证明:方法1:如图2,过点B '作//B G CD '交AD 于点G ,B ,B '关于AD 对称,12∴∠=∠,AB AB =',//B G CD ' ,//AB CD ,//B G AB ∴'.23∴∠=∠,13∴∠=∠,B A B G ∴'=',AB CD = ,AB AB =',B G CD ∴'=,//B G CD ' ,4D ∴∠=∠,B FG CFD ∠'=∠ ,在△B FG '与CFD ∆中4D B FG DFC B G CD ∠=∠⎧⎪∠'=∠⎨⎪'=⎩,∴△()B FG CFD AAS '≅∆,FB FC ∴'=,F ∴是CB '的中点;方法2:连接BB '交直线AD 于H 点,B ,B '关于AD 对称,AD ∴是线段B B '的垂直平分线,B H HB ∴'=,//AD BC ,∴1B F B HFC HB''==,FB FC ∴'=.F ∴是CB '的中点;方法3:连接BB ',BF ,B ,B '关于AD 对称,AD ∴是线段B B '的垂直平分线,B F FB ∴'=,12∴∠=∠,//AD BC ,B B BC ∴'⊥,90B BC ∴∠'=︒,1390∴∠+∠=︒,2490∠+∠=︒,34∴∠=∠,FB FC ∴=,B F FB FC ∴'==,F ∴是CB '的中点;(3)解:取B E '的中点G ,连结GF ,由(2)得,F 为CB '的中点,//FG CE ∴,12FG CE =,135ABC ∠=︒ ,ABCD 中,//AD BC ,18045BAD ABC ∴∠=︒-∠=︒,∴由对称性,45EAD BAD ∠=∠=︒,//FG CE ,//AB CD ,//FG AB ∴,45GFA FAB ∴∠=∠=︒,90FGA ∴∠=︒,GA GF =,sin 2FG EAD AF AF ∴=∠= ,∴由①,②可得CEAF=.例3.解:(1)①在ABC ∆中,AB BC =,BD AC ⊥于点D ,ABD CBD ∴∠=∠,AD CD =,90ABC ∠=︒ ,45ACB ∴∠=︒,CE 平分ACB ∠,22.5ECB ACE ∴∠=∠=︒,67.5BEF CFD BFE ∴∠=∠=∠=︒,BE BF ∴=,BEF ∴∆是等腰三角形;②如图,延长AB 至M ,使得BM AB =,连接CM ,//BD CM ∴,12BD CM =,45BCM DBC ABD BMC ∴∠=∠=∠=∠=︒,BFE MCE ∠=∠,BC BM ∴=,由①得,BEF BFE ∠=∠,BE BF =,BFE MCE BEF ∴∠=∠=∠,EM MC ∴=,11()22BD EM BC BF ∴==+;(2)14ACE ABC ∠=∠.求解ACE ∠与ABC ∠关系的思路:a ,延长AB 至P ,使得BP AB =,连接CP ,与(1)②同理可得//BD PC ,12BD PC =,BP BC =;b ,由1()2BD BC BE =+,可证明PEC ∆和BEF ∆分别是等腰三角形;c ,由180BEF BFE EBF ∠+∠+∠=︒以及90FCD DFC ∠+∠=︒,可得180902EBFDCF ︒-∠=︒-∠,即可证明14ACE ABC ∠=∠.巩固训练答案1.B[解析]在Rt △ABC 中,∠ACB=90°,∠A=30°,BC=2,∴AB=4,CD=21AB ,∴CD=21×4=2.∵E ,F 分别为AC ,AD 的中点,∴EF=21CD=21×2=1.故选B .2.C 3.B[解析]如图,连结AC ,CF ,∵正方形ABCD 和正方形CEFG 中,BC=1,CE=3,∴AC=2,CF=32,∠ACD=∠GCF=45°,∴∠ACF=90°,由勾股定理得,AF===25,∵H 是AF 的中点,∴CH=21AF=21×25=5.故选B .4.B [解析]在Rt △ABC 中,∠C=90°,AB=5,BC=4,∴AC=3,过点D 作DE ⊥BC 于点E ,易证△ABC ∽△DQE ,∵BD 平分∠ABC ,PQ ∥AB ,∴BQ=QD ,设QD=BQ=4x ,则AP=3x ,DP=4x ,∴PQ=8x ,CP=524x ,∴AC=539x=3,∴x=135,AP=3x=1315.故选B .5.D[解析]如图①,连结AF 并延长与BC 的延长线相交于点M ,易证△ADF ≌△MCF ,∴AF=MF ,AD=MC.又∵AD=BC ,DC=AB=2AD ,∴AB=BM ,∴∠ABC=2∠ABF ,故①正确.如图②,延长EF ,BC 相交于点G.易得△DEF ≌△CGF ,∴FE=FG.∵BE ⊥AD ,AD ∥BC ,∴∠EBG=90°.根据直角三角形斜边上的中线等于斜边的一半,得EF=BF ,故②正确.如图②,由于BF 是△BEG 的中线,∴S △BEG =2S △BEF ,而S △BEG =S 四边形DEBC ,∴S 四边形DEBC =2S △EFB ,故③正确.如图②,设∠DEF=x ,∵AD ∥BC ,∴∠DEF=∠G=x ,又∵FG=FB ,∴∠G=∠FBG=x ,∴∠EFB=2x.∵CD=2AD ,F 为CD 的中点,BC=AD ,∴CF=CB ,∴∠CFB=∠CBF=x ,∴∠CFE=∠CFB+∠BFE=x+2x=3x=3∠DEF ,故④正确.故选D .6.4[解析]解此题时可取AB 的中点,然后再利用三角形的中位线定理和平行四边形的判定和性质.取AB 的中点M ,连结ME ,则ME ∥BC ,ME=21BC.∵EF ∥CD ,∴M ,E ,F 三点共线,∵EF=2CD ,CD=21BC ,∴MF=BD ,∴四边形MBDF 是平行四边形,∴DF=BM=21AB=21×8=4.7.219[解析]如图,连结DE.∵D ,E 分别为AB ,BC 的中点,∴DE ∥AC ,DE=21AC=2,EC=2.∵EF ⊥AC ,∴DE ⊥EF ,∴△DEG 为直角三角形.在Rt △EFC 中,EC=2,∠C=60°,∴EF=3.∵G 为EF 的中点,∴EG=23.在Rt △DEG 中,DE=2,EG=23,由勾股定理,得DG=219.故答案为219.8.42[解析]如图,连结BE ,由E ,F 分别为OA ,OD 的中点可知EF=21AD ,EF ∥AD ,易证△BEC 是等腰直角三角形,EM 三线合一,可证得△EFN ≌△MBN ,可得到BN=FN=10,tan ∠NBM=21,就能求出BM=22,所以BC=42.9.22[解析]如图①,∵F 为EC 上一动点,P 为DF 中点,∴点P 的运动轨迹为△DEC 的中位线MN ,∴MN ∥EC.如图②,连结ME ,则四边形EBCM 为正方形,连结BM ,则BM ⊥CE ,易证BM ⊥MN ,故此时点P 与点M 重合,点F 与点C 重合,BP 取到最小值,在Rt △BCP 中,BP=22.10.33π[解析]如图,连结BA 1,取BC 的中点O ,连结OQ ,BD.∵四边形ABCD 是矩形,∴∠BAD=90°,∴tan ∠ABD=AB AD =3,∴∠ABD=60°,∵A 1Q=QC ,BO=OC ,∴OQ=21BA 1=21AB=23,∴点Q 的运动轨迹是以O 为圆心,OQ 为半径的圆弧,圆心角为120°,∴点Q 的运动路径长==33π.故答案为33π.11.证明:连结AE ,∵点E ,F 分别是边BC ,AC 的中点,∴EF 是△ABC 的中位线,∴EF ∥AB ,即EF ∥AD ,且EF=21AB ,又∵AD=21AB ,∴AD=EF ,∴四边形ADFE 是平行四边形,∴DF=AE.∵在Rt △ABC 中,点E 是BC 的中点,∴AE=21BC=BE=CE ,∴BE=DF.12.解:(1)AG=FG.证明如下:在BC 边上取一点M ,使BM=BE ,连结EM ,AF.∵四边形ABCD 是正方形,∴AB=BC ,∴AE=CM.∵∠CEF=90°,∴∠AEF+∠BEC=90°.∵∠BEC+∠BCE=90°,∴∠AEF=∠BCE.又∵CE=EF ,∴△AEF ≌△MCE ,∴∠EAF=∠EMC=135°.又∵∠BAD=90°,∴∠DAF=45°.又∵FG ⊥AD ,∴∠AFG=∠DAF=45°,∴AG=FG.(2)DH ⊥GH.证明如下:延长GH 交CD 于点Q.∵H 为CF 的中点,∴FH=CH.∵四边形ABCD 是正方形,∴AD ⊥CD.∵FG ⊥AD ,∴FG ∥CD ,∴∠GFH=∠DCH.又∵∠GHF=∠CHQ ,FH=CH ,∴△FGH ≌△CQH ,∴GH=HQ ,FG=CQ ,∴AG=CQ ,∴DG=DQ ,∴△DGQ 是等腰三角形,∴DH ⊥GH.13.解:(1)操作发现:线段GM 与GN 的数量关系为GM=GN ;位置关系为GM ⊥GN.(2)类比思考:上述结论仍然成立.理由如下:如图①,连结CD ,BE 相交于点O ,BE 交AC 于点F.①②∵点M ,G 分别是BD ,BC 的中点,∴MG ∥CD ,MG=21CD.同理可得GN ∥BE ,GN=21BE.∵∠DAB=∠EAC ,∴∠DAC=∠BAE.又∵AD=AB ,AC=AE ,∴△ADC ≌△ABE ,∴∠AEB=∠ACD ,DC=BE ,∴GM=GN.∵∠AEB+∠AFE=90°,∴∠OFC+∠ACD=90°,∴∠FOC=90°,易得∠MGN=90°,∴GM ⊥GN.(3)深入探究:△GMN 是等腰直角三角形.证明如下:如图②,连结BE ,CD ,CE 与GM 相交于点H.∵点M ,G 分别是BD ,BC 的中点,∴MG ∥CD ,MG=21CD.同理GN ∥BE ,GN=21BE.∵∠DAB=∠EAC ,∴∠DAC=∠BAE.又∵AD=AB ,AC=AE ,∴△ADC ≌△ABE ,∴∠AEB=∠ACD ,DC=BE ,∴GM=GN.∵GM ∥CD ,∴∠MHC+∠HCD=180°,∴∠MHC+(45°+∠ACD )=180°,∴∠MHC+45°+∠AEB=180°,∴∠MHC+45°+(45°+∠CEB )=180°,∴∠MHC+∠CEB=90°,∴∠GNH+∠GHN=90°,∴∠NGM=90°,即GM ⊥GN ,∴△GNM 是等腰直角三角形.。
中点的联想

D
E
F
C
B
合肥滨湖寿春中学精品课例集
本节课学习了哪些知识? 课堂小结 1、从复杂图形联想关于中点的基本图形;
2、根据中点构造“8 字型”全等三角形;
中点的联想
例:
练:
草
教
板书设计
师
板
板
演
演
区
区
稿
板
演
区
区
教学反思
非常感谢在此次公开课中给予我指导的陈长星组长,殷文谦组长、孟利斌组长及组内的同 仁。通过这次的课我收获了很多具体如下: 1、精细的备课才能在课堂上游刃有余,才能更好的引导学生的更容易接受知识,这样才能 提高课堂效率。 2、本节课的设计不到位,例如在例 1 的 1、2 小问有点重复,关键还没给学生总结中点的 几种用途给学生罗列出来,造成了班级还是有部分孩子不知道该如何去破题,更不知道如 何去联想。 3、本节课设计的课程容量也有些大,尤其前面的题目设计也有点不合理,在后半程没能更 多的顾忌到班级的后一部分学生有些赶课煮了夹生饭,好多学生没有应用好之前总结方法。
重点:探索弧长及扇形面积计算公式;用公式解决实际问题。由圆 教学重点 的周长和面积迁移到弧长和扇形面积公式的过程。
教学难点 难点:探索弧长及扇形面积计算公式;用公式解决实际问题. 教学用具 多媒体课件,直尺。
教学过程
合肥滨湖寿春中学精品课例集
环节
教师活动
学生活动
设计意图
情境引入
我们已学过哪些与线段中 点有关的图形? 1、垂直平分线; 2、三线合一; 3、直角三角形斜边上的中 线; 4、三角形的中位线; 5、(类)倍长中线; 6、面积的一半; 7、垂径定理。 这些图形具有什么性质?
中考数学专题复习中点的联想-构造法公开课精品课件

间的数量关系
;
在(1)的条件下,过点O作OG∥AB,交AD于 G,且OE=GF=3时(如图),求BE的值.
谢谢大家
2.为BC的中点,连结DF,
AB = 5,AC = 2,则 DF 的长为 __1__.5______
3.如图 ,在 △ABC 中,D 是 AB 的中点,AC⊥
CD,tan∠BCD
=
1 3
,求
∠A 的正切值.
探究:如图①,点A在直线MN上,点B在直线MN外,连结AB,过线段AB的 中点P作PC∥MN,交∠MAB的平分线AD于点C,连结BC,求证:BC⊥AD.
遇到中点作特殊三角形的中线 遇到中线要倍长中线构造全等 遇到中点结论为比例式作平行线
…………
如图,在△ABD中,AB=AD,∠BAD=α,点O为BD边 的中点,BF⊥AD于F,OE⊥AB于E. (1)当0 <α<90 ,(如图),求证:AF+2BE=AB;
(2)当90 <α<180 ,(如图),则AE、BF、AB之
初三数学专题复习--
中点的联想—构造法
线段中点的定义
把一条线段分成两条相等的线段的点叫线段的中点.
BD CD 1 BC 2
你能回忆一下我们学过哪些结论与中点有关?
1.如图 ,O 是矩形 ABCD 的对角线 AC 的中点, M 是 AD 的中点,若 AB = 5,AD = 12,则四边
形 ABOM 的周长为 ___2_0______
应用:如图②,点B在∠MAN内部,连结AB,过线段AB的中点P作PC∥AM,
交∠MAB的平分线AD于点C;作PE∥AN,交∠NAB的平分线AF于点E,连结
BC、BE.若∠MAN=150°,则∠CBE的大小为
度.
2020年中考数学专题突破2 关于中点的联想

例5题解图②
微专题 中点问题六大模型
专题一
关于中点的联想
基本模型
模型分析 1.倍长中线构造全等三角形:当已知条件中出现中线时,常利用倍长中 线构造全等三角形解决问题; 2.倍长类中线构造全等三角形:当已知条件中出现类中线(中点有关的线 段)时,常利用倍长类中线构造全等三角形解决问题.
微专题 中点问题六大模型
微专题 中点问题六大模型
专题一
关于中点的联想
4. 如图,在△ABC中,D是AB上一点,AD=AC,AE平分∠CAD,交 CD于点E,F是BC的中点,若BD=16,则EF的长为___8_____.
第4题图
微专题 中点问题六大模型
专题一
关于中点的联想
模型四 遇到三角形一边垂线过这边中点,考虑垂直平分线的性质
微专题 中点问题六大模型
专题一
关于中点的联想
设CE=x,连接AE, ∵DE是线段AB的垂直平分线, ∴AE=BE=BC+CE=3+x, ∴在Rt△ACE中,AE2=AC2+CE2,即 (3+x)2=42+x2, 解得x= 7/6 . 故答案为:7/6.
微专题 中点问题六大模型
专题一
关于中点的联想
虑构造中位线;或出现一个中点,要证明平行线段或线段倍分关系时也常考 虑构造中位线.利用三角形中位线的性质定理:DE∥BC,且DE=12 BC , △ADE∽△ABC,则可得线段之间的相等或比例关系及平行关系.
微专题 中点问题六大模型
专题一
关于中点的联想
模型二 遇到直角三角形斜边上的中点,考虑构造斜边上的中线
专题一
关于中点的联想
针对训练
6. 如图,已知AB=24,AB⊥BC于点B,AB⊥AD于点A,AD=10,BC= 20.若点E是CD的中点,则AE的长是___1_3____.
中考数学复习专题--关于中点的联想
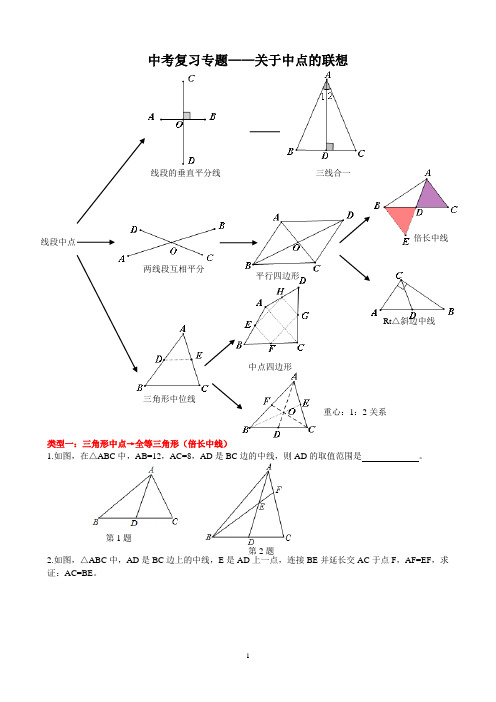
1 第1题第2题中考复习专题——关于中点的联想类型一:三角形中点→全等三角形(倍长中线)1.如图,在△ABC 中,AB=12,AC=8,AD 是BC 边的中线,则AD 的取值范围是 。
2.如图,△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,连接BE 并延长交AC 于点F ,AF=EF ,求证:AC=BE 。
线段中点 线段的垂直平分线 三线合一两线段互相平分 平行四边形倍长中线 Rt △斜边中线 三角形中位线 重心:1:2关系 中点四边形2第3题第4题第5题第6题第7题第8题第9题第10题第11题类型二、等腰+底边中点→等腰三角形(三线合一)3.如图,在△ABC中,AB=AC=5,BC=6,点M是BC中点,MN⊥AC于点N,则MN= 。
4.如图,AB是半圆O的直径,△ABC的两边BC、AC分别交半圆O与点D、E,且D为BC的中点,已知∠BAC=50°,则∠C= 。
类型三、中点+中点→中位线5.(2018苏州)如图,在△ABC中,延长BC到D,使CD=BC21,过AC的中点E作EF∥CD(点F在点E右侧),且EF=2CD,连接DF,若AB=8,则DF的长为---------------------------------------------()A.3B.4C.32 D. 236.(2017株洲)如图,点E、F、G、H分别为四边形ABCD的各边中点,则关于四边形EFGH的下列说法正确的是-----------------------------------------------------------------------------------------------------------------()A.一定不是平行四边形 B.一定不是中心对称图形C.可能是轴对称图形D.当AC=BD时,它是矩形7.(2018天津)如图,在边长为4的等边△ABC中,D、E分别为AB、BC的中点,EF⊥AC于点F,G 是EF的中点,连接DG,则DG的长为。
提分微课01 关于中点的联想

11.如图W1-11,在矩形ABCD中,AB=3,
BC=2,H是AB的中点,将△CBH沿CH折叠,
点B落在矩形内点P处,连接AP,则
tan∠HAP=
.
图W1-11
[答案]4
3
[解析]如图所示,连接 PB 交 CH 于点 O.
∵ H 是 AB 的中点,∴ HB=12AB=32.∵ 将△ CBH
沿 CH 折叠,点 B 落在矩形内点 P 处,
6.如图W1-6,在边长为4的等边三角形ABC中,D,E分别为AB,BC的中点,EF⊥AC于点
F,G为EF的中点,连接DG,则DG的长为
.
图W1-6
[答案] 19
2
[解析]连接 DE, ∵ D,E 分别为 AB,BC 的中点,∴ DE∥AC,2DE=AC=4,EC=2, ∵ EF⊥AC,∴ DE⊥EF.∴ △ DEG 为直角三角形, 在 Rt△ EFC 中,EC=2,∠C=60°, ∴ EF= 3. ∵ G 为 EF 的中点,∴ EG= 23. 在 Rt△ DEG 中,DE=2,EG= 23,由勾股定理得,DG= ������������2 + ������������2= 219. 故答案为 219.
图W1-14
解:(1)证明:如图①,连接AD. ∵ ∠BAC=90°,AB=AC, ∴ ∠BDA=∠EDF=90°, ∴ ∠BDE+∠EDA=∠EDA+∠ADF. ∴ ∠BDE=∠ADF. 又∵ D为BC的中点,△ABC是等腰直角三角形, ∴ BD=AD,∠B=∠DAC=45°. ∴ △BDE≌△ADF(ASA).∴ BE=AF.
类型二 构造中位线法
4.如图 W1-4,在△ ABC 中,延长 BC 至 D,使得 [答案]B
初中数学《关于中点的联想》培优拔高(奥数)专题讲义

初中数学《关于中点的联想》培优拔高(奥数)专题讲义阅读与思考线段的中点把线段分成相等的两部分,图形中出现中点,可以引起我们丰富的联想:首先它和三角形的中线紧密联系;若中点是在直角三角形的斜边上,又可以引用“斜边上的中线等于斜边的一半”结论;其次,中点又与中位线息息相关;另外,中点还可以与中心对称相连.解答中点问题的关键是恰当地添加辅助线,如作中线倍长、作直角三角形的斜边上的中线、构造三角形、梯形中位线、构造中心对称图形等,如图所示:例题与求解【例1】如图,△ABC边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP ⊥AD,M为BC的中点,则PM的值为___________. (安徽省竞赛试题)例2题图例1题图F解题思路:∠A的平分线与BP边上的垂线互相重合,通过作辅助线,点P可变为某线段的中点,利用三角形中位线定理解题.【例2】如图,边长为1的正方形EFGH在边长为3的正方形ABCD所在的平面上移动,始终保持EF ∥AB,线段CF,DH的中点分别为M,N,则线段MN的长度为( ) (北京市竞赛试题)A.102B.172C.173D.2103解题思路:连接CG,取CG的中点T,构造三角形中位线、梯形中位线.求证:CD =2EC . (宁波市竞赛试题)解题思路:图形中有两个中点E ,B ,联想到与中点相关的丰富知识,将线段倍分关系的证明转化为线段相等关系的证明,关键是恰当添加辅助线.【例4】如图1,P 是线段AB 上一点,在AB 的同侧作△APC 和△BPD ,使∠APC =∠BPD ,PC =P A ,PD =PB ,连接CD ,点E ,F ,G ,H 分别是AC ,AB ,BD ,CD 的中点,顺次连接E ,F ,G ,H .(1) 猜想四边形EFGH 的形状,直接回答,不必说明理由;(2) 当点P 在线段AB 的上方时,如图2,在△APB 的外部作△APC 和△BPD ,其他条件不变,(1)中的结论还成立吗?说明理由;(3) 如果(2)中,∠APC =∠BPD =90°,其他条件不变,先补全图3,再判断四边形EFGH 的形状,并说明理由. (营口市中考试题)BAPAFP BG D H CE HGF E PABC D图① 图② 图③解题思路:结论随着条件的改变也许发生变化,但解决问题的方法是一致的,即通过连线,为三角形中位线定理的应用创造条件.例3图CA D【例5】如图,以△ABC 的AB ,AC 边为斜边向形外作直角三角形ABD 和ACE ,且使∠ABD =∠ACE ,M 是BC 的中点,求证:DM =EM . (“祖冲之杯”邀请赛试题)解题思路:显然△DBM 不全等于△ECM ,必须通过作辅助线,构造全等三角形证明DM =EM .【例6】如图,已知△ABC 中,∠ACB =90°,AB 边上的高CH 与△ABC 的两条内角平分线AM ,BN 分别交于P ,Q 两点,PM ,QN 的中点分别为E ,F ,求证:EF ∥AB . (全国初中数学联赛题)解题思路:从图形的形成过程,逐步探索相应结论.将原问题分解为多个小问题.○能 ○力 ○训 ○练 A 级1.如图,若E ,F ,G ,H 分别是四边形ABCD 各边的中点,则四边形EFGH 是____________.(1)如果把条件中的四边形ABCD 依次改为矩形、菱形、正方形或等腰梯形,其他条件不变,那么所得的四边形EFGH 分别为_______________________;(2)如果把结论中的平行四边形EFGH 依次改为矩形、菱形、正方形,那么原四边形ABCD 应具备的条件是_______________________. (湖北省黄冈市中考试题)2.如图,已知AG ⊥BD ,AF ⊥CE ,BD ,CE 分别是∠ABC 和∠ACB 的角平分线,若BF =2,ED =3,GC =4,则△ABC 的周长为_______________. (重庆市竞赛试题)例5图 EDMABC例6图CB D第1题图第2题图C3.如图,在△ABC 中,AB =AC ,AD ⊥BC 于点D ,E 是AC 的中点,若BC =16,DE =5,则AD =______________. (南京市中考试题)4.如图,在△ABC 中,AB =AC ,M ,N 分别是AB ,AC 的中点,D ,E 为BC 上的点,连接DN ,EM ,若AB =13cm ,BC =10cm ,DE =5cm ,则图中阴影部分的面积为________________.(北京市中考试题)5.A ′,B ′,C ′,D ′顺次为四边形ABCD 的各边的中点,下面条件中使四边形A ′B ′C ′D ′为正方形的条件是( )A .四边形ABCD 是矩形B .四边形ABCD 是菱形C .四边形ABCD 是等腰梯形 D .四边形ABCD 中,AC ⊥BD 且AC =BD 6.若等腰梯形的两条对角线互相垂直,中位线长为8cm ,则该等腰梯形的面积为( ) A .16cm 2 B .32cm 2 C .64cm 2 D .112cm 27.如图,梯形ABCD 中,AD ∥BC ,E ,F 分别是BD ,AC 的中点,若AD =6cm ,BC =18cm ,则EF 的长为( )A .8cmB .7cmC .6cmD .5cm8.如图,在梯形ABCD 中,AD ∥EF ∥GH ∥BC ,AE =EG =GB ,AD =18,BC =32,则EF +GH =( )A .40B .48C .50D .56 (泰州市中考试题)MD B第8题图 第9题图9.如图,在△ABC 中,∠B =2∠C ,AD ⊥BC 于点D ,M 是BC 的中点,求证:DM =12AB .第4题图第3题图A第7题图10. 如图,在△ABC 中,BD =CE ,BE ,CD 的中点分别是M ,N ,直线MN 分别交AB ,AC 于点P ,Q ,求证:AP =AQ .11.在图1至图3中,点B 是线段AC 的中点,点D 是线段CE 的中点.四边形BCGF 和CDHN 都是正方形.AE 的中点是M .(1)如图1,点E 在AC 的延长线上,点N 与点G 重合时,点M 与点C 重合,求证:FM = MH ,FM ⊥MH ; (2)将图1中的CE 绕点C 顺时针旋转一个锐角,得到图2,求证:△FMH 是等腰直角三角形; (3)将图2中的CE 缩短到图3的情况,△FMH 还是等腰直角三角形吗?(不必说明理由) (2009年河北省中考试题)12.在六边形ABCDEF 中,AB ∥DE ,BC ∥EF ,CD ∥F A ,AB +DE =BC +EF ,A 1,B 1,D 1,E 1分别是边AB ,BC ,DE ,EF 的中点,A 1D 1=B 1E 1.求证:∠CDE =∠AFE .第12题图E第10题图图1AHC (M )DEBFG (N )G图2AHC DEBFNMAHCDE图3BFG MNB 级1.如图,正方形ABCD 两条对角线相交于点E ,∠CAD 的平分线AF 交DE 于点G ,交DC 于点F ,若GE =24,则FC =_________________.2.如图,四边形ABCD 的对角线AC ,BD 相交于点F ,M ,N 分别是AB ,CD 的中点,MN 分别交BD ,AC 于点P ,Q ,且∠FPQ =∠FQP ,BD =10,则AC =_________. (重庆市竞赛试题)3.如图,在△ABC 中,∠BAC =120°,以AB ,AC 为边分别向形外作正三角形ABD 和正三角形ACE ,M 为AD 的中点,N 为AE 的中点,P 为BC 的中点,则∠MPN =_________. (北京市竞赛试题)4.如图,已知A 为DE 的中点,设△DBC ,△ABC ,△EBC 的面积分别为S 1,S 2,S 3,则S 1,S 2,S 3之间的关系是( )A .S 2=32(S 1+S 3)B .S 2=12(S 3―S 1)C .S 2=12(S 1+S 3)D .S 2=32(S 3―S 1)5.如图,在图形ABCD 中,AB ∥DC ,M 为DC 的中点,N 为AB 的中点,则 ( ) A .MN >12(AD +BC ) B .MN <12(AD +BC )C .MN =12(AD +BC ) D .无法确定MN 与12(AD +BC )的关系6.如图,凸四边形ABCD 的面积是a ,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,那么图中的阴影部分的面积为( )A .18aB .16aC .14aD .12a(江苏省竞赛试题)7.如图,在△ABC 中,D 为AB 的中点,分别延长CA ,CB 到点E ,F ,使DE =DF ,过E ,F 分别作CA ,CB 的垂线,相交于点P .求证:∠P AE =∠PBF . (全国初中数学联赛试题)第5题图DC M 第2题图CF第1题图F第3题图第4题图D第6题图ABE第7题图EPF8.如图,锐角△ABC 中,作高BD 和CE ,过顶点B ,C 分别作DE 的垂线BF 和CG ,求证:EF =DG .(全俄奥林匹克数学竞赛试题)9. 如图,在△ABC 中,AD 是BC 边上的中线,点M 在AB 边上,点N 在AC 边上,并且∠MDN =90°,如果BM 2+CN 2=DM 2+DN 2.求证:AD 2=14(AB 2+AC 2). (北京市竞赛试题)10.已知:△ABD 和△ACE 都是直角三角形,且∠ABD =∠ACE =90°.如图1,连接DE ,设M 为DE 的中点.(1)求证:MB =MC ;(2)设∠BAD =∠CAE ,固定△ABD ,让Rt △ACE 绕顶点A 在平面内旋转到图2的位置,试问:MB =MC 是否还成立?请说明理由. (江苏省竞赛试题)图2图1第9题图 ABC D第8题图BG11.已知△OAB ,△OCD 都是等腰直角三角形,∠AOB =∠COD =90°. (1) 如图1,点C 在OA 边上,点D 在OB 边上,连接AD ,BC ,M 为线段AD 的中点,求证:OM ⊥BC . (2) 如图2,在图1的基础上,将△OCD 绕点O 逆时针旋转α(α为锐角),M 为线段AD 的中点.①求证:OM =12BC ;②OM ⊥BC 是否还成立?若成立,请证明;若不成立,请说明理由.图1图2BBODDC12.如图1,在△ABC 中,点P 为BC 边的中点,直线a 绕顶点A 旋转,若点B ,P 在直线a 的异侧,BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接PM ,PN .(1)延长MP 交CN 于点E (如图2). ①求证:△BPM ≌△CPE ; ②求证:PM =PN .(2)若直线a 绕点A 旋转到如图3的位置时,点B ,P 在直线a 的同侧,其他条件不变,此时PM =PN 还成立吗?若成立,请证明;若不成立,请说明理由.(3) )若直线a 绕点A 旋转到与BC 边平行的位置时,其他条件不变.请直接判断四边形MBCN 的形状及此时PM =PN 是否成立.不必说明理由. (沈阳市中考试题)图3图2图1BB。
