台湾92第一次基测数学

合集下载

台湾省(新版)2024高考数学统编版真题(自测卷)完整试卷

台湾省（新版）2024高考数学统编版真题(自测卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题甲、乙、丙、丁、戊五只猴子在一棵枯树上玩耍，假设它们均不慎失足下落，已知：（1）甲在下落的过程中依次撞击到树枝，，；（2）乙在下落的过程中依次撞击到树枝，，；（3）丙在下落的过程中依次撞击到树枝，，；（4）丁在下落的过程中依次撞击到树枝，，；（5）戊在下落的过程中依次撞击到树枝，，，则下列结论正确的是（）A．最高处的树枝定是B．最低处的树枝一定是C．九根树枝从高到低不同的顺序共有种D．九根树枝从高到低不同的顺序共有种第(2)题若函数的图像关于直线对称，则为A．B．C．D．任意实数第(3)题若对于任意的，，，则的取值范围是（）A．B．C．D．第(4)题学生的语文、数学成绩均被评定为三个等级，依次为“优秀”“合格”“不合格”．若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”．如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，那么这组学生最多有( )A．2人B．3人C．4人D．5人第(5)题如图，已知复数z在复平面内所对应的向量是，图中每个小正方形网格的边长均为1，则（）A．1＋2i B．1＋3i C．3＋i D．2＋i第(6)题已知定义在上的可导函数，满足，且.若，则满足的的取值范围是（）A．B．C．D．第(7)题已知数列满足：对任意的，都有，且，则（）A．B．C．D．第(8)题已知等比数列中，各项都是正数，且成等差数列，则A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题在数列中，若对，都有（为常数），则称数列为“等差比数列”，为公差比，设数列的前项和是，则下列说法一定正确的是（）A．等差数列是等差比数列B．若等比数列是等差比数列，则该数列的公比与公差比相同C．若数列是等差比数列，则数列是等比数列D．若数列是等比数列，则数列等差比数列第(2)题设是一个随机试验中的两个事件，且，则（）A．B．C．D．第(3)题已知正方体棱长为，为棱的中点，为底面上的动点，则下列说法正确的是（）A．存在点，使得B．存在唯一点，使得C．当，此时点的轨迹长度为D．当为底面的中心时，三棱锥的外接球体积为三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知向量，，若，则______．第(2)题已知，，点是线段（包括端点）上的动点，则的取值范围是 ________．第(3)题已知抛物线，过其焦点F的直线l与其交与A、B两点，，其准线方程为___________．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题由个不同的数构成的数列中，若时，（即后面的项小于前面项），则称与构成一个逆序，一个有穷数列的全部逆序的总数称为该数列的逆序数．如对于数列3，2，1，由于在第一项3后面比3小的项有2个，在第二项2后面比2小的项有1个，在第三项1后面比1小的项没有，因此，数列3，2，1的逆序数为；同理，等比数列的逆序数为．（1）计算数列的逆序数；（2）计算数列（）的逆序数；（3）已知数列的逆序数为，求的逆序数．第(2)题某中学为了解本校高二年级学生阅读水平现状，从该年级学生中随机抽取100人进行一般现代文阅读速度的测试，以每位学生平均每分钟阅读的字数作为该学生的阅读速度，将测试结果整理得到如下频率分布直方图：(1)若该校高二年级有1500人，试估计阅读速度达到620字/分钟及以上的人数；(2)用频率估计概率，从该校高二学生中随机抽取3人，设这3人中阅读速度达到540字/分钟及以上的人数为，求的分布列与数学期望；(3)若某班有10名学生参加测试，他们的阅读速度如下：506，516，553，592，617，632，667，693，723，776，从这10名学生中随机抽取3人，设这3人中阅读速度达到540字/分钟及以上的人数为，试判断数学期望与（2）中的的大小.第(3)题已知函数．(1)求不等式的解集；(2)将函数的图象与直线围成的封闭图形的面积记为，若正数a、b、c满足，求证：．第(4)题已知函数.（1）证明：函数在区间上存在唯一的极小值点；（2）证明：函数有且仅有两个零点.第(5)题凸四边形中，，，，．(1)当，且时，证明：；(2)求四边形的面积的最大值．。

台湾省(新版)2024高考数学人教版质量检测(押题卷)完整试卷

台湾省（新版）2024高考数学人教版质量检测(押题卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题复数满足，则（）A．1B．C．D．2第(2)题等差数列的首项为5，公差不等于零．若，，成等比数列，则（）A．B．C．D．-2014第(3)题要想得到正弦曲线，只需将余弦曲线（）A．向右平移个单位B．向左平移个单位C．向右平移个单位D．向左平移个单位第(4)题已知，那么命题的一个必要不充分条件是（）A．B．C．D．第(5)题已知是定义在上的单调函数，且对任意的，都有，则方程的解所在的区间是A． B．C．D．第(6)题圆的圆心坐标和半径分别为（）A．B．C．D．第(7)题等差数列{a n}中，a4+a8=10，a10=6，则公差d等于（）A．B．C．2D．-第(8)题已知复数，则在复平面内对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知抛物线，为坐标原点，过作轴的垂线交直线于点，点满足，过作轴的平行线交于点（在的右侧），若，则（）A．B．C．D．的面积为第(2)题在正四棱柱中，是棱的中点，则（）A．直线与所成的角为B．直线与所成的角为C．平面平面D．直线与平面所成角的正弦值为第(3)题下图是样本甲与样本乙的频率分布直方图，下列说法判断正确的是（）A．样本乙的极差一定大于样本甲的极差B．样本乙的众数一定大于样本甲的众数C．样本甲的方差一定大于样本乙的方差D．样本甲的中位数一定小于样本乙的中位数三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题在中，A，B，C所对应的边分别是a，b，c，若其面积，则____________．第(2)题若一个圆台的侧面展开图是半圆面所在的扇环，且扇环的面积为，圆台上､下底面圆的半径分别为，（），则___________.第(3)题如图，半径为1的球O的直径AB垂直于平面，垂足为B，是平面内的等腰直角三角形，其中，线段AC、AD分别与球面交于点M、N，则三棱锥的体积为_________.四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题如图1，在四边形中，，．将四边形沿折起，使得，得到如图2所示的几何体．(1)若为的中点，证明：平面；(2)若为上一动点，且二面角的余弦值为，求的值．第(2)题在三棱柱中，平面平面，侧面为菱形，，，，E是AC的中点.(1)求证：平面(2)确定在线段上是否存在一点P，使得AP与平面所成角为，若存在，求出的值;若不存，说明理由.第(3)题在中，角的对边分别是，从下列条件中任选一个补充到题中解决题.条件：①：; ②：; ③：.(1)求的值;(2)，求的取值范围．第(4)题已知椭圆的左焦点为，且．(1)求椭圆的方程；(2)斜率为的直线与椭圆交于不同的两点，设点，直线，分别与椭圆交于不同的点，若和点共线，求的值．第(5)题设函数，，为的导函数．(1)当时，过点作曲线的切线，求切点坐标；(2)若，，且和的零点均在集合中，求的极小值．。

台湾省(新版)2024高考数学统编版(五四制)能力评测(自测卷)完整试卷

台湾省（新版）2024高考数学统编版（五四制）能力评测(自测卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题设集合，，则（）A．B．C．D．第(2)题设，则“”是“”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不允分也不必要条件第(3)题总体由编号为00,01，，28,29的30个个体组成.利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第6列和第7列开始从左往右依次选取两个数字，则选出来的第5个个体的编号为（）0842 2689 5319 6450 9303 2320 9025 6015 9901 90252909 0937 6707 1528 3113 1165 0280 7999 7080 1573A．19B．02C．11D．16第(4)题如图四棱锥P-ABCD中，底面ABCD为正方形，且各棱长均相等，E是PB的中点，则异面直线AE与PC所成角的余弦值为（）A．B．C．D．第(5)题在中，角、、的对边分别为、、，若，，的平分线的长为，则边上的中线的长等于（）A．B．C．D．第(6)题已知直线恒在曲线的上方，则的取值范围是（）A．B．C．D．第(7)题在下列四个函数中，满足性质：“对于区间上的任意，恒成立”的只有（）A．B．C．D．第(8)题在正方体中，下列结论正确的是（）①；②平面平面；③；④平面.A．①②④B．①②③C．②③④D．①③④二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题新中国成立至今，我国一共进行了7次全国人口普查，历次普查得到的全国人口总数如图1所示，城镇人口比重如图2所示.下列结论正确的有（）A．与前一次全国人口普查对比，第五次总人数增长量高于第四次总人数增长量B．对比这7次全国人口普查的结果，我国城镇人口数量逐次递增C．第三次全国人口普查城镇人口数量低于2亿D．第七次全国人口普查城镇人口数量超过第二次全国人口普查总人口数第(2)题积性函数指对于所有互质的整数和有的数论函数．则以下数论函数是积性函数的有（）A．高斯函数表示不大于实数的最大整数B．最大公约数函数表示正整数与的最大公约数（是常数）C．幂次函数表示正整数质因数分解后含的幂次数（是常数）D．欧拉函数表示小于正整数的正整数中满足与互质的数的数目第(3)题约翰逊多面体是指除了正多面体､半正多面体（包括13种阿基米德多面体､无穷多种侧棱与底棱相等的正棱柱､无穷多种正反棱柱）以外，所有由正多边形面组成的凸多面体．其中，由正多边形构成的台塔是一种特殊的约翰逊多面体，台塔，又叫帐塔､平顶塔，是指在两个平行的多边形（其中一个的边数是另一个的两倍）之间加入三角形和四边形所组成的多面体．各个面为正多边形的台塔，包括正三､四､五角台塔．如图是所有棱长均为1的正三角台塔，则该台塔（）A．共有15条棱B．表面积为C．高为D．外接球的体积为三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知的内角A，B，C的对边分别为a，b，c，若，则的取值范围___________.第(2)题已知，，则____________.第(3)题已知一簇双曲线：，设双曲线的左､右焦点分别为､，是双曲线右支上一动点，的内切圆与轴切于点，则___________.四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知椭圆C的中心在原点，焦点在x轴上，长轴长为4，且点椭圆C上．(1)求椭圆C的方程；(2)设P是椭圆C长轴上的一个动点，过P作方向向量的直线l交椭圆C于A、B两点，求证：为定值．第(2)题已知数列的前项和为,且满足,且.(1)求证:数列为常数列,并求的通项公式;(2)若使不等式成立的最小整数为,且,求和的最小值.第(3)题选修4-4：坐标系与参数方程在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为（Ⅰ）写出直线的极坐标方程与曲线的直角坐标方程；（Ⅱ）已知与直线平行的直线过点，且与曲线交于两点，试求第(4)题现有甲，乙，丙，丁四位同学课余参加巴蜀爱心社和巴蜀文学风的活动，每人参加且只能参加一个社团的活动，并且参加每个社团都是等可能的.（1）求巴蜀爱心社和巴蜀文学风都至少有1人参加的概率；（2）求甲，乙在同一个社团，丙，丁不在同一个社团的概率.第(5)题现在常常可以看到人们在走路、吃饭或乘车时低着头玩手机，长期下来，就很容易使颈椎损伤，患上颈椎病.某学习小组调查研究“长期使用智能手机对颈椎病的影响”，随机选取了100名手机用户得到部分统计数据如下表，约定日使用手机时间超过4小时为“频繁使用手机”.已知“频繁使用手机”的人数比“非频繁使用手机”的人数少24人.非频繁使用手机频繁使用手机合计颈椎病人数8非颈椎病人数16合计100(1)求表中p，q的值，并补全表中所缺数据；(2)根据2×2列联表，判断是否有99.9%的把握认为“频繁使用手机”对颈椎病有影响.附：，其中.0.100.050.010.0050.0012.7063.8416.6357.87910.828。

2103台湾国民中学学生基本学力测验数学题

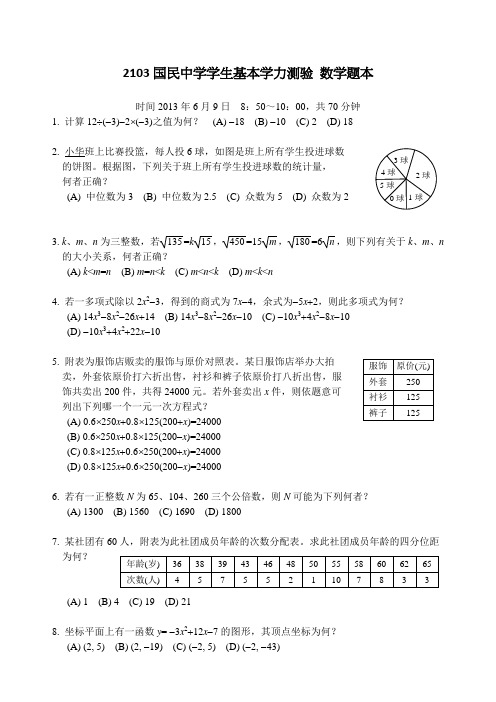
12. 解一元一次不等式 12(2x5)7x3，得其解的范围为何？ 10 (A) x 9 20 (B) x 9 10 (C) x 9 20 (D) x 9
13. 以下表示小勋到商店购买 2 个单价相同的布丁和 10 根单价相同的棒棒糖的经过。小勋：「我要 2 个布丁和 10 根棒棒糖。」老板：「谢谢！这是您要的 2 个布丁和 10 根棒棒糖，总共 200 元！」老板：「小朋友，我钱算错了，我多算 2 根棒棒糖的钱，我退还你 20 元。」根据上文，判断布丁和棒棒糖的单价相差多少元？ (A) 20 (B) 30 (C) 40 (D) 50 14. 如图，△ABC 中，D 为￣ AB 中点，E 在￣ AC 上，且￣ BE ￣ AC 。若￣ DE =10，￣ AE =16，则￣ BE 的长度为何？ (A) 10 (B) 11 (C) 12 (D) 13
B A G D F E C
24. 下列何者是 22x783x621x5 的因式？ (A) 2x3 (B) x2(11x7) (C) x4(11x3) (D) x6(2x7)
25. 附图的长方体与下列选项中的立体图形均是由边长为 1 公分的小正方体紧密堆砌而成。若下列有一立体图形的表面积与附图的表面积相同，则此图形为何？ (A) (B) (C) (D)
甲图( )
乙
甲图()
17. 如图，圆 O 与正方形 ABCD 的两边￣ AB 、￣ AD 相切，且￣ DE 与圆 O 相切于 E 点。若圆 O 的半径为 5，且￣ AB =11，则￣ DE 的长度为何？ (A) 5 (B) 6 (C) 30 11 (D) 2
A O E B
D
C
18. 附图为八个全等的正六边形紧密排列在同一平面上的情形。根据图中标示的各点位置，判断△ACD 与下列哪一个三角形全等？ (A) △ACF (B) △ADE (C) △ABC (D) △BCF

台湾省(新版)2024高考数学人教版摸底(自测卷)完整试卷

台湾省（新版）2024高考数学人教版摸底(自测卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题已知，则的大关系为（）A．B．C．D．第(2)题随机变量的分布列如下表，且，则（）02A．10B．15C．40D．45第(3)题已知等比数列满足，，则的值为（）A．1B．4C．D．9第(4)题某地为响应“扶贫必扶智，扶智就扶知识、扶技术、扶方法”的号召，建立了农业科技图书馆，供农民免费借阅．现收集了该图书馆五年的借阅数据如下表：年份20162017201820192020年份代码x12345年借阅量y（万册） 4.9 5.1 5.5 5.7 5.8根据上表，可得y关于x的线性回归方程为，则下列说法中错误的是（）．A．B．借阅量4.9，5.1，5.5，5.7，5.8的第75百分位数为5.7C．y与x的线性相关系数D．2021年的借阅量一定少于6.12万册第(5)题已知，且，则（）A．B．C．D．第(6)题将5名学生分配到3个社区当志愿者，每个社区至少分配1名学生，则不同的分配方法种数是（）A．24B．50C．72D．150第(7)题设命题：，，则为（）A．，B．，C．，D．，第(8)题把曲线先沿轴向右平移个单位，再沿轴向下平移1个单位，得到的曲线方程为A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题如图，已知正方体的棱长为2，M､N分别是､的中点，平面与棱的交点为E，点F为线段上的动点，则下列说法正确的是（）A．B．三棱锥体积为C．若则平面D．若，则直线与所成角的正弦值为第(2)题已知数列满足，，且，记数列的前n项和为，前n项积为，则下列说法正确的有（）A．，使得B．C．D．第(3)题某班级到一工厂参加社会实践劳动，加工出如图所示的圆台，轴截面ABCD为等腰梯形，且满足.下列说法正确的是（）A．该圆台轴截面ABCD的面积为B．该圆台的表面积为C．该圆台的体积为D．该圆台有内切球，且半径为三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题南宋数学家杨辉所著的《详解九章算法·商功》中出现了如图所示的形状,后人称为“三角垛”.“三角垛”的最上层有1个球,第2层有3个球,第3层有6个球,…,则第10层球的个数______.第(2)题设复数满足（其中为虚数单位），则的模为______ _第(3)题在三棱锥中，，则三棱锥外接球的表面积为______．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题在中，角的对边分别为，已知（1）求的值；（2）若，（i）求的值：（ii）求的值.第(2)题在平面直角坐标系中，曲线的参数方程为（，为参数），在以为极点，轴的正半轴为极轴的极坐标系中，曲线是圆心在极轴上，且经过极点的圆已知曲线上的点对应的参数，射线与曲线交于点（1）求曲线，的方程；（2）若点，在曲线上，求的值第(3)题已知m＝(cosωx＋sinωx，cosωx)，n＝(cosωx－sinωx，2sinωx)，其中ω＞0，若函数f(x)＝m·n，且f(x)的对称中心到f(x)的对称轴的最近距离不小于.（I）求ω的取值范围；（II）在△ABC中，a，b，c分别是内角A，B，C的对边，且a＝1，b＋c＝2，当ω取最大值时，f(A)＝1，求△ABC的面积.第(4)题如图，已知四棱锥的底面是平行四边形，且.（1）求证：平面；（2）若点分别是棱，的中点，求证：平面.第(5)题已知函数为奇函数，其图象在点处的切线与直线垂直，导数的最小值为，求的值．。

台湾省(新版)2024高考数学人教版质量检测(备考卷)完整试卷

台湾省（新版）2024高考数学人教版质量检测(备考卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题集合，若的充分条件是，则实数的取值范围是（）A．B．C．D．第(2)题已知关于的不等式在上恒成立（其中、），则（）A．当时，存在满足题意B．当时，不存在满足题意C．当时，存在满足题意D．当时，不存在满足题意第(3)题已知单位向量，的夹角为，向量，且，则的值为（）A．1B．C．D．2第(4)题已知展开式的常数项的取值范围为，且恒成立.则的取值范围为（）A．B．C．D．第(5)题将函数图像上各点的横坐标变为原来的倍，纵坐标不变，得到函数的图像，若对于满足的，，都有，则的值为（）A．B．C．D．第(6)题函数的图象大致是（）A．B．C．D．第(7)题设二元一次不等式组所表示的平面区域为M，使函数的图象过区域M的a的取值范围是( ) A．[1，3]B．C．[2，9]D．第(8)题已知集合，则等于（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题若均为不相等实数，下列命题中正确的是（）A．若，，则B．若，，，则C．若，，则D．当时，不等式成立第(2)题等腰梯形的上下底边之比为，若绕该梯形的对称轴旋转一周所得几何体的表面积为，则该梯形的周长可能为（）A．B．8C．D．16第(3)题数列首项，对一切正整数，都有，则（）A．数列是等差数列B．对一切正整数都有C．存在正整数，使得D．对任意小的正数，存在，使得三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题某工厂生产一种溶液，按市场要求该溶液的杂质含量不得超过0.1％，这种溶液最初的杂质含量为3％，现进行过滤，已知每过滤一次杂质含量减少，则至少经过______次过滤才能达到市场要求．（参考数据：，）第(2)题已知向量，，若，的方向是沿方向绕着点按逆时针方向旋转角得到的，则称经过一次变换得到.已知向量经过一次变换后得到，经过一次变换后得到，…，如此下去，经过一次变换后得到，设，则__________.第(3)题已知函数，若函数，则函数的图象的对称中心为______；若数列为等差数列，，______．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知函数，为的导函数．(1)证明：当时，函数在区内存在唯一的极值点，；(2)若在上单调递减，求整数a的最小值．第(2)题如图，在四棱锥中，平面平面，底面为直角梯形，为等边三角形，，，．(1)求证：；(2)点在棱上运动，求面积的最小值；(3)点为的中点，在棱上找一点，使得平面，求的值．第(3)题如图，已知斜三棱柱中，底面是正三角形，，点O是点A1在下底面内的正投影.(1)求证：(2)若点O是的中心，求高度A1O；(3)在（2）的条件下求二面角的余弦值.第(4)题已知在时取得极大值．(1)讨论在上的单调性；(2)令，试判断在上零点的个数．第(5)题已知等差数列，记为的前项和，从下面①②③中再选取一个作为条件，解决下面问题．①；②；③．(1)求的最小值；(2)设的前项和为，求．。

台湾省(新版)2024高考数学部编版质量检测(自测卷)完整试卷

台湾省（新版）2024高考数学部编版质量检测(自测卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题若是上周期为5的奇函数，且满足，则A ．－1B ．1C ．－2D ．2第(2)题在底面是正方形的四棱锥中，底面，点为棱的中点，点在棱上，平面与交于点，且，，则四棱锥的外接球的表面积为( )A．B ．C ．D ．第(3)题函数的部分图象为（）A ．B ．C ．D ．第(4)题已知对任意正数恒成立，则实数的最大值为（）A．B ．1C ．2D ．第(5)题复数（）A．B ．C ．D ．第(6)题执行如图所示的程序框图，则输出的值为（）A．B ．C ．D ．2第(7)题在上定义的函数是偶函数，且，若在区间上是减函数，则（）A ．在区间上是增函数，在区间上是增函数B ．在区间上是增函数，在区间上是减函数C ．在区间上是减函数，在区间上是增函数D ．在区间上是减函数，在区间上是减函数第(8)题向量，，则（）A ．B ．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知函数的相邻对称轴之间的距离为，且图象经过点，则下列说法正确的是（）A．该函数解析式为B．函数的一个对称中心为C．函数的定义域为D ．将函数的图象向右平移个单位，得到函数的图象，且函数的图象关于原点对称，则b的最小值为.第(2)题已知函数，其图象相邻对称轴间的距离为，点是其中一个对称中心，则下列结论正确的是（）A．函数的最小正周期为B．函数图象的一条对称轴方程是C．函数在区间上单调递增D ．将函数图象上所有点横坐标伸长为原来的2倍，纵坐标缩短为原来的一半，再把得到的图象向左平移个单位长度，可得到正弦函数的图象第(3)题已知点，，，则下列说法正确的是（）A．B．若，则C．若，则D．若，的夹角为锐角，则且三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题公比的等比数列的前n项和为，且，，则______．第(2)题过抛物线上且在第一象限内的一点作倾斜角互补的两条直线，分别与抛物线另外交于，两点，若直线的斜率为，则的最大值为__________．第(3)题已知是第三象限角，是终边上的一点，若，则______.四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题如图，在三棱锥中，M为AC边上的一点，，，，．(1)证明：平面平面；(2)若直线PA与平面ABC所成角的正弦值为，且二面角为锐二面角，求二面角的正弦值．第(2)题已知函数.（1）当时，讨论函数在上的单调性；（2）当时，求证：函数(为自然对数的底数)存在唯一极值点且.第(3)题在平面直角坐标系中，曲线的参数方程为（为参数）.以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为.(1)求的普通方程和的直角坐标方程；(2)设直线与轴相交于点，动点在上，点满足，点的轨迹为，试判断曲线与曲线是否有公共点.若有公共点，求出其直角坐标；若没有公共点，请说明理由.第(4)题函数的部分图象如图所示.（1）求函数的解析式；（2）若，且，求.第(5)题已知函数.(1)若函数，讨论的单调性；(2)从下面①②两个问题中任意选择一个证明，若两个都证明，则按第一个证明计分.①若函数，，且，证明：.②若函数，证明：.。

2022年台湾省中考数学试卷(解析版)

2022年台湾省中考数学试卷第一部分：选择题（1～25题）1．如图数线上的A、B、C、D四点所表示的数分别为a、b、c、d，且O为原点．根据图中各点的位置判断，下列何者的值最小？（）A．|a|B．|b|C．|c|D．|d|2．计算多项式6x2+4x除以2x2后，得到的余式为何？（）A．2B．4C．2x D．4x3．下列何者为156的质因数？（）A．11B．12C．13D．144．如图为一个长方体的展开图，且长方体的底面为正方形．根据图中标示的长度，求此长方体的体积为何？（）A．144B．224C．264D．3005．算式+﹣（﹣）之值为何？（）A．B．C．D．6．的值介于下列哪两个数之间？（）A．25，30B．30，35C．35，40D．40，457．已知坐标平面上有一直线L与一点A．若L的方程式为x＝﹣2，A点坐标为（6，5），则A点到直线L的距离为何？（）A．3B．4C．7D．88．多项式39x2+5x﹣14可因式分解成（3x+a）（bx+c），其中a、b、c均为整数，求a+2c之值为何？（）A．﹣12B．﹣3C．3D．129．箱子内有分别标示号码1～6的球，每个号码各2颗，总共12颗．已知小茹先从箱内抽出5颗球且不将球放回箱内，这5颗球的号码分别是1、2、2、3、5．今阿纯打算从此箱内剩下的球中抽出1颗球，若箱内剩下的每颗球被他抽出的机会相等，则他抽出的球的号码，与小茹已抽出的5颗球中任意一颗球的号码相同的机率是多少？（）A．B．C．D．10．已知一元二次方程式（x﹣2）2＝3的两根为a、b，且a＞b，求2a+b之值为何？（）A．9B．﹣3C．6+D．﹣6+11．根据如图中两人的对话纪录，求出哥哥买游戏机的预算为多少元？（）A．3800B．4800C．5800D．680012．已知p＝7.52×10﹣6，下列关于p值的叙述何者正确？（）A．小于0B．介于0与1两数之间，两数中比较接近0C．介于0与1两数之间，两数中比较接近1D．大于113．如图，AB为圆O的一弦，且C点在AB上．若AC＝6，BC＝2，AB的弦心距为3，则OC的长度为何？（）A．3B．4C．D．14．某国主计处调查2017年该国所有受雇员工的年薪资料，并公布调查结果如图的直方图所示．已知总调查人数为750万人，根据图中信息计算，该国受雇员工年薪低于平均数的人数占总调查人数的百分率为下列何者？（）A．6%B．50%C．68%D．73%15．如图，△ABC中，D点在AB上，E点在BC上，DE为AB的中垂线．若∠B＝∠C，且∠EAC＞90°，则根据图中标示的角，判断下列叙述何者正确？（）A．∠1＝∠2，∠1＜∠3B．∠1＝∠2，∠1＞∠3C．∠1≠∠2，∠1＜∠3D．∠1≠∠2，∠1＞∠316．缓降机是火灾发生时避难的逃生设备，如图是厂商提供的缓降机安装示意图，图中呈现在三楼安装缓降机时，使用此缓降机直接缓降到一楼地面的所需绳长（不计安全带）．若某栋建筑的每个楼层高度皆为3公尺，则根据如图的安装方式在该建筑八楼安装缓降机时，使用此缓降机直接缓降到一楼地面的所需绳长（不计安全带）为多少公尺？（）A．21.7B．22.6C．24.7D．25.617．如图为两直线L、M与△ABC相交的情形，其中L、M分别与BC、AB平行．根据图中标示的角度，求∠B的度数为何？（）A．55B．60C．65D．7018．某鞋店正举办开学特惠活动，如图为活动说明．小彻打算在该店同时购买一双球鞋及一双皮鞋，且他有一张所有购买的商品定价皆打8折的折价券．若小彻计算后发现使用折价券与参加特惠活动两者的花费相差50元，则下列叙述何者正确？（）A．使用折价券的花费较少，且两双鞋的定价相差100元B．使用折价券的花费较少，且两双鞋的定价相差250元C．参加特惠活动的花费较少，且两双鞋的定价相差100元D．参加特惠活动的花费较少，且两双鞋的定价相差250元19．如图，△ABC的重心为G，BC的中点为D，今以G为圆心，GD长为半径画一圆，且作A点到圆G的两切线段AE、AF，其中E、F均为切点．根据图中标示的角与角度，求∠1与∠2的度数和为多少？（）A．30B．35C．40D．4520．如图1为一张正三角形纸片ABC，其中D点在AB上，E点在BC上．今以DE为折线将B点往右折后，BD、BE分别与AC相交于F点、G点，如图2所示．若AD＝10，AF ＝16，DF＝14，BF＝8，则CG的长度为多少？（）A．7B．8C．9D．1021．有一直径为AB的圆，且圆上有C、D、E、F四点，其位置如图所示．若AC＝6，AD ＝8，AE＝5，AF＝9，AB＝10，则下列弧长关系何者正确？（）A．+＝，+＝B．+＝，+≠C．+≠，+＝D．+≠，+≠22．已知坐标平面上有二次函数y＝﹣（x+6）2+5的图形，函数图形与x轴相交于（a，0）、（b，0）两点，其中a＜b．今将此函数图形往上平移，平移后函数图形与x轴相交于（c，0）、（d，0）两点，其中c＜d，判断下列叙述何者正确？（）A．（a+b）＝（c+d），（b﹣a）＜（d﹣c）B．（a+b）＝（c+d），（b﹣a）＞（d﹣c）C．（a+b）＜（c+d），（b﹣a）＜（d﹣c）D．（a+b）＜（c+d），（b﹣a）＞（d﹣c）23．△ABC的边上有D、E、F三点，各点位置如图所示．若∠B＝∠F AC，BD＝AC，∠BDE ＝∠C，则根据图中标示的长度，求四边形ADEF与△ABC的面积比为何？（）A．1：3B．1：4C．2：5D．3：8请阅读下列叙述后，回答问题．表（一）、表（二）呈现P A、PB两种日光灯管的相关数据，其中光通量用来衡量日光灯管的明亮程度．表（一）P A灯管类别直径（毫米）长度（毫米）功率（瓦）光通量（流明）P A﹣2025.4580201440P A﹣3025.4895302340P A﹣4025.41198403360表（二）PB灯管类别直径（毫米）长度（毫米）功率（瓦）光通量（流明）PB﹣1415.8549141200PB﹣2815.8114928260024．已知日光灯管的发光效率为光通量与功率的比值，甲、乙两人根据表（一）、表（二）的信息提出以下看法：（甲）P A﹣20日光灯管的发光效率比PB﹣14日光灯管高（乙）P A日光灯管中，功率较大的灯管其发光效率较高关于甲、乙两人的看法，下列叙述何者正确？（）A．甲、乙皆正确B．甲、乙皆错误C．甲正确，乙错误D．甲错误，乙正确25．有一间公司请水电工程厂商安装日光灯管，厂商提供两种方案如表（三）所示．表（三）方案施工内容施工费用（含材料费）45000元基本方案安装90支P A﹣40日光灯管60000元省电方案安装120支PB﹣28日光灯管已知n支功率皆为w瓦的灯管都使用t 小时后消耗的电能（度）＝×w×t，若每支灯管使用时间皆相同，且只考虑灯管消耗的电能并以每度5元计算电费，则两种方案相比，灯管使用时间至少要超过多少小时，采用省电方案所节省的电费才会高于两者相差的施工费用？（）A．12200B．12300C．12400D．12500第二部分：非选择题（26～27题）26．健康生技公司培养绿藻以制作「绿藻粉」，再经过后续的加工步骤，制成绿藻相关的保健食品．已知该公司制作每1公克的「绿藻粉」需要60亿个绿藻细胞．请根据上述信息回答下列问题，完整写出你的解题过程并详细解释：（1）假设在光照充沛的环境下，1个绿藻细胞每20小时可分裂成4个绿藻细胞，且分裂后的细胞亦可继续分裂．今从1个绿藻细胞开始培养，若培养期间绿藻细胞皆未死亡且培养环境的光照充沛，经过15天后，共分裂成4k个绿藻细胞，则k之值为何？（2）承（1），已知60亿介于232与233之间，请判断4k个绿藻细胞是否足够制作8公克的「绿藻粉」？27．一副完整的扑克牌有4种花色，且每种花色皆有13种点数，分别为2、3、4、5、6、7、8、9、10、J、Q、K、A，共52张．某扑克牌游戏中，玩家可以利用「牌值」来评估尚未发出的牌之点数大小．「牌值」的计算方式为：未发牌时先设「牌值」为0；若发出的牌点数为2至9时，表示发出点数小的牌，则「牌值」加1；若发出的牌点数为10、J、Q、K、A时，表示发出点数大的牌，则「牌值」减1．例如：从一副完整的扑克牌发出了6张牌，点数依序为3、A、8、9、Q、5，则此时的「牌值」为0+1﹣1+1+1﹣1+1＝2．请根据上述信息回答下列问题，完整写出你的解题过程并详细解释：（1）若一副完整的扑克牌发出了11张点数小的牌及4张点数大的牌，则此时的「牌值」为何？（2）已知一副完整的扑克牌已发出28张牌，且此时的「牌值」为10．若剩下的牌中每一张牌被发出的机会皆相等，则下一张发出的牌是点数大的牌的机率是多少？2022年台湾省中考数学试卷参考答案与试题解析第一部分：选择题（1～25题）1．如图数线上的A、B、C、D四点所表示的数分别为a、b、c、d，且O为原点．根据图中各点的位置判断，下列何者的值最小？（）A．|a|B．|b|C．|c|D．|d|【分析】根据绝对值的定义：数轴上一个数表示的点到原点的距离是这个数的绝对值即可得出答案．【解答】解：∵a表示的点A到原点的距离最近，∴|a|最小，故选：A．【点评】本题考查了绝对值，数轴，掌握绝对值的定义：数轴上一个数表示的点到原点的距离是这个数的绝对值是解题的关键．2．计算多项式6x2+4x除以2x2后，得到的余式为何？（）A．2B．4C．2x D．4x【分析】利用多项式除以单项式的法则进行计算，即可得出答案．【解答】解：（6x2+4x）÷2x2＝3...4x，∴余式为4x，故选：D．【点评】本题考查了整式的除法，掌握多项式除以单项式的法则是解决问题的关键．3．下列何者为156的质因数？（）A．11B．12C．13D．14【分析】将156进行质因数分解，可得156＝2×2×3×13，即可求解．【解答】解：∵156＝2×2×3×13，∴156的质因数有2，3，13，故选：C．【点评】本题考查有理数的乘法，一个数的质因数，解题的关键是掌握分解一个数的质因数的方法．4．如图为一个长方体的展开图，且长方体的底面为正方形．根据图中标示的长度，求此长方体的体积为何？（）A．144B．224C．264D．300【分析】根据展开图，可以求得原来长方体的底面的边长和高，然后根据长方体的面积公式计算即可．【解答】解：设展开图的长方形的长为a，宽为b，12＝3b，2b+a＝22，解得a＝14，b＝4，∴长方体的体积为：4×4×14＝224，故选：B．【点评】本题考查几何体的展开图，解答本题的关键是明确题意，利用数形结合的思想解答．5．算式+﹣（﹣）之值为何？（）A．B．C．D．【分析】根据有理数的加减运算法则计算即可．【解答】解：+﹣（﹣）＝＝（）+（）＝﹣+1＝．故选：A．【点评】本题考查有理数的加减混合运算，熟练掌握有理数的加减运算法则是解答本题的关键．6．的值介于下列哪两个数之间？（）A．25，30B．30，35C．35，40D．40，45【分析】估算2022介于哪两个平方数之间便可．【解答】解：∵442＝1936，452＝2025，1936＜2022＜2025，∴44＜＜45，故选：D．【点评】本题考查估算无理数的大小，掌握算术平方根的意义是得出正确答案的前提．7．已知坐标平面上有一直线L与一点A．若L的方程式为x＝﹣2，A点坐标为（6，5），则A点到直线L的距离为何？（）A．3B．4C．7D．8【分析】根据L的方程式为x＝﹣2，A点坐标为（6，5），可知A点到直线L的距离为：6﹣（﹣2），然后计算即可．【解答】解：∵L的方程式为x＝﹣2，A点坐标为（6，5），∴A点到直线L的距离为：6﹣（﹣2）＝6+2＝8，故选：D．【点评】本题考查坐标与图形性质，解答本题的关键是明确题意，求出点A到直线L的距离．8．多项式39x2+5x﹣14可因式分解成（3x+a）（bx+c），其中a、b、c均为整数，求a+2c之值为何？（）A．﹣12B．﹣3C．3D．12【分析】根据十字相乘法可以将多项式39x2+5x﹣14分解因式，然后再根据多项式39x2+5x ﹣14可因式分解成（3x+a）（bx+c），即可得到a、b、c的值，然后计算出a+2c的值即可．【解答】解：∵39x2+5x﹣14＝（3x+2）（13x﹣7），多项式39x2+5x﹣14可因式分解成（3x+a）（bx+c），∴a＝2，b＝13，c＝﹣7，∴a+2c＝2+2×（﹣7）＝2+（﹣14）＝﹣12，故选：A．【点评】本题考查因式分解—十字相乘法，解答本题的关键是明确题意，会用十字相乘法分解因式．9．箱子内有分别标示号码1～6的球，每个号码各2颗，总共12颗．已知小茹先从箱内抽出5颗球且不将球放回箱内，这5颗球的号码分别是1、2、2、3、5．今阿纯打算从此箱内剩下的球中抽出1颗球，若箱内剩下的每颗球被他抽出的机会相等，则他抽出的球的号码，与小茹已抽出的5颗球中任意一颗球的号码相同的机率是多少？（）A．B．C．D．【分析】根据箱内剩下的球中的号码为1，3，4，4，5，6，6和小茹已抽出的5颗球中任意一颗球的号码相同的号码是1，3，5，根据概率公式即可得到结论．【解答】解：∵箱内剩下的球中的号码为1，3，4，4，5，6，6，∴阿纯打算从此箱内剩下的球中抽出1颗球与小茹已抽出的5颗球中任意一颗球的号码相同的号码是1，3，5，∴与小茹已抽出的5颗球中任意一颗球的号码相同的机率是，故选：C．【点评】本题考查概率公式，熟练掌握概率公式是解题的关键．10．已知一元二次方程式（x﹣2）2＝3的两根为a、b，且a＞b，求2a+b之值为何？（）A．9B．﹣3C．6+D．﹣6+【分析】先利用直接开平方法解方程得到a＝2+，b＝2﹣，然后计算代数式2a+b 的值．【解答】解：（x﹣2）2＝3，x﹣2＝或x﹣2＝﹣，所以x1＝2+，x2＝2﹣，即a＝2+，b＝2﹣，所以2a+b＝4+2+2﹣＝6+．故选：C．【点评】此题主要考查了直接开平方法解方程，正确掌握解题方法是解题关键．11．根据如图中两人的对话纪录，求出哥哥买游戏机的预算为多少元？（）A．3800B．4800C．5800D．6800【分析】设哥哥买游戏机的预算为x元，根据题意列出一元一次方程，解方程，即可得出答案．【解答】解：设哥哥买游戏机的预算为x元，由题意得：（x+1200）×0.8＝x﹣200，解得：x＝5800，故选：C．【点评】本题考查了一元一次方程的应用，根据题意正确列出一元一次方程是解决问题的关键．12．已知p＝7.52×10﹣6，下列关于p值的叙述何者正确？（）A．小于0B．介于0与1两数之间，两数中比较接近0C．介于0与1两数之间，两数中比较接近1D．大于1【分析】由0＜7.52×10﹣6＜1，且比较接近0，可得出答案．【解答】解：0＜7.52×10﹣6＜1，且比较接近0．故选：B．【点评】本题考查科学记数法﹣表示较小的数、有理数的大小比较，熟练掌握科学记数法表示较小的数的概念是解答本题的关键．13．如图，AB为圆O的一弦，且C点在AB上．若AC＝6，BC＝2，AB的弦心距为3，则OC的长度为何？（）A．3B．4C．D．【分析】根据垂径定理可以得到CD的长，根据题意可知OD＝3，然后根据勾股定理可以求得OC的长．【解答】解：作OD⊥AB于点D，如图所示，由题意可知：AC＝6，BC＝2，OD＝3，∴AB＝8，∴AD＝BD＝4，∴CD＝2，∴OC＝＝＝，故选：D．【点评】本题考查垂径定理、勾股定理，解答本题的关键是求出CD的长．14．某国主计处调查2017年该国所有受雇员工的年薪资料，并公布调查结果如图的直方图所示．已知总调查人数为750万人，根据图中信息计算，该国受雇员工年薪低于平均数的人数占总调查人数的百分率为下列何者？（）A．6%B．50%C．68%D．73%【分析】由受雇员工年薪低于平均数的人数除以总人数．再乘以100%，即可求得．【解答】解：该国受雇员工年薪低于平均数的人数占总调查人数的百分率为：×100%＝68%，故选：C．【点评】本题考查的是频数分布直方图．读懂统计图，从统计图中得到必要的信息是解决问题的关键．15．如图，△ABC中，D点在AB上，E点在BC上，DE为AB的中垂线．若∠B＝∠C，且∠EAC＞90°，则根据图中标示的角，判断下列叙述何者正确？（）A．∠1＝∠2，∠1＜∠3B．∠1＝∠2，∠1＞∠3C．∠1≠∠2，∠1＜∠3D．∠1≠∠2，∠1＞∠3【分析】根据线段垂直平分线的性质，等腰三角形的性质解答即可．【解答】解：∵DE为AB的中垂线，∴∠BDE＝∠ADE，BE＝AE，∴∠B＝∠BAE，∴∠1＝∠2，∵∠EAC＞90°，∴∠3+∠C＜90°，∵∠B+∠1＝90°，∠B＝∠C，∴∠1＞∠3，∴∠1＝∠2，∠1＞∠3，故选：B．【点评】本题主要考查了线段垂直平分线的性质和等腰三角形的性质，熟练掌握相关的性质定理是解答本题的关键．16．缓降机是火灾发生时避难的逃生设备，如图是厂商提供的缓降机安装示意图，图中呈现在三楼安装缓降机时，使用此缓降机直接缓降到一楼地面的所需绳长（不计安全带）．若某栋建筑的每个楼层高度皆为3公尺，则根据如图的安装方式在该建筑八楼安装缓降机时，使用此缓降机直接缓降到一楼地面的所需绳长（不计安全带）为多少公尺？（）A．21.7B．22.6C．24.7D．25.6【分析】根据线段的和差定义求解．【解答】解：该建筑八楼安装缓降机时，使用此缓降机直接缓降到一楼地面的所需绳长＝3×7﹣（1，6﹣0.4﹣0，5）＝21.7（公尺），故选：A．【点评】本题考查线段的和差定义，解题的关键是理解题意，灵活运用所学知识解决问题．17．如图为两直线L、M与△ABC相交的情形，其中L、M分别与BC、AB平行．根据图中标示的角度，求∠B的度数为何？（）A．55B．60C．65D．70【分析】由两直线平行，同旁内角互补可得出∠A和∠C的度数，再根据三角形内角和可得出∠B的度数．【解答】解：因为L、M分别与BC、AB平行，所以∠C+120°＝180°，∠A+115°＝180°，所以∠C＝60°，∠A＝65°，所以∠B＝180°﹣∠C＝∠A＝55°．故选：A．【点评】本题主要考查平行线的性质，三角形内角和定理等知识，根据两直线平行，同旁内角互补得出∠A和∠C的度数是解题的关键．18．某鞋店正举办开学特惠活动，如图为活动说明．小彻打算在该店同时购买一双球鞋及一双皮鞋，且他有一张所有购买的商品定价皆打8折的折价券．若小彻计算后发现使用折价券与参加特惠活动两者的花费相差50元，则下列叙述何者正确？（）A．使用折价券的花费较少，且两双鞋的定价相差100元B．使用折价券的花费较少，且两双鞋的定价相差250元C．参加特惠活动的花费较少，且两双鞋的定价相差100元D．参加特惠活动的花费较少，且两双鞋的定价相差250元【分析】设两双鞋子的价格分别为x，y（x＜y），则特惠活动花费0.6x+y，使用折价券花费0.8（x+y），由0.6x+y﹣0.8（x+y）＝﹣0.2x+0.2y＝0.2（y﹣x）＞0可得使用折价券的花费较少，由0.2（y﹣x）＝50可得y﹣x＝250，即两双鞋定价相差250元，即可求解．【解答】解：设两双鞋子的价格分别为x，y（x＜y），∴特惠活动花费：0.6x+y，使用折价券花费：0.8（x+y），∵0.6x+y﹣0.8（x+y）＝﹣0.2x+0.2y＝0.2（y﹣x）＞0，∴使用折价券的花费较少，∵0.2（y﹣x）＝50，∴y﹣x＝250，∴两双鞋定价相差250元，故选：B．【点评】本题考查列代数式，解题的关键是正确列出代数式．19．如图，△ABC的重心为G，BC的中点为D，今以G为圆心，GD长为半径画一圆，且作A点到圆G的两切线段AE、AF，其中E、F均为切点．根据图中标示的角与角度，求∠1与∠2的度数和为多少？（）A．30B．35C．40D．45【分析】连接AD、EG、FG，根据G为△ABC的重心，可得EG＝DG＝FG＝AG，又AE、AF是⊙G的切线，可得∠EAG＝∠F AG＝30°，而∠B＝40°，∠C＝45°，即可得∠1+∠2＝∠BAC﹣∠EAF＝35°．【解答】解：连接AD、EG、FG，如图：∵G为△ABC的重心，∴DG＝AG，∵以G为圆心，GD长为半径画一圆，∴EG＝DG＝FG＝AG，∵AE、AF是⊙G的切线，∴∠AEG＝∠AFG＝90°，∴∠EAG＝∠F AG＝30°，∴∠EAF＝60°，∵∠B＝40°，∠C＝45°，∴∠BAC＝95°，∴∠1+∠2＝∠BAC﹣∠EAF＝95°﹣60°＝35°，故选：B．【点评】本题考查是三角形的重心，涉及直角三角形性质、圆的切线等知识，解题的关键是掌握三角形重心定理，得到∠EAG＝∠F AG＝30°．20．如图1为一张正三角形纸片ABC，其中D点在AB上，E点在BC上．今以DE为折线将B点往右折后，BD、BE分别与AC相交于F点、G点，如图2所示．若AD＝10，AF ＝16，DF＝14，BF＝8，则CG的长度为多少？（）A．7B．8C．9D．10【分析】根据三角形ABC是正三角形，可得∠A＝∠B＝60°，△AFD∽△BFG，即可求出FG＝7，而AD＝10，DF＝14，BF＝8，可得AB＝32＝AC，故CG＝AC﹣AF﹣FG＝9．【解答】解：∵三角形ABC是正三角形，∴∠A＝∠B＝60°，∵∠AFD＝∠BFG，∴△AFD∽△BFG，∴＝，即＝，∴FG＝7，∵AD＝10，DF＝14，BF＝8，∴AB＝32，∴AC＝32，∴CG＝AC﹣AF﹣FG＝32﹣16﹣7＝9；故选：C．【点评】本题考查等边三角形中的翻折问题，解题的关键是掌握翻折的性质，证明△AFD ∽△BFG，从而求出FG的长度．21．有一直径为AB的圆，且圆上有C、D、E、F四点，其位置如图所示．若AC＝6，AD ＝8，AE＝5，AF＝9，AB＝10，则下列弧长关系何者正确？（）A．+＝，+＝B．+＝，+≠C．+≠，+＝D．+≠，+≠【分析】根据圆中弧、弦的关系，圆周角定理解答即可．【解答】解：连接BD，BF，∵AB直径，AB＝10，AD＝8，∴BD＝6，∵AC＝6，∴AC＝BD，∴，∴，∵AB直径，AB＝10，AF＝9，∴BF＝，∵AE＝5，∴，∴+≠，∴B符合题意，故选：B．【点评】本题主要考查了圆中弧、弦的关系和圆周角定理，熟练掌握相关定理是解答本题的关键．22．已知坐标平面上有二次函数y＝﹣（x+6）2+5的图形，函数图形与x轴相交于（a，0）、（b，0）两点，其中a＜b．今将此函数图形往上平移，平移后函数图形与x轴相交于（c，0）、（d，0）两点，其中c＜d，判断下列叙述何者正确？（）A．（a+b）＝（c+d），（b﹣a）＜（d﹣c）B．（a+b）＝（c+d），（b﹣a）＞（d﹣c）C．（a+b）＜（c+d），（b﹣a）＜（d﹣c）D．（a+b）＜（c+d），（b﹣a）＞（d﹣c）【分析】画出图形，利用抛物线的对称性判断出a+b＝c+d＝﹣12，可得结论．【解答】解：如图，∵y＝﹣（x+6）2+5的对称轴是直线x＝﹣6，平移后的抛物线对称轴不变，∴＝﹣6，＝﹣6，∴a+b＝﹣12，c+d＝﹣12，∴a+b＝c+d，且b﹣a＜d﹣c，故选：A．【点评】本题考查二次函数的性质，抛物线与x轴的交点，二次函数的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．23．△ABC的边上有D、E、F三点，各点位置如图所示．若∠B＝∠F AC，BD＝AC，∠BDE ＝∠C，则根据图中标示的长度，求四边形ADEF与△ABC的面积比为何？（）A．1：3B．1：4C．2：5D．3：8【分析】证明△CAF∽△CBA，推出CA2＝CF•CB，推出AC＝4，可得＝＝，推出S△ACF：S△ACB＝5：16，同法S△BDE：S△ABC＝5：16，由此可得结论．【解答】解：∵∠C＝∠C，∠CAF＝∠B，∴△CAF∽△CBA，∴＝，∴CA2＝CF•CB，∴CA2＝5×16＝80，∵AC＞0，∴AC＝4，∴＝＝，∴S△ACF：S△ACB＝5：16，同法可证△BDE∽△BCA，∵BA＝AC，∴＝，∴S△BDE：S△ABC＝5：16，∴S四边形ADEF：S△ABC＝（16﹣5﹣5）：16＝3：8，故选：D．【点评】本题考查相似三角形的判定和性质，解题的关键是正确寻找相似三角形解决问题，属于中考选择题中的压轴题．请阅读下列叙述后，回答问题．表（一）、表（二）呈现P A、PB两种日光灯管的相关数据，其中光通量用来衡量日光灯管的明亮程度．表（一）P A灯管类别直径（毫米）长度（毫米）功率（瓦）光通量（流明）P A﹣2025.4580201440P A﹣3025.4895302340P A﹣4025.41198403360表（二）PB灯管类别直径（毫米）长度（毫米）功率（瓦）光通量（流明）PB﹣1415.8549141200PB﹣2815.8114928260024．已知日光灯管的发光效率为光通量与功率的比值，甲、乙两人根据表（一）、表（二）的信息提出以下看法：（甲）P A﹣20日光灯管的发光效率比PB﹣14日光灯管高（乙）P A日光灯管中，功率较大的灯管其发光效率较高关于甲、乙两人的看法，下列叙述何者正确？（）A．甲、乙皆正确B．甲、乙皆错误C．甲正确，乙错误D．甲错误，乙正确【分析】根据“日光灯管的发光效率为光通量与功率的比值”表示出各日光灯管的发光效率然后进行比较即可．【解答】解：根据题意，P A﹣20日光灯管的发光效率为＝72，PB﹣14日光灯管的发光效率为，∵72＜，∴PB﹣14日光灯管发光效率高，故甲错误；P A﹣20日光灯管的发光效率为＝72，P A﹣30日光灯管的发光效率为＝78，P A﹣40日光灯管的发光效率为＝84，∵20＜30＜40时，72＜78＜84，∴P A日光灯管中，功率较大的灯管其发光效率较高，故乙正确，故选：D．【点评】本题考查了统计表，表示出各日光灯管的发光效率是解题的关键．25．有一间公司请水电工程厂商安装日光灯管，厂商提供两种方案如表（三）所示．表（三）方案施工内容施工费用（含材料费）基本方案安装90支45000元P A﹣40日光灯管60000元省电方案安装120支PB﹣28日光灯管已知n支功率皆为w瓦的灯管都使用t 小时后消耗的电能（度）＝×w×t，若每支灯管使用时间皆相同，且只考虑灯管消耗的电能并以每度5元计算电费，则两种方案相比，灯管使用时间至少要超过多少小时，采用省电方案所节省的电费才会高于两者相差的施工费用？（）A．12200B．12300C．12400D．12500【分析】根据“采用省电方案所节省的电费才会高于两者相差的施工费用”列一元一次不等式，求解即可．【解答】解：根据题意，得，解得t＞12500，∴灯管使用时间超过12500小时，采用省电方案所节省的电费才会高于两者相差的施工费用，故选：D．【点评】本题考查了一元一次不等式的应用，理解题意并根据题意建立一元一次不等式是解题的关键．第二部分：非选择题（26～27题）26．健康生技公司培养绿藻以制作「绿藻粉」，再经过后续的加工步骤，制成绿藻相关的保健食品．已知该公司制作每1公克的「绿藻粉」需要60亿个绿藻细胞．请根据上述信息回答下列问题，完整写出你的解题过程并详细解释：（1）假设在光照充沛的环境下，1个绿藻细胞每20小时可分裂成4个绿藻细胞，且分裂后的细胞亦可继续分裂．今从1个绿藻细胞开始培养，若培养期间绿藻细胞皆未死亡且培养环境的光照充沛，经过15天后，共分裂成4k个绿藻细胞，则k之值为何？（2）承（1），已知60亿介于232与233之间，请判断4k个绿藻细胞是否足够制作8公克的「绿藻粉」？【分析】（1）由1个绿藻细胞每20小时可分裂成4个绿藻细胞，可知经过15天，即360小时，分裂成418个绿藻细胞，故k之值为18；（2）根据每1公克的「绿藻粉」需要60亿个绿藻细胞，60亿介于232与233之间，可得制作8公克的「绿藻粉」需要60×8亿个绿藻细胞，且235＜60×8亿＜236，又418＝（22）18＝236，即得418个绿藻细胞足够制作8公克的「绿藻粉」．【解答】解：（1）15天＝15×24小时＝360小时，∵1个绿藻细胞每20小时可分裂成4个绿藻细胞，∴从1个绿藻细胞开始培养，经过20小时分裂成4个绿藻细胞，经过20×2＝40（小时），分裂成42个绿藻细胞，经过20×3＝60（小时），分裂成43个绿藻细胞，.....．经过20×18＝360（小时），分裂成418个绿藻细胞，∴k之值为18；（2）∵每1公克的「绿藻粉」需要60亿个绿藻细胞，∴制作8公克的「绿藻粉」需要60×8亿个绿藻细胞，∵60亿介于232与233之间，∴232×8＜60×8亿＜233×8，即235＜60×8亿＜236，而418＝（22）18＝236，∴60×8亿＜418，∴418个绿藻细胞足够制作8公克的「绿藻粉」．【点评】本题考查有理数的乘方，解题的关键是读懂题意，根据已知找到规律求出k的值．27．一副完整的扑克牌有4种花色，且每种花色皆有13种点数，分别为2、3、4、5、6、7、8、9、10、J、Q、K、A，共52张．某扑克牌游戏中，玩家可以利用「牌值」来评估尚未发出的牌之点数大小．「牌值」的计算方式为：未发牌时先设「牌值」为0；若发出的牌点数为2至9时，表示发出点数小的牌，则「牌值」加1；若发出的牌点数为10、J、Q、K、A时，表示发出点数大的牌，则「牌值」减1．例如：从一副完整的扑克牌发出了6张牌，点数依序为3、A、8、9、Q、5，则此时的「牌值」为0+1﹣1+1+1﹣1+1＝2．请根据上述信息回答下列问题，完整写出你的解题过程并详细解释：（1）若一副完整的扑克牌发出了11张点数小的牌及4张点数大的牌，则此时的「牌值」为何？（2）已知一副完整的扑克牌已发出28张牌，且此时的「牌值」为10．若剩下的牌中每一张牌被发出的机会皆相等，则下一张发出的牌是点数大的牌的机率是多少？【分析】（1）利用「牌值」的计算方式解答即可；（2）利用方程组的思想求得已发出的28张牌中的点数大的张数与点数小的张数，从而得到剩余的牌中点数大的张数与点数小的张数，再利用计算概率的方法解答即可．【解答】解：（1）11×1+4×（﹣1）＝7，∴若一副完整的扑克牌发出了11张点数小的牌及4张点数大的牌，则此时的「牌值」为7；（2）设一副完整的扑克牌已发出的28张牌中点数小的张数为x张，点数大的张数为y 张，∴．解得：，∴已发出的28张牌中点数小的张数为19张，点数大的张数为9张，∴剩余的24张牌中点数大的张数为17张，点数小的张数为7张，∵剩下的牌中每一张牌被发出的机会皆相等，∴下一张发出的牌是点数大的牌的机率是．【点评】本题主要考查了有理数的混合运算，用样本估计总体的思想方法，事件概率的计算方法，本题是阅读型题目，理解题干中的定义并熟练应用是解题的关键．。

[2008中考试卷]2008年台湾第一次初中升学测验数学题本

2008年台湾第一次初中升学测验数学科题本( D ) 1. 下列哪一个式子计算出来的值最大？ (A) 8.53⨯109-2.17⨯108 (B) 8.53⨯1010-2.17⨯109 (C) 9.53⨯109-2.17⨯108 (D) 9.53⨯1010-2.17⨯109 。

( C ) 2. 若a ：b =3：2，b ：c =5：4，则a ：b ：c =？ (A) 3：2：4 (B) 6：5：4 (C) 15：10：8 (D) 15：10：12 。

( D ) 3. 在五边形ABCDE 中，若∠A =100︒，且其余四个内角度数相等，则∠C =？ (A) 65︒ (B) 100︒ (C) 108︒ (D) 110︒ 。

( A ) 4. 图(一)表示数在线四个点的位置关系，且它们表示的数分别为p 、q 、r 、s 。

若 | p －r |=10， | p －s |=12，| q －s |=9，则 | q －r |=？图(一)(A) 7 (B) 9 (C)11 (D) 13 。

( B ) 5. 如图(二)，坐标平面上有一透明片，透明片上有一拋物线及一点P ，且拋物线为二次函数y =x 2的图形，P 的坐标(2,4)。

若将此透明片向右、向上移动后，得拋物线的顶点座标为(7,2)，则此时P(A) (9,4) (B) (9,6) (C) (10,4) (D) (10,6) 。

( C ) 7. 有两个多项式M =2x 2＋3x ＋1，N =4x 2－4x －3，则下列哪一个为M 与N 的公因式？ (A) x ＋1 (B) x －1 (C) 2x ＋1 (D) 2x －1 。

( D ) 8. 若二元一次联立方程式⎩⎨⎧=-=-34332y x y x 的解为x ＝a ，y ＝b ，则a ＋b ＝？(A) 1 (B) 6 (C) 53 ((D) 512。

1992_1_日本算术奥林匹克

1992年第1届日本算术奥林匹克竞赛预赛问题1三位数加上396后,答案也正好和所选的三位数的数字顺序相反的话,可以选出若干组这样的三位数,那么,请回答下列问题:①请写出全部的百位是4的这样的三位数(除去428).②如果选包括百位是4的任意三位数加上396,使答案的三位数和所选的三位数的数字顺序相反的话,一共可以选出几个这样的三位数?问题2和子去鱼店买了以下几种鱼,每种鱼都超过1条,正好花了3600日元,请问和子买了几条竹荚鱼?(注:100A君、B君、C君、D君等4人参加了画“○”和画“×”的考试.一道题是10分,10道题一共是100分.4人问题4如果站在游泳池中用手拍打水面,就会有水波从拍打处向四周扩散,这时水波的速度仅仅和水的深度有关,如果游泳池的水深都一样的话,那么不管是站立打水,还是边走边打水、强烈打水、轻轻打水、水波的扩散速度都将是一样的,水波真是奇怪的东西.在一个游泳池(水深都一样)里,放入一台10秒钟可以打出6个水波的机器.这台机器带有轮子,所以也可以以一定的速度前进.水波是以每10秒钟12米的速度扩散.水波的最高处叫波峰,最低处叫波谷,请问:①这台机器静止不动打水,从一个波峰到另一个相邻的波峰的距离是多少米?②太郎以每10秒钟4米的速度面向正在静止站立打水的机器走去,太郎在10秒钟内可以碰上几个波峰?(时间的计算是一个波谷正好到太郎面前开始的)③这回是机器以每10秒钟4米的速度朝着站立不动的太郎边走边打水,太郎在10秒钟内可以碰上几个波峰?(时间的计算同上)④太郎和机器分别以每10秒钟4米的速度面对面地走,太郎在10秒钟内可以碰上几个波峰?(时间的计算同上)问题5如图所示,一个多边形的每条边长是1cm,一共有12条边;空白部分是正三角形,一共有12个.请算出阴影部分的面积.1cm问题6图1是一个边长为5cm的正方体,这个正方体是由边长为1cm的小正方体组成的.A、B、C、D、E、F、G、H分别是正方体的各个顶点,P是ABCD面的对角线的交点,请回答下列问题.图1图2①如图2所示,用一个通过EPF三点的平面将正方体切开,这时被切开的面是什么形状?②通过①切开后剩下的立方体(包括E、F、G、H面)的体积是多少?③再用通过F、P、G三点的平面进一步切开②剩余的立体,然后用通过P、G、H三点的平面再进一步切开,最后用通过P、H、E三点的面进行切断,将得到一个包括E、F、G、H面的立体,请写出此立体的名称(即是何形状的立体).④这个最后剩下的立体中,包括几个完整的棱长是1cm的小正方体?问题7这里有8个人在说话,他们说的话都包括自己在内,请认真读他们说的话,然后回答问题.请问说错话的人是谁?1992年第1届日本算术奥林匹克竞赛决赛问题1一些确定的并排排列的数叫做数列,数列中的一个一个数叫做项,如果对于第一项乘上一个数可以得出第二项,第二项再乘上相同的数可以得出第三项,以此类推的话,可以得到一个数列,叫做等比数列.乘数不限于整数.例如{3、6、12、24、48、96、192}是每项乘上2得到的一个等比数列,共有7项.现在请你写出一个由100以上、1000以下的整数组成的、项尽可能多的等比数列.(注意:不包括乘以1的数列.请列出此等比数列的每一项)问题2由一个工厂制造一种产品,此产品卖一个可以得到1000日元,一共做了11个产品,但是其中有一个是次品不能卖出去.现在用一种机器来检验产品质量,此机器有以下性能:①一次可以检验任何数量的产品.②每检验一次,需要花费1000日元手续费.③检验中没发现次品,则每一个产品可卖1000日元.④如果在一次检验中发现次品的话,则此次检验的产品全部报销,一个也不能卖出去.假如用这个机器一次检验一个产品的话,有下面几种情况出现:运气非常好的情况:第一次被检产品是次品.这样剩下的10个产品都是正品,可以卖出去.检验一次需1000日元手续费,因此可以得到1000×10－1000＝9000日元的收入.运气最坏的情况:检验第10个产品时,发现是次品,这样前9个产品可分别卖1000日元,但检验费每次是1000日元,则等于没有收入.下面的问题请按运气最坏的情况考虑.请问:根据一次检验的个数及顺序可以有几种检验方法,如果在运气最坏的情况下想得到最高的收入的话,采用什么样的检验方法最好?并请答出此收入是多少?问题3从图A 看出,不论哪二个相邻圈里的数的差都正好是下面圈中的数,六个圈中正好是从1到6的数,一个数在一个圈里,请按这个规则将图B 的圈中填上从1到10的数(不能有重复的数出现),最下面的圈中数字为3.如果仅仅是左右的数字互换,则算为一种答案,如图A 和图C.解答不只一种,解答栏中写出4组,但不一定都填出,有几种解答就填几种.图A图B图C问题4图1是由3个正方体连接组成的看不出接缝的部件.图2是用9个这样的部件组成的正方体.请你从图2的底面看一下,画出部件的接缝.不限于一种答案,解答栏中可回答出6种,但不一定全部使用.图1问题5如图所示,无数量限制的黑、白色的正方形拼在一起.注意,相同的正方形不能用边相连,只能是顶点(角)相连.首先铺第一块正方形(颜色随意),选好顶点,然后以这个顶点作为中心画出一个圆(不要画出所铺的面积).无论是用大半径、小半径,所画出的圈中包括的黑色、白色的面积都正好相等,请考虑这是为什么,并说明理由.答案：白与黑的面积相等不管画什么样的圆，都可以沿着正方形的边画出作为对称轴的直径线。

2009年台湾第一次中考数学科试题(含答案)

A
80° lonyal
ADC 的长度分别为 7π 、11π，则 BAD 的长度为何？
(A) 4π (B) 8π (C) 10π (D) 15π 。 9 3 2 15. 已知 a=1.6×10 ，b=4×10 ，则 a ÷2b=？ (A) 2×107 (B) 4×1014 (C) 3.2×105 (D) 3.2×1014 。 16. 若 a、b 为方程式 x2 −4(x+1)=1 的两根，且 a>b，则 (A) −5 (B) −4 (C) 1
P 圖(十)
C
35 8
(D)
56 。 5
26. 某天，5 个同学去打羽球，从上午 8：55 一直到上午 11：15。若这段时间内，他们一直玩双打(即须 4 人同时上场)，则平均一个人的上场时间为几分钟？ (A) 112 (B) 136 (C) 140 (D) 175 。
-3-
27. 已知 1~99 中有 49 个偶数，从这 49 个偶数中取出 48 个数，其平均数为 49 的数字为何？ (A) 20 (C) 72
C
70 °
D
70 ° 50 ° 60 ° 50 ° 60 ° 50 °
F
70 ° 60 ° 50 °
I
70 ° 60 °
K
70 ° 50 ° 60 °
A
圖(三) (A) 甲=乙=丙
B
A
E 圖(四)
B
A
J 圖(五)
(D )丙<乙<甲。
B
(B) 甲<乙<丙
(C) 乙<丙<甲
12. 图(六)表示数在线不等式 x −1<0 解的范围，则下列选项中，何者可表示数在线不等式 3x +15>5x−9 解的范围？ (A) 0 3 (B) 0 12 (C) 0 3

对台湾“中学生基本学力测验”数学测验的思考

图２
圉３
例８（一次测验第２第４题）已知有大、小两种：纸杯与甲、乙两桶果汁，其中小纸杯与大纸杯的容量
比为２：３，甲桶果汁与乙桶果汁的体积比为４：５，若甲桶内的果汁刚好装满小纸杯１０个。则乙桶内的２果汁最多可装满几个大纸杯？
至
图８
Ａ
在数学学习的过程中，除了理解概念之外，台湾学生一般也做相当数量的练习题，透过不同的问题、
不同的条件等，多方面地、深刻地认识数学对象。经过一连串命题给定、推论、回答问题的数学活动，学
间，也提醒后续考生须加深对数学本质的理解，有利
于促进学生的数学思维、数学观念与数学素养的全面
提升。
轨迹长度为何？
Ａ．霄Ｂ．叮２ＴＣ－叮３ｒ
Ｏ
４试题设计强调数学思维，体现可带着走的知．
Ｄ．ｒ４叮
识、能力。
试题注重对数学思维的考查，问题的呈现上也颇
费心思，如此，使测验题既体现章节学习的内容要
求，又体现着初中系统学习后的各种能力要求（带可
ｏＢｏＢ
着走的生活基本知识、能力）。

2020年台湾地区学测（数学）选择题赏析

2020年台湾地区学测（数学）选择题赏析作者：***来源：《中学数学杂志(高中版)》2020年第03期1 前言台湾地区学科能力测试（简称“学测”）包括国文、英文、数学、社会、自然五科，旨在测验考生是否具有接受大学教育的基本学科能力，是大学校系初步筛选学生的门槛. 2020年台湾地区数学测试考试共20道題，其中单选题7道（试题1-7），多选题6道（试题8-13），选填题7道.考试时间共100分钟，满分100分.本文对台湾地区学测考试（数学）的选择题进行解析和点评，并对其特点进行总结，旨在让读者大致了解台湾地区学测考试的主要内容和特点.2 试题赏析试题1 已知两个直角三角形三边长分别为3、4、5，5、12、13，α，β分别为它们的一角，如图1所示. 试选出正确的选项（）.解析根据图形可知，sinα=35，sinβ=513，因为sin30°=12，又因为513<12<35，所以sinβ<sin30°<sinα，所以选（2）.点评本题考查了正弦在直角三角形中的定义，根据正弦函数y=sinx，x∈0，π2的单调性比较数值大小即可得到答案，属于一道较容易题.试题2 空间中有相异四点A，B，C，D，已知内积AB·AC=AB·AD.试选出正确的选项.（1）AB·CD=0;（2）AC=AD;（3）AB与CD平行;（4）AD·BC=0;（5）A，B，C，D四点在同一平面上.解析根据题意可知AB·AC=AB·AD，所以AB·AC-AB·AD=0AB·AC-AD=0AB·CD=0，所以选项（1）正确，故选（1）.点评本题无需计算出数量积的具体数值，只需要稍作变形即可得到答案.实际上，根据AB·AC=AB·AD可知AC，AD在AB上的投影相等，且C，D是不同的两点，所以有AB·CD=0.试题3 如图2所示，O为正六边形之中心.试问下列哪个向量的终点P落在△ODE内部（不含边界）？解析要使终点P在△ODE内（不含边界），不仅要结果向量的方向在边界内，而且还要使结果向量的终点落在△ODE区域内.据向量加法的几何意义，选项（1）对应的点P在射线OD上，且OP=OD=OC+OE，同理，根据向量加法的几何意义知选项（3）（4）（5）对应的点P（OP的方向）均不在△ODE区域内，所以选项（2）正确.点评本题考查了向量的有关运算（向量的加法和数乘），本题不需要设坐标进行代数运算，只需要了解和理解向量加法的几何意义即可.本题以特殊的平面图形——正六边形为载体，从形的方面考查对向量加法几何意义本质的理解.试题4 令I=1001，A=1134，B=I+A+A-1，试选出代表BA的选项.（1）1001;（2）6006;（3）4-1-31;（4）1134;（5）661824.解析因为B=I+A+A-1，等式两边同乘以矩阵A可得.因为BA=IA+A2+A-1A=10011134+11342+1001=661824，所以BA=661824，故选（5）.点评本题考查了矩阵的加法和乘法运算，特别注意的是运算技巧，不要首先将矩阵B算出来，再与矩阵A相乘，这样比较复杂. 同样也不要将计算矩阵BA的值算成计算矩阵AB的值.一般情况下，矩阵的乘法不满足交换律.实际上，上面的计算过程还可以简化为BA=IA+A2+A-1A=IA+A2+I=（I+A）A+I，同样可以得到正确的结果.试题5 试问数线上有多少个整数点与101的距离小于5，但与点38的距离大于3？（1）1个;（2）4个;（3）6个;（4）8个;（5）10个.解析因为10<101<11，所以数线上与101小于5的整数点有x=6，7，8，9，10，11，12，14，15，共10个;又因为6<38<7，所以数线上到38的距离大于3的整数点满足x10或x≤3. 所以，满足与101的距离小于5，且与点38的距离大于3的整数点有x=10，11，12，13，14，15，共6个，故选（3）.点评本题考查了绝对值不等式的解法，将同时满足两个条件的整数点在数线（即数轴）上表示出来，不难得出共6个整数点满足条件.实质上，本题考查了数形结合的思想和估算的能力，考生若能运用数形结合的思想，并在估算方面能力较强，不需要运算就可以又快又准地得出答案.试题6 连续投掷一公正骰子两次，设出现的点数依序为a，b.试问发生log（a2）+logb>1的概率为多少？（1）13;（2）12;（3）23;（4）34;（5）56.解析投掷一公正骰子两次，共有6×6=36种可能结果.又因为loga2+logb>1，所以a2b>10.我们先考虑a2b≤10的情况：当a=1时，b=1，2，3，4，5，6，共6种结果;当a=2时，b=1，2，共2种结果;当a=3时，b=1，共1种结果.所以，发生log（a2）+logb>1的概率p=36-（6+2+1）36=2736=34，故选（4）.点评本题为一道求古典概率题，从正面求满足a2b>10的整数对（a，b）的个数较多，所以从反面求a2b≤10的整数对（a，b）的个数（共6+2+1=9（个）），体现了处理数学问题时正难则反的思想.本题将求古典概率与对数函数的变形交汇，在知识的交汇处命题.值得注意的是这里loga表示以10为底a的对数，等同于大陆教材中常用符号lga.试题7 坐标平面上，函数图形y=-3x3上有两点P，Q到原点距离皆为1.已知点P坐标为cosθ，sinθ，试问点Q坐标为？（1）（cos（-θ），sin（-θ））;（2）（-cosθ，sinθ）;（3）（cos（-θ），-sinθ）;（4）（-cosθ，sin（-θ））;（5）（cosθ，-sinθ）.解析因为y=-3x3是奇函数，其图形关于原点成中心对称，P，Q到原点距离皆为1，所以P，Q两点关于原点成中心对称，因为Pcosθ，sinθ，所以Q（-cosθ，-sinθ），即Q（-cosθ，sin （-θ）），所以选（4）.点评本题考查的知识点有幂函数和三角函数的性质，关键是根据P，Q两点到原点距离皆为1推导出P，Q关于原点成中心对称.试题8 有一个游戏的规则如下：丢三颗公正的骰子，若所得的点数恰满足下列（A）或（B）两个条件之一，可得到奖金100元;若两个条件都满足，则共得200元奖金;若两个条件都不满足，则无奖金.（A）三个点数皆为奇数或者皆为偶数（B）三个点数由小排到大为等差数列若已知有两颗骰子的点数分别为1，3，且所得的奖金为100元，则未知的骰子点数可能为何？（1）2;（2）3;（3）4;（4）5;（5）6.解析因为所得奖金为100元，则三个点数满足条件（A）（B）之一.当未知的骰子的点数为2时，符合条件（B），但不符合条件（A），所以选项（1）正确;当未知的骰子的点数为3时，符合条件（A），但不符合条件（B），所以选项（2）正确;当未知的骰子的点数为4时，条件（A）（B）均不满足，选项（3）错误;当未知的骰子的点数为5时，条件（A）（B）均满足，选项（4）错误;当未知的骰子的点数为6时，条件（A）（B）均不满足，选项（5）错误.故选（1）（2）.点评本题是多项选择题，较为容易，认真审题即可得到正确答案.试题9 在坐标平面上，有一通过原点O的直线L，以及一半径为2、圆心为原点O的圆Γ.P，Q为Γ上相异两点，且OP，OQ分别与L所夹的锐角皆为30°，试选出内积OP·OQ之值可能发生的选项.（1）23;（2）-23;（3）0;（4）-2;（5）-4.解析根据题意可知，OP，OQ的夹角可能为60°，120°，180°，所以OP·OQ=|OP||OQ|cos 〈OP，OQ〉.当〈OP，OQ〉=60°时，OP·OQ=22cos60°=2;当〈OP，OQ〉=120°时，OP·OQ=22cos120°=-2;当〈OP，OQ〉=180°时，OP·OQ=22cos180°=-4;所以，正确的选项为（4）（5）.点评本题考查了考生的分类讨论的思想和向量的数量积等知识的运用，注意到直线和向量的区别. 根据题意，OP，OQ的夹角有3种情形，如图3所示，即〈OP，OQ〉=180°，〈OP，OQ1〉=60°，〈OP，OQ2〉=120°.值得一提的是，选项中并没有答案为“2”这一选项，也就是说，在多项选择题的命制中，选项不一定要覆盖所有可能值.試题10 已知多项式f（x）=3x4+11x2-4，试选出正确的选项.（1）y=f（x）的图形与y轴交点的y坐标小于0;（2）f（x）=0有4个实根;（3）f（x）=0至少有一个有理根;（4）f（x）=0有一根介于0与1之间;（5）f（x）=0有一根介于1与2之间.解析对于选项（1）来说，y=f（x）的图形与y轴交点的y坐标，即当x=0时y的值，显然有y=f（0）=-4<0，选项（1）正确;对于选项（2），因为f（x）=3x4+11x2-4=（3x2-1）（x2+4），当f（x）=0时，有3x2-1=0或x2+4=0，显然，f（x）=0只有两个不同的实根x1，2=±33，其余两个根为虚根x3，4=±2i（i为虚数单位，即i2=-1），故选项（2）错误;对于选项（3），由选项（2）可知，f（x）=0没有一个有理根，4个根分别为两个无理根，两个虚根，故选项（3）错误;对于选项（4），因为0<33<1，故f（x）=0有一根介于0与1之间，选项（4）正确，选项（5）错误.点评本题从多个方面考查了多项式函数（次数为4）的图形和性质，如图形与y轴交点的纵坐标的正负，根的类型和根的范围等等. 首先，遇到与多项式函数有关的问题时，因式分解是关键，将高次降为低次进行问题解决. 其次，若不能够因式分解，则运用多形式函数的有关定理，如余数定理、综合除法、虚根成对定理、代数基本定理和插值公式来解决问题.试题11 设a，b，c为实数且满足loga=1.1，logb=2.2，logc=3.3.试选出正确的选项.（1）a+c=2b;（2）1<a<10;（3）1000<c<2000;（4）b=2a;（5）a，b，c成等比数列.解析对于选项（1），因为loga+logc=2logb，所以有b2=ac，并不能推导出a+c=2b，故选项（1）错误;实际上，因为c=a3，b=a2，若a+c=2b，则有a+a3=2a2，又因为a>10，所以a+a3=2a2无解，所以a+c=2b错误;试题7 坐标平面上，函数图形y=-3x3上有两点P，Q到原点距离皆为1.已知点P坐标为cosθ，sinθ，试问点Q坐标为？（1）（cos（-θ），sin（-θ））;（2）（-cosθ，sinθ）;（3）（cos（-θ），-sinθ）;（4）（-cosθ，sin（-θ））;（5）（cosθ，-sinθ）.解析因为y=-3x3是奇函数，其图形关于原点成中心对称，P，Q到原点距离皆为1，所以P，Q两点关于原点成中心对称，因为Pcosθ，sinθ，所以Q（-cosθ，-sinθ），即Q（-cosθ，sin （-θ）），所以选（4）.点评本题考查的知识点有幂函数和三角函数的性质，关键是根据P，Q两点到原点距离皆为1推导出P，Q关于原点成中心对称.试题8 有一个游戏的规则如下：丢三颗公正的骰子，若所得的点数恰满足下列（A）或（B）两个条件之一，可得到奖金100元;若两个条件都满足，则共得200元奖金;若两个条件都不满足，则无奖金.（A）三个点数皆为奇数或者皆为偶数（B）三个点数由小排到大为等差数列若已知有两颗骰子的点数分别为1，3，且所得的奖金为100元，则未知的骰子点数可能为何？（1）2;（2）3;（3）4;（4）5;（5）6.解析因为所得奖金为100元，则三个点数满足条件（A）（B）之一.当未知的骰子的点数为2时，符合条件（B），但不符合条件（A），所以选项（1）正确;当未知的骰子的点数为3时，符合条件（A），但不符合条件（B），所以选项（2）正确;当未知的骰子的点数为4时，条件（A）（B）均不满足，选项（3）错误;当未知的骰子的点数为5时，条件（A）（B）均满足，选项（4）错误;当未知的骰子的点数为6时，条件（A）（B）均不满足，选项（5）错误.故选（1）（2）.点评本题是多项选择题，较为容易，认真审题即可得到正确答案.试题9 在坐标平面上，有一通过原点O的直线L，以及一半径为2、圆心为原点O的圆Γ.P，Q为Γ上相异两点，且OP，OQ分别与L所夹的锐角皆为30°，试选出内积OP·OQ之值可能发生的选项.（1）23;（2）-23;（3）0;（4）-2;（5）-4.解析根据题意可知，OP，OQ的夹角可能为60°，120°，180°，所以OP·OQ=|OP||OQ|cos 〈OP，OQ〉.当〈OP，OQ〉=60°时，OP·OQ=22cos60°=2;当〈OP，OQ〉=120°时，OP·OQ=22cos120°=-2;当〈OP，OQ〉=180°时，OP·OQ=22cos180°=-4;所以，正确的选项为（4）（5）.点评本题考查了考生的分类讨论的思想和向量的数量积等知识的运用，注意到直线和向量的区别. 根据题意，OP，OQ的夹角有3种情形，如图3所示，即〈OP，OQ〉=180°，〈OP，OQ1〉=60°，〈OP，OQ2〉=120°.值得一提的是，选项中并没有答案为“2”这一选项，也就是说，在多项选择题的命制中，选项不一定要覆盖所有可能值.试题10 已知多项式f（x）=3x4+11x2-4，试选出正确的选项.（1）y=f（x）的图形与y轴交点的y坐标小于0;（2）f（x）=0有4个实根;（3）f（x）=0至少有一个有理根;（4）f（x）=0有一根介于0与1之间;（5）f（x）=0有一根介于1与2之间.解析对于选项（1）来说，y=f（x）的图形与y轴交点的y坐标，即当x=0时y的值，显然有y=f（0）=-4<0，选项（1）正确;对于选项（2），因为f（x）=3x4+11x2-4=（3x2-1）（x2+4），当f（x）=0时，有3x2-1=0或x2+4=0，显然，f（x）=0只有两个不同的实根x1，2=±33，其余两个根为虚根x3，4=±2i（i为虚数单位，即i2=-1），故选项（2）错误;对于选项（3），由选项（2）可知，f（x）=0没有一个有理根，4个根分别为两个无理根，两个虚根，故选项（3）错误;对于选项（4），因为0<33<1，故f（x）=0有一根介于0与1之间，选项（4）正确，选项（5）错误.点评本题从多个方面考查了多项式函数（次数为4）的图形和性质，如图形与y轴交点的纵坐标的正负，根的类型和根的范围等等. 首先，遇到与多项式函数有关的问题时，因式分解是关键，将高次降为低次进行问题解决. 其次，若不能够因式分解，则运用多形式函数的有关定理，如余数定理、综合除法、虚根成对定理、代数基本定理和插值公式来解决问题.试题11 设a，b，c为实数且滿足loga=1.1，logb=2.2，logc=3.3.试选出正确的选项.（1）a+c=2b;（2）1<a<10;（3）1000<c<2000;（4）b=2a;（5）a，b，c成等比数列.解析对于选项（1），因为loga+logc=2logb，所以有b2=ac，并不能推导出a+c=2b，故选项（1）错误;实际上，因为c=a3，b=a2，若a+c=2b，则有a+a3=2a2，又因为a>10，所以a+a3=2a2无解，所以a+c=2b错误;。

2010年台湾省中考数学试卷与答案

2010年台湾第一次国民中学学生基本学力测验(台湾中考)数学科题本1. 下列何者是0.000815的科学记号？ (A) 8.15⨯10-3(B) 8.15⨯10-4(C) 815⨯10-3(D) 815⨯10-6。

2. 小芬买15份礼物，共花了900元，已知每份礼物内鄱有1包饼干及每支售价20元的棒棒糖2支，若每包饼干的售价为x 元，则依题意可列出下列哪一个一元一次方程式？ (A) 15(2x +20)=900 (B) 15x +20⨯2=900 (C) 15(x +20⨯2)=900 (D) 15⨯x ⨯2+20=900 。

3. 下列选项中，哪一段时间最长？ (A) 15分 (B)114小时 (C) 0.3小时 (D) 1020秒。

4. 图(一)表示D 、E 、F 、G 四点在△ABC 三边上的位置，其中DG 与EF 交于H 点。

若∠ABC =∠EFC =70︒，∠ACB =60︒，∠DGB =40︒，则下列哪一组三角形相似？(A) △BDG ，△CEF (B) △ABC ，△CEF (C) △ABC ，△BDG (D) △FGH ，△ABC 。

5. 计算 | -1-(-35) |-| -611-67| 之值为何？ (A) -37 (B) -31 (C) 34 (D) 311。

6. 下列何者为5x 2+17x -12的因式？ (A) x +1 (B) x -1 (C) x +4 (D) x -4 。

7. 计算106⨯(102)3÷104之值为何？ (A) 108(B) 109(C) 1010(D) 1012。

8. 如图(二)，AB 为圆O 的直径，C 、D 两点均在圆上，其中OD 与AC 交于 E 点，且OD ⊥AC 。

若OE =4，ED =2，则BC 长度为何？ (A) 6 (B) 7 (C) 8 (D) 9 。

9. 有数颗等重的糖果和数个大、小砝码，其中大砝码皆为5克、大砝码皆为1克，且图(三)是将糖果与砝码A BCD E H图(一)AB CE O 图(二)圖(三)放在等臂天平上的两种情形。

台湾省高级中学九十二学年度化学科能力竞赛笔试试题(甲...

台灣省高級中學九十二學年度化學科能力競賽筆試試題(甲)(台中地區)(試題共三面，第一面) 組別﹕第組一﹑選擇題（單選及複選，第16、17題為複選,每題3分，共51分）1.等量(0.5 g) 的制酸藥片，何者可中和最多量的胃酸？(K=39.10amu，Na=22.99amu，Mg=24.31amu，Al=26.98amu)(A) K2CO3(B) NaHCO3(C ) MgO (D) Al(OH)32.- 4.為題組若以一強鹼的標準液來滴定樣本，樣本中所包含的物質分別在問題中敘述。

標示出不同樣本的滴定曲線圖形：(H3PO4: pK1 = 2.1, pK2 = 7.2, pK3 = 12.0)pH滴定體積 (mL)2.樣本中只含有H3PO4(A) Curve A,(B) Curve B, (C) Curve C,(D) Curve D3.樣本中只含有 NaH2PO4(A) Curve A,(B) Curve B, (C) Curve C, (D) Curve D.4.樣本中含有H3PO4和 NaH2PO4，其莫耳數比為2：1(A) Curve A,(B) Curve B, (C) Curve C, (D) Curve D.5.一燃料/助燃劑系統中含有N,N-dimethylhydrazine (二甲基肼) (CH3)2NNH2與N2O4 (二物質均為液體)。

此系統通常作為太空船之推進劑，若將此二物質以化學計量比例混合，則其產物僅為N2、 CO2及Η2Ο (全部為氣態)。

試問燃燒1莫耳的(CH3)2NNH2將產生多少莫耳的氣體。

(A) 8 (B) 9 (C) 10 (D) 11 (E) 12 .6.下列那一個元素有最大的第三游離能?(A) B (B) C (C) N (D) Mg (E) Al7.下表中為某元素的前六個游離能(IE)數值(單位為 eV)，試問此元素(第二週期中)為何?IE1IE2IE3IE4IE5IE611 24 48 64 392 490(A) B (B) C (C) N (D) O (E) F8.在某一濃度與溫度狀況下，HNO3與 Zn 作用，生成了Zn(NO3)2，NO2及NO，若產物中NO2及NO莫耳數比為1:3，試問1莫耳的Zn總共要消耗多少莫耳的 HNO3?(A) 2.2 (B) 2.4 (C) 2.6 (D) 2.8 (E) 3.0 (F) 3.29.一碳氫化合物含有85.6%的碳與14.4%的氫，此氣體在STP下的密度為3.75g/L。

2019年台湾地区初中教育会考(第一次中考)数学科题本与解析

2019年台湾初中教育会考(第一次中考) 数学科题本与解析(2019年5月18日 10:50~12:10)第一部分：选择题 (1~27题)1. 算式( 6 + 10 ⨯ 15 ) ⨯ 3 之值为何？(A) 242 (B) 12 5 (C) 1213 (D) 18 2 [解] 原式=3 2 +15 2 =18 2 。

答：(D)。

◎ 方根运算基本2. 若A 为一数，且A =25 ⨯76 ⨯114，则下列选项中所表示的数，何者是A 的因子？ (A) 24 ⨯5 (B) 77 ⨯113 (C) 24 ⨯74 ⨯114 (D) 26 ⨯76 ⨯116 [解] 答：(C)。

◎ 因子, 指数基本3. 如图(一)，梯形ABCD 中，AD ￣ // BC ￣，E 点在BC ￣上，且AE ￣ ⊥ BC ￣。

若AB ￣=10，BE ￣=8，DE ￣=6 3 ，则AD ￣的长度为何？(A) 8 (B) 9 (C) 6 2 (D) 6 3[解] 直角△ABE 中，AB ￣=10，BE ￣=8，⇒AE ￣=6。

直角△ADE 中，AE ￣=6，DE ￣=6 3 ，⇒AD ￣=6 2 。

答：(C)。

◎ 平行, 勾股基本4. 有一箱子装有3张分别标示4、5、6的号码牌，已知小武以每次取一张且取后不放回的方式，先后取出2张牌，组成一个二位数，取出第1张牌的号码为十位数，第2张牌的号码为个位数，若先后取出2张牌组成二位数的每一种结果发生的机会都相同，则组成的二位数为6的倍数的机率为何？ (A) 1 6 (B) 1 4 (C) 1 3 (D) 12[解] 每次取一张且取后不放回共有6种可能情况，其中组成的二位数为6的倍数只有54，故机率为 16 。

答：(A)。

◎ 机率基本5. 算式743 ⨯ 369 - 741 ⨯ 370之值为何？ (A) -3 (B) -2 (C) 2 (D) 3[解] 原式=743 ⨯(370-1) - 741 ⨯ 370=370⨯(743-741)-743=370⨯2-743= -3。

台湾省(新版)2024高考数学统编版(五四制)能力评测(预测卷)完整试卷

台湾省（新版）2024高考数学统编版（五四制）能力评测(预测卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题等差数列中，其前n项和为，则“”是“为递减数列”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件第(2)题某公司有家直营店，现需将箱货物运送至直营店进行销售，各直营店出售该货物以往所得利润统计如下表所示.根据此表，该公司获得最大总利润的运送方式有（）A．种B．种C．种D．种第(3)题已知两个圆锥的轴截面均为等边三角形，两个圆锥的表面积分别为，，体积分别为，.若，则（）A．2B．C．3D．4第(4)题若三棱锥的四个面都为直角三角形，且平面，，，则其外接球的表面积为（）A．B．C．D．第(5)题设集合，，则（）A．B．C．D．第(6)题在的展开式中，项的系数为（）A．B．C．D．第(7)题若函数既有极大值也有极小值，则（）A．B．C．D．第(8)题设集合S={x|x＞﹣2}，T={x|x2+3x﹣4≤0}，则（∁R S）∪T=（）A．（﹣2，1]B．（﹣∞，﹣4]C．（﹣∞，1]D．[1，+∞）二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知三棱锥，，为棱上一点，且，过点作平行于直线和的平面，分别交棱于．下列说法正确的是（）A．四边形为矩形B．四边形的周长为定值C．四边形的面积为定值D．当时，平面分三棱锥所得的两部分体积相等第(2)题下列命题正确的是（）A ．正实数x，y满足，则的最小值为4B．“”是“”成立的充分条件C．若随机变量，且，则D．命题，则p的否定：第(3)题若图像上存在两点，关于原点对称，则点对称为函数的“友情点对”（点对与视为同一个“友情点对”）.若，且，，，则（）A．有无数个“友情点对”B．恰有个“友情点对”C．D．三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知球是底面半径为4、高为的圆锥的内切球，若球内有一个内接正三棱柱，则当该正三棱柱的侧面积最大时，正三棱柱的体积为______．第(2)题方程组的增广矩阵是______________.第(3)题已知狄利克雷函数，黎曼函数，则_________.四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知函数．(1)若，求的极值；(2)当时，证明：不存在两个零点．第(2)题已知函数.(1)当时，求的单调区间；(2)若对恒成立，求a的取值范围.第(3)题在直角坐标系xOy中，直线l的参数方程是（t是参数）.在以O为极点，x轴正半轴为极轴的极坐标系中，曲线.（1）当，时，求直线l与曲线C的直角坐标方程；（2）当时，若直线l与曲线C相交于A，B两点，设，且，求直线l的倾斜角.第(4)题如图，在四棱锥中，底面四边形是平行四边形，平面，且，的中点为．(1)求证：平面平面；(2)求二面角的余弦值．第(5)题现已知甲、乙两公司员工月薪情况统计如下：甲公司月薪范围/千元频率0.20.40.30.1乙公司(1)根据上述信息，如果你是求职者，你会选择哪一家公司？说明理由；(2)已知甲公司员工月薪在8000—10000元的人数为300，乙公司员工月薪在8000—10000元的人数为400，求甲、乙两公司所有员工中，月薪不低于10000元的频率；(3)某猎头公司对1000名求职者的就业意愿进行了调查，得到如下统计表格：年龄结构就业意愿95后00后选择甲公司200250选择乙公司200350根据表格，是否有的把握认为“就业意愿与年龄结构有关”？附：（其中）.0.0500.0250.0100.0053.8415.0246.6357.879。

台湾省(新版)2024高考数学人教版考试(综合卷)完整试卷

台湾省（新版）2024高考数学人教版考试(综合卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题在平面四边形中，，，，，则的最大值为（）A．B．2C．3D．第(2)题设命题甲为“”，命题乙为“”，那么甲是乙的（）A．充分而不必要条件B．充分必要条件C．必要而不充分条件D．既不充分也不必要条件第(3)题已知抛物线的焦点为，则的值为（）A．B．C．1D．2第(4)题已知等差数列满足，，数列满足．记数列的前项和为，则使的的最小值为（）A．B．C．D．第(5)题已知集合，则（）A．B．C．D．第(6)题已知正方体的棱长为2，棱的中点为S，则三棱锥的外接球的表面积为（）A．B．C．D．第(7)题在三棱锥中，平面ABC，，与的外接圆圆心分别为，，若三棱锥的外接球的表面积为，设，，则的最大值是（）A．B．C．D．第(8)题已知函数图象与函数图象相邻的三个交点依次为A，B，C，且是钝角三角形，则的取值范围是（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题定义在上的偶函数满足，当时，.设函数，则下列结论正确的是（）A．的图象关于直线对称B．的图象在处的切线方程为C．D．的图象与的图象所有交点的横坐标之和为10第(2)题若，，，则（）A．B．C．D．第(3)题设等差数列的前项和是，若，则（）A ．B ．C ．D ．三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题知数列，，，，，则该数列的第3项是______，是它的第______项．第(2)题在边长为1的正三角形ABC 中，E ，F 分别为边AB ，AC 上的动点，满足，，且，则的最小值为___________，设点M ，N 满足，，若，则___________.第(3)题若命题“，”为真命题，则实数的取值范围为______．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题近年来，我国科技成果斐然，北斗三号全球卫星导航系统已开通多年，北斗三号全球卫星导航系统由24颗中圆地球轨道卫星、3颗地球静止轨道卫星和3颗倾斜地球同步轨道卫星，共30颗卫星组成．北斗三号全球卫星导航系统全球范围定位优于，实测的导航定位精度都是2~3m ，全球服务可用性，亚太地区性能更优．现从地球静止轨道卫星和倾斜地球同步轨道卫星中任选两颗进行信号分析．(1)求恰好选择了地球静止轨道卫星和倾斜地球同步轨道卫星各一颗的概率；(2)求至少选择了一颗倾斜地球同步轨道卫星的概率．第(2)题已知．（1）若，解不等式；（2）若不等式无解，求实数a 的取值范围．第(3)题已知等比数列的公比，前项和为（）.数列是等差数列，且满足，，，.（1）求数列和的通项公式；（2）记，证明：当时，.第(4)题对于定义域为的函数，若存在实数使得对任意恒成立，则称函数具有性质.(1)判断函数与是否具有性质，若具有性质，请写出一个的值，若不具有性质，请说明理由；(2)若函数具有性质，且当时，，解不等式；(3)已知函数，对任意，恒成立，若由“具有性质”能推出“恒等于”，求正整数的取值的集合.第(5)题一盒中装有12个球，其中5个红球，4个黑球，2个白球，1个绿球．从中随机取出1球，求：(1)取出1球是红球或黑球的概率；(2)取出1球是红球或黑球或白球的概率．。

台湾省(新版)2024高考数学统编版能力评测(备考卷)完整试卷

台湾省（新版）2024高考数学统编版能力评测(备考卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题设集合A＝{x|－1＜x＜2}，集合B＝{x|1＜x＜3}，则A∪B＝A．{x|－1＜x＜3}B．{x|－1＜x＜1}C．{x|1＜x＜2}D．{x|2＜x＜3}第(2)题下列四个条件中，p是q的必要不充分条件的是 ( )A．p：a>b　q：a2>b2B．p：a>b　q：2a>2bC．p：ax2＋by2＝c为双曲线　q：ab<0D．p：ax2＋bx＋c>0　q：＋＋a>0第(3)题已知函数，，若函数在区间上恰有两个不同的零点，则实数的取值范围（）A．B．C．D．第(4)题设i是虚数单位，则复数A．-i B．-3i C．i D．3i第(5)题(2015新课标全国Ⅰ理科)=A．B．C．D．第(6)题某班四名同学去学校食堂就餐，他们在食堂一楼、二楼、三楼都可能就餐，如果他们中有同学在一楼就餐，则他们在食堂各层楼的就餐情况有（）种A．24B．37C．48D．65第(7)题如图，在中，，，是边的中点，过点作于点，延长交于点，则（）A．B．C．D．第(8)题在直角中，是斜边上的高，则下列等式不成立的是A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题若，则的值可能是（）A．B．C ．2D ．3第(2)题已知圆，点在直线上，若在圆上存在一点，使得，则满足条件的的值可能为（）A ．0B ．1C ．2D．第(3)题某个家庭中有若干个小孩，假定生男孩和生女孩是等可能的，设M =“该家庭中有男孩、又有女孩”，N =“该家庭中最多有一个女孩”，则下列结论正确的是()A ．若该家庭中有两个小孩，则M 与N 互斥B ．若该家庭中有两个小孩，则M 与N 不相互独立C ．若该家庭中有三个小孩，则M 与N 不互斥D ．若该家庭中有三个小孩，则M 与N 相互独立三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题如图，已知和是圆的两条弦，过点作圆的切线与的延长线相交于.过点作的平行线与圆交于点,与相交于点,,,,则线段的长为_____________第(2)题在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c，且．若角C 的平分线交AB 于D 点，且，则的最小值为______．第(3)题一工厂生产了某种产品16800件，它们来自甲、乙、丙3条生产线，为检查这批产品的质量，决定采用分层抽样的方法进行抽样，已知甲、乙、丙三条生产线抽取的个体数组成一个等差数列，则乙生产线生产了_____件产品．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线（为参数）．(1)求的极坐标方程；(2)已知点，曲线的极坐标方程为，与的交点为，与的交点为，，求的面积．第(2)题已知函数，，.（1）当时，存在,，使得成立，求实数的取值范围；（2）证明：当时，对任意，都有.第(3)题如图，在三棱锥中，是边长为的等边三角形，，是的中点，．(1)证明：平面平面；(2)若，求点到平面的距离．第(4)题已知函数，其中a为正实数．（1）若函数在处的切线斜率为2，求a的值；（2）若函数有两个极值点，，求证：．第(5)题已知等差数列的前项和为．（1）请从下面的三个条件中选择两个作为已知条件，求数列的通项公式；①；②；③；注：如果采用多种条件组合作答，则按第一个解答计分.（2）在（1）的条件下，令，求数列的前项和．。

台湾指考数学真题答案解析

台湾指考数学真题答案解析1. 前言台湾指考是台湾地区高中生进行升学考试的重要内容之一，其中数学部分被认为是相对较难的一部分。

本文将针对近年来的数学真题进行解析，帮助考生更好地掌握考点和解题技巧。

2. 解析篇2.1 选择题解析在选择题中，考生常常会遇到一些看似简单但实际上需要一定思维方式的题目。

例如，一道常见的平面几何题目是求解两直线之间的夹角。

在解决这类问题时，考生需要先明确两直线的斜率，然后利用斜率之间的关系求解夹角。

2.2 解答题解析解答题往往需要考生深入理解题目要求和解题方法。

例如，一道较难的函数题目要求考生求函数的反函数。

在解决这类问题时，考生需要充分理解函数的定义、反函数的性质，运用函数的图像、方程和性质来推导反函数的表达式。

2.3 应用题解析应用题往往是考察学生将数学理论与实际问题相结合的能力。

例如，一道常见的几何应用题是求解两点的距离。

在解决这类问题时，考生需要利用勾股定理或坐标系来计算距离，同时要注意将题目中涉及的实际情境与数学理论相结合。

3. 考点总结3.1 平面几何平面几何是数学中的重要内容之一，包括直线、角度、相似、圆等知识点。

通过分析真题，可以发现常考的平面几何考点主要包括：平行线、垂直线、相似三角形、圆的性质等。

对于这些考点，考生需要熟练掌握定义、定理和推导过程，灵活运用解题方法。

3.2 函数、方程与不等式函数、方程与不等式是数学中的基础内容，也是指考数学中的重点内容之一。

通过分析真题，可以发现常考的函数、方程与不等式考点主要包括：一次函数、二次函数、指数函数、对数函数、三角函数、复合函数等。

对于这些考点，考生需要掌握函数图像、方程与不等式的性质、解题方法和应用情境。

3.3 统计与概率统计与概率是数学中的实际应用内容，也是指考数学中的重要内容之一。

通过分析真题，可以发现常考的统计与概率考点主要包括：数据的收集与整理、概率计算、统计推断等。

对于这些考点，考生需要熟悉数据处理的方法、概率计算的原理和统计推断的过程，能够灵活应用于实际问题的解决。