2016年安徽自主招生数学模拟题：抛物线

合集下载

(完整word版)2016年安徽省淮南一中自主招生试题数学(无答案)

2016年淮南一中自主招生试题数学一、选择题（共4小题，每题4分，满分16分）1.已知，且，，，00><∈b a R c b a 则下列不等式中一定成立的是( )A.22b a <B.22bc ac >C. b a 11>D. a b a 11>- 2.抛物线2ax y =与直线，，，，2131====y y x x 围成的长方形有公共点，则实数a 的取值范围（）A.191≤≤a B.291≤≤a C.131≤≤a D. 231≤≤a3.若1>b 且a 是正有理数，，32=+-a a bb 则a a b b --的值是（） A ．22B ．3C ．10D ．32 4.若，⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=2222201611...411311211S 则S 的值为（） A ． 20162013 B ．20162015 C ．40322015 D ． 40322017 二、填空题（共4小题，每题4分，满分16分）5.若关于x 的方程0342=-+x ax 有唯一实数解，则a 的值为________.6.已知，1223=++c b a 且bc ac ab c b a ++=++222则=--c b a 23_________.7.已知函数，322--=x x y 则使m y =成立的x 值恰好有三个，则m 的值为________8.如图，AB 是半圆O 的直径，弦AD 、BC 相交于点P ，且CD 、AB 是一元二次方程01582=+-x x 的两根，则=∠APC sin ________.三、解答题（共4题，满分48分）9.（10分）已知ABC ∆的两边AC AB 、的长是关于x 的一元二次方程()0655222=++++-k k x k x 两个实数根，第三边长为5。

（1）当k 为何值时，△ABC 是以BC 为斜边的直角三角形；（2）当k 为何值时，△ABC 是等腰三角形，并求出此时△ABC 的周长．10.（12分）如图，在梯形ABCD 中，DC AB //，︒=∠90BCD ，且AB=2，BC=3，3tan =∠ADC .（1）求证：DC=BC ；（2）E 是梯形内的一点，F 是梯形外的一点，且，，BF DE FBC EDC =∠=∠试判断ECF ∆的形状，并证明你的结论。

安徽2016中考数学模拟考试试题

安徽省2016年初中毕业学业考试数学模拟试题一、选择题（本大题共10小题，每小题4分，满分40分） 1．在实数032-，｜－2｜中，最小的数是 ( ) A ．32-B ．0C D ．｜－2｜2．为了实现街巷硬化工程高质量“全覆盖”，我省今年1﹣4月公路建设累计投资92．7亿元，该数据用科学记数法可表示为( )A ． 0.927×1010B ．92.7×108C ．9.27×1010D ．9.27×109 3．下列运算正确的是 ( )A ．222()a b a b -=- B ． 11()33-= C ． 3(2)8-= D ．633a a a -=4．在数轴上表示不等式组102x +>⎧⎨的解集，正确的是 ( )A.B.C.D.5．下列函数：①y x =-；②2y x =；③1y x=-；④2y x =．当0x <时，y 随x 的增大而减小的函数有 ( )A ．1 个B ．2 个C ．3 个D ．4 个 6．如图，点O 是线段BC 的中点，点A 、D 、C 到点O 的距离相等。

若30=∠ABC °，则ADC ∠的度数是 ( )A ．30°B ．60°C ．120°D ．150°7．如图三棱柱ABC -111C B A 的侧棱长和底面边长均为2，且侧棱⊥1AA 底面ABC ，其主视图是边长为2的正方形，则此三棱柱左视图的面积为 ( ) A ．3B ．23C ．22D ．4（第6题）（第7题）（第8题）8．古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”，而把1、4、9、16 … 这样的数称为“正方形数”．从图8中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是 ( ) A ．13 = 3+10B ．25 = 9+16C ．36 = 15+21D ．49 = 18+319．某市2012年国内生产总值（GDP ）比2011年增长了12%，由于受到国际金融危机的影响，预计今年比2012年增长7%，若这两年GDP 年平均增长率为x %，则x %满足的关系是 ( )A ．12%7%%x +=B ．(112%)(17%)2(1%)x ++=+C ．%2%7%12x =+D ．2(112%)(17%)(1%)x ++=+10．二次函数)0(12≠++=a bx ax y 的图象的顶点在第一象限，且过点（﹣1，0）．设1++=b a t 则t 值的变化范围是 ( ) A ．10<<tB ．20<<tC ．21<<tD ．11<<-t二、填空题（本大题共4小题，每小题5分，满分20分） 11. 因式分解：39ab ab -．12. 甲、乙两名射击运动员在一次训练中，每人各打10发子弹，根据命中环数求得为方差6.0=甲s ，8.0=乙s ，则运动员的成绩比较稳定．13．如图，在平面直角坐标系中，⊙P 的圆心是（2，a ）(a ＞2)，半径为2，函数x y =的图象被⊙P 所截得的弦AB 的长为a 的值是．14. 如图，在△ABC 中，∠ABC 和∠ACB 的平分线相交于点O ，过点O 作EF ∥BC 交AB 于E ，交AC 于F ，过点O 作OD ⊥AC于D ．下列四个结论：①∠BOC ＝90º＋ 12∠A ； ②EF=BE+CF ；③设OD ＝m ，AE ＋AF ＝n ，则S △AEF ＝21mn ； ④EF是△ABC 的中位线．其中正确的结论是_____________．（第13题）（第14题）三、（本大题共2小题，每小题8分，满分16分）15．先化简，再求值：(21+a -1)÷212+-a a ，其中a ＝13+16．小民在教学楼的点P 处观察对面的办公大楼．为了测量点P 到对面办公大楼上部 AD 的距离，小强测得办公大楼顶部点A 的仰角为45°，测得办公大楼底部点B 的俯角为60°，已知办公大楼高46米，CD ＝10米．求点P 到AD 的距离（用含根号的式子表示）．四、（本大题共2小题，每小题8分，满分16分）17. 如图所示，正方形网格中，ABC △（1）把ABC △沿BA 方向平移后，点A 移到点1A ，在网格中画出平移后得到的11A B C 1△；（2）把11A B C 1△绕点1A 按逆时针方向旋转90°，在网格中画出旋转后的22A B C 1△（3）如果网格中小正方形的边长为1，求点B 经过（1）、（2）变换的路径总长．18．为实施“留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成了如下两幅不完整的统计图：（1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；（2）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．五、（本大题共2小题，每小题10分，满分20分） 19．已知一次函数m x y +=1的图象与反比例函数xy 62=的图象交于A 、B 两点，已知当1>x 时，21y y >；当10<<x 时，21y y <.（1）求一次函数的解析式；（2）已知双曲线在第一象限上有一点C 到y 轴的距离为3，求ABC ∆的面积.20．已知：如图，在平行四边形ABCD 中，点M 在边AD 上，且DM AM =．CM 、BA 的延长线相交于点E ．求证：（1）AB AE =；（2）如果BM 平分ABC ∠，求证：CE BM ⊥．六、（本题满分12分） 21．(1)解下列方程：①32=+x x 根为；②56=+x x 根为；③712=+xx 根为； (2)根据这类方程特征，写出第n 个方程为，其根为．(3)请利用(2)的结论，求关于x 的方程4232+=-++n x nn x （n 为正整数）的根．七、（本题满分12分）22．为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元．该产品每月销售量y （万件）与销售单价x （元）之间的函数关系如图所示．（1）求月销售量y （万件）与销售单价x （元）之间的函数关系式；（2）当销售单价定为50元时，为保证公司月利润达到5万元（利润＝销售额－生产成本－员工工资－其它费用），该公司可安排员工多少人？（3）若该公司有80名员工，则该公司最早可在几个月后还清无息贷款？八、（本题满分14分）23．在锐角△ABC 中，AB =4，BC =5，∠ACB =45°，将∆ABC 绕点B 按逆时针方向旋转，得到∆A 1BC 1．（1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数；（2）如图2，连接AA 1，CC 1．若△ABA 1的面积为4，求∆CBC 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在∆ABC 绕点B 按逆时针方向旋转过程中，点P 的对应点是点P 1，求线段EP 1长度的最大值与最小值．2014年安徽省中考数学仿真模拟试卷参考答案与试题解析一、选择题1．（4分）（2014•安徽模拟）在实数0，﹣，，|﹣2|中，最小的是（B）﹣2．（4分）（2012•山西）为了实现街巷硬化工程高质量“全覆盖”，我省今年1﹣4月公路建设累计投资92.7亿元，该数据用科学记数法可表示为（D）3．（4分）（2014•安徽模拟）下列运算正确的是（B）C4．（4分）（2008•茂名）在数轴上表示不等式组的解集，正确的是（C）B5．（4分）（2011•黔南州）下列函数：①y=﹣x；②y=2x；③y=﹣；④y=x2（x＜0），y随x的增大而减小的函数有（B）6．（4分）（2014•安徽模拟）如图，O是线段BC的中点，A、D、C到O点的距离相等．若∠ABC=30°，则∠ADC的度数是（D）7．（4分）（2014•安徽模拟）如图，三棱柱ABC﹣A1B1C1的侧棱长和底面边长均为2，且侧棱AA1⊥底面ABC，其正（主）视图是边长为2的正方形，则此三棱柱侧（左）视图的面积为（B）8．（4分）（2009•河北）古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（C）9．（4分）（2009•安徽）武汉市2010年国内生产总值（GDP）比2009年增长了12%，由于受到国际金融危机的影响，预计今年比2010年增长7%，若这两年GDP年平均增长率为x%，则x%满足的关系是（D）10．（4分）（2012•乐山）二次函数y=ax+bx+1（a≠0）的图象的顶点在第一象限，且过点（﹣1，0）．设t=a+b+1，则t值的变化范围是（B）二、填空题（本大题共4小题，每小题5分，满分20分）11．（5分）（2014•安徽模拟）因式分解：9a3b﹣ab=ab（3a+1）（3a﹣1）．12．（5分）（2012•湖州）甲、乙两名射击运动员在一次训练中，每人各打10发子弹，根据命中环数求得方差分别是=0.6，=0.8，则运动员甲的成绩比较稳定．13．（5分）（2014•安徽模拟）在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y=x的图象被⊙P截得的弦AB的长为，则a的值是．AE=PD=a=PD+DC=2+．2+14．（5分）（2014•安徽模拟）如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC=90°+∠A；②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切；③设OD=m，AE+AF=n，则S△AEF=mn；④EF是△ABC的中位线．﹣∠°∠=AF m=（m=三、（本大题共2小题，每小题8分，满分16分）15．（8分）（2014•安徽模拟）先化简，再求值：（﹣1）÷，其中a=．﹣．16．（8分）（2012•资阳）小强在教学楼的点P处观察对面的办公大楼．为了测量点P到对面办公大楼上部AD的距离，小强测得办公大楼顶部点A的仰角为45°，测得办公大楼底部点B的俯角为60°，已知办公大楼高46米，CD=10米．求点P到（米））解得，=18四、（本大题共2小题，每小题8分，满分16分）17．（8分）（2009•本溪）如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．（1）把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；（2）把△A1B1C1绕点A1按逆时针方向旋转90°，在网格中画出旋转后的△A1B2C2；（3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．）=18．（8分）（2011•重庆）为实施“农村留守儿童关爱计划”，某校结全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：（1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；（2）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．解：（1）该校班级个数为4÷20%=20（个），只有2名留守儿童的班级个数为：20﹣（2+3+4+5+4）=2（个），该校平均每班留守儿童的人数为：=4（名），则所选两名留守儿童来自同一个班级的概率为：=五、（本大题共2小题，每小题10分，满分20分）19．（10分）（2012•德阳）已知一次函数y1=x+m的图象与反比例函数的图象交于A、B两点．已知当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2．（1）求一次函数的解析式；（2）已知双曲线在第一象限上有一点C到y轴的距离为3，求△ABC的面积．代入反比例函数解析式，=2，解得，=4+20．（10分）（2014•安徽模拟）已知：如图，在平行四边形ABCD中，点M在边AD上，且AM=DM．CM、BA的延长线相交于点E．求证：（1）AE=AB；（2）如果BM平分∠ABC，求证：BM⊥CE．，∴△AM=BE六、（本题满分12分）21．（12分）（2014•安徽模拟）（1）解下列方程：①根为x1=1，x2=2；②根为x1=2，x2=3；③根为x1=3，x2=4；（2）根据这类方程特征，写出第n个方程为x﹣3+=2n+1，其根为x1=n，x2=n+1．（3）请利用（2）的结论，求关于x的方程（n为正整数）的根．七、（本题满分12分）22．（12分）（2009•长沙）为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元．该产品每月销售量y（万件）与销售单价x（元）之间的函数关系如图所示．（1）求月销售量y（万件）与销售单价x（元）之间的函数关系式；（2）当销售单价定为50元时，为保证公司月利润达到5万元（利润=销售额﹣生产成本﹣员工工资﹣其它费用），该公司可安排员工多少人？（3）若该公司有80名员工，则该公司最早可在几个月后还清无息贷款？则，解得故y=×x+8﹣（（八、（本题满分14分）23．（14分）（2012•义乌市）在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．（1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；（2）如图2，连接AA1，CC1．若△ABA1的面积为4，求△CBC1的面积；（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．∴，∠∴；=。

2016年安徽省淮南一中自主招生试题数学(无答案)

2016年淮南一中自主招生试题25•若关于x 的方程ax 4x 3 0有唯一实数解，则a 的值为6.已知 3a 2b c 12,且 a 2 b 2 c 2 ab ac be 则 a 3 b 2 c ______________________ . 7•已知函数y x 2 2x 3,则使y m 成立的x 值恰好有三个，贝y m 的值为 ____________________ 8.如图，AB 是半圆O 的直径，弦ADBC 相交于点P,且CDAB 是一元二次方程 x 2 8x 15 0 的两根，则sin APC ________ .1.已知 a ， b ， c R ， a 0且 b 0,则下列不等式中一定成立的是（ )2 . 2 2 .21 1 1 1A. a bB. ac bcC.-- D. --------— a a b a b a22.抛物线y ax 与直线x 1, x 3, y 1, y 2,围成的长方形有公共点, 值范围（）1 , 1 1 1 cA. — a 1B.- a 2C.- a 1D. - a 29 9 3 3、选择题（共4小题，每题4分，满分16 分）a b a 的值是（ 3若b 1且a 是正有理数, ）则实数 a 的取2 3,则 b a b a 2.2 C . 10 D . 231 1 2013 2016 1 承… 2015 2016 丄乜，则S 的值为（2016 2015 C . 4032 20174032二、填空题（共 4小题，每题 4分，满分16分）三、解答题（共4题，满分48分）9. （10分）已知ABC的两边AB、AC的长是关于x的一元二次方程2 2x 2k 5 x k 5k 6 0两个实数根，第三边长为5。

（1 ）当k为何值时，△ ABC是以BC为斜边的直角三角形；（2）当k为何值时，△ ABC是等腰三角形，并求出此时△ ABC的周长.10. （12 分）如图，在梯形ABCD 中，AB//DC , BCD 90，且AB=2 , BC=3 , tan ADC 3. （1）求证：DC=BC ;（2）E是梯形内的一点，F是梯形外的一点，且EDC FBC, DE BF,试判断ECF的形状，并证明你的结论。

2016年安徽师大附中高中自主招生数学试卷

2016年安徽师大附中高中自主招生数学试卷一、选择题（本大题共6小题，每小题8分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（8分）设a，b，c的平均数为M，a与b的平均数为N，N与c的平均数为P，若a＞b＞c，则M与P的大小关系是（）A．M=P B．M＞P C．M＜P D．不能确定2．（8分）已知a＞b，且a≠0，b≠0，a+b≠0，则函数y=ax+b与y=同一坐标系中的图象一定不可能是（）A．B．C．D．3．（8分）如图，⊙O中，弦AD∥BC，DA=DC，∠BCO=15°，则∠AOC等于（）A．120°B．130°C．140° D．150°4．（8分）已知实数a≠b，且满足（a+1）2=3﹣3（a+1），3（b+1）=3﹣（b+1）2，则b+a的值为（）A．﹣23 B．23 C．13 D．﹣135．（8分）如果二次方程x2﹣px﹣q=0（其中p，q均是大于0的整数）的正根小于3，那么这样的二次方程有（）A．4个 B．5个 C．6个 D．7个6．（8分）如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为（）A．140°B．130°C．120° D．110°二、填空题（本大题共6小题，每小题0分，共48分）7．若函数f（x）=定义域为一切实数，则实数k的取值范围为．8．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n（n是大于0的整数）个图形需要黑色棋子的个数是．9．已知a、b、x、y都为实数，且y+|﹣2|=1﹣a2，|x﹣4|=3y﹣3﹣b2．则a+b+x+y 的值为．10．如图，正方形ABCD的边长为1，E是CD边外的一点，满足：CE∥BD，BE=BD，则CE=．11．实数x，y，z满足x+y+z=5，xy+yz+zx=3，则z的最大值是．12．如图，已知⊙O1、⊙O2的半径分别为r1、r2，⊙O2经过点O1，且两圆相交于点A、B，C为⊙O2上的点，连接AC交⊙O1于点D，再连接BC、BD、AO1、AO2、O1O2有如下四个结论：①∠BDC=∠AO1O2；②=③AD=DC ④BC=DC，其中正确结论的序号为．三．解答题（本题共3小题，每小题16分，共54分）答题应写出文字说明、证明过程或演算步骤）13．（16分）设[x]表示不超过x的最大整数，如[4.3]=4，[﹣4，3]=﹣5．化简：++…+（结果用n表示，其中n 是大于0的整数）．14．（18分）如图，在梯形PMNQ中，PQ∥MN，对角线PN和MQ相交于点O，并把梯形分成四部分，记这四部分的面积分别为S1，S2，S3，S4．试判断S1+S2和S3+S4的大小关系，并证明你的结论．15．（18分）如图，将OA=6，AB=4的矩形OABC放置在平面直角坐标系中，动点M，N以每秒1个单位的速度分别从点A，C同时出发，其中点M沿AO向终点O运动，点N沿CB向终点B运动，当两个动点运动了t秒时，过点N作NP ⊥BC，交OB于点P，连接MP．（1）点B的坐标为；用含t的式子表示点P的坐标为；（2）记△OMP的面积为S，求S与t的函数关系式（0＜t＜6）；并求t为何值时，S有最大值？（3）试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△ONC 分割成三角形和四边形两部分，且三角形的面积是△ONC面积的？若存在，求出点T的坐标；若不存在，请说明理由．2016年安徽师大附中高中自主招生数学试卷参考答案与试题解析一、选择题（本大题共6小题，每小题8分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（8分）（2016•镜湖区校级自主招生）设a，b，c的平均数为M，a与b的平均数为N，N与c的平均数为P，若a＞b＞c，则M与P的大小关系是（）A．M=P B．M＞P C．M＜P D．不能确定【解答】解：由题意得：a+b+c=3M，a+b=2N，N+c=2P；∴M=，又∵a＞b＞c，∴a+b＞2c，∴M﹣p=，∴M＞P；故选B．2．（8分）（2016•镜湖区校级自主招生）已知a＞b，且a≠0，b≠0，a+b≠0，则函数y=ax+b与y=同一坐标系中的图象一定不可能是（）A．B．C．D．【解答】解：A、由函数y=ax+b过一、三、四象限可知，a＞0，b＜0；由函数y=图象可知，a+b＞0，与已知a＞b，且a≠0，b≠0，a+b≠0，相吻合，故可能成立；B、由直线的图象知a＜0，b＜0，故a+b＜0，所以y=的图象在二四象限，C、由函数y=ax+b过一、三、四象限可知，a＞0，b＜0；由函数y=的图象可知，a+b＜0，与已知a＞b，且a≠0，b≠0，a+b≠0，相吻合，故可能成立；D、由函数y=ax+b过一、三、四象限可知，a＜0，b＜0；由函数y=的图象可知，a+b＜0，与已知a＞b，且a≠0，b≠0，a+b≠0，相吻合，故可能成立；故选：B．3．（8分）（2016•镜湖区校级自主招生）如图，⊙O中，弦AD∥BC，DA=DC，∠BCO=15°，则∠AOC等于（）A．120°B．130°C．140° D．150°【解答】解：连接AC，设∠AOC=2x∵∠B=∠AOC=x∴∠D=180°﹣x∵AD=CD，OA=OC∴∠DAC=∠ACD=x，∠OCA=∠OAC=90°﹣x∵AD∥BC∴∠ACB=∠DAC=x，∴∠BCO=x﹣（90°﹣x）=x﹣90°=15°，∴x=70°，∴∠AOC=140°．故选：C．4．（8分）（2016•镜湖区校级自主招生）已知实数a≠b，且满足（a+1）2=3﹣3（a+1），3（b+1）=3﹣（b+1）2，则b+a的值为（）A．﹣23 B．23 C．13 D．﹣13【解答】解：∵a、b是关于x的方程（x+1）2+3（x+1）﹣3=0的两个根，整理此方程，得x2+5x+1=0，∵△=25﹣4＞0，∴a+b=﹣5，ab=1．故a、b均为负数．因此b+a=﹣﹣=﹣=﹣=﹣23．故选A．5．（8分）（2016•镜湖区校级自主招生）如果二次方程x2﹣px﹣q=0（其中p，q 均是大于0的整数）的正根小于3，那么这样的二次方程有（）A．4个 B．5个 C．6个 D．7个【解答】解：由△=p2+4q＞0，﹣q＜0，知方程的根为一正一负．设f（x）=x2﹣px﹣q，则f（3）=32﹣3p﹣q＞0，即3p+q＜9．由于p，q均是正整数，所以p=1，q≤5或p=2，q≤2．于是共有7组（p，q）符合题意．故选：D．6．（8分）（2016•镜湖区校级自主招生）如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为（）A．140°B．130°C．120° D．110°【解答】解：如下图，作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值．作DA延长线AH，∵∠DAB=120°，∴∠HAA′=60°，∴∠AA′M+∠A″=∠HAA′=60°，∵∠MA′A=∠MAA′，∠NAD=∠A″，且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2（∠AA′M+∠A″）=2×60°=120°．故选：C．二、填空题（本大题共6小题，每小题0分，共48分）7．（2016•镜湖区校级自主招生）若函数f（x）=定义域为一切实数，则实数k的取值范围为[0，）．【解答】解：函数f（x）=定义域为一切实数，可转化为：∀x∈R，kx2+4kx+3≠0．令w=kx2+4kx+3，下面分三类求解：一类：当k=0，由于3≠0，显然符合题意二类：当k＞0，要想使二次函数w=kx2+4kx+3≠0，只需△＜0，即（4k）2﹣4×3×k＜0即三类：当k＜0，要想使二次函数w=kx2+4kx+3≠0，只需△＜0，即（4k）2﹣4×3×k＜0即（不合，舍去）综上所述：[0，）．故答案为：[0，）．8．（2016•镜湖区校级自主招生）如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n（n是大于0的整数）个图形需要黑色棋子的个数是n（n+2）．【解答】解：第1个图形是三角形，有3条边，每条边上有2个点，重复了3个点，需要黑色棋子2×3﹣3个，第2个图形是四边形，有4条边，每条边上有3个点，重复了4个点，需要黑色棋子3×4﹣4个，第3个图形是五边形，有5条边，每条边上有4个点，重复了5个点，需要黑色棋子4×5﹣5个，按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是（n+1）（n+2）﹣（n+2）=n（n+2）；故答案为n（n+2）．9．（2016•镜湖区校级自主招生）已知a、b、x、y都为实数，且y+|﹣2|=1﹣a2，|x﹣4|=3y﹣3﹣b2．则a+b+x+y的值为5．【解答】解：∵3（y﹣1）=|x﹣4|+b2≥0，∴y≥1，∵1﹣y=|﹣2|+a2≥0，∴y≤1，则y=1，∴x﹣4=0，即x=4，b=0，a=0，则a+b+x+y=0+0+4+1=5，故答案为：5．10．（2016•镜湖区校级自主招生）如图，正方形ABCD的边长为1，E是CD边外的一点，满足：CE∥BD，BE=BD，则CE=．【解答】解：，设CF=x，则，DF=1﹣x，EF=﹣，由△BDF～△ECF，得，即有，所以，，则，再由，即，所以，故答案为：11．（2016•镜湖区校级自主招生）实数x，y，z满足x+y+z=5，xy+yz+zx=3，则z 的最大值是．【解答】解：∵x+y=5﹣z，xy=3﹣z（x+y）=3﹣z（5﹣z）=z2﹣5z+3，∴x、y是关于t的一元二次方程t2﹣（5﹣z）t+z2﹣5z+3=0的两实根．∵△=（5﹣z）2﹣4（z2﹣5z+3）≥0，即3z2﹣10z﹣13≤0，（3z﹣13）（z+1）≤0．∴﹣1≤z≤，当x=y=时，z=；故z的最大值为；故答案为：．12．（2016•镜湖区校级自主招生）如图，已知⊙O1、⊙O2的半径分别为r1、r2，⊙O2经过点O1，且两圆相交于点A、B，C为⊙O2上的点，连接AC交⊙O1于点D，再连接BC、BD、AO1、AO2、O1O2有如下四个结论：①∠BDC=∠AO1O2；②=③AD=DC ④BC=DC，其中正确结论的序号为①②④．【解答】解：延长O2O1交圆O1于M，连接AB、AM、BM、O2B，∵圆O1与圆O2交于A、B，∴O2O1是AB的垂直平分线，∵O1A=O1B，∴∠AO1O2=∠AO1B=∠AMB，∵四边形AMBD是圆O1的内接四边形，∴∠AMB=∠BDC，∴①正确；∵O1A=O1B，∴∠C=∠AO2B=∠AO2M，∠AO1O2=∠AMB，∴△BDC∽△AO1O2，∴=，∴②正确；∵△BDC∽△AO1O2，∴∠O2AO1=∠DBC，∠BDC=∠AO1O2，∵O2A=O2B，∴∠AO1O2=∠O2AO1，∴∠DBC=∠BDC，∴DC=BC，∴④正确；无法证出∠C=∠DBC，即BD≠DC，∵AD=BD，∴③错误．故答案为：①②④．三．解答题（本题共3小题，每小题16分，共54分）答题应写出文字说明、证明过程或演算步骤）13．（16分）（2016•镜湖区校级自主招生）设[x]表示不超过x的最大整数，如[4.3]=4，[﹣4，3]=﹣5．化简：++…+（结果用n表示，其中n 是大于0的整数）．【解答】解：由题意，[x]表示不超过x的最大整数，设n为正整数，则，于是，，∴， ∴原式==．14．（18分）（2016•镜湖区校级自主招生）如图，在梯形PMNQ 中，PQ ∥MN ，对角线PN 和MQ 相交于点O ，并把梯形分成四部分，记这四部分的面积分别为S 1，S 2，S 3，S 4．试判断S 1+S 2和S 3+S 4的大小关系，并证明你的结论．【解答】解：设PQ=m ，MN=n ， ∵△PMN 和△QMN 同底等高， ∴S △PMN =S △QMN ，∴S 3+S 2=S 4+S 2，即：S 3=S 4． ∵△POQ ∽△NOM ， ∴，∴．∵S 1：S 3=OQ ：OM=m ：n ， ∴．∴（S 1+S 2）﹣（S 3+S 4）=S 1++S 2﹣2•S 1=S 1（1+﹣）=S 1（1﹣）2．∵，∴S 1+S 2＞S 3+S 4．15．（18分）（2016•镜湖区校级自主招生）如图，将OA=6，AB=4的矩形OABC放置在平面直角坐标系中，动点M，N以每秒1个单位的速度分别从点A，C同时出发，其中点M沿AO向终点O运动，点N沿CB向终点B运动，当两个动点运动了t秒时，过点N作NP⊥BC，交OB于点P，连接MP．（1）点B的坐标为（6，4）；用含t的式子表示点P的坐标为（）；（2）记△OMP的面积为S，求S与t的函数关系式（0＜t＜6）；并求t为何值时，S有最大值？（3）试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△ONC 分割成三角形和四边形两部分，且三角形的面积是△ONC面积的？若存在，求出点T的坐标；若不存在，请说明理由．【解答】解：（1）由题意，OA=6，AB=4，∴B（6，4）；延长NP角AB与Q，NB=6﹣t，则OQ=t，设QP=x，则NP=4﹣x，△OPQ和△NPB相似，即可得x=∴P（），=×OM×，（2）∵S△OMP∴S=×（6﹣t）×=t2+2t=（0＜t＜6）．∴当t=3时，S有最大值．（3）存在．由（2）得：当S有最大值时，点M、N的坐标分别为：M（3，0），N（3，4），则直线ON的函数关系式为：y=．设点T 的坐标为（0，b ），则直线MT 的函数关系式为：y=，解方程组，得∴直线ON 与MT 的交点R 的坐标为．∵S △OCN =×4×3=6，∴S △ORT =S △OCN =2．①当点T 在点O 、C 之间时，此时T 记为T 1，分割出的三角形是△OR 1T 1，如图，作R 1D 1⊥y 轴，D 1为垂足，则S △OR1T1=R 1D 1•OT=••b=2．∴3b 2﹣4b ﹣16=0，b=．∴b 1=，b 2=（不合题意，舍去）此时点T 1的坐标为（0，）．②当点T 在OC 的延长线上时，分割出的三角形是△R 2NE ，如图，设MT 交CN 于点E ，∵点E 的纵坐标为4，∴由①得点E 的横坐标为，作R 2D 2⊥CN 交CN 于点D 2，则 S △R2NE =•EN•D 2=••==2．∴b 2+4b ﹣48=0，b=．∴b 1=﹣2，b 2=（不合题意，舍去）．∴此时点T 2的坐标为（0，）．综上所述，在y 轴上存在点T 1（0，），T 2（0，）符合条件．参与本试卷答题和审题的老师有：刘老师；lcb001；whgcn；zlzhan；lily2011；danbo7801；左杰（排名不分先后）菁优网2017年5月25日。

2016年安徽自主招生数学模拟试题：参数方程与普通方程的互化

2016年某某自主招生数学模拟试题:参数方程与普通方程的互化【试题内容来自于相关和学校提供】1：曲线(为参数)的焦距是( )A、3B、6C、8D、102：若直线的参数方程为（为参数），则直线的斜率为（）A、B、C、D、3：曲线的参数方程为(t是参数)，则曲线是（）A、线段B、直线C、圆D、射线4：曲线的参数方程为(t是参数)，则曲线是（）A、线段B、双曲线的一支C、圆D、射线5：若直线的参数方程为，则直线的斜率为（）A、B、C、D、6：（坐标系与参数方程选做题）直线(为参数)与曲线(为参数)的交点个数为____________.7：在直角坐标系中,曲线的参数方程为（t为参数），在极坐标系（与直角坐标系取相同的长度单位，且以原点为极点,以轴正半轴为极轴）中，曲线的极坐标方程为,则与的两个交点之间的距离等于.8：在直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系.已知直线与曲线（为参数）相交于A,B两点，若为线段AB的中点，则直线OM的斜率为_______.9：已知直线（为参数），（为参数）, 若，则实数。

10：在平面直角坐标系中，直线的参数方程为（参数），圆的参数方程为（参数），则圆心到直线的距离为_______.11：以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的长度单位。

已知直线的参数方程为 (t 为参数，0<><>)，曲线C的极坐标方程为。

（I）求曲线C的直角坐标方程；（II）设直线l 与曲线C相交于A、B两点，当a变化时，求|AB|的最小值。

<>12：已知曲线的极坐标方程是，直线的参数方程是（为参数）。

（Ⅰ）将曲线的极坐标方程化为直角坐标方程；（Ⅱ）设直线与轴的交点是,是曲线上一动点,求的最大值.13：(本题满分12分)（学选修4-4的选做题1，没学的选做题2）题1：已知点M是椭圆C:+ ＝1上的任意一点,直线l:x+2y-10＝0.(1)设x＝3cosφ,φ为参数,求椭圆C的参数方程；(2)求点M到直线l距离的最大值与最小值.14：选修4—4:坐标系与参数方程(本题满分l0分)在直角坐标系中，以O为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为。

(2021年整理)2016年安徽自主招生数学模拟试题：程序框图

(完整版)2016年安徽自主招生数学模拟试题：程序框图编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)2016年安徽自主招生数学模拟试题：程序框图）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)2016年安徽自主招生数学模拟试题：程序框图的全部内容。

（完整版）2016年安徽自主招生数学模拟试题：程序框图编辑整理：张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是我们任然希望（完整版）2016年安徽自主招生数学模拟试题:程序框图这篇文档能够给您的工作和学习带来便利。

同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉,前进的动力.本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为〈（完整版)2016年安徽自主招生数学模拟试题：程序框图〉这篇文档的全部内容。

2016年安徽自主招生数学模拟试题:程序框图【试题内容来自于相关网站和学校提供】1：阅读右图所示的程序框图，运行相应的程序，若,则输出的值为 ( ）A、3B、4C、5D、62：阅读右边的程序框图，运行相应的程序，当输入x的值为-25时，输出x的值为A、-1B、1C、3D、93：执行下面的程序框图，如果输入的t∈［－1，3］，则输出的s属于( )A、[－3,4］B、［－5,2]C、[－4，3］D、[－2,5]4：右图给出的是计算的值的一个程序框图，判断其中框内应填入的条件是( ）A、B、C、D、5：某算法的程序框图如图所示，则输出S的值是（）A、6B、24C、120D、8406:下图是选修1－2中《推理与证明》一章的知识结构图, 请把“①合情推理”,“②类比推理”,“③综合法"，“④反证法”填入适当的方框内.（填序号即可）A填___ _B填_____ _C填_____ _D填________7:如图是一个算法的程序框图,若输出的结果是31，则判断框中的正整数的值是___________。

2016年168中学自主招生数学试题

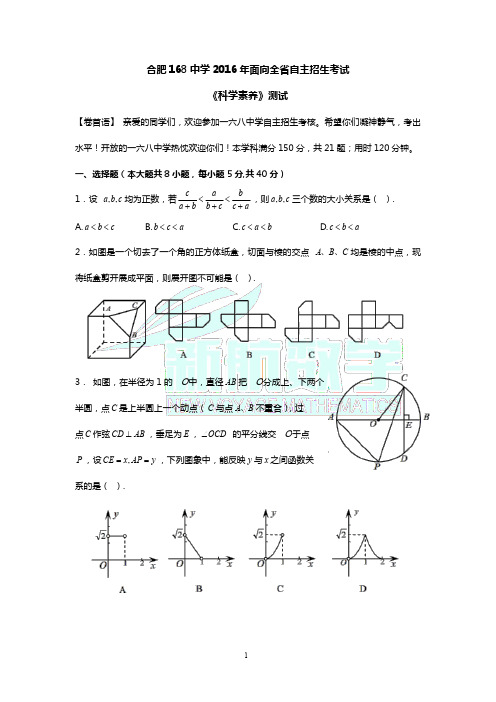
1．设
a,b, c
均为正数，若
a
c
b

b
a
c

c
b
a
，则
a,b, c
三个数的大小关系是（
）.
A. a b c
B. b c a
C. c a b
D. c b a
2．如图是一个切去了一个角的正方体纸盒，切面与棱的交点 A、B、C 均是棱的中点，现
将纸盒剪开展成平面，则展开图不可能是（）．
差 10 米，乙距离终点差 20 米；甲到达终点时，乙距离终点差 10.1 米，经过计算，这条跑
道长度不标准，则这条跑道比 1000 米多______米. 14．如图，在 ABC 中， AB AC 15, cosBAC 4 ,点 D 在
5 边 AB 上，且 AD 2BD ,点 E 是边 AC 上的一个动点，把 ADE
95 D. 5
5．如图，矩形 ABCD 被分成 8 块，图中的数字是其中 5 块的面积数，则图中阴影部分的
面积为（）.
A．80
B．85
C . 90
D．95
6．已知 a 为实常数，关于 x 的方程 a2 2a x2 4 6a x 8 0 的解都是整数，则 a 的值的
个数为（）
1
4．如图，在 AOB 中，已知 AOB 90o ， AO 3, BO 6 ，将 AOB 绕顶点 O 逆时针旋转
到 A'O ' B ' 处，此时线段 A' B ' 与 BO 的交点 E 为 BO 的中点，那么线段 B ' E 的长度为( ).
A. 6 5 5
75 B. 5

2016安徽中考数学模拟试题及答案

2015安徽省模拟中考数学一、选择题（本题共10 小题，每小题4 分，满分40分）每一个小题都给出代号为A 、B 、C 、D 的四个结论，其中只有一个是正确的，把正确结论的代号写在题后的括号。

每一小题：选对得 4 分，不选、选错或选出的代号超过一个的（不论是否写在括号内）一律得0分。

1.34相反数是【】 A.43 B.43- C.34 D. 34-2.今年“五一”黄金周，我省实现社会消费的零售总额约为94亿元。

若用科学记数法表示，则94亿可写为【】A.0.94×109B. 9.4×109C. 9.4×107D. 9.4×1083. 如图，直线1l ∥2l ，∠1＝550，∠2＝650，则∠3为【】A ）500. B ）550C ）600D ）6504.如图，在⊙O 中，∠ABC=50°，则∠AOC 等于【】A.50°B.80°C.90°D. 100°5. 分式方程112x x =+的解是【】 A. x=1 B. x=－1 C. x=2 D. x=－26.如图是某几何体的三视图及相关数据，则判断正确的是…【】A. a ＞cB. b ＞cC. 4a 2+b 2=c 2D. a 2+b 2=c 27.如图，已知AB ∥CD ，AD 与BC 相交于点P ，AB=4，CD=7，AD=10，则AP 的长等于【】A.4011 B.407 C.7011 D. 7048.挂钟分针的长10cm ，经过45分钟，它的针尖转过的弧长是【】 A.152cm p B. 15cm p C. 752cm pD. 75cm p9.一张正方形的纸片，剪去两个一样的小矩形得到一个“E”图案，如图所示，设小矩形的长和宽分别为x 、y ，剪去部分的面积为20，若2≤x≤10，则y 与x 的函数图象是…【】 10.如图，△PQR 是⊙O 的内接正三角形，四边形ABCD 是⊙O 的内接正方形，BC ∥QR ，则∠AOQ=【】A.60°B. 65°C. 72°D. 75° 二、填空题（本题共 4 小题，每小题 5 分，满分 20 分） 11. 不等式组⎩⎨⎧≤-<+-843,24x x 的解集是_______________.12.如图，已知∠1=100°，∠2=140°，那么∠3=______13. 如图，AD 是△ABC 的边BC 上的高，由下列条件中的某一个就能推出△ABC 是等腰三角形的是__________________。

2016安徽中考数学模拟试卷、答案

2016安徽中考数学模拟试卷题号一二三四五六七八总分得分考生注意：本卷共八大题，23小题，满分150分，考试时间120分钟一、选择题(本大题共10小题，每小题4分，满分40分)每小题都给出了A 、B 、C 、D 四个选项，其中只有一个是正确的，请把正确选项的代号写在题后的括号内，选对得4分，不选、错选或选出的代号超过一个的（不论是否写在括号内）一律得0分．题号 1 2 3 4 5 6 7 8 9 10 答案1. 计算36---的结果为【】A .－9 B .－3 C .3 D .92.计算 (m 3)2÷m 3的结果等于【】A ．2m B ．3m C ．4m D ．6m 3.某几何体的主视图和左视图均如左下图所示，则该几何体的俯视图不可能是【】4.下列整式中能直接运用完全平方公式分解因式的为【】A ．21x - B ．221x x ++ C ．232x x ++ D ．22x y +5.不等式组215,3112x x x -<⎧⎪⎨-+≥⎪⎩的解集在数轴上表示正确的是【】6.如图，在ABC ∆中，DE ∥BC ，12AD DB =，4DE =，则BC 的长是【】 A ．8 B ．10 C ．11 D ．127.某奥体中心的构造如图所示，其东、西面各有一个入口A 、B ，南面为出口C ，北面分别有两个出口D 、E .聪聪若任选一个入口进入，再任选一个出口离开，那么他从入口A 进入并从北面出口离开的概率为【】 A ．16 B ．15 C ．13D ．12班级姓名考场号座位号学号………………………………装………………………………订………………………………线………………………………8. 如图，直径为10的⊙A经过点C(0,5)和点O(0,0)，B是y轴右侧⊙A优弧上一点，则tan OBC∠的值为【】A．12B．32C ．33D．39.如下左图，矩形ABCD中，AB＝1，BC＝2，点P从点B出发，沿B→C→D向终点D匀速运动，设点P走过的路程为x，ABP∆的面积为S，能正确反映S与x之间函数关系的图象是【】10.如图所示，在33⨯的网格中，每个网格线的交点称为格点，已知图中A、B为两格点，请在图中再寻找另一格点C，使ABC∆成为等腰三角形.则满足条件的C点的个数为【】A．10个B．8个C．6个D．4个二、填空题（本大题共4小题，每小题5分，满分20分）11.2015年3月29日，习近平同出席博鳌亚洲论坛年会的中外企业家代表座谈时说：通过“一带一路”，我们希望用10年左右的时间，使中国同沿线国家的年贸易额突破2.5万亿美元，2.5万亿用科学记数法表示为： .12. 已知关天x的一元二次方程2(1)10m x x-++=有实数根，则m的取值范围是．13.已知，△ABC，按如下步骤作图：（1）以A为圆心，AC长为半径画弧；（2）以B为圆心，BC长为半径画弧，与前一条弧相交于点D，（3）连接CD.若AC=6，CD=8，则sin∠CAB= ．第10题图第8题图第7题图第6题图14.将矩形纸片ABCD 折叠，使点B 落在边CD 上的B '处，折痕为AE ，过B '作B P '∥BC ，交AE 于点P ，连接BP .已知BC ＝3，1CB '=，下列结论：①AB ＝5；②3sin 5ABP ∠=；③四边形BEB P '为菱形；④1ECB S S ''∆-=四边形BEB P ，其中正确的是 .（把所有正确结论的序号都填在横线上）三、（本大题共2小题，每小题8分，满分16分） 15.计算：2011(2)1(2015)()2π----+--.16. 我们学习了勾股定理后，都知道“勾三、股四、弦五” ．观察：3、4、5； 5、12、13； 7、24、25； 9、40、41；……，发现这些勾股数的勾都是奇数，且从3起就没有间断过．（1）请你根据上述的规律写出下一组勾股数：；（2）若第一个数用字母n （n 为奇数，且3n ≥）表示，那么后两个数用含n 的代数式分别表示为和，请用所学知识说明它们是一组勾股数．四、（本大题共2小题,每小题8分,满分16分）17. 如图,在正方形网络中，△ABC 的三个顶点都在格点上，点A 、B 、C 的坐标分别为（－2，4）、（－2，0）、（－4，1），结合所给的平面直角坐标系解答下列问题：（1）画出△ABC 关于原点O 对称的△A 1B 1C 1．（2）平移△ABC ，使点A 移动到点A 2（0，2），画出平移后的△A 2B 2C 2并写出点B 2、C 2的坐标．第14题图第13题图（3）在△ABC 、△A 1B 1C 1、△A 2B 2C 2中，△A 2B 2C 2与成中心对称，其对称中心的坐标为．18.合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面，自A 点看壁画上部D 的仰角为045，看壁画下部C 的仰角为030，求壁画CD 的高度.（参考数据：3 1.7≈，2 1.4≈，精确到十分位）五、（本大题共2小题，每小题10分，满分20分） 19. 在平面直角坐标系XOY 中，一次函数223y x =-+的图象与反比例函数ky x=(0k ≠)的图象交于二、四象限内的A 、B 两点，若点A 纵、横坐标绝对值的比为4:3．（1）求反比例函数解析式；（2）求△AOB 的面积．学号……………………………20.如图，AB 是O e 的切线，B 为切点，圆心O 在AC 上，030A ∠=，D 为»BC的中点.（1）求证：AB ＝BC .（2）试判断四边形BOCD 的形状，并说明理由.六、（本题满分12分）21.由于各地雾霾天气越来越严重，2015年春节前夕，蚌埠市某校团委向全校3000名学生发出“减少空气污染，少放烟花爆竹”倡议书，并围绕“A 类：不放烟花爆竹；B 类：少放烟花爆竹；C 类：不会减少烟花爆竹数量；D 类：使用电子鞭炮”四个选项对100名学生进行问卷调查，并将调查结果绘制成如下两幅统计图表（不完整），请根据图表，回答下列问题：（1）表格中a = ，b = ，并补全条形统计图；（2）如果绘制扇形统计图，请求出C 类所占的圆心角的度数；（3）根据抽样结果，请估计全校“不放烟花爆竹”或“使用电子鞭炮”的学生有多少名？七、（本大题满分12分）22.某服装经销商发现某款新型运动服市场需求量较大，经过市场调查发现年销售量y （件）与销售单价x （元）之间存在如图所示的一次函数关系，而该服装的进价z （元）与销售量y （件）之间的关系如下表所示.已知每年支付员工工资和场地租金等费用总计2万元. 类别频数频率Aa m B 35 0.35 C 200.20D bn合计1001.00销售数量y （件） … 300 400 500 600 … 进货价格z （元） …340320300280…（1）求y 关于x 的函数关系式.（2）写出该经销商经销这种服装的年获利W （元）关于销售单价x （元）的函数关系式.当销售单价x 为何值时，年获利最大？并求出这个最大值.（3）若经销商希望该服装一年的销售获利不低于2.2万元，请你根据图象帮助确定销售单价的范围.在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？八、（本大题满分14分）23.类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题：（1）已知：如图1，四边形ABCD 是等对角四边形，A C ∠≠∠，070A ∠＝，B ∠0＝75，则C ∠＝，D ∠＝ . （2）在探究等对角四边形性质时：①小红画了一个如图2所示的等对角四边形ABCD ，其中ABC ADC ∠∠＝，AB ＝AD ，此时她发现CB ＝CD 成立，请你证明该结论； ②由此小红猜想：“对于任意等对角四边形，当一组邻边相等时，另一组邻边也相等” .你认为她的猜想正确吗？若正确，请给与证明；若不正确，请举出反例.（3）已知：在等对角四边形ABCD 中，060DAB ∠＝，090ABC ∠＝，AB ＝5，AD ＝4，求对角线AC 的长.2014-2015学年度第二学期九年级第二次质量检测数学参考答案及评分标准 2015年5月一、选择题（本大题共10小题，每小题4分，满分40分）1 2 3 4 5 6 7 8 9 10 A B C B A D C C C B二、填空题（本大题共4小题，每小题5分，满分20分） 11.122.510⨯ 12. 54m ≤且1m ≠ 13.23 14. ①③④三、（本大题共2小题，每小题8分，满分16分）图1图215. 原式＝4－1+1－2 ……………… 4分＝2 ……………… 8分 16. （1）11，60，61 …………………………………… 2分（2）后两个数表示为212n -和212n + ……………… 4分∵2424222212121()244n n n n n n n --++++=+=，2422121()24n n n +++=， ∴2222211()()22n n n -++=．又∵3n ≥，且n 为奇数， ∴由n ，212n -，212n +三个数组成的数是勾股数． …… 8分四、（本大题共2小题，每小题8分，满分16分）17. （1）略 …………………… …… 2分（2）平移后的△A 2B 2C 2点B 2、C 2的坐标分别为（0，－2），（－2，－1） 6分（3）△A 1B 1C 1 （1，－1）． ……………………8分 18. 过A 点作AB ⊥DC 于点B ，则AB ＝15，在Rt ABD ∆中，045DAB ∠=，∴BD ＝AB ＝15 ……… 3分在Rt ABC ∆中，030BAC ∠=， ∴03tan 301553BC AB ==⨯=g ………… 6分 ∴CD ＝BD －BC ＝15－53155 1.7 6.5≈-⨯=答：壁画CD 的高度为6.5米 …………… 8分五、（本大题共2小题，每小题10分，满分20分）19. （1）过A 作AC ⊥x 轴于C ，设A 点坐标是（a ，b ），则43b a =- ①，把A 点坐标代入一次函数，得223b a =-+ ②， ①②联合解得34a b =-⎧⎨=⎩，把（-3，4）代入反比例函数，得12k =-，……4分∴反比例函数的解析式是12y x=-； ……… 5分∴3432922AOB AOD BOD S S S ∆∆∆=+=⨯⨯+⨯⨯=． ……… 10分 20. （1）∵AB 是O e 的切线，∴090OBA ∠=，000903060AOB ∠=-=. ∵OB ＝OC ，∴OBC OCB ∠=∠，030OCB A ∠==∠，∴AB ＝BC . ………………………………………… 5分（2）四边形BOCD 为菱形，理由如下： ……………………………………… 6分连接OD 交BC 于点M ，∵D 是»BC的中点，∴OD 垂直平分BC . 在Rt OMC ∆中，∵030OCM ∠=，∴OC ＝2OM ＝OD∴OM ＝OD ，∴四边形BOCD 为菱形. ……………………………………… 10分六、（本题满分12分）21.（1）30 15 图略 ……………………………… 4分（2）C 类圆心角的度数为002036072100⨯= …………………… 8分（3）这两类学生的人数估计为(3015)10030001350+÷⨯= ………… 12分七、（本题满分12分）22.（1）设y 关于x 的函数关系式为y kx b =+，则500300400400k b k b =+⎧⎨=+⎩，解得1800k b =-⎧⎨=⎩∴800y x =-+ …………………………… 4分（2）设z 关于y 的函数关系式为11y k y b =+，则1111340300320400k b k b =+⎧⎨=+⎩，解得1115400k b ⎧=-⎪⎨⎪=⎩∴14005z y =-+ …………………………………… 6分则z 关于x 的函数关系式为11(800)40024055z x x =--++=+年获利w 关于销售单价x 的函数关系式为：()20000w x z y =--1(240)(800)200005x x x =---+-248802120005x x =-+-24(550)300005x =--+ 当550x =时，30000W 最大＝，最大获利3万元 …………………………… 10分（3）由图象可知，要使年获利不低于2.2万元，销售单价应在450元到650元之间，又由于销售单价越低，销售最越大，所以销售单价应定为450元 …………… 12分八、（本题满分14分）23. （1）0140C ∠＝ 075D ∠＝ ………………………………… 2分（2）①证明：连接BD ，∵AB ＝AD ，∴ABD ADB ∠∠＝.∵四边形ABCD 为等对角四边形，∴ABC ADC ∠∠＝.∴CBD CDB ∠∠＝，即CB ＝CD . ………………………………… 5分 ②不正确 ………………………………… 6分如图，在等对角四边形ABCD 中，A C ∠∠＝，B D ∠≠∠，AB ＝BC ，但显然AD DC ≠ ………………………………… 8分（3）当090ABC ADC ∠∠＝＝时，如图延长BC 、AD 相交于点E∵060DAB ∠＝，∴030E ∠＝.∵AB ＝5，∴AE ＝10，BE ＝53.又∵AD ＝4， ∴DE ＝6.在Rt DCE ∆中，043cos30DE CE == ∴BC ＝BE －CE ＝53433-=在Rt ABC ∆中，2227AC AB BC =+= ……………………………… 11分当060DAB DCB ∠=∠=时，如图过D 点作DE ⊥AB ，DF ⊥BC ，垂足分别为点E 、F ，则四边形BEDF 为矩形在Rt ADE ∆中，01cos60422AE AD ==⨯=g ，DE ＝03sin 60423AD =⨯=g ∴DF ＝BE ＝AB －AE ＝5－2＝3在Rt CDF ∆，03tan 603DFCF ===∵BF ＝DE ＝23，∴BC ＝BF +CF ＝33在Rt ABC ∆中，22213AC AB BC =+= ……………………………… 14分。

2016年安徽自主招生数学模拟试题：古典概型

2016年自主招生数学模拟试题:古典概型【试题容来自于相关和学校提供】1：甲从正方形四个顶点中任意选择两个顶点连成直线,乙从该正方形四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是( )A.B.C.D.2：某校毕业生毕业后有回家待业，上大学和补习三种方式，现取一个样本调查如图所示。

若该校每个学生上大学的概率为，则每个学生补习的概率为（）A、B、C、D、3：一个盒子中装有4卡片,上面分别写着如下四个定义域为R的函数:f1(x)=x3,f2(x)=|x|,f3(x)=sinx,f4(x)=cosx,现从盒子中任取2卡片,将卡片上的函数相乘得到一个新函数,所得函数为奇函数的概率是( )A、B、C、D、4：已知一组抛物线，其中为2、4、6、8中任取的一个数，为1、3、5、7中任取的一个数，从这些抛物线中任意抽取两条，它们在与直线交点处的切线相互平行的概率是（）A、B、C、D、5：将9个（含甲、乙）人平均分成三组，甲、乙分在同一组的概率为------------ ( )A、B、C、D、6：从1，2，……，9这九个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是7：假设小军、小燕和小明所在的班级共有50名学生，并且这50名学生早上到校先后的可能性相同，则“小燕比小明先到校，小明又比小军先到校”的概率为____________.8：已知集合，集合，在集合A中任取一个元素p，则p∈B的概率是。

9：(2014·模拟)设数列{a n}满足：a 3=8,(a n+1-a n-2)·(2a n+1-a n)=0(n∈N *),则a 1的值大于20的概率为________.10：从集合A＝{－1，1，2}中随机选取一个数记为k，从集合B＝{－2，1，2}中随机选取一个数记为b，则直线y＝kx＋b不经过第三象限的概率为________。

11：春节前，有超过20万名某某，等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年，为防止摩托车驾驶人员因长途疲劳驾驶，手脚僵硬影响驾驶操作而引发交通事故，市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾驶人员休息站，让过往返乡过年的摩托车驾驶人员有一个停车休息的场所。

2016年安徽自主招生数学模拟试题：导数的实际应用

2016年自主招生数学模拟试题:导数的实际应用【试题容来自于相关和学校提供】1：已知函数，则（）A、0B、1C、2D、2：已知点是曲线上的一个动点，则点到直线的距离的最小值为（）A、B、C、D、3：设f（x），g（x）分别是定义在R上的奇函数和偶函数。

当x<0时，f′（x）g（x）＋f（x）g′（x）> 0，且g（－3）＝0，则不等式f（x）g（x）<0的解集是（）A、（－3,0）∪（3，＋∞）B、（－3,0）∪（0,3）C、（－∞，－3）∪（3，＋∞）D、（－∞，－3）∪（0,3）4：某工厂要围建一个面积为512 m2的矩形堆料场，一边可以用原有的墙壁，其他三边需要砌新的墙壁，当砌壁所用的材料最省时堆料场的长和宽分别为（）A、32 m，16 mB、30 m，15 mC、40 m，20 mD、36 m，18 m5：函数f(x)＝ln x的图像与函数g(x)＝x 2－4x＋4的图像的交点个数为( )A、0B、1C、2D、36：设,若函数有小于零的极值点，则实数的取值围是。

7：的极大值是，极小值是。

8：电动自行车的耗电量与速度之间有如下关系：，为使耗电量最小，则速度应定为。

9：设函数，对任意，恒有，其中M是常数，则M的最小值是 .10：已知函数的图象在处的切线方程为，则的值是 .11：若函数，(Ⅰ)当时，求函数的单调增区间；(Ⅱ)函数是否存在极值.12：（12分）已知设的反函数为。

（I）求的单调区间；（II）若对任意，不等式恒成立，数的取值围。

13：已知函数在（1,2）上是增函数，在（0,1）上是减函数。

求的值；当时，若在恒成立，数的取值围; 求证：方程在有唯一解.14：已知实数，函数。

(Ⅰ)若函数有极大值32，数的值；(Ⅱ)若对，不等式恒成立，数的取值围。

15：已知函数，. （1）当时，求在闭区间上的最大值与最小值；（2）若线段：与导函数的图像只有一个交点，且交点在线段的部，试求的取值围。

安徽省2016年中考数学模拟试题(含答案)

安徽省2016年中考数学模拟试题（一）时间：120分钟满分：150分一、选择题（共10小题、每题4分，计40分）1．的相反数是（）12-A ．﹣2B ．2C ．D ．12±2．如图所示，下列选项中，正六棱柱的左视图是（）A ．B ．C ．D ．3．下列运算正确的是（）A ．x •x 2=x 2B ．（xy ）2=xy 2C ．（x 2）3=x 6D ．x 2+x 2=x 44．若分式的值为0，则x 的值为（）A ．﹣1B ．3C ．﹣1或3D ．﹣3或15．某班50名学生的年龄统计结果如下表所示，这个班学生年龄的众数、中位数是（）年龄13141516人数422231A ．23，15B ．23，22C ．1，22D ．15，146．把直线y=﹣3x 向上平移后得到直线AB ，直线AB 经过点（m 、n ），且3m+n=10，则直线AB 的解析式（）A ．y=﹣3x ﹣5B ．y=﹣3x ﹣10C ．y=﹣3x+5D ．y=﹣3x+107．如图，△ABC 是⊙O 的内接三角形，AC 是⊙O 的直径，∠C=50°，∠ABC 的平分线BD 交⊙O 于点D ，则∠BAD 的度数是（）A ．45°B ．85°C ．90°D ．95°8．关于x 的一元二次方程（m ﹣2）2x 2+（2m+1）x+1=0有两个不相等的实数根，则m 的取值范围是（）A ．m ＜B ．m ＞且m ≠2C ．m ≤D ．m ≥且m ≠29．如图，菱形ABCD 的边长为8cm ，∠A=60°，DE ⊥AB 于点E ，DF ⊥BC 于点F ，则四边形BEDF 的面积为（）cm 2．A．16 B．64C．8D．810．如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=3时，这两个二次函数的最大值之和等于（）A．B．C．3D．4二、填空题（共4小题、每题5分、共计20分）11．分解因式：a2﹣b2﹣2a+1= ．12．在一次社会实践活动中，某班可筹集到的活动经费最多900元．此次活动租车需300元，每个学生活动期间所需经费15元，则参加这次活动的学生人数最多为．13．如图，双曲线y=经过Rt△OMN斜边上的点A，与直角边MN相交于点B，已知OA=2AN，△OAB的面积为5，则k的值是．14．如图，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE，那么DE长的最小值是．三、（本大题共2小题，每小题8分，满分16分）15．计算：|﹣4|﹣（）﹣2+4π0．16．先化简，再求值：，其中．四、（本大题共2小题，每小题8分，满分16分）17．“低碳生活，绿色出行”，自行车正逐渐成为人们喜爱的交通工具。

安徽省2016届中考数学一模试卷解析版

数列通项与求和：注意数列的项数和公差，以及求和公式的正确应用。
三角函数与解三角形：注意三角函数的周期性和图像变换，以及解三角形中的边角关系。
立体几何：注意空间想象力和计算能力，以及几何定理的正确应用。
计算错误：由于粗心大意导致的简单计算错误。
理解偏差：对题目要求理解不准确，导致解题思路出现偏差。
概念模糊：对数学概念理解不清晰，导致应用错误。
忽略细节：在解题过程中忽略细节，导致答案不完整或错误。
仔细审题，避免因理解错误而失分
计算过程要规范，避免扣分
注意答题顺序，先易后难
掌握时间分配，避免时间不够用
掌握数学基础知识，如公式、定理和概念，确保理解透彻。
定期复习巩固，避免遗忘，可利用思维导图等方式梳理知识框架。
题目：解答题 456
解析：本题考查了反比例函数的图象和性质，熟练掌握反比例函数的图象和性质是解题的关键。
直接法：根据题目的条件，通过计算、推理或证明，直接得出结论。
排除法：通过排除不符合条件的选项，选出正确答案。
特殊值法：选取符合条件的特殊值或特殊情况，进行验
证或推理。
保证充足的睡眠时间，避免熬夜和疲劳过度
强化计算能力，提高解题速度和准确性。
注重细节，仔细审题，避免因粗心导致失分。
掌握基础知识：确保对数学基础知识的掌握，包括公式、定理和概念。练习解题技巧：通过大量的练习，熟练掌握各种解题技巧和方法。提高思维品质：培养数学思维能力，如逻辑推理、归纳总结和演绎推理等。反思与总结：在练习和考试后，及时反思和总结解题的经验和教训。
数形结合法：根据题目的条件，画出图形或图像，通过数形结合的方法解决问题。

2016年安徽自主招生数学模拟试题：(中心投影)平行投影与直观图

2016年自主招生数学模拟试题:（中心投影）平行投影与直观图【试题容来自于相关和学校提供】1：有一个几何体的主视图、左视图、俯视图从左到右如下图所示，则这个几何体应是一个( )A、棱台B、棱锥C、棱柱D、都不对2：A、B、C、D、3：已知三棱锥S—ABC的三条侧棱两两垂直，且SA=2，SB=SC=4，则该三棱锥的外接球的半径为A、3B、6C、36D、94：一个正四棱锥的正(主)视图如右图所示，该四棱锥侧面积和体积分别是（）A、，B、，C、，D、，5：已知某几何体的三视图如图所示，根据图中标注的尺寸（单位cm）可得该几何体的体积是（）A、B、C、D、6：若一个四棱锥的三视图如图所示，其中正视图与侧视图都是边长为2的等边三角形，则该四棱锥的四条侧棱长之和等于_____________ 7：如图是一个正三棱柱的三视图，若三棱柱的体积是，则____________________. 8：水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3, B′C′=2,则AB边上的中线的实际长度为 .9：如右上图，在正方体中，点P是上底面一动点，则三棱锥的主视图与左视图的面积的比值为____ 10：某几何体的三视图如右图所示，若该几何体各顶点都在一球面上，则这个球的表面积为 . 11：(12分) 已知四棱锥，底面ABCD，其三视图如下，若M是PD的中点⑴求证：PB//平面MAC；⑵求直线PC与平面MAC所成角的正弦值。

12：用小方块搭一个几何体,使得它的正视图和俯视图如图所示,这样的几何体只有一种吗?它至少需要多少个小立方块?最多需要多少个小立方块?13：如图,已知几何体的三视图,用斜二测画法画出它的直观图.14：根据图1-2-7中物体的三视图,画出物体的形状. 图1-2-715：(本题满分12分)作图（不要求写出作法，请保留作图痕迹）（１）画出下图几何体的三视图（尺寸自定）；（２）画出一个底面直径为４ｃｍ，高为２ｃｍ的圆锥的直观图答案部分1、A从俯视图来看，上、下底面都是正方形，但是大小不一样，可以判断是棱台，选A.2、D由三视图可知,几何体为正方体切一角故3、A因为三棱锥S—ABC的三条侧棱两两垂直，所以该三棱锥的外接球就是以三棱锥S—ABC的三条侧棱为棱的长方体的外接球；长方体的外接球的直径等于长方体对角线；所以外接球的半径为故选A4、B试题分析：侧面三角形的高为，侧面积为，体积为. 考点：三视图，棱锥侧面积与体积公式.5、C由三视图可知该几何体是有一条侧棱垂直于底面的三棱锥，其中底面是等腰三角形，底边长为2，底边上的高为2，三棱锥的高也为2，所以，故选C6、试题分析：由三视图可知该四棱锥的四个侧面是底边长为2，高为2的全等的等腰三角形，所以每条侧棱长都等于，所以四条侧棱长之和为。