信号与系统 期中考试答案
信号与系统试卷及参考答案

试卷及答案信号与系统试卷(1)(满分:100分,所有答案一律写在答题纸上)考试班级学号姓名成绩考试日期:年月日,阅卷教师:考试时间120分钟,试卷题共2页一一线性非时变离散系统,具有一初始状态x(0),当激励为时f(k),响应为y(k)=((1/2)k+1)u(k);若初始状态不变,当激励为-f(k)时,响应y(k)=((-1/2)k-1)u(k)为;试求当初始状态2x(0)为,激励为4f(k)时,系统的响应?(10分)二绘出下列函数的图形(1).已知一连续时间信号x(t)如图所示,试概略画出信号y(t)=x(2-t/3)的波形图。
(8分)t(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。
(8分)三 计算下列函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt (4分) (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h (t) (8分)(3). f(k)=1, k=0,1,2,3, h(k)=1, k=0,1,2,3, y(k)=f(k)*h (k) (8分) (4) 已知f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换 (8分) (5)y’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? (8分) (6). y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2, 试求零输入响应y x (k)=? 零状态响应y f (k)=? (8分)四 一线性非时变因果系统,当激励为u(t)时,响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ,求当激励f(t)=δ(t)时的响应)(t h 。
(10分)五 某一子系统,当输入f(t)=e -t u(t)时,零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时,总系统的冲激响应。
信号与系统期中考试试卷(答案)
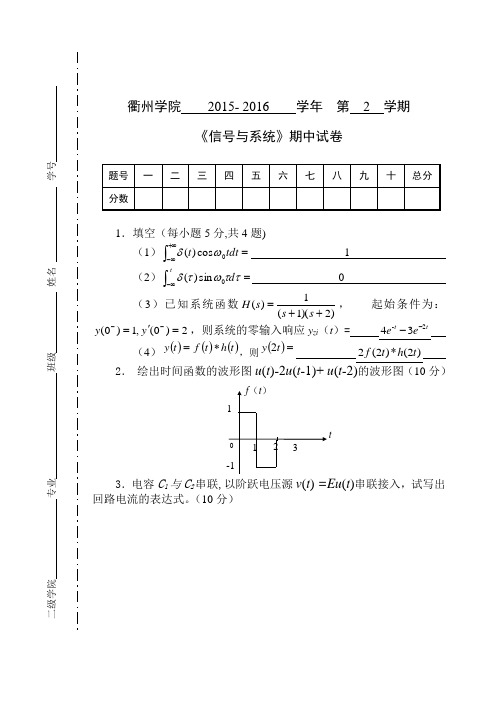
衢州学院 2015- 2016 学年 第 2 学期《信号与系统》期中试卷1.填空(每小题5分,共4题)(1)⎰+∞∞-=tdt t 0cos )(ωδ 1(2)⎰∞-=td ττωτδ0sin )( 0(3)已知系统函数)2)(1(1)(++=s s s H , 起始条件为:2)0(,1)0(='=--y y ,则系统的零输入响应y zi (t )= t t e e 2-34--(4)()()()t h t f t y *=,则()=t y 2 )2(*)2(2t h t f2. 绘出时间函数的波形图u (t )-2u (t -1)+ u (t -2)的波形图(10分)1t123f (t )-13.电容C 1与C 2串联,以阶跃电压源v (t ) =Eu (t )串联接入,试写出回路电流的表达式。
(10分)题号 一 二 三 四 五 六 七 八 九 十 总分 分数班级 姓名 学号dtt dv c c c c t i d i c c c c d i c d i c t v ttt )()()()(1)(1)(2121212121+=⇒+=+=⎰⎰⎰∞-∞-∞-ττττττ4.如下图所示,t<0时,开关位于“1”且已达到稳态,t=0时刻,开关由“1”转到“2”,写出t ≥0时间内描述系统的微分方程,求v (t )的完全响应。
(10分)解:设回路电流为)(t i ,则)()(t Ri t v =,由KVL 方程由:)()()()(1t V t Ri dtt di L dt t i C in t =++⎰∞- 整理后得到: dt t dV t v RC dt t dv dt t v d R L in )()(1)()(22=++ 代入参数得到: )t t v dtt dv dt t v d (10)(10)(10)(68522δ=++ 特征根: 423110*9.9,102-≈⨯-≈αα 初始值: 610)0()0(')0(',0)0(==⨯==++++L v LRi R v v 得到: t t e e t v 2131.10-31.10)(αα=5.信号f (t )如图1所示,求=)(ωj F F )]([t f ,并画出幅度谱)(ωj F 。
信号与系统(带答案)

第一套第1题,下列信号的分类方法不正确的是(A)A、数字信号和离散信号B、确定信号和随机信号C、周期信号和非周期信号:D、因果信号与反因果信号第2题,以下信号属于连续信号的是(B)A、e-nTB、e-at sin(ωt)C、cos(nπ)D、sin(nω0)第3题,下列说法正确的是(D)A、两个周期信号x(t),y(t)的和x(t)+y(t)一定是周期信号。
B、两个周期信号x(t),y(t)的周期分别为2和2开根号,其和信号x(t)+y(t)是周期信号。
C、两个周期信号x(t),y(t)的周期分别为2和Pi,其和信号x(t)+y(t)是周期信号。
D、两个周期信号x(t),y(t)的周期分别为2和3,其和信号x(t)+y(t)是周期信号。
第4题,将信号f(t)变换为( A ) 称为对信号f(t)的平移或移位。
A、f(t-t0)B、f( k -k0)C、f(at)D、f(-t)第五题,下列基本单元属于数乘器的是(A )A、B、C、D、第六题、下列傅里叶变换错误的是(D)А.1<-->2πδ(ω)B.ejω0t<-- > 2πδ(ω-ω0 )С.соѕ(ω0t) < -- > π[δ(ω-ω0 ) +δ (ω+ω0 )]D. ѕіn(ω0t)<-> jπ[δ(ω+ω0)+ δ(ω- ω0)]第7题、奇谐函数只含有基波和奇次谐波的正弦和余弦项,不会包含偶次谐波项。
(对)第8题、在奇函数的傅里叶级数中不会含有正弦项,只可能含有直流项和余弦项。
(错)第9题、满足均匀性和____条件的系统称为线性系统。
(叠加性)第10题.根据激励信号和内部状态的不同,系统响应可分为零输入响应和__响应(零状态)第二套1、当周期信号的周期增大时,频谱图中谱线的间隔( C)A:增大B:无法回答C:减小D:不变2、δ(t)的傅立叶变换为( A)。
A:1B: u(t)C: 0D:不存在3、已知f(t),为求f(3-2t)则下列运算正确的是(B)A:f(-2t)左移3/2B:f(-2t)右移3/2C:f(2t)左移3D:f(2t)右移3 ,4、下列说法不正确的是(D)。
中科大信号与系统2014期中考试答案

1)是线性系统;所以为线性。
考虑到对输入有限制,部分的a*x(t)可能无对应的输出,所以此题按此思路答非线性也判为对。
2)不是线性系统对应的输出并不等于是或者分情况讨论,b为0是为线性系统,b不为0是为非线性系统3)是线性,时不变,非因果系统线性:计算对应的输出发现等于时不变性:计算对应的输出等于因果性:与未来的时刻有关故为非因果系统;或者分情况讨论:当t<0时,若h==0,则为因果,否则,非因果。
4)线性,时不变,可逆系统线性与时不变型:写出输入为的输出与原系统对比可得输出,或者考虑到零输入对应零输出需要要求,对此分情况讨论也给分。
时不变性同理。
可逆。
或者将y(t)写成,在进行后面的判断。
二经分析,当或者时,y(t)=0;当时,当时,当时,(0,3)在各个端点都是连续的,所以连续。
对1的结果求导即可当时,当时,当时,方法二:由卷积性质先计算,,然后积分计算y(t),计算量比较少三四1)特征方程解得那么齐次方程为代入求解可得零输入响应为2)考虑两个LTI 系统级联第一个LTI 系统的单位冲激响应为第二个LTI 系统的单位冲激响应满足同样解齐次方程得那么当 时3)4)5)不稳定因为五770171.cos 3cos 41()4周期为2,1==,其余为04X ()[()()(7)(7)]2j t j t j t j t t te e e e X X ππππππωππωδωπδωπδωπδωπ--±±=+++==-+++-++2.cost+cos2t非周期X ()=[(1)(1)(2)(2)]πωπδωδωδωπδωπ-+++-++ 12122213.非周期,sin (){0,1所以,x(t)=cos 0.51=-sin((0.5))t 0.5()()别的形式的答案:X(j )=-)sgn()],或:2有一般的卷积方法:,01(){sgn()0.5,0co j j j j tj X j t t t t X j eX j e j j X j e j e t j ωωωωπωππωωωπππωωπωωπωπωωωππωω----<=<---=--+->==--<2122s ()[()()]1()*2[sgn()sgn()]2j t j X j X j X X e ωπωωπδωπδωπωππωπωπ-=++-==---+六(t)Xc(nT)(t nT)(jw)Xc(nT)e (1)(e )Xd(n)e (nT)e (2)由(1)(2)式可得(e )(j /)1(jw)(j(w ))12(e)(j())(j(n jwnT n j j n j n n n j s n j s n s s s Xp Xp Xd Xc Xd Xp T Xp Xc nw T n Xd Xc f Xc T T T δπ+∞=-∞+∞-=-∞+∞+∞Ω-Ω-Ω=-∞=-∞Ω+∞=-∞+∞Ω=-∞=-====Ω=-Ω=-=Ω-∑∑∑∑∑∑2))s n n f π+∞=-∞∑。
(完整word版)信号与系统考试试题及答案,推荐文档

长沙理工大学拟题纸课程编号 1拟题教研室(或老师)签名 教研室主任签名 符号说明:)sgn(t 为符号函数,)(t δ为单位冲击信号,)(k δ为单位脉冲序列,)(t ε为单位阶跃信号,)(k ε为单位阶跃序列。
一、填空(共30分,每小题3分)1. 已知)()4()(2t t t f ε+=,求_______)("=t f 。
)('4)(2)("t t t f δε+2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ,求______)()(=*k h k f 。
}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。
0)(t j Kej H ωω-=4. 若)(t f 最高角频率为m ω,则对)4(t f 取样的最大间隔是______。
m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。
101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =,试判断该系统是否为线性时不变系统______。
故系统为线性时变系统。
7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ,求该信号的傅立叶变换)(ωj F =______。
故傅立叶变换)(ωj F 不存在。
8. 已知一离散时间系统的系统函数2121)(---+=z z z H ,判断该系统是否稳定______。
故系统不稳定。
9. =+-+⎰∞∞-dt t t t )1()2(2δ______。
310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数,试问)(t f 有何种对称性______。
关于t=3的偶对称的实信号。
二、计算题(共50分,每小题10分)1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示,试由时域求解该系 统的零状态响应)(t y ,画出)(t y 的波形。
信号与系统期中考试参考答案_326004751

《信号与系统》期中考试试题2011年11月 A 卷一、填空(25分)1、(3分)已知2()(e )()t f t t u t -=+,则()f t ''=(2e )()()()t u t t t δδ-'+-+。
解:2()(2e )()(e )()(2e )()()t t t f t t u t t t t u t t δδ---'=-++=-+()(2e )()(2e )()()(2e )()()()t t t f t u t t t t u t t t δδδδ---''''=++-+=+-+2、(3分)若()f t 的最高截止频率为m ω,则对(/2)(4)f t f t 抽样的最大时间间隔为2/(9)m πω。
解:{}{}{}11(/2)(4)(/2)*(2)(2)*(/4)24f t f t f t f t F F ωωππ==FF F , (2)F ω的截止频率为0.5m ω,(/4)F ω的截止频率为4m ω,根据卷积性质知(/2)(4)f t f t 的最高截止频率为4.5m ω,因此最低抽样频率为9s m ωω=,最大时间间隔2/(9)m m T πω=。
3、(3分)已知实信号()f t 的频谱可写成(2/2)()()e j F A ωπωω-+=,其中()A ω为实奇函数,试问该信号波形满足何种对称性(2)(2)f t f t -+=-+。
解:由题意知2()j ()j F e A ωωω=,而[][]*j ()j ()A A ωω=-,即*j 2j2()()F e F e ωωωω⎡⎤=-⎣⎦,从而(2)(2)f t f t -+=-+,即()f t 关于2t =反对称。
4、(3分)由Parseval 定理计算2sin d t t t π+∞-∞⎛⎫= ⎪⎝⎭⎰2π。
解:{}[]sin()()()()t Sa t u u t ππππωπωπ⎧⎫==+--⎨⎬⎩⎭F F ,因此2sin d t t t π+∞-∞⎛⎫= ⎪⎝⎭⎰21d 2πππωππ2-=⎰。
信号与系统期中考试答案,DOC

一、(15%)已知连续时间信号x t ()和离散时间信号x n []的波形图如下图所示。
画出下列各信号的波形图,并加以标注。
1.()()11xt x t =-,2.()()221x t x t =-,3.3()()x x t ττ=-第三个自变量不为t !! 4.{}1[][][]e x n x n Even x n ==,5.2[][][1]x n x n n δ=-答案二、(25%)简要回答下列问题。
1. 推导离散时间信号[]0j n xn e ω=成为周期信号的条件(3%);若是周期信号,给出基波周期的求法(3%)。
答案:若为周期信号,则00()j nj n N e e n ωω+=∀,。
推出01j N e ω=,再推出02,,0N k k z k ωπ=∈≠。
得出02k Nωπ=为有理分数。
2.指出离散时间信号[]j n x n e ω=频率取值的主值范围(2%),指出它的最低频率和最高频率(2%)。
答案2πωπωπ-≤<≤<或0。
min max 02,21),k k z k k z ωπωππ=∈=+∈或。
而或(。
3. 断下列两个系统是否具有记忆性。
①()()()()222y t x t x t =-,(1%)②[][][]0.51y n x n x n =--。
(1%)答案①无记忆性②有记忆性4.简述连续时间和离散时间线性时不变(LTI )系统的因果性、稳定性与单位冲激响应(Unitimpulseresponse )的关系(4%)。
答案因果性与()()()[][][]h t h t u t h n h n u n ==或互为充要条件。
稳定性与|()||[]|n h t dt h n +∞+∞=-∞-∞<+∞<+∞∑⎰或互为充要条件。
5. 很广泛一类因果系统可用常系数微分方程:()()00k k NM k k k k k k d y t d x t a b dt dt ===∑∑表征,画出该类系统的增量线性系统结构(2%),用该结构说明全响应的构成方法及每一部分的物理含义(4%),在什么条件下该类系统为LTI 系统(3%)? 答案()()()x i y t y t y t =+,()()*()x y t x t h t =是仅由输入信号引起响应:零状态响应,()i y t 是仅由初始状态引起的响应:零输入响应。
信号与系统期中考试答案3

信号与系统期中考试答案一、共八小题 1、⎰-=++232)2()(dt t t t δ 2⎰∞-=-+td ττδτ)2()1( 3u(t-2)3、判别下列系统是否线性。
其中x (t 0)为初始状态,f (t )为输入。
)(7)(d )(d 3)(t f t ty tt y a =+线性系统)(6)(5)( )(0t tf t x t y b +=线性系统4、求下列信号的奈奎斯特抽样频率和抽样间隔 (1))70100cos(︒-t π最大的角频率ωm=100π rad/s奈奎斯特抽样频率fs=2fm=100Hz 奈奎斯特抽样间隔Ts=1/fs=0.01s; (2) )20()100(2t sa t sa ππ-最大的角频率ωm=100π rad/s奈奎斯特抽样频率fs=2fm=100Hz 奈奎斯特抽样间隔Ts=1/fs=0.01s; 5、一个系统的系统频域函数ωωω3sin 23cos 2)(j j H -=,该系统是否为无失真传输系统?ωωωω323s i n 23c o s 2)(j ej j H -=-=,是无失真传输系统 6、已知一线性系统的输入)1(3)(-=t t f δ,系统的单位冲激响应)(2)(3t u e t h t -=, 求系统的零状态响应。
零状态响应)1(3)(2*)1(3)(*)()()1(33-=-==---t u e t u e t t h t f t y t t f δ7、已知一线性系统当输入)(2)(t u t f =时,系统的零状态响应)(2)(3t u e t y t f -=,当输入)1()(2)(--=t u t t f δ时, 求系统的零状态响应。
系统的零状态响应是: )1()(6)(22)]1(2[)](2[)()1(33)1(33---=--=------t u et u et t u et u edt d t y t tt tf δ8、已知某一理想低通滤波器系统函数⎩⎨⎧><=- 50|| 050|| 5.0)(2πωπωωωj e j H ,系统的输入)30100cos(4)1020cos(2)(︒-+︒+=t t t f ππ,求系统的零状态响应。
东南大学信号与系统期中考试试卷及答案

F { f (t )} = 2 Sa (ω ) − 2 e
'
− jω
= jω F ( jω )
2 − jω F ( jω ) = [ Sa (ω ) − e ] jω
4。 计算卷积: 2 * t[ε(t+2)-ε(t-2)] 。 (5分)
2
f1 (t )
0
−2 2
t
f 2 (t )
0 2
t
= ∫ τ [ε (τ + 2) − ε (τ − 2)]2dτ
解: 引入辅助函数q(t), 得
d 3 q (t ) d 2 q (t ) dq ( t ) 4 5 + + + 6 q (t ) = e (t ) 3 2 dt dt dt dq ( t ) r (t ) = 7 + 8 q (t ) dt
7
e (t )
Σ
q ′′′
∫
-4 -5 -6
q ′′
∫
q′
(t ) = (t ) =
e
− 2 t
− 2 c
e
− 2 t
, t ≥
在输入为零时 r(0+)= r(0-)= 0,r´(0+)= r´(0-)= 2, 代入上列二式
c1 + c 2 = 0 , → − 2 c 2 = 2 ∴ r zi ( t ) = ( 1 − e
(2)系统转移算子为:
解法2:因 e(t)=5,(-∞<t<∞),故由直流稳态解,可设 r(t)=A (常数),代入系统方程,得 5A=3x5, ∴ r(t)= A =3
3. 利用傅里叶变换的性质求下列波形信号的傅里叶 变换。 (8分)
信号与系统期中考试答案

1、一连续LTI系统在相同初始条件下,输入为f(t)
时,全响应为y(t)=2e-t+cos2t,当输入为2f(t)时,全 响应为y(t)=e-t+2cos2t。则在相同初始条件下,求 输入为4f(t)时的全响应y(t)。
• 1、解:
• 设:y(t)= yzi (t)+ yzs(t) • 输入为f(t)时:y(t)=2e-t+cos2t,
• 即: yzi (t)+ yzs(t) = 2e-t+cos2t
(1)
• 输入为2f(t)时:y(t) =e-t+2cos2t,
• 即: yzi (t)+2 yzs(t) = e-t+2cos2t
(2)
• 由(1)、(2)得: yzs(t) =cos2t- e-t ,yzi (t)=3 e-t
• 所以输入为4f(t)时
d 2 y(t) 5 d y(t) 6 y(t) 2 d f (t) 8 f (t)
dt
dt
dt
yzs (t) (3et 4e2t e3t ) (t)
yzi (t) (11e2t 8e3t ) (t)
y(t) (3et 7e2t 7e3t ) (t)
y'(t) (t) (10e2t 15e3t ) (t) h(t)
•
H ( j)
由模拟框图得:
(
( j)2 6 j)2 5 j
6
H(
j)
(
j
( j)2
)2 a(
c
j)
b
或H(
p)
p2 c p2 ap b
信号与系统期中考试题(答案201X.5)

.武夷学院期末考试试卷( 2010 级 电子信息技术 专业2012~2013学年度 第 2 学期) 课程名称 信号与系统 期中 卷 考试形式 开 卷 考核类型 考 试 本试卷共三 大题,卷面满分100分,答题时间120分钟。
一、选择题:(本大题共15小题,每小题2分,共30分每题给出四个答案,其中只有一个正确的)1、下列关于冲激函数性质的表达式不正确的是( B )。
A 、)()0()()(t f t t f δδ= B 、()t aat δδ1)(=C 、)(d )(t tεττδ=⎰∞- D 、)()-(t t δδ=2、积分dt t t ⎰∞∞---)21()2(δ等于( D )。
A 1.25B 2.5C -1.5D 53、周期信号的频谱和非周期信号的频谱分别为( A )A 离散频谱和连续频谱B 连续频谱和离散频谱C 均为离散频谱D 均为连续频谱4、将信号f (t )变换为( A )称为对信号f (t )的尺度变换。
A f (at )B f (t –k 0)C f (t –t 0)D f (-t ) 5、下列关于冲激函数性质的表达式不正确的是( D )。
A 、⎰∞∞-='0d )(t t δ B 、)0(d )()(f t t t f =⎰+∞∞-δC 、)(d )(t tεττδ=⎰∞- D 、⎰∞∞-=')(d )(t t t δδ6、某系统的系统函数为 H ( s ),若同时存在频响函数 H ( j ω),则该系统必须满足条件( C )A 时不变系统B 因果系统C 稳定系统D 线性系统 7、设定某系统的系统函数为)2)(1()2(2)(-++=s s s s s H ,则其极点为( D )A 0、-2B -2C 1、-2D -1、28、对因果系统,只要判断H(s)的极点,即A(s)=0的根(称为系统特征根)在平面上的位置,即可判定系统是否稳定。
下列式中对应的系统可能稳定的是( D ) A s 3+4s 2-3s+2 B s 3+4s 2+3s C s 3-4s 2-3s-2 D s 3+4s 2+3s+29、有两个系统分别为(1)y (t)= cost·f(t),(2)y (t )= 4f 2(t) +3f(t)则这两个系统分别为( B )A 都是时变系统B (1)是时变系统 (2)是时不变系统C 都是时不变系统D (1)是时不变系统 (2)是时变系统 10、下列说法不正确的是( D )。
信号与系统期中考试答案

一、(15%)已知连续时间信号x t ()和离散时间信号x n []的波形图如下图所示。
画出下列各信号的波形图,并加以标注。
1. ()()11x t x t =-, 2. ()()221x t x t =-, 3. 3()()x x t ττ=-第三个自变量不为t !! 4. {}1[][][]e x n x n Even x n ==, 5. 2[][][1]x n x n n δ=-答案二、(25%)简要回答下列问题。
1. 推导离散时间信号[]0j n x n e ω=成为周期信号的条件(3%);若是周期信号,给出基波周期的求法(3%)。
答案:若为周期信号,则00()j nj n N e e n ωω+=∀,。
推出01j N e ω=,再推出02,,0N k k z k ωπ=∈≠。
得出02kNωπ=为有理分数。
0002min ,1k N N z k z k πω⎧⎫⎪⎪=∈∈≥⎨⎬⎪⎪⎩⎭,且2.指出离散时间信号[]j n x n e ω=频率取值的主值范围(2%),指出它的最低频率和最高频率(2%)。
答案2πωπωπ-≤<≤<或0。
min max 02,21),k k z k k z ωπωππ=∈=+∈或。
而或(。
3.断下列两个系统是否具有记忆性。
① ()()()()222y t x t x t =-,(1%)② [][][]0.51y n x n x n =--。
(1%)答案 ① 无记忆性 ② 有记忆性4. 简述连续时间和离散时间线性时不变(LTI )系统的因果性、稳定性与单位冲激响应(Unit impulse response )的关系(4%)。
答案因果性与()()()[][][]h t h t u t h n h n u n ==或互为充要条件。
稳定性与|()||[]|n h t dt h n +∞+∞=-∞-∞<+∞<+∞∑⎰或互为充要条件。
5. 很广泛一类因果系统可用常系数微分方程:()()00k k NM k kk k k k d y t d x t a b dt dt ===∑∑表征,画出该类系统的增量线性系统结构(2%),用该结构说明全响应的构成方法及每一部分的物理含义(4%),在什么条件下该类系统为LTI 系统(3%)? 答案()()()x i y t y t y t =+, ()()*()x y t x t h t =是仅由输入信号引起响应:零状态响应,()i y t 是仅由初始状态引起的响应:零输入响应。
信号与系统(含答案)试卷

课程测试试题(A 卷)
一、选择题 (本大题共 10 小题,20 分, 每题 2 分) 1.积分 ∫ (t − 3)δ (−2t + 4)dt 等于
−5 5
(A) -1 (B) -0.5 (C) 0 (D) 0.5 2.已知实信号 f (t ) 的傅里叶变换 F (= jω ) R(ω ) + jx(ω ) ,信号 1 ) (t ) [ f (t ) + f (−t )] 的傅里叶变换 Y ( jω ) 等于( y= 2 (A) R(ω ) (B) 2 R(ω ) (C) 2 R(2ω ) (D)
is
1Ω
iR
uc -
课程测试试题答卷()
一、
(1) C (9)D
选择题 (本大题共 10 小题,20 分, 每题 2 分)
(2) B (10)D (3) B (4) D (5) B (6) A (7) D (8) A
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分) 1.
g (t )
(B)
8.单边拉氏变换 F ( s ) =
e− s 的原函数为 s2 + 1 (A) sin(t − 1)u (t − 1) (B) sin(t − 1)u (t ) (C) cos(t − 1)u (t − 1) (D) cos(t − 1)u (t )
9. 为使 LT1 连续系统是稳定的,其系统函数 H ( s ) 的极点必须在 s 平面的 (A) 单位圆内 (B) 单位圆外 (C) 左半平面 (D) 右半平面 10.积分 ∫ (t 2 + 1)δ (t − 2)d (t ) 的值为
1 (1 − e −2t )δ (t ) ,则其冲激响应 h(t ) = 2
信号与系统考试题及答案(共8套)

信号与系统考试题及答案(一)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
08信号与系统期中答案
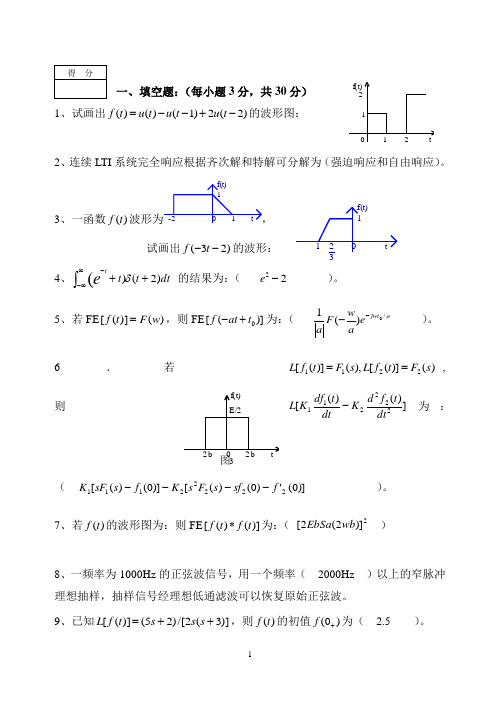
一、填空题:(每小题3分,共30分) 1、试画出)2(2)1()()(-+--=t u t u t u t f 的波形图:2、连续LTI 系统完全响应根据齐次解和特解可分解为(强迫响应和自由响应)。
3、一函数)(t f 波形为tf(t)0-211,试画出)23(--t f 的波形:4、dt t t et)2()(++⎰∞∞--δ 的结果为:( 22-e )。
5、若FE )()]([w F t f =,则FE )]([0t at f +-为:(a j w t e a wF a/0)(1-- )。
)()]([),()]([2211s F t f L s F t f L ==,6.若])()([222211dt t f d K dt t df K L -为:则( )]0(')0()([)]0()([22222111f sf s F s K f s sF K ---- )。
7、若)(t f 的波形图为:则FE )]()([t f t f *为:( 2)]2(2[wb EbSa )8、一频率为1000Hz 的正弦波信号,用一个频率( 2000Hz )以上的窄脉冲理想抽样,抽样信号经理想低通滤波可以恢复原始正弦波。
9、已知)]3(2/[)25()]([++=s s s t f L ,则)(t f 的初值)0(+f 为( 2.5 )。
-11t(A)121tf(t)(B)120-11tf(t)(C)1221tf(t)(D)12tf(t)0-12132bE/2tf(t)图 3-2b10、已知at e t f -=)(,则该函数进行拉斯变换后的收敛域为( a ->σ )。
二、计算题:(共7题,共52分)11、求右图所示信号的傅里叶级数。
(10分)解:21)(12000EEdt T dt t f T a TT ⎰⎰===002)sin(2)cos(2)cos()(2200====⎰⎰T nw nwt T E dt nwt E T dt nwt t f T a TT n )cos 1(02)cos(2)sin(2)sin()(2200ππn n E T nw nwt T E dt nwt E T dt nwt t f T b TT n -=-⋅===⎰⎰ ⎪⎩⎪⎨⎧=02πn E ,...6,4,2,...5,3,1==n n)sin(22)(1nwt n EE t f n ∑∞=+=π,7,5,3,1=n12、试求右图所示信号的傅里叶变换。
信号与系统期中考试标准答案
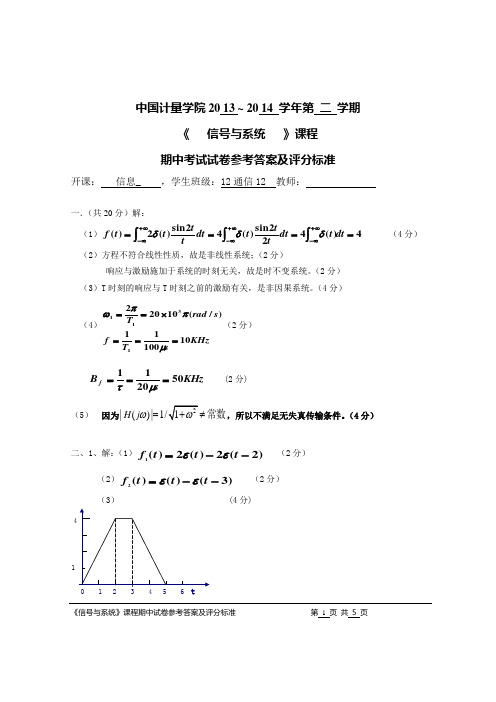
《信号与系统》课程期中试卷参考答案及评分标准 第 1 页 共 5 页中国计量学院20 13 ~ 20 14 学年第 二 学期《 信号与系统 》课程 期中考试试卷参考答案及评分标准开课: 信息_ ,学生班级:12通信12 教师:一.(共20分)解: (1)4)(422sin )(42sin )(2)(====⎰⎰⎰∞+∞-∞+∞-∞+∞-dt t dt ttt dt t t t t f δδδ (4分)(2)方程不符合线性性质,故是非线性系统;(2分)响应与激励施加于系统的时刻无关,故是时不变系统。
(2分)(3)T 时刻的响应与T 时刻之前的激励有关,是非因果系统。
(4分)(4)KHz sT f s rad T 1010011)/(102021311===⨯==μππω(2分)KHz sB f 502011===μτ(2分) (5)因为|()|1/ω=常数H j ,所以不满足无失真传输条件。
(4分)二、1、解:(1))2(2)(2)(1--=t t t f εε (2分)(2))3()()(2--=t t t f εε (2分)(3) (4分)1《信号与系统》课程期中试卷参考答案及评分标准 第 2 页 共 5 页2、(8分)解:f(t)为周期信号,T=2,其基波角频率Ω=π。
在间隔(-1,1)内,f(t)表示为δ(t),f(t)的傅里叶级数展开式为 21)(1,)(11===⎰∑-ΩΩ-∞-∞=dt e t Tc ec t f tin n tjn n n δ其中, 所以,∑-∑=-=∑=∑=∞-∞=∞-∞=-∞-∞=-∞-∞=n n tjn n ntjn n nn n eF c ec F t f F )()(221][][)]([πωδπΩωπδΩΩ3、(8分)解:211)(j ωω+=Hωωϕa r c t a n )(-=)4sin(21sin π-⇒t t ,)sin(sin 632512-⇒t t ,)sin(sin 7231013-⇒t t所以,)723sin(101)632sin(51)4sin(21)( -+-+-=t t t t y π三.(12分) 解:⎪⎫⎛==⎰--)(21ωττωττωSa A dt Ae j F t j (4分)(4分)(2) 2 (4分)四、(10分)将f(t)展开成三角函数形式的傅立叶级数,考虑到f(t)偶对称性质,故正弦分量bn 全为零,其中:12/2/21T ωπππ===,τπ=,E A = !!!!第 3 页共 5 页故:01/2a = ,1sin(/2)2*/2A A a πππππ== 3sin(3/2)2*3/23A A a πππππ==等,如下,其它偶次项0n a =)7cos 715cos 513cos 31(cos 22)( +-+-+=t t t t A A t f π (5分) 考虑到该系统是一个带通滤波器,只将2到7 rad/s 的频率成分保留,故除3,5,7三个频率分量保留外,其它分量全部滤除!!又因为该系统的通带内的增益为1,所以输出信号的直接就是f(t)的三个频率分量!!如下所示:)7c o s 715c o s 513c o s 31(2)(t t t A t f +--=π (5分)五、解:1《信号与系统》课程期中试卷参考答案及评分标准 第 4 页 共 5 页(8分)2、将y(t)与2cos30000πt 相乘,得到信号的频谱为:将2y(t) cos30000πt 经过截止频率为15kHz 的低通滤波器,则可以恢复到m(t)的频谱,即恢复为m(t).所以解密器与加密器的结构完全相同。
信号与系统期中考试题(答案201X.5)

.武夷学院期末考试试卷( 2010 级 电子信息技术 专业2012~2013学年度 第 2 学期) 课程名称 信号与系统 期中 卷 考试形式 开 卷 考核类型 考 试 本试卷共三 大题,卷面满分100分,答题时间120分钟。
一、选择题:(本大题共15小题,每小题2分,共30分每题给出四个答案,其中只有一个正确的)1、下列关于冲激函数性质的表达式不正确的是( B )。
A 、)()0()()(t f t t f δδ= B 、()t aat δδ1)(=C 、)(d )(t tεττδ=⎰∞- D 、)()-(t t δδ=2、积分dt t t ⎰∞∞---)21()2(δ等于( D )。
A 1.25B 2.5C -1.5D 53、周期信号的频谱和非周期信号的频谱分别为( A )A 离散频谱和连续频谱B 连续频谱和离散频谱C 均为离散频谱D 均为连续频谱4、将信号f (t )变换为( A )称为对信号f (t )的尺度变换。
A f (at )B f (t –k 0)C f (t –t 0)D f (-t ) 5、下列关于冲激函数性质的表达式不正确的是( D )。
A 、⎰∞∞-='0d )(t t δ B 、)0(d )()(f t t t f =⎰+∞∞-δC 、)(d )(t tεττδ=⎰∞- D 、⎰∞∞-=')(d )(t t t δδ6、某系统的系统函数为 H ( s ),若同时存在频响函数 H ( j ω),则该系统必须满足条件( C )A 时不变系统B 因果系统C 稳定系统D 线性系统 7、设定某系统的系统函数为)2)(1()2(2)(-++=s s s s s H ,则其极点为( D )A 0、-2B -2C 1、-2D -1、28、对因果系统,只要判断H(s)的极点,即A(s)=0的根(称为系统特征根)在平面上的位置,即可判定系统是否稳定。
下列式中对应的系统可能稳定的是( D ) A s 3+4s 2-3s+2 B s 3+4s 2+3s C s 3-4s 2-3s-2 D s 3+4s 2+3s+29、有两个系统分别为(1)y (t)= cost·f(t),(2)y (t )= 4f 2(t) +3f(t)则这两个系统分别为( B )A 都是时变系统B (1)是时变系统 (2)是时不变系统C 都是时不变系统D (1)是时不变系统 (2)是时变系统 10、下列说法不正确的是( D )。
《信号与系统》试题及答案

信号与系统》试题及答案2012 年度教学质量综合评估测验卷《信号与系统》试题 题组::1、开课学院:信息工程学院学院 题组2、:题纸上。
电子3、类适专用业班级:信息工程学院通信工程专业及 电子4、类在专答业写所要求填 卷面题型及分值:)题 答 不 内 线 封 密名姓研12组0 分钟,所有答案均写在答 发两张答题纸上认真填 。
总总分二 三 四 五 六 七 八 九 十100 20 20 60一、选择题(每小题 2 分,共 10小题。
每一小题仅有一个选项是正确的。
共计 20 分)列说法不正确的是( 一般周期信号为功率信号。
时限信号 (仅在有限时间区间不为零的非周期信号 )为能量信号。
ε(t)是功率信号; 1、 A 、 B 、 C 、)。
D 、 e t 为能量信号 列关于冲激函数性质的表达式不正确的是( 2、 A 、 C 、 3、 A 、 4、 f (t) (t) f (0) (t)H(s)B、(at))d (t)D 、 1ta(-t)(t)(s2s 1()s (s 2)2),属于其极点的是(B 、2C 、 )。
1 If f1(t) ←→ F1(j ω), f2(t) ←→ F2(j ω) A 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) *b F2(j ω) ] B 、[a f1(t) + b f2(t) ] ←→ [aF1(j ω) - b F2(j ω) ] C 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) + b F2(j ω) ] D 、[a f1(t) + b f2(t) ] ←→ [a F1(j ω) /b F2(j ω) ] 5、下列说法不正确的是( )。
A 、H(z)在单位圆内的极点所对应的响应序列为衰减的。
即当趋于 0。
Then[ D 、-2k →∞时,响应均B 、H(z)在单位圆上的一阶极点所对应的响应函数为稳态响应。
C 、H(z) 在单位圆上的高阶极点或单位圆外的极点, 其所对应的响应序列都是递 增的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1 已知系统的微分方程为()())(4)(23322t u e t r dt t dr dtt r d t -=++ 且初始条件为,4)0( ,3)0(='=--r r 求系统的完全响应、自由响应、强迫响应、零输入响应、零状态响应。
【解】:(一)自由响应()h r t ,即齐次解,可以按照如下方法求得:令()()2232()0d r t dr t r t dt dt++=, 特征方程为:2320λλ++= ,特征根:11λ=- ,22λ=-,特征模式为t e -,2t e -,于是212()t t h r t A e A e --=+(二)强迫响应()p r t ,即特解,可以按照如下方法求得(参见表2-3):因为原方程中的强迫项为34()te u t -,所以3()t p r Be t -=,将此特解代入原方程,得到2B = (三)完全解()r t ,可以按照如下方法求得:3212()()()2t t h p t r t r t r t Ae A e e ---=+=++ 由于完全解通常是在0t > 的条件下求得,因此需要知道初始条件(0)r + ,(0)r +' 。
观察原方程可以看出,方程的右边不含冲激函数()t δ ,且在0t = 附近有界,于是在0t = 附近()r t '' 有界,()r t ' 连续,()r t 连续,因此(0)(0)3r r +-==, (0)(0)4r r +-''==根据以上初始条件,可以解出完全解()r t 中的常数1212, 11A A ==- ,故23()12112t t t r t e e e ---=-+(四)零输入响应()zi r t令()()2232()0d r t dr t r t dt dt++=,按照步骤(一)同样的方法可以得到: 212()t t zi r t C e C e --=+,由于输入信号为零,系统没有外部输入信号的激励作用,只在系统内部储能的作用下,按照系统固有的特征模式(t e -和2t e -)运动,此时系统保持连续平稳的运动状态,初始条件不会产生跃变,因此(0)(0)3zi zi r r +-==, (0)(0)4zizi r r +-''== ,将它们代入()zi r t 的表达式,得到1210, C 7C ==-,故2()107t t zi r t e e --=-(五)零状态相应()zs r t此时的微分方程可以写成()()23232()4()zs zs t zs d r t dr t r t e u t dt dt-++= 初始条件为(0)0, (0)0zs zsr r --'==。
根据完全解的表达式可以得到1322()2t t zs t r t D e D e e ---=++用步骤(三)同样的分析方法可以知道(0)(0)0zs zs r r +-==,(0)(0)0zszs r r +-''==,将它们代入()zs r t 的表达式,得到122, D 4D ==-,故23()242t s t t z r t e e e ---=-+2-2 求系统)(3)(2)( t e t r t r =+'的冲激响应。
【解】:方法一:时域经典法令()()e t t δ= ,系统方程变为()2()3()r t r t t δ'+=,由于冲激响应是一种零状态响应,初始条件为(0)0r -= ,因此,需要考虑从0-到0+状态的跳变问题,以求得(0)r +。
根据冲激函数平衡法,观察方程两边可以知道,()r t ' 中含有()t δ ,()r t 中不含()t δ,故()r t 在0t = 附近有界,即|()|r t M ≤(M 是某个正实数),000000()|()|0r t dt r t dt Mdt +++---≤==⎰⎰⎰ , 对系统方程两边从0-到0+积分000000() 2()3()r t dt r t dt t dt δ+++---'+=⎰⎰⎰ [](0)(0)03r r +--+=(0)3r +=于是,我们可以写出0t > 时的系统微分方程和初始条件:()2()0r t r t '+=,(0)3r +=这是一个齐次方程。
至此,求解冲激响应的问题就转化为当0t >时求解齐次方程的问题。
解此方程,得到:2()t r t Ae-=(0t >) ,代入初始条件得到3A = ,因此,该系统的冲激响应为 2()3()t h t e u t -=()h t 中乘上()u t 是为了含摄0t >的条件。
方法二:冲激函数系数匹配法(参见教材2.6节例2-9)观察系统方程 ()2()3()r t r t t δ'+=可以知道,()r t 中不含冲激函数()t δ,于是()r t 中只含有系统固有的特征运动模式2t e - (特征方程为20λ+= ,特征根为2λ=- ),因此 2()()t r t Ae u t -=(特征模式2t e -乘上()u t 是为了含摄0t >的条件) ,222()2()()2()()t t t r t Ae u t Ae t Ae u t A t δδ---'=-+=-+将()r t 和()r t '代入系统方程,222()()2()3()t t Ae u t A t Ae u t t δδ---++=注意上面的式子中,特征模式2t e -的系数自动平衡,这是由特征方程20λ+=所保证的。
比较()t δ 的系数,可以得到3A = ,故2()3()t r t e u t -=或者写作2()3()t h t eu t -=2-3 如图2-3所示电路,激励信号为)(t e ,求当)()(t t e δ=和)()(t u t e =时的响应信号)(t v L 。
图2-3 【解】()()L di t v t L dt = ,1()()t L i t v t dt L -∞=⎰ , 根据基尔霍夫电压定律,列出方程()()()L R v t v t e t +=()()()t L L R v t v t dt e t L -∞+=⎰ 两边对t 求导,得到()()()L L dv t R de t v t dt L dt+= 当()()e t t δ= 时,系统方程变为()()()L L dv t R d t v t dt L dtδ+= 根据冲激函数平衡法(参见教材2.6节例2-9),可以知道()L v t 中含有()t δ,再加上系统固有的特征运动模式R t L e - ,于是系统的冲激响应具有如下形式()()()R t L L v t A t Be u t δ-=+()()()()()()()R R Rt t t L L L L dv t d t BR d t BR A e u t Be t A e u t B t dt dt L dt Lδδδδ---=-+=-+, 将()L v t 和()L dv t dt 代入系统方程,比较()d t dtδ和()t δ的系数,得到1A = ,R B L =- ,故 ()()()Rt L L R v t t e u t Lδ-=- 或者写作()()()Rt L R h t t e u t Lδ-=- 类似地,当()()e t u t =时,可以求得系统的阶跃响应()()R t L g t eu t -= 可以验证冲激响应是阶跃响应的导数()()dg t h t dt=2-4 一个系统的冲激响应为)()()(t u e t t h t-+=δ,激励信号为)()(t tu t e =,试求系统的零状态响应)()()(t h t e t r zs *=。
【解】:这是一个求卷积的问题,首先注意到()()()f t t f t δ*=对于任意函数()f t 均成立(参见教材第77页(2-71)式),于是[][][]()()000()()()()*()()()*()()*()()()()()()()()()(1)()(21)()zs t t t t t t t tt t r t e t h t tu t t e u t tu t t tu t e u t tu t u e u t d tu t e d u t tu t e e d u t tu t e e u t t e u t ττττδδτττττττττ--∞---∞-----=*⎡⎤=+⎣⎦⎡⎤=+⎣⎦=+-⎡⎤=+⎢⎥⎣⎦⎡⎤=+⎢⎥⎣⎦⎡⎤=+-⎣⎦=-+⎰⎰⎰其中第4个等式中的积分的上下限由()()u u t ττ- 给出,只有当0t τ<< 时,被积函数才不为零,因此积分下限为0,积分上限为t ,而且t>0,故整个积分的外面要乘上u(t)。
2-5试求图2-5所示两信号的卷积,并画出波形。
图2-53-1设()()ωF t f ↔,试用()ωF 表示下列各信号的频谱。
(1)()[]t t f m 0cos 1ω+;(2)()()t f t 2+; (3)()dtt df et j 0ω-; (4)()()3-*t f t f ; 【解】:(1)运用公式000cos()[()()]w t w w w w πδδ↔++-,00()*()()f t t t f t t δ-=-(参见(2-72)式),以及频域卷积定理得到 000[1()]cos()cos()()cos()mf t w t w t mf t w t +=+0000[()()][()()]2m w w w w F w w F w w πδδ↔++-+++-(2)根据频域微分定理:()()dF w jtf t dw -↔,得到 )(2)()(2)()()2(w F w F j t f t tf t f t +'↔+=+(3)根据时域微分定理)()(w jwF dtt df ↔,以及频移性质,得到 )()()(000w w F w w j dtt df e t jw ++↔- (4)根据时移性质w j e w F t f 3)()3(-↔-,以及时域卷积定理,得到:w j w j e w F e w F w F t f t f 323)()().()3(*)(--=↔-3-2先求如下图(a)所示信号()t f 的频谱()ωF 的具体表达式,再利用傅里叶变换的性质由()ωF 求出其余信号(b )(c )(d )的频谱的具体表达式。
【解】:(a )()(1)[()(1)]f t t u t u t =---,对f(t)求一阶和二阶导数得到[()(1)][()(1)][()(1)][]()(1()()(1)()(1)())u t u t t u t u t u t u t t u d d f t dt dtt u t t t t t t δδδδδ'=-------=---=----+-其中()0t t δ= ,(1)(1)t t t δδ-=-)1()()()(++-'=''t t t t f δδδ()1jw f t jw e -''↔-+ 根据时域微分定理)()(w jwF dtt df ↔,可知 1()jwjw e f t jw--+'↔ 21()()jwjw e f t jw --+↔ 21()(1)jw F w jw e w-=-- (b )由于)1()(1-=t f t f故 jw jw jw e e jw we w F w F -----==)1(1)()(21 (c ))1()()(12+-=-=tf t f t fjw jw e e jw ww F w F )1(1)()(212-+=-= (d)根据尺度变换和时移性质231()[(2)]2(2)2j w f t f t F w e -=--↔- 2232()(12)2j w j w e F w j w e w-=+-3-3 如图3-3所示余弦脉冲信号为⎪⎩⎪⎨⎧><+=1, 0 1 ),cos 1(5.0)(t t t t f π,试利用线性和频域卷积性质求)(t f 频谱。
