三线摆法测刚体的转动惯量所用近似方法对测量结果的影响

合集下载

三线摆法测转动惯量实验改进实验

三线摆法测转动惯量实验改进实验摘要: 本文介绍了针对传统三线摆测转动惯量实验进行的装置及算法的改进，简化了人工操作并且减小了传统实验的误差。

关键字: 三线摆;转动惯量；装置；算法；改进；误差1. 引言转动惯量是刚体在转动中惯性大小的量度，它与刚体的总质量、形状和转轴的位置有关。

对于形状较简单的刚体，可以通过数学方法计算出它绕特定轴的转动惯量。

但是，对于形状较复杂的刚体，用数学方法计算它的转动惯量非常困难，故大都用实验方法测定。

由于三线摆具有结构简单、操作简便、等优点，因此许多大学物理实验教材都选用该实验方法。

但是传统的实验操作复杂，且存在许多需通过人工测量的数据，因而产生了一定误差。

本文针对传统实验中存在的一些问题进行改进，再减少人力花费的同时也减少了一定的实验误差。

2. 实验方案（设计思想）一、传统实验：三线摆是将一个匀质圆盘，以等长的三条细线对称地悬挂在一个水平的小圆盘下面构成的。

每个圆盘的三个悬点均构成一个等边三角形。

如图1所示，当底圆盘B 调成水平，三线等长时，B 盘可以绕垂直于它并通过两盘中心图1 三线摆示意图的轴线O 1O 2作扭转摆动，扭转的周期与下圆盘(包括其上物体)的转动惯量有关，三线摆法正是通过测量它的扭转周期去求已知质量物体的转动惯量。

当摆角很小，三悬线很长且等长，悬线张力相等，上下圆盘平行，且只绕O 1O 2轴扭转的条件下，下圆盘B 对O 1O 2轴的转动惯量I 0为：202004T HgRrm I π= (1)式中m 0为下圆盘B 的质量，r 和R 分别为上圆盘A 和下圆盘B 上线的悬点到各自圆心O 1和O 2的距离 (注意r 和R 不是圆盘的半径)，H 为两盘之间的垂直距离，T 0为下圆盘扭转的周期。

若测量质量为m 的待测物体对于O 1O 2轴的转动惯量I ，只须将待测物体置于圆盘上，设此时扭转周期为T ，对于O 1O 2轴的转动惯量为：220014)(T HgRr m m I I I π+=+= (2)于是得到待测物体对于O 1O 2轴的转动惯量为：02204)(I T HgRr m m I -+=π·······(3) 为了测量出R 与r ，我们通过测量悬点间的距离，因为三点构成一个等边三角形，根据几何关系可得：a r33=，同理，b R 33=。

大学物理实验之用三线摆测物体的转动惯量

大学物理【2 】试验之用三线摆测物体的迁移转变惯量1、懂得三线摆道理,并以此测物体的迁移转变惯量.2、控制秒表.游标卡尺等测量对象的应用办法,控制测周期的办法.3、加深对迁移转变惯量概念的懂得.1、三线摆测迁移转变惯量的道理.2、精确测量三线摆扭摆周期.讲解.评论辩论与演示相联合.3学时.迁移转变惯量是刚体迁移转变惯性的量度,它的大小与物体的质量及其散布和转轴的地位有关.对证量散布平均.外形规矩的物体,经由过程外形尺寸和质量的测量,就可以算出其绕定轴的迁移转变惯量,而质量散布不平均.外形不规矩物体的迁移转变惯量则要由试验测出.本试验应用三线摆测出圆盘和圆环对中间轴的迁移转变惯量并与理论值进行比较.三线扭摆法测量迁移转变惯量的长处是：仪器简略,操作便利.精度较高.一.试验目标1.懂得三线摆道理,并以此测物体的迁移转变惯量.2.控制秒表.游标卡尺等测量对象的应用办法,控制测周期的办法.3.加深对迁移转变惯量概念的懂得.二.试验仪器三线摆仪,秒表,游标卡尺,钢直尺,水准器,待测圆环.三.试验道理三线摆试验道理如图所示,圆盘(下盘)由三根悬线吊挂于启动盘(上盘)之下,两圆盘圆心位于统一竖直轴上.轻扭上盘,在悬线扭力的感化下.圆盘可绕个中间竖轴作小幅扭摆活动.设圆盘的质量为m 0.高低盘的间距为H .高低盘的受力半径为r 与R.圆盘的扭摆角为θ（θ很小）.因为θ很小,所以圆盘在扭摆中升起的高度很小,可以以为在此进程中高低盘的间距H 保持不变.在此情形下,依据三角关系可以导出悬线拉力N 对圆盘的扭力矩为:0/M m gRrSin H θ=.因为Sin θθ≈,所以0/M m gRr H θ=.设圆盘的迁移转变惯量为J 0,且M 与角位移θ的偏向相反,依据迁移转变定律可得：2002m gRr d M J H d tθθ==-由此可知圆盘的扭摆为简谐振动,解此微分方程得圆盘的振动周期为：02T =于是: 200024m gRrT J Hπ= 三线摆道理图此即为圆盘对中间竖轴迁移转变惯量的试验公式.在圆盘上齐心叠放上质量为m 的圆环后,测出盘环体系的扭摆周期T ,则盘环体系的迁移转变惯量为: 2002()4m m gRrT J J J Hπ+=+=总由此可得圆环迁移转变惯量的试验公式：()22000024gRr J J J m m T m T Hπ⎡⎤=-=+-⎣⎦总圆盘.圆环迁移转变惯量的理论公式为：20012J m R =’.22121()2J m R R =+’式中R 0.R 1.R 2分离为圆盘半径及圆环的表里半径.四.试验内容及步骤1.用水准器调三线摆仪底座程度及下盘程度.2.使下盘静止,然后朝统一偏向轻转上盘,使下盘作小幅扭摆.控制摆角不超过5.3.待下盘扭摆稳固后,用秒表测出持续摆动50个周期的时光,反复5次,然后算出周期T 0的平均值.4.将圆环齐心肠放置于圆盘上,反复步骤2.3,测出周期T 的平均值.5.用钢直尺在不同地位测量高低盘之间的垂直距离5次.用游标卡尺在不同地位分离测量高低盘悬线孔间距各5次.盘算H.a.b的平均值,并由此算出受力半径r与R的平均值.6.用游标卡尺沿不同偏向测量圆盘直径.圆环表里径各5次.算出2R0.2R1.2R2的平均值.7.记载圆盘.圆环的质量m0.m及本地的重力加快度g.五.留意事项1.调下圆盘水日常平凡,松开固定悬线的螺母后要留意控制住调节悬线长度的螺母,防止悬线滑落.2.圆盘（或盘环）要在静止状况下开端启动,以防止在扭摆时消失晃悠,圆盘扭摆的角度θ须≤50.3.圆盘（或盘环）启动后可持续测完5个50次周期,不必每次从新启动.4.留意游标卡尺的零点修改.秒表与米尺的最小分度值及估读.六.教室指点1.圆盘程度的调节办法.2.圆盘启摆的请求.办法及摆幅控制.3.圆盘扭摆周期的不雅察办法.4.游标卡尺的应用办法.七.思虑题1.三线摆的振幅受空气的阻尼会逐渐变小,它的周期也会随时光变化吗？答：振幅反应出谐振的强度;周期反应的是谐振的频率,这是两个意义不同的物理量.阻尼振动的周期T =阻尼系数β是常数,所以周期不随时光而变化.2.试剖析：加了待测物之后,三线摆的扭摆周期是否必定大于空盘的扭摆周期？答：不必定.∵()00J J J +>,∴()22000m m T m T +>,或00m m m ⎛⎫+ ⎪⎝⎭·20T T ⎛⎫⎪⎝⎭＞１.因为00m m m +＞１,所以0TT 不必定大于1,即T 不必定大于0T （可以大于.等于或小于）.八.数据处理1.数据记载及表格①下盘质量m0= 1.163 （kg）; 园环质量m= 0.371 （kg）;g = 9.781 m/s2②几何尺寸测量：钢直尺最小分度值 1 mm;游标卡尺最小分度值 0.02 mm;零点修改值 0.00 mm③周期测量：秒表最小分度值__0.1__s;零点修改值__0.00__s班级序号姓名教师签字日期2.数据处理①盘算圆盘.圆环迁移转变惯量的试验值0J .J26232000222 1.1639.78192.5443.7110 1.433 5.277104 3.1445.40104m g RrT J kg mHπ---⨯⨯⨯⨯⨯===⨯⋅⨯⨯⨯()()62200023222329.78192.5443.71101.1630.3714 3.1445.401041.415 1.163 1.433 1.51010g Rr J m m T m T Hkg m π---⨯⨯⨯⎡⎤=+-=⨯+⎡⎣⎢⎥⎣⎦⨯⨯⨯⎤⨯-⨯=⨯⋅⎦②盘算圆盘.圆环迁移转变惯量的理论值0J ’.J ’262320001 1.163190.3710 5.2681028J m R kg m --⨯⨯===⨯⋅’22622321210.371(100.30150.16)10() 1.5121028J m R R kg m --⨯+⨯=+==⨯⋅’③盘算试验值与理论值的相对误差000||100%0.17%J J J-⨯=’’||100%0.13%J J J-⨯=’’九.教授教养跋文1.用水准仪调圆盘水日常平凡须要技能,须对学生解释.2.试验中要留意巡查,不雅察学生的操作,随时指出他们的问题.3.周期测量是否精确对试验成果的影响最大,其次是孔间距.要解释圆盘（或盘环）启摆的要乞降办法,以及摆幅的请求.只有圆盘（或盘环）的扭摆合乎请求,才能保证周期测量的精确性.测孔间距现实上是测两线孔中悬线间的距离,所以在测量中尺要留意瞄准悬线的地位.。

用三线摆法测刚体的转动惯量

用三线摆法测刚体的转动惯量在物理学中，转动惯量是描述物体旋转惯性的重要参数。

在研究刚体的转动运动时，测量刚体转动惯量是一项基本任务。

三线摆法是一种常用的测量刚体转动惯量的实验方法。

本文将介绍三线摆法测量刚体转动惯量的原理、步骤和注意事项。

一、原理任何物体都有转动惯量，它是物体质量分布与轴线位置相对关系的函数。

对于一个旋转的刚体而言，它的转动惯量大小与轴线与刚体质量分布的几何形状密切相关。

刚体的质量分布越偏离轴线，转动惯量就越大。

转动惯量的单位是千克·米²。

三线摆法是一种通过比较不同轴线下刚体的摆动周期来测量刚体转动惯量的方法。

实验中将刚体悬挂在三根垂直的细线上，分别取不同位置的细线作为转轴，使刚体绕不同的轴线转动。

在相同的初始条件下，测量刚体围绕不同轴线的摆动周期，利用以下公式计算刚体转动惯量：I=ml²(Δt/T)²其中，I表示刚体的转动惯量；m表示刚体质量；l表示刚体距离轴线的距离；Δt表示两次摆动周期之差；T表示平均摆动周期。

通过多次测量，取平均值得到最终转动惯量的测量值。

二、步骤1、实验器材准备实验器材包括刚体、三根细线、支架、计时器等。

刚体的质量和形状可以根据实验需求选择，通常选择球体或圆柱体形状。

细线长度应保持一致，不得有较大的弯曲。

计时器精度应足够高，一般要求在毫秒级别。

2、实验装置设置将刚体悬挂在三根相互垂直的细线上。

通过调整细线长度和悬挂位置，使刚体能够沿不同轴线旋转。

为了避免干扰，需要保证细线的振动不会影响刚体的摆动。

支架应保持稳定，防止发生震动。

3、实验测量首先记录刚体在重力作用下自由下落的时间，确定初始角度。

然后，分别选取三根垂直的细线作为转轴，计时器计时并记录刚体摆动的周期。

每个轴线至少重复三次，取平均值作为摆动周期。

4、数据处理用公式计算刚体围绕不同轴线的转动惯量。

一般情况下，需要进行多组测量并取平均值，以提高测量的精度。

如果多组测量结果差异较大，则说明实验数据存在较大误差，需要检查实验条件和测量方法是否正确。

《用三线摆法测定物体的转动惯量》简明实验报告

《用三线摆法测定物体的转动惯量》简明实验报告实验目的：通过使用三线摆法，测定不同物体的转动惯量，并探究物体质量、几何形状及质心位置对转动惯量的影响。

实验原理：转动惯量是描述物体转动惯性的物理量，表示了物体对转动所表现出的惯性大小。

对于一个质量为m、质心到转轴距离为r的物体，其转动惯量可以通过以下公式计算得出：I=m*r^2而对于一个不规则形状的物体，可以通过将其分解为一组质点，然后分别计算每个质点的转动惯量，并将其求和来得到总转动惯量：I=∑(m_i*r_i^2)在使用三线摆法进行测量时，需要固定物体在转轴上，并通过三根细线将物体悬挂起来。

当物体开始转动时，通过测量物体的摆动周期T和细线长度L，可以利用以下公式计算出转动惯量：I=(T^2*m*g*L)/(4π^2)实验装置：1.一个三线摆装置2.不同形状、不同质量的物体（如圆环、长方体、球体等）3.量角器4.绳子5.计时器6.秤实验步骤：1.将三线摆装置固定在桌面上，并调整好其水平度。

2.选择一个物体，将其通过一根细线绑在摆装置上，并调整好细线的长度，使得物体可以自由摆动。

3.将量角器放在与物体摆动平面垂直的位置，用来测量摆动的振幅角。

4.将绳子固定在物体上，并通过一张纸卡片保持绳子长度不变。

这样可以控制绳子长度的一致性。

5.用计时器测量物体的摆动周期T，反复测量多次以取得平均值。

6.用秤测量物体的质量m，并记录下来。

7.将摆装置往一侧推动，观察物体的摆动情况。

如果摆动不稳定，要重新调整摆装置和细线的位置。

8.重复步骤2-7，测量其他不同形状、不同质量的物体。

实验结果：根据测量得到的摆动周期T、细线长度L、质量m以及重力加速度g，可以计算出物体的转动惯量I。

将测量结果整理成表格，并绘制转动惯量与物体质量、几何形状及质心位置的关系图。

实验讨论：通过实验结果可以看出，质量、几何形状及质心位置都对物体的转动惯量有影响。

质量越大的物体，其转动惯量也越大；几何形状越复杂的物体，其转动惯量也越大；质心离转轴越远的物体，其转动惯量也越大。

三线摆测量刚体转动惯量及其误差分析

科研应用三线摆测量刚体转动惯量及其误差分析毕江林沈一鸣王威*(沈阳工业大学辽宁·沈阳110870)中图分类号：O313.3文献标识码：A文章编号：1672-7894（2013）28-0086-02摘要本文研究了三线摆法测量刚体转动惯量的误差影响因素并对误差的来源和原因进行了分析，在此基础上对实验操作提出了一些改进的方法，以提高实验的精度。

关键词三线摆转动惯量误差分析操作改进The Error Analysis of Measuring the Inertia of Rigid Body with Three-Wire Pendulum //Bi Jianglin,Shen Yiming,Wang Wei*Abstract In this paper,the rotating inertias of rigid body such as the cylindrical and the ring are measured by three wire pendulum and their experimental error sources are analyzed.Several meth-ods have been put forward to improve the precision of the experi-ment.Key words three wire pendulum;moment of inertia;analysis oferrors;modified operation1引言转动惯量是刚体转动惯性大小的量度，其量值取决于刚体的形状、质量、质量分布及其转轴的位置。

刚体的转动惯量有着重要的物理意义，在科学实验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。

对于几何形状简单、质量分布均匀的刚体可以直接用公式计算出它相对于某一确定转轴的转动惯量。

而对于外形复杂和质量分布不均匀的物体只能通过实验的方法来测定物体的转动惯量，因而实验方法就显得十分重要。

三线摆测量刚体转动惯量实验的不确定度分析

2
2
2
式, 可得 E r ( I ) = 8 4% , 则 I 的合成不确定度为 u C ( I ) = E r ( I ) I = 0 6 # 10- 4 kg m 2 圆环转动惯量的最终结果表达式为: 30
I = ( 6 8 ∃ 0 6) # 10 E r( I ) = 8 4% . 4 结论
∀ ( Hi- H ∀) 2 i= 1 n( n - 1)
= 0 058mm, B 类不确定 u B( H ∀) =
仪
3
= 0 29mm 各直接测量量的 A 类
不确定度、 B 类不确定度、合成不确定度和相对不确定度的计算结果见表 3
表 3 各测量量的不确定度不确定度 m 0/ g m/ g T 0/ s T/ s a/ mm b / mm H / mm A 类不确定度 0 0 0 0096 0 011 0 012 0 2 0 058 B 类不确定度 0 003 0 003 0 0058 0 0058 0 012 0 012 0 29 合成不确定度 0 003 0 003 0 012 0 013 0 017 0 2 0 3 相对不确定度 Er 0 0001 % 0 002 % 4 6% 7% 0 03% 0 2% 0 06%
3 2 1 直接测量量的不确定评定摆动周期 T 、上圆盘两悬点间距 a 、下圆盘两悬点间距 b 、上下圆盘间距 H 以上各被测量中质量为单次测量 , 其余各量均为多次重复测量其中 A 类不确定度可由公式 u A ( x ) = t ( t = 1) 计算得出而 B 类 n ( n - 1) 不确定度这里只考虑由仪器的极限误差引起的部分, 并且视为均匀分布, 则 B 类不确定度可由公式 u B ( x ) =

科学性分析三线摆法测刚体转动惯量的实验改进

科学性分析三线摆法测刚体转动惯量的实验改进摘要通过光电门测试三线摆的转动周期，从而更精确的测量三线摆的转动惯量，并通过实验对比分析实验改进前后的精确度和误差，得出改进实验后，误差有一定程度的减小。

关键词三线摆；光电门；转动惯量前言转动惯量是大学物理教学中的重要内容，大一学生开始上大学物理就接触到转动惯量，而高中阶段未接触过，学生难以理解。

因此，在实验中学习测量刚体的转动惯量是大学物理实验教学中的一个基础性的实验项目，对学生理解转动惯量非常重要。

对于形状规则、质量分布均匀的物体可以通过理论计算的方法算出刚体的转动惯量，但是对于几何形状复杂或者质量分布不均匀的刚体，则只能通过实验的方法测出转动惯量。

测量刚体转动惯量的方法很多，例如三线摆法[1]、扭摆法[2]等。

董英伟等[3]导出摆角与转动惯量之间的表达式，探讨了摆角、摆动次数的选择和空气阻尼对测量精度的影响；陈庆东等[4]对三线摆测量刚体的转动惯量进行了改进，在竖直支杆上刻上刻度直接读出两水平圆盘之间的垂直距离，在上圆盘上方加一个固定的圆盘，同时在下圆盘的圆心位置刻一个圆形洞口，改进后的仪器在某种程度上减少了实验误差；张国玺等[5]对三线摆实验进行了改进，实验改进后精确度提高了18倍之多，但是该实验采用了电脑通用计数器、He-Ne激光器、气垫导轨光电门等，实验改进后，实验效果很好，但是设计比较复杂，对学生做实验来说要掌握的东西较多，比较难懂。

我们仅仅采用最简单的设备光电门对实验进行改进，比较适合学生实验，提高实验的精确度，减小误差，并且我们在现有的仪器进行改造，比较容易施行。

桂林理工大学是理工科学校，大多数学生都要学习大学物理课程，而三线摆实验是一个非常重要的实验，但是以往实验中采用秒表测试三线摆的周期，但是在计算公式中，周期是一个二次方项，对结果计算影响较大。

本实验采用实验室已有的设备-数字毫秒计对实验进行改装，研究了改进的实验对结果的影响。

1 实验原理我们实验室采用YJ-SP-1型三线摆测刚体的转动惯量。

三线摆测量物体的转动惯量实验过程分析和实验数据处理

三线摆测物体的转动惯量7．预习思考题回答(1)用三线摆测刚体转动惯量时，为什么必须保持下盘水平？答：扭摆的运动可近似看作简谐运动，以便公式推导，利用根据能量守恒定律和刚体转动定律均可导出物体绕中心轴的转动惯量公式。

(2)在测量过程中，如下盘出现晃动，对周期有测量有影响吗？如有影响，应如何避免之？答：有影响。

当三线摆在扭动的同时产生晃动时，这时下圆盘的运动已不是一个简谐振动，从而运用公式测出的转动惯量将与理论值产生误差，其误差的大小是与晃动的轨迹以及幅度有关的。

(3)三线摆放上待测物后，其摆动周期是否一定比空盘的转动周期大？为什么？答：不一定。

比如，在验证平行轴定理实验中，d=0,2,4,6cm 时三线摆周期比空盘小；d=8cm 时三线摆周期比空盘大。

理论上，220100020[()]04x gRrI I I m m T m T H π=-=+-> 所以22000()0m m T m T +->=〉0/T T >1，并不能保证0/1T T >，因此放上待测物后周期不一定变大。

(4)测量圆环的转动惯量时，若圆环的转轴与下盘转轴不重合，对实验结果有何影响？答：三线摆在扭摆时同时将产生晃动时，这时下圆盘的运动已不是一个简谐振动，从而运用公式测出的转动惯量将与理论值产生误差。

8．数据记录及处理g(重力加速度)= 9.793 m/s 2 m 0（圆盘） = 380 g m 1（圆环） = 1182 g m 21（圆柱）= 137 gm 22（圆柱）= 137 g x(两圆柱离中心距离)= 4.50 cm表 1 待测刚体的有关尺寸数据的记录及简单计算表 2 待测刚体的摆动时间的数据表（周期数为35）二、实验过程记录1）各个多次测量的物理量的平均值及不确定度：501049.45()5ii t t s ===∑；00.04t s ==0.04t u===; t 0=49.45±0.04(s) 511148.92()5ii tt s ===∑；1)t S s =10.05t u==（s ）; t 1=48.92±0.05(s) 521247.08()5ii tt s ===∑;2)t S s =20.25()t s u==; t 2=47.08±0.25(s) 2）待测物体的转动惯量下盘加圆环： a ）空盘的转动惯量：32222200000222200321182109.7937.6681016.091049.45()1212 3.1444.89103545.347510(.)m gRr m gab I T T H H kg m ππ-----⨯⨯⨯⨯⨯⨯===⨯⨯⨯=⨯ b ）空盘加圆环的转动惯量：232212102212032()(3801182)109.7937.6681016.0951048.92()12 3.1444.891035126.966810(.)m m gabT H kg m I π-----++⨯⨯⨯⨯⨯⨯==⨯⨯⨯=⨯c ）圆环的转动惯量平均值：33210(6.9668 5.3475)10 1.619310(.)I I I kg m --=-=-⨯=⨯ 圆环转动惯量结果表示：I u ===521.66310(.)kg m -=⨯=〉32(1.6190.017)10()0.017100%100%1%1.619I I Ir I I u k u u I-⎧=±=±⨯⎪⎨=⨯=⨯=⎪⎩g.m 下盘与两圆柱体：22222020202122002122002200222232242[()][()]4129.7937.6681016.0951047.0849.45[(1371371182)()1182()]1012 3.1444.891035356.258710(.)x gRr gabI I I m m m T m T m m m T m T H H kg m ππ-----=-=++-=++-⨯⨯⨯⨯=++⨯-⨯⨯⨯⨯⨯=⨯x I u ====526.307410(.)kg m -=⨯结果表示：42(6.30.6)10(.)100%9%xxx x I I Ixr x I I u kg m u u I -⎧=±=±⨯⎪⎨=⨯=⎪⎩ 理论公式： 3)百分误差的计算a)圆环的转动惯量理论公式：223224321121I ()38010(10.01615.010)10 1.546710(.)448D D m kg m ---=+=⨯⨯⨯+⨯=⨯内外理论相对误差：1.6193 1.5467100%100% 4.7%1.5467I I I --⨯=⨯=理论理论 b)圆柱的转动惯量理论公式：22212221222122123222242I ()()()2224113710[(2.49010)(4.510)]82.88010(.)m m x x m m D D kg m ----++++=+=⨯⨯⨯⨯+⨯=⨯2122x 理论相对误差：2 6.2587 2.8802100%100%8.7%2 2.8802x I I I --⨯⨯=⨯=⨯理论理论9.数据分析圆环的相对不确定度波动较小，为1%。

三线摆测刚体转动惯量误差分析及改进

四川工商学院学术新视野Academic New Vision of Sichuan Technology and Business University 2020年6月Jun.2020第5卷第2期Vol.5No.2•理学与工学•三线摆测刚体转动惯量误差分析及改进余江妹(四川工商学院计算机学院，四川成都611745)摘要：文章阐述了三线摆测刚体转动惯量的基本原理，分析了实验中产生误差的几种因素，并就主要因素提出了相应的改进方法。

关键词：三线摆；转动惯量；误差中图分类号：04-33文献标识码：AThe Error Analysis and Improvement Methods of Measuring the Moment of I nertia of Rigid Body withThree-Wire PendulumYu Jiangmei(School of C omputer Science,Sichuan Technology and Business University,Chengdu611745China)Abstract：In this study,the basic principle of measuring the moment of inertia of a rigid body with a three line pendulum is described,and several factors causing errors in the experiment are analyzed.At the same time,the corresponding improvement methods for the main factors are put forward.Key words：Three-wire pendulum；Moment of inertia;Error1引言转动惯量是描述刚体在转动中转动惯性大小的量度，是刚体力学中一个非常重要的物理量。

三线摆测物体转动惯量实验报告

三线摆测物体转动惯量实验报告一、实验目的1、掌握三线摆测量物体转动惯量的原理和方法。

2、学会使用秒表、游标卡尺、米尺等测量工具。

3、研究物体的转动惯量与其质量分布、形状和转轴位置的关系。

二、实验原理三线摆是由三根等长的悬线将一圆盘水平悬挂而成。

当圆盘绕中心轴扭转一个小角度后，在重力作用下圆盘将做简谐振动。

其振动周期与圆盘的转动惯量有关。

设圆盘的质量为＄m_0$，半径为＄R$，对于通过其中心且垂直于盘面的轴的转动惯量为＄J_0$，上下圆盘之间的距离为＄H$，扭转角为＄＼theta$。

当下圆盘转过角度＄＼theta$ 时，圆盘的势能变化为：＄＼Delta E_p ＝ m_0g ＼Delta h$其中，＄＼Delta h$ 为下圆盘重心的升高量，可近似表示为：＄＼Delta h ＝＼frac{R^2 ＼theta^2}｛2H}＄根据能量守恒定律，圆盘的势能变化等于其动能变化，即：＄＼frac{1}｛2} J_0 ＼omega^2 ＝ m_0g ＼frac{R^2 ＼theta^2}｛2H}＄又因为圆盘做简谐振动，其角频率＄＼omega ＝＼frac{2\pi}｛T}＄，所以有：＄T^2 ＝＼frac{4\pi^2 J_0}｛m_0gR^2} ＼cdot ＼frac{H}｛R^2}＄设待测物体的质量为＄m$，放在下圆盘上，此时系统的转动惯量为＄J$，则系统的振动周期为＄T'＄，有：＄T'＾2 ＝＼frac{4\pi^2 J}｛（m ＋ m_0)gR^2} ＼cdot ＼frac{H}｛R^2}＄则待测物体对于中心轴的转动惯量为：＄J ＝＼frac{T'＾2 （m ＋ m_0)gR^2 H}｛4\pi^2 R^2} J_0$三、实验仪器三线摆实验装置、游标卡尺、米尺、秒表、待测物体（圆柱体、圆环等）、天平。

四、实验步骤1、用天平测量下圆盘、待测物体的质量。

2、用游标卡尺测量下圆盘、待测物体的直径和高度。

用三线扭摆法测定物体转动惯量及其实验误差

用三线扭摆法测定物体转动惯量及其实验误差（东南大学电气工程学院,南京 211189）摘要：通过实验熟悉秒表、水平仪、游标卡尺、米尺等仪器的使用，掌握质量和周期等量的测量方法；了解用三线摆测转动惯量的原理和方法，研究刚体转动惯量与质量分布的关系；最后巩固误差并对测试结果做了分析。

摘要：转动惯量；质量分布；三线扭摆；平行轴定理；实验误差Measuring Moment of Inertia Using Trilinear Pendulum and its Experimental Error(School of Electrical Engineering, Nanjing, 211189)Abstract: Through the experiment with stopwatch, level gauge, vernier caliper, meter and instrument using, grasp the quality and cycle equivalent measurement method; learn to use the three wire pendulum for measuring moment of inertia of the principle and method of moment of inertia of rigid body, and mass distribution of the relationship; consolidate finally error and the test results were analyzed.key words: Moment of intertia; Mass distribution; torsional pendulum; parallel exis theorem; Experimental error转动惯量是刚体转动惯性大小的量度，它与刚体的质量、转轴位置及质量相对转轴的分布情况有关。

4-3三线摆实验(终稿)

实验4—3 三线摆实验转动惯量是刚体转动惯性大小的量度，是表征刚体特性的一个物理量。

转动惯量的大小除与刚体的质量有关外，还与转轴的位置和刚体的质量分布（即形状、大小和密度）有关。

如果刚体形状简单、且质量分布均匀，则可直接计算出它绕特定轴的转动惯量。

但在工程实践中，我们常碰到大量形状复杂、且质量分布不均匀的刚体，用理论计算其转动惯量将极为复杂，有时甚至不可能，因此通常采用实验方法来测定。

测量刚体的转动惯量时，一般都是使刚体以一定的形式运动。

通过表征这种运动特征的物理量与转动惯量之间的关系，进行转换测量。

测量刚体转动惯量的方法有多种，三线摆法是具有较好物理思想的实验方法，它具有设备简单、直观、测试方便等优点。

【实验目的】1. 学会用三线摆测定刚体的转动惯量。

2. 学会用累积放大法测量周期运动的周期。

图4-3-1 三线摆实验装置3. 了解摆角大小和摆线长短对测量周期的影响。

4. 验证转动惯量的平行轴定理。

【实验原理】三线摆实验装置如图4-3-1所示，上、下圆盘均处于水平，且悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘可绕中心轴O O ′作扭摆运动。

当下盘转动角度很小，且略去空气阻力时，扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中心轴的转动惯量（推导过程见本实验附录）。

O O ′ 200004T H gRr m I π= （4-3-1）式中各物理量的意义如下：为下盘的质量；0m r 、R 分别为上下悬点离各自圆盘中心的距离；为平衡时上下盘间的垂直距离；T 0H 0为下盘作简谐运动的周期；g 为重力加速度（连云港地区g =9.797m/s 2）。

将质量为的待测刚体放在下盘上，并使待测刚体的转轴与m O O ′轴重合。

测出此时下盘运动周期和上下圆盘间的垂直距离1T H 。

同理可求得待测刚体和下圆盘对中心转轴轴的总转动惯量为：O O ′大学物理实验66 212014)(T HgRr m m I π+= （4-3-2）如不计因重量变化而引起的悬线伸长，则有。

用三线摆测刚体转动惯量实验报告

用三线摆测刚体转动惯量实验报告实验目的：1. 掌握使用三线摆测定刚体转动惯量的方法；2. 理解刚体转动惯量的概念及其在物体转动中的作用。

实验器材：1. 三线摆实验装置：包括一个固定在架子上的支持轴、一个可绕轴转动的支架；2. 不同形状和质量的刚体：如圆柱体、长方体等；3. 黄铜环：用于挂载刚体；4. 轻质细线：用于连接黄铜环和支架；5. 增重片：用于调整刚体的质量。

实验原理：1. 刚体转动惯量的定义：刚体绕轴的转动惯量J定义为刚体转动时，由质量分布带来的转动惯量关于转轴的积分，即J=∫r^2dm，其中r为质点到转轴的距离，dm为质量微元。

2. 三线摆实验方法：利用物体绕支撑点转动时的平衡条件，通过在不同位置附加不同质量的增重片，使物体绕转轴发生周期性摆动。

通过测量周期和刚体实际质量，计算出刚体的转动惯量。

实验步骤：1. 将三线摆装置安装于平稳的实验台上，并将刚体挂载在黄铜环上，使其悬吊在三线摆装置上；2. 调整黄铜环的位置，使刚体能够自由摆动，并找到刚体摆动的平衡位置；3. 测量刚体的长度L，以及黄铜环与刚体重心的距离d；4. 测量刚体的质量m，并记录刚体的形状；5. 在黄铜环上附加适量的增重片，使刚体产生微小摆动；6. 启动计时器，并记录刚体进行n个周期的时间T；7. 根据实验数据，计算刚体的转动惯量J=4π²(L+d)⁴m/nT²。

实验数据记录与处理：在进行实验时，根据实际情况记录以下数据：1. 刚体的形状、质量和长度；2. 增重片的质量；3. 进行n个周期的时间T。

根据记录的数据，利用实验原理中的公式计算刚体的转动惯量，并进行数据处理与分析。

实验注意事项：1. 实验过程中要小心操作，避免刚体与装置碰撞或摩擦造成误差；2. 实验时要确保刚体摆动的幅度足够小，以保证计算中的近似条件成立；3. 注意记录实验数据时的精确度，尽量减小测量误差；4. 实验完成后要对仪器进行清理，保持实验室的整洁。

三线摆测物体转动惯量实验报告

三线摆测物体转动惯量实验报告一、实验目的本次实验的主要目的是通过三线摆测量物体转动惯量的实验，帮助同学们更好地理解转动惯量的概念，掌握三线摆的原理和使用方法，提高实验操作能力和数据处理能力。

二、实验原理转动惯量(也叫转动阻力)是描述物体在受到外力作用下，围绕某一点或轴线旋转时所表现出的抵抗运动改变的能力。

简单来说，就是物体在旋转过程中，抵抗自身发生旋转的能力。

转动惯量的单位是千克·米2。

三、实验器材1. 三线摆：一根长杆，中间连接一个质量块，下面吊一个质量块，形成一个三角形。

2. 计时器：用于记录物体旋转的时间。

3. 加速度计：用于测量物体的加速度。

4. 角度仪：用于测量物体旋转的角度。

5. 数据处理软件：用于处理实验数据，计算出物体的转动惯量。

四、实验步骤1. 将三线摆调整到水平状态，然后将质量较大的物体放在三角形的顶点，质量较小的物体放在底端。

确保两个物体之间的距离适中，以免影响实验结果。

2. 用角度仪测量物体开始旋转前的角度，然后启动计时器，记录物体旋转一周所需的时间。

重复多次，取平均值作为实验数据。

3. 在物体旋转过程中，用加速度计测量其加速度。

同样地，取多次实验数据的平均值作为实验数据。

4. 将实验数据导入数据处理软件，按照公式计算出物体的转动惯量。

五、实验结果与分析通过本次实验，我们成功地测量出了物体的转动惯量。

在实验过程中，我们需要注意以下几点：1. 确保三线摆的状态稳定，避免因为摆动过大而影响实验结果。

2. 在测量加速度时，要保持加速度计与物体的距离恒定，以免误差过大。

3. 在计算转动惯量时，要严格按照公式进行计算，避免出现错误。

通过这次实验，我们不仅掌握了三线摆测量物体转动惯量的原理和方法，还锻炼了自己的实验操作能力和数据处理能力。

希望大家在今后的学习生活中，能够将所学知识运用到实际中去，不断提高自己的综合素质。

三线摆测物体转动惯量实验报告

三线摆测物体转动惯量实验报告摘要：本实验通过使用三线摆装置，测量不同物体在转动过程中的角加速度，进而计算得出物体的转动惯量。

实验结果表明，不同形状和质量的物体具有不同的转动惯量，验证了转动惯量与物体形状和质量分布有关的结论。

引言：转动惯量是描述物体转动惯性的物理量，对于研究旋转运动以及理解物体在转动过程中的稳定性具有重要意义。

本实验使用三线摆装置，通过测量物体的加速度与力矩的关系，来研究物体转动惯量与其形状和质量分布的相关性。

实验装置与原理：1. 实验装置：三线摆装置、电子计时器、物体（包括圆环、圆盘等不同形状和质量的物体）2. 实验原理：三线摆实验是利用释放物体后，通过测量物体的加速度来推导出转动惯量。

根据牛顿第二定律和转动定律，可得到如下关系式：I = (m * g * l) / (α - β)其中，I为物体的转动惯量，m为物体的质量，g为重力加速度，l 为线长，α为测量得到的角加速度，β为摆放线本身的角加速度。

实验步骤与数据处理：1. 搭建三线摆装置，并调整每根线的长度一致，保持摆放线与竖直方向的夹角为20°。

2. 选择不同形状和质量的物体进行实验。

首先测量物体的质量m，并计算出物体的质心到摆放线的垂直距离l。

3. 将物体固定在摆放线上，释放摆线并使物体进行自由旋转。

4. 同时用电子计时器测量摆放线上一定长度内的自由旋转时间t，并记录下物体自由旋转的圈数n。

5. 重复以上实验步骤3-4多次，取得多组测量数据并计算平均旋转时间t和平均圈数n。

6. 通过角度关系计算得到物体的角加速度α=(2πn)/t。

7. 根据实验原理中的公式，计算得到物体的转动惯量I。

实验结果与分析：将实验得到的数据整理如下：物体形状质量(m) 距离(l) 旋转时间(t) 圈数(n) 角加速度(α) 转动惯量(I)圆环 0.2kg 0.3m 1.64s 5 3.82 rad/s^2 0.16 kg·m^2圆盘 0.3kg 0.4m 2.02s 6 5.95 rad/s^2 0.18 kg·m^2...通过实验结果可以观察到不同形状和质量的物体具有不同的转动惯量。

刚体转动惯量测定实验报告

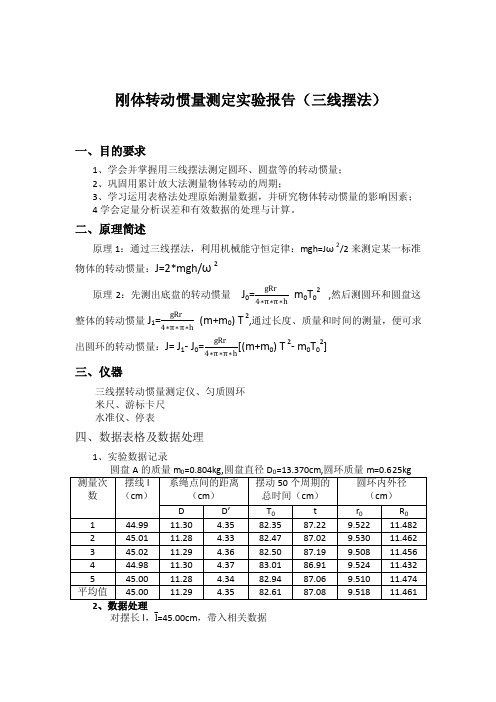
刚体转动惯量测定实验报告（三线摆法）一、目的要求1、学会并掌握用三线摆法测定圆环、圆盘等的转动惯量；2、巩固用累计放大法测量物体转动的周期；3、学习运用表格法处理原始测量数据，并研究物体转动惯量的影响因素；4学会定量分析误差和有效数据的处理与计算。

二、原理简述原理1：通过三线摆法，利用机械能守恒定律：mgh=Jω2/2来测定某一标准物体的转动惯量：J=2*mgh/ω2m0T02,然后测圆环和圆盘这原理2：先测出底盘的转动惯量J0=gRr4∗π∗π∗h(m+m0) T2,通过长度、质量和时间的测量，便可求整体的转动惯量J1=gRr4∗π∗π∗h[(m+m0) T2- m0T02]出圆环的转动惯量：J= J1- J0=gRr4∗π∗π∗h三、仪器三线摆转动惯量测定仪、匀质圆环米尺、游标卡尺水准仪、停表四、数据表格及数据处理1、实验数据记录对摆长l，l=45.00cm，带入相关数据∆l =（li −l ）ni =1n ∗（n −1）=（li −l ）5i=15∗（5−1）=0.01cm则l=l ±∆l =45.00±0.01cm同理，可得出，D ，D ’，t 0，t ，R ，r下圆盘系点间的距离D=D±∆D =11.29±0.01cm 上系点间的距离D ’=D′±∆D′=4.35±0.01cm 盘摆动50个周期所用时间t 0t 0= t0±∆t0=82.61±0. 14s 圆盘与圆环这整体摆动50个周期所用时间tt= t ±∆t =87.08±0.07s 圆环内径r 0=9.518±0.004cm 圆环外径R 0=11.461±0.008cm同时，由系点组成的上下圆半径：r =33D′，R = 33D周期，T0 =t050=1.67s ，T =t50=1.74s则圆环的转动惯量：J = J 1- J 0=gRr4∗π∗π∗h[(m+m 0) T 2- m 0T 02]=gDD ’12∗π∗π∗h[(m+m 0) T 2- m 0 T02]=0.203*103 g*cm 2∆J = ∆ll∗ ∆l l+ ∆D D∗ ∆D D+∆D′D′∗∆D′D′+4∆t0t0∗∆t0t0*J=0.085*103 g*cm 2J=J ±∆J =(0.203±0.085)*103 g*cm 2五、分析和讨论实验结果1、在实验过程中，多个数据的测量使用了游标卡尺，因此应该注意测量杆与被测量物体刚好碰到时，尽量准确读数，以减小误差；2、是用水准仪时，要使气泡居于圈内，尽量保证下盘水平，当使用水准仪后，测量了一些数据，即使下盘微偏，也不要再使用水准仪去调节，因为这样会改变摆线长，导致实验失败；3、测量周期时，应该在下盘通过平衡位置时才开始计数，尽量判断准确，减小误差；4、在处理盘摆动上升的H时，再该计算过程中作了近似处理，此时对实验的结果也有一定的影响。

三线摆法测量物体的转动惯量2015

实验三线摆法测量物体的转动惯量转动惯量是刚体转动惯性大小的量度，是表征刚体特征的一个物理量。

转动惯量的大小除与物体质量有关外，还与转轴的位置和质量分布（即形状、大小和密度）有关。

如果刚体形状简单，且质量分布均匀，可以直接计算出它绕特定轴的转动惯量。

但是工程实践中，我们常常碰到大量的形状复杂，且质量分布不均匀刚体，理论计算将极其复杂，通常采用实验方法来测定。

转动惯量的测量，一般都是使刚体以一定的形式运动。

通过表征这种运动特征的物理量与转动惯量之间的关系，进行转换测量。

测量刚体转动惯量的方法有多种，三线摆法具有设备简单、直观、测试方便的优点。

一.实验目的1. 学会用三线摆测量物体的转动惯量。

2. 学会用积累放大法测量扭摆运动的周期。

3. 验证转动惯量的平行轴定理。

二. 实验仪器DH4601转动惯量测试仪，计时器，圆环，圆柱体，游标卡尺，米尺，水平仪三. 实验原理图1是三线摆实验装置的示意图。

上、下圆盘均处于水平，悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘转动角很小，且略去空气阻力时，扭摆的运动可以近似的看作简谐运动。

根据能量守恒定律和刚体的转动定律均可以导出物体绕中心轴OO ’的转动惯量（推导过程见附录）：2002004T H gRr m I π=（1-1）式中各物理量的含义如下：0m 为下盘的质量r 、R 分别为上下悬点离各自圆盘中心的距离 0H 为平衡时上下盘间的垂直距离0T 为下盘作简谐运动的周期，g 为重力加速度。

将质量为m 的待测圆环放在下盘上，并使待测圆环的转轴与OO ’轴重合。

测出此时摆运动的周期1T 和上下圆盘间的垂直距离H 。

那么，可以求得待测圆环和下圆盘对中心转轴OO ’的总转动惯量为：212014T HgRr m m I π)(+=（1-2）图1 三线摆实验示意图如果不计因重量变化而引起的悬线伸长，则有0H H ≈。

那么，待测圆环绕中心轴OO ’的转动惯量为：01I I I -= （1-3）因此，通过长度、质量和时间的测量，便可以求出刚体绕某轴的转动惯量。

三线摆法测刚体的转动惯量所用近似方法对测量结果的影响

1986 . 77～83 .
The influence of measuring method to the result in the experiment of trilinear pendulum
SHEN G Zhong2zhi , YI De2wen , YAN G Wu’ e
( College of Science ,Central Sout h Forestry University , Zhuzhou , Hunan 412006 , China)
=
2r
H
2
2
sin2θ
( 11)
由式 ( 11) 可知 , 该比值与摆角 ( 角位移) 有关 . 实验室中常用的三线摆的典型数据约为 : H = 50 cm , r = 3 cm , R = 7 cm . 表 1 给出了不同摆角下平动动能与转
由表 3 可知 , 三线摆下圆盘离开平衡位置的最 θ θ 大角位移 θ ≈ 近似影响较大 . 当最 0 对采用 sin 2 2 大角位移 θ 时, 由此引起的误差达到 0 为 15° 0153 % , 已不可忽略 .
湖南科学技术出版社 , 1995 . 8～12 .
[4 ] 潘人培 . 物理实验 [ M ]. 南京 : 南京工学院出版社 ,
三线摆上、下两圆盘之间的距离 . 其中以式 ( 13) 和式 ( 15) 的影响较大 . 当最大角位移 θ 时 , 综合 4 0 为 15°
衡位置的最大角位移为 20° 时 , 平动动能与转动动能之比也小于 0 . 084 % , 故这一近似对测量结果的影响不大 .
3. 2 采用 H = B C≈ B C1 近似的影响
这是一简谐振动方程 , 该振动的周期平方为 π2 J 0 l 4 2 T0 =

实验四用三线摆法测定物体的转动惯量

实验4—3 三线摆实验转动惯量是刚体转动惯性大小的量度，是表征刚体特性的一个物理量。

转动惯量的大小除与刚体的质量有关外，还与转轴的位置和刚体的质量分布（即形状、大小和密度）有关。

如果刚体形状简单、且质量分布均匀，则可直接计算出它绕特定轴的转动惯量。

测量刚体的转动惯量时，一般都是使刚体以一定的形式运动。

通过表征这种运动特征的物理量与转动惯量之间的关系，进行转换测量。

测量刚体转动惯量的方法有多种，三线摆法是具有较好物理思想的实验方法，它具有设备简单、直观、测试方便等优点。

【实验目的】1. 学会用三线摆测定刚体的转动惯量。

2. 学会用累积放大法测量周期运动的周期。

图4-3-1 三线摆实验装置3. 了解摆角大小和摆线长短对测量周期的影响。

4. 验证转动惯量的平行轴定理。

【实验原理】三线摆实验装置如图4-3-1所示，上、下圆盘均处于水平，且悬挂在横梁上。

三个对称分布的等长悬线将两圆盘相连。

上圆盘固定，下圆盘可绕中心轴O O ′作扭摆运动。

当下盘转动角度很小，且略去空气阻力时，扭摆的运动可近似看作简谐运动。

根据能量守恒定律和刚体转动定律均可以导出物体绕中心轴的转动惯量（推导过程见本实验附录）。

O O ′ 2002004T H gRr m I π= （4-3-1）式中各物理量的意义如下：为下盘的质量；0m r 、R 分别为上下悬点离各自圆盘中心的距离；为平衡时上下盘间的垂直距离；T 0H 0为下盘作简谐运动的周期；g 为重力加速度（连云港地区g =9.797m/s 2）。

将质量为的待测刚体放在下盘上，并使待测刚体的转轴与m O O ′轴重合。

测出此时下盘运动周期和上下圆盘间的垂直距离1T H 。

三线摆摆线质量对转动惯量精确测量的影响

三线摆摆线质量对转动惯量精确测量的影响葛宇宏;葛志利【期刊名称】《力学与实践》【年(卷),期】2012(034)006【摘要】三线摆法是测量转动惯量的常用方法,理论上通常都是把摆线作理想处理（即摆线质量趋于0）,但在工程测量中,被测工件往往较重,摆线不再是轻质细线,摆线质量势必会对空载悬盘的转动惯量测量产生影响.本文应用哈密顿原理和变量替换,导出三线摆摆线的变张力弦振动方程,通过对摆线与悬盘连接点（x=0）的运动状态讨论,推得摆线质量不能忽略情形下的对称式三线摆的转动惯量计算式,并借助于MATLAB软件快速便利地进行计算.%Using the three wire-pendulum to measure the moment of inertia is a common practice. The cycloid is usually assumed in an ideal state theoretically (i.e the mass of the cycloid approaches 0). But actually, if the workpiece measured is heavy, the mass of the cycloid can not be neglected, we have to consider the mass of the cycloid in the moment of inertia of the empty turning wheel. This paper uses the Halmiltonian theory and the variable substitution to derive the variable tension string vibration equation of the threewire-pendulum cycloid. And from the state of the point in the junction of the cycloid and the turning wheel (x = 0), we obtain a computational formula for the moment of inertia by using the three wire-pendulum without neglecting the mass of the cycloid. In addition, we can make calculations by MATLAB.【总页数】5页(P50-54)【作者】葛宇宏;葛志利【作者单位】南京化工职业技术学院,南京210048;南京化工职业技术学院,南京210048【正文语种】中文【中图分类】O4-34【相关文献】1.三线摆测转动惯量时高度对测量结果的影响 [J], 朱瑜;邵雪纯2.Tracker软件在三线摆测量刚体转动惯量实验中的应用 [J], 高寒;张黔;谢媛;伊志鑫3.三线摆法测刚体的转动惯量所用近似方法对测量结果的影响 [J], 盛忠志;易德文;杨恶恶4.不同摆角对三线摆测量转动惯量的影响 [J], 朱瑜;潘永丰;左安友5.三线摆实验中用大摆角测量转动惯量 [J], 周艳明;翦知渐;谢中因版权原因，仅展示原文概要，查看原文内容请购买。