重庆南开中学2015届高三9月月考数学试题(文)含答案

合集下载

重庆市南开中学2015届高三10月月考语文试题 Word版含答案

重庆南开中学高2015级10月月考语文试题卷语文试题卷共8页。

考试时间l50分。

第1至6题、第8至10题为选择题，27分；第7题、第11至22题为非选择题，123分。

满分150分。

注意事项：1．答题前，务必将自己的姓名、考号填写在答题卡规定的位置上。

2．答第1至6题、第8至10题时，务必使用2B铅笔将答题卡上对应题目答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3．答第7题、第11至22题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定位置上。

4．所有题目必须在答题卡上作答，在试卷上答题无效。

5．考试结束后，将答题卡交回。

一、(本大题共4小题，每小题3分，共12分)1．下列词语中，字形和加点字的读音全都正确的一组是A．宣泄披沙拣金佣．工yòng 洗涮．shuànB．震撼展露才华踮．脚diǎn 生肖．xiào ．C．烦躁一愁莫展症．结zhāng 恫．吓dòngD．既使委曲求全癖．pǐ好拘泥．nì2．下列语句中，加点的词语使用正确的一项是A．这些文明成就积淀在文化中，又通过教育传授给新一代，从而．．使新一代获得比前代更高的起点。

B．蜀南竹海旅游景区内翠竹森森，遮天蔽日，浩如烟海．．．．，四季皆可观：春看竹雾，夏赏竹绿，秋览竹浪，冬观竹翠。

C．随着网络的普及，网络文学创作蔚然成风，出现了一批脍炙人口的精品，但也有许多不忍卒读．．．．的作品，内容低俗，文字粗劣。

D．他为人不错，只是过于固执，喜欢钻牛角尖，丁是丁，卯是卯．．．．．．．，一点也不晓得变通。

3．下列选项中，标点符号使用正确的一项是A．如何调动农民的积极性，避免水利工程只修不管的现象，从一些地方经验看，以“谁投资、谁受益、谁所有”的原则推进产权改革，是一个好办法。

B．《易经》的作者说：“上古结绳而治，后世圣人易之以书契。

”他不说“仓颉”，只说“后世圣人”；不说“造”，只说“易”，真是谨慎得很。

重庆市巴蜀2024-2025学年高三上学期9月月考数学试题含解析

数学试卷（答案在最后）注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚.2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.在试题卷上作答无效.3．考试结束后，请将本试卷和答题卡一并交回.满分150分，考试用时120分钟.一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.命题“x ∀∈R ，2210x x ++≥”的否定是（）A.x ∃∈R ，2210x x ++≥B.x ∃∈R ，2210x x ++<C.x ∀∈R ，2210x x ++>D.x ∀∈R ，2210x x ++<【答案】B 【解析】【分析】利用全称量词命题的否定即可解答.【详解】命题“x ∀∈R ，2210x x ++≥”为全称量词命题，它的否定是存在量词命题，即x ∃∈R ，2210x x ++<，故选：B.2.今年高二（1）班的同学参加语文和数学两个学科的结业水平考试，每科满分为100分．考试成绩非常优秀，每个同学都至少有一科成绩在90分以上，其中语文90分以上的有45人，数学90分以上的有48人，这两科均在90分以上的有40人，高二（1）班共有（）个同学．A.45B.48C.53D.43【答案】C 【解析】【分析】由题意设出集合,A B 得到集合,A B 以及A B ⋂中元素的个数，即可得出A B 中元素的个数．【详解】设集合A 表示语文在90分以上的学生，则集合中有45个元素，集合B 表示数学在90分以上的学生，则集合中有48个元素，A B ⋂表示两科均在90分以上的学生，则集合A B ⋂中有40个元素，A B 表示至少有一科成绩在90分以上的学生，由题意可知A B 中有个45484053+-=元素，又因为每个同学都至少有一科成绩在90分以上，所以高二（1）班共有53人，故选：C ．3.关于x 的不等式lg lg lg 10k x x k x ⋅+-<对一切x +∈R 恒成立，则k 的取值范围是（）A.(,4]-∞-B.(,4][0,)-∞-+∞C.(4,0)-D.(4,0]-【答案】D 【解析】【分析】当0k =时，可知不等式恒成立；当0k ≠时，由二次函数图象和性质可得不等式组，解不等式组求得结果.【详解】x 的不等式2lg lg lg 1lg lg 10k x x k x k x k x ⋅+-=+-<对一切x +∈R 恒成立，当0k =时，不等式对一切x +∈R 恒成立，当0k ≠时，x +∈R 时lg x ∈R ，则有2Δ40k k k <⎧⎨=+<⎩，解得40k -<<，所以k 的取值范围是(4,0]-.故选：D4.19世纪美国天文学家西蒙·纽康和物理学家本·福特从实际生活得出的大量数据中发现了个现象，以1开头的数出现的频数约为总数的三成，并提出本·福特定律，即在大量10进制随机数据中，以()n n +∈N 开头的数出现的概率为1()lgn P n n+=，如斐波那契数、阶乘数、素数等都比较符合该定律．后来常有数学爱好者用此定律来检验某些经济数据、选举数据等大数据的真实性．若()193333log 8log 2(),19log 2log 5n k P n k k +=-=∈≤+∑N （说明符号()1,,jk i i j k i a a a a k i j ++==+++∈∑N ），则k 的值为（）A.3B.5C.7D.9【答案】B 【解析】【分析】根据题意利用对数的运算法则可得19()lg 4n kP n ==∑，再由符号说明表达式即可求得5k =.【详解】易知19333333log 8log 2log ()lg 4log o 4102log 5l g n kP n =-===+∑，由1()lg n P n n +=可得191212()lg l 19g lg lg l 2020201119g n kk k k k k k k k k P n =++++⎛⎫=++⋅⋅⋅+=⨯⨯⋅⋅⋅⨯= ⎭++⎪⎝∑；所以lglg 420k=，解得5k =.故选：B5.某机器上有相互啮合的大小两个齿轮（如图所示），大轮有25个齿，小轮有15个齿，大轮每分钟转3圈，若小轮的半径为2cm ，则小轮每秒转过的弧长是（）cm．A.10πB.5πC.π3D.π6【答案】C 【解析】【分析】根据给定条件，求出小轮每分钟转的圈数，再借助弧长公式计算即得.【详解】由大轮有25个齿，小轮有15个齿，大轮每分钟转3圈，得小轮每分钟转的圈数为325515⨯=，因此小轮每秒钟转的弧度数为52ππ606⨯=，所以小轮每秒转过的弧长是2cm cm ππ63⨯=.故选：C6.已知函数32()6f x x x =-，若()()g x f x a b =+-为奇函数，则（）A.2a =，16b =B.2a =-，16b =-C .2a =-，16b = D.2a =，16b =-【答案】D 【解析】【分析】根据奇函数定义可得()()0f x a b f x a b +-+-+-=恒成立，化简可求,a b .【详解】因为()()g x f x a b =+-为奇函数，32()6f x x x =-，所以()()0f x a b f x a b +-+-+-=，所以()()()()3232660x a x a b x a x a b +-+-+-+--+-=，所以()()()()3232660x a x a b x a x a b +-+------=，所以()23261221220a x a a b -+--=，所以6120a -=，3221220a a b --=，所以2a =，16b =-，故选：D.7.若函数32()(1)(5)2f x x k x k x =+-+++在区间(0,3)上不单调，则k 的取值范围是（）A.(4,3)--B.(5,2)-- C.(5,3)-- D.(4,2)--【答案】B 【解析】【分析】求出函数()f x 的导数()f x '，利用()f x '在(0,3)上有变号零点列式求解即得.【详解】函数32()(1)(5)2f x x k x k x =+-+++，求导得2()32(1)5f x x k x k '=+-++，由函数()f x 在区间(0,3)上不单调，得()f x '在(0,3)上有变号零点，由()0f x '=，得2232(1)50(21)325x k x k k x x x +-++=⇔-+=-+，则24(21)3(2)4220k x x x -+=-⋅+，令21(1,7)x t +=∈，于是2243(1)4(1)2031027kt t t t t -=--⋅-+=-+，即有943(10k t t-=+-，令9()3()10,17g t t t t=+-<<，函数()g t 在(1,3]上单调递减，函数值从20减小到8，在[3,7)上单调递增，函数值从8增大到1047，由()f x '在(0,3)上有变号零点，得直线4y k =-与函数(),17y g t t =<<的图象有交点，且当有两个交点时，两个交点不重合，因此8420k <-<，解得52k -<<-，所以k 的取值范围是(5,2)--.故选：B8.已知函数()e e x x f x -=+，若关于x 的方程()2f x x k +=有4个不同的实数根，则k 的取值范围是（）A.11442,e e -⎛⎫+ ⎪⎝⎭B.()222,e e -+ C.11222,e e -⎛⎫+ ⎪⎝⎭ D.11114422e e ,e e --⎛⎫++ ⎪⎝⎭【答案】A 【解析】【分析】先得到()e e x x f x -=+的奇偶性和单调性，从而令2x x t +=，若()f t k =仅有一个实数根0t ，则00t =，2k =，此时推出只有两个根，不合要求，若()f t k =有两个实数根12,t t ，由对称性可知21t t =-，故210x x t +-=和210x x t ++=均有两个解，有根的判别式得到11144t -<<且10t ≠，结合函数单调性和奇偶性得到11441()2,e e k f t -⎛⎫=∈+ ⎪⎝⎭.【详解】()e e x x f x -=+的定义域为R ，且()e e ()x x f x f x --=+=，故()e e x x f x -=+为偶函数，且当0x >时，0()e e x x f x -=->'恒成立，故()e e x x f x -=+在0,+∞上单调递增，由对称性可知()f x 在(),0∞-上单调递减，()min ()02f x f ==，令2x x t +=，若()f t k =仅有一个实数根0t ，则00t =，2k =，此时20x x +=，解得10x =或1-，仅有2个实数根，不合要求，舍去；若()f t k =有两个实数根12,t t ，由对称性可知21t t =-，需要满足21x x t +=和21x x t +=-均有两个解，即210x x t +-=和210x x t ++=均有两个解，由11140,140t t ∆=+>∆=->，解得11144t -<<，又10t ≠，故11144t -<<且10t ≠，即1111441()e e 2,e e t t k f t --⎛⎫==+∈+ ⎪⎝⎭.故选：A【点睛】方法点睛：复合函数零点个数问题处理思路：①利用换元思想，设出内层函数；②分别作出内层函数与外层函数的图象，分别探讨内外函数的零点个数或范围；③内外层函数相结合确定函数交点个数，即可得到复合函数在不同范围下的零点个数.二、多项选择题（本大题共3个小题，每小题6分，共18分，在每个给出的四个选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分）9.若tan α=，则下列与角α的终边可能相同的角是（）A.4π3B.5π3C.ππ3k +，k ∈Z D.2π2π3k -，k ∈Z 【答案】ACD 【解析】【分析】通过正切函数值相等，分析判断对应角的终边是否相同.【详解】对于A ，4πtan 3=，因此A 正确；对于B ，5πtan3=B 不正确；对于C ，πtan π3k ⎛⎫+=⎪⎝⎭，因此C 正确；对于D ，2πtan 2π3k ⎛⎫-= ⎪⎝⎭，因此D 正确。

【名师解析】重庆南开中学2015届高三9月月考物理试题 Word版含解析

重庆南开中学高2015级9月月考理科综合能力测试试题卷【试卷综析】本试卷是高三开学模拟试题，包含了高中物理的必修一、必修二，选修3-3内容，主要包含受力分析、牛顿运动定律、动能定理、万有引力与航天热力学定理等内容，在考查问题上以基本定义、基本规律为主，以基础知识和基本技能为载体，以能力测试为主导。

物理（共110分）一、选择题（本大题共5小题，每小题6分，共30分．在每小题给出的四个选项中，只有一项符合题目要求）【题文】1．关于物体受力和力与运动的关系，下列说法正确的是A．竖直向上运动的物体，一定受到竖直向上的力的作用B．有一个力出现时，一定有两个与该力相关的物体C．只有在相互接触的物体之间才能有力的作用D．摩擦力一定是阻碍物体运动的阻力【知识点】弹性形变和范性形变；力的概念及其矢量性；摩擦力的判断与计算．B2 B3 【答案解析】B 解析：A、竖直向上运动的物体，不一定受到竖直向上的力的作用，如竖直上抛运动只受重力，故A错误；B、力是物体间的相互作用，有一个力出现时，一定有两个与该力相关的物体，故B正确；C、力是物体间的相互作用，发生相互作用的两个物体不一定要接触，故C错误；D、摩擦力一定是阻碍物体间的相对运动，但与速度方向可以相同，故D错误；故选：B．【思路点拨】力是改变物体运动状态的原因；平衡状态是指静止状态或匀速直线运动状态，处于平衡状态的物体受平衡力作用；原来运动的物体，当不受外力时，物体将做匀速直线运动状态；原来静止的物体，当不受外力时，物体将保持原来静止的状态．力是改变速度的原因，不是维持速度的原因，即力是产生加速度的原因．【题文】2．如图所示，质量相等的A、B两物体在同一水平线上，当A物体被水平抛出的同时，B物体开始自由下落（空气阻力忽略不计），曲线AC为A物体的运动轨迹，直线BD为B物体的运动轨迹，两轨迹相交于O点，则关于两物体在O点的物理量，下列说法正确的是A．经O点时速率相等B．运动到O点的时间不相等C．运动到O点的速度改变量相等D．在O点时重力的功率一定不相等【知识点】平抛运动．D2【答案解析】C 解析： A、两物体经O点时，两个物体重力做功相同，即竖直方向分速度相等，平抛运动的A物体在O点有水平速度，根据速度的合成可知平抛运动的物体经过O点的速度较大，则在O点v A＞v B，故A错误．B、C、两物体在竖直方向做自由落体运动，下∆=∆，故B错误，C正确；D、O点的重力功率P=mgv y，可知P相等，落时间相等，利用v g t故D错误．故选C【思路点拨】速率表示瞬时速度的大小，到C点的速度可以通过平抛运动和自由落体运动的公式求出；恒力的功率，可用公式P=Fvcosθ去求．【题文】3．如图所示，质量为所的物块始终固定在倾角为θ的斜面上，下列说法中错．误．的是A．若斜面向右匀速移动距离s，斜面对物块没有做功B．若斜面向上匀速移动距离s，斜面对物块做功mgsC．若斜面向左以加速度a移动距离s，斜面对物块做功masD．若斜面向下以加速度a移动距离s．斜面对物块做功m(g+a)s【知识点】功的计算．E1【答案解析】D 解析： A．斜面向右匀速运动，物块也是匀速运动，受力平衡，斜面对物块的力等于其重力，方向竖直向上，运动方向（位移矢量）始终与斜面作用力垂直，所以不做功，故A正确；B．物块和斜面一起竖直向上匀速运动，物块受力平衡，斜面对物块的力大小等于物块的重力mg，方向竖直向上，位移方向也向上，所以W=mgs，故B正确；C．物块和斜面一起向左以加速度a移动距离s，物块所受的合力做的功等于mas，物块受到重力和斜面对物块的力，所以，重力做的功加上斜面对物块做的功之和等于mas，又因为重力做功为零，所以斜面对物块做的功等于mas，故C正确；D．物块和斜面一起竖直向下以加速度a移动距离s，物块所受的合力做的功等于mas，物块受到重力和斜面对物块的力，所以，重力做的功加上斜面对物块做的功之和等于mas，又因为重力做功为mgs，所以斜面对物块做的功等于mas-mgs，故D错误．故选D．【思路点拨】（1）力对物体做功的条件是：要有力作用在物体上，并在力的方向上产生一段位移；（2）功的计算方式一般有两种，一种是根据功的计算公式W=FLcosθ进行计算，一般计算恒力做功，第二种是根据动能定理求解，一般求变力做功．（3）求合力做功时可以先求各个力做的功，再求代数和，也可以先求出合力，再根据W=F合Lcosθ进行计算．该题考查了力做功的条件以及功的计算方法，求合力做功时可以先求各个力做的功，再求代数和，也可以先求出合力，再根据W=F合Lcosθ进行计算，求变力做功可据动能定理求解，该题难度适中．【题文】4．宇宙间存在一些离其它恒星较远的三星系统，其中有一种三星系统如图所示，三颗质量均为m 的星位于等边三角形的三个顶点，三角形边长为L ，忽略其它星体对它们的引力作用，三星在同一平面内绕三角形中心O 做匀速圆周运动，则：A. 当质量m 变为原来的2倍，距离L 也变为原来的2倍时，周期变为原来的2倍B ．当质量m 变为原来的2倍，距离L 也变为原来的2倍时，线速度变为原来的2倍C ．该三星系统运动的周期跟两星间距离L 无关，只与星的质量m 有关D. 该三星系统运动的周朔跟星的质量m 无关，只与两星间距离L 有关【知识点】万有引力定律及其应用．D5【答案解析】A 解析：任意两个星星之间的万有引力为：F=G 2mm L 每一颗星星受到的合力为：F 1=，恒星的转动半径L，根据万有引力的合力提供圆周运动向心力有222243mm G L L T π== A 、可得周期可知当质量m 和L 均变为原来的2倍，可知周期变为原来的2倍，故A 正确；B 、可得线速度，可知当质量m 和L 均变为原来的倍时，可知线速度保持不变，故B 错误；CD 、由周期周期既与恒星的质量m 有关也与恒星的距离有关，故CD 错误．故选：A ．【思路点拨】先写出任意两个星星之间的万有引力，求每一颗星星受到的合力，该合力提供它们的向心力．然后用L 表达出它们的轨道半径，最后写出用周期和线速度表达的向心力的公式，整理即可的出结果．解决该题首先要理解模型所提供的情景，然后能够列出合力提供向心力的公式，才能正确解答题目．【题文】5．在广场游玩时，一小孩将一充有氢气的气球用细绳系于一个小石块上，并将小石块置于水平地面上，如图所示．若水平的风力逐渐增大（设气球所受空气的浮力不变），则A．细绳的拉力逐渐减小B．小石块有可能连同气球一起被吹离地面C．地面受到小石块的压力逐渐减小D．小石块滑动前受到地面施加的摩擦力逐渐增大，滑动后受到的摩擦力不变【知识点】共点力平衡的条件及其应用；力的合成与分解的运用．B3 B4【答案解析】 D 解析： A、以气球为研究对象，分析受力如图1所示：重力G1、空气的浮力F1、风力F、绳子的拉力T．设绳子与水平方向的夹角为α，当风力增大时，α将减小．根据平衡条件得竖直方向：F1=G1+Tsinα，当α减小时，sinα减小，而F1、G1都不变，则绳子拉力T增大．故A错我．C、D、以气球和石块整体为研究对象，分析受力如图2，根据平衡条件得竖直方向：N+F1=G1+G2，水平方向：f=F气球所受的浮力F1、气球的重力G1、石块的重力G2都不变，则地面对石块的支持力N不变，地面受到小石块的压力也不变．在石块滑动前，当风力F增大时，石块所受的摩擦力增大，当石块滑动后受到的摩擦力f=μN保持不变．故C错误，D正确．B、由于地面对石块的支持力N=G1+G2-F1保持不变，与风力无关，所以当风力增大时，小石块连同气球一起不可能被吹离地面．故B错误．故选：D．【思路点拨】分析气球的受力情况，根据平衡条件得出细绳的拉力与绳子与水平方向夹角的表达式，再分析绳子拉力的变化．以气球和石块整体为研究对象，由平衡条件分析小石块所受地面的支持力如何变化，再由牛顿第三定律判断地面受到小石块的压力变化，判断小石块能否滑动．本题是两个物体的平衡问题，一是要灵活选择研究对象，二是要抓住浮力、重力等不变的条件进行分析．二、非选择题（本大题共4小题，共68分）【题文】6.(19分)(1)某学生用打点计时器研究小车的匀变速直线运动．实验时得到一条纸带．他在纸带上便于测量的地方选取第一个计时点A，已知相邻两计时点间的时间间隔为T 且测量时发现AC两点间的B点已模糊不清，如图所示，于是他测得AC长为S1，DE长为S2，EF 长为S 3（CD 间还有一些相邻计时点未标出），则打B 点时小车的瞬时速度大小为__ __，小车运动的加速度大小为__ __．【知识点】测定匀变速直线运动的加速度．A7 【答案解析】12S T ,312S S T- 解析：根据匀变速直线运动中时间中点的速度等于该过程中的平均速度得：v B ＝122AC x s T T =根据匀变速直线运动的推论公式△x=aT 2得：a=312S S T- 【思路点拨】根据匀变速直线运动的推论公式△x=aT 2可以求出加速度的大小，根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上D 点时小车的瞬时速度大小．要提高应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用．(2)如图，质量为M 的滑块A 放在气垫导轨B 上，C 为位移传感器，它能将滑块A 到传感器C 的距离数据实时传送到计算机上，经计算机处理后在屏幕上显示滑块A 的位移一时间(s-t )图像和速率一时间(v-t ) 图像．整个装置置于高度可调节的斜面上，斜面的长度为l 、高度为h ．①现给滑块A 一沿气垫寻轨向上的初速度，A 的v-t 图线如题6图所示。

重庆市南开中学2015届高三12月月考数学(文)试题Word版含答案

重庆南开中学高2015级高三12月月考数学试题(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦擦干净后，再选涂其他答案标号．3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上． 4．所有题目必须在答题卡上作答，在试题卷上答题无效．第Ⅰ卷(选择题共50分)一．选择题：本大题共10小题，每小题5分。

共50分．在每小题给出的四个备选项中。

只有一项是符合题目要求的。

1．圆122=+y x C ：关于直线2=x 对称的圆的方程为( ) A ．()1422=+-y x B ．()1422=++y xC ．()1422=-+y x D ．()1422=++y x2．已知(){}2,x y y x A ==，(){}x y y x B ==,，则B A = ( )A ．RB ．[0，+∞)C ．(1，1)D ．()(){}1100，，，3．在某次测量中得到的A 样本数据如下：82，84，84，86，86，86，88，88，88，88．若B 样本恰好是A 样本每个数据都加2后所得数据，则A ，B 两样本的下列数字特征对应相同的是( )A ．众数B ．平均数C ．中位数D ．标准差4．已知等比数列{}n a 满足253=a a ，则7241a a a 的值是( )A ．2B ．4C ．8D ． 165．某三棱锥的三视图如右图所示，则该三棱锥最长棱的棱长为( )`A ．32B ．6C ．22D ．3 6．下列说法错误的是( )A ．若命题“q p ∧”为真命题，则“q p ∨”为真命题B ．命题“若0＞m ，则方程02=-+m x x 有实根”的逆命题为真命题C ．命题“022=-∈∃x x R x ，”的否定是“022≠-∈∀x x R x ，”D ．“1＞x ”是“0＞x ”的充分不必要条件7．已知平面点集()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≤--≥-≥+=2211y x y x y x y x M ，，平面点集(){}122≤+y x y x ，，在集合M中任取一点P ，则点P 落在集合N 中的概率为( ) A ．122-π B ．1232-π C ．62-π D ．632-π 8．已知()x f y =是定义域为R 的奇函数，且当0＞x 时，()423-+=x x f x ，若存在I x ∈0，使得()00=x f ，则区间I 不可能是( )A ．()12--，B ．()11，-C ．()21， D ．()01，- 9．阅读右面的程序框图，若输入的n 是100，则输出的变量S 和T 的值依次是( )A ．2450，2500B ．2550，2450C ．2500，2550D ．2550，250010．已知双曲线()0012222＞，＞b a by a x =-上一点C ，过双曲线中心的直线交双曲线于A ，B 两点，记直线AC ，BC 的斜率分别为21k k ，，当2121ln ln 2k k k k ++最小时，双曲线离心率为( )A ．2B ．3C ．2+1D ．2第Ⅱ卷(非选择题，共l00分)二．填空题：本大题共5小题，每小题5分。

重庆南开中学初2015级初三(上)12月数学月考试卷

重庆南开中学初2015级九年级(上)阶段测试(二)数学试题 2014.12参考公式：抛物线)0(2≠++=a c bx ax y 的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 4422，，对称轴为直线a b x 2-= 一、选择题(本大题12个小题，每小题4分，共48分)在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案。

其中只有一个是正确的，请将答卷上对应的方框涂黑。

1．上下楼梯时，如果将上3步台阶记为+3，那么下3步台阶应该记为(▲)·A ．﹣3B ．3C ．+3D ．02．计算()23x 的结果是(▲)。

A ．5x B ．6x C ．9x D ．32x3．下面的图形中，既是轴对称图形又是中心对称图形的是(▲)。

4．函数x y -=3中，自变量x 的取值范围是(▲)。

A ．x ≠3B ．3≥xC ．3＜xD ．3≤x5．下列调查中，调查方式选择正确的是(▲)。

A ．为了了解某品牌手机的屏幕是否耐摔，选择全面调查B ．为了了解玉兔号月球车的零部件质量，选择抽样调查C ．为了了解南开步行街平均每天的人流量，选择抽样调查D ．为了了解中秋节期间重庆市场上的月饼质量，选择全面调查6．如图，直线m l ∥，将含︒45角的三角板ABC 的直角顶点C 放在直线m 上，若︒=∠251，则2∠的度数为(▲)。

A ．20°B ．25°C ．30°D ．35°7．如图，在ABCD 中，E 为CD 上一点，且32：：=CE DE ，连结AE 、BD 相交于点F ，则△DEF 和△ABF 的面积之比为(▲)。

A ．2：3B ．4：9C ．2：5D ．4：258．分式方程0347=-+x x 的根是(▲)。

A ．3-=x B ．3=x C ．1-=x D ． 1=x9．如图，△ABC 的三个顶点都在O 上，连结CO 、BO ，已知︒=∠55A ，则BCO ∠ 的度数是(▲)。

2024-2025学年重庆市南开中学高一数学上学期9月考试卷附答案解析

2024-2025学年重庆市南开中学高一数学上学期9月考试卷试卷满分150分，考试时间120分钟.第I 卷（选择题）一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．下列各项中，不可以组成集合的是A ．所有的正数B ．等于2的数C ．接近于0的数D ．不等于0的偶数2．已知命题1:0,2p x x x∀>+>，则p ⌝为（）A ．0x ∀>，12x x +≤B ．0x ∀≤，12x x +≤C ．0x ∃≤，12x x+≤D ．0x ∃>，12x x+≤3．{}2{1,,},1,,2A x y B x y ==，若A B =，则实数x 的取值集合为（）A ．12⎧⎫⎨⎬⎩⎭B ．11,22⎧⎫-⎨⎩⎭C ．10,2⎧⎫-⎨⎬⎩⎭D ．110,,22⎧⎫-⎨⎬⎩⎭4．满足{1，2，3}M {1，2，3，4，5，6}的集合M 的个数是（）A ．8B ．7C ．6D ．55．如图，I 是全集，M P S 、、是I 的3个子集，则阴影部分所表示的集合是（）A ．()M P S ⋂⋂B ．()M P S ⋂⋃C ．()I M P S ⋂⋂ðD ．()I M P S⋂⋃ð6．设常数a ∈R ，集合A={x|（x ﹣1）（x ﹣a ）≥0}，B={x|x≥a ﹣1}，若A ∪B=R ，则a 的取值范围为（）A ．（﹣∞，2）B ．（﹣∞，2]C ．（2，+∞）D ．[2，+∞）7．若A 、B 、C 为三个集合，A B B C ⋃=⋂，则一定有（）A ．A C⊆B ．C A⊆C ．A C¹D ．A =∅8．设集合{123456}M =，，，，，，12k S S S ，，，都是M 的含两个元素的子集，且满足：对任意的{}i i i S a b =，，{}j j j S a b =，（i≠j ，{123}i j k ∈ 、，，，，），都有min min j j i i i i j j a b a b b a b a ⎧⎫⎧⎫⎪⎪≠⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭，，（min{}x y ，表示两个数x y，中的较小者），则k 的最大值是（）A ．10B ．11C ．12D ．13二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，有选错的得0分，部分选对的得部分分.9．已知“1x <”是“x a ”的充分不必要条件，则a 的值可能为（）A ．0B ．1C ．2D ．410．设{}{},31,,31,a b A xx m m c B x x k k ∈==+∈∈==-∈Z Z ∣∣，则（）A ．a b A +∈B ．ab A ∈C ．a b B+∈D ．ac B∈11．集合{}S x m x l =≤≤∣，且若a S ∈，则2a S ∈，那么下列说法正确的有（）A ．若1m =，则1l =B ．12l =，则202m ≤≤C ．||1,||1m l ≤≤D ．若1l =，则10m -≤≤第II 卷（非选择题）三、填空题：本大题3个小题，每小题5分，共15分.各题答案必须填写在答题卡上相应位置（只填结果，不写过程）.12．设全集{}*6U x x =∈<N ∣，集合{}1,3A =，{}3,5B =，则()U C A B ⋃=．13．南开中学高一某班报名数学、物理竞赛班，两科都不参加的占全班的13，只参加数学的占全班的25，参加物理的比参加数学的少11人，两门都参加的有5人，则全班有人.14．已知集合(){}22,1,,A x y xy x y =+≤∈Z ，(){},1,1,,B x y x y x y =≤≤∈Z ，定义集合()()(){}12121122,,,,A B x x y y x y A x y B ⊕=++∈∈，则A B ⊕中元素的个数为.四、解答题15．（1）若集{}2R310A x ax x =∈++=∣中有且仅有一个元素，求实数a 的所有取值.（2）已知集合{}2{10},320A xmx B x x x =-==-+=∣∣，若A B ⊆，求实数m 的值.16．设集合{}{}{}23217,280,321A x x B x x x C x a x a =-<+<=+->=-<<+.(1)求()A B ⋂R ð(2)若()A B C ⋃⊆R ð，求实数a 的取值范围.17．已知全集R U =，集合22{|30},{|(2)(34)0}A x x x b B x x x x =-+==-+-=．(1)若b ＝4时，存在集合M 使得AMB ，求出所有这样的集合M ；(2)集合A ，B 能否满足()U B A =∅ ð？若能，求实数b 的取值范围；若不能，请说明理由．18．已知{}{}22{(,)2},(,),(,)2(42)A x y y x k B x y y x C x y y x k x k ==+====+--∣∣∣.(1)若A B =∅ ，求实数k 的取值范围;(2)若()()A B A C ⋂⊆⋂，求实数k 的取值范围.19．设集合{1,2,3,,n S n = ），若X 是n S 的子集，把X 中所有元素的和称为X 的"容量"（规定空集的容量为0），若X 的容量为奇（偶）数，则称X 为n S 的奇（偶）子集.(1)写出4S 的所有奇子集;(2)求证：n S 的奇子集与偶子集个数相等；(3)求证：当3n ≥时，n S 的所有奇子集的容量之和等于所有偶子集的容量之和.1．C【详解】试题分析：集合中的元素满足三要素：确定性、互异性、无序性；“接近于0的数”是不确定的元素故接近于0的数不能组成集合故选C ．考点：集合的含义．2．D【分析】根据题意，结合全称量词命题与存在性量词命题的关系，准确改写，即可求解.【详解】根据全称量词命题与存在性量词命题的关系，可得：命题1:0,2p x x x ∀>+>的否定是10,2x x x∃>+≤．故选：D 3．A【分析】两个集合相等，则元素相同，据此分类讨论求解即可.【详解】由题意1x ≠，22x y y x =⎧⎨=⎩或22x x y y ⎧=⎨=⎩，∴1214x y ⎧=⎪⎪⎨⎪=⎪⎩或00x y =⎧⎨=⎩，由集合元素互异性可知1214x y ⎧=⎪⎪⎨⎪=⎪⎩，则实数x 的取值集合为12⎧⎫⎨⎬⎩⎭.故选：A.4．C【分析】根据条件，列举出满足条件的集合M ，即可求解.【详解】由题意可知，{}1,2,3,4M =,{}1,2,3,5,{}1,2,3,6,{}1,2,3,4,5,{}1,2,3,4,6,{}1,2,3,5,6，共有6个集合满足条件.故选：C 5．C【分析】直接根据阴影部分的位置得答案.【详解】图中阴影部分不在集合S 中，在集合,M P 中，故阴影部分所表示的集合是()I M P S ⋂⋂ð.故选：C.6．B【详解】试题分析：当时，，此时成立，当时，，当时，，即，当时，，当时，恒成立，所以a的取值范围为，故选B.考点：集合的关系7．A【分析】由已知等式可推导得到A B C ⊆⊆，由此可依次判断各个选项得到结果.【详解】因为A B B C ⋃=⋂，所以⊆ A B B ，A B C ⊆ ，B B C ⊆ ，所以,,A B A C B C ⊆⊆⊆,所以A B C ⊆⊆，对于A ，因为A B C ⊆⊆，所以A C ⊆，故A 正确；对于B ，当且仅当A B C ==时，C A ⊆，故B 错误；对于C ，当A B C ==时，满足A B C ⊆⊆，故C 错误；对于D ，当A ≠∅时，满足A B C ⊆⊆，故D 错误.故选：A.8．B 【分析】根据题意，首先分析出M 的所有含2个元素的子集数目，进而对其特殊的子集分析排除，注意对{},,(,j j i i i i j j a b a b min min min x y b a b a ⎧⎫⎧⎫⎪⎪≠⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭表示两个数x 、y 中的较小者）的把握，即可得答案．【详解】解：根据题意，对于M ，含2个元素的子集有15个，但{1，2}、{2，4}、{3，6}只能取一个；{1，3}、{2，6}只能取一个；{2，3}、{4，6}只能取一个，故满足条件的两个元素的集合有11个；故选：B ．9．BCD【分析】由充分不必要条件求出a 的范围即可找到选项.【详解】因为“1x <”是“x a ≤”的充分不必要条件，所以1a ≥.故选：BCD 10．BCD【分析】利用数的特征及元素与集合的关系计算即可.【详解】设()31,31,31a u b v c w u v w =+=+=-∈Z 、、，而()()32311a b u v u v B +=++=++-∈，即A 错误，C 正确；()()931331ab uv u v uv u v A =+++=+++∈，即B 正确；()()931331ac uw w u uw u w B =+--=-+-∈，即D 正确.故选：BCD.11．AB【分析】根据集合的定义，由m S ∈，l S ∈，得到2m S ∈，2l S ∈，即2m m ≥，2l l ≤，然后利用一元二次不等式的解法化简后逐项判断.【详解】∵非空集合{}S x m x l =≤≤满足：当a S ∈时，有2a S ∈∴m S ∈，l S ∈，m l ≤.则2m S ∈，2l S ∈，且2m m ≥，2l l ≤.即0m ≤或1m ≥，01l ≤≤且1m ≤，对于A ，当1m =时，有1l =，故A 正确；对于B ，当12l =时，2m S ∈，所以212m ≤，所以02m ≤≤，故B 正确；对于C ，因为0m ≤或1m ≥，故C 错误；对于D ，当1l =时，可知10m -≤≤或1m =，故D 错误.故选：AB 12．{2,4}【分析】由全集{}*6U x x =∈<N ∣，可得{1,2,3,4,5}U =，然后根据集合混合运算的法则即可求解．【详解】{}1,3A = ，{}3,5B =，{1,3,5}A B ∴⋃=，{}*{|6}1,2,3,4,5U x x =∈<=N ，(){}2,4U C A B ∴⋃=，故答案为：{2,4}．13．45【分析】引入参数x ，只参加数学的占参加了竞赛班的比例列方程即可求解.【详解】设只参加物理的有x 个人，则只参加数学的有()11x +个人，因为两科都不参加的占全班的13，所以参加了竞赛班的占全班的23，所以只参加数学的占参加了竞赛班的()2311115251152163x x x x x ++===++++，解得7x =，所以全班有7114525+=人.故答案为：45.14．21【分析】首先用列举法表示集合A 、B ，从而得到A B ⊕，即可得解.【详解】因为(){}()()()()(){}22,1,,0,1,0,1,1,0,1,0,0,0A x y xy x y =+≤∈=--Z ，(){},1,1,,B x y x y x y =≤≤∈Z()()()()()()()()(){}1,1,1,0,1,1,0,1,0,0,0,1,1,1,1,0,1,1=------，又()()(){}12121122,,,,A B x x y y x y A x y B ⊕=++∈∈，所以()()()()()()()(){2,1,2,0,2,1,1,0,1,1,1,2,1,1,1,2,A B ⊕=-----------()()()()()0,0,0,1,0,2,0,1,0,2--，()()()()()()()()1,0,1,1,1,2,1,1,1,2,2,0,2,1,2,1}---，所以A B ⊕中元素的共21个.故答案为：2115．（1）0，94；（2）0，12，1.【分析】（1）分a 是否等于0两种情况讨论即可；（2）分m 是否等于0两种情况讨论即可.【详解】（1）情形一：若0a =，则{}1R3103A x x ⎧⎫=∈+==-⎨⎬⎩⎭∣中只有13-这一个元素，故0a =符合题意；情形二：若0a ≠，且集合A 中只有一个元素，这意味着当且仅当一元二次方程2310ax x ++=有两个相等的实数根，从而940a ∆=-=，解得94a =；综上所述，实数a 的所有取值可能为：0，94；（2）{}{}23201,2B xx x =-+==∣，情形一：当0m =时，{}{10}|010A xmx x x =-==⋅-==∅∣，此时满足A B ⊆，故0m =符合题意；情形二：当0m ≠时，1{10}A xmx m ⎧⎫=-==⎨⎩⎭∣，若要A B ⊆，则当且仅当11m =或12m=，解得12m =或1m =；综上所述，实数m 的值可能是：0，12，1.16．(1){}22x x -<≤(2)233a a ⎧⎫-≤≤-⎨⎬⎩⎭【分析】（1）先解不等式求出集合,A B ，再利用交集、补集的概念计算即可；（2）先求出,A B 并集的补集，再根据集合间的基本关系计算即可.【详解】（1）由3217x -<+<得{}23A x x =-<<，由2280x x +->得2x >或<4x -，即B ={2x x >或<4x -}，所以{}42B x x =-≤≤R ð，故(){}22A B x x ⋂=-<≤R ð；（2）由上知A B = {2x x >-或<4x -}，所以(){}42A B x x ⋃=-≤≤-R ð，而()A B C ⋃⊆R ð，则32132412a a a a -<+⎧⎪-≤-⎨⎪+≥-⎩，解之得233a -≤≤-，即a 的取值范围为233a a ⎧⎫-≤≤-⎨⎬⎩⎭.17．(1){}{}{}{}{}{}4,1,2,4,1,4,2,1,2---；(2)能，{}9(,)24+∞ .【分析】（1）当4b =时，由0∆<，得到A =∅，求得{4,1,2}B =-，结合条件即可求解；（2）由()U B A =∅ ð，得到A B ⊆，分A =∅和A ≠∅，两种情况讨论，结合集合的包含关系，即可求解.【详解】（1）解：当4b =时，可得2{|330}A x x x =-+=，因为2(3)440∆=--⨯<，所以A =∅，又由2{|(2)(34)0}{4,1,2}B x x x x =-+-==-，又因为AMB ，所以这样的集合M 共有如下6个：{}{}{}{}{}{}4,1,2,4,1,4,2,1,2---.（2）解：能；由()U B A =∅ ð，可得A B ⊆，若A =∅时，此时满足A 是B 的一个子集，此时940b ∆=-<，解得94b >；若A ≠∅时，由（1）知{4,1,2}B =-，当4A -∈时，28b =-，此时{4,7}A =-，此时A 不是B 的一个子集；当1A ∈时，2b =，此时{1,2}A =，此时A 是B 的一个子集；当2A ∈时，2b =，此时{1,2}A =，此时A 是B 的一个子集，综上可得，当A =∅或{1,2}A =时，满足()U B A =∅ ð，此时实数b 的取值范围为{}9(,)24+∞ .18．(1)(),1∞--(2)1k <-或3k =【分析】（1）由交集为空集得到一元二次方程无解，再由判别式小于等于零可解出；（2）分A B =∅ 和A B ≠∅ 时，分别求出k 的范围，注意A B ≠∅ 时A B ⋂中的点都在集合C 中，即可解出；【详解】（1）由22y x ky x=+⎧⎨=⎩得220--=x x k ，①因为A B =∅ ，所以①的440k ∆=+<，解得1k <-，所以实数k 的取值范围为(),1∞--，（2）①若A B =∅ ，由（1）可得1k <-，②若A B ≠∅ ，且其中的点都在集合C 中，也符合题意，此时1k ≥-，联立22y x ky x=+⎧⎨=⎩，得220--=x x k ，且Δ440k =+≥，解得()(){}1,1A B k k⋂=+-，将1x =C 中，整理可得82y k =+-令822y k k =++=--，整理得())310k -+=，解得3k =，同理，把1x =C ，得(()(221421882y k k k k =-+---=-+，令2y k =-，整理并化简可得()(310k -=，所以3k =，综上，实数k 的取值范围为1k <-或3k =.19．(1){1}、{3}、{1,2}、{1,4}、{3,4}、{2,3}、{1,2,4}、{2,3,4}；(2)证明见解析(3)证明见解析【分析】（1）根据题意，分析4S 的子集，对应奇子集的定义，即可得4S 的所有奇子集；（2）设S 为n S 的奇子集，根据奇子集和偶子集的定义，按1是否属于S 进行分类，则得到奇子集和偶子集之间的关系，分析即可证得结论；（3）根据（2）中的结论，计算奇子集容量之和时，元素i 的贡献是22n i -，即可求得奇子集的容量之和，从而得到偶子集的容量之和，即可得到结论．【详解】（1）由题意可知，当4n =时，4{1s =，2，3，4}，X 的容量为奇数，则X 为n S 的奇子集，∴所有的奇子集应为{1}、{3}、{1,2}、{1,4}、{3,4}、{2,3}、{1,2,4}、{2,3,4}；（2）设奇数n k S ∈，对于n S 的每个奇子集A ，当k A ∈时，取{|B x x A =∈且}x k ≠．当k A ∉时，取{}B A k = ，则B 为n S 的偶子集．反之，亦然．11所以，n S 的奇子集与偶子集是一一对应的．所以，n S 的奇子集与偶子集个数相等．（3）对任一(1)i i n ≤≤，含i 的子集共有12n -个，用上面的对应方法可知，其中必有一半是奇子集，一半是偶子集，从而对于每个数i ，在奇子集的和与偶子集的和中，i 所占的个数是一样的．于是在计算奇子集容量之和时，元素i 的贡献是22n i -，∴奇子集容量之和是2312(1)2nn n i i n n --==+⋅∑，根据上面所说，这也是偶子集的容量之和，两者相等，故当3n ≥时，n S 的所有奇子集的容量之和等于所有偶子集的容量之和．【点睛】方法点睛：对于新型集合，首先要了解集合的特性，抽象特性和计算特性，抽象特性是将集合可近似的当作数列或者函数分析.计算特性，将复杂的关系通过找规律即可利用已学相关知识求解.。

重庆南开中学2024年九年级上学期9月月考模拟数学试卷+答案

重庆市南开中学2024-2025学年九年级上学期数学9月第一次考试模拟试卷一．选择题（共10小题，满分40分，每小题4分）1．（4分）下列社交软件的标志中，是中心对称图形的是（）A．B．C．D．2．（4分）下列计算正确的是（）A．a2•a3＝a6B．a+2a2＝3a3C．（﹣3ab）2•2ab2＝﹣18a3b4D．6ab3÷（﹣2ab）＝﹣3b23．（4分）如图，在Rt△ABC中，CD是斜边AB上的高，∠A≠45°，下列比值中等于sin A的是（）A．B．C．D．4．（4分）如图，△ABC和△A′B′C′是以点O为位似中心的位似图形，点A在线段OA′上．若OA：AA′＝1：2，则△ABC和△A′B′C′的周长之比为（）A．1：2B．1：4C．4：9D．1：35．（4分）下列命题中，不一定是真命题的是（）A．平行四边形的两条对角线长度相等B．菱形的两条对角线互相垂直C．矩形的两条对角线长度相等且互相平分D．正方形的两条对角线长度相等，并且互相垂直平分6．（4分）某公司上半年生产甲、乙两种型号的无人机若干架，已知甲种型号无人机架数比总架数的一半多11架，乙种型号无人机架数比总架数的三分之一少2架．设甲种型号无人机x架，乙种型号无人机y架，根据题意可列出的方程组是（）A．B．C．D．7．（4分）估算的值（）A．在3和4之间B．在4和5之间C．在2和3之间D．在5和6之间8．（4分）①个图形中一共有8个正方形，第②个图形中一共有15个正方形，第③个图形中一共有22个正方形，…，按此规律排列，则第⑨个图形中正方形的个数为（）A．50B．60C．64D．729．（4分）已知四边形ABCD和DEFG都是正方形，点F在线段AB上，连接AE、BD，BD交FG于点H．若∠AEF＝α，则∠BHF＝（）10．（4分）在多项式a+b﹣c﹣d﹣e中，除首尾项a、﹣e外，其余各项都可去掉，去掉项的前面部分和其后面部分都加上绝对值，并用减号连接，则称此为“消减操作”．每种“消减操作”可以去掉的项数分别为一项，两项，三项．“消减操作”只针对多项式a+b﹣c﹣d﹣e进行．例如：+b“消减操作”为|a|﹣|﹣c﹣d﹣e|，﹣c与﹣d同时“消减操作”为|a+b|﹣|﹣e|，…，下列说法：①存在对两种不同的“消减操作”后的式子作差，结果不含与e相关的项；②若每种操作只去掉一项，则对三种不同“消减操作”的结果进行去绝对值，共有8种不同的结果；③若可以去掉的三项+b，﹣c，﹣d满足：（|+b|+|+b+2|）（|﹣c+1|+|﹣c+4|）（|﹣d+1|+|﹣d﹣6|）＝42，则2b+c﹣d的最大值为14．其中正确的个数是（）A．0个B．1个C．2个D．3个二．填空题（共8小题，满分32分，每小题4分）11．（4分）已知，△ABC中，∠A是锐角，sin A＝，则∠A的度数是．12．（4分）一个多边形的内角和是720°，这个多边形的边数是．13．（4分）如图，分别过矩形ABCD的顶点A、D作直线l1、l2，使l1∥l2，l2与边BC交于点P，若∠1＝38°，则∠BPD的度数为．14．（4分）已知a、b是一元二次方程x2﹣x﹣1＝0的两个根，则代数式3a2+2b2﹣3a﹣2b的值等于．15．（4分）如图，点B在x的正半轴上，且BA⊥OB于点B，将线段BA绕点B逆时针旋转60°到BB′的位置，且点B′的坐标为（1，）．若反比例函数y＝（x＞0）的图象经过A点，则k＝．16．（4分）若关于x的一元一次不等式组有且只有2个整数解，且关于y的分式方程的解为正数，则所有满足条件的整数a的值之和为．17．（4分）如图，点E在矩形ABCD的边CD上，将△ADE沿AE翻折，点D恰好落在边BC的点F处，如果BC ＝10，，那么EC＝．18．（4分）一个四位自然数，若满足千位数字与十位数字的差比百位数字与个位数字的差多1，则称这样的四位数为“多一数”，如：9675，9﹣7＝6﹣5+1，9765是“多一数”；又如：6973，∵6﹣7≠9﹣3+1，∴6973不是“多一数”．现有一个“多一数”M，千位数字为a，百位数字为b，十位数字为c，个位数字为d（1≤c≤a≤9，0≤d≤b≤9），将M的千位数字与十位数字交换，百位数字与个位数字交换，得到新的四位数N，若，F（M）能被6整除，则a﹣c＝；规定，若G（M）为完全平方数，则满足条件的“多一数”M中，最大值与最小值的差是．三．解答题（共8小题，满分78分）19．（8分）计算：（1）因式分解：9（x+y）2﹣25（x﹣y）2；（2）计算：．20．（10分）解方程：（1）x2﹣2x﹣2＝0；（2）．21．（10分）在第18章学习了三角形的中位线定理后，小明对这一知识进行了拓展性研究．他发现，连接梯形两腰中点的线段也具有类似的性质．探究过程如下：（1）用直尺和圆规，作线段CD的垂直平分线，垂足为点F，连接EF，连接AF并延长AF交线段BC的延长线于点M（只保留作图痕迹）；（2）已知：在四边形ABCD中，AD∥BC，E为AB中点，F为CD中点，连接EF．猜想：EF∥AD∥BC，且．证明：∵F是CD中点，∴．∵AD∥BC，∴∠DAF＝∠在△ADF和△MCF中，，∴△ADF≌△MCF（AAS）．∴AF＝FM，AD＝CM．∵在△ABM中，E是AB中点，F是AM中点，∴EF∥BM且．∵BM＝BC+CM，∴BM＝BC+AD．∴．∵EF∥BM，AD∥BC，∴EF∥AD∥BC．请你根据该探究过程完成下面命题：连接梯形两腰中点的线段平行于两底并且．22．（10分）重庆市自发布“重庆市长江10年禁鱼通告”后，忠县内的黄钦水库自然生态养殖鱼在市场上热销，并被誉为“清凉五月天，黄钦自有贤”的美誉.2024年五一假期依依同学旅游到此，并购买了若干桂花鱼和大罗非，她发现用840元买的桂花鱼的数量比用同样价钱买大罗非的数量多20斤，且大罗非的单价是桂花鱼的1.5倍．（1）求桂花鱼、大罗非两种鱼的单价分别为多少元；（2）两种鱼在得到一致好评后，依依决定再次购买这两种鱼作为“伴手礼”．由于商家对老顾客让利，其中桂花鱼按照原单价购买，大罗非的单价每斤降低m（m＞0）元，则购买的数量会比第一次购买大罗非的数量增加2m斤，第二次一共购买80斤鱼共用了1340元．求m的值．23．（10分）如图矩形ABCD中，AB＝4，BC＝6，点F为BC边上的三等分点（CF＜BF），动点P从点A出发，沿折线A→D→C运动，到C点停止运动．点P的运动速度为每秒2个单位长度，设点P运动时间为x秒，△APF 的面积为y1．（1）请直接写出y1关于x的函数解析式，并注明自变量x的取值范围；（2）若函数，请在平面直角坐标系中画出函数y1，y2的图象，并写出函数y1的一条性质；（3）结合函数图象，直接写出当y1≤y2时x的取值范围（保留一位小数，误差不超过0.2）．24．（10分）已知图1是某超市购物车，图2是超市购物车的侧面示意图，现已测得支架AC＝72cm，BC＝54cm，两轮轮轴的距离AB＝90cm（购物车车轮半径忽略不计），DG、EH均与地面平行．（参考数据：）（1）猜想两支架AC与BC的位置关系并说明理由；（2）若FG的长度为80cm，∠EHG＝60°，求购物车把手F到AB的距离．（结果精确到0.1）25．（10分）如图，直线与双曲线交于A，B两点，点A的坐标为（m，﹣3），点C是双曲线第一象限分支上的一点，连接BC并延长交x轴于点D，且BC＝2CD．（1）求k的值并直接写出点B的坐标；（2）点M、N是y轴上的动点（M在N上方）且满足MN＝1，连接MB，NC，求MB+MN+NC的最小值；（3）点P是双曲线上一个动点，是否存在点P，使得∠ODP＝∠DOB，若存在，请直接写出所有符合条件的P 点的横坐标．26．（10分）在△ABC中，AB＝AC，∠B＝30°，过A作AD⊥BC于点D．（1）如图1，过D作DE⊥AB于点E，连接CE，若AE＝2，求线段CE的长；（2）如图2，H为平面内一点，连接AH、CH，在△AGH中，AG＝AH，∠GAH＝120°，延长AG与CB交于点F，过点H作HP∥AF交BC于点P，若C、H、G在一条直线上，求证：BF＝CP；（3）如图3，M为AD上一点，连接BM，N为BM上一点，若，，∠BAN﹣∠CBN＝30°，连接CN，请直接写出线段CN的长．重庆市南开中学2024-2025学年九年级上学期数学9月第一次考试模拟试卷参考答案与试题解析一．选择题（共10小题，满分40分，每小题4分）1．（4分）下列社交软件的标志中，是中心对称图形的是（）A．B．C．D．【解答】解：中心对称图形，即把一个图形绕一个点旋转180°后能和原来的图形重合，A、C、D都不符合；是中心对称图形的只有B．故选：B．2．（4分）下列计算正确的是（）A．a2•a3＝a6B．a+2a2＝3a3C．（﹣3ab）2•2ab2＝﹣18a3b4D．6ab3÷（﹣2ab）＝﹣3b2【解答】解：a2•a3＝a5，故A错误，不符合题意；a与2a2不能合并，故B错误，不符合题意；（﹣3ab）2•2ab2＝18a3b4，故C错误，不符合题意；6ab3÷（﹣2ab）＝﹣3b2，故D正确，符合题意；故选：D．3．（4分）如图，在Rt△ABC中，CD是斜边AB上的高，∠A≠45°，下列比值中等于sin A的是（）A．B．C．D．【解答】解：在Rt△ABC中，sin A＝，在Rt△ACD中，sin A＝，∵∠A+∠B＝90°，∠B+∠BCD＝90°，∴∠A＝∠BCD，在Rt△BCD中，sin∠BCD＝sin A＝．故选：B．4．（4分）如图，△ABC和△A′B′C′是以点O为位似中心的位似图形，点A在线段OA′上．若OA：AA′＝1：2，则△ABC和△A′B′C′的周长之比为（）A．1：2B．1：4C．4：9D．1：3【解答】解：∵OA：AA′＝1：2，∴OA：OA′＝1：3，∵△ABC和△A′B′C′是以点O为位似中心的位似图形，∴AC∥A′C′，∴△AOC∽△A′OC′，∴AC：A′C′＝OA：OA′＝1：3，∴△ABC和△A′B′C′的周长之比为1：3，故选：D．5．（4）A．平行四边形的两条对角线长度相等B．菱形的两条对角线互相垂直C．矩形的两条对角线长度相等且互相平分D．正方形的两条对角线长度相等，并且互相垂直平分【解答】解：A、平行四边形的两条对角线长度不一定相等，故本选项命题不一定是真命题，符合题意；B、菱形的两条对角线互相垂直，是真命题，不符合题意；C、矩形的两条对角线长度相等且互相平分，是真命题，不符合题意；D、正方形的两条对角线长度相等，并且互相垂直平分，是真命题，不符合题意；故选：A．6．（4分）某公司上半年生产甲、乙两种型号的无人机若干架，已知甲种型号无人机架数比总架数的一半多11架，乙种型号无人机架数比总架数的三分之一少2架．设甲种型号无人机x架，乙种型号无人机y架，根据题意可列出的方程组是（）A．B．C．D．【解答】解：设甲种型号无人机x架，乙种型号无人机y架，根据题意可列出的方程组是：．故选：D．7．（4分）估算的值（）A．在3和4之间B．在4和5之间C．在2和3之间D．在5和6之间【解答】解：∵25＜31＜36，∴5＜＜6，∴3＜﹣2＜4．故选：A．8．（4分）下列图形都是由正方形按一定规律组成的，其中第①个图形中一共有8个正方形，第②个图形中一共有15个正方形，第③个图形中一共有22个正方形，…，按此规律排列，则第⑨个图形中正方形的个数为（）A．50B．60C．64D．72【解答】解：观察图形发现第一个图形有8个正方形，第二个图形有8+7＝15个正方形，第三个图形有8+7×2＝22个正方形，…第n个图形有8+7（n﹣1）＝7n+1个正方形，当n＝9时，7n+1＝7×9+1＝64个正方形．故选：C．9．（4分）已知四边形ABCD和DEFG都是正方形，点F在线段AB上，连接AE、BD，BD交FG于点H．若∠AEF＝α，则∠BHF＝（）A．2αB．45°+αC．22.5°+αD．90°﹣α【解答】解：过点E作EM⊥AB于点M，作EN⊥AD，交DA的延长线于N，设EF与AD交于T，如图所示：则∠N＝∠EMB＝∠EMA＝90∵四边形ABCD和DEFG都是正方形，∴∠BEF＝∠BAD＝∠EFG＝∠ADC＝∠EDG＝90°，DE＝EF，∴∠N＝∠EMA＝∠MAN＝90°，∴四边形AMEN为矩形，∴∠1+∠DTE＝90°，∠2+∠FTA＝90°，∵∠DTE＝∠FTA，∴∠1＝∠2，在△DME和△FNE中，，∴△DME≌△FNE（AAS），∴EM＝EN，∴AE平分∠DAN，∴∠EAD＝45°，∴∠EAF＝∠BAD+∠EAD＝90°+45°＝135°，∴∠2＝180°﹣∠EAF﹣AEF＝180°﹣135°﹣α＝45°﹣α，∴∠1＝∠2＝45°﹣α，∵BD是正方形ABCD的对角线，∴∠ADB＝45°，∴∠EDH＝∠1+∠ADB＝45°﹣α+45°＝90°﹣α，∴∠HDG＝∠EDG﹣∠EDH＝90°﹣（90°﹣α）＝α，∴∠BHF＝∠DHG＝90°﹣∠HDG＝90°﹣α．故选：D．10．（4分）在多项式a+b﹣c﹣d﹣e中，除首尾项a、﹣e外，其余各项都可去掉，去掉项的前面部分和其后面部分都加上绝对值，并用减号连接，则称此为“消减操作”．每种“消减操作”可以去掉的项数分别为一项，两项，三项．“消减操作”只针对多项式a+b﹣c﹣d﹣e进行．例如：+b“消减操作”为|a|﹣|﹣c﹣d﹣e|，﹣c与﹣d同时“消减操作”为|a+b|﹣|﹣e|，…，下列说法：①存在对两种不同的“消减操作”后的式子作差，结果不含与e相关的项；②若每种操作只去掉一项，则对三种不同“消减操作”的结果进行去绝对值，共有8种不同的结果；③若可以去掉的三项+b，﹣c，﹣d满足：（|+b|+|+b+2|）（|﹣c+1|+|﹣c+4|）（|﹣d+1|+|﹣d﹣6|）＝42，则2b+c﹣d的最大值为14．其中正确的个数是（）A．0个B．1个C．2个D．3个【解答】解：①﹣d“闪减操作”后的式子|a+b﹣c|﹣|﹣e|，﹣c﹣d“闪减操作”后的式子|a+b|﹣|﹣e|对这两个式子作差，得（|a+b﹣c|﹣|﹣e|）﹣（|a+b|﹣|﹣e）＝|a+b﹣c|﹣|﹣e|﹣|a+b|+|﹣e|＝|a+b﹣c|﹣|a+b|，结果不含与e相关的项，∴①正确；②若每种操作只闪退一项，则分三种情况：+b闪减操作”后的结果|a|﹣|﹣c﹣d﹣e|，当a≥0，﹣c﹣d﹣e≥0时，|a|﹣|﹣c﹣d﹣e|＝a+c+d+e，当a≥0，﹣c﹣d﹣e≤0时，|a|﹣|﹣c﹣d﹣e|＝a﹣c﹣d﹣e，当a≤0，﹣c﹣d﹣e≥0时，|a|﹣|﹣c﹣d﹣e|＝﹣a+c+d+e，当a≤0，﹣c﹣d﹣e≤0时，|a|﹣|﹣c﹣d﹣e|＝﹣a﹣c﹣d﹣e，﹣c“闪减操作”后的结果|a+b|﹣|﹣d﹣e|，当a+b≥0，﹣d﹣e≥0时，|a+b|﹣|﹣d﹣e|＝a+b+d+e，当a+b≥0，﹣d﹣e≤0时，|a+b|﹣|﹣d﹣e|＝a+b﹣d﹣e，当a+b≤0，﹣d﹣e≥0时，|a+b|﹣|﹣d﹣e|＝﹣a﹣b+d+e，当a+b≤0，﹣d﹣e≤0时，|a+b|﹣|﹣d﹣e|﹣a﹣b﹣d﹣e，﹣d“闪减操作”后的结果|a+b﹣c|﹣|﹣e|，当a+b﹣d≥0，﹣e≥0时，|a+b﹣c|﹣|﹣e|＝a+b﹣c+e，当a+b﹣d≥0，﹣e≤0时，|a+b﹣c|﹣|﹣e|＝a+b﹣c﹣e，当a+b﹣d≤0，﹣e≥0时，|a+b﹣c|﹣|﹣e|＝﹣a﹣b+c+e，当a+b﹣d≤0，﹣e≤0时，|a+b﹣c|﹣|﹣e|＝﹣a﹣b+c﹣e，共有12种不同的结果，∴②错误；③∵|+b|+|+b+2|＝|b﹣0|+|b﹣（﹣2）|，在数轴上表示点b与0和﹣2的距离之和，∴当距离取最小值0﹣（﹣2）＝2时，b的最小值为﹣2，同理|﹣c+1|+|﹣c+4|＝|1﹣c|+|4﹣c|，在数轴上表示点c与1和4的距离之和，∴当距离取最小值4﹣1＝3时，c的最小值为1，|﹣d+1|+|﹣d﹣6|＝|1﹣d|+|﹣6﹣d|，在数轴上表示点d与1和﹣6的距离之和，∴当距离取最小值1﹣（﹣6）＝7时，d的最小值为﹣6，∴当|+b|+|+b+2|，|﹣c+1|+|﹣c+4|，|﹣d+1|+|﹣d﹣6|都取最小值时，（|+b|+|+b+2|）（|﹣c+1|+|﹣c+4|）（|﹣d+1|+|﹣d﹣6|）＝2×3×7＝42，∴③正确，故选：C．二．填空题（共8小题，满分32分，每小题4分）11．（4分）已知，△ABC中，∠A是锐角，sin A＝，则∠A的度数是30° ．【解答】解：∵∠A是锐角，sin A＝，∴∠A＝30°，故答案为：30°．12．（4分）一个多边形的内角和是720°，这个多边形的边数是6．【解答】解：∵多边形的内角和公式为（n﹣2）•180°，∴（n﹣2）×180°＝720°，解得n＝6，∴这个多边形的边数是6．故答案为：6．13．（4分）如图，分别过矩形ABCD的顶点A、D作直线l1、l2，使l1∥l2，l2与边BC交于点P，若∠1＝38°，则∠BPD的度数为142° ．【解答】解：∵l1∥l2，∠1＝38°，∴∠ADP＝∠1＝38°，∵四边形ABCD为矩形，∴AD//BC，∴∠BPD+∠ADP＝180°，∴∠BPD＝180°﹣38°＝142°．故答案为：142°．14．（4分）已知a、b是一元二次方程x2﹣x﹣1＝0的两个根，则代数式3a2+2b2﹣3a﹣2b的值等于5．【解答】解：根据题意得a2﹣a＝1，b2﹣b＝1，所以3a2+2b2﹣3a﹣2b＝3a2﹣3a+2b2﹣2b＝3（a2﹣a）+2（b2﹣b）＝3+2＝5．故填515．（4分）如图，点B在x的正半轴上，且BA⊥OB于点B，将线段BA绕点B逆时针旋转60°到BB′的位置，且点B′的坐标为（1，）．若反比例函数y＝（x＞0）的图象经过A点，则k＝8．【解答】解：如图，过点B′作B′D⊥x轴于点D，∵BA⊥OB于点B，∴∠ABD＝90°．∵线段BA绕点B逆时针旋转60°到BB′的位置，∴∠ABB′＝60°，∴∠B′BD＝90°﹣60°＝30°．∵点B′的坐标为（1，），∴OD＝1，B′D＝，∴BB′＝2B′D＝2，BD＝＝3，∴OB＝1+3＝4，AB＝BB′＝2，∴A（4，2），∴k＝4×2＝8．故答案为：8．16．（4分）若关于x的一元一次不等式组有且只有2个整数解，且关于y的分式方程的解为正数，则所有满足条件的整数a的值之和为8．【解答】解：，解得：，∴，解得2＜a≤5.5，解分式方程得y＝2a﹣5，∵y的值解为正数，∵2a﹣5＞0，且2a﹣5≠3，∵a＞2.5且a≠4，∴满足条件的整数a的值有3和5，∴3+5＝8．故答案为：8．17．（4分）如图，点E在矩形ABCD的边CD上，将△ADE沿AE翻折，点D恰好落在边BC的点F处，如果BC ＝10，，那么EC＝3．【解答】解：∵四边形ABCD∴AD＝BC＝10，∠B＝∠C＝∠D＝90°，由折叠的性质可得AF＝AD＝10，∠AFE＝∠D＝90°，在Rt△ABF中，，∴，∴CF＝BC﹣BF＝4，在Rt△ABF，由勾股定理得，∴，∵∠BAF+∠BF A＝90°＝∠BF A+∠CFE，∴∠BAF＝∠CFE，∴在Rt△EFC中，，∴，故答案为：3．18．（4分）一个四位自然数，若满足千位数字与十位数字的差比百位数字与个位数字的差多1，则称这样的四位数为“多一数”，如：9675，9﹣7＝6﹣5+1，9765是“多一数”；又如：6973，∵6﹣7≠9﹣3+1，∴6973不是“多一数”．现有一个“多一数”M，千位数字为a，百位数字为b，十位数字为c，个位数字为d（1≤c≤a≤9，0≤d≤b≤9），将M的千位数字与十位数字交换，百位数字与个位数字交换，得到新的四位数N，若，F（M）能被6整除，则a﹣c＝5；规定，若G（M）为完全平方数，则满足条件的“多一数”M中，最大值与最小值的差是2222．【解答】解：根据题意可知0≤a﹣c≤8，a﹣c＝b﹣d+1．M＝1000a+100b+10c+d，N＝1000c+100d+10a+b．＝，＝，＝10（a﹣c）+b﹣d＝10（a﹣c）+a﹣c﹣1，＝11（a﹣c）﹣1，∵F（M）能被6整除，∴a﹣c＝5．∵c≥1，∴a≥6．当a＝6时，c＝1．∵a﹣c＝b﹣d+1，∴d＝b﹣4．∴，∵G（M）为完全平方数，∴b＝3．∴d＝﹣1（舍去）．同理，当a＝7时，c＝2，M＝7420；当a＝8时，c＝3，M＝8531；当a＝9时，c＝4，M＝9642；∴满足条件的“多一数”M中，最大值与最小值的差＝9642﹣7420＝2222．故答案为：5；2222．三．解答题（共8小题，满分78分）（1）因式分解：9（x+y）2﹣25（x﹣y）2；（2）计算：．【解答】解：（1）9（x+y）2﹣25（x﹣y）2＝（3x+3y+5x﹣5y）（3x+3y﹣5x+5y）＝﹣4（4x﹣y）（x﹣4y）；（2）＝1﹣•＝1﹣＝＝﹣．20．（10分）解方程：（1）x2﹣2x﹣2＝0；（2）．【解答】解：（1）x2﹣2x﹣2移项得x2﹣2x＝2，配方得x2﹣2x+1＝2+1，即（x+1）2＝3，开方得，解得；；（2），去分母，得m﹣4+m+2＝0，解得m＝1，经检验，m＝1是原方程的根．21．（10分）在第18章学习了三角形的中位线定理后，小明对这一知识进行了拓展性研究．他发现，连接梯形两腰中点的线段也具有类似的性质．探究过程如下：（1）用直尺和圆规，作线段CD的垂直平分线，垂足为点F，连接EF，连接AF并延长AF交线段BC的延长线（2）已知：在四边形ABCD中，AD∥BC，E为AB中点，F为CD中点，连接EF．猜想：EF∥AD∥BC，且．证明：∵F是CD中点，∴DF＝CF．∵AD∥BC，∴∠DAF＝∠CMF．在△ADF和△MCF中，，∴△ADF≌△MCF（AAS）．∴AF＝FM，AD＝CM．∵在△ABM中，E是AB中点，F是AM中点，∴EF∥BM且．∵BM＝BC+CM，∴BM＝BC+AD．∴．∵EF∥BM，AD∥BC，∴EF∥AD∥BC．请你根据该探究过程完成下面命题：连接梯形两腰中点的线段平行于两底并且等于两底边之和的一半．【解答】（1）解：如图所示．.（2）证明：∵F是CD中点，∴DF＝CF．∵AD∥BC，∴∠DAF＝∠CMF．在△ADF和△MCF中，，∴△ADF≌△MCF（AAS）．∴AF＝FM，AD＝CM．∵在△ABM中，E是AB中点，F是AM中点，∴EF∥BM且．∵BM＝BC+CM，∴BM＝BC+AD．∴．∵EF∥BM，AD∥BC，∴EF∥AD∥BC．连接梯形两腰中点的线段平行于两底并且等于两底边之和的一半．故答案为：DF＝CF；∠AFD＝∠MFC；；等于两底边之和的一半．22．（10分）重庆市自发布“重庆市长江10年禁鱼通告”后，忠县内的黄钦水库自然生态养殖鱼在市场上热销，并被誉为“清凉五月天，黄钦自有贤”的美誉.2024年五一假期依依同学旅游到此，并购买了若干桂花鱼和大罗非，她发现用840元买的桂花鱼的数量比用同样价钱买大罗非的数量多20斤，且大罗非的单价是桂花鱼的1.5倍．（1）求桂花鱼、大罗非两种鱼的单价分别为多少元；（2）两种鱼在得到一致好评后，依依决定再次购买这两种鱼作为“伴手礼”．由于商家对老顾客让利，其中桂花鱼按照原单价购买，大罗非的单价每斤降低m（m＞0）元，则购买的数量会比第一次购买大罗非的数量增加2m斤，第二次一共购买80斤鱼共用了1340元．求m的值．【解答】解：（1）设桂花鱼的单价是x元，则大罗非的单价是1.5x元，根据题意得：﹣＝20，解得：x＝14，经检验，x＝14是所列方程的解，且符合题意，∴1.5x＝1.5×14＝21（元）．答：桂花鱼的单价是14元，大罗非的单价是21元；（2）第一次购买大罗非的数量是840÷21＝40（斤）．根据题意得：14（80﹣40﹣2m）+（21﹣m）（40+2m）＝1340，整理得：m2+13m﹣30＝0，解得：m1＝2，m2＝﹣15（不符合题意，舍去）．答：m的值为2．23．（10分）如图矩形ABCD中，AB＝4，BC＝6，点F为BC边上的三等分点（CF＜BF），动点P从点A出发，沿折线A→D→C运动，到C点停止运动．点P的运动速度为每秒2个单位长度，设点P运动时间为x秒，△APF 的面积为y1．（1）请直接写出y1关于x的函数解析式，并注明自变量x的取值范围；（2）若函数，请在平面直角坐标系中画出函数y1，y2的图象，并写出函数y1的一条性质；（3）结合函数图象，直接写出当y1≤y2时x的取值范围（保留一位小数，误差不超过0.2）．【解答】解：（1）当0≤x≤3时，y1＝＝4x，当3＜x≤5时，y1＝﹣×6×（2x﹣6）﹣＝﹣4x+24，∴y1＝；（2）函数y1，y2的图象如图：函数y1的性质：当0≤x≤3时，y随x的增大而增大，当3＜x≤5时，y随x的增大而减小；（3）由两个函数图像可知，当y1≤y2时x的取值范围为0＜x≤2.1或x＝5．24．（10分）已知图1是某超市购物车，图2是超市购物车的侧面示意图，现已测得支架AC＝72cm，BC＝54cm，两轮轮轴的距离AB＝90cm（购物车车轮半径忽略不计），DG、EH均与地面平行．（参考数据：）（1）猜想两支架AC与BC的位置关系并说明理由；（2）若FG的长度为80cm＝60°，求购物车把手F到AB的距离．（结果精确到0.1）【解答】解：（1）AC⊥BC，理由如下：∵AC＝72cm，BC＝54cm，AB＝90cm，∴AC2+BC2＝722+542＝8100，AB2＝8100，∴AC2+BC2＝AB2，∴∠ACB＝90°，∴AC⊥BC．（2）过F作FN⊥AB交AB延长线于N，过C作CM⊥AB于M，延长DG交FN于K，∵EH∥DG∥AB，∴GK⊥FN，∴四边形MNKC是矩形，∴NK＝CM，∵△ABC的面积＝AB•CM＝AC•BC，∴90CM＝72×54，∴CM＝43.2（cm），∴NK＝CM＝43.2（cm），∵EH∥DG，∴∠FGK＝∠EHG＝60°，∴sin∠FGK＝sin60°＝＝，∵FG＝80cm，∴FK＝40≈69.28（cm），∴FN＝FK+NK＝69.28+43.2≈112.5（cm）．∴购物车把手F到AB的距离约是112.5cm．25．（10分）如图，直线与双曲线交于A，B两点，点A的坐标为（m，﹣3），点C是双曲线第一象限分支上的一点，连接BC并延长交x轴于点D，且BC＝2CD．（1）求k的值并直接写出点B的坐标；（2）点M、N是y轴上的动点（M在N上方）且满足MN＝1，连接MB，NC，求MB+MN+NC的最小值；（3）点P是双曲线上一个动点，是否存在点P，使得∠ODP＝∠DOB，若存在，请直接写出所有符合条件的P 点的横坐标．【解答】解：（1）根据题意可知点A（m，﹣3）在直线和双曲线的图象上，∴，解得m＝﹣2，∴点A的坐标为（﹣2，﹣3），代入双曲线得：k＝（﹣2）×（﹣3）＝6，由图象可知点B与点A关于原点对称，∴B（2，3）；（2）过点B、C分别作x轴的垂线，垂足分别为E、F，作点B关于y轴的对称点点B'，并向下平移一个单位记为B''，连接B''C，则BE∥CF，B'B''＝1，∴△DCF∽△DBE，∴，∵BC＝2CD，B（2，3），B'（﹣2，3），B''（﹣2，2），∴，BE＝3，∴CF＝1，即点C的纵坐标为1，∵点C在反比例函数的图象上，∴C（6，1），B''C＝，∴MB+MN+NC的最小值即为B'B''+B''C＝1+；（3）当∠ODP＝∠DOB时，当DP在x轴下方时，DP∥AB，设直线BC的解析式为y＝kx+b，由（2）可知：B（2，3），C（6，1），∴解得，∴，当y＝0时，，解得x＝8，∴D（8，0），∵DP∥AB，直线AB的解析式为，∴设直线DE的解析式为，把D（8，0）代入得：12+m＝∴m＝﹣12，∴，由P是直线DE与反比例函数的交点可得：，解得，此时点P在第三象限，符合题意，当DP在x轴上方时，则与下方的DP关于x轴对称，可得直线DP的解析式为：，再解方程组得，此时点P在第一象限，两个都符合题意，∴点P的横坐标为：．．26．（10分）在△ABC中，AB＝AC，∠B＝30°，过A作AD⊥BC于点D．（1）如图1，过D作DE⊥AB于点E，连接CE，若AE＝2，求线段CE的长；（2）如图2，H为平面内一点，连接AH、CH，在△AGH中，AG＝AH，∠GAH＝120°，延长AG与CB交于点F，过点H作HP∥AF交BC于点P，若C、H、G在一条直线上，求证：BF＝CP；（3）如图3，M为AD上一点，连接BM，N为BM上一点，若，，∠BAN﹣∠CBN＝30°，连接CN，请直接写出线段CN的长．【解答】解：（1）∵∠B＝30°，AD⊥BC，∴∠BAD＝60°，∴AD＝2AE＝4，∴AB＝2AD＝8，BD＝AD＝4，∴BE＝AB﹣AE＝6，∴EF＝BE＝3，BF＝BE＝3，∵AB＝AC，∴BD＝CD，∴CF＝2BD﹣BF＝8﹣3＝5，∴CE＝＝2，（2）证明：∵∠ABC＝30°，AB＝AC，∴∠BAC＝120°，又∵∠GAH＝120°，∴∠F AB＝∠CAH，∵AH＝AG，∴∠AHG＝30°＝∠ABC，∴∠ABF＝∠AHC，∴△ABF∽△AHC，∴＝，∵PH∥FG，∴△CHP∽△CGF，∴＝，又∵△ABC∽△AGH，∴＝，∴＝，∴＝，∵＝，∴＝＝+1＝+1＝，∴CP＝FB；（3）延长BM交AC于F，延长AN到E，使NE＝BN，连接BE，如图3：∵∠BAN﹣∠CBN＝30°，∴∠BAN＝∠CBN+30°，∴∠BNE＝∠BAN+∠ABN＝∠CBN+∠ABN+30°＝60°，∵NE＝BN，∴△BEN是等边三角形，∴∠E＝60°，∵∠ANB＝180°﹣∠BNE＝120°＝∠BAC，∴△ABN∽△FBA，∴＝＝，∠BAE＝∠AFB，∴△ANF∽△BEA，∴＝＝，∴FN＝＝＝，∴BF＝FN+BN＝，∴AB2＝BN•BF＝5+，过F作FG⊥BC于F，过N作NH⊥BC于H，∵∠ACB＝30°，∴FG＝FC＝（AB﹣AF）＝AB，CG＝AB，∴BG＝BC﹣CG＝AB﹣AB＝AB，∵NH∥CF，∴＝＝＝，∴NH＝AB，BH＝AB，∴CH＝BC﹣BH＝AB，∴CN2＝CH2+NH2＝9，∴CN＝3．。

重庆市南开中学2015届高三12月月考语文试题含答案

重庆南开中学高2015级高三12月月考语文试题卷语文试题卷共8页。

考试时间150分钟。

第l至5题、第7至9题为选择题，24分；第6题、第10至21题为非选择题，126分。

满分l50分。

注意事项：1．答题前，务必将自己的姓名、考号填写在答题卡规定的位置上。

2．答第1至5题、第6至9题时，务必使用2B铅笔将答题卡上对应题目答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3．答第6题、第11至21题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定位置上。

4．所有题目必须在答题卡上作答，在试卷上答题无效。

5．考试结束后，将答题卡交回。

一、(本大题共3小题。

每小题9分。

共12分)1．字形和加点字的读音全部正确的一组是A．蒸汽机斧底游鱼剽悍．piāo雪泥鸿爪．zhuǎB．大姆指和衣而眠氛．围fēn汗流浃．背jiāC．绿茵场棉里藏针躯．壳qiào 解．甲归田jiěD．一炷香谈笑风生谂．知shěn爱憎．分明zēng2．下列语句中，加点的词语使用不正确．．．的一项是A．1849年，美国加州有个木匠在溪沟旁拾到一个沉甸甸的金块。

消息不翼而飞．．．．，人们像潮水般一涌向旧金山，掀起了著名的“西部淘金热”。

B．11月l2日，科幻巨制《星际穿越》登陆内地各大院线，截至．．17日晚，《星际穿越》上映首周狂卷3亿元人民币，登顶内地票房周冠军。

C．依靠自身技术优势长期在汽车制造业中执牛耳．．．的美国通用汽车公司，由于生产成本居高不下，八十年代末开始走下坡路，风光不再。

D．刚面世的《全宋诗》汇集了宋代所有诗歌，长篇短制，细大不捐．．．．，即使是断章残句，也有所收录，堪称一项辉煌卓绝的伟业。

3．依次填入下边一段话的语句，与上下文衔接最恰当的一组是一个人的记忆，是源于诸多细胞的相互联络，诸多经验的积累、延续和创造；。

个人之于人类，正如细胞之于肌体，。

但这里面常常有一种悲哀，，而将其他人的话语变成沉默的大多数。

重庆市南开中学2015届高三12月月考数学(理)试题Word版含答案

重庆南开中学高2015级高三12月月考数学试题(理科)考试说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．(1)答题前，考生先将自己的姓名、准考证号码填写清楚；(2)选择题必须使用2B 铅笔填涂，非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整，字迹清楚；(3)请按照题号顺序在各题目的答题区域内作答．超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效；(4)保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀．第Ⅰ卷(选择题共50分)一．选择题：本大题共l0小题，每小题5分，共50分．在每小题给出的四个备选项中，只有一项是符合题目要求的。

1．关于x 的不等式ax +b >0的解集不可能．．．是( ) (A)R (B)φ (C) ⎭⎬⎫⎩⎨⎧-a b x x ＞ (D)⎭⎬⎫⎩⎨⎧≠a b x x 2．抛物线x y 42=的焦点到准线的距离为( ) (A)41 (B)21(C)2 (D)4 3．已知⎪⎭⎫⎝⎛∈ππ，2a ，5102cos 2sin =-a a ，则=a cos ( ) (A)54-(B)53- (C)54 (D)534．等比数列{}n a 的前n 项和为n S ，且4a ，2a 2，a 3成等差数列，若a 1=1。

则S 4=( ) (A)7 (B)8 (C)15 (D)165．已知单位向量a ，b 夹角为3π，则b a -2=( )(A)2 (B)3 (C)2 (D)56．已知直线()00022＞，＞b a by ax =+-平分圆014222=+-++y x y x C ：的圆周长，则ba 21+的最小值为( ) (A) 24 (B) 223+ (C)4 (D)67．已知定义在R 上的偶函数()x f 满足：当x ≥0时，()83-=x x f ，则关于x 的不等式：()122＞-x f 的解集为( )(A){}20＞或＜x x x (B) {}40＞或＜x x x (C) {}42＞或＜x x x - (D) {}22＞或＜x x x - 8．下列说法正确的个数是( )①命题“0123≤+-∈∀x x R x ，”的否定是“0120300＞，+-∈∃x x R x ”； ②“ac b =”是“三个数a ，b ，c 成等比数列”的充要条件；⑨“1-=m ”是“直线01)12(=+-+y m mx 和直线023=++my x 垂直”的充要条件： ④“复数()R b a bi a Z ∈+=，是纯虚数的充要条件是0=a ”是真命题．(A)1 (B)2 (C)3 (D)49．设21F F ，为双曲线C ：()0012222＞，＞b a by a x =-的左、右焦点，过坐标原点O 的直线与双曲线C 在第一象限内交于点P ，若a PF PF 621=+，且21F PF ∆为锐角三角形，则直线OP 斜率的取值范围是( )(A)⎪⎪⎭⎫⎝⎛34332， (B)⎪⎭⎫ ⎝⎛334， (C)⎪⎪⎭⎫ ⎝⎛3321， (D) ⎪⎪⎭⎫⎝⎛2332， 10．存在实数a ，使得对函数()x g y =定义域内的任意x ，都有()x g a ＜成立，则称a 为 g(x)的下界，若a 为所有下界中最大的数，则称a 为函数()x g 的下确界．已知+∈R z y x ，，且以z y x ，，为边长可以构成三角形，则()()2z y x zxyz xy z y x f ++++=，，的下确界为( )(A)61 (B)41 (C) 31 (D) 21第Ⅱ卷(非选择置共100分)二、填空置：本大题共5小题，每小题5分，共25分．把答案填写在答题卡相应位置上。

重庆南开中学2015届高三9月月考数学(文)试题(含答案)

重庆南开中学高2015级高三9月月考数学试题（文史类）本试卷分第1卷（选择题）和第II 卷（非选择题）两部分，满分150分，考试时间120分钟．注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上．2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号．3．答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上． 4．所有题目必须在答题卡上作答，在试题卷上答题无效． 5．考试结束后，将试题卷和答题卡一并收回，第1卷（选择题共50分）一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个备选项中，只有一项是符合题目要求的．1．设集合M ={1,2,3}，N ={x |1log 2>x ），则N M ⋂=( ) A ．{3} B ．{2,3} C ．{1,3} D ．{1,2,3}2．已知等比数列{n a }满足：9273π=⋅a a ．等，则5cos a =( )A ．21-B ．31-C ．±21D ．±233．已知31)2sin(=+a π，则a 2cos 的值为( ) A ．31 B ．31- C ．97 D ．97-4．已知命题x x R x p lg 2,:>-∈∃，命题0,:2>∈∀x R x q ,则( ) A ．命题q p ∨是假命题 B ．命题q p ∧是真命题 C ．命题)(q p ⌝∧是真命题 D ．命题)(q p ⌝∨是假命题5．若x >0, y >0且12)21(2-=y x ，则yx 11+的最小值为( ) A ．3 B ．22 C ．2 D ．3+226．函数2ln 4)(x x x f -=的大致图象是( )7．若)(x f 是奇函数，且0x 是函数xe xf y -=)(的一个零点，则0x -一定是下列哪个函数的零点( )A ．1)(--=xe xf y B ．1)(+=-xex f y C ．1)(+=x e x f y D ．1)(-=x e x f y8．在△ABC 中，内角A ,B ,C 所对的边分别是a ,b ,c ,已知a c b 41=-，C B sin 3sin 2=，则cos A =( ) A ．41-B ．41C ．87D ．1611 9．已知),(y x P 为区域⎩⎨⎧≤≤≤-ax x y 0022内的任意一点，当该区域的面积为4时，y x z -=2的最大值是( )A ．6B ．0C ．2D ．2210．在△ABC 中，E ，F 分别在边AB ,AC 上，D 为BC 的中点，2||||||===AC FA EB ，0=⋅DF DE ,则 cos A = ( )A ．0B ．23 C ．43 D ．169第Ⅱ卷（非选择题共100分）二．填空题：本大题共5小题，每小l15分，共25分，把答案填写在答题卡相应位置上． 11．已知),(23R b a i b iia ∈-=+，其中i 为虚数单位，则b a +=____________. 12．已知等差数列{n a }的前n 项和为n S ，若648a a -=，则9S =____________. 13.已知a 为单位向量，3|2|),4,3(=-=b a b ,则=⋅b a ____________.14．设m ，n ，p ∈R ，且p n m -=+2，22212p n m -=+，则p 的最大值和最小值的差为__ __．15．函数⎪⎪⎪⎩⎪⎪⎪⎨⎧<-≤≤>-=0,1)21(20,2sin 2),1(log )(2015x x xx x x f xπ，若a,b,c,d 是互不相等的实数，且)()()()(d f c f b f a f ===，则a+b+c+d 的取值范围为___ .三．解答题：本大题6个小题，共75分．解答应写出文字说明、证明过程或演算步骤． 16．（13分）等差数列{n a }足：642=+a a ，36S a =，其中n S 为数列{n a }前n 项和． (I)求数列{n a }通项公式；(II)若*N k ∈，且k a ，k a 3，k S 2成等比数列，求k 值．17．（13分）某中学高二年级的甲、乙两个班中，需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛，已知这次预赛他们取得的成绩（满分100分）的茎叶图如图所示，其中甲班5名学生成绩的平均分是83，乙班5名学生成绩的中位数是86．(I)求出x ，y 的值，且分别求甲、乙两个班中5名学生成绩的方差21S 、22S ，并根据结果，你认为应该选派哪一个班的学生参加决赛？(II)从成绩在85分及以上的学生中随机抽取2名．求至少有1名来自甲班的概率．18．（13分）已知函数)(ln )(R a x a x x f ∈-=(I)当a =2时，求曲线)(x f y =在点A (1，f （1）)处的切线方程； (II)讨论函数f (x )的单调性与极值．19．（12分）设函数)0(41cos cos )6sin()(2>-+⋅-=ϖϖϖπϖx x x x f 图像上的一个最高点为A ，其相邻的一个最低点为B ，且|AB|=2． (I)求ϖ的值；(II)设△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，且b+c =2，3π=A ，求)(a f的值域．20.（12分）已知数列{n a }的前n 项和为n S ，且满足*)(2N n a n S n n ∈=+． (I)证明：数列}1{+n a 为等比数列，并求数列{n a }的通项公式；(II)数列{n a }满足*))(1(log 2N n a a b n n n ∈+⋅=，其前n 项和为n T ，试求满足201522>++n n T n 的最小正整数n ．21.（12分）对于函数)(x f y =与常数a ，b ，若b x af x f +=)()2(恒成立，则称（a ，b ）为函数)(x f 的一个“P 数对”：设函数)(x f 的定义域为+R ，且f (1)=3． (I)若（a ，b ）是)(x f 的一个“P 数对”，且6)2(=f ，9)4(=f ，求常数a ，b 的值； (Ⅱ)若(1，1)是)(x f 的一个“P 数对”，求*))(2(N n f n∈；(Ⅲ)若(0,2-)是)(x f 的一个“P 数对”，且当)2,1[∈x 时，|32|)(--=x k x f ，求k 的值及)(x f 茌区间*))(2,1[N n ∈上的最大值与最小值．重庆南开中学高2015级高三9月月考数学试题（文史类）参考答案一、选择题ABDCD BCAAD二、填空题11．5 12．36 13．5 14．31615．）20174（,三、解答题16．【解】（Ⅰ）由条件，111113615331n a d a d a a n a d a d d +++==⎫⎧⇒⇒=⎬⎨+=+=⎩⎭；（Ⅱ）(1)2n n n S +=， ∵22329(21)4k k k a a S k k k k k =⋅⇒=⋅+⇒=．17．【解】(Ⅰ)甲班的平均分为1748284(80)908355x x x +++++==⇒=，易知6y =．2127.2S =；又乙班的平均分为283x =， ∴2257.2S =；∵12x x =，2212S S <，说明甲班同学成绩更加稳定，故应选甲班参加．(Ⅱ) 85分及以上甲班有2人，设为,a b ；乙班有3人，设为z y x ,,，从这5人中抽取2人的选法有：,,,,,,,,,ab ax ay az bx by bz xy xz yz ，共10种，其中甲班至少有1名学生的选法有7种，则甲班至少有1名学生被抽到的概率为710P =.18．【解】（Ⅰ）2a =时，()2ln f x x x =-，2()1f x x'=-， ∴(1)1k f '==-，又(1)1f =，故切线方程为：11(1)y x -=--即2y x =-+.（Ⅱ）函数()f x 的定义域为(0,)+∞，令()10af x x a x'=->⇒> ① 当0a ≤时，()f x 在(0,)+∞上单调递增，无极值；② 当0a >时，()f x 在(0,)a 上单调递减，在(,)a +∞上单调递增，()ln f f a a a a ==-极小，无极大值.19．【解】(Ⅰ) )62sin(21)(πω+=x x f ，由条件，2222πωωπ=⇒==T .(Ⅱ)由余弦定理：bc bc c b A bc c b a 343)(cos 22222-=-+=-+=又1022≤<⇒≥+=bc bc c b ，故412<≤a ，又a c b >+=2，故21<≤a由)6sin(21)(ππ+=a a f ，613667ππππ<+≤a ，所以)(a f 的值域为)41,21[-.20．【解】（Ⅰ）当1n =时，111121a a a +=⇒=；当2n ≥时，1111212221(1)2n nn n n n n n n S n a a a a a a S n a ----+=⎫⇒+=-⇒=+⎬+-=⎭；即112(1)n n a a -+=+（2n ≥），且112a +=，故{}1n a +为等比数列1221n n n n a a +=⇒=-（*n N ∈）.（Ⅱ）(21)2n n n b n n n =-⋅=⋅-设231222322n n K n =⨯+⨯+⨯++⨯… ………………①23121222(1)22n n n K n n +=⨯+⨯++-⨯+⨯… …………②①-②：231112(12)222222(1)2212n nn n n n K n n n +++--=++++-⨯=-⨯=-⨯--…∴1(1)22n n K n +=-⨯+， ∴1(1)(1)222n n n n T n ++=-⨯+-， 21(1)22201582n n n n T n n +++=-⨯+>⇒≥，∴满足条件的最小正整数8n =.21．【解】（Ⅰ）由题意知⎩⎨⎧=+=+)4()2()2()1(f b af f b af ，即⎩⎨⎧=+=+9663b a b a ，解得：⎩⎨⎧==31b a（Ⅱ）由题意知(2)()1f x f x =+恒成立，令2(*)N k x k =∈，可得1(2)(2)1k k f f +=+，∴{(2)}k f 是公差为1的等差数列故0(2)(2)n f f n =+，又0(2)(1)3f f ==，故(2)3n f n =+．（Ⅲ）当[1,2)x ∈时，()|23|f x k x =--，令1x =，可得(1)13f k =-=，解得4k =，所以，[1,2)x ∈时，()4|23|f x x =--，故()f x 在[1,2)上的值域是[3,4]．又(2,0)-是()f x 的一个“P 数对”，故(2)2()f x f x =-恒成立，当1[2,2)k k x -∈(*)N k ∈时，1[1,2)2k x -∈，()2()4()24x x f x f f =-==…11(2)()2k k xf --=-，故k 为奇数时，()f x 在1[2,2)k k -上的取值范围是11[32,2]k k -+⨯；当k 为偶数时，()f x 在1[2,2)k k -上的取值范围是11[2,32]k k +---⨯．所以当1n =时，()f x 在[1,2)n 上的最大值为4，最小值为3；当3n ≥且为奇数时，()f x 在[1,2)n 上的最大值为12n +，最小值为2n -；当n 为偶数时，()f x 在[1,2)n 上的最大值为2n ，最小值为12n +-．。

重庆市南开中学校2025届高三上学期7月月考数学试题(含答案)

重庆南开中学高2025级高三7月月考数学试题本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．满分150分，考试时间120分钟．第Ⅰ卷和第Ⅱ卷都答在答题卷上．第Ⅰ卷（选择题共58分）一、单项选择题：本题共8小题，每小题5分，共40分．在每道题给出的四个选项中，只有一项符合题目要求．1．已知集合，集合，则（）A ．B ．C ．D ．2．函数的单调递增区间为（）A ．B ．C ．D ．3．命题p ：“函数在区间上单调递增”是命题q ：“”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知f （x ）是定义在R 上的奇函数，当时，，则（）A ．4B ．C ．5D ．5．若正实数x ，y 满足，则xy 的取值范围为（）A ．（0，4]B ．C ．D ．6．若函数在时有极小值，则（）A ．B ．C ．D ．7．已知函数的图象与函数的图象有且只有一个交点，则实数（）A ．B ．1C ．D ．28．已知函数是R 上的偶函数，且，当时，，函数f （x ）在区间的零点个数为（）A ．7B ．8C ．9D ．10二、多项选择题：本小题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．{A x y =={}2x B y y ==A B = (](),50,-∞-+∞ [)1,+∞()0,+∞[)[)5,01,-+∞ ()()2ln 1f x x =-()0,+∞(),0-∞()1,+∞(),1-∞()313f x x ax =-[]1,1-1a ≤0x >()21f x x =+()2f '-=4-5-40x y xy +-=[)2,+∞[)4,+∞[)16,+∞()()2e x f x ax b =+1x =2e -ab =2-3-e-1-()()ln f x x m =+()()ln g x x =--m =1-2-()1f x +()()220f x f x ++-=(]0,1x ∈()25log 22f x x ⎛⎫=-+ ⎪⎝⎭[]3,3-9．下列关于幂函数的说法正确的有（）A ．函数f （x ）的定义域为RB ．函数f （x ）的值域为C ．函数f （x ）为偶函数D ．不等式的解集为10．已知函数f （x ）在定义域内恒大于0，且满足，则下列不等式正确的是（）A ．B ．C ．D ．11．已知函数（且），则（）A ．当时，函数g （x ）有3个零点B ．当时，函数g （x ）在上单调递减C ．当函数g （x ）在处的切线经过坐标原点时，有或D ．当时，若函数恰有两个零点、，则第Ⅱ卷（非选择题共92分）三、填空题：本题共3小题，每小题5分，共15分．12．若，则f （x ）的解析式为______．13．已知函数的值域为，则______．14．已知函数，若且，有恒成立，则实数a 的取值范围是______．四、解答题：本小题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（13分）已知函数在点处的切线l 与直线平行．（1）求k 的值及切线l 的方程；（2）求f （x ）的单调区间和极值．16．（15分）()43f x x -=()0,+∞()1f x <()1,1-()1,+∞()()ln 0f x xf x x '->()()2ln 33ln 2f f >()()2ln 33ln 2f f <()()224f f >()()224f f <()[)()[]cos ,0,2ππ2sin 1,2π,3πax x x g x a x x ⎧-∈⎪=⎨-∈⎪⎩a ∈R 0a >1a =12a =4π5π,33⎛⎫⎪⎝⎭()00,P x y 0001sin cos 2x x x +=00tan 1x x ⋅=12a ⎡∈⎢⎣()()f x g x t =-1x 2x 122πx x +>()2212f x x x -=-()()sin 1202520252cos 3xf x x x =+-≤≤-[],m M M m +=()()1e ln xf x x x x =--()12,0,x x ∀∈+∞12x x ≠()()122212f x f x a x x ->-()2ln 1f x x x kx =+-+()()2,2f 320x y -=已知函数为偶函数．（1）求a 的值及函数f （x ）的值域；（2）设，若，都有恒成立，求实数m 的取值范围．17．（15分）2024年4月26日至10月28日，世界园艺博览会在成都主办，主题为“公园城市，美好人居”．本次展览的主会场内部规划了中华园艺展区，国家园艺展区，天府人居展区，公园城市展区等7个展区．暑假期间，甲乙两人相约游览世园会，恰逢7月6日小署至，“花语成都”诗词活动正在火热进行，一场场沉浸式、高互动的成都行歌正在线下演绎．（1）由于园区太大，甲乙两人决定在7个展区中随机选出3个展区游玩，求他们至少选中中华园艺展区，国家园艺展区，天府人居展区，公园城市展区这4个展区中2个展区的概率．（2）甲乙两人各自独立的参加了诗词活动中的“诗词填白”游戏，参加的人只要准确填出抽中的诗中空白的诗句，则视为闯关成功．已知甲和乙闯关成功的概率分别为p 和．（i ）记甲乙两人闯关成功的人数之和为X ，求X 的分布列；（ii ）若甲乙两人闯关成功的人数之和的期望大于1，求p 的取值范围．18．（17分）已知椭圆C ：，、分别为椭圆C 的左、右焦点，过作与x 轴不重合的直线l 与椭圆交于A 、B 两点．当l 垂直于x 轴时，．（1）求椭圆C 的标准方程；（2）若点D 、E 分别为线段、的中点，点M 、N 分别为线段AE 、BD 的中点．（i ）求证：为定值；（ii ）设面积为S ，求S 的取值范围．19．（17分）定义可导函数p （x ）在x 处的函数为p （x ）的“优秀函数”，其中为p （x ）的导函数．若，都有成立，则称p （x ）在区间D 上具有“优秀性质”且D 为（x ）的“优秀区间”．已知．（1）求出f （x ）的“优秀区间”；（2）设f （x ）的“优秀函数”为g （x ），若方程有两个不同的实数解、()()93x xaf x a +=∈R ()()()()22g x mf x f x m m =++∈R x ∀∈R ()0g x <12112p p ⎛⎫-<< ⎪⎝⎭()222210x y a b a b+=>>()11,0F -()21,0F 2F 3AB =1F A 1F B MNAB1F MN △()()()xq x p x p x '=⋅()p x 'x D ∀∈()1q x >()()e 10xf x x =-≠()()ln e xx m g x +=1x．（ⅰ）求m 的取值范围；（ⅱ）证明：（参考数据：）．参考答案一、单选题12345678B CAADBDC二、多选题91011BC ACABD三、填空题12．13．214．四、解答题15．（1），，故f （x ）在处的切线斜率为．，解得．因此．故l ：，即．（2）f （x ）的定义域为．又．令，解得或；令，解得．故f （x ）在区间上单调递增，在上单调递减，在上单调递增．综上所述，f （x ）的单调递增区间为和，单调递减区间为．且在处取得极大值，在处取得极小值．16．（1）∵f （x ）为偶函数，，，，()212x x x <121ln x x m e++< 2.718e ≈()22x x f x 2=+1,2⎛⎤-∞ ⎥⎝⎦()12f x x k x '=+-()922f k '=-2x =92k -9322k ∴-=3k =()2ln 2461ln 21f =+-+=-()()3ln 2122y x --=-3ln 242y x =+-()0,+∞()()()2211123123x x x x f x x x x x---+'=+-==()0f x '>1x >12x <()0f x '<112x <<10,2⎛⎫ ⎪⎝⎭1,12⎛⎫ ⎪⎝⎭()1,+∞10,2⎛⎫ ⎪⎝⎭()1,+∞1,12⎛⎫⎪⎝⎭12x =111ln 224f ⎛⎫=- ⎪⎝⎭1x =()11f =-()()f x f x ∴=-9919333x x xx x xa a a --+++⋅∴==919x x a a ∴+=+⋅即对恒成立，．（当且仅当时取等）故值域为．（2），令，则．对恒成立，即对恒成立．，故原式子又等价于对恒成立．令，则，则h （t ）在上单调递增．故，．故m 的取值范围为．17．（1）记“他们至少选中其中的两个园区”为事件A ．则．（2）（ⅰ）由可知：X 可取0，1，2．列出分布列如下：X 012P（ⅱ）由（ⅰ）可知，解得．18．（1）在椭圆C 中，令，可得，故有，而，，解得，，，故椭圆C 的标准方程为．（2）（ⅰ）设l ：，将l 与C 联立可得：．设，，则，．()191xa a -⋅=-x ∀∈R 1a ∴=()1323x x f x ∴=+≥=0x =[)2,+∞()()()2233233x x x x g x m m --=++++()332xxt t -=+≥222332x x t -+=-()()2220g x m t t m ∴=-++<2t ∀≥()2120m t t -+<2t ∀≥210t -> 221tm t <--2t ∀≥()221th t t =--()()2222201t h t t +'=>-()2,+∞()()423h t h ≥=-43m ∴<-4,3⎛⎫-∞- ⎪⎝⎭()11343437C C C 22C 35P A +==()()()201121242P X p p p p ==---=-+⎡⎤⎣⎦()()()()21121121451P X p p p p p p ==--+--=-+-⎡⎤⎣⎦()()22212P X p p p p==-=-2242p p -+2451p p -+-22p p-()()()22145122311E X p p p p p =⋅-+-+⋅-=->213p >>x c =2b y a =±223b a =1c =222a b c =+24a =23b =21c =22143x y +=1x ty =+()2234690t y ty ++-=()11,A x y ()22,B x y 122634t y y t -+=+122934y y t -=+则，，，．①当l 与x 轴垂直时，，此时，故；②当l 与x 轴不垂直时，也有．综上，．故，而，故．（ⅱ）由（ⅰ）可知：，故：．令，解得．恒过定点．设到MN 与AB 的距离分别为与，的面积为，则．故令，则，因为在上单调递增，故，则．综上所述，S 的取值范围为．19．（1）当时，．令，则，令，解得；令，解得．111,222x y D ⎛⎫-⎪⎝⎭221,222x y E ⎛⎫- ⎪⎝⎭12121,24424x x y y M ⎛⎫+-+ ⎪⎝⎭21211,24424x x yy N ⎛⎫+-+ ⎪⎝⎭12x x =13144M N x x x =-=MN AB ∥1212121244M N MNAB M N y y y y y y k k x x x x x x ---====---MN AB ∥MN AB ∥2AB y =-14N MN y AB =-=14MN AB =MN AB ∥MN l 1212124224x x y y x t y ⎛⎫⎛⎫⎛⎫-+-=--⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0y =121212121111124424244242x x y y ty ty y y x t t ++⎛⎫⎛⎫=+--+=+--+= ⎪ ⎪⎝⎭⎝⎭MN l 1,02R ⎛⎫⎪⎝⎭1F 1d 2d 1F AB △1S 111122113214162MN d F R S S F F AB d ===112121233131616216S S F F y y y y ==⋅⋅-=-=94==)1r r =≥()2299911443143143r r S r r r r=⋅=⋅=⋅+-++13y r r =+[)1,+∞134r r +≥916S ≤90,16⎛⎤⎥⎝⎦()e 1xf x =-()()1e 1e 11e 1e 1xxx x x x g x -+-=-=--()()1e 1xh x x =-+()e xh x x '=()0h x '>0x >()0h x '<0x <当时，h （x ）单调递减；当时，h （x ）单调递增，故．当时，，则，f （x ）不具有“优秀性质”；当时，，则，f （x ）具有“优秀性质”．故f （x ）的“优秀区间”为．（2）（ⅰ）原式．令，，令，解得；令，解得．故当时，k （x ）单调递减；时，k （x ）单调递增．当时，；时，，，故．即m 的取值范围为．（ⅱ）由、为方程的两个解可知：，则，令，，令，，则N （x ）在单调递增，故．令，解得．故M （x ）在（0，1）上单调递减，上单调递增．则．令，，令，则，故G （x ）在上单调递增，．即，故Q （x ）在上单调递增．故(),0x ∈-∞()0,x ∈+∞()()00h x h >=(),0x ∈-∞e 10x -<()10g x -<()0,x ∈+∞e 10x ->()10g x ->()0,+∞()e ln 1ln 1e 1ln 0e 1x xx x x x m x x x mx m x--⇔+=⇔---=⇔=-()e ln 1x x x k x x --=()()()21e 1x x k x x --'=()0k x '>1x >()0k x '<01x <<()0,1x ∈()1,x ∈+∞0x →()k x →+∞x →+∞()k x →+∞()11k e =-1m e >-()1,e -+∞1x 2x 2222e 1ln x m x x x =--1201x x <<<()1212212222221e 1e 11ln ln ln x x x x m x x x x e x x x x e++<=--⇔<---()e 11x M x x x x e =---()()()21e 1xx x M x x ---'=()e 1xN x x =--()e 10xN x '=->()0,+∞()()00N x N >=()0M x '>1x >()1,+∞()()22121 2.72 2.710.89120e e M x M e e e e e---⨯-≥=--=>=>()()()11Q x k x k x x ⎛⎫=-> ⎪⎝⎭()()()()221e e 111x xx x x Q x k x k x x x --+-⎛⎫'''=+= ⎪⎝⎭()e e 1,1x x G x x x x =-+->()1111e e e 1e e e 10x xx xx x G x x x x x'=-++>-++>()1,+∞()()10G x G >=()0Q x '>()1,+∞，即，成立．因为，则，又，，k （x ）在（0，1）单调递减，则，即，故．所以．()()10Q x Q >=()1k x k x ⎛⎫> ⎪⎝⎭1x ∀>1201x x <<<()()1221k x k x k x ⎛⎫=>⎪⎝⎭101x <<2101x <<121x x <121x x <()12ln 0x x <()212222e 11ln 0x x x x x x e <<---。

理综卷(生物解析)·2015届重庆南开中学高三9月月考(2014.09)

重庆南开中学高2015级9月月考理科综合能力测试试题卷理科综合能力测试试卷分分为物理、化学、生物三个部分，物理部分1至4页，化学部分5至8页，生物部分9至12页，共12页，满分300分，考试时间150分钟。

【题文】2．下图是人体某组织结构示意图，①②③④分别表示人体内不同部位的液体。

据图判断下列说法正确的是 ( )A．人体的内环境是由①②③④组成的B．②中含激素、乳酸、消化液、CO2等物质C．若该组织为胰岛，则进食后短时间内左侧血液中胰岛素的含量低于右侧D．血浆中的氧进入组织细胞的途径是②→③→④【答案】【知识点】H1人体内环境与稳态及水和无机盐的平衡【答案解析】D解析：由图可知，①是淋巴、②是血浆、③是组织液、④是细胞内液，人体的内环境主要是由淋巴、血浆、组织液，A错；消化液存在于消化道内，血液中没有消化液，B错；胰岛素具有降血糖的作用，若该组织为胰岛，则进食后短时间内左侧血液中胰岛素的含量高于右侧，C错；组织细胞直接从组织液中吸收氧气，D正确。

重庆南开中学九年级下学期月考数学试题(含答案)

重庆南开中学九年级数学下学期月考试题(全卷共五个大题，满分l50分，考试时间l20分钟)注意事项：1．试题的答案书写在答题卡．．．上不得在试卷上直接作答； 2．作答前认真阅读答题卡上的注意事项；3．作图(包括作辅助线)，请一律用黑色．．签字笔完成； 4．考试结束，由监考人员将试题和答题卡．．．一并收回．参考公式：抛物线()02≠++=a c bx ax y 的定点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 4422，，对称作为ab x 2-=．一、选择题：(本大题共l2个小题，每小题4分，共48分)在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将答题卡．．．上题号右侧正确答案所对应的方框涂黑．1．实数4的倒数是(▲)A ．4B ．41C ．-4D ．41- 2．计算()232x 的结果是(▲) A ．64x B ．62x C ．54x D ．52x 3．下列商标是轴对称图形的是(▲)4．在代数式12+x 中，x 的取值范围是(▲) A ．0＞x B ．0≤x C ．x ≠-1 D ．x ≠0 5．下列调查中，适合采用普查方式的是(▲)A ．调查市场上粽子的质量情况B ．调查某品牌圆珠笔芯的使用寿命C ．调查乘坐飞机的旅客是否携带了违禁物品D ．调查我市市民收看重庆新闻的情况6．ABC ∆与DEF ∆的相似比为3：4，则ABC ∆与DEF ∆的周长比为(▲)A ．3：2B ．3：4C ．4：5D ．9：167．如图，a ∥b ，将—块三角板的直角顶点放在直线a 上，若︒=∠421，则2∠的度数为(▲)A ．46°B ．48°C ．56°D ．72°8．如图，A 、B 、C 是O 上的三点，︒=∠40ACB ，则AOB ∠的度数为(▲)A ．20°B ．40°C ．60°D ．80°9．不等式组⎪⎩⎪⎨⎧-+≤-1321022x x x ＞的解集是(▲) A ．1≥x B ．14≤-x ＞ C ．4＜xD ．1≤x10．五一假期，刘老师开车自驾前往荣昌，他开车离开家时，由于车流量大，行进非常缓慢，十几分钟后，终于行驶在畅通无阻的高速公路上，大约五十分钟后，汽车顺利到达荣昌收费站，经停车缴费后，进入车流量较小的道路，很快就到达了荣昌县城．在以上描述中，汽车行驶的路程s(千米)与所经历的时间t(小时)之间的大致函数图象是(▲)11．下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有3颗棋子，第②个图形一共有9颗棋子，第③个图形一共有l8颗棋子，…，则第⑥个图形中棋子的颗数为(▲)12．如图，Rt OAB ∆的直角边OA 在x 轴正半轴上，︒=∠60AOB ，反比例函数()03＞x xy =的图象与Rt OAB ∆两边OB ，AB 分别交于点C ，D ．若点C 是OB 边的中点，则点D 的坐标是(▲)A ．()3,1B ．()1,3 C ．⎪⎪⎭⎫ ⎝⎛23,2 D ．⎪⎪⎭⎫ ⎝⎛43,4二、填空题：(本大题共6个小题，每小题4分，共24分)请将每小题的答案直接填在答．题卡．．中对应的横线上． 13．化简()()11-+a a 的结果为 ▲ ．14．某校乒乓球训练队共有7名队员，他们的年龄(单位：岁)分别为：l2，13，14，12，l3，15，l3，则他们年龄的众数为 ▲ 岁．15．计算()120153121-⎪⎭⎫ ⎝⎛--+-的值为 ▲ ． 16．如图，AB 为半圆O 的直径，点C 在AB 的延长线上，CD 与半圆O 相切于点D ，且42==CD AB ，则图中阴影部分的面积为 ▲ ．(结果保留π)17．从23-，1-，0，1这四个数中，任取一个数作为m 的值，恰好使得关于x ，y 的二元一次方程组⎩⎨⎧-=--=-232y x m y x 有整数解，且使以x 为自变量的一次函数()331-++=m x m y的图象不经过第二象限，则取到满足条件的m 值的概率为 ▲ ．18．如图，ABC ∆中，4==AC AB ，︒=∠120BAC ，以A 为一个顶点的等边三角形ADE 绕点A 在BAC ∠内旋转，AD 、AE 所在的直线与BC 边分别交于点F 、G ，若点B 关于直线AD 的对称点为'B ，当'FGB ∆是以点G 为直角顶点的直角三角形时，BF 的长为 ▲ ．三、解答题：(本大题共2个小题。

2015届重庆南开中学高三9月月考理综卷(2014.09)

重庆南开中学高2015届9月月考理科综合能力测试试题卷理科综合能力测试试卷分分为物理、化学、生物三个部分，物理部分1至4页，化学部分5至8页，生物部分9至12页，共12页，满分300分，考试时间150分钟。

注意事项；1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上．2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦擦干净后，再选涂其它答案标号．3．答非选择题和选做题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上．4．所有题目必须在答题卡上作答，在试题卷上答题无效．5．考试结束后，将试题卷带走，仅将答题卡交回，物理（共110分）一、选择题（本大题共5小题，每小题6分，共30分．在每小题给出的四个选项中，只有一项符合题目要求）1．关于物体受力和力与运动的关系，下列说法正确的是A．竖直向上运动的物体，一定受到竖直向上的力的作用B．有一个力出现时，一定有两个与该力相关的物体C．只有在相互接触的物体之间才能有力的作用D．摩擦力一定是阻碍物体运动的阻力2．如图所示，质量相等的A、B两物体在同一水平线上，当A物体被水平抛出的同时，B物体开始自由下落（空气阻力忽略不计），曲线AC为A物体的运动轨迹，直线BD为B物体的运动轨迹，两轨迹相交于O点，则关于两物体在O点的物理量，下列说法正确的是A．经O点时速率相等B．运动到O点的时间不相等C．运动到O点的速度改变量相等D．在O点时重力的功率一定不相等3．如图所示，质量为所的物块始终固定在倾角为的斜面上，下列说法中错误．．的是A．若斜面向右匀速移动距离s，斜面对物块没有做功B．若斜面向上匀速移动距离s，斜面对物块做功mgsC．若斜面向左以加速度a移动距离s，斜面对物块做功masD．若斜面向下以加速度a移动距离s．斜面对物块做功m(g+a)s4．宇宙间存在一些离其它恒星较远的三星系统，其中有一种三星系统如图所示，三颗质量均为m的星位于等边三角形的三个顶点，三角形边长为L，忽略其它星体对它们的引力作用，三星在同一平面内绕三角形中心O做匀速圆周运动，则：A. 当质量m变为原来的2倍，距离L也变为原来的2倍时，周期变为原来的2倍B．当质量m变为原来的2倍，距离L也变为原来的2倍时，线速度变为原来的2倍C．该三星系统运动的周期跟两星间距离L无关，只与星的质量m有关D. 该三星系统运动的周朔跟星的质量m无关，只与两星间距离L有关5．在广场游玩时，一小孩将一充有氢气的气球用细绳系于一个小石块上，并将小石块置于水平地面上，如图所示．若水平的风力逐渐增大（设气球所受空气的浮力不变），则A．细绳的拉力逐渐减小B．小石块有可能连同气球一起被吹离地面C．地面受到小石块的压力逐渐减小D．小石块滑动前受到地面施加的摩擦力逐渐增大，滑动后受到的摩擦力不变二、非选择题（本大题共4小题，共68分）6.(19分)(1)某学生用打点计时器研究小车的匀变速直线运动．实验时得到一条纸带．他在纸带上便于测量的地方选取第一个计时点A，已知相邻两计时点间的时间间隔为T且测量时发现AC两点间的B点已模糊不清，如图所示，于是他测得AC长为S1，DE长为S2，EF长为S3（CD间还有一些相邻计时点未标出），则打B点时小车的瞬时速度大小为__ __，小车运动的加速度大小为__ __．(2)如图，质量为M的滑块A放在气垫导轨B上，C为位移传感器，它能将滑块A到传感器C的距离数据实时传送到计算机上，经计算机处理后在屏幕上显示滑块A的位移一时间(s-t)图像和速率一时间(v-t)图像．整个装置置于高度可调节的斜面上，斜面的长度为l、高度为h．①现给滑块A一沿气垫寻轨向上的初速度，A的v-t图线如题6图所示。

重庆南开中学初2015级九上数学第一次月考试题

重庆一中初2015级13—14学年度上期期末考试数学试题2014．1（本试卷满分150分，考试时间120分钟）一．选择题（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A ．B ．C ．D 的四个答案，其中只有一个是正确的，请将正确的答案填入下面的表格内.1. 4的算术平方根是（）A ．－2B ． 2C ．±2D ．±4 2. 在平面直角坐标系中，点A （2，－3）在第( )象限． A. 一 B. 二 C. 三 D. 四 3x 的取值范围是（） A ．x =1 B ．x ≥1 C ．x ＞1 D ．x ≤1 4.如图，已知AB ∥CD ，AB=AC ，∠ABC=68°，则∠ACD 的度数为（） A.22o B. 32o C. 44o D.34o5. 如图，在△ABC 中，DE 垂直平分AB ，垂足为E ，交BC 于点D ，连接AD ．已知AC=5cm ，△ADC 的周长为17cm ，则BC 的长为（）A ．7cmB ．10cmC ．12cmD ．22cm6. 已知△ABC 的各边长分别为3cm 、4cm 、5cm ，则连结各边中点所得△DEF 的周长为（） A ．2cm B ．7cmC ．5cmD ．6cm 7. 已知一个多边形的内角和是o 540，则这个多边形是( )A. 四边形B. 五边形 C . 六边形 D. 七边形 8. 对于一组统计数据：2，4，4，5，6，9．下列说法错误的是（） A ．众数是4 B ．中位数是5 C ．极差是7 D ．平均数是5A BCDE（第5题）（第4题）B(第6题)9. 某地受灾后，灾区急需帐篷．某企业急灾区之所急，准备捐助甲、乙两种型号的帐篷共 1500顶，其中甲种帐篷每顶安置6人，乙种帐篷每顶安置4人，共安置8000人．设该企业捐助甲种帐篷x 顶、乙种帐篷y 顶，那么下面列出的方程组中正确的是（）A ．x 4y 15004x y 8000+=⎧⎨+=⎩B ．x 4y 15006x y 8000+=⎧⎨+=⎩C ．x y 15004x 6y 8000+=⎧⎨+=⎩D ．x y 15006x 4y 8000+=⎧⎨+=⎩10. 对于函数y=﹣3x+1，下列结论正确的是( )A ．它的图象必经过点（﹣1，3）B ．它的图象经过第一、二、三象限C ．当x ＞1时，y ＜0D ．y 的值随x 值的增大而增大11. 一辆公共汽车从车站开出，加速行驶一段时间后匀速行驶，过了一段时间，汽车到达下一个车站．乘客上下车后汽车开始加速，一段时间后又开始匀速行驶，下面可以近似地刻画出汽车在这段时间内的速度变化情况的图象是（）12. 如图，在□ABCD 中，90,2,3o ABC AB BC ∠===, 点E 在BC 边上，2EC BE =,点F 为CD 边的中点，连接,BF DE ,过点A 作AM BF M ⊥于点，.A N D E N ⊥于点则:AM AN 的值为 ( )A ．2:3 B． CD．二．填空题（本大题6个小题，每小题4分，共24分）请将每小题的答案填在下面表格内.13. 若函数2131m y x-=+是关于x 的一次函数，则m 的值为 .14. 在平面直角坐标系中，点P （－2，a ）与点Q （b ，3）关于y 轴对称，则a b +的值为；15.若一条直线经过点（﹣1，1）和点（1，5），则这条直线的解析式为； 16. 在平面直角坐标系中，已知点A （2，3），在x 轴上找一点P ，使得△AOP 是等腰三角形，则这样的点P 共有个．A ．．．B ．C ．D ．E F(第12题)17. 如图是一组密码的一部分．为了保密，许多情况下可采用不同的密码，请你运用所学知识找到破译的“钥匙”．目前，已破译出“今天考试”的真实意思是“努力发挥”．破译“正做数学”的真实意思是；18.如图，△ABC 中，∠C=90o ，BC=2AC ，''A B C ∆≌ABC ∆,线段''A B 与BC 的交点M 为BC 的中点，则':'A M B M = .三．解答题（本大题2个小题，每小题7分，共14分）解答每小题都必须写出必要的演算过程或推理步骤. 19.计算：)()2201412133-⎛⎫-+-+- ⎪⎝⎭20.解方程组：6328x y x y +=⎧⎨-=⎩A B C A ’B ’ M（第18题）（第17题）四．解答题（本大题4个小题，每小题10分，共40分）解答每小题都必须写出必要的演算过程或推理步骤.21. 已知：如图， EC=AC ，∠BCE=∠DCA ，∠A=∠E ；求证：BC=DC ．22.如图，已知直线1:5l y x =-+，直线2:22l y x =+，两直线交于点A ，1l 交x 轴于C 点，2l 交y 轴于点B ，交x 轴于点D.（1）求出A 、B 、C 三点的坐标；（2）求ABC ∆的面积.B23.为了了解学生对体育活动的喜爱情况，某校对参加足球、篮球、乒乓球、羽毛球这四个课外活动小组的人员分布情况进行抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图，请根据图中提供的信息，解答下面问题：（1）此次共调查了多少名同学？（2）将条形统计图补充完整；（3）根据调查情况探求，如果该校共有1000名学生参加这四个课外活动小组，而每个教师最多．．只能辅导本组的20名学生，请通过计算确定这四个课外活动小组至少．．共．需要．．准备多少名教师？24.如图，在□ABCD 中，延长CD 至点E ，使DE ＝CD ，连接BE 交AD 于点F ，交AC 于点G. （1）求证：AF ＝DF ；（2）若BC ＝2AB ，DE ＝1，∠ABC＝60°，求FG五．解答题（本大题2个小题，每小题12分，共24分）解答每小题都必须写出必要的演算过程或推理步骤.25. 甲、乙两车分别从M 、N 两地相向而行，甲车出发1小时后乙车出发，并以各自的速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是甲、乙两车之间的距离S （千米）与甲车出发时间t （小时）之间的函数关系图象，其中D 点表示甲车到达N 地，停止行驶. （1）A 、B 两地的距离千米；甲车出发小时后与乙车相遇；甲车的速度是千米/时；乙车的速度是千米/时；（2）求出a 的值；（3）甲车出发多长时间后两车相距330千米？26.如图，ABC ∆为直角三角形，90oACB ∠=,30oABC ∠=，AC =PMN ∆为等边三角形，4MN =，点M 、N 、B 、C 在同一直线上，将PMN ∆沿水平方向向右以每秒1个单位的速度移动，直至点M 与点C 重合时停止运动.设运动时间为t 秒，当0t =时，点B 与点N 重合.（1）求点P 与点A 重合时的t 值；（2）在运动过程中，设PMN ∆与ABC ∆重叠部分的面积为S ，请直接写出．．．．S 与t 的函数关系式，并注明自变量t 的取值范围；（3）若点D 为AB 边中点，点E 为AC 边中点，在运动过程中，是否存在点M ，使得DEM ∆为等腰三角形？若存在，请求出对应的t 值；若不存在，请说明理由.命题：石含军审题：吴献B(N)重庆一中初2015级13—14学年度上期期末考试数学试题参考答案一．选择题（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A ．B ．C ．D 的四个答案，其中只有一个是正确的，请将正确的答案填入下面的表格内.二．填空题（本大题6个小题，每小题4分，共24分）请将每小题的答案填在下面表格内.19.解：原式=13139-+++………………………….5分 =11…………………………………………..7分20.解: 6328x y x y +=⎧⎨-=⎩由①×2+②得:520x =4x =………………………..3分将4x =代入①,得:2y =………………….6分∴原方程组的解为:42x y =⎧⎨=⎩………………..7分21.证明：∵∠BCE=∠DCA∴∠BCE ＋∠ACE ＝∠DCA ＋∠ACE即：∠BCA ＝∠DCE ………………………………………………3分在△BCA 与△DCE 中，A E AC ECBCA DCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BCA ≌△DCE （ASA ）……………………………………..8分 ∴BC=DC ………………………………………………………….10分①②22．解：（1）在直线：1:5l y x =-+中，令0y =，则：50x -+=，解得：5x =∴点C 坐标为：（5，0）………………………………………………….2分在直线：2:22l y x =+中，令0x =，则：y 2022=⨯+=∴点B 坐标为（0，2）……………………………………………………4分联立：522y x y x =-+⎧⎨=+⎩，解得：14x y =⎧⎨=⎩∴点A 坐标为（1，4）…………………………………（2）在直线：2:22l y x =+中，令0y =，则：220x +=，解得：1x =-∴直线2l 与x 轴的交点D 的坐标为（-1，0）…………∴CD=5(1)6C D x x -=--=112211=6462221266ABC ACD BCD A B S S S CD y CD y ∆∆∆=-=⋅⋅-⋅⋅⨯⨯-⨯⨯=-= ∴ABC ∆的面积为6…………………………………………10分23.解：（1）90÷45%=200．故此次共调查了200名同学；.................................................3分（2）由200-20-30-90=60为参加羽毛球项目的学生数，所以补全的条形图如下所示；……………………………………………………………5分（3）足球组：1000×45%÷20=22.5，至少需要准备23名教师；篮球组：1000×10%÷20=5，至少需要准备5名教师；乒乓球组：30÷200×1000÷20=7.5，至少需要准备8名教师；羽毛球组：60÷200×1000÷20=15人，至少需要准备15名教师．故这四个小组至少共需教师：23+5+8+15=51（名）…………………………….……..10分24.(1)证明：∵四边形ABCD 是平行四边形 ∴AB//CD ，AB=CD∴∠ABF ＝∠E ………………………..1分又∵CD=DE∴AB=DE ………………………………2分在△ABF 与△DEF 中，ABF E AFB DFE AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABF ≌△DEF （AAS ）...............................................4分 ∴AF=DF ……………………………………………………………………………….5分（2）解：过点A 作AN ⊥BG 于点M ，交BC 于点N. ∵四边形ABCD 是平行四边形∴AD=BC ，AD//BC ，∠BAD ＋∠ABC ＝180o 由（1）知：AF=DF 而：BC=2AB ∴AF=12AD=12BC=AB ∵∠ABC=60o∴∠BAF=180o -∠ABC=120o∴∠ABF ＝∠AFB=30o ，∠BAM ＝∠FAM=60o ∴∠ANB ＝∠ABC ＝∠BAM ＝60o∴△ABM 是等边三角形……………………………………………………………6分 ∵DE=1∴AB=AN=BN=1 ∴CN=AN=1又∠ANC=180o -∠ANB=120o∴∠NAC=∠NCA=300则：∠AFG ＝∠FAG=30o∴GA=GF ……………………………………………………………………………..7分令：FG=x ，则：MG=12AG=12x 又∵AF=AB=1，AM=12AN=12在Rt △AMF 中，由勾股定理得：AM 2+MF 2=AF 2即：22211122x x ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭………………………………………………………..9分解得：3x =∴线段FG的长为3. ……………………………………………………………..10分MN25.解: (1) 560 、 3 、 120 、 100 ；……………..4分（2）相遇后甲车到达B 地的时间为：（3﹣1）×100÷120= （小时）所以，a=（120+100）×=（千米）……….8分（3）设直线BC 的解析式为S=k 1t+b 1（k 1≠0），将B （1，440），C （3，0）代入得，，解得，所以，S=﹣220t+660，当﹣220t+660=330时，解得t=1.5，………………………………………………….10分直线CD 的解析式为S=k 2t+b 2（k 2≠0），点D 的横坐标为+3=，将C （3，0），D （，）代入得，，解得，所以，S=220t ﹣660，当220t ﹣660=330时，解得t=4.5，…………………………………………………………..12分答：甲出发多长1.5小时或4.5小时后两车相距330千米．（3）解法二：设甲车出发x 小时后两车相距330千米当两车相遇前，得：120100-1330560x x ++=（）解得： 1.5x =当两车相遇后，得：120100(1)560330x x +-=+ 解得： 4.5x =所以，甲车出发1.5小时或4.5小时后两车相距330千米。

重庆南开中学高2015届高三3月月考试题

重庆南开中学高2015届高三3月月考试题高三2011-03-11 18:02重庆南开中学高2011级高三3月月考试题语文卷一、(本大题共4小题，每小题3分，共12分)1．下列词语中，字形全都正确，加点字的读音全都一致的一项是A．依附本埠老师付物阜民丰B．稗草裨益碧螺春弊帚自珍C．觊觎侪辈荠菜汤济济一堂D．蛊惑鼓噪绩优股余勇可贾2．下列词语中，加点的词语使用不当的一项是A．我们试图从流行文化各个分战场的阵势来窥视未来流行文化发展的端倪：能够与美国一争高下的挑战者出现了吗?B．今年春晚表演的魔术被行家们一一破解，但对于我这个只是爱好魔术的半瓶醋来说还是觉得个中奥妙无穷。

C．适当地使用方言，能使人物形象鲜活，乡土气息浓郁；可是不分青红皂白地滥用方言，却会在一定程度上影响读者对作品的理解。

D．曼联的弗格森和阿森纳的温格，这对似乎视彼此为天敌的主教练，近两年已缓解了敌对情绪，然而两个俱乐部的关系始终剑拔弩张。

3．下列各句中，没有语病的一句是A．衡量教育是否成功，不是看分数，而是看受教育者对所学知识的兴趣越来越大还是越来越小。

B．有国外媒体评论，中国是从埃及接返国民的国家中相关工作速度最快、效率最高、启动最早、规模最大的国家之一。

C．该场招聘会有150家单位参与，提供了超过4000多个岗位，其中电子制造业占百分之七十五左右。

D．从目前我国快递物流行业的发展水平来看，远远滞后于电子商务的发展速度，要打通节日期间物流瓶颈尚需时日。

4．依次填入下面一段文字横线处的语句，衔接最恰当的一组是我一生最爱雪，可我偏偏客居南方一座不下雪的城市，为此很遗憾。

随笔志感，聊释雪馑。

①难得上个月上海下了一场雪，雪花漫天飞扬，宛如柳絮鹅毛，飘飘洒洒。

②尽管是刹那间的挑逗，却也让我无限眷慕。

③也只有睡梦中重温故乡雪的往事——凭窗看飘雪，执笤扫积雪，踏雪嬉戏，炉边烹雪，灯下咏雪，纸上画雪……真是情趣无穷，诗意盎然。

④可惜这美景只显现了十分钟，大地还没有粉妆，尘垢尚未冰封，便匆匆猝然而止!⑤只有在荧屏上欣赏哈尔滨的雪、瑞士的雪和北海道的雪。

重庆南开中学2015届高三10月月考生物试题(word版)

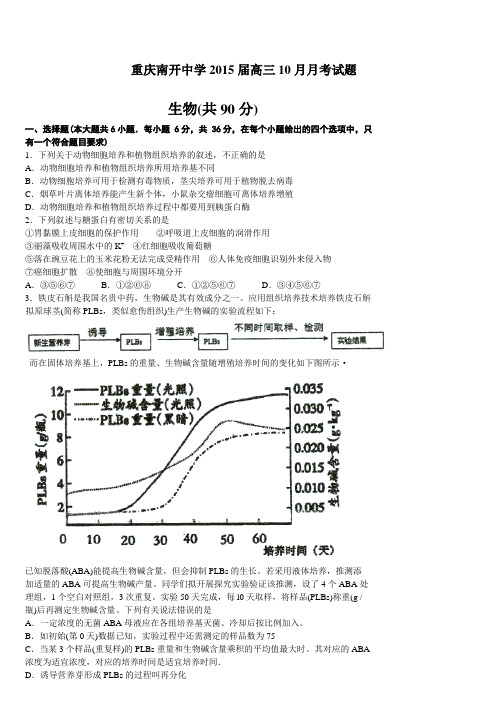
重庆南开中学2015届高三10月月考试题生物(共90分)一、选择题(本大题共6小题．每小题 6分，共 36分，在每个小题给出的四个选项中，只有一个符合题目要求)1．下列关于动物细胞培养和植物组织培养的叙述，不正确的是A．动物细胞培养和植物组织培养所用培养基不同B．动物细胞培养可用于检测有毒物质，茎尖培养可用于植物脱去病毒C．烟草叶片离体培养能产生新个体，小鼠杂交瘤细胞可离体培养增殖D．动物细胞培养和植物组织培养过程中都要用到胰蛋白酶2．下列叙述与糖蛋白有密切关系的是①胃黏膜上皮细胞的保护作用②呼吸道上皮细胞的润滑作用③丽藻吸收周围水中的K+④红细胞吸收葡萄糖⑤落在豌豆花上的玉米花粉无法完成受精作用⑥人体免疫细胞识别外来侵入物⑦癌细胞扩散⑧使细胞与周围环境分开A．③⑤⑥⑦B．①②⑥⑧C．①②⑤⑥⑦D．③④⑤⑥⑦3．铁皮石斛是我国名贵中药，生物碱是其有效成分之一。

应用组织培养技术培养铁皮石斛拟原球茎(简称PLBs，类似愈伤组织)生产生物碱的实验流程如下：而在固体培养基上，PLBs的重量、生物碱含量随增殖培养时间的变化如下图所示·已知脱落酸(ABA)能提高生物碱含量，但会抑制PLBs的生长。

若采用液体培养，推测添加适量的ABA可提高生物碱产量。

同学们拟开展探究实验验证该推测，设了4个ABA处理组，1个空白对照组，3次重复。

实验50天完成，每l0天取样，将样品(PLBs)称重(g / 瓶)后再测定生物碱含量。

下列有关说法错误的是A．一定浓度的无菌ABA母液应在各组培养基灭菌、冷却后按比例加入。

B．如初始(第0天)数据已知，实验过程中还需测定的样品数为75C．当某3个样品(重复样)的PLBs重量和生物碱含量乘积的平均值最大时。

其对应的ABA 浓度为适宜浓度，对应的培养时间是适宜培养时间．D．诱导营养芽形成PLBs的过程叫再分化4．生物技术安全性和伦理问题是社会关注的热点。

下列叙述，正确的是A．对转基因生物安全性的争论主要集中在食物安全、生物安全和环境安全这三个方面B．对于克隆人和治疗性克隆，我国的态度是明令禁止C．设计试管婴儿须在植入前对胚胎进行产前诊断D．新型鼠疫病毒和重组流感病毒属于生化毒剂类生物武器，应当严令禁止生产5．下列有关高中生物学实验的说法，不正确的是A．如果材料用具中无双缩脲试剂，而有斐林试剂和蒸馏水等，也能检测蛋白质B．分离绿叶中的色素，发现叶绿素b和胡萝卜素在层析液中的溶解度差异最大C．检测人体血液中的葡萄糖时，可加入新配制的斐林试剂，结果出现了砖红色沉淀D．向豚鼠的胰腺腺泡细胞中注射3H标记的氨基酸，会发现放射性依次出现在附有核糖体的内质网、高尔基体和靠近细胞膜内侧的运输蛋白质的囊泡中6．下图表示鲤鱼体内某蛋白质中氨基酸及相关基团的数目，下列有关叙述中正确的是A．该蛋白质的R基中共含有l6个氨基B．该蛋白质对应的mRNA(不考虑终止密码子)逆转录所得的cDNA连续复制两次，需要消耗2268个游离的脱氧核苷酸C．鲤鱼体内蛋白质种类繁多，其直接原因在于组成各种蛋白质的氨基酸数目、排列顺序、空间结构的千差万别D．若该蛋白质是有氧呼吸第二阶段的关键酶，当它的合成出现障碍时，鲤鱼细胞内呼吸产生的CO2与消耗的O2的比值将会增大二、非选择题(每空两分，共54分)7．(30分)1．(16分)科学家通过诱导黑鼠体细胞去分化获得诱导性多能干细胞(iPS)．继而利用iPS细胞培育出与黑鼠遗传特性相同的克隆鼠，流程如下：(1)从黑鼠体内获得组织块后，用________ 处理将其分散成单个细胞。

重庆市南开中学校2024-2025学年高三上学期10月月考语文试题

重庆市高2025 届高三第二次质量检测、语文试题 2024.10命审单位：重庆南开中学注意事项：1.本试卷满分150分，考试时间150分钟。

2.答卷前，考生务必将自己的姓名和座位号填写在答题卡上。

3.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

4.考试结束后，将本试卷和答题卡一并交回。

一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5 小题，19分)阅读下面的文字，完成1~5题。

材料一：全球经济与社会活动的各个领域已无处不见互联网技术的参与，互联网用户数量早已超过世界总人口的一半。

其中，未成年用户占到了总数的三分之一。

未成年人正以极其快速的适应能力融入这场数字变革中。

与此同时，触网的低龄化特征愈发突出。

无处不在的全球互联与匿名开放的网络世界正在迅速瓦解传统线下社会为未成年人建立的保护屏障，给未成年人的成长带来前所未有的巨大挑战，其中数字负能的挑战日益严峻。

数字负能包括数字鸿沟、网络成瘾与网络伤害。

数字鸿沟主要表现为由于对信息、网络技术的拥有程度、应用程度以及创新能力的差别而造成的信息落差，网络伤害则侧重强调未成年人面临的安全、隐私与身心健康等巨大挑战，但无论政府还是学术界都较少关注网络伤害。

一是因为未成年人面临的风险与伤害并不只是数字时代特有的现象，而是一直以来都存在的普遍性问题；二是因为网络世界中的伤害风险只是一种潜在可能，人们容易掉以轻心，致使目前还没有一套完善的保护未成年人免受网络伤害的机制措施。

由于互联网能够突破线下社会的时空限制，大大增加了未成年人面临风险与伤害的概率，传统线下社会为未成年人构建的保护措施越来越难以适应数字时代的需要。

在数字时代，没有任何一个上网的未成年人能够远离网络风险与伤害，而本身在传统线下社会已经处于困境的最为弱势的未成年人则更容易受到伤害。

重庆南开中学2015届高三9月月考文综试题(无答案)

重庆南开中学高2015级高三9月月考文科综合能力测试试题卷文科综合能力测试试题卷分为思想政治、历史、地理三个部分。

思想政治部分1至4页，历史部分5至8页，地理部分9至12页，共12页。

满分300分。

考试时间150分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3．答综合题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试题卷上答题无效。

5．考试结束后，将答题卡交回，试题卷自行保存。

思想政治(共100分)一、选择题(本大题共12小题，每小题4分，共48分)在每小题给出的四个备选项中，只有一项是最符合题目要求的。

曾经号称高仿真的HD编号的假钞让人们成了惊弓之乌，随着公安部门对假钞打击力度的加强，各种假钞曾经销声匿迹，然而，近期以TJ55、AZ88、WL15、YX86开头的新版假钞开始在全国部分地区出现。

回答1~2题。

1．我国对伪造人民币的违法行为一向严厉打击，甚至有人因伪造人民币上亿元而被判处死刑。

对于公安部门的上述做法，理解正确的是A．货币是经济的血液，保护货币流通，才能保护经济的正常发展B．发挥市场的决定作用，才能解决制造、使用假币的违法问题C．国家应适当使用法律手段，过多、过严执法伤害市场经济的活力D．公民鉴别假钞能力偏低是导致假钞屡禁不绝的根本原因2．伪造人民币违法，使用或持有(包括收藏)假人民币也违法，不能给假币任何生存空间。

这是因为①人民币是我国唯一法定货币，因此假币不具备合法地位②人民币发行权在国家，由中国人民银行执行，任何其他机构不得发行③假币的滥用会推动人民币升值，影响人民生活水平④姑息制造假币、使用假币的行为会扭曲人们的金钱观A．②③B．①④C．②④D．①③A．该家庭恩格尔系数上升，更多投资性消费B．该家庭恩格尔系数下降，食品支出变少，消费结构改善C．2013年该家庭投资模式较2012年实际收益更高D．2012年该家庭投资模式较2013年风险更小继人民币对日元、澳元、新西兰元开展直接交易后，今年人民币对英镑也绕开了美元，可以进行直接交易．央行还公布消息称，中国建设银行(伦敦)有限公司担任伦敦人民币业务清算行，这将助推伦敦成为欧洲人民币离岸结算中心。

重庆市南开中学校2025届高三7月月考数学试题

重庆市南开中学校2025届高三7月月考数学试题一、单选题1．已知集合{A x y ==，集合{}2x B y y ==，则A B =I （）A ．(](),50,-∞-+∞UB ．[)1,+∞C ．()0,∞+D ．[)[)5,01,-+∞U2．函数()()2ln 1f x x =-的单调递增区间为（）A ．()0,∞+B ．(),0-∞C ．()1,+∞D ．(),1-∞3．命题p ：“函数()313f x x ax =-在区间[]1,1-上单调递增”是命题q ：“1a ≤”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知f x 是定义在R 上的奇函数，当0x >时，()21f x x =+，则()2f '-=（）A ．4B ．4-C ．5D ．5-5．若正实数x ，y 满足40x y xy +-=，则xy 的取值范围为（） A ．(]0,4B ．[)2,+∞C ．[)4,+∞D ．[)16,+∞6．若函数()()2e xf x ax b =+在1x =时有极小值2e -，则ab =（）A ．2-B ．3-C ．e -D ．1-7．已知函数()()ln f x x m =+的图象与函数()()ln g x x =--的图象有且只有一个交点，则实数m =（） A ．1-B ．1C ．2-D ．28．已知函数()1f x +是R 上的偶函数，且()()220f x f x ++-=，当(]0,1x ∈时，()25log 22f x x ⎛⎫=-+ ⎪⎝⎭，函数f （x ）在区间[]3,3-的零点个数为（）A ．7B ．8C ．9D ．10二、多选题9．下列关于幂函数()43f x x -=的说法正确的有（） A ．函数()f x 的定义域为R B ．函数()f x 的值域为()0,∞+ C ．函数()f x 为偶函数D ．不等式()1f x <的解集为()1,1-10．已知函数()f x 在定义域 1,+∞ 内恒大于0，且满足()()ln 0f x xf x x '->，则下列不等式正确的是（）A ．()()2ln33ln 2f f >B ．()()2ln33ln 2f f <C ．()()224f f >D ．()()224f f <11．已知函数()[)()[]cos ,0,2ππ2sin 1,2π,3πax x x g x a x x ⎧-∈⎪=⎨-∈⎪⎩（R a ∈且0a >），则（） A ．当1a =时，函数()g x 有3个零点 B ．当12a =时，函数()g x 在4π5π,33⎛⎫⎪⎝⎭上单调递减 C ．当函数()g x 在P x 0,y 0 处的切线经过坐标原点时，有0001sin cos 2x x x +=或00tan 1x x ⋅=D．当12a ⎡∈⎢⎣⎦时，若函数()()f x g x t =-恰有两个零点1x 、2x ，则122πx x +>三、填空题12．若()2212f x x x -=-，则()f x 的解析式为．13．已知函数()()sin 1202520252cos 3xf x x x =+-≤≤-的值域为[],m M ，则M m +=．14．已知函数()()1e ln xf x x x x =--，若()12,0,x x ∀∈+∞且12x x ≠，有()()122212f x f x a x x ->-恒成立，则实数a 的取值范围是．四、解答题15．已知函数()2ln 1f x x x kx =+-+在点()()22f ,处的切线l 与直线320x y -=平行．(1)求k 的值及切线l 的方程；(2)求()f x 的单调区间和极值．16．已知函数()()9R 3x xaf x a +=∈为偶函数． (1)求a 的值及函数f （x ）的值域；(2)设()()()()22R g x mf x f x m m =++∈，若R x ∀∈，都有()0g x <恒成立，求实数m 的取值范围．17．2024年4月26日至10月28日，世界园艺博览会在成都主办，主题为“公园城市，美好人居”．本次展览的主会场内部规划了中华园艺展区，国家园艺展区，天府人居展区，公园城市展区等7个展区．暑假期间，甲乙两人相约游览世园会，恰逢7月6日小暑至，“花语成都”诗词活动正在火热进行，一场场沉浸式、高互动的成都行歌正在线下演绎． (1)由于园区太大，甲乙两人决定在7个展区中随机选出3个展区游玩，求他们至少选中中华园艺展区，国家园艺展区，天府人居展区，公园城市展区这4个展区中2个展区的概率． (2)甲乙两人各自独立的参加了诗词活动中的“诗词填白”游戏，参加的人只要准确填出抽中的诗中空白的诗句，则视为闯关成功．已知甲和乙闯关成功的概率分别为p 和12112p p ⎛⎫-<< ⎪⎝⎭．（i ）记甲乙两人闯关成功的人数之和为X ，求X 的分布列；（ii ）若甲乙两人闯关成功的人数之和的期望大于1，求p 的取值范围．18．已知椭圆C ：()222210+=>>x y a b a b，()11,0F -、()21,0F 分别为椭圆C 的左、右焦点，过2F 作与x 轴不重合的直线l 与椭圆交于A 、B 两点．当l 垂直于x 轴时，3AB =． (1)求椭圆C 的标准方程；(2)若点D 、E 分别为线段1F A 、1F B 的中点，点M 、N 分别为线段AE 、BD 的中点．（i ）求证：MN AB为定值；（ii ）设1F MN △面积为S ，求S 的取值范围． 19．定义可导函数p （x ）在x 处的函数()()()xq x p x p x '=⋅为p （x ）的“优秀函数”，其中()p x '为p （x ）的导函数．若x D ∀∈，都有()1q x >成立，则称p （x ）在区间D 上具有“优秀性质”且D 为（x ）的“优秀区间”．已知()()e 10xf x x =-≠．(1)求出f （x ）的“优秀区间”；(2)设f （x ）的“优秀函数”为g （x ），若方程()()ln e xx m g x +=有两个不同的实数解1x 、()212x x x <．（ⅰ）求m 的取值范围；（ⅱ）证明：121ln ex x m ++<（参考数据：e 2.718≈）．。