中考几何最值问题(含答案)
中考数学重难点突破专题十一:几何、代数最值问题试题(含答案)

专题十一 几何、代数最值问题类型1 利用对称、线段公理求最小值1.(2017·临沂)如图,在平面直角坐标系中,反比例函数y =k x (x >0)的图象与边长是6的正方形OABC 的两边AB ,BC 分别相交于M ,N 两点,△OMN 的面积为10.若动点P 在x 轴上,则PM +PN 的最小值是( C )A .6 2B .10C .226D .229解:由已知得M(6,k 6),N(k 6,6),∴BN =6-k 6,BM =6-k 6,∵△OMN 的面积为:6×6-12×6×k 6-12×6×k 6-12×(6-k 6)2=10,∴k =24,∴M(6,4),N(4,6),作M 关于x 轴的对称点M′,连接NM′交x 轴于P ,则NM′的长=PM +PN 的最小值,∵AM =AM′=4,∴BM′=10,BN =2,∴NM′=BM′2+BN 2=102+22=226.2.(2017·枣庄)如图,直线y =23x +4与x 轴、y 轴分别交于点A 和点B ,点C 、D 分别为线段AB 、OB 的中点,点P 为OA 上一动点,PC +PD 值最小时点P 的坐标为( C )A .(-3,0)B .(-6,0)C .(-32,0)D .(-52,0) 解:(方法一)作点D 关于x 轴的对称点D′,连接CD′交x 轴于点P ,此时PC +PD 值最小,如图1所示.可求点B(0,4);A(-6,0).∵点C 、D 分别为线段AB 、OB 的中点,∴点C(-3,2),点D(0,2).∵点D′和点D 关于x 轴对称,∴点D′的坐标为(0,-2).设直线CD′的解析式为y =kx +b ,∵直线CD′过点C(-3,2),D′(0,-2),可求CD′的解析式为y =-43x -2.令y =-43x -2中y =0,则0=-43x -2,解得:x =-32,∴点P(-32,0).(方法二)连接CD ,作点D 关于x 轴的对称点D′,连接CD′交x 轴于点P ,此时PC +PD 值最小,如图2所示.3.(2017·贵港)如图,在Rt △ABC 中,∠ACB =90°,将△ABC 绕顶点C 逆时针旋转得到△A′B′C ,M 是BC 的中点,P 是A′B′的中点,连接PM.若BC =2,∠BAC =30°,则线段PM 的最大值是( B )A .4B .3C .2D .1解:如图连接PC .在Rt △ABC 中,∵∠A =30°,BC =2,∴AB =4,根据旋转不变性可知,A ′B ′=AB =4,∴A ′P =PB ′,∴PC =12A ′B ′=2,∵CM =BM =1,又∵PM ≤PC +CM ,即PM ≤3,∴PM 的最大值为3(此时P 、C 、M 共线).4.(2017·菏泽)如图,矩形ABOC 的顶点A 的坐标为(-4,5),D 是OB 的中点,E 是OC 上的一点,当△ADE 的周长最小时,点E 的坐标是( B )A .(0,43)B .(0,53)C .(0,2)D .(0,103)解:作A 关于y 轴的对称点A ′,连接A ′D 交y 轴于E ,则此时,△ADE 的周长最小,∵四边形ABOC 是矩形,∴AC ∥OB ,AC =OB ,∵A 的坐标为(-4,5),∴A ′(4,5),B (-4,0),∵D 是OB 的中点,∴D (-2,0),设直线DA ′的解析式为y =kx +b ,可求直线DA ′的解析式为y =56x +53,当x =0时,y =53,∴E (0,53).5.(2017·天水)如图所示,正方形ABCD 的边长为4,E 是边BC 上的一点,且BE =1,P 是对角线AC 上的一动点,连接PB 、PE ,当点P 在AC 上运动时,△PBE 周长的最小值是__6__.解:连接DE 于AC 交于点P′,连接BP′,则此时△BP′E 的周长就是△PBE 周长的最小值,∵BE =1,BC =CD =4,∴CE =3,DE =5,∴BP′+P′E =DE =5,∴△PBE 周长的最小值是5+1=6.6.(2017·徐州)如图,将边长为6的正三角形纸片ABC 按如下顺序进行两次折叠,展平后,得折痕AD ,BE(如图1),点O 为其交点.(1)探求AO 与OD 的数量关系,并说明理由;(2)如图2,若P ,N 分别为BE ,BC 上的动点.①当PN +PD 的长度取得最小值时,求BP 的长度;②如图3,若点Q 在线段BO 上,BQ =1,则QN +NP +PD 的最小值=__10__.解:(1)AO =2OD ,理由:∵△ABC 是等边三角形,∴∠BAO =∠ABO =∠OBD =30°,∴AO =OB ,∵BD =CD ,∴AD ⊥BC ,∴∠BDO =90°,∴OB =2OD ,∴OA =2OD ;(2)如图2,作点D 关于BE 的对称点D′,过D′作D′N ⊥BC 于N 交BE 于P ,则此时PN+PD 的长度取得最小值,∵BE 垂直平分DD′,∴BD =BD′,∵∠ABC =60°,∴△BDD′是等边三角形,∴BN =12BD =32,∵∠PBN =30°,∴BN PB =32,∴PB =3;(3)如图3,作Q 关于BC 的对称点Q′,作D 关于BE 的对称点D′,连接Q′D′,则D′Q′的长度即为QN +NP +PD 的最小值.在Rt △D′BQ′中,D′Q′=32+12=10.∴QN +NP +PD 的最小值=10.类型2 利用函数性质求最值7.(2017·济宁)已知函数y =mx 2-(2m -5)x +m -2的图象与x 轴有两个公共点.(1)求m 的取值范围,并写出当m 取范围内最大整数时函数的解析式;(2)题(1)中求得的函数记为C 1,①当n ≤x ≤-1时,y 的取值范围是1≤y ≤-3n ,求n 的值;②函数C 2:y =m(x -h)2+k 的图象由函数C 1的图象平移得到,其顶点P 落在以原点为圆心,半径为5的圆内或圆上,设函数C 1的图象顶点为M ,求点P 与点M 距离最大时函数C 2的解析式.解:(1)∵函数图象与x 轴有两个交点,∴m ≠0且[-(2m -5)]2-4m(m -2)>0,解得:m <2512且m ≠0.∵m 为符合条件的最大整数,∴m =2.∴函数的解析式为y =2x 2+x. (2)抛物线的对称轴为x =-b 2a =-14.∵n ≤x ≤-1<-14,a =2>0,∴当n ≤x ≤-1时,y 随x 的增大而减小.∴当x =n 时,y =-3n.∴2n 2+n =-3n ,解得n =-2或n =0(舍去).∴n 的值为-2.(3)∵y =2x 2+x =2(x +14)2-18,∴M(-14,-18).如图所示:当点P 在OM 与⊙O 的交点处时,PM 有最大值.设直线OM 的解析式为y =kx ,将点M 的坐标代入解得:k =12.∴OM 的解析式为y =12x.设点P 的坐标为(x ,12x).由两点间的距离公式可知:OP =x 2+(12x )2=5,解得:x =2或x =-2(舍去). ∴点P 的坐标为(2,1).∴当点P 与点M 距离最大时函数C 2的解析式为y =2(x -2)2+1.8.(2017·毕节)如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P 是直线BC 下方抛物线上一动点.(1)求这个二次函数的解析式;(2)是否存在点P ,使△POC 是以OC 为底边的等腰三角形?若存在,求出P 点坐标;若不存在,请说明理由;(3)动点P 运动到什么位置时,△PBC 面积最大,求出此时P 点坐标和△PBC 的最大面积.解:(1)抛物线解析式为y =x 2-3x -4;(2)作OC 的垂直平分线DP ,交OC 于点D ,交BC 下方抛物线于点P ,如图1,∴PO =PC ,此时P 点即为满足条件的点,∵C(0,-4),∴D(0,-2),∴P 点纵坐标为-2,代入抛物线解析式可得x 2-3x -4=-2,解得x =3-172(小于0,舍去)或x =3+172,∴存在满足条件的P 点,其坐标为(3+172,-2);(3)∵点P 在抛物线上,∴可设P(t ,t 2-3t -4),过P 作PE ⊥x 轴于点E ,交直线BC 于点F ,如图2,可求直线BC 解析式为y =x -4,∴F(t ,t -4),∴PF =(t -4)-(t 2-3t -4)=-t2+4t,∴S△PBC=S△PFC+S△PFB=12(-t2+4t)×4=-2(t-2)2+8,∴当t=2时,S△PBC最大值为8,此时t2-3t-4=-6,∴当P点坐标为(2,-6)时,△PBC的最大面积为8.。
中考真题分类整理:几何最值(附答案)

一、选择题12.(2020·长沙)如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+5 BD的最小值是【】A.25B.45C.53D.10【答案】B二、填空题16.(2020·黄冈)如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8.点M为AB的中点.若∠CMD=120°,则CD的最大值是.【答案】14【解析】将△CAM沿CM翻折到△CA′M,将△DBM沿DM翻折至△DB′M,则A′M=B′M,∠AMC=∠A′MC,∠DMB=∠DMB′,∵∠CMD=120°,∴∠AMC+∠DMB=∠A′MC+∠DMB′=60°,∴∠A′MB′=180°-(∠AMC+∠DMB+∠A′MC+∠DMB′)=60°,∴△A′MB′是等边三角形,又∵AC=2,BD=8,AB=8.点M为AB的中点,∴A′B′=A′M=B′M=AM=12AB=4,CA′=AC=2,DB′=DB=8,又CD≤CA′+A′B′+DB′=2+4+8=14.三、解答题24.(2019山东威海,24,12分)如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止,设△BEF的面积为ycm2,E点的运动时间为x秒.(1)求证:CE =EF ;(2)求y 与x 之间关系的函数表达式,并写出自变量x 的取值范围; (3)求△BEF 面积的最大值. 【解题过程】(1)证明:过E 作MN ∥AB ,交AD 于M ,交BC 于N , ∵四边形ABCD 是正方形,∴AD ∥BC ,AB ⊥AD , ∴MN ⊥AD ,MN ⊥BC , ∴∠AME =∠FNE =90°=∠NFE +∠FEN , ∵AE ⊥EF ,∴∠AEF =∠AEM +∠FEN =90°, ∴∠AEM =∠NFE , ∵∠DBC =45°,∠BNE =90°, ∴BN =EN =AM .∴△AEM ≌△EFN (AAS ). ∴AE =EF .∵四边形ABCD 是正方形, ∴AD =CD ,∠ADE =∠CDE , ∵DE =DE ,∴△ADE ≌△CDE (SAS ), ∴AE =CE =EF .(2)在Rt △BCD 中,由勾股定理得:BD=,∴0≤x ≤. 由题意,得BE =2x ,∴BN =EN x.由(1)知:△AEM ≌△EFN , ∴ME =FN ,∵AB =MN =10,∴ME =FN =10x ,如图(1),当0≤x 时, ∴BF =FN -BN =10x x =10-x . ∴y =12BF ·EN =1(102-=-2x 2+(0≤x ≤2); 如图(2),当2<x ≤∴BF =BN -FN-(10x)=-10, ∴y =12BF ·EN=12-=2x 2-(2≤x≤.∴222(0);22(2x x y x x ⎧-+≤≤⎪⎪=⎨⎪-<≤⎪⎩(1) (2) (3)y =-2x 2+5x =-2(x-52)2+254,∵-2<0, ∴当x =524时,y 有最大值是;即△BEF 面积的最大值是;<x ≤ y =2x 2-=22(4x --254, 此时2>0,开口向上,对称轴为直线x =4, ∵对称轴右侧,y 随x 的增大而增大, ∴当x =y 最大值=50.∴当x =BEF 面积的最大值是50.【知识点】四边形综合运用,二次函数的解析式,二次函数的最值问题,三角形全等的判定. 25.(2019山东省威海市,题号25,分值12) (1)方法选择如图①,四边形ABCD 是OO 的内接四边形,连接AC ,BD .AB =BC =AC . 求证:BD =AD +CD .小颖认为可用截长法证明:在DB 上截取DM =AD ,连接AM ..…… 小军认为可用补短法证明:延长CD 至点N ,使得DN =AD …… 请你选择一种方法证明.(2)类比探究【探究1】如图②,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD .BC 是⊙O 的直径,AB =AC .试用等式表示线段AD ,BD ,CD 之间的数量关系,并证明你的结论. 【探究2】如图③,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD .若BC 是⊙O 的直径,∠ABC =30°,则线段AD ,BD ,CD 之间的等量关系式是. (3)拓展猜想如图④,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD .若BC 是O 0的直径,BC :AC :AB =a :b :c ,则线段AD ,BD ,CD 之间的等量关系式是.【思路分析】(1)选小颖的截长法,如图①,在DB 上截取DM =AD ,连接AM ,由旋转全等得BM =CD ,∴BD =MD +BM =AD +CD(2)【探究1】数量关系为:BDAD +CD如图②,在DB 上截取AD =AN ,连接AN ,可得△AND 为等腰直角三角形,∴NDAD ,由旋转全等得BN =CD ,∴BD =ND +BNAD +CD 【探究2】数量关系为:BD =2ADCD如图③,在DB 上截取2AD =PD ,连接AP ,可得△APD 为30°的直角三角形, 由旋转相似得BP,∴BD =PD +BP =2AD(3)拓展猜想数量关系为:BD =a bAD +cb CD如图④,过A 作AQ ⊥AD 交BD 于Q ,连接AQ ,由旋转相似得=BQ AB c CD AC b =,=DQ BC aAD AC b=, 图①图②B图③BC 图④BC∴BQ =c b CD ,BQ =a b AD ,∴BD =PD +BP =a bAD +c b CD【解题过程】(1)选小颖的截长法,如图①,在DB 上截取DM =AD ,连接AM ,可得△AMD 为等边三角形,可证△BAM ≌△CAD (SAS )得BM =CD ,∴BD =MD +BM =AD +CD(2)【探究1】数量关系为:BDAD +CD如图②,在DB 上截取AD =AN ,连接AN ,可得△AND 为等腰直角三角形,∴NDAD ,∠BAN =∠CAD ,可证△BAN ≌△CAD (SAS )得BN =CD ,∴BD =ND +BNAD +CD【探究2】数量关系为:BD =2ADCD如图③,在DB 上截取2AD =PD ,连接AP ,可得△APD 为30°的直角三角形,∴=tan 30AP ABAD AC=︒,∠BAP =∠CAD ,可证△BAP ∽△CAD 得BPCD ,∴BD =PD +BP =2ADCD答案图①答案图②B(3)拓展猜想数量关系为:BD =a bAD +c b CD如图④,过A 作AQ ⊥AD 交BD 于Q ,连接AQ ,可得∠BAQ =∠CAD ,∠ABQ =∠ACD ,∠ADQ =∠ACB ,∠BAC =∠QAD ∴△BAP ∽△CAD ,△ADQ ∽△ACB ∴=BQ AB c CD AC b =,=DQ BC aAD AC b=, ∴BQ =c b CD ,BQ =a b AD ,∴BD =PD +BP =a bAD +cb CD26.(2020·益阳)如图,在半面直角坐标系xOy 中,矩形ABCD 的边AB=4,BC=6.若不改变矩形ABCD 的形状和大小,当形顶点A 在x 轴的正半轴上左右移动时,矩形的另一个顶点D 始终在y 轴的正半上随之上下移动. (1)当∠OAD=30°时,求点C 的坐标;(2)设AD 的中点为M ,连接OM 、MC ,当四边形 OMCD 的面积为221时,求OA 的长; (3)当点A 移动到某一位置时,点C 到点O 的距离有最大值,请直接写出最大值,并求此时cos ∠OAD 的值.第26题图 第26题备用图【解题过程】(1)如图1,过点C 作CE ⊥y 轴,垂足为E.答案图③B答案图④BC第26题答图1∵矩形ABCD 中,CD ⊥AD , ∴∠CDE+∠ADO=90°, 又∵∠OAD+∠ADO=90°, ∴∠CDE=∠OAD=30°. 在Rt △CED 中,CE=21CD=2, ∴DE=32242222=-=-CE CD ; 在Rt △OAD 中,∠OAD=30°, ∴OD=21AD=3. ∴点C 的坐标为(2,323+). (2)∵M 为AD 的中点, ∴DM=3,6=DCM S △. 又∵221=OMCD S 四边形, ∴29=ODM S △, ∴9=OAD S △. 设OA=x ,OD=y ,则⎪⎩⎪⎨⎧==+9213622xy y x , ∴xy y x 222=+, 即0)(2=-y x , ∴x=y.将x=y 代入3622=+y x 得182=x , 解得23=x (23-不合题意,舍去), ∴OA 的长为23.(3)OC 的最大值为8.理由如下: 如图2,第26题答图2 ∵M 为AD 的中点,∴OM=3,522=+=DM CD CM .∴OC ≤OM+CM=8,当O 、M 、C 三点在同一直线时,OC 有最大值8.连接OC ,则此时OC 与AD 的交点为M ,过点O 作ON ⊥AD ,垂足为N. ∵∠CDM=∠ONM=90°,∠CMD=∠OMN , ∴△CMD ∽△OMN , ∴OM CMMN DM ON CD ==, 即3534==MN ON , 解得59=MN ,512=ON , ∴56=-=MN AM AN . 在Rt △OAN 中, ∵55622=+=AN ON OA , ∴55cos ==∠OA AN OAD . 26.(2020·衡阳)如图,在等边△ABC 中,AB =6cm ,动点P 从点A 出发以cm/s 的速度沿AB 匀速运动.动点Q 同时从点C 出发以同样的速度沿BC 延长线方向匀速运动.当点P 到达点B 时,点P 、Q 同时停止运动.设运动时间为t(s).过点P作PE⊥AC于E,连接PQ交AC边于D.以CQ、CE为边作平行四边形CQFE.(1)当t为何值时,△BPQ为直角三角形;(2)是否存在某一时刻t,使点F在∠ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;(3)求DE的长;(4)取线段BC的中点M,连接PM,将△BPM沿直线PM翻折,得△B′PM,连接AB′,当t为何值时,AB′的值最小?并求出最小值.解:(1)∵△ABC为等边三角形,∴∠B=60°,∵BP⊥PQ,∴2BP=BQ即2(6-t)=6+t,解得t=2.∴当t为2时,△BPQ为直角三角形;(2)存在.作射线BF,∵PE⊥AC,∴AE=0.5t.∵四边形CQFE是平行四边形,∴FQ=EC=6-0.5t,∵BF 平分∠ABC,∴∠FBQ+∠BQF=90°.∵BQ=2FQ,BQ=6+t,∴6+t=2(6-0.5t),解得t=3.(3)过点P作PG∥CQ交AC于点G,则△APG是等边三角形.∵BP⊥PQ,∴EG=12AG.∵PG∥CQ,∴∠PGD=∠QCD,∵∠PDG=∠QDC,PG=PA=CG=t,∴△PGD≌△QCD.∴GD=12GC.∴DE=12AC=3.(4)连接AM,∵△ABC为等边三角形,点M是BC的中点,∴BM=3.由勾股定理,得AM=.由折叠,得BM′=3.当A 、B′、M在同一直线上时,AB′的值最小,此时AB′=3.过点B′作B′H⊥AP于点H,则cos30°=AHAB',即2t,解得t=9-∴t为9-AB′的值最小,最小值为-3.MMM QB C1.(2020·重庆A 卷)如图,在平面在角坐标系中,抛物线y =x 2-2x -3与x 轴交与点A ,B (点A 在点B 的左侧)交y 轴于点C ,点D 为抛物线的顶点,对称轴与x 轴交于点E .(1)连结BD ,点M 是线段BD 上一动点(点M 不与端点B ,D 重合),过点M 作MN ⊥BD 交抛物线于点N (点N 在对称轴的右侧),过点N 作NH ⊥x 轴,垂足为H ,交BD 于点F ,点P 是线段OC 上一动点,当MN 取得最大值时,求HF +FP +13PC 的最小值;(2)在(1)中,当MN 取得最大值,HF +FP +13PC 取得小值时,把点P 向上平移个2单位得到点Q ,连结AQ ,把△AOQ 绕点O 顺时针旋转一定的角度α(0°<α<360°),得到△A OQ '',其中边A Q ''交坐标轴于点G ,在旋转过程中,是否存在一点G ,使得OG Q Q ''∠=∠?若存在,请直接写出所有满足条件的点Q '的坐标;若不存在,请说明理由.解:(1)由题意得A (-1,0),B (3,0),C (0,-3),D (1,-4),直线BD :y =2x -6. 如答图1,连接DN 、BN ,则S △BDN =12BD •MN ,而BD 为定值,故当MN 最大时,S △BDN 取最大值.此时由S △BDN =S △DFN +S △BFN =12EH •FN +12BH •FN =12BE •FN =FN ,从而S △BDN 取最大值时,即为FN 有最大值.令N (m ,m 2-2m -3),则F (m ,2m -6),从而FN =(2m -6)-(m 2-2m -3)=-m 2+4m -3=-(m -2)2+1,此时,当且仅当m =2,FN 有最大值为1,于是N (2,-3),F (2,-2),H (2,0). 在直角三角形中,设最小的直角边为a ,斜边为3a ,较长直角边为3,即可求出a =324,于是在x 轴上取点H B'M FD E QA BP yxOEDCBA第26题备用图第26题图K (-324,0),连接KC ,易求直线KC :y =-22x -3.如答图1,过点F 作FR ⊥CK 于点R ,交OC 于点P ,作FT ⊥OC ,交CK 于点T ,则∠OCK =∠TFR ,于是,由△PCR ∽△ACO ∽△TFR ,得133PR OK a PC KC a ===,从而PR =13PC ,因此由FH 为定值,再由定点F 到直线的垂直线最短,可知MN 取得最大值时,HF +FP+13PC 最小值=HF +FR .在y =-22x -3中,当y =-2,x =-24,于是FT =2+24.在Rt △FTR 中,由223FR FT =,得FR =223FT =223(2+24)=14233+,故HF +FP +13PC 最小值=2+14233+=7423+.(2)4525(,)55--,2545(,)55-,4525(,)55,2545(,)55-. 第26题答图4第26题答图5第26题答图1 T KR QP HF NMyxO ED CBA第26题答图2第26题答图32.(2020·重庆B 卷)在平面直角坐标系中,抛物线2y =++与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,顶点为D ,对称轴与x 轴交于点Q .(1)如图1,连接AC ,BC .若点P 为直线BC 上方抛物线上一动点,过点P 作PE ∥y 轴交BC 于点E ,作PF⊥BC 于点F ,过点B 作BG ∥AC 交y 轴于点G .点H ,K 分别在对称轴和y 轴上运动,连接PH ,HK .当△PEF 的周长最大时,求PH +HKKG 的最小值及点H 的坐标. (2)如图2,将抛物线沿射线AC 方向平移,当抛物线经过原点O 时停止平移,此时抛物线顶点记作D ’,N 为直线DQ 上一点,连接点D ’,C ,N ,△D ’CN 能否构成等腰三角形?若能,直接写出满足条件的点N 的坐标;若不能,请说明理由.解:(1)∵2y x =+与x 轴交于A ,B 两点, ∴当y=0时,即20=+,∴122,4x x =-=,即A (-2,0),B (4,0), 设直线BC 的解析式为y =kx +b ,∵C (0,,B (4,0),∴40b k b ⎧=⎪⎨+=⎪⎩,∴b k ⎧=⎪⎨=⎪⎩,∴直线BC的解析式为y =+设点2(,4),P m m +<< ∵PE ∥y 轴且点E 在直线BC上,∴(,E m +∠PEF =∠OCE ,∴2(04),PE m =<< ∵PF ⊥BC ,∴∠PFE =∠COB =90°,∴△PEF ∽△BCO ,设△PEF 的周长为1l ,△BCO 的周长为2l , 则12l PEl BC=,∵B (4,0),C (0,,∴BC=24l =+∴21)(04),l m =+<< 备用图图1图2∴当m=2时,1l此时点P 的坐标为(2,, ∵A (-2,0),C (0,,∴∠ACO =30°,∠CAO =60°, ∵BG ∥AC ,∴.∠BGD =30°,∠OBG =60°,∴G (0,-, 直线BG解析式为y -PM解析式为y =,过点G 作GN ⊥BG ,过点P 作PM ⊥GN 于点M ,如图1,此时,点H 为PM 与对称轴的交点,K 为PM 与y 轴的交点,点K 与点O 重合, 则KM=OMKG ,PH +HKKG 的最小值为线段PM 的长.(此问题是胡不归问题).解法一:(作一线三直角利用相似求解)如图2,过点P 作PQ ∥x 轴交对称轴于点T , 过点M 作MQ ⊥y 轴交PT 于点Q ,过点G 作GJ ⊥MQ 交MQ 于点J.设点Q (n,,∴J (n,-,∴PQ =2-n ,2-n ), ∵GJ =-n ,∴MJ=,∴MQ +MJ =CG=(--=2-n )+()=n =-3,∴Q (-3,,∴PQ =5, ∴PM =2PQ =10,∴PH +HKKG 的最小值为10, ∵∠OGM =60°,∠PHT=30°,∠HPT=60°,∴PT =1,∴HTH (1.图1N解法二:由上面的解法可知MG ⊥BG ,直线MG的解析式为:y =- 如图3,过点P 作PR ⊥x 轴交MG 于点R ,∴R (2,, 由第一种解法可知∠PRG =60°,∴PMP R()=10, ∴PH +HKKG 的最小值为10,同理可求H (1.(2)这样的N 点存在.当△'CD N 为等腰三角形时,这样的N有:1N,2N,3N,4N,5N .【提示】由(1)可知∠ACO=30°,∠OAC=60°,又∵221)y x =++=-D (1, ∵抛物线按射线AC的方向平移,设平移后顶点'(D a +,平移后的抛物线解析式为21)y x a =--++该抛物线经过原点,则201)a =--+图2NN∴2280a a --=,∴a =4或a =-2(舍去),即D .设点N (1,b )'CD =CN ='ND 如图4,当△'CD N 为等腰三角形时,分三种情况: ①当'CD CN ==,可得1N,2N ; ②当''CD D N ==3N,4N ,③当'CN D N ==可得5N , ∴当△'CD N 为等腰三角形时,这样的N有:1N,2N,3N,4N,5N .3.(2020·天津)已知抛物线y=x 2-bx+c(b,c 为常数,b>0)经过点A (-1,0),点M(m,0)是x 轴正半轴上的动点,(1)当b=2时,求抛物线的顶点坐标;(2)点D(b,y D )在抛物线上,当AM=AD,m=5时,求b 的值; (3)点Q(1b ,2+y Q )2QM +时,求b 的值. 解:(1)∵抛物线y=x 2-bx+c 经过点A (-1,0), ∴1+b+c=0,∴c=-1-b 当b=2时,c=-3,∴抛物线的解析式为y=x 2-2x-3, ∴顶点坐标为(1,-4) (2)由(1)知,c=-1-b , ∵点D(b,y D )在抛物线上, ∴y D =-b-1,∵b>0,∴b 02b >>,-b-1<0,∴D(b,-b-1)在第四象限,且在抛物线对称轴2bx =的右侧.如图,过点D 作DE ⊥x 轴于E ,则E (b ,0),∴AE=b+1=DE,所以1)b +, ∵m=5,∴AM=5-(-1)=6, ∴1)b +∴b=(3)∵点Q(1b ,2+y Q )在抛物线上, ∴yQ=2113)()12224b b b b b +-+--=--(, ∴点Q (1b ,2+3-24b -)在第四象限,且在直线x=b 的右侧,2QM +的最小值为4,A(-1,0) ∴取点N(0,1),如图,过点Q 作QH ⊥x 轴于H ,作QG ⊥AN 于G,QG 与x 轴交于点M ,则H (1b ,2+0),∠GAM=45°,∴GM=2AM ,∵M (m,0),∴AM=m+1,MH=1b 2m +-,QH=324b +, ∵MH=QH,∴1b 2m +-=324b +, ∴m=1-24b ,∴AM=13-12424b b +=+,3)24b =+2QM +33)2())24244b b +++=,∴b=4. 4.(2020·自贡)如图,已知直线AB 与抛物线:y =ax 2+2x +c 相交于点A (-1,0)和点B (2,3)两点. (1)求抛物线C 函数解析式;(2)若点M 是位于直线AB 上方抛物线上的一动点,以MA 、MB 为相邻的两边作平行四边形MANB ,当平行四边形MANB 的面积最大时,求此时平行四边形MANB 的面积S 及点M 的坐标; (3)在抛物线C 的对称轴上是否存在顶点F ,使抛物线C 上任意一点P 到F 的距离等于到直线y =174的距离,若存在,求出定点F 的坐标;若不存在,请说明理由.解:(1)将A (-1,0)和B (2,3)代入抛物线解析式得{a −2+c =04a +4+c =3解得,{a =−1c =3∴抛物线解析式为y =-x 2+2x +3.(2)过M 作MH ∥y 轴,交AB 于H ,设直线AB 为y =kx +b ,将A ,B 坐标代入得,{−k +b =02k +b =3解得,{k =1b =1.∴直线AB 的解析式为y =x +1.设M 为(m ,-m 2+2m +3),则H (m ,m +1) ∴MH =y M -Y H =(-m 2+2m +3)-( m +1)=-m 2+m +2. ∴S △ABM =S △AMH +S △BMH =12·MH ·(x B -x A ) =12·(-m 2+m +2)·(2+1)=-32(m 2-m )+3 =-32(m -12)2+278.∵四边形MANB 是以MA 、MB 为相邻的两边的平行四边形, ∴△ABM ≌△BAN .∴S 四边形MANB =2 S △ABM =-3(m -12)2+274,∵a =-3<0且开口向下,∴当m =12时,S 四边形MANB 的最大值为274. 此时,M 坐标为(12,154). (3)存在,理由如下:过P 作直线y =174的垂线,垂足为T ,∵抛物线为y =-x 2+2x +3=-(x -1)2+4.∴抛物线的对称轴为直线x =1,顶点坐标为(1,4). 当P 为顶点,即P (1.4)时, 设F 点坐标为(1,t ), 此时PF =4-t ,PT =174-4=14.∵P 到F 的距离等于到直线y =174的距离,∴4-t =14,即t =154.∴F 为(1,154)设P 点为(a ,-a 2+2a +3),由勾股定理,PF 2=(a -1)2+(-a 2+2a +3-154)2=a 4-4a 3+132a 2-5a +2516.又∵PT 2=[174-(-a 2+2a +3)]2= a 4-4a 3+132a 2-5a +2516. ∴PF 2=PT 2,即PF =PT .∴当F 为(1,154)时,抛物线C 上任意一点P 到F 的距离等于到直线y =174的距离 .27.(2020·淮安)如图①,在△ABC 中,AB=AC=3,∠BAC=100°,D 是BC 的中点.小明对图①进行了如下探究:在线段AD 上任取一点P ,连接PB.将线段PB 绕点P 按逆时针方向旋转80°,点B 的对应点是点E ,连接BE ,得到△BPE.小明发现,随着点P 在线段AD 上位置的变化,点E 的位置也在变化,点E 可能在直线AD 的左侧,也可能在直线AD 上,还可能在直线AD 的右侧. 请你帮助小明继续探究,并解答下列问题: (1)当点E 在直线AD 上时,如图②所示. ①∠BEP=°;②连接CE ,直线CE 与直线AB 的位置关系是.(2)请在图③中画出△BPE ,使点E 在直线AD 的右侧,连接CE.试判断直线CE 与直线AB 的位置关系,并说明理由.(3)当点P 在线段AD 上运动时,求AE 的最小值.【解题过程】(1)①由题意得,PE=PB ,∠BPE=80°,∴∠BEP=︒=︒-︒50280180; ②如图所示,∵AB=AC ,D 是BC 的中点,∠BAC=100°, ∴∠ABC=︒=︒-︒402100180,∵∠BEP=50°,∴∠BCE=∠CBE=40°, ∴∠ABC=∠BCE , ∴CE ∥AB.答案:①50°;②平行(2)在DA 延长线上取点F ,使∠BFA=∠CFA=40°,总有△BPE ∽△BFC. 又∵△BPF ∽△BEC , ∴∠BCE=∠BFP=40°, ∴∠BCE=∠ABC=40°, ∴CE ∥AB.(3)当点P 在线段AD 上运动时,由题意得PB=PE=PC ,∴点B 、E 、C 在以P 为圆心、PB 为半径的圆上, 如图所示:∴AE 的最小值为AC=3.5.(2020·凉山州)如图,抛物线y = ax 2+bx +c 的图象过点A (-1,0)、B (3,0)、C (0,3). (1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在一点P ,使得△P AC 的周长最小,若存在,请求出点 P 的坐标及△P AC 的周长;若不存在,请说明理由;(3)在(2)的条件下,在x 轴上方的抛物线上是否存在点M (不与C 点重合),使得 S △P AM =S △P AC ,若存在,请求出点M 的坐标;若不存在,请说明理由.解:(1)由题知⎪⎩⎪⎨⎧==++=+-30390c c b a c b a ,解得⎪⎩⎪⎨⎧==-=321c b a ,∴抛物线的解析式为y = -x 2+2x +3;(2)存在.连接BC 交抛物线对称轴于点P ,此时△P AC 的周长最小.设BC :y =kx +3,则3k +3=0,解得k =-1,∴BC :y =-x +3.由抛物线的轴对称性可得其对称轴为直线x =1,当x =1时,y =-x +3=2,∴P (1,2).在Rt △OAC 中,AC =2231+=10;在Rt △OBC 中,BC =2233+=32.∵点P 在线段AB 的垂直平分线上,∴P A =PB ,∴△P AC 的周长=AC +PC +P A = AC +PC +PB =AC +BC =10+32.综上,存在符合条件的点P ,其坐标为(1,2),此时△P AC 的周长为10+32;(3)存在.由题知AB =4,∴S △P AC =S △ABC -S △P AB =21×4×3-21×4×2=2.设:AP :y =mx +n ,则⎩⎨⎧=+=+-20n m n m ,解得⎩⎨⎧==11n m ,∴AP :y =x +1. ①过点C 作AP 的平行线交x 轴上方的抛物线于M ,易得CM :y =x +3,由⎩⎨⎧++-=+=3232x x y x y 解得⎩⎨⎧==3011y x ,⎩⎨⎧==4122y x ,∴M (1,4);②设抛物线对称轴交x 轴于点E (1,0),则S △P AC =21×2×2=2=S △P AC .过点E 作AP 的平行线交x轴上方的抛物线于M ,设EM :y =x +t ,则1+t =0,∴t =-1,∴EM :y =x -1. 由⎩⎨⎧++-=-=3212x x y x y 解得⎪⎪⎩⎪⎪⎨⎧--=-=2171217111y x (舍),⎪⎪⎩⎪⎪⎨⎧+-=+=2171217122y x ,∴M (2171+,2171+-). 综上,存在符合条件的点M ,其坐标为(1,4)或(2171+,2171+-).27.(2020·苏州,26,10)已知矩形ABCD 中,AB =5cm ,点P 为对角线AC 上的一点,且AP =.如图①,动点M 从点A 出发,在矩形边上沿着A →B →C 的方向匀速运动(不包含点C ).设动点M 的运动时间为t (s ),△APM 的面积为S (cm 2),S 与t 的函数关系如图②所示. (1)直接写出动点M 的运动速度为 cm/s ,BC 的长度为 cm ;(2)如图③,动点M 重新从点A 出发,在矩形边上按原来的速度和方向匀速运动,同时,另一个动点N 从点D 出发,在矩形边上沿着D →C →B 的方向匀速运动,设动点N 的运动速度为v (cm/s ).已知两动点M ,N 经过时间x (s )在线段BC 上相遇(不包含点C ),动点M ,N 相遇后立即同时停止运动,记此时△APM 与△DPN 的面积分别为S 1(cm 2),S 2(cm 2) ①求动点N 运动速度v (cm/s )的取值范围;②试探究S 1•S 2是否存在最大值,若存在,求出S 1•S 2的最大值并确定运动时间x 的值;若不存在,请说明理由.图① 图② 图③(第27题)【解题过程】解:(1)∵t =2.5s 时,函数图象发生改变,∴t =2.5s 时,M 运动到点B 处,∴动点M 的运动速度为52.5=2cm/s ,∵t =7.5s 时,S =0,∴t =7.5s 时,M 运动到点C 处,∴BC =(7.5﹣2.5)×2=10(cm ), 故答案为2,10;(2)①∵两动点M ,N 在线段BC 上相遇(不包含点C ),∴当在点C 相遇时,v 527.53==(cm/s ),当在点B 相遇时,v 5102.5+==6(cm/s ),∴动点N 运动速度v (cm/s )的取值范围为23cm/s <v ≤6cm/s ; ②过P 作EF ⊥AB 于F ,交CD 于E ,如图所示:则EF ∥BC ,EF =BC =10,∴AF APAB AC=,∵AC==∴5AF =解得AF =2,∴DE =AF =2,CE =BF =3,PF ==4, ∴EP =EF ﹣PF =6,∴S 1=S △APM =S △APF +S 梯形PFBM ﹣S △ABM 12=⨯4×212+(4+2x ﹣5)×312-⨯5×(2x ﹣5)=﹣2x +15,S 2=S △DPM =S △DEP +S 梯形EPMC ﹣S △DCM 12=⨯2×612+(6+15﹣2x )×312-⨯5×(15﹣2x )=2x ,∴S 1•S 2=(﹣2x +15)×2x =﹣4x 2+30x =﹣4(x 154-)22254+,∵2.5154<<7.5,在BC 边上可取,∴当x 154=时,S 1•S 2的最大值为2254.第27题答图6.(2020·巴中)如图,抛物线y =ax 2+bx -5(a ≠0)经过x 轴上的点A(1,0)和点B 及y 轴上的点C,经过B,C 两点的直线为y =x+n.①求抛物线的解析式;②点P 从A 出发,在线段AB 上以每秒1个单位的速度向B 运动,同时点E 从B 出发,在线段BC 上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t描,求t为何值时,△PBE的面积最大,并求出最大值.③过点A作AM⊥BC与点M,过抛物线上一动点N(不与点B,C重合)作直线AM的平行线交直线BC于点Q,若点A,M,N,Q为顶点的四边形是平行四边形.求点N的横坐标.第26题图分析:①由点A和直线y=x+n可得方程组,解出系数,求得二次函数的解析式;②根据题意表示出三角形面积,利用二次函数最值进行求解;③分析得到AM平行且等于NQ,设出坐标,利用坐标关系列方程进行求解,并检验.解:①因为点B,C在y=x+n上,所以B(-n,0),C(0,n),因为点A(1,0)在抛物线上,所以25050 5a ban bnn,解得,a=-1,b=6,所以抛物线的解析式为:y=-x2+6x-5.②由题意得:PB=4-t,,BE=2t,由①可知:∠OBC=45°,点P到BC上的高h=BPsin45(4-t),所以S△PBE=12BE h =222222t,当t=2时,S取得最大值为③因为l BC:y=x-5,所以B(5,0), 因为A(1,0),所以AB=4,在Rt△ABM中,∠ABM=45°,AMAB=M(3,-3),过点N作x轴的垂线交直线BC于点P交x轴于点H, 设N(m,-m2+6m-5),则H(m,0),P(m,m-5),易证△PQN为等腰直角三角形,即NQ=PQ=所以PN=4.当NH+HP=4时,即-m2+6m-5-(m-5)=4, 解之得,m1=1,m2=4.当m1=1时,点N与点A重合,故舍去;当NH+HP=4时,即m-5-(-m2+6m-5)=4,解得,m1541,m2541,因为m>5,所以m 541;当NH-HP=4,即-(-m2+6m-5)-[-(m-5)]=4,解得,m1541,m2541,因为m<0,所以m 541.综上所述,要使点A,M,N,Q 为顶点的四边形是平行四边形,点N 的横坐标为:4541或541.第26题答图7.(2020·淄博)如图,顶点为M 的抛物线y =ax 2+bx +3与x 轴交于A (3,0),B (-1,0)两点,与y 轴交于点C .(1)求这条抛物线对应的函数表达式;(2)问在y 轴上是否存在点P ,使得△P AM 为直角三角形?若存在,求出点P 的坐标;若不存在,说明理由. (3)若在第一象限的抛物线下方有一动点D ,满足DA =OA ,过D 作DG ⊥x 轴于点G ,设△ADG 的内心为I ,试求CI 的最小值.解:(1)将A 、B 两点坐标代入抛物线表达式,得933030a b a b ++=⎧⎨-+=⎩,解得12a b =-⎧⎨=⎩.∴y =-x 2+2x +3.(2)假设存在点P ,使△P AM 是直角三角形.当点M 为直角顶点,过M 作CD ⊥y 轴,过A 作AD ⊥x 轴,交CD 于D ,CD 交y 轴于C ,∵∠AMP =90°, ∴∠CMP +∠AMD =90,∴∠CMP =∠MAD ,又∵∠DM =∠PCM ,∴△CPM ∽△DMA ,∴CM AD =PCMD, ∴14=2PC ,∴PC =12,∴P 1(0,72); 当点A 为直角顶点,过A 作CD ⊥x 轴,过M 作MD ⊥y 轴交AD 于D ,过P 作PC ⊥y 轴交CD 于C ,同上△CP A∽△DAM ,∴PC AD =AC MD ,∴34=2AC ,∴AC =32,∴P 2(0,-32); 当点P 为直角顶点,过M 作CM ⊥y 轴于C ,∴△CPM ∽△OAP ,∴PC AO =CM PO ,∴3PC =14-PC,∴PC =1或3,∴P 3(0,3),P 4(0,1).图综上所述,使△P AM 是直角三角形的点P 的是P 1(0,72),P 2(0,-32),P 3(0,3),P 4(0,1).(3)(方法1)由(1)得DA =OA =3,设D (x ,y ),△ADG 的内切圆半径为r ,则△ADG 的内心I 为(x +r ,r ), ∴DG =y ,AG =3-x由两点距离公式可得()2222339DA x y =-+==①由等面积法得r =()33+22y x DG AG DA +---==2y x-②∴()()2223CI x r r =++-③由①②③得(2229123124CI x y -⎡⎤⎡⎤⎛⎫=-+-+ ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦,2CI 在3335=512105x y =--,最小,此时CI 也最小,()()min 912253=10-242CI -=(方法2)简解:如图,由内心易知:∠DIA =135°,∠DAI =∠OAI ,△DAI ≌△OAI (SAS ),∴∠DIA =∠OIA =135°,则I 在圆周角∠OIA =135°⊙T 的圆周上运动,且半径R =322,圆心T 为(32,32),∴CI =3102在△CIA 中,CI ≥CT -IT =()310-22,当C 、I 、T 三点一线时,()min 3=10-22CI .8.(2020·枣庄)已知抛物线y =ax 2+32x+4的对称轴是直线x =3,与x 轴相交于A 、B 两点(点B 在点A 的右侧),与y 轴交于点C.(1)求抛物线的解析式和A 、B 两点的坐标;(2)如图1,若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合),是否存在点P ,使四边形PBOC 的面积最大?若存在,求点P 的坐标及四边形PBOC 面积的最大值;若不存在,请说明理由.(2)答图1Iy 12(3)如图2,若点M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求点M 的坐标.解:(1)抛物线y=ax2+32x+4的对称轴为:x=332224ba a a-=-=-=3,∴a=14-,∴抛物线的解析式为:y=14-x2+32x+4,令y=0,得14-x2+32x+4=0,解之,得,x1=-2,x2=8,∵点B在点A的右侧,∴A(-2,0),B(8,0);(2)连接BC,在抛物线y=14-x2+32x+4中,令x=0,得y=4,∴C(0,4),∴OC=4,OB=8,∴S△OBC=16,∵B(8,0),C(0,4),设l BC:y=kx+b,得0=8k+b,4=b,∴k=12-,b=4,l BC:y=12-x+4,∴过点P作PD∥y轴交BC于点D,过点C作CE垂直PD于点E,过点B作BF⊥PD于点F,则S△PBC=S△PCD+S△PBD=12PD×CE+12PD×BF=12PD×(CE+BF)=12PD×(x B-x C)=12PD×8=4PD,∵点P在抛物线上,设点P(x,14-x2+32x+4),∵PD∥y轴,点D在直线BC上,∴D(x,12-x+4),∵点P在B,C间的抛物线上运动,∴PD=y P-y D=14-x2+32x+4-(12-x+4)=14-x2+2x,S△PBC=4PD=4(14-x2+2x)=-x2+8x=-(x-4)2+16,∴当x=4时,S△PBC取最大值16,∴此时S四边形OBPC=S△OBC+S△PBC=32;第25题答图(3)∵MN∥y轴,∴设M,N的横坐标为m,∵点M在抛物线上,设点M(m,n),其中n=14-m2+32m+4,点N在直线BC上,∴N(m,12-m+4),∵点M是抛物线上任意一点,∴点M和点N的上下位置关系不确定,∴MN=|14-m2+32m+4-(12-m+4)|=|14-x2+2x|,∵MN=3,∴|14-x2+2x|=3,即14-x2+2x=3或14-x2+2x=-3,解这两个方程,得m1=2,m2=6, m3=4+4=4-∴n1=6, n2=4, n3-1, n4-1,∴M1(2,6), M2(6,4), M3(4+-1), M 4(4-1).9.(2020· 聊城)如图,在平面直角坐标系中,抛物线y =ax 2+bx+c 与x 轴交于点A(-2,0),点B(4,0),与y 轴交于点C(0,8),连接BC,又已知位于y 轴右侧且垂直于x 轴的动直线l,沿x 轴正方向从O 运动到B(不含O 点和B 点),且分别交抛物线,线段BC 以及x 轴于点P,D,E. (1)求抛物线的表达式;(2)连接AC,AP,当直线l 运动时,求使得△PEA 和△AOC 相似的点P 的坐标; (3)作PF ⊥BC,垂足为F,当直线l 运动时,求Rt △PFD 面积的最大值.第25题图解:(1)由已知,将C(0,8)代入y =ax 2+bx+c,∴c =8,将点A(-2,0)和B(4,0)代人y =ax 2+bx+8,得428016480a b a b -+=⎧⎨++=⎩,解得12a b =-⎧⎨=⎩,∴抛物线的表达式为y =-x 2+2x+8; (2)∵A(-2,0),C(0,8),∴OA =2,OC =8,∵l ⊥x 轴,∠PEA =∠AOC =90°,∵∠PAE ≠∠CAO,只有当∠PAE =∠ACO 时,△PEA ∽△AOC.此时AE PECO AO=,∴AE =4PE.设点P 的纵坐标为k,则PE =k,AE =4k,∴OE =4k -2,P 点的坐标为(4k -2,k),将P(4k -2,k)代入y =-x 2+2x+8,得-(4k -2)2+2(4k -2)+8=k,解得k 1=0(舍去),k 2=2316,当k =2316时,4k -2=154,∴P 点的坐标为(154,2316). (3)在Rt △PFD 中,∠PFD =∠COB =90°,∵l ∥y 轴,∴∠PDF =∠OCB,∴Rt △PFD ∽Rt △BOC,∴2PFD=S PD S BC ⎛⎫ ⎪⎝⎭△△BOC,∴S △PFD =2PD S BC ⎛⎫⋅ ⎪⎝⎭△BOC ,由B(4,0)知OB =4,又∵OC =8,∴BC 又S △BOC =12OB OC ⋅=16,∴S △PFD =215PD ,∴当PD 最大时,S △PFD 最大.由B(4,0),C(0,8)可解得BC 所在直线的表达式为y =-2x+8,设P(m,-m 2+2m+8),则D(m,-2m+8),∴PD =-(m -2)2+4,当m =2时,PD 取得最大值4,∴当PD =4时,S △PFD =165,为最大值.10.(2020·济宁)如图1,在矩形ABCD 中,AB =8,AD =10,E 是CD 边上一点,连接AE ,将矩形ABCD 沿AE 折叠,顶点D 恰好落在BC 边上点F 处,延长AE 交BC 的延长线于点G . (1)求线段CE 的长;(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN=y.①写出y关于x的函数解析式,并求出y的最小值;②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.解:(1)由折叠可得AF=AD=10,EF=ED,矩形ABCD中,∠B=90°,∴AB2+BF2=AF2,∴6, BF===∴CF=BC-BF=AD-BF=10-6=4.设CE=x,则EF=DE=CD-CE=AB-CE=8-x,∵EF2=CE2+CF2.∴(8-x)2=x2+42.∴x=3,∴CE=3.(2)①∵矩形ABCD中,AD∥BC,∴∠DAG=∠AGF,∵∠DAG=∠F AG, ∠DAG=∠AGF,∴∠F AG=∠AGF,∴AF=FG=10,∴BG=BF+FG=6+10=16.∵矩形ABCD中∠B=90°,∴AB2+BG2=AG2,∴AG==∵AD=FG,AD∥FG,∴四边形AFGE是平行四边形,又∵AD=AF,∴平行四边形AFGE是菱形,∴DG=DA=10,∴∠DAG=∠DGA,∵∠DMG=∠DMN+∠NAG=∠DAM+∠ADM, ∠DMN=∠DAM,∴∠NMG=∠ADM.在△ADM和△MNG中,∠ADM=∠NMG, ∠DAG=∠DGA,∴△ADM∽△GMN.∴AD AMMG NG=10xy=-,∴2110105y x x=-+,∵110>0,∴当51210x=-=⨯时,y有最小值为214101021410⎛⨯⨯-⎝⎭=⨯.∴y关于x的函数解析式是:211010y x x=-+,当x=y有最小值为2.②在△DMN 和△DMG 中,∠DMN =∠DGM ,∠MDG =∠MDG ,∴△DMN 和△DMG 是相似三角形. 当△DMG 是等腰三角形时,△DMN 也是等腰三角形.∵M 不与A 重合,∴DM ≠DG ,∴△DMG 是等腰三角形只有GM =GD 或DM =GM 两种情况:(1)如图3,当△DMG 中GM =GD =10时,△DMN 也是等腰三角形,即x =AG -MG =10;(2)如图4,当△DMG 中DM =GM 时,△DMN 也是等腰三角形,∴∠MDG =∠DGM ,∴∠DAG =∠MDG =∠MDG ,∴△ADG ∽△DMG ,∴AD AGMG DG =,=x综上:当x 的值为2△DMN 是等腰三角形.11.(2020·滨州)如图①,抛物线y =-x 2+x +4与y 轴交于点A ,与x 轴交于点B ,C ,将直线AB 绕点A 逆时针旋转90°,所得直线与x 轴交于点D . (1)求直线AD 的函数解析式;(2)如图②,若点P 是直线AD 上方抛物线上的一个动点 ①当点P 到直线AD 的距离最大时,求点P 的坐标和最大距离; ②当点P 到直线AD 的距离为时,求sin ∠P AD 的值.解:(1)当x =0时,y =4,则点A 的坐标为(0,4),………………………………………1分 当y =0时,0=-x 2+x +4,解得x 1=-4,x 2=8, 则点B 的坐标为(-4,0),点C 的坐标为(8,0),∴OA=OB=4,∴∠OBA=∠OAB=45°.∵将直线AB绕点A逆时针旋转90°得到直线AD,∴∠BAD=90°,∴OAD=45°,∴∠ODA=45°,∴OA=OD,∴点D的坐标为(4,0).………………………………………………………………………2分设直线AD的函数解析式为y=kx+b,,得,即直线AD的函数解析式为y=-x+4.……………………………………………………………4分(2)作PN⊥x轴交直线AD于点N,如右图①所示,设点P的坐标为(t,-t2+t+4),则点N的坐标为(t,-t+4),∴PN=(-t2+t+4)-(-t+4)=-t2+t,………………………………………………6分∴PN⊥x轴,∴PN∥y轴,∴∠OAD=∠PNH=45°.作PH⊥AD于点H,则∠PHN=90°,∴PH==(-t2+t)=t=-(t-6)2+,∴当t=6时,PH取得最大值,此时点P的坐标为(6,),………………………………8分即当点P到直线AD的距离最大时,点P的坐标是(6,),最大距离是.………………9分②当点P到直线AD的距离为时,如右图②所示,则t=,解得t1=2,t2=10,………………………………………………………………………10分则P1的坐标为(2,),P2的坐标为(10,-).当P1的坐标为(2,),则P1A==,∴sin∠P1AD==;…………………………………………………………12分当P 2的坐标为(10,-),则P 2A ==,∴sin ∠P 2AD ==;由上可得,sin ∠P AD 的值是或.……………………………………………14分二、填空题16.(2020·南充)如图,矩形硬纸片ABCD 的顶点A 在y 轴的正半轴及原点上滑动,顶点B 在x 轴的正半轴及原点上滑动,点E 为AB 的中点,24AB =,5BC =.给出下列结论:①点A 从点O 出发,到点B 运动至点O 为止,点E 经过的路径长为12π;②OAB ∆的面积最大值为144;③当OD 最大时,点D 的坐标为,.其中正确的结论是 .(填写序号)【答案】②③ 【解析】点E 为AB 的中点,24AB =,1122OE AB ∴==, AB ∴的中点E 的运动轨迹是以点O 为圆心,12为半径的一段圆弧,90AOB ∠=︒,∴点E 经过的路径长为90126180ππ⨯⨯=,故①错误; 当OAB ∆的面积最大时,因为24AB =,所以OAB ∆为等腰直角三角形,即OA OB =, E 为AB 的中点,OE AB ∴⊥,1122OE AB ==, ∴124121442AOB S ∆=⨯⨯=,故②正确;如图,当O 、E 、D 三点共线时,OD 最大,过点D 作DF y ⊥轴于点F , 5AD BC ==,1122AE AB ==,∴13DE ===,131225OD DE OE ∴=+=+=, 设DF x =,∴OF =,四边形ABCD 是矩形,90DAB ∴∠=︒,DFA AOB ∴∠=∠,DAF ABO ∴∠=∠, DFA AOB ∴∆∆∽∴DF DA OA AB =,∴524x OA =,∴245x OA =, E 为AB 的中点,90AOB ∠=︒,AE OE ∴=,AOE OAE ∴∠=∠,DFO BOA ∴∆∆∽,∴OD OF AB OA=,∴25245=,解得x =x =舍去,∴OF =,∴D .故③正确. 故答案为:②③.【知识点】直角形的性质;矩形的性质;相似三角形的判定和性质三、解答题17. (2019 · 镇江)如图,菱形ABCD 的顶点B 、C 在x 轴上(B 在C 的左侧),顶点A 、D 在x 轴上方,对角线BD(2,0)E -为BC 的中点,点P 在菱形ABCD 的边上运动.当点(0,6)F 到EP 所在直线的距离取得最大值时,点P 恰好落在AB 的中点处,则菱形ABCD 的边长等于( )A .103BC .163D .3【答案】A【解析】如图1中,当点P 是AB 的中点时,作FG PE ⊥于G ,连接EF .(2,0)E -,(0,6)F ,2OE ∴=,6OF =,EF ∴=90FGE ∠=︒,FG EF ∴,∴当点G 与E 重合时,FG 的值最大.如图2中,当点G 与点E 重合时,连接AC 交BD 于H ,PE 交BD 于J .设2BC a =.PA PB =,BE EC a ==,//PE AC ∴,BJ JH =,四边形ABCD 是菱形,AC BD ∴⊥,BH DH ==BJ PE BD ∴⊥,90BJE EOF PEF ∠=∠=∠=︒,EBJ FEO ∴∠=∠, BJE EOF ∴∆∆∽, ∴BE BJ EF EO=,∴62=, 53a ∴=, 1023BC a ∴==, 故选:A .【知识点】菱形的性质;平面直角坐标系;相似三角形的判定和性质;垂线段最短。
中考几何最值问题(含答案)

几何最值问题一.选择题(共6小题)1.(2015孝感一模)如图,已知等边△ABC的边长为6,点D为AC的中点,点E为BC的中点,点P为BD上一点,则PE+PC的最小值为()A.3B.3C.2D.3考点:轴对称-最短路线问题.分析:由题意可知点A、点C关于BD对称,连接AE交BD于点P,由对称的性质可得,PA=PC,故PE+PC=AE,由两点之间线段最短可知,AE即为PE+PC的最小值.解答:解:∵△ABC是等边三角形,点D为AC的中点,点E为BC的中点,∴BD⊥AC,EC=3,连接AE,线段AE的长即为PE+PC最小值,∵点E是边BC的中点,∴AE⊥BC,∴AE===3,∴PE+PC的最小值是3.故选D.点评:本题考查的是轴对称﹣最短路线问题,熟知等边三角形的性质是解答此题的关键.2.(2014•鄂城区校级模拟)如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm和40cm,B点到y轴的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,则这个值为()A.50B.50C.50﹣50D.50+50考点:轴对称-最短路线问题;坐标与图形性质.专题:压轴题.分析:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交X,Y轴分别为P,Q点,此时四边形PABQ的周长最短,根据题目所给的条件可求出周长.解答:解:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F 点,截取NF=AF,连接MN交x,y轴分别为P,Q点,过M点作MK⊥x轴,过N点作NK⊥y轴,两线交于K点.MK=40+10=50,作BL⊥x轴交KN于L点,过A点作AS⊥BP交BP于S点.∵LN=AS==40.∴KN=60+40=100.∴MN==50.∵MN=MQ+QP+PN=BQ+QP+AP=50.∴四边形PABQ的周长=50+50.故选D.点评:本题考查轴对称﹣最短路线问题以及坐标和图形的性质,本题关键是找到何时四边形的周长最短,以及构造直角三角形,求出周长.3.(2014秋•贵港期末)如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数为()A.30°B.40°C.50°D.60°考点:轴对称-最短路线问题.分析:根据要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=70°,进而得出∠MAB+∠NAD=70°,即可得出答案.解答:解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值,作DA延长线AH,.∵∠DAB=110°,∴∠HAA′=70°,∴∠AA′M+∠A″=∠HAA′=70°,∵∠MA′A=∠MAB,∠NAD=∠A″,∴∠MAB+∠NAD=70°,∴∠MAN=110°﹣70°=40°.故选B.点评:本题考查的是轴对称﹣最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.4.(2014•无锡模拟)如图,∠MON=90°,矩形ABCD的顶点A,B分别在OM、ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=.运动过程中,当点D到点O的距离最大时,OA长度为()A.B.C.2D.考点:勾股定理;三角形三边关系;直角三角形斜边上的中线.分析:取AB的中点,连接OE、DE,根据直角三角形斜边上的中线等于斜边的一半求出OE,利用勾股定理列式求出DE,然后根据三角形的任意两边之和大于第三边判断出O、E、D三点共线时点D到点O的距离最大,过点A作AF⊥OD于F,利用∠ADE的余弦列式求出DF,从而得到点F是OD的中点,判断出AF垂直平分OD,再根据线段垂直平分线上的点到两端点的距离相等可得OA=AD.解答:解:如图,取AB的中点,连接OE、DE,∵∠MON=90°,∴OE=AE=AB=×2=1,∵三边形ABCD是矩形,∴AD=BC=,在Rt△ADE中,由勾股定理得,DE===2,由三角形的三边关系得,O、E、D三点共线时点D到点O的距离最大,此时,OD=OE+DE=1+2=3,过点A作AF⊥OD于F,则cos∠ADE==,即=,解得DF=,∵OD=3,∴点F是OD的中点,∴AF垂直平分OD,∴OA=AD=.故选B.点评:本题考查了勾股定理,三角形的任意两边之和大于第三边,直角三角形斜边上的中线等于斜边的一半的性质,线段垂直平分线上的点到两端点的距离相等的性质,作辅助线并判断出OD最大时的情况是解题的关键,作出图形更形象直观.5.(2015•鞍山一模)如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是()A.B.C.D.1考点:轴对称-最短路线问题;正方形的性质.分析:根据题意得出作EF∥AC且EF=,连结DF交AC于M,在AC上截取MN=,此时四边形BMNE的周长最小,进而利用相似三角形的判定与性质得出答案.解答:解:作EF∥AC且EF=,连结DF交AC于M,在AC上截取MN=,延长DF交BC 于P,作FQ⊥BC于Q,则四边形BMNE的周长最小,由∠FEQ=∠ACB=45°,可求得FQ=EQ=1,∵∠DPC=∠FPQ,∠DCP=∠FQP,∴△PFQ∽△PDC,∴=,∴=,解得:PQ=,∴PC=,由对称性可求得tan∠MBC=tan∠PDC==.故选:A.点评:此题主要考查了正方形的性质以及相似三角形的判定与性质,得出M,N的位置是解题关键.6.(2015•江干区一模)如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为()A.B.C.2D.考点:圆的综合题.分析:根据等腰三角形的性质可得点D是AB的中点,然后根据三角形中位线定理可得DP=BG,然后利用两点之间线段最短就可解决问题.解答:解:连接BG,如图.∵CA=CB,CD⊥AB,AB=6,∴AD=BD=AB=3.又∵CD=4,∴BC=5.∵E是高线CD的中点,∴CE=CD=2,∴CG=CE=2.根据两点之间线段最短可得:BG≤CG+CB=2+5=7.当B、C、G三点共线时,BG取最大值为7.∵P是AG中点,D是AB的中点,∴PD=BG,∴DP最大值为.故选A.点评:本题主要考查了圆的综合题,涉及了等腰三角形的性质、三角形中位线定理、勾股定理、两点之间线段最短等知识,利用三角形中位线定理将DP转化为BG是解决本题的关键.二.填空题(共3小题)7.(2014•江阴市校级模拟)如图,线段AB的长为4,C为AB上一动点,分别以AC、BC 为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.考点:等腰直角三角形.分析:设AC=x,BC=4﹣x,根据等腰直角三角形性质,得出CD=x,CD′=(4﹣x),根据勾股定理然后用配方法即可求解.解答:解:设AC=x,BC=4﹣x,∵△ABC,△BCD′均为等腰直角三角形,∴CD=x,CD′=(4﹣x),∵∠ACD=45°,∠BCD′=45°,∴∠DCE=90°,∴DE2=CD2+CE2=x2+(4﹣x)2=x2﹣4x+8=(x﹣2)2+4,∴当x取2时,DE取最小值,最小值为:4.故答案为:2.点评:本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.8.(2012•河南校级模拟)如图,矩形ABCD中,AB=4,BC=8,E为CD边的中点,点P、Q 为BC边上两个动点,且PQ=2,当BP=4时,四边形APQE的周长最小.考点:轴对称-最短路线问题.专题:压轴题.分析:要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC 的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H 点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度.解答:解:如图,在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC 交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.∵GH=DF=6,EH=2+4=6,∠H=90°,∴∠GEH=45°.设BP=x,则CQ=BC﹣BP﹣PQ=8﹣x﹣2=6﹣x,在△CQE中,∵∠QCE=90°,∠CEQ=45°,∴CQ=EC,∴6﹣x=2,解得x=4.故答案为4.点评:本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.9.(2013•武汉)如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是﹣1.考点:正方形的性质.专题:压轴题.分析:根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.解答:解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,在△ABE和△DCF中,,∴△ABE≌△DCF(SAS),∴∠1=∠2,在△ADG和△CDG中,,∴△ADG≌△CDG(SAS),∴∠2=∠3,∴∠1=∠3,∵∠BAH+∠3=∠BAD=90°,∴∠1+∠BAH=90°,∴∠AHB=180°﹣90°=90°,取AB的中点O,连接OH、OD,则OH=AO=AB=1,在Rt△AOD中,OD===,根据三角形的三边关系,OH+DH>OD,∴当O、D、H三点共线时,DH的长度最小,最小值=OD﹣OH=﹣1.(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆上运动当O、H、D三点共线时,DH长度最小)故答案为:﹣1.点评:本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,确定出DH最小时点H的位置是解题关键,也是本题的难点.三.解答题(共1小题)10.(2015•黄冈中学自主招生)阅读下面材料:小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).请你回答:AP的最大值是6.参考小伟同学思考问题的方法,解决下列问题:如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是(或不化简为).(结果可以不化简)考点:旋转的性质;全等三角形的判定与性质;等边三角形的性质;勾股定理;等腰直角三角形.专题:几何综合题.分析:(1)根据旋转的性质知A′A=AB=BA′=2,AP=A′C,所以在△AA′C中,利用三角形三边关系来求A′C即AP的长度;(2)以B为中心,将△APB逆时针旋转60°得到△A'P'B.根据旋转的性质推知PA+PB+PC=P'A′+P'B+PC.当A'、P'、P、C四点共线时,(P'A′+P'B+PC)最短,即线段A'C最短.然后通过作辅助线构造直角三角形A′DC,在该直角三角形内利用勾股定理来求线段A′C的长度.解答:解:(1)如图2,∵△ABP逆时针旋转60°得到△A′BC,∴∠A′BA=60°,A′B=AB,AP=A′C∴△A′BA是等边三角形,∴A′A=AB=BA′=2,在△AA′C中,A′C<AA′+AC,即AP<6,则当点A′A、C三点共线时,A′C=AA′+AC,即AP=6,即AP的最大值是:6;故答案是:6.(2)如图3,∵Rt△ABC是等腰三角形,∴AB=BC.以B为中心,将△APB逆时针旋转60°得到△A'P'B.则A'B=AB=BC=4,PA=P′A′,PB=P′B,∴PA+PB+PC=P′A′+P'B+PC.∵当A'、P'、P、C四点共线时,(P'A+P'B+PC)最短,即线段A'C最短,∴A'C=PA+PB+PC,∴A'C长度即为所求.过A'作A'D⊥CB延长线于D.∵∠A'BA=60°(由旋转可知),∴∠1=30°.∵A'B=4,∴A'D=2,BD=2,∴CD=4+2.在Rt△A'DC中A'C====2+2;∴AP+BP+CP的最小值是:2+2(或不化简为).故答案是:2+2(或不化简为).点评:本题综合考查了旋转的性质、等腰直角三角形的性质、勾股定理以及等边三角形的判定与性质.注意:旋转前、后的图形全等.。
【中考冲刺】初三数学培优专题 25 平面几何的最值问题(含答案)(难)

平面几何的最值问题阅读与思考几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值. 求几何最值问题的基本方法有:1.特殊位置与极端位置法:先考虑特殊位置或极端位置,确定最值的具体数据,再进行一般情形下的推证.2.几何定理(公理)法:应用几何中的不等量性质、定理.3.数形结合法等:揭示问题中变动元素的代数关系,构造一元二次方程、二次函数等.例题与求解【例1】在Rt △ABC 中,CB =3,CA =4,M 为斜边AB 上一动点.过点M 作MD ⊥AC 于点D ,过M 作ME ⊥CB 于点E ,则线段DE 的最小值为 .(四川省竞赛试题)解题思路:四边形CDME 为矩形,连结CM ,则DE = CM ,将问题转化为求CM 的最小值.【例2】如图,在矩形ABCD 中,AB =20cm ,BC =10cm .若在AC ,AB 上各取一点M ,N ,使BM +MN 的值最小,求这个最小值.(北京市竞赛试题)ADMN解题思路:作点B 关于AC 的对称点B ′,连结B ′M ,B ′A ,则BM = B ′M ,从而BM +MN = B ′M +MN .要使BM +MN 的值最小,只需使B ′M 十MN 的值最小,当B ′,M ,N 三点共线且B ′N ⊥AB 时,B ′M +MN 的值最小.【例3】如图,已知□ABCD ,AB =a ,BC =b (b a ),P 为AB 边上的一动点,直线DP 交CB 的延长线于Q .求AP +BQ 的最小值. (永州市竞赛试题)PDA BQ解题思路:设AP =x ,把AP ,BQ 分别用x 的代数式表示,运用不等式以ab b a 222≥+或a +b ≥2ab(当且仅当a =b 时取等号)来求最小值. 【例4】阅读下列材料:问题 如图1,一圆柱的底面半径为5dm ,高AB 为5dm ,BC 是底面直径,求一只蚂蚁从A 点出发沿圆柱表面爬行到C 点的最短路线. 小明设计了两条路线:图2图1摊平沿AB 剪开ACBBA路线1:侧面展开图中的线段AC .如图2所示.设路线l 的长度为l 1,则l 12 =AC 2=AB 2 +BC 2 =25+(5π) 2=25+25π2. 路线2:高线AB 十底面直径BC .如图1所示.设路线l 的长度为l 2,则l 22 = (BC +AB )2=(5+10)2 =225.∵l 12 – l 22 = 25+25π2-225=25π2-200=25(π2-8),∴l 12 >l 22 ,∴ l 1>l 2 . 所以,应选择路线2.条路线才能使蚂蚁从点A 出发沿圆柱表面爬行到C 点的路线最短. (衢州市中考试题)解题思路:本题考查平面展开一最短路径问题.比较两个数的大小,有时比较两个数的平方比较简便.比较两个数的平方,通常让这两个数的平方相减.【例5】如图,已知边长为4的正方形钢板,有一个角锈蚀,其中AF =2,BF =1.为了合理利用这块钢板,将在五边形EABCD 内截取一个矩形块MDNP ,使点P 在AB 上,且要求面积最大,求钢板的最大利用率. (中学生数学智能通讯赛试题)NME DAB解题思路:设DN =x ,PN =y ,则S =xy .建立矩形MDNP 的面积S 与x 的函数关系式,利用二次函数性质求S 的最大值,进而求钢板的最大利用率.【例6】如图,在四边形ABCD 中,AD =DC =1,∠DAB =∠DCB =90°,BC ,AD 的延长线交于P ,求AB ·S △P AB 的最小值. (中学生数学智能通讯赛试题)1ABD解题思路:设PD =x (x >1),根据勾股定理求出PC ,证Rt △PCD ∽Rt △P AB ,得到PCPACD AB ,求出AB ,根据三角形的面积公式求出y =AB ·S △P AB ,整理后得到y ≥4,即可求出答案.能力训练A 级1.如图,将两张长为8、宽为2的矩形纸条交叉,使重叠部分是一个菱形.容易知道当两张纸条垂直时,菱形的周长有最小值,那么菱形周长的最大值是 . (烟台市中考试题)2.D 是半径为5cm 的⊙O 内一点,且OD =3cm ,则过点O 的所有弦中,最短的弦AB = cm . (广州市中考试题)3.如图,有一个长方体,它的长BC =4,宽AB =3,高BB 1=5.一只小虫由A 处出发,沿长方体表面爬行到C 1,这时小虫爬行的最短路径的长度是 . (“希望杯”邀请赛试题)DD 1第1题图 第3题图 第4题图 第5题图4.如图,在△ABC 中,AB =10,AC =8,BC =6,经过点C 且与边AB 相切的动圆与CB ,CA 分别相交于点E ,F ,则线段EF 长度的最小值是( ) (兰州市中考试题)A .42B .4. 75C .5D .4. 85.如图,圆锥的母线长OA =6,底面圆的半径为2.一小虫在圆锥底面的点A 处绕圆锥侧面一周又回到点A ,则小虫所走的最短距离为( ) (河北省竞赛试题) A .12B .4πC .62D .636.如图,已知∠MON = 40°,P 是∠MON 内的一定点,点A ,B 分别在射线OM ,ON 上移动,当△P AB 周长最小时,∠APB 的值为( ) (武汉市竞赛试题) A .80° B .100° C .120° D .140° 7.如图, ⌒AD 是以等边三角形ABC 一边AB 为半径的四分之一圆周,P 为AD 上任意一点.若AC =5,则四边形ACBP 周长的最大值是( ) (福州市中考试题) A .15B .20C .15+52D .15+55NM NMAOPBDCBCA DBA PE第6题图 第7题图 第8题图 8.如图,在正方形ABCD 中,AB =2,E 是AD 边上一点(点E 与点A ,D 不重合),BE 的垂直平分线交AB 于M ,交DC 与N .(1) 设AE =x ,四边形ADNM 的面积为S ,写出S 关于x 的函数关系式.(2) 当AE 为何值时,四边形ADNM 的面积最大?最大值是多少? (山东省中考试题)9.如图,六边形ABCDEF 内接于半径为r 的⊙O ,其中AD 为直径,且AB =CD =DE =F A . (1) 当∠BAD =75°时,求⌒BC 的长; (2) 求证:BC ∥AD ∥FE ;(3) 设AB =x ,求六边形ABCDEF 的周长l 关于x 的函数关系式,并指出x 为何值时,l 取得最大值.10.如图,已知矩形ABCD 的边长AB =2,BC =3,点P 是AD 边上的一动点(P 异于A 、D ).Q 是BC边上任意一点.连结AQ,DQ,过P作PE∥DQ交于AQ于E,作PF//AQ交DQ于F.(1) 求证:△APE∽△ADQ;(2) 设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?(3) 当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必证明)(无锡市中考试题)B Q11.在等腰△ABC中,AB=AC=5,BC=6.动点M,N分别在两腰AB,AC上(M不与A,B重合,N不与A,C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.(1)当MN为何值时,点P恰好落在BC上?(2)设MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式,当x为何值时,y的值最大,最大值是多少?(宁夏省中考试题)B CAB级1.已知凸四边形ABCD中,AB+AC+CD= 16,且S四边彤ABCD=32,那么当AC= ,BD= 时,四边形ABCD面积最大,最大值是.(“华杯赛”试题)2.如图,已知△ABC的内切圆半径为r,∠A=60°,BC=23,则r的取值范围是.(江苏省竞赛试题)DBAB CAA第2题图第3题图第4题图第5题图3.如图⊙O的半径为2,⊙O内的一点P到圆心的距离为1,过点P的弦与劣弧⌒AB组成一个弓形,则此弓形面积的最小值为.4.如图,△ABC的面积为1,点D,G,E和F分别在边AB,AC,BC上,BD<DA,DG∥BC,DE ∥AC ,GF ∥AB ,则梯形DEFG 面积的最大可能值为 .(上海市竞赛试题)5.已知边长为a 的正三角形ABC ,两顶点A ,B 分别在平面直角坐标系的x 轴,y 轴的正半轴上滑动,点C 在第一象限,连结OC ,则OC 的最大值是 .(潍坊市中考试题)6.已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当P A + PD 取最小值时,△APD 中边AP 上的高为( ) (鄂州市中考试题)A .17172B .17174C .17178D .3QADBCA BDCPP第6题图 第7题图 第8题图7.如图,正方形ABCD 的边长为4cm ,点P 是BC 边上不与点B ,C 重合的任意一点,连结AP ,过点P 作PQ ⊥AP 交DC 于点Q .设BP 的长为x cm ,CQ 的长为y cm . (1) 求点P 在BC 上运动的过程中y 的最大值;(2) 当y =41cm 时,求x 的值. (河南省中考试题)8.如图,y 轴正半轴上有两点A (0,a ),B (0,b ),其中a >b >0.在x 轴上取一点C ,使∠ACB 最大,求C 点坐标. (河北省竞赛试题)9.如图,正方形ABCD 的边长为1,点M ,N 分别在BC ,CD 上,使得△CM N 的周长为2.求: (1) ∠MAN 的大小;(2) △MAN 的面积的最小值. (“宇振杯”上海市竞赛试题)10,如图,四边形ABCD 中,AD = CD ,∠DAB =∠ACB =90°,过点D 作DE ⊥AC 于F ,DE 与AB相交于点E .(1) 求证:AB ·AF =CB ·CD ; (2)已知AB =15cm ,BC =9cm ,P 是射线DE 上的动点,设DP =x cm(x >0),四边形BCDP 的面积为y cm 2. ①求y 关于x 的函数关系式;②当x 为何值时,△PBC 的周长最小?求出此时y 的值.(南通市中考试题)MNExCB第6题图 第7题图 第8题图 第9题图11.如图,已知直线l :k kx y 42-+=(k 为实数).(1) 求证:不论k 为任何实数,直线l 都过定点M ,并求点M 的坐标;(2) 若直线l 与x 轴、y 轴的正半轴交于A ,B 两点,求△AOB 面积的最小值.(太原市竞赛试题)12.如图,在Rt △ABC 中,∠C =90°,BC =2,AC =x ,点F 在边AB 上,点G ,H 在边BC 上,四边形EFGH 是一个边长为y 的正方形,且AE =AC . (1) 求y 关于x 的函数解析式;(2) 当x 为何值时,y 取得最大值?求出y 的最大值.(上海市竞赛试题)平面几何的最值问题例1125提示:当CM ⊥AB 时,CM 值最小,CM =125AC BC AB ⋅= 例2 如图,B ′M +MN 的最小值为点B ′到AB 的距离B ′F ,BE =45AB BCAC⋅=cm ,BB ′=85cm ,AE =()2222204585AB BE --=.在△ABB ′中,由12BB ′•AE =12AB •B ′F ,得B ′F =16cm .故BM +MN 的最小值为16cm . 例3 由△APD ∽△BPQ ,得AP AD BP BQ =,即BQ =()b a x AD BP AP x-⋅=,∴AP +BQ =x +ab b x -.∵x +ab x ≥2ab x ab x ⋅=仅当x =abx即x ab ,上式等号成立.故当AP ab ,AP +BQ 最小,其最小值为ab-b .例4 ⑴22125l π=+,22l =49,l 1<l 2,故要选择路线l 较短. ⑵()2221l h r π=+,()2222l h r =+,()2221244l l r r h π⎡⎤-=--⎣⎦.当r =244h π-时,2212l l =,当r >244h π-时,2212l l >,当r <244hπ-时,2212l l <. 例5 设DN =x ,PN =y ,则S =xy ,由△APQ ∽△ABF ,得()41242y x -=--即x =10-2y ,代入S =xy 得S =xy =y (10-2y ),即S =-2252522y ⎛⎫-+ ⎪⎝⎭,因3≤y ≤4,而y =52不在自变量y 的取值范围内,所以y =52不是极值点,当y =3时,S (3)=12,当y =4时,S (4)=8,故S max =12.此时,钢板的最大利用率21214212-⨯⨯=80%. 例6 设PD =x (x >1),则PC 21x -,由R t △PCD ∽△P AB ,得AB =21CD PA PC x ⋅=-y =AB •S △P AB ,则y =12AB ×P A ×AB =()()2121x x +-,求y 的最小值,有下列不同思路:①配方:y =21212242121x x x x --++=+--1221x x -=-x =3时,y 有最小值4.②运用基本不等式:y =122221x x -++≥- 321221x x -⋅-+2=4,∴当12x -=21x -,即当x =3时,y 有最小值4. ③借用判别式,去分母,得x 2+2(1-y )x +1+2y =0,由△=4(1-y )2-4(1+2y )=4y (y -4)≥0,得y ≥4,∴y 的最小值为4. A 级1. 17 提示:当两张纸条的对角重合时,菱形周长最大.2. 83.74 4. D 5. D 6. B7. C 提示:当点P 与点D 重合时,四边形ACBP 的周长最大.8. (1)连结ME ,过N 作NF ⊥AB 于F ,可证明Rt △EB A ≌Rt △MNF ,得MF =AE =x. ∵ME 2=AE 2+AM 2,故MB 2=x 2+AM 2,即(2-AM )2=x 2+AM 2,AM =1-14x 2,∴S =2AM DN +×AD =2AM AF+×2=AM +AM +MF =2 AM +AE =2(1-14x 2)+x =-12x 2+x +2.(2)S =-12(x 2-2 x +1)+52=-12(x -1)2+52. 故当AE =x =1时,四边形ADNM 的面积最大,此时最大值为52. 9. (1)BC 长为23rπ. (2)提示:连结BD . (3)过点B 作BM ⊥AD 于M ,由(2)知四边形ABCD为等腰梯形,从而BC =AD -2 AM =2r -2 AM . 由△BAM ∽△DAB ,得AM =2AB AD =22x r ,∴BC =2r-2x r . 同理,EF =2 r -2x r . l =4 x +2(2 r -2x r )=-xr(x -r )2+6 r (0<x 2 r ). . 当x =r时,l 取得最大值6 r .10. (1)∵∠APE =∠ADQ ,∠AEP =∠AQD ,∴△APE ∽△ADQ . (2)由△APE ∽△ADQ ,△PDF ∽△ADQ ,S △PEF =12S □PEQF ,得S △PEF =-13x 2+x =-13(x -32)2+34. 故当x =32时,即P 是AD 的中点时,S △PEF 取得最大值,(3)作A 关于直线BC 的对称点A′,连结DA′交BC 于Q ,则这个Q 点就是使△ADQ 周长最小的点,此时Q 是BC 的中点.11. (1)点P 恰好在BC 上时,由对称性知MN 是△ABC 的中位线,∴当MN =12BC =3时,点P 在BC 上. (2)由已知得△ABC 底边上的高h =225-3=4. ①当0<x ≤3时,如图1,连结AP 并延长交BC 于点D ,AD 与MN 交于点O .由△AMN ∽△ABC ,得AO =23x ,y =S △PMN =S △AMN =12·x ·23x =13x 2即y =13x 2. 当=3时,y 的值最大,最大值是3. ②当3<x <6时,如图2,设△PMN 与BC 相交于点E ,F ,AP 与BC 相交于D . 由①中知AO =23x ,∴AP =43x ,∴PD =AP -AD =43x -4,∵△PEF ∽△ABC . ,∴PEFABC S S ∆∆=(PD AD )2=(4434x -)2,即PEF ABC S S ∆∆=2-3)9x (. ∵S △ABC =12,∴S △PEF =43(x -3)2. ∴y =S △AMN -S △PEF =13x 2-43(x -3)2=-x 2+8x -12=-(x -4)2+4. 故当x =4时,y 的最大值为4. 综上,当x =4时,y 的值最大,最大值为4. B 级1. 8 2 32 提示:当∠CAB =∠ACD =90°时,四边形ABCD 的面积达到最大值.2. 0<r ≤1 提示:设BC =a ,CA =b ,AB =c ,b +c =3(r +1),又12bc sin60°=S △ABC =12(a +b +c )r ,即12bc ·32=12[33r +1)]r ,. bc =4r (r +2). b ,c 为方程x 2-3r +1)x +4r (r +2)=0的两个根,由△≥0,得(r +1)≤22. 因r >0,r +1>0,故r +1≤2,即0<r ≤1. 3.249π3提示:过P 作垂直于OP 的弦AB ,此时弓形面积最小. 4.13 提示:设AD AB =x ,则BD BA =1-x =CG CA ,ADGABCS S ∆∆=x 2,BDE ABC S S ∆∆=(1-x )2=CFG ABC S S ∆∆,S 梯形DEFG=1―x 2―2(1-x )2=-3(x -23)2+13.5. 312+a 提示:当OA =OB 时,OC 的长最大.6. C7. (1)由Rt △ABP ∽Rt △PCQ ,得BP CQ =AB CP ,即x y =44x -,y =-14(x -2)2+1(0<x <4). 当x =2时, y 最大值=1cm. (2)由14=-14(x -2)2+1,得x =(2+3)cm 或(2-3)cm. 8. 当过A ,B 两点的圆与x 轴正半轴相切时,切点C 为所求. 作O′D ⊥A B 于D . ,O′D 2= O′B 2-BD 2=2()2a b +-2()2a b -=ab ,O′D =ab 故点C 坐标为(ab ,0).9. (1)如图,延长CB 到L ,使BL =DN ,则Rt △ABL ≌Rt △ADN ,得AL =AN ,∠1=∠2,又∵N =2―CN ―CM =DN +BM =BL +BM =ML ,且AM =AM ,∠NAL =∠DAB =90°. ∴△AMN ≌△AML ,故∠MAN =∠MAL=902=45°. (2)设CM =x ,CN =y ,MN =z ,则2222222,2,x y z x y z x y z x y z ++==--⎧⎧⇔⎨⎨+=+=⎩⎩,于是,(2―y ―z )2+y 2=z 2. 整理得2y 2+(2z -4)y +(4-4z )=0. ∵y >0,故△=4(z -2)2-32(1-z )≥0,即(z +2+22)(z +2-22)≥0. 又∵z >0,故z ≥22-2,当且仅当x =y =2-2时等号成立. 由于S △AMN =S △AML =12·ML ·AB =12 MN ×1=2z ,因此,△AMN 的面积的最小值为2-1.10. (1)提示:证明△ADF ∽△BAC . (2)①AB =15,BC =9,∠ACB =90°,∴AC 22AB BC -=2215912-=,∴CF =AF =6,∴()()19632702y x x x =+⨯=+>.②∵BC =9(定值),∴△PBC 的周长最小,就是PB +PC 最小,由(1)知,点C 关于直线DE 的对称点是点A ,所以PB +PC =PB +P A ,故只要求PB +P A 最小.显然当P 、A 、B 三点共线时PB +P A 最小,此时DP =DE ,PB +P A =AB .由(1),角∠ADF =∠F AE ,∠DF A =∠ACB =90°,得△DAF ∽△ABC .EF ∥BC ,得AE =BE =12AB =152,EF =92.∴ AF ∶BC =AD ∶AB ,即6∶9=AD ∶15,∴AD =10.Rt △ADF 中,AD =10,AF =6,∴DF =8.∴DE =DF +FE =8+92=252. ∴当x =252时,△PBC 的周长最小,此时y =1292. 11.(1)令k =1,得y =x +2;令k =2,得y =2x +6,联立解得x =4,y =2,故定点(4,2). (2)取x =0,得OB =2-4k (k <0),取y =0,得OA =()420k k k-<.于是△ABO 的面积()()114224022k S OA OB k k k-==-<,化简得()28820k S k +-+=.由()28640S ∆=--≥得2160S S -≥,故S ≥16.将S =16代入上述方程,得k =12-.故当k =12-,S 值最小. 12.(1)如图,延长EF 交AC 于点D ,DF ∥BC ,Rt △ADF ∽Rt △ACB ,AE =AC =x ,()2222DE x x y xy y =--=-22xy y y x y x -+-=,2x -2y -xy =22x xy y -,两边平方整理得(x 2+2x +2)y 2-(x 3+2x 2+4x )y +2x 2=0.解得2222x y x x =++(y =x 舍去) . (2)由(1)22122222y x x ==+++≤ .当且仅当2x x =,即2x =,上式等号成立.故当2x =,y 去最大21.。
初中数学几何最值存在性问题(word版+详解答案)

几何最值的存在性问题【考题研究】在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。
从历年的中考数学压轴题型分析来看,经常会考查到距离或者两条线段和差最值得问题,并且这部分题目在中考中失分率很高,应该引起我们的重视。
几何最值问题再教材中虽然没有进行专题讲解,到却给了我们很多解题模型,因此在专题复习时进行压轴训练是必要的。
【解题攻略】最值问题是一类综合性较强的问题,而线段和(差)问题,要归归于几何模型:(1)归于“两点之间的连线中,线段最短”凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.(2)归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,PA与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′.解决线段和差的最值问题,有时候求函数的最值更方便,建立一次函数或者二次函数求解最值问题.【解题类型及其思路】解决平面几何最值问题的常用的方法有:(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;(2)应用垂线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用二次函数求最值;(5)应用其它知识求最值。
【典例指引】类型一【确定线段(或线段的和,差)的最值或确定点的坐标】【典例指引1】(2018·天津中考模拟)如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x 轴、y轴的正半轴上.点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC 交于点E.(I)证明:EO=EB;(Ⅱ)点P是直线OB上的任意一点,且△OPC是等腰三角形,求满足条件的点P的坐标;(Ⅲ)点M是OB上任意一点,点N是OA上任意一点,若存在这样的点M、N,使得AM+MN最小,请直接写出这个最小值.【举一反三】(2020·云南初三)如图,抛物线y=ax2+bx+3经过点B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.(1)求抛物线的表达式;(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.类型二【确定三角形、四边形的周长的最值或符合条件的点的坐标】【典例指引2】(2020·重庆初三期末)如图,抛物线2y ax bx =+(0a >)与双曲线k y x =相交于点A 、B ,已知点A 坐标()1,4,点B 在第三象限内,且AOB ∆的面积为3(O 为坐标原点).(1)求实数a 、b 、k 的值;(2)在该抛物线的对称轴上是否存在点P 使得POB ∆为等腰三角形?若存在请求出所有的P 点的坐标,若不存在请说明理由.(3)在坐标系内有一个点M ,恰使得MA MB MO ==,现要求在y 轴上找出点Q 使得BQM ∆的周长最小,请求出M 的坐标和BQM ∆周长的最小值.【举一反三】(2019·重庆实验外国语学校初三)如图1,已知抛物线y =﹣23384x +x +3与x 轴交于A 和B 两点,(点A 在点B 的左侧),与y 轴交于点C .(1)求出直线BC 的解析式.(2)M 为线段BC 上方抛物线上一动点,过M 作x 轴的垂线交BC 于H ,过M 作MQ ⊥BC 于Q ,求出△MHQ 周长最大值并求出此时M 的坐标;当△MHQ 的周长最大时在对称轴上找一点R ,使|AR ﹣MR |最大,求出此时R 的坐标.(3)T 为线段BC 上一动点,将△OCT 沿边OT 翻折得到△OC ′T ,是否存在点T 使△OC ′T 与△OBC 的重叠部分为直角三角形,若存在请求出BT 的长,若不存在,请说明理由.类型三 【确定三角形、四边形的面积最值或符合条件的点的坐标】【典例指引3】(2019·甘肃中考真题)如图,已知二次函数y =x 2+bx+c 的图象与x 轴交于点A (1,0)、B (3,0),与y 轴交于点C .(1)求二次函数的解析式;(2)若点P 为抛物线上的一点,点F 为对称轴上的一点,且以点A 、B 、P 、F 为顶点的四边形为平行四边形,求点P 的坐标;(3)点E 是二次函数第四象限图象上一点,过点E 作x 轴的垂线,交直线BC 于点D ,求四边形AEBD 面积的最大值及此时点E 的坐标.【举一反三】(2019·内蒙古中考真题)如图,在平面直角坐标系中,已知抛物线22(0)y ax bx a =++≠与x 轴交于()1,0A -),()3,0B 两点,与y 轴交于点C ,连接BC .(1)求该抛物线的解析式,并写出它的对称轴;(2)点D 为抛物线对称轴上一点,连接CD BD 、,若DCB CBD ∠=∠,求点D 的坐标;(3)已知()1,1F ,若(),E x y 是抛物线上一个动点(其中12x <<),连接CE CF EF 、、,求CEF ∆面积的最大值及此时点E 的坐标.(4)若点N 为抛物线对称轴上一点,抛物线上是否存在点M ,使得以,,,B C M N 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M 的坐标;若不存在,请说明理由.【新题训练】1.如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.(1)求二次函数的表达式;(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴,y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F、E的坐标.2.(2019·江苏中考真题)如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.(1)如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为_____;(2)如图2,当PB=5时,若直线l//AC,则BB’的长度为;(3)如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;(4)当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.3.(2019·湖南中考真题)如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y 轴的正半轴上随之上下移动.(1)当∠OAD=30°时,求点C的坐标;(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为212时,求OA的长;(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.4.(2018·江苏中考真题)如图,在平面直角坐标系中,一次函数y=﹣23x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.(1)当t=13秒时,点Q的坐标是;(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.5.(2020·江苏初三期末)已知二次函数223y x x =--+的图象和x 轴交于点A 、B ,与y 轴交于点C ,点P 是直线AC 上方的抛物线上的动点.(1)求直线AC 的解析式.(2)当P 是抛物线顶点时,求APC ∆面积.(3)在P 点运动过程中,求APC ∆面积的最大值.6.(2020·江苏初三期末)如图,抛物线265y ax x =+-交x 轴于A 、B 两点,交y 轴于点C ,点B 的坐标为()5,0,直线5y x =-经过点B 、C .(1)求抛物线的函数表达式;(2)点P 是直线BC 上方抛物线上的一动点,求BCP ∆面积S 的最大值并求出此时点P 的坐标;(3)过点A 的直线交直线BC 于点M ,连接AC ,当直线AM 与直线BC 的一个夹角等于ACB ∠的3倍时,请直接写出点M 的坐标.7.(2019·石家庄市第四十一中学初三)如图,在平面直角坐标系中,抛物线y =x (x ﹣b )﹣与y 轴相交于A 点,与x 轴相交于B 、C 两点,且点C 在点B 的右侧,设抛物线的顶点为P .(1)若点B 与点C 关于直线x =1对称,求b 的值;(2)若OB =OA ,求△BCP 的面积;(3)当﹣1≤x≤1时,该抛物线上最高点与最低点纵坐标的差为h ,求出h 与b 的关系;若h 有最大值或最小值,直接写出这个最大值或最小值.8.(2020·江西初三期中)如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(-3,0),与y轴交于点C.(1)求抛物线的解析式;(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.9.(2020·山东初三期末)如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.(1)求直线CD 的解析式;(2)求抛物线的解析式;(3)将直线CD 绕点C 逆时针方向旋转45°所得直线与抛物线相交于另一点E ,求证:△CEQ ∽△CDO ; (4)在(3)的条件下,若点P 是线段QE 上的动点,点F 是线段OD 上的动点,问:在P 点和F 点移动过程中,△PCF 的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由. 10.(2020·盘锦市双台子区第一中学初三月考)如图①,已知抛物线y=ax 2+bx+c 的图像经过点A (0,3)、B (1,0),其对称轴为直线l :x=2,过点A 作AC ∥x 轴交抛物线于点C ,∠AOB 的平分线交线段AC 于点E ,点P 是抛物线上的一个动点,设其横坐标为m.(1)求抛物线的解析式;(2)若动点P 在直线OE 下方的抛物线上,连结PE 、PO ,当m 为何值时,四边形AOPE 面积最大,并求出其最大值;(3)如图②,F 是抛物线的对称轴l 上的一点,在抛物线上是否存在点P 使△POF 成为以点P 为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.11.(2020·四川初三)如图,一次函数122y x =-+的图像与坐标轴交于A 、B 两点,点C 的坐标为(1,0)-,二次函数2y ax bx c =++的图像经过A 、B 、C 三点.(1)求二次函数的解析式(2)如图1,已知点(1,)D n 在抛物线上,作射线BD ,点Q 为线段AB 上一点,过点Q 作QM y ⊥轴于点M ,作QN BD ⊥于点N ,过Q 作//QP y 轴交抛物线于点P ,当QM 与QN 的积最大时,求点P 的坐标;(3)在(2)的条件下,连接AP ,若点E 为抛物线上一点,且满足APE ABO ∠=∠,求点E 的坐标.12.(2019·广东初三)如图,已知抛物线y =﹣3x 2+bx +c 与x 轴交于原点O 和点A (6,0),抛物线的顶点为B .(1)求该抛物线的解析式和顶点B 的坐标;(2)若动点P 从原点O 出发,以每秒1个长度单位的速度沿线段OB 运动,设点P 运动的时间为t (s ).问当t 为何值时,△OPA 是直角三角形?(3)若同时有一动点M 从点A 出发,以2个长度单位的速度沿线段AO 运动,当P 、M 其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t (s ),连接MP ,当t 为何值时,四边形ABPM 的面积最小?并求此最小值.13.(2019·山东初三期中)如图,已知抛物线经过两点A (﹣3,0),B (0,3),且其对称轴为直线x =﹣1.(1)求此抛物线的解析式.(2)若点Q 是对称轴上一动点,当OQ +BQ 最小时,求点Q 的坐标.(3)若点P 是抛物线上点A 与点B 之间的动点(不包括点A ,点B ),求△PAB 面积的最大值,并求出此时点P 的坐标.14.(2019·四川中考真题)如图,抛物线212y x bx c =-++过点(3,2)A ,且与直线72y x =-+交于B 、C两点,点B 的坐标为(4,)m .(1)求抛物线的解析式;(2)点D 为抛物线上位于直线BC 上方的一点,过点D 作DE x ⊥轴交直线BC 于点E ,点P 为对称轴上一动点,当线段DE 的长度最大时,求PD PA +的最小值;(3)设点M 为抛物线的顶点,在y 轴上是否存在点Q ,使45AQM ︒∠=?若存在,求点Q 的坐标;若不存在,请说明理由.15.(2019·天津中考真题)已知抛物线2y x bx c =-+(b c ,为常数,0b >)经过点(1,0)A -,点(,0)M m 是x 轴正半轴上的动点.(Ⅰ)当2b =时,求抛物线的顶点坐标;(Ⅱ)点(,)D D b y 在抛物线上,当AM AD =,5m =时,求b 的值;(Ⅲ)点1(,)2QQ b y+在抛物线上,当22AM QM+的最小值为3324时,求b的值.16.(2019·湖南中考真题)如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.(1)求抛物线的解析式;(2)F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;(3)在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为610?若存在,求出点P的坐标;若不存在,请说明理由;(4)矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL 平分矩形的面积时,求抛物线平移的距离.17.(2019·辽宁中考真题)如图,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线经过点D(﹣2,﹣3)和点E(3,2),点P是第一象限抛物线上的一个动点.(1)求直线DE和抛物线的表达式;(2)在y 轴上取点F (0,1),连接PF ,PB ,当四边形OBPF 的面积是7时,求点P 的坐标;(3)在(2)的条件下,当点P 在抛物线对称轴的右侧时,直线DE 上存在两点M ,N (点M 在点N 的上方),且MN =22,动点Q 从点P 出发,沿P→M→N→A 的路线运动到终点A ,当点Q 的运动路程最短时,请直接写出此时点N 的坐标.18.(2019·湖南中考真题)已知抛物线2(0)y ax bx c a =++≠过点(1,0)A ,(3,0)B 两点,与y 轴交于点C ,=3OC .(1)求抛物线的解析式及顶点D 的坐标;(2)过点A 作AM BC ⊥,垂足为M ,求证:四边形ADBM 为正方形;(3)点P 为抛物线在直线BC 下方图形上的一动点,当PBC ∆面积最大时,求点P 的坐标; (4)若点Q 为线段OC 上的一动点,问:12AQ QC +是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.几何最值的存在性问题【考题研究】在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。
2024年中考复习-11 几何图形中求线段,线段和,面积等最值问题(4题型)(解析版)
抢分秘籍11几何图形中求线段,线段和,面积等最值问题(压轴通关)目录【中考预测】预测考向,总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题,讲解通关策略(含新考法、新情境等)几何图形中求线段、线段和、面积最值题是全国中考的热点内容,更是全国中考的必考内容。
每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分。
1.从考点频率看,几何图形中的性质综合问题,是高频考点、也是必考点。
2.从题型角度看,以解答题的最后一题或最后二题为主,分值12分左右,着实不少!题型一线段最值问题【例1】(2024·四川成都·一模)如图1,在四边形ABFE 中,90F ∠=︒,点C 为线段EF 上一点,使得AC BC ⊥,24AC BC ==,此时BF CF =,连接BE ,BE AE ⊥,且AE BE =.(1)求CE 的长度;(2)如图2,点D 为线段AC 上一动点(点D 不与A ,C 重合),连接BD ,以BD 为斜边向右侧作等腰直角三角形BGD .①当DG AB ∥时,试求AD 的长度;②如图3,点H 为AB 的中点,连接HG ,试问HG 是否存在最小值,如果存在,请求出最小值;如果不存在,请说明理由.DC =,即可得出DM GF =,证明DMG GFB ≌,进而证明G 在EF 上,根据已知条件证明D 在EB 上,然后解直角三角形,即可求解;②如图所示,过点H 作HP EF ⊥于点P ,连接EH ,由①可得G 在EF 上运动,当HG EF ⊥时,HG 取得最小值,即,G P 重合时,HP 的长即为HG 的最小值,由①可得103AT =,求得sin 10ETA ∠=,根据45HEF ETA α∠=+︒=∠,即可求解.【详解】(1)解:如图所示,取AB 的中点H ,连接,EH HC ,∵BF CF =,90F ∠=︒,∴45BCF ∠=︒,BC =,又∵AC BC⊥∴45ECA ∠=︒∵AE BE =,BE AE⊥∴45EBA ∠=︒∴45ECA ABE ∠=∠=︒∴FEB CAB∠=∠∵24AC BC ==,∴2BC =∴BF CF ==∴1tan 2CB CAB AC ∠==∴1tan tan 2FB FEB CAB EF ∠==∠=∴12BF EF =∴EF =∴CE EF CF =-=(2)①如图所示,过点D 作DM EF ⊥于点M ,过点D 作DN AB ⊥于点N,由(1)可得45ACE ABE ∠=∠=︒∴CDM V 是等腰直角三角形,∴CD =,∵,CBF DBG 都是等腰直角三角形,∴CB DB BF BG =∴BD BG BC BF=又∵DBG CBF∠=∠∴DBC GBF∠=∠∴DBC GBF∽∴DC DB GF GB==∴DC =∴DM GF=在,DMG GFB 中,DM GF DMG F DG BG =⎧⎪∠=∠⎨⎪=⎩∴DMG GFB≌∴MGD FBG∠=∠∵90FBG FGB ∠+∠=︒∴90MGD FGB ∠+∠=︒又∵90DGB ∠=︒∴180MGF ∠=︒∴G 在EF 上,∵DG AB ∥,90DGB ∠=︒∴90GBA ∠=︒∵45,45ABE DBG ABD∠=︒∠=︒=∠∴D 在EB 上,∵1tan 2CAB ∠=,∴12DN AN =,则AD ==∵,45DN AB ABE ⊥∠=︒∴DN DB=∴3AB DN =,∵4AC =,2CB =∴AB =∴133DN AB ==,∴103AD ==,②如图所示,过点H 作HP EF ⊥于点P ,连接EH ,由①可得G 在EF 上运动,∴当HG EF ⊥时,HG 取得最小值,即,G P 重合时,HP 的长即为HG 的最小值,设,AC EB 交于点T ,即与①中点D 重合,由①可得103AT =∵AB =∴AE =,12EH AB ==∴sin 10103AE ETA AT ∠==设FEB CAB α∠=∠=则45HEF ETA α∠=+︒=∠,在Rt PEH △中,sin sin 102PH HEF EH ETA EH =∠⨯=∠⨯=⨯.【点睛】证明G 点在EF 上是解题的关键.本题考查了相似三角形的性质与判定,等腰三角形的性质,全等三角形的性质与判定,解直角三角形.【例2】(2024·天津红桥·一模)在平面直角坐标系中,点()0,0O ,()2,0A,(2,B ),C ,D 分别为OA ,OB 的中点.以点O 为中心,逆时针旋转OCD ,得OC D '' ,点C ,D 的对应点分别为点C ',D ¢.(1)填空∶如图①,当点D ¢落在y 轴上时,点D ¢的坐标为_____,点C '的坐标为______;(2)如图②,当点C '落在OB 上时,求点D ¢的坐标和BD '的长;(3)若M 为C D ''的中点,求BM 的最大值和最小值(直接写出结果即可).(),D为OB中点,B2,23()∴,D1,3()22132OD∴=+=,∵以点O为中心,逆时针旋转由(1)知60AOB ∠=︒,30GD O '∴∠=︒,112OG OD '∴==,D G '()1,3D ∴'-,()2,23B ,∵C ,D 分别为OA ,OB 的中点,此时M 在BO 的延长线上,()2,23B ,()222234OB ∴=+=,742BM OB OM ∴=+=+;即BM 最大值为742+;此时M 在线段OB 上,BM BM ∴最小值为427-;综上所述,BM 最大值为1.(2024·山东济宁·模拟预测)已知,四边形ABCD 是正方形,DEF 绕点D 旋转(DE AB <),90EDF ∠=︒,DE DF =,连接AE CF ,.(1)如图1,求证:ADE CDF ≅ ;(2)直线AE 与CF 相交于点G .①如图2,BM AG ⊥于点M ,⊥BN CF 于点N ,求证:四边形BMGN 是正方形;②如图3,连接BG ,若6AB =,3DE =,直接写出在DEF 旋转的过程中,线段BG 长度的最小值为.【详解】(1)证明: 四边形ABCD 是正方形,AD DC ∴=,90ADC ∠=︒,DE DF = ,90EDF ∠=︒,ADC EDF ∴∠=∠,ADE CDF \Ð=Ð,在ADE V 和CDF 中,DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩,SAS ADE CDF ∴() ≌.(2)解:①证明:如图2中,设AG 与CD 相交于点P ,90ADP ∠=︒ ,90DAP DPA ∴∠+∠=︒,ADE CDF ≅ ,DAE DCF ∴∠=∠,DPA GPC ∠∠= ,90DAE DPA GPC GCP ∠∠∠∠∴+=+=︒,90PGN ∠∴=︒,BM AG ⊥ ,BN GN ⊥,∴四边形BMGN 是矩形,90MBN ∴∠=︒,四边形ABCD 是正方形,AB BC ∴=,90ABC MBN ∠∠==︒,ABM CBN ∴∠=∠,又90AMB BNC ∠∠==︒ ,AMB CNB ∴≅ ,MB NB ∴=,∴矩形BMGN 是正方形;∵DAH BAM ∠+∠=∠∴DAH ABM ∠=∠,又∵AD BA =,DHA ∠∴AMB DHA ≌△△,BM AH ∴=,222AH AD DH =- ,DH ∴最大时,AH 最小,即点(1)若AC AB AD BC >⊥,,当点E 在线段AC 上时,AD BE ,交于点F ,点F 为BE 中点.①如图1,若37BF BD AD ===,,求AE 的长度;②如图2,点G 为线段AF 上一点,连接GE 并延长交BC 的延长线于点H .若点E 为GH 中点,602BAC DAC EBC ∠=︒∠=∠,,求证:12AG DF AB +=.(2)如图3,若360AC AB BAC ︒==∠=,.当点E 在线段AC 的延长线上时,连接DE ,将DCE △沿DC 所在直线翻折至ABC 所在平面内得到DCM △,连接AM ,当AM 取得最小值时,ABC 内存在点K ,使得ABK CAK ∠=∠,当KE 取得最小值时,请直接写出2AK 的值.AD BC EG AD ⊥⊥ ,,90BDF ∴∠=︒,EGF ∠=BDF EGF ∴∠=∠,在Rt BDF △中,90BDF ∠=(22DF BF BD ∴=-=AD BC ⊥ ,90ADC ∴∠=︒,点E 为GH 的中点,GE HE ∴=,在AGE 和KHE △中,12AE KE =⎧⎪∠=∠⎨,由题意可知:160∠=︒,AC 30CAM ∴∠=︒,1322CM AC ∴==,32CE CM ∴==,(1)如图①,在ABC 中,点M ,N 分别是AB ,AC 的中点,若BC =MN 的长为__________.问题探究:(2)如图②,在正方形ABCD 中,6AD =,点E 为AD 上的靠近点A 的三等分点,点F 为AB 上的动点,将AEF △折叠,点A 的对应点为点G ,求CG 的最小值.问题解决:(3)如图③,某地要规划一个五边形艺术中心ABCDE ,已知120ABC ∠=︒,60BCD ∠=︒,40m AB AE ==,80m BC CD ==,点C 处为参观入口,DE 的中点P 处规划为“优秀”作品展台,求点C 与点P 之间的最小距离.∵点E为AD上的靠近点∴11633 AE AD==⨯在Rt EDC中,EC 根据折叠的性质,EG(1)如图1,点D 为ABC 的边BC 上一点,连接2,,3BD AD BDA BAC AB ∠=∠=,若ABD △的面积为4,则ACD 的面积为______;【问题探究】(2)如图2,在矩形ABCD 中,6,5AB BC ==,在射线BC 和射线CD 上分别取点E F 、,使得65BE CF =,连接AE BF 、相交于点P ,连接CP ,求CP 的最小值;【问题解决】(3)如图3,菱形ABCD 是某社区的一块空地,经测量,120AB =米,60ABC ∠=︒.社区管委会计划对该空地进行重新规划利用,在射线AD 上取一点E ,沿BE CE 、修两条小路,并在小路BE 上取点H ,将CH 段铺设成某种具有较高观赏价值的休闲通道(通道宽度忽略不计),根据设计要求,BHC BCE ∠=∠,为了节省铺设成本,要求休闲通道CH 的长度尽可能小,问CH 的长度是否存在最小值?若存在,求出CH 长度的最小值;若不存在,请说明理由.【答案】(1)5;(2)343-;(3)存在,最小值为403米【分析】(1)证明C ABD BA ∽△△,利用相似三角形的性质得到994CBA ABD S S == ,即可得到ACD 的面积;(2)证明ABE BCF ∽△△,进一步得到90APB ∠=︒,则证明点P 在矩形ABCD 内部以AB 为直径的O 上运动,连接,OP OC ,OC 交O 于点P ',进一求出3,34OP OP OB OC '====,则343CP OC OP ''=-=-,由CP OC OP ≥-,即可得到CP 的最小值;(3)证明,CBH EBC ∽得到2BC BE BH =⋅,则2AB BE BH =⋅,再证明,ABH EBA ∽得到120AHB EAB ∠=∠=︒,证明点H 在O 的劣弧 AB 上运动,求得90OBC ∠=︒,进一步求得403OH AO BO ===米,勾股定理可得803OC =米,记OC 与O 相交于点H ',则403OH OH '==米,求出403CH OC OH ''=-=米,由403CH OC OH '≥-=米,即可得到答案.【详解】(1)解:∵,BDA BAC ∠=∠B B ∠=∠,∴C ABD BA ∽△△,∴2439ABDCBA S BD S AB ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ,∴994CBA ABD S S == ,∴ACD 的面积为945CBA ABD S S -=-= ,故答案为:5(2)∵四边形ABCD 是矩形,∴90ABE BCF ∠=∠=︒,∵65BE CF =,6,5AB BC ==,∴65BE AB CF BC ==,∴ABE BCF ∽△△,∴BAE CBF ∠=∠,∵90CBF ABP ∠+∠=︒∴90BAE ABP ∠+∠=︒∴()18090APB BAE ABP ∠=︒-∠+∠=︒∴点P 在矩形ABCD 内部以AB 为直径的O 上运动,则1602BM AM AB ===米,题型二线段和的最小值问题【例1】(2024·四川达州·模拟预测)【问题发现】(1)如图1,在OAB 中,3OB =,若将OAB 绕点O 逆时针旋转120︒得OA B '',连接BB ',则BB '=________.【问题探究】(2)如图2,已知ABC 是边长为BC 为边向外作等边BCD △,P 为ABC 内一点,连接AP BP CP ,,,将BPC △绕点C 逆时针旋转60︒,得DQC △,求PA PB PC ++的最小值;【实际应用】(3)如图3,在长方形ABCD 中,边1020AB AD ==,,P 是BC 边上一动点,Q 为ADP △内的任意一点,是否存在一点P 和一点Q ,使得AQ DQ PQ ++有最小值?若存在,请求出此时PQ 的长,若不存在,请说明理由.在OAB 中,3OB =,将 120BOB '∴∠=︒,OB OB '==OBB OB B ''∴∠=∠,OBB OB B B OB '''∠+∠+∠=PA PB PC PA ∴++=+∴当点D、Q、P、A⊥连接AD,作DE AC∠=∠=︒DCB BCA60本题主要考查了等边三角形的性质与判定,矩形的性质与判定,旋转的性质,勾股定理,含30度角的直角三角形的性质,解题的关键在于利用旋转构造等边三角形,从而把三条不在一条直线的线段之和的问题,转换成几点共线求线段的最值问题是解题的关键.【例2】(2024·贵州毕节·一模)在学习了《图形的平移与旋转》后,数学兴趣小组用一个等边三角形继续进 是边长为2的等边三角形.行探究.已知ABC(1)【动手操作】如图1,若D为线段BC上靠近点B的三等分点,将线段AD绕点A逆时针旋转60︒得到线段AE,连接CE,则CE的长为________;(2)【探究应用】如图2,D 为ABC 内一点,将线段AD 绕点A 逆时针旋转60︒得到线段AE ,连接CE ,若,,B D E 三点共线,求证:EB 平分AEC ∠;(3)【拓展提升】如图3,若D 是线段BC 上的动点,将线段AD 绕点D 顺时针旋转60︒得到线段DE ,连接CE .请求出点D 在运动过程中,DEC 的周长的最小值.(3)由ABD ACE ≌△△,得CE BD =,可得DEC 的周长BC DE =+,而DE AD =,知AD 的最小时,DEC 的周长最小,此时AD BC ⊥,即可求得答案.∵ABD ACE ≌△△,∴CE BD =,∴DEC 的周长DE CE =+∴当点D 在线段BC 上时,∵DEC 为等边三角形,1.(2024·陕西·二模)在平面直角坐标系中,A 为y 轴正半轴上一点,B 为x 轴正半轴上一点,且4OA OB ==,连接AB .(1)如图1,C 为线段AB 上一点,连接OC ,将OC 绕点O 逆时针旋转90︒得到OD ,连接AD ,求AC AD +的值.(2)如图2,当点C 在x 轴上,点D 位于第二象限时,90ADC ∠=︒,且AD CD =,E 为AB 的中点,连接DE ,试探究线段AD DE +是否存在最小值?若存在,求出AD DE +的最小值;若不存在,请说明理由.又90AOB ∠=︒,∴四边形DMON 是矩形,∴90MDN ∠=︒,大值和最小值分别是______和______;(2)如图2,在矩形ABCD 中,4AB =,6AD =,点P 在AD 上,点Q 在BC 上,且AP CQ =,连接CP 、QD ,求PC QD +最小时AP 的长;(3)如图3,在ABCD Y 中,10AB =,20AD =,点D 到AB 的距离为,动点E 、F 在AD 边上运动,始终保持3EF =,在BC 边上有一个直径为BM 的半圆O ,连接AM 与半圆O 交于点N ,连接CE 、FN ,求CE EF FN ++的最小值.如图,当点P 在AO 的延长线上时,此时PA 的最大值为:PO OA +故答案为:11;3;(2)延长BA 至点B ',使AB ∵在矩形ABCD 中,4AB =,∴DAB BAP CBA '∠=∠=∠=∠∴DA 垂直平分BB ',∴PB PB '=,(3)如图,过点F 作FG EC ∥,交BC OG ',NO ,∵在ABCD Y 中,10AB =,20AD =,点∴AD BC ∥,即EF CG ∥,BC AD =∴四边形EFGC 是平行四边形,∴3GC EF ==,FG EC =,【点睛】本题考查圆的基本性质,全等三角形的判定和性质,相似三角形的判定和性质,矩形的性质,平行四边形的判定和性质,对称的性质,勾股定理,三角形三边关系定理,两点之间线段最短等知识点.灵活运用所学知识、弄清题意并作出适当辅助线是解题的关键.3.(2024·陕西西安·三模)【问题提出】(1)如图①,AB 为半圆O 的直径,点P 为半圆O 的 AB 上一点,BC 切半圆O 于点B ,若10AB =,12BC =,则CP 的最小值为;【问题探究】(2)如图②,在矩形ABCD 中,3AB =,5BC =,点P 为矩形ABCD 内一点,连接PB 、PC ,若矩形ABCD 的面积是PBC 面积的3倍,求PB PC +的最小值;【问题解决】(3)如图③,平面图形ABCDEF 为某校园内的一片空地,经测量,AB BC ===60B ∠︒,150BAF BCD ∠=∠=︒,DE DC ⊥,20CD =米,劣弧 EF所对的圆心角为90︒, EF 所在圆的圆心在AF 的延长线上,10AF =米.某天活动课上,九(1)班的同学准备在这块空地上玩游戏,每位同学在游戏开始前,在BC 上选取一点P ,在弧 EF上选取一点Q ,并在点P 和点Q 处各插上一面小旗,从点A 出发,先到点P 处拔下小旗,再到点Q 处拔下小旗,用时最短者获胜.已知晓雯和晓静的跑步速度相同,要使用时最短,则所跑的总路程()AP PQ +应最短,问AP PQ +是否存在最小值?若存在,请你求出AP PQ +的最小值;若不存在,请说明理由.【答案】(1)8;(2)41;(3)AP PQ +存在最小值,最小值为()20310m -.【分析】(1)连接OC 交O 于点1P ,则1CP是CP 的最小值,求出1CP 的长即可,(2)过点P 作PH BC ⊥于点H ,作EF BC ∥,连接BC ',BP C P '+的最小值,即为BC '的长度,求出BC '即可,(3)连接AC ,作点A 关于BC 的对称点A ',连接PA ',A Q ',AA ',过A '作A N ED '⊥,分别交ED 、AC 的延长线于点N 、M ,分别延长AF ,DE 交于点O ,连接OQ ,OA ',当A Q '取得最小值时,AP PQ +的值最小,即A Q ''的长,求出A Q ''即可.解:(1)如图,连接OC 交O 于点1P ,连接OP ,点P 为半圆O 的AB上一点,∴当点P 与点1P 不重合时,CP OC OP >-,当点P 与点1P 重合时,1CP CP OC OP ==-,CP OC OP ∴≥-,CP ∴的最小值OC OP =-,BC 切半圆O 于点B ,90ABC ∴∠=︒,152OB OP AB === ,12BC =,2212513OC ∴=+=,CP ∴的最小值1358OC OP =-=-=,故答案为:8.(2)过P 作PH BC ⊥,如图,矩形ABCD 的面积是13553PBC S ∴=⨯⨯= 2PH ∴=,60ABC ∠=︒ ,AB BC ==ABC ∴ 是等边三角形,60BAC BCA ∴∠=∠=︒,150BAF BCD ∠=∠=︒ ,DE ACD MCD CAO ∴∠=∠=∠=AA M '∴ 和OA N '△都是直角三角形,四边形,E G分别作,,⊥⊥与EF交于点F,连接CF.EF AD FG AB FG特例感知(1)以下结论中正确的序号有______;ED CF BG为边围成的三角形不是直①四边形AGFE是矩形;②矩形ABCD与四边形AGFE位似;③以,,角三角形;类比发现(2)如图2,将图1中的四边形AGFE绕着点A旋转,连接BG,观察CF与BG之间的数量关系和位置关系,并证明你的发现;拓展应用(3)连接CE ,当CE 的长度最大时,①求BG 的长度;②连接,,AC AF CF ,若在ACF △内存在一点P ,使CP AP ++的值最小,求CP AP ++的最小值.∴HF DE =,CH BG =∴CHF 是直角三角形,∵四边形ABCD 是矩形,∴43AB CD ==,AD =∴228AC AB BC =+=,则由(2)知,90CEF ∠=︒,∵2247CF CE EF =+=∴3221BG CF ==;根据旋转,可得30PAF KAL ∠=∠=∴3KL PF =,过P 作PS AK ⊥于S ,则12PS AP =∴32KS AK AS AP =-=,则tan ∠题型三面积的最小值问题【例1】(新考法,拓视野)(2024·陕西西安·一模)【问题提出】(1)如图1,已知在边长为5的等边ABC 中,点D 在边BC 上,3BD =,连接AD ,则ACD 的面积为;【问题探究】(2)如图2,已知在边长为6的正方形ABCD 中,点E 在边BC 上,点F 在边CD 上,且45EAF ∠=︒,若5EF =,求AEF △的面积;【问题解决】(3)如图3是某座城市廷康大道的一部分,因自来水抢修在4AB =米,AD =ABCD 区域内开挖一个AEF △的工作面,其中B 、F 分别在BC CD 、边上(不与B 、C 、D 重合),且60EAF ∠=︒,为了减少对该路段的拥堵影响,要求AEF △面积最小,那么是否存在一个面积最小的AEF △?若存在,请求出AEF △面积的最小值;若不存在,请说明理由.(2)如图所示,延长∵四边形ABCD 是正方形,∴AB AD D =,∠∴ABG ADF ≌∴AG AF DAF =,∠(3)把ADF △绕点A ∴33AG AF FAG =,∠∵60EAF ∠=︒,∴30EAG ∠=︒,本题主要考查了圆周角定理,勾股定理,旋转的性质,解直角三角形,正方形的性质,等边三角形的性质与判定,矩形的性质与判定,全等三角形的性质与判定等等,通过作出辅助线构造直角三角形,全等三角形是解题的关键.【例2】(2024·陕西西安·二模)图形旋转是解决几何问题的一种重要方法.如图1,正方形ABCD 中,E F 、分别在边AB BC 、上,且45EDF ∠=︒,连接EF ,试探究AE CF EF 、、之间的数量关系.解决这个问题可将ADE V 绕点D 逆时针旋转90︒到CDH △的位置(易得出点H 在BC 的延长线上),进一步证明DEF 与DHF △全等,即可解决问题.(1)如图1,正方形ABCD 中,45,3,2EDF AE CF ∠=︒==,则EF =______;(2)如图2,正方形ABCD 中,若30EDF ∠=︒,过点E 作EM BC ∥交DF 于M 点,请计算AE CF +与EM 的比值,写出解答过程;(3)如图3,若60EDF ∠=︒,正方形ABCD 的边长8AB =,试探究DEF 面积的最小值.,,,D F H G 四点共圆;进而可得30FHG ∠=,根据13tan 30AE CF CH CF FH EM GH GH ++====︒,即可求解;(3)过点E 作EK CD ⊥于K ,交DF 于M ,作FT EK ⊥于T ,得出4DEF S EM = ,进而根据(2)的方法得出3EM GH FH ==,根据FC AE CH ==时,面积最小,得出32163OF =-,即可求解.【详解】(1)解:∵将ADE V 绕点D 逆时针旋转90︒,∴90DCH A DCB ∠=∠=︒=∠,DH DE HDC EDA=∠=∠,∴点H 在BC 的延长线上,∵四边形ABCD 是正方形∴90ADC ∠=︒,∵45EDF ∠=︒,∴45HDF CDH FDC ADE FDC EDF∠=∠+∠=∠+∠=︒=∠又∵DF DF =,∴DEF ()SAS DHF ≌,∴235EF FH FC CH FC AE ==+=+=+=,故答案为:5.(2)解:将ADE V ,DEM △绕点D 逆时针旋转90︒,得,DCH DHG∴,AED CHD DEM DHG ∠=∠∠=∠,∵EM BC ∥,则EM AB ⊥,∴90AEM ∠=︒,∴90CHG CHD DHG AED DEM AEM ∠=∠+∠=∠+∠=∠=︒,∵30EDF ∠=︒,EM BC ∥则EM AD ∥,∴ADE CDH ∠=∠,30GDH MDE ∠=∠=︒,∵EM BC ∥,∴EMF DFC ∠=∠,∴180EMD EMF EMD DFC ∠+∠=∠+∠=︒,即180DFC DGH ∠+∠=︒,∴,,,D F H G 四点共圆;∴30GFH GDH ∠=∠=︒,又30FHG ∠=︒∴1tan 30AE CF CH CF FH EM GH GH ++====︒(3)如图,过点E 作EK CD ⊥于K ,交DF 于M ,作FT EK ⊥于T ,90FTK TKC BCD ∠=∠=∠=︒∴四边形CFTK 是矩形,FT CK∴=8DK CK DK FT ∴+=+=111()4222DEF EMD EMF S S S DK EM FT EM DK FH EM ∴=+=⋅+⋅=+= 同(2)将ADE V ,DEM △绕点D 逆时针旋转90︒,得,DCH DHG ,可得60GFH EDM ∠=∠=︒,EM GH=∵2220-+=≥,∴FH x y =+≥当且仅当x y =时取得等于号,此时FC AE CH ==,设,,,D F H G 的圆心为O ,∵DC FH ⊥,FC CH =,∴DC 经过点O ,∴OF OD =,sin 602OC OF OF =︒=∵8OD OC +=即82OF +=解得:32OF =-∴232FH FC OF ===-∴48GH ==-,∴()44448192DEF S EM GH ===-=- ,即DEF 面积的最小为192-.【点睛】本题考查了旋转的性质,正方形的性质、全等三角形的判定与性质、四点共圆等知识,解直角三角形,熟练掌握旋转的性质是解题的关键.1.(2023·陕西西安·一模)问题发现(1)在ABC 中,2AB =,60C ∠=︒,则ABC 面积的最大值为;(2)如图1,在四边形ABCD 中,6AB AD ==,90BCD BAD ∠=∠=︒,8AC =,求BC CD +的值.问题解决(3)有一个直径为60cm 的圆形配件O ,如图2所示.现需在该配件上切割出一个四边形孔洞OABC ,要求60O B ∠=∠=︒,OA OC =,并使切割出的四边形孔洞OABC 的面积尽可能小.试问,是否存在符合要求的面积最小的四边形OABC ?若存在,请求出四边形OABC 面积的最小值及此时OA 的长;若不存在,请说明理由.∴当点C 在C '的位置,即∴C A C B ''=,BD =∴ABC '△是等边三角形,∴2C B AB '==,∴B ADE ∠=∠,BAC ∠∵6AB AD ==,BCD ∠∴180B ADC ∠+∠=︒,∵180ADE ADC ∠+∠=∵60AOC ∠=︒,OA OC =∴将AOB 绕O 点顺时针旋转∴60BOE ∠=︒,OE OB =∴BOE △是等边三角形,∴160302BE OB ==⨯=,(1)如图①,已知ABC 是面积为AD 是BAC ∠的平分线,则AB 的长为______.问题探究:(2)如图②,在ABC 中,90C ∠=︒,AC BC =,4AB =,点D 为AB 的中点,点E ,F 分别在边AC ,BC 上,且90EDF ∠=︒.证明:DE DF =.问题解决:(3)如图③,李叔叔准备在一块空地上修建一个矩形花园ABCD ,然后将其分割种植三种不同的花卉.按照他的分割方案,点P ,Q 分别在AD ,BC 上,连接PQ 、PB 、PC ,60BPC ∠=︒,E 、F 分别在PB 、PC 上,连接QE 、QF ,QE QF =,120EQF ∠=︒,其中四边形PEQF 种植玫瑰,ABP 和PCD 种植郁金香,剩下的区域种植康乃馨,根据实际需要,要求种植玫瑰的四边形PEQF 的面积为2,为了节约成本,矩形花园ABCD 的面积是否存在最小值?若存在,请求出矩形ABCD 的最小面积,若不存在,请说明理由.当PQ BC ⊥时,矩形ABCD 的面积最小,根据2ABCD PEQF S S =四边形四边形,即可求解.【详解】解:(1)∵ABC 是面积为AD 是BAC ∠的平分线,∴12BD CD AB ==设ABC 的边长为a∴2AD a =∴2112224ABC S BC AD a a a =�创=∴24a =解得:4a =,故答案为:4.(2)如图所示,连接CD,∵在ABC 中,90C ∠=︒,AC BC =,4AB =,点D 为AB 的中点,∴CD AD =,90ADC ∠=︒,45A DCF ∠=∠=︒又∵90EDF ∠=︒∴ADE ADC CDE EDF EDC CDF∠=∠-∠=∠-∠=∠在,ADE CDF △△中,45A DCF ADE CDF AD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴ADE CDFV V ≌∴DE DF =;(3)如图所示,∵60BPC ∠=︒,120EQF ∠=︒,∴36060120180PFQ PEQ ∠+∠=︒-︒-︒=︒将QFP △绕点Q 逆时针旋转120︒,得到EQG ,∴,,P E G 三点共线,∴四边形PEQF 的面积等于PQG ,又∵120,PQG PQ GQ ∠=︒=,∴30QPG QGP ∠=∠=︒过点Q 作QN PG ⊥于点N ,则12QN PQ =设PQ b =,则1,22NQ b PN b ==∴2PG PN ==∴21112224PQG S PG NQ b b =⨯=⨯⨯=∵四边形PEQF 的面积为∴16b =,即16PQ =,如图所示,作QM PM ⊥于点M ,∵30EPQ FPQ ∠=∠=︒,QM PM ⊥,QN PG ⊥,则QN QM =,在,ENQ FMQ 中,QN QM EQ FQ=⎧⎨=⎩∴()HL ENQ FMQ ≌,同理可得PNQ PMQ≌则2PNQPEQF S S = 四边形∴PEQF PNQM S S =四边形四边形,作点Q 关于PE 的对称点T ,连接PT ,则PTQ 是等边三角形,则PTQ S = ,如图所示,依题意,当PQ BC ⊥时,矩形ABCD 的面积最小,此时,E F 与,N M 重合,,∴22128ABCD PEQF S S ==⨯四边形四边形∴矩形ABCD 的最小面积为2【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质与判定,等腰三角形的性质与判定,勾股定理,旋转的性质,综合运用以上知识是解题的关键.3.(2024·陕西榆林·二模)(1)如图1,AB CD ∥,1,2AB CD ==,AD ,BC 交于点E ,若4=AD ,则AE =;(2)如图2,矩形ABCD 内接于O ,2,AB BC ==,点P 在 AD 上运动,求PBC 的面积的最大值;(3)为了提高居民的生活品质,市政部门计划把一块边长为120米的正方形荒地ABCD (如图3)改造成一个户外休闲区,计划在边AD ,BC 上分别取点P ,Q ,修建一条笔直的通道PQ ,要求2CQ AP =,过点B 作BE PQ ⊥于点E ,在点E 处修建一个应急处理中心,再修建三条笔直的道路BE CE DE ,,,并计划在CDE 内种植花卉,DEP 内修建老年活动区,BCE 内修建休息区,在四边形ABEP 内修建儿童游乐园.问种植花卉的CDE 的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.∵四边形ABCD 是矩形,90ABC ∴∠=︒,AC ∴是O 的直径.在Rt ABC △中,tan BC BAC AB∠=60BPC BAC ∴∠=∠=︒过点O 作OE BC ⊥,垂足为E ,延长连接P B P C ₂,₂,此时P BC ₂的面积最大.理由:在 AD 上任意另取一点P。
专题05 解析几何中的最值问题 (解析版)

专题05 解析几何中的最值问题常见考点考点一 面积最值问题典例1.已知椭圆C ∶22221(0)x y a b a b+=>>经过点P32),O 为坐标原点,若直线l 与椭圆C交于A ,B 两点,线段AB 的中点为M ,直线l 与直线OM 的斜率乘积为-14. (1)求椭圆C 的标准方程;(2)若OM =AOB 面积的最大值.【答案】(1)221123x y +=(2)3 【解析】 【分析】(1)根据椭圆经过点P32),得到223914a b+=,再利用点差法,根据直线l 与直线OM 的斜率乘积为-14,得到 2214b a -=-求解;(2)当AB x ⊥轴时,易得12AOBSOM AB =⋅AB 与x 轴不垂直时,设直线AB 的方程为y kx t =+,联立221123x y y kx t ⎧+=⎪⎨⎪=+⎩,根据OM =k ,t 的关系,再求得AB 和点O 到直线AB 的距离为d ,由12AOB S AB d =⋅⋅求解.(1)解:因为椭圆经过点P32), 所以223914a b +=, 设()()1122,,,A x y B x y ,因为直线l 与椭圆C 交于A ,B 两点,所以22112222222211x y a b x y ab ⎧+=⎪⎪⎨⎪+=⎪⎩,两式相减得2121221212y y x x b x x a y y -+=-⋅-+,因为线段AB 的中点为M ,且直线l 与直线OM 的斜率乘积为-14,所以 2214b a -=-,解得223,12b a ==,所以椭圆方程为:221123x y +=;(2)当AB x ⊥轴时,点M 在x 轴上,且OM AB ⊥,由OM =3AB =,所以12AOBSOM AB =⋅ 当直线AB 与x 轴不垂直时,设直线AB 的方程为y kx t =+,由221123x y y kx t ⎧+=⎪⎨⎪=+⎩,消去y 得()2221484120k x ktx t +++-=, 则21212228412,1414kt t x x x x k k -+=-⋅=++,224,1414kt t M k k ⎛⎫- ⎪++⎝⎭,由OM =()2222314116k t k +=+,因为AB =点O 到直线AB 的距离为d =所以12AOBSAB d =⋅⋅=3≤=,当且仅当221214k k =+,即218k =时,等号成立,综上 AOB 面积的最大值是3.变式1-1.已知椭圆221221x y C a b+=:的焦距为2,且过点(P .若直线AB 为椭圆1C 与抛物线2C :22(0)y px p =>的公切线.其中点,A B 分别为1C ,2C 上的切点.(1)求椭圆1C 的标准方程:(2)求OAB 面积的最小值.【答案】(1)2212x y +=;(2)2. 【解析】 【分析】(1)根据给定条件,列出关于22,a b 的方程,求解作答.(2)设出直线AB 的方程,分别与抛物线2C ,椭圆1C 的方程联立,求出切点纵坐标,再求出面积的函数关系,借助均值不等式计算作答. (1)椭圆半焦距c ,依题意,1c =,221112a b+=,又2221a b c -==,解得22a =,21b =, 所以椭圆1C 的标准方程为:2212x y +=. (2)显然直线AB 不垂直于坐标轴,设直线AB 的方程为(0)x my t m =+≠,()11,A x y ,()22,B x y ,由22y px x my t⎧=⎨=+⎩消去x 并整理得:2220y pmy pt --=, 则22480p m pt ∆=+=,即22t p m =-,22ty pm m==-, 由2222x y x my t⎧+=⎨=+⎩ 消去x 并整理得:()2222220m y mty t +++-=, 则()()222244220m t m t '∆=-+-=,即222t m =+,1222mt mt my m t t --===-+,点O 到直线AB 的距离为d =∴1211222OABm tS AB d y y t t m =⋅=-=⋅-+221212414(||)2222||t m m m m m m m +=-+=-+=+≥=, 当且仅当4||||m m =,即2m =±时取“=”, 所以OAB 面积的最小值为2.变式1-2.已知曲线C 上任一点到点()3,0F 的距离等于该点到直线3x =-的距离.经过点()3,0F 的直线l 与曲线C 交于A 、B 两点. (1)求曲线C 的方程;(2)若曲线C 在点A 、B 处的切线交于点P ,求PAB △面积的最小值. 【答案】(1)212y x = (2)36 【解析】 【分析】(1)分析可知曲线C 是以点()3,0F 为焦点,以直线3x =-为准线的抛物线,由此可求得曲线C 的方程;(2)先证明结论:抛物线212y x =在其上一点()00,Q x y 上一点的切线方程为()006y y x x =+,设直线l 的方程为3x ty =+,设点()11,A x y 、()22,B x y ,将直线l 的方程与抛物线C 的方程联立,列出韦达定理,求出AB ,写出抛物线C 在A 、B 两点处的切线方程,求出点P 的坐标,进而求出点P 到直线l 的距离,利用三角形的面积公式结合二次函数的性质可求得PAB △面积的最小值. (1)解:由题意可知,曲线C 是以点()3,0F 为焦点,以直线3x =-为准线的抛物线,设抛物线C 的标准方程为()220y px p =>,则32p ,可得6p ,因此,曲线C 的方程为212y x =. (2)解:先证明结论:抛物线212y x =在其上一点()00,Q x y 上一点的切线方程为()006y y x x =+, 由题意可得20012y x =,联立()002612y y x x y x⎧=+⎨=⎩,可得()200x x -=,解得0x x =,因此,抛物线212y x =在其上一点()00,Q x y 上一点的切线方程为()006y y x x =+. 若直线l 与x 轴重合,则直线l 与抛物线C 只有一个交点,不合乎题意. 设直线l 的方程为3x ty =+,设点()11,A x y 、()22,B x y ,联立2312x ty y x=+⎧⎨=⎩,可得212360y ty --=,21441440t ∆=+>,由韦达定理可得1212y y t +=,1236y y =-,()2121AB t ==+,抛物线212y x =在点A 处的切线方程为()2111662y y y x x x =+=+,同理可知抛物线212y x =在点A 处的切线方程为22262y y y x =+,联立2112226262y y y x y y y x ⎧=+⎪⎪⎨⎪=+⎪⎩,解得121231262y y x y y y t ⎧==-⎪⎪⎨+⎪==⎪⎩,即点()3,6P t -, 点P 到直线l 的距离为261t d +==所以,()3221361362PABS AB d t =⋅=+≥△,当且仅当0=t 时,等号成立. 因此,PAB △面积的最小值为36. 【点睛】方法点睛:圆锥曲线中的最值问题解决方法一般分两种:一是几何法,特别是用圆锥曲线的定义和平面几何的有关结论来求最值;二是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用基本不等式、函数的单调性或三角函数的有界性等求最值.变式1-3.已知椭圆E :22221(0)x y a b a b +=>>,且过点⎛- ⎝⎭. (1)求E 的方程;(2)若()3,0M ,O 为坐标原点,点P 是E 上位于第一象限的一点,线段PM 的垂直平分线交y 轴于点N ,求四边形OPMN 面积的最小值.【答案】(1)22162x y +=(2)【解析】 【分析】(1)根据椭圆的离心率以及椭圆上的点,列出方程组,解得a.b ,可得答案.(2)设P 点坐标,表示出直线PM 的斜率,进而可得其中垂线方程,求得N 点坐标,从而表示出四边形OPMN 的面积,结合基本不等式,即可求得答案. (1)设E 的焦距为2c,则()222222211c a a b a b c ⎧=⎪⎪⎪⎪-⎪⎝⎭+=⎨⎪-=⎪⎪⎪⎪⎩,解得2a b c ⎧=⎪⎪=⎨⎪=⎪⎩所以E 的方程是22162x y +=.(2)由题意,设()(000,0P x y y <,线段MP 的中点为A ,则点A 的坐标为003,22x y+⎛⎫⎪⎝⎭,且直线MP 的斜率003PM y k x =-,故直线AN 的斜率为0031AN PM x k k y -=-=, 从而直线AN 的方程为00003322y x x y x y -+⎛⎫-=- ⎪⎝⎭, 又2200162x y +=,则220063x y =-, 令0x =,得2200092x y y y +-=,化简得200230,2y N y ⎛⎫-- ⎪⎝⎭,所以四边形OPMN 的面积2000231133222OPMN OMNOPMy S SSy y --=+=⨯⨯+⨯⨯200023322y y y ⎛⎫+=+ ⎪⎝⎭003332222y y ⎛⎫=+≥⨯= ⎪⎝⎭当且仅当0y =所以四边形OPMN面积的最小值为考点二 其他最值问题典例2.如图,已知椭圆C :22212x y a +=的左、右焦点为1F 、2F ,左、右顶点分别为1A 、2A ,离心率e =M 为椭圆C 上动点,直线1A M 交y 轴正半轴于点A ,直线2A M 交y 轴正半轴于点B (当M 为椭圆短轴上端点时,A ,B ,M 重合).(1)求椭圆C 的方程;(2)若3OA OB =,求直线MA 的方程;(3)设直线2MA 、2AA 的斜率分别为1k 、2k ,求12k k +的最大值.【答案】(1)22142x y +=(2)y =(3)【解析】 【分析】(1)根据离心率可求a ,从而可得椭圆方程.(2)设()00,M x y ,则可以用M 的坐标表示,A B ,再根据3OA OB =可求0x ,从而可求M 的坐标,故可求直线MA 的方程.(3)结合(2)可得12k k +,利用M 在椭圆上可化简前者,利用其纵坐标的范围可求最大值. (1)因为椭圆的离心率为e =c a =即22212a a -=,故24a =,所以椭圆的方程为:22142x y +=.设()00,M x y ,因为直线1A M 交y 轴正半轴于点A ,则02x ≠±,00y >,又()00:22y AM y x x =++,故0020,2y A x ⎛⎫⎪+⎝⎭,()00:22y MM y x x =--,故0020,2y B x ⎛⎫- ⎪-⎝⎭, 因为3OA OB =,故000022322yyx x =-⨯+-,所以01x =-,所以0y =故()2:212AM y x x =+=-+y =. (3)由(2)可得0102y k x =-,而0020202022y x y k x -+==--+, 故00002200000124422242y y y y k y k x x x y =-==-=--+-+,因为00y <2y -≤12k k +的最大值为 变式2-1.已知曲线C 上任意一点(),P x y2=,(1)求曲线C 的方程;(2)若直线l 与曲线C 在y 轴左、右两侧的交点分别是,Q P ,且0OP OQ ⋅=,求22||OP OQ +的最小值.【答案】(1)2212y x -=(2)8 【解析】 【分析】(1)根据双曲线的定义即可得出答案;(2)可设直线OP 的方程为()0y kx k =≠,则直线OQ 的方程为1=-y x k ,由2212y x y kx⎧-=⎪⎨⎪=⎩,求得2OP ,同理求得2OQ ,从而可求得2211||||OP OQ +的值,再结合基本不等式即可得出答案. (1)解:设())12,F F ,2=,等价于12122PF PF F F -=<,∴曲线C 为以12,F F 为焦点的双曲线,且实轴长为2,焦距为故曲线C 的方程为:2212y x -=;(2)解:由题意可得直线OP 的斜率存在且不为0,可设直线OP 的方程为()0y kx k =≠,则直线OQ 的方程为1=-y x k ,由2212y x y kx ⎧-=⎪⎨⎪=⎩,得222222222x k k y k ⎧=⎪⎪-⎨⎪=⎪-⎩, 所以()2222221||2k OP x y k+=+=-,同理可得,()2222212121||1212k k OQ k k⎛⎫+ ⎪+⎝⎭==--, 所以()()()22222222211111||||22121k k k OP OQ k k -+-++===++,()()22222222112222228||||OQ OP OP OQ OP OQOP OQ OP OQ ⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥+=++=++≥+= ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 当且仅当2OP OQ ==时取等号,所以当2OP OQ ==时,22||OP OQ +取得最小值8.变式2-2.已知椭圆2222:1(0)x y C a b a b +=>>过点(0,1)P,椭圆上的任意一点到焦点距离的最小值为2(1)求椭圆C 的方程;(2)设不过点P 的直线l 与椭圆相交于,A B 两点,若直线PA 与直线PB 斜率之和为1-,求点P 到直线l 距离的最大值.【答案】(1)2214x y +=(2)【解析】【分析】(1)根据题意可得21b =且2a c -=a ,b ,c 之间的关系,解得a ,c ,b ,即可得出答案. (2)当直线l 垂直于y 轴时,直线PA 与直线PB 的斜率和为0,不符合题意,设直线l 的方程为x my n =+,则111PA y k x -=,221PB y k x -=,联立直线l 与椭圆C 的方程,可得244181()10n m y y m n x m n x---+⋅+=++,PA k ,PB k 是该二次方程的两根,利用韦达定理结合条件可得到21PA PB k k n m+=-=--,即可得出答案. (1)因为椭圆过点(0,1)P,椭圆上的任意一点到焦点距离的最小值为2, 所以21b =且2a c -= 又22221a b c c =+=+, 解得2a =,c =所以椭圆的方程为2214x y +=.(2)当直线l 垂直于y 轴时,直线PA 与直线PB 的斜率和为0,不符合题意, 故设直线l 的方程为x my n =+, 由于直线l 不过点(0,1)P ,故0m n +≠, 设1(A x ,1)y ,2(B x ,2)y ,10x ≠,20x ≠, 则111PA y k x -=,221PB y k x -=, 直线l 的方程可改写为(1)1x m y m n m n--=++, 椭圆C 的方程可改写为224(1)8(1)0x y y +-+-=, 两者联立,可得22(1)4(1)8(1)[]0x m y x y y m n m n-+-+-⋅-=++, 0x ≠时,整理可得244181()10n m y y m n x m n x---+⋅+=++①, 若n m =,则直线l 与椭圆C 的一个交点为(0,1)-, 此时直线PA 的斜率不存在,不符合题意, 故n m ≠,且PA k ,PB k 是以上二次方程①的两根, 由韦达定理有21PA PB k k n m+=-=--,于是2n m =+,直线l 的方程为2x my m =++,所以直线l 经过定点(2,1)-,则当点P 与该定点的连线与l 垂直时,点P 到直线l 距离的最大,最大值.. 【点睛】本题考查椭圆的方程,直线与椭圆的相交问题,解答时要注意便是德技巧,解题中需要一定的计算能力,属于较难题.变式2-3.已知点()0,2R -,()0,2Q ,双曲线C 上除顶点外任一点(),M x y 满足直线RM 与QM 的斜率之积为4. (1)求C 的方程;(2)若直线l 过C 上的一点P ,且与C 的渐近线相交于A ,B 两点,点A ,B 分别位于第一、第二象限,2AP PB =,求AP PB ⋅的最小值.【答案】(1)2214y x -=(2)1 【解析】 【分析】 (1)由题意得224+-⋅=y y x x,化简可得答案, (2)求出渐近线方程,设点()00,P x y ,()11,2A x x ,()22,2B x x -,1>0x ,20x <,由2AP PB =可得12023x x x +=,120243-=x x y 代入双曲线方程化简可得1298⋅=-x x ,然后表示AP PB ,的坐标,再进行数量积运算,化简后利用基本不等式可得答案 (1)由题意得224+-⋅=y y x x ,即2244-=y x, 整理得2214y x -=,因为双曲线的顶点坐标满足上式,所以C 的方程为2214y x -=.(2)由(1)可知,曲线C 的渐近线方程为2y x =±, 设点()00,P x y ,()11,2A x x ,()22,2B x x -,1>0x ,20x <, 由2AP PB =,得()()01012020,22,2--=---x x y x x x x y , 整理得12023x x x +=,120243-=x x y ①,把①代入220014y x -=,整理得1298⋅=-x x ②, 因为()121201012244,2,33-+--⎛⎫=--=⎪⎝⎭x x x x AP x x y x , ()2121202022,2,33---⎛⎫=---= ⎪⎝⎭x x x x PB x x x y , 所以()22121211010129⋅=++⋅AP PB x x x x .由1298=-x x ,得1298=-x x , 则()22221212221199192710101210101210219988982⎡⎤⎛⎫⎛⎫⎢⎥⋅=++⋅=-+-⨯≥⨯⨯-= ⎪⎪⎝⎭⎢⎥⎝⎭⎣⎦AP PB x x x x x x ,当且仅当24x =-时等号成立,所以AP PB ⋅的最小值是1.巩固练习练习一 面积最值问题1.点P 与定点()1,0F 的距离和它到定直线:4l x =的距离之比为1:2. (1)求点P 的轨迹方程;(2)记点P 的轨迹为曲线C ,直线l 与x 轴的交点M ,直线PF 与曲线C 的另一个交点为Q .求四边形OPMQ 面积的最大值.(O 为坐标原点)【答案】(1)22143x y +=(2)6 【解析】 【分析】(1)设出点(),P x y ,直接法求出轨迹方程;(2)求出4OM =,设出直线方程,表达出四边形OPMQ 面积,使用换元及基本不等式求出面积最大值. (1)设点(),P x y ,则PF =P 到直线:4l x =的距离为4x -,12=,解得:22143x y +=.(2)由题意得:()4,0M ,则4OM =,设当直线l 斜率为0时,即0y =,此时四边形OPMQ 不存在,故舍去;设直线l 为1x ky =+,与22143x y +=联立得:()2234690k y ky ++-=,设()()1122,,,P x y Q x y ,则由韦达定理得:122634k y y k -+=+,122934y y k-=+,则12y y -==, 四边形OPMQ面积1211422S OM y y =⋅-=⨯=,t =()1t ≥,则221k t =-,224241313t S t t t==++,其中13y t t =+在[)1,t ∈+∞上单调递增,故当1t =时,13y t t=+取得最小值为4,此时面积S 取得最大值6 【点睛】求解轨迹方程通常方法有:直接法,定义法,相关点法,交轨法,本题中使用的是直接法.2.设椭圆E :22143x y +=的右焦点为F ,点A ,B ,P 在椭圆E 上,点M 是线段AB 的中点,点F是线段MP 中点(1)若M 为坐标原点,且△ABP 的面积为3,求直线AB 的方程; (2)求△ABP 面积的最大值. 【答案】(1)32y x =或32y x =- (2)【解析】 【分析】(1)分斜率存在和不存在讨论,当斜率存在时设直线方程与椭圆方程联立消元,利用弦长公式和点到直线的距离公式表示出面积,根据已知列方程可解;(2)分直线过原点和不过原点,当不过原点时设直线方程与椭圆方程联立消元,利用韦达定理表示出M 坐标,再由中点坐标公式得P 点坐标,代入椭圆方程可得k 和b 的关系,然后利用弦长公式和点到直线的距离公式表示出面积(注意2ABPABFS S=),然后用导数求最值.(1)在椭圆22143x y +=中,2,1a b c ===,此时点P 坐标为(2,0),当直线AB的斜率不存在时,易知AB =122ABPS=⨯=,不满足题意.故设直线方程为y kx =,代入椭圆方程得22234120x k x +-=,即22(43)120k x +-=,由弦长公式得AB =P 到直线AB 的距3=,解得32k =±,所以直线AB 的方程为32y x =或32y x =-.(2)由(1)知,当直线过原点且斜率存在时,ABPS==故此时面积最大值为ABP S =△当直线不过原点时,易知直线斜率一定存在,设方程为y kx m =+,代入椭圆方程整理可得()2224384120k x kmx m +++-=…①,记112200(,),(,),(,)A x y B x y M x y ,则21212228412,4343km m x x x x k k -+=-=++,002243,4343km mx y k k =-=++,00(2,)P x y -- 则22003(2)412x y -+=,将002243,4343km m x y k k =-=++代入上式得222243324124343km m k k ⎛⎫⎛⎫++= ⎪ ⎪++⎝⎭⎝⎭,整理得4m k =-,代入①得2222(43)3264120k x k x k +-+-=,又点F 到直线AB,则ABPSAB k ===+ABPS=2t k =,2(14)()(43)t t g t t -=+,则()()332843t g t t -=+',易知当3028t <<时,()0g t '>,函数单调递增,当328t >时,()0g t '<,函数单调递减,故当328t =时,max 31()()28192g t g ==,所以ABPS≤=又直线与椭圆有两个交点,所以422644(43)(6412)0k k k ∆=-+⨯->,解得214k <,故当2328k =,即k =ABP综上,△ABP 面积的最大值为【点睛】设而不求是圆锥曲线中最常用的方法之一,本题通过各点之间的关系,结合韦达定理表示出M 坐标,进而得到点P 坐标,借助P 点在椭圆上作为突破口进行求解,考察学生的转化能力和运算能力,属难题.3.设椭圆()2222:10x y E a b a b+=>>,点1F ,2F 为E 的左、右焦点,椭圆的离心率12e =,点31,2P ⎛⎫ ⎪⎝⎭在椭圆E 上.(1)求椭圆E 的方程;(2)M 是直线4x =上任意一点,过M 作椭圆E 的两条切线MA ,MB ,(A ,B 为切点). ①求证:2⊥MF AB ; ②求MAB △面积的最小值.【答案】(1)22143x y +=;(2)①证明见解析;②92. 【解析】【分析】(1)由题得222222123121c a a b a b c ⎧=⎪⎪⎪⎛⎫⎪⎪⎪⎝⎭+=⎨⎪=+⎪⎪⎪⎪⎩,即得;(2)由题可得在点(),A A A x y ,(),B B B x y 处的切线方程,进而可得直线AB 方程,再利用斜率关系即证,联立直线AB 方程,与椭圆方程,利用韦达定理可得(222291212MAB t S AB MF t +=⋅⋅=+△,再通过换元,利用函数的性质可求. (1)由题可得,222222123121c a a b a b c ⎧=⎪⎪⎪⎛⎫⎪⎪⎪⎝⎭+=⎨⎪=+⎪⎪⎪⎪⎩,解得224,3,a b ⎧=⎨=⎩ ∴椭圆E 的标准方程为22143x y +=.(2)①先求在椭圆上一点的切线方程,设椭圆上一点为()x y x y ≠≠0000,,0,0,切线方程为()00y y k x x -=-,联立方程组()0022143y y k x x x y ⎧-=-⎪⎨+=⎪⎩,可得()()()22200003484120k x k y kx x y kx ++-+--=,∴()()()222000084344120k y kx k y kx ⎡⎤⎡⎤∆=--⨯+--=⎣⎦⎣⎦,∴()()22200004230x k kx y y -++-=,即2220000432034y x k kx y ++=,∴034x k y =-, 故切线方程为()000034x y y x x y -=--,即00143x x y y +=, 设(),A A A x y ,(),B B B x y ,()4,M t . 椭圆E 在点(),A A A x y 的切线AM 的方程为:143A A x x y y+=, 在点(),B B B x y 处的切线BM 方程为:143B B x x y y +=. 又直线AM ,BM 过点()4,M t ,即41434143A A B B x ty x ty ⎧+=⎪⎪⎨⎪+=⎪⎩,即3333A A B B x ty x ty +=⎧⎨+=⎩,故点(),A A A x y ,(),B B B x y ,在直线33x ty +=上,故直线AB 方程为:33x ty +=, 当0=t ,即()4,0M 时,直线AB 方程为:1x =,则2⊥MF AB . 当0t ≠时,直线AB 方程为:33y x t t=-+.右焦点()21,0F ,则23MF t k =,所以2313MF AB t k k t ⎛⎫⋅=⋅-=- ⎪⎝⎭,即2⊥MF AB .②直线AB 方程为:33x ty +=与椭圆E 联立得;()22126270t y ty +--=,2612A B t y y t +=+,22712A By y t -=+,(222291212MABt S AB MF t +=⋅⋅==+△令m =3m ≥,则(23223292213123MABt m S t m m m +===+++△在[)3,m ∈+∞上单调递增,所以当3m =时,MAB S 取最小值92.4.已知抛物线2:4C y x =的焦点为F ,过点F 的直线l 与抛物线C 交于,A B 两点. (1)证明:以AB 为直径的圆与直线1x =-相切;(2)设(1)中的切点为,P O 为坐标原点,直线OP 与C 的另一个交点为E ,求ABE △面积的最小值. 【答案】(1)证明见解析 (2)【解析】 【分析】(1)利用直线与圆相切等价于圆心到直线的距离等于半径来证明;(2)先设直线AB 的方程为1x my =+,以m 为参数表示出点P 以及点E 的坐标,进而求出E 点到直线的距离,即为ABE △的高,最后把ABE △的面积表示成m 的函数,求其最值. (1)证明:抛物线24y x =的焦点为()1,0F ,准线方程为1x =-. 设()()()()()11221212,,,,112A x y B x y AB AF BF x x x x =+=+++=++, 弦AB 的中点1212,22x x y y M ++⎛⎫⎪⎝⎭, 则M 到准线1x =-的距离为()121211222AB x x x x++--=+=, 所以以AB 为直径的圆与直线1x =-相切. (2)解:由题可知直线l 的斜率不能为0,设直线l 的方程为1x my =+,由21,4x my y x=+⎧⎨=⎩整理得2440y my --=, 又()()1122,,,A x y B x y , 则12124,4y y m y y +==-,所以2AB =()()21212444x x m y y m ++=++=+.点P 的坐标为()1,2m -,于是直线OP 的方程为2y mx =-, 代入24y x =,整理得0x =或21x m =, 从而212,E mm ⎛⎫-⎪⎝⎭ 则点E 到直线AB211+=故()()32221442ABESm m =+=.[),1,t t ∈+∞,()()()()223222232,11t t t f t f t t t -=--'= 则()f t在⎡⎣上单调递减,在)+∞上单调递增,故min ()f t f ==练习二 其他最值问题5.已知抛物线()2:20E x py p =>的焦点为F ,直线4x =分别与x 轴交于点P ,与抛物线E 交于点Q ,且54QF PQ =.(1)求抛物线E 的方程;(2)如图,设点,,A B C 都在抛物线E 上,若ABC 是以AC 为斜边的等腰直角三角形,求AB AC ⋅的最小值.【答案】(1)24x y = (2)32 【解析】 【分析】(1)设()04,Q y ,列方程组000216524py p y y =⎧⎪⎨+=⎪⎩,求出2p =,即可得到抛物线E 的方程;(2)设点()222312123123,,,,,444x x x A x B x C x x x x ⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,利用ABC 是以AC 为斜边的等腰直角三角形,表示出()()32211k x k k --+,用坐标表示出AB AC =()()32221611k k k ++利用基本不等式求出AB AC 的最小值.(1)设点()04,Q y ,由已知000216524py p y y =⎧⎪⎨+=⎪⎩,则8102p p p +=,即24p =. 因为0p >,则2p =,所以抛物线E 的方程是24x y =. (2)设点()222312123123,,,,,444x x x A x B x C x x x x ⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,直线AB 的斜率为()0k k >,因为AB BC ⊥,则直线BC 的斜率为1k-. 因为AB BC =,则212232111x x k x x k -+=-+,得()2312x x k x x -=-,① 因为22121212444x x x x k x x -+==-,则124x x k +=,即124x k x =-,②因为223223231444x x x x k x x -+-==-,则234x x k +=-,即324x x k=--③将②③代入①,得()2242420x k k x k +--=,即()()322212120k k x k k k-+---=,则()()32211k x k k -=+, 所以()()()()22222122··cos 451421AB AC AB AC AB x x k k x k ︒===-+=-+ ()()()()()2332222411614111k k k k k k k k ⎡⎤-+⎢⎥=-+=++⎢⎥⎣⎦因为212k k +≥,则()22214k k +≥,又()22112k k ++≥,则()()3222121k k k +≥+,从而()()3222121k k k +≥+,当且仅当1k =时取等号,所以AB AC 的最小值为32.6.已知双曲线C :()222210,0x y a b a b-=>>的左右顶点分别为()1,0A -,()10B ,,两条准线之间的距离为1.(1)求双曲线C 的标准方程;(2)若点P 为右准线上一点,直线P A 与C 交于A ,M ,直线PB 与C 交于B ,N ,求点B 到直线MN 的距离的最大值.【答案】(1)2213y x -=(2)1【解析】【分析】(1)求得双曲线C 的的,a b ,即可求得双曲线C 的标准方程;(2)以设而不求的方法先判定直线MN 过定点,再去求点B 到直线MN 的距离的最大值.(1)由题意得1a =.设双曲线C 的焦距为2c ,则221a c⨯=,所以2c =.所以b所以双曲线C 的标准方程2213y x -=. (2) 设1,2P t ⎛⎫ ⎪⎝⎭,则直线P A 的方程为:()213t y x =+. 由()2213213y x t y x ⎧-=⎪⎪⎨⎪=+⎪⎩,得()222242784270t x t x t -+++=.因为直线P A 与C 交于A ,M ,所以24270t -≠,所以t ≠. 因为22427427A M M t x x x t +=-=-,所以22427427M t x t +=--, ()22222427361133427427M M t t t t y x t t ⎛⎫+-=+=-+= ⎪--⎝⎭, 所以22242736,427427t t M t t ⎛⎫+-- ⎪--⎝⎭. 因为直线PB 的方程为()21y t x =--,由()221321y x y t x ⎧-=⎪⎨⎪=--⎩,得()2222438430t x t x t --++=.因为直线PB 与C 交于B ,N ,所以2430t -≠,所以t ≠ 因为224343B N N t x x x t +==-,所以224343N t x t +=-, ()222431*********N N t t y t x t t t ⎛⎫+-=--=--= ⎪--⎝⎭,所以2224312,4343t t N t t ⎛⎫+- ⎪--⎝⎭. 所以当32t ≠±时,直线MN 的方程为222222222123612434342743427434343427t t t t t t y x t t t t t t -+⎛⎫+--+=- ⎪++--⎝⎭+--. 令0y =,得()()22422222222221243649610821236434274443431327438843427t t t t x t t t t t t t t t t t t ++-=⨯+==--+++--+-+---. 所以直线MN 过定点()2,0D . 当32t =±时,222242743242743t t t t ++-==--,所以直线MN 过定点()2,0D . 所以当BD MN ⊥时,点B 到直线MN 的距离取得最大值为1.7.如图,已知点()2,2P 是焦点为F 的抛物线()2:20C y px p =<上一点,A ,B 是抛物线C 上异于P 的两点,且直线P A ,PB 的倾斜角互补,若直线P A 的斜率为()1k k <.(1)求抛物线方程;(2)证明:直线AB 的斜率为定值并求出此定值;(3)令焦点F 到直线AB 的距离d ,求d d FA FB -的最大值.【答案】(1)22y x =(2)证明见解析,12-【解析】【分析】(1)待定系数法求解抛物线方程;(2)设出直线方程,联立后得到A 点纵坐标,同理得到B 点纵坐标,从而求出直线AB 的斜率;(3)在前两问基础上用斜率k表达出2454516k d d k FA FB k k --=⎛⎫-+ ⎪⎝⎭,换元后使用基本不等式求出最大值.(1)将点()2,2P 代入抛物线方程可得:1p =,抛物线2:2C y x =(2)设()():221-=->PA y k x k ,与抛物线方程联立可得:22440-+-=ky y k ,∴4422--=⇒=A P A k k y y y k k ,用k -代k 可得:22+=-B k y k因此,2221222A B A B AB A B A B A B y y y y k y y x x y y --===--+-=,即12AB k =-. (3) 由(1)可知,12AB k =-,()222122,⎛⎫-- ⎪ ⎪⎝⎭k k A k k ,()222122,⎛⎫+-+ ⎪ ⎪⎝⎭k k B k k 因此()22222122122:202⎛⎫----=--⇒+-= ⎪ ⎪⎝⎭k k k AB y x x y k k k 1,02F ⎛⎫ ⎪⎝⎭到直线AB的距离2==d . 11d d d FA FB FA FB ⎛⎫-=- ⎪ ⎪⎝⎭∵()342113211112524162422B A B A A B A B A B FB FA x x x x k FA FB FA FB k k x x x x x x ----====⋅-+⎛⎫⎛⎫++++⋅+ ⎪ ⎪⎝⎭⎝⎭∴()22342425432252416252416k k d d k FA FB k k k k --==-+-+22244551642524516--==⎛⎫-+-+ ⎪⎝⎭k k k k k k k k ,令45=-t k k,由1k >得1t >∴211616d d tFA FB t tt-=≤=++当且仅当4454=⇒-=⇒=t k kk.d dFA FB-【点睛】求解抛物线取值范围问题,把要求解的问题转化为单元问题,常使用的工具有换元,基本不等式,或导函数.8.已知抛物线()2:20C y px p=>的焦点为F,A,B是该抛物线上不重合的两个动点,O为坐标原点,当A点的横坐标为4时,3cos5OFA∠=-.(1)求抛物线C的方程;(2)以AB为直径的圆经过点()1,2P,点A,B都不与点P重合,求AF BF+的最小值.【答案】(1)24y x=;(2)11.【解析】【分析】(1)作出辅助线,利用焦半径与余弦值求出p的值,进而求出抛物线方程;(2)设出直线方程,与抛物线方程联立,根据PA PB⊥得到等量关系,求出25n m=+,从而表达出212124112AF BF x x m⎛⎫+=++=++⎪⎝⎭,求出最小值.(1)设()04,A y,因为3cos05OFA∠=-<,所以42p>,42pAF=+,过点A作AD⊥x轴于点D,则42pDF=-,432cos542pDFDFApAF-∠===+,解得:2p=,所以抛物线方程为24y x=.(2)设直线AB 为x my n =+,()()1122,,,A x y B x y ,由方程x my n =+与24y x =联立得:2440y my n --=,所以()24160m n ∆=-+>,即20m n +>,且124y y m +=,124y y n =-,所以()21212242x x m y y n m n +=++=+,222121216y y x x n ⋅==,因为以AB 为直径的圆经过点()1,2P ,所以PA PB ⊥,即()()11221,21,20PA PB x y x y ⋅=--⋅--=,即()()12121212250x x x x y y y y -++-++=,所以()22424850n m n n m -+--+=,所以()()22322n m -=+,所以25n m =+或21n m =-+, 当21n m =-+时,直线AB 为12x my m =+-过点P ,此时与题干条件A ,B 都不与点P 重合矛盾,不合题意,舍去;当25n m =+时,直线AB 为25x my m =++,满足要求,所以2212424410x x m n m m +=+=++,则22121244124112AF BF x x m m m ⎛⎫+=++=++=++ ⎪⎝⎭,所以当12m =-时,AF BF +最小,且最小值为11.。
中考数学回归教材重难点07 几何最值问题(解析版)

回归教材重难点07 几何最值问题几何最值问题是初中几何章节的重点内容,考查的范围比较广,把几何图形性质与平移、翻折等图形变换结合起来。
在中考数学中,主要是以压轴题形式出现。
通过熟练的几何模型的应用,提升数学学科素养,提高逻辑思维推断能力。
本考点是中考五星高频考点,在全国各地的中考试卷中均有出现,题目难度较大,甚至有些地方将其作为选填题的压轴题。
1.将军饮马模型;2.瓜豆模型;3.隐圆模型1.(2021·辽宁盘锦·中考真题)如图,四边形ABCD为矩形,AB=23AD=2点P为边AB上一点.以DP为折痕将△DAP翻折,点A的对应点为点A'.连结AA',AA' 交PD于点M,点Q为线段BC上一点,连结AQ,MQ,则AQ+MQ的最小值是________【答案】42【分析】如图,作点A关于BC的对称点T,取AD的中点R,连接BT,QT,RT,RM.想办法求出RM,RT,求出MT的最小值,再根据QA+QM=QM+QT≥MT,可得结论.【详解】解:如图,作点A关于BC的对称点T,取AD的中点R,连接BT,QT,RT,RM.△四边形ABCD 是矩形,△△RAT =90°,△AR =DR 2AT =2AB =3△RT 2222(2)(43)52AR AT ++△A ,A′关于DP 对称,△AA′△DP ,△△AMD =90°, △AR =RD ,△RM =12AD 2△MT ≥RT −RM ,△MT 2, △MT 的最小值为2△QA +QM =QT +QM ≥MT ,△QA +Q M 2,△QA +QM 的最小值为2.故答案为:2【点睛】本题考查翻折变换,矩形的性质,解直角三角形等知识,解题的关键是求出MT 的最小值,属于中考常考题型.2.(2021·四川成都·中考真题)如图,在矩形ABCD 中,4,8AB AD ==,点E ,F 分别在边,AD BC 上,且3AE =,按以下步骤操作:第一步,沿直线EF 翻折,点A 的对应点'A 恰好落在对角线AC 上,点B 的对应点为'B ,则线段BF 的长为_______;第二步,分别在,'EF A B 上取点M ,N ,沿直线MN 继续翻折,使点F 与点E 重合,则线段MN 的长为_______.【答案】 1 5【分析】第一步:设EF 与AA’交于点O ,连接AF ,易证明△AOE △ADC ,利用对应边成比例可得到OA =2OE ,由勾股定理可求出OE 35从而求得OA 及OC ;由AD △BC ,易得△AOE △△COF ,由对应边成比例可得AE 、FC 的关系式,设BF =x ,则FC =8-x ,由关系式可求得x 的值;第二步:连接NE ,NF ,根据折叠的性质,得到NF =NE ,设B’N =m ,分别在Rt △NB F '和Rt △ EA N '中,利用勾股定理及NF =NE 建立方程,可求得m ,最后得出结果.【详解】如图所示,连接AF ,设EF 与AA’交于点O ,由折叠的性质得到AA’△EF , 3A E AE '==△四边形ABCD 是矩形△△ADC =90°,CD =AB =4 ,AD △BC△△AOE =△ADC ,△OAE =△DAC △△AOE △ADC ,△12OE CD OA AD == ,△OA =2OE , 在直角△AOE 中,由勾股定理得:2249OE OE += ,△OE 35,△OA 65, 在Rt △ADC 中,由勾股定理得到:AC 224845+=,△OC =6514545 令BF =x ,则FC =8-x ,△AD △BC ,△△AOE △△COF ,△37OA AE OC FC == ,即7AE =3FC △3(8-x )=7×3解得:1x =,△BF 的长为1. 连接NE ,NF ,如图,根据折叠性质得:BF =B’F =1,MN △EF ,NF =NE ,设B’N =m ,则22222213(4)NF m NE m =+==+- ,解得:m =3,则NF 10,△EF 222425+=△MF 5△MN 5故答案为:15【点睛】本题主要考查了折叠的性质、勾股定理、三角形相似的判定与性质,矩形的性质等知识,熟练运用这些知识是解决本题的关键,本题还涉及到方程的运用.3.(2021·内蒙古鄂尔多斯·中考真题)如图,已知正方形ABCD 的边长为6,点F 是正方形内一点,连接,CF DF ,且ADF =DCF ∠∠,点E 是AD 边上一动点,连接,EB EF ,则EB EF +长度的最小值为___________.【答案】3133【分析】根据正方形的性质得到△ADC =90°,推出△DFC =90°,点F 在以DC 为直径的半圆上移动,,如图,设CD 的中点为O ,作正方形ABCD 关于直线AD 对称的正方形APGD ,则点B 的对应点是P ,连接PO 交AD 于E ,交半圆O 于F ,则线段FP 的长即为BE +FE 的长度最小值,根据勾股定理即可得到结论.【详解】解:△四边形ABCD 是正方形,△△ADC =90°,△△ADF +△CDF =90°,△ADF =DCF ∠∠,△△DCF +△CDF =90°,△△DFC =90°,△点F 在以DC 为直径的半圆上移动,如图,设CD 的中点为O ,作正方形ABCD 关于直线AD 对称的正方形APGD ,则点B 的对应点是P , 连接PO 交AD 于E ,交半圆O 于F ,则线段FP 的长即为BE +FE 的长度最小值,OF =3,△△G =90°,PG =DG =AB =6,△OG =9,△OP 222269313PG OG +=+△FP =3133, △BE +FE 的长度最小值为3133,故答案为:3133.【点睛】本题考查了轴对称−最短路线问题,正方形的性质,勾股定理以及圆的基本性质.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.4.(2021·山东聊城·中考真题)如图,在直角坐标系中,矩形OABC 的顶点O 在坐标原点,顶点A ,C 分别在x 轴,y 轴上,B ,D 两点坐标分别为B (﹣4,6),D (0,4),线段EF 在边OA 上移动,保持EF =3,当四边形BDEF 的周长最小时,点E 的坐标为__________.【答案】()0.4,0-【分析】先得出D 点关于x 轴的对称点坐标为H (0,-4),再通过转化,将求四边形BDEF 的周长的最小值转化为求FG +BF 的最小值,再利用两点之间线段最短得到当F 、G 、B 三点共线时FG +BF 的值最小,用待定系数法求出直线BG 的解析式后,令y =0,即可求出点F 的坐标,最后得到点E 的坐标.【详解】解:如图所示,△D (0,4),△D 点关于x 轴的对称点坐标为H (0,-4),△ED =EH ,将点H 向左平移3个单位,得到点G (-3,-4),△EF =HG ,EF △HG ,△四边形EFGH 是平行四边形,△EH =FG ,△FG =ED ,△B (-4,6),△BD ()()224064=25--+-又△EF =3,△四边形BDEF 的周长=BD +DE +EF +BF =25FG +3+BF ,要使四边形BDEF 的周长最小,则应使FG +BF 的值最小,而当F 、G 、B 三点共线时FG +BF 的值最小, 设直线BG 的解析式为:()0y kx b k =+≠△B (-4,6),G (-3,-4),△4634k b k b -+=⎧⎨-+=-⎩,△1034k b =-⎧⎨=-⎩,△1034y x =--, 当y =0时, 3.4x =-,△()3.4,0F -,△()0.4,0E -,故答案为:()0.4,0-.【点睛】本题综合考查了轴对称的性质、最短路径问题、平移的性质、用待定系数法求一次函数的解析式等知识,解决问题的关键是“转化”,即将不同的线段之间通过转化建立相等关系,将求四边形的周长的最小值问题转化为三点共线和最短的问题等,本题蕴含了数形结合与转化的思想方法等.5.(2021·广东·中考真题)在ABC 中,90,2,3ABC AB BC ∠=︒==.点D 为平面上一个动点,45ADB ∠=︒,则线段CD 长度的最小值为_____. 52-【分析】由已知45ADB ∠=︒,2AB =,根据定角定弦,可作出辅助圆,由同弧所对的圆周角等于圆心角的一半可知,点D 在以O 为圆心OB 为半径的圆上,线段CD 长度的最小值为CO OD -.【详解】如图: 以12AB 为半径作圆,过圆心O 作,ON AB OM BC ⊥⊥, 以O 为圆心OB 为半径作圆,则点D 在圆O 上,45ADB ∠=︒90AOB ∠=︒∴2AB =,1AN BN ==,22112AO ∴=+112ON OM AB ===,3BC =,221(31)5OC ∴=+-=52CO OD ∴-=CD 长度的最小值为52-52-【点睛】本题考查了圆周角与圆心角的关系,圆外一点到圆上的线段最短距离,勾股定理,正确的作出图形是解题的关键.6.(2021·河南周口·三模)如图,在边长为4的正方形ABCD 中,动点E ,F 分别在BC ,AB 上移动,AF =BE ,AE 和DF 交于点P ,点M 为边AB 上一动点,点N 为平面上一动点,CN =1,则NM +MP 的最小值是 ___.【答案】133【分析】首先证明△APD =90°,推出点P 在以AD 为直径的圆上运动,设圆心为T ,作点T 关于AB 的对称点R ,以R 为圆心,AR 为半径作△R ,则点P 关于AB 的对称点L ,在△R 上,连接CR ,R L ,ML .根据RL +ML +MN +NC ≥CR ,MP =ML ,求出CR ,可得结论.【详解】解:如图,△四边形ABCD 是正方形,△△B =△DAF =90°,AD =AB ,在△AB E 和△DAF 中,AB DA B DAF BE AF =⎧⎪∠=∠⎨⎪=⎩,△△ABE △△DAF (SAS ),△△BAE =△ADF ,△△BAE +△DAP =90°,△△ADP +△DAE =90°,△△APD =90°,△点P 在以AD 为直径的圆上运动,设圆心为T ,作点T 关于AB 的对称点R ,以R 为圆心,AR 为半径作△R ,则点P 关于AB 的对称点L ,在△R 上,连接CR ,RL ,ML .△CN =1,△点N 在以C 为圆心,半径为1的△C 上运动,在Rt △CD R 中,CR 22DR CD +2264+13△RL +ML +MN +NC ≥CR ,MP =ML ,△PM +MN 132-1,△PM +MN 133,△PM +MN 的最小值为133.【点睛】本题考查轴对称最短问题,正方形的性质,勾股定理,轨迹等知识,解题的关键是学会把问题转化为两点之间线段最短,属于中考填空题中的压轴题.7.(2021·河南郑州·一模)如图,在边长为4的正方形ABCD 中,P 是AB 边上一动点(不与点A ,B 重合),连接PD ,过点B 作BM △PD 交DP 的延长线于点M ,连接AM ,过点A 作AN △AM 交PD 于点N ,连接BN ,CN ,则△BNC 面积的最小值为________.【答案】1242-【分析】点N 在正方形内部,所以S △AND +S △BNC =12S 正方形ABCD =14482⨯⨯=,由BM △PD 可得点M 在以BD 中点为圆心,12BD 长为半径的圆上,先证明△AMB 与△ADN 全等,然后求△ABM 最大面积即可求出△BNC 的最小面积.【详解】解:△四边形ABCD 为正方形, △AD =AB ,△BAD =△BAN +△NAD =90°,△△MAB +△BAN =△MAN =90°,△△MAB =△NAD ,△△BMP +△BPM +△MBP =△P AD +△PDA +△APD =180°,△MPB =△APD ,△BMP =△DAP =90°,△△MBP =△ADP , 在△AMB 和△AND 中,MAB NAD MBA NDA AB AD ∠∠⎧⎪∠∠⎨⎪=⎩==,△△AMB △△AND (ASA ).△S △AMB =S △AND , △S △AND +S △BNC =12S 正方形ABCD =14482⨯⨯=,△当S △AMB 面积最大时,S △BNC 面积最小, △△BMD =90°,△点M 在以BD 中点为圆心,12BD 长为半径的圆上,当△ABM面积最大时,OM △AB ,如图,△点O 为BD 中点,OM △AD ,△OK =12AD =2,△BD 2=42△OM =12BD =22△MK =OM ﹣OK =222,△S △AMB =12AB •MK =424, △S △BNC =8﹣S △AMB =8﹣(424)=1242-故答案为:1242-【点睛】本题考查正方形的性质、三角形面积计算、全等三角形的判定、圆周角定理等知识点,将求△BNC 的最小面积转化为求△ABM 最大面积并找出M 点运动轨迹是解题关键.8.(2021·河南·三模)如图,在正方形ABCD 中,AB =8,点E ,F 分别为边AB ,AD 上的动点,且EF =6,点G ,M 分别为边BC ,CD 的中点,连接BM ,DG 交于点O .将△EF A 沿EF 折叠得到△EF A ',点H 是边EF 上一动点,连接A 'H ,HO ,OA '.当A 'H +HO 的值最小时,OA '的长为 __________________.16216- 【分析】连接AH 、AO ,由折叠的性质,点A 与点A '关于直线EF 对称,则可得当A 、H 、O 三点共线时,A 'H +HO 的值最小,连接OC 、AH ,过点O 作NO △BC 于点N ,可知四边形AF A 'E 是正方形,△ACB =45°,设CN =x ,则ON =CN =x ,BN =8﹣x ,可证明△BON △△BMC ,可求出CN =83,CO =823,在Rt △ABC 中,由勾股定理得AC =2A 'O =AC ﹣AA '﹣OC 162. 【详解】解:连接AH 、AO ,如图,由折叠的性质,点A 与点A '关于直线EF 对称,AH A H '∴= A H HO AH HO AO '∴+=+≥A H O ∴、、三点共线时,A H HO '+的值最小,连接OC 、AH ,过点O 作NO △BC 于点N ,如图2,∴四边形AFA E '是正方形,6AA EF '∴==,A O C 、、三点共线,45ACB ∴∠=︒M 是DC 中点,4MC ∴=设CN =x ,则ON =CN =x ,BN =8﹣x ,BNO BCM ∠=∠,BON BMC ∴~,ON MC BN BC ∴=即488x x =-,83x ∴=,83CN ∴= 822CO CN ∴==在Rt ABC 中,由勾股定理得,2282AC AB BC =+=8216282616A O AC AA OC ''∴=--== 16216-. 【点睛】本题考查相似的判定与性质、折叠的性质、正方形的性质、勾股定理等知识,是重要考点,掌握相关知识是解题关键.9.(2021·四川绵阳·一模)等边△ABC 的边长为6,P 是AB 上一点,AP =2,把AP 绕点A 旋转一周,P 点的对应点为P ′,连接BP ′,BP ′的中点为Q ,连接CQ .则CQ 长度的最小值是_____.【答案】331【分析】取AB中点D,连接DQ,CD,AP',利用等边三角形求出CD=33根据三角形中位线定理得到DQ=1,利用三角形三边关系得出结果.【详解】解:如图,取AB中点D,连接DQ,CD,AP',△AP=2,把AP绕点A旋转一周,△AP'=2,△等边△ABC的边长为6,点D是AB中点,△BD=AD=3,CD△AB,△CD22226333BC BD--△点Q是BP'是中点,△BQ=QP',又△AD=BD,△DQ=12AP'=1,在△CDQ中,CQ≥DC﹣DQ,△CQ的最小值为31,故答案为331.【点睛】本题考查最短路径、中位线、等边三角形等知识,解决问题的关键是已知中点的常见思路:等腰三角形中构造三线合一,一般三角形中构造中位线.10.(2021·福建·厦门五缘实验学校二模)如图,在平面直角坐标系中,反比例函数ykx=(k>0)的图象与半径为5的△O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是______.【答案】2【详解】设点M(a,b),N(c,d),先求出a2+b2=c2+d2=25,再求出ac()227k c a-=,同理:bd()227k b d-=,即可得出ac﹣bc=0,最后用两点间的距离公式即可得出结论.【解答】解:如图,设点M(a,b),N(c,d),△ab=k,cd=k,△点M,N在△O上,△a2+b2=c2+d2=25,作出点N关于x轴的对称点N'(c,﹣d),△MN'即为PM+PN的最小值△S△OMN12=k12+(b+d)(a﹣c)12-k=3.5,△ad﹣bc=7,△kc kaa c-=7,△ac()227k c a-=,同理:bd()227k b d-=,△ac﹣bc()()2222777k c a k b d k--=-=[(c2+d2)﹣(a2+b2)]=0,△M(a,b),N'(c,﹣d),△MN'2=(a﹣c)2+(b+d)2=a2+b2+c2+d2﹣2ac+2bd=a2+b2+c2+d2﹣2(ac﹣bd)=50,△MN'=2故答案为:2【点睛】此题主要考查了反比例函数的性质、圆的性质、两点间的距离公式,判断出ac-bd=0是解本题的关键.11.(2021·广东·雷州市第八中学一模)如图,把矩形ABCD沿EF对折,使B与D重合,折痕EF交BD于G,连AG,若tan△AGE7BF=8,P为DG上一个动点,则PF+PC的最小值为_____.【答案】10【分析】如图,连接BE,CE,PE,取BE的中点O,连接OA,OG.首先证明△EGD△△FGB(ASA),推出BF=DE=8,EG=FG,再证明PF=PE,推出PF+PC=PE+PC≥EC,想办法求出EC即可解决问题.【详解】解:如图,连接BE,CE,PE,取BE的中点O,连接OA,OG.由题意,EF 垂直平分线段BD ,△EB =ED ,BG =GD ,△四边形ABCD 是矩形,△AD △BC ,△△EDG =△FBG ,△△EGD =△FGB ,△△EGD △△FGB (ASA ),△BF =DE =8,EG =FG ,△DB △EF ,△PE =PF ,△PF +PC =PE +PC ≥EC ,△△BAE =△BGE =90°,OB =OE ,△OA =OB =OE =OG ,△A ,B ,G ,E 四点共圆,△△ABE =△AGE ,△tan△ABE =tan△AGE 7AE AB , 设AE 7,AB =3k ,△AB 2+AE 2=BE 2,BE =DE =8,△7k )2+(3k )2=82,△k =2,△AB =CD =6,△△EDC =90°,△EC 222268CD DE ++,△PF +PC ≥10,△PF +PC 的最小值为10.故答案为:10.【点睛】本题考查翻折变换,矩形的性质,全等三角形的判定和性质,线段的垂直平分线的判定和性质,解直角三角形,四点共圆等知识,本题综合性比较强. 12.(2022·上海·一模)如图,在ABC 中,90ACB ∠=︒,2AC 22BC =ABC 绕点C 按逆时针方向旋转得到DEC ,连接AD ,BE ,直线AD ,BE 相交于点F ,连接CF ,在旋转过程中,线段CF 的最大值为__________.10【分析】取AB 的中点H ,连接CH 、FH ,设EC ,DF 交于点G ,在△ABC 中,由勾股定理得到AB 10由旋转可知:△DCE △△ACB ,从而△DCA =△BCE ,△ADC =△BEC ,由△DGC =△EGF ,可得△AFB =90º,由直角三角形斜边上的中线等于斜边的一半,可得FH=CH=12AB10△FCH中,当F、C、H在一条直线上时,CF10【详解】取AB的中点H,连接CH、FH,设EC,DF交于点G,在△ABC中,△ACB=90º,△AC2,BC2△AB2210AC BC+由旋转可知:△DCE△△ACB,△△DCE=△ACB,DC=AC,CE=CB,△△DCA=△BCE,△△ADC=12(180º-△ACD) ,△BEC=12(180º-△BCE),△△ADC=△BEC,△△DGC=△EGF,△△DCG=△EFG=90º,△△AFB=90º,△H是AB的中点,△FH=12AB,△△ACB=90º,△CH=12AB,△FH=CH=12AB10在△FCH中,FH+CH>CF,当F、C、H在一条直线上时,CF 101010=△线段CF10.10【点睛】本题考查了旋转的性质、勾股定理,解决本题的关键是掌握全等的性质.13.(2022·重庆·一模)如图,已知ABC ,外心为O ,18BC =,60BAC ∠=︒,分别以AB ,AC 为腰向形外作等腰直角三角形ABD △与ACE ,连接BE ,CD 交于点P ,则OP 的最小值是______.【答案】933-【分析】由ABD △与ACE 是等腰直角三角形,得到90BAD CAE ∠=∠=︒,DAC BAE ∠=∠,根据全等三角形的性质得到ADC ABE ∠=∠,求得在以BC 为直径的圆上,由ABC 的外心为O ,60BAC ∠=︒,得到120BOC ∠=︒,如图,当PO BC ⊥时,OP 的值最小,解直角三角形即可得到结论.【详解】解:ABD 与ACE 是等腰直角三角形,90BAD CAE ∴∠=∠=︒,DAC BAE ∴∠=∠,在DAC △与BAE 中,AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩,DAC ∴△()BAE SAS ,ADC ABE ∴∠=∠,90PDB PBD ∴∠+∠=︒, 90DPB ∴∠=︒,P ∴在以BC 为直径的圆上,ABC 的外心为O ,60BAC ∠=︒,120BOC ∴∠=︒,如图,当PO BC ⊥时,OP 的值最小,18BC =,9BH CH ∴==,12OH OB =,223BH OB OH OH ∴- 33OH ∴=9PH =,933OP ∴=-OP 的最小值是933-,故答案为:933-【点睛】本题考查了三角形的外接圆与外心,全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.。
中考常见的几何最值问题

中考常见的几何最值问题1. 已知单位正方形ABCD 内或边界上有一点P ,则PD PC PB PA ⋅⋅⋅的最大值为__________.(165)2. 如图,在矩形ABCD 中,AB =4,BC =3,E 、F 分别为AB 、CD 边的中点,动点P 从点E 出发沿EA 向点A 运动,同时,动点Q 从点F 出发沿FC 向点C 运动,连接PQ ,过点B 作BH ⊥PQ 于点H ,连接DH ,若点P 的速度是点Q 速度的2倍,在点P 从点E 运动至点A 的过程中,线段PQ 长度的最大值为__________,线段DH 长度的最小值为__________.(213,23-)3. 如图,在矩形纸片ABCD 中,AB =8,BC =6,E 是AD 的中点,F 是AB 上一动点,将△AEF 沿直线EF 折叠,点A 落在点'A 处,在EF 上任取一点G ,连接',',CA GA GC ,则'CGA ∆的周长的最小值为__________.(737+)4. 如图,在□ABCD 中,56=BC ,对角线BD =10,21tan =∠DBC ,E 是线段BC 上的动点,连接DE ,过点D 作DP ⊥DE ,在射线DP 上取点F ,使得∠DFE =∠DBC ,连接CF ,则△DCF 周长的最小值为__________.(210102+)5. 如图,在矩形ABCD 中,已知AB =3,BC =4,P 是边BC 上一动点(点P 不与点B 、C 重合),连接AP ,作点B 关于直线AP 的对称点M ,连接MP ,作∠MPC 的平分线交边CD 于点N ,则线段MN 的最小值为__________.(34)6. 如图,点O 是矩形ABCD 的对角线的交点,AB =15,BC =8,直线EF 经过点O ,分别与边CD 、AB 相交于点E 、F (其中2150<<DE ),现将四边形ADEF 沿直线EF 折叠得到四边形EF D A '',点A 、D 的对应点分别为','D A ,过点'D 作GD G D ⊥'于点G ,则线段G D '的长的最大值是__________,此时折痕EF 的长为__________.(534829,)7. 如图,在平面直角坐标系中,)3,0(,)0,1(B A ,过点B 作直线BC ∥x 轴,点P 是直线BC 上的一个动点,以AP 为边在AP 右侧作Rt △APQ ,使∠APQ =90°,且PQ AP : 3:1=,连接AB 、BQ ,则△ABQ 周长的最小值为__________.(2132+)8. 如图,在Rt △ABC 中,∠ACB =90°,∠A =60°,32=AC ,P 为AB 边上的一个动点,连接PC ,过点P 作PQ ⊥PC 交BC 边于点Q ,则BQ 的最大值为__________.(2)9. 如图,在矩形ABCD 中,AB =4,BC =3,以点C 为圆心作⊙C 与直线BD 相切,点P 是⊙C 上一点,连接AP 交BD 于点T ,则TAPA 的最大值是__________.(3)10. 将一个平行四边形放入平面直角坐标系中,它的四个顶点坐标分别表示如下:),(,),(,)4,0(,)0,8(b a D n n C B A -,其中n b a ,,为任意满足条件的实数,则线段CD 长的最小值为__________.(26)11. 如图,在∠ABC 内部有一点M ,过点M 作MA ∥BC 交AB 边于点A ,作MC ∥AB 交BC 边于点C ,若∠ABC =45°,23=AB ,BC =6,D 为线段AB 中点,P 为线段BC 上一动点,连接DP ,将线段DP 绕点D 逆时针旋转90°至'DP ,连接','CP MP ,则''CP MP +的最小值是__________.(103)12. 在△ABC 中,BC =2,高AD =2,点P 、E 、F 分别在边BC 、AC 、AB 上,且四边形PEAF 是平行四边形,则四边形PEAF 的面积的最大值为__________.(1)13. 在四边形ABCD 中,AD =DC =2,∠DAB =∠DCB =90°,BC ,AD 的延长线交于点P ,则PAB S AB ∆⋅的最小值为__________.(32)14. 已知边长为6的等边△ABC 中,E 是高AD 所在直线上的一个动点,连接BE ,将线段BE 绕点B 顺时针旋转60°得到BF ,连接DF ,则在点E 运动的过程中,当线段DF 长度最小时,2DE 的值为__________.(427)15. 如图,△ABC 中,AB =CB ,AC =10,60=∆ABC S ,E 为AB 上一动点,连接CE ,过A 作AF ⊥CE 于F ,连接BF ,则BF 的最小值是__________.(7)16. 如图,在矩形ABCD 中,AB =4,AD =2,M 是AD 边的中点,N 是AB 边上的一动点,将△AMN 沿MN 所在直线翻折得到MN A '∆,连接C A ',在MN 上存在一动点P ,连接CP P A ,',则PC A '∆周长的最小值是__________.(15217-+)17. 如图,在△ABC 中,∠ACB =90°,AC =5,BC =3,点P 是线段AC 上的一个动点,连接BP ,将线段BP 绕点P 逆时针旋转90°得到线段PD ,连接AD ,则线段AD 的最小值是__________.(2)18. 如图,长方形ABCD 中,AB =2,BC =4,正方形AEFG 的边长为1,正方形AEFG 绕点A 旋转的过程中,线段CF 的长的最小值为__________.(252-)19. 如图,P 为∠MBN 内部一定点,PD ⊥BN ,PD =3,BD =5,过点P 的直线与BM 和BN 分别相交于点E 和点F ,A 是BM 边上任意一点,过点A 作AC ⊥BN 于点C ,有3=BCAC ,则△BEF 面积的最小值是__________.(24)20. 如图,在长方形纸片ABCD 中,3,31=+=CD AD ,将长方形纸片折叠,使B 点落在AD 上的点E 处,折痕为AF ,打开纸片,再沿DF 折叠,使C 点落在点G 处,在折痕FD 上有一动点H ,连接GH ,则DH GH +2的最小值是__________.(3)21. 如图,在△ABC 中,∠ABC =45°,∠ACB =60°,434+=BC ,D 是BC 边上异于点B 、C 的一动点,将△ABD 沿AB 翻折得到1ABD ∆,将△ACD 沿AC 翻折得到2ACD ∆,连接21D D ,则四边形21BCD D 的面积最大值为__________.(31636+)22. 如图,在△ABC 中,AB =AC =8,∠ABC =30°,点M 、N 分别在AB 、AC 上,将 △AMN 沿MN 翻折,点A 落在点'A 处,则线段'BA 长度的最小值为__________.(838-)23. 如图所示,点O 是边长为1的等边△ABC 的中心,直线EF 经过点O ,分别与边BC 、AC 相交于点E 、F ,现将△CEF 沿直线EF 折叠得到△DEF ,点C 的对应点为点D ,则 △ABD 周长的最大值是__________.(1332+)24. 如图,在△ABC 中,∠B =45°,232,22+==BC AB ,等腰直角△DAE 中,∠DAE =90°,且点D 是边BC 上一点.(1)求AC 的长;(2)如图1,当点E 恰在AC 上时,求点E 到BC 的距离;(3)如图2,当点D 从点B 向点C 运动时,求点E 到BC 的距离的最大值。
几何最值问题(讲义及答案)

4
11. (2020 扬州)如图,在□ABCD 中,∠B=60°,AB=10, BC=8,点 E 为边 AB 上的一个动点,连接 ED 并延长至点 F,使得 DF= 1 DE,以 EC,EF 为邻边构造□EFGC,连接 4 EG,则 EG 的最小值为__________.
A E
DF
G
B
C
12. 如图,在△A1B1C1 中,A1B1=8,∠A1B1C1=60°,∠B1A1C1=75°, P 是 B1C1 上的任意点,连接 A1P,将 A1P 绕点 A1 按顺时针方 向旋转 75°,得到线段 A1Q,连接 B1Q.则线段 B1Q 长度的最 小值为__________.
在∠AOB 内有一点 P(4,3),M,N 分别是 OA,OB 边上的动
点,连接 PM,PN,MN,则△PMN 周长的最小值是_______.
y A
M
P
O
N Bx
6. 如图,在正方形 ABCD 中,AB=8,AC 与 BD 交于点 O,N
是 AO 的中点,点 M 在 BC 边上,且 BM=6,P 为对角线 BD
几何最值问题(讲义)
知识点睛
1. 解决几何最值问题的理论依据: 两点之间,线段最短(已知两个定点) 垂线段最短(已知一个定点、一条定直线) 三角形三边关系(已知两边长固定或其和、差固定) 过圆内一点,最长的弦为直径,最短的弦为垂直于直径的弦
2. 解决几何最值问题的处理思路 ①分析定点、动点,寻找不变特征; ②若属于常见模型、结构,调用模型、结构解决问题; 若不属于常见模型,要结合所求目标,根据不变特征转化为 基本定理或表达为函数解决问题. 转化原则: 尽量减少变量,向定点、定线段、定图形靠拢,或使用同一 变量表达所求目标.
中考几何最值问题含答案

几何最值问题一.选择题〔共6小题〕1.〔2021 •孝感一模〕如图,等边△ABC的边长为6,点D为AC 的中点,点E为BC的中点,点P为BD上一点,那么PE+PC的最小值为〔〕A.3B.3C.2D.3考点:轴对称-最短路线问题.分析:由题意可知点A、点C关于BD对称,连接AE交BD于点P,由对称的性质可得,PA=PC,故PE+PC=AE,由两点之间线段最短可知,AE即为PE+PC的最小值.解答:解:∵△ABC是等边三角形,点D为AC的中点,点E为BC 的中点,∴BD⊥AC,EC=3,连接AE,线段AE的长即为PE+PC最小值,∵点E是边BC的中点,∴AE⊥BC,∴AE===3,∴PE+PC的最小值是3.应选D.点评:此题考察的是轴对称﹣最短路线问题,熟知等边三角形的性质是解答此题的关键.2.〔2021•鄂城区校级模拟〕如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm与40cm,B点到y 轴的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,那么这个值为〔〕A.50B.50C.50﹣50D.50+50考点:轴对称-最短路线问题;坐标与图形性质.专题:压轴题.分析:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交X,Y轴分别为P,Q点,此时四边形PABQ的周长最短,根据题目所给的条件可求出周长.解答:解:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A 点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交x,y 轴分别为P,Q点,过M点作MK⊥x轴,过N点作NK⊥y轴,两线交于K点.MK=40+10=50,作BL⊥x轴交KN于L点,过A点作AS⊥BP交BP于S点.∵LN=AS==40.∴KN=60+40=100.∴MN==50.∵MN=MQ+QP+PN=BQ+QP+AP=50.∴四边形PABQ的周长=50+50.应选D.点评:此题考察轴对称﹣最短路线问题以及坐标与图形的性质,此题关键是找到何时四边形的周长最短,以及构造直角三角形,求出周长.3.〔2021秋•贵港期末〕如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN 的度数为〔〕A.30°B.40°C.50°D.60°考点:轴对称-最短路线问题.分析:根据要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC与CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=70°,进而得出∠MAB+∠NAD=70°,即可得出答案.解答:解:作A关于BC与CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,那么A′A″即为△AMN的周长最小值,作DA延长线AH,.∵∠DAB=110°,∴∠HAA′=70°,∴∠AA′M+∠A″=∠HAA′=70°,∵∠MA′A=∠MAB,∠NAD=∠A″,∴∠MAB+∠NAD=70°,∴∠MAN=110°﹣70°=40°.应选B.点评:此题考察的是轴对称﹣最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质与垂直平分线的性质等知识,根据得出M,N的位置是解题关键.4.〔2021•无锡模拟〕如图,∠MON=90°,矩形ABCD的顶点A,B分别在OM、ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=.运动过程中,当点D到点O的距离最大时,OA长度为〔〕A.B.C.2D.考点:勾股定理;三角形三边关系;直角三角形斜边上的中线.分析:取AB的中点,连接OE、DE,根据直角三角形斜边上的中线等于斜边的一半求出OE,利用勾股定理列式求出DE,然后根据三角形的任意两边之与大于第三边判断出O、E、D三点共线时点D到点O的距离最大,过点A作AF⊥OD于F,利用∠ADE的余弦列式求出DF,从而得到点F是OD的中点,判断出AF垂直平分OD,再根据线段垂直平分线上的点到两端点的距离相等可得OA=AD.解答:解:如图,取AB的中点,连接OE、DE,∵∠MON=90°,∴OE=AE=AB=×2=1,∵三边形ABCD是矩形,∴AD=BC=,在Rt△ADE中,由勾股定理得,DE===2,由三角形的三边关系得,O、E、D三点共线时点D到点O的距离最大,此时,OD=OE+DE=1+2=3,过点A作AF⊥OD于F,那么cos∠ADE==,即=,解得DF=,∵OD=3,∴点F是OD的中点,∴AF垂直平分OD,∴OA=AD=.应选B.点评:此题考察了勾股定理,三角形的任意两边之与大于第三边,直角三角形斜边上的中线等于斜边的一半的性质,线段垂直平分线上的点到两端点的距离相等的性质,作辅助线并判断出OD最大时的情况是解题的关键,作出图形更形象直观.5.〔2021 •鞍山一模〕如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为的线段MN在AC上运动,当四边形BMNE 的周长最小时,那么tan∠MBC的值是〔〕A.B.C.D.1考点:轴对称-最短路线问题;正方形的性质.分析:根据题意得出作EF∥AC且EF=,连结DF交AC于M,在AC上截取MN=,此时四边形BMNE的周长最小,进而利用相似三角形的判定与性质得出答案.解解:作EF∥AC且EF=,连结DF交AC于M,在AC上截答:取MN=,延长DF交BC于P,作FQ⊥BC于Q,那么四边形BMNE的周长最小,由∠FEQ=∠ACB=45°,可求得FQ=EQ=1,∵∠DPC=∠FPQ,∠DCP=∠FQP,∴△PFQ∽△PDC,∴=,∴=,解得:PQ=,∴PC=,由对称性可求得tan∠MBC=tan∠PDC==.应选:A.点评:此题主要考察了正方形的性质以及相似三角形的判定与性质,得出M,N的位置是解题关键.6.〔2021 •江干区一模〕如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,那么DP的最大值为〔〕A.B.C.2D.考圆的综合题.点:分析:根据等腰三角形的性质可得点D是AB的中点,然后根据三角形中位线定理可得DP=BG,然后利用两点之间线段最短就可解决问题.解答:解:连接BG,如图.∵CA=CB,CD⊥AB,AB=6,∴AD=BD=AB=3.又∵CD=4,∴BC=5.∵E是高线CD的中点,∴CE=CD=2,∴CG=CE=2.根据两点之间线段最短可得:BG≤CG+CB=2+5=7.当B、C、G三点共线时,BG取最大值为7.∵P是AG中点,D是AB的中点,∴PD=BG,∴DP 最大值为.应选A.点评:此题主要考察了圆的综合题,涉及了等腰三角形的性质、三角形中位线定理、勾股定理、两点之间线段最短等知识,利用三角形中位线定理将DP转化为BG是解决此题的关键.二.填空题〔共3小题〕7.〔2021•江阴市校级模拟〕如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD与等腰直角△BCE,那么DE长的最小值是 2 .考点:等腰直角三角形.分析:设AC=x,BC=4﹣x,根据等腰直角三角形性质,得出CD=x,CD′=〔4﹣x〕,根据勾股定理然后用配方法即可求解.解答:解:设AC=x,BC=4﹣x,∵△ABC,△BCD′均为等腰直角三角形,∴CD=x,CD′=〔4﹣x〕,∵∠ACD=45°,∠BCD′=45°,∴∠DCE=90°,∴DE2=CD2+CE2=x2+〔4﹣x〕2=x2﹣4x+8=〔x﹣2〕2+4,∴当x取2时,DE取最小值,最小值为:4.故答案为:2.点评:此题考察了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.8.〔2021•河南校级模拟〕如图,矩形ABCD中,AB=4,BC=8,E为CD边的中点,点P、Q为BC边上两个动点,且PQ=2,当BP= 4 时,四边形APQE的周长最小.考点:轴对称-最短路线问题.专题:压轴题.分析:要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,那么此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度.解答:解:如图,在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC 的延长线于H点.∵GH=DF=6,EH=2+4=6,∠H=90°,∴∠GEH=45°.设BP=x,那么CQ=BC﹣BP﹣PQ=8﹣x﹣2=6﹣x,在△CQE中,∵∠QCE=90°,∠CEQ=45°,∴CQ=EC,∴6﹣x=2,解得x=4.故答案为4.点评:此题考察了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.9.〔2021•武汉〕如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.假设正方形的边长为2,那么线段DH长度的最小值是﹣1 .考点:正方形的性质.专压轴题.题:分析:根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边〞证明△ABE与△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS〞证明△ADG与△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.解答:解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,在△ABE与△DCF中,,∴△ABE≌△DCF〔SAS〕,∴∠1=∠2,在△ADG与△CDG中,,∴△ADG≌△CDG〔SAS〕,∴∠2=∠3,∴∠1=∠3,∵∠BAH+∠3=∠BAD=90°,∴∠1+∠BAH=90°,∴∠AHB=180°﹣90°=90°,取AB的中点O,连接OH、OD,那么OH=AO=AB=1,在Rt△AOD中,OD===,根据三角形的三边关系,OH+DH>OD,∴当O、D、H三点共线时,DH的长度最小,最小值=OD﹣OH=﹣1.〔解法二:可以理解为点H是在Rt△AHB,AB 直径的半圆上运动当O、H、D三点共线时,DH长度最小〕故答案为:﹣1.点评:此题考察了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,确定出DH最小时点H的位置是解题关键,也是此题的难点.三.解答题〔共1小题〕10.〔2021 •黄冈中学自主招生〕阅读下面材料:小伟遇到这样一个问题:如图1,在△ABC〔其中∠BAC是一个可以变化的角〕中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.小伟是这样思考的:利用变换与等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解〔如图2〕.请你答复:AP 的最大值是 6 .参考小伟同学思考问题的方法,解决以下问题:如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,那么AP+BP+CP的最小值是〔或不化简为〕.〔结果可以不化简〕考点:旋转的性质;全等三角形的判定与性质;等边三角形的性质;勾股定理;等腰直角三角形.专题:几何综合题.分析:〔1〕根据旋转的性质知A′A=AB=BA′=2,AP=A′C,所以在△AA′C中,利用三角形三边关系来求A′C即AP的长度;〔2〕以B为中心,将△APB逆时针旋转60°得到△A'P'B.根据旋转的性质推知PA+PB+PC=P'A′+P'B+PC.当A'、P'、P、C四点共线时,〔P'A′+P'B+PC〕最短,即线段A'C最短.然后通过作辅助线构造直角三角形A′DC,在该直角三角形内利用勾股定理来求线段A′C的长度.解答:解:〔1〕如图2,∵△ABP逆时针旋转60°得到△A′BC,∴∠A′BA=60°,A′B=AB,AP=A′C∴△A′BA是等边三角形,∴A′A=AB=BA′=2,在△AA′C中,A′C<AA′+AC,即AP<6,那么当点A′A、C三点共线时,A′C=AA′+AC,即AP=6,即AP的最大值是:6;故答案是:6.〔2〕如图3,∵Rt△ABC是等腰三角形,∴AB=BC.以B为中心,将△APB逆时针旋转60°得到△A'P'B.那么A'B=AB=BC=4,PA=P′A′,PB=P′B,∴PA+PB+PC=P′A′+P'B+PC.∵当A'、P'、P、C四点共线时,〔P'A+P'B+PC〕最短,即线段A'C最短,∴A'C=PA+PB+PC,∴A'C长度即为所求.过A'作A'D⊥CB延长线于D.∵∠A'BA=60°〔由旋转可知〕,∴∠1=30°.∵A'B=4,∴A'D=2,BD=2,∴CD=4+2.在Rt△A'DC中A'C====2+2;∴AP+BP+CP的最小值是:2+2〔或不化简为〕.故答案是:2+2〔或不化简为〕.点评:此题综合考察了旋转的性质、等腰直角三角形的性质、勾股定理以及等边三角形的判定与性质.注意:旋转前、后的图形全等.。
初中数学几何最值问题(将军饮马、将军过河、费马点、隐圆、瓜豆、胡不归、阿氏圆)
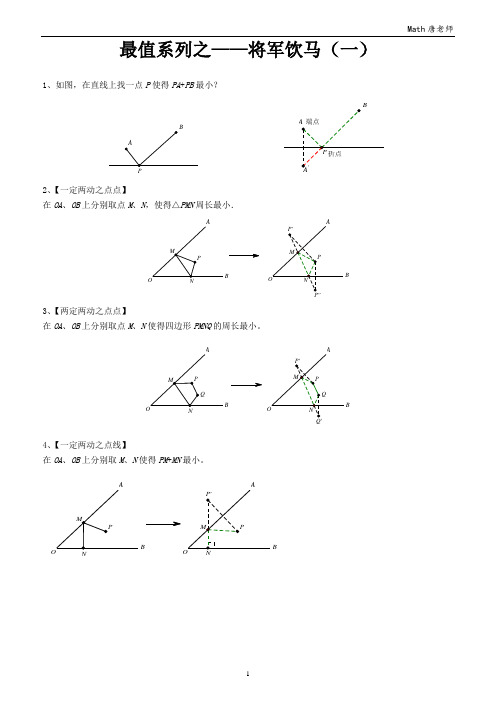
1、如图,在直线上找一点P使得PA+PB最小?2、【一定两动之点点】在OA、OB上分别取点M、N,使得△PMN周长最小.B3、【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
BB4、【一定两动之点线】在OA、OB上分别取M、N使得PM+MN最小。
BB【将军过桥】1.已知将军在图中点A 处,现要过河去往B 点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?2.已知A 、B 两点,MN 长度为定值,求确定M 、N 位置使得AM +MN +NB 值最小?军营河1.如图,在平面直角坐标系中,矩形ABCD 的顶点B 在原点,点A 、C 在坐标轴上,点D 的坐标为(6,4),E 为CD 的中点,点P 、Q 为BC 边上两个动点,且PQ =2,要使四边形APQE 的周长最小,则点P 的坐示应为______________.x2.如图,矩形ABCD 中,AD =2,AB =4,AC 为对角线,E 、F 分别为边AB 、CD 上的动点,且EF ⊥AC 于点M ,连接AF 、CE ,求AF +CE 的最小值.AB CDEFM几何图形中的将军饮马正方形中的将军饮马1. 如图,正方形ABCD 的边长是4,M 在DC 上,且DM =1, N 是AC 边上的一动点,则△DMN 周长的最小值是___________.NMD CBA2.如图,在Rt △ABO 中,∠OBA =90°,A (4,4),点C 在边AB 上,且AC :CB =1:3,点D 为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PDBC 周长最小的点P 的坐标为( )A .(2,2)B .5(2,5)2C .8(3,8)3D .(3,3)3.如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在BC 上,BD =3,DC =1,点P 是AB 上的动点,则PC +PD 的最小值为( )PDCBAA .4B .5C .6D .7三角形中的将军饮马1.如图,在等边△ABC 中,AB =6, N 为AB 上一点且BN =2AN , BC 的高线AD 交BC 于点D ,M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值是___________.A BCDMN2. 如图,在Rt △ABC 中,∠ACB =90°,AC =6.AB =12,AD 平分∠CAB ,点F 是AC 的中点,点E 是AD 上的动点,则CE +EF 的最小值为( )E AFCDBA .3B .4C .33D .233. 如图,在锐角三角形ABC 中,BC =4,∠ABC =60°, BD 平分∠ABC ,交AC 于点D ,M 、N 分别是BD ,BC 上的动点,则CM +MN 的最小值是( )NMDCBAA .3B .2C .23D .44.如图,△ABC 中,∠BAC =75°,∠ACB =60°,AC =4,则△ABC 的面积为_;点D ,点E ,点F 分别为BC ,AB ,AC 上的动点,连接DE ,EF ,FD ,则△DEF 的周长最小值为 .矩形、菱形中的将军饮马1. 如图,在菱形ABCD 中,AC=BD =6,E 是BC 的中点,P 、M 分别是AC 、AB 上的动点,连接PE 、PM ,则PE +PM 的最小值是( )EPDCBAMA .6 B.C.D .4.52.如图,矩形ABOC 的顶点A 的坐标为(-4,5),D 是OB 的中点,E 是OC 上的一点,当△ADE 的周长最小时,点E 的坐标是( )A .4(0,)3B .5(0,)3C .(0,2)D .10(0,)33.如图,在矩形ABCD 中,AB =6,AD =3,动点P 满足13PAB ABCD S S ∆=矩形,则点P 到A 、B 两点距离之和PA +PB的最小值为( )DCBAPA. B.C.D4.如图,矩形ABCD 中,AB =10,BC =5,点E 、F 、G 、H 分别在矩形ABCD 各边上,且AE =CG ,BF =DH ,则四边形EFGH 周长的最小值为( )H FGEDCB AA.B. C. D.特殊角的对称1. 如图,∠AOB =60°,点P 是∠AOB 内的定点且OPM 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是( )ABMOPNABC .6D .32. 如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N (3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB =30°,要使PM +PN 最小,则点P 的坐标为 .x3. 如图,已知正比例函数y =kx (k >0)的图像与x 轴相交所成的锐角为70°,定点A 的坐标为(0,4),P 为y 轴上的一个动点,M 、N 为函数y =kx (k >0)的图像上的两个动点,则AM +MP +PN 的最小值为____________.求两线段差的最大值问题基本图形解析:在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A-P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
中考数学《几何中的最值问题》专项练习(附答案解析)

中考数学《几何中的最值问题》专项练习(附答案解析)一、单选题1.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是()A.12 B.24 C.36 D.482.将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是()A.4cm2B.8cm2C.12cm2D.16cm23.如图,已知直线5-512y x与x轴、y轴分别交于B、C两点,点A是以D(0,2)为圆心,2为半径的⊙D上的一个动点,连接AC、AB,则△ABC面积的最小值是()A.30 B.29 C.28 D.274.如图,∠AOB=45°,点M、N分别在射线OA、OB上,MN=6,△OMN的面积为12,P是直线MN上的动点,点P关于OA对称的点为P1,点P关于OB对称点为P2,当点P在直线NM上运动时,△OP1P2的面积最小值为()A.6 B.8 C.12 D.185.如图,矩形ABCD中,AB=8,AD=4,E为边AD上一个动点,连接BE,取BE的中点G,点G 绕点E逆时针旋转90°得到点F,连接CF,则△CEF面积的最小值是()A.16 B.15 C.12 D.11二、填空题6.如图,在△ABC中,AB=AC,∠BAC=120°,点D为AB边上一点(不与点B重合),连接CD,将线段CD绕点D逆时针旋转90°,点C的对应点为E,连接BE.若AB=6,则△BDE面积的最大值为_________.7.如图,⊙O的直径为5,在⊙O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A,B重合),过C作CP的垂线CD交PB的延长线于D点.则△PCD的面积最大为______________.8.已知AB为半圆的直径,AB=2,DA⊥AB,CB⊥AB,AD=1,BC=3,点P为半圆上的动点,则AD,AB,BC,CP,PD围成的图形的面积的最大值是_____.9.如图,在矩形ABCD中,∠ACB=30°,,点E是边BC上一动点(点E不与B,C重合),连接AE,AE的中垂线FG分别交AE于点F,交AC于点G,连接DG,GE.设AG=a,则点G到BC边的距离为_____(用含a的代数式表示),ADG的面积的最小值为_____.10.如图,直线AB交坐标轴于A(-2,0),B(0,-4),点P在抛物线1(2)(4)2y x x=--上,则△ABP面积的最小值为__________.三、解答题11.如图,已知抛物线23y ax bx =++与x 轴交于A 、B 两点,过点A 的直线l 与抛物线交于点C ,其中A 点的坐标是(1,0),C 点坐标是(4,3).(1)求抛物线的解析式;(2)抛物线的对称轴上是否存在点D ,使△BCD 的周长最小?若存在,求出点D 的坐标,若不存在,请说明理由;(3)点P 是抛物线上AC 下方的一个动点,是否存在点p ,使△PAC 的面积最大?若存在,求出点P 的坐标,若不存在,请说明理由.12.已知,如图,矩形ABCD 中,AD =6,DC =7,菱形EFGH 的三个顶点E ,G ,H 分别在矩形ABCD 的边AB ,CD ,AD 上,AH =2,连接CF .(1)当四边形EFGH 为正方形时,求DG 的长;(2)当DG =6时,求△FCG 的面积;(3)求△FCG 的面积的最小值.13.如图,抛物线2y ax bx c =++与x 轴交于点(1,0)A -,点(3,0)B ,与y 轴交于点C ,且过点(2,3)D -.点P 、Q 是抛物线2y ax bx c =++上的动点.(1)求抛物线的解析式;(2)当点P 在直线OD 下方时,求POD ∆面积的最大值.(3)直线OQ 与线段BC 相交于点E ,当OBE ∆与ABC ∆相似时,求点Q 的坐标.14.已知抛物线y =a (x ﹣1)2过点(3,4),D 为抛物线的顶点.(1)求抛物线的解析式;(2)若点B 、C 均在抛物线上,其中点B (0,1),且∠BDC =90°,求点C 的坐标:(3)如图,直线y =kx +1﹣k 与抛物线交于P 、Q 两点,∠PDQ =90°,求△PDQ 面积的最小值.15.如图,已知二次函数213222y x x =-++的图象交x 轴于A (-1,0),B (4,0),交y 轴于点C ,点P 是直线BC 上方抛物线上一动点(不与B ,C 重合),过点P 作PE ⊥BC ,PF ∥y 轴交BC 与F ,则△PEF 面积的最大值是___________.16.如图,已知点P 是∠AOB 内一点,过点P 的直线MN 分别交射线OA ,OB 于点M ,N ,将直线MN 绕点P 旋转,△MON 的形状与面积都随之变化.(1)请在图1中用尺规作出△MON ,使得△MON 是以OM 为斜边的直角三角形;(2)如图2,在OP 的延长线上截取PC =OP ,过点C 作CM ∥OB 交射线OA 于点M ,连接MP 并延长交OB 于点N .求证:OP 平分△MON 的面积;(3)小亮发现:在直线MN 旋转过程中,(2)中所作的△MON 的面积最小.请利用图2帮助小亮说明理由.17.如图,已知A ,B 是线段MN 上的两点,4MN =,1MA =,1MB >,以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M ,N 两点重合成一点C ,构成ABC ,设AB x =.(1)求x 的取值范围;(2)求ABC 面积的最大值.18.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM与PN的数量关系是,位置关系是;(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.19.问题提出(1)如图①,在Rt△ABC中,∠ABC=90°,AB=12,BC=16,则AC=;问题探究(2)如图②,在Rt△ABC中,∠ABC=90°,AC=10,点D是AC边上一点,且满足DA=DB,则CD=;问题解决(3)如图③,在Rt△ABC中,过点B作射线BP,将∠C折叠,折痕为EF,其中E为BC中点,点F在AC边上,点C的对应点落在BP上的点D处,连接ED、FD,若BC=8,求△BCD面积的最大值,及面积最大时∠BCD的度数.20.如图,已知边长为6的菱形ABCD 中,∠ABC =60°,点E ,F 分别为AB ,AD 边上的动点,满足BE AF =,连接EF 交AC 于点G ,CE 、CF 分别交BD 于点M ,N ,给出下列结论:①△CEF 是等边三角形;②∠DFC =∠EGC ; ③若BE =3,则BM =MN =DN ;④222EF BE DF =+; ⑤△ECF .其中所有正确结论的序号是______21.如图,抛物线2y ax bx c =++与坐标轴交于点()()()0, 31,03,0A B E --、、,点P 为抛物线上动点,设点P 的横坐标为t .(1)若点C 与点A 关于抛物线的对称轴对称,求C 点的坐标及抛物线的解析式;(2)若点P 在第四象限,连接PA PE 、及AE ,当t 为何值时,PAE ∆的面积最大?最大面积是多少?(3)是否存在点P ,使PAE ∆为以AE 为直角边的直角三角形,若存在,直接写出点P 的坐标;若不存在,请说明理由.22.如图,在平面直角坐标系xOy 中,抛物线y =ax 2﹣2ax ﹣3a (a <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),经过点A 的直线l :y =kx+b 与y 轴负半轴交于点C ,与抛物线的另一个交点为D ,且CD =4AC .(1)直接写出点A 的坐标,并求直线l 的函数表达式(其中k 、b 用含a 的式子表示);(2)点E 是直线l 上方的抛物线上的动点,若△ACE 的面积的最大值为54,求a 的值; (3)设P 是抛物线的对称轴上的一点,点Q 在抛物线上,当以点A 、D 、P 、Q 为顶点的四边形为矩形时,请直接写出点P 的坐标.23.如图1,抛物线2y x bx c =-++与x 轴交于A 、B 两点,与y 轴交于点C ,已知点B 坐标为(3,0),点C 坐标为(0,3).(1)求抛物线的表达式;(2)点P 为直线BC 上方抛物线上的一个动点,当PBC 的面积最大时,求点P 的坐标;(3)如图2,点M 为该抛物线的顶点,直线MD x ⊥轴于点D ,在直线MD 上是否存在点N ,使点N 到直线MC 的距离等于点N 到点A 的距离?若存在,求出点A 的坐标;若不存在,请说明理由.24.如图,已知边长为10的正方形ABCD E ,是BC 边上一动点(与B C 、不重合),连结AE G ,是BC 延长线上的点,过点E 作AE 的垂线交DCG ∠的角平分线于点F ,若FG BG ⊥.(1)求证:ABE EGF ∽△△; (2)若2EC =,求CEF △的面积;(3)请直接写出EC 为何值时,CEF △的面积最大.参考答案与解析一、单选题1.【答案】D【解答】由图2知,AB=BC=10,当BP⊥AC时,y的值最小,即△ABC中,BC边上的高为8(即此时BP=8),即可求解.【解答】解:由图2知,AB=BC=10,当BP⊥AC时,y的值最小,即△ABC中,BC边上的高为8(即此时BP=8),当y=8时,PC===6,△ABC的面积=×AC×BP=×8×12=48,故选:D.【点评】本题是运动型综合题,考查了动点问题的函数图象、解直角三角形、图形面积等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.2.【答案】B【分析】当AC⊥AB时,重叠三角形面积最小,此时△ABC是等腰直角三角形,面积为8cm2.【解答】解:如图,当AC⊥AB时,三角形面积最小,∵∠BAC=90°∠ACB=45°∴AB=AC=4cm,∴S△ABC =12×4×4=8cm2.故选:B.【点评】本题考查了折叠的性质,发现当AC⊥AB时,重叠三角形的面积最小是解决问题的关键.3.【答案】B【分析】过D作DM⊥BC于M,连接BD,则由三角形面积公式得,12BC×DM=12OB×CD,可得DM,可知圆D上点到直线5-512y x的最小距离,由此即可解决问题.【解答】过D作DM⊥BC于M,连接BD,如图,令0y =,则12x =,令0x =,则5y =-,∴B (12,0),C (0,-5),∴OB=12,OC=5,=, 则由三角形面积公式得,12BC ×DM=12OB ×CD , ∴DM=8413, ∴圆D 上点到直线5-512y x =的最小距离是845821313-=, ∴△ABC 面积的最小值是1581329213⨯⨯=. 故选:B .【点评】本题考查了一次函数的应用、勾股定理的应用、圆的有关性质,解此题的关键是求出圆上的点到直线BC 的最大距离以及最小距离.4.【答案】B【分析】连接OP ,过点O 作OH ⊥NM 交NM 的延长线于H .首先利用三角形的面积公式求出OH ,再证明△OP 1P 2是等腰直角三角形,OP 最小时,△OP 1P 2的面积最小.【解答】解:连接OP ,过点O 作OH ⊥NM 交NM 的延长线于H .∵S △OMN =12•MN •OH =12,MN =6,∴OH =4,∵点P 关于OA 对称的点为P 1,点P 关于OB 对称点为P 2,∴∠AOP =∠AOP 1,∠POB =∠P 2OB ,OP =OP 1=OP 2∵∠AOB =45°,∴∠P 1OP 2=2(∠POA+∠POB )=90°,∴△OP 1P 2是等腰直角三角形,∴OP =OP 1最小时,△OP 1P 2的面积最小,根据垂线段最短可知,OP 的最小值为4,∴△OP 1P 2的面积的最小值=12×4×4=8, 故选:B .【点评】本题考查轴对称,三角形的面积,垂线段最短等知识,解题的关键是证明△OP 1P 2是等腰直角三角形,属于中考常考题型.5.【答案】B【分析】过点F 作AD 的垂线交AD 的延长线于点H ,则△FEH ∽△EBA ,设AE=x ,可得出△CEF 面积与x 的函数关系式,再根据二次函数图象的性质求得最小值.【解答】解:过点F 作AD 的垂线交AD 的延长线于点H ,∵∠A=∠H=90°,∠FEB=90°,∴∠FEH=90°-∠BEA=∠EBA ,∴△FEH ∽△EBA ,∴ ,HF HE EF AE AB BE == G 为BE 的中点,1,2FE GE BE ∴==∴ 1,2HF HE EF AE AB BE === 设AE=x , ∵AB 8,4,AD ==∴HF 1,4,2x EH == ,DH AE x ∴==CEF DHFC CED EHF S S S S ∆∆∆∴=+-11111(8)8(4)422222x x x x =++⨯--⨯• 2141644x x x x =+--- 2116,4x x =-+ ∴当12124x -=-=⨯ 时,△CEF 面积的最小值1421615.4=⨯-+= 故选:B .【点评】本题通过构造K 形图,考查了相似三角形的判定与性质.建立△CEF 面积与AE 长度的函数关系式是解题的关键.二、填空题6.【答案】818【分析】作CM ⊥AB 于M ,EN ⊥AB 于N ,根据AAS证得EDN ≌DCM ,得出EN =DM ,然后解直角三角形求得AM =3,得到BM =9,设BD =x ,则EN =DM =9﹣x ,根据三角形面积公式得到S △BDE =12BD EN ⋅=12x (9﹣x )=﹣12(x ﹣4.5)2+818,根据二次函数的性质即可求得. 【解答】解:作CM ⊥AB 于M ,EN ⊥AB 于N ,∴∠EDN +∠DEN =90°,∵∠EDC =90°,∴∠EDN +∠CDM =90°,∴∠DEN =∠CDM , 在EDN 和DCM 中DEN CDM END DMC 90ED DC ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩∴EDN ≌DCM (AAS ),∴EN =DM ,∵∠BAC =120°,∴∠MAC =60°,∴∠ACM =30°,∴AM =12AC =12⨯6=3, ∴BM =AB +AM =6+3=9,设BD =x ,则EN =DM =9﹣x ,∴S △BDE =12BD EN ⋅=12x (9﹣x )=﹣12(x ﹣4.5)2+818, ∴当BD =4.5时,S △BDE 有最大值为818, 故答案为:818. 【点评】此题主要考查旋转综合题、全等三角形的判定及性质、直角三角形的性质和求最值,解题的关键是熟知全等三角形的判定与性质和利用二次函数求最值.7.【答案】503【分析】由圆周角定理可知A P ∠=∠,再由90ACB PCD ∠=∠=︒可证明~ACB PDC ,最后根据相似三角形对应边成比例,及已知条件BC :CA =4:3,结合三角形面积公式解题即可.【解答】AB 为直径,90ACB ∴∠=︒PC CD ⊥,90PCD ∴∠=︒又CAB CPD ∠=∠~ACB PDC ∴AC BC CP CD∴= BC :CA =4:3,43CD PC ∴= 当点P 在弧AB 上运动时,12PCD S PC CD =⋅△ 2142233PCD S PC PC PC ∴=⨯⋅= 当PC 最大时,PCD S 取得最大值而当PC 为直径时最大,22505=33PCD S ∴=⨯. 【点评】本题考查圆周角定理、三角形面积、相似三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.8.【答案】【分析】五边形ABCDP 的面积=四边形ABCD 的面积﹣△CPD 的面积只要求出△CDP 面积的最小值,作EF//CD ,且与⊙O 相切于点P ,连接OP 延长OP 交AD 于H ,易知此时点P 到CD 的距离最小,此时△CDP 的面积最小.【解答】解:∵五边形ABCDP 的面积=四边形ABCD 的面积﹣△CPD 的面积,∴只要求出△CDP 面积的最小值,作EF//CD ,且与⊙O 相切于点P ,连接OP 延长OP 交AD 于H ,易知此时点P 到CD 的距离最小,此时△CDP 的面积最小,易知AD =,∵四边形ABCD 的面积=12(1+3)×2=4=12×1×1+12•AD •OH+12•1•3,∴OH ,∴PH ﹣11,∴△CAD 的面积最小值为2,∴五边形ABCDP 面积的最大值是4﹣(2)=.故答案为.【点评】本题主要考查了求解多边形的面积知识点,结合圆的切线的性质进行求解是解题的重要步骤.9.【答案】42a - 【分析】先根据直角三角形含30度角的性质和勾股定理得AB=2,AC=4,从而得CG 的长,作辅助线,构建矩形ABHM 和高线GM ,如图2,通过画图发现:当GE ⊥BC 时,AG 最小,即a 最小,可计算a 的值,从而得结论.【解答】∵四边形ABCD 是矩形,∴∠B=90°,∵∠ACB=30°,,∴AB=2,AC=4,∵AG=a ,∴CG=4a -,如图1,过G 作MH ⊥BC 于H ,交AD 于M ,Rt△CGH中,∠ACB=30°,∴GH=12CG=42a-,则点G到BC边的距离为42a-,∵HM⊥BC,AD∥BC,∴HM⊥AD,∴∠AMG=90°,∵∠B=∠BHM=90°,∴四边形ABHM是矩形,∴HM=AB=2,∴GM=2﹣GH=422a--=2a,∴S△ADG11222a AD MG=⋅=⨯=当a最小时,△ADG的面积最小,如图2,当GE⊥BC时,AG最小,即a最小,∵FG是AE的垂直平分线,∴AG=EG,∴42aa -=,∴43a =,∴△ADG 的面积的最小值为4233=,故答案为:42a -. 【点评】本题主要考查了垂直平分线的性质、矩形的判定和性质、含30度角的直角三角形的性质以及勾股定理,确定△ADG 的面积最小时点G 的位置是解答此题的关键.10.【答案】152【分析】根据直线AB 交坐标轴于A(-2,0),B(0,-4),计算得直线AB 解析式;平移直线AB 到直线CD ,直线CD 当抛物线相交并只有一个交点P 时,△ABP 面积为最小值,通过一元二次方程和抛物线的性质求得点P 坐标;再利用勾股定理逆定理,证明ABP △为直角三角形,从而计算得到△ABP 面积的最小值.【解答】设直线AB 为y kx b =+∵直线AB 交坐标轴于A(-2,0),B(0,-4)∴024k b b=-+⎧⎨-=⎩ ∴24k b =-⎧⎨=-⎩∴直线AB 为24y x =--如图,平移直线AB 到直线CD ,直线CD 为2y x p =-+当2y x p =-+与抛物线1(2)(4)2y x x =--相交并只有一个交点P 时,△ABP 面积为最小值∴()()21242y x p y x x =-+⎧⎪⎨=--⎪⎩∴22820x x p -+-= ∴()44820p ∆=--=∴72p =∴2210x x -+= ∴1x =将1x =代入1(2)(4)2y x x =--,得32y =∴31,2P ⎛⎫⎪⎝⎭∴()2223451224AP ⎛⎫=++= ⎪⎝⎭2231251424BP ⎛⎫=++=⎪⎝⎭2222420AB∴222AB AP BP +=∴ABP △为直角三角形,90BAP ∠=∴1115=2222ABP AB A S P ⨯=⨯=△ 即△ABP 面积的最小值为152故答案为:152. 【点评】本题考查了二次函数、一次函数、平移、一元二次方程、勾股定理逆定理的知识;解题的关键是熟练掌握二次函数、一次函数、平移、一元二次方程、勾股定理逆定理的性质,从而完成求解.三、解答题11.【答案】(1)抛物线y =x 2-4x +3;(2)D(2,1);(3)点P 的坐标为5(2,3)4- 【分析】(1)(1) 将A 、C 坐标代入即可;(2)由于BC 长度不变, 要周长最小, 就是让DB DC 最小, 而A 、B 关于对称轴对称, 所以AC 就是DB DC 的最小值, 此时D 点就是AC 与抛物线对称轴的交点; 【解答】解:(1)抛物线23y ax bx =++经过点(1,0)A ,点(4,3)C ,∴3016433a bab,解得14a b ==-⎧⎨⎩,所以,抛物线的解析式为243y x x =-+;(2)243(1)(3)yx xx x ,(3,0)∴B ,抛物线的对称轴为2x =;BC 长度不变,BDDC 最小时,BCD ∆的周长最小,A 、B 是关于抛物线对称轴对称的,∴当D 点为对称轴与AC 的交点时,BD DC +最小, 即BCD ∆的周长最小, 如图,∴21x yx ,解得:21x y =⎧⎨=⎩,(2,1)D ∴,∴抛物线对称轴上存在点(2,1)D ,使BCD ∆的周长最小;(3)存在,如图,设过点P 与直线AC 平行线的直线为y x m =+,联立243y x m yx x,消掉y 得,2530x x m ,2(5)41(3)0m ,解得:134m =-, 即134m =-时,点P 到AC 的距离最大,ACP ∆的面积最大, 此时52x =,5133244y , ∴点P 的坐标为5(2,3)4-,设过点P 的直线与x 轴交点为F ,则13(4F ,0), 139144AF, 直线AC 的解析式为1y x =-,45CAB ∴∠=︒,∴点F 到AC 的距离为9292sin 45428AF , 又223(41)32AC ,∴∆的最大面积127ACE=⨯=.28【点评】本题考查了二次函数综合题型,主要考查了待定系数法求二次函数解析式,待定系数法求一次函数解析式,利用轴对称确定最短路线问题,联立两函数解析式求交点坐标,利用平行线确定点到直线的最大距离问题,熟悉相关性质是解题的关键.12.【答案】(1)2‘(2)1;(3)(.【分析】(1)当四边形EFGH为正方形时,则易证AHE≌△DGH,则DG=AH=2;(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于AB∥CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,从而有FM=HA=2(即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2),进而可求三角形面积;=7-x,在△AHE中,AE≤AB=7,利用勾股定理可得HE2(3)先设DG=x,由第(2)小题得,S△FCG≤53,在Rt△DHG中,再利用勾股定理可得x2+16≤53,进而可求x,从而可得当时,△GCF的面积最小.【解答】解:(1)∵四边形EFGH为正方形,∴HG=HE,∠EAH=∠D=90°,∵∠DHG+∠AHE=90°,∠DHG+∠DGH=90°,∴∠DGH=∠AHE,∴△AHE≌△DGH(AAS),∴DG=AH=2;(2)过F作FM⊥DC,交DC延长线于M,连接GE,∵AB∥CD,∴∠AEG=∠MGE,∵HE∥GF,∴∠HEG=∠FGE , ∴∠AEH=∠MGF ,在△AHE 和△MFG 中,∠A=∠M=90°,HE=FG , ∴△AHE ≌△MFG (AAS ), ∴FM=HA=2,即无论菱形EFGH 如何变化,点F 到直线CD 的距离始终为定值2, 因此S △FCG =12×FM ×GC=12×2×(7-6)=1; (3)设DG=x ,则由(2)得,S △FCG =7-x , 在△AHE 中,AE ≤AB=7, ∴HE 2≤53, ∴x 2+16≤53,∴x∴S △FCG 的最小值为,此时,∴当时,△FCG 的面积最小为(.【点评】本题属于四边形综合题,考查了矩形、菱形的性质、全等三角形的判定和性质、勾股定理.解题的关键是学会添加常用辅助线,构造全等三角形解决问题. 13.【答案】(1)抛物线的表达式为:223y x x =--;(2)POD S ∆有最大值,当14m =时,其最大值为4916;(3) Q -或(或1122⎛⎫-+- ⎪ ⎪⎝⎭或1322⎛⎫-+ ⎪ ⎪⎝⎭. 【分析】(1)函数的表达式为:y=a (x+1)(x-3),将点D 坐标代入上式,即可求解;(2)设点()2,23P m m m --,求出32OG m =+,根据()12POD D P S OG x x ∆=⨯-1(32)(2)2m m =+-2132m m =-++,利用二次函数的性质即可求解;(3)分∠ACB=∠BOQ 、∠BAC=∠BOQ ,两种情况分别求解,通过角的关系,确定直线OQ 倾斜角,进而求解.【解答】解:(1)函数的表达式为:(1)(3)y a x x =+-,将点D 坐标代入上式并解得:1a =,故抛物线的表达式为:223y x x =--…①;(2)设直线PD 与y 轴交于点G ,设点()2,23P m m m --,将点P 、D 的坐标代入一次函数表达式:y sx t =+并解得,直线PD 的表达式为:32y mx m =--,则32OG m =+,()12POD D P S OG x x ∆=⨯-1(32)(2)2m m =+-2132m m =-++, ∵10-<,故POD S ∆有最大值,当14m =时,其最大值为4916; (3)∵3OB OC ==,∴45OCB OBC ︒∠=∠=,∵ABC OBE ∠=∠,故OBE ∆与ABC ∆相似时,分为两种情况:①当ACB BOQ ∠=∠时,4AB =,BC =,AC =, 过点A 作AH ⊥BC 与点H ,1122ABC S AH BC AB OC ∆=⨯⨯=⨯,解得:AH =, ∴CH则tan 2ACB ∠=,则直线OQ 的表达式为: 2 y x =-…②,联立①②并解得:x =故点Q -或(; ②BAC BOQ ∠=∠时,3tan 3tan 1OC BAC BOQ OA ∠====∠, 则直线OQ 的表达式为: 3 y x =-…③,联立①③并解得:12x -±=,故点1322Q ⎛-- ⎝⎭或⎝⎭;综上,点Q -或(或⎝⎭或⎝⎭. 【点评】本题考查的是二次函数综合运用,涉及到解直角三角形、三角形相似、面积的计算等,其中(3),要注意分类求解,避免遗漏.14.【答案】(1)y =(x ﹣1)2;(2)点C 的坐标为(2,1);(3)1 【分析】(1)将点(3,4)代入解析式求得a 的值即可;(2)设点C 的坐标为(x 0,y 0),其中y 0=(x 0﹣1)2,作CF ⊥x 轴,证△BDO ∽△DCF 得BO DFDO CF=,即1=00x 1y -=()01x 1-,据此求得x 0的值即可得;(3)过点D 作x 轴的垂线交直线PQ 于点G ,则DG =4,根据S △PDQ =12DG •MN 列出关于k 的等式求解可得.【解答】解:(1)将点(3,4)代入解析式,得:4a =4,解得:a =1,所以抛物线解析式为y =(x ﹣1)2; (2)由(1)知点D 坐标为(1,0), 设点C 的坐标为(x 0,y 0),(x 0>1、y 0>0), 则y 0=(x 0﹣1)2,如图1,过点C 作CF ⊥x 轴,∴∠BOD =∠DFC =90°,∠DCF+∠CDF =90°, ∵∠BDC =90°, ∴∠BDO+∠CDF =90°, ∴∠BDO =∠DCF , ∴△BDO ∽△DCF , ∴BO DFDO CF=, ∴1=00x 1y -=()01x 1-,解得:x 0=2,此时y 0=1, ∴点C 的坐标为(2,1).(3)设点P 的坐标为(x 1,y 1),点Q 为(x 2,y 2),(其中x 1<1<x 2,y 1>0,y 2>0), 如图2,分别过点P 、Q 作x 轴的垂线,垂足分别为M 、N , 由y=(x-1)2 ,y=kx+1-k ,得x 2﹣(2+k )x+k =0. ∴x 1+x 2=2+k ,x 1•x 2=k . ∴MN =|x 1﹣x 2|=|2﹣k|.则过点D 作x 轴的垂线交直线PQ 于点G ,则点G 的坐标为(1,1), 所以DG =1,∴S △PDQ =12DG •MN =12×1×|x 1﹣x 2|12|2﹣k|, ∴当k =0时,S △PDQ 取得最小值1.【点评】本题主要考查二次函数的综合问题,解题的关键是熟练掌握待定系数法求函数解析式、相似三角形的判定与性质及一元二次方程根与系数的关系等知识点.15.【答案】45【分析】先证明△PEF ∽△BOC,得出PE EF PF BO OC BC ==,再根据122y x =-+,得出关于x 的二次函数方程,根据顶点坐标公式,求得则△PEF 面积最大值.【解答】解:设213,222P x x x ⎛⎫-++⎪⎝⎭(0<x<4), 抛物线213222y x x =-++与y 轴交于C 点,故C(0,2),∵PF ∥y 轴,PE ⊥BC , ∴∠PFE=∠BCO, 又∵∠PEF=∠BOC=90°, ∴△PEF ∽△BOC, ∴PE EF PF BO OC BC== ,把B(4,0),C(0,2)代入直线BC 的解析式为122y x =-+, 点1,22F x x ⎛⎫-+ ⎪⎝⎭,∴221312(2)22222P F x PF y y x x x x =-=-++--+=-+,∴PE=BO ·PF BC =42212x x -+== , EF=OC ·PFBC=222211122(2)x x x x x x -+-+-== , ∴221(2)1225PEFx x SPE EF -=⋅= =2221(2)(2)42520x x x ⎡⎤-⎢⎥⎡⎤--+⎣⎦⎣⎦=, 当2x =时,PEF S △取值最大,∴PEF S △的最大值为244205=, 故答案为45. 【点评】本题考查了三角形的面积及相似三角形的判定与性质.熟练掌握相似三角形的判定与性质及用含x 的代数式表示出三角形的面积是解题的关键.16.【答案】(1)见解析;(2)见解析;(3)当点P 是MN 的中点时S △MON 最小.理由见解析. 【分析】(1)根据尺规作图,过P 点作PN ⊥OB 于N ,交OA 于点M ; (2)证明三角形全等得P 为MN 的中点,便可得到结论;(3)过点P 作另一条直线EF 交OA 、OB 于点E 、F ,设PF <PE ,与MC 交于于G ,证明△PGM ≌△PFN ,得△PGM 与△PFN 的面积相等,进而得S 四边形MOFG =S △MON . 便可得S △MON <S △EOF ,问题得以解决.【解答】(1)①在OB 下方取一点K ,②以P 为圆心,PK 长为半径画弧,与OB 交于C 、D 两点,③分别以C 、D 为圆心,大于12CD 长为半径画弧,两弧交于E 点, ④作直线PE ,分别与OA 、OB 交于点M 、N ,故△OMN 就是所求作的三角形;(2)∵CM ∥OB ,∴∠C =∠PON ,在△PCM 和△PON 中,C PON PC POCPH OPN ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△PCM ≌△PON (ASA ),∴PM =PN ,∴OP 平分△MON 的面积;(3)过点P 作另一条直线EF 交OA 、OB 于点E 、F ,设PF <PE ,与MC 交于于G ,∵CM ∥OB ,∴∠GMP =∠FNP ,在△PGM 和△PFM 中,PMG PNF PM PNMPG NPF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△PGM ≌△PFN (ASA ),∴S △PGM =S △PFN∴S 四边形MOFG =S △MON .∵S 四边形MOFG <S △EOF ,∴S △MON <S △EOF ,∴当点P 是MN 的中点时S △MON 最小.【点评】本题主要考查了图形的旋转性质,全等三角形的性质与判定,三角形的中线性质,关键证明三角形全等.17.【答案】(1)12x <<;(2)2. 【分析】(1)由旋转可得到AC=MA=x ,BC=BN=3-x ,利用三角形三边关系可求得x 的取值范围;(2)过点C 作CD ⊥AB 于D ,设CD=h ,利用勾股定理表示出AD 、BD ,再根据BD=AB-AD 列方程求出h 2,然后求出△ABC 的面积的平方,再根据二次函数的最值问题解答.【解答】解:(1)∵4MN =,1MA =,AB x =,∴413BN x x =--=-.由旋转的性质,得1MA AC ==,3BN BC x ==-,由三角形的三边关系,得31,31,x x x x --<⎧⎨-+>⎩①② 解不等式①得1x >,解不等式②得2x <,∴x 的取值范围是12x <<.(2)如图,过点C 作CD AB ⊥于点D ,设CD h =,由勾股定理,得AD =,BD ==, ∵BD AB AD =-,x =-34=-x ,两边平方整理,得()222832=x x h x -+-.∵ABC 的面积为1122AB CD xh ⋅=, ∴()2222113183222422S xh x x x ⎛⎫⎛⎫==-⨯-+=--+ ⎪ ⎪⎝⎭⎝⎭, ∴当32x =时,ABC 面积最大值的平方为12,∴ABC . 【点评】本题考查了旋转的性质,三角形的三边关系,勾股定理,二次函数的最值问题,(1)难点在于考虑利用三角形的三边关系列出不等式组,(2)难点在于求解利用勾股定理列出的无理方程.18.【答案】(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【解答】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点,//PM CE ∴,12PM CE =, AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒,PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =,PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒,AM ∴=在Rt ABC ∆中,10AB AC ==,AN =MN ∴=最大,22211114922242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点评】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.19.【答案】(1)20;(2)5;(3)S △BCD =16;∠BCD =45°【分析】(1)由勾股定理可求解;(2)由等腰三角形的性质可得∠A =∠DBA ,由余角的性质可得∠DBC =∠C ,可得DB =DC =AD =12AC =5; (3)由中点的性质和折叠的性质可得DE =EC =4,则当DE ⊥BC 时,S △BCD 有最大值,由三角形面积公式和等腰直角三角形的性质可求解.【解答】解:(1)∵∠ABC =90°,AB =12,BC =16,∴20AC ==,故答案为:20;(2)∵DA =DB ,∴∠A =∠DBA ,∵∠ABC =90°∴∠A +∠C =90°,∠ABD +∠DBC =90°,∴∠DBC =∠C ,∴DB=DC,∴DB=DC=AD=12AC=5,故答案为:5;(3)∵E为BC中点,BC=8,∴BE=EC=4,∵将∠C折叠,折痕为EF,∴DE=EC=4,当DE⊥BC时,S△BCD有最大值,S△BCD=12×BC×DE=12×8×4=16,此时∵DE⊥BC,DE=EC,∴∠BCD=45°.故答案为:S△BCD=16;∠BCD=45°.【点评】本题主要考查了勾股定理、直角三角形斜边中线问题以及三角形中的折叠问题;题目较为综合,其中熟练掌握定义定理是解题的关键.20.【答案】①②③⑤【分析】由“SAS”可证△BEC≌△AFC,可得CF=CE,∠BCE=∠ACF,可证△EFC是等边三角形,由三角形内角和定理可证∠DFC=∠EGC;由等边三角形的性质和菱形的性质可求MN=DN=BM=由勾股定理即可求解EF2=BE2+DF2不成立;由等边三角形的性质可得△ECF面积2,则当EC⊥AB时,△ECF【解答】解:∵四边形ABCD是菱形,∴AB=BC=CD=AD=6,∵AC=BC,∴AB=BC=CD=AD=AC,∴△ABC,△ACD是等边三角形,∴∠ABC=∠BAC=∠ACB=∠DAC=60°,∵AC=BC,∠ABC=∠DAC,AF=BE,∴△BEC≌△AFC(SAS)∴CF=CE,∠BCE=∠ACF,∴∠ECF =∠BCA =60°,∴△EFC 是等边三角形,故①正确;∵∠ECF =∠ACD =60°,∴∠ECG =∠FCD ,∵∠FEC =∠ADC =60°,∴∠DFC =∠EGC ,故②正确;若BE =3,菱形ABCD 的边长为6,∴点E 为AB 中点,点F 为AD 中点,∵四边形ABCD 是菱形,∴AC ⊥BD ,AO =CO ,BO =DO ,∠ABO =12∠ABC =30°,∴AO =12AB =3,BO =∴BD =,∵△ABC 是等边三角形,BE =AE =3,∴CE ⊥AB ,且∠ABO =30°,∴BE EM =3,BM =2EM ,∴BM =同理可得DN =∴MN =BD −BM −DN =∴BM =MN =DN ,故③正确;∵△BEC ≌△AFC ,∴AF =BE ,同理△ACE ≌△DCF ,∴AE =DF ,∵∠BAD ≠90°,∴EF 2=AE 2+AF 2不成立,∴EF 2=BE 2+DF 2不成立,故④错误,∵△ECF 是等边三角形,∴△ECF 2, ∴当EC ⊥AB 时,△ECF 面积有最小值,此时,EC =ECF 面积的最小值为4,故⑤正确; 故答案为:①②③⑤.【点评】本题是四边形综合题,考查菱形的性质,全等三角形的判定和性质,等边三角形的判定和性质,勾股定理等知识,熟练掌握性质定理是解题的关键.21.【答案】(1)223;y x x =--(2)当32t =时,S 有最大值278;(3)()()2,5,1,4-- 【分析】(1)根据抛物线上的对称点B 和E ,求出对称轴从而可求出C 点坐标.然后设出抛物线的交点式,再把点A 代入求出a 值即可求出抛物线的解析式;(2)过点P 作y 轴的平行线交AE 于点H ,分别根据抛物线和直线AE 的解析式表示出点P 和点H 的坐标,从而求出线段PH 的长,最后用含t 的式子表示∆APE 的面积,利用二次函数的性质求解;(3)根据两直线垂直时,它们的斜率之积为-1,可求得与直线AE 垂直的直线方程,最后联立方程组可求点P 的坐标.【解答】解:(1)抛物线2y ax bx c =++经过点()()1,03,0,B E -、∴抛物线的对称轴为1,x =点()0,3A -,点()2,3C -抛物线表达式为()()()23123,.y a x x a x x =-+=--33a ∴-=-,解得1,a =∴抛物线的表达式为223;y x x =--()2如图,过点P 作y 轴的平行线交AE 于点H由点,A E 的坐标得直线AE 的表达式为3,y x =-设点()2,23P t t t --,则(),3H t t -()()22213333273233222228PAES PH OE t t t t t t ∆⎛⎫∴=•=--++=-+=--+ ⎪⎝⎭ 当32t =时,S 有最大值278()3直线AE 表达式中的k 值为1,则与之垂直的直线表达式中的k 值为1-① 当90PEA ︒∠=时,直线PE 的表达式为1,y x b =-+将点E 的坐标代人并解得13b =,直线PE 的表达式为3,y x =-+联立得2233y x x y x ⎧=--⎨=-+⎩解得2x =-或3(不合题意,舍去)故点P 的坐标为()2,5-② 当90PAE ︒∠=时,直线PA 的表达式为2,y x b =-+将点A 的坐标代人并解得23b =,直线PE 的表达式为3,y x =--联立得2233y x x y x ⎧=--⎨=--⎩ 解得1x =或0(不合题意,舍去)故点()1,4P -综上,点P 的坐标为()2,5-或(1,-4)【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质;会利用待定系数法求二次函数解析式;会解一元二次方程;理解坐标与图形性质,记住两直线垂直时它们的斜率之积为-1;会利用分类讨论的思想解决数学问题.。
中考数学专题:几何最值问题
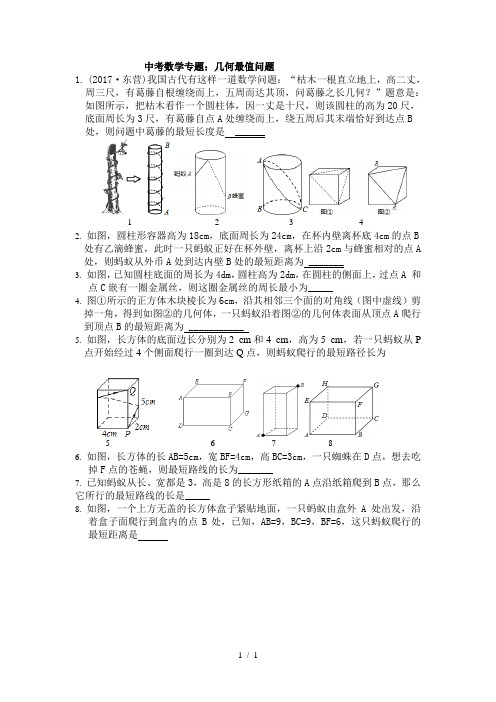
中考数学专题:几何最值问题
1. (2017·东营)我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B
处,则问题中葛藤的最短长度是 ______
1 2 3 4
2.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B 处有乙滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A 处,则蚂蚁从外币A处到达内壁B处的最短距离为 _______
3.如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A 和
点C嵌有一圈金属丝,则这圈金属丝的周长最小为_____
4.图①所示的正方体木块棱长为6cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为 ___________
5.如图,长方体的底面边长分别为2 cm和4 cm,高为5 cm,若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为_______
5 6 7 8
6.如图,长方体的长AB=5cm,宽BF=4cm,高BC=3cm,一只蜘蛛在D点,想去吃
掉F点的苍蝇,则最短路线的长为_______
7.已知蚂蚁从长、宽都是3,高是8的长方形纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是_____
8.如图,一个上方无盖的长方体盒子紧贴地面,一只蚂蚁由盒外A处出发,沿
着盒子面爬行到盒内的点B处,已知,AB=9,BC=9,BF=6,这只蚂蚁爬行的最短距离是
1 / 1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何最值问题一.选择题(共6小题)1.(2015•孝感一模)如图,已知等边△ABC的边长为6,点D为AC的中点,点E为BC的中点,点P为BD上一点,则PE+PC的最小值为()A.3 B.3C.2D.3考点:轴对称-最短路线问题.分析:由题意可知点A、点C关于BD对称,连接AE交BD于点P,由对称的性质可得,PA=PC,故PE+PC=AE,由两点之间线段最短可知,AE即为PE+PC的最小值.解答:解:∵△ABC是等边三角形,点D为AC的中点,点E为BC的中点,∴BD⊥AC,EC=3,连接AE,线段AE的长即为PE+PC最小值,∵点E是边BC的中点,∴AE⊥BC,∴AE===3,∴PE+PC的最小值是3.故选D.点评:本题考查的是轴对称﹣最短路线问题,熟知等边三角形的性质是解答此题的关键.2.(2014•鄂城区校级模拟)如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm和40cm,B点到y轴的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,则这个值为()A.50 B.50C.50﹣50 D.50+50考点:轴对称-最短路线问题;坐标与图形性质.专题:压轴题.分析:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交X,Y轴分别为P,Q点,此时四边形PABQ的周长最短,根据题目所给的条件可求出周长.解答:解:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交x,y轴分别为P,Q点,过M点作MK⊥x轴,过N点作NK⊥y轴,两线交于K点.MK=40+10=50,作BL⊥x轴交KN于L点,过A点作AS⊥BP交BP于S点.∵LN=AS==40.∴KN=60+40=100.∴MN==50.∵MN=MQ+QP+PN=BQ+QP+AP=50.∴四边形PABQ的周长=50+50.故选D.点评:本题考查轴对称﹣最短路线问题以及坐标和图形的性质,本题关键是找到何时四边形的周长最短,以及构造直角三角形,求出周长.3.(2014秋•贵港期末)如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数为()A.30°B.40°C.50°D.60°考点:轴对称-最短路线问题.分析:根据要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=70°,进而得出∠MAB+∠NAD=70°,即可得出答案.解答:解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值,作DA延长线AH,.∵∠DAB=110°,∴∠HAA′=70°,∴∠AA′M+∠A″=∠HAA′=70°,∵∠MA′A=∠MAB,∠NAD=∠A″,∴∠MAB+∠NAD=70°,∴∠MAN=110°﹣70°=40°.故选B.点评:本题考查的是轴对称﹣最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.4.(2014•无锡模拟)如图,∠MON=90°,矩形ABCD的顶点A,B分别在OM、ON上,当B 在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=.运动过程中,当点D到点O的距离最大时,OA长度为()A.B.C.2 D.考点:勾股定理;三角形三边关系;直角三角形斜边上的中线.分析:取AB的中点,连接OE、DE,根据直角三角形斜边上的中线等于斜边的一半求出OE,利用勾股定理列式求出DE,然后根据三角形的任意两边之和大于第三边判断出O、E、D三点共线时点D到点O的距离最大,过点A作AF⊥OD于F,利用∠ADE的余弦列式求出DF,从而得到点F是OD的中点,判断出AF垂直平分OD,再根据线段垂直平分线上的点到两端点的距离相等可得OA=AD.解答:解:如图,取AB的中点,连接OE、DE,∵∠MON=90°,∴OE=AE=AB=×2=1,∵三边形ABCD是矩形,∴AD=BC=,在Rt△ADE中,由勾股定理得,DE===2,由三角形的三边关系得,O、E、D三点共线时点D到点O的距离最大,此时,OD=OE+DE=1+2=3,过点A作AF⊥OD于F,则cos∠ADE==,即=,解得DF=,∵OD=3,∴点F是OD的中点,∴AF垂直平分OD,∴OA=AD=.故选B.点评:本题考查了勾股定理,三角形的任意两边之和大于第三边,直角三角形斜边上的中线等于斜边的一半的性质,线段垂直平分线上的点到两端点的距离相等的性质,作辅助线并判断出OD最大时的情况是解题的关键,作出图形更形象直观.5.(2015•鞍山一模)如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是()A.B.C.D.1考点:轴对称-最短路线问题;正方形的性质.分析:根据题意得出作EF∥AC且EF=,连结DF交AC于M,在AC上截取MN=,此时四边形BMNE的周长最小,进而利用相似三角形的判定与性质得出答案.解答:解:作EF∥AC且EF=,连结DF交AC于M,在AC上截取MN=,延长DF交BC于P,作FQ⊥BC于Q,则四边形BMNE的周长最小,由∠FEQ=∠ACB=45°,可求得FQ=EQ=1,∵∠DPC=∠FPQ,∠DCP=∠FQP,∴△PFQ∽△PDC,∴=,∴=,解得:PQ=,∴PC=,由对称性可求得tan∠MBC=tan∠PDC==.故选:A.点评:此题主要考查了正方形的性质以及相似三角形的判定与性质,得出M,N的位置是解题关键.6.(2015•江干区一模)如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE 为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为()A.B.C.2D.考点:圆的综合题.分析:根据等腰三角形的性质可得点D是AB的中点,然后根据三角形中位线定理可得DP=BG,然后利用两点之间线段最短就可解决问题.解答:解:连接BG,如图.∵CA=CB,CD⊥AB,AB=6,∴AD=BD=AB=3.又∵CD=4,∴BC=5.∵E是高线CD的中点,∴CE=CD=2,∴CG=CE=2.根据两点之间线段最短可得:BG≤CG+CB=2+5=7.当B、C、G三点共线时,BG取最大值为7.∵P是AG中点,D是AB的中点,∴PD=BG,∴DP最大值为.故选A.点评:本题主要考查了圆的综合题,涉及了等腰三角形的性质、三角形中位线定理、勾股定理、两点之间线段最短等知识,利用三角形中位线定理将DP转化为BG是解决本题的关键.二.填空题(共3小题)7.(2014•江阴市校级模拟)如图,线段AB的长为4,C为AB上一动点,分别以AC、BC 为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是 2 .考点:等腰直角三角形.分析:设AC=x,BC=4﹣x,根据等腰直角三角形性质,得出CD=x,CD′=(4﹣x),根据勾股定理然后用配方法即可求解.解答:解:设AC=x,BC=4﹣x,∵△ABC,△BCD′均为等腰直角三角形,∴CD=x,CD′=(4﹣x),∵∠ACD=45°,∠BCD′=45°,∴∠DCE=90°,∴DE2=CD2+CE2=x2+(4﹣x)2=x2﹣4x+8=(x﹣2)2+4,∴当x取2时,DE取最小值,最小值为:4.故答案为:2.点评:本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.8.(2012•河南校级模拟)如图,矩形ABCD中,AB=4,BC=8,E为CD边的中点,点P、Q 为BC边上两个动点,且PQ=2,当BP= 4 时,四边形APQE的周长最小.考点:轴对称-最短路线问题.专题:压轴题.分析:要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC 的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度.解答:解:如图,在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.∵GH=DF=6,EH=2+4=6,∠H=90°,∴∠GEH=45°.设BP=x,则CQ=BC﹣BP﹣PQ=8﹣x﹣2=6﹣x,在△CQE中,∵∠QCE=90°,∠CEQ=45°,∴CQ=EC,∴6﹣x=2,解得x=4.故答案为4.点评:本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.9.(2013•武汉)如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是﹣1 .考点:正方形的性质.专题:压轴题.分析:根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.解答:解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,在△ABE和△DCF中,,∴△ABE≌△DCF(SAS),∴∠1=∠2,在△ADG和△CDG中,,∴△ADG≌△CDG(SAS),∴∠2=∠3,∴∠1=∠3,∵∠BAH+∠3=∠BAD=90°,∴∠1+∠BAH=90°,∴∠AHB=180°﹣90°=90°,取AB的中点O,连接OH、OD,则OH=AO=AB=1,在Rt△AOD中,OD===,根据三角形的三边关系,OH+DH>OD,∴当O、D、H三点共线时,DH的长度最小,最小值=OD﹣OH=﹣1.(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆上运动当O、H、D三点共线时,DH长度最小)故答案为:﹣1.点评:本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,确定出DH最小时点H的位置是解题关键,也是本题的难点.三.解答题(共1小题)10.(2015•黄冈中学自主招生)阅读下面材料:小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).请你回答:AP的最大值是 6 .参考小伟同学思考问题的方法,解决下列问题:如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是(或不化简为).(结果可以不化简)考点:旋转的性质;全等三角形的判定与性质;等边三角形的性质;勾股定理;等腰直角三角形.专题:几何综合题.分析:(1)根据旋转的性质知A′A=AB=BA′=2,AP=A′C,所以在△AA′C中,利用三角形三边关系来求A′C即AP的长度;(2)以B为中心,将△APB逆时针旋转60°得到△A'P'B.根据旋转的性质推知PA+PB+PC=P'A′+P'B+PC.当A'、P'、P、C四点共线时,(P'A′+P'B+PC)最短,即线段A'C最短.然后通过作辅助线构造直角三角形A′DC,在该直角三角形内利用勾股定理来求线段A′C的长度.解答:解:(1)如图2,∵△ABP逆时针旋转60°得到△A′BC,∴∠A′BA=60°,A′B=AB,AP=A′C∴△A′BA是等边三角形,∴A′A=AB=BA′=2,在△AA′C中,A′C<AA′+AC,即AP<6,则当点A′A、C三点共线时,A′C=AA′+AC,即AP=6,即AP的最大值是:6;故答案是:6.(2)如图3,∵Rt△ABC是等腰三角形,∴AB=BC.以B为中心,将△APB逆时针旋转60°得到△A'P'B.则A'B=AB=BC=4,PA=P′A′,PB=P′B,∴PA+PB+PC=P′A′+P'B+PC.∵当A'、P'、P、C四点共线时,(P'A+P'B+PC)最短,即线段A'C最短,∴A'C=PA+PB+PC,∴A'C长度即为所求.过A'作A'D⊥CB延长线于D.∵∠A'BA=60°(由旋转可知),∴∠1=30°.∵A'B=4,∴A'D=2,BD=2,∴CD=4+2.在Rt△A'DC中A'C====2+2;∴AP+BP+CP的最小值是:2+2(或不化简为).故答案是:2+2(或不化简为).点评:本题综合考查了旋转的性质、等腰直角三角形的性质、勾股定理以及等边三角形的判定与性质.注意:旋转前、后的图形全等.实用标准文档文案大全。
