2018年高三最新 北京市西城区2018年第二学期期中抽样测试高三数学(理科)20182018 精品
2018年高三最新 北京市西城区2018年抽样测试高三数学试卷(理科)2018018 精品

北京市西城区2018年抽样测试高三数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合要求的. 1.sin600°+tan240°的值是A .23-B .23 C .321+-D .321+ 2. 函数)0(12>+=x x y 的反函数是 A .)0(12>-=x x y B .)0(12>--=x x yC .)1(12>-=x x yD .)1(12>--=x x y3.等差数列6427531,4,}{a a a a a a a a n ++=+++则中=A .3B .4C .5D .64.设命题p :若001:;11,<⇔<<>ab bq b a b a 则.给出下列四个复合命题: ①p 或q ;②p 且q ;③ p ;④ q ,其中真命题的个数有A .0个B .1个C .2个D .3个5.直线ky x k y x 1=-=+与的交点A .在直线上B .在圆上C .在椭圆上D .在双曲线上6.两个平面α与β相交但不垂直,直线m 在平面α内,则在平面β内 A .一定存在与直线m 平行的直线 B .一定不存在与直线m 平行的直线C .一定存在与直线m 垂直的直线D .不一定存在与直线m 垂直的直线7.某人上午7:00乘汽车以匀速1υ千米/时(30≤1υ≤100),从A 地出发到距300公里的B地,在B 地不作停留,然后骑摩托车以匀速2υ千米/时(4≤2υ≤20)从B 地出发到距50公里的C 地,计划在当天16:00至21:00到达C 地。
设乘汽车、摩托车行驶的时间分别是x 、y 小时,则在xOy 坐标系中,满足上述条件的x ,y 的范围用阴影部分表正确的是8.若},6,5,4,3,2,1{)2,1,0(},1010|{,0122∈=+⨯+⨯=∈i a a a a x x n m i 其中并且606=+n m ,则实数对(m ,n )表示平面上不同点的个数为A .32个B .30个C .62个D .60个8.若},6,5,4,3,2,1{)2,1,0(},1010|{,0122∈=+⨯+⨯=∈i a a a a x x n m i 其中并且606=+n m ,则实数对(m ,n )表示平面上不同点的个数为 A .32个 B .30个 C .62个D .60个二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中横线上.9.=-+-+→254lim 221x x x x x . 10.把点A (2,2)按向量)2,2(-=a 平移到点B ,此时点B 分OC (O 为坐标原点)的比为2-,则点C 的坐标为 .11.6)21(x -展开式中所有项的系数之和为 ;63)21)(1(x x -+展开式中5x 的系数为 .12.若椭圆11:22=++y m x C 的一条准线方程为2-=x ,则=m ;此时,定点)0,21(与椭圆C 上动点距离的最小值为 .13.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,点D 到平面ACD 1的距离为 ,若点P 为△BCD 的重心,则D 1P 与平面ADD 1A 1所成角的大小为 . 14.设}{n a 是公比为q 的等比数列,其前n 项的积为T n ,并且满足条件,01,1100991>->a a a 01110099<--a a .给出下列结论:①0<q<1;②T 198<1;③a 99a 101<1;④使T n <1成立的最小自然数n 等于199. 其中正确结论的编号是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分) 有6件产品,其中含有3种次品,现逐个抽取检查(不放回),求: (1)前4次恰好查出2件产品的概率;(2)设查出全部次品时检查产品的个数为ξ,求ξ的分布列、期望. 16.(本小题满分13分)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且满足C b B c a cos cos )2(=-.(1)求角B 的大小;(2)设n m k k n A A m ⋅>==),1)(1,4(),2cos ,(sin 的最大值为5,求k 的值. 17.(本小题满分13分)已知函数).,0(,ln )(e x x x f ∈-=曲线)(x f y =在点))(,(t f t 处的切线与x 轴和y 轴分别交于A 、B 两点,设O 为坐标原点,求△AOB 面积的最大值.18.(本小题满分13分) 如图,四棱锥S —ABCD 中,平面SAC 与底面ABCD 垂直,侧棱SA 、SB 、SC 与底面ABCD 所成的角均为45°,AD//BC ,且AB=BC=2AD.(1)求证:四边形ABCD 是直角梯形; (2)求异面直线SB 与CD 所成角的大小; (3)求直线AC 与平面SAB 所成角的大小. 19.(本小题满分14分)双曲线)0,0(12222>>=-b a by a x 的离心率为3,A 、F 分别是双曲线的左顶点、右焦点,过点F 的直线l 交双曲线的右支于P 、Q 两点,交y 轴于R 点,AP 、AQ 分别交右准线于M 、N 两点.(1)若5=,求直线l 的斜率; (2)证明:M 、N 两点的纵坐标之积为234a -. 20.(本小题满分14分) 已知实数0≥c ,曲线c x y l x y C -==::与直线的交点为P (异于原点O ),在曲线C 上取一点),,(111y x P 过点P 1作P 1Q 1平行于x 轴,交直线l 于点Q 1,过点Q 1作Q 1P 2平行于y 轴,交曲线C 于点P 2(x 2,y 2),接着过点P 2作P 2Q 2平行于x 轴,交直线l 于点Q 2,过点Q 2作直线Q 2P 3平行于y 轴,交曲线C 于点P 3(x 3,y 3),如此下去,可以得到点P 4(x 4,y 4),P 5(x 5,y 5),…,P n (x n ,y n ),….设点P 的坐标为.0,),,(1a b b x a a <<= (1)试用c 表示a ,并证明1≥a ;(2)试证明)(,12*∈<>N n a x x x n 且;(2)当).,(22)(:,21,0121*=++∈<-≥=∑N n k x x x b c nk k k k 求证时北京西城区数学(理)参考答案一、选择题1.B2.C3.A4.C5.D6.C7.B8.D二、填空题(一题两空的题目,第一个空2分,第二个空3分)9.2 10.(0,2) 11.1;-132 12. 23,1 13.510arctan ,3314.①③④(注:全部选对得5分;选出错误选项②得0分;其余情况得2分) 三、解答题(限于篇幅,每题只给出一种答案,其他答案仿此给分) 15.解:(1)前4次恰好查出2件次品的概率53464423231==A A C C P ;(2)根据题意,ξ的取值可以是3、4、5、6.其中,;201)3(3633===A A P ξ21)6(;103)5(;203)4(6655135644132346131313=========A A C P A A C C P A A C C P ξξξ所以,25.5216103520342013=⨯+⨯+⨯+⨯=ξE16.解:(I )因为,cos cos )2(C b B c a =- 所以,cos sin cos )sin sin 2(C B B C A =- 整理得,cos sin cos sin cos sin 2B C C B B A += 所以A C B B A sin )sin(cos sin 2=+=,因为3,21cos ,0sin ),,0(ππ==≠∈B B A A 所以所以.(2)A A k 2cos sin 4+=⋅)32,0(,1sin 4sin 22π∈++-=A A k A 其中设]1,0(,142],1,0(sin 2∈++-=⋅∈=t kt t t A 则 所以,当t ⋅=,1时取得最大值.依题意23,5142==++-k k 解得,符合题意.所以,23=k .17.解:(I )由已知,1)(xx f -='所以曲线)(x f y =在点))(,(t f t 处的切线方程为),(1ln t x tt y --=+令y=0,得A 点的横坐标为)ln 1(t t x A -=,令x=0,得B 点的纵坐标为t x B ln 1-=,当0,0,),0(>>∈B A x x e t 时,此时△AOB 的面积,)ln 1(212t S -= ),1)(ln 1(ln 21+-='t t S解e t e S e t S <<<'<<>'1,0;10,0得解得.所以)1,0(e是函数2)ln 1(21t t S -=的增区间;),1(e e是函数的减区间.所以,当e t 1=时△AOB 的面积最大,最大值为ee e 2)1ln 1(1212=-⨯. 18.解:方法一(1)证明:作SO ⊥AC 交AC 于点O ,连接OB.因为面SAC ⊥ABCD ,所以SO ⊥ABCD , 因为侧棱SA 、SB 、SC 与底面ABCD 所成的角均为45°, 所以∠SAO=∠SBO=∠SCO=45°, 所以△SAO ≌△SBO ≌△SCO ,所以SA=SB=SC ,OA=OB=OC , 所以AC 是△ABC 外接圆的直径,所以AB ⊥BC , 又AD//BC ,AD ≠BC ,所以四边形ABCD 是直角梯形. (2)分别取BC 中点M ,SC 中点N ,连结AM ,AN ,MN ,则MN//SB , 又AD//BC ,AD=21BC=MC ,所以,ADCM 为平行四边形, 所以AM//DC ,所以∠AMN 是异面直线SB 与CD 所成角. 由(1),△SAO ,△SBO ,△SCO 是全等的等腰直角三角形,AB=BC ,所以,△SAC ,△BAC 是全等的等腰直角三角形. 设SO=a ,则MN=21SB=a22,AM=,1022a a BM AB =+ 因为AM=AN ,所以在等腰三角形AMN 中,.10521cos ==AM MNAMN 所以,异面直线SB 与CD 所成角为.105arccos(3)取SB 中点E ,连结AE 、CE 、OE ,由(2)知AE ⊥SB ,CE ⊥SB ,所以,SB ⊥平面AEC , 所以,平面SAB ⊥平面AEC ,且交线就是AE , 所以AC 在平面SAB 上的射影是AE , 所以∠CAE 是AC 与平面SAB 所成的角 在等腰直角三角形SOB 中,E 是SB 的中点, 所以,22tan ,.2222==∆==AO OE OAE AOE Rt AO SO OE 中在所以直线AC 与平面SAB 所成角的大小是.22arctan方法二(1)证明:作SO ⊥AC 交AC 于点O ,连OB , 因为面SAC ⊥面ABCD ,所以SO ⊥面ABCD 因为侧棱SA 、SB 、SC 与底面 ABCD 所成的角均为45°, 所以∠SAO=∠SBO=∠SCO=45°, 所以△SAO ≌△SBO ≌△SCO , 所以SA=SB=SC ,OA=OB=OC=OS 又AB=BC ,所以OB ⊥AC , 以OA 、OB 、OS 所在射线分别作为非负x 轴、非负y 轴、 非负z 轴建立空间直角坐标系, 设OS=a , 则A (a ,0,0),B (0,a ,0),C (-a ,0,0),S (0,0,a ) 所以,0)0,,()0,,(22=-=--⋅-=⋅a a a a a a所以,,//.,BC AD BC AD BC AB ≠⊥⊥又即所以四边形ABCD 是直角梯形. (2)由(1),△SAO ,△SBO ,△SCO 是全等的等腰直角三角形, 所以△SAC ,△BAC 是全等的等腰直角三角形.则),,,0(),0,21,23(),0,21,21(a a SB a a CD a a D -=-=-,105210221||||,cos 2-=⋅-=⋅<aa a CD SB 所以异面直线SB ,CD 所成角的大小是.105arccos(3)设),,(111z y x =是平面SAB 的法向量.则由⎩⎨⎧=+-=-⎪⎩⎪⎨⎧=⋅=⋅00001111ay ax az ax 得取),1,1,1(,11==x 得则,33232||||cos -=⋅-=⋅>=⋅<aa AC n AC n设AC 和面SAB 所成的角的大小为α,则,36,sin cos >=<=α所以AC 和面SAB 所成的角的大小是36arccos .19.(1)解:设),(),,(2211y x Q y x P ,因为双曲线的离心率为3,所以a b a c 2,3==,双曲线方程为22222a y x =-,因为5=,所以c x 652=, 因为直线),(:c x k y l -=所以62ck y -=,点Q 是双曲线上一点,所以2222)6()65(2a ck c =--,整理得,,23613650222=-k e e 解得.26±=k(2)证明:设),,(),,(2211y x Q y x P 由已知)(:),(:2211a x ax y y AQ a x a x y y AP ++=++=, 所以)(),(222211a ca a x y y a c a a x y y N M ++=++=, 所以222212121222211)()()(a ca a x x a x x y y a c a a x y a x y y y N M ++++=++⋅+=, 由,22)(222⎩⎨⎧=--=ay x c x k y 得022)2(222222=--+-a c k cx k x k 所以22,222222212221-+=-=+k a c k x x k c k x x ,222])([))((222222121221221--=++-=--=k c a kc x x c x x k c x c x k y y ,2)()(22222121-+=+++k c a ka x x a x x所以,222222234)()()(2a c c a a c a c a y y N M -=+⋅+-=20.解:(I )点P 的坐标),(a a 满足方程组c a a xy c x y -=⎩⎨⎧=-=所以,, 解)4121(21,2411,0c c a c a c a a +++=++==--所以得因为.1,24121,0≥≥+++≥a c c c 所以所以 (2)由已知),,(),,(),,(211c b c b P b c b Q b b P +++即,,21c b x b x +==),1)((,)1(,1212-+-=--+=--=-+=-b a b a b a a b x x a a c b c b x x 所以由因为,12,1,0x x a a b >≥<<所以. 下面用数学归纳法证明).(*∈<N n a x n.,,0,,,,;,1111a a a x c x x x c y x a x k n a b x n k k k k k k k <-+=+=>+=<=>==++所以由已知时假设当时当综上)(*∈<N n a x n(3)当),(,121,01*+∈===<≤=N n x y x a b c n n n 时所以122)21()21(1)21(2211-=====--n bxxxx n n n因为42413221,,)21(,1,21<≥≥≥≥++k k x x x k b 所以时所以当又01)21()21(1>-=--+k k bbx x k k所以,21211,12111=-<-=<<=≤x x a x x b n n所以,.22)(2)(2)(414111421<-=-≤-+=+=++∑∑k k n k k k nk k k k x x x x x x x。
北京市西城区2018届高三二模试题理科综合试卷含答案
西城区高三模拟测试理科综合2018.5本试卷共17页,共300分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共120分)本部分共20小题,每小题6分,共120分。
在每小题列出的四个选项中,选出最符合题目要求的一项。
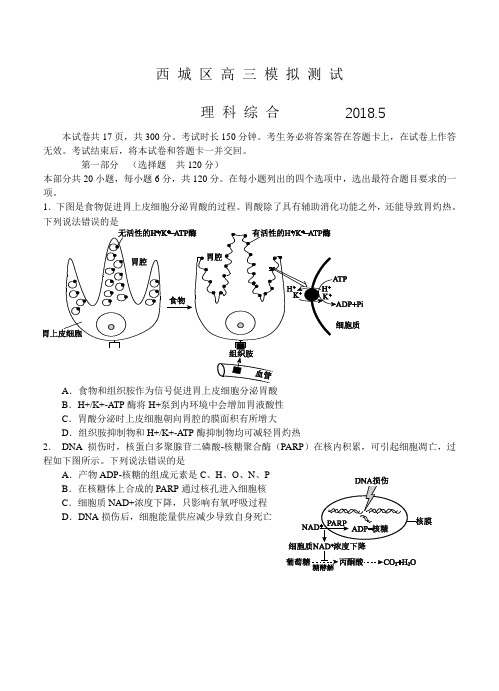
1.下图是食物促进胃上皮细胞分泌胃酸的过程。
胃酸除了具有辅助消化功能之外,还能导致胃灼热。
下列说法错误的是A.食物和组织胺作为信号促进胃上皮细胞分泌胃酸B.H+/K+-ATP酶将H+泵到内环境中会增加胃液酸性C.胃酸分泌时上皮细胞朝向胃腔的膜面积有所增大D.组织胺抑制物和H+/K+-ATP酶抑制物均可减轻胃灼热2.DNA损伤时,核蛋白多聚腺苷二磷酸-核糖聚合酶(PARP)在核内积累,可引起细胞凋亡,过程如下图所示。
下列说法错误的是A.产物ADP-核糖的组成元素是C、H、O、N、PB.在核糖体上合成的PARP通过核孔进入细胞核C.细胞质NAD+浓度下降,只影响有氧呼吸过程D.DNA损伤后,细胞能量供应减少导致自身死亡3.脱落酸(ABA)和赤霉素(GA)在种子萌发中起重要作用。
用35S-甲硫氨酸“饲喂”不同激素处理的大麦种子,提取蛋白质进行电泳,结果如右图。
下列说法错误的是A.在图中所示的蛋白质中,α-淀粉酶分子最大B.35S-甲硫氨酸是合成淀粉酶等蛋白质的原料C.ABA能拮抗GA诱导的α-淀粉酶合成D.GA通过抑制某些蛋白质合成抑制萌发4.栎树是某森林中主要的生产者,舞毒蛾啃食栎树。
栎树盛果期时丰富的果实会把白尾鹿吸引到森林中,鹿身上的扁虱会跳到森林地面产卵。
大量的栎树果实也吸引着白足鼠,扁虱卵孵化出的幼虫吸食白足鼠血和人血,同时会将白足鼠体内的螺旋菌传播给人类,使人类患上莱姆病。
下列相关分析错误的是A.扁虱与鼠、鹿、人之间的寄生关系导致螺旋菌传播到人B.舞毒蛾数量增加使栎树减产,人类患莱姆病的风险增加C.栎树盛果期时,该区域人类患上莱姆病的风险明显提高D.生物多样性是维持生态系统结构和功能稳态的必要条件5.利用竞争酶联免疫检测技术,检测抗虫棉中Bt抗虫蛋白表达量,原理如下图所示。
2018年高三最新 北京市西城区2018年抽样测试高三数学

北京市西城区2018年抽样测试高三数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、圆x 2+y 2-2x =0的圆心到直线y =的距离是( )A 、12BC D2、函数11y x=-的图象是( )3、极坐标方程2cos21ρθ=表示的曲线是( ) A 、椭圆 B 、双曲线 C 、抛物线 D 、圆4、等差数列{a n }中,已知113a =,a 2+a 5=4,a n =33,则n 为( )A 、48B 、49C 、50D 、51 5、圆锥侧面展开图扇形圆心角的弧度数为θ,则圆锥母线与底面所成角的余弦值是( ) A 、πθ B 、θπ C 、2πθ D 、2θπ6、使不等式2log 1x x <-成立的x 的取值范围是( )A 、(0 ,1)B 、1(,1)2C 、(1 ,+∞)D 、1(0,]27、将3种农作物都种植在如图的4块试验田里,每块种植一种农作物,要求相邻的试验田不能种植同一种作物,则不同的种植方法共有( )A 、6种B 、12种C 、18种D 、24种8、关于函数f (x )=1x x-(x ∈R 且x ≠0),有下列三个结论: ①f (x )的值域为R ;②f (x )是R 上的增函数;③对任意x ∈R ,有f (-x )+f (x )=0成立其中全部正确的结论是( )A 、①、②、③B 、①、③C 、①、②D 、②、③二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上9、设集合A ={-3,-2,-1,0,1,2,3},映射f :A →B 把集合A 中的元素k 映射到B 中的元素|k |,则在影射f 下,-2的象是 ;若集合B 中每个元素都有原象,则集合B 中的元素个数是 个。
10、将参数方程{1cos sin x y θθ=+= (θ为参数)转化为直角坐标方程是 ;该曲线上的点与定点A(-1,1)距离的最小值是 11、设z ∈C ,且(1-i )z =2i ,则z = ;| z |= 12、直线x +y =0的倾斜角是 ;它与直线5()12y tgx π= 的夹角是 13、已知m 、n 表示直线,α表示平面,给出下列两个命题:①m ⊥α,n ∥α,则m ⊥n ; ②m ⊥α,m ⊥n ,则n ∥α 其中错误的一个命题是 (填命题序号);因为当 时,该结论不成立 14、设函数f (x )= log 2x -2log 2(x +1),则f (x )的定义域是 ;f (x )的最小值是 。
西城区2018届高三二模理综化学试题及答案(word版)

西 城 区 高 三 模 拟 测 试理 科 综 合 2018.5本试卷共17页,共300分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分 (选择题 共120分)本部分共20小题,每小题6分,共120分。
在每小题列出的四个选项中,选出最符合题目要求的一项。
6.下列物质的分离方法中,利用粒子大小差异的是A .过滤豆浆B .酿酒蒸馏C .精油萃取D .海水晒盐7.4种短周期元素在周期表中的位置如下图,X 原子最外层有6个电子。
下列说法不正确...的是 A .离子半径:X 2−<Y 2− B .非金属性:W <XC .还原性:Y 2−<Z − D .酸性:H 2YO 4<HZO 48.下列关于pH =3的CH 3COOH 溶液的叙述正确的是 A .溶液中H 2O 电离出的c (OH −)=1.0×10−3 mol·L −1 B .加入少量CH 3COONa 固体后,溶液pH 升高C .加0.1 mol·L −1 CH 3COONa 溶液使pH >7,则c (CH 3COO −)=c (Na +)D .与等体积pH =11的NaOH 溶液混合,所得溶液呈中性 9.下列说法正确的是A .分别向等物质的量浓度的Na 2CO 3和NaHCO 3溶液中滴加2滴酚酞溶液,后者红色更深W XYZB.分别向2 mL5%H2O2溶液中滴加1 mL 0.1 mol·L−1 FeCl3和CuSO4溶液,产生气泡快慢不相同C.蛋白质溶液遇饱和Na2SO4溶液或醋酸铅溶液均产生沉淀,沉淀均可溶于水D.加热NH4Cl和Ca(OH)2固体的混合物,可将二者分离10.聚氨酯类高分子材料PU用途广泛,其合成反应为:下列说法不正确的是...A.HO(CH2)4OH的沸点高于CH3CH2CH2CH3B.高分子材料PU在强酸、强碱中能稳定存在C.合成PU的两种单体的核磁共振氢谱中均有3个吸收峰D.以1,3-丁二烯为原料,可合成HO(CH2)4OH11.在金属Pt、Cu和铱(Ir)的催化作用下,密闭容器中的H2可高效转化酸性溶液中的硝态氮(NO3−)以达到消除污染的目的。
2018年高三最新 北京市西城区2018年高三年级抽样测试数学(理科) 精品

北京市西城区2018年抽样测试高三数学试卷(理科)2018.1本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
共150分。
考试时间120分钟。
第一卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合要求的。
)1.已知集合P = {1,2 },那么满足Q ⊆P 的集合Q 的个数是 ( )A .4个B .3分C .2个D .1个2.若函数f ( x )的反函数为1-f ( x ) = 12+x 则f (1)的值为 ( )A .4B .-4C .1D .-13.设等比数列{a n }的前n 项和为Sn ,且a 2 =321,415=a ,则∞→n lim S n = ( )A .3B .2C .1D .214.若函数f ( x ) =[)[]⎪⎩⎪⎨⎧∈-∈⎪⎭⎫ ⎝⎛,1,0,4,0,1,41x x xx则f ( lig 4 3 ) = ( )A .31B .3C .31 D .45.从甲单位的3人和乙单位的2人中选出3人参加一项联合调查工作,要求这3 人中两个单位的人都要有,则不同的选法共有 ( ) A .9种 B .10种 C .18种 D .20种6.已知两直线的方程分别为l 1:x + ay + b = 0,l 2:x + cy + d = 0,它们在坐标系中的位置如图所示,那么 ( ) A .b >0,d <0,a <c B .b >0,d <0,a >c C .b <0,d >0,a >c D .b <0,d >0,a <c 7.在(a 2-312a )n 的展开中 ( )A .没有常数项B .当且仅当n = 2时,展开式中有常数项C .当且仅当n = 5时,展开式中党龄数项D 当n = 5k (k ∈N *)时,展开式中有常数项8.已知方程x 2 +(1+ a )x + 1 + a + b = 0的两根为x 1,x 2,并且0<x 1<1<x 2,则a b的取值范围是 ( )A .⎥⎦⎤ ⎝⎛--21,1B .(-1,21-) C .⎥⎦⎤ ⎝⎛--21,2D (-2,21-) 第二卷(非选择题 共110分)二、填空题(本大题共6小题,每小题5分,共30分,把答案填在题中横线上。
北京市西城区2018届高三二模试题理科综合试卷(Word版-含答案)
西城区高三模拟测试理科综合2018.5本试卷共17页,共300分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共120分)本部分共20小题,每小题6分,共120分。
在每小题列出的四个选项中,选出最符合题目要求的一项。
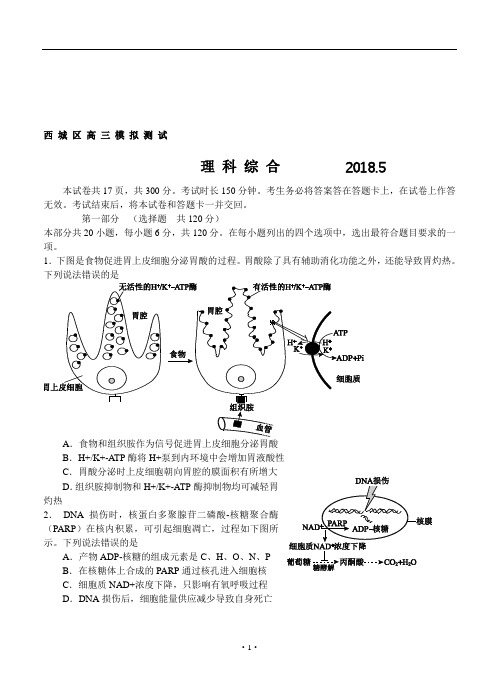
1.下图是食物促进胃上皮细胞分泌胃酸的过程。
胃酸除了具有辅助消化功能之外,还能导致胃灼热。
下列说法错误的是A.食物和组织胺作为信号促进胃上皮细胞分泌胃酸B.H+/K+-ATP酶将H+泵到内环境中会增加胃液酸性C.胃酸分泌时上皮细胞朝向胃腔的膜面积有所增大D.组织胺抑制物和H+/K+-ATP酶抑制物均可减轻胃灼热2.DNA损伤时,核蛋白多聚腺苷二磷酸-核糖聚合酶(PARP)在核内积累,可引起细胞凋亡,过程如下图所示。
下列说法错误的是A.产物ADP-核糖的组成元素是C、H、O、N、PB.在核糖体上合成的PARP通过核孔进入细胞核C.细胞质NAD+浓度下降,只影响有氧呼吸过程D.DNA损伤后,细胞能量供应减少导致自身死亡3.脱落酸(ABA)和赤霉素(GA)在种子萌发中起重要作用。
用35S-甲硫氨酸“饲喂”不同激素处理的大麦种子,提取蛋白质进行电泳,结果如右图。
下列说法错误的是A.在图中所示的蛋白质中,α-淀粉酶分子最大B.35S-甲硫氨酸是合成淀粉酶等蛋白质的原料C.ABA能拮抗GA诱导的α-淀粉酶合成D.GA通过抑制某些蛋白质合成抑制萌发4.栎树是某森林中主要的生产者,舞毒蛾啃食栎树。
栎树盛果期时丰富的果实会把白尾鹿吸引到森林中,鹿身上的扁虱会跳到森林地面产卵。
大量的栎树果实也吸引着白足鼠,扁虱卵孵化出的幼虫吸食白足鼠血和人血,同时会将白足鼠体内的螺旋菌传播给人类,使人类患上莱姆病。
下列相关分析错误的是A.扁虱与鼠、鹿、人之间的寄生关系导致螺旋菌传播到人B.舞毒蛾数量增加使栎树减产,人类患莱姆病的风险增加C.栎树盛果期时,该区域人类患上莱姆病的风险明显提高D.生物多样性是维持生态系统结构和功能稳态的必要条件5.利用竞争酶联免疫检测技术,检测抗虫棉中Bt抗虫蛋白表达量,原理如下图所示。
最新-北京市西城区2018年抽样测试(数学理) 精品

北京市西城区2018年抽样测试高三数学试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,选出符合要求的一项 1. 设集合{1,2,3,4,5}U =,{1,2,3}A =,{3,4,5}B =,则C U ()A B 等于A .{1,2,3,4,5}B .{1,2,4,5}C .{1,2,5}D .{3}2. “ln 1x >”是“1x >”的A .充分不必要条件 √B .必要不充分条件C .充要条件D .既不充分也不必要条件 3. 若0b a <<,则下列不等式中正确的是 A .11a b> B .a b > C .2b aa b +> D .a b ab +>4. 如图,三棱柱111ABC A B C -的侧棱长和底面边长均为2,且侧棱1AA ⊥底面ABC ,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为AB. C. D .45. 数列{}n a 满足11a =,23a =,1(2)n n a n a λ+=-(1,2,n =),则3a 等于A .15B .10C .9D .5 6. 在数列{}n a 中,11a =,1n n a a n -=+,2n ≥.为计算这个数列前10项的和,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是A .8i ≥B .9i ≥C .10i ≥D .11i ≥7. 设集合{129}S =,,,,集合123{,,}A a a a =是S 的子集,且123,,a a a 满足123a a a <<,326a a -≤,那么满足条件的子集A 的个数为 A . 78 B .76 C .84 D .83正(主)视图ABCA 1B 1C 18. 如图,在等腰梯形ABCD 中,//AB CD ,且2A B A D =. 设DAB θ∠=,(0,)2πθ∈,以A ,B 为焦点且过点D 的双曲线的离心率为1e ,以C ,D 为焦点且过点A 的椭圆的离心率为2e ,则A .随着角度θ的增大,1e 增大,12e e 为定值B .随着角度θ的增大,1e 减小,12e e 为定值C .随着角度θ的增大,1e 增大,12e e 也增大D .随着角度θ的增大,1e 减小,12e e 也减小 二、填空题:本大题共6小题,每小题5分,共30分. 9. 某区高二年级的一次数学统考中,随机抽取200名同学的成绩,成绩全部在50分至100分之间,将成绩按如下方式分成5组:第一组,成绩大于等于50分且小于60分;第二组,成绩大于等于60分且小于70分;……第五组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.则这200名同学中成绩大于等于80分且小于90分的学生有______名.10. 在261()x x+的展开式中,常数项是______.(结果用数值表示)11. 如图,ABC ∆是圆的内接三角形,PA 切圆于点A ,PB 交圆于点D.若60ABC ∠=,1PD =,8BD =,则PAC∠=________,PA =________.12. 圆1,:2x C y θθ⎧=⎪⎨=+⎪⎩(θ为参数)的半径为______, 若圆C 与直线0x y m -+=相切,则m =______.13. 设,,a b c 为单位向量,,a b 的夹角为60,则()++⋅a b c c 的最大值为_____.14. 已知函数()e ln xf x a x =+的定义域是D ,关于函数()f x 给出下列命题:①对于任意(0,)a ∈+∞,函数()f x 是D 上的减函数;B②对于任意(,0)a ∈-∞,函数()f x 存在最小值;③存在(0,)a ∈+∞,使得对于任意的x D ∈,都有()0f x >成立; ④存在(,0)a ∈-∞,使得函数()f x 有两个零点.其中正确命题的序号是_____.(写出所有正确命题的序号)②、④三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)如图,在四边形ABCD 中,3AB =,2AD BC CD ===,60A =. (Ⅰ)求sin ABD ∠的值; (Ⅱ)求BCD ∆的面积.16.(本小题满分13分)一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、4、5,现从盒子中随机抽取卡片.(Ⅰ)若从盒子中有放回的取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;(Ⅱ)若从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当取到一张记有偶数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X 的分布列和期望.17.(本小题满分13分)如图,四棱柱1111ABCD A B C D -中,1A D ⊥平面ABCD ,底面ABCD 是边长为1的正方形,侧棱12AA =.(Ⅰ)求证:1//C D 平面11ABB A ;(Ⅱ)求直线1BD 与平面11AC D 所成角的正弦值; (Ⅲ)求二面角11D AC A --的余弦值. ABCDD 1A 1B 1C 1ABCD18.(本小题满分13分)已知0a ≥,函数2()f x x ax =+.设1(,)2a x ∈-∞-,记曲线()y f x =在点11(,())M x f x 处的切线为l ,l 与x 轴的交点是2(,0)N x ,O 为坐标原点.(Ⅰ)证明:21212x x x a=+;(Ⅱ)若对于任意的1(,)2a x ∈-∞-,都有916aOM ON ⋅>成立,求a 的取值范围.19.(本小题满分14分)如图,椭圆22:14y C x +=短轴的左右两个端点分别为,A B ,直线:1l y kx =+与x 轴、y 轴分别交于两点,E F ,与椭圆交于两点,C D ,.(Ⅰ)若CE FD =,求直线l 的方程;(Ⅱ)设直线,AD CB 的斜率分别为12,k k ,若12:2:1k k =,求k 的值.20.(本小题满分14分)在数列{}n a 和{}n b 中,n n a a =,(1)n b a n b =++,1,2,3,n =,其中2a ≥且a ∈*N ,b ∈R .(Ⅰ)若11a b =,22a b <,求数列{}n b 的前n 项和;(Ⅱ)证明:当2,a b =={}n b 中的任意三项都不能构成等比数列; (Ⅲ)设123{,,,}A a a a =,123{,,,}B b b b =,试问在区间[1,]a 上是否存在实数b 使得C A B =≠∅.若存在,求出b 的一切可能的取值及相应的集合C ;若不存在,试说明理由.北京市西城区2018年抽样测试参考答案 高三数学试卷(理科) 2018.5一、选择题:本大题共8小题,每小题5分,共40分.二、填空题:本大题共6小题,每小题5分,共30分.9. 40 10. 15 11. 60,312.3或1- 13.1 14. ②④注:两空的题目,第一个空2分,第二个空3分.14题②④选对一个命题得两分,选出错误的命题即得零分.三、解答题:(本大题共6小题,共80分.若考生的解法与本解答不同,正确者可参照评分标准给分.)15、解:(Ⅰ)已知60A =,由余弦定理得2222cos7BD AB AD AB AD A =+-⋅=, 解得BD = …………………3分由正弦定理,sin sin AD BD ABD A=∠,所以sin sin ADABD A BD∠=. …………………5分 ==. …………………7分 (Ⅱ)在BCD ∆中,2222cos BD BC CD BC CD C =+-⋅,所以744222cos C =+-⨯⨯,1cos 8C =, …………………9分 因为(0,)C ∈π,所以sin 8C =…………………11分 所以,BCD ∆的面积1sin 24S BC CD C =⋅⋅=. …………………13分 16、解:(Ⅰ)设A 表示事件“有放回地抽取3次卡片,每次抽取一张,恰有两次取到的卡片上数字为偶数”,A B CD由已知,每次取到的卡片上数字为偶数的概率为25, …………………2分 则2232336()()55125P A C =⨯=. …………………5分 (Ⅱ)依题意,X 的可能取值为1,2,3,4. …………………6分2(1)5P X ==, …………………7分 323(2)5410P X ⨯===⨯, …………………9分3221(3)5435P X ⨯⨯===⨯⨯, …………………10分3211(4)54310P X ⨯⨯===⨯⨯, …………………11分X …………………12分2311()12342510510E X =⨯+⨯+⨯+⨯=. …………………13分17、(Ⅰ)证明:四棱柱1111ABCD A BC D -中,11//BBCC , 又1CC ⊄面11ABB A ,所以1//CC 平面11ABB A , …………………2分ABCD 是正方形,所以//CD AB ,又CD ⊄面11ABB A ,所以//CD 平面11ABB A , …………………3分 所以平面11//CDD C 平面11ABB A ,所以1//C D 平面11ABB A .…………………4分 (Ⅱ)解:ABCD 是正方形,AD CD ⊥,因为1A D ⊥平面ABCD ,所以1A DAD ⊥,1A D CD ⊥,如图,以D 为原点建立空间直角坐标系D xyz -,. …………………5分 在1ADA ∆中,由已知可得1A D =, 所以11(0,0,0),(1,0,0),(1,1D A A C -,11(0,1(1(1,1,0)B D B -,11(2,1BD =--, ………6分因为1A D ⊥平面ABCD , 所以1A D ⊥平面1111A B C D ,111A D B D ⊥,又1111B D AC ⊥,所以11B D ⊥平面11AC D ,…………………7分所以平面11AC D 的一个法向量为(1,1,0)=n , …………………8分 设1BD 与n 所成的角为β, 则113cos 42BD BD β⋅===-n n , …………………9分所以直线1BD 与平面11AC D 所成角的正弦值为34. …………………10分 (Ⅲ)解:设平面11AC A 的法向量为(,,)a b c m =,则1110,0AC A A ⋅=⋅=m m , 所以0a b -+=,0a=,令c =m =, …………………12分 设二面角11D AC A --的大小为α,则cos 7α⋅===m nm n所以二面角11D AC A --. …………………13分 18、解:(Ⅰ)对()f x 求导数,得()2f x x a '=+,故切线l 的斜率为12x a +, …………………2分由此得切线l 的方程为21111()(2)()y x ax x a x x -+=+-. …………………4分令0y =,得22111211122x ax x x x x a x a +=-+=++. …………………5分 (Ⅱ)由2211111(,),(,0)2x M x x ax N x a ++,得3112x OM ON x a⋅=+. …………6分所以0a =符合题意, ………………7分当0a >时,记3111()2x g x x a=+,1(,)2a x ∈-∞-.对1()g x 求导数,得211121(43)()(2)x x a g x x a +'=+, …………………8分令1()0g x '=,得13(,)42a a x =-∈-∞-. 当1(,)ax ∈-∞-时,1()g x '的变化情况如下表:所以,函数1()g x 在(,)4-∞-上单调递减,在(,)42--上单调递增,……10分 从而函数1()g x 的最小值为2327()432a g a -=. …………………11分 依题意22793216a a >, …………………12分 解得23a >,即a 的取值范围是2(,)3+∞. …………………13分综上,a 的取值范围是2(,)3+∞或0a =.19、解:(Ⅰ)设1122(,),(,)C x y D x y ,由2244,1x y y kx ⎧+=⎨=+⎩得22(4)230k x kx ++-=, 222412(4)1648k k k ∆=++=+,12224k x x k -+=+,12234x x k -=+, …………………2分 由已知1(,0),(0,1)E F k -,又CE FD =,所以11221(,)(,1)x y x y k---=- …………………4分 所以121x x k --=,即211x x k +=-, …………………5分所以2214k k k-=-+,解得2k =±, …………………6分符合题意,所以,所求直线l 的方程为210x y -+=或210x y +-=. …………………7分 (Ⅱ)2121y k x =+,1211y k x =-,12:2:1k k =, 所以2112(1)2(1)1y x y x -=+, …………………8分平方得22212212(1)4(1)y x y x -=+, …………………9分 又221114y x +=,所以22114(1)y x =-,同理22224(1)y x =-,代入上式, 计算得2112(1)(1)4(1)(1)x x x x --=++,即121235()30x x x x +++=,…………………12分所以231030k k -+=,解得3k =或13k =, …………………13分 因为2112(1)2(1)1y x y x -=+,12,(1,1)x x ∈-,所以12,y y 异号,故舍去13k =,所以3k =. …………………14分20、解:(Ⅰ)因为11a b =,所以1a a b =++,1b =-, …………………1分由22a b <,得2210a a --<,所以11a << …………………3分因为2a ≥且a ∈*N ,所以2a =, …………………4分所以 31n b n =-,{}n b 是等差数列, 所以数列{}n b 的前n 项和2131()222n n n S b b n n =+=+. …………………5分 (Ⅱ)由已知3n b n =,假设3m,3n,3t 成等比数列,其中,,m n t ∈*N ,且彼此不等,则2(3(3n m t =, …………………6分所以29292n mt ++=+++,所以233(2n mt m t n -=+-,若20m t n +-=,则2330n mt -=,可得m t =,与m t ≠矛盾; ………7分 若20m t n +-≠,则2m t n +-为非零整数,(2m t n +-所以233n mt -为无理数,与233n mt -是整数矛盾. …………………9分 所以数列{}n b 中的任意三项都不能构成等比数列. (Ⅲ)设存在实数[1,]b a ∈,使C AB =≠∅,设0m C ∈,则0m A ∈,且0m B ∈,设0()t m a t =∈*N ,0(1)()m a s b s =++∈*N ,则(1)ta a sb =++,所以1t a bs a -=+,因为,,a t s ∈*N ,且2a ≥,所以ta b -能被1a +整除. …………………10分 (1)当1t =时,因为[1,]b a ∈, [0,1]a b a -∈-,所以1a bs a -=∉+*N ; …………………11分 (2)当2()t n n =∈*N 时,22212[(1)1](1)(1)1n n n n a b a b a C a b -=+--=++-++-,由于[1,]b a ∈,所以1[0,1]b a -∈-,011b a ≤-<+,所以,当且仅当1b =时,ta b -能被1a +整除. …………………12分 (3)当21()t n n =+∈*N 时,212121121[(1)1](1)(1)1n n n n a b a b a C a b ++++-=+--=++++--, 由于[1,]b a ∈,所以1[2,1]b a +∈+,所以,当且仅当11b a +=+,即b a =时,ta b -能被1a +整除. ……13分 综上,在区间[1,]a 上存在实数b ,使C AB =≠∅成立,且当1b =时,2{,}n C y y a n ==∈*N ;当b a =时,21{,}n C y y an +==∈*N . …………14分。
2018年高三最新 北京西城区2018高三理科数学二模试卷

北京市西城区2018年抽样测试高三数学试卷(理科)(2018.6)参考公式:三角函数的和差化积公式2cos2sin2sin sin βαβαβα-+=+2sin 2cos 2sin sin βαβαβα-+=-2cos 2cos 2cos cos βαβαβα-+=+2sin 2sin cos cos βαβαβα-+-=-正棱台、圆台的侧面积公式l c c S )'(21+=台侧 其中c',c 分别表示上、下底面周长,l 表示斜高或母线长。
一、选择题:本大题共12小题;每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合要求的。
每小题选出答案后,用铅笔在下表中将对应答案标号涂黑。
1.)335(π-ctg 的值是( ). A .33- B.3 C.33D. 3-2.设 {}R x x y y P ∈==,2 {}R x y y Q X∈==,2 则( ).A. Q=PB. P Q ⊂C. }{)4,2(=⋂Q PD.P ∩Q={(2,4)}3.双曲线116922=-y x 的一个焦点到一条渐近线的距离等于( ). A. 3 B.3C. 4D. 24.圆θρcos 2=上与极点距离为3的一个点的极坐标是( ). A .(3,3π) B. (3,6π) C. (-3,3π) D. (-3,6π) 5.在△ABC 中,sinA: sinB:sinC=3:2:4,则cosC 的值为( ). A.41- B.41C.32-D.32 6.某企业2001年12月份的产值是这年1月份产值的p 倍,则该企业2001年年度产值的月平均增长率为( )。
A.1-P P B.111-P C.11P D.111-P7.学校要选派4名爱好摄影的同学中的3名分别参加校外摄影小组的3期培训(每期只派1名),由于时间上的冲突,甲、乙两位同学都不能参加第1期培训,则不同的选派方式有( )。
A. 6种 B. 8种 C. 10种 D. 12种8.一圆锥被平行于底面的截面截成一个小圆锥和一个圆台,若小圆锥的体积为y,圆台的体积为x,则y 关于x 的函数图象的大致形状为( ).9. 已知点M(cos α, sin α),N(cos β,sin β),若直线MN 的倾斜角为θ,0<α<π<β<2π,则θ等于( ) A .)(21βαπ++B.)(21βα+ C.)(21πβα-+ D.)(21αβ-10.直平行六面体1111D C B A ABCD -的棱长均为2,∠BAD=60°,则对角线C A 1与侧面11D DCC 所成角的正弦值为( )。
2018年高三最新 北京市西城区2018年抽样测试高三数学

北京市西城区2018年抽样测试高三数学试卷(理科)2018.5学校______________ 班级_______________ 姓名______________参考公式:三角函数的和差化积公式2cos2sin2sin sin βαβαβα-+=+2sin 2cos 2sin sin βαβαβα-+=-2cos 2cos 2cos cos βαβαβα-+=+2sin 2sin 2cos cos βαβαβα-+=-正棱台、圆台的侧面积公式l c c S )'(21+=台侧 其中'c 、c 分别表示上下底面周长,l 表斜高或母线长 球体的体积公式334R V π=球一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.双曲线116922=-x y 的两条准线方程是( ) A .59±=x B .516±=x C .59±=y D .516±=y 2.不等式(2x-1)(1-|x|)<0成立的充要条件是( )A .x>1,或21<x B .x>1,或211<<-x C .211<<-x D .x<-1,或21>x3.在极坐标系中,定点)2,1(πA ,点B 在直线0sin cos 3=-θρθρ上移动.当线段AB 最短时,点B 极的坐标是( )A .)6,21(π B .)6,23(π C .)3,21(π D .)3,23(π 4.已知α,β表示平面,m ,n 表示直线.下列命题中正确的是( ) A .若α//β,α⊂m ,β⊂n 则m//nB .若α⊥β,α⊂m ,β⊂n ,则m ⊥nC .若m ⊥α,n ⊥β,m//n ,则α//βD .若m//α,n//β,m ⊥n ,则α⊥β 5.函数)1(12<+=x y x 的反函数是( )A .)1(log 2-=x y ,x ∈(1,3)B .x y 2log 1+-=,x ∈(1,3)C .)1(log 2-=x y ,x ∈(1,3]D .x y 2log 1+-=,x ∈(1,3]6.在复平面内,向量→AB 对应的复数是2+i ,向量→CB 对应的复数是-1-3i ,则向量→CA对应的复数为( )A .1-2IB .-1+2IC .3+4ID .-3-4i7.设集合A={1,2,3,4,5},a 、b ∈A ,则方程122=+by a x 表示焦点位于y 轴上的椭圆有( )A .5个B .10个C .20个D .25个8.人口问题是我国最大的社会问题之一,估计人口数量和发展趋势是我们制定一系列相关政策的基础.由人口统计年监,可查得我国从1974年至1999年人口数据资料如下:(单位:亿)由此可估算出我国2018年的人口数为( )A .13.18亿B .13.22亿C .13.42亿D .13.66亿二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.9.如果函数⎩⎨⎧<>-=)0( , )()0(,32x x f x x y 是奇函数,则f(x)=_________.10.设正方体的棱长为a ,则以其六个面的中心为顶点的多面体的体积是_________.11.函数)10(≠>=a a a y x且在[1,2]上最大值比最小值大2a ,则a 的值是_________. 12.直线l 截圆0222=-+y y x 所得弦AB 的中点是)23,21(-,则直线l 的方程为_________________;|AB|=___________.13.函数))(cos 3(sin sin R x x x x y ∈+⋅=的最大值是__________,14.如图,)4(2≥n n 个正数排成n 行n 列方阵.符号),1,1(N j i n j n i a ij ∈≤≤≤≤、表示位于第i 行第j 列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都等于q .若2111=a ,124=a ,4132=a .则q=___________;________=ij a .nnn n n n n a a a a a a a a a a a a 32122322211131211三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本题满分12分) 设x ∈R ,函数)20,0(21)(cos )(2πϕωϕω<<>-+=x x f .已知f(x)的最小正周期为π,且41)8(=πf .(Ⅰ)求ω和ϕ的值;(Ⅱ)求f(x)的单调递增区间. 16.(本题满分14分)如图,正三棱柱111C B A ABC -中,E 是AC 中点. (Ⅰ)求证:平面111A ACC BEC 平面⊥; (Ⅱ)求证:11//BEC AB 平面;(Ⅲ)若221=AB A A ,求二面角C BC E --1的大小.17.(本题满分13分)设函数f(x)=)1(log xaa -,其中0<a <1. (Ⅰ)证明f(x)是(a ,+∞)上的减函数;(Ⅱ)解不等式f(x)>1. 18.(本题满分14分)已知定点A (-2,-4),过点A 作倾斜角为45°的直线l .交抛物线px y 22=(p >o)于B 、C 两点,且|AB|,|BC|,|AC|成等比数列. (Ⅰ)求抛物线方程;(Ⅱ)在(Ⅰ)中的抛物线上是否存在点D ,使得|DB|=|DC|成立?如果存在,求出点D 的坐标;如果不存在,请说明理由.19.(本题满分13分)如图,工厂检验员通常用一个直径为2cm 的标准圆柱和一个直径为1cm 的标准圆柱检测一个直径为3cm 的圆柱状洞口.为了保证质量,有时再插入两个合适的同号标准圆柱,分别与三圆柱相切.记A 、B 、C 依次为直径2cm 、3cm 、1cm 的圆柱截面圆的圆心,求插入的两个标准圆柱的直径.20.(本题满分14分)已知正项数列{}n a 和{}n b 中,a a =1(0<a <1),a b -=11.当n ≥2时,21111,----=⋅=n n n n n n a b b b a a . (Ⅰ)证明:对任意N n ∈,有1=+n n b a ; (Ⅱ)求数列{}n a 的通项公式;(Ⅲ)记12+⋅=n n n b a c ,n S 为数列{}n c 的前n 项和.求∞→n lin n S 的值.高三数学(理科)参考答案及评分标准一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.B 3.D 4.C 5.A 6.D 7.B 8.B二、填空题:本大题共6小题,每小题5分,共30分.9.2x+3 (5分) 10.63a (5分) 11.2321或 (只答对一个给2分)12.2 0;2y -x =+ (第一个空2分,第二个空3分).13.23(5分) 14.21;ij )21(⋅(第一个空2分,第二个空3分)三、解答题:本大题共6小题,共80分,其它解法,请仿此给分. 15.(本题满分12分)(Ⅰ)解:21)]22cos(1[2121)(cos )(2-++=-+=ϕωϕωx x x f =)22cos(21ϕω+x ……………………………………………………4分 ∵f(x)的最小正周期为π, ∴1,22==ωπωπ…………………………………6分 ∵41)24cos(21)8(=+=ϕππf ∴21)24cos(=+ϕπ∵20πϕ<<, ∴45244πϕππ<+<∴324πϕπ=+ ∴24πϕ=…………………………………………8分(Ⅱ)解:由(Ⅰ)得,).122cos(21)(π+=x x f ∴当ππππk x k 21222≤+≤-时,即)(242413Z k k x k ∈-≤≤-ππππ时,f(x)单调递增. ∴f(x)的单调递增区间是)(],24,2413[Z k k k ∈--ππππ………………………………12分16.(本题满分14分)(Ⅰ)证明:∵111C B A ABC -是正三棱柱, ∴,1ABC AA 平面⊥ ∴1AA BE ⊥∵△ABC 是正三角形,E 是AC 中点, ∴AC,BE ⊥∴11A ACC BE 平面⊥, 又∵1BEC BE 平面⊂∴平面111A ACC BEC 平面⊥……………………………………………………4分 (Ⅱ)证明:连.,111D C B BC C B =⋂设∵111C B A ABC -是正三棱柱, ∴B BCC 1是矩形,D 是C B 1的中点. ∵E 是AC 的中点,∴1AB ∥DE . ∵1BEC DE 平面⊂,11BEC AB 平面⊄∴1AB ∥平面1BEC ………………………………………………………………8分 (Ⅲ)解:作F EC CF 于1⊥,1BC FG ⊥于G ,连CG . ∵平面111A ACC BEC 平面⊥,∴1BEC CF 平面⊥………………………………………………………………9分 ∴FG 是CG 在平面1BEC 上的射影. ∴根据三垂线定理得,1BC CG ⊥∴∠CGF 是二面角C BC E --1的平面角……………………………………11分 设a AB =,∵221=AB A A ,则a A A 221=.在1ECC Rt ∆中,a EC CC EC CF 6611=⋅=,在1BCC Rt ∆中,a BC CC BC CG 3311=⋅=.在CFG Rt ∆中, ∵22sin ==∠CG CF CGF ,∴︒=∠45CGF . ∴二面角C BC E --1的大小是45°………………………………14分 17.(本题满分13分)(Ⅰ)证明:任取),(,21+∞∈a x x ,且21x x <,)()(log )1(log )1(log )()(21122121a x x a x x x ax a x f x f a a a --=---=-…………3分 ∵)()()()()(1)()(21212121122112a x x x x a a x x a x x a x x a x x a x x --=----=---,…………5分∵21,10x x a a <<<<,∴01)()(,0)()(21122112<--->--a x x a x x a x x a x x 且.即1)()(02112<--<a x x a x x ,∴0)()(log 2112>--a x x a x x a .∴)()(21x f x f >,∴),()(+∞a x f 是上的减函数.……………………7分 (Ⅱ)解:[解法1] ∵10<<a ,∴⎪⎪⎩⎪⎪⎨⎧<->-⇔>-⇔>)2( 1)1( 01log )1(log 1)(a xa xax a x f a a ……………………10分解不等式(1)得,x>a 或x<0, 解不等式(2)得,aax -<<10, ∵0<a<1,∴aa a -<1 ∴原不等式解集为}1|{aax a x -<<……………………………………13分 [解法2] 函数f(x)的定义域为{x|x>a 或x<0}………………………………8分 ∵0<a<1,∴当x<0时,11>-xa, ∴0)1(log )(<-=xax f a ,不合题意.…………………………10分 当x>a 时,解方程f(x)=1,得aax -=1.由(Ⅰ)知f(x)是),(+∞a 上的减函数,∴f(x)>1时,aax -<1.∵a a a -<1,∴原不等式解集为}1|{aax a x -<<.……………………13分 18.(本题满分14分)(Ⅰ)解:直线l 方程为y=x-2,将其代入px y 22=,整理为,04)2(22=++-x p x .①……………………2分∵p>0,∴016)2(42>-+=∆p . 设),(),,(2211y x C y x B .∴4,242121=⋅+=+x x p x x .…………………………4分 ∵|AB|,|BC|,|AC|成等比数列, ∴||||||2AC AB BC ⋅=. ∴)2(2)2(2|)|2(21212+⋅+=-x x x x ,整理为,045)(2)(2121221=-⋅---+x x x x x x . 将4,242121=⋅+=+x x p x x 代入上式,解得p=1. ∴抛物线方程x y 22=.………………………………7分(Ⅱ)解:假设在抛物线x y 22=上存在点),(33y x D ,使得|DB|+|DC|成立, 记线段BC 中点为),(00y x E .则11||||1-=-=⇔⊥⇔=K K BC DE DC DB DE .………………10分 当p=1时,①式成为0462=+-x x . ∴32210=+=x x x ,1200=-=x y . ∴点),(33y x D 应满足⎪⎩⎪⎨⎧-=--=13123323x y x y .…………………………12分解得,⎩⎨⎧-==⎩⎨⎧==48223333y x y x 或. ∴存在点)2,2(D 或(8,-4),使得|DB|=|DC|成立…………………………14分 19.(本题满分13分)解:以经过三圆心A 、B 、C 的直线为x 轴,B 为原点,建立直角坐标系.……………1分设所求圆D 的半径为rcm ,连结DA 、DC , 连BD 并延长交⊙B 于点E . ∵r DB r DA -=+=23||,1|| ∴||25||||AB DB DA >=+. ∴点D 在以A 、B 为焦点,长轴长为25的椭圆上. ∵212,252==c a ,∴23222=-=c a b .∴该椭圆方程为13225)41(1622=++y x ……………………5分又∵r DC r DB +=-=21||,23||,∴|DB|+|DC|=2>|BC|同理,点D 还在以B 、C 为焦点,长轴长为2的椭圆上,其方程为134)21(22=+-y x …………………………………………9分 由⎪⎪⎩⎪⎪⎨⎧=+-=++134)21(13225)41(162222y x y x ,解得⎪⎪⎩⎪⎪⎨⎧==76149y x 或⎪⎪⎩⎪⎪⎨⎧-==76149y x .………………11分 ∴73)76()149(2322=+-=-=BD BE r . ∴插入的两个标准圆柱的直径是76cm .……………………………………………13分 20.(本题满分14分)(Ⅰ)证明:用数学归纳法证明:①当n=1时,1)1(11=-+=+a a b a ,命题成立;…………………………………1分 ②假设n=k 时命题成立,即1=+k k b a ,则当n=k+1时,111)1(112221111==-=-+=-+-⋅=+⋅=+++++k kk k kk k k k k k k k k k k k b b a b a a b a b a b a b b a b a . ∴当n=k+1时,命题也成立.综合①、②知,1=+n n b a 对N n ∈恒成立.……………………………………5分 (Ⅱ)解:∵n nnn n n n n n n n a a a a a a b a b a a +=--⋅=-⋅=⋅=++11)1(12211, ∴11111+=+=+nn n n a a a a ,即1111=-+n n a a .③…………………………………8分 ∴数列⎭⎬⎫⎩⎨⎧n a 1是公差为1的等差数列,其首项是a a 111=.∴1)1(11⨯-+=n aa n ,从而a n a a n )1(1-+=.………………………………10分 (Ⅲ)解:∵1112)(+++⋅=⋅=⋅=n n n n n n n n a a b a a b a c ,③式变形为11++-=⋅n n n n a a a a ,∴1+-=n n n a a c ,………………………………………………………………12分 ∴)()()(1322121--++-+-=+++=n n n n a a a a a a c c c S naaa a a n +-=-=+111.∴ ⎝⎛=⎪⎭⎫+-=→→a na a a S xn n xn 1lim lim .……………………………………………14分 [注:如果学生未证出(Ⅰ),而使用(Ⅰ)的结论正确解答出(Ⅱ)、(Ⅲ),则独立给(Ⅱ)、(Ⅲ)的分数]。
北京市西城区高三数学第二学期期中抽样测试word资料23页

北京市西城区高三数学第二学期期中抽样测试(理科)一、选择题:本大题共 8 小题,每小题 5 分,共 40 分. 1. 在复平面内,复数21i+ 对应的点与原点的距离是( )A. 1B.C.2D.2. 函数 (2)2xy x x =>-的反函数的定义域为( ) A. (1)+∞, B. (0)+∞, C. (01), D.(12),3. 若双曲线221x ky +=的离心率是2,则实数k 的值是( )A.3-B. 13- C. 3 D. 134. 函数()sin (cos sin )f x x x x =⋅-的最小正周期是( )A.4π B. 2πC. πD. 2π5. 下列四个正方体图形中,A B 、为正方体的两个顶点,M N P 、、分别为其所在棱的中点,能得出//AB 平面MNP 的图形的序号是( )A. ①、③B. ①、④C. ②、③D. ②、④6. 若集合2{|540}A x x x =-+<,{|||1}B x x a =-<,则“(23)a ∈,”是“B A ⊆”的( )A. 充分但不必要条件B. 必要但不充分条件C.充要条件D. 既不充分又不必要条件7. 设a ∈R ,函数()e e x x f x a -=+⋅的导函数是()f x ',且()f x '是奇函数 . 若曲线()y f x =的一条切线的斜率是32,则切点的横坐标为( ) A. ln 22- B.ln 2- C.ln 22D.ln 28. 设不等式组123350x a y x y ≥⎧⎪≥⎨⎪+-≤⎩,,表示的平面区域是W ,若W 中的整点(即横、纵坐标均为整数的点)共有91个,则实数a 的取值范围是( )A.(21]--,B.[10)-,C. (01],D. [12), 二、填空题:本大题共 6 小题,每小题 5 分,共 30 分. 把答案填在题中横线上 . 9. 已知{}n a 是公比为q 的等比数列,且243a a a ,,成等差数列,则q =__________ . 10. 在10()x a -的展开式中,7x 的系数是15,则实数a =__________ .11. 5人排成一排照相,要求甲不排在两端,不同的排法共有 种. (用数字作答)12. 已知A B C ,,三点在球心为O ,半径为3的球面上,且几何体O ABC -为正四面体,那么A B ,两点的球面距离为__________;点O 到平面ABC 的距离为__________ .13. 已知两点(10)A ,,(0)B b ,,若抛物线24y x =上存在点C 使ABC ∆为等边三角形,则b =_________ .14. 已知点G 是ABC ∆的重心,()AG AB AC λμλμ=+∈R u u u r u u u r u u u r,,那么λμ+=_____;若︒=∠120A ,2AB AC ⋅=-u u u r u u u r,则的最小值是__________ .三、解答题:本大题共 6 小题,共 80 分. 解答应写出文字说明,证明过程或演算步骤.15.(本小题满分12分)在ABC ∆中,5cos A =,10cos B =. (Ⅰ)求角C ;(Ⅱ)设2AB =,求ABC ∆的面积. 16. (本小题满分13分)盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得1-分 . 现从盒内任取3个球.(Ⅰ)求取出的3个球颜色互不相同的概率; (Ⅱ)求取出的3个球得分之和恰为1分的概率;(Ⅲ)设ξ为取出的3个球中白色球的个数,求ξ的分布列和数学期望. 17.(本小题满分14分)如图,在三棱锥P ABC -中,PA PB =, PA PB ⊥,30AB BC BAC ⊥∠=︒,,平面PAB ⊥平面ABC .(Ⅰ)求证:PA PBC ⊥平面 ; (Ⅱ)求二面角P AC B --的大小;(Ⅲ)求异面直线AB 和PC 所成角的大小. 18.(本小题满分13分)已知函数()ln f x x x =.(Ⅰ)求()f x 的最小值;(Ⅱ)若对所有1x ≥都有()1f x ax ≥-,求实数a 的取值范围. 19.(本小题满分14分)已知定点)01(,-C 及椭圆5322=+y x ,过点C 的动直线与椭圆相交于A B ,两点. (Ⅰ)若线段AB 中点的横坐标是12-,求直线AB 的方程;(Ⅱ)在x 轴上是否存在点M ,使MB MA ⋅为常数?若存在,求出点M 的坐标;若不存在,请说明理由. 20.(本小题满分14分)数列{}n a 中,11a =,2112n n n a a a c +=-+ (1c >为常数,1,2,3,n =L ) ,且321.8a a -=(Ⅰ)求c 的值;(Ⅱ)① 证明:1n n a a +<;② 猜测数列{}n a 是否有极限?如果有,写出极限的值(不必证明); (Ⅲ)比较11nk ka =∑与14039n a +的大小,并加以证明. 高三数学(理科)参考答案一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.1. B2. A3. B4. C5. B6. A7. D8. C二、填空题:本大题共 6 小题,每小题 5 分,共 30 分.9. 12-或1 10. 12- 11. 72 12. π13. 5或13- 14.23;23注:两空的题目,第一个空2分,第二个空3分;两解的题目少一解给2分,有错解不给分.三、解答题:本大题共 6 小题,共 80 分. 15.(本小题满分12分) (Ⅰ)解:由cos 5A =,cos 10B =, 得02A B π⎛⎫∈ ⎪⎝⎭、,, 所以sin sin A B == ………….. 3分因为cos cos[()]cos()cos cos sin sin 2C A B A B A B A B π=-+=-+=-+=, ……….. 6分且0C π<<, 故.4C π=………….. 7分(Ⅱ)解: 根据正弦定理得sin sin sin sin AB AC AB B AC C B C ⋅=⇒==, ………….. 10分 所以ABC ∆的面积为16sin .25AB AC A ⋅⋅= ………….. 12分 16. (本小题满分13分) (Ⅰ)解:记 “取出1个红色球,1个白色球,1个黑色球”为事件A , 则11123439C C C 2()C 7P A ==. ………….. 3分 (Ⅱ)解:记 “取出1个红色球,2个白色球”为事件B ,“取出2个红色球, 1个黑色球”为事件C , 则122123243399C C C C 5()()()C C 42P B C P B P C +=+=+=. (6)分 (Ⅲ)解:ξ可能的取值为0123,,,. ………….. 7分3639C 5(0)C 21P ξ===, 123639C C 45(1)C 84P ξ===,213639C C 3(2)C 14P ξ===,3339C 1(3)C 84P ξ===. ………….. 11分ξ的分布列为: ξ 0123P5214584314184………….. 12分ξ的数学期望545310123121841484E ξ=⨯+⨯+⨯+⨯=. ………….. 13分 17.(本小题满分14分) 解法一: (Ⅰ)证明:Q 平面PAB ⊥平面ABC ,平面PAB I 平面ABC AB =,且BC AB ⊥,BC PAB ∴⊥平面 . ………….. 2分PA ⊂Q 平面 PAB , PA BC ∴⊥.又 PA PB ⊥Q ,∴PA PBC ⊥平面 . ………….. 4分(Ⅱ)解:作PO AB ⊥于点O ,OM AC ⊥于点M ,连结PM .Q 平面PAB ⊥平面ABC , PO ABC ∴⊥平面 ,根据三垂线定理得 PM AC ⊥,PMO∴∠是二面角P AC B --的平面角. ………….. 6分设6PA PB ==, PA PB ⊥Q , 233AB PO BO AO ∴==== , .30OM AM MAO ⊥∠=︒Q ,, sin 302AOOM AO ∴=⋅︒=, tan 2PO AOPMO OM OM∴===, ………….. 8分 即二面角P AC B--的大小是arctan 2. ………….. 9分(Ⅲ)解:在底面ABC 内分别过A C 、作BC AB 、的平行线,交于点D , 连结OC OD PD ,,.则PCD ∠是异面直线AB 和PC 所成的角或其补角. ….. 11分30AB BC BAC ⊥∠=︒Q ,,tan302BC AB ∴=⋅︒=, 227OC OB BC =+=,22 10PC PO CO ∴=+=.易知底面ABCD 为矩形,从而OC OD =,.PC PD = 在PCD∆中,1302cos 10CDPCD PC ==, ………….. 13分 ∴异面直线AB 和PC 所成角的大小为30arccos. ………….. 14分 解法二:作PO AB ⊥于点O ,Q 平面PAB ⊥平面ABC ,PO ∴⊥平面ABC .过点O 作BC 的平行线,交AC 于点D .如图,以O 为原点,直线OD OB OP ,,分别为x 轴,y 轴,z 轴,建立空间直角坐标系 . ………….. 2分6PA PB ==设. PA PB ⊥Q ,233AB PO BO AO ∴==== , .30AB BC BAC ⊥∠=︒Q ,,tan302BC AB ∴=⋅︒=.(0 0 0)(0 3 0)(0 3 0)(2 3 0)O A B C ∴-,,,,,,,,,,,,(0 0 3)P ,,,(1 0 0).D ,, …………..4分(Ⅰ)证明:(0 33)(2 00)PA BC =--=u u u r u u u r Q ,,, ,,,0PA BC ∴=u u u r u u u rg , PA BC ∴⊥.又 PA PB ⊥Q ,∴PA PBC ⊥平面 . ………….. 7分 (Ⅱ)解:作OM AC ⊥于点M ,连结PM .PO ⊥Q 平面ABC , 根据三垂线定理得 PM AC ⊥, PMO∴∠是二面角P AC B --的平面角. ………….. 8分在Rt AMO ∆中,sin 302AO OM AO =⋅︒==,3 04M ⎛⎫∴ ⎪ ⎪⎝⎭,,从而33044MO MP ⎛⎫⎛=-=- ⎪ ⎪ ⎝⎭⎝u u u u r u u u r , ,cos MO MP MO MP MO MP∴〈〉==u u u u r u u u ru u u u r u u u r g u u u u r u u u r , ………….. 10分 即二面角P AC B --的大小是………….. 11分 (Ⅲ)解:()( 02AB PC ==u u u r u u u r Q , ,cos AB PC AB PC AB PC∴〈〉==u u u r u u u ru u u r u u u r g u u u r u u u r ,, ∴ 异面直线AB 和PC 所成角的大小为. ………….. 14分 18.(本小题满分13分) (Ⅰ)解:()f x 的定义域为0∞(,+), ….. 1分 ()f x 的导数()1ln f x x '=+. ………….. 3分令()0f x '>,解得1e x >;令()0f x '<,解得10ex <<. 从而()f x 在10e ⎛⎫ ⎪⎝⎭,单调递减,在1e ⎛⎫∞ ⎪⎝⎭,+单调递增. ………….. 5分 所以,当1ex =时,()f x 取得最小值1e-. ………….. 6分 (Ⅱ)解:解法一:令()()(1)g x f x ax =--,则()()1ln g x f x a a x ''=-=-+, ………….. 8分① 若1a ≤,当1x >时,()1ln 10g x a x a '=-+>-≥, 故()g x 在(1)∞,+上为增函数, 所以,1x ≥时,()(1)10g x g a ≥=-≥,即()1f x ax ≥-. ………….. 10分② 若1a >,方程()0g x '=的根为 10e a x -=,此时,若0(1)x x ∈,,则()0g x '<,故()g x 在该区间为减函数.所以,0(1)x x ∈,时,()(1)10g x g a <=-<,即()1f x ax <-,与题设()1f x ax ≥-相矛盾. ………….. 12分 综上,满足条件的a的取值范围是(1]-∞,. ………….. 13分 解法二:依题意,得()1f x ax ≥-在[1)+∞,上恒成立, 即不等式1ln a x x≤+对于[1)x ∈+∞,恒成立 . ………….. 8分 令1()ln g x x x=+, 则21111()1g x x x x x ⎛⎫'=-=- ⎪⎝⎭. ………….. 10分 当1x >时,因为11()10g x x x⎛⎫'=-> ⎪⎝⎭,故()g x 是(1)+∞,上的增函数, 所以 ()g x 的最小值是(1)1g =, ………….. 12分从而a 的取值范围是(1]-∞,. ………….. 13分19.(本小题满分14分) (Ⅰ)解:依题意,直线AB 的斜率存在,设直线AB 的方程为(1)y k x =+,将(1)y k x =+代入5322=+y x , 消去y 整理得 2222(31)6350.k x k x k +++-= ………….. 2分设1122() () A x y B x y ,,,, 则4222122364(31)(35)0 (1)6. (2)31k k k k x x k ⎧∆=-+->⎪⎨+=-⎪+⎩, ………….. 4分由线段AB 中点的横坐标是12-, 得2122312312x x k k +=-=-+, 解得k =±,适合(1). ………….. 5分所以直线AB 的方程为10x +=,或10x +=. ………….. 6分(Ⅱ)解:假设在x 轴上存在点(,0)M m ,使MB MA ⋅为常数.① 当直线AB 与x 轴不垂直时,由(Ⅰ)知 22121222635. (3)3131k k x x x x k k -+=-=++,所以212121212()()()()(1)(1)MA MB x m x m y y x m x m k x x ⋅=--+=--+++u u u r u u u r22221212(1)()().k x x k m x x k m =++-+++ ………….. 8分将(3)代入,整理得 222222114(2)(31)2(61)5333131m k m m k MA MB m m k k -+----⋅=+=+++u u u r u u u r 2216142.33(31)m m m k +=+--+注意到⋅是与k 无关的常数, 从而有761403m m +==-,, 此时4.9MA MB ⋅=u u u r u u u r ..11分② 当直线AB 与x 轴垂直时,此时点A B ,的坐标分别为11⎛⎛-- ⎝⎝、,, 当73m =-时, 亦有4.9MA MB ⋅=u u u r u u u r ………….. 13分综上,在x 轴上存在定点703M ⎛⎫- ⎪⎝⎭,,使MB MA ⋅为常数. ………….. 14分 20.(本小题满分14分) (Ⅰ)解:依题意,222211322111111.222222a a a c c a a a c c ⎛⎫=-+=-=-+=-+ ⎪⎝⎭,由3218a a -=,得21111122228c c ⎛⎫⎛⎫-+--= ⎪ ⎪⎝⎭⎝⎭, 解得2c =,或1c =(舍去). ………….. 3分 (Ⅱ)解:① 证明:因为2211122(2)022n n nn n a a a a a +-=-+=-≥, 当且仅当2n a =时,1n n a a +=. 因为11a =,所以10n n a a +->,即1n n a a +<(1,2,3,n =L ) . .............. 5分 ② 数列{}n a 有极限, .. (6)分 且lim 2n n a →∞=. ………….. 7分(Ⅲ)解:由21122n n n a a a +=-+,可得11()(2)(2)n n n n n a a a a a ++-=--,从而111122n n n a a a +=---. 因为11a =,所以 1111111111111.22222nnk k k k k n n a a a a a a ==+++⎛⎫=-=-=- ⎪-----⎝⎭∑∑ 所以21111111111404139(53)(813)1401401.3923939(2)39(2)nn n n n n n k kn n n a a a a a a a a a a ++++++=+++--+--=--==-⋅-⋅-∑………….. 9分因为11a =,由(Ⅱ)① 得 1n a ≥ (*n ∈N ). (1) 下面证明:对于任意*n ∈N ,有2n a <成立. 当1n =时,由11a =,显然结论成立. 假设结论对 (1)n k k =≥时成立,即 2.k a <因为2211132(1)222n n n n a a a a +=-+=-+,且函数213(1)22y x =-+在1x ≥时单调递增,所以2113(21)222k a +<-+=.即当1n k =+时,结论也成立. 于是,当*n ∈N 时,有2n a <成立. (2) 根据(1)(2)、得12n a ≤<. (12)分由11a = 及21122n n n a a a +=-+, 经计算可得23313.28a a ==,所以,当1n =时, 2114039a a <; 当2n =时,312114039a a a +=; 当3n ≥时,由11328n a +<<, 得1111111(53)(813)1401400 3939(2)39nnn n n n k k k n k a a a a a a a ++++==++--=>⇒>⋅-∑∑. ………….. 14分昌平区数学第二学期高三第二次统练试 卷(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分.考试时间120分钟.第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项,并将答案填在题后的答题表中..............) 1. 已知向量a (2,1)=, b (,2)x =-,且a +b 与2a -b 平行,则实数x 的值是 A .-6 B .6 C .4 D . -4 2.函数2sin sin cos y x x x =+⋅的最小正周期为A .π2B . πC . 2π D .4π3.若二项式n xx )2(-的展开式的第5项为常数项,则n 的值为A .6B .10C .12D .154.设集合(){}(){}2220A x y x y B x y x y n =+==-+≤,,,,则“2n =-”是 “A B ⊆”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件5. 在等比数列185721010{},6,5,n a a a a a a a =+=中则的值为A .2332--或B .32C .23D .2332或6.下列四个正方体中,直线l 是正方体的一条对角线,点M 、N 、P 分别为其所在棱的中点,不能得出l ⊥平面MNP 的是A. B. C.D. 7.在ABC ∆中,(2,0)B -,(2,0)C ,且满足条件1sin sin sin 2C B A -=,则顶点A 的轨迹方程是A .221(0)3y x y -=≠ B. 221(1)3y x x -=≥C .221(1)3y x x -=> D.221(1)3y x x -=<-8.在一次台球比赛中,两名选手约定:以先赢6局为胜.后比赛因故中断,不能进行,此时选手甲赢得5局比赛,选手乙赢得2局.试问总奖金两名选手应按如下哪种比例分配才合理?A .5:2 B.10:1 C. 15:1 D.4:1第一大题(选择题)答题表昌平区2007-2008学年第二学期高三第二次统练 数 学 试 卷(理科) 2008.5 第Ⅱ卷(共110分)注意事项:1. 用钢笔或圆珠笔将答案直接写在试卷上. 2. 答卷前将密封线内的项目填写清楚.151617181920得分二、 填空题(本大题共6小题,每小题5分,共30分.请把答案填在题中横线上.)9.若复数()()2433i z m m m =-++-是纯虚数,则实数m = . 10.已知数列{n a }的通项公式为52n a n =-+,其前n 项和为n S ,则2lim nn S n ∞=→ .11.已知向量a 与b 都是单位向量,它们的夹角为120,且|k a +b|3=k 的值是 .12.市内某公共汽车站有10个候车位(排成一排),现有4名乘客随便坐在某个座位上候车,则恰好有5个连续空座位的候车方式共有_______________种.13. 在正三棱锥P ABC -中,,M N 分别是侧棱,PB PC 的中点,若截面AMN ⊥侧面PBC ,则此三棱锥的侧棱与底面所成角的正切值是 .14.下列命题:①要得到函数y=sin(24x π-)的图象,只需将函数y=sin 2x 的图象向右平移4π位;②函数y=1xx -的图象关于直线y x =对称; ③函数()f x 的定义域为R ,则函数()y f x =--的图象关于原点成中心对称;④设随机变量ξ服从正态分布2(2,)N σ,且(4)0.84P ξ≤=,则(02)0.34P ξ≤≤=.其中正确命题的序号是______________________.三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)15.(本小题满分12分)在ABC ∆中,,,a b c 分别是角,,A B C 所对的边, 0cos )cos(=++B c B A b . (Ⅰ)判断ABC ∆的形状; (Ⅱ)若3sin 3B b ==,求ABC ∆的面积. 16.(本小题满分13分)PMN B A一台仪器每启动一次都随机地出现一个6位的二进制数A =1236a a a a L ,其中A 的各位数字中,161a a ==,(2,3,4,5,6)k a k =出现0的概率为13,出现1的概率为23.例如:100111A =,其中230a a ==,451a a ==,记1236a a a a ξ=++++L .当启动仪器一次时,(Ⅰ)求3ξ=的概率;(Ⅱ)求随机变量ξ的分布列和数学期望. 17. (本小题满分14分)如图,正三棱柱111ABC A B C -的底面边长的3,侧棱1AA =,233D 是CB 延长线上一点,且BD BC =.(Ⅰ)求证:直线1BC //平面1AB D ; (Ⅱ)求二面角1B AD B --的大小; (Ⅲ)求三棱锥11C ABB -的体积. 18.(本小题满分14分)已知函数()()(),(,R)f x x x a x b a b =--∈.(Ⅰ)若,0,a b ab ≠≠过两点O (0,0)、(,0)A a 的中点作与x 轴垂直的直线,此直线与函数()y f x =的图像交于点00(,())P x f x .求证:函数()y f x =在点P 处的切线过点B (b ,0);(Ⅱ)若a =b (a >0),且当[0,1]x a ∈+时,2()2f x a <恒成立,求实数a 的取值范围. 19.(本小题满分13分)已知椭圆22122:1(0)x y C a b a b +=>>的一条准线方程是254x =,其左、右顶点分别是,A B ,双曲线22222:1(0)x y C a b a b-=>>的一条渐近线350x y -=.(Ⅰ)求椭圆1C 的方程;(Ⅱ)在第一象限内取双曲线2C 上一点P ,连结AP 交椭圆1C 于点M ,连结PB 并延长交椭圆1C 于点N ,若AM MP =u u u u r u u u r,求证:MN AB ⊥.DA 1B 1C 1ABC20.(本小题满分14分)已知函数2()(1)2ln (N*)k f x x x k =--∈g .(I)讨论函数()f x 的单调性;(II) k 是偶数时,正项数列{}n a 满足21131,'()n n na a f a a +-==,求{}n a 的通项公式;(III )k 是奇数,*N n ∈时,求证:1['()]2'()2(22)n n n n n f x f x --≥-g .数学试卷参考答案及评分标准(理)2一、选择题(本大题共8小题,每小题5分,共40分.)二、填空题(本大题共6小题,每小题5分,共30分.) 9、1 10、52- 11、 2或-112、480 13、、②④. 三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)⒂(本小题满分12分)解:(I )0cos )cos(=++B c B A b Θ,0cos sin )cos(sin =++∴B C B A B0cos sin )cos(sin =+-B C C B π0cos sin cos sin =+-B C C B ……………………………………….3分0)sin(=-B C在ABC ∆中,C=B ,即ABC ∆为等腰三角形…………………………………6分(2)∵C=B 02B π∴<<sin cos B B =∴=Qsin sin[()]sin[2]sin 22sin cos A B C B B B B ππ∴=-+=-===11sin 33223ABC S bc A ∆∴==⨯⨯⨯=..12分 ⒃(本小题满分13分)(I) 解:(1)设3=ξ时为事件A ,即2345a a a a 中恰有一位数字1.则818)31()32()(3114==C A P ………………………………………………………….5分 (II) ξ可能取值为2、3、4、5、6811)31()32()2(4004===C P ξ818)31()32()3(3114===C P ξ8124)31()32()4(2224===C P ξ 8132)31()32()5(1334===C P ξ 8116)31()32()6(0444===C P ξξ∴的分布列为2345581818181813E ξ=⨯+⨯+⨯+⨯+⨯=………………………….13分⒄ (本小题满分14分)(Ⅰ)证明:CD//C 1B 1,又BD=BC=B 1C 1, ∴ 四边形BDB 1C 1是平行四边形, ∴BC 1//DB 1.又DB 1⊂平面AB 1D ,BC 1⊄平面AB 1D ,∴直线BC 1//平面AB 1D ……………..4分(Ⅱ)解:过B 作BE ⊥AD 于E ,连结EB 1,∵B 1B ⊥平面ABD ,∴B 1E ⊥AD ,∴∠B 1EB 是二面角B 1—AD —B 的平面角, (6)分∵BD=BC=AB , ∴E 是AD 的中点, .2321==AC BE在Rt △B 1BE中,112tan 32B B B BE BE∠===∴∠B 1EB=60°.即二面角B 1—AD —B 的大小为60° (9)分(Ⅲ)解法一:过A 作AF ⊥BC 于F ,∵B 1B ⊥平面ABC ,∴平面ABC ⊥平面BB 1C 1C ,∴AF ⊥平面BB 1C 1C ,且AF 为点A 到平面BB 1C 1的距离 (11)分∴AF=∴=⨯,323323 AF S V V C B B C BB A ABB C ⋅==∆--1111111131 .827233)323321(31=⨯⨯⨯=即三棱锥C 1—ABB 1的体积为.827……………………………………….14分解法二:在三棱柱ABC —A 1B 1C 1中,11111111111C B A A B AA C ABB C B AA ABB V V V S S ---∆∆==∴=Θ.827233)3434(313121111=⨯⨯⨯=⋅=∆AA S CB A 即三棱锥C 1—ABB 1的体积为.827………….14分⒅ (本小题满分14分)解:(I )由已知22(,()),'()3(22)242a a aP b f x x a b x ab -=-++所求切线斜率为22'()3()(22),2224a a a a f ab ab =-+⋅+=-∴在点P 处的切线方程为22()()4242a a a ay b x +-=--………………………….4分令y=0,解得x =b.所以函数,)(x f y =在点P 处的切线过点B (b ,0)………..……………………6分(II )因为b a =,所求2)()(a x x x f -=)3)((34322ax a x a ax x y --=+-='∵a >0时,函数)3,()(a x f y -∞=在上单调递增,在),3(a a单调递减,在),(+∞a 上单调递增。
2018西城高三数学二模考试答案解析理科

2018西城高三二模数学(理科)参考答案及评分标准2018.5一、选择题:本大题共8小题,每小题5分,共40分.1.C 2.A 3.D 4.B 5.D 6.C 7.A 8.A二、填空题:本大题共6小题,每小题5分,共30分.9.π,65 10.6 11.1312.2n -+(答案不唯一) 13.1[,3]214.D注:第9题第一空3分,第二空2分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)解:(Ⅰ)因为函数tan y x =的定义域是π{|π,}2x x k k ∈≠+∈R Z ,所以()f x 的定义域为π{|π,}2x x k k ∈≠+∈R Z . ……………… 4分(Ⅱ)()(1tan )sin 2f x x x =+⋅sin (1)sin 2cos xxx =+⋅……………… 5分 2sin 22sin x x =+ ……………… 6分sin2cos21x x =-+ ……………… 7分π)14x -+. ……………… 8分由()2f α=,得πsin(2)4α-= ……………… 9分因为 0πα<<,所以ππ7π2444α-<-<, ………………10分 所以 ππ244α-=,或π3π244α-=. ………………11分解得 π4α=,或π2α=(舍去). ………………13分16.(本小题满分14分)解:(Ⅰ)因为 //CD EF ,且CD EF =, 所以 四边形CDFE 为平行四边形,所以 //DF CE . …… 2分因为 DF ⊄平面BCE ,…… 3分所以 //DF 平面BCE .…… 4分 (Ⅱ)在平面ABEF 内,过A 作Az AB ⊥.因为 平面ABCD ⊥平面ABEF ,平面ABCD 平面ABEF AB =, 又 Az ⊂平面ABEF ,Az AB ⊥, 所以 Az ⊥平面ABCD ,所以 AD AB ⊥,AD Az ⊥,Az AB ⊥.如图建立空间直角坐标系A xyz -. ……………… 5分 由题意得,(0,0,0)A ,(0,4,0)B ,(2,2,0)C,E,F . 所以 (2,2,0)BC −−→=-,(0,BF −−→=-. 设平面BCF 的法向量为(,,)x y z =n ,则 0,0,BC BF −−→−−→⎧⋅=⎪⎨⎪⋅=⎩n n即220,30.x y y -=⎧⎪⎨-+=⎪⎩令1y =,则1x =,z ==n . ……………… 7分 平面ABF 的一个法向量为 (1,0,0)=v , ……………… 8分 则cos ,||||⋅〈〉=n v n v n v 所以 二面角C BF A --. ………………10分 (Ⅲ)线段CE 上不存在点G ,使得AG ⊥平面BCF ,理由如下: ………………11分解法一:设平面ACE 的法向量为111(,,)x y z =m ,则 0,0,AC AE −−→−−→⎧⋅=⎪⎨⎪⋅=⎩m m即1111220,30.x y y +=⎧⎪⎨+=⎪⎩令11y =,则11x =-,1z =(1,1,=-m . ………………13分因为 0⋅≠m n ,所以 平面ACE 与平面BCF 不可能垂直,从而线段CE 上不存在点G ,使得AG ⊥平面BCF . ………………14分 解法二:线段CE 上不存在点G ,使得AG ⊥平面BCF ,理由如下: …………11分 假设线段CE 上存在点G ,使得AG ⊥平面BCF , 设 CG CE λ−−→−−→=,其中[0,1]λ∈.设 222(,,)G x y z,则有222(2,2,)(2,)x y z λλ--=-, 所以 222x λ=-,22y λ=+,2z =,从而(22,2,)G λλ-+,所以(22,2)AG λλ−−→=-+. ………………13分 因为 AG ⊥平面BCF ,所以 //AG n . 所以有22211λλ-+==, 因为 上述方程组无解,所以假设不成立.所以 线段CE 上不存在点G ,使得AG ⊥平面BCF . ………………14分17.(本小题满分13分)解:(Ⅰ)根据分层抽样原则,容量为100的样本中,患病者的人数为 3.4100408.5⨯=人.… 2分 10.100.350.250.150.100.05a =-----=,10.100.200.300.40b =---=. ……………… 4分(Ⅱ)指标检测数据为4的样本中,有患病者400.208⨯=人,未患病者600.159⨯=人. ……………… 6分 设事件A 为“从中随机选择2人,其中有患病者”.则 29217C 9(A)C 34P ==, ……………… 8分所以 25(A)1(A)34P P =-=. ……………… 9分 (Ⅲ)使得判断错误的概率最小的0 4.5X =. ………………11分 当0 4.5X =时,判断错误的概率为21100. ………………13分 18.(本小题满分14分)解:(Ⅰ)由 21,4y kx y x=+⎧⎪⎨=⎪⎩ 得 22(24)10k x k x +-+=. ① ……………… 2分依题意,有0k ≠,且22(24)40k k ∆=--=.解得 1k =. ……………… 3分所以直线l 的方程为1y x =+. ……………… 4分 将 1k = 代入①,解得 1x =,所以点P 的坐标为(1,2). ……………… 5分 (Ⅱ)设 (,)Q m n , 则 24n m =,所以 12(,)22m n A ++. ……………… 7分 依题意,将直线 22n y +=分别代入抛物线C 与直线l , 得 2(2)2(,)162n n M ++,2(,)22n n N +. ……………… 8分因为 22(2)444441||16216164n n n n m n m n MN +-+-+-+=-===, ……… 10分 221(2)(88)(44)||21616m n m n n AM +++-++=-=(88)(444)1164m m n m n +-++-+==, ………………12分 所以 ||||AM MN =. ………………13分 又 A 为PQ 中点,所以P Q ,两点到直线AN 的距离相等,所以 12S S =. ………………14分19.(本小题满分13分)解:(Ⅰ)()f x 的导函数为221ln ()x ax f x x --'=, ……………… 2分所以(1)1f a '=-. 依题意,有 (1)(1)112f a --=--,即1112a a -+=--, ……………… 4分 解得 1a =. ……………… 5分(Ⅱ)由(Ⅰ)得221ln ()x xf x x --'=.当0<<1x 时,210x ->,ln 0x ->,所以()0f x '>,故()f x 单调递增;当>1x 时,210x -<,ln 0x -<,所以()0f x '<,故()f x 单调递减.所以 ()f x 在区间(0,1)上单调递增,在区间(1,)+∞上单调递减. ……………… 8分因为 101b b<<<, 所以 ()f x 最大值为(1)1f =-. ……………… 9分 设 111()()()()ln h b f b f b b b b b b =-=+-+,其中1b >. ………………10分则 21()(1)ln 0h b b b'=->,故 ()h b 在区间(1,)+∞上单调递增. ………………11分所以 ()(1)0h b h >=, 即 1()()f b f b>, ………………12分故 ()f x 最小值为11()ln f b b b b=--. ………………13分20.(本小题满分13分)解:(Ⅰ)满足条件的数列3A 为:1,1,6--;1,0,4-;1,1,2-;1,2,0-. ……………… 3分 (Ⅱ)11a =-. ……………… 4分否则,假设11a ≠-,因为10a ≠,所以11a ≥.又23,,,1n a a a -≥,因此有12312312222n n n n n a a a a a ----⋅+⋅+⋅++⋅+ 1232(1)2(1)2(1)2(1)n n n ---+-⋅+-⋅++-⋅+-≥123222211n n n ---=-----=,这与123123122220n n n n n a a a a a ----⋅+⋅+⋅++⋅+=矛盾!所以11a =-. ……………… 8分 (Ⅲ)先证明如下结论:{1,2,,1}k n ∀∈-,必有12122220n n n k k a a a ---⋅+⋅++⋅≤.否则,令 12122220n n n k k a a a ---⋅+⋅++⋅>,注意左式是2n k -的整数倍,因此 12122222n n n k n k k a a a ----⋅+⋅++⋅≥.所以有:12312312222n n n n na a a a a ----⋅+⋅+⋅++⋅+ 122(1)2(1)2(1)2(1)n kn k n k -----+-⋅+-⋅++-⋅+-≥1222221n k n k n k -----=-----1=,这与123123122220n n n n n a a a a a ----⋅+⋅+⋅++⋅+=矛盾!所以 12122220n n n k k a a a ---⋅+⋅++⋅≤. ………………10分因此有:112123121212312210,20,420,2220,2220.k k k k n n n n a a a a a a a a a a a a a a -------<⋅+⋅+⋅+⋅+⋅++⋅+⋅+⋅++⋅+≤≤≤≤将上述1n -个不等式相加得 12121(21)(21)(21)0n n n a a a ---⋅-+⋅-++⋅-<, ①又 123123122220n n n n n a a a a a ----⋅+⋅+⋅++⋅+= ,②两式相减即得 120n a a a +++>. ………………13分。
北京市西城区届高三二模试卷理科数学Word版含答案

、选择题:本大题共合题目要求的一项1 .已知集合北京市西城区2018年高三二模试卷数学(理科) 第I卷(选择题共40分)8小题,每小题A 二{x|x -2 ::0},2 .在复平面内,复数(A )第一象限(C)第三象限2018.5 5分,共40分.在每小题列出的四个选项中,选出符B二{x | x ::: a},若A「| B二A,则实数a的取值范围是(B) [-2, ::) (C) (-::,2]2z=(1 2i)对应的点位于(B )第二象限(D )第四象限(D) [2,::)2x 3 .直线y = 2x为双曲线C: 一2a 七=1(a 0,b 0)的一条渐近线,则双曲线bC的离心率是()(A) ...5 (B(C) 3(D)4 •某四棱锥的三视图如图所示,记 A 为此棱锥所有棱的长度的集合,则(A) 2? A ,且 4? A(B)v 2? A ,且4? A(C) 2? A ,且 2、5? A (D) ,2 ? A ,且...17 ? A5•设平面向量a ,b ,c 均为非零向量,则“ a (b-c ) =0 ”是“ b 二c ”的()(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件6•如图,阴影区域是由函数 y^cosx 的一段图象与 xx >0,7.在平面直角坐标系 xOy 中,不等式组 y 》0, 所表示的平面区域是〉,不等式组x y -8< 0'所表示的平面区域是 P .从区域G 中随机取一点P (x, y ),则P 为区域B 内的点的 0< y <10概率是()/八133 1 (A)-(B )-(C )-(D )-4545轴围成的封闭图形,那么这个阴影区域的面积是( )'y才O n x2 2(A) 1(C )7C(D) n)侧(左)视图8.设门为平面直角坐标系 xOy 中的点集,从中的任意一点 P 作x 轴、y 轴的垂线,垂足 分别为M ,N ,记点M 的横坐标的最大值与最小值之差为 x (「),点N 的纵坐标的最大值 与最小值之差为y (「).若门是边长为1的正方形,给出下列三个结论: ①x (门)的最大值为.2 ;D x (「)• y (「)的取值范围是[2, 2,2];第H 卷(非选择题共110 分)、填空题:本大题共 6小题,每小题5分,共30分.1 69. ______________________________________ (x+—)的二项展开式中,常数项为 •x110. 在厶 ABC 中,若 a=4 , b=3 , cosA = —,贝U sinA= _____ ; B= ____311 .如图,AB 和CD 是圆0的两条弦,AB 与CD 相交于点 E ,且CE = DE = 4 ,12 •执行如图所示的程序框图,输出的a 值为 ______ xCO -yC 1)恒等于 0.AE: BE =4:1,贝U AE -AC开始BDi=i+1213.设抛物线C: y =4x 的焦点为F , M 为抛C其中所有正确结论的序号是()a =3,i=11N(2,2) U|MF | • |MN |的取值范围是14.已知f是有序数对集合M二{(x, y)|x挝N ,y N }上的一个映射,正整数数对(x,y)在映射f下的象为实数乙记作f (x, y) = z.对于任意的正整数m, n (m> n),映射f由下表给出:则f (3,5)= _________ ,使不等式f(2x, x) < 4成立的x的集合是__________________三、解答题:本大题共6小题,共80分•解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)在平面直角坐标系xOy中,点A(cosr「2sin旳,B(sin二0),其中"R .2 n T(I)当时,求向量AB的坐标;3n T(H)当才[0,—]时,求|AB |的最大值.216.(本小题满分13分)为了解某校学生的视力情况,现采用随机抽样的方式从该校的 A , B两班中各抽5名学生进行视力检测.检测的数据如下:A班5名学生的视力检测结果: 4.3, 5.1, 4.6, 4.1, 4.9.B班5名学生的视力检测结果: 5.1 , 4.9, 4.0, 4.0, 4.5.(I)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?(n)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)(川) 现从A班的上述5名学生中随机选取3名学生,用X表示其中视力大于 4.6的人数,求X的分布列和数学期望17.(本小题满分14分)如图,在三棱锥P—ABC中,PA_底面ABC , AC _ BC , H为PC的中点,M为AH 的中点,PA=AC=2,BC=1.(I)求证:AH _ 平面PBC ;(H)求PM与平面AHB成角的正弦值;PN(川)设点N在线段PB上,且,MN//平面ABC,求实数■的值.PB18.(本小题满分13分)x +e已知函数f(x)二一2,其中a R.ax +4x +4(I)若a=0,求函数f (x)的极值;(n)当a・1时,试确定函数f(x)的单调区间19.(本小题满分14分)2 2设A,B是椭圆W:亍•器1上不关于坐标轴对称的两个点,直线AB交x轴于点M(与点代B不重合),0为坐标原点(I)如果点M是椭圆W的右焦点,线段MB的中点在y轴上,求直线AB的方程;(n)设N为x轴上一点,且OM QN =4,直线AN与椭圆W的另外一个交点为C,证明:点B与点C关于x轴对称.20.(本小题满分13分)在无穷数列{a*}中,印=1,对于任意n • N*,都有a* • N , a n:::a n彳•设N* , 记使得a* < m成立的n的最大值为b m.(I)设数列{a*}为1, 3, 5,乙…,写出b i, b2, b3的值;(n)若{b n}为等差数列,求出所有可能的数列{a n};(川)设a^q , a i • a2 • 111 a^ A,求b i J|| ■ b q的值.(用p,q, A 表示)北京市西城区2018年高三二模试卷参考答案及评分标准sin r - COST - sinN — cos2n 1;33一云…一云吟6所以AB高三数学(理科)2018.5 、 选择题: 本大题共 8小题, 每小题5分,共40分. 1. D 2 . B 3 . A 4 . D 5.B 6 . B7 .C8 . D _ 、 填空题:本大题共 6小题,每小题5分,共30分.202、.2 冗 910. 一3 4118212 1313[3,+::)14. 8{1,2}三、解答题:本大题共 6小题,共80分.其他正确解答过程,请参照评分标准给分15. (本小题满分13分)(I)解:由题意,得AB = (sin v - cos 二 一2 sin v), 2).(n )解:因为注:第10, 11, 14题第一问2分,第二问3分.AB = (sin v - COST , 2 sin 旳,所以|AB|2=(si n 八cos*2(-・ 2 si nJ2=1 -sin 2^ 2sin J .................. 8 分=1 -si n2^ 1-cos2 二.......... 9 分=2 - ,2sin(2寸n). .......... 10分4n因为0 w 寸w —,2n n , 5 n 所以—w 2— w ........... 11分444所以当•亠 2时,|忑|2取到最大值| AB|^^-,2 ( 「2)=3 ,……12分4 42n即当时,|AB|取到最大值.3........... 13分16. (本小题满分13分)从数据结果来看A 班学生的视力较好. 解:B 班5名学生视力的方差较大则X 的所有可能取值为0 , 1, 2.C 31所以P (x ;P (X =1)=晋=| ;C 5 5所以随机变量X 的分布列如下:12分13 3 6 故 E (X ) =01 2 - 解:A 班5名学生的视力平均数为 x A =4.3+5.1+4.6+4.1 4.9=4.6,B 班5名学生的视力平均数为 x B =5.1+4.9+4.0+4.0 4.5=4.5.(出解:由(I )知,A 班的5名学生中有2名学生视力大于4.6.10分c ;c 2P (X =2)诗唏11分13分10 510 5 17.(本小题满分14分)(I)证明:因为PA _底面ABC , BC二底面ABC ,所以PA_BC ,又因为AC _ BC , PA" AC 二A ,所以BC _平面PAC ,又因为AH 平面PAC ,所以BC _ AH •因为PA二AC, H是PC中点,所以AH _ PC ,又因为PC「|BC二C ,所以AH —平面PBC. .......... 5分(n)解:在平面ABC中,过点A作AD//BC,因为BC _平面PAC,所以AD _平面PAC,由PA_底面ABC,得PA,AC,AD两两垂直,所以以A为原点,AD,AC,AP所在直线分别为x轴,y轴,z轴如图建立空间直角坐标系,则A(0,0,0),P(0,0,2),B(1,2,0),C(0,2,0),1 15,M(0,2,2).设平面AHB的法向量为n = (x, y, z),因为AH =(0,1,1)"AB =(120)n AH =0,由得n AB =0, y z = 0, x 2y = 0,令z =1,得n =(2, -1,1). .......... 8分设PM与平面AHB成角为二,因为PM6分PM即 sin (2115)15(川)解:因为詣=(1,2,-2), "PN = PB ,所以 PN =( ■ ,2 ■ , -2 ),-* 1 3又因为PM =(0,丄,),2 2所以 sin 日=cos v PM , n > =PM n 27 + (—1)x 丄十仆(一卫)2 210分所以因为1 3MN =PN - PM -( ,2 , 2 ).••…2 2MN //平面ABC,平面ABC的法向量-(0,0,2),12分所以MNAP解得14分18.(本小题满分13分)ex +(I)解:函数f (x) 的定义域为{X I x • R,且x = -1} . .......... 1分4x +4e x 1(4x 4) -4e x 1(4x +4)24xe (4x 4)2.令f (x) =0,得x = 0,当x变化时,f (x)和f (x)的变化情况如下:故f(x)的单调减区间为(-::,-1), (-1,0);单调增区间为(0, • ::) •e所以当x =0时,函数f(x)有极小值f(0)................. 6分4(n)解:因为a 1 ,2 2 2所以 ax 4x 4 =(x 2) (a -1)x 0 ,所以函数f (x)的定义域为R ,4令 f (x) =0,得 x , =0 , X 2 =2,........... 9 分a当 1 : :a : 2 时,X 2 : x , 当x44故函数f (x)的单调减区间为(2,0),单调增区间为(-::,2) , (0,.a a.......... 11分当 a 2 时,x 2 x 1,当x 当a =2时, x2 二片,因为f (x)二2e x 1x 2 .22》0 ,(当且仅当X=0时,f (x) =0 )(2x 2 4x 4)2所以函数f(x)在R 单调递增.12分求导,得f (xr 皿 +4x +4) -e x 卑(2ax + 4) 2 2(ax 4x 4)e x ^x(ax + 4 _2a)(ax 2 4x 4)2 '4 4故函数f(x)的单调减区间为(0,2 ),单调增区间为(-::,0) , (2 .a a4 4综上,当1 :: a :: 2时,f (x)的单调减区间为(2 ,0),单调增区间为(-::,2 ),a a (0, •::);当a =2时,函数f(x)在R单调递增;当a 2时,函数f (x)的单调减区间为4 413分(0,2 );单调增区间为(-::,0) , (2 -一,,:).a a19.(本小题满分14分)(I)解:椭圆W的右焦点为M(1,0),............... 1分因为线段MB的中点在y轴上,所以点B的横坐标为-1, 因为点B在椭圆W上,3将X - -1代入椭圆W的方程,得点B的坐标为(-1,_—). ................. 3分2所以直线AB (即MB )的方程为3x-4y-3 = 0或3x,4y-3 = 0. .................. 5分(n)证明:设点B关于x轴的对称点为B1(在椭圆W上),要证点B与点C关于x轴对称,只要证点B1与点C重合,.又因为直线AN与椭圆W的交点为C (与点A不重合),所以只要证明点A , N , B1三点共线. ........... 7分以下给出证明:由题意,设直线AB 的方程为y 二kx • m(k =0) , A(x1, y1), B(x2, y2),则B1(x2^y2).得(3 4k2)x2 8kmx 4m2-12=0,所以厶=(8km)2-4(3 4k2)(4m2-12) 0,28km 4m -12x1 x2 2,X t X2〒1 2 3 4k2 1 2 3 4k2在y二kx・m中,令y=0,得点M的坐标为(一m ,0),k由OM ON =4,得点N的坐标为(-坐,0),m8m 2k -24k -8m 2k -32k 324k 32k 33+4k 2=0,所以 k NA - k NB 1- 0,所以点A ,N ,B 1三点共线, 即点B 与点C 关于x 轴对称.20.(本小题满分13分)(I)解:4=1 , b 2 =1, 6=2.................. 3分(n)解:由题意,得 1 = a 1 ::: a 2 ::: a 3 ::: 11( ::: a* :::()| , 结合条件a* • N ,得a n >10分11分设直线NA ,NB 1的斜率分别为k NA , k N B 1,,乂 4k 4kX2% y 1 xy y 2_______ m m“ 4k 、“ 4k ,(x)(X )* 议 =4k 一 4k _为 X 2m m中斗 4k 4k 因为 x 2y ( y 1 ^y 2 y 2m m4k 4k= x 2(k% m) (kx-! m) x 1 (kx 2 m) (kx 2 m) ——则 k NA - k NB 112分= 2^2 (m M)(x 1 x 2) 8km =2k (4m 2 -12 3 4k 2)(m4k 2m)( 8 km 3 4k 213分14分n . ........... 4分又因为使得a* < m成立的n的最大值为b m,使得a* < m 1成立的n的最大值为b m d 所以b1 =1,b m < b m1(m・N *). ................ 5 分设a2 = k,则k》2.假设k 2,即a2 = k >2 ,则当*》2时,a* 2 ;当*》3时,a*> k 1.所以b2 =1 , b k = 2 .因为{b*}为等差数列,所以公差d = b2—bi =0 ,所以b* =1,其中*• N*.这与b k = 2(k 2)矛盾,所以a2 = 2 . ................. 6分又因为a1 p :::丨1( ::: a*汕I ,所以b2 =2 ,由{b*}为等差数列,得b*二*,其中*■ N . ........... 7分因为使得a*< m成立的*的最大值为b m ,所以a*< * ,由a*> *,得a* = *. .......... 8 分(川)解:设a^k (k . 1),因为印:::a2 心3 ::: |1( ::: a n 训 | ,所以b] =||(=bk」=1,且bk = 2 ,所以数列{b n}中等于1的项有k -1个,即a2 - a,个;........... 9分设a3 =l (Ik),则b k =b k 1 =|l(二b 丄=2 ,且b| =3 ,所以数列{b n}中等于2的项有I - k个,即a3 -a2个;........... 10分以此类推,数列{b n}中等于p -1的项有a p-a p」个. ........... 11分所以b b2 111 b q -aj 2(a3 -a2)• ()1 (p -1)(a^a p d) p 二-a1 - a2 T I ( - a p 二• ( P - 1)a p p=pap p -⑻ a2 111 • ap」ap)二p(q 1)-A.即b1 b2 • III b q = p(q,1) - A . ........... 13分21 / 15。
2018年高三最新 北京市西城区2018年抽样测试高三数学

北京市西城区2018年抽样测试高三数学试卷(理科)第 Ⅰ 卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合A ⊂{1,2,3},且A 的元素中至少含有一个奇数,则满足条件的集合A 共有( )A .6个B .5个C .4个D .3个 2.若q p x q x p 是则,2|1:|,0)1lg(:<-<-的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知函数)()(),1,0(log 1)(1x f x fa a x x f a 是且-≠>+=的反函数. 若)(1x f -的图象过点(3,4),则a 等于( )A .2B .3C .33D .24.在正三棱锥P —ABC 中,D ,E 分别是AB ,BC 的中点,有下列三个论断: ①PB AC ⊥;②AC //平面PDE ; ③PDE AB 平面⊥.其中正确论断的个数为 ( )A .0个B .1个C .2个D .3个5.若420443322104,)1(a a a x a x a x a x a a x ++++++=-则的值为 ( )A .9B .8C .7D .66.已知a ,b 是不共线的向量,∈+=+=μλμλ,(,b a AC b a AB R )那么A ,B ,C 三点共线的充要条件为( )A .2=+μλB .1=-μλC .λμ=-1D .λμ=17.设双曲线)0,0(12222>>=-b a by a x 的半焦距为c ,离心率为45.若直线kx y =与双曲线的一个交点的横坐标恰为c ,则k 等于( )A .54±B .53±C .209±D .259±8.如图,正五边形ABCDE 中,若把顶点A 、B 、C 、D 、E 染上红、黄、绿、三种颜色中的一种,使得相邻顶点所染颜色不≠相同,则不同的染色方法共有 ( ) A .30种 B .27种 C .24种D .21种第Ⅱ卷(非选择题 共110分)二、填空题(本大题共6小题,每小题5分,共30分. 把答案填在题中横线上.) 9.设甲、乙、丙三个加工厂共生产玩具6000件,其中甲厂生产了1440件. 现采用分层抽样的方法从三个加工厂抽取一个容量为500件的样本进行质量检测,则应从甲加工厂抽取件玩具.10.若∈+=-b a i b i ia ,,2其中R ,i 是虚数单位,则22b a += . 11.)221(lim 220xx x x x ---→= . 12.设∈x R ,函数)23sin(sin x x k y -+⋅=π的最小值是-2,则实数k = . 13.已知正四棱柱ABCD —A 1B 1C 1D 1的底面ABCD 边长为1,高AA 1=2,它的八个顶点都在同一球面上,那么球的半径是 ;A ,B 两点的球面距离为 . 14.按下列程序框图运算: 规定:程序运行到“判断结果是否大于244”为1次运算.若x =5,则运算进行 次才停止;若运算进行k ∈k (N *)次才停止,则x 的取值范围是 .三、解答题(本大题共6小题,共80分. 解答应写出文字说明,证明过程或演算步骤.) 15.(本小题满分12分)已知α为第二象限的角,βα,53sin =为第三象限的角,34tan =β. (I )求)tan(βα+的值. (II )求)2cos(βα-的值.16.(本小题满分12分)设甲、乙两套试验方案在一次试验中成功的概率均为p ,且这两套试验方案中至少有一套试验成功的概率为0.51. 假设这两套试验方案在试验过程中,相互之间没有影响. (I )求p 的值;(II )设试验成功的方案的个数为ξ,求ξ的分布列及数学期望E ξ.17.(本小题满分14分)如图,正三棱柱ABC —A 1B 1C 1中,D 是BC 的中点,AA 1=AB =1.(I )求证:A 1C //平面AB 1D ; (II )求二面角B —AB 1—D 的大小; (III )求点c 到平面AB 1D 的距离.18.(本小题满分14分)设直线)1(:+=x k y l 与椭圆)0(3222>=+a a y x 相交于A 、B 两个不同的点,与x 轴相交于点C ,记O 为坐标原点.(I )证明:222313kk a +>; (II )若OAB ∆=求,2的面积取得最大值时的椭圆方程.19.(本小题满分14分)设a >0,函数a x a x x f ++-=1)(2.(I )若)(x f 在区间]1,0(上是增函数,求a 的取值范围; (II )求)(x f 在区间]1,0(上的最大值.20.(本小题满分14分)设2021,,,a a a 是首项为1,公比为2的等比数列. 对于满足190≤≤k 的整数k ,数列⎩⎨⎧=-++,,,,,202021k n k n n a a b b b b 由 ⎩⎨⎧≤<--≤≤,2020,201时当时当n k k n 确定. 记∑==201n n n b a M . (I )当k =1时,求M 的值;(II )求M 的最小值及相应的k 的值.参考答案一、选择题:本大题共8小题,每小题5分,共40分.1.B 2.A 3.D 4.C 5.B 6.D 7.C 8.A 二、填空题:本大题共6小题,每小题5分,共30分. 9.120 10.5 11.21-12.3± 13.1(2分),3π(3分) 14.4(2分),(]k k x k x k --++∈>+∞∈=6531,31,2);,82(,1时时(3分) 三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分12分)(I )解:因为α为第二象限的角,53sin =α, 所以,54sin 1cos 2-=--=αα,………………………………………2分 .43cos sin tan -==ααα ……………………………………………………… 4分 又34tan =β,所以,.247tan tan 1tan tan )tan(=⋅-+=+βαβαβα …………………………… 6分(II )解:因为β为第三象限的角,34tan =β, 所以,.53cos ,54sin -=-=ββ …………………………………………8分 又257sin 212cos ,2524cos sin 22sin 2=-=-==ααααα,………10分 所以,.53sin 2sin cos 2cos )2cos(=+=-βαβαβα ………………12分16.(本小题满分12分)(I )解:记这两套试验方案在一次试验中均不成功的事件为A ,则至少有一套试验成功的事件为.A由题意,这两套试验方案在一次试验中不成功的概率均为1-p .所以,2)1()(p A P -=,从而,.)1(1)(2p A P --=令.3.0,51.0)1(12==--p p 解得 ………………………………………6分 (II )解:ξ的可取值为0,1,2. ……………………………………………7分,42.0)3.01(3.02)1(,49.0)3.01()0(2=-⨯⨯===-==ξξP P.09.03.0)2(2===ξP ……………………………………………………10分所以ξ的分布列为ξ的数学期望.6.0)2(2)1(1)0(0==⨯+=⨯+=⨯=ξξξξP P P E ……12分 17.(本小题满分14分)解法一(I )证明:连接A 1B ,设A 1B ∩AB 1 = E ,连接DE. ∵ABC —A 1B 1C 1是正三棱柱,且AA 1 = AB , ∴四边形A 1ABB 1是正方形, ∴E 是A 1B 的中点, 又D 是BC 的中点,∴DE ∥A 1C. ………………………… 3分 ∵DE ⊂平面AB 1D ,A 1C ⊄平面AB 1D , ∴A 1C ∥平面AB 1D. ……………………4分(II )解:在面ABC 内作DF ⊥AB 于点F ,在面A 1ABB 1内作FG ⊥AB 1于点G ,连接DG.∵平面A 1ABB 1⊥平面ABC , ∴DF ⊥平面A 1ABB 1,∴FG 是DG 在平面A 1ABB 1上的射影, ∵FG ⊥AB 1, ∴DG ⊥AB 1 ∴∠FGD 是二面角B —AB 1—D 的平面角 …………………………7分 设A 1A = AB = 1,在正△ABC 中,DF=.43 在△ABE 中,82343=⋅=BE FG , 在Rt △DFG 中,36tan ==FG DF FGD , 所以,二面角B —AB 1—D 的大小为.36arctan…………………………9分 (III )解:∵平面B 1BCC 1⊥平面ABC ,且AD ⊥BC ,∴AD ⊥平面B 1BCC 1,又AD ⊂平面AB 1D ,∴平面B 1BCC 1⊥平面AB 1D.在平面B 1BCC 1内作CH ⊥B 1D 交B 1D 的延长线于点H ,则CH 的长度就是点C 到平面AB 1D 的距离. ……………………………12分 由△CDH ∽△B 1DB ,得.5511=⋅=D B CD BB CH即点C 到平面AB 1D 的距离是.55……………………………………14分 解法二:建立空间直角坐标系D —xyz ,如图, (I )证明:连接A 1B ,设A 1B ∩AB 1 = E ,连接DE. 设A 1A = AB = 1, 则).0,0,21(),21,43,41(),1,23,0(),0,0,0(1C E A D - ),21,43,41(),1,23,21(1-=--=∴A.//,211DE C A DE C A ∴-=∴ …………………………3分 D AB C A D AB DE 111,平面平面⊄⊂ ,.//11D AB C A 平面∴ ……………………………………4分(II )解:)1,0,21(),0,23,0(1-B A , )1,0,21(),0,23,0(1-==∴D B AD , 设),,(1r q p n =是平面AB 1D 的法向量,则0,0111=⋅=⋅B n n 且, 故)1,0,2(,1.021,0231===-=-n r r p q 得取; 同理,可求得平面AB 1B 的法向量是).0,1,3(2-=n ……………………7分 设二面角B —AB 1—D 的大小为θ,515||||cos 2121=⋅=n n n n θ , ∴二面角B —AB 1—D 的大小为.515arccos…………………………9分 (III )解由(II )得平面AB 1D 的法向量为)1,0,2(1=n ,取其单位法向量).0,0,21(),51,0,52(==n 又∴点C 到平面AB 1D 的距离.55||=⋅=n d ……………………14分 18.(本小题满分14分)(I )解:依题意,直线l 显然不平行于坐标轴,故.11)1(-=+=y kx x k y 可化为 将x a y x y k x 消去代入,311222=+-=,得 .012)31(222=-+-+a y k y k① ………………………… 3分由直线l 与椭圆相交于两个不同的点,得3)31(,0)1)(31(4422222>+>---=∆a ka kk 整理得, 即.313222kk a +> …………………………………………………… 5分 (II )解:设).,(),,(2211y x B y x A 由①,得221312k ky y +=+因为212,2y y -==得,代入上式,得.31222kky +-= ……………8分 于是,△OAB 的面积 ||23||||21221y y y OC S =-⋅=.23||32||331||32=<+=k k k k ………………11分 其中,上式取等号的条件是.33,132±==k k 即 ……………………12分 由.33,312222±=+-=y k k y 可得 将33,3333,3322=-=-==y k y k 及这两组值分别代入①,均可解出.52=a 所以,△OAB 的面积取得最大值的椭圆方程是.5322=+y x ………………14分 19.(本小题满分14分)(I )解:对函数.11)(,)(2+-='x ax x f x f 得求导数 ……………………… 2分要使(]1,0)(在区间x f 上是增函数,只要(]1,0011)(2在≥+-='x ax x f 上恒成立,即(]1,011122在x x x a +=+≤上恒成立 ……………………………………4分 因为(]1,0112在x +上单调递减,所以(]1,0112在x+上的最小值是2, 注意到a > 0,所以a 的取值范围是(].2,0 ……………………………………6分 (II )解:①当20≤<a 时,由(I )知,(]1,0)(在区间x f 上是增函数, 此时(]1,0)(在区间x f 上的最大值是.)21(1)1(a f -+= ……………………8分 ②当011)(,22=+-='>x ax x f a 令时,解得).1,0(112∈-=a x ……………………………………………………10分因为0)(,111;0)(,11022<'<<->'-<<x f x a x f a x 时时, 所以)1,11(,)11,0()(22--a a x f 在上单调递增在上单调递减,此时(]1,0)(在区间x f 上的最大值是.1)11(22--=-a a a f ………… 13分综上,当20≤<a 时,(]1,0)(在区间x f 上的最大值是a )21(1-+; 当2>a 时,(]1,0)(在区间x f 上的最大值是.12--a a ……………14分 20.(本小题满分14分)(I )解:显然.201,21≤≤=-n a n n 其中 ……………………………………1分当⎩⎨⎧=≤≤==+.20,,191,,111时时当时n a n a b k n n ……………………………………3分所以,∑∑∑∑=-==--++=+⋅=+==2011911911911912191120122222n n n n n nn n nnn a a aa b a M.2322212]1)2[(21939192192+-=+--= …………………………6分 (II )解:∑∑∑∑∑=---=-+-=--+-=--++⋅+⋅==+==2012012021212021112011201202222n k n kn k n kn n k n kn n k n n kn nn n a a a a aa b a M∑∑-=-=-+-++=kn kn k n k n 20120212222222………………………………………………9分)22(31)22(3114142141422020402020k k k k kk k k-+----+-=--⋅+--⋅= .32222312222312113120202020-=⋅-≥⎪⎪⎭⎫ ⎝⎛+-=k k ………………12分 当.322,10,222113120-===M k k k时即 所以,M 的最小值为.10,3221131=-k 此时 ………………………………14分。
2018年高三最新 北京市西城区2018年抽样测试数学(理)试卷及评分标准 精品

北京市西城区2018年抽样测试高三数学试卷(理科)学校_____________ 班级_____________ 姓名_____________参考公式:三角函数的和差化积公式正棱台、圆台的侧面积公式其中c'、c分别表示上下底面周长,l表示斜高或母线长球体的体积公式一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 函数是R上的偶函数,则的值是()A. 0B.C.D.2. 圆锥曲线的准线方程是()A. B.C. D.3. 若圆锥与球的体积相等,且圆锥底面半径与球的直径相等,则圆锥侧面积与球面积之比为()A. B. C. D.4. 两个集合A与B之差记作“A/B”,定义为:,如果集合,那么A/B等于()A. B.C. D.5. 设,则下列不等式中一定成立的是()A. B.C. D.6. 已知双曲线中心在原点且一个焦点为,点P位于该双曲线上,线段PF1的中点坐标为(0,2),则双曲线的方程是()A. B.C. D.7. 函数f(x)的部分图象如下图所示,则f(x)的解析式可以是()A.B.C.D.8. 某航空公司经营A、B、C、D这四城市之间的客运业务。
它的部分机票价格如下:A—B为2000元,A—C为1600元;A—D为2500元;B—C为1200元;C—D为900元。
若这家公司规定的机票价格与往返城市间的直线距离成正比,则B—D的机票价格为()(注:计算时视A、B、C、D四城市位于同一平面内)A. 1000元B. 1200元C. 1400元D. 1500元二、填空题:本大题共6小题,每小题5分,共30分。
把答案填在题中横线上。
9. 正四棱锥S—ABCD的底面边长为2,高为,则异面直线AB与SC所成角的大小是_____________。
10. 从3名男同学1名女同学中选3人,分别担任班长、体委、宣委职务,其中女同学不能担任体委职务,那么不同的任职方案共有_____________种(用数字作答)。
北京市西城区2018年高三二模试卷理数 精品

北京市西城区2018年高三二模试卷数学(理科) 2018.5第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分. 在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知集合{0,1}A =,{1,0,3}B a =-+,且A B ⊆,则a 等于 (A )1(B )0(C )2-(D )3-2.已知i 是虚数单位,则复数23z i+2i 3i =+所对应的点落在 (A )第一象限 (B )第二象限 (C )第三象限(D )第四象限3.在ABC ∆中,“0AB BC ⋅>u u u r u u u r”是“ABC ∆为钝角三角形”的(A )充分不必要条件 (B )必要不充分条件 (C )充要条件(D )既不充分又不必要条件4.已知六棱锥P ABCDEF -的底面是正六边形, PA ⊥平面ABC .则下列结论不正确...的是 (A )//CD 平面PAF (B )DF ⊥平面PAF (C )//CF 平面PAB (D )CF ⊥平面PAD5.双曲线22221x y a b-=的渐近线与圆22(2)1x y +-=相切,则双曲线离心率为(A )2(B )3(C )2(D )3 6.函数sin()(0)y x ϕϕ=π+>的部分图象如右图所示,设P 是图象的最高点,,A B 是图象与x 轴的交点,则tan APB ∠=xA BPyO(A )10 (B )8(C )87(D )477.已知数列{}n a 的通项公式为13n a n =-,那么满足119102k k k a a a +++++=L 的整数k(A )有3个 (B )有2个 (C )有1个(D )不存在8.设点(1,0)A ,(2,1)B ,如果直线1ax by +=与线段AB 有一个公共点,那么22a b +(A )最小值为15 (B)最小值为5 (C )最大值为15(D)最大值为5第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9.在ABC ∆中,若2B A =,:a b =A =_____. 10.在521()x x+的展开式中,2x 的系数是_____. 11.如图,AB 是圆O 的直径,P 在AB 的延长线上,PD切圆O 于点C .已知圆O2OP =,则PC =______;ACD ∠的大小为______.12.在极坐标系中,点(2,)2A π关于直线:cos 1l ρθ=的对称点的一个极坐标为_____.13.定义某种运算⊗,a b ⊗的运算原理如右图所示.设()(0)(2)f x x x x =⊗-⊗.则(2)f =______;()f x 在区间[2,2]-上的最小值为______.14.数列{}n a 满足11a =,11n n n a a n λ+-=+,其中λ∈R ,⋅⋅⋅=,2,1n .①当0λ=时,20a =_____;②若存在正整数m ,当n m >时总有0n a <,则λ的取值范围是_____.三、解答题:本大题共6小题,共80分. 解答应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分13分)已知函数cos 2()sin()4x f x x π=+.(Ⅰ)求函数()f x 的定义域; (Ⅱ)若4()3f x =,求sin 2x 的值.16.(本小题满分13分)如图,已知菱形ABCD 的边长为6,60BAD ∠=o ,AC BD O =I .将菱形ABCD 沿对角线AC 折起,使32BD =,得到三棱锥B ACD -.(Ⅰ)若点M 是棱BC 的中点,求证://OM 平面ABD ; (Ⅱ)求二面角A BD O --的余弦值;(Ⅲ)设点N 是线段BD 上一个动点,试确定N 点的位置,使得42CN =,并证明你的结论.17.(本小题满分13分)甲班有2名男乒乓球选手和3名女乒乓球选手,乙班有3名男乒乓球选手和1名女乒乓球选手,学校计划从甲乙两班各选2名选手参加体育交流活动.(Ⅰ)求选出的4名选手均为男选手的概率.(Ⅱ)记X 为选出的4名选手中女选手的人数,求X 的分布列和期望. M18.(本小题满分14分)已知函数()(1)e (0)x a f x x x=->,其中e 为自然对数的底数.(Ⅰ)当2a =时,求曲线()y f x =在(1,(1))f 处的切线与坐标轴围成的面积;(Ⅱ)若函数()f x 存在一个极大值点和一个极小值点,且极大值与极小值的积为5e ,求a 的值.19.(本小题满分14分)已知椭圆2222:1x y M a b+=(0)a b >>的离心率为3,且椭圆上一点与椭圆的两个焦点构成的三角形周长为246+.(Ⅰ)求椭圆M 的方程;(Ⅱ)设直线l 与椭圆M 交于,A B 两点,且以AB 为直径的圆过椭圆的右顶点C , 求ABC ∆面积的最大值.20.(本小题满分13分)若,,21A A …m A 为集合,2,1{=A …,n}(n ≥2且)n ∈*N 的子集,且满足两个条件: ②U U 21A A …A A m =U ;②对任意的A y x ⊆},{,至少存在一个,3,2,1{∈i …,m},使}{},{x y x A i =⋂或}{y . 则称集合组,,21A A …m A 具有性质P .如图,作n 行m 列数表,定义数表中的第k 行第l 列的数为⎩⎨⎧∉∈=)(0)(1l l kl A k A k a .(Ⅰ)当4n =时,判断下列两个集合组是否具有性质P ,如果是请画出所对应的表格,如果不是请说明理由;集合组1:123{1,3},{2,3},{4}A A A ===; 集合组2:123{2,3,4},{2,3},{1,4}A A A ===.(Ⅱ)当7n =时,若集合组123,,A A A 具有性质P ,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合123,,A A A ;(Ⅲ)当100n =时,集合组12,,,t A A A L 是具有性质P 且所含集合个数最小的集合组,求t 的值及++21A A …+i A 的最小值.(其中||i A 表示集合i A 所含元素的个数)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市西城区2018-2018年第二学期期中抽样测试高三数学(理科) 2018.4一、选择题:本大题共 8 小题,每小题 5 分,共 40 分. 1. 在复平面内,复数21i+ 对应的点与原点的距离是( )A. 1B.C.2D.2. 函数 (2)2xy x x =>-的反函数的定义域为( ) A. (1)+∞, B. (0)+∞, C. (01), D. (12),3. 若双曲线221x ky +=的离心率是2,则实数k 的值是( ) A.3- B. 13- C. 3 D.134. 函数()sin (cos sin )f x x x x =⋅-的最小正周期是( ) A.4π B. 2πC. πD. 2π 5. 下列四个正方体图形中,A B 、为正方体的两个顶点,M N P 、、分别为其所在棱的中点,能得出//AB 平面MNP 的图形的序号是( )A. ①、③B. ①、④C. ②、③D. ②、④6. 若集合2{|540}A x x x =-+<,{|||1}B x x a =-<,则“(23)a ∈,”是“B A ⊆”的( )A. 充分但不必要条件B. 必要但不充分条件C. 充要条件D. 既不充分又不必要条件7. 设a ∈R ,函数()e e x xf x a -=+⋅的导函数是()f x ',且()f x '是奇函数 . 若曲线()y f x =的一条切线的斜率是32,则切点的横坐标为( )A. ln 22-B.ln 2-C.ln 22D. ln 28. 设不等式组123350x a y x y ≥⎧⎪≥⎨⎪+-≤⎩,,表示的平面区域是W ,若W 中的整点(即横、纵坐标均为整数的点)共有91个,则实数a 的取值范围是( )A.(21]--,B.[10)-,C. (01],D. [12),二、填空题:本大题共 6 小题,每小题 5 分,共 30 分. 把答案填在题中横线上 . 9. 已知{}n a 是公比为q 的等比数列,且243a a a ,,成等差数列,则q =__________ . 10. 在10()x a -的展开式中,7x 的系数是15,则实数a =__________ .11. 5人排成一排照相,要求甲不排在两端,不同的排法共有 种. (用数字作答) 12. 已知A B C ,,三点在球心为O ,半径为3的球面上,且几何体O ABC -为正四面体,那么A B ,两点的球面距离为__________;点O 到平面ABC 的距离为__________ .13. 已知两点(10)A ,,(0)B b ,,若抛物线24y x =上存在点C 使ABC ∆为等边三角形,则b =_________ .14. 已知点G 是ABC ∆的重心, ()AG AB AC λμλμ=+∈R,,那么λμ+=_____;若︒=∠120A , 2AB AC ⋅=-的最小值是__________ .三、解答题:本大题共 6 小题,共 80 分. 解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分12分)在ABC ∆中,cos A =,cos B =(Ⅰ)求角C ;(Ⅱ)设AB =,求ABC ∆的面积.16. (本小题满分13分)盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得1-分 . 现从盒内任取3个球.(Ⅰ)求取出的3个球颜色互不相同的概率; (Ⅱ)求取出的3个球得分之和恰为1分的概率;(Ⅲ)设ξ为取出的3个球中白色球的个数,求ξ的分布列和数学期望.17.(本小题满分14分)如图,在三棱锥P ABC -中,PA PB =, PA PB ⊥, 30AB BC BAC ⊥∠=︒,,平面PAB ⊥平面ABC .(Ⅰ)求证:PA PBC ⊥平面 ; (Ⅱ)求二面角P AC B --的大小; (Ⅲ)求异面直线AB 和PC 所成角的大小.18.(本小题满分13分)已知函数()ln f x x x =. (Ⅰ)求()f x 的最小值;(Ⅱ)若对所有1x ≥都有()1f x ax ≥-,求实数a 的取值范围.19.(本小题满分14分)已知定点)01(,-C 及椭圆5322=+y x ,过点C 的动直线与椭圆相交于A B ,两点. (Ⅰ)若线段AB 中点的横坐标是12-,求直线AB 的方程; (Ⅱ)在x 轴上是否存在点M ,使MB MA ⋅为常数?若存在,求出点M 的坐标;若不存在,请说明理由.20.(本小题满分14分)数列{}n a 中,11a =,2112n n n a a a c +=-+ (1c >为常数,1,2,3,n = ) ,且321.8a a -=(Ⅰ)求c 的值;(Ⅱ)① 证明:1n n a a +<;② 猜测数列{}n a 是否有极限?如果有,写出极限的值(不必证明); (Ⅲ)比较11nk ka =∑与14039n a +的大小,并加以证明.北京市西城区2018-2018年第二学期期中抽样测试高三数学(理科)参考答案 2018.4一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.1. B2. A3. B4. C5. B6. A7. D8. C 二、填空题:本大题共 6 小题,每小题 5 分,共 30 分.9. 12-或1 10. 12- 11. 72 12. π 13. 5或13- 14. 23;23注:两空的题目,第一个空2分,第二个空3分;两解的题目少一解给2分,有错解不给分.三、解答题:本大题共 6 小题,共 80 分. 15.(本小题满分12分) (Ⅰ)解:由cos A =,cos B = 得02A B π⎛⎫∈ ⎪⎝⎭、,, 所以sin sinA B == ………….. 3分因为c o C π=, ………….. 6分且0C π<<,故.4C π=………….. 7分 (Ⅱ)解: 根据正弦定理得sinsin sin sin AB AC AB B AC C B C ⋅=⇒==, ………….. 10分 所以ABC∆的面积为16sin .25AB AC A ⋅⋅= ………….. 12分16. (本小题满分13分)(Ⅰ)解:记 “取出1个红色球,1个白色球,1个黑色球”为事件A , 则11123439C C C 2()C 7P A ==. …………..3分(Ⅱ)解:记 “取出1个红色球,2个白色球”为事件B ,“取出2个红色球, 1个黑色球”为事件C , 则122123243399C C C C 5()()()C C 42P B C P B P C +=+=+=. …………..6分(Ⅲ)解:ξ可能的取值为0123,,,. ………….. 7分3639C 5(0)C 21P ξ===, 123639C C 45(1)C 84P ξ===, 213639C C 3(2)C 14P ξ===,3339C 1(3)C 84P ξ===. ………….. 11分ξ的分布列为:………….. 12分ξ的数学期望545310123121841484E ξ=⨯+⨯+⨯+⨯=. ………….. 13分17.(本小题满分14分)解法一: (Ⅰ)证明:平面PAB ⊥平面ABC ,平面PAB 平面ABC AB =,且BC AB ⊥, BC PAB ∴⊥平面 . ………….. 2分PA ⊂ 平面 PAB , PA BC ∴⊥.又 PA PB ⊥ ,∴ P A P B C ⊥平面 .………….. 4分 (Ⅱ)解:作PO AB ⊥于点O ,OM AC ⊥于点M ,连结PM .平面PAB ⊥平面ABC , PO ABC ∴⊥平面 ,根据三垂线定理得 PM AC ⊥,PMO∴∠是二面角P AC B--的平面角. ………….. 6分设PA PB =, PA PB ⊥ , 3A B P O B O A ∴===, . 30OM AM MAO ⊥∠=︒ ,, sin 302AOOM AO ∴=⋅︒=, tan 2PO AOPMO OM OM∴===, ………….. 8分 即二面角P A--的大小是a r . ………….. 9分(Ⅲ)解:在底面ABC 内分别过A C 、作BC AB 、的平行线,交于点D , 连结OC OD PD ,,.则PCD ∠是异面直线AB 和PC 所成的角或其补角. ….. 11分 30AB BC BAC ⊥∠=︒ ,,tan 302BC AB ∴=⋅︒=, OC ==PC ∴易知底面ABCD 为矩形,从而OC OD =,.PC PD = 在PCD∆中,12cos 10CDPCD PC ==, ………….. 13分 ∴ 异面直线AB 和PC 所成角的大小为………….. 14分 解法二:作PO AB ⊥于点O ,平面PAB ⊥平面ABC ,PO ∴⊥平面ABC .过点O 作BC 的平行线,交AC 于点D .如图,以O 为原点,直线OD OB OP ,,分别为x 轴, y 轴,z 轴,建立空间直角坐标系 . ………….. 2分PA PB ==设 PA PB ⊥ ,AB PO BO AO ∴====, .30AB BC BAC ⊥∠=︒ ,,tan 302BC AB ∴=⋅︒=.(0 0 0)(0 (0(2O A B C ∴,,,,,,,(0 0P ,(1 0 0).D ,, ………….. 4分 (Ⅰ)证明:(0 (2 00)PA BC == ,, ,,, 0PA BC ∴=, PA BC ∴⊥.又 PA PB ⊥ ,∴P A P B C ⊥平面 . …………..7分(Ⅱ)解:作OM AC ⊥于点M ,连结PM .PO ⊥ 平面ABC , 根据三垂线定理得 PM AC ⊥, PMO∴∠是二面角P AC B--的平面角. ………….. 8分 在Rt AMO ∆中,sin 302AO OM AO =⋅︒==3 04M ⎛⎫∴ ⎪ ⎪⎝⎭,,从而33044MO MP ⎛⎫⎛=-=- ⎪ ⎪ ⎝⎭⎝ , ,cos MO MP MO MP MO MP∴〈〉==,, ………….. 10分 即二面角P A--的大小是ac c o s ………….. 11分(Ⅲ)解:()( 02AB PC == , ,cos AB PC AB PC AB PC∴〈〉==,, ∴异面直线AB和PC所成角的大小为………….. 14分18.(本小题满分13分) (Ⅰ)解:()f x 的定义域为0∞(,+), ….. 1分 ()f x 的导数()1ln f x x '=+. ………….. 3分令()0f x '>,解得1e x >;令()0f x '<,解得10ex <<. 从而()f x 在10e ⎛⎫ ⎪⎝⎭,单调递减,在1e ⎛⎫∞ ⎪⎝⎭,+单调递增. ………….. 5分 所以,当1ex =时,()f x 取得最小值1e-. ………….. 6分 (Ⅱ)解: 解法一:令()()(1)g x f x ax =--,则()(g x f x a ax''=-=-+, ………….. 8分 ① 若1a ≤,当1x >时,()1ln 10g x a x a '=-+>-≥, 故()g x 在(1)∞,+上为增函数,所以,1x ≥时,()(1)10g x g a ≥=-≥,即()1f xa x ≥-. …………..10分② 若1a >,方程()0g x '=的根为 10e a x -=,此时,若0(1)x x ∈,,则()0g x '<,故()g x 在该区间为减函数.所以,0(1)x x ∈,时,()(1)10g x g a <=-<,即()1f x ax <-,与题设()1f x ax ≥-相矛盾.………….. 12分 综上,满足条件的a的取值范围是(1-∞,. ………….. 13分 解法二:依题意,得()1f x ax ≥-在[1)+∞,上恒成立, 即不等式1ln a x x≤+对于[1x ∈+∞,恒成立 . ………….. 8分令1()ln g x x x=+, 则21111()1g x x x x x ⎛⎫'=-=- ⎪⎝⎭. ………….. 10分 当1x >时,因为11()10g x x x ⎛⎫'=-> ⎪⎝⎭, 故()g x 是(1)+∞,上的增函数, 所以 ()g x 的最小值是(1)1g =, ………….. 12分从而a的取值范围是(-∞,. ………….. 13分19.(本小题满分14分) (Ⅰ)解:依题意,直线AB 的斜率存在,设直线AB 的方程为(1)y k x =+, 将(1)y k x =+代入5322=+y x , 消去y整理得2222(31)6350.k x k x k +++-= ………….. 2分设1122() ()A x yB x y ,,,, 则4222122364(31)(35)0 (1)6. (2)31k k k k x x k ⎧∆=-+->⎪⎨+=-⎪+⎩, ………….. 4分 由线段AB 中点的横坐标是12-, 得2122312312x x k k +=-=-+, 解得k =,适合(1). ………….. 5分所以直线AB的方程为10x +=,或10x +=. ………….. 6分(Ⅱ)解:假设在x 轴上存在点(,0)M m ,使MB MA ⋅为常数.① 当直线AB 与x 轴不垂直时,由(Ⅰ)知 22121222635. (3)3131k k x x x x k k -+=-=++, 所以212121212()()()()(1)(1)MA MB x m x m y y x m x m k x x ⋅=--+=--+++22221212(1)()().k x x k m x x k m=++-+++ ………….. 8分 将(3)代入,整理得 222222114(2)(31)2(61)5333131m k m m k MA MB m m k k -+----⋅=+=+++ 2216142.33(31)m m m k +=+--+ 注意到MB MA ⋅是与k 无关的常数, 从而有761403m m +==-,, 此时4.9M A M B ⋅= .. 11分② 当直线AB 与x 轴垂直时,此时点A B ,的坐标分别为11⎛⎛-- ⎝⎝、, 当73m =-时, 亦有4.9M A M B ⋅= ………….. 13分综上,在x 轴上存在定点703M ⎛⎫- ⎪⎝⎭,,使MB MA ⋅为常数. ………….. 14分20.(本小题满分14分) (Ⅰ)解:依题意,222211322111111.222222a a a c c a a a c c ⎛⎫=-+=-=-+=-+ ⎪⎝⎭,由3218a a -=,得21111122228c c ⎛⎫⎛⎫-+--= ⎪ ⎪⎝⎭⎝⎭,解得2c =,或1c =(舍去). …………..3分(Ⅱ)解:① 证明:因为2211122(2)022n n n n n a a a a a +-=-+=-≥, 当且仅当2n a =时,1n n a a +=. 因为11a =,所以10n n a a +->,即1n n a a +<(1,2,3,n = ) . ………….. 5分 ②数列{}n a 有极限,………..6分且lim 2n n a →∞=. ………….. 7分(Ⅲ)解:由21122n n n a a a +=-+,可得11()(2)(2)n n n n n a a a a a ++-=--,从而111122n n n a a a +=---. 因为11a =,所以 111111111111 1.22222nnk k k k k n n a a a a a a ==+++⎛⎫=-=-=- ⎪-----⎝⎭∑∑ 所以21111111404139(53)(813)1401401.3923939(2)39(2)nn n n n n n k k n n n a a a a a a a a a a ++++++=+++--+--=--==-⋅-⋅-∑ ………….. 9分因为11a =,由(Ⅱ)① 得 1n a ≥ (*n ∈N ). (1) 下面证明:对于任意*n ∈N ,有2n a <成立. 当1n =时,由11a =,显然结论成立. 假设结论对 (1)n k k =≥时成立,即 2.k a <因为2211132(1)222n n n n a a a a +=-+=-+,且函数213(1)22y x =-+在1x ≥时单调递增,所以2113(21)222k a +<-+=. 即当1n k =+时,结论也成立. 于是,当*n ∈N 时,有2n a <成立. (2) 根据(、得12n a ≤<. ………….. 12分由11a = 及21122n n n a a a +=-+, 经计算可得23313.28a a ==,所以,当1n =时,2114039a a <; 当2n =时,312114039a a a +=; 当3n ≥时,由11328n a +<<, 得1111111(53)(813)1401400 3939(2)39nnn n n n k k k n k a a a a a a a ++++==++--=>⇒>⋅-∑∑. ………….. 14分。
