八年级数学上册第十二章整式的乘除12.1幂的运算练习新版华东师大版
2019秋八年级数学上册第12章整式的乘除12.1幂的运算12.1.3积的乘方习题课件新版华东师大版
3.
计
算
2 3
2016
×(
－
1.
5)2017×( － 1)2018
的结果是
(C )
A.
3 2
B.
2 3
C．－23
D．－23
h
10
4. 计算(－4×103)2×(－2×103)3 的结果为( B )
A．1. 28×1017
B．－1. 28×1017
C．4. 8×1016
D．－2. 4×1016
h
11
h
17
(2)(0. 5×323)2017×(－2×131)2018. 解：原式＝(12×131)2017×(2×131)2018 ＝(12×131×2×131)2017×(2×131) ＝161.
h
18
11. 已知 an＝2，b2n＝3，求(a3b4)2n 的值． 解：原式＝a6nb8n＝(an)6(b2n)4＝26×34＝5184.
－18
．
h
8
1. 下列计算：①(ab)2＝ab2；②(4ab)3＝12a3b3；③(－
2x3)4＝－16x12；④(23a)3＝83a3，其中正确的有( A )
A．0 个
B．1 个
C．2 个
D．3 个
h
9
2. 若(a3·ax)y＝a20，则当 x＝2 时，y 等于( A )
A．4BΒιβλιοθήκη 5C．14D．15
h
13
【解析】∵2×103×4×102×8×10＝64×106＝(4×102)3， ∴能有一个正方体贮水池将这些废水正好装完，且这个 正方体的棱长为 4×102 dm .
h
14
9. 计算： (1)(－a2)2·(－2a3)2； 解：原式＝a4·4a6＝4a10； (2)(－2a)6－(－3a3)2－[－(2a)2]3； 解：原式＝64a6－9a6＋64a6＝119a6；
八年级数学上册第12章整式的乘除幂的运算练习题新版华东师大版(含答案)
八年级数学上册：12.1 幂的运算一、选择题(每题4分,共28分)1.计算(a2)4的结果是（)A.2a4B.4a2C.a8D.a62.计算(-2a3)2的结果是（)A.-4a5B.4a5C.-4a6D.4a63.计算(-x)2·x3的结果是（)A.x5B.-x5C.x6D.-x64.计算下列代数式,结果为x5的是（)A.x2+x3B.x·x5C.x6-xD.2x5-x55.x4m+2可以写成（)A.x4m÷x2B.(x2m+1)2C.(x·x4m)2D.x4m+x26.下列计算不正确的是（)A.=x6y2B.(x-y)3÷(y-x)2=x-yC.x2·x4=x6D.(-x2)3=-x57.若3x=2,3y=5,则32x-y的值是（)A.-1B.C.20D.二、填空题(每题5分,共30分)8.计算(-a)2·(-a)3的结果为.9.一个长方体的长、宽、高分别为a2,a,a3,则这个长方体的体积是.10.计算:(a7÷a)÷(a4÷a2)=.11.若m-n=2,则10m÷10n=.12.计算:(-3)2020×=.13.若2a=m,2b=m2,则a,b之间的数量关系是.三、解答题(共42分)14.(10分)计算:(1)(-2x2)2+x3·x-x5÷x;(2)(104)2÷(102)3×(103)2.15.(8分)已知m,n都是正整数,且x m÷x n=x6,x m·x n=x10,求m,n的值.16.(10分)已知10a=2,10b=3,求:(1)102a×103b的值;(2)102a-3b的值.17.(14分)(1)填空:因为(23)2=,(22)3=,所以(23)2=(22)3.因为(32)3=,(33)2=,所以.因为[(-4)3]4=,[(-4)4]3=,所以.…(2)由上面的计算,你能发现什么?请用字母表示出你发现的规律:.(3)请用上面的规律解答下面的问题:若2x=m,求8x的值.答案1.C[解析] 根据“幂的乘方,底数不变,指数相乘”的运算法则计算即可.(a2)4=a2×4=a8.故选C.2.D[解析] 原式=4a6.故选D.3.A[解析] 根据积的乘方法则、同底数幂的乘法运算法则,计算后直接选取答案.(-x)2·x3=x 2·x3=x2+3=x5.故选A.4.D[解析] x2与x3不是同类项,不能合并同类项,故A不合题意;x·x5=x6,故B不合题意;x6与x不是同类项,不能合并同类项,故C不合题意;2x5-x5=x5,故D符合题意.故选D.5.B6.D[解析] 这是一道综合运用幂的乘方与积的乘方、同底数幂的乘法和除法的选择题.可根据幂的乘方与积的乘方、同底数幂的乘法和除法运算法则逐一计算作出判断.A项,=x6y2,正确;B项,(x-y)3÷(y-x)2=x-y,正确;C项,x2·x4=x6,正确;D项,(-x2)3=-x6,不正确.故选D.7.D[解析] 因为3x=2,3y=5,所以32x-y=32x÷3y=(3x)2÷3y=22÷5=.故选D.8.-a5[解析] (-a)2·(-a)3=(-a)5=-a5.故答案为-a5.9.a610.a4[解析] (a7÷a)÷(a4÷a2)=a6÷a2=a4.11.100[解析] 10m÷10n=10m-n=102=100.12.-13.b=2a [解析] 因为2a=m,2b=m2,所以2b=(2a)2=22a,所以b=2a.故答案为b=2a.14.解:(1)原式=4x4+x4-x4=4x4.(2)(104)2÷(102)3×(103)2=108÷106×106=108-6+6=108.15.解:由已知,得x m-n=x6,x m+n=x10,于是解得即m,n的值分别为8,2.16.解:(1)102a×103b=(10a)2×(10b)3=4×27=108.(2)102a-3b=102a÷103b=(10a)2÷(10b)3=4÷27=.17.解:(1)26263636(32)3=(33)2 412412[(-4)3]4=[(-4)4]3(2)(a m)n=(a n)m(m,n为正整数)(3)因为2x=m,所以8x=(23)x=(2x)3=m3.。
八年级数学上册第12章整式的乘除12.2_12.3练习题新版华东师大版
12.2~12.3一、选择题(每题3分,共24分)1.以下运算正确的选项是〔)A.a2·a2=2a2B.a2+a2=a4C.(1+2a)2=1+2a+4a2D.(-a+1)(a+1)=1-a22.假设单项式-8x a y和x2y b的积为-2x5y6,那么ab的值为〔)A.2B.30C.-15D.153.计算(x+y)2-(x-y)(x+y),正确的结果是()A.2xyB.2y2C.2xy+2y2D.xy+2y24.(x+3)(2x-m)与2x2+x+n的值相等,那么m,n的值分别是〔)A.5,15B.5,-15C.-5,15D.-5,-155.(m-n)2=8,(m+n)2=2,那么m2+n2等于〔)A.10B.6C.5D.36.在多项式4x2+1中添加一个单项式,使其成为一个多项式的完全平方,那么添加的单项式不正确的选项是〔)A.-4xB.4xC.-4x2D.4x47.如图1,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影局部沿虚线剪开,拼成右侧的长方形.根据图形的变化过程写出的一个正确的等式是〔)图1A.(a-b)2=a2-2ab+b2B.a(a-b)=a2-abC.(a-b)2=a2-b2D.a2-b2=(a+b)(a-b)8.a2+a-4=0,那么代数式a2(a+5)的值是〔)A.4B.8C.12D.16二、填空题(每题3分,共21分)9.计算:4y·(-2xy2)=.10.光年是计量天体间距离的单位,其意思是指光在真空中沿直线传播一年的距离.如果光速为3×105千米/秒,一年的时间按3.2×107秒计算,那么一光年为千米.11.a+b=4,ab=3,那么代数式(a+1)(b+1)的值为.12.计算:399×401+1=.13.假设M(x2-y)=x4-y2,那么代数式M应是.14.当整数k=时,多项式x2+4kx+4恰好可以写成一个多项式的平方.15.假设一个正方形的边长增加2 cm,它的面积就增加12 cm2,那么这个正方形的边长是.三、解答题(共55分)16.(6分)计算:(1)(x+1)2-x(x+2);(2)(a+2)(1-4a)+(2a-1)2.17.(8分)先化简,再求值:(x-2)(x+2)-x(x-1),其中x=3.18.(8分)周末杨阳来到农科所水稻试验基地参加社会实践活动,图2是水稻专家李教授和杨阳的对话:图2请聪明的你也动手算一下吧!19.(9分)有四个连续奇数,最小的奇数为2n-1,王老师要求同学们计算最小奇数与最大奇数的积减去中间两个奇数积的差,并选择你喜欢的一个正整数代替n,求出结果,聪聪认为n只要任取一个正整数代入都有相同结果.你认为他说得有道理吗?请说明理由.20.(12分)A是关于x的二次整式,且二次项系数为1,A与多项式(x+2)相乘后的结果为两项的多项式,求多项式A.21.(12分)(1)通过计算,探索规律:152=225,可写成100×1×(1+1)+25;252=625,可写成100×2×(2+1)+25;352=1225,可写成100×3×(3+1)+25;……752=5625,可写成;852=7225,可写成;(2)从(1)的计算结果,归纳猜测得:(10n+5)2=.(3)根据上面的归纳猜测,计算:20252.答案1.D[解析]A.因为a2·a2=a4,所以A错误;B.因为a2+a2=2a2,所以B错误;C.因为(1+2a)2=1+4a+4a2,所以C错误;D.因为(-a+1)(a+1)=1-a2,所以D正确.应选D.2.D[解析]-8x a y·x2y b=-2x a+2y b+1=-2x5y6,所以a+2=5,b+1=6,解得a=3,b=5,所以ab=3×5=15.应选D.3.C[解析] 原式=x2+2xy+y2-x2+y2=2xy+2y2.应选C.4.B[解析] 由(x+3)(2x-m)=2x2+(6-m)x-3m,可知6-m=1,n=-3m,那么m=5,n=-15.5.C6.C[解析]A.因为(2x-1)2=4x2+1-4x,所以添上-4x后是一个多项式的完全平方,故A不符合题意;B.因为(2x+1)2=4x2+1+4x,所以添上4x后是一个多项式的完全平方,故B不符合题意;C.因为4x2+1-4x2=12,所以添上-4x2后不是一个多项式的完全平方,故C符合题意;D.因为(2x2+1)2=4x2+1+4x4,所以添上4x4后是一个多项式的完全平方,故D不符合题意.应选C.7.D[解析] 第一个图形中阴影局部的面积是a2-b2,第二个图形的面积是(a+b)(a-b),那么a2-b2=(a+b)(a-b).应选D.8.D[解析] 因为a2+a-4=0,所以a2=-a+4,a2+a=4,所以a2(a+5)=(-a+4)(a+5)=-a2-a+20=-(a2+a)+20=-4+20=16.应选D.9.-8xy310.9.6×101211.8[解析] 原式=ab+a+b+1=ab+(a+b)+1.当a+b=4,ab=3时,原式=3+4+1=8.故答案为8.12.16000013.x2+y [解析](x2+y)(x2-y)=x4-y2.14.1或-1[解析] 由于4可以看作是22, 也可以看作是(-2)2,按照“首平方,尾平方,积的2倍在中央〞的两数和(差)的平方公式构成特征,中间一项应是2·2x或2·(-2)x,即4x或-4x,因此k的值是1或-1.15.2cm[解析] 设这个正方形的边长为a cm,那么(a+2)2-a2=12,a2+4+4a-a2=12,4a=8,解得a=2.16.[解析](1)先根据两数和的平方公式和单项式乘以多项式的法那么将原式展开,再合并同类项.(2)先利用两数差的平方公式和多项式乘以多项式的法那么去括号,然后再合并同类项.解:(1)原式=x2+2x+1-x2-2x=1.(2)原式=a-4a2+2-8a+4a2-4a+1=-11a+3.17.解:(x-2)(x+2)-x(x-1)=x2-4-x2+x=x-4.当x=3时,原式=x-4=-1.18.[解析] 长方形稻田的面积为(2x+3y)(2x-3y)m2,正方形稻田的面积为(2x+3y)2m2,作差比拟即可.解:根据题意,得长方形稻田的面积为(2x+3y)(2x-3y)m2,正方形稻田的面积为(2x+3y)2m2,(2x+3y)2-(2x+3y)(2x-3y)=4x2+12xy+9y2-(4x2-9y2)=4x2+12xy+9y2-4x2+9y2=m2.所以这块正方形稻田比长方形稻田的面积多(12xy+18y2)m2.19.解:有道理.理由:由题意得四个连续奇数分别为2n-1,2n+1,2n+3,2n+5,最小奇数与最大奇数的积减去中间两个奇数积的差为(2n-1)(2n+5)-(2n+1)(2n+3)=4n2+8n-5-4n2-8n-3=-8,结果为常数,故任取一个正整数代入都有相同结果.20.解:设A=x2+ax+b,那么A·(x+2)=(x2+ax+b)·(x+2)=x3+(a+2)x2+(2a+b)x+2b.因为相乘后的结果为两项的多项式,所以应分三种情况讨论:①a+2=0且2a+b=0,解得a=-2,b=4,所以A=x2-2x+4;②a+2=0且2b=0,解得a=-2,b=0,所以A=x2-2x;③2a+b=0且2b=0,解得a=0,b=0,所以A=x2.故多项式A为x2-2x+4或x2-2x或x2.21.解:(1)100×7×(7+1)+25100×8×(8+1)+25(2)100n(n+1)+25(3)20252=100×202×(202+1)+25=4100625.。
华师大版八年级数学上册单元测试 第12章 整式的乘除(含部分答案)
华师版八年级数学上册单元测试卷第12章整式的乘除班级姓名第一卷(选择题共30分)一、选择题(每题3分 ,共30分)1．以下运算正确的选项是( A)A．|2－1|＝2－1 B．x3·x2＝x6C．x2＋x2＝x4 D．(3x2)2＝6x42．以下计算 ,正确的选项是( C)A．a2·a2＝2a2 B．a2＋a2＝a4C．(－a2)2＝a4 D．(a＋1)2＝a2＋13．以下式子变形是因式分解的是( D)A．x2－2x－3＝x(x－2)－3B．x2－2x－3＝(x－1)2－4C．(x＋1)(x－3)＝x2－2x－3D．x2－2x－3＝(x＋1)(x－3)4．假设a－b＝8, a2－b2＝72 ,那么a＋b的值为( A)A．9 B．－9 C．27 D．－275．利用因式分解计算57×99＋44×99－99 ,正确的选项是( B) A．99×(57＋44)＝99×101＝9999B．99×(57＋44－1)＝99×100＝9900C．99×(57＋44＋1)＝99×102＝10098D．99×(57＋44－99)＝99×2＝1986．通过计算比拟图1、图2中阴影局部的面积 ,可以验证的计算式子是( D) A．a(a－2b)＝a2－2abB．(a－b)2＝a2－2ab＋b2C．(a＋b)(a－b)＝a2－b2D．(a＋b)(a－2b)＝a2－ab－2b27．因式分解3y2－6y＋3 ,结果正确的选项是( A)A．3(y－1)2 B．3(y2－2y＋1)C．(3y－3)2 D.3(y－1)28．多项式x－a与x2＋2x－1的乘积中不含x2项 ,那么常数a的值是( D)A．－1 B．1 C．－2 D．29．m＋n＝3 ,那么m2＋2mn＋n2－6的值为( C)A．12 B．6 C．3 D．010．a＝2019x＋2019 ,b＝2019x＋2019 ,c＝2019x＋2020 ,那么a2＋b2＋c2－ab－ac－bc的值是( D)A．0 B．1 C．2 D．3第二卷(非选择题共70分)二、填空题(每题3分 ,共18分)11．n是正整数 ,且x2n＝5 ,那么(3x2n)2的值为__225__．12．计算：a(a2÷a)－a2＝__0__．13．假设ab＝2 ,a－b＝1 ,那么代数式a2b－ab2的值等于__2__．14．将x2＋6x＋3配方成(x＋m)2＋n的形式 ,那么m＝__3__．15．x＝m时 ,多项式x2＋2x＋n2的值为－1 ,那么x＝－m时 ,该多项式的值为__3__．16．在日常生活中如取款、上网等都需要密码 ,有一种用“因式分解〞法产生的密码方便记忆 ,原理是：如对多项式x4－y4因式分解的结果是(x－y)(x＋y)(x2＋y2) ,假设取x＝9 ,y＝9时 ,那么因式x－y＝0 ,x＋y＝18 ,x2＋y2＝162 ,于是就可以把“018 162〞作为一个六位数的密码 ,对于多项式4x3－xy2 ,取x＝10 ,y＝10时 ,用上述方法产生的密码是__103__010 ,101__030或301__010__．(写出一个即可)三、解答题(共52分)17．(4分)化简[2019·舟山] (m＋2)(m－2)－m3×3m.18．(8分)先化简 ,再求值：(1)x(x－2)＋(x＋1)2 ,其中x＝1.(2)3a2－4a－7＝0 ,求代数式(2a－1)2－(a＋b)(a－b)－b2的值．19．(7分)x＋y＝7 ,xy＝2 ,求：(1)2x2＋2y2的值；(2)(x－y)2的值．20．(7分)将多项式(x－2)(x2＋ax－b)展开后不含x2项和x项．求2a2－b的值．21．(8分)对于任意有理数a、b、c、d ,我们规定符号(a ,b)·(c ,d)＝ad－bc ,例如：(1 ,3)·(2 ,4)＝1×4－2×3＝－2.(1)(－2 ,3)·(4 ,5)的值为__－22__；(2)求(3a＋1 ,a－2)·(a＋2 ,a－3)的值 ,其中a2－4a＋1＝0.22．(8分)阅读以下文字：,图2),图3) ,图4)我们知道 ,对于一个图形 ,通过两种不同的方法计算它的面积 ,可以得到一个数学等式 ,例如由图1可以得到(a＋2b)(a＋b)＝a2＋3ab＋2b2.请解答以下问题：(1)写出图2中所表示的数学等式__(a＋b＋c)2＝a2＋b2＋c2＋2ab＋2ac＋2bc__；(2)利用(1)中所得到的结论 ,解决下面的问题：a＋b＋c＝11 ,ab＋bc＋ac＝38 ,求a2＋b2＋c2的值；(3)图3中给出了假设干个边长为a和边长为b的小正方形纸片及假设干个边长分别为a、b的长方形纸片．①请按要求利用所给的纸片拼出一个几何图形 ,并画在图4所给的方框中 ,要求所拼出的几何图形的面积为2a2＋5ab＋2b2；②再利用另一种计算面积的方法 ,可将多项式2a2＋5ab＋2b2分解因式．即2a2＋5ab ＋2b2＝__(2a＋b)(a＋2b)__．23．(10分)材料阅读：假设一个整数能表示成a2＋b2(a、b是正整数)的形式 ,那么称这个数为“完美数〞．例如：因为13＝32＋22 ,所以13是“完美数〞；再如：因为a2＋2ab＋2b2＝(a＋b)2＋b2(a、b是正整数) ,所以a2＋2ab＋2b2也是“完美数〞．(1)请你写出一个大于20小于30的“完美数〞 ,并判断53是否为“完美数〞；(2)试判断(x2＋9y2)·(4y2＋x2)(x、y是正整数)是否为“完美数〞 ,并说明理由．。
八年级数学上册 第12章 整式的乘除本章总结提升练习 (新版)华东师大版
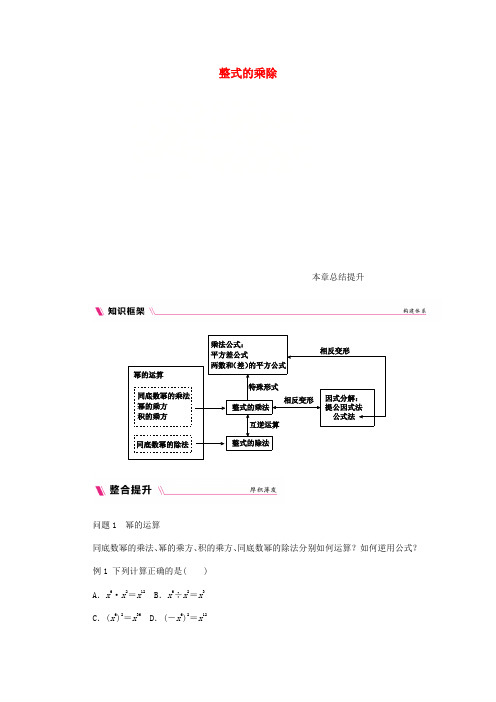
整式的乘除本章总结提升问题1 幂的运算同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法分别如何运算？如何逆用公式？例1 下列计算正确的是( )A．x6·x2＝x12 B．x6÷x2＝x3C．(x6)2＝x36 D．(－x6)2＝x12问题2 整式的乘法单项式与单项式、单项式与多项式、多项式与多项式相乘分别如何计算？怎样将多项式乘单项式转化为单项式的相乘？多项式乘多项式是如何转化为单项式相乘的？例2 计算：5x (x 2＋2x ＋1)－(2x ＋3)(x －5)．问题3 乘法公式本章学习了哪几个乘法公式？你能说出它们的结构特点吗？你能从几何直观的角度用图形解释乘法公式吗？例3 计算：49.82－39.8×40.2.[全品导学号：90702074]问题4 整式的除法单项式除以单项式怎样计算？怎样将多项式除以单项式转化为单项式的除法呢？例4 先化简，再求值：[(x －y )2＋(x －y )(x ＋y )]÷x ，其中x ＝－1，y ＝12.问题5 因式分解什么是因式分解？因式分解与整式乘法有什么关系？因式分解有哪些方法？它们各有什么特点？例5 把下列各式分解因式：(1)12x 2－2x ＋2； (2)(x －2)(x －4)＋1；(3)(a ＋b )2＋4(a ＋b ＋1)．【归纳总结】在多项式分解因式时，有公因式的先提公因式，再考虑用公式法分解因式．分解因式时要分解到每个因式都不能再分解为止．详解详析本章总结提升【整合提升】例1 [解析] D 对照幂的各种运算法则，选项A ，B ，C 的正确答案分别是x 8，x 4，x 12. 例2 解：5x(x 2＋2x ＋1)－(2x ＋3)(x －5)＝5x·x 2＋5x·2x＋5x·1－2x(x －5)－3(x －5)＝5x 3＋10x 2＋5x －2x 2＋10x －3x ＋15＝5x 3＋8x 2＋12x ＋15.例3 解：49.82－39.8×40.2＝(50－0.2)2－(40－0.2)×(40＋0.2)＝502－2×50×0.2＋0.22－(402－0.22)＝880.08.例4 解：方法一：原式＝(x 2－2xy ＋y 2＋x 2－y 2)÷x ＝(2x 2－2xy)÷x＝2x －2y.当x ＝－1，y ＝12时，原式＝2×(－1)－2×12＝－3. 方法二：原式＝(x －y)(x －y ＋x ＋y)÷x ＝2(x －y)．当x ＝－1，y ＝12时，原式＝2×⎝⎛⎭⎪⎫－1－12＝－3. 例5 [解析] (1)中虽无公因式，但系数是分数与整数混杂，为了统一，可先提取12.(2)中先做乘法后做加法，然后再分解因式．(3)原式两项既无公因式可提，又无公式可套用，但由此结构特点可视a ＋b 为一个整体，局部展开后或许能运用两数和(差)的平方公式．解：(1)12x 2－2x ＋2＝12(x 2－4x ＋4)＝12(x －2)2. (2)(x －2)(x －4)＋1＝x 2－6x ＋8＋1＝x 2－6x ＋9＝(x －3)2.(3)(a ＋b)2＋4(a ＋b ＋1)＝(a ＋b)2＋4(a ＋b)＋4＝(a ＋b ＋2)2.。
八年级数学上册第12章整式的乘除12.1幂的运算4同底数幂的除法作业（新版）华东师大版
八年级数学上册第12章整式的乘除12.1幂的运算4同底数幂的除法作业（新版）华东师大版[12.1 4.同底数幂的除法]一、选择题1．xx·重庆计算x 6÷x 2的正确结果是( )A ．3B ．x 3C ．x 4D ．x 82．计算(－a )6÷a 2的结果是( )A ．a 4B ．－a 4C ．a 3D ．－a 33．若x m ÷x 2n ＝x ，则m ，n 的关系是( )A ．m ＝2nB ．m ＝－2nC ．m －2n ＝1D ．m ＋2n ＝14．计算(a 2)3÷(a 2)2的结果是( )A ．aB ．a 2C ．a 3D ．a 45．已知2a ＝3，2b ＝5，则2a －b 等于( )A ．15B ．8 C.35 D.536．xx·南京计算106×(102)3÷104的结果是( )A ．103B ．107C ．108D ．1097．计算4m ·8m －1÷2m 的结果为( )A ．24m －3B ．16m －1C ．4m －1D ．25m －38．已知a m ＝6，a n ＝3，则a 2m －3n 的值为( )A ．9 B.34 C ．2 D.43二、填空题9．计算：m 3÷m 2＝________，(－a )5÷a 3＝________．10．若m·2×23＝28，则m等于________．11．地球的体积约为1012立方千米，太阳的体积约为1.4×1018立方千米，太阳的体积约是地球体积的________倍．12．化简：[(a 5)4÷a 8]2÷a 5＝________．13．xx·资阳安岳永清辖区期中已知3x ＝5，3y ＝4，则32x －y ＝________.三、解答题14．计算：(1)(－m )12÷(－m )9；(2)x 2m ＋2÷x m ＋2；(3)(xy )38÷(－xy )12； (4)(x －y )5÷(y －x )3.15．已知3×9m ×27m ＝321，求(－m 2)3÷(m 3·m 2)的值．16．若10x ＝20，10y ＝15，求4x ÷22y 的值．17．某长方体的体积为1024立方厘米，长为108厘米，宽为107厘米，求此长方体的高．规律探究题60300000÷3000＝xx0，可改写为(6.03×107)÷(3×103)＝2.01×104.仿照上面改写的方法，你会发现(a ×10m )÷(b ×10n )的算法有什么规律吗？请你用发现的规律直接计算：(7.329×109)÷(2.1×104)÷(2×102)．详解详析【课时作业】[课堂达标]1．[解析] C 先判断题目属于两个同底数幂相除，然后根据“同底数幂的除法：底数不变，指数相减”，得x 6÷x 2＝x 6－2＝x 4.2．A 3.C 4.B 5.C6．[解析] C 根据乘方的意义及幂的乘方，可知106×(102)3÷104＝106×106÷104＝108.7．A 8.D 9.m －a 210．[答案] 16[解析] m ＝28÷(2×23)＝28÷24＝28－4＝24＝16.11．1.4×10612．[答案] a 19[解析] 原式＝(a 20÷a 8)2÷a 5＝a 24÷a 5＝a 19.13．[答案]254 [解析] 32x －y ＝32x ÷3y ＝(3x )2÷3y ＝52÷4＝254. 14．解：(1)原式＝(－m)12－9＝(－m)3＝－m 3.(2)原式＝x 2m ＋2－(m ＋2)＝x 2m ＋2－m －2＝x m .(3)原式＝(xy)38÷(xy)12＝(xy)38－12＝(xy)26＝x 26y 26.(4)原式＝(x －y)5÷[－(x －y)3]＝－(x －y)2.15．解：∵3×9m ×27m ＝3×32m ×33m ＝31＋5m ＝321，∴1＋5m ＝21，∴m ＝4，∴(－m 2)3÷(m 3·m 2)＝－m 6÷m 5＝－m ＝－4.16．解：4x ÷22y ＝4x ÷(22)y ＝4x ÷4y ＝4x －y .因为10x ＝20，10y ＝15，所以10x ÷10y＝20÷15，即10x －y ＝100＝102，所以x －y ＝2，所以4x －y ＝42＝16.17．解：1024÷(108×107)＝1024÷1015＝109(厘米)．答：此长方体的高为109厘米．[素养提升]解：根据题意，得(a×10m )÷(b×10n )＝(a÷b )×10m －n ，故(7.329×109)÷(2.1×104)÷(2×102)＝(7.329÷2.1÷2)×109－4－2＝1.745×103.感谢您的支持，我们会努力把内容做得更好！。
八年级数学上册第12章整式的乘除测试题新版华东师大版
第12章整式的乘除一、选择题(每题3分,共24分)1.以下运算中正确的选项是〔)A.a5+a5=a10B.a7÷a=a6C.a3·a2=a6D.(-a3)2=-a62.以下计算正确的选项是〔)A.(a4b)3=a7b3B.-2b(4a-b2)=-8ab-2b3C.a·a3+a2·a2=2a4D.(a-5)2=a2-253.假设(x-2y)2=(x+2y)2+m,那么m等于〔)A.4xyB.-4xyC.8xyD.-8xy4.以下因式分解正确的选项是〔)A.x2-x=x(x+1)B.a2-3a-4=(a+4)(a-1)C.a2+2ab-b2=(a-b)2D.x2-y2=(x+y)(x-y)5.边长为a的正方形,其边长减少b后,所得正方形的面积比原正方形的面积减少〔)A.a2B.b2C.(a-b)2D.2ab-b26.对于任意非零整数n,按图1所示的程序计算应输出的答案为〔)图1A.n2-n+2B.3-nC.n2-2D.27.长方形的面积为4a2-6ab+2a,且它的一边长为2a,那么其周长为〔)A.4a-3bB.8a-6bC.4a-3b-1D.8a-6b+28.10x=m,10y=n,那么102x+3y等于〔)A.2m+3nB.m2+n2C.6mnD.m2n3二、填空题(每题4分,共24分)9.因式分解:a2+ab-a=.10.计算:(-12)2021×=.11.假设x2+2x+m恰好可以写成一个多项式的平方,那么m=.12.假设2m×8n=32,2m÷4n=16,那么m+n的值为.13.假设x2-2x-2=0,那么(2x+3)(x-2)-3x=.14.分解因式:(x-y)2-6x+6y+9=.三、解答题(共52分)15.(6分)计算:(1)x(x2+x-1)-(2x2-1)(x-4);(2)[5xy2(x2-3xy)+(3x2y2)3]÷(5xy)2.16.(6分)把以下多项式分解因式:(1)(x-1)2+2(x-5);(2)-ab(a-b)2+a(b-a)2.17.(6分)先化简,再求值:(3x+2)(3x-2)+(x-2)2-5x(x-1),其中x=-1.18.(8分)凤燕与丽君做游戏,两人各报一个整式,丽君报的整式作为除式,凤燕报的整式作为被除式,要求商式必须是4x2y.(1)假设凤燕报的整式是x7y5-4x5y4+16x2y,那么丽君报的整式是什么?(2)假设凤燕报的整式是(-2x3y2)2+5x3y2,那么丽君能报出一个整式吗?请说明理由.19.(8分)如图2,2021年8月,上海自贸区临港新片区成立,为了进一步引进人才,临港自贸区要用一块长方形地打造新的住宅区和商圈,请你根据条件求出商场用地的面积(图中数据单位:米).图220.(8分)如图3①,边长为a的大正方形中有一个边长为b(b<a)的小正方形,图②是由图①中阴影局部拼成的一个长方形.(1)观察图①②,当用不同的方法表示图中阴影局部的面积时,可以获得一个因式分解公式,这个公式是;(2)如果大正方形的边长a比小正方形的边长b多3,它们的面积相差57,试利用(1)中的公式,求a,b的值.图321.(10分)定义新运算:对于任意实数a,b,都有a⊕b=(a+b)(a-b)+2b(a+b),等式右边是通常的加法、减法及乘法运算.例如:2⊕5=(2+5)×(2-5)+2×5×(2+5)=-21+70=49.(1)求(-2)⊕3的值;(2)通过计算,验证等式a⊕b=b⊕a成立.答案1.B[解析]a5+a5=2a5,故A不符合题意;a7÷a=a6,故B符合题意;a3·a2=a5,故C不符合题意;(-a3)2=a6,故D不符合题意.应选B.2.C[解析](a4b)3=a12b3,故A不符合题意;-2b(4a-b2)=-8ab+2b3,故B不符合题意;a·a3+a2·a2=2a4,故C符合题意;(a-5)2=a2-10a+25,故D不符合题意.应选C.3.D[解析] 将等式两边分别展开,两边对应相等,进而求得m.4.D[解析]x2-x=x(x-1),故A错误;a2-3a-4=(a-4)(a+1),故B错误;a2+2ab-b2不能分解因式,故C错误;x2-y2=(x+y)(x-y),故D正确.应选D.5.D[解析] 原正方形的面积为a2,新正方形的面积为(a-b)2,所以新正方形的面积比原正方形的面积减少a2-(a-b)2=[a+(a-b)][a-(a-b)]=(a+a-b)(a-a+b)=b(2a-b)=2ab-b2.6.D[解析] 运算过程如下:(n2+2n)÷n-n=n(n+2)÷n-n=n+2-n=2.7.D[解析] 另一边长为(4a2-6ab+2a)÷2a=2a-3b+1,所以其周长为2·2a+2(2a-3b+1)=8a-6b+2.8.D[解析]102x+3y=102x·103y=(10x)2·(10y)3=m2n3.应选D.9.a(a+b-1)10.144[解析](-12)2021×=(-12)2×(-12)2021×=(-12)2×=(-12)2=144.故答案为144.11.112.[解析] 因为2m×8n=2m×23n=2m+3n=32=25,2m÷4n=2m÷22n=2m-2n=16=24,所以m+3n=5,m-2n=4,两式相加,得2m+n=9,那么原式=(2m+n)=.故答案为.13.-2[解析] 因为x2-2x-2=0,所以x2-2x=2,所以(2x+3)(x-2)-3x=2x2-x-6-3x=2x2-4x-6=2(x2-2x)-6=4-6=-2.14.(x-y-3)2[解析] 观察题中的特点,把-6x+6y提取公因式-6以后变成了-6(x-y),假设将(x-y)看成一个整体,就可以套两数差的平方公式进行因式分解了.(x-y)2-6x+6y+9=(x-y)2-6(x-y)+9=(x-y-3)2.15.解:(1)原式=x3+x2-x-(2x3-8x2-x+4)=x3+x2-x-2x3+8x2+x-4=-x3+9x2-4.(2)[5xy2(x2-3xy)+(3x2y2)3]÷(5xy)2=(5x3y2-15x2y3+27x6y6)÷25x2y2=x-y+x4y4.16.解:(1)原式=x2-2x+1+2x-10=x2-9=(x+3)(x-3).(2)-ab(a-b)2+a(b-a)2=-ab(a-b)2+a(a-b)2=-a(a-b)2(b-1).17.解:原式=9x2-4+x2-4x+4-5x2+5x=5x2+x.当x=-1时,原式=5×(-1)2+(-1)=5-1=4.18.解:(1)丽君报的整式为(x7y5-4x5y4+16x2y)÷4x2y=x5y4-x3y3+4.(2)丽君能报出一个整式.理由:[(-2x3y2)2+5x3y2]÷4x2y=(4x6y4+5x3y2)÷4x2y=x4y3+xy,即丽君能报出一个整式,为x4y3+xy.19.解:由题意可得[(5a+2b)-(3a+b)]·(4a-3b)=(5a+2b-3a-b)(4a-3b)=(2a+b)(4a-3b)=8a2-2ab-3b2,那么商场用地的面积是(8a2-2ab-3b2)平方米.20.解:(1)a2-b2=(a+b)(a-b)[解析] 由图①可得阴影局部的面积=a2-b2,由图②可得阴影局部的面积=(a-b)(a+b), 所以可得公式为a2-b2=(a+b)(a-b).故答案为a2-b2=(a+b)(a-b).(2)由题意,得a-b=3,a2-b2=57.因为a2-b2=(a+b)(a-b)=57,所以a+b=19,所以解得所以a,b的值分别是11,8.21.解:(1)-2⊕3=(-2+3)×(-2-3)+2×3×(-2+3)=1×(-5)+2×3×1=-5+6=1.(2)因为a⊕b=(a+b)(a-b)+2b(a+b)=a2-b2+2ab+2b2=(a+b)2,b⊕a=(b+a)(b-a)+2a(b+a)=b2-a2+2ab+2a2=(a+b)2,所以a⊕b=b⊕a成立.。
2020八年级数学上册第12章整式的乘除12.1幂的运算3积的乘方作业(新版)华东师大版
[12.1 3.积的乘方]一、选择题1．2017·乌鲁木齐计算(ab 2)3的结果是( )A ．3ab 2B ．ab 6C ．a 3b 5D ．a 3b 62．计算(－2x 2)3的结果是( )A ．－2x 5B ．－8x 6C ．－2x 6D ．－8x 53．下列等式错误的是( )A ．(2mn )2＝4m 2n 2B ．(－2mn )2＝4m 2n 2C ．(2m 2n 2)3＝8m 6n 6D ．(－2m 2n 2)3＝－8m 5n 54．如果(2a m b n )3＝8a 9b 15成立，那么( )A ．m ＝3，n ＝5B ．m ＝3，n ＝3C ．m ＝6，n ＝－2D ．m ＝2，n ＝55．计算a ·a 5－(2a 3)2的结果为( )A ．a 6－2a 5B ．－a 6C ．a 6－4a 5D ．－3a 66．计算(23)2018×(－1.5)2019的结果为( )A.23 B ．－1.5 C ．－1 D ．20177．若a 8＝5，b 8＝3，则(－ab )8的值为( )A ．8B ．15C ．－8D ．－15二、填空题8．计算：(－5ab )3＝________；⎝ ⎛⎭⎪⎫32x 2y 2＝________；(4×103)2＝________． 9．若5n ＝2，4n ＝5，则20n 的值是________．三、解答题10．计算：(1)⎝ ⎛⎭⎪⎫43ab 2c 33； (2)[(－3a 2b 3)3]2；(3)(－3×103)2； (4)⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1223×(23)3. 链接听课例2归纳总结11．计算：(1)3a 2b 6－(2ab 3)2；(2)(－2xy 2)6＋(－3x 2y 4)3.12．已知x 2n ＝7，求(－2x 2n )3－7(x 2)2n 的值．13．某市环保局欲将一个长为2×103 dm ，宽为4×102 dm ，高为8×10 dm 的长方体废水池中的满池废水注入正方体贮水池净化，请你考虑一下，是否有一个正方体贮水池能将这些废水正好装完？若有，请你求出这个正方体贮水池的棱长，若没有，请说明理由．,方法技巧题用简便方法计算：(12018×12017×12016×…×13×12×1)2018×(2018×2017×2016×…×3×2×1)2018.详解详析【课时作业】[课堂达标]1．[解析] D 根据积的乘方和幂的乘方法则，知(ab 2)3＝a 3·(b 2)3＝a 3b 6.故选D .2．B 3.D 4.A5．[解析] D 原式＝a 6－4a 6＝－3a 6.故选D .6．[解析] B (23)2018×(－1.5)2019＝⎣⎢⎡⎦⎥⎤（23）2018×（－1.5）2018×(－1.5)＝⎣⎢⎡⎦⎥⎤23×（－1.5）2018×(－1.5)＝(－1)2018×(－1.5)＝－1.5.7．B 8．－125a 3b 3 94x 4y 2 1.6×107 9．10 [解析] 20n ＝(4×5)n ＝4n ×5n ＝2×5＝10.10．解：(1)⎝ ⎛⎭⎪⎫43ab 2c 33＝⎝ ⎛⎭⎪⎫433·a 3·(b 2)3·(c 3)3＝6427a 3b 6c 9. (2)[(－3a 2b 3)3]2＝[(－3)3·(a 2)3·(b 3)3]2＝(－27a 6b 9)2＝729a 12b 18.(3)(－3×103)2＝(－3)2×(103)2＝9×106.(4)原式＝⎝ ⎛⎭⎪⎫126×29 ＝⎝ ⎛⎭⎪⎫126×26×23 ＝⎝ ⎛⎭⎪⎫12×26×23 ＝16×23＝8.[点拨] 运用积的乘方法则时，要注意每个因式都要乘方，同时要注意符号．11．解：(1)原式＝3a 2b 6－4a 2b 6＝－a 2b 6.(2)(－2xy 2)6＋(－3x 2y 4)3＝64x 6y 12－27x 6y 12＝37x 6y 12.12．解：原式＝－8(x 2n )3－7(x 2n )2.因为x 2n ＝7，所以原式＝－8×73－7×72＝－2744－343＝－3087.13．解：长方体废水池中水的体积为2×103×4×102×8×10＝64×106＝(4×102)3(dm 3)，所以有一个正方体贮水池能将这些废水正好装完，该正方体贮水池的棱长为4×102 dm .[素养提升]解：原式＝(12018×12017×12016×…×13×12×1×2018×2017×2016×…×3×2×1)2018 ＝12018＝1.。
八年级数学上册第十二章整式的乘除12.1幂的运算作业新版华东师大版(20200217174253)
（ 1）（ ）·（ ）；
（ 2）（ 2x - y ）·（ 2x - y）·（ 2x - y ）； （ 3） a· a-2 a· a-3 a· a.
11. 一台电子计算机每秒可运行 4×10 次运算，它工作 5×10 秒可作多少次运算？
12. 水星和太阳的平均距离约为 5.79 ×10 km，冥王星和太阳的平均距离约是水星和太阳的平
A ． x B.
x C.
x
D.
x
4. a
· a=a. （在括号内填数）
5. 若 10·10=10，则 m=. 6.2 ·8=2，则 n=. 7.- a·（ - a） =； x· x · xy=. 8. a· a+a· a– a· a+a· a=. 9. （ a- b）·（ a- b） =；（ x+y）·（ x +y ） =. 10. 化简计算：
12.1 幂的运算
1. 下列各式正确的是（）
A ． 3a·５a=15a
B.-3
x·（ -2 x） =-6 x
C ． 3x·２x=6x
D.
2. 设 a=8， a=16，则 a=（）
（ - b）·（ - b） =b
A ． 24 B.32
C.64
D.128
3. 若 x ·x·（） =x ，则括号内应填 x 的代数式为（）
（2） a★ b 与 b★ a 的运算结果相等，
a★ b=10a×10b=10a+b
b★
a=10b
×
a
10
b+a
=10 ，
∴a★ b=b★a．
参考答案： 1.D 2.D 3.A 4.16 5.2001 6.12 7. axy 8. 2 a 9.( a- b) ( x + y)
2022八年级数学上册 第12章 整式的乘除12.1 幂的运算2 幂的乘方习题课件(新版)华东师大版
15、一个人炫耀什么，说明他内心缺 少什么 。。2022年5月 上午9时24分22.5.609:24May 6, 2022
16、业余生活要有意义，不要越轨。2022年5月6日 星期五9时24分 9秒09:24:096 May 2022
17、一个人即使已登上顶峰，也仍要 自强不 息。上 午9时24分9秒 上午9时 24分09:24:0922.5.6
谢谢收看
15、一个人炫耀什么，说明他内心缺 少什么 。。2022年5月 上午9时24分22.5.609:24May 6, 2022
16、业余生活要有意义，不要越轨。2022年5月6日 星期五9时24分 9秒09:24:096 May 2022
17、一个人即使已登上顶峰，也仍要 自强不 息。上 午9时24分9秒 上午9时 24分09:24:0922.5.6
15、一个人炫耀什么，说明他内心缺 少什么 。。2022年5月 上午9时24分22.5.609:24May 6, 2022
16、业余生活要有意义，不要越轨。2022年5月6日 星期五9时24分 9秒09:24:096 May 2022
17、一个人即使已登上顶峰，也仍要 自强不 息。上 午9时24分9秒 上午9时 24分09:24:0922.5.6
12、人乱于心，不宽余请。09:24:0909:24:0909:24Fri day, May 06, 2022
13、生气是拿别人做错的事来惩罚自 己。22.5.622.5.609:24:0909:24:09May 6, 2022
14、抱最大的希望，作最大的努力。2022年5月6日 星期五 上午9时 24分9秒09:24:0922.5.6
12、人乱于心，不宽余请。09:24:0909:24:0909:24Fri day, May 06, 2022
八年级数学上册第十二章整式的乘除12.1幂的运算作业新版华东师大版word版本
102倍，那么冥王星和太阳的均匀距离约为多少
km？
13.计算
（1）2x5?x5+（﹣x）2?x?（﹣x）7；
（2）32×3×27﹣3×81×3．
14.已知am=2，an=8，求am+n．
15.我们商定：a★b=10a×10b，比如3★4=103×104=107．
（1）试求2★5和3★17的值；
（2）猜想：a★b与b★a的运算结果能否相等？说明原因．
参照答案：
1.D
2.D
3.A
4.16
5.2001
6.12
7.a8x6y
8. 2an 5
9.(a-b)8
(
x+y)5
10.(1) (
1)7
(2) (2
x-y)8
(3)பைடு நூலகம்4am 4
10
11.2×1012
12.5.91×109
13.解：（1）原式=2x10﹣x10=x10；
12.1幂的运算
1.以下各式正确的选项是（）
A．3a2
·5a3
=15a6
B.-3
x4·（-2x2）=-6x
6
C．3x3·2x4=6x12
D.
（-b）3·（-b）5=b8
2.设am=8，an=16，则am n=（）
A．24B.32C.64D.128
3.若x2·x4·（）=x16，则括号内应填x的代数式为（）
10.化简计算：
（1）（1）4·（1）3；
1010
（2）（2x-y）3·（2x-y）·（2x-y）4；
（3）am 1·a3-2am·a4-3a2·am 2.
11.一台电子计算机每秒可运转4×109次运算，它工作5×102秒可作多少次运算？
八年级数学上册 第12章 整式的乘除本章总结提升练习 (新版)华东师大版
整式的乘除本章总结提升问题1 幂的运算同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法分别如何运算？如何逆用公式？例1 下列计算正确的是( )A．x6·x2＝x12 B．x6÷x2＝x3C．(x6)2＝x36 D．(－x6)2＝x12问题2 整式的乘法单项式与单项式、单项式与多项式、多项式与多项式相乘分别如何计算？怎样将多项式乘单项式转化为单项式的相乘？多项式乘多项式是如何转化为单项式相乘的？例2 计算：5x(x2＋2x＋1)－(2x＋3)(x－5)．问题3 乘法公式本章学习了哪几个乘法公式？你能说出它们的结构特点吗？你能从几何直观的角度用图形解释乘法公式吗？例3 计算：49.82－39.8×40.2.[全品导学号：90702074]问题4 整式的除法单项式除以单项式怎样计算？怎样将多项式除以单项式转化为单项式的除法呢？例4 先化简，再求值：[(x －y )2＋(x －y )(x ＋y )]÷x ，其中x ＝－1，y ＝12.问题5 因式分解什么是因式分解？因式分解与整式乘法有什么关系？因式分解有哪些方法？它们各有什么特点？例5 把下列各式分解因式：(1)12x 2－2x ＋2； (2)(x －2)(x －4)＋1；(3)(a ＋b )2＋4(a ＋b ＋1)．【归纳总结】在多项式分解因式时，有公因式的先提公因式，再考虑用公式法分解因式．分解因式时要分解到每个因式都不能再分解为止．详解详析本章总结提升【整合提升】例1 [解析] D 对照幂的各种运算法则，选项A ，B ，C 的正确答案分别是x 8，x 4，x 12. 例2 解：5x(x 2＋2x ＋1)－(2x ＋3)(x －5)＝5x·x 2＋5x·2x＋5x·1－2x(x －5)－3(x －5)＝5x 3＋10x 2＋5x －2x 2＋10x －3x ＋15＝5x 3＋8x 2＋12x ＋15.例3 解：49.82－39.8×40.2＝(50－0.2)2－(40－0.2)×(40＋0.2)＝502－2×50×0.2＋0.22－(402－0.22)＝880.08.例4 解：方法一：原式＝(x 2－2xy ＋y 2＋x 2－y 2)÷x＝(2x 2－2xy)÷x＝2x －2y.当x ＝－1，y ＝12时，原式＝2×(－1)－2×12＝－3. 方法二：原式＝(x －y)(x －y ＋x ＋y)÷x ＝2(x －y)．当x ＝－1，y ＝12时，原式＝2×⎝⎛⎭⎪⎫－1－12＝－3. 例5 [解析] (1)中虽无公因式，但系数是分数与整数混杂，为了统一，可先提取12.(2)中先做乘法后做加法，然后再分解因式．(3)原式两项既无公因式可提，又无公式可套用，但由此结构特点可视a ＋b 为一个整体，局部展开后或许能运用两数和(差)的平方公式．解：(1)12x 2－2x ＋2＝12(x 2－4x ＋4)＝12(x －2)2. (2)(x －2)(x －4)＋1＝x 2－6x ＋8＋1＝x 2－6x ＋9＝(x －3)2.(3)(a ＋b)2＋4(a ＋b ＋1)＝(a ＋b)2＋4(a ＋b)＋4＝(a ＋b ＋2)2.。
八年级数学上册第12章整式的乘除12.1幂的运算1同底数幂的乘法作业新版华东师大版
[12.1 1.同底数幂的乘法],一、选择题1．xx·丽水计算a2·a3的正确结果是( )A．a5 B．a6 C．a8 D．a92．xx·呼伦贝尔化简(－x)3·(－x)2，结果正确的选项是( ) A．－x6 B．x6 C．x5 D．－x53．计算(－a)2·a3的结果是( )A．a5 B．a6 C．－a5 D．－a64．以下计算结果为m14的是( )A．m2·m7 B．m7＋m7C．m·m6·m7 D．m·m8·m65．以下计算结果与a2m＋3不相等的是( )A．a m＋3·a m B．a2m＋1·a2C．a2m＋3·a D．a m＋1·a m＋26．在以下各式中，填入“－a〞后成立的是( )A．a12＝－a3·( )4B．a12＝(－a)7·( )5C．a12＝－a6·( )6D．a12＝a13＋( )7．如果a2·a x－3＝a6，那么x的值为( )A．－1 B．5 C．6 D．78．10m＝2，10n＝3，那么10m＋n的值是( )A ．4B ．6C ．9 D.239．以下各式中能用同底数幂的乘法法那么进展运算的是( )A ．(x ＋y )2·(x －y )2B ．(－x －y )·(x ＋y )2C ．(x ＋y )2＋(x ＋y )2D ．－(x －y )2·(－x －y )210．假设x ，y 为正整数，且2x ·2y ＝25，那么x ，y 的值有() A ．4对 B ．3对 C ．2对 D ．1对二、填空题11．计算：a ·a 2·________＝a 9.12．假设27×3n ＝32n －1，那么n ＝________．三、解答题13．计算：(1)－a 2·a 6； (2)(－x )·(－x )3；(3)(m －n )3·(n －m )2； (4)x 3·x 2＋x 4·x .14．(1)2x ＝3，求2x ＋3的值；(2)假设42a ＋1＝64，求a 的值．15．假设2a ＝3，2b ＝6，2c ＝18，试求a ，b ，c 之间的关系．,阅读理解阅读材料：求1＋2＋22＋23＋24＋…＋2xx ＋2xx 的值．解：设S＝1＋2＋22＋23＋24＋…＋2xx＋2xx，将等式两边同时乘以2，得2S＝2＋22＋23＋24＋25＋…＋2xx＋22021，用下式减去上式，得2S－S＝22021－1，即S＝22021－1，即1＋2＋22＋23＋24＋…＋2xx＋2xx＝22021－1.请你仿照此法计算：(1)1＋2＋22＋23＋24＋ (210)(2)1＋3＋32＋33＋34＋…＋3n(其中n为正整数)．详解详析【课时作业】[课堂达标]1．[解析] A根据同底数幂的乘法法那么，知a2·a3＝a2＋3＝a5.应选A. 2．[解析] D(－x)3·(－x)2＝(－x)3＋2＝－x5.3．[解析] A(－a)2·a3＝a2·a3＝a2＋3＝a5.4．C 5.C 6.B7．[解析] D根据同底数幂的乘法法那么，有2＋x－3＝6，解得x＝7. 8．B9．[解析] B(－x－y)·(x＋y)2＝－(x＋y)·(x＋y)2＝－(x＋y)3. 10．A11．a612．[答案] 4[解析] 27×3n＝32n－1可化为33×3n＝32n－1，即3n＋3＝32n－1，所以n＋3＝2n－1，解得n＝4.13．解：(1)原式＝－a2＋6＝－a8.(2)原式＝(－x)1＋3＝(－x)4＝x4.(3)原式＝(m－n)3·(m－n)2＝(m－n)3＋2＝(m－n)5.(4)原式＝x5＋x5＝2x5.14．解：(1)2x＋3＝2x·23＝2x·8＝3×8＝24.(2)∵42a＋1＝64，∴42a＋1＝43，∴2a ＋1＝3，∴a ＝1.15．解：2c ＝18＝3×6＝2a ·2b ＝2a ＋b ，所以c ＝a ＋b. [素养提升]解：(1)设S ＝1＋2＋22＋23＋24＋ (210)将等式两边同时乘以2，得2S ＝2＋22＋23＋24＋…＋210＋211，用下式减去上式，得2S －S ＝211－1，即S ＝211－1，那么1＋2＋22＋23＋24＋…＋210＝211－1.(2)设S ＝1＋3＋32＋33＋34＋…＋3n ，将等式两边同时乘以3，得3S ＝3＋32＋33＋34＋…＋3n ＋3n ＋1， 用下式减去上式，得3S －S ＝3n ＋1－1，即S ＝12(3n ＋1－1)， 那么1＋3＋32＋33＋34＋…＋3n ＝12(3n ＋1－1)． 如有侵权请联系告知删除，感谢你们的配合！。
华师大版八年级上册数学第12章 整式的乘除含答案(必刷题)
华师大版八年级上册数学第12章整式的乘除含答案一、单选题(共15题，共计45分)1、下列计算正确的是（）A.a 6÷a 2=a 4B.a 3•a 2=a 6C.2a+3b=5abD.（﹣2a 3）2=﹣4a 62、把多項式a2﹣4a分解因式，结果正确的是（）A.a（a+2）（a﹣2）B.a（a﹣4）C.（a+2）（a﹣2） D.（a﹣2）2﹣43、下列从左到右的变形是分解因式的有（）①6a3b2=2a2b•3b；②x2−＝(x+)(x−)；③（m-2n）2=m2-4mn+4n2；④x2-4x+4=（x-2）2．A.一个B.二个C.三个D.四个4、已知，则的值等于（）．A. B. C. D.5、方程(x-3)(x+4)=(x+5)(x-6)的解是( )A.x=9B.x=-9C.x=6D.x=-66、计算（－3a2）2的结果是（）A.3a 4B.－3a 4C.9a 4D.－9a 47、下计算正确的是（）.A. B. C. D.8、下列运算正确的是（）A. B. C. D.9、如果一个正整数可以表示为两个连续奇数的平方差，那么称该正整数为“友好数”如（，即8,16均为“友好数”），在不超过2020的正整数中，所有的“友好数”之和为（）A.255054B.255064C.250554D.25502410、下列计算正确的是（）A.|﹣2|=﹣2B.C.D.11、下列各多项式从左到右变形是因式分解，并分解正确的是（）A.(a-b) 3-b(b-a) 2=(b-a) 2(a-2b)B.(x+2)(x+3)=x 2+5x+6C.4a 2-9b 2=(4a-9b)(4a+9b)D.m 2-n 2+2=(m+n)(m-n)+212、下列运算正确的是（）A. B. C. D.13、下列运算正确的是（）A. B. C.D.14、下列各式分解因式正确的是（）A.x 2+6xy+9y 2=（x+3y）2B.2x 2﹣4xy+9y 2=（2x﹣3y）2C.2x 2﹣8y 2=2（x+4y）（x﹣4y）D.x（x﹣y）+y（y﹣x）=（x﹣y）（x+y）15、下列各式计算正确的是（）A.2a+2=3a 2B.（﹣b 3）2=﹣b 6C.c 2•c 3=c 5D.（m﹣n）2=m 2﹣n 2二、填空题(共10题，共计30分)16、计算的结果等于________．17、计算：________．18、计算：（－2）2018×0.52019=________．19、分解因式:4a2－16＝________．20、计算：（﹣x2y）2=________（﹣2）﹣2=________﹣2x2•（﹣x）3=________（﹣0.25）2014×42015=________．（﹣1）2015+（﹣π）0+2﹣2=________．21、已知a m=3，a n=9，则a3m﹣n=________22、分解因式：ab2－4ab＋4a＝________.23、已知x= +2，y= ﹣2，则x2+2xy+y2的值是________．24、分解因式：________.25、若，互为相反数，则________.三、解答题(共5题，共计25分)26、已知求的值.27、因式分解：28、如图，公园里有A、B两个花坛，A花坛是长为20米，宽为米的长方形，花坛中间16横竖各铺设一条小路（阴影部分），竖着的小路宽为0.5米，横着的小路宽为1米，剩余部分栽种花卉；B花坛是直径为米的半圆，其中修建一个半圆形水池（阴影部分），剩余部分栽种花卉，求B花坛比A花坛栽种花卉的面积大多少？（取）29、图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．（1）将图②中的阴影部分面积用2种方法表示可得一个等式，求等式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
12.1 幂的运算
1．计算（-a）÷（-a）的结果是（）
A．a B.-a C.-a D. a
2.如果a÷a=a，那么x等于（）
A．3 B.-2m C.2m D.-3 3．计算：
（1）m9÷m7=_________；
（2）（﹣a）6÷（﹣a）2=_________；
（3）（x﹣y）6÷（y﹣x）3÷（x﹣y）=_________．
4．已知2m=8，2n=4，
求（1）2m﹣n的值．（2）2m+2n的值．
5．（1）已知x m=8，x n=5，求x m﹣n的值；
（2）已知10m=3，10n=2，求103m﹣2n的值．
6．已知a m=4，a n=3，a k=2，求a m﹣3k+2n的值．
7．计算：（﹣3x2n+2y n）3÷[（﹣x3y）2]n
8．已知：a n=2，a m=3，a k=4，试求a2n+m﹣2k的值．
9．已知5x﹣3y﹣2=0，求1010x÷106y的值．
10.计算下列各题：
（1）（m-1）÷（m-1）；
（2）（x-y）÷（y-x）÷（x-y）；
（3）（a）×（-a）÷(a);
11．一颗人造地球卫星的速度是2.88×10m/h，一架喷气式飞机的速度是1.8×10m/h，这颗人造地球卫星的速度是这架喷气式飞机的速度的多少倍？
12．光明小学图书馆藏书约3.6×10册，学校现有师生1.8×10人，每个教师或学生假期平均最多可以借阅多少册图书？
13. 地震的强度通常用里克特震级表示，描绘地震级数的数字表示地震的强度是10的若干次幂.例如用里克特表示地震是8级，说明地震的强度是10，1992年4月，荷兰发生5级地震，12天后，加利福尼亚发生了7级地震，加利福尼亚的地震强度是荷兰地震强度的多少倍？
14.化简求值：（2x-y）÷[（2x-y）]÷[（y-2x）]，其中x=2，y=-1.
参考答案：
1.C
2.B
3. （1）m9÷m7=m9﹣7=m2；
（2）（﹣a）6÷（﹣a）2=（﹣a）6﹣2=a4；
（3）（x﹣y）6÷（y﹣x）3÷（x﹣y）
=（x﹣y）6÷[﹣（x﹣y）]3÷（x﹣y）
=﹣（x﹣y）6﹣3﹣1
=﹣（x﹣y）2．
4．∵2m=8=23，2n=4=22，∴m=3，n=2，
（1）2m﹣n=23﹣2=2；
（2）2m+2n=23+4=27=128．
5．（1）∵x m=8，x n=5，
∴x m﹣n=x m÷x n，=8÷5=；
（2）∵10m=3，10n=2，
∴103m=（10m）3=33=27，102n=（10n）2=22=4，∴103m﹣2n=103m÷102n=27÷4=
6．∵a m=4，a n=3，
∴a m﹣3k+2n=a m÷a3k•a2n
=a m÷（a k）3•（a n）2
=4÷23×32=
7．（﹣3x2n+2y n）3÷[（﹣x3y）2]n
=﹣27x6n+6y3n÷（﹣x3y）2n
=﹣27x6n+6y3n÷x6n y2n
=﹣27x6y n
8．∵a n=2，a m=3，a k=4，
∴a2n+m﹣2k=a2n•a m÷a2k
=（a n）2•a m÷（a k）2
=4×3÷16=．
9．由5x﹣3y﹣2=0，得5x﹣3y=2．
∴1010x÷106y=1010x﹣6y=102（5x﹣3y）=102×2=104．
故1010x÷106y的值是104 10.（1）（m-1）
（2）-（x-y）
（3）原式=a·a÷a-a=0
11.16倍
12.20册
13.100倍
14.原式=2x-y=4-（-1）=5.。