湖北省随县2014年初中数学毕业生学业水平能力测试暨升学适应.
湖北省,随县2014年,初中,毕业生,学业水平能力测试,暨升学适应性考试,文综试题及答案(扫描版)

随县2014年九年级升学适应性考试思品试题参考答案一、选择题部分(每题2分,共计22分)二、非选择题部分(共计18分)33、情景一:①找个借口离开现场,立即向有关部门举报(或识别这里的低价消费陷阱,坚决不予购买)(1分)②理由:违背了诚实信用原则;侵犯了消费者的安全权、知情权和公平交易权;违反了我国食品安全管理法律法规,是违法行为。
(3分)情景二:①应该勇敢地拿起法律武器,采用自己与侵权人协商、请求司法保护等方式,要求侵权人停止侵害、赔礼道歉;若因此造成较大的精神痛苦,还有权要求精神损失赔偿。
(2分)②公民个人隐私受法律保护。
侵扰他人私生活、公开他人隐私的行为,既是违反社会道德的行为,也是违法行为;能够自觉地尊重和维护隐私及隐私权,是现代文明的标志,也是社会进步的体现。
(2分)34、(1)①当今世界,科学技术日益渗透到经济发展、社会进步和人类生活的各个领域,成为生产力中最活跃的因素,科学技术是第一生产力。
(1分)②未来科学技术的发展,必将对人类社会的发展产生更加深刻的影响。
(1分)③各国之间激烈的经济竞争和科技竞争,归根到底是教育的竞争、人才的竞争。
(1分)④从一定意义上说,教育决定一个国家和民族的未来,是民族振兴和社会进步的基石(1分)。
(2)(3分)①根本原因:开辟了中国特色社会主义道路,形成了中国特色社会主义理论体系;②坚持了以经济建设为中心,大力发展了生产力;③国家实施了科教兴国和人才强国战略;④我国形成了“尊重知识、尊重人才、尊重劳动、尊重创造”的良好社会氛围(此题为开放性试题,只要学生观点正确,符合题意,可酌情给分,答案不少于3个观点)。
(3)(3分)①树立崇高而远大的理想;②树立报效祖国的决心;③努力学习科学文化知识,提高自身素质,掌握过硬本领;④努力探索、注重实践,养成勤动脑、勤动手的好习惯;⑤树立创新意识,培养勇于质疑、敢为人先的精神;⑥积极参加科技小发明、小制作活动。
(此题为开放性试题,只要学生观点正确,言之有理,即可给分。
随县2014年初中毕业生适应性考试数学试题

随县2014年初中毕业生适应性考试数 学 试 题一、选择题(每小题3分,共计30分) ( )1、下列计算正确的是:A 、9)31(2=- B 、2)2(2-=- C 、1)2(0-=- D 、235=--( )2、67500用科学记数法表示为:A 、31075.6⨯ B 、41075.6⨯ C 、51075.6⨯ D 、41075.6-⨯ ( )3、下列计算正确的是:A 、532x x x =+B 、4)2(22-=-x x C 、53222x x x =⋅D 、743)(x x = ( )4、下列说法不正确的是:A 、某种彩票中奖概率是10001,买1000张应该种彩票一定会中奖B 、了解一批电视机的使用寿命适合用抽样调查C 、甲乙两组数据的方差分别为1和0.001,则乙组数据比甲组稳定D 、在一个装有白球与黑球的袋子中,摸出黑球是不可能事件( )5、如图,AB ∥CD ,AD 平分∠BAC ,若∠ABD=65º,那么∠ACD 等于:A 、35ºB 、40ºC 、45ºD 、50º( )6、一个几何体的三视图如图所示,则这个几何体是:A 、B 、C 、D 、( )7、:甲乙两人在一段长为1200m 的笔直公路上进行跑步,甲乙跑步的速度分别是4m/s 和6m/s ,起跑前乙在起点,甲在乙前100m 处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲乙两人之间的距离)(m y 与时间)(s t 的函数图象是:A 、B 、C 、D 、( )8、如图,DC 是⊙O 直径,弦AB ⊥CD 于F ,连接BC 、DB ,则下列结论不一定正确的是:A 、弧AD=弧BD B 、AF=BF C 、OF=CF D 、∠DBC=90º ( )9、已知关于x 的一元二次方程012)1(2=+--x x k 有两个不相等的实数根,则k 的取值范围是:A 、2-<kB 、1,2-≠<k kC 、2>kD 、1,2≠<k k ( )10、将图1中的正方形剪开得到图2,图2中共有4个正方形;将图2中的正方形剪开得到图3,图3中共有7个正方形;将图3中的正方形剪开得到图4,图4中共有10个正方形;…;如此下去,则第2014个图中共有正方形的个数为:A 、2014 B 、2017 C 、6040 D 、6044二、填空题(每小题3分,共计18分)11、在学校舞蹈比赛中,10名学生参赛成绩统计如图所示,极差和中位数的和等于__________。
湖北省2014年中考数学试卷汇总(12份)

湖北省2014年中考数学试卷汇总(12份)湖北省鄂州市2014年中考数学试卷学校:________考生姓名:________准考证号:注意事项:1.本试卷共6页,满分120分,考试时间120分钟。
2.答题前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
3.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试题卷上无效。
4.非选择题用0.5毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内。
答在试题卷上无效。
5.考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
6.考生不准使用计算器。
一、选择题(每小题3分,共30分)1.的绝对值的相反数是()A.B.C.D.2.下列运算正确的是()A.B.C.D.3.如图所示,几何体是由一些正方体组合而成的立体图形,则这个几何体的左视图是()第3题图ABCD4.如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠B=70°,则∠2的度数为()A.20°B.40°C.30°D.25°]5.点A为双曲线上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为()A.B.±C.D.±6.圆锥体的底面半径为2,侧面积为8,则其侧面展开图的圆心角为()A.90°B.120°C.150°D.180°第4题图7.在矩形ABCD中,AD=3AB,点G、H分别在AD、BC上,连BG、DH,且BG∥DH,当()时,四边形BHDG为菱形.A.B.C.D.第7题图8.近几年,我国经济高速发展,但退休人员待遇持续偏低.为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工李师傅2011年月退休金为1500元,2013年达到2160元.设李师傅的月退休金从2011年到2013年年平均增长率为x,可列方程为()A.B.C.D.9.如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形,再顺次连接四边形各边中点,得到四边形,如此进行下去,得到四边形.下列结论正确的是()①四边形是菱形②四边形是矩形③四边形周长为④四边形面积为A.①②③B.②③④C.①③④D.①②③④第9题图10.已知抛物线的顶点为的顶点为,点在该抛物线上,当恒成立时,的最小值为()A.1B.2C.4D.3二、填空题:(每小题3分,共18分)11.的算术平方根为.12.小林同学为了在体育中考获得好成绩,每天早晨坚持练习跳绳,临考前,体育老师记载了他5次练习成绩,分别为143、145、144、146、a,这五次成绩的平均数为144.小林自己又记载了两次练习成绩为141、147,则他七次练习成绩的平均数为.13.如图,直线过A(-1,2)、B(-2,0)两点,则的解集为第13题图第15题图第16题图14.在平面直角坐标中,已知点A(2,3)、B(4,7),直线与线段AB 有交点,则k的取值范围为.15.如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径.求阴影部分的面积.16.如图,正方形ABCD边长为1,当M、N分别在BC,CD上,使得△CMN的周长为2,则△AMN的面积的最小值为.三.解答题(17-20每题8分,21-22每题9分,23题10分,24题12分,共72分)17.(本题满分8分)先化简,再求值:,其中18.(本题满分8分)在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证:(1)(4分)BH=DE.(2)(4分)BH⊥DE.第18题图19.(本题满分8分)学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下:甲班:乙班:等级成绩(S)频数A90<S≤100xB80<S≤9015C70<S≤8010DS≤703合计30第19题图根据上面提供的信息回答下列问题⑴(3分)表中x=,甲班学生成绩的中位数落在等级中,扇形统计图中等级D部分的扇形圆心角n=.⑵(5分)现学校决定从两班所有A等级成绩的学生中随机抽取2名同学参加市级征文比赛.求抽取到两名学生恰好来自同一班级的概率(请列树状图或列表求解).20.(本题满分8分)一元二次方程⑴(4分)若方程有两实数根,求的范围.⑵(4分)设方程两实根为,且,求m.21.(本题满分9分)小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°. (1)(5分)求AD的长.(2)(4分)求树长AB.第21题图22.(本题满分9分)如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.(1)(5分)求证:CD为⊙O的切线.(2)(4分)若,求cos∠DAB.第22题图23.(本题满分10分)大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:x(天)123 (50)p(件)118116114 (20)销售单价q(元/件)与x满足:当.(1)(2分)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.(2)(4分)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.(3)(4分)这50天中,该超市第几天获得利润最大?最大利润为多少?24.(本题满分12分)如图,在平面直角坐标系xoy中,一次函数的图象与x轴交于A(-1,0),与y轴交于点C.以直线x=2为对称轴的抛物线经过A、C两点,并与x轴正半轴交于点B.(1)(3分)求m的值及抛物线的函数表达式.(2)(5分)设点,若F是抛物线对称轴上使得△ADF的周长取得最小值的点,过F任意作一条与y轴不平行的直线交抛物线于两点,试探究是否为定值?请说明理由.(3)(4分)将抛物线C1作适当平移,得到抛物线,若当时,恒成立,求m的最大值.鄂州市2014年中考数学参考答案一、选择题(30分)1——5BCDAD6——10DCBAD二、填空题(18分)11、12、14413、14、15、16、17、原式=…………………………………………………5′当时,原式=…………………………8′18、(1)证明△BCH△DCE,则BH=DE…………………5′(2)设CD与BH相交于G,则∠MBC+∠CGB=90°又∵∠CDE=∠MBC,∠DGH=∠BGC∵∠CDE+∠DGH=90°∴∠GMD=90°∴DE⊥BH……………8′19、(1)X=2Bn=36°……………………………………………3′(2)………………………………………8′20、(1)∴>0………………4′(2)x1+x2=2若x1>x2则x1-x2=1∴∴=8若x1<x2则x2-x1=1∴∴=8∴=8………………8′21、(1)过A作AH⊥CB于H,设AH=x,CH=x,DH=x,∵CH-DH=CD∴x-x=10∴x=……………………………3′∴AD=x=……………………………5′(2)过B作BM⊥AD于M∵∠1=75°,∠ADB=45°,∴∠DAB=30°设MB=m∴AM=mDM=m∵AD=AM+DM∴=m+m∴m=…………………7′∴AB=2m=……………………9′22、(1)连CO,证OC∥AD则OC⊥CD即可………………………………………5′(2)设AD交圆O于F,连BFBC在直角△ACD中,设CD=3k,AD=4k∴AC=5k△ACD~△ABC∴,∴AB=又BF⊥AD,∴OC⊥BF,∴BF=2CD=6k在直角△ABF中AF=,∴∠DAB=……………………………………9′23、(1)……………………………………………………………………3′(2)…………………7′(3)∴x=20时,y的最大值为3200元x=25时,y的最大值为3150元∴该超市第20天获得最大利润为3200元…………………………………10′24、(1),抛物线……………………………………3′(2)要使△ADF周长最小,只需AD+FD最小,∵A与B关于x=2对称∴只需BF+DF最小又∵BF+DF≥BD∴F为BD与x=2的交点BD直线为,当x=2时∴∵∴同理∴又∵∴∴∴………………………………8′(3)法一:设的两根分别为∵抛物线可以看成由左右平移得到,观察图象可知,随着图象向右移,的值不断增大∴当学习恒成立时,最大值在处取得∴当时,对应的即为的最大值将代入得∴10′将代入有∴∴的最大值为9…………………………………12′法二:恒成立化简得,,恒成立设,如图则有10′即∴∴的最大值为9…………………………。
2014年湖北省随州市随县洪山镇九年级上第一次月考数学试题【新课标人教版】

洪山镇九年级第一次月考数学试题一.选择题(本题有10个小题,每小题3分,共30分。
每个小题给出的四个选项中,只有一个是正确的) 1.方程(x-2)(x+3)=0的解是( )A.k <12B.k ≥-12 且k ≠0C.-12 ≤k <12 D.22<≤-k 且0≠k3.若关于x 的一元二次方程为ax 2+bx+5=0(a≠0)的一个根是x=1,则2014-a-b 的值( ) A .2019B .2009C .2014D .20124. 已知一元二次方程:①x 2+2x+3=0②x 2-2x-3=0,下列说法正确的是( )A.①②都有实数解B.①无实数解②有实数解C .①有实数解②无实数解D.①②都无实数解 5. 二次函数22(1)3y x =-+的图象的顶点坐标是( )A .(13),B .(13)-,C .(13)-, D .(13)--, 6.已知二次函数y=3(x-1) 2+k 的图象上有三点A ( 2 ,y 1),B (2,y 2),C (﹣ 5 ,y 3) 则123y y y 、、的大小关系为( )A.2 B . 8 C.4 D.16 8.函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是( )9.函数y =ax 2+bx +c 的图象如图所示,那么关于x 的一元二次方程 ax 2+bx +c -4=0的根的情况是( )A .有两个不相等的实数根B .有两个异号的实数根C .有两个相等的实数根D .没有实数根10.小轩从如图所示的二次函数y=ax 2+bx+c(a ≠0)的图象中,观察得出了下面五条信息:①ab >0;②a+b+c <0;③b+2c >0;④a-2b+4c >0;⑤a= 32 b,你认为正确的信息的条数为( )A.2B.3C.4D.5xOx4O1-1第7题图二.填空题(本题有6个小题,每小题3分,共18分)11. 若关于x 的一元二次方程(m ﹣2)x 2+3x+m 2﹣4=0的一根为0,则m 的值等于 12. 将二次函数y =2x 2+8x +3化为y =a(x -h)2+k 的形式是____ ___ 其顶点坐标为 13.已知函数y=x 2-2014x+2013与x 轴交点是(m,0),(n,0), 则(m 2-2015m+2013) (n 2-2015n+2013)的值是14.已知二次函数223y x =-的图像经过(1x ,5),(2x ,5)(1x ≠2x ),则当x 取 13(1x +2x )时,函数值为________.三. 解答题 (共9题,共72分.解答题必须写出必要的演算步骤.文字说明或证明过程)17.(本题满分9分)解下列方程(1)(6x-1)2=25 (2)x 2-4x+2=0(3) (3-x)(4-x)=48-20x+2x 218.(本题满分6分)已知x 关于的方程x 2-2(k-1)x+k 2=0有两个实数根x 1,,x 2 (1)求k 的取值范围(2)若︱x 1+x 2 ︳=x 1x 2-1,求k 的值19. (本题满分8分) 汽车产业是随州市支柱产业之一,产量和效益逐年增如.据统计,2012年随州市某种品牌汽 车的年产量为6.4万辆,到2014年,该品牌汽车的年产量达到10万辆.若该品牌汽车年产量的年平均增长率从2012年开始五年内保持不变, (1)求该品牌汽车的年平均增长率 (2)2015的年产量为多少万辆?20.(本题满分6分)已知关于x 的方程0)21(4)12(2=-++-k x k x .(1)求证:无论k 取什么实数值,这个方程总有实根.(2)若等腰△ABC 的一边长a=4,另两边b 、c 恰好是这个方程的两根,求△ABC 的周长.21. (本题满分6分)如图所示,已知在△ABC 中,∠B=90°,AB=6cm ,BC=12cm ,点P 从点A 开始沿 AB 边向点B 以1cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以2cm/s 的速度移动.(1)如果P 、Q 分别从A 、B 两点出发,那么几秒后,△PBQ 的面积等于82cm ?(2)在(1)中,△PBQ 的面积能否等于102cm ?试说明理由.22.(本题满分8分)某商场销售一种名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元? (2)当每件衬衫售价为多少元时,商场每天获利最大23.(本题满分8分)已知抛物线y 1=ax 2+bx+3与直线y 2=3x+1交于A(-2,m),B(1,n), (1)求出A,B 的坐标. (2)求抛物线y 1解析式(3)在同一坐标系中画出y 1, y 2的图象(草图),并说明当x 为何值时,y1>y224. (本题满分9分)如图,直线33+=x y 交x 轴于A 点,交y 轴于B 点,过A 、B 两点的抛物线交x 轴于另一点C (3,0). (1) 求抛物线的解析式;(2) 在抛物线的对称轴上是否存在点Q ,使△ABQ是等腰三角形?若存在,求出符合条件的Q 点坐标;若不存在,请说明理由.第24题图第21题图 A C25.(本题满分12分)如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.(1)求该抛物线的解析式;(2)若点P是该抛物线对称轴l上的一个动点,当△PBC周长的最小时求P点的坐标;(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.E。
湖北省孝感市2014年中考适应性考试数学试卷(无答案)

2004年宜昌市中考试卷以下数据和公式供参考:扇形面积S n r ==π23603032,°cos 频率分布直方图中小长方形的面积=频率=频数数据总数第I 卷(选择题、填空题,共45分)一. 选择题:(下列各小题都给出了四个选项,其中只有一项是符合题目要求的,请将符合要求的选项前面的字母代号填写在第II 卷上指定的位置,本大题共10小题,每小题3分,度30分)1. -2的倒数是( ) A. 2B. -12C.12D. -22. 若a ≠0,下列等式成立的是( )A. a a a +=23B. ()aa 339= C. a a a 623÷= D. a a a 2222⋅=3. 实数x 在数轴上的位置如图所示,则( ) A. ||x <-1 B. ||x <0 C. ||x >1D. ||x =04. 下列二次根式中,是最简二次根式的为( ) A. 12B. a b 2C. abD. x 45. 如图所示,AB//CD ,那么∠+∠+∠=A C AEC ( ) A. 360°B. 270°C. 200°D. 180°6. 以下列长度的三条线段为边,能组成三角形的是( ) A. 3、3、3 B. 3、3、6 C. 3、2、5 D. 3、2、67. 衡量样本和总体的波动大小的特征数是( )A. 平均数B. 方差C. 众数D. 中位数8. 如图所示,AB 为圆O 的直径,CD 为弦,CD AB E ⊥于, 则下列结论中错误的是( )A. ∠=∠COE DOEB. CE DE =C. AE BE =D. BC BD ⋂=⋂9. 如图所示,在平行四边形ABCD 中,F 是AD 延长线上一点, 连结BF 交DC 于点E ,则图中的相似三角形共有( )A. 0对B. 1对C. 2对D. 3对10. 直线y x =与双曲线y kx=的一个分支 (k x ≠>00,)相交,则该分支的图象大致是下面的图( )二. 填空题(请将答案填写在第II 卷上指定的位置,本大题共5小题,每小题3分,计15分)11. 当a________时,括号中两个数的和等于0。
2014年湖北中考数学真题卷含答案解析

2014年武汉市初中毕业生学业考试数学试题(含答案全解全析)第Ⅰ卷(选择题,共30分)一、选择题(共10小题,每小题3分,共30分)下列各题中均有四个备选答案,其中有且只有一个是正确的.1.在实数-2、0、2、3中,最小的实数是( )A.-2B.0C.2D.32.若代数式√x-3在实数范围内有意义,则x的取值范围是( )A.x≥-3B.x>3C.x≥3D.x≤33.光速约为300000千米/秒,将数字300000用科学记数法表示为( )A.3×104B.3×105C.3×106D.30×1044.在一次中学生田径运动会上,参加跳高的15名运动员的成绩如下表所示:成绩(m) 1.50 1.60 1.65 1.70 1.75 1.80人数124332那么这些运动员跳高成绩的众数是( )A.4B.1.75C.1.70D.1.655.下列代数运算正确的是( )A.(x3)2=x5B.(2x)2=2x2C.x3·x2=x5D.(x+1)2=x2+16.如图,线段AB两个端点的坐标分别为A(6,6)、B(8,2),以原点O为位似中心,在第一象限后得到线段CD,则端点C的坐标为( )内将线段AB缩小为原来的12A.(3,3)B.(4,3)C.(3,1)D.(4,1)7.下图是由4个大小相同的正方体组合而成的几何体.其俯视图是( )8.为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为( )A.9B.10C.12D.159.观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…….按此规律第5个图中共有点的个数是( )A.31B.46C.51D.6610.如图,PA、PB切☉O于A、B两点,CD切☉O于点E,交PA、PB于C、D,若☉O的半径为r,△PCD 的周长等于3r,则tan∠APB的值是( )A.512√13 B.125C.35√13 D.23√13第Ⅱ卷(非选择题,共90分)二、填空题(共6小题,每小题3分,共18分)11.计算:-2+(-3)= .12.分解因式:a3-a= .13.如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为.14.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为米.15.如图,若双曲线y=kx与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=3BD,则实数k的值为.16.如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为.三、解答题(共9小题,共72分)下列各题解答应写出文字说明、证明过程或演算步骤.17.(本小题满分6分)解方程:2x-2=3 x .18.(本小题满分6分)已知直线y=2x-b经过点(1,-1),求关于x的不等式2x-b≥0的解集.19.(本小题满分6分)如图,AC和BD相交于点O,OA=OC,OB=OD,求证:AB∥CD.20.(本小题满分7分)如图,在直角坐标系中,A(0,4),C(3,0).(1)①画出线段AC关于y轴对称的线段AB;②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;(2)若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值.21.(本小题满分7分)袋中装有大小相同的2个红球和2个绿球.(1)先从袋中摸出1个球后放回..,混合均匀后再摸出1个球.①求第一次摸到绿球,第二次摸到红球的概率;②求两次摸到的球中有1个绿球和1个红球的概率;(2)先从袋中摸出1个球后不放回...,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.22.(本小题满分8分)⏜上两点,AB=13,AC=5.如图,AB是☉O的直径,C,P是AB⏜的中点,求PA的长;(1)如图①,若点P是AB⏜的中点,求PA的长.(2)如图②,若点P是BC图①图②23.(本小题满分10分)九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:时间x(天)1≤x<5050≤x≤90售价(元/件)x+4090每天销量(件)200-2x已知该商品的进价为每件30元,设销售该商品的每天利润为y元.(1)求出y与x的函数关系式;(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.24.(本小题满分10分)如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm 的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连结PQ.(1)若△BPQ与△ABC相似,求t的值;(2)连结AQ、CP,若AQ⊥CP,求t的值;(3)试证明:PQ的中点在△ABC的一条中位线上.25.(本小题满分12分)x2交于A、B两点.如图,已知直线AB:y=kx+2k+4与抛物线y=12(1)直线AB总经过一个定点C,请直接写出点C的坐标;时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;(2)当k=-12(3)若在抛物线上存在定点D使∠ADB=90°,求点D到直线AB的最大距离.备用图答案全解全析:一、选择题1.A∵-2<0<2<3,∴最小的实数是-2,故选A.评析本题考查了实数的大小比较,属容易题.2.C要使√x-3在实数范围内有意义,则需x-3≥0,解得x≥3.故选C.评析本题考查二次根式有意义的条件,即被开方数大于等于零,属容易题.3.B300000用科学记数法可表示为3×105.故选B.评析本题考查科学记数法的表示方法.科学记数法的表示形式为a×10n,其中1≤|a|<10,n 为整数,属容易题.4.D∵1.65出现了4次,出现的次数最多,∴这些运动员跳高成绩的众数是1.65,故选D.评析本题考查了众数的定义,众数是一组数据中出现次数最多的数,属容易题.5.C(x3)2=x6,故A选项错误;(2x)2=4x2,故B选项错误;x3·x2=x5,故C选项正确;(x+1)2=x2+2x+1,故D选项错误.故选C.6.A∵线段AB两个端点的坐标分别为A(6,6)、B(8,2),以原点O为位似中心,在第一象限后得到线段CD,∴端点C的坐标为(3,3).故选A.内将线段AB缩小为原来的12评析本题主要考查位似图形的性质,属容易题.7.C从上面看可得到一行正方形,其个数为3,故选C.评析本题考查了三视图的知识,俯视图是从物体的上面看得到的视图,属容易题.8.C由题图可知,10天中在同一时段通过该路口的汽车数量超过200辆的有4天,频率为4=0.4,所以估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为1030×0.4=12,故选C.评析 本题考查了折线统计图及用样本估计总体的思想,属容易题.9.B 第1个图中共有1+1×3=4个点,第2个图中共有1+1×3+2×3=10个点,第3个图中共有1+1×3+2×3+3×3=19个点,…,第n 个图中有1+1×3+2×3+3×3+…+3n 个点. 所以第5个图中共有点的个数是1+1×3+2×3+3×3+4×3+5×3=46.故选B. 评析 本题是规律探索题,属容易题.10.B 连结OA 、OB 、OP,延长BO 交PA 的延长线于点F.∵PA、PB 切☉O 于A 、B 两点,CD 切☉O 于点E, ∴∠OAP=∠OBP=90°,CA=CE,DB=DE,PA=PB.∵△PCD 的周长=PC+CE+DE+PD=PC+AC+PD+DB=PA+PB=3r,∴PA=PB=32r. 在Rt △OAF 和Rt △BFP 中,{∠FAO =∠FBP,∠OFA =∠PFB,∴Rt △AFO ∽Rt △BFP. ∴AF FB =AO BP =r 32r =23,∴AF=23FB. 在Rt △FBP 中,PF 2-PB 2=FB 2, ∴(PA+AF)2-PB 2=FB 2,∴(32r +23BF)2-(32r)2=BF 2,解得BF=185r,∴tan ∠APB=BFPB =185r 32r=125,故选B.评析 本题主要考查切线的性质,相似三角形的判定及三角函数的定义,属难题.二、填空题 11.答案 -5解析 -2+(-3)=-(2+3)=-5.评析 本题考查有理数加法的运算,属容易题. 12.答案 a(a+1)(a-1)解析 a 3-a=a(a 2-1)=a(a+1)(a-1).评析 本题考查利用提公因式法和公式法分解因式,属容易题. 13.答案 37解析 ∵一个转盘被分成7个相同的扇形,红色的有3个,∴指针指向红色的概率为37. 14.答案 2 200解析 设小明的速度为a 米/秒,小刚的速度为b 米/秒,由题意,得{1 600+100a =1 400+100b,1 600+300a =1 400+200b,解得{a =2,b =4,∴这次越野跑的全程为1 600+300×2=2 200(米).评析 本题考查了行程问题的数量关系及二元一次方程组的解法,属容易题.15.答案9√34解析 过点C 作CE ⊥x 轴于点E,过点D 作DF ⊥x 轴于点F, 设BF=x,则DF=√3x,BD=2x.因为OC=3BD,所以OE=3x,CE=3√3x, 所以C(3x,3√3x),D(5-x,√3x). 因为点C 、D 都在双曲线上,所以3x ·3√3x=√3x ·(5-x), 解得x 1=12,x 2=0(舍去),所以C (32,3√32), 故k=3√32×32=9√34.评析 本题考查了反比例函数图象上点的坐标特征,解答本题的关键是利用k 的值相同建立方程,属中等偏难题. 16.答案 √41解析 作AD'⊥AD,且使AD'=AD,连结CD',DD',如图.由已知条件可得∠BAC+∠CAD=∠DAD'+∠CAD,即∠BAD=∠CAD'. 在△BAD 与△CAD'中,{BA =CA,∠BAD =∠CAD',AD =AD',∴△BAD ≌△CAD'(SAS), ∴BD=CD'.又∠DAD'=90°,由勾股定理得DD'=√AD 2+(AD')2 =√32=4√2,易知∠D'DA+∠ADC=90°,由勾股定理得CD'=√DC 2+(DD')2=√9+32=√41, ∴BD=CD'=√41.评析 本题考查了等腰直角三角形的性质、勾股定理、全等三角形的判定与性质,属难题. 三、解答题17.解析 方程两边同乘以x(x-2),得2x=3(x-2). 解得x=6.检验:当x=6时,x(x-2)≠0. ∴x=6是原分式方程的解.评析 本题考查了解分式方程,解分式方程一定要注意验根,属容易题. 18.解析 ∵直线y=2x-b 经过点(1,-1), ∴-1=2×1-b. ∴b=3.∴不等式2x-b ≥0即为2x-3≥0,解得x ≥32.19.证明 在△AOB 和△COD 中,{OA =OC,∠AOB =∠COD,OB =OD,∴△AOB ≌△COD. ∴∠A=∠C,∴AB ∥CD. 20.解析 (1)如图所示:(2)43.评析 本题考查利用旋转、轴对称变换作图,属容易题.21.解析 (1)分别用R 1,R 2表示2个红球,G 1,G 2表示2个绿球,列表如下:第二次第一次 R 1 R 2 G 1 G 2R 1 R 1R 1 R 1R 2 R 1G 1 R 1G 2 R 2 R 2R 1 R 2R 2 R 2G 1 R 2G 2 G 1 G 1R 1 G 1R 2 G 1G 1 G 1G 2 G 2 G 2R 1 G 2R 2 G 2G 1 G 2G 2由上表可知,有放回地摸2个球共有16个等可能结果. ①其中第一次摸到绿球,第二次摸到红球的结果有4个. ∴第一次摸到绿球,第二次摸到红球的概率P=416=14;②其中两次摸到的球中有1个绿球和1个红球的结果有8个. ∴两次摸到的球中有1个绿球和1个红球的概率P=816=12. 画树形图法按步骤给分(略). (2)23.22.解析 (1)如图,连结PB,BC.∵AB 是☉O 的直径,P 是AB⏜的中点, ∴PA=PB,∠APB=90°. ∵AB=13,∴PA=√22AB=13√22.(2)如图,连结PB,BC.连结OP 交BC 于D 点.∵P 是BC⏜的中点,∴OP ⊥BC 于D,BD=CD. ∵OA=OB,∴OD=12AC=52.∵OP=12AB=132,∴PD=OP -OD=132-52=4.∵AB 是☉O 的直径,∴∠ACB=90°.∵AB=13,AC=5,∴BC=12,∴BD=12BC=6.∴PB=√PD 2+BD 2=2√13.∵AB 是☉O 的直径,∴∠APB=90°,∴PA=√AB 2-PB 2=3√13.23.解析 (1)y={-2x 2+180x +2 000(1≤x <50),-120x +12 000(50≤x ≤90).(2)当1≤x<50时,y=-2x 2+180x+2 000=-2(x-45)2+6 050.∵-2<0,∴当x=45时,y 有最大值,最大值为6 050元.当50≤x ≤90时,y=-120x+12 000,∵-120<0,∴y 随x 的增大而减小.当x=50时,y 有最大值,最大值为6 000元.∴当x=45时,当天的销售利润最大,最大利润为6 050元.(3)41天.评析 本题考查利用函数的性质解决实际问题,属中等难度题.24.解析 (1)由题意知,BP=5t cm,CQ=4t cm,∴BQ=(8-4t)cm.当△PBQ ∽△ABC 时,有BP AB =BQ BC .即5t 10=8-4t 8,解得t=1. 当△QBP ∽△ABC 时,有BQ AB =BP BC .即8-4t 10=5t 8,解得t=3241.∴△PBQ 与△ABC 相似时,t=1或3241.(2)如图,过点P 作PD ⊥BC 于D.依题意,得BP=5t cm,CQ=4t cm.则PD=PB ·sin B=3t cm,∴BD=4t cm,CD=(8-4t)cm.∵AQ ⊥CP,∠ACB=90°,∴tan ∠CAQ=tan ∠DCP.∴CQ AC =PD CD .∴4t 6=3t 8-4t ,∴t=78.(3)证明:如图,过点P 作PD ⊥AC 于D,连结DQ 、BD,BD 交PQ 于M,则PD=AP ·cos ∠APD=AP ·cos ∠ABC=(10-5t)×810=(8-4t)cm.而BQ=(8-4t)cm,∴PD=BQ,又PD ∥BQ,∴四边形PDQB 是平行四边形.∴点M 是PQ 和BD 的中点. 过点M 作EF ∥AC 交BC,BA 于E,F 两点.则BE EC =BM MD =1,即E 为BC 的中点.同理,F 为BA 的中点.∴PQ 的中点M 在△ABC 的中位线EF 上.25.解析 (1)(-2,4).(2)如图,直线y=-12x+3与y 轴交于点N(0,3).在y 轴上取点Q(0,1),易得S △ABQ =5. 过点Q 作PQ ∥AB 交抛物线于点P.则PQ 的解析式为y=-12x+1,由{y =-12x +1,y =12x 2,解得{x =-2,y =2,或{x =1,y =12, ∴P 点坐标为(-2,2)或(1,12).(3)如图,设A (x 1,12x 12),B (x 2,12x 22),D (m,12m 2). 联立{y =kx +2k +4,y =12x 2,消去y 得x 2-2kx-4k-8=0. ∴x 1+x 2=2k,x 1·x 2=-4k-8.过点D 作EF ∥x 轴,过点A 作y 轴的平行线交EF 于点E,过点B 作y 轴的平行线交EF 于点F. 由△ADE ∽△DBF,得AE DF =DE BF . ∴12x 12-12m 2x 2-m =m -x 112x 22-12m 2,整理,得x 1x 2+m(x 1+x 2)+m 2=-4.∴2k(m -2)+m 2-4=0. 当m-2=0,即m=2时,点D 的坐标与k 无关,∴点D 的坐标为(2,2).又∵C(-2,4),所以CD=2√5,过点D 作DM ⊥AB,垂足为M.则DM ≤CD.当CD ⊥AB 时,点D 到直线AB 的距离最大,最大距离为2√5.评析本题考查解方程组、一元二次方程、一元二次方程根与系数的关系、勾股定理、相似三角形的判定与性质等知识,考查了通过解方程组求两函数图象交点坐标等,综合性比较强,属难题.。
湖北省随州市随县2019届九年级初中毕业生学业水平能力测试暨升学适应性考试数学试题(扫描版)

∵E 是BD的中点,
⌒⌒
∴DE=EB,
∴∠EAB=∠EAD, ……………………1 分
∵∠ACB=2∠EAB,
∴∠ACB=∠DAB, ……………………2 分
∵AB 是⊙O 的直径,
∴∠ADB=90°,
∴∠DAC+∠ACB=90°,
∴∠DAC+∠DAB=90°,即∠BAC=90°,
∴AC⊥AB, ……………………3 分
,解得
……………………2 分
∴销售量 p 与 x 的函数关系式为:p=-2x+120 ……………………3 分 (2)由题意知该超市销售该新型商品第 x 天获得的利润为 y 元 关于 x 的函数关系分两种情况 当 1≤x<25 时,销售单价 q=x+60 ∴y=(x+60-40)(-2x+120) 整理得 y=-2x2+80x+2400 ……………………5 分
解得:m=
……………………5 分
∵m= <2 ……………………6 分
∴符合条件的 m 的值为
19. (10 分) 解:(1)
……………………7 分
……………………2 分
(2)72 ……………………4 分 (3)根据题意,得
答:估计该校参加这次海选比赛的 2000 名学生中成绩“优等”的约有 700 人. ……………………6 分
如图,在△ABN,△AM1B 中, ∠BAN=∠M1AB,∠ABN=∠AM1B, ∴△ABN∽△AM1B,得:AB2=AN•AM1; 由勾股定理,得 AB2=(-2)2+(-6)2=40, …………10 分 又∵AN=OA-ON=6-2=4, ∴AM1=40÷4=10,OM1=AM1-OA=10-6=4 OM2=OM1=4 AM2=OA-OM2=6-4=2. …………11 分 综上所述,AM 的长为 10 或 2. …………12 分
2014年湖北省随州市中考数学试题及参考答案(word解析版)

2014年湖北省随州市中考数学试题及参考答案与解析一、选择题(每小题3分,共30分) 1.2的相反数是( ) A .12 B .﹣2 C .2 D .12- 2.如图所示的物体的俯视图是( )A .B .C .D .3.2013年,我市以保障和改善民生为重点的“十件实事”全面完成,财政保障民生支出达74亿元,占公共财政预算支出的75%,数据74亿元用科学记数法表示为( ) A .74×108元 B .7.4×108元 C .7.4×109元 D .0.74×1010元4.如图,在△ABC 中,两条中线BE 、CD 相交于点O ,则S △DOE :S △COB =( )A .1:4B .2:3C .1:3D .1:25.计算3212xy ⎛⎫- ⎪⎝⎭,结果正确的是( )A .2414x y B .3618x y - C .3618x y D .3518x y - 6.在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )A .18,18,1B .18,17.5,3C .18,18,3D .18,17.5,17.如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()A.100米B.C米D.50米8.关于反比例函数2yx的图象,下列说法正确的是()A.图象经过点(1,1)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.当x<0时,y随x的增大而减小9.在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是()A.AE∥BC B.∠ADE=∠BDC C.△BDE是等边三角形D.△ADE的周长是9 10.某通讯公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80分钟通话时间,超过80分钟的部分,以每分钟0.15元的价格计费.下列结论:①如图描述的是方式1的收费方法;②若月通话时间少于240分钟,选择方式2省钱;③若月通讯费为50元,则方式1比方式2的通话时间多;④若方式1比方式2的通讯费多10元,则方式1比方式2的通话时间多100分钟.其中正确的是()A.只有①②B.只有③④C.只有①②③D.①②③④二、填空题(每小题3分,共18分) 11.计算:)|3|1-= .12.不等式组11223x x ⎧⎪⎨⎪-⎩≤<的解集是 .13.将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 度.14.某小区2010年屋顶绿化面积为2000平方米,计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是 .15.圆锥的底面半径是2cm ,母线长6cm ,则这个圆锥侧面展开图的扇形圆心角度数为 度. 16.如图1,正方形纸片ABCD 的边长为2,翻折∠B 、∠D ,使两个直角的顶点重合于对角线BD 上一点P 、EF 、GH 分别是折痕(如图2).设AE=x (0<x <2),给出下列判断: ①当x=1时,点P 是正方形ABCD 的中心; ②当12x =时,EF+GH >AC ; ③当0<x <2时,六边形AEFCHG 面积的最大值是114; ④当0<x <2时,六边形AEFCHG 周长的值不变. 其中正确的是 (写出所有正确判断的序号).三、解答题(共72分) 17.(6分)先简化,再求值:221111aa a a a ⎛⎫-÷⎪+--⎝⎭,其中1a =. 18.(7分)已知:如图,在矩形ABCD 中,M 、N 分别是边AD 、BC 的中点,E 、F 分别是线段BM 、CM 的中点.(1)求证:△ABM≌△DCM;(2)填空:当AB:AD=时,四边形MENF是正方形.19.(7分)近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m 名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表:请你根据图表中提供的信息解答下列问题:(1)表中m的值为,n的值为;(2)补全条形统计图;(3)若该校九年级有学生500名,估计该校大约有多少名毕业生的升学意向是职业高中?20.(7分)某市区一条主要街道的改造工程有甲、乙两个工程队投标.经测算:若由两个工程队合做,12天恰好完成;若两个队合做9天后,剩下的由甲队单独完成,还需5天时间,现需从这两个工程队中选出一个队单独完成,从缩短工期角度考虑,你认为应该选择哪个队?为什么?21.(7分)四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.22.(8分)如图,⊙O中,点C为AB的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.(1)求证:AD与⊙O相切;(2)若点C到弦AB的距离为2,求弦AB的长.23.(8分)楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x 的函数关系式;(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么月需售出多少辆汽车?(注:销售利润=销售价﹣进价)24.(10分)已知两条平行线l1、l2之间的距离为6,截线CD分别交l1、l2于C、D两点,一直角的顶点P在线段CD上运动(点P不与点C、D重合),直角的两边分别交l1、l2与A、B两点.(1)操作发现如图1,过点P作直线l3∥l1,作PE⊥l1,点E是垂足,过点B作BF⊥l3,点F是垂足.此时,小明认为△PEA∽△PFB,你同意吗?为什么?(2)猜想论证将直角∠APB从图1的位置开始,绕点P顺时针旋转,在这一过程中,试观察、猜想:当AE满足什么条件时,以点P、A、B为顶点的三角形是等腰三角形?在图2中画出图形,证明你的猜想.(3)延伸探究在(2)的条件下,当截线CD与直线l1所夹的钝角为150°时,设CP=x,试探究:是否存在实数x,使△PAB的边AB的长为25.(12分)平面直角坐标系中,四边形ABCD是菱形,点C的坐标为(﹣3,4),点A在x轴的正半轴上,O为坐标原点,连接OB,抛物线y=ax2+bx+c经过C、O、A三点.(1)直接写出这条抛物线的解析式;(2)如图1,对于所求抛物线对称轴上的一点E,设△EBO的面积为S1,菱形ABCD的面积为S2,当S1≤14S2时,求点E的纵坐标n的取值范围;(3)如图2,D(0,52-)为y轴上一点,连接AD,动点P从点O/秒的速度沿OB方向运动,1秒后,动点Q从O出发,以2个单位/秒的速度沿折线O﹣A﹣B方向运动,设点P运动时间为t秒(0<t<6),是否存在实数t,使得以P、Q、B为顶点的三角形与△ADO相似?若存在,求出相应的t值;若不存在,请说明理由.参考答案与解析一、选择题(每小题3分,共30分)1.2的相反数是()A.12B.﹣2 C.2 D.12-【知识考点】相反数.【思路分析】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.【解答过程】解:2的相反数是﹣2.故选B.【总结归纳】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.2.如图所示的物体的俯视图是()。
2024年湖北省随州市随县中考数学适应性试卷(含解析)

2024年湖北省随州市随县中考数学适应性试卷一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.−34的绝对值是( )A. −34B. 34C. −43D. 432.太阳半径约696000千米,则696000千米用科学记数法可表示为( )A. 0.696×106米B. 6.96×108米C. 0.696×107米D. 6.96×105米3.下列计算中,结果是a7的是( )A. a3−a4B. a3⋅a4C. a3+a4D. a3÷a44.下列图形既是轴对称图形,又是中心对称图形的是( )A. B.C. D.5.下列语句所描述的事件是随机事件的是( )A. 任意画一个四边形,其内角和为180°B. 经过任意两点画一条直线C. 任意画一个菱形,是中心对称图形D. 过平面内任意三点画一个圆6.如图,AB//CD,E为CD上一点,射线EF经过点A,EC=EA.若∠CAE=30°,则∠BAF=( )A. 30°B. 40°C. 50°D. 60°7.如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )A. 50°B. 55°C. 60°D. 65°8.如图,填在各方格中的三个数之间均具有相同的规律,根据此规律,n的值是( )A. 48B. 56C. 63D. 749.如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为xs,△APQ的面积为ycm2,则下列图象中能大致表示y与x的函数关系的是( )A. B.C. D.10.如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x=5,2连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )A. 点B坐标为(5,4)B. AB=ADC. a=−1D. OC⋅OD=166二、填空题:本题共5小题,每小题3分,共15分。
湖北省随县2014年初中毕业生学业水平能力测试暨升学适应性考试数学试题(扫描版)

随县2014年初中毕业生学业水平能力测试暨升学适应性考试数学试题参考答案一、选择题(每小题3分,共30分)二、填空题(每小题3分,共18分)11. 15,90 12. 14 13. 2x y =14. π 15.(35,-4) 16. 1三、解答题(共72分) 17. (本题满分5分) 解:原式=y x y x y x y x y x x --+⨯-+2))(())((2 =yx x-22 ………………………2分 由题意得⎩⎨⎧=--=-01202y x x 此时,2=x ,12=-y x ………………4分 当2=x ,12=-y x 时,原式=4. ………………5分 18. (本题满分6分)解:设某游客一年中进入该公园x 次,依题意得不等式组20x >200 (1)5x +100>200 (2) ………………2分 解(1)得:x >10, 解(2)得:x >20.∴不等式组的解集为x >20. ………………5分答:某游客一年进入该公园超过20次时,办理金卡最合算。
………………6分 19. (本题满分7分) 解:∵∠DBA =∠DAB =45°,∴△DAB 是等腰直角三角形. ………………1分 过点D 作DE ⊥AB 于点E ,则DE =21AB . ………………2分 设DE =x ,则AB =2x .在Rt △CDE 中,∠DCE =30°,则CE =3DE =3x .………………4分 在Rt △BDE 中,∠DBE =45°, 则DE =BE =x ,由题意得,CB =CE -BE ∴3x -x =36×41, ………………5分 解得: x ≈12.3, ……………… 6分答:中国海监船离钓鱼岛最近距离为12.3海里.……………… 7分 20. (本题满分7分)解:(1)设捐10元的人数为4x 人,根据题意得4x =12解得:x =3∴一共调查了3x +4x +5x +6x +2x =20x =20×3=60(人) ………………2分 (2)捐款为20元的圆心角度数为:360°×206=108°………………4分 (3)全校学生共捐款:10006030620181515101259⨯⨯+⨯+⨯+⨯+⨯=15500(元) …………7分21. (本题满分7分)解:(1)设袋子里2号球的个数为x 个. 根据题意得:4121=++x x解得:x =1.经检验:x =1是原分式方程的解 ………………3分 (2)由题意画树形图如下:∵共有12种等可能的结果,点A (x ,y )在直线y =x 上的有2个,∴点A (x ,y )在直线y =x 上的概率为:P =122=61………………7分 22. (本题满分8分) (1)证明:连OB.∵OA =OB ,∴∠OAC =∠OBA . ∵CD =DB ,∴∠DBC =∠DCB =∠ACO .∴∠ACO +∠OAC =∠OBA +∠CBD . ………………2分 ∵AO ⊥OD ,∴∠ACO +∠OAC =90°. ∴∠OBD =90°.∴BD 是⊙O 的切线. ………………4分 (2)解:过D 作DE ⊥BC 于E 在Rt △OBD 中,OB =2245-=3 ∴OA =OB=3 ………………5分 在Rt △OAC 中,AC =2213+=10 ∵∠ACO =∠DCE ,∠AOC =∠DEO , ∴Rt △AOC ∽Rt △DEC . ………………6分 ∴ECOCCD AC =. ∵CD =BD ,CE =BC 21,∴BC 211410=, ∴BC =1054. ………………8 【如果没有去掉条件AC ,请参照: (2)解:过D 作DE ⊥BC 于E ∵∠ACO =∠DCE ,∠AOC =∠DEO , ∴Rt △AOC ∽Rt △DEC . ………………6分 ∴ECOCCD AC =.∵CD =BD ,CE =BC 21,∴BC 21143 , ∴BC =38. ………………8分】23. (本题满分10分)解:(1)设一次至少买x 件,才能以最低价购买,由题意,得200-(x -10)×1=160,解得:x =50.答:一次至少买50件,才能以最低价购买.………………3分 (2)当0<x ≤10时,y =(200-120)x =80x当10<x ≤50时,y =[(200-120)-(x -10)×1] ×x =-x 2+90x , 当x >50时,y =(160-120)x =40x . 综上:y 与x 的关系式为80x (0<x ≤10且x 为整数)y = -x 2+90x ( 10<x ≤50且x 为整数)40x ( x >50且x 为整数) ………………7分 (3)由y =-x 2+90x =-(x -45)2+2025 知对称轴x =45,当45<x ≤50时,y 随x 的增大而减小,即当卖的件数越多时,利润越小.即出现了卖46件赚的钱比卖50件嫌的钱多的现象. ………………9分 当x =45时,最低售价为200-(45-10)=165(元).∴为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每件160元至少提高到165元. ………………10分 24. (本题满分10分)(1)解:∵长方形CEFD 绕点C 顺时针旋转至CE ′F ′D ′, ∴CD ′=CD =2,在Rt △CED ′中,CD ′=2,CE =1,∴sin ∠CD ′E =21, ∴∠CD ′E =30°,∵CD ∥EF ,∴∠α=30°;………………3分 (2)证明:∵G 为BC 中点, ∴CG =1, ∴CG =CE ,∵长方形CEFD 绕点C 顺时针旋转至CE ′F ′D ′, ∴∠D ′CE ′=∠DCE =90°,CE =CE ′=CG , ∴∠GCD ′=∠DCE ′=90°+α, 在△GCD ′和△E ′CD 中⎪⎩⎪⎨⎧'='∠='∠='E C CG E DC D GC CD D C ∴△GCD ′≌△E ′CD (SAS ), ∴GD ′=E ′D ; ………………7分(3)解:能,α的值为135°或315°. ………………10分 25. (本题满分12分)解:(1)过C 点作CE ⊥x 轴于点E , ∵Rt △AOB 中,tan ∠ABO =3,AB =10, ∴OA =3,OB =1,……1分由△AOB ≌△BEC 得BE =3,CE =1,∴C (4,1),………………2分 由题意得A (0,3),B (1,0),C (4,1).设过A ,B ,C 的抛物线的解析式为32++=bx ax y ,得⎩⎨⎧=++=++1341603b a b a 解得a =65,b =623- ∴所求函数解析式为3623652+-=x x y ………………3分 (2)作PF ⊥x 轴于点F ,连接AC .因为P 是正方形的对称中心,根据平行线等分线段定理可求得OF =2,所以可得PF 为直角梯形AOEC 的中位线,可求得PF=2,所以P (2,2) ……………… 6分 (3)存在令y =0得03623652=+-x x , 解得x 1=1,x 2=3.6 ∵B (1,0), ∴E (3.6,0)………………7分作E 关于直线OP 的对称点E ',连接E B ',交直线OP 于点H ,根据两点之间线段最短知H 是满足△BHE 周长最小的点 ∵P ((2,2), ∴ OP 是∠AOB 的平分线, ∴E '在y 轴上, ∴E '(0,518),………………8分 ∴△BHE 周长为513349)1518(1)518(22+=-++. ………………9分(4)当CR ∥AB 时, t =413. ………………10分 当AR ∥BC 时,t =29. ………………11分当BR ∥AC 时,t =31. ………………12分。
湖北省随州市随县2019届九年级初中毕业生学业水平能力测试暨升学适应性考试数学试题

湖北省随州市随县2019届九年级初中毕业生学业水平能力测试暨升学适应性考试数学试题一、选择题1.-的绝对值为()A. B. 4 C. D.2.下列运算正确的是()A. B. C. D.3.如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠BEF,若∠1=48°,则∠2的度数是()A. B. C. D.4.在一次中学生田径运动会上,参加跳远的15名运动员的成绩如下表所示则这些运动员成绩的中位数、众数分别是()A. 、B. 、C. 、D. 、5.如图,D是△ABC的AB边上的一点,过点D作DE∥BC交AC于E.已知AD:DB=2:3.则S△ADE:S BCED=()A. 2:3B. 4:9C. 4:5D. 4:216.一个立体图形的三视图如图所示.根据图中数据求得这个立体图形的表面积为()A.B.C.D.7.甲、乙两人在一条长为600m的笔直马路上进行跑步,速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面50m处,若两人同时起跑,则从起跑出发到其中一人先到达终点的过程中,两人之间的距离y(m)与时间t(s)的函数图象是()A. B. C. D.8.如图,将△ABC绕点C顺时针旋转60°得到△A'B'C',已知AC=6,BC=4,则线段AB扫过的图形面积为()A.B.C.D. 以上答案都不对9.《孙子算经》是唐初作为“算学“教科书的著名的《算经十书)之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼“问题是其中之一,原题如下:今有雉(鸡)兔同笼,上有三十五头,下有九十四足.问雉、兔各几何?()A. 雉23只,兔12只B. 雉12只,兔23只C. 雉13只,兔22只D. 雉22只,兔13只10.如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③abc<0;④b2+8a<4ac.其中正确的结论有()A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共6小题,共18.0分)11.计算:(-)-2-|-2|+2cos45°-(3-π)0=______.12.如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于______.13.如图,直线y=x+2与反比例函数y=的图象在第一象限交于点P,若OP=,则k的值为______.14.如图,E(-6,0),F(-4,-2),以O为位似中心,按比例尺1:2把△EFO放大,则点F的对应点F'的坐标为______.15.如图中每一个小方格的面积为1,则可根据面积计算得到如下算式:1+3+5+7+…+(2n-1)=______(用n表示,n是正整数)16.如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+.其中正确结论的序号是______.三、计算题(本大题共1小题,共6.0分)17.先化简,再求值:先化简÷(-x+1),然后从-2<x<的范围内选取一个合适的整数作为x的值代入求值.四、解答题(本大题共7小题,共66.0分)18.已知关于x的一元二次方程x2-2x+m-1=0有两个实数根x1,x2.(1)求m的取值范围;(2)当x12+x22=6x1x2时,求m的值.19.《中国汉字听写大会》唤醒了很多人对文字基本功的重视和对汉字文化的学习,我市某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:抽取的200名学生海选成绩分组表请根据所给信息,解答下列问题:(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为______,表示C组扇形的圆心角θ的度数为______度;(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?(4)经过统计发现,在E组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?20.如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:,AB=10米,AE=15米.(i=1:是指坡面的铅直高度BH与水平宽度AH的比)(1)求点B距水平而AE的高度BH;(2)求宣传牌CD的高度.(结果精确到0.1米.参考数据:≈1.414,≈1.732)21.如图,AB是⊙O的直径,BC交⊙O于点D,E是的中点,AE与BC交于点F,∠C=2∠EAB.(1)求证:AC是⊙O的切线;(2)已知CD=4,CA=6,①求CB的长;②求DF的长.22.大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+.(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.(3)这50天中,该超市第几天获得利润最大?最大利润为多少?23.观察下列等式:12×231=132×21,13×341=143×31,23×352=253×32,34×473=374×43,62×286=682×26,…以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:①52×______=______×25;②______×396=693×______.(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.(-2,0),C两点.(1)求此抛物线的函数关系式和顶点D的坐标;(2)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1,若新抛物线y1的顶点P在△ABC内,求m的取值范围;(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,直接写出AM的长.。
2014年湖北省随州市初中毕业升学考试数学试卷

2014年湖北省随州市初中毕业升学考试数学试卷一、选择题(每小题3分,共30分)1.2的相反数是()A.B.﹣2 C.2 D.考点:相反数.菁优网版权所有解析:根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.2的相反数是﹣2.答案:B2.如图所示的物体的俯视图是()A.B.C.D.考点:简单组合体的三视图.菁优网版权所有解析:找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.从上面向下看,易得到横排有3个正方形.答案:D3.2013年,我市以保障和改善民生为重点的“十件实事”全面完成,财政保障民生支出达74亿元,占公共财政预算支出的75%,数据74亿元用科学记数法表示为()A.74×108元B.7.4×108元C.7.4×109元D.0.74×1010元考点:科学记数法—表示较大的数.菁优网版权所有解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.74亿=74 0000 0000=7.4×109,答案:C4.如图,在△ABC中,两条中线BE、CD相交于点O,则S△DOE:S△COB=()A. 1:4 B.2:3 C.1:3 D.1:2考点:相似三角形的判定与性质;三角形中位线定理.菁优网版权所有解析:根据三角形的中位线得出DE∥BC,DE=BC,根据平行线的性质得出相似,根据相似三角形的性质求出即可.解:∵BE和CD是△ABC的中线,∴DE=BC,DE∥BC,∴=,△DOE∞△COB,∴=()2=()2=,答案:A5.计算(﹣xy2)3,结果正确的是()A.x2y4B.﹣x3y6C.x3y6D.﹣x3y5考点:幂的乘方与积的乘方.菁优网版权所有解析:根据积的乘方的性质进行计算,然后再选取答案.原式=﹣()3x3y6=﹣x3y6.答案:B6.在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是()A. 18,18,1 B.18,17.5,3 C.18,18,3 D.18,17.5,1考点:方差;折线统计图;中位数;众数.菁优网版权所有解析:根据众数、中位数的定义和方差公式分别进行解答即可.这组数据18出现的次数最多,出现了3次,则这组数据的众数是18;把这组数据从小到大排列,最中间两个数的平均数是(18+18)÷2=18,则中位数是18;这组数据的平均数是:(17×2+18×3+20)÷6=18,则方差是:[2×(17﹣18)2+3×(18﹣18)2+(20﹣18)2]=1;答案:A7.如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()A. 100米B.50米C.米D.50米考点:解直角三角形的应用.菁优网版权所有解析:过B作BM⊥AD,根据三角形内角与外角的关系可得∠ABC=30°,再根据等角对等边可得BC=AC,然后再计算出∠CBM的度数,进而得到CM长,最后利用勾股定理可得答案.解:过B作BM⊥AD,∵∠BAD=30°,∠BCD=60°,∴∠ABC=30°,∴AC=CB=100米,∵BM⊥AD,∴∠BMC=90°,∴∠CBM=30°,∴CM=BC=50米,∴BD==50米,答案:B8.关于反比例函数y=的图象,下列说法正确的是()A.图象经过点(1,1)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.当x<0时,y随x的增大而减小考点:反比例函数的性质.菁优网版权所有解析:根据反比例函数的性质,k=2>0,函数位于一、三象限,在每一象限y随x的增大而减小.A、把点(1,1)代入反比例函数y=得2≠1不成立,答案:项错误;B、∵k=2>0,∴它的图象在第一、三象限,答案:项错误;C、图象的两个分支关于y=﹣x对称,故错误.D、当x>0时,y随x的增大而减小,答案:项正确.答案:D9.在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是()A.AE∥BC B.∠ADE=∠BDCC.△BDE是等边三角形D.△ADE的周长是9考点:旋转的性质;等边三角形的性质.菁优网版权所有解析:首先由旋转的性质可知∠AED=∠ABC=60°,所以看得AE∥BC,先由△ABC是等边三角形得出AC=AB=BC=5,根据图形旋转的性质得出AE=CD,BD=BE,故可得出AE+AD=AD+CD=AC=5,由∠EBD=60°,BE=BD即可判断出△BDE是等边三角形,故DE=BD=4,故△AED的周长=AE+AD+DE=AC+BD=9,问题得解.解:∵△ABC是等边三角形,∴∠ABC=∠C=60°,∵将△BCD绕点B逆时针旋转60°,得到△BAE,∴∠AEB=∠C=60°,∴AE∥BC,答案:项A正确;∵△ABC是等边三角形,∴AC=AB=BC=5,∵△BAE△BCD逆时针旋旋转60°得出,∴AE=CD,BD=BE,∠EBD=60°,∴AE+AD=AD+CD=AC=5,∵∠EBD=60°,BE=BD,∴△BDE是等边三角形,答案:项C正确;∴DE=BD=4,∴△AED的周长=AE+AD+DE=AC+BD=9,答案:项D正确;而选项B没有条件证明∠ADE=∠BDC,∴结论错误的是B,答案:B10.某通讯公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80分钟通话时间,超过80分钟的部分,以每分钟0.15元的价格计费.下列结论:①如图描述的是方式1的收费方法;②若月通话时间少于240分钟,选择方式2省钱;③若月通讯费为50元,则方式1比方式2的通话时间多;④若方式1比方式2的通讯费多10元,则方式1比方式2的通话时间多100分钟.其中正确的是()A.只有①②B.只有③④C.只有①②③D.①②③④考点:一次函数的应用.菁优网版权所有解析:根据题意得:方式一的函数解析式为y=0.1x+20,方式二的函数解析式为y=0.15x+8,①当x=80时,方式一的收费是28元,故①说法正确;②0.1x+20>0.15x+8,解得x<240,故②的说法正确;③当y=50元时,方式一0.1x+20=50,解得x=300分钟,方式二0.15x+8=50,解得x=280分钟,故③说法正确;④0.1x+20﹣0.15x﹣8=10,解得x=40,故④说法错误;答案:C二、填空题(每小题3分,共18分)11.计算:|﹣3|++(﹣1)0= .考点:实数的运算;零指数幂.菁优网版权所有解析:原式第一项利用绝对值的代数意义化简,第二项利用立方根定义化简,最后一项利用零指数幂法则计算即可得到结果.原式=3﹣2+1=2.答案:2.12.不等式组的解集是.考点:解一元一次不等式组.菁优网版权所有解析:分别求出各不等式的解集,再求出其公共解集即可.解:,由①得x≤1,由②得x>﹣1,故此不等式的解集为:﹣1<x≤2.答案:﹣1<x≤2.13.将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为度.考点:三角形内角和定理;平行线的性质.菁优网版权所有解析:根据三角形三内角之和等于180°求解.解:如图.∵∠3=60°,∠4=45°,∴∠1=∠5=180°﹣∠3﹣∠4=75°.答案:75.14.某小区2010年屋顶绿化面积为2000平方米,计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是.考点:一元二次方程的应用.菁优网版权所有解析:本题需先设出这个增长率是x,再根据已知条件找出等量关系列出方程,求出x 的值,即可得出答案.解:设这个增长率是x,根据题意得:2000×(1+x)2=2880解得:x1=20%,x2=﹣220%(舍去)答案:20%.15.圆锥的底面半径是2cm,母线长6cm,则这个圆锥侧面展开图的扇形圆心角度数为___________度.考点:圆锥的计算.菁优网版权所有解析:根据展开图的扇形的弧长等于圆锥底面周长计算.解:∵圆锥的底面半径是2cm,∴圆锥的底面周长为4π,设圆心角为n°,根据题意得:=4π,解得n=120.答案:120.16.如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:①当x=1时,点P是正方形ABCD的中心;②当x=时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的是(写出所有正确判断的序号).考点:翻折变换(折叠问题);正方形的性质.菁优网版权所有解析:(1)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,∴△BEF和△三DGH是等腰直角三角形,∴当AE=1时,重合点P是BD的中点,∴点P是正方形ABCD的中心;故①结论正确,(2)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,∴△BEF∽△BAC,∵x=,∴BE=2﹣=,∴=,即=,∴EF=AC,同理,GH=AC,∴EF+GH=AC,故②结论错误,(3)六边形AEFCHG面积=正方形ABCD的面积﹣△EBF的面积﹣△GDH的面积.∵A E=x,∴六边形AEFCHG面积=22﹣BE•BF﹣GD•HD=4﹣×(2﹣x)•(2﹣x)﹣x•x=﹣x2+2x+2=﹣(x﹣1)2+3,∴六边形AEFCHG面积的最大值是3,故③结论错误,(4)当0<x<2时,∵EF+GH=AC,六边形AEFCHG周长=AE+EF+FC+CH++HG+AG=(AE+CF)+(FC+AG)+(EF+GH)=2+2+2=4+2故六边形AEFCHG周长的值不变,故④结论正确.答案:①④.三、解答题(共72分)17.先简化,再求值:(﹣)+,其中a=+1.考点:分式的化简求值.菁优网版权所有解析:原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,将a的值代入计算即可求出值.解:原式=•(a+1)(a﹣1)=a2﹣3a,当a=+1时,原式=3+2﹣3﹣3=﹣.18.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.(1)求证:△ABM≌△DCM;(2)填空:当AB:AD= 时,四边形MENF是正方形.考点:矩形的性质;全等三角形的判定与性质;正方形的判定.菁优网版权所有解析:(1)根据矩形性质得出AB=DC,∠A=∠D=90°,根据全等三角形的判定推出即可;(2)求出四边形MENF是平行四边形,求出∠BMC=90°和ME=MF,根据正方形的判定推出即可.(1)证明:∵四边形ABCD是矩形,∴AB=DC,∠A=∠D=90°,∵M为AD的中点,∴AM=DM,在△ABM和△DCM中∴△ABM≌△DCM(SAS).(2)解:当AB:AD=1:2时,四边形MENF是正方形,理由是:∵AB:AD=1:2,AM=DM,AB=CD,∴AB=AM=DM=DC,∵∠A=∠D=90°,∴∠ABM=∠AMB=∠DMC=∠DCM=45°,∴∠BMC=90°,∵四边形ABCD是正方形,∴∠ABC=∠DCB=90°,∴∠MBC=∠MCB=45°,∴BM=CM,∵N、E、F分别是BC、BM、CM的中点,∴BE=CF,ME=MF,NF∥BM,NE∥CM,∴四边形MENF是平行四边形,∵ME=MF,∠BMC=90°,∴四边形MENF是正方形,即当AB:AD=1:2时,四边形MENF是正方形,答案:1:2.19.近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表:(1)表中m的值为,n的值为;(2)补全条形统计图;(3)若该校九年级有学生500名,估计该校大约有多少名毕业生的升学意向是职业高中?考点:条形统计图;用样本估计总体;统计表.菁优网版权所有解析:(1)由省级示范高中人数除以占的百分比得到总学生数,确定出m的值;进而确定出职业高中学生数,求出占的百分比,确定出n的值;(2)补全条形统计图,如图所示;(3)由职业高中的百分比乘以500即可得到结果.解:(1)根据题意得:15÷25%=60(人),即m=60,职业高中人数为60﹣(15+15+9+3)=18(人),占的百分比为18÷60×100%=30%,则n=1﹣(25%+25%+30%+5%)=15%;答案:60;15%;(2)补全条形统计图,如图所示:(3)根据题意得:500×30%=150(名),则估计该校大约有150名毕业生的升学意向是职业高中.20.某市区一条主要街道的改造工程有甲、乙两个工程队投标.经测算:若由两个工程队合做,12天恰好完成;若两个队合做9天后,剩下的由甲队单独完成,还需5天时间,现需从这两个工程队中选出一个队单独完成,从缩短工期角度考虑,你认为应该选择哪个队?为什么?考点:分式方程的应用.菁优网版权所有解析:设甲队单独完成工程需x天,则甲队的工作效率为,等量关系:甲乙9天的工作量+甲5天的工作量=1,可得方程,解出即可.解:设甲队单独完成工程需x天,由题意,得:×9+×5=1,解得:x=20,经检验得:x=20是方程的解,∵﹣=,∴乙单独完成工程需30天,∵20<30,∴从缩短工期角度考虑,应该选择甲队.21.四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.考点:列表法与树状图法.菁优网版权所有解析:由四张扑克牌的牌面是5的有2种情况,不是5的也有2种情况,可求得方案A 中,小亮获胜的概率;首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小亮获胜的情况,再利用概率公式即可求得答案;比较其大小,即可求得答案.解:小亮选择A方案,使他获胜的可能性较大.方案A:∵四张扑克牌的牌面是5的有2种情况,不是5的也有2种情况,∴P(小亮获胜)==;方案B:画树状图得:∵共有12种等可能的结果,两张牌面数字之和为偶数的有4种情况,不是偶数的有8种情况,∴P(小亮获胜)==;∴小亮选择A方案,使他获胜的可能性较大.22.如图,⊙O中,点C为的中点,∠ACB=120°,OC的延长线与AD交于点D,且∠D=∠B.(1)求证:AD与⊙O相切;(2)若点C到弦AB的距离为2,求弦AB的长.考点:切线的判定;解直角三角形.菁优网版权所有解析:(1)连接OA,由=,得CA=CB,根据题意可得出∠O=60°,从而得出∠OAD=90°,则AD与⊙O相切;(2)设OC交AB于点E,由题意得OC⊥AB,求得CE=2,Rt△BCE中,由三角函数得BE=2,即可得出AB的长.(1)证明:如图,连接OA,∵=,∴CA=CB,又∵∠ACB=120°,∴∠B=30°,∴∠O=2∠B=60°,∵∠D=∠B=30°,∴∠OAD=180°﹣(∠O+∠D)=90°,∴AD与⊙O相切;(2)解:设OC交AB于点E,由题意得OC⊥AB,∴CE=2,在Rt△BCE中,BE==2×=2.∴AB=2BE=4.23.楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么月需售出多少辆汽车?(注:销售利润=销售价﹣进价)考点:一元二次方程的应用;分段函数.菁优网版权所有解析:(1)根据分段函数可以表示出当0<x≤5,5<x≤30时由销售数量与进价的关系就可以得出结论;(2)由销售利润=销售价﹣进价,由(1)的解析式建立方程就可以求出结论.解:(1)由题意,得当0<x≤5时y=30.当5<x≤30时,y=30﹣0.1(x﹣5)=﹣0.1x+30.5.∴y=;(2)当0<x≤5时,(32﹣30)×5=10<25,不符合题意,当5<x≤30时,[32﹣(﹣0.1x+30.5)]x=25,解得:x1=﹣25(舍去),x2=10.答:该月需售出10辆汽车.24.已知两条平行线l1、l2之间的距离为6,截线CD分别交l1、l2于C、D两点,一直角的顶点P在线段CD上运动(点P不与点C、D重合),直角的两边分别交l1、l2与A、B两点.(1)操作发现如图1,过点P作直线l3∥l1,作PE⊥l1,点E是垂足,过点B作BF⊥l3,点F是垂足.此时,小明认为△PEA∽△PFB,你同意吗?为什么?(2)猜想论证将直角∠APB从图1的位置开始,绕点P顺时针旋转,在这一过程中,试观察、猜想:当AE满足什么条件时,以点P、A、B为顶点的三角形是等腰三角形?在图2中画出图形,证明你的猜想.(3)延伸探究在(2)的条件下,当截线CD与直线l1所夹的钝角为150°时,设CP=x,试探究:是否存在实数x,使△PAB的边AB的长为4?请说明理由.考点:几何变换综合题.菁优网版权所有解析:(1)根据题意得到:∠EPA+∠APF=90°,∠FPB+∠APF=90°,从而得到∠EPA=∠FPB,然后根据∠PEA=∠PFB=90°证得△PEA∽△PFB;(2)根据∠APB=90°得到要使△PAB为等腰三角形,只能是PA=PB,然后根据当AE=BF 时,PA=PB,从而得到△PEA≌△PFB,利用全等三角形的性质证得结论即可;(3)在Rt△PEC中,CP=x,∠PCE=30°从而得到PE=x,然后利用PE+BF=6,BF=AE 得到AE=6﹣x,然后利用勾股定理得到PE2+AE2=PA2,代入整理后得到一元二次方程x2﹣12x﹣8=0,求得x的值后大于12,从而得到矛盾说明不存在满足条件的x.解:(1)如图(1),由题意,得:∠EPA+∠APF=90°,∠FPB+∠APF=90°,∴∠EPA=∠FPB,又∵∠PEA=∠PFB=90°,∴△PEA∽△PFB;(2)证明:如图2,∵∠APB=90°,∴要使△P AB为等腰三角形,只能是PA=PB,当AE=BF时,PA=PB,∵∠EPA=∠FPB,∠PEA=∠PFB=90°,AE=BF,∴△PEA≌△PFB,∴PA=PB;(3)如图2,在Rt△PEC中,CP=x,∠PCE=30°,∴PE=x,由题意,PE+BF=6,BF=AE,∴AE=6﹣x,当AB=4时,由题意得PA=2,Rt△PEA中,PE2+AE2=PA2,即()2+(6﹣x)2=40,整理得:x2﹣12x﹣8=0,解得:x=6﹣2<0(舍去)或x=6+2,∵x=6+2>6+6=12,又CD=12,∴点P在CD的延长线上,这与点P在线段CD上运动相矛盾,∴不合题意,综上,不存在满足条件的实数x.25.平面直角坐标系中,四边形ABCD是菱形,点C的坐标为(﹣3,4),点A在x轴的正半轴上,O为坐标原点,连接OB,抛物线y=ax2+bx+c经过C、O、A三点.(1)直接写出这条抛物线的解析式;(2)如图1,对于所求抛物线对称轴上的一点E,设△EBO的面积为S1,菱形ABCD的面积为S2,当S1≤S2时,求点E的纵坐标n的取值范围;(3)如图2,D(0,﹣)为y轴上一点,连接AD,动点P从点O出发,以个单位/秒的速度沿OB方向运动,1秒后,动点Q从O出发,以2个单位/秒的速度沿折线O﹣A﹣B 方向运动,设点P运动时间为t秒(0<t<6),是否存在实数t,使得以P、Q、B为顶点的三角形与△ADO相似?若存在,求出相应的t值;若不存在,请说明理由.考点:二次函数综合题.菁优网版权所有解析:(1)求得菱形的边长,则A的坐标可以求得,然后利用待定系数法即可求得函数的解析式;(2)首先求得菱形的面积,即可求得S1的范围,当S1取得最大值时即可求得直线的解析式,则n的值的范围即可求得;(3)分当1<t<3.5时和3.5≤t≤6时两种情况进行讨论,依据相似三角形的对应边的比相等,即可列方程求解.解:(1)根据题意得:,解得:,则抛物线的解析式是:y=x2﹣x;(2)设BC与y轴相交于点G,则S2=OG•BC=20,∴S1≤5,又OB所在直线的解析式是y=2x,OB==2,∴当S1=5时,△EBO的OB边上的高是.如图1,设平行于OB的直线为y=2x+b,则它与y轴的交点为M(0,b),与抛物线对称轴x=交于点E(,n).过点O作ON⊥ME,点N为垂足,若ON=,由△MNO∽△OGB,得OM=5,∴y=2x﹣5,由,解得:y=0,即E的坐标是(,0).∵与OB平行且到OB的距离是的直线有两条.∴由对称性可得另一条直线的解析式是:y=2x+5.则E′的坐标是(,10).由题意得得,n的取值范围是:0≤n≤10且n≠5.(3)如图2,动点P、Q按题意运动时,当1<t<3.5时,OP=t,BP=2﹣t,OQ=2(t﹣1),连接QP,当QP⊥OP时,有=,∴PQ=(t﹣1),若=,则有=,又∵∠QPB=∠DOA=90°,∴△BPQ∽△AOD,此时,PB=2PQ,即2﹣t=(t﹣1),10﹣t=8(t﹣1),∴t=2;当3.5≤t≤6时,QB=10﹣2(t﹣1)=12﹣2t,连接QP.若QP⊥BP,则有∠PBQ=∠ODA,又∵∠QPB=∠AOD=90°,∴△BPQ∽△DOA,此时,PB=PB,即12﹣2t=(2﹣t),12﹣2t=10﹣t,∴t=2(不合题意,舍去).若QP⊥BQ,则△BPQ∽△DAO,此时,PB=BQ,即2﹣t=(12﹣2t),2﹣t=12﹣2t,解得:t=.则t的值为2或.。
湖北省随县2015届初中数学毕业生学业水平能力测试暨升学适应.

湖北省随县2015届初中数学毕业生学业水平能力测试暨升学适应性考试试题机密*启用苗随>2013年利中毕业生罕业朮平能力测试螢升芋逢皿性考试数学试題注宜事项:I芋笔前,专虫爭处將金巴芍社主M甘订奇填石衣貳题靈利體减卡上+捋豁沦才逞養序珂整福农答趨卡上的拾定注苣-九时林酯若隶都用0」基報盟巴賛字笔直快各從苦建卡上对应醇苦痺医疑內二苦莊蛊观蕊上无盘“3.考生融類泾持备變卡的荃賦.希试桔朿后,请将本试題班和备疫卡一舟上更,一■、选择分.共如分}L下列运釁止備的是f )A- □;* *jt3z J£S R. JC**±A=£C2.如果甘式扌;;;的值为Q •则的值肥()Al B.4 C3.如朗.□知HEf AC,團屮釉/ C相寺的拾£(随县•敌学试西第1页(共4页)D. ±14.如图’中H仆别足ZMC的中点侧耳肿H AA.li 2B.b 3C. it 4>苦去于工円一元一状厅却卅- h-1 =◎有两个不相予旳戈包艰,IB;戈:数飪円承直叶甬尼(}A.JL> - I R. i <1 £Lt^0 C. - I 且丄护0 D.Jt> - I £.fc?£Q&- •张卓子上崔故着若T个卿子*以二牛肓向上看―种现图即卜屈所示侧这弹桌子上艾石球子肌◎◎Oo oO;:住¥扎石个G 12牛IX 17 牛D Z/3BJ?D.2t 37*亍休制瓯在一次采』:中同耐丈出两帯上虬毎佇那订畑 元出帕咼按戍相|■笫英中一 件蛊利25%T J5件右本笳%'则这京买卖中他(}扎不略不mt 曲略9元&年1$元 D.聃岱元乳如图*有一圆心甬为12U 。
,半卅怏沟Em 的扇形,科朴招亜音后围成一岡惟罰曲.瑯 么S1«E的盘是〔 )扎B. -/'SJimC2r'gniD*2^3VE虫小离从家U 口骑车£单隹匕IL 先走T 路刘达盒扎再走上坡齬创达 卜氏,, 虑E,最厉謳下坡路到这丄非甲位,所用的时间与跻稈的关托如图斯 _____________________________示-下班岭•如呆他沽匣路返回•且走平路、上独路、下坡路的極度分[2 駅聚持列上班时色*捧虫他从单位御家门u 霍幣的时回杲()匕# L12井帥R.15曲和iC.25^钟D.27井钟10如图,已知点4的坐标为(訂.3 KABlx 轴.垂足为阻连搖厲仮比因丙] 魏丁二⑴的阳虻线淮 叽個分划交干点匸及十価二3肋型 \ :! 点丄为岡心,心的■壬借的丘为半径作FH.麵谨圆与廿轴的宜遇艾条& 八匕f f \\O B __总相离山相切二殖空盘(毎小題了分,井駡井] 押分解因式:^-^ =呛-懈址计血北省鲫4 V I 〔业生产总直突破4万亿亓JI 附学记如珈为 ______________ 7T一计算心• ; j "-3uM a + (l -血严- . 1斗』间*巳知甬数严怠+ 2与甫数尸耐-4的際&交十点血根翩歩可知不等式fcf+2< FTW-d 的解集昱15-如图,AAEC 瞬点A 咽时托吐转45嘲到也刖■芒帛・9tT f AH -AC-2 T Ml£l 屮阴戲琲心窗先伽耐徐吟耳誉心+曲亠底甌县+数学址題 带2页(共4页)分的面觀等于_______________ ■J6.加图,用围摂了按h 商的如tt 摆團形侧摆第n 牛图形需要词抿丁的枚数呆三踊答罢(共9玄題,及分)LIJLU^ 定i 艮简分呷忆两名学•土和宇仲打一篇字的立罩与乙扌】一篇彌 宇的文卒所 用的时间柏同启如甲毎分铀比乙母分怦务扎5个宇顾甲、乙网人每舲事打寧少宇219.(7分》如因,00的半廉为4T B 是OO 外一点,连楼阳,且朋"「过点B 玮的切绒出""切点为认延绘UO 交观丁点儿过点兀作切建BD 的 垂线*旻JL 为C (丄)草证:AP 平分£的门 (即求越;谊(20, (7分)菜稅逡鬥-交通安金卿识"直怜培训后逋齐了 ■次圖试’怙牛Z 分授标唯期分育不 合幡冶船浪好、优脊聊个竽紙沟了輕全校的石试情况.狀在校的学牛随机紬样闊査•醤 闻如1圉⑴所示的-东琢卄国'希合统计團回答卜一列问題:(对抽样小不合洛的人融是 ________ 人,占彼调杏人敦的TT 分比是 _________(盯若已知该校九彳1级冇学生50Q^,ffl (2)是各勺製人数占全桩人数百分比的闻羽罔 ■:'圈中岡心角粧爭分),淆祢怙H 全H 优良(良如与优秀}的人数约右需少人?刘.(了分)期I 图是-秤鞘椅及其简住芽构示直圉•扶手*45与座板仞 都平齐十地面,靠背DM 屯也架血Y 行血文架他打后乂架阳分别屯 仙兗丁点&和点D.a 七IWW 处丁点 A . S 得乙就加‘二別4*’r ODC = 3U\U> = 4(kni 』G = 3Utm.(□求两支架卿点E 』之问的距离;⑵若血V-60cm’求躺榆时高度(点間创地面的距牌盘果取整数). (券石散Ifiisin 时七、曲3 ・;,ian6C fi -/3-l +73)I(H 谏校拙样碉誉的于生人数沟D C处-门分}四孤虞地甜同的卡片妁周听录,捋卡片洗匀冇,背呵期上畝 肾在皇血匕(丄)求菠机瞬 张卡片,恰刘褂到数字去的軽率§(打小川和小品更用以上艸素F 片做游題*掘戏燜團庇怙息曲.你 认为这个游戏公平码?请用列表达或倉树務图袪说明理由.若 认为不鱼平"请垛憧收规則,偿辭我空褂公平-23.临分)如图.在矩形旣片ABCD 屮,屈=3 r BC=4.把A 战;0帘对甬线HD 折叠■使点C 落 在底处立肋十点F.⑴康血心网(2)求tan 丄一迪F 的值】【3)達fiHU 交脈十点硏求侦的托加.莎)菜商场要经件•种新上巾的立氏”逬价为划元/件.试杵期阶段加现;当销售单 榆足25元时,每天的错棒量为250 fh 销恃单析每上注1元,毎天的销悴量就恥闪杵一(1)巧出曲场捫俘逮种文rv 撷大和省的钳售划洞«(JL )与销售单悅巩九)之间前函魏关 帝式匚(2)求销售单价为多少」L 时*该文具何大的销習利涧燉大;(站商场的昔谓祁结台丄述情况"樹出r kP 两种营谓方秦;方案A :陵丈具的钳皆单价髙丁进析瓦不)1过30皿方秦职毎天谓店呈不少f io rr 口每件文只的和涧至少为巧元- 审比校哪种方案的最大利侗吏高•井说明理di.25.(13分)如图,在平面虫角坐标杲屮.抛^y = f ^+^+c (f ^Q )的张点为占柑」),且过 ^4(0-2).育裁y=x 与抛物线交十点D 風也E 在对称轴的右圖)•拋物罐的对称轴交育 线工=£于点:交務轴于点A EF 丄乂牠.垂圧为点只心卩也拋物罐上,且侦于对稀轴刖 右値,把《丄卫轴.垂足为点皿为寺边二甬骸d )求谏籬物戟的套达式中 (2)求点F 的坐标:(SJCWUWCL -L , ii-.*并说明理由*⑷违楼皿Uii 轴3耐的右测是否仔Ti —点w 淮庖cwv 与△即E 全等?若存往,试 求山点声的聿标:若不■存在,请说明理由.「 |/ \彳 r<i w & X萌奥*敷学试题 界4页(共4厦)3T«!<M 、fTFi.押“石活.乙 ! fa j r2tl.此*日藏灯%.aJk£J CA Jit.ft - 生U 片上苗短生牛Mhi ■吕随县2015年初中毕业生学业水平能力测试暨升学适应性考试数学试题参考答案、填空题(每小题3分,共18分)11. m( n+3) (m—3)12. 4x 101213.-3 3 - 214. x v—315. 2 2-216. 6n—1三、解答题(共72分)17.(本题满分6分)解:原式(a b)(a—b) 2 2亠2ab-b -a(a b)(a -b) aa _(a _b)2a b—b -a .把a = 1 ■ 2 , b =1 - 2代入得a b= 2 2= _ 2............................... 6 分b-a 1 - ”2-1-、2 218.(本题满分6分)解:设甲每分钟打x个字,则乙每分钟打(x —5)个字,依题意得:1分1000 900 八x x -5解得:x = 50 .经检验x = 50是方程的解.4分x —5= 45.答:甲每分钟打50个字,乙每分钟打45个字.19.(本题满分7分)(1) 证明:(1)证明:连接0D••• BD是O 0的切线,•••ODL BD ..................................... 1 分••• AC L BD•0D// AC:丄2=1 3, ............................... 2 分•••0AOD:丄仁/3, ............................... 3分•••/ 仁/2,即AD平分/ BAC .................................. 4分(2)解:T OD/ AC•••△BOD^A BAC ................................ 5 分•OD = BOAC BA '• 4 _ 6 ............................"AC 10,20解得:AO20 . .................320. (本题满分7分)(1)50,良好. .....................(2)8, 16%.抽样中不及格的人数是8人.占被调查人数的百分比是16% ......... 4分4(3)解:500- = 1500 , ................... 5 分12281500 X =840 (人). ................ 6 分50所以全校优良的人数大约有840人. ..................... 7分21. (本题满分7分)解:(1)连接EF.•••CD平行于地面,•GD/ EF.•OG _ OG = GD OE OG EG EF又• AB// EF,19.(本题满分7分)••• AB// CD而 OE/ DM则四边形OGD 是平行四边形. ........................ 1分 •OGDN GDON•••ON=40cm / EOI =90°,Z ODC 30 ° ,1 • GD=40cm OG —.2GD 20cm,又 EG=30cm,• EF = 100 ( cm ).(2)延长 MD 交EF 于点 H 过点 M 作MPL EF 于点P. •••四边形ONH 是平行四边形,• NH=OE=50cm, / MH F / E = 60°.由于 MN= 60cm •- MH= 110cm.在 Rt △ MHP 中, MP= MH in / MHP ........................亦即 MP =110sin60 ° = 110 x ' = 55x 1.73 〜95(cm) 2答:躺椅的高度约为 95cm. ............................. 7分22. (本题满分7分)2 1解:(1) P (抽到 2)= — = _................. 2 分4 2(2)不公平 ................... 1分 根据题意可画如下树形图:抽 2 2 3 6_ a a //\\ a第一庆抽 2236223^ 22 36 2236............. 3分(用列表法参照给分)从树状图可以看出所有可能结果共有16种,符合条件的有10种,10 5• P (两位数不超过 32 )=—=—,16 8•游戏不公平•................. 5分20 20 3040 EF可按如下方法调整规则:方案一:将游戏规则中的32换成26〜31 (包括26和31)之间的任何一个数都能使游戏公平;方案二:游戏规则改为:抽到的两位数不超过32的得3分,抽到的两位数不超过的得5分,能使游戏公平;方案三:游戏规则改为:组成的两位数中,若个位数字是2,小贝胜,反之小晶胜•................ 5分(答一条即可,只要合理均可给分)23. (本题满分8分)(1)证明:••• △EBD是由厶CBD折叠而得,••• ED= DC BE= BC;............................ 1 分•••四边形ABCD!矩形,•AB=CD / BAD-Z BED- 90°•ED- AB 而Z EFD=Z AFD•△AFB^A EFD•AF= EF ................................... 2 分(2 )设AF= x•/AB=3, BC=BE=4, AF= EFBF= 4—x•••Z BAF= 90°•…丁二<7 .................................. 3 分x2+32=(4 —x)2• x=787tan Z ABF=AF——8=7................ 4分AB324(3)•••四边形ABCD^矩形,• Z BAD- 90°, AD/ BC•AC=」『卞•△AGF^ A CGB32AF AG Be - GC设 AG = m 则 CG = 5- m24. (本题满分11分) 解:(1)由题意得,销售量=250- 10 (x — 25)=- IO x +500, .............................. 1 分则 w =( x - 20) (- 10X +500) =-10x 2+700x - 10000; (3 分)2 2(2) w =- 10x +700x -10000 = - 10 (x -35) +2250....................•••—10v 0,.••函数图象开口向下, w 有最大值,当x = 35时,w max = 2250,故当单价为35元时,该文具每天的利润最大.............................. 6分(3) A 方案利润高.理由如下:A 方案中:20v x < 30,故当x = 30时,w 有最大值, 此时 W A = 2000;................ 8 分B 方案中:『-10x +500> 10 ,x - 20> 25故x 的取值范围为:45< x < 49,•.•函数 w =- 10 (x -35) +2250,对称轴为 x = 35, .•.当x = 45时,w 有最大值, 此时 W B = 1250, ( 10 分) ■/ w > w , ••• A 方案利润更高. ................ 11分25. (本题满分13分)解之得:m =35,即 AG=色39 392解:(1 )•••抛物线y = ax bx c(^J 0)的顶点为B(2, 1),x 2 = 4 -2(2y 2 = 4 - 2 •. 2•••可设抛物线的解析式为 y = a(x _2)2 • 1.2 1将 A (0, 2)代入,得 2 =a(0 -2)2 1,解得 a . 4•该抛物线的表达式 y =J (x _2)2 • 1. .............................. 2分 4(2)将 x =2代入 y =x ,得 y =2 ,•点C 的坐标为(2, 2),即CG 2.•••△ PCM 为等边三角形,•/ CMP 60°, CMPM I••• PMLx 轴,,CM =30° • CM 4, GM2 ... 3. •0M2 2 .. 3 , PM=4. •••点P 的坐标为(2 2 3,4)(3)相等.理由如下:联立y = x 禾口 y 1 2 =—(x — 2) +1 得* 4 y = x1(x -2)21,4 ••• x 2 =4 - 2 •一 2 2不合题意,舍去,• EF =4 2,2,点 E 的坐标为(4 • 2・,2 , 4 2 2 ) . ........ 6 分 •- OE 」EF 2 OF 2 =4 2 2又••• OC = J CG 2 OG 2 = 2 2 ,• CE =OE -OC =4 4、2-2、、2 =4 2 2. •CE=EF(4)不存在.理由如下: 10分假设在x 轴上点M 的右侧存在一点N ,使厶CMN2 △ CPE 贝U CN t CE, / MCN / PCE 10分•••/ MCP 60。
2024年湖北省随县中考适应性考试数学试题(含答案)
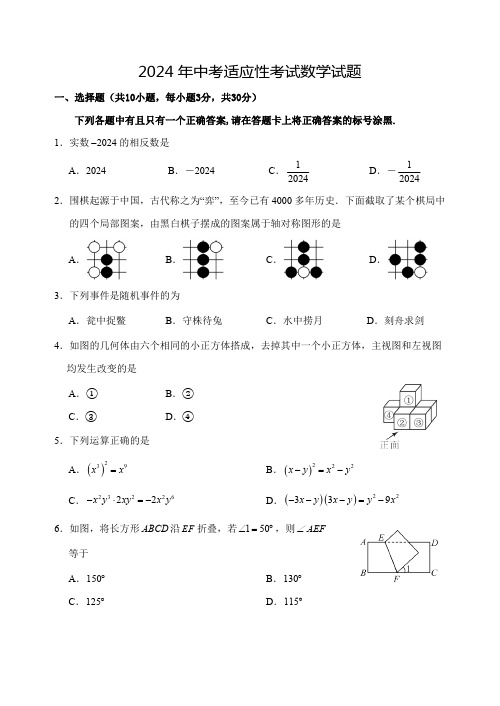
2024年中考适应性考试数学试题一、选择题(共10小题,每小题3分,共30分)下列各题中有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.1.实数的相反数是A .2024B .-2024C .D .-2.围棋起源于中国,古代称之为“弈”,至今已有4000多年历史.下面截取了某个棋局中的四个局部图案,由黑白棋子摆成的图案属于轴对称图形的是A .B .C .D .3.下列事件是随机事件的为A .瓮中捉鳖B .守株待兔C .水中捞月D .刻舟求剑4.如图的几何体由六个相同的小正方体搭成,去掉其中一个小正方体,主视图和左视图均发生改变的是A .①B .②C .③D .④5.下列运算正确的是A .B .C .D .6.如图,将长方形沿折叠,若,则等于A .B .C . D.2024-1202412024()239x x =()222x y x y -=-2322622x y xy x y -⋅=-()()22339x y x y y x ---=-ABCD EF 150∠=︒AEF∠150︒130︒125︒115︒7.通常情况下酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.一次化学课上,学生用酚酞溶液检测四瓶标签被污染无法分辨的无色溶液的酸碱性.已知四瓶溶液分别是A :盐酸(呈酸性),B :硝酸钾溶液(呈中性),C :氢氧化钠溶液(呈碱性),D :氢氧化钾溶液(呈碱性).小周将任选的两瓶溶液滴入酚酞溶液进行检测,则两瓶溶液恰好都变红色的概率是A. B . C . D .8.学校举行篮球比赛.图中的四个点分别描述了甲、乙、丙、丁四位同学投篮的命中率y (投进的次数占尝试投篮次数的百分率)与尝试投篮次数x 的情况,其中所有投进的球记2分,描述乙、丁两位同学情况的点恰好在同一个反比例函数的图像上,则投篮得分最多的是A .甲 B .乙 C .丙 D .丁9.在边长为1的正五边形内,所有到点的距离大于且到点的距离小于1的点组成图形的面积是A .B .C .D .10.下列不可能是函数图象的是AB C D 二、填空题(共6小题,每小题3分,共18分)下列各题不需要写出解答过程,请将结果直接填写在答题卡指定的位置.121416112ABCDE A C 1072cos π-1072sin π- 3023π-3043π-c bx ax y ++=211.2024年全国新注册登记的新能源汽车预计约有1335万辆,将数据1335万用科学记数法表示为 .12.写出一个图象经过第一、二、四象限的一次函数解析式是 .13.化简的结果是 .14.2024年4月25日20时59分,运载火箭托举着神舟十八号载人飞船,在酒泉卫星发射中心点火升空,送航天员奔赴“天宫”.如图,神舟十八号载人飞船从地面O 处成功发射,当飞船到达点A 时,地面D 处的雷达站测得AD =4000米,仰角为37°,0.3秒后,飞船直线上升到达点B 处,此时地面C 处的雷达站测得B 处的仰角为45°,点O ,C ,D 在同一直线上,已知C ,D 两处相距460米,则飞船从A 到B 处的平均速度为 米/秒.(结果精确到1米;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)15.已知抛物线与轴的两交点的横坐标为m ,n ,满足.下列结论:①;②若,当时,随的增大而减小;③若有一个根是大于的负数,则;④.其中正确的结论是________.(填写序号)16.如图,在中,分别是边上的点,且.则的最大值是 .2211++-x x x x c bx ax y ++=2x n m <<<-010>+-c b a 0>a 21-<x y x 01))((=---n x m x a m a ac b 442-<-0))(2(2>-+--c a c b a ab a ABC ∆E D ,AB BC ,DAC EDA B ∠=∠=∠ABC ADE S S ∆∆三、解答题(共8小题,共72分)下列各题需要在答题卡指定的位置写出文字说明、证明过程、演算步骤或画出图形.17.(本小题满分8分)求满足不等式组的整数解.18.(本小题满分8分)如图,在平行四边形中,点E ,F ,G ,H 分别在边AB ,BC ,CD ,DA 上,且.(1)求证:≌;(2)请添加一个条件,使四边形为矩形(不需说明理由).19.(本小题满分8分)为了解武汉市初中生每周锻炼身体的时长t (单位:小时)的情况,在武汉市随机抽取部分初中生进行调查,按五个组别:A 组(3t <4),B 组(4t <5),C 组(5t <6),D 组(6t <7),E 组(7t <8)进行整理,绘制如下两幅不完整的统计图.所抽取学生周锻炼时长的频数直方图 所抽取学生周锻炼时长的扇形统计图(1)这次抽样调查的样本容量为______;≤≤≤≤≤21135x x x +<-⎧⎨+≥⎩①②ABCD ,AE CG BF DH ==AEH ∆CGF ∆EFGH(2)抽取的样本中,每周锻炼身体时长的中位数落在______组,A 组所在扇形的圆心角大小是______;(3)若武汉市共有250000名初中生,请估计每周锻炼时间不低于6小时的学生人数.20.(本小题满分8分)如图,AC 是⊙O 的弦,OD ⟂AC ,连接OA ,OC ,点B 在⊙O 外,AB=AC ,连接BC 交OD 于E ,交OA 于F ,.(1)求证:AB 是⊙O 的切线;(2)若,,求⊙O 的半径.21.(本小题满分8分)如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,A ,B ,C 都是格点.仅用无刻度的直尺在给定网格中完成画图.(1)先在上画点,使平分,再画的中点;(2)先画点,使四边形为平行四边形,再将绕点旋转得,使得的对应点落在直线上.22.(本小题满分10分)乒乓球是我国国球.球台长为2.8m ,中间处球网的高度为1.5dm .现有一台乒乓球发球器,球从发球器出口到第一次接触台面的运动轨迹近似为一条直线.从第一次接触台面到第二次接触台面的运动轨迹近似为一条抛物线.乒乓球第一次接触台面在球网左侧,越OF OE =3=OF 53sin =∠AOD 714⨯BC M AM BAC ∠AM N P ACPB ABC ∆C EFC ∆A E CP过球网(擦网不影响球运动轨迹)后,第二次接触台面在球网右侧为成功发球.乒乓球大小忽略不计.如图,当发球器放在球台左端时,通过测量得到球距离台面高度y (单位:dm )与球距离发球器出口的水平距离x (单位:dm )的相关数据,如下表所示:x (dm )024********…y (dm ) 3.36 2.52 1.680.840 1.40 2.403…(1)直接写出球从发球器出口到第一次接触台面时y 关于x 的函数解析式;(写出自变量的取值范围)(2)求乒乓球第二次接触台面时与发球器出口的水平距离;(3)发球器有一个滑轨,可以让发球口向右平移,若要成功发球,发球口最多向右平移多少dm ?23.(本小题满分10分)问题提出:如图1,是正方形边上一点,延长至使,四边形是正方形,,连,探究与的数量关系.问题探究:(1)先将问题特殊化,如图2,当与重合时,直接写出与的数量关系;(2)再探究一般情形,如图1,求与的数量关系.问题拓展:(3)如图3,是矩形边上一点,,在的延长线上且,,矩形满足,若,求与的数量关系.E ABCD BC CD F BE DF =EGHI EC EG=FH AI ,AI FH G C AI FH AI FH E ABCD BC 2,1==EC BE F CD AE FA ⊥27=CF EGHI 34,2==HG EG DF CD >AI FH图1 图2 图324.(本小题满分12分)抛物线交轴于A ,B 两点(A 在B 的左边),交y 轴于点C .(1)如图1,当时,①直接写出A ,B ,C 三点的坐标;②抛物线的顶点为D ,求证:∠DAB =∠ACB ;(2)如图2,将抛物线平移得到抛物线,其顶点为原点.过点P (0,1)的直线与抛物线交于M ,N 两点.直线QM ,QN 与抛物线只有一个交点,连接PQ ,若PQ ⟂MN 恒成立,求a .图1 图232:21-+=x ax y C x 1=a 1C 2C 2C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省随县2014年初中数学毕业生学业水平能力测试暨升学适应性考试试题(考试时间120分钟,满分120分)一、选择题(本题有10个小题,每小题3分,共30分)1.下列计算正确的是()A.2193-⎛⎫=⎪⎝⎭B.2=- C. (﹣2)0=﹣1 D. |﹣5﹣3|=22.中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为()A. 6.75×104吨B. 6.75×103吨C. 6.75×105吨D. 6.75×10﹣4吨3.下列运算正确的是()A. x2+x3=x5B. (x﹣2)2=x2﹣4C. 2x2•x3=2x5D. (x3)4=x74.下列说法不正确的是()A. 某种彩票中奖的概率是,买1000张该种彩票一定会中奖B. 了解一批电视机的使用寿命适合用抽样调查C. 若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定D. 在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件5.如图,AB∥CD,AD平分∠BAC,若∠BAD=65°,那么∠ACD度数为()A. 40°B. 35°C. 50°D. 45°6.一个几何体的三视图如图所示,则这个几何体是()7.已知关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则k的取值范围是()A. k<﹣2 B. k<2 C. k>2 D. k<2且k≠18.如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()A. B. AF=BF C. OF=CF D. ∠DBC=90°9.甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y(m)与时间t(s)的函数图象是()10.将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形;…;如此下去,则第2014个图中共有正方形的个数为()A. 2014B. 2017C. 6040D.6044二、填空题(本题有6个小题,每小题3分,共18分)11.在学校舞蹈比赛中,10名学生参赛成绩统计如图,极差和中位数分别是_________ ,_________ .12.如图,在△ABC中,AB=10,BC=8,AD垂直平分BC,垂足为D,点E是AC的中点,连接DE,则△CDE 的周长为_________ .13.将抛物线y=(x﹣1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为_________ .14.如图,将量角器和含30°角的一块直角三角板紧靠着放在同一平面内,使D,C,B在一条直线上,且DC=2BC,过点A作量角器圆弧所在圆的切线,切点为E,如果AB=6cm,则的长是_________cm.15.如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为_________ .16.如图,在平面直角坐标系中,∠OAB=60°,∠AOB=90°,反比例函数y1=的图象经过点A,反比例函数y2=﹣的图象经过点B,则m的值为_________ .三、解答题(本题有9小题,共72分)17.(5分)化简并求值:(+)÷,其中x,y满足(x﹣2)2+|2x﹣y﹣1|=0.18.(6分)某公园门票为20元/张,为增加公园人气,特推出办卡业务(从办卡日起,可供持卡者使用一年),卡分金卡,银卡两种:金卡每张200元,持卡者每次可直接进入公园,无需再购票;银卡每张100元,持卡者进入公园时需再购买每次5元的门票,某游客一年中进入该公园至少要超过多少次时,办理金卡最合算?19.(7分)如图,中国海监船在钓鱼岛附近海域沿正西方向航行执行巡航任务,在A处望见钓鱼岛在南偏西45°方向,海监船航行到B处时望见钓鱼岛在南偏45°方向,又航行了15分钟到达C 处,望见钓鱼岛在南偏60°方向,若海监船的速度为36海里/小时,求中国海监船离钓鱼岛最近距离为多少海里?(≈1.732,结果精确到0.1海里).20.(7分)某校学生会对学校倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图1中从左到右各长方形A、B、C、D、E高度之比为3:4:5:6:2,已知此次调查中捐10元的人数为12人.(1)他们一共抽查了多少人?(2)图2中,捐款数为20元的D部分所在的扇形的圆心角的度数是多少?(3)若该校共有1000名学生,请求出全校学生共捐款多少元?21.(7分)一个有透明的袋子里装有编号分别为1,2,3的球(除编号以为,其余都相同),其中1号球1个,3号球2个,从中随机摸出一个球是2号球的概率为.(1)求袋子里2号球的个数.(2)甲、乙两人分别从袋中摸出一个球(不放回),甲摸出球的编号记为x,乙摸出球的编号记为y,用列表法或画树形图求点A(x,y)在直线y=x上的概率.22.(8分)如图,AB为⊙O的弦,若OA⊥OD且BD=CD.(1)求证:BD是⊙O的切线;(2)当AC=3,OC=1,BD=4时,求BC的长.23.(10分)一服装批发店出售星星童装,每件进价120元,批发价200元,多买优惠;凡是一次买10件以上的,每多买一件,所买的全部服装每件就降低1元,但是最低价为为每件160元,(1)求一次至少买多少件,才能以最低价购买?(2)写出服装店一次销售x件时,民获利润y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围;(3)一天,甲批发了46件,乙批发了50件,店主却发现卖46件赚的钱反而比卖50件赚的钱多,你能用数学知识解释这一现象吗?为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每件160元至少提高到多少?24.(10分)如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABE F.现将小长方形CEFD绕点C顺时针旋转至CE′F′D′,旋转角为a.(1)当点D′恰好落在EF边上时,求旋转角a的值;(2)如图2,G为BC中点,且0°<a<90°,求证:GD′=E′D;(3)小长方形CEFD绕点C顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角a的值;若不能说明理由.25.(12分)如图,点A在y轴上,点B在x轴上,以AB为边作正方形ABCD,P为正方形ABC D的对称中心,正方形ABCD的边长为,ta n∠ABO=3.(1)求经过A,B,C三点的抛物线的解析式;(2)求点P的坐标;(3)若(1)中的抛物线与x轴另一交点为E,在直线OP上是否存在一点H,使△BHE的周长最小?如有,求出△BHE周长的最小值;(4)点R从原点O出发沿OP方向以个单位每秒速度运动,设运动时间为t秒,直接写出以A,B,C,R为顶点的四边形是梯形时t的值.2014年湖北省随县初中毕业生学业水平能力测试暨升学适应性考试数学试题参考答案二、填空题(每小题3分,共18分)11. 15,90 12. 14 13. 2x y = 14. π 15.(35,-4) 16. 1 三、解答题(共72分) 17. (本题满分5分) 解:原式=y x y x y x y x y x x --+⨯-+2))(())((2=yx x-22 ………………………2分由题意得⎩⎨⎧=--=-01202y x x 此时,2=x ,12=-y x ………………4分当2=x ,12=-y x 时,原式=4. ………………5分18. (本题满分6分)解:设某游客一年中进入该公园x 次,依题意得不等式组 20x >200 (1)5x +100>200 (2) ………………2分 解(1)得:x >10, 解(2)得:x >20.∴不等式组的解集为x >20. ………………5分答:某游客一年进入该公园超过20次时,办理金卡最合算。
………………6分 19. (本题满分7分)解:∵∠DBA=∠DAB=45°,∴△DAB 是等腰直角三角形. ………………1分 过点D 作DE⊥AB 于点E ,则DE =21AB . ………………2分 设DE =x ,则AB =2x在Rt△CDE 中,∠DCE=30°,则CE =3DE =3x .………………4分 在Rt△BDE 中,∠D BE =45°,则DE =BE =x ,由题意得,CB =CE -BE∴3x -x =36×41, ………………5分 解得: x ≈12.3, ……………… 6分答:中国海监船离钓鱼岛最近距离为12.3海里.……………… 7分 20. (本题满分7分)解:(1)设捐10元的人数为4x 人,根据题意得 4x=12 解得:x=3∴一共调查了3x+4x+5x+6x+2x=20x =20×3=60(人) ………………2分 (2)捐款为20元的圆心角度数为:360°×206=108°………………4分 (3)全校学生共捐款:10006030620181515101259⨯⨯+⨯+⨯+⨯+⨯=15500(元) …………7分21. (本题满分7分)解:(1)设袋子里2号球的个数为x 个. 根据题意得:4121=++x x解得:x =1.经检验:x =1是原分式方程的解 ………………3分 (2)由题意画树形图如下:∵共有12种等可能的结果,点A (x ,y )在直线y =x 上的有2个, ∴点A (x ,y )在直线y =x 上的概率为:P =122=61………………7分 22. (本题满分8分) (1)证明:连OB.∵OA=OB ,∴∠OAC=∠OBA.∵CD=DB ,∴∠DBC=∠DCB=∠ACO.∴∠ACO+∠OAC=∠OBA+∠CBD. ………………2分 ∵AO⊥OD,∴∠ACO+∠OAC=90°. ∴∠OBD=90°.∴BD 是⊙O 的切线. ………………4分 (2)解:过D 作DE ⊥BC 于E 在Rt △OBD 中,OB =2245-=3 ∴OA =OB=3 ………………5分在Rt △OAC 中,AC =2213+=10 ∵∠ACO=∠DCE ,∠AOC=∠DEC ,∴Rt △AOC ∽Rt △DEC . ………………6分∴ECOCCD AC =. ∵CD =BD ,CE =BC 21,∴BC 211410=, ∴BC =1054. ………………8分 【如果没有去掉条件AC ,请参照: (2)解:过D 作DE ⊥BC 于E∵∠ACO=∠DCE ,∠AOC=∠DEC ,∴Rt △AOC ∽Rt △DEC . ………………6分∴ECOCCD AC =. ∵CD =BD ,CE =BC 21,∴BC 21143=,∴BC =38. ………………8分】23. (本题满分10分)解:(1)设一次至少买x 件,才能以最低价购买,由题意,得 200-(x -10)×1=160, 解得:x =50.答:一次至少买50件,才能以最低价购买.………………3分 (2)当0<x ≤10时,y =(200-120)x =80x当10<x ≤50时,y =[(200-120)-(x -10)×1] ×x =-x 2+90x , 当x >50时,y =(160-120)x =40x . 综上:y 与x 的关系式为80x (0<x ≤10且x 为整数)y = -x 2+90x ( 10<x ≤50且x 为整数)40x ( x >50且x 为整数) ………………7分 (3)由y =-x 2+90x =-(x -45)2+2025 知对称轴x =45,当45<x ≤50时,y 随x 的增大而减小,即当卖的件数越多时,利润越小.即出现了卖46件赚的钱比卖50件嫌的钱多的现象. ………………9分当x =45时,最低售价为200-(45-10)=165(元). ∴为了不出现这种现象,在其他优惠条件不变的情况下,店家应把最低价每件160元至少提高到165元. ………………10分 24. (本题满分10分)(1)解:∵长方形CEFD 绕点C 顺时针旋转至CE ′F ′D ′, ∴CD ′=CD =2,在Rt △CED ′中,CD ′=2,CE =1,∴sin ∠CD ′E =21, ∴∠CD ′E =30°, ∵CD ∥EF ,∴∠α=30°;………………3分 (2)证明:∵G 为BC 中点, ∴CG =1, ∴CG =CE ,∵长方形CEFD 绕点C 顺时针旋转至CE ′F ′D ′, ∴∠D ′CE ′=∠DCE=90°,CE =CE ′=CG , ∴∠GCD ′=∠DCE ′=90°+α, 在△GCD ′和△E ′CD 中⎪⎩⎪⎨⎧'='∠='∠='E C CG E DC D GC CD D C ∴△GCD ′≌△E ′CD (SAS ),∴GD ′=E ′D ; ………………7分(3)解:能,α的值为135°或315°. ………………10分 25. (本题满分12分)解:(1)过C 点作CE⊥x 轴于点E , ∵Rt△AOB 中,tan∠ABO=3, AB =10,∴OA=3,OB =1,……1分由△AOB≌△BEC 得BE =3,CE =1,∴C(4,1),………………2分 由题意得A(0,3),B(1,0),C(4,1).设过A ,B ,C 的抛物线的解析式为32++=bx ax y ,得⎩⎨⎧=++=++1341603b a b a 解得a =65,b =623- ∴所求函数解析式为3623652+-=x x y ………………3分 (2)作PF⊥x 轴于点F ,连接AC .因为P 是正方形的对称中心,根据平行线等分线段定理可求得OF =2,所以可得PF 为直角梯形AOEC 的中位线,可求得PF =2,所以P(2,2) (6)分(3)存在 令y =0得03623652=+-x x , 解得x 1=1,x 2=3.6 ∵B(1,0), ∴E(3.6,0)………………7分作E 关于直线OP 的对称点E ',连接E B ',交直线OP 于点H ,根据两点之间线段最短知H 是满足△BHE 周长最小的点∵P((2,2), ∴ OP 是∠AOB 的平分线, ∴E '在y 轴上, ∴E '(0,518),………………8分 ∴△BHE 周长为513349)1518(1)518(22+=-++. ………………9分 (4)当CR∥AB 时, t =413. ………………10分 当AR∥BC 时,t =29. ………………11分 当BR∥AC 时,t =31. ………………12分。
