2019力学竞赛材料力学辅导(拉压)
合集下载
材料力学S02拉压
B
qx
l
C
F1
F1
23
第二章
轴向拉伸和压缩
拉压变形计算例题
例7： 支架，F=20kN， E=200GPa ，杆1截面d=0.022m， θ0=30°；杆2长度为l2=2m，截面为No.10工字钢， A2=1.435×10-3m2 。试计算结构中的最大应力和A点位 移。 d
B
(1)
FN 1
C
( 2)
l l
(a)
第二章
d
轴向拉伸和压缩
(b)
34
2. 低碳钢的拉伸力学性质
2.1 学习重点 材料的拉伸曲线（应力-应变或载荷-位移曲线） 重要参数 D 2.2 曲线 F 四个阶段： B 弹性，屈服 C 强化，颈缩 A
' '
轴向拉伸和压缩
F
b
b b
F
泊松比ν
第二章
l
20
拉压变形计算例题
F
例6： A 如图直径为d的圆截面的桩被外力F打入土中， 假设土对桩体的阻力为均匀分布，其线分布 B 集度为qx，土对桩头的阻力F1=0.3qxl，桩体 材料的弹性模量为E。试计算桩体最大应力 和总变形量。 q
F
O
x
x
该杆件上的载荷力系关于杆件中截面C反对称，FN的分 布关于杆件中截面C也是反对称的。
第二章 轴向拉伸和压缩 9
第三节
应力 拉压应力
Fi1
1. 应力 单位截面积上作用着的内力 平均应力 p ΔF
m
m
ΔA
ΔFn
ΔFt
一点应力
ΔA ΔF ΔF m n m t ΔA ΔA ΔF p lim ΔA 0 ΔA ΔF ΔF lim n lim t ΔA0 ΔA ΔA0 ΔA
材料力学第二章拉压(2)
李禄昌
通知
请各班班长、课代表，到院馆204室 找曲维波老师，商定力学实验安排。
曲老师电话：13306388861。
1
李禄昌
第2-4节 拉伸和压缩时材料的机械性能
材料的力学性能(机械性质):是指材料在外力作用下表现出的变 形、破坏等方面的特性，它是在常温、静载荷作用条件下，由 实验来测定。
铁碳合金中碳含量：0.02% ~ 0.25% 、0.3%~ 0.55%、0.6%~2.11%、
注意电动葫芦在什么位置时 构件受力最大？应分析。
FW
28
2．确定两杆件的轴力
以节点A为研究对象，画受力图。设AB和
AC杆的轴力均为正方向，分别为FN1和FN2。 由平衡条件：
Fx＝0， Fy＝0，
FN1 FN2cos＝0 FW FN2sin＝0
sin＝1 ， cos＝ 3
2
2
FN1＝ 1.73FW , FN2＝2FW
19
李禄昌
第2-7节 失效、许用应力与强度条件
的性各能种、问构使题件用用要：不求同构是材不件料同制的工造。作，不时同材，料只有不要同使的机其械性危能险，不截同构件对材料 1、失效面或、破危坏：险构点件最在外大力应作力用下不丧大失于正常极工限作应能力力。，
对构于塑件性就材是料，安当全应的力达吗到？σs 时，构件将产生明显的塑性变
S AB
B
QG
QG
解：(1)计算拉杆轴力：
注意电动葫芦 的位置。
Y 0, SBC sin (G Q) 0
得：
SBC
GQ
sin
又由三角关系知： sin lAC
lBC
代入上式得：
SBC
5 15 0.352
56.8KN
通知
请各班班长、课代表，到院馆204室 找曲维波老师，商定力学实验安排。
曲老师电话：13306388861。
1
李禄昌
第2-4节 拉伸和压缩时材料的机械性能
材料的力学性能(机械性质):是指材料在外力作用下表现出的变 形、破坏等方面的特性，它是在常温、静载荷作用条件下，由 实验来测定。
铁碳合金中碳含量：0.02% ~ 0.25% 、0.3%~ 0.55%、0.6%~2.11%、
注意电动葫芦在什么位置时 构件受力最大？应分析。
FW
28
2．确定两杆件的轴力
以节点A为研究对象，画受力图。设AB和
AC杆的轴力均为正方向，分别为FN1和FN2。 由平衡条件：
Fx＝0， Fy＝0，
FN1 FN2cos＝0 FW FN2sin＝0
sin＝1 ， cos＝ 3
2
2
FN1＝ 1.73FW , FN2＝2FW
19
李禄昌
第2-7节 失效、许用应力与强度条件
的性各能种、问构使题件用用要：不求同构是材不件料同制的工造。作，不时同材，料只有不要同使的机其械性危能险，不截同构件对材料 1、失效面或、破危坏：险构点件最在外大力应作力用下不丧大失于正常极工限作应能力力。，
对构于塑件性就材是料，安当全应的力达吗到？σs 时，构件将产生明显的塑性变
S AB
B
QG
QG
解：(1)计算拉杆轴力：
注意电动葫芦 的位置。
Y 0, SBC sin (G Q) 0
得：
SBC
GQ
sin
又由三角关系知： sin lAC
lBC
代入上式得：
SBC
5 15 0.352
56.8KN
材料力学拉压资料重点
材料力学拉压资料重点材料力学是研究物质内部组织结构和形态变化与力学性能之间关系的学科，是材料科学中非常重要的一个分支。
在材料力学中，拉压是常见的一种力学行为。
下面将介绍材料力学中拉压的相关知识，并重点讨论拉压行为对材料性能的影响。
首先，拉压是指施加在物体上的拉力和压力。
拉力是指物体在两端受到的拉伸作用力，而压力是指物体从左右两侧受到的压缩作用力。
拉压在实际应用中非常常见，例如钢筋的拉压试验、纤维材料的拉压性能测试等。
在材料力学中，拉压行为对材料性能有着重要的影响。
首先，拉压行为能够直接反映材料的强度和刚度。
强度是指材料抵抗外部拉压应力的能力，在拉压过程中体现为材料是否能够承受足够大的拉力或压力而不发生破裂。
而刚度则是指材料对拉力或压力的变形程度，刚度越大，变形越小，材料的性能越好。
其次，拉压行为还能够反映材料的延展性和脆性。
延展性是指材料在拉压过程中发生塑性变形的能力，脆性则是指材料在受到拉压应力时发生破裂的能力。
在拉压过程中，如果材料能够发生塑性变形而不发生破裂，表明材料具有较好的延展性；反之，如果材料容易发生破裂，表明材料较为脆性。
第三，拉压行为还能够反映材料的弹性和塑性行为。
弹性和塑性是材料的两种基本变形行为。
弹性是指材料在受到拉压应力后能够恢复原状态的能力，塑性则是指材料在受到拉压应力后存在永久性变形的能力。
拉压过程中，如果材料的应力-应变曲线显示出较大的线性区域，且应力-应变曲线在应变达到一定值之后开始呈现非线性变化，则说明材料具有较好的弹性行为；反之，如果应力-应变曲线出现较大的非线性变化区域，并呈现出较明显的塑性特性，则说明材料具有较强的塑性行为。
最后，拉压行为还能够反映材料的抗蠕变和抗疲劳性能。
抗蠕变性能是指材料在长时间受到拉压应力作用时不发生塑性变形的能力，抗疲劳性能则是指材料在受到拉压应力循环加载和卸载过程中不发生疲劳断裂的能力。
在实际应用中，材料常常会遭受到长时间的拉压应力加载和卸载，因此对于材料的抗蠕变性能和抗疲劳性能的评估非常重要。
材料力学竞赛辅导1
T
＋
＋ －
M
－
6、弯曲 Q
＋
＋ －
－
外力分析
内力分析
N
应力
N A
强度
max
N A
0
n
胡克定律 E 变形 截面位移
L L1 L
b b1 b
应变
b b
L L
刚度
L
0 b
N L EA
b1 b
=
ζs
n
或
ζb
n
3、强度计算
N max A ≤
ζ
max
=
ζ
(1) 强度校核
(2) 许用载荷计算
ηmax
T ≤［η］ = Wp
(3) 截面尺寸设计
四、变形 1、概念 2 、应变
ε 无量纲 拉为正，压为负 rad
γ
ζ
线应变
ε=
lim Δu Δs →0 Δs
Δs +Δu
Δs
3、Hooke 定律
ζ= E ε η= Gγ
〔 θ max 〕
∫
l
0
T (x) dx G I p(x)
3、刚度计算
梁横截面上的正应力
N dA 0
A
外力分析
内力分析 弯矩M 胡克定律
M z y d A M
A
max
M WZ
应力
强度
d dx
M y IZ
E E y
变形
截面位移 转角θ bb
应变
y d dx
秋季学期工程力学材料力学实验拉压
可以拷取本讲义
(桌面)
重要通知
说明：第十五周的周五和周六所提供的第四个“三选一” 实验：弯扭组合变形实验，由于开设的单元组数 过少，已经做了重新调整，请如下同学务必注意： （1）已选本实验的同学请重新上网及时预约； （2）由于“测弹性模量E”和“叠梁弯曲”两个实验已 经预约满员导致无法再预约的同学，请尽快上 网预约。
(4)在颈缩阶段，试件出现颈缩之后，横截
面积急剧缩小，出现颈缩，材料变形增大应力反而下降，最后材被拉断。2．铸铁的拉伸
(1)平断口，无屈服，无颈缩 (2)非线性变形，弹性模量 E 近似用割线斜率代替 (3)拉伸强度极限很低，只有 = 110～160Mpa
(4)延伸率很小 δ 0.5% 。
3．低碳钢的压缩
(1)弹性模量、比例极限、弹性极限、 屈服极限 ， 与拉伸时几乎相同。
(2)试件最后压缩变扁，不会断裂，由于两端 摩擦力影响，形成“腰鼓状”。
(3)测不出抗压强度极限
4．铸铁的压缩
(1)近450斜断口 (2)延伸率远大于拉伸（接近5%）
(3)弹性模量E 与拉伸时不同
(4)抗压强度极限远高于抗拉强度（接近4倍）。
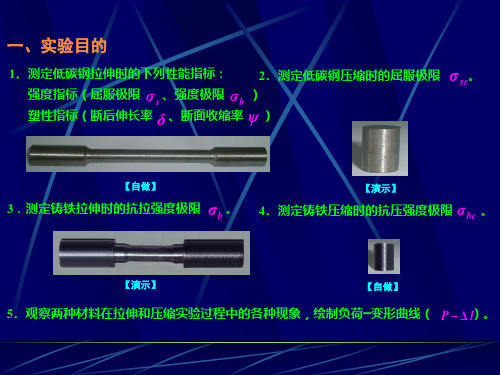
一、实验目的
1．测定低碳钢拉伸时的下列性能指标：
2．测定低碳钢压缩时的屈服极限 σ sc。
强度指标（屈服极限 σ s 、强度极限 σb ）
塑性指标（断后伸长率 δ 、断面收缩率 ψ ）
【自做】
3．测定铸铁拉伸时的抗拉强度极限 σb 。
【演示】
4．测定铸铁压缩时的抗压强度极限 σbc 。
【演示】
【自做】
强化阶段
低
低
碳 钢
Ps
屈服阶段
碳
Psc
拉伸实验
材料力学-拉压
§5–4
拉(压)杆的变形·胡克定律
P
P
杆在拉力P作用下产生的纵向 伸长为：
Δ =L −L L 1
L L1
胡克 定律: 拉杆的纵向线应变：
当杆的应力不超过材料的某一限 值时，杆的伸长 ΔL与其所受的力P、 杆的原长L成正比，而与其横截面 A成反比 ：
ΔL ε= L
∵ σ = Eε
PL ∴ ΔL = EA
[σ ] =
σu
n
n是一个大于1的系数，称为安全系数
§5–5
强度条件·安全系数·许用应力
为确保拉(压)杆不致因强度不足而破坏的强度条件:
σ max ≤ [σ ]
对于等截面直杆，拉伸(压缩)时的强度条件，则为
N max ≤ [σ ] A
§5–5
强度条件·安全系数·许用应力
拉压杆的强度条件
[σ ] =
例：圆截面等直杆沿轴向受力如图示，材料为铸铁，抗拉许用应 力[σ t ] ＝60Mpa，抗压许用应力 [σ c ] ＝120MPa，设计横截面直径。 20KN 20KN 30KN 30KN
30 ×1033 20 ×10 ≤ [σ ct ] ≤σ 2 2 πd 2 1 4
4 × 20 × 103 4 × 30 × 103 = 20.6mm ≥ dd1 ≥ 2 π [σ ] = 17.8mm
1. 已知ε D
F NCD
Δ L CD ε = a
Δ L CD = ε a
δ B = 2 Δ L CD = 2 ε a
F B B1 a 已知EA
Δ L CD F NCD a = EA
A L 2
C C1
刚杆 L 2
∑m
A
=0
F NCD = 2 F
材料力学之拉压
σs—屈服极限
σb—强度极限
30
试验设备： 万能试验机：用来强迫试样变形并 测定试样抗力的机器。
变形仪：用来将试样的微小变形放大到 试验所需精度范围内的仪器。
31
塑性指标
1. 延伸率
l1 l0 100% l0
2. 断面收缩率
A0 A1 100% A0
l1 —试件拉断后的标距长度 l0 —试件标距长度
36
二 . 金属材料压缩时的力学性能 1. 低碳钢压缩实验：
400
s(MPa)
低碳钢压缩应力 —— 应变曲线
200
低碳钢拉伸—— 应力应变曲线
比例极限 spy , 屈服极限 ssy ， 弹性模量 Ey 基本与拉伸时相同。
e
O
0.1
0.2
37
2. 铸铁压缩实验：
s
sby
灰铸铁的 压缩曲线 sbL 灰铸铁的 拉伸曲线
A1——试件拉断后断口处的 最小横截面面积 δ ＜5%—脆性材料
32
δ ≥5%—塑性材料
冷作硬化现象
构件处于强化阶段实施卸载。如卸载后重新加载， 曲线将沿卸载曲线上升。 如对试件预先加载, 使其达到强化阶段, 然后卸载, 当再加载时, 试件的线弹性阶段将增加, 同时其塑性降低。 ——称为冷作硬化现象
2. 轴力正负号规定： 规定: 引起杆件拉伸时的轴力为正, 即拉力为正； 压缩时的轴力为负, 即压力为负。 FN F F FN 正 负
3. 轴力图: 用图线表示轴力沿杆件轴线变化的规律 作法： a). 用截面法求出各段轴力的大小； b). 选一个坐标系, 用其横坐标表示横截面的位置， 纵坐标表示相应截面上的轴力； c). 拉力绘在坐标轴的上侧, 压力绘在坐标轴的下侧。
北大材料力学--第一章拉压
1、低碳钢和铸铁拉伸\压缩时的力学性能
在工程上使用最广泛，力学性能最典型
2019/10/25
材料力学
# 实验用试件
（1）材料类型： 低碳钢： 塑性材料的典型代表； 灰铸铁： 脆性材料的典型代表；
标距
L0
（2）标准试件：
d0
标点
尺寸符合国标的试件；
2．标用标于距准测：试试件的：等截面部分长度；
圆截面试件标距：L0=10d0或5d0
P
P
P
P
说明杆内纵向纤维的伸长量是相同的，或者
说横截面上每一点的伸长量是相同的
2019/10/25
材料力学
根据前面的实验，我么可以得出结论，即横截面 上每一点存在相同的拉力
P
N
如果杆的横截面积为：A
N
A
2019/10/25
材料力学
做轴力图并求各个截面应力
1 f20 4kN
1
2 6kN
延伸率 δ < 5%
断裂前有很大塑性变形
断裂前变形很小
抗压能力与抗拉能力相近 抗压能力远大于抗拉能力
可承受冲击载荷，适合于 适合于做基础构件或外壳 锻压和冷加工
材料的塑性和脆性会因为制造方法工艺条件 的改变而改变
2019/10/25
材料力学
2-7 轴向拉伸压缩时的强度计算
1、材料的极限应力
材料的极限应力是指保证正常工作条件下，该材料所能 承受的最大应力值。
2019/10/25
p
sin
sin
cos
2
sin 2
材料力学
2-5 轴向拉压的变形分析 P
细长杆受拉会变长变细， 受压会变短变粗
在工程上使用最广泛，力学性能最典型
2019/10/25
材料力学
# 实验用试件
（1）材料类型： 低碳钢： 塑性材料的典型代表； 灰铸铁： 脆性材料的典型代表；
标距
L0
（2）标准试件：
d0
标点
尺寸符合国标的试件；
2．标用标于距准测：试试件的：等截面部分长度；
圆截面试件标距：L0=10d0或5d0
P
P
P
P
说明杆内纵向纤维的伸长量是相同的，或者
说横截面上每一点的伸长量是相同的
2019/10/25
材料力学
根据前面的实验，我么可以得出结论，即横截面 上每一点存在相同的拉力
P
N
如果杆的横截面积为：A
N
A
2019/10/25
材料力学
做轴力图并求各个截面应力
1 f20 4kN
1
2 6kN
延伸率 δ < 5%
断裂前有很大塑性变形
断裂前变形很小
抗压能力与抗拉能力相近 抗压能力远大于抗拉能力
可承受冲击载荷，适合于 适合于做基础构件或外壳 锻压和冷加工
材料的塑性和脆性会因为制造方法工艺条件 的改变而改变
2019/10/25
材料力学
2-7 轴向拉伸压缩时的强度计算
1、材料的极限应力
材料的极限应力是指保证正常工作条件下，该材料所能 承受的最大应力值。
2019/10/25
p
sin
sin
cos
2
sin 2
材料力学
2-5 轴向拉压的变形分析 P
细长杆受拉会变长变细， 受压会变短变粗
材料力学拉压
二、
工 程 实 例
轴 向 拉 压 的 工 程 实 例
轴向拉压的工程实例
轴向拉压的工程实例
§2–2 拉压时的内力 、应力
一、内力 指由外力作用所引起的、物体内相邻部分之间的相互
作用力。
内力的计算是分析构件强度、刚度、稳定性等问题的 基础。求内力的一般方法是截面法。
截面法的基本步骤：① 截开、② 代替、③ 平衡
当a = 90°时，
(s a )min 0
当a = ± 45°时，|a|maxs20 (45 °斜截面上剪应力达到最大)
当a = 0,90°时， |a |min 0
补充：应力状态 1.一点的应力状态：过一点有无数的截面，这一点的各个截面
上的应力情况总体，称为这点的应力状态
2。、单元体：单元体—构件内的点的代表物，是包围被研究点的
A
斜截面上全应力：pa
s cosa
斜截面上全应力： pa s cosa F
k
分解：
a
sa pa cosas 0cos2a
k
k
pa
F
a
pa
s
ina
s
0
c
osas
ina
s 0
2
sin2a
a
k
反映：通过构件上一点不同截面上应力变化情况。
F
sa
a pa
a
当a = 0°时， (sa )maxs 0 (横截面上存在最大正应力)
FN2 A
BC
PB
PC
FN3
C
PC FN4
BC
FN PA
2P +
PB 5P PC
+
P
– 3P
材料力学习题拉压
拉伸与压缩基 本 概 念 题一、 选择题 (如果题目有5个备选答案选出其中2—5个正确答案，有4个备选答案选出其中一个正确答案。
)1．若两等直杆的横截面面积为A ，长度为l ，两端所受轴向拉力均相同，但材料不同，那么下列结论正确的是( )。
A ．两者轴力相同应力相同B ．两者应变和仲长量不同C ．两者变形相同D ．两者强度相同E ．两者刚度不同2．一圆截面直杆，两端承受拉力作用，若将其直径增大一倍，其它条件不变，则（）。
A ．其轴力不变B ．其应力将是原来的1/4C ．其强度将是原来的4倍D ．其伸长量将是原来的1/4E ．其抗拉强度将是原来的4倍3．设ε和1ε分别表示拉压杆的轴向线应变和横向线应变，μ为材料的泊松比，则下列结论正确的是（ ）。
A ．εεμ1=B ．εεμ1-=C ．εεμ1= D ．εεμ1-= E ．常数时，=≤μσσ p 4．钢材经过冷作硬化处理后，其性能的变化是（ ）。
A ．比例极限提高B ．屈服极限提高C ．弹性模量降低D ．延伸率提高E ．塑性变形能力降低5．低碳钢的拉伸σ-ε曲线如图1-19所示若加载至强化阶段的C 点，然后卸载，则应力回到零值的路径是（ ）。
A ．曲线cbaoB ．曲线cbf (bf ∥oa )C ．直线ce (ce ∥oa )D ．直线cd (cd ∥o σ轴)-3-6．低碳钢的拉伸σ-ε曲线如图l —19，若加载至强化阶段的C 点时，试件的弹性应变和塑性应变分别是（ ）。
A ．弹性应变是ofB ．弹性应变是oeC ．弹性应变是edD ．塑性应变是ofE ．塑性应变是oe7．图l-2l 表示四种材料的应力—应变曲线，则：(1)弹性模量最大的材料是（ ）；(2)强度最高的材料是（ ）；(3)塑性性能最好的材料是（ ）。
8．等截面直杆承受拉力，若选用三种不同的截面形状：圆形、正方形、空心圆，比较材料用量，则（ ）。
A ．正方形截面最省料B ．圆形截面最省料C ．空心圆截面最省料D ．三者用料相同9．若直杆在两外力作用下发生轴向拉伸(压缩)变形，则此两外力应满足的条件是A ．等值B ．反向C ．同向D ．作用线与杆轴线重合E ．作用线与轴线垂直10．轴向受拉杆的变形特征是（ ）。
材料力学拉压资料重点
pa
Fa Aa
F cos a s cos a
A
斜截面上全应力：pa
s cosa
斜截面上全应力： pa s cosa F
k
分解：
a
sa pa cosas 0cos2a
k
k
pa
F
a
pa
s
ina
s
0
c
osas
ina
s 0
2
sin2a
a
k
反映：通过构件上一点不同截面上应力变化情况。
F
sa
a pa
危险点：应力最大的点。
s
max
max(
FN ( x) A( x)
)
4. 公式的应用条件： • 等截面直杆； • 外力的作用线与轴线重合。 5. Saint-Venant原理：
离开载荷作用处一定距离，应力分布与大小不受外载荷作 用方式的影响。
6. 应力集中（Stress Concentration）： 在截面尺寸突变处，应力急剧变大。
上的应力情况总体，称为这点的应力状态
例如： 截面法求A截面处的内力FN。
F
A
F
截开：
F
ቤተ መጻሕፍቲ ባይዱ
A F
简图
代替： 平衡：
F A
Fx 0 FN F 0
FN
FN F
轴力——轴向拉压杆的内力，用FN 表示。
轴力的正负规定:
FN 与外法线同向,为正轴力(拉力) FN
FN
FN 与外法线反向,为负轴力(压力) FN
FN
轴力图—— FN (x) 的图象表示。
二、
工 程 实 例
轴 向 拉 压 的 工 程 实 例
材料力学_拉压1
拉、压杆的变形分析
♣ 相对变形 正应变
拉、压杆的变形分析
♣ 相对变形 正应变
FPl Δ =± l EA
对于杆件沿长度方向均匀变形的情形，其相对伸长量 ∆l/l 表示轴向变形的程度，是这种情形下杆件的正应变， 用 εx 表示。
εx =
Δl l
σ x = FP / A
FPl ∆l σ εx = ＝ EA = x l l E
第1章 最简单材料力学问题 最简单材料力学问题
第1章 最简单材料力学问题 最简单材料力学问题
斜拉桥承受拉力的钢缆
第1章 最简单材料力学问题 最简单材料力学问题
杆件在轴向载荷作用下的内力与应力 拉、压杆的变形分析 应力与变形算例 强度设计概述 拉伸和压缩时材料的应力一应变曲线 常温、静载下材料的力学性能 强度失效与失效控制 强度计算过程与算例 结论与讨论
o
1 2
1 2
应力与变形算例
例 题 1
解：2、计算杆的总伸长量 因为杆各段的轴力不等，且横截面面 积也不完全相同，因而必须分段计算各 段的变形，然后相加。 应用杆件承受轴向载荷时的轴向变形 公式
Δ =± l FPl EA
应力与变形算例
例 题 1
解：2、计算杆的总伸长量
Δ =± l FPl EA
计算各段杆的轴向变形分别为：
ε y = −νεx
ν为材料的另一个弹性常数，称为泊松比 泊松比(Poisson ratio),为无 泊松比
量纲量。
第1章 最简单材料力学问题 最简单材料力学问题
应力与变形算例
返回总目录
返回
应力与变形算例
例 题 1
已知: 已知 : 阶梯形直杆受力如图 示。材料的弹性模量E＝200GPa； 杆各段的横截面面积分别为 A1 ＝ A2 ＝2500mm2 ， A3 ＝1000mm2 ； 杆各段的长度标在图中。 试求： 1．杆AB、BC、CD段横截面 上的正 应力； 2 ． 杆 AB 段 上 与 杆 轴 线 夹 45°角 (逆时针方向)斜截面上 的正应力和切应力；杆的总伸 长量。
材料力学——拉压
B 1
解：(a) 求内力。用截面法求1、2杆的内力
FN1
30o A
C
2 P
FN2
30o
A
P
∑X = 0: ∑Y = 0 :
− F N 1 cos300 − F N 2 = 0
1 N ( x ) = ∫ − kx d x = − kx 2 2
x 0
N ( x ) max
N O
–
1 2 = − kL 2
x
kL2 2
轴向拉压杆件截面上的应力及强度条件
应力 : 1.平面截面假设 由外力引起的内力 集度 原为平面的横截面在变形后仍为平面， 纵向纤维变形相同。
P
a´ c´
b´ d´
题：图示杆件 BC段的横截面面积为 A ，AB和 CD段的横截面面积是 2A ，求杆件各 段的内力和应力。
在图示结构中，若钢拉杆 BC的横截面直径为 10mm，试求拉杆内的应力。设由 BC联接的两部分均为刚体。
零件上的拉力 P=38kN，零件内最大拉应 力发生于哪个横截面上？并求其值。 分析三个可能的危险截面：
∆l =ε l
σ
e f
σb σs σe σ P
O ● 弹性阶段 (Oab 段)：卸载后，变形完全恢复 ★ a
b
c
ε
Oa 段(直线 )：应力与应变成正比， σ= Eε，比例常数 E称作弹性模量；应力极限是比例极限σp
★ ab段 (曲线 )：应力与应变成非线性关系；应力极限是弹性极限 σe ● 屈服阶段 (bc段)：应力基本保持不变，应变有明显加大，下屈服极限应力是屈服极限 σs ● 强化阶段 (ce 段)：恢复抵抗变形能力，即增加变形必须增加应力；极限应力是强度极限 σb， ● 局部变形阶段 (ef阶段)：试件在局部范围内横向尺寸突然缩小，试件在 f点被拉断
全国大学生力学竞赛—材料力学专题
拉压 扭转 弯曲
组合 变形
Tension or compression :
(x) N(x)
A( x) N N(x)
N ( x)
l l EA d x
max
N(x) [ ]
A(x) max
l [l]
Equilibrium of forces Harmunious equations Physical equations
yx xy
zy
x
x
z
zx xz
x xy xz
T yx
y
yz
zx zy z
单元体微分面上的应力实际上就是 A 点处三 个相互垂直平面上的应力情况.
虎克定律
E G
y
yz
yx xy
zy
拉压 ( tension & compression ) 扭转 ( torsion )
弯曲 ( bending )
剪切 ( shearing )
组合变形 (combined deformations)
P
3. 材料力学的基本概念
强度 刚度 稳定性 内力 应力 应变 单元体 虎克定律
内力: 是材料力学问题的出发点.
P/ 2 P/ 2 a
L
H
H v
F
F v
P/ 2 P/ 2 a
L
H
H v
F
F v
P/ 2 P/ 2 a
L
材料力学
理论体系
1. 材料力学的主要任务
材料力学的研究对象
以杆件和杆件结构系统为研究对象
材料力学的任务
组合 变形
Tension or compression :
(x) N(x)
A( x) N N(x)
N ( x)
l l EA d x
max
N(x) [ ]
A(x) max
l [l]
Equilibrium of forces Harmunious equations Physical equations
yx xy
zy
x
x
z
zx xz
x xy xz
T yx
y
yz
zx zy z
单元体微分面上的应力实际上就是 A 点处三 个相互垂直平面上的应力情况.
虎克定律
E G
y
yz
yx xy
zy
拉压 ( tension & compression ) 扭转 ( torsion )
弯曲 ( bending )
剪切 ( shearing )
组合变形 (combined deformations)
P
3. 材料力学的基本概念
强度 刚度 稳定性 内力 应力 应变 单元体 虎克定律
内力: 是材料力学问题的出发点.
P/ 2 P/ 2 a
L
H
H v
F
F v
P/ 2 P/ 2 a
L
H
H v
F
F v
P/ 2 P/ 2 a
L
材料力学
理论体系
1. 材料力学的主要任务
材料力学的研究对象
以杆件和杆件结构系统为研究对象
材料力学的任务
材料力学——拉压.
： BC
Fx 0 FN 2 F2 F1
10
25
x
FN2 F1 F2 10 20 10kN
10
CD ： Fx 0 FN3 F4 25kN
横截面 §3 截面上的应力
应力
横截面 §3 截面上的应力
应力
横截面 §3 截面上的应力
应力
Aa
a表示斜截 面与轴线 夹角
a
pa
cosa
cos2 a
2
(1 cos2a )
a
pa
s in a
sina cosa
2
sin 2a
•一点应力分量随截面方位的改变而变化
的特性，称为应力状态。
•应力状态与强度有关。
•横截面正应力最大
•45o截面切应力最大
•纵截面应力为0
约为0.25~0.33
横向应变
例2－6 已知组合杆承载如图所示，杆
AB为铝材，Eal=70GPa, AAB=58.1mm2; 杆 BC为铜材，Eco=120GPa, ABC=77.4mm2;杆 CD为钢材，Est=200GPa, ACD=38.7mm2。 试求A和D之间的相对位移。
解：
§10 拉压应变能
外力作功 全部转化为应变能
W
VS
1 2
Fl
F1在d(l1)作功
dW F1dl1
l
l
W 0
F1d l1
ห้องสมุดไป่ตู้0
l1EA l
dl1
F
1 Fl 2
Vs
材料力学 第2章_拉压
解：1． 确定螺栓所受轴力 FN＝FP＝20 kN 2． 计算螺栓横截面上的正应力 FN FP 4 FP 4 20 103 N ＝ ＝ 2 ＝ 2 ＝ ＝113.2MPa 2 2 A πd πd π 15 mm 4 3．许用应力 ＝ S 240 160MPa n 1.5 4．强度校核
FN1 F1 10kN
F
x
0
FN2 F1 F2 10kN
CD段
FN kN
FN3 F4 25kN
x
F
x
0
2.绘制轴力图
返回
例题 2-1 1 B 1 F2 FN1 FN2 F2 FN3
25 10 10
已知 F1=10kN；F2=20kN；
F3=35kN；F4=25kN； 2 C 2 3 D F4 3.用截面一侧外力计算轴力
A A1 l1 l 100% 100% 断面收缩率 A l
式中，l1为断裂后标距长度；A1为断口处最小面积。
≥5%为塑性材料
＜5%为脆性材料
返回
3. 低碳钢拉伸时的主要性能指标
e
b
P
a
c
s
b
f
弹性常数 弹性模量：
o
E tan
泊松比：
返回
4. 卸载定律
d
e
b
f
卸载定律——在卸载过程中， 应力和应变按直线规律变化。 d点卸载后，弹性应变消 失，留下塑性应变。d点的 应变包括两部分：
P
a
o
d g
f h
弹性应变： d ’g
塑性应变： od ’ f点的应变与断后伸长率有何不同？
FN1 F1 10kN
F
x
0
FN2 F1 F2 10kN
CD段
FN kN
FN3 F4 25kN
x
F
x
0
2.绘制轴力图
返回
例题 2-1 1 B 1 F2 FN1 FN2 F2 FN3
25 10 10
已知 F1=10kN；F2=20kN；
F3=35kN；F4=25kN； 2 C 2 3 D F4 3.用截面一侧外力计算轴力
A A1 l1 l 100% 100% 断面收缩率 A l
式中，l1为断裂后标距长度；A1为断口处最小面积。
≥5%为塑性材料
＜5%为脆性材料
返回
3. 低碳钢拉伸时的主要性能指标
e
b
P
a
c
s
b
f
弹性常数 弹性模量：
o
E tan
泊松比：
返回
4. 卸载定律
d
e
b
f
卸载定律——在卸载过程中， 应力和应变按直线规律变化。 d点卸载后，弹性应变消 失，留下塑性应变。d点的 应变包括两部分：
P
a
o
d g
f h
弹性应变： d ’g
塑性应变： od ’ f点的应变与断后伸长率有何不同？
材料力学拉压
F
FN 图
FN max 3F （在OB段）
材料力学
§3
拉压杆内的应力
轴向拉伸与压缩
O
1
B 4F
C 3F 3
3
D 2F
4、分段求 max
1
FN 1 3F 1 , 2A 2A 2F max 3 A
材料力学
FN 3 2 F 3 A A
（在CD段）
§3
拉压杆内的应力
§3
拉压杆内的应力
轴向拉伸与压缩
正负号规定： ：横截面外法线转至斜截面的外法线，逆时针
转向为正，反之为负；
：拉应力为正，压应力为负；
：对脱离体内一点产生顺时针力矩的切应
力为正，反之为负；
材料力学
§3
拉压杆内的应力
轴向拉伸与压缩
讨论：
1、当 0, cos0 1, sin 0 0,
B F
C
2
FN 1 28.3 103 1 A1 202 106 4 90 106 Pa 90MP a
FN 1
FN 2
45°
y
B F
x
FN 2 2010 2 2 A2 15 106
6
3
8910 Pa 89MPa
材料力学
§3
拉压杆内的应力
轴向拉伸与压缩
圣维南原理：力作用于杆端的分布方式的不同，只
影响杆端局部范围的应力分布，影响区的轴向范围约
离杆端1~2个杆的横向尺寸。
如用与外力系静力等效的合力来代替原力，则
除了原力系起作用区域内有明显差别外，在离外力 作用区域略远处，上述代替的影响就非常微小，可 以不计。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
P/2 P/2 B
E③
②E
45o 45o
D
④
Δl 12
=
N1 l － EA
N2 l = EA
l (P－2N2) EA
N2
G
Δl 12
Δl 3
Δl 3 =Δl 4
N4 l = EA
N 1= 2 P/ 3
N 2= P/ 3 N 3 = N 4= √2 P/ 6
例题3： 图示由五根等直杆与刚性梁
AB 组成的平面结构。各杆的E、A、l 与 b 均相同且已知。在刚性梁上距杆 1 为 a 处作用一铅垂载荷 P ，今欲通过 电测方法测定 P 和 a 的值。 试
x1
FB
h－ c
x2
c
∫ （3）物理方程 h－c Δl 1 = q x1 dx1 = 0 E1 A
γA (h－ c ) 2
A FA
2E1 A 假定C截面为应力零截面
∫ Δl 2 = c q x2 dx2= γA c 2
解一元二次方程，并去掉负值解：
0 E2 A
2E2 A
E1 c 2 = E2 (h－ c ) 2
12345
Aa
B
P
FN1
=
P(3b − 5b
a)
FN 2
=
P(4b − 10b
a)
FN 3
=
P 5
FN 4
=
Pa 10b
FN 5
=
P(a − b) 5b
2017 第11届全国赛——第一部分6题
FN2 FN1
（1）对B点的力矩平衡方程
FN1 ⋅ 2a − FN 2 ⋅ a cosθ = 0 2FN1 − FN 2 cosθ = 0
能量法
动应力
压杆稳定
外力分析
材料力学的主线
内力分析 应力
强度
胡克定律 变形 截面位移 应变 刚度
外力分析
轴向载荷
一 轴向拉压
内力分析
FN
应力
σ = FN
A
强度
σ max
=
FN A
≤ [σ ]
胡克定律 σ=E⋅ε
[σ ] = σ u
n
变形
截面位移 应变 刚度
Δl = FN l EA
ε = ΔL
L
Δl ≤ [Δl]
杆系问题 静不定杆系
①C
P/2 P/2
B
③
②E
D
45o 45o ④
G
解：1）静力平衡方程 设各杆轴力为 N i
N2
N3
45o 45o
N4
N 1+ N 2= P N 3= N 4
G
N1
①C
2 N 3 cos 45o = N 2
P/2 P/2
（2）变形协调方程
Δl 12 cos 45o = Δl 3
（3）物理方程
（2）协调方程 Δl1 + 2Δl2 / cosθ = δ
请同学自己画出变形图
1、两同学在实验室作试验时需用一根长为1m、直径为10mm的拉 杆，但手头只有两根长为0.52m直径为10mm的圆杆和胶水（该种
胶的许用拉应力为[σ] ，许用切应力为[τ]=0.75[σ] ，圆杆材料的
许用拉应力为 [σ 0 ] = 3[σ ] ，他们应该如何粘结以获得强度最大的
tanθ ≤ 4
2、一矩形截面的等直杆，承受轴向拉力F作用，若在杆受力
前，其表面画有直角，且BC边与杆轴线的夹角为α ，杆材料
的弹性模量为E，泊松比为u。则杆受力后，
求：1）线段BC的变形；2）直角的改变量；3）角α 的改变量。
A
C
F
α
B
h F
b
3、图示对称桁架，在铰A处受荷载F作用。已知桁架中各杆的 材料相同，横截面面积也相同。问有何办法可使各杆同时达到 材料的许用应力[σ]？
ε ′ = Δ b = b1 − b < 0
b
b
ε′ 、7题 第三届竞赛第12题
2、拉压变形，静不定问题
赛题：第二届竞赛第1、7、10题、 第三届竞赛第1、2、11题 第五届竞赛第1、3、4题 第11届第一部分6题
例题1：确定图示变截面柱体在强度充分发挥的情况
全国周培源大学生 力学竞赛辅导
材料力学
建立力学模型
约束？ 构件？
载荷？
利用分析方法
变形？ 应力？
内力？
应用基础知识
理论？
强度？ 稳定？
刚度？
求解
公式？ 数学方法？
几何分析：杆件横截面上点与点
材料力学的研究方法 之间或杆件系统中杆与杆之间变
形的协调关系
几何分析
物理分析
力学分析
物理分析：分析杆件的外力 和变形之间的关系
aB P/2
Δl3 = 0 Δl1 = Δl5 = 2Δl2 = 2Δl4
F '' N3
=
0
FN"1
=
F '' N5
=
2FN'' 2
=
2FN'' 4
求解得：
FN1
=
P(3b − 5b
a)
FN 3
=
P 5
FN 5
=
P(a − b) 5b
FN 2
=
P(4b − a) 10b
FN 4
=
Pa 10b
（1）给出最佳贴片方案：应变片的 片数。应变片各贴在何处。 （2）给出 P 和 a 与测得的应变值
P
x
l
x
实际工程中，为便于浇注，可改为多段等截面柱，像桥墩。
例题2： 高为 h 的直立圆柱只受容重为γ的自重作 B
用，若将其上、下端固定且保持柱的原长 h 不变，
若柱材料抗拉弹性模量 E1 不等于抗压弹性模量
E2 ，试确定当σ= 0 时，z = c 中的 c 值。
h
（第三届竞赛题）
杆件
自重 两端固定端约束
第七届3题
将载荷分解
b bb b l
12345
Aa
B
P
=
b bb b
l
12345
+
Aa
aB
P/2
P/2
对称载荷
b bb b l
12345
Aa P/2
aB P/2
反对称载荷
变形、内力对称
变形、内力反对称
b bb b
+ l
12345
Aa P/2
aB P/2
变形协调条件：
Δl1 = Δl2 = Δl3 = Δl4 = Δl5
A FA
σ+ max
σ− max
=
γ (h − c) γc
=
h−c c
=
h c
−1
=
E1 E2
c = E1E2 − E2 h = h
E1 − E2
1+ E1
E2
例题2： 图示结构，各杆的抗拉（压）刚度均为EA ，杆 ①、②、③、④长度均为 l ，在E处作用力P。求各杆的 轴力 N i 。（第三届全国竞赛1题）
[σ ](A + dA) − [σ ]A = ρgAdx x
dA = ρg ⋅ dx A [σ ] ln A = ρg x + C
[σ ]
ln
A
=
ρg [σ ]
x
+
C
A(x)
当x=0，根据强度条件求初始截面A0。
强度条件：
A0
=
P
[σ ]
C = ln P
[σ ]
A=
P
ρg x
e [σ ]
[σ ]
等强度柱
b bb b l
12345
（1）给出最佳贴片方案：应变片的片 A a P
B
数。应变片各贴在何处。 （2）
给出 P 和 a 与测得的应变值εi 的关
系式。（第二届全国竞赛10题）
静不定结构
5根杆相同，结构对称，
利用对称性求解
第一届竞赛第3、6、8题，
第二届2、5、10题，
第三届1、4题，第四届2题，
第五届2、4、6、8题，
轴力满足：
FN' 1
=
FN' 2
=
FN' 3
=
FN' 4
=
FN' 5
=
P 5
力矩平衡方程：
P 2
(4b
−
2a)
−
FN" 2
⋅
2b
−
F '' N1
⋅
4b
=
0
F '' N2
=
F '' N4
=
P(2b − a) 10b
FN"1
=
F '' N5
=
P(2b − a) 5b
b bb b l
12345
Aa P/2
利用装配应力实现
拉杆，所能承受的最大拉力是多少。
0.48m
0.52m
θ θ
思路：1、拉杆满足强度条件 2、胶接面的正应力强度、切应力强度都满足要求 3、杆件总长度满足要求拉杆满足强度条件
F A
≤
[σ
0
]
F
=
πd 2
4
⋅[σ 0 ]
[σ 0 ]cos2 θ ≤ [σ ] [σ 0 ] sin 2θ ≤ [τ ]
2
60o < θ < 76o
c 2 (1 －
E1 )
－2hc+h2