相似形的综合运用(一)
第八讲 二次函数与几何图形的综合运用1(含答案)

第八讲 二次函数与几何图形的运用一、知识梳理二次函数与三角形的综合运用:1、求面积及最值2、与三角形的综合运用3、与相似三角形的综合运用4、与四边形的综合运用二、例题例1:如图,已知抛物线y=﹣x 2+mx+3与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0)(1)求m 的值及抛物线的顶点坐标.(2)点P 是抛物线对称轴l 上的一个动点,当PA+PC 的值最小时,求点P 的坐标.变式 1 如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0). (1)求该抛物线的解析式;(2)动点P 在x 轴上移动,当△PAE 是直角三角形时,求点P 的坐标.例2、如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.(1)当抛物线F经过点C时,求它的表达式;(2)设点P的纵坐标为y P,求y P的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.例3:在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.例4:已知二次函数y=ax2﹣2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B 两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3(1)求A、B两点的坐标;(2)若tan∠PDB=,求这个二次函数的关系式.例5、如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.(1)写出点D的坐标.(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c (a≠0)的图象过点A.①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x ﹣4)、y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H 作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.三、课堂练习1、如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE.设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是 ( )A.y=32x2 B.y=3x2 C.y=23x2 D.y=33x22、已知抛物线y=2x2+bx+c与直线y=﹣1只有一个公共点,且经过A(m﹣1,n)和B(m+3,n),过点A,B分别作x轴的垂线,垂足记为M,N,则四边形AMNB的周长为.3、直线y=kx+b与抛物线y=x2交于A(x1,y1)、B(x2,y2)两点,当OA⊥OB时,直线AB 恒过一个定点,该定点坐标为.4、如图,抛物线y=ax2+bx﹣经过点A(1,0)和点B(5,0),与y轴交于点C.(1)求抛物线的解析式;(2)以点A为圆心,作与直线BC相切的⊙A,请判断⊙A与y轴有怎样的位置关系,并说明理由;(3)在直线BC上方的抛物线上任取一点P,连接PB、PC,请问:△PBC的面积是否存在最大值?若存在,求出这个值和此时点P的坐标;若不存在,请说明理由.5、如图,在平面直角坐标系中,抛物线y=ax 2+bx+c 的顶点坐标为(2,9),与y 轴交于点A (0,5),与x 轴交于点E 、B . (1)求二次函数y=ax 2+bx+c 的表达式;(2)过点A 作AC 平行于x 轴,交抛物线于点C ,点P 为抛物线上的一点(点P 在AC 上方),作PD 平行与y 轴交AB 于点D ,问当点P 在何位置时,四边形APCD 的面积最大?并求出最大面积;(3)若点M 在抛物线上,点N 在其对称轴上,使得以A 、E 、N 、M 为顶点的四边形是平行四边形,且AE 为其一边,求点M 、N 的坐标.六、课后作业1、已知抛物线y=ax 2﹣3x+c (a ≠0)经过点(﹣2,4),则4a+c ﹣1= .2、a 、b 、c 是实数,点A (a+1、b )、B (a+2,c )在二次函数y=x 2﹣2ax+3的图象上,则b 、c 的大小关系是b c (用“>”或“<”号填空)3、已知二次函数n mx x y ++=2的图像经过点()1,3-P ,对称轴是经过()0,1-且平行于y轴的直线。
相似三角形对应高的比等于相似比.7 相似三角形的性质(一)教学设计

第四章图形的相似7.相似三角形的性质(一)一、教学目标1.经历探索相似三角形中对应线段比值与相似比的关系的过程,理解相似三角形的性质。
利用相似三角形的性质解决一些实际问题.2.培养学生的探索精神和合作意识;通过运用相似三角形的性质,增强学生的应用意识.在探索过程中发展学生类比的数学思想及全面思考的思维品质.3.在探索过程中发展学生积极的情感、态度、价值观,体现解决问题策略的多样性.一、学生知识状况分析学生在之前七年级已经学习了全等图形判定和性质,对全等三角形的对应边的比已有所了解。
在本章又学习了相似图形的判定条件,对相似图形,特别是相似三角形已有一定的认识。
通过前面的学习学生已经经历了一些关于相似三角形性质的探究。
例如,利用相似三角形测量旗杆的高度等实际问题,感受到了数学的实际价值,利用相似三角形的性质的解决问题的活动经验。
本节主要研究相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比这一性质,九年级学生在以前的数学学习中已经经历了很多合作学习过程,具有了一定的学习经验,学生间相互评价、相互提问的积极性高,因此,参与有关性质的实践探究活动的热情应该是比较高的。
二、教学任务分析教材基于学生对相似三角形的性质的基础上,提出了本课的学习任务:理解相似三角形的性质,让学生经历探索相似三角形性质的过程,并在探索过程中,发展学生积极的情感、态度、价值观、体现解决问题策略的多样性,同时也力图在学习过程中,逐步达成学生的有关情感态度目标。
为此本节课的教学目标是:(一)知识目标:经历探索相似三角形中对应线段比值与相似比的关系的过程,理解相似三角形的性质。
利用相似三角形的性质解决一些实际问题.(二)能力目标:培养学生的探索精神和合作意识;通过运用相似三角形的性质,增强学生的应用意识.在探索过程中发展学生类比的数学思想及全面思考的思维品质.(三)情感与价值观目标:在探索过程中发展学生积极的情感、态度、价值观,体现解决问题策略的多样性.二、教学过程第一环节:探究相似三角形对应高的比.在前面我们学习了相似三角形的定义和判定条件,知道相似三角形的对应角相等,对应边成比例。
初中数学_图形的相似教学设计学情分析教材分析课后反思

《相似三角形》练习学案【教学目标】 1、理解相似图形的性质,灵活运用相似三角形的判定及性质进行计算和证明。
2、利用相似解决一些实际问题。
【教学重点】相似三角形的性质和判定【教学难点】相似三角形的性质和应用【教学过程】 一、知识梳理(课前预习,学生独立完成,小组互评) 1、相似三角形: (1)相似三角形的性质:相似三角形的对应角,对应边(2)相似三角形的判定:① ② ③ 2、如何寻找和发现相似三角形? 两个三角形相似,一般说来必须具备下列图形之一:一线三等角条件∠APD=∠B=∠C 只要能在复杂图形中辨认出上述基本图形,并能根据问题需要添加适当的辅助线,构造出基本图形,从而使问题得以解决.二、基础练习(课前预习,学生独立完成,小组互评)1、如图共有( )对相似三角形。
A 、1B 、2C 、3D 、4 2、如图,已知D 、E 分别是△ABC 的边,AB 、AC 上的点,DE ∥BC ,且S △ADE :S 四边形DBCE=1:8,那么,AE :AC=( ) A 、1:9 B 、1:3 C 、1:8 D 、1:23、如图,△DEF 是由△ABC 经过位似变换得到的,点O 是位似中心,D ,E ,F 分别是OA ,OB ,E D A D C B A B C _ F_ E _ C _ B _ AOC 的中点,则△DEF 与△ABC 的面积比是( )A . 1:2B .1:4C .1:5D .1:64、若两个相似三角形对应高的比为2:3,他们的周长的差是25 ,那么较大三角形的周长是 。
5、两个相似多边形的相似比为3:2,面积之差为25cm 2,则这两个多边形的面积为 。
三、典例解析(小组内讨论,学生展示,互相质疑,教师点评)例1、变式练习A 组:(原型题)如图所示,给出下列条件:①B ACD ∠=∠; ②ADC ACB ∠=∠;③AC AB CD BC=; ④2AC AD AB =. 其中能够判定ABC ACD △∽△的个数为( )A .1B .2C .3D .4(变式题)如图在△ABC 中,点D 、E分别是AB 、AC 边上的点,AE =2,AC=4,DE =3,则BC 的长是B 组:(原型题)点P 是Rt △ABC 的斜边上 A 异于B 、C 的一点,过点P 作直线截△ABC , P使截得的三角形与△ABC 相似,满足这样条件的直线可作 条。
相似三角形复习

E
C
Rt△ACD∽Rt△CBD △ ∽ △
A D B
AE AD = CF CD
AC=AE BC=CF
……
需证∠ 需证∠DAE=∠DCF ∠
需证△ 需证△ADE∽△CDF ∽ 结论1 结论
需证 ∠ADE=∠CDF ∠
CD⊥AB ⊥
DE⊥DF ⊥ 结论2 结论
练习2:如图, 、 分别是 分别是△ 的高, 练习 :如图,AD、CF分别是△ABC的高,在AB上截取 的高 上截取 AE=AD,EG∥BC交AC于G,求证:EG=CF , ∥ 交 于 ,求证:
③∠F=∠C, ∠
AF AE = AC AB
则△ABC∽△AEF ( 错 ) △ ∽
B D
(2)如图 △ABC和△CDB中, 如图:△ 如图 和 中 ∠ABC=∠CDB=90° ∠ °
BC 2 = AC • BD
则Rt△ABC∽Rt△CDB ( 对 ) △ ∽ △
A
C
是边AB上一点 例1。已知△ABC中,P是边 上一点,连结 。已知△ 中 是边 上一点,连结CP ①∠ACP满足什么条件时,△ACP∽△ABC? 满足什么条件时, ∽ ? 满足什么条件时 满足什么条件时, ②AC:AP满足什么条件时,△ACP∽△ABC? : 满足什么条件时 ∽ ?
结论) (结论)
引申:证明一个结论,可以从条件出发,围绕条件找条件, 引申:证明一个结论,可以从条件出发,围绕条件找条件,直
到找到所需的条件。也可以从结论开始分析, 到找到所需的条件。也可以从结论开始分析,证此结论需要什么 条件,从题中证出所需条件,从而找到解题思路。 条件,从题中证出所需条件,从而找到解题思路。
指出下列判断是否正确,为什么 指出下列判断是否正确 为什么? 为什么
人教版相似知识点总结

人教版相似知识点总结一、相似三角形在平面几何中,相似三角形是指有相同形状但不一定相同大小的三角形。
相似三角形的性质和判定方法是初中数学重要的知识点之一。
1. 相似三角形的性质a. 性质1:对应角相等两个相似三角形的对应角相等,即如果两个三角形ABC和A'B'C'相似,则∠A=∠A',∠B=∠B',∠C=∠C'。
b. 性质2:对应边成比例两个相似三角形的对应边成比例,即如果两个三角形ABC和A'B'C'相似,则AB/A'B'=BC/B'C'=AC/A'C'。
c. 性质3:相似三角形的面积成比例如果两个三角形ABC和A'B'C'相似,则它们的面积之比等于边长之比的平方,即S(ABC)/S(A'B'C')=(AB/A'B')^2=(BC/B'C')^2=(AC/A'C')^2。
2. 相似三角形的判定方法a. 直角三角形的判定方法:两个直角三角形如果有一个角相等,则它们相似;或者两个直角三角形的三条边分别成比例,则它们相似。
b. 三边成比例的判定方法:两个三角形的三条边分别成比例,则它们相似。
c. 边角边(或角边角)的判定方法:两个三角形的两个角分别相等,且夹在两边成比例,则它们相似。
d. 已知相似三角形内部某个角相等的判定方法:如果两个三角形相似且三角形内部有一个角相等,则其他两个角也相等。
相似三角形的性质和判定方法在初中数学中具有重要的理论和实际应用价值,对于几何图形的相似性质和相关计算都有重要的指导作用。
二、比例比例是数学中重要的概念,主要用来描述两个量之间的相对关系。
在人教版初中数学中,比例是一个重要的知识点,包括比例的性质、比例的计算、比例的应用等内容。
1. 比例的性质a. 比例的传递性:如果a:b=c:d,则a/c=b/d;如果a/c=b/d,则a:b=c:d。
《相似形》全章复习与巩固--知识讲解(提高)

《相似形》全章复习与巩固--知识讲解(提高)撰稿:康红梅 审稿:杜少波 【学习目标】1.了解比例的基本性质,线段的比、成比例线段;2.掌握黄金分割的定义、性质及应用;3.探索并掌握相似三角形的判定方法及性质,并能利用这些性质和判定方法解决生活中的一些实际问题;4.了解图形在平面直角坐标系中的位似变换.【知识网络】【要点梳理】 要点一、比例线段比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的比与另两条线段的比相等,如a :b =c :d ,我们就说这四条线段是成比例线段,简称比例线段. 要点诠释:(1)若a :b =c :d ,则ad=bc ;(d 也叫第四比例项) (2)若a :b=b :c ,则2b =ac (b 称为a 、c 的比例中项). 要点二、黄金分割1.定义:如图,将一条线段AB 分割成大小两条线段AP 、PB ,若小段与大段的长度之比等于大段的长度与全长之比,即ABAPAP PB (此时线段AP 叫作线段PB 、AB 的比例中项),则P 点就是线段AB 的黄金分割点(黄金点),这种分割就叫黄金分割.2.黄金三角形:顶角为36°的等腰三角形,它的底角为72°,恰好是顶角的2倍,人们称这种三角形为黄金三角形.黄金三角形性质:底角平分线将其腰黄金分割. 要点三、相似三角形 1. 相似三角形的判定:平行于三角形一边的直线和其他两边相交,截得的三角形和原三角形相似.定理1:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似. 定理2:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似. 特别地,如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. 2. 相似三角形的性质:定理1:相似三角形对应高,对应中线,对应角平分线的比都等于相似比. 定理2:相似三角形的周长的比等于相似比.定理3:相似三角形面积的比等于相似比的平方.要点诠释:要特别注意“对应”两个字,在应用时,要注意找准对应线段. 要点四、图形的位似变换1.位似图形定义: 如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.2.位似图形的性质:(1)位似图形的对应点和位似中心在同一条直线上;(2) 位似图形的对应点到位似中心的距离之比等于相似比; (3)位似图形中不经过位似中心的对应线段平行. 要点诠释:(1)位似图形与相似图形的区别:位似图形是一种特殊的相似图形,而相似图形未必能构成位似图形.(2)位似变换中对应点的坐标变化规律:在平面直角坐标系中,如果位似变换是以原点 为位似中心,相似比为k ,那么位似图形对应点的坐标的比等于k 或-k. 【典型例题】 类型一、相似三角形1. 已知:如图,∠ABC =∠CDB =90°,AC =a ,BC =b ,当BD 与a 、b 之间满足怎样的关系时,这两个三角形相似?【答案与解析】∵AC =a ,BC =b , ∴AB=22a b -,①当△ABC ∽△BDC 时,BD BCAB AC=, 即22b a b BD a-=.②当△ABC∽△CDB时,BD BCCB AC=,即2b BDa=.【总结升华】相似三角形中未明确对应点和对应边时,要注意分类讨论.举一反三【变式】如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.(1)求证:△COM∽△CBA;(2)求线段OM的长度.【答案】(1)证明:Q A与C关于直线MN对称,∴AC⊥MN,∴∠COM=90°,在矩形ABCD中,∠B=90°,∴∠COM=∠B ,又Q∠ACB=∠ACB,∴△COM∽△CBA ,(2)Q在Rt△CBA中,AB=6,BC=8,∴AC=10 ,∴OC=5,Q△COM∽△CBA,∴OC OM=BC AB,∴OM=15 4.2.如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=23,则四边形MABN的面积是()A .63B .123C .183D .243【答案】C ;【解析】由MC =6,NC =23,∠C=90°得S △CMN =63,再由翻折前后△CMN ≌△DMN 得对应高相等;由MN∥AB 得△CMN ∽△CAB 且 相似比为1:2,故两者的面积比为1:4,从而得S △CMN :S 四边形MABN =1:3,故选C.【总结升华】本题综合考查了直角三角形的面积算法、翻折的性质、由平行得相似的三角形相似的判定方法、相似图形的面积比等于相似比的平方等一些类知识点.知识点丰富;考查了学生综合运用知识来解决问题的能力.难度较大.类型二、相似三角形的综合应用3. 如图,点D 是△ABC 的边AB 的延长线上一点,点F 是边BC 上的一个动点(不与点B 重合).以BD 、BF 为邻边作平行四边形BDEF ,又AP //BE (点P 、E 在直线AB 的同侧),如果AB BD 41=,求△PBC 的面积与△ABC 面积之比. PGF EDCB A【答案与解析】连接FP, 延长AP 交BC 的延长线于H, 过点A 、P 分别作,AM BC PN BC ⊥⊥,垂足M 、N.NMD A CB∵四边形BDEF 是平行四边形,EF ∥AD,又AP //BE ,∴E 、F 、P 共线,即PF ∥AB,四边形APEB 是平行四边形,∴EP=AB , 又∵ABBD 41=,∴ EF=DB=14AB=13PF,∴PF=34AB, ∵△ABH ∽△PFH,∴34PN PF AM AB ==, ∴34PBC ABC S PN S AM ==△△. 【总结升华】此题应用了平行四边形,相似三角形和三角形面积的相关知识,能够合理作出辅助线是解决本题的关键,4.如图所示,已知AB 为⊙O 的直径,弦CD ⊥AB ,垂足为H.(1)求证;(2)若过A 的直线与弦CD(不含端点)相交于点E ,与⊙O 相交于点F ,求证:;(3)若过A 的直线与直线CD 相交于点P ,与⊙O 相交于点Q ,判断是否成立(不必证明).【答案与解析】(1)证明:连结CB ,因为AB 是⊙O 的直径, 所以∠ACB=90°.而∠CAH=∠BAC ,所以△CAH ∽△BAC , 所以,即.(2)证明:连结FB ,易证△AHE ∽△AFB , 所以AE ·AF=AH ·AB , 所以. (3)解:结论成立.【总结升华】本题考查了圆有关的性质和相似三角形知识的综合运用,并且渗透了转化思想,即将等积式转化为比例式. 举一反三:【变式】如图,M 为线段AB 的中点,AE 与BD 交于点C ,∠DME=∠A=∠B=α ,且DM 交AC 于F ,ME 交BC 于G .(1)写出图中三对相似三角形,并证明其中的一对;(2)连结FG ,如果α=45°,AB =42,AF =3,求FG 的长.【答案】(1)△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM以下证明△AMF∽△BGM.∵∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B ∴△AMF∽△BGM.(2)当α=45°时,可得AC⊥BC 且AC =BC∵M 为AB 的中点,∴AM=BM =22, 又∵AMF∽△BGM,∴AF BMAM BG=, ∴3832222=⨯=⋅=AF BM AM BG ,又∵α=45°,AB =42,∴AC=BC=4, ∴84433CG =-=,431CF =-=, ∴2222451()33FG CF CG =+=+= .5. 如图,已知在四边形ABCD 中,AD //BC ,AD =2,BC =4,点M 是AD 的中点,△MBC 是等边三角形.动点P 、Q 分别在线段BC 和MC 上运动,且∠MPQ=60°保持不变. 设PC =x ,MQ =y ,求y 与x 的函数关系式.【答案与解析】在等边MBC △中,4MB MC BC ===,60MBC MCB ==︒∠∠, 又∵60MPQ =︒∠,∴120BMP BPM BPM QPC +=+=︒∠∠∠∠, ∴BMP QPC =∠∠, ∴BMP CQP △∽△, ∴PC CQBM BP=, ∵PC x MQ y ==, ∴44BP x QC y =-=-, ,∴444x yx-=- , ∴2144y x x =-+.【总结升华】利用相似三角形得到的比例式,构建线段关系求得函数关系,关键是能够灵活运用所学知识来解题.举一反三【变式】如图所示,在Rt △ABC 中,∠A=90°,AB=8,AC=6.若动点D 从点B 出发,沿线段BA 运动到点A 为止,运动速度为每秒2个单位长度.过点D 作DE ∥BC 交AC 于点E ,设动点D 运动的时间为x 秒,AE 的长为y .(1)求出y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)当x 为何值时,△BDE 的面积S 有最大值,最大值为多少?【答案】(1)因为DE ∥BC ,所以△ADE ∽△ABC ,所以.又因为AB=8,AC=6,,,所以,即, 自变量x 的取值范围为. (2).所以当时,S 有最大值,且最大值为6.类型三、黄金分割6.如图,用纸折出黄金分割点:裁一张正方的纸片ABCD ,先折出BC 的中点E ,再折出线段AE ,然后通过折叠使EB 落到线段EA 上,折出点B 的新位置B ′,因而EB ′=EB .类似地,在AB 上折出点B ″使AB ″=AB ′.这是B ″就是AB 的黄金分割点.请你证明这个结论.【答案与解析】设正方形ABCD 的边长为2, E 为BC 的中点, ∴BE=1∴AE=225AB BE +=,又B ′E=BE=1,∴AB ′=AE-B ′E=5-1,∵AB″=AB′=5-1∴AB″:AB=(5-1):2∴点B″是线段AB的黄金分割点.【总结升华】本题考查了黄金分割的应用,知道黄金比并能求出黄金比是解题的关键.举一反三【变式】如图,已知△ABC中,D是AC边上一点,∠A=36°,∠C=72°,∠ADB=108°.求证:(1)AD=BD=BC;(2)点D是线段AC的黄金分割点.【答案】(1)∵∠A=36°,∠C=72°,∴∠ABC=72°,∠ADB=108°,∴∠ABD=36°,∴△ADB、△BDC是等腰三角形,∴AD=BD=BC.(2)∵∠DBC=∠A=36°,∠C=∠C,∴△ABC∽△BDC,∴BC:AC=CD:BC,∴BC2=AC•DC,∵BC=AD,∴AD2=AC•DC,∴点D是线段AC的黄金分割点.。
相似三角形性质与判定的综合运用专题及答案

相似三角形性质与判定的综合运用一、解答题1.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边上的点C1处,点D落在点D1处,C1D1交线段AE于点G.(1)求证:△BC1F∽△AGC1;(2)若C1是AB的中点,AB=6,BC=9,求AG的长.2.已知:如图,在正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.(1)求证:EF=AE−BE.(2)连接BF,如果AFBF =DFAD,求证:EF=EP.3.如图,四边形ABCD、CDEF、EFGH都是正方形.(1)△ACF与△ACG相似吗?说说你的理由.(2)求∠1+∠2的度数.4.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;(2)若AB=8,AD=6√3,AF=4√3,求AE的长.5.如图,花丛中一根灯杆AB上有一盏路灯A,灯光下,小明在D点处的影长DE=3米,沿BD方向走到点G,DG=5米,这时小明的影长GH=4米,如果小明的身高为1.7米,求路灯A离地面的高度.6.已知:如图,△ABC为等腰直角三角形,∠ACB=90°,点E、F是AB边所在直线上的两点,且∠ECF=135°.(1)求证:△ECA∽△CFB;(2)若AE=3,设AB=x,BF=y,求y与x之间的函数关系式,并写出x的取值范围.7.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,(1)求证:AC2=AB⋅AD;(2)求证:△AFD∽△CFE.8.如图,在四边形ABCD中,AB//DC,BC>AD,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).(1)求证:△ACD∽△BAC;(2)求DC的长;(3)试探究:△BEF可以为等腰三角形吗?若能,求t的值;若不能,请说明理由.9.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE//AC,EF//AB.(1)求证:△BDE∽△EFC.(2)设AFFC =12,①若BC=12,求线段BE的长;②若△EFC的面积是20,求△ABC的面积.10.小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米?.答案和解析1.【答案】解:(1)证明:由题意可知∠A=∠B=∠GC1F=90∘,∴∠BFC1+∠BC1F=90∘,∠AC1G+∠BC1F=90∘,∴∠BFC1=∠AC1G,∴△BC1F∽△AGC1.(2)∵C1是AB的中点,AB=6,∴AC1=BC1=3,∵CF=C1F,∴C1F=BC−BF=9−BF,∵∠B=90∘,∴BF2+BC12=C1F2,即BF2+32=(9−BF)2,解得BF=4,由(1)得△AGC1∽△BC1F,∴AGBC1=AC1BF,∴AG3=34,解得AG=94.【解析】本题考查相似三角形的判定与性质、矩形的性质、翻折变化,解答本题的关键是明确题意,找出所求问题需要的条件,利用三角形的相似和勾股定理解答.(1)根据题意和图形可以找出△BC1F∽△AGC1的条件,从而可以解答本题;(2)根据勾股定理和(1)中的结论可以求得AG的长.2.【答案】证明:(1)∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°.∵BE⊥AP,DF⊥AP,∴∠BEA=∠AFD=90°.∵∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3.在△ABE和△DAF中,∵{∠BEA=∠AFD,∠1=∠3,AB=DA,∴△ABE≌△DAF,∴BE=AF,∴EF=AE−AF=AE−BE.(2)如图,∵AFBF =DFAD,而AF=BE.∴BEBF =DFAD,∴BEDF =BFAD,∴Rt△BEF∽Rt△DFA,∴∠4=∠3.∵∠1=∠3,∴∠4=∠1.∵∠5=∠1,∴∠4=∠5.即BE平分∠FBP,而BE⊥EP,∴EF=EP.【解析】本题主要考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.也考查了全等三角形的判定与性质和正方形的性质.(1)利用正方形的性质得AB=AD,∠BAD=90°,根据等角的余角相等得到∠1=∠3,则可判断△ABE≌△DAF,则BE=AF,然后利用等线段代换可得到结论;(2)利用AFBF =DFAD和AF=BE得到BEDF=BFAD,则可判定Rt△BEF∽Rt△DFA,所以∠4=∠3,再证明∠4=∠5,然后根据等腰三角形的性质可判断EF=EP.3.【答案】解:(1)相似.理由:设正方形的边长为a,AC=√a2+a2=√2a,∵ACCF =√2aa=√2,CGAC=√2a=√2,∴ACCF =CGAC,∵∠ACF=∠ACF,∴△ACF∽△GCA;(2)∵△ACF∽△GCA,∴∠1=∠CAF,∵∠CAF+∠2=45°,∴∠1+∠2=45°.【解析】(1)设正方形的边长为a,求出AC的长为√2a,再求出△ACF与△GCA中夹∠ACF 的两边的比值相等,根据两边对应成比例、夹角相等,两三角形相似,即可判定△ACF 与△GCA相似;(2)根据相似三角形的对应角相等可得∠1=∠CAF,再根据三角形的一个外角等于和它不相邻的两个内角的和,∠2+∠CAF=∠ACB=45°,所以∠1+∠2=45°.本题主要利用两边对应成比例,夹角相等两三角形相似的判定和相似三角形对应角相等的性质以及三角形的外角性质,求出两三角形的对应边的比值相等是解本题的关键.4.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AB//CD,AD//BC,∴∠C+∠B=180°,∠ADF=∠DEC.∵∠AFD+∠AFE=180°,∠AFE=∠B,∴∠AFD=∠C.∴△ADF∽△DEC.(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.由(1)知△ADF∽△DEC,∴ADDE =AFCD,∴DE=AD⋅CDAF =√3×84√3=12.在Rt△ADE中,由勾股定理得:AE=√DE2−AD2=6.【解析】(1)根据四边形ABCD为平行四边形,利用平行四边形的对边平行且相等,得到一对同旁内角互补,一对内错角相等,根据已知角相等,利用等角的补角相等得到两组对应角相等,从而推知:△ADF∽△DEC;(2)由△ADF∽△DEC,得比例,求出DE的长.利用勾股定理求出AE的长.此题考查了相似三角形的判定与性质,以及平行四边形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.5.【答案】解:∵CD//AB,∴△EAB∽△ECD,∴CDAB =DEBE,即1.7AB=33+BD①,∵FG//AB,∴△HFG∽△HAB,∴FGAB =HGHB,即1.7AB=4BD+5+4②,由①②得33+BD =4BD+5+4,解得BD=15,∴1.7AB =315+3,解得AB=10.2.答:路灯A离地面的高度为10.2m.【解析】根据相似三角形的判定,由CD//AB 得△EAB∽△ECD ,利用相似比有1.7AB =33+BD ,同理可得1.7AB =4BD+5+4,然后解关于AB 和BD 的方程组求出AB 即可.本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决. 6.【答案】(1)证明:∵△ABC 为等腰直角三角形,∠ACB =90°,∴AC =BC ,∴∠CAB =∠CBA =45°,∴∠CAE =180°−45°=135°,同理∠CBF =135°,∴∠CAE =∠CBF ,∵∠ECF =135°,∠ACB =90°,∴∠ECA +∠BCF =45°,∵∠ECA +∠E =∠CAB =45°,∴∠E =∠BCF ,∵∠CAE =∠CBF ,∴△ECA∽△CFB ;(2)解:∵AB =x ,∠CAB =45°,∠ACB =90°,AC =BC ,∴sin45°=CB x , ∴CB =√22x =AC ,∵由(1)知△ECA∽△CFB ,∴AE CB =AC BF ,∴3√22x =√22x y ,∴y =16x 2,x 的取值范围是x >0,即y 与x 之间的函数关系式是y =16x 2,x 的取值范围是x >0.【解析】(1)根据等腰直角三角形性质求出∠CAE =∠CBF =135°,求出∠ECA +∠BCF =45°,∠E +∠ACE =45°,推出∠E =∠BCF ,即可推出两三角形相似;(2)根据等腰直角三角形性质和锐角三角函数定义求出AC和BC长,根据两时间相似得出比例式,代入即可求出答案.本题考查了相似三角形的性质和判定,等腰直角三角形性质,锐角三角函数的定义等知识点,通过做此题培养了学生的分析问题和解决问题的能力.7.【答案】(1)证明:∵AC平分∠DAB,∴∠DAC=∠CAB,∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴AD:AC=AC:AB,∴AC2=AB⋅AD;(2)证明:∵E为AB的中点,∴CE=BE=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE//AD,∴△AFD∽△CFE.【解析】(1)根据两组对角对应相等的两个三角形相似证明即可;(2)根据直角三角形的性质得到CE=BE=AE,根据等腰三角形的性质得到∠EAC=∠ECA,推出AD//CE即可解决问题;本题考查的是相似三角形的判定和性质、平行线的判定,掌握相似三角形的判定定理和性质定理是解题的关键.8.【答案】(1)证明:∵CD//AB,∴∠BAC=∠DCA又AC⊥BC,∠ACB=90°,∴∠D=∠ACB=90°,∴△ACD∽△BAC;(2)解:在Rt△ABC中,AC=√AB2−BC2=8,由(1)知,△ACD∽△BAC,∴DCAC =ACBA,即 DC 8=810 解得:DC =6.4; (3)能.由运动知,BF =2t ,BE =t ,△EFB 若为等腰三角形,可分如下三种情况:①当 BF =BE 时,10−2t =t ,解得t =103秒.②当EF =EB 时,如图,过点E 作AB 的垂线,垂足为G ,则BG =12BF =12(10−2t).此时△BEG∽△BAC∴BEAB =BGBC ,即t 10=12(10−2t)6, 解得:t =258;③当FB =FE 时,如图2,过点F 作AB 的垂线,垂足为H则BH =12BE =12t.此时△BFH∽△BAC∴BFAB =BHBC ,即10−2t 10=12t 6, 解得:t =6017综上所述:当△EFB 为等腰三角形时,t 的值为103秒或258秒或6017秒.【解析】(1)利用平行线判断出∠BAC =∠DCA ,即可得出结论;(2)先根据勾股定理求出AC =8,由(1)知,△ACD∽△BAC ,得出DC AC =ACBA ,即可得出结论;(3)分三种情况,利用等腰三角形的性质构造出相似三角形,得出比例式建立方程求解即可得出结论.此题是相似形综合题,主要考查了平行线的性质,相似三角形的判定和性质,等腰三角形的性质,构造出相似三角形得出比例式是解本题的关键. 9.【答案】(1)证明:∵DE//AC ,∴∠DEB =∠FCE ,∵EF//AB,∴∠DBE=∠FEC,∴△BDE∽△EFC;(2)解:①∵EF//AB,∴BEEC =AFFC=12,∵EC=BC−BE=12−BE,∴BE12−BE =12,解得:BE=4;②∵AFFC =12,∴FCAC =23,∵EF//AB,∴△EFC∽△BAC,∴S△EFCS△ABC =(FCAC)2=(23)2=49,∴S△ABC=94S△EFC=94×20=45.【解析】(1)由平行线的性质得出∠DEB=∠FCE,∠DBE=∠FEC,即可得出结论;(2)①由平行线的性质得出BEEC =AFFC=12,即可得出结果;②先求出FCAC =23,易证△EFC∽△BAC,由相似三角形的面积比等于相似比的平方即可得出结果.本题考查了相似三角形的判定与性质、平行线的性质等知识;熟练掌握相似三角形的判定与性质是解题的关键.10.【答案】解:根据题意可得:∠AEB=∠CED,∠BAE=∠DCE=90°,∴△ABE∽△CDE,∴ABCD =AECE,∴AB1.6=212.5,∴AB=13.44(米).答:教学大楼的高度AB是13.44米.【解析】根据反射定律,∠1=∠2,又因为FE⊥EC,所以∠3=∠4,再根据垂直定义得到∠BAE=∠DCE,所以可得△BAE∽△DCE,再根据相似三角形的性质解答.本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.。
沪教版九年级上学期-相似三角形讲义(含解析) (1)
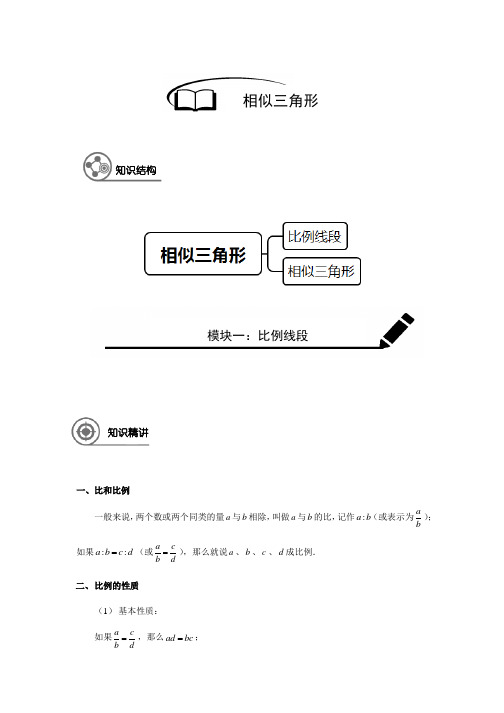
一、比和比例一般来说,两个数或两个同类的量a与b相除,叫做a与b的比,记作:a b(或表示为ab );如果::a b c d=(或a cb d=),那么就说a、b、c、d成比例.二、比例的性质(1)基本性质:如果a cb d=,那么ad bc=;相似三角形知识结构模块一:比例线段知识精讲2 / 34如果a cb d =,那么b d ac =,a b cd =,c d a b=. (2) 合比性质: 如果a cb d =,那么a bc db d++=; 如果a cb d =,那么a bc db d--=. (3) 等比性质: 如果a c kb d ==,那么ac a c k bd b d+===+.三、比例线段的概念对于四条线段a 、b 、c 、d ,如果::a b c d =(或表示为a cb d=),那么a 、b 、c 、d 叫做成比例线段,简称比例线段. 四、黄金分割如果点P 把线段AB 分割成AP 和PB (AP PB >)两段(如下图),其中AP 是AB 和PB 的比例中项,那么称这种分割为黄金分割,点P 称为线段AB 的黄金分割点.其中,510.6182AP AB -=≈,称为黄金分割数,简称黄金数.五、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例. 如图,已知ABC ∆,直线l // BC ,且与AB 、AC 所在直线交于点D 和点E ,那么AD AEDB EC=.APBlAB CDEAB C DEAB CDE ll六、三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.如图,点D 、E 分别在ABC ∆的边AB 、AC 上, 如果DE // BC ,那么DE AD AE BC AB AC==. 七、三角形的重心定义:三角形三条中线交于一点,三条中线交点叫三角形的重心.性质:三角形重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍. 八、三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.九、三角形一边的平行线判定定理推论如果一条直线截三角形的两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.如图,在ABC ∆中,直线l 与AB 、AC 所在直线交于点D 和点E ,如果ADAEDB EC=,那么l //BC .ABCD EA BCDEAB CDEABCD E4 / 34十、平行线分线段成比例定理两条直线被三条平行的直线所截,截得的对应线段成比例. 如图,直线1l //2l //3l ,直线m 与直线n 被直线1l 、2l 、3l所截,那么DF EGFB GC=.十一、平行线等分线段定理两条直线被三条平行的直线所截,如果一条直线上截得的线段相等,那么另一条直线上 截得的线段也相等.【例1】 如图,点D 、E 分别在ABC ∆的边AB 和BC 上.下列所给的四个条件中,不一定能得到DE // AC 的条件是( ) A .BE BCBD BA =B .CE ADBE BD =C .BD DEBA AC=D .BC CEAB AD=【难度】★ 【答案】C .例题解析A BCDEF BC D E F G【解析】如图,作DF DE =,则DF DE AC AC =,∴BD DEBA AC=不能判定DE // AC ,故选C . 【总结】本题考查了平行线分线段成比例定理,找准对应关系,避免错选.【例2】 在比例尺为1 : 40000的一张地图上,量得A 、B 两地的距离是37 cm ,那么A 、B两地的实际距离是______km .【难度】★ 【答案】14.8.【解析】设A 、B 两地的实际距离是x km ,则51371040000x -⨯=,解得:14.8x =. 【总结】本题考查了比例尺的有关计算,注意单位的换算.【例3】 如图,已知1l //2l //3l ,DE = 4,DF = 6,那么下列结论正确的是( )A .BC : EF = 1 : 1B .BC : AB = 1 : 2 C .AD : EF = 2 : 3 D .BE : CF = 2 : 3 【难度】★ 【答案】B .【解析】::1:2BC AB EF DE ==,故B 正确. 【总结】本题考查了平行线分线段成比例定理的运用.【例4】 如果线段a = 4 cm ,b = 9 cm ,那么它们的比例中项是______cm . 【难度】★ 【答案】6.【解析】设它们的比例中项是x cm ,则由题意得249x =⨯,解得:6x =. 【总结】本题考查了比例中项的概念及计算.6 / 34BC DE FGA【例5】 四边形ABCD 是平行四边形,点E 在边BA 的延长线上,CE 交边AD 于点F ,交对角线BD 于点G .求证:CG 是EG 与FG 的比例中项. 【难度】★ 【答案】详见解析.【解析】∵四边形ABCD 是平行四边形,∴AD ∥BC ,AB ∥CD ,∴CG BG FG GD =,EG BGCG GD=, ∴CG EGFG CG=, ∴CG 是EG 与FG 的比例中项. 【总结】本题考查了平行线分线段成比例定理的运用.【例6】 已知线段AB = 10,P 是线段AB 的黄金分割点(AP > PB ),则AP =______. 【难度】★ 【答案】555.【解析】由题意得51AP AB -=555AP =. 【总结】本题考查了黄金分割的有关计算.【例7】 已知23a c eb d f ===,18ac e =--,0bd f ++≠,求b d f ++的值. 【难度】★★ 【答案】27.【解析】∵23a c eb d f ===,0b d f ++≠,∴23a c e b d f ++=++, ∵18a c e =--,∴18a c e ++=,∴27b d f ++=.【总结】本题考查了等比性质的应用.【例8】 如果直角三角形的斜边长为18,那么这个三角形的重心到直角顶点的距离为______.【难度】★★ 【答案】6.【解析】如图,易得192CD AB ==,∴263CG CD ==. 【总结】本题考查了重心的性质及直角三角形斜边上的中线等于斜边的一半.【例9】 如图,已知AD // EF // BC ,AE = 3BE ,AD = 2,EF = 5,那么BC =______.【难度】★★ 【答案】6.【解析】作AN ∥DC 分别交EF 、BC 于点M 、N ,由题意得2NC MF AD ===,EM AEBN AB=, 即334BN =,∴4BN =,∴6AB =. 【总结】本题考查了平行线分线段成比例定理的运用.【例10】 如图,点E 、F 分别在正方形ABCD 的边AB 、BC 上,EF 与对角线BD 交于点G ,如果BE = 5,BF = 3,那么FG : EF 的比值是_______.【难度】★★A BCDEF M NA BCDEFGH【答案】38.【解析】作GH AB⊥于点H,易得GH BH=,∵GH EHBF EB=,535GH GH-=,解得:158GH=,∴38 FG BHEF BE==.【总结】本题考查了平行线分线段成比例定理的运用,注意比和比值的区别.【例11】如图,BD是ABC∆的角平分线,点E、F分别在BC、AB上,且DE // AB,DEF A∠=∠.(1)求证:BE = AF;(2)设BD与EF交于点M,联结AE,交BD于点N,求证:BN MD BD ND=.【难度】★★【答案】详见解析.【解析】(1)∵DE // AB,DEF A∠=∠,∴AD∥EF,∴四边形AFED是平行四边形,∴AF DE=,ABD EDB∠=∠,∵BD是ABC∆的角平分线,∴ABD EBD∠=∠,∴EDB EBD∠=∠,∴BE DE=,∴BE AF=;(2)∵DE // AB,∴BN AB ND ED=,∵AD∥EF,∴BD ABMD AF=,MAFB E CDN8/ 34ABCDEFM∵ED AF =,∴BD AB MD ED =,∴BN BDND MD=, ∴BN MD BD ND ⋅=⋅.【总结】本题考查了平行四边形的判定及平行线分线段成比例定理.【例12】 如图,在直角梯形ABCD 中,AD // BC ,90DAB ABC ∠=∠=︒,E 为CD 的中点,联结AE 并延长交BC 的延长线于F ; (1)联结BE ,求证:BE = EF .(2)联结BD 交AE 于M ,当AD = 1,AB =2,AM = EM 时,求CD 的长. 【难度】★★【答案】(1)详见解析;(2)5CD =.【解析】(1)∵AD // BC ,DE EC =,易得ADE ∆≌FCE ∆, ∴E 为AF 的中点,∵90DAB ABC ∠=∠=︒, ∴BE EF =;(2)∵AM EM =,∴13AM MF =,∴13AD BF =, ∵1AD CF ==,∴3BF =,2BC =,∵2AB =,∴()225DC BC AD AB -+.【总结】本题考查了直角三角形的性质、平行线分线段成比例定理及勾股定理等.10 / 34一、 相似三角形的定义如果一个三角形的三个角与另一个三角形的三个角对应相等,且它们各有的三边对应成比例,那么这两个三角形叫做相似三角形.如图,DE 是ABC ∆的中位线,那么在ADE ∆与ABC ∆中, A A ∠=∠, ADE B ∠=∠,AED C ∠=∠;12AD DE AE AB BC AC ===.由相似三角形的定义,可知这两个三角形相似.用符号来表示,记作ADE ∆∽ABC ∆,其中点A 与点A 、点D 与点B 、点E 与点C 分别是对应顶点;符号“∽”读作“相似于”.用符号表示两个相似三角形时,通常把对应顶点的字母分别写在三角形记号“∆”后相应的位置上.根据相似三角形的定义,可以得出:(1)相似三角形的对应角相等,对应边成比例;两个相似三角形的对应边的比,叫做这两个三角形的相似比(或相似系数).(2)如果两个三角形分别与同一个三角形相似,那么这两个三角形也相似. 二、 相似三角形的预备定理平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似.模块二:相似三角形DABCE知识精讲AB C A 1B 1C 1如图,已知直线l 与ABC ∆的两边AB、AC 所在直线分别交于点D 和点E , 则ADE ∆∽ABC ∆.三、 相似三角形判定定理1如果一个三角形的两角与另一个三角形的两角对应相等,那么这两个三角形相似. 可简述为:两角对应相等,两个三角形相似.如图,在ABC ∆与111A B C ∆中,如果1A A ∠=∠、1B B ∠=∠,那么ABC ∆∽111A B C ∆.常见模型如下:ABCDEAB C DEAB CDE12 / 34AB C AB CABC A 1B 1C 1四、 相似三角形判定定理2如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.可简述为:两边对应成比例且夹角相等,两个三角形相似. 如图,在ABC ∆与111A B C ∆中,1A A ∠=∠,1111AB ACA B AC =,那么ABC ∆∽111A B C ∆.五、 相似三角形判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似. 可简述为:三边对应成比例,两个三角形相似.如图,在ABC ∆与111A B C ∆中,如果111111AB BC CAA B B C C A ==,那么ABC ∆∽111A B C ∆.六、 直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例,那么这两个直角三角形相似.可简述为:斜边和直角边对应成比例,两个直角三角形相似. 如图,在Rt ABC ∆和111Rt A B C ∆中,如果190C C ∠=∠=︒,1111AB BCA B B C =, 那么ABC ∆∽111A B C ∆.七、 相似三角形性质定理相似三角形性质定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都 等于相似比.相似三角形性质定理2:相似三角形周长的比等于相似比. 相似三角形性质定理3:相似三角形的面积的比等于相似比的平方.例题解析ABCA 1B 1C 114/ 34AB CDEF【例13】在下列44⨯的正方形网格图中,每个小正方形的边长都是1,三角形的顶点都在格点上,那么与图1中ABC∆相似的三角形所在的网格图是()A.B.C.D.【难度】★【答案】B.【解析】由图易得ABC∆为直角三角形,且:1:2BC AB=,故选B.【总结】本题考查了相似三角形的判定.【例14】已知ABC∆∽DEF∆,且相似比为3 : 4,2ABCS∆=cm2,则DEFS∆=______ cm2.【难度】★【答案】329.【解析】由题意得234ABCDEFSS∆∆⎛⎫= ⎪⎝⎭,∴329DEFS∆=cm2.【总结】本题考查了相似三角形的性质.【例15】如图,已知点D是ABC∆中的边BC上的一点,BAD C∠=∠,ABC∠的平分线交边AC于点E,交AD于F,那么下列结论中错误的是()A.BAC∆∽BDA∆B.BFA∆∽BEC∆图1ABCDABCD EF C .BDF ∆∽BEC ∆ D .BDF ∆∽BAE ∆【难度】★ 【答案】C .【解析】∵BAD C ∠=∠,ABD CBA ∠=∠,∴BAC ∆∽BDA ∆; ∵BAD C ∠=∠,ABF CBF ∠=∠,∴BFA ∆∽BEC ∆;∵BAE BDF ∠=∠,ABF CBF ∠=∠,∴BDF ∆∽BAE ∆;故C 错误.【总结】本题考查了相似三角形的判定.【例16】 如图,已知点D 在ABC ∆的边AB 上,且ACD B ∠=∠,:1:3ACD DBC S S ∆∆=.求AC AB的值. 【难度】★【答案】12.【解析】∵ACD B ∠=∠,CAD BAC ∠=∠,∴CAD BAC ∆∆,∴22::CAD BAC S S AC AB ∆∆=,∵:1:3ACD DBC S S ∆∆=,∴:1:4CAD BAC S S ∆∆=,∴12AC AB =. 【总结】本题考查了相似三角形的判定及性质.【例17】 如图,已知点E 、F 分别在矩形ABCD 的边BC 和CD 上,EF AE ⊥,BE = 3 cm ,AB = 6 cm ,矩形ABCD 的周长为28 cm ,求CF 的长.【难度】★16 / 34ABCDEAMG【答案】52CF =cm . 【解析】∵AB = 6 cm ,矩形ABCD 的周长为28 cm , ∴8BC =cm ,∴5EC =cm ,∵EF AE ⊥, 易证ABE ∆∽ECF ∆,∴AB BE EC CF =,即635CF =,解得:52CF =cm . 【总结】本题考查了一线三等角基本模型的运用.【例18】 如图,已知点D 、E 分别在ABC ∆边AB 、AC 上,DE // BC ,BD = 2AD ,那么:DEB EBC S S ∆∆等于( )A .1 : 2B .1 : 3C .1 : 4D .2 : 3【难度】★★ 【答案】B .【解析】∵BD = 2AD ,∴2BDE ADE S S ∆=,∵DE // BC ,∴9ABC ADE S S ∆∆=,∴6EBC ADE S S ∆∆=,∴:DEB EBC S S ∆∆1:3=.【总结】本题考查了相似三角形的性质及同底等高模型的综合运用.【例19】 如图,ABC ∆中,如果AB = AC ,AD ⊥BC 于点D ,M 为AC 中点,AD 与BM 交于点G ,那么:GDM GAB S S ∆∆的值为_______.【难度】★★ABCDEF【答案】14. 【解析】∵AB = AC ,AD ⊥BC , ∴BAD CAD ∠=∠,BD DC =, ∵M 为AC 中点,∴DM AM =,∴BAD MDA ∠=∠, ∴GDM ∆∽GAB ∆,∵点G 为ABC ∆的重心,∴214GDM GAB S GD S GA ∆∆⎛⎫== ⎪⎝⎭. 【总结】本题考查了相似三角形的判定及性质,同时考查了重心的性质.【例20】 如图,已知ABC ∆中,AB = AC ,CD 是边AB 上的高,且CD = 2,AD = 1,四边形BDEF 是正方形.CEF ∆和BDC ∆相似吗?试证明你的结论.【难度】★★【答案】相似,详见解析.【解析】由题意,可得:5AC AB =∴51BD DE EF ===,∴35CE =∴51BD DC -=355151CE EF --==-,∴BD CEDC EF=,∵BDC CEF∠=∠,∴CEF∆∽BDC∆.【总结】本题考查了相似三角形的判定.【例21】已知:如图,点E是四边形ABCD的对角线BD上一点,且BAC BDC DAE∠=∠=∠.(1)求证:ABE∆∽ACD∆;(2)求证:BC AD DE AC=.【难度】★★【答案】详见解析.【解析】(1)∵BAC BDC DAE∠=∠=∠,∴BAE CAD∠=∠,∵BEA EDA DAE∠=∠+∠,CDA EDA BDC∠=∠+∠,∴BEA CDA∠=∠,∴ABE∆∽ACD∆;(2)由(1)知AB AEAC AD=,∴AB ACAE AD=,又∵BAC EAD∠=∠,∴ABC∆∽AED∆,∴BC ACED AD=,∴BC AD DE AC=.【总结】本题考查了相似三角形的判定及性质的综合运用.EDCBA18/ 34ABCD EFGHA BCD EF 【例22】 如图,已知:四边形ABCD 是平行四边形,点E 在边BA 的延长线上,CE 交AD于点F ,ECA D ∠=∠. (1)求证:ECA ∆∽ECB ∆; (2)若DF = AF ,求AC : BC 的值. 【难度】★★【答案】(1)详见解析;(22. 【解析】(1)∵四边形ABCD 是平行四边形, ∴B D ∠=∠,∵ECA D ∠=∠,∴ECA B ∠=∠, 又∵E E ∠=∠, ∴ECA ∆∽ECB ∆; (2)∵DF AF =,易证DC AE AB ==,∴2EB EA =,由(1)得AC EC EA BC EB EC ==,即2EC EAEA EC=,∴2EC EA =, ∴22AC EA BC EC ==. 【总结】本题考查了相似三角形的判定及性质的应用.【例23】 如图,BD 是平行四边形ABCD 的对角线,若45DBC ∠=︒,DE BC ⊥于E ,BF CD ⊥于F ,DE 与BF 相交于H ,BF 与AD 的延长线相交于G .求证:(1)CD = BH ; (2)AB 是AG 和HE 的比例中项. 【难度】★★ 【答案】详见解析.【解析】(1)∵45DBC ∠=︒,DE BC ⊥, ∴ED EB =,∵BF CD ⊥,∴EBH CDE ∠=∠,∴EDC ∆≌EBH ∆,20 / 34∴CD BH =;(2)∵四边形ABCD 是平行四边形,∴C A ∠=∠,∴BHE A ∠=∠,∵EBH BGA ∠=∠,∴EBH ∆∽BGA ∆,∴AG ABHB HE=, ∵HB CD AB ==,∴AG ABAB HE=,∴AB 是AG 和HE 的比例中项. 【总结】本题考查了全等及相似三角形的判定.【例24】 如图,已知等腰ABC ∆中,AB = AC ,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E .(1)求证:CAD ECB ∠=∠;(2)点F 是AC 的中点,联结DF ,求证:2BD FC BE =.【难度】★★ 【答案】详见解析.【解析】(1)∵AD ⊥BC ,CE ⊥AB , ∴BAD ECB ∠=∠, ∵AB = AC ,∴BAD CAD ∠=∠, ∴CAD ECB ∠=∠; (2)由题意得12ED BC BD ==,∴DBE DEB ∠=∠, ∵点F 是AC 的中点,∴12DF AC FC ==,∴DCF FDC ∠=∠, ∵DBE DCF ∠=∠,∴CDF ∆∽BED ∆, ∴CD FC BE BD =,∵CD BD =,∴BD FCBE BD=, ∴2BD FC BE =.CBADEFABC D E F G【总结】本题考查了直角三角形的性质及相似三角形的判定.【例25】 如图,已知在梯形ABCD 中,AD // BC ,90A ∠=︒,AB = AD .点E 在边AB 上,且DE CD ⊥,DF 平分EDC ∠,交BC 于点F ,联结CE 、EF . (1)求证:DE = DC ;(2)如果2BE BF BC =,求证:BEF CEF ∠=∠. 【难度】★★ 【答案】详见解析.【解析】(1)作CH AD ⊥的延长线于点H , ∵AD // BC ,90A ∠=︒,AB = AD ,∴CH AD =,∵DE CD ⊥,∴ADE HCD ∠=∠, ∴ADE ∆≌HCD ∆,∴DE DC =;(2)∵2BE BF BC =,B B ∠=∠,∴BEF ∆∽BCE ∆,∴BEF BCE ∠=∠, ∵DF 平分EDC ∠,DE DC =,∴DEF ∆≌DCF ∆,∴DEF DCF ∠=∠,∵DEC DCE ∠=∠,∴CEF BCE ∠=∠,∴BEF CEF ∠=∠.【总结】本题考查了一线三直角模型及相似和全等三角形的综合应用.【例26】 已知:如图,在ABC ∆中,AB = AC ,点D 、E 分别是边AC 、AB 的中点,DF ⊥AC ,DF 与CE 相交于点F ,AF 的延长线与BD 相交于点G .(1)求证:2AD DG BD =;(2)联结CG ,求证:ECB DCG ∠=∠. 【难度】★★ 【答案】详见解析.【解析】(1)∵AB = AC ,点D 、E 分别是边AC 、AB 的中点,A BCDEFH∴ACE∆≌ABD∆,∴ABD ACE∠=∠,∵DF⊥AC,∴FAD FCD∠=∠,∴ABD FAD∠=∠,∴DAG∆∽DBA∆,∴AD DG BD AD=,∴2AD DG BD=;(2)∵AD DC=,∴DC DG BD DC=,∵CDG BDC∠=∠,∴CDG∆∽BDC∆,∴DBC DCG∠=∠,∵ABC ACB∠=∠,∴ABD GCB∠=∠,∴ACE GCB∠=∠,∴ECB DCG∠=∠.【总结】本题考查了相似三角形的判定及性质.ABCD EFG【例27】 如图,直角梯形ABCD 中,90B ∠=︒,AD // BC ,BC = 2AD ,点E 为边BC 的中点.(1)求证:四边形AECD 为平行四边形;(2)在CD 边上取一点F ,联结AF 、AC 、EF ,设AC 与EF 交于点G ,且EAF CAD ∠=∠.求证:AEC ∆∽ADF ∆;(3)在(2)的条件下,当45ECA ∠=︒时,求:FG : EG 的比值. 【难度】★★【答案】(1)详见解析;(2)详见解析;(3)45.【解析】(1)∵BC = 2AD ,点E 为边BC 的中点, ∴AD EC =,∵AD // BC ,∴四边形AECD 为平行四边形;(2)∵EAF CAD ∠=∠,∴EAC DAF ∠=∠, ∵四边形AECD 为平行四边形,∴AEC D ∠=∠, ∴AEC ∆∽ADF ∆;(3)∵45ECA ∠=︒,∴AB BC =,设1AD =,则1BE EC ==,2AB =,∴5AE =∵AEC ∆∽ADF ∆,∴AD DFAE EC=,解得5DF =,∴45FC , ∴45FG FC EG AE ==.24 / 34【总结】本题考查了平行四边形的判定、勾股定理、相似三角形的判定及性质的综合运用,综合性较强,解题时注意进行分析.【例28】 如图,已知在ABC ∆中,P 是边BC 上的一个动点,PQ // AC ,PQ 与边AB 相交于点Q ,AB = AC = 10,BC = 16,BP = x ,APQ ∆的面积为y . (1)求y 关于x 的函数解析式;(2)试探索:APQ ∆与ABP ∆能否相似?如果能相似,请求出x 的值,如果不能相似,请说明理由.【难度】★★★【答案】(1)()23301616y x x x =-<<;(2)能相似,394x =. 【解析】(1)作AH BC ⊥于点H ,ABCPQ H∵AB = AC = 10,BC = 16,∴6AH =,∴1482ABC S BC AH ∆=⋅⋅=,132ABP S BP AH x ∆=⋅⋅=, ∵PQ // AC ,∴BPQ ∆∽BCA ∆,∴22256BPQ BCAS BP x S BC ∆∆⎛⎫== ⎪⎝⎭,∴2316BPQ x S ∆=,∴23316APQ ABP BPQ S S S x x ∆∆∆=-=-,即()23301616y x x x =-<<; (2)能相似,此时394x =,详解如下: ∵BPQ ∆∽BCA ∆,∴BQ BP BA BC =,∴58BQ x =,∵AQP B ∠>∠,∴AQP APB ∠=∠,∴APQ ∆∽ABP ∆,∴AP PQ AB BP =,即5810xAP x =,解得:254AP =,∵AQ PQ AP BP =,即551088254x xx -=,解得:394x =, 综上,APQ ∆与ABP ∆能相似,此时394x =. 【总结】本题考查了相似三角形的性质及相似三角形的存在性问题.26 / 34ABCMN【习题1】 如果两个相似三角形的面积的比为4 : 9,那么它们对应的角平分线的比是______. 【难度】★ 【答案】2:3.【解析】相似三角形面积比等于相似比的平方. 【总结】本题考查了相似三角形的性质.【习题2】 如图,ABC ∆和AMN ∆都是等边三角形,点M 是ABC ∆的重心,那么AMNABCS S ∆∆的值为( ) A .23B .13C .14D .49【难度】★★ 【答案】B .【解析】∵点M 是ABC ∆的重心,设2AM =,则可得23AB =,∴AMN ABC S S ∆∆213AM AB ⎛⎫== ⎪⎝⎭,故选B . 【总结】本题考查了相似三角形及重心的性质的综合运用.【习题3】 如图,AB // DC ,DE = 2AE ,CF = 2BF ,且DC = 5,AB = 8,则EF =______. 【难度】★★随堂检测CDMABCDEF O P【答案】7.【解析】延长AD 、BC 交于点M ,∵AB // DC ,∴MD MCDA CB=, ∵DE = 2AE ,CF = 2BF ,∴MD MCDE CF=,∴EF // DC , 过点D 作DH ∥CB ,易求7EF =.【总结】本题考查了本题考查了平行线分线段成比例定理的运用.【习题4】 已知,如图,D 、E 、F 分别是ABC ∆的边BC 、AB 、AC 的中点,AD 与EF 相交于点O ,线段CO 的延长线交AB 于点P ,求证:AB = 3AP .【难度】★★【答案】详见解析.【解析】∵D 、E 、F 分别是ABC ∆的边BC 、AB 、AC 的中点, ∴EF ∥BC ,22BD CD OE OF ===,设PE k =,则14PE OE PB BC ==,∴4PB k =,3BE k =,∴3AE k =, ∴2AP k =,6AB k =,∴3AB AP =.【总结】本题考查了三角形一边平行线的性质定理及中位线性质定理的运用.【习题5】 如图,在平行四边形ABCD 中,AE ⊥BC 于E ,AF ⊥CD 于F .(1)求证:CD DF BC BE =;(2)若M 、N 分别是AB 、AD 中点,且60B ∠=︒,求证:EM // FN .ABCDEFMNG28 / 34ABCDEF【难度】★★ 【答案】详见解析.【解析】(1)∵四边形ABCD 是平行四边形, ∴B D ∠=∠, ∵AE ⊥BC ,AF ⊥CD ,∴ABE ∆∽ADF ∆,∴AB BEAD DF=,∵AB CD =,AD BC =, ∴CD DF BC BE =;(2)延长EM 、DA 交于点G ,∵M 、N 分别是AB 、AD 中点,AE ⊥BC ,AF ⊥CD ,∴EM BM =,FN ND =, ∵60B ∠=︒,∴BME ∆、DFN ∆为等边三角形, ∴60BEM DNF ∠=∠=︒,∵G BEM ∠=∠,∴G DNF ∠=∠,∴EM // FN .【总结】本题考查了相似三角形的判定及直角三角形的有关性质.【习题6】 如图,Rt ABC ∆中,90ACB ∠=︒,D 是边BC 上一点,点E 、F 分别是线段AB 、AD 中点,联结CE 、CF 、EF . (1)求证:CEF ∆≌AEF ∆;(2)联结DE ,当BD = 2CD 时,求证:DE = AF .【难度】★★【答案】详见解析.【解析】(1)∵90ACB∠=︒,点E、F分别是线段AB、AD中点,∴12CF AD AF==,12CE AB AE==,∵EF EF=,∴CEF∆≌AEF∆;(2)∵点E、F分别是线段AB、AD中点,∴EF∥BD,12EF BD=,∵BD = 2CD,∴EF CD=,∴四边形CFED是平行四边形,∴DE CF=,∵CF AF=,∴DE AF=.【总结】本题考查了直角三角形的性质、三角形全等及平行四边形的判定和性质的综合运用.【习题7】已知正方形ABCD的对角线相交于点O,CAB∠的平分线分别交BD、BC于点E、F,作BH AF⊥,垂足为H ,BH的延长线分别交AC、CD于点G、P.(1)求证:AE = BG;(2)求证:GO AG CG AO=.【难度】★★【答案】详见解析.【解析】(1)∵ABCD为正方形,∴OA OB=,AC BD⊥,∵BH AF⊥,∴BGO BEH∠=∠,∵AEO BEH∠=∠,∴BGO AEO∠=∠,∴AEO∆≌BGO∆,∴AE BG=;(2)∵AF为CAB∠的平分线,∴OAE BAF∠=∠,∵CBP BAF∠=∠,∴OAE∆∽CBP∆,∴OE PCAO BC=,∵AB BC=,GO OE=,∴GO PCAO AB=,A BCD PGOFHE30 / 34ABCDE F∵PC ∥AB ,∴CG PCAG AB=, ∴GO CGAO AG=,∴GO AG CG AO =. 【总结】本题考查了正方形的性质及相似三角形的判定.【作业1】 若ABC ∆∽111A B C ∆(其中点A 和1A 、B 和1B 、C 和1C 分别对应),且AB = 4,11A B= 6,则ABC ∆的周长和111A B C ∆的周长之比是( )A .9 : 4B .4 : 9C .2 : 3D .3 : 2【难度】★ 【答案】C .【解析】相似三角形的周长比等于相似比. 【总结】本题考查了相似三角形的性质.【作业2】 已知,如图,在Rt ABC ∆中,90ACB ∠=︒,点D 为AB 的中点,BE CD ⊥,垂足为点F ,BE 交AC 于点E ,CE = 1cm ,AE = 3 cm . 求证:(1)ECB ∆∽BCA ∆;(2)求斜边AB 的长.课后作业【难度】★【答案】详见解析.【解析】(1)∵BE CD⊥,90ACB∠=︒,∴ACD CBE∠=∠,∵点D为AB的中点,∴CD AD=,∴ACD DAC∠=∠,∴CBE A∠=∠,∴ECB∆∽BCA∆;(2)由(1)得CB CECA CB=,解得:2CB =cm,∴2225AB AC BC=+=cm.【总结】本题考查了相似三角形的判定及性质,注意观察母子形.【作业3】已知:如图,线段AB // CD,AC CD⊥,AC、BD相交于点P,E、F分别是线段BP和DP的中点.(1)求证:AE // CF;(2)如果AE和DC的延长线相交于点Q,M、N分别是线段AP和DQ的中点,求证:MN = CE.【难度】★★【答案】详见解析.【解析】(1)∵AB // CD,∴AP BP PC PD=,∵E、F分别是线段BP和DP的中点,A BCDEFPQNM32 / 34∴22AP PE PEPC PF PF==, ∴AE // CF ;(2)∵AC CD ⊥,E 、F 分别是线段BP 和DP 的中点,∴AE EP EB ==,∵EA EBEQ ED=,∴ED EQ =, ∵M 、N 分别是线段AP 和DQ 的中点,∴EM AC ⊥,EN DQ ⊥,∴四边形MNCE 是矩形,∴MN CE =.【总结】本题考查了平行线分线段成比例定理和矩形的判定及性质.【作业4】 如图,已知在四边形ABCD 中,AD // BC ,对角线AC 、BD 相交于点O ,BD 平分ABC ∠,过点D 作DF // AB ,分别交AC 、BC 于点E 、F . (1)求证:四边形ABFD 是菱形;(2)设AC AB ⊥,求证:AC OE AB EF =. 【难度】★★ 【答案】详见解析.【解析】(1)∵AD // BC ,DF // AB ,∴四边形ABFD 是平行四边形, ∵BD 平分ABC ∠,∴ABD DBC ∠=∠,∵ADB DBC ∠=∠, ∴ABD ADB ∠=∠,∴AB AD =,∴四边形ABFD 是菱形; (2)连接OF ,易证AOB ∆≌FOB ∆,∵AC AB ⊥,∴OF BC ⊥,∵DF // AB ,∴EF OC ⊥,∴CEF ∆∽FEO ∆,∴EF CEEO EF=, ∵CE EF AC AB =,即CE AC EF AB =,∴EF ACEO AB=,∴AC OE AB EF =. 【总结】本题考查了菱形的判定及相似三角形的判定及性质的综合运用.ABC DEFO【作业5】 已知:如图,四边形ABCD 是菱形,点E 在边CD 上,点F 在BC 的延长线上,CF = DE ,AE 的延长线与DF 相交于点G . (1)求证:CDF DAE ∠=∠;(2)如果DE = CE ,求证:AE = 3EG .【难度】★★ 【答案】详见解析.【解析】(1)∵四边形ABCD 是菱形,∴AD DC =,ADE DCF ∠=∠,∵CF = DE ,∴ADE ∆≌DCF ∆,∴CDF DAE ∠=∠;(2)延长AG 、BF 交于点M , ∵DE = CE ,易证ADE ∆≌MCE ∆,∴AE EM =,AD CM =, 设1DE =,则2AD DC CM ===,1CF FM ==,∴12MG MF AG AD ==,设MG k =,则2AG k =,1322AE AM k ==,∴12EG k =,∴3AE EG =.【总结】本题考查了全等三角形的判定及相似三角形的性质.【作业6】 已知:如图,在正方形ABCD 中,点E 是边AD 的中点,联结BE ,过点A 作AF BE ⊥,分别交BE 、CD 于点H 、F ,联结BF . (1)求证:BE = BF ;(2)联结BD ,交AF 于点O ,联结OE .求证:AEB DEO ∠=∠. 【难度】★★ 【答案】详见解析.EDCG FABMAB CDEFHO【解析】(1)∵四边形ABCD 是正方形,AF BE ⊥, ∴AB AD =,DAF ABE ∠=∠,∴DAF ∆≌ABE ∆,∴AE DF =,∴点F 为DC 中点,∴CBF ∆≌ABE ∆,∴BE BF =;(2)∵DE DF =,EDO FDO ∠=∠,DO DO =, ∴EDO ∆≌FDO ∆,∴DEO DFO ∠=∠,由(1)得AEB DFO ∠=∠,∴AEB DEO ∠=∠.【总结】本题考查了全等三角形的判定及正方形的性质的综合运用.。
人教版九年级数学下27.2相似三角形小结优秀教学案例

1.利用生活情境,引发学生兴趣。
在导入新课时,我会利用与生活相关的情境,引发学生的学习兴趣。例如,我可以展示一些建筑设计图,让学生观察并思考:如何在设计中利用相似三角形的性质?这样既能激发学生的学习兴趣,又能引导学生思考相似三角形在实际生活中的应用。
2.回已有知识,为新课学习做好铺垫。
(五)作业小结
1.设计具有针对性的作业,巩固所学知识。
在布置作业时,我会设计一些具有针对性的题目,让学生通过完成作业,巩固所学知识。例如,我可以设计一些关于相似三角形的判定和性质的练习题,让学生在完成作业的过程中,加深对知识的理解和运用。
2.鼓励学生进行自我反思,提高自我监控能力。
在布置作业时,我会鼓励学生进行自我反思,让学生思考自己在学习过程中的优点和不足,从而提高学生的自我监控能力。例如,我可以让学生在作业中总结自己在学习相似三角形时的思维方式和方法,以及遇到的困难和解决方法。
2.培养学生运用数学知识解决实际问题的能力,提高学生的创新思维。
在教学过程中,我会以一个实际问题为背景,让学生分组讨论,探讨相似三角形在实际问题中的应用,培养学生的合作意识和解决问题的能力。同时,我会鼓励学生提出问题,引导他们通过讨论、思考解决问题,从而提高学生的思维能力和创新能力。
(二)过程与方法
在教学过程中,我会引导学生分工合作,完成一些具有挑战性的任务。例如,在讲解相似三角形的判定时,我可以让学生分组进行实验,通过实际操作验证相似三角形的性质,从而提高学生的团队协作能力。
(四)反思与评价
1.引导学生进行自我反思,提高学生的自我监控能力。
在教学过程中,我会引导学生进行自我反思,让学生思考自己在学习过程中的优点和不足,从而提高学生的自我监控能力。例如,在讲解相似三角形的性质时,我可以让学生回顾自己的学习过程,思考自己在解决问题时的思维方式和方法。
(完整word版)圆与相似的综合运用

3
4、如图,在平面直角坐标系 xoy 中, M 是 x 轴正半轴上一点,⊙ M与 x 轴的正半轴交于
A,B 两点,A 在 B 的左侧,且 OA,OB 的长是方程 x2 12x 27 0 的两根,ON 是⊙ M 的切线, N 为切点, N 在第四象限.
B
N
F
3
P
G
M
1
2
O
CA
x
∴Rt△ MOC∽Rt△ CAN
∴OAMC
=
OC AN
∵直线 y=-m(x – 4)交 x 轴于点 A,交 y 轴于点 B,
∴A(4,0),
∴AC =CO = 2∵ OM= x,AN = y,
∵x2
=
2 y
∴y =
4 x
(3)∵ OM = 1,∴ AN =y = 4,此时 S 四边形 ANMO = 10 ∵直线 AB 平分梯形 ANMO 的面积,
二、典例精析
例 1.如图,点 A,B,C,D 在 e O 上,AB ,AD 与 BC 相交于点 E ,AE 1 ED , 2
延长 DB 到点 F ,使 FB 1 BD ,连结 AF . 2
(1)证明 △BDE ∽△FDA ; (2)试判断直线 AF 与 e O 的位置关系,并给出证明.
由 AO BE 知, AO FA .∴直线 FA 与 e O 相切.
【点评】.这是一道利用圆内的有关性质,得出三角形相似的结论。再次巩固了全等三角形,
相似三角形,平行线的知识,得出直线与圆的位置关系.同时同学们在做题的过程中,要注意
思维的逻辑性和书写的规范性.
[数学]-专题34 利用相似解决四边形问题——几何综合(原版)
![[数学]-专题34 利用相似解决四边形问题——几何综合(原版)](https://img.taocdn.com/s3/m/c45f872c49d7c1c708a1284ac850ad02de8007d4.png)
专题34 利用相似解决四边形问题——几何综合(原卷版)专题诠释:几何综合题是中考必考题型。
试题一般以全等或相似为中心 , 以四边形为重点 , 常常是三角形、四边形、相似三角形、锐角三角函数等知识的综合运用.解题策略:解答几何综合题应注意 :(1) 注意观察、分析图形 , 把复杂的图形分解成几个基本图形 , 通过添加辅助线补全或构造基本图形 .(2) 掌握常规的证题方法和思路 ;(3) 运用转化的思想解决几何证明问题 , 运用方程的思想解决计算问题。
另外还用结合数学思想和方法。
第一部分 专题典例剖析类型一 利用相似解决平行四边形问题1.(2022•贺州)如图,在平行四边形ABCD 中,点E ,F 分别在AD ,BC 上,且ED =BF ,连接AF ,CE ,AC ,EF ,且AC 与EF 相交于点O .(1)求证:四边形AFCE 是平行四边形;(2)若AC 平分∠F AE ,AC =8,tan ∠DAC =34,求四边形AFCE 的面积.2.(2022•杭州)如图,在△ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,连接DE ,EF .已知四边形BFED 是平行四边形,DE BC =14. (1)若AB =8,求线段AD 的长.(2)若△ADE 的面积为1,求平行四边形BFED 的面积.3.(2021•长春)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=4,BD=8,点E在边AD上,AE=13AD,连结BE交AC于点M.(1)求AM的长.(2)tan∠MBO的值为.类型二利用相似解决矩形问题4.(2022•玉林)如图,在矩形ABCD中,AB=8,AD=4,点E是DC边上的任一点(不包括端点D,C),过点A作AF⊥AE交CB的延长线于点F,设DE=a.(1)求BF的长(用含a的代数式表示);(2)连接EF交AB于点G,连接GC,当GC∥AE时,求证:四边形AGCE是菱形.5.(2022•泰安)如图,矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.(1)若BE平分∠CBD,求证:BF⊥AC;(2)找出图中与△OBF相似的三角形,并说明理由;(3)若OF=3,EF=2,求DE的长度.6.(2022秋•苏州期末)如图,矩形ABCD 中,AD =3,CD =4,点P 从点A 出发,以每秒1个单位长度的速度在射线AB 上向右运动,运动时间为t 秒,连接DP 交AC 于点Q .(1)求证:△DCQ ∽△P AQ ;(2)若△ADQ 是以AD 为腰的等腰三角形,求运动时间t 的值.类型三 利用相似解决菱形问题7.(2022•长春)如图,在Rt △ABC 中,∠ABC =90°,AB <BC .点D 是AC 的中点,过点D 作DE ⊥AC 交BC 于点E .延长ED 至点F ,使得DF =DE ,连结AE 、AF 、CF .(1)求证:四边形AECF 是菱形;(2)若BE EC =14,则tan ∠BCF 的值为 .8.(2022秋•海淀区校级期末)如图,在菱形ABCD 中,∠A =60°,经过点C 的直线分别与AB ,AD 的延长线相交于点P ,Q ,QB ,PD 相交于点O .(Ⅰ)求证:BD 2=PB •DQ ;(Ⅱ)求证:BD 2=OD •PD .9.(2022秋•汝州市期末)如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.(1)求证:四边形ODEC是矩形;(2)连接AE,交CD于点F,当∠ADB=60°,AD=4√3时,直接写出EA的长.10.(2022秋•白塔区月考)如图,在菱形ABCD中,DE⊥BC交BC的延长线于点E,连结AE交BD于点F,交CD于点G,连结CF.(1)求证:AF2=EF•GF;(2)若菱形ABCD的边长为2,∠BAD=120°,求FG的长.类型一利用相似解决正方形问题11.(2022秋•青浦区校级期末)如图,在三角形ABC中,∠C=90°,四边形DEFC是边长为4的正方形,且D、E、F分别在边AC、AB、BC上.把三角形ADE绕点E逆时针旋转一定的角度.(1)当点D与点F重合时,点A的对应点G落在边BC上,此时四边形ACGE的面积为;(2)当点D的对应点D1落在线段BE上时,点A的对应点为点A1,在旋转过程中点A经过的路程为l1,点D经过的路程为l2,且l1:l2=3:2,求线段AD1的长.12.(2022秋•成华区期末)如图,点E是正方形ABCD的对角线CA延长线上一点,连接BE,将BE绕点B顺时针旋转90°至BF,连接EF,EF交AD于点G.(1)求证:△ABE∽△AEG;(2)若正方形ABCD的边长为4,点G为AD的中点,求AE的长.13.(2022秋•洛阳期末)如图,把边长为3的正方形OABC绕点O逆时针旋转n°(0°<n<90°)得到正方形ODEF,DE与BC交于点P,ED的延长线交AB于点Q,交OA的延长线于点M,若BQ:AQ =4:1,求AM的值.14.(2022秋•邹平市校级期末)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;(2)若AB=4,AD=3,AE=3,求AF的长.第二部分 专题提优训练1.(2023•偃师市一模)如图,在△ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,连接DE ,EF .已知四边形BFED 是平行四边形,DE BC =14.(1)若AB =12,求线段AD 的长.(2)若△ADE 的面积为1,求平行四边形BFED 的面积.2.(2022秋•济南期末)如图,点F 是平行四边形ABCD 的边AD 上的一点,直线CF 交线段BA 的延长线于点E .(1)求证:△AEF ∽△DCF ;(2)若AF :DF =1:2,AE =√2,S △AEF =23.①求AB 的长;②求△EBC 的面积.4.(2022秋•惠济区校级期末)如图1,在矩形ABCD 中,AC ,BD 相交于点O ,点E 为BD 上的一个动点,连接CE 并延长到点F ,使EF =CE ,连接AF .(1)若点E 与点B 重合(如图2),判断AF 与BD 的数量关系和位置关系,并说明理由;(2)若以A ,F ,B ,E 为顶点的四边形是平行四边形,BD =3,请直接写出线段BE 的长度.5.(2022秋•路南区校级期末)如图,矩形ABCD中,AB=16,BC=8,点P为AB边上一动点,DP交AC于点Q.(1)求证:△APQ∽△CDQ;(2)P点从A点出发沿AB边以每秒2个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?8.(2022秋•运城期末)如图,矩形ABCD的对角线AC、BD相交于点F,延长BC到点E,使CE=BC,连接DE,连接AE交BD于点G,交CD于点H.(1)求证:四边形ACED是平行四边形;(2)求证:DG2=FG•BG;(3)若AB=14,BC=24,求线段GH的长度.9.(2021秋•三原县期末)如图,在菱形ABCD中,∠C=60°,AB=4,点E是边BC的中点,连接DE、AE、BD.(1)求DE的长;(结果保留根号)(2)点F为边CD上的一点,连接AF,交DE于点G,连接EF,AF⊥EF.①求证:△AGE∽△DGF;②求DF的长.(提示:过点E作EH⊥CD于点H.)10.(2022•江西)如图,四边形ABCD为菱形,点E在AC的延长线上,∠ACD=∠ABE.(1)求证:△ABC∽△AEB;(2)当AB=6,AC=4时,求AE的长.11.(2021秋•宝塔区校级期末)如图,在菱形ABOC中,对角线AO,BC相交于点D,BE⊥AC于点E,A0与BE交于点H.(1)求证:△BAD∽△HBD;(2)延长OC交BE的延长线于点F.求证:HB2=HE•HF.12.(2022秋•未央区校级期末)已知有一块三角形材料∠ABC,其中BC=120cm,高AD=80cm,现需要在三角形ABC上裁下一个正方形材料做零件,使得正方形EFGH的顶点E、F分别在边AB,AC上,H、G在BC上,裁下的正方形EFGH的边长是多少?27.(2022秋•东明县校级期末)如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F.(1)如图①,当CEEB =13时,求S△CEFS△CDF的值;(2)如图②,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=12BG.。
《相似形》复习课教案

相似形复习课教案教学目标1.掌握相似形的定义及相关概念。
2.理解并能运用相似形的性质解决实际问题。
3.能够判断两个图形是否相似,并对不同的判断情况进行分析。
教学内容1.相似形的定义。
2.相似形的性质。
3.相似形的判定方法。
教学重难点1.相似形的判定方法。
2.能够将相似形的性质运用到实际问题中。
教学过程复习1.复习前几节课所学内容,包括平移、旋转、翻转等。
2.回顾相似形的定义和性质。
引入1.引导学生观察两个图形,发现它们之间的相似性。
2.提出问题:如何判断两个图形是否相似?讲解1.定义相似形:如果两个图形之间的对应角度相等,对应边成比例,那么这两个图形就是相似形。
2.讲解相似形的性质:–对应角度相等。
–对应边成比例。
–相似形的比值等于对应边的比值。
–相似形的面积比等于对应边长度的平方。
3.讲解相似形的判定方法:–角-边-角相似法:如果两个角分别对应相等,且它们之间夹着一个对应边成比例的边,那么这两个图形相似。
–边-角-边相似法:如果两个边分别对应相等,且它们之间夹着一个对应角相等的角,那么这两个图形相似。
实践1.给出实际问题,如已知一条杆子的长度和另一条杆子与它的夹角,求另一条杆子的长度。
2.让学生自己判断使用哪种相似形的性质解决问题,并进行计算。
总结1.总结相似形的定义,性质,以及两种相似形的判定方法。
2.强调相似形在生活和工作中的应用。
课后作业1.完成课堂练习。
2.按照教师要求完成作业。
沪科版数学九年级上册《相似三角形的综合应用》教学设计1

沪科版数学九年级上册《相似三角形的综合应用》教学设计1一. 教材分析《相似三角形的综合应用》是沪科版数学九年级上册的一章内容。
本章主要介绍了相似三角形的性质和判定方法,以及相似三角形在实际问题中的应用。
相似三角形是中学数学中的一个重要概念,它在几何学和其他学科中都有广泛的应用。
通过本章的学习,学生可以加深对相似三角形的理解,提高解决实际问题的能力。
二. 学情分析九年级的学生已经学习了三角形的基本性质,对三角形的内角和、边长关系等有一定的了解。
然而,学生对于相似三角形的概念和相关性质可能还不够熟悉,需要通过本章的学习来进一步掌握。
此外,学生可能对于将相似三角形应用于实际问题中还存在一定的困难,需要通过实例分析和练习来提高。
三. 说教学目标1.知识与技能目标:学生能够掌握相似三角形的性质和判定方法,并能够应用于实际问题中。
2.过程与方法目标:学生能够通过观察、分析和推理等方法,探索相似三角形的性质,培养解决问题的能力。
3.情感态度与价值观目标:学生能够积极参与课堂活动,与同伴合作解决问题,培养团队合作精神。
四. 说教学重难点1.教学重点:相似三角形的性质和判定方法。
2.教学难点:相似三角形在实际问题中的应用。
五. 说教学方法与手段1.教学方法:采用问题驱动的教学方法,通过引导学生观察、分析和推理等思维活动,探索相似三角形的性质。
2.教学手段:利用多媒体课件和实物模型等辅助教学,帮助学生直观地理解相似三角形的概念和性质。
六. 说教学过程1.引入新课:通过展示一些实际问题,引发学生对相似三角形的思考,激发学生的学习兴趣。
2.探究相似三角形的性质:引导学生观察和分析一些几何图形,引导学生通过推理得出相似三角形的性质。
3.应用相似三角形的性质:通过一些实际问题,让学生运用相似三角形的性质解决问题,巩固所学知识。
4.总结与拓展:引导学生总结本节课所学的知识,并给出一些拓展问题,激发学生的进一步学习兴趣。
七. 说板书设计板书设计要简洁明了,突出相似三角形的性质和判定方法。
相似三角形的判定数学教学教案(优秀6篇)

相似三角形的判定数学教学教案(优秀6篇)(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如总结报告、心得体会、策划方案、合同协议、条据文书、竞聘演讲、心得体会、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as summary reports, insights, planning plans, contract agreements, documentary evidence, competitive speeches, insights, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please stay tuned!相似三角形的判定数学教学教案(优秀6篇)学习可以这样来看,它是一个潜移默化、厚积薄发的过程。
九年级数学上册《相似三角形的性质及其应用》教案、教学设计

6.课后布置综合性、实践性作业,让学生将所学知识应用于实际情境,提高学生的几何建模和解决问题的能力。
-例如,让学生设计一幅利用相似三角形原理的图案,或解决生活中的实际问题。
7.开展课后辅导和个性化教学,关注学生的个体差异,使每个学生都能在原有基础上得到提高。
(2)学生通过观察、分析,总结相似三角形的性质,如对应角相等、对应边成比例等。
(3)教师引导学生运用相似三角形的性质解决实际问题,如求线段长度、角度大小等。
(4)教师讲解相似三角形判定方法,如AA、SAS、SSS等,并结合实例进行分析。
(三)学生小组讨论
1.教学内容:相似三角形性质的应用问题。
2.教学活动设计:
-对于学习困难的学生,教师可以提供针对性的辅导,帮助他们克服难点,提高学习效果。
四、教学内容与过程
(一)导入新课
1.教学活动设计:通过展示实际生活中含有相似三角形元素的图片,如建筑物的立面图、艺术作品等,引发学生对相似三角形的关注。
教师引导学生观察这些图片,并提出问题:“这些图片中有什么共同特征?它们在几何学中有什么特别之处?”
(1)学生分享本节课的收获,教师点评并补充。
(2)教师强调相似三角形在实际生活中的重要性,激发学生学习兴趣。
(3)教师布置课后作业,巩固所学知识。
(4)教师鼓励学生继续探索相似三角形的相关知识,为后续学习打下基础。
五、作业布置
为了巩固学生对相似三角形性质的理解和应用,以及培养学生的几何思维和问题解决能力,特布置以下作业:
(二)教学难点
1.相似三角形性质的推导和应用,尤其是相似三角形面积比等于相似比的平方这一结论的理解。
利用相似三角形求线段的长(专题)

相似三角形的综合运用(利用相似三角形求线段的长) 姓名____________学号___________1、已知CD AB //,AD 、BC 交于点O ,2=AO ,3=DO ,5=CD ,求AB 的长。
2、如图,在ABC Rt ∆中,︒=∠90C ,D 是AC 边上的一点,AB DE ⊥于点E ,若2=DE ,3=BC ,6=AC ,求AD 的长。
3、如图,在△ABC 中,∠ACB =90°,D 为AC 的中点,DE ⊥AB 于点E ,AC =8,AB =10.求AE 的长.4、如图,正方形ABCD 的边长是4cm ,E 是AD 的中点,EC BM ⊥,垂足为M ,求BM 的长。
5、如图,在矩形ABCD 中,点E 在边AD 上,CE BE ⊥(1)ABE ∆与ECB ∆相似吗,请说明理由;(2)如图,4=AE ,9=BC ,求BE 的长。
6、如图,在矩形ABCD 中,E 是边AB 的中点,连接DE 交对角线AC 于点F ,若4=AB ,3=AD ,求CF 的长。
7、如图,在△ABC 中,D ,E 分别是边AB ,AC 上的点,连接DE ,且∠A =60°,∠ADE =50°,∠B =70°.(1)求证:△ADE∽△ACB .(2)如果E 是AC 的中点,AD =8,AB =10,求AE 的长.8、如图,在ABC Rt ∆中,︒=∠90B ,D 为AB 上一点,以BD 为直径的半⊙O 与AC 相切于点E ,若6==BC BD ,求斜边AC 的长。
9、如图,AB 是⊙O 的直径,点E 在AB 的延长线上,AC 平分∠DAE 交⊙O 于点C ,AD ⊥DE 于点D .(1)求证:直线DE 是⊙O 的切线.(2)如果BE =2,CE =4,求线段AD 的长.10、如图,AB 是⊙O 的直径,CD 与⊙O 相切于点C ,与AB 的延长线交于D .(1)求证:△ADC∽△CDB ;(2)若2=AC ,CD AB 23=,求⊙O 半径.。
数学教学设计小学数学的相似三角形

数学教学设计小学数学的相似三角形数学教学设计:小学数学的相似三角形引言:数学是一门基础学科,对学生的逻辑思维和问题解决能力有着重要的培养作用。
在小学数学教学中,相似三角形是一个重要的概念,它不仅能够帮助学生理解三角形的特性,还能够应用于实际问题的解决中。
本文将介绍一种适用于小学数学教学的相似三角形教学设计。
一、教学目标:通过本次教学,学生将能够:1. 理解相似三角形的定义及其性质;2. 能够判断两个三角形是否相似;3. 能够应用相似三角形解决实际问题;4. 培养学生的观察力、分析能力和解决问题的能力。
二、教学准备:1. 教师准备:投影仪、白板、黑板笔、课件、练习题;2. 学生准备:笔、纸、教材。
三、教学过程:1. 导入(5分钟):- 引导学生回顾三角形的定义和特性。
- 引出相似三角形的概念,让学生思考相似三角形与三角形之间的关系。
2. 概念解释(10分钟):- 通过使用投影仪展示相似三角形的定义,让学生理解相似三角形的概念。
- 解释相似三角形的性质,如边长比例相等、对应角相等等。
3. 判断相似三角形(15分钟):- 教师以示例的方式,先引导学生观察两组三角形的边长关系。
- 引导学生发现边长之间的比例关系,通过观察角度是否相等确定是否为相似三角形。
- 分组让学生自行判断一些给定的三角形是否相似。
4. 拓展应用(20分钟):- 提供一些实际问题,让学生利用相似三角形的性质解决问题。
- 引导学生运用相似三角形的知识计算高度、距离等实际应用题。
5. 总结巩固(10分钟):- 通过提问的方式,让学生总结相似三角形的定义、性质以及应用方法。
- 开展小组讨论,让学生互相交流、分享学习心得和解题思路。
6. 练习与评价(10分钟):- 发放练习题,让学生独立完成。
- 对学生的练习进行评价,及时给予指导和反馈。
四、教学扩展:1. 针对学生的不同水平,可以提供不同难度的练习题,满足学生的个性化学习需求。
2. 可以引导学生探究相似三角形的一些性质,如周长比例、面积比例等。
利用相似三角形测高优秀教案

利用相似三角形测高【教学目标】1.知识与技能:使学生掌握和综合运用三角形相似的判定条件和性质。
2.过程与方法:通过测量旗杆的高度,使学生运用所学知识解决问题,以课后分组合作活动的方法进行实践以及进行全班交流,进一步积累数学活动经验。
3.情感与态度:通过问题情境的设置,培养学生积极的进取精神,增强学生数学学习的自信心。
实现学生之间的交流合作,体现数学知识解决实际问题的价值。
【教学重点】综合运用相似三角形判定、性质解决实际问题。
【教学难点】解决学生在操作过程中如何与课本中有关知识相联系。
【教学过程】(一)拓展思维、探究方法学生课前预习、教师课堂引导、学生课上讨论,归纳总结出测量一些不能直接测量的物体的高度的方法:1.利用阳光下的影子来测量旗杆的高度,如图1:图1操作方法:一名学生在直立于旗杆影子的顶端处测出该同学的影长和此时旗杆的影长。
点拨:图4皮尺等测量工具。
2.教师在活动中要加强巡视观察、引导,对学生测量中的不当之处要立即纠正。
3.学生实际测量后回教室进行计算,小组间交流测量结果。
4.在实际测量时,充分调动学生原有的生活经验和知识基础,去解决生活中的实际问题,体验成功的喜悦,轻松愉快地学习数学。
5.进入小组汇报总结阶段时,应引导学生比较各种方法的优点和缺点,寻求最优化意识。
(三)丰富联想通过以下问题的解决,充分发挥学生的聪明才智。
(想一想)同学们经历了上述三种方法,你还能想出哪些测量旗杆高度的方法?你认为最优化的方法是哪种?思路点拨:1.如果旗杆周围有足够地空地使旗杆在太阳光照射下影子都在平地上,并能测出影子的长度,那么,可以在平地垂直树一根小棒,等到小棒的影子恰好等于小棒的高度时,再量旗杆的影子,此时旗杆的影子长度就是这个旗杆的高度。
2.可以采用立一个已知长度的参照物在旗杆旁照相后量出照片中旗杆与参照物的长度根据线段成比例来进行计算。
3.拿一根知道长度的直棒,手臂伸直,不断调整自己的位置,使直棒刚好完全挡住旗杆,量出此时人到旗杆的距离、人手臂的长度和棒长,就可以利用三角形相似来进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似形的综合运用(一)
知识考点:
会综合运用相似三角形的有关概念、定理解答有关问题。
另外,直角三角形被斜边上的高分成的两个直角三角形与原三角形相似的性质运用,是近几年中考的热点题型。
精典例题:
【例1】如图,已知,在边长为1的正方形ABCD的一边上取一点E,使AE=AD,从AB 的中点F作HF⊥EC于H。
[来源:学+科+网]
(1)求证:FH=FA;
(2)求EH∶HC的值。
证明:(1)连结EF,FC,在正方形ABCD中,AD=AB=BC,∠A=∠B=900
∵AE=AD,F为AB的中点,∴
∴△EAF∽△FBC,∴∠AEF=∠BFC,∠EFA=∠CFB
∴∠EFC=900,
又∵∠EFC=∠B=900 ∴△EFC∽△FBC
∴∠HEF=∠B FC,∠ECF=∠BCF
∴∠AEF=∠HEF,∠AFE=∠HFE
∴△EAF≌△HEF ∴FH=FA
(2)由(1)得,由(1)易证△EHF∽△EFC,从而可得,同理,于是EH∶HC=∶=1∶4
变式:如图,在矩形ABCD中,,点E在BC上,点F在CD上,且EC=BC,FC=CD,FG⊥AE于G,。
求证:AG=4GE 。
(提示:证△ECF∽△FDA得EF∶AF=1∶2,再证△EFG∽△EAF∽△FAG即可)
【例2】已知,在△ABC中,∠ACB=900,过C作CD⊥AB于D,AD=,BD=,∶=2∶1,又关于的方程的两实数根的差的平方小于192,求整数、的值。
分析:如图,易证△ABC∽△ADC,∶=AD∶BD=∶=2∶1,即,再由方程两根差的平方小于192可得,又由判别式△≥0知≤2
∴<≤2,又为整数,∴=1,2
∴=2,=1或=4,=2
探索与创新:
【问题一】已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC(AB>AE)。
(1)△AEF与△EFC是否相似,若相似,证明你的结论;若不相似,请说明理由。
(2)设=,是否存在这样的值,使得△AEF 与△BFC相似,若存在,证明你的结论并求出的值;若不存在,说明理由。
解:(1)相似,如图
证明:延长FE与CD的延长线交于点G。
在Rt△AEF与Rt△DEG中
∵E是AD的中点
∴AE=ED,∠AEF=∠DEG,∠A=∠EDG
∴△AFE≌△DGE
∴E为FG的中点。
又CE⊥FG,∴FC=GC ∴∠CFE=∠G。
∴∠AFE=∠EFC,又△AEF 与△EFC均为直角三角形
∴△AEF∽△EFC。
(2)①存在。
如果∠BCF=∠AEF,即=时,△AEF∽△BCF。
证明:当时,。
∴∠ECG=300。
∴∠ECG=∠ECF=∠AE F=300,∴∠BCF=900-600=300。
又△AEF和△BCF均为直角三角形。
∴△AEF∽△BCF。
②因为EF不平行于BC,∴∠BCF≠∠AFE。
∴不存在第二种相似情况。
跟踪训练:
一、填空题:
1、在Rt△ABC中,∠BAC=900,AD⊥BC于D,AB=2,DB=1,则DC=,AD =。
[来源:学。
科。
网]
2、在△ABC中,AB=12,AC=15,D为AB上一点,BD=AB,在AC上取一点E,得△ADE,当AE的长为时,图中的两个三角形相似。
3、在Rt△ABC中,AD为斜边上的高,,则AB∶BC=。
二、选择题:
在△ABC中,∠A∶∠B∶∠C=1∶2∶3,CD⊥AB于D,AB=,则DB=()
A、B、C、D、
三、解答题:
1、如图,在△ABC中,∠ACB=900,CD⊥AB于D,为了求出AC,在图中你能找出哪些适当的条件?
2、如图,CD是Rt△ABC的斜边AB上的高,E是BC上任意一点,EF⊥AB于F。
求证:。
3、如图,在Rt△ABC中,CD是斜边AB上的高,点M在CD上,DH⊥BM且与AC的延长线交于点E。
求证:
(1)△AED∽△CBM;
(2)
4、已知,如图,在Rt△ABC中,∠ACB=900,AD平分∠CAB交BC于点D,过点C作CE⊥AD,垂足为E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G,,,求EG的长。
[来源:学科网]
跟踪训练参考答案
一、填空题:
1、3,;
2、10或;
3、1∶2;[来源:学&科&网Z&X&X&K]
二、选择题:A[来源:]
三、解答题:
1、AD、DC;AB、BC;AD、AB;AD、BD;AB、BD;CD、BD;BD、BC ;BC、CD;AD、BC;AB、CD等。
2、由△ADC∽△ACB得,又由△ACD∽△EBF得,所以
3、略
4、4。
