第四、五章气体动理论和热力学的补充题
气体动理论补充习题

07 气体动理论补充习题1. 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常数,R 为普适气体常量,则该理想气体的分子数为: [ ](A) pV /m . (B) pV /kT . (C) pV /RT . (D) pV /mT .2. 一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m .根据理想气体的分子模型和统计假设,分子速度在x 方向的分量平方的平均 [ ]2(A) v x =2() v x B =2() v 3/x C kT m = 2() v /x D kT m =3. 在一密闭容器中,理想气体的平均速率变为原来的2倍,则 [ ]A.温度和压强都变为原来的2倍;B.温度为原来的2倍,压强为原来的4倍;C.温度为原来的4倍,压强为原来的2倍;D.温度和压强都变为原来的4倍.4.可视为刚性分子的氧气压强 2.026p =Pa ,体积23310V m -=⨯,则其内能为 [ ](A) 0.02J . (B) 0.03J . (C) 0.05J . (D) 0.06J .5. 有一个电子管,其真空度(即电子管内气体压强)为 1.0×10-5 mmHg ,则27 ℃ 时管内单位体积的分子数为(玻尔兹曼常量k =1.38×10-23 J/K , 1 atm=1.013×105 Pa =76 cmHg )[ ](A) 3.2×1015 /m 3 (B) 3.2×1016 /m 3 (C) 3.2×1017 /m 3 (D) 3.2×1018 /m 36. 1 mol 氧气(视为刚性双原子分子的理想气体)贮于一氧气瓶中,温度为27℃,这瓶氧气的内能为 (摩尔气体常量 R = 8.31 J·mol -1·K -1 玻尔兹曼常量 k = 1.38×10-23J·K -1)[ ](A) 6.23×103J (B) 6.23×104J (C) 6.23×105J (D) 6.23×106J7.气缸内盛有一定量的氢气(可视作理想气体),当温度不变而压强增大一倍时,氢气分子的平均碰撞频率的变化情况是:[](A) 增大一倍 (B) 减为原来的一半 (C) 不变 (D) 不能确定8.两种不同的理想气体,若他们的最概然速率相等,则他们的[](A)平均速率相等,方均根速率相等(B)平均速率相等,方均根速率不相等(C)平均速率不相等,方均根速率相等 (D)平均速率不相等,方均根速率不相等9. 有2×103 m3 刚性双原子分子理想气体,其内能为6.75×102 J.(1) 试求气体的压强;(2) 设分子总数为 5.4×1022个,求分子的平均平动动能及气体的温度。
大学物理吉林大学第5章气体动理论练习及答案

解 (1) pV m RT M mRT RT 28.0 103kg
M
pV p
(2) 2 3RT 493m / s
M
(3)
E平
n 3 kT 2
3 2
p
1.5 103 J
3 设某系统由N个粒子组成,粒子的速率分布如图所示。 求
5.三个容器A、B、C 中装有同种理想气体,其
分子数密度相同,而方均根速率之比为1:2:4, 则其压强之比pA : pB : pC为: A.1 ∶ 2 ∶ 4 B.4∶ 2 ∶ 1 C.1 ∶ 4 ∶ 16 D.1∶ 4 ∶ 8
2 T
p nkT
6.在一封闭容器内,理想气体分子的平均速率
提高为原来的2倍,则
第五章 气体动理论
一、选择题
k
3 2
kT
p nkT
1.两瓶不同种类的气体,其分子的平均平动动能相等,
但分子密度不同,则
A.温度相同,压强相同; B.温度不同,压强相同
C.温度相同,压强不同 ; D.温度不同,压强不同
2.在一密闭容器中,储有A、B、C三种理想气体,
处于平衡状态.A种气体的分子数密度为n1,它产生 的压强为p1,B种气体的分子数密度为2n1,C种气体 的分子数密度为3 n1,则混合气体的压强p为( )
3R
4R
5R
2R
10.设 代表气体分子运动的平均速率。 P代表
气体分子运动的最可几速率, 2代表气体分子运动
的方均根速率。处于平衡状态下的理想气体,三
种速率的关系为
A. 2 P
B. P 2
C.P 2
D. P 2
气体动、热练习题(含答案)

(温度、气体动理论及热力学基础)1.如图所示,一绝热密闭的容器,用隔板分成相等的两部分,左边盛有一定量的理想气体,压强为p 0,右边为真空.今将隔板抽去,气体自由膨胀,当气体达到平衡时,气体的压强为 。
2. 对于室温下的双原子分子理想气体,在等压膨胀的情况下,系统对外所作的功与从外界吸收的热量之比W / Q 等于。
3.已知f (v )为麦克斯韦速率分布函数,v p 为分子的最概然速率.则()⎰p f v v v 0d 表示 ;速率v >v p 的分子的平均速率表达式为 .4. 一超声波源发射超声波的功率为10 W .假设它工作10 s ,并且全部波动能量都被1 mol 氧气吸收而用于增加其内能,则氧气的温度升高了多少?(氧气分子视为刚性分子,普适气体常量R =8.31 J·mol -1·K -1 )5. 设以氮气(视为刚性分子理想气体)为工作物质进行卡诺循环,在绝热膨胀过程中气体的体积增大到原来的两倍,求循环的效率.6. 一瓶氦气和一瓶氮气分子数密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则氦气的温度 氮气的温度,氦气的压强 氮气的压强。
(选填:相等、大于、小于)7. 一定量的理想气体,从a 态出发经过①或②过程到达b 态,acb 为等温线(如图),则①、②两过程中外界对系统传递的热量Q 1、Q 2是(A) Q 1>0,Q 2>0. (B) Q 1<0,Q 2<0.(C) Q 1<0,Q 2>0. (D) Q 1>0,Q 2<0.8.给定理想气体(比热比为γ),从标准状态(p 0,V 0,T 0)开始作绝热膨胀,体积增大到2倍.膨胀后温度T 、压强p 与标准状态时T 0、p 0之关系为 (A) 021T T γ)(=; 0121p p -=γ)(. (B) 0121T T -=γ)(;021p p γ)(=. (C) 021T T γ-=)(;0121p p -=γ)( (D) 0121T T -=γ)(;021p p γ-=)(.9.对一定质量的理想气体进行等温压缩.若初始时每立方米体积内气体分子数为1.96×1024,则当压强升高到初始值的两倍时,每立方米体积内气体分子数应为__________.10.一定量的某种理想气体,先经过等体过程使其热力学温度升高为原来的4倍;再经过等温过程使其体积膨胀为原来的2倍,则分子的平均碰撞频率变为原来的__________倍.11.一定量的理想气体处于热动平衡状态时,此热力学系统的不随时间变化的三个宏观量是_____________________,而随时间不断变化的微观量是_______________________. 12.当氢气和氦气的压强、体积和温度都相等时,求它们的质量比()()e H H 2M M 和内能比()()e H H 2E E .(将氢气视为刚性双原子分子气体)13.计算下列一组粒子的平均速率和方均根速率.14.如果一定量的理想气体,其体积和压强依照2 p a V =的规律变化,其中a 为已知常量.试求: (1) 气体从体积V 1膨胀到V 2所作的功; (2) 气体体积为V 1时的温度T 1与体积为V 2时的温度T 2之比.15.如图所示,AB 、DC 是绝热过程,CEA 是等温过程,BED 是任意过程,组成一个循环。
气体动理论练习题

气体动理论练习题练习1一、选择题1. 在一密闭容器中,储有A 、B 、C 三种理想气体,处于平衡状态。
A 种气体的分子数密度为n 1,它产生的压强为p 1,B 种气体的分子数密度为2n 1,C 种气体的分子数密度为3n 1,则混合气体的压强p 为 ( )A. 3p 1;B. 4p 1;C. 5p 1;D. 6p 1.2. 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻 尔兹曼常量,R 为普适气体常量,则该理想气体的分子数为 ( )A. pV m ⁄;B. pV kT ⁄;C. pV RT ⁄;D. pV mT ⁄。
3. 一定量某理想气体按pV 2=恒量的规律膨胀,则膨胀后理想气体的温度( )A. 将升高;B. 将降低;C. 不变;D. 升高还是降低,不能确定。
二、填空题1. 解释下列分子动理论与热力学名词:(1) 状态参量: ;(2) 微观量: ;(3) 宏观量: 。
2. 在推导理想气体压强公式中,体现统计意义的两条假设是:(1) ;(2) 。
练习2一、选择题1. 一个容器内贮有1摩尔氢气和1摩尔氦气,若两种气体各自对器壁产生的压强分别为p1和p2,则两者的大小关系是( )A. p1>p2; B. p1<p2; C. p1=p2; D. 不能确定。
2. 两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数为n,单位体积内的气体分子的总平动动能为E kV⁄,单位体积内的气体质量为ρ,分别有如下关系( )A. n不同,E k V⁄不同,ρ不同;B. n不同,E k V⁄不同,ρ相同;C. n相同,E k V⁄相同,ρ不同;D. n相同,E k V⁄相同,ρ相同。
3. 有容积不同的A、B两个容器,A中装有刚体单原子分子理想气体,B中装有刚体双原子分子理想气体,若两种气体的压强相同,那么,这两种气体的单位体积的内能E A和E B的关系( )A. E A<E B;B. E A>E B;C. E A=E B;D.不能确定。
大学物理基础教程答案第05章习题分析与解答

5-1 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常数,R 为摩尔气体常数,则该理想气体的分子数为( )。
(A )PV m (B )PV kT (C )PV RT (D ) PVmT解:由N p nkT kT V ==得,pVN kT=,故选B 5-2 两个体积相同的容器,分别储有氢气和氧气(视为刚性气体),以1E 和2E 分别表示氢气和氧气的内能,若它们的压强相同,则( )。
(A )12E E = (B )12E E > (C )12E E < (D ) 无法确定 解:pV RT ν=,式中ν为摩尔数,由于两种气体的压强和体积相同,则T ν相同。
又刚性双原子气体的内能52RT ν,所以氢气和氧气的内能相等,故选A 5-3 两瓶不同种类的气体,分子平均平动动能相同,但气体分子数密度不同,则下列说法正确的是( )。
(A )温度和压强都相同 (B )温度相同,压强不同 (C )温度和压强都不同(D )温度相同,内能也一定相等解:所有气体分子的平均平动动能均为32kT ,平均平动动能相同则温度相同,又由p nkT =可知,温度相同,分子数密度不同,则压强不同,故选B5-4 两个容器中分别装有氦气和水蒸气,它们的温度相同,则下列各量中相同的量是( )。
(A )分子平均动能 (B )分子平均速率 (C )分子平均平动动能 (D )最概然速率解:分子的平均速率和最概然速率均与温度的平方根成正比,与气体摩尔质量的平方根成反比,两种气体温度相同,摩尔质量不同的气体,所以B 和D 不正确。
分子的平均动能2i kT ε=,两种气体温度相同,自由度不同,平均动能则不同,故A 也不正确。
而所有分子的平均平动动能均为k 32kT ε=,只要温度相同,平均平动动能就相同,如选C 5-5 理想气体的压强公式 ,从气体动理论的观点看,气体对器壁所作用的压强是大量气体分子对器壁不断碰撞的结果。
第四章气体动理论

第四章 气体动理论2-4-1选择题:1、处于平衡状态的一瓶氦气和一瓶氮气的分子数密度相同,分子的平均平动动能也相同,都处于平衡态。
以下说法正确的是:(A )它们的温度、压强均不相同。
(B )它们的温度相同,但氦气压强大于氮气压强。
(C )它们的温度、压强都相同。
(D) 它们的温度相同,但氦气压强小于氮气压强。
2、三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,方均根速率之比4:2:1::222=C B A v v v ,则其压强之比C B A p p p ::为:(A) 1 : 2 : 4 (B) 1 : 4 : 8 (C) 1 : 4 : 16 (D) 4 : 2 : 13、一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m . 根据理想气体的分子模型和统计假设,分子速度在x 方向的分量平方的平均值为: (A) 2xv =m kT 3 (B) 2x v = m kT331 (C) 2xv = m kT 3 (D) 2x v = m kT4、关于温度的意义,有下列几种说法:(1) 气体的温度是分子热运动平均平动动能的量度.(2) 气体的温度是大量气体分子热运动的集体表现,具有统计意义.(3) 温度的高低反映物质内部分子热运动剧烈程度的不同.(4) 从微观上看,气体的温度表示每个气体分子的冷热程度.上述说法中正确的是(A ) (1)、(2)、(4) (B ) (1)、(2)、(3)(C ) (2)、(3)、(4) (D) (1)、(3)、(4)5、两容器内分别盛有氢气和氦气,若它们的温度和质量分别相等,则:(A) 两种气体分子的平均平动动能相等.(B) 两种气体分子的平均动能相等.(C) 两种气体分子的方均根速率相等.(D) 两种气体的内能相等.6、一容器内装有N 1个单原子理想气体分子和N 2个刚性双原子理想气体分子,当该系统处在温度为T 的平衡态时,其内能为(A)⎪⎭⎫ ⎝⎛++kT kT N N 2523)(21 (B) ⎪⎭⎫ ⎝⎛++kT kT N N 2523)(2121(C)kT N kT N 252321+ (D) kT N kT N 232521+7、有一截面均匀的封闭圆筒,中间被一光滑的活塞分割成两边,如果其中的一边装有0.1kg 某一温度的氢气,为了使活塞停留在圆筒的正中央则另一边应装入同一温度的氧气质量为:(A ) kg 161 (B) 0.8 kg (C ) 1.6 kg (D) 3.2 kg8、若室内生火炉以后,温度从15°C 升高到27°C ,而室内的气压不变,则此时室内的分子数减少了:(A) 0.5% (B) 4% (C) 9% (D) 21%9、有容积不同的A 、B 两个容器,A 中装有单原子分子理想气体,B 中装有双原子分子理想气体。
大物第五章答案

气体动理论一. 基本要求1. 了解气体分子热运动的图象及理想气体分子的微观模型。
2. 理解气体压强、温度的统计意义,通过气体压强公式的推导,了解从提出模型、进行统计平均、建立宏观量与微观量的联系到阐明宏观量的微观本质的思想和方法。
3. 了解玻耳兹曼能量分布律及等温气压公式,并用它们来处理一些有关的简单问题。
4. 了解麦克斯韦速率分布律、分布函数、分布曲线的物理意义,了解气体分子的热运动的最概然速率、平均速率、方均根速率的意义及求法。
5. 理解内能的概念及能量均分定理,会用能均分定理计算理想气体的内能。
6. 了解气体分子的平均自由程、平均碰撞频率的意义及其简单计算。
二. 内容提要1. 理想气体的状态方程 理想气体处于平衡态时,其态参量压强p 、体积V 及温度T 之间存在的关系式RTM MpV mol=利用状态方程可以由一些已知的态参量推算另一些未知的态参量。
2. 压强公式 反映理想气体的压强P 与气体分子平均平动动能k ε及分子数密度n 之间的关系式,其数学表达式为)(2v 213232m n n P k =ε=式中221v m k =ε代表一个分子的平均平动动能,m 代表分子的质量。
3. 温度公式 描述气体温度与气体分子平均平动动能之间的关系式,其数学表达式为kTk 23=ε式中,k 为玻耳兹曼常量。
由压强公式和温度公式可以得到理想气体物态方程的另一种形式nkTP =4. 能量均分定理 当气体处于平衡态时,分布与每一个自由度(平动、转动)上的平均能量均为kT 21。
利用能均分定理很容易计算理想气体的内能。
5. 理想气体的内能 气体分子所具有的各种平均动能的总和。
质量为M 的理想气体的内能RTi M M E mol 2=式中mol M 为气体的摩尔质量,i 为自由度。
6. 麦克斯韦速率分布律 气体处于平衡态时,分布在速率区间v ~ v +d v 内的分子数d N 与总分子数N 的比率按速率v 的分布规律。
大学物理课后答案第四章

第四章 气体动理论一、基本要求1.理解平衡态的概念。
2.了解气体分子热运动图像和理想气体分子的微观模型,能从宏观和统计意义上理解压强、温度、内能等概念。
3.初步掌握气体动理论的研究方法,了解系统的宏观性质是微观运动的统计表现。
4.理解麦克斯韦速率分布律、速率分布函数和速率分布曲线的物理意义,理解气体分子运动的最概然速率、平均速率、方均根速率的意义,了解玻尔兹曼能量分布律。
5.理解能量按自由度均分定理及内能的概念,会用能量均分定理计算理想气体的内能。
6.了解气体分子平均碰撞频率及平均自由程的意义及其简单的计算。
二、基本内容1. 平衡态在不受外界影响的条件下,一个系统的宏观性质不随时间改变的状态。
2. 理想气体状态方程在平衡态下,理想气体各参量之间满足关系式pV vRT =或 n k T p =式中v 为气体摩尔数,R 为摩尔气体常量 118.31R J mol K --=⋅⋅,k 为玻尔兹曼常量 2311.3810k J K --=⨯⋅3. 理想气体压强的微观公式21233t p nm n ε==v4. 温度及其微观统计意义温度是决定一个系统能否与其它系统处于热平衡的宏观性质,在微观统计上32t kT ε=5. 能量均分定理在平衡态下,分子热运动的每个自由度的平均动能都相等,且等于2kT 。
以i 表示分子热运动的总自由度,则一个分子的总平均动能为2t i kT ε=6. 速率分布函数()dNf Nd =v v麦克斯韦速率分布函数232/22()4()2m kT m f e kTππ-=v v v7. 三种速率最概然速率p =≈v 平均速率==≈v 方均根速率==≈8. 玻尔兹曼分布律平衡态下某状态区间(粒子能量为ε)的粒子数正比于kT e /ε-。
重力场中粒子数密度按高度的分布(温度均匀):kT m gh e n n /0-=9. 范德瓦尔斯方程采用相互作用的刚性球分子模型,对于1mol 气体RT b V V ap m m=-+))((2 10. 气体分子的平均自由程λ==11. 输运过程 内摩擦dS dz du df z 0)(η-=, 1133mn ηλρλ==v v 热传导dSdt dz dT dQ z 0)(κ-= 13v c κρλ=v 扩散dSdt dz d D dM z 0)(ρ-= 13D λ=v三、习题选解4-1 一根铜棒的两端分别与冰水混合物和沸水接触,经过足够长的时间后,系统也可以达到一个宏观性质不随时间变化的状态。
第4章气体动理论

00:30
kT B. v v v m0
2 x 2 y 2 z
3kT C. v v v m0
2 x 2 y 2 z
2 2 D. v x v2 v y z 0
投票人数:0
5. 关于温度的意义,有下列几种说法: 00:30 (1)气体的温度是分子平均平动动能的量度; (2)气体的温度是大量气体分子热运动的集体表现,具 有统计意义; (3)温度的高低反映物质内部分子运动剧烈程度的不同; (4)从微观上看,气体的温度表示每个气体分子的冷热 程度。 上述说法中正确的是( )。 A. B. C. D. (1)(2)(4) (1)(2)(3) (2)(3)(4) (1)(3)(4)
投票人数:0
23. 麦克斯韦速率分布曲线如图4-4所示,图中A,B
两部分面积相等,则由图可知( )。 00:30
A O B
f (v )
A. v0 为最概然速率
B. v0 为平均速率
C. v0 为方均根速率
D. 速率大于和小于 v0 的 分子数各占一半
v0 图4-4
v
投票人数:0
24. 一定量的理想气体,在容积不变的条件下,当温
H2 O2
)。
00:30
D. 无法判断
图4-1
投票人数:0
2. 一密闭容器中储有4 kg氢气和4 kg氦气,它们处于 平衡状态。那么,氢气和氦气的体积比和压强比分别 为( A. B. C. D. )。 2:1,1:1 2:1,2:1 1:1,1:1 1:1,2:1 00:30
投票人数:0
3. 在没有外力场作用下,分子质量为m0的大量气体分 子处于热动平衡态时,下列各式中成立的是( )。
气体动理论

能有如下关系:
()
(A)和都相等;
(B)相等,而不相等;
(C)相等,而不相等; (D)和都不相等。
15.刚性多原子分子所具有的平均能量为
()
(A) (B) (C) (D)
16.1mol刚性双原子分子理想气体,当温度为T时,其内能为(式中R为
摩尔气体常量,k为玻尔兹曼常量)
()
(A);
(B);
(C);
Байду номын сангаас
压强分别为P1和P2,则两个的大小关系是
()
(A)P1>P2; (B)P1<P2; (C)P1=P2; (D)不能确定
14.下列各试中哪一式表示气体分子的平均平动动能?(式中M为气体
的质量,m为气体分子的质量,N为气体分子的总数目,n为气体分
子数密度) ( )
(A); (B); (C); (D)
15.1mol氮气,由状态A(P1,V)变到状态B(P2,V),气体内能的增量为 ()
(C)刚性双原子理想气体分子的平均能量为;
(D)单原子理想气体分子的平均平动能量为。
11.对一定量气体来说,下列说法中哪个是正确的?
()
(A)当温度不变时,气体对器壁的压强随体积的减少而增大;当体积不
变时,压强随温度升高而增加;
(B)当温度不变时,气体对器壁的压强随体积的减少而减少;当体积不
变时,压强随温度升高而增加;
(A) 2倍 (B) 4倍 (C) 6倍 (D) 34倍 21.三个容器A、B、C中装有同种理想气体,其分子数密度n相同,而方
均根速率之比为=1∶2∶4,则其压强之比∶∶为: ()
(A) 1∶2∶4; (C) 1∶4∶16;
(B) 1∶4∶8; (D) 4∶2∶1。
大学物理-气体动理论-热力学基础-复习题及答案详解

第12章 气体动理论一、填空题:1、一打足气的自行车内胎,假设在7℃时轮胎中空气压强为4.0×510pa .则在温度变为37℃,轮胎内空气的压强是 。
〔设内胎容积不变〕2、在湖面下深处〔温度为℃〕,有一个体积为531.010m -⨯的空气泡升到水面上来,假设湖面的温度为℃,则气泡到达湖面的体积是 。
〔取大气压强为50 1.01310p pa =⨯〕3、一容器内储有氧气,其压强为50 1.0110p pa =⨯,温度为℃,则气体分子的数密度为 ;氧气的密度为 ;分子的平均平动动能为 ;分子间的平均距离为 。
〔设分子均匀等距排列〕4、星际空间温度可达2.7k ,则氢分子的平均速率为 ,方均根速率为 ,最概然速率为 。
5、在压强为51.0110pa ⨯下,氮气分子的平均自由程为66.010cm -⨯,当温度不变时,压强为 ,则其平均自由程为。
6、假设氖气分子的有效直径为82.5910cm -⨯,则在温度为600k ,压强为21.3310pa ⨯时,氖分子1s 内的平均碰撞次数为 。
7、如图12-1所示两条曲线(1)和(2),分别定性的表示一定量的某种理想气体不同温度下的速率分布曲线,对应温度高的曲线 是 .假设图中两条曲线定性的表示相同温度下的氢气和氧气的速率分布曲线,则表示氧气速率分布曲线的是 .8、试说明以下各量的物理物理意义: 〔1〕12kT , 〔2〕32kT , 〔3〕2i kT , 〔4〕2i RT , 〔5〕32RT , 〔6〕2M i RT Mmol 。
参考答案:1、54.4310pa ⨯2、536.1110m -⨯ 图12-13、25332192.4410 1.30 6.2110 3.4510m kg m J m ----⨯⋅⨯⨯ 4、2121121.6910 1.8310 1.5010m s m s m s ---⨯⋅⨯⋅⨯⋅ 5、6.06pa 6、613.8110s -⨯ 7、〔2〕 ,〔2〕8、略二、选择题:教材习题12-1,12-2,12-3,12-4. 〔见课本p207~208〕参考答案:12-1~12-4 C, C, B, B.第十三章热力学基础一、选择题1、有两个相同的容器,容积不变,一个盛有氦气,另一个盛有氢气〔均可看成刚性分子〕它们的压强和温度都相等,现将 5 J 的热量传给氢气,使氢气温度升高,如果使氦气也升高同样的温度,则应向氦气传递的热量是 〔 〕〔A 〕 6 J 〔B 〕 5 J 〔C 〕 3 J 〔D 〕 2 J2、一定量理想气体,经历某过程后,它的温度升高了,则根据热力学定理可以断定:〔1〕该理想气体系统在此过程中作了功;〔2〕在此过程中外界对该理想气体系统作了正功;〔3〕该理想气体系统的内能增加了;〔4〕在此过程中理想气体系统既从外界吸了热,又对外作了正功。
气体动理论习题解答

(3)速率小于 的粒子数占总粒子数的百分比
8-14图中I、II两条曲线是两种不同气体(氢气和氧气)在同一温度下的麦克斯韦速率分布曲线。试由图中数据求:(1)氢气分子和氧气分子的最概然速率;(2)两种气体所处的温度。
解:(1)由习题8-14图可知:
(2)由
8-15在容积为×10-2m3的容器中装有×10-2kg气体,容器内气体的压强为104Pa,求气体分子的最概然速率。
解:
8-3容积V=1 m3的容器内混有N1=×1023个氢气分子和N2=×1023个氧气分子,混合气体的温度为400 K,求:
(1)气体分子的平动动能总和;(2)混合气体的压强。
解:(1)
(2)
8-4储有1mol氧气、容积为1 m3的容器以 =10 m/s的速率运动。设容器突然停止,其中氧气的80%的机械运动动能转化为气体分子热运动动能。问气体的温度及压强各升高多少(将氧气分子视为刚性分子)
*8-20试求上升到什么高度时大气压强减至地面的75%设空气温度为0℃,空气的摩尔质量为0.0289 kg/mol。
解:由
8-21(1)求氮气在标准状态下的平均碰撞次数和平均自由程;(2)若温度不变,气压降低到×10-4Pa,平均碰撞次数又为多少平均自由程为多少(设分子有效直径为10-10m)
解:
8-22真空管的线度为10-2m,真空度为×10-3Pa,设空气分子有效直径为3×10-10m,求27℃时单位体积内的空气分子数、平均自由程和平均碰撞频率。
解: (1)
(2)
所以此气体分子为CO或N2
(3)
(4)
(5)
8-10一容器内储有氧气,其压强为×105Pa,温度为27.0℃,求:(1)分子数密度;(2)氧气的密度;(3)分子的平均平动动能;(4)分子间的平均距离。(设分子间均匀等距排列)
大学物理第5章练习答案

第五章 气体动理论练 习 一一. 选择题1. 一个容器内贮有1摩尔氢气和1摩尔氦气,若两种气体各自对器壁产生的压强分别为1p 和2p ,则两者的大小关系是( C )(A) 21p p >; (B) 21p p <; (C) 21p p =; (D) 不确定的。
2. 一定量的理想气体贮于某一容器中,温度为T ,气体分子的质量为m. 根据理想气体的分子模型和统计假设,分子速度在x 方向的分量平方的平均值为( D )(A) 2x v =m kT 3; (B) 2x v = (1/3)m kT 3 ; (C) 2x v = 3kT /m ; (D) 2x v = kT/m 。
3. 设M 为气体的质量,m 为气体分子质量,N 为气体分子总数目,n 为气体分子数密度,0N 为阿伏伽德罗常数,下列各式中哪一式表示气体分子的平均平动动能( A )(A)pV M m ⋅23; (B)pV M M mol ⋅23; (C) npV 23; (D) 023N pV M M mol ⋅。
4. 关于温度的意义,有下列几种说法,错误的是( D ) (A) 气体的温度是分子平动动能的量度;(B) 气体的温度是大量气体分子热运动的集体表现,具有统计意义; (C) 温度的高低反映物质内部分子运动剧烈程度的不同; (D) 从微观上看,气体的温度表示每个气体分子的冷热程度。
二.填空题1. 在容积为10?2m 3的容器中,装有质量100g 的气体,若气体分子的方均根速率为200m/s ,则气体的压强为ap 51034⨯。
2. 如图1所示,两个容器容积相等,分别储有相同质量的N 2和O 2气体,它们用光滑细管相连通,管子中置一小滴水银,两边的温度差为30K ,当水银滴在正中不动时,N 2和O 2的温度为2N T = 210k ,2O T = 240k 。
( N 2的摩尔质量为28×10-3kg/mol,O 2的摩尔质量为32×10-3kg/mol)3.分子物理学是研究大量微观粒子的集体运动的统计表现 的学科, 它应用的方法是 统计学 方法。
气体动理论和热力学答案

衡水学院理工科专业《大学物理B》气体动理论热力学基础习题解答命题教师:张郡亮试题审核人:郑永春一、填空题(每空1分)1、 ________________________________________________________________________________________________________________ 有一个电子管,其真空度(即电子管内气体压强)为X10-5 mmHg,则27 °C时管内单位体积的分子数为___________________________________ .答:X 10iT /m32、 ___________________________________________________________________ 在温度为127 °C时,1 mol氧气(其分子可视为刚性分子)的内能为_____________________________________________________________ J,其中分子转动的总动能为 _______________ •答:X103X1033、 ________________________________________________________________________________________________________________ 一泄量理想气体,从月状态(2a,%)经历如图1所示的直线过程变到万状态(a,2Q,则仙过程中系统作功护 = _____________________________ :内能改变 & __________.答:汕04、给泄的理想气体(比热容比丫为已知),从标准状态(以、%、養)开始,作绝热膨胀,体积增大到三倍,膨胀后的温度T= ____________ ,压强P- ___________•答:(I)', (|)Z Po5、有一卡诺热机,用290 g空气为工作物质,工作在27°C的高温热源与-73°C的低温热源之间,此热机的效率.若在等温膨胀的过程中气缸体积增大到倍,则此热机每一循环所作的功为___________________ •(空气的摩尔质量为29XW5 kg/mol)答:%:X105 J二、单项选择题(每小题2分)(C ) 1、一个容器内贮有1摩尔氢气和1摩尔氨气,若两种气体各自对器壁产生的压强分別为a和a,则两者的大小关系是:(A) pi> g (B) pi< R・(0 A=A. (D)不确定的.■(B) 2、关于温度的意义,表述正确的是(1)气体的温度是分子平均平动动能的量度.(2)气体的温度是大疑气体分子热运动的集体表现,具有统计意义.(3)温度的高低反映物质内部分子运动剧烈程度的不同.(4)从微观上看,气体的温度表示每个气体分子的冷热程度.⑷⑴、⑵、(4). ⑻⑴、⑵、(3).(0 (2)、(3)、(4). (D)⑴、(3)、(4).(B ) 3、宜于容器内的气体,如果气体内各处压强相等,或气体内各处温度相同,则这两种情况下气体的状态(A)一泄都是平衡态.(B)不一泄都是平衡态.(0前者一左是平衡态,后者一泄不是平衡态.(D)后者一泄是平衡态,前者一定不是平衡态.(C ) 4、一左疑的理想气体,经历某过程后,温度升髙了.则根拯热力学泄律可以断泄:①该理想气体系统在此过程中吸了热.②在此过程中外界对该理想气体系统作了正功.③该理想气体系统的内能增加了.④在此过程中理想气体系统既从外界吸了热,又对外作了正功.以上正确的断言是:⑷①、③.(B)②、③.(0③.(D)③、④.(D )5、有人设计一台卡诺热机(可逆的).每循环一次可从400 K的高温热源吸热1800 J,向300 K的低温热源放热800 J.同时对外作功1000 J,这样的设计是(A)可以的,符合热力学第一泄律.(B)可以的,符合热力学第二泄律.(0不行的,卡诺循环所作的功不能大于向低温热源放出的热量.(D)不行的,这个热机的效率超过理论值.三、判断题(每小题1分,请在括号里打上丁或X)(X ) 1、气体的平衡态和力学中的平衡态相同。
《大学物理》气体动理论练习题及答案解析

《大学物理》气体动理论练习题及答案解析一、简答题1、你能够从理想气体物态方程出发 ,得出玻意耳定律、查理定律和盖吕萨克定律吗? 答: 方程RT Mm pV '=描述了理想气体在某状态下,p ,V ,T 三个参量所满足的关系式。
对给定量气体(Mm '不变),经历一个过程后,其初态和终态之间有222111T V p T V p =的关系。
当温度不变时,有2211V p V p =,这就是玻意耳定律;当体积不变时,有2211T p T p =,这就是查理定律;当压强不变时,有2211T V T V =,这就是盖吕萨克定律。
由上可知三个定律是理想气体在经历三种特定过程时所表现出来的具体形式。
换句话说,遵从玻意耳定律、查理定律和盖吕萨克定律的气体可作为理想气体。
2、为什么说温度具有统计意义? 讲一个分子具有多少温度,行吗?答:对处于平衡态的理想气体来说,温度是表征大量分子热运动激烈程度的宏观物理量,是对大量气体分子热运动状态的一种统计平均,这一点从公式kT v m 23212=中的2v 计算中就可以看出(∑∑=iii Nv N v22),可见T 本质上是一种统计量,故说温度具有统计意义,说一个分子的T 是毫无意义的。
3、解释下列分子运动论与热力学名词:(1) 状态参量;(2) 微观量;(3) 宏观量。
答:(1)状态参量:在一定的条件下,物质系统都处于一定的状态下,每个状态都需用一组物理量来表征,这些物理量称为状态参量。
(2)微观量:描述个别分子运动状态的物理量。
(3)宏观量:表示大量分子集体特征的物理量。
4、一定量的理想气体处于热动平衡状态时,此热力学系统的不随时间变化的三个宏观量和不随时间变化的微观量分别有哪些?建议:本题“不随时间变化的微观量分别有哪些”不知道通过该设问需要学生掌握什么东西。
其实从微观角度来讲,分子的任何量,如分子速度,动能,动量,严格说来甚至质量也是变化的。
可能会有人回答为平均速度、平均速率、平均自有程等,但那又是一种统计行为,该值对应着某些宏观量,这只能称为统计量,与微观量和宏观量相区别。
大学物理第5章题库(含答案)

05章 气体动理论一、填空题 (一)易(基础题)1、一定质量的气体处于平衡态,则气体各部分的压强 相等 (填相等或不相等),各部分的温度 相等 (填相等或不相等)。
2、根据能量按自由度均分原理,设气体分子为刚性分子,分子自由度为i ,则当温度为T时,(1)一个分子的平均能量为(平均总动能) 12i kT ⋅;(2)ν摩尔理想气体的内能为2i RT ν⋅ ;(3)一个双原子分子的平均转动动能为 kT 。
3、对于单原子分子理想气体,①32RT 代表的物理意义为: 1mol 单原子分子理想气体的内能; ②R 23代表的物理意义为:单原子分子理想气体的定体摩尔热容 。
4、自由度数为i 的一定量的刚性分子理想气体,其体积为V,压强为p 时,其内能E=2iPV 。
5.两瓶不同种类的理想气体,它们温度相同,压强也相同,但体积不同,则它们分子的平均平动动能 相同,单位体积内分子的总平动动能 相同。
(均填相同或不相同) 6.一定量的某种理想气体,装在一个密闭的不变形的容器中,当气体的温度升高时,气体分子的平均动能 增大 ,气体分子的密度 不变 ,气体的压强 增大 ,气体的内能 增大 。
(均填增大、不变或减少)7、理想气体的压强公式为 P nkT = ,理想气体分子的平均平动动能与温度的关系为 32k kT ε=。
8、有两瓶气体,一瓶是氧气,另一瓶是氢气(均视为刚性分子理想气体),若它们的压强、体积、温度均相同,则氧气的内能是氢气的▁▁1▁▁倍。
9、一容器内贮有气体,其压强为1atm,温度为27ºC,密度为31.3kg m -⋅,则气体的摩尔质量为__33210-⨯____1kg mol -⋅,由此确定它是__氧____气.10、()Nf d u u 表示的物理意义是 表示速率分布在~d υυυ+内的分子数 ------------------------------------。
11、21()f d u u u u ò表示的物理意义是 表示速率分布在12~υυ范围内的分子数占总分子数的比率.12、在相同条件下,氧原子的平均动能是氧分子的平均动能的___35___倍.(二)中(一般综合题)1、如图1所示,两条曲线分别表示相同温度下,氢气和氧气分子的速率分布曲线,则a 表示▁氧▁▁气分子的速率分布曲线;b 表示▁▁氢▁气分子的速率分布曲线。
第四章 气体动理论

第四章气体动理论第四章气体动理论一.选择题1. 把一容器用隔板分成相等的两部分,左边装CO2 ,右边装H2,两边气体质量相同,温度相同,如果隔板与器壁无摩擦,则隔板应(A) 向右移动. (B) 向左移动. (C) 不动.(D) 无法判断是否移动.2.关于平衡态,以下说法正确的是(A) 描述气体状态的状态参量p、V、T不发生变化的状态称为平衡态;(B) 在不受外界影响的条件下,热力学系统各部分的宏观性质不随时间变化的状态称为平衡态;(C) 气体内分子处于平衡位置的状态称为平衡态; (D) 处于平衡态的热力学系统,分子的热运动停止. 3.关于热量Q,以下说法正确的是(A) 同一物体,温度高时比温度低时含的热量多; (B) 温度升高时,一定吸热;(C) 温度不变时,一定与外界无热交换; (D) 温度升高时,有可能放热.4. 气缸中有一定量的氦气(视为理想气体),经过绝热压缩,体积变为原来的一半,问气体分子的平均速率变为原来的几倍?(A) 22 / 5 . (B) 21 / 5 . (C) 22 / 3 .(D) 21 / 3 .5. 刚性三原子分子理想气体的压强为P,体积为V,则它的内能为( )5PV 27 C.3PV D.PV26. 一瓶刚性双原子分子理想气体处于温度为T的平衡态,据能量按自由度均分定理,可以断定()A.分子的平均平动动能大于平均转动动能B.分子的平均平动动能小于平均转动动能C.分子的平均平动动能等于平均转动动能D.分子的平均平动动能与平均转动动能的大小视运动情况而定A.2PVB.7. 1 mol 单原子分子理想气体和1 mol双原子分子理想气体分别处于平衡态,它们的温度相同,则它们的一个分子的平均平动动能( ) A.相同,它们的内能相同 B.不同,它们的内能相同 C.相同,它们的内能不同D.不同,它们的内能不同8. 理想气体分子的平均速率与温度T的关系为() A.与T成正比 C.与T成正比B.与T成反比 D.与T成反比9.处于平衡态的双原子气体分子的平均平动动能为0.03eV,则分子的平均转动动能为()A.0.02eV C.0.04 eVB.0.03 eV D.0.05 eV10.处于平衡态的氧气和氮气,它们的分子平均速率相同,则它们的分子最概然速率()A.不同,它们的温度不同 C.相同,它们的温度相同B.不同,它们的温度相同 D.相同,它们的温度不同11.温度相同的氦气和氧气,它们分子的平均动能?和平均平动动能?t有如下关系() A.?和?t都相等 C. ?t相等,而?不相等B.?相等,而?t不相等 D. ?和?t都不相等12.当刚性双原子分子理想气体处于平衡态时,根据能量按自由度均分定理,一个分子的平均平动动能() A.大于一个分子的平均转动动能 B.小于一个分子的平均转动动能 C.等于一个分子的平均转动动能D.与一个分子平均转动动能谁大谁小是随机变化的13.一瓶单原子分子理想气体与一瓶双原子分子理想气体,它们的温度相同,且一个单原子分子的质量与一个双原子分子的质量相同,则单原子气体分子的平均速率与双原子气体分子的平均速率()A.相同,且两种分子的平均平动动能也相同 B.相同,而两种分子的平均平动动能不同 C.不同,而两种分子的平均平动动能相同 D.不同,且两种分子的平均平动动能也不同 14.氢气和氧气的温度和压强相同,则它们的() A.分子密度相同,分子的平均动能相同B.分子密度相同,分子的平均动能不同C.分子密度不同,分子的平均动能相同 D.分子密度不同,分子的平均动能不同 15.一瓶单原子分子理想气体的压强、体积、温度与另一瓶刚性双原子分子理想气体的压强、体积、温度完全相同,则两瓶理想气体的() A.摩尔数相同,内能不同 B.摩尔数不同,内能不同 C.摩尔数相同,内能相同 D.摩尔数不同,内能相同 16. 氦气和氧气的温度相同,则它们的() A.分子的平均动能相同,分子的平均速率相同 B.分子的平均动能相同,分子的平均速率不同 C.分子的平均动能不同,分子的平均速率相同D.分子的平均动能不同,分子的平均速率不同感谢您的阅读,祝您生活愉快。
热力学定律与分子动理论与气体的练习题
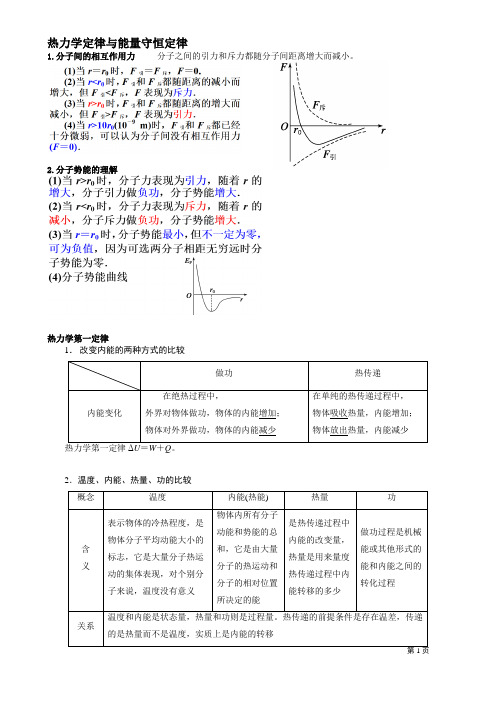
热力学定律与能量守恒定律1.分子间的相互作用力分子之间的引力和斥力都随分子间距离增大而减小。
2.分子势能的理解热力学第一定律1.改变内能的两种方式的比较做功热传递内能变化在绝热过程中,外界对物体做功,物体的内能增加;物体对外界做功,物体的内能减少在单纯的热传递过程中,物体吸收热量,内能增加;物体放出热量,内能减少热力学第一定律ΔU=W+Q。
2.温度、内能、热量、功的比较概念温度内能(热能)热量功含义表示物体的冷热程度,是物体分子平均动能大小的标志,它是大量分子热运动的集体表现,对个别分子来说,温度没有意义物体内所有分子动能和势能的总和,它是由大量分子的热运动和分子的相对位置所决定的能是热传递过程中内能的改变量,热量是用来量度热传递过程中内能转移的多少做功过程是机械能或其他形式的能和内能之间的转化过程关系温度和内能是状态量,热量和功则是过程量。
热传递的前提条件是存在温差,传递的是热量而不是温度,实质上是内能的转移第1页热力学第二定律的两种表述(1)克劳修斯表述:热量不能自发地从低温物体传到高温物体。
(2)开尔文表述:不可能从单一热库吸收热量,使之完全变成功,而不产生其他影响。
或表述为“第二类永动机是不可能制成的。
”两类永动机的比较第一类永动机第二类永动机不需要任何动力或燃料,却能不断地对外做功的机器从单一热库吸收热量,使之完全变成功,而不产生其他影响的机器违背能量守恒,不可能制成 不违背能量守恒,违背热力学第二定律,不可能制成理想气体物态方程RT M MPV molR 称为“普适气体常数 ”(1)理想气体分子本身的大小可以忽略不计,分子可视为质点.(2)理想气体分子除碰撞外,无相互作用的引力和斥力,故无分子势能,理想气体的内能等于所有分子热运动动能之和,一定质量的理想气体内能只与温度有关.练习题:1.某种气体在不同温度下的气体分子速率分布曲线如图所示,图中f (v )表示v 处单位速率区间内的分子数百分率,所对应的温度分别为T I ,T II ,T III ,则下列正确的是( A ) A .T Ⅰ>T Ⅱ>T Ⅲ B .T Ⅲ>T Ⅱ>T Ⅰ C .T Ⅱ>T Ⅰ,T Ⅱ>T Ⅲ D .T Ⅰ=T Ⅱ=T Ⅲ2.分子间有相互作用势能,规定两分子相距无穷远时两分子间的势能为零.设分子a 固定不动,分子b 以某一初速度从无穷远处向a 运动,直到它们之间的距离最小.在此过程中,a 、b 之间的势能( B ) A .先减小,后增大,最后小于零 B .先减小,后增大,最后大于零 C .先增大,后减小,最后小于零 D .先增大,后减小,最后大于零3.如图为两分子系统的势能E p 与两分子间距离r 的关系曲线。
热学习题第四章气体动理论

第四章气体动理论4.1 关于理想气体的基本假设是什么?【答】理想气体是气体分子运动论和热学所研究的,由大量做无规则热运动的分子组成的最简单的系统,它是客观实际存在的许多真实气体的理想化的物理模型。
关于理想气体的基本假设如下:(1)气体的密度很小,因而气体分子问的平均距离比,分子本身的几何线度大很多’(2)气体分子之间的相互作用力随分子间距离的增大,而急剧地减小,当分子问的距离超过分子本身的几何线度很。
多时,分子间的相互作用力变得非常小,以至于可以忽略不-计;(3)气体分子是完全弹性的刚性球,因此,气体分子之间的相互碰撞以及气体分子与容器壁的碰撞都是完全的弹-性碰撞;(4)气体分子之间的相互碰撞很少,即在绝大部分时间内,气体分子都是自由运动的。
也就是说,气体分子的运动轨道是由许多直线段组成的不规则的折线,各直线线段的长度比分子本身的几何线度大很多;(5)气体分子的运动速度很大,因此单位时间内气体分子之间的相互碰撞次数很多,在标准状态下,一般气体分子的运动速度为500米/秒左右,一个分子在1秒内所经历的碰撞10次。
次数为大约8上述五条即是关于理想气体的基本假设,做了这样的基本假设后,气体的许多主要性质被突出了,例如,理想气体服从状态方程: PV=nRT这就为我们研究气体各状态参量——压强P、体积V和温度T之间的关系提供了方便。
做了上述基本假定之后,这样的理想气体虽然并不真实存在,它只是客观存在的真实气体的理想模型,但它与一般状态下的气体,例如,氢气、氨气和氧气等非常接近。
实际上,在压强不太高,温度不特别低的情况下,很多种真实气体都可以用理想气体来近似。
换句话说,由于对理想气体的基本假设是抓住了问题的本质,忽略了次要因素,因此,理想气体具有很好的普遍性和适用性,成为气体分子运动论和热学的典型的研究对象。
4.2 什么是动力学规律性?什么是统计规律性?【答】动力学规律性是从经典力学、经典电磁场理论以及其他物理学科的研究中总结出来的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三、四章 气体动理论及热力学习题
一、选择题
1.某理想气体状态变化时,内能随压强的变化关系如图中
直线AB 所示,则A 至B 变化过程为:( ) (A )等温过程 (B )等容过程
(C )等压过程
(D )绝热过程
2. 一定量的理想气体,处在某一初始状态,现在要使它的温度经过一系列状态变化后回到初始状态的温度,可能实现的过程为 ( )
(A )先保持压强不变而使它的体积膨胀,接着保持体积不变而增大压强; (B )先保持压强不变而使它的体积减小,接着保持体积不变而减小压强; (C )先保持体积不变而使它的压强增大,接着保持压强不变而使它体积膨胀; (D )先保持体积不变而使它的压强减小,接着保持压强不变而使它体积膨胀。
3. 压强、体积和温度都相同(常温条件)的氧气和氦气在等压过程中吸收了相等的热量,它们对外作的功之比为 ( )
(A )1:1; (B )5:9; (C )5:7; (D )9:5。
4. 一绝热密闭的容器,用隔板分成相等的两部分,左边盛有一定量的理想气体,压强为0p ,右边为真空,今将隔板抽去,气体自由膨胀,当气体达到平衡时,气体的压强是( )
(A )0p ; (B )0p /2; (C )02p γ; (D )γ2/0p 。
)/(v p C C =γ 5. 在V p 图上有两条曲线abc 和adc ,由此可以得出以下结论: ( )
(A )其中一条是绝热线,另一条是等温线; (B )两个过程吸收的热量相同; (C )两个过程中系统对外作的功相等; (D )两个过程中系统的内能变化相同。
6. 一定量的理想气体向真空作自由膨胀,体积由1V 增至2V ,此过程中气体的( )
(A )内能不变,熵增加; (B )内能不变,熵减少; (C )内能不变,熵不变; (D )内能增加,熵增加。
7. 一热机由温度为727℃的高温热源吸热,向温度为527
℃的低温热源放热,若热机在最
大可能效率下工作、且吸热为2000焦耳,热机作功约为 ( )
(A )400J ; (B )1450J ; (C )1600J ; (D )2000J ; (E )2760J 。
8. 在功与热的转变过程中,下面的那些叙述是正确的? ( )
(A )能制成一种循环动作的热机,只从一个热源吸取热量,使之完全变为有用功; (B )其他循环的热机效率不可能达到可逆卡诺机的效率,因此可逆卡诺机的效率最高; (C )热量不可能从低温物体传到高温物体; (D )绝热过程对外作正功,则系统的内能必减少。
二、填空题
1. 一定量的理想气体从同一初态) , (00V p a 出发,分别经两个准静态过程ab 和ac ,b 点的压强为1p ,C 点的体积为1V ,如图所示,若两个过程中系统吸收的热量相同,则该气体的
==
v
p c c γ_________________。
2. 对下表所列的理想气体各过程,并参照下图,填表判断系统的内能增量E ∆,对外作功
A 和吸收热量Q 的正负(用符号+,-,0表示):
图(a ) 图(b )
1
p p
3. 1mol 双原子刚性分子理想气体,从状态a (p 1,V 1)沿p —V 图所示直线变到状态b (p 2,V 2),则(1)气体内能的增量
E ∆=___________________;(2)气体对外界所作的功A =______________;(3)气体吸收的热量Q =______________。
4. 如图所示,容器中间为隔板,左边为理想气体,右边为真空。
今突然抽去隔板,则系统对外作功A =______________。
5. 一卡诺热机(可逆的),低温热源为27℃,热机效率为40%,其高温热源温度为________K 。
今欲将该热机效率提高到50%,且低温热源保持不变,则高温热源的温度增加________K 。
6. 一卡诺机从373K 的高温热源吸热,向273K 的低温热源放热,若该热机从高温热源吸收1000J 热量,则该热机所做的功A =________,放出热量Q 2=________。
7. 有v 摩尔理想气体,作如图所示的循环过程acba ,其中acb 为半圆弧,ba 为等压过程,a c p p 2=,在此循环过程中气体净吸收热量为Q _______)(a b p T T vC -。
(填:>、<或=)。
8.热力学第二定律的两种表述:
开尔文表述: ____________________________________________________________________________克劳修斯表述:
____________________________________________________________________________
b
a
p p。
