“反比例函数的图象与性质”教学设计案例
八年级数学下册 17.4.2 反比例函数的图象和性质教案 (新版)华东师大版

反比例函数的图象和性质
(1)是非零常数;
学做思一:你能作出反比例函数的图像
例:画出函数
导学:画出函数图象一般分为列表,描点、连线三个步骤,
这个
的取值
范围是不等于零的一切
用表里各组对
在直角坐
.连线:用平滑的曲线将第一象限各点依次连起来,得到图象的第一个分支;用平滑的曲线将第三象限各点依次连起来,得到图象的另一分支。
这两个分支合起来,就是反比例函数的图象,如图所示。
这种
画出函数的图象。
学
教师注意指导画函数图象有困难的学生,并评
这个函数的图象在哪两个象限
联系一次函数的性质,你能否总结出反比例函随着自变量
导做:在充分讨论、交流后达成共识:
时,函数的图象在第一、三象限,在每个象限内,曲线从左向右下降,也就是在每个象跟内
时,函数的图象在第二、四象限,在
3。
反比例函数的图象和性质教案(教学设计)

反比例函数的图像和性质【教学目标】1.了解反比例函数图像的形状特征。
2.会画反比例函数的图像。
3.经历探究反比例函数性质的过程,掌握反比例函数的性质。
4.学会利用反比例函数的性质解决简单的实际问题。
【教学重难点】1.会画反比例函数的图像。
2.学会利用反比例函数的性质解决简单的实际问题。
【教学过程】1.复习导入(1)反比例函数是怎样定义的?(2)确定反比例函数的解析式需要什么条件?2.课前热身请同学们展示各自在上节课实践活动中所画出的问题2的函数图像,比一比谁画得最好?(学生互评在上节课的实践活动中所画出的问题2的函数图像,形成对反比例函数图像的初步感形认识。
)3.合作探究(1)整体感知我们知道一次函数y=kx+b(k≠0)的图像是直线,其性质随着k的正负发生变化,那么反比例函数y=kx(k≠0)的图像又具有什么特征?其性质是否随着k的正负发生变化呢?本课我们着重探讨这两个问题。
(2)四边互动互动1师:利用多媒体演示幻灯片。
例1:画出函数y=6x的图像。
师:在未知函数图像的形状特征时,我们画函数的图像通常用什么方法?这个函数自变量的取值范围是什么?由此猜想这个函数的图像是连在一起的吗? 用描点法画该函数的图像,在列表应注意哪些? 生:逐个举手回答问题,达成共识。
师:利用多媒体展现画图过程。
(1)列表:这个函数中自变量x 的取值范围是不等于零的一切实数,列出x 与y 的对应值表:──┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬── x │…│-6│-3│-2│-1│…│1 │2 │3 │6 │… ──┼─┼─┼─┼─┼─┼─┼─┼─┼─┼─┼── y │…│-1│-2│-3│-6│…│6 │3 │2 │1 │… ──┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴──(2)描点:由这些有序实数对,可以在直角坐标系中描出相应的点(-6,-1),(-3,-2),(-2,-3)等。
(3)连线:用光滑曲线将各点依次连起来,就得到反比例函数的图像,如图所示:师:请同学们用透明纸放在课本的该函数图像上复制这个图像,并用大头钉固定上下坐标系原点,再把上面的图像绕着原点旋转180°,结果你发现什么现象?生:动手操作,并提出发现的问题。
反比例函数的图象与性质教案

反比例函数的图象与性质教案•相关推荐反比例函数的图象与性质教案范文(通用8篇)作为一名教师,时常会需要准备好教案,教案是教学蓝图,可以有效提高教学效率。
那么大家知道正规的教案是怎么写的吗?下面是小编精心整理的反比例函数的图象与性质教案范文,欢迎阅读与收藏。
反比例函数的图象与性质教案篇1教学目标知识与技能:1、进一步熟悉作函数图象的主要步骤,会作反比例函数的图象。
2、体会函数的三种表示方法的相互转换,对函数进行认识上的整合。
3、培养学生从函数图象中获取信息的能力,初步探索反比例函数的性质。
过程与方法:通过学生自己动手列表,描点,连线,提高学生的作图能力;通过观察图象,概括反比例函数图象的有关性质,训练学生的概括总结能力、情感、态度与价值观:让学生积极参与到数学学习活动中去,增强他们对数学学习的好奇心和求知欲。
教学重难点1) 重点:画反比例函数图象并认识图象的特点。
2)难点:画反比例函数图象。
教学关键:教师画图中要规范,为学生树立一个可以学习的模板。
教学方法:激发诱导,探索交流,讲练结合三位一体的教学方式。
教学手段:教师画图,学生模仿。
教具:三角板,小黑板。
学法:学生动手、动眼,、动耳、采用自主,合作、探究的学习方法。
教学过程一:课前检测:1、什么叫做反比例函数;(一般地,如果两个变量x、y之间的关系可以表示成y= (k为常数,k0)的形式,那么称y是x的反比例函数。
)2、反比例函数的定义中需要注意什么?(1)k为常数,k0(2)从y= 中可知x作为分母,所以x不能为零。
二:激发兴趣导入新课问题1:对于一次函数 y = kx + b ( k 0 )的图象与性质,我们是如何研究的?y=kx+b y=kxK0 一、二、三一、三b0 一、三、四K0 一、二、四二、四b0 二、三、四问题2:对于反比例函数 y=k/x ( k是常数,k 0 ),我们能否象一次函数那样进行研究呢?可以问题3:画图象的步骤有哪些呢?(1)列表(2)描点(3)连线(教学片断:师:上一节课我们研究了反比例函数,今天我们继续研究反比例函数,下面哪位同学说一下自己对反比例函数的了解。
反比例函数教案(优秀7篇)

反比例函数教案(优秀7篇)反比例函数教案篇一一、背景分析1.对教材的分析本节课讲述内容为北师大版教材九年级下册第五章《反比例函数》的第二节,也这一章的重点。
本节课是在理解反比例函数的意义和概念的基础上,进一步熟悉其图象和性质的过程。
本节课前一课时是在具体情境中领会反比例函数的意义和概念。
函数的性质蕴涵于概念之中,对反比例函数性质的探索是对其内在规定性的的认识,也是对函数的概念的深化。
同时,本节课也是下一节课《反比例函数的应用》的基础,有了本节课的知识储备,便于学生利用函数的观点来处理问题和解释问题。
传统教材在内容和编写意图的比较:传统教材里反比例函数的内容仅有一节,新教材里反比例函数的内容增加至一章。
本节课中的作函数图象的要求在新旧教材中并不一样,旧教材对画图只是一带而过,而新教材中让学生反复作反比例函数的图象,为下一步性质的探索打下良好的基础。
因为在学生进行函数的列表、描点作图是活动中,就已经开始了对反比例函数性质的探索,而且通过对函数的三种表示方式的整和,逐步形成对函数概念的整体性认识。
在旧教材中对反比例函数性质只是简单观察以后,由老师讲解得到,但是在新教材中注重从操作、观察、概括和交流这些数学活动中得到性质结论,从而逐步提高从函数图象中获取信息的能力。
这也充分体现了重视获取知识过程体验的新课标的精神。
(1)教学目标:进一步熟悉作函数图象的主要步骤,会作反比例函数的图象;体会函数三种方式的相互转换,对函数进行认识上的整和;逐步提高从函数图象中获取知识的能力,探索并掌握反比例函数的主要性质。
(2)重点:会作反比例函数的图象;探索并掌握反比例函数的主要性质。
(3)难点:探索并掌握反比例函数的主要性质。
2、对学情的分析九年级学生在前面学习了一次函数之后,对函数有了一定的认识,虽然他们在小学已经接触了反比例,但都处于浅显的、肤浅的知识表面,这对于他们理解反比例函数的图象与性质没有多大的帮助,但由于本节课采用z+z智能教育平台进行教学,比较形象,便于学生接受。
反比例函数的图象和性质优秀教案

欧姆定律
在电路中,利用反比例函 数表示电阻、电流和电压 之间的关系。
万有引力定律
描述两物体间引力与它们 质量、距离之间的关系时 ,可以使用反比例函数。
在经济问题中应用
供需关系
劳动生产率
通过反比例函数表示商品价格与需求 量之间的关系,以及价格与供应量之 间的关系。
在经济学中,可以用反比例函数来表 示劳动生产率与劳动投入量之间的关 系。
反比例函数的图象和性质 优秀教案
汇报人:XXX 2024-01-22
目录
• 课程介绍与目标 • 反比例函数基本概念 • 反比例函数图像绘制方法 • 反比例函数性质分析 • 反比例函数应用举例 • 课程总结与拓展延伸
01
课程介绍与目标
教学目标
知识与技能
使学生理解反比例函数的概念,掌握反比例 函数的图象特征及其性质,能利用反比例函 数的性质解决简单问题。
感谢您的观看
THANKS
采用启发式、探究式、讨论式等 多种教学方法,引导学生主动思 考、积极探究。
教学手段
利用多媒体课件、几何画板等教 学工具辅助教学,提高教学效果 。
02
反比例函数基本概念
反比例函数定义
一般形式
$y = frac{k}{x}$ (其中 $k$ 是非零 常数)
变量关系
当 $x$ 增大时,$y$ 减小;当 $x$ 减 小时,$y$ 增大。
工程中的应用
探讨反比例函数在工程领域的应 用,如电阻、电容、电感等电子 元件的特性描述。
社会科学Байду номын сангаас的应用
讨论反比例函数在社会科学中的 应用,如人口增长模型、传播模 型等。
01
物理中的应用
介绍反比例函数在物理中的应用 ,如万有引力定律、库仑定律等 。
人教版九年级数学下册26.1.2反比例函数的图象与性质优秀教学案例

在学生掌握了反比例函数的基本性质后,我会组织小组讨论。每个小组选取一个或几个反比例函数,通过绘制图象、分析性质,探讨反比例函数在实际问题中的应用。我会鼓励学生尝试用反比例函数解决一些简单的几何问题,如求两个反比例函数交点的问题。
(四)总结归纳
在总结归纳环节,我会邀请几个小组代表展示他们的讨论成果,让学生通过对比和讨论,总结出反比例函数的普遍性质和图象特征。我会引导学生从数形结合的角度,理解反比例函数的本质,并强调反比例函数在实际问题中的应用价值。
二、教学目标
(一)知识与技能
1.理解反比例函数的定义,掌握反比例函数的一般形式,并能准确表述。
2.学会绘制反比例函数的图象,分析图象特征,总结反比例函数的性质。
3.能够运用反比例函数的性质解决实际问题,提高数学应用能力。
4.掌握反比例函数与一次函数、二次函数等其他类型函数之间的关系,拓展函数知识体系。
(五)实施多元化评价
本案例采用多元化的评价方式,包括自评、互评、师评等,全面评价学生的学习过程和结果。这种评价方式有助于激发学生的学习动力,促使学生反思自己的学习,不断提高。
(二)问题导向
在教学过程中,我将采用问题导向法,引导学生发现问题、提出问题、解决问题。首先,通过提出问题“反比例函数的图象有什么特点?”让学生进行独立思考。然后,组织学生进行小组讨论,共同探讨反比例函数的性质。在学生掌握性质后,再提出问题:“反比例函数在实际生活中有哪些应用?”引导学生将所学知识运用到实际问题中。
(五)作业小结
为了巩固本节课的学习内容,我会布置以下作业:
1.绘制并分析至少三个不同反比例函数的图象,总结它们的性质。
2.结合实际情境,编写至少两个反比例函数的应用问题,并解答。
反比例函数的图象和性质(教案)
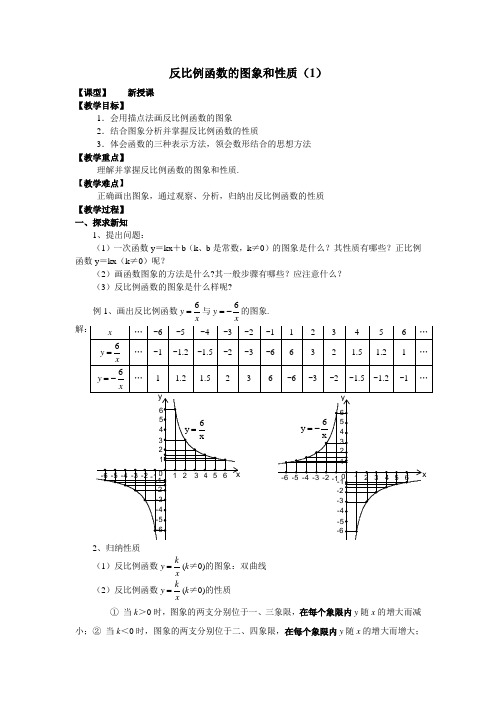
反比例函数的图象和性质(1)【课型】 新授课 【教学目标】1.会用描点法画反比例函数的图象2.结合图象分析并掌握反比例函数的性质3.体会函数的三种表示方法,领会数形结合的思想方法 【教学重点】理解并掌握反比例函数的图象和性质. 【教学难点】正确画出图象,通过观察、分析,归纳出反比例函数的性质 【教学过程】 一、探求新知1、提出问题:(1)一次函数y =kx +b (k 、b 是常数,k ≠0)的图象是什么?其性质有哪些?正比例函数y =kx (k ≠0)呢?(2)画函数图象的方法是什么?其一般步骤有哪些?应注意什么? (3)反比例函数的图象是什么样呢?例1、画出反比例函数y 6=与y 6-=的图象.小;② 当k <0时,图象的两支分别位于二、四象限,在每个象限内y 随x 的增大而增大;③ 图象的两个分支都无限接近x 轴、y 轴,但都与x 轴、y 轴不相交;④ k 越大,图象的弯曲度越小,曲线越平直,越远离坐标轴;⑤ 图象关于直线y =±x 对称.注:双曲线的两个分支是断开的,研究反比例函数的增减性时,要对两个分支分别讨论,不能一概而论.二、例题分析例2.见教材P48,用描点法画图,注意强调: (1)列表取值时,x ≠0,因为x =0函数无意义,为了使描出的点具有代表性,可以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y 值(2)由于函数图象的特征还不清楚,所以要尽量多取一些数值,多描一些点,这样便于连线,使画出的图象更精确(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线(4)由于x ≠0,k ≠0,所以y ≠0,函数图象永远不会与x 轴、y 轴相交,只是无限靠近两坐标轴例3.(补充)已知反比例函数32)1(--=m x m y 的图象在第二、四象限,求m 值,并指出在每个象限内y 随x 的变化情况?分析:此题要考虑两个方面,一是反比例函数的定义,即1-=kx y (k ≠0)自变量x 的指数是-1,二是根据反比例函数的性质:当图象位于第二、四象限时,k <0,则m -1<0,不要忽视这个条件解:∵ 32)1(--=m xm y 是反比例函数∴ m 2-3=-1,且m -1≠0又∵ 图象在第二、四象限∴ m -1<0解得2±=m 且m <1 ∴ 2-=m例4.(补充)如图,过反比例函数xy 1=(x >0)的图象上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,设△AOC 和△BOD 的面积分别是S 1、S 2,比较它们的大小,可得( )(A )S 1>S 2 (B )S 1=S 2(C )S 1<S 2 (D )大小关系不能确定分析:从反比例函数xky =(k ≠0)的图象上任一点P (x ,y )向x 轴、y 轴作垂线段,与x 轴、y 轴所围成的矩形面积k xy S ==,由此可得S 1=S 2 =21,故选B三、课堂练习1.已知反比例函数xky -=3,分别根据下列条件求出字母k 的取值范围 (1)函数图象位于第一、三象限(2)在第二象限内,y 随x 的增大而增大 2.函数y =-ax +a 与xay -=(a ≠0)在同一坐标系中的图象可能是( )3.在平面直角坐标系内,过反比例函数xky =(k >0)的图象上的一点分别作x 轴、y 轴的垂线段,与x 轴、y 轴所围成的矩形面积是6,则函数解析式为四、课后作业1.课本习题第2、3题.2.若函数x m y )12(-=与xmy -=3的图象交于第一、三象限,求m 的取值范围. 3. 反比例函数xy 2-=,当x =-2时,y = ;当x <-2时;y 的取值范围是 ; 当x >-2时;y 的取值范围是4. 已知反比例函数y a x a=--()226,当x >0时,y 随x 的增大而增大,求该函数关系式. 五、课堂小结1、反比例函数的图象及性质.2、双曲线的两个分支是断开的,研究反比例函数的增减性时,要对两个分支分别讨论.3、在解决函数问题时,注意数形结合. 【课后反思】。
反比例函数的图象和性质教案(完美版)

在线分享文档:麦群超反比例函数的图象和性质【知识与技能】1. 会用描点法画反比例函数的图象;2. 理解反比例函数的性质.【过程与方法】 经历实验操作、探索思考、观察分析的过程中,培养学生探究、归纳及概括的能力.【情感态度】在通过画图探究反比例函数图象及其性质过程中,发展学生的合作交流意识,增强求知欲望.【教学重点】画反比例函数图象,理解反比例函数的简单性质【教学难点】 理解反比例函数性质,能用性质解决简单的问题.一、情境导入,初步认识问题 我们知道,一次函数y = 6x 的图象是一条直线,那么反比例函数y =6x 的图象是什么形状呢?你能用“描点”的方法画出函数的图象?【教学说明】教师提出问题,学生思考、交流,尝试着解决问题,教师巡视,关注学生的画图,及时纠正个别同学在画图中的不足和失误之处,帮助学生尽可能得到其合适的图象.二、思考探究,获取新知问题1 在同一坐标系中画出反比例函数y =6x 和y =12x的图象; 【教学说明】将全班同学分成两大组,分别完成问题y =6x 、y =12x的画图,在学生探索画反比例函数的图象过程中,教师应给予恰当点拨:如学生列表时,由于自变量x ≠0,故在x <0和x >0时,应各取三个以上的数据,以便使描点画图更精确些;在连线上,x <0和x >0 的两个分支应根据变化趋势用平滑曲线连接,但它们是不能相交的;列表中数据,描点时点的位置等不能出错,以保证图象更能反映出反比例函数的性质.在线分享文档让每个人平等地提升自我:麦群超 问题2 反比例函数y =-6x 和y =-12x的图象有什么共同特点?它们之间有什么关系?反比例函数y = 6x 和y =-6x的图象呢?同学间相互交流. 【教学说明】让两组同学分别交流,找出图象的特征,教师可分别参与讨论,帮助学生获取正确认知. 【归纳结论】由图象可发现:(1)它们都是由两条曲线组成,并且随|x|的不断增大(或减 小),曲线越来越接近x 轴(或y 轴),但这两条曲线永不相交;(2) y = 6x 和y =-6x 及y =12x 和y =-12x 的图象分别关于x 轴对称,也关于y 轴对称. 思考 观察函数y = 6x 和y =-6x 以及y =12x 和y =-12x 的图象. (1)你能发现它们的共同特征以及不同点吗?(2)每个函数的图象分别位于哪几个象限? (3)在每个象限内y 随x 的变化如何变化? 【归纳结论】反比例函数y =k x 的图象及其性质: (1)反比例函数y=k x (k 为常数,且k 0)的图象是双曲线; (2)当k >0时,双曲线的两个分支分别位于第一、三象限,在每个象限内,y 随x 值的增大而减小;(3)当k <0时,双曲线的两个分支分别位于第二、四象限,在每个象限内y 随x 值的增大而增大.三、典例精析,掌握新知例 如图,一次函数y = kx 十b 的图象与反比例函数y =m x 的图象相交于A 、B 两点.(1)根据图象,分别写出A 、B 的坐标;(2)求出两函数的解析式;(3)根据图象回答:当x 为何值时,一次函数的函数值大于反比例函数的函数值. 【分析】(1)观察图象,可直接写出A 、B 两点的坐标;(2)利用A 、B 两点的坐标,用待定系数法建立方程组求解,可确定两函数的解析式;(3 )通过两函数的交点A 、B 的坐标得出答案.解:(1)观察图象可知A ( -6,-2),B (4,3)在线分享文档地提升自我By :麦群超(2)由点B 在反比例函数y =m x 的图象上,所以把B (4,3)代入y =m x 得3 =4m ,故m =12,所以y=12x.由点A 、B 在一次函数y =kx 十b 的图象上,所以把A 、B 两点坐标代入y = kx 十b 得14326+2,1k b k k b b ⎧+==⎧⎪⎨⎨-=-⎩⎪=⎩解得 . 所以一次函数解析式为y = 12x+1.(3)由图象可知,当一6<x <0或x >4时,一次函数的函数值大于反比例函数的函数值.【教学说明】本例有一定难度,教师可将题目展开,分步讲解,辅导学生克服对大题的恐惧.本题考查了从图象获取信息,应用待定系数法确定反比例函数与一次函数的关系式,以及利用图象比较函数值的大小等知识点. 四、运用新知,深化理解 1 .若反比例函数 y =21m x -的图象的一个分支在第三象限,则m 的取值范围是 . 2.如图是某一函数的一部分,则这个函数的表达式可能是( )A.y=5xB.y=-x+3C.y=-6xD.y=4x 【教学说明】学生独立完成,然后相互交流,谈谈自己的看法,教师应参与学生的讨论, 加深学生对反比例函数的图象及其性质的认识和理解,从而更好地掌握本节知识.在完成上述题目后,教师引导学生完成创优作业中本课时的“名师导学”部分. 【答案】1.m >122. C 五、师生互动,课堂小结 本节课学习了哪些知识?在知识应用过程中需要注意什么?你有哪些收获?1.布置作业:从教材“习题”中选取.在线分享文档让每个人平等2.完成创优作业中本课时的“课时作业”部分.“反比例函数的图象和性质”是反比例函数的教学重点,学生需要在理解的基础上熟练运用.在学习反比例函数图象和性质时k >0时,双曲线的两个分支在一、三象限;k <0时,双曲线的两个分支在二、四象限),学生可由画法观察图象得知.而增减性由解析式y =k x (k 0)可得到,学生也容易理解.但从图象观察增减性较难,借助计算机的动态演示就容易多了,所以本课教学最好用多媒体,因为运用多媒体比较函数图象,可以使学生更直观、更清楚地看清函数的变化,从而使学生加深对函数性质的理解.通过本课的教学,教师可深刻地体会到运用信息技术可加强数学课堂教学中的灵活性、直观性. 虽然制作起来比较麻烦,但能使课堂教学达到预想不到的效果,使课堂教学效率也明显提高.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
17.4“反比例函数的图象与性质”教学设计案例
善堂镇第一初级中学张军朋
教学目标:
1.知识与能力目标:
(1)能画出反比例函数的图象,了解其特征。
(2)根据反比例函数的图象和解析表达式探索并理解反比例函数的性质:当k>0或k<0时,图象的变化情况。
2.过程与方法目标:
经过阅读钻研教材,绘画观察反比例函数图象,了解反比例函数的特征,再通过对k的取值不同的反比例函数图象的观察、比较与分析,获得反比例函数图象的性质。
3.情感与态度目标:
再次领会函数图象是研究函数的重要直观工具,数形结合是学习和研究函数的不可少的重要数学思想方法,认识正比例函数与反比例函数的区别。
教学重点:反比例函数图象的特征与性质。
教学难点:对反比例函数图象性质的理解与应用。
教学方法:六部探究教学法。
教学过程:
一、:督预示标
1.一次函数、正比例函数的图象,确定一次函数图象的条件。
2.什么是中心对称。
3.反比例函数的解析表达式,它的图象是怎样的呢?
4、出示本节课教学目标
二、合作探究,发现新知:
请同学们独立阅读、研究教材,在纸上画一画函数y=6/x的图象。
(绝大多数学生开始阅读课本,尝试画图,教师巡视)
提问:1.画函数图象的关键问题是什么?
答:合理、正确地选值列表。
2.在选值时,你认为要注意什么问题?
答:(1)由于这个函数的图象的特点还不清楚,应多选几个点较好;
(2)不能选x=0,因为x=0时函数无意义;
(3)选取整数可以较好计算和描点。
这个问题中最核心的一点是关于x≠0的问题,提醒学生注意。
现在你能不能完成y=6/x的图象了呢?
学生在练习本上列表、描点、连线,教师在黑板上板演,到连线时暂停,让学生先连完线之后找同学上黑板连线,然后就这位学生的连线加以讨论、评价并总结:
注意:(1)一般地,反比例函数y=k/x(k≠0)的图象有两条曲线组成,叫做双曲线。
(2)这两条曲线不相交。
(3)这两条曲线无限延伸,无限地逼近x轴、y轴,但永远不会与x轴、y轴相交。
关于注意(3)问学生:为什么图象与x轴和y轴不相交?
在这个问题环节中,引导学生可以通过代数的方法分析反比例函数的解析式,由分母不能为零,得x不能为零;由k≠0,得y必不为零,从而验证了反比例函数的图象。
当两个分支无限延伸时,可以无限地逼近x 轴、y轴,但永远不会与两轴相交。
随即强调画图时要注意准确性。
通过这个问题既可以加深学生对反比例函数图象的记忆,又可培养学生思维的灵活性与深刻性。
教师安排学生练习画反比例函数y=-6/x的图象。
三、观察图象,得出性质:
师:请同学们观察函数的图象,你发现了什么?
生:当k>0时,反比例函数图象在第一、三象限;当k<0时,反比例函数图象在第二、四象限。
师:你是怎样发现的?
生1:通过图象观察可以得到。
生2:我是从解析式中得到的,当k<0时,x、y同号;所以在第一象限;当k<0时,x、y异号,所以在第三象限。
师:谁还可以说说反比例函数的增减性呢?
生:当k<0时,y随x的增大而减小;当k<0时,y随x的增大而增大。
师:这位同学的说法正确吗?
生:对(大部分学生表示赞同)。
师:真的对吗(教师给学生留一点时间思考)?
有学生开始举反例:不对,对于反比例函数y=6/x,当x=-2时,y=-3;
当x=2时,y=3,y就不随x的增大而减小。
师:这个反例讲得很好,看来在整个坐标系中,y就不一定随x的增大而减小(当k>0时)。
那么怎样讲才是正确的呢?
教师总结:由于反比例函数的图象是断开的,所以在归纳它的图象的增减性时,我们要与一次函数的增减性要有区别,因为一次函数的图象是直线,它是连续的。
板书:对于反比例函数y=k/x(k≠0):
(1)当k>0时,函数的图象在第一、三象限;在每一象限内,y随x的增大而减小;当k<0时,函数的图象在第二、四象限,在每一象限内,y随x的增大而增大。
师:继续观察图象,还有其它性质吗?
学生讨论后发现,双曲线是关于原点O成中心对称的,原点O是它的对称中心。
四、应用拓展,鼓励创新:
师:反比例函数y=k/x与正比例函数y=kx的解析式中都含有k,且k≠0,而k决定了它们图象在平面直角坐标系中的位置,观察以下两个图,图中的A点与B点有什么关系?
学生思考、讨论、合作探究,发现:A点与B点是关于原点O成中心对称的,若A点坐标是(a,b),则B点坐标是(-a,-b)。
通过这个问题使学生把学过的相关知识有机地联系起来,便于记忆和应用。
五、整理反思,促进提高:
1.这节课我们学习了哪些内容,你能总结一下吗?
2.通过这节课学习,我们有哪些收获?
六、课后思考探究:
教师出示本节课探究内容(多媒体显示)
案例研究:
一、设计理念:
数学教学是数学活动的教学,是师生之间、学生之间交往互动与共同发展的过程。
教学中教师既要把握好教学的导向作用,又要发现学生思维的闪光点,及时调整自己的教学方案,活跃课堂气氛,使学生产生学习情趣。
新课标下的教学设计,既要为学生的今天服务,又要为学生明天的发展奠基,改变课程实施过于强调接受学习、死记硬背、机械训练的现状,倡导学生主动参与、乐于探究、勤于动手,培养学生搜集和处理信息的能力,获取新知识的能力,分析和解决问题的能力以及合作交流的能力。
我们要准确把握数学新课程的本质与内涵,坚持“以学生发展为本”的教学设计基本理念,把学生的起点作为教师的起点,把传授书本知识服务于学生有个性、可持续、全面和谐的发展。
二、设计概要:
为了让学生充分理解反比例函数图象的特征与性质,初步形成数形结合的数学思想,再次领会函数解析式与函数图象之间的联系,突出两者间的转化对分析解决问题有特殊作用。
教学中通过学生自己主动探索、同学之间的讨论交流,体验知识的形成过程,体会观察、分析、归纳解决问题
的技能与方法。
在教学中,教师应重视引导师生间、学生间的多边探索活动,进行有条理地交流,让学生清晰地阐述自己的想法,同时运用不同的手段和方式评价学生,使学生感受探索带来的喜悦。
三、教学反思:
在本课的教学中,教师要运用一切有效的手段,启发学生的学习兴趣,给学生较多的独立思考和自我发展的机会,以促进学生生动、活泼、主动地学习和探索。
1.先学后教:学生是课堂的主人,是学习的主人,教师在课堂教学中,只有不断确定学生的主体地位,唤起学生的主体意识,发挥学生的主动精神,才能取得良好的教学效果,教师的教才能替代学生的学,把学习的主动权交给学生。
作为教师要做教学的热心人,尽力捕捉时机,引导学生将阅读提升为研读、探究。
2.精讲诱导:为了保证学生有充足的自学时间、探讨时间,教师要研究“讲”的策略,教师不可以不讲,但多讲,“满堂灌”绝不是好教师,可以画龙点睛地讲、启发性地讲、点拨性地讲、归纳性地讲,留出更多时间,让学生去思考、去探索。
本节课中,我的做法是:凡是学生能看懂的,我不教;凡是学生自己能学的,我不教;凡是学生能探索出结论的,我不教;凡是学生自己能做的活儿,我不做。
我只在“导”上和“点拨”上下功夫,点拨要精,要切中要害,激发学生的求知欲,让多数学生体验成功的愉悦。
3.质疑启思:在教学中,包含了许多对学生来说是“疑问”的东西,“疑”是学习的需要、是思维的开端、是求知的基础、是探索的起点,有
“疑”才有“思”。
本课中,反比例函数的增减性要将两个图象分支分别讨论,对学生来说是一个疑点,这也是激发学生探索知识的兴趣与热情地又一个起点,为了让它成为学生进行自主探索学习的动力,教师应努力营造轻松愉快的教学环境,让学生做到敢思、敢问、敢讨论,从而培养学生具有独特见解、敢想敢说的创造性思维,使学生在不断思索中前进。
4.引导探究:探究式的课堂教学的教学效果直接与教师的引导有关,教学中笔者从以下两方面引导学生进行探究,一是引导学生参与知识的形成探究,即反比例函数的图象的形状、特征及性质;二是引导学生参与知识的建构性探究,即反比例函数图象与正比例函数图象联系起来可以得到什么结论。
学生探究之后交流其成果,先是组内交流,达成共识,进而再在全班交流。
