结构切线刚度矩阵与割线刚度矩阵之间的关系
高温下钢框架荷载效应方法

高温下钢框架荷载效应研究方法综述摘要:随着钢结构越来越广泛的应用于实际生产和生活中,对钢结构的防火性能的研究也不断得到重视。
本文通过查阅文献,对高温下钢框架结构荷载效应的研究方法进行综述,得出各种方法存在的问题和缺陷,并对以后的研究发展进行了展望。
关键词:高温钢框架温度应力0 引言钢结构由于强度高、自重轻、延性好、施工周期短等优点,在建筑结构中被广泛应用。
但是由于钢材的导热系数大,高温作用下,钢材温度升高快,强度和弹性模量迅速下降,使钢结构在较短的时间内达到极限状态而发生破坏。
目前,对于钢框架柱荷载效应的研究方法主要有理论分析、试验研究和数值模拟三种方法。
1 高温下钢框架荷载效应的研究方法1.1理论分析1990 年,李国强提出了广义 clough 模型[1],其后,该校的谭巍[2]、曹文衔[3]分别根据广义 clough 模型建立了高温钢结构梁单元切线刚度方程。
文献[4]中也基于该模型,同时考虑了温度沿单元截面非均匀分布的影响,建立了高温下钢结构梁单元的切线刚度方程。
1994 年,李国强、金福安根据火灾时钢构件的内部温度分布及性能,进行了结构温度内力和钢框架非线性静力反应分析,并基于分析结果提出一种钢框架结构抗火极限状态的实用分析方法[5]。
1999年李国强,蒋首超,林桂祥编写的《钢结构抗火计算与设计》[6]一书中,提出了一种用结构力学处理超静定结构温度变化的方法。
2000年蒋首超,李国强[7]利用结构力学的原理, 提出了局部火灾下钢框架温度内力的计算方法。
具体步骤为:①计算梁、住端轴向变形约束刚度;②计算杆端转动约束刚度。
③根据下式求得带弹性杆端约束构件的温度应力:具体参数参见文献[7]2000年赵金城[8]提出一种直接迭代方法来分析受火钢框架的反应。
该方法可以计算相应于特定荷载水平和温度分布的结构总体反应,在推导有限元方程时,采用了割线刚度矩阵,而不是常用的切线刚度矩阵,然后采用直接迭代法求解。
切线刚度法

切线刚度法尊敬的供应商:我们,作为采购方,特此向您发出预留采购份额分包承诺书,以确保您的参与和合作。
根据我们之间的合作协议,在本次采购项目中,我们将保留一定份额供您参与分包。
您的参与对于项目的成功和顺利进行至关重要,我们将竭尽所能提供支持和帮助。
请注意,我们承诺保持公平、公正的采购环境,并根据合理的标准进行供应商选择和评估。
我们将依法遵守相关采购法规,并不歧视任何潜在供应商。
请您务必在约定的时间内提交相关文件和资料,以便我们对您的参与进行评估和确认。
一旦确认您的资格和能力符合要求,我们将与您进一步协商合作细节。
请知悉,本承诺书并不构成采购合同的一部分,而仅是我们之间的合作意向表达。
我们希望能够共同努力,实现双方的共赢。
谢谢您的支持与合作!此致敬礼(采购方名称)切线刚度法(tangent stiffness method)是结构力学中一种求解线性结构的静力分析方法。
在切线刚度法中,结构被建模为由节点和单元组成的网格结构。
节点代表结构的连接点,而单元则代表结构的构件(如杆件、梁等)。
每个节点都有与之相连的单元,这些单元通过节点与相邻单元连接。
切线刚度法的基本思想是,通过计算结构在各个节点处的位移、应力和应变,进而求解结构各个部分的受力情况。
在每个节点处,通过求解节点处的切线刚度矩阵(tangent stiffness matrix),可以计算出节点处的受力和位移。
这样,通过对整个结构的各个节点进行切线刚度矩阵的累加,就可以得到整个结构的切线刚度矩阵,从而求解结构的位移、应力和应变。
切线刚度法的主要优点是能够高效、准确地求解线性结构的静力问题,尤其在复杂结构中应用较为广泛。
然而,切线刚度法只适用于线性结构的静力分析,对于非线性结构或动力分析问题,则需要采用其他更加精确的方法。
结构的原始刚度矩阵

结构的原始刚度矩阵结构的原始刚度矩阵是描述结构刚度特性的重要工具,它是一种用于表示结构中杆件或单元的刚度关系的矩阵形式。
通过原始刚度矩阵,我们可以计算结构的整体刚度矩阵,进而分析和计算结构的位移、应力和应变等力学性能。
一、原始刚度矩阵的定义原始刚度矩阵是指在结构的局部坐标系下,描述单个杆件或单元刚度关系的矩阵。
它是由结构的几何形状、材料性质和截面特性等因素决定的。
在结构的分析和计算中,我们可以通过将各个单元的原始刚度矩阵组合起来,得到整个结构的总刚度矩阵。
这样,我们就可以利用刚度矩阵进行结构的力学性能分析和计算。
二、原始刚度矩阵的计算原始刚度矩阵的计算需要考虑结构的几何形状、材料性质和截面特性等因素。
对于简单的结构单元,如梁单元、柱单元等,其原始刚度矩阵可以通过解析公式或数值计算方法得到。
而对于复杂的结构单元,如板单元、壳单元等,其原始刚度矩阵则需要通过有限元法等数值方法进行计算。
在计算原始刚度矩阵时,需要考虑结构的各向异性和非线性特性。
对于各向同性结构单元,其刚度矩阵通常是对称正定的。
而对于各向异性结构单元,其刚度矩阵则可能是非对称的。
此外,在计算原始刚度矩阵时,还需要考虑结构的边界条件和约束条件等因素,以保证计算结果的准确性和可靠性。
三、原始刚度矩阵的应用原始刚度矩阵在结构力学领域有着广泛的应用。
通过原始刚度矩阵,我们可以计算结构的整体刚度矩阵,并根据位移边界条件和载荷条件等信息,求解结构的位移、应力和应变等力学性能。
此外,原始刚度矩阵还可以用于结构的优化设计和参数敏感性分析等工作。
通过对原始刚度矩阵的计算和分析,我们可以更好地理解和评估结构的刚度特性,为结构的设计和分析提供科学依据。
总结:结构的原始刚度矩阵是描述结构刚度特性的重要工具,通过它我们可以计算结构的整体刚度矩阵,进而分析和计算结构的力学性能。
原始刚度矩阵的计算需要考虑结构的几何形状、材料性质和截面特性等因素,可以通过解析公式或数值计算方法得到。
静力弹塑性分析(Pushover分析)两种方法剖析
静力弹塑性分析(Pushover分析)■简介Pushover分析是考虑构件的材料非线性特点,分析构件进入弹塑性状态直至到达极限状态时结构响应的方法。
Pushover分析是最近在地震研究及耐震设计中经常采用的基于性能的耐震设计(Performance-BasedSeismicDesign,PBSD)方法中最具代表性的分析方法。
所谓基于性能的耐震设计就是由用户及设计人员设定结构的目标性能(targetperformance),并使结构设计能满足该目标性能的方法。
Pushover分析前要经过一般设计方法先进行耐震设计使结构满足小震不坏、中震可修的规范要求,然后再通过pushover分析评价结构在大震作用下是否能满足预先设定的目标性能。
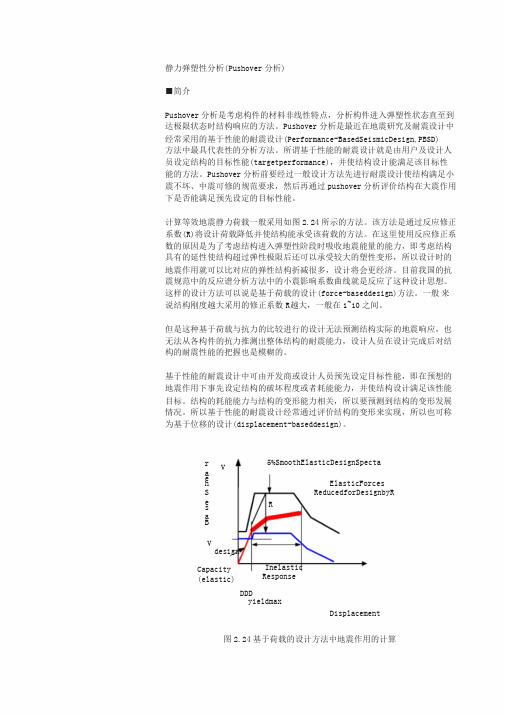
计算等效地震静力荷载一般采用如图2.24所示的方法。
该方法是通过反应修正系数(R)将设计荷载降低并使结构能承受该荷载的方法。
在这里使用反应修正系数的原因是为了考虑结构进入弹塑性阶段时吸收地震能量的能力,即考虑结构具有的延性使结构超过弹性极限后还可以承受较大的塑性变形,所以设计时的地震作用就可以比对应的弹性结构折减很多,设计将会更经济。
目前我国的抗震规范中的反应谱分析方法中的小震影响系数曲线就是反应了这种设计思想。
这样的设计方法可以说是基于荷载的设计(force-baseddesign)方法。
一般来说结构刚度越大采用的修正系数R越大,一般在1~10之间。
但是这种基于荷载与抗力的比较进行的设计无法预测结构实际的地震响应,也无法从各构件的抗力推测出整体结构的耐震能力,设计人员在设计完成后对结构的耐震性能的把握也是模糊的。
基于性能的耐震设计中可由开发商或设计人员预先设定目标性能,即在预想的地震作用下事先设定结构的破坏程度或者耗能能力,并使结构设计满足该性能目标。
结构的耗能能力与结构的变形能力相关,所以要预测到结构的变形发展情况。
所以基于性能的耐震设计经常通过评价结构的变形来实现,所以也可称为基于位移的设计(displacement-baseddesign)。
大跨度钢结构非线性分析论文

大跨度钢结构非线性分析研究【摘要】随着现代计算机技术和结构计算理论的发展,钢结构高等分析法被应用到结构设计中,高等分析法是考虑了结构的非线性响应、各种缺陷以及其他影响结构承载能力的因素,通过对结构进行一次全过程的整体分析研究结构的响应。
本文对结构非线性分析理论进行了研究,并通过具体的算例验证了非线性分析在工程中的应用。
【关键词】钢结构;非线性;有限元1 前言钢结构具有材料强度高、塑性韧性好、重量轻、材质均匀、工业化生产程度高等优点,目前在国内外的工程建设中得到了越来越广泛的应用。
由于钢材强度高,构件一般板件较薄,长细比大[1],更容易出现失稳现象,同时,耐腐蚀性差、高温下容易软化、在低温下容易发生脆断等,导致了钢结构事故的发生。
对于大型公共建筑,结构体系复杂,设计难度高,投资大,人员密集,因此对其安全性要求极高。
传统的钢结构设计采用的是两阶段设计法,第一阶段是按线弹性理论计算结构内力,第二阶段是进行构件设计,通过计算长度系数考虑构件之间的影响,然后按照规范对构件进行单独验算和设计,通过计算长度系数考虑构件之间的相互影响。
目前各国规范基本都采用两阶段设计法,但该方法也有一定的不合理性,如结构的内力分析模式与构件承载力计算模式不一致、不能考虑内力重分布等等。
因此,结构设计若仅进行强度、稳定性、刚度进行计算和验算,无法保证其可靠性,不能满足现代结构设计的需求,必须发展对结构进行非线性分析和设计的方法。
2 非线性理论从本质上讲,工程中所有的力学问题都是非线性的[2],一些经典的力学理论都是对实际问题基于某些假定的简化处理,如小变形假定、线性弹性假定、边界条件保持不变假定等,不满足上述假定中的任意一种假定,就产生非线性现象。
一般地,力学中的非线性问题包括三类:(1)几何非线性。
在小变形假定下,通常是在未变形的结构上建立平衡。
当结构在荷载作用下产生较大的变形,小变形假定不成立,就必须考虑几何非线性的影响,平衡应建立在结构变形后的构形上,考虑内力的二阶效应,几何方程应包括位移的高阶项。
桥梁结构的材料几何非线性分析-文档在线预览

(2) 迭代求解方法 用迭代方法求解材料非线性问题的平衡方程,可分为
变刚度迭代法 常刚度迭代法 (a)变刚度迭代法 变刚度法分为割线刚度法(直接刚度法)和切线刚度法。如果 材料的本构关系能够表示成
则应力位移关系
刚度矩阵
平衡方程迭代公式
迭代步骤如下
①首先取
,则
②由式
③取 ,算得 ④ ⑤多次迭代直止
当
时为加载,且满
足;
当
时为卸载,且满
足
⑥在卸载后某应力 下重新加载,
则当
时,
⑦由卸载转入反向加载,应力应 变关系继续依线性关系,一直 到反向屈服。
若
,称此材料为理想塑性材料
若
,称此为硬化现象或加工硬化。
理想塑性材料
(b)增量形式的弹塑性矩阵通式 在复杂应力状态下,判断材料是否屈服,可用应力的某种函数表示
桥梁结构的材料几何非线性分析
■ 桥梁结构的非线性问题 ■ 桥梁结构材料非线性分析 ■ 桥梁结构几何非线性分析 ■ 活载非线性分析 ■ 小结 ■ 本章参考文献 ■ 本章附录:几种常见单元的切线刚度矩阵
桥梁结构的非线性问题
从20世纪中起,科学为困扰人们的非线性问题奠定了力学基础 上世纪60年代末,有限元法与计算机相结合,使工程中的非线 性问题逐步得以解决; 目前,求解桥梁结构非线性问题,已经不是特别困难,而重要 的是提高精度、节省计算机时和寻找合理有效的本构模型及其复杂 问题的简化方法。 经典线性理论基于:
迭代步骤如下
①已知 ,求得 ,切线弹性矩阵
,
②算出
及
,则
③重复①、②步骤,直到接近真实解,使
给定小数
计算时,可取
matlab有限元切线刚度矩阵编程

题目:使用MATLAB编程实现有限元切线刚度矩阵计算一、引言有限元法是一种用于求解复杂工程问题的数值分析方法,它将连续介质划分为许多小的单元,通过对每个单元进行离散化处理,再用数学方法对这些单元进行组装,最终得到整个结构的解。
在有限元方法中,刚度矩阵是求解结构问题的关键步骤之一,而有限元切线刚度矩阵的计算则是其中的重要内容之一。
本文将介绍如何使用MATLAB编程实现有限元切线刚度矩阵的计算。
二、有限元切线刚度矩阵的基本概念1. 切线刚度矩阵在有限元方法中,切线刚度矩阵是描述结构对外部载荷作用下的应变-应力关系的重要矩阵。
它描述了结构在外部载荷下的变形行为,是求解结构变形和应力的重要工具。
2. 切线刚度矩阵的计算切线刚度矩阵的计算是通过对单元的局部坐标系进行刚度矩阵的求解,并进行坐标变换得到全局坐标系下的切线刚度矩阵。
在实际计算中,需要考虑单元的几何形状、材料性质等因素,以及在单元上施加的外部载荷。
三、MATLAB编程实现有限元切线刚度矩阵的基本步骤1. 单元刚度矩阵的计算我们需要编写MATLAB函数来实现对单元刚度矩阵的计算。
这个函数需要考虑单元的几何形状、材料性质等因素,以及在单元上施加的外部载荷。
通常情况下,我们可以利用数值积分的方法来进行刚度矩阵的计算。
2. 坐标变换矩阵的计算在得到单元刚度矩阵之后,我们需要计算坐标变换矩阵,将单元刚度矩阵从局部坐标系变换到全局坐标系。
这也需要编写一个MATLAB函数来实现坐标变换矩阵的计算。
3. 矩阵组装我们需要将所有单元的切线刚度矩阵组装成整体刚度矩阵。
这通常需要考虑到单元之间的连接关系,以及边界条件等因素。
在MATLAB中,我们可以利用矩阵的组合和相加等运算来实现整体刚度矩阵的计算。
四、编程实例这里我们以一个简单的弹簧-弹簧系统为例,介绍如何使用MATLAB编程实现有限元切线刚度矩阵的计算。
我们需要定义系统的几何形状、材料性质等参数,然后编写MATLAB函数来进行刚度矩阵的计算,坐标变换矩阵的计算,以及矩阵的组装,最终得到整体刚度矩阵,并求解系统的变形和应力。
砂土 切线刚度 割线刚度

砂土切线刚度割线刚度砂土的切线刚度和割线刚度是土工力学中的重要参数,用来描述砂土在变形过程中的抗剪性能和变形特征。
本文将对砂土的切线刚度和割线刚度进行简要介绍,并探讨其在土壤力学研究和工程实践中的应用。
一、砂土的切线刚度砂土的切线刚度是指在规定的剪应力水平下,砂土抗剪强度对剪应变的敏感程度。
它可以用来衡量砂土在抗剪性能方面的刚性和稳定性。
切线刚度的计算方法一般采用试验数据进行拟合。
在一般的三轴剪切试验中,可以通过测量剪应力-剪应变关系曲线的斜率来求得切线刚度。
切线刚度与砂土的配比、颗粒形状、含水率等因素有关。
在实际工程中,砂土的切线刚度可以直接影响着土体的变形特征和承载力。
切线刚度越大,砂土的刚性和稳定性越好,其抗剪能力也更强。
因此,对于要求较高的工程项目,需要选择切线刚度较大的砂土。
二、砂土的割线刚度砂土的割线刚度是指土体在一定剪切应变范围内的变形能力。
它可以用来描述砂土的变形特征和抗剪性能的变化规律。
割线刚度的计算方法一般也是根据试验数据进行拟合得到。
通过测量剪应力-剪应变关系曲线上某一剪切应变范围内的斜率来求得割线刚度。
砂土的割线刚度会随着剪切应变的增大而逐渐减小。
在土壤力学研究中,砂土的割线刚度常用于剪切变形分析和变形特征研究。
砂土的割线刚度能反映土体的变形能力和剪切应力状态的变化,对于理解砂土的变形特征和预测土体的稳定性具有重要作用。
三、砂土切线刚度和割线刚度的应用砂土的切线刚度和割线刚度在土工力学研究和工程实践中有着广泛的应用。
1. 土工力学研究:砂土的切线刚度和割线刚度是研究土体抗剪特性和变形特征的重要参数,可以用于土体的力学性质分析、变形机理研究等领域。
2. 土壤力学计算:在土体力学计算中,切线刚度和割线刚度是经常使用的参数。
通过合理选择切线刚度和割线刚度的数值,可以对土体的承载能力、变形特征和稳定性进行准确的分析和预测。
3. 岩土工程设计:砂土的切线刚度和割线刚度可以用于岩土工程中的土体模型建立和参数确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a ela niee e e tm ehod sw l sf t l m n t i .
Ke r s g o t c n ni e rt tn e t t n s t x s c n t f e s ar ; o e t l n r y y wo d : e me r o l ai i n y; a g n i e smar ; e a t i n s ti p tn i e g sf i sf m x ae
1 引言
非线性 稳 定性 分析 中常 用 到割线 刚度 矩 阵与切 线 刚度 矩 阵 ,其 中,前 者用 于全 量形 式 的平衡 方 程 ,后者 用 于增量 形 式 的平 衡 方程 。 线 刚度 矩 阵常 用于 判断 临界 点 的稳 定性和 对 临界 点进行 分类 。 切 基 于有 限元 法 ,考虑 了结构 可 能存在 初始 缺 陷 的情 况 ,从 结 构 的能量表 达 式 出发 ,推导 了二 者之 间 的数 学关系 。具 体做 法是 :针对 具有 任 意 多 自由度和 任 意参 数变量 ( 任意 荷载 或初 始缺 陷 ) 的结 如
间 的关 系
王天英 邓长根
( 济大 学 土 木 工 程 学 院 , 上 海 同 209 ) 002
摘要 : 从结构 的总势 能泰勒级数展 开式出发, 导了结构 的切 线刚度矩阵和割线刚度矩阵之间的数量关系 。 推
其结果 可用于 结构非线 性稳 定性分析 ,并且 不仅可 用于有 限元法 ,还可用 于瑞利一 李兹 法( al g olg f iiE gn e n , o gi i ri , hn h i 0 0 2 C ia C l e vl n ier g T n jUnv sy S a g a2 0 9 , hn ) e oC i e t
A bs r c - nt i pe , ege r ahe ai e ai ns p t e n sr t a e nta d a t a t I h spa r t ne a m t m tcr l to hi bew e tucur ls ca h l n tnge tsif s a c s n tfne sm  ̄i e
构 ,从结构的通用总势能泰勒级数展开式出发,推导得出结构的切线刚度矩阵和割线刚度矩阵之 间
的数 量关 系 。结论 可广 泛 应用于 离 散化算 法 中 ,如有 限元 法 ,瑞利 一李兹法 ( yeg— i to) RalihRtme d、 z h
收稿 日期:2 0 —41 ;修回 日期 :2 0 —9 1 0 70 —0 0 70 —0 基金项 目:国家 自然科 学基金资助项 目 ( 0 7 17 54 8 0 ) 作者简介 :王天英(9 2) 17 一,女,工程 师,博士生 ,研究方 向:结构稳 定理论 、失稳监测和稳 定控制 ;(0 02 209) 上海 市杨浦 区密云路 5 8弄博士生 5号楼 10 —# 2 4 15 .
Ge e a ea i n h p b t e t u t r l e a t n a g n t f e s n r l l to s i e we n sr c u a c n d t n e t i n s r s a sf
m a rc s t ie
W ANG a -i g Tin- n y DENG Cha g- n n - ge
维普资讯
20 0 8年 4月 第3 5卷第 2期
强 度 与 环 境
S TRUCTURE & ENVI RoNM ENT ENGI NEERI NG
A p .00 r2 7 Vl13 No. 0 .5. 2
结构切线 刚度矩 阵与割线 刚度矩 阵之
K U, u =P ( v) () 1
式 中 , K 为割 线刚度 矩 阵 ; U为节 点位 移 列 向量 ; V 为参 数 向量 ; P为节 点荷 载 列 向量 。
me o ) t d 、伽 辽 金 法 ( l ri to ) 。 h Ga knme d等 e h
关键 词:几何非线性 ;切线刚度矩阵 ;割线刚度矩 阵;势 能 中图分类号 :T 1. U3 1 2 文献标识码 :A 文章编号 :10 .992 0 )20 3 —5 0 63 1(0 80 —0 10
i e e o e n d t l a e nTa l rs re x r si n o et tl o e ta n r y T er s l i sd v l p d i e a s d o y o e se p e so ft a p t n l e e g . h e u t si o t n e i b i h o i mp ra tt t Oh a ay i fs u t r o l e rsa i t . o e v r i C eu e y eg — t t o G ae k n m e od, c, n sso t cu a n n i a tb l y M r o e , t a b s d i Ra li h Ri me d l r i t l r l n i n n z h h et.
维普资讯
3 2
强 度 与 环 境
20 0 8笠
伽 辽金 法( aeknme o ) 。 G l i t d等 r h
2 切线刚度矩 阵与割线刚度矩阵关系式推导
2t 平 衡 方 程 的两 种 形 式 . 几何 非线 性 分析 的全 量形 式 的平衡 方程 可表 示 为矩 阵形 式 的非线 性代 数方 程 组 :
