HotZ-雷达系统(第一章)波形模糊函数
雷达波形模糊图专业训练课设报告

专业综合课程设计报告课设题目:雷达波形模糊图学院:信息与电气工程学院专业:电子信息工程班级:姓名:学号:指导教师:哈尔滨工业大学(威海)2013年11月28日一、设计任务模糊函数是对雷达信号进行分析研究和波形设计的有效工具, 是雷达信号理论中极为重要的一个概念。
模糊函数最初是在研究雷达分辨力问题时提出的, 并从衡量两个不同距离和不同径向速度目标的分辨度出发提出了模糊函数的定义。
但模糊函数不仅可以说明分辨力, 还可以说明测量精度、测量模糊度以及抗干扰状况等问题。
雷达信号的模糊函数与雷达信息的提取紧密相关, 它不仅涉及了雷达的精度, 还涉及了雷达的抗干扰、自适应以及雷达信号的处理方式。
本次课程设计目标是:画出某线性调频和相位编码信号的模糊图;根据模糊图分析多普勒频移对匹配滤波的影响;产生雷达回波数据并匹配滤波,根据仿真结果分析各参数对匹配滤波结果的影响。
二、 方案设计设计某线性调频和相位编码信号线性调频波形的定义为()⎪⎭⎫⎝⎛=2cos t t x τβπ τ≤≤t 0 (1)使用复数表达式,有()()t j tj e e t x θτπβ==/2τ≤≤t 0 (2)该波形的瞬时频率是相位函数的微分()()t dt t d t F i τβθπ==21 (3)假设0>β,在s τ的脉宽内()t F i 线性地扫过了整个Hz β带宽。
当βτ=50时,()t F 就是一个线性调频波。
画出其模糊图并分析模糊图的特征模糊函数是波形设计与分析的工具,它可以方便地刻画波形与对应匹配滤波器的特征。
模糊函数在分析分辨率、副瓣性能,以及多普勒和距离模糊方面非常有用,另外也可以用于对距离-多普勒耦合的分析。
考虑当输入为多普勒频移响应想()()t F j t x D π2ex p 时波形()t x 的匹配滤波器输出。
同时,假设滤波器具有单位增益(1=α),并且设计为在0=M T 时达到峰值。
这仅仅意味着滤波器输出端的时间轴与目标距离期望的峰值输出时间相关。
雷达模糊函数

雷达模糊函数雷达模糊函数是一种常见的信号处理技术,用于处理雷达接收到的信号并提取出目标信息。
雷达系统通过发射电磁波并接收回波来探测目标,而雷达模糊函数则可以帮助我们更好地理解这些回波信号。
雷达模糊函数在雷达信号处理中扮演着至关重要的角色。
它可以帮助我们确定目标的位置、速度和形状等信息,从而实现雷达系统的目标跟踪和识别功能。
雷达模糊函数通常包括距离模糊函数、速度模糊函数和角度模糊函数等,每种模糊函数都有其特定的应用场景和处理方法。
距离模糊函数是指雷达接收到的信号中存在距离信息上的不确定性,导致无法准确确定目标的距离。
这种模糊通常是由于雷达发射的脉冲信号在传播过程中受到多径效应、大气扰动等因素的影响所致。
为了解决距离模糊问题,我们可以采用多普勒处理、脉冲压缩等技术来提高雷达系统的分辨率和抗干扰能力。
速度模糊函数是指雷达接收到的信号中存在速度信息上的不确定性,导致无法准确确定目标的速度。
这种模糊通常是由于目标本身的运动状态、雷达系统的参数设置等因素所致。
为了解决速度模糊问题,我们可以采用脉冲多普勒处理、MTI滤波器等技术来提取目标的速度信息并实现速度测量。
角度模糊函数是指雷达接收到的信号中存在角度信息上的不确定性,导致无法准确确定目标的方位角。
这种模糊通常是由于天线指向精度、目标散射截面积等因素的影响所致。
为了解决角度模糊问题,我们可以采用波束形成、空时处理等技术来提高雷达系统的方位角分辨率和目标识别能力。
总的来说,雷达模糊函数在雷达信号处理中起着至关重要的作用。
通过对雷达接收到的信号进行模糊函数分析,我们可以更准确地获取目标信息并实现雷达系统的各种功能。
因此,深入了解雷达模糊函数的原理和应用对于提高雷达系统性能和效率具有重要意义。
希望通过本文的介绍,读者对雷达模糊函数有了更深入的了解,为相关领域的研究和应用提供参考和指导。
模糊函数

Property 4 says that adding LFM modulation shears the resulting ambiguity function. The meaning of the shear will be demonstrated following the proof of property 4. This important property is the basis for an important pulse compression technique.
Radar Signals, By Nadav Levanon and Eli Mozeson ISBN 0-471-47378-2 Copyright 2004 John Wiley & Sons, Inc.
34
MAIN PROPERTIES OF THE AMBIGUITY FUNCTION
then adding linear frequency modulation (LFM), which is equivalent to a quadratic-phase modulation, implies that u(t) exp(j πkt 2 ) ⇔ |χ(τ, ν − k τ)| (3.6)
Property 2: To prove this property, we rewrite χ(τ, ν), replacing ν with −f : χ(τ, −f ) =
∞ −∞
[u(t)u∗ (t + τ)] exp(−j 2πf t) dt
(3.10)
which is recognized as the Fourier transform χ(τ, −f ) = F [β(τ, t)] of the function β(τ, t) = u(t)u∗ (t + τ) (3.11)
雷达波形

第3章 雷达波形在雷达系统中,波形类型和信号处理技术的选取在很大程度上取决于雷达具体的任务和作用㊂与某种波形的软硬件实现相关的成本和复杂性是决策过程中的主要考虑因素㊂雷达系统可以使用连续波形(CW)㊁调制或未调制的脉冲波形㊂调制技术既可以是模拟的,也可以是数字的㊂距离分辨率及多普勒分辨率与特定波形的频率特征直接相关,因此,了解一种波形的功率谱密度非常关键㊂一般来说,信号或波形可以用时域或频域的技术来分析㊂本章我们将介绍许多常用的雷达波形㊂某种特定波形的相关应用将在它的时域和频域特征中描述㊂在本书中,术语 波形”和 信号”交互使用,表示相同的意思㊂3.1 低通㊁带通信号和正交分量如果信号包含的主要频率处于包括直流(DC)在内的低频频带,则称其为低通(LP)信号㊂如果信号包含的主要频率处于离开原点的某个频率附近,则称其为带通(BP)信号㊂一个实带通信号x(t)在数学上可表示为(3.1)其中,r(t)是幅度调制或包络,x(t)为相位调制,f0是载波频率,r(t)和x(t)所包含的频率成分都比f0明显要小,调制频率为(3.2)瞬时频率为(3.3)如果信号带宽为B,并且f0远大于B,则信号x(t)被称为窄带信号㊂带通信号也可以用两个称为正交分量的低通信号表示,此时式(3.1)可以重写为(3.4)其中,x I(t)和x Q(t)是称为正交分量的实低通信号,分别表示为(3.5)图3.1说明了正交分量是如何被提取的㊂图3.1 正交分量的提取3.2 解析信号在式(3.1)中定义的正弦信号x (t )可以写为复信号(t )的实部,更具体的表示为(3.6)定义 解析信号”为(3.7)其中(3.8)并且(3.9)()是(t )的傅里叶变换,X()是x (t )的傅里叶变换㊂式(3.9)可以写为(3.10)其中,U()为频域阶跃函数㊂由此可以得出(t )为(3.11)~x 是x (t )的希尔伯特变换㊂利用式(3.6)和式(3.11),可以得出(这里只给出结果,没有证明)(3.12)这与式(3.44)相似,只是这里的=2πf 0㊂根据帕塞瓦尔(Parseval)定理,可以看出x (t )的能量为(3.13)3.3 连续和脉冲波形一个给定信号的频谱描述了其能量在频域的分布㊂一个能量信号(有限能量)的特征可以由它的能量谱密度(ESD)函数来表示,而一个功率信号(有限功率)的特征可以由它的功率谱密度(PSD)函数来表示㊂ESD 的单位为J /Hz,PSD 的单位为W /Hz㊂信号带宽是指信号非零谱的频率范围㊂一般说来,一个信号可以由它的时间(时域)和带宽(频域)来定义㊂如果信号的带宽是有限的,那么就说这个信号是带限的㊂具有有限持续时间(时间有限)的信号具有无限的带宽,而带宽有限的信号具有无限的持续时间㊂极限情况是一个连续正弦信号,它的带宽是无限小的㊂一个时域信号f (t )的傅里叶变换(FT)如下:(3.14)而逆傅里叶变换(IFT)为(3.15)信号自相关函数R f (τ)为(3.16)89雷达系统设计MATLAB 仿真式中,星号表示复共轭㊂信号幅度谱为|F()|㊂如果是能量信号,则其ESD 为|F()|2;如果是功率信号,则其PSD 为⎺S f(),是其自相关函数的傅里叶变换,即(3.17)首先,考虑CW波形为(3.18)f 1(t )的傅里叶变换为(3.19)其中,δ(㊃)是狄拉克δ(Dirac⁃δ)函数,0=2πf 0㊂如图3.2中的幅度谱所示,信号f 1(t )有无限小的带宽,位于±f 0处㊂图3.2 一个连续正弦波形的幅度谱接下来考虑时域函数f 2(t ),为(3.20)它的傅里叶变换为(3.21)其中(3.22)f 2(t )的幅度谱如图3.3所示㊂此时,带宽是无限的㊂由于无限带宽是物理不可实现的,因此信号的带宽近似为2π/τrad /s 或者是1/τHz㊂实际上,这种近似得到广泛的认可,因为它把信号大部分的能量都计算在内㊂下面考虑相干加窗连续波形f 3(t )为(3.23)显然f 3(t )是周期的,其中T 为周期(回忆f r =1/T 即为PRF)㊂利用复指数傅里叶级数,f 3(t )可重写为(3.24)其中,傅里叶级数的系数F n 为99第3章 雷达波形(3.25) f3(t)的傅里叶变换为(3.26) f3(t)的幅度谱如图3.4所示㊂此时,幅度谱具有对应于F n的(sin x)/x形状的包络,谱线之间的间隔都等于雷达的脉冲重复频率f r ㊂图3.3 单脉冲或非相干脉冲串的幅度谱图3.4 无限长相干脉冲串的幅度谱最后,定义函数f4(t)为(3.27)注意,f4(t)为f3(t)的一个有限时宽信号㊂f4(t)的傅里叶变换为(3.28)001雷达系统设计MATLAB仿真其中,操作符(㊃)表示卷积㊂此时,频谱如图3.5所示,包络仍然是对应于脉宽的(sin x )/x ,但是谱线被对应于时宽NT 的(sin x )/x 谱替换㊂图3.5 有限长相干脉冲串的幅度谱3.4 线性调频波形频率或相位调制信号用来得到宽得多的工作带宽㊂线性调频(LFM)是常用的方式㊂在这种情况下,频率在脉宽内线性扫描,或者向上(上调频)或者向下(下调频)㊂匹配滤波器的带宽与扫描的带宽成比例,与脉宽无关㊂图3.6是一个典型的LFM 波形样本,脉宽为τ,带宽为B ㊂LFM 上变频波形的瞬时相位可以表示为(3.29)其中,f 0为雷达中心频率,μ=(2πB )/τ是LFM 系数㊂因此,瞬时频率为(3.30)同理,下变频波形的瞬时相位和频率分别为(3.31)(3.32)典型的线性调频信号可以表示为(3.33)其中,rect(t /τ)表示宽度为τ的矩形脉冲,则式(3.33)可写为(3.34)其中101第3章 雷达波形(3.35)是s1(t)的复包络㊂图3.6 典型LFM波形信号s1(t)的频谱由它的复包络s(t)决定㊂式(3.34)中的复指数项表示中心频率f0的频移㊂将s(t)进行傅里叶变换,得到(3.36)令μ′=2πμ=2πB/τ,进行变量替换为(3.37)因此,式(3.36)可写为(3.38)(3.39)其中(3.40)(3.41)用C(x)和S(x)表示菲涅耳积分,定义如下:(3.42)(3.43)菲涅耳积分近似为(3.44)201雷达系统设计MATLAB仿真(3.45)注意,C(-x)=-C(x),S(-x)=-S(x)㊂图3.7给出了C(x)和S(x)在0≤x≤4.0时的图形㊂该图可以使用3.12节的清单3.1中的MATLAB程序 fig37.m”得到㊂在式(3.39)中使用式(3.42)和式(3.43),进行积分得到(3.46)图3.8显示了线性调频信号实部㊁虚部及幅度谱的典型图形㊂图3.8(c)中的类似方形的频谱就是广为人知的菲涅耳谱㊂该图可由3.12节的清单3.2中的MATLAB程序 fig38.m”得到㊂开发了一个MATLAB GUI[见图3.8(d)],用来输入LFM数据并显示图3.8所示的输出㊂文件名为 LFM gui.m”,其输入是未压缩的脉宽和调制带宽㊂图3.7 菲涅耳积分(a)典型LFM波形,实部图3.8301第3章 雷达波形(b)典型LFM 波形,虚部(c)LFM波形的典型谱(d)GUI 工作空间 LFM gui.m”图3.8(续)401雷达系统设计MATLAB 仿真3.5 高距离分辨率在第1章中,得到了一个用脉宽τ表示距离分辨率ΔR 的表达式㊂当未使用脉冲压缩时,雷达接收机的瞬时带宽B 通常和脉冲的带宽匹配㊂在大多数雷达应用中,这是通过令B =1/τ实现的㊂因此,距离分辨率为(3.47)雷达使用者和设计者不约而同地通过最小化ΔR 来寻求实现高距离分辨率(HRR)㊂然而如式(3.47)所示,为了得到高距离分辨率,必须使用短脉冲,从而导致平均发射功率的减小,并且强加了对大工作带宽的需求㊂在得到好的距离分辨率的同时保持足够的平均发射功率,可以通过使用脉冲压缩技术来实现,这将在第5章中进行讨论㊂利用频率或相位调制,脉冲压缩可以使我们获得相当长脉冲的平均发射功率,同时得到对应非常短脉冲的距离分辨率㊂例如,考虑一个LFM 波形,其带宽为B ,未压缩脉宽为τ㊂经过脉冲压缩后,压缩后的脉宽表示为τ′,其中τ′<<τ,HRR为(3.48)经常使用线性调频和调频(FM)连续波信号来得到HRR㊂高距离分辨率也可以通过一种称为 步进频波形”(SFM)的波形来合成㊂与LFM 或FM⁃CW 相比,步进频波形需要更加复杂的硬件实现;不过,对雷达工作带宽要求较低㊂这是因为接收机的瞬时带宽与SFM 子脉冲带宽相匹配,其远小于LFM 或FM⁃CW 带宽㊂下一节将对SFM 波形进行简要讨论㊂3.6 步进频波形步进频波形(SFW)产生合成的HRR 目标距离像,这是因为目标距离像是通过实际目标距离像的频域样本的逆离散傅里叶变换(IDFT)计算的㊂产生合成的高分辨率距离像的过程在Wehner ①的著作中描述,总结如下:1.发射n 个窄带脉冲序列,从一个脉冲到下一个脉冲的频率以固定的频率步长步进㊂每组的n 个脉冲称为一个脉冲串(burst)㊂2.接收信号以对应于每个脉冲中心频率的速率进行采样㊂3.收集并保存每个脉冲串的正交分量㊂4.对正交分量进行频谱加权(为了降低距离旁瓣电平),进行目标速度㊁相位和幅度变化的校正㊂5.计算每个脉冲串加权后正交分量的IDFT,以合成该脉冲串的距离像㊂对N 个脉冲串重复处理,以得到连续的合成高分辨率距离像㊂图3.9显示了典型的SFW 脉冲串㊂脉冲重复间隔(PRI)为T ,脉宽为τ′㊂每个脉冲可以有自己的LFM,或者其他类型的调制㊂此书假设为LFM㊂第i个步进的中心频率为(3.49)501第3章 雷达波形①Wehner,D.R.,High Resolution Radar ,second edition,Artech House,1993.图3.9 步进频波形脉冲串在一个脉冲串内,第i个步进的发射波形可以描述为(3.50)其中,θi 为相对相位,C i 为常数㊂在距离R 0处的目标在时间t =0时的接收信号为(3.51)其中,C′i 为常数,往返时延τ(t )为(3.52)c 为光速,v 为目标的径向速度㊂为了提取正交分量,接收信号下变频到基带㊂准确地说,s ri (t )和下面信号混频(3.53)经过低通滤波器后,正交分量为(3.54)其中,A i 为常数,并且(3.55)现在,f i =Δf ㊂对于每个脉冲,正交分量的采样时刻为(3.56)τr 是与对应于距离像起点的距离有关的时延㊂正交分量的复数形式可以表示为(3.57)式(3.57)表示基于单个脉冲串的目标反射性的频域样本㊂该信息可以利用IDFT 转化为一系列距离时延的反射性(即为距离像)大小,表示如下:601雷达系统设计MATLAB 仿真(3.58)将式(3.57)和式(3.55)代入式(3.58)中,合并同类项得到(3.59)相对于n归一化,并且假设A i=1,目标为静止的(即v=0),则式(3.59)可以写为(3.60)在式(3.60)中,利用f i=iΔf得到(3.61)其可以简化为(3.62)其中(3.63)最后,合成的距离像为(3.64) 3.6.1 SFW的距离分辨率和距离模糊一般来说,距离分辨率由总的系统带宽来决定㊂假设一个SFW具有n个步进,步长为Δf,则对应的距离分辨率等于(3.65)SFM的距离模糊可以通过检验对应于在距离R0的点散射体的相位来决定㊂更准确地说,(3.66)那么(3.67)或等价于(3.68)从式(3.68)可以明显看出,当Δ=Δ+2nπ时,存在距离模糊㊂因此(3.69)不模糊距离窗为(3.70)因此,关于对应于脉冲串时延的绝对距离,使用特定SFW合成的距离像表示在不模糊距离窗内所有散射体的相对距离反射性㊂另外,如果一个特定目标的范围大于R u,则落在不模糊距离窗外的所有散射体将重叠在一起,出现在合成距离像上㊂这种重叠问题与使用快速傅里叶变换(FFT)分辨某个信号的频率分量时出现的频谱混叠是一样的㊂例如,考虑一个频率分辨率为Δf=50Hz,长度为NFFT=64的FFT㊂此时,这个FFT可以分辨的音频在-1600Hz 到1600Hz之间㊂当这个FFT被用来分辨一个正弦音调为1800Hz的频率分量时,就会发生频谱混叠,在第4个FFT单元(即200Hz)会出现谱线㊂因此,为了在合成距离像中避免混叠,频率步进Δf必须满足(3.71)其中,E为目标长度,单位为m㊂另外,脉冲宽度也必须足够大,以包括整个目标长度,所以(3.72)实际中(3.73)为了减小由于考察目标周围的杂波而引起的合成距离像的污染,这是必要的㊂MATLAB函数 hrr profile.m”函数 hrr profile.m”计算并画出特定SFW的合成HRR像(见3.12节的清单3.3)㊂该函数使用一个长度为步进数两倍的逆傅里叶变换(IFFT)㊂还假设采用同样大小的汉明窗㊂调用语法如下:[hl]=hrr profile(nscat,scat range,scat rcs,n,deltaf,prf,v,r0,winid)其中,符号含义如下表所示㊂符 号描 述单 位状 态nscat组成目标的散射体个数无输入scat range包含散射体距离的向量m输入scat rcs包含散射体RCS的向量m输入n步进数无输入deltaf步进频率Hz输入prf SFW的PRF Hz输入v目标速度m/s输入r0像起始距离m输入winid数值>0为汉明窗数值<0为不加窗无输入hl距离像dB输出例如,假设距离像起始点为R0=900m处,且nscat tau n deltaf prf v 3100μs6410MHz10KHz0.0这种情况下因此,间隔大于0.235m的散射体将会在合成距离像上显示为不同的尖峰㊂假设两种情况,第1种:[scat range]=[908,910,912]m,第2种:[scat range]=[908,910,910.2]m㊂在这两种情况下,令[scat rcs]=[100,10,1]m2㊂图3.10显示了第1种情况下利用函数 hrr profilr.m”在没有使用汉明窗时所产生的合成距离像㊂图3.11与图3.10类似,除了此时使用了汉明窗㊂图3.12显示了对应于第2种情况的合成距离像(使用汉明窗)㊂注意在图3.10和图3.11中,所有3个散射体都可以被分辨;而在图3.12中,最后两个散射体没有被分辨,因为它们的间隔小于ΔR㊂图3.10 3个被分辨散射体的合成距离像,未加窗图3.11 3个散射体的合成距离像,汉明窗接下来考虑另外一种情况,其中[scat range]=[908,912,916]m㊂图3.13显示了对应的距离像㊂在这种情况下,出现了混叠,最后一个散射体出现在合成距离像的近段部分㊂再考虑这种情况,其中[scat range]=[908,910,923]m图3.12 3个散射体的合成距离像,两个不能分辨图3.14显示了对应的距离像㊂在这种情况下,第1个和第2个散射体出现了模糊,因为它们的间隔为15m㊂两者都出现在相同的距离单元㊂3.6.2 目标速度的影响由式(3.64)定义的距离像是在假设检验目标静止的情况下得到的㊂将式(3.55)和式(3.56)代入到式(3.58)中,可以确定目标速度对合成距离像的影响,得到(3.74)图3.13 3个散射体的合成距离像,第3个散射体出现混叠式(3.74)中的附加相位项使合成距离像失真㊂为了说明这种失真,考虑前一节描述的SFW,并且假设第1种情况下的3个散射体,而且假设目标速度v=100m/s㊂图3.15显示了这种情况下的合成距离像㊂比较图3.11和图3.15,清楚地显示了由于未补偿目标速度而产生的失真㊂图3.16与图3.15类似,除了速度v=-100m/s㊂注意在任意一种情况下,目标由预定的位置偏移了(向左或向右)Disp=2×n×v/PRF(1.28m)㊂图3.14 3个散射体的合成距离像,第1个和第2个散射体出现在相同的FFT单元图3.15 由于目标速度引起的距离像失真这种失真可以通过将每个脉冲的复接收数据乘以下面的相位项消除(3.75)和分别是目标速度和距离的估计值㊂这种修订正交分量相位的过程通常被称为 相位旋转”㊂事实上,当不能得到和好的估计时,目标速度的影响可以通过在SFW中前后脉冲之间使用调频来减小㊂此时,每个子脉冲的频率由一个预定的编码来选取㊂这种类型的波形通常称为频率编码波形(FCW)㊂Costas波形或信号就是这种类型波形的一个很好的例子㊂图3.17是一个RCS为=10m2,v=15m/s的运动目标的合成距离像㊂目标的原始距离为R=912m㊂其他所有参数与前面一样㊂这幅图形可以使用3.12节的清单3.4中的MATLAB程序 fig317.m”得到㊂图3.17 一个运动目标的合成距离像(4s长)3.7 匹配滤波器匹配滤波器最独特的特征是当输入端出现信号与加性白噪声时,其在输出端产生最大可实现瞬时SNR㊂此噪声不必为高斯的㊂接收机输出端的峰值瞬时SNR可以通过将雷达接收机传输函数与接收信号匹配来得到㊂下面将证明匹配滤波器输出端的峰值瞬时信号功率除以平均噪声功率,等于两倍的输入信号能量除以输入噪声功率,无论雷达采用何种波形㊂这就是为什么我们常说匹配滤波器是SNR意义下的最优滤波器的原因㊂注意,在雷达方程(SNR)推导中使用的峰值功率表示在脉冲持续期间的平均信号功率,而不是在匹配滤波器情况下的峰值瞬时信号功率㊂事实上,实现理想的匹配滤波有时是很困难的㊂这时可以使用准最佳滤波器㊂由于这种失配,输出信噪比会降低㊂考虑一个使用有限持续时间的能量信号s i(t)的雷达系统㊂用τ′表示脉宽,并且假设使用匹配滤波器接收机㊂我们需要回答的主要问题是:当输入为延迟的信号s i(t)加上加性白噪声时,使接收机输出端的瞬时SNR最大的滤波器冲激或频率响应是什么样的?匹配滤波器的输入信号可以表示为(3.76)其中,C为常数,t1是正比于目标距离的未知时延,n i(t)是输入白噪声㊂因为输入噪声是白色的,所以其对应的自相关和功率谱密度(PSD)函数分别为(3.77)(3.78)其中,N0为常数㊂s0(t)和n0(t)分别表示信号和噪声的滤波器输出㊂更准确地可定义(3.79)其中(3.80)(3.81)操作符*表示卷积,h(t)为滤波器的冲激响应(假设滤波器为线性时不变的)㊂用R h(t)表示滤波器的自相关函数,则输出噪声的自相关函数和功率谱密度函数分别为(3.82)(3.83)其中,H()为滤波器冲激响应h(t)的傅里叶变换㊂总的平均输出噪声功率等于⎺Rn o(t)在t=0处的值,更精确的表示为(3.84)在t时刻的输出信号功率为|Cs o(t-t1)|2,并且利用式(3.80)可以得到(3.85)在t时刻输出SNR的一般表达式可以写为(3.86)将式(3.84)和式(3.85)代入式(3.86),得到(3.87) Schwartz不等式为(3.88)其中,等号仅当P=kQ*时成立,这里k为常数可以假定为1㊂则将式(3.88)作用于式(3.87)的分子上,得到(3.89)式(3.89)告诉我们,当等号成立时[即根据式(3.88),h=ks*i],出现峰值瞬时SNR㊂更准确地,如果我们假设等号出现在t=t0时刻,并且k=1,那么(3.90)最大瞬时SNR为(3.91)式(3.91)可以利用Parseval定理简化为(3.92)其中,E代表输入信号的能量㊂因此,可以将输出端峰值瞬时SNR写为(3.93)因此可得出结论:峰值瞬时SNR仅依赖于信号能量和输入噪声功率,而与雷达使用的波形无关㊂最后,可以由式(3.90)定义匹配滤波器的冲激响应㊂如果期望在t0=t1时刻出现峰值,我们得到非因果的匹配滤波器冲激响应为(3.94)另一方面,因果的冲激响应为(3.95)这时的峰值出现在t0=t1+τ时刻㊂h nc(t)和h c(t)的傅里叶变换分别为(3.96)(3.97)其中,Si()为s i(t)的傅里叶变换㊂因此,H()和S i()的模是相等的,而相位响应是相反的㊂例题计算线性滤波器输出端最大瞬时SNR,其冲激响应与信号x(t)=exp(-t2/2T)相匹配㊂解:信号能量为最大瞬时SNR为其中,N0/2为输入噪声功率谱密度㊂。
雷达原理及系统课件:hotz-雷达系统-第一章

PART 06
Hotz-雷达系统的性能评 估
雷达系统性能指标
探测距离
指雷达能够探测到的 最远距离,通常以千 米为单位。
分辨率
指雷达区分两个相邻 目标的能力,通常以 角度、距离和速度来 表示。
精度
指雷达测量目标参数 的准确性,包括位置、 速度和姿态等。
抗干扰能力
指雷达在面对各种干 扰信号时的性能表现, 包括压制式干扰和欺 骗式干扰。
系统集成
将多个雷达系统集成在一起,实现信息共享和协同探测 ,提高整体性能。
ABCD
软件优化
通过改进雷达系统的信号处理算法,提高其抗干扰能力 和可靠性。
应用拓展
将Hotz-雷达系统应用于更多领域,如无人驾驶、无人机 侦察等,以满足不同需求。
WENKU DESIGN
WENKU DESIGN
2023-2026
目标跟踪与定位
目标跟踪算法
采用跟踪算法对检测到的目标进行连续跟踪,记录目标的运动轨迹。
数据关联与滤波
利用数据关联算法和滤波算法,对跟踪数据进行处理,减小测量误差 和干扰因素的影响。
目标定位
根据多个接收站接收到的信号,采用定位算法计算出目标的精确位置。
系统性能评估
根据实际应用需求,对Hotz-雷达系统的性能进行评估,包括探测距 离、定位精度、跟踪稳定性等指标。
天线
定向发送和接收电 磁波。
控制单元
控制雷达系统的运 行和操作。
Hotz-雷达系统的特点与优势
高精度测距和测速
利用电磁波的往返时间,计算 出目标物体的距离和速度。
抗干扰能力强
采用特定的编码和调制方式, 有效降低干扰的影响。
实时性强
雷达原理与系统-杂波与杂波抑制

主瓣杂波
地面雷达的杂波包括从主瓣和旁瓣进入 的杂波,RCS的计算可描述为:
C MBc SLc
旁瓣 杂波区
旁瓣 杂波区
主瓣 杂波区
MBc 是主瓣杂波RCS, SLc是旁瓣杂波
图5.7地基雷达杂波几何图(侧视图和下视图)
14
由图5.7可以导出如下关系:
r arcsin(hr / R) e arcsin((ht hr ) / R) Rg R cosr
波也会表现出多普勒展宽,而且成片海杂波散射单元之间的相关性也比地杂波强。
海杂波的后向散射系数与海况、风速、波束相对于风向和波浪的 观测角、入射余角、工作频率、极化方式等因素有关。
不同掠射角下海杂波反射系数的统计结果
不同风速下海杂波的平均反射系数
(2)影响海杂波的参数
与地杂波的散射特性相比,海杂波的散射特性与其特殊性,不仅会因海情的
不同表现出不同的散射系数,而且海浪是运动的,即使对于固定的雷达平台,海杂
雷达原理与系统 杂波特征与杂波抑制
1
教学内容
✓ 概述 ✓ 杂波特征 ✓ 杂波抑制的性能指标 ✓ 动目标显示(Moving Target Indicator, MTI) ✓ 动目标检测(Moving Target Detection, MTD) ✓ 脉冲多普勒(PD)雷达
2
5.1: 概 述
“杂波”(Clutter,原意为混乱、杂乱的状态)表示自然环境中客观 存在的不需要的回波。杂波包括来自地面及地面人造物体和结构(例 如楼房、桥梁、公路、铁路、车辆、高压电缆塔、风电设备等)、海 洋、天气(特别是雨)、鸟群以及昆虫等的回波。由于地形的不同(农地、 林地、城市、沙漠等),或者海面的不同(海况、相对于雷达观测角 的风向),杂波也会在相邻区域上发生变化。通常杂波的功率比目标 回波强得多,容易产生假目标信息,“扰乱了”雷达工作,使得雷达难 以对目标进行有效的检测。因此,雷达需要排除杂波信号。
雷达模糊函数

雷达模糊函数雷达模糊函数是雷达信号处理中经常使用的一种数学模型,用于描述雷达系统中目标的位置和速度信息。
雷达系统通过发送和接收无线信号来探测目标的位置和速度,但由于各种环境因素的影响,接收到的信号往往会受到干扰和衰减,导致信号的模糊化。
雷达模糊函数就是用来描述这种信号模糊化程度的函数。
雷达模糊函数通常由雷达系统的特性和目标的运动状态等因素决定。
在雷达系统中,信号的传播会受到大气折射、多路径传播、目标散射等因素的影响,导致信号在传播过程中发生衰减和失真。
同时,目标的运动状态也会对接收到的信号产生影响,比如目标的速度越高,接收到的信号就会越模糊。
因此,雷达模糊函数可以用来描述在不同环境条件下接收到的雷达信号的模糊程度。
雷达模糊函数的形式通常是一个复杂的数学函数,包括各种参数和变量。
通过对雷达系统和目标的特性进行建模和分析,可以得到相应的雷达模糊函数,从而帮助雷达系统更准确地探测目标的位置和速度。
在实际的雷达信号处理中,工程师们会根据具体的情况选择合适的雷达模糊函数,以提高雷达系统的性能和探测精度。
除了用于描述信号模糊化程度外,雷达模糊函数还可以应用于雷达信号的处理和分析。
通过对雷达信号进行模糊函数的计算和处理,可以更好地理解和解释雷达系统的工作原理,从而为雷达系统的优化和改进提供参考。
同时,雷达模糊函数还可以用于目标跟踪、碰撞预警、地图绘制等领域,为相关应用提供支持和指导。
总的来说,雷达模糊函数在雷达信号处理中起着至关重要的作用,它不仅可以描述信号的模糊化程度,还可以用于雷达系统的优化和改进。
通过对雷达模糊函数的研究和应用,可以提高雷达系统的性能和可靠性,为雷达技术的发展和应用提供有力支持。
希望未来能够进一步深入研究雷达模糊函数的理论和应用,为雷达技术的发展做出更大的贡献。
第一章 模糊数学引 言

我国的模糊技术研究
1) 70年代后期传到我国,起步晚,但发展快
2) 理论研究居世界领先地位,但应用与发达国家有差距
3)“模糊技术产业化”
3) 近几年国内掀起了模糊控制技术的研究与开发热,成绩喜人
- 企业:大型加电集团已成功开发了国产模糊控制洗衣机 如: “小天鹅”,“海尔”,“小鸭”,“金羚”
等名牌智能洗衣机
“模糊逻辑与神经网络---理论研究与探索”刘增良,北京航空航天大学出版社
“模糊技术与神经网络选编”,北京航空航天大学出版社
第十三页,共14页
杂志
1.模糊数学与系统 2.控制与决策 3.系统工程理论与实践 4.计算机学报 5.人工智能与模式识别 6.Fuzzy Sets And Systems
rmation Science 8.IEEE Tran.on Fuzzy Systems
如:“人”的内涵=所有人具有的共同属性 如:有语言、会思考、发明创造等
“人”的外延=世界上所有人组成的集合(康托集)
注:康托 集合论是现代数学的基础,康托(德国数学家,1845-1918)
第二页,共14页
Cantor Set:“把一些明确的,彼此有区别的对象的全体”
(康托)
A a p(a)
如:N 1,2,3,... 实数集R r r是实数
第三页,共14页
二.模糊与精确的关系
模糊性与精确性: 对立统一,相互依存,可互相转化。
- 精确的概念可表达模糊的意思: 如“望庐山瀑布”
“飞流直下三千尺,凝是银河落九天” - Fuzzy的概念也能表达精确的意思:
模糊数学不是让数学变成模模糊糊的东西,
而是让数学进入模糊现象这个禁区,即用 精确的数学方法去研究处理模糊现象
HotZ-雷达系统(第一章)波形模糊函数 ppt课件

1.1 常见雷达波形 1.2 雷达信号模糊函数
1
背景
发射机 收发开关
天线
目标
终端 显示
信号 处理
接收机
R
雷达依赖天线向空间辐射电磁波,并接收由目标散 射的电磁波,以确定目标的存在。
雷达发射的电磁波具有一定的形式:连续波或脉冲 串,单频的或调频、调幅或相位编码的
2
雷达波形要求
要实现目标的有效检测,雷达信号波形必须同时满 足以下条件:
待测目标尺寸
调制类型
动目标检测
极化方式
多目标检测
波形、环境匹配 (模糊函数) 雷达成像
8
长度参数 距离像 目标识别
常见雷达波形介绍
连续波(Continuous Wave,CW) 频率调制连续波(Frequncey Modulated CW,FMCW) 脉冲(Pulsed)
9
常见雷达波形介绍
CW Radar
-可有效测量固定目标距离 单基系统存在收发隔离问题,双基系统较好
11
常见雷达波形介绍
Pulsed Radar
发射机由发射脉冲开、关 当发射机关闭时,接收机打开 在脉冲间的距离门上感知目标
-可有效测量目标距离 单基地系统的发射机与接收机隔离不是问题 可以测量距离变化率
12
常见雷达波形介绍
足够的能量(看得见) 足够的目标分辨率(看得准) 对需要的回波有很好的选择、屏蔽能力
(选择、对抗能力) 选择的雷达波形要与雷达用途、目标类型、目标环 境“匹配”
3
基本概念
波是一种可在媒介或空间中传播的,连续或突发的 周期性扰动,其到达均值的位移是时间,或空间, 或两者的函数。 电磁波直观解释是发射到空中的能量,这种能量部 分以电场的形式存在,部分的以磁场的形式存在。 电磁波的基本特性有:速度、方向、极化、强度、 波长、频率和相位。 波形是波的周期变化量的瞬时值沿时间表示的图形
外辐射源雷达互模糊函数的两种快速算法_高志文

分级抽取 FFT 算法流程 如图 1 所示, 初始化 时 l = 0, 算法的具体步骤概括如下: Step1: 计算 rN ( n , l ) = u ( n) v ( n + l) , n = 0, 1, ,,il[ N h1/ D 1 ] , ceil 表 示对 N h1 / D 1 朝正无穷大 方向取 整, c = mod( m, C) , c = 0, 1, ,, C 1. 为避免预加权 的数 据互 相重 叠, 需 要存储 C 个不 同 的 ucc ( mD + i) . 以三级抽取为例 说明预 加权方法, 三级 抽取 中的 第一级 滤波 器阶数 N h 1 通常 为第一 级抽取 比 D 1 的 2~ 3 倍, 假设 C = ceil[ N h1/ D 1] = 3, 第一级抽取的 预加权框图如图 3 所示. 将 图 1、 图 2 和 图 3 结合 起来, 可得到预加权三级抽取 FFT 算法流程图. 预加权三级抽
针 对外辐射源雷达 ( 无源雷达、 被动雷达 ) 利用 互模糊函数测量时延 差和多普勒频移的 运算量大 , 直接
计算难以满足系统实时性要求的问题 , 本文提出了 外辐射源雷达互模糊函数的两种快速算法 : 分级抽取 FFT 算法和预 加权分级抽取 FFT 算法 . 分级抽取 FFT 算法降低了 抗混叠滤波器的阶 数 , 明 显地节省了 计算量和 存储量 ; 预加权 分级 抽取 FFT 算法使第一级滤波的乘法运算在时延的循环外进行 , 进一 步提高了计 算效率 , 代价是存 储量有所 增加 . 实测 结果表明本文所提两种快速算法有效地提高了计算效率 . 关键词 : 外辐射源雷达 ; 互模糊函数 ; 分级抽取 ; 预加权 中图分类号 : TN957. 51 文献标识码 : A 文章编号 : 0372 - 2112 ( 2009) 3 - 0669 - 04
雷达信号处理

雷达信号处理技术与系统设计第一章绪论1.1 论文的背景及其意义近年来,随着电子器件技术与计算机技术的迅速发展,各种雷达信号处理技术的理论与应用研究成为一大热门领域。
雷达信号的动目标检测(MAD)是利用动目标、地杂波、箔条和气象干扰在频谱上的差别,抑制来自建筑物、山、树、海和雨之类的固定或低速杂波信号。
区分运动目标和杂波的基础是它们在运动速度上的差别,运动速度不同会引起回波信号频率产生的多普勒频移不相等,这就可以从频率上区分不同速度目标的回波。
固定杂波的中心频率位于零频,很容易设计滤波器将其消除。
但对于运动杂波,由于其多普勒频移未知,不能像消除固定杂波那样很容易地设计滤波器,其抑制就变得困难了从本质上来讲,雷达信号的检测问题就是对某一坐标位置上目标信号“有”或“无”的判断问题。
最初,这一任务由雷达操作员根据雷达屏幕上的目标回波信号进行人工判断来完成。
后来,出现了自动检测技术,一开始为固定或半固定门限检测,这种体制下当干扰和杂波功率水平增加几分贝,虚警概率将急剧增加,以至于显示器画面饱和或数据处理过载,这时即使信噪比很大,也不能作出正确的判断。
为克服这些问题进而发展了自适应恒虚警(Constant FalseAlarm Rate,CFAR)检测。
CFAR 检测使得雷达在多变的背景信号中能够维持虚警概率的相对稳定,这种虚警概率的稳定性对于大多数的雷达,如搜索警戒雷达、跟踪雷达、火控雷达等。
第二章 雷达信号数字脉冲压缩技术2.1 引言雷达脉冲压缩器的设计实际上就是匹配滤波器的设计。
根据脉冲压缩系统实 现时的器件不同,通常脉冲压缩的实现方法分为两类,一类是用模拟器件实现的 模拟方式,另一类是数字方式实现的,主要采用数字器件实现。
脉冲压缩处理时必须解决降低距离旁瓣的问题,否则强信号脉冲压缩的旁瓣 会掩盖或干扰附近的弱信号的反射回波。
这种情况在实际工作中是不允许的。
采 用加权的方法可以降低旁瓣,理论设计旁瓣可以达到小于-40dB 的量级。
雷达原理笔记之模糊与盲区

参数 PRF1 PRT2 距离门宽度 目标所在的距离门数(PRF1相对应) 目标的视在距离(测量距离)
根据PRF1和PRT2计算得到最大不模糊距离:
数值 25kHz 41 150m
20
则,目标的可能距离:
则可根据目标在PRT2对应的距离门求解出真实距离:
目标真实距离/km
PRT2对应的距离/km
3
1. 回波信号的脉冲包络有起伏(目标起伏特性、加性噪声、天线扫描对脉冲 幅度的调制【空域滤波】)
2. 相参处理时间有限(时域截短,频谱展宽【相当于加窗】) 3. 杂波谱线展宽的原因,除1和2还有固定目标的内部运动(地面扬尘、路人
行走等)
1.1.3 盲区出现原因
雷达对接收的回波信号进行FFT处理前首先经过MTI杂波对消处理。而杂波的频 谱位置就是在单值测速区间的0多普勒点。如果运动目标的多普勒频移等于PRF的整 数倍,那么由于频谱的周期重现在单值测速区间,该运动目标的频谱也处在0多普勒 点附近。因此在做MTI杂波对消处理的同时也将运动目标给对消处理了。因此在后续 的FFT处理中就很难再发现运动目标,造成测速盲区。
1.3.2 其他方法
示踪脉冲法(实践起来较复杂) 脉冲舍弃法(常用)
1.1.4 危害
对运动目标的 运动方向 和 速度大小 难以判断甚至无法探测。如下仿真截 图,目标速度120.11m/s,但是测出来的速度却是1.96m/s。相差很大。极限情 况如果目标的多普勒频移fd等于PRF,运动目标会被对消,产生周期性的测速 盲区。
1.2 距离模糊与盲区
1.2.1 模糊出现原因
3 mod(6.15)=3
9
9 mod(6.15)=2.85
15
15 mod(6.15)=2.7
HotZ-雷达系统(第六章)合成孔径雷达

3 108 c 25 m Rr 6 2 BR sin 2 15.55 10 sin( 23 )
合成孔径雷达:在不同位置 接收同一地物的回波信号。 雷达成像结果
真实孔径雷达:在同位置 接收目标的回波信号。
Range Resolution(距离分辨率)
Slant range(斜距)
c p / 2 Rr where c velocity of light p length of pulse
把同一地物的多次成像合成为一幅图像antennaformingverylongantennathusimprovingazimuthresolution等效于增大天线形成一根很长的天线从而改善分辨率sketchmap示意图fromglobesarprogramccrsmultipleimaging多次成像分解示意图synthesismultipleimaging合成objectsexperienceilluminationovertimeintervalcompletehistoryreflections记录和保存了完整回波信号permitsreconstructionreflectedsignals反射信号重建dopplerfrequencyshiftcausedrelativemovementbetweenfrequencyshiftsthussynthesisingcorrespondingechoesazimuthresolutioncansharpenedsarfocusingtechnique根据多普勒频移合成相应的回波改善方位分辨率称为sar成像或聚焦过程courtesy
雷达信号理论与应用-

d T
0
1 e 1 j 2 f d t e dt T j 2 f d T
j 2 f d t
d T
0
j 2 f d T d
1
j 2 f d
j f T j f T 1 j fd T d e d d e d d e T j 2 f d
* Case3: | d | T u(t )u (t d ) 0
d , f d 0, | d | T
Slide 6
6.1 简单脉冲信号
6.1.2 矩形脉冲信号的模糊函数 综合Case1~Case3,得到模糊函数的表达式
d , f d e
2 3
T 0.2887T
3
T 1.814T
多普勒主瓣分辨率(近似) Eq3.17 2 1
f 2 Te
6 1 1 0.78 T T
时延主瓣分辨率
1 2 2 1 1.414 2 Be Be Be
Slide 2
6.1 简单脉冲信号
6.1.1 矩形脉冲信号的波形参量
T
T
T
1 1 ( d , f d ) d d 2 T 2 0
雷达信号理论与应用
Radar Signals:Theory & Application
哈尔滨工业大学 电子工程系
2014 .秋季学期
Slide 0
Lecture 6
简单脉冲与脉压信号
6.1 简单脉冲信号
6.2 脉冲压缩信号 6.3 雷达信号分类
Slide 1
6.1 简单脉冲信号
雷达系统导论第5-6章作业答案分析
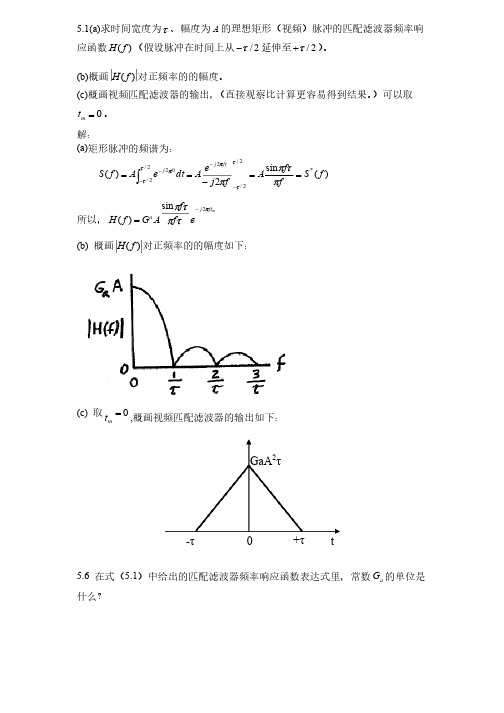
5.1(a)求时间宽度为t 、幅度为A 的理想矩形(视频)脉冲的匹配滤波器频率响应函数)(f H (假设脉冲在时间上从2/t -延伸至2/t +)。
(b)概画)(f H 对正频率的的幅度。
对正频率的的幅度。
(c)概画视频匹配滤波器的输出,(直接观察比计算更容易得到结果。
)可以取0=m t 。
解:解:(a)矩形脉冲的频谱为:矩形脉冲的频谱为:)(sin 2)(*2/2/2/2/22f S ff Af j e A dt e A f S ftj ft j ==-==----òp t p p t t t t p p 所以,mft j a e f f A G f H p t p t p 2sin )(-=(b) 概画)(f H 对正频率的的幅度如下:对正频率的的幅度如下:(c) 取0=mt ,概画视频匹配滤波器的输出如下:概画视频匹配滤波器的输出如下:5.6 在式(5.1)中给出的匹配滤波器频率响应函数表达式里,常数a G 的单位是什么?什么? t0 +τ -τ GaA 2τ解:解: 由式(5.1))2exp()()(*m a ft j f S G f H p -=,式中)2exp(m ft j p -部分没有单位,常数a G 的单位是能量的单位的倒数1()VT -。
5.9 (a )画出相关接收机的方框图。
(b )解释为什么在检测性能上相关接收机可以认为等同于匹配接收机。
(c )如果可能,在什么情况下可以选择制造相关接收机而不是匹配接收机?收机而不是匹配接收机?解:解:(a )输入信号()in y t 首先乘以发射信号的延迟的()R s t T -(RT 是估计的目标回波信号的时延估计值),然后把乘积通过低通滤波器完成积分。
,然后把乘积通过低通滤波器完成积分。
(b )(参看P211P211)因为匹配滤波器的输出是接收信号和发射信号的互相关函数,)因为匹配滤波器的输出是接收信号和发射信号的互相关函数,所以匹配滤波器和互相关接收机在数学上是等价的,在检测性能上相关接收机可以认为等同于匹配接收机。
matlab 雷达信号处理 模糊函数

matlab 雷达信号处理模糊函数文章题目: Matlab雷达信号处理中的模糊函数摘要:雷达信号处理是现代雷达系统中至关重要的一个环节。
随着科技的进步,Matlab 已成为研究雷达信号处理领域的主要工具之一。
而在雷达信号处理中,模糊函数是一种常用的数学工具,用于处理雷达信号的模糊问题。
本文将一步一步回答关于Matlab雷达信号处理中模糊函数的相关问题,以帮助读者深入了解该主题。
引言:雷达信号处理是通过对雷达接收到的信号进行分析和处理,以获取目标位置、速度等信息的过程。
而在这个过程中,我们常常需要处理一些模糊问题,例如雷达信号的模糊性、模糊目标的检测等。
而Matlab作为一款功能强大、易于使用的科学计算软件,为我们提供了很多方便快捷的工具,其中包括了一些常用的模糊函数。
接下来,我们将介绍这些模糊函数的使用方法以及在雷达信号处理中的应用。
一、模糊函数基础知识1.1 定义模糊函数是一种将模糊集映射到一组实数上的函数。
可以将其看作是一种模糊逻辑的扩展,常用于描述和处理模糊性问题。
1.2 成员函数模糊函数通常由一组成员函数组成,例如三角形函数、梯形函数、高斯函数等。
每个成员函数都描述了一个特定的模糊概念。
二、Matlab中的模糊函数2.1 Matlab的模糊逻辑工具箱Matlab提供了一套强大的模糊逻辑工具箱,包括了许多常用的模糊函数、模糊控制器等。
在使用这些工具之前,我们需要先安装并加载模糊逻辑工具箱。
2.2 模糊逻辑工具箱的基本使用要使用模糊逻辑工具箱,我们需要先定义输入输出变量、成员函数以及规则库。
在定义好这些基本元素之后,我们就可以进行模糊推理和模糊控制等操作了。
三、雷达信号处理中的模糊函数应用3.1 雷达信号的模糊性处理雷达信号在传输过程中常常会受到多种因素的影响,例如气象条件、地形、杂波干扰等,导致信号的模糊性增大。
而模糊函数可以帮助我们对这种模糊信号进行处理,从而提高信号的可靠性和准确性。
3.2 模糊目标的检测在雷达信号处理中,我们经常需要对目标进行检测和跟踪。
HotZ 雷达系统第一章波形模糊函数

31
2
距离模糊函数与距离分辨率
时延分辨常数 的频域形式
的自相关函数
:信号的 自相关函数 和功率谱 是一对傅立叶变换对 :帕斯瓦尔关系式
频域形式为:
32
2
距离模糊函数与距离分辨率
有效相关带宽定义:
★有效相关带宽
距离分辨力
逼近
时域 : 反映了
的能力
频域 :反映了
1( 均匀谱)
(信号功率谱逼近均匀谱的能力)
采用固有分辨力定义的缺陷 :
只考虑了主瓣内邻近目标的分辨能力, 没有考虑旁瓣干 扰对目标分辨的影响
30
2
距离模糊函数与距离分辨率
时延分辨常数的数学表达式定义为:
将主瓣、基底旁瓣和模 糊瓣的全部能量都计算 在内,再除以主瓣顶点 的功率所得的时间宽度
表示信号能量集中 在 区域的能力
越趋近于冲激函数 分辨力
??
?
fd )df
信号的频率自相关函数
再根据对偶关系:? ? fd u(t) ? U ( f )
? ? ? ( fd ) ?
? ??
U ( f )U *( f
?
fd )df
?
? (?) ? ? u(t)u*(t ? ?)dt ??
? ? ( fd ) ?? F ? u(t) 2
39
2
速度模糊函数与速度分辨率
42
2
关于距离、径向速度分辨力的结论
结论1:信号频谱越宽 ,距离分辨力越高 结论2:信号时域持续期越宽 ,速度分辨力越好
对一般信号而言:时宽? ? 频宽 ?
有没有时宽、频宽都大的信号? 如,LFM脉冲信号
43
2
距离-速度模数函数与其联合分辨力
雷达模糊函数

雷达模糊函数函数名称:radar_blur函数功能:对雷达信号进行模糊处理函数参数:- signal:雷达信号,类型为一维数组- blur_radius:模糊半径,类型为整数函数返回值:处理后的雷达信号,类型为一维数组函数实现:```pythondef radar_blur(signal, blur_radius):"""对雷达信号进行模糊处理Args:signal: 雷达信号,类型为一维数组blur_radius: 模糊半径,类型为整数Returns:处理后的雷达信号,类型为一维数组"""# 初始化结果数组result = [0] * len(signal)# 处理每个点for i in range(len(signal)):# 计算当前点的模糊范围start = max(0, i - blur_radius)end = min(len(signal) - 1, i + blur_radius)# 对当前点进行模糊处理for j in range(start, end + 1):result[i] += signal[j]result[i] /= (end - start + 1)return result```函数说明:该函数实现了对雷达信号进行模糊处理的功能。
输入参数包括一个一维数组signal表示原始的雷达信号以及一个整数blur_radius表示模糊半径。
输出结果也是一个一维数组,表示经过模糊处理后的雷达信号。
函数的实现过程如下:首先,初始化一个长度为原始信号长度的数组result,用于存储处理后的信号。
然后,遍历原始信号中的每个点,计算该点的模糊范围,并对该范围内的所有点进行加权平均处理。
最后,将处理结果存储到result数组中,并返回该数组作为输出结果。
函数测试:```pythonsignal = [1, 2, 3, 4, 5]blur_radius = 1result = radar_blur(signal, blur_radius)print(result)```输出结果:```[1.5, 2.0, 3.0, 4.0, 4.5]```说明:对于输入信号[1,2,3,4,5]和模糊半径1,经过处理后得到的输出信号为[1.5,2.0,3.0,4.0,4.5]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
– 单基系统存在收发隔离问题,双基系统较好
– 简单的CW雷达无法测量距离
-波形缺乏“时间标志”
2020/1/16
10
常见雷达波形介绍
• FMCW Radar
– 发射被一频率序列调制的连续正弦波 – 发射机与接收机始终处于工作状态 – 通过频差发现目标
-可有效测量固定目标距离
– 单基系统存在收发隔离问题,双基系统较好
从距离和径向速度二维进行分辨
fd
目标A为基准,则:
f
' d
fd' fd
fd
发射信号为参考
2020/1/16
A B
A的回波复包络为 u(t)
B的回波复包络为 u(t )e j2 fdt
为两个目标距离差对应的时间间隔
tr tr
为两个目标相对径向速度差对应的 多普勒频移
t
23
距离模糊函数与距离分辨率
脉冲重复频率: 占空比:
2020/1/16
平均功率:
13
常见雷达波形介绍
• 发射脉冲串波形时可能产生距离模糊
2020/1/16
14
常见雷达波形介绍
• 两大类脉冲串波形:相参脉冲串和非相参 脉冲串
A.源正弦波
B.相参脉冲串
C.非相参脉冲串
2020/1/16
15
常见雷达波形介绍
• 相参脉冲串频谱
• 衡量两个信号为“不同”的参数:均方差
值
设信号是 维几何空间 中的点或矢量
用两点间的距离 度量点 和点 的可分辨程度
2020/1/16
对
24
误差的均方,或均方差
距离模糊函数与距离分辨率
• 距离分辨问题描述
A、B相对雷达径向速度相同
fd
仅有距离差
时延
17
常见雷达波形介绍
• 脉冲重复频率(PRF)
不同类型PRF的距离、多普勒频率模糊特性
PRF
距离
多普勒
低
不模糊
模糊
中
模糊
模糊
高
模糊
不模糊
PRF参差 PRF交织
2020/1/16
在一个停留时间 内有多种PRF
18
常见雷达波形介绍
连续波信号 相参脉冲串信号 PRI捷变波形 频率捷变信号 频率分集信号 极化捷变信号 双脉冲信号 双路信号 脉冲压缩信号 分布频谱信号 沃尔什函数信号 冲激信号 (《雷达系统》,向敬成.表1-1)
第一章 雷达系统基础
1.1 常见雷达波形 1.2 雷达信号模糊函数
2020/1/16
1
背景
发射机 收发开关
天线
目标
终端 显示
信号 处理
接收机
R
雷达依赖天线向空间辐射电磁波,并接收由 目标散射的电磁波,以确定目标的存在。
雷达发射的电磁波具有一定的形式:连续波或脉冲 串,单频的或调频、调幅或相位编码的
2020/1/16
21
基本概念
• 模糊函数 研究雷达波形的数学工具,反映了雷达波
形在距离和径向速度二维上的精度和分辨力 波形性能可通过所定义的分辨常数和模糊
函数进行比较 模糊与分辨是对立概念。
2020/1/16
22
目标分辨场景
• 目标分辨问题
有两个相同的点目标A和B,它们相对雷达 是视角相同的邻近目标
2020/1/16
11
常见雷达波形介绍
• Pulsed Radar
– 发射机由发射脉冲开、关 – 当发射机关闭时,接收机打开 – 在脉冲间的距离门上感知目标
-可有效测量目标距离
– 单基地系统的发射机与接收机隔离不是问题 – 可以测量距离变化率
2020/1/16
12
常见雷达波形介绍
• 脉冲串是一种常见雷达波形
f0
Tr
2020/1/16
f0
fr
1
16
相参脉冲串频谱
sin x x
非相参脉冲串频谱
常见雷达波形介绍
• 相参脉冲串雷达的速度模糊问题
有多普勒频移的 CW信号的频谱图
相干脉冲串频谱 (固定目标-无多普勒频移)
将含有多普勒频移目标的中心波瓣区域展开
中心波瓣 滤波器
有多普勒频移 的目标回波
2020/1/16
• 雷达系统设计考虑:
工作频率
应用类型、雷达硬件 ★最重要
连续波或脉冲 硬件复杂程度
峰值功率 脉冲时宽 脉冲带宽 重复频率
作用距离 、系统灵敏度 (雷达方程)
待测目标尺寸
调制类型
动目标检测
极化方式
多目标检测
波形、环境匹配 (模糊函数) 雷达成像
2020/1/16
8
长度参数 距离像 目标识别
常见雷达波形介绍
2020/1/16
19
第一章 雷达系统础
1.1 常见雷达波形 1.2 雷达信号模糊函数
2020/1/16
d
20
基本概念
• 雷达分辨力 在多目标环境中,雷达区分两个或两个以
上邻近目标的能力(距离、速度、角度进行 分辨)。
发射信号波形决定 天线方向图(波束)
波形设计
理论依据、工具
模糊函数
决定雷达分辨力的三个因素: 信噪比 信号形式 信号固有分辨力 信号处理方法
电磁波直观解释是发射到空中的能量,这种 能量部分以电场的形式存在,部分的以磁场 的形式存在。电磁波的基本特性有:速度、 方向、极化、强度、波长、频率和相位。
波形是波的周期变化量的瞬时值沿时间表示 的图形
2020/1/16
4
基本概念
相位是在单个周期内波或信号与同频率参考 信号相一致的程度。通常用信号幅度正向穿 越零点的这个时间点来定义,因此,信号的 相位是这些过零点相对于参考信号过零点的 超前量或滞后量。 参考信号
2020/1/16
2
雷达波形要求
要实现目标的有效检测,雷达信号波形必须 同时满足以下条件:
• 足够的能量(看得见)
• 足够的目标分辨(率看得准)
•
对需要的回波有很好的选择、屏蔽能力
(选择、对抗能力)
选择的雷达波形要与雷达用途、目标类型、目标环
境“匹配”
2020/1/16
3
基本概念
波是一种可在媒介或空间中传播的,连续或 突发的周期性扰动,其到达均值的位移是时 间,或空间,或两者的函数。
2020/1/16
5
基本概念
波前是一个假设的面,在这个面上辐射电磁 波的相位处处相等。
极化电场方向即为极化方向。
电磁波
电场 磁场
垂直极化
水平极化
2020/1/16
6
基本概念
• RF波形属性
积累(同相)
部分积累(不完全同相)
抵消(反相)
2020/1/16
非相参信号(噪声)
7
雷达系统及其波形
• 雷达波形及其指标是决定任何雷达系统设 计与性能的基本部分
• 连续波(Continuous Wave,CW)
• 频率调制连续波(Frequncey Modulated CW, FMCW)
• 脉冲(Pulsed)
2020/1/16
9
常见雷达波形介绍
• CW Radar
– 发射连续的单频正弦波信号
– 发射机与接收机始终处于工作状态
– 通过多普勒频移发现目标
-可有效测量目标的距离变化率
