【志鸿优化设计】2016届高考数学(文)一轮复习课件 第四章 三角函数、解三角形4.8
【优化设计】高考数学(人教版,文科)一轮总复习精品课件: 三角函数的图象与性质(共31张PPT)

{y|-1≤ y≤1}
R
3.3 三角函数的图象与性质 第三章
5-5-
在 - π + 2kπ, π + 2kπ
2
2
单 上递增,k∈Z;
调 性
在 π + 2������π, 3π + 2kπ
2
2
上递减,k∈Z
x= π+2kπ (k∈Z)时,
2
最 ymax=1; 值 x=-π+2kπ (k∈Z)时,
2
在
π 4
,
5π 4
单调递减,所以要使函数
f(x)=sin
������������
+
π 4
在
π 2
,π
单调递减,需满足
π 4
×
5π 4
×
���1������1���≤≥π2π,,解得12≤ω≤54.
关闭
A
考点一 考点二 考点三 考点四 思想方法
解析 答案
第三章
3.3 三角函数的图象与性质
-1188-
考点一 考点二 考点三 考点四 思想方法
关闭
解析 答案
第三章
3.3 三角函数的图象与性质
-1166-
方法提炼
1.熟记 y=sin x,y=cos x,y=tan x 的单调区间是求复杂的三角函数单调区 间的基础.
2.求形如 y=Asin(ωx+φ)+k 的单调区间时,只需把 ωx+φ 看作一个整体 代入 y=sin x 的相应单调区间即可,注意 A 的正负以及要先把 ω 化为正数. 求 y=Acos(ωx+φ)+k 和 y=Atan(ωx+φ)+k 的单调区间类似.
2016届人教A版高考数学大一轮复习课件 第4章 三角函数、解三角形 第4讲

()
基础诊断
考点突破 课堂总结 第二十页,编辑于星期五:十八点 四十二分。
解析 (1)2ωπ=254π-π4,即 ω=1, ∴f(x)=sin(x+φ), ∴fπ4=sinπ4+φ=±1. ∵0<φ<π,∴π4<φ+π4<54π, ∴φ+π4=π2,∴φ=π4. (2)y=2cos2x-π4-1=cos2x-π2=sin 2x 为奇函数,最小正 周期 T=22π=π. 答案 (1)A (2)A
当 t=1 时,ymax=1; 当 t=- 2时,ymin=-12- 2.
∴函数的值域为-12-
2,1.
答案
(1)x2kπ+π4≤x≤2kπ+54π,k∈Z
(2)-12-
2,1
基础诊断
考点突破 课堂总结 第十八页,编辑于星期五:十八点 四十二分。
考点二 三角函数的奇偶性、周期性、对称性
【例 2】 (1)已知 ω>0,0<φ<π,直线 x=π4和 x=54π是函数 f(x)
法二 利用三角函数线, 画出满足条件的终边范围(如图阴影部分所示).
∴定义域为x2kπ+π4≤x≤2kπ+54π,k∈Z
.
基础诊断
考点突破 课堂总结 第十六页,编辑于星期五:十八点 四十二分。
法三 sin x-cos x= 2sinx-π4≥0,将 x-π4视为一个整体,
由正弦函数 y=sin x 的图象和性质可知 2kπ≤x-π4≤π+2kπ,
基础诊断
考点突破 课堂总结 第十四页,编辑于星期五:十八点 四十二分。
【训练 1】 (1)函数 y= sin x-cos x的定义域为________. (2)函数 y=sin x-cos x+sin xcos x 的值域为________.
【志鸿优化设计】(山东专用)高考数学一轮复习 第四章三角函数、解三角形4.2同角三角函数的基本关系及三角

课时作业19 同角三角函数的基本关系及三角函数的诱导公式一、选择题1.点M (2,tan 300°)位于( ). A .第一象限 B .第二象限 C .第三象限 D .第四象限2.锐角α终边上一点A 的坐标为(2sin 3,-2cos 3),则角α的弧度数为( ). A .3 B .π-3C .3-π2D .π2-33.记cos(-80°)=k ,那么tan 100°等于( ).A .1-k 2kB .-1-k 2k C .k1-k2D .-k1-k24.(2013山东师大附中高三模拟)已知tan α=2,则π+αcos ⎝ ⎛⎭⎪⎫π2+α的值为( ).A .-12B .-2C .12D .25.若cos α=-45,α是第三象限的角,则sin ⎝ ⎛⎭⎪⎫α+π4等于( ). A .-7210 B .7210C .-210 D .2106.若3sin α+cos α=0,则1cos 2α+sin 2α的值为( ).A .103B .53C .23D .-2 7.已知sin α+3cos α3cos α-sin α=5,则sin 2α-s in αcos α的值是( ).A .25B .-25C .-2D .2 二、填空题8.若函数f (x )=⎩⎪⎨⎪⎧-cos πx ,x >0,f x ++1,x ≤0,则f ⎝ ⎛⎭⎪⎫-43的值为__________.9.sin 29π6+cos ⎝ ⎛⎭⎪⎫-29π3-tan 25π4=__________.10.sin 21°+sin 22°+…+sin 290°=__________. 三、解答题11.已知f (α)=π-απ-α-α+π--α-π-π-α.(1)化简f (α);(2)若α是第三象限角,且cos ⎝⎛⎭⎪⎫α-3π2=15,求f (α)的值.12.已知sin θ,cos θ是关于x 的方程x 2-ax +a =0(a ∈R )的两个根.(1)求cos 3⎝ ⎛⎭⎪⎫π2-θ+sin 3⎝ ⎛⎭⎪⎫π2-θ的值;(2)求tan(π-θ)-1tan θ的值.参考答案一、选择题1.D 解析:∵tan 300°=tan(360°-60°)=-tan 60°=-3, ∴M (2,-3).故点M (2,tan 300°)位于第四象限.2.C 解析:tan α=-2cos 32sin 3=-1tan 3=tan ⎝⎛⎭⎪⎫3-π2,且α与3-π2的范围均在⎝ ⎛⎭⎪⎫0,π2上,所以α=3-π2. 3.B 解析:∵cos(-80°)=cos 80°=k ,∴sin 80°=1-cos 280°=1-k 2.∴tan 100°=-tan 80°=-sin 80°cos 80°=-1-k2k.4.C 解析:cos(π+α)cos ⎝ ⎛⎭⎪⎫π2+α=-cos α-sin α=1tan α=12,选C.5.A 解析:由cos α=-45,α是第三角限角,得sin α=-35,则sin ⎝⎛⎭⎪⎫α+π4=22(sin α+cos α)=-7210.6.A 解析:由3sin α+cos α=0,有tan α=-13.∴1cos 2α+sin 2α=cos 2α+sin 2αcos 2α+2sin αcos α=1+tan 2α1+2tan α=103. 7.A 解析:由sin α+3cos α3cos α-sin α=5,得tan α+33-tan α=5,即tan α=2. 所以sin 2α-sin αcos α=sin 2α-sin αcos αsin 2α+cos 2α =tan 2α-tan αtan 2α+1=25. 二、填空题 8.52 解析:由已知,得f ⎝ ⎛⎭⎪⎫-43=f ⎝ ⎛⎭⎪⎫-13+1=f ⎝ ⎛⎭⎪⎫23+2=-cos 2π3+2=52. 9.0 解析:原式=sin ⎝ ⎛⎭⎪⎫4π+5π6+cos ⎝ ⎛⎭⎪⎫-10π+π3-tan ⎝⎛⎭⎪⎫6π+π4 =sin 5π6+cos π3-t an π4=sin ⎝⎛⎭⎪⎫π-π6+12-1 =sin π6-12=12-12=0.10.4512解析:原式=(sin 21°+sin 289°)+(sin 22°+sin 288°)+…+(sin 244°+sin 246°)+sin 245°+sin 290°=(sin 21°+cos 21°)+(sin 22°+cos 22°)+…+(sin 244°+cos 244°)+12+1=441111++++个+12+1=4512.三、解答题11.解:(1)f (α)=sin(π-α)cos(2π-α)tan(-α+π)-tan(-α-π)sin(-π-α)=sin αcos α(-tan α)tan αsin α=-cos α.(2)∵α是第三象限角,且cos ⎝ ⎛⎭⎪⎫α-3π2=-sin α=15, ∴sin α=-15,∴cos α=-1-sin 2α-1-⎝ ⎛⎭⎪⎫-152=-265.∴f (α)=-cos α=265.12.解:由已知原方程的判别式Δ≥0,即(-a )2-4a ≥0,∴a ≥4或a ≤0.又⎩⎪⎨⎪⎧sin θ+cos θ=a ,sin θcos θ=a ,(sin θ+cos θ)2=1+2sin θcos θ,则a 2-2a -1=0,从而a =1-2或a =1+2(舍去),因此sin θ+cos θ=sin θcos θ=1- 2.(1)cos 3⎝ ⎛⎭⎪⎫π2-θ+sin 3⎝ ⎛⎭⎪⎫π2-θ=sin 3θ+cos 3θ=(sin θ+cos θ)(sin 2θ-s inθcos θ+cos 2θ)=(1-2)[1-(1-2)]=2-2.(2)tan(π-θ)-1tan θ=-tan θ-1tan θ=-⎝ ⎛⎭⎪⎫sin θcos θ+cos θsin θ=-1sin θcos θ =-11-2=1+ 2.。
2016届高考数学一轮复习课件 第四章 三角函数、解三角形4.4

图象及应用
第一页,编辑于星期五:二十点 四十二分。
第四章
4.4
考纲要求
1.了解函数 y=Asin(ωx+φ)的物
理意义;能画出 y=Asin(ωx+φ)
的图象,了解参数 A,ω,φ 对函数
图象变化的影响.
2.了解三角函数是描述周期变
化现象的重要函数模型,会用
三角函数解决一些简单实际问
2
12
关闭
π
π
π
y=
2sin
3
+
=
2sin
3
+
的图象,故选 A.
√
√
A
12
2
4
解析
解析
答案
答案
第十一页,编辑于星期五:二十点 四十二分。
4.4
第四章
函数y=Asin(ωx+φ)的图象及应用
考情概览
考点一
考点二
知识梳理
核心考点
核心考点
学科素养
考点三
π
10
2.将函数 y=sin x 的图象上所有点向右平移 个单位长度,再把所得各
(1)定点:如下表所示.
-φ 3 -φ 2-φ
φ
-φ
2
x
2
ω
ω
ω
ω
ω
3
0
π
2π
ωx+φ
2
2
y=Asin(ωx+φ)
0
A
0
-A
0
(2)作图:在坐标系中描出这五个关键点,用平滑的曲线顺次连接得到
y=Asin(ωx+φ)在一个周期内的图象.
2016届人教A版高考数学大一轮复习课件 第4章 三角函数、解三角形 第1讲

考点突破
课堂总结
第一页,编辑于星期五:十八点 四十二分。
第1讲 任意角、弧度制及任意角的三角函数
最新考纲 1.了解任意角的概念;2.了解弧度制的概念,能进行 弧度与角度的互化;3.理解任意角的三角函数(正弦、余弦、正 切)的定义.
基础诊断
考点突破
课堂总结
第二页,编辑于星期五:十八点 四十二分。
解析 设扇形圆心角为 α,半径为 r,则 2r+|α|r=4,∴|α|=4r-2. ∴S 扇形=12|α|·r2=2r-r2=-(r-1)2+1, ∴当 r=1 时,(S 扇形)max=1, 此时|α|=2. 答案 1 2 1
基础诊断
考点突破
课堂总结
第二十六页,编辑于星期五:十八点 四十二分。
微型专题 三角函数线的应用 三角函数线是三角函数的几何特征,具有重要的意义,考生 在平时的备考中总认为它是概念性内容,事实并不然,其应 用十分广泛,除了用来比较三角函数值的大小,解三角不等 式外,还是数形结合的有效工具,借助它不但可以准确画出 三角函数图象,还可以讨论三角函数的性质.
=
()
A.45
B.35
C.-35
D.-45
解析 由三角函数的定义知 cos α= --442+32=-45 .
故选 D.
答案 D
基础诊断
考点突破
课堂总结
第十页,编辑于星期五:十八点 四十二分。
5.(人教A必修4P10A6改编)一条弦的长等于半径,这条弦所对 的圆心角大小为_________弧度.
答案
解 (1)设弧长为 l,弓形面积为 S 弓,则
α=60°=π3,R=10,l=π3×10=103π (cm),
S 弓=S 扇-S△=12×103π×10-12×102×sin
【志鸿优化设计】(湖南专用)高考数学一轮复习 第四章三角函数、解三角形4.1任意角和弧度制及任意
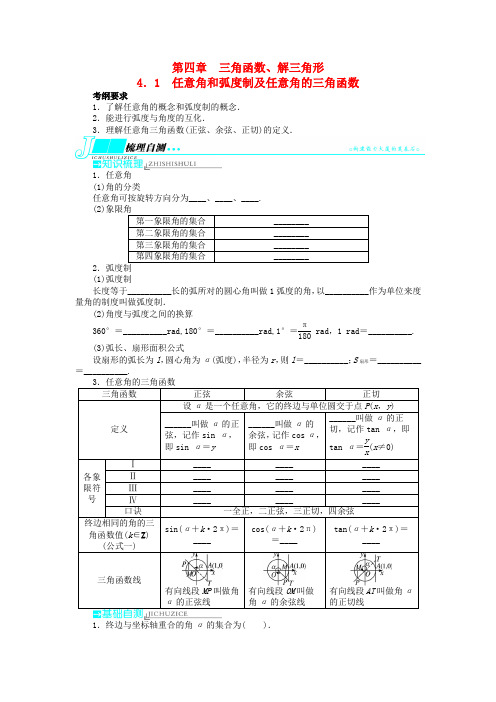
第四章 三角函数、解三角形4.1 任意角和弧度制及任意角的三角函数考纲要求1.了解任意角的概念和弧度制的概念. 2.能进行弧度与角度的互化.3.理解任意角三角函数(正弦、余弦、正切)的定义.1.任意角 (1)角的分类任意角可按旋转方向分为____、____、____. (2)2(1)弧度制长度等于__________长的弧所对的圆心角叫做1弧度的角,以__________作为单位来度量角的制度叫做弧度制.(2)角度与弧度之间的换算360°=__________rad,180°=__________rad,1°=π180rad ,1 rad =__________.(3)弧长、扇形面积公式 设扇形的弧长为l ,圆心角为α(弧度),半径为r ,则l =__________;S 扇形=__________=__________.有向线段MP 叫做角的正弦线 有向线段OM 叫做α的余弦线 有向线段AT 叫做角的正切线1.终边与坐标轴重合的角α的集合为( ).A .{α|α=k ·360°,k ∈Z }B .{α|α=k ·180°,k ∈Z }C .{α|α=k ·90°,k ∈Z }D .{α|α=k ·180°+90°,k ∈Z }2.设角α终边上一点P (-4a,3a )(a <0),则sin α的值为( ). A .35 B .-35 C .45 D .-453.已知2弧度的圆心角所对的弦长为2,则这个圆心角所对的弧长是( ).A .2B .sin 2C .2sin 1D .2sin 14.已知sin θ<0,tan θ>0,那么θ是( ). A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角5.若点P 在角23π的终边上,且|OP |=2,则点P 的坐标为__________.一、象限角及终边相同的角【例1-1】若α是第三象限的角,则π-12α是( ).A .第一或第二象限的角B .第一或第三象限的角C .第二或第三象限的角D .第二或第四象限的角【例1-2】已知角α是第一象限角,确定2α,α2的终边所在的位置.方法提炼1.对与角α终边相同的角的一般形式α+k ·360°的理解. (1)k ∈Z ;(2)α是任意角;(3)终边相同的角不一定相等,但相等的角终边一定相同.终边相同的角有无穷多个,它们相差360°的整数倍.2.已知α的终边位置,确定k α,αk(k ∈N *)的终边的方法:先用终边相同角的形式表示出角α的范围,再写出k α或αk 的范围,然后就k 的可能取值讨论k α或αk的终边所在位置.提醒:不少同学往往容易把“小于90°的角”等同于“锐角”,把“0°~90°的角”等同于“第一象限的角”.其实锐角的集合是{α|0°<α<90°},第一象限角的集合为{α|k ·360°<α<k ·360°+90°,k ∈Z }.请做演练巩固提升1二、扇形的弧长、面积公式的应用【例2】已知一扇形的圆心角为α(α>0),所在圆的半径为R .(1)若α=60°,R =10 cm ,求扇形的弧长及该弧所在的弓形的面积;(2)若扇形的周长是一定值C (C >0),当α为多少弧度时,该扇形有最大面积? 方法提炼(1)在弧度制下,计算扇形的面积和弧长比在角度制下更方便、简捷. (2)从扇形面积出发,在弧度制下使问题转化为关于α的不等式或利用二次函数求最值的方法确定相应最值.(3)记住下列公式:①l =αR ;②S =12lR ;③S =12αR 2.其中R 是扇形的半径,l 是弧长,α(0<α<2π)为圆心角,S 是扇形面积.请做演练巩固提升2不理解三角函数的定义而致误【典例】 已知角θ的顶点为坐标原点,始边为x 轴的正半轴.若P (4,y )是角θ终边上的一点,且sin θ=-255,则y =__________.错解:因P (4,y )是角θ终边上的一点,且sin θ=-255.∴sin θ=y =-255.错因:题中P 点不在单位圆,不能直接用定义表示sin θ,而应利用下列方法求解, 若角α终边上任意一点P (x ,y ),|OP |=r ,则sin α=y r ,cos α=x r ,tan α=y x这两个定义是等价的.正解:P (4,y )是角θ终边上的一点,由三角函数的定义知sin θ=y16+y2,又sin θ=-255,∴y 16+y2=-255,解得y =-8. 答案:-8答题指导:对于三角函数的定义要牢固记忆,并且与单位圆中的要区分开,要知道只有在单位圆中点的纵坐标才是角θ的正弦,而本题的错因恰是对三角函数的定义理解不清而导致.1.若α=k ·180°+45°(k ∈Z ),则α在( ). A .第一或第三象限 B .第一或第二象限 C .第二或第四象限 D .第三或第四象限2.已知扇形的周长是6 cm ,面积是2 cm 2,则扇形的圆心角的弧度数是( ). A .1 B .4 C .1或4 D .2或43.(2012大纲全国高考)正方形ABCD 的边长为1,点E 在边AB 上,点F 在边BC 上,AE =BF =13.动点P 从E 出发沿直线向F 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当点P 第一次碰到E 时,P 与正方形的边碰撞的次数为( ).A .8B .6C .4D .34.角α的终边上有一点P (3t,4t )(t ∈R 且t ≠0),则sin α的值是__________. 5.已知角α的终边在直线3x +4y =0上,求sin α,cos α,tan α的值.参考答案基础梳理自测知识梳理1.(1)正角 负角 零角 (2){α|2k π<α<2k π+π2,k ∈Z } {α|2k π+π2<α<2k π+π,k ∈Z }{α|2k π+π<α<2k π+3π2,k ∈Z } {α|2k π+3π2<α<2k π+2π,k ∈Z } 2.(1)半径 弧度 (2)2π π ⎝ ⎛⎭⎪⎫180π° (3)|α|r 12lr 12|α|r 23.y x yx正 正 正 正 负 负负 负 正 负 正 负 sin α cos α tan α基础自测1.C 解析:当角α的终边在x 轴上时,可表示为k ·180°,k ∈Z .当角α的终边在y 轴上时,可表示为k ·180°+90°,k ∈Z .∴当角α的终边在坐标轴上时,可表示为k ·90°,k ∈Z . 2.B 解析:设P 与原点的距离为r , ∵P (-4a,3a ),a <0,∴r =(-4a )2+(3a )2=|5a |=-5a .∴sin α=3a r =-35.3.C 解析:由已知可得该圆的半径为1sin 1.∴2弧度的圆心角所对的弧长为2×1sin 1=2sin 1.4.C 解析:∵sin θ<0,∴θ在第三或第四象限或在y 轴的非正半轴上, 又tan θ>0,∴θ在第一或第三象限, ∴θ在第三象限.5.(-1,3) 解析:根据三角函数的定义,x =|OP |cos 23π=2×⎝ ⎛⎭⎪⎫-12=-1,y =|OP |sin 23π=2×32= 3.∴P 点的坐标为(-1,3).考点探究突破【例1-1】B 解析:由已知,得2k π+π<α<2k π+32π(k ∈Z ),∴-k π+π4<π-α2<-k π+π2(k ∈Z ).∴π-α2是第一或第三象限的角.【例1-2】 解:∵α是第一象限的角,∴k ·2π<α<k ·2π+π2(k ∈Z ).(1)k ·4π<2α<k ·4π+π(k ∈Z ). 即2k ·2π<2α<2k ·2π+π(k ∈Z ).∴2α的终边在第一象限或第二象限或y 轴的非负半轴上.(2)k ·π<α2<k ·π+π4(k ∈Z ),当k =2n (n ∈Z )时,2n π<α2<2n π+π4(n ∈Z ).∴α2的终边在第一象限.当k =2n +1(n ∈Z )时,(2n +1)π<α2<(2n +1)π+π4(n ∈Z ),即2n π+π<α2<2n π+5π4(n ∈Z ),∴α2的终边在第三象限. 综上,α2的终边在第一象限或第三象限.【例2】 解:(1)设弧长为l ,弓形面积为S 弓,则α=60°=π3,R =10,l =|α|R =π3×10=10π3(cm), S 弓=S 扇-S △=12×10π3×10-12×102×sin π3=50π3-5032=50⎝ ⎛⎭⎪⎫π3-32(cm 2).(2)扇形周长C =2R +l =2R +αR ,∴R =C2+α,∴S 扇=12α·R 2=12α·⎝ ⎛⎭⎪⎫C 2+α2 =C 22α·14+4α+α2 =C 22·14+α+4α≤C 216. 当且仅当α2=4,即α=2弧度时,扇形面积有最大值为C 216cm 2.演练巩固提升1.A 解析:当k 为奇数时,α在第三象限;当k 为偶数时,α在第一象限.2.C 解析:设扇形的半径为r ,弧长为l ,则由题意得⎩⎪⎨⎪⎧2r +l =6,12rl =2.解得r =1,l =4或r =2,l =2.3.B 解析:如图,由题意:tan∠BEF =12,∴KX 21=12,∴X 2为HD 中点,X 2D X 3D =12,∴X 3D =13, X 4C X 3C =12,∴X 4C =13, X 5H X 4H =12,∴X 5H =12, X 5A X 6A =12,∴X 6A =13,∴X 6与E 重合, 故选B.4.±45解析:∵P (3t,4t ),∴原点O 到P 点的距离|OP |=5|t |,∴sin α=4t 5|t |=±45.5.解:∵角α的终边在直线3x +4y =0上,∴在角α的终边上任取一点P (4t ,-3t )(t ≠0),设P 到原点的距离为r , 则x =4t ,y =-3t .r =x 2+y 2=(4t )2+(-3t )2=5|t |,当t >0时,r =5t ,sin α=y r =-3t 5t =-35,cos α=x r =4t 5t =45.tan α=y x =-3t 4t =-34;当t <0时,r =-5t ,sin α=y r =-3t -5t =35.cos α=x r =4t -5t =-45.tan α=y x =-3t 4t =-34.。
高三数学一轮课件 第四章 三角函数与解三角形 4.4 函数y=Asin(ωx+φ)的图象及应用

解得 x=������2π + 1π2-θ,k∈Z.
由于函数 y=g(x)的图象关于点
5π 12
,0
成中心对称,令������2π + 1π2-
θ=51π2,k∈Z,解得 θ=������2π − π3,k∈Z. 由 θ>0 可知,当 k=1 时,θ 取得最小值π6.
考点1
考点2
考点3
-16-
解题心得1.函数y=Asin(ωx+φ)(A>0,ω>0)的图象的两种作法:
3
上所有点的纵坐标伸长到原来的 2 倍(横坐标不变),
即可得到 y=2sin
2������ + π
3
的图象.
-20-
考点1
考点2
考点3
考点 2 求函数 y=Asin(ωx+φ)的解析式(多考向)
考向一 由函数的图象求函数y=Asin(ωx+φ)的解析式
例2函数y=Asin(ωx+φ)的部分图象如图所示,则( )
=2sin x'.
列表:
x
x'=2x+������
3
y=sin x' y=2sin 2x + ������
3
-���6���
������ 12
������
0
2
01
02
������ 7������ 3 12
3������ π
2 0 -1
0 -2
5������ 6 2π
0 0
-19-
考点1
考点2
考点3
高三数学一轮复习教学课件
第四章 三角函数、解三角形
4.4 函数y=Asin(ωx+φ)的图象及应用
【志鸿优化设计】(湖南专用)高考数学一轮复习 第四章三角函数、解三角形4.3三角函数的图象与性质

课时作业19 三角函数的图象与性质一、选择题1.(2013届湖南师大附中月考)若点(m,4)在函数y =2x的图象上,则函数y =sin ⎝ ⎛⎭⎪⎫12mx +π3的最小正周期为 ( ).A .πB .π2C .2πD .4π2.下列函数中,周期为π,且在⎣⎢⎡⎦⎥⎤π4,π2上为减函数的是( ). A .y =sin ⎝ ⎛⎭⎪⎫2x +π2 B .y =cos ⎝ ⎛⎭⎪⎫2x +π2 C .y =sin ⎝ ⎛⎭⎪⎫x +π2 D .y =cos ⎝⎛⎭⎪⎫x +π23.(2012福建高考)函数f (x )=sin ⎝⎛⎭⎪⎫x -π4的图象的一条对称轴是( ).A .x =π4B .x =π2C .x =-π4D .x =-π24.将函数y =sin x -3cos x 的图象沿x 轴向右平移a (a >0)个单位长度,所得函数的图象关于y 轴对称,则a 的最小值是( ).A.7π6B.π2C.π6D.π35.函数f (x )=1-2sin 2x +2cos x 的最小值和最大值分别为( ).A .-1,1B .-32,-1C .-32,3D .-2,326.函数y =sin x +tan x -|sin x -tan x |在区间⎝ ⎛⎭⎪⎫π2,32π内的取值范围是( ). A .(-∞,0] B .[0,+∞) C .[-2,0] D .[0,2]7.已知函数f (x )的导函数的图象如图所示.若△ABC 为锐角三角形,则一定成立的是( ).A .f (sin A )>f (cosB ) B .f (sin A )<f (cos B )C .f (sin A )>f (sin B )D .f (cos A )<f (cos B )二、填空题8.函数y =1-tan x 的定义域是__________.9.函数y =cos ⎝ ⎛⎭⎪⎫x +π3,x ∈⎝⎛⎦⎥⎤0,π3的值域是__________.10.函数f (x )=sin x +2|sin x |,x ∈[0,2π]的图象与直线y =k 有且仅有两个不同的交点,则k 的取值范围是__________.三、解答题11.已知f (x )=23cos 2x +sin 2x -3+1(x ∈R ). (1)求f (x )的最小正周期; (2)求f (x )的单调递增区间;(3)若x ∈⎣⎢⎡⎦⎥⎤-π4,π4时,求f (x )的值域. 12.是否存在实数a ,使得函数y =sin 2x +a cos x +58a -32在闭区间⎣⎢⎡⎦⎥⎤0,π2上的最大值是1?若存在,求出对应的a 值;若不存在,请说明理由.参考答案一、选择题1.D 解析:当a =1或a =-1时,相邻两交点间的距离最大,为2π.2.A 解析:C ,D 两项中函数的周期都为2π,不合题意,排除C ,D ;B 项中y =cos ⎝⎛⎭⎪⎫2x +π2=-sin 2x ,该函数在⎣⎢⎡⎦⎥⎤π4,π2上为增函数,不合题意;A 项中y =sin ⎝⎛⎭⎪⎫2x +π2=cos 2x ,该函数符合题意,故选A.3.C 解析:函数f (x )=sin ⎝⎛⎭⎪⎫x -π4的图象的对称轴是x -π4=k π+π2,k ∈Z ,即x=k π+3π4,k ∈Z .当k =-1时x =-π+3π4=-π4.故选C.4.C 解析:∵y =sin x -3cos x =2sin ⎝⎛⎭⎪⎫x -π3,经平移后的函数图象所对应解析式为y =2sin ⎝⎛⎭⎪⎫x -a -π3,它关于y 轴对称,∴-a -π3=k π+π2,k ∈Z .又a >0,由分析可知a 的最小值为π6.故选C.5.C 解析:∵f (x )=1-2sin 2x +2cos x =1-2(1-cos 2x )+2cos x =2cos 2x +2cos x-1=2⎝⎛⎭⎪⎫cos x +122-32, 又∵x ∈R ,∴cos x ∈[-1,1].∴当cos x =-12时,f (x )min =-32;当cos x =1时,f (x )max =3.选C.6.A 解析:∵y =sin x +tan x -|sin x -tan x |=⎩⎪⎨⎪⎧2tan x ,π2<x ≤π,2sin x ,π<x <32π,当π2<x ≤π时,2tan x ∈(-∞,0], 当π<x <32π时,2sin x ∈(-2,0).∴y 的值域为(-∞,0].7.A 解析:因为△ABC 为锐角三角形,所以A +B >π2,即A >π2-B .又A ,π2-B ∈⎝ ⎛⎭⎪⎫0,π2,所以sin A >sin ⎝ ⎛⎭⎪⎫π2-B =cos B >0. 由图象知,在(0,+∞)上f ′(x )>0, 所以f (x )在(0,+∞)上单调递增. 所以f (sin A )>f (cos B ).故选A. 二、填空题8.⎝⎛⎦⎥⎤k π-π2,k π+π4(k ∈Z ) 解析:由1-tan x ≥0,得tan x ≤1,∴k π-π2<x ≤k π+π4(k ∈Z ).9.⎣⎢⎡⎭⎪⎫-12,12 解析:∵0<x ≤π3, ∴π3<x +π3≤23π, 又y =cos x 在[0,π]上是减函数,∴cos 23π≤cos ⎝⎛⎭⎪⎫x +π3<cos π3,即-12≤y <12.10.(1,3) 解析:f (x )=sin x +2|sin x |=3sin x ,x ∈[0,π], -sin x ,x ∈(π,2π].如图所示,则k 的取值范围是1<k <3.三、解答题11.解:f (x )=sin 2x +3(2cos 2x -1)+1=sin 2x +3cos 2x +1=2sin ⎝ ⎛⎭⎪⎫2x +π3+1.(1)函数f (x )的最小正周期为T =2π2=π.(2)由2k π-π2≤2x +π3≤2k π+π2,得2k π-5π6≤2x ≤2k π+π6.∴k π-5π12≤x ≤k π+π12(k ∈Z ).∴函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-5π12,k π+π12(k ∈Z ). (3)∵x ∈⎣⎢⎡⎦⎥⎤-π4,π4, ∴2x +π3∈⎣⎢⎡⎦⎥⎤-π6,5π6.∴sin ⎝⎛⎭⎪⎫2x +π3∈⎣⎢⎡⎦⎥⎤-12,1. ∴f (x )∈[0,3].12.解:y =1-cos 2x +a cos x +58a -32=-⎝⎛⎭⎪⎫cos x -a 22+a 24+58a -12.∵0≤x ≤π2,∴0≤cos x ≤1.①若a2>1.即a >2,则当cos x =1时,y max =a +58a -32=1⇒a =2013<2(舍去);②若0≤a2≤1,即0≤a ≤2,则当cos x =a 2时,y max =a 24+58a -12=1,∴a =32或a =-4<0(舍去);③若a2<0,即a <0,则当cos x =0时,y max =58a -12=1 a =125>0(舍去).综上可知存在a =32符合题意.。
【志鸿优化设计】(安徽专用)高考数学一轮复习 第四章三角函数、解三角形4.5三角恒等变换试题 新人教A版

课时作业22 三角恒等变换一、选择题1.计算1-2sin 222.5°的结果等于( ). A .12 B .22 C .33 D .322.已知tan α=-43,则tan ⎝ ⎛⎭⎪⎫π4-α的值为( ).A .-7B .7C .-17D .173.已知sin θ=45,sin θ-cos θ>1,则sin 2θ=( ).A .-2425B .-1225C .-45D .24254.已知tan(α+β)=25,tan ⎝ ⎛⎭⎪⎫β-π4=14,则tan ⎝⎛⎭⎪⎫α+π4=( ). A .1318 B .1322 C .322 D .165.已知向量a =⎝ ⎛⎭⎪⎫sin ⎝ ⎛⎭⎪⎫α+π6,1,b =(4,4cos α-3),若a ⊥b ,则sin ⎝⎛⎭⎪⎫α+4π3=( ).A .-34B .-14C .34D .146.函数f (x )=3cos(3x -θ)-sin(3x -θ)是奇函数,则θ为( ).A .k π,(k ∈Z )B .k π+π6,(k ∈Z )C .k π+π3,(k ∈Z )D .-k π-π3,(k ∈Z )7.(2012四川高考)如图,正方形ABCD 的边长为1,延长BA 至E ,使AE =1,连结EC ,ED ,则sin∠CED =( ).A .31010B .1010C .510 D .515 二、填空题 8.已知tan α=2,则2sin 2α+1sin 2α=__________.9.函数f (x )=sin ⎝⎛⎭⎪⎫2x -π4-22sin 2x 的最小正周期是__________.10.若sin ()π-α=45,α∈⎝⎛⎭⎪⎫0,π2,则sin 2α-cos 2α2的值等于__________.三、解答题11.(2013届安徽皖南八校联考)△AB C 中,角A ,B ,C 所对的边分别为a ,b ,c ,若(a +b +c )(sin A -sin B +sin C )=3a sin C .(1)求角B ;(2)若f (x )=cos(2x -B )+2sin 2x ,求f (x )的最小正周期及单调递增区间.12.已知cos ⎝ ⎛⎭⎪⎫α-β2=-45,sin ⎝⎛⎭⎪⎫β-α2=513,且π2<α<π,0<β<π2,求cos α+β2的值.参考答案一、选择题1.B 解析:1-2sin 222.5°=cos 45°=22. 2.A 解析:tan ⎝ ⎛⎭⎪⎫π4-α=tan π4-tan α1+tan π4·tan α=1-⎝ ⎛⎭⎪⎫-431+⎝ ⎛⎭⎪⎫-43=-7. 3.A 解析:由题意知cos θ<0,又sin θ=45,∴cos θ=-35,故sin 2θ=2sin θcos θ=-2425.4.C 解析:因为α+π4=(α+β)-⎝⎛⎭⎪⎫β-π4, 所以tan ⎝⎛⎭⎪⎫α+π4 =ta n ⎣⎢⎡⎦⎥⎤(α+β)-⎝⎛⎭⎪⎫β-π4 =tan(α+β)-tan ⎝⎛⎭⎪⎫β-π41+tan(α+β)tan ⎝⎛⎭⎪⎫β-π4=322.故选C.5.B 解析:a ·b =4sin ⎝⎛⎭⎪⎫α+π6+4cos α-3=23sin α+6cos α-3=43sin ⎝⎛⎭⎪⎫α+π3-3=0, ∴sin ⎝⎛⎭⎪⎫α+π3=14. ∴sin ⎝ ⎛⎭⎪⎫α+4π3=-sin ⎝⎛⎭⎪⎫α+π3=-14.故选B. 6.D 解析:f (x )=3cos(3x -θ)-sin(3x -θ)=2cos ⎝⎛⎭⎪⎫3x -θ+π6,由函数为奇函数得-θ+π6=k π+π2(k ∈Z ),解得θ=-k π-π3(k ∈Z ),故选D.7.B 解析:因为四边形ABCD 是正方形,且AE =AD =1,所以∠AED =π4.又因为在Rt△EBC 中,EB =2,BC =1,所以sin∠BEC =55,cos∠BEC =255.于是sin∠CED =sin ⎝ ⎛⎭⎪⎫π4-∠BEC =sin π4cos∠BEC -co s π4sin∠BEC=22×255-22×55=1010.故选B. 二、填空题8.134 解析:2sin 2α+1sin 2α=3sin 2α+cos 2α2sin αcos α=3tan 2α+12tan α=3×22+12×2=134.9.π 解析:f (x )=22(sin 2x -cos 2x )-2(1-cos 2x )=22(sin 2x +cos 2x )-2=sin ⎝ ⎛⎭⎪⎫2x +π4-2,故f (x )的最小正周期T =2π2=π. 10.425 解析:∵sin (π-α)=45,∴sin α=45.又∵α∈⎝⎛⎭⎪⎫0,π2,∴cos α=35.∴sin 2α-cos 2α2=2sin αcos α-1+cos α2=2×45×35-1+352=425.三、解答题11.解:(1)由(a +b +c )(sin A -sin B +sin C )=3a sin C , 得(a +b +c )(a -b +c )=3ac ,即(a +c )2-b 2=3ac ,∴a 2+c 2-b 2=ac ,由余弦定理,得cos B =12,∴B =π3;(2)f (x )=cos ⎝⎛⎭⎪⎫2x -π3+2sin 2x =cos 2x cos π3+sin 2x sin π3+1-cos 2x ,f (x )=32sin 2x -12cos 2x +1 =sin ⎝⎛⎭⎪⎫2x -π6+1, ∴f (x )的最小正周期T =2π2=π.由2k π-π2≤2x -π6≤2k π+π2,∴k π-π6≤x ≤k π+π3(k ∈Z ),故f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π6,k π+π3(k ∈Z ). 12.解:∵π2<α<π,0<β<π2,∴α-β2∈⎝ ⎛⎭⎪⎫π4,π,β-α2∈⎝ ⎛⎭⎪⎫-π2,π4. ∴sin ⎝ ⎛⎭⎪⎫α-β2=1-cos 2⎝ ⎛⎭⎪⎫α-β2=35,cos ⎝⎛⎭⎪⎫β-α2=1-sin 2⎝⎛⎭⎪⎫β-α2=1213.∵⎝⎛⎭⎪⎫α-β2+⎝ ⎛⎭⎪⎫β-α2=α+β2,∴cos α+β2=cos ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫α-β2+⎝ ⎛⎭⎪⎫β-α2=cos ⎝ ⎛⎭⎪⎫α-β2cos ⎝ ⎛⎭⎪⎫β-α2-sin ⎝ ⎛⎭⎪⎫α-β2·sin ⎝⎛⎭⎪⎫β-α2 =⎝ ⎛⎭⎪⎫-45×1213-35×513=-6365.。
高考数学文一轮分层演练:第4章三角函数与解三角形 第3讲 Word版含解析

[学生用书P225(单独成册)]一、选择题 1.cos 15°+sin 15°cos 15°-sin 15°的值为( )A .33 B . 3 C .-33D .- 3解析:选B.原式=1+tan 15°1-tan 15°=tan 45°+tan 15°1-tan 45°tan 15°=tan(45°+15°)= 3. 2.(1+tan 18°)·(1+tan 27°)的值是( )A . 3B .1+ 2C .2D .2(tan 18°+tan 27°) 解析:选C.原式=1+tan 18°+tan 27°+tan 18°tan 27°=1+tan 18°tan 27°+tan 45°(1-tan 18°tan 27°)=2,故选C.3.已知sin α+cos α=13,则sin 2(π4-α)=( )A .118B.1718 C .89D.29解析:选B.由sin α+cos α=13两边平方得1+sin 2α=19,解得sin 2α=-89,所以sin 2(π4-α)=1-cos (π2-2α)2=1-sin 2α2=1+892=1718.4.已知cos ⎝⎛⎭⎫α-π6+sin α=435,则sin ⎝⎛⎭⎫α+7π6的值是( ) A .-235B .235C .45D .-45解析:选D.由cos ⎝⎛⎭⎫α-π6+sin α=435,可得32cos α+12sin α+sin α=435,即32sin α+32cos α=435,所以3sin ⎝⎛⎭⎫α+π6=435,sin ⎝⎛⎭⎫α+π6=45, 所以sin ⎝⎛⎭⎫α+7π6=-sin ⎝⎛⎭⎫α+π6=-45. 5.已知cos(π3-2x )=-78,则sin(x +π3)的值为( )A .14B .78C .±14D .±78解析:选C.因为cos [π-(π3-2x )]=cos(2x +2π3)=78,所以有sin 2(x +π3)=12(1-78)=116,从而求得sin(x +π3)的值为±14,故选C.6.3cos 10°-1sin 170°=( )A .4B .2C .-2D .-4解析:选 D.3cos 10°-1sin 170°=3cos 10°-1sin 10°=3sin 10°-cos 10°sin 10°cos 10°=2sin (10°-30°)12sin 20°=-2sin 20°12sin 20°=-4,故选D.二、填空题7.已知cos θ=-513,θ∈⎝⎛⎭⎫π,3π2,则sin ⎝⎛⎭⎫θ-π6的值为________. 解析:由cos θ=-513,θ∈⎝⎛⎭⎫π,3π2得sin θ=-1-cos 2θ=-1213,故sin ⎝⎛⎭⎫θ-π6=sin θcos π6-cos θsin π6=-1213×32-⎝⎛⎭⎫-513×12=5-12326.答案:5-123268.已知cos ⎝⎛⎭⎫x -π6=-33,则cos x +cos ⎝⎛⎭⎫x -π3=________. 解析:cos x +cos ⎝⎛⎭⎫x -π3 =cos x +12cos x +32sin x=32cos x +32sin x =3cos ⎝⎛⎭⎫x -π6 =3×⎝⎛⎭⎫-33=-1. 答案:-1 9.2cos 10°-sin 20°sin 70°的值是________.解析:原式=2cos (30°-20°)-sin 20°sin 70°=2(cos 30°cos 20°+sin 30°sin 20°)-sin 20°sin 70°=3cos 20°cos 20°= 3.答案: 310.设α为锐角,若cos ⎝⎛⎭⎫α+π6=45,则sin ⎝⎛⎭⎫2α+π12的值为________. 解析:因为α为锐角,cos ⎝⎛⎭⎫α+π6=45, 所以sin ⎝⎛⎭⎫α+π6=35,sin ⎣⎡⎦⎤2⎝⎛⎭⎫α+π6=2425, cos ⎣⎡⎦⎤2⎝⎛⎭⎫α+π6=725, 所以sin ⎝⎛⎭⎫2α+π12=sin ⎣⎡⎦⎤2⎝⎛⎫α+π6-π4 =2425×22-725×22=17250. 答案:17250三、解答题11.已知函数f (x )=sin ⎝⎛⎭⎫x +π12,x ∈R . (1)求f ⎝⎛⎫-π4的值; (2)若cos θ=45,θ∈⎝⎛⎭⎫0,π2,求f ⎝⎛⎭⎫2θ-π3的值. 解:(1)f ⎝⎛⎭⎫-π4=sin ⎝⎛⎭⎫-π4+π12 =sin ⎝⎛⎭⎫-π6=-12. (2)f ⎝⎛⎭⎫2θ-π3=sin ⎝⎛⎭⎫2θ-π3+π12=sin ⎝⎛⎭⎫2θ-π4=22(sin 2θ-cos 2θ). 因为cos θ=45,θ∈⎝⎛⎭⎫0,π2, 所以sin θ=35.所以sin 2θ=2sin θcos θ=2425,cos 2θ=cos 2 θ-sin 2θ=725,所以f ⎝⎛⎭⎫2θ-π3=22(sin 2θ-cos 2θ) =22×⎝⎛⎭⎫2425-725=17250. 12.已知α∈⎝⎛⎭⎫π2,π,且sin α2+cos α2=62. (1)求cos α的值;(2)若sin(α-β)=-35,β∈⎝⎛⎭⎫π2,π,求cos β的值. 解:(1)因为sin α2+cos α2=62,两边同时平方,得sin α=12.又π2<α<π, 所以cos α=-1-sin 2α=-32. (2)因为π2<α<π,π2<β<π,所以-π2<α-β<π2.又由sin(α-β)=-35,得cos(α-β)=45.所以cos β=cos[α-(α-β)] =cos αcos(α-β)+sin αsin(α-β) =-32×45+12×⎝⎛⎭⎫-35 =-43+310.。
【志鸿优化设计】(湖南专用)高考数学一轮复习 第四章三角函数、解三角形4.6正、余弦定理及其应用

4.6 正、余弦定理及其应用举例考纲要求1.掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.2.能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.在视线和水平线所成的角中,视线在水平线__________的角叫仰角,在水平线______的角叫俯角(如图①).3.方位角从指北方向顺时针转到目标方向线的水平角,如B 点的方位角为α(如图②). 4.方向角相对于某一方向的水平角(如图③).图③(1)北偏东α°:指北方向向东旋转α°到达目标方向. (2)东北方向:指北偏东45°或东偏北45°. (3)其他方向角类似. 5.坡角和坡比坡角:坡面与水平面的夹角(如图④,角θ为坡角).图④坡比:坡面的铅直高度与水平长度之比(如图④,i 为坡比).1.(2012广东高考)在△ABC 中,若∠A =60°,∠B =45°,BC =32,则AC =( ).A .4 3B .2 3 C. 3 D.322.在△ABC 中,cos 2B 2=a +c 2c(a ,b ,c 分别为角A ,B ,C 的对边),则△ABC 的形状为( ). A .等边三角形 B .直角三角形 C .等腰三角形或直角三角形 D .等腰直角三角形3.一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是( ).A .5海里/时B .5 3 海里/时C .10海里/时D .10 3 海里/时4.如图,为了测量隧道AB 的长度,给定下列四组数据,无法求出AB 长度的是( ).A .α,a ,bB .α,β,aC .a ,b ,γD .α,β,γ5.△ABC 中,若a =32,cos C =13,S △ABC =43,则b =__________.一、利用正弦、余弦定理解三角形【例1-1】 (2012辽宁高考)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .角A ,B ,C 成等差数列.(1)求cos B 的值;(2)边a ,b ,c 成等比数列,求sin A sin C 的值.【例1-2】 △ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,tan C =sin A +sin Bcos A +cos B,sin(B-A )=cos C .(1)求A ,C ;(2)若S △ABC =3+3,求a ,c . 方法提炼应熟练掌握正、余弦定理及其变形.解三角形时,有时可用正弦定理,也可用余弦定理,应注意用哪一个定理更方便、简捷就用哪一个定理.二、三角形形状的判定【例2-1】△ABC 满足sin B =cos A sin C ,则△ABC 的形状是( ). A .直角三角形 B .等腰三角形C .等腰直角三角形D .等腰三角形或直角三角形 【例2-2】 在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C .(1)求A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状. 方法提炼判断三角形的形状的基本思想是:利用正、余弦定理进行边角的统一.即将条件化为只含角的三角函数关系式,然后利用三角恒等变换得出内角之间的关系式;或将条件化为只含有边的关系式,然后利用常见的化简变形得出三边的关系.结论一般为特殊的三角形.如等边三角形、等腰三角形、直角三角形、等腰直角三角形等.另外,在变形过程中要注意A ,B ,C 的范围对三角函数值的影响.提醒:1.在△ABC 中有如下结论sin A >sin B a >b .2.当b 2+c 2-a 2>0时,角A 为锐角,若可判定其他两角也为锐角,则三角形为锐角三角形;当b 2+c 2-a 2=0时,角A 为直角,三角形为直角三角形;当b 2+c 2-a 2<0时,角A 为钝角,三角形为钝角三角形. 请做演练巩固提升2三、与三角形面积有关的问题【例3】在△ABC 中,内角A ,B ,C 对边的边长分别是a ,b ,c ,已知c =2,C =π3.(1)若△ABC 的面积等于3,求a ,b ;(2)若sin C +sin(B -A )=2sin 2A ,求△ABC 的面积. 方法提炼1.正弦定理和余弦定理并不是孤立的,解题时要根据具体题目合理选用,有时还需要交替使用;在解决三角形问题中,面积公式S =12ab sin C =12bc sin A =12ac sin B 最常用,因为公式中既有边也有角,容易和正弦定理、余弦定理联系起来.2.解三角形过程中,要注意三角恒等变换公式的应用. 请做演练巩固提升5四、应用举例、生活中的解三角形问题【例4-1】 某人在塔的正东沿着南偏西60° 的方向前进40米后,望见塔在东北方向,若沿途测得塔的最大仰角为30°,求塔高.【例4-2】 如图,为了解某海域海底构造,在海平面内一条直线上的A ,B ,C 三点进行测量.已知AB =50 m ,BC =120 m ,于A 处测得水深AD =80 m ,于B 处测得水深BE =200 m ,于C 处测得水深CF =110 m ,求∠DEF 的余弦值.方法提炼1.测量距离问题,需注意以下几点:(1)利用示意图把已知量和待求量尽量集中在有关的三角形中,建立一个解三角形的模型;(2)利用正、余弦定理解出所需要的边和角,求得该数学模型的解; (3)应用题要注意作答. 2.测量高度时,需注意:(1) 要准确理解仰、俯角的概念;(2)分清已知和待求,分析(画出)示意图,明确在哪个三角形内应用正、余弦定理; (3)注意铅垂线垂直于地面构成的直角三角形.3.测量角度时,要准确理解方位角、方向角的概念,准确画出示意图是关键. 请做演练巩固提升6忽视三角形中的边角条件而致误【典例】 在△ABC 中,a ,b ,c 分别为内角A ,B ,C 所对的边长,a =3,b =2,1+2cos(B +C )=0,求边BC 上的高.错解:由1+2cos(B +C )=0,知cos A =12,∴A =π3.根据正弦定理a sin A =b sin B 得:sin B =b sin A a =22,∴B =π4或3π4.以下解答过程略.错因:忽视三角形中“大边对大角”的定理,产生了增根. 正解:∵在△ABC 中,cos(B +C )=-cos A ,又∵1+2cos(B +C )=0,∴1-2cos A =0,∴A =π3.在△ABC 中,根据正弦定理a sin A =bsin B,得sin B =b sin A a =22. ∴B =π4或3π4.∵a >b ,∴B =π4.∴C =π-(A +B )=512π.∴sin C =sin(B +A )=sin B cos A +cos B sin A =22×12+22×32=6+24. ∴BC 边上的高为b sin C =2×6+24=3+12. 答题指导:1.考查解三角形的题在高考中一般难度不大,但稍不注意,会出现“会而不对,对而不全”的情况,其主要原因就是忽视三角形中的边角条件.2.解三角函数的求值问题时,估算是一个重要步骤,估算时应考虑三角形中的边角条件.1.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .若a cos A =b sin B ,则sin A cos A +cos 2B =( ).A .-12B .12C .-1D .12.(2012湖南高考)在△ABC 中,AC =7,BC =2,B =60°,则BC 边上的高等于( ).A .32B .332C .3+62D .3+3943.在△ABC 中,(a +b +c )(a +b -c )=3ab ,且a cos B =b cos A ,则△ABC 的形状为__________.4.(2012陕西高考)在△ABC 中,角A ,B ,C 所对边的长分别为a ,b ,c .若a =2,B =π6,c =23,则b =______.5.(2012山东高考)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知sin B (tan A +tan C )=tan A tan C .(1)求证:a ,b ,c 成等比数列;(2)若a =1,c =2,求△ABC 的面积S .6.某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O 北偏西30°且与该港口相距20海里的A 处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v 海里/时的航行速度匀速行驶,经过t 小时与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少? (2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.参考答案基础梳理自测知识梳理1.asin A=bsin B=csin Cb 2+c 2-2bc ·cos A c 2+a 2-2ca ·cos B a 2+b 2-2ab ·cos C ①2R sin A 2R sin B 2R sin C ②a 2Rb 2Rc 2R③sin A ∶sin B ∶sin C b 2+c 2-a 22bc c 2+a 2-b 22ca a 2+b 2-c 22ab2.上方 下方 基础自测1.B 解析:由正弦定理得BC sin A =AC sin B ,即32sin 60°=ACsin 45°,解得AC =2 3.2.B 解析:∵cos 2B 2=a +c 2c , ∴2cos 2B 2-1=a +c c -1, ∴cos B =a c,∴a 2+c 2-b 22ac =a c,∴c 2=a 2+b 2.3.C 解析:如图,A ,B为灯塔,船从O 航行到O ′,OO ′BO =tan 30°, OO ′AO=tan 15°,∴BO =3OO ′, AO =(2+3)OO ′. ∵AO -BO =AB =10,∴OO ′·[(2+3)-3]=10, ∴OO ′=5,∴船的速度为512=10海里/时.4.D 解析:利用余弦定理,可由a ,b ,γ或α,a ,b 求出AB ;利用正弦定理,可由a ,α,β求出AB ,当只知α,β,γ时,无法计算AB .5.2 3 解析:由cos C =13,得sin C =223,∴S △ABC =12ab sin C =12×32×b ×223=43.∴b =2 3.考点探究突破【例1-1】 解:(1)由已知2B =A +C ,A +B +C =180°,解得B =60°,所以cos B=12. (2)方法一:由已知b 2=ac ,及cos B =12,根据正弦定理得sin 2B =sin A sin C ,所以sin A sin C =1-cos 2B =34.方法二:由已知b 2=ac ,及cos B =12,根据余弦定理得cos B =a 2+c 2-ac2ac ,解得a =c ,所以B =A =C =60°,故sin A sin C=34. 【例1-2】 解:(1)因为tan C =sin A +sin Bcos A +cos B,即sin C cos C =sin A +sin B cos A +cos B, 所以sin C cos A +sin C cos B =cos C sin A +cos C sin B , 即sin C cos A -cos C sin A =cos C sin B -sin C cos B , 得sin(C -A )=sin(B -C ).所以C -A =B -C ,或C -A =π-(B -C )(不成立),即2C =A +B ,得C =π3,所以B +A =2π3.又因为sin(B -A )=cos C =12,则B -A =π6或B -A =5π6(舍去),得A =π4,B =5π12.(2)S △ABC =12ac sin B =6+28ac =3+3,又a sin A =c sin C ,即a 22=c 32,得a =22,c =2 3.【例2-1】 A 解析:∵sin B =cos A ·sin C ,∴b =b 2+c 2-a 22bc·c .∴b 2+a 2=c 2.∴△ABC 为直角三角形,选A.【例2-2】 解:(1)由已知,根据正弦定理得2a 2=(2b +c )b +(2c +b )c ,即a 2=b 2+c 2+bc .①由余弦定理得a 2=b 2+c 2-2bc cos A ,故cos A =-12,A =120°.(2)由①得,sin 2A =sin 2B +sin 2C +sin B sin C . 又sin B +sin C =1,故sin B =sin C =12.因为0°<B <90°,0°<C <90°,故B =C . 所以△ABC 是等腰钝角三角形.【例3】 解:(1)由余弦定理及已知条件,得a 2+b 2-ab =4,又因为△ABC 的面积等于3,所以12ab sin C =3,得ab =4.联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,ab =4,解得⎩⎪⎨⎪⎧a =2,b =2.(2)由题意得sin(B +A )+sin(B -A )=4sin A cos A ,即sin B cos A =2sin A cos A .当cos A =0时,A =π2,B =π6,a =433,b =233.所以△ABC 的面积 S =12ab sin C =12×433×233×32=233; 当cos A ≠0时,得sin B =2sin A , 由正弦定理得b =2a ,联立方程组⎩⎪⎨⎪⎧a 2+b 2-ab =4,b =2a .解得⎩⎪⎨⎪⎧a =233,b =433.所以△ABC 的面积S =12ab sin C =12×233×433×32=233.综上知,△ABC 的面积为233.【例4-1】 解:依题意画出图,某人在C 处,AB 为塔高,他沿CD 前进,CD =40米,此时∠DBF =45°,从C 到D 沿途测塔的仰角,只有B 到测试点的距离最短,即BE ⊥CD 时,仰角才最大,这是因为tan∠AEB =AB BE,AB 为定值,BE 最小时,仰角最大.在△BCD 中,CD =40,∠BCD =30°,∠DBC =135°. 由正弦定理,得CDsin∠DBC =BDsin∠BCD,∴BD =40sin 30°sin 135°=20 2.在Rt△BED 中,∠BDE =180°-135°-30°=15°,BE =BD sin 15°=202×6-24=10(3-1).在Rt△ABE 中,∠AEB =30°,∴AB =BE tan 30°=103(3-3)(米).∴所求的塔高为103(3-3)米.【例4-2】 解:作DM ∥AC 交BE 于N ,交CF 于M .DF =MF 2+DM 2=302+1702=10298, DE =DN 2+EN 2=502+1202=130,EF =(BE -FC )2+BC 2=902+1202=150. 在△DEF 中,由余弦定理,cos∠DEF =DE 2+EF 2-DF 22DE ×EF=1302+1502-102×2982×130×150=1665.演练巩固提升1.D 解析:根据正弦定理a sin A =bsin B=2R 得,a =2R sin A ,b =2R sin B , ∴a cos A =b sin B 可化为sin A cos A =sin 2B .∴sin A cos A +cos 2B =sin 2B +cos 2B =1. 2.B 解析:在△ABC 中,由余弦定理可知:AC 2=AB 2+BC 2-2AB ·BC cos B ,即7=AB 2+4-2×2×AB ×12.整理得AB 2-2AB -3=0.解得AB =-1(舍去)或AB =3.故BC 边上的高AD =AB ·sin B =3×sin 60°=332.3.等边三角形 解析:∵(a +b +c )(a +b -c )=3ab ,∴(a +b )2-c 2=3ab . ∴a 2+b 2-c 2=ab .∴cos C =a 2+b 2-c 22ab =12.∴C =π3.∵a cos B =b cos A ,∴sin A cos B =sin B cos A . ∴sin(A -B )=0. ∴A =B .故△ABC 为等边三角形.4.2 解析:∵b 2=a 2+c 2-2ac cos B =4+12-2×2×23×32=4, ∴b =2.5.(1)证明:在△ABC 中,由于sin B (tan A +tan C )=tan A tan C ,所以sin B ⎝ ⎛⎭⎪⎫sin A cos A +sin C cos C =sin A cos A ·sin C cos C,因此sin B (sin A cos C +cos A sin C )=sin A sin C , 所以sin B sin(A +C )=sin A sin C , 又A +B +C =π,所以sin(A +C )=sin B ,因此sin 2B =sin A sinC .由正弦定理得b 2=ac , 即a ,b ,c 成等比数列. (2)解:因为a =1,c =2,所以b =2,由余弦定理得cos B =a 2+c 2-b 22ac =12+22-(2)22×1×2=34,因为0<B <π,所以sin B =1-cos 2B =74,故△ABC 的面积S =12ac sin B =12×1×2×74=74.6.解:(1)解法一:设相遇时小艇的航行距离为s 海里,则s =900t 2+400-2·30t ·20·cos (90°-30°)=900t 2-600t +400=900⎝ ⎛⎭⎪⎫t -132+300.故当t =13时,s min =103,v =10313=30 3.即小艇以303海里/时的速度航行,相遇时小艇的航行距离最小.解法二:若相遇时小艇的航行距离最小,又轮船沿正东方向匀速行驶,则小艇航行方向为正北方向,如图,设小艇与轮船在C 处相遇.在Rt△OAC 中,OC =20c os 30°=103,AC =20sin 30°=10. 又AC =30t ,OC =vt ,此时,轮船航行时间t =1030=13,v =10313=30 3.即小艇以303海里/时的速度航行,相遇时小艇的航行距离最小.(2)如图,设小艇与轮船在B 处相遇,由题意,可得(vt )2=202+(30t )2-2·20·30t ·cos(90°-30°).化简,得v 2=400t 2-600t +900=400⎝ ⎛⎭⎪⎫1t -342+675. 由于0<t ≤12,即1t≥2, 所以当1t=2时,v 取得最小值1013, 即小艇航行速度的最小值为1013海里/时.。
【志鸿优化设计】(湖南专用)高考数学一轮复习 第四章三角函数、解三角形4.1任意角和弧度制及任意

课时作业17 任意角和弧度制及任意角的三角函数一、选择题1.若-π2<α<0,则点P (tan α,cos α)位于( ).A .第一象限B .第二象限C .第三象限D .第四象限2.若α=m ·360°+θ,β=n ·360°-θ(m ,n ∈Z ),则α,β终边的位置关系是( ).A .重合B .关于原点对称C .关于x 轴对称D .关于y 轴对称3.若α是第三象限角,则y =⎪⎪⎪⎪⎪⎪sin α2sin α2+⎪⎪⎪⎪⎪⎪cos α2cosα2的值为( ).A .0B .2C .-2D .2或-24.已知点P ⎝⎛⎭⎪⎫sin 3π4,cos 3π4落在角θ的终边上,且θ∈[0,2π),则θ的值为( ).A.π4B.3π4C.5π4D.7π45.若一个扇形的周长与面积的数值相等,则该扇形所在圆的半径不可能等于( ). A .5 B .2 C .3 D .46.一段圆弧的长度等于其圆内接正三角形的边长,则其圆心角的弧度数为( ). A.π3 B.2π3C. 3D. 2 7.(2012上海高考)若S n =sin π7+sin 2π7+…+sin n π7(n ∈N *),则在S 1,S 2,…,S 100中,正数的个数是( ).A .16B .72C .86D .100 二、填空题8.已知点P (tan α,cos α)在第三象限,则角α的终边在第__________象限.9.若角α的终边落在射线y =-x (x ≥0)上,则sin α1-sin 2α+1-cos 2αcos α=__________. 10.若β的终边所在直线经过点P ⎝⎛⎭⎪⎫cos 3π4,sin 3π4,则sin β=__________,tan β=__________.三、解答题11.已知角α终边经过点P (x ,-2)(x ≠0),且cos α=36x .求sin α,tan α的值.12.已知扇形AOB 的周长为8,(1)若这个扇形的面积为3,求圆心角的大小;(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB .参考答案一、选择题1.B 解析:∵-π2<α<0,∴tan α<0,cos α>0, ∴点P 在第二象限. 2.C3.A 解析:∵α是第三象限角, ∴α2是第二或第四象限角. 当α2为第二象限角时,y =1+(-1)=0; 当α2为第四象限角时,y =-1+1=0. ∴y =0.4.D 解析:设P 到坐标原点的距离为r ,r =sin23π4+cos 23π4=1, 由三角函数的定义,tan θ=cos3π4sin3π4=-1.又∵sin 3π4>0,cos 3π4<0,∴P 在第四象限.∴θ=7π4.5.B 解析:设扇形的半径为R ,圆心角为α,则有2R +R α=12R 2α,即2+α=12R α,整理得R =2+4α,由于4α≠0,∴R ≠2.6.C 解析:设圆的半径为R ,由题意可知:圆内接正三角形的边长为3R ,∴圆弧长为3R .∴该圆弧所对圆心角的弧度数为3RR= 3.7.C 解析:由sin π7=-sin 8π7,sin 2π7=-sin 9π7,…,sin 6π7=-sin 13π7,sin7π7=sin 14π7=0,所以S 13=S 14=0.同理S 27=S 28=S 41=S 42=S 55=S 56=S 69=S 70=S 83=S 84=S 97=S 98=0, 所以在S 1,S 2,…,S 100中,其余各项均大于0. 故选C. 二、填空题8.二 解析:由已知⎩⎪⎨⎪⎧tan α<0cos α<0,∴α是第二象限的角.9.0 解析:由题意,角α的终边在第四象限.∴sin α1-sin 2α+1-cos 2αcos α=sin α|cos α|+|sin α|cos α=sin αcos α-sin αcos α=0.10.22或-22 -1 解析:因为β的终边所在直线经过点P ⎝⎛⎭⎪⎫cos 3π4,sin 3π4,所以β的终边所在直线为y =-x ,则β在第二或第四象限.所以sin β=22或-22,tanβ=-1.三、解答题11.解:∵P (x ,-2)(x ≠0),∴P 到原点的距离r =x 2+2.又cos α=36x ,∴cos α=x x 2+2=36x . ∵x ≠0,∴x =±10, ∴r =2 3.当x =10时,P 点坐标为(10,-2),由三角函数定义,有sin α=-66,tan α=-55;当x =-10时,P 点坐标为(-10,-2),∴sin α=-66,tan α=55.12.解:设扇形AOB 的半径为r ,弧长为l ,圆心角为α, (1)由题意可得⎩⎪⎨⎪⎧2r +l =8,12lr =3,解得⎩⎪⎨⎪⎧r =3,l =2或⎩⎪⎨⎪⎧r =1,l =6,∴α=l r =23或α=lr=6.(2)∵2r +l =8,∴S 扇=12lr =14l ·2r ≤14⎝ ⎛⎭⎪⎫l +2r 22=14×⎝ ⎛⎭⎪⎫822=4,当且仅当2r =l ,即α=l r=2时,扇形面积取得最大值4.∴r =2,∴弦长AB =2sin 1×2=4sin 1.。
【志鸿优化设计】高考数学一轮复习 第四章 三角函数、解三角形4.5三角恒等变换教学案 理 新人教A版

4.5 三角恒等变换考纲要求1.会用向量的数量积推导出两角差的余弦公式.2.能利用两角差的余弦公式导出两角差的正弦、正切公式.3.能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.4.能运用两角和与差的正弦、余弦、正切公式以及二倍角的正弦、余弦和正切公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆).1.两角和与差的正弦、余弦和正切公式公式名 公式 两角和与差的正弦 sin(α±β)=__________ 两角和与差的余弦 cos(α±β)=__________ 两角和与差的正切 tan(α±β)=__________ 2.二倍角的正弦、余弦、正切公式公式名 公式 二倍角的正弦 sin 2α=______ 二倍角的余弦 cos 2α=______=______=______ 二倍角的正切 tan 2α=______ 3.半角公式4.形如a sin α+b cos α的化简a sin α+b cos α=a 2+b 2sin(α+φ),其中cos φ=__________,sin φ=__________,即tan φ=b a.1.(2012重庆高考)sin 47°-sin 17°cos 30°cos 17°=( ).A .-32B .-12C .12D .322.化简2+cos 2-sin 21的结果是( ). A .-cos 1 B .cos 1C .3cos 1D .-3cos 13.若sin ⎝ ⎛⎭⎪⎫θ+π4=a ,则cos ⎝⎛⎭⎪⎫θ-π4等于( ). A .-a B .aC .1-aD .1+a4.函数f (x )=2sin x -2cos x 的值域是__________.5.若1+tan α1-tan α=2 013,则tan 2α+1cos 2α=__________.一、两角和与差的三角函数公式的应用【例1-1】在△ABC 中,角C =120°,tan A +tan B =233,则tan A tan B 的值为( ).A.14B.13C.12D.53【例1-2】 化简:2cos 4x -2cos 2x +122tan ⎝ ⎛⎭⎪⎫π4-x sin 2⎝ ⎛⎭⎪⎫π4+x .方法提炼1.运用两角和与差的三角函数公式时,不但要熟练,准确,而且要熟悉公式的逆用及变形,如tan α+tan β=tan(α+β)·(1-tan αtan β)和二倍角的余弦公式的多种变形等.2.应熟悉公式的逆用和变形应用,公式的正用是常见的,但逆用和变形应用则往往容易被忽视,公式的逆用和变形应用更能开拓思路,培养从正向思维向逆向思维转化的能力,只有熟悉了公式的逆用和变形应用后,才能真正掌握公式的应用.提醒:在T (α+β)与T (α-β)中,α,β,α±β都不等于k π+π2(k ∈Z ),即保证tan α,tan β,tan(α+β)都有意义;若α,β中有一角是k π+π2(k ∈Z ),可利用诱导公式化简.请做演练巩固提升2 二、角的变换【例2-1】 已知sin ⎝ ⎛⎭⎪⎫x +π4=-34,则sin 2x =__________.【例2-2】 已知0<β<π4<α<34π,cos ⎝ ⎛⎭⎪⎫π4-α=35,sin ⎝ ⎛⎭⎪⎫3π4+β=513,求sin(α+β)的值.方法提炼1.当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式; 2.当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”.3.常见的配角技巧:α=2·α2;α=(α+β)-β;α=β-(β-α);α=12[(α+β)+(α-β)];β=12[(α+β)-(α-β)];π4+α=π2-⎝ ⎛⎭⎪⎫π4-α. 提醒:特殊的角也看成已知角,如α=π4-⎝ ⎛⎭⎪⎫π4-α. 请做演练巩固提升3三、三角函数式的化简、求值【例3-1】 化简:+sin α+cos α⎝ ⎛⎭⎪⎫sin α2-cos α22+2cos α(π<α<2π).【例3-2】 已知34π<α<π,tan α+1tan α=-103,求5sin2α2+8sin α2cos α2+11cos 2α2-82sin ⎝⎛⎭⎪⎫α-π2的值.方法提炼1.三角函数式的化简要遵循“三看”原则.(1)一看“角”,这是最重要的一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式;(2)二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,常见的有“切化弦”;(3)三看“结构特征”,分析结构特征,可以帮助我们找到变形的方向,常见的有“遇到分式要通分”等.2.三角函数的求值主要有三种类型,即给角求值、给值求值、给值求角.(1)给角求值的关键是正确地选用公式,以便把非特殊角的三角函数相约或相消,从而化为特殊角的三角函数.(2)给值求值的关键是找出已知式与待求式之间的联系及函数的差异,一般可以适当变换已知式,求得另外某些函数式的值,以备应用.同时也要注意变换待求式,便于将已知式求得的函数值代入,从而达到解题的目的.(3)给值求角的关键是先求出该角的某一三角函数的值,其次判断该角对应的区间,从而达到解题的目的.请做演练巩固提升5 四、三角恒等式的证明【例4-1】 求证:cos 2α1tanα2-tan α2=14sin 2α.【例4-2】 已知0<α<π4,0<β<π4,且3sin β=sin(2α+β),4tan α2=1-tan2α2,证明:α+β=π4. 方法提炼1.证明三角恒等式的实质是消除等式两边的差异,有目的的化繁为简、左右归一或变更论证.2.三角恒等式的证明主要有两种类型:绝对恒等式与条件恒等式.(1)证明绝对恒等式要根据等式两边的特征,化繁为简,左右归一,变更论证,通过三角恒等式变换,使等式的两边化异为同.(2)条件恒等式的证明则要认真观察,比较已知条件与求证等式之间的联系,选择适当途径.常用代入法、消元法、两头凑等方法.请做演练巩固提升6不能挖掘隐含条件而增解【典例】 若sin θ,cos θ是关于x 的方程5x 2-x +a =0(a 是常数)的两根,θ∈(0,π),求cos 2θ的值.错解:由题意知:sin θ+cos θ=15,∴(sin θ+cos θ)2=125.∴sin 2θ=-2425.∵θ∈(0,π),∴2θ∈(0,2π).∴cos 2θ=±1-2sin 22θ=±725.正解:由题意知:sin θ+cos θ=15,∴(sin θ+cos θ)2=125.∴sin 2θ=-2425,即2sin θcos θ=-2425<0.则sin θ与cos θ异号.又sin θ+cos θ=15>0,∴π2<θ<3π4.∴π<2θ<3π2. 故cos 2θ=-1-sin 22θ=-725.答题指导:涉及到角的终边、函数符号和同角函数关系问题时,应深挖隐含条件,处理好开方、平方关系,避免出现增解与漏解的错误.1.(2012辽宁高考)已知sin α-cos α=2,α∈(0,π),则sin 2α=( ).A .-1B .-22 C. 22D .12.如果cos 2α-cos 2β=a ,则sin(α+β)sin(α-β)等于( ). A .-a 2B.a2 C .-a D .a 3.已知tan ⎝ ⎛⎭⎪⎫α-π6=37,tan ⎝ ⎛⎭⎪⎫π6+β=25,则tan(α+β)的值为( ).A.2941B.129C.141 D .1 4.+3-cos 20°cos 80°·1-cos 20°=__________.5.化简:sin 2αsin 2β+cos 2αcos 2β-12cos 2αcos 2β.6.已知sin β=m sin(2α+β)(m ≠1),求证:tan(α+β)=1+m1-mtan α.参考答案基础梳理自测知识梳理1.sin αcos β±cos αsin β cos αcos β∓sin αsin β tan α±tan β1∓tan αtan β2.2sin αcos α cos 2α-sin 2α 2cos 2α-11-2sin 2α 2tan α1-tan 2α3.2α α 1-2sin 2α2 2cos 2α2-1±1-cos α2±1+cos α2 sin α1+cos α 1-cos αsin α 4.a a 2+b2ba 2+b 2基础自测1.C 解析:因为sin 47°=sin(30°+17°)=sin 30°cos 17°+sin 17°cos 30°,所以原式=sin 30°cos 17°+sin 17°cos 30°-sin 17°cos 30°cos 17°=sin 30°=12, 故选C.2.C 解析:2+cos 2-sin 21=1-sin 21+1+cos 2=cos 21+2cos 21=3cos 1.3.B 解析:∵sin ⎝⎛⎭⎪⎫θ+π4=a =22(sin θ+cos θ), 又cos ⎝⎛⎭⎪⎫θ-π4=22(sin θ+cos θ),∴cos ⎝ ⎛⎭⎪⎫θ-π4=a . 4.[-22,22]解析:f (x )=22sin ⎝⎛⎭⎪⎫x -π4,又-1≤sin ⎝⎛⎭⎪⎫x -π4≤1,∴-22≤f (x )≤2 2.5.2 013 解析:tan 2α+1cos 2α=1+sin 2αcos 2α=(cos α+sin α)2cos 2α-sin 2α=cos α+sin αcos α-sin α =1+tan α1-tan α=2 013. 考点探究突破【例1-1】 B 解析:由题意得 tan C =tan[π-(A +B )]=-tan(A +B )=-tan A +tan B1-tan A tan B=-3,又tan A +tan B =233,解得tan A tan B =13.故选B.【例1-2】 解:原式=12(4cos 4x -4cos 2x +1)2×sin ⎝ ⎛⎭⎪⎫π4-x cos ⎝ ⎛⎭⎪⎫π4-x ·cos 2⎝ ⎛⎭⎪⎫π4-x=(2cos 2x -1)24sin ⎝ ⎛⎭⎪⎫π4-x cos ⎝ ⎛⎭⎪⎫π4-x=cos 22x 2sin ⎝ ⎛⎭⎪⎫π2-2x=cos 22x 2cos 2x =12cos 2x . 【例2-1】 18 解析:sin 2x =-cos ⎝ ⎛⎭⎪⎫π2+2x =-cos 2⎝ ⎛⎭⎪⎫π4+x =2sin 2⎝ ⎛⎭⎪⎫π4+x -1=2×⎝ ⎛⎭⎪⎫-342-1=18.【例2-2】 解:∵π4<α<3π4,∴-3π4<-α<-π4,-π2<π4-α<0.又∵cos ⎝ ⎛⎭⎪⎫π4-α=35,∴sin ⎝ ⎛⎭⎪⎫π4-α=-45. ∵0<β<π4,∴3π4<3π4+β<π.又∵sin ⎝ ⎛⎭⎪⎫3π4+β=513,∴cos ⎝ ⎛⎭⎪⎫3π4+β=-1213, ∴sin(α+β)=-cos ⎣⎢⎡⎦⎥⎤π2+(α+β)=-cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫3π4+β-⎝ ⎛⎭⎪⎫π4-α =-cos ⎝ ⎛⎭⎪⎫3π4+βcos ⎝ ⎛⎭⎪⎫π4-α-sin ⎝ ⎛⎭⎪⎫3π4+βsin ⎝ ⎛⎭⎪⎫π4-α=-⎝ ⎛⎭⎪⎫-1213×35-513×⎝ ⎛⎭⎪⎫-45=3665+2065=5665.【例3-1】 解:原式=⎝ ⎛⎭⎪⎫2cos 2α2+2sin α2cos α2⎝ ⎛⎭⎪⎫sin α2-cos α22·2cos2α2=2cos α2⎝ ⎛⎭⎪⎫cos α2+sin α2⎝ ⎛⎭⎪⎫sin α2-cos α22⎪⎪⎪⎪⎪⎪cos α2=cos α2·(-cos α)⎪⎪⎪⎪⎪⎪cos α2.又∵π<α<2π,∴π2<α2<π.∴cos α2<0.∴原式=cos α2·(-cos α)-cosα2=cos α.【例3-2】 解:∵tan α+1tan α=-103,∴3tan 2α+10tan α+3=0,解得tan α=-3或tan α=-13.又∵3π4<α<π,∴tan α=-13.∵5sin 2α2+8sin α2cos α2+11cos 2α2-82sin ⎝⎛⎭⎪⎫α-π2=5·1-cos α2+4sin α+11·1+cos α2-8-2cos α=5-5cos α+8sin α+11+11cos α-16-22cos α=8sin α+6cos α-22cos α=8tan α+6-22=-526.【例4-1】 证明:∵左边=cos 2αcos α2sin α2-sin α2cos α2=cos 2αcos 2α2-sin 2α2sin α2cosα2=cos 2αsin α2cos α2cos 2α2-sin2α2=cos 2αsin α2cos α2cos α=cos αsin α2cos α2=12sin αcos α=14sin 2α=右边. ∴原式成立.【例4-2】 证明:∵3sin β=sin(2α+β), 即3sin(α+β-α)=sin(α+β+α), ∴3sin(α+β)cos α-3cos(α+β)sin α =sin(α+β)cos α+cos(α+β)sin α, ∴2sin(α+β)cos α=4cos(α+β)sin α, ∴tan(α+β)=2tan α.又∵4tan α2=1-tan 2α2,∴tan α=2tanα21-tan2α2=12.∴tan(α+β)=2tan α=1.∵α+β∈⎝⎛⎭⎪⎫0,π2,∴α+β=π4.演练巩固提升1.A 解析:将sin α-cos α=2两端同时平方得,(sin α-cos α)2=2, 整理得1-2sin αcos α=2,于是sin 2α=2sin αcos α=-1,故选A. 2.C 解析:sin(α+β)sin(α-β)=(sin αcos β+cos αsin β)(sin αcos β-cos αsin β)=sin 2αcos 2β-cos 2αsin 2β=(1-cos 2α)cos 2β-cos 2α(1-cos 2β)=cos 2β-cos 2α=-a . 3.D 解析:tan(α+β)=tan ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α-π6+⎝ ⎛⎭⎪⎫π6+β=tan ⎝ ⎛⎭⎪⎫α-π6+tan ⎝ ⎛⎭⎪⎫π6+β1-tan ⎝ ⎛⎭⎪⎫α-π6tan ⎝ ⎛⎭⎪⎫π6+β=37+251-37×25=29352935=1,故选D. 4. 2 解析:∵sin 50°(1+3tan 10°)=sin 50°·cos 10°+3sin 10°cos 10°=sin 50°·2sin 40°cos 10°=2sin 40°cos 40°cos 10°=sin 80°cos 10°=cos 10°cos 10°=1,cos 80°·1-cos 20°=sin 10°·2sin 210°=2sin 210°.∴sin 50°(1+3tan 10°)-cos 20°cos 80°1-cos 20°=1-cos 20°2sin 210°= 2. 5.解:解法一:原式=sin 2α·sin 2β+cos 2α·cos 2β-12(2cos 2α-1)(2cos 2β-1)=sin 2α·sin 2β+cos 2α·cos 2β-12(4cos 2αcos 2β-2cos 2α-2cos 2β+1)=sin 2α·sin 2β-cos 2α·cos 2β+cos 2α+cos 2β-12=sin 2α·sin 2β+cos 2α·sin 2β+cos 2β-12=sin 2β+cos 2β-12=1-12=12.解法二:原式=1-cos 2α2·1-cos 2β2+1+cos 2α2·1+cos 2β2-12cos 2α·cos2β=14(1+cos 2α·cos 2β-cos 2α-cos 2β)+14(1+cos 2α·cos 2β+cos 2α+cos 2β)-12cos 2α·cos 2β=12+12cos 2α·cos 2β-12cos 2α·cos 2β=12.6.证明:由β=(α+β)-α,2α+β=(α+β)+α得sin[(α+β)-α]=m ·sin[(α+β)+α],即sin(α+β)cos α-cos(α+β)sin α=m [sin(α+β)cos α+cos(α+β)sin α],即(1-m )sin(α+β)cos α=(1+m )cos(α+β)sin α. 两边同除以(1-m )cos(α+β)cos α,得tan(α+β)=1+m1-mtan α(m ≠1),即等式成立.。
【志鸿优化设计】(安徽专用)高考数学一轮复习 第四章三角函数、解三角形4.4函数y=Asin(ω

课时作业21 函数y =A sin(ωx +φ)的图象与性质一、选择题1.将函数y =sin x 的图象上所有的点向右平移π10个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( ).A .y =sin ⎝ ⎛⎭⎪⎫2x -π10B .y =sin ⎝ ⎛⎭⎪⎫2x -π5C .y =sin ⎝ ⎛⎭⎪⎫12x -π10D .y =sin ⎝ ⎛⎭⎪⎫12x -π20 2.(2013届安徽省示范高中摸底)若把函数f (x )=sin ωx 的图象向左平移π3个单位,恰好与函数y =cos ωx 的图象重合,则ω的值可能是( ).A .13B .12C .23D .323.函数y =2sin 3x ⎝ ⎛⎭⎪⎫π6≤x ≤5π6与函数y =2的图象围成一个封闭图形,这个封闭图形的面积是( ).A .43B .π3C .4π3D .1 4.已知函数y =2sin(ωx +θ)为偶函数(0<θ<π),其图象与直线y =2的某两个交点的横坐标为x 1,x 2,若|x 2-x 1|的最小值为π,则( ).A .ω=2,θ=π2B .ω=12,θ=π2C .ω=12,θ=π4D .ω=2,θ=π45.若把函数y =cos x -3sin x +1的图象向右平移m (m >0)个单位长度,使点⎝ ⎛⎭⎪⎫π3,1为其对称中心,则m 的最小值是( ).A .πB .π2C .π3D .π66.(2012山东高考)函数y =2sin ⎝ ⎛⎭⎪⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为( ).A .2- 3B .0C .-1D .-1- 37.函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π4,给出下列三个命题:①函数f (x )在区间⎣⎢⎡⎦⎥⎤π2,5π8上是减函数;②直线x =π8是函数f (x )的图象的一条对称轴;③函数f (x )的图象可以由函数y=2sin 2x 的图象向左平移π4个单位得到.其中正确的是( ). A .①③ B.①② C .②③ D.①②③ 二、填空题8.已知f (x )=sin ⎝ ⎛⎭⎪⎫ωx +π3(ω>0),f ⎝ ⎛⎭⎪⎫π6=f ⎝ ⎛⎭⎪⎫π3且f (x )在区间⎝ ⎛⎭⎪⎫π6,π3内有最小值,无最大值,则ω=__________.9.已知函数y =sin ωx (ω>0)在一个周期内的图象如图所示,要得到函数y =sin⎝ ⎛⎭⎪⎫12x +π12的图象,则需将函数y =sinωx 的图象向__________平移__________个单位长度.10.水渠横断面为等腰梯形,如图所示,渠道深为h ,梯形面积为S ,为了使渠道的渗水量达到最小,应使梯形两腰及底边CD 之和达到最小.此时α应该是__________.三、解答题11.已知函数f (x )=sin(ωx +φ)(ω>0,|φ|<π)的图象如图所示:(1)求ω、φ的值;(2)设g (x )=f (x )f ⎝⎛⎭⎪⎫x -π4,求函数g (x )的单调递增区间.12.(2012安徽合肥一中模拟)已知向量a =⎝⎛⎭⎪⎫sin x ,cos 2x -12,b =(cos x ,-3),其中x ∈R ,函数f (x )=5a ·b -3.(1)求函数f (x )的最小正周期; (2)确定函数f (x )的单调递增区间;(3)函数f (x )的图象可以由函数y =5sin 2x 的图象经过怎样的变化而得到?参考答案一、选择题1.C 解析:函数y =sin x 的图象上的点向右平移π10个单位长度可得函数y =sin ⎝ ⎛⎭⎪⎫x -π10的图象;再把各点的横坐标伸长到原来的2倍(纵坐标不变)可得函数y =sin ⎝ ⎛⎭⎪⎫12x -π10的图象,所以所求函数的解析式是y =sin ⎝ ⎛⎭⎪⎫12x -π10.故选C. 2.D 解析:将函数y =sin ωx 的图象向左平移π3个单位,则得到函数y =sin ω⎝⎛⎭⎪⎫x +π3=sin ⎝ ⎛⎭⎪⎫ωx +ωπ3的图象,因为y =cos ωx =cos(-ωx )=sin ⎝ ⎛⎭⎪⎫π2+ωx ,所以ωπ3=π2+2k π,ω=32+6k ,k ∈Z ,所以当k =0时,ω=32,选D.3.C 解析:在同一坐标系中画出函数y =2sin 3x ⎝ ⎛⎭⎪⎫π6≤x ≤5π6和函数y =2的图象,如图,根据图象的对称性,所求的面积即为图中所示阴影部分的面积,为4π3.4.A 解析:∵y =2sin(ωx +θ)为偶函数,0<θ<π,∴θ=π2.∵图象与直线y =2的两个交点的横坐标为x 1,x 2,|x 2-x 1|min =π, ∴2πω=π,ω=2.故选A. 5.D 解析:y =cos x -3sin x +1=2cos ⎝ ⎛⎭⎪⎫x +π3+1,把该函数图象向右平移m (m>0)个单位后所得函数的解析式为y =2cos ⎝ ⎛⎭⎪⎫x -m +π3+1,由平移后⎝ ⎛⎭⎪⎫π3,1为其对称中心得1=2cos ⎝ ⎛⎭⎪⎫π3-m +π3+1,所以cos ⎝ ⎛⎭⎪⎫2π3-m =0, ∴2π3-m =k π+π2(k ∈Z ),解得m =-k π+π6(k ∈Z ),故m 的最小值是π6. 6.A 解析:由0≤x ≤9可得,-π3≤π6x -π3≤7π6,所以-3≤2sin ⎝ ⎛⎭⎪⎫π6x -π3≤2,所以最大值为2,最小值为-3,最大值与最小值之差为2- 3.7.B 解析:∵π2≤x ≤5π8,∴5π4≤2x +π4≤3π2, ∴f (x )在⎣⎢⎡⎦⎥⎤π2,5π8上是减函数,故①正确.f ⎝ ⎛⎭⎪⎫π8=2sin ⎝ ⎛⎭⎪⎫π4+π4=2,故②正确. y =2sin 2x 向左平移π4个单位得y =2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +π4=2cos2x ≠f (x ),故③不正确.故选B.二、填空题 8.143 解析:∵f ⎝ ⎛⎭⎪⎫π6=f ⎝ ⎛⎭⎪⎫π3且f (x )在区间⎝ ⎛⎭⎪⎫π6,π3上有最小值,无最大值, ∴f (x )在x =12×⎝ ⎛⎭⎪⎫π6+π3=π4处取得最小值.∴π4ω+π3=2k π-π2(k ∈Z ). ∴ω=8k -103(k ∈Z ).∵ω>0,∴当k =1时,ω=8-103=143;当k =2时,ω=16-103=383,此时函数在区间⎝ ⎛⎭⎪⎫π6,π3内已存在最大值.故ω=143. 9.左 π6 解析:由图象知函数y =sin ωx 的周期为T =3π-(-π)=4π,∴ω=2πT =12,故y =sin 12x .又y =sin ⎝ ⎛⎭⎪⎫x 2+π12=sin 12⎝ ⎛⎭⎪⎫x +π6,所以将函数y =sin 12x 的图象向左平移π6个单位长度,即可得到函数y =sin ⎝ ⎛⎭⎪⎫x 2+π12的图象.10.60° 解析:设CD =a ,由题意知CB =h sin α,AB =a +2htan α,∴S =12⎝ ⎛⎭⎪⎫a +a +2h tan α·h ,∴a =S h -htan α.设两腰与底边CD 之和为l ,则l =a +2CB =S h -h tan α+2hsin α=S h +2-cos αsin α·h =Sh +1+2sin2α22sin α2cosα2·h=Sh +3sin 2α2+cos2α22sin α2cosα2·h =S h +⎝⎛⎭⎪⎪⎫32tan α2+12tan α2·h ≥S h +⎝⎛⎭⎪⎪⎫232tan α2×12tan α2·h =S h+3·h , 当且仅当32tan α2=12tanα2,即tan α2=33时,上式取等号,∴α2=30°,即α=60°. 三、解答题11.解:(1)由图可知T =4⎝ ⎛⎭⎪⎫π2-π4=π, ω=2πT =2,又由f ⎝ ⎛⎭⎪⎫π2=1, 得sin(π+φ)=1,sin φ=-1.∵|φ|<π,∴φ=-π2.(2)由(1)知f (x )=sin ⎝⎛⎭⎪⎫2x -π2=-cos 2x . 因为g (x )=-cos 2x ⎣⎢⎡⎦⎥⎤-cos ⎝⎛⎭⎪⎫2x -π2 =cos 2x sin 2x =12sin 4x ,所以2k π-π2≤4x ≤2k π+π2(k ∈Z ),即k π2-π8≤x ≤k π2+π8(k ∈Z ). 故函数g (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π2-π8,k π2+π8(k ∈Z ).12.解:f (x )=5a ·b -3=5sin x cos x +5⎝ ⎛⎭⎪⎫cos 2x -12·(-3)-3=5sin x cos x -53cos 2x +532-3=52sin 2x -53·1+cos 2x 2+532-3=52sin 2x -532cos 2x -3 =5sin ⎝⎛⎭⎪⎫2x -π3-3.(1)T =2π2=π.(2)递增区间:⎣⎢⎡⎦⎥⎤k π-π12,k π+512π(k ∈Z ). (3)先向右平移π6个单位,再向下平移3个单位.。
高考数学一轮复习第四章三角函数解三角形第4讲三角函数的图象与性质第1课时三角函数的图象与性质一课件

数学
01
基础知识 自主回顾
02
核心考点 深度剖析
03
方法素养 助学培优
04
高效演练 分层突破
一、知识梳理
1.正弦、余弦、正切函数的图象与性质
函数
y=sin x
y=cos x
图象
y=tan x
函数 定义域
值域
函数的 最值
y=sin x
y=cos x
y=tan x
R
R
{x|x≠kπ+π2,k∈Z}
则 3tan x-
3>0,即
tan
x>
3 3.
所以π6+kπ<x<π2+kπ,k∈Z.
答案:π6+kπ,π2+kπ,k∈Z
2.函数 y= sin x-cos x的定义域为__________. 解析:要使函数有意义,需 sin x-cos x≥0, 即 sin x≥cos x. 解得 2kπ+π4≤x≤2kπ+54π(k∈Z),故原函数的定义域为2kπ+π4,2kπ+54π(k∈Z). 答案:2kπ+π4,2kπ+54π(k∈Z)
[-1,1]
[-1,1]
R
最大值 1,当且
最大值 1,当且
仅当__x_=__2_k_π___ _+__π2_,__k_∈__Z_;
仅当__x_=__2_k_π_,__ ___k_∈__Z____;
无最大值和最小值
最小值-1,当 最小值-1,当且 且仅当_x_=__2_k_π_-__π2_, 仅当_x_=__2_k_π_-__π_,
【迁移探究 2】 (变条件)本例(2)f(x)变为:f(x)=sin2x-π3,试讨论 f(x)在区间-π4,π4上 的单调性. 解:令 z=2x-π3,易知函数 y=sin z 的单调递增区间是-π2+2kπ,π2+2kπ,k∈Z. 由-π2+2kπ≤2x-π3≤π2+2kπ,得-1π2+kπ≤x≤51π2+kπ,k∈Z. 设 A=-π4,π4,B=x|-1π2+kπ≤x≤51π2+kπ,k∈Z,易知 A∩B=-1π2,π4. 所以,当 x∈-π4,π4时,f(x)在区间-1π2,π4上单调递增,又因为π4--π4=π2<T,所以 f(x)在区间-π4,-1π2上单调递减.
高三数学一轮课件 第四章 三角函数与解三角形 4.7 解三角形

于是由余弦定理可得 c= ������2 + ������2-2������������cos������
=
22 + 32-2 × 2 × 3 ×
-
1 4
=4.
-21-
考点1
考点2
考点3
考点4
(2)解:①由正弦定理可知,2cos A(sin Bcos C+sin Ccos B)=sin A,
即2cos Asin A=sin A.
-7-
知识梳理 双基自测
1234
4.实际问题中的常用角 (1)仰角和俯角:与目标视线在同一铅垂平面内的水平视线和目标 视线的夹角,目标视线在水平视线 上方 的角叫做仰角,目标视 线在水平视线 下方 的角叫做俯角(如图①).
-8-
知识梳理 双基自测
1234
(2)方向角:相对于某正方向的水平角,如南偏东30°、北偏西45°、 西偏北60°等.
关闭
D
解析 答案
-11BC的内角A,B,C的对边分别为a,b,c.已知C=60°,b= √6 ,c=3,
则A=
.
关闭
关闭
D
解析 答案
-12-
知识梳理 双基自测
123456
4.△ABC的内角A,B,C的对边分别为a,b,c,若2bcos B=acos C+ccos
-5-
知识梳理 双基自测
1234
2.三角形中的常见结论 (1)在△ABC中,A+B+C=π. (2)在△ABC中,A>B⇔a>b⇔sin A>sin B. (3)任意两边之和大于第三边,任意两边之差小于第三边.
-6-
知识梳理 双基自测
