三角形知识结构图
八年级各章知识结构图

知识结构图
第二十五章概率初步
知识结构图
第二十六章二次函数
知识结构图
第二十七章相似
知识结构图
第二十八章锐角三角函数
知识结构图
第二十九章投影与视图
知识结构图
第一章有理数
知识结构图
第二章整式的加减
知识结构图
知识结构图
第四章图形的认识初步
知识结构图
第五章相交线与平行线
知识结构图
第六章平面直角坐标系
知识结构图
第七章三角形
知识结构图
第八章二元一次方程组
知识结构图
第九章不等式与不等式组
知识结构图
第十章数据的收集、描述与整理
知识结构图
第十一章全等三角形
知识结构图
第十二章轴对称
知识结构图
等十三章实数
知识构图
第十四章一次函数
知识结构图
第十五章整式的乘除与因式分解
知识结构图
第十六章分式
知识结构图
第十七章反比例函数
知识结构图
第十八章勾股定理
知识结构图
第十九章四边形
知识结构图
第二十章数据的分析
知识结构图
第二十一章二次根式
知识结构图
第二十二章一元二次方程
知识结构图
第二十三章旋转
知识结构图
初中数学知识结构图
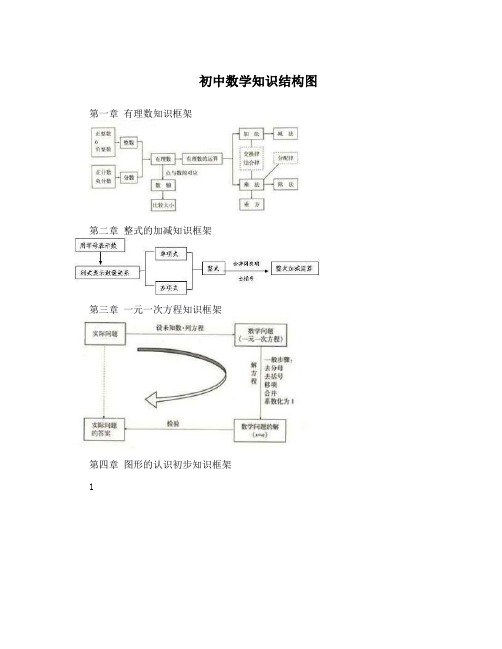
初中数学知识结构图第一章有理数知识框架
第二章整式的加减知识框架
第三章一元一次方程知识框架
第四章图形的认识初步知识框架
1
第五章相交线与平行线知识框架
第六章平面直角坐标系知识框架
第七章三角形知识框架
2
第八章二元一次方程组知识结构图
第九章不等式与不等式组知识框架
3
第十章数据的收集、整理与描述知识框架
全面调查收整描分得集理述析出数数数数结论据据据据抽样调查
第十一章全等三角形知识框架
第十二章轴对称知识框架
第十三章实数知识框架:
有理数
实数
无理数
4
第十四章一次函数知识框架
第十五章整式的乘除与分解因式知识框架整式乘法乘法法则
整式除法因式分解
第十六章分式知识框架
第十七章反比例函数知识框架
5
第十八章勾股定理知识框架
第十九章四边形知识框架
6
第二十章数据的分析知识框架
第二十一章二次根式知识框架
第二十二章一元二次方程知识框架7
第二十三章旋转知识框架
8
第二十四章圆知识框架
第二十五章概率
知识框架
第二十六章二次函数知识框架
9
第二十七章相似知识框架
第二十八章锐角三角函数知识框架
第二十九章投影与视图知识框架10
11。
北师大版九年级上第四章相似三角形复习课件

6. 四边形ABCD是平行四边形,点E是 BC的延长线 上的一点,而CE:BC=1:3,则 △ADG和△EBG的周 长比3:4 , 9:16 为面积比。
A
D
GF
B
CE
7. 举例说明三角形类似的一些应用. 例如用类似测物体的高度
测山高
测楼高
D
E 1.2m
A 1.6m B 8.4m C
8. 如图,△ABC是一块锐角三角形材料,边BC=120mm,高AD= 80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两 个顶点分别在AB、AC上,这个正方形零件的边长是多少?
3.如图,DE∥BC,AD:DB=1:2,DC,BE交于点O, 则△DOE与△BOC的周长之比是__1_:_3___, 面积比是___1_:_9___.
A
D
E
O
B
C
4、 两类似三角形对应高之比为3∶4,周长之和为28cm, 则两个三角形周长分别为 12cm与16cm
5、 两类似三角形的类似比为3∶5,它们的面积和为 102cm2,则较大三角形的面积为 75cm2
C2
A
C
B
A2
C1 B2
A
A1 B1
C
B
4、如图,在△ABC中,∠BAC=90°,AB=6, BC=12,点P从A点出发向B以1m/s的速度移动,点Q 从B点出发向C点以2m/s的速度移动,如果P、Q分别 从A、B两地同时出发,几秒后△ PBQ与原三角形类 似?
C
Q Q
B PP A
学以致用:
5.如图⊿ABC中,AB=8cm,BC=16cm ,点P从A点开始沿AB边向点B以2cm/s 的速度移动,点Q从点B开始沿BC边向 点C以4cm/s的速度移动。若点P、Q从A 、B处同时出发,经过几秒钟后, ⊿PBQ与⊿ABC类似?
《三角形的分类》三角形PPT优秀课件

在地理测量中,利用三角形的性质可 以计算两点之间的距离,这种方法在 航海、航空等领域也有广泛应用。
24
物理领域:力学平衡问题、光学成像原理等
力学平衡
在力学中,三角形结构常被用于解决平衡问题。例如,一个均质杠杆在平衡时,其重心、支点和力点构成的三角 形满足平衡条件。
光学成像
在光学中,三角形原理被应用于成像过程。例如,人眼通过晶状体将光线聚焦到视网膜上形成倒立的三角形图像 ,大脑再将其转换为正立的视觉感知。
20
相似和全等关系在解决实际问题中应用举例
建筑设计中的应用
地理测量中的应用
在建筑设计中,相似和全等关系可用于计 算建筑物的比例和尺寸,确保建筑物的稳 定性和美观性。
在地理测量中,相似和全等关系可用于计 算两点之间的距离、高度和角度等参数, 为地图制作和导航提供准确数据。
机械制造中的应用
艺术绘画中的应用
各类三角形的特点
等腰三角形有两条等边和两个等角;等边三角形三边相等,三个角都是60度;直角三角 形有一个90度的角和两条垂直的边;锐角三角形三个角都小于90度;钝角三角形有一个 角大于90度。
28
易错难点剖析及解决方法分享
易错点一
忽视三角形的定义和性质,导致 在解题过程中出现错误。解决方 法:牢记三角形的定义和性质,
在机械制造中,相似和全等关系可用于设 计和制造精确的机械零件和组件,确保机 械设备的正常运转和性能稳定。
在艺术绘画中,相似和全等关系可用于绘 制符合透视原理和比例关系的作品,使画 面更加逼真和生动。
2024/1/24
21
05
三角形在生活中的应用 场景举例
2024/1/24
22
建筑领域:桥梁设计、房屋结构稳定性分析等
八年级上第十一章至第十五章知识点梳理
7
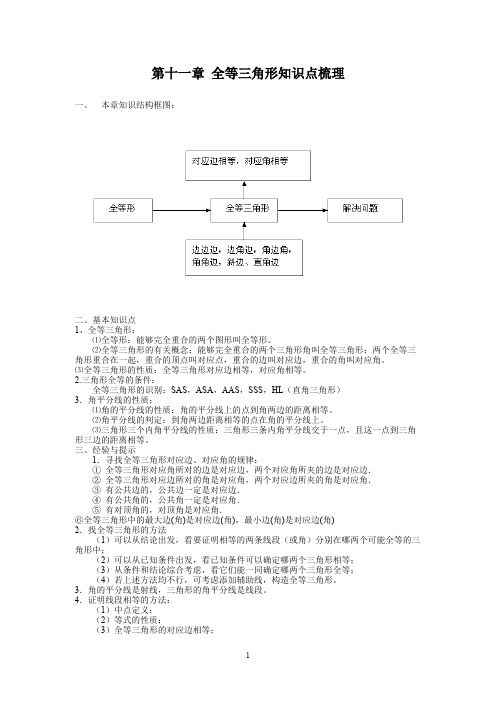
a 按定义分
正整数
正有理数
实数有理数负零有理数负 负正分 整分数 数数有限小数或无限循环小数
无理数负正无无理理数数无限不循环小数
b 按大小分:
正实数 实数 零
4、如图,每个图中是由若干个盆花组成的图案,每条边(包括两个顶点)有 n 盆花, 每个图案的花盆总数是 S,求 S 与 n 之间的关系式.
9
2、函数的概念
一般的,在一个变化过程中,如果有两个变量 x 和 y,并且对于 x 的每一个确定的值,
y 都有惟一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数。如果当 x=a 时,
6
第十三章
(一)本章知识结构框图
实数知识点汇总
1.本章知识的内在结构如下图所示:
2.本章知识的展开顺序如下图所示:
(二)知识点梳理: 本章主要内容包括算术平方根、平方根、立方根以及实数的有关概念和运算。本章的
重点是算术平方根和平方根的概念和求法,本章难点是平方根和实数的概念
1.有理数,无理数概念: 有理数:任何有限小数和无限循环小数都是有理数。 无理数:无限不循环小数叫做无理数。
负实数
在数轴上表示的两个实数,右边的数总比左边的数大. 5.与实数有关的概念:在实数范围内,相反数,倒数,绝对值的意义与有理数 范围内的意义完全一致;在实数范围内,有理数的运算法则和运算律同样成立。 每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表 示一个实数,即实数和数轴上的点是一一对应的。因此,数轴正好可以被实数 填满。
例 1、写出下列各问题中所满足的关系式,并指出各个关系式中,哪些量是变量,哪 些量是常量?
八年级(初二)数学-等腰三角形的知识结构图(思维导图)

八年级(初二)数学-等腰三角形的知识结构图(思维导图)文章格式已经无法更改,以下是文章的修改版本:在今天的社会中,信息技术已经成为了人们生活中不可或缺的一部分。
它们给我们带来了无数的便利和改变,但同时也带来了一些问题。
首先,信息技术的快速发展已经对传统的职业造成了很大的冲击。
许多传统行业的工作已经被自动化取代,导致很多人失去了工作。
此外,信息技术还带来了新的职业,这些职业需要人们具备新的技能和知识。
其次,信息技术的普及也带来了一些道德和隐私问题。
人们的个人信息和隐私已经变得更加容易受到侵犯。
此外,网络上存在大量的虚假信息和不良内容,这些对人们的价值观和思想观念产生了负面影响。
最后,信息技术的便利性也带来了一些负面影响。
人们越来越依赖于技术,导致他们失去了一些基本的技能和知识。
此外,过度使用电子设备也会对人们的健康产生负面影响,例如眼睛疲劳和颈椎病等。
总之,信息技术对我们的生活产生了巨大的影响,既带来了便利和改变,也带来了一些问题。
我们需要认真思考这些问题,并采取适当的措施来解决它们。
等腰三角形是初中数学中的一个重要知识点。
下面将介绍等腰三角形的定义、性质和判定方法。
1.定义:等腰三角形是指两边长度相等的三角形。
2.性质:等腰三角形的底角(即两边不等的角)相等,顶角(即两边相等的角)的角平分线也是底边中线。
3.判定:如果一个三角形的两边长度相等,则这个三角形是等腰三角形。
等腰直角三角形是指一个直角三角形中,两条直角边长度相等的三角形。
1.性质:等腰直角三角形的斜边长度是直角边长度的根号2倍,顶角(即直角所在的角)的角平分线也是底边中线。
2.判定:如果一个直角三角形的两条直角边长度相等,则这个三角形是等腰直角三角形。
等边三角形是指三条边长度相等的三角形。
1.定义:等边三角形的三个内角都是60度。
2.性质:等边三角形的三条高、三条中线、三条角平分线、三条垂直平分线都重合。
3.判定:如果一个三角形的三条边长度相等,则这个三角形是等边三角形。
八年级(初二)数学-等腰三角形的知识结构图(思维导图)

1.
1.1.
有两条边相等的三角形叫做等腰三角形.
1.2.
两腰相等
两底角相等
三线合一
顶角平分线
底边上的中线
底边上的高
轴对称图形
1.3.
①有两条边相等的三角形是等腰三角形.
②有两个角相等的三角形是等腰三角形.
2.
2.1.
顶角等于90°;
底角等于45°;
两直角边相等;
2.2.
①顶角为90°的等腰三角形.
②底角为45°的等腰三角形.
3.
3.1.
有三条边相等的三角形叫做等边三角形.
3.2.
三条边都相等;
三个角பைடு நூலகம்等于60°;
三个角都相等;
三线合一
顶角平分线
底边上的中线
底边上的高
3.3.
①三条边都相等的三角形是等边三角形.
②三个角都相等的三角形是等边三角形.
③有一个角是60°的等腰三角形是等边三角形.
三角形的三边关系课件

本节课知识点总结回顾
三角形的基本概念和性质
01
三角形是由三条不在同一直线上的线段首尾顺次连接所组成的
封闭图形。
三角形三边关系定理
02
三角形任意两边之和大于第三边,任意两边之差小于第三边。
三角形按边的分类
03
根据三角形的边长关系,可以将三角形分为等边三角形、等腰
三角形和一般三角形。
学生自我评价报告展示
交通网络优化
三角形的三边关系还可以应用于交通网络的优化。通过分析交通网络中各个节 点之间的连接关系,可以合理规划道路布局,提高交通网络的通行效率和便捷 性。
其他领域应用举例
机械设计
在机械设计中,三角形的稳定性原理被用于设计各种支撑 结构和连接件。例如,三角形的支架可以用于支撑机械部 件,确保其稳定性和可靠性。
对于多边形,可以将其划分成若 干个三角形,然后利用三角形的 三边关系定理来推断多边形的边 长关系。
实际应用
在建筑、工程等领域中,经常需 要利用三角形的三边关系定理来 解决实际问题,如测量距离、设 计结构等。同时,对于多边形边 长关系的探索也可以为相关领域 的研究提供新的思路和方法。
THANK YOU
02
三角形三边关系定理
三角形两边之和大于第三边
对于任意三角形ABC,有AB + BC > AC,AC + BC > AB,AB
+ AC > BC。
三角形两边之和大于第三边是三 角形的基本性质之一,也是判断 三条线段能否构成三角形的必要
条件。
若三条线段满足三角形两边之和 大于第三边的条件,则它们可以 构成一个三角形;反之,则不能。
当两点之间直线距离不可达时, 可以通过构造三角形并利用三 边关系找到最短路径。
人教版八年级各章知识结构图

⼈教版⼋年级各章知识结构图第⼀章有理数
知识结构图
第⼆章整式的加减
知识结构图
第三章⼀元⼀次⽅程知识结构图
第四章图形的认识初步知识结构图
第五章相交线与平⾏线知识结构图
第六章平⾯直⾓坐标系知识结构图第七章三⾓形
知识结构图
第⼋章⼆元⼀次⽅程组
知识结构图
第九章不等式与不等式组
知识结构图
第⼗章数据的收集、描述与整理知识结构图
第⼗⼀章全等三⾓形知识结构图
第⼗⼆章轴对称
知识结构图
等⼗三章实数
知识结构图
第⼗四章⼀次函数知识结构图
第⼗五章整式的乘除与因式分解知识结构图
第⼗六章分式
知识结构图
第⼗七章反⽐例函数
知识结构图
第⼗⼋章勾股定理
知识结构图
第⼗九章四边形
知识结构图
第⼆⼗章数据的分析知识结构图
第⼆⼗⼀章⼆次根式知识结构图
第⼆⼗⼆章⼀元⼆次⽅程知识结构图
第⼆⼗三章旋转
知识结构图
第⼆⼗四章圆
知识结构图
第⼆⼗五章概率初步知识结构图
第⼆⼗六章⼆次函数知识结构图
知识结构图。
三角形知识结构图

三角形知识结构图定义:多边形多边形内角和:1. 三角形的三边关系:(1) 三角形两边的和大于第三边(2) 三角形两边的差小于第三边2. 判断三条已知线段a、b、c能否组成三角形.当a最长,且有b+c>a时,就可构成三角形.3. 确定三角形第三边的取值范围:两边之差<第三边<两边之和.△ABC的三边分别为a,b,ca+b>c<c4. 三角形的三条高线(或高线所在直线)交于一点锐角三角形三条高线交于三角形内部一点,直角三角形三条高线交于直角顶点,钝角三角形三条高线所在直线交于三角形外部一点。
5、三角形的三条中线交于三角形内部一点。
6. 三角形的三条角平分线交于三角形内部一点。
7. 三角形的分类(2) 按边分8. 三角形的主要线段(1)、三角形的高线定义:从三角形的一个顶点向它的对边所在直线作垂线,_______________的线段叫做三角形的高线.(2)、三角形角平分线的定义:三角形一个角的平分线与它的对边相交,这个角的之间的线段叫做三角形的角平分线。
(3)、三角形的中线定义:连结三角形一个的线段叫做三角形的中线。
9. 三角形木架的形状不会改变,而四边形木架的形状会改变.这就是说,三角形具有稳定性,而四边形没有稳定性。
10. 三角形内角和定理三角形的内角和等于180°直角三角形的两个锐角互余。
11. 三角形外角和定理:三角形的外角和等于360°12. 三角形的外角与内角的关系(1)三角形的一个外角等于与它不相邻的两个内角的和。
(2)三角形的一个外角大于与它不相邻的任何一个内角。
13、n边形的内角和等于(n-2)·180 .多边形的外角和都等于360°.我们通过把多边形划分为若干个三角形,用三角形内角和去求多边形内角和,从而得到多边形的内角和公式为(n-2)×180°。
单元教学结构图
实践活动
利用这三条线段摆一个三角形,动手量一量给出来的三角形,以小组为单位先画4个不同类型的三角形,利用手中的工具分别计算三角形三个内角的和各是多少度。
作业设计
《索认识三角形的特性,。
2、探索三角形的内角和是180°
3、知道三角形任意两边之和大于第三边
4、灵活运用所学知识解释生活中的相关现象并解决简单的实际问题。
创新点
本单元是从学生的生活实践出发,,给予学生充分从事数学活动的时间和空间,让他们通过观察、操作、有条理的思考和推理、交流等活动,经历从现实空间抽象出几何图形的、探索;图形性质及其变化规律的过程,从而获得对图形的认识,发展窨观念。
单元教学目标
科目
第8册第五单元
执教
单元内容
三角形
教学目标
认知目标
1、认识三角形的特性,知道三角形任意两边之和大于第三边
2、会根据三角形的边、角特点给三角形分类,
3、三角形的内角和是180°
情感目标
1、注重培养学生的思维灵活性和创新意识。
2、加强直观演示和实践操作,引导学生积极参与知识的形成过程,感受成功的体验。
3、注重引导学生参与小组合作学习,培养学生的合作、交流意识。
操作目标
1、经历度量三角形边长的实践活动,理解三角形三边不等的关系。
2、通过动手操作,会按角的特征及边的特征给三角形进行分类。
3、通过动手操作,使学生理解并掌握三角形的内角和是180°的结论
探究能力
基础知识
学生已有一定的“空间与图形”的知识和经验,形成一定的抽象思维能力。
初中数学知识结构图

初中数学知识结构图(总11页)
--本页仅作为文档封面,使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
第一章有理数知识框架
第二章整式的加减知识框架
第三章一元一次方程知识框架
第四章图形的认识初步知识框架
第五章相交线与平行线知识框架
第六章平面直角坐标系知识框架
第七章三角形知识框架
第八章二元一次方程组知识结构图
第九章不等式与不等式组知识框架
第十章数据的收集、整理与描述知识框架
第十一章全等三角形知识框架
第十二章轴对称知识框架
第十三章实数知识框架:
有理数
实数
无理数
全面调查
抽样调查
收
集
数
据
描
述
数
据
整
理
数
据
分
析
数
据
得
出
结
论
第十四章 一次函数知识框架
第十五章 整式的乘除与分解因式知识框架
第十六章 分式知识框架
第十七章 反比例函数知识框架
整式乘法
整式除法
因式分解
乘法法则
第十八章勾股定理知识框架
第十九章四边形知识框架
第二十章数据的分析知识框架
第二十一章二次根式知识框架
第二十二章一元二次方程知识框架
第二十三章旋转知识框架
第二十四章圆知识框架
第二十五章概率
知识框架
第二十六章二次函数知识框架
第二十七章相似知识框架
第二十八章锐角三角函数知识框架
第二十九章投影与视图知识框架。
