2014年普通高等学校招生全国统一考试浙江卷(理科)精校版

合集下载

2014年全国高考浙江省数学(理)试卷及答案【精校版】

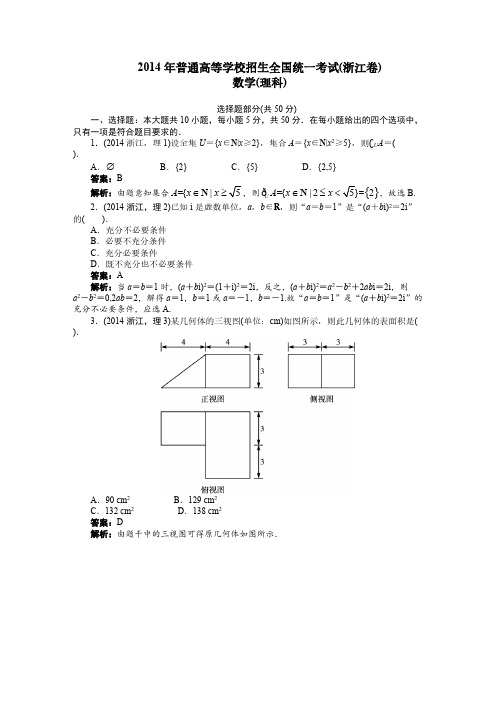
2014年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，则=A C U （）A. ∅B. }2{C. }5{D. }5,2{（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是 A. 902cm B. 1292cm C. 1322cm D. 1382cm4.为了得到函数x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（）A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位5.在46)1()1(y x ++的展开式中，记nm yx 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（）A.45B.60C.120D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f （） A.3≤c B.63≤<c C.96≤<c D. 9>c7.在同一直角坐标系中，函数x x g x x x f a alog )(),0()(=≥=的图像可能是（）8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩，,min{,},y x yx y x x y≥⎧=⎨<⎩，设a,b 为平面向量，则（）A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+ D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球()3,3m n ≥≥，从乙盒中随机抽取()1,2i i =个球放入甲盒中. （a ）放入i 个球后，甲盒中含有红球的个数记为()1,2ii ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为()1,2i p i =. 则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<< 10.设函数21)(x x f =，),(2)(22x x x f -=|2sin |31)(3x x f π=，99,,2,1,0,99==i ia i ，记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ，.3,2,1=k 则( )A.321I I I <<B. 312I I I <<C. 231I I I <<D. 123I I I <<二、填空题：本大题共7小题，每小题4分，共28分.11.若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12.随机变量ξ的取值为0,1,2，若()105P ξ==，()1E ξ=，则()D ξ=________. 13.当实数x ，y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，14ax y ≤+≤恒成立，则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ，则实数a 的取值范围是______15.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x （0a b >>）两条渐近线分别交于点B A ,，若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________17、如图，某人在垂直于水平地面的墙面前的点处进行射击训练.已知点到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若则的最大EA值。

2014年全国高考浙江省高中数学理科试卷和答案

2014年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，则=A C U （） A. ∅ B. }2{ C. }5{ D. }5,2{（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是 A. 902cm B. 1292cm C. 1322cm D. 1382cm4.为了得到函数x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（）A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位5.在46)1()1(y x ++的展开式中，记n m y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（）A.45B.60C.120D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f （）A.3≤cB.63≤<cC.96≤<cD. 9>c 7.在同一直角坐标系中，函数x x g x x x f a a log )(),0()(=≥=的图像可能是（）8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩，,min{,},y x yx y x x y≥⎧=⎨<⎩，设a,b 为平面向量，则（）A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球()3,3m n ≥≥，从乙盒中随机抽取()1,2i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为()1,2i i ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为()1,2i p i =.则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<<10.设函数21)(x x f =，),(2)(22x x x f -=|2sin |31)(3x x f π=，99,,2,1,0,99==i ia i ，记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ，.3,2,1=k 则( )A.321I I I <<B. 312I I I <<C. 231I I I <<D.123I I I <<二、填空题：本大题共7小题，每小题4分，共28分.11.若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12.随机变量ξ的取值为0,1,2，若()105P ξ==，()1E ξ=，则()D ξ=________.13.当实数x ，y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，14ax y ≤+≤恒成立，则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ，则实数a 的取值范围是______15.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x （0a b >>）两条渐近线分别交于点B A ,，若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________ 17、如图，某人在垂直于水平地面的墙面前的点处进行射击训练.已知点到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若则的最大值。

2014年全国高考理综试题及答案-浙江卷

2014年普通高等学校招生全国统一考试（浙江卷）理科综合化学试题7．下列说法不正确．．．的是A．光催化还原水制氢比电解水制氢更节能环保、更经济B．氨氮废水(含NH4+及NH3)可用化学氧化法或电化学氧化法处理C．某种光学检测技术具有极高的灵敏度，可检测到单个细胞(V=10－12L)内的数个目标分子，据此可推算该检测技术能测量到细胞内浓度约为10－12～10－11mol ·L－1的目标分子D．向汽油中添加甲醇后，该混合燃料的热值不变8．下列说法正确的是A．金属汞一旦洒落在实验室地面或桌面时，必须尽可能收集，并深埋处理B．用pH计、电导率仪(一种测量溶液导电能力的仪器)均可检测乙酸乙酯的水解程度C．邻苯二甲酸氢钾可用于标定NaOH溶液的浓度，假如称量邻苯二甲酸氢钾时电子天平读数比实际质量偏大，则测得的NaOH溶液浓度比实际浓度偏小D．向某溶液中加入茚三酮试剂，加热煮沸后溶液若出现蓝色，则可判断该溶液含有蛋白质Array 9．如表所示的五种元素中，W、X、Y、Z为短周期元素，这四种元素的原子最外层电子数之和为22。

下列说法正确的是A．X、Y、Z三种元素最低价氢化物的沸点依次升高B．由X、Y和氢三种元素形成的化合物中只有共价键C．物质WY2、W3X4、WZ4均有熔点高、硬度大的特性D．T元素的单质具有半导体的特性，T与Z元素可形成化合物TZ410．下列说法正确的是A．乳酸薄荷醇酯( )仅能发生水解、氧化、消去反应B．乙醛和丙烯醛( )不是同系物，它们与氢气充分反应后的产物也不是同系物C．淀粉和纤维素在酸催化下完全水解后的产物都是葡萄糖D．CH3COOCH2CH3与CH3CH2COOCH3互为同分异构体，1H－NMR谱显示两者均有三种不同的氢原子且三种氢原子的比例相同，故不能用1H－NMR来鉴别11．镍氢电池(NiMH)目前已经成为混合动力汽车的一种主要电池类型。

NiMH中的M表示储氢金属或合金。

2014年浙江省数学(理)高考真题含答案(超完美word版)

2014年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，则=A C U （）A. ∅B. }2{C. }5{D. }5,2{（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是 A. 902cm B. 1292cm C. 1322cm D. 1382cm4.为了得到函数x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（）A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 5.在46)1()1(y x ++的展开式中，记nmy x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（）A.45B.60C.120D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f （） A.3≤c B.63≤<c C.96≤<c D. 9>c7.在同一直角坐标系中，函数x x g x x x f a alog )(),0()(=≥=的图像可能是（）A. B. C. D.8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩，,min{,},y x yx y x x y ≥⎧=⎨<⎩，设a,b 为平面向量，则（）A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+ D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球()3,3m n ≥≥，从乙盒中随机抽取()1,2i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为()1,2ii ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为()1,2i p i =. 则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<< 10.设函数21)(x x f =，),(2)(22x x x f -=|2sin |31)(3x x f π=，99,,2,1,0,99==i ia i ，记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ，.3,2,1=k 则( )A.321I I I <<B. 312I I I <<C. 231I I I <<D. 123I I I << 二、填空题：本大题共7小题，每小题4分，共28分.11.若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12.随机变量ξ的取值为0,1,2，若()105P ξ==，()1E ξ=，则()D ξ=________. 13.当实数x ，y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，14ax y ≤+≤恒成立，则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ，则实数a 的取值范围是______15.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x （0a b >>）两条渐近线分别交于点B A ,，若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________ 17、如图，某人在垂直于水平地面的墙面前的点处进行射击训练.已知点到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若则的最大值。

[精品]2014年全国高考浙江省高中数学理科试卷和答案

2014年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，则=A C U （） A. ∅ B. }2{ C. }5{ D. }5,2{（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是A. 902cmB. 1292cmC. 1322cmD. 1382cm4.为了得到函数x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（）A.向右平移4π个单位B.向左平移4π个单位C.向右平移12π个单位D.向左平移12π个单位5.在46)1()1(y x ++的展开式中，记n m y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（）A.45B.60C.120D. 210 6.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f （） A.3≤c B.63≤<c C.96≤<c D.9>c7.在同一直角坐标系中，函数x x g x x x f a a log )(),0()(=≥=的图像可能是（）8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩，,min{,},y x yx y x x y ≥⎧=⎨<⎩，设a,b 为平面向量，则（）A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球()3,3m n ≥≥，从乙盒中随机抽取()1,2i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为()1,2i i ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为()1,2i p i =. 则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<< 10.设函数21)(x x f =，),(2)(22x x x f -=|2sin |31)(3x x f π=，99,,2,1,0,99==i ia i ，记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ，.3,2,1=k 则( )A.321I I I <<B. 312I I I <<C. 231I I I <<D.123I I I <<二、填空题：本大题共7小题，每小题4分，共28分.11.若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12.随机变量ξ的取值为0,1,2，若()105P ξ==，()1E ξ=，则()D ξ=________.13.当实数x ，y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，14ax y ≤+≤恒成立，则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ，则实数a 的取值范围是______15.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x （0a b >>）两条渐近线分别交于点B A ,，若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________EA17、如图，某人在垂直于水平地面的墙面前的点处进行射击训练.已知点到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若则的最大值。

2014年高考试题——理综(浙江卷)含答案

2014年普通高等学校招生全国统一考试（浙江卷）理科综合化学试题相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5 K-39 Ca-40 Fe-56 Cu-64 Ba-1377．下列说法不正确．．．的是A．光催化还原水制氢比电解水制氢更节能环保、更经济B．氨氮废水（含NH4+及NH3）可用化学氧化法或电化学氧化法处理C．某种光学检测技术具有极高的灵敏度，可检测到单个细胞（V ≈10－12L）内的数个目标分子，据此可推算该检测技术能测量细胞内浓度约为10－12~10－11mol·L－1的目标分子D．向汽油中添加甲醇后，该混合燃料的热值不变8．下列说法正确的是A．金属汞一旦洒落在实验室地面或桌面时，必须尽可能收集，并深埋处理B．用pH计、电导率仪（一种测量溶液导电能力的仪器）均可监测乙酸乙酯的水解程度C．邻苯二甲酸氢钾可用于标定NaOH溶液的浓度。

假如称量邻苯二甲酸氢钾时电子天平读数比实际质量偏大，则测得的NaOH溶液浓度比实际浓度偏小D．向某溶液中加入茚三酮试剂，加热煮沸后溶液若出现蓝色，则可判断该溶液含有蛋白质9．如表所示的五种元素中，W、X、Y、Z为短周期元素，这四种元素的原子最外层电子数之和为22。

下列说法正确的是A．X、Y、Z三种元素最低价氢化物的沸点依次升高B．由X、Y和氢三种元素形成的化合物中只有共价键C．物质WY2、W3X4、WZ4均有熔点高、硬度大的特性D．T元素的单质具有半导体的特性，T与Z元素可形成化合物TZ410．下列说法正确的是A．乳酸薄荷醇酯（）仅能发生水解、氧化、消去反应B．乙醛和丙烯醛（）不是同系物，它们与氢气充分反应后的产物也不是同系物C．淀粉和纤维素在酸催化下完全水解后的产物都是葡萄糖D．CH3COOCH2CH3与CH3CH2COOCH3互为同分异构体，1H-NMR 谱显示两者均有三种不同的氢原子且三种氢原子的比例相同，故不能用1H-NMR来鉴别11．镍氢电池（NiMH）目前已经成为混合动力汽车的一种主要电池类型。

2014年高考浙江理科数学试题及答案

2014 年一般高等学校招生全国一致考试（浙江卷）数学（理科）第Ⅰ卷（选择题共50分）一、选择题：本大题共10 小题，每题 5 分，共50 分，在每题给出的四个选项中，只有一项切合题目要求．（ 1）【 2014 年浙江，理1， 5 分】设全集 U { x N | x 2} ，会合 A{ x N | x25} ，则e U A（）（ A）（B） {2}（ C） {5}（ D） {2,5}【答案】 B【分析】 A { x25}{ x N | x5} ， C U A { x N | 2x5}{2}，应选 B．N | x【评论】本题主要考察全集、补集的定义，求会合的补集，属于基础题．（ 2）【 2014 年浙江，理2， 5 分】已知i是虚数单位，a,b R ，则“ a b1”是“ ( a bi) 22i ”的（）（ A）充足不用要条件（ B）必需不充足条件（C）充足必需条件（ D）既不充足也不用要条件【答案】 A【分析】当 a b1时，(a bi) 2(1 i) 22i ，反之， (a bi) 22i，即 a 2b22abi 2i ，则 a 2b20 ，2 ab2a1a1解得或b ，应选 A．b11【评论】本题考察的知识点是充要条件的定义，复数的运算，难度不大，属于基础题．（ 3）【 2014 年浙江，理 3， 5 分】某几何体的三视图（单位：cm）以下图，则此几何体的表面积是（）2（B） 129 cm 2（ C）132 cm22（ A）90 cm（ D） 138 cm 【答案】 D【分析】由三视图可知直观图左侧一个横放的三棱柱右边一个长方体，故几何体的表面积为：S 2 4 6 2 3 4 3 633343 5 213 4138，应选 D．2【评论】本题考察了由三视图求几何体的表面积，依据三视图判断几何体的形状及数据所对应的几何量是解题的重点．（ 4）【 2014 年浙江，理4，5 分】为了获取函数y sin3 x cos3x 的图像，能够将函数 y 2 cos3x 的图像（）（ A）向右平移个单位（ B）向左平移4个单位（ C）向右平移12个单位（ D）向左平移个单位【答案】 C412【分析】 y sin3 x cos3x 2 sin(3x) 2 sin[3( x)] ，而 y 2 cos3x 2 sin(3 x) = 2 sin[3( x6)] ，4122由 3(x)3( x) ，即 x x12，故只要将 y 2 cos3x 的图象向右平移个单位，应选 C．61212【评论】本题考察两角和与差的三角函数以及三角函数的平移变换的应用，基本知识的考察．（ 5 ）【 2014年浙江，理 5，5分】在(1x)6 (1y) 4的展开式中 , 记 x m y n项的系数 f (m, n)，则f (3,0) f (2,1) f (1,2) f (0,3) =（）（ A）45（ B）60（ C） 120（ D） 210【答案】 C【分析】令 x y ，由题意知 f (3,0) f (2,1) f (1,2) f (0,3) 即为(1x)10睁开式中 x3的系数，故 f (3,0) f (2,1) f (1,2) f (0,3) =C107120 ，应选 C．【评论】本题考察二项式定理系数的性质，二项式定理的应用，考察计算能力．（ 6）【 2014 年浙江，理6， 5 分】已知函数 f (x)x3ax2bx c ，且 0 f ( 1) f ( 2) f ( 3) 3 （）（ A）c 3（ B）3 c6（ C）6 c 9（ D）c 9【答案】 C【分析】由 f ( 1)f ( 2) f ( 3) 得1 a b c 8 4a 2b c ，解得 a 6 ，1 a b c 27 9a 3b cb 11 所以 f (x) x 3 6x 2 11xc ，由 0 f ( 1) 3，得 01 6 11 c 3 ，即 6 c9 ，应选 C ．【评论】本题考察方程组的解法及不等式的解法，属于基础题．（ 7）【 2014 年浙江，理 7，5 分】在同向来角坐标系中，函数f ( x) x a (x 0) ， g( x) log a x 的图像可能是（）（ A ）（ B ）（C ）（D ）【答案】 D【分析】函数 f (x)x a ( x 0) ， g( x) log a x 分其他幂函数与对数函数答案 A 中没有幂函数的图像 , 不切合；答案 B 中，( ) x a ( x 0) 中 a 1 ，g(x) log a x 中 0 a 1，不切合；答案 C 中，f (x) a(x 0) 中 0 a 1， fxx g(x) log a x 中 a 1 ，不切合；答案 D 中， f (x)x a (x 0) 中 0 a 1 ， g( x) log a x 中 0a 1 ，切合，应选 D ．【评论】本题考察的知识点是函数的图象，娴熟掌握对数函数和幂函数的图象和性质，是解答的重点．（ 8）【 2014 年浙江，理 8， 5 分】记 max{ x, y}r r r r min{| r r （ A ） min{| a b |,| a b |} a |,| b |} r r 2 r r 2 r 2 r 2 （ C ） max{| a b | ,| a b | } | a | |b | 【答案】 Dr【分析】由向量运算的平行四边形法可知 min{| a x, x y， min{ x, y} y, x r r y ，设 a,b 为平面向量，则（） y, x y r x, x y r rr r r min{|（ B ） min{| a b |,| a b |} a |,| b |}r r 2 r r 2 r 2 r 2（ D ） max{| a b | ,| a b | } | a | | b | r r r r rb |,| a b |} 与 min{| a |,| b |} 的大小不确立，平行四边形法可知r r r r90r rr rrrmax{| ab |,| ab |} 所对的角大于或等于，由余弦定理知 max{| a b |2,| a b |2} | a |2|b |2，r r 2 r r r r r r r r r 2r 2| a b |2 | a b |2 2(| a |2 | b |2 ) 2 ），应选 D ．（或 max{| a b | ,| a b | } 2 r 2| a | | b | r r r r r【评论】本题在办理时要联合着向量加减法的几何意义，将a ，b ， a b ， a b 放在同一个平行四边形中进行比较判断，在详细解题时，本题采纳了清除法，对错误选项进行举反例说明，这是高考取做选择题的常用方法，也不失为一种迅速有效的方法，在高考选择题的办理上，未必每一题都要写出详细解答步骤，针对选择题的特色，有时“清除法”，“确立法”，“特别值”代入法等或许是一种更迅速，更有效的方法．（ 9）【 2014 年浙江，理 9，5 分】已知甲盒中仅有1 个球且为红球，乙盒中有 m 个红球和 n 个篮球 ( m 3,n 3) ，从乙盒中随机抽取 i (i 1,2) 个球放入甲盒中．（ a ）放入 i 个球后，甲盒中含有红球的个数记为i(i 1,2) ；（ b ）放入 i 个球后，从甲盒中取1 个球是红球的概率记为p i (i 1,2) ．则（）（ A ） p 1 p 2 ,E( 1 )E( 2 ) （ B ） p 1p 2 , E( 1 ) E( 2 ) （ C ） p 1 p 2 , E( 1 ) E( 2 ) （ D ） p 1p 2 ,E( 1 ) E( 2 )【答案】 A【分析】解法一：p 1m n1 2m n， p 2C n 21 C m 1C n 1 2C m 2 =3m 23m 2mnn 2 n， m nmn 22( m n )2g2g 23(mn)(m n1)Cm n3Cm n3 Cm n∴ p 1p 22m n － 3m 23m 2mn n 2 n = 5mn n( n 1)1)0 ，故 p 1 p 2 ．2( m n) 3(m n)( m n 1) 6(m n)( m n又∵P(11)m n，P(12) m ，∴ E( 1) 1 nn2m n 2m n ，nm n mm m n 又P( 2C n 2n(n 1)， P(C n 1C m 12mn ，1)(m n)( m n 22)(mn)( m nC m 2 n 1)C m2n1) P (23)C m 2m (m1)C m 2( m n )( m n 1)n∴E( 2)1n( n 1)22mn n 1) 3 (m m(m 1)1) = 3m 2n 2 3m n 4mn( mn)(m n 1)( m n)( m n)( m n (m n)(m n 1)3m 2 n 23m n 4mn － 2m n = m( m 1)mnE( 2 ) E( 1)=0 ，所以 E( 2) E( 1) ，应选 A ．(mn)(m n 1)n)( m n 1) m n ( m解法二：在解法一中取 mn3 ，计算后再比较，应选A ．【评论】正确理解ii1,2 的含义是解决本题的重点．本题也能够采纳特别值法，不如令m n3 ，也能够很快求解．（ 10）【 2014 年浙江，理 10，5 分】设函数 f 1 ( x) x 2， f 2 ( x)2( x x 2) ， f 3 ( x) 1 | sin 2 x |， a ii， i 0,1, 2 ，399 L , 99 ，记 I k | f k ( a 1 ) f k (a 0 ) | | f k (a 2 ) f k (a 1) | L| f k ( a 99 ) f k (a 98 ) | ， k 1,2,3 ，则（）（A ） I 1I 2 I 3（B ） I 2I 1I 3（C ） I 1I 3I 2（D ） I 3I 2I 1【答案】 B【分析】解法一：221 135299 1 1 992由ii 11 g2i 1，故 I 1L(99 9999)g1 ，9999 99 9999 99 99 99ii 1 i2i 1 21 | 99 (2i 1)|，故 I 2150(98 0)98g 100 由 2222 1 ，9999999999 9999 2 9999 99I 31 1 ) | |sin(2 0 g 2 |sin(2 1 |sin(29998( |sin(2 g g ) | | sin(2 ) | g ) | L g ) | | sin(2 g ) |)3 99 99 99 999999 = 1 25 741，故 I 2I 1I 3，应选 B ．[2sin(2 g ) 2sin(2 g)]3 9999解法二：估量法： I k 的几何意义为将区间 [0,1] 平分为 99 个小区间，每个小区间的端点的函数值之差的绝对值之和．如图为将函数f 1 (x)2的区间 [0,1] 平分为4 个小区间的情况，因f 1 (x) 在 [0,1] 上递加，此时xI 1 | f (a 1 ) f (a 0 ) | | f (a 2 ) f (a 1 ) | | f (a 3 ) f (a 2 ) | | f ( a 4 ) f ( a 3 ) |= A 1H 1A 2H 2 A 3H 3A 4H 4f (1)f (0)1，同理对题中给出的 I 1 ，相同有 I 1 1；而 I 2 略小于 21 ，11 42I 3 略小于 4，所以估量得 I 2 I 1I 3，应选 B ．33【评论】本题主要考察了函数的性质，重点是求出这三个数与1 的关系，属于难题．第Ⅱ卷（非选择题共 100 分）二、填空题：本大题共 7 小题，每题4 分，共 28 分．（ 11）【 2014 年浙江，理 11，5 分】若某程序框图以下图，当输入 50 时，则该程序运算后输出的结果是．【答案】 6【分析】第一次运转结果S 1,i 2 ；第二次运转结果 S 4,i 3；第三次运转结果 S 11,i 4 ；第四次运转结果 S 26,i 5；第五次运转结果 S 57,i 6；此时 S 57 50 ，∴输出 i 6 ．【评论】本题考察了直到型循环构造的程序框图，依据框图的流程模拟运转程序是解答此类问题的常用方法．（ 12）【 2014 年浙江，理 12，5 分】随机变量的取值为 0,1,2 ，若 P( 0)1，E( )1，则D( )=．【答案】250 1251 时的概率为p ，P1p1 p1 【分析】设的散布列为：551 13由E( ) 0 1 p2 (1 p 1 ，解得 p5 ) 55 的散布列为即为 0 1 2P1315 55故E( ) (01) 2 1 (1 1) 2 3 (2 1) 2 12 ． 5 55 5 【评论】本题综合考察了散布列的性质以及希望、方差的计算公式．x 2 y 4 0（ 13）【 2014 年浙江，理 13， 5 分】当实数 x, y 知足 xy 1 0 时， 1 axy4 恒成立，则实数 a 的取值范x1围是__ ．【答案】 [1,3]2【分析】解法一：x 2 y 4 0作出不等式组xy1 0所表示的地区如图，由1 axy4 恒成立，x 1故 A(1,0), B(2,1), C(1,3) ，三点坐标代入 11 a 43ax y 4 ，均成立得1 2a 1 4 解得 1 a，∴实数 a2321 a42的取值范围是 [1, 3 ] ．解法二：2x 2 y 4 0作出不等式组xy1 0所表示的地区如图，由 1 axy4 得，由图剖析可知， a0 且在 A(1,0) 点x 1a 1，得 1 a3，故实数 a 的取值范围是 [1, 3 ]．获得最小值，在 B(2,1) 获得最大值，故12a 4 2 2 【评论】本题考察线性规划，考察了数形联合的解题思想方法，考察了数学转变思想方法，训练了不等式组得解法，是中档题．（ 14）【2014 年浙江，理 14，5 分】在 8 张奖券中有一、二、三等奖各 1 张，其他 5 张无奖．将这 8 张奖券分派给 4 个人，每人 2 张，不一样的获奖状况有种（用数字作答）．【答案】 60【分析】解法一：不一样的获奖分两种，一是有一人获两张奖券，一人获一张奖券，共有C 32 A 42 36 ，二是有三人各获取一张奖券，共有 A 43 24 ，所以不一样的获奖状况共有 36 24 60 种．解法二：将一、二、三等奖各 1 张分给 4 个人有 43 64 种分法，此中三张奖券都分给一个人的有 4 种分法，所以不一样的获奖状况共有 64 4 60 种．【评论】本题考察摆列、组合及简单计数问题，考察学生的计算能力，属于基础题．x 2 x, x 0（ 15）【 2014 年浙江，理 15，5 分】设函数 f ( x) 2x 若 f ( f (a)) 2 ，则实数 a 的取值范围是．x , 0 【答案】 ( , 2] ．【分析】由题意f (a ) 02 或 f (a) 0 ，解得 f (a) 2 ∴当 a 0 或 a0 ，解得 a 2 ． f 2 (a) f (a) f 2 (a) 2 a 2 a 2 a 2 2【评论】本题主要考察分段函数的应用，其他不等式的解法，表现了数形联合的数学思想，属于中档题．2 2（ 16）【 2014 年浙江，理 16， 5 分】设直线 x 3 y m0 ( m 0 ) 与双曲线xy1 （ a 0,b 0 ）两条渐近a 2b 2线分别交于点 A ， B ．若点P( m,0)知足| PA | | PB |，则该双曲线的离心率是．【答案】 52【分析】解法一：由双曲线的方程可知，它的渐近线方程为ybx 和 ybx ，分别与直线 l ：aax 3y m0 联立方程组，解得， A(a am , bm) ， B ( am , bm )，设 AB 中3b a 3b a 3b a 3bam ambm bm点为 Q ，由 |PA| |PB|得，则 Q(a3ba 3b , a3b a3b) ，223b 2 m22122即 Q(a m,3b m 2 )， PQ 与已知直线垂直，∴ k PQ gk l1 ，即a9b1 ，22 29b2 m ga9b aa 3a 2 9b 2 m2即得 2a28b 2 ，即 2a28(c2a 2) ，即c 5，所以 ec52a．解法二：a42不如设 a 1 ，渐近线方程为 x 2y 20 即 b 2 x 2 y 20 ，由 b 2 x 2 y 2 0 消去 x ，12b 2x 3 y m 0得 (9b 2 1) y 2 6b 2my b 2 m 0 ，设 AB 中点为 Q(x 0 , y 0 ) ，由韦达定理得： y 0 3b 2 m ① ，2 19b 3b 2m 3又 x 0 3y 0 m ，由 k PQ gk l 1得 y 0 1 1 ，即得 y 0 1 1 得 y 0 3m 代入①得 m ，x 0 g g 5 2m 33 y 0 2m 3 9b 1 5得 b 21 ，所以 c2 a 2 b 2 1 1 5，所以 c 5 ，得 e c c 5 ．4 4 4 2 a 2【评论】本题考察双曲线的离心率，考察直线的地点关系，考察学生的计算能力，属于中档题．（ 17）【 2014 年浙江，理 17， 5 分】如图，某人在垂直于水平川面ABC 的墙眼前的点 A 处进行射击训练．已知点 A 到墙面的距离为 AB ，某目标点 P 沿墙面上的射击线 CM 挪动，这人为了正确对准目标点 P ，需计算由点 A 察看点 P 的仰角的大小．若， 25m ， BCM 30 ，则 tan 的最大值是（仰AB 15m AC角为直线 AP 与平面 ABC 所成角）．【答案】5 39【分析】解法一：∵ AB15cm ， AC25cm ， ABC90 ，∴ BC20cm ，过 P 作 PPBC ，交 BC 于 P ，1当 P 在线段BC 上时，连结AP ，则 tanPP'，设 BPx ，则 CP20 x ，AP '（x 20 ）由BCM30 ，得 PP'CP 'tan 303(20 x) ．3在直角 ABP 中，2PP '3 20 x20 x，则函数在AP '225x∴ tanAP '3 g，令y225 x 2225 x 2x0,20 单一递减，∴x 0 时， tan 获得最大值为3 g 2020 3 4 33225 24592当 P 在线段 CB 的延伸线上时，连结AP ，则 tanPP'，设 BPx ，AP '则 CP20 x ，（ x0 ）由BCM30 ，得 PP'CP 'tan 303 (20x) ，3在直角 ABP 中， AP '225x 2 ，∴ tanPP ' 3 g 20 x ，AP ' 3 225 x 2令 y20 x ，则 y '225 20x，当 0x 22545 时 y ' 0 ；当 x 45时 y ' 0 ，x 2 )225 x 2(225 225 x 2204420 45 5355 3所以当x 45时 y max 4 ，此时x45时， tan获得最大值为，33g 94225( 45 ) 2434综合 1， 2 可知 tan获得最大值为5 3 ．9解法二：如图以 B 为原点， BA 、 BC 所在的直线分别为x ， y 轴，成立以下图的空间直角坐标系，∵ AB15cm ， AC25cm ， ABC90 ，∴ BC 20cm ，由 BCM 30 ，可设 P(0, x,3x))(20x 20）， P '(0, x,0) ， A(15,0,0) ，3（此中3x)PP '(20320 x所以 tan3152 x 2g，AP '3225 x 2设 f (x)tan3 20xx20) ， f '(x)3g225 20x，3 g(3 x 2 )225 x 2225x 2(225所以，当 x225 45 时 y '0 ；当 45x 20 时 y '0 ，20444545453 205 35 3所以当时 f ( x) max f ()4tan． x获得最大值为4 3 g9 ，所以94225 (45) 24解法三：剖析知，当 tan 获得最大时，即最大，最大值即为平面ACM 与地面 ABC所成的锐二面角的胸怀值，如图，过B 在面 BCM 内作 BD BC 交CM 于D ，过B 作BH AC 于 H ，连 DH ，则 BHD 即为平面 ACM 与地面 ABC 所成的二面角的平面角，tan 的最大值即为tan BHD ，在 Rt ABC 中，gg20 3由等面积法可得 AB BC15 2012，DB BC gtan30，BHAC253DB2035 3所以(tan ) max tan BHD3 ．BH12 9【评论】本题考察利用数学知识解决实质问题，考察函数的单一性，考察学生剖析解决问题的能力，属于中档题．三、解答题：本大题共 5 题，共 72 分．解答应写出文字说明，演算步骤或证明过程．（ 18）【 2014 年浙江，理 18，14 分】在 ABC 中，内角 A ， B ， C 所对的边分别为 a ， b ， c ．已知 a b,c3 ，cos 2 A cos 2 B 3sin AcosA 3sin BcosB ．（ 1）求角 C 的大小；（ 2）若 sin A4 ，求 ABC 的面积．5解：（ 1）由题得1 cos2 A1 cos2B3 sin 2 A 3 sin 2B ，即 3 sin 2 A 1 cos2 A 3 sin 2B 1 cos2B ，2222 2 2 2 2sin(2 A)sin(2B) ，由 a b 得 AB ，又 AB (0,) ，得 2 A2B 6，666即 AB 2 ，所以 C．33（ 2） c3 ， sin A4 ，a c ，得 a 8，由 ac 得 AC ，进而 cos A3 ，5sin AsinC55故 sin B sin( AC ) =sinAcosC cosAsinC43 3，所以，ABC 的面积为 S 1 ac sin B8 3 18 ．102 25【评论】本题主要考察二倍角公式、两角和差的三角公式、正弦定理的应用，属于中档题．（ 19）【 2014 年浙江，理 19，14 分】已知数列 { a n } 和 { b n } 知足 a 1a 2a 3 L a n ( 2) b n (n N *) ．若 { a n } 为等比数列，且 a 1 2,b 3 6 b 2 ．（ 1）求 a n 与 b n ；（ 2）设 c n1 1(n N *) ．记数列 { c n } 的前 n 项和为 S n ．a nb n（ⅰ）求 S n ；（ⅱ）求正整数 k ，使得对随意 nN * 均有 S kS n ．解：（ 1）∵ a 1a 2 a 3 L a n (2) b n(n N *)①，当 n2 ， nN * 时， a 1a 2 a 3 L a n 1 (2) bn 1②，由①②知：当 n2 时， a n ( 2) b n b n 1，令 n 3，则有 a 3 ( 2) b 3b 2，∵ b 3 6 b 2 ，∴ a 3 8．∵ a n 为等比数列，且a 1 2 ，∴a n 的公比为q ，则 q 2a 3 4 ，由题意知a n 0 ，∴ q0 ，a 2∴．∴n*b n123nb nq2 a ＝2（ nN ）( 2)(nN*) ，得： 222L2( 2)，n．又由 a 1a 2a 3 L a nn( n 1)* 即2b n2( 2)，∴ b （n n1）（ nN ）n．（ 2）（ⅰ）∵ c n1 1 11 1( 1 1 ) ，a nb n 2nn(n 1) 2 nnn1∴ S n c 1 c 2 c 31 1 1 1 1 1 1 1 1 ) L c n = () 2 ( ) L n( n 2 1 2 2 2 32n 1= 1 1L1(11 ) = 1 111 = 1 1 ．2 222nn 12nn 1 n 1 2 n（ⅱ）因为 c 10 ， c 20， c 30 ， c 4 0 ；当 n5 时， c n 1 n(n 1)1] ，n(n 1) [ 2 n而 n (n 1)(n 1)(n2) (n 1)(n 2) 0 ，得n(n1)5g(5 1)1 ，2 n 2n 12n 12n25所以，当 n5 时， c n 0 ，综上，对随意nN * 恒有 S 4S n ，故 k 4 ．【评论】本题考察了等比数列通项公式、乞降公式，还考察了分组乞降法、裂项乞降法和猜想证明的思想，证明能够用二项式定理，还能够用数学概括法．本题计算量较大，思想层次高，要修业生有较高的剖析问题解决问题的能力．本题属于难题．（ 20）【 2014 年浙江，理 20，15 分】如图，在四棱锥 A BCDE 中，平面 ABC平面 BCDE ， CDEBED 90 ，AB CD2， DE BE 1， AC2 ．（ 1）证明： DE 平面 ACD ；（ 2）求二面角 B AD E 的大小．解：（ 1）在直角梯形BCDE 中，由DE BE 1 ， CD 2，得 BD BC 2 ，由 AC 2 ，AB 2 得 AB 2 AC 2 BC 2，即 AC BC ，又平面 ABC 平面 BCDE ，进而 AC 平面 BCDE ，所以 AC DE ，又 DE DC ，进而 DE 平面 ACD ．（ 2）解法一：作 BF AD ，与 AD 交于点 F ，过点 F 作 FG//DE ，与 AB 交于点 G ，连结 BG ，由（ 1）知 DE AD ，则 FG AD ，所以 BFG 就是二面角 B AD E 的平面角，在直角梯形 BCDE 中，由 CD 2 BC 2 BD 2 ，得 BD BC ，又平面 ABC 平面 BCDE ，得 BD 平面 ABC ，进而 BD AB ，因为 AC 平面 BCDE ，得 AC CD ．在 Rt ACD 中，由 DC 2 ， AC2，得 AD 6 ；在 Rt AED 中，由ED1， AD6得 AE7 ；在 Rt ABD 中，由 BD2 ， AB 2， AD6 ，得 BF2 3 ， AF2 3AD ，进而3GF2，在ABE ，ABG 中，利用余弦定理分别可得cos BAE5 7，BC2．在 BFG 中，3143cos BFGGF2BF 2 BG 23 ，所以，BFG，即二面角 BAD E 的大小为．2BF gGF26 6解法二：以 D 的原点，分别以射线DE ， DC 为 x ， y 轴的正半轴，成立空间直角坐标系D xyz ，如图所示．由题意知各点坐标以下： D(0,0,0) ， E (1,0,0) ， C (0,2,0) ， A(0,2, 2) ， B(1,1,0) ．ADE 的法向量为 ur ABD 的法向量为 r设平面 m (x 1 , y 1 , z 1 ) ，平面 n ( x 2 , y 2 , z 2 ) ，uuur uuur uuur ur uuur 0(0, 2, 2, (1,1,0) ，由 mgAD ，可算得： AD 2) ， AE (1, 2)，DB ur uuur 0r uuur mgAEur2 y 1 2 z 1 0 (0,1, 2) ，由 n AD 0 2 y 2 2z 2 0即，可取 m r uuur 即 x 2 y 2 01 1 10 n BD 0 x 2 y 2z ur rrur r 33(0, 1, 2) ，于是 | cos | m n |可取 n m, n | ur r 3 2 ．| m | | n | 2由题意可知，所求二面角是锐角，故二面角B AD E 的大小为．6【评论】本题主要考察空间点、线、面地点关系，二面角等基础知识，同时考察空间想象能力，推理论证能力和运算求解能力．2 2（ 21）【 2014 年浙江，理 21，15 分】如图，设椭圆 C: xy1(a b 0) 动直线 l 与椭圆 C 只有一个公共点 P ，且点 P 在第一象限．a 2b 2（ 1）已知直线 l 的斜率为 k ，用 a,b, k 表示点 P 的坐标；（ 2）若过原点 O 的直线 l 1 与 l 垂直，证明：点P 到直线 l 1 的距离的最大值为 a b ．解：（ 1）解法一：y kx m y 得： (b 2 a 2 k 2 )x 22a 2 kmx a 2 m 2 a 2b 2设 l 方程为 ykx m( k 0) ，x 2 y 2 ，消去 0 ，a 2b 2 1因为直线 l 与椭圆 C 只有一个公共点P ，故0 222 20 ，解得点 P 的坐标为，即 bma kP(a 2km 2 ,b 2 m2 ) ，又点 P 在第一象限，故点P 的坐标为 P( a 2k ,b 2) ．222a 2kb 2a 2k 2b 2b a k ba 2 k 2解法二：xx 'x 2 y 2作变换a ，则椭圆C ： 1(a b 0) 变成圆C '： x' 2y ' 21 ，切点 P(x 0 , y 0 ) 变成点y a 2 b 2y 'bP'( x'0 , y'0 ) ，切线 l : y y 0 k( x x 0 ) （ k0) ，变成 l ': by' y 0 k(ax'x 0 ) ．x '01y ' mx '1 m 2在圆 C ' 中设直线O'P ' 的方程为y ' mx' （ m0 ），由，解得，x '2 y '21 y '0m1 m2即 P'(1 1 ,1 m ) ，因为 O' P'l ' ，所以 k O ' P ' gk l ' 1，得 m ak1 ，即 mb ，m 2m 2bak1bakbx'xaka代入得 P'(, ) ，即 P '(,) ，利用逆变换b 2 b 2 a 2k 2 b 2b 2 y1 1a 2 k 2y '( ak)2b( ak)2代入即得： P( a 2k , b 2 ) ．a 2k 2b 2 a 2 k 2b 2（ 2）因为直线l 1 过原点 O 且与直线l 垂直，故直线 l 1 的方程为x ky 0 ，所以点P 到直线 l 1 的距离|a 2 kb 2 k |222b2a 2 k2b2da 2 k2，整理得: da b，因为 a 2 k 2b 2ab ，1 k2b2b 2a 22k 22kak 2a2b2a2b2所以 da b ，当且仅当2b时等号成立．222k2aba2a 222bbaba k2k所以，点 P 到直线 l 1 的距离的最大值为 a b ．【评论】本题主要考察椭圆的几何性质、点到直线间的距离、直线与椭圆的地点关系等基础知识，同时考察分析几何的基本思想方法、基本不等式应用等综合解题能力．（ 22）【 2014 年浙江，理 22， 14 分】已知函数f x 33 x a (aR) ．x（ 1）若 f x 在1,1 上的最大值和最小值分别记为M ( a), m(a ) ，求 M ( a) m(a) ；（ 2）设 bR, 若fx b 24 对 x1,1 恒成立，求 3a b 的取值范围．解：（ 1）∵ f (x)x 3 3| xa |x 3 3 x 3a , xa，∴ f '(x) 3x 2 3, x a ，因为 1 x1 ，x 33x 3a , x a 3x 23, x a（ⅰ）当 a 1 时，有x a ，故 f ( x) x 33x 3a ，所以，f x 在 ( 1,1)上是增函数，所以 M ( a)f (1) 4 3a ， m( a)f ( 1)4 3a ，故 M ( a) m(a) (4 3a) (4 3a ) 8 ．（ⅱ）当1 a 1时，若 xa,1 ， f ( x)x 3 3x 3a ，在 a,1 上是增函数；若x1,a， f ( x) x 3 3x3a ，在 1,a 上是减函数，∴M (a ) max{ f (1), f ( 1)} ， m(a ) f (a ) a 3 ，因为 f (1)f ( 1)6a 2 ，所以当1 a1 时， M (a ) m( a)a 3 3a 4 ；3当 1a 1 时， M (a) m(a )a 3 3a 2 ；3x 3（ⅲ）当 a 1 时，有 x a ，故 f ( x)3 x 3a ，此时 f ( x) 在 ( 1,1)上是减函数，所以 M (a)f ( 1)2 3a ， m( a) f (1)2 3a ，故 M ( a)m(a) 4 ；8 ,a 1a 3 3a 4 , 1 a 1综上， M (a)m( a)13 ． a33a2 ,a 134 ,a 1（ 2）令 h(x)f ( x)b ，则 h(x)x33x 3a b , x a ， h '(x)3x23, x ax 33 x 3a b , x a3x 2，3, x a因为 f xb 2 4 对 x 1,1 恒成立，即 2 h( x) 2 对 x 1,1 恒成立，所以由（1）知，（ⅰ）当a 1 时， h( x) 在 ( 1,1)上是增函数， h(x) 在 [ 1,1] 上的最大值是h(1)4 3a b ，最小值 h( 1)4 3a b ，则 4 3a b2 且 4 3a b 2矛盾；（ⅱ）当1 a1时， h( x) 在 [ 1,1] 上的最小值是h( a) a 3 b ，最大值是h(1) 43a b ，33b 2 且 4 3ab2，进而2 33a3a b6a 2且 0 a1 ，所以 aa3令 t(a)2 a33a ，则 t '(a) 3 3a20 ，∴ t (a ) 在 (0, 1) 上是增函数，故t(a)t (0)2 ，2 3a b0 ；3所以（ⅲ）当 1 a 1 时， h( x) 在 [ 1,1] 上的最小值是h(a)a 3b ，最大值是h( 1) 3a b 2 ，3所以由a3b2且3a b22，解得283a b0 27（ⅳ）当 a1时，h(x)在[1,1] 上的最大值是 h(1)3a b 2 ，最小值是h(1) 3a b 2 ，所以由3a b22且3a b22，解得3a b0．综上，3a b 的取值范围是23a b0 ．【评论】本题考察导数的综合运用，考察函数的最值，考察分类议论、化归与转变的数学思想，难度大．。

2014年浙江高考理综试题含答案解析(同名5328)

2014年浙江高考理综试题含答案解析(同名5328)2014年普通高等学校招生全国统一考试（浙江卷）理科综合化学试题相对原子质量：H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 S-32 Cl-35.5 K-39 Ca-40 Fe-56 Cu-64 Ba-1377．下列说法不正确．．．的是A．光催化还原水制氢比电解水制氢更节能环保、更经济B．氨氮废水（含NH4+及NH3）可用化学氧化法或电化学氧化法处理C．某种光学检测技术具有极高的灵敏度，可检测到单个细胞（V≈10－12L）内的数个目标分子，据此可推算该检测技术能测量细胞内浓度约为10－12~10－11mol·L－1的目标分子D．向汽油中添加甲醇后，该混合燃料的热值不变8．下列说法正确的是A．金属汞一旦洒落在实验室地面或桌面时，必须尽可能收集，并深埋处理B．用pH计、电导率仪（一种测量溶液导电能力的仪器）均可监测乙酸乙酯的水解程度C．邻苯二甲酸氢钾可用于标定NaOH溶液的浓度。

假如称量邻苯二甲酸氢钾时电子天平读数比实际质量偏大，则测得的NaOH溶液浓度比实际浓度偏小D．向某溶液中加入茚三酮试剂，加热煮沸后溶液若出金。

该电池在充电过程中的总反应方程式是：Ni(OH)2 + M = NiOOH + MH已知：6NiOOH + NH3 + H2O + OH－=6 Ni(OH)2 + NO2－下列说法正确的是A．NiMH 电池放电过程中，正极的电极反应式为：NiOOH + H2O + e－= Ni(OH)2 + OH－B．充电过程中OH－离子从阳极向阴极迁移C．充电过程中阴极的电极反应式：H2O + M + e－= MH + OH－，H2O中的H被M还原D．NiMH电池中可以用KOH溶液、氨水等作为电解质溶液12．氯在饮用水处理中常用作杀菌剂，且HClO的杀菌能力比ClO－强。

25℃时氯气-氯水体系中存在以下平衡关系：Cl2(g) Cl2(aq) K1=10－1.2Cl2(aq)+ H2O HClO + H+ +Cl－K2=10－3.4HClO H+ + ClO－K a=?其中Cl2(aq)、HClO和ClO－分别在三者中所占分数（α）随pH变化的关系如图所示。

2014年高考浙江省理科数学试题及答案解析(名师精校版)

（A）向右平移个单位（B）向左平移个单位（C）向右平移个单位（D）向左平移个单位
4
4
12
12
【答案】C
【解析】 y sin 3x cos 3x 2 sin(3x ) 2 sin[3(x )] ，
4
12
而 y 2 cos 3x 2 sin(3x ) = 2 sin[3(x )] ，
（A）充分不必要条件（B）必要不充分条件（C）充分必要条件（D）既不充分也不必要条件
【答案】A
【解析】当
a

b
1 时，(a

bi)2

(1
i)2

2i ，反之，(a

bi)2

2i
，即
a2
b2

2abi

2i
，则
a
2
b2

0
，
2ab 2
a 1 a 1 解得 b 1 或 b 1 ，故选 A．
注意事项：
1.答题前，考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试卷和答题纸规
定的位置上。
2.每小题选出答案后，用 2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，
再选涂其他答案标号。不能答在试题卷上。
参考公式
如果事件 A, B 互斥，那么 P(A B) P(A) P(B) 如果事件 A, B 相互独立，那么 P(A B) P(A) P(B) 如果事件 A 在一次试验中发生的概率为 P , 那么 n 次独立重复试验中事件 A 恰好发生 k

2014年高考浙江理科数学试题及标准答案(精校版)

2０1４年普通高等学校招生全国统一考试（浙江卷)数学（理科）一. 选择题:本大题共１0小题，每小题5分，共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集{|2}U x N x =∈≥，集合2{|5}A x N x =∈≥,则U C A =（）A ． ∅ Ｂ. {2} C. {5} D. {2,5}２. 已知i 是虚数单位，,a b R ∈,则“1a b ==”是“2()2a bi i +=”的（ )A. 充分不必要条件Ｂ. 必要不充分条件Ｃ. 充分必要条件 D. 既不充分也不必要条件3．某几何体的三视图(单位：cm)如图所示,则此几何体的表面积是（ )A. 902cm B ． 1２92cmC. 1322cm D ． 13８2cm4. 为了得到函数sin 3cos3y x x =+的图像，可以将函数2cos 3y x =的图像( ）Ａ．向右平移4π 个单位 B. 向左平移4π个单位C. 向右平移12π个单位 D ．向左平移12π个单位5.在64(1)(1)x y ++的展开式中，记m n x y 项的系数(,)f m n ,则(3,0)(2,1)(1,2)(0,3)f f f f +++= （ )A. 45B. ６0C. 120D ． 2１０6. 已知函数32()f x x ax bx c =+++ ，且0(1)(2)(3)3f f f <-=-=-≤( ）A ．3c ≤ Ｂ.36c <≤ C ．69c <≤ D. 9c >７. 在同一直角坐标系中,函数()(0)a f x x x =≥，()log a g x x = 的图像可能是( )8．记,max{,},x x y x y y x y ≥⎧=⎨<⎩，y,min{,}x,x y x y x y ≥⎧=⎨<⎩，设,a b 为平面向量，则( ） A.min{||,||}min{||,||}a b a b a b +-≤Ｂ． min{||,||}min{||,||}a b a b a b +-≥Ｃ． 2222max{||,||}||||a b a b a b +-≤+D. 2222max{||,||}||||a b a b a b +-≥+９. 已知甲盒中仅有1个球且为红球,乙盒中有m 个红球和n 个篮球(3,3)m n ≥≥,从乙盒中随机抽取(1,2)i i =个球放入甲盒中.（ａ)放入i 个球后,甲盒中含有红球的个数记为(1,2)i i ξ=;（b)放入i 个球后，从甲盒中取1个球是红球的概率记为(1,2)i p i =.则 ( )A.1212,()()p p E E ξξ><B. 1212,()()p p E E ξξ<>C. 1212,()()p p E E ξξ>>D. 1212,()()p p E E ξξ<<10. 设函数21()f x x =,22()2()f x x x =-，31()|sin 2|3f x x π=，99i a i =，,2,1,0=i 99, ,记10219998|()()||()()||()()|k k k k k k k I f a f a f a f a f a f a =-+-++-,1,2,3k = 则( )A.123I I I <<B. 213I I I <<C. 132I I I << Ｄ. 321I I I <<二. 填空题:本大题共７小题，每小题4分，共28分.11. 若某程序框图如图所示，当输入50时,则该程序运算后输出的结果是_______＿.1２. 随机变量ξ的取值为0，1,2,若1(0)5P ξ==，()1E ξ=，则()D ξ＝＿_____＿_. 13．当实数,x y 满足240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时,14ax y ≤+≤恒成立，则实数a 的取值范围是_＿_＿__＿_.14. 在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给４个人，每人2张,不同的获奖情况有＿____种（用数字作答）．1５.设函数22,0(),0x x x f x x x ⎧+<⎪=⎨-≥⎪⎩若(())2f f a ≤,则实数a 的取值范围是___＿_＿16.设直线30x y m -+=(0m ≠) 与双曲线。

高考浙江理科数学试题及答案精校版

高考浙江理科数学试题及答案精校版Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-2014年普通高等学校招生全国统一考试（浙江卷）数学（理科）一.选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设全集{|2}U x N x =∈≥，集合2{|5}A x N x =∈≥，则U C A =（）A. ∅B. {2}C. {5}D. {2,5}2. 已知i 是虚数单位，,a b R ∈,则“1a b ==”是“2()2a bi i +=”的（）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件3. 某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是( )A. 902cmB. 1292cmC. 1322cmD. 1382cm4. 为了得到函数sin 3cos3y x x =+的图像，可以将函数2cos 3y x =的图像（）A. 向右平移4π 个单位B. 向左平移4π个单位C. 向右平移12π个单位 D. 向左平移12π个单位5.在64(1)(1)x y ++的展开式中,记m n x y 项的系数(,)f m n ，则(3,0)(2,1)(1,2)(0,3)f f f f +++=（）A. 45B. 60C. 120D. 2106. 已知函数32()f x x ax bx c =+++ ，且0(1)(2)(3)3f f f <-=-=-≤（）A.3c ≤B.36c <≤C.69c <≤D. 9c >7. 在同一直角坐标系中，函数()(0)a f x x x =≥，()log a g x x = 的图像可能是（）8. 记,max{,},x x y x y y x y ≥⎧=⎨<⎩，y,min{,}x,x y x y x y ≥⎧=⎨<⎩，设,a b为平面向量，则（）A ．min{||,||}min{||,||}a b a b a b +-≤B. min{||,||}min{||,||}a b a b a b +-≥C. 2222max{||,||}||||a b a b a b +-≤+D. 2222max{||,||}||||a b a b a b +-≥+9. 已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球(3,3)m n ≥≥，从乙盒中随机抽取(1,2)i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为(1,2)i i ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为(1,2)i p i =. 则 ( )A.1212,()()p p E E ξξ><B. 1212,()()p p E E ξξ<>C. 1212,()()p p E E ξξ>>D. 1212,()()p p E E ξξ<<10. 设函数21()f x x =，22()2()f x x x =-，31()|sin 2|3f x x π=，99ia i =，,2,1,0=i99, ，记10219998|()()||()()||()()|k k k k k k k I f a f a f a f a f a f a =-+-++-，1,2,3k = 则 ( )A.123I I I <<B. 213I I I <<C. 132I I I <<D.321I I I <<二.填空题：本大题共7小题，每小题4分，共28分.11. 若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12. 随机变量ξ的取值为0,1,2，若1(0)5P ξ==，()1E ξ=，则()D ξ=________.13.当实数,x y 满足240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，14ax y ≤+≤恒成立，则实数a 的取值范围是________.14. 在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数22,0(),0x x x f x x x ⎧+<⎪=⎨-≥⎪⎩若(())2f f a ≤，则实数a 的取值范围是______ 16.设直线30x y m -+=(0m ≠) 与双曲线12222=-by a x （0,0a b >>）两条渐近线分别交于点A ，B.若点(,0)P m 满足||||PA PB =,则该双曲线的离心率是__________17、如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A到墙面的距离为AB ，某目标点P 沿墙面上的射击线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小.若15AB m = ，25AC m =，30BCM ∠=︒,则tan θ的最大值是 (仰角θ 为直线AP 与平面ABC 所成角)三. 解答题：本大题共5小题，共72分。

【精校】2014年普通高等学校招生全国统一考试(浙江卷)数学理

2014年普通高等学校招生全国统一考试（浙江卷）数学理一、选择题(每小题5分，共50分)1.设全集U={x∈N|x≥2}，集合A={x∈N|x2≥5}，则∁U A=( )A.B. {2}C. {5}D. {2，5}解析：∵全集U={x∈N|x≥2}，集合A={x∈N|x2≥5}={x∈N|x≥3}，则C U A={x∈N|x＜3}={2}，答案：B.2.已知i是虚数单位，a，b∈R，则“a=b=1”是“(a+bi)2=2i”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件解析：当“a=b=1”时，“(a+bi)2=(1+i)2=2i”成立，故“a=b=1”是“(a+bi)2=2i”的充分条件；当“(a+bi)2=a2-b2+2abi=2i”时，“a=b=1”或“a=b=-1”，故“a=b=1”是“(a+bi)2=2i”的不必要条件；综上所述，“a=b=1”是“(a+bi)2=2i”的充分不必要条件；故选A3.某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是( )A. 90cm2B. 129cm2C. 132cm2D. 138cm2解析：由三视图知：几何体是直三棱柱与直四棱柱的组合体，其中直三棱柱的侧棱长为3，底面是直角边长分别为3、4的直角三角形，四棱柱的高为6，底面为矩形，矩形的两相邻边长为3和4，∴几何体的表面积S=2×4×6+3×6+3×3+2×3×4+2××3×4+(4+5)×3=48+18+9+24+12+27=138(cm2).答案：D.4.为了得到函数y=sin3x+cos3x的图象，可以将函数y=cos3x的图象( )A. 向右平移个单位B. 向左平移个单位C. 向右平移个单位D. 向左平移个单位解析：函数y=sin3x+cos3x=，故只需将函数y=cos3x的图象向右平移个单位，得到y==的图象.答案：C.5.在(1+x)6(1+y)4的展开式中，记x m y n项的系数为f(m，n)，则f(3，0)+f(2，1)+f(1，2)+f(0，3)=( )A. 45B. 60C. 120D. 210解析：(1+x)6(1+y)4的展开式中，含x3y0的系数是：=20.f(3，0)=20；含x2y1的系数是=60，f(2，1)=60；含x1y2的系数是=36，f(1，2)=36；含x0y3的系数是=4，f(0，3)=4；∴f(3，0)+f(2，1)+f(1，2)+f(0，3)=120.答案：C.6.已知函数f(x)=x3+ax2+bx+c，其0＜f(-1)=f(-2)=f(-3)≤3，则( )A. c≤3B. 3＜c≤6C. 6＜c≤9D. c＞9解析：由f(-1)=f(-2)=f(-3)得，解得，f(x)=x3+6x2+11x+c，由0＜f(-1)≤3，得0＜-1+6-11+≤3，即6＜c≤9，故选C.7.在同一直角坐标系中，函数f(x)=x a(x≥0)，g(x)=log a x的图象可能是( )A.B.C.D.解析：当0≤a＜1时，函数f(x)=x a(x≥0)，g(x)=log a x的图象为：此时答案D满足要求，当a＞1时，函数f(x)=x a(x≥0)，g(x)=log a x的图象为：无满足要求的答案，综上：故选D8.记max{x，y}=，min{x，y}=，设，为平面向量，则( )A. min{|+|，|-|}≤min{||，||}B. min{|+|，|-|}≥min{||，||}C. max{|+|2，|-|2}≤||2+||2D. max{|+|2，|-|2}≥||2+||2解析：对于选项A，取⊥，则由图形可知，根据勾股定理，结论不成立；对于选项B，取，是非零的相等向量，则不等式左边min{|+|，|-|}=，显然，不等式不成立；对于选项C，取，是非零的相等向量，则不等式左边max{|+|2，|-|2}=|+|2=4，而不等式右边=||2+||2=2，显然不成立.由排除法可知，D选项正确.答案：D.9.已知甲盒中仅有1个球且为红球，乙盒中有m个红球和n个蓝球(m≥3，n≥3)，从乙盒中随机抽取i(i=1，2)个球放入甲盒中.(a)放入i个球后，甲盒中含有红球的个数记为ξi(i=1，2)；(b)放入i个球后，从甲盒中取1个球是红球的概率记为p i(i=1，2).则( )A. p1＞p2，E(ξ1)＜E(ξ2)B. p1＜p2，E(ξ1)＞E(ξ2)C. p1＞p2，E(ξ1)＞E(ξ2)D. p1＜p2，E(ξ1)＜E(ξ2)解析：，，，所以P1＞P2；由已知ξ1的取值为1、2，ξ2的取值为1、2、3，所以，==，E(ξ1)-E(ξ2)=.答案：A10.设函数f1(x)=x2，f2(x)=2(x-x2)，，，i=0，1，2，…，99.记I k=|f k(a1)-f k(a0)|+|f k(a2)-f k(a1)丨+…+|f k(a99)-f k(a98)|，k=1，2，3，则( )A. I1＜I2＜I3B. I2＜I1＜I3C. I1＜I3＜I2D. I3＜I2＜I1解析：由，故==1，由，故＜1，+=，故I2＜I1＜I3，答案：B.二、填空题11.(4分)在某程序框图如图所示，当输入50时，则该程序运算后输出的结果是.解析：由程序框图知：第一次循环S=1，i=2；第二次循环S=2×1+2=4，i=3；第三次循环S=2×4+3=11，i=4；第四次循环S=2×11+4=26，i=5；第五次循环S=2×26+5=57，i=6，满足条件S＞50，跳出循环体，输出i=6.答案：6.12.(4分)随机变量ξ的取值为0，1，2，若P(ξ=0)=，E(ξ)=1，则D(ξ)= . 解析：设P(ξ=1)=p，P(ξ=2)=q，则由已知得p+q=，，解得，，所以.答案：13.(4分)当实数x，y满足时，1≤ax+y≤4恒成立，则实数a的取值范围是.解析：由约束条件作可行域如图，联立，解得C(1，).联立，解得B(2，1).在x-y-1=0中取y=0得A(1，0).要使1≤ax+y≤4恒成立，则，解得：1.∴实数a的取值范围是.答案：.14.(4分)在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有种(用数字作答).解析：分类讨论，一、二、三等奖，三个人获得，共有=24种；一、二、三等奖，有1人获得2张，1人获得1张，共有=36种，共有24+36=60种.答案：60.15.(4分)设函数f(x)=，若f(f(a))≤2，则实数a的取值范围是.解析：∵函数f(x)=，它的图象如图所示：由f(f(a))≤2，可得f(a)≥-2.由f(x)=-2，可得-x2=-2，即x=，故当f(f(a))≤2时，则实数a的取值范围是a≤，答案：(-∞，].16.(4分)设直线x-3y+m=0(m≠0)与双曲线(a＞0，b＞0)的两条渐近线分别交于点A，B.若点P(m，0)满足|PA|=|PB|，则该双曲线的离心率是 .解析：双曲线(a＞0，b＞0)的两条渐近线方程为y=±x，则与直线x-3y+m=0联立，可得A(，)，B(-，)，∴AB中点坐标为(，)，∵点P(m，0)满足|PA|=|PB|，∴=-3，∴a=2b，∴=b，∴e==.答案：.17.(4分)如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A 到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若AB=15cm，AC=25cm，∠BCM=30°，则tanθ的最大值是 .(仰角θ为直线AP与平面ABC所成角)解析：∵AB=15cm，AC=25cm，∠ABC=90°，∴BC=20cm，过P作PP′⊥BC，交BC于P′，连接AP′，则tanθ=，设BP′=x，则CP′=20-x，由∠BCM=30°，得PP′=CP′tan30°=(20-x)，在直角△ABP′中，AP′=，∴tanθ=•，令y=，则函数在x∈[0，20]单调递减，∴x=0时，取得最大值为=.答案：.三、解答题18.(14分)在△ABC中，内角A，B，C所对的边分别为a，b，c.已知a≠b，c=，cos2A-cos2B=sinAcosA-sinBcosB.(Ⅰ)求角C的大小；(Ⅱ)若sinA=，求△ABC的面积.解析：(Ⅰ)△ABC中，由条件利用二倍角公式化简可得-2sin(A+B)sin(A-B)=2·cos(A+B)sin(A-B).求得tan(A+B)的值，可得A+B的值，从而求得C的值.(Ⅱ)由 sinA=求得cosA的值.再由正弦定理求得a，再求得 sinB=sin[(A+B)-A]的值，从而求得△ABC的面积为的值.答案：(Ⅰ)∵△ABC中，a≠b，c=，cos2A-cos2B=sinAcosA-sinBcosB，∴-=sin2A-sin2B，即 cos2A-cos2B=sin2A-sin2B，即-2sin(A+B)sin(A-B)=2•cos(A+B)sin(A-B).∵a≠b，∴A≠B，sin(A-B)≠0，∴tan(A+B)=-，∴A+B=，∴C=.(Ⅱ)∵sinA=＜，C=，∴A＜，或A＞(舍去)，∴cosA==.由正弦定理可得，=，即=，∴a=.∴sinB=sin[(A+B)-A]=sin(A+B)cosA-cos(A+B)sinA=-(-)×=，∴△ABC的面积为=×=.19.(14分)已知数列{a n}和{b n}满足a1a2a3…a n=(n∈N*).若{a n}为等比数列，且a1=2，b3=6+b2.(Ⅰ)求a n和b n；(Ⅱ)设c n=(n∈N*).记数列{c n}的前n项和为S n.(i)求S n；(ii)求正整数k，使得对任意n∈N*均有S k≥S n.解析：(Ⅰ)先利用前n项积与前(n-1)项积的关系，得到等比数列{a n}的第三项的值，结合首项的值，求出通项a n，然后现利用条件求出通项b n；(Ⅱ)(i)利用数列特征进行分组求和，一组用等比数列求和公式，另一组用裂项法求和，得出本小题结论；(ii)本小题可以采用猜想的方法，得到结论，再加以证明.答案：(Ⅰ)∵a1a2a3…a n=(n∈N*) ①，当n≥2，n∈N*时，②，由①②知：，令n=3，则有.∵b3=6+b2，∴a3=8.∵{a n}为等比数列，且a1=2，∴{a n}的公比为q，则=4，由题意知a n＞0，∴q＞0，∴q=2.∴(n∈N*).又由a1a2a3…a n=(n∈N*)得：，，∴b n=n(n+1)(n∈N*).(Ⅱ)(i)∵c n===.∴S n=c1+c2+c3+…+c n====；(ii)因为c1=0，c2＞0，c3＞0，c4＞0；当n≥5时，，而=＞0，得，所以，当n≥5时，c n＜0，综上，对任意n∈N*恒有S4≥S n，故k=4.20.(15分)如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=.(Ⅰ)证明：DE⊥平面ACD；(Ⅱ)求二面角B-AD-E的大小.解析：(Ⅰ)依题意，易证AC⊥平面BCDE，于是可得AC⊥DE，又DE⊥DC，从而DE⊥平面ACD；(Ⅱ)作BF⊥AD，与AD交于点F，过点F作FG∥DE，与AB交于点G，连接BG，由(Ⅰ)知DE⊥AD，则FG⊥AD，所以∠BFG就是二面角B-AD-E的平面角，利用题中的数据，解三角形，可求得BF=，AF=AD，从而GF=，cos∠BFG==，从而可求得答案.答案：(Ⅰ)在直角梯形BCDE中，由DE=BE=1，CD=2，得BD=BC=，由AC=，AB=2得AB2=AC2+BC2，即AC⊥BC，又平面ABC⊥平面BCDE，从而AC⊥平面BCDE，所以AC⊥DE，又DE⊥DC，从而DE⊥平面ACD；作BF⊥AD，与AD交于点F，过点F作FG∥DE，与AB交于点G，连接BG，由(Ⅰ)知DE⊥AD，则FG⊥AD，所以∠BFG就是二面角B-AD-E的平面角，在直角梯形BCDE 中，由CD2=BC2+BD2，得BD⊥BC，又平面ABC⊥平面BCDE，得BD⊥平面ABC，从而BD⊥AB，由于AC⊥平面BCDE，得AC⊥CD.在Rt△ACD中，由DC=2，AC=，得AD=；在Rt△AED中，由ED=1，AD=得AE=；在Rt△ABD中，由BD=，AB=2，AD=得BF=，AF=AD，从而GF=，在△ABE，△ABG中，利用余弦定理分别可得cos∠BAE=，BC=.在△BFG中，cos∠BFG==，所以，∠BFG=，二面角B-AD-E的大小为.21.(15分)如图，设椭圆C：(a＞b＞0)，动直线l与椭圆C只有一个公共点P，且点P在第一象限.(Ⅰ)已知直线l的斜率为k，用a，b，k表示点P的坐标；(Ⅱ)若过原点O的直线l1与l垂直，证明：点P到直线l1的距离的最大值为a-b.解析：(Ⅰ)设直线l的方程为y=kx+m(k＜0)，由，消去y得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0，利用△=0，可求得在第一象限中点P的坐标；(Ⅱ)由于直线l1过原点O且与直线l垂直，设直线l1的方程为x+ky=0，利用点到直线间的距离公式，可求得点P到直线l1的距离d=，整理即可证得点P到直线l1的距离的最大值为a-b..答案：(Ⅰ)设直线l的方程为y=kx+m(k＜0)，由，消去y得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0.由于直线l与椭圆C只有一个公共点P，故△=0，即b2-m2+a2k2=0，解得点P的坐标为(-，)，又点P在第一象限，故点P的坐标为P(，).(Ⅱ)由于直线l1过原点O且与直线l垂直，故直线l1的方程为x+ky=0，所以点P到直线l1的距离d=，整理得：d=，因为a2k2+≥2ab，所以≤=a-b，当且仅当k2=时等号成立.所以，点P到直线l1的距离的最大值为a-b.22.(14分)已知函数f(x)=x3+3|x-a|(a∈R).(Ⅰ)若f(x)在[-1，1]上的最大值和最小值分别记为M(a)，m(a)，求M(a)-m(a)；(Ⅱ)设b∈R，若[f(x)+b]2≤4对x∈[-1，1]恒成立，求3a+b的取值范围.解析：(Ⅰ)利用分段函数，结合[-1，1]，分类讨论，即可求M(a)-m(a)；(Ⅱ)令h(x)=f(x)+b，则h(x)=，h′(x)=，则[f(x)+b]2≤4对x∈[-1，1]恒成立，转化为-2≤h(x)≤2对x∈[-1，1]恒成立，分类讨论，即可求3a+b的取值范围.答案：(Ⅰ)∵f(x)=x3+3|x-a|=，∴f′(x)=，①a≤-1时，∵-1≤x≤1，∴x≥a，f(x)在(-1，1)上是增函数，∴M(a)=f(1)=4-3a，m(a)=f(-1)=-4-3a，∴M(a)-m(a)=8；②-1＜a＜1时，x∈(a，1)，f(x)=x3+3x-3a，在(a，1)上是增函数；x∈(-1，a)，f(x)=x3-3x-3a，在(-1，a)上是减函数，∴M(a)=max{f(1)，f(-1)}，m(a)=f(a)=a3，∵f(1)-f(-1)=-6a+2，∴-1＜a≤时，M(a)-m(a)=-a3-3a+4；＜a＜1时，M(a)-m(a)=-a3+3a+2；③a≥1时，有x≤a，f(x)在(-1，1)上是减函数，∴M(a)=f(-1)=2+3a，m(a)=f(1)=-2+3a，∴M(a)-m(a)=4；(Ⅱ)令h(x)=f(x)+b，则h(x)=，h′(x)=，∵[f(x)+b]2≤4对x∈[-1，1]恒成立，∴-2≤h(x)≤2对x∈[-1，1]恒成立，由(Ⅰ)知，①a≤-1时，h(x)在(-1，1)上是增函数，最大值h(1)=4-3a+b，最小值h(-1)=-4-3a+b，则-4-3a+b≥-2且4-3a+b≤2矛盾；②-1＜a≤时，最小值h(a)=a3+b，最大值h(1)=4-3a+b，∴a3+b≥-2且4-3a+b≤2，令t(a)=-2-a3+3a，则t′(a)=3-3a2＞0，t(a)在(0，)上是增函数，∴t(a)＞t(0)=-2，∴-2≤3a+b≤0；③＜a＜1时，最小值h(a)=a3+b，最大值h(-1)=3a+b+2，则a3+b≥-2且3a+b+2≤2，∴-＜3a+b≤0；④a≥1时，最大值h(-1)=3a+b+2，最小值h(1)=3a+b-2，则3a+b-2≥-2且3a+b+2≤2，∴3a+b=0.综上，3a+b的取值范围是-2≤3a+b≤0.考试高分秘诀是什么？试试这四个方法，特别是中考和高考生谁都想在考试中取得优异的成绩，但要想取得优异的成绩，除了要掌握好相关的知识定理和方法技巧之外，更要学会一些考试技巧。

2014年普通高等学校招生考试浙江理数

2014年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，zxxk 则=A C U （） A. ∅ B. }2{ C. }5{ D. }5,2{（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是 A. 902cm B. 1292cm C. 1322cm D. 1382cm4.为了得到函数zxxk x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（） A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位5.在46)1()1(y x ++的展开式中，记n m y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（）A.45B.60C.120D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f （）A.3≤cB.63≤<cC.96≤<cD. 9>c 7.在同意直角坐标系中，函数x x g x x x f a a log )(),0()(=≥=的图像可能是（）8.记,max{,},x x y x y y x y ≥⎧=⎨<⎩，,min{,},y x yx y x x y≥⎧=⎨<⎩，设,a b 为平面向量，则（）A.min{||,||}min{||,||}a b a b a b +-≤B.min{||,||}min{||,||}a b a b a b +-≥C.2222min{||,||}||||a b a b a b +-≥+ D.2222min{||,||}||||a b a b a b +-≤+9.已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球 ()3,3m n ≥≥，从乙盒中随机抽取()1,2i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为()1,2ii ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为zxxk ()1,2i p i =. 则A.()()1212,p p E E ξξ><B.()()1212,p p E E ξξ<>C.()()1212,p p E E ξξ>>D.()()1212,p p E E ξξ<<10.设函数21)(x x f =，),(2)(22x x x f -=|2sin |31)(3x x f π=，99,,2,1,0,99==i ia i ，记|)()(||)()(||)()(|98991201a f a f a f a f a f a f I k k k k k k k -++-+-= ，.3,2,1=k 则A.321I I I <<B. 312I I I <<C. 231I I I <<D. 123I I I << 二、填空题：本大题共7小题，每小题4分，共28分.11.若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12.随机变量ξ的取值为0,1,2，若()105P ξ==，()1E ξ=，则()D ξ=________. 13.当实数x ，y 满足240,10,1,x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，zxxk 14ax y ≤+≤恒成立，则实数a 的取值范围是________.14.在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数()⎪⎩⎪⎨⎧≥-<+=0,0,22x x x x x x f 若()()2≤a f f ，则实数a 的取值范围是______16.设直线)0(03≠=+-m m y x 与双曲线12222=-by a x （0a b >>）两条渐近线分别交于点B A ,，若点)0,(m P 满足PB PA =,则该双曲线的离心率是__________17、如图，某人在垂直于水平地面的墙面前的点处进行射击训练. 已知点到墙面的距离为，某目标点沿墙面的射击线移动，此人为了准确瞄准目标点，需计算由点观察点的仰角的大小.若则的最大值三．解答题：本大题共5小题，共72分。

2014年普通高等学校招生全国统一考试(浙江卷)_数学(理)-推荐下载

π 4
a 6,

3x＋cos
2
cos
3
D．210
x
因此需将函数
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电通，力1根保过据护管生高线0产中不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置，机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资22负料，荷试而下卷且高总可中体保资配障料置各试时类卷，管调需路控要习试在题验最到；大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资，常料要工试加况卷强下安看2与全22过，22度并22工且22作尽2下可护1都能关可地于以缩管正小路常故高工障中作高资；中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整，高核或中对者资定对料值某试，些卷审异弯核常扁与高度校中固对资定图料盒纸试位，卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置，地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中，案资要，料求编5试技写、卷术重电保交要气护底设设装。备备4置管高调、动线中试电作敷资高气，设料中课并3技试资件且、术卷料拒管中试试调绝路包验卷试动敷含方技作设线案术，技槽以来术、及避管系免架统不等启必多动要项方高方案中式；资，对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资，件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调，并试合且技理进术利行，用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活：。。在对对分于于线调差盒试动处过保，程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试，题技应，术采作是用为指金调发属试电隔人机板员一进，变行需压隔要器开在组处事在理前发；掌生同握内一图部线纸故槽资障内料时，、，强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试，卷卷线试切缆验除敷报从设告而完与采毕相用，关高要技中进术资行资料检料试查，卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

2014年全国高考理综试卷(浙江卷)

2014年普通高等学校招生全国统一考试（浙江卷）理科综合化学试题7．下列说法不正确．．．的是 A ．光催化还原水制氢比电解水制氢更节能环保、更经济 B ．氨氮废水(含NH 4+及NH 3)可用化学氧化法或电化学氧化法处理 C ．某种光学检测技术具有极高的灵敏度，可检测到单个细胞(V=10－12L)内的数个目标分子，据此可推算该检测技术能测量到细胞内浓度约为10－12～10－11mol ·L－1的目标分子D ．向汽油中添加甲醇后，该混合燃料的热值不变 8．下列说法正确的是A ．金属汞一旦洒落在实验室地面或桌面时，必须尽可能收集，并深埋处理B ．用pH 计、电导率仪(一种测量溶液导电能力的仪器)均可检测乙酸乙酯的水解程度C ．邻苯二甲酸氢钾可用于标定NaOH 溶液的浓度，假如称量邻苯二甲酸氢钾时电子天平读数比实际质量偏大，则测得的NaOH 溶液浓度比实际浓度偏小D ．向某溶液中加入茚三酮试剂，加热煮沸后溶液若出现蓝色，则可判断该溶液含有蛋白质9．如表所示的五种元素中，W 、X 、Y 、Z 为短周期元素，这四种元素的原子最外层电子数之和为22。

下列说法正确的是 A ．X 、Y 、Z 三种元素最低价氢化物的沸点依次升高 B ．由X 、Y 和氢三种元素形成的化合物中只有共价键 C ．物质WY 2、W 3X 4、WZ 4均有熔点高、硬度大的特性D ．T 元素的单质具有半导体的特性，T 与Z 元素可形成化合物TZ 4 10．下列说法正确的是A ．乳酸薄荷醇酯( )仅能发生水解、氧化、消去反应B ．乙醛和丙烯醛( )不是同系物，学科网它们与氢气充分反应后的产物也不是同系物C ．淀粉和纤维素在酸催化下完全水解后的产物都是葡萄糖D ．CH 3COOCH 2CH 3与CH 3CH 2COOCH 3互为同分异构体，1H －NMR 谱显示两者均有三种不同的氢原子且三种氢原子的比例相同，故不能用1H－NMR来鉴别11．镍氢电池(NiMH)目前已经成为混合动力汽车的一种主要电池类型。

2014年浙江高考数学(理科)试卷(含答案)

2014年普通高等学校招生全国统一考试（浙江卷）数学（理科）一. 选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1. 设全集{|2}U x N x =∈≥，集合2{|5}A x N x =∈≥，则U C A =（）A. ∅B. {2}C. {5}D. {2,5} 2. 已知i 是虚数单位，,a b R ∈,则“1a b ==”是“2()2a bi i +=”的（） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件3. 某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是( )A. 902cm B. 1292cmC. 1322cm D. 1382cm4. 为了得到函数sin 3cos3y x x =+的图像，可以将函数2cos 3y x =的图像（）A. 向右平移4π 个单位B. 向左平移4π个单位 C. 向右平移12π个单位 D. 向左平移12π个单位5.在64(1)(1)x y ++的展开式中,记m nx y项的系数(,)f m n ，则(3,0)(2,1)(1,2)(0,3)f f f f +++= （）A. 45B. 60C. 120D. 2106. 已知函数32()f x x ax bx c =+++ ，且0(1)(2)(3)3f f f <-=-=-≤（） A.3c ≤ B.36c <≤ C.69c <≤ D. 9c >7. 在同一直角坐标系中，函数()(0)af x x x =≥，()log a g x x = 的图像可能是（）8. 记,max{,},x x y x y y x y ≥⎧=⎨<⎩，y,min{,}x,x yx y x y≥⎧=⎨<⎩，设,a b 为平面向量，则（）A ．min{||,||}min{||,||}a b a b a b +-≤ B. min{||,||}min{||,||}a b a b a b +-≥C. 2222max{||,||}||||a b a b a b +-≤+ D. 2222max{||,||}||||a b a b a b +-≥+9. 已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球(3,3)m n ≥≥，从乙盒中随机抽取(1,2)i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为(1,2)i i ξ=；（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为(1,2)i p i =. 则 ( )A.1212,()()p p E E ξξ><B. 1212,()()p p E E ξξ<>C. 1212,()()p p E E ξξ>>D. 1212,()()p p E E ξξ<<10. 设函数21()f x x =，22()2()f x x x =-，31()|sin 2|3f x x π=，99i a i =，,2,1,0=i 99, ，记10219998|()()||()()||()()|k k k k k k k I f a f a f a f a f a f a =-+-++-，1,2,3k = 则 ( )A.123I I I <<B. 213I I I <<C. 132I I I <<D. 321I I I <<二. 填空题：本大题共7小题，每小题4分，共28分.11. 若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是________.12. 随机变量ξ的取值为0,1,2，若1(0)5P ξ==，()1E ξ=，则()D ξ=________.13.当实数,x y 满足240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩时，14ax y ≤+≤恒成立，则实数a 的取值范围是________.14. 在8张奖券中有一、二、三等奖各1张，其余5张无奖.将这8张奖券分配给4个人，每人2张，不同的获奖情况有_____种（用数字作答）.15.设函数22,0(),0x x x f x x x ⎧+<⎪=⎨-≥⎪⎩若(())2f f a ≤，则实数a 的取值范围是______16.设直线30x y m -+=(0m ≠) 与双曲线12222=-by a x （0,0a b >>）两条渐近线分别交于点A ，B.若点(,0)P m 满足||||PA PB =,则该双曲线的离心率是__________17、如图，某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练.已知点A 到墙面的距离为AB ，某目标点P 沿墙面上的射击线CM 移动，此人为了准确瞄准目标点P ，需计算由点A 观察点P 的仰角θ的大小.若15AB m = ，25AC m =，30BCM ∠=︒,则tan θ的最大值是 (仰角θ 为直线AP 与平面ABC 所成角)三. 解答题：本大题共5小题，共72分。