六年级数学下册课件比例的意义和基本性质第3课时解比例人教版
合集下载
六年级下册数学课件1.比例的意义和基本性质解比例(人教版)PPT课件
亲爱的同学们，再见！ 4.初步形成宽容他人的良好品质。 5 . 通 过 具体 事例体 验宽容 对己对 人带来 的慰藉 。 6. 传统的 节日也 应有时 代的价 值，不 符合时 代需要 的，应 该淘汰 。 7. 生活中 ，伴随 着我们 成长有 许多风 俗，其 中不少 体现了 尊老的 传统美 德。
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
1. 独立思考用比例解决的方法 2. 在小组中交流各自的方法 3. 归纳总结本小组的解决方法 4. 准备向全班同学展示
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
用字母表示比例的基本性质：
a∶b＝c∶d(b、d≠0)
x∶320＝1∶10
或a
c
＝
b
d
ad＝bc
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
根据比例的基本性质，如果已知比例中 任何三项，就可以求出这个比例中的另 外一个未知项。求比例中的未知项，叫 做解比例。
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
练习八第8、 9、10题。
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
1. 独立思考用比例解决的方法 2. 在小组中交流各自的方法 3. 归纳总结本小组的解决方法 4. 准备向全班同学展示
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
用字母表示比例的基本性质：
a∶b＝c∶d(b、d≠0)
x∶320＝1∶10
或a
c
＝
b
d
ad＝bc
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
根据比例的基本性质，如果已知比例中 任何三项，就可以求出这个比例中的另 外一个未知项。求比例中的未知项，叫 做解比例。
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
练习八第8、 9、10题。
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
六年级下册数学课件1．比例的意义和 基本性 质解比 例（人 教版） PPT课 件
人教版六年级下册比例的意义和基本性质ppt课件
应用比例的意义判断下面的 比例是否正确：
1.
20 ：5 = 1 ：4 (错)
2.
1 2
：1 3
= 6 ：4
(对)
3.
0.6 ：0.2 = 3 ：1 44
(对)
4.
6 ：10 = 9 ：15 (对)
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
＝ 2.4︰1.6 60︰40
外项
内项
＝ 2.4
60
1.6
40
内项
外项
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
6∶9 和 9∶12
比例的意义： 因为： 6 ∶ 9 ＝ 2
3 9∶12 = 3
4 2 ≠3 34
比例的基本性质： 因为： 6 × 12 ＝ 72
9 × 9 ＝ 81
72 ≠ 81
所以： 6∶9 和 9∶12
所以： 6∶9 和 9∶12
不能组成比例。
不能组成比例。
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
1.
20 ：5 = 1 ：4 (错)
2.
1 2
：1 3
= 6 ：4
(对)
3.
0.6 ：0.2 = 3 ：1 44
(对)
4.
6 ：10 = 9 ：15 (对)
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
＝ 2.4︰1.6 60︰40
外项
内项
＝ 2.4
60
1.6
40
内项
外项
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
6∶9 和 9∶12
比例的意义： 因为： 6 ∶ 9 ＝ 2
3 9∶12 = 3
4 2 ≠3 34
比例的基本性质： 因为： 6 × 12 ＝ 72
9 × 9 ＝ 81
72 ≠ 81
所以： 6∶9 和 9∶12
所以： 6∶9 和 9∶12
不能组成比例。
不能组成比例。
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
1比例的意义和基本性质第3课时 解比例
43
解：1 x 10 1
3
4
1x 5 32
解： 1.2x=0.4×2 x 0.4 2 1.2 x2
2.4 x 解：12x=2.4×3
12x=7.2 x=0.6
x = 7.5
3
2. 餐馆给餐具消毒，要用100mL消毒液配成消毒水，
如果消毒液与水的比是1∶150，应加入多少升水？
【教材P40 做一做 第2题】
方法一：57÷10=5.7(m) 方法二：57× 1 =5.7(m)
10
探索新知
长征五号运载火箭总长约为57m。 有一个长征五号运载火箭的模型， 它的总长与火箭总长的比是1∶10。 这个模型总长约为多少米？
模型总长 火箭总长 ＝1∶10 模型总长∶火箭总长＝1∶10
方法三
模型总长∶火箭总长＝1∶10
（1）解：设杭州湾跨海大桥实际长 x cm。 7.2∶x=1∶500000 x=3600000 3600000cm=36km
（2）解：设港珠澳大桥模型长 y cm。
55km=5500000cm y∶5500000=1∶500000
y=11
新课导入
3∶9＝( 5 )∶15
根( 据)÷比1例5=的13 ，意这义个，未3÷知9项= 13是，5。
根据比例的基本性质，把比例写成 9×( )=3×15，求出这个未知项是5。
新课导入
3∶9＝( 5 )∶15
根据比例的基本性质，如果已知比例中的 任意三项，就可以求出这个比例中的另外 一个未知项。
求比例中的未知项，叫作解比例。
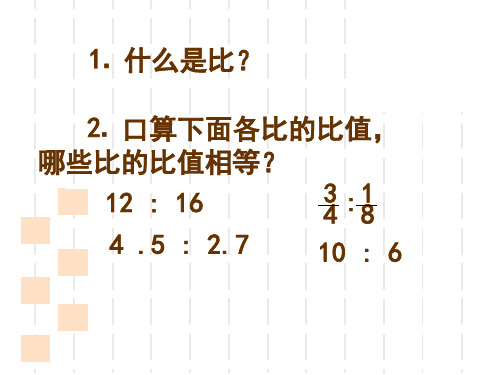
1.解比例。 12 : x 6 : 4 x8
1 ：5 x : 9 24 6
x 9 20
8 = 0.4 21 x x 1.05
2021年人教版六年级数学下册《比例的意义和基本性质》优质教学课件.ppt
仔细观察，你 发现了什么？
＝ 2.4 ︰ 1.6 6600 ︰40
内项 外项
外项积是： 2.4 × 40 ＝ 96 内项积是： 1.6 × 60＝96
×＝ ×
做一做 计算下面比例的外项积和内项积．
4.5∶2.7 = 10 ∶6
6 ∶10 = 9 ∶15
外项积：4.5 × 6 = 27 外项积： 6 × 15 = 90
2 ∶3 = 4 ∶6
6 ∶4 = 3 ∶2
2 ∶4 = 3 ∶6
6 ∶3 = 4 ∶2
4 ∶2 = 6 ∶3
3 ∶6 = 2 ∶4
4 ∶6 = 2 ∶3
3 ∶2 = 6 ∶4
复习
什么叫做比例？ 表示两个比相等的式子叫做比例。
什么叫做比例的基本性质？ 在比例里，两个外项的积等于两个内项的积。
判断下列各组比能否组成比例：
⑴ 6 ：12 和 4 ：8
()
⑵ 24：8 和 0.6：2
⑶ 4 ：7 和 6 ：5
56
74
⑷ 12 和 3 2 .4 6
() () ()
侦探柯南之神秘脚印:
一个月黑风高的夜晚，一家珠宝店失 窃了。第二天早上，小侦探柯南经过仔 细勘察，在案发现场发现了一枚犯罪嫌 疑人留下的脚印，根据这枚脚印，柯南 很快判断出了犯罪嫌疑人的身高，你们 知道，他是怎样判断的吗？
2．我是小法官，对错我来判判。
（1）比例是由任意两个比组成的。 （×） （2）在比例里，两个内项的积与两个外项的积的
差是0。 （√ ） （3）比例式中有四个外项，四个内项。（√ ）
3.把握知识点，做题不困难。
（1）（ C ）与 3 : 5 能组成比例。
A. 10:6 B.
比和比例(课件)-六年级数学下册人教版
答：需要糖0.1千克，水1.9千克。
➢ 用正、反比例的知识解决问题
甲工程队铺一条路，前5天 乙工程队铺路，原计划每天
铺了16千米，照这样的速度， 铺3.2千米，15天铺完。实
铺完这条路用了15天。这条 际每天铺4千米，实际需要
路长多少千米？ 正比例
多少天铺完？ 反比例
在练习本上解 答这两题。
➢ 用正、反比例的知识解决问题 • 解题步骤 ✓ 分析数量关系，判断成什么比例关系。 ✓ 找等量关系。若成正比例，则按“等比”找等量关系式; 若成反比例，则按“等积”找等量关系式。 ✓ 列比例。设未知数x，并代入等量关系式。 ✓ 解比例。 ✓ 检验写答。
＝
5 32
前比 后
比
项号 项
值
3∶ 2 ＝ 6 ∶4
内项 外项
➢ 比和比例的区别
• 基本性质
化简比 的根据
比的基本性质：比的前项和后项同时乘或除以 解比例 相同的数（0除外），比值相等。
的根据
比例的基本性质：在比例里，两个外项的积等于
两个内项的积。
➢ 比和比例的联系 • 比是比例的基础，比例是比的扩展； • 两个相等的比可以组成比例。
➢ 判断正、反比例的方法
一找：分析数量关系，确定哪两种量是相关联的量 二看：分析这两种相关联的量，看它们之间的关系是
乘积一定还是比值一定 三判断：如果乘积一定，成反比例
如果比值一定，成正比例 如果乘积和比值都不一定，不成比例
用比和比例的知识解决问题
➢ 按一定的比分配问题
一种糖水是糖与水按1∶19的比例配制而成的。要配制 这种糖水2千克，需要糖和水各多少千克？
成整数比再化简。 把比的前、后项同时乘分母的最小公倍数，转化成整 分数比 数比再化简。
人教版数学六年级下册 第4单元 比例 比例的意义和基本性质 第3课时 解比例 课件
的埃菲尔铁塔高
度约320m。北京的世界公园里 有一座埃菲尔铁塔的模型，它 的高度与原塔高度的比是1:10. 这座模型的高多少米？
解：设这座模型的高度是x m 可以列出式子： x∶320=1∶10
x∶320=1∶10，你能 试着计算出来吗？
怎样把比例式转化为方 程式？
根据比例的基本性质 转化。
四、课堂小结
求比例中的未知项叫做解比例。 解比例无论在书写格式还是验算方法上它与解方程都是相同 的。解比例时，先根据比例的基本性质把比例转化为方程，再按 解方程的方法进行解答。
五、课后练习
不能组成比例 不能组成比例
能组成比例，30:2=120:8 能组成比例，100:5=200:10
4. 李叔叔承包了两块水稻田，面积分别是0.5公顷 和0.8公顷。秋收时，两块水稻田的产量分别为3.75 吨和6吨。 （1）两块水稻田的产量与面积之比，是否可以组成 比例？
5.甲乙两个车间原有工人的比是4:3，甲车间的人数减少48 人后，甲乙两个车间人数比是2:3，甲乙两个车间原有多少 人？
解：设甲车间原有4x人，乙车间原有3x人，则 （4x-48）：3x=2：3
2×3x=3×（4x-48） 6x=12x-144 x=24
4x=96 3x=72 答：甲车间原有96人，乙车间原有72人。
回顾一下
1、什么叫做比例?
2、什么叫做比例的基本性质?怎样用比例的基本性质 判断两个比能否组成比例?那么组成一个比例需要几项 呢?
3、比例有几种表示形式?
一、新课导入
这节课，我们就要继续学习有关 比例的知识，就是解比例。
根据比例的基本性质，如 果已知比例中的任何三项，就可 以求出这个比例中的另外一个未 知项。
x ＝ 3.75
度约320m。北京的世界公园里 有一座埃菲尔铁塔的模型，它 的高度与原塔高度的比是1:10. 这座模型的高多少米？
解：设这座模型的高度是x m 可以列出式子： x∶320=1∶10
x∶320=1∶10，你能 试着计算出来吗？
怎样把比例式转化为方 程式？
根据比例的基本性质 转化。
四、课堂小结
求比例中的未知项叫做解比例。 解比例无论在书写格式还是验算方法上它与解方程都是相同 的。解比例时，先根据比例的基本性质把比例转化为方程，再按 解方程的方法进行解答。
五、课后练习
不能组成比例 不能组成比例
能组成比例，30:2=120:8 能组成比例，100:5=200:10
4. 李叔叔承包了两块水稻田，面积分别是0.5公顷 和0.8公顷。秋收时，两块水稻田的产量分别为3.75 吨和6吨。 （1）两块水稻田的产量与面积之比，是否可以组成 比例？
5.甲乙两个车间原有工人的比是4:3，甲车间的人数减少48 人后，甲乙两个车间人数比是2:3，甲乙两个车间原有多少 人？
解：设甲车间原有4x人，乙车间原有3x人，则 （4x-48）：3x=2：3
2×3x=3×（4x-48） 6x=12x-144 x=24
4x=96 3x=72 答：甲车间原有96人，乙车间原有72人。
回顾一下
1、什么叫做比例?
2、什么叫做比例的基本性质?怎样用比例的基本性质 判断两个比能否组成比例?那么组成一个比例需要几项 呢?
3、比例有几种表示形式?
一、新课导入
这节课，我们就要继续学习有关 比例的知识，就是解比例。
根据比例的基本性质，如 果已知比例中的任何三项，就可 以求出这个比例中的另外一个未 知项。
x ＝ 3.75
人教版六年级数学下册第四单元第3课时《解比例》(授课课件)
(3)若 4∶a＝21∶45，则 a＝(
32 5
)。
知识点 2 依据比例的基本性质解比例
2．解比例。
(1)x∶8＝12∶32
解：x＝
（
8 ）×（ 12 ） （ 32 ）
x＝ ( 3 )
(2)25∶71＝21∶x x＝258
(3) 2x5＝17.52
解：x＝
（ 25 ）×（ 1.2 ） （ 75 ）
x＝7.5
1.2x÷1.2＝0.8÷1.2 2
x＝ 3
探究点 2
ac
解形如 ＝ 的比例
bd
解比例
2.4 1.5
＝
6。 x
写成分数形式的比例，你会解吗？试一试并把你想
提醒大家的在组内交流。
解：2.4x＝1.5×6
x＝
(1.5 )×( ( 2.4 )
6)
x＝（ 3.75 ）
提示：
在将分数形式的比例改写成乘 积相等的式子时，一般要把含 有x的乘积写在等号的左边。
(3)若4∶a＝ 1∶4 ，则a＝( 32 )。
25
5
(4)在一个比例中，两个内项互为倒数，一个外项
是最小的质数，另一个外项是(
1 )。
2
(5)大、小齿轮的齿数之比是7∶4，大齿轮有56个
齿，则小齿轮有( 32 )个齿。
2．选择。(将正确答案的字母填在括号里)
(1) 如果0.6∶15＝x∶10，那么( A )。
x＝ ( 0.4 )
(4) 40..62＝8x x＝283
知识点 3 利用比例解决问题
3．手机专卖店按10∶1的比制作手机模型。 (1)A品牌手机模型的长是150 cm，A品牌手机的实际长度
是多少厘米？解：设A品牌手机的实际长度是x cm。 10∶1＝150∶x x＝15 答：A品牌手机的实际长度是15 cm。
六年级下册数学说课稿《4.1.比例的意义和基本性质第3课时解比例》人教版
六年级下册数学说课稿《 4.1.比例的意义和基本性质第3课时解比例》人教版一. 教材分析《4.1.比例的意义和基本性质》是人教版六年级下册数学的一个重要内容。
本节课主要让学生理解比例的意义，掌握比例的基本性质，并能运用比例解决实际问题。
本节课是本单元的第三课时，主要教学解比例。
通过前两节课的学习，学生已经掌握了比例的概念和基本性质，本节课将进一步引导学生运用比例解决实际问题，培养学生的解决问题的能力。
二. 学情分析六年级的学生已经具备了一定的数学基础，对比例的概念和基本性质有了初步的了解。
但是，学生在解决实际问题时，还存在着一定的困难，需要通过本节课的学习，进一步加强对比例的理解和运用。
此外，学生的学习兴趣和学习积极性也需要进一步激发和引导。
三. 说教学目标1.知识与技能目标：学生能理解比例的意义和基本性质，并能运用比例解决实际问题。
2.过程与方法目标：学生在解决实际问题的过程中，进一步培养观察、思考、解决问题的能力。
3.情感态度与价值观目标：学生通过学习，培养对数学的兴趣，增强自信心，培养合作意识。
四. 说教学重难点1.教学重点：学生能理解比例的意义和基本性质，并能运用比例解决实际问题。
2.教学难点：学生能灵活运用比例解决实际问题，特别是在解决问题时，能正确找出比例关系，列出比例式。
五. 说教学方法与手段本节课采用情境教学法、问题教学法和小组合作学习法。
情境教学法通过创设生活情境，让学生在情境中感受比例的意义和基本性质；问题教学法通过提出问题，引导学生思考和解决问题；小组合作学习法通过小组讨论，培养学生的合作意识和团队精神。
此外，利用多媒体教学手段，如PPT、教学视频等，可以丰富教学形式，提高学生的学习兴趣。
六. 说教学过程1.导入：通过创设一个生活情境，如购物场景，让学生观察和发现比例关系，引出本节课的主题——解比例。
2.教学新课：讲解比例的意义和基本性质，通过示例和练习，让学生理解和掌握比例的运用。
最新人教版数学六年级下册《比例的意义和基本性质》精品教学课件
从左往右看，比的前项、后项同时除以 相同的数（2除外），比值不变；
↑ 最简整数比
从右往左看，比的后项乘以比值等于比 的前项，比的前项除以后项等于比值。
小
试
牛
刀
最简整数比：
指的是比的前项和后项都是整数,且这两个整数互素
（即分子、分母只有公因数 1，不能进行约分）。
PART THREE
总结回顾
3
温馨提示
比的性质
比的前项和后项同时乘以或除以相同的数（零除外），比值不 变。
PART TWO
按部就班
2
张丽用时是李兰的几倍呢？
我们还可以把这两个数量之间的关系用比来表示。 5 ÷ 4 可以写成 5∶4 或 都读作“5 比 4”。 两个数相除又叫做这两个数的比。
想一想
下面有两杯糖水哪一杯糖水更甜？
做个观察家 最简分数 ↓
内在联系
比的前项相当于被除数、分子， 比的后项相当于除数、分母，
比值相当于商、分数值， 比号相当于除号、分数线。
比值相当于商和分数值。
转化
PART FOUR
大显身手
4
把下面的比化成最简整数比。 指出下列每个比的前项和后项，并求出比值。
（1）右图中长方形的长与宽的比 是（ ），比值是（ ）。
（2）把 25 g 盐溶解到 10 kg 水中， 盐与水的比是（ ），最简整数 比是（ ）；盐与盐水的比是 （ ），比值是（ ）。
复习感悟
01 今天的课堂你收获了什么？
课后研讨
学完这节课，你收获了 什么？有什么样的感悟？ 与同学相互交流讨论。
课后作业
1.从课后习题中选取； 2.完成练习册本课时的习题。
教师寄语
大千世界，充满着无数的奥秘，希望 同学们能遇事独立，积极探索钻研，解决 更多的难题。
六年级数学下册课件-4.1比例的意义和基本性质(第3课时)解比例人教版 (共24张PPT)
9 = 4.5 1.6 0.8
3：9=（ ）：15
9 × 0.8=1.6× 4.5 3×15=9×（ ）
3.填一填 利用比例的基本性质： a:b=c:d ad=bc ( 1 ):5=2:10
1.8:( 10 )=0.9:5 72:9=64：( 8 )
想一想：
（1）比例中共有几项？有什么关系？ （2）根据比例的基本性质，如果已知 比例中的任何三项，能不能求出这个 比例中的另外一个未知项？
解比例 2.4 = 6
1.5 x
解：2.4x = 1.5×6 1.5 × 6
x= 2.4
x = 3.75
餐馆给餐具消毒，要用100ml消毒液配 成消毒水，如果消毒液与水的比是1:150， 应加入水多少毫升?
解：设应加水 x ml 100:x=1:150 x=150×100 x=15000
答：应加水15000ml。
（2）麦片的单价是28元，饼干的 单价是多少？
解：设饼干单价为x元。 3:2=x：28
x=42
课堂小结
定义： 求比例中的未知项。
解
比 例
方法：利用比例的基本性质，把比例式 转化为方程，再通过解方程求出
未知项的值。
课后作业 数学书44页：11. 12. 13题
人教版 六年级数学下册 第4单元 比例
4.1 比例的意义和基本性质（第3课时）
解比例
1.什么叫做比例？ 表示两个比相等的式子叫做比例。
2.什么叫做比例的基本性质？
在比例里两个外项的积等于两个 内项的积。
复习
根据比例的基本性质，将下列各比例 改写成其他等式。
3∶8 = 15∶40 3 × 40 = 8 × 15
3.依照下面的条件列出比例，并且解比例。
新版六年级数学下册课件 1.比例的意义和基本性质 第3课时 解比例 人教版(共10P)
第四单元 比 例
1.比例的意义和基本性质
一、填一填。 1.六（1）班男生和女生人数的比是5∶6，六（1） 班男生有25人，女生有（ 30 ）人。 2.一种猪肉水饺的馅主要是由猪肉和葱调制成的， 其中猪肉和葱的质量的比是7∶2，现在有0.35 kg 猪肉，要调制这种馅，需要（ 0.1 ）kg葱。二、解一解。（解比例）9∶24 = x∶12
解：24x=9×12
x=9×2412
x=
9 2
1.8 11
=
x 22
解：11x=1.8×22
x=1.81×1 22 x=3.6
三、解决问题。 1.一种喷洒果树的农药，是用药液和水按1∶120的 质量比配制而成的。 （1）如果用5.5 kg药液配制农药，需要加水多少 千克？ 解：设需要加水x kg。 5.5∶x=1∶120 x=660
（2）配制这种农药，420 kg水中需要加入药液多少千克？
解：设需要加入药液y kg。 y∶420=1∶120 y=3.5
2.国庆节期间，某超市洗衣液搞促销活动。 （1）促销活动中，洗衣液和洗洁精是按照怎样的数量 比进行搭配的？
3∶1
（2）现在有240桶洗衣液，需要准备多少瓶洗洁精？
解：设需要准备x瓶洗洁精。 240∶x=3∶1 x=80
甲、乙两个图形部分重叠在一起，重叠部分的面积
是甲的
1 3
，是乙的
1 4
。已知图形乙的面积是48cm2，图形
甲的面积是多少平方厘米？
重叠部分面积=
1 3
甲=
1 4
乙，则甲∶乙=3∶4。
解：设图形甲的面积是xcm2。
x∶48=3∶4
x=36
1.比例的意义和基本性质
一、填一填。 1.六（1）班男生和女生人数的比是5∶6，六（1） 班男生有25人，女生有（ 30 ）人。 2.一种猪肉水饺的馅主要是由猪肉和葱调制成的， 其中猪肉和葱的质量的比是7∶2，现在有0.35 kg 猪肉，要调制这种馅，需要（ 0.1 ）kg葱。二、解一解。（解比例）9∶24 = x∶12
解：24x=9×12
x=9×2412
x=
9 2
1.8 11
=
x 22
解：11x=1.8×22
x=1.81×1 22 x=3.6
三、解决问题。 1.一种喷洒果树的农药，是用药液和水按1∶120的 质量比配制而成的。 （1）如果用5.5 kg药液配制农药，需要加水多少 千克？ 解：设需要加水x kg。 5.5∶x=1∶120 x=660
（2）配制这种农药，420 kg水中需要加入药液多少千克？
解：设需要加入药液y kg。 y∶420=1∶120 y=3.5
2.国庆节期间，某超市洗衣液搞促销活动。 （1）促销活动中，洗衣液和洗洁精是按照怎样的数量 比进行搭配的？
3∶1
（2）现在有240桶洗衣液，需要准备多少瓶洗洁精？
解：设需要准备x瓶洗洁精。 240∶x=3∶1 x=80
甲、乙两个图形部分重叠在一起，重叠部分的面积
是甲的
1 3
，是乙的
1 4
。已知图形乙的面积是48cm2，图形
甲的面积是多少平方厘米？
重叠部分面积=
1 3
甲=
1 4
乙，则甲∶乙=3∶4。
解：设图形甲的面积是xcm2。
x∶48=3∶4
x=36
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：设应加水 x ml 100:x=1:150 x=150×100 x=15000
答：应加水15000ml。
1.在下面括号里填上合适的数。
24:9=8:（ 3 ）
（ 10 ）= 2
15 3
（ 1 ）:3=8:24
4:（ 1 ）=36:9
2.解比例
（1） 1：5 =x : 9
36
解： 5 x=9 1
5.妈妈买了2盒饼干和3袋麦片，饼干 和麦片所花的钱数相等。
（1）饼干和麦片的单价之比是多少？
解：设饼干和麦片的单价分别为x元、y元。
2x=3y x：y=3:2
（2）麦片的单价是28元，饼干的 单价是多少？
解：设饼干单价为x元。 3:2=x：28
x=42
课堂小结
定义： 求比例中的未知项。
解
比 例
解： x：7=9:2.1 2.1x=7×9 x=63÷2.1 x=30
4.莉莉在电脑上把下面的照片按比例放 大，放大后的照片长是13.5厘米，宽是 多少厘米？
6厘米
4厘米
解：设放大后的照片宽是x厘米。
13.5:6=x：4
13.5: x 6 : 4
6x=13.5×4
x=9
答：放大后的照片宽是9厘米。
例3：解比例： 交叉相乘改写为等式 12—..55 ＝ —X6
解： 1.5 X＝ 2.5 × 6 X＝ 2.5 × 6 1.5 X＝ 10
练习
解比例 2.4 = 6
1.5 x
解：2.4x = 1.5×6 1.5 × 6
x= 2.4
x = 3.75
餐馆给餐具消毒，要用100ml消毒液配 成消毒水，如果消毒液与水的比是1:150， 应加入水多少毫升?
9 = 4.5 1.6 0.8
3：9=（ ）：15
9 × 0.8=1.6× 4.5 3×15=9×（ ）
3.填一填 利用比例的基本性质： a:b=c:d ad=bc ( 1 ):5=2:10
1.8:( 10 )=0.9:5 72:9=64：( 8 )
想一想：
（1）比例中共有几项？有什么关系？ （2）根据比例的基本性质，如果已知 比例中的任何三项，能不能求出这个 比例中的另外一个未知项？
埃菲尔铁塔模型的高度：320=1：10
解:设这座模型高X 米。
X : 320 = 1 : 10
根据比例的基本性质
10X = 320×1
X=
320×1 10
X =32
答:这座模型高 32米。
根据比例的基本性质，如果已 知比例中的任何三项，就可以求出 这个比例中的另外一个未知项。
求比例中的未知项，叫做解比例。
人教版 六年级数学下册 第4单元 比例
4.1 比例的意义和基本性质（第3课时）
解比例
1.什么叫做比例？ 表示两个比相等的式子叫做比例。
2.什么叫做比例的基本性质？
在比例里两个外项的积等于两个 内项的积。
复习
根据比例的基本性质，将下列各比例 改写成其他等式。
3∶8 = 15∶40 3 × 40 = 8 × 15
6
3
x=3 5
6
x= 18
5
（2）
8 21
=
0.4 x
解： 8x=210.4
x=8.4 8
x=1.05
3.依照下面的条件列出比例，并且解比例。
（1）12
与x的比等于
3 4
与
1 8
的比。
解：
1 2
：x
=
3 4
：1
8
3 4
x=
1 2
பைடு நூலகம்
×18
x=
1 12
（2）比的两内项分别是7和9，两外 项分别是x和2.1.
艾菲尔铁塔高320米, 它不仅是一座吸引游 人观光的纪念塔，还 是巴黎这座具有悠久 历史的美丽城市的象 征。
例2：法国巴黎的埃 菲尔铁塔高320米,北 京的“世界公园”里 有一座埃菲尔铁塔的 模型,它的高度与原塔 高度的比是1:10。这 座模型高多少米?
埃菲尔铁塔模型的高度：埃菲尔铁塔的高度=1：10
方法：利用比例的基本性质，把比例式 转化为方程，再通过解方程求出
未知项的值。
课后作业 数学书44页：11. 12. 13题
答：应加水15000ml。
1.在下面括号里填上合适的数。
24:9=8:（ 3 ）
（ 10 ）= 2
15 3
（ 1 ）:3=8:24
4:（ 1 ）=36:9
2.解比例
（1） 1：5 =x : 9
36
解： 5 x=9 1
5.妈妈买了2盒饼干和3袋麦片，饼干 和麦片所花的钱数相等。
（1）饼干和麦片的单价之比是多少？
解：设饼干和麦片的单价分别为x元、y元。
2x=3y x：y=3:2
（2）麦片的单价是28元，饼干的 单价是多少？
解：设饼干单价为x元。 3:2=x：28
x=42
课堂小结
定义： 求比例中的未知项。
解
比 例
解： x：7=9:2.1 2.1x=7×9 x=63÷2.1 x=30
4.莉莉在电脑上把下面的照片按比例放 大，放大后的照片长是13.5厘米，宽是 多少厘米？
6厘米
4厘米
解：设放大后的照片宽是x厘米。
13.5:6=x：4
13.5: x 6 : 4
6x=13.5×4
x=9
答：放大后的照片宽是9厘米。
例3：解比例： 交叉相乘改写为等式 12—..55 ＝ —X6
解： 1.5 X＝ 2.5 × 6 X＝ 2.5 × 6 1.5 X＝ 10
练习
解比例 2.4 = 6
1.5 x
解：2.4x = 1.5×6 1.5 × 6
x= 2.4
x = 3.75
餐馆给餐具消毒，要用100ml消毒液配 成消毒水，如果消毒液与水的比是1:150， 应加入水多少毫升?
9 = 4.5 1.6 0.8
3：9=（ ）：15
9 × 0.8=1.6× 4.5 3×15=9×（ ）
3.填一填 利用比例的基本性质： a:b=c:d ad=bc ( 1 ):5=2:10
1.8:( 10 )=0.9:5 72:9=64：( 8 )
想一想：
（1）比例中共有几项？有什么关系？ （2）根据比例的基本性质，如果已知 比例中的任何三项，能不能求出这个 比例中的另外一个未知项？
埃菲尔铁塔模型的高度：320=1：10
解:设这座模型高X 米。
X : 320 = 1 : 10
根据比例的基本性质
10X = 320×1
X=
320×1 10
X =32
答:这座模型高 32米。
根据比例的基本性质，如果已 知比例中的任何三项，就可以求出 这个比例中的另外一个未知项。
求比例中的未知项，叫做解比例。
人教版 六年级数学下册 第4单元 比例
4.1 比例的意义和基本性质（第3课时）
解比例
1.什么叫做比例？ 表示两个比相等的式子叫做比例。
2.什么叫做比例的基本性质？
在比例里两个外项的积等于两个 内项的积。
复习
根据比例的基本性质，将下列各比例 改写成其他等式。
3∶8 = 15∶40 3 × 40 = 8 × 15
6
3
x=3 5
6
x= 18
5
（2）
8 21
=
0.4 x
解： 8x=210.4
x=8.4 8
x=1.05
3.依照下面的条件列出比例，并且解比例。
（1）12
与x的比等于
3 4
与
1 8
的比。
解：
1 2
：x
=
3 4
：1
8
3 4
x=
1 2
பைடு நூலகம்
×18
x=
1 12
（2）比的两内项分别是7和9，两外 项分别是x和2.1.
艾菲尔铁塔高320米, 它不仅是一座吸引游 人观光的纪念塔，还 是巴黎这座具有悠久 历史的美丽城市的象 征。
例2：法国巴黎的埃 菲尔铁塔高320米,北 京的“世界公园”里 有一座埃菲尔铁塔的 模型,它的高度与原塔 高度的比是1:10。这 座模型高多少米?
埃菲尔铁塔模型的高度：埃菲尔铁塔的高度=1：10
方法：利用比例的基本性质，把比例式 转化为方程，再通过解方程求出
未知项的值。
课后作业 数学书44页：11. 12. 13题