高中数学知识框架图
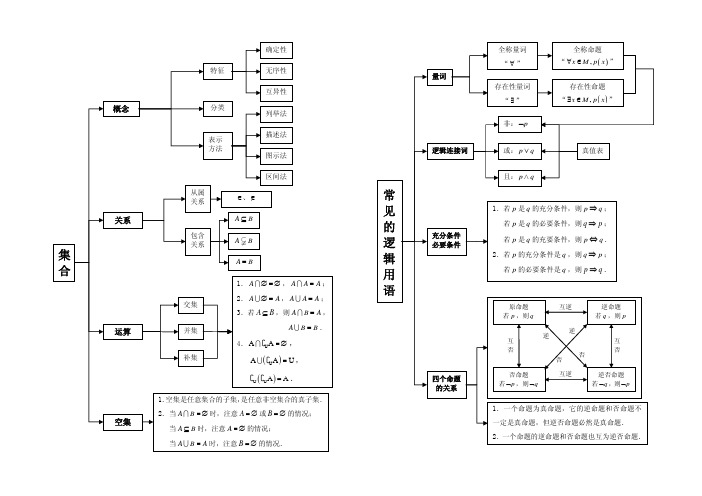
高中数学知识结构图 全部
,
+∞
⎞ ⎠⎟
为减函数.
① 图像是双曲线;
当 k < 0 时,
② 定义域为{x x ∈ R, x ≠ 0} ,
值域为{y y ∈ R, y ≠ 0} ;
③ 奇函数. ④ 没有零点;
在 (−∞,0) 和 (0, +∞) 为增函数
①
值域为
⎡ ⎢ ⎣
4ac − 4a
b2
,
+∞
⎞ ⎟ ⎠
②
在
⎛ ⎜⎝
−∞,
−
顶点坐标是
⎛ ⎜ ⎝
−
b 2a
,
4ac − 4a
b2
⎞ ⎟ ⎠
④ 当 b = 0 时是偶函数;
⑤ 当 Δ > 0 ,有两个零点;当 Δ = 0 ,
有一个零点;当 Δ < 0 ,没有零点.
①
值域为
⎛ ⎜ ⎝
−∞,
4ac − 4a
b2
⎤ ⎥ ⎦
②
在
⎛ ⎜⎝
−∞,
−
b 2a
⎞ ⎟⎠
为增函数,
在
⎛ ⎜⎝
−
b 2a
辑
2.若 p 的充分条件是 q ,则 q ⇒ p ;
用
若 p 的必要条件是 q ,则 p ⇒ q .
语
原命题 若 p ,则 q
互 否
互逆
逆
逆
否 否
逆命题 若 q ,则 p
互 否
四个命题 的关系
否命题 若 ¬p ,则 ¬q
互逆
逆否命题 若 ¬q ,则 ¬p
1.一个命题为真命题,它的逆命题和否命题不 一定是真命题,但逆否命题必然是真命题. 2.一个命题的逆命题和否命题也互为逆否命题.
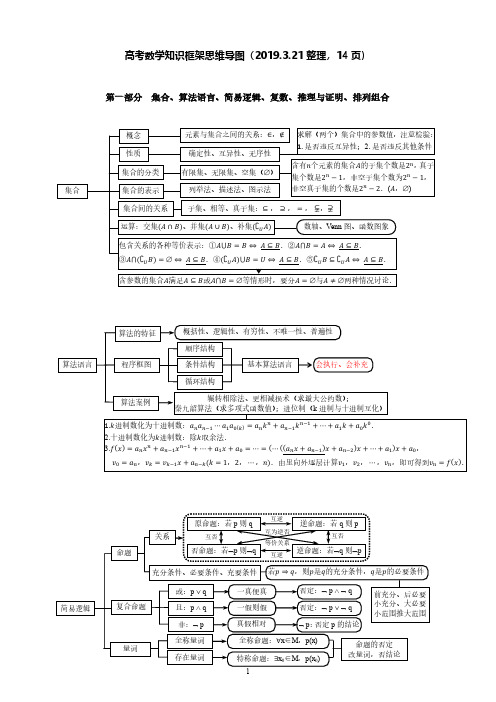
高中数学知识框架思维导图
i.
①(1 ± i)2 = ±2i;
②1+i = i;1−i = −i;
1−i
1+i
③������ + ������i = i(������ − ������i),
如3+4i = i(4−3i) = i;
4−3i 4−� = ������ + ������i、复平面内点 Z(������, ������)、向量���⃗⃗���⃗⃗���⃗��� = (������, ������)的一一对应关系; 复数模的几何意义:|������| = |������ + ������i| = √������2 + ������2 = |���⃗⃗���⃗⃗���⃗���|
2.对数的运算性质(������>0,且������ ≠1,������>0,������>0):①log������(������ ∙ ������) = log������������ + log������������;
简易逻辑
命题
关系
原命题:若 p 则 q
互否
否命题:若p 则q
互逆
互为逆否 等价关系
互逆
逆命题:若 q 则 p
互否
逆命题:若q 则p
充分条件、必要条件、充要条件 若������ ⇒ ������,则������是������的充分条件,������是������的必要条件
复合命题 量词
或:p q 且:p q 非: p 全称量词 存在量词
2
映射
函数
函数图象 及其变换
第二部分 函数、导数及微积分
������: ������ → ������:一对一,或多对一
2021年高中数学知识结构框图(人教版)

高中数学知识结构框图(必修 1)第一章 集合与函数概念含义与表示集合基本关系基本运算列举法 {a,b,c,…}描述法 {x|p(x)}图象法韦恩图; 数轴包含关系 相等关系子集; 真子集交集:A∩B={x|x∈A 且 x∈B}并集:A∪B={x|x∈A 或 x∈B}函数 映射概念 表示补集: 定义域 对应关系 值域 解析法 图象法 列表法单调性性质映射的概念奇偶性1定义 图象特征 定义最值上升或 下降图象特征:对称性第二章 基本初等函数(Ⅰ)根式指分数指数幂指数数与无理数指数幂指数运算性质函数 定义指基 本数 函图象: “一撇或一捺”, 过点(0,1).见教材 P56初 等数性质: 位于 x 轴上方,以 x 轴为渐近线函数定义:(Ⅰ对数对运算性质数与对数函换底公式:数定义: 对数 函图象:位于 y 轴右侧,以 y 轴为渐近线.见教材 P71数性质:过点(1,0)定义:图象见 P77 图 2.3-幂函数具体的五个幂函数特征:过点(1,1),当时在上递增;当时,在上递减。
2第三章 函数的应用函 数 与 方 程函 数 的 应 用函 数 模 型 及 其 应 用方程的根与 函数零点的关函数零点的存在性用二分法求方程的近似解 几种不同增长的函数模型 用已知函数模型解决问题 建立实际问题的函数模型直线上升 指数爆炸 对数增长指数函数,对数函数, 幂函数增长速度的比 较。
见教材 P98~1003数学二 第一章 空间几何体的知识结构框架第二章 点、直线、平面之间的位置关系的知识结构框架4第三章 直线与方程的知识结构框架 第四章 圆与方程的知识结构框架5数学三数学四 本章知识结构如下:本章知识结构如下:6本章知识结构如下:7。
高中数学知识体系框架

高中数学知识体系框架第一章集合、映射、函数、导数及微积分集合学习要点:(1)理解集合、子集、补集、交集、并集的概念;了解空集和全集的意义;了解属于、包含、相等关系的意义;掌握有关的术语和符号,并会用它们正确表示一些简单的集合;(2)理解逻辑联结词“或”、“且”、“非”的含义理解四种命题及其相互关系;掌握充分条件、必要条件及充要条件的意义。
映射学习要点:((1)了解映射的概念,理解函数的概念;(2)了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法;(3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数;(4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像和性质;(5)理解对数的概念,掌握对数的运算性质;掌握对数函数的概念、图像和性质;(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题。
函数学习要点:数三要素是定义域,对应法则和值域,而定义域和对应法则是起决定作用的要素,因为这二者确定后,值域也就相应得到确定,因此只有定义域和对应法则二者完全相同的函数才是同一函数。
导数学习要点:(1)了解导数概念的某些实际背景;(2)理解导数的几何意义;(3)掌握函数,y=c(c为常数)、y=xn(n∈N+)的导数公式,会求多项式函数的导数;(4)理解极大值、极小值、最大值、最小值的概念,并会用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值;(5)会利用导数求某些简单实际问题的最大值和最小值.微积分学习要点:(1)微积分基本定理揭示了导数与定积分之间的联系,同时它也提供了计算定积分的一种有效方法;(2)根据定积分的定义求定积分往往比较困难,而利用微积分基本定理求定积分比较方便。
知识体系框架结构图:第二章三角函数与平面向量三角函数学习要点:(1)理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算;(2)掌握任意角的正弦、余弦、正切的定义;了解余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式;了解周期函数与最小正周期的意义;(3)掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式;(4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明;(5)理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图,理解A.ω、φ的物理意义;(6)会由已知三角函数值求角,并会用符号arcsinx\arc-cosx\arctanx表示;(7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形;(8)“同角三角函数基本关系式:sin2α+cos2α=1,sinα/cosα=tanα,tanα•cosα=1”。
高中数学必修一知识点思维导图

高中数学必修一知识点思维导图一、函数与映射1. 函数的概念- 定义- 函数的表示方法- 函数的组成:定义域、值域、对应关系2. 函数的性质- 单调性- 奇偶性- 周期性- 有界性3. 特殊函数- 一次函数- 二次函数- 指数函数- 对数函数- 三角函数4. 函数的运算- 函数的加法、减法、乘法、除法- 复合函数- 反函数二、集合与运算1. 集合的基本概念- 集合的定义- 元素与集合的关系- 集合的表示法2. 集合间的关系- 子集、真子集- 并集、交集、补集3. 集合的运算- 集合的并、交、补运算的性质 - 德摩根定律三、不等式与不等式组1. 不等式的性质- 基本性质- 特殊不等式(如柯西不等式)2. 不等式的解集- 一元一次不等式的解集- 一元二次不等式的解集3. 不等式组- 定义- 解集的求解方法- 线性规划四、数列与数学归纳法1. 数列的概念- 数列的定义- 数列的表示方法2. 等差数列与等比数列- 定义与性质- 通项公式- 求和公式3. 数学归纳法- 原理- 证明方法- 应用五、初等几何1. 平面几何- 点、线、面的基本性质- 圆的性质- 相似三角形- 圆与直线的关系2. 空间几何- 空间图形的基本概念- 空间直线与平面的位置关系- 立体角的概念- 柱、锥、台的体积与表面积计算六、概率与统计1. 概率的基本概念- 随机事件- 概率的定义- 条件概率2. 随机变量及其分布- 离散型随机变量- 连续型随机变量- 概率分布与概率密度函数3. 统计基础- 数据的收集与整理- 描述性统计量(均值、中位数、众数等)- 抽样与估计以上是高中数学必修一知识点的思维导图结构。
每个部分都应该详细展开,包含具体的公式、定理、性质和例子。
这份思维导图旨在帮助学生系统地复习和掌握必修一的数学知识,为进一步学习打下坚实的基础。
高中数学知识框架思维导图(2019.3.21整理,14页)

两个原理
分类加法计算原理和分步乘法计算原理 排列数:������������ ������ = ������(������ − 1) ⋯ (������ − ������ + 1) = (������−������)!
������!
计算原理
排列与组合
������! m 组合数:C n = ������!(������−������)!
高考数学知识框架思维导图(2019.3.21 整理,14 页)
陈永清
第一部分
集合、算法语言、简易逻辑、复数、推理与证明、排列组合
概念 性质 集合的分类 集合 集合的表示 集合间的关系
Hale Waihona Puke 元素与集合之间的关系:∈,∉ 确定性、互异性、无序性 有限集、无限集、空集() 列举法、描述法、图示法
求解(两个)集合中的参数值,注意检验: 1.是否违反互异性;2.是否违反其他条件 含有������个元素的集合������的子集个数是2������ , 真子 ������ ������ 集个数是2 − 1,非空子集个数为2 − 1, 非空真子集的个数是2������ − 2.(������,)
性质
C n =C n
m
m
n-m
Cn+1=C n +C
m
m-1 n
应用
捆绑法、插空法、优先法、隔板法、间接法、建模法、分类法、树状图
0 ������ ������ + ������ 1 ������ ������−1 ������ + ⋯ + ������ ������ ������ ������−������ ������ ������ + ⋯ + ������ ������−1 ������1 ������ ������−1 + ������ ������ ������ ������ (������∈N*). (������ + ������)������ = ������������ ������ ������ ������ ������
数学高一知识点框架图

数学高一知识点框架图数学是一门广泛应用于各个领域的学科,而高中数学则是数学学科中最基础、最重要的一部分。
理解和掌握高一数学的知识点是我们深入学习数学的首要任务。
为此,我整理了数学高一知识点的框架图,以便于我们更好地理解和记忆这些知识。
一、函数与方程1.函数的概念与性质2.函数的表示与运算3.一次函数与二次函数4.指数函数与对数函数5.三角函数与周期性函数6.函数的应用问题7.方程与不等式的基本性质8.一元一次方程与一元二次方程的解法9.绝对值方程与不等式的解法10.分式方程与分式不等式二、数列与数学归纳法1.数列的概念与性质2.等差数列与等比数列的性质3.递推公式与通项公式4.数列的求和与数学归纳法三、平面几何1.平面几何基本概念和性质2.直线与角的性质3.三角形的性质与分类4.平行线与三角形的性质5.勾股定理与直角三角形的性质6.相似三角形与勾股定理的应用7.圆的性质与弧度制8.圆的切线与切圆问题9.圆与直线的位置关系四、空间几何1.空间几何基本概念和性质2.二面角与直线垂直的判定3.平面与空间中直线的位置关系4.棱柱与棱锥的性质5.平行四边形与平行四边体的性质6.球的性质与球与圆柱的位置关系7.空间中直线与平面的位置关系8.等腰三角形与正三角形的性质9.平面与空间中的位置关系与图形的投影五、概率与统计1.随机事件与概率的基本概念2.古典概型与几何概型3.概率的加法定理与乘法定理4.条件概率与独立事件5.排列与组合的基本原理6.样本空间与事件的概率7.统计图表的制作与分析8.均值、中位数和众数的计算和比较六、解析几何与立体几何1.直线与直线的位置关系2.圆与直线的位置关系3.曲线的方程与图像4.空间中的直线与平面的位置关系5.空间中的曲线与曲面的位置关系6.线性规划与最值问题的求解7.球和球面的性质和计算以上就是数学高一知识点的框架图,通过这个框架图可以清楚地了解到高一数学的主要知识点。
接下来,我们可以根据这个框架图,有针对性地进行学习和复习,以便更好地掌握高一数学。
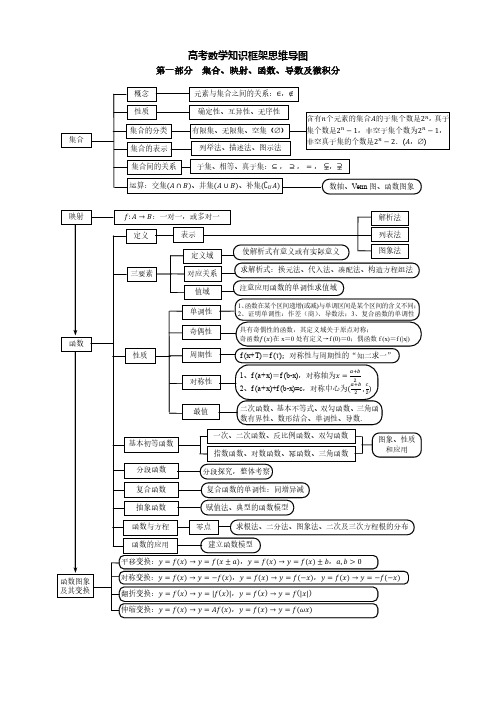
高中数学知识框架思维导图(整理版)
柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan , =
倾斜角和斜率
重合
A1B2-A2B1=0,C1B2-C2B1=0
平行
A1B2-A2B1=0,C1B2-C2B1≠0
相交
A1B2-A2B1≠0
垂直
直线的方程
z 的几何意义:
过可行域内一点(, )
向直线 = , = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
对称性
y=Asin(x+)+b
化简、求值、
证明(恒等变形)
)
值域
图象
对称轴(正切函数除外)经过函数图象
的最高(或低)点且垂直 x 轴的直线,
对称中心是正余弦函数图象的零点,正
切函数的对称中心为( ,0)(k∈Z).
最值
2
①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
(完整版)高中数学知识结构框图
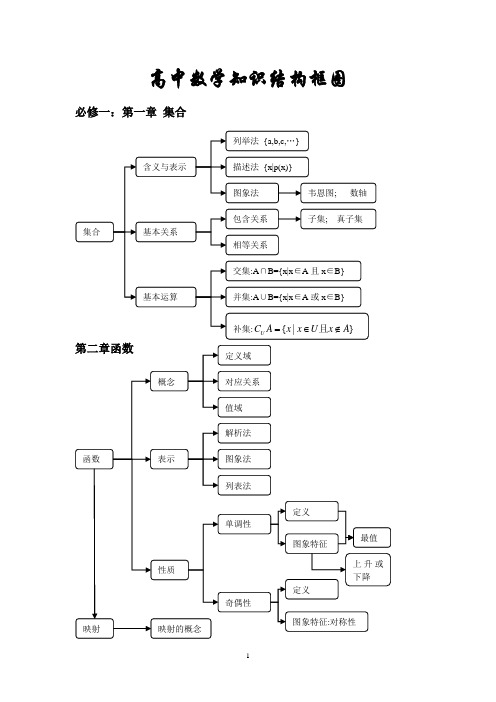
必修一:第一章集合
第三章基本初等函数(Ⅰ)
指数函数
对数数函数
定义域
值域
图象
性质
过定点
过定点
减函数
增函数
减函数
增函数
幂函数
奇函数
偶函数
第一象限性质
减函数
增函数
过定点
必修二:第一章立体几何初步
第二章 平面解析几何初步
必修三:第一章 算法初步
第二章 统计
第三章 概率
必修四:第一章 基本初等函数(II)
函
数
性Байду номын сангаас
质
图象
定义域
值域
最值
当 时, ;当
时, .
当 时,
;当
时, .
既无最大值也无最小值
周期性
奇偶性
奇函数
偶函数
奇函数
单调性
在
上是增函数;在
上是减函数.
在
上是增函数;在
上是减函数.
在
上是增函数.
对称性
对称中心
对称轴
对称中心
对称轴
对称中心
无对称轴
第二章平面向量
第三章三角恒等变换
必修五:第一章解三角形
第二章 数列
高中数学知识方法树状图
正余弦定理综合
运用边角互化功能解决解三角形的具体题型
运用正余弦定理解决与几何图形结合的题型 基本几何知识
用正余弦定理处理实际生活问题
平均变化率 瞬时变化率
导数的定义
导数的加法与减法法则 导数的乘法与除法法测
常见函数的导数 复合函数求导
导数的几何意义
求切线方程
切线中含参求值问题 旋转动直线问题
简单的离散型随机变量分布列的求法 离散型随机变量的均值与方差的求法及其性质
利用排列组合求解随机变量取值及对应概率 利用数字特征解决实际应用问题
两角和与差的正余弦公式
两角和与差的正切公式 两角和差公式的运用 辅助角公式的推导及其应用 辅助角公式的运用
倍半角公式的推导
倍半角公式的运用 积化和差公式 和差化积公式
三角恒等变换及化简求值 三角函数的恒等式证明 三角恒等变换的综合问题
正弦定理及其推导
正弦定理的应用
余弦定理及其推导
余弦定理的应用
余弦定理的应用
轨迹问题 定点定值问题 弦长与面积问题
弦长与面积问题
共线比例问题 角度相关问题
四级名称 平方差公式 完全平方差公式 立方差公式 二次根式的概念 分母有理化 二次根式的意义 用零点分段法化简绝对值或求值 提公因式法
公式法 十字相乘法 分组分解法 判别式与根个数的关系 因式分解法
配方法 求根公式法 韦达定理内容
映射的概念与象与原象
映射的个数 利用一一映射解题
函数的概念 数集的区间表示法
简单的函数求值 相同函数的判断
定义域的分类 具体函数的定义域 抽象函数的定义域 定义域已知求参数范围
值域的概念
二次函数的值域
高中数学知识框架

高中数学知识框架一、代数基础加减法:实数、有理数、整式的加减法,结合律、交换律、分配律的应用。
乘法:实数、有理数、整式的乘法,乘法交换律、结合律、分配律的应用。
除法:实数、有理数、整式的除法,除法交换律、结合律、分配律的应用。
二、平面几何点:坐标、对称、轨迹。
线:平行、垂直、相交、角平分线、中垂线、等角对等边等概念。
面:三角形、四边形、圆形等基本几何形体的性质与判定定理。
距离:两点间距离、点到直线距离、直线间距离等概念的计算和应用。
角:锐角、直角、钝角、平角、周角等概念,以及相关的性质与判定定理。
三、立体几何体:立方体、长方体、圆柱体等基本几何体的性质与判定定理。
线:直线、平面、直角坐标系等概念,以及相关的性质与判定定理。
面:三角形、四边形、圆形等基本几何形体的性质与判定定理。
体积:立方体、长方体等基本几何体的体积计算方法。
表面积:立方体、长方体等基本几何体的表面积计算方法。
四、解析几何坐标系:二维坐标系和三维坐标系的建立与表示方法。
直线:斜率、截距、两点式方程等概念,以及直线的性质与判定定理。
圆:圆心、半径、标准方程等概念,以及圆的相关性质与判定定理。
椭圆:焦点、长轴、短轴等概念,以及椭圆的相关性质与判定定理。
抛物线:焦点、准线等概念,以及抛物线的相关性质与判定定理。
双曲线:焦点、实轴、虚轴等概念,以及双曲线的相关性质与判定定理。
五、概率与统计概率:事件概率、独立事件概率、互斥事件概率等概念的计算和应用。
样本空间:样本空间的概念和表示方法。
概率分布:离散型概率分布和连续型概率分布的概念和计算方法。
超几何分布:超几何分布的概念和计算方法。
二项分布:二项分布的概念和计算方法。
正态分布:正态分布的概念和计算方法,以及正态分布曲线族的特点和应用。
六、函数与方程函数:函数的概念和表示方法,函数的单调性、奇偶性等性质。
方程:方程的概念和表示方法,以及方程的解法。
根:根的概念和表示方法,以及根与系数的关系。
高中数学专题知识框架及应用结构图(彩色版)-01集合与简易逻辑基本知识总结

一、集合概念概念指定的某些对象的全体称为集合元素与集合元素与集合的关系有且仅有两种:属于(∈)或不属于(∉).元素特性确定性、互异性、无序性常用数集实数集R;有理数集Q;整数集Z;自然数集N;正整数集N*(或N+)表示方法列举法、描述法基本关系子集A⊆B①空集是任何集合的子集.②空集是任何非空集合的真子集.③若A⊆B,B⊆C,则A⊆C.④A=B⇔A⊆B且B⊆A.⑤有限集合的子集个数:n个元素的集合有2n个子集;其中有2n-1个真子集;有2n-1个非空子集;有2n-2个非空真子集.真子集A⊂B相等集合A=B基本运算交集A∩B A∩B={x|x∈A且x∈B}A∩B⊆AA∩B⊆BA∩Ø=Ø并集A∪B A∪B={x|x∈A或x∈B}B⊆A∪BA⊆A∪BA∪Ø=A补集∁U A∁U A={x|x∈U且x∉A}A∪(∁U A)=UA∩(∁U A)=Ø∁U(∁U A)=A二、简易逻辑命题概念能够判断真假的语句四种命题原命题:若p,则q逆命题:若q,则p否命题:若¬p,则¬q逆否命题:若¬q,则¬p充要条件充分条件p⇒q,p是q的充分条件若命题p对应集合A,命题q对应集合B,则:p⇒q等价于A⊆B;p⇒q且q⇒p等价于A=B.必要条件p⇒q,q是p的必要条件充要条件p⇒q且q⇒p,p、q互为充要条件逻辑联结词且命题“p∧q”:一假则假,同真为真.类比集合的“交”或命题“p∨q”:一真则真,同假为假.类比集合的“并”非命题“¬p”:真假相反类比集合的“补”量词全称量词∀,含全称量词的命题叫全称命题,其否定为特称命题.存在量词∃,含存在量词的命题叫特称命题,其否定为全称命题.。
