三角形、梯形中位线练习题
三角形的中位线基础题30道选择题附详细答案

9.5 三角形的中位线基础题汇编(1)...2=...7+9.5 三角形的中位线基础题汇编(1)参考答案与试题解析一.选择题(共30小题)1.(2014•河北)如图,△ABC中,D,E分别是边AB,AC的中点.若DE=2,则BC=()2.(2014•北海)如图△ABC中,D、E分别是边AB、AC的中点,已知DE=5,则BC的长为()3.(2014•泸州)如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为()4.(2014•宜昌)如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是()MN=MN=AB5.(2014•牡丹江一模)如图,⊙O的半径为5,弦AB=8,点C在弦AB上,且AC=6,过点C作CD⊥AB交OB 于点D,则CD的长为()AB=4EO=1.5=47.(2013•怀化)如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=14米,则A、B间的距离是()AB8.(2013•昆明)如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为()BC EF=则新三角形的周长为AC BC EF=(∴等边三角形的中位线长是:12.(2013•巴中)如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、CD的中点且EF=6,则AD+BC的值是()EF=.C D.×(14.(2013•德庆县二模)已知△ABC的三边长分别为3cm,4cm,5cm,D,E,F分别为△ABC各边的中点,则△DEF15.(2013•潮安县模拟)如图,△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为()DAB=4BC=216.(2013•南岗区三模)如图,在△ABC中,∠ACB=90°,AC=BC=4,M是CB中点,P、N分别在AC、AB上,若△APN的面积与△ANM的面积相等,则AP长为()DPG=ANAP=AC=17.(2012•台州)如图,点D、E、F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为()18.(2012•聊城)如图,在△ABC中,点D、E分别是AB、AC的中点,则下列结论不正确的是()D=BC=19.(2012•佛山)依次连接任意四边形各边的中点,得到一个特殊图形(可认为是一般四边形的性质),则这个图AC EF=AC EF=AC.cm ∴相似比是21.(2012•朝阳)如图,C、D分别为EA、EB的中点,∠E=30°,∠1=110°,则∠2的度数为()BC AC EF=AB BC EF=23.(2012•邵阳)如图所示,在△ABC中,AB=AC,∠A<90°,边BC、CA、AB的中点分别是D、E、F,则四边形AFDE是()ABAC24.(2012•德城区三模)如图,在△ABC中,BC=6,M、N分别是AB、AC的中点,则MN等于()DMN=25.(2012•黄埔区一模)如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的周长为()AD=BD=AC BCAB=2AC=2BC=226.(2012•长宁区一模)如图,若DE是△ABC的中位线,△ABC的周长为1,则△ADE的周长为()D.AD=,的周长为边长的.27.(2012•盐田区二模)如图,▱ABCD的对角线AC、BD相交于点O,E是BC边的中点,OE=1.那么AB=().29.(2011•黔南州)如图,△ABC中,AB=AC=6,BC=8,AE平分∠BAC交BC于点E,点D为AB的中点,连接DE,则△BDE的周长是()+2BE=CE=AB=3AC=330.(2011•义乌市)如图,DE是△ABC的中位线,若BC的长为3cm,则DE的长是()BC。
中位线习题及答案

1.如图,在四边形ABCD中,BD⊥CD,AC⊥AB,E为BC的中点,∠EDA=60°,求证:AD=DE2.如图,在△ABC中,AD⊥CB、BE⊥AC,且相交于O点,N、M是CO、AB的中点,连接MN、ED,求证:MN是ED的中垂线证明:连接ME、MD、NE、ND(注:DE与MN交于P点)因AD⊥CB、BE⊥AC ,可得EM为直角△AEB斜边AB上的中线,EM=1/2 AB;MD为直角△ADB斜边AB上的中线,MD=1/2 AB∴EM=MDNE为直角△CEO斜边CO上的中线,NE=1/2 CO ND为直角△CDO斜边CO上的中线,ND=1/2 CO ∴NE=ND又MN=MN∴△MEN≌△MDN所以∠EMN=≌∠DMN又ME=MD,MP=MP∴△EMP≌△DMP∴EP=DP∠EPM = ∠DPM = 180°÷2 = 90°即:MN是ED的中垂线3、如图所示,BD、CE是三角形ABC的两条高,M、N分别是BC、DE的中点求证:MN⊥DE∵BD,CE为△ABC的两条高,∴BD⊥AC,CE⊥AB,∴∠BEC=∠BDC=90°,在Rt△BEC中,M为斜边BC的中点,∴EM=2分之一的BC,同理在Rt△BDC中,M为斜边BC的中点,可得DM=2分之一BC(不知可是这图?= =格式出了一点问题。
)∴EM=DM,∴M在线段ED的垂直平分线上,又N为ED的中点,∴N也在线段ED的垂直平分线上,∴MN垂直平分ED.M C4、如图,四边形ABCD中,∠DAB=∠DCB=90o,点M、N分别是BD、AC的中点。
MN、AC的位置关系如何?证明你的猜想。
DAB5、已知梯形ABCD中,∠B+∠C=90o,EF是两底中点的连线,试说明BC-AD =2EF解:作EM//AB,EN//CD,又AD//BC,则四边形AEMB,CDEN是平行四边形,AE=BM,ED=CN,∠EMN=∠B,∠ENM=角∠C∠B+∠C=90°,则△MEN是直角三角形。
三角形中位线专题

∵ AF=CF,
∴ △ADF≌ △FEC (SAS)
∴ DF=EC ∵ BE=EC, 三角∴形中位D线F专=题BE
此课件下载可自行编辑修改,供参考! 感谢你的支持,我们会努力做得更好!
三角形中位线专题
三角形中位线专题
拓展应用:
在△ABC中,∠BAC=90°,延长BA到点D,使
AD=1/2AB,点E,F分别为BC,AC的中点,试说DF=BE理
由
D
理由: ∵ 点E,F分别为BC,AC的中点 ∴ EF ∥AB,EF=1/2AB ∴ ∠DAC= ∠EFC=90 °
A
F B
E
C
∵ AD=1/2AB, ∴ AD=EF,
三角形中位线专题
• 如图7,△ABC的周长为1,连接△ABC三边 的中点构成第二个三角,再连接第二个三角形 三边中点构成第三个三角形,依此类推,第 2003个三角形的周长为 .
三角形中位线专题
• 已知如图,E、F、G、H分别是AB、BC、CD、 DA的中点。
• 求证:四边形EFGH是平行四边形
三角形中位线专题
三角形中位线专题
复习巩固
定义:把连接三角形两边中点的线段 叫做三角形的中位线 A
中位线定理
D
E
三角形的中位线平行于三角形
的第三边,且等于第三边的一半 B
C
中位线定理 的推理格式
∵AD=BD,AE=CE
∴DE∥BC且DE=
1 2
BC
三角形中位线专题
基础练习:
1、已知三角形的各边长分别为6cm,8cm,12cm, 求连结各边中点所成三角形的周长_1_3c。m 2、直角三角形两条直角边分别是6cm,8cm, 则连接着两条直角边中点的线段长为_5_cm。
三角形中位线经典测试题

三角形中位线经典测试题1、已知三角形ABC,其中AC与BD交于点O,BC边中点为E,OE=1,求AB的长。
2、已知三角形ABC,其中DE是BC边的中位线,DE=2cm,求BC的长。
3、已知三角形ABC,要测量A、B两点间的距离,取OA的中点C,OB的中点D,测得CD=30米,求AB的长。
4、顺次连结任意四边形各边中点所得到的四边形一定是平行四边形。
5、以三角形的三个顶点及三边中点为顶点的平行四边形共有4个。
6、已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,线段EF的长不变。
7、已知三角形三边长分别为6、8、10,则它的中位线构成的三角形的面积为24.8、已知△ABC中,AD=11/44AB,AE=AC,BC=16,求DE的长。
9、已知四边形ABCD中,M、N、P、Q分别为AB、BD、CD、AC的中点,证明四边形MNPQ是平行四边形。
10、已知四边形ABCD中,AD∥BC,BC=3AD,E、F分别是对角线AC、BD的中点,证明四边形ADEF是平行四边形。
11、已知四边形ABCD中,AB=CD,E、F分别为BC、AD的中点,BA、EF的延长线交于点M,CD、EF的延长线交于点N,证明∠AME=∠XXX。
12、已知△ABC中,P是中线AD的中点,连接BP并延长交AC于E,F为BE的中点,证明AF∥DE。
13、已知四边形ABCD中,M是OB的中点,连接AM并延长至P,使MP=AM,连接DP交AC于N,证明(1)MN∥AD;(2)S四边形MPNQ=S△XXX。
14、已知△ABC中,AD是外角平分线,CD⊥AD于D,E是BC的中点,证明(1)DE∥AB;(2)DE=1/2(AB+AC)。
15、已知等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC,对角线相交于点O,∠AOB=60°,且E、F、M分别是OD、OA、BC的中点,证明△EFM是等边三角形。
三角形、梯形中位线(练习)

《三角形、梯形的中位线》基础练习姓名班级学号成绩【知识要点】1.三角形、梯形中位线的概念及其性质,并利用中位线的性质解决有关问题.2.三角形中位线定理:3.梯形中位线定理:4.梯形面积公式可用来表达.5.图形中出现多个中点时一些添加辅助线的基本思想和方法.一.填空题(3分×10 = 30分)1.若等腰梯形的腰长等于中位线的长,周长为48㎝,则中位线长为㎝.2.已知梯形的高是4,面积是32,上底长为4,则梯形的中位线长为.3.已知等腰梯形的上、下底长分别为2㎝和6㎝,且它的两条对角线互相垂直,则这个梯形的面积为.4.已知直角梯形的一条对角线把梯形分成一个直角三角形和一个边长为8㎝的等边三角形,则此梯形的中位线长为㎝.5.梯形的上、下底长分别为6、10,则由中位线分得的两个梯形的面积之比为.6.梯形的两条对角线的中点的连线长为7,上底长为8,则下底长为.7.若等腰梯形的腰长是5cm,中位线是6cm,则它的周长是㎝.8.若梯形的一底长是14cm,中位线长是16cm,则另一底长为㎝.9.已知梯形中位线长是5cm,高是4cm,则梯形的面积是.10.梯形上底与中位线之比是2:5,则梯形下底与中位之比是.二.选择题(3分×6 = 18分)1.顺次连结矩形四边的中点所得的四边形是()(A)矩形(B)菱形(C)正方形(D)以上都不对2.如果四边形的对角线互相垂直,那么顺次连结四边形中点所得的四边形是()(A)矩形(B)菱形(C)正方形(D)以上都不对3.若顺次连结四边形各边中点组成的四边形是菱形,那么原四边形的对角线()(A)互相平分(B)互相垂直(C)相等(D)相等且互相平分4.顺次连结下列各四边形中点所得的四边形是矩形的是()(A)等腰梯形(B)矩形(C)平行四边形(D)菱形或对角线互相垂直的四边形5.已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是()(A)3cm (B)26cm (C)24cm (D)65cm6.已知直角梯形中,上底和斜腰长均为a ,且斜腰和下底的夹角是60°,则梯形中位线长为( )(A )a 43 (B ) (C )a 45 (D )都不对 三.解答题 (6分×6 + 8分×2 = 52分)1.如图,已知△ABC 中,D 是AB 上一点,AD =AC ,AE ⊥CD 于E ,F 是BC 的中点.求证:BD =2EF .2.已知在△ABC 中,M 是BC 的中点,AP 是∠BAC 的平分线,BP ⊥AP 于点P .求证:AC -AB =2PM .3.已知在△ABC 中,BC =15,D 、G 为BC 的三等分点,AD =13,AG =12,E 、F 分别为AB 、AC 的中点.求四边形EFGD 的周长和面积.4.如图,矩形ABCD 的对角线相交于点O ,点E 、F 、G 、H 分别是OA 、OB 、OC 、DO 的中点,四边形EFGH 是矩形吗?为什么?A BD H G FE o D C A P M CB A5.如图,在平行四边形ABCD 中,E 、F 分别是BC 、AD 的中点,AE 与BF 相交于点G ,DE 与CF 相交于点H ,试说明GH ∥AD 且GH=21AD .6.如图,已知CD 是△ABC 的高,E 、F 、G 分别是BC 、AB 、AC 上的中点.求证:FG =DE .7.如图,梯形ABCD 中,AD ∥BC ,AB =CD ,EF 是中位线,∠ABC =60°,BD 平分∠ABC , EF =12㎝.求梯形ABCD 的面积.8.对角线互相垂直且相等的四边形一定是菱形吗?试画出图形加以说明.如果取这样四边形各边中点并顺次联结起来,构成的四边形是什么四边形?FED C B A。
三角形、梯形中位线定理教师版

三角形、梯形中位线定理应用练习课、复习题组1知识要点(1)如图1,三角形中位线性质定理的条件是结论是三角形中位线判定定理的条件是结论是(2)如图2,梯形中位线性质定理的条件是_结论是_ 梯形中位线判定定理的条件是_结论是_2.基本方法三角形、梯形中位线定理不仅反映了线段的相等关系,也反映了线段间的倍半关系。
此外,证明线段相等或倍半关系还有其他方法,你能指出一些其他的常用方法吗?(1)全等三角形对应边相等;(2)等角对等边,等腰三角形“三线合一”性质;(3)线段垂直平分线上的点到线段两端点的距离相等;⑷ 角平分线上的点到角的两边距离相等;(5)直角三角形斜边上的中线等于斜边的一半;(6)直角三角形中,30°角所对的直角边等于斜边的一半;(7)平行四边形(包括矩形、菱形、正方形)的性质;(8)等腰梯形的两腰相等,两条对角线相等。
二、基本题组1.__________________________________________________ 顺次连结四边形各边中点所得的四边形是_________________________________________ ;2.顺次连结平行四边形各边中点所得的四边形是 _____________________3._________________________________________________ 顺次连结矩形各边中点所得的四边形是___________________________________________ ;4._________________________________________________ 顺次连结菱形各边中点所得的四边形是___________________________________________ ;5.__________________________________________________ 顺次连结正方形各边中点所得的四边形是_________________________________________ ;6._________________________________________________ 顺次连结梯形各边中点所得的四边形是___________________________________________ 。
226三角形梯形的中位线

.
对角线相等且互相垂直的四边形的“中点四边形”是 正方形 .
课堂小结
通过本课的学习你有何收获?
1、三角形中位线的概念
联结三角形两边的中点的线段叫做三角形的中位线 .
2、三角形中位线定理
A
在△ABC 中,
D
E
∵ ∴
ADDE=∥BBDC,,A且E =DCEE,? 1
BC
2
(三角形的中位线平行于第三边,并且等于
形变质△O不BC变的中位
线,且这两个
三角形有公共 边BC.
结论 四边形 DEFG 是
平行四边形.
课堂练习
求证:顺次联结四边形四条边的中点,所得的四边形是平行四边形 . 已知:如图,四边形ABCD 中, E、F、G、H分别是AB 、BC、CD、 DA的中点, 求证:四边形DEFG 是平行四边形. 证明:联结BD.
∵AD=BD,AD=CF, . .
适如时何小证结明:四边
∴DB=CF.
形D倍BC长F中是位平线
∴(四一边组形对边BC平FD行是且根助平相据线行等实,四的验构边四操造形边作与形,△是如AD平何E行添全四辅等边形),也添行是方四辅法边助之形线一?的. 常 ∴∴DDFE∥ ∥BBCC,,且且DD的FE=三?B角C1 .B形C?.
B
C 第三边的一半).
GF 、DE 分别是 △ABC 和△OBC的中 位线,且这两个三角 形有公共边BC.
DE∥BC, DE ? 1 BC. 2
GF∥BC, GF ? 1 BC. 2
GF ∥DE ,GF ? DE .
如何证明?
例题讲解
例题6 已知:如图,点O是△ABC 内任意一点,D、E、F、G分 别是OB、 OC、AC、AB 的中点. 求证:四边形DEFG 是平行四边形.
梯形及中位线(习题及答案)
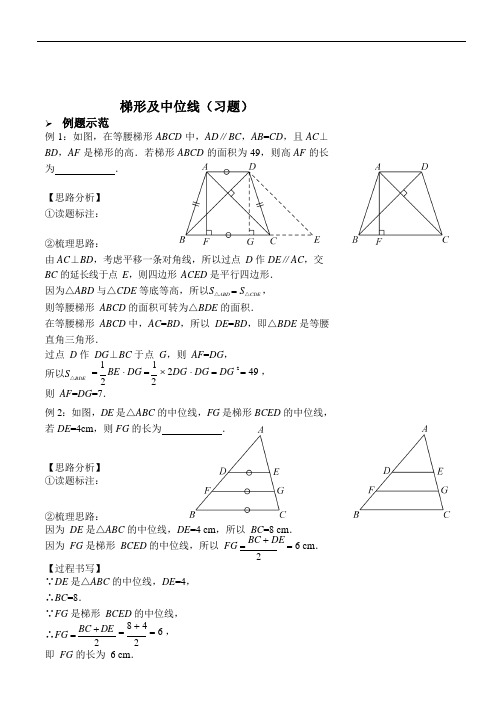
梯形及中位线(习题)➢ 例题示范 例 1:如图,在等腰梯形 ABCD 中,AD ∥BC ,AB =CD ,且 AC ⊥ BD ,AF 是梯形的高.若梯形 ABCD 的面积为 49,则高 AF 的长为.【思路分析】 ①读题标注:②梳理思路:由 AC ⊥BD ,考虑平移一条对角线,所以过点 D 作 DE ∥AC ,交BC 的延长线于点 E ,则四边形 ACED 是平行四边形. 因为△ABD 与△CDE 等底等高,所以S △ABD = S △CDE , 则等腰梯形 ABCD 的面积可转为△BDE 的面积.在等腰梯形 ABCD 中,AC =BD ,所以 DE =BD ,即△BDE 是等腰 直角三角形.过点 D 作 DG ⊥BC 于点 G ,则 AF =DG ,所以S △BDE= 1 BE ⋅ DG = 1 ⨯ 2DG ⋅ DG = DG 2 = 49 , 2 2则 AF =DG =7.例 2:如图,DE 是△ABC 的中位线,FG 是梯形 BCED 的中位线, 若 DE =4cm ,则 FG 的长为.【思路分析】 ①读题标注:②梳理思路:因为 DE 是△ABC 的中位线,DE =4 cm ,所以 BC =8 cm .因为 FG 是梯形 BCED 的中位线,所以 FG = BC + DE= 6 cm .2【过程书写】∵DE 是△ABC 的中位线,DE =4, ∴BC =8.∵FG 是梯形 BCED 的中位线,∴FG =BC + DE = 8 + 4 = 6 ,1例3:如图,在四边形ABCD 中,E,F,G,H 分别为AD,BD,BC,AC 的中点.要使四边形EFGH 是菱形,则应满足的条件是()A.AC⊥BD B.AC=BDC.AB=CD D.AD=BC【思路分析】题目中出现多个中点,考虑中点四边形.EF 是△ABD 的中位线,EF∥AB,EF =1AB ;2HG 是△ABC 的中位线,HG∥AB,HG =1AB ;2所以EF∥HG,EF=HG,根据一组对边平行且相等的四边形是平行四边形,可得四边形EFGH 是平行四边形.当AB=CD 时,EF=EH,根据有一组邻边相等的平行四边形是菱形,可得四边形EFGH 是菱形.故选C.➢巩固练习1.如图,在矩形ABCD 中,E,F,G,H 分别为边AB,BC,CD,AD 的中点.若AB=2,AD=4,则图中阴影部分的面积为()A.8 B.6C.4 D.32.下列图形:①等边三角形;②矩形;③等腰梯形;④直角梯形;⑤角;⑥圆.其中既是轴对称图形,又是中心对称图形的有()A.1 个B.2 个C.3 个D.4 个3.下列美丽的图案,是中心对称图形的是()A.B .C.D.4.下列正多边形:①正六边形;②正五边形;③正方形;④正三角形.其中能够铺满地面的正多边形有()A.1 种B.2 种C.3 种D.4 种5.已知等腰梯形的上底为6cm,下底为8cm,高为腰长为.cm,则其6.若直角梯形的一腰长为18cm,这条腰和一个底所成的角是30°,则其另一条腰长为.7.在直角梯形ABCD 中,AB∥CD,AD⊥CD 于点D.若AB=1,AD=2,CD=4,则BC 的长为.8.如图,在梯形ABCD 中,AD∥BC,∠B=50°,∠C=80°.若AD=2,BC=5,则CD 的长为.第8 题图第9 题图9.如图,在梯形ABCD 中,AD∥BC,若AC⊥BD,AC=6cm,BD=8cm,则该梯形的面积为.10.如图,A,B 两点被池塘隔开,在A,B 外选一点C,连接AC,BC,并分别找出AC 和BC 的中点M,N,如果测得MN=20m,那么A,B 两点间的距离为.311.如图,在Rt△ABC 中,∠ACB=90°,D,E 分别是AC,AB 的中点.若DE=3,CE=5,则AC 的长为.第11 题图第12 题图12.如图,在△ABC 中,AB=AC=9cm,AD⊥BC,M 为AD 的中点,直线CM 交AB 于点E,F 为CE 的中点,连接DF,则DF 的长为.13.如图,在四边形ABCD 中,P 是对角线BD 的中点,E,F 分别是AB,CD 的中点.若AD=BC=8,EF=7.6,则△PEF 的周长为.第13 题图第14 题图14.如图,DE 是△ABC 的中位线,FG 是梯形BCED 的中位线,若BC=10cm,则FG 的长为.15.若梯形中位线的长是梯形高的2 倍,且梯形的面积为18cm2,则这个梯形的高为()A.6 cm B.6cm C.3 cm D.3cm 2216.顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.如图,四边形EFGH 为中点四边形,当AC=BD 时,四边形EFGH 是形;当AC⊥BD 时,四边形EFGH 是形;当四边形EFGH 是正方形时,AC 与BD 满足的关系是.由此可见,中点四边形的形状与外围四边形的对角线有关.➢思考小结1. 对于梯形,我们的处理方式往往是通过做辅助线,把它转化为平行四边形或者是特殊的三角形进行处理.请添加合适的辅助线,将以下梯形转化为平行四边形或特殊三角形.【参考答案】➢ 巩固练习1. C2. B3. B4. C5. 2 cm6. 9 cm7. 138. 39. 24 cm210. 40 m11. 812. 3 cm13. 15.614.15cm 215. D16.菱,矩,AC=BD 且AC⊥BD ➢思考小结1. 略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形、梯形中位线
一、选择
1.三角形的三边长分别为12cm、16cm、20cm,则它的中位线构成的三角形的周长与面积分别为____ 和___ .
2.在Rt△ABC中,∠C=90°,D、E、F分别为AB、BC、AC边上的中点,AC=4 cm ,BC=6 cm,那么四边形CEDF为__________,它的边长分别为_________________.
3.三角形一条中位线分三角形所成的新三角形与原三角形周长之和为60 cm ,则原三角形的周长为_______.
4. 已知梯形的上底长为3cm,下底长为7cm,则此梯形中位线长为__________cm.
5.等腰三角形的两条中位线长分别是3和4,则它的周长是
____________.
6. 已知D、E、F分别是△ABC三边的中点,当△ABC满足条件___________时,四边形AFDE是菱形.
7.已知等腰梯形的周长为80cm,中位线长与腰长相等,则它的中位线长等于_____cm.
8.如图,已知等腰梯形的中位线的长为,腰的长为,则这个等腰梯形的周长为 .
9.如图,沿折叠后,点落在边上的处,若点为边的中点,,则的度数为 .
10、等腰梯形上、下底长分别为
,且两条对角线互相垂直,则这个梯形的面积为
.
二、选择题:
1、如果顺次连结四边形各边中点组成的四边形是菱形,那么原来的四边形的对角线()
A.互相平分
B.互相垂直
C.相等
D.相等且互相平分
2、顺次连结下列各四边形中点所得的四边形是矩形的是().
A.等腰梯形B.矩形C.平行四边形D.菱形或对角线互相垂直的四边形
3、已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是().
A.3cm B.26cm C.24cm D.65cm
4.已知DE是△ABC的中位线,则△ADE和△ABC的面积之比是( )
(A) 1:1 (B) 1:2 (C) 1:3 (D ) 1:4
5.若梯形中位线的长是高的2倍,面积是18cm2,则这个梯形的高等于( )
(A)6cm (B)6cm (C)3cm (D)
B
A
D
C
E
F
D
O
6.如图,梯形ABCD中,AD//BC,BD为对角线,中位线EF交
BD于O点,若FO-EO=3,则BC-AD等于( )A.4 B.6 C.8 D.10
7.如图,△中,、分别为、边上的点,∥,为边上的中线,若
=5,=3,=4,则的长为()
A. B. C. D.
8.小明作出了边长为的第1个正△A1B1C1,算出了正△A1B1C1的
面积。
然后分别取△A1B1C1的三边中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积。
用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积……,由此可得,第10个正△A10B10C10的面积是
A B C D.
三、解答题:
1、梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=5cm,BD=12cm,求该梯形的中位线长.
2、已知,如图,△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点。
求证:EF=DG且EF∥DG。
3、如图,在锐角三角形ABC中,AB<AC,AD⊥BC,
交BC与点D,E、F、G分别是BC、CA、AB的中点。
求证:四边形DEFG是等腰梯形
4. 如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分
线CF交AD于点F.
点E是AB的中点,连结EF.
F
E
D
C
B
A
(1)求证:EF∥BC;
(2)若△ABD的面积是6.求四边形BDFE的面积
5、 如图,在平行四边形ABCD中,E、F分别是BC、AD的中点,AE与BF相交于点G,
DE与CF相交于点H,试说明GH∥AD且GH=AD
6、
如图,梯形ABCD中,AD∥BC,点E是AB中点,连结EC、ED、CE⊥DE,CD、AD与BC三条线段之间有什么样的数量关系?请说明理由。
7、
在△ABC中,AH⊥BC于H,D,E,F分别是BC,CA,AB的中点.求证:∠DEF=∠HFE.
8、 已知,如图梯形ABCD中,AD//BC,对角线AC与BD垂直相交于O,
MH是梯形中位线,∠DBC=30o,猜想MN与AC什么关系?并证明猜想
9、如图,四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、CD分别交于点E、F。
试说明∠BEN=∠NFC.
10、如图.D,E分别在AB,AC上,BD=CE,BE,CD的中点分别是M,N,
直线MN分别交AB,AC于P,Q.求证AP=AQ.
11、已知:如图5,在梯形ABCD中,A B∥CD,E,F分别是AC和BD 的中点。
求证:EF=(AB-CD)
图5
B
E
D
F
C
A
12、如图8,等腰梯形ABCD的周长为80cm,如果它的中位线与腰长相等,
它的高是12cm,求这个梯形的面积。
图8
B
E
D
F
C
A
想一想
如图7,在四边形ABCD中,AB与CD不平行,E,F分别是AD,BC的中点。
那么,
图7
B
E
D
F
C
A
EF=(AB+CD)成立吗?为什么?。
