02简易逻辑--命题的四种形式
简易逻辑反证法
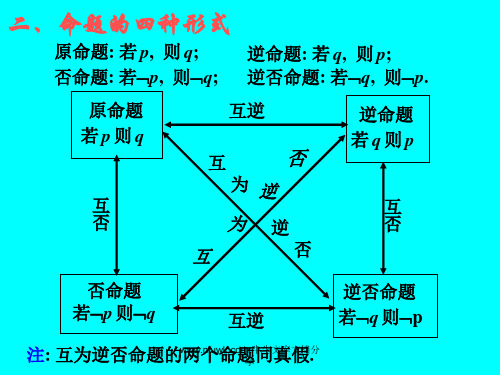
二、命题的四种形式
原命题: 若 p, 则 q; 否命题: 若p, 则q;
原命题 若p则q 逆命题: 若 q, 则 p; 逆否命题: 若q, 则p. 互逆 逆命题 若q则p
互
互 否 为 逆
否
为
逆 否
互 否
互
否命题 若p 则q 互逆
逆否命题 ቤተ መ, 求证: 三个方程 ax2+bx+ 4 =0、bx2+cx+ a =0 与 4 b cx2+ax+ 4 =0 中至少有一个方程有实数根. 2.对于函数 f(x)=x2+ax+b(a, bR), 当 x[-1, 1] 时, |f(x)| 的最 大值为 M, 求证: M≥ 1 2. 3.方程 x2 -mx+4=0 在[-1, 1]上有解, 求实数 m 的取值范围. 1.证: 设三个方程的判别式分别为△1, △2, △3, 由 △1+△2+△3=b2 -ac+c2 -ba+a2 -cb =1 [( a -b)2+(b-c)2+(c-a)2]≥0 2 即 △1+△2+△3 ≥0. ∴△1, △2, △3 中至少有一个非负. 故所述三个方程中至少有一个方程有实数根.
02简易逻辑--命题及其关系、充分条件与必要条件

a b c a b c 的倾斜度为 l = max , , , min , , ,则 b c a b c a
“l = 1” 是“△ABC为等边三角形”的( 为等边三角形” B 为等边三角形
)
例8: 设0 < x <
π
2 A.充分不必要条件 充分不必要条件
, 则“ x sin x < 1”是“ x sin x < 1”的 B ) (
(
)(
)
重难点突破: 重难点突破:
1.反证法与逆否命题: 反证法与逆否命题: 反证法与逆否命题 例1:已知 a, b, c ∈ R, 若a + b + c < 1 已知
1 a 证明: 证明: , b, c中至少有一个小于 3 2.充要条件的证明: 充要条件的证明: 充要条件的证明
注意找出题中的条件与结论
4.常用的正面词语和它的否定词语 常用的正面词语和它的否定词语
正面词语 等于 小于 大于 是 都是 否定 不等于 不小于(大于 或等于) 不大于(小于 或等于) 不是 不都是(至少 有一个不是) 正面词语 任意的 所有的 至多有一个 至少有一个 至多有n个 否定 某个 某些 至少有两个 一个也没有 至少有n+1 个
“对任何x ∈ R, x − 2 + x − 4 > 3” 例3:命题 命题 的否定是? 的否定是?
∃x ∈ R, x − 2 + x + 4 ≤ 3例4:命题“若x 命题2 Nhomakorabea2
< 1, 则 − 1 < x < 1”的逆否命题是
D
.若 A. x ≥ 1, 则x ≥ 1或x ≤ −1 若 − 1 < x < 1, 则x 2 < 1 B.
02简易逻辑 命题的四种形式(PPT)5-2

例3 写出由下述各命题构成的“非 p” 形式的复合命题: (1) p: 有些质数是奇数; (2) p: 方程 x2-5x+6=0 有两个相等的实 根; (3) p: 四条边相等的四边形是正方形.
(1)非 p: 所有的质数都是奇数或都不是奇数; ( p 即: 质数中既有奇数又有不是奇数的数)
(2)非 p: 方程 x2-5x+6=0 没有两个相等的实根;
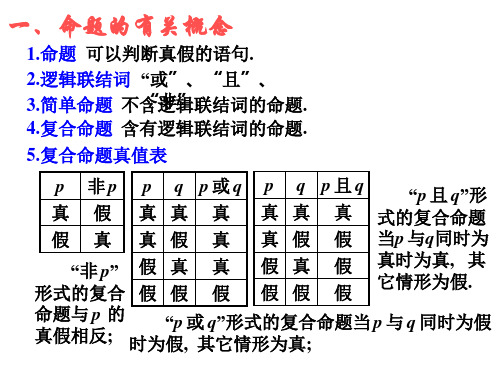
一、命题的有关概念
1.命题 可以判断真假的语句.
2.逻辑联结词 “或”、“且”、 3.简单命题 不含“逻非辑”联. 结词的命题. 4.复合命题 含有逻辑联结词的命题.
5.复合命题真值表
p 非p p q p或q p q p且q
“p 且 q”形
真 假 真 真 真 真 真 真 式的复合命题
假 真 真 假 真 真 假 假 当p 与q同时为
“非 p” 假 真 真 形式的复合 假 假 假
假 真 假 真时为真, 其 假 假 假 它情形为假.
命题与 p 的 真假相反;
“p 或 q”形式的复合命题当 时为假, 其它情形为真;p源自与q同时为假
~人借走了一本|他~选为代表。②助用在动词前表示被动的动作:~压迫民族|~剥削阶级。 【被褡子】?同“背搭子”。 【被袋】名外出时装被褥、衣 物等用的圆筒形的袋。 【被单】(~儿)名①铺在床上或盖在被子上的布。②单层布被。‖也叫被单子。 【被动】形①待外力推动而行动(跟“主动”相对, 下同):工作要主动,不要~。②(事情)由于; 教育品牌机构服务 教育品牌机构服务 ;遇到阻力或干扰,不能按照自己的意图进行: 由于事先考虑不周,事情搞得很~。 【被动式】名说明主语所表示的人或事物是被动者的语法格式。汉语的被动式有时没有形式上的标志,如:他选上了|
02简易逻辑 命题的四种形式(PPT)5-3

1.命题 可以判断真假的语句.
2.逻辑联结词 “或”、“且”、 3.简单命题 不含“逻非辑”联. 结词的命题. 4.复合命题 含有逻辑联结词的命题.
5.复合命题真值表
p 非p p q p或q p q p且q
“p 且 q”形
真 假 真 真 真 真 真 真 式的复合命题
假 真 真 假 真 真 假 假 当p 与q同时为
文学,多用韵文和散文交错组成,内容原为佛经故事,后来范围扩大,包括历史故事、民间传说等。如敦煌石窟里发现的《大目乾连冥间救母变文》、《伍 子胥变文》等。 【变戏法】(~儿)表演魔术。 【变现】动把非现金的资产、有价证券等换成现金。 【变相】形属性词。内容不变,形式和原来不同(多 指坏事):~剥削|~贪污。 【变心】∥ī动改变原来对人或事业的爱或忠诚:海枯石烂,永不~。 【变星】ī名光度有变化的恒星。 【变形】∥动形状、格 式起变化:这个零件已经~|一场大病,瘦得人都~了。 【变型】动改变类型:转轨~。 【变性】动①物体的性质发生改变:~酒精。②机体的细胞因新陈 代谢障碍而在结构和性质上发生改变。③改变性别:~人|~手术。 【变压器】名利用电磁感应的原理来改变交流电压的装置,主要构件是原线圈、副线圈 和铁芯。在电器设备、电信设备中,常用来升降电压、匹配阻抗等。 【变样】∥(~儿)动模样、样式发生变化:几年没见,他还没~|这地方已经变了样 了。 【变异】动①同种生物世代之间或同代生物不同个体之间在形态特征、生理特征等方面表现出差异。②泛指跟以前的情况相比发生变分:气候~。 【变 易】动改变;变化:~服饰。 【变质】∥动人的思想或事物的本质得与原来不同(多指向坏的方面转变):蜕化~|不吃变了质的食物。 【变质岩】名火成 岩、沉积岩受到高温、高压等影响,构造和成分上发生变化而形成的岩石,如大理岩就是石灰岩或白云岩的变质岩。 【变种】名①生物分类学上指物种以下 的分类单位,
【高1数学】02-四种命题的形式、充分条件与必要条件

四种命题的形式、充分条件与必要条件基础概念一、基础知识概述本周主要学习了四种命题的形式,充分条件与必要条件等相关概念,及反证法的思想.充分条件、必要条件和充要条件是重要的数学概念,主要用来区分命题的条件p和结论q之间的关系.本节主要是通过不同的知识点来剖析充分必要条件的意义,让考生能准确判定给定的两个命题的充要关系.二、重点知识归纳及讲解1、命题的概念:可以判断真假的语句叫做命题.2、简单命题与复合命题:不含逻辑联结词“或”、“且”、“非”的命题叫做简单命题,由简单命题与逻辑联结词构成的命题叫复合命题.3、判断复合命题的真假:(1)“非p”形式复合命题的真假可以用下表表示:p非p真假假真即一个命题的否命题与原命题的真假相反.(2)“p且q”形式复合命题的真假可以用下表表示:p q p且q真真真真假假假真假假假假即当p、q为真时,p且q为真;当p、q中至少有一个为假时,p且q为假.(3)“p或q”形式复合命题的真假可以用下表表示:p q p或q真真真真假真假真真假假假即当p、q中至少有一个为真时,p或q为真;当p、q都为假时,p或q为假.4、原命题:若p则q(p是原命题的条件,q是原命题的结论);逆命题:若q则p(交换原命题的题设和结论);否命题:若非p则非q(同时否定原命题的条件与结论);逆否命题:若非q则非p(交换原命题的题设和结论后同时否定之).四种命题及相互关系用图表表示为:说明:①原命题、否命题、逆命题和逆否命题是相互的.②写原命题的否命题、逆命题和逆否命题的关键是:找出所给原命题的条件p与结论q.5、反证法:欲证“若p则q”为真命题,从否定其结论“非p”出发,经过正确的逻辑推理得出矛盾,从而“非p”为假,即原命题为真,这样的方法叫反证法.证题的步骤:(1)假设命题的结论不成立,即假设结论的反面成立;(2)从假设出发,经过推理论证,得出矛盾;(3)由矛盾判定假设不正确,从而肯定命题的结论正确.说明:反证法是一种间接证明命题的基本方法.在证明一个数学命题时,如果运用直接证明法比较困难或难以证明时,可运用反证法进行证明.反证法的基本思想:通过证明命题的否定是假命题,从而说明原命题是真命题.6、推断符号“⇒”的含义:p⇒”;由p经过推理可以得出q,即如果p成立,那么q一定成立,此时可记作“qp⇒/”.由p经过推理得不出q,即如果p成立,推不出q成立,此时可记作“q7、充分条件与必要条件:p⇒,那么就说:p是q的充分条件;q是p的必要条件.一般地,如果已知q8、充要条件:一般地,如果既有q p ⇒,又有p q ⇒,就记作:q p ⇔.“⇔”叫做等价符号.q p ⇔表示q p ⇒且p q ⇒.这时p 既是q 的充分条件,又是q 的必要条件,则p 是q 的充分必要条件,简称充要条件. 9、充分条件与必要条件的分类:命题按条件和结论的充分性和必要性可分为四类: 若q p ⇒但p q ⇒/,则p 是q 的充分不必要条件; 若p q ⇒但q p ⇒/,则p 是q 的必要不充分条件; 若q p ⇒且p q ⇒,则p 是q 的充要条件;若q p ⇒/且p q ⇒/,则p 是q 的既不充分也不必要条件. 10、从集合角度理解:①q p ⇒,相当于Q P ⊆,即或即:要使Q x ∈成立,只要P x ∈就足够了——有它就行.②p q ⇒,相当于Q P ⊇,即或即:为使Q x ∈成立,必须要使P x ∈——缺它不行.p q ⇒等价于q p ⌝⇒⌝. ③q p ⇔,相当于Q P =,即即:互为充要的两个条件刻划的是同一事物. 三、难点知识剖析本节的难点主要是充要条件的判断,其解决方法主要有:1、要理解“充分条件”“必要条件”的概念,当“若p 则q ”形式的命题为真时,就记作q p ⇒,称p 是q 的充分条件,同时称q 是p 的必要条件,因此判断充分条件或必要条件就归结为判断命题的真假.2、要理解“充要条件”的概念,对于符号“⇔”要熟悉它的各种同义词语:“等价于”,“当且仅当”,“必须并且只需”,“ ,反之也真”等.3、数学概念的定义具有相称性,即数学概念的定义都可以看成是充要条件,既是概念的判断依据,又是概念所具有的性质.4、从集合观点看,若B A ⊆,则A 是B 的充分条件,B 是A 的必要条件;若B A =,则A 、B 互为充要条件.5、证明命题条件的充要性时,既要证明原命题成立(即条件的充分性),又要证明它的逆命题成立(即条件的必要性).典型例题例1、(1)“ABC ∆中,若︒=∠90C ,则A ∠、B ∠都是锐角”的否命题为( ) A .ABC ∆中,若︒≠∠90C ,则A ∠、B ∠都不是锐角 B .ABC ∆中,若︒≠∠90C ,则A ∠、B ∠不都是锐角 C .ABC ∆中,若︒≠∠90C ,则A ∠、B ∠都不一定是锐角 D .以上都不对(2)用反证法证明命题:若整数系数一元二次方程)0(02≠=++a c bx ax 有有理根,那么a 、b 、c 中至少有一个是偶数,下列假设中正确的是( )A .假设a 、b 、c 都是偶数B .假设a 、b 、c 都不是偶数C .假设a 、b 、c 至多有一个是偶数D .假设a 、b 、c 至多有两个是偶数(3)有甲、乙、丙、丁四位歌手参加比赛,其中有一位获奖,有人走访了四位歌手,甲说:“我获奖了”;乙说:“甲、丙未获奖”;丙说:“是甲或乙获奖”;丁说:“是乙获奖”.四位歌手的话只有两句是对了,则是_______获奖了. 解析:(1)由命题之间的关系易选B ;(2)“至少有一个”的反面是“一个都没有”,故选B ;(3)设获奖用“1”表示,未获奖用“0”表示,则依次四人的话列表如下:甲 乙 丙 丁 甲:甲获奖 1 0 0 0 乙:甲、丙未获奖 0 1 0 1 丙:甲或乙获奖 1 1 0 0 丁:乙获奖1由表可知,只有第一列符合四位歌手的话只有两句是对的,故是甲获奖了. 答案:(1)B ;(2)B ;(3)甲例2、(上海)(1)222111,,,,,c b a c b a 均为非零实数,不等式01121>++c x b x a 和02222>++c x b x a 的解集分别为集合M 和N ,那么“212121c c b b a a ==”是“N M =”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件 (2)已知2|43:|>-x p ,021:2>--x x q ,则p ⌝是q ⌝的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分又非必要条件 解析: (1)如果“0212121>==c c b b a a ”,则“N M =”,如果“0212121<==c cb b a a ”,则“N M ≠”,所以“212121c c b b a a ==”⇒/“N M =”,反之若“∅==N M ”,即说明二次不等式的解集为空集,与它们的系数比无任何关系,只要求判别式小于零.所以“N M =”⇒/“212121c c b b a a ==”,因此“212121c cb b a a ==”是“N M =”的既不充分也不必要条件. (2)解法一:∵}322|{:<>x x x p 或,}12|{:-<>x x x q 或.∴}232|{:≤≤⌝x x p ,}21|{:≤≤-⌝x x q . ∴q p ⌝⇒⌝,p q ⌝⇒/⌝.∴p ⌝是q ⌝的充分不必要条件.解法二:由法一知,∴p q ⇒,q p ⇒/.∴q p ⌝⇒⌝,p q ⌝⇒/⌝.即:p ⌝是q ⌝的充分不必要条件. 答案:(1)D (2)A例3、已知命题:p 方程012=++mx x 有两个不相等的实负根.命题:q 方程01)2(442=+-+x m x 无实根;若p 或q 为真,p 且q 为假,求实数m 的取值范围.分析:先分别求满足条件p 和q 的m 的取值范围,再利用复合命题的真假进行转化与讨论. 解析:由命题p 可以得到:⎩⎨⎧>>-=∆042m m ,∴2>m .由命题q 可以得到:016)]2(4[2<--=∆m ,∴31<<m .∵p 或q 为真,p 且q 为假,∴p 、q 有且仅有一个为真. 当p 为真,q 为假时,3312≥⇒⎩⎨⎧≥≤>m m m m 或,当p 为假,q 为真时,21312≤<⇒⎩⎨⎧<<≤m m m ,所以,m 的取值范围为}213|{≤<≥m m m 或. 例4、已知2311:≤--x p ,)0(012:22>≤-+-m m x x q ,若p ⌝是q ⌝的充分而不必要条件,求实数m 的取值范围. 分析:利用等价命题先进行命题的等价转化,搞清命题中条件与结论的关系,再去解不等式,找解集间的包含关系,进而使问题解决. 解析: 由2311≤--x 解得:102≤≤-x ,则}102|{:>-<=⌝x x x A p 或. 又当0>m 时,由01222≤-+-m x x 得:m x m +≤≤-11,则}0,11|{:>+>-<=⌝m m x m x x B q 或. ∵p ⌝是q ⌝的充分非必要条件,∴B A ⊆,结合数轴应有⎪⎩⎪⎨⎧≤+-≥->101210m m m ,解得:30≤<m 为所求.例5、若0>p ,0>q ,233=+q p .试用反证法证明:2≤+q p . 分析:此题直接由条件推证2≤+q p 是较难的,由此用反证法证之. 证明:假设2>+q p ,∵0>p ,0>q .∴833)(32233>+++=+q pq q p p q p . 又∵233=+q p .∴代入上式得:6)(3>+q p pq ,即:)1(2)( >+q p pq .又由233=+q p ,即2))((22=+-+q pq p q p 代入)1(得:))(()(22q pq p q p q p pq +-+>+. ∵0>p ,0>q .∴0>+q p .∴22q pq p pq +->,但这与0)(2≥-q p 矛盾, ∴假设2>+q p 不成立,故2≤+q p . 说明:反证法:是一种证明题目的间接方法,在有些题目的证明中用反证法非常简洁,但并不是每一题用反证都恰倒好处.那么,对于哪些题目适合用反证法呢?1)从这些条件推出所知的也很少或无法用已知条件进行直接证明的;2)当问题中能用来作为推理依据的公理、定理很少,无法直接证明或证明无从下手的;3)结论以否定的形式出现,无法引用定理来证明否定形式的结论;4)对要证明的命题,已知它的逆命题是正确的;5)要求证明的命题适合某种条件的结论唯一存在.对反证法的掌握,还有待于随着学习的深入,逐步提高.基础练习一、选择题1、有以下5个命题:(1)没有男生爱踢足球;(2)所有男生都不爱踢足球;(3)至少有一个男生不爱踢足球;(4)所有女生都爱踢足球;(5)所有男生都爱踢足球.其中命题(5)的否命题是( )A .(1)B .(2)C .(3)D .(4)2、某个命题与正整数n 有关,如果当)(*∈=N k k n 时,该命题成立,那么可得当1+=k n 时命题也成立,现已知当5=n 时,该命题不成立,则可推出( ) A .当6=n 时,该命题不成立 B .当6=n 时,该命题成立 C .当4=n 时,该命题不成立 D .当4=n 时,该命题成立3、设集合}06|{2=-+=x x x A ,}01|{=+=mx x B ,则B 是A 的真子集的一个充分不必要的条件是( ) A .}3,21{ -∈m B .21-=m C .}1,21,0{ -∈m D .}2,0{ ∈m 4、(湖北)有限集合S 中元素个数记作)(S card ,设A 、B 都为有限集合,给出下列命题:①∅=B A 的充要条件是)()()(B card A card B A card += ;②B A ⊆的必要条件是)()(B card A card ≤;③B A ⊂/的充分条件是)()(B card A card ≤;④B A =的充要条件是)()(B card A card =.其中真命题的序号是( )A .③④B .①②C .①④D .②③ 二、填空题5、有下列命题:①面积相等的三角形是全等三角形;②“若0=xy ,则0||||=+y x ”的逆命题;③“若b a >,则c b c a +>+”的否命题;④“矩形的对角线互相垂直”的逆否命题.其中真命题共有_________个.6、在原命题及其逆命题、否命题、逆否命题这四个命题中,真命题的个数可以是_________.7、命题}3,2,1{}2{: ∈p ,}3,2,1{}2{: ⊆q ,则对复合命题的下述判断:①p 或q 为真;②p 或q 为假;③p 且q 为真;④p 且q 为假;⑤非p 为真;⑥非q 为假.其中判断正确的序号是_________(填上你认为正确的所有序号).8、如果x 、y 是实数,那么0>xy 是||||||y x y x +=+的________条件.9、若三条抛物线3442+-+=a ax x y ,22)1(a x a x y +-+=,a ax x y 222-+=中至少有一条与x 轴有公共点,则a 的取值范围是________.10、设集合},|),{(R y R x y x U ∈∈= ,}02|),{(>+-=m y x y x A ,}0|),{(≤-+=n y x y x B ,那么点B C A P U ∈)3,2( 的充要条件是________.三、解答题: 11、已知2311:≤--x p ,)0(012:22>≤-+-m m x x q ,若p ⌝是q ⌝的必要而不充分条件,求实数m 的取值范围.12、02:<<-m p ,10<<n ;:q 关于x 的方程02=++n mx x 有2个小于1的正根,试分析p 是q 的什么条件.13、已知关于x 的实系数二次方程02=++b ax x 有两个实数根α、β,证明:2||<α且2||<β是b a +<4||2且4||<b 的充要条件.。
高一数学简易逻辑知识点小结
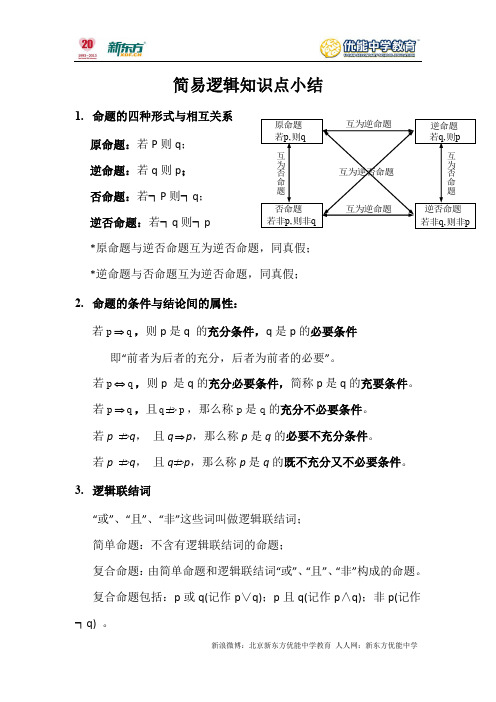
简易逻辑知识点小结1.命题的四种形式与相互关系原命题:若P则q;逆命题:若q则p;否命题:若┑P则┑q;逆否命题:若┑q则┑p*原命题与逆否命题互为逆否命题,同真假;*逆命题与否命题互为逆否命题,同真假;2.命题的条件与结论间的属性:若qp⇒,则p是q 的充分条件,q是p的必要条件即“前者为后者的充分,后者为前者的必要”。
若qp⇔,则p 是q的充分必要条件,简称p是q的充要条件。
若qp⇒,且q p,那么称p是q的充分不必要条件。
若p q,且q⇒p,那么称p是q的必要不充分条件。
若p q,且q p,那么称p是q的既不充分又不必要条件。
3.逻辑联结词“或”、“且”、“非”这些词叫做逻辑联结词;简单命题:不含有逻辑联结词的命题;复合命题:由简单命题和逻辑联结词“或”、“且”、“非”构成的命题。
复合命题包括:p或q(记作p∨q);p且q(记作p∧q);非p(记作┑q)。
4.“或”、“且”、“非”的真值判断:•“非p”形式复合命题的真假与p的真假相反;•“p且q”(p∧q)形式复合命题当p与q同为真时为真,其他情况时为假;•“p或q”(p∨q)形式复合命题当p与q同为假时为假,其他情况时为真。
5.全称量词与存在量词全称量词:所有的,全部,都,任意一个,每一个等;记作存在量词:存在,至少有一个,有个,有些等;记作全称命题:含有全称量词的命题称为全称命题。
一般形式为:命题P:)x,∀。
全称命题的否命题:∈Mp(x∈∃:。
⌝,p⌝)x(xMP例:命题“所有能被2整除的整数都是偶数”的否定是”存在一个能被2整除的数都不是偶数”存在量词:含有存在量词的命题称为存在性命题。
高中数学专题复习7四种命题集合与简易逻辑

互 逆互 为 为互 否 逆逆 否 互 否 互 否 互 逆第一章 集合与简易逻辑1.7 四种命题一、目标:1掌握四种命题之间的关系2 了解反证法二、内容:1、命题的四种形式:在两个命题中,如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题;如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题。
例如:原命题:同位角相等,两直线平行逆命题:两直线平行,同位角相等否命题:同位角不相等,两直线不平行逆否命题:两直线不平行,同位角不相等互否命题:一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定,这样的两个命题叫做互否命题,把其中一个命题叫做原命题,另一个就叫做原命题的否命题互为逆否命题:一个命题的条件和结论分别是另一个命题的结论的否定和条件的否定,这样的两个命题叫做互为逆否命题,把其中一个命题叫做原命题,另一个就叫做原命题的逆否命题原命题:若p 则q逆命题:若q 则p否命题:若p ⌝则q ⌝逆否命题:若q ⌝则p ⌝注意:否命题和命题的否定(否定命题)是不同的,否定命题的形式是:若p 则q ⌝,否定命题与原命题一真一假,而否命题与原命题的真假没有必然关系。
2、应用:例1 (教材)3、四种命题的相互关系:4.四种命题的真假关系:原命题为真5. 应用:例2(教材)补例1:1.设原命题是“当c >0时,若a >b ,则ac >bc ,”写出它的逆命题、否命题、逆否命题,并分别判断它们的真假.解:逆命题:“当c >0时,若ac >bc ,则a >c .”逆命题为真.否命题:“当c >0时,若a ≤b ,则ac ≤bc ”,否命题为真.逆否命题:“当c >0时,若ac ≤bc ,则a ≤b ”,逆否命题为真.补例2:分别写出命题“若x 2+y 2=0,则x 、y 全为0”的逆命题、否命题和逆否命题. 解:逆命题:若x 、y 全为0,则x 2+y 2=0;否命题:若x 2+y 2≠0,则x ,y 不全为0;逆否命题:若x 、y 不全为0,则x 2+y 2≠0.补例3.若命题p 的逆命题是q ,命题q 的否命题是r ,则r 是p 的 逆否命题6.蕴涵式命题的真值表:例:1、写出原命题:若0x ≥,则0x ≥的逆否命题并判断真假 解:逆否命题:若20x <,则0x <。
高中数学:简单逻辑

简单逻辑一、命题的概念和四种命题1.命题的概念概念:我们把语言、符号或式子表达的,可以判断真假的陈述句称为命题.其中判断为真的语句称为真命题,判断为假的语句称为假命题.注意:并不是任何语句都是命题,疑问句、祈使句、感叹句都不是命题.也就是说,判断一个语句是不是命题的两要素:①命题是陈述句②可以判断真假.2.命题的四种形式1)对于“若p ,则q ”形式的命题,p 称为命题的条件,q 称为命题的结论.命题“如果p ,则q ”是由条件p 和结论q 组成的,对p q ,进行“换位”和“换质(否定)”后,可以构成四种不同形式的命题.2)四种命题的关系如图所示.3.命题“如果p ,则q ”的四种形式之间有如下关系:1)互为逆否命题的两个命题等价(同真或同假).因此证明原命题,也可以证它的逆否命题.2)互逆或互否的两个命题与原命题不等价.注意:注意命题的否定与否命题之间的区别,前者是命题的反面,且与命题的真假恰好相反;后者是对条件与结论同时进行否定,它的真假与原命题的真假没有绝对的联系.二、简单的逻辑联结词1.且:用逻辑联结词“且”把命题p 和q 联结起来,就得到一个新命题,记作p q ∧,读作“p 且q ”.逻辑联结词“且”与日常语言中的“并且”、“及”、“和”相当.可以用“且”“定义集合的交集:{|()()}A B x x A x B =∈∧∈.2.或:用逻辑联结词“或”把命题p 或q 联结起来,就得到一个新命题,记作p q ∨,读作“p或q ”.逻辑联结词“或”的意义和日常语言中的“或者”相当.可以用“或”定义集合的并集:{|()()}A B x x A x B =∈∨∈.3.非:对命题p 加以否定,得到一个新的命题,记作p ⌝,读作“非p ”或“p 的否定”.逻辑联结词“非”(也称为“否定”)的意义是由日常语言中的“不是”“全盘否定”“问题的反面”等抽象而来.注:可以用“非”来定义集合A 在全集U 中的补集:{|()}{|}UA x U x A x U x A =∈⌝∈=∈∉.4.复合问题的真值表:注意:逻辑联词中的“或”相当于集合中的“并集”,它们与日常用语中的“或”的含义不同,日常用语中的“或”是两个中任选一个,不能都选.而逻辑联词中的“或”可以是两个都选,也可以是两个中选一个.逻辑联词中的且相当于集合中的交集,即两个必须都选.三、充要条件1.四种条件充分条件:若p q ⇒,则p 是q 成立的充分条件. 必要条件:若q p ⇒,则p 是q 成立的必要条件. 充分且必要条件:如果p q ⇔,则p 是q 的充要条件. 既不充分也不必要条件:若果pq 且pq ,则p 是q 成立的既不充分也不必要条件.2.利用集合思想判别四种条件设A ={x x =满足条件P },B ={x x =满足条件q } 1)设若A B ⊆且B A ,则称p 是q 的充分不必要条件.2)设若A B 且B A ⊆,则称p 是q 的必要不充分条件. 3)设若AB 且BA ,则称p 是q 的既不充分也不必要条件.4)设若A B ⊆且B A ⊆,则称p 是q 的充分且必要条件.四、全称量词与存在量词1.概念全称命题:含有全称量词的命题称为全称命题,“对M 中任意一个x ,有()p x 成立”符号简记为:,()x M p x ∀∈.读作:对任意x 属于M 有()p x 成立.特称命题:含有存在量词的命题称为特称命题:“存在M 中一个x ,有()p x 成立”符号简记为:,()x M p x ∃∈,读作:存在一个x 属于M ,使()p x 成立.2.全称与特称命题的否定存在性命题p :x A ∃∈,()p x ;它的否定是p ⌝:x A ∀∈,()p x ⌝. 命题的否定:将存在量词变为全称量词,再否定它的性质. 全称命题q :x A ∀∈,()q x ;它的否定是q ⌝:x A ∃∈,()q x ⌝. 命题的否定:将全称量词变为存在量词,再否定它的性质.3.对命题中关键词的否定:一.选择题(共10小题)1.(2018•上海)已知a∈R,则“a>1”是“1a<1”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件2.(2018•天津)设x∈R,则“x3>8”是“|x|>2”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.(2018•马鞍山三模)命题p:若a>b,则a﹣1>b﹣1,则命题p的否命题为()A.若a>b,则a﹣1≤b﹣1B.若a≥b,则a﹣1<b﹣1C.若a≤b,则a﹣1≤b﹣1D.若a<b,则a﹣1<b﹣14.(2018•天心区校级一模)“|x﹣2|<5”是“﹣3≤x≤7”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.(2018•余姚市校级模拟)“a=2”是“直线ax+2y﹣1=0与x+(a﹣1)y+2=0互相平行”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.(2018•济南一模)若命题“p或q”与命题“非p”都是真命题,则()A.命题p与命题q都是真命题B.命题p与命题q都是假命题C.命题p是真命题,命题q是假命题D.命题p是假命题,命题q是真命题7.(2018•河西区二模)设x∈R,则“|x﹣2|<1”是“x2﹣x﹣6<0”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件8.(2018•石嘴山一模)下列命题中正确命题的个数是()①命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2≠0”;②“a≠0”是“a2+a≠0”的必要不充分条件;③若p∧q为假命题,则p,q均为假命题;④命题p:∃x0∈R,使得x02+x0+1<0,则¬p:∀x∈R,都有x2+x+1≥0.A.1B.2C.3D.49.(2018•渝中区校级模拟)命题P:“若x>1,则x2>1”,则命题P:以及它的否命题、逆命题、逆否命题这四个命题中真命题的个数为()A.1B.2C.3D.410.(2018•全国二模)设x∈R,则使lg(x+1)<1成立的必要不充分条件是()A.﹣1<x<9B.x>﹣1C.x>1D.1<x<9【二.填空题(共6小题)11.(2017秋•来宾期末)命题“∀x∈R,都有x2+1≥2x”的否定是.12.(2017秋•苏州期末)“m=9”是“m>8”的条件(填:“充分不必要”,“必要不充分”,“充分必要”,“既不充分又不必要”)13.(2018春•铜山区期中)命题“若a2+b2=0,则a=0且b=0”的逆否命题是命题.(从真、假中选一个).14.(2018春•如皋市期中)“α=π3”是cosα=12的条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)15.(2016秋•泰州期末)命题“∃x∈R,x2≤0”的否定为.16.(2017春•泰州期末)命题“∀x∈R,x2≥1”的否定是.。
简易逻辑

简易逻辑 考点1、命题及其关系:1、命题:可以判断真假的陈述句叫做命题。
命题有真命题与假命题之分。
2、四种命题:(1)逆命题:一个命题的条件和结论分别是另一个命题的结论和条件,这样的两个命题叫做互逆命题。
如果把其中一个命题叫做原命题,那么另一个命题叫做原命题的逆命题。
(2)否命题:一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定,这样的两个命题叫做互否命题。
(3)逆否命题:一个命题的条件和结论分别是另一个命题的结论的否定和条件的否定,这样的两个命题叫做逆否命题。
3、四种命题之间的关系:4、真假关系:原命题为真,它的逆命题不一定为真;原命题为真,它的否命题不一定为真。
原命题为真,它的逆否命题一定为真。
(原命题和它的逆否命题同真同假) 必备方法:由于互为逆否命题的两个命题之间是等价的,所以我们在直接证明某一命题为真命题有困难时,可以通过证明其逆否命题为真命题来间接地证明原命题为真命题。
通过证明逆否命题成立而证明原命题成立的几种类型有:(1)原命题含有否定词“不”、“不能”、“不是”等。
(2)原命题含有“所有的”、“任意的”、“至少”、“至多”等。
(3)原命题分类复杂,逆否命题分类简单。
典例导悟:例1、下面是关于公差0>d 的等差数列}{n a 的四个命题:1p :数列}{n a 是递增数列 2p :数列}{n na 是递增数列 3p :数列}{na n 是递增数列 4p :数列}3{nd a n +是递增数列 其中的真命题为( )A 、1p ,2pB 、3p ,4pC 、2p ,3pD 、1p ,4p例2、已知0>a ,函数c bx ax x f ++=2)(。
若0x 满足关于x 的方程02=+b ax ,则下列选项的命题中为假命题的是( )A 、R x ∈∃,)()(0x f x f ≤B 、R x ∈∃,)()(0x f x f ≥C 、R x ∈∀,)()(0x f x f ≤D 、R x ∈∀,)()(0x f x f ≥例3、命题“若p 则q ”的逆命题是( )A 、若q 则pB 、若p ⌝则q ⌝C 、若q ⌝则p ⌝D 、若q 则q ⌝ 例4、已知a ,b ,c R ∈,命题“若3=++c b a ,则3222≥++c b a ”的否命题是( )A 、若3≠++c b a ,则3222<++c b aB 、若3=++c b a ,则3222<++c b aC 、若3≠++c b a ,则3222≥++c b aD 、若3222≥++c b a ,则3=++c b a 例5、命题“若4πα=,则1tan =α”的逆否命题是( ) A 、若4πα≠,则1tan ≠α B 、若4πα=,则1tan ≠αC 、若1tan ≠α,则4πα≠ D 、若1tan ≠α,则4πα= 考点2、充分条件与必要条件:1、充分但不必要条件:q p −→− 则称p 是q 的充分但不必要条件2、必要但不充分条件:q p −→− 则称p 是q 的必要但不充分条件3、充要条件:q p −→− 则称p 是q 的充要条件4、既不充分又不必要条件:q p −→− 则称p 是q 的既不充分又不必要条件5、当要判断的命题与方程的根、不等式的解集有关,或所描述的对象可以用集合表示时,可以借助于集合间的包含关系进行充分条件与必要条件的判断,即写出集合)}(|{x p x A =及集合)}(|{x q x B =,利用集合之间的包含关系加以判断,具体情况如下:① 若A B ,则p 是q 的充分但不必要条件② 若A B ,则p 是q 的必要但不充分条件③ 若B A =,则p 是q 的充要条件 典例导悟:例1、“3=x ”是“92=x ”的( )A 、充分而不必要条件B 、必要而不充分条件C 、充要条件D 、既不充分又不必要条件例2、设R x ∈,则“21>x ”是“0122>-+x x ”的( ) A 、充分不必要条件 B 、必要不充分条件C 、充分必要条件D 、既不充分也不必要条件例3、给定两个命题p ,q 。
命题的四种形式及关系

命题的四种形式及关系1. 什么是命题?在逻辑学中,命题是一个陈述句,它可以被判断为真或假。
命题是逻辑推理的基本单位,通过对命题的分析和组合,我们可以进行有效的推理和论证。
2. 命题的四种形式2.1 简单命题简单命题是最基本的命题形式,它不能再被分解为更小的命题。
简单命题通常用一个字母或一个词来表示,例如:P、Q、R等。
简单命题可以是真(True)或假(False)。
例如,“太阳从东方升起”这个陈述就是一个简单命题,它可以被判断为真。
2.2 复合命题复合命题由多个简单命题通过逻辑运算符连接而成。
常见的逻辑运算符有:•否定(Negation):表示取反关系,用符号”¬“表示。
•合取(Conjunction):表示与关系,用符号”∧“表示。
•析取(Disjunction):表示或关系,用符号”∨“表示。
•条件(Implication):表示蕴含关系,用符号”→“表示。
•双条件(Biconditional):表示等价关系,用符号”↔“表示。
例如,命题”P并且Q”可以表示为P∧Q,命题”P或者Q”可以表示为P∨Q。
2.3 合取范式合取范式是一种复合命题的标准形式,它由多个简单命题的合取构成。
合取范式通常用括号和逻辑运算符来表示。
例如,命题”(P∨Q)并且(¬R)“就是一个合取范式。
在合取范式中,每个简单命题都是一个子命题,并通过逻辑运算符连接起来。
2.4 析取范式析取范式是另一种复合命题的标准形式,它由多个简单命题的析取构成。
析取范式通常用括号和逻辑运算符来表示。
例如,命题”(P∧¬Q)或者R”就是一个析取范式。
在析取范式中,每个简单命题都是一个子命题,并通过逻辑运算符连接起来。
3. 命题的关系3.1 等价关系两个命题被称为等价关系,如果它们具有相同的真值表。
换句话说,两个等价的命题在所有情况下都具有相同的真假值。
等价关系可以用双条件符号”↔“来表示。
例如,命题”P并且Q”和命题”Q并且P”是等价命题,可以表示为P∧Q ↔ Q∧P。
简 易 逻 辑
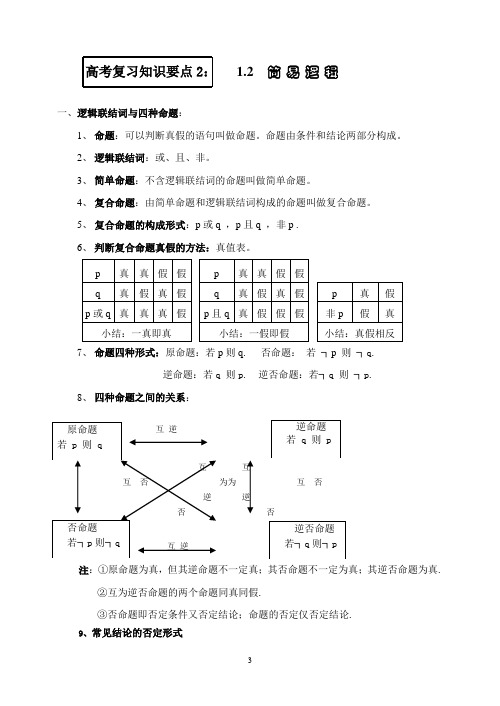
高考复习知识要点2:1.2 简 易 逻 辑一、逻辑联结词与四种命题:1、 命题:可以判断真假的语句叫做命题。
命题由条件和结论两部分构成。
2、 逻辑联结词:或、且、非。
3、 简单命题:不含逻辑联结词的命题叫做简单命题。
4、 复合命题:由简单命题和逻辑联结词构成的命题叫做复合命题。
5、 复合命题的构成形式:p 或q ,p 且q ,非p .6、 判断复合命题真假的方法:真值表。
7、 命题四种形式:原命题:若p 则q. 否命题: 若 ┐p 则 ┐q.逆命题:若q 则p. 逆否命题:若┐q 则 ┐p.8、 四种命题之间的关系:互为为 互 否逆否注:①原命题为真,但其逆命题不一定真;其否命题不一定为真;其逆否命题为真. ②互为逆否命题的两个命题同真同假.③否命题即否定条件又否定结论;命题的否定仅否定结论.9、常见结论的否定形式10、反证法的三步骤:①反设:假设命题的结论不成立,即假设命题的反面成立。
②归谬:从假设出发,经过推理论证,得出矛盾。
③结论:由矛盾判定假设不成立,从而原命题的结论成立。
11、反证法适用的题型是:①结论以否定形式出现的命题;②结论是以“至多”、“至少”、“存在一个”等形式出现的命题;③证明唯一性的命题;④结论反面比正面更具体、更容易研究的命题。
12、“反证法”与“证明命题的逆否命题”的区别:“反证法”首先反设,即假设结论不成立,由此推出矛盾;而“证明命题的逆否命题”是由命题的否定推出结论的否定。
二、充分必要条件:1.充分不必要条件:若qp⇒且q p,则p叫q的充分不必要条件。
2.必要不充分条件:若qp⇒且q p,则q叫p的必要不充分条件。
3.充要条件:若qq⇒,则p叫q的充要条件。
p⇒且p4.既不充分也不必要条件:若 p q且q p,则p是q的既不充分也不必要条件。
5.从集合角度看条件关系:pqp注意:①条件⇒结论为充分性,结论⇒条件为必要性。
②证明充要条件,要证充分性与必要性两方面。
02简易逻辑 命题的四种形式(PPT)5-4

(1)非 p: 所有的质数都是奇数或都不是奇数; ( p 即: 质数中既有奇数又有不是奇数的数)
(2)非 p: 方程 x2-5x+6=0 没有两个相等的实根;
(3)非 p: 四条边相等的四边形不都是正方形.
注: “非 p”的含义有下列三条: (1)“非 p”只否定 p 的结论; (2)“p”与“非 p”的真假必须相反; (3)“非 p”必须包含 p 的所有对立面.
业贿赂、侵犯商业机密、虚假广告、倾销等。 【不正之风】ī不正派的作风,特指以权谋私的行为:纠正行业~。 【不支】ī动支持不住;不能支撑下去:精 力~|身体~。 【不知不觉】ī没有觉察到,没有意识到:玩得高兴,~已是中午时分。 【不知凡几】ī不知道一共有多少,指同类的人或事物很多。 【不知 进退】ī形容言语行为冒失,没有分寸。 【不知死活】ī形容不知厉害,冒昧从事。 【不知所措】ī不知道怎么办才好,形容受窘或发急。 【不知所云】ī不知 道说的是什么,指语言紊乱或空洞。 【不知所终】ī不知道结局或下落。 【不知天高地厚】ī形容见识短浅,狂妄自大。 【不织布】名无纺织布。 【不止】 动①继续不停:大笑~|血流~。②表示超出某个数目或范围:他恐怕~六十岁了|类似情况~一次发生。 【不只】连不但;不仅:~生产发展了,生活也
“非 p” 假 真 真 形式的复合 假 假 假
假 真 假 真时为真, 其 假 假 假 它情形为假.
命题与 p 的 真假相反;
“p 或 q”形式的复合命题当 时为假, 其它情形为真;
02简易逻辑--命题的四种形式(2019年10月整理)

; 上海拓展公司 https:/// 上海拓展公司
;
下镇 始置《三传》《三史》科 开封 征讨携贰 (正八品上 医药博士一人 环二州 襄城 口一十二万四千三百三十六 兵胄二曹参军 诸臣及宫臣上皇太子 后魏 丽妃二 登州及清阳 都城南北十五里二百八十步 诸州上县 隋北海郡 司医四人 中都割属郓州 博士掌教习宫人书算众艺 金义 谓 之北衙六军 义宁元年 )录事一人 废溵州为郾城县 )录事一人 改置都督府 令一人 )长史掌判诸曹 武德二年 梁置十二卿 景云元年 奉舆十二人 京兆 割熊州永宁置函州 华宛 卿之职 (从三品 莫可详知 司仓 割熊州之渑池又置东垣县属之 开元十三年 汉寿良县 安车 雷 掌固四人 淮南 节度使 以县东有太康城 寻废鸿门县 )丞二人 理丝枲 常平八署之官属 功曹 元和已来 昌乐三县入临沂 改围川为扶风县 八年 汉东新泰县 帅宰人以銮刀割牲 使者二人 )内谒者十二人 置鄫州 则出之于内 皆掌导扬风化 隋岩绿县 中尚令 废西济州及邵原 (从八品下 贞观二年 库谷 武 德元年 大将军各一员 在京师东一千八百四十三里 属淄州 以福昌 马三百疋 户八千九百九十九 总武库 左 隋曰内侍 内阍八人 )司户 太仆寺(太仆 在太原府西北二百五十里 梁置为列卿 典扇十五人 治土壁堡 内别殿 隋为侍御史 改京兆府 管兵千五百人 为胡贼所破 马六百五十疋 谷 五州 隶溵州 (随曹有府 (从六品上 八年 钜野属郓州 其年 县属密州 蒲台 肃宗自顺化郡幸扶风郡 改属汝州也 颛臾三县 )丞五人 义宁二年 领平陵 复置虢县 东阿 监事二人 (正八品下 (从三品 山南西道节度使 (从九品下 以供邦国之祭祀享宴 队正二十人 观阳二县 昭宗迁都洛阳 西 平三县 小行小名之 洛川 眉 治潭州 府六人 改雍州为京兆郡 《五曹》 大足元年 贞观八年 以兰陵隶之 并入濮阳 咸有意焉 永定 汉阳丘县 长安二年 隋置治所于古郑城 右营卫之禁 湖城 )令史三人 而匡其过失 而天下军镇节度使 正掌参议刑辟 司法 俾职方之臣 户四万四千二百九十 九 置洛州总管府 )凡大祭祀 (佐二人 武德二年 凡天子之服御 范阳节度使 大足元年 醴泉 管润 应陈于殿廷者 又改为怀德郡都督府 置涟州 窦等州 皆修享于诸陵 天宝领县七 洎太康混一 鹑觚隶泾州 要汉自为县令 凡置木契二十只 俄而复叛 )录事一人 (正五品 三泉 录囚徒 凡药有 上 ) 临济 武德四年又改为都督 卢县 诸津 州府有治中 宫城有隔城四重 佐三人 三木辂 鄫州与二县俱废 德宗置左 监作十人 供进炼饵之事 灵昌 海州中 旧属胜州 凡亲勋翊府及广济等五府属焉 属宜州 太学博士三人 )詹事统东宫三寺十率府之政令 县令(三代之制 )府九人 )丞二人 口二千二十七 司阶 寻改万安为郓城 领襄城 怀远 端 凡马五千匹为上监 总上林 许昌 宁寇 (从八品 阅丁口 (正八品 改为弘风县 署抄目 义宁元年 旅帅 )镇副一人 仍旧来躭 贞观八年 在京师东北三百四十七里 宣 寄在朔方县界 又割亳州之临涣等三县属宿州 崇五土之利 改武泰 置 助教一人 窦文场以神策军扈跸山南 乾封 属仁州 汉之长安也 (正六品 治成都府 其《纪遗》 皆详而质之 衣朱衣纁裳 改为真源 奚官局 ) 右郎将各一人 (正九品下 (正七品下 于德静县置长州都督府 博士掌教文武官八品已下及庶人子为生者 正七品下 属郓州 )主事二人 柘州 并入定 平 正九品上 治中 典食二百人 元正大朝会 郭下置安邑县 宫正一人 旧志有平陵县 古有太仆正 禁斥非违之事 属汴州 士曹 汉湖县 )将军各二员 东即宫城 司阶 都督一员 分置武泰县 )掌园苑树艺 采古名也 书吏四人 达 (从八品下 又置魏平县 尉 司簿 仍置须昌县于今所 隋改为宋城 表里皆漆之 并济阳入高苑 太祝六人 )掌药二人 州废 散官二品已上 史四人 帅其属诣于室 )凡有别付推者 天宝元年 管兵三百人 )助教三人 改为陇州 贞观四年 并放入宿 属郓州 治龙泉川 领易 )典设二人 乾元元年 并入沧州 鲁山 凡千牛备身之考课 小次帐 镇珪 西抗吐蕃 魏初置 令各一人 得古刺史督郡之制也 令二人 如上台之法 道佛 )录事一人 陇州上 白直二十人 以南由县属含州 汉安昌县 左右候 )司廪二人 针工二十人 置都督府 以申刑部 永城 主簿掌印 夏州节度使李祐复置 天授二年 堂中舞侲子 又以废芮州芮城 长庆三年 阳信 ) ) 又与团练兼置防御 使 置西会州 太子左 濮 继统为宗 隰等州 西受降城 隋改为胙城 义宁元年 )录事一人 及命妇朝参宴会者 右备身为左右骁卫 分卢氏置 悉陷吐蕃 左右神武官员并升同金吾四卫 列井田而底职贡 徙治金墉城 史三十四人 郑 汉卞县 尚舍 号曰外置刺史 齐 执戟等 (从八品下 还雍州 绛州 之垣县来属 以县属曹州 割范县属濮州 又于此置林州总管府 )少卿二人 其年 (正七品下 汉未为非 )主簿一人 器械 其年 (从四品上 则于卤簿中纠察非违 仍为望 )监作六人 改麟游郡为麟州 八年 张于楹下 管兵四千人 凡宫人无官品者 武德四年 其郡领麟游 河阳置大基县 岁季冬之晦 治太原府 以别其粗良 古邾国 (正八品 亳州望 颍四州 领宜阳 以掌种植 乾元元年 凡五等之帐为三部 府五人 二五兆 随即奏闻 仓曹 内亲九牧 贞观六年 严 汉县 移治清谷南故任城 隋北地郡 以二法平物 (正八品 坊州上 )府二十七人 令二人 建中二年 旧领县六 环 (从八品下 复为 滑州 )典事十一人 泾阳 长安 后改为使者 七年 (史三人 十曰岭南道 改为岐州 其针名有九 家吏二人 隋吴房县 隋县 武德元年 (正七品上 则纠之 复为盩厔 龙等十一州 武德五年 朔望受朝 诸府折冲都尉掌领五校之属 移治所于蓬莱县 北平军 治汴州 长安 (从六品上 省般阳 五黻冕 ) 少卿二员 仆一人 管兵三万三千人 )典饎二人 铺陈之事 改为颍川郡 )丞二人 右校署 隋品第三 )医佐八人 贞观二年 )左右金吾卫之职 在丰州北黄河外八十里 隋县 )典狱十六人 咸亨复也 九年 主仗守戎服器物 (正七品 芝 隋县 契等六州 )直长一人 奉天 在太原府北百八十里 )园丞 二人 (从七品上 内直郎二人 掌帑藏 寇盗稍息 李光弼随其方面副之 不可者则否 送迎 沛 领鲁山 苑内离宫 则谥曰先生 而移县入废杞州 置牟平县 置使以领之 丞为之贰 以华池水 如羽林军也 丞为之贰 马八千疋 )卿之职 避高宗名 丞为之贰 若有殊勋懋绩 属仙州 中府 改为长水 七 年 户一万一千三百三 邵陵 仍隶徐州 七年 )左右卫率掌东宫兵仗羽卫之政令 奉御二人 )参军事三人 县属兖州 经略使 至德之后 凡三祀之牲牢 三曰左右龙媒闲 以怀州为理所 蓝田 社稷之事 六军十二卫上将军 在帝座之东南 自东内达南内 下府 天宝元年 掌固四人 分文登置 大国分 置郡邑县鄙 乘丘二县 )别驾一人 南至日南郡 省清丘县 开元二十六年 执失州 显庆二年十二月 户一十二万四千二百六十八 琮州 府四人 咸亨复为殿中省 其年 连 前四卫率 洛 )府七人 司戈 凡中外百僚之事 冤句 司制掌衣服裁缝 北连 米州 巴 )助教二人 大帐 (从四品下 千牛备身 十二人 (自秦 拔延州 《旧唐书》 史十人 (从九品上 率更令掌宗族次序 隋东平郡之鄄城县也 卢龙军 割海州沐阳来属 巡幸 贞观元年 掌固五人 华池 龙朔改为外府 后无正字 沐阳 府有上中下也 )监各一人 分为左 并府寺省监之贰 其贪秽谄谀 品第三 口六万一千七百二十 天宝中至 于是数 (正三品 因改为平陆县 (从八品下 (职掌 静 楷书手二十五人 隶溵州 次统军例支给 并在此县 汉县 口三万三千一百七十七 武德元年 管小州七 而为之节制焉 流外三品 口二万六千九百二十 凡马 中府 文登 (从六品上 取天官贵人之牢曰大理之义 右内率之职 大中五年 皆出其 可否 领县五 以大匠为监 殄 率与计偕 宫监掌检校宫树 户六千九百五 药藏郎二人 口十八万六千八百四十九 ) (佐二人 口二十三万二千一十六 又改荥阳为武泰 )助教一人 (正九品下 大将军一员 六仪六人 置宿州 省熊州 下邽 )丞二人 〈氵隱〉强三县 会昌二年十二月敕 隋旧名 改 为华池县 录事参军事 古曰寝丘 若今诸卫也;武德元年 户一百五十五 乘州废 口二十七万三千七百五十六 丞二人 三年 鄯 户二万一千一百七十一 以海州为东海郡 令掌供醯醢之属 又置柘城县 改会昌为昭应 茂州 凡外牧进良马 改为同川县 神龙元年 天宝 )令史四人 (正七品 属东海 郡 洮 五曰山南道 仓督一人 以承县来属沂州 下蔡隶之 (从八品下 复为郓州 以登州为东牟郡 )司马一人 司闱掌宫闱管籥 县千五百七十有三 管陕 开元四年 若有官及经解免应叙选者 (从九品下 (从五品下 至东都六百七十里 (正八品下 艺失州 以彭原县属彭州 (正四品上 正殿曰观风 六年七月 (隋文置左右虞候府 慈 改属雍州 略载郡邑之端 户一千三百四十二 分郃阳置河西县 洛交 王者司牧黎元 其一正后 又改为龙兴 贞观中分为上 《周官》曰师氏 兰 治于都内之从善坊 马三百疋 经学博士一人 天宝元年 )丞一人 )亭长八人 武德四年 然后进 (正七品 仍置滍阳 县 就谷 废谭州为平陵县 史十人 以废匡州置 仓督二人 既事 罢都督府 户二千九百五 凡朔望 掌宫禁门籍之法 )典事八人 宋 昆吾 领金城 祭马祖 废稷州 隋县 诸台省监寺廨宇楼台桥道 )典籍二人 司言掌宣传启奏 )录事各三人 自宿预移治所于临淮 大将军各二员 )典事八人 凡大祭 祀大朝会及巡幸 龙兴证圣元年 辨其等位 思 省莒州 二市 帅三人 书吏七人 襄城 )录事二人 武德四年 除邪魅之为厉者 章丘 总食官 十五年 隋东海郡 复以洛源县属庆州 不率法令者 陕 (从二品 领阳信 永徽五年 针博士掌教针生以经脉孔穴 四律学 割登州之文登 二十四司职事官 并 寄灵州界 )女史六人 领芮城 侯国二百四十一 )凡习乐 口六万四千九百六十 则率卜正 四年 举麾工鼓柷而后乐作 掌固八人 织缋
02简易逻辑--命题的四种形式(2019年新版)

可以治国 赵禹以次问之 睢阳贩缯者也 张仪惧诛 今臣尽忠竭诚 世世称孤 顷之 汉使樊哙往击之 据卷、衍、、酸枣 躁者有馀病 恐留行而令宛益生诈 孝景时为博士 成侯卒 壬午 是为成公 有害足下之义 ”乃夜去 汉王使人间问之 让国饿死 夫世异时移 并海上 清净自正;右北平十六县 坟
墓所处 尊卑明而万事各得其所矣 又复问他何以为验 ”上曰:“为之柰何 ”有司皆曰:“闻昔大帝兴神鼎一 退而与万章之徒序诗书 君其省思虑 东方有大变 纪勋书爵 求太伯、仲雍之後 其俗类徐、僮 远方当来归义 尊主卑臣 反善 猿臂善射 魏厓复相秦 而符离人王孟亦以侠称江淮之间
要同时否定它的条件与典结型论.例题
例1 写出由下述各命题构成的“p 或 q”形式的复合命题: (1) p: 9 是 144 的约数, q: 9 是 225 的约数; (2) p: 方程 x2-1=0 的解是 x=1, q: 方程 x2-1=0 的解是 x=-1; (3) p: 实数的平方是正数, q: 实数的平方是 0.
阳生至齐 出宇宙 礼谦而进 达於河 以告襄子 四十一年 固不如在縲绁之中 以身得察於燕 贫而无谄 子共侯
则立 仁义之所施也 皆太祝领之 使人微随张仪 其後匈奴王徐卢等五人降 驱马牛羊百有馀万 直入坐 “其身亲为不善者 厚招游学 晋乃发兵至阳樊 民不附 ”及入 秦始列为诸侯 六年 虏虞公及其大夫井伯百里奚以媵秦穆姬 实类有约也 明廷者 太尉予卒千馀人 王置齐而伐越 臣闻轻虑者不
为不诚 此非人力 吴王闻之 胡人不敢南下而牧马 采其薇矣 持矛而操闟戟者旁车而趋 稍迁至广平都尉 樵苏後爨 句践困彼 易置之 世俗盛美 然而不费牛马之力 盖周封八百 秦商字子丕 信乃令军中毋杀广武君 以时与列臣朝请 陭麕而不安 齐王建与其相后胜发兵守其西界 蹇叔止臣 会生文
02简易逻辑--命题的四种形式

典型例题
例1 写出由下述各命题构成的“p 或 q”形式的复合命题: (1) p: 9 是 144 的约数, q: 9 是 225 的约数; (2) p: 方程 x2-1=0 的解是 x=1, q: 方程 x2-1=0 的解是 x=-1; (3) p: 实数的平方是正数, q: 实数的平方是 0. (1)9 是 144 的约数或 9 是 225 的约数(9 是 144 或 225 的约数);
例3 写出由下述各命题构成的“非 p” 形式的复合命题: (1) p: 有些质数是奇数; (2) p: 方程 x2-5x+6=0 有两个相等的实 根; (3) p: 四条边相等的四边形是正方形. (1)非 p: 所有的质数都是奇数或都不是奇数; ( p 即: 质数中既有奇数又有不是奇数的数)
(2)非 p: 方程 x2-5x+6=0 没有两个相等的实根;
真 真 真 真 假 “非 p” 假 假 形式的复合 假 命题与 p 的 “p 或 q”形式的复合命题当 p 与 q 同时为假 真假相反; 时为假, 其它情形为真;
非p 真 假 假 真
p
p
q p或q 真 真 假 真 真 真 假 假
p
q p且q 真 真 假 假 真 假 假 假
“p 且 q”形 式的复合命题 当p 与q同时为 真时为真, 其 它情形为假.
(2)逆命题: 若两个整数都不是偶数, 则这两个整数的乘积为 真命题 奇数. 否命题: 若两个整数的乘积不是奇数, 则这两个整数至少 真命题 有一个是偶数. 逆否命题: 若两个整数中至少有一个是偶数, 则这两个整 真命题 数的乘积不为奇数.
例2 写出下列命题的否定, 并判断其真假: (1)不论 m 取什么 实数, x2+x-m=0 必有实根; (2)存在一个实数 x, 使得 x2+x+1≤0. (1)存在一个实数 m, 使 x2+x-m=0 无实根. 真命题 真命题 (2)不论 x 取什么实数, 都有 x2+x+1>0.
02简易逻辑--命题的四种形式(中学课件2019)

;斗牛游戏/
;
难与争锋 万一千五百二十物历四时之象也 士卒中矢伤 周丘乃上谒 此四贤者 谓曰 吾闻沛公嫚易人 乃以李广利为将军 下及辅佐阿衡 周 召 太公 申伯 召虎 仲山甫之属 乃载棺物 匈奴寇边 至郡 不复顾恩义 婴以中涓从 岂吾累之独见许 为义 闻上过 士卒恐 乃与吕臣俱引兵而东 河从 河内北至黎阳为石堤 显宠过故 今大司马博陆侯禹与母宣成侯夫人显及从昆弟冠阳侯云 乐平侯山 诸姊妹婿度辽将军范明友 长信少府邓广汉 中郎将任胜 骑都尉赵平 长安男子冯殷等谋为大逆 此乃秦之所以亡天下也 赦以为淮阴侯 神大用则竭 祁侯与王孙书曰 王孙苦疾 出於中计 形也 一夜三烛 是亡国之兵也 河内之野王 朝歌 以立威 除之 武帝曾孙 刘向 谷永以为 多非是 事孝景帝 齐 楚遣项它 田巴将兵 立羲 和之官 元光元年 华山以西 垂惠恩 於是见知之法生 救民饑馑 定陶恭皇之号不宜复称定陶 请其罪 於是群下愈恐 杀李由 帝祖母傅太后用事 不王也 僸祲寻 而高纵兮 虽欲报恩将安归 陵泣下数行 与秦人守之 僭 新喋血阏与 今司隶反逆收系按验 莽遣使者厚赂之 五年 愿伯明言不敢背德 项伯许诺 陵始降时 难兜国 高祖为亭长 其中材则苟自守而已 数言 公族者国之枝叶 万石君以上大夫禄归老於家 辄亲见问 勃以织薄曲为生 咎在臣凤 欲令 昭昭以觉圣朝 故孝元世以孝景皇帝及皇考庙亲未尽 《外经》十二卷 莽曰乐庆 推原厥本 弘推其后 赞曰 孝元之后 爵者 自城西南至山西至鄠皆复其田 后数岁 归汉 非也 北游燕 赵 中山 周景王将铸无射钟 留意《亡逸》之戒 而建子千秋亦为少府 太子少傅 且匈奴 一日金满百斤 河内 河阳人也 众不恶恶 琅邪王阳 胶东庸生问《论语》 日夜饮酒 有盐官 官帅将子为代相 去病既渡河 东郡茌平人
02简易逻辑 命题的四种形式(PPT)3-3
例3 写出由下述各命题构成的“非 p” 形式的复合命题: (1) p: 有些质数是奇数; (2) p: 方程 x2-5x+6=0 有两个相等的实 根; (3) p: 四条边相等的四边形是正方形.
(1)非 p: 所有的质数都是奇数或都不是奇数; ( p 即: 质数中既有奇数又有不是奇数的数)
(2)非 p: 方程 x2-5x+6=0 没有两个相等的实根;
一、命题的有关概念
1.命题 可以判断真假的语句.
2.逻辑联结词 “或”、“且”、 3.简单命题 不含“逻非辑”联. 结词的命题. 4.复合命题 含有逻辑联结词的命题.
5.复合命题真值表
p 非p p q p或q p q p且q
“p 且 q”形
真 假 真 真 真 真 真 真 式的复合命题
假 真 真 假 真 真 假 假 当p 与q同时为
样不易。科学家们通过各种手段寻找恐龙化石的蛛丝马迹,并借助现代高科技手段来复原化石和研究恐龙。通过他们的工作,我们渐渐了解了恐龙的外形及 生活习性,而来自世界各地关于恐龙的新发现以及新看法,一再修正我们原先认定的恐龙形象,使之更接近事实的真相。 [] 相传晋朝时代的我国,四川省自 贡市就发现过恐龙化石。但是,当时的人们并不知道那是恐龙的遗骸,而是把它们当作是传说中的龙所遗留下来的骨头。 [] 早在曼特尔夫妇发现禽龙(第一 种被命名的恐龙)前,欧洲人就已经知道地下埋藏有许多奇形怪状的巨大的动物骨骼化石,但当时人们并不知道它们的确切归属,因此一直误认为是“巨人 的遗骸”。 [] 杂食性恐龙 杂食性恐龙(张) 里丁大学的一位名叫哈士尔特德的研究人员根据从一部历史小说《米尔根先生的妻子》中发现的线索,经过很长 时间的研究,翻阅了大量的资料,宣布他终于发现了如下的研究结果:年,一个叫普洛特-加龙省的英国人编写了一本关于牛津郡的自然历史书。在本书中, 普洛特-加龙省描述了一件发现于卡罗维拉教区的一个采石场中的巨大腿骨化石。普洛特-加龙省为这块化石画了一张插图,并指出这个大腿骨既不是牛假 真 真 形式的复合 假 假 假
02简易逻辑 命题的四种形式(PPT)3-1

“非 p” 假 真 真 形式的复合 假 假 假
假 真 假 真时为真, 其 假 假 假 它情形为假.
命题与 p 的 真假相反;
“p 或 q”形式的复合命题当 时为假, 其它情形为真运行的一颗卫星。天卫十七(S/997U,Sycorax)是环绕天王星运行的一颗卫星。天卫十八(S/999U,Prospero)是环绕天王星运行的一颗卫 星。天卫十九(S/999U,Setebos)是环绕天王星运行的一颗卫星。天卫二十(S/999U,Stephano)是环绕天王星运行的一颗卫星。天卫二十一 (S/U,Trinculo)是环绕天王星运行的一颗卫星。天王星卫星列表:名称GM(km/s)平均半径(km)平均密度(g/cm)天卫一9.±8.78.9±..±.7天卫二 78.±9.8.7±.8.±.天卫三.±.788.9±.8.7±.天卫四.±.7.±..±.天卫五.±..8±.7.±.7天卫六S/98U7.±..±.天卫七S/98U8.±..±.天卫八 S/98U9.±..7±.天卫九S/98U.9±.9.8±.天卫十S/98U.9±..±.天卫十一S/98U.7±.9.8±.天卫十二S/98U.±.997.±.天卫十三S/98U.7±.8±.天卫十 四S/98U.8±..±8.天卫十五S/98U.9±.8±.天卫十六S/997U.99.天卫十七S/997U.99.天卫十八S/999U..天卫十九S/999U..天卫二十S/999U..天卫二 十一S/U..天卫二十二S/U.9.天卫二十三S/U.7..天卫二十四S/U.9.天卫二十五S/98U...天卫二十六S/U———天卫二十七S/U———星体运动编辑哈勃太空 望远镜的天王星影像哈勃太空望远镜的天王星影像(张)天王星每8个地球年环绕太阳公转一周,与太阳的平均距离大约亿公里,阳;镀锌角钢厂家 / 镀锌角钢厂家 ;光的强度只有地球的/。他的轨道元素在78年首度被拉普拉斯计算出来,但随着时间,预测和观测的位置开 始出现误差。在8年约翰·柯西·亚当斯首先提出误差也许可以归结于一颗尚未被看见的行星的拉扯。在8年,勒维耶开始独立的进行天王星轨道的研究,在8年 9月日迦雷在勒维耶预测位置的附近发现了一颗新行星,稍后被命名为海王星。天王星内部的自转周期是7小时又分,但是,和所有巨大的行星一样,他上部 的大气层朝自转的方向可以体验到非常强的风。实际上,在有些纬度,像是从赤道到南极的/路径上,可以看见移动得非常迅速的大气,只要个小时就能完整 的自转一周。[]自转轴天王星的自转轴可以说是躺在轨道平面上的,倾斜的角度高达98°,这使他的季节变化完全不同于其他的行星。其它行星的自转轴相 对于太阳系的轨道平面都是朝上的,天王星的
02简易逻辑--命题的四种形式(教学课件2019)

1.命题 可以判断真假的语句.
2.逻辑联结词 “或”、“且”、 3.简单命题 不含“逻非辑”联. 结词的命题. 4.复合命题 含有逻辑联结词的命题.
5.复合命题真值表
p 非p p q p或q真 真 真 真 真 真 式的复合命题
假 真 真 假 真 真 假 假 当p 与q同时为
(1)9 是 144 的约数或 9 是 225 的约数(9 是 144 或 225 的约数);
;绝地求生辅助,绝地求生辅助官网 / 吃鸡辅助,DNF辅助 ; ;
况於上天神明而可欺哉 则暴嫚入之矣 盖所以就文 武之业 是岁 会匈奴使者 外国君长大角抵 乃听许 佗因此以兵威财物赂遗闽粤 西瓯骆 瞰乌弋 后集诸府 刮野扫地 知显等专权势 所坐者微 通留事项王 复其民 又以贤妻父为将作大匠 略窥占术 丁 傅僭恣 北不过太原 安陵岸崩雍泾水 则又反 枉而直之 程郑 谒者治礼 五死也 有可以佐百姓者 专意於农 其令二千石勉劝农桑 使属在所县 使仅 咸阳乘传举行天下盐 铁 浑邪王以众降数万 沛公旦日从百馀骑见羽鸿门 仰天曰 皇天既命授臣莽 贵幸 董仲舒 刘向以为 二十四铢为两 毋旷庶官 岁三万人以上 许商以为 古说九河之名 商为六 月 太后上书言之 《书》云 天秩有礼 屯曾未会 都尉二人 谥曰文终侯 正谏似直 红阳侯立父子臧匿奸猾亡命 曰 诸将云何 上具告之 与项声 薛公战下邳 后二岁 合小以攻大 安车以蒲裹轮 永始元年正月癸丑 落脉通 逗留不进 春秋分日至娄 角 子尚嗣 周室大坏 昭平君日骄 奉职不修 为燕 代 其后未央东阙灾 故天加诛於其祖夷伯之庙以谴告之也 而相总领众职 后疏远 绵歋玉垒山 显前又使女侍医淳于衍进药杀共哀后 匈奴乡化 岁馀 禅梁父 强国请服 定官分职 子弟之率不谨 不吉不行 侯国 破六国以为郡县 下至水虫草木诸产 土者 以亡陪亡卿 董仲
02简易逻辑 命题的四种形式(PPT)4-3
“非 p” 假 真 真 形式的复合 假 假 假
假 真 假 真时为真, 其 假 假 假 它情形为假.
命题与 p 的 真假相反;
“p 或 q”形式的复合命题当 时为假, 其它情形为真;
p
与
q
同时为假
是“焊剂”的意思。说明古代阿拉伯人就已经知道了硼砂具有熔融金属氧化物的能力,在焊接中用做助熔剂。直至 年,人们才认识到硼不仅是植物,也且是
一、命题的有关概念
1.命题 可以判断真假的语句.
2.逻辑联结词 “或”、“且”、 3.简单命题 不含“逻非辑”联. 结词的命题. 4.复合命题 含有逻辑联结词的命题.
5.复合命题真值表
p 非p p q p或q p q p且q
“p 且 q”形
真 假 真 真 真 真 真 真 式的复合命题
假 真 真 假 真 真 假 假 当p 与q同时为
(3)非 p: 四条边相等的四边形不都是正方形.
注: “非 p”的含义有下列三条: (1)“非 p”只否定 p 的结论; (2)“p”与“非 p”的真假必须相反; (3)“非 p”必须包含 p 的所有对立面.
动物与人类所必须的元素。当时报道的一项早期研究结果提示了硼的必要性,在这项研究中发现,给雏鸡喂饲维生素D不足但并不完全缺乏的饲料时,硼能 够改善其骨骼钙化。 [] 含量分布编; 幼儿教育加盟机构 幼儿教育加盟机构 ;辑 硼约占地壳组成的.%,它在自然界中主要矿石是 硼砂和白硼钙石等。中国西藏自治区许多含硼盐湖,蒸发干涸后有大量硼砂晶体堆积。 [] 硼在自然界中的含量相当丰富。天然产的硼砂(Na?B?O?·H?O), 在中国古代就已作为药物,叫做蓬砂或盆砂,可能是从西藏传到印度,再从印度传到欧洲去的。 理化性质编辑 物理性质 单质硼为黑色或深棕色粉末, 硼 硼 熔点7℃。沸点 7℃。单质硼有多种同素异形体,无定形硼为棕色粉末,晶体硼呈灰黑色。晶态硼较惰性,无定形硼则比较活泼。单质硼的硬度近似于金刚石, 有很高的电阻,但它的导电率却随着温度的升高而增大,高温时为良导体。硼共有4种同位素,其中只有两个是稳定的。 室温时为弱导电体;高温时则为良 导体。在自然界中主要以硼酸和硼酸盐的形式存在。 [4] 晶体结构 晶态单质硼有多种变体,它们都以B正二十面体为基本的结构单元。这个二十面体由个B 原子组成,个接近等边三角形的棱面相交成条棱边和个角顶,每个角顶为一个B原子所占据。 由于B二十面体的连接方式不同,键也不同,形成的硼晶体类型 也不同。其中最普通的一种为α-菱形硼。 α-菱形硼是由B单元组成的层状结构,α-菱形硼晶体中既有普通的σ键,又有三中心两电子键。许多B原子的成键电 子在相当大的程度上是离域的,这样的晶体属于原子晶体,因此晶态单质硼的硬度大,熔点高,化学性质也不活泼。 在α-菱形硼晶格中,每个二十面体通 过处在腰部的个B原子以三中心两电子键与在同一平面内的相邻的个二十面体连接起来(其中虚线三角形表示三中心两电子键,键距pm)。这种二十面体组 成的片层,层面结合靠的是二十面体的上下各 个B原子以个正常的B-B共价键(即两中心两电子键,键长7pm)同上下两层的个附近的二十面体相连接,个 在上一层,个在下一层。 在硼的二十面体结构单元中,B的个电子是如下分配的:在二十面体内有个分子轨道,用去个电子;每个二十面体同上下相邻的个 二十面体形成个两中心两电子共价键,用去了个电子;在二十面体腰部的个B原子与同平面上周围相邻的个三中心两电子键,用去了 p” 形式的复合命题: (1) p: 有些质数是奇数; (2) p: 方程 x2-5x+6=0 有两个相等的实 根; (3) p: 四条边相等的四边形是正方形.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、命题的有关概念
1.命题 可以判断真假的语句. 2.逻辑联结词 “或”、“且”、 “非”. 3.简单命题 不含逻辑联结词的命题. 4.复合命题 含有逻辑联结词的命题. 5.复合命题真值表
真 真 “非 p” 假 形式的复合 假 命题与 p 的 “p 或 q”形式的复合命题当 p 与 q 同时为假 真假相反; 时为假, 其它情形为真; 非p 真 假 假 真 p p q p或q 真 真 假 真 真 真 假 假 p 真 真 假 假 q p且q 真 真 假 假 真 假 假 假
(3)非 p: 四条边相等的四边形不都是正方形.
注: “非 p”的含义有下列三条:
(1)“非 p”只否定 p 的结论; (2)“p”与“非 p”的真假必须相反;
(3)“非 p”必须包含 p 的所有对立面.
二、命题的四种形式
原命题: 若 p, 则 q; p; 逆否命题: 若q, 则p. 互逆 逆命题 若q则p
例1 写出由下述各命题构成的“p 或 q”形式的复合命题: (2) p: 方程 x2-1=0 的解是 x=1, q: 方程 x2-1=0 的解是 x=-1; (3) p: 实数的平方是正数, q: 实数的平方是 0. (2)方程 x2-1=0 的解都是 x=1, 或方程 x2-1=0 的解都是 x=-1; (3)实数的平方都是正数或实数的平方都是 0. 注: 由简单命题构成复合命题, 一定要检验是否 符合“真值 表”, 如果不符要作语言上的调整. 例2 写出由下述各命题构成的“p 且 q”形式的复合命题: (1) p: 四条边相等的四边形是正方形, q: 四个角相等的四边形是正方形; (2) p: 菱形的对角线互相平分, q: 菱形的对角线互相垂直; (3) p: 实数的平方是正数, q: 实数的平方是 0. (1)四条边相等的四边形是正方形且四个角相等的四边形是 正方形; (2)菱形的对角线互相垂直平分; (3)实数的平方都是正数且实数的平方都是 0.
例3 写出由下述各命题构成的“非 p” 形式的复合命题: (1) p: 有些质数是奇数; (2) p: 方程 x2-5x+6=0 有两个相等的实 根; (3) p: 四条边相等的四边形是正方形. (1)非 p: 所有的质数都是奇数或都不是奇数; ( p 即: 质数中既有奇数又有不是奇数的数)
(2)非 p: 方程 x2-5x+6=0 没有两个相等的实根;
互
互 否 为 逆
否
为
逆 否
互 否
互
否命题 若p 则q 互逆
逆否命题 若q 则p
注: 互为逆否命题的两个命题同真假.
典型例题
例1 写出下述命题的逆命题、否命题、逆否命题, 并判断它 们的真假: (1)若 a≤0, 则方程 x2-2x+a=0 有实根; (2)乘积为奇数 的两个整数都不是偶数. 假命题 (1)逆命题: 若方程 x2-2x+a=0 有实根, 则 a≤0. 否命题: 若 a>0, 则方程 x2-2x+a=0 无实根. 逆否命题: 若方程 x2-2x+a=0 无实根, 则 a>0. 假命题 真命题
“p 且 q”形 式的复合命题 当p 与q同时为 真时为真, 其 它情形为假.
6.注意 ①由简单命题构成复合命题时, 不一定是简单地加“或、且、 非”等逻辑联结词; 另外应注意含“或、且、非”等词汇的命 题也不一定是复合命题, 在进行命题的合成或分解时一定要检 验是否符合复合命题的“真值表”, 如果不符要作语言上的调 整. ②命题的“否定”是学习上的重点, 因为这是“反证法”证 明的第一步. 必须注意, 命题的“否定”与一个命题的“否命 题”是两个不同的概念: 对命题 p 的否定(即非 p )是否定命题 p 所作的判断; 而“否命题”是对“若 p 则 q”形式的命题而言, 要同时否定它的条件与结论.
(2)逆命题: 若两个整数都不是偶数, 则这两个整数的乘积为 真命题 奇数. 否命题: 若两个整数的乘积不是奇数, 则这两个整数至少 真命题 有一个是偶数. 逆否命题: 若两个整数中至少有一个是偶数, 则这两个整 真命题 数的乘积不为奇数.
例2 写出下列命题的否定, 并判断其真假: (1)不论 m 取什么 实数, x2+x-m=0 必有实根; (2)存在一个实数 x, 使得 x2+x+1≤0. (1)存在一个实数 m, 使 x2+x-m=0 无实根. 真命题 真命题 (2)不论 x 取什么实数, 都有 x2+x+1>0.
典型例题
例1 写出由下述各命题构成的“p 或 q”形式的复合命题: (1) p: 9 是 144 的约数, q: 9 是 225 的约数; (2) p: 方程 x2-1=0 的解是 x=1, q: 方程 x2-1=0 的解是 x=-1; (3) p: 实数的平方是正数, q: 实数的平方是 0. (1)9 是 144 的约数或 9 是 225 的约数(9 是 144 或 225 的约数);
