浙教版九年级数学下《22切线长定理》同步练习有答案MnPUnP
浙教版数学九年级下册《切线长定理》习题.docx

《切线长定理》习题1.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于()A.21 B.20 C.19 D.182.如图,P A、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠P AB相等的角(不包括∠P AB本身)有()A.1个B.2个C.3个D.4个3.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的()A.三条中线的交点B.三条高的交点C.三条角平分线的交点D.三条边的垂直平分线的交点4.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是()A.120°B.125°C.135°D.150°5.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25cm,∠MPN=60 ,则OP=()A.50cm B.253cmC.3350cm D.503cm6.如图,P A、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=().B ACPOA.60°B.75°C.105°D.120°7.如图,在△ABC中,5cmAB AC==,cosB35=.如果⊙O的半径为10cm,且经过点B、C,那么线段AO=__________cm.8.如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且ο60=∠AEB,则=∠P_____度.9.如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC的周长.10.如图,已知AB为⊙O的直径,AD、BC、CD为⊙O的切线,切点分别是A、B、E,则有一下结论:(1)CO⊥DO;(2)四边形OFEG是矩形.试说明理由.GFECB初中数学试卷鼎尚图文**整理制作。
浙教版九年级数学下册第2章直线与圆的位置关系2.2切线长定理同步测试-附答案
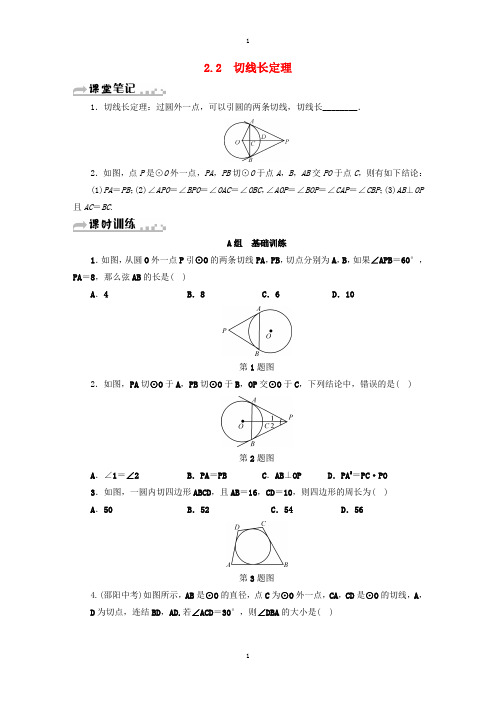
2.2 切线长定理1.切线长定理:过圆外一点,可以引圆的两条切线,切线长________.2.如图,点P是⊙O外一点,PA,PB切⊙O于点A,B,AB交PO于点C,则有如下结论:(1)PA=PB;(2)∠APO=∠BPO=∠OAC=∠OBC,∠AOP=∠BOP=∠CAP=∠CBP;(3)AB⊥OP 且AC=BC.A组基础训练1.如图,从圆O外一点P引⊙O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )A.4 B.8 C.6 D.10第1题图2.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是( )第2题图A.∠1=∠2 B.PA=PB C.AB⊥OP D.PA2=PC·PO3.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )A.50 B.52 C.54 D.56第3题图4.(邵阳中考)如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连结BD,AD.若∠ACD=30°,则∠DBA的大小是( )第4题图A.15° B.30° C.60° D.75°5.如图,过⊙O外一点P作⊙O的两条切线PA,PB,切点分别为A,B.下列结论中:①OP 垂直平分AB;②∠APB=∠BOP;③△ACP≌△BCP;④PA=AB;⑤若∠APB=80°,则∠OBA =40°.正确的是________.第5题图1.如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是________°.第6题图7.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2,AD=4.则BE=________,BC=________.第7题图2.如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是________.第8题图9.如图,AB为半圆O的直径,在AB的同侧作AC,BD切半圆O于点A,B,CD切半圆O 于点E.若AC=4,BD=9,求⊙O的半径.第9题图10.如图,PA,PB,DE分别切⊙O于点A,B,C,D在PA上,E在PB上.(1)若PA=30,求△PDE的周长;(2)若∠P=50°,求∠O的度数.第10题图B组自主提高11.如图,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点,若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确( )第11题图A.AB>CE>CD B.AB=CE>CD C.AB>CD>CE D.AB=CD=CE12.如图,直尺、三角尺都和⊙O相切,B是切点,且AB=8cm.求⊙O的直径.第12题图13.如图,PA,PB分别切⊙O于点A,B,连结PO,AB相交于点D,C是⊙O上一点,∠C=60°.(1)求∠APB的大小;(2)若PO=20cm,求△AOB的面积.第13题图C组综合运用14.如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB长为半径的圆与AB交于点E,与AC相切于点D,直线ED交BC的延长线于点F.(1)求证:BC=FC;(2)若AD∶AE=2∶1,求tanF的值.第14题图2.2 切线长定理【课堂笔记】 1.相等 【课时训练】 1-4.BDBD 5. ①③⑤ 6. 99 7. 6 6 8. 29. r =6.法一:可在△COD 中,连结OE ,有OE 2=CE×DE=36,∴r =6.法二:过C 作CH⊥BD 于点H ,在△CDH 中,CD =13,DH =5,∴CH =AB =12,即r =6.10. (1)∵PA、PB 是⊙O 切线,∴PA =PB ,∵DE 是⊙O 切线,∴DC =DA ,EC =EB ,∴△PDE 的周长=PD +PE +DC +CE =PD +DA +PE +EB =PA +PB =60; (2)连结AO ,BO ,CO ,可证:∠AOD=∠COD,∠COE =∠BOE,∴∠DOE =12∠AOB ,∵∠AOB +∠P=180°,∠P =50°,∴∠AOB =130°,∴∠DOE =65°.11. A12. 连结AO ,BO ,∵AB 是⊙O 的切线,AC 是⊙O 的切线,∴∠ABO =90°,∠BAO =12∠BAC =60°,在Rt △AOB 中,OB =AB·tan ∠BAO =8×tan 60°=83,∴⊙O 的直径为163cm .13. (1)∵PA,PB 分别为⊙O 的切线,∴OA ⊥PA ,OB ⊥PB ,∴∠OAP =∠OBP=90°.∵∠C =60°,∴∠AOB =2∠C=120°,∴在四边形APBO 中,∠APB =360°-∠OAP-∠OBP-∠AOB =360°-90°-90°-120°=60°; (2)在Rt △PAO 与Rt △PBO 中,∵OA =OB ,PO =PO ,∴Rt △PAO ≌Rt △PBO ,∴∠APO =∠BPO=12∠APB =30°,∴PO ⊥AB ,∴∠DAO =∠APO=30°,∴OA =sin ∠APO ×OP =12×20=10(cm ).在Rt △AOD 中,∠DAO =30°,OA =10cm ,∴AD =cos∠DAO ×OA =32×10=53(cm ),OD =sin ∠DAO ×OA =12×10=5(cm ),∴AB =2AD =103(cm ),∴S △AOB =12AB ×OD =12×103×5=253(cm 2).14. (1)连结BD.∵BE 为⊙O 的直径,∴∠BDE =90°,∴∠EBD =90°-∠BED.∵∠EBF =90°,∴∠F =90°-∠BEF.∴∠F=∠EBD.∵AC 切⊙O 于点D ,∴∠EBD =∠ADE=∠CDF.∴∠F=∠CDF,∴DC =FC.∵OB⊥BC,∴BC 是⊙O 的切线,∴DC =BC.∴BC=FC; (2)在△ADE 和△ABD 中,∵∠A =∠A,∠ADE =∠ABD,∴△ADE ∽△ABD ,DE BD =AE AD =12.又∵∠F=∠EBD,∴tan F =tan ∠EBD =DE BD =12.。
浙教版数学九年级数学下册 2.2切线长2.3三角形的内切圆同步测试试题

切线长定理一、选择题(只有一个选项是正确的,请把它选出来)1. 点P是⊙O外一点,PA,PB是圆的切线,切点分别为A,B,若PA=12,则PB的长为()(A)6. (B)8. (C)12. (D)14.2. (原创)如图1,点P是⊙O外一点,PA,PB是圆的切线,切点分别为A,B,PO与AB交于点C,则图中直角三角形的个数为()(A)4个. (B)5个. (C)6个. (D)8个.图 13. 如图2,点P是⊙O外一点,PA,PB是圆的切线,切点分别为A,B,E点是劣弧AB上一点,过E点的切线CD,交PA,PB分别于点D,C,若圆的半径为3,PO=5,则三角形PCD的周长为()(A)6. (B)8. (C)10. (D)12.图 24. (原创)如图3,点A是⊙O外一点,AB,AC是圆的切线,切点分别为B,C,若∠BOC=120°,则三角形ABC的形状是()(A)等腰三角形. (B)等边三角形. (C)等腰直角三角形. (D)直角三角形.图 3二、填空题(答案要简洁)5. (原创) 如图4,点A是⊙O外一点,AB,AC是圆的切线,切点分别为B,C,若AB⊥AC,则四边形ABOC的形状是 .图 46. (原创)如图5,点P是⊙O外一点,PB,PA是圆的切线,切点分别为B,A,C是优弧AB上一点,且∠ACB=84°.则∠P的度数是 .图 57. (原创)如图6,点P是⊙O外一点,PB,PA是圆的切线,切点分别为B,A,C是PA的中点,CD切圆O于点D,则AD,PD,PB三者之间的关系是 .图 68. (原创) 如图7,已知点P是⊙O外一点,PB,PA是圆的切线,切点分别为B,A,B是OC 的中点,∠POB=70°,则∠APC的度数为 .图 7三、解答题9. (原创)如图8,已知半⊙O与等腰三角形ABC的边AB,AC分别相切,切点分为D,E,半圆的直径FG在边BC上.求证:DF=EG.图 810. (原创) 如图9,已知点P是⊙O外一点,PB,PA是圆的切线,切点分别为B,A,连接AB,PO 二线交于点E,以AB为一边作矩形ABCD,连接OB,若OB=3,PO=5,求矩形ABCD的面积.图 9三角形的内切圆一、选择题(只有一个选项是正确的,请把它选出来)1.三角形的内心是()(A)三角形三条中线的交点.(B)三角形三条垂直平分线的交点.(C)三角形三条高线的交点.(D)三角形三条角平分线的交点.2. 如图1,⊙G是三角形ABC的内切圆,切点分别是D,E,F,则三角形EDF的形状是()(A)直角三角形. (B)锐角三角形. (C)等边三角形. (D)无法确定.3. 如图2,⊙O是三角形ABC的内切圆,切点分别是D,E,F,∠C=78°,则∠EDF的度数是()(A)51°. (B)62°. (C)78°. (D)84°.4. (原创) 如图3,圆与直角三角形ABC的三边都相切,切点分别是D,E,F,已知斜边AB=10,直角边BC=6,则CD,AE,BF 的长分别是 ( ) (A )2、6、4. (B )2、4、6. (C )2、4、5. (D )2、5、4.二、填空题(答案要简洁)5. (原创) Rt △ABC 中,∠C=90°,AC=3cm ,BC=4cm ,r 为半径作圆与三角形的三边都相切,则点A 到圆心的距离为_______.6.三角形ABC 的内心与外心重合,则三角形ABC 的形状是 .7. 如图4,Rt△ABC 的内切圆⊙O 与两直角边AB ,BC 分别相切与点D 、E ,过劣弧DE (不包括端点D ,E )上任一点P 作⊙O 的切线MN 与AB ,BC 分别交于点M ,N ,若⊙O 的半径为r ,则Rt△MBN 的周长为 .8. (原创) 如图4,CD 是Rt△ABC 斜边AB 上高,⊙E 是三角形ABC 的内切圆,半径为R ,⊙F 是三角形ACD 的内切圆,半径为1R ,⊙G 是三角形BCD 的内切圆,半径为2R ,设三角形ABC 的三边长分别为a,b,c ,则12R R R= .(用a,b,c 表示)三、解答题9. 原创如图5,,CD是Rt△ABC斜边AB上高,⊙1O是三角形ACD的内切圆,半径为1R,⊙2O是三角形BCD的内切圆,半径为2R,设三角形ABC的三边长分别为a,b,c.(1)用a,b,c分别表示1R,2R;(2)计算12RR的值.10.原创如图6,Rt△ABC中,⊙O是三角形ABC的内切圆,半径为1R;如图7,⊙1O,⊙2o是两个等圆,两圆外切,且⊙1O与AB,BC都相切,⊙2o与AC,BC都相切,半径为2R;如图8,⊙1O,⊙2o,⊙3O是等圆,自左到右依次外切,且⊙1O与AB,BC都相切,⊙3O与AC,BC都相切,半径为3R,设三角形ABC的三边长分别为a,b,c.(1)求1R,2R,3R;(2)有n个等圆⊙1O,⊙2o,⊙3O…⊙nO,自左到右依次外切,且⊙1O与AB,BC都相切,⊙nO与AC,BC都相切,半径为2R,仔细观察(1)中的规律,直接写出nR.探究题:如图9,直角三角形ABC中,∠C=90°,AB=c,BC=a,AC=b,⊙0与直角三角形的三边相切,圆的半径r.则r=2()abcc a b c++.(2)如图10,直角三角形ABC中,∠C=90°,AB=c,BC=a,AC=b,⊙0、⊙I是两个等圆,且⊙0与直角三角形的两边相切,⊙I与直角三角形的两边相切,⊙0与⊙I相外切,圆的半径r.则r=22()abcc a b c ab+++.(3)如图11,直角三角形ABC中,∠C=90°,AB=c,BC=a,AC=b,⊙0、⊙I是n个等圆中的两个,且⊙0与直角三角形的两边相切,⊙I与直角三角形的两边相切,n个等圆两两相切,圆的半径r,则r= .切线长定理一、选择题 1.(C )提示:根据切线长定理PB=12. 2. (C )提示:根据切线的性质,知道三角形PAO,PBO 是直角三角形,根据切线长定理,等腰三角形三线合一,知道三角形PAC,PBC,OAC,OBC 都是直角三角形. 3.(B )提示: 三角形PCD 的周长为PA+PB=2PA ,根据勾股定理,PA=4. 4.. (B ) 提示:利用切线性质,四边形内角,确定∠A=60°. 二、填空题 5. 正方形提示:切线性质,得到两个直角,矩形+邻边相等. 6. 12°提示:利用圆心角与圆周角关系定理,得∠AOB=168°,利用四边形内角和定理可求. 7. 222AD PD PB +=提示:根据切线长定理,得PA=PB,AC=CD=CP ,所以三角形APD 是直角三角形. 8. 60°提示:切线长定理,等腰三角形三线合一,确定∠APO=∠OPB=∠BPC=20°.三、解答题 9.证明:连接OA ,因为AD,AE 是圆的切线,所以OA 平分∠BAC ,AD=AE , 所以AB-AD=AC-AE ,所以BD=CE. 因为OA 平分∠BAC,AB=AC ,所以OB=OC,所以OB-OF=OC-OG ,所以BF=CG ,因为∠B=∠C ,所以△DBF ≌△EGC , 所以DF=EG.10.解:因为PB 是圆的切线,所以三角形POB 是直角三角形,所以PB=4, 所以BD=8.因为PA,PB 是圆的切线,所以PE ⊥AB ,所以PB g OB=PO g BE , 所以BE=125,所以AB=245, 所以2222248()5BD AB -=-325, 所以矩形的面积AB g AD=245×325=76825.三角形的内切圆一、选择题 1.(D )提示:根据三角形内心的定义判断. 2. (B )提示:连接EG,FG ,则∠EGF <180°,所以12∠EGF <90°,所以∠EDF 是锐角,同理可证其余两个角也是锐角.3. (A )提示:先求∠EOF=102°,后求解即可. 4.(A )提示:先求AC=8,再求CF=2,AE=6,BF=4.二、填空题提示:r=1,AC 上点A 到切点的距离为2,根据勾股定理求解. 6. 等边三角形提示:等边三角形的三线合一判定. 7.2r提示:三角形的周长为2BD ,BD 就是r. 8.a bc+ 提示:设CD=h ,AD=x ,BD=y ,则R=2a b c +-,1R =2h x b +-,2R =2h y a+- 所以1R +2R =2h x b +-+2h y a +-=2()2h x y a b ++-+=2()2h c a b +-+,因为h=ab c ,所以1R +2R =222()()22ab ab c a b cc a b c c +-++-+= =2222()()()22ab a b a b ca b a b c c c++-++-+==()()22a b a b c a b a b c a b R c c c++-++-+==•g ,所以12R R R +=a b c+.三、解答题 9.解:(1)因为三角形ABC 的面积是定值,所以CD=abc.易证△ADC ∽△ACB , 所以AD=2b c,因为⊙1O 是三角形ACD 的内切圆,半径为1R ,所以AD-1R +CD-1R =AC所以1R =2AD CD AC +-=2()22b abbb a bc c c c+-+-=; 同理可证, 2R =()2a a b c c+-;(2)因为1R =()2b a b c c +-,2R =()2a a b c c+-,所以12R R =b a .10. 解:(1)如图6 连接OA,OC,OB,因为⊙O 是三角形ABC 的内切圆,半径为1R ,三角形ABC 的三边长分别为a,b,c ,所以三角形AOC 的面积=12×AC ×1R ,三角形BOC 的面积=12×BC ×1R ,三角形AOB 的面积=12×AB ×1R ,三角形ABC 的面积=12×a ×b , 所以12×AC ×1R +12×BC ×1R +12×AB ×1R =12×a ×b , 所以1R =ab a c b ++;如图7 连接1O A, 1O C, 1O B, 等圆的半径为2R 三角形ABC 的三边长分别为a,b,c , 所以三角形A 1O C 的面积=12×AC ×22R ,三角形B 1O C 的面积=12×BC ×2R ,三角形A 1O B 的面积=12×AB ×2R ,三角形ABC 的面积=12×a ×b , 所以12×AC ×22R +12×BC ×2R +12×AB ×2R =12×a ×b , 所以2R =2ab a c b ++;同理可证,3R =3ab a c b++; (2)n R =ab a c nb ++.探究题:解:(1)连接OA,OC ,OB ,则三角形AOC 的面积=12×AC ×r ,三角形BOC 的面积=12×BC ×r , 三角形AOB 的面积=12×AB ×r ,三角形ABC 的面积=12×a ×b , 因为三角形AOC 的面积+三角形BOC 的面积+三角形AOB 的面积=三角形ABC 的面积, 所以12×AC ×r+12×BC ×r+12×AB ×r=12×a ×b , 所以12(a+b+c )r=12×a ×b,所以r=ab a b c ++,所以r=2()abc c a b c++. (2)连接OA,OC,IC,IB,OI,OE,IF,作高CD,交OI 于点G ,则三角形AOC 的面积=12×AC ×r ,三角形BIC 的面积=12×BC ×r ,三角形AOF 的面积=12×AF ×r ,三角形BIF 的面积=12×BF ×r ,三角形OIF 的面积=12×OI ×IF ,三角形OCI 的面积=12×OI ×CG ,三角形ABC 的面积=12×a ×b ,因为三角形AOC 的面积+三角形BIC 的面积+三角形AOF 的面积+三角形BIF 的面积+三角形OIF 的面积+三角形OCI 的面积=三角形ABC 的面积, 所以12×AC ×r+12×BC ×r+12×AF ×r+12×BF ×r+12×OI ×IF+12×OI ×CG=12×a ×b , 所以12(a+b+c )r+12×OI ×CD=12×a ×b,且CD=ab c ,整理得:r=22()abc c a b c ab +++.(3)规律隐藏在ab 分母中ab 的系数中,且系数与等圆的个数n 的关系是:系数=2(n-1),于是结论为r=221()()abc c a b c n ab +++-.。
浙教版九年级数学下册2.2:切线长定理 同步练习题(含解析)
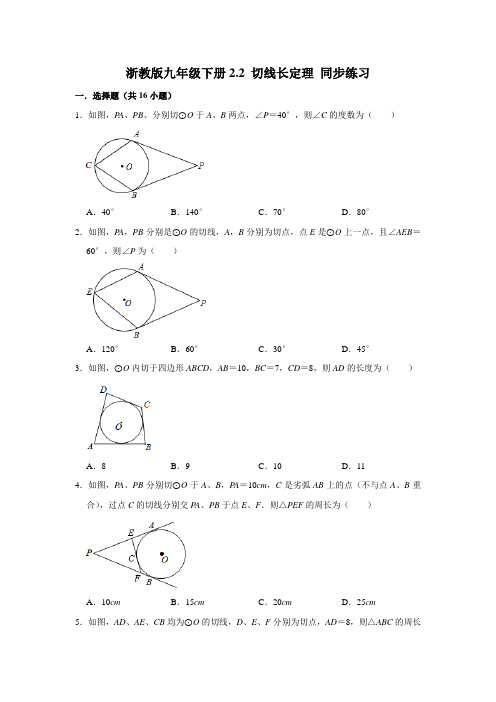
浙教版九年级下册2.2 切线长定理同步练习一.选择题(共16小题)1.如图,P A、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为()A.40°B.140°C.70°D.80°2.如图,P A,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为()A.120°B.60°C.30°D.45°3.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8B.9C.10D.114.如图,P A、PB分别切⊙O于A、B,P A=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交P A、PB于点E、F.则△PEF的周长为()A.10cm B.15cm C.20cm D.25cm5.如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为()A.8B.10C.12D.166.如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有()个①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.A.1B.2C.3D.47.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°8.如图,已知P A,PB分别切⊙O于点A、B,∠P=60°,P A=8,那么弦AB的长是()A.4B.8C.4D.89.如图所示,P A,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是()A.P A=PB B.∠APO=20°C.∠OBP=70°D.∠AOP=70°10.如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为()A.20B.30C.40D.5011.如图,从圆O外一点P引圆O的两条切线P A,PB,切点分别为A,B.如果∠APB=60°,P A=8,那么弦AB的长是()A.4B.8C.D.12.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD =6,则CB长()A.4B.5C.6D.无法确定13.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()A.50B.52C.54D.5614.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为()A.5B.10C.7.5D.415.已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=()A.4B.C.D.16.如图,P A、PB分别切⊙O于A、B两点,如果∠P=60°,P A=2,那么AB的长为()A.1B.2C.3D.4二.填空题(共4小题)17.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为.18.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为.19.如图,P A,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=°.20.如图,四边形ABCD外切于圆,AB=16,CD=10,则四边形的周长是.三.解答题(共7小题)21.如图,P A、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P 的度数.22.如图,P A、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)P A的长;(2)∠COD的度数.23.如图,P A、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交P A、PB于点E、F,已知P A=12cm,∠P=40°①求△PEF的周长;②求∠EOF的度数.24.如图,P A、PB、DE切⊙O于点A、B、C、D在P A上,E在PB上,(1)若P A=10,求△PDE的周长.(2)若∠P=50°,求∠O度数.25.如图,P A,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.(1)求∠BAC的度数;(2)当OA=2时,求AB的长.26.已知:如图,P A、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O 的切线,交P A、PB于E、F点,已知P A=12cm,求△PEF的周长.27.如图,已知AB为⊙O的直径,P A,PC是⊙O的切线,A,C为切点,∠BAC=30°.(Ⅰ)求∠P的大小;(Ⅱ)若AB=2,求P A的长(结果保留根号).参考答案一.选择题(共16小题)1.如图,P A、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为()A.40°B.140°C.70°D.80°【分析】连接OA,OB根据切线的性质定理,切线垂直于过切点的半径,即可求得∠OAP,∠OBP的度数,根据四边形的内角和定理即可求的∠AOB的度数,然后根据圆周角定理即可求解.【解答】解:∵P A是圆的切线.∴∠OAP=90°,同理∠OBP=90°,根据四边形内角和定理可得:∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,∴∠ACB=∠AOB=70°.故选:C.2.如图,P A,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=60°,则∠P为()A.120°B.60°C.30°D.45°【分析】连接OA,BO,由圆周角定理知可知∠AOB=2∠E=120°,P A、PB分别切⊙O 于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠P =180°﹣∠AOB=60°.【解答】解:连接OA,BO;∵∠AOB=2∠E=120°,∴∠OAP=∠OBP=90°,∴∠P=180°﹣∠AOB=60°.故选:B.3.如图,⊙O内切于四边形ABCD,AB=10,BC=7,CD=8,则AD的长度为()A.8B.9C.10D.11【分析】根据圆外切四边形的性质对边和相等进而得出AD的长.【解答】解:∵⊙O内切于四边形ABCD,∴AD+BC=AB+CD,∵AB=10,BC=7,CD=8,∴AD+7=10+8,解得:AD=11.故选:D.4.如图,P A、PB分别切⊙O于A、B,P A=10cm,C是劣弧AB上的点(不与点A、B重合),过点C的切线分别交P A、PB于点E、F.则△PEF的周长为()A.10cm B.15cm C.20cm D.25cm【分析】根据切线长定理由P A、PB分别切⊙O于A、B得到PB=P A=10cm,由于过点C的切线分别交P A、PB于点E、F,再根据切线长定理得到EA=EC,FC=FB,然后三角形周长的定义得到△PEF的周长=PE+EF+PF=PE+EC+FC+PF,用等线段代换后得到三角形PEF的周长等于P A+PB.【解答】解:∵P A、PB分别切⊙O于A、B,∴PB=P A=10cm,∵EA与EC为⊙的切线,∴EA=EC,同理得到FC=FB,∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF=PE+EA+FB+PF=P A+PB=10+10=20(cm).故选:C.5.如图,AD、AE、CB均为⊙O的切线,D、E、F分别为切点,AD=8,则△ABC的周长为()A.8B.10C.12D.16【分析】由AD、AE、CB均为⊙O的切线,D、E、F分别为切点,根据切线长定理,可得CE=CF,BD=BF,AE=AD=8,继而可求得△ABC的周长为AE+AD的和.【解答】解:∵AD、AE、CB均为⊙O的切线,D、E、F分别为切点,∴CE=CF,BD=BF,AE=AD=8,∴△ABC的周长为:AC+BC+AB=AC+CF+BF+AB=AC+CE+BD+AB=AE+AD=16.故选:D.6.如图,⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,下列结论一定正确的有()个①AF=BG②CG=CH③AB+CD=AD+BC④BG<CG.A.1B.2C.3D.4【分析】根据切线长定理(从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角)对以下选项进行分析.【解答】解:如图,连接OE、OF、OH、OG.①∵⊙O是四边形ABCD的内切圆,切点依次是E、F、G、H,∴BF=BG、AF=AE,只有当点F是边AB的中点时,AF=BF=BG,否则,等式AF=BG不成立;故本选项不一定正确;②根据题意,知,CG、CH都是⊙O的切线,∴CG=CH.故本选项正确;③根据题意,知AF=AE,DH=DE,BF=BG,CG=CH,则AF+BF+CH+DH=AE+BG+CG+DE,即AB+CD=AD+BC.故本选项正确;④当点G是边BC的中点时,BG=CG.故本选项错误;综上所述,正确的说法有2个;故选:B.7.如图,AB、AC是⊙O的切线,B、C为切点,∠A=50°,点P是圆上异于B、C,且在上的动点,则∠BPC的度数是()A.65°B.115°C.115°或65°D.130°或65°【分析】连接OB、OC,根据四边形的内角和定理,求得∠BOC=130°,再由圆周角定理求得∠P的度数即可.【解答】解:如图,连接OB、OC,∵AB、AC是⊙O的切线,∴∠OBA=∠OCA=90°,∵∠A=50°,∴∠BOC=130°,∵∠BOC=2∠P,∴∠BPC=65°;故选:AC.8.如图,已知P A,PB分别切⊙O于点A、B,∠P=60°,P A=8,那么弦AB的长是()A.4B.8C.4D.8【分析】根据切线长定理和等边三角形的判定方法,发现等边三角形即可求解.【解答】解:∵P A,PB分别切⊙O于点A、B,∴P A=PB,又∠P=60°,∴△APB是等边三角形,∴AB=P A=8.故选:B.9.如图所示,P A,PB是⊙O的切线,且∠APB=40°,下列说法不正确的是()A.P A=PB B.∠APO=20°C.∠OBP=70°D.∠AOP=70°【分析】根据切线长定理得A,B是正确的;再根据切线的性质定理以及直角三角形的两个锐角互余得D是正确的;根据切线的性质定理得C错误.【解答】解:∵P A,PB是⊙O的切线,且∠APB=40°,∴P A=PB,∠APO=∠BPO,∠A=∠B=90°,∴∠OBP=∠OAP,∴C是错误的.故选:C.10.如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为()A.20B.30C.40D.50【分析】根据切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,将△ABC 的周长转化为切线长求解.【解答】解:据切线长定理有AD=AE,BE=BF,CD=CF;则△ABC的周长=AB+BC+AC=AB+BF+CF+AC=AB+BE+AC+CD=AD+AE=2AD=40.故选:C.11.如图,从圆O外一点P引圆O的两条切线P A,PB,切点分别为A,B.如果∠APB=60°,P A=8,那么弦AB的长是()A.4B.8C.D.【分析】根据切线长定理知P A=PB,而∠P=60°,所以△P AB是等边三角形,由此求得弦AB的长.【解答】解:∵P A、PB都是⊙O的切线,∴P A=PB,又∵∠P=60°,∴△P AB是等边三角形,即AB=P A=8,故选:B.12.如图,圆O的圆心在梯形ABCD的底边AB上,并与其它三边均相切,若AB=10,AD =6,则CB长()A.4B.5C.6D.无法确定【分析】方法1、设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH,则圆的半径R,可以看作△BOC,△COD,△AOD的高,根据S梯形ABCD=S△BOC+S△COD+S△DOA,以及梯形的面积公式即可求解.方法2、利用切线的性质得出∠ADO=∠ODC,进而得出∠ADO=∠AOD,即可得出OA =6,即:OB=4,同理:BC=OB即可得出结论.【解答】解:方法1、设圆O的半径是R,圆O与AD、DC、CB相切于点E、F、H,连接OE、OD、OF、OC、OH.设CD=y,CB=x.设S梯形ABCD=S则S=(CD+AB)R=(y+10)R﹣﹣﹣﹣(1)S=S△BOC+S△COD+S△DOA=xR+yR+×6R﹣﹣﹣﹣(2)联立(1)(2)得x=4;方法2、连接OD.OC∵AD,CD是⊙O的切线,∴∠ADO=∠ODC,∵CD∥AB,∴∠ODC=∠AOD,∴∠ADO=∠AOD∴AD=OA∵AD=6,∴OA=6,∵AB=10,∴OB=4,同理可得OB=BC=4,故选:A.13.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()A.50B.52C.54D.56【分析】根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边和相等,从而可求得四边形的周长.【解答】解:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2(16+10)=52.故选:B.14.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为()A.5B.10C.7.5D.4【分析】由切线长定理,可知:AF=AD,CF=CE,BE=BD,用未知数设AF的长,然后表示出BD、CF的长,即可表示出BE、CE的长,根据BE+CE=5,可求出AF的长.【解答】解:设AF=x,根据切线长定理得AD=x,BD=BE=9﹣x,CE=CF=CA﹣AF =6﹣x,则有9﹣x+6﹣x=5,解得x=5,即AF的长为5.故选:A.15.已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=()A.4B.C.D.【分析】在Rt△POA中,用勾股定理,可求得P A的长,进而可根据∠APO的正弦值求出AC的长,即可求出AB的长.【解答】解:如图所示,P A、PB切⊙O于A、B,因为OA=4,PO=8,则AP==4,∠APO=30°,∵∠APB=2∠APO=60°故△P AB是等边三角形,AB=AP=4故选:C.16.如图,P A、PB分别切⊙O于A、B两点,如果∠P=60°,P A=2,那么AB的长为()A.1B.2C.3D.4【分析】由切线长定理知P A=PB,根据已知条件即可判定△P AB是等边三角形,由此可求得AB的长.【解答】解:∵P A、PB分别切⊙O于A、B,∴P A=PB;∵∠P=60°,∴△P AB是等边三角形;∴AB=P A=2,故选B.二.填空题(共4小题)17.如图,四边形ABCD是⊙O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为50.【分析】根据切线长定理得到AE=AH,BE=BF,CF=CG,DH=DG,得到AD+BC=AB+CD=25,根据四边形的周长公式计算,得到答案.【解答】解:∵四边形ABCD是⊙O的外切四边形,∴AE=AH,BE=BF,CF=CG,DH=DG,∴AD+BC=AB+CD=25,∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50,故答案为:50.18.如图,菱形ABCD,∠B=60°,AB=4,⊙O内切于菱形ABCD,则⊙O的半径为.【分析】作辅助线,构建直角△AOB,分别计算OA、OB的长,根据面积法可得OE的长.【解答】解:设AB和BC上的切点分别为E、F,连接OA、OE、OB、OF,则OE⊥AB,OF⊥BC,∵⊙O内切于菱形ABCD,∴OE=OF,∴OB平分∠ABC,∵∠ABC=60°,∴∠ABO=30°,同理得∠BAO=60°,∴∠AOB=90°,∴AO=AB=2,OB=2,∴S△AOB=AB•OE=AO•OB,4OE=2×,OE=,故答案为:.19.如图,P A,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=76°.【分析】由切线的性质得出P A=PB,P A⊥OA,得出∠P AB=∠PBA,∠OAP=90°,由已知得出∠PBA=∠P AB=90°﹣∠OAB=52°,再由三角形内角和定理即可得出结果.【解答】解:∵P A,PB是⊙O的切线,∴P A=PB,P A⊥OA,∴∠P AB=∠PBA,∠OAP=90°,∴∠PBA=∠P AB=90°﹣∠OAB=90°﹣38°=52°,∴∠P=180°﹣52°﹣52°=76°;故答案为:76.20.如图,四边形ABCD外切于圆,AB=16,CD=10,则四边形的周长是52.【分析】利用圆外切四边形的性质定理可以得出,四边形的周长是对边和的2倍,即可得.【解答】解:由题意可得圆外切四边形的两组对边和相等,所以四边形的周长=2(16+10)=52.故答案为:52.三.解答题(共7小题)21.如图,P A、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=20°,求∠P 的度数.【分析】根据切线长定理得等腰△P AB,运用三角形内角和定理求解即可.【解答】解:根据切线的性质得:∠P AC=90°,所以∠P AB=90°﹣∠BAC=90°﹣20°=70°,根据切线长定理得P A=PB,所以∠P AB=∠PBA=70°,所以∠P=180°﹣70°×2=40°.22.如图,P A、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)P A的长;(2)∠COD的度数.【分析】(1)可通过切线长定理将相等的线段进行转换,得出三角形PDE的周长等于P A+PB的结论,即可求出P A的长;(2)根据三角形的内角和求出∠ADC和∠BEC的度数和,然后根据切线长定理,得出∠EDO和∠DEO的度数和,再根据三角形的内角和求出∠DOE的度数.【解答】解:(1)∵CA,CE都是圆O的切线,∴CA=CE,同理DE=DB,P A=PB,∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=P A+PB=2P A=12,即P A的长为6;(2)∵∠P=60°,∴∠PCE+∠PDE=120°,∴∠ACD+∠CDB=360°﹣120°=240°,∵CA,CE是圆O的切线,∴∠OCE=∠OCA=∠ACD;同理:∠ODE=∠CDB,∴∠OCE+∠ODE=(∠ACD+∠CDB)=120°,∴∠COD=180﹣120°=60°.23.如图,P A、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交P A、PB于点E、F,已知P A=12cm,∠P=40°①求△PEF的周长;②求∠EOF的度数.【分析】①根据切线长定理得出P A=PB,EB=EQ,FQ=F A,由PE+EF+PF=PE+EQ+FQ+PF即可求出答案.②连接OE,OF,求出∠OEF+∠OFE的度数,即可得出∠EOF的度数.【解答】解:①∵P A、PB是⊙O的切线,∴P A=PB,又∵直线EF是⊙O的切线,∴EB=EQ,FQ=F A,∴△PEF的周长=PE+PF+EF=PE+PF+EB+F A=P A+PB=2P A=24cm;②连接OE,OF,则OE平分∠BEF,OF平分∠AFE,则∠OEF+∠OFE=(∠P+∠PFE)+∠(P+∠PEF)=(180°+40°)=110°,∴∠EOF=180°﹣110°=70°.24.如图,P A、PB、DE切⊙O于点A、B、C、D在P A上,E在PB上,(1)若P A=10,求△PDE的周长.(2)若∠P=50°,求∠O度数.【分析】(1)于P A、PB、DE都是⊙O的切线,可根据切线长定理将切线P A、PB的长转化为△PDE的周长;(2)连接OA、OC、0B,利用切线长定理即可得到∠O=∠AOB,根据四边形的内角和可得∠AOB+∠P=180°,进而求出∠O的度数.【解答】解:(1)∵P A、PB、DE分别切⊙O于A、B、C,∴P A=PB,DA=DC,EC=EB;∴C△PDE=PD+DE+PE=PD+DA+EB+PE=P A+PB=10+10=20;∴△PDE的周长为20;(2)连接OA、OC、0B,∵OA⊥P A,OB⊥PB,OC⊥DE,∴∠DAO=∠EBO=90°,∴∠P+∠AOB=180°,∴∠AOB=180°﹣50°=130°∵∠AOD=∠DOC,∠COE=∠BOE,∴∠DOE=∠AOB=×130°=65°.25.如图,P A,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.(1)求∠BAC的度数;(2)当OA=2时,求AB的长.【分析】(1)根据切线长定理推出AP=BP,根据等腰三角形性质和三角形的内角和定理求出∠P AB=60°,求出∠P AO=90°即可;(2)根据直角三角形性质求出OP,根据勾股定理求出AP,根据等边三角形的判定和性质求出即可.【解答】解:(1)∵P A,PB是⊙O的切线,∴AP=BP,∵∠P=60°,∴∠P AB=60°,∵AC是⊙O的直径,∴∠P AC=90°,∴∠BAC=90°﹣60°=30°.(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,∴OP=4,由勾股定理得:,∵AP=BP,∠APB=60°,∴△APB是等边三角形,∴.26.已知:如图,P A、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O 的切线,交P A、PB于E、F点,已知P A=12cm,求△PEF的周长.【分析】根据切线长定理得出P A=PB,EB=EQ,FQ=F A,代入PE+EF+PF=PE+EQ+FQ+PF即可求出答案.【解答】解:∵P A、PB是⊙O的切线,切点分别是A、B,∴P A=PB=12,∵过Q点作⊙O的切线,交P A、PB于E、F点,∴EB=EQ,FQ=F A,∴△PEF的周长是:PE+EF+PF=PE+EQ+FQ+PF,=PE+EB+PF+F A=PB+P A=12+12=24,答:△PEF的周长是24.27.如图,已知AB为⊙O的直径,P A,PC是⊙O的切线,A,C为切点,∠BAC=30°.(Ⅰ)求∠P的大小;(Ⅱ)若AB=2,求P A的长(结果保留根号).【分析】(Ⅰ)根据切线的性质及切线长定理可证明△P AC为等边三角形,则∠P的大小可求;(Ⅱ)由(Ⅰ)知P A=PC,在Rt△ACB中,利用30°的特殊角度可求得AC的长.【解答】解:(Ⅰ)∵P A是⊙O的切线,AB为⊙O的直径,∴P A⊥AB,∴∠BAP=90°;∵∠BAC=30°,∴∠CAP=90°﹣∠BAC=60°.又∵P A、PC切⊙O于点A、C,∴P A=PC,∴△P AC为等边三角形,∴∠P=60°.(Ⅱ)如图,连接BC,则∠ACB=90°.在Rt△ACB中,AB=2,∠BAC=30°,∵cos∠BAC=,∴AC=AB•cos∠BAC=2cos30°=.∵△P AC为等边三角形,∴P A=AC,∴P A=.。
浙教版九年级数学下册作业本:2.2 切线长定理

2.2切线长定理1.切线长定理:过圆外一点,可以引圆的两条切线,切线长________.2.如图,点P是⊙O外一点,P A,PB切⊙O于点A,B,AB交PO于点C,则有如下结论:(1)P A=PB;(2)∠APO=∠BPO=∠OAC=∠OBC,∠AOP=∠BOP=∠CAP=∠CBP;(3)AB⊥OP且AC=BC.A组基础训练1.如图,从圆O外一点P引⊙O的两条切线PA,PB,切点分别为A,B,如果∠APB =60°,PA=8,那么弦AB的长是()A.4B.8C.6D.10第1题图第2题图2.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是()A.∠1=∠2B.PA=PB C.AB⊥OP D.PA2=PC·PO3.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()A.50B.52C.54D.56第3题图第4题图4.(邵阳中考)如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连结BD,AD.若∠ACD=30°,则∠DBA的大小是() A.15°B.30°C.60°D.75°5.如图,过⊙O外一点P作⊙O的两条切线PA,PB,切点分别为A,B.下列结论中:①OP垂直平分AB;②∠APB=∠BOP;③△ACP≌△BCP;④PA=AB;⑤若∠APB=80°,则∠OBA=40°.正确的是________.第5题图第6题图6.如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E =46°,∠DCF=32°,则∠A的度数是________°.7.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2,AD=4.则BE=________,BC=________.第7题图第8题图8.如图,PA,PB切⊙O于A,B,若∠APB=60°,⊙O半径为3,则阴影部分面积为____________.9.如图,AB为半圆O的直径,在AB的同侧作AC,BD切半圆O于点A,B,CD 切半圆O于点E.若AC=4,BD=9,求⊙O的半径.第9题图10.如图,PA,PB,DE分别切⊙O于点A,B,C,D在PA上,E在PB上.(1)若PA=30,求△PDE的周长;(2)若∠P=50°,求∠O的度数.第10题图B组自主提高第11题图11.如图,在平面直角坐标系xOy中,直线AB经过点A(6,0)、B(0,6),⊙O的半径为2(O为坐标原点),点P是直线AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为()A.7B.3C.32 D.14第12题图12.(深圳中考)如图,一把直尺,60°的直角三角板和光盘如图摆放,A为60°角与直尺交点,AB=3,则光盘的直径是________cm.13.如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,求⊙O的半径.第13题图C组综合运用14.如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB长为半径的圆与AB交于点E,与AC相切于点D,直线ED交BC的延长线于点F.(1)求证:BC=FC;(2)若AD∶AE=2∶1,求tanF的值.第14题图参考答案【课堂笔记】1.相等【课时训练】1-4.BDBD 5.①③⑤ 6.99 7.6 6 8.93-3π9.r =6.法一:可在△COD 中,连结OE ,有OE 2=CE ×DE =36,∴r =6. 法二:过C 作CH ⊥BD 于点H ,在△CDH 中,CD =13,DH =5,∴CH =AB =12,即r =6. 10.(1)∵PA 、PB 是⊙O 切线,∴PA =PB ,∵DE 是⊙O 切线,∴DC =DA ,EC =EB ,∴△PDE 的周长=PD +PE +DC +CE =PD +DA +PE +EB =PA +PB =60; (2)连结AO ,BO ,CO ,可证:∠AOD =∠COD ,∠COE =∠BOE ,∴∠DOE =12∠AOB ,∵∠AOB +∠P =180°,∠P =50°,∴∠AOB =130°,∴∠DOE =65°. 11.D 12.6 3第13题图13.如图,设⊙O 与AC ,BC ,AB 相切于D ,E ,F ,连结OD 、OE ,∵⊙O 与△ABC 中AB 、AC 的延长线及BC 边相切,∴AF =AD ,BE =BF ,CE =CD ,OD ⊥AD ,OE ⊥BC ,∵∠ACB =90°,∴四边形ODCE 是正方形,设OD =r ,则CD =CE =r ,∵BC =3,∴BE =BF =3-r ,∵AB =5,AC =4,∴AF =AB +BF =5+3-r ,AD =AC +CD =4+r ,∴5+3-r =4+r ,r =2,则⊙O 的半径是2. 14.(1)连结BD.∵BE 为⊙O 的直径,∴∠BDE =90°,∴∠EBD =90°-∠BED.∵∠EBF =90°,∴∠F =90°-∠BEF.∴∠F =∠EBD.∵AC 切⊙O 于点D ,∴∠EBD =∠ADE =∠CDF.∴∠F =∠CDF ,∴DC =FC.∵OB ⊥BC ,∴BC 是⊙O 的切线,∴DC =BC.∴BC =FC ; (2)在△ADE 和△ABD 中,∵∠A =∠A ,∠ADE =∠ABD ,∴△ADE ∽△ABD ,DE BD =AE AD =12.又∵∠F =∠EBD ,∴tan F =tan ∠EBD =DE BD =12.。
九年级下册第2章直线与圆的位置关系2、2切线长定理习题新版浙教版

证明:连结 OE, ∵AM,DE 是⊙O 的切线,切点分别为点 A,E, ∴DA=DE,易证△ AOD≌△EOD, ∴∠AOD=∠EOD=12∠AOE, 又∵∠ABE=12∠AOE, ∴∠AOD=∠ABE,∴OD∥BE.
(2)猜想:OF与CD有何数量关系?并说明理由. 解:OF=12CD. 理由:∵AM,BN,DC 是⊙O 的切线, ∴AD=DE,BC=CE,∴AD+BC=DE+CE. 即 AD+BC=CD. 由 AB 是⊙O 的直径,且点 F 是 CD 的中点,易得 OF=12(AD+BC)=12CD.即 OF=12CD.
2 如图,从⊙O 外一点 P 引⊙O 的两条切线 PA,PB,切 点分别为 A,B.如果∠APB=60°,PA=8,那么弦 AB 的长是( B ) A.4 B.8 C.4 3 D.8 3
3 如图,PA,PB为圆O的切线,切点分别为 A,B,PO 交AB于点C,PO的延长线交圆O于点D.下列结论不一 定成立的是( B ) A.△BPA为等腰三角形 B.AB与PD相互垂直平分 C.点A,B都在以PO为直径的圆上 D.PC为△BPA的边AB上的中线
10 【中考·甘肃】如图,在Rt△ABC中,∠ACB=90°, 以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
证明:如图,连结OD. ∵DE是⊙O的切线,∴∠ODE=90°. ∴∠ADE+∠BDO=90°. ∵∠ACB=90°,∴∠A+∠B=90°. ∵OD=OB,∴∠B=∠BDO. ∴∠A=∠ADE.
【点拨】 如图,连结OC,OD,OE. ∵BC切⊙O于点E,AC切⊙O于点D, ∴OE⊥BC,OD⊥AC. ∴∠OEB=∠OEC=∠ODC=∠ODA=∠ACB=90°. ∴四边形ODCE是矩形. 又∵DO=OE,∴四边形ODCE是正方形.
浙教版数学九年级下册2.2切线长定理.doc

2.2切线长定理一、选择题1. 如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为()A.130°B.120°C.110°D.100°2. 如图,P A、PB分别切⊙O于A、B两点,如果∠P=60°,P A=2,那么AB的长为()A.1 B.2 C.3 D.43. 如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()A.50 B.52 C.54 D.564. 如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是()A.9 B.10 C.12 D.145. 如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为()A.5 B.10 C.7.5 D.46. 如图,从圆O外一点P引圆O的两条切线P A,PB,切点分别为A,B.如果∠APB=60°,P A=8,那么弦AB的长是()A .4B .8C .34D .38二、填空题7. 如图,⊙O 的半径为3cm ,点P 到圆心的距离为6cm ,经过点P 引⊙O 的两条切线,这两条切线的夹角为 .8. 如图,⊙O 与△ABC 中AB 、AC 的延长线及BC 边相切,且∠ACB =90°,∠A ,∠B ,∠C 所对的边长依次为3,4,5,则⊙O 的半径是 .9. 如图:EB 、EC 是⊙O 的两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E =46°,∠DCF =32°,则∠A 的度数是 °.10. 如图,⊙O 的半径为3cm ,点P 到圆心的距离为6cm ,经过点P 引⊙O 的两条切线,则∠APO =°.11. 如图,P A 、PB 分别切⊙O 于A 、B .P A =5,在劣弧AB 上取点C ,过C 作⊙O 的切线,分别交P A ,PB 于D ,E ,则△PDE 的周长等于 .12.如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为 .三、解答题13.已知:⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P和⊙O的两条切线,求这两条切线的夹角及切线长.参考答案2.2切线长定理一、选择题1.C2.B3.B4.D5.A6.B二、填空题7.60度8.29.9910.3011.1012.24三、解答题13.初中数学试卷鼎尚图文**整理制作。
九年级数学下册第2章直线与圆的位置关系2.2切线长定理同步测试浙教版

2.2 切线长定理1.切线长定理:过圆外一点,可以引圆的两条切线,切线长________.2.如图,点P是⊙O外一点,PA,PB切⊙O于点A,B,AB交PO于点C,则有如下结论:(1)PA=PB;(2)∠APO=∠BPO=∠OAC=∠OBC,∠AOP=∠BOP=∠CAP=∠CBP;(3)AB⊥OP 且AC=BC.A组基础训练1.如图,从圆O外一点P引⊙O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )A.4 B.8 C.6 D.10第1题图2.如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是( )第2题图A.∠1=∠2 B.PA=PB C.AB⊥OP D.PA2=PC·PO3.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )A.50 B.52 C.54 D.56第3题图4.(邵阳中考)如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连结BD,AD.若∠ACD=30°,则∠DBA的大小是( )第4题图A.15° B.30° C.60° D.75°5.如图,过⊙O外一点P作⊙O的两条切线PA,PB,切点分别为A,B.下列结论中:①OP 垂直平分AB;②∠APB=∠BOP;③△ACP≌△BCP;④PA=AB;⑤若∠APB=80°,则∠OBA =40°.正确的是________.第5题图1.如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是________°.第6题图7.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2,AD=4.则BE=________,BC=________.第7题图2.如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是________.第8题图9.如图,AB为半圆O的直径,在AB的同侧作AC,BD切半圆O于点A,B,CD切半圆O 于点E.若AC=4,BD=9,求⊙O的半径.第9题图10.如图,PA,PB,DE分别切⊙O于点A,B,C,D在PA上,E在PB上.(1)若PA=30,求△PDE的周长;(2)若∠P=50°,求∠O的度数.第10题图B组自主提高11.如图,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点,若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确( )第11题图A.AB>CE>CD B.AB=CE>CD C.AB>CD>CE D.AB=CD=CE12.如图,直尺、三角尺都和⊙O相切,B是切点,且AB=8cm.求⊙O的直径.第12题图13.如图,PA,PB分别切⊙O于点A,B,连结PO,AB相交于点D,C是⊙O上一点,∠C=60°.(1)求∠APB的大小;(2)若PO=20cm,求△AOB的面积.第13题图C组综合运用14.如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB长为半径的圆与AB交于点E,与AC相切于点D,直线ED交BC的延长线于点F.(1)求证:BC=FC;(2)若AD∶AE=2∶1,求tanF的值.第14题图2.2 切线长定理【课堂笔记】 1.相等 【课时训练】 1-4.BDBD 5. ①③⑤ 6. 99 7. 6 6 8. 29. r =6.法一:可在△COD 中,连结OE ,有OE 2=CE×DE=36,∴r =6.法二:过C 作CH⊥BD 于点H ,在△CDH 中,CD =13,DH =5,∴CH =AB =12,即r =6.10. (1)∵PA、PB 是⊙O 切线,∴PA =PB ,∵DE 是⊙O 切线,∴DC =DA ,EC =EB ,∴△PDE 的周长=PD +PE +DC +CE =PD +DA +PE +EB =PA +PB =60; (2)连结AO ,BO ,CO ,可证:∠AOD=∠COD,∠COE =∠BOE,∴∠DOE =12∠AOB ,∵∠AOB +∠P=180°,∠P =50°,∴∠AOB =130°,∴∠DOE =65°.11. A12. 连结AO ,BO ,∵AB 是⊙O 的切线,AC 是⊙O 的切线,∴∠ABO =90°,∠BAO =12∠BAC =60°,在Rt △AOB 中,OB =AB·tan ∠BAO =8×tan 60°=83,∴⊙O 的直径为163cm .13. (1)∵PA,PB 分别为⊙O 的切线,∴OA ⊥PA ,OB ⊥PB ,∴∠OAP =∠OBP=90°.∵∠C =60°,∴∠AOB =2∠C=120°,∴在四边形APBO 中,∠APB =360°-∠OAP-∠OBP-∠AOB =360°-90°-90°-120°=60°; (2)在Rt △PAO 与Rt △PBO 中,∵OA =OB ,PO =PO ,∴Rt △PAO ≌Rt △PBO ,∴∠APO =∠BPO=12∠APB =30°,∴PO ⊥AB ,∴∠DAO =∠APO=30°,∴OA =sin ∠APO ×OP =12×20=10(cm ).在Rt △AOD 中,∠DAO =30°,OA =10cm ,∴AD =cos∠DAO ×OA =32×10=53(cm ),OD =sin ∠DAO ×OA =12×10=5(cm ),∴AB =2AD =103(cm ),∴S △AOB =12AB ×OD =12×103×5=253(cm 2).14. (1)连结BD.∵BE 为⊙O 的直径,∴∠BDE =90°,∴∠EBD =90°-∠BED.∵∠EBF =90°,∴∠F =90°-∠BEF.∴∠F=∠EBD.∵AC 切⊙O 于点D ,∴∠EBD =∠ADE=∠CDF.∴∠F=∠CDF,∴DC =FC.∵OB⊥BC,∴BC 是⊙O 的切线,∴DC =BC.∴BC=FC; (2)在△ADE 和△ABD 中,∵∠A =∠A,∠ADE =∠ABD,∴△ADE ∽△ABD ,DE BD =AE AD =12.又∵∠F=∠EBD,∴tan F =tan ∠EBD =DE BD =12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2 切线长定理
一、选择题
1.如图K -49-1,P A ,PB 分别切⊙O 于点A ,B ,E 是⊙O 上一点,且∠AEB =60°,则∠P 的度数为( )
A .45°
B .50°
C .55°
D .60°
图K -49-1
2.一个钢管放在V 形架内,图K -49-2是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN =60°,那么OP 的长为( )
图K -49-2
A .50 cm
B .25 3cm C.50 33
cm D .50 3cm
3.如图K -49-3,P A ,PB 是⊙O 的切线,切点分别是A ,B .若∠APB =60°,P A =4,则⊙O 的半径为( )
A .4 B.433C.3
4
3D .3
图K -49-3
4.如图K -49-4,P A ,PB 分别切⊙O 于点A ,B ,AC 是⊙O 的直径,连结AB ,BC ,OP ,则与∠P AB 相等的角(不包括∠P AB 本身)有( )
图K -49-4
A .1个
B .2个
C .3个
D .4个
5.2017·无锡如图K -49-5,菱形ABCD 的边AB =20,面积为320,∠BAD <90°,⊙O 与边AB ,AD 都相切,AO =10,则⊙O 的半径等于( )
图K -49-5
A .5
B .6
C .2 5
D .3 2 二、填空题
6.如图K -49-6,AE ,AD ,BC 分别切⊙O 于点E ,D ,F .若AD =20,则△ABC 的周长为________.
图K -49-6
7.如图K -49-7,在△ABC 中,AB =AC =5 cm ,cos ∠ABC =3
5
.如果⊙O 的半径为10cm ,且经过点
B ,
C ,那么线段AO =________ cm.
图K -49-7
8.从圆外一点向半径为9的圆作切线,已知切线长为18,从这点到圆的最短距离为________. 9.2017·衢州如图K -49-8,在直角坐标系中,⊙A 的圆心A 的坐标为(-1,0),半径为1,P 为直线y =-3
4
x +3上的一动点,过点P 作⊙A 的切线,切点为Q ,则切线长PQ 的最小值是________.
图K -49-8
三、解答题
10.如图K-49-9,已知正方形ABCD的边长为2,M是BC的中点,P是线段MC上的一个动点,P 不与M和C重合,以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E.求四边形CDFP的周长.
图K-49-9
11.如图K-49-10,AB,CD分别与半圆O切于点A,D,BC切⊙O于点E.若AB=4,CD=9,求⊙O 的半径.
图K-49-10
12.如图K-49-11,P A,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,AC,PB的延长线相交于点D.
(1)若∠1=20°,求∠APB的度数;
(2)当∠1为多少度时,OP=OD?并说明理由.
图K-49-11
13.2017·遵义如图K-49-12,P A,PB是⊙O的切线,A,B为切点,∠APB=60°.连结PO并延长与⊙O交于点C,连结AC,BC.
(1)求证:四边形ACBP是菱形;
(2)若⊙O的半径为1,求菱形ACBP的面积.
图K-49-12
14分类讨论如图K-49-13,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=24 cm,BC =26 cm,AB为⊙O的直径.动点P从点A开始沿AD边向点D以1 cm/s的速度运动,动点Q从点C开始沿CB边向点B以3 cm/s的速度运动,P,Q两点同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t s,求t分别为何值时,直线PQ与⊙O相切、相离、相交.
图K-49-13
1.[答案]D 2.[答案]A 3.[答案]B 4.[答案]C
5.[解析]C 如图,连结AC ,BD ,交点为P ,过点P 作PQ ⊥AB 于点Q ,过点O 作OE ⊥AB 于点E ,∴OE ∥PQ.
∵⊙O 与边AB ,AD 都相切,∴点O 在AC 上.
∵菱形ABCD 的面积为320,∴1
2AC·BD =320,∴AP ·BP =160.
∵AB =20,∴20PQ =AP·BP =160, ∴PQ =8.
由AC ⊥BD ,PQ ⊥AB ,可证△APQ ∽△PBQ , ∴
AQ PQ =PQ BQ ,即AQ 8=8
20-AQ
, ∴AQ =16或 AQ =4(不合题意,舍去).
∴在Rt △APQ 中,AP =AQ 2+PQ 2=162+82=8 5. ∵OE ∥PQ ,∴OE OA =PQ AP ,即OE 10=885,
∴OE =2 5.
∴⊙O 的半径等于2 5. 6.[答案] 40
[解析]∵AD ,AE 分别切⊙O 于点D ,E , ∴AD =AE =20.
∵AD ,BF 分别切⊙O 于点D ,F , ∴BD =BF.同理CF =CE.
∴C △ABC =AB +BC +AC =AB +BF +FC +AC =AB +BD +EC +AC =AD +AE =40. 7.[答案] 5
8.[答案] 9 5-9
9.[答案] 2 2
[解析] 如图,连结PA,PQ,AQ,有PQ2=PA2-AQ2,∴PQ=PA2-AQ2.又AQ=1,故当AP有最小值时PQ最小.过点A作AP′⊥MN,则有AP′最小=3,此时PQ最小=32-12=2 2.
10.解:∵四边形ABCD是正方形,
∴∠A=∠B=90°,∴OA⊥AD,OB⊥BC.
∵OA,OB是半径,
∴AF,BP都是⊙O的切线.
又∵PF是⊙O的切线,
∴FE=FA,PE=PB,
∴四边形CDFP的周长为AD+DC+CB=2×3=6.
11.解:如图,过点B作BF⊥CD于点F.
∵AB,CD与半圆O分别切于点A,D,
∴∠BAD=∠CDA=∠BFD=90°,
∴四边形ADFB为矩形.
∵AB与BC分别切⊙O于点A,E,
∴AB=BE.同理CE=CD.
∵DF=AB=4,CE=CD=9,
∴BC=BE+CE=13,CF=CD-DF=9-4=5.
在Rt△BFC中,BF=BC2-CF2=132-52=12,
∴⊙O的半径为6.
12.解:(1)∵PA 是⊙O 的切线, ∴∠BAP =90°-∠1=70°. 又∵PA ,PB 是⊙O 的切线, ∴PA =PB ,
∴∠BAP =∠ABP =70°, ∴∠APB =180°-70°×2=40°. (2)当∠1=30°时,OP =OD. 理由如下:
当∠1=30°时,由(1)知∠BAP =∠ABP =60°, ∴∠APB =180°-60°×2=60°. ∵PA ,PB 是⊙O 的切线, ∴∠OPB =1
2
∠APB =30°.
又∵∠D =∠ABP -∠1=60°-30°=30°, ∴∠OPB =∠D ,∴OP =OD.
13.解:(1)证明:如图,连结OA ,则∠OAP =90°. ∵PA ,PB 是⊙O 的切线,∠APB =60°, ∴PA =PB ,∠APC =∠BPC =30°, ∠AOP =60°.
∵OA =OC ,∴∠ACO =30°, 同理∠BCO =30°, ∴AP ∥BC ,BP ∥AC , ∴四边形ACBP 是平行四边形. 又∵∠APC =∠BPC , ∴四边形ACBP 是菱形.
(2)如图,连结AB 交CP 于点M ,连结OA ,
∴AB 垂直平分CP.
在Rt △AOM 中,OA =1,∠AOM =60°, ∴∠OAM =30°,
∴OM =12OA =1
2,
∴AM =OA 2-OM 2=32
, ∴CM =3
2
,
即PC =3,AB =3,
∴菱形ACBP 的面积=12×3×3=33
2
.
14解:设运动t s 时,直线PQ 与⊙O 相切于点G ,过点P 作PH ⊥BC 于点H ,
则PH =AB =8,BH =AP , 可得HQ =26-3t -t =26-4t. 由切线长定理得AP =PG ,QG =BQ ,
则PQ =PG +QG =AP +BQ =t +26-3t =26-2t. 由勾股定理得PQ 2=PH 2+HQ 2, 即(26-2t)2=82+(26-4t)2, 整理,得 3t 2-26t +16=0, 解得t 1=2
3
,t 2=8,
所以,当t =2
3或 t =8时直线PQ 与⊙O 相切.
当t =0时,直线PQ 与⊙O 相交;
当t =26
3时,点Q 运动到点B ,点P 尚未运动到点D ,但也停止运动,直线PQ 也与⊙O 相交.
综上可知:
当t =2
3或 t =8时,直线PQ 与⊙O 相切;
当0≤t <23或8<t ≤26
3时,直线PQ 与⊙O 相交;
当2
3<t <8时,直线PQ 与⊙O 相离.。
