第六章 刚体基本运动
合集下载
理论力学6—刚体的基本运动
34.8
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
1、角速度矢量和角加速度矢量
角速度矢量
dj
ww
dt
大小
角速度矢沿轴线，弯向表示刚体转动的方向。
指向用右手螺旋法则。
w wk
角加速度矢量
dw dw
k k
dt
dt
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
2
例6-6
某定轴转动刚体通过点M0（2，1，3），其角速度矢w 的方向
余弦为0.6，0.48，0.64，角速度 的大小ω=25rad/s 。求：刚体上点
M（10，7，11）的速度矢。
解：角速度矢量
w wn
其中 n （0.6，0.48，0.64）
M点相对于转轴上一点M0的矢径
r rM rM0 10,7,11 2,1,3 8,6,8
Z2=60，Z3=12，Z4=70。(a)求减速箱的总减速比i13 ；(b)如
果n1=3000r/min，求n3.
1
n1
2
n2
3
n3
4
解：求传动比：
n1 n1 n2 Z 2 Z 4
i13
34.8
n3 n2 n3 Z1 Z 3
则有：
n1 3000
n3
86r / min
i13
4 rad
dw dw d
dw
w
dt
d dt
d
dw
w
0.2
d
解：
w
w wdw
0
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
1、角速度矢量和角加速度矢量
角速度矢量
dj
ww
dt
大小
角速度矢沿轴线，弯向表示刚体转动的方向。
指向用右手螺旋法则。
w wk
角加速度矢量
dw dw
k k
dt
dt
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
2
例6-6
某定轴转动刚体通过点M0（2，1，3），其角速度矢w 的方向
余弦为0.6，0.48，0.64，角速度 的大小ω=25rad/s 。求：刚体上点
M（10，7，11）的速度矢。
解：角速度矢量
w wn
其中 n （0.6，0.48，0.64）
M点相对于转轴上一点M0的矢径
r rM rM0 10,7,11 2,1,3 8,6,8
Z2=60，Z3=12，Z4=70。(a)求减速箱的总减速比i13 ；(b)如
果n1=3000r/min，求n3.
1
n1
2
n2
3
n3
4
解：求传动比：
n1 n1 n2 Z 2 Z 4
i13
34.8
n3 n2 n3 Z1 Z 3
则有：
n1 3000
n3
86r / min
i13
4 rad
dw dw d
dw
w
dt
d dt
d
dw
w
0.2
d
解：
w
w wdw
0
刚体的基本运动
转速：刚体每分钟转过的圈数。单位：r / min。 转速 n 与角速度 2n n 60 30
的关系：
（7-6）
角加速度
d d 2 lim 2 t 0 t dt dt
（7-7）
刚体的角加速度（Angular acceleration）
等于其角速度对时间的一阶导数，也等于其转角对
v r 0.4 50 20 m / s
an r 0.4 50 1000 m /s
2 2
2
例7-4 定轴轮系如图7-9所示，主动轮I通过轮齿
与从动轮II轮齿啮合实现转动传递。主动轮I和从动轮 II的节圆半径分别为r1、r2，齿数分别为z1、z2。设I轮 的角速度为 1 （转数为n1），角加速度为 1 ；II轮的 角速度为 2（转数为n2），角加速度为 2 。试求上
2 a a2 an (r )2 (rω2 )2 r 2 ω4
tan
a an
ω
2
（7-13）
在给定瞬时，刚体的角速度和角加速度有确 定的值，对刚体上任何点都是一样。因而，在同一瞬 时，转动刚体上各点的速度 v 和加速度 a 的大小均与
该点的转动半径 r 成正比；各点速度 v 的方向都垂直
O轴作定轴转动，其转动方程为 t 2 4t （1）当t = 1 s时，试求轮缘上M点速度和加速度；
（2）若轮上绕一不可伸长的绳索，并在绳索下端
悬一物体A，求当t = 1 s时，物体A的速度和加速度。 解：圆轮在任一瞬时的角速 a M 度和角加速度为 d 2t 4 rad / s
当
t 1s，直杆AB上D点的速度和加速度。
解：由于O1A与O2B平行等
06刚体的基本运动
τ
vC = v0 = 1.5m/s
α
ω0
ϕ N = = 2 .86 ( 转） 2π
17
内的行程； ②重物B在3s内的行程；
ϕ = ω 0t +
1 α t 2 = 18 rad 2
s = r ϕ = 0 .3 × 18 = 5 .4 m
时的速度； ③重物B在ｔ＝3s时的速度；
aC 1 α= = = 2 rad/s 2 R 0.5 vC 1 .5 ω0 = = = 3 rad/s R 0 .5
5
加速度： 加速度：
刚体平动的特点： 刚体平动的特点： 平动刚体在任一瞬时各点的运动轨迹、速度、 平动刚体在任一瞬时各点的运动轨迹、速度、加速度都 一样。 一样。 结论：平动刚体的运动可以简化为一个点的运动，研究刚体 结论：平动刚体的运动可以简化为一个点的运动， 的平动可归结为研究点的运动。 的平动可归结为研究点的运动。
ϕ = f(t)
8
四、定轴转动的角速度和角加速度 1. 角速度： 角速度：
∆ ϕ dϕ & = =ϕ 定义 : ω = lim ∆t → 0 ∆ t dt ( 代数量 )
角位移
单位： 单位： rad/s 工程中常用转速： 工程中常用转速： n ： 转/分(r/ min)（rpm) n与ω 的关系为： 与 的关系为：
ds ∆s v= = lim dt ∆t → 0 ∆t
∆ϕ ⋅ R v = lim = ωR ∆t → 0 ∆t
R
v = ωR
O
12
二、角加速度α 与 an 、aτ 的关系
dv d dω aτ = = (ωR ) = R = Rα dt dt dt
ϕ
α
(ωR)2 an = = = Rω 2 R ρ v2
《理论力学》第六章 刚体的简单运动ppt课件
r r M r M 0 1 0 , 7 , 1 1 2 , 1 , 3 8 , 6 , 8
i jk
vrnr0.6 0.48 0.648j6k
86 8
例6-3
一矢量绕z轴以角速度ω转动，假设a =常量
求：d a
dt
解： 将矢量的端点A看成是绕z轴作定轴转动刚体上的一点
rA a
② 传动比
i12
1 2
R2 R1
z2 z1
２.带轮传动
r 11 v A v A v B v B r 22
i12
1 2
r2 r1
§6-5 以矢量表示角速度和角加速度 以矢积表示点的速度和加速度
1.角速度矢量和角加速度矢量
角速度矢量
大小
d
dt
作用线 沿轴线 滑动矢量
指向 右手螺旋定那么
知：刚体绕定轴转动，知转轴经过坐标原点O,角速度矢
为
5sinπ 2 ti5cosπ 2 tj53 。k
求：t =1s时,刚体上点M〔0，2，3〕的速度矢及
加速度矢。
解：
i
j
k
v r 5sin πt 5cos πt 5 3
2
2
0
2
3
1 03 i 1 5 j 1 0 k
arvdrv
dt 1 2 5π753 i200j75k
例6-2 知：某定轴转动刚体经过点M0〔2，1，3〕，其角
速度矢 的方向余弦为0.6，0.48，0.64，角速度
的大小ω=25rad/s 。 求：刚体上点M〔10，7，11〕的速度矢。 解： 角速度矢量
n 其中 n ( 0 . 6 , 0 . 4 , 0 . 6 8 )4
M点相对于转轴上一点M0的矢径
i jk
vrnr0.6 0.48 0.648j6k
86 8
例6-3
一矢量绕z轴以角速度ω转动，假设a =常量
求：d a
dt
解： 将矢量的端点A看成是绕z轴作定轴转动刚体上的一点
rA a
② 传动比
i12
1 2
R2 R1
z2 z1
２.带轮传动
r 11 v A v A v B v B r 22
i12
1 2
r2 r1
§6-5 以矢量表示角速度和角加速度 以矢积表示点的速度和加速度
1.角速度矢量和角加速度矢量
角速度矢量
大小
d
dt
作用线 沿轴线 滑动矢量
指向 右手螺旋定那么
知：刚体绕定轴转动，知转轴经过坐标原点O,角速度矢
为
5sinπ 2 ti5cosπ 2 tj53 。k
求：t =1s时,刚体上点M〔0，2，3〕的速度矢及
加速度矢。
解：
i
j
k
v r 5sin πt 5cos πt 5 3
2
2
0
2
3
1 03 i 1 5 j 1 0 k
arvdrv
dt 1 2 5π753 i200j75k
例6-2 知：某定轴转动刚体经过点M0〔2，1，3〕，其角
速度矢 的方向余弦为0.6，0.48，0.64，角速度
的大小ω=25rad/s 。 求：刚体上点M〔10，7，11〕的速度矢。 解： 角速度矢量
n 其中 n ( 0 . 6 , 0 . 4 , 0 . 6 8 )4
M点相对于转轴上一点M0的矢径
6 运动学 刚体的基本运动
例 题
A
v0
h
x
角速度为
角加速度为
Theoretical Mechanics
hv0 d 2 22 dt h v0 t 3 2hv0 t d 2 32 2 dt (h v0 t )
h
返回首页
6.5 刚体的定轴转动
定轴转动：在运动过程 中，刚体内（或其扩展 部分）有一条直线始终 保持不动。 转轴：固定不动的直线
1 2 1 1 t1 10.46 5 2 130.8 rad 2 2
例 题
从t1＝5s后，电动机作匀速转动，到t2＝10s时， 转过的角度为,
2 t 52.3(10 5) 262 rad。
所以，电动机在10秒内共转过的角度为
1 2 130.8 262 392.8 rad
返回首页
6.4 刚体的平行移动 平行移动（平动）：在运动过程中，刚体上任 一直线与其初始位置始终保持平行。
直线平移
Theoretical Mechanics
返回首页
6.4 刚体的平行移动 荡木AB的运动 曲线平移
平移刚体上任一点的轨迹可能是直线或曲线 AB: 平移刚体上任取两点, 矢量BA为一常量 ，刚体 在运动过程中，A、B 两 点所描绘出的轨迹曲线的 形状彼此相同。
方向一致。法向加速度总是沿着转动半径的方向,指
向圆心。
Theoretical Mechanics 返回首页
6.6 转动刚体上点的速度和加速度 M点的加速度a等于其切向加 速度和法向加速度的矢量和
6.3.3 加速度
a a an
大小
2 a a2 an R 2 4
tan
第6章.刚体的基本运动
Ⅱ
上式称为刚体定轴转动的运动 转动方程。 方程，简称刚体的转动方程。 转动方程
2012-4-27
图6—2
7
3.角速度 角速度ω 角速度
角速度定义为 刚体的瞬时角速度 角速度 ∆ϕ dϕ & ω = lim = =ϕ ∆t →0 ∆t dt
(6 - 5)
刚体的角速度等于其转角对时间的一阶导数 工程中常用单位：转/分钟（n/min） 设刚体的转速为n r/min，以rad/s为单位表示的角速度
s = Rϕ
( 6 - 7)
10
2012-4-27
2.速度 速度
ds d & v= = ( Rϕ ) = Rϕ (6 - 8) dt dt v = Rω 转动刚体内任一点的速度的大小，等于刚体的角速度 与该点到轴线的垂直距离的乘积，它的方向沿圆周的切线 而指向转动的一方。
v
速度分布规律
ω
在同一瞬时，刚体上 各点的速度大小 速度大小与其转动 速度大小 半径成正比，其方向与转 动半径垂直，如图6—4所 示；
2012-4-27
x x
图6—6
14
s 5t 2 ϕ= = = = 10t 2 rad R R 0.5
鼓轮的角速度和角加速度分别为：
dϕ d ω= = (10t 2 ) = 20t rad/s dt dt dϕ d α= = ( 20t ) = 20 rad / s 2 dt dt
轮缘上点M的速度和加速度为：
2012-4-27 12
点M的加速度a的大小和方向按下式确定：
a = aτ + a n = R α 2 + ω 4
2 2
(6 - 11) (6 - 12)
aτ α θ = arctan = arctan 2 an ω
工程力学6第六章
点的曲线运动与刚体的定轴转动的比较 运动性质 匀速运动 点的曲线运动 刚体定轴转动
s s0 vtv为常量 0 t 为常量
v v0 a t
0 at
1 2 0 0t t 2
匀变速 运动
2 2 v 2 v0 2a s s0 2 0 2 0
• 例6-2 • 作业：导学篇P88 1、6、7
按自然法 ds d s R , v R R dt dt dv d a R R dt dt v2 an R 2 R
M点全加速度
2 a a2 an R 2 4
tan
a an
2
例：已知轮1的角速度和角加速度，轮2的角速度与 角加速度？
则角速度为 d lim f `t t 0 t dt 即刚体绕定轴转动的角速度等于 转角对时间的一阶导数, 单位：rad / s
3.角加速度
角加速度是反映角速度变化快慢的物理量 如右图所示刚体， 设在瞬时t， 刚体的角速度为 到瞬时t t角速度变为 刚经过t时间后， 角速度的改变量为
• 二、以矢积表示转动刚体上点的速度与加速度 • 如图6-7
M点的速度 v r , 三者按右手法则确定方向。 矢积的 r 大小 : r r sin R v M点的加速度 dv d dr a r r v dt dt dt r ( r ) a a n 矢积 r 的大小： r r sin R a 矢积 v 的大小： v v sin 90 R 2
如何确定刚体在空间的位置?
6 刚体的基本运动
= 0
第六章 刚体的基本运动
vB = v A aB = a A
刚体的平行移动(平动 平动) §1 . 刚体的平行移动 平动 刚体平动特点总结： 刚体平动特点总结： 1、其上任一直线始终平行于它的初始位置； 、其上任一直线始终平行于它的初始位置； 2、任一点的轨迹可是直线也可是曲线； 、任一点的轨迹可是直线也可是曲线； 3、各点的运动轨迹形状相同； 、各点的运动轨迹形状相同； 4、任一瞬时各点的速度、加速度相等。 、任一瞬时各点的速度、加速度相等。 平动刚体的运动可以简化为一个点的运动 即:平动刚体的运动可以简化为一个点的运动。 平动刚体的运动可以简化为一个点的运动。
速度分布图
第六章 刚体的基本运动
加速度分布图
§3 轮系的传动比 1）齿轮传动： 传动比:
v = r1ω1 = r2ω2
ω1 r1
ω2 r2
ω1 r2 z2 i12 = = = ω2 r1 z1
2）带轮传动：
v
ω1 r1 r2 ω2
ω1 r2 i12 = = ω2 r1
第六章 刚体的基本运动
传动比？ 传动比？
第六章 刚体的基本运动
§2 刚体的定轴转动 转动刚体上点的运动几何特点： 转动刚体上点的运动几何特点： 1）轨迹： 在垂直于转轴的平面内作圆周运动。 在垂直于转轴的平面内作圆周运动。 2）速度：
v= d S d (ϕ R ) = = ωR dt dt
方向沿圆周的切线与角速度转向一致。 方向沿圆周的切线与角速度转向一致。 2）加速度： dv d dω v 2 (ωR ) 2 = (ωR ) = R =α R at = an = = = Rω 2 dt d t dt R ρ
第六章 刚体的基本运动
第六章 刚体的基本运动
第六章 刚体的基本运动
vB = v A aB = a A
刚体的平行移动(平动 平动) §1 . 刚体的平行移动 平动 刚体平动特点总结： 刚体平动特点总结： 1、其上任一直线始终平行于它的初始位置； 、其上任一直线始终平行于它的初始位置； 2、任一点的轨迹可是直线也可是曲线； 、任一点的轨迹可是直线也可是曲线； 3、各点的运动轨迹形状相同； 、各点的运动轨迹形状相同； 4、任一瞬时各点的速度、加速度相等。 、任一瞬时各点的速度、加速度相等。 平动刚体的运动可以简化为一个点的运动 即:平动刚体的运动可以简化为一个点的运动。 平动刚体的运动可以简化为一个点的运动。
速度分布图
第六章 刚体的基本运动
加速度分布图
§3 轮系的传动比 1）齿轮传动： 传动比:
v = r1ω1 = r2ω2
ω1 r1
ω2 r2
ω1 r2 z2 i12 = = = ω2 r1 z1
2）带轮传动：
v
ω1 r1 r2 ω2
ω1 r2 i12 = = ω2 r1
第六章 刚体的基本运动
传动比？ 传动比？
第六章 刚体的基本运动
§2 刚体的定轴转动 转动刚体上点的运动几何特点： 转动刚体上点的运动几何特点： 1）轨迹： 在垂直于转轴的平面内作圆周运动。 在垂直于转轴的平面内作圆周运动。 2）速度：
v= d S d (ϕ R ) = = ωR dt dt
方向沿圆周的切线与角速度转向一致。 方向沿圆周的切线与角速度转向一致。 2）加速度： dv d dω v 2 (ωR ) 2 = (ωR ) = R =α R at = an = = = Rω 2 dt d t dt R ρ
第六章 刚体的基本运动
第六章 刚体的基本运动
第6章刚体的基本运动
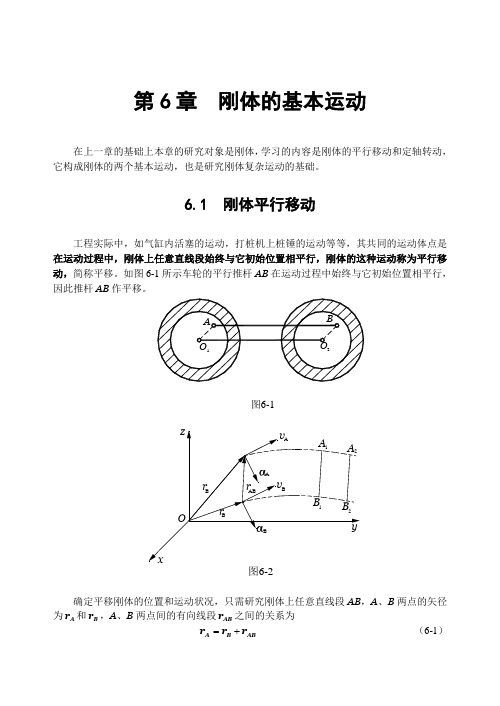
第6章 刚体的基本运动在上一章的基础上本章的研究对象是刚体，学习的内容是刚体的平行移动和定轴转动，它构成刚体的两个基本运动，也是研究刚体复杂运动的基础。
6.1 刚体平行移动工程实际中，如气缸内活塞的运动，打桩机上桩锤的运动等等，其共同的运动体点是在运动过程中，刚体上任意直线段始终与它初始位置相平行，刚体的这种运动称为平行移动，简称平移。
如图6-1所示车轮的平行推杆AB 在运动过程中始终与它初始位置相平行，因此推杆AB 作平移。
确定平移刚体的位置和运动状况，只需研究刚体上任意直线段AB ，A 、B 两点的矢径为A r 和B r ，A 、B 两点间的有向线段AB r 之间的关系为AB B A r r r += （6-1）图6-1图6-2由平动定义知AB r 为恒矢量，A 、B 两点的轨迹只相差AB r 的恒矢量，即A 、B 两点的轨迹形状相同。
式（6-1）对时间求导，得B A v v = （6-2） B A a a = （6-3）结论：（1）平移刚体上各点的轨迹形状相同；（2）在同一瞬时平移刚体上各点的速度相等，各点的加速度相等。
因此，刚体的平行移动可以转化一点的运动来研究，即点的运动学。
6.2 刚体的定轴转动工程实际中绕固定转动的物体很多，如飞论、电动机的转子、卷扬机的鼓轮、齿轮等均绕定轴转动。
这些刚体的运动特点是：在运动过程中，刚体上存在一条不动的直线段，刚体的这种运动称为刚体的绕定轴转动，简称转动，转动刚体的不动的直线段称为刚体的转轴。
6.2.1转动刚体的运动描述如图6-3所示，选定参考坐标系oxyz ，设z 轴与刚体的转轴重合，过z 轴作一个不动的平面0P （称为静平面），再作一个与刚体一起转动的平面P （称为动平面），令静平面0P 位于oxz 面上，初始瞬时这两个平面重合，当刚体转动到t 瞬时，两个平面间的夹角为ϕ，ϕ称为刚体的转角，用来描述转动刚体的代数量。
按照右手螺旋法则规定转角ϕ的符号，其单位为弧度（rad ）。
教学要求1、理解刚体平动的概念及其特性,掌握刚体平动时速度、(精)
和R2，在轮上绕有不可伸长的细绳，绳端挂重物A。 若重物自静止开始以匀加速度a下降，带动轮Ⅰ和轮
Ⅱ转动。求当重物下降h时，轮Ⅱ边缘上B点的速度
和加速度的大小。
解题分析与步骤： ①分析运动
Ⅰ
R1
R2 B1 B2
Ⅱ
重物为直线平动，轮Ⅰ和轮Ⅱ固连为定
轴转动。
A
②根据公式求未知量
h
重物自静止开始以匀加速度a下降高
过的圈数和t=2s时转子的角速度、角加速度。
解题步骤：由于转子的转动方程已知，可直接
应用公式计算。
将t=2s代入转动方程，则
φ=t3=23=8rad
于是，转子转过的圈数为
N=φ/2л=8 /2л=1.27圈
于是:ω=dφ/dt=3t2
α=dω/dt=6t
当t=2s时，有
ω=3t2=3×22=12rad/s
aB2 a2B2 a2B2n (aR2 / R1)2 (2ahR2 / R12 )2 R2a R12 4h2 / R1
度h时，其初速度v0=0，由公式 v2-v02= 2ah
得
v=√2ah
轮Ⅰ和轮Ⅱ的角速度、角加速度为:
ω= vB1/R1=√2ah/R1 α=aB1τ/R1=a/R1
轮Ⅱ边缘上B点的速度和加速度为
vB2 = R2ω= R2√2ah / R1 aB2τ= R2α=aR2/R1aB2n= R2ω2=2ahR2/R12
v ds R d R
dt dt
aτ
dv dt
R d
dt
R
an
v2
R
R 2
a
a
O
an
Ⅱ转动。求当重物下降h时，轮Ⅱ边缘上B点的速度
和加速度的大小。
解题分析与步骤： ①分析运动
Ⅰ
R1
R2 B1 B2
Ⅱ
重物为直线平动，轮Ⅰ和轮Ⅱ固连为定
轴转动。
A
②根据公式求未知量
h
重物自静止开始以匀加速度a下降高
过的圈数和t=2s时转子的角速度、角加速度。
解题步骤：由于转子的转动方程已知，可直接
应用公式计算。
将t=2s代入转动方程，则
φ=t3=23=8rad
于是，转子转过的圈数为
N=φ/2л=8 /2л=1.27圈
于是:ω=dφ/dt=3t2
α=dω/dt=6t
当t=2s时，有
ω=3t2=3×22=12rad/s
aB2 a2B2 a2B2n (aR2 / R1)2 (2ahR2 / R12 )2 R2a R12 4h2 / R1
度h时，其初速度v0=0，由公式 v2-v02= 2ah
得
v=√2ah
轮Ⅰ和轮Ⅱ的角速度、角加速度为:
ω= vB1/R1=√2ah/R1 α=aB1τ/R1=a/R1
轮Ⅱ边缘上B点的速度和加速度为
vB2 = R2ω= R2√2ah / R1 aB2τ= R2α=aR2/R1aB2n= R2ω2=2ahR2/R12
v ds R d R
dt dt
aτ
dv dt
R d
dt
R
an
v2
R
R 2
a
a
O
an
第六章刚体的基本运动
h高度时，轮Ⅱ边缘上B2点的速度和加速度的大小。
R Ⅰ 1
R2
B1 B2
Ⅱ
A
h
图6.21
第7章 运动力学基础 解 重物自静止下降了高度h时，其速度大小为v2= v20+2ah, 其中v0=0，故 v 2ah 。轮Ⅰ和轮Ⅱ的角速度、角加速度分别 为
v1 v 2ah R1 R1 R1 a R1 R1
dv d a R R dt dt
（6.29）
即转动刚体上任一点切向加速度的大小等于其转动半径与角加
速度的乘积，其方向垂直于转动半径，指向与角加速度的转向 一致， 如图6.18所示。
第7章 运动力学基础 M点法向加速度的大小为
v 2 ( R )2 an R 2 R R
为正，反之为负。转角φ的单位是rad。
第7章 运动力学基础
（2） 角速度。角速度是描述刚体转动快慢和转动方向的物
理量，用符号ω表示，它是转角φ对时间t的一阶导数，即
d dt
(6.23)
角速度是代数量，其正负表示刚体的转动方向。当ω＞0时， 刚体逆时针转动；反之则瞬时针转动。角速度的单位是rad/s。 工程上常用每分钟转过的圈数表示刚体转动的快慢， 称为 转速，用符号n表示，单位是r/min。转速n与角速度ω的关系为
第7章 运动力学基础 若以转速n表示刚体转动的快慢，则直径为D的圆周上各 点的速度可表示为
Dn Dn v R m/s 2 30 60
或
v=πDn m/min
(6.28)
第7章 运动力学基础
2） 转动刚体上各点的加速度
由于定轴转动刚体上的各点作圆周运动，因此其加速度分为 切向加速度和法向加速度。 M点切向加速度的大小为
《理论力学》第六章 刚体的基本运动习题全解
第六章 刚体的基本运动 习题全解[习题6-1] 物体绕定轴转动的运动方程为334t t -=ϕ（ϕ以rad 计，t 以s 计）。
试求物体内与转动轴相距m r 5.0=的一点，在00=t 与s t 11=时的速度和加速度的大小，并问物体在什么时刻改变它的转向？ 解：角速度： 2394)34(t t t dt ddt d -=-==ϕω 角加速度：t t dtddt d 18)94(2-=-==ωα速度： )94(2t r r v -==ω)/(2)094(5.0|20s m r v t =⨯-⨯===ω)/(5.2)194(5.0|21s m v t -=⨯-⨯==切向加速度：rt t r a t 18)18(-=-==ρα法向加速度：22222)94()]94([t r rt r v a n -=-==ρ 加速度： 422222222)94(324])94([)18(t t r t r rt n a a n t -+=-+-=+=)/(8165.0)094(0324|24220s m r a t =⨯=⨯-+⨯== )/(405.1581.305.0)194(1324|24221s m r a t =⨯=⨯-+⨯== 物体改变方向时，速度等于零。
即：0)94(2=-=t r v )(667.0)(32s s t ==[习题6-2] 飞轮边缘上一点Ｍ，以匀速ｖ＝１０ｍ／ｓ运动。
后因刹车，该点以)/(1.02s m t a t =作减速运动。
设轮半径Ｒ＝０.４ｍ，求Ｍ点在减速运动过程中的运动方程及ｔ＝２ｓ时的速度、切向加速度与法向加速度。
解：t dtd a t 1.04.022-===ϕρα （作减速运动，角加速度为负）t dt d 25.022-=ϕ12125.0C t dtd +-=ϕ2130417.0C t C t ++-=ϕ12124.005.0)125.0(4.0C t C t dtd R v +-=+-⨯==ϕ104.0005.0|120=+⨯-==C v t图题46-251=C0000417.0|2130=+⨯+⨯-==C C t ϕ 02=C ，故运动方程为： t t 250417.03+=ϕt t t t R s 100167.0)250417.0(4.033+-=+-==ϕ速度方程：1005.02+-=t v)/(8.910205.0|22s m v t =+⨯-== 切向加速度：)/(2.021.01.0|22s m t a t t -=⨯-=-== 法向加速度：222)25125.0(4.0+-⨯==t a n ρω)/(1.240)252125.0(4.0|2222s m a t n =+⨯-⨯==[习题6-3] 当起动陀螺罗盘时，其转子的角加速度从零开始与时间成正比地增大。
刚体的基本运动
刚体的基本运动
答案：
刚体的基本运动形式包括平动、转动（分为定轴转动和非定轴转动）以及平面运动（随质心的平动、绕质心的转动）。
平动是指刚体在运动过程中，整体上以同一速度沿直线运动的现象，其特点是刚体内各点的运动轨迹完全相同。
转动则是刚体绕某一轴心进行旋转的运动，根据轴心的位置不同，可以分为定轴转动和非定轴转动。
平面运动则包括了随质心的平动和绕质心的转动，这种运动形式在工程实际中也是常见的。
复合运动，即平动和转动的组合运动，是刚体运动的一种特殊形式。
例如，自行车在平地上行驶时，既有整车质心的平动，又有轮胎相对于地面的转动。
因此，复合运动确实是刚体的基本运动形式之一。
延伸：
刚体指在运动中和受力作用后，形状和大小不变，而且内部各点相对位置不变的物体。
绝对刚体实际上只是一种理想模型，因为任何物体在受力作用后，都或多或少地变形，如果变形的程度相对于物体本身几何尺寸来说极为微小，在研究物体运动时变形就可以忽略不计。
把许多固体视为刚体，所得到的结果在工程上一般已有足够的准确度。
刚体的特点：刚体上任意两点的连线在平动中是平行且相等的。
刚体上任意质元的位置矢量不同，相差一恒矢量，但各质元的位移、速度和加速度却相同。
因此，常用“刚体的质心”来研究刚体的平动。
第六章 刚体的基本运动
dω dr dv d = （ω× r ) = × r + ω× a= dt dt dt dt
z R a M
n
a = α × r + ω× v
aτ = α × r
α × r = α ⋅ r sin θ = α ⋅ R
O
aτ
v
α ω θ r
ω× r
a
n
= ω × v
ω ⋅ v = ω ⋅ ω ⋅ R = ω
dθ = ωo 其中： dt
所以： bcosθ ⋅ ω o = rcos(θ + ϕ ) ⋅ (ω o + ω )
dϕ =ω dt
*
rcos(θ + ϕ ) ω 解得： ω o = bcosθ − rcos(θ + ϕ )
方程*两边对时间取导数，得：
bcosθ ⋅ ω o = rcos(θ + ϕ ) ⋅ (ω o + ω )
一 、角速度的矢量表示
z
ω
k k
ω
z
ω=ω k
右手螺旋规则：右手的四指代表转动的方向，拇指代表角 速度矢量 ω 的方向。
二、角加速度的矢量表示
角加速度矢量定义：
dω α= dt
角加速度矢
α 为角速度矢 ω 对时间的一阶导数
d dω α = ( ωk) = k dt dt
dω d ϕ = 2 α= dt dt
为描述变速的程度，引入传动比的概念。
ω1 R2 z 2 = = 传动比： i12 = ω 2 R1 z1
ω1 n1 α1 R2 z 2 i12 = = = = = ω 2 n2 α 2 R1 z1
二 、皮带轮传动
n1 R1
vB A vA B R2
z R a M
n
a = α × r + ω× v
aτ = α × r
α × r = α ⋅ r sin θ = α ⋅ R
O
aτ
v
α ω θ r
ω× r
a
n
= ω × v
ω ⋅ v = ω ⋅ ω ⋅ R = ω
dθ = ωo 其中： dt
所以： bcosθ ⋅ ω o = rcos(θ + ϕ ) ⋅ (ω o + ω )
dϕ =ω dt
*
rcos(θ + ϕ ) ω 解得： ω o = bcosθ − rcos(θ + ϕ )
方程*两边对时间取导数，得：
bcosθ ⋅ ω o = rcos(θ + ϕ ) ⋅ (ω o + ω )
一 、角速度的矢量表示
z
ω
k k
ω
z
ω=ω k
右手螺旋规则：右手的四指代表转动的方向，拇指代表角 速度矢量 ω 的方向。
二、角加速度的矢量表示
角加速度矢量定义：
dω α= dt
角加速度矢
α 为角速度矢 ω 对时间的一阶导数
d dω α = ( ωk) = k dt dt
dω d ϕ = 2 α= dt dt
为描述变速的程度，引入传动比的概念。
ω1 R2 z 2 = = 传动比： i12 = ω 2 R1 z1
ω1 n1 α1 R2 z 2 i12 = = = = = ω 2 n2 α 2 R1 z1
二 、皮带轮传动
n1 R1
vB A vA B R2
06 刚体的基本运动
3 1 ln 3 1 3 0 t
6.4 已知轮 I、II、III 的半径分别为 r1＝30cm，r2＝75cm，r3＝40cm，轮 I 的转速 n1＝ 100rpm。求物块 M 的上升速度，胶带 AB、BC、CD、DA 各段上点的加速度的大 小。 B A
r3
r2
n1
O1 DБайду номын сангаас
r1
2
O2
1
C
v
I
当 d＝r=5cm 时，
II
50 50 2 2 (rad/s2) 2 r 5 2n I II 20 (rad/s) 60
所以，当 d＝r 时，轮 II 边缘上的一点的全加速度的大小
2 4 a R II II 15 (2 )2 (20 )4 59218 (cm/ s2 )
a A a
n n aM aA a 2 ,
M 点：∵AB 杆作曲线平动，∴ vM v A a , 6.3
a M a A a
如图所示，一飞轮绕固定轴 O 转动，其轮缘上任一点 M 的全加速度在某运动 过程中与轮半径的交角恒为 60o。当运动开始时，其转角 0 0 ，角速度为0。求 飞轮的转动方程以及角速度与转角的关系。
M
解：
1
n1
30
， 2
1 r1
r2
AB 和 CD 之间各点作匀速直线运动， AD 和 BC 之间各点作匀速圆周运动，所以
a AD r112 32.9 (cm/s2)
2 a BC r2 2 13.16 (cm/s2)
aAB aCD 0 ， 物块 M 的上升速度 v M r3 2 1.676 (cm/s)
第6 章 刚体的基本运动.
B
A
O
i15 i12 i23i34 i45
OA z2 z4 1 1 z1 z3 5
z1 z3 z2
z4 z 5
R
OA
z2 z4 z 2 z 4 v BC 5 z1 z3 z1 z3 R
C
7
z 2 z 4 s 24 32 1 4 rad z1 z3 R 68 4
第6章 刚体的基本运动
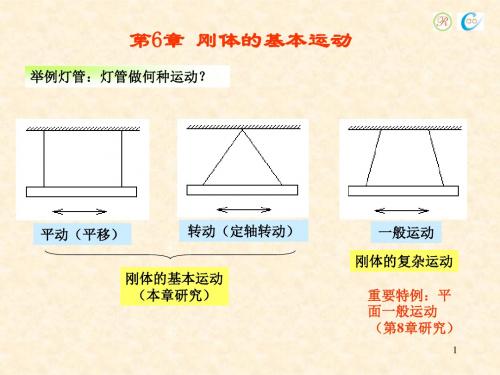
举例灯管：灯管做何种运动？
平动（平移）
转动（定轴转动） 刚体的基本运动 （本章研究）
一般运动 刚体的复杂运动
重要特例：平 面一般运动 （第8章研究）
1
再来看一个例子。
研究刚体运动两个问题
刚体自身运动规律 刚体上点的运动规律
2
§6-1 刚体的平动
定义。直线平动与曲线平动。让同学举例。 刚体上各点运动规律相同——回答了研究刚体平动的两个问题。 注意：只有平动刚体可以谈其速度、加速度，因其可简化为一点的运动。
j 1
6
n 1
例2：(老书题7-13)
图示仪表机构，已知各齿轮齿数 z1=6, z2=24, z3=8, z4=32, 齿轮5的半 径R = 4 cm。如齿条BC下移s = 1cm，求指针OA转过的角度 。
分析： 利用轮系总传动比公式，求 OA 与轮 5 的角速 度关系，即其转角的关系，从而得BC与OA的 位移关系。 解:
解：
v r
求导得：0
dr dr dA 1 v ( v ) 而 dt dA dt 2 r 2 r
dr d r dt dt
d dr dt r dt
(Hale Waihona Puke )dA v dt4
《刚体的基本运动》PPT课件
轮系的传动比
齿轮传动
转速n与w 的关系：
26n0 12nn12成正比
即i1 ,2 ： 1 2n n 1 2r r1 2z z1 2
当： | i1,2 | 1 时, 2 1 , 为升速转动； | i1,2 | 1 时, 2 1 , 为降速转动。
轮系的传动比
皮带传动
轮系的传动比
皮带传动
vAvB ArABrB
aτr0.36m s－ 2
a nr2 0 .64 m 8 s－ 2
A点： vAvM0.36 m s－ 1
aAaτ0.36 m s－ 2
转动刚体内各点的速度和加速度 例题3
转动刚体内各点的速度和加速度
例题3
已知：O1A＝ O1B ＝l； O1A杆的角速度 和角 加速度 a 。
求：C点的运动
轨迹、速度和加 速度。
《刚体的基本运动》PPT课件
本课件仅供大家学习学习 学习完毕请自觉删除
谢谢 本课件仅供大家学习学习
学习完毕请自觉删除 谢谢
第6章 刚体的简单运动
刚体的平行移动 刚体绕定轴的转动 转动刚体内各点的 速度和加速度 轮系的传动比 以矢量表示角速度
和角加速度
第6章 刚体的简单运动
刚体的平行移动
刚体的平行移动
刚体的平行移动
例题1
O1
O2
0
sinπ 4
t
v
π4l0
c
osπt 4
l
l
aM
aτ 1π26l0sinπ4t
A M
M点:
t (s)
B
vM
(rad)
v (m·s－1)
an
1π26l02c
o2sπt 4
at (m·s－2)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：
因为板平动， 因为板平动， ∴vC=vA =l ω ∴aCn =aAn = l ω 2 ∴aCτ=aAτ = l ε
aAn aCn aAτ vA aCτ vC
§2-4 以矢量表示角速度和角加速度以 矢积表示转动刚体内点的速度和加速度 一、角速度矢量和角加速度矢量
角速度矢量
dϕ ω =ω = 大小 dt 作用线 沿轴线滑动矢量 指向 右手螺旋规则
4、特殊情况： 特殊情况： 匀速转动： ω =常量, α = 0 匀速转动：
ϕ =ϕ0 +ω t
匀变速转动： 匀变速转动： α =常量
转动方程
ω = ω 0+ α t ϕ =ϕ0 +ω 0 t +1/2 α t 2 转动方程 ω2 -ω0 2 =2α (ϕ -ϕ0 )
三、定轴转动刚体上各点的运动 各点轨迹为圆， 各点轨迹为圆，选弧坐标
2、角速度： 角速度：
描述转角变化的快慢
ω =dϕ /dt 单位：rad /s (1 /s) 单位： 符号：同转角 ϕ，是代数量 符号：
3、角加速度： 角加速度：
描述角速度变化的快慢
α =dω /dt =d2ϕ /dt2 单位：rad /s2 (1 /s2) 单位： 符号：同转角 ϕ, 是代数量 符号：
第2章 刚体的基本运动
平行移动 定轴转动
§2-1 刚体的平行移动
一、定义 刚体运动过程中， 刚体运动过程中，其上任意直线始终平行 于这一直线的初始位置。 于这一直线的初始位置。 实例1 汽车沿直线行驶时车身的运动.
实例2
滑动窗户的运动.
二、平动的特点 轨迹： 轨迹：
y
A B B′
A′ A″ B″
一、定轴齿轮传动
①
啮合条件
Rω1 = vA = vB = R2ω2 1
② 传动比
ω1 R2 z2 i12 = ± = ± = ± ω2 R1 z1
外啮合
内啮合
二、带轮传动
rω1 = vA = v′ = v′ = vB = r2ω2 1 A B
ω1 r2 i12角速度 ω（逆时针）和角加速度 ε（逆时针） , （逆时针）和角加速度 已知： 点的运动轨迹、 已知：O1A＝ O1B ＝l；求：C点的运动轨迹、速度和加 速度
o
x
A″B″≡ A′B′≡ AB A A′ A″弧 ≡ BB′ B″弧
各点轨迹相同
即 B点轨迹与 A点轨迹完全相同
运动方程: 运动方程
rB = rA + AB
AB是常矢量
速度： 速度： ɺ ɺ rB = rA + AB
∵ AB = 0
y
，
A B rB rA B′
A′ A″ B″ x
∴ vB = v A
加速度： 加速度：
o
ɺɺ = ɺɺ rB rA
a A = aB
各点速度、加速度相同 各点速度、
结论: 结论:
* 刚体上的各点具有形状相同的运动轨迹； 刚体上的各点具有形状相同的运动轨迹； * 刚体上的各点在某一瞬时具有相同的速度 和加速度； 和加速度； * 刚体平移时的运动分析可以简化为其上任 意一点(一般取为质心或已知点)运动分析. 意一点(一般取为质心或已知点)运动分析.
§2-2 刚体绕定轴转动
一、定义 刚体在运动过程中，有一直线始终保持不动。 刚体在运动过程中，有一直线始终保持不动。
转轴 转角ϕ
二、定轴转动刚体的整体运动描述 1、运动方程
描述转动刚体位置的变化
转角：ϕ =ϕ（t） 转角： 单位：rad 单位： 符号：逆时为正 符号：
（或右手螺旋法） 或右手螺旋法）
1、运动方程 、 2、速度 、 3、加速度 、
S = Rϕ v= ds/dt =Rω aτ= dv/dt =R α an = v2 /R =Rω2
a = (aτ ) + (an ) = R α +ω
2 2 2
4
aτ α tanθ = = 2 an ω
4 、速度与加速度分布图
§2-3 轮系的传动比
= α × r +ω × v = at + an
at =α ×r M点切向加速度
an =ϖ ×v =ϖ ×(ϖ ×r ) M点法向加速度
作业3： P117: 6 -1 6 -6
作业2： P171: 8 -2 8 -8 8 -9
ω
ω = ωk
角加速度矢量
dω dω α= = k = αk dt dt
二、用矢积表示刚体上点的速度与加速度
大小 ω ⋅ r sinθ = ω R = v 速度 v = ω×r 方向 矢积方向 dv d = (ω× r ) 加速度 a = dt dt
dω dr = × r +ω × dt dt