极坐标系下二重积分计算的参数范围的确定曹兆龙
极坐标系下二重积分的计算

二、计算下列二重积分:
1、 ln(1 x 2 y 2 )d ,其中D 是由圆周x 2 y 2 1
D
及坐标轴所围成的在第一象限内的区域.
2、 ( x 2 y 2 )d 其中D 是由直线y x ,
D
y x a, y a, y 3a(a 0)所围成的区域.
D: , 0 r ( ).
f ( x, y)dxdy
D
r ( )
D
o
A
f (r cos , r sin )rdrd
D
d
0
(
)
f
(r cos ,
r sin ) r
dr.
3、区域特征如图
0 2 , 0 r ( ).
r ( )
D
f ( x, y)dxdy
D
o
A
f (r cos , r sin )rdrd
极坐标系下二重积分的计算
一、极坐标系下二重积分的一般公式
1、面积元素
d r drd . 或 dxdy r drd .
r ri ri r ri
2、一般公式
f ( x, y)dxdy
o
D
f (r cos , r sin )rdrd .
D
i i
i D
i A
二、极坐标系下二重积分化为累次积分的
例 4 计算 ( x2 y2 )dxdy。
D
x r cos
y
r
sin
其中 D 为由圆 x2 y2 2 y, x2 y2 4 y及直
线 x 3 y 0, y 3 x 0 所围的闭区域.
解: x 3 y 0
1
6
x2 y2 4 y r 4sin
二重积分极坐标计算公式

二重积分极坐标计算公式二重积分是微积分中的重要概念之一,用于计算在二维区域上的一些函数的平均值、面积、质心等数值特征。
极坐标系统是一种常用的描述平面点的坐标系,由径向和角度两个坐标变量组成。
在极坐标下,二重积分有一套特定的计算公式。
一、极坐标变换在直角坐标系下,点P的坐标为(x,y),在极坐标系下,P的坐标可以表示为(r,θ),其中r为点P到原点的距离,θ为点P到正半轴的角度。
我们可以通过以下公式将直角坐标系下的二重积分转换为极坐标下的二重积分:∬R f(x, y) dxdy = ∬D f(rcosθ, rsinθ) r drdθ其中,R为直角坐标系下的二维区域,D为其对应的极坐标系下的二维区域。
f(x,y)为被积函数。
二、极坐标下的积分区域在极坐标下,二重积分的积分区域通常是一个由两个角度θ1和θ2以及两个径向r1和r2确定的扇形区域,可以表示为:D={(r,θ),r1≤r≤r2,θ1≤θ≤θ2}其中,r和θ的取值范围由具体问题决定。
三、极坐标下的积分公式在极坐标下,二重积分的计算公式包括被积函数的转换、积分区域的确定和积分的计算三个部分。
具体的计算步骤如下:(1)将被积函数f(x, y)转换为极坐标下的形式f(rcosθ, rsinθ),并根据具体问题进行简化和化简。
(2)确定积分区域D的极坐标表达式,即确定r的取值范围和θ的取值范围。
(3)将被积函数f(rcosθ, rsinθ)乘以极坐标的雅可比行列式r,并根据r和θ的取值范围进行积分计算。
具体的计算公式如下:∬D f(x, y) dxdy = ∬D f(rcosθ, rsinθ) r drdθ四、极坐标下的面积计算二重积分在极坐标下的一个重要应用是计算二维区域的面积。
对于一个在极坐标下表示的简单闭合曲线,其面积可以通过以下公式进行计算:A=1/2∬Dr^2dθ其中,A为二维区域的面积,D为二维区域在极坐标下的表示,r为点到极坐标原点的距离。
在极坐标系下二重积分的计算

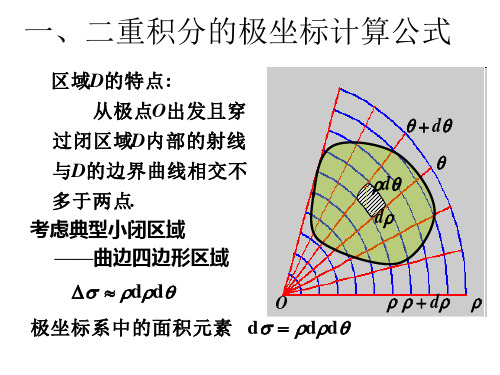
第九节 在极坐标系下二重积分的计算根据微元法可得到极坐标系下的面积微元θσr d r dd = 注意到直角坐标与极坐标之间的转换关系为,c o s θr x = ,sin θr y =从而就得到在直角坐标系与极坐标系下二重积分转换公式为⎰⎰⎰⎰=D D rdrd r r f dxdy y x f θθθ)sin ,cos (),( (9.1)内容分布图示★ 利用极坐标系计算二重积分★ 二重积分化为二次积分的公式★ 例1 ★ 例2 ★ 例3★ 例4 ★ 例5 ★ 例6★ 例7 ★ 例8★ 内容小结 ★ 课堂练习★ 习题6-9★ 返回内容提要:一、二重积分的计算1.如果积分区域D 介于两条射线βθαθ==,之间,而对D 内任一点),(θr ,其极径总是介于曲线)(),(21θϕθϕ==r r 之间(图6-9-2),则区域D 的积分限).()(,21θϕθϕβθα≤≤≤≤r于是 ⎰⎰⎰⎰=D D rdrd r r f dxdy y x f θθθ)sin ,cos (),( .)sin ,cos ()()(21⎰⎰=θϕθϕβαθθθrdr r r f d (9.2)具体计算时,内层积分的上、下限可按如下方式确定:从极点出发在区间),(βα上任意作一条极角为θ的射线穿透区域D (图6-9-2),则进入点与穿出点的极径)(),(21θϕθϕ就分别为内层积分的下限与上限.2.如果积分区域D 是如图6-9-3所示的曲边扇形,则可以把它看作是第一种情形中当)()(,0)(21θϕθϕθϕ==的特例,此时,区域D 的积分限).(0,θϕβθα≤≤≤≤r 于是.)sin ,cos (),()(0⎰⎰⎰⎰=θϕβαθθθrdr r r f d dxdy y x f D (9.3)3.如果积分区域D 如图6-9-4所示,极点位于D 的内部,则可以把它看作是第二种情形中当πβα2,0==的特例,此时,区域D 的积分限).(0,20θϕπθ≤≤≤≤r于是.)sin ,cos (),()(020⎰⎰⎰⎰=θϕπθθθrdr r r f d dxdy y x f D (9.4)注:根据二重积分的性质3,闭区域D 的面积σ在极坐标系下可表示为⎰⎰⎰⎰==DD rdrd d θσσ (9.5) 如果区域D 如图6-9-3所示,则有⎰⎰⎰⎰⎰===βαθϕβαθθϕθθσd rdr d rdrd D )(21)(0 (9.6) 例题选讲:例1(讲义例1)计算⎰⎰++D yx dxdy 221,其中D 是由122≤+y x 所确定的圆域. 例2(讲义例2) 计算⎰⎰++D dxdy y x y x 2222)sin(π, 其中积分区域D 是由4122≤+≤y x 所确定的圆环域.例3(讲义例3)计算⎰⎰D dxdy x y 22, 其中D 是由曲线x y x 222=+所围成的平面区域. 例4(讲义例4)写出在极坐标系下二重积分⎰⎰Ddxdy y x f ),(的二次积分,其中区域}.10,11|),{(2≤≤-≤≤-=x x y x y x D 例5 计算dxdy y x D)(22+⎰⎰,其中D 为由圆y y x y y x 4,22222=+=+及直线03=-y x , 03=-x y 所围成的平面闭区域.例 6 将二重积分σd y x f D⎰⎰),(化为极坐标形式的二次积分,其中D 是曲线,222a y x =+ 42222a y a x =+⎪⎭⎫ ⎝⎛-及直线0=+y x 所围成上半平面的区域.例7(讲义例5)求曲线)(2)(222222y x a y x -=+和a y x ≥+22所围成区域D 的面积.例8(讲义例6)求球体22224a z y x ≤++被圆柱面ax y x 222=+)0(>a 所截得的(含在圆柱面内的部分)立体的体积(图6-9-9).课堂练习1.计算⎰⎰--D y x dxdy e22, 其中D 是由中心在原点, 半径为a 的圆周所围成的闭区域.2.计算,|2|22⎰⎰-+D d y x σ 其中3:22≤+y x D .。
二重积分在极坐标系下的计算
f ( x, y)dxdy
O
D
f ( cos , sin )dd
D
d
d d
d
计算方法——化为二次积分
D : 1( ) 2( ),
其中1( ), 2( ) C[ , ], 0 1( ) 2( ), 0 2π.
2( )
D
1( )
O
在[ , ]上取定 ,
解 根据对称性 SD 4SD1 .
( x2 y2 )2 2a2( x2 y2 )
D1
a 2cos 2
x2 y2 a2 a
a
a
2cos2 得交点(a, π).
6
S dxdy 4 dxdy
D
D1
π
a 2cos2
4 6 d
0
a
d
a 2 ( 3 π). 3
例7 计算一个球体 x2 y2 z2 4a2 被圆柱面 x2 y2 2ax(a 0) 所截得的含在圆柱面内的那 部分立体的体积.
0
0
0
I1 ex2 y2dxdy
D1
π
2 d
R e 2 d
π (1 eR2 );
0
0
4
同理
I2
e x2 y2dxdy
D2
π (1 e2R2 ); 4
因为 I1 I I2,
所以 π (1 eR2 ) ( R e x2dx)2 π (1 e2R2 );
4
0
4
当R 时,
0
0
D
π(1 ea2 ).
例2 将 f ( x, y)dxdy 化为极坐标形式的二次积分,
D
其中D {(x, y)1 x y 1 x2 ,0 x 1}.
二重积分极坐标r范围

二重积分极坐标r范围
二重积分极坐标r范围是指在极坐标系中,对于一个被积函数f(x,y),其被积区域在极坐标下的极径r的范围。
这个范围可以表示成一个圆环或者扇形区域。
对于一个圆环区域,其极径的范围为r1到r2,其中r1和r2都是正实数,r1<r2。
这个区域在极坐标系下表示为:r1≤r≤r2,0≤θ≤2π。
对于一个扇形区域,其极角范围为θ1到θ2,其中θ1和θ2是角度。
这个区域在极坐标系下表示为:r≥0,θ1≤θ≤θ2。
当被积区域在极坐标下是一个非标准区域时,我们可以将其分解为多个标准区域的组合,然后再进行积分计算。
在进行二重积分极坐标r范围的计算时,我们需要根据被积函数的特点,选择合适的积分方法,比如极坐标下的面积元素法、极坐标下的乘积法等。
同时,我们也需要注意在极坐标下进行积分时,要将被积函数中的x和y用极坐标的形式表示出来。
- 1 -。
极坐标计算二重积分

极坐标计算二重积分极坐标是一种用于计算平面上的点坐标的坐标系。
在极坐标系中,一个点的位置由它到原点的距离(称为径向偏移)和与极轴的夹角(称为角度)确定。
极坐标系对于描述与圆形相关的问题非常有用,因为其使用极坐标可以更简洁地表示圆形的方程。
对于一个给定的函数f(r,θ),其中r是距离,θ是角度,我们可以使用二重积分来计算函数在极坐标系下的积分。
要计算在极坐标系下的二重积分,我们需要将二重积分的微元符号替换为极坐标系的微元符号。
在直角坐标系下,二重积分的微元符号是dA,在极坐标系下它被替换为rdrdθ。
因此,对于给定的函数f(r,θ),在极坐标系下的二重积分可以表示为:∬f(r,θ)dA = ∬f(r,θ)rdrdθ其中,∬表示积分号,dA表示微元面积或微元面积。
在计算二重积分之前,我们需要确定积分的范围。
在极坐标系中,范围由两个角度θ1和θ2以及两个距离r1和r2决定。
这些限制可以是常数或者其他变量的函数。
当函数f(r,θ)在极坐标系中具有圆对称性时,即当函数与极轴无关时,可以进一步简化计算。
举个例子,假设我们要计算函数f(r,θ)=r^2在极坐标系下的二重积分。
首先,我们需要确定积分的范围。
假设我们将积分范围设置为θ从0到2π,r从0到R,则二重积分可以表示为:∬r^2dA = ∫[0,2π]∫[0,R](r^2)rdrdθ我们可以首先对r进行积分,然后对θ进行积分。
对于r的积分,我们可以得到:∫[0,2π]∫[0,R](r^2)rdrdθ = ∫[0,2π][(1/4)R^4]dθ对于θ的积分,我们可以得到:∫[0,2π][(1/4)R^4]dθ=(1/4)R^4∫[0,2π]dθ=(1/4)R^4(2π-0)=(1/4)R^4(2π)因此,函数f(r,θ)=r^2在极坐标系下的二重积分为(1/4)R^4(2π)。
以上是关于极坐标计算二重积分的简要介绍。
在实际应用中,我们可以通过将问题转换为极坐标系,并使用适当的积分限制和计算方法,来计算复杂函数在极坐标系下的二重积分。
利用极坐标系计算二重积分共30页

s in i
)ri ri i
D
i
f (r cos,r sin)rdrd
o
A
iD 1 2 ( r i r i) 2 i 1 2 r i2 i 1 2(2ri ri) rii
r i r i i 1 2 ( r i)2 i ri ri i(11 2 rr ii)
二重积分化为二次积分的公式(1)
0
0
0
I 1 e x 2 y 2 dxdy
D 1
2dRer2rdr(1eR2);
00
4
同 理 I 2 D 2 e x 2 y 2 dx 4(1d e2R2y );
I 1 I I 2 ,
( 1 e R 2 ) (R e x 2 d ) 2 x ( 1 e 2 R 2 );
解 在 极 坐 标 系 下
x 2 y 2 a 2 r a , D1
( x 2 y 2 ) 2 2 a 2 ( x 2 y 2 )
ra2 co 2 ,s
由 rar 2cao2s,
得 交 点 A (a, ), 6
∵ D=2D1
所 求 面 积 dx 2ddy xdy
a
26d
2co2s
x
3y01
6
x2y22y r2sin
(x2y2)dxdy 3d4sinr2rdr15( 3).
D
6
2s in
2
例5 求由球面x2+y2+z2=4a2与柱面x2+y2=2ay所围立体的体积。
解: 计算第一挂限部分体积
z
y
V1 4a2x2y2dxdy
D1
2as in
2d
4a2r2rdr
00
d f(r co ,r ssi)r n .dr 00
极坐标系下二重积分的计算方法和例题

计算 I f ( x, y)d
D
用一族同心圆 =常数 一族射线 =常数划分 D
d ?
i
0
i +i i
i
D
i
1 2
(
i
i )2 i
1 2
i2i
i
(i
2
i )
ii
i ii
d dd
取 i i cosi ,
解
由对称性有 V 4 4a 2 x 2 y2 dxdy .
D
其中 D : 0 π , 0 2a cos .
2
V=4
4a2 x2 y2 dxdy =4
π
2 d
2a cos
4a2 2 d
0
0
D
= 32 a 3 3
π
2 (1 sin 3 )d
I 2(R) R e x2dx 0
R e x2dy
0
R e x2 dx R e y2 dy
0
0
e( x2 y2 )dxdy
S
例 计算: e x2 dx 0
解 设 S : 0 x R,0 y R ,
D1 : x 2 y 2 R2 , x 0, y 0 , D2 : x 2 y2 2R2 , x 0, y 0 , 由于 e x2 y2 >0,所以有
e x2 y2 dxdy <
e x2 y2 dxdy < e x2 y2 dxdy
D1
S
D2
e x2 y2 dxdy = π (1 e R2 ) ,
在极坐标系下二重积分的计算

第九节 在极坐标系下二重积分的计算根据微元法可得到极坐标系下的面积微元θσrdrd d =注意到直角坐标与极坐标之间的转换关系为,cos θr x = ,sin θr y =从而就得到在直角坐标系与极坐标系下二重积分转换公式为⎰⎰⎰⎰=DD rdrd r r f dxdy y x f θθθ)sin ,cos (),( (9.1)内容分布图示★ 利用极坐标系计算二重积分★ 二重积分化为二次积分的公式★ 例1 ★ 例2 ★ 例3★ 例4 ★ 例5 ★ 例6★ 例7 ★ 例8★ 内容小结 ★ 课堂练习★ 习题6-9★ 返回内容提要:一、二重积分的计算1.如果积分区域D 介于两条射线βθαθ==,之间,而对D 内任一点),(θr ,其极径总是介于曲线)(),(21θϕθϕ==r r 之间(图6-9-2),则区域D 的积分限).()(,21θϕθϕβθα≤≤≤≤r于是⎰⎰⎰⎰=DD rdrd r r f dxdy y x f θθθ)sin ,cos (),(.)sin ,cos ()()(21⎰⎰=θϕθϕβαθθθrdr r r f d (9.2)具体计算时,内层积分的上、下限可按如下方式确定:从极点出发在区间),(βα上任意作一条极角为θ的射线穿透区域D (图6-9-2),则进入点与穿出点的极径)(),(21θϕθϕ就分别为内层积分的下限与上限.2.如果积分区域D 是如图6-9-3所示的曲边扇形,则可以把它看作是第一种情形中当)()(,0)(21θϕθϕθϕ==的特例,此时,区域D 的积分限).(0,θϕβθα≤≤≤≤r于是.)sin ,cos (),()(0⎰⎰⎰⎰=θϕβαθθθrdr r r f d dxdy y x f D (9.3)3.如果积分区域D 如图6-9-4所示,极点位于D 的内部,则可以把它看作是第二种情形中当πβα2,0==的特例,此时,区域D 的积分限).(0,20θϕπθ≤≤≤≤r于是.)sin ,cos (),()(020⎰⎰⎰⎰=θϕπθθθrdr r r f d dxdy y x f D (9.4)注:根据二重积分的性质3,闭区域D 的面积σ在极坐标系下可表示为⎰⎰⎰⎰==DD rdrd d θσσ (9.5)如果区域D 如图6-9-3所示,则有⎰⎰⎰⎰⎰===βαθϕβαθθϕθθσd rdr d rdrd D )(21)(0 (9.6)例题选讲:例1(讲义例1)计算⎰⎰++Dy x dxdy 221,其中D 是由122≤+y x 所确定的圆域. 例2(讲义例2) 计算⎰⎰++D dxdy y x y x 2222)sin(π, 其中积分区域D 是由4122≤+≤y x 所确定的圆环域. 例3(讲义例3)计算⎰⎰Ddxdy x y 22, 其中D 是由曲线x y x 222=+所围成的平面区域. 例4(讲义例4)写出在极坐标系下二重积分⎰⎰Ddxdy y x f ),(的二次积分,其中区域}.10,11|),{(2≤≤-≤≤-=x x y x y x D例5 计算dxdy y x D )(22+⎰⎰,其中D 为由圆y y x y y x 4,22222=+=+及直线03=-y x ,03=-x y 所围成的平面闭区域.例 6 将二重积分σd y x f D ⎰⎰),(化为极坐标形式的二次积分,其中D 是曲线,222a y x =+ 42222a y a x =+⎪⎭⎫ ⎝⎛-及直线0=+y x 所围成上半平面的区域. 例7(讲义例5)求曲线)(2)(222222y x a y x -=+和a y x ≥+22所围成区域D 的面积.例8(讲义例6)求球体22224a z y x ≤++被圆柱面ax y x 222=+)0(>a 所截得的(含在圆柱面内的部分)立体的体积(图6-9-9).课堂练习1.计算⎰⎰--D y x dxdy e 22, 其中D 是由中心在原点, 半径为a 的圆周所围成的闭区域. 2.计算,|2|22⎰⎰-+D d y x σ 其中3:22≤+y x D .。
3.2.2极坐标系下二重积分的计算

D
D
= 2 d
2a cos
4a2 2 d
0
0
=8 a3
2 (1 sin3 )d
= 8 a(3 - 2)
30
3 23
4a2 x2 y2dxdy, D : x2 y2 2ax,( y 0)
D
•几何意义
4a2 x2 y2dxdy 是球面 z 4a2 x2 y2,
1,
1x
1
sin cos
D :1 x y 1 x2 , 0 x 1,
于是
D:
1
1, 0
sin cos
2
y
1
1
sin cos
f ( x, y)d
D
1
2 d 0
1
f cos , sin d
D
圆柱面 y 2ax x2 , xOz面及xOy面所围成
z
的立体的体积.
顶:z 4a2 x2 y2 O
y
2a
D
x
小结
一、利用极坐标将二重积分化为二次积分
若积分区域
D :1( ) 2( ), D
面积元素 d dd
1( )
须划分为四个子域注意到圆考虑在极坐标下求二重积分极坐标下面积元素用极坐标曲线网常数同心圆族常数射线族来划分积分域
3.2.2 极坐标下的二重积分计算
有些二重积分在直角坐标系下计算比较 复杂或无法计算,就需要尝试在其他坐标系 下来处理.
问题:
计算 f (x, y)d 其中D :1 x2 y2 4. D 在直角坐标系下,若把积分区域看作X型,
11.3 极坐标系下二重积分的计算法

在原点,半径为 a 的圆周所围成的闭区域.
解
在极坐标系下
D: 0 r a , 0 2 .
e
D
x2 y2
dxdy d e
0 0
a2
2
a
r 2
rdr
(1 e
).
上页 下页 返回
例7 计算I e
D
y x y
dxdy, 其中D是由直线
D1
sin( x 2 y 2 ) sin( x 2 y 2 ) dxdy 2 2 x 2 y 2 dxdy 4 x y D1 D
sin r 4 d rdr 4. 0 1 r
2
2
上页
下页
返回
D
2 f x , y d , f x , y f x , y ; f ( x , y )d D f x , y f x , y . 0,
x0
(2)设积分区域 D 关于 x 轴对称,则
D
2 f x , y d , f x , y f x , y ; D f ( x , y )d f x , y f x , y . 0,
x2 y2 1
1 直线方程为r , sin cos
所以圆方程为 r 1,
x y 1
f ( x, y )dxdy
D
2
0
d
1
1 sin cos
f ( r cos , r sin )rdr .
上页 下页 返回
练习 计算二重积分 y x 2 y 2 dxdy, 其中D为圆周
1 ( ) r 2 ( ).
一利用极坐标系计算二重积分二小结

3
6
二、小结
二重积分在极坐标下的计算公式
f ( x, y)d f (r cos , r sin )rdrd
D
D
d 2( )
1( )
f (r cos , r sin )rdr.
d
(
0
)
f
(r
cos
,r
sin
)rdr.
02
d
(
0
)
f
(r
cos
,r
sin
)rdr.
作业:110页 1,2,3,4,5,
D
x r cos
y
r
sin
其中 D 为由圆 x2 y2 2 y, x2 y2 4 y及直
线 x 3 y 0, y 3 x 0 所围的闭区域.
解
x 3y0
1
6
x2 y2 4 y r 4sin
y
3x 0
2
3
x2 y2 2 y r 2sin
r 4sin
r 2sin
区域特征如图
r 1( )
,
D:
1( ) r 2( ).
f ( x, y)dxdy
D
D
o
f (r cos , r sin )rdrd
D
d 2( )
1( )
f (r cos ,
r sin ) r
dr.
r 2( )
A
区域特征如图
,
D:
1( ) r 2( ).
r 1( ) DD
D 可表示为
22ຫໍສະໝຸດ ,0 r 4cos .
r 4cos
2
2
o
4A
12-6.极坐标系下计算二重积分PPT

当R T8 时,11 T 4, 11 T 4,
J 故当R T 8时,I T :,即( e~x2dx)2 ,
8 e - x 2 dx =重
J 所求广义积分
2
例 2 求曲线(x2 + y2)2= 2a2(x2 - y2)的外 部和
x2 + y2 = a a的外部所围成图形的面积.
解 根据对称性有D = 4D1在极坐标系下x2 + y2 = a2 n r = a, (x2 + y2)2 = 2a 2( x2 — y2) n r = a J 2cos2。,
Ii = JJ e ~ x 2 ~ y 2 dxdy
=£ 站 e" rdr =f (1 - e -R 2);
Jo o
4
22
JJ 同理I2 =
ห้องสมุดไป่ตู้
-x - y
eDi-x 2 - y 2 dxdy4 = - (1 - e -2 R 2);
I v I v L, ・--・(14-(1e-eR丿2)vv (dJ*oReed7x丿2dxvV4V(1 -e (丿1 一e一2R2)
o-
-A
JJ f (pcos^, pSn 饥 pdpdp
D
宜
rp(。)
J 极=Jo坐d标(p系下区f域(pc的os面p,积psbin饥= pJdJpp・dpdp.
D
3■例题
例1计算JJe72顼dxdy,其中D是由中心在原
D
点,半径为a的圆周所围成的闭区域,进而计算
广义积分『e - x 2 dx.
解(1)在极坐标系下
o
分变量的变换
JJ f ( x, y y)dxdy = JJ f (pcos?, psin?}pdpd?.
二重积分 极坐标

二重积分极坐标二重积分是微积分中的重要概念,它在许多领域中都有广泛的应用。
其中,极坐标系是一种常用的坐标系,用于描述平面上的点的位置。
本文将介绍二重积分在极坐标系下的应用。
我们来回顾一下二重积分的定义。
在直角坐标系下,二重积分可以理解为对一个平面区域进行分割,并计算每个小区域的面积之和。
而在极坐标系下,我们是通过对一个平面区域进行分割,并计算每个小区域的面积乘以一个权重因子的和来定义二重积分。
在极坐标系下,一个点的位置可以由极径(r)和极角(θ)来描述。
以极点为原点,极径为正方向的射线为极轴,极角为正方向的射线为极角轴。
对于一个平面区域,我们可以将其分割成许多小扇形区域,每个小扇形区域的面积可以近似地表示为Δθ乘以Δr乘以r。
其中Δθ是极角的增量,Δr是极径的增量,r是极径。
在计算二重积分时,我们需要确定积分的范围。
在直角坐标系下,我们通过确定矩形区域的边界来确定积分的范围。
而在极坐标系下,我们可以通过确定极径和极角的范围来确定积分的范围。
例如,如果我们要计算一个圆形区域的面积,可以将极径的范围设定为0到圆的半径,极角的范围设定为0到2π。
接下来,我们来看一个具体的例子。
假设我们要计算极坐标下的二重积分∫∫_D r^2 dA,其中D是一个由圆心为原点、半径为R的圆所围成的区域。
我们可以将积分区域D分割成许多小扇形区域,每个小扇形区域的面积为Δθ乘以Δr乘以r。
因此,二重积分可以表示为∫∫_D r^2 dA = ∫_0^(2π) ∫_0^R r^2 r dr dθ。
根据上述积分的定义,我们可以将其计算过程分为两步。
首先,我们对极径r进行积分,积分的范围是从0到R。
这一步的结果是一个关于极角θ的函数。
然后,我们对极角θ进行积分,积分的范围是从0到2π。
这一步的结果是一个数值。
最后,将这两步的结果相乘,即可得到整个二重积分的结果。
二重积分在极坐标系下的应用非常广泛。
例如,在物理学中,我们经常需要计算旋转体的体积或质量分布。
极坐标二重积分θ范围

极坐标二重积分θ范围1. 引言极坐标是描述平面上点的一种坐标系统,它使用极径和极角来表示点的位置。
在数学中,极坐标常用于描述圆形、环形和对称图形等问题。
在本文中,我们将讨论极坐标下的二重积分,并研究如何确定θ的范围。
2. 极坐标系简介首先,让我们回顾一下极坐标系的定义。
在二维平面上,一个点P可以用两个数值(r, θ)来表示,其中r是点P到原点O的距离,θ是从正半轴到线段OP所成角度。
这样,我们就可以唯一地确定一个点P的位置。
3. 极坐标下的二重积分在直角坐标系中,二重积分用于计算曲线包围的面积或曲面包围的体积。
类似地,在极坐标系中也可以进行二重积分。
设有一个函数f(r, θ),定义在一个闭区域D上。
则f(r, θ)在D上的二重积分可以表示为:∬D f(r, θ) dA = ∫θ1θ2 ∫r1(θ)r2(θ) f(r, θ) r dr dθ其中,r1(θ)和r2(θ)是极角为θ时,曲线D上的两个极径。
4. 确定θ的范围在进行极坐标二重积分时,我们需要确定θ的范围。
一般情况下,θ的范围可以根据问题的几何特性来确定。
4.1 环形区域考虑一个环形区域,内半径为a,外半径为b。
我们希望计算该区域上某个函数f(r, θ)的二重积分。
首先,我们需要确定θ的范围。
由于环形区域是对称的,我们可以将整个环形分成若干个等角度的扇形区域。
假设一个扇形区域对应的角度为Δθ,则整个环形对应的角度范围为2π。
因此,我们可以将二重积分转化为对每个扇形区域进行积分,并将结果相加:∬D f(r, θ) dA = ∑i=1n ∫r1(θi)r2(θi) f(r, θ) r dr dθ其中,n为扇形区域的个数,r1(θi)和r2(θi)分别是第_i_个扇形区域上的内外极径。
4.2 对称图形对称图形是指具有某种对称性质的图形,例如圆形、椭圆等。
在处理对称图形时,我们可以利用其对称特点来简化计算。
考虑一个对称图形D,它关于极轴(即θ=0)具有对称性。
利用极坐标求二重积分

利用极坐标求二重积分一、引言积分是微积分的重要概念之一,用于求解曲线下面的面积、体积、质量等问题。
在二重积分中,我们需要求解平面上某个区域的面积,通常使用直角坐标系来描述这个区域。
然而,在某些情况下,使用极坐标系可以更加简化计算过程,尤其是对于具有旋转对称性的区域。
本文将介绍如何利用极坐标求解二重积分的方法。
二、极坐标系的基本概念极坐标系是一种描述平面上点位置的坐标系统,它由极径和极角两个参数组成。
极径表示点到原点的距离,极角表示点与正半轴的夹角。
在极坐标系中,一点的坐标可以表示为(r,θ),其中r表示极径,θ表示极角。
三、利用极坐标求解二重积分的方法对于一个在直角坐标系下给定的区域D,我们希望求解其面积A。
利用极坐标系,我们可以将区域D表示为极坐标下的形式。
具体而言,我们可以找到一个极坐标系下的函数r=f(θ),使得区域D可以表示为r的范围为[a,b],θ的范围为[α,β]的区域。
3.1 将二重积分转换为极坐标下的积分根据极坐标系的定义,我们可以将二重积分转换为极坐标下的积分形式。
对于一个在直角坐标系下的函数z=g(x,y),其对应的极坐标形式可以表示为z=g(rcos(θ),rsin(θ))。
因此,二重积分可以表示为:∬g D (x,y)dA=∫∫gbaβα(rcos(θ),rsin(θ))rdrdθ其中,dA表示直角坐标系下的面积元素,r表示极径。
3.2 求解极坐标下的积分在得到极坐标下的积分形式后,我们可以根据具体的函数g(rcos(θ),rsin(θ))来求解积分。
求解极坐标下的积分与求解直角坐标下的积分类似,可以使用数值积分方法或者利用已知函数的积分性质进行计算。
四、实例分析为了更好地理解利用极坐标求解二重积分的方法,我们将通过一个具体的实例来进行分析。
4.1 实例描述假设我们需要求解区域D 的面积,其中D 由直角坐标系下的函数y =x 2和x =y 2所围成。
4.2 转换为极坐标下的形式首先,我们需要将区域D 转换为极坐标下的形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常见的二重积分的计算方法主要是在直角坐标系或在 极坐标系下将二重积分化为二次积分,但在极坐标系下将 二重积分化为二次积分,经常以一些单位圆,或标准圆为例 题进行讲解,导致部分同学对一些运用极坐标系下计算的 习题积分限的确定难以把握.本人在教学实践中,运用划线 的方法,帮助同学正确的确定积分的上下限.划线法主要是 针对内层积分,在极坐标系下,规定从极点向外划线,先于 积分区域边界相交的为积分下限,后与积分区域边界相交 的为积分上限.
2
dθ
2acosθ 1 r2·rdr
-π
0a
2
π
乙 =
1 a
2 -π
16a4cos4θ 4
dθ
2
π
乙 =4a3 2 cos4θdθ= 3 πa3.
-
π 2
2
通过例 1,例 2 的观察,一些二重积分习题用常规的直
角坐标系下进行计算,虽然在直角坐标系下,参数范围比较
容易确定,但由于积分表达式比较复杂,很多时候还是无从
当二重积分出现以下两种情况(1)积分区域用极坐标 表示比较简单时或(2)被积函数用极坐标表示比较简单时, 我们需要考虑采用极坐标来计算二重积分.直角坐标系下的 二重积分转化到极坐标下来计算,要注意三个转换:一是被 积函数的转换,这个问题只要将 x=ρcosθ,y=ρsinθ 代入原来 的被积函数 f(x,y)即可;二是面积元素的转换,这只要将 dσ 或 dxdy 换成 ρdρdθ 就可以了;三是直角坐标系下积分限的 转换为极坐标系下的积分限,这个是最难的,我们这篇文章 主要是通过一些不典型的习题帮助同学学会如何正确地确 定极坐标系下的积分限.
-2asinθ
= dθ
ρ2
dρ
-
π 4
0
姨4a2-ρ2
乙 乙 0
-θ
令 ρ=2asint dθ 2a2(1-cos2t)dt
-
π 4
0
=a2(
π2 16
-
1 2
).
例 2 求由曲面 x2+y2=2ax,az=x2+y2(a>0)及平面 z=0 所围
成立体积为一曲顶柱体
第 28 卷 第 9 期(下) 2012 年 9 月
赤 峰 学 院 学 报( 自 然 科 学 版 ) Journal of Chifeng University(Natural Science Edition)
Vol. 28 No. 9 Sep. 2012
极坐标系下二重积分计算的参数范围的确定
曹兆龙
的体积,可用二重积分计算,关键是要确定柱体的曲顶以及
坐标平面的投影区域.
解 x2+y2=2ax 是一母线平行于 z 轴的圆柱面,顾可知
所围立体是一曲顶柱体,其顶为抛物面 z= 1 (x2+y2).立体在 a
xOy 面上的投影区域 Dxy 为:x2+y2≤2ax.如图 3 所示. 我们首先可以确定参数 θ 的范围,然后用划线法确定
蓦 蓦 f(x,y)dxdy= f(ρcosθ,ρsinθ)ρdρdθ
D
D
乙 乙 β
φ2(θ)
= dθ f(ρcosθ,ρsinθ)ρdρ
α
φ1(θ)
下面举例说明:
蓦 例 1 计算二重积分 I= 姨x2+y2 dσ,其中 D 是由 D 姨4-x2-y2 直线 y=-x 和曲线 y=-a+ 姨a2-x2 (a>0)围成. 思路探索:被积函数含有 x2+y2,积分区域 D 也与圆或圆 弧有关,故想到可以利用极坐标计算二重积分. 解 积分区域 D 如图 2 所示,利用划线法帮助确定积 分的限.首先,我们从积分区域的函数表达式和图形可以得 出参数 θ 的范围,然后我们从极点 O 作一些射线,发现从极 点发出的射线与积分区域先相交交点始终就是极点本身, 而后相交的一个交点则落在圆 y=-a+ 姨a2-x2 (a>0)上,利用
先回顾一下二重积分在极坐标下先对 ρ 后对 θ,是如何 确定积分的上下限的.
ρ=φ1(θ) ;
β α O
D 图1
ρ=φ2(θ) x
先确定 θ 的变化范围,即看积分区域 D 被哪两条从极 点 O 发出的射线夹住,我们就以小的作为 θ 的积分下限,大 的作为 θ 的积分上限. 如图 1 中的积分区域 D 被射线 θ=α, θ=β 夹住,故 α≤θ≤β.
参数 r 的范围,发现从极点发出的射线与积分区域先相交的
交点始终就是极点本身,而后相交的交点则落在圆
图3
x2+y2=2ax 上,将该圆方程转化为极坐标方程.故极坐标系下
积分区域表示为:
-
π 2
≤θ≤ π 2
,0≤γ≤2acosθ.所求立体的体积为:
蓦 V= 1 (x2+y2)dxdy a Dxy
π
乙 乙 =
(盐城工学院 基础教学部,江苏 盐城 224002)
摘 要:本文探讨了二重积分在极坐标系下的计算过程中参数范围如何确定的问题,并用例题进行了说明. 关键词:二 重 积 分 ;极 坐 标 ;划 线 法 中图分类号:O172.2 文献标识码:A 文章编号:1673- 260X(2012)09- 0013- 02
然后开始用划线法帮助确定 ρ 的范围 (一般可以用 θ 的函数表示).用任意的 φ∈[α,β],将 φ 固定,从极点作该极 角,从极点 O 引出的另一条射线穿过积分区域,只允许该射 线与积分区域至多有两个交点(若交点多于两个,则积分区 域需要分割),观察:与积分区域先交的交点落在哪一条曲 线上,则该曲线作为 ρ 的积分下限,与积分区域后交的交点 落在哪一条曲线上,则该曲线作为 ρ 的积分上限.这样我们 就可以将直角坐标系下的二重积分转换为极坐标系下的二 次积分.如图 1 中的积分区域 D 首先与边界曲线 ρ=φ1(θ)相 交,然后与边界曲线 ρ=φ2(θ)相交,故 φ1(θ)≤ρ≤φ2(θ).
下手.在这种情况下,我们通过观察被积函数和积分区域,如
果发现通过极坐标变换以后积分函数变的简单,或者积分
区域是与圆或圆环有关的图形,我们就可以选择在极坐标
系下计算二重积分,借助划线的方法确定有关参数的上下
- 13 -
y
O
a
x
-a
y
O
a
x
图2
极坐标,D 可以表示为 D=
-
π 4
≤θ≤0
,
0≤ρ≤-2asinθ
蓦 则 I=
姨x2+y2 dxdy
D 姨4a2-x2-y2
蓦=
姨ρ2cos2θ+ρ2sin2θ ρdρdθ
D 姨4a2-ρ2sin2θ-ρ2cos2θ
蓦=
ρ ρdρdθ
D 姨4a2-ρ2
乙 乙 0
