运筹学课件——第8讲 网络优化
合集下载
运筹学课件 第8章 网络计划

• 美国海军武器局—计划评审技术PERT:类似流程 图的箭线图,它描绘出项目包含的各种活动的先 后顺序,表明每项活动的时间或相关的成本。主 要用于研究与开发项目。
基本概念
• 网络图(赋权有向图):由箭线和节点构成,用 来表示工作流程的有向、有序的网状图形。它反 映整个工程任务的分解和合成。
5
1
2
a
网络计划
网络图 时间参数的计算 网络计划的优化和实施管理 图解评审法简介
基本概念
• 网络计划是通过网络图的制作,进行计划的优化, 通过其关键路线,实现管理者对工程项目的进度 控制。简单说,就是用网络分析的方法进行工程 项目计划和控制的一项管理技术。
• 杜邦公司—关键路线法CPM:是一个动态系统, 会随着项目的进度不断更新。主要用于以往在类 似工程中已取得一定经验的承包工程。
还要注意以下规则:
(1)网络图只能有一个总起点事项,一个总终 点事项
3
4
1
6
7
9
2
5
8
(2)网络图是有向图,不允许有回路
3
5
1
2
6
7
4
(3)节点i、j之间不允许有两个或两个以上的工 作
b
1
2
a
(4)虚工序的运用
3
4
7
1
6
9
2
5
8
(5)必须正确表示工作之间的前行、后继关系
b a
c
a c
b
1a
c4
• 路线的长度:完成该路线上的各项工序持续时间 的长度之和。
• 关键路线:网路中花费时间最长的时间和活动的 序列
• 次关键路线:花费时间次长的时间和活动的序列 • 关键工序:关键路线上的工序 • 工序时间(权),完成工序的时间消耗
基本概念
• 网络图(赋权有向图):由箭线和节点构成,用 来表示工作流程的有向、有序的网状图形。它反 映整个工程任务的分解和合成。
5
1
2
a
网络计划
网络图 时间参数的计算 网络计划的优化和实施管理 图解评审法简介
基本概念
• 网络计划是通过网络图的制作,进行计划的优化, 通过其关键路线,实现管理者对工程项目的进度 控制。简单说,就是用网络分析的方法进行工程 项目计划和控制的一项管理技术。
• 杜邦公司—关键路线法CPM:是一个动态系统, 会随着项目的进度不断更新。主要用于以往在类 似工程中已取得一定经验的承包工程。
还要注意以下规则:
(1)网络图只能有一个总起点事项,一个总终 点事项
3
4
1
6
7
9
2
5
8
(2)网络图是有向图,不允许有回路
3
5
1
2
6
7
4
(3)节点i、j之间不允许有两个或两个以上的工 作
b
1
2
a
(4)虚工序的运用
3
4
7
1
6
9
2
5
8
(5)必须正确表示工作之间的前行、后继关系
b a
c
a c
b
1a
c4
• 路线的长度:完成该路线上的各项工序持续时间 的长度之和。
• 关键路线:网路中花费时间最长的时间和活动的 序列
• 次关键路线:花费时间次长的时间和活动的序列 • 关键工序:关键路线上的工序 • 工序时间(权),完成工序的时间消耗
网络计划优化PPT课件

假想的两道工序(A+B)和(B+C)在各施工段上的施工时间如所示。 最优施工次序为:Ⅱ→Ⅰ→Ⅴ→Ⅳ→Ⅲ。
工期优化
方法4:优选工作的可变顺序
树枝图法
当m个施工段三道工序的施工次序问题不能满足条件
min
{t iA
} ≥max {t
}或
iB
min
{t iC
}≥max
{t iB
}时,
就不能按上述方法确定施工顺序,可以采用树枝图法。
工期优化
方法4:优选工作的可变顺序
分析法
案例剖析:
按Ⅴ→Ⅰ→Ⅳ→Ⅲ→Ⅱ顺序组织流水施工的总工期为25d。若不按此原则确定施工顺序,一般不 能取得最短的施工周期。
例如,若按Ⅰ→Ⅱ→Ⅲ→Ⅳ→Ⅴ的次序施工,总工期需要33d。从数学上可以证明,在五个施工 段的120种排序方案中,25d是工期最短的方案。
最优施工顺序的网络计划图
(2)第三道工序C在各施工段上持续时间的最小值min{tiC}大于或等于第二道工序B在各施工
{ } { } 段上持续时间的最大值max{tiB} ,即: min t iC ≥max t iB
或者符合上述二个条件之一时,则可将三道工序的施工顺序问题转化成两个工序的施工顺序问题 予以解决。即三个工序可列出三个工期,取大值即max{TA,TB,TC}为其下限,TA TB TC分别为:
工期优化
方法4:优选工作的可变顺序
分析法
约翰逊法则
美国学者约翰逊(S.M.Johnson)-贝尔曼(R.Bellman)在1954年提出了一种简单的寻求 最短施工时间的排序方法,通常称为“约翰逊.-贝尔曼”法则,这个法则的基本原理是:必须 在tmB和t1A中挑其最小值,先行工序排在前面,后续工序排在最后。挑出一个以后,任务数量 减少一项,但仍可列出上述关系,只是任务项数为(m-1)个而已。排序方法按此顺序进行, 最终可得到最佳施工顺序。
工期优化
方法4:优选工作的可变顺序
树枝图法
当m个施工段三道工序的施工次序问题不能满足条件
min
{t iA
} ≥max {t
}或
iB
min
{t iC
}≥max
{t iB
}时,
就不能按上述方法确定施工顺序,可以采用树枝图法。
工期优化
方法4:优选工作的可变顺序
分析法
案例剖析:
按Ⅴ→Ⅰ→Ⅳ→Ⅲ→Ⅱ顺序组织流水施工的总工期为25d。若不按此原则确定施工顺序,一般不 能取得最短的施工周期。
例如,若按Ⅰ→Ⅱ→Ⅲ→Ⅳ→Ⅴ的次序施工,总工期需要33d。从数学上可以证明,在五个施工 段的120种排序方案中,25d是工期最短的方案。
最优施工顺序的网络计划图
(2)第三道工序C在各施工段上持续时间的最小值min{tiC}大于或等于第二道工序B在各施工
{ } { } 段上持续时间的最大值max{tiB} ,即: min t iC ≥max t iB
或者符合上述二个条件之一时,则可将三道工序的施工顺序问题转化成两个工序的施工顺序问题 予以解决。即三个工序可列出三个工期,取大值即max{TA,TB,TC}为其下限,TA TB TC分别为:
工期优化
方法4:优选工作的可变顺序
分析法
约翰逊法则
美国学者约翰逊(S.M.Johnson)-贝尔曼(R.Bellman)在1954年提出了一种简单的寻求 最短施工时间的排序方法,通常称为“约翰逊.-贝尔曼”法则,这个法则的基本原理是:必须 在tmB和t1A中挑其最小值,先行工序排在前面,后续工序排在最后。挑出一个以后,任务数量 减少一项,但仍可列出上述关系,只是任务项数为(m-1)个而已。排序方法按此顺序进行, 最终可得到最佳施工顺序。
运筹学课件 第八章 图与网络分析

运筹学教程
例:哥尼斯堡七桥问题 哥尼斯堡(现名加里宁格勒)是欧洲一
个城市,Pregei河把该城分成两部分,河中 有两个小岛,十八世纪时,河两边及小岛之 间共有七座桥,当时人们提出这样的问题: 有没有办法从某处(如A)出发,经过各桥 一次且仅一次最后回到原地呢?
A C
B
运筹学教程
D
运筹学教程
最后,数学家Euler在1736年巧妙地给出 了这个问题的答案,并因此奠定了图论的基 础,Euler把A、B、C、D四块陆地分别收缩 成四个顶点,把桥表示成连接对应顶点之间 的边,问题转化为从任意一点出发,能不能 经过各边一次且仅一次,最后返回该点。这 就是著名的Euler问题。
第二阶段是从十九世纪中叶到二十世纪 中叶,这时,图论问题大量出现,如 Hamilton问题,地图染色的四色问题以 及可平面性问题等,这时,也出现用图 解 决 实 际 问 题 , 如 Cayley 把 树 应 用 于 化 学领域,Kirchhoff用树去研究电网络等.
运筹学教程
第三阶段是二十世纪中叶以后,由生产管 理、军事、交通、运输、计算机网络等方 面提出实际问题,以及大型计算机使大规 模问题的求解成为可能,特别是以Ford和 Fulkerson建立的网络流理论,与线性规划、 动态规划等优化理论和方法相互渗透,促 进了图论对实际问题的应用。
e5
运筹学教程
v2
v3
e2
e6
v4
v5
e8
运筹学教程
二、连通图
定义8:如果图中的某些点、边可以排列成点和边的交错序列 (v0 ,e1 ,v1 ,e2 ,v2,e3 ,v3 ,…,vn-1 , en , vn ) ,ei=(vi-1,vi),则称 此为一条链。 由两两相邻的点及其相关联边构成的点边序列。 初等链:链中无重复的点和边; 定义9:无向图中,如一条链中起点和终点重合,则称此链为 圈。 初等圈:圈中无重复的点和边; 有向图中,当链(圈)上的边方向相同时,为道路(回路)。
运筹与决策PPT:网络优化问题
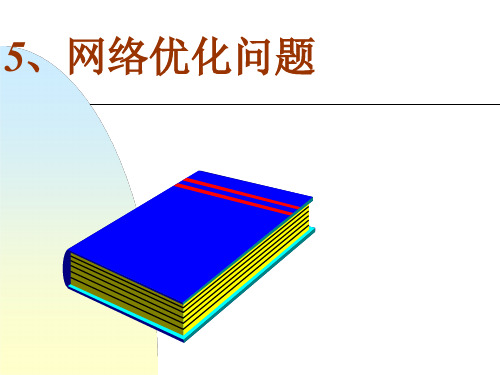
▪ SUMIF(向量1,v,向量2)
若向量1的第i个分量=v,则 SUMIF = SUMIF +向量2的第i个分量值
该函数可用于计算流出或流入节点v的流量
5.2 最大流问题
最大流问题,是要在网络中找出一个可 行流方案,使得通过网络的流量最大。
案例2: BMZ公司的配送中心问题
▪ BMZ是欧洲的一家豪华汽车制造商,其对美国的出口 至关重要;
5.1 最小费用流问题
最小费用流问题,也即网络配送问题, 解决如何以最小成本在一个配送网络中运输 货物。
案例1: Distribution Unlimited公司问题
▪ 该公司有两个工厂,生产一种产品,运往两个仓库;
– 工厂 1 生产 80 单位 – 工厂 2 生产 70 单位 – 仓库 1 需要 60 单位 – 仓库 2 需要 90 单位
C
To Rotterdam Bordeaux
Lisbon New York New York New Orleans New Orleans Los Angeles Los Angeles
▪工厂 1 与仓库 1 之间、工厂 2 与仓库 2 之间分别有铁 路相连;
▪ 也可通过卡车先将产品运至配送中心(DC),再从 配送中心运至仓库(每车至多装50单位)
问题:如何运输才能使费用最小?
配送网络图
80 units produced
F1
$700/unit
W1
60 units needed
$300/unit
Bordeaux
[40 units max.]
[50 units max.]
LI Lisbon [30 units max.]
BMZ问题的网络模型
若向量1的第i个分量=v,则 SUMIF = SUMIF +向量2的第i个分量值
该函数可用于计算流出或流入节点v的流量
5.2 最大流问题
最大流问题,是要在网络中找出一个可 行流方案,使得通过网络的流量最大。
案例2: BMZ公司的配送中心问题
▪ BMZ是欧洲的一家豪华汽车制造商,其对美国的出口 至关重要;
5.1 最小费用流问题
最小费用流问题,也即网络配送问题, 解决如何以最小成本在一个配送网络中运输 货物。
案例1: Distribution Unlimited公司问题
▪ 该公司有两个工厂,生产一种产品,运往两个仓库;
– 工厂 1 生产 80 单位 – 工厂 2 生产 70 单位 – 仓库 1 需要 60 单位 – 仓库 2 需要 90 单位
C
To Rotterdam Bordeaux
Lisbon New York New York New Orleans New Orleans Los Angeles Los Angeles
▪工厂 1 与仓库 1 之间、工厂 2 与仓库 2 之间分别有铁 路相连;
▪ 也可通过卡车先将产品运至配送中心(DC),再从 配送中心运至仓库(每车至多装50单位)
问题:如何运输才能使费用最小?
配送网络图
80 units produced
F1
$700/unit
W1
60 units needed
$300/unit
Bordeaux
[40 units max.]
[50 units max.]
LI Lisbon [30 units max.]
BMZ问题的网络模型
网络优化图及网络(运筹学)

详细描述
最短路径问题有多种算法,如Dijkstra算法和Bellman-Ford算法。这些算法通 过不断优化路径长度,最终找到最短路径。在现实生活中,最短路径问题广泛 应用于交通网络、通信网络和电力网络等领域。
最小生成树问题
总结词
最小生成树问题是图论中的另一个经典问题,旨在在给定连 通图中找到一棵包含所有节点且总权重最小的树。
网络优化图及网络(运筹学)
目 录
• 网络优化图概述 • 网络(运筹学)基础 • 网络优化模型 • 网络优化算法 • 网络优化实例分析 • 网络(运筹学)的未来发展与挑战
01
网络优化图概述
定义与特点
定义
网络优化图是一种数学模型,用于描 述现实世界中各种网络系统的结构和 行为。
特点
网络优化图具有节点和边的概念,能 够表示各种对象之间的关系和交互作 用,同时可以引入各种参数和约束条 件,以实现特定的优化目标。
详细描述
大数据的爆炸式增长使得传统的数据 处理和分析方法难以应对,需要采用 新的数据处理和分析技术,如分布式 计算、流处理等,以提高数据处理效 率。
人工智能与网络优化
总结词
人工智能技术的发展为网络优化提供了 新的思路和方法,可以更好地解决复杂 的问题。
VS
详细描述
人工智能技术如机器学习、深度学习等可 以用于网络优化,例如通过学习历史数据 来预测未来的流量和需求,从而更好地进 行资源调度和路径选择。
遗传算法通过模拟生物进化 过程中的自然选择和遗传机 制,不断迭代和优化种群中 的个体,最终找到最优解。
遗传算法适用于多目标优化、 约束满足问题等复杂问题,具 有较好的鲁棒性和全局搜索能
力。
05
网络优化实例分析
最短路径问题
最短路径问题有多种算法,如Dijkstra算法和Bellman-Ford算法。这些算法通 过不断优化路径长度,最终找到最短路径。在现实生活中,最短路径问题广泛 应用于交通网络、通信网络和电力网络等领域。
最小生成树问题
总结词
最小生成树问题是图论中的另一个经典问题,旨在在给定连 通图中找到一棵包含所有节点且总权重最小的树。
网络优化图及网络(运筹学)
目 录
• 网络优化图概述 • 网络(运筹学)基础 • 网络优化模型 • 网络优化算法 • 网络优化实例分析 • 网络(运筹学)的未来发展与挑战
01
网络优化图概述
定义与特点
定义
网络优化图是一种数学模型,用于描 述现实世界中各种网络系统的结构和 行为。
特点
网络优化图具有节点和边的概念,能 够表示各种对象之间的关系和交互作 用,同时可以引入各种参数和约束条 件,以实现特定的优化目标。
详细描述
大数据的爆炸式增长使得传统的数据 处理和分析方法难以应对,需要采用 新的数据处理和分析技术,如分布式 计算、流处理等,以提高数据处理效 率。
人工智能与网络优化
总结词
人工智能技术的发展为网络优化提供了 新的思路和方法,可以更好地解决复杂 的问题。
VS
详细描述
人工智能技术如机器学习、深度学习等可 以用于网络优化,例如通过学习历史数据 来预测未来的流量和需求,从而更好地进 行资源调度和路径选择。
遗传算法通过模拟生物进化 过程中的自然选择和遗传机 制,不断迭代和优化种群中 的个体,最终找到最优解。
遗传算法适用于多目标优化、 约束满足问题等复杂问题,具 有较好的鲁棒性和全局搜索能
力。
05
网络优化实例分析
最短路径问题
R820-运筹学-第8章 网络计划

• 从起始节点开始沿箭线方向自左往右,通过一系列 箭线和节点,到达终点节点的通路,称为线路。
2. 紧前工作和紧后工作
• 紧前工作是指紧排在本工作之前的工作;且开始或完 成后,才能开始本工作。紧后工作是指紧排在本工作 之后的工作;本工作开始或结束后,才能开始或结束 的工作。如图11-3中,只有工作A 完成后工作B,C,D,E 才能开始,工作A 是B,C,D,E 的紧前工作;而工作 B,C,D,E 则是工作A 的紧后工作。
2
2.2 计算关系式 这些时间参数的关系可以用下图11-6表示工作的关 系状态。
TF i-j=LFi-j-EFi-j ESi-j 工作持续时间 D i-j i 工作 A 工作a的总时差 EFi-j 工作 A LFi-j 工作 A 的紧后工作 B ESj-k LSi-k EFj-k LFj-k 最早开始 最迟开始
⑦ 10 15 ⑧ 7 16
13
③
17
⑥
7
12
(d)
第2节 网络计划图的时间参数计算。
• 网络计划的时间参数计算有几种类型:双代号网络 计划有工作计算法和节点计算法;单代号网络计划 有节点计算法。以下仅介绍工作计算法。 网络图中工作的时间参数。它们是: • 工作持续时间(D); • 工作最早开始时间(ES); • 工作最早完成时间(EF); • 工作最迟开始时间(LS); • 工作最迟完成时间(LF); • 工作总时差(TF); • 工作自由时差(FF)。
表11-1
序号
1 2 3 4 5 6 7 8 9 10
工作名称
产品设计和工艺设计 外购配套件 锻件准备 工装制造1 铸件 机械加工1 工装制造2 机械加工2 机械加工3 装配与调试
工作代号
A B C D E F G H K L
2. 紧前工作和紧后工作
• 紧前工作是指紧排在本工作之前的工作;且开始或完 成后,才能开始本工作。紧后工作是指紧排在本工作 之后的工作;本工作开始或结束后,才能开始或结束 的工作。如图11-3中,只有工作A 完成后工作B,C,D,E 才能开始,工作A 是B,C,D,E 的紧前工作;而工作 B,C,D,E 则是工作A 的紧后工作。
2
2.2 计算关系式 这些时间参数的关系可以用下图11-6表示工作的关 系状态。
TF i-j=LFi-j-EFi-j ESi-j 工作持续时间 D i-j i 工作 A 工作a的总时差 EFi-j 工作 A LFi-j 工作 A 的紧后工作 B ESj-k LSi-k EFj-k LFj-k 最早开始 最迟开始
⑦ 10 15 ⑧ 7 16
13
③
17
⑥
7
12
(d)
第2节 网络计划图的时间参数计算。
• 网络计划的时间参数计算有几种类型:双代号网络 计划有工作计算法和节点计算法;单代号网络计划 有节点计算法。以下仅介绍工作计算法。 网络图中工作的时间参数。它们是: • 工作持续时间(D); • 工作最早开始时间(ES); • 工作最早完成时间(EF); • 工作最迟开始时间(LS); • 工作最迟完成时间(LF); • 工作总时差(TF); • 工作自由时差(FF)。
表11-1
序号
1 2 3 4 5 6 7 8 9 10
工作名称
产品设计和工艺设计 外购配套件 锻件准备 工装制造1 铸件 机械加工1 工装制造2 机械加工2 机械加工3 装配与调试
工作代号
A B C D E F G H K L
运筹学第8章 网络规划

欧拉回路:经过每边且仅一次 厄尼斯堡七桥问题、邮路问题
充要条件:图中无奇点
哈密尔顿回路:经过每点且仅一次 货郎担问题、快递送货问题
2016/9/7
10
例8-4 节目排序问题
8个节目,首尾为A, H或H,A;10名演员,不连续出演。如何安排? 节 目 A B C D E F G H √ √ √ √ √ √ 11 √ √ 演 员 1 √ √ √ 2 3 √ √ √ √ √ √ √ √ √ √ √ 4 5 √ 6 √ 7 √ 8 9 √ 10
从\至
T l1 =(0 3 4 )
1 0 3 2
2 3 0
3 4 4 0
4 0 1
5 5 0
1 2 3 4 5
T l2 =(0 3 1 3 2 ) T l3 (0 3 1 0 1) T l4 (0 3 1 0 1)
定理8-2:点集V的非空子集 (i, k)必在最小树中。
V S S ,连结两子集的最小边
16
1、破圈算法 步骤:
(1)在给定的赋权的连通图上任找一个圈。
(2)在所找的圈中去掉一个权数最大的边(如果有两条或
两条以上的边都是权数最大的边,则任意去掉其中一条)。
(3)如果所余下的图已不包含圈,则计算结束,所余下的 图即为最小树,否则返回第1步。
12
8.2
最小树问题
v1 v2 v8
树是图论中的重要概念,所谓树就是一个无圈的连通图。
v1 v2 v6 v5 v7 v6 v8 v9 v3 v4 v2 v4 v1 v3 v5 v8
v3 v4 v5 v7 v6 v9
(a)
(b)
图8-4
运筹学( 图与网络优化)

七桥问题
七桥问题图形
原理及方法
七桥问题是图论中的著名问题。1736年,Euler巧妙 地将此问题化为图的不重复一笔画问题,并证明了 该问题不存在肯定回答。原因在于该图形有顶点连 接奇数条边。
§10.1
图的基本概念
一个图(Graph) 定义为三元有序组
(V (G ), E (G ), G )
几何实现图例
在一个图的几何实现中,两条边的交点可能不是图的顶 点。例如下图 中,它共有4个顶点,6条边;而e 3 与e 4 的交点不是这个图的顶点。
v1
e1
v2 e4
e2
v3
e3
e5
v4
e6
e3
v1
v4
e1 e4
v2
e2
v3 e6
e5
v4
平面图
一个图称为平面图,如它有一个平面图形,使得边与边仅在
u 1
f5 u3 f6
f2 f4
u2
u4
同构
给定两个图
G (V (G), E(G), G )
H (V ( H ), E( H ), H )
称G和H是同构的,记为 G H , 如果存在两个一一对应 ( , )
: V (G) V ( H )
: E (G) E ( H )
e7
v2
e3 v3
e6
v4
e4
关联矩阵性质
图G的关联矩阵M=(mij)为m×n矩阵;则每行元
素之和等于相应顶点的度;每列元素之和等于 2。
因此,图G的关联矩阵M所有元素之和既等于所
有顶点的度之和,又等于边数的2倍。 定理 设G是一个图,则
vV ( G )
d (v) 2
运筹学第8章 图与网络优化R52

v4 a5 v3 a6 a4 D=(V, A) a3 a2 v2 v1 v4 e5 v3 e6 e4 G(D) e3 e2 v2 v1
基础图
25
有向图、弧、路、初等路
设有向图的弧为a=(u ,v),则起点为u,终点为v; 路: 初等路: 各顶点都不相同的路; 初等回路:u = v 的初等路; 连通图: 若不考虑方向是无向连通图; 强连通图:任两点有路;
26
v3 a2 v1 a1 v2 a3 a4
a8
v5 a10
v7 a9 v6
•路 • 初等路 • 回路
a6
a5 v4
a11
a7
( v 1 , a 2 , v 3 , a 4 , v 4 , a 7 , v 6 )是 从 v 1 到 v 6 的 路 , 也 是 一 条 初 等 路 。 在 上 图 中 , ( v 3 , a 3 , v 2 , a 5 , v 4 , a 6 , v 5 , a 8 , v 3 )是 一 个 回 路 。
v3 v1 v2
v5
v7
v6
v4
15
端点,关联边,相邻
若边e可表示为e=[vi,vj],称vi和vj是
边e的端点,称边e为点vi或vj的关联 边。若点vi,vj与同一条边关联,称 点vi和vj相邻;若边ei和ej具有公共 的端点,称边ei和ej相邻。 e2 v2 e6 v4
e1 v1 e4 e3
e5 e7
vV2 vV
vV1
2m为偶数,且偶点的次之和 d (v ) 也为偶数,所以 d (v ) 必为偶 vV2 数,即奇数点的个数必为偶数。
19
链,圈,初等链,初等圈,简单链(圈)
• 链: 由两两相邻的点及其相关联的边构成的点边 交错序列, 如: (v0 ,e1 ,v1 ,e2 ,v2 ,e3 ,v3 ,…,vn-1 ,en , vn ); 其中v0 ,vn分别为链的起点和终点, v1 ,v2 ,…,vn-1称 为中间点 ; • 圈: 起点与终点重合的链; • 简单链(圈):链(圈)中所含的边均不相同; • 初等链(圈):链(圈)中所含的点均不相同,也 称通路;
基础图
25
有向图、弧、路、初等路
设有向图的弧为a=(u ,v),则起点为u,终点为v; 路: 初等路: 各顶点都不相同的路; 初等回路:u = v 的初等路; 连通图: 若不考虑方向是无向连通图; 强连通图:任两点有路;
26
v3 a2 v1 a1 v2 a3 a4
a8
v5 a10
v7 a9 v6
•路 • 初等路 • 回路
a6
a5 v4
a11
a7
( v 1 , a 2 , v 3 , a 4 , v 4 , a 7 , v 6 )是 从 v 1 到 v 6 的 路 , 也 是 一 条 初 等 路 。 在 上 图 中 , ( v 3 , a 3 , v 2 , a 5 , v 4 , a 6 , v 5 , a 8 , v 3 )是 一 个 回 路 。
v3 v1 v2
v5
v7
v6
v4
15
端点,关联边,相邻
若边e可表示为e=[vi,vj],称vi和vj是
边e的端点,称边e为点vi或vj的关联 边。若点vi,vj与同一条边关联,称 点vi和vj相邻;若边ei和ej具有公共 的端点,称边ei和ej相邻。 e2 v2 e6 v4
e1 v1 e4 e3
e5 e7
vV2 vV
vV1
2m为偶数,且偶点的次之和 d (v ) 也为偶数,所以 d (v ) 必为偶 vV2 数,即奇数点的个数必为偶数。
19
链,圈,初等链,初等圈,简单链(圈)
• 链: 由两两相邻的点及其相关联的边构成的点边 交错序列, 如: (v0 ,e1 ,v1 ,e2 ,v2 ,e3 ,v3 ,…,vn-1 ,en , vn ); 其中v0 ,vn分别为链的起点和终点, v1 ,v2 ,…,vn-1称 为中间点 ; • 圈: 起点与终点重合的链; • 简单链(圈):链(圈)中所含的边均不相同; • 初等链(圈):链(圈)中所含的点均不相同,也 称通路;
运筹学8图与网络分析PPT课件

v2
[v3 ,v4],[v1 ,v4],
[v2 ,v4], [v3 ,v3]}
v3 v4
图8.4
第12页/共166页
图8.5 是一个有向图D=(V,A)
其中V={v1 ,v2 ,v3 ,v4 ,v5 ,v6 ,v7}
A={(v1,v2),(v1,v3),(v3 ,v2)(v3 ,v4),(v2 ,v4),(v4 ,v5),
定理8.1 所有顶点度数之和等于所有边数
的2倍。
证明:因为在计算各个点的度时,每条边
被它的两个端点个用了一次。
第18页/共166页
定理8.2 在任一图中,奇点的个数必为偶数。 证明:设 V1,V2 分别是图G中奇点和偶点的
集合,由定理8.1 ,有
d(v) d(v) d(v) 2q
vV1
随着科学技术的进步,特别是电子计算 机技术的发展,图论的理论获得了更进一步 的发展,应用更加广泛。如果将复杂的工程 系统和管理问题用图的理论加以描述,可以 解决许多工程项目和管理决策的最优问题。 因此,图论越来越受到工程技术人员和经营 管理人员的重视。
关于图的第一篇论文是瑞士数学家欧拉 (E. Euler)在1736年发表的解决“哥尼
(v4 ,v6),(v5 ,v3),(v5 ,v4), (v5 ,v6),(v6 ,v7)}
v3
v5
v7
v1 v6
v2
v4
图8.5
第13页/共166页
下面介绍一些常用的名词:
一 个 图 G 或 有 向 图 D 中 的 点 数 , 记 作 P(G) 或 P(D),简记作P,边数或者弧数,记作q(G)或者q(D), 简记作q 。
简单链:链中所含的边均不相同;
初等链:链中所含的点均不相同, 也称通路; 圈:若 v0 ≠ vn 则称该链为开链,否则称 为闭链或回路或圈;
运筹学―第八章 图与网络分析PPT课件
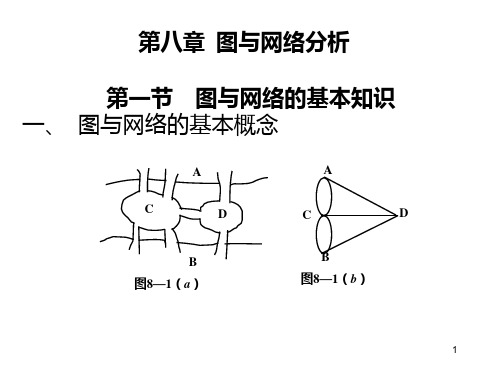
12
二、 图的生成树 定义10 设图 K(V,E1)是图G=(V , E )的一支撑子图, 如果图 K(V,E1) 是一个树,那么称K 是G 的一个生 成树(支撑树),或简称为图G的树。
作G=(V,E),连接点的边记作[vi , vj],或者[vj , vi]。
如果一个图是由点和弧所构成的,那么称它为有向图,
记作D=(V, A),其中V表示有向图D的点集合,A表示有向
图D的弧集合。一条方向从vi指向vj 的弧,记作(vi , vj)。
V = {v1 , v2 , v3 , v4 , v5 , v6 },
e1 {v1,v2} e2 {v1,v2}
v6
e3 {v2,v3} e4 {v3,v4}
e9
e5 {v1,v3} e6 {v3,v5}
e7 {v3,v5} e8 {v5,v6}
e9 {v6,v6} e10{v1,v6}
e1
e2
v2
e5 e3 e4 v4
e8
e6
v5 e7 v3
图8—2
3
如果一个图是由点和边所构成的,则称其为无向图,记
第八章 图与网络分析
第一节 图与网络的基本知识 一、 图与网络的基本概念
A
C
D
A
C
D
B 图8—1(a)
B 图8—1(b)
1
整体概述
概述一
点击此处输入
相关文本内容
概述二
点击此处输入
相关文本内容
概述三
点击此处输入
相关文本内容
2
定义1 一个图是由点集 Vvj和 V 中元素的无序对的一
个集合 E {ek}构成的二元组,记为G=(V,E),其中V中的
二、 图的生成树 定义10 设图 K(V,E1)是图G=(V , E )的一支撑子图, 如果图 K(V,E1) 是一个树,那么称K 是G 的一个生 成树(支撑树),或简称为图G的树。
作G=(V,E),连接点的边记作[vi , vj],或者[vj , vi]。
如果一个图是由点和弧所构成的,那么称它为有向图,
记作D=(V, A),其中V表示有向图D的点集合,A表示有向
图D的弧集合。一条方向从vi指向vj 的弧,记作(vi , vj)。
V = {v1 , v2 , v3 , v4 , v5 , v6 },
e1 {v1,v2} e2 {v1,v2}
v6
e3 {v2,v3} e4 {v3,v4}
e9
e5 {v1,v3} e6 {v3,v5}
e7 {v3,v5} e8 {v5,v6}
e9 {v6,v6} e10{v1,v6}
e1
e2
v2
e5 e3 e4 v4
e8
e6
v5 e7 v3
图8—2
3
如果一个图是由点和边所构成的,则称其为无向图,记
第八章 图与网络分析
第一节 图与网络的基本知识 一、 图与网络的基本概念
A
C
D
A
C
D
B 图8—1(a)
B 图8—1(b)
1
整体概述
概述一
点击此处输入
相关文本内容
概述二
点击此处输入
相关文本内容
概述三
点击此处输入
相关文本内容
2
定义1 一个图是由点集 Vvj和 V 中元素的无序对的一
个集合 E {ek}构成的二元组,记为G=(V,E),其中V中的
第八讲网络最优化模型【共61张PPT】

第八讲 网络最优化模型
最短路模型
最短路模型的求解
求解最短路问题实际上就是找一条总长度最短的路 线,对于这样的最短路问题,可以建立0-1整数规划数学
模型求解(如下图)。
第八讲 网络最优化模型
最短路模型
最短路模型的求解
为简化求解过程,可以建立专门的最短路求解模型 ,用计算机求解:可以将图中各条边和每条边是的权数 直接录入到求解模型中,直接得到结果。因此可以称下 图就是一个最短路问题的数学表述模型。
条路,使两点间的总距离为最短。
第八讲 网络最优化模型
最短路模型
例8.1 如下图所示,某人每天从住处S开车到工作地T上
班,图中各弧旁的数字表示道路的长度(千米),试问 他从家出发到工作地,应选择哪条路线,才能使路上行 驶的总距离最短?
第八讲 网络最优化模型
最短路模型的基本特征
最短路模型
1、在网络中选择一条路,始于发点(源点),终于收点(目的
条道路及道路维修。工期和所需劳动力见下表。该公司共 有劳动力120人,任一工程在一个月内的劳动力投入不能超 过80人,问公司应如何分配劳动力以完成所有工程,是否能按
期完成?
工程 A.地下通道 B.人行天桥 C.新建道路 D.道路维修
工期和所需劳动力
工期 5~7月 6~7月 5~8月
8月
需要劳动力(人) 100 80 200 80
赵●
(v1)
e1
e3
钱● (v2)
●孙 (v3) e4
●李 (v4)
第八讲 网络最优化模型
基本概念
图
7、 回路 始点和终点重合的路叫做回路。上图中(v3,v5,v6
,v7,v4 ,v3)就是一条回路。
网络优化图及网络运筹学
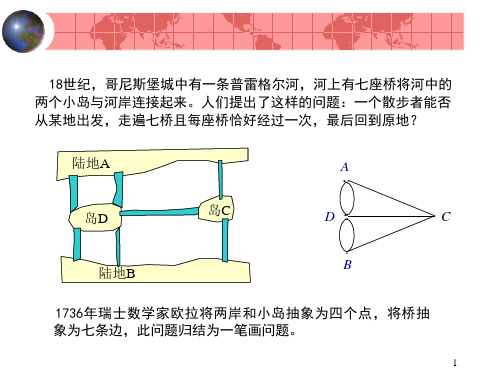
24
(13,v3)
(18,v5)
(22,v6)
(0,s) (10,v1)
(14,v3)
(16,v5)
实际中我们还可以从各点的标号找到v1到各点的距离, 以及从v1到各点最短路径.例如,从v4的标号(18,v5) 可知v1到v4的距离为18,并可找到v1到v4的最短路径为
25
例11:求节点1-6之间的最短路。
32
应用举例
例12 设备更新问题。某企业使用一台设备,在每年年初都要 决定是购置新设备还是继续使用旧的。购置新设备要支付一定 的购置费,使用旧设备则要支付维修费。制定一个五年内的设 备更新计划,使得总支付费用最少。
已知该设备在各年年初的价格为:
第一年 11
第二年 11
第三年 12
第四年 12
第五年 13
原问题图画为:
43
基本思路:
(1)找出一条从发点到收点的路,在这条路上的每一条弧的可用容 量都大于零。如果不存在这样的路,则已求得最大流。 (2)找出这条路上各条弧的最小的可用容量Pf,通过这条路增加网络 的流量Pf 。 (3)在这条路上,减少每一条弧的可用容量Pf ,同时增加这些弧的 流量Pf ,返回步骤(1)。 当然由于在步骤(1)中所选择的路不一样,计算过程也不一样,但 最终所求得的最大流量应该是一样的,为了使算法更快捷有效。 我们一般在步骤(1)中尽量选择包含弧数最少的路。
边,这样一个电话线网就可以用
一个图来表示。显然,这个图必
v4
须是连通的,而且是不含圈的连 通图。如左图所示。
3
例3 某工厂的组织机构如下图所示
行
生产计划科
政 办
技术科
设计组 工艺组
公
供销科
(13,v3)
(18,v5)
(22,v6)
(0,s) (10,v1)
(14,v3)
(16,v5)
实际中我们还可以从各点的标号找到v1到各点的距离, 以及从v1到各点最短路径.例如,从v4的标号(18,v5) 可知v1到v4的距离为18,并可找到v1到v4的最短路径为
25
例11:求节点1-6之间的最短路。
32
应用举例
例12 设备更新问题。某企业使用一台设备,在每年年初都要 决定是购置新设备还是继续使用旧的。购置新设备要支付一定 的购置费,使用旧设备则要支付维修费。制定一个五年内的设 备更新计划,使得总支付费用最少。
已知该设备在各年年初的价格为:
第一年 11
第二年 11
第三年 12
第四年 12
第五年 13
原问题图画为:
43
基本思路:
(1)找出一条从发点到收点的路,在这条路上的每一条弧的可用容 量都大于零。如果不存在这样的路,则已求得最大流。 (2)找出这条路上各条弧的最小的可用容量Pf,通过这条路增加网络 的流量Pf 。 (3)在这条路上,减少每一条弧的可用容量Pf ,同时增加这些弧的 流量Pf ,返回步骤(1)。 当然由于在步骤(1)中所选择的路不一样,计算过程也不一样,但 最终所求得的最大流量应该是一样的,为了使算法更快捷有效。 我们一般在步骤(1)中尽量选择包含弧数最少的路。
边,这样一个电话线网就可以用
一个图来表示。显然,这个图必
v4
须是连通的,而且是不含圈的连 通图。如左图所示。
3
例3 某工厂的组织机构如下图所示
行
生产计划科
政 办
技术科
设计组 工艺组
公
供销科
运筹学图与网络优化133页PPT

26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
16、云无心以出岫,鸟倦飞而知还。 17、童孺纵行歌,斑白欢游诣。 18、福不虚至,祸不易来。 19、久在樊笼里,复得返自然。 20、羁鸟恋旧林,池鱼思故渊。
运
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 教材 教材P79例2.4 例
• 若公司能提前完成工程的话,有可能得到奖励。下表 若公司能提前完成工程的话,有可能得到奖励。 为建筑工程中每项工序的时间成本平衡的数据, 为建筑工程中每项工序的时间成本平衡的数据,现在 的问题是: 的问题是: 1.若要用额外的资金来加速工程进度的话,怎样才能以最 若要用额外的资金来加速工程进度的话, 若要用额外的资金来加速工程进度的话 低的成本在40周内完工? 低的成本在 周内完工? 周内完工 2.若要把工程完成时间下降到 周之内,则对一些工序进 若要把工程完成时间下降到40周之内 若要把工程完成时间下降到 周之内, 行应急处理最节省的途径是什么? 行应急处理最节省的途径是什么
3 18 在关键线路上确定缩短工期 (工作的延续时间可在一定条 4 90 件下和一定范围内以增加费用 6 20 为代价而缩短) 5 21 6 3 3 1 3 43 16 25 10 33
J工期 工期8→6单代号网络图时间参数的计算 工期 单代号网络图时间参数的计算
计算顺序指标 工序 代号 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 工序 名称 S A B C D E F G H I J K L M N T 紧前 工序 — — A B C C E D E,G C F,I J J H K,L N 后续 工序 A B C D,E,I G F,H J H M J K,L N N T T 工期 Di 0 2 4 10 6 4 5 7 9 7 8→6 4 5 2 6 0 ↓ ES 0 0 2 6 16 16 20 22 20/29=29 16 25/23=25 33 →31 33 →31 38 37 (35) /38(36)=38 (36) 44 →42 ↓ EF 0 2 6 16 22 20 25 29 38 23 33 →31 37 →35 38 →36 40 44 →42 44 →42 ↑ LS 0 0 2 6 20 →18 16 20 26 →24 33 →31 18 25 34 →32 33 →31 42 →40 38 (36) 44 →42 ↑ LF 0 2 6 16/20(18)/18=16 26 →24 33(31)/20=20 25 33 →31 42 →40 25 34/33=33(32/31=31) 38 →36 38 →36 44 →42 44 →42 44 →42 ↓ TF 0 0 0 0 4(2) 0 0 4(2) 3(2) 2 0 1 0 4(2) 0 0
0 1 0 0 1 0
7 — — — — — — — 9
—:为总时差,人力限制10人。 :为总时差,人力限制 人
调整后各工序所需人力资源- 调整后各工序所需人力资源-时间图
时间—费用的优化 时间 费用的优化
• 最小直接费用的关键工序调整法: 最小直接费用的关键工序调整法: 费用分为:间接费用和直接费用。 费用分为:间接费用和直接费用。 1.直接费用:包括直接生产工人的工资及附加费, 直接费用:包括直接生产工人的工资及附加费, 直接费用 设备能源、 设备能源、工具及材料消耗等直接与完成工序有 关的费用。为了缩短工作的作业时间, 关的费用。为了缩短工作的作业时间,须采用一 些技术组织措施,相应会增加一些费用, 些技术组织措施,相应会增加一些费用,在一定 范围内,工作的时间越短,直接费用越大。 范围内,工作的时间越短,直接费用越大。 2.间接费用:包括管理费、办公费等。间接费用常 间接费用:包括管理费、办公费等。 间接费用 按任务期的长短分摊,在一定条件下,工期越长, 按任务期的长短分摊,在一定条件下,工期越长, 间接费用越大。 间接费用越大。
S A Yes — B Yes A C — D B E Yes B,D , T E
工期:12( 工期:12(天)
双代号网络图
1Leabharlann A 7 C 62B 3 4 3
E 2
5
3
D
双代号图计算事项最早时间
7 0 1 A 7 C 6 3 6 2 B 3 3 D 工期:12 工期: 4 10
E 2
12 5
双代号图计算事项最迟时间
工序 内容
紧前工 序 正常 时间
突击 时间 4 2 4 1 1
直接费用 率(元/ 天) 100 150 200 150 250
A B C D E
检查Ⅰ 检查Ⅰ 调节Ⅰ 调节Ⅰ 检查Ⅱ 检查Ⅱ 调节Ⅱ 调节Ⅱ 测试系统
— A — B B,D ,
7 3 6 3 2
• 要求:10日内完工,应该采用什么措施? 要求:10日内完工,应该采用什么措施? 日内完工
单代号网络图
A S C
B E D T
单代号网络图求CPM
工序 紧前 工序 Di 0 7 3 6 3 2 0 ES 0 0 7 0 6 10 12 EF LS LF 0 7 10 6 9 12 12 0 0 7 1 7 10 12 0 7 10 7 10 12 12 TF 总时差 0 0 0 1 1 0 0
工 程 工 序 费 用 ) (
费用与工期的关系
费用 费 费
总费用
直接费用 接费用
T′
T′
费用
直接费用与工序所需工时的关系
直 接 费 用 A(极限工序)
从正常工时每缩短一个单位 时间所增加的费用
成本斜率si =
cd i − c Di Di − d i
cd i
c Di
B(正常工序)
di
Di
工时
例:设备维修问题
试求以下方案的关键工序
• 方案一:突击工序A紧缩2天; 方案一:突击工序A紧缩2 • 方案二:突击工序A,B,D各紧缩1天; 方案二:突击工序A 各紧缩1 • 方案三:突击工序A紧缩2天,突击工 方案三:突击工序A紧缩2 紧缩1 序D紧缩1天; • 哪个方案是10天完工的最佳方案? 哪个方案是10天完工的最佳方案? 10天完工的最佳方案 • 本问题的最佳方案是否唯一? 本问题的最佳方案是否唯一?
网络图的优化
• 1.时间 资源的优化 时间—资源的优化 时间 • 资源优化的要求:保证关键线路上的资 资源优化的要求: 源;利用非关键线路上工序的总时差调 整平衡资源;在资源受到限制时, 整平衡资源;在资源受到限制时,可适 当推迟完工时间。 当推迟完工时间。 • 2.时间 费用的优化 时间—费用的优化 时间 • 最小直接费用的关键工序调整法
调整后的工程进度表(单位: 调整后的工程进度表(单位:天)
工 序 工 时 t 总 时 差 TF
工程进度(天 工程进度 天) 1 6 3 2 6 9 9 9 3 3 — 7 7 5 — 4 5 4 5 4 1 1 1 1 3 4 5 6 7 8 9 10 11
A B C D E F G
2 4 2 3 3 3 4
建筑工程中每项工序的时间成本平衡的数据
工序 (红色为关键工序 红色为关键工序) 红色为关键工序 A B C D E F G H I J K L M N 时间(周 时间 周) 正常 2 4 10 6 4 5 7 9 7 8 4 5 2 6 应急 1 2 7 4 3 成本(万元 成本 万元) 万元 正常 18 32 62 26 41 应急 28 42 86 34 57 26 102 38 27 49 20 35 20 51 每周的 应急成本 10(6 #) 5(3 #) 8(5 #) 4 16(7 #) 4(2 #) 4 6 3 3(1# ) 4 5(3 #) 10 6(4 #)
7 2 7
0 0
1
A 7 C 6
B 3 4 10 10
E 2
12 5 12
3 3 6 7 D
工序的总时差
• 工序总时差 (i,j):指在不影响整个工期的前提下, 工序总时差TF( ) 指在不影响整个工期的前提下 指在不影响整个工期的前提下, 工序最早开始(或结束)的时间可以推迟的时间。 工序最早开始(或结束)的时间可以推迟的时间。工 序总时差=最迟开工时间 最迟开工时间-最早开工时间 序总时差 最迟开工时间 最早开工时间 =最迟完工时间 最早完工时间 最迟完工时间-最早完工时间 最迟完工时间 • TF(i,j)= tLF(i,j)- tEF(i,j) ( ) (i,j)(i,j)= tLF(i,j)- [tE(i) + t (i,j)] (j)=tL(j)- tE(i) - t (i,j) 箭头事项最迟时间-箭尾事项最早时间–工序作业时间 =箭头事项最迟时间-箭尾事项最早时间 工序作业时间
工序的作业时间(期望 与方差 工序的作业时间 期望)与方差 期望
t a + 4t m + tb 2 tb − t a 2 t= ,σ = ( ) 6 6
• 概率型网络图假设: 概率型网络图假设: 1.各工序的时间分布相互随机独立; 各工序的时间分布相互随机独立; 各工序的时间分布相互随机独立 2.关键线路一直比其他任何线路所需时间都长; 关键线路一直比其他任何线路所需时间都长; 关键线路一直比其他任何线路所需时间都长 3.工程时间的概率分布是一个正态分布。 工程时间的概率分布是一个正态分布。 工程时间的概率分布是一个正态分布
计算总时差, 计算总时差,确定关键工序
7 2 7
0 0
0 1
A 7 6
B 3 0
C1
3 6 7
4 3 10 1 D 10
E0 2
12 5 12
工期:12 工期:
方案一:突击工序A紧缩2 方案一:突击工序A紧缩2天
5 0 1 A 5 C 6 3 6 2 B 3 3 D 1 4 9
E 2
11 5 工期:11 工期: 关键工序? 关键工序?
特别提醒:下周星期一交作业! 特别提醒:下周星期一交作业!
谢 谢! 再 见!
2.2概率型网络图 概率型网络图
• 在不具备定额和类似工序作业时间消耗的统计资料, 在不具备定额和类似工序作业时间消耗的统计资料, 且作业时间较长, 且作业时间较长,未知的和难估计的因素较多的情况 对完成工序可估计三种时间, 下,对完成工序可估计三种时间,之后计算它们的平 均时间作为该工序的作业时间。 均时间作为该工序的作业时间。 • 三种时间是 1.乐观时间:ta 乐观时间: 乐观时间 2.最可能时间:tm 最可能时间: 最可能时间 3.悲观时间:tb 悲观时间: 悲观时间
